第二节 离心泵的基本方程式
合集下载
水泵特性曲线H=f
§2.4 离心泵的基本方程
动量矩(角动量)，指的是描述物体转动状态的量，即物体中所
有质点的动量对一点或一轴之矩的和。
动量矩定理
动力学普遍定理之一，它给出质点系的动量矩与质点系
受机械作用的冲量矩之间的关系。动量矩定理有微分形式
和积分形式两种。 质点系的总动能在某个力学过程中的改变量，等于质点 系所受的诸外力和诸内力在此过程中所做功的总和。
§2.4 离心泵的基本方程
单位时间里控制面内恒定总流的动量矩变化（流出的动量矩与流入的 动量矩之差）等于该控制面内的合外力矩。
J 2 J1 M
J2——单位时间内流出控制面内液体所具有 的动量矩； J1——单位时间内流入控制面内液体所具有 的动量矩；
C
M——作用于控制面内液体上的合外力矩。
开动一定时间后，外界使用条件不变时，这一条件假定基本上可以认
为是能满足的。
§2.4 离心泵的基本方程
□ 关于叶槽内，液流均匀一致，叶轮同半径处液流同名速度相等的问题
实际叶轮转动时，叶槽内水流的惯性，反抗水流本身被叶槽带着旋转，趋 向于保持水流的原来位置，因而相对于叶槽产生了“反旋现象”，从而导致叶 槽中流速的实际分布是不均匀的。
α2
推导过程略
P18~P19
离心泵的基本方程式
HT
1 (u2C2u u1C1u ) g
§2.4 离心泵的基本方程
HT
三、基本方程式的讨论
（1）当α1=90°，即C1u=0； H T
1 u2C2u g
1 (u2C2u u1C1u ) g
为提高离心泵的扬程和改善吸水性能，大多数离
心泵均在水流进入叶轮时，α1=90°；为获取正值扬 程（HT>0）必须使α2<90°；α2越小HT就越大，实 际工程运用中水泵厂一般采用α2在6~15°左右。
二、离心泵的基本方程式
二、离心泵的基本方程式离心泵基本方程式从理论上表达了泵的压头与其结构、尺寸、转速及流量等因素之间的关系，它是用于计算离心泵理论压头的基本公式。
离心泵的理论压头是指在理想情况下离心泵可能达到的最大压头。
所谓理想情况就是：①叶轮为具有无限多叶片(叶片的厚度当然为无限薄)的理想叶轮，因此液体质点将完全沿着叶片表面流动，不发生任何环流现象；②被输送的液体是理想液体，因此无粘性的液体在叶轮内流动时不存在流动阻力。
这样，离心泵的理论压头就是具有无限多叶片的离心泵对单位重量理想液体所提供的能量。
显然，上述假设是为了便于分析研究液体在叶轮内的运动情况，从而导出离心泵的基本方程式。
(一)液体通过叶轮的流动离心泵工作时，液体一方面随叶轮作旋转运动，同时又经叶轮流道向外流动，因此液体在叶轮内的流动情况是十分复杂的。
如图2—5所示，液体质点沿着轴向以绝对速度co进入叶轮，在叶片人口处转为径向运动，此时液体一方面以圆周速度u1随叶轮旋转，其运动方向与液体质点所在处的圆周的切线方向一致，大小与所在处的半径及转速有关；另一方面以相对速度侧，在叶片间作相对于旋转叶轮的相对运动，其运动方向是液体质点所在处的叶片切线方向，大小与液体流量及流道的形状有关。
两者的合速度为绝对速度c1，此即为液体质点相对于泵壳(固定于地面)的绝对运动速度。
同样，在叶片出口处，圆周速度为u2，相对速度为ws，两者的合速度即为液体在叶轮出口处的绝对速度c2。
图2—5 液体在离心泵中的流动由上述三个速度所组成的矢量图，称为速度三角形。
如图2—5中出口速度三角形所示，α表示绝对速度与圆周速度两矢量之间的夹角，β表示相对速度与圆周速度反方向延线的夹角，一般称之为流动角。
α及β的大小与叶片的形状有关。
根据速度三角形可确定各速度间的数量关系。
由余弦定律得知111212121cos 2αu c u c w -+=(2—1)222222222cos 2αu c u c w -+=(2—1a)由此可知，叶片的形状影响液体在泵内的流动情况以及离心泵的性能。
2012-3离心泵基本方程式
理论流量可表示为在叶轮出口处的液体径 向速度和叶片末端圆周出口面积之乘积， 即QT=cr2πD2b2 由出口的速度三角形： （cu2=）c2cosα2=u2-cr2ctgβ2
HT
g
(C2R2cosa2 - C1R1cosa1)
1 (u 2C 2u u1Cu1) g
3 基本方程的讨论
所以
离心泵的理论压头就是具有无限多叶片的 离心泵对单位重量理想液体所提供的能量
为了分析液体在叶轮内的运动，了解液体与叶 轮之间的相互作用和能量转换的过程，必需首 先了解叶轮叶槽内液体的运动情况 运动特性 当叶轮旋转时，叶轮叶槽中每液体质点在随叶 轮一起作旋转运动的同时，还在叶轮产生的离 心力作用下，相对于旋转叶轮作相对运动
液体沿轴向从泵的入口进入叶轮中央。现以叶片入口处的 一小团液体考虑，其质量为mkg。此小团液体进入叶片后 的运动方向与底面平行，其运动速度是由两个分速度合成 的。其一为沿着叶片而运动的速度U1 ，在叶片入口与 叶片相切；其二为随叶轮带动旋转的圆周速度W1，在叶 片入口处与旋转圆周相切，二者的合成速度为Ｃ1，即为 小团液体在叶片入口处的绝对速度。同理，叶片外缘端点 处的一小团液体，其相对速度为U2，圆周速度为W2，二 者的合成速度Ｃ2为小团液体在叶片外缘端点处的绝对速 度。
泵与泵站
第四节 离心泵的基本方程式
市政与环境工程系 于海琴 2013
第四节 离心泵的基本方程式
离心泵在工作过程中：叶轮旋转抽吸水
问题
1 工作水流在旋转的叶轮中是如何运动的? 2 一个旋转的叶轮能够产生多大的扬程? 离心泵的基本方程式的推导和分析就是说明上 述问题和规律的
教学内容和基本要求
速度三角形 水流质点在叶轮内的流动: (1)沿叶片的相对运动 (2)随叶轮旋转的圆周运动
叶片泵的基本性能参数-离心泵的基本方程
水泵的理论流量QT与实际流量Q。
2017/8/12 叶片式水泵 2
第二讲
泵及泵站
2.3 水泵的性能参数——扬程
2、扬程（总扬程）H
水泵对单位重量的液体所作的功，即单位重量的液体流 过水泵后其能量的增值。 数学表示：以水泵出口的单位重量能量E2与水泵入口单位 重量的能量E1之差表示。
H E2 E1
Vacuum Head）
定义：指水泵在标准状况下（水温：20°C，当地压强1 atm）
运转时，水泵吸入口测压孔处所允许的最大真空高度。
要求： HV ≤ HS
其中：HV — 入口真空表读数。
数值： 依据气蚀实验确定。 单位：m H2O。
特点：对不同的海拔高程和水温需要修正。
用途：保证水泵在正常运行时不发生气蚀；用以计算、确
量纲：[ML2T-3]
水泵有效功率Nu：水泵输入液体的功率。 N u gHQ ( N m / s W )
2017/8/12 叶片式水泵 5
第二讲
泵及泵站
2.3 水泵的性能参数——功率单位换算 功率单位 1 W （瓦特）= N·m/s; 1 kgf ·m/s （公斤力米每秒）= 9.80665 W;
第二讲
泵及泵站
2.3 水泵的性能参数——流量
1、流量（抽水量）Q：在单位时间内水泵所输送 的液体数量。
体积流量QV—— 单位：m3/s，m3/h，m3/d，l/s等； 量纲：[L3T-1]。
质量流量QM—— 单位：kg/s，kg/h，t/h等； 量纲：[MT-1]。
பைடு நூலகம்
换算关系： QM = ρQV
ρ—— 液体密度；单位：kg/m3；量纲：[ML-3]。
1 kW =1000 W = 102 kgf ·m/s = 1.36 HP;
3离心泵的基本方程式
三点假定(简化分析推理过程)： 1.液体是恒定流 2.叶槽中液流均匀一致，叶轮同半径处液流的同名 速度相等 3.液流为理想流体
离心泵叶轮中液体的流动情况分析
两个坐标系统： 动坐标系统—旋转着的叶轮 静坐标系统—泵座
运动情况分析： 相对运动→相对速度W 液体质点对动坐标系（叶轮） 牵连运动→牵连速度U 叶轮对静坐标系（泵座） 绝对运动→绝对速度C 液体质点对静坐标系（泵座）
β1/β2 ：叶片进水角\出水角 α1/α2 ：进口\出口工作角
外力矩（∑M）分析
∑M:作用在叶槽内整股 水流上的所有外力矩
组成∑M的外力有：
1.叶片迎水面和背水面作用 于水的压力P1 和P2 ；
2.作用在ab与cd面上的水压 力P3和P4; （沿着径向， 对转轴没有力矩）
3.作用于水流的摩擦阻力P5 及P6，（理想流体，不予 考虑）
=
ω
g
(C2
cosα
2
R2
−
C1
cos α1 R1 )
方程式的推导
又∵u1＝R1·ω
u2＝R2·ω
∴
HT
=
1 g
(C2u2 cosα2
− C1u1 cosα1)
叶轮出口的速度三角形分析
由图可知： C2u＝C2COSα2 ＝u2－C2rctgβ2 C2r＝C2sinα2
∴
HT
=
1 g
(u2C2u
− u1C1u )
2g
2g
2g
又由能量方程：
HT
=
E2
− E1
= (Z2
+
p2
γ
)
−
(Z1
+
p1 ) +
离心泵叶轮中液体的流动情况分析
两个坐标系统： 动坐标系统—旋转着的叶轮 静坐标系统—泵座
运动情况分析： 相对运动→相对速度W 液体质点对动坐标系（叶轮） 牵连运动→牵连速度U 叶轮对静坐标系（泵座） 绝对运动→绝对速度C 液体质点对静坐标系（泵座）
β1/β2 ：叶片进水角\出水角 α1/α2 ：进口\出口工作角
外力矩（∑M）分析
∑M:作用在叶槽内整股 水流上的所有外力矩
组成∑M的外力有：
1.叶片迎水面和背水面作用 于水的压力P1 和P2 ；
2.作用在ab与cd面上的水压 力P3和P4; （沿着径向， 对转轴没有力矩）
3.作用于水流的摩擦阻力P5 及P6，（理想流体，不予 考虑）
=
ω
g
(C2
cosα
2
R2
−
C1
cos α1 R1 )
方程式的推导
又∵u1＝R1·ω
u2＝R2·ω
∴
HT
=
1 g
(C2u2 cosα2
− C1u1 cosα1)
叶轮出口的速度三角形分析
由图可知： C2u＝C2COSα2 ＝u2－C2rctgβ2 C2r＝C2sinα2
∴
HT
=
1 g
(u2C2u
− u1C1u )
2g
2g
2g
又由能量方程：
HT
=
E2
− E1
= (Z2
+
p2
γ
)
−
(Z1
+
p1 ) +
离心泵的基本方程式
r2
r1
2 ）叶轮中相邻的两叶片构成自中心向外沿逐渐扩大的液体流道，液体通
过时部分动能转化为静压能，这部分静压能的增加可表示为：
w12 w2 2 2g
单位重量流体经 叶轮后的静压能 增加为:
根据余弦定理，上述速度之间的关系可表示为：
代入（a）式，并整理可得到：
一般离心泵的设计中，为提高理论压头，使 α1=90°，即cosα1=0
4)两个速度的合成速度就是液体质点在点1或点2处相对于静 止的壳体的速度，称为绝对速度，用c1、c2来表示。
5）单位重量理想液体，通过无数叶片的旋转，获得的能量 称作理论压头，用H∞表示。 6）单位重量液体由点1到点2获得的机械能为:
在高速旋转的随叶轮旋转 ； 经叶轮流道向外流动。 液体与叶轮一起旋转的速度u1或u2方向与所处圆周的切线方向一致，大 小为：
离心泵的基本方程式
主讲人：韩二涛
1. 离心泵基本方程式的导出 假设如下理想情况： 1 ）泵叶轮的叶片数目为无限多个，也就是说叶片的厚度 为无限薄，液体质点沿叶片弯曲表面流动，不发生任 何环流现象。 2）输送的是理想液体，流动中无流动阻力。
3)液体沿叶片表面运动的速度w1、w2，方向为液体质点所处 叶片的切线方向，大小与液体的流量、流道的形状等有关。
——离心泵的基本方程式 ——离心泵理论压头的表达式
理论压头与理论流量QT关系 ：
流量可表示为叶轮出口处的径向速度与出口截面积
的乘积：
径向速度：
出口截面积 ：
从点2处的速度三角形可以得出：
代入 H=u2c2cosα2/g, 得：
H
——离心泵基本方程式
表示离心泵的理论压头与理论流量，叶轮的转速和 直径、叶轮的几何形状间的关系。
离心泵的基本方程式
离心泵的基本方程式
基本方程式的说明
泵把机械能转换成液体的能量是在叶轮内进行的。
叶轮带着液体旋转时把力矩传给液体，使液体的运动状态发生变化，从而完成能量的转换。
泵的基本方程式就是定量地表示液体流经叶轮前后运动状态的变化与叶轮传给单位重量液体的能量(即理论扬程)之间的关系式，也就是泵理论扬程的计算公式。
离心泵的基本方程式为式中H,——泵的理论扬程(m)。
离心泵基本方程式是泵理论中最重要的公式，现对其做如下说明：
1）基本方程式的实质是能量平衡方程，它建立了叶轮的外特性(理论扬程Ht)和叶轮前后液体运动参数Vu.之间的关系。
对于既定的叶轮，求得叶轮前后的Vu1，和Vu2后，代入方程式即可算出理论扬程。
2)基本方程式可用速度矩表示、速度矩的实质是单位质量的动量矩。
在叶轮中由于叶片对液体施加外力矩，速度矩是增加的。
如果无叶片，外力矩M=O,就
是说在没有外力矩作用于液体的情况下，液体的速度矩等于常数，称此为速度矩保
持定理。
以后在研究泵中其他过流部分的流动时常会遇到这种情况
3)从基本方程式可以看出，用液柱高度表示的理论扬程与液体的种类
和性质无关，只与其运动状态有关。
对于同一台泵，抽送不同的介质，如水、空气和水银时、所产生的理论扬程是相同的，但因介质密度不同，泵产生的压力和所需的功率不同。
本文由华威熔盐泵编辑整理。
离心泵的基本方程式
离心泵的基本方程式
基本方程式的说明
泵把机械能转换成液体的能量是在叶轮内进行的。
叶轮带着液体旋转时把力矩传给液体，使液体的运动状态发生变化，从而完成能量的转换。
泵的基本方程式就是定量地表示液体流经叶轮前后运动状态的变化与叶轮传给单位重量液体的能量(即理论扬程)之间的关系式，也就是泵理论扬程的计算公式。
离心泵的基本方程式为式中H,——泵的理论扬程(m)。
离心泵基本方程式是泵理论中最重要的公式，现对其做如下说明：
1）基本方程式的实质是能量平衡方程，它建立了叶轮的外特性(理论扬程Ht)和叶轮前后液体运动参数Vu.之间的关系。
对于既定的叶轮，求得叶轮前后的Vu1，和Vu2后，代入方程式即可算出理论扬程。
2)基本方程式可用速度矩表示、速度矩的实质是单位质量的动量矩。
在叶轮中由于叶片对液体施加外力矩，速度矩是增加的。
如果无叶片，外力矩M=O,就
是说在没有外力矩作用于液体的情况下，液体的速度矩等于常数，称此为速度矩保
持定理。
以后在研究泵中其他过流部分的流动时常会遇到这种情况
3)从基本方程式可以看出，用液柱高度表示的理论扬程与液体的种类
和性质无关，只与其运动状态有关。
对于同一台泵，抽送不同的介质，如水、空气和水银时、所产生的理论扬程是相同的，但因介质密度不同，泵产生的压力和所需的功率不同。
本文由华威熔盐泵编辑整理。
离心泵的基本方程式
HT
u 2C g
2u
为了获得正值扬程，必须使a2=0°，a2愈小，水泵的理论扬程 愈大。在实际应用中，水泵厂一般选用a2 ＝6 ° ～15 °左右。
• 2．水流通过水泵时，比能的增值(HT)与圆 周速度u2有关。而u2=(nлD2)/60，因此，水 流在叶轮中所获得的比能与叶轮的转速(n)、 叶轮的外径(D2)有关。增加转速(n)和加大 轮径(D2)，可以提高水泵之扬程。 • • 3．基本方程式适用于各种理想流体。这表 明，离心泵的理论扬程与液体的容重无关。 （抽水和抽气时扬程是一样的）
• 4.水泵的扬程是由两部分能量所组成的，
势扬程和动扬程组成，由于动能转化 为压能过程中，伴有能量损失，因此， 希望动扬程在水泵总扬程中所占的百 分比愈小，泵壳内水力损失就愈小， 水泵效率提高。
四、基本方程式的修正
• • • • 由于假定与实际应用不符，必须进行修正： 1.叶槽中，液流实际不均匀一致； 2.考虑泵壳内水力损失。 修正公式为：水泵的实际扬程
H h
H率和轴功率？它们之间有何 关系？ • 3、动力机的旋转机械能是如何传递给液体的？在能量 的传递过程中会产生哪些损失？ 如何将这些损失减至 最小程度？ • 4 ．离心泵装置上的真空表与压力表读数各表示什么意 义？ • 5 ．液体在叶轮内的运动是什么运动？各运动间有什么 关系？
离心泵的基本方程式
• 离心泵是靠叶轮的旋转来抽送水的，那么，工作 水流在旋转的叶轮中究竟是如何运动的呢? • 一个旋转的叶轮能够产生多大的扬程? • 对于这些运动规律，我们将借助于离心泵的基本 方程式的推导和分析，逐一得到进一步的了解。 •
一、叶轮中液体的流动情况
r
C 2 u C 2 cos α 2 u 2 C 2 r ctg β 2 C 2 r C 2 sin α 2
1.2离心泵基本方程式
D u2
2
要会从上述5个关系式分析
HT∞
b）叶片形状
HT
u u cot 2 2 2 QT g gD2b2
w2
2>90° （前弯叶轮）理论上更好,此时cot2为负值，HT∞更大
C2
w2
α β
u2
β
u2
β
w2
u2
后弯叶轮
径向叶轮
前弯叶轮
4
Chapter2第一节 离心泵 1-2离心泵基本方程式
Chapter2 第一节 离心泵
1-2离心泵基本方程式( 寻找压头He与流量的关系) 一、条件 a）叶轮数无穷多，且无厚度
b）μ=0（理想流体）
二、公式推导 叶轮宽度为B，半径R2，合成速度c 叶轮入口与叶轮出口间应用B.e.q(能衡)：
H T p 2 p1 c 2 2 c1 2 H p Hc g 2
（1）
2
Chapter2第一节 离心泵
1-2离心泵基本方程式 理论压头 流道面积 流 量
H T u 2 c 2 cos 2 g
（1）
A D 2 b2 Q D2 b2 c r 2
将cr2 用u表示（叶轮线速度）
（2）
（3）
w2
β
Cr2 C2 α u2
c2cosα2=u2-cr2cotβ2
三、关于基本方程式的讨论 3)理论流量及实际流量与压头关系
HT∞ H 机械损失 容积损失 水力损失
Q H与Q关系曲线
6
(A)
理论压头HT∞，m=J/N，单位质量力的物质所获得能量离心力做功动能转为静 压能
1
Chapter2 第一节 离心泵
1-2离心泵基本方程式
2
要会从上述5个关系式分析
HT∞
b）叶片形状
HT
u u cot 2 2 2 QT g gD2b2
w2
2>90° （前弯叶轮）理论上更好,此时cot2为负值，HT∞更大
C2
w2
α β
u2
β
u2
β
w2
u2
后弯叶轮
径向叶轮
前弯叶轮
4
Chapter2第一节 离心泵 1-2离心泵基本方程式
Chapter2 第一节 离心泵
1-2离心泵基本方程式( 寻找压头He与流量的关系) 一、条件 a）叶轮数无穷多，且无厚度
b）μ=0（理想流体）
二、公式推导 叶轮宽度为B，半径R2，合成速度c 叶轮入口与叶轮出口间应用B.e.q(能衡)：
H T p 2 p1 c 2 2 c1 2 H p Hc g 2
（1）
2
Chapter2第一节 离心泵
1-2离心泵基本方程式 理论压头 流道面积 流 量
H T u 2 c 2 cos 2 g
（1）
A D 2 b2 Q D2 b2 c r 2
将cr2 用u表示（叶轮线速度）
（2）
（3）
w2
β
Cr2 C2 α u2
c2cosα2=u2-cr2cotβ2
三、关于基本方程式的讨论 3)理论流量及实际流量与压头关系
HT∞ H 机械损失 容积损失 水力损失
Q H与Q关系曲线
6
(A)
理论压头HT∞，m=J/N，单位质量力的物质所获得能量离心力做功动能转为静 压能
1
Chapter2 第一节 离心泵
1-2离心泵基本方程式
泵与泵站第二讲
`
四、基本方程式的修正
1、假定条件中认为液体是恒定流。 水泵启动，关闭阶段不是恒定流，正常运转 时，基本是恒定流。 2、叶槽中的水流不是均匀一致的，与假定不 同，叶槽迎水面压力大，流速小； 叶槽背水面压力小，流速大。修正： HT ′ HT = 1+ P
P—修正系数；由实验定。 `
3、非理想流体：有粘性，有冲击，有紊 动，有摩擦。及气蚀余量（HSV）： HS—水泵在标准状态下（水温200C；水 表面为一个标准大气压。）运转时，水泵所允 许的最大吸上真空高度（mH2O）。它反映了水 泵的吸水性能。 HSV—指水泵吸口处，单位重量液体所具 有的超过饱和蒸汽压力的富裕压能。单位： mH2O 有时用H来表示。常用于轴流泵；锅炉给 水泵；渣浆泵等。
`
1，水流质点在叶槽中以W速度沿叶片流动。是对动坐标 的相对运动。 2，水流质点随叶轮以角速度ω做圆周运动。 线速度: u=Rω，是对静坐标的速度,又称为牵连速度。 3，合成速度： C （平行四边形法则，或三角形法则） 图中：C1与u1和C2与u2 的夹角为α1；α2。 W1与u1 ；W2与u2 的反向延长线的夹角，β1β2称为进水角 和出水角。水泵设计中 β1β2均小于900，叶片与旋转方向 呈后弯式。 这种设计的特点：流槽平缓，弯度小，水力损失小，有 利提高泵的效率。 β2一般在200—300之间。 `
∴
HT
u 2C 2 u = g
欧拉方程
C2u——叶轮外缘扭捲速度。
`
2、比能的增值（扬程HT）与u2的关系： u 2C 2 u HT = g
nπD2 Q u2 = g
∴ n ↗和D2 ↗⇒HT ↗
`
3.方程式中没有了ρ。HT与ρ理论上无关。(基 本方程式在推导过程中，液体的容重ρ并没起 作用而被消掉的，因此，该方程可适用于各种 理想流体。) 据有一定ρ的液体在一定的转速下，所受到的 离心力与液体的质量（也就是密度）有关。但 液体受离心力作用而获得扬程，相当于离心力 所造成的压强，除以液体的ρg。这样， ρg对 扬程的影响就消除了。
离心泵
(3)泵发生汽蚀时的条件 NPSHa＞NPSHr，泵不发生汽蚀 NPSHa＝NPSHr，泵开始发生汽蚀 NPSHa＜NPSHr，泵严重汽蚀 上式即为离心泵发生汽蚀的判别式，亦 称为汽蚀基本方程式。
(4)临界汽蚀余量NPSHc 当NPSHa降到使pk=pv时, 液体开始汽化, 因此,此时的NPSHa就是使泵不发生汽蚀的临 界值,称为临界汽蚀余量,用NPSHc表示,即: NPSHa＝NPSHc＝NPSHr 通过汽蚀实验确定的就是临界汽蚀余量 NPSHc。
q pB p A L Hg AB AB g 2g
2 V
LST AB
2 qV 2g
(3)离心泵与管路联合工作 --工作点的确定 满足能量平衡,流量平衡的条件. (4)泵的不稳定工况 泵的特性曲线为驼峰型曲线时,可能和管 路特性曲线相交于K和N两点。其中N点为稳 定工况，而K点为不稳定工况,当泵在K点工 作时，会因某种扰动因素而离开K点。
(5)允许汽蚀余量[NPSH] 在实际使用中,为了避免泵内发生汽蚀,常 考虑一定的安全余量,即得允许汽蚀余量 [NPSH]。 [NPSH]= NPSHc + (0.3-0.5) m 或 [NPSH]= (1.1-1.3)NPSHc 则防止汽蚀的条件为: NPSHa≥ [NPSH]
(6)吸上真空高度 如储液池液面上的压力为pa，则
2 s
(7)吸入特性 [NPSH]-qv曲线:向上弯曲的二次抛物线; [Hs]-qv曲线:向下弯曲的二次抛物线; (8)泵的允许几何安装高度[Hg] 由 NPSHa≥[NPSH] 或 Hs≤[Hs] 离心泵不发生汽蚀的条件确定泵的允许 几何安装高度,使Hg≤[Hg]。
4.3.1.3提高离心泵抗汽蚀性能的措施 (1)提高离心泵本身抗汽蚀性能-NPSHr↓ ▲改进泵的吸入口至叶轮叶片入口附近的结构 设计 ●增大叶片入口宽度b1，b1↑,则w1↓； ●将叶片进口边向吸入口延伸,使液流提前 增加能量; ●采用长短叶片叶轮,改善入口处液流分布;
泵基本方程式
影响泵扬程的因素
1、叶轮直径、转速的影响
1 由 HT∞= U 2 (U 2 C2 r ctg ) g D n 2 U2 ＝ r2w ＝ 而 知： 60
知： U2 D2
HT∞
n
HT∞
影响泵扬程的因素
叶片弯曲形状对理论扬程的影响
Hale Waihona Puke 影响泵扬程的因素1、叶片弯曲形状对理论扬程的影响
径向式叶片 β ＝90° Ctgβ＝0
后弯式叶片
β ＜90°
Ctgβ＞0
前弯式叶片
β ＞90°
Ctgβ＜0
影响泵扬程的因素
1、叶片弯曲形状对理论扬程的影响 β2
HT∞
但其绝对速度C2也增加，液体阻力提高，反而降低 了效率。
离心泵总是采用后弯式叶片，并且一般β2 ＝20 °～30 °
密度不随时间而变化。
泵的基本方程式
液体在旋转叶轮的流道中流动，从叶轮处获得了能量，这种
能量传递过程可用流体力学中的动量矩定理来推导。
导出公式： HT∞=
1 (U 2C2U U1C1U ) g
欧拉方程式
HT∞:无限多叶片时的理论扬程，单位m g: 重力加速度,单位：m/s2
U1、 U2：叶轮进口、出口处的圆周速度，单位m/s C1U、 C2U：叶轮进口、出口处的圆周分速度，单位m/s
离心泵的基本方程式
离心泵的基本方程式
速度分析
速度三角形
泵的基本方程式
三个假设条件：
1、叶轮的叶片为无限多而又无限薄，此时液体完全
沿着叶片的型线流动，即β1和β2分别等于叶片的安
装角β1 a、β2a
2、泵内流动的液体为理想液体，可不考虑液体的摩
擦阻力
第二章 泵与风机的基本理论
c1u = c1 cos α 1 c 2 u = c 2 cos α 2
（4） ）
欧拉方程II式 将（4）式代于（1）式后，得：欧拉方程 式 ）式代于（ ）式后，
H T∞
u 2 c 2 cos α 2 − u1c1 cos α 1 u 2 c 2 u − u1c1u = = g g
基本方程式的修正
c1u = c1conα 1
qt q 径向分速度： c1r = = A1 π D1b1ϕ 圆周速度： u1 =
π D1n
60
ϕ
• 式中 式中：
ϕ
——叶片厚度对断面影响系数。取 q ——理论流量（设计流量）。
=0.9~0.95。
• 叶轮上的速度：
w2
β
C2
α2 β2
C2
u2
α2
w2
C2r
β2
w1
β1A
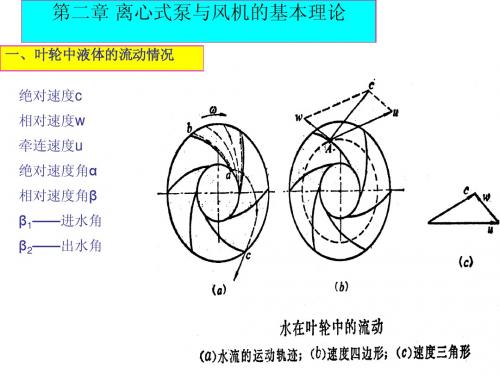
第二章 离心式泵与风机的基本理论
一、叶轮中液体的流动情况
绝对速度c 相对速度w 牵连速度u 绝对速度角α 相对速度角β β1——进水角 β2——出水角
一、叶轮中液体的流动情况
绝对速度c 绝对速度角α 相对速度w 相对速度角β 牵连速度c β1——进水角 β2——出水角
• 一 . 泵叶轮进、出口速度三角形 泵叶轮进、 1 . 进出口速度三角形 c1=u1+w1
α1 β1
C2u
C1
u2
w1
u1
C1 1 β1 α
ω
u1
2. 叶轮出口速度三角形
C2=u2+w2
绝对速度： c = c + c
2 2 2 2r 2 2u
分速度： c2 r = c2 sin α 2
1-2 离心泵的基本方程
w
w
c u
u
c=u+w
ω
ω
ω
(a) 相对运动 (b) 圆周运动 (c) 绝对运动
1-2 离心泵的基本方程
一、速度三角形 牵连速度指与所求液体质点瞬时重合点的叶轮圆周速度， 牵连速度 用矢量u表示，其方向垂直于叶轮圆半径，指向叶轮旋转方 u 向。
w
w3;w
ω
(a) 相对运动
(b) 圆周运动 (c) 绝对运动
《泵与压缩机》
1-2 离心泵的基本方程
培黎石油工程学院 李 鲤
1-2 离心泵的基本方程
一、速度三角形
(1)通过叶轮的液体为理想液体，即 液体在叶轮内流动时无能量损失。 两 点 假 设
只有在叶 片数无穷 多情况下 才能实现
(2)液体在叶片间的流动呈轴对称， 即每一液体质点在流道内的相对运 动轨迹与叶片曲线的形状完全一致。 在同一半径的圆周上，液体质点的 相对速度大小相同，其液流角相等。
T时刻ABCD 研究对象
C' C A' A B B' D
D'
t + dt 时刻
A′B ′C ′D ′
由连续性方程，有：
∑m
ABB′A′
= ∑ mCDD′C ′ = ρQT dt
1-2 离心泵的基本方程
二、离心泵的基本方程式 在dt时间内流过叶轮的液流动量矩的变化值：
dLo = ρQT dt (c2 ∞l2 − c1∞l1 )
叶轮角速度
驱动机传递给叶轮的功率：
N T∞ = M Oω
叶轮叶片数为无限多 的情况下的理论扬程
′ 理想状态下液体得到的功率： NT∞ = ρQT H T∞
1-2 离心泵的基本方程
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
思考题:
1 泵扬程是什么意义？说泵扬程50m，是否可把介 质送高50m? 复习工程力学中的动量矩定理。 扬程与压差的关系，以m表示，以J/kg表示
2 3
p H ( J / kg 表示） p gH （m表示） （Pa） ( Pa)
4 5 6
轴功率N、有效功率的含义。 泵效率的含义 熟练掌握速度三角形，
绝对速度 (absolute velocity)
矢量 c表示， 液体相对于壳体的运动。 大小、方向由矢量合成 而定。
总结：速度三角形的概念
相对速度矢量 w 牵连速度矢量 u 绝对速度矢量 c
cuw
对照上页图认识以下参数:
cr
cu
α
β
βA
后面推导中还会用到的参数:
D — 叶轮直径，单位 m b — 叶轮轴面流道宽度，单位 m Z — 叶片数目
下标:
1： 叶片进口 参数 2： 叶片出口 参数 ∞ ： 叶片无限多的叶轮中流动时的参数
思考:速度三角形的构成
速度三角形底边u 1.
u Dn
(u1 D 1n
u 2 D 2n )
速度三角形的高与流量、流道面积有关，cr ，考虑叶片厚cr 2. 假设cr
QT cr Db
Leonhard Euler (1707-1783)1750年建立以上方程
轴向吸入的离心泵，液流在叶轮入口无预旋，即
c1u 0
H T u2 c2u HT
结论：
J / kg m
1 u2c2u g
1、与进出口处的速度有关，即与D、n、Q 等 有关。 2、与液体性质无关，对每公斤质量介质所给 能量相同，水、气、油。
第二节 离心泵的基本方程式
内容：研究叶轮与流体之间能量传递过程，确定泵 使液体获得有效能量多少。
一 液体在叶轮中的流动—速度三角形 (velocity triangle)
两点假设： （1）通过叶轮的液体为理想液体，即液体在叶轮内流动时 无能量损失。 （2）液体在叶片中间流动呈轴对称：每个液体质点在流道 内相对运动轨迹与叶片曲线形状一致。在同一半径上液体质 点的相对速度大小相同，液流角相等。
QT ：理论流量（不计泄漏）m 3 / s
式中 ：阻塞系数
D2 2
Z 2 sin 2A D2
：叶轮出口叶片厚度。
3. 进口：一般设计成无预旋c1u 0 出口：2 2A
叶轮叶片进、出口的速度三角形
w2 cr2 c2 u大小方向已知
u nD 60
叶轮中液体动量矩对时间的导数 dL0 M0 QT (c2 r2 cos 2 c1 r1 cos 1 ) dt
力矩 M0 是流量为QT时轴上作用力矩，驱动机的做 功力矩。
NT M 0
驱动机的角速度
前述理想情况下（无损失、叶片无限多）流体得到 功率
NT ' QT HT
根据连续性原理，两部分的质量应相等
mABB' A mCDD'C QT dt
在dt时间流过叶轮的流体动量矩的变化 是流入、流出两部分动量矩之差
dL0 QT dt (c2l2 c1l1 )
l1 r1 cos 1 c1 对O轴垂直距离
l2 r2 cos 2
c2 对O轴垂直距离
此时 NT ' NT无损失，理想情况下 M 0 NT ' NT 及 H T QT H T QT (c2 r2 cos 2 c1 r1 cos 1 ) QT u2 u1 u r , r2 r1 cu c cos
“两点假设”的理论条件：叶片无限多、无限薄。 补充条件：稳定流动 重点概念
相对速度：(relative
velocity)
矢量w表示 其方向与叶片方向一致（无 限多叶片）即叶片切线。
牵连速度 (peripheral velocity) 矢量u表示，叶轮在转动， 专指某一瞬时与液体质点 重合时的叶轮圆周速度， 方向垂直于叶轮半径。
H T ( u2
c2u
u1
c1u ) J / kg
c2u c2 cos 2 c1u c1 cos 1
H T u2c2u u1c1u
用2c2u u1c1u ) g
m
欧拉公式是适用于一切离心式机器的基本方程。
Daniel Bernoulli (1700-1782)
u、w、c、、、cr、cu
7 欧拉公式几种表示
HT u2c2u u1c1u
H T u2c2u
J / kg （表示）
1 1 HT ＝ (u2c2u u1c1u ) H T u2c2u m （表示） g g
dL0 M0 dt
其中: L0— 液体对O轴的动量矩 M0— 诸外力对O轴的力矩和
取轴O为叶轮轴
为求
dL0 取叶轮前后盖板及两叶片进 dt
出口边之间的液体来分析。 在定常流下，t时刻ABDC间的液体在t+dt 时刻流到A'B'D'C'位置，其中A'B'DC这部 分 液 体 对 O 轴 动 量 矩 不 变 。 ABCD 与 A'B'C'D' 之 间 的 变 化 仅 发 生 在 ABB'A' 和 CDD'C'动量矩之差。
u2 cr只与流量和叶轮流道 的流通面积有关,大小 方向已知。
A2
2
cu2 c1 cr1
1
QT cr Db
叶道进口:一般设计进口 无预旋,则cu1=0，即 c1= cr1
u1
叶道出口:相对速度方 向已知, 2 =A2
二
离心泵的基本方程式
研究叶轮如何将驱动机的能量传给液体及液体获得 能头大小与哪那些因素有关？ 常用方法：建立叶轮对液体所做的功与液体运动状 态变化之间的关系，可用动量矩定理推导。 动量矩定理(工程力学): 质点系对某一轴线的动量矩对时间的导数等于作用于该质 点系诸外力对该轴力矩之和。