第3章 分析化学中的误差与数据处理(2)
分 析 化 学第三章 误差和分析数据处理

(二)已知样本标准偏差(s) 对于有限次测定,须根据t分布进行统计处理 1. 使用单次测定值
μ = x t p,f s
2. 使用样本平均值
μ = x t p,f s x = x t p,f
t值可通过p90表4-3查得
s n
t分布的意义 真值虽然不知,但可以通过由有限次
测定值计算出一个范围,它将以一定的置
x-μ u= σ
y = Φ(u) = 1 e 2π
u2 2
标准正态分布曲线
【特点】曲线的形状与µ 和σ的大小无关。
三、随机误差的区间概率
正态分布曲线与横坐标之间所包围的总面积,
表示来自同一总体的全部测定值或随机误差在上
述区间出现的概率总和为100%。
+
-
1 + Φ(u)du = e du = 1 2π -
正态分布曲线
(二)正态分布曲线的讨论
1.测定值的正态分布(x分布)
(1)x = μ时,其概率密度最大,曲线以x=μ
这一点的垂线为对称轴分布。 (2)精密度不同的两组测定值的正态分布曲 线,σ 值较小的相应的曲线陡峭,σ 值较大的曲 线较平坦。(☆)
(3)µ 和σ是正态分布的基本参数,一旦µ和
σ确定后,正态分布曲线的位置和形状就确了,这
二、正态分布
(一)正态分布曲线的数学表达式 测定次数无限增加,其测定值服从正态分布 的规律,其数学表达式为:
1 y = f(x) = e σ 2π (x-μ)2 2σ 2
σ-总体标准偏差,µ -总体平均值,在无系统 误差存在时,µ 就是真值T。y为测定次数无限时,
测定值xi出现的概率密度。 以x横坐标,y纵坐标 作图,得测定值的正态分布曲线。
第3章-分析化学中的误差与数据处理

分 析 化 学 中 的 误 差
系统误差与随机误差的比较
项目 产生原因 分类 性质 影响 系统误差 固定因素 随机误差 不定因素,总是存在
2.乘除法 是各测量步骤相对标准偏差的平方总和
R A B C 和 R m A B C
S R
2 R 2
S A
2 A 2
S B
2 B 2
S C
2 C 2
分 析 化 学 中 的 误 差
3.指数关系运算时( R mA
n
)则为
SR R
分 析 化 学 中 的 误 差
§3-1 分析化学中的误差
关键词: 误 差 系统误差 偶然误差 公 差
偏
差
准 确 度
精 密 度
分 析 化 学 中 的 误 差
课程学习要点
1、理解真值、中位数、极差、偏差的含义。
2、掌握系统误差和随机误差的产生、特点及消除方法。
3、理解准确度与误差、精密度与偏差的含义及二者关系
二、平均值(算术平均值):
n次测量:
x
x1 x 2 x n n
x n
i 1
1
n
i
分 析 化 学 中 的 误 差
三、中位数(xM)
将测定数据由小到大排列, 当n为奇数时,最中间的数据为中位数。 X1、 X2 、 X3 、 X4 、 X5 、 X6 、 X7、 当n为偶数时,中间两位数的平均数为中位数。 X1、 X2 、 X3 、 X4 、 X5 、 X6、
分析化学第六版第3章分析化学中的误差与数据处理及答案

第三章分析化学中的误差与数据处理一、判断题(对的打√, 错的打×)1、滴定分析的相对误差一般要求为小于%,滴定时消耗的标准溶液体积应控制在10~15mL。
( B )2、、分析测定结果的偶然误差可通过适当增加平行测定次数来减免。
( A )3、标准偏差可以使大偏差能更显著地反映出来。
( A )4、所谓终点误差是由于操作者终点判断失误或操作不熟练而引起的。
( B )5、测定的精密度好,但准确度不一定高,消除了系统误差后,精密度好,测定结果的准确度就高。
( A )6、置信区间的大小受置信度的影响,置信度越大,置信区间越小。
( B )二、选择题:1、下列论述中错误的是( D )A、方法误差属于系统误差B、系统误差具有单向性C、系统误差又称可测误差D、系统误差呈正态分布2、下列论述中不正确的是( C )A、偶然误差具有随机性B、偶然误差服从正态分布C、偶然误差具有单向性D、偶然误差是由不确定的因素引起的3、下列情况中引起偶然误差的是( A )A、读取滴定管读数时,最后一位数字估计不准B、使用腐蚀的砝码进行称量C、标定EDTA溶液时,所用金属锌不纯D、所用试剂中含有被测组分4、分析天平的称样误差约为克,如使测量时相对误差达到%,试样至少应该称( C )A、克以上B、克以下C、克以上D、克以下5、分析实验中由于试剂不纯而引起的误差是( A )A、系统误差B、过失误差C、偶然误差D、方法误差6、定量分析工作要求测定结果的误差 ( C )A、没有要求B、等于零C、在充许误差范围内D、略大于充许误差7、可减小偶然误差的方法是( D )A、进行仪器校正B、作对照试验C、作空白试验D、增加平行测定次数8、从精密度就可以判断分析结果可靠的前提是( B )A、偶然误差小B、系统误差小C、平均偏差小D、标准偏差小9、[×-]/1000结果应以几位有效数字报出( B )A、5B、4C、 3D、210、用失去部分结晶水的Na2B4O7·10H2O标定HCl溶液的浓度时,测得的HCl浓度与实际浓度相比将( B )A、偏高B、偏低C、一致D、无法确定11、pH 有几位有效数字( B )A、4B、 3C、 2D、 112、某人以差示光度法测定某药物中主成分含量时,称取此药物,最后计算其主成分含量为%,此结果是否正确;若不正确,正确值应为( D )A、正确B、不正确,%C、不正确,98%D、不正确,%13、一个样品分析结果的准确度不好,但精密度好,可能存在 ( C )A、操作失误B、记录有差错C、使用试剂不纯D、随机误差大14、某学生用4d法则判断异常值的取舍时,分以下四步进行,其中错误的步骤为( A )A、求出全部测量值的平均值B、求出不包括待检值(x)的平均偏差C、求出待检值与平均值之差的绝对值D、将平均偏差与上述绝对值进行比较15、有一组平行测定所得的分析数据,要判断其中是否有异常值,应采用 ( B )A、t检验B、格鲁布斯法C、F检验D、方差分析16、标定某标准溶液的浓度,其3次平行测定的结果为:,, mol·L-1。
分析化学第三章 分析化学中的误差与数据处理_OK

分类
方法误差、仪器与试剂 环境的变化因素、主
误差、主观误差
观的变化因素等
性质
重现性、单向性(或周 服从概率统计规律、
期性)、可测性
不可测性
影响
准确度
精密度
消除或减 小的方法
校正
增加测定的次数 12
系统误差的校正
• 方法系统误差——方法校正 • 主观系统误差——对照实验校正(外检) • 仪器系统误差——对照实验校正 • 试剂系统误差——空白实验校正
误差
10
• 随机误差: • 由某些不固定偶然原因造成,使测定结果在一定范围内波动,大小、正负不定,难以
找到原因,无法测量。 • 特点:不确定性;不可避免性。 • 只能减小,不能消除。每次测定结果无规律性,多次测量符合统计规律。 • 过失、错误误差
11
系统误差与随机误差的比较
项目
系统误差
随机误差
产生原因 固定因素,有时不存在 不定因素,总是存在
相对误差: 绝对误差占真值的百分比,用Er表示
Er =E/xT = x - xT /xT×100%
2
相对误差反映误差在真值中所占的比例
误差以真值为标准
真值:某一物理量本身具有的客观存在的真实值。真值是
未知的、客观存在的量。在特定情况下认为 是已知的:
理论真值(如化合物的理论组成)(如,NaCl中Cl的 含量) 计量学约定真值(如国际计量大会确定的长度、质 量、物质的量单位等等) 相对真值(如高一级精度的测量值相对于低一级精 度的测量值)(例如,标准样品的标准值)
6 15.99 34 0.172
7 16.02 55 0.278
8 16.06 40 0.202
9 16.09 20 0.101
第3章 分析化学中的误差及数据处理

b:如何确定滴定体积消耗?(滴定的相对误差
小于0.1% )
0~10ml; 20~30ml; 40~50ml
万分之一的分析天平可称准至±0.1mg
常量滴定管可估计到±0.01mL
一般常量分析中,分析结果的精密度以平均相 对偏差来衡量,要求小于0.3%;准确度以相对误差 来表示,要求小于0.3%。
误差传递,每一个测定步骤应控制相对误差更小 如,称量相对误差小于0.1%
使用计算器作连续运算时,过程中可不必对每一步 的计算结果进行修约,但要注意根据准确度要求,正确 保留最后结果的有效数字位数。
四、有效数字在分析化学中的应用
1. 正确地记录数据 2. 正确地选取用量和适当的仪器 3. 正确表示分析结果
问题: 分析煤中含硫量时,称样量为3.5g,甲、乙 两人各测2次,甲报结果为0.042%和0.041%,乙报结 果为0.04201%和0.04199%,谁报的结果合理?
5. 大多数情况下,表示误差或偏差时,结果取一位 有效数字,最多取两位有效数字。
6. 对于组分含量>10%的,一般要求分析结果保留4 位有效数字;对于组分含量1%~10%的,一般要求分析 结果保留3位有效数字;对于组分含量<1%的,一般要 求分析结果保留2位有效数字。
7. 为提高计算的准确性,在计算过程中每个数据可 暂时多保留一位有效数字,计算完后再修约。
3)pH,lgK等对数值 有效数字的位数仅取决于小数部分数字(尾数)的位数。
4)不是测量得到的倍数、比率、原子量、化合价、 π、e等可看作无限多位有效数字。
5)不能因为变换单位而改变有效数字的位数。
二、有效数字的修约规则
应保留的有效数字位数确定之后,舍弃多余数字的 过程称为数字修约
修约规则:“四舍六入五成双”
分析化学知识点归纳 第三章

第三章分析化学中的误差与数据处理1、误差⑴绝对误差绝对误差是测量值是真实值之间的差值。
绝对误差的单位与测量值相同,误差越小表示测量值与真实值越接近,准确度越高;反之,误差越大,准确度越低。
当测量值大于真实值时,误差为正值,表示测量结果偏高;反之,误差为负值,表示测量结果偏低。
⑵相对误差响度误差是指绝对误差相当于真实值的百分率。
相对误差有大小、正负之分,反应的是误差在真实值中所占的比例大小,因此绝对误差相同的条件下,待测组分含量越高,相对误差越小;反之相对误差越大。
⑶真值真值是某一物理量本身具有的客观存在的真实值。
严格的说任何物质中各组分的真实含量是不知道的,用测量方法是得不到真值的。
在分析化学中常将以下的作为真值①理论真值化合物的理论组成等;②计算学约定真值国际剂量大会上确定的长度、质量、物质的量的单位等;③相对真值人们设法采用各种可靠的分析方法,使用最精密的仪器,经过不同的实验室、不同人员进行平行分析,用数理统计方法对分析结果进行处理,确定出各组分相对准确的含量,此值称为标准值,一般用标注值代表该物质中各组分的真实含量。
2、偏差偏差是指测量值与各次测量结果的算术平均值之间的差值(中位数与平均值相比优点是受离群数据影响较小,缺点是不能充分利用数据)。
偏差有正有负,还有一些偏差可能为零。
如果将单次测定的偏差相加,其和为零或接近于零。
平均偏差是指单次测定偏差绝对值的平均数,代表一组测量数据中任何一个数据的偏差,没有正负号。
因此,它最能表示一组数据的重现性。
在一般分析工作中平行测定的次数不多时,常用平均偏差表示分析结果精密度。
相对平均偏差是平均偏差在各次测量结果平均值中所占的百分比例。
标准偏差的表达式是()112--=∑=nxxsnii,相对标准偏差(RSD,rs)又称变异系数,是指标准偏差在平均值中所占的百分比例。
标准偏差通过平方运算能将较大的偏差更显著的表现出来,因此标准偏差能更好的反映测定值的精密度,实际工作中,都用RSD表示分析结果精密度。
分析化学第三章 误差与分析数据的处理

2019/5/12
analytical chemistry
13
3、标准偏差(standard deviation, SD):突出较大偏差值的影响
当测定为无限多次时,标准偏差 的数学表达式为
总体标准偏差
n
(xi )2
i 1
n
为无限多次测定的总体平均 值,当测定次数趋向无穷大, 其可看做真值
2
2019/5/12
analytical chemistry
24
(三)极值误差法
在分析过程中,当不需要严格定量计算,只需要粗略 估计整个过程可能出现的最大误差时,可用极值误差表示。 极值误差法的计算:
①和、差的极值误差等于各测量植极值误差绝对值的和。 ②积、商的相对极值误差等于各测量值相对极值误差的和。
由某些不确定的偶然因素引起的误差(不可避免!!)
特点: a) 大小、正负不定
决定测量结果的精密度
b) 服从统计学规律
大误差出现的概率小
小误差出现的概率大
绝对值相同的正、负误差出现的概率大致相等
c) 通过增加平行测定次数,可以减小偶然误差,但不能
通过校正的方法消除偶然误差。
产生原因:a)晃动、震动等随机因素;b)估读数
2
xi x
s i1
n 1
相对偏差:
相对平均偏差:
d %= d 100% x
相对标准偏差: RSD(%) s 100%
x
2019/5/12
analytical chemistry
16
(三) 准确度与精密度的关系**
谁才是未来的神枪手???
2019/5/12
analytical chemistry
第3章-2 分析化学中的数据处理
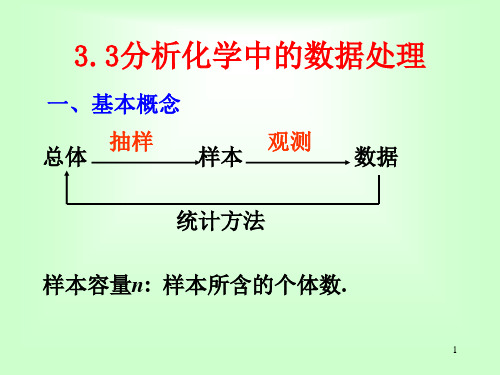
表3.2 正态分布概率积分表
随机误差出现的区间
测量值出现的区间
概率
(以σ为单位) u=±1 u=±1.96 u=±2 u=±2.58 u=±3
x=μ±1σ x=μ±1.96σ x=μ±2σ x=μ±2.58σ x=μ±3σ
68.3% 95.0% 95.5% 99.0% 99.7%
12
例1 已知某试样中质量分数的标准值为1.75%, σ=0.10%,又已知测量时没有系统误差,求分析 结果落在(1.75±0.15)%范围内的概率。 解: x x 1.75% 0.15%
(47.60 0.13)%
(47.60 0.23)%
置信度越高,置信区间就越大,所 估计的区间包括真值的可能性也就 越大,置信度定在 95%或 90%。
23
3.4 显著性检验
1. 平均值与标准值的比较-t检验法
步骤:a.将 x ,μ 和 n代入 t x n ,求t计
x 10.79%, s 0.042%
9 1.43
t
x s
n
10.79% 10.77% 0.042%
查表 ,P=0.95,f=8 时, t0.05 , 8=2.31 。 t<t0.05 , 8 ,故 x 与 μ 之间不存在显著性差异,即采用新方法后,没有 引起明显的系统误差。 25
涉及到的是测量值较少时的平均偏差;但在用统
计学处理数据时,广泛采用标准偏差来衡量数据
的分散程度。
2
总体标准偏差:
(测量次数为无限多次时)
σ
x
n
2
样本标准偏差:
(测量值不多时)
s
x x
n 1
2
第三章分析化学中的误差与数据处理

2.计量学约定真值(如国际计量大会确定的长度、质量、 物质的量单位等)由标准参考物质证书上给出的数值或有 经验的人用可靠方法多次测定的平均值,确认消除系统误 差;
3.相对真值,认定精度高一个数量级的测量值作为低一级 精度的测量值的真值,这种真值是相对比较而言的(如科 学实验中使用的标准试样及管理试样中组分的含量等)。
随机误差的传递
1.加减法
Y k k a A kb B k c C s k s k s k s
2 Y 2 2 a A 2 2 b B 2 2 c C
2.乘除法
3.指数关系
Y m An
2 2 sY s 2 A n Y2 A2
4.对数关系
Y m lg A
AB Y m C 2 2 2 2 sY s A sB sC 2 2 2 2 Y A B C
滴定剂体积应为20~30mL
Er 0.1% 1%
0.02 mL 0.02 mL
称样质量应大于0.2g
E 0.2 mg 0.2 mg
Er 0.1% 1%
例3:测定含铁样品中w(Fe), 比较结果的准确度。
A. 铁矿中,
xT 62.38%, x 62.32% Ea x xT 0.06%
示 : 1000 (1.0×103 ,1.00×103,1.000 ×103 )。
零的具体作用: *在1.0008中,“0” 是有效数字; *在0.0382中,“0”定位作用,不是有效数字; *在0.0040中,前面3个“0”不是有效数字, 后面一个“0”是有效数字。 *在3600中,一般看成是4位有效数字,但它可能是 2位或3位有效数字,分别写3.6×103,3.60×103或 3.600×103较好。
02第3章误差与分析数据处理(精)
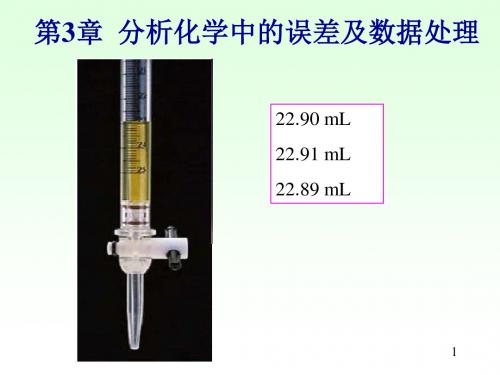
2
( n1 1) s1 ( n2 1) s2 n1 n2 2
2
f n1 n2 2
SR为合并的标准偏差(pooled standard deviation) 若t计≥t表,则两组平均值间存在显著性差异,反之无显著性 差异。
解:
t
|x μ| s
n
0.1080 0.1075 0.0005
5 2.24
查表 t0.95,4=2.776。因t< t0.95,4, 故平均值与标 准值之间无显著性差异,测定不存在系统误差。测定 结果可靠。
32
(2)两组平均值的比较
当t检验用于两组测定值的比较时,用下式计 算统计量t
Er Er Ea T Ea T
Ea x T 0.002%
100% -0.06 / 62.38 0.1% 100% 0.002 / 0.042 5%
5
3.1.2 偏差与精密度
精密度表示平行测定的结果互相靠近的程度, 一般用偏差表示。 绝对偏差 :单次测量值与平均值之差
称样质量应大于0.2g
Ea 0.2 mg 0.2 mg
Er 0.1% 1%
4
例1 测定含铁样品中w(Fe), 比较结果的准确度。 A. 铁矿中,
T 62.38%, x 62.32% Ea x T 0.06%
B. Li2CO3试样中,T 0.042%, x 0.044% A. B.
-3 -2 -1 0 f = 1 2 n-1
3 t
26
总体均值的置信区间 —对μ的区间估计
在一定的置信度P下(把握性),
分析化学教案 第3章 分析天平 误差及分析数据处理

第三章分析天平、误差与数据处理天平是定量分析中用来称取物质质量的一种精密仪器。
一般分为普通天平(即托盘天平)和分析天平。
第一节分析天平一天平的工作原理1 机械天平的工作原理杠杆原理:A__________C___________BQ PQ×AC=P×BC若力臂相等,即AC=BC,则Q=P所以m物g = m砝码gm= m砝码物2 电子天平的原理通电导线在磁场中会产生电磁力。
被称物重力向下,电磁力方向向上,二者平衡时,则电流大小与被称物的质量成正比。
mg=F=k×I二分析天平的种类和构造目前无比较完善的、准确的分类方法。
通常按构造特点,分为等臂双盘天平和不等臂单盘天平。
双盘天平又分为阻尼天平和无阻尼天平(摇摆天平)。
按天平的精度,分为“万分之一天平”、“十万分之一天平”、“百万分之一天平”。
1双盘自动分析天平分为部分机械加码(半自动)分析天平和全部机械加码(全自动)分析天平。
主要部件及其作用(参见课本P61、63的图 )(1)横梁上有三个互相平行、并位于同一水平的玛瑙刀口。
中间的一个刀口向下,作为杠杆的支点;两端的刀口向上,承载两个天平盘上的重量。
(2) 立柱支承横梁,上部有一玛瑙平板(刀垫)。
柱上有支架,下部有升降枢钮。
开动枢钮时,支架上升并托住横梁,天平处于休止状态;支架下降时,横梁上玛瑙刀刃落在支承平板上,天平处于工作状态。
(3) 装码装置吊耳盘托:天平休止时,托住天平盘盒式砝码(半自动天平有)(4)空气阻尼盒(5)光学读数装置2 单盘电光天平(略)三天平的灵敏度天平的灵敏度:天平一个盘增加1mg质量所引起的指针偏移的程度。
单位:格/ mg实际中,用“感量”来表示其灵敏度。
是灵敏度的倒数,mg / 格。
天平的灵敏度和三个玛瑙刀口的棱边锋利程度、三个玛瑙平板的光滑程度有关。
刀口越锋利,刀垫越光滑,就越灵敏。
四分析天平的使用基本步骤:检查调零等——进行称量(左物右码,半自动分析天平)——读数——再测天平零点——还原归位。
分析化学第3章

下列计算结果应包含几位有效数字: (1)213.64+4.402+0.3244 5位 (2)pH=4.32的c(H+)
2位
(3) 0.1000
(25.00 1.52) 246.47 1.000 1000
4位
(4)
0 . 1010 ( 25 . 00 18 . 80 ) 1000
四、提高分析结果准确度的方法
1. 消除测定过程中的系统误差 1)对照实验: 用标准试样或标准方法来检验所选
用的分析方法是否可靠。
2)空白实验:不加试样的情况下,按照试样的分
析步骤和条件进行测定,求出空白值。
3)校准仪器 4)方法校正:选用公认的标准方法与所采用的方法
进行比较,找出校正数据。或加样回收,以检验是 否存在方法误差。
100 %, 或 RE
x
100 %
相对误差亦有正、负
例:用分析天平称量两个试样,测定值分 别是0.1990g和1.1990g,假定真实值分别是 0.1991g和1.1991g。求E、RE。 -0.0001,-0.0001,-0.05%,-0.008%
说明:相对误差更能反映测定的准确度。 注:1)测高含量组分,RE可小
比色法
40.20% ±2.0%×40.20%
3.2 有效数字及其运算规则
3.2.1 有效数字(significant figure) 1)定义:指实际能测到的数字。 2)构成: 全部准确数字+最后一位估计的可疑数字 如滴定管读数23.45mL,23.4是准确 的,而第四位5可能是4也可能是6,虽然 是可疑的,但又是有效的。
3.2.2 有效数字的修约 1)修约(rounding)规则 表述一:四舍六入五留双 表述二:四舍六入、过五进位、恰五留 双
分析化学中的误差

确定某种方法是否可用,判断实验室测定结果准确性
实用文档
可疑数据的取舍 过失误差的判断
Q 检验法
步骤:
(1) 数据排列 x1 x2 …… xn
(2) 求极差
xn - x1
(3) 求可疑数据与相邻数据之差
xn - xn-1 或 x2 -x1
(4) 计算: Qxnxn1 或Qx2x1
解:两者称量的绝对误差分别为 E = x – xT = 1.6380-1.6381 = – 0.0001 (g)
E = x – xT = 0.1637-0.1638 = – 0.0001 (g) 两者称量的相对误差分别为
Er =E/xT ×100%= – 0.0001 /1.6381 ×100%= –0.006% Er =E/xT ×100%= – 0.0001 /0.1638 ×100%= –0.06%
yi: xi时的测量值; y: xi时的预测值 a=yA-bxA b= ∑(xi-xA)(yi-yA)/ ∑(xi-xA)2
其中yA和xA分别为x,y的平均值
实用文档
A
0.35
0.30
0.25
y=a+bx
0.20
r=0.9993
0.15
0.10
0.05
0.00
0
12Leabharlann 3456
7
8
相关系数
concentration
尾数≤4时舍; 尾数≥6时入
尾数=5时, 若后面数为0, 舍5成双;若5后面还有 不是0的任何数皆入
例 下列值修约为四位有效数字 0.324 74 0.324 75 0.324 76 0.324 85
第03章 分析化学中的误差与数据处理

R m lg A
),则为
SA S R 0.434m A
例:P47
.34.
(三) 极值误差 1. 加减法是各测量值的绝对误差的绝对值累加
R=A+mB-C
ER max EA m EB EC
.35.
2.乘除法是各测量值相对误差的绝对值累加
A B A B R 和 R m C C
准确度 校正 精密度 增加测定的次数
.24.
3.1.10 误差的传递
分析结果通常是经过一系列测量步骤之后获得的,其中每 一步骤的测量误差都会反映到分析结果中去。 设测定值为A,B,C, 其绝对误差为EA,EB,EC, 相对误差为EA/A, EB/B, EC/C, 标准偏差分别为SA、SB、SC, 分析结果R: 绝对误差为ER, 相对误差为ER/R, 标准偏差为SR.
RR R
max
EC EA EB A B C
.36.
3.2 有效数字及运算规则
量筒
容量瓶
容量仪器
烧杯
锥形瓶 .37.
3.2 有效数字及其运算规则
记录的数字不仅表示数量的大小,而且要正确地反映测 量的精确程度。
3.2.1 有效数字:
分析工作中实际上能测量到的数字,表示量的同时反映测量 准确程度。
.26.
(一) 系统误差的传递 1.加减法 若R为A,B,C 三个测量值相减的结果 R=A+mB-C
则绝对误差E是各测量步骤结果绝对误差的系 数的代数和。
ER=EA+mEB-EC
.27.
2.乘除法
相对系统误差是各测量步骤相对误差的代数和
R是A,B,C 三个测量值的结果
A B A B R 和 R m C C
【最新试题库含答案】《分析化学》思考题答案(第四版,武汉大学版)

《分析化学》思考题答案(第四版,武汉大学版) :篇一:分析化学_第四版_(武汉大学_著)_高等教育出版社_课后答案分析化学课后习题答案123篇二:化学分析(武汉大学编_第五版)上册课后习题答案从第三章开始。
前面的大家应该都不需要吧、、、第3章分析化学中的误差与数据处理1.根据有效数字运算规则,计算下列算式:(1)19.469+1.537-0.0386+2.54 (2) 3.6?0.0323?20.59?2.12345 45.00?(24.00?1.32)?0.12451.0000?1000(3)(4) pH=0.06,求+[H]=? 解:a. 原式=19.47+1.54-0.04+2.54=23.51b. 原式=3.6×0.032×21×2.1=5.1c. 原式=+-0.06d. [H]=10=0.87( mol/L ) 2. 返滴定法测定试样中某组分含量时,按下式计算:已知V1=(25.00±0.02)mL,V2=(5.00±0.02)mL,m =(0.2000±0.0002)g,设浓度c及摩尔质量Mx的误差可忽略不计,求分析结果的极值相对误差。
解:?xxmax45.00?22.68?0.1245=0.12711.000?10002c(V1?V2)Mx?x??100%m=EVEm?Vm=0.040.0002?200.2=0.003=0.3%3.设某痕量组分按下式计算分析结果:,A为测量值,C为空白值,m 为试样质量。
已知sA=sC=0.1,sm=0.001,A=8.0,C=1.0,m=1.0,求sx。
解:22222s(A?C)sxsmsA?sCsm0.12?0.120.0012?4???????4.09?10x2(A?C)2m2( A?C)2m2(8.0?1.0)21.022x?A?Cm且故s??0.144. 测定某试样的含氮量,六次平行测定的结果为20.48%,20.55%,20.58%,20.60%,20.53%,20.50%。
(完整版)分析化学答案(武汉五版)第3章

第三章分析化学中的误差与数据处理1.根据有效数字运算规则,计算下列算式:(1)19.469+1.537-0.0386+2.54(2) 3.6⨯0.0323⨯20.59⨯2.12345(3)(4) pH=0.06,求[H+]=?解:a. 原式=19.47+1.54-0.04+2.54=23.51b. 原式=3.6×0.032×21×2.1=5.1c. 原式=d. [H+]=10-0.06=0.87( mol/L )2、返滴定法测定试样中某组分含量时,按下式计算:已知V1=(,V2=(,m=(,设浓度c及摩尔质量M x的误差可忽略不计,求分析结果的极值相对误差。
解:在加减运算中,结果的极差是各测量值相对误差的绝对值之和,设V=V1-V2,V的极值差,。
在乘除运算中,结果的极值相对误差是各测量值相对误差的绝对值之和,所以运算结果的极值相对误差为3.设某痕量组分按下式计算分析结果:,A为测量值,C为空白值,m为试样质量。
已知s A=s C=0.1,s m=0.001,A=8.0,C=1.0,m=1.0,求s x。
解:且故4、测定某试样的含氮量,六次平行测定的结果为20.48%,20.55%,20.58%,20.60%,20.53%,20.50%。
解:平均值中位值全距平均偏差标准偏差标准相对偏差b.已知,则绝对误差为相对误差为5. 反复称量一个质量为 1.0000g的物体,若标准偏差为0.4mg,那么测得值为1.0000 1.0008g的概率为多少?解:由故有即查表得 P=47.73%6.按正态分布x落在区间的概率是多少?解:。
根据题意,x落在区间内的概率,即正态分布N(0,1)中,u落在(-1.0,0.5)之间的概率。
查表得=0.5时,面积为0.1915,=1时,面积为0.3413。
所以概率为0.3413+0.1915=0.5328=53.28%7.要使在置信度为95%时平均值的置信区间不超过±s,问至少应平行测定几次?解:查表,得:8. 若采用已经确定标准偏差为0.041%的分析氯化物的方法,重复三次测定某含氯试样,测得结果的平均值为21.46%,计算:a.90%置信水平时,平均值的置信区间;b.95%置信水平时,平均值的置信区间。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
0.007
1
7.026
4
pH=5.36
2
91.40
4
1000
不确 定
pKa=9.26
2
6.00×10-5
3
27
3. 2. 2 有效数字的修约规则
一、“四舍六入五成双”
1、被修约的数≤4时将其舍去;
2、被修约的数≥6时就进位; 3、被修约的数为5时,分为两种情况: (1)当5后面无数或为“0”时,是否进位决定于 “5”前面的数字, “奇进偶舍”
(2)标准溶液的浓度为4 位有效数字, (3)平衡常数为2 位有效数字, (4)误差和偏差一般保留1~2位有效数字。
33
四、分析结果合理
结果报告:与方法精度一致, 由误差最大的一步确定
例10:两位分析者同时测定某一试样中硫的质量分
数,称取试样均为3.5g,分别报告结果如下:
甲: 0.042%,0.041%;
0.2 E r1 100 % 0.3% 0.0600 1000
0.2 Er 2 100 % 0.02% 1.0000 1000
结论:在绝对误差相同的情况下,真实值越 大,相对误差越小。
8
三、偏差(deviation)
测量值(x)与平均值(mean,x )的差值,即
x 10.0%
d 0.24%
s1 0.28%
s2 0.33%
14
3. 1. 2
准确度和精密度
一、准确度(accuracy)
测量值与真值相接近பைடு நூலகம்程度。
因此,误差是衡量准确度高低的尺度。
如:铁矿石中含铁量真值为71.68%
准确 度低
甲 69.50% 乙 71.47%
E=69.50%-71.68%= -2.18% E=71.47%-71.68%= -0.21%
潍坊学院化学化工与环境工程学院
李丽敏
1
第3章 分析化学中的误差与数据处理
3. 1 3. 2 3. 3 3. 4 3. 5 3. 7 分析化学中的误差 有效数字及其运算规则 分析化学中的数据处理 显著性检验 可疑值取舍 提高分析结果准确度的方法
2
3. 1 分析化学中的误差
3. 1 .1 误差与偏差 一、有关概念 1、真值( xT)true value
25
2、对数
lgK、pH、pM、pKa等对数和负对数值,其 有效数字的位数仅取决于小数点后面数字的位数, 其整数部分只说明了该数的方次。
3、常数
e、π等常数,计算式中的倍数、分数关系, 不是测量所得到的,可视为任意位数的有效数字。
4、不能因为变换单位而改变有效数字的位数。
26
例1:下列数据的有效数字位数各是多少?
(2)当5后面还有不是“0”的任何数时,都必须 进位,无论“5” 前面的数字是奇数还是偶数。
二、一次修约
28
例2:将下列数字修约为三位有效数字
3.144 =3.14 3.135 =3.14 3.1350 =3.14
3.136
3.145
=3.14 =3.14
3.135013 =3.14
例3:将数字2.3457修约到两位 2.3457 → 2.3 正确 2.3457 → 2.346 → 2.35 → 2.4
结论:n次测量结果的绝对偏差之和等于零。
10
例3:某分析人员对试样测定5次,求得各次
测量值 xi 与平均值 x 的偏差分别为:+0.04, -0.02,+0.01,-0.01,+0.06。问此计算结果 是否正确? 答:计算结果不正确,因为单次测量值的 绝对偏差之和应等于零。
11
2、平均偏差(average deviation)
20
二、随机误差(random error)
是由某些难以控制且无法避免的偶然因素 造成的,又称为偶然误差或不可测误差 。
1、特点:大小和正负都难以预测,不可避免 不可被校正,但服从统计规律。 2、消除方法:增加平行测定次数。 过 失 误 差 由粗心大意引起,可以避免。
重做!
21
三、系统误差和随机误差与 准确度和精密度的关系
系统误差和随机误差决定测定结果的准确度。 随机误差决定结果的精密度。
3. 1. 4
公差
公差是生产部门对于分析结果允许误差的 一种表示方法。
22
作
业
书面作业:武大本P75习题4
课外思考题:武大本P74思考题2
23
3. 2 有效数字及其运算规则
3. 2. 1 有效数字(significant figure)
真值
137 .33 xT 100 % 56 .22 % 244 .27
E x xT 56.15% 56.22% 0.07%
E 0.07% Er 100% 100% 0.12% xT 56.22%
7
例2:某分析天平的称量误差为±0.1mg,如果称 取试样0.0600g,相对误差是多少?如称样为 1.0000g,相对误差又是多少?这些结果说明什么 问题?(P74思考题4) 解:相对误差分别为:
18
2、分类(根据产生的原因)
(1)方法误差(method error):由于分析方法 本身不够完善或有缺陷所造成的。 (2)仪器误差(instrumental error):由于仪 器本身不够精确或未经校准所引起的。 (3)试剂误差:由于试剂不纯和蒸馏水中含有 微量杂质引起的。 (4)操作误差(personal error):由于分析人 员操作不当造成的。 (5)主观误差:又称个人误差。由分析人员本 身的一些主观因素造成。
d xx
偏差的表示方法:
绝对偏差
平均偏差 相对平均偏差
标准偏差
极差
相对标准偏差
9
1、绝对偏差di (个别测定值的偏差):
单次测量结果与多次测量结果平均值之差。 设 n次测量结果为x1,x2,…,xn,其平均值
为 x ,用di 来表示绝对偏差,则
di x x i
( i = 1,2,…, n )
最合适的仪器是 ( C )
A.100mL量筒 C.100mL移液管 B.100mL烧杯有刻度的烧杯 D.100mL容量瓶
32
三、常见分析结果有效数字的保留
(1)百分含量的有效数字为小数点后2 位,高含
量的(>10%)保留4位,中等含量的(1~10
%)保留3位,微量的(<1%)保留2位,如:
66.81%,5.34%,0.21%
将一组测量数据按大小顺序排列,中间一 个数据即为中位数。当测量值的个数为偶数时, 中位数为中间相邻两个测量值的平均值。
5
二、误差(error)
1、绝对误差(absolute error)
测定值与真实值之差
E = x - xT
2、相对误差(relative error)
绝对误差在真实值中所占的百分率
例4:见武大本P42例2 例5:测定某铜合金中铜的质量分数(%),得到 两组测定值,分别求其平均偏差和标准偏差。
1组 10.3 9.8 9.6 10.2 10.1 10.4 10.0 9.7 10.2 9.7
2组 10.1 9.9 9.3 10.2 10.1 10.5 10.3 9.9 9.9 9.8
准确 度高
15
二、精密度
一组平行测定结果相互接近的程度。
因此,偏差是衡量精密度高低的尺度。 例如:测定铁矿石中铁含量的测定结果如下 甲组: 55.62% 56.70% 57.80%
d 0.73%
乙组: 56.40% 56.50% 56.52%
精密 度低
精密 度高
16
d 0.05%
三、准确度与精密度的关系
30
3. 2. 4 有效数字运算规则在分析化学中的应用
一、正确记录测量数据
m ◇台秤(称至0.1g): 12.8g, 0.5g, 1.0g ◆分析天平(称至0.1mg): 2.8218g, 0.5020g V ★滴定管(量至0.01mL): 26.32mL,3.97mL
★容量瓶: 50.00mL,100.0mL,250.0mL
某一物理量本身具有的客观存在的真 实数据,即为该量的真值。
3
理论真值 计量学约定真值
如某化合物的理 论组成 如国际计量大会 上确定的长度、 质量、物质的量 单位等 认定精度高一个数 量级的测定值作为 低一级的测量值的 真值
4
相对真值
2、平均值( x )
3、中位数(xM) median
又称 (算术平均偏差),指单次测量偏差的绝对值
的平均值,没有正负之分,用
d 表示
d1 d 2 d n 1 d di n n
3、相对平均偏差(relation mean deviation)
d d r 100% x
12
4、标准偏差(standard deviation,s)
注意:在乘除运算中,如果有效数字位数最少的
数字的首位数≥9,则积和商的有效数字的位数
可以比这个因数多取一位。 例11:9.6×3.587×1.89
35
作
业
书面作业:武大本P74习题1
课外练习题:武大本P74思考题5、8
错误
29
3. 2. 3 运算规则
一、加减法(尾数取齐法) 运算结果的有效数字的位数决定于这些数 据中绝对误差最大者。(以小数点后位数最少 的数为准例 ) 4:0.0121 + 25.64 + 1.05782 二、乘除法(位数取齐法 ) 运算结果的有效数字的位数决定于这些数 据中相对误差最大者。(以有效数字位数最少 的数为准) 例5:0.0325×5.103×60.064 ÷1.398 三、混合运算 例6:5.994÷0.6957-5.02 先乘除,后加减;有括号时,先括号里, 后括号外。 例7:0.1010 × (25.00-24.80) ÷ 1.0000
