静定结构的内力分析习题解答分解
静定结构的内力计算图文

30 30
4m
4m
4m
4m
12kN
12kN 12kN
M 图(kN·m)
9kN
9kN
2kN/m
7kN
5kN
9kN
4.5kN
7.5kN
39
第40页/共76页
作业
习题3-5、3-6、3-9 习题3-10、3-12
40
第41页/共76页
§3-3 三铰拱
41
第42页/共76页
一、 概述
1、定义:
通常杆轴线为曲线,在竖向荷载作用下,支座产生水平反力的结构。
AC段受力图:
q
MC
t
C
FNC
FQC
n
x
FAY
FAYSinα
(2)求内力方程:
MC = 0 Ft = 0 Fn= 0
M = 1 qlx 1 qx2 (0 x l) 22
FN
=
q(1 l 2
x) sin
(0 x l)
FQ
=
q(1 2
l
x) cos
(0 x l)
FAYcosα
FAY
M中 =162 / 8 6.23/ 2 =1.385kN.m(下拉)
弯矩图见下图。
1kN/m
6.23 D
C 1.385
6.23 E
1.385kN A
4.5kN
M 图(kN.m)
B 1.385kN
1. 5kN
38
第39页/共76页
例:主从刚架弯矩图。
12kN
2kN/m
36 36
6m
12 42 30
F
F
曲梁
拱
f / l : 高跨比(1~1/10)
结构力学课后习题答案重庆大学
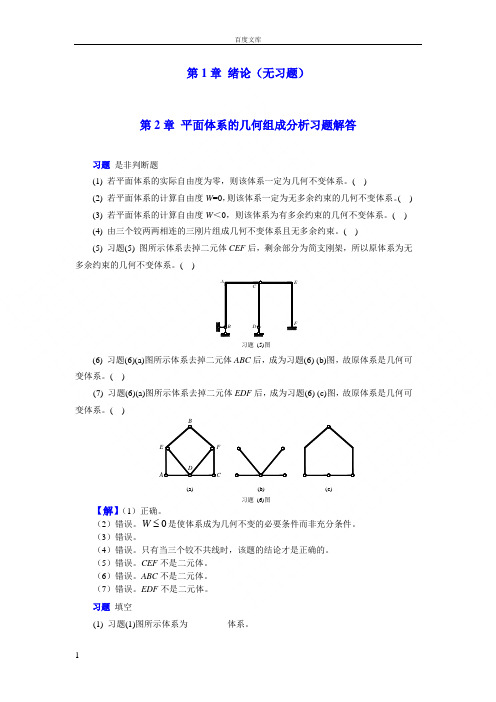
第1章 绪论(无习题)第2章 平面体系的几何组成分析习题解答习题 是非判断题(1) 若平面体系的实际自由度为零,则该体系一定为几何不变体系。
( )(2) 若平面体系的计算自由度W =0,则该体系一定为无多余约束的几何不变体系。
( ) (3) 若平面体系的计算自由度W <0,则该体系为有多余约束的几何不变体系。
( ) (4) 由三个铰两两相连的三刚片组成几何不变体系且无多余约束。
( )(5) 习题(5) 图所示体系去掉二元体CEF 后,剩余部分为简支刚架,所以原体系为无多余约束的几何不变体系。
( )B DACEF习题 (5)图(6) 习题(6)(a)图所示体系去掉二元体ABC 后,成为习题(6) (b)图,故原体系是几何可变体系。
( )(7) 习题(6)(a)图所示体系去掉二元体EDF 后,成为习题(6) (c)图,故原体系是几何可变体系。
( )(a)(b)(c)D习题 (6)图【解】(1)正确。
(2)错误。
0W 是使体系成为几何不变的必要条件而非充分条件。
(3)错误。
(4)错误。
只有当三个铰不共线时,该题的结论才是正确的。
(5)错误。
CEF 不是二元体。
(6)错误。
ABC 不是二元体。
(7)错误。
EDF 不是二元体。
习题 填空(1) 习题(1)图所示体系为_________体系。
习题(1)图(2) 习题(2)图所示体系为__________体系。
习题2-2(2)图(3) 习题(3)图所示4个体系的多余约束数目分别为_______、________、__________、__________。
习题(3)图(4) 习题(4)图所示体系的多余约束个数为___________。
习题(4)图(5) 习题(5)图所示体系的多余约束个数为___________。
习题(5)图(6) 习题(6)图所示体系为_________体系,有_________个多余约束。
习题(6)图(7) 习题(7)图所示体系为_________体系,有_________个多余约束。
《结构力学习题集》2-静定结构内力

第二章 静定结构内力计算一、是非题1、 静定结构的全部内力及反力,只根据平衡条件求得,且解答是唯一的。
2、静定结构受外界因素影响均产生内力,内力大小与杆件截面尺寸无关。
3、静定结构的几何特征是几何不变且无多余约束。
4、图示结构||M C =0。
aa5、图示结构支座A 转动ϕ角,M AB = 0, R C = 0。
BCaaAϕ2a26、荷载作用在静定多跨梁的附属部分时,基本部分一般内力不为零。
7、图示静定结构,在竖向荷载作用下, AB 是基本部分,BC 是附属部分。
ABC8、图示结构B 支座反力等于P /2()↑。
9、图示结构中,当改变B 点链杆的方向(不通过A 铰)时,对该梁的影响是轴力有变化。
AB10、在相同跨度及竖向荷载下,拱脚等高的三铰拱,水平推力随矢高减小而减小。
11、图示桁架有9根零杆。
12、图示桁架有:N 1=N 2=N 3= 0。
aaaa13、图示桁架DE 杆的内力为零。
a a14、图示对称桁架在对称荷载作用下,其零杆共有三根。
15、图示桁架共有三根零杆。
16、图示结构的零杆有7根。
17、图示结构中,CD 杆的内力 N 1=-P 。
a 418、图示桁架中,杆1的轴力为0。
4a19、图示为一杆段的M 、Q 图,若Q 图是正确的,则M 图一定是错误的。
图M Q 图二、选择题1、对图示的AB 段,采用叠加法作弯矩图是:A. 可以;B. 在一定条件下可以;C. 不可以;D. 在一定条件下不可以。
2、图示两结构及其受载状态,它们的内力符合:A. 弯矩相同,剪力不同;B. 弯矩相同,轴力不同;C. 弯矩不同,剪力相同;D. 弯矩不同,轴力不同。
PPP2 l ll l3、图示结构M K(设下面受拉为正)为:A. qa22;B. -qa2;C. 3qa22;D. 2qa2。
2a4、图示结构M DC(设下侧受拉为正)为:A. -Pa;B.Pa;C. -Pa;D. Pa。
a a5、在径向均布荷载作用下,三铰拱的合理轴线为:A.圆弧线;B.抛物线;C.悬链线;D.正弦曲线。
3静定结构的内力分析习题解答
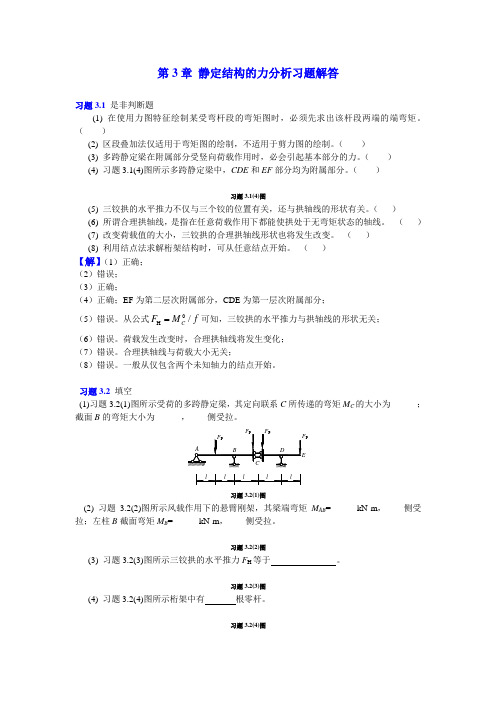
第3章 静定结构的力分析习题解答习题3.1 是非判断题(1) 在使用力图特征绘制某受弯杆段的弯矩图时,必须先求出该杆段两端的端弯矩。
( )(2) 区段叠加法仅适用于弯矩图的绘制,不适用于剪力图的绘制。
( ) (3) 多跨静定梁在附属部分受竖向荷载作用时,必会引起基本部分的力。
( ) (4) 习题3.1(4)图所示多跨静定梁中,CDE 和EF 部分均为附属部分。
( )习题3.1(4)图(5) 三铰拱的水平推力不仅与三个铰的位置有关,还与拱轴线的形状有关。
( ) (6) 所谓合理拱轴线,是指在任意荷载作用下都能使拱处于无弯矩状态的轴线。
( ) (7) 改变荷载值的大小,三铰拱的合理拱轴线形状也将发生改变。
( ) (8) 利用结点法求解桁架结构时,可从任意结点开始。
( )【解】(1)正确;(2)错误; (3)正确;(4)正确;EF 为第二层次附属部分,CDE 为第一层次附属部分;(5)错误。
从公式0H /C F M f 可知,三铰拱的水平推力与拱轴线的形状无关;(6)错误。
荷载发生改变时,合理拱轴线将发生变化; (7)错误。
合理拱轴线与荷载大小无关;(8)错误。
一般从仅包含两个未知轴力的结点开始。
习题3.2 填空(1)习题3.2(1)图所示受荷的多跨静定梁,其定向联系C 所传递的弯矩M C 的大小为______;截面B 的弯矩大小为______,____侧受拉。
P习题3.2(1)图(2) 习题3.2(2)图所示风载作用下的悬臂刚架,其梁端弯矩M AB =______kN·m ,____侧受拉;左柱B 截面弯矩M B =______kN·m ,____侧受拉。
习题3.2(2)图 (3) 习题3.2(3)图所示三铰拱的水平推力F H 等于 。
习题3.2(3)图 (4) 习题3.2(4)图所示桁架中有 根零杆。
习题3.2(4)图【解】(1)M C = 0;M C = F P l,上侧受拉。
第十三章静定结构内力分析(一

如图13-3d、e所示。
2020/1/31
第13章 第1节 多跨静定梁及斜梁
15
例题 13-1
2020/1/31
第13章 第1节 多跨静定梁及斜梁
16
图13-4
2020/1/31
图13-5
一、多跨静定梁的内力分析
1.多跨静定梁的组成
▪ 将若干根短梁彼此用铰相联接,并用若干支座 再与基础联接而组成的无多余约束的几何不变 体系,称为多跨静定梁。
图13-1a所示为一静定公路桥梁结构图,图131b是其计算简图,由图13-1c可清楚地看到梁 各部分之间的依存关系和力的传递层次。因此, 称图13-1c为多跨静定梁的层叠图或层次图。
(V)和轴力N。根据平衡条件列出K截面的各内力
方程:
2020/1/31
第13章 第1节 多跨静定梁及斜梁
23
以上内力方程与相应的水平梁(图13-8f、g、h、i)
相比较,得
上式中 、为相应水平梁的弯矩和剪力。
2020/1/31
第13章 第1节 多跨静定梁及斜梁
24
(3)绘制内力图
绘制内力图时,一般以梁轴线为基准线, 且内力图的竖标与梁的轴线垂直
为附属部分 图13-2除左边开始第一、三、五跨为基
本部分外,其余二跨的BC、DE均为附属 部分。其层叠图如图13-2C所示。
2020/1/31
第13章 第1节 多跨静定梁及斜梁
11
多跨静定梁力的传递关系
基本部分上的荷载作用,不传递给附属部 分 。即附属部分不产生内力和外力;
而附属部分的荷载作用,则一定传递给基本 部分。即基本部分一定要产生内力和外力。
建筑力学之 静定结构的内力分析知识详解

第二个脚标表示该截面所属杆件的另一端。例如 则表M示BA AB杆B端截面的弯矩。
表M示AB AB杆A端截面的弯矩,
❖ (3)内力图绘制
❖ 静定刚架内力图有弯矩图、剪力图、轴力图。刚架的内力图由各杆的内力图组合 而成,而各杆的内力图,只需求出杆端截面的内力后,即可按照梁内力图的绘制 方法画出。
❖ 6.平面刚架计算步骤
第十一章 静定结构的内力分析
❖ 第一节 楼梯斜梁和多跨静定梁 ❖ 1. 楼梯斜梁 ❖ 楼梯斜梁承受的荷载主要有两种,一种是沿
斜梁水平投影长度分布的荷载,如楼梯上人群 的重量等;另一种是沿倾斜的梁轴方向分布的 竖向荷载,如梁的自重等。 ❖ 一般在计算时,为计算简便可将沿梁轴方 向分布的竖向荷载按等值转换为沿水平方向分 布的竖向荷载,如图11-1 (a),沿梁轴线方向分 布 则的 由荷 于载 是等′值转转换换为,沿所水q 以平有方:向分布的荷q 载 ,
❖ (2)杆端内力的表示:如:FNAB 、 、 、 FNBA FQAB FQBA 、M AB 、M BA 等。 ❖ 注意:刚结点处不同方向有不同的杆端内力。
❖ 为了明确表示刚架上不同截面的内力,特别是为了区别汇交于同一结点的不同杆
端截面的内力,在内力符号右下角采用两个脚标;第一个脚标表示内力所属截面,
❖ 详解见教材
图11-21
❖ (6)结点法与截面法的联合应用 ❖ 欲求图11-23所示a杆的内力,如果只用结点法计算,不论取哪个结
点为隔离体,都有三个以上的未知力无法直接求解;如果只用截面法 计算,也需要解联立方程。 ❖ 为简化计算,可以先作Ⅰ-Ⅰ截面,如图所示,取右半部分为隔离 体,由于被截的四杆中,有三杆平行,故可先求1B杆的内力,然后以 B结点为隔离体,可较方便地求出3B杆的内力,再以3结点为隔离体, 即可求得a杆的内力。
建筑力学:静定结构的内力分析

静定结构的内力分析第一节多跨静定梁、斜梁一、多跨静定梁若干根梁用中间铰连接在一起,并以若干支座与基础相连,或者搁置于其他构件上而组成的静定梁,称为多跨静定梁。
在实际的建筑工程中,多跨静定梁常用来跨越几个相连的跨度。
图13—1a所示为一公路或城市桥梁中,常采用的多跨静定梁结构形式之一,其计算简图如图13—1b所示。
在房屋建筑结构中的木檩条,也是多跨静定梁的结构形式,如图13—2a所示为木檩条的构造图,其计算简图如图13—2b所示。
连接单跨梁的一些中间铰,在钢筋混凝土结构中其主要形式常采用企口结合(图13—1a),而在木结构中常采用斜搭接或并用螺栓连接(图13—2a)。
从几何组成分析可知,图13—1b中AB梁是直接由链杆支座与地基相连,是几何不变的。
且梁AB本身不依赖梁B C和CD就可以独立承受荷载,所以,称为基本部分。
如果仅受竖向荷载作用,CD梁也能独立承受荷载维持平衡,同样可视为基本部分。
短梁BC是依靠基本部分的支承才能承受荷载并保持平衡,所以,称为附属部分。
同样道理在图13—2b 中梁AB,CD和EF均为基本部分,梁BC和梁DE为附属部分。
为了更清楚地表示各部分之间的支承关系,把基本部分画在下层,将附属部分画在上层,分别如图13—1c和图13—跨梁的内力图连在一起,便得到多跨静定梁的内力图。
要依靠AC 梁才能保证其几何不变性,所以CE 梁为附属部分。
(2)计算支座反力从层叠图看出,应先从附属部分CE 开始取隔离体,如图13-3c 所示。
∑=0CM 04680=⨯-⨯D V kN V D 120=(↑) ∑=0DM04280=⨯-⨯C V kN V C 40=(↓)将C V 反向,作用于梁AC 上,计算基本部分∑=0X 0=AH∑=0AM -40×10+V B ×8+10×8×4-64=0 ∑=0BM-40×2-10×8×4-64+V A ×8=0V A =58kN (↑) V B =18kN (↓) 校核:由整体平衡条件得∑Y =—80十120—18十58—10×8=0, 无误。
静定结构内力分析

FQ图
FP
自由端无外力偶则自由端截面无弯矩.
例3-4 不求支反力,直接作图示
A
梁弯矩图、剪力图.
FPl/2 FP
B
B FPl/2
l
铰接杆端无外力偶则该截面无弯矩. FP/2
l/2
FP
练习 :不求支座反力,直接作弯矩图、剪力图。
3FPl
3FP
FPl
FP
l
l
2FP
l
FP
3FP
FPl
FP
FP
FPl
l
l
l
M图 FQ图
2ql 2
D FQDE
q
ql 2
11ql/4
E FQED
M D 0 2 q 2 4 q l 2 l l q 2 F Q E l 4 l D 0 FQED
11ql 4
F y 0F Q D F E Q E D 4 q 0 l
FQD E
5 4
2l
l
自由端有外力偶, 弯矩等于外力偶
练习: 不求支座反力,直接作弯矩图,剪力图
FPl
FP
M
l
l
l
M
l
M MБайду номын сангаас
M/l
2M
MM
l
l
练习: 不求支座反力,直接作弯矩图,剪力图
M
M
l
M
M
l
M
lM
M
l
5.叠加法作弯矩图
ql2/4
q
ql2/4
l
ql2/4
=
ql2/4
ql2/8 + q
ql2/8
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
静定结构内力分析习题集锦(一)徐丰武汉工程大学第3章 静定结构的内力分析习题解答习题3.1 是非判断题(1) 在使用内力图特征绘制某受弯杆段的弯矩图时,必须先求出该杆段两端的端弯矩。
( )(2) 区段叠加法仅适用于弯矩图的绘制,不适用于剪力图的绘制。
( ) (3) 多跨静定梁在附属部分受竖向荷载作用时,必会引起基本部分的内力。
( ) (4) 习题3.1(4)图所示多跨静定梁中,CDE 和EF 部分均为附属部分。
( )习题3.1(4)图(5) 三铰拱的水平推力不仅与三个铰的位置有关,还与拱轴线的形状有关。
( ) (6) 所谓合理拱轴线,是指在任意荷载作用下都能使拱处于无弯矩状态的轴线。
( ) (7) 改变荷载值的大小,三铰拱的合理拱轴线形状也将发生改变。
( ) (8) 利用结点法求解桁架结构时,可从任意结点开始。
( )【解】(1)正确;(2)错误; (3)正确;(4)正确;EF 为第二层次附属部分,CDE 为第一层次附属部分;(5)错误。
从公式0H /C F M f 可知,三铰拱的水平推力与拱轴线的形状无关;(6)错误。
荷载发生改变时,合理拱轴线将发生变化; (7)错误。
合理拱轴线与荷载大小无关;(8)错误。
一般从仅包含两个未知轴力的结点开始。
习题3.2 填空(1)习题3.2(1)图所示受荷的多跨静定梁,其定向联系C 所传递的弯矩M C 的大小为______;截面B 的弯矩大小为______,____侧受拉。
P习题3.2(1)图(2) 习题3.2(2)图所示风载作用下的悬臂刚架,其梁端弯矩M AB =______kN·m ,____侧受拉;左柱B 截面弯矩M B =______kN·m ,____侧受拉。
习题3.2(2)图(3) 习题3.2(3)图所示三铰拱的水平推力F H等于。
习题3.2(3)图(4) 习题3.2(4)图所示桁架中有根零杆。
习题3.2(4)图【解】(1)M C = 0;M C = F P l,上侧受拉。
CDE部分在该荷载作用下自平衡;(2)M AB=288kN·m,左侧受拉;M B=32kN·m,右侧受拉;(3)F P/2;(4)11(仅竖向杆件中有轴力,其余均为零杆)。
习题3.3作习题3.3图所示单跨静定梁的M图和QF图。
(a)(b)qP(c) (d)2(e) (f)习题3.3图【解】C DM图(单位:kN·m)F Q图(单位:kN)(a)2aF24F P5M图F Q图(b)8ql22ql8ql5M图F Q图(c)F3P4M图F Q图(d)qa21.5qa22qaM图F Q图(e)M 图 (单位:kN·m )F Q 图(单位:kN )(f)习题3.4 作习题3.4图所示单跨静定梁的内力图。
(a)(b)m(c) (d)习题3.4图【解】M 图 (单位:kN·m ) F Q 图(单位:kN )(a)M 图 (单位:kN·m ) F Q 图(单位:kN )(b)M 图 (单位:kN·m ) F Q 图(单位:kN )(c)M 图 (单位:kN·m ) F Q 图(单位:kN )(d)习题3.5 作习题3.5图所示斜梁的内力图。
习题3.5图【解】M 图 (单位:kN·m ) F Q 图(单位:kN ) F N 图(单位:kN )习题3.6 作习题3.6图所示多跨梁的内力图。
(a)(b)A(c)(d) 习题3.6图【解】DM 图 (单位:kN·m ) F Q 图(单位:kN )(a)21M 图 (单位:kN·m ) F Q图(单位:kN )(b)AM 图(单位:kN·m )AF Q 图(单位:kN )(c)M 图(单位:kN·m )F Q图(单位:kN)(d)习题3.7 改正习题3.7图所示刚架的弯矩图中的错误部分。
(a) (b)(c)(d) (e)(f)习题3.7图【解】(a) (b)(c)(d) (e) (f)习题3.8 作习题3.8图所示刚架的内力图。
(a) (b) (c)q(d) (e) (f)习题3.8图【解】M 图 (单位:kN·m ) F Q 图(单位:kN ) F N 图(单位:kN )(a)M 图 (单位:kN·m ) F Q 图(单位:kN ) F N 图(单位:kN )(b)M 图 (单位:kN·m ) F Q 图(单位:kN ) F N 图(单位:kN )(c)M 图 F Q 图 F N 图(d)3.5M 图 (单位:kN·m ) F Q 图(单位:kN ) F N 图(单位:kN )(e)F PM 图 F Q 图 F N 图(f)习题3.9 作习题3.9图所示刚架的弯矩图。
(a) (b) (c)(d) (e)(f)(g) (h) (i)习题3.9图【解】P(a) (b) (单位:kN·m)(c)(单位:kN·m)(d) (e)(f)(单位:kN·m)aF P(g) (单位:kN·m)(h) (i) (单位:kN·m)习题3.10试用结点法求习题3.10图所示桁架杆件的轴力。
P(a) (b)习题3.10图【解】(1)提示:根据零杆判别法则有:N13N43F F==;根据等力杆判别法则有:N24N46F F=。
然后分别对结点2、3、5列力平衡方程,即可求解全部杆件的内力。
(2)提示:根据零杆判别法则有:N18N17N16N27N36N450F F F F F F ======;根据等力杆判别法则有:N12N23N34F F F ==;N78N76N65F F F ==。
然后取结点4、5列力平衡方程,即可求解全部杆件的内力。
习题3.11 判断习题3.11图所示桁架结构的零杆。
P(a) (b)(c)习题3.11图【解】P(a) (b)(c)提示:(c)题需先求出支座反力后,截取Ⅰ.Ⅰ截面以右为隔离体,由30M=∑,可得N120F =,然后再进行零杆判断。
习题3.12 用截面法求解习题3.12图所示桁架指定杆件的轴力。
(a)(b)(c) (d)习题3.12图【解】 (1) N P 32a F F =-;N P 12b F F =;N P 2c F F = 提示:截取Ⅰ.Ⅰ截面可得到N b F 、N c F ;根据零杆判断法则,杆26、杆36为零杆,则通过截取Ⅱ.Ⅱ截面可得到N a F 。
(2) N 0a F =;N P b F ;N 0c F =提示:截取Ⅰ.Ⅰ截面可得到N b F ;由结点1可知N 0a F =;截取Ⅱ.Ⅱ截面,取圆圈以内为脱离体,对2点取矩,则N 0c F =。
Ⅰ(3) N 12kN a F =-;N 10kN 3b F =;N 28kN 3c F = 提示:先计算支座反力。
取Ⅰ.Ⅰ截面以左为脱离体,由0AM=∑,得N a F ;由0B M =∑,得N c F ;再取结点A 为脱离体,由0yF=∑,得N b F 。
=N F N c(4) N 5.66kN a F =-;N 1.41kN b F =-;N 8kN c F =-提示:先计算支座反力。
取Ⅰ.Ⅰ截面以左为脱离体,将N a F 移动到2点,再分解为x 、y 的分力,由10M=∑,得4kN ya F =-,则N 5.66kN a F =-;取Ⅱ.Ⅱ截面以左为脱离体,由0yF=∑,得1kN yb F =-,则N 1.41kN b F =-;取Ⅲ.Ⅲ截面以右为脱离体,注意由结点4可知N340F =,再由10M=∑,得N 8kN c F =-。
习题3.13 选择适当方法求解习题3.13图所示桁架指定杆件的轴力。
(a)(b)(c)(d)(e)(f)(g) (h)习题3.13图【解】(1)N PaF F=;NbF=;NcF=。
提示:由4M=∑,可得60yF=。
则根据零杆判别原则,可知N Nb cF F==。
根据结点5和结点2的构造可知,N23N35F F==,再根据结点3的受力可知N PaF F=。
(2) N 12.73kN a F =;N 18.97kN b F =;N 18kN c F =-。
提示:先计算支座反力。
取Ⅰ.Ⅰ截面以左为脱离体,由0AM =∑,可得N 12.73kN aF =;取B 结点为脱离体,由0yF=∑,得N 12.73kN BD F =-;由0x F =∑,可得N 18kN cF =-;取Ⅱ.Ⅱ截面以右为脱离体,由0CM=∑,可得N 18.97kN b F =。
N B DN cF(3) N 0a F =;N P 3b F F =;N P c F F =。
提示:先计算支座反力。
取Ⅰ.Ⅰ截面以左为脱离体,由0yF=∑,可得N 0a F =;由30M=∑,可得N12/3P F F =;由0x F =∑,可得N34/3P F F =-;取结点3为脱离体,由0xF =∑,可得N b F;取结点A 为脱离体,由0xF =∑,可得N cF。
注意N1N12A F F =。
N 341A(4) N P 13a F F -=;N P 3b F F =;N 0c F =。
提示:先计算支座反力。
取Ⅰ.Ⅰ截面以上为脱离体,由10M=∑,可得N a F ;取Ⅱ.Ⅱ截面以右为脱离体,由0yF=∑,可得N b F ;取Ⅲ.Ⅲ截面以右为脱离体,注意由结点B 可知N 0BC F =,再由30M=∑,得N c F 。
(5) N P a F F =;N P b F =。
提示:根据求得的支反力可知结构的受力具有对称性,且结点A 为K 形结点,故可判别零杆如下图所示。
再取结点B 为脱离体,由0yF=∑,可得N N P b BC F F ==;由0xF=∑,可得N P a F F =。
(6) N 0a F =;N P /2b F F =;N 0ac F =。
提示:原结构可分为以下两种情况的叠加。
对于状态1,由对称性可知,R 0B F =,则根据零杆判别法则可知1N 0a F =。
取Ⅰ.Ⅰ截面以右为脱离体,由0DM=∑,可得1N 0b F =;根据E 、D 结点的构造,根据零杆判别法则,可得1N 0c F =。
对于状态2,根据零杆判别法则和等力杆判别法则,易得到:2N 0a F =;2N P /2b F F =;2N 0c F =。
将状态1和状态2各杆的力相加,则可得到最终答案。
222F P F P F P22F P F P 状态1 状态2 (7) N 0a F =;N 0b F =;N 40/3kN c F =-。
提示:先计算支座反力。
取Ⅰ.Ⅰ截面以右为脱离体,将N a F 移动到B 点,再分解为x 、y 的分力,由0AM=∑,可得0ya F =,则N 0a F =;根据结点B 的构造和受力,可得N 0b F =; 取结点C 为脱离体,可得N 40/3kN c F =-。
