九年级数学上学期课时知识同步测试9
2022-2023学年全国初中九年级上数学新人教版同步练习(含解析)

2022-2023学年全国九年级上数学同步练习考试总分:24 分 考试时间: 120 分钟学校:__________ 班级:__________ 姓名:__________ 考号:__________注意事项:1.答题前填写好自己的姓名、班级、考号等信息; 2.请将答案正确填写在答题卡上;卷I (选择题)一、 选择题 (本题共计 4 小题 ,每题 3 分 ,共计12分 )1. 如图,在中,,按如下步骤作图:以点为圆心,小于的长为半径作弧,分别交,于点,;分别以点,为圆心,大于的长为半径作弧,两弧相交于点,作射线,交于点,过点作交于点.已知,,则的长为( )A.B.C.D.2. 如图,点、、在上,,则的度数是( )A.B.C.D.Rt △ABC ∠C =90∘①A AC AC AB M N ②M N MN 12P AP BC D D DE ⊥BC AB E DE =2∠B =30∘AC 5–√3+15–√23–√A B C ⊙O ∠AOB =40∘∠ACB 10∘20∘30∘403. 如图,和是两个全等的正三角形,它们各边的交点均为各边的三等分点.若从该图形中随机取一点,则该点取自其中阴影部分的概率为 A.B.C.D.4. 如图,中,弦与交于点,,,则的度数是( )A.B.C.D.卷II (非选择题)二、 填空题 (本题共计 3 小题 ,每题 3 分 ,共计9分 )5. 在圆的内接四边形中,、、的度数之比为,则的度数是________.6. 如图,一张扇形纸片,=,=,连接,,,若=,则图中阴影部分的面积为________(结果保留).△ABC △DEF ()12233458⊙O AB CD M ∠A =45∘∠AMD =75∘∠B 15∘20∘25∘30∘ABCD ∠A ∠B ∠C 2:3:4∠D ∘OAC ∠AOC 120∘OA 8AB BC AC OA AB π7. 如图,在菱形中,,点、分别在边、上,与关于直线对称,点的对称点是点,且点在边上.若,则的长为________.三、 解答题 (本题共计 1 小题 ,共计3分 )8.(3分) 如图,中, ,为上的一点,以为直径的交于,连接交于,交于,连接,求证:与相切;若,,则的半径________;若,,求(用的代数式表示).ABCD ∠BAD =120∘E F AB BC △BEF △GEF EF B G C AD EG ⊥AC,AB =62–√FC △ABC ∠ACB =90∘D AB CD ⊙O AC E BE CD P ⊙O F DF ∠ABC =∠EFD.(1)AB ⊙O (2)AD =4BD =6⊙O =(3)PC =2PF BF =a CP a参考答案与试题解析2022-2023学年全国九年级上数学同步练习一、 选择题 (本题共计 4 小题 ,每题 3 分 ,共计12分 )1.【答案】B【考点】作图—复杂作图角平分线的性质平行线的性质含30度角的直角三角形【解析】由作图知平分,由直角三角形性质可得,由平分,则,由,可得,则,故,由可得解.【解答】解:由作图步骤可知:平分,,,,,,,,,,平分,,,,,,,.故选.2.AD ∠CAB 30∘BE =2DE =4AD ∠CAB ∠CAD =∠BAD AC//DE ∠CAD =∠EDA ∠BAD =∠EDA AE =DE =2AB =AE +BE AD ∠CAB ∵DE ⊥BC ∴∠BDE =90∘∵∠B =30∘∴DE =BE 12∵DE =2∴BE =2DE =2×2=4∵∠C =90∘∴∠BDE =∠C =90∘∴AC//DE ∴∠CAD =∠EDA ∵AD ∠CAB ∴∠CAD =∠BAD ∴∠BAD =∠EDA ∴AE =DE =2∴AB =AE +BE =2+4=6∵∠C =90∘∠B =30∘∴AC =AB =×6=31212B【答案】B【考点】圆周角定理【解析】根据圆周角定理得到,即可计算出.【解答】解:∵,∴.故选.3.【答案】A【考点】几何概型计算(与长度、角度、面积、体积有关的几何概型)【解析】设正六边形的边长为,与的交点为,由已知求得,,,进一步求出阴影部分的面积,由测度比是面积比得答案.【解答】解:根据题意可得图形外侧的个小三角形均全等,且为正三角形.设一个小三角形面积为,则该图形的面积为,阴影部分的面积为,所以从该图形中随机取一点,则该点取自其中阴影部分的概率 ,故选4.【答案】∠ACB =∠AOB 12∠ACB ∠AOB =40∘∠ACB =∠AOB =1220∘B 2AC BE G BG AG CG 6S 12S 6S P ==6S 12S12A.D【考点】圆周角定理三角形的外角性质【解析】此题暂无解析【解答】解:根据圆周角定理可知:,∵,∴.故选.二、 填空题 (本题共计 3 小题 ,每题 3 分 ,共计9分 )5.【答案】【考点】圆内接四边形的性质【解析】根据圆内接四边形的性质得到,设,,的度数分别为、、,根据圆内接四边形的性质列出方程,解方程求出,计算即可.【解答】解:∵四边形是圆内接四边形,∴,设,,的度数分别为、、,则,解得,,则,∴.故答案是:.6.【答案】∠D =∠A =45∘∠AMD =∠B +∠D =75∘∠B =−∠D =75∘30∘D 90∠A +∠C =∠B +∠D ∠A ∠B ∠C 2x 3x 4x x ABCD ∠A +∠C =∠B +∠D =180∘∠A ∠B ∠C 2x 3x 4x 2x +64=180∘x =30∘∠B =3x =90∘∠D =−∠B =180∘90∘90【考点】扇形面积的计算【解析】此题暂无解析【解答】此题暂无解答7.【答案】【考点】切线的性质垂径定理勾股定理【解析】此题暂无解析【解答】解:如图,∵四边形是菱形,,∴,,∴,是等边三角形,∵,∴,∵,∴,∴,∴,∴,∴.故答案为:.三、 解答题 (本题共计 1 小题 ,共计3分 )36–√ABCD ∠BAD =120∘AB =BC =CD =AD ∠CAB =∠CAD =60∘△ABC △ACD EG ⊥AC ∠AEG =∠AGE =30∘∠B =∠EGF =60∘∠AGF =90∘FG ⊥BC 2⋅=BC ⋅FG S △ABC 2××(6=6⋅FG 3–√42–√)22–√FG =36–√36–√8.【答案】证明:∵,∴.∵,,∴.∵,∴,即.∴.∴与相切.解:如图,连接.∵是的直径,∴,∴.∵,,∴.∵,∴,又∵,∴,∴.∴.∵,∴,即.∵,∴.【考点】圆周角定理直角三角形的性质切线的判定三角形的外角性质相似三角形的性质与判定【解析】(1)∠ACB =90∘∠CEB +∠CBE =90∘∠ABC =∠EFD ∠EFD =∠FDB +∠FBD ∠EBC =∠FDB ∠CEB =∠CDF ∠CDF +∠FDB =90∘CDB =90∘CD ⊥AB AB ⊙O 6–√(3)CF CD ⊙O ∠CFD =90∘∠DCF +∠CDF =90∘∠CDB =90∘∴∠FDB +∠CDF =90∘∠FDB =∠DCF ∠EBC =∠FDB ∠EBC =∠DCF ∠CPF =∠BPC △PCF∽△PBC ==PC PB PF PC 12PB =2PC =4PF PB =PF +BF 4PF =PF +BF PF =BF =a1313PC =2PF CP =a 23∠CEB +∠CBE =90∘(1)根据直角三角形的两个锐角互余可得,根据三角形外角的性质可得,然后等量替换结合圆周角定理即可得到,进一步根据切线的判定可得结论.(2)利用已知条件证明,然后根据相似三角形的性质可以求出直径的长,进一步可求半径的长.(3)连接,然后证明,再根据相似三角形的性质可得和的关系,再结合即可得出的长.【解答】证明:∵,∴.∵,,∴.∵,∴,即.∴.∴与相切.解:∵,,∴.∵,∴,∴,∴.∴.∴的半径.故答案为:.解:如图,连接.∵是的直径,∴,∴.∵,,∴.∵,∴,又∵,∴,∴.∴.∵,∴,即.∵,∠CEB +∠CBE =90∘∠EFD =∠FDB +∠FBD ∠CDF +∠FDB =90∘△ACD ∼△CBD CD CF △PCF ∼△PBC PB PC PB =PF +BF PC (1)∠ACB =90∘∠CEB +∠CBE =90∘∠ABC =∠EFD ∠EFD =∠FDB +∠FBD ∠EBC =∠FDB ∠CEB =∠CDF ∠CDF +∠FDB =90∘CDB =90∘CD ⊥AB AB ⊙O (2)∠ACD +∠A =90∘∠ABC +∠A =90∘∠ACD =∠ABC ∠ADC =∠BDC =90∘△ACD ∽△CBD =CD BD AD CD C =AD ⋅BD =4×6=24D 2CD ==224−−√6–√⊙O =CD =126–√6–√(3)CF CD ⊙O ∠CFD =90∘∠DCF +∠CDF =90∘∠CDB =90∘∴∠FDB +∠CDF =90∘∠FDB =∠DCF ∠EBC =∠FDB ∠EBC =∠DCF ∠CPF =∠BPC △PCF ∽△PBC ==PC PB PF PC 12PB =2PC =4PF PB =PF +BF 4PF =PF +BFPF =BF =a 1313PC =2PF P =a2∴.CP =a 23。
人教版初中九年级数学上册课堂同步试题及答案 全册

21.1二次根式(1)中学初三数学备课组一、选择题1.下列式子中,一定是二次根式的是()A.BC D.x2.下列式子中,不是二次根式的是()A BC D.1 x3.已知一个正方形的面积是5,那么它的边长是()A.5 B C.15D.以上皆不对4一定是二次根式的个数是().A.4 B.3 C.2 D.1二、填空题5.形如________的式子叫做二次根式.6.面积为a的正方形的边长为________.三、解答题7.某工厂要制作一批体积为1m3的产品包装盒,其高为0.2m,按设计需要,•底面应做成正方形,试问底面边长应是多少?8=0,求x y的值.21.1二次根式(2)中学初三数学备课组一、选择题1.下列各式中一定是二次根式的是( )A.10- B.22-aC.327D.132+x2.下列计算正确的是( ) A.()2552=B.()332-=-C.416±=D.749=3.如果a 为任意实数,那么下列各式中正确的是( ) A.a ≥0 B.a -≥0C.2a ≥0D.a -≥0二、填空题4.若a 的算式平方根是21,则a =_______________. 5.计算:(1)()=222-_______;(2)=⎪⎭⎫⎝⎛--221________. 6.已知一个直角三角形的两直角边分别为x 和y ,则斜边用代数式表示为_________________;当x =6,y =8时,斜边长为__________.三、解答题7.当x 是多少时,下列各式在实数范围内有意义? (1)x 2-;(2)121-x .8.当5=a 时,求式子221a a a +-+的值.21.2二次根式的乘除(1)中学 初三数学备课组一、选择题1.已知12)1(2-•=-x x ,则有( )A.x >1 B.x <1C.x ≥1 D.x ≤12.计算xx 2•的结果是( ) A.xB.2C.xD.23.下列计算正确的是( ) A.3163838=⨯ B.652535=⨯C.562234=⨯D.15125236=⨯二、填空题4.=⨯44__________,.__________62=⨯ 5.化简38)2(2⨯⨯-的结果是____________.三、解答题6.化简:(1)16925⨯;(2)429y x .7.若直角三角形两条直角边长分别为15cm 和12cm ,求此直角三角形的面积.21.2二次根式的乘除(2)中学 初三数学备课组一、选择题1.下列各式是最简二次根式的为( )A.12+x B.32y xC.12- D.5.22.化简231+的结果为( )A.23+B.23-C.2 D.13.已知a aa a -=-112,则a 的取值范围是( )A.a ≤0 B.a <0C.0<a ≤1D.a >0二、填空题4.__________2385=÷,___________3=÷a b a .5.___________3625=,___________3611214=⨯.三、解答题6.把下列各式化为最简二次根式(1)326-;(2)328a a.7.已知长方形的面积是48,一边长是12,则另一边长是多少?21.2二次根式的乘除(3)中学 初三数学备课组一、选择题1.下列化简中,正确的是( )A.1535925=⨯=⨯B.632=⨯C.222543=+D.33-12= 2.下列计算正确的是( )A .3232--=-- B .a a 3313=C .a a=33D .a a333= 3.把(a -1)11-a根号外的因式移入根号内,其结果是( ) A .1-a B .-1-a C .a -1 D .-a -1二、填空题4.= . 5.把aa 1-中根号外面的因式移到根号内的结果是三、解答题6.计算:(1)213675÷⨯7.已知x+y=4,xy=2.求;xyy x+的值。
2022-2023学年新人教版九年级上数学同步练习(含解析)

2022-2023学年初中九年级上数学同步练习学校:____________ 班级:____________ 姓名:____________ 考号:____________考试总分:48 分 考试时间: 120 分钟注意事项:1.答题前填写好自己的姓名、班级、考号等信息; 2.请将答案正确填写在答题卡上;卷I (选择题)一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )1. 已知,且,,则的值为()A.B.C.D.2. 用配方法解方程,则方程可变形为( )A.B.C.D.3. 设,是方程的两个实数根,则的值为( )A.B.C.D.4. 已知,是关于的方程的两根,下列结论一定正确的是( )mn ≠15+2019m +9=0m 29+2019n +5=0n 2mn −402599567033−6x +2=0x 2(x −3=)2233(x −1=)223(3x −1=1)2(x −1=)213m n +x −1001x 2=0+2m +n m 2−100110011000−1000x 1x 2x +mx −1x 2=0≠A.B.C.D.,5. 将抛物线 向左平移个单位长度,再向下平移个单位长度,得到的抛物线的函数表达式为 A.B.C.D.6. 抛一个铁球,在泥地上砸了一个直径,深的坑,这个铁球的直径是( )A.B.C.D.7. 如图,中,半径弦于点,点在上,,,则线段等于( )A.B.C.D.8. 如图,在中,是的直径,,点,是的三等分点,是上一动点,则的最小值是 ≠x 1x 2+<0x 1x 2⋅>0x 1x 2>0x 1<0x 2y =x 223()y =(x +2−3)2y =(x +2+3)2y =(x −2+3)2y =(x −2+3)28cm 2cm 12cm10cm8cm2–√6cm3–√⊙O OC ⊥AB D E ⊙O ∠E =22.5∘AB =4CD 2–√12−22–√32⊙O AB ⊙O AB =12C D AB ˆM AB CM +DM ()A.B.C.D.9. 下列说法中,正确的是( )A.在同圆或等圆中,相等的圆心角所对的弧相等B.平分弦的直径垂直于弦C.长度相等的两条弧是等弧D.圆的切线垂直于半径10. 如图,点、、在上,,则的度数是( )A.B.C.D.卷II (非选择题)二、 解答题 (本题共计 6 小题 ,每题 3 分 ,共计18分 )11.;;;161286A B C ⊙O ∠AOB =40∘∠ACB 10∘20∘30∘40(1)+x =2x 23–√(2)6000=8640(1+x)2(3)−6x −7=0x 2(2−3x)+=02. 12. 某商品现在的售价为每件元,每星期可卖出件,市场调查反映,如调整价格,每降价元,每星期可多卖出件,已知商品的进价为每件元.该商品每件降价多少元,商场可以获利元?该商品每件降价多少元,才能使利润最大?13. 设椭圆的右焦点为,过的直线与交于,两点,点的坐标为.(1)当与轴垂直时,求直线的方程;(2)设为坐标原点,求的值.14. 已知关于的一元二次方程.求证:此方程有两个不相等的实数根;如果方程的两个实数根为,且,求的值.15. 抛物线经过点,,直线过点,,点是抛物线上点,间的动点(不含端点,),过作轴于点,连接,.求抛物线与直线的解析式;求证:为定值;若的面积为,求满足条件的点的坐标.16. 某广告公司设计一幅周长为米的矩形广告牌,广告设计费为每平方米元. 设矩形一边长为,面积为平方米.求与之间的函数关系式,并写出自变量的取值范围;设计费能达到元吗?为什么?当是多少米时,设计费最多?最多是多少元?(4)(2−3x)+=0(3x −2)26030012040(1)3000(2)C :+=1x 22y 2F F l C A B M (2,0)l x AM O ∠OMA ∠OMB x −(2m −2)x +(−2m)=0x 2m 2(1)(2),x 1x 2+=10x 12x 22m y =a +b x 2A (4,0)B (0,−4)EC E (4,−1)C (0,−3)P A B A B P PD ⊥x D PC PE (1)CE (2)PC +PD (3)△PEC 1P 162000x S (1)S x x (2)24000(3)x参考答案与试题解析2022-2023学年初中九年级上数学同步练习一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )1.【答案】C【考点】根与系数的关系【解析】此题暂无解析【解答】解:将变形得:,,∴与为方程的两个解,则,故选.2.【答案】D【考点】解一元二次方程-配方法【解析】先移项得到,再把方程两边都除以,然后把方程两边加上即可得到.【解答】解:移项得,二次系数化为得,9+2009n +5=0n 25×+2009×+9=0()1n 21n 5+2009m +9=0m 2m 1m 5+2009x +9=0x 2m ⋅==1n m n 95C 3−6x =−2x 231(x −1=)2133−6x =−2x 21−2x =−x 2232x +1=−+12方程两边加上得,所以.故选.3.【答案】C【考点】列代数式求值根与系数的关系一元二次方程的解【解析】由于、是方程的两个实数根,根据根与系数的关系可以得到,并且,然后把变形为,把前面的值代入即可求出结果.【解答】解:,是方程的两个实数根,该一元二次方程,二次项系数,一次项系数,常数项,根据根与系数的关系,可得到.又,,.故选.4.【答案】A【考点】根与系数的关系根的判别式【解析】先计算判别式的值得到=,根据判别式的意义可判断方程有两个不相等的实数解,再利用根与系数的关系得到、异号,然后对各选项进行判断.【解答】解:,,1−2x +1=−+1x 223(x −1=)213D m n +x −1001=0x 2m +n =−1+m −1001=0m 2+2m +n m 2(+m)+(m +1)m 2m n +x −1001=0x 2a =1b =1c =−1001m +n =−=−1b a +m −1001=0m 2+m =1001m 2+2m +n =(+m)+(m +n)m 2m 2=1001−1=1000C △+4>0m 2x 1x 2A Δ=−4×(−1)m 2=+4>0m 2∴方程有两个不相等的实数解,∴.故选项正确;,,不能确定是否小于,故选项错误;,,故选项错误;,,,异号,但不能确定大小,故选项错误.故选.5.【答案】A【考点】二次函数图象与几何变换【解析】先确定抛物线的顶点坐标为,再根据点平移的规律得到点平移后所得对应点的坐标为,然后根据顶点式写出平移后的抛物线解析式.【解答】解:抛物线 向左平移个单位长度,得到,再向下平移个单位长度,则得到的抛物线的函数表达式为:.故选.6.【答案】B【考点】垂径定理的应用【解析】根据题意画出草图,建立数学模型.根据勾股定理和垂径定理求解.【解答】设该铅球的半径是.在由铅球的半径、小坑的半径即半弦和弦心距组成的直角三角形中,根据勾股定理,得=,解得=,故=.7.【答案】≠x 1x 2B +=−m x 1x 20C x 1x 2=−1<0D x 1x 2=−1<0x 1x 2A y =x 2(0,0)(0,0)(−2,−3)y =x 22y =(x +2)23y =(x +2−3)2A rcm r 2(r −2+16)2r 52r 10C【考点】圆周角定理垂径定理勾股定理【解析】直接利用垂径定理进而结合圆周角定理得出是等腰直角三角形,进而得出答案.【解答】解:∵半径弦于点,∴,∴,∴,∴是等腰直角三角形,∵,∴,则半径等于:,∴.故选.8.【答案】B【考点】垂径定理的应用【解析】作点关于的对称点,连接与相交于点,根据轴对称确定最短路线问题,点为的最小值时的位置,根据垂径定理可得,然后求出为直径,从而得解.【解答】解:如图,作点关于的对称点,连接与相交于点,此时,点为的最小值时的位置,由垂径定理,,△ODB OC ⊥AB D =ACˆBC ˆ∠E =∠BOC =1222.5∘∠BOD =45∘△ODB AB =4DB =OD =2OB =2+2222−−−−−−√2–√CD =2−22–√C C AB C'C'D AB M M CM +DM =AC ˆAC'ˆC'D C AB C'D C ′AB M M CM +DM =AC ˆAC ′ˆˆˆ∴,∵,为直径,∴为直径,即的最小值是.故选.9.【答案】【考点】圆心角、弧、弦的关系【解析】此题暂无解析【解答】此题暂无解答10.【答案】B【考点】圆周角定理【解析】根据圆周角定理得到,即可计算出.【解答】解:∵,∴.故选.二、 解答题 (本题共计 6 小题 ,每题 3 分 ,共计18分 )11.【答案】解:原式可化为,则,解得,.=BD ˆAC ′ˆ==AC ˆCD ˆBD ˆAB D C ′CM +DM 12B ∠ACB =∠AOB 12∠ACB ∠AOB =40∘∠ACB =∠AOB =1220∘B (1)+x −2=0x 23–√x =−±3–√3+8−−−−√2=x 1−+3–√11−−√2=x 2−−3–√11−−√2x +1=8640原式可化为,即,则,解得,.移项,得,配方,得,即,则,解得,.原式可化为,则,所以或,解得,,【考点】解一元二次方程-因式分解法解一元二次方程-公式法解一元二次方程-配方法解一元二次方程-直接开平方法【解析】无无无无【解答】解:原式可化为,则,解得,.原式可化为,即,则,解得,.移项,得,配方,得,即,则,解得,.(2)(x +1=)286406000(x +1=)23625x +1=±65=x 115=−x 2115(3)−6x =7x 2−6x +9=16x 2(x −3=16)2x −3=±4=7x 1=−1x 2(4)(2−3x)+(2−3x =0)2(2−3x)(2−3x +1)=02−3x =02−3x +1=0=x 123=1x 2(1)+x −2=0x 23–√x =−±3–√3+8−−−−√2=x 1−+3–√11−−√2=x 2−−3–√11−−√2(2)(x +1=)286406000(x +1=)23625x +1=±65=x 115=−x 2115(3)−6x =7x 2−6x +9=16x 2(x −3=16)2x −3=±4=7x 1=−1x 2(4)(2−3x)+(2−3x =0)2原式可化为,则,所以或,解得,,12.【答案】解:设该商品每件降价元,根据题意,得解得:,(不符合题意,舍去),答:该商品每件降价元.设商品每件降价元,获得的利润为元,根据题意,得,,当时,有最大值,即最大值为,答:商品每件降价元,才能使利润最大.【考点】一元二次方程的应用二次函数的最值二次函数的应用【解析】本小题考查一元二次方程的应用.设该商品每件降价元,则每件利润为元,可卖件数为件,根据利润=每件利润件数列出方程为,求解即可.注意:要检验是否符合题意.本题考查二次函数的应用.利用二次函数最值求解.先设商品每件降价元,获得的利润为元,根据利润每件商品的单价件数列出二次函数,再根据二次函数最值求法求解即可.【解答】解:设该商品每件降价元,根据题意,得解得:,(不符合题意,舍去),答:该商品每件降价元.设商品每件降价元,获得的利润为元,根据题意,得,,当时,有最大值,即最大值为,答:商品每件降价元,才能使利润最大.13.(4)(2−3x)+(2−3x =0)2(2−3x)(2−3x +1)=02−3x =02−3x +1=0=x 123=1x 2(1)x (60−40−x)(300+20x)=3000=15x 1=−10x 215(2)x y y =(60−40−x)(300+20x)=−20+100x +6000x 2=−20+6125(x −)522∵−20<0∴x =52y 612552(1)x (60−40−x)(300+20x)×(60−40−x)(300+20x)=3000(2)x y =×(1)x (60−40−x)(300+20x)=3000=15x 1=−10x 215(2)x y y =(60−40−x)(300+20x)=−20+100x +6000x 2=−20+6125(x −)522∵−20<0∴x =52y 612552【答案】解:(1)由已知得,的方程为,由已知可得,点的坐标为或.所以的方程为或.(2)由题意知直线的斜率不为,当与轴不垂直时,设的方程为,,,直线,的斜率之和为,由,得,将代入得,所以,.则,从而,故,的倾斜角互补,所以.当与轴垂直时,由椭圆方程的对称性可知,.所以.【考点】直线与椭圆的位置关系【解析】【解答】解:(1)由已知得,的方程为,由已知可得,点的坐标为或.所以的方程为或.F(1,0)l x =1A (1,)2–√2(1,−)2–√2AM y =−x +2–√22–√y =x −2–√22–√l 0l x l y =k(x −1)(k ≠0)A (,)x 1y 1B (,)x 2y 2MA MB +=+k MA k MB y 1−2x 1y 2−2x 2=k (−1)y 1x 1=k (−1)y 2x 2+=k MA k MB 2k −3k (+)+4k x 1x 2x 1x 2(−2)(−2)x 1x 2y =k(x −1)+=1x 22y 2(2+1)−4x +2−2=0k 2x 2k 2k 2+=x 1x 24k 22+1k 2=x 1x 22−2k 22+1k 22k −3k (+)+4kx 1x 2x 1x 2==04−4k −12+8+4k k 3k 3k 32+1k 2+=0k MA k MB MA MB ∠OMA =∠OMB l x ∠OMA =∠OMB =1∠OMA ∠OMBF(1,0)l x =1A (1,)2–√2(1,−)2–√2AM y =−x +2–√22–√y =x −2–√22–√l(2)由题意知直线的斜率不为,当与轴不垂直时,设的方程为,,,直线,的斜率之和为,由,得,将代入得,所以,.则,从而,故,的倾斜角互补,所以.当与轴垂直时,由椭圆方程的对称性可知,.所以.14.【答案】证明:由题意得:,∴此方程有两个不相等的实数根.解:∵,∴,即,∴,解得或.【考点】根与系数的关系根的判别式【解析】此题暂无解析l 0l x l y =k(x −1)(k ≠0)A (,)x1y 1B (,)x2y 2MA MB +=+k MA k MB y 1−2x 1y 2−2x 2=k (−1)y 1x 1=k (−1)y 2x 2+=k MA k MB 2k −3k (+)+4kx 1x 2x 1x 2(−2)(−2)x 1x 2y =k(x −1)+=1x 22y 2(2+1)−4x +2−2=0k 2x 2k 2k 2+=x 1x 24k 22+1k 2=x 1x 22−2k 22+1k 22k −3k (+)+4kx 1x 2x1x2==04−4k −12+8+4kk 3k 3k 32+1k 2+=0k MA k MB MA MB ∠OMA =∠OMB l x ∠OMA =∠OMB =1∠OMA ∠OMB(1)Δ=[−(2m −2)−4(−2m)=4>0]2m 2(2)+=2m −2,=−2m x 1x 2x 1x 2m 2+=x 12x 22(+−2=10x 1x 2)2x 1x 2(2m −2−2(−2m)=10)2m 2−2m −3=0m 2m =−1m =3【解答】证明:由题意得:,∴此方程有两个不相等的实数根.解:∵,∴,即,∴,解得或.15.【答案】解:将,代入 ,得∴抛物线的解析式为.设直线的解析式为 ,将点,代入得解得∴直线的解析式为.证明:过点作轴于点,如图,设点, ,则, ,, ,(1)Δ=[−(2m −2)−4(−2m)=4>0]2m 2(2)+=2m −2,=−2m x 1x 2x 1x 2m 2+=x 12x 22(+−2=10x 1x 2)2x 1x 2(2m −2−2(−2m)=10)2m 2−2m −3=0m 2m =−1m =3(1)A (4,0)B (0,−4)y =a +b x 2{16a +b =0,b =−4,a =,14b =−4,y =−414x 2CE y =mx +n E (4,−1)C (0,−3)y =mx +n {4m +n =−1,n =−3,m =,12n =−3,CE y =x −312(2)P PF ⊥y F P (t,−4)14t 20<t <4PF =t FC =|−4+3|=|−1|14t 214t 2PD =4−14t 2PC ===+1+t 2(−1)14t 22−−−−−−−−−−−−−√(+1)14t 22−−−−−−−−−−√14t 2C +PD =(+1)+(4−)=511∴为定值.解:设与的交点为,设,①如图,当点在点上方时,,∵,∴,解得, (负根舍去),∴ ,即.②如图,当点在点下方时,,∵,∴,解得,(负根舍去),∴ ,即,综上所述,满足条件的点有 ,.【考点】PC +PD =(+1)+(4−)=514t 214t 2(3)DP EC G P (x,−4)14x 2G P =×4×[(x −3)−(−4)]S △PEC 121214x 2=−+12(x −1)252=1S △PEC−+=112(x −1)252=1+x 13–√=1−x 23–√y =×−4=−314(1+)3–√23–√2(1+,−3)P 13–√3–√2G P =×4×[(−4)−(x −3)]S △PEC 1214x 212=−12(x −1)252=1S △PEC −=112(x −1)252=1+x 37–√=1−x 47–√y =×−4=−214(1+)7–√27–√2(1+,−2)P 27–√7–√2(1+,−3)P 13–√3–√2(1+,−2)P 27–√7–√2待定系数法求二次函数解析式待定系数法求一次函数解析式二次函数综合题二次函数图象上点的坐标特征勾股定理三角形的面积【解析】暂无暂无暂无【解答】解:将,代入 ,得∴抛物线的解析式为.设直线的解析式为 ,将点,代入得解得∴直线的解析式为.证明:过点作轴于点,如图,设点, ,则, ,, ,(1)A (4,0)B (0,−4)y =a +b x 2{16a +b =0,b =−4,a =,14b =−4,y =−414x 2CE y =mx +n E (4,−1)C (0,−3)y =mx +n {4m +n =−1,n =−3,m =,12n =−3,CE y =x −312(2)P PF ⊥y F P (t,−4)14t 20<t <4PF =t FC =|−4+3|=|−1|14t 214t 2PD =4−14t 2PC ===+1+t 2(−1)14t 22−−−−−−−−−−−−−√(+1)14t 22−−−−−−−−−−√14t 2C +PD =(+1)+(4−)=511∴为定值.解:设与的交点为,设,①如图,当点在点上方时,,∵,∴,解得, (负根舍去),∴ ,即.②如图,当点在点下方时,,∵,∴,解得,(负根舍去),∴ ,即,综上所述,满足条件的点有 ,.16.【答案】PC +PD =(+1)+(4−)=514t 214t 2(3)DP EC G P (x,−4)14x 2G P =×4×[(x −3)−(−4)]S △PEC 121214x 2=−+12(x −1)252=1S △PEC −+=112(x −1)252=1+x 13–√=1−x 23–√y =×−4=−314(1+)3–√23–√2(1+,−3)P 13–√3–√2G P =×4×[(−4)−(x −3)]S △PEC 1214x 212=−12(x −1)252=1S △PEC−=112(x −1)252=1+x 37–√=1−x 47–√y =×−4=−214(1+)7–√27–√2(1+,−2)P 27–√7–√2(1+,−3)P 13–√3–√2(1+,−2)P 27–√7–√2(1)解:∵矩形的一边长为米,周长为米,∴另一边长为米,∴,其中.能,理由如下:当设计费为元时,面积为(平方米),即,解得:或,符合,故设计费能达到元.∵,∴当时,,∴当米时,矩形的最大面积为平方米,设计费最多,最多是元.【考点】二次函数的应用一元二次方程的应用【解析】(1)由矩形的一边长为、周长为得出另一边长为,根据矩形的面积公式可得答案;(2)由设计费为元得出矩形面积为平方米,据此列出方程,解之求得的值,从而得出答案;(3)将函数解析式配方成顶点式,可得函数的最值情况.【解答】解:∵矩形的一边长为米,周长为米,∴另一边长为米,∴,其中.能,理由如下:当设计费为元时,面积为(平方米),即,解得:或,符合,故设计费能达到元.∵,∴当时,,∴当米时,矩形的最大面积为平方米,设计费最多,最多是元.(1)x 16(8−x)S =x(8−x)=−+8x x 20<x <8(2)2400024000÷2000=12−+8x =12x 2x =2x =60<x <824000(3)S =−+8x =−(x −4+16x 2)2x =4=16S max x =41632000x 168−x 2400012x (1)x 16(8−x)S =x(8−x)=−+8x x 20<x <8(2)2400024000÷2000=12−+8x =12x 2x =2x =60<x <824000(3)S =−+8x =−(x −4+16x 2)2x =4=16S max x =41632000。
【新人教版九年级数学上册同步测试及答案】专题九 圆周角定理的综合运用同步测试 (新版)新人教版

圆周角定理的综合运用一巧作辅助线求角度教材P89习题24.1第7题)求证:圆内接平行四边形是矩形.已知:如图1,已知平行四边形ABCD是⊙O的内接四边形.求证:平行四边形ABCD是矩形.图1证明:∠A+∠C=180 °(圆内接四边形对角互补)又∠A=∠C(平行四边形对角相等)∴∠A=∠C=90 °所以圆内接平行四边形是矩形.如图2,△ABC内接于⊙O,OD⊥BC于D,∠A=50°,则∠OCD的度数是( A )A.40°B.45°C.50°D.60°图2变形1答图【解析】 如图,连接OB ,∵∠A =50°,∴∠BOC =2∠A =100°.∵OB =OC ,∴∠OCD =∠OBC =180°-∠BOC 2=40°.如图3,点A ,B ,C ,D 在⊙O 上,O 点在∠D 的内部,四边形OABC 为平行四边形,则∠OAD +∠OCD =__60°__.图3变形2答图 【解析】 如图,连接DO 并延长,∵四边形OABC 为平行四边形,∴∠B =∠AOC .∵∠AOC =2∠ADC ,∴∠B =2∠ADC .∵四边形ABCD 是⊙O 的内接四边形,∴∠B +∠ADC =180°,∴3∠ADC =180°,∴∠ADC =60°,∴∠B =∠AOC =120°.∵∠1=∠OAD +∠ADO ,∠2=∠OCD +∠CDO ,∴∠OAD +∠OCD =(∠1+∠2)-(∠ADO +∠CDO )=∠AOC -∠ADC =120°-60°=60°.[2012·青岛]如图4,点A ,B ,C 在⊙O 上,∠AOC =60°,则∠ABC 的度数是__150°__.【解析】 在优弧ADC ︵上取点D ,连接AD ,CD ,∵∠AOC =60°,∴∠ADC =12∠AOC =30 °. ∵∠ABC +∠ADC =180°,∴∠ABC =180°-∠ADC =180°-30°=150°.故答案为150°.图4图5如图5,若AB是⊙O的直径,CD是⊙O的弦,∠ABD=55°,则∠BCD的度数为( A )A.35° B.45° C.55° D.75°如图6,A,P,B,C是半径为8的⊙O上的四点,且满足∠BAC=∠APC=60°.(1)求证:△ABC是等边三角形;(2)求圆心O到BC的距离OD.解:(1)在△ABC中,∵∠BAC=∠APC=60°,又∵∠APC=∠ABC,∴∠ABC=60°,∴∠ACB=180°-∠BAC-∠ABC=180°-60°-60°=60°,∴△ABC是等边三角形;(2)如图,连接OB,OC,则∠BOC=2∠BAC=120°.∵OB=OC,OD⊥BC,∴∠OBC=∠OCB=12(180°-∠BOC)=30°.在Rt△BOD中,∠ODB=90°,∠OBC=30°,∴OD=12OB=12×8=4.图6变形5答图二 圆周角定理与垂径定理的综合教材P89习题24.1第5题)如图7,OA ⊥BC ,∠AOB =50°,试确定∠ADC 的大小.图7解:∵OA ⊥BC ,∴AC ︵=AB ︵,∴∠ADC =12∠AOB =25°. 【思想方法】 垂径定理与圆周角定理的综合运用一般是通过圆周角定理进行角度、弧度转换,利用垂径定理求解.如图8,⊙O 的弦AB 垂直半径OC 于点D ,∠CBA =30°,OC =3 3 cm ,则弦AB 的长为( A )图8A .9 cmB .3 3 cmC.92 cmD.332cm 解:∵∠CBA =30°,∴∠AOC =2∠CBA =60°,∵AB ⊥OC ,∴∠ADO =90°,∴∠OAD =30°,∴OD =12OA =12×33=323(cm), 由勾股定理得:AD =OA 2-OD 2=4.5 cm ,∵AB ⊥OC ,OC 过O ,∴AB =2AD =9(cm),故选A.如图9,⊙O 的半径OD ⊥弦AB 于点C ,连接AO 并延长交⊙O 于点E ,连接EC .若AB =8,CD =2,则EC 的长为( D )图9 变形2答图A .215B .8C .210D .213【解析】 ∵⊙O 的半径OD ⊥弦AB 于点C ,AB =8,∴AC =BC =4,设⊙O的半径为r,则OC=r-2,在Rt△AOC中,∵AC=4,OC=r-2,∴OA2=AC2+OC2,即r2=42+(r-2)2,解得r=5,∴AE=2r=10,连接BE,∵AE是⊙O的直径,∴∠ABE=90°,在Rt△ABE中,∵AE=10,AB=8,∴BE=AE2-AB2=102-82=6,在Rt△BCE中,∵BE=6,BC=4,∴CE=BE2+BC2=62+42=213.故选D.如图10,半圆O的直径AB=10,弦AC=6 cm,AD平分∠BAC,则AD的长为( A )图10 变形3答图A.4 5 cm B.3 5 cmC.5 5 cm D.4 cm【解析】连接OD,OC,作DE⊥AB于E,OF⊥AC于F,∵∠CAD =∠BAD (角平分线的性质),∴CD ︵=BD ︵,∴∠DOB =∠OAC =2∠BAD ,∴△AOF ≌△OED ,∴OE =AF =12AC =3 cm , 在Rt △DOE 中,,DE =OD 2-OE 2=4 cm ,在Rt △ADE 中,AD =DE 2+AE 2=4 5 cm ,故选A.如图11,AB 是⊙O 的一条弦,点C 是⊙O 上一动点,且∠ACB =30°,点E ,F 分别是AC ,BC 的中点,直线EF 与⊙O 交于G ,H 两点,若⊙O 的半径为7,则GE +FH 的最大值为__10.5__.图11 变形4答图【解析】 如图,当GH 为⊙O 的直径时,GE +FH 有最大值.∵⊙O 的半径为7,∴GH =14.连接OA ,OB .∵∠ACB =30°,∴∠AOB =2∠ACB =60°,∵OA =OB ,∴△AOB 为等边三角形,∴AB =OA =OB =7,∵点E ,F 分别是AC ,BC 的中点,∴EF =12AB =3.5, ∴GE +FH =GH -EF =14-3.5=10.5.故答案为10.5.如图12,在⊙O 中,直径AB 与弦CD 相交于点P ,∠CAB =40°,∠APD =65°.(1)求∠B 的大小;(2)已知AD =6,求圆心O 到BD 的距离.图12变形5答图 解:(1)∵∠APD =∠C +∠CAB ,∴∠C =∠APD -∠CAB =65°-40°=25°.∴∠B =∠C =25°.(2)如图,过点O 作OE ⊥BD 于点E ,则DE =BE .又∵AO =BO ,∴OE =12AD =12×6=3.∴圆心O 到BD 的距离为3.如图13所示,AB 是⊙O 的一条弦,E 在⊙O 上,设⊙O 的半径为4 cm ,AB =4 3cm ,(1)求圆心O 到弦AB 的距离OD ;(2)求∠AEB 的度数.解:(1)连接OA ,OB .∵OD ⊥AB ,∴AD =12AB =2 3 cm. 在Rt △ODA 中,OA =4 cm ,∴OD =OA 2-AD 2=16-12=2 (cm);(2)Rt △ODA 中,OA =4 cm ,OD =2 cm ,∴∠OAD =30°,∴∠AOD =60°.∵OA =OB ,OD ⊥AB ,∴∠AOB =2∠AEB =120°,∴∠AEB =12∠AOB =60°.图13图14 如图14,已知在⊙O 中,AB =43,AC 是⊙O 的直径,AC ⊥BD 于F ,∠A =30°,求BD 及OF 的长.解:∵AB =43,AC ⊥BD 于F ,∠A =30°,∴BF =12AB =43×12=23,AF =AB 2-BF 2=(43)2-(23)2=6. ∵AC 是⊙O 的直径,∴BD =2BF =2×23=4 3.设OF =x ,则OB =AF -OF =6-x ,在Rt △OBF 中,OB 2=BF 2+OF 2,即(6-x )2=(23)2+x 2,解得x =2,即OF =2.答:BD 的长是43,OF 的长是2.如图15,AB 是⊙O 的直径,AC 是⊙O 的弦,以OA 为直径的⊙D 与AC 相交于点E . (1)若AC =16,求AE 的长.(2)若C 点在⊙O 上运动(不包括A ,B 两点),则在运动的过程中AC 与AE 有何特殊的数量关系?请把你探究得到的结论填写在横线上____________________________________________________________________.图15变形8答图解:(1)如图,连接OE ,∵AO 是⊙D 的直径,∴∠OEA =90°,∴OE ⊥AC .∵OE 过⊙O 的圆心O ,∴AE =CE =12AC =12×16=8. (2)若C 点在⊙O 上运动(不包括A ,B 两点),则在运动的过程中AE =12AC .如何学好初中数学经典介绍浅谈如何学好初中数学数学是必考科目之一,故从初一开始就要认真地学习数学。
2020年人教版初中数学九年级上册课堂同步练习(含答案)

2020年人教版初中数学九年级上册课堂同步练习《第21章 一元二次方程》同步练习测试1 一元二次方程的有关概念及直接开平方法 学习要求1.掌握一元二次方程的有关概念,并应用概念解决相关问题. 2.掌握一元二次方程的基本解法——直接开平方法. 课堂学习检测 一、填空题1.一元二次方程中,只含有______个未知数,并且未知数的______次数是2.它的一般形式为__________________.2.把2x 2-1=6x 化成一般形式为__________,二次项系数为______,一次项系数为______,常数项为______.3.若(k +4)x 2-3x -2=0是关于x 的一元二次方程,则k 的取值范围是______. 4.把(x +3)(2x +5)-x (3x -1)=15化成一般形式为______,a =______,b =______,c =______.5.若-3=0是关于x 的一元二次方程,则m 的值是______. 6.方程y 2-12=0的根是______. 二、选择题7.下列方程中,一元二次方程的个数为( ). (1)2x 2-3=0 (2)x 2+y 2=5 (3) (4) A .1个B .2个C .3个D .4个8.在方程:3x 2-5x =0,7x 2-6xy +y 2=0,=0, 3x 2-3x =3x 2-1中必是一元二次方程的有( ).A .2个B .3个C .4个D .5个9.x 2-16=0的根是( ).x x m -m+-222)(542=-x 2122=+x x ,5312+=+x x 322,052222--=+++xx x x axA .只有4B .只有-4C .±4D .±810.3x 2+27=0的根是( ). A .x 1=3,x 2=-3 B .x =3C .无实数根D .以上均不正确三、解答题(用直接开平方法解一元二次方程) 11.2y 2=8. 12.2(x +3)2-4=0.13. 14.(2x +1)2=(x -1)2.综合、运用、诊断 一、填空题15.把方程化为一元二次方程的一般形式(二次项系数为正)是__________,一次项系数是______.16.把关于x 的一元二次方程(2-n )x 2-n (3-x )+1=0化为一般形式为_______________,二次项系数为______,一次项系数为______,常数项为______.17.若方程2kx 2+x -k =0有一个根是-1,则k 的值为______. 二、选择题18.下列方程:(x +1)(x -2)=3,x 2+y +4=0,(x -1)2-x (x +1)=x ,其中是一元二次方程的有( ).A .2个B .3个C .4个D .5个19.形如ax 2+bx +c =0的方程是否是一元二次方程的一般形式,下列说法正确的是( ).A .a 是任意实数B .与b ,c 的值有关.25)1(412=+x x x x +=-2232,01=+xx ,5)3(21,42122=+=-+x x xC .与a 的值有关D .与a 的符号有关20.如果是关于x 的方程2x 2+3ax -2a =0的根,那么关于y 的方程y 2-3=a 的解是( ).A .B .±1C .±2D .21.关于x 的一元二次方程(x -k )2+k =0,当k >0时的解为( ). A .B .C .D .无实数解三、解答题(用直接开平方法解下列方程) 22.(3x -2)(3x +2)=8. 23.(5-2x )2=9(x +3)2.24.25.(x -m )2=n .(n 为正数)拓广、探究、思考26.若关于x 的方程(k +1)x 2-(k -2)x -5+k =0只有唯一的一个解,则k =______,此方程的解为______.27.如果(m -2)x |m |+mx -1=0是关于x 的一元二次方程,那么m 的值为( ).A .2或-2B .2C .-2D .以上都不正确28.已知关于x 的一元二次方程(m -1)x 2+2x +m 2-1=0有一个根是0,求m 的值.29.三角形的三边长分别是整数值2cm ,5cm ,k cm ,且k 满足一元二次方程2k 2-9k -5=0,求此三角形的周长.21=x 5±2±k k +k k -k k -±.063)4(22=--x测试2 配方法与公式法解一元二次方程 学习要求掌握配方法的概念,并能熟练运用配方法与公式法解一元二次方程. 课堂学习检测 一、填空题1._________=(x -__________)2. 2.+_________=(x -_________)2. 3._________=(x -_________)2. 4.+_________=(x -_________)2.5.关于x 的一元二次方程ax 2+bx +c =0(a ≠0)的根是______.6.一元二次方程(2x +1)2-(x -4)(2x -1)=3x 中的二次项系数是______,一次项系数是______,常数项是______.二、选择题7.用配方法解方程应该先变形为( ).A .B .C .D .8.用配方法解方程x 2+2x =8的解为( ). A .x 1=4,x 2=-2B .x 1=-10,x 2=8C .x 1=10,x 2=-8D .x 1=-4,x 2=29.用公式法解一元二次方程,正确的应是( ). A . B . C .D . 10.方程mx 2-4x +1=0(m <0)的根是( ). A .B .+-x x 82x x 232-+-px x 2x ab x -201322=--x x 98)31(2=-x 98)31(2-=-x 910)31(2=-x 0)32(2=-x x x 2412=-252±-=x 252±=x 251±=x 231±=x 41mm-±42C .D .三、解答题(用配方法解一元二次方程) 11.x 2-2x -1=0. 12.y 2-6y +6=0.四、解答题(用公式法解一元二次方程) 13.x 2+4x -3=0. 14.五、解方程(自选方法解一元二次方程) 15.x 2+4x =-3. 16.5x 2+4x =1.综合、运用、诊断 一、填空题17.将方程化为标准形式是______________________,其中a =______,b =______,c =______.18.关于x 的方程x 2+mx -8=0的一个根是2,则m =______,另一根是______. 二、选择题19.若关于x 的二次三项式x 2-ax +2a -3是一个完全平方式,则a 的值为( ).A .-2B .-4C .-6D .2或620.4x 2+49y 2配成完全平方式应加上( ). A .14xyB .-14xymm-±422mmm -±42.03232=--x x x x x 32332-=++C .±28xyD .021.关于x 的一元二次方程的两根应为( ). A . B ., C .D .三、解答题(用配方法解一元二次方程) 22.3x 2-4x =2. 23.x 2+2mx =n .(n +m 2≥0).四、解答题(用公式法解一元二次方程) 24.2x -1=-2x 2. 25.26.2(x -1)2-(x +1)(1-x )=(x +2)2.拓广、探究、思考27.解关于x 的方程:x 2+mx +2=mx 2+3x .(其中m ≠1)28.用配方法说明:无论x 取何值,代数式x 2-4x +5的值总大于0,再求出当x 取何值时,代数式x 2-4x +5的值最小?最小值是多少?ax a x 32222=+22a±-a 2a 22422a±a 2±x x 32132=+测试3 一元二次方程根的判别式 学习要求掌握一元二次方程根的判别式的有关概念,并能灵活地应用有关概念解决实际问题.课堂学习检测 一、填空题1.一元二次方程ax 2+bx +c =0(a ≠0)根的判别式为=b 2-4ac ,(1)当b 2-4ac ______0时,方程有两个不相等的实数根; (2)当b 2-4ac ______0时,方程有两个相等的实数根; (3)当b 2-4ac ______0时,方程没有实数根.2.若关于x 的方程x 2-2x -m =0有两个相等的实数根,则m =______. 3.若关于x 的方程x 2-2x -k +1=0有两个实数根,则k ______. 4.若方程(x -m )2=m +m 2的根的判别式的值为0,则m =______. 二、选择题5.方程x 2-3x =4根的判别式的值是( ). A .-7B .25C .±5D .56.一元二次方程ax 2+bx +c =0有两个实数根,则根的判别式的值应是( ). A .正数B .负数C .非负数D .零7.下列方程中有两个相等实数根的是( ). A .7x 2-x -1=0B .9x 2=4(3x -1)C .x 2+7x +15=0D .8.方程有( ). A .有两个不等实根 B .有两个相等的有理根 C .无实根D .有两个相等的无理根三、解答题9.k 为何值时,方程kx 2-6x +9=0有:(1)不等的两实根;(2)相等的两实根;(3)没有实根.02322=--x x 03322=++x x10.若方程(a -1)x 2+2(a +1)x +a +5=0有两个实根,求正整数a 的值.11.求证:不论m 取任何实数,方程都有两个不相等的实根.综合、运用、诊断 一、选择题12.方程ax 2+bx +c =0(a ≠0)根的判别式是( ).A .B .C .b 2-4acD .abc13.若关于x 的方程(x +1)2=1-k 没有实根,则k 的取值范围是( ). A .k <1B .k <-1C .k ≥1D .k >114.若关于x 的方程3kx 2+12x +k +1=0有两个相等的实根,则k 的值为( ).A .-4B .3C .-4或3D .或15.若关于x 的一元二次方程(m -1)x 2+2mx +m +3=0有两个不等的实根,则m 的取值范围是( ).A .B .且m ≠1C .且m ≠1D . 16.如果关于x 的二次方程a (1+x 2)+2bx =c (1-x 2)有两个相等的实根,那么以正数a ,b ,c 为边长的三角形是( ).A .锐角三角形B .钝角三角形C .直角三角形D .任意三角形02)1(2=++-mx m x 242ac b b -±-ac b 42-2132-23<m 23<m 23≤m 23>m二、解答题17.已知方程mx2+mx+5=m有相等的两实根,求方程的解.18.求证:不论k取任何值,方程(k2+1)x2-2kx+(k2+4)=0都没有实根.19.如果关于x的一元二次方程2x(ax-4)-x2+6=0没有实数根,求a的最小整数值.20.已知方程x2+2x-m+1=0没有实根,求证:方程x2+mx=1-2m一定有两个不相等的实根.拓广、探究、思考21.若a,b,c,d都是实数,且ab=2(c+d),求证:关于x的方程x2+ax +c=0,x2+bx+d=0中至少有一个方程有实数根.测试4 因式分解法解一元二次方程学习要求掌握一元二次方程的重要解法——因式分解法.课堂学习检测一、填空题(填出下列一元二次方程的根) 1.x (x -3)=0.______2.(2x -7)(x +2)=0.______3.3x 2=2x .______ 4.x 2+6x +9=0.______ 5.______6.______ 7.(x -1)2-2(x -1)=0.______. 8.(x -1)2-2(x -1)=-1.______ 二、选择题9.方程(x -a )(x +b )=0的两根是( ). A .x 1=a ,x 2=b B .x 1=a ,x 2=-b C .x 1=-a ,x 2=bD .x 1=-a ,x 2=-b10.下列解方程的过程,正确的是( ). A .x 2=x .两边同除以x ,得x =1. B .x 2+4=0.直接开平方法,可得x =±2.C .(x -2)(x +1)=3×2.∵x -2=3,x +1=2, ∴x 1=5, x 2=1.D .(2-3x )+(3x -2)2=0.整理得3(3x -2)(x -1)=0,三、解答题(用因式分解法解下列方程,*题用十字相乘法因式分解解方程) 11.3x (x -2)=2(x -2). 12.*13.x 2-3x -28=0. 14.x 2-bx -2b 2=0.*15.(2x -1)2-2(2x -1)=3. *16.2x 2-x -15=0..03222=-x x .)21()21(2x x -=+.1,3221==∴x x .32x x =四、解答题17.x 取什么值时,代数式x 2+8x -12的值等于2x 2+x 的值.综合、运用、诊断一、写出下列一元二次方程的根18..______________________. 19.(x -2)2=(2x +5)2.______________________. 二、选择题20.方程x (x -2)=2(2-x )的根为( ). A .-2B .2C .±2D .2,221.方程(x -1)2=1-x 的根为( ). A .0B .-1和0C .1D .1和022.方程的较小的根为( ). A .B .C .D .三、用因式分解法解下列关于x 的方程 23. 24.4(x +3)2-(x -2)2=0.25.26.abx 2-(a 2+b 2)x +ab =0.(ab ≠0)四、解答题27.已知关于x 的一元二次方程mx 2-(m 2+2)x +2m =0. (1)求证:当m 取非零实数时,此方程有两个实数根; (2)若此方程有两个整数根,求m 的值.0222=-x x 0)43)(21()43(2=--+-x x x 43-218543.2152x x =-.04222=-+-b a ax x测试5 一元二次方程解法综合训练 学习要求会用适当的方法解一元二次方程,培养分析问题和解决问题的能力. 课堂学习检测一、填空题(写出下列一元二次方程的根) 1.3(x -1)2-1=0.__________________ 2.(2x +1)2-2(2x +1)=3.__________________ 3.3x 2-5x +2=0.__________________ 4.x 2-4x -6=0.__________________ 二、选择题5.方程x 2-4x +4=0的根是( ). A .x =2B .x 1=x 2=2C .x =4D .x 1=x 2=46.的根是( ). A .x =3B .x =±3C .x =±9D .7.的根是( ). A .B .C .x 1=0,D .8.(x -1)2=x -1的根是( ). A .x =2 B .x =0或x =1 C .x =1D .x =1或x =2三、用适当方法解下列方程 9.6x 2-x -2=0. 10.(x +3)(x -3)=3.11.x 2-2mx +m 2-n 2=0.12.2a 2x 2-5ax +2=0.(a ≠0)5.27.0512=+x 3±=x 072=-x x 77=x 77,021==x x 72=x 7=x四、解下列方程(先将你选择的最佳解法写在括号中) 13.5x 2=x .(最佳方法:______)14.x 2-2x =224.(最佳方法:______)15.6x 2-2x -3=0.(最佳方法:______)16.6-2x 2=0.(最佳方法:______)17.x 2-15x -16=0.(最佳方法:______)18.4x 2+1=4x .(最佳方法:______)19.(x -1)(x +1)-5x +2=0.(最佳方法:______)综合、运用、诊断 一、填空题20.若分式的值是0,则x =______.1872+--x x x21.关于x 的方程x 2+2ax +a 2-b 2=0的根是____________. 二、选择题22.方程3x 2=0和方程5x 2=6x 的根( ). A .都是x =0 B .有一个相同,x =0 C .都不相同D .以上都不正确23.关于x 的方程abx 2-(a 2+b 2)x +ab =0(ab ≠0)的根是( ). A . B . C .D .以上都不正确三、解下列方程24.(x +1)2+(x +2)2=(x +3)2. 25.(y -5)(y +3)+(y -2)(y +4)=26.26. 27.kx 2-(k +1)x +1=0.四、解答题28.已知:x 2+3xy -4y 2=0(y ≠0),求的值.29.已知:关于x 的方程2x 2+2(a -c )x +(a -b )2+(b -c )2=0有两相等实数根.求证:a +c =2b .(a ,b ,c 是实数)bax a b x 2,221==ba x a bx ==21,0,2221=+=x abb a x .02322=+-x x yx yx +-拓广、探究、思考30.若方程3x 2+bx +c =0的解为x 1=1,x 2=-3,则整式3x 2+bx +c 可分解因式为______________________.31.在实数范围内把x 2-2x -1分解因式为____________________. 32.已知一元二次方程ax 2+bx +c =0(a ≠0)中的两根为请你计算x 1+x 2=____________,x 1·x 2=____________.并由此结论解决下面的问题:(1)方程2x 2+3x -5=0的两根之和为______,两根之积为______. (2)方程2x 2+mx +n =0的两根之和为4,两根之积为-3,则m =______,n =______.(3)若方程x 2-4x +3k =0的一个根为2,则另一根为______,k 为______. (4)已知x 1,x 2是方程3x 2-2x -2=0的两根,不解方程,用根与系数的关系求下列各式的值:①② ③|x 1-x 2|;④ ⑤(x 1-2)(x 2-2).测试6 实际问题与一元二次方程 学习要求会灵活地应用一元二次方程处理各类实际问题. 课堂学习检测 一、填空题1.实际问题中常见的基本等量关系。
2022-2023学年新人教版九年级上数学同步练习(含解析)

2022-2023学年初中九年级上数学同步练习学校:____________ 班级:____________ 姓名:____________ 考号:____________考试总分:24 分 考试时间: 120 分钟注意事项:1.答题前填写好自己的姓名、班级、考号等信息; 2.请将答案正确填写在答题卡上;卷I (选择题)一、 选择题 (本题共计 4 小题 ,每题 3 分 ,共计12分 )1. 如图,切于点,若=,则的度数为( )A.B.C.D.2. 如图,在中,=,=,=.以为圆心作圆与相切,则该圆的半径等于( )A.B.C.D.3. 如图,、分别与相切于、两点,点为上一点,连接、,若=,则的度数为( )A.B.C.D.PA ⊙O A ∠P 25∘∠AOP 75∘65∘55∘45∘△ABC ∠ACB 90∘AC 3BC 4B AC 2.5345PA PB O A B C O AC BC ∠P 50∘∠ACB 115∘130∘65∘75∘4. 如图,是外一点,射线、分别切于点、点,切于点,分别交、于点、点,若=,则的周长( )A.B.C.D.卷II (非选择题)二、 填空题 (本题共计 2 小题 ,每题 3 分 ,共计6分 )5. 在中,,若将沿直线折叠,使点落在直线上的点处,若,则的长为________.6. 如图,切于点,割线经过圆心,,绕点逆时针旋转到,则的长为________.三、 解答题 (本题共计 2 小题 ,每题 3 分 ,共计6分 )7. 如图,在平面直角坐标系中,抛物线交轴于,两点,已知点坐标为,.求抛物线解析式;点是抛物线位于第三象限上一动点,过点作轴的平行线,分别交线段,轴于,两点,请问线段是否存在最大值,若存在,求出点的坐标,若不存在,请说明理由;在抛物线对称轴上存在点,使得,请直接写出点的坐标.8. 如图,梯形中,,为坐标原点,,,,动点从点出发,以每秒个单位的速度沿线段运动到点后,再以每秒个单位的速度沿线段运动,到点停止,过点作轴于,以为一边向左作正方形,设运动时间为(秒),正方形与梯形重叠的面积为(平方单位).求点的坐标;求与的函数关系式;连接,中点为,正方形在变化过程中,使点在正方形的边上的值为________.P ⊙O PA PB ⊙O A B CD ⊙O E PA PB D C PB 4△PCD 46810△ABC AB =AC =5△ABC BD C AC C ′A =3C ′BC PA ⊙O A PBC O OB =PB =1OA O 60∘OD PD y =a +bx−3x 2x A B A (−4,0)AO =2BO (1)(2)D D y AC x E F DE E (3)P ∠OAC =∠OPC P OABC CB//OA O A(4,0)C(0,4)tan ∠BAO =2P C 1CB B 5–√BA A P PQ ⊥x Q PQ PQRS t PQRS OABC S (1)B (2)S t (3)OB OB M PQRS M PQRS t参考答案与试题解析2022-2023学年初中九年级上数学同步练习一、选择题(本题共计 4 小题,每题 3 分,共计12分)1.【答案】B【考点】切线的性质【解析】此题暂无解析【解答】此题暂无解答2.【答案】C【考点】切线的性质【解析】此题暂无解析【解答】此题暂无解答3.【答案】A【考点】切线的性质【解析】此题暂无解析【解答】此题暂无解答4.【答案】C【考点】切线的性质【解析】此题暂无解析【解答】此题暂无解答二、 填空题 (本题共计 2 小题 ,每题 3 分 ,共计6分 )5.【答案】或【考点】相似三角形的性质与判定菱形的判定与性质翻折变换(折叠问题)平行线的判定与性质【解析】此题暂无解析【解答】解:如图,分两种情况:①如图①,当在线段上时;,则,;在中,,;由勾股定理得:,则;②如图②,当在线段的延长线上时;,则,;在中,,,由勾股定理得:,则;故的长为或.故答案为:或.6.【答案】【考点】与圆有关的比例线段【解析】10−−√210−−√C'AC AC'=3CC'=2C'D =CD =1Rt △ABD AB =5AD =AC'+C'D =4BD =3BC ==B +C D 2D 2−−−−−−−−−−√10−−√C'CA AC'=3CC'=8C'D =CD =4Rt △ABD AD =1AB =5B =A −A =24D 2B 2D 2BC ==2B +C D 2D 2−−−−−−−−−−√10−−√BC 10−−√210−−√10−−√210−−√7–√解法一:如图根据题设条件可求得角的大小,由于,,由余弦定理求长度即可.解法二:由图形知,若能求得点到线段的距离与线段的长度,在直角三角形中用勾股定理求即可.【解答】解:法一:∵切于点,为中点,∴,∴,∴,在中由余弦定理,得:.∴.法二:过点作垂足为,∵,∴,可得,,在中,有.三、 解答题 (本题共计 2 小题 ,每题 3 分 ,共计6分 )7.【答案】解:点的坐标为,,得点的坐标为,设抛物线解析式为:,且过点,,解得:,抛物线解析式为:,即:.存在,点坐标为,依题意作图,理由如下:设直线的解析式为,将点坐标代入得:,直线的解析式为:.设点坐标为,则点坐标为,.,当时,有最大值为,此时点坐标为.点的坐标为,.以线段为直径构,分别交抛物线对称轴于,两点,连接,,作,垂足为,如图,DOP OD =1OP =2D OC DE OE PED PD PA ⊙O A B PO AB =OB =OA ∠AOB =60∘∠POD =120∘△POD P =P +−2PO ⋅DOcos ∠POD =4+1−4×(−)=7D 2O 2DO 212PD =7–√D DE ⊥PC E ∠POD =120∘∠DOC =60∘OE =12DE =3–√2Rt △PED PD ===P +D E 2E 2−−−−−−−−−−√+25434−−−−−−−√7–√(1)∵A (−4,0)AO =2BO B (2,0)y =a(x+4)(x−2)C(0,−3)∴−8a =−3a =38∴y =(x+4)(x−2)38y =+x−338x 234(2)E (−2,−)32AC y =kx−3A (−4,0)y =kx−3k =−34∴AC y =−x−334D (m,+m−3)38m 234E (m,−m−3)34∴=(−m−3)−(+m−3)y DE 3438m 234=−−m=−+38m 23238(m+2)232∵a =−<038∴m=−2y DE 32E (−2,−)32(3)P (−1,−+)3221−−√2(−1,−−)3221−−√2AC ⊙M P 1P 2MP 1MP 2MN ⊥P 1P 2N∵点的坐标为,点的坐标为),∴的中点的坐标为(.∵抛物线的对称轴为直线,∴.由勾股定理得,∴.在中,,,.由垂径定理得,点的坐标为,点的坐标为,点的坐标为.由圆周角定理知,故点的位置有,两个,故点的坐标为,.【考点】待定系数法求二次函数解析式二次函数综合题二次函数的最值垂径定理圆周角定理【解析】【解答】解:点的坐标为,,得点的坐标为,设抛物线解析式为:,且过点,,解得:,抛物线解析式为:,即:.存在,点坐标为,依题意作图,A (−4,0)C (0,−3AC M −2,−)32y =+x−338x 234x =−1MN =−1−(−2)=1AC =5M =M =AC =P 1P 21252Rt △MNP 1M =P 152MN =1∴N ==P 1(−52)212−−−−−−−−√21−−√2N =N P 1P 2∵N (−1,−)32∴P 1(−1,−+)3221−−√2P 2(−1,−−)3221−−√2∠O C =∠O C =∠OAC P 1P 2P P 1P 2P (−1,−+)3221−−√2(−1,−−)3221−−√2(1)∵A (−4,0)AO =2BO B (2,0)y =a(x+4)(x−2)C(0,−3)∴−8a =−3a =38∴y =(x+4)(x−2)38y =+x−338x 234(2)E (−2,−)32理由如下:设直线的解析式为,将点坐标代入得:,直线的解析式为:.设点坐标为,则点坐标为,.,当时,有最大值为,此时点坐标为.点的坐标为,.以线段为直径构,分别交抛物线对称轴于,两点,连接,,作,垂足为,如图,∵点的坐标为,点的坐标为),∴的中点的坐标为(.∵抛物线的对称轴为直线,∴.由勾股定理得,∴.在中,,,.由垂径定理得,点的坐标为,点的坐标为,点的坐标为.由圆周角定理知,故点的位置有,两个,故点的坐标为,.8.【答案】解:如图,过作轴于点,∵,,∴,.∵四边形为矩形,∴,,在中,,∵,AC y =kx−3A (−4,0)y =kx−3k =−34∴AC y =−x−334D (m,+m−3)38m 234E (m,−m−3)34∴=(−m−3)−(+m−3)y DE 3438m 234=−−m=−+38m 23238(m+2)232∵a =−<038∴m=−2y DE 32E (−2,−)32(3)P (−1,−+)3221−−√2(−1,−−)3221−−√2AC ⊙M P 1P 2MP 1MP 2MN ⊥P 1P 2N A (−4,0)C (0,−3AC M −2,−)32y =+x−338x 234x =−1MN =−1−(−2)=1AC =5M =M =AC =P 1P 21252Rt △MNP 1M =P 152MN =1∴N ==P 1(−52)212−−−−−−−−√21−−√2N =N P 1P 2∵N (−1,−)32∴P 1(−1,−+)3221−−√2P 2(−1,−−)3221−−√2∠O C =∠O C =∠OAC P 1P 2P P 1P 2P (−1,−+)3221−−√2(−1,−−)3221−−√2(1)B BD ⊥x D A(4,0)C(0,4)OA =4OC =4BDOC BC =OD BD =OC =4Rt △ABD ∠BDA =90∘tan ∠BAO ===2BD AD 4AD∴,∴,∴.分三种情况讨论:①当点在边上运动时,,∵四边形为矩形,∴,∴正方形与梯形重叠的面积为;②如图,当点在边上运动时,则,由可知,,∴,在中,,∴,设,则,根据勾股定理,得,又,∴,即,∴,,∴,∴正方形与梯形重叠的面积为;③如图,当点在边上运动时,同理,得到,此时重合部分为正方形,则.秒或秒【考点】解直角三角形动点问题全等三角形的性质与判定三角形中位线定理【解析】(1)过作垂直于轴于点,由的坐标得出的长,再由的坐标得出的长,根据四边形为矩形,得到对边相等,即,,在直角三角形中,利用锐角三角函数定义表示出,根据及的长,求出的长,同时利用勾股定理求出的长,由求出的长,由与的长,及在第一象限,写出的坐标即可;(2)根据的位置分三种情况考虑:当在边上时,正方形与梯形重叠的面积为矩形的面积,而,,表示出与的关系式,并写出此时的范围;当在边上,且在轴左侧时,如图所示,在边上运动的时间是秒,在边上运动由时间秒,根据每秒个单位的速度沿线段运动,利用路程时间速度,表示出的长,由表示出,在直角三角形中,由,设,则有,利用勾股定理表示出,列出关于的方程,求出方程的解表示出与,由求出的长,由矩形的两条边与的乘积即可得出与的关系式,并写出此时的范围;当在边上,且在轴右侧时,如图所示,此时重合部分为正方形,由表示出的,即可表示出此时与的关系式,并求出此时的范围;(4)分两种情况考虑:当在边上时,若过点,由为的中点,得到,再由与平行,利用两AD =2OD =OA−AD =4−2=2B(2,4)(2)P BC CP =t PQOC PQ =OC =4PQRS OABC S =CP ⋅OC =4t(0≤t ≤2)P BA BP =(t−2)5–√(1)AB =25–√AP =AB−BP =2−(t−2)=(4−t)5–√5–√5–√Rt △APQ ∠AQP =90∘tan ∠BAO ==2PQ AQAQ =x PQ =2x AP =x 5–√AP =(4−t)5–√x =(4−t)5–√5–√x =4−t AQ =4−t PQ =8−2t OQ =OA−AQ =4−(4−t)=t PQRS OABC S =OQ ⋅PQ =t(8−2t)=−2+8t(2≤t <)t 283P BA PQ =8−2t PQRS S =P =(8−2t =4−32t+64(≤t <4)Q 2)2t 28313B BD x D C OC A OA BDOC BC =OD BD =OC ABD tan ∠BAO tan ∠BAO =2BD AD AB OA−AD OD BD OD B B P (I)P BC PQRS ABCD PQOC PQ =OC =4CP =t S t t (II)P AB S y P BC 2P BA (t−2)P 5–√BA =×BP AB−BP AP APQ tan ∠BAO =2AQ =x PQ =2x AP x AQ PQ OA−AQ OQ OQ PQ S t t P AB S y PQRS PQ S t t (I)P BC PQ M M OB BM =OM BC OA直线平行得到两对内错角相等,利用可得出三角形与三角形全等,利用全等三角形的对应边相等得到,而,得到,,列出关于的方程,求出方程的解即可得到的值;当在边上运动时,此时与重合,由为的中点,平行于,利用平行线等分线段定理得到为的中点,即为三角形的中位线,利用中位线定理得到为的一半,求出的长,即为此时正方形的边长,由,令等于求出的边长列出关于的方程,求出方程的解即可得到此时的值.【解答】解:如图,过作轴于点,∵,,∴,.∵四边形为矩形,∴,,在中,,∵,∴,∴,∴.分三种情况讨论:①当点在边上运动时,,∵四边形为矩形,∴,∴正方形与梯形重叠的面积为;②如图,当点在边上运动时,则,由可知,,∴,在中,,∴,设,则,根据勾股定理,得,又,∴,即,∴,,∴,∴正方形与梯形重叠的面积为;③如图,当点在边上运动时,同理,得到,此时重合部分为正方形,则.分两种情况讨论:①如图,当点在边上,且过点时,AAS PBM OMQ PB =OQ OQ =CP =t CP =PB PB =CB−CP =2−t t t (II)P AB S M M OB MP OA P AB MP AOB MP OA MP PQ =8−2t 8−2t t t (1)B BD ⊥x D A(4,0)C(0,4)OA =4OC =4BDOC BC =OD BD =OC =4Rt △ABD ∠BDA =90∘tan ∠BAO ===2BD AD 4AD AD =2OD =OA−AD =4−2=2B(2,4)(2)P BC CP =t PQOC PQ =OC =4PQRS OABC S =CP ⋅OC =4t(0≤t ≤2)P BA BP =(t−2)5–√(1)AB =25–√AP =AB−BP =2−(t−2)=(4−t)5–√5–√5–√Rt △APQ ∠AQP =90∘tan ∠BAO ==2PQ AQAQ =x PQ =2x AP =x 5–√AP =(4−t)5–√x =(4−t)5–√5–√x =4−t AQ =4−t PQ =8−2t OQ =OA−AQ =4−(4−t)=t PQRS OABC S =OQ ⋅PQ =t(8−2t)=−2+8t(2≤t <)t 283P BA PQ =8−2t PQRS S =P =(8−2t =4−32t+64(≤t <4)Q 2)2t 283(3)P BC PQ M∵为中点,∴,又,∴,,∴,∴.∵,,∴,即,解得;②如图,当点在边上,且过点时(此时与重合),∵为的中点,,∴为的中点,即为的中位线,∴,即正方形的边长为,又,即,解得,综上所述,点在正方形的边上的值为秒或秒.故答案为:秒或秒.M OB BM =OM BC//OA ∠BPM =∠MQO ∠PBM =∠QOM △BPM ≅△OQM(AAS)PB =OQ OQ =CP =t CB =2PB =2−t 2−t =t t =1P AB SR M S M M OB MP //OA P AB MP △AOB MP =OA =212PQRS 2PQ =8−2t 8−2t =2t =3M PQRS t 1313。
2023年九年级数学上半期课时练习同步练习

选择题如图,准确表示小岛A相对于灯塔O的位置是()A. 北偏东60°B. 距灯塔2 km处C. 北偏东30°且距灯塔2 km处D. 北偏东60°且距灯塔2 km处【答案】D【解析】根据方向角的定义,确定OA相对于正南、北或正东西的方向即可确定.解:相对灯塔O而言,小岛A的位置是北偏东60°且距灯塔2km处.故选:D.填空题某军事行动中,对军队部署的方位,采用钟代码的方式来表示、例如,北偏东30°方向45千米的位置,与钟面相结合,以钟面圆心为基准,时针指向北偏东30°的时刻是1:00,那么这个地点就用代码010045来表示、按这种表示方式,南偏东40°方向78千米的位置,可用代码表示为________.【答案】044078【解析】南偏东40°方向,时针正好指到4点40分,因而代码前4位是:0440,78千米的位置则代码的后两位是78.则代码是:044078.填空题如果用(8,3)表示8排3号,那么(5,2)表示_______,10排15号表示为________.【答案】5排2号(10,15)【解析】根据有序数对(a,b),a表示排,b表示号,可得答案.解:用(8,3)表示电影院的座位号是8排3号,那么(5,2)表示5排2号;10排15号可表示为(10,15),故答案为:5排2号;(10,15).选择题象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图,是一局象棋残局,已知表示棋子“馬”和“車”的点的坐标分别为(4,3),(-2,1),则表示棋子“炮”的点的坐标为( )A. (-3,3)B. (3,2)C. (0,3)D. (1,3)【答案】D【解析】如图所示:棋子“炮”的点的坐标为:(1,3).故选:D.解答题如图是某学校的平面示意图,在8×8的正方形网格中,如果实验楼所在位置的坐标为(-2,-4),旗杆所在位置的坐标为(0,-1).(1)请画出符合题意的平面直角坐标系;(2)在(1)的平面直角坐标系内表示下列位置:校门________;图书馆________;教学楼________.【答案】(1)详见解析;(2)校门(-4,-1),图书馆(-5,2),教学楼(-1,1).【解析】(1)实验楼向右2个单位,向上4个单位确定出坐标原点,然后建立平面直角坐标系即可;(2)根据平面直角坐标系写出各位置的坐标即可.解:(1)建立平面直角坐标系如图所示.(2)校门(-4,-1),图书馆(-5,2),教学楼(-1,1).填空题已知A(-2,1),B(-6,0),若白棋A飞挂后,黑棋C尖顶,黑棋C 的坐标为(_______),_____).【答案】-1 1【解析】根据,,建立平面直角坐标系如图所示:所以C(-1,1),故答案为:-1,1.填空题如图,每个小方格的边长均为1,若用(1,3)→(2,3)→(3,3)→(4,3)→(4,2)→(4,1)表示由A到B的路径,请你试写出一条由A到C的路径:________________________.【答案】(1,3)→(2,3)→(2,4)→(3,4)(本题是开放性问题,有多种答案)【解析】根据从点A到点C的途径依次写出即可.解:路径: (1,3)→(2,3)→(2,4)→(3,4).故答案为:(1,3)→(2,3)→(2,4)→(3,4).填空题如图是一台雷达探测相关目标后得到的结果,若记图中目标A的位置为(2,90°),则目标B,D的位置分别记为________和________.【答案】(5,30°) (3,300°)【解析】根据坐标的第一个数表示到中心的距离,第二个数表示角度,分别写出各目标的坐标即可.解:B(5,30°) ,D(3,300°).故答案为:(5,30°),(3,300°).填空题在一次“寻宝”游戏中,“寻宝”人在如图23-6-9所示的藏宝图中找到了两个标志点A(2,3),B(4,1),A,B两点到“宝藏”点的距离相等,则“宝藏”点的可能坐标是________(填一个即可).【答案】如(0,-1)或(1,0)或(2,1)或(3,2)或(4,3)或(5,4)或(6,5)等【解析】根据线段垂直平分线上的点到两端点的距离相等可得“宝藏”在AB的垂直平分线上,然后根据平面直角坐标系写出点的坐标即可.答案不唯一,如(0,-1)或(1,0)或(2,1)或(3,2)或(4,3)或(5,4)或(6,5)等[解析] 如图,“宝藏”的可能坐标是(0,-1),(1,0),(2,1),(3,2),(4,3),(5,4),(6,5)等.解答题如图所示为某市几个旅游景点分布示意图(图中每个小正方形的边长均为1个单位),如果用(0,0)表示公园,用(2,2)表示西湖.(1)图中风云堂、碧水池的位置如何表示?(2)用距离和方向角表示风云堂相对于西湖的位置.【答案】(1)风云堂表示为(5,5),碧水池表示为(6,1).(2)风云堂位于西湖的北偏东45°方向且距西湖3个单位处.【解析】先画出直角坐标系,然后利用方格图写出各景点的坐标和距离和方向角表示出风云堂相对于西湖的位置.解:如图,(1)风云堂表示为(5,5),碧水池表示为(6,1).(2)风云堂位于西湖的北偏东45°方向且距西湖3个单位处.解答题如图,某校7年级的学生从学校O点出发,要到某地P处进行探险活动,他们先向正西方向走8km到A处,又往正南方向走4km到B 处,又折向正东方向走6km到C处,再折向正北方向走8km到D处,最后又往正东方向走4km才到探险地P;取点O为原点,取点O的正东方向为x轴的正方向,取点O的正北方向为y轴的正方向,以2km为一个单位长度建立平面直角坐标系.(1)在平面直角坐标系中画出探险路线图;(2)分别写出A、B、C、D、P点的坐标.【答案】解:(1)探险路线如图所示:(2)A、B、C、D、P点的坐标分别为(-4,0)、(-4,-2)、(-1,-2)、(-1,2)、(1,2)、【解析】根据题意建立平面直角坐标系即可画出探险路线图,从而得到A、B、C、D、P点的坐标.填空题如图,某小区有东西方向的街道3条,南北方向的街道4条,从位置A出发沿街道行进到达位置B,要求路程最短,研究共有多少种不同的走法.小东是这样想的:要使路程最短,就不能走“回头路”,只能分五步来完成,其中三步向右行进,两步向上行进,如果用数字“1”表示向右行进,数字“2”表示向上行进,那么“11221”与“11212”就表示两种符合要求的不同走法,请你思考后回答:符合要求的不同走法共有________种.【答案】10【解析】由于只能分五步来完成,其中三步向右行进,两步向上行进;因此1、1、1、2、2这五个数有多少种组合方法,就有多少种不同的走法.解:根据题意,则不同的走法有:11122;11221;11212;12112;12211;12121;22111;21112;21121;21211.因此共有10种不同的走法.。
九年级数学上学期知识点同步练习卷,精品29套含详细答案,成才系列

九年级数学上学期知识点同步练习卷精品29套含详细答案,成才系列班级:__________ 姓名:__________一、你还记得什么是频数、什么叫频率、什么叫概率吗?试举例说明.二、将一枚硬币抛起,使其自然下落,每抛两次作为一次实验,当硬币落定后,一面朝上,我们叫做“正”,另一面朝上,我们叫做“反”.(1)一次实验中,硬币两次落地后可能出现几种情况图片来源,百度搜索→硬币.(2)做20次实验,根据实验结果,填写下表.(3)根据上表,制作相应的频数分布直方图.(4)经观察,哪种情况发生的频率较大.(5)实验结果为“正反”的频率是多大.(6)5个同学结成一组,分别汇总其中两人,三人,四人,五人的实验数据,得到40次,60次,80次,100次的实验结果,将相应数据填入下表。
(7)依上表,绘制相应的折线统计图.(8)计算“正反”出现的概率.(9)经过以上多次重复实验,所得结果为“正反”的频率与你计算的“正反”的概率是否相近.参考答案发生的频率.概率:某一事件发生的可能程度.二、(1)可能出现“正正”“反反”“正反”三种情况.(2)~(7)无标准答案1.(8)“正反”出现的概率为2(9)当实验次数无限大时,频率与概率会更接近.一、判断题(下列方程中,是一元二次方程的在括号内划“√”,不是一元二次方程的,在括号内划“×”)1.5x2+1=0 ()2.3x2+x1+1=0 ()3.4x2=ax(其中a为常数) ()4.2x2+3x=0 ()5.5132+x =2x ()6.22)(xx+ =2x ()7.|x2+2x|=4 ()二、填空题1.一元二次方程的一般形式是__________.2.将方程-5x2+1=6x化为一般形式为__________.3.将方程(x+1)2=2x化成一般形式为__________.4.方程2x2=-8化成一般形式后,一次项系数为__________,常数项为__________.5.方程5(x 2-2x +1)=-32x +2的一般形式是__________,其二次项是__________,一次项是__________,常数项是__________.6.若ab ≠0,则a1x 2+b1x =0的常数项是__________.7.如果方程ax 2+5=(x +2)(x -1)是关于x 的一元二次方程,则a __________.8.关于x 的方程(m -4)x 2+(m +4)x +2m +3=0,当m __________时,是一元二次方程,当m __________时,是一元一次方程.三、选择题1.下列方程中,不是一元二次方程的是_________.[ ]A .2x 2+7=0B .2x 2+23x +1=0C .5x 2+x1+4=0 D .3x 2+(1+x ) 2+1=02.方程x 2-2(3x -2)+(x +1)=0的一般形式是_________.[ ]A .x 2-5x +5=0B .x 2+5x +5=0C .x 2+5x -5=0D .x 2+5=03.一元二次方程7x 2-2x =0的二次项、一次项、常数项依次是_________.[ ]A.7x2,2x,0 B.7x2,-2x,无常数项C.7x2,0,2x D.7x2,-2x,04.方程x2-3=(3-2)x化为一般形式,它的各项系数之和可能是_________.[ ] A.2 B.-2 C.32- D.3+21-25.若关于x的方程(ax+b)(d-cx)=m(ac≠0)的二次项系数是ac,则常数项为_________.[ ] A.m B.-bd C.bd-m D.-(bd-m)6.若关于x的方程a(x-1)2=2x2-2是一元二次方程,则a的值是_________.[ ] A.2 B.-2 C.0 D.不等于27.若x=1是方程ax2+bx+c=0的解,则_________.[ ] A.a+b+c=1 B.a-b+c=0C.a+b+c=0 D.a-b-c=08.关于x2=-2的说法,正确的是_________.[ ] A.由于x2≥0,故x2不可能等于-2,因此这不是一个方程B.x2=-2是一个方程,但它没有一次项,因此不是一元二次方程C.x2=-2是一个一元二次方程D.x2=-2是一个一元二次方程,但不能解四、解答题现有长40米,宽30米场地,欲在中央建一游泳池,周围是等宽的便道及休息区,且游泳池与周围部分面积之比为3∶2,请给出这块场地建设的设计方案,并用图形及相关尺寸表示出来。
2022-2023学年新人教版九年级上数学同步练习(含解析)

2022-2023学年初中九年级上数学同步练习学校:____________ 班级:____________ 姓名:____________ 考号:____________考试总分:27 分 考试时间: 120 分钟注意事项:1.答题前填写好自己的姓名、班级、考号等信息; 2.请将答案正确填写在答题卡上;卷I (选择题)一、 选择题 (本题共计 3 小题 ,每题 3 分 ,共计9分 )1. 已知的半径为,圆心到直线的距离为,则直线与的位置关系是( )A.不能确定B.相离C.相切D.相交2. 如图,是外一点,射线、分别切于点、点,切于点,分别交、于点、点,若=,则的周长( )A.B.C.D.3. 如图,在中,=,=,的垂直平分线交于点,交边于点,则的度数是( )A.⊙O 3O L 2L ⊙O P ⊙O PA PB ⊙O A B CD ⊙O E PA PB D C PB 4△PCD 46810△ABC ∠A 30∘∠C 110∘AB AB D AC E ∠EBC 10∘15∘B.C.D.卷II (非选择题)二、 填空题 (本题共计 4 小题 ,每题 3 分 ,共计12分 )4. 已知矩形中,=,=,以点为圆心为半径作圆,且与边有唯一公共点,则的取值范围是________.5. 如图,为的切线,交于、两点,连接,若,则的度数为________.6. 在中,,,,在上取一点,使,过点作交的延长线于点,若,则________.7. 如图,在四边形中,,,分别为,上的动点,则的最小值为________.15∘20∘25∘ABCD AB 4BC 3B r ⊙B CD r PA ⊙O PC ⊙O B C AC AC =BC,∠P =30∘∠C Rt △ABC ∠ACB =90∘BC =2cm CD ⊥AB AC E EC =BC E EF ⊥AC CD F EF =5cm AE =cm ABCD ∠ABC =,AB =3,BC =4,CD =5,DA =1090∘5–√M N CD AD AM +MN三、 解答题 (本题共计 2 小题 ,每题 3 分 ,共计6分 )8. 如图,正方形的边在的边上,顶点,分别在边和上.已知的边,高,求正方形的边长.9. 如图,是的直径,是的一条弦,是的切线.作并与交于点,延长交于点,交于点,连接.求证:;若的半径,,求的长.DEFG EF △ABC BC D G AB AC △ABC BC =20AH =16DEFG AC ⊙O AB ⊙O AP ⊙O BM =AB AP M MB AC E ⊙O D AD (1)AB =BE (2)⊙O R =2.5MB =3AD参考答案与试题解析2022-2023学年初中九年级上数学同步练习一、 选择题 (本题共计 3 小题 ,每题 3 分 ,共计9分 )1.【答案】D【考点】直线与圆的位置关系【解析】判断直线和圆的位置关系:设的半径为,圆心到直线的距离为.①直线和相交②直线和相切③直线和相离.【解答】解:∵的半径为,圆心到直线的距离为,∴,,∴,∴直线与圆相交,故选.2.【答案】C【考点】切线的性质【解析】此题暂无解析【解答】此题暂无解答3.【答案】A⊙O r O l d l ⊙O ⇔d <r l ⊙O ⇔d =r l ⊙O ⇔d >r ⊙O 3O L 2r =3d =2d <r D【考点】线段垂直平分线的性质【解析】此题暂无解析【解答】此题暂无解答二、 填空题 (本题共计 4 小题 ,每题 3 分 ,共计12分 )4.【答案】【考点】直线与圆的位置关系矩形的性质【解析】由于,根据点与圆的位置关系得到.【解答】∵矩形中,=,=,∴=,==,==,∵以点为圆心作圆,与边有唯一公共点,∴的半径的取值范围是:;5.【答案】【考点】切线的性质【解析】此题暂无解析【解答】解:连接并延长交于,连接,,3≤r ≤5BD >AB >BC 3≤r ≤5ABCD AB 4BC 3BD AC ==5A +B B 2C 2−−−−−−−−−−√AD BC 3CD AB 4B ⊙B CD ⊙B r 3≤r ≤540∘AO ⊙O E AB BE ∠C =∠E,∠ABE =90∘则,∴,∴,∵为的切线,∴,∴,∴,∵,∴∴,∴.故答案为:.6.【答案】【考点】全等三角形的性质与判定【解析】根据直角三角形的两锐角互余的性质求出,然后利用“角边角”证明和全等,根据全等三角形对应边相等可得,再根据,代入数据计算即可得解.【解答】解:∵,∴,∵,∴,∴(等角的余角相等),在和中,,∴,∴,∵,,,∴.故答案为:.7.【答案】∠C =∠E,∠ABE =90∘∠E +∠BAE =90∘∠C +∠BAB =90∘PA ⊙O ∠PAE =90∘∠PAB +∠BAE =90∘∠PAB =∠C AC =BC ∠ABC =(−∠C)12180∘+∠C =(−∠C)30∘12180∘∠C =40∘40∘3∠ECF =∠B △ABC △FCE AC =EF AE =AC −CE ∠ACB =90∘∠ECF +∠BCD =90∘CD ⊥AB ∠BCD +∠B =90∘∠ECF =∠B △FCE △ABC∠ECF =∠B EC =BC ∠ACB =∠FEC =90∘△ABC ≅△FCE(ASA)AC =EF AE =AC −CE BC =2cm EF =5cm AE =5−2=3cm 3【考点】切线的性质三角形的外接圆与外心旋转的性质矩形的性质三角形中位线定理线段的性质:两点之间线段最短【解析】解:在中,,由勾股定理得,.再根据勾股定理的逆用,∵,∴.作,垂足为,作,垂足为,并交延长线于点,点是关于直线的的对称点,此时,并且其值也最小.如图所示:∵,∴.在中,,即对边等于邻边的一半.8Rt △ABC AB =3,BC =4AC =5(CD =(AC +(DA )2)2)2∠DAC =90∘AM ⊥CD M N ⊥AD N ′N ′NN ′AM N ′N ′l N AM +MN =AM +M N ′AM ⊥CD ∠AMC =∠AMD =90∘Rt △ACD tan ∠ADC ==AC AD12M =DM1∴在中,,已知,设,则,在中,由勾股定理得,解得,即,【解答】解:在中,,由勾股定理得,.再根据勾股定理的逆用,∵,∴.作,垂足为,作,垂足为,并交延长线于点,点是关于直线的的对称点,此时,并且其值也最小.如图所示:∵,∴.在中,,即对边等于邻边的一半.∴在中,,已知,设,则,在中,由勾股定理得,解得,即,三、 解答题 (本题共计 2 小题 ,每题 3 分 ,共计6分 )8.【答案】解:设正方形的边长为.由正方形得,,即,,∴,∵,Rt △AMD AM =DM 12AD =10AM =x DM =2x Rt △AMD x =2–√AM =,DM =22–√2–√Rt △ABC AB =3,BC =4AC =5(CD =(AC +(DA )2)2)2∠DAC =90∘AM ⊥CD M N ⊥AD N ′N ′NN ′AM N ′N ′l N AM +MN =AM +M N ′AM ⊥CD ∠AMC =∠AMD =90∘Rt △ACD tan ∠ADC ==AC AD 12Rt △AMD AM =DM 12AD =10AM =x DM =2x Rt △AMD x =2–√AM =,DM =22–√2–√x DEFG DG//EF DG//BC ∵AH ⊥BC AM ⊥DG DG//BC △ADG ∽△ABC∴,∴.∵,,∴,,即,由,,,得,解得.∴正方形的边长是.【考点】勾股定理正方形的性质相似三角形的性质与判定【解析】由得,利用相似三角形对应边上高的比等于相似比,列方程求解.【解答】解:设正方形的边长为.由正方形得,,即,,∴,∵,∴,∴.∵,,∴,,即,由,,,得,解得.∴正方形的边长是.9.【答案】证明:∵是的切线,∴,∴,.又∵,△ADG ∽△ABC =DG BC AM AH GF ⊥BC DE ⊥BC GF//DE AM =AH −MH =DG BC AH −MH AH BC =20AH =16DE =DG =x =x 2016−x 16x =809DEFG 809DG//BC △ADG ∼△ABC x DEFG DG//EF DG//BC ∵AH ⊥BC AM ⊥DG DG//BC △ADG ∽△ABC =DG BC AM AH GF ⊥BC DE ⊥BC GF//DE AM =AH −MH =DG BC AH −MH AH BC =20AH =16DE =DG =x =x 2016−x 16x =809DEFG 809(1)AP ⊙O ∠EAM=90∘∠BAE +∠MAB =90∘∠AEB +∠AMB =90∘AB =BM ∠MAB =∠AMB∴,∴,∴.解:如图,连接,∵是的直径,∴.在中,,,∴.∵,∴.由知,,∴,∴,,即,∴.又∵,∴,∴.【考点】切线的性质相似三角形的性质与判定【解析】(1)根据切线的性质得出=,等腰三角形的性质=,根据等角的余角相等得出=,即可证得=;(2)证得,求得=,,由=,求得=,即可证得=.【解答】证明:∵是的切线,∴,∴,.又∵,∴,∴,∠MAB =∠AMB ∠BAE =∠AEB AB =BE (2)BC AC ⊙O ∠ABC=90∘Rt △ABC AC =5AB =MB =3BC =4BE =AB =MB EM =6(1)∠BAE =∠AEB △ABC ∼△EAM ∠C =∠AME =EM AC AM BC=65AM 4AM =245∠D =∠C ∠D =∠AMD AD =AM =245∠EAM 90∘∠MAB ∠AMB ∠BAE ∠AEB AB BE △ABC ∽△EAM ∠C ∠AME AM =485∠D ∠C ∠D ∠AMD AD AM =485(1)AP ⊙O ∠EAM=90∘∠BAE +∠MAB =90∘∠AEB +∠AMB =90∘AB =BM ∠MAB =∠AMB ∠BAE =∠AEB AB =∴.解:如图,连接,∵是的直径,∴.在中,,,∴.∵,∴.由知,,∴,∴,,即,∴.又∵,∴,∴.AB =BE (2)BC AC ⊙O ∠ABC=90∘Rt △ABC AC =5AB =MB =3BC =4BE =AB =MB EM =6(1)∠BAE =∠AEB △ABC ∼△EAM ∠C =∠AME =EM AC AM BC =65AM 4AM =245∠D =∠C ∠D =∠AMD AD =AM =245。
九年级上册(人教版)数学课时同步检测卷:二次函数与一元二次方程

二次函数与一元二次方程1.如图所示,抛物线y=ax2+bx+c(a≠0)与x轴的两个交点分别为A(-1,0)和B(2,0),当y<0时,x的取值范围是___________.2.已知抛物线y=ax2+bx+c=0(a≠0) 与x轴交于x,x两点,若点x的坐标为(−2,0),线段xx的长为8,则抛物线的对称轴为直线________________.3.若二次函数y=x2+3x-c(c为整数)的图象与x轴没有交点,则c的最大值是________.4.设关于x的方程x2 +(k-4)x-4k =0 有两个不相等的实数根x1,x2,且0<x1<2<x2,那么k的取值范围是__________. 5.不论x取何值,二次函数y=-x2+6x+c的函数值总为负数, 则c 的取值范围为_______.6.若直线x=x+x与抛物线x=x2+3x有交点,则m的取值范围是()A.x≥−1B.x≤−1C.x>1D.x<17.函数y=ax2+2ax+m(a<0)的图象过点(2,0),则使函数值y<0成立的x的取值范围是()A.x<﹣4或x>2 B.﹣4<x<2 C.x<0或x>2 D.0<x<28.二次函数y=2x2−8x+m满足以下条件:当−2<x<−1时,它的图象位于x轴的下方;当6<x<7时,它的图象位于x轴的上方,则m的值为()A.8 B.−10C.−42D.−249.若抛物线y=x2-6x+c-2的顶点到x轴的距离是3,则c的值等于()A.8;或14 B.14;C.-8 D.-8或-1410.二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,顶点坐标为(﹣2,﹣9a),下列结论: 4a+2b+c>0; 5a ﹣b+c=0; 若方程a(x+5)(x﹣1)=﹣1有两个根x1和x2,且x1<x2,则﹣5<x1<x2<1; 若方程|ax2+bx+c|=1有四个根,则这四个根的和为﹣4.其中正确的结论有()A.1个B.2个C.3个D.4个11.关于x的方程(x-3)(x-5)=m(m>0)有两个实数根x,x( x<x),则下列选项正确的是()A.3<x<x<5 B.3<x<5<x C.x<2<x<5 D.x<3且x>512.如图是抛物线y=ax2+bx+c的大致图象,则一元二次方程ax2+bx+c=0 ()A.有两个不等的实数根B.有两个相等的实数根C.没有实数根D.无法确定13.如图,抛物线x=−23x2+103x+4分别交x轴于A,B两点,与y轴交于点C,动点P从x(0,2)出发,先到达x轴上的某点E,再到达抛物线对称轴上的某点F,最后运动到点C,求点P运动的最短路径长为() A.√61B.8 C.7 D.914.已知二次函数y=x2+bx+c的图象经过点A(-1,12),B(2,-3).(1)求这个二次函数的解析式;(2)求这个图象的顶点坐标及与x轴的交点坐标.15.已知二次函数x=2(x−1)(x−x−3)(x为常数).(1)求证:不论x为何值,该函数的图像与x轴总有公共点;(2)当x取什么值时,该函数的图像与x轴的交点在x轴的上方?16.如图,已知抛物线y1=x2-2x-3与x轴相交于点A,B(点A在B的左侧),与y轴相交于点C,直线y2=kx+b经过点B,C.(1)求直线BC的函数关系式;(2)当y1>y2时,请直接写出x的取值范围.参考答案1.x<-1或x>22.x=2或x=-63.-34.−2<x<05.c<-96.A7.A8.D9.B10.B11.D12.A13.A14.(1)y=x2-6x+5;(2)(1,0)(5,0)15.(1)证明略;(2)x>−3时,该函数的图像与x轴的交点在x轴的上方. 16.(1)y=x-3;(2)当y1>y2时,x<0和x>3.第3页/共3页。
人教九年级数学上册同步练习题及答案教学文稿

人教九年级数学上册同步练习题及答案九年级(上)第21章二次根式1、 当X ________ 时,二次根式 X 3在实数范围内有意义2、 计算:• 64 = _______ ; 3 、计算:(..3) 2 = 4、 计算:(-•._ 2) 2 =J 3 X5、 代数式 丄厘 有意义,则X 的取值范围是1 X&计算:.42 = 7、 计算(2)2 =8、 已知卡—2 + b 1 =0,则 a= ,b=9、 若 X 2 =36,则 X= 10、已知一个正数X 的平方根3X-5,另一个平方根是1-2X ,求X 的值二次根式(第2课时)二次根式(第 1课时)1、 25的平方根是( ) A.5 B.-5 C. ± D.,52、16的算术平方根是( )A.4 B.-4 C. ±4 D.256 3、 下列计算中,正确的是( )A.(-2) 0=0 B.9 =3C.-24、 4的平方根是5、 36的算术平方根是2=-9、课前练习、课堂练习2=4 D.3一、课前练习1、计算:..(3)22、计算:(「5)2= ______ ;3、化简:124、若,3m 1有意义,则m的取值范围是()1111A. m= -B.m> -C.mD.m -3 3 3 35、下列各式中属于最简二次根式的是()A. 、X 1B. X2Y5C. , 12D. . 0.5二、课堂练习1、下面与.、2是同类二次根式的是()A. ,3B. J2C. ,8D. , 2 -12、下列二次根式中,是最简二次根式的是()A. ,8B. X2 1C.D. 3X 2Y33、化简:J27 = ________ ;4、化简:屮1 = ______ ;5、计算(3 J2 )2 = 6 计算:.、12 • 27= _______ ; 7、化简8X2Y3 =8、当X>1时,化简.X22X 19、若最简二次根式2X Y 5和X X 3Y 11是同类二次根式,求X、Y的值二次根式的乘法(第3课时)1、计算:X、、2 = ________ ;2、2 X. 5 =3、2 XY • 1 = ;4、、XY 2、1 =\ Y V X5、、49 121 =二、课堂练习1、计算:.288 .. 1 = ;2、计算:255 =V723、 化简: 16ab 2c 3 = ________ ;4、 计算 2- ,9 的结果是( ) A.1 B.-1 C.-7 D.55、 下列计算中,正确的是( )A.. 23 = ., 6 B. . 2+ .-3 = .-5 C. .. 8 =4. 2 D. ..4 -、. 2 = . 2&下列计算中,正确的是( )A.■:-2 + :/3 = :.[5 B. 』2 • 3 =吋6 C.:『8 =4D. ( 3) 2 =-37、 计算:-.、10 3 152 18、 计算:-.,8 6 .339、 计算:(,3+ ,5)( 3,5)10、计算:402242次根式的除法(第4课时)、课前练习二、课堂练习1、化简:、1 = ________ ;2、••• 2-1的倒数是\ 23、计算:\30 .5= ________ ;4、计算(巧-2) 2 =11 I --------------④—48 +-121、计算:.15 53、 化简:25 y 236X5、 化简:75、下列式子中成立的是()A. .. ( 13)2 =13B.- 3.6 =-0.6C. .. ( 13)2 =-13D. 36= 616、若、3- 1=a,求a+ —的值a7、若X= 2+1,求1 2X X1 2的值8、计算:(.5+1)( .. 5 +3)19、已知X=1+ 2,丫=1- ,2 ,求—的值X Y10、已知a=2+ , 3 ,b=2- 3,求a2 b-ab 2的值二次根式的加减(第5课时)一、课前练习1、化简.18= _______ 、. 27= _______ ,12 = __________ , 20 =2、在、30、、24、ab、. x2y2、、a3b3中,_________ 是最简二次根式,__________ 与________ 是同类二次根式•3、化简1= 1= ,.'2- = I9\ 3 \ 8 \ 2 \ 24、如果..a与.3是同类二次根式,则a=5、2a +5 a -3「a =二、课堂练习1、在,12、, 27、.. 75、.. 30中,____________ 与、.3不是同类二次根式2、计算:①.20a + . 45a ②•. 75 - . 12 + •. 27③(27 + 18)-(2 ,3- ,8)2 22、计算:①.80- .125 +2.5二、课堂练习 计算:①.45 + .50 - .75③已知X= 2 +1,Y —2-1,求X 2 -Y 2的值④已知a=^,求.a 3 1+ ■ a的值、课前练习计算:◎(3^-2) 2二次根式的加减6课时)、化简卜列二次根式 :,54 =796 = .108 =、.32 =1 ------ 50a51 -----1 -----\248 = 54 =2 -=、课前练习3 1 || || ------------------------------------------------②.12 + .. 32 -(6二次根式的加减7课时)3 - -2)2②18-8冷二、课堂练习©( 5、3 )(、5+、3 )3 .x+ y )(3 x - . y )3( 2、.3 S2 ) 22、96-3、6 ) 3⑤已知a- 3^.2 ,求a+1的值a a第22章一元二次方程22.1 —兀二次方程、基础训练1、下列方程中,一元二次方程是()A 、3x + 4=02B 、4x +2y-仁0C 、2 2 , cx + -仁0x2D 、3x -2x +1=02、方程x2 -3 =-3x化成一般形式后,它的各项系数是A0, -3,-3, B 1,-3,3C1, -3, -3 D 1,3,-33若关于的方程(m-1)x2+nx+p=O是一元方程,则有()36x -5 = x2 + 3 xA m=0B m M 0C m=1D m^ 14、一元二次方程的一般形式是5、已知2是关于的方程3x=2a的一个解,贝U a=二、综合训练:1、如果x=3是方程x2-mx=6的根,贝U m=2、已知x=1是方程3x2-2b=1的解,贝U b2-1 =3、方程X2-16=0的根是()4、将下列方程化成一元二次方程的一般形式,并写出其中的二次项系数、一次项系数及常数项;(1) 9 x2 -3 = 3x +1 (2) 5x ( 2x + 3 ) = 3x -22.2.1配方法(第一课时)一、课前小测1、方程x2 -4 =0的根是2、将方程化成一元二次方程的一般形式,并写出其中的二次项系数、一次项系数及常数项;(2) 2x -7 = x ( 2x -9 )、基础训练1、用适当的数值填空,使下列各式成立(1)X2+2X+ _= (x+ _)2(2)x 2 -6x + 一= (x - _)2(3)x4 5 +px + _=(X + _)22、式子x2 -4x +—是一个完全平方式3、把方程x2 +8x +9 =0配成(x + m)2 = n的形式是4、方程3x2 -27=0的根是5、当n=_,时形如(x +m)2 =n的方程可以求解三、综合训练:1、方程(2X-1)2=9的根是2、当x=—时,代数式2x2 -3的值等于53、方程x 2=0的实数根个数是()个A1 B2 C0 D无限多22.2.1配方法(第二课时)一、课前小测:1、方程x 2 -81 = 0的根是2、把方程x2- 2x -3 =0配方后得3、把方程2x 2-8x -1=0配方后得4、方程(x- 2)2 = 9的根是5、方程(3x -1)2 =0的根是二、基础训练:1、若x 2+10x+a是一个完全平方式,则a=2、用适当的数填空:4 x2 +x + _= ( x + _)2⑶ 9x2 -18x + _ = (3x - - )2⑵ x 2 -x + —=(x - _ )23、用配方法解下列方程:三、综合训练:1、方程x 2+4X = -4的根是2、如果x2 +ax +9是一个完全平方式,则a=3、已知x满足4x2 -4x +仁0则2x +—=2x4、求证:6x2 -24 x +27的值恒大于零22. 2. 2公式法(第一课时)一、课前小测1、用配方法解下列方程:x2 +8x +7 =02、将方程x ( x -2 )=8化成一般形式是3、方程5x2= 3x + 2 中,a =_ , b=_ , c _ ,二、基础训练:1、在方程x2+9x=6,b2 -4ac =2、用公式法解下列方程(1) 3x 2-5x -2 =0(2) 4x 2-3x +1 =0三、综合训练;1、当x=—时, X2x 2分式的值为0(1) x2 -2x -8 =0 (2)2« -4x +1=02、若代数式x 2+ 4x -5的值和代数式x -1的值相等,贝U x=3、用公式法解下列方程:(1) y2— 3y +2=0(2) (x -7)(x+3)=2522. 2. 2公式法(第二课时)课前小测:1、一元二次方程ax2+bx+c=0 (a^ 0)的求根公式是_________ 条件是_________ .2、一元二次方程5x2-2x-1=0 中,a= ___ ,b= ____ ,c= ___ .用公式法解下列方程.3、2x2-3x=04、3x2-2 3x+1=025、4x2+x+1=0基础训练:1、一元二次方程ax2+bx+c=0 (a^ 0)的根的判别式是:_______________ 。
人教版九年级数学上册同步测试 23.1 --23.3 基础知识检测题含答案

人教版九年级数学上册同步测试23.1 --23.3 基础知识检测题含答案23.1 图形的旋转一、选择题(共18小题)1.如图,△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移,得到△A′B′C′,再将△A′B′C′绕点A′逆时针旋转一定角度后,点B′恰好与点C重合,则平移的距离和旋转角的度数分别为()A.4,30°B.2,60°C.1,30°D.3,60°2.如图,四边形ABDC中,△EDC是由△ABC绕顶点C旋转40°所得,顶点A恰好转到AB上一点E的位置,则∠1+∠2=()A.90°B.100°C.110°D.120°3.如图,将△AOB绕点O按逆时针方向旋转60°后得到△COD,若∠AOB=15°,则∠AOD的度数是()A.15°B.60°C.45°D.75°4.如图,线段AB放在边长为1个单位的小正方形网格中,点A、B均落在格点上,先将线段AB 绕点O逆时针旋转90°得到线段A1B1,再将线段AB向下平移3个单位得到线段A2B2,线段AB,A1B1,A2B2的中点构成三角形面积为()A.B.15 C.3 D.5.如图,将△AOB绕点O按逆时针方向旋转45°后得到△A′OB′,若∠AOB=21°,则∠AOB′的度数是()A.21°B.45°C.42°D.24°6.如图,四边形ABCD是正方形,点E在CB的延长线上,连结AE,将△ABE绕点A逆时针旋转90°,得到△ADF,点E落在DC上的点F处,AF的延长线交BC延长线于点G.若AB=3,AE=,则CG的长是()A.1.5 B.1.6 C.1.8 D.27.如图,△ABC中,∠C=67°,将△ABC绕点A顺时针旋转后,得到△AB′C′,且C′在边BC上,则∠B′C′B的度数为()A.56°B.50°C.46°D.40°8.如图,在Rt△ABC中,∠BAC=90°.如果将该三角形绕点A按顺时针方向旋转到△AB1C1的位置,点B1恰好落在边BC的中点处.那么旋转的角度等于()A.55°B.60°C.65°D.80°9.如图,在△ABC中,∠ACB=90°,∠ABC=30°,AB=2.将△ABC绕直角顶点C逆时针旋转60°得△A′B′C,则点B转过的路径长为()A.B.C. D.π10.如图,ABCD为正方形,O为对角线AC、BD的交点,则△COD绕点O经过下列哪种旋转可以得到△DOA()A.顺时针旋转90°B.顺时针旋转45°C.逆时针旋转90°D.逆时针旋转45°11.如图,在4×4的正方形网格中,每个小正方形的边长为1,若将△AOC绕点O顺时针旋转90°得到△BOD,则的长为()A.πB.6πC.3πD.1.5π12.如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=20°,则∠B的度数是()A.70°B.65°C.60°D.55°13.在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=5,BD=4.则下列结论错误的是()A.AE∥BC B.∠ADE=∠BDCC.△BDE是等边三角形D.△ADE的周长是914.如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上.若AC=,∠B=60°,则CD的长为()A.0.5 B.1.5 C.D.115.将两个斜边长相等的三角形纸片如图①放置,其中∠ACB=∠CED=90°,∠A=45°,∠D=30°.把△DCE绕点C顺时针旋转15°得到△D1CE1,如图②,连接D1B,则∠E1D1B的度数为()A.10°B.20°C.7.5°D.15°16.如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕点C顺时针旋转至△A′B′C,使得点A′恰好落在AB上,则旋转角度为()A.30°B.60°C.90°D.150°17.如图,Rt△ABC中,∠ACB=90°,AC=BC=2,在以AB的中点O为坐标原点,AB所在直线为x轴建立的平面直角坐标系中,将△ABC绕点B顺时针旋转,使点A旋转至y轴正半轴上的A′处,则图中阴影部分面积为()A.π﹣2 B.πC.πD.π﹣218.如图,△ABC,△EFG均是边长为2的等边三角形,点D是边BC、EF的中点,直线AG、FC 相交于点M.当△EFG绕点D旋转时,线段BM长的最小值是()A.2﹣B. +1 C.D.﹣1二、填空题(共6小题)19.如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AC=1,将Rt△ABC绕点A逆时针旋转30°后得到△AB′C′,则图中阴影部分的面积是.20.如图,在△ABC中,∠B=50°,在同一平面内,将△ABC绕点A逆时针方向旋转到△AB′C′的位置,使得AB′⊥BC,连接CC′,则∠AC′C=度.21.如图,在正方形ABCD中,AD=1,将△ABD绕点B顺时针旋转45°得到△A′BD′,此时A′D′与CD交于点E,则DE的长度为.22.如图,AB是⊙O的直径,分别以OA,OB为直径作半圆.若AB=4,则阴影部分的面积是.23.如图,在△ABC中,AB=2,AC=4,将△ABC绕点C按逆时针方向旋转得到△A′B′C,使CB′∥AB,分别延长AB、CA′相交于点D,则线段BD的长为.24.如图,在△ABC中,AC=BC=8,∠C=90°,点D为BC中点,将△ABC绕点D逆时针旋转45°,=.得到△A′B′C′,B′C′与AB交于点E,则S四边形ACDE三、解答题(共6小题)25.如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,点D刚好落在AB边上.(1)求n的值;(2)若F是DE的中点,判断四边形ACFD的形状,并说明理由.26.如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线平移至△FEG,DE、FG相交于点H.(1)判断线段DE、FG的位置关系,并说明理由;(2)连结CG,求证:四边形CBEG是正方形.27.将一副三角尺(在Rt△ABC中,∠ACB=90°,∠B=60°;在Rt△DEF中,∠EDF=90°,∠E=45°)如图①摆放,点D为AB的中点,DE交AC于点P,DF经过点C.(1)求∠ADE的度数;(2)如图②,将△DEF绕点D顺时针方向旋转角α(0°<α<60°),此时的等腰直角三角尺记为△DE′F′,DE′交AC于点M,DF′交BC于点N,试判断的值是否随着α的变化而变化?如果不变,请求出的值;反之,请说明理由.28.已知△ABC中,M为BC的中点,直线m绕点A旋转,过B、M、C分别作BD⊥m于D,ME ⊥m于E,CF⊥m于F.(1)当直线m经过B点时,如图1,易证EM=CF.(不需证明)(2)当直线m不经过B点,旋转到如图2、图3的位置时,线段BD、ME、CF之间有怎样的数量关系?请直接写出你的猜想,并选择一种情况加以证明.29.在同一平面内,△ABC和△ABD如图①放置,其中AB=BD.小明做了如下操作:将△ABC绕着边AC的中点旋转180°得到△CEA,将△ABD绕着边AD的中点旋转180°得到△DFA,如图②,请完成下列问题:(1)试猜想四边形ABDF是什么特殊四边形,并说明理由;(2)连接EF,CD,如图③,求证:四边形CDEF是平行四边形.30.两个长为2cm,宽为1cm的长方形,摆放在直线l上(如图①),CE=2cm,将长方形ABCD 绕着点C顺时针旋转α角,将长方形EFGH绕着点E逆时针旋转相同的角度.(1)当旋转到顶点D、H重合时,连接AE、CG,求证:△AED≌△GCD(如图②).(2)当α=45°时(如图③),求证:四边形MHND为正方形.参考答案一、选择题(共18小题)1.如图,△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移,得到△A′B′C′,再将△A′B′C′绕点A′逆时针旋转一定角度后,点B′恰好与点C重合,则平移的距离和旋转角的度数分别为()A.4,30°B.2,60°C.1,30°D.3,60°【考点】旋转的性质;平移的性质.【分析】利用旋转和平移的性质得出,∠A′B′C=60°,AB=A′B′=A′C=4,进而得出△A′B′C是等边三角形,即可得出BB′以及∠B′A′C的度数.【解答】解:∵∠B=60°,将△ABC沿射线BC的方向平移,得到△A′B′C′,再将△A′B′C′绕点A′逆时针旋转一定角度后,点B′恰好与点C重合,∴∠A′B′C=60°,AB=A′B′=A′C=4,∴△A′B′C是等边三角形,∴B′C=4,∠B′A′C=60°,∴BB′=6﹣4=2,∴平移的距离和旋转角的度数分别为:2,60°.故选:B.2.如图,四边形ABDC中,△EDC是由△ABC绕顶点C旋转40°所得,顶点A恰好转到AB上一点E的位置,则∠1+∠2=()A.90°B.100°C.110°D.120°【考点】旋转的性质.【分析】由旋转的性质可知AC=EC,BC=DC,∠BCD=∠ACE=40°,在△BCD中,由内角和定理求∠1,根据外角定理可求∠2.【解答】解:在△BCD中,∠BCD=∠ACE=40°,BC=CD,∴△BCD为等腰三角形,∴∠1=(180°﹣40°)=70°,∵∠BEC为△ACE的外角,∴∠2+∠DEC=∠ACE+∠A,而∠DEC与∠A为对应角,∴∠2=∠ACE=40°,∴∠1+∠2=70°+40°=110°,故选C.3.如图,将△AOB绕点O按逆时针方向旋转60°后得到△COD,若∠AOB=15°,则∠AOD的度数是()A.15°B.60°C.45°D.75°【考点】旋转的性质.【分析】根据∠AOD=∠DOB﹣∠AOB求解.【解答】解:∵将△AOB绕点O按逆时针方向旋转60°后得到△COD,∴∠BOD=60°,∵∠AOB=15°,∴∠AOD=∠DOB﹣∠AOB=60°﹣15°=45°.故选:C.4.如图,线段AB放在边长为1个单位的小正方形网格中,点A、B均落在格点上,先将线段AB 绕点O逆时针旋转90°得到线段A1B1,再将线段AB向下平移3个单位得到线段A2B2,线段AB,A1B1,A2B2的中点构成三角形面积为()A.B.15 C.3 D.【考点】旋转的性质;平移的性质.【专题】网格型.【分析】首先作出线段A1B1和A2B2,确定线段AB,A1B1,A2B2的中点,作出三角形,利用三角形的面积公式求解.【解答】解:三角形的面积是:×3×5=.故选A.5.如图,将△AOB绕点O按逆时针方向旋转45°后得到△A′OB′,若∠AOB=21°,则∠AOB′的度数是()A.21°B.45°C.42°D.24°【考点】旋转的性质.【分析】如图,首先运用旋转变换的性质求出∠BOB′的度数,结合∠AOB=21°,即可解决问题.【解答】解:如图,由题意及旋转变换的性质得:∠BOB′=45°,∵∠AOB=21°,∴∠AOB′=45°﹣21°=24°,故选D.6.如图,四边形ABCD是正方形,点E在CB的延长线上,连结AE,将△ABE绕点A逆时针旋转90°,得到△ADF,点E落在DC上的点F处,AF的延长线交BC延长线于点G.若AB=3,AE=,则CG的长是()A.1.5 B.1.6 C.1.8 D.2【考点】旋转的性质;勾股定理;相似三角形的判定与性质.【专题】计算题.【分析】先根据正方形的性质得AB=AD=CD=3,再根据旋转的性质得AF=AE=,则可根据勾股定理计算出DF=2,所以CF=CD﹣DF=1,然后证明△CGF∽△DAF,再利用相似比可计算出CG.【解答】解:∵四边形ABCD是正方形,∴AB=AD=CD=3,∵△ABE绕点A逆时针旋转90°,得到△ADF,∴AF=AE=,在Rt△ADF中,∵AD=3,AF=,∴DF==2,∴CF=CD﹣DF=3﹣2=1,∵AD∥CG,∴△CGF∽△DAF,∴=,即=,∴CGF=1.5.故选A.7.如图,△ABC中,∠C=67°,将△ABC绕点A顺时针旋转后,得到△AB′C′,且C′在边BC上,则∠B′C′B的度数为()A.56°B.50°C.46°D.40°【考点】旋转的性质;等腰三角形的性质.【专题】几何图形问题.【分析】利用旋转的性质以及等腰三角形的性质得出∠AC′C=∠AC′B′=67°,进而得出∠B′C′B的度数.【解答】解:∵将△ABC绕点A顺时针旋转后,得到△AB′C′,∴AC′=AC,∴∠C=∠AC′C=67°,∴∠AC′B=180°﹣67°=113°,∵∠AC′C=∠AC′B′=67°,∴∠B′C′B=∠AC′B﹣∠AC′B′=113°﹣67°=46°.故选:C.8.如图,在Rt△ABC中,∠BAC=90°.如果将该三角形绕点A按顺时针方向旋转到△AB1C1的位置,点B1恰好落在边BC的中点处.那么旋转的角度等于()A.55°B.60°C.65°D.80°【考点】旋转的性质.【分析】利用直角三角形斜边上的中线等于斜边的一半,进而得出△ABB1是等边三角形,即可得出旋转角度.【解答】解:∵在Rt△ABC中,∠BAC=90°,将该三角形绕点A按顺时针方向旋转到△AB1C1的位置,点B1恰好落在边BC的中点处,∴AB1=BC,BB1=B1C,AB=AB1,∴BB1=AB=AB1,∴△ABB1是等边三角形,∴∠BAB1=60°,∴旋转的角度等于60°.故选:B.9.如图,在△ABC中,∠ACB=90°,∠ABC=30°,AB=2.将△ABC绕直角顶点C逆时针旋转60°得△A′B′C,则点B转过的路径长为()A.B.C. D.π【考点】旋转的性质;弧长的计算.【专题】几何图形问题.【分析】利用锐角三角函数关系得出BC的长,进而利用旋转的性质得出∠BCB′=60°,再利用弧长公式求出即可.【解答】解:∵在△ABC中,∠ACB=90°,∠ABC=30°,AB=2,∴cos30°=,∴BC=ABcos30°=2×=,∵将△ABC绕直角顶点C逆时针旋转60°得△A′B′C,∴∠BCB′=60°,∴点B转过的路径长为:=π.故选:B.10.如图,ABCD为正方形,O为对角线AC、BD的交点,则△COD绕点O经过下列哪种旋转可以得到△DOA()A.顺时针旋转90°B.顺时针旋转45°C.逆时针旋转90°D.逆时针旋转45°【考点】旋转的性质.【专题】几何图形问题.【分析】因为四边形ABCD为正方形,所以∠COD=∠DOA=90°,OC=OD=OA,则△COD绕点O 逆时针旋转得到△DOA,旋转角为∠COD或∠DOA,据此可得答案.【解答】解:∵四边形ABCD为正方形,∴∠COD=∠DOA=90°,OC=OD=OA,∴△COD绕点O逆时针旋转得到△DOA,旋转角为∠COD或∠DOA,故选:C.11.如图,在4×4的正方形网格中,每个小正方形的边长为1,若将△AOC绕点O顺时针旋转90°得到△BOD,则的长为()A.πB.6πC.3πD.1.5π【考点】旋转的性质;弧长的计算.【专题】计算题.【分析】根据弧长公式列式计算即可得解.【解答】解:的长==1.5π.故选:D.12.如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=20°,则∠B的度数是()A.70°B.65°C.60°D.55°【考点】旋转的性质.【专题】几何图形问题.【分析】根据旋转的性质可得AC=A′C,然后判断出△ACA′是等腰直角三角形,根据等腰直角三角形的性质可得∠CAA′=45°,再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠A′B′C,然后根据旋转的性质可得∠B=∠A′B′C.【解答】解:∵Rt△ABC绕直角顶点C顺时针旋转90°得到△A′B′C,∴AC=A′C,∴△ACA′是等腰直角三角形,∴∠CAA′=45°,∴∠A′B′C=∠1+∠CAA′=20°+45°=65°,由旋转的性质得∠B=∠A′B′C=65°.故选:B.13.在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=5,BD=4.则下列结论错误的是()A.AE∥BC B.∠ADE=∠BDCC.△BDE是等边三角形D.△ADE的周长是9【考点】旋转的性质;平行线的判定;等边三角形的性质.【专题】几何图形问题.【分析】首先由旋转的性质可知∠EBD=∠ABC=∠C=60°,所以看得AE∥BC,先由△ABC是等边三角形得出AC=AB=BC=5,根据图形旋转的性质得出AE=CD,BD=BE,故可得出AE+AD=AD+CD=AC=5,由∠EBD=60°,BE=BD即可判断出△BDE是等边三角形,故DE=BD=4,故△AED的周长=AE+AD+DE=AC+BD=9,问题得解.【解答】解:∵△ABC是等边三角形,∴∠ABC=∠C=60°,∵将△BCD绕点B逆时针旋转60°,得到△BAE,∴∠EAB=∠C=∠ABC=60°,∴AE∥BC,故选项A正确;∵△ABC是等边三角形,∴AC=AB=BC=5,∵△BAE△BCD逆时针旋旋转60°得出,∴AE=CD,BD=BE,∠EBD=60°,∴AE+AD=AD+CD=AC=5,∵∠EBD=60°,BE=BD,∴△BDE是等边三角形,故选项C正确;∴DE=BD=4,∴△AED的周长=AE+AD+DE=AC+BD=9,故选项D正确;而选项B没有条件证明∠ADE=∠BDC,∴结论错误的是B,故选:B.14.如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上.若AC=,∠B=60°,则CD的长为()A.0.5 B.1.5 C.D.1【考点】旋转的性质.【分析】解直角三角形求出AB,再求出CD,然后根据旋转的性质可得AB=AD,然后判断出△ABD 是等边三角形,根据等边三角形的三条边都相等可得BD=AB,然后根据CD=BC﹣BD计算即可得解.【解答】解:∵∠B=60°,∴∠C=90°﹣60°=30°,∵AC=,∴AB=AC•tan30°=×=1,∴BC=2AB=2,由旋转的性质得,AB=AD,∴△ABD是等边三角形,∴BD=AB=1,∴CD=BC﹣BD=2﹣1=1.故选:D.15.将两个斜边长相等的三角形纸片如图①放置,其中∠ACB=∠CED=90°,∠A=45°,∠D=30°.把△DCE绕点C顺时针旋转15°得到△D1CE1,如图②,连接D1B,则∠E1D1B的度数为()A.10°B.20°C.7.5°D.15°【考点】旋转的性质;全等三角形的判定与性质;等腰直角三角形.【分析】根据直角三角形两锐角互余求出∠DCE=60°,旋转的性质可得∠BCE1=15°,然后求出∠BCD1=45°,从而得到∠BCD1=∠A,利用“边角边”证明△ABC和△D1CB全等,根据全等三角形对应角相等可得∠BD1C=∠ABC=45°,再根据∠E1D1B=∠BD1C﹣∠CD1E1计算即可得解.【解答】解:∵∠CED=90°,∠D=30°,∴∠DCE=60°,∵△DCE绕点C顺时针旋转15°,∴∠BCE1=15°,∴∠BCD1=60°﹣15°=45°,∴∠BCD1=∠A,在△ABC和△D1CB中,,∴△ABC≌△D1CB(SAS),∴∠BD1C=∠ABC=45°,∴∠E1D1B=∠BD1C﹣∠CD1E1=45°﹣30°=15°.故选:D.16.如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕点C顺时针旋转至△A′B′C,使得点A′恰好落在AB上,则旋转角度为()A.30°B.60°C.90°D.150°【考点】旋转的性质.【专题】几何图形问题.【分析】根据直角三角形两锐角互余求出∠A=60°,根据旋转的性质可得AC=A′C,然后判断出△A′AC 是等边三角形,根据等边三角形的性质求出∠ACA′=60°,然后根据旋转角的定义解答即可.【解答】解:∵∠ACB=90°,∠ABC=30°,∴∠A=90°﹣30°=60°,∵△ABC绕点C顺时针旋转至△A′B′C时点A′恰好落在AB上,∴AC=A′C,∴△A′AC是等边三角形,∴∠ACA ′=60°,∴旋转角为60°.故选:B .17.如图,Rt △ABC 中,∠ACB=90°,AC=BC=2,在以AB 的中点O 为坐标原点,AB 所在直线为x 轴建立的平面直角坐标系中,将△ABC 绕点B 顺时针旋转,使点A 旋转至y 轴正半轴上的A ′处,则图中阴影部分面积为( )A .π﹣2B .πC .πD .π﹣2【考点】旋转的性质;扇形面积的计算.【分析】根据等腰直角三角形的性质求出AB ,再根据旋转的性质可得A ′B=AB ,然后求出∠OA ′B=30°,再根据直角三角形两锐角互余求出∠A ′BA=60°,即旋转角为60°,再根据S 阴影=S 扇形ABA ′+S △A ′BC ′﹣S △ABC ﹣S 扇形CBC ′=S 扇形ABA ′﹣S 扇形CBC ′,然后利用扇形的面积公式列式计算即可得解. 【解答】解:∵∠ACB=90°,AC=BC ,∴△ABC 是等腰直角三角形,∴AB=2OA=2OB=AC=2,∵△ABC 绕点B 顺时针旋转点A 在A ′处,∴BA ′=AB ,∴BA ′=2OB ,∴∠OA ′B=30°,∴∠A ′BA=60°,即旋转角为60°,S 阴影=S 扇形ABA ′+S △A ′BC ′﹣S △ABC ﹣S 扇形CBC ′,=S 扇形ABA ′﹣S 扇形CBC ′, =﹣,=π﹣π,=π.故选C.18.如图,△ABC,△EFG均是边长为2的等边三角形,点D是边BC、EF的中点,直线AG、FC 相交于点M.当△EFG绕点D旋转时,线段BM长的最小值是()A.2﹣B. +1 C.D.﹣1【考点】旋转的性质;四点共圆;线段的性质:两点之间线段最短;等边三角形的性质;勾股定理;相似三角形的判定与性质.【专题】压轴题.【分析】取AC的中点O,连接AD、DG、BO、OM,如图,易证△DAG∽△DCF,则有∠DAG=∠DCF,从而可得A、D、C、M四点共圆,根据两点之间线段最短可得BO≤BM+OM,即BM≥BO﹣OM,当M在线段BO与该圆的交点处时,线段BM最小,只需求出BO、OM的值,就可解决问题.【解答】解:AC的中点O,连接AD、DG、BO、OM,如图.∵△ABC,△EFG均是边长为2的等边三角形,点D是边BC、EF的中点,∴AD⊥BC,GD⊥EF,DA=DG,DC=DF,∴∠ADG=90°﹣∠CDG=∠FDC,=,∴△DAG∽△DCF,∴∠DAG=∠DCF.∴A、D、C、M四点共圆.根据两点之间线段最短可得:BO≤BM+OM,即BM≥BO﹣OM,当M在线段BO与该圆的交点处时,线段BM最小,此时,BO===,OM=AC=1,则BM=BO﹣OM=﹣1.故选:D.二、填空题(共6小题)19.如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AC=1,将Rt△ABC绕点A逆时针旋转30°后得到△AB′C′,则图中阴影部分的面积是.【考点】旋转的性质;扇形面积的计算.【专题】计算题.【分析】根据含30度的直角三角形三边的关系得到AB=2AC=2,BC=AC=,根据互余得到∠CAB=60°,再根据旋转的性质得到AC′=AC=1,AB′=AB=2,B′C′=BC=,∠B′AB=30°,∠C′AB′=∠CAB=60°,则∠C′AD=∠C′AB′∠BAB′=30°,接着在Rt△AC′D中,利用∠C′AD=30°可得C′D=AC′=,所以B′D=B′C′﹣C′D=,然后根据三角形面积公式、扇形面积公式和图中阴影部分的面积=S﹣S△ADB′进行计算即可.扇形BAB′【解答】解:∵∠C=90°,∠ABC=30°,∴∠CAB=60°,AB=2AC=2,BC=AC=,∵Rt△ABC绕点A逆时针旋转30°后得到△AB′C′,∴AC′=AC=1,AB′=AB=2,B′C′=BC=,∠B′AB=30°,∠C′AB′=∠CAB=60°,∴∠C′AD=∠C′AB′∠BAB′=30°,在Rt△AC′D中,∵∠C′AD=30°,∴C′D=AC′=,∴B′D=B′C′﹣C′D=﹣=,∴图中阴影部分的面积=S﹣S△ADB′扇形BAB′=﹣××1=.故答案为:.20.如图,在△ABC中,∠B=50°,在同一平面内,将△ABC绕点A逆时针方向旋转到△AB′C′的位置,使得AB′⊥BC,连接CC′,则∠AC′C=70度.【考点】旋转的性质.【分析】首先证明∠CAC′=40°然后证明∠ACC′=∠AC′C;然后运用三角形的内角和定理求出∠AC′C=70°即可解决问题.【解答】解:∵∠B=50°,AB′⊥BC,∴∠B′AB=40°,∴旋转角为40°,∴∠CAC′=40°,由题意得:AC=AC′,∴∠ACC′=∠AC′C;∴∠AC′C=70°,故答案为7021.如图,在正方形ABCD中,AD=1,将△ABD绕点B顺时针旋转45°得到△A′BD′,此时A′D′与CD交于点E,则DE的长度为2﹣.【考点】旋转的性质.【专题】几何图形问题.【分析】利用正方形和旋转的性质得出A′D=A′E,进而利用勾股定理得出BD的长,进而利用锐角三角函数关系得出DE的长即可.【解答】解:由题意可得出:∠BDC=45°,∠DA′E=90°,∴∠DEA′=45°,∴A′D=A′E,∵在正方形ABCD中,AD=1,∴AB=A′B=1,∴BD=,∴A′D=﹣1,∴在Rt△DA′E中,DE==2﹣.故答案为:2﹣.22.如图,AB是⊙O的直径,分别以OA,OB为直径作半圆.若AB=4,则阴影部分的面积是2π.【考点】旋转的性质.【分析】首先计算出圆的面积,根据图示可得阴影部分面积为半圆的面积,进而可得答案.【解答】解:∵AB=4,∴BO=2,∴圆的面积为:π×22=4π,∴阴影部分的面积是:×4π=2π,故答案为:2π.23.如图,在△ABC中,AB=2,AC=4,将△ABC绕点C按逆时针方向旋转得到△A′B′C,使CB′∥AB,分别延长AB、CA′相交于点D,则线段BD的长为6.【考点】旋转的性质;相似三角形的判定与性质.【专题】几何图形问题.【分析】利用平行线的性质以及旋转的性质得出△CAD∽△B′A′C,再利用相似三角形的性质得出AD的长,进而得出BD的长.【解答】解:∵将△ABC绕点C按逆时针方向旋转得到△A′B′C,∴AC=CA′=4,AB=B′A′=2,∠A=∠CA′B′,∵CB′∥AB,∴∠B′CA′=∠D,∴△CAD∽△B′A′C,∴=,∴=,解得AD=8,∴BD=AD﹣AB=8﹣2=6.故答案为:6.24.如图,在△ABC中,AC=BC=8,∠C=90°,点D为BC中点,将△ABC绕点D逆时针旋转45°,=28.得到△A′B′C′,B′C′与AB交于点E,则S四边形ACDE【考点】旋转的性质.【专题】几何图形问题.=S△ACB﹣S△BDE求出即【分析】利用旋转的性质得出∠B=∠BDE=45°,BD=4,进而由S四边形ACDE可.【解答】解:由题意可得:∠B=∠BDE=45°,BD=4,则∠DEB=90°,∴BE=DE=2,∴S△BDE=×2×2=4,∵S△ACB=×AC×BC=32,=S△ACB﹣S△BDE=28.∴S四边形ACDE故答案为:28.三、解答题(共6小题)25.如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,点D刚好落在AB边上.(1)求n的值;(2)若F是DE的中点,判断四边形ACFD的形状,并说明理由.【考点】旋转的性质;含30度角的直角三角形;直角三角形斜边上的中线;菱形的判定.【专题】几何图形问题.【分析】(1)利用旋转的性质得出AC=CD,进而得出△ADC是等边三角形,即可得出∠ACD的度数;(2)利用直角三角形的性质得出FC=DF,进而得出AD=AC=FC=DF,即可得出答案.【解答】解:(1)∵在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,∴AC=DC,∠A=60°,∴△ADC是等边三角形,∴∠ACD=60°,∴n的值是60;(2)四边形ACFD是菱形;理由:∵∠DCE=∠ACB=90°,F是DE的中点,∴FC=DF=FE,∵∠CDF=∠A=60°,∴△DFC是等边三角形,∴DF=DC=FC,∵△ADC是等边三角形,∴AD=AC=DC,∴AD=AC=FC=DF,∴四边形ACFD是菱形.26.如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线平移至△FEG,DE、FG相交于点H.(1)判断线段DE、FG的位置关系,并说明理由;(2)连结CG,求证:四边形CBEG是正方形.【考点】旋转的性质;正方形的判定;平移的性质.【专题】几何图形问题.【分析】(1)根据旋转和平移可得∠DEB=∠ACB,∠GFE=∠A,再根据∠ABC=90°可得∠A+∠ACB=90°,进而得到∠DEB+∠GFE=90°,从而得到DE、FG的位置关系是垂直;(2)根据旋转和平移找出对应线段和角,然后再证明是矩形,后根据邻边相等可得四边形CBEG是正方形.【解答】(1)解:FG⊥ED.理由如下:∵△ABC绕点B顺时针旋转90°至△DBE后,∴∠DEB=∠ACB,∵把△ABC沿射线平移至△FEG,∴∠GFE=∠A,∵∠ABC=90°,∴∠A+∠ACB=90°,∴∠DEB+∠GFE=90°,∴∠FHE=90°,∴FG⊥ED;(2)证明:根据旋转和平移可得∠GEF=90°,∠CBE=90°,CG∥EB,CB=BE,∵CG∥EB,∴∠BCG=∠CBE=90°,∴四边形BCGE是矩形,∵CB=BE,∴四边形CBEG是正方形.27.将一副三角尺(在Rt△ABC中,∠ACB=90°,∠B=60°;在Rt△DEF中,∠EDF=90°,∠E=45°)如图①摆放,点D为AB的中点,DE交AC于点P,DF经过点C.(1)求∠ADE的度数;(2)如图②,将△DEF绕点D顺时针方向旋转角α(0°<α<60°),此时的等腰直角三角尺记为△DE′F′,DE′交AC于点M,DF′交BC于点N,试判断的值是否随着α的变化而变化?如果不变,请求出的值;反之,请说明理由.【考点】旋转的性质;相似三角形的判定与性质.【分析】(1)根据直角三角形斜边上的中线等于斜边的一半可得CD=AD=BD=AB,根据等边对等角求出∠ACD=∠A,再求出∠ADC=120°,再根据∠ADE=∠ADC﹣∠EDF计算即可得解;(2)根据同角的余角相等求出∠PDM=∠CDN,再根据然后求出△BCD是等边三角形,根据等边三角形的性质求出∠BCD=60°,再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠CPD=60°,从而得到∠CPD=∠BCD,再根据两组角对应相等,两三角形相似判断出△DPM和△DCN 相似,再根据相似三角形对应边成比例可得=为定值.【解答】解:(1)∵∠ACB=90°,点D为AB的中点,∴CD=AD=BD=AB,∴∠ACD=∠A=30°,∴∠ADC=180°﹣30°×2=120°,∴∠ADE=∠ADC﹣∠EDF=120°﹣90°=30°;(2)∵∠EDF=90°,∴∠PDM+∠E′DF=∠CDN+∠E′DF=90°,∴∠PDM=∠CDN,∵∠B=60°,BD=CD,∴△BCD是等边三角形,∴∠BCD=60°,∵∠CPD=∠A+∠ADE=30°+30°=60°,∴∠CPD=∠BCD,在△DPM和△DCN中,,∴△DPM∽△DCN,∴=,∵=tan∠ACD=tan30°=,∴的值不随着α的变化而变化,是定值.28.已知△ABC中,M为BC的中点,直线m绕点A旋转,过B、M、C分别作BD⊥m于D,ME ⊥m于E,CF⊥m于F.(1)当直线m经过B点时,如图1,易证EM=CF.(不需证明)(2)当直线m不经过B点,旋转到如图2、图3的位置时,线段BD、ME、CF之间有怎样的数量关系?请直接写出你的猜想,并选择一种情况加以证明.【考点】旋转的性质;全等三角形的判定与性质;梯形中位线定理.【专题】证明题.【分析】(1)利用垂直于同一直线的两条直线平行得出ME∥CF,进而利用中位线的性质得出即可;(2)根据题意得出图2的结论为:ME=(BD+CF),图3的结论为:ME=(CF﹣BD),进而利用△DBM≌△KCM(ASA),即可得出DB=CK,DM=MK即可得出答案.【解答】解:(1)如图1,∵ME⊥m于E,CF⊥m于F,∴ME∥CF,∵M为BC的中点,∴E为BF中点,∴ME是△BFC的中位线,∴EM=CF.(2)图2的结论为:ME=(BD+CF),图3的结论为:ME=(CF﹣BD).图2的结论证明如下:连接DM并延长交FC的延长线于K又∵BD⊥m,CF⊥m∴BD∥CF∴∠DBM=∠KCM在△DBM和△KCM中,∴△DBM≌△KCM(ASA),∴DB=CK,DM=MK由题意知:EM=FK,∴ME=(CF+CK)=(CF+DB)图3的结论证明如下:连接DM并延长交FC于K 又∵BD⊥m,CF⊥m∴BD∥CF∴∠MBD=∠KCM在△DBM和△KCM中,∴△DBM≌△KCM(ASA)∴DB=CK,DM=MK,由题意知:EM=FK,∴ME=(CF﹣CK)=(CF﹣DB).29.在同一平面内,△ABC和△ABD如图①放置,其中AB=BD.小明做了如下操作:将△ABC绕着边AC的中点旋转180°得到△CEA,将△ABD绕着边AD的中点旋转180°得到△DFA,如图②,请完成下列问题:(1)试猜想四边形ABDF是什么特殊四边形,并说明理由;(2)连接EF,CD,如图③,求证:四边形CDEF是平行四边形.【考点】旋转的性质;平行四边形的判定;菱形的判定.【专题】几何综合题.【分析】(1)根旋转的性质得AB=DF,BD=FA,由于AB=BD,所以AB=BD=DF=FA,则可根据菱形的判定方法得到四边形ABDF是菱形;(2)由于四边形ABDF是菱形,则AB∥DF,且AB=DF,再根据旋转的性质易得四边形ABCE为平行四边形,根据平行四边形的性质得AB∥CE,且AB=CE,所以CE∥FD,CE=FD,所以可判断四边形CDEF是平行四边形.【解答】(1)解:四边形ABDF是菱形.理由如下:∵△ABD绕着边AD的中点旋转180°得到△DFA,∴AB=DF,BD=FA,∵AB=BD,∴AB=BD=DF=FA,∴四边形ABDF是菱形;(2)证明:∵四边形ABDF是菱形,∴AB∥DF,且AB=DF,∵△ABC绕着边AC的中点旋转180°得到△CEA,∴AB=CE,BC=EA,∴四边形ABCE为平行四边形,∴AB∥CE,且AB=CE,∴CE∥FD,CE=FD,∴四边形CDEF是平行四边形.30.两个长为2cm,宽为1cm的长方形,摆放在直线l上(如图①),CE=2cm,将长方形ABCD 绕着点C顺时针旋转α角,将长方形EFGH绕着点E逆时针旋转相同的角度.(1)当旋转到顶点D、H重合时,连接AE、CG,求证:△AED≌△GCD(如图②).(2)当α=45°时(如图③),求证:四边形MHND为正方形.【考点】旋转的性质;全等三角形的判定与性质;矩形的性质;正方形的判定.【专题】几何综合题.【分析】(1)由全等三角形的判定定理SAS证得:△AED≌△GCD(如图②);(2)通过判定四边形MHND四个角是90°,且邻边DN=NH来判定四边形MHND是正方形.【解答】证明:(1)如图②,∵由题意知,AD=GD,ED=CD,∠ADC=∠GDE=90°,∴∠ADC+∠CDE=∠GDE+∠CDE,即∠ADE=∠GDC,在△AED与△GCD中,,∴△AED≌△GCD(SAS);(2)如图③,∵α=45°,BC∥EH,∴∠NCE=∠NEC=45°,CN=NE,∴∠CNE=90°,∴∠DNH=90°,∵∠D=∠H=90°,∴四边形MHND是矩形,∵CN=NE,∴DN=NH,∴矩形MHND是正方形.23.2 中心对称一、选择题1. 下列图形中,一定既是轴对称图形又是中心对称图形的是()A.等边三角形B.直角三角形C.平行四边形D.正方形2. 如图,在△ABC中,AB=AC,△ABC与△FEC关于点C对称,连接AE,BF,当∠ACB=______时,四边形ABFE为矩形()A.90°B.60°C.45°D.30°3. 如图,两个半圆分别以P,O为圆心,它们成中心对称,点A1,P,B1,B2,O,A2在同一条直线上,则对称中心为()A.A2P的中点B.A1B2的中点C.A1O的中点D.PO的中点4. 把△ABC各点的横坐标都乘-1,纵坐标都乘-1,符合上述要求的图是()5. 如图,将△ABC以点O为旋转中心旋转180°后得到△A′B′C′.ED是△ABC的中位线,经旋转后变为线段E′D′.已知BC=4,则线段E′D′的长度为()A.2 B.3 C.4 D.1.56. 如图,已知菱形ABCD与菱形EFGH关于直线BD上的某个点中心对称,则点B的对称点是()A .点EB .点FC .点GD .点H7. 2019·襄阳期末 如图,在正方形网格中,格点三角形ABC 绕某点顺时针旋转α度(0<α<180),得到格点三角形A 1B 1C 1,点A 与点A 1,点B 与点B 1,点C 与点C 1是对应点,则α的值为( )A .50B .60C .90D .1208. 若点P (-a ,a -3)关于原点对称的点是第二象限内的点,则a 满足( )A .a >3B .0<a ≤3C .a <0D .a <0或a >39. 在如图所示的平面直角坐标系中,△OA 1B 1是边长为2的等边三角形,作△B 2A 2B 1与△OA 1B 1关于点B 1对称,再作△B 2A 3B 3与△B 2A 2B 1关于点B 2对称……如此作下去,则△B 2n A 2n +1B 2n +1(n 是正整数)的顶点A 2n +1的坐标是( )A .(4n -1,3)B .(2n -1,3)C .(4n +1,3)D .(2n +1,3)10. 2020·河北模拟 如图所示,A 1(1,3),A 2(32,32),A 3(2,3),A 4(3,0).作折线OA 1A 2A 3A 4关于点A 4中心对称的图形,得折线A 8A 7A 6A 5A 4,再作折线A 8A 7A 6A 5A 4关于点A 8中心对称的图形……以此类推,得到一个大的折线.现有一动点P 从原点O 出发,沿着折线以每秒1个单位长度的速度运动,设运动时间为t 秒.当t =2020时,点P 的坐标为( )A.(1010,3) B.(2020,3 2)C.(2016,0) D.(1010,3 2)二、填空题11. 如图所示,在△ABC中,已知∠ACB=90°,AC=BC=2.若以AC的中点O为旋转中心,将这个三角形旋转180°,点B落在点B′处,则BB′=________.12. 如图,直线a,b垂直相交于点O,曲线C是以点O为对称中心的中心对称图形,点A的对称点是点A′,AB⊥a于点B,A′D⊥b于点D.若OB=3,OD=2,则阴影部分的面积为________.13. 已知▱ABCD的顶点A在第三象限,对角线AC的中点在坐标原点,一边AB与x轴平行且AB=2.若点A的坐标为(a,b),则点D的坐标为________________.14. 如图,点A,B,C的坐标分别为(2,4),(5,2),(3,-1).若以点A,B,C,D为顶点的四边形既是轴对称图形,又是中心对称图形,则点D的坐标为________.15. 如图,将△ABC绕点C(0,1)旋转180°得到△A′B′C,设点A的坐标为(a,b),则点A′的坐标为____________.。
2023年沪科版九年级上册数学同步周测试卷及答案 (9)
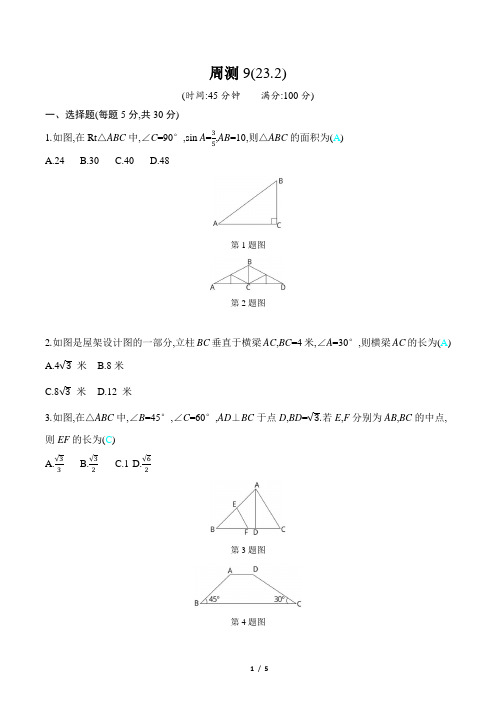
周测9(23.2)(时间:45分钟满分:100分)一、选择题(每题5分,共30分)1.如图,在Rt△ABC中,∠C=90°,sin A=35,AB=10,则△ABC的面积为(A)A.24B.30C.40D.48第1题图第2题图2.如图是屋架设计图的一部分,立柱BC垂直于横梁AC,BC=4米,∠A=30°,则横梁AC的长为(A)A.4√3米B.8米C.8√3米D.12 米3.如图,在△ABC中,∠B=45°,∠C=60°,AD⊥BC于点D,BD=√3.若E,F分别为AB,BC的中点,则EF的长为(C)A.√33B.√32C.1D.√62第3题图第4题图4.如图,拦水坝的横断面为梯形ABCD ,其中AD ∥BC ,∠ABC =45°,∠DCB =30°,斜坡AB 长为8 m,则斜坡CD 的长为(B ) A.6√2 mB.8√2 mC.4√6 mD.8√3 m5.如图,小明先在凉亭A 处测得湖心岛C 在其北偏西15°的方向上,又从A 处向正东方向行驶200米到达凉亭B 处,测得湖心岛C 在其北偏西60°的方向上,则凉亭B 与湖心岛C 之间的距离为(B ) A.400米B.(100√3+100)米C.(100√2+100)米D.(100√3-100)米第5题图第6题图6.如图,延长Rt △ABC 的斜边AB 到点D ,使BD =AB ,连接CD.若tan ∠BCD =13,则tan A =(A ) A.32 B.1 C.13 D.23二、填空题(每题5分,共20分)7.一条上山直道的坡度为1:7,沿这条直道上山,每前进100米所上升的高度为 10√2 米. 8.如图,矩形ABCD 的对角线AC ,BD 相交于点O ,过点O 作OE ⊥BC ,垂足为点E ,过点A 作AF ⊥OB ,垂足为点F.若BC =2AF ,CD =6,则BE 的长为 3√3 .第8题图第9题图9.如图,大楼AD高30 m,远处有一座塔BC,某人在楼底A处测得塔顶的仰角为45°,爬到楼顶D 测得塔顶的仰角为30°,则塔高BC为(45+15√3)m.10.如图1是一台手机支架,图2是其侧面示意图,AB,BC可分别绕点A,B转动,已知BC=8cm,AB=16 cm.当AB,BC转动到∠BAE=60°,∠ABC=50°时,点C到AE的距离约为6.3 cm.(结果保留一位小数,参考数据:sin 70°≈0.94,√3≈1.73)图1图2三、解答题(共50分)11.(14分)如图,点A,B在池塘的两端,在池塘外选一点C,连接AC,BC.测得BC=221 m,∠ACB=45°,∠ABC=58°.根据测得的数据,求AB的长.(结果取整数,参考数据:sin 58°≈0.85,cos 58°≈0.53,tan 58°≈1.60)解:过点A作AD⊥BC,垂足为点D.∵∠ACB=45°,∴AD=CD.设AB=x.在Rt△ABD中,AD=AB·sin 58°≈0.85x,BD=AB·cos 58°≈0.53x.又∵BC=221,即CD+BD=221,∴0.85x+0.53x=221,解得x≈160.答:AB的长约为160 m.12.(18分)如图是某人行天桥的引桥部分的示意图,梯面AD,BE互相平行,且与地面成37°的夹角,DE是一段水平歇台,离地面高度3米.已知天桥高度BC为6.6米,引桥水平跨度AC为11米,求歇台DE的长.(参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75)解:过点D,E分别作DF⊥AC,EG⊥BC,垂足分别为点F,G.在Rt△ADF中,∠A=37°,DF=3,∴AF=3tan37°≈30.75=4.∵AD∥BE,DE∥AC,∴∠BEG=∠A=37°.在Rt△BEG中,BG=BC-CG=3.6,∴EG= 3.6tan37°≈ 3.60.75=4.8,∴DE=AC-EG-AF=11-4.8-4=2.2(米).答:歇台DE的长约为2.2米.13.(18分)某校“综合与实践”活动小组的同学要测量AB,CD两座楼之间的距离,他们借助无人机设计了如下测量方案:无人机在AB,CD两楼之间上方的点O处,点O距地面AC的高度为60 m,此时观测到楼AB底部点A处的俯角为70°,楼CD上点E处的俯角为30°,沿水平方向由点O 飞行24 m到达点F,测得点E处俯角为60°,其中点A,B,C,D,E,F,O均在同一竖直平面内.请根据以上数据求楼AB与CD之间的距离AC的长.(结果精确到1 m,参考数据:sin 70°≈0.94,cos 70°≈0.34,tan 70°≈2.75,√3≈1.73)解:延长AB,CD分别与直线OF交于点G,H.由题意,得AG=60 m,GH=AC,∠AGO=∠EHO=90°.在Rt△AGO中,∠AOG=70°,∴OG=AGtan70°≈602.75≈21.8(m).∵∠HFE是△OFE的一个外角,∴∠OEF=∠HFE-∠FOE=30°,∴∠FOE=∠OEF,∴EF=OF=24 m,∴FH=12EF=12 m,∴AC=GH=OG+OF+FH=21.8+24+12≈58(m).答:楼AB与CD之间的距离AC的长约为58 m.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
22.1.2二次函数y=ax2的图象和性质[见A本P14]
1.关于二次函数y=8x2的图象,下列说法错误的是(C)
A.它的形状是一条抛物线
B.它的开口向上,且关于y轴对称
C.它的顶点是抛物线的最高点
D.它的顶点在原点处,坐标为(0,0)
【解析】∵抛物线y=8x2中二次项系数为8,∴此抛物线的开口向上,顶点为(0,0),它应是抛物线的最低点.
2.对于二次函数y=-3
4x
2,下列说法错误的是(A)
A.开口向上
B.对称轴为y轴
C.顶点坐标为(0,0)
D.当x=0时,y有最大值0
【解析】当a=-3
4
<0时,二次函数的图象开口向下.
3.若二次函数y=ax2的图象过点P(-2,4),则该图象必经过点(A) A.(2,4)B.(-2,-4)
C.(-4,-2) D.(4,-2)
4.已知二次函数:y=2 013x2,y=-2 013x2,y=
1
2 014x
2,y=-
1
2 014x
2,它们
图象的共同特点为(D)
A.都关于原点对称,开口方向向上
B.都关于x轴对称,y随x增大而增大
C.都关于y轴对称,y随x增大而减小
D.都关于y轴对称,顶点都是原点
【解析】根据y=ax2的图象特征判断.D正确.
5.下列函数中,当x>0时,y随x的增大而减小的是(D)
A .y =x 2
B .y =x -1
C .y =34x
D .y =1
x
【解析】 A 不正确,二次函数y =x 2的对称轴为x =0,在对称轴右侧y 随x 的增大而增大;B 、C 中y 随x 的增大而增大,均不正确,D 正确.
图22-1-7
6.函数y =x 2,y =1
2x 2,y =2x 2的图象大致如图22-1-7所示,则图中从里到外的三条抛物线对应的函数依次是( D ) A .y =1
2x 2,y =x 2,y =2x 2 B .y =x 2,y =1
2x 2,y =2x 2 C .y =2x 2,y =1
2
x 2,y =x 2
D .y =2x 2,y =x 2
,y =12x 2
【解析】 |a |越大,抛物线y =ax 2的开口越小.
7.抛物线y =-2
3x 2的开口向__下__,顶点坐标为(0,0),顶点是抛物线的最高点,当x =__0__时,函数有最大值为__0__.
8.若二次函数y =(m +2)xm 2-3的图象开口向下,则m =. 【解析】 根据题意知⎩⎪⎨⎪⎧m +2<0,
m 2-3=2,
解得m =- 5.
9.一个二次函数的图象如图22-1-8所示,图象过点(-2,3),则它的解析式为__y =3
4x 2__,当x =__0__时,函数有最__小__值为__0__,若另一个函数图象与此图象关于x 轴对称,那么另一个函数的解析式为__y =-3
4x 2__,当x =__0__时,函数y 有最__大__值为__0__.
图22-1-8
【解析】 设y =ax 2,则3=4a ,a =34,∴y =3
4x 2.
当x =0时,y 有最小值.关于x 轴对称的抛物线的解析式中a 值互为相反数. 10.在同一直角坐标系中,画出下列函数的图象:y =1
2x 2,y =x 2,y =-x 2. 解:列表:
描点、连线画图象.
(1)完成上述表格,在图22-1-9中画出其余的两个函数的图象;
(2)由图22-1-9中的三个函数图象,请总结二次函数y =ax 2中a 的值与它的图象有什么关系?
图22-1-9
解:(1)第二行依次填92,12,12,92; 第三行依次填4,0,1,9;
第四行依次填-9,-4,0,-4.图象略.
(2)a的符号决定抛物线的开口方向,|a|的大小决定抛物线的开口大小.
11.已知a≠0,在同一直角坐标系中,函数y=ax与y=ax2的图象有可能是(C)
【解析】在同一平面直角坐标系中,a值的正、负情况应保持一致,只有A、C 符合条件,又因为两图象应有两个交点,故选C.
12.已知抛物线y=ax2经过点A(-2,-8).
(1)求此抛物线的函数解析式;
(2)判断点B(-1,-4)是否在此抛物线上;
(3)求出此抛物线上纵坐标为-6的点的坐标.
解:(1)把(-2,-8)代入y=ax2,
得-8=a×(-2)2,解出a=-2,
所求抛物线的函数解析式为y=-2x2.
(2)因为-4≠-2×(-1)2,
所以点B(-1,-4)不在此抛物线上.
(3)由-6=-2x2,得x2=3,x=±3,
所以抛物线上纵坐标为-6的点有两个,它们分别是(3,-6),(-3,-6).
图22-1-10
13.如图22-1-10,已知直线l过A(4,0),B(0,4)两点,它与二次函数y=ax2
的图象在第一象限内相交于点P.若△AOP的面积为9
2,求a的值.
解:设点P(x,y),直线AB的解析式为y=kx+b,将A(4,0),B(0,4)分别代入y=kx+b,
得k=-1,b=4,故y=-x+4,
∵△AOP的面积为9
2=1
2×4×y
∴y=9
4
再把y=9
4代入y=-x+4,得x=7
4
,
所以P(7
4,9 4)
把P(7
4,9
4)代入到y=ax
2中得:a=36
49.
14.问题情境:
如图22-1-11,在x轴上有两点A(m,0),B(n,0)(n>m>0),分别过点A,点B作x轴的垂线,交抛物线y=x2于点C,点D,直线OC交直线BD于点E,直线OD交直线AC于点F,点E,点F的纵坐标分别为y E,y F.
特例探究:
填空:
当m=1,n=2时,y E=________,y F=________;
当m=3,n=5时,y E=________,y F=________.
归纳证明:
对任意m,n(n>m>0),猜想y E与y F的大小关系,并证明你的猜想.
拓展应用:
(1)若将“抛物线y=x2”改为“抛物线y=ax2(a>0)”,其他条件不变,请直接写出y E与y F的大小关系;
(2)连接EF,AE.当S四边形OFEB=3S△OFE时,直接写出m与n的关系及四边形OFEA 的形状.
图22-1-11
解:221515
归纳证明:猜想:y E=y F.
证明:∵AC⊥x轴,BD⊥x轴,A,B的坐标分别为A(m,0),B(n,0),
∴C,D的横坐标分别为m,n.
∵C,D在抛物线y=x2上,
∴C点的坐标为(m,m2),D点的坐标为(n,n2).
设直线OC的解析式为y=k1x,直线OD的解析式为y=k2x,∴m2=k1m,n2=k2n,解得k1=m,k2=n,
∴直线OC的解析式为y=mx.
直线OD的解析式为y=nx,
把E,F的横坐标分别代入y=mx与y=nx得
y E=mn,y F=mn,∴y E=y F.
拓展应用:(1)y E=y F.
(2)n=2m,四边形OAEF为平行四边形.。
