2011学而思杯五年级数学试题及答案
第一讲五年级学而思答案解析

第一讲 金字塔的影子
4 6 k 5 7 k 885 24 k 35k 885 59 k 885 k 15
5 2 k 4 3k 3 5k 91 10 k 12 k 15k 91 7 k 91 k 13
x 26 z 65
2 1 : 4:5 5 2 1 2 2 y, 5 14 5 , ; (2) 10 : 7 ; (3) 4 : 5 13 9
【例 4】 (难度等级 ※※※)
解下列方程 (1) x :111 99 : 37 (2) (2 x 3) : (4 x 5) 6 : 7 (3) (本题提高班、基础班选做)
第一讲 金字塔的影子
(3) 五年级一班的男生占一半, 五年级二班的男生占五分之二. 已知两个班男生人数相等, 那么一班和二班的总人数之比是________. 【答案】 (1)18,25,15,12.5, 【解析】 (1)略; (2)略; (3)设一班总人数为 x 人,二班总人数为 y 人,则可得: x 那么 x : y
【解析】 (1)
x :111 99 : 37 37 x 111 99 x 111 99 37 x 297
x 8 101 99 99 x 808 x 808 9
(2)
(2 x 3) : (4 x 5) 6 : 7 6(4 x 5) 7(2 x 3) 24 x 30 14 x 21 10 x 51 x 5.1 x y 78
(2)求比值
72 : 24 ________ 2.015 : 4.03 ________ 135 : 60 ________
6 8 : ________ 5 7
31 32 : ________ 32 33
小学思维数学讲义:位值原理-带详解

⼩学思维数学讲义:位值原理-带详解位值原理1. 利⽤位值原理的定义进⾏拆分2. 巧⽤⽅程解位值原理的题位值原理当我们把物体同数相联系的过程中,会碰到的数越来越⼤,如果这种联系过程中,只⽤我们的⼿指头,那么到了“⼗”这个数,我们就⽆法数下去了,即使象古代墨西哥尤⾥卡坦的玛雅⼈把脚趾也⽤上,只不过能数⼆⼗。
我们显然知道,数是可以⽆穷⽆尽地写下去的,因此,我们必须把数的概念从实物的世界中解放出来,抽象地研究如何表⽰它们,如何对它们进⾏运算。
这就涉及到了记数,记数时,同⼀个数字由于所在位置的不同,表⽰的数值也不同。
既是说,⼀个数字除了本⾝的值以外,还有⼀个“位置值”。
例如,⽤符号555表⽰五百五⼗五时,这三个数字具有相同的数值五,但由于位置不同,因此具有不同的位置值。
最右边的五表⽰五个⼀,最左边的五表⽰五个百,中间的五表⽰五个⼗。
但是在奥数中位值问题就远远没有这么简单了,现在就将解位值的三⼤法宝给同学们。
希望同学们在做题中认真体会。
1.位值原理的定义:同⼀个数字,由于它在所写的数⾥的位置不同,所表⽰的数值也不同。
也就是说,每⼀个数字除了有⾃⾝的⼀个值外,还有⼀个“位置值”。
例如“2”,写在个位上,就表⽰2个⼀,写在百位上,就表⽰2个百,这种数字和数位结合起来表⽰数的原则,称为写数的位值原理。
2.位值原理的表达形式:以六位数为例:abcdef =a ×100000+b ×10000+c ×1000+d ×100+e ×10+f 。
3.解位值⼀共有三⼤法宝:(1)最简单的应⽤解数字谜的⽅法列竖式(2)利⽤⼗进制的展开形式,列等式解答(3)把整个数字整体的考虑设为x ,列⽅程解答模块⼀、简单的位值原理拆分【例 1】⼀个两位数,加上它的个位数字的9倍,恰好等于100。
这个两位数的各位数字的和是。
【考点】简单的位值原理拆分【难度】2星【题型】填空【关键词】希望杯,4年级,初赛,7题,六年级,初赛,第8题,5分【解析】这个两位数,加上它的个位数字的9倍,恰好等于100,也就是说,⼗位数字的10倍加上个位数字的10倍等于100,所以⼗位数字加个位数字等于100÷10=10。
学而思人教版小学五年级数学期末检测试卷及答案

“学而思”人教版小学五年级(上册)数学期末检测试卷18分)一、填空题。
(每空1分,共27层,地面以下第2层,地面以上第7层记作+1.南京某饭店有37层高,地面以下有)层。
层记作( 24平方厘米,2.右边平行四边形的面积是)平方厘米。
涂色部分的面积是(;里面有一个十和( ) 4个百分之一组成的数是( )3.5个一和个十分之一。
年“五一”黄2008.全国假日办发布的《2008年“五一”黄金周旅游统计报告》显示:4)“万人次”作单位的数是(金周期间,某市共接待游客1236000人次。
把它改写成用。
万人次,再把改写后的数保留整数写出近似数是( ) 。
个图形是()5.○☆☆☆○○☆☆☆○○☆☆☆○……按这种规律,第29 。
的商保留两位小数是( )( ).×的积是位小数,16÷236。
=”里填上“﹥”、“﹤”或“7.在米米÷÷××=( )平方千米=( )平方米 5000公顷8. 公顷B=( )。
则A÷9. 已知A=……096,B=……03, 2007个0个20080二、判断题。
(对的画“√”,错的画“×”,5分)1. 0既不是正数,也不是负数。
……………………………………………()2.小数点的后面添上“0”或去掉“0”,小数的大小不变。
…………………()3.平行四边形面积是梯形面积的2倍。
…………………………………()4.小数不一定比整数小。
…………………………………………………()5.-(+)=-+= …………………………()三、选择题。
(把正确答案的序号填在括号里,6分)1.大于而小于的小数( )。
)一个也没有3(个9)有2()有无数个1(2.一排学生从前往后按1、2、3、1、2、3……依次重复报数,从前往后数小明是第24个,他应该报()。
(1)1 (2)2 (3)33.00≈()。
(1)20亿(2)21亿(3)205亿4.小明的房间面积是15( )。
2011学而思杯五年级试卷及详解

考试科目:数学考试时间: 80分钟总分: 120分填空题(共20题,每题6分直接写出答案)1.11111111 1357911131517 612203042567290 ++++++++=2.小镜是个小学生,最近参加一次数学竞赛,并获得了好成绩,小司问她:“姐姐,你考了多少分?得了第几名?”小镜说:“我的年龄、得分和名次相乘的积是776。
”小镜的年龄、得分、名次的和是。
3.布袋中有许多4种不同颜色的小球,每次摸两个,要保证有10次所摸的结果是一样的,那么至少要摸次。
4.牧场上有一片匀速生长的草地,如果有30头牛吃,可以吃6天;如果有25头牛吃,可以吃8天。
那么20头牛吃,可以吃天。
5.用8个棱长是1厘米的小正方体拼成1个大的长方体,这个长方体的表面积最大与最小的差是平方厘米。
6.用绳子测井深,把绳对折一次来测量,井外余6米,将绳对折两次来测量,还差2米,那么井深米。
7.如图所示,正方形ABCD的面积是16平方厘米,5BE=厘米,三角形DOE的面积是平方厘米。
O AB DE8.在如图所示○内填入不同的数,使得三条边上的三个数的和都是12,若A、B、C的和为18,则三个顶点的三个数的和是_______。
2011第六届学而思综合素质测评五年级C BA9.将一张纸剪成6块,从所得纸片中取出若干块,每块各剪成6块,再从所得纸片中取出若干块,每块各剪成6块……如此进行下去,到剪完某一次后停止,所得纸块总数可能是2005、2006、2007、2008、2009、2010、2011、2012这几个数中的_________。
(写出所有可能的答案)10.一个四位数,减去它各个数位上的数字之和,差是四位数658 , 中应填________。
11.如图所示,P为长方形ABCD内的一点,PAB∆的面积等于5,PBC∆的面积等于13,PBD∆的面积是。
AB CP12.将自然数N接在任一自然数的右面(例如将2接在35的右面得352),如果所得的新数都能被N整除,那么称N为神奇数,那么在小于100的自然数中,神奇数有1、。
五年级A

绝密★启用前2011年首届全国学而思综合能力测评(学而思杯)数学试卷(五年级A 卷) 时间:13:30~14:50 满分:150分考生须知: 1. 请在答题纸上认真填写考生信息;2. 所有答案请填写在答题纸上,否则成绩无效一.填空题(每题8分,共40分)1. (视听题)杯子中有浓度为5%的盐水150克,那么其中含有______克盐. 【分析】浓度问题求溶质。
浓度=溶质÷溶液×100 %。
因此溶质=浓度×溶液。
1505%7.5⨯=克。
2. (视听题)杯子中有浓度为5%的盐水150克,向杯子中加入100克水,盐水的浓度变为______%. 【分析】浓度=溶质÷溶液×100 %。
()7.5150100100%3%÷+⨯=3. (视听题)杯子中有浓度为10%的盐水100克,向杯子中加入浓度为20%的盐水150克,混合均匀.新的盐水的浓度是______%.【分析】溶质总重量为10010%15020%40⨯+⨯=克;溶液总重量为100150250+=克。
因此溶液浓度为:40250100%16%÷⨯=4. 计算:10.253464155⨯+⨯+÷=______.【分析】=0.2(534641)28⨯++=原式5. 2011年3月11日,日本发生里氏9级大地震。
在3月15日,日本本州岛东海岸附近海域再次发生5级地震。
已知里氏地震级数每升2级,地震释放能量扩大到原来的1000倍,那么3月11日的大地震释放能量是3月15日东海岸地震的______倍. 【分析】差了4级,差了1000×1000=1,000,000倍. 二.填空题(每题10分,共50分)1. 横式“+=学理科到学而思学而思杯”中,相同的汉字代表相同的数字,不同的汉字代表不同的汉字,那么四位数“学而思杯”的最大值为______.【分析】确定“学”最大为8,那么到为7,而最大为6,此时有算式:825+7869=8694,那么四位数的最大值为86942.今天是2011年4月9日,20110409这个九位数是9的倍数,则方框里应填入的数字是______.【分析】容易得13.用若干个1×1×1的小立方体堆积成一个立体图形(小立方体不能悬空),它的正视图、左视图、俯视图都是下图的样子,那么堆积成满足条件的小立方体最少需要______个小立方体.【分析】如图,最小的体积为9立方厘米。
2011-2015年学而思杯五年级数学试题汇总

一、填空题(每题7分,共28分)1.今天是2012年4月7日,欢迎同学们参加“第二届全国学而思综合能力测评(学而思杯)”。
请先计算20120407 除以11的余数是___________。
(张宇鹏老师供题)2.算式:11111201212450310062012×−+−+− 的计算结果是___________。
(齐志远老师供题)3.水泊梁山共聚108名将领,受招安后奉命征讨“方腊”(人名)。
征讨过程中战死将领占总人数的3554,征讨得胜后辞官将领占总人数的118,那么,队伍中还有___________名将领。
(董博聪老师供题)3.如图,是一个由2个半圆、2个扇形、1个正方形组成的“心型”。
已知半圆的直径为10,那么,“心型”的面积是___________。
(注:π取3.14 )(胡浩老师供题)二、填空题(每题9分,共36分)5.定义:A □B 为A 和B 乘积的约数个数,那么,1□8+2□7+3□6+4□5=___________。
(崔梦迪老师供题)6.由24个棱长为1的小正方体组成一个大的长方体,那么,组成后长方体的表面积最大为___________。
(刘斌老师供题)7.“2012A”是一个最简真分数,那么,满足条件的 有___________个。
(贺赓帆老师供题)8.在一个盛有部分水的长方体容器中,插有两根木棒,木棒露在外面的长度比是3∶7,当水面的高度升高10厘米后,木棒露在外面长度比变成2∶5。
当木棒露在外面长度比变成1∶3时,还需要升高_______厘米的水。
(郭忠秀老师供题)三、填空题(每题10分,共40分)9.下图为学而思标志中的字母“S”,被分成52个完全相同的小正方形。
那么,在右下图中共有___________个“”。
(注:“L”型可旋转)(李响老师供题)10.北京某水族馆饲养鲨鱼,偶数颗牙齿的鲨鱼总说实话,奇数颗牙齿的鲨鱼总说谎话。
一天,绿鲨鱼、蓝鲨鱼、紫鲨鱼、白鲨鱼在一起聊天。
2011年学而思杯数学试题答案

1.简单小数计算2011-201.1+20.11-2.011+0.001【解析】18282.分小四则混合运算541??1)12.3?(3.85??1854541【解析】??1)??12.3?(3.8518544?(3.85?3.6?12.3?1.8)?94????1.8?12.37.7?94?36?9?16 3 已知N*等于N的因数个数,比如4*=3,则(2011*+10*+6*)*=_______【解析】(2011*+10*+6*)*=(2+4+4)*=44用字母表示数一个非等腰三角形,一边长为6,一边长为7,还有一边长为6k,已知k是自然数,则三角形的周长为______.【解析】k=2,周长为6+7+12=25.5基础类型应用题1红光大队用拖拉机耕地,2台3小时耕75亩,照这样计算,4台5小时耕____亩.【解析】2台1小时可耕75 ÷3=25亩,4台5小时可耕地25×2×5=250亩6基础类型应用题2一个骗子到商店买了5元的东西,他付给店员50元钱,然后店员把剩下的钱找给了他;这时他又说自己有零钱,于是给店员5元的零钱,并且要回了开始给出的50元。
则这个骗子一共骗了______钱?【解析】由于一开始骗子并没有骗钱,产生骗钱的是后用零钱换50元,所以共骗得50-5=45元。
7约数倍数已知A、B两数的最小公倍数是120,B、C两数的最小公倍数是180,A、C两数的最小公倍数是72,则A、B、C三数的最小公倍数是______.3×3×5【解析】120=222180=2×3×53272=2×332×3×所以最小公倍数是25=3608简单的逻辑推理2011年8月14日,伦敦羽毛球世锦赛进入最后一个比赛日。
在女单决赛中,中国选手王仪涵2比0完胜中华台北选手郑韶婕,首次夺得世锦赛冠军,中国队也实现了女单项目的八连冠。
学而思杯五年级数学

隔是 4 分钟. 【答案】4 分钟.
15. 在 5 5 的棋盘的左下角的格子中放置一个“国王”,规定“国王”每一步只能向右、向上或向右上方走一格,那
么走到棋盘右上角的格子的方法一共有________种. 【解析】标数法,如图. 1 9 7 5 3 1 41 25 13 5 1 129 63 25 7 1 321 129 41 9 1
6.
二、 填空题Ⅱ(每题 6 分,共 30 分,将答案填在下面的空格处) 7. 图中有________个三角形.
2.
答 题
10 个棱长为 2 的小立方体堆成如下图形,表面积为________.
禁 止
线 内
年级____________________
密
封
【解析】前后各 10 个小正方形,左右各 4 个正方形,上下个 4 个正方形,表面积相当于 36 个小正方形,每个小 正方形的面积是 4,表面积共 144. 【答案】144.
解析边长为1的三角形有16个边长为2的三角形有7个边长为3的三角形有3个边长为4的三角形有一个三位数的2倍它的数字和是原来三位数数字和的一半这样的三位数最小是
绝密※启用前 2015 年学而思综合能力测评(深圳) 五年级 数学
座位号____________________
【解析】倒数第二行的 6 说明第一行的空格可以是 1,可以是 6,枚举尝试, 31 65=2015 或 36 67=2412 . 【答案】2015 或 2412. 动物王国中有一个奇怪的猫村.已知猫村共有 60 只猫,其中有漂亮尾巴的 27 只,漂亮毛色的 45 只.所有猫 毛色或尾巴至少一项漂亮,则两样都漂亮的有________只. 【解析】 27 45 60 12 . 【答案】12.
-学而思杯五年级数学试题汇总

一、填空题(每题7分,共28分)1.今天是2012年4月7日,欢迎同学们参加“第二届全国学而思综合能力测评(学而思杯)”。
请先计算20120407 除以11的余数是___________。
(张宇鹏老师供题)2.算式:11111201212450310062012×−+−+− 的计算结果是___________。
(齐志远老师供题)3.水泊梁山共聚108名将领,受招安后奉命征讨“方腊”(人名)。
征讨过程中战死将领占总人数的3554,征讨得胜后辞官将领占总人数的118,那么,队伍中还有___________名将领。
(董博聪老师供题)3.如图,是一个由2个半圆、2个扇形、1个正方形组成的“心型”。
已知半圆的直径为10,那么,“心型”的面积是___________。
(注:π取3.14 )(胡浩老师供题)二、填空题(每题9分,共36分)5.定义:A □B 为A 和B 乘积的约数个数,那么,1□8+2□7+3□6+4□5=___________。
(崔梦迪老师供题)6.由24个棱长为1的小正方体组成一个大的长方体,那么,组成后长方体的表面积最大为___________。
(刘斌老师供题)7.“2012A”是一个最简真分数,那么,满足条件的 有___________个。
(贺赓帆老师供题)8.在一个盛有部分水的长方体容器中,插有两根木棒,木棒露在外面的长度比是3∶7,当水面的高度升高10厘米后,木棒露在外面长度比变成2∶5。
当木棒露在外面长度比变成1∶3时,还需要升高_______厘米的水。
(郭忠秀老师供题)三、填空题(每题10分,共40分)9.下图为学而思标志中的字母“S”,被分成52个完全相同的小正方形。
那么,在右下图中共有___________个“”。
(注:“L”型可旋转)(李响老师供题)10.北京某水族馆饲养鲨鱼,偶数颗牙齿的鲨鱼总说实话,奇数颗牙齿的鲨鱼总说谎话。
一天,绿鲨鱼、蓝鲨鱼、紫鲨鱼、白鲨鱼在一起聊天。
学而思2011年寒假.五年级优秀儿童作业答案

五年级优秀体系寒假班课后作业答案第1讲 1.[分析](1)(2)不是.(3)是,公比为13.2.[分析]第5项是第1,9项的中间项.那么22551919252.510a a a a a a =⇒===.3.[分析]先算公比231255aq q a ==⇒=,那么41755875a =⨯=.4.[分析]211939÷==,因此2小时后细菌能充满瓶子,即下午2点(14点).5.[分析]把算式的整数部分和分数部分分开:()1111248......1024 (248)10241023204821024102320461024⎛⎫=+++++++++ ⎪⎝⎭=-+=原式第2讲1.[分析]最容易观察到的一次重合是12时整.不难看出,在10时至12时之间,还应有一次重合.这一重合过程可以理解为一追及问题:分针在环形的跑道上追时针.现在将表盘一周分为60格,分针在时针后面50格,分针一分钟走1格,时针一小时走5格.这样,就可以计算本题了.将表盘分成60份,则分针的速度是每分钟走1格,时针的速度是每分钟走5÷60=112.现在是10时整,分针在时针后50格处,则追及时间为:150(1)1265411÷-=分钟.下次追上,可以理解为现在分针在时针后面60格,则再次追及时间为:160(1)125 65 11÷-=分钟.综上所述,经过65411分钟,分针与时针第一次重合;再经过56511分钟,分针与时针再次相合.2.[分析]分针每分钟走1格,时针每分钟走112格.当它们成75︒角时,中间相差7525603602⨯=(格),需要追赶25554022-=(格).需要时间为551(1)30212÷-=(分钟).3.[分析]可以想象,这道题的答案应该有2个.8点的时候,时针在分针前240度,而到时针与分针的夹角是60度时,时针在分针前或后60度,所以分针应该比时针多运动180度或300度,而一个小时分针比时针多运动36030330-=度,所以要构成符合条件的角度,要经过618033011÷=小时,即83211分钟,或1030033011÷=小时,即65411分钟,所以在8点83211分或8点65411分时分针和时针成60°.4.[分析](1)根据题意闹钟与标准时间的速度比为63:60,所以标准钟走了7606360400⨯÷⨯=格,走了24006063÷=时,即当闹铃响起时,标准时间是5点40分.(2)根据题意手表与标准时间的速度比为56:6014:15=,所以标准钟走了7601415450⨯÷⨯=格,走了450607.5÷=时,即当这只表指向下午3点的时候,标准时间是3点30分.5.[分析]分针速度为:10°/分钟;时针速度为:53o/分钟;3点时分针与时针成180°,18分钟后分针追上时针5 18101503⎛⎫⨯-=⎪⎝⎭°所以此时,分针与时针所成的锐角为30°.1. 2.3. 4.5.1.[分析]顺水速度为25328÷=(小时).+=(千米/时),需要航行1402852.[分析]从甲到乙顺水速度:234926÷=(千米/时),船速÷=(千米/时),从乙到甲逆水速度:2341318是:(2618)222+÷=(千米/时),水速是:(2618)24-÷=(千米/时).3.[分析]从甲地到乙地的顺水速度为15318⨯=(千米),从乙+=(千米/时),甲、乙两地路程为188144地到甲地的逆水速度为15312-=(千米/时),返回所需要的时间为1441212÷=(小时).4.[分析]乙船顺水速度为120260÷=(千米/时),所以水流速度为÷=(千米/时),逆水速度为120430()6030215-÷=(千米/时),甲船顺水速度为120340-⨯=(千米/时),÷=(千米/时),逆水速度为4015210返回原地比去时多用的时间为1201039÷-=(小时).5.[分析]在两船的船速相同的情况下,一船顺水,一船逆水,它们的航程差是什么造成的呢?不妨设甲船顺水,乙船逆水.甲船的顺水速度=船速+水速,乙船的逆水速度=船速-水速,故:速度差=(船速+水速) -(船速-水速)2⨯=(千米).3小时的距离差为=⨯水速,即:每小时甲船比乙船多走428⨯=(千米).83241.[分析]周期问题,先找出周期.2,3,6,8,8,4,2,8,6,8,8……6位一循环.()10026162-÷= ,那么第100个数是循环中的第2个.第100个数是8.2.[分析]根据观察,这一列数的个位为:3、 4、 7、1、8、9、7、6、3、9、2、1、3、4、7、1…,12个数为一个周期,由于501242÷= ,共有4个周期且余数为2,所以从8开始连续50 个数的和最大,为:89604257++⨯=. 3.[分析]13589+++⋯+=()18945202520102+⨯=>, 13587+++⋯+=()18744193620102+⨯=<.所以擦去的奇数是2025201015-=. 4.[分析](1)首先观察规律.数表里面出现的是从0开始的连续偶数;每两行中有7个数,其中第1行有3个数,从小到大排在第3,4,5号位置;第2行有4个数,从大到小排在第1,2,3,4号位置.那么前98行中有7982343⨯÷=个数,其中第343个数是()34312684-⨯=.第99行最右边的数是该行的第3个数,它是:6846690+=. (2)2006是第2006211004÷+=个数.100471433÷= ,那么第1004个数在第14321287⨯+=行的第3个数,那么就是第287行的第5列.5.[分析]左上角的数为:123891015161781++++++++=.由于每向右移动一位,即增加9,最多可向右移动4次,向下移动一位可增加63. 由于:(1)()1997811916,1916633026-=÷= , 不是9的倍数; (2)()2016811935,1935633045-=÷= ,无法向右移动5次; (3)()2349812268,22686336-=÷=; 所以,只有2349是可以的,应向下移动36次, 所以最大的数为:73617269⨯+=1.[分析]既不是4的倍数,也不是6的倍数的同学,以及既是4的倍数,也是6的倍数的同学是面朝老师的.[][][]5050450625012501282438-÷-÷+⨯÷=--+⨯=(名) 2.[分析]设不能被2整除,又不能被3整除,还不能被5整除的数有x 个,则在0123P x P P P -=-+中,0100P =,1100100100103235P ⎡⎤⎡⎤⎡⎤=++=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦,21001001001610632232535P ⎡⎤⎡⎤⎡⎤=++=++=⎢⎥⎢⎥⎢⎥⨯⨯⨯⎣⎦⎣⎦⎣⎦,31003235P ⎡⎤==⎢⎥⨯⨯⎣⎦,因此100103323x -=-+,解得26x =,从而x 占总数的26%. 3.[分析]这个题需要韦恩图辅助分析,搞清楚已知和所求.如图示,“///”阴影表示爱喝红茶的10人,“\\\”阴影表示不爱喝红茶却爱喝绿茶的12人,空白为只爱喝花茶的x 人,从而3010128x =--=人.花茶4.[分析]唐僧与徒弟共同渡过了81378-=难,设师徒四人共同渡过了x 难,根据容斥原理有77656264616078x ++---+= 解得,59x =因此师徒四人共同渡过了59难. 5.[分析]由于每人最多参加两科,也就是说有参加2科的,有参加1科的,要求参加的人最少,那么尽可能让每人都参加两科,所以理论上至少有(8911)214++÷=人参加竞赛,1495-=,14113-=,参加语文和英语竞赛的有5人,参加语文和数学竞赛的有3人,参加数学和英语竞赛的有6人,符合题意,因此至少有14人参加竞赛.1.[分析] (法1)被除数2143=-除数-商-余数2143=-除数3352--2058=-除数, 被除数=除数⨯商+余数,所以除数33522058⨯+=-除数, 则除数(205852)3459=-÷=,被除数2058591999=-=.(法2)从被除数中减掉余数52后,被除数就是除数的33倍,所以可以得到:2143335252(331)---=+⨯除数,求得除数59=,被除数3359521999=⨯+= 2.[分析]这是把带有余数的问题转化成整除性的问题,也就是要找出能整除(1094)-的所有的两位数.进一步,要找出能整除105的两位数,很简单的方法就是把105分解质因数,从所得到的质因子中去凑两位数.1094105357-==⨯⨯.因此这样的两位数是:15,35,21. 3.[分析]30024357-=,24320538-=,所以这个数是57,38的大于1的公约数,而57,38的公约数只有1和19,所以所求自然数为19. 4.[分析]n 能整除639112925258++-=.因为25381÷= ,所以n 是258大于8的约数.显然,n 不能大于63.符合条件的只有43. 5.[分析]因为246111223÷= ,13511123÷= ,6047115498÷= ,根据余数性质⑤,2461135604711⨯⨯÷的余数等于83811⨯⨯÷的余数,而838192⨯⨯=,19211175÷= ,所以2461135604711⨯⨯÷的余数为5.1.[分析]第一问要用乘法原理,当分子有5种可能时,分母有4种可能,即5×4=20种,所以这样的分数有20个.第二问中,分母为3的真分数有1个,分母为5的真分数有2个,分母为7的真分数有3个,分母为11的真分数有4个,所以真分数共有1+2+3+4=10个. 2.[分析]10个. 3.[分析]这个数加1能同时被2,3,4,5,6整除,而 [2,3,4,5,6]=60 所以这个数最小是 60-1=59. 4.[分析]我们可以先去考虑到100的所有自然数中与100不互质的数,因为100=2×2×5×5,故1到100中所有含因子2或5的数都与100不互质.其中含因子2的有2,4,6,8…,100(即为50个数),他们的和是(2+100)×50÷2=2550; 含因子5的有5,10,15,20…,100,他们的和是(5+100)×20÷2=1050; 既含2又含5的有10,20…,100,他们得的和是(10+100)×10÷2=550; 则与100不互质的所有数的和为2550+1050-550=3050; 而1到100所有自然数的和为(1+100)×100÷2=5050;所以符合题意的从1到100所有自然数中与100互质的数的和为:5050-3050=2000. 5.[分析]360=3223 ×5=1×2×4×5×9,所以a 的最大值为95421.1.[分析]()108022.51080182216m ÷+÷⨯=. 2.[分析]两腰合并,形成一个直角三角形(勾3、股4、弦5),所以梯形的高为:341255⨯=. 所以梯形的面积为18.3.[分析]梯形蝴蝶定理.梯形被对角线分成的四个部分的比为:22::::::9:15:15:25COD AOD BOC AOB S S S S CD CD AB CD AB AB ∆∆∆∆=⨯⨯=.那么252525491515256416AOB ABCD S S ∆==⨯=+++. 4.[分析]地震监测点接收到纵波时,横波距离检测点还有2.58 6.917.802⨯=(千米),纵波每秒比横波多走3.96 2.58 1.38-=(千米),那么纵波总时间为17.802 1.3812.9÷=(秒),那么可以知道地震中心距离监测点3.9612.951.084⨯=(千米). 5.[分析]如图所示,令AB ,BC ,CA 间的距离分别为a ,b ,c .CBA c ba从而根据题意有:10a b +=,13b c +=,11a c +=,从而有:101311172a b c ++++==,分别求得:171341711617107a b c =-==-==-=可见距离最近的是AB 间的距离为4千米.。
学而思杯数学试题(五年级)答案解析

2013 年第三届全国学而思综合能力测评(学而思杯)数学试卷(五年级)详解一.填空题(每题5 分,共20 分)1. 两个质数的和是9,那么这两个质数的乘积是.【考点】数论,质数性质【难度】☆【答案】14【分析】两质数和为奇数,必有偶质数2,另一质数为7,故答案为2 ⨯ 7 = 14 .2. 如右图,共有个正方形.【考点】组合,几何计数【难度】☆【答案】10【分析】1⨯1的正方形有4 个,2 ⨯ 2 的正方形有5 个,4 ⨯ 4 的正方形有1 个,共10 个.3. 学而思教研部一共购买了300 本书,其中有五分之二是数学书,三分之一是语文书,其余是英语书.那么,英语书共有本.【考点】应用题,分数应用题【难度】☆【答案】80【分析】300 ⨯ (1 - 2-1) = 300 - 120 - 100 = 80 (本).5 34. 如右图,正方形ABCD 边长为40 厘米,其中M、N、P、Q 为所在边的中点;分别以正方形的顶点为圆心,以边长的一半为半径做直角扇形,那么形成图中阴影部分的面积是平方厘米.(π取3.14)【考点】几何,圆与扇形面积【难度】☆☆【答案】344【分析】阴影面积的实质是整体减空白:边长40 厘米的正方形面积减去半径为20 厘米的圆的面积(4 个扇形刚好拼成一个整圆),故答案为402 - 3.14 ⨯ 202 = 400 ⨯ (4 - 3.14) = 344 平方厘米.5. 对一个大于1 的自然数进行如下操作:如果是偶数则除以2,如果是奇数则先减去1 再除以2,如此进行直到得数为1,操作停止.那么,所有经过3 次操作结果为1 的数中,最大的数是.【考点】数论,奇偶性,倒推【难度】☆☆【答案】15【分析】从1 向前倒推,寻找原数的最大值;但发现若上一步是偶数,则须本数⨯2 ;若上一步是奇数,则须本数⨯2 + 1 ;明显每次向前推出奇数可使原数更大,倒推过程为:1→3→7→15;故15 为原数的可能达到的最大值.6. 定义:∆( A, B,C, D) = A ⨯ 4 + B ⨯ 3 + C ⨯ 2 + D ⨯1 ,那么,∆(2, 0,1, 3) =_ .【考点】计算,定义新运算【难度】☆【答案】13【分析】按定义式,∆(2, 0,1,3) = 2 ⨯ 4 + 0 ⨯ 3 + 1⨯ 2 + 3 ⨯1 = 13 .7. 一项工程,由甲队单独做10 天后,乙队加入,甲、乙两队又合作了8 天完成;这项工程,如果全部由乙队单独做,20 天可以完成.那么,如果全部由甲队单独做,天可以完成.【考点】应用题,工程问题【难度】☆☆【答案】30【分析】把总工作量看做单位“1”,则乙队的工作效率为每天做120,故可在甲乙合作的条件中求出甲队的工作效率为每天做(1 - 1⨯ 8) ÷ (10 + 8) =3÷18 =1;故答案为30.20 5 308. 如右图,大正方体的棱长为2 厘米,两个小正方体的棱长均为1厘米,那么,组合后整个立体图形的表面积为平方厘米.【考点】几何,立体几何,表面积【难度】☆☆【答案】32【分析】三个立方体原总表面积为12 ⨯ 6 + 12 ⨯ 6 + 22 ⨯ 6 = 36 平方厘米,之后放在一起时缺失了4 个1⨯1 的表面,故答案为36 - 12 ⨯ 4 = 32 平方厘米;或者可用三视图法求表面积:(5 + 5 + 6) ⨯ 2 = 32 平方厘米.9.甲、乙、丙 3 人共有 2013 块巧克力,甲拿走了乙、丙各 3 块巧克力后,甲、乙、丙 3 人的巧克 力数比为 4: 2: 5 ,那么,甲原.有.【考点】应用题,比例应用题 【难度】☆☆☆ 【答案】726块巧克力.【分析】之后甲的巧克力块数易由 3 人的块数比求得,为 2013 ⨯732 - 3 ⨯ 2 = 726 块.4 4 + 2 + 5= 732 块,故甲原有巧克力10. 在 5×5 的方格中,将其中的一些小方格染成红色,使得对于图中任意的2×2 的方格中,均有至少 1 个小方格是红色的.那么,至少要将个小方格染成红色. 【考点】组合,构造与论证 【难度】☆☆ 【答案】4【分析】论证:为了保证 4 个角上的互不重叠的 4 个 2 ⨯ 2 的方格中都至少有 1个红色方格,可知答案必不小于 4; 构造:如右图,4 是可能的; 综上,答案为 4.11. 一个五位数,各.位.数.字.互.不.相.同.,并且满足:从左往右,第一位是 2 数是 3 的倍数,前三位组成的三位数是 5 的倍数,前四位组成的四位数是 7 的倍数,这个五位数 是 11 的倍数.那么,这个五位数最小是 .【考点】数论,整除特征,最值 【难度】☆☆☆ 【答案】21076【分析】考虑最值确定各位数字:万位是 2 的倍数,故万位最小应为 2; 前两位组成的数是 3 的倍数,故前两位最小应为 21; 前三位组成的数是 5 的倍数,故前三位最小应为 210;前四位组成的数是 7 的倍数,最小为 2100,但要求各位数字不同,故应为 2107; 这个五位数是 11 的倍数,故此数应为 21076.12. 右边的乘法竖式中,相.同.汉字代表相.同.数字,不.同.汉字代表不.同.数字,那么,“大自然”代表的三位数是.【考点】数论,数字谜【难度】☆☆☆☆【答案】958我爱大自然⨯ 4 大自然爱我【分析】由个位可知“我”为偶数,再分析最高位即可知“我”只能为2;故“然”为3 或8;(还可分析知五个汉字所代表的数字之和必为3 的倍数,这个小结论可以辅助之后的分析)若“然”= 8,①则分析万位知“大”只能为9,故千位“爱”乘以4 后向万位进1,可知“爱”为3 或4;②若“爱”= 4,此时十位:“自⨯4 + 3 ”的末位数字为4,这表示“自⨯4 ”的末位数字为1,奇偶性矛盾!故确定“爱”只能为3;③若“爱”= 3,此时十位:“自⨯4 + 3 ”的末位数字为3,这表示“自⨯4 ”的末位数字为0,“自”为0或5;若“自”= 0,千位要接受进位8,这不可能;若“自”= 5,则有答案23958 ⨯ 4 = 95832 ;若“然”= 3,①分析万位知“大”为9 或8;②若“大”= 9,则千位“爱”乘以4 后向万位进1,可知“爱”只能为4;此时十位:“自⨯4 + 1 ”的末位数字为4,这表示“自⨯4 ”的末位数字为3,奇偶性矛盾!故知只能“大”= 8;③若“大”= 8,分析十位可知“爱”为奇数,再分析千位可知“爱”= 1;④此时无论十位的“自”为0 还是为5,式子的百位和千位都是错误的(21803 ⨯ 4 = 80312 错误;21853 ⨯ 4 = 85312 错误),故知“然”= 3 时无解;综上,本数字谜只有唯一解:23958 ⨯ 4 = 95832 ,本题答案为958.四.填空题(每题8 分,共32 分)13. 有A、B、C、D、E、F 六个人围坐在圆桌吃饭,A 会讲英语,1B 会讲汉语、英语和法语,C 会讲汉语、英语和德语,D 会讲6 2汉语和德语,E 会讲汉语,F 会讲法语和德语.如果每个人都能与他相邻的两个人交流,那么,共有种不同的排座位方式.(经过旋转、对称后重合的方式不.算.做.一.种.)【考点】组合,逻辑推理 5 3【难度】☆☆☆4【答案】24【分析】本题突破口在于A,由于A 只会说英语,英语也只有A、B、C 三人会说,故座位顺序中必然有紧邻的BAC(或CAB),此时分析F 可知F 必须与B 或C 中的一个相邻,E 必须在D、F 的中间;综上,得到两种圆排列方式:①BACEDF;②BACFDE;每种圆排列方式都有旋转、对称的12 种排座方式,故答案为12 ⨯ 2 = 24 种.⎨ ⎩ Q14. A 、B 两地相距 120 千米.甲、乙从 A 地,丙从 B 地同时出发,相向而行.当甲、丙相遇时,乙行了 20 千米.甲到达 B 地后立即原路返回,当乙、丙相遇在途中 C 地时,甲也恰好到达 C 地. 那么,当丙到达 A 地时,乙共行了 千米.【考点】行程问题,比例法解行程问题 【难度】☆☆☆ 【答案】72【分析】本题关键点在于甲丙速度之和与乙的速度之比为 120 : 20 = 6 :1 ;设甲、乙、丙三人到达 C 点⎧z + y = 120时各走了 x 、y 、z 千米,则有方程组:⎪x - z = 120,解得 y = 3 (可以解出 x 、y 、z 的具体值, ⎪(x + z ) : y = 6 :1 z 5但其实不必要);故丙走了 120 千米时,乙走了120 ⨯ 3= 72 千米.515. 如右图,三角形 ABC 是直角三角形,M 是斜边 BCA 的中点,MNPQ 是正方形,N 在 AB 上,P 在 AC 上. NP如果,AB 的长度是 12 厘米,AC 的长度是 8 厘米. 那么,正方形 MNPQ 的面积是 平方厘米.Q【考点】几何,面积,弦图 BMC【难度】☆☆☆ 【答案】20【分析】如下图,过 M 点作 AB 的垂线,垂足为 D ;以 AD 为外围正方形的一边,做出以 MNPQ 为内含正方形的弦图,;则 MD 为△ABC 的中位线, MD = AC = 4cm , AD = AB= 6cm ;故弦图中外2 2围正方形边长为 6cm , AN = MD = 4cm , DN = 6 - 4 = 2cm ;故所求面积为 62 - 2 ⨯ 4⨯ 4 = 20cm 2 .2AANP NPDD FBMCMQE16. 有一个自然数A,它的平方有9 个约数,老师把9 个约数写在9 张卡片上,发给学学三张、思思三张.学学说:“我手中的三个数乘积是A3 .”思思说:“我手中的三个数乘积就是A2 ,而且我知道你手中的三个数和是625.”那么,思思手中的三个数和是.【考点】数论,约数个数定理,幻方【难度】☆☆☆☆☆【答案】55【分析】A2 有9 个约数,故由约数个数定理可逆推出:A 的质因数分解形式为p4 或pq (p、q 为不相同的质数);若A = p4 ,那么可把A2 的9 个约数写成如下的表格形式(幻方):学学手中必拿到了一行或一列或一条对角线;思思手中拿到的可能是(1、p 、p7 )(1、p2 、p6 )(1、p3 、p5 )(p 、p2 、p5 )(p 、p3 、p4 );只有后两组才能确定学学手中的牌,但后两组所确定的数需要1 + p4 + p8 = 625 或1 + p5 + p7 = 625 ,可是这两种情况p 均无解;故知A 的质因数分解形式不能为p4 ,只能为pq ;若A = pq ,那么可把A2 的9 个约数写成如下的表格形式思思手中拿到的可能是(1、p 、pq2 )(1、q 、p2 q )(1、p2 、q2 )(p 、q 、pq );经分析可知,只有当思思拿到(p、q、pq)时,才一定能确定学学手中的牌,此时学学手中的牌为(1、p2 q 、pq2 ),故1 + p2 q + pq2 = 625 ,(可用枚举法,或因数分析)解得A 的两个质因数p、q 为3 和13,故思思手中的牌为(3、13、39),所求答案为3 + 13 + 39 = 55 .五. 解答题(每题 8 分,共 16 分)17. 计算:(1) 0.27 ⨯103 + 0.19 (4 分)(2) 2013⨯ 2.3+ 201 3÷ 0.4 - 2013 ⨯ 1(4 分) 10 4 【考点】计算、巧算 【难度】☆☆ 【答案】28;4697【分析】(1)原式 = 0.27 ⨯100 + (0.27 ⨯ 3 + 0.19) = 27 + 1 = 28 ;(2)原式 = 2013 ⨯ 7 + 2013 ÷ 4 - 2013 ÷ 4 = 2013 ⨯ 7= 4697 .3 318. 解方程:(1) 4(2x - 1) - 3(x - 2) = 7 (4 分) (2) 2 x + 5 = 4 x - 7 (4 分) 3 5【考点】计算、解方程【难度】☆☆ 【答案】 x = 1 ; x = 23【分析】(1)注意去第 2 个括号时要变号;原方程化为: 8x - 4 - 3x + 6 = 7 ,即 5x = 5 ,解得 x = 1 ;(2)通分,原方程化为:5(2x + 5) = 3(4x - 7) ,即10x + 25 = 12x - 21 ,即 2x = 46 ,解得 x = 23 .六.解答题(每题 15 分,共 30 分)19. 如图,将 1、2、3……按规律排成一个沙漏型的数表,那么,12 13 14 15上 3 行(1)下 5 行从左向右数的第 5 个数是多少?(4 分) (2)上 6 行最左边的数是多少?(4 分)(3)2013 排在哪一行的从左向右数的第多少个?(7 分) 【考点】计算、数列与数表6 7 82 3 1 5 4 11 10 9上 2 行 上 1 行 0 行下 1 行下 2 行 【难度】☆☆☆☆【答案】37;42;上 44 行从左向右第 34 个19 18 17 16下3 行【分析】(1)下 n 行从左向右第 (n + 1) 个数(即最右数)为 (n + 1)2 ;故下 5 行从左向右第 6 个数为 36,下 5 行从左向右第 5 个数为 37;(2)上 n 行从左向右第 1 个数(即最左数)为 n (n + 1) ;故上 6 行最左数为 42; (3)上 44 行从左向右第 1 个数为 44 ⨯ 45 = 1980 ,故 2013 为上 44 行从左向右第2013 - 1980 + 1 = 34 个数.20. 思思编了一个计算机程序,在屏幕上显示所有由0、1、2、3 组成的四位编码(数字可以重复使用),每个四位编码都是红、黄、蓝、绿四种颜色中的一种.并且,如果两个编码的每一位数字均不相同,那么这两个编码的颜色也不相同.如果,0000 是红色的、1000 是黄色的、2000 是蓝色的,那么:(1)下列编码中,一定不是红色的是()(2 分)A. 0102B. 0312C. 2222D. 0123(2)编码3111 是什么颜色的?(5 分)(3)编码2013 是什么颜色的?(8 分)【考点】组合,构造与论证【难度】☆☆☆☆【答案】C;绿色;蓝色【分析】(1)2222 与0000 的每一位数字均不相同,故2222 一定不是红色的,选C;(2)3111 与0000、1000、2000 的每一位数字均不相同,故3111 不是红色的,不是黄色的,也不是蓝色的,故3111 是绿色的;(3)0222 与1000、2000、3111 的每一位数字均不相同,故0222 是红色的;1222 与0000、2000、3111 的每一位数字均不相同,故1222 是黄色的;3222 与0000、1000、2000 的每一位数字均不相同,故3222 是绿色的;2013 与0222、1222、3222 的每一位数字均不相同,故2013 是蓝色的.。
学而思杯11届数学试题

2014 年春·超常班&目标班选拔考试·数学·五升六
考试时间:120 分钟 考 生 须 知 考试科目:五升六数学 总 分:120 分 1. 请考生务必认真填写试卷上的考生信息以方便正常通知; 2. 请使用蓝色或黑色签字笔或者钢笔作答; 3. 请将答案写在答题纸上,在试卷上作答无效;考试结束后需上交答题纸。
A
D
B
C
二、 解答题。 (每题 8 分,共 40 分) 21. 一个非零自然数, 如果从左到右顺读和从右到左逆读都是一样的, 则这个数称为“回文数”, 如 8 、66 、 151 、 5335 都是回文数,而 332 不是回文数.那么从小到大的第 2014 个回文数是多少?
22. 如图所示:在三角形 ABC 中, DC 3BD ,DE EA ,若三角形 ABC 的面积是 1 ,那么阴影部分的面 积是多少?
一、 填空题。 (每题 4 分,共 80 分) 1. 计算: 1 19 2 19 3 19 37 19 ________.
17 37 39 37 39 31 17 37 39 31 37 39 ________. 2. 计算: 31 53 91 53 91 51 31 53 91 51 53 91
15. 学校运动会开幕式的旗手们排成一行,首先从左向右 1 至 3 循环报数,最右端的旗手报 2 ;然后从右 向左 1 至 4 循环报数, 最左端的旗手报 3 , 两次都报 1 的旗手有 12 人. 那么, 开幕式一共有旗手________ 人. 16. 正整数 A ,B 满足
1 1 1 ,其中 A 是一个三位数,则 A ________. A B 2014
2011年“学而思杯”初一数学试卷及答案

2011年“学而思杯”中学生理科能力大赛初 一 数 学 试 卷学校______________ 姓名_________ 准考证号________ 成绩_________一、填空题(本题共60分,每小题5分)1. 计算:()3179111315231220304256⎛⎫-+-+-⨯-= ⎪⎝⎭ _________.2. 如图,MN PQ ∥,A B 、分别在MN PQ 、上,70ABP ∠=︒,BC 平分ABP ∠,且20CAM ∠=︒,则C ∠的度数为______________.3. 当2x =时,代数式31ax bx -+的值等于17-,那么当1x =-时,代数式31235ax bx --的值等于__________.4. 已知关于x 的方程3243a x x x ⎡⎤⎛⎫--= ⎪⎢⎥⎝⎭⎣⎦和3151128x a x +--=有相同的解,那么这个解是x =_______.5. 已知ABC △中,90BAC ∠≠︒,AD BC ⊥,BE AC ⊥,且AD BE 、交于点H ,连接CH , 则ACH BAE ∠+∠=_______.6. a b c 、、三个有理数满足0a b c <<<,且1a b c ++=,b c M a +=,a c N b +=,a bP c+=, 则M N P 、、之间的大小关系是________________.7. 如图,ABC △中,D 在AC 上,E 在AB 上,且BD CE 、相交于O ,OB OD =,2OC OE =,若2BOC S =△,则ABC S =△__________.CBAQP N M OEDCBA8. 平面直角坐标系xOy 中有两个点()44A -,,()62B --,,则AOB △的面积为___________.9. 若关于x 的方程()42a x b bx a -+=-+-有无穷多个解,则323a b +的值为__________.10. 如图,ABC △中,90C ∠=︒,ABC ∠和EAC ∠的平分线交于点D ,ABD ∠和BAD ∠的平分线交于点F ,则AFB ∠的度数为_________.11. 若21234m m --+=,则m 的取值范围是_____________12. 已知ABC △中,AB AC =,D 为BC 边上一点,若ACD △和ABD △都是等腰三角形,则C ∠的度数为_______________.二、解答题(本题共40分,每小题10分)13. 如图,M N 、为四边形ABCD 的边AD BC 、的中点,AN BM 、交于P 点,CM DN 、交于Q 点. 若四边形ABCD 的面积为150,四边形MPNQ 的面积为50,求阴影部分的面积之和.FEDC BA14. 数形结合思想是中学数学解题中常用的数学思想,利用这种思想,可以将代数问题转化为几何问题,也可以将几何问题转化为代数问题。
2011学而思数学及答案

绝密★启用前2011 年首届全国学而思综合能力测评(学而思杯)数学试卷(二年级A 卷)时间:13:30~14:50 满分:150 分考生须知:1. 请在答题纸上认真填写考生信息;2. 所有答案请填写在答题纸上,否则成绩无效一.填空题(每题8 分,共40 分)1. (视听题)82 - 47 +18 - 53 =2. (视听题)1+ 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 =3. (视听题)5 个小朋友围成一圈。
球从A开始,按照A→B→C →D→E → A 的顺序传球,那么,传20 次后,球在哪个小朋友手里?4. (视听题)把小动物放在篮子里,篮子上面栓气球,让它们飞起来。
1 只猫1 只狗->5 个气球2 只狗1 只兔子->7 只气球2 只猫->4 个气球2 只兔子->几个气球5. (视听题)下面两个图形,可以分割成4 个大小相等,形状相同的图形。
下面A、B、C、D 四个选项中的哪个图形?二.填空题(每题10 分,共50 分)1. 106÷□,余数是7,□表示的数最小是.2. 一箱桔子,小玲第一次拿3 个,第二次拿6 个,以后每次比前一次多拿3 个,10 次拿完,这箱桔子有个.3. 下面的图中共有12 个小图形,每一个不同的小图形表示1 到9 这九个数字中的一个,每行三个小(A)(B)(C)(D)图形都表示一个三位数,这四行表示四个三位数:521,146,658 和692.那么第三行图形表示的三位数是.4. 图中总共包含有各种大小的正方形共个.5. 下图中,从整体上看第一幅图是五边形,第二幅图是五角星,第三幅图是五边形,第四幅图是五角星,……每幅图下方的数字是该图中基本线段的数量.请问,第40 幅图是图形,这个图中共有条基本线段.……5 15 20 30 35 45 50 ……三.填空题(每题12 分,共60 分)1. 康康在喝一杯饮料时做了实验,他将一根吸管垂直插入杯底,他量了一下被水浸湿部分,正好是8 厘米;他又把吸管调个头,将另一端垂直插入杯底,这时他发现现在吸管干的部分正好是整个浸湿部分的一半.这根吸管长有厘米.2. 小华、小俊都有一些玻璃球.如果小华给小俊4 个,小华的玻璃球的个数就和小俊一样多;原来小华的玻璃球的个数就是小俊的5 倍.小华原来有个玻璃球,小俊原来有个玻璃球.3. 农场里所有大鸭子的重量均相同,所有小鸭子的重量均相同.已知3 只大鸭子和2 只小鸭子共重32 千克,4 只大鸭子和3 只小鸭子共重44 千__________克,请问1 只大鸭子共重千克.4. 下面竖式中,“学理科到学而思”的每一个汉字表示0 到9 这10 个数字中的一个,相同的汉字表示相同的数字,不同的汉字表示不同的数字,四位数“学而思到”的最大值是_____.2 0 1 1学理科到学而思5. 甲、乙、丙、丁四个盒子中依次放:8 个、5 个、3 个、2 个玻璃小球,第一个小朋友找到放球最多的盒子,从中拿出3 个小球放到其它盒子中各1 个球;第二个小朋友找到放球最多的盒子,从中拿出3 个小球放到其它盒子中各1个球……当第83 个小朋友放完后,甲、乙、丙、丁四个盒子中各有玻璃小球个,个,个,个.2011年北京“学而思杯”二年级数学答案二年级答案第一题第1题第2题第3题第4题第5题答案0 80 A 2 D第二题第1题第2题第3题第4题第5题答案9 165 146 27 五角星、300第三题第1题第2题第3题第4题第5题答案24 10、2 8 1792 3、4、6、5。
第11届学而思数学联考XMO一试试题及答案

第十一届学而思数学竞赛联考一试试题时间:80分钟一、填空题(本大题共8小题,每小题8分,共64分)1.方程2log2(x−2)+log2(x+1)=1的所有实数解为x=.2.已知实数k∈R,平面上的向量|−→b|=1,若满足−→a,−→b的夹角为150◦,且(−→a+−→b)⊥(−→a+k−→b)的非零向量−→a恰好有两个,则实数k的取值范围为.3.已知正实数a,b,c依次构成等比数列,并恰好是△ABC的三边长,则a+cb的取值范围是.4.已知F为椭圆C:x225+y216=1的右焦点,P为C上一点,Q(7,8),则|P F|+|P Q|的取值范围是.5.如下图,对于正实数r(1<r<√2),以点A为球心,半径为r的球面与单位立方体ABCD−A1B1C1D1的棱产生6个交点,不难发现这六个点在同一个平面上.则这六个点构成的凸六边形的面积与周长的比值的取值范围是.6.设集合A={x|ax2+3x−2a=0}(其中a为实常数);集合B={x|2x2−5x−42≤0},如果A∩B=A,则参数a的取值范围是.7.多项式(1+x+x2+···+x203)3的展开式在合并同类项以后,x300这一项的系数为8.从4×4的方格表中随机选5个不同的方格,则选出的5个方格构成连通区域的概率是.注:连通区域是指,对于区域内部(不含边界)任意两点,均存在一条完全落在区域内部(不含边界)的折线连接这两个点.二、解答题(本大题共3小题,第9题16分,第10,11题各20分,共56分)9.已知x,y∈R,且满足(4x3−3x)2+(4y3−3y)2=1.求x+y的最大值.10.设复数x,y,z满足:|x|=|y|=|z|=1,并且ty =1x+1z,其中t∈C为给定的复数;求|2xy+2yz+3xzx+y+z|的值.(用含t的代数式表示)11.设p 为给定的正整数,点F 是抛物线Γ:y 2=2px 的焦点,点S 在x 轴上,且满足−→OS =m −−→OF ,其中m 是给定的正奇数;设经过点S 且不与坐标轴垂直的动直线l 与抛物线Γ交于A,B 两点,线段AB 的中垂线与AB 以及x 轴分别交于M,T 两点,记N 为线段MT 的中点,点N 的轨迹记为ω.(1)确定ω的形状以及方程,并证明:在ω上存在无穷多个整点(整点就是横纵坐标都是整数的点).(2)如果正整数p 满足:p 的任意大于1的因数都不是完全平方数,求证:ω上的任意一个整点到原点O 的距离都不是整数.第十一届学而思数学竞赛联考一试试题时间:80分钟一、填空题(本大题共8小题,每小题8分,共64分)1.方程2log 2(x −2)+log 2(x +1)=1的所有实数解为x =.解答(刘涵祚陈乐恒供题)1+√3原方程可以转化为(x −2)2(x +1)=2,化简得(x −1)(x 2−2x −2)=0,得出x =1或x =1±√3,又由于x ≥2,得出原方程的解为x =1+√3.2.已知实数k ∈R ,平面上的向量|−→b |=1,若满足−→a ,−→b 的夹角为150◦,且(−→a +−→b )⊥(−→a +k −→b )的非零向量−→a 恰好有两个,则实数k 的取值范围为.解答(刘涵祚陈乐恒供题)(−∞,0]∪{13}∪{3}由于(−→a +−→b )⊥(−→a +k −→b ),则(−→a +−→b )·(−→a +k −→b )=0;即:|−→a |2−√3(k +1)2|−→a ||−→b |+k |−→b |2=0所以,|−→a |2−√3(k +1)2|−→a |+k =0.不难发现,上述方程在(0,+∞)上恰好有一个实根.当k ≤0时,显然该方程有一正根和一非正根,满足条件;当k >0时,该方程的判别式∆=34(k +1)2−4k =0,化简得:3k 2−10k +3=0解得:k =3或k =13.综上所述,k 的取值范围是(−∞,0]∪{13}∪{3}.3.已知正实数a,b,c 依次构成等比数列,并恰好是△ABC 的三边长,则a +cb的取值范围是.解答(李纪琛供题)[2,√5)不妨设a =1,b =x,c =x 2(x ≥1),则c 为该三角形的最长边,于是1+x >x 2,得出:1≤x <1+√52.而a +c b=1+x 2x=x +1x .设上述关于x 的对勾函数为f (x ),则不难发现在[1,1+√52)上,2≤f (x )<√5.第5页,共12页4.已知F 为椭圆C :x 225+y 216=1的右焦点,P 为C 上一点,Q (7,8),则|P F |+|P Q |的取值范围是.解答(刘涵祚陈乐恒供题)[4√5,10+2√41]不难发现,F (3,0),一方面,|P F |+|P Q |≥|F Q |=4√5,并且在点P 位于线段F Q 与椭圆C 的交点时,可以取等;另一方面,考虑左焦点E (−3,0),则|P F |+|P Q |=|P Q |+10−|P E |≤10+|EQ |=10+2√41在点P 位于QE 的延长线与椭圆C 的交点时可以取等;综上即得答案.5.如下图,对于正实数r (1<r <√2),以点A 为球心,半径为r 的球面与单位立方体ABCD −A 1B 1C 1D 1的棱产生6个交点,不难发现这六个点在同一个平面上.则这六个点构成的凸六边形的面积与周长的比值的取值范围是.解答(李纪琛供题)(√612,√68]如左图,不难发现这个六边形对边互相平行,并且每个内角均为120◦,并且其六条边长依次为x,√2−x,x,√2−x,x,√2−x ,其中x ∈R 且0<x <√2.于是,其周长C =3(x +(√2−x ))=3√2.如右图,我们将这个六边形补成一个正三角形,即可得出其面积S =√34(√2+x )2−3√34x 2=−√32(x 2−√2x −1)=−√32(x −√22)2+3√34于是我们有√32<S ≤3√34.再结合C =3√2,则√612<S C ≤√68第6页,共12页6.设集合A ={x |ax 2+3x −2a =0}(其中a 为实常数);集合B ={x |2x 2−5x −42≤0},如果A ∩B =A ,则参数a 的取值范围是.解答(李纪琛供题)(−∞,−917]∪{0}∪[4241,+∞)不难得出,B =[−72,6],我们需要A ⊆B ;当a =0时,A ={0},满足条件;当a =0时,此时方程ax 2+3x −2a =0为二次方程,其判别式∆=9+8a 2>0并且根据韦达定理,其两个根x 1,x 2满足:x 1x 2=−2aa=−2<0则这两根必然是一正一负,再结合A ⊆B ,我们需要满足以下条件即可:f (0)=0;f (0)f (−72)≤0;f (0)f (6)≤0解得:a ≤−917或者a ≥4241综上所述,参数a 的取值范围是:(−∞,−917]∪{0}∪[4241,+∞).7.多项式(1+x +x 2+···+x 203)3的展开式在合并同类项以后,x 300这一项的系数为解答(李纪琛供题)31192根据乘法分配律,这个问题等价于求方程x +y +z =300满足0≤x,y,z ≤203的整数解的组数;首先,该方程的非负整数解的组数为(3022)=45451;下面来考虑该方程有超出203的解的组数,不难发现x,y,z 中恰有一个数超过203,不妨设为z ,我们设w =z −204,即转化为求方程x +y +w =96的非负整数解的组数,为(982),再结合x,y,z,的对称性,则原方程有超出203的非负整数解的组数为3(982)=14259;那么满足条件的解的组数为:45451−14259=31192.8.从4×4的方格表中随机选5个不同的方格,则选出的5个方格构成连通区域的概率是.注:连通区域是指,对于区域内部(不含边界)任意两点,均存在一条完全落在区域内部(不含边界)的折线连接这两个点.解答(王正供题)611092.我们按照这5格的形状来分类计算个数(旋转后重合也视为不同的形状).(1)若包含一个1×4矩形,此时1×4矩形有横竖两种,剩下的一格有8种不同的位置可以选,因此共16种形状.而每种形状在4×4方格表中的位置有3种,因此共16×3=48种选法.(下面假设不含1×4矩形)(2)若包含两个1×3矩形,则其必为一横一竖且有一个交点,此时共9种形状,每种形状在4×4矩形中的位置有4种,因此共9×4=36种选法.(3)若只包含一个1×3矩形,且剩下两格在该1×3矩形的异侧,此时1×3矩形有横竖两种,剩下两格有6种选法,因此共12种形状.每种形状在4×4矩形中的位置有4种,因此共12×4=48种选法.第7页,共12页(4)若只包含一个1×3矩形,且剩下两格在该1×3矩形的同侧且均和1×3矩形相邻,此时1×3矩形有横竖两种,剩下两格有6种选法,因此共12种形状.每种形状在4×4矩形中的位置有6种,因此共12×6=72种选法.(5)若只包含一个1×3矩形,且剩下两格在该1×3矩形的同侧且有一格不和1×3矩形相邻,此时1×3矩形有横竖两种,剩下两格有4种选法,因此共8种形状.每种形状在4×4矩形中的位置有3种,因此共8×3=24种选法.(6)若不含1×3矩形,则必为如图所示的形状旋转或对称得到,共4种形状.每种形状在4×4矩形中的位置有4种,因此共4×4=16种选法.综上,共244种选法构成连通区域,而总的选法有(165)种,因此构成连通区域的概率为244(165)=61 1092.二、解答题(本大题共3小题,第9题16分,第10,11题各20分,共56分)9.已知x,y ∈R ,且满足(4x 3−3x )2+(4y 3−3y )2=1.求x +y 的最大值.解答((刘涵祚陈乐恒供题))√6+√22令4x 3−3x =cos 3θ,3y −4y 3=sin 3θ,θ∈R .再设x =cos α,不难发现cos 3α=cos 3θ,类似的,设y =sin β,则sin 3β=sin 3θ.注意到用π−β来代替β不会影响y 的取值,则可以不妨设α−β=2tπ3(t∈Z ),此时会产生如下三种情况:情形一:α=β此时x +y =√2sin(α+π4)≤√2.情形二:α=β−2π3此时x +y =sin(α+2π3)+cos α=2cosπ12cos(α+π12)≤√6+√22.情形三:α=β−4π3此时x +y =cos α+sin(α+4π3)=2cos(α+π12)cos 5π12≤√6−√22.综上所述,x +y 的最大值为√6+√22.10.设复数x,y,z满足:|x|=|y|=|z|=1,并且ty =1x+1z,其中t∈C为给定的复数;求|2xy+2yz+3xzx+y+z|的值.(用含t的代数式表示)解答(刘涵祚陈乐恒供题)|2t+3t+1|先证明一个结论:|x+y+z|=|xy+yz+xz|结合|x|=|y|=|z|=1,我们有,|x+y+z|2=(x+y+z)(¯x+¯y+¯z)=3+∑cyc x¯y+∑cyc¯x y|xy+yz+zx|2=(xy+yz+zx)(¯x¯y+¯y¯z+¯z¯x)=3+∑cyc x¯y+∑cyc¯x y所以,|x+y+z|=|xy+yz+xz|.回到原题,则有|2xy+2yz+3xzx+y+z |=|2xy+2yz+3xzxy+yz+zx|=|2+zxxy+yz+zx|=|2+1yz+yx+1|又由于yz +yx=y(1x+1z)=y·ty=t;那么|2xy+2yz+3xzx+y+z|=|2+1yz+yx+1|=|2+1t+1|=|2t+3t+1|.11.设p 为给定的正整数,点F 是抛物线Γ:y 2=2px 的焦点,点S 在x 轴上,且满足−→OS =m −−→OF ,其中m 是给定的正奇数;设经过点S 且不与坐标轴垂直的动直线l 与抛物线Γ交于A,B 两点,线段AB 的中垂线与AB 以及x 轴分别交于M,T 两点,记N 为线段MT 的中点,点N 的轨迹记为ω.(1)确定ω的形状以及方程,并证明:在ω上存在无穷多个整点(整点就是横纵坐标都是整数的点).(2)如果正整数p 满足:p 的任意大于1的因数都不是完全平方数,求证:ω上的任意一个整点到原点O 的距离都不是整数.解答(李纪琛供题)(1)不难得出F (p2,0),则S (mp 2,0),我们设直线l 的方程为:l :x =ky +mp 2(k =0)与抛物线Γ联立得:y 2−2pky −mp 2=0.由韦达定理,y 1+y 2=2pk ,则x 1+x 2=k (y 1+y 2)+mp =2pk 2+mp.点M 为线段AB 的中点,其坐标为(pk 2+mp 2,pk ).再结合AB 的中垂线与l 垂直,则中垂线的方程为:y =−kx +pk 3+(m +2)pk 2得出点T (pk 2+(m +2)p 2,0),则T M 中点N (pk 2+(m +1)p 2,pk 2).不难发现点N 的轨迹方程为:4y 2=p (x −(m +1)p 2)(y =0)其形状为一条去掉顶点的抛物线.并且由于m 为正奇数,则m +12为正整数,记它等于n ,则ω的方程可转化为:ω:4y 2=p (x −np )对于正整数t ,不难得知,点(p (4t 2+n ),pt )是ω上的整点,显然这样的点有无穷多个.(2)由(1)中的分析,我们得知ω的方程为:ω:4y 2=p (x −np ).反证法,若ω上存在整点到原点的距离为正整数;当p =1时,必然存在正整数x,y,a 满足:x 2+y 2=a 24y 2=x −n不难发现a ≥x +1,则x >x −n 4=y 2=a 2−x 2=(a −x )(a +x )≥a +x >x 产生矛盾.当p为大于1的奇数时,必然存在正整数x,y,a满足:x2+y2=a24y2=p(x−np)不难发现p|y2,又由于p没有平方因子,则p|y,进而得出p|x,则p|a.我们记x=px1,y=py1,a=pa1,其中x1,y1,a1∈Z+,那么x21+y21=a21 4y21=x1−n这转化为p=1的情况,产生矛盾.当p为偶数时,由于p无平方因子,设p=2q,其中q为不含平方因子的奇数,此时必然存在正整数x,y,a满足:x2+y2=a22y2=q(x−2nq)容易得出,x为偶数,记x=2x1,则4x21+y2=a2 y2=q(x1−nq)易证q|y,q|x1,则q|a,我们令y=qy2,x1=qx2,a=qa2,其中x2,y2,a2∈Z+,那么(2x2)2+y22=a22 y22=x2−n显然a2≥2x2+1,则2x2>x2−n=y22=a22−(2x2)2=(a2−2x2)(a2+2x2)≥a+2x2>2x2产生矛盾.综上所述,ω上不存在整点到原点的距离为整数.。
2011年学而思杯奥数试题及答案
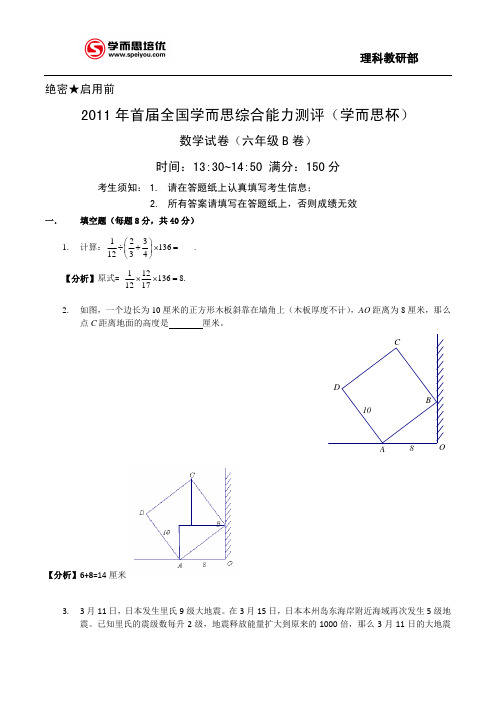
绝密★启用前2011年首届全国学而思综合能力测评(学而思杯)数学试卷(六年级B 卷) 时间:13:30~14:50 满分:150分考生须知: 1. 请在答题纸上认真填写考生信息;2. 所有答案请填写在答题纸上,否则成绩无效一.填空题(每题8分,共40分)1. 计算:123136___.1234⎛⎫÷+⨯= ⎪⎝⎭【分析】原式= 1121368.1217⨯⨯=2. 如图,一个边长为10厘米的正方形木板斜靠在墙角上(木板厚度不计),AO 距离为8厘米,那么点C 距离地面的高度是 厘米。
【分析】6+8=14厘米3. 3月11日,日本发生里氏9级大地震。
在3月15日,日本本州岛东海岸附近海域再次发生5级地震。
已知里氏的震级数每升2级,地震释放能量扩大到原来的1000倍,那么3月11日的大地震BCODA810释放能量是15日东海岸地震的倍.【分析】差了4级,差了1000×1000=1,000,000倍.4. 今天是2011年4月9日,20110409这个九位数是9的倍数,则方框里应填入的数字是。
【分析】容易知道为15. 一列数,我们可以用:1x 、2x …表示,已知:12x =,112n nx x +=-()1,2,3n = ,如213222x =-=,则2011____x =。
【分析】由于213222x =-=;324233x =-=;435244x =-=;找规律,可知:1n n x n +=,所以201120122011x =。
二.填空题(每题10分,共50分)1. 在梯形ABCD 中,对角线AC 与BD 相交于O 点,而三角形ABO 的面积为9,三角形BOC 的面积为27,DO 上有一点E ,而三角形ADE 的面积为1.2,则阴影部分三角形AEC 的面积为【分析】根据题意,由于三角形ADO 的面积为3,则阴影三角形AEO 的面积为1.2,所以有三角形EOC 的面积为3.6,则阴影部分的面积为4.8.2. 有四个人说话,分别如下:A :我们中至少有一个人说的是正确的B :我们中至少有两个人说的是正确的C :我们中至少有一个人说的是错误的D :我们中至少有两个人说的是错误的 请问:说错话的有人.【分析】方法一:若没人说对,则CD 说对,矛盾;若1人说对,则ACD 说对,矛盾;若2人说对,则ABCD 说对,矛盾;若3人说对,则ABC 说对,D 错,成立;若4人说对,则AB 说对,CD 说错,矛盾,因此只能是ABC 说对,D 说错.方法二:因为四个人,所以至少有两人说错或两人说对,因此AB 一定是正确的,剩下的就容易知道D 是错的.3. n 是一个三位数,且组成它的各位数码是从左到右是从大到小的连续数字。
学而思杯五年级数学试卷

L(12)=4,R(12)=3.
根据题意,解下列问题:
(1)判断对错(每空 1 分,共 4 分):
L(4)=3
()
L(20)=5
()
R(4)=2 R(20)=3
() ()
(2)若 n=1000,计算: L(n)= ________.(2 分) R(n)= ________.(3 分)
(3)若 n 201744 ,计算 L R n 的结果,并写出分析过程.(6 分)
链.的.长.度.,R(n) 表示 n 的最.长.因.数.链.的.条.数..
例如:当 n 6 时,有1, 2, 6 和1, 3, 6 共 2 条最长因数链,所以有 L(6)=3,R(6)=2.
当 n 12 时,有 1, 2, 4,12 、 1, 2, 6,12 和 1,3, 6,12 共 3 条最长因数链,所以有
1
1
1
(1) 666 666 666
2
3
6
1 1 1
(2)
1
2
2
3
ห้องสมุดไป่ตู้
3
4
120
18. 解下列方程或者方程组,写出简要的解方程过程与方程的解:
x 1 x 1 (1)
23
2x y 5 (2)
x 2 y 20
六、 解答题(共 2 道小题,每题 15 分,共 30 分) 19. 如图一所示,梯形 ABCD 中 AB∥CD 且 CD=2AB,E 为 BC 边中点,连接 AC 和 BD 相
绝密★启用前
2017 年第十一届北京市小学生综合能力测评(学而思杯)
五年级数学试卷
考试时间:90 分钟 满分:150 分
考生须知:请将填空题答案填涂在答.题.卡.上,解答题答写在答.题.纸.上 第Ⅰ卷(填空题共 104 分)
2011年“学而思杯”初二数学试卷及答案

2011年“学而思杯”中学生理科能力大赛初 二 数 学 试 卷一、填空题(本题共60分,每小题5分)1. 点()1x x --,不可能在第________象限.2. 函数y =x 的取值范围是______________.3. 已知()2x y -+的算术平方根和()21x y +-互为相反数,则3yx-的平方根为___________.4. 如图,在矩形ABCD 中,E 是BC 的中点,30BAE ∠=︒,2AE =, 则矩形ABCD 的面积为___________.5. 已知,函数y kx m =+和y ax b =+的图象交于点P ,则根据图象 可得不等式组0kx m ax b kx m +>⎧⎨+>+⎩的解集为___________.6. 如图,直线1y x =--交两坐标轴于A 、B 两点,平移线段AB 到CD ,使两点都落在反比例函数()0ky x x=>的图象上,DM y ⊥轴于点M ,DN x ⊥轴于点N ,则DM DN -= .EDCBA7. 如果实数a b ,满足2840a a --=,2840b b --=,则b aa b+的值为 .8. 已知x y a 、、都是实数,且1x a =-,()()2211y a a a =---,则31x y a +++的值为________.9. 设实数a b c ,,满足2142a b c +++=,那么ba c-的值为_______.10. 如图,Rt ABC △中,E D F 、、分别在AB BC AC 、、上,且四边形AEDF 是正方形.已知8CD =,12BD =,则阴影部分的面积为_____________.11. 若实数,x y 满足333333331343615456x y x y ⎧+=⎪⎪++⎨⎪+=⎪++⎩,则x y +的值是 _____ .12. 已知正方形ABCD 所在平面内的直线满足:⑴ 正方形四个顶点到这条直线的距离只有两种; ⑵ 两种距离中,较大的是较小的三倍. 那么符合上述条件的直线一共有 条二、解答题(本题共40分,每小题10分)13. 如图,直角梯形ABCD 中,AB CD ∥,90DAB ∠=︒,12CD AB =,2245BC AD =, ⑴ 求证:AD AB =.⑵ AC BD 、交于点E ,AO BD ⊥交BD 于O ,交BC 于F ,求证:CE CF =. ⑶ 作点F 关于点O 的对称点H ,试判断BH 与AE 的关系,并证明你的结论.HFEO DC BA14. 如图1,已知直线12y x m=-+与反比例函数kyx=的图象在第一象限内交于A B、两点(点A在点B的左侧),分别与x y、轴交于点C D、,AE x⊥轴于E.⑴若12OE CE⋅=,求k的值.⑵如图2,作BF y⊥轴于F,求证:EF CD∥.⑶在⑴⑵的条件下,EFAB=P是x轴正半轴上一点,且PAB△是以P为直角顶点的等腰直角三角形,求P点的坐标.15. 如图,D 为ABC △中线AM 的中点,过M 作AB 、AC 边的垂线,垂足分别为P 、Q .过P 、Q分别作DP 、DQ 的垂线交于点N .⑴ 求证:PN QN =; ⑵ 求证:MN BC ⊥.16. 若x y z ,,满足1x y z ++=,2222x y z ++=,3333x y z ++=,求444x y z ++的值.2011年“学而思杯”中学生理科能力大赛初二数学答案一、填空题(每小题5分,答对得5分,答错、不答或答不全均不得分)QP N M DCB A二、解答题(每小题10分,按解题过程分步给分,若只有答案且正确,给2分) 13. ⑴ 过C 点作CM AB ⊥于M ,∵AB CD ∥,90DAB ∠=︒,∴四边形AMCD 是矩形,∴AM CD =………………………………………………………………1分∵12CD AB =,∴AM BM = ∴AC BC =………………………………………………………………2分 ∵在Rt ACD △中,90ADC ∠=︒,∴2222AD CD AC BC +==, ∵2245BC AD =,∴2214CD AD =,即12CD AD =, ∴AD AB =.……………………………………………………………4分 ⑵ 由⑴知:45ADB ABD ∠=∠=︒,又AC BC =,∴CAB CBA ∠=∠,∴CAF CBE ∠=∠,……………………………………………………5分 ∴在ACF △和DCE △中, ACF BCE AC BCCAF CBE ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴()ASA ACF BCE △≌△, ∴CE CF =.……………………………………………………………7分 ⑶ 解法一:延长BH 交AE 于N .由⑵可得:AE BF =,∵F H 、关于点O 对称,∴BH BF =,OBF OBH ∠=∠,∴BH AE =………………………………………………………………8分 ∵CAF CBE ∠=∠,∴OBH CAF ∠=∠,∴90ANH BOH ∠=∠=︒,即BH AE ⊥.……………………………10分 解法二:延长BH 交AE 于N ,∵F H 、关于点O 对称,∴BH BF =,OBF OBH ∠=∠, ∵CAF CBE ∠=∠,∴OBH CAF ∠=∠,∴90ANH BOH ∠=∠=︒,即BH AE ⊥.…………………………9分 ∵AO BD ⊥,∴AO BO =,90AOE BOH ∠=∠=︒, ∴AOE BOH △≌△,∴AE BH =.………………………………………………………10分 14. ⑴ 设OE a =,∴12A a a m ⎛⎫-+ ⎪⎝⎭,,∵点A 在反比例函数图象上,∴12a a m k ⎛⎫-+= ⎪⎝⎭,即212k a am =-+,……2分由一次函数解析式可得()20C m ,,∴2CE m a =-, ∴()22212OE CE a m a a am ⋅=-=-+=,……………………3分∴()211212622k a am =-+=⨯=.……………………………4分 ⑵ 连接AF BE 、,过E F 、分别作FM AB ⊥,EN AB ⊥, ∴FM EN∥.∵AE x ⊥轴,BF y ⊥轴,∴AE BF ⊥N MA BCD OE F H122AEF k S AE OE =⋅=△,122BEF k S BF OF =⋅=△, ∴AEF BEF S S =△△, …………………………………………5分 ∴FM EN =,∴四边形EFMN 是矩形,∴EF CD ∥.………………………………………………7分 ⑶由⑵可知,EF AD BC ==,∴CD =.由直线解析式可得OD m =,2OC m =, ∴4OD =,又EF CD ∥,∴2OE OF =,∴1OF =,2OE =,………………………………………8分 ∴3DF =,∴3AE DF ==,∵AB =AP =∴1EP =,…………………………………………………9分∴()30P ,.………………………………………………10分 15. ⑴ 连接DN ,由已知得APM △和AQM △都是直角三角形,AM 是公共斜边,∵D 是AM 的中点,∴12PD AM QD ==,……………………………………2分 ∵PN PD ⊥,QN QD ⊥,∴DPN DQN ∠=∠,∴Rt Rt DPN DQN △≌△()HL ,∴NP NQ =.……………………………………………………………………4分 ⑵ 取BM 、MC 的中点S 、T ,连结SP 、SN 、TQ 、TN . 1122SP BM MC TQ ===,…………………………………………………………5分9090SPN BPS NPM B DPA ∠=︒-∠-∠=︒-∠-∠ 9090B BAM AMC =︒-∠-∠=︒-∠9090DMQ QMT DQM MQT =︒-∠-∠=︒-∠-∠TQN =∠.………………………………………………7分∴SPN TQN △≌△()SAS .∴SN TN =,……………………………………………8分 ∵SM TM =,∴MN BC ⊥.…………………………10分16. ∵()2222222x y z x y z xy yz zx ++=+++++, ∴()111222xy yz zx ++=-=-,…………………………………2分 ∵()()3332223x y z xyz x y z x y z xy yz zx ++-=++++---, ∴16xyz =.………………………………………………………4分 ()()24442222222222x y z x y z x y y z z x ++=++-++,…………6分又()()22222222111222612x y y z z x xy yz zx xyz x y z ⎛⎫++=++-++=--⨯=- ⎪⎝⎭,……………8分∴444212522126x y z ⎛⎫++=-⨯-= ⎪⎝⎭.…………………………………………………………10分NQ。
