1.1.探究与发现:解三角形的进一步讨论
1.1.3解三角形的进一步讨论

1.1.3解三⾓形的进⼀步讨论1.1.3 解三⾓形的进⼀步讨论【学习⽬标】1.掌握已知三⾓形的两边及其中⼀边的对⾓时对解个数的讨论; 2.三⾓形各种形状的判断⽅法;【学习重难点】1.已知三⾓形的两边及其中⼀边的对⾓时对解个数的讨论;2.正弦、余弦定理的综合运⽤;⼀、情景问题:我们在解三⾓形时可以会出现⼀些我们预想不到的结果,现在请⼤家思考下⾯问题:在ABC ?中,已知 133,25,22===A cm b cm a ,解三⾓形。
⼆、探索研究:问题:在ABC ?中,已知A b a ,,,讨论三⾓形解的情况,并画图表⽰。
讨论1:当A 为钝⾓时三⾓形解的情况:讨论2:当A 为锐⾓时三⾓形解的情况:结论:;三、解题研究:例1:在ABC ?中,已知 45,100,80===A b a ,讨论三⾓形解的情况;例2:在ABC ?中,已知 45,2,===B b x a ,如果利⽤正弦定理解三⾓形时有两解,求实数x 的取值范围。
例3:在ABC ?中,已知3,5,7===c b a ,判断三⾓形的类型。
对于上述问题你有什么结论吗?变式训练:1.在?ABC 中,已知sin :sin :sin ::A B C =654,试判断△ABC 的形状;2.在△ABC 中,已知⾓A ,B ,C 的对边分别为a ,b ,c ,且bcosB +ccosC =acosA ,试判断△ABC 的形状。
例4:设2,1,++x x x ,是钝⾓三⾓形的三边长,求实数x 的取值范围。
变式训练:已知锐⾓三⾓形的三边长为:2,3,x ,求实数x 的取值范围。
四、尝试⼩结:五、课后作业:P11 B 组T2 六、课后练习:1.在?ABC 中,c o s c o s s i n s i n A B A B >,则ABC 是: A.锐⾓三⾓形 B.直⾓三⾓形 C.钝⾓三⾓形 D.正三⾓形2.在?ABC 中,A 、B 均为锐⾓,且cos sin A B >,则?ABC 是_________3.在△ABC 中,∠A ,∠B 的对边分别为a,b ,且∠A=60°,4a b =,那么满⾜条件的△ABC :A.有⼀个B.有两个C.不存在D.不能确定个数 3.设A 是△ABC 中的最⼩⾓,且1cos 1a A a -=+,则实数a 的取值范围是:A.a ≥3B.a >-1C.-1<a ≤3D.a >04.关于x 的⽅程22cos cos cos 02C x x A B -??-=有⼀个根为1,则△ABC ⼀定是: A.等腰三⾓形 B.直⾓三⾓形 C.锐⾓三⾓形 D.钝⾓三⾓形5.钝⾓三⾓形的三边长为2,1,++a a a ,其最⼤⾓不超过0120,则a 的取值范围是:A .30<323<≤a C .32≤51<≤a6.在△ABC 中,已知cos 2B+cos 2C=1+cos 2A,sinA=2sinBcosC, cosC=sinB.求证:△ABC 是以A 为直⾓顶点的等腰直⾓三⾓形.7.根据下⾯条件判断,已知形状在ABC ?中,有)sin()()sin()(2222B A b a B A b a +-=-+。
1.1.3 解三角形的进一步讨论

1.1.3 解三角形的进一步讨论三维目标一、知识与技能1.掌握已知三角形的两边及其中一边的对角解三角形时,有两解或一解或无解等情形;2.三角形各种形状的判定方法;3.三角形面积定理的应用.二、过程与方法通过引导学生分析,解答三个典型例子,使学生学会综合运用正、余弦定理,三角函数公式及三角形有关性质求解三角形问题.三、情感态度与价值观通过正、余弦定理,在解三角形问题时沟通了三角形的有关性质和三角函数的关系,反映了事物之间的必然联系及一定条件下相互转化的可能,从而从本质上反映了事物之间的内在联系.教学过程一、情境导入1、回顾一下正、余弦定理的内容正弦定理:;余弦定理:2、正弦定理、余弦定理实质上反映了三角形内的边角关系,运用定理可以进行边与角之间的转换.这一节,我们将通过例题分析来学习正、余弦定理的边角转换功能在判断三角形形状和证明三角恒等式时的应用.二、新课探究1、思考在△ABC中,已知A=22cm,B=25cm,A=133°,解三角形.阅读课本第9页解答过程并思考.从此题的分析我们发现,在已知三角形的两边及其中一边的对角解三角形时,在某些条件下会出现无解的情形.下面进一步来研究这种情形下解三角形的问题.2、探究分析探究一在△ABC中,已知A,B,a,讨论三角形解的情况.师:分析:先由可进一步求出;则,从而.一般地,已知两边和其中一边的对角解三角形,有两解、一解、无解三种情况.1.当A为钝角或直角时,必须a>b才能有且只有一解;否则无解.2.当A为锐角时,如果a≥b,那么只有一解;如果a<b,那么可以分下面三种情况来讨论:(1)若a>bsinA,则有两解;(2)若a=bsinA,则只有一解;(3)若a<bsinA,则无解.注意:在已知三角形的两边及其中一边的对角解三角形时,只有当A为锐角且bsinA<a<b时,有两解;其他情况时则只有一解或无解.(1)A为直角或钝角(2)A为锐角探究二在△ABC中,已知a=7,b=5,c=3,判断△ABC的类型.分析:由余弦定理可知a2=b2+c2A是直角△ABC是直角三角形,a2>b2+c2A是钝角△ABC是钝角三角形,a2<b2+c A是锐角△ABC是锐角三角形。
人教版高中必修5探究与发现解三角形的进一步讨论课程设计

人教版高中必修5探究与发现解三角形的进一步讨论课程设计一、课程目标•理解余弦定理、正弦定理的原理和应用;•掌握利用余弦定理、正弦定理求解三角形的面积和角度的方法;•能够综合运用知识解决实际问题;•培养学生自主思考、团队协作、解决问题的能力。
二、教学内容1.余弦定理和正弦定理的原理和应用;2.利用余弦定理、正弦定理求解三角形的面积和角度的方法;3.实际问题的应用。
三、教学方法1.活动导入:通过探究一道三角形问题的方法引出余弦定理、正弦定理;2.课堂授课:讲解余弦定理、正弦定理的原理和应用,并引导学生掌握求解三角形面积和角度的方法;3.小组讨论:分组讨论三角形实际问题,并给出解决方案;4.展示讨论结果:每个小组选出代表展示讨论结果,其他小组给予点评;5.教师点评:对学生讨论结果进行点评并给予指导;6.作业布置:巩固本课内容,并涉及到课前所学知识。
四、教学重点1.掌握余弦定理、正弦定理的应用;2.利用余弦定理、正弦定理求解三角形的面积和角度。
五、教学难点1.实际问题的应用;2.解决问题的方法。
六、课时安排本课程计划为4学时,具体安排如下:时间教学内容第1学时活动导入、授课第2学时小组讨论、展示第3学时教师点评、作业布置第4学时作业讲解、扩展课程七、教学资源1.电子白板;2.课件PPT;3.教学实例。
八、预期效果1.学生理解余弦定理、正弦定理的原理和应用;2.学生掌握利用余弦定理、正弦定理求解三角形的面积和角度的方法;3.学生能够综合运用知识解决实际问题;4.学生具备自主思考、团队协作、解决问题的能力。
备课教案资料(1.1.3 解三角形的进一步讨论)

备课资料一、正、余弦定理的边角互换功能对于正、余弦定理,同学们已经开始熟悉,在解三角形的问题中常会用到它,其实,在涉及到三角形的其他问题中,也常会用到它们.两个定理的特殊功能是边角互换,即利用它们可以把边的关系转化为角的关系,也可以把角的关系转化为边的关系,从而使许多问题得以解决. 【例1】已知A 、B 为△ABC 的边,A 、B 分别是A 、B 的对角,且23sin sin =B A 求b ba +的值. 解:∵B bA a sin sin =, ∴b a B A =sin sin . 又32sin sin =B A (这是角的关系), ∴23=b a (这是边的关系).于是,由合比定理得 25223=+=+b b a . 【例2】已知△ABC 中,三边A 、B 、C 所对的角分别是A 、B 、C ,且a 、b 、c 成等差数列. 求证:sin A +sin C =2sin B .证明:∵a 、b 、c 成等差数列, ∴a +c =2B (这是边的关系).①又CcB b A a sin sin sin ==, ∴B C b a sin sin =,②BCb c sin sin =.③ 将②③代入①,得b BCb B A b 2sin sin sin sin =+=2B .整理得sin A +sin C =2sin B (这是角的关系).二、正、余弦定理的巧用某些三角习题的化简和求解,若能巧用正、余弦定理,则可避免许多繁杂的运算,从而使问题较轻松地获得解决,现举例说明如下: 【例3】求sin 220°+co s 280°+3sin20°co s80°的值.解:原式=sin 220°+sin 210°-2sin20°sin10°co s150°, ∵20°+10°+150°=180°, ∴20°、10°、150°可看作一个三角形的三个内角.设这三个内角所对的边依次是A 、B 、C ,由余弦定理得a 2+b 2-2abco s150°=C 2.(*)而由正弦定理知A =2Rsin20°,B =2Rsin10°,C =2Rsin150°, 代入(*)式得sin 220°+sin 210°-2sin20°sin10°co s150°=sin 2150°=41. ∴原式=41.三、构造正三角通常,我们使用标尺作正三角形.以标尺作正三角形,只需相异两点A 、B ,再配合工具即可.分别以A 、B 点为圆心,AB 长为半径作圆,两圆相交于C 点,△ABC 就是正三角形了.因为,圆A 中,AB =AC (半径);而且圆B 中,BA =BC (半径),所以AB =BA =AC .(参见上图)如果没了圆规,我们要如何作出正三角形呢?再者连标尺也没了,那么万能的双手又要如何作出正三角形呢?这时我们可以考虑折纸来协助完成.取适当大小的矩形纸张,先对折,取得一边的中垂线;再以A 点为基点,将此边向内翻折,并使得顶点落在中垂线上B 点;最后再将B 点和A 、C 点连成三角形(参见右图),就是正三角形了.因为,AC =AB ,又B 点在中垂线上,所以,BA =BC ,因此,AB =BC =CA .1.1.3 解三角形的进一步讨论从容说课本节课中,应先通过分析典型例题,帮助学生理解并掌握正弦定理和余弦定理;应指出正弦定理和余弦定理是相通的,凡是能用正弦定理解的三角形,用余弦定理也可以解,反之亦然.但解题的时候,应有最佳选择.教学过程中,我们应指导学生对利用正弦定理和余弦解斜三角形时可用的定理和公式适用类型备注余弦定理a 2=b 2+c 2-2bcco s A b 2=a 2+c 2-2acco s B c 2=b 2+a 2-2baco s C (1)已知三边(2)已知两边及其夹角类型(1)(2)有解时只有一解正弦定理R CcB b A a 2sin sin sin === (3)已知两角和一边 (4)已知两边及其中一边的对角类型(3)在有解时只有一解,类型(4)可有两解、一解或无解 三角形面积公式==A bc S sin 21=B ac sin 21C ab sin 21(5)已知两边及其夹角主要途径有两条:(1)化边为角,然后通过三角变换找出角与角之间的关系,进而解决问题;(2)化角为边,将三角问题转化为代数问题加以解决.一般地,当已知三角形三边或三边数量关系时,常用余弦定理;若既有角的条件,又有边的条件,通常利用正弦定理或余弦定理,将边化为角的关系,利用三角函数公式求解较为简便.总之,关键在于灵活运用定理及公式.教学重点 1.在已知三角形的两边及其中一边的对角解三角形时,有两解或一解或无解等情形;2.三角形各种形状的判定方法;3.三角形面积定理的应用.教学难点1.利用正、余弦定理进行边角互换时的转化方向; 2.三角恒等式证明中结论与条件之间的内在联系的寻求; 3.正、余弦定理与三角形的有关性质的综合运用. 教具准备 投影仪、幻灯片第一张:课题引入图片(记作1.1.3A) 正弦定理:R CcB b A a 2sin sin sin ===; 余弦定理:a 2=b 2+c 2-2bcco s A ,b 2=c 2+a 2-2caco s B ,c 2=a 2+b 2-2abco sC ,bc a c b A 2cos 222-+=,ca b a c B 2cos 222-+= ,abc b a C 2cos 222-+=.第二张:例3、例4(记作1.1.3B )[例3]已知△ABC , BD 为角B 的平分线,求证: AB ∶BC =AD ∶DC . [例4]在△ABC 中,求证:a 2sin2B +b 2sin2A =2ab sin C . 第三张:例5(记作1.1.3C)[例5]在△ABC 中,bco s A =aco s B ,试判断三角形的形状.三维目标一、知识与技能1.掌握在已知三角形的两边及其中一边的对角解三角形时,有两解或一解或无解等情形;2.三角形各种形状的判定方法;3.三角形面积定理的应用. 二、过程与方法通过引导学生分析,解答三个典型例子,使学生学会综合运用正、余弦定理,三角函数公式及三角形有关性质求解三角形问题. 三、情感态度与价值观通过正、余弦定理,在解三角形问题时沟通了三角形的有关性质和三角函数的关系,反映了事物之间的必然联系及一定条件下相互转化的可能,从而从本质上反映了事物之间的内在联系.教学过程导入新课师 前面两节课,我们一起学习了正弦定理、余弦定理的内容,并且接触了利用正、余弦定理解三角形的有关题型.下面,我们先来回顾一下正、余弦定理的内容 (给出幻灯片1.1.3A ).从幻灯片大体可以看出,正弦定理、余弦定理实质上反映了三角形内的边角关系,运用定理可以进行边与角之间的转换,这一节,我们将通过例题分析来学习正、余弦定理的边角转换功能在判断三角形形状和证明三角恒等式时的应用. 推进新课思考:在△ABC 中,已知A =22c m ,B =25c m,A =133°,解三角形.(由学生阅读课本第9页解答过程)从此题的分析我们发现,在已知三角形的两边及其中一边的对角解三角形时,在某些条件下会出现无解的情形.下面进一步来研究这种情形下解三角形的问题. 【例1】在△ABC 中,已知A ,B ,A ,讨论三角形解的情况. 师 分析:先由a A b B sin sin =可进一步求出B ;则C =180°-(A +B ),从而ACa c sin sin =. 一般地,已知两边和其中一边的对角解三角形,有两解、一解、无解三种情况.1.当A 为钝角或直角时,必须a >b 才能有且只有一解;否则无解.2.当A 为锐角时,如果a ≥b ,那么只有一解;如果a <b ,那么可以分下面三种情况来讨论: (1)若a >b sin A ,则有两解; (2)若a =b sin A ,则只有一解; (3)若a <b sin A ,则无解.(以上解答过程详见课本第9到第10页)师 注意在已知三角形的两边及其中一边的对角解三角形时,只有当A 为锐角且b sin A <a <b 时,有两解;其他情况时则只有一解或无解. (1)A 为直角或钝角(2)A 为锐角【例2】在△ABC 中,已知a =7,b =5,c =3,判断△ABC 的类型. 分析:由余弦定理可知a 2=b 2+c 2⇔A 是直角⇔△ABC 是直角三角形, a 2>b 2+c 2⇔A 是钝角⇔△ABC 是钝角三角形, a 2<b 2+c ⇔A 是锐角/△ABC 是锐角三角形。
人教版高中数学必修五第一章《解三角形的进一步讨论-解三角形中的一类倍角问题》教学设计

解三角形的进一步讨论——解三角形中的一类倍角问题1.教学内容解析“正弦定理和余弦定理”是高中数学必修5中“解三角形”的一节内容.本节教学内容与前后知识联系紧密,涉及多种数学思想方法,主要工具是正弦定理、余弦定理、三角形面积公式和三角形内角和定理,通过对任意三角形边角关系的探究,发现并掌握三角形中边角之间的数量关系.有些问题的求解还会用到三角函数中的和、差角公式和二倍角公式.根据问题的不同类型和不同形式,广泛联想、合理选择、灵活运用公式是求解问题的关键.2.教学目标设置教学目标:(1)掌握并熟练运用正弦、余弦定理转化三角形中的边角关系;(2)理解三角形中有关边角关系的几何意义,如cos a B 、sin b A 、22a b bc 、2A B ,并对以此为背景的试题进行深入的探究,理解其数学本质;(3)通过对问题背景与变式探究学习,激发学生参与数学活动的兴趣与热情.教学重难点:(1)能够熟练运用正弦、余弦定理转化三角形中的边角关系;(2)理解三角形中有关边角关系的几何意义,如cos a B 、sin b A 、22a b bc 、2A B ,探究其数学本质.3.学生学情分析学生通过必修5的学习,已了解正弦和余弦定理的内容,但如何合理选择、灵活运用定理解决解三角形综合问题,怎样合理选择定理进行边角关系转化进而解决三角形综合问题,还需通过复习指导有待进一步提高.4.教学策略分析(1)问题引入,激发求知欲望(2)广泛联想,挖掘数形背景(3)分析例题,落实核心知识(4)重视应用,培养实践能力设计思路:(1)重视教学各环节的合理安排;(2)重视多种教学方法有效整合,以小组讨论、讲练结合、分析引导、变式训练、扩展训练等多种方法贯穿整个教学过程;(3)重视提出问题、解决问题策略的指导.在教学中引导学生发现问题、提出问题,并指导学生掌握观察、分析、归纳、类比、抽象、概括、猜想等解决问题的科学思维方法.5.教学过程过程问题驱动下的教学设计(1)问题引入【引题】人教A 版必修五第25页B 组练习3:研究一下,是否存在一个三角形具有以下性质:(1)三边是连续的三个自然数;(2)最大角是最小角的2倍.【设计意图】通过引题的解决,回顾正弦定理和余弦定理的内容,初步体问题引入揭示本质变式探究探究不止知识重建会通过三角恒等变换和正、余弦定理实现三角形边角关系转化,从而求解三角形的作用.【提问】一般地,在ABC中,由等式2B A可以得到什么结论?(2)问题探究揭示本质【探究一】一般地,在ABC中,由等式2B A可以得到什么结论?它具有什么代数特征呢?【设计意图】通过发散性探究,学生能够体会正、余弦定理在转化三角形边角关系中的作用,以及在解三角形的过程中三角恒等变换的作用.在问题的解决过程中,引导学生发现等式2B A的代数特征.【提问】反之是否成立呢?【探究二】一般地,在ABC中,若22b a ac,则2B A.【设计意图】通过探究,进一步体会正、余弦定理在转化三角形边角关系中的作用.同时,通过两次探究,我们得到了一个重要的推论:一般地,在ABC中,222a b bc A B.并能利用正弦定理和余弦定理证明该推论,感受正弦定理和余弦定理的内在联系.【提问】在ABC中,222a b bc A B,这个代数恒等式具有怎么样的几何意义呢?【设计意图】引导学生发现其几何背景,从几何角度看清问题本质,感受在三角形中的数与形的统一性,培养数学抽象与数形结合的能力,了解此类问题的命题策略,(3)应用探究尝试解决【练习】在ABC中,,,a b c分别为角,,A B C所对的边,已知B C A,且2,4,8B A c a b,求,a b的值.【设计意图】通过微调题目条件,增加了思维容量,培养学生综合运用正弦定理和余弦定理的能力,并在问题的解决过程中,引导学生体会等式2B A的代数特征.【高考链接】(2019年高考北京卷(理))在ABC中,,,a b c分别为角,,A B C 所对的边,若3,26,2a b B A.(I)求cos A的值; (II)求c的值.【高考链接】(2019年浙江高考)在ABC中,内角,,A B C所对的边分别为,,a b c.已知2cosb c a B.(I)证明:2A B;(II)若ABC的面积2=4aS,求角A的大小.【设计意图】进一步熟悉正弦、余弦定理,注重推论的应用性,引导学生落实核心知识,培养实践能力.(4)直通自招探究不止(2019上海交大自招)是否存在三边长为连续自然数的三角形,使得(1)最大角是最小角的两倍;(2)最大角是最小角的三倍.若存在,求出该三角形;若不存在,请说明理由.【探究三】一般地,在ABC中,由等式3B A可以得到什么结论?它具有什么代数特征和几何意义呢?【设计意图】体会推论应用的广泛性,培养学生数学抽象,逻辑推理,数学运算等能力,树立用数学的眼光观察现实世界,用数学的思维思考现实世界的数学核心素养.(5)自主命题总结反思【学生命题】以三角形中有关边角关系的几何意义为背景,如cosa B、sinb A、22a b bc、2A B(或者其它自选),命制一道解答题.【学生归纳】1.正弦定理、余弦定理体现了三角形中边与角存在的一种内在联系,其主要作用是将已知的边、角互化或统一;2.理解三角形中有关边角关系的几何意义,如cosa B、sinb A、22a b bc、2A B,掌握此类问题的“源”与“流”;【设计意图】学生通过归纳,回顾自己在本节课所学得知识要点与思想方法,并与同学,老师交流,完善知识结构与思维方式;通过自主命题,旨在引导学生与命题者对话,加深对问题本质的理解,拓展探究学习的维度.(6)作业布置1.书本P25 B组练习3;2.小组合作完成探究三;3.以三角形中有关边角关系的几何意义为背景命制一道解答题.。
高中数学《探究与发现 解三角形的进一步讨论》省级名师优质课教案比赛获奖教案示范课教案公开课教案

高中数学人教A版必修5第一章《探究与发现解三角形的进一步讨论》省级名师优质课教案比赛获奖教案示范课教案
公开课教案
【省级名师教案】
1教学目标
1.正弦定理的概念;
2.正弦定理的证明及其基本应用.
2重点难点
1.正弦定理的探索和证明;
2.已知两边和其中一边的对角解三角形时判断解的个数.
3教学过程
3.1第一学时
教学活动
1【讲授】正弦定理
导入新课
师如右图,固定△ABC的边CB及∠B,使边AC绕着顶点C转动.
师思考:∠C的大小与它的对边AB的长度之间有怎样的数量关系?
生显然,边AB的长度随着其对角∠C的大小的增大而增大.
师能否用一个等式把这种关系精确地表示出来?
师在初中,我们已学过如何解直角三角形,下面就首先来探讨直角三角形中,角与边的等式关系.如右图,在Rt△ABC中,设BC =A,AC =B,AB =C,根据锐角三角函数中正弦函数的定义,有=sinA, =sinB,又sinC=1= ,则 .从而在直角三角形ABC中,
.
推进新课
[合作探究]。
人教版高中必修5探究与发现解三角形的进一步讨论课程设计 (2)

课程设计:人教版高中必修5探究与发现解三角形的进一步讨论一、教学目标1. 知识目标•了解解三角形的概念和方法•掌握利用正弦定理、余弦定理、正切定理及海伦公式等解决三角形相关问题的方法•根据实际问题,运用相关知识解决三角形的相关问题2. 能力目标•培养学生观察、归纳和总结的能力•培养学生沟通、合作和创新思维的能力•提高学生运用数学知识解决实际问题的能力3. 情感目标•激发学生学习数学的兴趣和热情•培养学生积极参与课堂讨论,自主学习的意识•培养学生正义、和谐、团结的价值观二、教学内容1. 概念介绍•解三角形的概念及相关术语说明2. 解三角形的方法•正弦定理的应用•余弦定理的应用•正切定理的应用•海伦公式的应用3. 相关问题探究•从实际问题出发,引导学生自主观察、归纳、总结•运用所学方法解决相关问题三、教学过程1. 课前预习•学生预习课本内容及课件•学生思考和准备提出解三角形有哪些方法2. 自主学习•小组合作,每个小组选择一个问题,研究并解决问题•学生自主寻找相关材料,进行学习和总结3. 讲授并讨论•介绍解三角形的概念及相关术语•分别讲解正弦定理、余弦定理、正切定理和海伦公式的应用•在每个方法讲解后,由学生提出实际问题并进行讨论解决4. 实践演练•学生分组,在白板上模拟相关问题,运用所学方法解决•学生自主寻找相关实际问题,进行解决练习5. 总结归纳•教师与学生共同总结本次课程所学内容,提出不足和进一步改进措施•学生进行总结自我反思,思考如何将所学知识应用到实际生活中四、作业•学生回去后继续以小组形式进行学习和讨论•选取1-2个相关问题,并利用所学方法进行解决,准备进行讲解展示•学生通过个人笔记记录所学重点及解决问题的过程五、教学评估•通过学生的课前预习讨论,了解学生的掌握程度及问题•在课堂讲授、讨论、实践过程中及时反馈和引导,检查学生的掌握情况•通过学生的课后作业和自我反思,了解学生的学习效果六、教学反思•通过本次课程的设计和实施,掌握了针对解三角形相关内容的教学思路和方法•鉴于学生学习数学实践应用的能力较为薄弱,课程设计应注重实践环节的拓展•下一步的工作将持续探索和实践,倡导学生以积极探究的心态参与数学学习,提升学生数学思维的发展。
1.3解三角形的进一步讨论

1.1.3 解三角形的进一步讨论三维目标一、知识与技能1.掌握在已知三角形的两边及其中一边的对角解三角形时,有两解或一解或无解等情形;2.三角形各种形状的判定方法;3.三角形面积定理的应用.二、过程与方法通过引导学生分析,解答三个典型例子,使学生学会综合运用正、余弦定理,三角函数公式及三角形有关性质求解三角形问题.三、情感态度与价值观通过正、余弦定理,在解三角形问题时沟通了三角形的有关性质和三角函数的关系,反映了事物之间的必然联系及一定条件下相互转化的可能,从而从本质上反映了事物之间的内在联系.重难点教学重点1.在已知三角形的两边及其中一边的对角解三角形时,有两解或一解或无解等情形;2.三角形各种形状的判定方法;3.三角形面积定理的应用. 教学难点1.利用正、余弦定理进行边角互换时的转化方向2.三角恒等式证明中结论与条件之间的内在联系的寻求;3.正、余弦定理与三角形的有关性质的综合运用.教具准备 投影仪、幻灯片 第一张:课题引入图片(记作1.1.正弦定理:R CcB b A a 2sin sin sin ===;余弦定理:a 2=b 2+c 2-2bcco s A ,b 2=c 2+a 2-2caco s B ,c 2=a 2+b 2-2abco s C ,bc a c b A 2cos 222-+=,ca b a c B 2cos 222-+= ,abc b a C 2cos 222-+=第二张:例3、例4(记作1.1.B[例3]已知△ABC , BD 为角B 的平分线,求证: AB ∶BC =AD ∶DC[例4]在△ABC 中,求证:a 2sin2B +b 2sin2A =2ab sin C第三张:例5(记作1.1.[例5]在△ABC 中,bco s A =aco s B ,试判断三角形的形状教学过程导入新课师 前面两节课,我们一起学习了正弦定理、余弦定理的内容,并且接触了利用正、余弦定理解三角形的有关题型.下面,我们先来回顾一下正、余弦定理的内容 (给出幻灯片 1.1.3A ).从幻灯片大体可以看出,正弦定理、余弦定理实质上反映了三角形内的边角关系,运用定理可以进行边与角之间的转换,这一节,我们将通过例题分析来学习正、余弦定理的边角转换功能在判断三角形形状和证明三角恒等式时的应用推进新课思考:在△ABC 中,已知A =22c m ,B =25c m,A =133°,解三角形.(由学生阅读课本第9页解答过程)从此题的分析我们发现,在已知三角形的两边及其中一边的对角解三角形时,在某些条件下会出现无解的情形.下面进一步来研究这种情形下解三角形的问题. 【例1】在△ABC 中,已知A ,B ,A ,讨论三角形解的情况师 分析:先由a A b B sin sin =可进一步求出B ;则C =180°-(A +B ),从而ACa c sin sin =一般地,已知两边和其中一边的对角解三角形,有两解、一解、无解三种情况.1.当A 为钝角或直角时,必须a >b 才能有且只有一解;否则无解.2.当A 为锐角时,如果a ≥b ,那么只有一解;如果a <b ,那么可以分下面三种情况来讨论:(1)若a>b sin A,则有两解;(2)若a=b sin A,则只有一解;(3)若a<b sin A,则无解.(以上解答过程详见课本第9到第10页)师注意在已知三角形的两边及其中一边的对角解三角形时,只有当A为锐角且b sin A<a<b 时,有两解;其他情况时则只有一解或无解.(1)A为直角或钝角(2)A为锐角【例2】在△ABC中,已知a =7,b=5,c =3,判断△ABC的类型.分析:由余弦定理可知a2=b2+c2⇔A是直角⇔△ABC是直角三角形,a2>b2+c2⇔A是钝角⇔△ABC是钝角三角形,a2<b2+c⇔A是锐角/△ABC是锐角三角形。
人教版高一数学教案-解三角形的进一步讨论
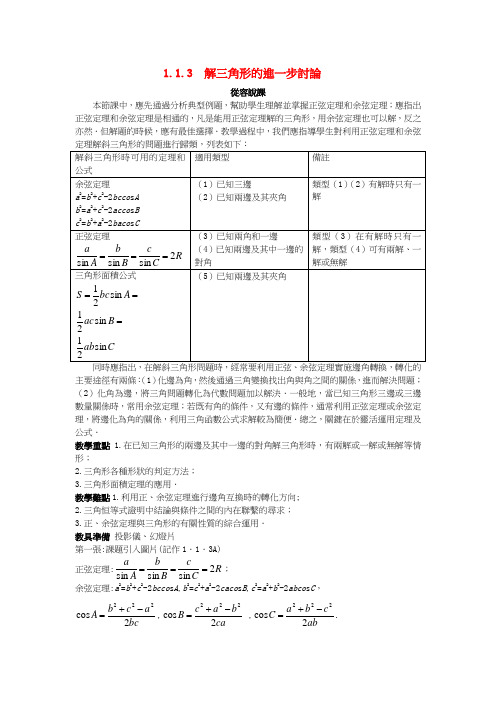
1.1.3 解三角形的進一步討論從容說課本節課中,應先通過分析典型例題,幫助學生理解並掌握正弦定理和余弦定理;應指出正弦定理和余弦定理是相通的,凡是能用正弦定理解的三角形,用余弦定理也可以解,反之亦然.但解題的時候,應有最佳選擇.教學過程中,我們應指導學生對利用正弦定理和余弦定理解斜三角形的問題進行歸類,列表如下: 解斜三角形時可用的定理和公式 適用類型 備註 余弦定理 a 2=b 2+c 2-2bcco s Ab 2=a 2+c 2-2acco s Bc 2=b 2+a 2-2baco s C(1)已知三邊 (2)已知兩邊及其夾角 類型(1)(2)有解時只有一解 正弦定理 R Cc B b A a 2sin sin sin === (3)已知兩角和一邊(4)已知兩邊及其中一邊的對角 類型(3)在有解時只有一解,類型(4)可有兩解、一解或無解 三角形面積公式 ==A bc S sin 21 =B ac sin 21 C ab sin 21 (5)已知兩邊及其夾角同時應指出,在解斜三角形問題時,經常要利用正弦、余弦定理實施邊角轉換,轉化的主要途徑有兩條:(1)化邊為角,然後通過三角變換找出角與角之間的關係,進而解決問題;(2)化角為邊,將三角問題轉化為代數問題加以解決.一般地,當已知三角形三邊或三邊數量關係時,常用余弦定理;若既有角的條件,又有邊的條件,通常利用正弦定理或余弦定理,將邊化為角的關係,利用三角函數公式求解較為簡便.總之,關鍵在於靈活運用定理及公式.教學重點1.在已知三角形的兩邊及其中一邊的對角解三角形時,有兩解或一解或無解等情形;2.三角形各種形狀的判定方法;3.三角形面積定理的應用.教學難點1.利用正、余弦定理進行邊角互換時的轉化方向;2.三角恒等式證明中結論與條件之間的內在聯繫的尋求;3.正、余弦定理與三角形的有關性質的綜合運用.教具準備 投影儀、幻燈片第一張:課題引入圖片(記作1.1.3A)正弦定理:R Cc B b A a 2sin sin sin ===; 余弦定理:a 2=b 2+c 2-2bcco s A ,b 2=c 2+a 2-2caco s B ,c 2=a 2+b 2-2abco s C ,bc a c b A 2cos 222-+=,ca b a c B 2cos 222-+= ,abc b a C 2cos 222-+=.第二張:例3、例4(記作1.1.3B )[例3]已知△ABC , BD 為角B 的平分線,求證: AB ∶BC =AD ∶DC .[例4]在△ABC 中,求證:a 2sin2B +b 2sin2A =2ab sin C .第三張:例5(記作1.1.3C)[例5]在△ABC 中,bco s A =aco s B ,試判斷三角形的形狀.三維目標 一、知識與技能1.掌握在已知三角形的兩邊及其中一邊的對角解三角形時,有兩解或一解或無解等情形;2.三角形各種形狀的判定方法;3.三角形面積定理的應用. 二、過程與方法通過引導學生分析,解答三個典型例子,使學生學會綜合運用正、余弦定理,三角函數公式及三角形有關性質求解三角形問題. 三、情感態度與價值觀通過正、余弦定理,在解三角形問題時溝通了三角形的有關性質和三角函數的關係,反映了事物之間的必然聯繫及一定條件下相互轉化的可能,從而從本質上反映了事物之間的內在聯繫.教學過程 導入新課師 前面兩節課,我們一起學習了正弦定理、余弦定理的內容,並且接觸了利用正、余弦定理解三角形的有關題型.下面,我們先來回顧一下正、余弦定理的內容 (給出幻燈片 1.1.3A ).從幻燈片大體可以看出,正弦定理、余弦定理實質上反映了三角形內的邊角關係,運用定理可以進行邊與角之間的轉換,這一節,我們將通過例題分析來學習正、余弦定理的邊角轉換功能在判斷三角形形狀和證明三角恒等式時的應用.推進新課思考:在△ABC 中,已知A =22c m ,B =25c m,A =133°,解三角形.(由學生閱讀課本第9頁解答過程)從此題的分析我們發現,在已知三角形的兩邊及其中一邊的對角解三角形時,在某些條件下會出現無解的情形.下面進一步來研究這種情形下解三角形的問題.【例1】在△ABC 中,已知A ,B ,A ,討論三角形解的情況.師 分析:先由a A b B sin sin =可進一步求出B ;則C =180°-(A +B ),從而A C a c sin sin =. 一般地,已知兩邊和其中一邊的對角解三角形,有兩解、一解、無解三種情況. 1.當A 為鈍角或直角時,必須a >b 才能有且只有一解;否則無解.2.當A 為銳角時,如果a ≥b ,那麼只有一解; 如果a <b ,那麼可以分下面三種情況來討論:(1)若a >b sin A ,則有兩解;(2)若a =b sin A ,則只有一解;(3)若a<b sin A,則無解.(以上解答過程詳見課本第9到第10頁)師注意在已知三角形的兩邊及其中一邊的對角解三角形時,只有當A為銳角且b sin A<a<b時,有兩解;其他情況時則只有一解或無解.(1)A為直角或鈍角(2)A為銳角【例2】在△ABC中,已知a =7,b=5,c =3,判斷△ABC的類型.分析:由余弦定理可知a2=b2+c2⇔A是直角⇔△ABC是直角三角形,a2>b2+c2⇔A是鈍角⇔△ABC是鈍角三角形,a2<b2+c⇔A是銳角/△ABC是銳角三角形。
高中数学人教版必修五《第一章 解三角形 探究与发现 解三角形的进一步讨论》课件

(4)余弦定理的变式:cos C a2 b2 c2
2ab
(5)三角形面积公式:SΔ
1 ah 2
,
SΔ
1 absinC 2
① sinA=sin(B+C),cosA=-cos(B+C),
tanA=-tan(B+C)
② sin A cos B C , cos A sin B C ,
2
2
2
2
2 则tan A ______
6、某海上缉私小分队驾驶缉私艇以40km/小时的速度由A处动身,沿北 偏东600方向,进行海面巡逻,当航行半小时到达B处时,发觉北偏西 450方向有一船C,若船C位于A处北偏东300方向上,则缉私艇在B处与 船C的距离是( )
A.5( 6 2 ) B.5( 6 2 ) C .10( 6 2 ) D.10( 6 2 )
苏教版 高中数学
解斜三角形
(1)正弦定理: a b c 2R
sinA sinB sinC
(2)余弦定理: c2=a2+b2-2abcosC
(3)正弦定理的变式:
a=2RsinA b=2RsinB c=2RsinC.
sin A a sinB b sinC c
2R
2R
2R
a : b : c sin A: sinB : sinC
tan A cot B C
2
2
③在△ABC中,c边为最大边,
若c2>a2+b2, 则C为钝角,△ABC为钝角三角形。 若c2=a2+b2, 则C为直角,△ABC为直角三角形。 若c2<a2+b2, 则C为锐角,△ABC为锐角三角形。
a b c 2R sinA sinB sinC
2022年高中数学新人教版A版精品教案《探究与发现 解三角形的进一步讨论》

正弦定理和余弦定理探究与发现解三角形的进一步讨论●教学目标知识与技能:掌握在三角形的两边及其中一边的对角解三角形时,有两解或一解或无解等情形;三角形各种类型的判定方法。
过程与方法:通过引导学生分析,解答三个典型例子,使学生学会综合运用正、余弦定理,三角函数公式及三角形有关性质求解三角形问题。
情感态度与价值观:通过正、余弦定理,在解三角形问题时沟通了三角形的有关性质和三角函数的关系,反映了事物之间的必然联系及一定条件下相互转化的可能,从而从本质上反映了事物之间的内在联系。
●教学重点在三角形的两边及其中一边的对角解三角形时,有两解或一解或无解等情形;三角形各种类型的判定方法。
●教学难点正、余弦定理与三角形的有关性质的综合运用。
●教学过程〔一〕复习归纳:1正弦定理:;或,,余弦定理:或,,2正弦定理可解决的类型:〔1〕两角和任一边,求其它两边及一角;〔2〕两边和其中一边对角,求另一边的对角。
余弦定理可解决的类型:〔1〕知三角形的任意两边及它们的夹角就可以求出第三边;〔2〕三角形的三条边就可以求出其它角。
〔二〕创设情景思考1:引申:将上题条件改为以下几种情况,结果如何?1 〔一解〕2 〔一解〕3 〔无解〕从此题的分析我们发现,在三角形的两边及其中一边的对角解三角形时,在某些条件下会出现无解,一解,两解的情形。
下面进一步来研究这种情形下解三角形的问题。
〔三〕讲授新课探索研究讨论三角形解的情况为钝角或直角时,必须才能有且只有一解;否那么无解。
为锐角时,如果,那么只有一解;如果,那么可以分下面三种情况来讨论:〔1〕假设,那么有两解;〔2〕假设,那么只有一解;〔3〕假设,那么无解。
评述:注意在三角形的两边及其中一边的对角解三角形时,只有当A为锐角且时,有两解;其它情况时那么只有一解或无解。
随堂练习1 不解三角形,判断三角形的个数〔1〕〔2〕〔3〕〔4〕 5 6解:思考2:能否用余弦定理求解两边及夹角?利用方程的思想和余弦定理:当等式中含有未知数时,等式便成为方程式中有四个量,知道任意三个,便可以解出另一个,运用此式可以求a或b或c或coA例:在ABC中,,解三角形。
解三角形的进一步讨论教学设计

解三角形的进一步讨论——教学设计一、教学内容分析本节课是《普通高中课程标准实验教科书·数学(5)》(人教A 版)第一章第一节第三课(1.1.3)《正、余弦定理及其应用》。
根据我所任教的学生的实际情况,我将《正、余弦定理及其应用》划分为三节课(正弦定理、余弦定理、解三角形的进一步讨论),这是第三节课“解三角形的进一步讨论”。
正余弦定理是解三角形的重要工具,是三角函数的重要应用,是在生活及生产实际中有着广泛的应用,所以正余弦定理应重点研究。
二、学生学习况情分析解三角形是在学生系统学习了正余弦定理,基本掌握了正余弦定理的各种变型形式的基础上进行研究的,是学生对正余弦定理的第一次应用。
教材在之前的学习中给出了实际例子,已经让学生感受到正余弦定理的实际背景。
本节课先设计一个看似简单的问题,通过不同的结果来激发学生学习新知的兴趣和欲望。
三、设计思想1. 正余弦定理在解三角形中占有很重要的位置。
如何突破这个即重要又抽象的内容,其实质就是将抽象的符号语言与直观的图象语言有机的结合起来,通过具有一定思考价值的问题,激发学生的求知欲望――持久的好奇心。
从实际实例出发,逐步体会不同情形下产生的不同结果,从看似杂乱的现象中发现规律、总结规律,形成直观、快速、准确的判断方法。
本节课,力图让学生从不同的角度去研究解三角形,对解三角形进行一个全方位的研究,并通过对比总结得到一般规律,让学生去体会这种的研究方法,以便能将其迁移到其他现象的研究中去。
2.在本课的教学中我努力实践以下两点:(1)在课堂活动中通过恰当的游戏式引入,让学生快速进入情景,迅速进入节奏。
(2)在教学过程中努力做到知识节点环环相扣、逐步深入,注重生生对话、师生对话,并且在对话之后重视体会、总结、反思,力图在培养和发展学生数学素养的同时让学生掌握一些学习、研究数学的方法。
(3)通过课堂教学活动向学生渗透数学思想方法。
四、教学目标根据任教班级学生的实际情况,本节课我确定的教学目标是:知识与技能:正余弦定理在解三角形中的应用讨论; 过程与方法:讨论总结,讲练结合;情感态度与价值观:体会数学中多角度看问题的思维,让学生在数学活动中感受数学思想方法之美;同时通过本节课的学习,使学生获得研究数学问题的规律和方法;培养学生主动学习、合作交流的意识。
北师大版高中数学必修5第二章《解三角形》之解三角形的进一步讨论

第三课时§2.1.3解三角形的进一步讨论一、教学目标1、知识与技能:掌握在已知三角形的两边及其中一边的对角解三角形时,有两解或一解或无解等情形;三角形各种类型的判定方法;三角形面积定理的应用。
2、过程与方法:通过引导学生分析,解答三个典型例子,使学生学会综合运用正、余弦定理,三角函数公式及三角形有关性质求解三角形问题。
3、情感态度与价值观:通过正、余弦定理,在解三角形问题时沟通了三角形的有关性质和三角函数的关系,反映了事物之间的必然联系及一定条件下相互转化的可能,从而从本质上反映了事物之间的内在联系。
二、教学重点:在已知三角形的两边及其中一边的对角解三角形时,有两解或一解或无解等情形;三角形各种类型的判定方法;三角形面积定理的应用。
教学难点:正、余弦定理与三角形的有关性质的综合运用。
三、教学方法:探析归纳,讲练结合四、教学过程Ⅰ.课题导入[创设情景]思考:在∆ABC 中,已知22a cm =,25b cm =,0133A =,解三角形。
(由学生阅读课本第9页解答过程)从此题的分析我们发现,在已知三角形的两边及其中一边的对角解三角形时,在某些条件下会出现无解的情形。
下面进一步来研究这种情形下解三角形的问题。
Ⅱ.探析新课[探索研究]:例1.在∆ABC 中,已知,,a b A ,讨论三角形解的情况 分析:先由sin sin b A B a=可进一步求出B ; 则0180()C A B =-+ 从而sin a C c A = 1.当A 为钝角或直角时,必须a b >才能有且只有一解;否则无解。
2.当A 为锐角时,如果a ≥b ,那么只有一解;如果a b <,那么可以分下面三种情况来讨论:(1)若sin a b A >,则有两解;(2)若sin a b A =,则只有一解;(3)若sin a b A <,则无解。
(以上解答过程详见课本第9:10页)评述:注意在已知三角形的两边及其中一边的对角解三角形时,只有当A 为锐角且 sin b A a b <<时,有两解;其它情况时则只有一解或无解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2 6 2 2 6 6 ( 5 ) =x +( ) -2x ( ). 3 3 6 2 即3x +4x 7 0.
2 2
A D E
7 x=1或x (舍) . 3
B
C
4 6 6 例2.在ABC中,已知:AB= ,cosB= ,AC边上的 3 6 中线BD= 5. 求sin A的值。
必须a>b,才能有且只有一解,否则无解。
C b a C b a
A
B
A
B
2.当A为锐角时, 如果a b,那么只有一解。
C b C a B2
a
A 如果a<b,那么可以分下面三种情况讨论: b
B
a B1
(1)若a>bsinA,则有两解。
A (2)若a=bsinA,则只有一解。 C b A a=bsinA B b
评述:注意在已知三角形的两边及其中一边的对角解三 角形时,只有当A为锐角且 b sin A a b 时,有两解; 其它情况时则只有一解或无解。
例1.在ABC中,已知a 80,b 100,A 45 , 试判断此三角形解的情况。
0
b sin A 100sin 45 解: sinB= = 1 a 80 又a<b, B有两解。 三角形有两解。
2
cos(A+B)[cos(A B ) +cos(A B )] =0,
2cos A cos B cosC =0,
A、B、C中至少有一个为900 , ABC为Rt.
1.在ABC中, A :sin B :sinC 1:2:3,判断ABC的类型。 sin
钝角三角形
2.已知ABC满足a cos A b cos B,判断ABC的类型。
2 2 2
b2 c2 a2 cos A 2bc a2 c2 b2 cos B 2bc 2 2 2 a b c cos C 2ab
(3)正弦定理的应用范围:
b sin A ①已知两角和任一边,求其它两边及一角;a sin B
②已知两边和其中一边对角,求另一边的对角。 (4)余弦定理的应用范围:
ABC为等腰或Rt .
例4.在ABC中,若acosA+bcosB=ccosC,试判断ABC的形状。
解:(边化角)由已知得sinAcosA+sinBcosB=sinCcosC,
sin2A+sin2B=sin2C,
sin2C=sin2[ -(A+B)]=sin[2 2 (A+B)]=-sin2(A+B), 2sin(A+B)cos(A-B)=-2sin(A+B)cos(A+B), sin(A+B)[cos(A-B)+cos(A+B)]=0, 2sin(A+B)cosAcosB=0, 0 A+B< , sin(A+B) 0, cosA=0或cosB=0,
a2(b 2 c2 a 2 ) 2(a 2 c2 b 2 ) 2(a 2 b 2 c2 ) +b =c , 2a2b 2 a 4 b4 = c4 ,
2 2 2 2 2 2
(a 2 b2 )2 c4 =0,
(a b c )(a b c ) =0, b2 a 2 c 2或a 2 b2 c 2,
等腰三角形或直角三角形
3.利用正弦定理、余弦定理证明三角形中的恒等式
例1.在ABC中,求证:a sin2B+b sin2A=2absinC.
2 2
证明:(边化角)
左边=4R2sin2A 2sinBcosB+4R2sin2B 2sinAcosA
=8R sinAsinB(sinAcosB+cosAsinB) =8R 2sinAsinBsin(A+B)
0
1 0 例2.在ABC中,a 1,c ,C 40 , 2 则符合题意的b的值有 __________ 个。 两个
a sinC 又a c, 解: sinA= =2sin400 1 c A有两解。 三角形有两解,b的值有两个。
例3.在ABC中,a xcm,b 2cm,B 450, 如果用正弦定理解三角形有两解,求x的取值范围。
A=900或B=900 ,
ABC是以角A或以角B为直角的Rt。
例4.在ABC中,若acosA+bcosB=ccosC,试判断ABC的形状。
解:(角化边)由已知得 b 2 c2 a 2 a 2 c2 b 2 a 2 b 2 c2 a +b =c , 2bc 2ac 2ab
=2(2RsinA)(2RsinB)sinC
2
=2absinC
即:a sin2B+b sin2A=2absinC.
ABC是以角A或以角B为直角的Rt。
例5.在ABC中,已知cos A+cos B+cos C=1, 试判断ABC的形状。
2 2 2
解:由cos2A+cos2B+cos2C=1, 1 cos2A 1 cos2B 1 cos2C + + =1, 2 2 2 cos2A+cos2B +cos2C =-1, 2cos(A+B)cos(A B ) +2cos C 1=-1, cos(A+B)cos(A B ) +cos2(A B ) =0,
2 2 2
b c a (1)已知三边求三个角; cos A 2bc (2)已知两边和它们的夹角,求第三边和其他两个角。
a sin A sin B b
c a b 2ab cos C
2 2 2
注意:利用正弦定理求角时,应先求较短边的对角 (一定是锐角)可避免讨论。
探究:在ABC中,已知a,b,A,讨论三角形解的情况。 b sin A 分析:由sinB= ,可求出角B, a a sin C 则C=1800 ( A B), 从而c= . sin A 1.当A为钝角或直角时,
C
a<bsinA B
(3)若a<bsinA,则无解。 A
若A为锐角时:
无解 a b sin A a b sin A 一解直角 b sin A a b 二解一锐、一钝 ab 一解锐角
若A为直角或钝角时:
a b 无解 a b 一解锐角
0
B
D
C
4 6 6 例2.在ABC中,已知:AB= ,cosB= ,AC边上的 3 6 中线BD= 5. 求sin A的值。 1 解:取BC中点E, 连DE, 则DE AB且DE= AB. 2 2 6 DE= . 3 2 2 2 设BE=x,在BDE中,BD =BE +DE -2BE DEcosBED.
B=C或B= -C(舍).
ABC为等腰直角三角形。
例3.在ABC中,已知tanA:tanB=a2:b2,试判断ABC的形状。
解法一: (边化角)
tan A a 2 2, tan B b
sin A cos B sin A 2 , 2 cos A sin B cos B cos B sin A 即 , cos A sin B
2
例1.在ABC中,a 7,b 5,c 3,判断ABC的形状。 b2 c2 a2 解:由余弦定理cosA= 可知: 2bc b 2 c 2 a 2 52 32 72 0 A为钝角.
2.利用正弦定理、余弦定理判断三角形的形状
ABC为钝角三角形.
总结:
sinC=sinAcosB,
即sin(A B ) sin A cos B ,
化简得:cosAsinB=0.
B 0, sinB 0,
cosA=0, A=900 .
又由b=asinC,得sinB=sinAsinC
而A=900, sin A 1
sinB=sinC,
B=C或B= -C(舍)
x=1,即BC=2.
在ABC中,AC2 =AB2 +BC2 -2AB BCcosABC.
4 6 2 2 4 6 6 84 2 21 AC =( ) +2 -2 2 = . AC= 3 3 6 9 3 AC BC 6 30 = . 由cosB= , sinB= . sin B sin A A 6 6 30 2 D 70 6 sin A . 14 2 21 B C E 3
即sin 2A sin 2B ,
2A 2B或2A 2B .
2 ABC为等腰或Rt .
A B或A B
.
例3.在ABC中,已知tanA:tanB=a2:b2,试判断ABC的形状。
解法二: (角化边)
tan A a 2, tan B b
2
sin A cos B sin A 2 , 2 cos A sin B cos B
a k sin A, b k sin B, c k sin C.(k 0)
a b c sin A ,sin B ,sin C R为外接圆半径 2R 2R 2R
b2 c2 a2 cos A 2bc
1.利用正弦定理、余弦定理解三角形
例1.在ABC中,已知:B=45 ,D是BC边上一点,AD=5, AC=7,DC=3,求AB的长。 AC 2 DC 2 AD2 72 32 52 11 解:在ADC中,cosC= 2AC DC 273 14 5 3 0<C< ,sinC= . 14 5 3 7 AC sin C 14 5 6 . 在ABC中,AB= sin B 2 2 A 2
ABC为等腰直角三角形。
