15-第15讲微分中值定理
微分中值定理

微分中值定理微分中值定理是微积分中的重要定理之一,它揭示了函数在某个区间内取得极值的一种方法。
微分中值定理包括拉格朗日中值定理和高尔的中值定理两种形式,下面将分别介绍这两种定理。
拉格朗日中值定理是微分学中的基本定理之一,它表明如果函数满足一些条件,那么在某个区间内一定存在一个点,它的导数等于函数在这个区间两个端点处的斜率。
具体来说,如果函数在闭区间[a,b]上连续,在开区间(a,b)上可导,并且a<b,那么存在一个点c∈(a,b),使得函数在点c处的导数等于函数在区间的两个端点处的斜率。
也就是说,存在c∈(a,b)使得:f'(c) = (f(b) - f(a)) / (b - a)这个定理的图像可以形象地理解为,曲线在某点的切线与连接两个端点的直线斜率相等。
高尔的中值定理是拉格朗日中值定理的一个推广,它是由高尔证明的。
高尔的中值定理的条件比拉格朗日中值定理更加宽松,它只要求函数在闭区间[a,b]上连续,在开区间(a,b)上可导。
具体来说,如果函数在闭区间[a,b]上连续,在开区间(a,b)上可导,并且函数在区间的两个端点处的斜率相等,那么存在一个点c∈(a,b),使得函数在点c处的导数等于函数在区间的两个端点处的斜率。
也就是说,存在c∈(a,b)使得:f'(c) = (f(b) - f(a)) / (b - a)高尔的中值定理可以看做拉格朗日中值定理的推广,它更加灵活,适用范围更广。
微分中值定理的证明可以通过利用拉格朗日中值定理或高尔的中值定理的定义和一些基本的微积分知识进行推导。
证明的过程比较复杂,需要运用到数学分析中的一些技巧与方法。
微分中值定理在微积分的应用中有着广泛的应用。
它可以用来证明一些数学定理,比如费马最值定理、罗尔定理和拉格朗日多重中值定理等。
此外,微分中值定理还可以用来求函数的零点、证明函数的单调性和判断函数的极值等。
在实际问题中,微分中值定理常常被用来解决一些最优化问题,比如求函数的最值、最小二乘法中的参数估计等。
中值定理 证明 解微分方程

中值定理证明解微分方程中值定理是微积分中的一个重要定理,它是解微分方程的基础。
本文将介绍中值定理的证明和如何利用它来解微分方程。
一、中值定理的证明中值定理也被称为罗尔定理或拉格朗日中值定理,它的表述如下:设函数 $f(x)$ 在闭区间 $[a,b]$ 上连续,在开区间 $(a,b)$ 内可导,则在 $(a,b)$ 内至少存在一点 $c$,使得 $f'(c)=\dfrac{f(b)-f(a)}{b-a}$。
证明如下:由于 $f(x)$ 在闭区间 $[a,b]$ 上连续,根据最值定理,$f(x)$ 在该区间内必有最大值 $M$ 和最小值 $m$,即 $m\leqf(x)\leq M$,且存在 $x_1,x_2\in[a,b]$,使得 $f(x_1)=M$,$f(x_2)=m$。
当 $f(x)$ 为常数函数时,结论显然成立。
当 $f(x)$ 不为常数函数时,存在 $x_0\in[a,b]$,使得 $f(x_0)\neq f(a)$,$f(x_0)\neq f(b)$。
不失一般性,假设 $f(x_0)>f(a)$。
若 $f(x_0)<f(b)$,则由连续性,$f(x)$ 在 $[a,b]$ 上取到$f(x_0)$ 的值,设为 $d$。
根据介值定理,存在 $[a,x_0]$ 和$[x_0,b]$ 上的某点 $c_1$ 和 $c_2$,使得 $f(c_1)=d$,$f(c_2)=d$。
由于 $f(x)$ 在 $(a,b)$ 内可导,根据导数的定义,有$$ f'(x_0)=\lim\limits_{h\to 0}\dfrac{f(x_0+h)-f(x_0)}{h} $$ 根据极限的性质,可以找到两个数列 $\{x_n\}$ 和 $\{y_n\}$,满足$$ \lim\limits_{n\to\infty}x_n=\lim\limits_{n\to\infty}y_n=x_ 0 $$$$ x_n\in(a,x_0),\ y_n\in(x_0,b) $$$$ f(x_n)<f(x_0),\ f(y_n)>f(x_0) $$于是有$$ f'(x_0)=\lim\limits_{n\to\infty}\dfrac{f(x_n)-f(x_0)}{x_n-x_0}=\lim\limits_{n\to\infty}\dfrac{f(y_n)-f(x_0)}{y_n-x_0} $$根据介值定理,存在 $\alpha\in[c_1,x_0]$ 和$\beta\in[x_0,c_2]$,使得 $f'(\alpha)=f'(\beta)=\dfrac{f(b)-f(a)}{b-a}$。
微分中值定理

1.微分中值定理微分中值定理分为罗尔中值定理、拉格朗日中值定理和柯西中值定理,又(统)称为微分学基本定理、有限改变量定理或有限增量定理,是微分学的基本定理之一,内容是说一段连续光滑曲线中必然有一点,它的斜率与整段曲线平均斜率相同(严格的数学表达参见下文)。
1.1.罗尔中值定理罗尔定理的几何意义如果函数满足1.在闭区间上连续;2.在开区间内可导;3.在区间端点处的函数值相等,即,那么在内至少有一点,使得。
这个定理称为罗尔定理。
1.2.拉格朗日中值定理拉格朗日中值定理的几何意义主条目:朗格朗日中值定理如果函数满足1.在闭区间上连续;2.在开区间内可导,那么在内至少有一点,使等式成立。
此定理称为拉格朗日中值定理。
拉格朗日中值定理是罗尔中值定理的推广,同时也是柯西中值定理的特殊情形。
1.3.柯西中值定理柯西中值定理的几何意义如果函数及满足1.在闭区间上连续;2.在开区间内可导,3.在对任意,那么在内至少有一点使等式成立。
此定理称为柯西中值定理。
2.积分中值定理积分中值定理分为积分第一中值定理和积分第二中值定理,它们各包含两个公式。
其退化状态均指在ξ的变化过程中存在一个时刻使两个图形的面积相等(严格表述在下面)。
2.1.积分第一中值定理设为一连续函数,为一正的可积函数,那么存在一点使得。
2.1.1.证明因为是闭区间上的连续函数,取得最大值和最小值。
于是。
对不等式求积分,我们有。
若,则。
可取上任一点。
设,那么。
因为是连续函数,则必存在一点,使得。
积分第一中值定理推论的几何意义2.1.2.推论(拉格朗日中值定理的积分形式)在上式中令,则可得出:设为一连续函数,则∃,使它也可以由拉格朗日中值定理推出:设在上可导,,则∃,使2.2.积分第二中值定理积分第二中值定理与积分第一中值定理相互独立,却又是更精细的积分中值定理。
它可以用来证明Dirichlet-Abel反常Rieman 积分判别法。
2.2.1.内容若f,g在[a,b]上黎曼可积且f(x)在[a,b]上单调,则存在[a,b]上的点ξ使;2.2.2.退化态的几何意义令g(x)=1,则原公式可化为:;进而导出:;此时易得其几何意义若连续y=f(x)在A(a,f(a)),B(b,f(b))两点间的每一点处都有不垂直于x轴的切线,则曲线在A,B间至少存在一点P(c,f(c)),使得该曲线在P点的切线与割线AB平行设f(x)在[1,2]上有二阶导数,且f(2)=0,又F(x)=(x-1)^2*f(x),证明:在区间(1,2)内至少存在一点§,使得F"(§)=0最佳答案由题设,f(x)在[1,2]上有2阶导数考察函数F(x)=(x-1)²f(x)显然F(x)在[1,2]上连续,在(1,2)可导且F(1)=(1-1)²f(1)=(2-1)²·0=(2-1)²f(2)=f(2)所以存在η∈(1,2)使得F'(η)=0现在考察区间[1,η]包含于[1,2)容易证明F'(x)在(1,η)可导,在[1,η]连续∵F'(x)=2(x-1)f(x)+(x-1)²f'(x)∴F'(1)=0·f(1)+0·f'(1)=0=F'(η)故存在ξ∈(1,η)使得F'(ξ)=0但是(1,η)包含于(1,2)所以ξ∈(1,2)证毕当x>1时,设f(t)=e^t,t∈[1,x].f(t)在[1,x]上连续,在(1,x)内可导,由拉格郎日中值定理,存在ξ∈(1,x),使得f'(ξ)=(f(x)-f(1))/(x-1).f'(x)=e^x,所以,e^ξ=(e^x-e)/(x-1).因为1<ξ<x,所以,e^ξ>e,所以,(e^x-e)/(x-1)>e,得e^x>ex.方法二:设f(t)=e^t-et,t∈[1,x],拉格郎日中值定理(e^x-ex)/(x-1)=e^ξ-e>0,得到结论方法三:取对数,设f(t)=lnt,t∈[1,x],拉格郎日中值定理lnx/(x-1)=1/ξ<1,得lnx<x-1,化为指数运算即得结论。
高等数学A1教学PPT课件1:15-第15讲 罗尔、拉格朗日中值定理

18
(2) 若 m M (即 M m) f (x) C([a, b])
f (x) 必在[a, b] 上取到它的最大值、 最小值至少各一次.
又 f (a) f (b) , 故 f (x) 不能同时在 x a 和 x b 处分别取到M和m .
即至少存在一点 (a, b), 使得 f ( ) M 或 f ( ) m.
g(x) 则由已知条件可知:
F (x) 在 [x1, x2 ] 上满足罗尔定理条件, 27
故至少存在一点 (x1, x2 ) , 使得
F( )
f ( )g( ) f ( )g( ) g( )2
0
从而 f ( )g( ) f ( )g( ) 0 , 与已知矛盾.
该矛盾说明命题为真 .
如果使用一次罗尔定理后, f (x) 仍满足罗尔定理条件, 能否再一次使用罗尔定理?
9
极值的定义
设 f (x) 在 U(x0 ) 内有定义 , 若
f (x) f (x0) x Uˆ (x0) ,
则称 f (x0 ) 为 f (x) 的极大值 , x0为函数的极大点.
f (x) f (x0) x Uˆ (x0) ,
则称 f (x0 ) 为 f (x) 的极小值 , x0为函数的极小点.
这些中值定理的创建要归功于费马、 拉格朗日、柯西等数学家.
6
首先, 从直观上来看看 “函数的差商与函数的导数间的基本关系式” 是怎么一回事.
7
导数与差商
y y f (x) 可微
P
B
点 P 处切线的斜率: k f (x0)
相等!
割线 AB 的斜率:
A
k f (x2 ) f (x1) x2 x1
取极大值 f ( ), 则有 f (x) C 是特殊情况
微分中值定理

定理证明
总结词
柯西中值定理的证明涉及到了微分学中的一 些基本概念和性质,如导数的定义、导数的 几何意义等。
Hale Waihona Puke 详细描述证明柯西中值定理,首先需要理解导数的定 义和性质,然后利用拉格朗日中值定理,再 结合闭区间上连续函数的性质,逐步推导, 最终得出结论。
定理应用
总结词
柯西中值定理在微分学中有广泛的应用,它可以用于研 究函数的单调性、极值等问题,还可以用于求解一些复 杂的微分方程。
详细描述
柯西中值定理的应用主要体现在两个方面,一是利用该 定理研究函数的单调性和极值问题,二是利用该定理求 解一些复杂的微分方程。通过柯西中值定理的应用,我 们可以更好地理解函数的性质,并且能够求解一些复杂 的数学问题。
06
罗尔中值定理
定理内容
总结词
罗尔中值定理是微分学中的基本定理之一,它指出如 果一个函数在闭区间上连续,在开区间上可导,并且 在区间的两端取值相等,那么在这个区间内至少存在 一点,使得函数在该点的导数为零。
定理应用
01
洛必达法则可以用于求极限,特别是当极限的形式为0/0或 者∞/∞时,可以通过洛必达法则求得极限值。
02
洛必达法则还可以用于判断函数的单调性,如果函数在某区间 的导数大于0,则函数在此区间单调递增;如果导数小于0,则
函数在此区间单调递减。
03
此外,洛必达法则还可以用于求函数极值,如果函数在某 点的导数等于0,则该点可能是函数的极值点。
定理应用
总结词
罗尔中值定理在微分学中有广泛的应 用,它可以用于证明其他中值定理、 研究函数的单调性、解决一些微分方 程问题等。
2. 研究函数的单调性
通过罗尔中值定理可以推导出一些关 于函数单调性的结论,例如如果函数 在区间上单调增加或减少,那么其导 数在该区间上非负或非正。
微分中值定理公式

微分中值定理公式
微分中值定理:
1、定义:如果函数f(x)在闭区间[a,b]上连续,且其在该区间上具有一阶导数,那么,存在一个c属于[a,b],使得f'(c)=(f(b)-f(a))/(b-a)
2、应用:
(1)求解函数f(x)在闭区间[a,b]中的最值。
(2)确定区间上函数的局部极大值和极小值,以及单调区间。
(3)确定函数凹凸变化,如果有拐点,则根据导数解一元二次不等式获取。
(4)计算凸函数f(x)的极限值,如极限存在的话,就用微分中值定理来确定它。
3、几何意义:围绕着函数曲线c,有两个相交面积相等,其一个为上和下凸函数组成的不规则四边形的面积,而另一个则为分别以端点a,b为对角的矩形的面积之和:S=(f(a)+f(b))(b-a)
4、优势:
(1)微分中值定理是由微积分中基础概念构成;
(2)它是通过计算数学原理而不是函数曲线平移,形变等操作来确定突变点;
(3)它是通过极值解决拐点计算的有力工具;
(4)它可以用来计算凸函数极限值,是一种快捷有效的方法。
微分中值定理解析

微分中值定理解析微分中值定理是微积分中一个重要的定理,它为我们提供了研究函数的性质和特点的重要工具。
本文将对微分中值定理进行解析,从定义、形式化表述、几何意义以及应用等方面进行论述。
一、定义微分中值定理是微积分中的一个重要定理,它是拉格朗日中值定理的推广和具体化。
该定理的核心思想是:若函数f(x)在[a, b]上满足一定条件,那么在(a, b)的某一点c处,函数的导数f'(c)与函数在[a, b]上的平均斜率相等。
二、形式化表述设函数f(x)在[a, b]上连续,在(a, b)上可导。
则存在某一点c∈(a, b),使得f'(c) = (f(b) - f(a))/(b - a)三、几何意义微分中值定理的几何意义是:在函数图像上,必然存在一条与割线平行的切线。
也即,函数在区间[a, b]上的斜率是局部变化率的平均值,那么在(a, b)的某一点c处,函数的斜率与该平均斜率相等。
四、应用微分中值定理在实际问题中有着广泛的应用,下面举几个例子进行说明:1. 高速公路行车速度问题:假设一辆汽车在时间t内,以速度v(t)行驶。
则根据微分中值定理,可以得知在某个时刻c,汽车的瞬时速度v'(c)等于汽车在整个行驶过程中的平均速度。
2. 生产线产品质量控制问题:假设某个生产线上,产品的质量由参数q(t)表示,其中t为生产时间。
根据微分中值定理,可以得知在某个时间点c,产品的质量变化率q'(c)等于该产品在整个生产过程中的平均变化率。
3. 就业市场薪水调查问题:假设在某个城市中,不同行业的毕业生就业薪水分别由函数f(x)表示,其中x表示毕业生的学历水平。
根据微分中值定理,可以得知在某个学历水平c处,不同行业的薪水增长率f'(c)等于整个就业市场中薪水增长的平均率。
五、总结微分中值定理是微积分中的一个重要定理,它通过连接函数的斜率、平均斜率和切线的关系,为我们提供了研究函数特性的重要工具。
微积分(第三版)课件:中值定理

例 试证 | arctanb arctan a || b a |.
证
设f
(x)=arctan
x
,
(a<b)
.
(arctan
x)
1
1 x2
显然arctan x在[a,b]上满足拉格朗日中值定理条件.
可知必定存在一点 (a,b) , 使得
arctanb arctana
1
1
2
(b a),
a
b.
拉格朗日 Joseph-Loouis Lagrange
(1736-1813)
f (x) x (0 x 1)
f
(x)
x 0
0 x1 x 1
原点处不可导
端点处值不等
端点处不连续
例 验证函数 f (x) x4 50x2 300 在区间 [ 8,8]符合罗尔定理.
显然多项式函数 f (x) 为偶函数,且连续可导.
满足罗尔定理条件 f (x) 4x3 100x
y
f (x) x4 50x2 300
微分中值定理
一、罗尔中值定理 二、拉格朗日中值定理 三、柯西中值定理
微分中值定理
导数在实际问题中具有广泛的应用,利用导数可 以求解未定式的极限问题;利用导数可以研究函数的 基本性态、函数图形的特征;利用导数可以解决实际 生活中的优化问题.
微分中值定理是利用导数研究函数在区间上整体 性质的有力工具和桥梁,微分中值定理主要包括罗尔 定理、拉格朗日定理和柯西定理。
例 f (x) (x 1)2在[0,3]上不满足罗尔定理的条件
( f (0) f (3)), 但是存在 1(0,3)使 f ( ) 0.
(2)罗尔定理的三个条件缺少其中任何一个条件定
微分积中值定理

微分积中值定理微分积中值定理是微积分中的重要定理,它指出了在一定条件下,函数的平均变化率等于它在某一点的导数值。
一般来说,微分积中值定理可以用于证明一些重要的基本定理,如拉格朗日中值定理和柯西中值定理等。
下面,我将详细介绍微分积中值定理的概念、证明以及应用。
微分积中值定理的概念微分积中值定理也称为罗尔中值定理,它是微积分中的基本定理之一。
定理的内容是:设函数$f(x)$在闭区间$[a,b]$上连续,在开区间$(a,b)$上可导,在闭区间$(a,b)$内取得了端点值$f(a)$和$f(b)$,则存在一点$c\in(a,b)$,使得$f'(c)=\dfrac{f(b)-f(a)}{b-a}$。
其中,$\dfrac{f(b)-f(a)}{b-a}$表示函数$f(x)$在闭区间$[a,b]$上的平均变化率。
微分积中值定理的证明微分积中值定理的证明可以通过画图来进行,主要分为以下几步:第一步:画出函数$f(x)$在闭区间$[a,b]$上的图像。
第二步:连结点$(a,f(a))$和$(b,f(b))$的线段,然后将这条线段的斜率设为$k$。
因为$f(x)$在开区间$(a,b)$上可导,所以函数$f(x)$在$(a,b)$处的导数$f'(x)$具有介值性,即在$(a,b)$中的任意一点$x$处,$f'(x)$都能够取到线段的斜率$k$。
因此,我们可以找到一个点$c\in(a,b)$,使得$f'(c)=k$。
第三步:去掉端点$(a,f(a))$和$(b,f(b))$的线段,将它们和点$(c,f(c))$连成两根直线,便可得到一个由三条线段组成的不封闭的折线。
因为函数$f(x)$在闭区间$[a,b]$上连续,所以这条折线一定会与函数$f(x)$在闭区间$[a,b]$上的图像相交。
设折线与$f(x)$的图像的交点为$(d,f(d))$,则$f(d)=f(c)+k(d-c)$。
第四步:由于函数$f(x)$在闭区间$[a,b]$上取得了端点值$f(a)$和$f(b)$,所以$f(a)\leqslant f(d)\leqslant f(b)$。
微积分学 P.P.t 标准课件15-第15讲导数概念

(2) 求函数由 x0 到 x0+ x 的平均变化率:
y f ( x0 x) f ( x0 ) ; x x
(3) 求 x 0 的极限:
y f ( x0 x) f ( x0 ) lim lim . x 0 x x 0 x
二.导数的概念
1. 导数的定义
e – x,
x>0
由可导性:
f (0 x) f (0) e x 1 x lim 1 lim lim x 0 x 0 x 0 x x x
f (0 x) f (0) (1 bx) 1 lim lim b x x x 0 x 0
称之为 f (x) 在 (a, b) 内的导函数. 通常我们仍称之
为 f (x) 在 (a, b) 内的导数:
y f ( x x) f ( x) f ( x) lim lim x x 0 x x 0
定义
若 f (x) 在 (a, b) 内可导, 且 f (a) , f (b) 存在,
f ( x0 ) a, y'| x x0 a,
dy d f ( x0 ) a, dx dx
x x0
a.
如果函数 f (x) 在点 x0 处可导, 则
f ( x) f ( x 0 ) f ' ( x0 ) lim ; x x0 x x0
f ( x0 x) f ( x0 ) f ( x0 ) lim x 0 x
高等院校非数学类本科数学课程
大 学 数 学(一)
—— 一元微积分学
第十五讲 导数的概念
脚本编写、教案制作:刘楚中 彭亚新 邓爱珍 刘开宇 孟益民
第四章 一元函数的导数与微分
微分中值定理复习

(
x
1)3
0
(x 0, 在 x
与 1 之间)
故所证不等式成立 .
法2 列表判别:
f (x) (x2 1) ln x (x 1)2 , f (1) 0
f
(
x)
2
x
ln
x
1 x
中的最大项 .
例11. 证明 ln(1 x) arctan x (x 0). 1 x
证: 设 (x) (1 x) ln(1 x) arctan x , 则 (0) 0
( x)
1 ln(1
x)
1
1 x
2
0
(x 0)
故 x 0 时, (x)单调增加 , 从而 (x) (0) 0
2. 解决最值问题 • 目标函数的建立与简化 • 最值的判别问题
3. 其他应用 : 求不定式极限 ; 几何应用 ; 相关变化率; 证明不等式 ; 研究方程实根等.
4. 补充定理 (见下页)
定理. 设函数 f (x) , g(x)在 [ a , ) 上具有n 阶导数, 且 (1) f (k) (a) g (k) (a) (k 0,1, 2, , n 1)
即所证不等式成立 .
例13. 证明:当0 x 1时, e2 x 1 x . 1 x
证: 只要证 (1 x) e2 x 1 x 0 (0 x 1)
设 f (x) (1 x) e2 x 1 x, f (x) (1 2x) e2 x 1,
则 f (0) 0 f (0) 0
f (x) 4x e2 x 0 (0 x 1)
例5. 设函数 f (x) 在[0, 3] 上连续, 在(0, 3) 内可导, 且
f (0) f (1) f (2) 3, f (3) 1, 试证必存在 (0,3), 使
微分中值定理的证明及应用

微分中值定理的证明及应用微分中值定理(Mean Value Theorem)是微积分中的一个重要定理,可以用来证明一些关于连续函数、可导函数以及函数的性质的定理,也可以用于解决一些实际问题。
下面将从两个方面,即证明与应用,进行详细讨论。
一、微分中值定理的证明1.拉格朗日中值定理的证明:设函数f(x)在[a,b]上连续,在(a,b)内可导。
根据费马定理,我们可以知道在(a,b)内存在一个点c,使得f'(c)=0。
即斜率为0.如果c点不是唯一,则取多个c点即可。
下面分两种情况进行讨论。
情况一:如果c=a或c=b,即在区间开头或结尾处取得斜率为0的点。
不妨设c=a,那么有f(a+h)-f(a)=f'(c)×h=0(因为斜率为0),所以得到f(b)-f(a)=0。
这个结论即为拉格朗日中值定理的结论。
情况二:如果c在(a,b)内,即在区间内部取得斜率为0的点。
定义一个新函数g(x) = f(x) - kc (k为实数),显然g(x)在[a,b]上连续,在(a,b)内可导,且g(a)=g(b)。
根据罗尔定理(Rolle's theorem),在(a,b)上存在一个点d,使得g'(d)=0,也就是说f'(d)-kc=0。
解得f'(d)=kc,而c点为f(x)在(a,b)上的极大值点或极小值点,即斜率为0。
故存在一个点d在(a,b)内,使得f'(d)=0;再利用拉格朗日中值定理的情况一即可得拉格朗日中值定理的结论。
2.柯西中值定理的证明:设函数f(x)和g(x)在[a,b]上连续,在(a,b)内可导,且g'(x)≠0,则存在一个点c在(a,b)内,使得(f(b)-f(a))g'(c)=(g(b)-g(a))f'(c)。
定义一个新函数h(x) = f(x) - kg(x)(k是实数),显然h(x)在[a,b]上连续,在(a,b)内可导,且h(a)=h(b)。
微分中值定理

T 与 l 平行
T
y = f (x)
(b, f (b))
l
这样的ξ可能有好多
f (b ) − f ( a ) y = f (a ) + ( x − a) b−a
(a, f (a))
O
a
ξ
ξ
b
x
Made by Huilai Li
一个特殊的例子:假设从A点运动到B点, 那么有许多种走法,首先我们来看一个例 子。
二、拉格朗日(Lagrange)中值定理
拉格朗日(Lagrange) 拉格朗日(Lagrange)中值定理
(1) 如果函数
f(x)在 在
闭区间[a, b]上连续,(2) 在开区间 (a, b) 内可导, 那末 上连续 , 内可导 , 在 (a, b)内至少有一点 ξ(a < ξ < b),使等式
f (b) − f (a) = f ' (ξ)(b − a) 成立. 成立.
设另有 x1 ∈ ( 0,1), x1 ≠ x 0 , 使 f ( x1 ) = 0.
Q f ( x ) 在 x0 , x1 之间满足罗尔定理的条 件, ∴ 至少存在一个 ξ (在 x0 , x1 之间), 使得 f ′(ξ ) = 0. 但 f ′( x ) = 5( x 4 − 1) < 0, ( x ∈ ( 0,1)) 矛盾 ∴ 为唯一实根 . 矛盾,
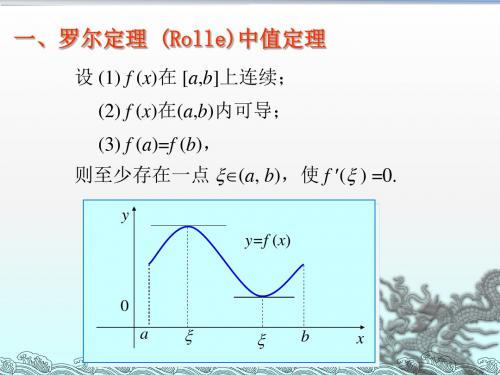
一、罗尔(Rolle)定理
( olle) 定理 如果函数 f (x)在 (1) 闭区间 [a, b]上 罗尔 Rolle) ( 连续, 内可导, 连续,(2) 在开区间 (a, b)内可导, 3) 且在区间端点的函数 值 相 等 , 即 f (a) = f (b) , 那 末 在 (a, b) 内 至 少 有 一 点 在该点的导数等于零, ξ(a < ξ < b),使得函数 f (x)在该点的导数等于零, 即f
微分中值定理主要作用

微分中值定理主要作用
首先从几何的角度讲,中值定理可以用来描述几何直观,比如Rolle定理、Lagrange中值定理和Cauchy中值定理的几何意义都是“存在与割线平行的切线”,Taylor中值定理的几何意义则比较复杂,可以理解成用高次曲线而非直线去代替割线。
只要去看一下单调性凹凸性等你认为特别有用的性质的具体讨论就会发现这些几何上很直观的性质严格证明并不容易,或者通俗地讲就是很多看着很显然的东西在逻辑上讲不清楚,而中值定理恰好可以把那些困难的地方给克服了,很好地把几何直观讲清楚,这样才把导数和那些实用的性质联系起来。
你不妨自己证明一下f'(x)在区间(a,b)上恒大于0,那么f(x)在(a,b)上严格单调递增,如果不用中值定理的话这个证明是很困难的(当年华罗庚先生曾试图回避中值定理,但是也没能完全做到这一点)。
微分中值定理条件

微分中值定理条件《微分中值定理条件》前两天我和我的好哥们小王在自习室学习,他正在为数学分析里的一道题发愁呢。
那题正好是关于微分中值定理的,他愁眉苦脸地看着我,说:“这微分中值定理的条件老搞混,题都没法做啊。
”这不,今天我就想好好讲讲这微分中值定理的条件。
首先呢,咱先说说罗尔定理。
这罗尔定理的条件有三条。
第一条要求函数在闭区间[a,b]上连续。
这就好比是一场接力赛,从起点a到终点b,函数这个小选手得一直待在赛道上,不能中途跑去别的地方,要是在中间某个地方突然消失了,那可不行。
第二条呢,函数在开区间(a,b)内可导。
这就像是小选手在跑道中间的那一段的时候,得能跑得顺滑,没有什么突然的阻碍让它跑不动或者走歪路,也就是每一点处都要有导数。
最后一条就是函数在区间端点的值相等,也就是f(a)=f(b)。
这就好比是在起点和终点的姿势得一样,有了这三条,那就保证了在开区间(a,b)内至少存在一点c,使得这个函数在点c处的导数为零。
就像这个小选手在跑道中间某个特殊的地方停止了加速似的。
再说拉格朗日中值定理,它和罗尔定理有点关系。
它要求函数在闭区间[a,b]上连续,在开区间(a,b)内可导。
这前面两条和罗尔定理有点像呀。
但是它就不需要f(a)=f(b)这个牵手的条件了。
它的结论是在开区间(a,b)内存在一点c,使得f(b) - f(a)=(b - a)f'(c)。
这就好比是说,虽然不要求起点和终点一样高了,但是肯定在中间有某个地方的“坡度”,也就是导数,和整个区间的“平均坡度”有关系。
柯西中值定理呢,它考虑的是两个函数的情况。
假设我们有两个函数f(x)和g(x),它要求f(x)和g(x)在闭区间[a,b]上连续,在开区间(a,b)内可导,而且在开区间(a,b)内g'(x)不等于零。
这就像是两个选手在跑道上跑,g(x)这个选手虽然一直在跑,但是不能一直停在原地不动(g'(x)不能为零)。
它的结论是存在一点c在开区间(a,b)内,使得[f(b) - f(a)]/[g(b) - g(a)] = f'(c)/g'(c)。
15微分中值定理
内的.
3
例5 选择题.函数 f (x) 2x2 x 1在区间[-1,3]上满
足拉格朗日中值定理的 =( ).
A. 3; B. 0; C. 3; D. 1 . 4
分析 由于 f (x) 2x2 x 1在[-1,3]上连续,在(-1,3)
内可导,因此f(x)在[-1,3]上满足拉格朗日中值
二、拉格朗日(Lagrange)中值定理
拉格朗日(Lagrange)中值定理 (1)如果函数 f(x)在
(2)
闭区间[a, b]上连续,在开区间(a, b) 内可导,那末在 (a, b)内至少有一点(a b),使等式
f (b) f (a) f ' ()(b a) 成立.
故
ln b ln a 1 (b a), ξ (a,b)
1 1 1 1 (b a) 1 (b a) 1 (b a)
b a b
a
b a ln b b a
b
ba
例9 证明当x 0时, x ln(1 x) x. 1 x
f (x2 ) f (x1) f '( )( x2 x1), (x1, x2 )
而 f () = 0, 故 f (x2)=f (x1)
由x1, x2 的任意性,f (x)=C, xI. (C为常数)
例10:设f (x) sin2 x cos2 x,试用微分中值定理证明: 对于一切x (,),,恒有f (x) 1。
证分明析:证明f (函x)数恒sin等2式x ,c主os要2 x是在利x用拉(格பைடு நூலகம்,朗日)定上理连的续推,且论:
如果函数f 'f((xx))在(区sin间2 xI上 c的o导s2 数x)恒' 为(s零in ,2 x那)'么(cfo(sx2)在x)'区间 I上是一个常数.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例2
设 f ( x)C ([a, b]) , 在 (a, b) 内可导, 证明
2 x ( f (b) f (a)) (b 2 a 2 ) f ( x) 令 F ( x) x 2 ( f (b) f (a )) (b 2 a 2 ) f ( x)
在 (a, b) 内至少有一根 .
f ( ) g ( ) f ( ) g ( ) F ( ) 0 2 g ( )
从而
f ( ) g ( ) f ( ) g ( ) 0 , 与已知矛盾 .
该矛盾说明命题为真 . 如果使用一次罗尔定理后, f ( x) 仍满足罗尔定理条件, 能否再一次使用罗尔定理? 如果需要, 当然可以使用.
a2 n 1 an a1 (1) 0 3 2n 1 a2 an 证 令 F ( x) a1 sin x sin 3x sin( 2n 1) x 3 2n 1 则 F (0) F ( ) 0 , 且满足罗尔定理其它条件, 2 故 (0, ) 使 2 F ( ) a1 cos a2 cos 3 an cos( 2n 1) 0
综上所述,
f ( x) 0 仅有三个实根 ,
分别在 (a, b), (b, c), (c, d ) 中.
例2
设 f ( x)C ([a, b]) , 在 (a, b) 内可导, 证明
2 x ( f (b) f (a)) (b 2 a 2 ) f ( x)
在 (a, b) 内至少有一根 .
最小值至少各一次.
又 f (a) f (b) ,
故 f ( x) 不能同时在 x a 和 x b 处分别取到M和m .
即至少存在一点 (a, b), 使得 f ( ) M 或 f ( ) m.
由费马定理可知: f ( ) 0
( a, b) .
例1
设 a, b, c, d 皆为实数, a b c d , f ( x) ( x a)( x b)( x c)( x d ) ,
不妨假设 x1 x2 . 并设方程 g ( x) 0 在 x1 与 x2 及其之间没有根 .
f ( x) 令 F ( x) ,(此时 g ( x) 0 ) . g ( x)
则由已知条件可知: F ( x) 在 [ x1 , x2 ] 上满足罗尔定理条件,
故至少存在一点 ( x1 , x2 ) , 使得
f (1 ) f ( 2 ) f (3 ) 0 . 其中, 1 (a, b) , 2 (b, c) , 3 (c, d ) .
即 f ( x) 0 至少有三个实根 .
f ( x) 是四次多项式 ,
f ( x) 是三次多项式 , f ( x) 0 至多有三个实根 .
分析
f ( x) f ( x) g ( x) f ( x) g ( x) g ( x) ( g ( x))2
如果 x1 , x2 是 f ( x) 0 的两个根 , 则
f ( x1 ) f ( x2 ) 0 ( 这时必须 g ( x) 0 ) . g ( x1 ) g ( x2 )
如何保证函 数在区间内 部取极值?
f ( x) f ( ) 0, x 0 x f ( x) f ( ) ( ) lim f 0, x 0 x
于是
f ( ) 0 .
(极小值类似可证)
f ( x) C ([a, b]) 可保证 f ( x)
在 [a, b] 内取到它的最大最小值.
y
y f (x)
但是……
O a
b
x
f ( x) C ([a, b])
f ( x) 在 (a, b) 存在
可保证在内部一点取到极值
f (a) f (b)
y
y f (x)
P
f ( ) 0
水平的
a
O
b
x
二. 罗尔中值定理
定理
设
(1) f ( x) C ([a, b]) ; (2) f ( x) 在 (a, b) 内可导 ; (3) f (a) f (b) ,
导数与差商
y
y f (x) 可微
点 P 处切线的斜率: k f ( x0 )
P
B
相等!
割线 AB 的斜率: f ( x2 ) f ( x1 ) k x2 x1
A
O
x1
x0
x2
x
将割线作平行移动, 那么它至少有一次会 达到这样的位置: 在曲线上与割线距离最远的那一点P 处成 为切线, 即在点P 处与曲线的切线重合. 也就是说, 至少存在一点 ( x1 , x2 ) , 使得
高等院校非数学类本科数学课程
高等 数 学(上)
—— 一元微积分学
第十五讲 微分中值定理
教案制作:吴洪武
作业
• 习题3-1(教材125页) • 1;2;3; 4; 5; 6 ;
第三章 微分中值定理与导数的应用
第一节 微分中值定理
一. 费马定理
二. 罗尔中值定理
三. 拉格朗日中值定理
四. 柯西中值定理
例4
设 f ( x) 、 ( x) C ([a, b]) , 在 (a, b) 内可导, g
且x (a, b), f ( x) g ( x) f ( x) g ( x) 0 . 证明方程
f ( x) 0 的两各根之间至少有 g ( x) 0 的一个根 .
证
设 x1 , x2 (a, b) 是 f ( x) 0 的两个根 .
费马定理的几何解释
y
如 何 证 明 ?
y f (x)
P
a
O
b
x
证
设 f ( x) 在区间 I 内有定义, 且在 x 处
f ( x) C 是特殊情况
ˆ x U( )
取极大值 f ( ), 则有
f ( x) f ( )
若 f ( ) 存在, 则
f ( ) lim
由罗尔定理, 至少存在一点 (a, b) 使得
即 方程在 (a, b) 内至少有一根 .
分析问题的条件, 作出 辅助函数是证明的关键 .
例3
在 0, (
证明方程 a1 cos x a2 cos 3x an cos( 2n 1) x 0
2
) 内至少有一根 , 其中实数 a1 , , an 满足
分析
2 x ( f (b) f (a )) (b 2 a 2 ) f ( x) 0 ( x 2 ( f (b) f (a)) (b 2 a 2 ) f ( x) ) 0
a 2 ( f (b) f (a )) (b 2 a 2 ) f (a ) b 2 ( f (b) f (a )) (b 2 a 2 ) f (b) a 2 f (b) b 2 f (a)
即方程在 0, (
2
) 内至少有一根 .
例4
设 f ( x) 、 g ( x) C ([a, b]) , 在 (a, b) 内可导,
且x (a, b), f ( x) g ( x) f ( x) g ( x) 0 . 证明方程
f ( x) 0 的两各根之间至少有 g ( x) 0 的一个根 .
x[ a , b ]
m min f ( x)
x[ a , b ]
(1) 若 M m m f ( x) M f ( x) m x [a, b] x [ a, b]
故 (a, b) , 均有 f ( ) 0 .
(2) 若 m M必在 [a, b] 上取到它的最大值、
f ( x) C ( [a, b],[b, c],[c, d ] ) , f (a) f (b) f (c) f (d ) 0 ,
证明方程 f ( x) 0 仅有三个实根, 并指出根所在区间.
证
又
f ( x) 是四次多项式, 在 (,) 内可微 , 在 [a, b] ,[b, c] ,[c, d ] 上运用罗尔中值定理 , 得
例5
设 f ( x), g ( x) C ([a, b]), 在 (a, b) 内二阶可导, 且 f (a) g (a), f (c) g (c), f (b) g (b), c (a, b),
证明 : 至少存在一点 (a, b), 使得 f ( ) g ( ).
f ( x) f ( x0 )
则称 f ( x0 ) 为 f ( x) 的极小值 , x0为函数的极小点 .
一. 费马定理
定理
设 f ( x) 在区间 I 内有定义, 且在 I 内某点
处取极大(小)值. 若 f ( ) 存在 , 则必有
f ( ) 0 .
可微函数在区间内部取极值的必要条件是 函数在该点的导数值为零.
证
则由 f ( x) 的连续性和可导性 , 得 F ( x) C ([a, b]) , F ( x) 在 (a, b) 内可导 ,
又 F (a) F (b) a 2 f (b) b 2 f (a) F ( ) 2 ( f (b) f (a )) (b 2 a 2 ) f ( ) 0
我们常常需要从函数的导数所给出 的局部的或“小范围”性质, 推出其整体的 或“大范围”性质. 为此, 我们需要建立函 数的差商与函数的导数间的基本关系式, 这些关系式称为“微分学中值定理”. 这些中值定理的创建要归功于费马、 拉格朗日、柯西等数学家.
首先, 从直观上来看看 “函数的差商与函数的导数间的基本关系式” 是怎么一回事.
f ( )
