频率分布直方图
频率分布直方图与折线图课件

优缺点分析
分别分析两种图表在展示 数据方面的优缺点,以便 在实际应用中选择合适的 图表。
实例对比
通过对比实际数据实例, 展示两种图表在展示数据 时的差异和效果。
感谢您的观看
THANKS
频率分布直方图的缺点
对于连续型数据或数据量较小的情况,直方图的表现力可能不够理想。
折线图的优点
能够直观地展示数据随时间或其他变量的变化趋势。能够清晰地展示 数据的趋势和变化。
折线图的缺点
对于数据点较少或数据变化不大的情况,折线图的表现力可能不够理 想。
05
实践练习
制作频率分布直方图
收集数据
首先需要收集一组数据,可以是 关于某班级学生的考试成绩、某
频率分布直方图与折线图课 件
目录
• 引言 • 频率分布直方图 • 折线图 • 比较频率分布直方图与折线图 • 实践练习
01
引言
课程目标
掌握频率分布直方图 和折线图的绘制方法
能够根据实际数据选 择合适的图表进行展 示
理解频率分布直方图 和折线图在数据分析 中的应用
学习内容概述
01
02
03
04
频率分布直方图的概念、特点 和绘制步骤
品牌产品的销售数据等。
确定组距
根据数据的特点和需求,确定 合适的组距,以便将数据分成 若干个区间。
计算频率
根据每个区间的数据个数,计 算出每个区间的频率。
绘制直方图
使用适当的图表软件,根据区间 和频率绘制出直方图,每个矩形
的高度代表该区间的频率。
制作折线图
01
02
03
04
准备数据
准备一组有序的数据点,可以 是时间序列数据或有序分类数
频率分布直方图

风险评估和预测模型构建
风险等级划分
01
在金融、保险等领域中,频率分布直方图可以用于划分风险等
级,评估不同风险水平下的损失分布情况。
预测模型构建
02
在构建预测模型时,频率分布直方图可以帮助确定输入变量的
分布特征,从而选择合适的模型类型和建模方法。
蛋白质表达水平
将蛋白质表达量按不同 水平分组,并通过直方 图呈现各组频数,有助 于分析蛋白质功能与疾 病的关系。
代谢物浓度分布
利用频率分布直方图展 示生物样本中代谢物的 浓度分布情况,为代谢 组学研究和疾病诊断提 供参考。
THANKS
感谢观看
处理异常值
在绘制频率分布直方图之前,可以对数据进行预处理,例如采用箱线图等方法识别并处理 异常值,以减少异常值对直方图形状的影响。同时,也可以在直方图上标注出异常值的位 置和数值,以便观察者更好地了解数据的分布情况。
06
案例:频率分布直方图在医学领域应
用
疾病发病率分布情况展示
发病率地域分布
通过频率分布直方图展示不同地区的疾病发病率,帮助医学研究 者识别高发区域和潜在风险因素。
图形表示不同
条形图用条形的长度表示各类别数 据的频数或频率,而频率分布直方 图用矩形的面积表示各组数据的频 数或频率。
横轴意义不同
条形图的横轴表示类别,而频率分 布直方图的横轴表示数据范围。
02
绘制频率分布直方图步骤
数据收集与整理
收集数据
根据研究目的确定需要收集的数据,并确保数据的准确性和 完整性。
频率分布直方图
汇报人:XX
• 频率分布直方图基本概念 • 绘制频率分布直方图步骤 • 频率分布直方图解读技巧 • 频率分布直方图在数据分析中应用 • 频率分布直方图优缺点及改进措施 • 案例:频率分布直方图在医学领域应
频率分布直方图与组距

通过分析不同特征的频率分布直方图,可以选择对目标变量影响较 大的特征进行建模。
模型评估
在建立预测模型后,可以利用频率分布直方图对模型的预测结果进 行评估,如检查预测值的分布情况是否与实际情况相符。
案例分析
• 数据收集:收集某次考试的成绩数据,包括学生的姓名、成绩等信息。 • 数据分组:根据成绩数据的分布情况,选择合适的组数和数据分组方式,将成绩数据进行分组。 • 绘制频率分布直方图:利用统计软件或编程语言绘制频率分布直方图,展示成绩数据的分布情况。 • 分析结果:通过观察频率分布直方图的形状、峰值、偏态等信息,可以分析考试成绩的分布情况。例如,如果
如果组距过小,则可能使得数据分布的规律性过 于明显,出现较多的异常值或者极端值。
如果组距过大,会导致数据分布的规律性不明显 ,无法准确反映数据的分布情况;
在选择组距时,可以先进行初步的数据分析,了 解数据的分布情况,然后根据实际情况进行调整 。同时,也可以参考一些经验值或者行业标准进 行选择。
03
确定数据分组
在统计学中,为了更好地分析数 据,经常需要将数据进行分组。 频率分布直方图可以帮助确定合 适的组数和数据分组方式。
探索数据规律
通过对频率分布直方图的分析, 可以发现数据中存在的规律,如 周期性变化、异常值等。
数据分析中的应用
数据预处理
在数据分析过程中,频率分布直方图可用于检查数据是否存在异常 值、缺失值等问题,以便进行数据预处理。
观察并比较不同组距下的频率分 布直方图,分析图形在形状、分 布和细节等方面的差异。
根据比较结果,分析不同组距对 频率分布直方图的影响,以及在 实际应用中的适用性和局限性。
05
频率分布直率分布直方图能够直观地展示 数据的分布情况,包括数据的集 中趋势、离散程度和偏态等。
频率分布直方图求平均数

频率分布直方图求平均数引言在统计学中,频率分布直方图是一种用于可视化数据集的方法。
它将数据集划分为一系列的区间,称为组或类别,并显示每个组中数据的频率或数量。
频率分布直方图不仅可以帮助我们了解数据的分布情况,还可以帮助我们计算数据的平均数。
本文将介绍如何使用频率分布直方图来计算数据集的平均数。
一、频率分布直方图的定义和构建频率分布直方图是一种以长方形的柱形来表示数据频率或数量的图表。
横轴表示数据的不同组或类别,纵轴表示频率或数量。
频率分布直方图的构建过程通常包括以下步骤:1. 确定组数和组宽:根据数据的范围和分布情况,确定合适的组数和组宽。
组数通常是一个正整数,而组宽则定义了每个组的范围。
2. 组织数据:将数据划分到各个组中。
每个组包含一个范围内的数据值。
3. 计算频率或数量:对于每个组,计算数据在该组内出现的次数或数量。
4. 绘制直方图:使用柱形来表示每个组的频率或数量。
横轴上的刻度表示各个组,纵轴上的刻度表示频率或数量。
二、频率分布直方图的计算平均数的方法频率分布直方图可以帮助我们计算数据集的平均数。
平均数是一个数据集的中心性度量,代表了数据的平均值。
使用频率分布直方图计算平均数的方法如下:1. 确定每个组的中点:对于每个组,计算该组的中点。
中点可以通过该组的上限和下限之间的平均值来计算。
2. 计算组中心的加权平均数:对于每个组,将该组的中点与该组的频率或数量相乘,得到组中心的加权值。
然后将所有组的加权值相加,除以数据集的总频率或数量,得到加权平均数。
三、示例分析为了更好地理解如何使用频率分布直方图来计算数据集的平均数,以下面的数据集为例进行分析:数据集:[1, 2, 3, 3, 4, 5, 5, 6, 7, 8]1. 确定组数和组宽:我们可以选择将数据集划分为4个组,每个组宽为2。
2. 组织数据:将数据划分到各个组中,得到如下分组情况:组1:[1, 2, 3]组2:[3, 4, 5]组3:[5, 6, 7]组4:[7, 8]3. 计算频率或数量:对于每个组,计算数据在该组内的频率或数量:组1:3个数据组2:3个数据组3:3个数据组4:2个数据4. 绘制直方图:根据频率或数量绘制直方图,得到如下图表:组 | 数据频率------------------组1 | ***组2 | ***组3 | ***组4 | **5. 计算平均数:对于每个组,计算该组的中点。
频数分布表和频率分布直方图课件

Excel制作频数分布表和频率分布直方图方法总结
频数分布表和频率分布直 方图
频数分布表和频率分布直方图是数据分析中常用的工具。通过本课件,我们 将介绍它们的定义、制作方法以及应用范围和重要性。
为什么需要频数分布表和频率 分布直方图?
频数分布表和频率分布直方图帮助我们更好地理解和解释数据。通过可视化 数据,我们可以发现模式、趋势和异常值,从而做出有意义的数据分析。
Excel提供了便捷的功能和工具来制作频数分布表和频率分布直方图。学习如 何使用Excel进行制作,并注意一些细节,可以更高效地进行数据分析。
结论
频数分布表和频率分布直方图在数据分析中应用广泛且具有重要性。它们帮助我们理解数据、发现规律,并为 数据分析提供有力支持。
参考资料
频数分布表知识点总结
频率分布直方图知识点总结
频数பைடு நூலகம்布表
频数是指某个数值或区间在数据集中出现的次数。制作频数分布表可以帮助 我们了解数据的分布情况和集中程度,从而更好地进行统计分析。
频率分布直方图
频率是指某个数值或区间在数据集中出现的频率或概率。通过制作频率分布 直方图,我们可以直观地展示数据的分布情况和集中程度。
使用Excel绘制频数分布表和频 率分布直方图
频率分布直方图第二课时

每个数据集都有其独特的特征,通过 频率分布直方图可以识别这些特征, 如分布的偏态、峰度等。
辅助决策制定过程
数据可视化支持
频率分布直方图作为一种 数据可视化工具,可以为 决策者提供直观的数据支 持。
数据驱动决策
通过对频率分布直方图的 分析和解读,决策者可以 基于数据制定更科学、合 理的决策。
风险评估与预测
不能展示原始数据
与散点图等图表类型相比,频率分布直方图不能直接展示 原始数据点,因此可能无法揭示数据中的某些特定模式或 关系。
适用场景探讨
描述性统计
在描述一组数据的分布情况时, 频率分布直方图是一种常用的工 具。它能够直观地展示数据的形
状、中心趋势和分散程度。
探索性数据分析
在数据分析的初步阶段,可以使用 频率分布直方图来探索数据的分布 情况,为后续的分析提供基础。
优点总结
直观性
频率分布直方图能够直观地展示 数据的分布情况,使得观察者可 以一目了然地看出数据的中心趋 势、分散程度以及可能存在的异
常值。
易于理解
相比于其他复杂的统计图表,频 率分布直方图的构造简单明了, 使得非专业人士也能够快速理解
数据的基本特征。
适用于连续变量
对于连续型数据,频率分布直方 图能够很好地展示其分布情况, 特别是当数据呈现出偏态或峰态
频率分布直方图第二课时
目
CONTENCT
录
• 频率分布直方图基本概念与性质 • 绘制频率分布直方图步骤与技巧 • 频率分布直方图在数据分析中应用 • 案例分析:频率分布直方图在实际
问题中运用 • 频率分布直方图优缺点及适用范围
讨论 • 课堂互动环节与课后作业布置
01
频率分布直方图基本概念与性质
频率分布直方图

频率分布直方图频率分布直方图是一种常用的统计图表,用于展示数据的分布情况。
它通过将数据分成若干个等距的区间,然后统计每个区间内的数据个数,并将统计结果以柱形图的形式呈现,从而直观地反映数据的分布。
本文将详细介绍频率分布直方图的概念、构建方法、应用场景以及注意事项。
一、频率分布直方图的概念频率分布直方图是一种数据可视化工具,用于展示数据的分布情况。
它将数据划分成若干个等距的区间,然后统计每个区间内的数据个数,最后以柱形图的形式呈现。
每个区间的宽度通常相等,但高度则表示该区间内数据的频数。
频率分布直方图可以帮助人们更好地理解数据的特征,比如中心位置、离散程度和偏态与峰态等。
二、频率分布直方图的构建方法构建频率分布直方图的步骤主要包括:确定划分区间、统计频数、绘制柱形图。
1. 确定划分区间在构建直方图之前,需要确定划分区间的个数和宽度。
划分区间的个数通常由数据的样本量和取值范围决定。
如果样本量较大,可以选择更多的区间,以便更准确地反映数据的细节;反之,如果样本量较小,可以选择较少的区间。
划分区间的宽度应该尽可能相等,以避免误导读者。
常用的划分区间方法有等距划分和等频划分。
等距划分是将整个取值范围等分成若干个区间,如每个区间的宽度为5;等频划分是根据数据的频数将取值范围划分为若干个区间,使每个区间内的频数相等。
2. 统计频数统计频数是指计算每个区间内数据的个数。
可以使用计数器或者计算机软件进行统计。
对于连续数据,需要考虑边界问题,即数据应该分到哪个区间中。
3. 绘制柱形图绘制柱形图是最后一步,通过将每个区间的频数表示为柱形的高度来反映数据的分布情况。
柱形图的横轴表示区间,纵轴表示频数。
每个区间的柱形应该相邻且不重叠。
为了增加可读性,可以在柱形上方标注频数的值。
三、频率分布直方图的应用场景频率分布直方图广泛应用于各个领域,可以帮助人们更好地理解数据的分布情况。
1. 经济学在经济学中,频率分布直方图可以用来展示收入、消费等经济指标的分布情况。
频率分布直方图(课堂PPT)

如果将频率分布直方图中各相邻的矩形的底边的中 点顺次连结起来 , 就得到一条折线 , 我们称这条折线 为本组数据的频率折线图 .
17
频率折线图的优点是它反映了数据的变化趋势 . 如 果将样本容量取得足够大 , 分组的组距取得足够小 , 则这条折线将趋于一条曲线 , 我们称这一曲线为总体 分布的密度曲线 .
167 154 159 166 169 159 156 166 162 158 159 156 166 160 164 160 157 156 157 161 160 156 166 160 164 160 157 156 157 161 158 158 153 158 164 158 163 158 153 157 162 162 159 154 165 166 157 151 146 151 158 160 165 158 163 163 162 161 154 165
162 162 159 157 159 149 164 168 159 153
在例子中我们可以直接获取下列信息:
①女生身高的最小值146cm。 ②女生身高的最大值169cm。 ③女生身高在146cm —169cm之间。 除此之外,很难发现其它有用信息。因此需要
借助图表和计算来分析数据,帮助我们找出规
频率分布直方图
09.06.2020 15:40:24
教学目标:
①使学生会列出频率分布表,画出频率分布 直方图,理解频率分布表和频率分布直方图 及其特点。用频率分布直方图解决简单实际 问题。 ②能根据样本频率分布表和频率分布直方图 估计总体分布,了解样本频率分布表和频率 分布直方图的随机性和规律性。
律,把信息转化成直观的易理解的形式。这节
课,我们就学习用频率分布表、频率分布直方
频率分布直方图-高中数学知识点讲解

频率分布直方图
1.频率分布直方图
【知识点的认识】
1.频率分布直方图:在直角坐标系中,横轴表示样本数据,纵轴表示频率与组距的比值,将频率分布表中的各组频率的大小用相应矩形面积的大小来表示,由此画成的统计图叫做频率分布直方图.
2.频率分布直方图的特征
①图中各个长方形的面积等于相应各组的频率的数值,所有小矩形面积和为 1.
②从频率分布直方图可以清楚地看出数据分布的总体趋势.
③从频率分布直方图得不出原始的数据内容,把数据表示成直方图后,原有的具体数据信息被抹掉.
3.频率分布直方图求数据
①众数:频率分布直方图中最高矩形的底边中点的横坐标.
②平均数:频率分布直方图各个小矩形的面积乘底边中点的横坐标之和.
③中位数:把频率分布直方图分成两个面积相等部分的平行于y 轴的直线横坐标.
【解题方法点拨】
绘制频率分布直方图的步骤:。
频率分布表和频率分布直方图课件

人口普查
在人口普查中,需要收集大量的人口数据。频率分布表和频率分布直方
图可以用于分析人口数据的分布情况,了解人口结构、年龄分布、性别
比例等情况。
05 练习与巩固
基础练习题
基础练习题1
根据给出的数据,制作频率分布表和 频率分布直方图。
基础练习题2
根据频率分布表和频率分布直方图, 计算各组的频数、频率和累计频率。
联系与区别
联系
频率分布表和频率分布直方图都是用于描述数据分布特征的 工具,它们都可以展示数据的频数、频率和分布情况。
区别
频率分布表是表格形式,可以提供更详细的数据信息,包括 频数、频率等,而频率分布直方图则更直观地展示数据的分 布形态,可以观察数据的集中趋势、离散程度和分布形态。
转换方法
将频率分布表转换为频率分布直方图
制作方法
数据分组
将数据按照一定的范围 进行分组,确定每个组 的上界和下界。
统计频数
统计每个组内的数据个 数,即频数。
计算频率
频率是频数与数据总数 的比值,用于表示该组 数据出现的相对频率。
制作表格
将分组情况、频数和频 率等信息整理成表格形 式。
实例分析
数据来源 数据分组 统计频数 计算频率 制作表格
在进行数据分析时,首先需要对数据进行探索性分析,以 了解数据的分布、变化规律和特征。频率分布表和频率分 布直方图是数据探索阶段的重要工具。
数据可视化
频率分布直方图是一种有效的数据可视化方法,可以直观 地展示数据的分布情况,帮助分析人员更好地理解数据。
比较分析
通过比较不同数据集的频率分布表和频率分布直方图,可 以分析它们之间的相似性和差异性,进而进行比较分析。
根据频数和频率数据,在坐标系中绘制条形图或直方图,每个条形或柱子的高度 代表该组的频数或频率。
苏教版频率分布直方图

推断统计中应用
01 估计参数
在参数估计中,频率分布直方图可以帮助我们了 解样本数据的分布情况,从而更好地估计总体参 数。
02 假设检验
在假设检验中,频率分布直方图可以帮助我们判 断样本数据是否符合某种理论分布,从而验证研 究假设。
03 预测未来趋势
通过分析历史数据的频率分布直方图,可以预测 未来数据的可能分布情况,为决策提供支持。
02
绘制频率分布直方图步骤
确定数据范围及组数选择
确定数据的最大值和最小值,计算数据范围。 01
根据数据范围选择合适的组数,通常选择5~15组 02 之间,以充分展示数据的分布情况。
确定各组的组距,即每组的宽度,通常选择等距 03 分组。
计算各组频数与频率
01 统计每个数据点落入的组别,得到各组的频数。
数据收集与整理过程回顾
01
02
03
数据收集
收集全班学生的数学成绩, 记录每个学生的分数
数据整理
将成绩按照一定的组距进 行分组,统计每个分数段 内的学生人数
数据呈现
将分组后的数据以表格形 式呈现,包括分数段和对 应的学生人数
频率分布直方图绘制步骤演示
绘制横坐标
将分数段作为横坐标,标注每个分数 段的起始和终止值
02 计算各组的频率,即该组频数与总频数的比值。
02 将频率转换为频率密度,即频率除以组距,以便 在直方图中表示。
绘制直方图并标注信息
在坐标轴上确定各组的位 置,横轴表示数据范围, 纵轴表示频率密度。
根据各组的频率密度绘制 矩形条,高度表示频率密 度,宽度表示组距。
在直方图上标注各组的数 据范围、频数、频率等信 息。
苏教版频率分布直方 图
频率分布直方图

例1:青少年“心理健康”问题引起社会关注,希望中学对全校600名
学生进行了一次“心理健康”知识测试,并从中抽取了部分学生的成 绩(得分取正整数,满分100分)作为样本, (1)填写频率分布表中的空格(2)画频率分布直方图 (3)若成绩在90分以上(不含90分)
为优秀,试估计该校成绩优秀
的有多少人
设抽取的学生人数为n,由已知条 件可得:
2
2
n 0.04, n 0.04 50
0.2
16
0.32
50
练习 1
1.某雷达测速区规定:凡车速大于或等于 70 km/h 的汽车视为“超速”,并将受到处罚, 如图是某路段的一个检测点对 200 辆汽车的车 速进行检测所得结果的频率分布直方图,则从 图中可以看出被处罚的汽车大约有( )
A.30 辆 B.40 辆 C.60 辆 D.80 辆
④列___频__率___分__布___表; ⑤画__频__率___分__布___直__方__图.
频率
在频率分布直方图中,纵轴表示 组距,数据落在各小 组内的频率用小长方形的面积表示,各小长方形的面积总
和等于 1 .
在频率分布直方图中,小矩形的高表示频率,对吗?
不对.小矩形的高表示“频率/组距”,小矩形的面积表示 频率.
A.6 B.8 C.12 D.18
解析:设样本容量为 n,
由题意,得(0.24+0.16)×1×n=20,解得 n=50.
所以第三组频数为 0.36×1×50=18.
因为第三组中没有疗效的有 6 人,所以第三组中有疗效的有 12
人.
答案:C
例【3例 2】 如图是根据部分城市某年 6 月份的平均气温(单位:℃)数据得到
练习 2 (2014·山东卷)为了研究某药品的疗效,选取若干名志愿者进行临床试验.所有志愿者的
频率分布直方图如下
(1)解:如图:茎为成绩的整环数,叶为小数点后的数字
甲
乙
85 2 74
7
1
8
57
4
9
112 78
8751
10
11
(2)乙成绩大致对称,甲成绩的中位数为9.05, 乙成绩的中位数为9.15,所以乙成绩较甲好, 乙成绩较集中于峰值,甲成绩分散
所以乙发挥的稳定性好,甲波动大
练习2:课本71页练习第三题
作业:课本71页练习1,上面的练习1和2。
优化设计
小结:1.什么是频率折线图
2.什么是总体密度曲线及其意义 3.1)认识茎叶图,如何做茎叶图 2)分析茎叶图,3)茎叶图的优缺点
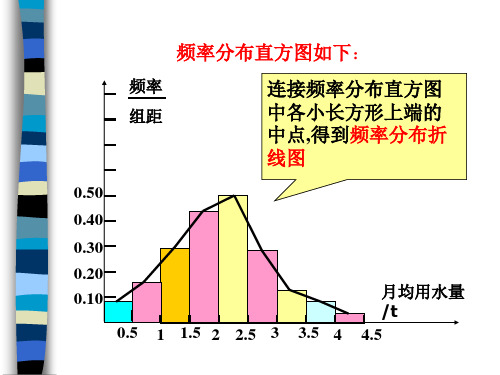
频率分布直方图如下:
频率
连接频率分布直方图
组距
中各小长方形上端的
中点,得到频率分布折
线图
0.50
0.40
0.30
0.20
0.10
月均用水量
/t
0.5 1 1.5 2 2.5 3 3.5 4 4.5
利用样本频率分布对总体分布进行相应估计
(1)上例的样本容量为100,如果增至1000, 其频率分布直方图的情况会有什么变化?假如增 至10000呢?
26
思考: 数据大于俩位数的整数时又如何选茎,叶?
数据为小数时又如何选茎,叶?
结论:1>当数据为整数时:通常个位数字在叶上, 其他位数在茎上(一位数时,茎为0)
2>当数据为小数时:通常小数部分在叶上, 整数部分在茎上
甲的茎叶图画法
也可以画一组数据的茎叶图,竖线左边为茎,
右边为叶。
茎
叶
08
1 364
甲的中位数为26,乙的中位数为36,所以乙较甲成绩要好, 另,乙的叶较甲的更集中于峰值附近,所以乙较甲发挥 更稳定
频数分布表和频率分布直方图课件

在医学领域,频数分布表和频率分布直方图可以用于分析病例数据 、药物疗效等,为医学研究和临床诊断提供支持。
05
制作频数分布表和频率分布直方图 的注意事项
数据来源的可靠性
确保数据来源可靠
在制作频数分布表和频率分布直 方图时,应确保所使用数据的来 源可靠,避免使用不准确或过时
的数据。
验证数据准确性
作用
方便地展示数据的分布情况,帮助我们了解数据的集中趋势、离散程度以及分布形态等特征,为进一步的数据 分析提供基础。
制作步骤
01
02
03
04
收集数据
首先需要收集需要分析的数据 。
数据分组
将数据按照一定的分类标准进 行分组,分组的方法可以根据
实际需求进行选择。
统计频数
统计每组数据的数量,即频数 。
制作表格
应用场景
频数分布表
适用于需要详细了解数据各组频数的场景,如人口普查、销 售数据统计等。
频率分布直方图
适用于需要直观展示数据分布的场景,如市场调研、产品质 量检测等。
实例对比
频数分布表
一个班级的考试成绩统计,可以得出各分数段的学生人数。
频率分布直方图
同个班级的考试成绩分布图,可以直观地看出成绩的集中区域和离散程度。
数据收集
收集需要分析的数据,并进行必要的整理 和筛选,确保数据的质量和准确性。
添加图表元素
在直方图中添加必要的图表元素,如坐标 轴、标题、图例等,以便更好地解释和展 示数据。
数据分组
将数据按照一定的规则进行分组,分组的 方法可以根据实际需求选择,常见的分组 方式有等距分组和等频分组等。
绘制直方图
根据频数和频率数据,绘制条形图来表示 每个数据组的分布情况,பைடு நூலகம்形图的高度代 表频率,宽度代表组距。
