比和比例专题讲解
小学数学知识要点三之比和比例

小学数学知识要点三之比和比例比和比例是小学数学中的一个重要概念。
在教学中,通常会有很多与比和比例相关的题目和问题,学好这一知识点对提升解题能力和数学思维非常重要。
本文将重点讲解比和比例的定义和基本性质,并提供一些相关的例题。
1.比的定义在数学中,比是指将两个数进行比较,用分数或者两个数的比值来表示它们之间的关系。
比的一般形式为a:b,读作“a比b”,其中a和b分别被称为比的两个项。
2.比的基本性质(1)比的大小关系:对于两个比a:b和c:d,如果ad=bc,则两个比相等;如果ad›bc,则a:b大于c:d;如果ad班级男女生人数的比是3:2,其中男生人数为15人,问女生人数是多少人?解:设女生人数为x,则3:2=15:x,将15和3约分得到5和1,所以5:x=15:3,再交叉相乘得到5x=45,解得x=9、所以女生人数是9人。
4.比例的定义比例是指两个或多个相等的比之间的关系。
比例可以用等式或者用冒号表示。
例如,如果两个比a:b和c:d相等,则可以表示为a:b=c:d或者a/b=c/d。
5.比例的基本性质(1)比例的保持性:如果两个比a:b和c:d相等,并且又有b和d不等于0,那么对于任意的正数m,am:bm=cm:dm也成立;(2)比例的逆比:如果a,b和c是三个不为零的实数,且a:b=c:d,则称比a:b和比c:d是互为逆比。
6.比例的延伸应用(1)比例换算:如果a:b=c:d,且已知一个比其中的三个数,可以求解另一个数。
例如,若已知a:b=3:5,且已知b=10,可以求解a=6;(2)合理运用比例:在实际生活中,我们经常用到比例的概念来解决问题。
例如,根据比例关系可以进行商业打折、计算图形的缩放比例等。
综上所述,比和比例是小学数学中的重要概念,学好比和比例的定义、基本性质和应用方法,对提高解题能力和培养数学思维非常重要。
希望本文的讲解能够帮助小学生更好地理解和掌握比和比例的知识。
比和比例讲义
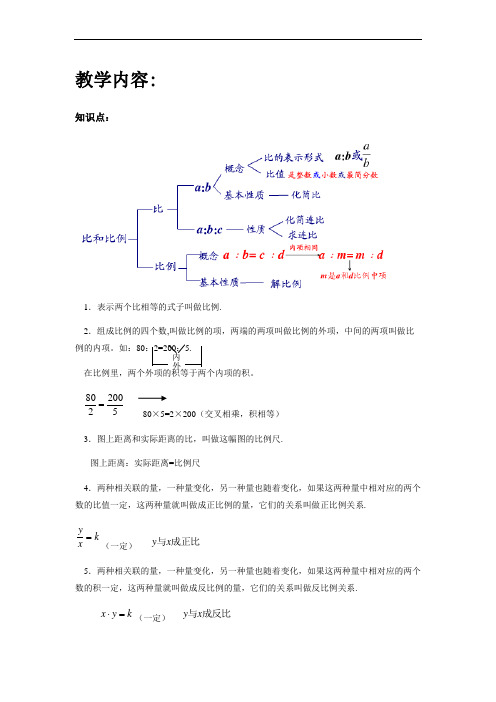
教学内容:知识点:1.表示两个比相等的式子叫做比例.2.组成比例的四个数,叫做比例的项,两端的两项叫做比例的外项,中间的两项叫做比例的内项。
如:80:2=200:5.在比例里,两个外项的积等于两个内项的积。
5200280= 80×5=2×200(交叉相乘,积相等) 3.图上距离和实际距离的比,叫做这幅图的比例尺.图上距离:实际距离=比例尺4.两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系.k x y =(一定) 成正比与x y5.两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系.k y x =⋅(一定) 成反比与x y内外例题讲解: 1.4:( )=2016=( )÷10=( )%解:设4:x =%102016z y =÷=,可以求得x =5,y =8, z =80.2.在3:5里,如果前项加上6,要使比值不变,后项应加 .解:在3:5里,如果前项加6,前项为3+6=9,即扩大了9÷3=3倍,要使比值不变,后项也应扩大3倍,即为5⨯3=15.后项应增加15-5=10.3.12:1的图纸上,精密零件的长度为6厘米,它的实际长度是 毫米.解:根据:实际距离=图上距离÷比例尺.可得:6÷(12:1)=0.5(厘米)=5(毫米).4.买甲、乙两种铅笔共210支,甲种铅笔每支价值3分,乙种铅笔每支价值4分,两种铅笔用去的钱相同,甲种铅笔买了 支.解:甲、乙两种铅笔单价之比为3:4,又两种笔用去的单价相同,故甲乙两种铅笔数之比为4:3.其中甲占总数的344+即74,甲种铅笔数为12074210=⨯(支).5.车库中停放若干辆双轮摩托车和四轮小卧车,车的辆数与车的轮子数的比是2:5.问:摩托车的辆数与小卧车的辆数的比是 .解:因为2:5=4:10,所以4辆车共有10个轮子,如果4辆车全是小卧车,那么轮子数应为16个,比实际多6个.故每4辆车中有摩托车(4⨯4-10)÷(4-2)=3(辆),有小卧车1辆.所以摩托车与小卧车的辆数之比为3:1.7.自然数A 、B 满足182111=-B A ,且A :B =7:13.那么,A +B = .解:设A =7K ,B =13K ,18219161317111==-=-K K K B A ,故K =12,从而A +B =20K =240.8.光明小学有三个年级,一年级学生占全校学生人数的25%,二年级与三年级学生人数的比是3:4,已知一年级比三年级学生少40人,一年级有学生 人.解:二、三年级占全校总数的1-25%=75%,故三年级占全校总数的75%73344=+⨯.一年级比三年级少的40人占全校的285%2573=-.于是全校有22428540=÷(人),一年级学生有224⨯25%=56(人).9.水泥、石子、黄砂各有5吨,用水泥、石子、黄砂按5:3:2拌制某种混凝土,若用完石子,水泥缺 吨.黄砂多 吨. 解:石子占总份数的2353++,即103.当石子用5吨时,混凝土共有32161035=÷(吨),因为水泥占总份数的2355++即21,那么3216吨混凝土中的水泥应为318213216=⨯(吨). 同法可求得3216吨混凝土中的黄砂为:313235216=++⨯(吨) 水泥缺3135318=-(吨),黄砂多3213135=-(吨). 10.甲、乙两人步行的速度比是13:11.如果甲、乙分别由A 、B 两地同时出发相向而行,0.5小时后相遇,如果它们同向而行,那么甲追上乙需要 小时.解:设甲的速度为每小时行13K 米,乙的速度为每小时行11K 千米,则两地相距(13K +11K )⨯0.5=12K 千米.甲追上乙需12K ÷(13K -11K )=6(小时).11.已知甲、乙两数的比为5:3,并且它们最大公约数与最小公倍数的和是1040,那么甲数是多少,乙数是多少.解:设甲和乙的最大公约数为K ,则甲数为5K ,乙数为3K ,它们的最小公倍数为15K .于是K +15K =1040,解得K =65.从而甲数为5⨯65=325,乙数为3⨯65=195.12.有一块铜锌合金,其中铜与锌的比是2:3.现在加入锌6克,共得新合金36克,求在新合金内铜与锌的比. 解:铜在旧合金中占52322=+,故旧合金中有铜125230=⨯(克),有锌30-12=18(克).新合金中,铜仍为12克,锌为18+6=24(克),于是铜与锌的比为12:24=1:2.13.一段路程分成上坡、平路、下坡三段,各段路程长之比依次是1:2:3.某人走各段路所用时间之比依次是4:5:6.已知他上坡时速度为每小时3千米.路程全长50千米.问:此人走完全程用了多少时间? 解:上坡路占总路程的613211=++,上坡路程为3256150=⨯(千米),上坡时间为9253325=÷(小时). 平路时间为3612545925=⨯(小时),下坡时间为3615046925=⨯(小时). 全程时间为125103615036125925=++(小时)14.一个圆柱体的容器中,放有一个长方形铁块.现在打开一个水龙头往容器中注水,3分钟时,水恰好没过长方体的顶面,又过了18分钟,水灌满容器.已知容器的高度是50厘米.长方体的高度是20厘米,那么长方体底面积:容器底面积等于多少?解:注满容器20厘米高的水与30厘米高的水所用时间之比为20:30=2:3.注20厘米的水的时间为123218=⨯(分),这说明注入长方形铁块所占空间的水要用时间为12-3=9(分).已知长方形铁块高为20厘米,因此它们底的面积比等于它们的体积之比,而它们的体积比等于所注入时间之比,故长方形底面面积:容器底面面积=9:12=3:4.厘米,那么长方体底面积:容器底面面积等于多少?二、练习:【热身训练】一、(1)某厂男工人比女工人多51,男工人与全厂职工人数的比是( )(2)行完全程,甲需8小时,乙需6小时,甲乙速度比是( )(3)一个正方体的棱长扩大2倍,得到的新正方体与原正方体的棱长之和之比是( ),表面积之比是( ),体积之比是( )。
比和比例总复习PPT课件

仔细审题 分析问题 建立模型 求解问题 验证答案
认真阅读题目,理解题意,明确解题目标。 对问题进行深入分析,确定解题思路和方法。 根据问题描述,建立数学模型,如比例关系、方程等。 运用数学知识和方法进行计算和推理,得出答案。 对得出的答案进行验证,确保答案的正确性和合理性。
03
比和比例的运算
比的化简
总结词
化简比是指将两个数的比值化简为最简形式,通常使用约分或交 叉相乘的方法。
详细描述
化简比的过程是将两个数的比值进行约分或交叉相乘,以消除公 因数,从而得到最简形式。例如,将比值 24:36 化简为最简形式 2:3。
比例的化简
总结词
化简比例是指将比例中的项进 约分或交叉相乘,以消除公因数 ,从而得到最简形式。
在工程中的运用
建筑设计
建筑师使用比例来设计建筑物的 外观、结构和功能布局,以达到
美观和实用的效果。
机械设计
工程师通过比较不同机械部件的性 能参数,选择合适的材料和工艺, 以确保机械设备的稳定性和可靠性。
电子工程
在电子工程中,比例用于描述电路 元件的电压、电流和阻抗之间的关 系,以确保电子设备的正常运行。
比和比例的综合运算
总结词
比和比例的综合运算是指将比和比例的 运算结合起来,进行一系列的计算和推 理。
VS
详细描述
在比和比例的综合运算中,需要运用化简 、转换等技巧,将问题转化为易于解决的 形式。例如,计算两个数的比值,然后将 结果代入另一个比例中进行计算。
04
比和比例的解题技巧
解题思路
01
02
比例的性质
总结词
比例的性质包括交叉相乘性质和合比 性质。
比和比例专题讲义

比和比例讲义一、知识点:1、两个数相除,又叫做这两个数的比,“:”是比号,比号前面的数叫做比的前项,比号后面的数叫做比的后项,前项除以后项所得的商叫做比值。
比的后项不能为0。
2、分数的基本性质:分数的分子和分母同时乘以或者除以相同的数(0除外),分数的大小不变。
乘积是1的两个数互为倒数。
1的倒数是1,0没有倒数。
3、商不变的规律:在除法里,被除数和除数同时扩大或者同时缩小相同的倍(0除外),商不变。
4、比的基本性质:比的前项和后项同时乘以或者除以相同的数(0除外),它们的比值不变。
5、小数的性质:在小数的末尾添上零或者去掉零小数的大小不变。
6、公因数只有1的两个数叫做互质数。
最简整数比:比的前项和后项是互质数。
7、比的化简:用商不变的性质、分数的基本性质或比的基本性质来化简。
8、比例:①表示两个比相等的式子叫做比例。
如:(3:4=9:12)。
比例有四个项,分别是两个内项和两个外项。
在3:4=9:12中,其中3与12叫做比例的外项,4与9叫做比例的内项。
比例的四个数均不能为0。
9、比例的基本性质:在一个比例中,两个外项的积等于两个内项的积。
10、比、比例、比例尺、百分数的后面不能带单位。
二、比和比例的比较:典型例题:判断两个量是否成正比例、反比例或不成比例。
一、写(写出数量关系式)1、根据数量间的关系或公式,写出数量关系式。
如,①宽一定,长方形的面积和长是否成正比例。
②圆锥的体积一定,底面积和高是否成反比例。
2、注意:写出的数量关系式,其中的一边(左边)只能有这两个相关联的量,不能有多余的量和数字。
二、看(1、看是否相关联2、看是否能变化3、看是否商(积)一定) 1、看是否相关联:也就是一个量变化了,另一个量是否也会随着变化。
2、看是否能变化:也就是这两个量都是能变化的,不是固定的。
3、看是否商(积)一定:也就是这两个量相除(或相乘)的结果是否固定不变的。
三、列(列出几组数据)列出几组数据,然后看这两个量是否相关联,比值或积是否一定。
比和比例知识点整理

比和比例知识点整理比和比例是初中数学中的重要概念,也是高中数学中的基础概念之一。
了解和掌握比和比例的相关知识,不仅是学好数学的前提,还是日常生活中进行比较和计算的基础。
本文将就比和比例的相关知识点进行整理和阐述。
一、比的概念比是指两个数之间的大小关系,通常用冒号“:”表示,如3:5。
其中,3称为比的前项,5称为比的后项。
比的大小可以用比的分数表示,即3:5=3/5。
二、比的性质1.比的前项和后项可以交换位置,但比的大小不变。
2.对比的前、后项同时乘以同一个非零数,比的大小不变。
3.对比的前、后项同时除以同一个非零数,比的大小不变。
三、比例的概念比例是指两个或两个以上的比之间的相等关系,通常用“=”号表示,如3:5=6:10。
其中,3和6称为比例的前项,5和10称为比例的后项。
四、比例的性质1.比例的前、后项同时乘以同一个非零数,比例不变。
2.比例的前、后项同时除以同一个非零数,比例不变。
3.如果两个比例的前项和后项分别相等,则它们相等。
五、比例的应用1.比例的简化:将比例的前、后项同时除以它们的最大公约数,得到的比例即为最简比例。
2.比例的扩大和缩小:将比例的前、后项同时乘以同一个数,得到的比例即为扩大或缩小后的比例。
3.求解未知量:利用已知比例中的三个量,可以求解出第四个量。
例如,已知3:5=6:x,可以通过横向对称法求解出x=10。
4.比例的混合运算:将比例和数值运算相结合,进行加减乘除等运算。
六、实际问题中的比例比例在实际问题中有广泛的应用,例如:1.商品打折:如一件原价为100元的商品打8折,其打折后的价格为80元,其中,原价和打折后的价格组成了一个比例关系。
2.地图比例尺:如1:50000表示地图上的1厘米对应实际地面上的50000厘米,这种比例关系是进行地图测量和规划的基础。
3.身高体重比例:如一个人身高为1.75米,体重为70公斤,则他的身高体重比例为1:40。
七、结语比和比例是数学中的基础概念,也是生活中经常使用的计算方法。
第四讲 比和比例(讲义)

第四讲比和比例(讲义)教学目标:1. 能够根据所给的比例求出未知数。
2. 能够正确比较两个或多个数的大小。
3. 能够灵活运用比和比例解决实际问题。
教学重点:1. 比例的概念与表示方法。
2. 比例中未知数的求解。
3. 比较数的大小。
教学难点:1. 支之所与比之关系的理解。
2. 在实际问题中灵活应用比和比例。
教学过程:一、导入新课(5分钟)老师先画一个下面宽,上面窄的梯形,再画一个下面宽,上面尖的箭头,让学生观察这两个形状,看哪一个更长,哪一个更短,引导学生发现这是在比较两个形状的大小,由此引出今天的主题--比和比例。
二、概念和表示方法(20分钟)1、比例的概念老师把两个相似的图形拿出来,让学生发现他们的长宽比是一样的,也就是说,这种关系叫做“比例”,定义为:用两个数或两个量之间的比值来表达它们的相对大小关系的式子,叫做比例。
比例是数学中一个极为常见、极其重要的概念,它在实际生活中应用比较广泛。
比如:材料的配比、身高、体重等比例关系等。
2、比例的表示方法老师拿出几组实例,让学生发现其中的比例关系,然后教授其表示方法,用两个数或两个量之间的比值来表示,常用冒号或分数表示。
如:3:5、3/5。
三、比例中未知数的求解(25分钟)1、比例中未知数的求解老师画一个小商店平时的进货和销售表格,让学生发现,进货价和售价都有数量和价格的两个要素,而在实际情况下,可能知道售价和数量,却不知道进货价,这时可以利用比和比例的知识来求解未知数。
老师拿出几个实例,给学生讲解具体步骤,即把已知量和未知量写成两个分数,使两个分数的值相等,求解未知量。
,如:如果5支笔的售价为40元,那么一支笔的售价是多少?2、解一次线性方程老师可以用此题目进行补充此概念,即用代数方法把一些问题表示成形如ax+b=c的式子,并求出未知数x的值。
四、比较数的大小(15分钟)老师可以用实例的形式介绍一下比较数的大小,如:“小区有300多户人家,张家家庭人口为5人,占小区人口的比例是多少?”学生经过计算可得:5/300≈0.017,如果将这个数改写为百分数,就是1.7%,张家占小区人口的比例很小,即居民家庭人口越小,占小区人口比例越小。
六年级比和比例知识点讲解

六年级比和比例知识点讲解比和比例是数学中重要的概念之一,对于六年级的学生来说,理解和掌握比和比例的概念非常重要。
本文将详细介绍比和比例的定义、性质以及应用,帮助学生更好地理解和运用比和比例知识。
一、比的概念及性质比是指两个量之间的大小关系,可以用分数或比例的形式表示。
比的一般形式为a:b,读作“a比b”。
其中,a称为比的前项,b称为比的后项。
比的两个项必须是同类的量,即具有相同的单位。
比的性质如下:1. 相等性:如果两个比的前项与后项互相相等,那么这两个比相等。
例如,4:6和2:3是相等的比。
2. 反比:两个比的前项与后项互为倒数时,这两个比称为反比。
例如,3:4和4:3是反比。
3. 异比:两个比的前项与后项既不相等,也不互为倒数时,这两个比称为异比。
例如,5:6和3:4是异比。
二、比例的概念及性质1. 比例的概念:当两个或多个比相等时,它们之间称为比例。
比例通常用冒号(:)或“=”符号表示。
2. 比例的性质:比例有以下几个重要的性质:a. 交换性:比例中的前、后项可以互换位置而保持比例不变。
例如,如果a:b=c:d,那么b:a=d:c。
b. 归结性:如果在一个比例中,两个比都是由同一个数相除而得到的,那么这两个比互为倒数。
例如,如果a:b=4:6,那么b:a=6:4=3:2。
c. 增量乘性:比例中的前、后项同时乘以同一个数,得到的新比例与原比例相等。
例如,如果a:b=4:6,那么2a:2b=8:12。
d. 变量比例:比例中的前项与后项都含有一个变量时,可以通过代入不同的值来求解这个变量的取值。
例如,如果a:b=3:5,且a=12,那么可以利用已知比例求解b的值。
三、比和比例的应用比和比例在日常生活和实际问题中有广泛的应用。
以下是一些常见的应用场景:1. 真实比例:在地图上,使用比例尺可以将真实世界的地理距离映射到纸面上,帮助我们进行测量和导航。
2. 长度比例:在实际测量中,我们可以使用比例来计算物体的长度、宽度等尺寸。
比和比例总结讲解+例题解析

比和比例总结讲解+例题解析比和比例是数学中常见的概念,在实际生活中也有很多应用。
本文将对比和比例的概念进行总结讲解,并提供一些例题解析。
一、比的概念比是两个数或物品在数量、大小、质量等方面的关系,用冒号(:)表示。
如2:3表示第一个数是第二个数的2/3。
二、比例的概念比例是两个或多个比之间的关系,用等号(=)表示。
如2:3=4:6表示前者的比是后者的比的相等关系。
三、比例的性质1.比例的交换律:a:b=c:d等于c:d=a:b。
2.比例的比例律:a:b=c:d, b:e=f:g,则a:e=c:g。
3.比例的倍数律:a:b=c:d,则ka:kb=kc:kd。
4.比例的倒数律:a:b=c:d,则b:a=d:c。
四、比例的应用1.求未知量在已知两个量的比例和其中一个量的值的情况下,可以求出另一个量的值。
如已知2:3=4:x,可以用比例的性质,将比例转化为等式,解出未知数x=6。
2.比例的分配在已知两个量的比例和其中一个量的值的情况下,可以求出另一个量在这个比例下的值。
如已知2:3=4:x,已知x=6,则2:3=4:6,可以求出x在这个比例下的值为9。
五、例题解析例题1:已知a:b=3:4,b:c=5:6,求a:b:c的大小关系。
解:由已知可得a:b=3:4,b:c=5:6,则a:b:c=3:4:6,即a:b:c=1:4/3:2。
例题2:已知a:b=4:5,c:b=6:7,求a:c的大小关系。
解:将两个比例的两个已知量对应相乘,得到a:c=24:35,即a:c=4:5/7。
总结:比和比例是数学中的基础概念,掌握了比例的性质和应用方法,可以在实际生活中解决一些问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
比和比例教学目标:1、比例的基本性质2、熟练掌握比例式的恒等变形及连比问题3、能够进行各种条件下比例的转化,有目的的转化;4、单位“1”变化的比例问题5、方程解比例应用题知识点拨:比例与百分数作为一种数学工具在人们日常生活中处理多组数量关系非常有用,这一部分内容也是小升初考试的重要内容.通过本讲需要学生掌握的内容有:一、比和比例的性质性质1:若a: b=c:d,则(a + c):(b + d)= a:b=c:d;性质2:若a: b=c:d,则(a - c):(b - d)= a:b=c:d;性质3:若a: b=c:d,则(a +x c):(b +x d)=a:b=c:d;(x为常数)性质4:若a: b=c:d,则a×d = b×c;(即外项积等于内项积)正比例:如果a÷b=k(k为常数),则称a、b成正比;反比例:如果a×b=k(k为常数),则称a、b成反比.二、主要比例转化实例①x ay b=⇒y bx a=;x ya b=;a bx y=;②x ay b=⇒mx amy b=;x may mb=(其中0m≠);③x ay b=⇒x ax y a b=++;x y a bx a--=;x y a bx y a b++=--;④x ay b=,y cz d=⇒x acz bd=;::::x y z ac bc bd=;⑤x的ca等于y的db,则x是y的adbc,y是x的bcad.三、按比例分配与和差关系⑴按比例分配例如:将x个物体按照:a b的比例分配给甲、乙两个人,那么实际上甲、乙两个人各自分配到的物体数量与x的比分别为():a a b+和():b a b+,所以甲分配到axa b+个,乙分配到bxa b+个.⑵已知两组物体的数量比和数量差,求各个类别数量的问题例如:两个类别A、B,元素的数量比为:a b(这里a b>),数量差为x,那么A的元素数量为axa b-,B的元素数量为bxa b-,所以解题的关键是求出()a b-与a或b的比值.四、比例题目常用解题方式和思路解答分数应用题关键是正确理解、运用单位“l”。
题中如果有几个不同的单位“1”,必须根据具体情况,将不同的单位“1”,转化成统一的单位“1”,使数量关系简单化,达到解决问题的效果。
在解答分数应用题时,要注意以下几点:1.题中有几种数量相比较时,要选择与各个已知条件关系密切、便于直接解答的数量为单位“1”。
2.若题中数量发生变化的,一般要选择不变量为单位“1”。
3.应用正、反比例性质解答应用题时要注意题中某一数量是否一定,然后再确定是成正比例,还是成反比例。
找出这些具体数量相对应的分率与其他具体数量之间的正、反比例关系,就能找到更好、更巧的解法。
4. 题中有明显的等量关系,也可以用方程的方法去解。
5. 赋值解比例问题例题精讲:模块一、比例转化【例 1】 已知甲、乙、丙三个数,甲等于乙、丙两数和的13,乙等于甲、丙两数和的12,丙等于甲、乙两数和的57,求::甲乙丙. 【解析】 由甲等于乙、丙两数和的13,得到甲等于三个数和的113+14=,同样的乙等于甲、丙两数和的112+13=,同样的丙等于甲、乙两个数和的557512=+ ,所以115::::3:4:54312==甲乙丙. 【例 2】 已知甲、乙、丙三个数,甲的一半等于乙的2倍也等于丙的23,那么甲的23、乙的2倍、丙的一半这三个数的比为多少?【解析】 甲的一半、乙的2倍、丙的23这三个数的比为1:1:1,所以甲、乙、丙这三个数的比为()121:12:123⎛⎫⎛⎫÷÷÷ ⎪ ⎪⎝⎭⎝⎭即132::22,化简为4:1:3,那么甲的23、乙的2倍、丙的一半这三个数的比为()214:12:332⎛⎫⎛⎫⨯⨯⨯ ⎪ ⎪⎝⎭⎝⎭即83:2:32,化简为16:12:9. 【例 3】 如下图所示,圆B 与圆C 的面积之和等于圆A 面积的45,且圆A 中的阴影部分面积占圆A 面积的16,圆B 的阴影部分面积占圆B 面积的15,圆C 的阴影部分面积占圆C 面积的13.求圆A 、圆B 、圆C 的面积之比.【解析】 设A 与B 的共同部分的面积为x ,A 与C 的共同部分的面积为y ,则根据题意有()()564A B C x y =+=+,5B x =,3C y =,于是得到()56453B C B C ⎛⎫+=+ ⎪⎝⎭,这条式子可化简为15B C =,所以()5204A B C C =+=.最后得到::20:15:1A B C =. 【例 4】 某俱乐部男、女会员的人数之比是3:2,分为甲、乙、丙三组.已知甲、乙、丙三组的人数比是10:8:7,甲组中男、女会员的人数之比是3:1,乙组中男、女会员的人数之比是5:3.求丙组中男、女会员人数之比.【解析】 以总人数为1,则甲组男会员人数为103310873110⨯=+++,女会员为31110310⨯=,乙组男会员为8511087535⨯=+++,女会员为1335525⨯=;丙组男会员为33113+210510⎛⎫-+= ⎪⎝⎭,女会员为21393+2102550⎛⎫-+= ⎪⎝⎭;所以,丙组中男、女会员人数之比为19:5:91050=. 【巩固】 一项公路的修建工程被平均分成两份承包给甲、乙个工程队建设,两个工程队建设了相同多的一段时间后,分别剩下60%、40%的任务没有完成,已知两个工程队的工作效率(建设速度)之比3:1,求这两个工程队原先承包的修建公路长度之比.【解析】 (法一)甲工程队以3倍乙工程队建设速度,仅完成了40%的承包任务,而乙工程队完成了60%,所以甲工程队承包任务的40%等于乙工程队承包任务的60%3180%⨯=,所以甲工程队的承包的任务是乙工程队承包任务的180%40%450÷=,所以两个工程队承包的修建公路长度之比为450%:19:2=. (法二)两个工程队完成的工程任务(修建公路长度)之比等于工作效率之比,等于3:1,而他们分别完成了各自任务的40%和60%,所以两个工程队承包的修建公路长度之比为()()340%:160%9:2÷÷=.【例 5】 某团体有100名会员,男女会员人数之比是14:11,会员分成三组,甲组人数与乙、丙两组人数之和一样多,各组男女会员人数之比依次为12:13、5:3、2:1,那么丙组有多少名男会员?【解析】 会员总人数100人,男女比例为14:11,则可知男、女会员人数分别为56人、44人;又已知甲组人数与乙、丙两组人数之和一样多,则可知甲组人数为50人,乙、丙人数之和为50人,可设丙组人数为x 人,则乙组人数为()50x -人,又已知甲组男、女会员比为12:13,则甲组男、女会员人数分别为24人、26人,又已知乙、丙两组男、女会员比例,则可得:5224(50)5683x x +-+=,解得18x =.即丙组会员人数为18人,又已知男、女比例,可得丙组男会员人数为218123⨯=人. 【例 6】 (2007年华杯赛总决赛)A 、B 、C 三项工程的工作量之比为1:2:3,由甲、乙、丙三队分别承担.三个工程队同时开工,若干天后,甲完成的工作量是乙未完成的工作量的二分之一,乙完成的工作量是丙未完成的工作量的三分之一,丙完成的工作量等于甲未完成的工作量,则甲、乙、丙队的工作效率的比是多少?【解析】 根据题意,如果把A 工程的工作量看作1,则B 工程的工作量就是2,C 工程的工作量就是3.设甲、乙、丙三个工程队的工作效率分别为x 、y 、z .经过k 天,则:()()()22133213kx ky ky kz kz kx =-⎧⎪=-⎨⎪=-⎩将⑶代入⑵,得()243kx ky +=, 将⑷代入⑴,得2223kx kx +=-,47x k=, 将47x k =代入⑴,得67y k =.代入⑶,得37z k=. 甲、乙、丙三队的.工作效率的连比是463::4:6:3777k k k=. 【巩固】 某次数学竞赛设一、二、三等奖.已知:①甲、乙两校获一等奖的人数相等;②甲校获一等奖的人数占该校获奖总人数的百分数与乙校相应的百分数的比为5:6;③甲、乙两校获二等奖的人数总和占两校获奖人数总和的20%;④甲校获三等奖的人数占该校获奖人数的50%;⑤甲校获二等奖的人数是乙校获二等奖人数的4.5倍.那么,乙校获一等奖的人数占该校获奖总人数的百分数等于多少?【解析】 由①、②可知甲、乙两校获奖总人数的比为6:5,不妨设甲校有60人获奖,则乙校有50人获奖.由③知两校获二等奖的共有(6050)20%22+⨯=人;由⑤知甲校获二等奖的有22(4.51) 4.518÷+⨯=人;由④知甲校获一等奖的有606050%1812-⨯-=人,那么乙校获一等奖的也有12人,从而所求百分数为1250100%24%÷⨯=.【例 7】 ①某校毕业生共有9个班,每班人数相等.②已知一班的男生人数比二、三班两个班的女生总数多1;③四、五、六班三个班的女生总数比七、八、九班三个班的男生总数多1.那么该校毕业生中男、女生人数比是多少?【解析】 如下表所示,由②知,一、二、三班的男生总数比二、三班总人数多1;由③知,等,则女生总数等于四个班的人数之和.所以,男、女生人数之比是5:4.模块二、按比例分配与和差关系(一)量倍对应【例 8】 一些苹果平均分给甲、乙两班的学生,甲班比乙班多分到16个,而甲、乙两班的人数比为13:11,求一共有多少个苹果?【解析】 一共有()()1613111311192÷-⨯+=个苹果.【巩固】 小新、小志、小刚三人拥有的藏书数量之比为3:4:6,三人一共藏书52本,求他们三人各自的藏书数量.【解析】 根据题意可知,他们三人各自的藏书数量分别占三人藏书总量的3346++、4346++、6346++,所以小新拥有的藏书数量为35212346⨯=++本,小志拥有的藏书数量为45216346⨯=++本,小刚拥有的藏书数量为65224346⨯=++本. 【巩固】 在抗洪救灾区活动中,甲、乙、丙三人一共捐了80元.已知甲比丙多捐18元,甲、乙所捐资的和与乙、丙所捐资的和之比是10:7,则甲捐 元,乙捐 元,丙捐 元.【解析】 由于甲比丙多捐18元,所以甲、乙所捐资的和比乙、丙所捐资的和多18元,那么甲、乙所捐资的和为:18(107)1060÷-⨯=(元),乙、丙所捐资的和为601842-=元.所以,甲捐了804238-=(元),乙捐了603822-=(元),丙捐了381820-=(元).【巩固】 有120个皮球,分给两个班使用,一班分到的13与二班分到的12相等,求两个班各分到多少皮球?【解析】 根据题意可知一班与二班分到的球数比11:3:223=,所以一班分到皮球31207232⨯=+个,二班分到皮球1207248-=个. 【例 9】 一班和二班的人数之比是8:7,如果将一班的8名同学调到二班去,则一班和二班的人数比变为4:5.求原来两班的人数.【解析】 原来一班的人数为两班总人数的888715=+,调班后一班的人数是两班人数的44459=+,调班前后一班人数的比值为84:6:5159=,所以一班原来的人数为()865648÷-⨯=人,二班原来的人数为488742÷⨯=人.【例 10】 幼儿园大班和中班共有32名男生,18名女生.已知大班男生数与女生数的比为5:3,中班男生数与女生数的比为2:1,那么大班有女生多少名?【解析】 由于男、女生人数有比例关系,而且知道总数,所以可以用鸡兔同笼的方法.假设18名女生全部是大班,则大班男生数:女生数5:330:18==,即男生应有30人,实际上男生有32人,相差2个人;又中班男生数:女生数2:16:3==,以3个中班女生换3个大班女生,每换一组可增加1个男生,所以需要换2组;所以,大班女生有183212-⨯=(名).【巩固】 参加植树的同学共有720人,已知六年级与五年级人数的比是3:2,六年级比四年级多80人,三个年级参加植树的各有多少人?【解析】 假设四年级和六年级人数同样多,则参加植树的同学共有72080800+=人,四、五、六三个年级的人数比为3:2:3,知道三个量的和及它们的比,就可以按比例分配,分别求出三个年级参加植树的人数.六年级:3800300323⨯=++人;五年级:2800200323⨯=++人;四年级:30080220-=人. 【巩固】 圆珠笔和铅笔的价格比是4:3,20支圆珠笔和21支铅笔共用71.5元.问圆珠笔的单价是每支多少元?【解析】 设圆珠笔的价格为4,那么铅笔的价格为3,则20支圆珠笔和21支铅笔的价格为20×4+21×3=143,则单位“1”的价格为71.5÷143=0.5元.所以圆珠笔的单价是O .5×4=2(元).【例 11】 甲、乙两只蚂蚁同时从A 点出发,沿长方形的边爬去,结果在距B 点2厘米的C 点相遇,已知乙蚂蚁的速度是甲的1.2倍,求这个长方形的周长.【解析】 两只蚂蚁在距B 点2厘米的C 点相遇,说明乙比甲一共多走了224⨯=(厘米).又知乙蚂蚁的速度是甲蚂蚁的1.2倍,相同时间内乙蚂蚁爬的路程与甲蚂蚁爬的路程比为:1.2:1=6:5,所以甲爬的路程是()465520÷-⨯=(厘米),乙爬的路程是20424+=(厘米),长方形的周长为202444+=(厘米).【例 12】 甲乙两车分别从 A , B 两地出发,相向而行.出发时,甲、乙的速度比是5∶4,相遇后,甲的速度减少20%,乙的速度增加20%,这样,当甲到达B 地时,乙离A 地还有10千米.问:A ,B 两地相距多少千米?【解析】 甲、乙原来的速度比是5∶4,相遇后的速度比是:[5×(1-20%)]∶[4×(1+20%)]=4∶4.8=5∶6.相遇时,甲、乙分别走了全程的95和94。
