第12讲-相对定向

合集下载

摄影测量学教案(第12-1讲相对定向).doc

（22）
1
同理可解算连续像对相对方位元素，结果如下：
1 1 f2 by (q2 q4 q6 ) ( 2 )(2q1 2q2 q3 q4 q5 q6 ) 3 6 2y f bz (q 4 q6 ) 2y f x (q3 q 4 q5 q 6 ) 2by f 2 (2q1 2q2 q3 q4 q5 q6 ) 4y 1 k (q1 q 2 q3 q 4 q5 q6 ) 3b （23）

BX x1 x2
BY y1 y2
BZ z1 0 z2
（2）
这便是连续像对系统的共面条件方程。
图2 图 2 表示在以基线坐标系为基础的单独像对系统中的情形，同样 a1 , a 2 是同名像点， R1 S1a1 ， R2 S 2 a2 。如果以 X 1、Y1、Z1 和 X 2、Y2、Z 2 表示 R1 , R2 在基线坐标系中的坐标分量，则（1）式可以用坐标分量的形式表示为：
从重建空间几何立体模型的角度引入相对定向的概念
三、共面条件方程
在恢复了像对的相对方位元素时，同名光线在各自的核面内对对相交，这些交点就构成了一个与实地相似的几何模型。从数学上表述构成这种几何模型的条件为：所有同名光线与基线共面。表示这个条件的方程便是共面条件方程。共面条件方程的基本形式是基线向量 B 与左右投影向量 R1 , R2 的混合积等于零，即：
F F0
其中：
F F F F F d d d x 2 d2 d 2 0 （9） x 2 2 2 提问： DLT
中的 11 个元素是相互独立的吗？
d 0 d 0 0 d x2 x2 x 2

第12讲空间前方交会

S Z
Y
B
BX
a
Y X A S
Z Y
S
X
BZ
BY
a
Z
X
Y S
[二]空间前方交会公式
XYN NXYB BYX
NX NY
(5)
ZNZBZ NZ Z
Y
B
(c)
N
BX Z BZ X XZ ZX
S
BX
a
N
BX Z BZ X XZ ZX
Z
Y X A
A
Z Y
S
S BZ
X
BY
a
Z
X
Y
[二]空间前方交会公式
B
B
2 X
B
2 Y
B
2 Z
[三]模型点坐标和地面点坐标的计算过程 1、模型点坐标的计算 a. 连续像对相对定向之后，模型点坐标的计算过程
原始数据
确定角方位元素和基线分量
计算左右片在摄测坐标系中旋转矩阵的方向余弦
a1 a2 a3
b1
b2
b3
E
c1 c2 c3
a1 a 2 a 3
b1
b 2
(X,Y,Z),(X,Y,Z)
计算投影系数 N和 N 计算模型点坐标（ X,Y,Z）
X NX
Y
1 2
(NY
NY
BY
)
Z NZ
为什么Y 取中数？
X,Z?
[三]模型点坐标和地面点坐标的计算过程 1、模型点坐标的计算 a. 连续像对相对定向之后，模型点坐标的计算过程
Z Y
Z
XYNNXYBBYX
Z
BZ
N f
[二]空间前方交会公式

学习测绘技术中的相对定向与绝对定向原理与方法

学习测绘技术中的相对定向与绝对定向原理与方法测绘技术是土地资源管理、城市规划、地形地貌、环境保护等领域中不可或缺的重要工具。

其中，相对定向和绝对定向是测绘技术中两个重要的概念。

本文将深入探讨相对定向与绝对定向的原理与方法。

一、相对定向的原理与方法相对定向是测绘技术中的一个基本概念，其主要目的是确定不同航片之间的相对方位关系。

相对定向的过程包括：图像坐标测量、航带布方、相对定向计算和网片平差。

1. 图像坐标测量图像坐标测量是相对定向的第一步，主要通过肉眼观察或计算机自动提取特征点进行。

常用的特征点有角点、交点等，可以通过这些特征点在航带上进行标注和测量，得到图像坐标。

2. 航带布方航带布方是相对定向的一个重要环节，其目的是实现不同航带之间的精确定位。

布方需要确定具有高精度的起始点、目标点和连接点作为基准，通过测量和计算航带之间的连线长度和角度，确定航带之间的相对位置关系。

3. 相对定向计算相对定向计算是相对定向的核心部分，其主要目的是通过空间后方交会等方法计算不同航带之间的相对方位关系。

常见的相对定向计算方法有解析解法和数值解法。

解析解法适用于简单的相对定向问题，而数值解法适合于复杂的相对定向问题。

4. 网片平差网片平差是相对定向的最后一步，其主要目的是通过调整和优化相对定向计算结果，消除误差。

常见的网片平差方法有最小二乘法和全球最小差法。

最小二乘法通过最小化观测值与估计值的残差平方和来求得最优解，而全球最小差法则通过迭代求解来优化结果。

二、绝对定向的原理与方法绝对定向是在相对定向的基础上，确定航片与地面坐标系之间的外方位元素。

绝对定向包括地面控制点选择、光束法平差、外方位元素计算以及精度评定等步骤。

1. 地面控制点选择地面控制点是绝对定向的基础，其目的是通过标志物或人工测量点将航片与地面实际坐标系联系起来。

选择合适的地面控制点需要兼顾数量、分布、均匀性以及观测条件等因素。

2. 光束法平差光束法平差是绝对定向的核心环节，其目的是根据航测数据和地面控制数据，通过光束法的原理进行计算和调整。

相对定向和绝对定向的解析过程(全面)

三、相对定向元素的计算过程
量测 5 个以上的同名点（定向点）明显点 1、2点：左、右片的像主点人工量测：六个标准点位 3、5点：X=0，Y值最大 4、6点：X=b，Y值最大
3
4
X
1
2
5
6
相对定向标准点位
计算框图：以连续像对的相对定向为例
输入像点坐标（x1,y1）,（x2,y2）确定初始值bu=(x1-x2)1 φ 2=ω 2=κ 2=μ =ν =0 计算右片旋转矩阵R2 计算像点的像空间辅助坐标(u1 v1 w1)和(u2 v2 w2) 逐点计算误差方程式系数和常数项否
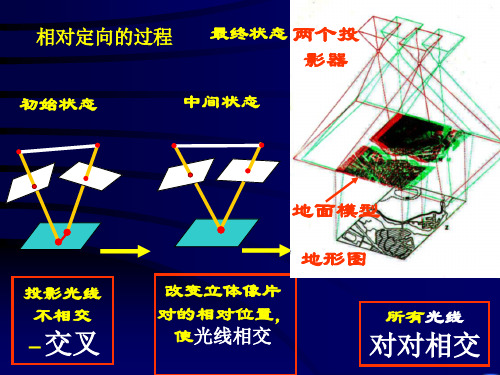
相对定向的过程
初始状态
最终状态两个投
影器
中间状态
地面模型地形图
投影光线不相交
－交叉改变立体像片对的相对位置，使光线相交所有光线
对对相交
1、连续像对相对定向元素：以左片为基准，右片相对于左片的相对方位元素 S1 u1v1w1 左片的像空间坐标系像空间辅助坐标系的选取： S2 u2v2 w2 与 S1 u1v1w1相应坐标轴平行 w2 左、右片相对方位元素 v2 左像片 S2 w1 u2 X S1 0, YS1 0, Z S1 0 y b B w v1 1 0, 1 0, 1 0 bv 右像片 S u
w1 w2
v1
S1 u1
y1
v2 b
S2
X S1 0, YS1 0, Z S1 0
u2
1 , 1 0, 1
右像片
X S 2 bu b, YS 2 bv 0, Z S 2 bw 0
y2
x2
1
1 2
1、1、2、2、2

摄影测量学教案(第121讲相对定向)

第14 次课首页教案正文第十四讲相对定向理论备注一、上讲内容回顾与相关知识复习● 直接线性变换（DLT ）形式的构像方程式 ● 像片纠正● 连续像对相对方位元素系统 ● 单独像对相对方位元素系统 ● 共面条件、上下视差、左右视差二、内容的引出、内容安排、难点重点介绍● 共面条件方程（重点） ● 连续像对相对定向方程（难点） ● 单独像对相对定向方程（难点） ● 相对方位元素的解算（重点）三、共面条件方程在恢复了像对的相对方位元素时，同名光线在各自的核面内对对相交，这些交点就构成了一个与实地相似的几何模型。

从数学上表述构成这种几何模型的条件为：所有同名光线与基线共面。

表示这个条件的方程便是共面条件方程。

共面条件方程的基本形式是基线向量B与左右投影向量21R R ,的混合积等于零，即：021 )(R R B（1）为了进行计算，必须使用共面条件的坐标表达式，因此在不同的坐标系统中，共面条件的表达式是不同的。

图1从重建空间几何立体模型的角度引入相对定向的概念图1表示在以左像空系为基础的连续像对系统中的情形。

图中，21aa,是同名像点，111aSR，222aSR。

如果以111zyx、、和222zyx、、表示21RR,在坐标系中的坐标分量，则（1）式可以用坐标分量的形式表示为：222111zyxzyxBBBZYX（2）这便是连续像对系统的共面条件方程。

图2图2表示在以基线坐标系为基础的单独像对系统中的情形，同样21aa,是同名像点，111aSR，222aSR。

如果以111ZYX、、和222ZYX、、表示21RR,在基线坐标系中的坐标分量，则（1）式可以用坐标分量的形式表示为：222111ZYXZYXBX（3）这便是单独像对系统的共面条件方程。

无论是（2）式还是（3）式，对于相对方位元素而言是非线性的，并且没有直接表达为相对方位元素的函数形式，为了便于解算相对方位元素，还需要进行线性化。

四、连续像对的相对定向方程将（2）式按第一行元素展开，为：221122112211yxyxBzxzxBzyzyBZYX（4）（4）式可改化为对比共线条件方程211222121122()x y x y y q d d f d x dk x dk f f f（19）六、相对方位元素的解算以单独像对相对定向为例，讨论相对方位元素的解算过程。

相对定向原理

8 求未知数新值，即初始值改正数。 9 检查未知数的改正数是否大于限差，若大于限
差，则重复（4）-（9）步的计算，直到所有改正数都小于限差为止。
作业
1、相对定向的原理是什么？连续法相对定向元素是什么？
2、相对定向的参数计算的实用步骤是什么？
系数约简
N2
BxZ1 X1Z2
BzX1 Z1X2
X1Z2
Z1X2
Bx N2
(Z1
Bz Bx
X1)N Bx2 Z1
又 Y1 N1Y1 N2Y2 By N2Y2 Y2 Z1 N1Z1 N2Z2 Bz N2Z2 Z2
Y1 Z1 Y2 Z2
X1Y2 X2Y1 Y2
Z1X2 X1Z2
Z2
BxY1 Z1X2 X1Z2
f Y1Z 2 Y2Z 1 Z 1Z 2
f Y1 f Y2
Z1
Z2
y t1 y t2
q
单独法相对定向中
常数项的几何意义
q为相当于像空
间辅助坐标系中一对理想像对上同名像点的上下视差
当一个立体像对完成相对定向， q＝0
当一个立体像对未完成相对定向，即同名光线不相交， q＝0
Y2 Z2
N2
BZ x(1Y X 1Y 22X Z11Z Z22)(Z2Y Z22 2)N2
BxX2Z1 Z1X2 X1Z2
N2X2
常数项约简
Bx By Bz
X1 Y1 Z1
F0
X2 Y2 Z2
Z1X2 X1Z2 Z1X2 X1Z2
Bx Bz
Bx Bz
X1 Z1
X2 Z1X2
Z2 X1Z2
相对定向数学模型的理解
相对定向的观测值是Q，与上下视差有关；每一对同名点，有一个Q，当重叠区域有5对同名点时，5个相对定向元素可唯一解出；实用时用6个同名点(也叫相对定向点、模型点)通过最小二乘平差计算；

相对定向—绝对定向解法

相对定向—绝对定向解法实验报告1、实验代码1.1根据所给同名像点的像平面坐标进行相对定向，求解相对的相对定向元素function xP= xiangduidingxiang( Lxy,Rxy,f )%UNTITLED Summary of this function goes here% Detailed explanation goes here%设置相对定向元素是初始值u=0;v=0;w=0;q=0;k=0;bu=Rxy(1,1)-Lxy(1,1);while (1)%求解余弦元素a1=cos(q)*cos(k)-sin(q)*sin(w)*sin(k);a2=-cos(q)*sin(k)-sin(q)*sin(w)*cos(k);a3=-sin(q)*cos(w);b1=cos(w)*sin(k);b2=cos(w)*cos(k);b3=-sin(w);c1=sin(q)*cos(k)+cos(q)*sin(w)*sin(k);c2=-sin(q)*sin(k)+cos(q)*sin(w)*cos(k);c3=cos(q)*cos(w);R=[a1,a2,a3;b1,b2,b3;c1,c2,c3];[n,m]=size(Lxy);u2=[];v2=[];w2=[];for i=1:nu2(i)=a1*Rxy(i,1)+a2*Rxy(i,2)-a3*f;v2(i)=b1*Rxy(i,1)+b2*Rxy(i,2)-b3*f;w2(i)=c1*Rxy(i,1)+c2*Rxy(i,2)-c3*f;endfor i=1:nu1(i)=Lxy(i,1);v1(i)=Lxy(i,2);w1(i)=-f;endbv=bu*u;bw=bu*v;for i=1:nN1(i)=(bu*w2(i)-bw*u2(i))/(u1(i)*w2(i)-u2(i)*w1(i));N2(i)=(bu*w1(i)-bw*u1(i))/(u1(i)*w2(i)-u2(i)*w1(i)); endfor i=1:na(i)=-u2(i)*v2(i)*N2(i)/w2(i);b(i)=-(w2(i)+v2(i)*v2(i)/w2(i))*N2(i);c(i)=u2(i)*N2(i);d(i)=bu;e(i)=-v2(i)*bu/w2(i);l(i)=N1(i)*v1(i)-N2(i)*v2(i)-bv;end%组成法方程系数阵AA=zeros(n,5); %c个控制点，A：c行，5列for i=1:nA(i,1)=a(i);A(i,2)=b(i);A(i,3)=c(i);A(i,4)=d(i);A(i,5)=e(i);L(i,1)=l(i);end%求解改正数XX=inv((A')*A)*(A')*L;q=q+X(1,1);w=w+X(2,1);k=k+X(3,1);u=u+X(4,1);v=v+X(5,1);%求解改正数绝对值的最大项，判断最大项是否小于限差Xabs=abs(X);aaa=max(Xabs);if aaa<0.00003 %当改正数中绝对值最大的改正数小于限差0.00003 break; %后跳出循环，计算结果已经收敛endxP=[u,v,q,w,k ];end1.2根据所给控制点的像平面坐标，求解控制点的模型坐标function M= calmodelcord(xP,Lxy,Rxy,f,m)h(1,:)=[0,0,0,0,0,0];bu=(Lxy(1,1)-Rxy(1,1))*m;bv=bu*xP(1);bw=bu*xP(2);h(2,:)=[bu,bv,bw,xP(3),xP(4),xP(5)];M= qianfang(h,Lxy,Rxy,f);end1.3利用控制点的地面摄影测量坐标和模型坐标求解相对立体模型的绝对定向元素function [jP,Accuracy]= jueduidingxiang(M,G)%UNTITLED Summary of this function goes here% Detailed explanation goes here%设置绝对定向元素是初始值Xs=0;Ys=0;Zs=0;q=0;w=0;k=0;r=1;[n,m]=size(G);gt=sum(G)/n;gm=sum(M)/n;for i=1:n%Mg(i,:)=M(i,:)-gm;%Gg(i,:)=G(i,:)-gt;Mg(i,:)=M(i,:) ;Gg(i,:)=G(i,:) ;end%组成法方程系数阵A%A=zeros(3*n,4); %c个控制点，A：2c行，6列A=zeros(3*n,7);for i=1:nA(3*i-2,:)=[1,0,0,Mg(i,1),-Mg(i,3),0,-Mg(i,2)];A(3*i-1,:)=[0,1,0,Mg(i,2),0,-Mg(i,3),Mg(i,1)];A(3*i-0,:)=[0,0,1,Mg(i,3),Mg(i,1),Mg(i,2),0];endwhile(1)%求解余弦元素a1=cos(q)*cos(k)-sin(q)*sin(w)*sin(k);a2=-cos(q)*sin(k)-sin(q)*sin(w)*cos(k);a3=-sin(q)*cos(w);b1=cos(w)*sin(k);b2=cos(w)*cos(k);b3=-sin(w);c1=sin(q)*cos(k)+cos(q)*sin(w)*sin(k);c2=-sin(q)*sin(k)+cos(q)*sin(w)*cos(k);c3=cos(q)*cos(w);R=[a1,a2,a3;b1,b2,b3;c1,c2,c3];L=zeros(3*n,1);for i=1:nl(i,:)=Gg(i,:)-r*Mg(i,:)*R'-[Xs,Ys,Zs];L(3*i-2)=l(i,1);L(3*i-1)=l(i,2);L(3*i-0)=l(i,3);end%求解改正数XX=inv((A')*A)*(A')*L;q=q+X(5,1);w=w+X(6,1);k=k+X(7,1);r=r+X(4,1);Xs=Xs+X(1,1);Ys=Ys+X(2,1);Zs=Zs+X(3,1) ;%q=q+X(1,1);w=w+X(2,1);k=k+X(3,1);r=r+X(4,1);%Xs=Xs+X(1,1);Ys=Ys+X(2,1);Zs=Zs+X(3,1) ;%求解改正数绝对值的最大项，判断最大项是否小于限差Xabs=abs(X);%X2=X(1:3);X2=X(1:7);aaa=max(X2);if aaa<0.00003 %当改正数中绝对值最大的改正数小于限差0.00003break; %后跳出循环，计算结果已经收敛endV=A*X-L;Qx=inv((A')*A);m=sqrt(V'*V/(3*n-7));mx=m*sqrt(Qx(1,1));my=m*sqrt(Qx(2,2));mz=m*sqrt(Qx(3,3));mr=m*sqrt(Qx(4,4));mq=m*sqrt(Qx(5,5));mw=m*sqrt(Qx(5,5));mk=m*sqrt(Qx(7,7));Accuracy=[m,mx,my,mz,mr,mq,mw,mk];jP=[Xs,Ys,Zs,q,w,k,r];end1.4根据同名像点在左右像片上的坐标，运用相对定向-绝对定向求解其对应的地面点在摄影测量坐标系中的坐标function G= modeltoground(M,jP)%UNTITLED Summary of this function goes here% Detailed exjPlanation goes here%设置绝对定向元素是初始值Xs=jP(1);Ys=jP(2);Zs=jP(3);q=jP(4);w=jP(5);k=jP(6);r=jP(7);%求解余弦元素a1=cos(q)*cos(k)-sin(q)*sin(w)*sin(k);a2=-cos(q)*sin(k)-sin(q)*sin(w)*cos(k);a3=-sin(q)*cos(w);b1=cos(w)*sin(k);b2=cos(w)*cos(k);b3=-sin(w);c1=sin(q)*cos(k)+cos(q)*sin(w)*sin(k);c2=-sin(q)*sin(k)+cos(q)*sin(w)*cos(k);c3=cos(q)*cos(w);R=[a1,a2,a3;b1,b2,b3;c1,c2,c3];[n,m]=size(M);G=zeros(n,3);for i=1:nG(i,:)=r*M(i,:)*R'+[Xs,Ys,Zs];endend2、实验结果内方位元素：f=152.000mm，x0=0，y0=0相对定向元素xP =-0.0233 0.0354 0.0160 0.0197 0.0159精度xAccuracy =0.0004 0.0139 0.0060 0.0110 0.0068 0.0047 控制点模型坐标M =156.936953481233 785.310912313082 -1489.78372028151 846.996568864545 777.568121579323 -1453.74298179100 137.064504568123 -813.912928625571 -1559.183******** 848.337950390061 -825.212755553314 -1567.93979157696 控制点地面摄影测量坐标G=5083.205 5852.099 527.9255780.02 5906.365 571.5495210.879 4258.446 461.815909.264 4314.283 455.484绝对定向元素jP=4989.990418301155058.391183895982015.932707725130.006366143570830820.0001719809659343390.08693178225995710.998202595968240精度jAccuracy=5.0713842812432411.33514559405495.624788573722556.218723144364650.002897437680264940.007221625088790500.007221625088790500.00292249179908379同名像点模型坐标M =156.936953481233 785.310912313082 -1489.78372028151 846.996568864545 777.568121579323 -1453.74298179100 137.064504568123 -813.912928625571 -1559.183******** 848.337950390061 -825.212755553314 -1567.93979157696 501.182474572058 786.460796681501 -1471.84466430219 147.511281621562 -2.32394422877021 -1533.84285172236 496.993543733293 -7.82730676502133 -1514.49516133642 847.202456098722 -13.2798292486915 -1493.16203433329 492.977274882422 -818.671550810105 -1556.71643881018同名像点地面摄影测量坐标G=5087.45817473871 5853.187******** 529.553768342082 5774.10439897111 5905.28632817327 569.910764342536 5206.73547144829 4261.155******** 460.763256117002 5915.06994836941 4311.56370026295 456.540224261176 5429.56672655585 5884.16218750909 549.644212500529 5146.62599969336 5069.12774757853 485.814766994366 5494.50969089619 5093.94002565289 507.347048180004 5843.09894966586 5118.86549598956 530.865748813818 5561.0564******* 4287.26877853566 465.485721912728。

计算相对定向元素的过程

计算相对定向元素的过程：1．假定第一象对左片的三个角元素0111===κωϕ，右片的三个角元素的初始值亦为零，0222===κωϕ，以假定相对定向元素μ，υ的初始值为零，0==υμ。

B 取用2点（标准点位）的左右视差，即2P B x =。

把每个点的观测数据x v 、y v 、p v 、q v ，换算为左像点的相片坐标1x 、1y ，右像点的相片坐标2x 、2y 。

2．把ϕ、ω、κ值代入公式κωϕκϕs i n s i n s i n c o s c o s 1-=aκωϕωϕc o s s i n s i n s i n c o s 2--=aωϕc o s s i n 3-=aκωs i n c o s 1=bκωc o s c o s 2=bωs i n 3-=bκωϕκϕs i n s i n c o s c o s s i n 1+=cκωϕκωc o s s i n c o s s i n s i n 2+-=cωϕc o s c o s3=c 分别计算左右两片的九个方向余弦，求得R 阵；再由R 阵计算左右两个同名像点的像空间坐标1X 、1Y 、1Z 、2X 、2Y 、2Z 。

计算公式为：⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡f y x c c c b b b a a a Z Y X321321321 3．根据计算出像点的像空间坐标由公式相对定向的误差方程式一般通式为l sd rd cd bd ad -++++=γμκωϕυ式中'222N Z Y X a -= '2222N Z Y Z b ⎪⎪⎭⎫ ⎝⎛+-='2N X c =x B r =x B Z Y s 22-=yB Y N NY Q l --==2'1计算误差方程式系数a 、b 、c 、r 、s 和常数项l 。

l 中的N 、'N 由公式 122122Z X Z X X B Z B N z x --= 122111'Z X Z X X B Z B N z x --=进行计算。

立体像对的解析法相对定向

1
3
4
1
o1
o2
2
P
5 6
x ( A PA) ( A Pl )
T T
V T PV 0 n5
Qxx ( AT PA) 1
ii mi 0 Q xx
第12讲立体像对的解析法相对定向
连续像对相对方位元素计算过程
1、读入原始数据
（x1，y1，x2，y2，f）
2、确定相对方位元素初值、计算右片方向余弦值（给出基线分量 Bx =x1 - x2，φ02=ω02=κ02=By0 =Bz0 =0 ）
第12讲立体像对的解析法相对定向
误差方程及法方程的建立
Y2 X 2Y2 Y22 vQ Bx Bx N 2 ( Z 2 ) N 2 X 2 N 2 Q Z2 Z2 Z2
量测 5 个以上的同名点可以按最小二乘平差法求相对定向元素
V Ax l ,
X2 x2 Y R 2 y 2 2 Z2 f

第12讲立体像对的解析法相对定向
四、单独像对相对定向元素的解算
各项乘以f/Bz1z2 令：Z1=Z2=-f
第12讲立体像对的解析法相对定向
四、单独像对相对定向元素的解算
yt1,yt2为左右相片上像点坐标化算为相对于基线的水平像片上的像点坐标
三、相对定向元素的解算
1、连续像对相对定向元素的解算
F F F F F F F 0
0
等式两边除以 Bx，省去二次以上小项
第12讲立体像对的解析法相对定向
三、相对定向元素的解算
1、连续像对相对定向元素的解算
有多余观测时的误差方程如下

第12讲绝对定向

这里 X T
XT YT Z T
• 给初值 0 , X 0 0
X00 0 Y0 , M 0 X 0 Z0
• 改正数为
dX 0 d , dX 0 dY0 , d ( M X ) dM M 0 X dZ 0
按泰勒级数展开：
XT XT YT YT
0 0 0
d = - 0, d = - 0, d = - 0, d X0 = X0 - X0 0, d Y0 = Y0 - Y0 0 , d Z0 = Z0 - Z0 0
X T X X X X dX0 T d T d T d T d X 0
a2 b2 c2
a3 X b3 Y c3 Z
一、绝对定向方程——空间相似变换
XT YT Z T
a1 b1 c 1
a2 b2 c2
a3 X X 0 b3 Y Y0 Z Z c3 0
0
( d )( E dM ) M X ( X 0 d X 0 )
0
0
M X X 0 dM 0 X 0 dMM0 X ddMM0 X d X 0
0 0
0
XT
0 0 0 X T0 M'0 X X dM X 00 X X dd M 0 dMM X dM 0 0
1 0 0 X 0 1 0 Y 0 0 1 Z
0 Z Y
Z 0 X
二、空间相似变换公式线性化
另外一种推导方法： • 空间相似变换公式
X T λM X X 0

相对定向--课程设计报告

课程设计报告相对定向元素计算2010 年 5 月15 日1 设计任务------------------------------------------------------------------------------------ 32 作业原理--------------------------------------------------------------------------------------- 33 已知条件及数据-------------------------------------------------------------------- 34 作业过程--------------------------------------------------------------------------- 35 程序流程----------------------------------------------------------------------------- 46 源程序----------------------------------------------------------------------------- 57 计算结果--------------------------------------------------------------------------- 10 8心得体会与建议----------------------------------------------------------------------------- 101 设计任务采用连续像对相对定向方法，计算出两张像片的相对定向元素，并运用一种高级语言解决此问题。

2作业原理解析法相对定向原理：根据同名光线对对相交这一立体像对内在的几何关系，通过量测的像点坐标，用解析计算的方法解求相对定向元素，建立与地面相似的立体模型，确定模型点的三维坐标。

相对定向,绝对定向,后方交会

#include<iostream>#include<cmath>#include<fstream>using namespace std;//-------------------------------------------------------------------------------------------------struct KBJ{double x;double y;};struct KZD{int num;double x;double y;double z;};struct XKZD{int num;double x;double y;double z;double x1;double y1;};struct XP{int num;double x;double y;double p;double q;};struct HFJH//前方交会{double x;double y;double z;double f;double w;double k;double jdx;double jdz;double jdf;double jdw;double jdk; };struct XD//相对定向{double u;double v;double f;double w;double k;double jdu;double jdv;double jdf;double jdw;double jdk; };struct XXD{double x1;double y1;double z1;double x2;double y2;double z2;double N1;double N2;double Q; };struct JD//绝对定向{double f;double w;double k;double l;double dx;double dy;double dz;double jdf;double jdw;double jdk;double jdx;double jdy;double jdz;};struct GS{double x;double y;double z;double f;double w;double k;double dx;double dy;double dz;double jdx;double jdy;double jdz;double jdf;double jdw;double jdk;double jddx;double jddy;double jddz;};//-------------------------------------------------------------------------------------------------struct GSF{int kzd;int num;double x;double y;double z;double x1;double y1;double x2;double y2;};KBJ kbj[2];//存放框标距KZD *kzd;//存放控制点XP *xp;//存放左右相片数据HFJH hfjh[2];//存放前方交会数据，一个存放左相片数据，一个存放右相片数据KZD *qfjh;//存放前方交会数据结果KZD *xddx;//存放相对定向数据XD xdwc;//存放相对定向数据KZD *xdkzd;KZD *jddx;//存放绝对定向JD jdwc;//存放绝对定向的误差GS gsz,gsy;//存放光束法左右相片的数据KZD *gszjg,*gsyjg;//光束法的结果int n;//存放控制点的个数int m;//存放相片的数据个数double zhuju;//主距double bilichi=12000;//比例尺//-------------------------------------------------------------------------------------------------void transpose(double *m1,double *m2,int tem1,int tem2) //矩阵转置{for(int i=0;i<tem1;i++)for(int j=0;j<tem2;j++)m2[j*tem1+i]=m1[i*tem2+j];return;}void inv(double *a,int n1)/*正定矩阵求逆*/{int i,j,k;for(k=0;k<n1;k++){for(i=0;i<n1;i++){if(i!=k)*(a+i*n1+k)=-*(a+i*n1+k)/(*(a+k*n1+k));}*(a+k*n1+k)=1/(*(a+k*n1+k));for(i=0;i<n1;i++){if(i!=k){for(j=0;j<n1;j++){if(j!=k)*(a+i*n1+j)+=*(a+k*n1+j)* *(a+i*n1+k);}}}for(j=0;j<n1;j++){if(j!=k)*(a+k*n1+j)*=*(a+k*n1+k);}}}void mult(double *m1,double *m2,double *result,int i_1,int j_12,int j_2)//矩阵相乘{int i,j,k;for(i=0;i<i_1;i++)for(j=0;j<j_2;j++){result[i*j_2+j]=0.0;for(k=0;k<j_12;k++)result[i*j_2+j]+=m1[i*j_12+k]*m2[j+k*j_2];}return;}void js_hfjh(int tem){XKZD *xkzd=new XKZD[n];//新控制点int tem1=0;if(tem==0){for(int i=0;i<n;i++)for(int j=0;j<m;j++)if(kzd[i].num==xp[j].num){xkzd[tem1].num=xp[j].num;xkzd[tem1].x=kzd[i].x;xkzd[tem1].y=kzd[i].y;xkzd[tem1].z=kzd[i].z;xkzd[tem1].x1=(xp[j].x-100)/1000;xkzd[tem1++].y1=(100-xp[j].y)/1000;}}if(tem==1){for(int i=0;i<n;i++)for(int j=0;j<m;j++)if(kzd[i].num==xp[j].num){xkzd[tem1].num=xp[j].num;xkzd[tem1].x=kzd[i].x;xkzd[tem1].y=kzd[i].y;xkzd[tem1].z=kzd[i].z;xkzd[tem1].x1=(xp[j].x-100-xp[j].p)/1000;xkzd[tem1++].y1=(100-xp[j].y-xp[j].q)/1000;}}for(int i=0;i<tem1;i++){hfjh[tem].x+=xkzd[i].x;hfjh[tem].y+=xkzd[i].y;hfjh[tem].z+=xkzd[i].z;}hfjh[tem].x/=tem1;hfjh[tem].y/=tem1;hfjh[tem].z=hfjh[tem].z/tem1+bilichi*zhuju;hfjh[tem].f=0.0;hfjh[tem].w=0.0;hfjh[tem].k=0.0;//六个外方位元素的初始值//-------------------------------------------------------------------------------------------------double X[6]={1,1,1,1,1,1};//存放外方位元素改正值double a[3],b[3],c[3];//存放旋转矩阵double *A=new double [12*tem1];double *B=new double [12*tem1];double *l=new double [2*tem1];double C[36],D[6];double *Xo=new double [tem1];double *Yo=new double [tem1];double *Zo=new double [tem1];//-------------------------------------------------------------------------------------------------while(fabs(X[0])>1e-6||fabs(X[1])>1e-6||fabs(X[2])>1e-6||fabs(X[3])>1e-6||fabs(X[4])>1e -6||fabs(X[5])>1e-6){a[0]=cos(hfjh[tem].f)*cos(hfjh[tem].k)-sin(hfjh[tem].f)*sin(hfjh[tem].w)*sin(hfjh[tem].k);a[1]=-cos(hfjh[tem].f)*sin(hfjh[tem].k)-sin(hfjh[tem].f)*sin(hfjh[tem].w)*cos(hfjh[tem].k);a[2]=-sin(hfjh[tem].f)*cos(hfjh[tem].w);b[0]=cos(hfjh[tem].w)*sin(hfjh[tem].k);b[1]=cos(hfjh[tem].w)*cos(hfjh[tem].k);b[2]=-sin(hfjh[tem].w);c[0]=sin(hfjh[tem].f)*cos(hfjh[tem].k)+cos(hfjh[tem].f)*sin(hfjh[tem].w)*sin(hfjh[tem].k); c[1]=-sin(hfjh[tem].f)*sin(hfjh[tem].k)+cos(hfjh[tem].f)*sin(hfjh[tem].w)*cos(hfjh[tem].k);c[2]=cos(hfjh[tem].f)*cos(hfjh[tem].w);//计算旋转矩阵R//-------------------------------------------------------------------------------------------------for(i=0;i<tem1;i++){Xo[i]=-zhuju*(a[0]*(xkzd[i].x-hfjh[tem].x)+b[0]*(xkzd[i].y-hfjh[tem].y)+c[0]*(xkzd[i].z-hfjh[tem ].z))/(a[2]*(xkzd[i].x-hfjh[tem].x)+b[2]*(xkzd[i].y-hfjh[tem].y)+c[2]*(xkzd[i].z-hfjh[tem].z));Yo[i]=-zhuju*(a[1]*(xkzd[i].x-hfjh[tem].x)+b[1]*(xkzd[i].y-hfjh[tem].y)+c[1]*(xkzd[i].z-hfjh[tem ].z))/(a[2]*(xkzd[i].x-hfjh[tem].x)+b[2]*(xkzd[i].y-hfjh[tem].y)+c[2]*(xkzd[i].z-hfjh[tem].z));Zo[i]=a[2]*(xkzd[i].x-hfjh[tem].x)+b[2]*(xkzd[i].y-hfjh[tem].y)+c[2]*(xkzd[i].z-hfjh[tem].z);A[12*i+0]=(a[0]*zhuju+a[2]*xkzd[i].x1)/Zo[i];A[12*i+1]=(b[0]*zhuju+b[2]*xkzd[i].x1)/Zo[i];A[12*i+2]=(c[0]*zhuju+c[2]*xkzd[i].x1)/Zo[i];A[12*i+3]=xkzd[i].y1*sin(hfjh[tem].w)-(xkzd[i].x1*(xkzd[i].x1*cos(hfjh[tem].k)-xkzd[i].y1*s in(hfjh[tem].k))/zhuju+zhuju*cos(hfjh[tem].k))*cos(hfjh[tem].w);A[12*i+4]=-zhuju*sin(hfjh[tem].k)-xkzd[i].x1*(xkzd[i].x1*sin(hfjh[tem].k)+xkzd[i].y1*cos(h fjh[tem].k))/zhuju;A[12*i+5]=xkzd[i].y1;A[12*i+6]=(a[1]*zhuju+a[2]*xkzd[i].y1)/Zo[i];A[12*i+7]=(b[1]*zhuju+b[2]*xkzd[i].y1)/Zo[i];A[12*i+8]=(c[1]*zhuju+c[2]*xkzd[i].y1)/Zo[i];A[12*i+9]=-xkzd[i].x1*sin(hfjh[tem].w)-(xkzd[i].y1*(xkzd[i].x1*cos(hfjh[tem].k)-xkzd[i].y1* sin(hfjh[tem].k))/zhuju-zhuju*sin(hfjh[tem].k))*cos(hfjh[tem].w);A[12*i+10]=-zhuju*cos(hfjh[tem].k)-xkzd[i].y1*(xkzd[i].x1*sin(hfjh[tem].k)+xkzd[i].y1*cos (hfjh[tem].k))/zhuju;A[12*i+11]=-xkzd[i].x1;l[2*i]=xkzd[i].x1-Xo[i];l[2*i+1]=xkzd[i].y1-Yo[i];}//计算A，L//-------------------------------------------------------------------------------------------------transpose(A,B,2*tem1,6);mult(B,A,C,6,2*tem1,6);mult(B,l,D,6,2*tem1,1);inv(C,6);mult(C,D,X,6,6,1);hfjh[tem].x+=X[0];hfjh[tem].y+=X[1];hfjh[tem].z+=X[2];hfjh[tem].f+=X[3];hfjh[tem].w+=X[4];hfjh[tem].k+=X[5];}double linshi=0;for(i=0;i<2*tem1;i++){linshi+=l[i]*l[i];}linshi=sqrt(linshi/(2*tem1-6));hfjh[tem].jdx=sqrt(C[0])*linshi;hfjh[tem].jdy=sqrt(C[7])*linshi;hfjh[tem].jdz=sqrt(C[14])*linshi;hfjh[tem].jdf=sqrt(C[21])*linshi;hfjh[tem].jdw=sqrt(C[28])*linshi;hfjh[tem].jdk=sqrt(C[35])*linshi;}void js_qfjh(){double Bx=hfjh[1].x-hfjh[0].x;double By=hfjh[1].y-hfjh[0].y;double Bz=hfjh[1].z-hfjh[0].z;double a[3],b[3],c[3],d[3],e[3],f[3];//-------------------------------------------------------------------------------------------------a[0]=cos(hfjh[0].f)*cos(hfjh[0].k)-sin(hfjh[0].f)*sin(hfjh[0].w)*sin(hfjh[0].k);a[1]=-cos(hfjh[0].f)*sin(hfjh[0].k)-sin(hfjh[0].f)*sin(hfjh[0].w)*cos(hfjh[0].k);a[2]=-sin(hfjh[0].f)*cos(hfjh[0].w);b[0]=cos(hfjh[0].w)*sin(hfjh[0].k);b[1]=cos(hfjh[0].w)*cos(hfjh[0].k);b[2]=-sin(hfjh[0].w);c[0]=sin(hfjh[0].f)*cos(hfjh[0].k)+cos(hfjh[0].f)*sin(hfjh[0].w)*sin(hfjh[0].k);c[1]=-sin(hfjh[0].f)*sin(hfjh[0].k)+cos(hfjh[0].f)*sin(hfjh[0].w)*sin(hfjh[0].k);c[2]=cos(hfjh[0].f)*cos(hfjh[0].w);//R1//-------------------------------------------------------------------------------------------------d[0]=cos(hfjh[1].f)*cos(hfjh[1].k)-sin(hfjh[1].f)*sin(hfjh[1].w)*sin(hfjh[1].k);d[1]=-cos(hfjh[1].f)*sin(hfjh[1].k)-sin(hfjh[1].f)*sin(hfjh[1].w)*cos(hfjh[1].k);d[2]=-sin(hfjh[1].f)*cos(hfjh[1].w);e[0]=cos(hfjh[1].w)*sin(hfjh[1].k);e[1]=cos(hfjh[1].w)*cos(hfjh[1].k);e[2]=-sin(hfjh[1].w);f[0]=sin(hfjh[1].f)*cos(hfjh[1].k)+cos(hfjh[0].f)*sin(hfjh[0].w)*sin(hfjh[0].k);f[1]=-sin(hfjh[1].f)*sin(hfjh[1].k)+cos(hfjh[0].f)*sin(hfjh[0].w)*sin(hfjh[0].k);f[2]=cos(hfjh[1].f)*cos(hfjh[1].w);//R2//-------------------------------------------------------------------------------------------------for(int i=0;i<m;i++){double X1=a[0]*(xp[i].x-100)/1000+a[1]*(100-xp[i].y)/1000-a[2]*zhuju;double Y1=b[0]*(xp[i].x-100)/1000+b[1]*(100-xp[i].y)/1000-b[2]*zhuju;double Z1=c[0]*(xp[i].x-100)/1000+c[1]*(100-xp[i].y)/1000-c[2]*zhuju;double X2=d[0]*(xp[i].x-100-xp[i].p)/1000+d[1]*(110-xp[i].y-xp[i].q)/1000-d[2]*zhuju;double Y2=e[0]*(xp[i].x-100-xp[i].p)/1000+e[1]*(110-xp[i].y-xp[i].q)/1000-e[2]*zhuju;double Z2=f[0]*(xp[i].x-100-xp[i].p)/1000+f[1]*(110-xp[i].y-xp[i].q)/1000-f[2]*zhuju;double N1=(Bx*Z2-Bz*X2)/(X1*Z2-X2*Z1);double N2=(Bx*Z2-Bz*X2)/(X1*Z2-X2*Z1);qfjh[i].num=xp[i].num;qfjh[i].x=hfjh[0].x+N1*X1;qfjh[i].y=hfjh[0].y+N1*Y1;qfjh[i].z=hfjh[0].z+N1*Z1;// cout<<X1<<" "<<Y1<<" "<<Z1<<" "<<X2<<" "<<Y2<<" "<<Z2<<" "<<N1<<" "<<N2<<endl;}}//-------------------------------------------------------------------------------------------------void js_xddx(){xdwc.f=0;xdwc.k=0;xdwc.u=0;xdwc.v=0;xdwc.w=0;double Bx=xp[0].p/1000;double *A=new double [m*5];//Adouble *L=new double [m];//Ldouble *B=new double [m*5];//Atdouble C[25];//AtAdouble *D=new double [m*5];//AtAAdouble X[5]={1,1,1,1,1};double a[3],b[3],c[3];XXD *point=new XXD[m];//-------------------------------------------------------------------------------------------------while(fabs(X[0])>1e-6||fabs(X[1])>1e-6||fabs(X[2])>1e-6||fabs(X[3])>1e-6||fabs(X[4])>1e -6){a[0]=cos(xdwc.f)*cos(xdwc.k)-sin(xdwc.f)*sin(xdwc.w)*sin(xdwc.k);a[1]=-cos(xdwc.f)*sin(xdwc.k)-sin(xdwc.f)*sin(xdwc.w)*cos(xdwc.k);a[2]=-sin(xdwc.f)*cos(xdwc.w);b[0]=cos(xdwc.w)*sin(xdwc.k);b[1]=cos(xdwc.w)*cos(xdwc.k);b[2]=-sin(xdwc.w);c[0]=sin(xdwc.f)*cos(xdwc.k)+cos(xdwc.f)*sin(xdwc.w)*sin(xdwc.k);c[1]=-sin(xdwc.f)*sin(xdwc.k)+cos(xdwc.f)*sin(xdwc.w)*cos(xdwc.k);c[2]=cos(xdwc.f)*cos(xdwc.w);for(int i=0;i<m;i++){point[i].x1=(xp[i].x-100.0)/1000;point[i].y1=(100.0-xp[i].y)/1000;point[i].z1=-zhuju;point[i].x2=a[0]*(xp[i].x-100.0-xp[i].p)/1000+a[1]*(110.0-xp[i].y-xp[i].q)/1000+a[2]*(-zhuju);point[i].y2=b[0]*(xp[i].x-100.0-xp[i].p)/1000+b[1]*(110.0-xp[i].y-xp[i].q)/1000+b[2]*(-zh uju);point[i].z2=c[0]*(xp[i].x-100.0-xp[i].p)/1000+c[1]*(110.0-xp[i].y-xp[i].q)/1000+c[2]*(-zhu ju);point[i].N1=(Bx*point[i].z2-Bx*xdwc.v*point[i].x2)/(point[i].x1*point[i].z2-point[i].z1*poin t[i].x2);point[i].N2=(Bx*point[i].z1-Bx*xdwc.v*point[i].x1)/(point[i].x1*point[i].z2-point[i].z1*poin t[i].x2);point[i].Q=point[i].N1*point[i].y1-point[i].N2*point[i].y2-Bx*xdwc.u;A[i*5]=Bx;A[i*5+1]=-point[i].y2/point[i].z2*Bx;A[i*5+2]=-point[i].x2*point[i].y2*point[i].N2/point[i].z2;A[i*5+3]=-(point[i].z2+point[i].y2*point[i].y2/point[i].z2)*point[i].N2;A[i*5+4]=point[i].x2*point[i].N2;L[i]=point[i].Q;}transpose(A,B,m,5);mult(B,A,C,5,m,5);inv(C,5);mult(C,B,D,5,5,m);mult(D,L,X,5,m,1);xdwc.u+=X[0];xdwc.v+=X[1];xdwc.f+=X[2];xdwc.w+=X[3];xdwc.k+=X[4];}//-------------------------------------------------------------------------------------------------double linshi=0;for(int i=0;i<m;i++){linshi+=L[i]*L[i];}linshi=sqrt(linshi/(2*m-6));xdwc.jdu=sqrt(C[0])*linshi;xdwc.jdv=sqrt(C[6])*linshi;xdwc.jdf=sqrt(C[12])*linshi;xdwc.jdw=sqrt(C[18])*linshi;xdwc.jdk=sqrt(C[24])*linshi;//-------------------------------------------------------------------------------------------------a[0]=cos(xdwc.f)*cos(xdwc.k)-sin(xdwc.f)*sin(xdwc.w)*sin(xdwc.k);a[1]=-cos(xdwc.f)*sin(xdwc.k)-sin(xdwc.f)*sin(xdwc.w)*cos(xdwc.k);a[2]=-sin(xdwc.f)*cos(xdwc.w);b[0]=cos(xdwc.w)*sin(xdwc.k);b[1]=cos(xdwc.w)*cos(xdwc.k);b[2]=-sin(xdwc.w);c[0]=sin(xdwc.f)*cos(xdwc.k)+cos(xdwc.f)*sin(xdwc.w)*sin(xdwc.k);c[1]=-sin(xdwc.f)*sin(xdwc.k)+cos(xdwc.f)*sin(xdwc.w)*cos(xdwc.k);c[2]=cos(xdwc.f)*cos(xdwc.w);xdkzd=new KZD[m];for(i=0;i<m;i++){point[i].x1=(xp[i].x-100.0)/1000;point[i].y1=(100.0-xp[i].y)/1000;point[i].z1=-zhuju;point[i].x2=a[0]*(xp[i].x-100.0-xp[i].p)/1000+a[1]*(110.0-xp[i].y-xp[i].q)/1000+a[2]*(-zh uju);point[i].y2=b[0]*(xp[i].x-100.0-xp[i].p)/1000+b[1]*(110.0-xp[i].y-xp[i].q)/1000+b[2]*(-zh uju);point[i].z2=c[0]*(xp[i].x-100.0-xp[i].p)/1000+c[1]*(110.0-xp[i].y-xp[i].q)/1000+c[2]*(-zhu ju);point[i].N1=(Bx*point[i].z2-Bx*xdwc.v*point[i].x2)/(point[i].x1*point[i].z2-point[i].z1*poin t[i].x2);point[i].N2=(Bx*point[i].z1-Bx*xdwc.v*point[i].x1)/(point[i].x1*point[i].z2-point[i].z1*poin t[i].x2);xdkzd[i].num=xp[i].num;xdkzd[i].x=point[i].N1*point[i].x1*bilichi;xdkzd[i].y=(point[i].N1*point[i].y1+point[i].N2*point[i].y2+Bx*xdwc.u)*0.5*bilichi;xdkzd[i].z=(point[i].N1*point[i].z1+zhuju)*bilichi;//}}//-------------------------------------------------------------------------------------------------void js_jddx(){XXD *jkzd=new XXD[m];jdwc.f=0;jdwc.w=0;jdwc.k=0;jdwc.l=1;jdwc.dx=0;jdwc.dy=0;jdwc.dz=0;int tem2=0;for(int i=0;i<n;i++)for(int j=0;j<m;j++)if(kzd[i].num==xp[j].num){jkzd[tem2].x1=kzd[i].x;jkzd[tem2].y1=kzd[i].y;jkzd[tem2].z1=kzd[i].z;jkzd[tem2].x2=xdkzd[j].x;jkzd[tem2].y2=xdkzd[j].y;jkzd[tem2++].z2=xdkzd[j].z;}double a[3],b[3],c[3];double *A=new double [tem2*3*7];//Adouble *L=new double [tem2*3];//Ldouble *B=new double [tem2*3*7];//Atdouble C[49];//AtAdouble *D=new double [tem2*3*7];//AtAAdouble X[7]={1,1,1,1,1,1,1};//-------------------------------------------------------------------------------------------------while(fabs(X[0])>1e-6||fabs(X[1])>1e-6||fabs(X[2])>1e-6||fabs(X[3])>1e-6||fabs(X[4])>1e -6||fabs(X[5])>1e-6||fabs(X[6])>1e-6){a[0]=cos(jdwc.f)*cos(jdwc.k)-sin(jdwc.f)*sin(jdwc.w)*sin(jdwc.k);a[1]=-cos(jdwc.f)*sin(jdwc.k)-sin(jdwc.f)*sin(jdwc.w)*cos(jdwc.k);a[2]=-sin(jdwc.f)*cos(jdwc.w);b[0]=cos(jdwc.w)*sin(jdwc.k);b[1]=cos(jdwc.w)*cos(jdwc.k);b[2]=-sin(jdwc.w);c[0]=sin(jdwc.f)*cos(jdwc.k)+cos(jdwc.f)*sin(jdwc.w)*sin(jdwc.k);c[1]=-sin(jdwc.f)*sin(jdwc.k)+cos(jdwc.f)*sin(jdwc.w)*cos(jdwc.k);c[2]=cos(jdwc.f)*cos(jdwc.w);for(i=0;i<tem2;i++){L[i*3]=jkzd[i].x1-jdwc.l*(a[0]*jkzd[i].x2+a[1]*jkzd[i].y2+a[2]*jkzd[i].z2)-jdwc.dx;L[i*3+1]=jkzd[i].y1-jdwc.l*(b[0]*jkzd[i].x2+b[1]*jkzd[i].y2+b[2]*jkzd[i].z2)-jdwc.dy;L[i*3+2]=jkzd[i].z1-jdwc.l*(c[0]*jkzd[i].x2+c[1]*jkzd[i].y2+c[2]*jkzd[i].z2)-jdwc.dz;A[21*i]=1;A[21*i+1]=0;A[21*i+2]=0;A[21*i+3]=jkzd[i].x2;A[21*i+4]=-jkzd[i].z2;A[21*i+5]=0;A[21*i+6]=-jkzd[i].y2;A[21*i+7]=0;A[21*i+8]=1;A[21*i+9]=0;A[21*i+10]=jkzd[i].y2;A[21*i+11]=0;A[21*i+12]=-jkzd[i].z2;A[21*i+13]=jkzd[i].x2;A[21*i+14]=0;A[21*i+15]=0;A[21*i+16]=1;A[21*i+17]=jkzd[i].z2;A[21*i+18]=jkzd[i].x2;A[21*i+19]=jkzd[i].y2;A[21*i+20]=0;}//-------------------------------------------------------------------------------------------------transpose(A,B,tem2*3,7);mult(B,A,C,7,tem2*3,7);inv(C,7);mult(C,B,D,7,7,tem2*3);mult(D,L,X,7,tem2*3,1);jdwc.dx+=X[0];jdwc.dy+=X[1];jdwc.dz+=X[2];jdwc.l+=X[3];jdwc.f+=X[4];jdwc.w+=X[5];jdwc.k+=X[6];}//求出绝对定向的数据//-------------------------------------------------------------------------------------------------double linshi=0;for(i=0;i<3*tem2;i++){linshi+=L[i]*L[i];}linshi=sqrt(linshi/(3*tem2-7));jdwc.jdx=sqrt(C[0])*linshi;jdwc.jdy=sqrt(C[8])*linshi;jdwc.jdz=sqrt(C[16])*linshi;jdwc.jdl=sqrt(C[24])*linshi;jdwc.jdf=sqrt(C[32])*linshi;jdwc.jdw=sqrt(C[40])*linshi;jdwc.jdk=sqrt(C[48])*linshi;//求各各值得精读//-------------------------------------------------------------------------------------------------a[0]=cos(jdwc.f)*cos(jdwc.k)-sin(jdwc.f)*sin(jdwc.w)*sin(jdwc.k);a[1]=-cos(jdwc.f)*sin(jdwc.k)-sin(jdwc.f)*sin(jdwc.w)*cos(jdwc.k);a[2]=-sin(jdwc.f)*cos(jdwc.w);b[0]=cos(jdwc.w)*sin(jdwc.k);b[1]=cos(jdwc.w)*cos(jdwc.k);b[2]=-sin(jdwc.w);c[0]=sin(jdwc.f)*cos(jdwc.k)+cos(jdwc.f)*sin(jdwc.w)*sin(jdwc.k);c[1]=-sin(jdwc.f)*sin(jdwc.k)+cos(jdwc.f)*sin(jdwc.w)*cos(jdwc.k);c[2]=cos(jdwc.f)*cos(jdwc.w);jddx=new KZD[m];for(i=0;i<m;i++){jddx[i].num=xdkzd[i].num;jddx[i].x=jdwc.l*(a[0]*xdkzd[i].x+xdkzd[i].y*a[1]+xdkzd[i].z*a[2])+jdwc.dx;jddx[i].y=jdwc.l*(b[0]*xdkzd[i].x+xdkzd[i].y*b[1]+xdkzd[i].z*b[2])+jdwc.dy;jddx[i].z=jdwc.l*(c[0]*xdkzd[i].x+xdkzd[i].y*c[1]+xdkzd[i].z*c[2])+jdwc.dz;}}int main(){//-------------------------------------------------------------------------------------------------ifstream fkbj("kbj.txt",ios::in);for(int i=0;i<2;i++){fkbj>>kbj[i].x>>kbj[i].y;}fkbj.close();//读入框标距//-------------------------------------------------------------------------------------------------ifstream fkzd("kzd.txt",ios::in);fkzd>>n;kzd=new KZD[n];for(i=0;i<n;i++){fkzd>>kzd[i].num>>kzd[i].y>>kzd[i].x>>kzd[i].z;}fkzd.close();//读入控制点//-------------------------------------------------------------------------------------------------ifstream fxp("xp1.txt",ios::in);fxp>>m>>zhuju;xp=new XP[m];for(i=0;i<m;i++){fxp>>xp[i].num>>xp[i].x>>xp[i].y>>xp[i].p>>xp[i].q;}fxp.close();//读入左相片数据zhuju/=1000;//-------------------------------------------------------------------------------------------------double tem2=kbj[0].x/kbj[1].x;double tem3=kbj[0].y/kbj[1].y;for(i=0;i<m;i++){xp[i].p*=tem2;xp[i].q*=tem3;xp[i].x*=tem2;xp[i].y*=tem3;}//-------------------------------------------------------------------------------------------------for(i=0;i<2;i++){hfjh[i].f=0;hfjh[i].jdf=0;hfjh[i].jdk=0;hfjh[i].jdw=0;hfjh[i].jdx=0;hfjh[i].jdy=0;hfjh[i].jdz=0;hfjh[i].k=0;hfjh[i].w=0;hfjh[i].x=0;hfjh[i].y=0;hfjh[i].z=0;}//-------------------------------------------------------------------------------------------------js_hfjh(0);//对左相片进展后交js_hfjh(1);//对右相片进展后交for(i=0;i<2;i++){cout<<"前方交会:"<<hfjh[i].x<<" "<<hfjh[i].y<<" "<<hfjh[i].z<<" "<<hfjh[i].f<<" "<<hfjh[i].w<<" "<<hfjh[i].k<<endl;cout<<"误差分析:"<<hfjh[i].jdx<<" "<<hfjh[i].jdy<<" "<<hfjh[i].jdz<<" "<<hfjh[i].jdf<<" "<<hfjh[i].jdw<<" "<<hfjh[i].jdk<<endl;}//-------------------------------------------------------------------------------------------------qfjh=new KZD[m];js_qfjh();cout<<endl<<"前方交会结果："<<endl;for(i=0;i<m;i++){cout<<qfjh[i].num<<" "<<qfjh[i].x<<" "<<qfjh[i].y<<" "<<qfjh[i].z<<endl;}cout<<endl;//-------------------------------------------------------------------------------------------------js_xddx();//相对定向cout<<endl<<"相对定向"<<xdwc.f<<" "<<xdwc.w<<" "<<xdwc.k<<" "<<xdwc.u<<" "<<xdwc.v<<endl;cout<<"误差分析"<<xdwc.jdf<<" "<<xdwc.jdw<<" "<<xdwc.jdk<<" "<<xdwc.jdu<<" "<<xdwc.jdv<<endl;//-------------------------------------------------------------------------------------------------js_jddx();cout<<endl<<"绝对定向"<<jdwc.dx<<" "<<jdwc.dy<<" "<<jdwc.dz<<" "<<jdwc.l<<" "<<jdwc.f<<" "<<jdwc.w<<" "<<jdwc.k<<endl;cout<<"误差分析"<<jdwc.jdx<<" "<<jdwc.jdy<<" "<<jdwc.jdz<<" "<<jdwc.jdl<<" "<<jdwc.jdf<<" "<<jdwc.jdw<<" "<<jdwc.jdk<<endl;cout<<"对左相片进展绝对定点结果："<<endl;for(i=0;i<m;i++)cout<<jddx[i].num<<" "<<jddx[i].x<<" "<<jddx[i].y<<" "<<jddx[i].z<<endl; }。

立体像对的相对定向与立体模型的绝对定向

授课教案
第 1页
立体像对的相对定向与立体模型的绝对定向
3.5 立体像对的相对定向——共面条件方程
立体像对的相对定向：恢复立体像对中两张像片（或光束）间的相对方位的过程，叫做立体像对的相对定向。
共面条件方程：通过讲述立体像对的基本定义时，我们知道相应光线和摄影基线共处于同一平面（核面）内，这也是恢复立体像对的相对方位的几何条件——共面条件，共面条件的解析表达，叫做共面条件方程。
相对定向的目的：恢复两张像片的相对位置，达到同名光线对对相交，建立起与地面相似的几何模型。
完成手段：解算五个相对方位元素。 3.5.1 共面条件方程的一般形式
同名光线对对相交，与摄影基线 B 共面，则有矢量 S1a1，S2a2 ，B 的混
合积等于零，即 S1S2 • (S1a1 S2a2 ) 0 。
N2 X 2
Q N1Y1 (N2Y2 By )
常数项的几何意义：Q 为定向点上模型上下视差，当一个立体像对完成相对定向，Q＝0。当一个立体像对未完成相对定向，即同名光线不相交，Q≠0。
3. 误差方程及法方程的建立：
vQ
Bx
Y2 Z2
Bx
X 2Y2 Z2
N2
(Z2
Y22 Z2
)
N2
X 2 N2
X 2 Y2 Z 2
2. 方程式线性化
按泰勒级数展开：F F 0 F F F F F 0
计算各偏导数：
010
F
Bx
X1
X2
Y1 Y2
Z1 Z2
Bx
X1 X2
Z1 Z2
Bx (X 2Z1 X1Z2 )
F
Bx ( X1Y2
X 2Y1 )
Bx By Bz

相对定向和绝对定向其他解法

实验二：相对定向和绝对定向
实验二：相对定向和绝对定向
数据记录
航摄像片3张，平交点4个
连续像对相对定向作业公式
2 F0 N 2 X 2Y2 Y2 N 2 d Z dW X 2 N 2 dK 2 bX Z1 Z2 Z2 Y2 bx d u bx dY Z2
相对定向和绝对定向?将像片p1与p2装到与摄影机相同的两个投影箱内保持两投影机的方位与摄影时方位相同但物镜间的距离缩小即投影器s2移到s2处s1与s2间距变小此时投影基线为s1s2b在投影器上经参数改正后用聚光灯照明则两投影器光束所有同名光线人对对相交构成空间的各个交点所有这些交点的集合构成与地图面相似的光学立体模型
实验二：相对定向和绝对定向
绝对定向的基本公式
X tp a1 Ytp b1 Z c 1 tp
a2 b2 c2
a3 X tp X b3 Ytp Y Z Z c3 tp
实验内容步骤
将多倍仪调平在模型的四角标注四个平交点，并调节角螺旋使图上的四个点与相应模型上的四个点完全重合：在三个投影器上装入航摄像片；固定左投影器，分别动螺旋，再用消除上下视差以达到相对定向的目的；经过定向后，戴上左右相应的红绿互补色眼镜，可视察出空间的立体模型；改变投影基线的长度，调整模型比例尺，用公共倾角φ，ω置平模型达到绝对定向；当完成绝对定向和相对定向后，将图纸固验二：相对定向和绝对定向
双像投影测图的原理，实际为投影过程的几何反转在进行连续像对的投影测图时，第二张由第一张定位，第三张由第二张定位，以次类推，但实际上都是以第一张标准定位的
上节回顾

工程摄影测量学--第12讲立体像对的相对定向和绝对定向理论

0 1
X 2 a a 2 1 Y2 b1 b2 c c 2 Z 2 1
0 2
a3 x2 a3 y2 a3 f
F ( 1 , , , 2 , ) 0
P1 J1
a1
o1 n1 S1 B n2
o2 a2
P2 J2
S2 WA A
10
2、共面条件方程共面条件的向量表达式
S1 S 2 ( S1 a1 S 2 a 2 ) 0
P1 J1
a1
o1 n1 S1 B n2
o2 a2
P2 J2
S2 WA A
B ( R1 R2 ) 0
y
X

原始图像
x
复习 Review
x f y f a1 ( X X S ) b1 (Y YS ) c1 ( Z Z S ) a3 ( X X S ) b3 (Y YS ) c3 ( Z Z S ) a2 ( X X S ) b2 (Y YS ) c2 ( Z Z S ) a3 ( X X S ) b3 (Y YS ) c3 ( Z Z S )
a2 b2 c2
a3 X b3 Y c3 Z
31
2、空间相似变换
XT Y ZT T

a1 a2 a 3
a2 b2 c2
a3 X b3 Y c3 Z
X0 Y0 Z 0
2、间接法
灰度内插
与赋值

相对定向理论和方法

相对定向理论和方法1 基本概念确定立体像对相对方位元素的过程称为立体像对的相对定向。

2 相对定向方程假设已求出立体像对的相对方位元素，恢复了两张像片的相对方位，则同名光线必然两两相交，在相对坐标系中构成一个立体模型。

此时，同名光线和摄影基线必然位于同一个空间平面内，如图 1 所示，这就是相对定向的共面条件。

由此条件得到的相对定向方程称为共面条件方程。

图1 共面条件由向量几何可知，三个向量共面的充分必要条件是三向量的混合积等于0，即0)(221121=⨯•S a S a S S (1)式中，“•”是数积运算符；“⨯”为向量积运算符。

在每种相对定向系统中，把(1)式化为坐标表示的形式，就是相应的相对定向方程。

2.1 连续像对系统的相对定向方程图2是连续相对定向系统的示意图。

按混合积的坐标表达方式，有图20222111==Z Y X Z Y X Bz By Bx F (2)式中。

Bz By Bx 、、是2S 在模型坐标系XYZ 中的坐标；111Z Y X 、、和222Z Y X 、、分别是像点21a a 、在XYZ 中的坐标。

由于连续相对定向系统是以左像空系为基准，所以⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡f y x f y x f y x R Z Y X 111111111100010001左 (3) ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡f y x R Z Y X 22222右 (4)此时，右R 是由相对方位元素κωϕ∆∆∆、、确定的旋转矩阵。

在近似垂直摄影条件下，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡∆∆∆-∆∆-∆-=111ωϕωϕk k R 右。

将(2)式展开，并在方程两侧同除以Bx ，有0221122112211=+-=Y X Y X Bx Bz Z X Z X Bx By Z Y Z Y F (5) 考虑到τ=BxBy、υ≈Bx Bz 后，展开(5)式，有0)()(212121212121=-+---=X Y Y X X Z Z X Y Z Z Y F υτ(6)显然，F 是υτκωϕ、、、、∆∆∆的函数，且是非线性方程。

立体像对的相对定向

(Y1Y2

Z1Z2 )d
-
X 2Z1dk

F0 bX
0
顾及点投影系数,得
Z1 X 2
-
Z2
X1

-
bX
Z1 - bZ N2
X1
- bX N2
(Z1
-bZ bXX1)- bX N2Z1
X1Y2
-
X 2Y1

-
bX Y1 - bY N2
X1

bX N2
(Y1
-
bY bX
X1)
bX N2
如何求解相对方位元素？
?
18
二、连续法解析相对定向原理
连续法相对定向是以左像片为基准，求出右像片相对于左像片的五个相对定向元素：
BY ， BZ ，2，2，2
在相对定向解析计算时，通常把基线B改写为b，b称为投影基线
B mb
19
二、连续法解析相对定向原理
s2
b

bZ
s1

bX
bY
bY bX tg bX
15
一、相对定向条件方程——共面条件方程
对共面条件方程的五点说明
(1)相应光线是否成对相交与摄影测量坐标系的选择无关，但适当选取可以使共面条件方程式的形式发生变化，便于实际应用。通常有二种选择：
• 选左像空系——连续像对系统
此时R1=E，或为前像对右片的旋转矩阵； BX BY BZ
X1 Y1 Z1 0
12
一、相对定向条件方程——共面条件方程 2、共面条件方程
共面条件的坐标分量表达式
连续像对系统
z1
y1 B
BX BY BZ X1 Y1 Z1 0 X 2 Y2 Z2