二次函数存在性问题
二次函数的存在性问题(面积)及答案

图12-2xCOy ABD 11二次函数的存在性问题(面积问题)1、[08云南双柏]已知:抛物线y =ax 2+bx +c 与x 轴交于A 、B 两点,与y 轴交于点C ,其中点B 在x 轴的正半轴上,点C 在y 轴的正半轴上,线段OB 、OC 的长(OB <OC )是方程x 2-10x +16=0的两个根,且抛物线的对称轴是直线x =-2. (1)求A 、B 、C 三点的坐标;(2)求此抛物线的表达式;(3)求△ABC 的面积; (4)若点E 是线段AB 上的一个动点(与点A 、点B 不重合),过点E 作EF ∥AC 交BC 于点F ,连接CE , 设AE 的长为m ,△CEF 的面积为S ,求S 与m 之间的函数关系式,并写出自变量m 的取值范围;(5)在(4)的基础上试说明S 是否存在最大值,若存在,请求出S 的最大值,并求出此时点E 的坐标, 判断此时△BCE 的形状;若不存在,请说明理由.2、 [09湖南益阳]阅读材料:如图12-1,过△ABC 的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC 的“水平宽”(a ),中间的这条直线在△ABC 内部线段的长度叫△ABC 的“铅垂高(h )”.我们可得出一种计算PABCAB 98SS =三角形面积的新方法:ah S ABC 21=∆,即三角形面积等于水平宽与铅垂高乘积的一半. 解答下列问题:如图12-2,抛物线顶点坐标为点C (1,4),交x 轴于点A (3,0),交y 轴于点B .(1)求抛物线和直线AB 的解析式;(2)点P 是抛物线(在第一象限内)上的一个动点,连结PA ,PB ,当P 点运动到顶点C 时,求△CAB 的铅垂高CD 及CAB S ∆; (3)是否存在一点P ,使PABCAB98S S =若存在,求出P 点的坐标;若不存在,请说明理由.图13、[09吉林长春]如图,在直角坐标系中,矩形ABCD 的边AD 在y 轴正半轴上,点A 、C 的坐标分别 为(0,1)(2,4).点P 从点A 出发,沿A →B →C 以每秒1个单位的速度运动,到点C 停止;点Q 在x 轴上,横坐标为点P 的横、纵坐标之和.抛物线c bx x y ++-=241经过A 、C 两点.过点P 作x 轴的垂线, 垂足为M ,交抛物线于点R .设点P 的运动时间为t (秒),△PQR 的面积为S (平方单位).(1)求抛物线对应的函数关系式.(2分) (2)分别求t=1和t=4时,点Q 的坐标.(3分)(3)当0<t ≤5时,求S 与t 之间的函数关系式,并直接写出S 的最大值.(5分)4、(07云南昆明)如图,在直角坐标系中,点A 的坐标为(-2,0),连结OA ,将线段OA 绕原点O 顺时针旋转120°,得到线段OB 。
二次函数存在性问题
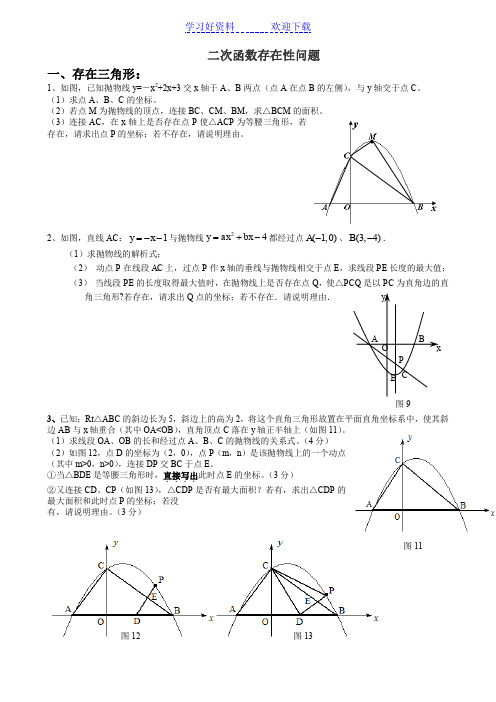
二次函数存在性问题一、存在三角形:1、如图,已知抛物线y=-x 2+2x+3交x 轴于A 、B 两点(点A 在点B 的左侧),与y 轴交于点C 。
(1)求点A 、B 、C 的坐标。
(2)若点M 为抛物线的顶点,连接BC 、CM 、BM ,求△BCM 的面积。
(3)连接AC ,在x 轴上是否存在点P 使△ACP 为等腰三角形,若存在,请求出点P 的坐标;若不存在,请说明理由。
2、如图,直线AC :1y x =--与抛物线24y ax bx =+-都经过点(1,0)A -、(3,4)B -.(1)求抛物线的解析式;(2) 动点P 在线段AC 上,过点P 作x 轴的垂线与抛物线相交于点E ,求线段PE 长度的最大值; (3) 当线段PE 的长度取得最大值时,在抛物线上是否存在点Q ,使△PCQ 是以PC 为直角边的直角三角形?若存在,请求出Q 点的坐标;若不存在.请说明理由.3、已知:Rt △ABC 的斜边长为5,斜边上的高为2,将这个直角三角形放置在平面直角坐标系中,使其斜边AB 与x 轴重合(其中OA<OB ),直角顶点C 落在y 轴正半轴上(如图11)。
(1)求线段OA 、OB 的长和经过点A 、B 、C 的抛物线的关系式。
(4分) (2)如图12,点D 的坐标为(2,0),点P (m ,n )是该抛物线上的一个动点(其中m >0,n >0),连接DP 交BC 于点E 。
①当△BDE 是等腰三角形时,直接写出....此时点E 的坐标。
(3分) ②又连接CD 、CP (如图13),△CDP 是否有最大面积?若有,求出△CDP 的最大面积和此时点P 的坐标;若没 有,请说明理由。
(3分)图11A B O C 图9 yx P E 图12 图13二、 存在四边形:1、如图,已知抛物线)0(2≠++=a c bx ax y 的顶点坐标为Q ()1,2-,且与y 轴交于点C ()3,0,与x 轴交于A 、B 两点(点A 在点B 的右侧),点P 是该抛物线上一动点,从点C 沿抛物线向点A 运动(点P 与A 不重合),过点P 作PD ∥y 轴,交AC 于点D . (1)求该抛物线的函数关系式;(2)当△ADP 是直角三角形时,求点P 的坐标;(3)在问题(2)的结论下,若点E 在x 轴上,点F 在抛物线上, 问是否存在以A 、P 、E 、F 为顶点的平行四边形?若存在, 求点F 的坐标;若不存在,请说明理由.2、在平面直角坐标系中,已知抛物线经过A )0,4(-,B )4,0(-,C )0,2(三点.(1)求抛物线的解析式;(2)若点M 为第三象限内抛物线上一动点,点M 的横坐标为m ,△AMB 的面积为S .求S 关于m 的函数关系式,并求出S 的最大值. (3)若点P 是抛物线上的动点,点Q 是直线x y -=上的动点,判断有几个位置能够使得点P 、Q 、B 、O 为顶点的四边形为平行四边形,直接写出相应的点Q 的坐标.3、如图,在平面直角坐标系中CDA Rt AOB Rt ∆≅∆,且)2,0(),0,1(B A -抛物线22-+=ax ax y 经过点C 。
二次函数中的存在性问题

⼆次函数中的存在性问题⼆次函数中的存在性问题存在性问题是指判断满⾜某种条件的事物是否存在的问题,这类问题的知识覆盖⾯较⼴,综合性较强,题意构思⾮常精巧,解题⽅法灵活,对学⽣分析问题和解决问题的能⼒要求较⾼,是近⼏年来各地中考的“热点”。
这类题⽬解法的⼀般思路是:假设存在→推理论证→得出结论。
若能导出合理的结果,就做出“存在”的判断,导出⽭盾,就做出“不存在”的判断。
以下⼏篇内容为⼏种典型的⼆次函数中出现的存在性问题,希望⼤家在以后的学习中如果遇到此类型时能够轻松解决。
⼀、特殊三⾓形的存在性问题(⼀)⼆次函数中的等腰三⾓形存在性问题如果△ABC是等腰三⾓形,那么存在①AB=AC,②BA=BC,③CA=CB三种情况.因此,解等腰三⾓形的存在性问题时,通常要进⾏分类讨论。
这类问题有⼏何法和代数法两种⽅法,我们要根据具体情况灵活选择简便的⽅法。
⼏何法⼀般分三步:分类、画图、计算.代数法⼀般也分三步:罗列三边长,分类列⽅程,解⽅程并检验.(⼆)⼆次函数中的直⾓三⾓形存在性问题如果△ABC是直⾓三⾓形,那么存在①∠A为直⾓,②∠B为直⾓,③∠C为直⾓三种情况.因此,解直⾓三⾓形的存在性问题时,通常要进⾏分类讨论。
这类问题有⼏何法和代数法两种⽅法,我们要根据具体情况灵活选择简便的⽅法。
⼏何法⼀般分三步:分类、画图、计算.代数法⼀般也分三步:罗列三边长,分类列⽅程,解⽅程并检验.(三)⼆次函数中的等腰直⾓三⾓形存在性问题在解决等腰直⾓三⾓形存在性问题时,往往要⽤到⼏何和代数相结合的⽅法,设出点的坐标后,利⽤等腰直⾓三⾓形的⼏何性质及函数关系式列⽅程求解,最常⽤到的有:①两直⾓边相等,直⾓边与斜边的⽐为1:√2;②斜边中线垂直于斜边,且等于斜边的⼀半。
③直⾓顶点处构造三垂直,得到全等三⾓形,利⽤对应边的等量关系求解。
专题22.8 二次函数中的存在性问题【八大题型】(人教版)(原卷版)

专题22.8 二次函数中的存在性问题【八大题型】【人教版】【题型1 二次函数中直角三角形的存在性问题】 (1)【题型2 二次函数中等腰三角形的存在性问题】 (3)【题型3 二次函数中等腰直角三角形的存在性问题】 (5)【题型4 二次函数中平行四边形的存在性问题】 (7)【题型5 二次函数中矩形的存在性问题】 (9)【题型6 二次函数中菱形的存在性问题】 (11)【题型7 二次函数中正方形的存在性问题】 (13)【题型8 二次函数中角度问题的存在性问题】 (15)【题型1 二次函数中直角三角形的存在性问题】【例1】(2022•柳州)已知抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B(m,0)两点,与y轴交于点C(0,5).(1)求b,c,m的值;(2)如图1,点D是抛物线上位于对称轴右侧的一个动点,且点D在第一象限内,过点D作x轴的平行线交抛物线于点E,作y轴的平行线交x轴于点G,过点E作EF⊥x轴,垂足为点F,当四边形DEFG 的周长最大时,求点D的坐标;(3)如图2,点M是抛物线的顶点,将△MBC沿BC翻折得到△NBC,NB与y轴交于点Q,在对称轴上找一点P,使得△PQB是以QB为直角边的直角三角形,求出所有符合条件的点P的坐标.【变式1-1】(2022•桐梓县模拟)在平面直角坐标系xOy中,已知抛物线y=−√36x2+2√33x+2√3与x轴交于A,B两点(点B在点A的右侧),与y轴交于点C,它的对称轴与x轴交于点D,直线L经过C,D两点,连接AC.(1)求A,B两点的坐标及直线L的函数表达式;(2)探索直线L上是否存在点E,使△ACE为直角三角形,若存在,求出点E的坐标;若不存在,说明理由.【变式1-2】(2022秋•日喀则市月考)如图,二次函数y=﹣x2+4x+5的图象与x轴交于A,B两点,与y 轴交于点C,M为抛物线的顶点.(1)求M点的坐标;(2)求△MBC的面积;(3)坐标轴上是否存在点N,使得以B,C,N为顶点的三角形是直角三角形?若存在,求出点N的坐标;若不存在,请说明理由.【变式1-3】(2022•平南县二模)如图,二次函数y=x2+bx+c的图象与x轴交于A、B两点,与y轴交于点C,且A(﹣1,0),对称轴为直线x=2.(1)求该抛物线的表达式;(2)直线l过点A与抛物线交于点P,当∠P AB=45°时,求点P的坐标;(3)在抛物线的对称轴上是否存在一点Q,使得△BCQ是直角三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.【题型2 二次函数中等腰三角形的存在性问题】【例2】(2022•沙坪坝区校级模拟)如图1,抛物线y=ax2+bx+2(a≠0)交x轴于点A(﹣1,0),点B (4,0),交y轴于点C.连接BC,过点A作AD∥BC交抛物线于点D(异于点A).(1)求抛物线的表达式;(2)点P是直线BC上方抛物线上一动点,过点P作PE∥y轴,交AD于点E,过点E作EG⊥BC于点G,连接PG.求△PEG面积的最大值及此时点P的坐标;个单位,得到新抛物线y1,在y1的对称轴上(3)如图2,将抛物线y=ax2+bx+2(a≠0)水平向右平移32确定一点M,使得△BDM是以BD为腰的等腰三角形,请写出所有符合条件的点M的坐标,并任选其中一个点的坐标,写出求解过程.【变式2-1】(2022•湘西州)定义:由两条与x轴有着相同的交点,并且开口方向相同的抛物线所围成的封闭曲线称为“月牙线”,如图①,抛物线C1:y=x2+2x﹣3与抛物线C2:y=ax2+2ax+c组成一个开口向上的“月牙线”,抛物线C1和抛物线C2与x轴有着相同的交点A(﹣3,0)、B(点B在点A右侧),与y轴的交点分别为G、H(0,﹣1).(1)求抛物线C2的解析式和点G的坐标.(2)点M是x轴下方抛物线C1上的点,过点M作MN⊥x轴于点N,交抛物线C2于点D,求线段MN 与线段DM的长度的比值.(3)如图②,点E是点H关于抛物线对称轴的对称点,连接EG,在x轴上是否存在点F,使得△EFG 是以EG为腰的等腰三角形?若存在,请求出点F的坐标;若不存在,请说明理由.【变式2-2】(2022秋•永嘉县校级期末)如图,在平面直角坐标系中,点A,B分别是y轴正半轴,x轴正x2+3x+k交y 半轴上两动点,OA=2k,OB=2k+3,以AO,BO为邻边构造矩形AOBC,抛物线y=−34轴于点D,P为顶点,PM⊥x轴于点M.(1)求OD,PM的长(结果均用含k的代数式表示).(2)当PM=BM时,求该抛物线的表达式.(3)在点A在整个运动过程中,若存在△ADP是等腰三角形,请求出所有满足条件的k的值.【变式2-3】(2022•杭州校级自主招生)如图,抛物线y=ax2﹣5ax+4经过△ABC的三个顶点,已知BC∥x轴,点A在x轴的负半轴上,点C在y轴上,且AC=BC.(1)求抛物线的对称轴;(2)求A点坐标并求抛物线的解析式;(3)若点P在x轴下方且在抛物线对称轴上的动点,是否存在△P AB是等腰三角形?若存在,求出所有符合条件的点P坐标;不存在,请说明理由.【题型3 二次函数中等腰直角三角形的存在性问题】【例3】(2022•顺城区模拟)如图,抛物线y=﹣x2+bx+c与x轴交于点A和B(5,0),与y轴交于点C (0,5).(1)求抛物线的解析式;(2)抛物线的对称轴与x轴交于点M,与BC交于点F,点D是对称轴上一点,当点D关于直线BC的对称点E在抛物线上时,求点E的坐标;(3)点P在抛物线的对称轴上,点Q在直线BC上方的抛物线上,是否存在以O,P,Q为顶点的三角形是等腰直角三角形,若存在,请直接写出点Q的坐标;若不存在,请说明理由.x2+bx+c的图象与x轴交于点A(﹣2,0),与【变式3-1】(2022•碑林区校级三模)已知抛物线C1:y=14y轴交于点C(0,﹣3),顶点为D.(1)求抛物线C1的表达式和点D的坐标;(2)将抛物线C1沿x轴平移m(m>0)个单位长度,所得新的抛物线记作C2,C2的顶点为D′,与抛物线C1交于点E,在平移过程中,是否存在△DED′是等腰直角三角形?如果存在,请求出满足条件的抛物线C2的表达式,并写出平移过程;如果不存在,请说明理由.【变式3-2】(2022•琼海二模)如图1,抛物线y=ax2+bx+3与x轴交于点A(3,0)、B(﹣1,0),与y 轴交于点C,点P为x轴上方抛物线上的动点,点F为y轴上的动点,连接P A,PF,AF.(1)求该抛物线所对应的函数解析式;(2)如图1,当点F的坐标为(0,﹣4),求出此时△AFP面积的最大值;(3)如图2,是否存在点F,使得△AFP是以AP为腰的等腰直角三角形?若存在,求出所有点F的坐标;若不存在,请说明理由.【变式3-3】(2022•枣庄)如图①,已知抛物线L:y=x2+bx+c的图象经过点A(0,3),B(1,0),过点A作AC∥x轴交抛物线于点C,∠AOB的平分线交线段AC于点E,点P是抛物线上的一个动点.(1)求抛物线的关系式;(2)若动点P在直线OE下方的抛物线上,连结PE、PO,当△OPE面积最大时,求出P点坐标;(3)将抛物线L向上平移h个单位长度,使平移后所得抛物线的顶点落在△OAE内(包括△OAE的边界),求h的取值范围;(4)如图②,F是抛物线的对称轴l上的一点,在抛物线上是否存在点P,使△POF成为以点P为直角顶点的等腰直角三角形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由.【题型4 二次函数中平行四边形的存在性问题】【例4】(2022•垦利区二模)已知抛物线y=ax2+bx+3的图象与x轴相交于点A和点B(1,0),与y轴交于点C,连接AC,有一动点D在线段AC上运动,过点D作x轴的垂线,交抛物线于点E,交x轴于点F,AB=4,设点D的横坐标为m.(1)求抛物线的解析式;(2)连接AE、CE,当△ACE的面积最大时,点D的坐标是;(3)当m=﹣2时,在平面内是否存在点Q,使以B,C,E,Q为顶点的四边形为平行四边形?若存在,请求出点Q的坐标;若不存在,请说明理由.【变式4-1】(2022•澄迈县模拟)在平面直角坐标系中,抛物线经过点A(﹣2,0),B(﹣3,3)及原点O,顶点为C.(1)求该抛物线的函数表达式及顶点C的坐标;(2)设该抛物线上一动点P的横坐标为t.①在图1中,当﹣3<t<0时,求△PBO的面积S与t的函数关系式,并求S的最大值;②在图2中,若点P在该抛物线上,点E在该抛物线的对称轴上,且以A,O,P,E为顶点的四边形是平行四边形,求点P的坐标;【变式4-2】(2022•福山区一模)如图,抛物线y=ax2+bx+c过点A(﹣1,0),点B(3,0),与y轴负半轴交于点C,且OC=3OA,抛物线的顶点为D,对称轴交x轴于点E.(1)求抛物线的函数表达式;(2)求直线BC的函数表达式;(3)若点P是抛物线上一点,过点P作PQ⊥x轴交直线BC于点Q,试探究是否存在以点E,D,P,Q为顶点的平行四边形.若存在,求出点P坐标;若不存在,请说明理由.【变式4-3】(2022•青羊区校级模拟)抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣3,0),B(1,0)两点,与y轴交于点C(0,3),点P是抛物线上的一个动点.(1)求抛物线的函数表达式;(2)如图1,点P在线段AC上方的抛物线上运动(不与A,C重合),过点P作PD⊥AB,垂足为D,PD交AC于点E.作PF⊥AC,垂足为F,求△PEF的面积的最大值;(3)如图2,点Q是抛物线的对称轴l上的一个动点,在抛物线上,是否存在点P,使得以点A,P,C,Q为顶点的四边形是平行四边形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由.【题型5 二次函数中矩形的存在性问题】【例5】(2022•齐齐哈尔三模)综合与实践如图,二次函数y=﹣x2+c的图象交x轴于点A、点B,其中点B的坐标为(2,0),点C的坐标为(0,2),过点A、C的直线交二次函数的图象于点D.(1)求二次函数和直线AC的函数表达式;(2)连接DB,则△DAB的面积为6;(3)在y轴上确定点Q,使得∠AQB=135°,点Q的坐标为;(4)点M是抛物线上一点,点N为平面上一点,是否存在这样的点N,使得以点A、点D、点M、点N 为顶点的四边形是以AD为边的矩形?若存在,请你直接写出点N的坐标;若不存在,请说明理由.【变式5-1】(2022•博山区一模)如图,已知抛物线y=ax2+bx﹣4与x轴交于A,B两点,与y轴交于点C,x﹣4.且点A的坐标为(﹣2,0),直线BC的解析式为y=12(1)求抛物线的解析式.(2)如图1,过点A作AD∥BC交抛物线于点D(异于点A),P是直线BC下方抛物线上一点,过点P作PQ∥y轴,交AD于点Q,过点Q作QR⊥BC于点R,连接PR.求△PQR面积的最大值及此时点P 的坐标.(3)如图2,点C关于x轴的对称点为点C′,将抛物线沿射线C′A的方向平移2√5个单位长度得到新的抛物线y′,新抛物线y′与原抛物线交于点M,原抛物线的对称轴上有一动点N,平面直角坐标系内是否存在一点K,使得以D,M,N,K为顶点的四边形是矩形?若存在,请直接写出点K的坐标;若不存在,请说明理由.【变式5-2】(2022•绥化)如图,抛物线y=ax2+bx+c交y轴于点A(0,﹣4),并经过点C(6,0),过点A作AB⊥y轴交抛物线于点B,抛物线的对称轴为直线x=2,D点的坐标为(4,0),连接AD,BC,BD.点E从A点出发,以每秒√2个单位长度的速度沿着射线AD运动,设点E的运动时间为m秒,过点E作EF⊥AB于F,以EF为对角线作正方形EGFH.(1)求抛物线的解析式;(2)当点G随着E点运动到达BC上时,求此时m的值和点G的坐标;(3)在运动的过程中,是否存在以B,G,C和平面内的另一点为顶点的四边形是矩形,如果存在,直接写出点G的坐标,如果不存在,请说明理由.【变式5-3】(2022•黔东南州)如图,抛物线y=ax2+2x+c的对称轴是直线x=1,与x轴交于点A,B(3,0),与y轴交于点C,连接AC.(1)求此抛物线的解析式;(2)已知点D是第一象限内抛物线上的一个动点,过点D作DM⊥x轴,垂足为点M,DM交直线BC 于点N,是否存在这样的点N,使得以A,C,N为顶点的三角形是等腰三角形.若存在,请求出点N的坐标,若不存在,请说明理由;(3)已知点E是抛物线对称轴上的点,在坐标平面内是否存在点F,使以点B、C、E、F为顶点的四边形为矩形,若存在,请直接写出点F的坐标;若不存在,请说明理由.【题型6 二次函数中菱形的存在性问题】【例6】(2022•烟台一模)如图,平面直角坐标系中,正方形ABCD的顶点A,B在x轴上,抛物线y=﹣x2+bx+c经过A,C(4,﹣5)两点,且与直线DC交于另一点E.(1)求抛物线的解析式;(2)P为y轴上一点,过点P作抛物线对称轴的垂线,垂足为Q,连接EQ,AP.试求EQ+PQ+AP的最小值;(3)N为平面内一点,在抛物线对称轴上是否存在点M,使得以点M,N,E,A为顶点的四边形是菱形?若存在,请直接写出点M的坐标;若不存在,请说明理由.【变式6-1】(2022•邵阳县模拟)如图,直线l:y=﹣3x﹣6与x轴、y轴分别相交于点A、C;经过点A、x2+bx+c与x轴的另一个交点为点B,其顶点为点D,对称轴与x轴相交于点E.C的抛物线C:y=12(1)求抛物线C的对称轴.(2)将直线l向右平移得到直线l1.①如图①,直线l1与抛物线C的对称轴DE相交于点P,要使PB+PC的值最小,求直线l1的解析式.②如图②,直线l1与直线BC相交于点F,直线l1上是否存在点M,使得以点A、C、F、M为顶点的四边形是菱形,若存在,求出点M的坐标;若不存在,请说明理由.【变式6-2】(2022•嘉定区二模)在平面直角坐标系xOy(如图)中,已知抛物线y=ax2+bx+3经过点A(3,0)、B(4,1)两点,与y轴的交点为C点.(1)求抛物线的表达式;(2)求四边形OABC的面积;(3)设抛物线y=ax2+bx+3的对称轴是直线l,点D与点B关于直线l对称,在线段BC上是否存在一点E,使四边形ADCE是菱形,如果存在,请求出点E的坐标;如果不存在,请说明理由.【变式6-3】(2022•山西模拟)综合与探究如图,二次函数y=ax2+bx+4的图象与x轴分别交于点A(﹣2,0),B(4,0),点E是x轴正半轴上的一个动点,过点E作直线PE⊥x轴,交抛物线于点P,交直线BC于点F.(1)求二次函数的表达式.EF,求此时点P的坐标.(2)当点E在线段OB上运动时(不与点O,B重合),恰有线段PF=12(3)试探究:若点Q是y轴上一点,在点E运动过程中,是否存在点Q,使得以点C,F,P,Q为顶点的四边形为菱形,若存在,直接写出点Q的坐标;若不存在,请说明理由.【题型7 二次函数中正方形的存在性问题】【例7】(2022•铁锋区二模)综合与探究如图,在平面直角坐标系中,直线y=x+b与x轴交于点A(4,0),与y轴交于点B,过A,B两点的抛物线交x轴于另一点C,且OA=20C,点F是直线AB下方抛物线上的动点,连接F A,FB.(1)求抛物线解析式;(2)当点F与抛物线的顶点重合时,△ABF的面积为;(3)求四边形F AOB面积的最大值及此时点F的坐标.(4)在(3)的条件下,点Q为平面内y轴右侧的一点,是否存在点Q及平面内另一点M,使得以A,F,Q,M为顶点的四边形是正方形?若存在,直接写出点Q的坐标;若不存在,说明理由.【变式7-1】(2022•陇县二模)在平面直角坐标系中,已知抛物线L1:y=ax2+bx+c经过A(﹣2,0),)两点,且与y轴交于点C,点B是该抛物线的顶点.B(1,−94(1)求抛物线L1的表达式;(2)将L1平移后得到抛物线L2,点D,E在L2上(点D在点E的上方),若以点A,C,D,E为顶点的四边形是正方形,求抛物线L2的解析式.【变式7-2】(2022秋•南宁期中)如图,抛物线与y轴交于点C(0,3),与x轴于点A(﹣1,0)、B(3,0),点P是抛物线的顶点.(1)求抛物线的解析式;(2)Q是抛物线上第一象限除点P外一点,△BCQ与△BCP的面积相等,求点Q的坐标;(3)若M、N为抛物线上两个动点,分别过点M、N作直线BC的垂线段,垂足分别为D、E.是否存在点M、N使四边形MNED为正方形?如果存在,求正方形MNED的边长;如果不存在,请说明理由.【变式7-3】(2022•南充)如图,抛物线顶点P(1,4),与y轴交于点C(0,3),与x轴交于点A,B.(1)求抛物线的解析式.(2)Q是抛物线上除点P外一点,△BCQ与△BCP的面积相等,求点Q的坐标.(3)若M,N为抛物线上两个动点,分别过点M,N作直线BC的垂线段,垂足分别为D,E.是否存在点M,N使四边形MNED为正方形?如果存在,求正方形MNED的边长;如果不存在,请说明理由.【题型8 二次函数中角度问题的存在性问题】【例8】(2022•西宁)如图,抛物线y=ax2+bx+3与x轴交于点A(3,0),与y轴交于点B,点C在直线AB上,过点C作CD⊥x轴于点D(1,0),将△ACD沿CD所在直线翻折,使点A恰好落在抛物线上的点E处.(1)求抛物线解析式;(2)连接BE,求△BCE的面积;(3)抛物线上是否存在一点P,使∠PEA=∠BAE?若存在,求出P点坐标;若不存在,请说明理由.,0),B(3,【变式8-1】(2022•鄂尔多斯)如图,在平面直角坐标系中,抛物线y=ax2+bx+2经过A(−127)两点,与y轴交于点C.2(1)求抛物线的解析式;(2)点P在抛物线上,过P作PD⊥x轴,交直线BC于点D,若以P、D、O、C为顶点的四边形是平行四边形,求点P的横坐标;(3)抛物线上是否存在点Q,使∠QCB=45°?若存在,请直接写出点Q的坐标;若不存在,请说明理由.【变式8-2】(2022•运城二模)如图,已知抛物线y=ax2+bx﹣8与x轴交于点A(﹣2,0),B(8,0)两点,与y轴交于点C,点P是直线BC下方抛物线上一动点,过点P作直线PE∥y轴,交直线BC于点D,交x轴于点F,以PD为斜边,在PD的右侧作等腰直角△PDF.(1)求抛物线的表达式,并直接写出直线BC的表达式;(2)设点P的横坐标为m(0<m<3),在点P运动的过程中,当等腰直角△PDF的面积为9时,请求出m的值;(3)连接AC,该抛物线上是否存在一点M,使∠ACO+∠BCM=∠ABC,若存在,请直接写出所有符合条件的点M的坐标,若不存在,请说明理由.x2+bx+c交x轴于A(﹣3,0),B(4,0)【变式8-3】(2022•罗湖区校级一模)如图,已知抛物线y=−13两点,交y轴于点C,点P是抛物线上一点,连接AC、BC.(1)求抛物线的表达式;(2)连接OP,BP,若S△BOP=2S△AOC,求点P的坐标;(3)在抛物线的对称轴上是否存在点Q,使得∠QBA=75°?若存在,直接写出点Q的坐标;若不存在,请说明理由.。
二次函数的存在性问题(Word版解析+答案)

中考压轴题解析二次函数的存在性问题【典例分析】【考点 1】二次函数与相似三角形问题例1】已知抛物线y ax2 bx 3与 x轴分别交于A( 3,0),B(1,0)两点,与 y轴交于点 C.2)点 F 是线段 AD 上一个动点.1AD .2ABC 相似?若相似,求出点 F 的坐标;若不相似,请说明理由.变式1-1】如图,抛物线y ax2 2x c经过A( 1,0),B两点,且与y轴交于点C(0,3) ,抛物线与直线y x 1交于A,E 两点.(1)求抛物线的解析式;(2)坐标轴上是否存在一点Q,使得AQE是以AE为底边的等腰三角形?若存在,请直接写出点Q 的坐标;若不存在,说明理由.(3)P点在x轴上且位于点B 的左侧,若以P,B,C为顶点的三角形与ABE相似,求点P的坐AF①如图 1,设k ,当 k 为何值时,CFAD1)求抛物线的表达式及顶点 D 的坐标;标.1【变式1-2】如图,已知抛物线y m(x 2)(x m)(m > 0)与 x 轴相交于点 A,B,与 y轴相交于点 C,且点 A 在点 B 的左侧 .( 1)若抛物线过点( 2, 2),求抛物线的解析式;(2)在( 1)的条件下,抛物线的对称轴上是否存在一点H ,使 AH+CH 的值最小,若存在,求出点 H 的坐标;若不存在,请说明理由;(3)在第四象限内,抛物线上是否存在点M ,使得以点 A,B,M 为顶点的三角形与△ACB 相似?若存在,求出 m 的值;若不存在,请说明理由 .考点 2】二次函数与直角三角形问题BC交于点D,连接AC 、AD ,求VACD的面积;3 点E为直线BC上的任意一点,过点E作x轴的垂线与抛物线交于点F ,问是否存在点E使VDEF 为直角三角形?若存在,求出点E 坐标,若不存在,请说明理由.例2】如图,抛物线y ax2bx c a 0的顶点坐标为2, 1 ,图象与y 轴交于点C 0,3 ,与x轴2 设抛物线对称轴与直线【变式2-1】如图,经过x 轴上A( 1,0), B(3,0)两点的抛物线y m(x 1)2 4m (m 0)交y 轴于点C ,设抛物线的顶点为D ,若以DB 为直径的⊙ G 经过点C ,求解下列问题:1)用含m的代数式表示出C,D 的坐标;2)求抛物线的解析式;3)能否在抛物线上找到一点Q,使△BDQ 为直角三角形?如能,求出Q点的坐标,若不能,请说明理由。
二次函数-存在性问题-备战2023年中考数学考点微专题

考向3.9 二次函数-存在性问题例1、(2021·湖南湘潭·中考真题)如图,一次函数333y x =-图象与坐标轴交于点A 、B ,二次函数233y x bx c =++图象过A 、B 两点. (1)求二次函数解析式;(2)点B 关于抛物线对称轴的对称点为点C ,点P 是对称轴上一动点,在抛物线上是否存在点Q ,使得以B 、C 、P 、Q 为顶点的四边形是菱形?若存在,求出Q 点坐标;若不存在,请说明理由.解:(1)对于33y x =:当x =0时,3y = 当y =0时,3303x -=,妥得,x =3 ∴A (3,0),B (0,3- 把A (3,0),B (0,3-23y bx c ++得: 33+3+=03b c c ⎧⎪⎨=-⎪⎩解得,233b c ⎧=⎪⎨⎪=⎩∴抛物线的解析式为:23233y =-(2)抛物线的对称轴为直线23312323b x a -=-=-=⨯故设P (1,p ),Q (m ,n ) ①当BC 为菱形对角线时,如图,∵B ,C 关于对称没对称,且对称轴与x 轴垂直, ∴∴BC 与对称轴垂直,且BC //x 轴 ∵在菱形BQCP 中,BC ⊥PQ ∴PQ ⊥x 轴 ∵点P 在x =1上, ∴点Q 也在x =1上, 当x =1时,232343113=333y =⨯-⨯--∴Q (1,433-); ②当BC 为菱形一边时,若点Q 在点P 右侧时,如图,∴BC //PQ ,且BC =PQ ∵BC //x 轴,∴令3y =23233=3y解得,120,2x x == ∴(2,3)C - ∴PQ =BC =2 ∵22(3)12+= ∴PB =BC =2 ∴迠P 在x 轴上, ∴P (1,0) ∴Q (3,0);若点Q 在点P 的左侧,如图,同理可得,Q (-1,0) 综上所述,Q 点坐标为(1,433-)或(3,0)或(-1,0)1、存在性问题的解题思路:假设存在,推理论证,得出结论;2、解決线段存在性问题的方法:将军饮马问题、垂线段问题、三角形三边关系、函数最值等;3、本题考查的知识点有用待定系数法求出二次函数的解析式,菱形的性质和判定,解一元二次方程,主要考查学生综合运用这些性质进行计算和推理的能力.同时注意用分类讨论思想解决问题。
二次函数存在性问题(题集)

二次函数存在性问题(题集)1.如图,抛物线y=﹣x2+bx+c与x轴交于A,B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A (﹣1,0),C(0,2).(1)求抛物线的解析式;(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出点P的坐标;如果不存在,请说明理由;(3)点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,求△CBF的最大面积及此时点E的坐标.2.在平面直角坐标系中,二次函数y=ax2+bx+2的图象与x轴交于A(﹣3,0),B(1,0)两点,与y轴交于点C.(1)求这个二次函数的关系解析式;(2)点M为抛物线上一动点,在x轴上是否存在点Q,使以A、C、M、Q为顶点的四边形是平行四边形?若存在,直接写出点Q的坐标;若不存在,说明理由.3.如图,在平面直角坐标系中,抛物线y=ax2+bx﹣3a经过点A(﹣1,0)、C(0,3),且与x轴交于另一点B,将抛物线的顶点记为D.(1)求该抛物线的表达式;(2)在对称轴右侧的抛物线上是否存在点P,使得△PDC为等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由.4.如图,已知二次函数y=﹣x2+bx+3的图象与x轴的两个交点为A(4,0)与点C,与y轴交于点B.(1)求此二次函数关系式和点C的坐标;(2)请你直接写出△ABC的面积;(3)在x轴上是否存在点P,使得△PAB是等腰三角形?若存在,请你直接写出点P的坐标;若不存在,请说明理由.BC上一动点,过点P作x轴的垂线交抛物线于点D.(1)求抛物线的表达式;(2)连接CD、DB.当△BDC的面积最大时,求△BDC面积的最大值以及此时点P的坐标?(3)是否存在点P,使得△PCD是等腰三角形,若存在,求出P点的坐标.若不存在,说明理由.6.如图,抛物线y=﹣+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).(1)求抛物线的解析式;(2)点E是线段BC上的一个动点(不与B、C重合),过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时点E的坐标.(3)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由.顶点,对称轴与x轴交于E.(1)求抛物线的解析式;(2)如图1,在抛物线的对称轴DE上求作一点M,使△AMC的周长最小,并求出点M的坐标和周长的最小值.(3)如图2,点P是x轴上的动点,过P点作x轴的垂线分别交抛物线和直线BC于F、G.设点P的横坐标为m.是否存在点P,使△FCG是等腰三角形?若存在,直接写出m的值;若不存在,请说明理由.8.如图,已知抛物线y=﹣x2+bx+c经过点A(﹣1,0),B(3,0),与y轴交于点C,点P是抛物线上一动点,连接PB,PC.(1)求抛物线的解析式;(2)如图1,当点P在直线BC上方时,过点P作PD⊥x轴于点D,交直线BC于点E.若PE=2ED,求△PBC 的面积;(3)抛物线上存在一点P,使△PBC是以BC为直角边的直角三角形,求点P的坐标.9.如图1,二次函数y=ax2+bx﹣2(a≠0)的图象与x轴交于A(﹣4,0)、B(1,0)两点,与y轴交于点C.(1)求这个二次函数的表达式:(2)点M在该抛物线的对称轴上,当△ACM是直角三角形时,求点M的坐标;(3)如图2,点D在y轴上,且CD=OA,连接AD,点E、F分别是线段OA,AD上的动点,求EF+OF的最小值.10.如图,抛物线y=ax2+bx过A(4,0),B(1,3)两点,点C、B关于抛物线的对称轴对称,过点B作直线BH ⊥x轴,交x轴于点H.(1)求抛物线的表达式;(2)点P是抛物线上一动点,且位于第四象限,当△ABP的面积为6时,求出点P的坐标;(3)若点M在直线BH上运动,点N在x轴上运动,当以点C、M、N为顶点的三角形为等腰直角三角形时,请直接写出此时△CMN的面积.11.如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且抛物线经过A(1,0),C(0,3)两点,与x轴的另一交点为点B.(1)若直线y=mx+n经过B,C两点,求直线BC和抛物线的解析式;(2)M为抛物线的对称轴x=﹣1上一点,设点M到点A的距离与到点C的距离之和为t,求t的最小值;(3)设点P为抛物线的对称轴x=﹣1上的一个动点,请直接写出使△BPC为直角三角形的点P的坐标.12.如图,抛物线y=x2﹣2x﹣8与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,连接AC,BC.点P是第四象限内抛物线上的一个动点,点P的横坐标为m,过点P作PM⊥x轴,垂足为点M,PM交BC于点Q.(1)求A,B,C三点的坐标;(2)试探究在点P运动的过程中,是否存在这样的点Q,使得以A、C、Q为顶点的三角形是等腰三角形?若存在,请求出此时点Q的坐标;若不存在,请说明理由.13.如图,在平面直角坐标系中,已知抛物线y=x2+bx+c过A,B,C三点,点A的坐标是(3,0),点C的坐标是(0,﹣3),动点P在抛物线上.(1)b=,c=,点B的坐标为;(2)是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;(3)是否存在点P使得∠PCA=15°,若存在,请直接写出点P的横坐标.若不存在,请说明理由.14.如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(﹣1,0),C(2,3)两点,与y轴交于点N.其顶点为D.(1)抛物线及直线AC的函数关系式;(2)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值.(3)在抛物线对称轴上是否存在一点M,使以A,N,M为顶点的三角形是直角三角形?若存在,请直接写出点M的坐标.若不存在,请说明理由.15.如图,抛物线y=﹣x2+bx+c与x轴相交于A、B两点,与y轴相交于点C,且点B与点C的坐标分别为B(3,0),C(0,3),点M是抛物线的顶点,点P为线段MB上一个动点,过点P作PD⊥x轴于点D,若OD=m.(1)求二次函数解析式;(2)设△PCD的面积为S,试判断S有最大值或最小值吗?若有,求出其最值,若没有,请说明理由;(3)在MB上是否存在点P,使△PCD为直角三角形?若存在,请写出点P的坐标;若不存在,请说明理由.16.综合与探究在平面直角坐标系中,二次函数y=ax2+bx+2的图象与x轴交于A(﹣3,0),B(1,0)两点,与y轴交点C.(1)求抛物线与直线AC的函数解析式;(2)若点P是直线AC上方抛物线上的一动点,过点P作PF⊥x轴于点F,交直线AC于点D,求线段PD的最大值.(3)点M为抛物线上一动点,在x轴上是否存在点Q,使以A、C、M、Q为顶点的四边形是平行四边形?若存在,直接写出点Q的坐标;若不存在,说明理由.17.如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A、B两点,与y轴交于C点,AC=,OB=OC=3OA.(1)求抛物线的解析式;(2)在第二象限内的抛物线上确定一点P,使四边形PBAC的面积最大,求出点P的坐标;(3)在(2)的结论下,点M为x轴上一动点,抛物线上是否存在一点Q,使点P、B、M、Q为顶点的四边形是平行四边形,若存在,请直接写出Q点的坐标;若不存在,请说明理由.18.如图,已知抛物线y=ax2+bx+c(a≠0)经过A(﹣1,0),C(0,2),对称轴为直线x=.(1)求该抛物线和直线BC的解析式;(2)点G是直线BC上方抛物线上的动点,设G点的横坐标为m,试用含m的代数式表示△GBC的面积,并求出△GBC面积的最大值;(3)设R点是直线x=1上一动点,M为抛物线上的点,是否存在点M,使以点B、C、R、M为顶点的四边形为平行四边形,若存在,请直接写出符合条件的所有点M坐标,不存在说明理由.19.如图,抛物线y=ax2+bx+6经过A(﹣2,0)、B(4,0)两点,与y轴交于点C,点D是抛物线上一动点,设点D的横坐标为m(1<m<4),连接AC、BC、DB、DC.(1)求抛物线的函数表达式.(2)当△BCD的面积等于△AOC的面积的时,求m的值.(3)当m=2时,若点M是x轴上一动点,点N是抛物线上一动点,试判断是否存在这样的点M,使得以点B、D、M、N为顶点的四边形是平行四边形?若存在,请直接写出点M的坐标;若不存在,请说明理由.20.如图,已知抛物线y=ax2+bx﹣5的经过点(﹣2,﹣15)、点(2,1).(1)求抛物线的表达式;(2)请用配方法求抛物线顶点A的坐标;(3)已知点M坐标为(2,﹣1).设动点P、Q分别在抛物线和对称轴l上,当以A,P,Q,M为顶点的四边形是平行四边形时,求P、Q两点的坐标.21.如图,已知抛物线y=x2+bx﹣3c经过点A(1,0)和点B(0,﹣3),与x轴交于另一点C.(1)求抛物线的解析式;(2)若点P是抛物线上的动点,点Q是抛物线对称轴上的动点,那么是否存在这样的点P,使以点A、C、P、Q为顶点的四边形为平行四边形?若存在,请求出点P的坐标;若不存在,请说明理由.22.如图,抛物线经过A(﹣2,0),B(4,0),C(0,﹣3)三点.(1)求抛物线的解析式;(2)在直线BC下方的抛物线上有一动点P,使得△PBC的面积最大,求点P的坐标;(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求出点N的坐标;若不存在,请说明理由.23.如图,抛物线y=﹣x2+2x+与x轴相交于A,B两点,点B在点A的右侧,与y轴相交于点C.(1)求点A,B,C的坐标;(2)在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标;(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.24.如图,抛物线y=﹣x2+mx+n与x轴交于A,B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2)(1)求抛物线的表达式;(2)点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标;(3)在y轴上是否存在点P使得∠OBP+∠OBC=45°?若存在,请直接写出点P的坐标,若不存在,请说明理由.25.如图,抛物线y=ax2+2x+c(a<0)与x轴交于点A和点B(点A在原点的左侧,点B在原点的右侧),与y轴交于点C,OB=OC=3.(1)求该抛物线的函数解析式;:S△(2)如图1,连接BC,点D是直线BC上方抛物线上的点,连接OD,CD,OD交BC于点F,当S△COF CDF=3:2时,求点D的坐标.(3)如图2,点E的坐标为(0,),在抛物线上是否存在点P,使∠OBP=2∠OBE?若存在,请直接写出符合条件的点P的坐标;若不存在,请说明理由.26.如图,抛物线y=﹣x2+bx+c与x轴交于A,B两点,其中A(3,0),B(﹣1,0),与y轴交于点C,抛物线的对称轴交x轴于点D,直线y=kx+b1经过点A,C,连接CD.(1)求抛物线和直线AC的解析式:(2)若抛物线上存在一点P,使△ACP的面积是△ACD面积的2倍,求点P的坐标;(3)在抛物线的对称轴上是否存在一点Q,使线段AQ绕Q点顺时针旋转90°得到线段QA1,且A1好落在抛物线上?若存在,求出点Q的坐标;若不存在,请说明理由.27.如图,已知抛物线y=ax2+bx+c与x轴相交于A(﹣3,0),B两点,与y轴相交于点C(0,2),对称轴是直线x=﹣1,连接AC.(1)求该抛物线的表达式;(2)若过点B的直线l与抛物线相交于另一点D,当∠ABD=∠BAC时,求直线l的表达式;=S (3)在(2)的条件下,当点D在x轴下方时,连接AD,此时在y轴左侧的抛物线上存在点P,使S△BDP.请直接写出所有符合条件的点P的坐标.△ABD28.如图1,抛物线y=ax2+c与x轴交于点A、B,与y轴交于点C,若OC=2OA=4.(1)求抛物线解析式;(2)如图2,过点A、C作直线,求直线AC的解析式;(3)若P为抛物线上一点且∠ABP=∠ACO,求点P的坐标.29.图①,二次函数y=ax2+bx+c(a≠0)的图象经过点A(﹣1,0),并且与直线y=x﹣2相交于坐标轴上的B、C两点,动点P在直线BC下方的二次函数的图象上.(1)求此二次函数的表达式;(2)如图①,连接PC,PB,设△PCB的面积为S,求S的最大值;(3)如图②,抛物线上是否存在点Q,使得∠ABQ=2∠ABC?若存在,则求出直线BQ的解析式及Q点坐标;若不存在,请说明理由.。
二次函数中点的存在性问题

二次函数中的存在性问题1.已知抛物线y=﹣x2+x﹣3与x轴交于A,B两点,与y轴交于点C.在直线CA上方的抛物线上是否存在一点D,使得△ACD的面积最大?若存在,求出点D的坐标;若不存在,请说明理由.2.已知y=ax2+bx+c(a≠0)图象与直线y=kx+4相交于A(1,m),B(4,8)两点,与x轴交于原点及点C.(1)求直线和抛物线解析式;(2)在x轴上方的抛物线上是否存在点D,使S△OCD=2S△OAB?如果存在,求出点D坐标,如果不存在,说明理由.3.已知直线y=x﹣3与x轴交于点A,与y轴交于点C,抛物线y=﹣x2+mx+n经过点A和点C.(1)求此抛物线的解析式;(2)在直线CA上方的抛物线上是否存在点D,使得△ACD的面积最大?若存在,求出点D的坐标;若不存在,说明理由.4.在平面直角坐标系xOy中,抛物线y=﹣x2+bx+c与x轴交于A、B两点(点A在点B的左侧),过点A的直线y=kx+1交抛物线于点C(2,3).(1)求直线AC及抛物线的解析式;(2)若直线y=kx+1与抛物线的对称轴交于点E,以点E为中心将直线y=kx+1顺时针旋转90°得到直线l,设直线l与y轴的交点为P,求△APE的面积;(3)若G为抛物线上一点,是否存在x轴上的点F,使以B、E、F、G为顶点的四边形为平行四边形?若存在,直接写出点F的坐标;若不存在,请说明理由.5.如图,在平面直角坐标系中,抛物线交x轴于A,B两点(A在B的左侧),交y轴于点C.(1)求直线BC的解析式;(2)求抛物线的顶点及对称轴;(3)若点Q是抛物线对称轴上的一动点,线段AQ+CQ是否存在最小值?若存在,求出点Q的坐标;若不存在,说明理由;(4)若点P是直线BC上方的一个动点,△PBC的面积是否存在最大值?若存在,求出点P的坐标及此时△PBC 的面积;若不存在,说明理由.1.已知抛物线y=﹣x2+x﹣3与x轴交于A,B两点,2.与y轴交于点C.在直线CA上方的抛物线上是否存在3.一点D,使得△ACD的面积最大?若存在,求出点D4.的坐标;若不存在,请说明理由.解答:解:对于抛物线y=﹣x2+x﹣3,令y=0,得到﹣x2+x﹣3=0,解得:x=1或x=4,∴B(1,0),A(4,0),令x=0,得到y=﹣3,即C(0,﹣3),设直线AC解析式为y=kx+b,将A与C坐标代入得:,解得:k=,b=﹣3,∴直线AC解析式为y=x﹣3,设平行于直线AC,且与抛物线只有一个交点的直线方程为y=x+m,此时直线与抛物线交于点D,使得△ACD的面积最大,与二次函数解析式联立消去y得:﹣x2+x﹣3=x+m,整理得:3x2﹣12x+4m+12=0,∴△=144﹣12(4m+12)=0,解得:m=0,∴此时直线方程为y=x,点D坐标为(2,).2.(2008•宁波校级自主招生)已知y=ax2+bx+c(a≠0)图象与直线y=kx+4相交于A(1,m),B(4,8)两点,与x轴交于原点及点C.(1)求直线和抛物线解析式;(2)在x轴上方的抛物线上是否存在点D,使S△OCD=2S△OAB?如果存在,求出点D坐标,如果不存在,说明理由.解答:解:(1)∵直线y=kx+4过A(1,m),B(4,8)两点,∴,解得,∴y=x+4,把O、A、B三点坐标代入抛物线解析式,得,,∴y=﹣x2+6x;∴S△OCD=2S△OAB=12,×6×h=12,解得h=4,由﹣x2+6x=4,得x=3±,∴D(3+,4)或(3﹣,4).3.(2014春•昌平区期末)已知直线y=x﹣3与x轴交于点A,与y轴交于点C,抛物线y=﹣x2+mx+n经过点A和点C.(1)求此抛物线的解析式;(2)在直线CA上方的抛物线上是否存在点D,使得△ACD的面积最大?若存在,求出点D的坐标;若不存在,说明理由.解答:解:(1)把x=0代入y=x﹣3得y=﹣3,则C点坐标为(0,﹣3),把y=0代入y=x﹣3得x﹣3=0,解得x=4,则A点坐标为(4,0),把A(4,0),C(0,﹣3)代入y=﹣x2+mx+n得,解得,所以二次函数解析式为y=﹣x2+x﹣3;(2)存在.过D点作直线AC的平行线y=kx+b,当直线y=kx+b与抛物线只有一个公共点时,点D到AC的距离最大,此时△ACD的面积最大,∵直线AC的解析式为y=x﹣3,∴k=,即y=x+b,由直线y=x+b和抛物线y=﹣x2+x﹣3组成方程组得,消去y得到3x2﹣12x+4b+12=0,∴△=122﹣4×3×(4b+12)=0,解得b=0,∴3x2﹣12x+12=0,解得x1=x2=2,把x=2,b=0代入y=x+b得y=,∴D点坐标为(2,).4.(2010•孝感模拟)在平面直角坐标系xOy中,抛物线y=﹣x2+bx+c与x轴交于A、B两点(点A在点B的左侧),过点A的直线y=kx+1交抛物线于点C(2,3).(1)求直线AC及抛物线的解析式;(3)若G为抛物线上一点,是否存在x轴上的点F,使以B、E、F、G为顶点的四边形为平行四边形?若存在,直接写出点F的坐标;若不存在,请说明理由.解答:解:(1)∵点C(2,3)在直线y=kx+1上,∴2k+1=3.解得k=1.∴直线AC的解析式为y=x+1.∵点A在x轴上,∴A(﹣1,0).∵抛物线y=﹣x2+bx+c过点A、C,∴解得∴抛物线的解析式为y=﹣x2+2x+3.(2)由y=﹣x2+2x+3=﹣(x﹣1)2+4,可得抛物线的对称轴为x=1,B(3,0).∴E(1,2).根据题意,知点A旋转到点B处,直线l过点B、E.设直线l的解析式为y=mx+n.将B、E的坐标代入y=mx+n中,联立可得m=﹣1,n=3.∴直线l的解析式为y=﹣x+3.∴P(0,3).过点E作ED⊥x轴于点D.∴S△PAE=S△PAB﹣S△EAB=AB•PO﹣AB•ED=×4×(3﹣2)=2.(3)存在,点F的坐标分别为(3﹣,0),(3+,0),(﹣1﹣,0)(﹣1+,0).5.(2013秋•红安县校级月考)如图,在平面直角坐标系中,抛物线交x轴于A,B两点(A在B的左侧),交y轴于点C.(1)求直线BC的解析式;(3)若点Q是抛物线对称轴上的一动点,线段AQ+CQ是否存在最小值?若存在,求出点Q的坐标;若不存在,说明理由;(4)若点P是直线BC上方的一个动点,△PBC的面积是否存在最大值?若存在,求出点P的坐标及此时△PBC 的面积;若不存在,说明理由.考点:二次函数综合题.专题:压轴题.分析:(1)令y=0,解关于x的一元二次方程求出点B的坐标,令x=0求出点C的坐标,设直线BC的解析式为y=kx+b,然后利用待定系数法求一次函数解析式解答即可;(2)把二次函数解析式整理成顶点式形式,然后写出顶点坐标与对称轴即可;(3)根据轴对称确定最短路线问题,直线BC与对称轴的交点即为使线段AQ+CQ最小的点Q,然后利用直线解析式求解即可;(4)过点P作PD∥y轴与BC相交于点D,根据抛物线解析式与直线BC的解析式表示出PD,再根据S△PBC=S△PCD+S△PBD列式整理,然后利用二次函数最值问题解答.解答:解:(1)令y=0,则﹣x2+x+2=0,整理得,x2﹣2x﹣3=0,解得x1=﹣1,x2=3,所以,点B的坐标为(3,0),令x=0,则y=2,所以,点C的坐标为(0,2),设直线BC的解析式为y=kx+b,则,解得,所以,直线BC的解析式为y=﹣x+2;(2)∵y=﹣x2+x+2,=﹣(x2﹣2x+1)+2+,=﹣(x﹣1)2+,∴顶点坐标为(1,),(3)由轴对称确定最短路线问题,直线BC与对称轴的交点即为使线段AQ+CQ最小的点,x=1时,y=﹣×1+2=,所以,存在Q(1,),使线段AQ+CQ最小;(4)如图,过点P作PD∥y轴与BC相交于点D,则PD=(﹣x2+x+2)﹣(﹣x+2)=﹣x2+2x,所以,S△PBC=S△PCD+S△PBD,=×(﹣x2+2x)×3,=﹣x2+3x,=﹣(x﹣)2+,所以,当x=时,△PBC的面积最大为,此时,y=﹣×()2+×+2=,所以,存在P(,),使S△PBC最大=.点评:本题是二次函数综合题型,主要利用了抛物线与x轴的交点坐标的求解,待定系数法求一次函数解析式,二次函数的顶点坐标与对称轴的求法,轴对称确定最短路线问题,二次函数的最值问题.。
二次函数中的存在性问题
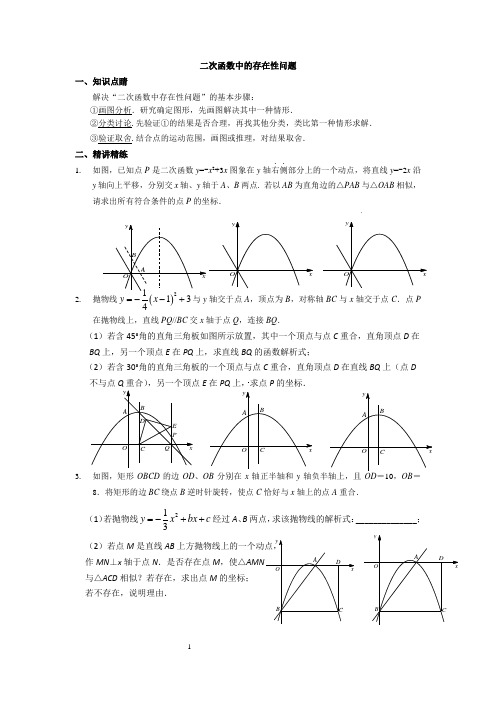
二次函数中的存在性问题一、知识点睛解决“二次函数中存在性问题”的基本步骤:①画图分析.研究确定图形,先画图解决其中一种情形.②分类讨论.先验证①的结果是否合理,再找其他分类,类比第一种情形求解.③验证取舍.结合点的运动范围,画图或推理,对结果取舍.二、精讲精练1.如图,已知点P是二次函数y=-x2+3x图象在y轴右侧..部分上的一个动点,将直线y=-2x沿y轴向上平移,分别交x轴、y轴于A、B两点. 若以AB为直角边的△PAB与△OAB相似,请求出所有符合条件的点P的坐标.2.抛物线()2134y x=--+与y轴交于点A,顶点为B,对称轴BC与x轴交于点C.点P 在抛物线上,直线PQ//BC交x轴于点Q,连接BQ.(1)若含45°角的直角三角板如图所示放置,其中一个顶点与点C重合,直角顶点D在BQ上,另一个顶点E在PQ上,求直线BQ的函数解析式;(2)若含30°角的直角三角板的一个顶点与点C重合,直角顶点D在直线BQ上(点D不与点Q重合),另一个顶点E在PQ上,求点P的坐标.3.如图,矩形OBCD的边OD、OB分别在x轴正半轴和y8.将矩形的边BC绕点B逆时针旋转,使点C恰好与x轴上的点A重合.(1)若抛物线cbxxy++-=231经过A、B两点,求该抛物线的解析式:______________;(2)若点M是直线AB作MN⊥x轴于点N.是否存在点M,使△与△ACD相似?若存在,求出点M的坐标;若不存在,说明理由.yOyxyyxO O xyyxOO xyxCOyBAxxA ByO C OyBA4. 已知抛物线2=23y x x --经过A 、B 、C 三点,点P (1,k )在直线BC :y=x -3上,若点M 在x 轴上,点N 在抛物线上,是否存在以A 、M 、N 、P 为顶点的四边形为平行四边形?若存在,请求出点M 的坐标;若不存在,请说明理由.5. 抛物线2212-+=x x y 与y 轴交于点C ,与直线y =x 交于A (-2,-2)、B (2,2)两点.如图,线段MN 在直线AB上移动,且M N =M 的横坐标为m ,过点M 作x 轴的垂线与x 轴交于点P ,过点N 作x 轴的垂线与抛物线交于点Q .以P 、M 、Q 、N 为顶点的四边形否为平行四边形?若能,请求出m 的值;若不能,请说明理由.A CyxO B精讲精练参考答案1.解:由题意,设OA =m ,则OB =2m ;当∠BAP =90°时, △BAP ∽△AOB 或△BAP ∽△BOA ; ① 若△BAP ∽△AOB ,如图1,可知△PMA ∽△AOB ,相似比为2:1;则P 1(5m ,2m ), 代入x x y 32+-=,可知2513=m ,)2526,513(1P② 若△BAP ∽△BOA ,如图2,可知△PMA ∽△AOB ,相似比为1:2;则P 2(2m ,2m ),代入x x y 32+-=,可知811=m ,)1611,411(2P当∠ABP =90°时,△ABP ∽△AOB 或△ABP ∽△BOA ; ③ 若△ABP ∽△AOB ,如图3,可知△PMB ∽△BOA ,相似比为2:1;则P 3(4m ,4m ), 代入x x y 32+-=,可知21=m ,)2,2(3P④ 若△ABP ∽△BOA ,如图4,可知△PMB ∽△BOA ,相似比为1:2;则P 4(m ,m 25), 代入x x y 32+-=,可知21=m ,415(,)24P2.解:(1)由抛物线解析式()21134y x =--+可得B 点坐标(1,3要求直线BQ 的函数解析式,只需求得点Q 坐标即可,即求CQ 长度过点D 作DG ⊥x 轴于点G ,过点D 作DF ⊥QP 于点F . 则可证△DCG ≌△DEF .则DG =DF , ∴矩形DGQF 为正方形.则∠DQG =45°,则△BCQ 为等腰直角三角形.∴CQ =BC =3,此时,Q 可得BQ 解析式为y =-x +4.(2)要求P 点坐标,只需求得点Q 坐标,然后根据横坐标相同来求点P 坐标即可. 而题目当中没有说明∠DCE =30°还是∠DCE =60°,所以分两种情况来讨论. ① 当∠DCE =30°时,a )过点D 作DH ⊥x 轴于点H ,过点D 作DK ⊥QP 于点K .则可证△DCH ∽△DEK .则D H D C D KD E==在矩形DHQK 中,DK =HQ,则D H H Q=在Rt △DHQ 中,∠DQC =60°.则在Rt △BCQ中,B C C Q=∴CQ,此时,Q 点坐标为(,0) 则P 点横坐标为代入()21134y x =--+可得纵坐标.∴P (94).b )又P 、Q 为动点,∴可能PQ 在对称轴左侧,与上一种情形关于对称轴对称.由对称性可得此时点P 坐标为(194)② 当∠DCE =60°时,a) 过点D 作DM ⊥x 轴于点M ,过点D 作DN ⊥QP 于点N .则可证△DCM ∽△DEN .则1D M D C D ND E==在矩形DMQN 中,DN =MQ,则1D M M Q=.在Rt △DMQ 中,∠DQM =30°. 则在Rt △BCQ中,B C C Q=∴CQBC=Q 点坐标为(1+0) 则P 点横坐标为1+代入()21134y x =--+可得纵坐标.∴P (1+154-).b )又P 、Q 为动点,∴可能PQ 在对称轴左侧,与上一种情形关于对称轴对称.由对称性可得此时点P 坐标为(1-154-)综上所述,P 点坐标为(94),(194),(1+154-)或(1-154-).4.解:满足条件坐标为:1(30)-M 2(30)+M 3(10)-+M 4(10)--M思路分析:A 、M 、N 、P 四点中点A 、点P 为顶点,则AP 可为平行四边形边、对角线; (1)如图,当AP 为平行四边形边时,平移AP ;∵点A 、P 纵坐标差为2 ∴点M 、N 纵坐标差为2; ∵点M 的纵坐标为0 ∴点N 的纵坐标为2或-2 ①当点N 的纵坐标为2时解:2232--=x x 得1=±x又∵点A 、P 横坐标差为2 ∴点M 的坐标为:1(30)-M 、2(30)+M②当点N 的纵坐标为-2时解:2232--=-x x 得1=±x又∵点A 、P 横坐标差为2 ∴点M 的坐标为: 3(10)-+M 、4(10)--M(2)当AP 为平行四边形边对角线时;设M 5(m ,0)MN 一定过AP 的中点(0,-1) 则N 5(-m ,-2),N 5在抛物线上 ∴2232+-=-m m1=-±m∴1=-+m∴5(10)-+M综上所述:符合条件点P 的坐标为:1(30)-M 2(30)+M 3(10)-+M 4(10)--M5.解:分析题意,可得:MP ∥NQ ,若以P 、M 、N 、Q 为顶点的四边形为平行四边形,只需MP =NQ 即可由题知:(,)M m m ,(,0)P m ,(1,1)N m m ++,21(1,(1)+(1)2)2Q m m m +++-故只需表达MP 、NQ 即可.表达分下列四种情况:①如图1,P M m =-,21(1)22Q N m =+-,令PM =QN ,解得:1=2+m -,2=2m --②如图2,P M m =-,21(1)+22Q N m =-+,令PM =QN ,解得:1=m (舍去),1=m -;③如图3,P M m =,21(1)+22Q N m =-+,令PM =QN ,解得:1=2+m -2=2m --;④如图4,P M m =,21(1)22Q N m =+-,令PM =QN ,解得:1=m ,1=m -(舍去);综上,m 的值为1=2m --、2=m -3=2+m -、4=m当我被上帝造出来时,上帝问我想在人间当一个怎样的人,我不假思索的说,我要做一个伟大的世人皆知的人。
二次函数解析几何--存在性问题

二次函数解析几何专题——存在性问题存在性问题是指判断满足某种条件的事物是否存在的问题,这类问题的知识覆盖面较广,综合性较强,题意构思非常精巧,解题方法灵活,对学生分析问题和解决问题的能力要求较高,是近几年来各地中考的“热点”。
这类题目解法的一般思路是:假设存在→推理论证→得出结论。
若能导出合理的结果,就做出“存在”的判断,导出矛盾,就做出不存在的判断。
由于“存在性”问题的结论有两种可能,所以具有开放的特征,在假设存在性以后进行的推理或计算,对基础知识,基本技能提出了较高要求,并具备较强的探索性,正确、完整地解答这类问题,是对我们知识、能力的一次全面的考验。
一、方法总结解存在性问题的一般步骤:(1)假设点存在;(2)将点的坐标设为参数;(3)根据已知条件建立关于参数的方程或函数。
二、常用公式(1)两点间距离公式:若A (x 1,y 1),B (x 2,y 2),则|AB|=221221)()(y y x x -+-(2)中点坐标公式:1212,22x x y y x y ++==(3)斜率公式:①;②(为直线与x 轴正方向的夹角)2121y y k x x -=-tan k θ=θ(4)①对于两条不重合的直线l 1、l 2,其斜率分别为k 1、k 2,则有l 1∥l 2⇔k 1=k 2②如果两条直线l 1、l 2的斜率存在,设为k 1、k 2,则l 1⊥l 2⇔k 1k 2=-1.题型一 面积问题例1.如图,抛物线y =-x 2+bx +c 与x 轴交于A (1,0),B (-3,0)两点.(1)求该抛物线的解析式;(2)在(1)中的抛物线上的第二象限内是否存在一点P ,使△PBC 的面积最大?,若存在,求出点P 的坐标及△PBC 的面积最大值;若不存在,请说明理由.变式练习:1.如图,在直角坐标系中,点A 的坐标为(-2,0),连结OA ,将线段OA 绕原点O 顺时针旋转120°,得到线段OB .(1)求点B 的坐标;(2)求经过A 、O 、B 三点的抛物线的解析式;(3)如果点P 是(2)中的抛物线上的动点,且在x 轴的下方,那么△PAB 是否有最大面积?若有,求出此时P 点的坐标及△PAB 的最大面积;若没有,请说明理由.O B A CyxA xy BO能力提升:1.(2013菏泽)如图1,△运动到何处时,四边形PDCQ的面积最小?此时四边形2.如图,已知抛物线y=x2+bx+c的图象与x轴的一个交点为B(5,0),另一个交点为A,且与y轴交于点C(0,5).(1)求直线BC与抛物线的解析式;(2)若点M是抛物线在x轴下方图象上的一动点,过点M作MN∥y轴交直线BC于点N,求MN的最大值;(3)在(2)的条件下,MN取得最大值时,若点P是抛物线在x轴下方图象上任意一点,以BC为边作平行四边形CBPQ,设平行四边形CBPQ的面积为S1,△ABN的面积为S2,且S1=6S2,求点P的坐标.3.如图,二次函数的图象与x轴相交于点A(-3,0)、B(-1,0),与y轴相交于点C(0,3),点P是该图象上的动点;一次函数y=kx-4k(k≠0)的图象过点P交x轴于点Q.(1)求该二次函数的解析式;(2)当点P的坐标为(-4,m)时,求证:∠OPC=∠AQC;(3)点M,N分别在线段AQ、CQ上,点M以每秒3个单位长度的速度从点A向点Q运动,同时,点N以每秒1个单位长度的速度从点C向点Q运动,当点M,N中有一点到达Q点时,两点同时停止运动,设运动时间为t秒.连接AN,当△AMN的面积最大时,①求t的值;②直线PQ能否垂直平分线段MN?若能,请求出此时点P的坐标;若不能,请说明你的理由.yD BMA CO xE 图1的坐标,并求出△POB的面积;若不存在,请说明理由.)中抛物线的第二象限图象上是否存在一点与△POC的坐标;若不存在,请说明理由;c的图象的顶点C的坐标为(0,-2),交m(m>1)与x轴交于D。
二次函数中的存在性问题(最新整理)

二次函数中的存在性问题1. 如图,矩形OABC在平面直角坐标系xOy中,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=4,OC=3,若抛物线的顶点在BC边上,且抛物线经过O,A两点,直线AC交抛物线于点D.(1)求抛物线的解析式;(2)求点D的坐标;(3)若点M在抛物线上,点N在x轴上,是否存在以A,D,M,N为顶点的四边形是平行四边形?若存在,求出点N的坐标;若不存在,请说明理由.4:解:(1)设抛物线顶点为E,根据题意OA=4,OC=3,得:E(2,3),设抛物线解析式为y=a(x﹣2)2+3,将A(4,0)坐标代入得:0=4a+3,即a=﹣,则抛物线解析式为y=﹣(x﹣2)2+3=﹣x2+3x;(2)设直线AC解析式为y=kx+b(k≠0),将A(4,0)与C(0,3)代入得:,解得:,故直线AC解析式为y=﹣x+3,与抛物线解析式联立得:,解得:或,则点D坐标为(1,);(3)存在,分两种情况考虑:①当点M在x轴上方时,如答图1所示:四边形ADMN为平行四边形,DM∥AN,DM=AN,由对称性得到M(3,),即DM=2,故AN=2,∴N1(2,0),N2(6,0);②当点M在x轴下方时,如答图2所示:过点D作DQ⊥x轴于点Q,过点M作MP⊥x轴于点P,可得△ADQ≌△NMP,∴MP=DQ=,NP=AQ=3,将y M=﹣代入抛物线解析式得:﹣=﹣x2+3x,解得:x M=2﹣或x M=2+,∴x N=x M﹣3=﹣﹣1或﹣1,∴N3(﹣﹣1,0),N4(﹣1,0).综上所述,满足条件的点N有四个:N1(2,0),N2(6,0),N3(﹣﹣1,0),N4(﹣1,0).2.如图,已知抛物线经过A(﹣2,0),B(﹣3,3)及原点O,顶点为C(1)求抛物线的函数解析式.(2)设点D在抛物线上,点E在抛物线的对称轴上,且以AO为边的四边形AODE是平行四边形,求点D的坐标.(3)P是抛物线上第一象限内的动点,过点P作PM⊥x轴,垂足为M,是否存在点P,使得以P,M,A为顶点的三角形与△BOC相似?若存在,求出点P的坐标;若不存在,请说明理由.解:(1)设抛物线的解析式为y=ax2+bx+c(a≠0),将点A(﹣2,0),B(﹣3,3),O(0,0),代入可得:,解得:.故函数解析式为:y=x2+2x.(2)当AO为平行四边形的边时,DE∥AO,DE=AO,由A(﹣2,0)知:DE=AO=2,若D在对称轴直线x=﹣1左侧,则D横坐标为﹣3,代入抛物线解析式得D1(﹣3,3),若D在对称轴直线x=﹣1右侧,则D横坐标为1,代入抛物线解析式得D2(1,3).综上可得点D的坐标为:(﹣3,3)或(1,3).(3)存在.如图:∵B(﹣3,3),C(﹣1,﹣1),根据勾股定理得:BO2=18,CO2=2,BC2=20,∵BO2+CO2=BC2,∴△BOC是直角三角形,假设存在点P,使以P,M,A为顶点的三角形与△BOC相似,设P(x,y),由题意知x>0,y>0,且y=x2+2x,①若△AMP∽△BOC,则=,即x+2=3(x2+2x),得:x1=13,x2=﹣2(舍去).当x=13时,y=59,即P(13,59),②若△PMA∽△BOC,则=,即:x2+2x=3(x+2),得:x1=3,x2=﹣2(舍去)当x=3时,y=15,即P(3,15).故符合条件的点P有两个,分别是P(13,59)或(3,15).3. 如图,直线y=2x+2与x轴交于点A,与y轴交于点B,把△AOB沿y轴翻折,点A落到点C,过点B的抛物线y=﹣x2+bx+c与直线BC交于点D(3,﹣4).(1)求直线BD和抛物线的解析式;(2)在第一象限内的抛物线上,是否存在疑点M,作MN垂直于x轴,垂足为点N,使得以M、O、N为顶点的三角形与△BOC相似?若存在,求出点M的坐标;若不存在,请说明理由;(3)在直线BD上方的抛物线上有一动点P,过点P作PH垂直于x轴,交直线BD于点H,当四边形BOHP是平行四边形时,试求动点P的坐标.8、解答:解:(1)∵y=2x+2,∴当x=0时,y=2,∴B(0,2).当y=0时,x=﹣1,∴A(﹣1,0).∵抛物线y=﹣x2+bx+c过点B(0,2),D(3,﹣4),∴解得:,∴y=﹣x2+x+2;设直线BD的解析式为y=kx+b,由题意,得,解得:,∴直线BD的解析式为:y=﹣2x+2;(2)存在.如图1,设M(a,﹣a2+a+2).∵MN垂直于x轴,∴MN=﹣a2+a+2,ON=a.∵y=﹣2x+2,∴y=0时,x=1,∴C(1,0),∴OC=1.∵B(0,2),∴OB=2.当△BOC∽△MON时,∴,∴,解得:a1=1,a2=﹣2M(1,2)或(﹣2,﹣4);如图2,当△BOC∽△ONM时,,∴,∴a=或,∴M(,)或(,).∵M在第一象限,(,);∴符合条件的点M的坐标为(1,2),(3)设P(b,﹣b2+b+2),H(b,﹣2b+2).如图3,∵四边形BOHP是平行四边形,∴BO=PH=2.∵PH=﹣b2+b+2+2b﹣2=﹣b2+3b.∴2=﹣b2+3b∴b1=1,b2=2.当b=1时,P(1,2),当b=2时,P(2,0)∴P点的坐标为(1,2)或(2,0).4.如图,点A在x轴上,OA=4,将线段OA绕点O顺时针旋转120°至OB的位置.(1)求点B的坐标;(2)求经过点A、O、B的抛物线的解析式;(3)在此抛物线的对称轴上,是否存在点P,使得以点P、O、B为顶点的三角形是等腰三角形?若存在,求点P的坐标;若不存在,说明理由.考点:二次函数综合题.专题:压轴题;分类讨论.分析:(1)首先根据OA的旋转条件确定B点位置,然后过B做x轴的垂线,通过构建直角三角形(2)和OB的长(即OA长)确定B点的坐标.(2)已知O、A、B三点坐标,利用待定系数法求出抛物线的解析式.(3)根据(2)的抛物线解析式,可得到抛物线的对称轴,然后先设出P点的坐标,而O、B坐标已知,可先表示出△OPB三边的边长表达式,然后分①OP=OB、②OP=BP、③OB=BP三种情况分类讨论,然后分辨是否存在符合条件的P点.解答:解:(1)如图,过B点作BC⊥x轴,垂足为C,则∠BCO=90°,∵∠AOB=120°,∴∠BOC=60°,又∵OA=OB=4,∴OC=OB=×4=2,BC=OB•sin60°=4×=2,∴点B的坐标为(﹣2,﹣2);(2)∵抛物线过原点O和点A、B,∴可设抛物线解析式为y=ax2+bx,将A(4,0),B(﹣2.﹣2)代入,得,解得,∴此抛物线的解析式为y=﹣x2+x(3)存在,如图,抛物线的对称轴是直线x=2,直线x=2与x轴的交点为D,设点P的坐标为(2,y),①若OB=OP,则22+|y|2=42,解得y=±2,当y=2时,在Rt△POD中,∠PDO=90°,sin∠POD==,∴∠POD=60°,∴∠POB=∠POD+∠AOB=60°+120°=180°,即P、O、B三点在同一直线上,∴y=2不符合题意,舍去,∴点P的坐标为(2,﹣2)②若OB=PB,则42+|y+2|2=42,解得y=﹣2,故点P的坐标为(2,﹣2),③若OP=BP,则22+|y|2=42+|y+2|2,解得y=﹣2,故点P的坐标为(2,﹣2),综上所述,符合条件的点P只有一个,其坐标为(2,﹣2),5.如图,抛物线y=ax2+bx+c经过A(﹣3.0)、C(0,4),点B在抛物线上,CB∥x轴,且AB平分∠CAO.(1)求抛物线的解析式;(2)线段AB上有一动点P,过点P作y轴的平行线,交抛物线于点Q,求线段PQ的最大值;(3)抛物线的对称轴上是否存在点M,使△ABM是以AB为直角边的直角三角形?如果存在,求出点M的坐标;如果不存在,说明理由.10、解答:解:(1)如图1,∵A(﹣3,0),C(0,4),∴OA=3,OC=4.∵∠AOC=90°,∴AC=5.∵BC∥AO,AB平分∠CAO,∴∠CBA=∠BAO=∠CAB.∴BC=AC.∴BC=5.∵BC∥AO,BC=5,OC=4,∴点B的坐标为(5,4).∵A(﹣3.0)∴解得:∴抛物线的解析式为y=﹣x2+x+4.(2)如图2,设直线AB的解析式为y=mx+n,∵A(﹣3.0)、B(5,4)在直线AB上,∴解得:∴直线AB的解析式为y=x+.设点P的横坐标为t(﹣3≤t≤5),则点Q的横坐标也为t.∴y P=t+,y Q=﹣t2+t+4.∴PQ=y Q﹣y P=﹣t2+t+4﹣(t+)=﹣t2+t+4﹣t﹣=﹣t2++=﹣(t2﹣2t﹣15)=﹣[(t﹣1)2﹣16]=﹣(t﹣1)2+.∵﹣<0,﹣3≤1≤5,∴当t=1时,PQ取到最大值,最大值为.∴线段PQ的最大值为.(3)①当∠BAM=90°时,如图3所示.抛物线的对称轴为x=﹣=﹣=.∴x H=x G=x M=.∴y G=×+=.∴GH=.∵∠GHA=∠GAM=90°,∴∠MAH=90°﹣∠GAH=∠AGM.∵∠AHG=∠MHA=90°,∠MAH=∠AGM,∴△AHG∽△MHA.∴.∴=.解得:MH=11.∴点M的坐标为(,﹣11).②当∠ABM=90°时,如图4所示.∵∠BDG=90°,BD=5﹣=,DG=4﹣=,∴BG===.同理:AG=.∵∠AGH=∠MGB,∠AHG=∠MBG=90°,∴△AGH∽△MGB.∴=.∴=.解得:MG=.∴MH=MG+GH=+=9.∴点M的坐标为(,9).综上所述:符合要求的点M的坐标为(,9)和(,﹣11).6.(2009•崇左)在平面直角坐标系中,现将一块等腰直角三角板ABC放在第二象限,斜靠在两坐标轴上,且点A(0,2),点C(﹣1,0),如图所示:抛物线y=ax2+ax﹣2经过点B.21教育网(1)求点B的坐标;(2)求抛物线的解析式;(3)在抛物线上是否还存在点P(点B除外),使△ACP仍然是以AC为直角边的等腰直角三角形?若存在,求所有点P的坐标;若不存在,请说明理由.考点:二次函数综合题.专题:压轴题.分析:(1)根据题意,过点B作BD⊥x轴,垂足为D;根据角的互余的关系,易得B到x、y 轴的距离,即B的坐标;21(2)根据抛物线过B点的坐标,可得a的值,进而可得其解析式;(3)首先假设存在,分A、C是直角顶点两种情况讨论,根据全等三角形的性质,可得答案.解答:解:(1)过点B作BD⊥x轴,垂足为D,∵∠BCD+∠ACO=90°,∠ACO+∠CAO=90°,∴∠BCD=∠CAO,(1分)又∵∠BDC=∠COA=90°,CB=AC,∴△BCD≌△CAO,(2分)∴BD=OC=1,CD=OA=2,(3分)∴点B的坐标为(﹣3,1);(4分)(2)抛物线y=ax2+ax﹣2经过点B(﹣3,1),则得到1=9a﹣3a﹣2,(5分)解得a=,所以抛物线的解析式为y=x2+x﹣2;(7分)(3)假设存在点P,使得△ACP仍然是以AC为直角边的等腰直角三角形:①若以点C为直角顶点;则延长BC至点P1,使得P1C=BC,得到等腰直角三角形△ACP1,(8分)过点P1作P1M⊥x轴,∵CP1=BC,∠MCP1=∠BCD,∠P1MC=∠BDC=90°,∴△MP1C≌△DBC.(10分)∴CM=CD=2,P1M=BD=1,可求得点P1(1,﹣1);(11分)②若以点A为直角顶点;则过点A作AP2⊥CA,且使得AP2=AC,得到等腰直角三角形△ACP2,(12分)过点P2作P2N⊥y轴,同理可证△AP2N≌△CAO,(13分)∴NP2=OA=2,AN=OC=1,可求得点P2(2,1),(14分)经检验,点P1(1,﹣1)与点P2(2,1)都在抛物线y=x2+x﹣2上.(16分)练习:1. 如图,二次函数y=x 2+bx+c 的图象与x 轴交于A 、B 两点,且A 点坐标为(-3,0),经过B 点的直线交抛物线于点D (-2,-3).(1)求抛物线的解析式和直线BD 解析式;(2)过x 轴上点E (a ,0)(E 点在B 点的右侧)作直线EF ∥BD ,交抛物线于点F ,是否存在实数a 使四边形BDFE 是平行四边形?如果存在,求出满足条件的a ;如果不存在,请说明理由.2.已知抛物线经过A (2,0). 设顶点为点P ,与x 轴的另一交点为点B . 36232++=bx x y (1)求b 的值,求出点P 、点B 的坐标;(2)如图,在直线 y=x 上是否存在点D ,使四边形OPBD 为平行四边形?若存在,3求出点D 的坐标;若不存在,请说明理由;(3)在x 轴下方的抛物线上是否存在点M ,使△AMP ≌△AMB ?如果存在,试举例验证你的猜想;如果不存在,试说明理由.4. 如图,已知抛物线y =x2+bx +3与x 轴交于点B (3,0),与y 轴交于点A ,P 是抛物线上的一个动点,点P 的横坐标为m (m >3),过点P 作y 轴的平行线PM ,交直线AB 于点M .(1)求抛物线的解析式;(2)若以AB 为直径的⊙N 与直线PM 相切,求此时点M 的坐标;(3)在点P 的运动过程中,△APM 能否为等腰三角形?若能,求出点M 的坐标;若不能,请说明理由.3. 已知:如图一次函数y =x +1的图象与x 轴交于点A ,与y 轴交于点B ;21二次函数y =x 2+bx +c 的图象与一次函数y =x +1的图象交于B 、C 两点,2121与x 轴交于D 、E 两点且D 点坐标为(1,0)(1)求二次函数的解析式;(2)求四边形BDEC 的面积S ;(3)在x 轴上是否存在点P ,使得△PBC 是以P 为直角顶点的直角三角形? 若存在,求出所有的点P,若不存在,请说明理由.4. 如图,抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,-3),设抛物线的顶点为D.(1)求该抛物线的解析式与顶点D的坐标;(2)以B、C、D为顶点的三角形是直角三角形吗?为什么?(3)探究坐标轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCD相似?若存在,请指出符合条件的点P的位置,并直接写出点P的坐标.。
中考 压轴专题02 二次函数的存在性问题 - 解析

压轴专题02:二次函数与存在性问题方法点拨:二次函数与动点存在性问题,平面上任意两点P 1(x 1,y 1),P 2(x 2,y 2) 距离为|P 1P 2|=221221)()(y y x x -+- 中点坐标:2,22121y y y x x x +=+=对于两条不重合的直线l 1,l 2,其斜率分别为k 1,k 2,则有l 1∥l 2⇔k 1=k 2l 1⊥l 2⇔k 1·k 2=-1,特殊情况:当一条直线斜率为零,另一条直线斜率不存在时,两条直线垂直. 把点用坐标表示出来,根据以上公式结合几何性质,代数化处理,构造方程解之即可。
【考点1】二次函数与相似三角形问题【例1】如图,抛物线2y ax bx c =++与x 轴交于点(1,0)A -,点(3,0)B ,与y 轴交于点C ,且过点(2,3)D -.点P 、Q 是抛物线2y ax bx c =++上的动点. (1)求抛物线的解析式;(2)直线OQ 与线段BC 相交于点E ,当OBE ∆与ABC ∆相似时,求点Q 的坐标.【分析】(1)函数的表达式为:y=a (x+1)(x-3),将点D 坐标代入上式,即可求解;(2)分∠ACB=∠BOQ 、∠BAC=∠BOQ ,两种情况分别求解,通过角的关系,确定直线OQ 倾斜角,进而求解. 【详解】解:(1)函数的表达式为:(1)(3)y a x x =+-,将点D 坐标代入上式并解得:1a =, 故抛物线的表达式为:223y x x =--…①; (2)∵3OB OC ==,∴45OCB OBC ︒∠=∠=,∵ABC OBE ∠=∠,故OBE ∆与ABC ∆相似时,分为两种情况: ①当ACB BOQ ∠=∠时,4AB =,32BC =,10AC =, 过点A 作AH ⊥BC 与点H ,1122ABC S AH BC AB OC ∆=⨯⨯=⨯,解得:22AH =,∴CH 2tan 2ACB ∠=, 则直线OQ 的表达式为: 2 y x =-…②,联立①②并解得:3x =±3,23)Q -或(3,3; ②BAC BOQ ∠=∠时,3tan 3tan 1OC BAC BOQ OA ∠====∠,则直线OQ 的表达式为:3 y x =-…③,联立①③并解得:1132x -±=,故点1133313Q -+-⎝⎭或1133313--+⎝⎭; 综上,点3,23)Q -或(3,3或113113-+-⎝⎭或1133313--+⎝⎭. 【点睛】本题考查的是二次函数综合运用,涉及到解直角三角形、三角形相似等,其中(2),要注意分类求解,避免遗漏.【变式1-1】如图,在平面直角坐标系中,抛物线y =﹣x 2+bx +c 经过点A (﹣1,0)和点C (0,4),交x轴正半轴于点B,连接AC,点E是线段OB上一动点(不与点O,B重合),以OE 为边在x轴上方作正方形OEFG,连接FB,将线段FB绕点F逆时针旋转90°,得到线段FP,过点P作PH∥y轴,PH交抛物线于点H,设点E(a,0).(1)求抛物线的解析式.(2)若△AOC与△FEB相似,求a的值.(3)当PH=2时,求点P的坐标.【详解】(1)点C(0,4),则c=4,二次函数表达式为:y=﹣x2+bx+4,将点A的坐标代入上式得:0=﹣1﹣b+4,解得:b=3,故抛物线的表达式为:y=﹣x2+3x+4;(2)tan∠ACO=AOCO=14,△AOC与△FEB相似,则∠FBE=∠ACO或∠CAO,即:tan∠FEB=14或4,∵四边形OEFG为正方形,则FE=OE=a,EB=4﹣a,则144aa=-或44aa=-,解得:a=165或45;(3)令y=﹣x2+3x+4=0,解得:x=4或﹣1,故点B(4,0);分别延长CF、HP交于点N,∵∠PFN+∠BFN=90°,∠FPN+∠PFN=90°,∴∠FPN=∠NFB,∵GN∥x轴,∴∠FPN=∠NFB=∠FBE,∵∠PNF=∠BEF=90°,FP=FB,∴△PNF≌△BEF(AAS),∴FN=FE=a,PN=EB=4﹣a,∴点P(2a,4),点H(2a,﹣4a2+6a+4),∵PH=2,即:﹣4a2+6a+4﹣4=|2|,解得:a=1或12317+317-舍去),故:点P的坐标为(2,4)或(1,4)或3+17,4).【考点2】二次函数与直角三角形问题【例2】如图,在平面直角坐标系中,直线122y x =-+与x 轴交于点A ,与y 轴交于点B ,抛物线223y x bx c =-++过点B 且与直线相交于另一点53,24C ⎛⎫ ⎪⎝⎭.(1)求抛物线的解析式;(2)点P 是抛物线上的一动点,当PAO BAO ∠=∠时,求点P 的坐标; (3)点5(,0)02N n n ⎛⎫<< ⎪⎝⎭在x 轴的正半轴上,点(0,)M m 是y 轴正半轴上的一动点,且满足90MNC ︒∠=.①求m 与n 之间的函数关系式;②当m 在什么范围时,符合条件的N 点的个数有2个? 【分析】(1)利用一次函数求出A 和B 的坐标,结合点C 坐标,求出二次函数表达式;(2)当点P 在x 轴上方时,点P 与点C 重合,当点P 在x 轴下方时,AP 与y 轴交于点Q ,求出AQ 表达式,联立二次函数,可得交点坐标,即为点P ; (3)①过点C 作CD ⊥x 轴于点D ,证明△MNO ∽△NCD ,可得MO NOND CD=,整理可得结果; ②作以MC 为直径的圆E ,根据圆E 与线段OD 的交点个数来判断M 的位置,即可得到m 的取值范围. 【详解】解:(1)∵直线122y x =-+与x 轴交于点A ,与y 轴交于点B ,令x=0,则y=2,令y=0,则x=4,∴A (4,0),B (0,2),∵抛物线223y x bx c =-++经过B (0,2),53,24C ⎛⎫⎪⎝⎭,∴2322554342c b c =⎧⎪⎨=-⨯++⎪⎩,解得:762b c ⎧=⎪⎨⎪=⎩,∴抛物线的表达式为:227236y x x =-++; (2)当点P 在x 轴上方时,点P 与点C 重合,满足PAO BAO ∠=∠, ∵53,24C ⎛⎫⎪⎝⎭,∴53,24P ⎛⎫ ⎪⎝⎭, 当点P 在x 轴下方时,如图,AP 与y 轴交于点Q , ∵PAO BAO ∠=∠,∴B ,Q 关于x 轴对称,∴Q (0,-2),又A (4,0),设直线AQ 的表达式为y=px+q ,代入,204q p q -=⎧⎨=+⎩,解得:122p q ⎧=⎪⎨⎪=-⎩,∴直线AQ 的表达式为:122y x =-,联立得:212227236y x y x x ⎧=-⎪⎪⎨⎪=-++⎪⎩,解得:x=3或-2,∴点P 的坐标为(3,12-)或(-2,-3), 综上,当PAO BAO ∠=∠时,点P 的坐标为:53,24⎛⎫⎪⎝⎭或(3,12-)或(-2,-3);(3)①如图,∠MNC=90°,过点C 作CD ⊥x 轴于点D ,∴∠MNO+∠CND=90°, ∵∠OMN+∠MNO=90°,∴∠CND=∠OMN,又∠MON=∠CDN=90°,∴△MNO ∽△NCD ,∴MO NO ND CD =,即5324m nn =-,整理得:241033m n n =-+;②如图,∵∠MNC=90°,以MC为直径画圆E,∵5 (,0)02N n n⎛⎫<<⎪⎝⎭,∴点N在线段OD上(不含O和D),即圆E与线段OD有两个交点(不含O和D),∵点M在y轴正半轴,当圆E与线段OD相切时,有NE=12MC,即NE2=14MC2,∵M(0,m),53,24C⎛⎫⎪⎝⎭,∴E(54,382m+),∴2382m⎛⎫+⎪⎝⎭=22153424m⎡⎤⎛⎫⎛⎫+-⎢⎥⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦,解得:m=2512,当点M与点O重合时,如图,此时圆E与线段OD(不含O和D)有一个交点,∴当0<m<2512时,圆E与线段OD有两个交点,故m的取值范围是:0<m<25 12.【点睛】本题是二次函数综合,考查了求二次函数表达式,相似三角形的判定和性质,圆周角定理,一次函数表达式,难度较大,解题时要充分理解题意,结合图像解决问题.【变式2-1】如图,抛物线24y ax bx=+-经过A(-3,6),B(5,-4)两点,与y轴交于点C,连接AB,AC,BC.(1)求抛物线的表达式;(2)求证:AB平分CAO∠;(3)抛物线的对称轴上是否存在点M,使得ABM∆是以AB为直角边的直角三角形.若存在,求出点M的坐标;若不存在,说明理由.【分析】(1)将A(-3,0),B(5,-4)代入抛物线的解析式得到关于a、b的方程组,从而可求得a、b 的值;(2)先求得AC的长,然后取D(2,0),则AD=AC,连接BD,接下来,证明BC=BD,然后依据SSS可证明△ABC≌△ABD,接下来,依据全等三角形的性质可得到∠CAB=∠BAD;(3)作抛物线的对称轴交x轴与点E,交BC与点F,作点A作AM′⊥AB,作BM⊥AB,分别交抛物线的对称轴与M′、M,依据点A和点B的坐标可得到tan∠BAE=12,从而可得到tan∠M′AE=2或tan∠MBF=2,从而可得到FM和M′E的长,故此可得到点M′和点M的坐标.【详解】解:(1)将A(-3,0),B(5,-4)两点的坐标分别代入,得9340,25544a ba b--=⎧⎨+-=-⎩,解得1,65,6ab⎧=⎪⎪⎨⎪=-⎪⎩故抛物线的表达式为y =215466y x x =--. (2)证明:∵AO=3,OC=4,∴AC=2234+=5.取D (2,0),则AD=AC=5.由两点间的距离公式可知BD=22(52)(40)-+--=5. ∵C (0,-4),B (5,-4),∴BC=5.∴BD=BC . 在△ABC 和△ABD 中,AD=AC ,AB=AB ,BD=BC , ∴△ABC ≌△ABD ,∴∠CAB=∠BAD ,∴AB 平分∠CAO ; (3)存在.如图所示:抛物线的对称轴交x 轴与点E ,交BC 与点F .抛物线的对称轴为x=52,则AE=112. ∵A (-3,0),B (5,-4),∴tan ∠EAB=12. ∵∠M′AB=90°.∴tan ∠M′AE=2.∴M′E=2AE=11,∴M′(52,11). 同理:tan ∠MBF=2.又∵BF=52,∴FM=5,∴M (52,-9). ∴点M 的坐标为(52,11)或(52,-9).【点睛】本题考查了二次函数的综合应用,主要应用了待定系数法求二次函数的解析式,全等三角形的性质和判定、锐角三角函数的定义,求得FM 和M′E 的长是解题的关键【考点3】二次函数与等腰三角形问题【例3】如图1,抛物线y =﹣x 2+bx +c 过点A (﹣1,0),点B (3,0)与y 轴交于点C .在x 轴上有一动点E (m ,0)(0<m <3),过点E 作直线l ⊥x 轴,交抛物线于点M . (1)求抛物线的解析式及C 点坐标;(2)当m =1时,D 是直线l 上的点且在第一象限内,若△ACD 是以∠DCA 为底角的等腰三角形,求点D 的坐标;(3)如图2,连接BM 并延长交y 轴于点N ,连接AM ,OM ,设△AEM 的面积为S 1,△MON 的面积为S 2,若S 1=2S 2,求m 的值.【分析】(1)用待定系数法即可求解;(2)若△ACD 是以∠DCA 为底角的等腰三角形,则可以分CD =AD 或AC =AD 两种情况,分别求解即可; (3)S 1=12AE ×y M ,2S 2=ON •x M ,即可求解. 【详解】解:(1)将点A 、B 的坐标代入抛物线表达式得-1-b+c=0-9+3b+c=0⎧⎨⎩,解得b=2c=3⎧⎨⎩,故抛物线的表达式为y =﹣x 2+2x +3,当x =0时,y =3,故点C (0,3); (2)当m =1时,点E (1,0),设点D 的坐标为(1,a ), 由点A 、C 、D 的坐标得,AC ()()220+1+3-0=10,同理可得:ADCD①当CD=AD,解得a=1;②当AC=AD时,同理可得a=(舍去负值);故点D的坐标为(1,1)或(1);(3)∵E(m,0),则设点M(m,﹣m2+2m+3),设直线BM的表达式为y=sx+t,则2-m+2m+3=sm+t0=3s+t⎧⎨⎩,解得:1s=-m+13t=m+1⎧⎪⎪⎨⎪⎪⎩,故直线BM的表达式为y=﹣1m+1x+3m+1,当x=0时,y=3m+1,故点N(0,3m+1),则ON=3m+1;S1=12⨯AE×y M=12×(m+1)×(﹣m2+2m+3),2S2=ON•x M=3m+1×m=S1=12×(m+1)×(﹣m2+2m+3),解得m=﹣舍去负值),经检验m2是方程的根,故m2.【点睛】本题考查的是二次函数综合运用,涉及到一次函数的性质、等腰三角形的性质、面积的计算等,其中(2),要注意分类求解,避免遗漏.【变式3-1】已知抛物线y=ax2+bx+c(a≠0)与x轴交于A、B两点(点A在点B的左边),与y轴交于点C(0,﹣3),顶点D的坐标为(1,﹣4).(1)求抛物线的解析式.(2)在y轴上找一点E,使得△EAC为等腰三角形,请直接写出点E的坐标.(3)点P是x轴上的动点,点Q是抛物线上的动点,是否存在点P、Q,使得以点P、Q、B、D为顶点,BD为一边的四边形是平行四边形?若存在,请求出点P、Q坐标;若不存在,请说明理由.【分析】(1)根据抛物线的顶点坐标设出抛物线的解析式,再将点C坐标代入求解,即可得出结论;(2)先求出点A,C坐标,设出点E坐标,表示出AE,CE,AC,再分三种情况建立方程求解即可;(3)利用平移先确定出点Q的纵坐标,代入抛物线解析式求出点Q的横坐标,即可得出结论.【详解】解:(1)∵抛物线的顶点为(1,﹣4),∴设抛物线的解析式为y=a(x﹣1)2﹣4,将点C(0,﹣3)代入抛物线y=a(x﹣1)2﹣4中,得a﹣4=﹣3,∴a=1,∴抛物线的解析式为y=a(x﹣1)2﹣4=x2﹣2x﹣3;(2)由(1)知,抛物线的解析式为y=x2﹣2x﹣3,令y=0,则x2﹣2x﹣3=0,∴x=﹣1或x=3,∴B(3,0),A(﹣1,0),令x=0,则y=﹣3,∴C(0,﹣3),∴AC10,设点E(0,m),则AE21m+CE=|m+3|,∵△ACE是等腰三角形,∴①当AC=AE1021m+∴m=3或m=﹣3(点C的纵坐标,舍去),∴E(3,0),②当AC=CE10=|m+3|,∴m=﹣310,∴E(0,﹣10)或(0,﹣310),③当AE=CE21m+|m+3|,∴m=﹣43,∴E(0,﹣43),即满足条件的点E的坐标为(0,3)、(0,﹣10)、(0,﹣310)、(0,﹣43 );(3)如图,存在,∵D(1,﹣4),∴将线段BD向上平移4个单位,再向右(或向左)平移适当的距离,使点B的对应点落在抛物线上,这样便存在点Q,此时点D的对应点就是点P,∴点Q的纵坐标为4,设Q(t,4),将点Q的坐标代入抛物线y=x2﹣2x﹣3中得,t2﹣2t﹣3=4,∴t=1+22或t=1﹣22,∴Q(1+22,4)或(1﹣22,4),分别过点D,Q作x轴的垂线,垂足分别为F,G,∵抛物线y=x2﹣2x﹣3与x轴的右边的交点B的坐标为(3,0),且D(1,﹣4),∴FB=PG=3﹣1=2,∴点P的横坐标为(1+22)﹣2=﹣1+22或(1﹣22)﹣2=﹣1﹣22,即P(﹣1+22,0)、Q(1+22,4)或P(﹣1﹣22,0)、Q(1﹣22,4).【考点4】二次函数与平行四边形问题【例4】如图,抛物线过点A(0,1)和C,顶点为D,直线AC与抛物线的对称轴BD的交点为B30),平行于y轴的直线EF与抛物线交于点E,与直线AC交于点F,点F的横坐标为433,四边形BDEF为平行四边形.(1)求点F的坐标及抛物线的解析式;(2)若点P为抛物线上的动点,且在直线AC上方,当△PAB面积最大时,求点P的坐标及△PAB面积的最大值;(3)在抛物线的对称轴上取一点Q,同时在抛物线上取一点R,使以AC为一边且以A,C,Q,R为顶点的四边形为平行四边形,求点Q和点R的坐标.【分析】(1)由待定系数法求出直线AB 的解析式为y 3,求出F 点的坐标,由平行四边形的性质得出﹣3a+1=163a ﹣8a+1﹣(﹣13),求出a 的值,则可得出答案; (2)设P (n ,﹣n 23n+1),作PP'⊥x 轴交AC 于点P',则P'(n 3),得出PP'=﹣n 2733,由二次函数的性质可得出答案; (3)联立直线AC 和抛物线解析式求出C 73343),设Q 3,m ),分两种情况:①当AQ 为对角线时,②当AR 为对角线时,分别求出点Q 和R 的坐标即可. 【详解】解:(1)设抛物线的解析式为y =ax 2+bx+c (a≠0),∵A (0,1),B 30),设直线AB 的解析式为y =kx+m ,∴3k m 0m 1+==⎪⎩,解得31k m ⎧=⎪⎨⎪=⎩∴直线AB 的解析式为y 3, ∵点F 43,∴F 343+1=﹣13,∴F 点的坐标为433,﹣13), 又∵点A 在抛物线上,∴c =1,对称轴为:x =﹣32ba=,∴b =﹣3a ,∴解析式化为:y =ax 2﹣23ax+1,∵四边形DBFE 为平行四边形.∴BD =EF ,∴﹣3a+1=163a ﹣8a+1﹣(﹣13),解得a =﹣1, ∴抛物线的解析式为y =﹣x 2+23x+1;(2)设P (n ,﹣n 2+23n+1),作PP'⊥x 轴交AC 于点P',则P'(n 3),∴PP'=﹣n 2733,S △ABP =12OB•PP'2372+n 2374936324n ⎝, ∴当n 736△ABP 49324,此时P 7364712). (3)∵231331y x y x x ⎧=+⎪⎨⎪=-++⎩,∴x =0或x 733C 73343),设Q 3m ), ①当AQ 为对角线时,∴R (473,33m +), ∵R 在抛物线y =2(3)x -+4上,∴m+73=﹣24333⎛ ⎝+4,解得m =﹣443, ∴Q 443,3⎫-⎪⎭,R 4373,33⎛⎫- ⎪⎝⎭;②当AR 为对角线时,∴R 1073,33m -), ∵R 在抛物线y =2(3)x -+4上,∴m ﹣27103333=-+4,解得m =﹣10,∴Q 310),R 10373,33-).综上所述,Q 443,3⎛⎫- ⎪⎝⎭,R 4373,33⎛⎫-- ⎪⎝⎭;或Q (3,﹣10),R (10373,33-). 【点睛】本题是二次函数综合题,考查了待定系数法,二次函数的性质,二次函数图象上点的坐标特征,平行四边形的性质等知识,熟练掌握二次函数的性质及方程思想,分类讨论思想是解题的关键.【变式4-1】如图,二次函数2y x bx c =++的图象交x 轴于点()30A -,,()10B ,,交y 轴于点C .点(),0P m 是x 轴上的一动点,PM x ⊥轴,交直线AC 于点M ,交抛物线于点N .(1)求这个二次函数的表达式;(2)①若点P 仅在线段AO 上运动,如图1.求线段MN 的最大值;②若点P 在x 轴上运动,则在y 轴上是否存在点Q ,使以M ,N ,C ,Q 为顶点的四边形为菱形.若存在,请直接写出所有满足条件的点Q 的坐标;若不存在,请说明理由. 【分析】(1)把(3,0),(1,0)A B -代入2y x bx c =++中求出b ,c 的值即可; (2)①由点(),0P m 得()2(,3),,23M m m N m m m --+-,从而得()2(3)23MN m m m =---+-,整理,化为顶点式即可得到结论;②分MN=MC 和2MC MN =两种情况,根据菱形的性质得到关于m 的方程,求解即可.【详解】解:(1)把(3,0),(1,0)A B -代入2y x bx c =++中,得093,01.b c x c =-+⎧⎨=++⎩ 解得2,3.b c =⎧⎨=-⎩∴223y x x =+-.(2)设直线AC 的表达式为y kx b =+,把(3,0),(0,3)A C --代入y kx b =+.得,03,3.k b b =-+⎧⎨-=⎩解这个方程组,得1,3.k b =-⎧⎨=-⎩∴3y x =--.∵点(),0P m 是x 轴上的一动点,且PM x ⊥轴.∴()2(,3),,23M m m N m m m --+-.∴()2(3)23MN m m m =---+-23m m =--23924m ⎛⎫=-++ ⎪⎝⎭.∵10a =-<,∴此函数有最大值. 又∵点P 在线段OA 上运动,且3302-<-<∴当32m =-时,MN 有最大值94. ②∵点(),0P m 是x 轴上的一动点,且PM x ⊥轴.∴()2(,3),,23M m m N m m m --+-.∴()2(3)23MN m m m =---+-23m m =--(i )当以M ,N ,C ,Q 为顶点的四边形为菱形,则有MN=MC ,如图,∵C (0,-3)∴222(0)(33)2m m m -+--+=∴223=2m m m --整理得,432670m m m ++= ∵20m ≠,∴2670m m ++=,解得,132m =-,232m =-32m =-+CQ=MN=322, ∴OQ=-3-(322)=321-∴Q(0,321-);当m=32--时,CQ=MN=-322-,∴OQ=-3-(-322-)=321-∴Q(0,321-); (ii)若2MC MN =,如图,则有223=22m m m --整理得,432650m m m ++= ∵20m ≠,∴2650m m ++=,解得,11m =-,25m =- 当m=-1时,MN=CQ=2,∴Q (0,-1), 当m=-5时,MN=-10<0(不符合实际,舍去)综上所述,点Q 的坐标为123(0,321),(0,1),(0,321)Q Q Q --- 【点睛】本题考查了二次函数综合题,解(1)的关键是待定系数法;解(2)的关键是利用线段的和差得出二次函数,又利用了二次函数的性质,解(3)的关键是利用菱形的性质得出关于m 的方程,要分类讨论,以防遗漏.。
二次函数存在性问题(菱形、平行四边形、矩形)

今天讲解二次函数背景下的四边形存在性问题.这里的四边形存在性问题,一般是以几种特殊的四边形为主,常考察的有平行四边形、菱形、 矩形、正方形.当然,三角形的存在性问题和四边形的存在性问题是一样, 如等腰三角形实际上和 菱形是一致的, 直角三角形和矩形是一样的, 等腰直角三角形和正方形是一致的.本文我们将重点讲解这类问题的求解逻辑以及注意事项,同时给大家理出一个比较通用的解题 模板.1如图,抛物线y = ax 2 + bx + 3 交x 轴于点A (−1, 0) 和点B (3, 0) ,与 y 轴交于点C ,连接BC , 交对称轴于点D .(1) 求抛物线的解析式;(2)点 P 是直线BC 上方的抛物线上点,连接PC ,PD .求 △PCD 的面积的最大值以及此时 点P 的坐标;(3)将抛物线y = ax 2 + bx + 3 向右平移 1 个单位得到新抛物线,新抛物线与原抛物线交于点E , 点F 是新抛物线的对称轴上的一点,点 G 是坐标平面内一点.当以D 、E 、F 、 G 四点为顶点的 四边形是菱形时,直接写出点F 的坐标,并写出求解其中一个点F 的坐标的过程.前两小问就不详说了,直接上结论, 抛物线解析式为y = −x 2 + 2x + 3 ;点 P | , | .( 3 15 )\2 4 )第 3 小问为菱形存在性问题, 以D 、E 、F 、 G 四点为顶点的四边形是菱形.四个点中, D , E 是定点,F 是平移后新抛物线对称轴上的动点,由于点F 的横坐标是确定的,只有纵坐标在变化, 我们可以称其为“G 如果只需要点F 的坐标,那么没有必要求解平移后抛物线的解析式.根据平移的性质,将原抛物线 向右平移 1 个单位长度, 那么原抛物线的对称轴也向右平移 1 个单位长度, 因此新抛物线的对称轴 为x = 2 ,几 F (2, m ) .但由于此时E 为量抛物线的交点,因此还是要把平移后的抛物线解析式求出 来,根据“左加右减”,平移后的抛物线解析式为y = − (x −1)2+ 2(x −1) + 3 = −x 2 + 4x ,联立两抛物(|y = −x 2 + 2x + 3 ( 3 15 ) 线〈|ly = −x 2 + 4x ,解得E |\2 , 4 )| .菱形的探究相对是比较简单的,对于这类探究性问题,一般都是先从确定的信息入手.菱形是 以D 、E 、F 、 G 为顶点, 其中DE 为定线段,那么存在的可能有DE 是一条边,也可能是一条对 对角线.前面提到,等腰三角形和菱形的分析是一致的,这里我们结合等腰三角形的存在性问题一 起分析.由于 G 是“自由点”,可以随机应变,因此讨论以D 、E 、F 为顶点的三角形是等腰三角 形.同样, 由于定线段DE 可能是等腰三角形的一条腰,也可能是底边.当DE 为一条腰时,第一种情形是点D 为顶点,即DE = DF ,也即半动点F 到D 的距离和E 到D 的距离相等,因此点F 在以点D 为圆心, DE 为半径的圆上,作出该圆,如图 1 所示,可知此时圆与新抛物线的对称轴有两个交点F 1 ,F 2 ,结合图象可以判断,此时两个点应该都是满足的.那么 再加上对应的“自由点” G ,就是以DE 为边菱形了.当DE 为一条腰时, 另一种情形是点E 为顶点, 即ED = EF ,也即半动点F 到E 的距离和D 到E 的距离相等,因此点F 在以点E 为圆心, ED 为半径的圆上,作出该圆,如图 2 所示,可知此时 圆与新抛物线的对称轴同样有两个交点F 1 ,F 2 ,结合图象, 此时的F 3 存在和DE 共线的风险,因此后续需要检验一下.根据坐标可以知道,x E =,通常像这类圆心可能为两个点中点的,一般都要留个心眼, 检验一下.此时再加上对应的“自由点” G ,也是以DE 为边菱形.当DE 为底边时,则F 为顶点, 即FD = FE ,即 F 到线段DE 的两端点的距离相等,可知此时F 在线段DE 的垂直平分线上,作出线段DE 的垂直平分线,如图 3 所示,可知此时有一个交点F 5 .加 上对应的“自由点” G ,此时便是以DE 为对角线的菱形.对于等腰三角形和菱形的存在性问题,如上图情形,我们称其为“两圆一线”法.由于这类题一般不需要书写完整过程,因此在解题过程中,把准备工作做好, 即对应的点坐标, 解析式等先求出来, 动点坐标假设好, 再把定线段DE ,半定线段DF 、EF 长度表示出来. 根据上 述分析,结合“两圆一线”分别使得三条线段两两相等建立方程,即DE = DF ,DE = EF ,DF = EF , 求解出动点坐标即可.(实际解题过程中, 一般使用线段平方的形式.此外, 只需关注下方解析中公 式计算部分即可,文字叙述部分可忽略)此题还是比较友善的,只需求出F 坐标.如果需要求解点G 的坐标,则还要加一个步骤.这里 以DEG 1F 1 为例,若要求 G 1 坐标,一般有两种比较常用的思路.一是利用菱形的对边平行且相等,即F 1G 1 可以看成是DE 平移得来的, 那么点D → F 1 的平移变化也即点E → G 1 的平移变化. 二是利用菱形的对角线相互平分,因此EF 1 的中点也即DG 1 的中点,利用中点坐标求解出 G 1 坐标.这两种处理 在平行四边形存在性问题中也是有力手段.(|y = −x 2 + 2x + 3 ( 3 15 ) 149 ( 149 )由题, y = −x 2 + 2x + 3 向右平移 1 个单位得到新抛物线y = − (x −1)2+ 2(x −1) + 3 = −x 2 + 4x ,联立〈|ly = −x 2 + 4x ,解得 E |\2 , 4 )| , 新抛物线的对称轴为x = 2 ,设 F (2, m ) ,由于 D (1, 2) ,则DE 2 =,EF 2 = + m −2= m 2 − m +,DF 2 = 1+ (m − 2)2= m 2 − 4m + 5 ,①当DE 、DF 为一组邻边时,则 DE 2 = DF 2 ,即 = m 2 − 4m + 5 ,37 ( ) ( )②当ED 、EF 为一组邻边时,则 ED 2 = EF 2 ,即 = m 2 − m + ,16 8 16 11 ( 11)③当EF 为对角线时,则FD = FE ,即 m 2 − m + = m 2 − 4m + 5 , 2 16解得m = ,此时 F 的坐标为|2, | ;( ) ( ) ( 149 )( 11) 当F |2, |时, y F + y D = 2y E ,x D + x F = 2x E ,即 E 为D 、F 中点, 不合题意, 舍去; 15 229 \ 2 )综上, F 点的坐标为||\2, 2 + 4 )|| 或||\2, 2 − 4 )|| 或(2, 2) 或|\2, 56 )| . 56 \ 56 )解得m = 2 或m = ,此时F 的坐标为(2, 2) 或|2, | ,2 \ 2 )解得m = 2 土 4 ,此时 F 的坐标为||\2, 2 + 4 )|| 或||\2, 2 − 4 )|| ;53 15 2291 .已知二次函数y = ax2 + bx − 2(a 丰 0)与x 轴交于A ( −, 0) ,B (4, 0) ,与 y 轴交于点C .(1) 求抛物线的解析式;(2) 连接AC ,BC ,点 P 是直线BC 下方抛物线上一点,过 P 作PD ∥AC 交直线BC 于点D ,PE ∥x 轴交直线BC 于点, E ,求△PDE 面积的最大值及此时点, P 的坐标;(3) 在(2)的条件下, 将原抛物线沿x 轴向左平移3个单位得到新抛物线,点 M 是新抛物线对称轴上一点, 点 N 是平面直角坐标系内一点, 当以点M 、 N 、P 、B 为顶点的四边形为菱形 时,请直接写出所有符合条件的N 点的坐标;并任选其中一个N 点,写出求解过程.立〈y= − 2 x 2 + 4x − 2 ,解得D 7 , 11 .1-1如图 1,抛物线y = ax 2 + bx + 4 交x 轴于A (−2, 0) ,B (4, 0) 两点,与y 轴交于点C ,连接 AC , BC .(1) 求抛物线的解析式;(2) P 是拋物线上位于直线BC 上方的一个动点,过点P 作PQ ∥y 轴交BC 于点Q , 过点P 作PE ⊥ BC 于点E ,过点 E 作EF ⊥ y 轴于点F ,求出2PQ + EF 的最大值及此时点P 的坐标;(3)如图 2,将抛物线y = ax 2 + bx + 4 沿着射线CB 的方向平移,使得新抛物线y ,过点(3,1) , 点D 为原抛物线y 与新抛物线y ,的交点,若点 G 为原抛物线的对称轴上一动点,点H 为新抛物线y , 上一动点,直接写出所有使得以 A ,D , G ,H 为顶点的四边形为平行四边形的点H 的坐标,并 把求其中一个点H 的坐标的过程写出来.抛物线解析式为y = − x 2 + x + 4 ;点 P | , | .相当于是沿着射线BC 方向平移,故舍去, 因此可得平移后抛物线的解析式为y = − x 2 + 4x − .联2 2 ( 1 13 y = − x 2 + x +4 \2 8 )这类平行四边的探究也并不难, 同样先从确定的信息入手.平行四边形是以A ,D ,G ,H 为 顶点,其中AD 是定线段, G 是半动点,H 在新的抛物线上.和菱形的讨论一样,我们要考虑AD 是 一条边的情形, 也要考虑AD 是对角线的情形.当 AD 是一条边时, 实际上此时也右两种情形,一是是平行四边形为ADHG ,也即AH ,DG 为 对角线;另一种则是平行四边形为ADGH ,也即 AG ,DH 为对角线.当然,不管是那种情形,由 于 AD 是一条边,根据平行四边形对边平行且相等的性质, GH 这条边可以看作是将AD 平移后得到1 (8 28 )2 \3 9 )第 3 小问中, 抛物线沿着射线CB 方向平移, 由于后续的点在新抛物线上, 因此还是要求出平移 后抛物线的解析式.这类沿着射线平移的,一般采用正交分解的形式平移,由点 C (0, 4) ,B (4, 0) 可 知,沿着射线 CB 平移,即向右平移t 个单位,则向下也平移t 个单位,因此假设平移后新抛物线的 解析式为y = − (x − t )2+ (x − t ) + 4 − t ,因为平移后经过点(3,1) ,代入可解得t = − 1 或t = 3 ,当 t = − 1 , 1 13的,由于半动点 G 在原抛物线对称轴x = 1 上,那么点 G 有可能是点 A 平移后得到的, 此时点H 就 是点D 平移后得到的,如图 1 所示;同理,当点 G 是点D 平移后得到的,那么此时点H 就是点A 平 移后得到的,如图 2 所示.设点 G (1, m ),根据平移的性质,结合点坐标的变化规律,当 A → G 时, 即(−2, 0) —(1, m ) ,则有D|2 , 8 )| —H | 2 , 8 + m )| ,由于点H 在新抛物线上, 且横坐标已知了,代入新抛物线即可 11 1 (13 213 13 13 (13 13 此外, 除了用平移性质得到H 点的坐标外,此时 AH 是一条对角线,也利用对角线相互平分, 则 A 、 H 的 中 点 和 D 、 G 的 中 点 是 同 一 个 , 利 用 中 点 坐 标 则 有 x A + x H = x D + x G ,故 13 13 13 (13 13 x H = x D + x G − x A = 2 ,将x = 2 代入新抛物线解析式,可求得H 点纵坐标y = − 8 ,故H | 2 , − 8 )|.当 AG 是一条对角线时, 则有x A + x G = x D + x H ,故 x H = x A + x G − x D = − ,代入新抛物线解析 277 ( 9 277式,可求得此时H 的纵坐标为 − ,故H |− , − | .8 2 8 ) 当 AD 是一条对角线时,则有x A + x D = x H + x G ,故 x H = x A + x D − x G = ,代入新抛物线解析式, 37 ( 1 37 可求得此时H 的纵坐标为 − ,故 H | , − | .8 2 8 )同样地,在解题过程中, 把准备工作做好,即对应的点坐标,解析式等先求出来,动点坐标假设好, 将点坐标表示列出来(通常都是横坐标),选定一个定点,如这里我们选定 x A ,将其与剩下 三点横坐标x D 、x G 、x H 两两组合,建立中点坐标关系式, 即x A + x D = x H + x G ,x A + x G = x D + x H 以 及x A + x H = x D + x G ,求解出点H 横坐标,再代入解析式中求出点H 纵坐标即可.求得纵坐标 8 + m = − 2 | 2 )| + 4 2 − 2 = − 8 ,此时H | 2 , − 8 )| . ( 7 11 (13 1113 (13 13)由题, 设平移后的抛物线解析式为y = − (x − t )2+ (x − t ) + 4− t ,因为平移后经过点(3,1),代入可解得t = − 1 (舍) 或t = 3 ,2 2联立〈y = − 2 x 2 + 4x − 2 ,解得 D 7 , 11 , y = − x 2 + x + 4 \2 8 )则x A =−2 ,x D = ,x G = 1,设 H 点横坐标为x H ,①当AH 为一条对角线时,x A + x H = x D + x G ,则 x H = ,代入可求得此时H | , − | ; 9 ( 9 277 )1 (1 37 )综上, H 的坐标为| , − |或|− , − |或| , − | .( 1 13 ③当AD 为一条对角线时,x A + x D = x H + x G ,则x H = ,代入可求得此时H | , − | ;(13 13) ( 9 277 ) (1 37 )2 \2 8 )\ 2 8 ) \ 2 8 ) \2 8 )②当AG 为一条对角线时,x A + x G = x D + x H ,则x H = − ,代入可求得此时H |− , − | ;2 \ 2 8 ) 2 \ 2 8 )故平移后抛物线的解析式为y = − x 2 + 4x − ,1 131.如图,在平面直角坐标系中,抛物线y= ax2 + bx+ 3(a 0) 与y轴交于点C,与x轴交于A,B两点(点A在点B的右侧),且点A的坐标为( 3, 0) ,连接BC,过点A作AD∥BC交y轴于点D,OB= 3OA.(1) 求抛物线的解析式;(2) 如图1,点E为射线AD上一点,点P为第二象限内抛物线上一点,求四边形PBEC面积的最大值及此时点P的坐标;(3) 如图2,将原抛物线沿x轴正方向平移得到新抛物线y,y经过点C,平移后点A的对应点为点A,点N为线段AD的中点,点Q为新抛物线y的对称轴上一点,在新抛物线y上存在一点M,使以点M,Q,A,N为顶点的四边形为平行四边形,请直接写出点M的坐标,并选择一个你喜欢的点写出求解过程.2.如图,抛物线y= x2 + bx+ c与x轴相交于点A(−1, 0) 和点B,交y轴于点C,tan 三ACO= .(1) 求抛物线的解析式;(2) 如图1 ,P点为一象限内抛物线上的一个动点,点D是BC中点,连接PD,BD,PB.求△BDP面积的最大值以及此时P点坐标;,M为新抛物线对称轴上(3) 如图2,将抛物线向左平移 1 个单位长度,得到新的抛物线y1一点,N为直线AC上一动点,在(2) 的条件下,是否存在点M,使得以点P、B、M、N为顶点的四边形为平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.| 4 21如图,已知抛物线y = ax 2 + bx − 4 与x 轴交于A ,B 两点, 与y 轴交于点C ,且点A 的坐标 为(−2, 0) ,直线BC 的解析式为y = x − 4 .(1) 求抛物线的解析式;(2)如图 1,过点 A 作 AD ∥BC 交抛物线于点D (异于点 A ), P 是直线BC 下方抛物线上一 点,过点P 作PQ ∥y 轴, 交AD 于点Q ,过点 Q 作QR ⊥ BC 于点R ,连接PR .求△PQR 面积的最 大值及此时点P 的坐标;(3) 如图 2,点 C 关于x 轴的对称点为点C ,将抛物线沿射线 C A 的方向平移2个单位长度得到新的抛物线y ,新抛物线y 与原抛物线交于点M ,原抛物线的对称轴上有一动点 N ,平面直 角坐标系内是否存在一点K ,使得以 D ,M ,N ,K 为顶点的四边形是矩形?若存在,请直接写 出点K 的坐标;若不存在, 请说明理由.抛物线解析式为y = x 2 − x − 4 ;S △PQR 的最大值为 9,点P (4, −6) .第 3 小问中,抛物线沿着射线C A 方向平移, 由于点M 为两抛物线交点, 因此需求出平移后抛 物线的解析式.根据A (−2, 0) ,C (0, 4) ,可知Rt △AOC 中AO : OC : AC = 1: 2 : ,因此将抛物线沿着射线C A 方向平移2个单位长度,则相当于向下平移 4 个单位长度,向左平移 2 个单位长度,因此平移后的抛物线为y = 1 (x + 2)2− 3 (x + 2) − 4 − 4 = 1 x 2 − 1 x −10 ,联立〈y = x 2 − x −10,解4 2 4 2y = x 2 − x − 4( 1得M (6, −4) .又 BC : y = 1 x − 4 ,可知 AD : y = 1 x + 1,联立〈 y = 2 x + 1,解得D (10, 6) .2 2 |y = 1 x 2 − 3x − 4因为以D ,M ,N ,K 为顶点的四边形是矩形,此时定线段是DM ,半动点为N ,自由点为K .和 前面讨论菱形、平行四边形时的流程基本大同小异,定线段DM 可能是矩形的边,也可能是矩形的 对角线,因此要分两种情形讨论.矩形的存在性问题和直角三角形的存在性问题是一致的,如本题 中,探究以D ,M ,N 为顶点的三角形是直角三角形. 同样地,先以直角三角形为例,那么D ,M ,1 3 4 2在实际解题中设 K (x , y ) 即可), 利用中点关系〈 M K D N ,则〈 K,整理得N 均有可能为直角顶点.当M 为直角顶点时,过M 作DM 垂线与对称轴交点即为点N 所在位置,如图 1 所示.对于N 点 坐标的求解,一方面,由于MN ⊥ DM ,则 k MN . k DM = − 1,结合点M 坐标,由此可求得直线MN 解 析式,将其与对称轴方程联立即可求得点N 坐标.另一方面,可以构造如图所示的K 型相似,即构DH MH1 腰直角三角形, 或者四边形中的正方形, 那么可以构造此类的K 型全等求解.在此直角三角形的基础上,加上自由点K ,就变成矩形问题了.对于矩形问题,同样可以求出点N 坐标后,利用平移关系或者对角线的中点关系,求相应的点K 的坐标.当然,如果是探究矩形 的存在性问题,也可以直接利用中点关系求得点K 的坐标.由点N (3, n ),设K (x K , y K ) (熟练后,(x + x = x + x (6 + x = 10 + 3 l y M + y K = y D + y N l−4 + y K = 6 + n 〈,再由对角线相等,即MK = DN ,代入即有1+ (y + 4)2= 49 + (16 − y )2,解得 y =,( 36 )同样适用.当D 为直角顶点时,三角形如图2 所示.同样, 加上自由点K ,就变成矩形问题了. 这里我们5 2 2 ( 44 )l y M + y N = y D + y K |y K = − \ 5 )对于直角三角形或矩形问题, 如上图情形,我们可以称其为“两线一圆”.若只求点N 坐标,一 般利用斜率关系,求出解析式后进一步求解.如果是矩形问题要求自由点的坐标,可以用对角线平 分且相等, 建立方程求解.当然, 先求点N ,利用点N 作为台阶进一步求解也是没问题的, 大家选 用自己顺手的方法即可.造 △MN 1G ∽△DMH ,利用 = ,可求出长度,进而得到点 N 坐标.更特殊地,如果是等以垂线方式求解.由于k DM = 2 ,则 k DN = − 5 ,故此时DN : y = − 5 x + 10 ,令x = 3 ,可解得N |\3, 5 )| , 由中点可知,〈(x M + x N = x D + x K ,可解得〈(|x K = − 16 ,此时 K −1,− 6 .l 5当N 为直角顶点时,则有NM ⊥ ND ,因此点N 在以DM 为直径的圆上.此种情形若只是求点N 坐标,策略比较多, 一方面,可以利用斜率, 由k ND . k NM= − 1求出点N 坐标;另一方面,可以利用线段长度求解,设DM 中点为为R ,则此时圆心为R ,因此NR = RD = DM ,由此也可求得点N 坐 标, 此外, 还可以利用勾股定理ND 2 + NM 2 = DM 2 .当加入自由点K ,变成矩形问题后,除了先求 出点N 坐标, 利用平移或中点求解点K 坐标外,也可以利用前面的对角线平分且相等来求解. 故此时K |7, | .此法借助的是矩形的对角线平分且相等的性质,该处理对于DM 是对角线的情形 \ 5 ) GM N G式和长度关系式子,即〈 M K D N 且MK 2 = DN 2 ,〈 M N D K 且MN 2 = DK 2 以及(x M + x D = x N + x K 4 2 4 2|l 4 2(x M + x K = x D + x N (6 + x = 10 + 3 (x = 7由MK 2 = DN 2 ,代入即有1+ (y + 4)2= 49 + (16 − y )2,解得 y = 36,故此时K 7,36;由MN 2 = DK 2 ,代入即有9 + (y +14)2 = 121+ (y − 6)2,解得 y = − 6 ,故此时K −1,− 6 ;(x M + x D = x N + x K (6 + 10 = 3 + x (x = 13 同样地,在解题过程中, 把准备工作做好,即对应的点坐标安排到位,动点坐标假设好,选定 一个定点, 如这里我们选定M ,将其与剩下三点横坐标D 、 N 、K 两两组合, 建立中点坐标关系 (x + x = x + x (x + x = x + xl y M + y K = y D + y N l y M + y N = y D + y K〈 且MD 2 = NK 2,利用方程组求解出对应的点K 的坐标. l y M + y D = y N + y K附:坐标平面内点A (x 1 , y 1 ) ,B (x 2 , y 2 ) ,其中x 1 丰 x 2 ,则过A 、B 两点的直线的斜率k =由题, 将抛物线沿着射线 C ,A 方向平移2个单位长度, 即将其向下平移 4 个单位长度, 向左平移 2 个单位长度, 因此平移后的抛物线为y =1(x + 2)2 − 3 (x + 2) − 4 − 4 = 1 x 2 − 1 x −10 , 联立〈y = x 2− x −10,解得M (6, −4) ,y = x 2 − x − 4( 1又 BC : y = 1 x − 4 ,可知 AD : y = 1 x + 1,联立〈 y = 2 x + 1,解得D (10, 6) ,2 2 |y = 1 x 2 − 3x − 4由M (6, −4) ,D (10, 6) ,设 N (3, n ) ,K (x , y ) ,①当MK 为一条对角线时,〈,即〈 ,整理得〈 , l y M + y K = y D + y N l −4 + y = 6 + n l n = y −105 \ 5 )②当MN 为一条对角线时,〈(x M + x N = x D + x K,即〈(6 + 3 = 10 + x,整理得〈(x = − 1l y M + y N = y D + y K l −4 + n = 6 + y l n = 10 + y5 \ 5 )③当MD 为一条对角线时,〈 ,即〈 ,整理得〈l y M + y D = y N + y K l−4 + 6 = n + y l n = 2 − y由MD 2 = NK 2 ,代入即有116 = 100 + (2 − 2y )2,解得y =− 1 或y = 3 ,故此时K (13, −1) 或(13,3) ; ( 36 ) ( 6 )综上, 点K 的坐标为|7, |或|−1,− |或(13, −1) 或(13,3) .\ 5 ) \ 5 ) y 1 − y 2. x 1 − x 21.如图1,二次函数y= ax2 + bx+ c(a丰0)与x轴交于点A(−2, 0) 、点B(点A在点B左侧),与y轴交于点C(0,3) ,tan 三CBO= .(1) 求二次函数解析式;(2)如图2,点P是直线BC上方抛物线上一点,PD∥y轴交BC于D,PE∥BC交x轴于点E,求PD+ BE的最大值及此时点P的坐标;(3) 在(2) 的条件下,当PD+ BE取最大值时,连接PC,将△PCD绕原点O顺时针旋转90。
二次函数中的十二大存在性问题(学生版)

二次函数中的十二大存在性问题【题型1二次函数中等腰三角形的存在性问题】【题型2二次函数中直角三角形的存在性问题】【题型3二次函数中等腰直角三角形的存在性问题】【题型4二次函数中全等三角形的存在性问题】【题型5二次函数中平行四边形的存在性问题】【题型6二次函数中菱形的存在性问题】【题型7二次函数中矩形的存在性问题】【题型8二次函数中正方形的存在性问题】【题型9二次函数中面积问题的存在性问题】【题型10二次函数中线段问题的存在性问题】【题型11二次函数中角度问题的存在性问题】【题型12二次函数中最值问题的存在性问题】【题型1二次函数中等腰三角形的存在性问题】1(2023春·甘肃张掖·九年级校考期中)如图甲,直线y=-x+3与x轴、y轴分别交于点B、点C,经过B、C两点的抛物线y=x2+bx+c与x轴的另一个交点为A,顶点为P.(1)求该抛物线的解析式;(2)当0<x<3时,在抛物线上求一点E,使△CBE的面积有最大值(图乙、丙供画图探究),并求出最大面积及E点的坐标.(3)在该抛物线的对称轴上是否存在点M,使以C、P、M为顶点的三角形为等腰三角形?若存在,请求出所符合条件的点M的坐标;若不存在,请说明理由;1(2023春·广西贵港·九年级统考期末)如图,抛物线y=ax2+3x+c a≠0和与x轴交于点A-2,0点B,与y轴交于点C0,8,点P为直线BC上方抛物线上的动点,连接CP,PB,直线BC与抛物线的对称轴l交于点E.(1)求抛物线的解析式;(2)求△BCP的面积最大值;(3)点M是抛物线的对称轴l上一动点.是否存在点M,使得△BEM为等腰三角形?若存在,求出点M的坐标;若不存在,请说明理由.2(2023春·山西晋城·九年级校考期末)如图1,抛物线y=ax2+bx+3与x轴交于A-1,0两,B4,0点,与y轴交于点C,顶点为D.点P是直线BC上方抛物线上的一个动点,过点P作PE⊥x轴于点E,交直线BC于点Q.(1)求抛物线的表达式;(2)求线段PQ的最大值;(3)如图2,过点P作x轴的平行线交y轴于点M,连接QM.是否存在点P,使得△PQM为等腰三角形?若存在,请直接写出点P的横坐标;若不存在,请说明理由.3(2023•沙坪坝区校级模拟)如图1,抛物线y=ax2+bx+2(a≠0)交x轴于点A(-1,0),点B(4,0),交y轴于点C.连接BC,过点A作AD∥BC交抛物线于点D(异于点A).(1)求抛物线的表达式;(2)点P是直线BC上方抛物线上一动点,过点P作PE∥y轴,交AD于点E,过点E作EG⊥BC于点G,连接PG.求△PEG面积的最大值及此时点P的坐标;(3)如图2,将抛物线y=ax2+bx+2(a≠0)水平向右平移32个单位,得到新抛物线y1,在y1的对称轴上确定一点M,使得△BDM是以BD为腰的等腰三角形,请写出所有符合条件的点M的坐标,并任选其中一个点的坐标,写出求解过程.【题型2二次函数中直角三角形的存在性问题】1(2023春·四川广安·九年级校考期中)如图,已知抛物线y=ax2+bx+c(a≠0)经过点A(-3,2),B(0,-2),其对称轴为直线x=52,C0,1 2为y轴上一点,直线AC与抛物线交于另一点D.(1)求抛物线的函数表达式;(2)试在线段AD下方的抛物线上求一点E,使得△ADE的面积最大,并求出最大面积;(3)在抛物线的对称轴上是否存在一点F,使得△ADF是直角三角形?如果存在,求点F的坐标;如果不存在,请说明理由.1(2023春·辽宁盘锦·九年级校考期中)如图,已知直线y=x+3与x轴交于点A,与y轴交于点B,抛物线y=-x2+bx+c经过A、B两点,与x轴交于另一个点C,对称轴与直线AB交于点E,抛物线顶点为D.(1)求抛物线的解析式;(2)在第三象限内,F为抛物线上一点,以A、E、F为顶点的三角形面积为3,求点F的横坐标;(3)点P是对称轴上的一动点,是否存在某一点P使P、B、C为顶点的三角形是以BC为直角边的直角三角形?若存在,请直接写出所有符合条件的P点坐标;不存在,说明理由.2(2023春·广东梅州·九年级校考期中)已知二次函数y=x2+bx+c的图象经过A(-2,5),B(-1,0),与x轴交于点C.(1)求这个二次函数的解析式;(2)点P直线AC下方抛物线上的一动点,求△PAC面积的最大值;(3)在抛物线对称轴上是否存在点Q,使△ACQ是直角三角形?若存在,直接写出点Q的坐标,若不存在,请说明理由.3(2023春·甘肃金昌·九年级统考期中)平面直角坐标系中,抛物线y=a(x-1)2+92与x轴交于A,B(4,0)两点,与y轴交于点C.(1)求抛物线的解析式,并直接写出点A,C的坐标;(2)在抛物线的对称轴上是否存在点P,使△BCP是直角三角形?若存在,请直接写出点P的坐标,若不存在,请说明理由;(3)如图,点M是直线BC上的一个动点,连接AM,OM,是否存在点M使AM+OM最小,若存在,请求出点M的坐标,若不存在,请说明理由;【题型3二次函数中等腰直角三角形的存在性问题】1(2023春·山西阳泉·九年级统考期末)综合与探究:在平面直角坐标系中,抛物线y=ax2+bx-2与x轴交于点A-1,0作平行于x轴的直线l,直线l与抛物线y,与y轴交于点C,过动点D0,m和点B4,0=ax2+bx-2相交于点E,F.(1)求抛物线的表达式;(2)求m的取值范围;(3)直线l上是否存在一点P,使得△BCP是以BC为直角边的等腰直角三角形?若存在,求m的值;若不存在,请说明理由.1(2023春·福建漳州·九年级校考期中)如图①,已知抛物线y=ax2+bx+3的图象经过点B1,0,与y 轴交于点A,其对称轴为直线l:x=2,过点A作AC∥x轴交抛物线于点C,∠AOB的角平分线交线段AC于点E,点P是抛物线上的一个动点,设其横坐标为m.(1)求抛物线的解析式;(2)若动点P在直线OE下方的抛物线上,连接PE、PO,当m为何值时,四边形AOPE面积最大,并求出其最大值;(3)如图②,F是抛物线的对称轴l上的一点,在抛物线上是否存在点P使△POF成为以点P为直角顶点的等腰直角三角形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由.2(2023春·湖南湘西·九年级统考期末)如图,在平面直角坐标系中,直线y =-x +3交x轴于点B ,交y 轴于点C ,直线AD 交x 轴于点A ,交y 轴于点D ,交直线BC 于点E -12,72,且CD =1.(1)求直线AD 解析式;(2)点P 从B 点出发沿线段BA 方向以1个单位/秒的速度向终点A 运动(点P 不与A ,B 两点重合),设点P 的运动时间为t ,则是否存在t ,使得△AEP 为等腰直角三角形?若存在,请求出t 的值,若不存在,请说明理由;(3)在(2)的条件下,点P 出发的同时,点Q 从C 点出发沿射线CO 方向运动,当点P 到达终点时,点Q 也停止运动,连接AQ ,PQ ,设△APQ 的面积为S ,S 与t 的函数关系式为S =32t 2-12t +2120≤t <1a t -1 t -7 1<t <7,其图象如图2所示,结合图1、图2的信息,请求出a 的值及当△APQ 的面积取得最大值时AQ 的长.3(2023春·北京通州·九年级统考期末)如图,抛物线y1=ax2-2x+c的图象与x轴交点为A和B,与y 轴交点为D0,3,与直线y2=-x-3交点为A和C.(1)求抛物线的解析式;(2)在直线y2=-x-3上是否存在一点M,使得△ABM是等腰直角三角形,如果存在,求出点M的坐标,如果不存在请说明理由.(3)若点E是x轴上一个动点,把点E向下平移4个单位长度得到点F,点F向右平移4个单位长度得到点G,点G向上平移4个单位长度得到点H,若四边形EFGH与抛物线有公共点,请直接写出点E的横坐标x E的取值范围.【题型4二次函数中全等三角形的存在性问题】1(2023·陕西咸阳·统考三模)如图,抛物线y=14x2-2x+3与x轴交于A、B两点,抛物线的顶点为C,对称轴为直线l,l交x轴于点D.(1)求点A、B、C的坐标;(2)点P是抛物线上的动点,过点P作PM⊥y轴于点M,点N在y轴上,且点N在点M上方,是否存在这样的点P、N,使得以点P、M、N为顶点的三角形与△BCD全等,若存在,请求出点P、N的坐标;若不存在,请说明理由.1(2023·甘肃陇南·统考一模)如图,抛物线y=x2+bx+c与x轴交于A-1,0,B两点,与y轴交于点C0,-3.(1)求抛物线的函数解析式;(2)已知点P m,n在抛物线上,当-1≤m<3时,直接写出n的取值范围;(3)抛物线的对称轴与x轴交于点M,点D坐标为2,3,试问在该抛物线上是否存在点P,使△ABP与△ABD全等?若存在,请求出所有满足条件的P点的坐标;若不存在,请说明理由.2(2023·陕西咸阳·统考三模)如图,抛物线y=14x2-2x+3与x轴交于A,B两点,抛物线的顶点为C,对称轴为直线l,l交x轴于点D.(1)求点A、B、C的坐标;(2)点P是抛物线上的动点,过点P作PM⊥y轴于点M,点N在y轴上,且点N在点M上方,是否存在这样的点P、N,使得以点P、M、N为顶点的三角形与△BCD全等,若存在,请求出点P、N的坐标;若不存在,请说明理由.3(2023·内蒙古通辽·统考中考真题)如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)的顶点为B(2,1),且过点A(0,2),直线y=x与抛物线交于点D,E(点E在对称轴的右侧),抛物线的对称轴交直线y=x于点C,交x轴于点G,EF⊥x轴,垂足为F,点P在抛物线上,且位于对称轴的右侧,PQ⊥x轴,垂足为点Q,△PCQ为等边三角形(1)求该抛物线的解析式;(2)求点P的坐标;(3)求证:CE=EF;(4)连接PE,在x轴上点Q的右侧是否存在一点M,使△CQM与△CPE全等?若存在,试求出点M的坐标;若不存在,请说明理由.[注:3+22=(2+1)2].【题型5二次函数中平行四边形的存在性问题】1(2023春·云南临沧·九年级统考期末)如图,抛物线y=ax2+bx-3与x轴交于A-1,0两点,、B3,0与y轴交于点C.(1)求抛物线的解析式;(2)若点D是抛物线上的一点,当△ABD的面积为10时,求点D的坐标;(3)点P是抛物线对称轴上的一点,在抛物线上是否存在一点Q,使得以B、C、P、Q为顶点的四边形是平行四边形?若存在,求出点Q的坐标;若不存在,请说明理由.1(2023春·山东东营·九年级校考期末)如图,已知抛物线y=ax2+bx+3与x轴交于A-1,0、B3,0两点,与y轴交于点C,连接BC.(1)求抛物线的解析式;(2)若点P为线段BC上的一动点(不与B、C重合),PM∥y轴,且PM交抛物线于点M,交x轴于点N,当△BCM的面积最大时,求点P的坐标;(3)在(2)的条件下,当△BCM的面积最大时,点D是抛物线的对称轴上的动点,在抛物线上是否存在点E,使得以A、P、D、E为顶点的四边形为平行四边形?若存在,请直接写出点E的坐标;若不存在,请说明理由.2(2023春·重庆梁平·九年级统考期末)如图1,在平面直角坐标系中,抛物线y=-2x2+4x+6与y轴交于点A,与x轴交于点E,B(E在B的左侧).(1)如图2,抛物线的顶点为点Q,求△BEQ的面积;(2)如图3,过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD 平行于y轴交AB于点D、交AC于点F,当点P在何位置时,PD+CF最大?求出最大值;(3)在(2)条件下,当PD+CF最大时,将抛物线y=-2x2+4x+6沿着射线AB平移,使得抛物线经过点C,此时得到新抛物y ,点N是原抛物线对称轴上一点,在新抛物线y 上是否存在一点M,使以点A,D,M,N为顶点的四边形为平行四边形,若存在,请直接写出点M的所有坐标,若不存在,请说明理由.3(2023春·重庆江北·九年级重庆十八中校考期末)如图1,抛物线y=ax2+bx+3a≠0与x轴正半轴交于点A,B,与y轴正半轴交于点C,且OC=OB=3OA,点D为抛物线的顶点.(1)求该抛物线的函数表达式;(2)点P为直线BC下方该抛物线上任意一点,点E为直线BC与该抛物线对称轴的交点,求△PBE面积的最大值;(3)如图2,将该抛物线沿射线CB的方向平移22个单位后得到新抛物线y ,新抛物线y 的顶点为D ,过(2)问中使得△PBE面积为最大时的点P作平行于y轴的直线交新抛物线y 于点M.在新抛物线y 的对称轴上是否存在点N,使得以点P,D ,M,N为顶点的四边形是平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.【题型6二次函数中菱形的存在性问题】1(2023春·重庆云阳·九年级校联考期中)如图1,抛物线y=ax2+bx+c(a≠0)与x轴相交于点A、B(点B在点A左侧),与y轴相交于点C(0,3).已知点A坐标为(1,0),△ABC面积为6.(1)求抛物线的解析式;(2)点P是直线BC上方抛物线上一动点,过点P作直线BC的垂线,垂足为点E,过点P作PF∥y轴交BC于点F,求△PEF周长的最大值及此时点P的坐标:(3)如图2,将该抛物线向左平移2个单位长度得到新的抛物线y ,平移后的抛物线与原抛物线相交于点D,点M为直线BC上的一点,点N是平面坐标系内一点,是否存在点M,N,使以点B,D,M,N为顶点的四边形为菱形,若存在,请直接写出点M的坐标;若不存在,请说明理由.1(2023春·甘肃庆阳·九年级统考期末)如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,与y轴交于点C0,-3,点P是直线BC下,点A在原点的左侧,点B的坐标为3,0方的抛物线上一动点.(1)求这个二次函数的表达式.(2)连接PO、PC,并把△POC沿CO所在直线翻折,得到四边形POP C,那么是否存在点P,使四边形POP C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.(3)当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的面积.点,抛物线y=-x2+bx+c经过点B,且与x轴交于点C(2,0).(1)求该抛物线的解析式;(2)已知点M是抛物线上的一个动点,并且点M在第一象限内,连接AM、BM,设点M的横坐标为m,四边形OAMB的面积为S,求S与m的函数表达式,并求出S的最大值;(3)若点P在平面内,点Q在直线AB上,平面内是否存在点P使得以O,B,P,Q为顶点的四边形是菱形.若存在,求出点P的坐标;若不存在,请说明理由.点,抛物线y=-x2+bx+c经过点B,且与x轴交于点C(2,0).(1)求该抛物线的解析式;(2)已知点M是抛物线上的一个动点,并且点M在第一象限内,连接AM、BM,设点M的横坐标为m,四边形OAMB的面积为S,求S与m的函数表达式,并求出S的最大值;(3)若点P在平面内,点Q在直线AB上,平面内是否存在点P使得以O,B,P,Q为顶点的四边形是菱形.若存在,求出点P的坐标;若不存在,请说明理由.【题型7二次函数中矩形的存在性问题】1(2023春·浙江湖州·九年级统考期末)如图,在平面直角坐标系xOy中,O为坐标原点,抛物线y=a(x+3)(x-1)(a>0)与x轴交于A,B两点(点A在点B的左侧).(1)求点A与点B的坐标;(2)若a=13,点M是抛物线上一动点,若满足∠MAO不大于45°,求点M的横坐标m的取值范围.(3)经过点B的直线l:y=kx+b与y轴正半轴交于点C.与抛物线的另一个交点为点D,且CD=4BC.若点P在抛物线对称轴上,点Q在抛物线上,以点B,D,P,Q为顶点的四边形能否成为矩形?若能,求出点P的坐标;若不能,请说明理由.1(2023·山东东营·东营市胜利第一初级中学校考三模)已知抛物线y=ax2+bx-4a≠0交x轴于点A4,0和点B-2,0,交y轴于点C.(1)求抛物线的解析式;(2)如图,点P是抛物线上位于直线AC下方的动点,过点P分别作x轴、y轴的平行线,交直线AC于点D,交x轴于点E,当PD+PE取最大值时,求点P的坐标及PD+PE最大值.(3)在抛物线上是否存在点M,对于平面内任意点N,使得以A、C、M、N为顶点且AC为一条边的四边形为矩形,若存在,请直接写出M、N的坐标,不存在,请说明理由.2(2023春·内蒙古通辽·九年级校考期中)如图,抛物线y=ax2+bx+3交x轴于A(3,0),B(-1,0)两点,交y轴于点C.(1)求抛物线的解析式和对称轴.SΔABC,求R的坐标.(2)若R为第一象限内抛物线上点,满足SΔRAC=12(3)若点P在抛物线的对称轴上,点Q是平面直角坐标系内的任意一点,是否存在点P使得A、C、P、Q为顶点的四边形是矩形,若存在,请直接写出所有符合条件的点P的坐标.3(2023春·广东江门·九年级校考期末)如图,在平面直角坐标系中,已知抛物线y=ax2+bx-2a≠0、B两点,交y轴于点C,其对称轴为x=1.5,交x轴于A-1,0(1)求该抛物线的函数解析式;(2)P为第四象限内抛物线上一点,连接PB,过点C作CQ∥BP交x轴于点Q,连接PQ,求△PBQ面积的最大值及此时点P的坐标.(3)在(2)的条件下,将抛物线y=ax2+bx-2a≠0向右平移经过点Q,得到新抛物线,点E在新抛物线的对称轴上,是否在平面内存在一点F,使得以A、P、E、F为顶点的四边形是矩形?若存在,直接写出点F的坐标;若不存在,请说明理由.【题型8二次函数中正方形的存在性问题】1(2023·辽宁阜新·阜新实验中学校考一模)如图,在平面直角坐标系中,抛物线y=ax2+bx-3与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C,点P为抛物线上的动点.(1)求该抛物线的函数表达式;(2)点D为直线y=x上的动点,当点P在第四象限时,求四边形PBDC面积的最大值及此时点P的坐标;(3)已知点E为x轴上一动点,点Q为平面内任意一点,是否存在以点P,C,E,Q为顶点的四边形是以PC为对角线的正方形,若存在,请直接写出点Q的坐标,若不存在,请说明理由.1(2023·陕西西安·校考模拟预测)如图,已知拋物线y=-x2+2x+c与x轴交于点A3,0,B与y轴交于点C.(1)求c的值及该抛物线的对称轴;(2)若点D在直线AC上,点E是平面内一点.是否存在点E,使得以点A,B,D,E为顶点的四边形为正方形?若存在,请求出点E的坐标;若不存在,请说明理由.2(2023·山西晋中·山西省平遥中学校校考模拟预测)如图,二次函数y=-x2+2x+3的图象与x轴交于A,B两点(点A在点B左侧),与y轴交于点C.连接BC.点P是抛物线第一象限内的一个动点,设点P的横坐标为m,过点P作直线PD⊥x轴于点D.交BC于点E.过点P作BC的平行线,交y轴于点M.(1)求A,B,C三点的坐标,并直接写出直线BC的函数表达式;(2)在点P的运动过程中,求使四边形CEPM为菱形时,m的值;(3)点N为平面内任意一点,在(2)的条件下,直线PM上是否存在点Q使得以P,E,Q,N为顶点的四边形是正方形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.3(2023·江西赣州·统考一模)已知二次函数C1:y=mx2-2mx+3(m≠0).(1)有关二次函数C1的图象与性质,下列结论中正确的有.(填序号)①二次函数C1的图象开口向上;②二次函数C1的图象的对称轴是直线x=1;③二次函数C1的图象经过定点(0,3)和(2,3);④函数值y随着x的增大而减小.(2)当m=1时,①抛物线C1的顶点坐标为;②将抛物线C1沿x轴翻折得到抛物线C2,则抛物线C2的表达式为;(3)设抛物线C1与y轴相交于点E,过点E作直线l∥x轴,与抛物线C1的另一交点为F,将抛物线C1沿直线l翻折,得到抛物线C3,抛物线C1,C3的顶点分别记为P,Q.是否存在实数m,使得以点E,F,P,Q为顶点的四边形为正方形?若存在,请求出m的值;若不存在,请说明理由.【题型9二次函数中面积问题的存在性问题】1(2023春·四川广安·九年级统考期末)如图1,抛物线y=ax2+bx+3经过A1,0两点,交y轴于,B3,0点C.(1)求抛物线的函数解析式.(2)在抛物线的对称轴上是否存在一点M,使得△ACM的周长最小?若存在,求出点M的坐标;若不存在,请说明理由.S△BCA,请直接写出点P的横坐(3)如图2,连接BC,若在BC下方的抛物线上存在一点P,使得S△BCP=12标.1(2023春·江西九江·九年级校考期中)如图,已知二次函数L1:y=x2+bx+c与x轴交于A、B两点,A点坐标(-1,0),B点坐标(3,0),与y轴交于点C,直线L2:y=x+n经过点A.(1)求二次函数L1的表达式及顶点P的坐标;(2)二次函数L3与二次函数L1关于X轴对称,直线L2与二次函数L3相交于A、D两点.①直接写出二次函数L3的表达式;②求出D点的坐标;③在直线L2上半部分的二次函数L3上,是否存在一点M,使得△AMD的面积最大?若存在,请求出M坐标,并求出最大面积.2(2023春·山东东营·九年级东营市实验中学校考期中)如图,抛物线y=ax2+bx+c a≠0与y轴交于点C0,4.,点B4,0,与x轴交于A-2,0(1)求抛物线的解析式;(2)若点M是抛物线上的一动点,且在直线BC的上方,当S△MBC取得最大值时,求点M的坐标;(3)在抛物线上是否存在点P,使三角形ABP的面积为12?若存在,直接写出点P的坐标;若不存在,请说明理由.3(2023春·福建泉州·九年级统考期末)如图,在平面直角坐标系xOy中,顶点为E1,4的抛物线y= ax2+bx+c与x轴从左到右依次交于A,B两点,与y轴的交点为C0,3,P是抛物线对称轴右侧图象上的一点,且在x轴的上方.(1)求此抛物线的解析式;(2)若直线BP与抛物线对称轴交于点D,当BD-CD取得最大值时,求点P的坐标;(3)若直线BC与抛物线对称轴交于点F,连接PC,PE,PF,记△PCF,△PEF的面积分别为S1,S2,判断2S1+S2是否存在最大值.若存在,求出最大值;若不存在,请说明理由.【题型10二次函数中线段问题的存在性问题】1(2023春·内蒙古巴彦淖尔·九年级校考期中)如图1,抛物线y=ax2+bx+c a≠0与x轴交于A-8,0.点E是第二象限内抛物线上的一个动点,设点E的横坐标 两点,与y轴交于点D0,4,C2,0为n,过点E作直线EB⊥x轴于点B,作直线AD交EB于点F.(1)求该抛物线的解析式;(2)如图1,当△EFD是以FD为底边的等腰三角形时,求点E的坐标;(3)如图2,连接CD,过点E作直线l∥CD,交y轴于点H,连接BH.试探究:在点E运动的过程中,是否存在点E,使得FD=BH,若存在,请求出点E的坐标;若不存在,请说明理由.1(2023春·四川南充·九年级统考期中)如图,平面直角坐标系中的Rt△AOB和Rt△COD全等,直角边OB、OD在x轴上.已知点C的坐标为4,2,过A、C两点的直线分别交x轴、y轴于点E、F,抛物线y=ax2+bx+c经过O、A、C三点.(1)写出点A的坐标并求该抛物线的函数解析式;(2)点G为抛物线上位于线段OC所在可直线上方部分的一动点,求G到直线OC的最大距离和此时点G 的坐标;(3)点P为线段OC上一个动点,过点P作y轴的平行线交抛物线于点M,交x轴于点N,问是否存在这样的点P,使得四边形ABPM的边AM与边BP相等?若存在,求出此时点P的坐标;若不存在,请说明理由.2(2023春·云南曲靖·九年级统考期末)已知抛物线y=x2+bx+c与x轴交于点A-1,0两,B3,0点,与y轴交于点C,连接BC.(1)求抛物线的解析式;(2)在抛物线上是否存在点M,使得B、C两点到直线AM的距离相等,如果存在,求出点M的坐标,如果不存在,请说明理由;(3)点P为x轴上一动点,以P为旋转中心,把线段BC逆时针旋转90°,得到线段GH,其中点B的对应点为点G,当抛物线的对称轴刚好经过GH中点时,求此时点P的坐标.3(2023春·安徽阜阳·九年级校考期末)如图,已知抛物线经过原点O和x轴上另一点A,它的对称轴x=-2与x轴交于点C,直线y=-2x+1经过抛物线上一点B2,m,且与y轴.直线x=-2分别交于点D、E.(1)求m的值及该抛物线对应的函数关系式;(2)①判断△CBE的形状,并说明理由;②判断CD与BE的位置关系;(3)若P x,y是该抛物线上的一个动点,是否存在这样的点P,使得PB=PE?若存在,试求出所有符合条件的点P的坐标;若不存在,请说明理由.【题型11二次函数中角度问题的存在性问题】1(2023春·辽宁葫芦岛·九年级统考期末)如图,在平面直角坐标系中,已知抛物线y=-x2+bx+c与x轴交于A,B4,0在抛物线上,点P是抛物线上一动点.两点,与y轴交于点C,点D3,4(1)求该抛物线的解析式;(2)如图1,连接OD,若OP平分∠COD,求点P的坐标;(3)如图2,连接AC,BC,抛物线上是否存在点P,使∠CBP+∠ACO=45°?若存在,请直接写出点P的坐标;若不存在,请说明理由.1(2023春·内蒙古鄂尔多斯·九年级统考期末)如图,直线y=-x+3与x轴、y轴分别交于B、C两点,抛物线y=-x2+bx+c经过点B、C,与x轴另一交点为A,顶点为D.(1)求抛物线的解析式;(2)在第四象限的抛物线上是否存在一点M,使△MBC的面积为27?若存在,求出M点坐标;若不存在,请说明理由.(3)在抛物线的对称轴上是否存在一点P,使得∠APB=∠OCB?若存在,求出P点坐标;若不存在,请说明理由.2(2023春·江苏盐城·九年级统考期末)如图,抛物线y=12x2+mx+n与x轴交于A,B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A-4,0,C0,-2.(1)求抛物线的函数表达式;(2)点E是线段AC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDAF的面积最大?求出四边形CDAF的最大面积及此时E点的坐标;(3)在y轴上是否存在点P,使得∠OAP+∠OAC=60°?若存在,请直接写出P点的坐标,若不存在,请说明理由.3(2023春·浙江湖州·九年级统考期末)如图,在平面直角坐标系中,直线y=12x-2与x轴交于点A,与y轴交于点C,抛物线y=12x2+bx+c经过A,C两点,与x轴的另一交点为点B,点P为抛物线上的一个动点.(1)求抛物线的函数表达式;(2)当△ACP的面积与△ABC的面积相等时,求点P的坐标;(3)是否存在点P,使得∠ACP=∠ABC-∠BAC,若存在,请直接写出点P的横坐标;若不存在,请说明理由.【题型12二次函数中最值问题的存在性问题】1(2023春·甘肃庆阳·九年级统考期中)如图,已知抛物线y=38x2-34x-3与x轴的交点为点A、D(点A在点D的右侧),与y轴的交点为点C.(1)直接写出A、D、C三点的坐标;(2)在抛物线的对称轴上找一点M,使得MD+MC的值最小,并求出点M的坐标;(3)设点C关于抛物线对称轴的对称点为点B,在抛物线上是否存在点P,使得以A、B、C、P四点为顶点的四边形为梯形?若存在,求出点P的坐标;若不存在,请说明理由.1(2023春·浙江宁波·九年级校考期中)对于给定的两个函数,任取自变量x 的一个值,当x <0时,它们对应的函数值互为相反数;当x ≥0时,它们对应的函数值相等,我们称这样的两个函数互为“伴随”函数.例如:一次函数y =x -3,它的“伴随”函数为y =-x +3x <0 x -3x ≥0 .(1)已知点M -2,1 在一次函数y =-mx +1的“伴随”函数的图象上,求m 的值.(2)已知二次函数y =-x 2+4x -12.①当点A a ,32 在这个函数的“伴随”函数的图象上时,求a 的值.②当-3≤x ≤3时,函数y =-x 2+4x -12的“伴随”函数是否存在最大值或最小值,若存在,请求出最大值或最小值;若不存在,请说明理由.。
二次函数动点存在性问题的破解策略

二次函数动点存在性问题的破解策略首先,要解决二次函数动点存在性问题,我们首先需要了解二次函数的基本性质。
二次函数的一般形式是:$y = ax^2 + bx + c$。
其中,$a$、$b$、$c$都是常数,$x$是自变量,$y$是因变量。
而要讨论二次函数的动点存在性问题,就是要找到函数图像上的其中一点,使得这个点满足特定的条件。
对于动点存在性问题,我们可以通过以下4个步骤来进行求解:第一步,确定二次函数的图像形状。
二次函数的图像形状主要与系数$a$的正负相关。
当$a>0$时,二次函数开口朝上,图像是一个U形;当$a<0$时,二次函数开口朝下,图像是一个倒U形。
通过确定函数的图像形状,可以帮助我们更好地理解函数的动点存在性。
第二步,求解二次函数的顶点坐标。
顶点坐标是二次函数图像的最高点(对于开口向上的二次函数)或最低点(对于开口向下的二次函数)。
顶点的横坐标可以通过以下公式来求解:$x = -\frac{b}{2a}$。
将$x$的值带入二次函数的方程中,即可求得顶点的纵坐标。
第三步,确定特定条件。
在解决动点存在性问题时,我们通常会有一些特定条件,例如点的坐标关系、点在坐标轴上的位置等。
根据具体条件,我们可以设置方程或不等式,将这些条件与二次函数的方程进行联立,从而获得更多的信息。
第四步,解决方程或不等式。
根据前面的步骤,我们已经获得了函数的图像形状、顶点坐标以及特定条件。
接下来,我们可以根据这些信息,将条件与二次函数的方程进行联立,解决方程或不等式,从而找到满足条件的解。
以上就是解决二次函数动点存在性问题的一般策略。
下面,我将结合一个具体的例子,进一步说明这些策略的应用。
例题:求解二次函数$y=x^2+4x+3$在坐标系中的动点存在性,并找出满足条件的点。
解析:首先,我们确定二次函数的图像形状。
由于$a=1>0$,所以二次函数开口朝上,图像是一个U形。
然后,我们可以根据题目的要求确定特定条件。
中考数学 二次函数存在性问题 及参考答案

中考数学二次函数存在性问题及参考答案中考数学二次函数存在性问题及参考答案一、二次函数中相似三角形的存在性问题1.如图,把抛物线 $y=x^2$ 向左平移1个单位,再向下平移4个单位,得到抛物线 $y=(x-h)^2+k$。
所得抛物线与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,顶点为D。
1)写出h、k的值;2)判断△ACD的形状,并说明理由;3)在线段AC上是否存在点M,使△AOM∽△ABC?若存在,求出点M的坐标;若不存在,说明理由。
2.如图,已知抛物线经过A($-2,0$),B($-3,3$)及原点O,顶点为C。
1)求抛物线的解析式;2)若点D在抛物线上,点E在抛物线的对称轴上,且A、O、D、E为顶点的四边形是平行四边形,求点D的坐标;3)P是抛物线上的第一象限内的动点,过点P作PM⊥x 轴,垂足为M,是否存在点P,使得以P、M、A为顶点的三角形△BOC相似?若存在,求出点P的坐标;若不存在,请说明理由。
二、二次函数中面积的存在性问题3.如图,抛物线 $y=ax^2+bx$ ($a>0$)与双曲线$y=\frac{k}{x}$ 相交于点A,B。
已知点B的坐标为($-2,-2$),点A在第一象限内,且 $\tan\angle AOX=4$。
过点A作直线AC∥x轴,交抛物线于另一点C。
1)求双曲线和抛物线的解析式;2)计算△ABC的面积;3)在抛物线上是否存在点D,使△ABD的面积等于△ABC的面积。
若存在,请写出点D的坐标;若不存在,请说明理由。
4.如图,抛物线 $y=ax^2+c$ ($a>0$)经过梯形ABCD的四个顶点,梯形的底AD在x轴上,其中A($-2,0$),B($-1,-3$)。
1)求抛物线的解析式;2)点M为y轴上任意一点,当点M到A、B两点的距离之和为最小时,求此时点M的坐标;3)在第(2)问的结论下,抛物线上的点P使$\triangle PAD=4\triangle ABM$ 成立,求点P的坐标。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A _ O
D _ x
B
C
2015 中考二轮复习专题
2.在平面直角坐标系 xOy 中,抛物线 y= -
m −1 2 x+ 4
5m x+m2-3m+2 4
ห้องสมุดไป่ตู้
与 x 轴的交点分别为原点 O 和点 A,点 B(2,n)在这条抛物线上。 (1) 求点 B 的坐标; (2) 点 P 在线段 OA 上,从 O 点出发向点运动,过 P 点作 x 轴的 垂线,与直线 OB 交于点 E。延长 PE 到点 D。使得 ED=PE。 以 PD 为斜边在 PD 右侧作等腰直角三角形 PCD(当 P 点运动 时,C 点、D 点也随之运动) 当等腰直角三角形 PCD 的顶点 C 落在此抛物线上时,求 OP 的长; 若 P 点从 O 点出发向 A 点作匀速运动,速度为每秒 1 个单位,同时线段 OA 上另 一点 Q 从 A 点出发向 O 点作匀速运动, 速度为每秒 2 个单位(当 Q 点到达 O 点时停止运动, P 点也同时停止运动)。过 Q 点作 x 轴的垂线,与直线 AB 交于点 F。延长 QF 到点 M,使 得 FM=QF,以 QM 为斜边,在 QM 的左侧作等腰直角三角形 QMN(当 Q 点运动时,M 点, N 点也随之运动)。若 P 点运动到 t 秒时,两个等腰直角三角形分 别有一条直角边恰好落在同一条直线上,求此刻 t 的值。 y D
2015 中考二轮复习专题
二次函数存在性问题(一)
1.如图,抛物线 y=ax2+c(a>0)经过梯形 ABCD 的四个顶点,梯形的底 AD 在 x 轴上, 其中 A(-2,0) ,B(-1, -3) . (1)求抛物线的解析式; (2)点 M 为 y 轴上任意一点,当点 M 到 A、B 两点的距离之和为最小时,求此时点 M 的 坐标; (3)在第(2)问的结论下,抛物线上的点 P 使 S△PAD=4S△ABM 成立,求点 P 的坐标.
y
E
C A x
B O
1
P 图1
x
O 1
2015 中考二轮复习专题
3. (2012 遵义)如图,已知抛物线 y=ax2+bx+c(a≠0)的图象经过原点 O,交 x 轴于点 A, 其顶点 B 的坐标为(3, ) . (1)求抛物线的函数解析式及点 A 的坐标; (2)在抛物线上求点 P,使 S△POA=2S△AOB; (3)在抛物线上是否存在点 Q,使△AQO 与△AOB 相似?如果存在,请求出 Q 点的坐标; 如果不存在,请说明理由.
