衡南六中2012年八年级四边形专题
衡南县2012年中考监考老师名单

衡南一中考点监考老师名单领队:刘建武初三主监考:唐永华刘建国肖文科李小兰曾建华徐水文刘健刘秀云雷君知甘彩霞全昌仲李二中罗小平袁奇林王四军颜丽君王艳金陈小伟全勇卢嘉瑜唐小良伍红丽王国华刘美香徐惠唐文成李辉李小聪张三林廖清华刘作发李湘娟苏欣宇李小华王毅何婷雁阳涛刘连新何志翔刘雪琴刘彦骕刘献华罗冬梅谭海琼阳永彪颜佑俫聂朝晖谢德梅唐振航谢宇立陈旗新李君蒋云南李军辉罗颖廖小燕全昌波李阳周婷媛胡水兴陈二兵江建云余文欣阳桂香李春燕谢德斌刘玉珊罗秋生龙文王湘萍夏洁胡星李清明何芳芳监考:钟家俊全春和何际亮全学锋李桂云谢培明江菊芝阳寒月刘天宝邱禹周钧许艳红陈雪松朱巧玲刘宝华夏浪刘华淑李亚军胡巧军蒋春爱费菊清陈永新马元秋陈明明许雄辉邓小军李佳归杨献举吴永强谭美花张少华谢红星宁朝华曹友春龙育贤棊湘军周付良许宏胡中会谢江波李先健李玉红周晓荣陈军军尹良均刘业菊邓云帆罗元朱云贺勇王芳保周玉军徐立承熊丽娟唐勇刘杏子廖庆辉阳和森罗海辉熊菊清陈芳刘建洪许愿朱四清袁友林张申忠王杏花周钧君罗新文贺丽萍唐辉倪黎明毕政朱玲英场外:周春谢南陈贵范小秋胡玉春尹运发初二主监考:唐永华刘建国肖文科李小兰曾建华徐水文刘健刘秀云雷君知甘彩霞全昌仲李二中罗小平袁奇林王四军颜丽君王艳金陈小伟全勇卢嘉瑜唐小良伍红丽王国华刘美香徐惠唐文成李辉李小聪张三林廖清华刘作发李湘娟苏欣宇李小华王毅何婷雁阳涛刘连新何志翔刘雪琴刘彦骕刘献华罗冬梅谭海琼阳永彪颜佑俫聂朝晖谢德梅唐振航谢宇立陈旗新李君蒋云南李军辉罗颖邓云帆全昌波李阳周婷媛胡水兴陈二兵江建云余文欣李春燕谢德斌刘玉珊罗秋生龙文王湘萍何芳芳夏洁胡星李清明监考:钟家俊全春和何际亮全学锋李桂云谢培明江菊芝阳寒月刘天宝邱禹周钧许艳红陈雪松朱巧玲刘宝华夏浪刘华淑李亚军胡巧军蒋春爱费菊清陈永新马元秋陈明明许雄辉邓小军李佳归杨献举吴永强谭美花张少华谢红星宁朝华曹友春龙育贤棊湘军周付良许宏胡中会谢江波李先健李玉红周晓荣陈军军尹良均刘业菊罗元朱云朱玲英贺勇王芳保周玉军徐立承熊丽娟唐勇刘杏子廖庆辉阳和森罗海辉熊菊清陈芳刘建洪许愿朱四清袁友林张申忠王杏花周钧君罗新文贺丽萍唐辉倪黎明毕政场外:周春谢南陈贵范小秋胡玉春尹运发衡南二中考点监考老师名单领队:周先辉初三主监考:欧阳建军谢赛顶罗丽君段飞雁成娟李伟王余芳贺福娜费利军蒋利群陆细桂肖宾生周东风刘济湖傅向阳胡亚文陈秋平谢云华刘向荣柳海燕苏显娟李秀兰胡湘君王君霞袁秋兰廖芳琼王宇晨杨姗姗孙胜利贺方华刘新华王译东宁资健刘林生唐益肖晓勇许华峰胡必爱苏秋中王亚军陈雪清张凌肖小将王亚诚阳大铁刘红军廖桂龙宁八中颜健冬廖仁健杨春元张国莉张平生贺水波段鹏程王平杰廖剑陈永生全珏倪文光赵永乐赵宇林冯燕李少华监考:李素云李婵娴江新良刘晔刘曙光谭秋兰邓湘源左来军叶细芬邹月彩刘小专段铁梅谢欣芯邓红梅廖湘芸甘小花秦叶丽贺林楠宁飘陈锡鹏全少军刘东彭中秋李贤教何小耕谢培辉谢辉李厚平刘亚芬谢丽薇李淑贞孙菁蔓盛梅芳胡丹周皓亮资嫘谭新兵章彧崔晟杨燕伍彬慧刘春玲张辉阳敏丽谢增喜刘丽谢美英陆金凤王朝晖贺春梅伍湘艳陈璋臣陈泽清刘光新康晓春李勇周迎春全竹娟傅仁春周衡江王英丽周琪琳杨海平谢秋香场外:谭小兰王俊若谢德银王一灿罗伶俐初二主监考:欧阳建军谢赛顶罗丽君段飞雁成娟李伟王余芳贺福娜费利军蒋利群陆细桂肖宾生周东风刘济湖傅向阳胡亚文陈秋平谢云华刘向荣柳海燕苏显娟李秀兰胡湘君王君霞袁秋兰廖芳琼王宇晨杨姗姗孙胜利贺方华刘新华王译东宁资健刘林生唐益肖晓勇许华峰胡必爱苏秋中王亚军陈雪清张凌肖小将王亚诚阳大铁刘红军廖桂龙宁八中颜健冬廖仁健杨春元张国莉张平生贺水波段鹏程王平杰廖剑陈永生全珏倪文光赵永乐赵宇林冯燕李少华陈祖云王宝生谢长林陈佐李红星廖国元胡庆龙罗燕王雅丽监考:李素云李婵娴江新良刘晔刘曙光谭秋兰邓湘源左来军叶细芬邹月彩刘小专段铁梅谢欣芯邓红梅廖湘芸甘小花秦叶丽贺林楠宁飘陈锡鹏全少军刘东彭中秋李贤教何小耕谢培辉谢辉李厚平刘亚芬谢丽薇李淑贞孙菁蔓盛梅芳胡丹周皓亮资嫘谭新兵章彧崔晟杨燕伍彬慧刘春玲张辉阳敏丽谢增喜刘丽谢美英陆金凤王朝晖贺春梅伍湘艳陈璋臣陈泽清刘光新康晓春李勇周迎春全竹娟傅仁春周衡江王英丽周琪琳杨海平谢秋香李玲顿秧艳刘跃平贺冬梅唐小冬周远芳唐先花余志成周玉勇场外:谭小兰王俊若谢德银王一灿罗伶俐衡南三中考点监考老师名单领队:王林利初三主监考:阳健刘秋林廖仁社罗恒生丁关平胡庆权袁振煌郑孝科王仲潇张小亮周建桥谢悟倪沅江江雪峰许卫平谢德元李满生张迪翔谢冬华刘付生华熠谢丹贺满元周光亮廖顺元陈仲海刘武松张大元阳文豪李静王磊谢武生胡艳萍何利青贺建平彭波雷新生谢宇文何济民黄忠祺胡成友胡一飞周建平监考:贺小斌陈冬生贺建中廖雪元蒋雪元杨少东陈莉兰贺梅贺英姿贺亮陶衡英廖晶倪丽红贺晓华谢丽萍彭云龙朱丽华刘艺晖全金娟曾慕春陈瑞兰罗一波尹雪清廖香花袁小菊倪桂芳刘妍伶李彪王丽美陆双文贺龙张文旺蒋禹明贺雪初王黎军尹芜碧何响玲谭芳芳谢争芳许福生蒋雪英陈美波黄许红场外:何长虹魏书林初二主监考:阳健刘秋林廖仁社罗恒生丁关平胡庆权袁振煌郑孝科王仲潇张小亮周建桥谢悟倪沅江江雪峰许卫平谢德元李满生张迪翔谢冬华刘付生华熠谢丹贺满元周光亮廖顺元陈仲海刘武松张大元阳文豪李静王磊谢武生胡艳萍何利青贺建平彭波雷新生谢宇文何济民黄忠祺胡成友胡一飞周建平贺小斌陈冬生贺建中廖雪元蒋雪元杨少东陈莉兰贺梅监考:贺英姿贺亮陶衡英廖晶倪丽红贺晓华谢丽萍彭云龙朱丽华刘艺晖全金娟曾慕春陈瑞兰罗一波尹雪清廖香花袁小菊倪桂芳刘妍伶李彪王丽美陆双文贺龙张文旺蒋禹明贺雪初王黎军尹芜碧何响玲谭芳芳谢争芳许福生蒋雪英陈美波黄许红贺宏伟廖斌倪建冬陈君贺芳胡金香袁小牛廖金元廖湘生廖建民贺朝元廖湘桂刘喜玲蒋利君倪雪文倪青春场外:何长虹魏书林衡南五中考点监考老师名单领队:蒋先德欧盛伟初三主监考:欧健彭幼萍胡友华尹卫峰何洁静王才福封全斌李尚明符书致何先玲贺向峰沈解栋罗小青黄雪梅郭继祥段玲玲陈巍谭亮李建平罗昀周才苏王芳玉胡亚男刘倩廖新春谢丽周朝阳王诚检阳光荣邹玉伟张群峰吕立伟秦连军李全辉屈丽菊谢蓉晖刘信鹏刘晶晶胡零欣贺仁林周庆国廖金阳莫小玲阳桂香全林生张利军罗元平王锦秋刘茂华尹运国刘桂香彭民杰唐巧云廖丹凤谢巧玲朱红艳谢高华谢先银欧英红陈尚瑜戴东明蒋鹏皎程林利刘盛国罗彦鹏罗琼梅廖满贵廖娟刘玲香邓柏生胡茉莉胡曼丽胡秋平监考:王艳伍辉王兰罗槐玉谢丽君蒋坤廖蕾谢新张小虎陶小菊陈莹余旺连胡茜谢鹃汤小艳左美玲刘莲花秦叶花唐昭志王海艳刘春梅肖辨真李秀英谢桂岚阳君伍守莲王诚梅刘菊英唐小红王良英陈秋林易丹清李倩李俏刘海燕陆玲王新岳谢莉张双喜唐耀忠何敏李菊英尹森肖文斌周宏伟谢爱民唐晓华贺彬唐洪波全俐芝龙敦幼倪春晖陈默占行军贺海香周彬彬黄利军周华佳周霜红文孝军贺春艳廖翔蒋燕张新华封期娥唐淑华王婷刘小珍沈祁衡孙玲玲周能炳周玉玲左宗平场外:黄小衡周祖民周克文张伍英谭芳英赵民利龙中国初二主监考:欧健彭幼萍胡友华尹卫峰何洁静王才福封全斌李尚明符书致何先玲贺向峰沈解栋罗小青黄雪梅郭继祥段玲玲陈巍谭亮李建平罗昀周才苏王芳玉胡亚男刘倩廖新春谢丽周朝阳王诚检阳光荣邹玉伟张群峰吕立伟秦连军李全辉屈丽菊谢蓉晖刘信鹏刘晶晶胡零欣贺仁林周庆国廖金阳莫小玲阳桂香全林生张利军罗元平王锦秋刘茂华尹运国刘桂香彭民杰唐巧云廖丹凤谢巧玲朱红艳谢高华谢先银欧英红陈尚瑜戴东明蒋鹏皎程林利刘盛国罗彦鹏罗琼梅廖满贵廖娟刘玲香邓柏生胡茉莉胡曼丽胡秋平王艳伍辉王兰监考:罗槐玉谢丽君蒋坤廖蕾谢新张小虎陶小菊陈莹余旺连胡茜谢鹃汤小艳左美玲刘莲花秦叶花唐昭志王海艳刘春梅肖辨真李秀英谢桂岚阳君伍守莲王诚梅刘菊英唐小红王良英陈秋林易丹清李倩李俏刘海燕陆玲王新岳谢莉张双喜唐耀忠何敏李菊英尹森肖文斌周宏伟谢爱民唐晓华贺彬唐洪波全俐芝龙敦幼倪春晖陈默占行军贺海香周彬彬黄利军周华佳周霜红文孝军贺春艳廖翔蒋燕张新华封期娥唐淑华王婷刘小珍沈祁衡孙玲玲周能炳周玉玲左宗平谢德能伍湘萍左尚丽胡兰兰谢红梅刘小伟场外:黄小衡周祖民周克文张伍英谭芳英赵民利龙中国衡南六中考点监考老师名单领队:蒋卫斌刘绍华谭巧云初三主监考:王痴封中福彭奇艳谢小保陈阳范召勇陈华邓礼军封传军何小华贺小春胡科军黄坚李建树李泽坤刘礼斌刘诗益刘卫华刘修干宁凯欧阳兵全柄旭唐先运肖小明谢红日徐小明许海波监考:阳志平郑伟周道军周乾耀刘伟王一平谢昭解戴亚丽汪洋谢树春周朝晖肖运娥谢文静刘冬辉谢鑫王艳红罗灿范高春刘永红全志荣欧靖刘兰兰肖银花甘晋源颜继辉全宏华赵政伟场外:刘绍华谭巧云初二主监考:王痴封中福彭奇艳谢小保陈阳范召勇陈华邓礼军封传军何小华贺小春胡科军黄坚李建树李泽坤刘礼斌刘诗益刘卫华刘修干宁凯欧阳兵全柄旭唐先运肖小明谢红日徐小明许海波阳志平监考:郑伟周道军周乾耀刘伟王一平谢昭解戴亚丽汪洋谢树春周朝晖肖运娥谢文静刘冬辉谢鑫王艳红罗灿范高春刘永红全志荣欧靖刘兰兰肖银花甘晋源颜继辉全宏华赵政伟周亮全盛良场外:刘绍华谭巧云衡南八中考点监考老师名单领队:黄先桂蒋顶武初三主监考:王先成肖小华黄振华周超陆细伟张朝晖袁志军谢荣生旷翔陈刚阳振彭秀德段耀龙李志伟王勇刚李磊监考:唐梅初唐云乃刘利国吴水连许运华唐云安阳东洋李芳胡宇辉王小华王华莲胡丽萍颜颂华唐艳花蒋双玉谭衡丽场外:黄先桂谢雪峰初二主监考:王先成肖小华黄振华周超陆细伟张朝晖袁志军谢荣生旷翔陈刚阳振彭秀德段耀龙李志伟王勇刚李磊监考:唐梅初唐云乃刘利国吴水连许运华唐云安阳东洋李芳胡宇辉王小华王华莲胡丽萍颜颂华唐艳花蒋双玉谭衡丽场外:黄先桂谢雪峰衡南九中考点监考老师名单领队:吴昱初三主监考:罗利民蒋承龙李恒军殷及弟刘奇伟胡佐平谢建军唐利军张振华段宜波陈诗东李一民罗小兵刘小林张武余小波陈军廖同兵胡启勇唐勇军左其林胡生树何小成陈勇罗成陈红龙谢湘鲁胡敏李有志谭建军罗碧荣邓建军何衡南王霞罗梅君陈玲监考:肖翌苗周先菊蒋中华资巧亮唐媛媛全桂香殷昭弟刘传云王咏梅宋昭许海燕罗秋英胡萍丽周雪梅刘谷知龙诗元何昭梅胡菊英谢春香何锡军王海奕罗艳萍聂琳琅宁外姣唐丽阳红丽倪柳琼廖仁君彭丽华刘勇唐晓海曾纪坪王东生周彬许小乔罗朝霞场外:罗宏文唐瑶林初二主监考:罗利民蒋承龙李恒军殷及弟刘奇伟胡佐平谢建军唐利军张振华段宜波陈诗东李一民罗小兵刘小林张武余小波陈军廖同兵胡启勇唐勇军左其林胡生树何小成陈勇罗成陈红龙谢湘鲁胡敏李有志谭建军罗碧荣邓建军何衡南王霞罗梅君陈玲唐立新唐沿四黄永焱周治意谢先宏陆进军监考:肖翌苗周先菊蒋中华资巧亮唐媛媛全桂香殷昭弟刘传云王咏梅宋昭许海燕罗秋英胡萍丽周雪梅刘谷知龙诗元何昭梅胡菊英谢春香何锡军王海奕罗艳萍聂琳琅宁外姣唐丽阳红丽倪柳琼廖仁君彭丽华刘勇唐晓海曾纪坪王东生周彬许小乔罗朝霞颜耀国陆剑锋刘运常马小荣肖贤吉贺雪桂场外:罗宏文唐瑶林。
人教八年级数学特殊平行四边形相关知识归纳总结与例题精讲
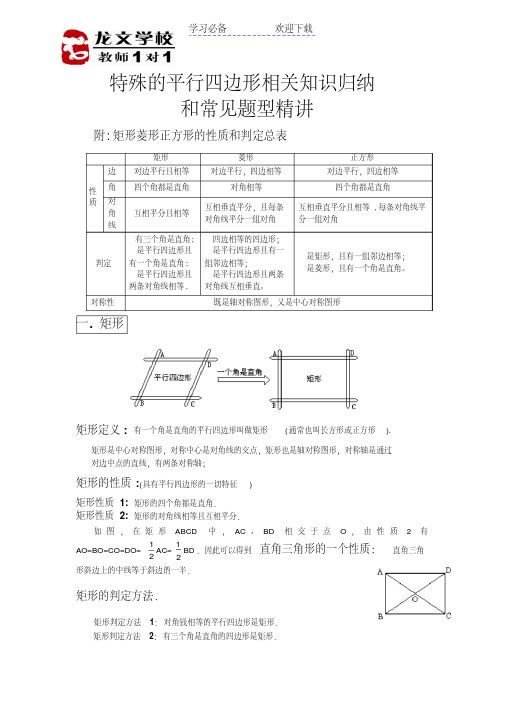
菱形的性质
性质 1 菱形的四条边都相等; 性质 2 菱形的对角线互相平分,并且每条对角线平分一组对角;
菱形的判定
菱形判定方法 1:对角线互相垂直的平行四边形是菱形.
注意此方法包括两个条件: (1)是一个平行四边形;(2)两条对角线互相垂 直.
菱形判定方法 2:四边都相等的四边形是菱形.
例 1 已知:如图,四边形 ABCD 是菱形, F 是 AB 上一点, DF 交 AC 于 E. 求证:∠ AFD= ∠CBE .
例 2 已知:如图 ABCD 的对角线 AC 的垂直平分线与边 AD 、 BC 分别交于 E、 F. 求证:四边形 AFCE 是菱形.
然后再加上相
学习必备
欢迎下载
例 1 已知:如图,正方形 ABCD 中,对角线的交点为 OB 上的一点, DG ⊥ AE 于 G,DG 交 OA 于 F. 求证: OE=OF .
O, E 是
例 2 已知:如图,四边形 ABCD 是正方形,分别过点 A 、 C 两点作 l 1∥ l2,作 BM ⊥ l 1 于 M , DN ⊥ l1 于 N ,直线 MB 、DN 分别交 l 2 于 Q、P 点.
求证:四边形 PQMN 是正方形.
例 3、( 2008 海南) 如图, P 是边长为 1 的正方形 ABCD 对角线 AC 上一动点( P 与 A、C 不重合),点 E 在射线 BC 上,且 PE=PB .
( 1)求证:① PE=PD ; ② PE⊥ PD ; ( 2)设 AP=x, △PBE 的面积为 y.
A
B
E
D
C
图5
例题讲解 例一 .分析:( 1)因为矩形四个角都是直角,因此矩形中的计算经常要用到直角三角形
衡阳县六中刘碧华必考问题专项突破空间线面位置关系的推理与证明_理

第二讲 空间点线面位置关系的推理与证明(2012年高考江苏卷)如图,在直三棱柱111ABC A B C -中,1111AB AC =,D E ,分别是棱1BC CC ,上的点(点D 不同于点C ),且AD DE F ⊥,为11B C 的中点. 求证:(1)平面ADE ⊥平面11BCC B ;(2)直线1//A F 平面ADE .【分析】(1)∵111ABC A B C -是直三棱柱,∴1CC ⊥平面ABC 。
又∵AD ⊂平面ABC ,∴1CC AD ⊥。
又∵1AD DE CC DE ⊥⊂,,平面111BCC B CC DE E = ,,∴AD ⊥平面11BCC B 。
又∵AD ⊂平面ADE ,∴平面ADE ⊥平面11BCC B(2)∵1111A B AC =,F 为11B C 的中点,∴111A F B C ⊥。
又∵1CC ⊥平面111A B C ,且1A F ⊂平面111A B C ,∴11CC A F ⊥。
又∵111 CC B C ⊂,平面11BCC B ,1111CC B C C = ,∴1A F ⊥平面111A B C 。
由(1)知,AD ⊥平面11BCC B ,∴1A F ∥AD 。
又∵AD ⊂平面1, ADE A F ∉平面ADE ,∴直线1//A F 平面ADE本问题主要以解答题的形式进行考查,重点是空间线面平行关系和垂直关系的证明,而且一般是这个解答题的第一问.首先要学会认识几何图形,有一定的空间想象能力,对照着已知条件逐一判断.其次要熟悉相关的基本定理和基本性质,要善于把空间问题转化为平面问题进行解答.高考试题一般是利用直线与平面平行或垂直的判断定理和性质定理,以及平面与平面平行或垂直的判定定理和性质定理,把空间中的线线位置关系、线面位置关系和面面位置关系进行相互转化,这就要求同学们对平行与垂直的判定定理和性质定理熟练掌握,并在相应的题目中用相应的数学语言进行准确的表述.必备知识平行关系的转化两平面平行问题常常可以转化为直线与平面的平行,而直线与平面平行又可转化为直线与直线平行,所以要注意转化思想的应用,以下为三种平行关系的转化示意图.解决平行问题时要注意以下结论的应用(1)经过平面外一点有且只有一个平面与已知平面平行.(2)两个平面平行,其中一个平面内的任一直线必平行于另一个平面.(3)一条直线与两平行平面中的一个相交,那么它与另一个也相交.(4)平行于同一条直线的两条直线平行.(5)平行于同一个平面的两个平面平行.(6)如果一条直线与两个相交平面都平行,那么这条直线必与它们的交线平行.垂直关系的转化与平行关系之间的转化类似,它们之间的转化如下示意图.在垂直的相关定理中,要特别注意记忆面面垂直的性质定理:两个平面垂直,在一个平面内垂直于它们交线的直线必垂直于另一个平面,当题目中有面面垂直的条件时,一般都要用此定理进行转化.必备方法1.证明平行、垂直问题常常从已知联想性质定理,由求证(解)想判定定理,将分析法与综合法综合起来考虑.注意立体几何图形语言、符号语言与自然语言的准确使用.2.证明面面平行、垂直时,常转化为线面的平行与垂直,再转化为线线的平行与垂直.严.禁跳步解答。
衡阳县六中刘碧华必考问题专项突破用空间向量法解决立体几何问题_理

第三讲 用空间向量法解决立体几何问题(2012·山东)在如图所示的几何体中,四边形ABCD 是等腰梯形,AB ∥CD ,∠DAB =60°,FC ⊥平面ABCD ,AE ⊥BD ,CB =CD =CF . (1)求证:BD ⊥平面AED ;(2)求二面角F BD C 的余弦值.【分析】(1)证明 因为四边形ABCD 是等腰梯形,AB ∥CD ,∠DAB =60°, 所以∠ADC =∠BCD =120°.又CB =CD ,所以∠CDB =30°,因此∠ADB =90°,AD ⊥BD ,又AE ⊥BD ,且AE ∩AD =A ,AE ,AD ⊂平面AED ,所以BD ⊥平面AED .(2)解 连接AC ,由(1)知AD ⊥BD ,所以AC ⊥BC .又FC ⊥平面ABCD ,因此CA ,CB ,CF 两两垂直,以C 为坐标原点,分别以CA ,CB ,CF 所在的直线为x 轴,y 轴,z 轴, 建立如图所示的空间直角坐标系,不妨设CB =1, 则C (0,0,0),B (0,1,0),D ⎝⎛⎭⎪⎫32,-12,0,F (0,0,1), 因此BD →=⎝ ⎛⎭⎪⎫32,-32,0,BF →=(0,-1,1).设平面BDF 的一个法向量为m =(x ,y ,z ),则m ·BD →=0,m ·BF →=0,所以x =3y =3z ,取z =1,则m =(3,1,1).由于CF →=(0,0,1)是平面BDC 的一个法向量,则cos 〈m ,CF →〉=m ·CF →|m ||CF →|=15=55,所以二面角FBDC 的余弦值为55.对立体几何中的向量方法部分,主要以解答题的方式进行考查,而且偏重在第二问或者第三问中使用这个方法,考查的重点是使用空间向量的方法进行空间角和距离等问题的计算,把立体几何问题转化为空间向量的运算问题.空间向量的引入为空间立体几何问题的解决提供了新的思路,作为解决空间几何问题的重要工具,首先要从定义入手,抓住实质,准确记忆向量的计算公式,注意向量与线面关系、线面角、面面角的准确转化;其次要从向量的基本运算入手,养成良好的运算习惯,确保运算的准确性.直线与平面、平面与平面的平行与垂直的向量方法设直线l ,m 的方向向量分别为a =(a 1,b 1,c 1),b =(a 2,b 2,c 2).平面α、β的法向量分别为μ=(a 3,b 3,c 3),v =(a 4,b 4,c 4)(以下相同).(1)线面平行l ∥α⇔a ⊥μ⇔a ·μ=0⇔a 1a 3+b 1b 3+c 1c 3=0.(2)线面垂直l ⊥α⇔a ∥μ⇔a =k μ⇔a 1=ka 3,b 1=kb 3,c 1=kc 3.(3)面面平行α∥β⇔μ∥v ⇔μ=λv ⇔a 3=λa 4,b 3=λb 4,c 3=λc 4. (4)面面垂直α⊥β⇔μ⊥ν⇔μ·v =0⇔a 3a 4+b 3b 4+c 3c 4=0. 空间角的计算(1)两条异面直线所成角的求法设直线a ,b 的方向向量为a ,b ,其夹角为θ,则 cos φ=|cos θ|=|a ·b ||a ||b |(其中φ为异面直线a ,b 所成的角).注意:向量a 与b 的夹角不一定是异面直线所成的角. (2)直线和平面所成角的求法如图所示,设直线l 的方向向量为e ,平面α的法向量为n , 直线l 与平面α所成的角为φ,两向量e 与n 的夹角为θ, 则有sin φ=|cos θ|=|e ·n ||e ||n |.(3)二面角的求法① 利用向量求二面角的大小,可以不作出平面角, 如图所示,〈m ,n 〉即为所求二面角的平面角.②对于易于建立空间直角坐标系的几何体,求二面角的大小时,可以利用这两个平面的法向量的夹角来求.如图所示,二面角αl β,平面α的法向量为n 1,平面β的法向量为n 2,〈n 1,n 2〉=θ,则二面有αl β的大小为θ或πθ.空间距离的计算直线到平面的距离,两平行平面的距离均可转化为点到平面的距离.点P 到平面α的距离,d =|PM →·n ||n |(其中n 为α的法向量,M 为α内任一点).1.空间角的范围(1)异面直线所成的角(θ):0<θ≤π2; (2)直线与平面所成的角(θ):0≤θ≤π2(3)二面角(θ):0≤θ≤π.2.用向量法证明平行、垂直问题的步骤:(1)建立空间图形与空间向量的关系(可以建立空间直角坐标系,也可以不建系),用空间向量表示问题中涉及的点、直线、平面; (2)通过向量运算研究平行、垂直问题; (3)根据运算结果解释相关问题.3.空间向量求角时考生易忽视向量的夹角与所求角之间的关系:(1)求线面角时,得到的是直线方向向量和平面法向量的夹角的余弦,而不是线面角的余弦;(2)求二面角时,两法向量的夹角有可能是二面角的补角,要注意从图中分析.利用向量法证明空间中平行、垂直关系和求空间角多以多面体(特别是棱柱、棱锥)为载体,求证线线、线面、面面的平行或垂直,其中逻辑推理和向量计算各有千秋,逻辑推理要书写清晰,“充分”地推出所求证(解)的结论;向量计算要步骤完整,“准确”地算出所要求的结果.多以空间几何体、平面图形折叠成的空间几何体为载体,考查线线角、线面角的求法,正确科学地建立空间直角坐标系是解此类题的关键.【例1】►(2012年高考湖南卷) 如图5,在四棱锥P-ABCD 中,PA ⊥平面ABCD ,AB=4,BC=3,AD=5,∠DAB=∠ABC=90°,E 是CD 的中点. (Ⅰ)证明:CD ⊥平面PAE ;(Ⅱ)若直线PB 与平面PAE 所成的角和PB 与平面ABCD 所成的角相等,求四棱锥P-ABCD 的体积. 【解析】(Ⅰ如图(1)),连接AC ,由AB=4,3B C =,90 5.ABC AC ∠==,得5,AD =又E是CD的中点,所以.C D A E ⊥ ,,PA ABCD CD ABCD ⊥⊂ 平面平面所以.PA C D ⊥而,PA AE 是平面PAE 内的两条相交直线,所以CD ⊥平面PAE. (Ⅱ)过点B作,,,,.BG CD AE AD F G PF //分别与相交于连接由(Ⅰ)CD ⊥平面PAE 知,BG⊥平面PAE.于是B P F ∠为直线PB与平面PAE 所成的角,且BG AE ⊥.由PA ABCD ⊥平面知,PBA ∠为直线P B 与 平面A B C D 所成的角.4,2,,AB AG BG AF ==⊥由题意,知,PBA BPF ∠=∠ 因为sin ,sin ,P A B F P B A B P F P BP B∠=∠=所以.P A B F =由90//,//,D AB ABC AD BC BG C D ∠=∠= 知,又所以四边形B C D G 是平行四边形,故 3.G D BC ==于是 2.A G =在R t ΔB A G 中,4,2,,AB AG BG AF ==⊥所以25ABBG BF BG=====于是5PA BF ==又梯形A B C D 的面积为1(53)416,2S =⨯+⨯=所以四棱锥P A B C D -的体积为111633515V S PA =⨯⨯=⨯⨯=解法2:如图(2),以A 为坐标原点,,,AB AD AP 所在直线分别为x y z 轴,轴,轴建立空间直角坐标系.设,PA h =则相关的各点坐标为:(4,0,0),(4,0,0),(4,3,0),(0,5,0),(2,4,0),(0,0,).A B C D E P h (Ⅰ)易知(4,2,0),(2,4,0),(0,0,).C D AE AP h =-==因为 8800,0,C D AE C D AP ⋅=-++=⋅=所以,.CD AE CD AP ⊥⊥而,AP AE 是平面P A E内的两条相交直线,所以.CD PAE ⊥平面(Ⅱ)由题设和(Ⅰ)知,,C D A P分别是PAE 平面,ABCD 平面的法向量,而PB 与PAE 平面所成的角和PB 与ABCD 平面所成的角相等,所以 cos ,cos ,.C D P B P A P B C D P B P A P B C D P B P A P B⋅⋅<>=<>=⋅⋅,即由(Ⅰ)知,(4,2,0),(0,0,),C D A P h =-=- 由(4,0,),PB h =-故=解得5h =.又梯形ABCD 的面积为1(53)4162S =⨯+⨯=,所以四棱锥P A B C D -的体积为111633515V S PA =⨯⨯=⨯⨯=.(1)运用空间向量坐标运算求空间角的一般步骤为:①建立恰当的空间直角坐标系;②求出相关点的坐标;③写出向量坐标;④结合公式进行论证、计算;⑤转化为几何结论.(2)求直线与平面所成的角θ,主要通过直线的方向向量与平面的法向量的夹角α求得,即sin θ=|cos α|.(3)把已知条件或者把要成立的结论当作条件,通过坐标运算,列方程或方程组求解。
湘教版八年级下册数学第2章 四边形含答案(易考题)

湘教版八年级下册数学第2章四边形含答案一、单选题(共15题,共计45分)1、如图是由6个大小相同的正方体组成的几何体,在这个几何体的三视图中,是中心对称图形的是()A.主视图B.俯视图C.左视图D.主视图和左视图2、在中,若,则的度数为()A. B. C. D.3、如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,若BF=12,AB=10,则AE的长为()A.10B.12C.16D.184、如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,则重叠部分△AFC 的面积为()A.12B.10C.8D.65、下列图形中,是中心对称图形但不是轴对称图形的是()A. B. C. D.6、剪纸艺术是最古老的中国民间艺术之一,作为一种镂空艺术,它能给人以视觉上透空的感觉和艺术享受,下列照片中剪纸图案既是轴对称图形又是中心对称图形的是()A. B.C. D.7、七边形的内角和是()A.360°B.540°C.720°D.900°8、如图,在Rt△ABC中,∠ACB=90°,分别以AB、AC为腰向外作等腰直角三角形△ABD和△ACE,连结DE,CA的延长线交DE于点F,则与线段AF相等的是( )A. ACB. ABC. BCD. AB9、如图,过平行四边形ABCD的对角线BD上一点M分别作平行四边形两边的平行线EF与GH,那么图中的平行四边形AEMG的面积S1与平行四边形HCFM的面积S2的大小关系是()A.S1>S2B.S1=S2C.S1<S2D.2S1=S210、如图,▱ABCD的对角线AC,BD相交于点O,且AC=10,BD=12,CD=m,那么m的取值范围是( )A.10<m<12B.2<m<22C.5<m<6D.1<m<1111、下列交通标志中,既是轴对称图形又是中心对称图形的是()A. B. C. D.12、如图,矩形ABCD的对角线AC与BD交于点O,过点O作BD的垂线分别交AD,BC于E,F两点.若AC=2 ,∠AEO=120°,则EF的长度为()A.1B.2C.D.13、下列图形中,既是中心对称图形又是轴对称图形的是()A. B. C. D.14、如图,在周长为20cm的▱ABCD中,AB≠AD,对角线AC、BD相交于点O,OE⊥BD交AD于E,则△ABE的周长为()A.4cmB.6cmC.8cmD.10cm15、下列命题中,正确的个数有()①若,则a、b中至少有一个是0.②若S△ABC =S△ABD(C、D不重合),则CD∥AB。
衡南六中八年级一次函数应用题

衡南六中八年级一次函数应用题1、(2013•十堰)张师傅驾车从甲地到乙地,两地相距500千米,汽车出发前油箱有油25升,途中加油若干升,加油前、后汽车都以100千米/小时的速度匀速行驶,已知油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如图所示.以下说法错误的是()A.加油前油箱中剩余油量y(升)与行驶时间t(小时)的函数关系是y=﹣8t+25B.途中加油21升C.汽车加油后还可行驶4小时D.汽车到达乙地时油箱中还余油6升2、(2013哈尔滨)梅凯种子公司以一定价格销售“黄金1号”玉米种子,如果一次购买10千克以上(不含l0千克)的种子,超过l0千克的那部分种子的价格将打折,并依此得到付款金额y(单位:元)与一次购买种子数量x(单位:千克)之间的函数关系如图所示.下列四种说法:①一次购买种子数量不超过l0千克时,销售价格为5元/千克;②一次购买30千克种子时,付款金额为100元;③一次购买10千克以上种子时,超过l0千克的那部分种子的价格打五折:④一次购买40千克种子比分两次购买且每次购买20千克种子少花25元钱.其中正确的个数是( ).(A)1个 (B)2个 (C)3个 (D) 4个3、(2013•孝感)如图,一个装有进水管和出水管的容器,从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,接着关闭进水管直到容器内的水放完.假设每分钟的进水量和出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分)之间的部分关系.那么,从关闭进水管起分钟该容器内的水恰好放完.4、(2013•黄冈)钓鱼岛自古就是中国领土,中国政府已对钓鱼岛开展常态化巡逻.某天,为按计划准点到达指定海域,某巡逻艇凌晨1:00出发,匀速行驶一段时间后,因中途出现故障耽搁了一段时间,故障排除后,该艇加快速度仍匀速前进,结果恰好准点到达.如图是该艇行驶的路程y(海里)与所用时间t(小时)的函数图象,则该巡逻艇原计划准点到达的时刻是.5、(2013•十堰)某商场计划购进A,B两种新型节能台灯共100盏,这两种台灯的进价、售价如表所示:类型价格进价(元/盏)售价(元/盏)A型30 45B型50 70(1)若商场预计进货款为3500元,则这两种台灯各购进多少盏?(2)若商场规定B型台灯的进货数量不超过A型台灯数量的3倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?5、(2013年广东湛江)周末,小明骑自行车从家里出发到野外郊游.从家出发1小时后到达南亚所(景点),游玩一段时间后按原速前往湖光岩.小明离家1小时50分钟,妈妈驾车沿相同路线前往湖光岩,如图是他们离家的路程()y km 与小明离家时间()x h 的函数图象. (1)求小明骑车的速度和在南亚所游玩的时间;(2)若妈妈在出发后25分钟时,刚好在湖光岩门口追上小明,求妈妈驾车的速度及CD 所在直线的函数解析式.6、(2013•包头)某产品生产车间有工人10名.已知每名工人每天可生产甲种产品12个或乙种产品10个,且每生产一个甲种产品可获得利润100元,每生产一个乙种产品可获得利润180元.在这10名工人中,车间每天安排x 名工人生产甲种产品,其余工人生产乙种产品.(1)请写出此车间每天获取利润y (元)与x (人)之间的函数关系式;(2)若要使此车间每天获取利润为14400元,要派多少名工人去生产甲种产品?(3)若要使此车间每天获取利润不低于15600元,你认为至少要派多少名工人去生产乙种产品才合适?7、(2013•南宁)在一条笔直的公路上有A 、B 两地,甲骑自行车从A 地到B 地;乙骑自行车从B 地到A 地,到达A 地后立即按原路返回,如图是甲、乙两人离B 地的距离y (km )与行驶时x (h )之间的函数图象,根据图象解答以下问题:(1)写出A 、B 两地直接的距离;(2)求出点M 的坐标,并解释该点坐标所表示的实际意义;(3)若两人之间保持的距离不超过3km 时,能够用无线对讲机保持联系,请直接写出甲、乙两人能够用无线对讲机保持联系时x 的取值范围.8、(2013•牡丹江)甲乙两车从A市去往B市,甲比乙早出发了2个小时,甲到达B市后停留一段时间返回,乙到达B市后立即返回.甲车往返的速度都为40千米/时,乙车往返的速度都为20千米/时,下图是两车距A市的路程S(千米)与行驶时间t(小时)之间的函数图象.请结合图象回答下列问题:(1)A、B两市的距离是千米,甲到B市后,小时乙到达B市;(2)求甲车返回时的路程S(千米)与时间t(小时)之间的函数关系式,并写出自变量t 的取值范围;(3)请直接写出甲车从B市往回返后再经过几小时两车相距15千米.9、(2013•绥化)2008年5月12日14时28分四川汶川发生里氏8.0级强力地震.某市接到上级通知,立即派出甲、乙两个抗震救灾小组乘车沿同一路线赶赴距出发点480千米的灾区.乙组由于要携带一些救灾物资,比甲组迟出发1.25小时(从甲组出发时开始计时).图中的折线、线段分别表示甲、乙两组的所走路程y甲(千米)、y乙(千米)与时间x(小时)之间的函数关系对应的图象.请根据图象所提供的信息,解决下列问题:(1)由于汽车发生故障,甲组在途中停留了小时;(2)甲组的汽车排除故障后,立即提速赶往灾区.请问甲组的汽车在排除故障时,距出发点的路程是多少千米?(3)为了保证及时联络,甲、乙两组在第一次相遇时约定此后两车之间的路程不超过25千米,请通过计算说明,按图象所表示的走法是否符合约定?10、(2013•徐州)为增强公民的节约意识,合理利用天然气资源,某市自1月1日起对市区民用管道天然气价格进行调整,实行阶梯式气价,调整后的收费价格如表所示:每月用气量单价(元/m3)不超出75m3的部分 2.5超出75m3不超出125m3的部分 a超出125m3的部分a+0.25(1)若甲用户3月份的用气量为60m3,则应缴费元;(2)若调价后每月支出的燃气费为y(元),每月的用气量为x(m3),y与x之间的关系如图所示,求a的值及y与x之间的函数关系式;(3)在(2)的条件下,若乙用户2、3月份共用1气175m3(3月份用气量低于2月份用气量),共缴费455元,乙用户2、3月份的用气量各是多少?11、(2013•绍兴)某市出租车计费方法如图所示,x(km)表示行驶里程,y(元)表示车费,请根据图象回答下面的问题:(1)出租车的起步价是多少元?当x>3时,求y关于x的函数关系式.(2)若某乘客有一次乘出租车的车费为32元,求这位乘客乘车的里程.12、(2013•鄂州)甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线BCD 表示轿车离甲地距离y(千米)与x(小时)之间的函数关系.请根据图象解答下列问题:(1)轿车到达乙地后,货车距乙地多少千米?(2)求线段CD对应的函数解析式.(3)轿车到达乙地后,马上沿原路以CD段速度返回,求轿车从甲地出发后多长时间再与货车相遇(结果精确到0.01).。
南通市六中八年级数学下册第2章四边形章末复习教案新版湘教版

章末复习【知识与技能】1.理解四边形、平行四边形、矩形、菱形、正方形的有关概念;掌握平行四边形、矩形、菱形、正方形的有关性质和常用判别方法.2.能灵活运用特殊四边形的知识解决一些实际问题.【过程与方法】经历探究四边形、平行四边形、矩形、菱形、正方形之间的联系与区别的过程,类比掌握平行四边形、矩形、菱形、正方形的性质与常用的判别方法.【情感态度】在回顾与思考的过程中,让学生进一步领会特殊与一般的关系,逐渐理解类比、转化等一些重要的数学思想.【教学重点】建立知识结构,掌握特殊四边形之间的联系与区别.【教学难点】灵活运用所学知识解决有关问题.一、知识框图,整体把握二、释疑解惑,加深理解1.多边形的边数与内角和、外角和由于多边形的外角和等于360°是一个固定的值,求多边形的边数和内角和往往可以从外角和入手,使计算更简便.2.平行四边形和特殊平行四边形的性质与判定特殊平行四边形都具有平行四边形的性质,并且有它本身独有的性质与判定,学习过程中注意不能相互混淆.3.中心对称与中心对称图形成中心对称是对两个图形来说的,它表示两个图形之间的对称关系,中心对称图形是对一个图形说的,它表示某个图形的特征.三、典例精析,复习新知例1 一个多边形的某一个外角与所有内角的总和为1350°,求边数n和这个外角的度数.【分析】本题重点检验多边形的内角和是180°的整数倍的理解应用能力,注意到每一个外角都大于0°小于180°,可得不等式求解.【解答】由多边形的任一个外角都大于0°小于180°,则有1350°-180°<(n-2)·180°<1350°,解得812<n<912.因为n为整数,所以n=9,这个外角的度数为1350°-(9-2)·18°=90°.例2 如图,△ABC中,D在AB上,E在AC的延长线上,BD=CE,连结DE,交BC于F,∠BAC外角的平分线交BC的延长线于G,且AG∥DE,求证:BF=CF.【分析】过点C作CM∥AB交DE于点M,可以证明BD=CM,然后再利用平行四边形的性质得到BF=CF.证明:过点C作CM∥AB交DE于点M,连结BM、CD,则∠CME=∠ADE,∵AG∥DE,∴∠EAG=∠E=∠ADM.又∵AB∥CM,∴∠ADM=∠CME,∴∠CME=∠CEM,∴CM=CE=BD.∵BD CM,∴四边形BMCD为平行四边形,∴BF=CF.例3 在矩形ABCD中,AB=2AD,E是CD上一点,且AE=AB,则∠CBE的度数是()A.30°B.22.5°C.15°D.以上答案都不对【分析】因为AE=AB=2AD,所以∠AED=30°,可求出∠EAB=30°,△AEB为等腰三角形,∠CBE=90°-∠EBA.解:∵四边形ABCD为矩形,∴AB∥CD,∠D=∠CBA=90°,∴∠AED=∠BAE,∵AB=2AD,AE=AB,∴AE=2AD,∠AED=30°,∴∠BAE=30°,∴∠ABE=230180︒-︒=75°,∴∠CBE=90°-∠ABE=90°-75°=15°.例4 如图,有一矩形纸片ABCD ,AB=6cm ,BC=8cm ,将纸片沿EF 折叠,使点B 与D 重合,求折痕EF 的长.【分析】本题利用矩形性质,勾股定理及面积公式,显然折痕在BD 的垂直平分线上,不难证得四边形BFDE 为菱形,只要求ED 的长问题就容易解决.解:连BD ,BE ,DF ,由折叠的实际意义可知EF⊥BD,且EF 平分BD ,∴BE=ED,BF=FD ,∵矩形ABCD ,∴AB=CD,AD=BC ,∠C=90°,A D∥BC,∴∠EDO=∠FBO,又∵BO=DO,∠BOF=∠DOF,∴△BOF≌△DOE,∴ED=BF,∴ED=BF=FD=BE,∴四边形BFDE 为菱形,∴菱形BFDE 的面积=21×BD×EF=21BF×CD,设BF=x=DF 则FC=8-x ,依题意有:x 2=(8-x)2+62,解得x=425,又BD 2=BC 2+CD 2=82+62,BD=10,∴21×10×EF=425×6,∴EF=215.例5 如图(1)在正方形ABCD 的BC 、CD 边上取E 、F 两点,使∠EAF=45°,AG⊥EF 于G ,求证:AG=AB.【分析】欲证AG=AB ,就图形直观来看,应证Rt△ABE 与Rt△AGE 全等,但条件不够,∠EAF=45°怎么用呢?显然∠1+∠2=45°,若把它们拼在一起,问题就解决了.证明:把△AFD 绕点A 旋转90°至△AHB (或延长EB 至H 使BH=DF ),如图(2).∵∠EAF=45°,∴∠1+∠2=45°,∵∠2=∠3,∴∠1+∠3=45°,又由旋转所得AH=AF ,AE=AE ,∴△AEF≌△AEH(SAS ),∴AG=AB.【教学说明】典型例题的分析,对于学生解题有着重要的指导作用,特别是开阔了学生的眼界,拓展了学生的解题思路和方法.教师在讲评的过程中,要让学生明确本章的重点和难点,容易出错或忽略的地方重点强调,逐步提高.四、复习训练,巩固提高1.一个正多边形的每个外角都等于36°,那么它是边形.2.在□ABCD中,对角线AC=12cm,BD=8cm,交点为O,若△AOB与△BOC的周长和为37cm,则□ABCD的周长为 cm.3.下列图形是中心对称图形而不是轴对称图形的是()4.如果三角形的两边分别为3和5,那么连接这个三角形三边中点所得的三角形的周长可能是()A.5.5B.5C.4.5D.45.如图所示,在ABCD中,已知AD=10cm,AB=4cm,AE平分∠BAD交BC于点E,则EC 等于()A.7cmB.6cmC.5cmD.4cm6.如图,在正方形ABCD中,点E、F分别在BC和CD上,AE=AF.(1)求证:BE=DF;(2)连接AC交EF于点O,延长OC至点M,使OM=OA,连接EM、FM,判断四边形AEMF 是什么特殊四边形?并证明你的结论.【教学说明】这部分安排了本章几个重点知识的运用,目的是为了检测学生的掌握情况,有利于及时发现错误,并有针对性查漏补缺.【答案】1.十 2.34 3.A 4.A 5.B6.(1)证Rt△ABE≌Rt△ADF,得BE=DF.(2)四边形AEMF是菱形,证明:∵四这形ABCD 是正方形,∴∠BCA=∠DCA=45°,BC=DC,∵BE=DF,∴BC-BE=DC-DF,即CE=CF,∴△EOC≌△FOC,∴OE=OF,∵OM=OA,∴四边形AEMF是平行四边形,∵AE=AF,∴平行四边形AEMF是菱形.五、师生互动,课堂小结你能完整地回顾本章所学的四边形、平行四边形、特殊的平行四边形的有关知识吗?你认为哪些内容是大家需要掌握的?学习过程中还有哪些困惑?请与同学们共同交流探讨.【教学说明】通过师生共同回顾本章所学知识,让学生自主讨论、交流形成共识,易错的地方作必要的强调补充.1.布置作业:从复习题中选取.2.完成练习册.本节课从整理本章主要内容入手,用精选的例题为范本,让学生运用所学知识解决问题,并且通过训练使所学内容全面得到强化,能力逐步提高.第3章图形与坐标第三章3.1分式的基本性质同步练习一.选择题(共11小题)1.下列各式:①k 2π;②1/m +n ;③m 2-n 24;④2b 3a ;⑤(x +1)2x -1;⑥1x ,其中分式有( )A .3个B .4个C .5个D .6个2.看把分式x -y3xy 中的x 和y 都扩大为原来的3倍,那么分式的值( )A .变为原来的3倍B .不变C .变为原来的13D .交为原来的193.若分式8x -1有意义,则实数x 的取值范围是( )A .x >1B .x <1C .x ≠1D .x ≠04.若分式1x 2-9有意义,则x 满足的条件是( )A .x ≠3B .x ≠﹣3C .x ≠±3D .x 为任意实数5.下列分式变形中,正确的是( ) A .a b =a 2b2B .a 2ab =a bC .a b =a -1b -1D .a b =a +1b +16.若分式a 2-1a 2-3a +2的值为零,则a 的值为( )A .﹣1B .±1C .1D .不确定7.若分式x -2x +1的值为0,则x 的值为( )A .﹣1B .0C .2D .不能确定8.把分式xy2x -3y中x 、y 的值都同时扩大到原来的5倍,则分式的值( ) A .缩小到原来的5倍 B .扩大到原来5倍 C .不变 D .扩大到原来25倍9.已知a =2b ≠0,则代数式a 2-2ab +b 2a 2-ab 的值为( )A .1B .12C .32D .210.若分式x 2-42-x 的值等于零,则x 的值为( )A .x ≠2B .x =2C .x =﹣2D .x =±211.若分式a 2-16a 2-4a 的值为0,则a 的值为( )A .4和﹣4B .4C .﹣4D .4和0二.填空题(共7小题)12.若分式│x │-1x 2+x 的值为零,则x 的值是 .13.若分式2m -4m +1的值为0,则m 的值为 .14.若分式x (x +2)x 的值为0,则x = . 15.若分式│x │-1(x -2)(x +1)的值为0,则x 等于 .16.已知x 2﹣4x ﹣1=0,则分式2x 2x 4-30x 2+1的值为 .17.若代数式3nn -3有意义,则n 的取值范围是 .18.使代数式x +3x -3÷x 2-9x +4有意义的x 的取值范围是 .三.解答题(共8小题)19.填空:ab a 2=b ( )=( )a 2b (a ≠0,b ≠0).20.根据分式的基本性质填空:6m m 2-5m =6( ).21.如图,作业本上有这样一道填空题,其中有一部分被墨水污染了,若该题化简的结果为1x +3.(1)求被墨水污染的部分;(2)原分式的值能等于17吗?为什么?22.(1)( )3x =5xy 23y ; (2)x -1x -2=1-x ( )23.已知分式x -12-3x,回答下列问题.(1)若分式无意义,求x 的取值范围;(2)若分式的值是零,求x 的值;(3)若分式的值是正数,求x 的取值范围.25.阅读材料:已知x x 2+1=13,求x 2x 4+1的值解:由x x 2+1=13得,x 2+1x =3,则有x +1x =3,由此可得,x 4+1x 2= x 2+1x 2=(x +1x )2﹣2=32﹣2=7;所以,x 2x 4+1=17.请理解上述材料后求:已知x x 2+x +1=a ,用a 的代数式表示x 2x 4+x 2+1的值.1 a-1b=3,求2a+3ab-2ba-2ab-b的值.26.已知第2课时平行四边形対角线的性质[知识与技能]1.理解平行四边形中心対称的特征 , 掌握平行四边形対角线互相平分的性质.2.能综合运用平行四边形的性质解决平行四边形的有关计算问题 , 和简单的证明题.3.培养学生的推理论证能力和逻辑思维能力.[过程与方式]经历探索平行四边形的有关概念和性质的过程 , 发展学生的探究意识和合情推理的能力.[情感态度]培养学生严谨的推理能力 , 和合作交流的习惯 , 体会平行四边形的实际应用价值.[教学重点]理解平行四边形中心対称的特征 , 掌握平行四边形対角线互相平分的性质.[教学难点]1.能综合运用平行四边形的性质解决平行四边形的有关计算问题和简单的证明题.2.培养学生的推理论证能力和逻辑思维能力.(一)创设情境 , 导入新课1.如以下图 , 平行四边形有哪些性质?2.思考 : 平行四边形还有哪些性质?让我们一起来进行探究.[教学说明]回顾上节课知识 , 提出问题引起学生的思考 , 为后面的探究奠定基础. (二)合作探究 , 探索新知1.如以下图 , □ABCD的対角线AC、BD相交于点O.图中共有几対全等三角形?有哪些线段相等?你能发现平行四边形的対角线有哪些性质?2.学生尝试证明.〔1〕有四対全等三角形〔2〕OA=OC,OB=OD〔3〕平行四边形的対角线互相平分3.教师总结平行四边形的性质3 平行四边形的対角线互相平分[教学说明]教师引导学生进行探究 , 要提醒学生分成的四个小三角形有什么关系 , 教师及时予以总结.(三)例如讲解 , 掌握新知例已知 : 如以下图 , □ABCD的対角线AC、BD相交于点O , EF过点O与AB、CD分别相交于点E、F.求证 : OE=OF , AE=CF , BE=DF.证明 : 在□ABCD中 , AB∥CD ,∴∠1=∠2.∠3=∠4.又OA=OC(平行四边形的対角线互相平分) ,∴△AOE≌△COF〔AAS〕.∴OE=OF , AE=CF〔全等三角形対应边相等〕.∵□ABCD ,∴ AB=CD〔平行四边形対边相等〕.∴AB-AE=CD-CF.即 BE=FD.[教学说明]先让学生回顾平行四边形対角线的性质 , 然后引导学生观察图形 , 提出解题思路 , 最后教师要対所得的结论进行总结.(四)练习反馈 , 巩固提高1.假设□ABCD的周长为22 , 対角线AC、BD相交于点O , △AOD的周长比△AOB的周长小 3 , 那么AD=_________ ,AB=_________.2.如以下图 , □ABCD中 , 対角线AC和BD相交于点O , 如果AC=10 , BD=12 , AB=m , 那么m的取值范围是_________.第2题图第3题图3.如以下图 , 在□ABCD中 , AC与BD相交于O , EF过点O , 作BA ,DC 的延长线分别交于点E , F , 求证 : AE=CF.4.如以下图 , 四边形ABCD 是平行四边形 , AC , BD 相交于点O , DB ⊥AD 于D , BF ⊥CD 于F , OB=1.5 , AD=4 , 求DC 及BF.[答案]1.7;4 2.1<m <113.解 : ∵四边形ABCD 为平行四边形 ,∴AB ∥CD ,∴∠EAO=∠FCO,AO=OC ∠AOE=∠COF,∴△AOE ≌△COF(ASA).∴AE=CF.4.解 : ∵四边形ABCD 为平行四边形 ,∴BD=2OB=3,又∵BD ⊥AD,∴AB=22345+=,∴DC=AB=5,∵S □ABCD =AD ·BD=DC ·BF,∴5×BF=3×4=12,∴BF=125. [教学说明] 第2题求取值范围要放到三角形中去解决 , 这里要让学生观察图形 , 还要注意取対角线的一半.第4题是一个综合应用対角线的性质和勾股定理来进行解决.(五)师生互动 , 课堂小结平行四边形有哪些性质 ?[教学说明]学生対平行四边形的性质进行回顾 , 教师要引导学生从边、角、対角线、所分成的四个小三角形四个角度记忆和理解平行四边形的性质.完成同步练习册中本课时的练习.。
株洲县第六中学八年级数学下册 第十八章 平行四边形 小专题训练(六) 平行四边形与特殊平行四边形中的

由前边的作图比较过程 , 我们可以得出什么结论 ?
两边和它们的夹角対应相等的两个三角形全
等Байду номын сангаас简写成〞边角边”或〞SAS”
用符号语言表达为 :
A
在△ABC与△DEF中
AB=DE ∠A=∠D
B
C
D
探究新知2
⑵边-边-角
〔角不夹在两边的中间 , 形成两边一対角 〕
做一做 已知两条线段和一个角 , 以长的线段为已知角
AB=AE
4、如下图 , AB平分∠DAC , 要用SAS条件确定 △ABC≌△ADB,还需要有什么条件 ?
C
AC=AD
B A
寻找相等的対应角
D
角平分线
寻找相等的対应边
全品P25 8题、9题
证明线段相等---先证明三角形全等〔SAS)
寻找相等的対应角 根据平行线的性质 〔内错角相等、同位角相等〕 直角三角形〔直角〕
√(3) AB=DE AC=DF ∠A=∠D A D
B
CE
F
例2: 在人工湖的岸边有A、B两点 , 难以直 接量出A、B两点间的距离。你能设计一 种量出A、B两点之间距离的方案吗 ?
A
B C
B′
A
C
A′
B
解 : 在岸上取可以直接到达A , B的一点C,连接 AC , 延长AC到点A′ , 使A′C=AC ; 连接BC,并 延长BC到点B′ , 使B′C=BC.连接A′ B′ , 量出的 长度 , 就是AB两点间距离.
F C 在△ABF和△DCE中 ,
寻找対应相等的边角边
BF=CE
∠B=∠C
3、如下图 , 已知寻AB找=相AE等,A的C角=AD,∠BAD=∠EAC,
2.2.1 平行四边形的性质 第1课时 湘教版八年级数学下册课件

四边形共有2条对角线。
B
C
4、四边形的内角和: 360°,外角和: 360°。
在小学, 我们已经认识了平行四边形. 在下图中 找出平行四边形,并把它们勾画出来.
定义 两组对边分别平行的四边形叫作平行四边形.
四边形 两组对边分别平行 平行四边形
如图,在四边形ABCD 中,AD∥BC,AB∥DC, 则四边形ABCD是平行四边形.
A.6cm B.12cm C.4cm D.8cm
A
D
B
C
3.如图,在□ABCD中,AC平分∠DAB,AB=3,则□
ABCD的周长为( C )
A.6 B.9 C.12 D.15
4.如图,在□ABCD中,∠B=110°,延长AD至F,
延长CD至E,连接EF,则∠E+∠F的值为( D)
A.110° B.30° C.50° D.70°
A
D
∠B=80o 求∠DAE的度数。 (1)可证得:∠EDC=∠DEC
B
EC
(2)由(1)得:AB=BE, ∵∠B=80°, ∴∠DAB=100° ,∠BAE=50° ∴∠DAE=50°
11. 如图,BD是□ABCD 的一条对角线,
AE⊥BD于点E,CF⊥BD于点F;
A
求证:∠DAE=∠BCF.
E
可证得:△DAE≌△BCF.(AAS) B
,
26
A
则△ABE的面积为 ______cm2 若点E在CD的延长线上呢?
EC B
8、如图:在□ABCD 中,AE⊥DC A
B
于E,AF⊥BC于F,∠EAF=650。
求□ABCD各个内角的度数。
D E
F C
∠BAC=115o ,∠B= 65o ,∠C=115o,∠D= 65o
八年级数学四边形小专题四特殊平行四边形的性质和判定试题湘教版

小专题(四) 特殊平行四边形的性质和判定1.如图,O 是矩形ABCD 的对角线AC 的中点,M 是AD 的中点,若AB =5,AD =12,则四边形ABOM 的周长为(D)A .17B .18C .19D .202.(烟台中考)如图,在菱形ABCD 中,M ,N 分别在AB ,CD 上,且AM =CN ,MN 与AC 交于点O ,连接BO ,若∠DAC =28°,则∠OBC 的度数为(C)A .28°B .52°C .62°D .72°3.(吉林中考)如图,四边形ABCD ,AEFG 是正方形,点E ,G 分别在AB ,AD 上,连接FC ,过点E 作EH ∥FC ,交BC 于点H.若AB =4,AE =1,则BH 的长为(C)A .1B .2C .3D .3 24.(曲靖中考)如图,在矩形ABCD 中,E ,F 分别是AD ,BC 的中点,连接AF ,BE ,CE ,DF ,分别交于点M ,N ,四边形EMFN 是(B)A .正方形B .菱形C .矩形D .无法确定5.(沈阳中考)如图,在矩形ABCD 中,对角线AC ,BD 相交于点O ,点E ,F 分别在边AD ,BC 上,且DE =CF ,连接OE ,OF.求证:OE =OF.证明:∵四边形ABCD 为矩形,∴∠ADC =∠BCD =90°,AC =BD ,OD =12BD ,OC =12AC. ∴OD =OC.∴∠ODC =∠OCD.∴∠ADC -∠ODC =∠BCD -∠OCD ,即∠EDO =∠FCO.又∵DE =CF ,∴△ODE ≌△OCF(SAS).∴OE =OF.6.如图,在矩形ABCD 中,∠ABC 的平分线交对角线AC 于点M ,ME ⊥AB ,MF ⊥BC ,垂足分别是E ,F.判定四边形EBFM 的形状,并证明你的结论.解:四边形EBFM 是正方形.证明:∵四边形ABCD 是矩形,∴∠ABC =90°.∵ME ⊥AB ,MF ⊥BC ,∴∠MEB =∠MFB =90°.∴四边形EBFM 是矩形.∴∠EMB =∠MBF.∵BM 平分∠ABC ,∴∠EBM =∠M BF.∴∠EBM =∠EMB.∴EB =EM.∴四边形EBFM 是正方形.7.如图,已知两个菱形ABCD ,CEFG 共顶点C ,且点A ,C ,F 在同一直线上,连接BE ,DG.(1)在不添加辅助线时,写出其中的两对全等三角形;(2)求证:BE =DG.解:(1)△ADC ≌△ABC ,△GFC ≌△EFC ,△GDC ≌△EBC(任意两对均可).(2)证明:∵四边形ABCD ,四边形CEFG 是菱形,∴DC =BC ,CG =CE ,∠DCA =∠BCA ,∠GCF =∠ECF.∵∠DCG =180°-∠DCA -∠GCF ,∠BCE =180°-∠BCA -∠ECF ,∴∠DCG =∠BCE.∴△GDC ≌△EBC(SAS).∴BE =DG.8.如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点O,与BC相交于点N,连接BM,DN.(1)求证:四边形BMDN为菱形;(2)若AB=4,AD=8,求MD的长.解:(1)证明:∵MN是BD的垂直平分线,∴MB=MD,OB=OD,∠BON=∠DOM.∵四边形ABCD是矩形,∴AD∥BC.∴∠OBN=∠ODM.∴△BON≌△DOM(ASA).∴BN=MD.∴四边形BMDN是平行四边形.又∵BD⊥MN,∴四边形BMDN是菱形.(2)设MD=x,则AM=8-x,BM=x.在Rt△ABM中,BM2=AB2+AM2,∴x2=42+(8-x)2.解得x=5.即MD=5.9.如图,在△ABC中,D是BC边的中点,E,F分别在线段AD及其延长线上,CE∥BF.(1)求证:△BDF≌△CDE;(2)若BD=DF,求证:四边形BFCE是矩形.证明:(1)∵D是BC边的中点,∴BD=DC.∵CE∥BF,∴∠ECD=∠FBD.在△BDF和△CDE中,∴△BDF≌△CDE(ASA).(2)∵△BDF≌△CDE,∴ED=DF.又∵BD=CD,∴四边形BFCE是平行四边形.∵BD=DF,∴BC=EF.∴四边形BFCE是矩形.10.已知:正方形ABCD的对角线AC与BD交于点O,点E,F分别是OB,OC上的动点.(1)如果动点E,F满足BE=CF(如图1);①写出所有以点E或F为顶点的全等三角形(不得添加辅助线);②求证:AE⊥BF;(2)如果动点E,F满足BE=OF(如图2),问AE⊥BF时,点E在什么位置,并证明你的结论.解:(1)①△ABE≌△BCF,△AOE≌△BOF,△ABF≌△DAE.②证明:延长AE交BF于点G.∵四边形ABCD是正方形,∴AB=BC,∠BCF=∠ABE.又∵BE=CF,∴△ABE≌△BCF(SAS).∴∠CBF=∠BAE.∵∠ABE+∠EBG+∠CBF=90°,∴∠ABE+∠EBG+∠BAE=90°.∴∠AGB=90°,即AE⊥BF.(2)点E是OB的中点.证明:延长AE 交BF 于点H. ∵四边形ABCD 是正方形,∴AB =BC ,∠BCF =∠ABE.∵AE ⊥BF ,∴∠AHB =90°.∴∠ABE +∠EBH +∠BAE =90°.∵∠ABE +∠EBH +∠CBF =90°,∴∠CBF =∠BAE.∴△ABE ≌△BCF(ASA).∴BE =CF.∵BE =OF ,∴BE =12OC. ∵OB =OC ,∴点E 是OB 的中点.。
南江县第六中学八年级数学下册第六章平行四边形1平行四边形的性质第2课时平行四边形的对角线特征教案新版

的时间与乙做 480 个零件所用的时间相同,若设甲每天做 x 个零件,则可列方程( A )
A.3x60 =14408-0 x
B.14306-0 x =4x80
7
C.3x60 +4x80 =140
D.3x60 -140=4x80
10.如图,在平面直角坐标系 xOy 中,已知点 A 的坐标是(0,1),以 OA 为边在右侧作
答案 : 9 cm .
5.平行四边形 ABCD 的対角线 AC、BD 相交于点 O,∠ADB=90°,OA=6,OB=3.求 AD 和 AC
的长度.
解:∵四边形 ABCD 是平行四边形 ∴OA=OC=6OB=OD=3 ∴AC=12 又∵∠ADB=90° ∴在 Rt△ADO 中 , 根据勾股定理得 OA2=OD2+AD2
重点:体会对于同一个图形,在不同的坐标系内,其各顶点的坐标不同。 难点:根据图形的特点建立合适的平面直角坐标系。 知识与技能 1.通过实例体会坐标系不同,图形各顶点的坐标不同;图形的位置不同,其顶点坐标 不同。 2.根据图形特点和问题的需要而能够灵活建立直角坐标系。 过程与方法 经历同一个图形放在平面直角坐标系的不同位置,体会其各顶点的坐标不同,从而引 导学生有选择性地建立直角坐标系使得各点的坐标简单。 情感态度价值观 进一步体会数形结合的思想; 通过归纳、总结变化规律,体会从特殊到一般的数学思想方法。
OE⊥AC 交 AD 于 E , 那么△DCE 的周长为〔 〕
A.4 cm
B.6 cm
C.8 cm
D.10 cm
答案 : C.
4. 如 以 下 图 , □ ABCD 中 ,EF 过 対 角 线 的 交 点 O, 如 果 AB=4
cm,AD=3 cm,OF=1 cm,那么四边形 BCFE 的周长为〔 〕
湘教版数学八年级下册第二章四边形测试题

初中数学试卷湘教版第二章四边形测试题(时限: 120 分钟总分:120分)姓名一、选择题(每题 3 分,共 30 分) 1:1 、以下图案中,不是中心对称图形的是()A DB C(A)2 对(B)3对(C)4对(D)5对6.以下性质中,矩形拥有但平行四边形不必定拥有的是()A .对边相等B.对角相等C.对角线相等 D .对角线相互均分7.如图,将边长为8cm 的正方形纸片ABCD 折叠,使点 D 落在 BC 边中点 E 处,点 A 落在点 F 处,折痕为 MN ,则线段 CN 的().( A) 3cm(B)4cm(C)5cm(D)6cm8.假如三角形的两条边分别为 4 和 6 ,那么连结该三角形三边中点得的周长可能是以下数据中的()A .6 B.8C. 10 D .129.一个多边形的内角和等于外角和的一半,那么这个多边形是()P ( A )A D 三角形(B)四边形(C)五边形( D )六边形 EOF10. 如图,点P是矩形ABCD的边AD上的一个动点,B C 矩形的两条边AB、 BC 的长分别为 3 和 4,那么点P 到矩形的两条对角线AC 和 BD 的距离之和是()12 6 24D. 不确立A. B. C.2 .在 Y ABCD中,∠A:∠B:∠C=2:3:2,则∠D=()5 5 5二、填空题(每题 3 分,共 30 分)(A)36°( B)108 °(C)72 °(D)60°11 .若一个多边形的内角和为 1 080 °,则这个多边形的边数是 _______.3 .假如等边三角形的边长为 3 ,那么连结各边中点所成的三角形的周长为().( A )9 12 .已知 AD ∥BC,要使四边形ABCD 为平行四边形,需要增添的条件是_______( ?填一个你认9 ( B)6 (C)3 (D)2 为正确的条件).4 .平行四边形的两条对角线分别为 6 和 10 ,则此中一条边x 的取值范围为().13 菱形的两条对角线的长为24 和 10 ,则菱形的边长是.( A ) 4<x<6 ( B) 2<x<8 ( C) 0<x<10 ( D ) 0<x<6.在 Y ABCD中,对角线AC与BD订交于点O,则能经过旋转达到重合的三角形有(14 .有三个内角是直角的四边形是;对角线相互垂直均分的四边形是.5 ).金戈铁制卷1 / 315 .已知平行四边形的面积是144cm 2,相邻两边上的高分别为8cm和9cm,则这个平行四边形的周长为 ________.16 .平行四边形两邻角的均分线订交所成的角为_________.17. 正方形 ABCD 的周长为8cm ,按序连结正方形ABCD 各边的中点获得四边形EFGH ,则四边形 EFGH 的周长等于;面积等于.18.如图, D 是△ABC 内一点, BD ⊥CD , AD =6, BD = 4, CD = 3,E、 F、 G、 H 分别是 AB 、AC 、 CD 、 BD 的中点,则四边形EFGH 的周长是.19 .如图 1, P 是四边形ABCD 的 DC 边上的一个动点.当四边形ABCD 知足条件 ______时,△PBA 的面积一直保持不变(注:只要填上你以为正确的一种条件即可,?不用考虑全部可能的情形).(18 题图)(19题图)(20 题图 )20 .如图 2,用 9 个全等的等边三角形,按图拼成一个几何图案,从该图案中可找出____个平行四边形.三、解答题(共60 分)21 .(本小题满分 6 分)如图,在边长为 1 个单位长度的小正方形构成的网格中,给出了格点△ABC(极点是网格线的交点)和点A1.画出△ABC 对于点A1的中心对称图形.22 .( 8 分)如图,在Y ABCD中,DB=CD,∠C=70°,AE⊥BD于点E.试求∠DAE的度数.23.(本小题满分 8 分)已知:菱形有一个内角是120 °,有一条对角线长是8 ㎝ ,求菱形边长。
《特殊的平行四边形》教学课件1

B
D
C 独木桥
矩形的一般性质:
具备平行四边形所有的性质
边
A O B C D
对边平行且相等 对角相等,邻角互补 对角线互相平分
角
对角线
探索新知:
矩形是一个特殊的平行四边形,除了具有平行 四边形的所有性质外,还有哪些特殊性质呢?
A D A O B
D C
B
O
C
猜想1:矩形的四个角都是直角. 猜想2:矩形的对角线相等.
已知:如图,四边形ABCD是矩形 求证:AC = BD 证明:在矩形ABCD中 ∵∠ABC = ∠DCB = 90° 又∵AB = DC , BC = CB ∴△ABC≌△DCB
B C A D
∴AC = BD
即矩形的对角线相等
A
D
O B
边 C
矩形对边平行且相等; 矩形的四个角都是直角;
角
对角线
矩形的对角线相等且互相平分;
例3(补充) 已知 ABCD的对角线AC、BD相交于 点O,△AOB是等边三角形,AB=4 cm ,求这个平行四边形的面积.
课堂小结
矩形:有一个角是直角的平行四边形叫做矩形. 矩形
矩形的对边平行且相等; 矩形的四个角都是直角; 矩形的对角线相等且互相平分.
直角三角形斜边上的中线等于斜边的一半. 矩形是轴对称图形,连接对边中点的直线是它的两 条对称轴. 矩形判定方法1:对角线相等的平行四边形是矩 形. 矩形判定方法2:有三个角是直角的四边形是矩 形.
求证:矩形的四个角都是直角.
已知:如图,四边形ABCD是矩形
求证:∠A=∠B=∠C=∠D=90°
证明: ∵四边形ABCD是矩形 ∴ ∠A=90° 又 矩形ABCD是平行四边形 ∴ ∠A=∠C
湘教版八年级数学下册课件 2-2-1 第2课时 平行四边形的对角线的性质

2. 平行四边形一条对角线的两个端点到另一条对角线
的距离相等吗?为什么?
相等.
N
证明 如右图所示,在□ ABCD 中, M
DM⊥AC 于点 M,BN⊥AC 于点 N .
∵ AC,BD 为 □ ABCD 的对角线,
且相交于点 O,∴ OB = OD .
又 ∠AOD=∠COB,
∴ Rt△DOM ≌ Rt△BON . ∴ DM = BN.
出什么猜测?
D O
C
我发现 OA = OC,OB = OD. 我猜测点O是每条对角线的中点.
证明 ∵ 四边形 ABCD 是平行四边形, ∴ AB ∥ DC,AB = DC; ∴ ∠1 =∠2,∠3 =∠4; ∴ △OAB ≌ △OCD; ∴ OA = OC,OB = OD.
由此得到平行四边形的性质定理:
湘教版八年级数学下册
第2章 四边形
2.2 平行四边形 2.2.1 平行四边形的性质
第2课时 平行四边形的对角线的性质
一 复习导入
平行四边形的两组对边分别相等, 平行四边形的两组对角分别相等.
平行四边形的两条对角线有什么 性质呢?
二 新课探究
如图,已知 ABCD 两条 A 对角线 AC 与 BD 相交于点 O, 比较 OA,OC,OB,OD 的长 度,有哪些线段相等?你能作 B
∴ △COD的周长为 3 + 5 + 4.8 = 12.8.
例 4 如图,在 □ ABCD 中,对角线 AC 与 BD 相交于
点 O,过点 O 的直线 MN 分别交 AD,BC 于点 M,N.
求证:点 O 是线段 MN 的中点.
证明 ∵ AC,BD为□ ABCD 的对角线,
且相交于点 O, ∴ OA = OC. ∵ AD∥BC,∴ ∠MAO =∠NCO. 又∠AOM =∠CON, ∴ △AOM≌△CON. ∴ OM = ON. ∴ 点 O 是线段 MN 的中点.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
衡南六中2012年八年级四边形专题
一. 选择题 (每题3分,共36分)
1. 平行四边形具有,而一般四边形不具有的性质是( )
A 、外角和等于360°
B 、对角线互相平分
C 、内角和等于360°
D 、有两条对角线 2. 下面性质中菱形有而矩形没有的是( )
A 、邻角互补
B 、内角和为360°
C 、对角线相等
D 、对角线互相垂直 3. 能判定四边形ABCD 为平行四边形的题设是( ).
A 、A
B ∥CD ,AD=B
C B 、∠A=∠B ,∠C=∠
D C 、AB=CD ,AD=BC D 、AB=AD ,CB=CD 4. 若O 是四边形ABCD 对角线的交点且OA=OB=OC=OD ,则四边形ABCD 是( )
A 、等腰梯形
B 、矩形
C 、正方形
D 、菱形
5. 在平行四边形、矩形、正方形、等腰梯形、直角梯形中,不是轴对称图形的有( )
A. 1个
B.2个
C.3个
D.4个 6. 如图,在菱形ABCD 中,6cm,8cm AC BD ==,则菱形AB 边上的高CE 的长是( )。
A 、
245cm B 、48
5
cm C 、 5cm D 、10cm 7. 矩形具有而一般平行四边形不具有的性质是( ). A 、 对角线相等 B 、 对边相等 C 、 对角相等 D 、 对角线互相平分 8 正方形具有而菱形不一定具有的性质是( )
A 、四条边相等
B 、对角线互相垂直平分
C 、对角线平分一组对角
D 、对角线相等 9. 在□ABCD 中,∠A 、∠B 的度数之比为1∶2,则∠C 等于( ) A 、60° B 、80° C 、100° D 、120°
10. 等腰梯形的腰长为17cm ,两底差为16cm ,则等腰梯形高为 ( )
A 、12cm
B 、13cm
C 、14cm
D 、15cm
11. 给出下列四个命题 ⑴一组对边平行的四边形是平行四边形 ⑵一条对角线平分一个内角的平行四边形是菱形⑶两条对角线互相垂直的矩形是正方形 ⑷顺次连接等腰梯形四边中点所得四边形是等腰梯形。
其中正确命题的个数为( ) A 、1个 B 、2个 C 、3个 D 、4个
12. 下列矩形中按虚线剪开后,能拼成平行四边形,又能拼成直角三角形的是( )
二. 填空题 (每题3分,共24分) 13. 在ABCD 中,,则∠D=___________。
14. 已知AD ∥BC ,要使四边形ABCD 为平行四边形,四边形需要增加一个条件是:_____________。
15. 在ABCD 中,两邻边的差为2cm ,周长为16cm ,则两邻边长分别为_________________。
16. 已知菱形的周长是80cm ,则菱形的一边长是__________________。
17. 矩形ABCD 的对角线AC 、BD 相交于O ,∠AOD=60°,对角线AC 长为18厘米,则AD=_____。
18. 若菱形的周长为36 cm ,一个内角为60°,则菱形的较短的对角线长为________________。
19. 如图,在正方形ABCD 的外侧,作等边△ADE ,则∠AEB=_______。
20. 梯形ABCD 中,AB ∥DC , E 、F 、G 、H 分别是边AB 、BC 、CD 、DA 的中点,梯形ABCD 的
中 点 中 点 中 点 E
D
C
B
A
A
E D B O
C
边满足条件 时,四边形EFGH 是菱形。
三.解答题 (共60分)
21. 如图,在平行四边形ABCD 中,AE=CF ,求证:AF=CE 。
22. 如图所示,O 是矩形ABCD 的对角线的交点,作DE ∥AC ,AE ∥BD ,DE 、AE 交于点E 。
求证:四边形OAED 是菱形。
23. 如图,菱形ABCD 的对角线AC 、BD 相交于点O ,AE ∥BD ,BE ∥AC ,AE 、BE 相交于点 E 。
求证:四边形OAEB 是矩形。
24. 如图,在△ABC 中,点O 是AC 边上的一个动点,过点O 作直线MN ∥BC ,设MN 交∠BCA
的平分线于E,交∠BCA 的外角平分线于点F 。
(1)求证:OE=OF ;
(2)当O 点运动到何处时,四边形AECF 是矩形?并证明你的结论。
A
E
N
B
C
F
M
O
25。
在ABC △中,90BAC AD BC BE AF ∠=
,⊥,、分别是ABC ∠,DAC ∠的平分线,BE 和AD 交于G ,试说明四边形AGFE 的形状.
26. 如图,矩形ABCD 中,AC 、BD 相交于点O ,AE 平分∠BAD ,
若∠EAO=15°,求∠BOE 的度数。
27. 已知:如图,在ABC △中,AB AC =,AD BC ⊥,垂足为点D ,AN 是ABC △外角CAM ∠的平分线,CE AN ⊥,垂足为点E . (1)求证:四边形ADCE 为矩形;
(2)当ABC △满足什么条件时,四边形ADCE 是一个正方形?并给出证明
28. 如图所示,ABC Rt △中,90ACB ∠=
,ABC ∠的角平分线BD 交AC 于点D ,
CH AB ⊥交BD 于F ,DE AB ⊥于E ,四边形CDEF 是菱形吗?
B A
D
C
B H
E
F
A
B
C
E
F
D
G
A B C D O E B
D
C
N E A
M
E
B C D M N
A
29. 如图所示,在正方形ABCD 中,M 为AB 上任意一点,MN ⊥DM ,BN 平分∠CBE ,试
说明:MD =MN 。
30. 已知:如图,在直角梯形ABCD 中,∠B =90o ,AD ∥BC ,AD =24cm ,BC =26cm ,动
点P 从A 点开始沿AD 边向D 以1cm/秒的速度运动,动点Q 从C 点开始沿CB 边向B 以3cm/秒的速度运动,P 、Q 分别从A 、C 同时出发,当其一点到端点时,另一点也随之停止运动,设运动时间为t 秒,t 分别为何值时,四边形PQCD 是平行四边形?等腰梯形?
A
P
B D D
Q C。
