广东省深圳市2015年高三第一次调研考试数学理试卷及答案(纯word版)

合集下载

2015年深圳市高三年级第一次调研考试数学(文科)试题与参考答案

2015年深圳市高三年级第一次调研考试数学（文科）试题与参考答案一、选择题：本大题共10小题，每小题5分，满分50分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1、已知集合}5,1,0,2{=U ，集合}2,0{=A ，则A C U ＝（）A.φ B 。

}2,0{ C 。

}5,1{ D 。

}5,1,0,2{2、i 是虚数单位，复数)1(2-i i 的虚部是（）A.i B 。

i - C 。

1 D 。

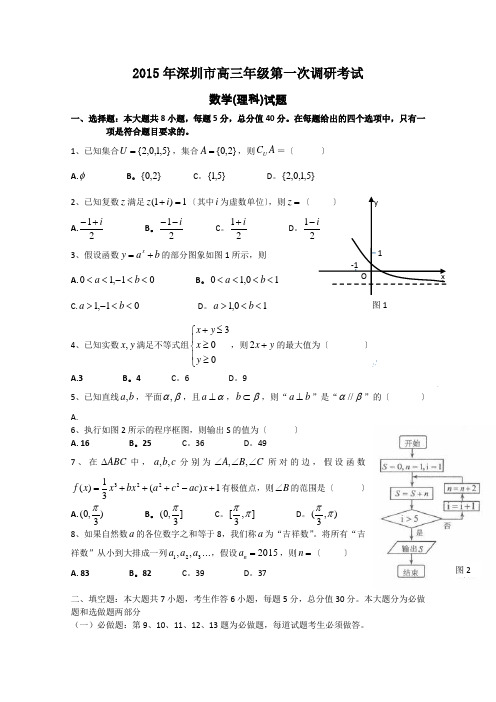
－13、在四边形ABCD 中，“AD AB AC +=”是“ABCD 是平行四边形”的（）A. 充分不必要条件B.充要条件C. 必要不充分条件D.既不充分也不必要条件4、若函数b a y x +=的部分图象如图1所示，则A.01,10<<-<<b a B 。

10,10<<<b a D 。

5、已知实数y x ,满足不等式组301≤⎪⎩⎪⎨⎧+≥≥y x y x ，则y x 2+的最大值为（） A.3 B 。

3 C 。

4 D 。

56、如图2，三棱锥A －BCD 中，AB ⊥平面BCD ，BC ⊥CD ，若AB ＝BC ＝CD ＝2，则该三棱锥的侧视图（投影线平行于BD ）的面积为（）A.2 B 。

2 C 。

22 D 。

327、在ABC ∆中，A ，B ，C 所对的边分别为c b a ,,，若A ＝060，3=a ，3=+c b ，则ABC ∆的面积为（） A.43 B 。

23 C 。

3 D 。

2 8、已知21,F F 分别是双曲线1:2222=-b y a x C （0,>b a ）的左、右焦点，点P 在C 上，若211F F PF ⊥，且211F F PF =，则C 的离心率是（）A.12- B 。

215+ C 。

12+ D 。

15- 9、函数axx x f 1)(+=在)1,(--∞上单调递增，则实数a 的取值范围是（） A.),1[+∞ B 。

2015年高考数学广东卷(理科)试卷及答案(word完整版)

绝密★启用前试卷类型：A2015年普通高等学校招生全国统一考试（广东卷）数学（理科）一、选择题：本大题共8小题，每小题5分，满分40分，在每小题给出的四个选项中，只有一个选项是符合题目要求的。

{}}{|(4)(1)0,|(4)(1)0M x x x N x x x =++==--=，则M N ⋂=}{A.1,4}{B.1,4--}{C.D.∅(32)z i i =-（i 是虚数单位），则z = A.23i -B.23i +C.32i +D.32i -3. 下列函数中，既不是奇函数，也不是偶函数的是A.y 1B.y x x=+1C.22x xy =+D.x y x e =+4. 袋中共有15个除了颜色外完全相同的球，其中有10个白球，5个红球，从袋中任取2个球，所取的2个球中恰好有1个白球，1个红球的概率为5A.2110B.2111C.21D.15. 平行于直线2++1=0x y 且与圆225x y +=相切的直线的方程是A.250250x y x y ++=+-=或B.2020x y x y +=+=或C.250250x y x y -+=--=或D.2020x y x y -=-=或6. 若变量,x y 满足约束条件4581302x y x y +≥⎧⎪≤≤⎨⎪≤≤⎩，则32z x y =+的最小值为A.4 23B.5C.6 31D.57. 已知双曲线2222:1x y C a b -=的离心率54e =，且其右焦点为2(5,0)F ，则双曲线C 的方程为22A.143x y -= 22B.1916x y -= 22C.1169x y -= 22D.134x y -= 8. 若空间中n 个不同的点两两距离都相等，则正整数n 的取值A.3至多等于B.4至多等于C.5等于D.5大于二、填空题：本大题共7小题，考生作答6小题，每小题5分，满分30分. （一）必做题（9-13题）9.在4）的展开式中，x 的系数为 .10. 在等差数列{}n a 中，若3456725a a a a a ++++=，则28a a += .11. 设ABC∆的内角A，B，C的对边分别为a，b，c，若a=1sin2B=，6Cπ=，则b= .12. 某高三毕业班有40人，同学之间两两彼此给对方仅写一条毕业留言，那么全班共写了条毕业留言。

广东省中山市第一中学等七校2015届高三第一次联考数学(理)试题 Word版含解析

2015届2014.8命题人：普宁二中陈左华潮阳一中黄绵凤【试卷综析】试题比较平稳，基本符合高考复习的特点，稳中有变，变中求新,适当调整了试卷难度，体现了稳中求进的精神.考查的知识涉及到函数、三角函数、数列、导数等几章知识，重视学科基础知识和基本技能的考察，同时侧重考察了学生的学习方法和思维能力的考察，这套试题以它的知识性、思辨性、灵活性，基础性充分体现了考素质，考基础，考方法，考潜能的检测功能.试题中无偏题，怪题，起到了引导高中数学向全面培养学生数学素质的方向发展的作用.一、选择题：本大题共8小题，每小题5分，满分40分。

在每小题给出的四个选项中，只有一项是符合题意要求的。

【题文】1设集合A={2|320x x x -+=}，则满足AB={0，1，2}的集合B 的个数是( )A 1B 3C 4D 6【知识点】并集及其运算 A1【答案解析】C 解析：解：A={x|x 2﹣3x+2=0}={x|x=1或x=2}={1，2}，若A∪B={0，1，2}，则0∈B ，则B={0}，{0，2}，{1，0}，{0，1，2}，共4个，故选：C 【思路点拨】先求出集合A 元素，根据集合关系和运算即可得到结论【题文】2. i 为虚数单位，复平面内表示复数z=(1+i )(2+i )的点在( )A.第一象限B.第二象限C.第三象限D.第四象限【知识点】复数代数形式的混合运算；复数的代数表示法及其几何意义L4 【答案解析】A 解析：解：复数z=（1+i ）（2+i ）=2+3i ﹣1=1+3i ，复数对应点为（1，3）．在第一象限．故选A【思路点拨】化简复数为a+bi 的形式，然后求出复数的对应点所在象限即可【题文】3．“1a =”是“函数ax sin ax cos y 22-=的最小正周期为π”的（）A ．必要不充分条件B ．充分不必要条件C ．充要条件D ．既不充分也不必要条件【知识点】三角函数的周期性及其求法；必要条件、充分条件与充要条件的判断A2,C3 【答案解析】A 解析：解：解：函数y=cos 2ax ﹣sin 2ax=cos2ax ，它的周期是，a=±1显然“a=1”可得“函数y=cos 2ax ﹣sin 2ax 的最小正周期为π”后者推不出前者，故选A ．【思路点拨】化简y=cos 2ax ﹣sin 2ax ，利用最小正周期为π，求出a ，即可判断选项．【题文】4.右图是一容量为100的样本的重量的频率分布直方图，则由图可估计样本重量的中位数为（）A ．11B ．11.5C ．12D ．12.5【知识点】众数、中位数、平均数K8【答案解析】C 解析：解：由题意，[5，10]的样本有5³0.06³100=30，[10，15]的样本有5³0.1³100=50，由于[10，15]的组中值为12.5，所以由图可估计样本重量的中位数12．故选：C【思路点拨】由题意，[5，10]的样本有5³0.06³100=30，[10，15]的样本有5³0.1³100=50，结合[10，15]的组中值，即可得出结论．【题文】5.执行上图所示的程序框图，则输出的结果是（）A ．5B ．7C ．9D ．11【知识点】程序框图L1【答案解析】C 解析：解：由程序框图知：第一次运行S=1+2=3，k=1+2=3；第二次运行S=1+2+6=9．k=3+2=5；第三次运行S=1+2+6+10=19，k=5+2=7；第四次运行S=1+2+6+10+14=33，k=7+2=9；此时不满足条件S ＜20，程序运行终止，输出k=9．故选：C ．【思路点拨】根据框图的流程依次计算运行的结果，直到不满足条件S ＜20，计算输出k 的值【题文】6、由曲线23,y x y x ==围成的封闭图形的面积为（）A ．712 B ．14 C ．13 D ．112【知识点】定积分在求面积中的应用B13【答案解析】D 解析：解：解：由题意得，两曲线的交点坐标是（1，1），（0，0）故积分区间是[0，1]所求封闭图形的面积为∫01（x 2﹣x 3）dx═，故选D【思路点拨】要求曲线y=x 2，y=x 3围成的封闭图形面积，根据定积分的几何意义，只要求∫01（x 2﹣x 3）dx 即可【题文】7．已知O 是坐标原点，点()1,0A -，若()y x M ,为平面区域⎪⎩⎪⎨⎧≤≤≥+212y x y x上的一个动点，则 OA OM +的取值范围是（）A []51，B []52，C []21，D []50，【知识点】简单线性规划E5 【答案解析】A 解析：解：+=（﹣1，0）+（x ，y ）=（x ﹣1，y ），则|+|=，设z=|+|=，则z 的几何意义为M 到定点D （1，0）的距离，由约束条件作平面区域如图，由图象可知当M 位于A （0，2）时，z 取得最大值z=，当M 位于C （1，1）时，z 取得最小值z=1， 1≤z≤，即|+|的取值范围是[1，]，故选：A【思路点拨】由题意作出可行域，由向量的坐标加法运算求得+的坐标，把||转化为可行域内的点M （x ，y ）到定点N （1，0）的距离，数形结合可得答案．【题文】8．对于集合A ，如果定义了一种运算“⊕”，使得集合A 中的元素间满足下列4个条件：（ⅰ）,a b A ∀∈，都有a b A ⊕∈；（ⅱ）e A ∃∈，使得对a A ∀∈，都有e a a e a ⊕=⊕=；（ⅲ）a A ∀∈，a A '∃∈，使得a a a a e ''⊕=⊕=；（ⅳ）,,a b c A ∀∈，都有()()a b c a b c ⊕⊕=⊕⊕，则称集合A 对于运算“⊕”构成“对称集”．下面给出三个集合及相应的运算“⊕”：①{}A =整数，运算“⊕”为普通加法；②{}A =复数，运算“⊕”为普通减法； ③{}A =正实数，运算“⊕”为普通乘法．其中可以构成“对称集”的有( ) A ①②B ①③C ②③D ①②③ 【知识点】元素与集合关系的判断A1【答案解析】B 解析：解：①A={整数}，运算“⊕”为普通加法，根据加法运算可知满足4个条件，其中e=0，a 、a′互为相反数；②A={复数}，运算“⊕”为普通减法，不满足4个条件； ③A={正实数}，运算“⊕”为普通乘法，根据乘法运算可知满足4个条件，其中e=1，a 、a′互为倒数．故选：B【思路点拨】根据新定义，对所给集合进行判断，即可得出结论二、填空题：本题共7小题，考生作答6小题，每小题5分，共30分 (一)必做题(9～13题)【题文】9. 若a x f xxlg 22)(-+=是奇函数，则实数a =_________。

广东省汕头市2015年普通高中毕业班上学期教学质量监测数学理试题(扫描版,word答案)

汕头市2015年普通高中毕业班监测(理科)答案一、选择题：1、C2、A3、B4、D5、C6、B7、D8、B 解析：3、B 2214322222,(2)(4)(2),212,6a a a a a a a a =-+=+=-=-8、B 解析：设i a A =，则20()a a A A ⊗⊗=等价于22i +被4除的余0，等价于i 是奇数.故a 可取135,,A A A . 二、填空题：9、24 10、⎭⎬⎫⎩⎨⎧≥21x x 11、70 12、6 13、（4） 14、⎪⎭⎫⎝⎛2,2π 15、32 三、解答题……………….3分………………6分（2）由题意可知道：1)32sin(2)32sin(2=+--+πθπθ，)2,0(πθ∈………………7分所以：3sin 2cos 3cos 2sin πθπθ+3sin )2cos(3cos )2sin(πθπθ----21= (8)所以213cos 2sin 2=πθ，即212sin =θ ……………………………9分因为)2,0(πθ∈，所以),0(2πθ∈ ……………………………10分所以62πθ=或652πθ=……………………………….11分所以12πθ=或125πθ= ……………………………….12分 17. 解(1):x 的可能值为0、2、10. ……………….1分153)2P 2623===C C x （ ……………….2分151)10P 2622===C C x （ ……………….3分1511)10()2(1)0P ==-=-==x P x P x （ ……………….4分……………….6分151615110153215110=⨯+⨯+⨯=Ex . ……………….8分（2）设摸一次得一等奖的事件为A ，摸一次得二等奖的事件为B.则151)A P 2622==C C （ 153)B P 2623==C C （ ……………….9分某人摸一次且获奖为事件A+B ，有因为A,B 互斥，所以154153151)B A P =+=+（ ……………….10分41154151B A P A P )B A A P =÷=+=+）（）（（ ……………….12分18、证明：(1)BC PA ABCD BC ABCD PA ⊥∴⊂⊥，平面，平面 …….1分.ABCD AB BC ⊥∴是矩形， …….2分，平面AB A,AB PA P BC ⊥=⋂ …………..3分BC AB ⊥∴⊂AF P AF ，平面又 …………..4分 .F PA AB PB AF PB ⊥∴=中点，是， …………..5分BC B BC PB P AF 平面，又⊥∴=⋂ . …………..6分(2)如图以A 为原点，分别以AD,AB,AP 为z y x ,,轴建系 . …………..7分设BE=a ，则)1,0,0(P ，)0,0,3(D ，)0,1,(E a ，)21,21,0(F . …………..8分 ),,(PDE z y x n =的法向量为设平面，则⎪⎩⎪⎨⎧=-=⋅=⋅=+-=-⋅=⋅03)1,0,3(),,(0)3()0,1,3(),,(z x z y x PD n y x a a z y x n. …………..10分 )3,3,1(,3,3,1a n z a y x -=∴=-==得令. …………..11分），，（的法向量为平面又21210PCE =AF . …………..12分635,2273222213cos 2=∴=+-⋅-==∴a a a an. ………..13分 045A -DE -P 635BE 为时，二面角当=∴. …………..14分 19、（1）设),y x （是)(x g 图像上任意一点，则)1,1(y x ---在)(x f 的图像上. ……2分 1111,111+=+-=∴---=-∴x xx y xy …………..4分 )1(,1)(≠+=∴x x x x g …………..5分0)1(1)(2>+='∴x x g …………..6分 ),1(),1,()(+∞---∞=∴的增区间为x g y …………..7分（2）0)(1,0>-=∴>>bb ac b a …………..8分3)(1)(3)(1)()(13=--≥-++-=-+=+∴bb a b b a b b a b b a b b a ac a ………10分43)3()(1-)(=≥+∴∞+=g c a g x g y ）上递增，，在（ ………….11分 43)(11111)()(≥+=+++=+++++>+++=+∴c a g c a c a c a c c a a c c a a c g a g 43)()(>+∴c g a g ………….14分 20、解：（1）若n c n =，因为5、6、7A ∉，所以5、6、7B ∈，由此可见，等差数列{}n b 的公差为1，而3是数列{}n b 中的项，所以3只可能是数列{}n b 中的第1、2、3项. …………..2分 ①若13b =，则2n b n =+； …………..3分②若23b =，则1n b n =+； …………..4分 ③若33b =，则n b n =. …………..5分（2）首先对元素2进行分类讨论：①若2是数列{}n c 的第2项，由{}n c 的前5项成等比数列，得34928c c ===，这显然不可能； …………..6分 ②若2是数列{}n c 的第3项，由{}n c 的前5项成等比数列，得212b =，因为数列{}n c 是将集合A B U 中的元素按从小到大的顺序排列构成的，所以0n b >，则1b =因此数列{}n c 的前5项分别为1、2、4，这样n b ，则数列{}n c 的前9项分别为12、4、、、8，上述数列符合要求. …………..8分③若2是数列{}n c 的第k 项（4k ≥），则2121b b -<-，即数列{}n b 的公差1d <，所以615257b b d =+<+=，而1、2、94c <，所以1、2、4在数列{}n c 的前8项中，由于Φ=⋂B A ，这样，1b 、2b 、…、6b 以及1、2、4共9项，它们均小于8，即数列{}n c 的前9项均小于8，这与98c =矛盾. …………..10分综上所述，n b =. …………..11分其次，当4n ≤时，154n n c c +=>，6554c c =<，764534c c =>. ………..12分当7n ≥时，n c ≥{}n b的等差数列，所以1n n c c +-≤….13分所以1115114n n n n n n n n n c c c c c c c c c ++++--==+≤+=，此时的n 不符合要求，所以符合要求的n 一共有5个. …………..14分 21、解：（Ⅰ）由题意可知：R k k x x k x x ∈>-+++++02)()(222令k x x t ++=2，则原不等式可以化为：022>-+t t ，解得：2-<t 或1>t即原不等式可以化为不等式①022<+++k x x 或不等式②012>-++k x x ……1分对于不等式①、②分别有:741--=∆k 与542+-=∆k 现做如下分类讨论：（1）当47-<k 时，01>∆，02>∆，此时不等式①、②对应的方程分别有不等根： 27411----=k x 与27412--+-=k x ；25413+---=k x 与25414+-+-=k x ；不难证明：4213x x x x <<<所以不等式①的解集为(,2741----∈k x )2741--+-k …………2分所以不等式②的解集为()2541,+---∞-∈k x ()∞++-+-,2541k …..3分所以当47-<k 时，函数)(x f 的定义域D =()2541,+---∞-k (,2741----k )2741--+-k ()∞++-+-,2541k ………….4分（2）当4547≤≤-k 时，01≤∆，02≥∆，结合（1）可知：不等式①的解集为Φ∈x 分 …………..5分不等式②的解集为()2541,+---∞-∈k x ()∞++-+-,2541k所以当4547≤≤-k 时，函数)(x f 的定义域 D =()2541,+---∞-k()∞++-+-,2541k …………..6分（3）当45>k 时，01<∆，02<∆，结合（1）可知：不等式①的解集为Φ∈x ；不等式②的解集为R x ∈所以当45>k 时，函数)(x f 的定义域D =R …………..7分综上所述：（1）当47-<k 时，函数)(x f 的定义域 D =()2541,+---∞-k (,2741----k )2741--+-k()∞++-+-,2541k（2）当4547≤≤-k 时，函数)(x f 的定义域 D =()2541,+---∞-k()∞++-+-,2541k（3）当45>k 时，函数)(x f 的定义域D =R …………..8分（Ⅱ）由（Ⅰ）知道：当2-<k 时，函数)(x f 的定义域D =()2541,+---∞-k(,2741----k )2741--+-k ()∞++-+-,2541k ………….9分令=)(x u 02)()(222>-+++++k x x k x x （2-<k ）,D x ∈则函数u y 2log =，显然函数u y 2log =在对应的定义域区间为单调递增函数，要求)(x f 的单调递增区间，我们只需要求出函数)(x u 在D x ∈上的单调递增区间。

2015深圳一模广东省深圳市2015年高三第一次调研考试文综地理试卷及答案

小时，其所处的自然带
是
。（6 分）
（2）波罗的海是世界上盐度最低的海域，其原因是什么？（8 分）
（3）卑尔根降水日数多的原因是什么？（6 分）
（4）丹麦被称为“欧洲的肉库和奶桶”，肉类、奶酪和黄油出口量居世界前列。请分析丹麦发展乳肉畜牧
业的有利条件。（8 分）
4
41.（28 分）根据下列材料，结合所学知识，完成（1）～（5）题。材料一: 滦河流域简图（图 15）
2015 年深圳市高三年级第一次调研考试
文科综合·地理
2015.1
一、选择题：本大题共 35 小题，每小题 4 分，共 140 分。在每小题列出的四个选项中，只有一项符合题目要求。
1．2014 年 12 月 12 日南水北调中线工程正式通水，通水现场施放“大黄鸭”测量水速。“大黄鸭”携带
的测速设备运用的地理信息技术是
100 90 80 70 60 50 40 30 20 10 0
1992
1993
1994
入库泥沙 1995 1996
出库泥沙
1997 1998 年份
拦截率（%） 1999 2000 2001
100 90 80 70 60 50 40 30 20 10 0
2002
图3
1
A．入库泥沙逐年减少
B．出库泥沙逐年增多
地面
图4
6．图 5 是我国某都市区 1982～2008 年空间扩张过程。此过程主要表现为
图5
A．郊区城市化 B．逆城市化 C．城市空心化 D．再城市化
7．图 6 是我国双季稻（一年中种植和收获两季水稻）主要种植区分布图。下列描述符合双季稻种植区特
点的是
A．形成双季稻种植区的主要因素是饮食习惯

广东省深圳市2015届高三上学期第一次五校联考数学(理)试题 Word版含答案

2015届高三年级第一次五校联考理科数学试卷本试卷共4页，21小题，满分150分．考试用时120分钟．命题人：二高董正林注意事项：1. 答卷前，考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上。

2. 选择题每小题选出答案后，用2B 铅笔把答题卡对应题目选项的答案信息点涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上．3. 非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目指定区域相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液。

不按以上要求作答的答案无效．4. 作答选做题时，请先用2B 铅笔填涂选做题的题号对应的信息点，再作答。

漏涂、错涂、多涂的，答案无效．5. 考生必须保持答题卡的整洁。

考试结束后，将试卷和答题卡一并交回．一、选择题（本大题共8小题，每小题5分，满分40分．在每小题给出的四个选项中，有且只有一项是符合题目要求的）1. 已知a b R ∈，，i 是虚数单位，若a i -与2bi +互为共轭复数，则()2a bi +＝（）A ．54i -B ．54i +C ．34i -D ．34i +2. 设集合{} 12A x R x =∈-<，{}2,xB y R y x R =∈=∈，则AB ＝（）A ．∅B ．[)0 3，C ．()0 3，D ．()1 3-， 3. 函数()2ln =-f x x x的零点所在的区间为（） A ．()0 1， B ．()1 2， C ．()2 3， D ．()3 4， 4. 已知m (),2a =-，n ()1,1a =-，则 “a ＝2”是“m //n ”的（） A ．充要条件 B ．充分而不必要条件C ．必要而不充分条件D ．既不充分也不必要条件5. 一个多面体的三视图如右图所示，则该多面体的体积为（）A ．233 B ．223C ．6D ． 76. 在《爸爸去哪儿》第二季第四期中，村长给6位“萌娃”布置一项搜寻空投食物的任务. 已知：①食物投掷地点有远、近两处； ②由于Grace 年纪尚小，所以要么不参与该项任务，但此时另需一位小孩在大本营陪同，要么参与搜寻近处投掷点的食物；③所有参与搜寻任务的小孩须被均分成两组，一组去远处，一组去近处。

广东省江门市普通高中2015届高三调研测试数学(理)试题 Word版含解析

江门市普通高中2015届高三（上）调考数学试卷（理科）参考答案与试题解析一、选择题：本大题共8小题，每小题5分，满分40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知R为实数集，A={x|2x﹣3＜3x}，B={x|x≥2}，则A∪B=（）A．{x|x≥2} B．{x|x＞﹣3} C．{x|2≤x＜3} D．R[品题]：求出不等式2x﹣3＜3x的解集A，再由并集的运算求出A∪B．解答：解：由2x﹣3＜3x得，x＞﹣3，则A={x|x＞﹣3}，又B={x|x≥2}，则A∪B={x|x＞﹣3}，故选：B．点拨：本题考查并集及其运算，属于基础题．2．i是虚数单位，则=（）A．1 B．﹣i C．i D．﹣i [品题]：利用复数代数形式的乘除运算法则求解．解答：解：=﹣﹣=．故选：D．点拨：本题考查复数的乘除运算，是基础题，解题时要注意运算法则的合理运用．3．已知三个实数：、、c=log3，它们之间的大小关系是（）A．a＞b＞c B．a＞c＞b C．b＞c＞a D．b＞a＞c[品题]：根据指数函数和对数函数的图象和性质，以0和1作为中间量，可比较出a，b，c的大小．解答：解：∵＞30=1、0＜=1、c=log3＜log31=0，∴a＞b＞c，故选：A点拨：本题考查的知识点是指数式与对数式的大小比较，熟练掌握指数函数和对数函数的图象和性质，是解答的关键．4．已知是非零向量，，则“”是“”成立的（）A．充分非必要条件B．必要非充分条件C．非充分非必要条件D．充要条件[品题]：根据“”成立，得到•（﹣）=0，结合是非零向量，，推出，根据充要条件的判定方法可得结论．解答：解：∵，∴•（﹣）=0，∵是非零向量，，∴，故选：D．点拨：题主要考查了数量积判断两个平面向量的垂直关系，以及必要条件、充分条件与充要条件的判断，属于基础题．5．如图，某几何体的正视图、侧视图和俯视图分别是直角三角形、等腰三角形和半圆，则该几何体的体积为（）A．4 B．8C．2πD．4π[品题]：根据几何体的三视图，得该几何体是底面为半圆的圆锥，求出几何体的体积即可．解答：解：根据几何体的三视图，得该几何体是底面为半圆的圆锥，∴该几何体的体积为V几何体=S底面h=××π××3=2π．故选：C．点拨：本题考查了空间几何体的三视图的应用问题，解题时应根据三视图，得出该几何体是什么几何图形．6．在△ABC中，∠A、∠B、∠C的对边分别为a、b、c，若∠A=75°，∠B=60°，c=10，则b=（）A．5B．5C．10D．10[品题]：由A与B的度数求出C的度数，根据sinB，sinC，以及c的值，利用正弦定理求出b的值即可．解答：解：∵在△ABC中，∠A=75°，∠B=60°，c=10，∴∠C=45°，由正弦定理=得：b===5，故选：B．点拨：此题考查了正弦定理，以及特殊角的三角函数值，熟练掌握正弦定理是解本题的关键．7．在同一直角坐标系中，直线=1与圆x2+y2+2x﹣4y﹣4=0的位置关系是（）A．直线经过圆心B．相交但不经过圆心C．相切D．相离[品题]：求出圆心到直线的距离大于零且小于半径，可得直线和圆相交但不经过圆心．解答：解：圆x2+y2+2x﹣4y﹣4=0，即（x+1）2+（y﹣2）2=9，表示以（﹣1，2）为圆心、半径等于3的圆．由于圆心到直线=1的距离为=2＜3，故直线和圆相交但不经过圆心，故选：B．点拨：本题主要考查直线和圆的位置关系，点到直线的距离公式的应用，属于基础题．8．已知函数f（x）=ax3﹣3x2+1，若f（x）存在唯一的零点x0，且x0＞0，则a的取值范围是（）A．（2，+∞）B．（1，+∞）C．（﹣∞，﹣2）D．（﹣∞，﹣1）[品题]：分类讨论：当a≥0时，容易判断出不符合题意；当a＜0时，由于而f（0）=1＞0，x→+∞时，f（x）→﹣∞，可知：存在x0＞0，使得f（x0）=0，要使满足条件f（x）存在唯一的零点x0，且x0＞0，则必须极小值f（）＞0，解出即可．解答：解：当a=0时，f（x）=﹣3x2+1=0，解得x=±，函数f（x）有两个零点，不符合题意，应舍去；当a＞0时，令f′（x）=3ax2﹣6x=3ax（x﹣）=0，解得x=0或x=＞0，列表如下：x （﹣∞，0）0 （0，）（，+∞）f′（x）+ 0 ﹣0 +f（x）单调递增极大值单调递减极小值单调递增∵x→﹣∞，f（x）→﹣∞，而f（0）=1＞0，∴存在x＜0，使得f（x）=0，不符合条件：f（x）存在唯一的零点x0，且x0＞0，应舍去．当a＜0时，f′（x）=3ax2﹣6x=3ax（x﹣）=0，解得x=0或x=＜0，列表如下：x （﹣∞，）（，0） 0 （0，+∞）f′（x）﹣0 + 0 ﹣f（x）单调递减极小值单调递增极大值单调递减而f（0）=1＞0，x→+∞时，f（x）→﹣∞，∴存在x0＞0，使得f（x0）=0，∵f（x）存在唯一的零点x0，且x0＞0，∴极小值f（）＞0，化为a2＞4，∵a＜0，∴a＜﹣2．综上可知：a的取值范围是（﹣∞，﹣2）．故选：C．点拨：本题考查了利用导数研究函数的单调性极值与最值、分类讨论的思想方法，考查了推理能力和计算能力，属于难题．二、填空题：本大题共5小题，考生作答6小题，每小题5分，满分25分．（一）必做题（9～13题）9．双曲线9x2﹣16y2=144的离心率等于．考点：双曲线的简单性质．专题：计算题；圆锥曲线的定义、性质与方程．[品题]：双曲线方程化为标准方程，可得a=5，b=3，c=4，从而可求双曲线的离心率．解答：解：双曲线9x2﹣16y2=144可化为，所以a=5，b=3，c=4，所以离心率e==．故答案为：．点拨：本题考查双曲线的标准方程，考查双曲线的几何性质，确定双曲线的几何量是关键．10．（5分）△ABC是等腰直角三角形，已知A（1，1），B（1，3），AB⊥BC，点C在第一象限，点（x，y）在△ABC内部，则点C的坐标为（3，3），z=2x﹣y的最大值是3．考点：简单线性规划．专题：不等式的解法及应用．根据等腰直角三角形的定义先求出C的坐标，利用线性规划的知识即可得到结论．[品题]：解答：解：∵A（1，1），B（1，3），AB⊥BC，点C在第一象限，∴|AB|=3﹣1=2，设C（x，y），则x＞0，y＞0，∵△ABC是等腰直角三角形，∴|BC|=|x﹣1|=2，解得x=3或x=﹣1（舍），即C（3，3），由z=2x﹣y得y=2x﹣z，平移直线y=2x﹣z，由图象可知当直线y=2x﹣z经过点C时，直线y=2x﹣z的截距最小，此时z最大，此时z=2x﹣y=2×3﹣3=3，故答案为：（3，3），3点拨：本题主要考查线性规划的应用，利用数形结合是解决本题的关键．11．（5分）（2012•四川）如图，在正方体ABCD﹣A1B1C1D1中，M、N分别是CD、CC1的中点，则异面直线A1M与DN所成的角的大小是90°．考点：异面直线及其所成的角．专题：计算题．[品以D为坐标原点，建立空间直角坐标系，利用向量的方法求出与夹角求出异题]：面直线A1M与DN所成的角．解答：解：以D为坐标原点，建立如图所示的空间直角坐标系．设棱长为2，则D（0，0，0），N（0，2，1），M（0，1，0），A1（2，0，2），=（0，2，1），=（﹣2，1，﹣2）•=0，所以⊥，即A1M⊥DN，异面直线A1M与DN所成的角的大小是90°，故答案为：90°．点拨：本题考查空间异面直线的夹角求解，采用了向量的方法．向量的方法能降低空间想象难度，但要注意有关点，向量坐标的准确．否则容易由于计算失误而出错．12．（5分）若f（x）=，则f（x）的最小值是﹣1．考点：函数的最值及其几何意义．专题：函数的性质及应用．[品根据分段函数的表达式，分别求出对应的取值范围即可得到结论．题]：解答：解：作出函数f（x）的图象如图：当x≤0，f（x）=﹣x≥0，当x＞0时，f（x）=x2﹣2x=（x﹣1）2﹣1≥﹣1，故当x=1时，函数f（x）取得最小值为﹣1，故答案为：﹣1点拨：本题主要考查函数最值的求解，根据分段函数的表达式结合函数的性质是解决本题的关键．13．（5分）已知数列{a n}满足a1=﹣，a n=1﹣（n＞1），计算并观察数列{a n}的前若干项，根据前若干项的变化规律推测，a2015=5．考点：归纳推理．专题：计算题；推理和证明．[品确定数列{a n}是以3为周期的周期数列，即可得出结论．题]：解答：解：∵a1=﹣，a n=1﹣，∴a2=5，a3=，a4=﹣，∴数列{a n}是以3为周期的周期数列，∴a2015=a2=5，故答案为：5．点拨：本题考查归纳推理，确定数列{a n}是以3为周期的周期数列是解题的关键．三.选做题（14、15题，考生只能从中选做一题）14．（5分）计算定积分：2．考点：定积分．专题：导数的概念及应用．[品题]：根据的导数为得到原函数是，写出当自变量取两个不同的值时，对应的函数值，让两个数字相减得到结果．解答：解：=4﹣2=2故答案为：2点拨：本题考查定积分，关键是求出原函数，属于一道基础题．15．已知定义在区间（﹣π，π）上的函数f（x）=xsinx+cosx，则f（x）的单调递增区间是，．考点：两角和与差的正弦函数．专题：导数的综合应用；三角函数的图像与性质．[品题]：根据求导公式和题意求出f′（x），结合定义域和余弦函数的性质求出f′（x）＞0是x的范围，奇求出函数f（x）的单调递增区间．解答：解：由题意得，f′（x）=sinx+xcosx﹣sinx=xcosx，根据余弦函数的性质得，当或时，f′（x）＞0，所以f（x）的单调递增区间是和，故答案为：和．点拨：本题考查余弦函数的性质，以及导数与函数的单调性关系，属于中档题．三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤．16．（12分）已知函数f（x）=2sinx（sinx+cosx），x∈R．（1）求f（x）的最小正周期T和最大值M；（2）若，求cosα的值．考点：三角函数中的恒等变换应用；三角函数的周期性及其求法．专题：三角函数的求值；三角函数的图像与性质．[品题]：（1）化简可得f（x）=，可求最小正周期，最大值；（2）依题意得，即，从而可求，．解答：解：（1）∵f（x）=sin2x+1﹣cos2x…（2分），=…（4分）∴最小正周期…（5分），最大值…（6分）（2）依题意，…（7分）即…（8分），∴…（10分）∴…（12分）点拨：本题主要考查了三角函数中的恒等变换应用，三角函数的周期性及其求法，属于基本知识的考查．17．（14分）已知{a n}是等差数列，a2=3，a3=5．（1）求数列{a n}的通项公式；（2）对一切正整数n，设b n=，求数列{b n}的前n项和S n．考点：数列的求和．专题：等差数列与等比数列．[品题]：（1）根据等差数列的通项公式由条件即可求出首项a1=1，公差d=2，所以可得到a n=2n ﹣1；（2）根据a n先求出b n并将它变成，看到该通项之后，可以想到能否在求和中使得一些项前后抵消，并且通过求前几项的和会发现是可以的，并且是有规律的，根据这个规律即可求出{b n}的前n项和S n．解答：解：（1）由得，a1=1，d=2；∴a n=1+2（n﹣1）=2n﹣1；（2）=；∴S n=b1+b2+b3+…+b n=；通过前几项的求和规律知：若n为奇数，则；若n为偶数，则．点拨：考查等差数列的通项公式，以及裂项的方法求数列前n项和，以及通过前几项求和的规律找到求数列前n项和的方法．18．（14分）如图，在四棱锥P﹣ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，PD=DC，E是PC的中点，作EF⊥PB交PB于点F．（1）证明PA∥平面EDB；（2）证明PB⊥平面EFD；（3）求二面角C﹣PB﹣D的大小．考点：用空间向量求平面间的夹角；直线与平面垂直的判定．专题：空间位置关系与距离；空间角．[品题]：方法一：（1）连结AC，AC交BD于O，连结EO，利用三角形中位线的性质，可得PA∥EO，利用线面平行的判定可得结论；（2）证明DE⊥PC，BC⊥平面PDC，DE⊥平面PBC，可得DE⊥PB，利用线面垂直的判定定理，可得PB⊥平面EFD；（3）确定∠EFD是二面角C﹣PB﹣D的平面角，利用正弦函数即可求解；方法二：建立空间直角坐标系，D为坐标原点，设DC=a（1）连结AC，AC交BD于G，连结EG，证明，这表明PA∥EG，可得结论；（2）利用向量的数量积公式，证明PB⊥DE，再利用线面垂直的判定定理，可得结论；（3）确定∠EFD是二面角C﹣PB﹣D的平面角，利用向量的夹角公式，即可解决．解答：方法一：（1）证明：连结AC，AC交BD于O，连结EO∵底面ABCD是正方形，∴点O是AC的中点在△PAC中，EO是中位线，∴PA∥EO而EO⊂平面EDB且PA⊄平面EDB，所以，PA∥平面EDB（2）证明：∵PD⊥底面ABCD且DC⊂底面ABCD，∴PD⊥DC∵PD=DC，可知△PDC是等腰直角三角形，而DE是斜边PC的中线，∴DE⊥PC ①同样由PD⊥底面ABCD，得PD⊥BC∵底面ABCD是正方形，有DC⊥BC，∴BC⊥平面PDC而DE⊂平面PDC，∴BC⊥DE ②由①和②推得DE⊥平面PBC而PB⊂平面PBC，∴DE⊥PB又EF⊥PB且DE∩EF=E，所以PB⊥平面EFD（3）解：由（2）知，PB⊥DF，故∠EFD是二面角C﹣PB﹣D的平面角由（2）知，DE⊥EF，PD⊥DB设正方形ABCD的边长为a，则，在Rt△PDB中，在Rt△EFD中，，∴所以，二面角C﹣PB﹣D的大小为；方法二：如图所示建立空间直角坐标系，D为坐标原点，设DC=a（1）证明：连结AC，AC交BD于G，连结EG依题意得∵底面ABCD是正方形，∴G是此正方形的中心，故点G的坐标为且∴，这表明PA∥EG而EG⊂平面EDB且PA⊄平面EDB，∴PA∥平面EDB（2）证明；依题意得B（a，a，0），又，故∴PB⊥DE由已知EF⊥PB，且EF∩DE=E，所以PB⊥平面EFD（3）解：设点F的坐标为（x0，y0，z0），，则（x0，y0，z0﹣a）=λ（a，a，﹣a）从而x0=λa，y0=λa，z0=（1﹣λ）a所以由条件EF⊥PB知，，即，解得∴点F的坐标为，且，∴即PB⊥FD，故∠EFD是二面角C﹣PB﹣D的平面角∵，且，，∴∴所以，二面角C﹣PB﹣D的大小为．点拨：本题考查线面平行、线面垂直、考查面面角，考查学生[品题]解决问题的能力，考查学生的计算能力，属于中档题．19．（12分）一艘船每小时的燃料费与船的速度的平方成正比，如果此船速度是10km/h，那么每小时的燃料费是80元．已知船航行时其他费用为500元/时，在100km航程中，航速多少时船行驶总费用最少？此时总费用多少元？考点：基本不等式在最值问题中的应用．专题：计算题；应用题；导数的综合应用；不等式的解法及应用．[品题]：设每小时燃料费与航速平方的比例系数为k，由条件求得k，设航速为xkm/h时，总费用为y元，求得y=80x+，可由基本不等式或函数的导数，即可得到最小值．解答：解：设每小时燃料费与航速平方的比例系数为k，则80=k×102，解得，设航速为xkm/h时，总费用为y元，则=．（方法一）令，解得x=25（负值舍去），当0＜x＜25时，y′＜0，x＞25时，y′＞0，∴x=25是极小值点，也是最小值点，此时（元）．（方法二）∵x＞0，∴=4000（元），等号成立当且仅当，解得x=25（负值舍去）．答：航速为25km/h时，总费用最少，此时总费用为4000元．点拨：本题考查函数的最值的应用题，考查运用导数求最值，运用基本不等式求最值，考查运算能力，属于中档题．20．（14分）在平面直角坐标系xoy中，点A，B的坐标分别是（0，﹣3），（0，3）直线AM，BM相交于点M，且它们的斜率之积是﹣．（1）求点M的轨迹L的方程；（2）若直线L经过点P（4，1），与轨迹L有且仅有一个公共点，求直线L的方程．考点：轨迹方程；直线的一般式方程．专题：计算题．[品题]：（1）求M点的轨迹方程，所以设M（x，y），根据直线AM，BM的斜率之积是﹣，即可求得关于x，y的等式，即点M的轨迹方程：x2+2y2=18；（2）若直线L不存在斜率，则容易判断它和轨迹L有两个交点，不合题意；存在斜率时设斜率为k，然后根据直线L经过点P可写出直线L的方程，将直线方程带入轨迹方程可得到关于x的方程，让该方程有一个解求k即可得到直线L的方程．解答：解：（1）设M（x，y），则：（x≠0）；∴点M的轨迹方程为：x2+2y2=18（x≠0）；（2）若直线L不存在斜率，则方程为：x=4；x=4带入轨迹方程可得y=±1，即直线L和轨迹L有两个公共点，不合题意；∴设直线L斜率为k，则方程为：y=kx﹣4k+1，带入轨迹方程并整理得：（1+2k2）x2+4k（1﹣4k）x+16（2k2﹣k﹣1）=0；∵直线L与轨迹L只有一个公共点，所以：△=16k2（1﹣4k）2﹣64（1+2k2）（2k2﹣k﹣1）=0；解得k=﹣2；∴直线L的方程为：y=﹣2x+9．点拨：考查轨迹与轨迹方程的概念，以及求轨迹方程的方法，斜率公式，直线的点斜式方程，一元二次方程有一个解时的判别式的取值如何．21．（14分）已知函数f（x）=x3+ax2﹣1（a∈R是常数）．（1）设a=﹣3，x=x1、x=x2是函数y=f（x）的极值点，试证明曲线y=f（x）关于点对称；（2）是否存在常数a，使得∀x∈[﹣1，5]，|f（x）|≤33恒成立？若存在，求常数a的值或取值范围；若不存在，请说明理由．（注：曲线y=f（x）关于点M对称是指，对于曲线y=f（x）上任意一点P，若点P关于M的对称点为Q，则Q在曲线y=f（x）上．）考点：利用导数研究曲线上某点切线方程．专题：导数的综合应用．[品题]：（1）把a=﹣3代入函数解析式，求出函数的导函数，得到导函数的零点，求出M的坐标，求出曲线y=f（x）上任意一点关于M对称的点Q，由Q 的坐标适合函数解析式说明结论成立；（2）把|f（x）|≤33恒成立转化为，然后构造两个函数，，由导数求其最值得答案．解答：（1）证明：当a=﹣3时，f（x）=x3﹣3x2﹣1，f′（x）=3x2﹣6x，由f′（x）=0，得x1=0，x2=2，∴=M（1，﹣3），曲线y=f（x）上任意一点关于M对称的点为，则，∴点Q在曲线y=f（x）上，∴曲线y=f（x）关于点M对称；（2）解：由|f（x）|≤33，即|x3+ax2﹣1|≤33，得﹣33≤x3+ax2﹣1≤33，x=0时，不等式恒成立；x≠0时，不等式等价于，作，，则，，解，得x1=4，解，得．列表：x [﹣1，0）（0，4）4 （4，5]﹣+ 0 ﹣g1（x）↘↗极大值↘+﹣﹣﹣g2（x）↗↘↘g1（﹣1）=﹣31，g1（4）=﹣6，在[﹣1，0）∪（0，5]的最大值为﹣6；g2（﹣1）=35，，在[﹣1，0）∪（0，5]的最小值为．综上所述，a的取值范围为．点拨：本题考查学生会利用导数求曲线上过某点切线方程的斜率，会利用导数研究函数的单调区间以及根据函数的增减性得到函数的最值，掌握不等式恒成立时所取的条件，是压轴题．。

数学理卷·2015届广东省惠州市高三第一次调研考试word典藏版

ì
1 ü ý 的前 n 项和为 Tn ，是否存在实数 M ，使得 Tn £ M 对一切正整数 n î an gan +1 þ
成立？若存在，求出 M 的最小值；若不存在，请说明理由．
20．（本小题满分 14 分）
x2 y 2 1 椭圆 C : 2 + 2 = 1 (a > b > 0) 的离心率为，其左焦点到点 P (2,1) 的距离为 10 ． a b 2
s 1 4 = = 2 ，故 s¢ p ´ p p 2 2 r r r
选A 8.【解析】由题意 v = u - (u - v ) = (1, 3) ，则 u + v = (3, 3) ， cos =
r
r
r
r
r
r
3 ，得 2
知
r r r 1 sin = ，由定 2 r r u u r r r r r r r 1 u ´ (u + v) = u gu + v sin = 2 ´ 2 3 ´ = 2 3 ，故选 D 2
3 3 3 2 A3 = 12 种，故共有没有重复数字的偶数 12 个。
C 1 1 O -1 【解析】由约束条件画出可行域如图所示，则目标函数 z = x + y 在点 B (2,1) 取得最大值，代入得 x + y = 3 ，故 x + y 的最大值为
3。
13．【解析】设函数 g ( x) = f ( x ) - 2 x - 4 ，则 g ¢( x ) = f ¢( x ) - 2 > 0 ，得函数 g ( x) 在 R 上为增函数，且 g ( -1) = f ( -1) - 2 ´ ( -1) - 4 = 0 ，所以当 f ( x ) > 2 x + 4 时，有 g ( x) > 0 ，得 x > -1 ，故不等式 f ( x ) > 2 x + 4 的解集为 ( -1, +¥) 14．【解析】由题意，直线 l : x - y + 5 = 0 ，圆的标准方程 x + ( y - 1) = 1 ，则圆心 (0,1) 到

2015 年深圳市高三年级第一次调研考试数学理科答案-精简修改版

解得 x1 0, x2
y kx m ， ……………………………………5 分联立直线 l 和椭圆 E 的方程，得 x 2 2 1 y 2
消去 y 并整理，得 2k 1 x 4kmx 2m 2 0 ，
2 2 2

…………………………6 分
5π 7π π π ) 2sin 2sin( π) 2sin 1 ． 12 6 6 6
………………………………5 分
（2）由 sin x0
1 3 2 得 cos 2 x0 1 2sin x0 ， ………………………………7 分 3 3 π 又 x0 (0, ) ， 2 x0 (0, π) ， ……………………………………………8 分 2
…………………………………2 分
12 6 4 个， ………………………………… 3 分 12 6 6 6 2 个，从“轻度污染”类城市中抽取 n2 ……………………………4 分 12 6 所以抽出的“良好”类城市为 4 个，抽出的“轻度污染”类城市为 2 个．
根据题意的所有可能取值为： 1, 2, 3 ．
………………………………14 分
a 2 b2 2 2 2 2 ，所以，解得 a 2b ， a 2 2
x2 y 2 故椭圆 E 的方程可设为 2 2 1 ，则椭圆 E 的右焦点坐标为 b, 0 ，过右焦点倾 2b b
斜角为 45 的直线方程为 l : y x b ．
②
……………………… 9 分
b1 1， b2 ， b3
1 ， 2
………………………………………10 分
若数列 bn } 为等比数列，则有 b2 2 b1b3 ，即 2 (1)(

2015年全国1卷高考理科数学试卷及答案(精校word详细解析版)

2015年普通高等学校招生全国统一考试理科数学一. 选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的.（1）设复数z 满足1+z1z-＝i ，则|z |＝(A )1 (B )2 (C )3 (D )2(2)sin 20°cos 10°－cos 160°sin 10°＝(A )32-(B )32 (C )12- (D )12(3)设命题P ：∃n ∈N ，2n >2n ，则⌝P 为(A )∀n ∈N ， 2n >2n (B )∃ n ∈N ， 2n ≤2n (C )∀n ∈N ， 2n ≤2n (D )∃ n ∈N ， 2n ＝2n(4)投篮测试中，每人投3次，至少投中2次才能通过测试.已知某同学每次投篮投中的概率为0.6，且各次投篮是否投中相互独立，则该同学通过测试的概率为 (A )0.648 (B )0.432 (C )0.36 (D )0.312 (5)已知M (x 0，y 0)是双曲线C ：=1 上的一点，F 1、F 2是C 的两个焦点，若12MF MF ⋅＜0，则y 0的取值范围是(A )(－33，33) (B )(－36，36) (C )(223-，223) (D )(233-，233) (6)《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题:“今有委米依垣内角，下周八尺，高五尺.问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图，米堆为一个圆锥的四分之一)，米堆底部的弧度为8尺，米堆的高为5尺，问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺，圆周率约为3，估算出堆放的米约有(A )14斛 (B )22斛 (C )36斛 (D )66斛 (7)设D 为ABC 所在平面内一点,3BC CD =，则(A ) 1433AD AB AC =-+ (B ) 1433AD AB AC =- (C ) 4133AD AB AC =+ (D ) 4133AD AB AC =-(8)函数f （x ）=cos （ωx+ϕ）的部分图像如图所示，则f (x )的单调递减区间为A ．（k π﹣，k π+，），k ∈z B ．（2k π﹣，2k π+），k ∈z C ．（k ﹣，k+），k ∈zD ．（，2k+），k ∈z(9)执行右面的程序框图，如果输入的t ＝0.01，则输出的n ＝(A )5 (B )6 (C )7 (D )8（10）25()x x y ++的展开式中，52x y 的系数为(A )10 (B )20 (C )30 (D )60（11）圆柱被一个平面截去一部分后与半球(半径为r )组成一个几何体，该几何体三视图中的正视图和俯视图如图所示.若该几何体的表面积为16 ＋ 20π，则r ＝(A )1 (B )2 (C )4 (D )812.设函数f (x )＝e x (2x －1)－ax ＋a ,其中a 1,若存在唯一的整数x 0，使得f (x 0)0，则a 的取值范围是( )A .[32e -，1) B . [33,24e -) C . [33,24e ) D . [32e，1)二、填空题：本大题共4小题，每小题5分 (13)若函数f (x )＝xln (x ＋2a x +)为偶函数，则a ＝ . (14)一个圆经过椭圆=1的三个顶点，且圆心在x 轴的正半轴上，则该圆的标准方程为 ______________________ .(15)若x ，y 满足约束条件10040x x y x y -≥⎧⎪-≤⎨⎪+-≤⎩，则y x 的最大值为 .(16)在平面四边形ABCD 中，∠A ＝∠B ＝∠C ＝75°，BC ＝2，则AB 的取值范围是 ______________________ .三.解答题：解答应写出文字说明，证明过程或演算步骤.(17)(本小题满分12分) S n 为数列{a n }的前n 项和.已知a n >0，2243n n n a a S +=+ (Ⅰ)求{a n }的通项公式；(Ⅱ)设 11n n n b a a +=，求数列}的前n 项和.(18) (本小题满分12分)如图,四边形ABCD 为菱形,∠ABC ＝120°E ，F 是平面ABCD 同一侧的两点，BE ⊥平面ABCD ，DF ⊥平面ABCD ，BE ＝2DF ，AE ⊥EC .(Ⅰ)证明：平面AEC ⊥平面AFC ;(Ⅱ)求直线AE 与直线CF 所成角的余弦值.(19) (本小题满分12分)某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费x (单位：千元)对年销售量y (单位：t )和年利润z (单位：千元)的影响，对近8年的年宣传费x i 和年销售量y i (i ＝1，2，···，8)数据作了初步处理，得到下面的散点图及一些统计量的值.xyw821()ii x x =-∑821()ii w w =-∑81()()iii x x y y =--∑ 81()()i ii w w yy =--∑46.6 563 6.8289.8 1.6 1469 108.8表中i i w x =8118i i w w ==∑(Ⅰ)根据散点图判断，y ＝a ＋bx 与y ＝c ＋x y 关于年宣传费x 的回归方程类型？(给出判断即可，不必说明理由)(Ⅱ)根据(Ⅰ)的判断结果及表中数据，建立y 关于x 的回归方程；(Ⅲ)已知这种产品的年利润z 与x ，y 的关系为z ＝0.2y －x .根据(Ⅱ)的结果回答下列问题：（ⅰ）年宣传费x ＝49时，年销售量及年利润的预报值是多少？（ⅱ）年宣传费x 为何值时，年利润的预报值最大？附：对于一组数据(u 1 v 1)，(u 2 v 2)…….. (u n v n )，其回归线v ＝αβ+u 的斜率和截距的最小二乘估计分别为：121()(),()niii nii u u v v v u u u βαβ==--==--∑∑A B C F E D(20)(本小题满分12分)在直角坐标系xoy 中，曲线C ：y ＝24x 与直线y ＝kx ＋a (a >0)交于M ，N 两点.(Ⅰ)当k ＝0时，分别求C 在点M 和N 处的切线方程；(Ⅱ)y 轴上是否存在点P ，使得当k 变动时，总有∠OPM ＝∠OPN ？说明理由.(21)(本小题满分12分)已知函数f (x )＝31,()ln 4x ax g x x ++=- .(Ⅰ)当a 为何值时，x 轴为曲线()y f x = 的切线；(Ⅱ)用min {},m n 表示m ，n 中的最小值，设函数}{()min (),()(0)h x f x g x x => ，讨论h (x )零点的个数.请考生在(22)、(23)、(24)三题中任选一题作答.如果多做，则按所做第一个题目计分. (22)(本题满分10分)选修4－1：几何证明选讲如图，AB 是⊙O 的直径，AC 是⊙O 的切线，BC 交⊙O 于点E ．（Ⅰ）若D 为AC 的中点，证明：DE 是⊙O 的切线；（Ⅱ）若OA= CE ，求∠ACB 的大小．(23)(本小题满分10分)选修4－4：坐标系与参数方程在直角坐标系xOy 中，直线1C : x ＝－2，圆2C ：(x －1)2＋(y －2)2＝1，以坐标原点为极点， x 轴的正半轴为极轴建立极坐标系. （Ⅰ）求1C ，2C 的极坐标方程；（Ⅱ）若直线3C 的极坐标方程为()4R πθρ=∈，设2C 与3C 的交点为M ，N ，求△C 2MN 的面积 .(24)(本小题满分10分)选修4—5：不等式选讲已知函数＝|x ＋1|－2|x －a |，a >0.(Ⅰ)当a ＝1时，求不等式f (x )>1的解集；(Ⅱ)若f (x )的图像与x 轴围成的三角形面积大于6，求a 的取值范围.2015年普通高等学校招生全国统一考试（新课标I ）理科数学答案一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的。

【恒心】2015届广东省13市高三上学期期末考试数学理试题分类汇编---导数及其应用【纯word精品版】

2015届广东省13市高三上学期期末考试数学理试题分类汇编导数及其应用整理：李炳璋一、填空题1、（潮州市2015届高三）曲线323y x x =-+在点1x =处的切线方程为2、（揭阳市2015届高三）函数()1x f x e =-的图象与x 轴相交于点P ，则曲线在P 处的切线方程是3、（深圳市2015届高三）设P 是函数x y ln =图象上的动点，则点P 到直线x y =的距离的最小值为4、（珠海市2015届高三）已知函数()f x 的导函数为()f x '，且满足3()=(2)f x x x f '-⋅，则函数()f x 在点（2，(2)f ）处的切线方程为二、解答题1、（潮州市2015届高三）已知函数()ln f x x a x =-，()1ag x x+=-（R a ∈）．（1）若1a =，求函数()f x 的极值；（2）设函数()()()h x f x g x =-，求函数()h x 的单调区间；（3）若在[]1,e （ 2.718e =⋅⋅⋅）上存在一点0x ，使得()()00f x g x <成立，求a 的取值范围．2、（佛山市2015届高三）已知函数()()ln x a f x x-=. （1）若1a =-,证明:函数()f x 是()0,+∞上的减函数；（2）若曲线()y f x =在点()()1,1f 处的切线与直线0x y -=平行,求a 的值；（3）若0x >,证明:()ln 1e 1x x xx +>-(其中e 2.71828=⋅⋅⋅是自然对数的底数).3、（广州市2015届高三）已知函数()2ln af x x x x=--，a ∈R . （1）讨论函数()f x 的单调性;（2）若函数()f x 有两个极值点1x ,2x , 且12x x <, 求a 的取值范围;（3）在（2）的条件下, 证明:()221f x x <-.4、（惠州市2015届高三）已知函数()(0)tf x x x x=+>，过点(1,0)P 作曲线()y f x =的两条切线PM ，PN ，切点分别为M ，N ．（1）当2t =时，求函数()f x 的单调递增区间；（2）设()g t MN =，求函数()g t 的表达式；（3）在（2）的条件下，若对任意的正整数n ，在区间642,n n ⎡⎤+⎢⎥⎣⎦内，总存在1m +个数121,,,,,m m a a a a +使得不等式121()()()()m m g a g a g a g a ++++<成立，求m 的最大值．5、（江门市2015届高三）已知函数1)(23-+=ax x x f （R a ∈是常数）．（1）设3-=a ，1x x =、2x x =是函数)(x f y =的极值点，试证明曲线)(x f y =关于点) )2( , 2(2121x x f x x M ++对称；（2）是否存在常数a ，使得] 5 , 1 [-∈∀x ，33|)(|≤x f 恒成立？若存在，求常数a 的值或取值范围；若不存在，请说明理由．（注：曲线)(x f y =关于点M 对称是指，对于曲线)(x f y =上任意一点P ，若点P 关于M 的对称点为Q ，则Q 在曲线)(x f y =上．）6、（揭阳市2015届高三）若实数x 、y 、m 满足||||-≤-x m y m ，则称x 比y 更接近m . （1）若23-x 比1更接近0，求x 的取值范围；（2）对任意两个正数a 、b ，试判断2()2+a b 与222+a b 哪一个更接近ab ？并说明理由；（3）当2≥a 且1≥x 时，证明：ex比+x a 更接近ln x .7、（清远市2015届高三）设函数()ln(1),()ln(1)1xf x a xg x x bx x=-+=+-+. （1）若函数()f x 在0x =处有极值，求函数()f x 的最大值；（2）①若b 是正实数，求使得关于x 的不等式()0g x <在()0,+∞上恒成立的b 取值范围； ②证明：不等式.)*(21ln 112N n n k knk ∈≤-+∑=．8、（汕头市2015届高三）已知函数R k k x x k x x x f ∈-+++++=]2)()[(log )(2222，（1）求函数)(x f 的定义域D （用区间表示）；（2）当2-<k 时，求函数)(x f 的单调递增区间．9、（汕尾市2015届高三）已知函数2()()x f x x bx b e =++的极值点为23x =-和1x =．（1）当1b =时，求函数()f x 的增区间；（2）当02b <≤时，求函数()f x 在[2,]b b -上的最大值．10、（韶关市2015届高三）已知函数()ln f x x a x =-，1()g x x=-，a R ∈；（1）设()()()h x f x g x =+，若()h x 在定义域内存在极值，求a 的取值范围；（2）设'()f x 是()f x 的导函数，若120x x <<，0a ≠，2121()()()f x f x f t x x -'=-12()x t x <<，求证：122x x t +<．11、（深圳市2015届高三）已知定义在]2,2[-上的奇函数)(x f 满足：当]2,0(∈x 时，)2()(-=x x x f ．（1）求)(x f 的解析式和值域；（2）设a ax x x g 2)2ln()(--+=，其中常数0>a ． ①试指出函数))(()(x f g x F =的零点个数；②若当11k+是函数))(()(x f g x F =的一个零点时，相应的常数a 记为k a ，其中1,2,,k n =．证明：1276n a a a +++<（*N ∈n ）．12、（珠海市2015届高三）已知函数21()ln (1)2f x a x x a x =+-+．（1）求函数()f x 的单调区间；（2）证明：m n N +∈、时，1111()[]ln()ln(1)ln(2)ln(1)m m n n m n m n m n m +++++>++-+-+．参考答案一、填空题1、3x -y -1=02、y x =-3、224、6160x y --= 二、解答题1、解：（1）()ln f x x a x =-的定义域为(0,)+∞． …………………1分当1a =时，()ln f x x x =-，11()1x f x x x-'=-=． ………………2分由'()0f x =，解得1x =.当01x <<时，'()0f x <，()f x 单调递减；当1x >时，'()0f x <，()f x 单调递增；所以当1x =时，函数()f x 取得极小值，极小值为(1)1ln11f =-=；……..4分（2）1()()()ln ah x f x g x x a x x+=-=-+，其定义域为(0,)+∞．又22221(1)(1)[(1)]'()1a a x ax a x x a h x x x x x +--++-+=--==．…………..5分①当10a +≤，即1a ≤-时，在(0,)x ∈+∞上'()0h x >，所以，函数()h x 在(0,)+∞上单调递增.…………6分 ②当10a +>，即1a >-时，在(0,1)x a ∈+上'()0h x <，在(1,)x a ∈++∞上'()0h x >，所以()h x 在(0,1)a +上单调递减，在(1,)a ++∞上单调递增；……………..……7分综上所述：当1a >-时，()h x 的递减区间为(0,1)a +；递增区间为(1,)a ++∞．当1a ≤-时，()h x 只有递增区间为(0,)+∞．…………………………….8分（3）若在[1,]e 上存在一点0x ，使得00()()f x g x <成立，即在[1,]e 上存在一点0x ，使得0()0h x <．则函数1()ln ah x x a x x+=-+在[1,]e 上的最小值小于零．…………………9分 ①当1a e +≥，即1a e ≥-时，由（2）可知()h x 在[1,]e 上单调递减．故()h x 在[1,]e 上的最小值为()h e ，由1()0a h e e a e+=+-<，可得211e a e +>-．因为2111e e e +>--．所以211e a e +>-； …………………………………10分 ②当11a +≤，即0a ≤时，由（2）可知()h x 在[1,]e 上单调递增．故()h x 在[1,]e 上最小值为(1)h ，由(1)110h a =++<，可得2a <-（满足0a ≤）；………………………………………………..…11分 ③当11a e <+<，即01a e <<-时，由（2）可知可得()h x 在[1,]e 上最小值为(1)2ln(1)h a a a a +=+-+．因为0ln(1)1a <+<，所以，0ln(1)a a a <+<．∴2ln(1)2a a a +-+>，即(1)2h a +>不满足题意，舍去．…..…………13分综上所述得2a <-，或211e a e +>-．∴实数a 的取值范围为21(,2)(,)1e e +-∞-+∞-．……………………….……14分 2、（1）当1a =-时,函数()f x 的定义域是()()1,00,-+∞,………………1分对()f x 求导得()()2ln 11xx x f x x-++'=,………………………………………………2分令()()ln 11xg x x x =-++,只需证:0x >时,()0g x ≤. 又()()()22110111xg x x x x '=-=-<+++,………………………………3分故()g x 是()0,+∞上的减函数,所以()()0ln10g x g <=-=…………………………5分所以()0f x '<,函数()f x 是()0,+∞上的减函数. ………………………………………6分（2）由题意知,()11x f x ='=,…………………………………………7分即()1ln 111a a --=-,()ln 101a a a--=-…………………………………8分令()()ln 1,11a t a a a a =--<-,则()()211011t a a a '=+>--,……………………9分故()t a 是(),1-∞上的增函数,又()00t =,因此0是()t a 的唯一零点,即方程()ln 101aa a--=-有唯一实根0,所以0a =,…………………………………10分 [说明]利用两函数1xy x=-与()ln 1y x =-图象求出0a =(必须画出大致图象),同样给至10分.（3）因为()ln e 11ln e e 1e 1e 1x x x x x x -+==---,故原不等式等价于()()ln e 11ln 1e 1xxx x -++>-,…11分由（1）知,当1a =-时,()()ln 1x f x x+=是()0,+∞上的减函数,………………………12分故要证原不等式成立,只需证明:当0x >时,e 1xx <-,令()e 1x h x x =--,则()e 10x h x '=->,()h x 是()0,+∞上的增函数,……………13分所以()()00h x h >=,即e 1xx <-,故()()1e x f x f >-,即()()ln e 11ln 1e 1e 1xx xx x x -++>=--…………………………………………………………14分3、（1）解: 函数()2ln af x x x x=--的定义域为()0,+∞, ()222221a x x af x x x x-+'=+-=, ………………………………………………1分令()0f x '=, 得220x x a -+=, 其判别式44a ∆=-,① 当0∆≤,即1a ≥时, 220x x a -+≥,()0f x '≥, 此时,()f x 在()0,+∞上单调递增;………………………2分② 当0∆>, 即1a <时, 方程220x x a -+=的两根为111x a =--,2111x a =+->,………………………3分若0a ≤, 则10x ≤, 则()20,x x ∈时, ()0f x '<, ()2,x x ∈+∞时, ()0f x '>,此时, ()f x 在()20,x 上单调递减, 在()2,x +∞上单调递增; ………………………4分若0a >,则10x >, 则()10,x x ∈时, ()0f x '>,()12,x x x ∈时, ()0f x '<,()2,x x ∈+∞时, ()0f x '>,此时, ()f x 在()10,x 上单调递增, 在()12,x x 上单调递减, 在()2,x +∞上单调递增. ……5分综上所述, 当0a ≤时, 函数()f x 在()20,x 上单调递减, 在()2,x +∞上单调递增; 当01a <<时, 函数()f x 在()10,x 上单调递增, 在()12,x x 上单调递减, 在()2,x +∞上单调递增;当1a ≥时, 函数()f x 在()0,+∞上单调递增. ………………………6分（2）解:由（1）可知, 函数()f x 有两个极值点1x ,2x ,等价于方程220x x a -+=在()0,+∞有两不等实根, 故01a <<. ………………………7分（3）证明: 由（1）, （2）得01a <<, 211x a =+-, 且212x <<, 2222a x x =-+. ………8分 ()22222222222212ln 12ln 1x x f x x x x x x x x -+-+=---+=--, …………………9分令()2ln 1g t t t =--, 12t <<, 则()221t g t t t-'=-=, ………………………………………………10分由于12t <<, 则()0g t '<, 故()g t 在()1,2上单调递减. ………………………11分故()()112ln110g t g <=--=. ………………………………………………12分 ∴()()22210f x x g x -+=<. ………………………………………………13分 ∴()221f x x <-. ………………………………………………14分 4、解：（1）当2t =时，2(),f x x x =+22222()10x f x x x-'=-=> --------1分解得(,2)(2,)x ∈-∞-+∞.------------------------------------------2分因为0x >所以函数()f x 有单调递增区间为)2,⎡+∞⎣--------------3分（2）设M ，N 两点的横坐标分别为1x 、2x ，2()1tf x x '=-所以切线PM 的方程为：11211()(1)().t ty x x x x x -+=-----------------4分所以切线PM 过点(1,0)P ，所以有112110()(1)(1).t tx x x x -+=--即21120.x tx t +-=……①同理，由切线PN 过点(1,0)P ，，得22220.x tx t +-=…… ②---------------5分由（1）、（2），可得212,20x x x tx t +-=是方程的两根，12122.x x t x x t +=-⎧∴⎨⋅=-⎩…… ③ -------------------------------------------------------------7分 22221212121212||()()()[1(1)]t t t MN x x x x x x x x x x =-++--=-+- 22121212[()4][1(1)]t x x x x x x =+-+--------------------------------------------8分把③式代入，得2||2020,MN t t =+因此，函数()g t 的表达式为2()2020g t t t =+ ----------------9分（3）易知()g t 在区间642,n n ⎡⎤+⎢⎥⎣⎦上为增函数， (2)()(1,2,,1).i g g a i m ∴≤=+则12(2)()()().m m g g a g a g a ⋅≤+++121()()()()m m g a g a g a g a ++++<n ∀恒成立，所以不等式64(2)()m g g n n⋅<+n ∀恒成立， 22646420220220()20(),m n n n n⨯+⨯<+++ 即216464[()()]6m n n n n<+++n ∀恒成立，--------------------------------12分 226416464113616,[()()][1616].663n n n n n n +≥∴+++≥+= 1363m ∴<，由于m 为正整数，6m ∴≤. --------------------------------------13 分又当6m =，存在1212,16,m m a a a a +=====任意的正整数n 满足条件因此，m 的最大值为6. --------------------------------------------------------14分5、证明与求解：⑴13)(23--=x x x f ，x x x f 63)(2/-=……1分解0)(/=x f 得01=x ，22=x ……2分，) )2( , 2 (2121x x f x x M ++即) 3 , 1(-M ……3分曲线)(x f y =上任意一点)13 , (20300--x x x P 关于M 对称的点为) 53 , 2(20300-+--x x x Q ……4分直接计算知，531)2(3)2()2(203020300-+-=----=-x x x x x f ，点Q 在曲线)(x f y =上，所以，曲线)(x f y =关于点M 对称……5分⑵（方法一）33|)(|≤x f 即33|1|23≤-+ax x ，3313323≤-+≤-ax x ……6分 0=x 时，不等式恒成立……7分；0≠x 时，不等式等价于23233432xx a x x -≤≤+-……8分作22313232)(x x x x x g --=+-=，22323434)(xx x x x g +-=-=，3/1641)(x x g +-=，3/2681)(xx g --=……9分，解0)(/1=x g 、0)(/2=x g 得41=x 、3268-=x ……10分x )0 , 1 [- )4 , 0( 4] 5 , 4( )(/1x g －＋ 0 － )(1x g↘ ↗ 极大值 ↘ )(/2x g ＋－－－ )(2x g↗↘↘……12分31)1(1-=-g ，6)4(1-=g ，23132)(xx x g +-=在]5 , 0()0 , 1[ -的最大值为6-；35)(2=-g ，2591)5(2-=g ，23234)(xx x g -=在]5 , 0()0 , 1[ -的最小值为2591-……13分综上所述，a 的取值范围为]2591, 6[--……14分（方法二）ax x x f 23)(2/+=，0=a 时，1)(3-=x x f 不符合题意，∴0≠a ，解0)(/=x f 得01=x ，322ax -=……6分当]5 , 1[322-∉-=ax 时，)(x f 在]5 , 1[-内的极值点为1x ……7分，33|)(|≤x f 当且仅当⎪⎪⎪⎩⎪⎪⎪⎨⎧≤≤-≤-<->-33|)5(|33|)1(|33|)0(|132532f f f a a 或……8分，即⎪⎪⎩⎪⎪⎨⎧≤+≤->-<33|12425|33|2|23215a a a a 或……9分，解集为空集φ……10分当]5 , 1[322-∈-=ax )(x f 在]5 , 1[-内的极值点为1x 、2x ……11分，33|)(|≤x f 当且仅当⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧≤≤-≤-≤≤-≤-33|)5(|33|)1(|33|)32(|33|)0(|5321f f a f f a (12)分，即⎪⎪⎪⎩⎪⎪⎪⎨⎧≤+≤-≤-≤≤-33|12425|33|2|33|1274|232153a a a a (13)分，解集为]2591 , 6[--，∵]2591 , 6[]2591 , 6[--=--φ ，∴a 的取值范围为]2591, 6[--……14分 6、解：（1）依题意可得2|3|1x -≤ ------------------------------------------------1分2131x ⇔-≤-≤22x ⇔-≤≤-或22≤≤x∴x 的取值范围为[2,2][2,2].--⋃---------------------------------------------3分（2）解法一：∵222|()|||22a b a b ab ab ++---22()()||||42a b a b --=----------------5分 22()()42a b a b --=-2()0,4a b -=-≤---------------------------------------------6分即222|()|||,22++-≤-a b a b ab ab ∴2()2+a b 比222+a b 更接近ab ；--------------------------------------------------7分【解法二：∵对任意两个正数a 、b ，有2(),2+≥a b ab 222+≥a b ab ，------------------4分 ∴2222222()|()|||()0,22224++++----=-=-≤a b a b a b a b a b ab ab 即222|()|||,22++-≤-a b a b ab ab ------------------------------------------------6分 ∴2()2+a b 比222+a b 更接近ab ；-------------------------------------------------7分】（3）令()ln ,()ln ,=-=+-ep x x q x x a x x则()p x 在区间[1,)+∞上单调递减，且()0,=p e由11()1,-'=-=x q x x x得当1x ≥时，()0,q x '≥ ∴()q x 在[1,)+∞上单调递增，且当1x ≥时，有()(1)0.q x q ≥=-----------------------8分 ①当1≤≤x e 时，∵()p x ≥0，2a ≥， ∴|()||()|ln (ln )120.e ep x q x x x a x x a e x x-=--+-=--≤--< ∴ex比+x a 更接近ln x .--------------------------------------------------------10分 ②当>x e 时，解法一：∵()p x <0，()0.q x >,∴|()||()|ln (ln )2ln 2ln 2.-=--+-=---<--e ep x q x x x a x x x a x x x x----------12分令()2ln 2,=--f x x x 则22()1.-'=-=xf x x x当>x e 时，()0.'<f x ∴()f x 在区间(,)+∞e 单调递减，当>x e 时，()()0.<=-<f x f e e ------------------13分综上可知，当1≥x 时，|ln ||ln |0.--+-≤e x x a x x 即|ln ||ln |.-≤+-ex x a x x∴ex比+x a 更接近ln x .--------------------------------------------------------14分【解法二：当>x e 时，∵()p x <0，()0.q x > ∴|()||()|ln (ln )2ln .-=--+-=---e ep x q x x x a x x x a x x-----------------------11分令()2ln =---e f x x x a x ，则22222()1.--'=-+=-e x x ef x x x x令'()0f x =，解得1211,11x e x e =++=-+，∵>x e ∴211x e =-+不合舍去，-------------------------------------------12分 ∵2(1)1,e e -<+ ∴11e e -<+ ∴1x e > ∵当1e x x <<时，()0.'>f x 当1x x >时，()0.'<f x∴()f x 在区间1(,)e x 单调递增，在1(,)x +∞单调递减，又13e x << ∴当>x e 时，1111()()2ln 2ln 320.ef x f x x x a e x ≤=---<--<------------------13分综上可知，当1≥x 时，|ln ||ln |0.--+-≤e x x a x x 即|ln ||ln |.-≤+-ex x a x x∴ex比+x a 更接近ln x .-------------------------------------------------------14分】7、解：（1）由已知得：()21()11a f x xx '=-++， ………1分又∵函数()f x 在0x =处有极值 ∴()21(0)01010af '=-=++，即1a = ……2分 ∴()ln(1),1x f x x x =-++ ()()2211()111x f x x x x -'=-=+++ ………3分 ∴,当()1,0x ∈-时，()0f x '>，()f x 单调递增；当()0,x ∈+∞时，()0f x '<，()f x 单调递减；………4分（或者列表） ∴函数()f x 的最大值为(0)0f =………5分（2）①由已知得：1()1g x b x'=-+………6分 (i)若1b ≥，则[)0,x ∈+∞时，1()01g x b x'=-≤+ ∴()ln(1)g x x bx =+-在[)0,+∞上为减函数，∴()ln(1)(0)0g x x bx g =+-<=在()0,+∞上恒成立； ………7分 (ii)若0b ≤，则[)0,x ∈+∞时，1()01g x b x'=->+ ∴()ln(1)g x x bx =+-在[)0,+∞上为增函数，∴()ln(1)(0)0g x x bx g =+->=，不能使()0g x <在()0,+∞上恒成立；…8分 (iii)若01b <<，则1()01g x b x '=-=+时，11x b =-，当10,1x b ⎡⎫∈-⎪⎢⎣⎭时，()0g x '≥，∴()ln(1)g x x bx =+-在10,1b ⎡⎫-⎪⎢⎣⎭上为增函数，此时()ln(1)(0)0g x x bx g =+->=，∴不能使()0g x <在()0,+∞上恒成立；9分综上所述，b 的取值范围是[)+∞,1. ………10分 ②由以上得：ln(1)(0)1xx x x x<+<>+, ………11分取1x n=得：111ln(1)1n n n <+<+ ………12分令21ln 1nn k kx n k ==-+∑， ………13分则112x =，()1222111ln 101111n n n n x x n n n n n n-⎛⎫-=-+<-=-< ⎪+-++⎝⎭. 因此1112n n x x x -<<⋅⋅⋅<=. ∴)*(21ln 112N n n k knk ∈≤-+∑= ………14分 8、解：（Ⅰ）由题意可知：R k k x x k x x ∈>-+++++02)()(222令k x x t ++=2，则原不等式可以化为：022>-+t t ，解得：2-<t 或1>t即原不等式可以化为不等式①022<+++k x x 或不等式②012>-++k x x ……1分对于不等式①、②分别有:741--=∆k 与542+-=∆k 现做如下分类讨论：（1）当47-<k 时，01>∆，02>∆，此时不等式①、②对应的方程分别有不等根： 27411----=k x 与27412--+-=k x ；25413+---=k x 与25414+-+-=k x ；不难证明：4213x x x x <<<所以不等式①的解集为(,2741----∈k x )2741--+-k …………2分所以不等式②的解集为()2541,+---∞-∈k x ()∞++-+-,2541k …..3分所以当47-<k 时，函数)(x f 的定义域D =()2541,+---∞-k (,2741----k )2741--+-k ()∞++-+-,2541k ………….4分（2）当4547≤≤-k 时，01≤∆，02≥∆，结合（1）可知：不等式①的解集为Φ∈x 分 …………..5分不等式②的解集为()2541,+---∞-∈k x ()∞++-+-,2541k所以当4547≤≤-k 时，函数)(x f 的定义域 D =()2541,+---∞-k()∞++-+-,2541k …………..6分（3）当45>k 时，01<∆，02<∆，结合（1）可知：不等式①的解集为Φ∈x ；不等式②的解集为R x ∈所以当45>k 时，函数)(x f 的定义域D =R …………..7分综上所述：（1）当47-<k 时，函数)(x f 的定义域 D =()2541,+---∞-k (,2741----k )2741--+-k()∞++-+-,2541k（2）当4547≤≤-k 时，函数)(x f 的定义域 D =()2541,+---∞-k()∞++-+-,2541k（3）当45>k 时，函数)(x f 的定义域D =R …………..8分（Ⅱ）由（Ⅰ）知道：当2-<k 时，函数)(x f 的定义域D =()2541,+---∞-k(,2741----k )2741--+-k ()∞++-+-,2541k ………….9分令=)(x u 02)()(222>-+++++k x x k x x （2-<k ）,D x ∈则函数u y 2log =，显然函数u y 2log =在对应的定义域区间为单调递增函数，要求)(x f 的单调递增区间，我们只需要求出函数)(x u 在D x ∈上的单调递增区间。

广东省实验中学2015届高三第一次阶段考试数学(理) Word版含答案

广东实验中学2015届高三阶段考试（一）理科数学一．选择题(5*8=40分)1．设集合A ＝{(x ，y )|x 24＋y 216＝1}，B ＝{(x ，y )|y ＝3x }，则A ∩B 的子集的个数是( )A ．4B ．3C ．2D ．1 2． 22log sinlog cos1212ππ+的值为（）A .-2B .–l C. 12D .13．已知x ，y ∈R ，则“1x y +=”是“14xy ≤”的（） A ．充分不必要条件 B ．必要不充分条件 C ．充要条件 D ．既不充分也不必要条件 4．已知函数cos21()sin 2x f x x-=，则有（）A ．函数()f x 的图像关于直线2x π=对称 B ．函数()f x 的图像关关于点(,0)2π对称C ．函数()f x 的最小正周期为2πD ．函数()f x 在区间(0,)π内单调递减5．已知0<a<b<l ．则（） A.11b a > B. 11()()22a b < C. 22(lg )(lg )a b < D. 11lg lg a b>6．已知函数 2()2cos f x x x =+，若 '()f x 是 ()f x 的导函数，则函数 '()f x 在原点附近的图象大致是（）A B C D7.已知函数213,1()log , 1x x x f x x x ⎧-+≤⎪=⎨>⎪⎩ ，若对任意的R x ∈，不等式23()4f x m m ≤-恒成立，则实数m 的取值范围是（） 111.(,].(,][1,).[1,).[,1]444A B C D -∞--∞-+∞+∞-8．已知关于x 的方程cos xk x=在(0,)+∞有且仅有两根，记为,()αβαβ<，则下列的四个命题正确的是（）A ．2sin 22cos ααα= B ．2cos 22sin ααα= C ．2sin 22sinβββ=- D ．2cos22sin βββ=-二．填空题（6*5=30分）（一）必做题：第9、10、11、12、13题为必做题，每道试题考生都必须作答。

广东省深圳市2015届高三第一次调研考试数学理试题-Word版含答案

2015年深圳市高三年级第一次调研考试数学(理科)试题一、选择题：本大题共8小题，每题5分，总分值40分。

在每题给出的四个选项中，只有一项是符合题目要求的。

1、已知集合}5,1,0,2{=U ，集合}2,0{=A ，则A C U ＝〔〕 A.φ B 。

}2,0{ C 。

}5,1{ D 。

}5,1,0,2{ 2、已知复数z 满足1)1(=+i z 〔其中i 为虚数单位〕，则=z 〔〕 A.21i +- B 。

21i -- C 。

21i+ D 。

21i -3、假设函数b a y x+=的部分图象如图1所示，则A.01,10<<-<<b a B 。

10,10<<<b a D 。

10,1<<>b a4、已知实数y x ,满足不等式组300≤⎪⎩⎪⎨⎧≥≥+y x y x ，则y x +2的最大值为〔〕A.3 B 。

4 C 。

6 D 。

95、已知直线b a ,，平面βα,，且α⊥a ，β⊂b ，则“b a ⊥”是“βα//”的〔〕 A.6、执行如图2所示的程序框图，则输出S 的值为〔〕 A. 16 B 。

25 C 。

36 D 。

497、在ABC ∆中，c b a ,,分别为C B A ∠∠∠,,所对的边，假设函数1)(31)(2223+-+++=x ac c a bx x x f 有极值点，则B ∠的范围是〔〕A.)3,0(π B 。

]3,0(π C 。

],3[ππ D 。

),3(ππ8、如果自然数a 的各位数字之和等于8，我们称a 为“吉祥数”。

将所有“吉祥数”从小到大排成一列321,,a a a …，假设2015=n a ，则=n 〔〕A. 83 B 。

82 C 。

39 D 。

37二、填空题：本大题共7小题，考生作答6小题，每题5分，总分值30分。

本大题分为必做题和选做题两部分（一）必做题：第9、10、11、12、13题为必做题，每道试题考生必须做答。

广东省深圳市2014届高三2月第一次调研数学理试题(WORD精校版)

绝密★启用前试卷类型：A2014年深圳市高三年级第一次调研考试数学（理科） 2014．2本试卷共6页，21小题，满分150分．考试用时120分钟．注意事项：1．答卷前，考生首先检查答题卡是否整洁无缺损，监考教师分发的考生信息条形码是否正确；之后务必用0．5毫米黑色字迹的签字笔在答题卡指定位置填写自己的学校、姓名和考生号，同时，将监考教师发放的条形码正向准确粘贴在答题卡的贴条形码区，请保持条形码整洁、不污损．2．选择题每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案，答案不能答在试卷上．不按要求填涂的，答案无效． 3．非选择题必须用0．5毫米黑色字迹的签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上，请注意每题答题空间，预先合理安排；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液．不按以上要求作答的答案无效．4．作答选做题时，请先用2B 铅笔填涂选做题的题号对应的信息点，再做答．漏涂、错涂、多涂的答案无效．5．考生必须保持答题卡的整洁，考试结束后，将答题卡交回．参考公式：如果事件A B 、互斥，那么P A B P A P B +=+()()()；如果事件A B 、相互独立，那么P AB P A P B =()()()；若锥体的底面积为S ，高为h ，则锥体的体积为13V Sh =．一、选择题：本大题共8个小题；每小题5分，共40分．在每小题给出的四个选项中，有且只有一项是符合题目要求的． 1.已知集合{2,0,1,4}A =，集合{04,R}=<≤∈B x x x ，集合C A B = ．则集合C 可表示为A ．{2,0,1,4}B ． {1,2,3,4}C ．{1,2,4}D ． {04,R}x x x <≤∈2.复数z 满足(1i)1z -=（其中i 为虚数单位），则z =A ．11i22- B ．11i 22+ C ．11i 22-+ D ．11i 22-- 3．下列函数中，为奇函数的是A ．122xx y =+B ．{},0,1y x x =∈C ．sin y x x =⋅D ．1,00,01,0x y x x <⎧⎪==⎨⎪->⎩4．“1ω=”是“ 函数()cos f x x ω=在区间[]0,π上单调递减”的A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件5．执行如图1所示的程序框图，则输出的a 的值为（注：“2a =”，即为“2a ←”或为“:2a =”．） A ．2B ．13C ．12-D ．3-6．412x x -(的展开式中常数项为A ．12B ．12-C ．32D ．32-7．如图2，在矩形OABC 内：记抛物线21y x =+与直线1y x =+ 围成的区域为M （图中阴影部分）．随机往矩形OABC 内投一点P ，则点P 落在区域M 内的概率是A ．118B ．112C ．16 D ．138.在平面直角坐标系中，定义两点11(,)P x y 与22(,)Q x y 之间的“直角距离”为1212(,)d P Q x x y y =-+-．给出下列命题：（1）若(1,2)P ，(sin ,2cos )()Q R ααα∈，则(,)d P Q 的最大值为3 （2）若,P Q 是圆221x y +=上的任意两点，则(,)d P Q 的最大值为 (3) 若(1,3)P ，点Q 为直线2y x =上的动点，则(,)d P Q 的最小值为12．其中为真命题的是A ．（1）（2）（3）B ．（1）（2）C ．（1）(3)D ． (2)(3)二、填空题：本大题共7小题，考生作答6小题，每小题5分，满分30分．本大题分为必做题和选做题两部分．（一）必做题：第9、10、11、12、13题为必做题，每道试题考生都必须作答． 9．函数f x =()的定义域为．10．某几何体的三视图如图3所示，其正视图是边长为2的正方形，侧视图和俯视图都是等腰直角三角形，则此几何体的体积是． 11+图411.已知双曲线2222:1x y C a b -=与椭圆22194x y +=有相同的焦点，且双曲线C 的渐近线方程为2y x =±，则双曲线C 的方程为．12. 设实数,x y 满足,102,1,x y y x x ≤⎧⎪≤-⎨⎪≥⎩向量2,x y m =-()a ，1,1=-()b ．若// a b ，则实数m 的最大值为．13.在数列{}n a 中，已知24a =， 315a =，且数列{}n a n +是等比数列，则n a = ．（二）选做题：第14、15题为选做题，考生只能选做一题，两题全答的，只计算前一题的得分． 14.（坐标系与参数方程选做题）在直角坐标系xOy 中，以原点O 为极点，x 轴的正半轴为极轴建立极坐标系．若曲线1C的参数方程为,x t y =⎧⎪⎨=⎪⎩（t 为参数），曲线2C 的极坐标方程为sin cos 1ρθρθ-=-．则曲线1C 与曲线2C 的交点个数为________个．15．（几何证明选讲选做题）如图4，已知AB 是⊙O 的直径，TA是⊙O 的切线，过A 作弦//AC BT ，若4AC =，AT =，则AB = ．三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤． 16.（本小题满分12分）已知函数()sin(2)(0π)f x x ϕϕ=+<<的图像经过点π(,1)12．（1）求ϕ的值；（2）在ABC ∆中，A ∠、B ∠、C ∠所对的边分别为a 、b 、c ，若222a b c ab +-=，且π(2122A f +=．求sin B ．17.（本小题满分12分）某网络营销部门为了统计某市网友2013年11月11日在某淘宝店的网购情况，随机抽查了该市当天60名网友的网购金额情况，得到如下数据统计表（如图5（1））：若网购金额超过2千元的顾客定义为“网购达人”，网购金额不超过2千元的顾客定义为“非网购达人”，已知“非网购达人”与“网购达人”人数比恰好为3:2．（1）试确定x ，y ，p ，q 的值，并补全频率分布直方图（如图5(2)）．（2）该营销部门为了进一步了解这60名网友的购物体验，从“非网购达人”、“网购达人”中用分层抽样的方法确定10人，若需从这10人中随机选取3人进行问卷调查．设ξ为选取的3人中“网购达人”的人数，求ξ的分布列和数学期望．18．（本小题满分14分）如图6所示，平面ABCD ⊥平面BCEF ，且四边形ABCD 为矩形，四边形BCEF 为直角梯形，//BF CE ，BC CE ⊥，4DC CE ==，2BC BF ==．（1）求证：//AF 平面CDE ；（2）求平面ADE 与平面BCEF 所成锐二面角的余弦值；（3）求直线EF 与平面ADE 所成角的余弦值．19.（本小题满分14分）已知数列{}n a 的前n 项和为n S ，且满足24(1)(1)(2)(N )n n n S n a n *++=+∈．图5 (1)(2)AD BC FE图6（1）求1a ，2a 的值；（2）求n a ；（3）设1n n n b a +=，数列{}n b 的前n 项和为n T ，求证：34n T <．20.（本小题满分14分）如图7，直线:(0)l y x b b =+>，抛物线2:2(0)C y px p =>，已知点(2,2)P 在抛物线C 上，且抛物线C 上的点到直线l（1）求直线l 及抛物线C 的方程；（2）过点(2,1)Q 的任一直线（不经过点P ）与抛物线C 交于A 、B 两点，直线AB 与直线l 相交于点M ，记直线PA ，PB ，PM 的斜率分别为1k ，2k ， 3k ．问：是否存在实数λ，使得123k k k λ+=？若存在，试求出λ的值；若不存在，请说明理由．图7yM PB Qx AOl21．（本小题满分14分）已知函数2901xf x a ax =>+()() ．（1）求f x ()在122[,]上的最大值；（2）若直线2y x a =-+为曲线y f x =()的切线，求实数a 的值；（3）当2a =时，设1214122x x x ,⎡⎤∈⎢⎥⎣⎦…,,, ，且121414x x x =…+++ ，若不等式1214f x f x +f x λ≤…()+()+()恒成立，求实数λ的最小值．2014年深圳市高三年级第一次调研考试数学(理科)答案及评分标准说明：一、本解答给出了一种或几种解法供参考，如果考生的解法与本解答不同，可根据试题的主要考查内容比照评分标准制订相应的评分细则．二、对计算题当考生的解答在某一步出现错误时，如果后续部分的解答未改变该题的内容和难度，可视影响的程度决定给分，但不得超过该部分正确解答应得分数的一半；如果后续部分的解答有较严重的错误，就不再给分．三、解答右端所注分数，表示考生正确做到这一步应得的累加分数．四、只给整数分数，选择题和填空题不给中间分数．二、填空题：本大题每小题5分，满分30分．9． {2}x x ≥； 10． 83； 11．2214y x -=； 12．6；13．123n n -⋅-； 14．1； 15．三、解答题16．（本小题满分12分）已知函数()sin(2)(0π)f x x ϕϕ=+<<的图像经过点π(,1)12．（1）求ϕ的值；（2）在ABC ∆中，A ∠、B ∠、C ∠所对的边分别为a 、b 、c ，若222a b c ab +-=，且π()2122A f +=．求sin B ．解：（1）由题意可得π()112f =，即πsin()16ϕ+=． ……………………………2分 0πϕ<< ，ππ7π666ϕ∴<+<， ππ62ϕ∴+=， π3ϕ∴=． ……………………………………………………………5分（2）222a b c ab +-= ，2221cos 22a b c C ab +-∴==， ……………………………………………………7分sin C ∴==． …………………………………………8分由（1）知π()sin(2)3f x x =+，π(+)sin()cos 21222A f A A π∴=+==． ()0,A π∈ ，sin 2A ∴==， ……………………………10分又sin sin(π())sin()B A C A C =-+=+ ，1sin sin cos cos sin 222B A C A C ∴=+=+=．……………12分【说明】本小题主要考查了三角函数)sin()(ϕω+=x A x f 的图象与性质，三角恒等变换，以及余弦定理等基础知识，考查了简单的数学运算能力． 17．（本小题满分12分）某网络营销部门为了统计某市网友2013年11月11日在某淘宝店的网购情况，随机抽查了该市当天60名网友的网购金额情况，得到如下数据统计表（如图5（1））：若网购金额超过2千元的顾客定义为“网购达人”，网购金额不超过2千元的顾客定义为“非网购达人”，已知“非网购达人”与“网购达人”人数比恰好为3:2．（1）试确定x ，y ，p ，q 的值，并补全频率分布直方图（如图5(2)）．（2）该营销部门为了进一步了解这60名网友的购物体验，从“非网购达人”、“网购达人”中用分层抽样的方法确定10人，若需从这10人中随机选取3人进行问卷调查．设ξ为选取的3人中“网购达人”的人数，求ξ的分布列和数学期望．解：（1）根据题意，有39151860,182.39153x y y x +++++=⎧⎪⎨=⎪+++⎩+ 解得9,6.x y =⎧⎨=⎩ …………………2分0.15p ∴=，0.10q =．补全频率分布直方图如图所示． ………4分（2）用分层抽样的方法，从中选取10人，则其中“网购达人”有210=45⨯人，“非网购达人”有310=65⨯人． …………………6分故ξ的可能取值为0，1，2，3；03463101(0)6C C P C ξ=== ， 12463101(1)2C C P C ξ===，21463103(2)10C C P C ξ===，30463101(3)30C C P C ξ===．…………………………10分所以ξ的分布列为：01236210305E ξ∴=⨯+⨯+⨯+⨯=． ……………………12分 )【说明】本题主要考察读图表、分层抽样、概率、随机变量分布列以及数学期望等基础知识，考查运用概率统计知识解决简单实际问题的能力，数据处理能力． 18．（本小题满分14分）如图6所示，平面ABCD ⊥平面BCEF ，且四边形ABCD 为矩形，四边形BCEF 为直角梯形，//BF CE ，BC CE ⊥，4DC CE ==，2BC BF ==．（1）求证：//AF 平面CDE ；（2）求平面ADE 与平面BCEF 所成锐二面角的余弦值；（3）求直线EF 与平面ADE 所成角的余弦值．解：（法一）（1）取CE 中点为G ，连接DG 、FG ，//BF CG 且BF CG =，∴四边形BFGC 为平行四边形，则//BC FG 且BC FG =． …………2分四边形ABCD 为矩形， //BC AD ∴且BC AD =，//FG AD ∴且FG AD =，∴四边形AFGD 为平行四边形，则//AF DG ．DG ⊂ 平面CDE ，AF ⊄平面CDE ，//AF ∴平面CDE ． ……………………………………………………4分（2）过点E 作CB 的平行线交BF 的延长线于P ，连接FP ，EP ，AP ，////EP BC AD ，∴A ，P ，E ，D 四点共面．四边形BCEF 为直角梯形，四边形ABCD 为矩形，∴EP CD ⊥，EP CE ⊥，又 CD CE C = ， EP ∴⊥平面CDE ，∴EP DE ⊥，又平面ADE 平面BCEF EP =，∴DEC ∠为平面ADE 与平面BCEF 所成锐二面角的平面角．……………………7分 4DC CE ==，∴cos 2CE DEC DE ∠==．即平面ADE 与平面BCEF所成锐二面角的余弦值为2． ……………………9分 ADBCFE图6GAD BCF EP（3）过点F 作FH AP ⊥于H ，连接EH ，根据（2）知A ，P ，E ，D 四点共面，////EP BC AD ，∴BC BF ⊥，BC AB ⊥，又 AB BF B = ， BC ∴⊥平面ABP ， ∴B C F H ⊥，则FH EP ⊥．又 FH AP ⊥， FH ∴⊥平面ADE ．∴直线EF 与平面ADE 所成角为HEF ∠． ……………………………11分 4DC CE ==，2BC BF ==，∴0sin 45FH FP ==EF ==HE =，∴cos 2HE HEF EF ∠===．即直线EF 与平面ADE． ……………………………14分（法二）（1）四边形BCEF 为直角梯形，四边形ABCD 为矩形，∴BC CE ⊥，BC CD ⊥，又平面ABCD ⊥平面BCEF ，且平面ABCD 平面BCEF BC =，DC ∴⊥平面BCEF ．以C 为原点，CB 所在直线为x 轴，CE 所在直线为y CD 所在直线为z 轴建立如图所示空间直角坐标系．根据题意我们可得以下点的坐标：(2,0,4)A ，(2,0,0)B ，(0,0,0)C ，(0,0,4)D ，(0,4,0)E ，(2,2,0)F ，则(0,2,4)AF =-，(2,0,0)CB =． ………………2分BC CD ⊥ ，BC CE ⊥， CB ∴为平面CDE 的一个法向量．又0220(4)00AF CB ⋅=⨯+⨯+-⨯=，//AF ∴平面CDE ． …………………………………………………………4分（2）设平面ADE 的一个法向量为1111(,,)n x y z = ，则110,0.AD n DE n ⎧⋅=⎪⎨⋅=⎪⎩(2,0,0)AD =- ，(0,4,4)DE =-，∴11120440x y z -=⎧⎨-=⎩，取11z =，得1(0,1,1)n = ． ……………………………6分 DC ⊥ 平面BCEF ，∴平面BCEF 一个法向量为(0,0,4)CD =，设平面ADE 与平面BCEF 所成锐二面角的大小为α，则11cos 2CD n CD n α⋅===⋅ ．因此，平面ADE 与平面BCEF． …………………9分（3）根据（2）知平面ADE 一个法向量为1(0,1,1)n =，(2,2,0)EF =- ，1111cos ,2EF n EF n EF n ⋅∴<>===-⋅，………12分设直线EF 与平面ADE 所成角为θ，则1cos sin ,2EF n θ=<>= ．因此，直线EF 与平面ADE所成角的余弦值为2． ………………………14分【说明】本题主要考察空间点、线、面位置关系，二面角及三角函数及空间坐标系等基础知识，考查空间想象能力、运算能力和推理论证能力，考查用向量方法解决数学问题的能力． 19．（本小题满分14分）已知数列{}n a 的前n 项和为n S ，且满足24(1)(1)(2)(N )n n n S n a n *++=+∈．（1）求1a ，2a 的值；（2）求n a ；（3）设1n n n b a +=，数列{}n b 的前n 项和为n T ，求证：34n T <．解：（1）当=1n 时，有2114(11)(+1=1+2a a ⨯+）（），解得1=8a ．当=2n 时，有21224(21)(1)(22)a a a ⨯+++=+，解得2=27a ．……………2分（2）（法一）当2n ≥时，有2(2)4(1)1nn n a S n ++=+, ……………①211(1)4(1)n n n a S n--++=． …………………② ①—②得：221(2)(1)41n n n n a n a a n n-++=-+，即：331(1)=n n a n a n -+．…………5分 ∴1223333===1(1)(1)3n n n a a a a n n n --==+-…．∴ 3=(1)n a n +(2)n ≥．………………………………………8分另解：33333121333121(1)42(1)(1)3n n n n n a a a n n a a n a a a n n ---+=⋅⋅⋅⋅=⋅⋅⋅⋅=+- ．又当=1n 时，有1=8a ， ∴3=(1)n a n +． …………………………8分（法二）根据1=8a ，2=27a ，猜想：3=(1)n a n +． ………………………………3分用数学归纳法证明如下：（Ⅰ）当1n =时，有318(11)a ==+，猜想成立．（Ⅱ）假设当n k =时，猜想也成立，即：3=(1)k a k +．那么当1n k =+时，有2114(11)(1)(12)k k k S k a +++++=++，即：211(12)4(1)11k k k a S k +++++=++，………………………①又 2(2)4(1)1kk k a S k ++=+， …………………………②①-②得：22223111(3)(2)(3)(2)(1)4=2121k k k k k a k a k a k k a k k k k ++++++++=--++++，解，得33+1(2)(11)k a k k =+=++．∴当1n k =+时，猜想也成立．因此，由数学归纳法证得3=(1)n a n +成立．………………………………………8分（3） 211111=(1(11n n n b a n n n n n +=<=-+++))， .................................10分 ∴1231=n n n T b b b b b -+++++ (22222)11111=234(1)n n ++++++ (2)11111<22323(1)(1)n n n n +++++⨯⨯-+… 111111111=()()()()4233411n n n n +-+-++-+--+… 1113=4214n +-<+．………………………………………14分【说明】考查了递推数列的通项公式、数列裂项求和公式、放缩法证明不等式等知识，考查了学生的运算能力，以及化归与转化的思想． 20．（本小题满分14分）如图7，直线:(0)l y x b b =+>，抛物线2:2(0)C y px p =>，已知点(2,2)P 在抛物线C 上，且抛物线C 上的点到直线l（1）求直线l 及抛物线C 的方程；（2）过点(2,1)Q 的任一直线（不经过点P ）与抛物线C 交于A 、B 两点，直线AB 与直线l 相交于点M ，记直线PA ，PB ，PM 的斜率分别为1k ，2k ， 3k ．问：是否存在实数λ，使得123k k k λ+=？若存在，试求出λ的值；若不存在，请说明理由．解：（1）（法一）点(2,2)P 在抛物线C 上， 1p ∴=． ……………………2分设与直线l 平行且与抛物线C 相切的直线l '方程为y x m =+，由2,2,y x m y x =+⎧⎨=⎩ 得22(22)0x m x m +-+=， 22(22)448m m m ∆=--=- ，∴由0∆=，得12m =，则直线l '方程为12y x =+．两直线l 、l '间的距离即为抛物线C 上的点到直线l 的最短距离，图7yM PB Qx AOl∴=2b =或1b =-（舍去）．∴直线l 的方程为2y x =+，抛物线C 的方程为22y x =． …………………………6分（法二）点(2,2)P 在抛物线C 上， 1p ∴=，抛物线C 的方程为22y x =．……2分设2(,))2t M t t R ∈（为抛物线C 上的任意一点，点M 到直线l的距离为d =象，有202t t b -+>，21)21]d t b ∴=-+-，t R ∈ ，d ∴4=，解得2b =．因此，直线l 的方程为2y x =+，抛物线C 的方程为22y x =．…………………6分（2）直线AB 的斜率存在，∴设直线AB 的方程为1(2)y k x -=-，即21y kx k =-+，由221,2,y kx k y x =-+⎧⎨=⎩ 得22420ky y k --+=，设点A 、B 的坐标分别为11(,)A x y 、22(,)B x y ，则122y y k +=，1224k y y k-=， 11121112222222y y k y x y --===-+- ，2222k y =+， …………………………9分 121212121222+82()82242242222()4324y y k k k k k y y y y y y k k⋅+++∴+=+===-++++++⋅+.…10分由21,2,y kx k y x =-+⎧⎨=+⎩ 得211M k x k +=-，411M k y k -=-，∴341221121321k k k k k k --+-==+--， ……………………………………………13分 1232k k k ∴+=．因此，存在实数λ，使得123k k k λ+=成立，且2λ=．…………………………14分【说明】本题主要考查抛物线的方程与性质、直线方程、直线与抛物线的位置关系，切线方程，点到直线距离，最值问题等基础知识，考查学生运算能力、推理论证以及分析问题、解决问题的能力，考查数形结合、化归与转化思想． 21．（本小题满分14分）已知函数2901xf x a ax=>+()() ．（1）求f x ()在122[,]上的最大值；（2）若直线2y x a =-+为曲线y f x =()的切线，求实数a 的值；（3）当2a =时，设1214122x x x ,⎡⎤∈⎢⎥⎣⎦…,,, ，且121414x x x =…+++ ，若不等式1214f x f x +f x λ≤…()+()+()恒成立，求实数λ的最小值．解：（1）2222229[1(1)2]9(1)()(1)(1)ax x ax ax f x ax ax ⋅+-⋅-'==++，…………………………2分令()0f x '=，解得x =（负值舍去），由122<<，解得144a <<．（ⅰ）当104a <≤时，由1[,2]2x ∈，得()0f x '≥，∴()f x 在1[,2]2上的最大值为18(2)41f a =+．…………………………………3分（ⅱ）当4a ≥时，由1[,2]2x ∈，得()0f x '≤，∴()f x 在1[,2]2上的最大值为118()24f a =+．……………………………………4分（ⅲ）当144a <<时，在12x a <<时，()0f x '>，在2x a <<时，()0f x '<，∴()f x 在1[,2]2上的最大值为f 5分（2）设切点为(,())t f t ，则()1,()2.f t f t t a '=-⎧⎨=-+⎩……………………………6分由()1f t '=-，有2229[1]1(1)at at -=-+，化简得2427100a t at -+=，即22at =或25at =， ……………………………① 由()2f t t a =-+，有2921ta t at=-+，……………②由①、②解得2a =或4a =． ……………………………………………9分（3）当2a =时，29()12xf x x =+，由（2）的结论直线4y x =-为曲线()y f x =的切线，(2)2f = ，∴点(2,(2))f 在直线4y x =-上，根据图像分析，曲线()y f x =在直线4y x =-下方． …………………………10分下面给出证明：当1[,2]2x ∈时，()4f x x ≤-．3222928104()(4)41212x x x x f x x x x x -+---=-+=++ 2221(2)12x x x--=+（）， ∴当1[,2]2x ∈时，()(4)0f x x --≤，即()4f x x ≤-．………………………12分∴12141214()()()414()f x f x f x x x x +++≤⨯-+++ ，121414x x x +++= ， 1214()()()561442f x f x f x ∴+++≤-= ．∴要使不等式1214()()()f x f x f x λ+++≤ 恒成立，必须42λ≥．……………13分又当12141x x x ==== 时，满足条件121414x x x +++= ，且1214()()()42f x f x f x +++= ，因此，λ的最小值为42． …………………………………………………14分【说明】本题主要考查函数的性质、导数运算法则、导数的几何意义及其应用、不等式的求解与证明、恒成立问题，考查学生的分类讨论，计算推理能力及分析问题、解决问题的能力及创新意识．。

2015年深圳市高三年级第一次调研考试文科数学参考答案

19．（本小题满分 14 分）已知各项为正的等差数列 {an } 的公差 d 1 ，且（1）求数列 {an } 的通项公式；
n 1 （2）若数列 {bn } 满足：b1 ，an 1bn 1 an bn (1) （ n N ），是否存在实数，
*
1 1 2 ． a1a2 a2 a3 3
侧面 SBC 是正三角形，
CE 3 ，…………………………………………………………………………………9 分
AC AE 2 CE 2 2 ， …………………………………………………………………10 分
ABC 是底边为 2 ，腰为 2 的等腰三角形，
2015 年深圳市高三年级第一次调研考试数学（文科）参考答案及评分标准
使得数列 {bn } 为等比数列？若存在，求出的值；若不存在，请说明理由．解：（1）法一：数列 an } 的首项为 a1 0 ，公差 d 1 ，
an a1 ( n 1) ，
1 1 1 ， an an1 an an1
………………………………………2 分
（A、甲）（B、甲）（C、甲）、、、、、、、、（B、C）（A、乙）（B、D）（B、乙）（C、D）（D、甲）（甲、乙）、、、共计 15 种可能; （C、乙）（D、乙）
………………… 8 分
（A、甲）其中既有“良好”类、又有“轻度污染”类城市选取可能为：、、（A、乙）（B、甲）（C、甲）（D、甲）、、、、、共计 8 种可能，（B、乙）（C、乙）（D、乙）
第 4 页共 14 页
即 SABC
7 ， 2
…………………………………………………………………11 分

深圳市2015年高三年级第一次调研考试数学理科试卷(扫描版,有答案)

2015年深圳市高三年级第一次调研考试数学(理科)答案及评分标准说明：一、本解答给出了一种或几种解法供参考，如果考生的解法与本解答不同，可根据试题的主要考查内容比照评分标准制订相应的评分细则．二、对计算题当考生的解答在某一步出现错误时，如果后续部分的解答未改变该题的内容和难度，可视影响的程度决定给分，但不得超过该部分正确解答应得分数的一半；如果后续部分的解答有较严重的错误，就不再给分．三、解答右端所注分数，表示考生正确做到这一步应得的累加分数．四、只给整数分数，选择题和填空题不给中间分数．二、填空题：本大题每小题5分，满分30分．9．23； 10． 18； 11．9； 12．13．2； 14．2； 15． 4．三、解答题 16．（本小题满分12分）函数π()2sin()3f x x ω=+（0ω>）的最小正周期是π．（1）求5π()12f 的值；（2）若0sin 3x =，且0π(0,)2x ∈，求0()f x 的值．解：（1）()f x Q 的周期πT =，即2ππω=， …………………………………………1分2ω∴=±，由0ω>，得2ω=，即π()2sin(2)3f x x =+． ……………………………………3分5π7πππ()2sin 2sin(π)2sin 112666f ∴==+=-=-． ………………………………5分（2）由0sin x =得2001cos 212sin 3x x =-=， ………………………………7分又0π(0,)2x ∈，∴02(0,π)x ∈， ……………………………………………8分 ∴0sin 23x ==， …………………………………………9分 000πππ2sin(2)2sin 2cos 2cos 2sin 333x x x +=+Q1122323=⨯⨯+⨯=．00π()2sin(2)3f x x ∴=+= …………………………………………12分【说明】本小题主要考查了三角函数)sin()(ϕω+=x A x f 的图象与性质，同角三角函数的关系式，诱导公式，两角和与差和二倍角的三角函数公式，考查了简单的数学运算能力．17．（本小题满分12分）空气质量指数（简称AQI ）是定量描述空气质量状况的指数，其数值越大说明空气污染越严重，为了及时了解空气质量状况，广东各城市都设置了实时监测站．下表是某网站公布的广东省内21个城市在2014年12月份某时刻实时监测到的数据：（1）请根据上表中的数据，完成下列表格：（2）统计部门从空气质量“良好”和“轻度污染”的两类城市中采用分层抽样的方式抽取6个城市，省环保部门再从中随机选取3个城市组织专家进行调研，记省环保部门“选到空气质量“良好”的城市个数为ξ”，求ξ的分布列和数学期望．解:（1）根据数据，完成表格如下：…………………………………2分（2）按分层抽样的方法，从“良好”类城市中抽取11264126n =⨯=+个， ………………………………… 3分从“轻度污染”类城市中抽取2662126n =⨯=+个， ……………………………4分所以抽出的“良好”类城市为4个，抽出的“轻度污染”类城市为2个．根据题意ξ的所有可能取值为：1,2,3．1242361(1)5C C P C ξ===Q , 2142363(2)5C C P C ξ===，3042361(3)5C C P C ξ===．………8分ξ∴的分布列为：所以1232555E ξ=⨯+⨯+⨯=． ………………………………………………11分答：ξ的数学期望为2个． …………………………………………………12分【说明】本题主要考察读图表、分层抽样、概率、随机变量分布列以及数学期望等基础知识，考查运用概率统计知识解决简单实际问题的能力，数据处理能力．18．（本小题满分14分）在三棱锥P ABC -中，已知平面PBC ⊥平面ABC ，AB 是底面△ABC 最长的边．三棱锥P ABC -的三视图如图5所示，其中侧视图和俯视图均为直角三角形．（1）请在图6中，用斜二测画法，把三棱锥P ABC-的直观图补充完整（其中点P 在 xOz 平面内），并指出三棱锥P ABC -的哪些面是直角三角形；（2）求二面角B PA C --的正切值；（3）求点C 到面PAB 的距离．正视图解：（1）三棱锥P ABC -直观图如图1所示；由三视图知ABC ∆和PCA ∆是直角三角形．（2）（法一）：如图2，过P 作PH BC ⊥交BC 于点H 由三视图知PBC ∆为等腰三角形，4BC =Q ，PH =4PB PC BC ∴===，取PC 的中点E ，过E 作EF PA ⊥且交PA 于点F ，连接BE ，BF ，因为BE PC ⊥，由三视图知AC ⊥面PBC ，且BE ⊂面PBC ，所以AC BE ⊥，又由AC PC C =I ，所以BE ⊥面PAC ，由PA ⊂面PAC ，所以BE PA ⊥， BE EF E =I ，所以PA ⊥面BEF ，由BF ⊂面BEF ，所以PA BF ⊥，所以BFE ∠是二面角B PA C --的平面角．………~PEF PAC ∆∆Q ，PE EFPA AC∴=， 2,4,PE AC PA ===Q EF ∴=， ∴在直角CFE ∆中，有tan BEBFE EF∠== 所以，二面角B PA C --． ………………………………………9分（法二）：如图3，过P 作PH BC ⊥交BC 于点H ，由三视图知PBC ∆为等腰三角形，4BC =，PH =由图3所示的坐标系，及三视图中的数据得：(0,0,0)B ，(4,0,0)C ，(2,0,P ，(4,4,0)A ，则(4,4,0)BA =u u u r ，(2,0,BP =u u u r ，(0,4,0)CA =u u u r， (2,0,CP =-u u u r,设平面PAB 、平面PAC 的法向量分别为m 、n ．设111(,,)x y z =m ，由0BA ⋅=u u u r m ，0BP ⋅=u u u r m ，得11420x ⎧⎪⎨+=⎪⎩，令11z =，得1x =1y =(=m ． …………………6分设222(,,)x y z =n ，由0CA ⋅=u u u r n ，0PA ⋅=u u u r n，得2224020y x =⎧⎪⎨-+=⎪⎩，令21=z ，得2x =，20y =，即=n ． ………………………7分cos ,7⋅∴<>===-m n m n m n，tan ,m n <>=8分而二面角B PA C --的大小为锐角，所以二面角B PA C --．…9分（3）（法一）：记C 到面PAB 的距离为h ，由（1）、（2）知4PA AB PB ===，PAB S ∆∴=，13C PAB PAB V S h -∆=⋅=， ………………………………12分三棱锥-P ABC的体积13-∆=⋅=P ABC ABC V S PH ， ……………………13分由P ABC C PAB V V --=，可得：7=h ． ………………………………………14分（法二）：由（2）知，平面PAB的法向量(=m ，(0,4,0)CA =u u u r记C 到面PAB 的距离为h ，CA h ⋅∴=u u u rmm== ………………………………………………14分【说明】本题主要考察空间点、线、面位置关系，三视图及几何体的直观图，二面角，三棱锥的体积，空间坐标系等基础知识，考查空间想象能力、运算能力和推理论证能力，考查用向量方法解决数学问题的能力．19．（本小题满分14分）已知首项大于0的等差数列{}n a 的公差1d =，且12231123a a a a +=．（1）求数列{}n a 的通项公式；（2）若数列{}n b 满足：11b =-，2b λ=，111(1)n n n nn b b n a -+--=+，其中2n ≥． ①求数列{}n b 的通项n b ；②是否存在实数λ，使得数列}{n b 为等比数列？若存在，求出λ的值；若不存在，请说明理由．解：（1）（法一）：Q 数列{}n a 的首项10a >，公差1d =，∴1(1)n a a n =+-，11111n n n n a a a a ++=-， ………………………………………2分 12231223111111()()a a a a a a a a ∴+=-+-131********a a a a =-=-=+， ……………3分整理得211230a a +-=解得11a =或13a =-（舍去）． ……………………………4分因此，数列{}n a 的通项n a n =． ………………………………………5分（法二）：由题意得1312231231123a a a a a a a a a ++==， …………………………………1分 Q 数列{}n a 是等差数列，∴1322a a a +=， ……………………………2分∴2123223a a a a =，即133a a =． ………………………………………………………3分又10,1a d >=Q ，∴11(2)3a a +=，解得11a =或13a =-（舍去）． …………………………………4分因此，数列{}n a 的通项n a n =． ………………………………………5分（2）①111(1)n n n n b b n n-+--=+Q ， 11(11(1)(1)n nn nnb n b ++-∴=+--）． ……………………………………………………6分令(1(1)nn nn b c -=-），则有2c λ=，11n n c c +=+(2)n ≥．∴当2n ≥时，2(2)2n c c n n λ=+-=-+，(21nn n b n λ-+=-)(-1)． ………8分因此，数列{}n b 的通项1, 1,(2,(2).1n n n b n n n λ-=⎧⎪=⎨-+≥⎪-⎩)(-1)． (9)分②11b =-Q ，2b λ=，312b λ+=-， ………………………………………10分∴若数列{}n b 为等比数列，则有2213b b b =，即21(1)()2λλ+=--，解得1λ=或12λ=-． …………………………………………………………11分当12λ=-时，(252)21n n n b n n -=≥-)(-1)（（），+1n n b b 不是常数，数列{}n b 不是等比数列，当1λ=时，11b =-，(1)(2)n n b n =-≥，数列{}n b 为等比数列．所以，存在实数1λ=使得数列{}n b 为等比数列． ………………………………14分【说明】考查了等差数列的基本量的计算、递推数列的通项公式、数列裂项求和公式、等比数列的定义，考查了学生的运算能力，以及化归与转化的思想． 20．（本小题满分14分）已知椭圆:E 22221(0)+=>>x y a b a b，过左焦点倾斜角为45︒的直线被椭圆截得的弦长为3．（1）求椭圆E 的方程；（2）若动直线l 与椭圆E 有且只有一个公共点，过点()1,0M 作l 的垂线垂足为Q ，求点Q 的轨迹方程．解：（1）因为椭圆E2=，解得222a b =，故椭圆E 的方程可设为222212x y b b+=，则椭圆E 的右焦点坐标为(),0b ，过右焦点倾斜角为45︒的直线方程为:l y x b '=-． ………………………………………2分设直线l '与椭圆E 的交点记为,A B ，由22221,2,x y b b y x b ⎧+=⎪⎨⎪=-⎩消去y ，得2340x bx -=，解得1240,3b x x ==，因为1233AB x =-==，解得1b =．故椭圆E 的方程为2212+=x y ． ……………………………………………………4分（2）（法一）（i ）当切线l 的斜率存在且不为0时，设l 的方程为y kx m =+，联立直线l 和椭圆E 的方程，得2212y kx m x y =+⎧⎪⎨+=⎪⎩， ……………………………………5分消去y 并整理，得()222214220k x kmx m +++-=， …………………………6分因为直线l 和椭圆E 有且仅有一个交点，()()222216421220k m k m ∴∆=-+-=， ………………………………………7分化简并整理，得2221m k =+． …………………………………………8分因为直线MQ 与l 垂直，所以直线MQ 的方程为：()11y x k=--，联立()11,,y x ky kx m ⎧=--⎪⎨⎪=+⎩ 解得221,1,1km x k k m y k -⎧=⎪⎪+⎨+⎪=⎪+⎩ ………………………9分 222222222222222222(1)()1(1)(1)1(1)(1)(1)1km k m k m k m k m m x y k k k k -++++++++∴+====++++，把2221m k =+代入上式得222x y +=． ① …………………………………11分（ii ）当切线l 的斜率为0时，此时(1,1)Q ，符合①式． …………………………12分（iii ）当切线l的斜率不存在时，此时Q或(0)，符合①式． ………13分综上所述，点Q 的轨迹方程为222x y +=． ………………………………………14分（法二）：设点Q 的坐标为00(,)Q x y ，（i ）当切线l 的斜率存在且不为0时，设l 的方程为y kx m =+，同解法一，得22210k m -+=， ① …………………………………………8分因为直线MQ 与l 垂直，所以直线MQ 的方程为：()11y x k=--，联立()11,,y x k y kx m ⎧=--⎪⎨⎪=+⎩解得002200001,,x k y x x y m y -⎧=⎪⎪⎨-+⎪=⎪⎩② …………………9分 ②代入①并整理，有()()()4222200000002212120+--+-+-=y x x y x x x ，…10分即()()2222000002210+-+-+=y x yx x ，由点Q 与点M 不重合， ()2222000002110y x x y x ∴+-+=+-≠，220020x y ∴+-=， ③ ……………………………………………………11分（ii ）当切线l 的斜率为0时，此时(1,1)Q ，符合③式． …………………………12分（iii ）当切线l的斜率不存在时，此时Q或(0)，符合③式． ………13分综上所述，点Q 的轨迹方程为222x y +=． ………………………………………14分（法三）：设点Q 的坐标为00(,)Q x y ，（i ）当切线l 的斜率存在且不为0时，设l 的方程为00()-=-y y k x x ，整理，得l 的方程为00=-+y kx kx y ， ……………………………………………………………5分联立直线l 和椭圆E 的方程，得002212=-+⎧⎪⎨+=⎪⎩y kx kx y x y ，消去y 并整理，得()()()2220000214220++-+--=k x k y kx x y kx ， ……………………6分因为直线l 和椭圆E 有且仅有一个交点，()()()222200001682110⎡⎤∴∆=--+--=⎣⎦k y kx k y kx ， ………………………7分化简并整理，得22200002210--+++=y x kx y k ， ① ………………………8分因为MQ 与直线l 垂直，有01-=x k y ， ②……………………………………9分 ②代入①并整理，有()()()4222200000002212120+--+-+-=y x x y x x x ，…10分即()()2222000002210+-+-+=y x yx x ，Q 点Q 与点M 不重合， ()2222000002110y x x y x ∴+-+=+-≠，220020x y ∴+-=， ③………………………………………………………………11分（ii ）当切线l 的斜率为0时，此时(1,1)Q ，符合③式． …………………………12分（iii ）当切线l的斜率不存在时，此时Q或(0)，符合③式． ………13分综上所述，点Q 的轨迹方程为222x y +=． ………………………………………14分【说明】本题主要考查轨迹方程和椭圆的定义、直线方程、直线与椭圆相切的位置关系，弦长问题，考查学生运算能力、推理论证以及分析问题、解决问题的能力，考查数形结合、化归与转化思想．21．（本小题满分14分）已知定义在]2,2[-上的奇函数)(x f 满足：当]2,0(∈x 时，)2()(-=x x x f ．（1）求)(x f 的解析式和值域；（2）设a ax x x g 2)2ln()(--+=，其中常数0>a ． ①试指出函数))(()(x f g x F =的零点个数；②若当11k+是函数))(()(x f g x F =的一个零点时，相应的常数a 记为k a ，其中 1,2,,k n =L ．证明：1276n a a a +++<L （*N ∈n ）．解：（1）()f x Q 为奇函数，(0)0f ∴=．当[)2,0x ∈-时，(]0,2x -∈，则()()()(2)(2)f x f x x x x x =--=----=-+，∴[][)(2)0,2,()(2)2,0,x x x f x x x x ⎧-∈⎪=⎨-+∈-⎪⎩ ………………………………………2分[0,2]x ∈Q 时，[]()1,0f x ∈-，[)2,0x ∈-，[]()0,1f x ∈，()f x ∴的值域为[]1,1-． …………………………………………………3分（2）①函数()f x 的图象如图a 所示，当0t =时，方程()f x t = 有三个实根；当1t =或1t =-时，方程()f x t =只有一个实根；当(0,1)t ∈或(1,0)t ∈-时，方程()f x t =有两个实根．（法一）：由()0g x =，解得ln(2)2x a x +=+，()f x Q 的值域为[]1,1-，∴只需研究函数ln(2)2x y x +=+在[]1,1-上的图象特征．设ln(2)()([1,1])2x h x x x +=∈-+，(1)0h -=，21ln(2)()(2)x h x x -+'=+，令()0h x '=，得e 2(0,1)x =-∈，1(e 2)eh -=． Q 当1e 2x -<<-时，()0h x '>，当e 21x -<<时，()0h x '<，又32ln 2ln 3<Q ，即ln 2ln 323<，由ln 2(0)2h =，ln 3(1)3h =，得(0)(1)h h <， ()h x ∴的大致图象如图b 所示．根据图象b 可知，当ln 2ln 2ln 310223a a a e<<<<=、、直线y a =与函数()y h x =的图像仅有一个交点，则函数()g x 在[1,1]-上仅有一个零点，记零点为t ，则t 分别在区间(1,0)-(0,1)、(0,1)上，根据图像a ，方程()f x t =有两个交点，因此函数()(())F x g f x =有两个零点． …………………………………………5分类似地，当ln 22a =时，函数()g x 在[1,1]-上仅有零点0，因此函数()F x 有1-、0、1这三个零点． ………………………………………………………………6分当ln 33a =时，函数()g x 在[1,1]-上有两个零点，一个零点是1，另一个零点在(0,1)内，因此函数()F x 有三个零点． …………………………………………………………7分当ln 313ea <<时，函数()g x 在[1,1]-上有两个零点，且这两个零点均在(0,1)内，因此函数()F x 有四个零点． ……………………………………………………………8分当1ea >时，函数()g x 在[]1,1-上没有零点，因此函数()F x 没有零点． ………9分（法二）：1()2g x a x '=-+ ，令0()0g x '=，得012x a=-，0a >Q ，()02,x ∴∈-+∞．当1(1,2)x a ∈--时，()0g x '>，当1(2,)x a∈-+∞时，()0g x '<， ∴当0x x =时，()g x 取得极大值01()ln 1g x a=-．（Ⅰ）当()g x 的极大值1ln10a -<，即1e a >时，函数()g x 在区间1,1-上无零点，因此函数()(())F x g f x =无零点．（Ⅱ）当()g x 的极大值1ln10a -=，即1ea =时， 02(0,1)x e =-∈，函数()g x 的图像如图c 所示，函数g由图a 可知方程()e 2f x =-有两不等的实根，因此函数()(())F x g f x =有两个零点．（Ⅲ）当()g x 的极大值1ln 10a ->且0121x a=->，即103a <≤时，()g x 在[1,1]-上单调递增，因为()10g a -=-<，222(0)ln 22ln 2ln ln1033e 3g a =->-=>=，函数()g x 的图像如图d 所示，函数()g x 在[]1,1-存在唯一零点1t ，其中1(1,0)t ∈-．由图a 可知方程1()f x t =有两不等的实根，因此函数()(())F x g f x =有两个零点．（Ⅳ）当()g x 的极大值1ln10a ->且0121x a =-<，即113ea <<时：由(0)ln 220g a =-=，得ln 22a =，由(1)ln 330g a =-=，得ln 33a =，根据法一中的证明有1ln 2ln 31323e<<<．（ⅰ）当1ln 232a <<时，(0)ln 220g a =->，(1)ln 330g a =->，函数()g x 的图像如图e 所示，函数()g x 在区间[1,1]-有唯一零点2t ，其中2(1,0)t ∈-．由图a 可知方程2()f x t =有两不等的实根，因此函数()(())F x g f x =有两个零点．（ⅱ）当ln 22a =时，(0)ln 220g a =-=， (1)ln 330g a =->，函数()g x 的图像如图f 所示，函数()g x 在区间[1,1]-有唯一零点0．由图a 可知方程()0f x =有三个不等的实根，因此函数()(())F x g f x =有三个零点．（ⅲ）当ln 2ln 323a <<时，(0)ln 220g a =-<，(1)ln 330g a =->，函数()g x 的图像如图g 所示，函数()g x 在区间[1,1]-有唯一零点3t ，其中3(0,1)t ∈．由图a 可知方程3()f x t =()(())F x g f x =有两个零点．（ⅳ）当ln 33a =时，(0)0g <，(1)ln 330g a =-=，函数()g x 的图像如图h 所示，函数()g x 在区间[1,1]-有两个零点，分别是1和4t ，其中4(0,1)t ∈．由图a 可知方程()1f x =有一个实根1-，方程4()f x t =有两个非1-的不等实根，因此函数()(())F x g f x =（ⅴ）当ln 313ea <<时，(0)0g <，(1)ln 33g a =-<函数()g x 的图像如图i 所示，函数()g x 在区间[1,1]-有两个零点5t 、6t ，其中56,(0,1)t t ∈．由图a 可知方程5()f x t =、6()f x t =且这四个根互不相等，因此函数()(())F x g f x =综上可得：当ln 2ln 2ln 310223a a a e <<<<=、、时，函数()F x 有两个零点；………………5分当ln 22a =、ln 33a =时，函数()F x 有三个零点； ………………………………7分当ln 313e a <<时，函数()F x 有四个零点； ……………………………………8分当1e a >时，函数()F x 无零点． ………………………………………………9分②因为k11+是函数))(()(x f g x F =的一个零点，所以有1((1))0g f k +=，(]110,2k +∈Q ，211(1)1f k k∴+=-，2221111((1))(1)ln(1)(1)0k g f g a k k k k ∴+=-=+-+=，221ln(1)11k k a k+∴=+，1,2,,k n =L ． …………………………………………10分记()ln(1)m x x x =+-，1()111xm x x x -'=-=++， Q 当(]0,1x ∈时，()0m x '<，∴当(]0,1x ∈时，()(0)0m x m <=，即ln(1)x x +<．故有2211ln(1)k k+<，则2222211ln(1)111111k k k a k k k +=<=+++()1,2,,k n =⋅⋅⋅． …11分当1n =时，11726a <<；当2n ≥时，（法一）：2211221121214k k k k <=-+-+-Q， ………………………………13分 123a a a ∴+++…++++++<+131121111222n a …112++n 1222222()()()235572121n n <+-+-+⋅⋅⋅+--+ 12272723216216n n =+-=-<++．综上，有++21a a (6)7<+n a ，*N ∈n ． ………………………………………14分（法二）：当2n =时，12117725106a a +<+=<；当3n ≥时，2211111()11211k k k k <=-+--+Q ， ………………………13分123a a a ∴+++…++++++<+131121111222n a …112++n 111111111[()()()]252243511n n <++-+-+⋅⋅⋅+--+ 111111167111677[]()2522316021606n n n n =+++--=-+<<++．综上，有++21a a (6)7<+n a ，*N ∈n ． ………………………………………14分【说明】本题主要考查函数的性质、分段函数、导数应用、一元二次方程的求解、连续函数的零点存在性定理，放缩法证明数列不等式，考查学生数形结合、分类讨论的数学思想，以及计算推理能力及分析问题、解决问题的能力及创新意识．。

广东省各地2015届高三上学期期中考试文科数学试题汇总(二)9份 Word版含答案

目录广东省广州市执信中学2015届高三上学期期中考试数学（文） Word 版含答案.doc 广东省广州市海珠区2015届高三摸底考试数学文试题 Word 版含解析.doc广东省广州市第六中学2015届高三上学期第一次质量检测数学文试题 Word 版含解析.doc 广东省广州市荔湾区2015届高三11月调研测试（二）数学文试题 Word 版含答案.doc 广东省惠州市2015届高三第二次调研考试数学（文）试题 Word 版含解析.doc广东省揭阳市一中、潮州金山中学、广大附中2015届高三上学期期中考试文数学Word 版答案广东省汕头市金山中学2015届高三第一学期期中考试数学（文）含部分答案 Word 版含答案.doc 广东省中山一中、潮阳一中等2015届高三七校联考数学（文） Word 版含解析.doc 广东省六校联盟2015届高三第二次联考数学（文）试题 Word 版含答案.doc广州市第六中学高三上学期第一次质量检测数学（文）【试卷综析】本试卷是高三文科试卷，以基础知识和基本技能为载体，以能力测试为主导，在注重考查学科核心知识的同时，突出考查考纲要求的基本能力，重视学生科学素养的考查.知识考查注重基础、注重常规、注重主干知识，兼顾覆盖面.试题重点考查：集合、不等式、向量、导数的综合应用、数列、函数的性质及图象、三角函数的性质、三角恒等变换与解三角形、简单的线性规划、立体几何、充分条件与必要条件等；考查学生解决实际问题的综合能力，是份较好的试卷.一、选择题(共10小题，每小题5分，共50分)【题文】1、已知全集U=R ，则正确表示集合M={－1,0,1}和{}20N x x x =+=关系的韦恩图是( )【知识点】集合的关系A1【答案解析】B 解析：因为{}{}201,0N x x x =+==-，所以N M ⊂，则选B.【思路点拨】先求出集合N ，再结合两个集合的关系判断其韦恩图即可.【题文】2、已知(3,2),(1,0)a b =- =- ，向量a b λ+ 与b 垂直，则实数λ的值为（） A ．3- B ．3 C ．13- D ．13【知识点】向量的数量积F3【答案解析】A 解析：因为向量a b λ+ 与b 垂直，则()230a b b a b b λλλ+∙=∙+=+=，得λ=-3，所以选A.【思路点拨】由两向量垂直，则两向量的数量积等于0，是解答本题的关键. 【题文】3、“”是“且”的（）A. 必要不充分条件B. 充分不必要条件C. 充分必要条件D. 既不充分也不必要条件【知识点】充分条件与必要条件A2 【答案解析】A解析：因为“”不一定有“且”，若“且”，由不等式的性质可知必有“”，所以选A.【思路点拨】判断充要条件时，可先分清命题的条件与结论，若由条件能推出结论，则充分性满足，若由结论能推出条件，则必要性满足. 【题文】4、已知角α为第二象限角，且3tan 4α=-，则sin()2πα+的值为（） A ．45 B ．45- C ．35 D ．35-【知识点】诱导公式，同角三角函数基本关系式C2【答案解析】B 解析：因为3tan 4α=-，所以22sin 3cos 4sin cos 1αααα⎧=-⎪⎨⎪+=⎩，又因为角α为第二象限角，所以解得4cos 5α=-，则4sin()cos 25παα+==-，所以选B. 【思路点拨】由角的正切求其余弦，可通过同角三角函数关系式的商数关系及平方关系得到正弦和余弦的方程组，解方程组即可.【题文】5、已知各项为正的等比数列}{n a 满足3a ·9a =254a ，2a =1，则1a = （）A ．12 B ．2 C ．22D ．2 【知识点】等比数列D3【答案解析】A 解析：因为2239654a a a a ∙==，又数列的各项为正数，所以公比652a q a ==,则2112a a q ==，所以选A . 【思路点拨】在遇到等比数列时，可先通过项数观察有无性质特征，有性质的用性质进行解答，无性质特征的用公式进行转化.【题文】6、设,x y 满足24,1,22,x y x y x y +≥⎧⎪-≥⎨⎪-≤⎩则z x y =+( )A.有最小值2，最大值3B.有最小值2，无最大值C.有最大值3，无最小值D.既无最小值，也无最大值【知识点】简单的线性规划E5【答案解析】B 解析：因为不等式组24,1,22,x y x y x y +≥⎧⎪-≥⎨⎪-≤⎩表示的平面区域如图ABCD 区域，显然当动直线z x y =+经过点A （2,0）时，目标函数取最小值为2，无最大值，所以选B..【思路点拨】解答线性规划问题，主要是利用数形结合的方法寻求目标函数的最值. 【题文】7、若函数2()()af x x a x=+∈R ，则下列结论正确的是（） A ．a ∀∈R ，()f x 在(0,)+∞上是增函数B ．a ∀∈R ，()f x 在(0,)+∞上是减函数 C ．a ∃∈R ，()f x 是偶函数 D ．a ∃∈R ，()f x 是奇函数【知识点】导数的应用、函数的单调性与奇偶性B3 B4 B12【答案解析】C 解析：因为()22'2a x af x x x x-=-= ，所以当a ≤0时，导数大于0，()f x 在(0,)+∞上是增函数，当a ＞0时，函数在（0，+∞）上不是单调函数，所以排除A,B ，当a=0时函数为偶函数，所以C 正确，当a ≠0时既不是奇函数也不是偶函数，所以D错误，综上知选C.【思路点拨】已知解析式判断函数的单调性，可利用导数进行判断，判断函数的奇偶性可利用其定义进行判断.【题文】8、给出四个函数，分别满足①)()()(y f x f y x f +=+；②)()()(y g x g y x g ⋅=+； ③)()()(y x y x ϕϕϕ+=⋅；④)()()(y x y x ωωω⋅=⋅，又给出四个函数的图象如下：则正确的配匹方案是（）A ．①—M ②—N ③—P ④—QB ．①—N ②—P ③—M ④—QC ．①—P ②—M ③—N ④—QD ．①—Q ②—M ③—N ④—P【知识点】指数函数、对数函数、幂函数B6 B7 B8 【答案解析】D 解析：图像M 为指数函数图像，由指数的运算性质得M 与②对应，则排除A,B,又图像Q 为过原点的一次函数，设f(x)=ax,则有f(x+y)=a(x+y)=ax+ay=f(x)+f(y),所以Q 与①对应，则排除C,所以选D. 【思路点拨】抓住指数函数、对数函数及幂函数的图像特征及对应的运算法则，利用排除法，即可确定选项.【题文】9、已知等差数列}{n a 的前n 项和S n 满足1021S S =，则下列结论正确的是（） A. 数列{}n S 有最大值 B. 数列{}n S 有最小值C. 150a =D. 160a = 【知识点】等差数列D2【答案解析】D 解析：因为1021S S =，结合等差数列的前n 项和的二次函数特征得函数的对称轴为102111522x +==，则15161516S S S a ==+，得160a =，所以选D. 【思路点拨】抓住等差数列n 项和的二次函数特征，利用对称性解答即可. 【题文】10、定义在R 上的函数f(x )满足f(x)= ⎩⎨⎧>---≤-0),2()1(0),1(log 2x x f x f x x ，则f （2015）的值为( )A. -1B. 0C.1D. 2【知识点】函数的周期性、分段函数B4【答案解析】C 解析：因为x ＞0时，f(x)=f(x ﹣1) ﹣f(x ﹣2),所以x ＞1时，f(x ﹣1)=f(x ﹣2) ﹣f(x ﹣3)，则有f(x)=f(x ﹣1) ﹣f(x ﹣2)= ﹣f(x ﹣3)=f(x ﹣6)，所以当x ＞4时以6为周期，则f （2015）=f(336×6－1)=f(－1)=1，所以选C.【思路点拨】由递推关系求自变量较大的函数值时，可考虑利用递推关系发现其周期特征，再进行解答.二、填空题（共4小题，每题5分，共20分）【题文】11、不等式260x x --+>的解集是_______________.x yOM xyOQ xy ON xy ON P【知识点】一元二次不等式E3【答案解析】()3,2- C 解析：由不等式260x x --+>得260x x +-< ，解得32x -<<，所以不等式的解集为()3,2-.【思路点拨】解一元二次不等式，一般先把不等式转化为二次项系数大于0，再结合对应的二次函数的图像进行解答.【题文】12、函数()cos f x x x =在点（,ππ -）处的切线方程是_______________. 【知识点】导数的应用B12【答案解析】y=－x 解析：因为()'cos sin f x x x x =-，所以切线的斜率为cos sin 1πππ-=-，则所求的切线方程为()y x ππ+=--即y=－x.【思路点拨】抓住切线的斜率等于在切点处的导数值，即可求出切线斜率，进而得出切线方程.【题文】13、数列{}n a 的通项公式为n a n nλ=+，若{}n a 为递增数列，则实数λ的取值范围是___________.【知识点】数列的单调性D1【答案解析】(),2-∞解析：因为数列{}n a 的通项公式为n a n nλ=+，{}n a 为递增数列，所以()1101n n a a n n λ+-=->+，即()1n n λ<+，而()12n n +≥，所以2λ<.【思路点拨】数列单调递增的充要条件是对于任意的n *N ∈,10n n a a +-=>恒成立，再利用不等式恒成立求λ的范围即可.【题文】14、如图，平行四边形ABCD 中，E 为CD 中点，F 在线段BC 上，且BC=3BF 。