材料力学下册第三章能量法
材料力学第三章 能量法

三、卡氏第二定理(线弹性体)
Di
Vc Fi
在线弹性范围内
余能定理 Vc V
Di
V Fi
卡氏第二定理: 线弹性杆件或杆系的应变能对于 作用在该杆件或杆系上的某一荷 载的变化率,就等于与该荷载相 应的位移。
卡氏第二定理适用于一切受力状态下的线弹性体。
卡氏第二定理公式D及i 含义VF:i
若结构的应变能 V 表示为F1、F2 …Fi …的函数,则应变 能对任一载荷Fi的偏导数等于Fi作用点沿Fi方向位移。
C
与需求位移相应的虚设外力
F。求偏导后令其为零。
(2)列弯矩方程
M
x
F 2
ql 2
x
qx 2 2
0
x
l 2
M
x
F 2
ql 2
x
qx 2 2
0
x
l 2
(3)求梁的应变能
M 2 l/2
x
1
V 2 0
dx
2EI
EI
l/2
0
F 2
ql 2
x
qx 2 2
2 dx
1 EI 1 EI
V W
一、杆件基本变形的应变能
(一)轴向拉伸(压缩)
1、杆的应变能
轴力沿轴线不变的情况:
dW Fd(Dl) W Dl1 Fd(Dl) 0
线弹性范围内 W 1 FDl
1
2
V
F
W
FN
2
F Dl Dl
FNl EA
应变能
V
FN2l 2EA
F
l
Dl
F
Dl d (Dl)
Dl1
Dl
(一)轴向拉伸(压缩)
材料力学-能量法

U
l
N 2( x)dx 2EA
l
M
2 n
(
x
)dx
2GI P
l
M 2( x)dx 2EI
(9-8)
注意:叠加法不能用于计算外力功和变形能。
例1 试分别计算图示各梁的变形能 例1图
解:求各梁的变形能 a b
c
Ua
0l
M 2( x)dx 2EI
0l
(
Px)2 2EI
dx
P 2l3 6EI
Ub
0l
M 2( x)dx 2EI
W 1 P
2
(9-2)
式中: P —— 广义力(力、力偶)
——广义位移(线位移、角位移)
广义力与广义位移相对应。如广义力是力,相应的广义
位移就是线位移(沿力方向的线位移);如广义力是力偶, 相应的广义位移就是角位移(在力偶作用处的角位移)。
(二)变形能和比能
1. 轴向拉伸与压缩时的变形能
a. 轴力为常量: ( N P,l Nl )
材料力学
能量法
一、外力功与变形能
本章考虑杆件在线弹性范围内的能量法计算问题。
能量法——利用功和能的概念来解决变形体的位移、变 形和内力等计算的方法。
在线弹性范围内,外力功 W 全部转变为变形能 U,不 考虑能量的损耗。因此有
W=U
(一)外力功
1. 常力作功(P 为恒力)
W P
(9-1)
2. 变力作功(P 从0逐渐增加到最终值)
EA
U W 1 Pl N 2l
2
2EA
(9-3)
u
U V
N2 2EA2
2
2E
1
2
u 为比能,即单位体积的变形能。
材料力学:能量法

P
P1
l
P
Δ1
o
d
1
外力作功为
W 0 P dΔ
Ve W Δ1
0
P dΔ
p
l
p
P
从拉杆中取出一个各边为 单位长 的单元体, 作用在单元体上,下两表面的力为 P= 1 1 =
其伸长量
l=1=
p
1
p
d
1
该单元体上外力作功为
0 d
§3-2
一、应变能
应变能 • 余能
1. 线弹性条件下,通过外力功求应变能 常力作功:常力 P 沿其方向线位移 上所作的功
W P
变力作功:在线弹性范围内,外力 P 与位移 间呈线性
关系。 (静荷载为变力)
P
P
l
P
o
轴向拉(压)杆外力作功
Pl F N l EA EA
FN
P P P l 2 sin a 2tga 2d
P
2 FN d l
l
d
a1
l
a1
FN
FN
d
A P1
P
2 FN d P l
FN l EA
d2 l l l 2 l 2 2l l
2
l
(
FNl ) EA
2
2l (
FN l ) EA
0
1 1 2 d E1 2 2E
2
扭转杆
G
ve
1
0
1 1 2 d G 1 2 2G
2
例 题: 在线弹性 范围内工作的杆, 已知: m、G、l、d 。 求:在加载过程中所积蓄的应变能 Ve。
材料力学第28讲 Chapter3-3第三章 能量法(超静定问题)

9
若将超静定梁的C支座改为 座的反力。
k
3EI l3
的弹簧,试求各支
q
A
EI ,l
B EI ,l
C
k
3EI l3
10
q
解: 选静定基同前
A 利用能量法建立补充方程
EI ,l
B EI ,l
C
3EI
k
dx dx 卡氏第二定理
V FC
FC
k
V ,BC
FA
1 l
(
FC
l
1 2
ql 2 )
FC
k
平衡: Fi cosi P1 i 1
k
Fi sin i P2
i 1
F1 F2i Fi 12 i k
P1 P2
Fk1 Fk1(F1, F2 Fk2 ) Fk Fk (F1, F2 Fk2 )
26
解(2): (k-2)次超静定问题 利用卡氏第一定理可写出 变形协调条件为:
V
(1, 2 ) 1
知量,这种以力为基本未知量求解超静 1 2 i k
定问题的方法,统称为力法。
方法(2)中,以未知的节点位移作为基 本未知量,这种以位移为基本未知量求解 超静定问题的方法,统称为位移法。
P1 P2
力法和位移法是求解超静定系统的两种基本方法。 通常力法应用较为广泛。关于力法和位移法的进一步讨论将在 结构力学课程中详细介绍。
K
1 n
(n 1)
2 1
1
( PF2 )n1
n1 K n An1 (2cos )n1
F1 (P F2 ) (2 cos ) O
VC V vCdV vC2 Al2 vC1 Al1 2
Al Al 2 1
材料力学第26讲 Chapter3-1第三章 能量法(应变能 余能)

能量方法是用有限元法解固体力学问题的重要基础。
4
能量方法用途很广:
不仅适用于线弹性问题; 也可用于非线性弹性问题; 曲杆问题;
5
本章要介绍的几种能量方法:
应变能原理-卡氏第一定理 余能原理-卡氏第二定理 虚位移原理及单位力法
6
§3–2 应变能 余能
应变能的计算:
I. 应变能
外力缓慢做功W ,无损失地转化为应变能 (不
转化成动能、热能) ,贮存于弹性体内部。
V W
7
一、 线弹性问题
1. 轴向拉压杆件应变能的计算
W 1 Fl
2
l Fl
W F 2l 2EA
F
EA
W=V 功能原理
V
EAl2
2l
F 2l V 2 EA
5P1P2l3 48EI
23
进一步分析
21
P1
P2
12
l
l
2
2
21P16(E 2l)Il2(3l2l)458P1E l3I
l
l
2
2
12P26(E 2l)Il2(3l2l)4 58 P2 E lI3
P112 P221 ====== 功的互等定理 ======
第一组力在第二组力作用所产生位移上做的功 等于第二组力在第一组力作用所产生位移上做的功。
17
4.3 弯曲杆件应变能的计算
V
V vdV
V
1 2
dV
V
1 2E
2dV
l
A21E(M Izy)2dAdl l
A21E(M Iz )2y2dAdl
d l dx M 2 l 2EIz
材料力学第29讲 Chapter3-4第三章 能量法(虚位移原理及单位力法)

实际载荷-系统1
FA
F1
F2
F3 F4
FB
A
B
E I,l
M MdM
1 2
d
1 2
d
1 2
d
1 2
d
dx
dx
F S FS dFS
1 2
d
dx
1 2
d
FA
A
虚位移
单位载荷-系统2
F 1
FB
B
E I,l
x
外力
内力
F 1, F A , F B
M ,FS
dW' dWi 0
dWi dW'
内力总虚功
Wi
l dW'
0
0l(MdFSd)
由虚位移原理 We Wi 0 得:
nF iil (M d F Sd F N d T d )
i 1
8
杆件的虚位移原理的具体表达式
nF iil (M d F Sd F N d T d )
i 1
在推导杆件的虚位移原理表达式时,完全没有涉及物性 方面的问题。因此,虚位移原理既不限定用于线性问题,也 不限定用于弹性问题。
3. 利用单位力法公式计算位移
x
E I,l M(x) x
o
1
l
(ME M IdxF SG sF A Sdx)
l
FN
FN EA
dx
1
5 5
F FNili Ni EA
1
P a
3
3 EA
3
A
1 3
3
1 3 B 1 3
1
i 1
5 3
材料力学能量法

材料力学能量法材料力学能量法是材料力学中的一种重要分析方法,它通过能量原理来研究材料的力学性能和行为。
能量法在工程应用中具有广泛的意义,可以用于解决各种复杂的材料力学问题。
本文将对材料力学能量法进行详细介绍,包括其基本原理、应用范围和计算方法等内容。
首先,我们来看一下材料力学能量法的基本原理。
能量法是以能量守恒原理为基础的一种力学分析方法,它认为在任何力学系统中,系统的总能量始终保持不变。
在材料力学中,通过能量方法可以方便地求解结构的变形、应力分布和稳定性等问题。
能量法的基本原理为系统的总能量等于外力对系统做功的总和,即系统的内能和外力对系统做功的总和保持恒定。
其次,材料力学能量法的应用范围非常广泛。
它可以用于分析材料的弹性、塑性、断裂等力学性能,也可以用于研究材料的疲劳、蠕变、冷却等行为。
在工程实践中,能量法可以应用于各种材料的设计、优化和性能评估,如金属材料、复合材料、土木工程材料等。
通过能量法分析,可以更好地理解材料的力学行为,为工程设计和材料选型提供科学依据。
最后,我们来介绍一下材料力学能量法的计算方法。
能量法的计算方法主要包括弹性能量法、弹塑性能量法和断裂能量法等。
在应用中,需要根据具体问题选择合适的能量方法,并结合数值计算和实验验证进行分析。
在计算过程中,需要考虑材料的本构关系、加载条件和边界约束等因素,以确保计算结果的准确性和可靠性。
综上所述,材料力学能量法是一种重要的力学分析方法,具有广泛的应用前景和深远的理论意义。
通过能量法分析,可以更好地理解材料的力学性能和行为,为工程实践提供科学依据。
在今后的研究和应用中,我们需要进一步深入理解能量法的基本原理和计算方法,推动其在材料力学领域的发展和应用。
材料力学(II)第三章 PPT课件
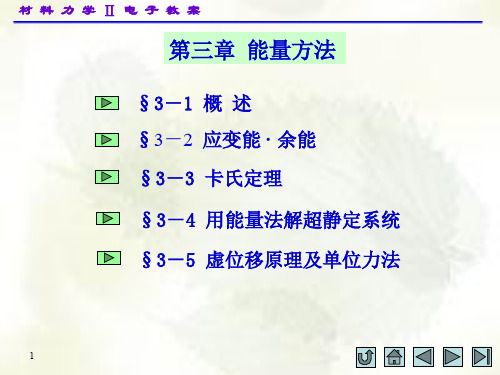
T 2l 2GIp
GIp 2l
2
5
材料力学Ⅱ电子教案
(c) 弯曲
第三章 能量方法
纯弯曲
Vε
W
1 2
M e
M e2l 2EI
M 2l 2EI
横力弯曲
Vε
l M 2 (x) d x 0 2EI
6
材料力学Ⅱ电子教案
第三章 能量方法
可以把应变能统一写成
Vε
W
1 2
FΔ
式中,F 为广义力,可以代表一个力,一个力偶,一对力或一
§3-2 应变能 ·余能
Ⅰ 应变能 (1)线弹性体
1. 基本变形形式【材料力学(Ⅰ)】 利用应变能 Vε 在数值上等于外力功W,可得
(a) 轴向拉(压)杆
4
Vε
W
1 2
FDl
FN2l 2EA
EA 2l
Dl 2
材料力学Ⅱ电子教案
第三章 能量方法
(b) 扭转
Vε
W
1 2
M
e
M e2l 2GIp
由结点A的平衡方程,得
F
FN 2sin
(3)
由于 为小角度,
所以 sin tan D
(4)
lLeabharlann 19材料力学Ⅱ电子教案
将(4)式代入(3)式,得
FN
Fl 2Δ
将(5)式代入(2)式,得
或写成
3
Δ
F
l
EA
F ( Δ)3 EA l
F 和D的关系如图b所示。
20
第三章 能量方法
2EA
材料力学 能量法

能量法一、变形能(应变能):变形固体在外力作用下由变形而储存的能量“”。
弹性变形能:变形固体在外力作用下产生的弹性变形而储存的能量1、性变形能具有可逆性。
2、塑性变形能不具有可逆性。
二、变形能的计算:利用能量守恒原理能量守恒原理:变形固体在外力作用下产生的变形而储存的能量,在数值上等于外力所作的外力功。
三、能量法:利用功能原理和功、能的概念进行计算的方法。
常见的能量法——功能原理、单位力(莫尔积分)、卡氏定理等。
在卡氏第二定理中应该注意的问题①、Vε——整体结构在外载作用下的线弹性变形能。
②、F i视为变量,结构反力和变形能等都必须表示为F i的函数②、Δi为F i作用点的、沿F i方向的变形③、Δi处要有相应的荷载,当无与Δi对应的F i时,可采用附加力法进行计算。
既先加一沿Δi方向的F i(在所求位移处沿所求位移的方向加上相对应的附加力),求偏导后,在令其为零,结果即为实际荷载作用的位移⑤、结果为正时,说明Δi与F i的方向相同;结果为负时,说明Δi与的F i方向相反。
单位力载荷法注意问题1、此种方法存在两个力系:一个为实际的力系;另一个为单位力系。
2、单位力必须与所求位移相对应:若求线位移——则单位力必须作用在所求点沿所求位移方向加单位的集中力;若求角位移——则单位力必须作用在所求点沿所求位移方向加单位的集中力偶。
2、内力的坐标系必须一致,每段杆的坐标系可自由建立。
莫尔积分必须遍及整个结构。
4、结果为“+”只说明所加的单位力的方向与实际的位移方向相同;“-”只说明所加的单位力的方向与实际的位移方向相反。
材料力学(能量法)

弹性变形阶段
01
外力作用下,材料发生弹性变形,此时外力所做的功全部转化
为应变能储存于材料内部。
塑性变形阶段
02
当外力继续增加,材料进入塑性变形阶段,部分应变能转化为
热能散失到环境中。
断裂破坏阶段
03
当材料达到强度极限时发生断裂破坏,此时储存的应变能迅速
释放并转化为断裂表面的新表面能和其他形式的能量。
非圆截面扭转时的能量可以通过实验或数值模拟等方法进 行计算,以获得准确的能量值。
扭转变形过程中能量转化
弹性变形能
在扭转变形过程中,部分能量以弹性变形能的形式储存在材料中。 当外力去除后,这部分能量可以释放并使材料恢复原状。
塑性变形能
当扭转变形超过材料的弹性极限时,部分能量会以塑性变形能的形 式消耗在材料中。这部分能量不可逆转,导致材料产生永久变形。
压缩过程中能量变化
外力做功
在压缩过程中,外力对杆件做 功,使其产生压缩变形和位移 。外力做功的大小与外力的大 小和杆件的位移成正比。
内力耗能
杆件在压缩过程中,材料内部 会产生应力和应变,从而消耗 能量。内力耗能的大小与材料 的应力-应变关系有关。
弹性势能
杆件在压缩过程中,由于材料 的弹性变形,会储存一定的弹 性势能。弹性势能的大小与材 料的弹性模量和变形量有关。
结构稳定性分析方法
能量准则
通过比较结构失稳前后的能量变 化,判断结构的稳定性。若失稳 后能量降低,则结构不稳定。
平衡路径跟踪法
通过逐步增加荷载或位移,跟踪 结构的平衡路径,观察结构从稳 定到不稳定的转变过程。
特征值分析法
基于结构刚度矩阵和质量矩阵, 求解特征值和特征向量,分析结 构的振动特性和稳定性。
孙训方版材料力学II第三章能量法

材料力学II 第三章能量法主讲:韩玉林东南大学工程力学系§3.1 概述在弹性范围内,弹性体在外力作用下发生变形而在体内积蓄的能量,称为弹性应变能,简称应变能。
物体在外力作用下发生变形,物体的应变Vε在数值上等于外力在加载过程中在相应位移上所做的功W,即Vε=W§3.2 杆件应变能•余能应变能的一般表达式若取单元体的边长为dx 、dy 、dz ,则该单元体的应变能为dV ε= v εdx dy dz令dx dy dz = dV则整个拉杆内的应变能为V dV dVεεευ==∫∫而外力P 1做功为:1ΔΔ(3.1)W P d =⋅∫1ΔΔW P d =⋅∫1d εευσε=⋅∫V dV dVεεευ==∫∫V Wε=应变能的一般表达式(适用于线性和非线性关系):整个杆件的应变能•整个杆件的应变能V ε与单位体积应变能v εVV v dVεε=∫若单位体积应变能v ε为常量,那么VV v dV v Vεεε==∫单位体积应变能v ε也称为应变能密度关于上述变形能计算的讨论:1以上计算公式仅适用于线弹性材料在小变形下的变形能的计算。
2变形能可以通过外力功计算,也可以通过杆件微段上的内力功等于微段的变形能,然后积分求得整个杆件上的变形能。
3 变形能为内力(或外力)的二次函数,故叠加原理在变形能计算中不能随便使用。
只有当杆件上任一载荷在其他载荷引起的位移上不做功时,才可应用。
4变形能是恒为正的标量,与坐标轴的选择无关,在杆系结构中,各杆可独立选取坐标系。
关于简单变形条件下,变形能计算的讨论(强调):•变形能的计算有两种方式:•一种由外力做功等价为变形能。
外力同位移间不一定是线性关系。
•另一种通过杆件微段上的内力功等于微段的变形能,然后积分求得整个杆件上的变形能。
如果是线弹性材料则实际上是通过最终应力乘以最终应变再除以2。
如果:•如果是线弹性材料,则实际上是通过单元体最终应力乘以最终应变再除以2(得到比能),再对整个杆件积分。
《材料力学(II)》第三章能量法

vc
1 d
0
余功与外力功
W 1 Fd 之和等于矩形面积 0
F11
F
F
曲线与纵 F1
dF
轴围成的
F
面积
11
o
1
材料力学Ⅱ电子教案
第三章 能量法
例题 图示等截面悬臂梁,E, I, A已知。在自由端受集中力F 和集中力偶M作用。设材料是线弹性的,试计算梁的应变能。 考虑两种不同的加载次序,略去剪力的影响.
第三章 能量法
例题 线弹性材料悬臂梁,受力如图所示,若F、EI、l等
均为已知,试用卡氏第二定理求: 1.加力点A处的挠度; 2.梁中点B处的挠度。
解:
F
x
1.加力点A处的挠度 C
B
l/2
l/2
A
弯矩: M Fx
Vε
M2 dx
l 2EI
F2 2EI
l 0
x 2dx
F 2l3 6EI
wA
Vε F
卡氏第二定理
i
V Fi
——卡氏第二定理
线弹性范围内,杆件的应变能对于杆件上某
一荷载的变化率,就等于与该荷载相应的位移。
28
材料力学Ⅱ电子教案
第三章 能量法
III. 卡氏第一定理和余(Δ1, Δ2 ,, Δi ,, Δn ) Vc f (F1, F2 ,, Fi ,, Fn )
(1 2
Δ12
Δ1 Δ2
1 2
Δ22 )
由卡氏第一定理,得
AB Δ1
Vε EA ( 4 Δ1 2l 2
2 Δ1
2 2
Δ2 )
0
BC
2 2
(1
2
)
Vε Δ2
材料力学能量法知识点总结

材料力学能量法知识点总结材料力学是工程力学的重要分支之一,研究材料在受力作用下的变形与破坏行为。
能量法是材料力学的基础理论之一,通过利用能量守恒原理,分析和求解材料的力学问题,具有重要的理论和实践价值。
本文将对材料力学能量法的基本概念、原理和应用进行总结。
1. 弹性势能与弹性应变能材料在受力作用下产生的变形能够存储为弹性势能,其中最常用的势能是弹性应变能。
弹性应变能是由于材料的弹性变形而储存的能量,可表示为弹性应变能密度。
2. 弹性势能的计算方法弹性应变能的计算方法主要有两种:一是通过力学平衡方程和材料力学性质的函数关系进行积分计算;二是通过应力-应变关系和应变能密度公式进行计算。
3. 弹性势能的应用弹性势能的应用涉及材料的变形、破裂、接头设计等问题。
通过计算弹性势能可以判断材料是否会发生破裂,并可用于材料的优化设计。
4. 塑性势能与塑性应变能材料在塑性变形时会产生塑性势能,塑性势能是由于材料的塑性变形而储存的能量。
塑性应变能可表示为塑性应变能密度。
5. 塑性势能的计算方法塑性势能的计算方法适用于材料的非弹性变形过程,常用的方法有等效应力法和Mises准则。
通过计算塑性势能可以估计材料在受力作用下的变形程度和破坏形式。
6. 塑性势能的应用塑性势能的应用主要涉及材料的变形、强度分析和塑性成形工艺等问题。
通过计算塑性势能可以评估材料的强度和变形能力,并可用于材料的成形优化。
7. 总势能与变分原理材料受到多种因素的叠加作用时,总势能是各种势能的代数和。
变分原理是能量法的基本原理之一,通过对总势能进行变分,得到材料力学问题的基本方程。
8. 总势能的应用总势能的应用主要涉及材料的稳定性分析和振动问题。
通过计算总势能可以判断材料的稳定性,预测振动频率和振动模式。
9. 耗散能与损伤模型材料在受力作用下会发生能量损耗,产生耗散能。
通过建立耗散能与应变的关系,可以描述材料的损伤行为,并建立损伤模型进行应力-应变分析。
材料力学能量法

材料力学能量法
材料力学是研究材料在外力作用下的变形、破坏和稳定性等问题的学科。
能量法是材料力学中的一种重要分析方法,它通过能量的守恒原理来分析材料的力学性能,为工程实践提供了重要的理论支撑。
本文将对材料力学能量法进行介绍,包括能量原理、应用范围、解题方法等内容,希望能为相关领域的研究人员和工程师提供一些参考。
在材料力学中,能量原理是指系统在外力作用下,能量的总变化等于外力所做的功。
根据这一原理,可以利用能量方法来分析材料的力学性能。
能量方法的应用范围非常广泛,可以用于分析材料的弹性、塑性、断裂等问题,也可以用于分析结构的稳定性和动力响应。
在工程实践中,能量方法被广泛应用于材料设计、结构优化和故障分析等领域。
在使用能量方法进行分析时,首先需要建立系统的能量平衡方程,然后根据系统的力学性能和外力条件,确定系统的势能和动能表达式。
接下来,可以利用能量平衡方程来推导系统的力学性能参数,比如应力、应变、位移等。
最后,通过求解能量平衡方程,可以得到系统的稳定性、破坏条件等重要信息。
除了上述基本方法外,能量方法还可以结合其他分析方法,比如有限元方法、变分原理等,来进行更复杂的问题分析。
在工程实践中,能量方法通常与实验测试和数值模拟相结合,可以为工程设计和材料选择提供重要的参考依据。
总之,材料力学能量法是一种重要的分析方法,它通过能量的守恒原理来分析材料的力学性能,为工程实践提供了重要的理论支撑。
希望本文的介绍能够对相关领域的研究人员和工程师有所帮助,也希望能够引起更多人对材料力学能量法的关注和研究。
材料力学能量法最经典解析PPT课件

能量法——利用定理求变形
极坐标方程是给一 个角度能够确定一 个挠度。因此该问 题是求任意位置角 的径向变形。
注意2个角度φ和θ的意义。 Φ用于表 示力F作用下任意位置上的弯矩。而θ 是用于表示任意位置的挠度,单位力 作用的位置。摩尔积分应该是对Φ积 分。 Φ在0到360度变化。
能量法——利用定理求变形
能量法——其他
超静定——与拉压杆相关
每根杆都沿杆的方 向线变形,后旋转 到变形后的位置。 变形用作垂线代替。
超静定——与拉压杆相关
此处注意CD杆
变形转换后是 BC杆变形的一 半。
超静定——与拉压杆相关
超静定——与拉压杆相关
广义胡克定律的应用。 每一点的应力状态为
p p
超静定——弯扭相关
此题仍然是有两个变 量,x是所求任意截面 的挠度值,而ξ是任意 截面的弯矩值,摩尔 积分是对ξ积分。
超静定——弯扭相关
超静定——弯扭相关
此类题目重点是分析圆盘 及2根杆的受力情况及变 形情况。
超静定——弯扭相关
该表达式上课过 程中没有出现过, 但是很容易推导 出来。
超静定——弯扭相关
超静定——弯扭相关
超静定——弯扭相关
超静定——弯扭相关
超静定——弯扭相关
此题目的重点是分析的方法和思路。由弹簧变 形与力和力矩之间的关系找到变形协调方程求 解超静定问题。
能量法——利用力做功求变形
能量法——利用力做功求变形
应力已知,计算应变能从而得到外力 功,最终获得力作用下的变形。
能量法——利用力做功求变形
能量法——利用力做功求变形
能量法——互等定理
该表达式上课过 程中没有出现过, 但是很容易推导 出来。积分求得 挠曲线后可得到 弯矩方程,进而 计算应变能。
材料力学第29讲 Chapter3-4第三章 能量法(虚位移原理及单位力法)

P
3
P
3
3. 利用单位力法公式计算位移
1
1
桁架结构:1
l
FN
FN EA
dx
1
F 5 5 FNili Ni EA
1
P a
3
3 EA
3
A
1 3
3
1 3 B 1 3
1
i 1
5 3
Pa EA
15
解: 本题也可用卡氏第二定理
P
P
V
5 i 1
FN2i li 2EA
3
3
PA
P 3
P
B
P
5
二单位力法11虚位移原理单位力法对系统2实际载荷系统1单位载荷系统212单位力法eaeigagieigaeagi推导单位力法时将虚设的单位力作为载荷将实际载荷引起的位移当作虚位移
材料力学 II
(4)
Energy Method—Part 4
第廿九讲
1
内容
1. 应变能和余能的计算 2. 卡氏定理 3. 用能量法解超静定系统 4. 虚位移原理及单位力法
l
1
Fl 2 2EI
2 3
l
M图
1
w A
1 EI
l 1
1 2
Fl
Fl 2 2EI
1 A
l
B
30
作业 P98:3-18(a) (第二册) P98:3-20(a)
P99:3-22(b)
下次课讲第二册第六章 动载荷和交变应力
31
M M dM
FB
dx
B
dx
1 2
d
1 2
d
FS FS dFS
1 2
材料力学能量法范文

材料力学能量法范文材料力学能量法是一种分析和计算物体的力学行为的方法,它基于能量守恒定律。
在这种方法中,物体或结构的变形和应力被视为能量的转化和传递过程。
通过确定系统的动能和势能,并将其与外部力和内部能力作为输入参数,可以计算系统的平衡状态和力学性能。
材料力学能量法的应用十分广泛,特别在工程领域中,例如结构分析、疲劳分析、材料强度计算和复杂系统的模拟等。
这种方法的基本原理是通过对物体的动能和势能之间的转化过程的考虑,来得到物体的平衡状态和力学性能。
在材料力学能量法中,物体的动能是由其质量和速度决定的,而势能是由物体的形变和应力分布决定的。
物体的动能包括其线性运动的动能和旋转运动的动能。
线性运动的动能可以通过物体的质量和速度平方的乘积来计算,而旋转运动的动能可以通过物体的惯性矩和角速度平方的乘积来计算。
物体的势能包括其弹性势能和塑性势能。
弹性势能是由物体的形变和应力分布引起的,而塑性势能是由物体在塑性变形时的能量损失引起的。
弹性势能可以通过弹性模量和物体的形变量的乘积来计算,而塑性势能可以通过材料的塑性应变和应力的乘积来计算。
在材料力学能量法中,系统的总能量是系统动能和势能的总和。
根据能量守恒定律,系统的总能量在无外部能量输入的情况下保持不变。
通过计算系统各个部分的动能和势能,可以确定系统的能量平衡状态和力学性能。
材料力学能量法的优点是可以考虑到物体的整体行为,并对动能和势能之间的转化过程进行分析。
它可以用来解决复杂的力学问题,并提供物体的应力和变形的直观理解。
此外,它还可以与其他力学方法相结合,例如有限元分析和基于能量的优化方法。
然而,材料力学能量法也有一些限制。
它通常只适用于小变形和较简单的物体形状,而对于大变形、非线性材料和复杂几何形状的物体,其精确性可能会降低。
此外,对于一些实际工程问题,由于存在其他影响因素,如温度和湿度等,材料力学能量法可能需要进一步修正和扩展。
总之,材料力学能量法是一种重要的力学分析方法,它基于能量守恒定律,通过对系统动能和势能之间的转化过程进行分析,来确定物体的平衡状态和力学性能。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
σ2
σ3
∫ ∫ ∫ Vε =
V vε dV =
( σ ε1 dε )dV
V0
∫ ∫ ∫ Vc =
V vc dV =
( σ1 ε dσ )dV
V0
Mechanics of Materials
三、应变能的计算
F
原理: W = Vε
线弹性体
1. 基本变形形式 F
轴向拉(压)杆
F
Vε
=W
=
1 2
FΔl
Δl = FN l EA
最终值——简单加载。
Clapeyron’s theorem (克拉贝依隆原理)
Vε
=
1 2
FwC
+
1 2
Meθ A
=
F 2l3 96EI
+
M
2 e
l
6EI
+
FMel 2 16EI
wC
=
Fl 3 48EI
+
Mel2 16EI
θA
=
Fl 2 16EI
+
Mel 3EI
Me
F
A
θθAAMF wCF C
wCM
T (x) + dT (x)
FN(x) M(x)
FN(x) +dFN(x) M(x) + dM(x)
dx
dVε
=
dW
=
1 2
FN
(
x
)
d
Δ
+
1 T( x)dϕ
2
+
1 2
M(x)dθ
= FN2 ( x)d x + T 2 ( x)d x + M 2 ( x)d x
2EA
杆的应变能为
2GIp
2EI
∫ ∫ ∫ ∫ Vε =
3 变形能是恒为正的标量,与坐标轴的选择无关, 在杆系结构中,各杆可独立选取坐标系。
4 应变能的大小与加载顺序无关(能量守恒)。
Mechanics of Materials
5 变形能为内力(或外力)的二次函数,故叠加原理 在变形能计算中不能使用。只有当杆件上任一载荷 在其他载荷引起的位移上不做功时,才可应用。
Mechanics of Materials
§10-3 卡氏定理
卡氏定理(Castigliano’s Theorem),是意大利工程 师卡斯蒂利亚诺(A.Castigliano )于1873年提出。
一、卡氏第一定理
图示为非线性弹性杆,Fi为广义力,Δi为广义位移。
Δ
O
Δ
Δ 2
O
Δ ≠ Δ 1+Δ2
Δ′ ≠ Δ11
Δ ΔΔ
2
Mechanics of Materials
例题:杆件受外载荷如图所示,已知杆的拉(压) 刚度为EA,求杆件内储存的应变能。
L q
x L
F 解:
Vε 1
=
F2L 2EA
∫ Vε 2 =
L (qx )2
dx 0 2EA
= q2 L3 6EA
Δ
=
Δ l1
sin α
+
Δl2
tan α
=
Fl
EA sin2 α
⎛ ⎜⎝
c
o
s
2
α
+
1
cosα
⎞ ⎟⎠
1
2 αA
l
A′ F
方法二 应变能原理 W = Vε
Vε
=
FN 12l1 2EA
+
FN 22l 2EA
=
F 2l
2EA sin2 α
⎛ ⎜⎝
c
o
s
2
α
+
1
cos α
⎞ ⎟⎠
W = FΔ 2
Δ
=
Fl
EA sin2 α
= F 2 L + FqL2 + q2 L3 F 2EA 2EA 6EA
Vε3 ≠ Vε1 + Vε2
应变能不能采用叠加原理进行计算
Mechanics of Materials
例题:求图示简支梁的应变能,EI为常量。
Me
F
A
θA
wC C
0.5l
0.5l
解:1. 由外力功求
F 和Me 同时作用在梁上,并 B 按同一比例由零逐渐增加到
l
l
解:计算位移Δ
α
Δ
α
杆的伸长量为
A
F
Δl = FN l EA
Δ = (l + Δl)2 − l2 = [l 2 + 2l(Δl ) + (Δl )2 ] − l 2 ≈ 2l(Δ l )
Δ= l⋅
2 FN EA
解:计算位移Δ
Δ = l ⋅ 2 FN EA
FN
=
F
2 sin α
sinα ≈ tanα = Δ
x
s --截面系数
矩形截面
αs
=
6 5
圆形截面
αs
=
10 9
Mechanics of Materials
变形形式 外力功 以内力表示的变形能
内力恒定 内力变化
F
轴扭基向转本拉变压形V下ε 变= W形1212能=FMΔ12的elϕF一Δ 般表达22FTGEN22式IAllp :
∫ FN2 ( x)dx
=
GIp 2l
ϕ2
m x
T 2(x)
∫ Vε = W =
dx l 2GI p
l
弯曲
纯弯曲
θ
ρ
Mechanics of Materials
M
M
M
M
θ
θ
l
Vε
=W
=
1 2
M eθ
1 = Me
ρ EI
θ = l = Mel ρ EI
Vε
=W
=
1 2
M eθ
=
M
2 e
l
2EI
=
M 2l 2EI
Mechanics of Materials
Mechanics of Materials
Me
F
2. 由内力方程直接求
A
x1 0.5l
FA
C
x2 B
0.5l
FB
FA
=
F 2
−
Me l
FB
=
F 2
+
Me l
AC:M ( x1 )
=
F (
2
−
Me l
) x1
+
Me
BC:
M(x2 )
=
F (
2
+
Me l
)x2
∫ ∫ Vε
= VεAC
+ VεBC
=
1 2EI
Mechanics of Materials
线弹性,位移可以叠加,但应变能不能叠加
F
F1
Vε1
O Δ1
F
F
F1+F2
Vε1
F2
Δ
O
Vε2
Δ2
Vε
Δ
Δ 1
Vε2
Δ
O
ΔΔ 2
Vε ≠ Vε1 + Vε 2
Mechanics of Materials
非线性弹性,位移也不可以叠加
F
F1
OΔ 1
F
F
F1+F2 F2
Mechanics of Materials
§3-1 概 述
回顾:计算节点A铅垂位移
1
2 αA
l
F
常规方法:平衡关系,几何关系,物理关系
Mechanics of Materials
FN1 = F sinα(拉), FN2 = F tanα(压)
方法一
Δ l1
=
FN 1l1 EA
, Δl2
=
FN 2l EA
l
Mechanics of Materials
l
l
α
Δ
α
FN A
FN
F
FN
=
Fl 2Δ
F
3
Δ=
F
⋅ l 或 F = ( Δ)3 EA
Δ
EA
l
Mechanics of Materials
3
Δ=
F
⋅ l 或 F = ( Δ)3 EA
EA
l
l
l
α
Δ
α
杆的应变能
A
F
∫ ∫ Vε = W =
Δ
FdΔ=
0
Δ⎛ 0 ⎜⎝
⎡ ⎢⎣
l
2
0
M
2(
x1
)dx1
+
l 2
0
M
2(
x2
)dx2
⎤ ⎥⎦
= F2l3 + Me2l + FMel2 96EI 6EI 16EI
Mechanics of Materials
例题:原为水平位置的杆系如图所示,试计算在荷 载F作用下的应变能。两杆的弹性模量均为E,横截 面面积均为A,且均为线弹性的。
Me
F
A
C
B
0.5l
0.5l
F2
Me
F1
Vε ≠ Vε (F ) + Vε (Me )
Vε = Vε (F1 ) + Vε (F2 ) + Vε (Me )
Mechanics of Materials
