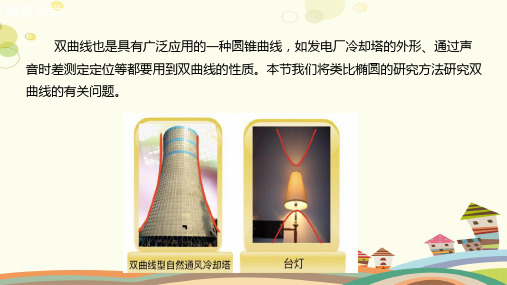
双曲线的标准方程PPT教学课件

③这两焦点的距离叫双曲线的焦距.
F1 o F2
定义中的“绝对值”三字去掉， 能否表示双曲线？
概念深化
• 如果动点到两个定点的距离的差是一个常数, 这个常数小于这两个定点的距离时是双曲线.
• 那么如果这个差等于这两点的距离呢?如果这 个差大于这两点间的距离呢?动点的轨迹各是 什么?
• ||MF1|-|MF2||<|F1F2|双曲线 • ||MF1|-|MF2||=|F1F2|两条射线 • ||MF1|-|MF2||>|F1F2|无轨迹
即c>a，所以c2
• － a2>0 ， 令 c2 － a2=b2 ， 其 中
b>0，代ax22入上by式22 得 1
(a 0, b 0)
双曲线的标准方程
y
M
y M
F1 O F2 x
F2 x
O
F1
x2 a2
y2 b2
1
y2 a2
x2 b2
1
(a 0，b 0,c2 a2b2) 演示
练习：写出以下双曲线的焦点坐标
ቤተ መጻሕፍቲ ባይዱWhat can’t Betty do?
She can’t speak Chinese.
1. x2 y2 1 16 9
3. y2 x2 1 16 9
2. x2 y2 1 9 16 y2 x2
4. 1 9 16
F(±5,0) F(0,±5)
典型例题
例1已知双曲线两个焦点的坐标为F1（－5，0）、F2（5， 0），双曲线上一点P到F1、F2的距离的差的绝对值等
于6，求双曲线的标准方程.
ride a bike
ride a horse
sing
swim
Match
Check the answer
Look,read and do
Play basketball Play table tennis
Play tennis Play Ridefoaotbbaiklel
Ride a Sing horse
F1 o F2 x
x
F1
方程
焦点
a.b.c 的关
x2 a2
y2 b2
1
y2 a2
x2 b2
1
F ( ±c, 0) F(0, ± c)
c2 a2 b2
当堂检测
1.求适合下列条件的双曲线的标准方程:
1 焦点在x轴上,a 4,b 3; 2 焦点为0, 6, (0, 6),且经过点(2, 5)
答案： (1) x2 y2 1; (2) y2 x2 1;
m 0
n
0
表示焦点在 x 轴上的双曲线；
m 0
n
0
表示焦点在 y 轴上的双曲线。
Teacher’s Name – X Grade
教学科目
Module 2 Me,my parents and my friends
Unit 1 I can speak English
Introduce yourself:
Swim
What can Lingling do ?
She can swim, play football and play tennis.
Listen and read
What can Betty do?
She can play football, play basketball and speak English.
• 双曲线上的点应满足的条件是什么？
• MF1 MF2 常数 （小于 |F1F2|）
演示
形成概念
• 类比椭圆的定义,你能给出双曲线的定义吗？
• 我们把平面内与两个定点F1、F2的距离的
差的绝对值等于常数（小于|F1F2|）的点的
轨迹叫做双曲线.
说明
M
①常数小于 |F1F2|； ②这两个定点叫做双曲线的焦点；
My name is …. I’m a …. I’m from …. I’m … years old. My favourite sport is ….
Sports
play basketball
play football
play tennis
play table tennis
play the piano
2 22
引入新课
• 问题3.如果把上述定义中的“距离的和”改为 “距离的差”那么点的轨迹会发生怎样的变化？
• 动点M所满足的几何条件是什么？
• 这个常数与|F1F2|的大小关系如何？为什么？
• 用同样的方法，使|MF2|-|MF1|<|F1F2| ，就得 到另一条曲线，这两条曲线合起来叫做双曲线， 每条叫做双曲线的一支。
双曲线的标准方程
知识回顾
• 问题1.椭圆的定义是什么？ • 我们把平面内与两个定点F1、F2的距离的
和等于常数（大于∣F1F2∣）的点的轨迹叫 椭圆.这两个定点叫椭圆的焦点，两焦点的 距离叫椭圆的焦距.
• 问 关题 系ax222如.b椭y何22 圆？1(的焦标点在准x轴 方上程) 是bx怎22 样ay的22 ？1(焦a点、在by、轴上c )
• ③列式。||MF1|-|MF2||=2a
• 即 (x c)2 y2 (x c)2 y2 2a
方程推导
• ④化简。
y
(x c)2 y2 (x c)2 y2 2a.
M
• 化简得(c2－a2)x2－a2y2=a2(c2－
a2).
F1
O
F
2
x
• 由双曲线的定义可知，2c>2a，
类比椭圆标准方程的建立过程,你能建立 双曲线的标准方程吗?
即
方程推导
• ①建系。使x轴经过两定点 F1、F2， 轴为线段F1F2的 垂直平分线。
y
M
• ②设点。设M(x,y)是双曲 线上任一点，焦距为2c，
F1
O
F
2
x
那么焦点F1(-c,0)、F2(c,0) ， ||MF1|-|MF2||=2a。
16 9
20 16
当堂检测
练习 1.判断下列方程是否表示双曲线？若是，求出 a、b、c 及焦点坐标。
（1） x 2 y 2 1 42
（2） x 2 y 2 1 22
（3） x2 y 2 1 42
（4） x2 y 2 1 (m 0, n 0) mn
② x 2 y 2 1 (mn 0) 是否为双曲线的方程？ mn
解：因为双曲线的焦点在x轴上，所以设它的
标准方程为： x2
a2
y2 b2
1(a
0, b
0)
∵2a=6,2c=10, ∴a=3,c=5. ∴b2=52－32=16
所以所求双曲线的标准方程为
x2 y2 1
9 16
小结
定义 图象
| |MF1|-|MF2| | =2a（2a<|F1F2|）
y
M
y
M F2