第十三章 弯曲变形与静不定梁
材料力学-弯曲变形

(向下)
qB
qmax
w(l)
Pl 2 2EI
(顺时针)
例题2
图示的等截面简支梁长为l,抗弯刚度为
EI,在右端受有集中力偶M0的作用,求梁任
一截面的转角和挠度。
y
解:
由整体平衡得 FAx=0, FAy= FBy= M0/l 从而,截面的弯矩为
M(x)= xFAy= xM0/l
FAx A x o
FAy
横截面变形:
线位移:长度变化
水平方向—小变形假定,挠曲轴平坦,忽略不计 垂直方向—挠度 w= w(x)
转角:角度变化
横截面相对于原位置转过的夹角,
一般用q (x)表示截面转角,并且以逆时针为正
q'
对于细长梁,略去剪力对变形影响 平截面假设成立: 变形的横截面与挠曲轴垂直
q q tan q dw
(l 2
a2)
y
例题3
P x
A
C
于是,梁的挠曲线方程为 FAx
l
w
w1 w2
(x) (x)
0 xa a xb
FAy
a
b
Pb
6 EIl
Pa
6 EIl
x3 (b2 l2 )x (l x)3 (a2 l2
)(l
x)
0 xa a xl
转角方程为
q w ww12((xx))
0 xa a xb
Pb 2EIl
x2
C1
ቤተ መጻሕፍቲ ባይዱdx
Pb 6EIl
x3
C1x
D1
同理,对CB段
w2
w2dx C2
Pa EIl
(l
x)dx
C2
材料力学(单辉祖)第十三章 能量法

第十三章能量法主讲人:张能辉1引言2-研究变形体方法:微体法,能量法引言微体法几何关系i ij u ~ε微体法静力学关系物理关系ijij εσ~平衡ij σd v ⇓V控制方程数学手段ij σ边界条件初值条件ijε3-引言能量法1P P 1P 外力作用线弹性体恢复22P 变形效应外力卸除原形i P →ij ij εσ~Hooke’s Law Lineariij u ~ε线弹性体f广义载荷δ广义位移δ∝f 引进比例常数δk f =下面看能量如何写?与外力有何关系?4由能量守恒WV =ε(外力功全部转化成应变能)P26488主平面微体应变能(P264 8-8)1ii εσυε2=应变能密度i =1,2,3)(,,)6外力功与应变能杆件应变能微段d x 储存应变能∫∫⋅==dVAdAdx dV dV εεευυdAxx体积分化为面积分d x dV整个梁存储应变能积分思想: 微段的叠加==dAdx dV V εεευ变∫∫∫AlV822 EA21 2NFdx EAd ml2ρ2p外力功与应变能弯曲(忽略切应力)21zM 21zM 2zEI ευ=2z lV dxEI ε=∫Conclusion外力功与应变能应变能特点C1: 与载荷终值有关,而与加载次序无关M(a) M 、F 同时作用(b)ABF (b)先F 后M (c) 先M 后F 三种加载历史等效?FM F M M FM M M M M =+=+19互等定理23互等定理讨论2F 独立加第I 组力系F 123411121:0;0;Δ→Δ→Δ先加第II 组力系,再加第I 组力系3F 2F 21110;0:Δ′→Δ′→Δ12344F ????;21211111Δ′=ΔΔ′=Δ问1F F =k Δ保证相等27互等定理线弹性体变形能特点:大小取决于加载终值而与加载次序无关21V V =414313222121Δ+Δ=Δ+Δ⇒F F F F 21F F I 组力系12I 组力系作用点43F F II 组力系,3,4力点II 组力系作用点2212,ΔΔII 组力系在I 组力系作用点引起的沿I 组力系方向的位移4131,ΔΔI 组力系在II 组力系作用点引起的沿II 组力系方向的位移28互等定理等定功的互等定理第I 组力系在第II 组力系引起位移上所做功等于第II 组力系在第I 组力系引起位移上所做功简化:If F 1---I; F 2---IIthen F =F FF =2then F 1Δ12= F 2Δ2112FF =1If F 1= F 2, then Δ12=Δ21位移互等定理弹在对于线弹性体,若在1,2处分别作用两个大小相等的载荷,则点1处由于点2处载荷引起的位移Δ12等于处由点点2处由于点1处载荷引起的位移Δ2129Example-1实测w 1 ,w 2 ,w 3方案:1F3211.三点装位移计浪费2.一个位移计逐点测费工1新方案(位移互等定理)F323.自由端加位移计逐点加载不影响原有力系30单位载荷法32Example-1E ample1qABlx已知:梁EI=const已知梁求:w=?θA=?A38Example-2M aCB B1x x FAa 2已知:刚架M B =F a 求:Δcy =?40E l3 Example-3BA1αβ2CF已知:桁架EA, l1l2? Δ?求: Δcx=? Δcy=?43Example-4 (P20 12-5)F FR已知:小曲率曲梁AB已知:小曲率曲梁,轴线曲率半径为R求:截面A和B的相对转角46E l5(P56)Example-5 (P56)F OA BϕCA B已知:小曲率曲梁,轴线曲率半径为R求求:A的铅垂位移48余能与卡氏第二定理50。
《工程力学》课程的知识体系和内容结构

《工程力学》课程的知识体系和内容结构1、课程的知识体系《工程力学》是一门是既与工程又与力学密切相关的技术基础课程,在基础课程和专业课程之间起桥梁作用。
通过本课程的学习,使学生掌握工程力学的理论和方法,具备从力学角度对工程问题的思维能力和初步解决此类问题的实践能力,并且获得大量的工程背景知识,为学习后续课程、掌握机械等工程设计技术打下牢固的基础。
本课程涵盖了“静力学”和“材料力学”两部分的内容。
“静力学”主要研究刚体的受力和平衡的规律;“材料力学”主要研究构件强度、刚度和稳定性的问题,在保证构件既安全适用又经济的条件下,为合理设计和使用材料提供理论依据。
静力学主要研究的问题:物体的受力分析、力系的简化和力系的平衡条件。
材料力学主要研究的问题:杆件在发生拉伸或压缩、剪切、扭转和弯曲基本变形时内力、应力和变形的计算,在各种基本变形下的强度和刚度计算;应力状态的基本理论;材料在复杂应力作用下破坏或失效规律及其应用;压杆稳定性问题。
2、课程的内容结构第一章介绍静力学的基本概念,常见的几类典型约束及约束力的特征,物体的受力分析。
第二章介绍汇交力系的简化和平衡条件。
第三章介绍力偶的概念及其对刚体的作用效应,力偶系的合成与平衡条件。
第四章介绍平面任意力系的简化、平衡条件和平衡方程,刚体系的平衡问题求解。
第五章介绍空间任意力系的简化和平衡条件。
第六章静力学专题:桁架杆件内力的求解;滑动摩擦、摩擦角和自锁现象、以及滚动摩擦的概念。
第七章介绍材料力学的研究对象、基本假设、外力和内力、应力和应变的概念。
第八章介绍拉压杆的内力、应力、变形及材料在拉伸与压缩时的力学性能,拉压杆的强度和刚度问题,简单静不定问题,拉压杆连接部分的强度计算。
第九章介绍圆轴扭转的外力、内力、应力与变形,圆轴的强度和刚度计算,静不定轴的扭转问题。
第十章介绍梁的外力和内力(剪力与弯矩),内力图的绘制。
第十一章介绍对称弯曲时梁的正应力、切应力、强度计算和梁的合理强度设计。
《弯曲变形超静定梁》课件

方法:采用有限元 分析方法进行优化 设计
优化参数:梁的截 面尺寸、材料属性 、加载方式等
优化策略:根据优化 目标,选择合适的优 化算法和优化参数, 进行迭代优化设计
弯曲变形超静定梁的优化设计实例
实例1:某桥梁的 弯曲变形超静定 梁优化设计
实例2:某高层建 筑的弯曲变形超 静定梁优化设计
实例3:某大型体 育场馆的弯曲变形 超静定梁优化设计
位移法求解
基本原理:通过求解位移场,得到结构内力 求解步骤:建立位移场方程,求解位移场,得到内力 适用范围:适用于求解超静定梁的位移和内力 优点:计算简便,易于实现自动化计算
混合法求解
混合法求解的基本 思想:将超静定梁 的求解问题转化为 静定梁的求解问题
混合法求解的步骤: 先求解静定梁,再 求解超静定梁
位移法:通过求解 位移法方程,得到 超静定梁的位移和 内力
混合法:结合力法 和位移法,求解超 静定梁的位移和内 力
矩阵法:通过建立 刚度矩阵和荷载向 量,求解超静定梁 的位移和内力
弯曲变形超静定 梁的分析
弯曲变形的产生原因
材料性质:材料的 弹性模量、泊松比 等参数影响弯曲变 形
载荷作用:外力作 用下,梁的弯曲变 形程度与载荷大小、 方向有关
确定超静定梁的边界条件 建立超静定梁的平衡方程 求解超静定梁的位移和应力 验证超静定梁的稳定性和强度
弯曲变形超静定 梁的求解方法
力法求解
基本原理:利用静力平衡条件求解超静定结构
求解步骤:建立平衡方程、求解未知力、求解位移
适用范围:适用于超静定梁、桁架等结构
优点:计算简便、易于理解
缺点:需要人工判断未知力的方向和数量,可能存在误差
优化设计的概念和意义
优化设计:通过数学模型和算法,寻找最优解,使结构满足设计要求 概念:在满足设计要求的前提下,使结构具有最优的性能和成本 意义:提高结构的稳定性、安全性和耐久性,降低成本和能耗 应用:广泛应用于建筑、桥梁、机械等领域
梁的弯曲(工程力学课件)

02 弯曲的内力—弯矩与剪力
3-3截面
M 3 q 2a a 2qa 2
4-4截面
qa 2
5qa 2
2
M 4 FB 2a M C
3qa
2
2
5-5截面
qa 2
M 5 FB 2a
2
02 弯曲的内力—弯矩与剪力
由以上计算结果可以看出:
(1)集中力作用处的两侧临近截面的弯矩相同,剪力不同,说明剪力在
后逐段画出梁的剪力图和弯矩图。
04 弯矩、剪力与载荷集度之间的关系
例8 悬臂梁AB只在自由端受集中力F作用,如图(a)所示,
试作梁的剪力图和弯矩图。
解:
1-1截面: Q1=-F M1=0
2-2截面: Q1=-F M1=-Fl
04 弯矩、剪力与载荷集度之间的关系
例9 简支梁AB在C点处受集中力F作用,如图(a)所示,作此梁的剪力
(2)建立剪力方程和弯矩方程;
(3)应用函数作图法画出剪力Q(x),弯矩M(x)的图线,即为剪力
图和弯矩图
03 弯矩图和剪力图
例9.3 悬臂梁AB在自由端B处受集中载荷F作用,如图(a)所示,试作
其剪力图和弯矩图。
解 :(1)建立剪力方程和弯矩方程
() = ( < < )
() = −( − ) ( ≤ ≤ )
方程和弯矩方程,并作剪力图和弯矩图。
解:(1)求支反力
(2)建立剪力方程和弯矩方程
03 弯矩图和剪力图
(3)绘制剪力图、弯矩图
计算下列5个截面的弯矩值:
03 弯矩图和剪力图
二、用简便方法画剪力图、弯矩图 (从梁的左端做起)
1.无载荷作用的梁段上 剪力图为水平线。 弯矩图为斜直线(两点式画图)。
工程力学(材料力学)8 弯曲变形与静不定梁

B
ql4 RBl3 0
8EI 3EI
q 约束反力为
B
RB
3 8
ql
RB
用变形比较法求解静不定梁的一般步骤:
(1)选择基本静定系,确定多余约束及反力。 (2)比较基本静定系与静不定梁在多余处的变形、确定 变形协调条件。 (3)计算各自的变形,利用叠加法列出补充方程。 (4)由平衡方程和补充方程求出多余反力,其后内力、 强度、刚度的计算与静定梁完全相同。
教学重点
• 梁弯曲变形的基本概念; • 挠曲线的近似微分方程; • 积分法和叠加法计算梁的变形; • 梁的刚度条件。
教学难点
• 挠曲线近似微分方程的推导过程; • 积分法和叠加法计算梁的变形; • 变形比较法求解静不定梁。
第一节 弯曲变形的基本概念
齿轮传动轴的弯曲变形
轧钢机(或压延机)的弯曲变形
例13-4 用叠加法求图示梁的 yC、A、B ,EI=常量。
M
P
解 运用叠加法
A
C
l/2
l/2
A
=
q
5ql4 Pl3 ml2
B
yC
384EI
48EI
16EI
A
ql3 24EI
Pl 2
16EI
ml 3EI
B
B
ql3 24EI
Pl2 16EI
ml 3EI
M
+
q
A
+
BA
B
二、梁的刚度条件
y max y,
A
max
A ql3
B
24EI
RA
q
A
θB
l
B θB RB
在梁跨中点 l /2 处有 最大挠度值
材料力学第十三章 能量法2013

§13-7 计算莫尔积分的图乘法 ★重点
(Energy methods)
§13-1 概述(Introduction)
能量方法 (Energy methods )
利用功能原理 U = W 来求解可变形固体的位移、变形和内 力等的方法.
功能原理(Work-energy principle) 外力功等于变形能
2
Me ( x) U dx l 2 EI ( x )
2
(Energy ( Strain energy density for pure shearing state of stresses )
1 u ηγ 2
将 = G 代如上式得
G 2 2 u γ 2 2G
F1a
F2
M图
a B x A
F1a+F2l
特点:在刚节点处,弯矩值连续 ;
(Chapter Thirteen)
(Energy Method)
(Energy methods)
第十三章 能量法 (Energy Methods)
§13-1 概述(Introduction) §13-2 杆件变形能的计算及普遍表达式 §13-3 互等定理(Reciprocal theorems) §13-4 卡氏定理(Castigliano’s Theorem) §13-5 虚功原理(了解) §13-6 单位荷载法 莫尔定理 ★重点
2、利用功能原理计算变形 (Work-energy principle for calculating deflection)
2 FN ( x) T 2 ( x) M 2 ( x) U dx dx dx l 2 EA( x ) l 2GI ( x ) l 2 EI ( x ) p
《弯曲变形静不定梁》课件

效果评估
通过对比优化前后的设计方案,评估 优化效果,如承载能力的提高、弯曲 变形的减小等。
改进建议
根据评估结果,提出进一步改进的建 议,如调整设计变量、优化算法的改 进等,为后续的优化设计提供参考。
06
结论与展望
本课程的主要结论
01 02 03 04
静不定梁在弯曲变形时,其挠度曲线与简支梁类似,但存在一定的差 异。
影响分析
弯曲变形会导致静不定梁的轴线发生弯曲,同时产生剪力和弯矩,这些力会对 梁的承载能力和稳定性产生影响。具体来说,弯曲变形会导致梁的承载能力降 低,稳定性变差,容易发生失稳和破坏。
弯曲变形静不定梁的实例分析
实例一
某桥梁的主梁在受到车辆荷载作 用时发生弯曲变形,导致承载能 力降低,需要进行加固或更换。
通过实例演示,展示弯曲变形 计算方法的实际应用和效果。05弯曲变形静不定梁的优化设计
优化设计的目标和方法
目标
提高梁的承载能力、减小弯曲变形和 振动。
方法
采用有限元分析、遗传算法、模拟退 火算法等优化算法,结合实际工程需 求进行设计。
优化设计的具体步骤和实例分析
2. 确定设计变量和约束条 件;
1. 建立梁的有限元模型;
梁性能的影响。
开展实验研究,验证不同类型静不定梁弯曲变形的理 论分析结果,提高理论模型的精度和可靠性。
进一步研究不同类型静不定梁的弯曲变形特性 ,如多跨静不定梁、连续静不定梁等。
结合实际工程应用,研究静不定梁在复杂环境下 的弯曲变形行为,为结构设计提供依据。
THANK YOU
感谢各位观看
静不定梁的定义
静不定梁
静不定次数
在结构分析中,当一个结构的几何形 状和边界条件不能完全确定时,该结 构被称为静不定梁。
《弯曲变形静不定梁》课件

THANK YOU
。
适用范围
适用于分析简单梁结构,计 算过程相对简单,但精度略 低于弹性力学方法和有限元 方法。
04
静不定梁的应用
工程结构
桥梁
静不定梁在桥梁设计中应用广泛 ,如斜拉桥、悬索桥等,能够承 受较大的弯曲和剪切力,提高桥 梁的稳定性和安全性。
建筑
在高层建筑、大跨度结构等建筑 设计中,静不定梁能够提供更好 的支撑和稳定性,保证建筑的安 全性和耐久性。
解法
通过求解弹性力学基本方程,可以得到梁的位 移、应变和应力等参数。
适用范围
适用于分析梁的精确解,但计算过程较为复杂。
有限元方法
基本思想
01
将连续的梁离散为有限个小的单元,对每个单元进行受力分析
,再通过单元的集合体来近似表示整个梁。
求解过程
02
通过迭代或直接求解方法,得到每个单元的位移和应力,再通
大跨度结构
大跨度结构如体育场馆、会展中心等需要承受较大的荷载和 变形,静不定梁能够提供更好的承载和支撑,保证大跨度结 构的稳定性和安全性。
05
静不定梁的优化设计
材料选择
钢材
高强度钢材具有较高的承载能力和耐久性,适用于需要承受较大 载荷的静不定梁。
铝合金
铝合金具有轻质、耐腐蚀的优点,适用于需要减轻自重的静不定梁 。
01
03
为了减小扭转变形的影响,可以通过增加梁的截面尺 寸、提高材料的剪切模量或改变截面形状等方式来实
现。
04
在静不定梁中,扭转变形的影响通常较小,但在某些 情况下,如梁的长度较大或受到较大的力矩作用时, 其影响可能会变得较为显著。
03
静不定梁的分析方法
弹性力学方法
第十三章-压杆稳定

例题13.8图13-8所示正方形桁架结构,由五根圆截面钢杆组成,连接处均为铰链,各杆直径均为d=40 mm,a=1 m。材料的λp=110,λs=60,E=200 GPa,经验公式为 ,nst=1.8。试求结构的许可载荷。
第十三章压杆稳定
1基本概念及知识要点
1.1基本概念
理想受压直杆、理想受压直杆稳定性、屈曲、临界压力。
1.2临界压力
细长压杆(大柔度杆)用欧拉公式计算临界压力(或应力);中柔度杆用经验公式计算临界压力(或应力);小柔度杆发生强度破坏。
1.3稳定计算
为了保证受压构件不发生稳定失效,需要建立如下稳定条件,进行稳定计算:
压杆的柔度
iy=iz=i
由于
所以,λ>λP压杆为大柔度杆
用欧拉公式计算临界压力
例题13.4所示工字钢直杆在温度t1=20℃时安装,此时杆不受力,已知杆长l=6m,材料的λP=132,E= 200GPa,线膨胀系数α=12.5×10-6/℃。试问当温度升高到多少度时杆将失稳。
[解]
随着温度的升高,直杆在杆端受到压力FA=FB,当两端压力达到压杆的临界压力即:FA=FB=Fcr时,压杆将失稳。
由压杆稳定条件
则许用外载荷
FP≤139.2kN
3.计算由AC杆稳定条件确定的许用外载荷
AB杆的柔度
用欧拉公式计算压杆的临界应力:
由压杆稳定条件
则许用外载荷
FP≤240.6kN
4.确定整个结构的许用载荷
由稳定计算结果可知,结构的许用载荷为
[FP]=139.2kN
解题指导:
对于这类题目,所确定的载荷要确保整个结构所有受压杆件匀不失稳。
材料力学 静不定系统
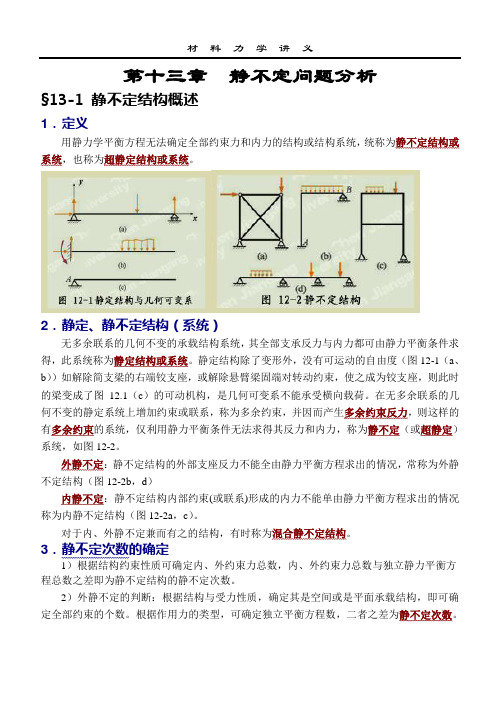
第十三章静不定问题分析§13-1 静不定结构概述1.定义用静力学平衡方程无法确定全部约束力和内力的结构或结构系统,统称为静不定结构或系统,也称为超静定结构或系统。
2.静定、静不定结构(系统)无多余联系的几何不变的承载结构系统,其全部支承反力与内力都可由静力平衡条件求得,此系统称为静定结构或系统。
静定结构除了变形外,没有可运动的自由度(图12-1(a、b))如解除简支梁的右端铰支座,或解除悬臂梁固端对转动约束,使之成为铰支座,则此时的梁变成了图12.1(c)的可动机构,是几何可变系不能承受横向载荷。
在无多余联系的几何不变的静定系统上增加约束或联系,称为多余约束,并因而产生多余约束反力,则这样的有多余约束的系统,仅利用静力平衡条件无法求得其反力和内力,称为静不定(或超静定)系统,如图12-2。
外静不定:静不定结构的外部支座反力不能全由静力平衡方程求出的情况,常称为外静不定结构(图12-2b,d)内静不定:静不定结构内部约束(或联系)形成的内力不能单由静力平衡方程求出的情况称为内静不定结构(图12-2a,c)。
对于内、外静不定兼而有之的结构,有时称为混合静不定结构。
3.静不定次数的确定1)根据结构约束性质可确定内、外约束力总数,内、外约束力总数与独立静力平衡方程总数之差即为静不定结构的静不定次数。
2)外静不定的判断:根据结构与受力性质,确定其是空间或是平面承载结构,即可确定全部约束的个数。
根据作用力的类型,可确定独立平衡方程数,二者之差为静不定次数。
如图12-3(b),外载荷为平面力系,则为三次外静不定静,而图12-3(c)为空间力系,则为六次外静不定。
3)内静不定次数确定桁架:直杆用铰相连接,载荷只作用于结点,杆只受拉压力的杆系,其基本几何不变系由三杆组成(图12-4a)。
图12-4(b)仍由基本不变系扩展而成,仍是静定系,而(c)由于在基本系中增加了一约束杆,因而为一次超静定。
刚架:杆以刚结点相连接,各杆可以承受拉、压、弯曲和扭转,这样的杆系为刚架(图12-5)。
北航材料力学-第十三章1-静不定问题分析

MECHANICS OF MATERIALS
➢ 外力静不定问题: 存在多余的外部约束
解除多余的外部约束,代之以支反力
相当系统
在解除约束处,建立变形协调条件
建立补充方程
M
A
l
BA
l
B
l
B
l
l
A RClCFra bibliotekHCRC
C 0 fC 0
C
A 0
fA 0
Page13
MECHANICS OF MATERIALS
3EI kAB l 3
3EI kCD l 3
Ql3 Q
3EI k
Q k
2 ( f ) 2 2 f 2 f 2
f 2
2
Page3
MECHANICS OF MATERIALS
➢ 讨论:
1、若 2Ql 3
3EI
2Ql 3 2Q
3EI k
Q k
2
B点与CD梁 刚好接触
( f ) 2 2 f 2 f 2
x1
M
l
A
B
以相当系统为真实载荷状态 将单位载荷加在基本系统上
l x2
M
1
HC C
M ( x1 ) ( l HC )x1 M ( x1 ) l x1 1
f 0 f (舍去)
2
2、若
Ql 3
EI
Ql 3 3Q
EI k
Q k
3
B点与CD梁 没有接触
2 ( f ) 3( 2 2 f 2 f 2) 方程无解
Page4
MECHANICS OF MATERIALS
第十三章 静不定问题分析 §13-1 引言
梁的变形计算

例题
解: 4. 利用约束条件和 连续条件确定积分常数
EI183FPx2 C1
EI2=8 3- FPx2+ 1 2FPx- 4 l2C2
EI1w 8 1FPx3C1xD1
E2 I= w8 1F - Px3 + 1 6F P x- 4 l 3C 2xD 2
ddw xl MEIxdxC
wll M ExIdxdxC xD
其中C、D为积分常数。
小挠度微分方程的积分与积分常数的确定
积分法中常数由梁的约束条件与连续条件确定。约 束条件是指约束对于挠度和转角的限制:
在固定铰支座和辊轴支座处,约束条件为挠 度等于零:w=0;
在固定端处,约束条件为挠度和转角都等于零:
FP、EI、l均为已知。
求:加力点B的挠度和
支承A、C处的转角。
例题
解:1. 确定梁约束力 2. 分段建立梁的弯矩方程 于是,AB和BC两段的弯矩方程分别为
AB段 BC段
M1x3 4FPx 0x4 l
M 2x3 4F Px - F P x - 4 l 4 lxl
例题
解: 3. 将弯矩表达式代入小挠度微分方程并分别积分
小挠度微分方程
d2w 0,M 0
dx2
d2w0,M 0 dx2
d2w M dx 2 EI
本书采用向下的w坐标系,有
d2w M
dx2 EI d2w M dx2 EI
小挠度微分方程
d2w M
dx 2
EI
对于等截面梁,应用确定弯矩方程的方法,写出弯 矩方程M(x),代入上式后,分别对x作不定积分,得到包 含积分常数的挠度方程与转角方程:
xE FP I8 3x21 2x4 l212 78l2
结构力学弯曲变形

梁的变形
梁的挠度和转角
基本概念
挠曲线:梁弯曲变形后的轴线,称为挠曲线。
挠曲线
y
p
c
w
x
挠曲线
挠曲线
位移 变形后的横截面位置相对于变形前的位置的改变。
挠度:梁变形后任一截面的形心C沿原轴线铅垂方向的线 位移,称为该截面的挠度;即挠曲线上相应点的y坐 标,记为w 。
转角:横截面在弯曲变形过程中对其原来位置所转过的角 度 ,称为该截面的转角;即挠曲线上 点切线与 x 轴的夹角。
例1 求图所示悬臂梁的挠曲线方程及转角方程,
并求自由端B 的挠度和转角。
解:1. 支座反力
y
RA
q
弯矩方程:
A
MA
x
Bx l
挠曲线微分方程: 连续积分两次得:
利用两个边界条件:
将其代入方程(a)、(b)则得梁的挠曲线方程和转角方程:
y q x
A
B
以x=l 代入以上方程可得自由端的挠度和转角:
解法二:选如图坐标系,显然
2EI B
l/2
B
p
EI C
l/2
p
c
wB
P MB=Pl/2
A
B
C
wc2
由梁的变形连续条件,直线BC因AB段的弯曲变形而移位到
的位置,使C点有相应的挠度
A
P MB=Pl/2
B
C
wc2
将图(b)和(c)两种情况的变形叠加后,即可求得自由 端 C 的挠度
p
B
c
这种分析方法叫做梁的逐段刚化法。
梁的刚度条件
求解超静定问题的基本方法
——平衡、变形协调、 物性关系。 物性关系体现为力与变形关系。
工程力学知到章节答案智慧树2023年贵州理工学院

工程力学知到章节测试答案智慧树2023年最新贵州理工学院第一章测试1.力对物体的作用效应取决于力的三要素,分别是()。
参考答案:力的大小;力的方向;力的作用点2.作用于刚体上的力,可以沿其作用线移至刚体内任意一点,而不改变它对刚体的作用效应。
()参考答案:对3.受力后几何形状和尺寸均保持不变的物体称为()。
参考答案:刚体4.两物体间相互作用的力总是同时存在,并且两力等值、反向共线,作用在同个物体上。
()参考答案:错5.柔体约束特点是限制物体沿绳索伸长方向的运动,只能给物体提供拉力。
()参考答案:对第二章测试1.指出以下力的多边形中,合力为零的有()。
参考答案:;2.F1、F2、F3及F4是作用在刚体上的平面汇交力系,其力矢之间的关系如图,这个汇交力系的合力FR为()。
参考答案:3.平面汇交力系有()个独立平衡方程。
参考答案:24.刚架ABCD,不计自重,仅受力F作用,铰链A反力F的作用线必定()。
参考答案:通过C点5.作用在物体上的多个力,如果各个力的作用线汇交于一点,这样的力系就称为平面汇交力系。
()错第三章测试1.力偶无合力,且力偶只能用力偶来等效。
()参考答案:对2.扳手所受力如图,已知,力F对O点之矩为()。
0.69kN·m3.关于力偶性质的下列说法中,正确的是()。
参考答案:力偶对其作用面上任意点之矩均相等,与矩心位置无关;力偶无合力;若力偶矩的大小和转动方向不变,可同时改变力的大小和力偶臂的长度,作用效果不变4.力偶对物体有移动效应。
()参考答案:错5.力的作用线通过矩心时,力矩为零。
()参考答案:对第四章测试1.司机操纵方向盘驾驶汽车时,可用双手对方向盘施加一个力偶,也可用单手对方向盘施加一个力,这两种方式能取得相同的效果,说明一个力与一个力偶可以等效。
()参考答案:错2.力线平移定理认为,作用在刚体上的力F可以平行移到刚体内任一点,但必须同时附加一个力偶,其力偶矩等于原力F对平移点的矩。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例13-4 用叠加法求图示梁的 13M P A C
l/2
yC、θ A、θ B,EI=常量。
解 运用叠加法
5ql 4 Pl 3 ml 2 yC = − − − 384 EI 48EI 16 EI
q B
l/2
ql 3 Pl 2 ml θA = − − − 24 EI 16 EI 3EI
=
B
A
ql 3 Pl 2 ml θB = + + 24 EI 16 EI 3EI
教学重点
梁弯曲变形的基本概念; 梁弯曲变形的基本概念; 挠曲线的近似微分方程; 挠曲线的近似微分方程; 积分法和叠加法计算梁的变形; 积分法和叠加法计算梁的变形; 梁的刚度条件。 梁的刚度条件。
教学难点
挠曲线近似微分方程的推导过程; 挠曲线近似微分方程的推导过程; 积分法和叠加法计算梁的变形; 积分法和叠加法计算梁的变形; 变形比较法求解静不定梁。 变形比较法求解静不定梁。
A C
B x
2.挠度和转角 挠度和转角 它们是度量梁变形后横截面位移的两个基本量。 它们是度量梁变形后横截面位移的两个基本量。 挠度( ) 即轴线上的点)在垂直于 挠度( y): 横截面形心 C (即轴线上的点 在垂直于 x 轴方向 即轴线上的点 的线位移,称为该截面的挠度。 的线位移,称为该截面的挠度。 转角( 转角(θ) :横截面对其初始位置的所转过的角度 , 称为该截 面的转角。 面的转角。
三、提高梁弯曲刚度的措施 梁的变形不仅与梁的受力和支承情况有关, 梁的变形不仅与梁的受力和支承情况有关,而且还 梁的材料、截面形状与大小和梁的长度有关 有关。 与梁的材料、截面形状与大小和梁的长度有关。 提高梁刚度的措施为 1.增大梁的抗弯刚度 ; 增大梁的抗弯刚度EI; 增大梁的抗弯刚度 2.减小梁的跨度; 减小梁的跨度; 减小梁的跨度 3.改变加载方式。 改变加载方式。 改变加载方式
M
+
q B A
A
B
+
二、梁的刚度条件
y max ≤ [ y ] ,
θ
max
≤ [θ ]
常见梁结构的许用挠度和许用转角如下: 常见梁结构的许用挠度和许用转角如下: 普通传动轴 齿轮轴 吊车梁 楼盖梁
[ y ] = (0.0003 ~ 0.0005)l [θ ] = 0.001 ~ 0.005rad
[θ ] = 0.001rad
d2 y <0 2 dx
d2y M (x) 所以 = ± 2 dx EI
x
o
d 2 y M ( x) = 2 dx EI
上式就是挠曲线近似微分方程。 上式就是挠曲线近似微分方程。
对于等截面直梁,挠曲线近似微分方程可写成如下形式 对于等截面直梁,挠曲线近似微分方程可写成如下形式:
d y M ( x) = 2 dx EI
第二节
梁的挠曲线近似微分方程
M = ρ EI 1
一、挠曲线近似微分方程
y
1 M ( x) ⇒ = ρ ( x) EI
小变形
M>0
d2 y >0 2 dx
o
x
d2 y 1 dx 2 =± dy ρ ( x) [1 + ( ) 2 ]3 / 2 dx
1 d2 y ≈ =± 2 ρ ( x) dx
y
M<0
P
M B = Pl
O
B
l/2
A
l/2
(2)MB单独作用时,A、B两截面变形位移可以直接从表中查出。 ) 单独作用时, 、 两截面变形位移可以直接从表中查出 两截面变形位移可以直接从表中查出。
(3)P和MB共同作用时,应用叠加法可得知,A截面挠度为两种载 ) 和 共同作用时,应用叠加法可得知, 截面挠度为两种载 荷的代数和, 截面的转角也为两者的代数和 截面的转角也为两者的代数和。 荷的代数和,B截面的转角也为两者的代数和。
P
解 由刚度条件可得
ymax
O
B
Pl 3 l = ≤ [ y] = 48EI 500
48 EI P≤ 500l 2
l/2
A
l/2
解得
120a z
所以得 [ P ] = 7.11kN 由梁的最大弯曲应力为
σ max =
M max Pl = = 60MPa ≤ [σ ] Wz 4Wz
因此,满足强度条件。 因此,满足强度条件。
例13-3 用叠加法求如图所示梁的截面A的挠度和截面B的转 角。EI=常量。 单独作用时, 解 (1)P单独作用时,梁的左半 ) 单独作用时
段OA的变形如同悬臂梁在末端受 的变形如同悬臂梁在末端受 集中力作用时的变形;右半段AB 集中力作用时的变形;右半段 部分梁没有变形位移, 部分梁没有变形位移,但其有刚体 位移。刚体位移可以看作是随A截 位移。刚体位移可以看作是随 截 面的平动与绕A截面的转动 截面的转动。 面的平动与绕 截面的转动。所以 B截面的转角等于 截面的转角。 截面的转角等于A截面的转角。 截面的转角等于 截面的转角
2
第三节
用叠加法计算梁的变形 梁的刚度条件
一、用叠加法求梁的弯曲变形 多个载荷同时作用于结构而引起的变形等于每个载荷单 独作用于结构而引起的变形的代数和。 独作用于结构而引起的变形的代数和。
θ ( P P2 ⋅ ⋅ ⋅ ⋅ ⋅ ⋅Pn ) = θ1 ( P ) + θ2 ( P2 ) + ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ +θn ( Pn ) 1 1
第一节
弯曲变形的基本概念
齿轮传动轴的弯曲变形
轧钢机(或压延机) 轧钢机(或压延机)的弯曲变形
1.挠曲线 挠曲线 梁变形后的轴线称为挠曲线 。 挠曲线方程为
y = f (x)
为该点的挠度。 式中 ,x 为梁变形前轴线上任一点的横坐标 ,y为该点的挠度。 为该点的挠度
y
转角θ 转角θ
C'
挠曲线
θ
y挠度 挠度
q θ = y' = (−l3 +6lx2 −4x3) 24EI qx y= (−l3 +2lx2 − x3) 24EI
在 x = 0 和 x = l 处转角的 绝对值相等且都是 最大值, 最大值,为
A
q
B
θB
θ
− =
θ
A
m ax
θ
B
ql =m 24EI
3
θA
θB
l
RA
RB
在梁跨中点 l /2 处有 最大挠度值
[ y] = ( 1 1 ~ )l 750 400
[ y] = (
1 1 ~ )l 400 250
如图所示工字钢梁, 例13-5 如图所示工字钢梁,l=8m, Iz=2370cm4, Wz=237cm3, , [ y ]= l/500,E=200GPa,[σ]=100MPa。试根据梁的刚度条件,确 / , , 。试根据梁的刚度条件, 定梁的许可载荷 [P],并校核强度。 ,并校核强度。
θ max = θ B
PL2 = 2 EI
( )
y max = y B
PL 3 = 3 EI
( )
的简支梁, 例13-2 图示一抗弯刚度为 EI 的简支梁 在全梁上受集度为 13q 的均布载荷作用。试求此梁的挠曲线方程和转角方程, 的均布载荷作用。试求此梁的挠曲线方程和转角方程 并确定其最大挠度 ymax 和最大转角 θmax 。 q
二、用积分法求梁的弯曲变形 微分方程的积分
2
d2 y E I = M(x) 2 dx
dy EI = EI θ ( x ) = ∫ M ( x ) d x + C dx
EIy ( x ) =
∫ [∫ M ( x ) d x ]d x + Cx + D
式中C、 为积分常数 可根据梁的边界条件和连续性条件确定。 为积分常数, 式中 、D为积分常数,可根据梁的边界条件和连续性条件确定。
B A
l
q
B A
l
RA
由对称性可知, 解: 由对称性可知,梁的两个支反力为
RB
ql RA = RB = 2
梁的 弯矩方程 及 挠曲线微分方程 分别为
ql 1 2 q M(x) = x − qx = (lx − x2 ) 2 2 2
q 2 E '' = M(x) = (lx − x ) Iy 2
q EIy'' = M(x) = (lx − x2) 2
x
(3)确定积分常数 。 确定积分常数 当
x = 0 时,
P EIy′ = x 2 − PLx + C 2 P PL 2 EIy = x 3 − x + Cx + D 6 2
θ A = y′A = 0 , y A = 0
求得
C =0; D = 0
y
L
P
B
θB
x
yB
(4)写出挠曲线近似方程并画出挠曲线的大致形 状。 Px 2 y(x) = (x − 3L) 6 EI (5)最大转角及最大挠度(绝对值最大)。 最大转角及最大挠度(绝对值最大)。
第十三章 弯曲变形与静不定梁
第一节 弯曲变形的基本概念 第二节 梁的挠曲线近似微分方程 第三节 用叠加法计算梁的变形 梁的刚度条件 第四节 静不定梁
教学目的和要求
本章介绍了梁的弯曲变形的基本知识, 本章介绍了梁的弯曲变形的基本知识,主要包括挠 曲线及梁的刚度条件。 曲线及梁的刚度条件。学习时要掌握梁的弯曲变形 的基本概念,了解程, 掌握积分法和叠加法计算梁的变形, 掌握积分法和叠加法计算梁的变形,同时了解提高 梁刚度的方法。 梁刚度的方法。了解变形比较法求静不定梁的计算 过程。 过程。
(图b)
y A = 0,
yB = 0
