上海静安数学暑假补习班高二数学暑假班

合集下载

高考保送生

就像蒲永杰同学所说的，自己的性格就是比较慢的那种，对细节很追求，做事不紧不慢，也不急躁，这可能和喜欢钻研问题有关，经常研究这些问题，形成了这种慢的性格，沉下去，精神放松才能更好地思考。
塞外
:注册用户军衔:上尉
贴子：825
积分：1594
人气：3250
在线：
注册：2008-08-23
个人空间发短消息
第4楼发表于:2012-04-20 10:05
他们的性格特点：做事不紧不慢，人缘好
就同学们自身的性格特点中，出现频率较高的是：不紧不慢、内心平静、耐心、仔细、随和、专注、稳重，20位同学在描述自己的性格时，都说到这其中的词语。在这类同学中，有的同学性格比较“从一而终”，有的则是经历了转变的。
因为参加竞赛班，谢佳在高一、高二的时候补过课，他说：“高一也补过理科的，主要是在周末补课，针对高考数学，上了高三了就没补了。”
雷浩然是通过化学竞赛奖取得保送生资格的，但是因为参加竞赛班耽误了其他科目的学习，所以他还是会去补课：“高中开始，周末是否补课要看高考内容，数学物理或者语文；高中开始，寒暑假也要补。”
刘俊琳：计算机编程。喜欢运动，特别是球类。
蒲永杰：对电子制作、机器人感兴趣，参加了9次省级以上的电子制作竞赛，也得过奖的。
毛运航：特别的算不上，但我参加了不少比赛，包括科技创新大赛、机器人大赛。
甘兰蕙子：喜欢唱歌、钢琴，也爱游泳、打羽毛球，学了5年多的英语口语，既爱好也擅长。
王船：体育好，跑步跑得比较快，校运动会100米、200米都是全校第四名，前三名都是体尖。爱好吧，喜欢打篮球。
邓佳豪：小学时就是中等偏上吧，不过初中成绩是名列前茅的。
王余愉：从小成绩就一直很好，都是排在前几名的。
高中开夜车吗？很少有，“晚上12点前必须睡”

2014培训学校暑假班课程安排

让学生喜欢写作文，爱上作文。
一至六年级
小学数学班
(小学1~6年级）
一年级班二年级班三年级班四年级班五年级班六年级班
1.数学基础知识和能力提高知识
2.奥数和数学思维训练
1.打好基础，培养数学思维，开发智力
2.包课本知识全掌握（基础班）
3.包班级中上游或前几名（提高班）
一至六年级
(3A~6B)小学牛津英语班
培训学校暑假班课程安排
2
小学班
班型
教学内容
教学效果
适合对象
幼儿升
一年级
衔接班
数学班
汉语拼音班
汉语拼音和数学
为上一年级打好基础
大班升
一年级学生
小学作文
和阅读班
(小学1~6年级）
一年级班二年级班三年级班四年级班五年级班六年级班
各种类型阅读和写作方法
好词好句好段的积累和运用
快速全面提高作文水平和阅读能力,
三年级班四年级班五年级班六年级班
小学牛津课本
1.口语、听力、语法很棒
2.包班级中上游或前几名
三至六年级
剑桥英语
(预备级
1~3级)
预备级班
一级班
二级班三级班
《剑桥英语》教材
口语和听力很棒
考级通过率100%
（1~4年级）
新概念英语
五年级班
六年级班
新概念英语教材
学完第一册相当于初中毕业水平
学完第二册相当于高中毕业水平
初三升高一
新高二班
英语班数学班
物理班化学班
先复习高一各知识点,然后上高二
新课,为高二学习打下坚实基础
高一升高二
新高三班
英语班数学班
物理班化学班

高一升高二数学暑假衔接班讲义第六讲(学)

第六讲圆的方程（一）热点透析考查目标 1.考查圆的方程的形式及应用；2.利用待定系数法求圆的方程．达成目标 1.熟练掌握圆的方程的两种形式及其特点；2.会利用代数法、几何法求圆的方程，注意圆的方程形式的选择．（二）知识回顾1．圆的定义在平面内，到的距离等于的点的集合叫圆． 2．确定一个圆最基本的要素是和 3．圆的标准方程(x －a )2＋(y －b )2＝r 2(r >0)，其中( )为圆心，为半径． 4．圆的一般方程x 2＋y 2＋Dx ＋Ey ＋F ＝0表示圆的充要条件是，其中圆心为⎝⎛⎭⎫－D 2，－E2，半径r ＝D 2＋E 2－4F2.5．确定圆的方程的方法和步骤确定圆的方程主要方法是待定系数法，大致步骤为： (1)根据题意，选择标准方程或一般方程；(2)根据条件列出关于a ，b ，r 或D 、E 、F 的方程组； (3)解出a 、b 、r 或D 、E 、F 代入标准方程或一般方程． 6．点与圆的位置关系点和圆的位置关系有三种．圆的标准方程(x －a )2＋(y －b )2＝r 2，点M (x 0，y 0) (1)点在圆上：； (2)点在圆外：； (3)点在圆内： . [难点正本疑点清源]1．确定圆的方程时，常用到的圆的三个性质(1)圆心在过切点且垂直切线的直线上；(2)圆心在任一弦的中垂线上；(3)两圆内切或外切时，切点与两圆圆心三点共线． 2．圆的一般方程的特征圆的一般方程：x 2＋y 2＋Dx ＋Ey ＋F ＝0，若化为标准式，即为⎝⎛⎫x ＋D 22＋⎝⎛⎭⎫y ＋E 22＝D 2＋E 2－4F 4.由于r 2相当于D 2＋E 2－4F4. 所以①当D 2＋E 2－4F >0时，圆心为⎝⎛⎭⎫－D 2，－E 2，半径r ＝D 2＋E 2－4F 2.②当D 2＋E 2－4F ＝0时，表示一个点⎝⎛⎭⎫－D 2，－E 2. ③当D 2＋E 2－4F <0时，这样的圆不存在．附件：当堂过手训练（快练五分钟，稳准建奇功！）1．若方程x 2＋y 2＋ax ＋2ay ＋2a 2＋a －1＝0表示圆，则a 的取值范围是______________．2． (2011·辽宁)已知圆C 经过A (5,1)，B (1,3)两点，圆心在x 轴上，则圆C 的方程为______________． 3． (2011·四川)圆x 2＋y 2－4x ＋6y ＝0的圆心坐标是( )A ．(2,3)B ．(－2,3)C ．(－2，－3)D ．(2，－3)4． (2012·辽宁)将圆x 2＋y 2－2x －4y ＋1＝0平分的直线是( )A ．x ＋y －1＝0B ．x ＋y ＋3＝0C ．x －y ＋1＝0D ．x －y ＋3＝05． (2012·湖北)过点P (1,1)的直线，将圆形区域{(x ，y )|x 2＋y 2≤4}分为两部分，使得这两部分的面积之差最大，则该直线的方程为( )A ．x ＋y －2＝0B ．y －1＝0C ．x －y ＝0D ．x ＋3y －4＝0二、高频考点专题链接题型一求圆的方程例1 根据下列条件，求圆的方程：(1)经过P (－2,4)、Q (3，－1)两点，并且在x 轴上截得的弦长等于6； (2)圆心在直线y ＝－4x 上，且与直线l ：x ＋y －1＝0相切于点P (3，－2)．探究提高求圆的方程时，应根据条件选用合适的圆的方程．一般来说，求圆的方程有两种方法：①几何法，通过研究圆的性质进而求出圆的基本量．②代数法，即设出圆的方程，用待定系数法求解．(1)已知圆C 与直线x －y ＝0及x －y －4＝0都相切，圆心在直线x ＋y ＝0上，则圆C 的方程为( )A ．(x ＋1)2＋(y －1)2＝2B ．(x －1)2＋(y ＋1)2＝2C ．(x －1)2＋(y －1)2＝2D ．(x ＋1)2＋(y ＋1)2＝2(2)经过点A (5,2)，B (3,2)，圆心在直线2x －y －3＝0上的圆的方程为 ____________________．题型二与圆有关的最值问题例2 已知实数x 、y 满足方程x 2＋y 2－4x ＋1＝0.(1)求yx 的最大值和最小值；(2)求y －x 的最大值和最小值．探究提高与圆有关的最值问题，常见的有以下几种类型：(1)形如μ＝y －bx －a形式的最值问题，可转化为动直线斜率的最值问题；(2)形如t ＝ax ＋by 形式的最值问题，可转化为动直线截距的最值问题；(3)形如(x－a)＋(y－b)形式的最值问题，可转化为动点到定点的距离的平方的最值问题．已知M为圆C：x2＋y2－4x－14y＋45＝0上任意一点，且点Q(－2,3)．(1)求|MQ|的最大值和最小值；(2)若M(m，n)，求n－3m＋2的最大值和最小值．题型三与圆有关的轨迹问题例3设定点M(－3,4)，动点N在圆x2＋y2＝4上运动，以OM、ON为两边作平行四边形MONP，求点P的轨迹．探究提高求与圆有关的轨迹问题时，根据题设条件的不同常采用以下方法：①直接法：直接根据题目提供的条件列出方程．②定义法：根据圆、直线等定义列方程．③几何法：利用圆的几何性质列方程．④代入法：找到要求点与已知点的关系，代入已知点满足的关系式等．点P(4，－2)与圆x2＋y2＝4上任一点连线的中点轨迹方程是() A．(x－2)2＋(y＋1)2＝1B．(x－2)2＋(y＋1)2＝4C．(x＋4)2＋(y－2)2＝4D．(x＋2)＋(y－1)＝1反思总结利用方程思想求解圆的问题典例：(12分)已知圆x2＋y2＋x－6y＋m＝0和直线x＋2y－3＝0交于P，Q两点，且OP⊥OQ(O为坐标原点)，求该圆的圆心坐标及半径．温馨提醒(1)在解决与圆有关的问题中，借助于圆的几何性质，往往会使得思路简捷明了，简化思路，简便运算．(2)本题中三种解法都是用方程思想求m值，即三种解法围绕“列出m的方程”求m值．(3)本题的易错点：不能正确构建关于m的方程，找不到解决问题的突破口，或计算错误．方法与技巧1．确定一个圆的方程，需要三个独立条件．“选形式、定参数”是求圆的方程的基本方法，是指根据题设条件恰当选择圆的方程的形式，进而确定其中的三个参数．2．解答圆的问题，应注意数形结合，充分运用圆的几何性质，简化运算．失误与防范1．求圆的方程需要三个独立条件，所以不论是设哪一种圆的方程都要列出系数的三个独立方程．2．过圆外一定点，求圆的切线，应该有两个结果，若只求出一个结果，应该考虑切线斜率不存在的情况．巩固练习(时间：35分钟，满分：57分)一、选择题(每小题5分，共20分)1．若圆x2＋y2－2ax＋3by＝0的圆心位于第三象限，那么直线x＋ay＋b＝0一定不经过() A．第一象限B．第二象限C．第三象限D．第四象限2．若点(1,1)在圆(x－a)2＋(y＋a)2＝4的内部，则实数a的取值范围是()A．－1<a<1 B．0<a<1C．a>1或a<－1 D．a＝±13．(2011·安徽)若直线3x＋y＋a＝0过圆x2＋y2＋2x－4y＝0的圆心，则a的值为() A．－1 B．1 C．3 D．－34．圆心在y轴上，半径为1，且过点(1,2)的圆的方程为() A．x2＋(y－2)2＝1 B．x2＋(y＋2)2＝1C．(x－1)2＋(y－3)2＝1 D．x2＋(y－3)2＝1二、填空题(每小题5分，共15分)5．若圆x2＋y2－4x＋2my＋m＋6＝0与y轴的两交点A，B位于原点的同侧，则实数m的取值范围是______________．6．以直线3x－4y＋12＝0夹在两坐标轴间的线段为直径的圆的方程为________________．7．已知点M(1,0)是圆C：x2＋y2－4x－2y＝0内的一点，那么过点M的最短弦所在直线的方程是__________．三、解答题(共22分)8．(10分)根据下列条件求圆的方程：(1)经过点P(1,1)和坐标原点，并且圆心在直线2x＋3y＋1＝0上；(2)过三点A(1,12)，B(7,10)，C(－9,2)．9．(12分)一圆经过A(4,2)，B(－1,3)两点，且在两坐标轴上的四个截距的和为2，求此圆的方程．拓展训练(时间：25分钟，满分：43分)一、选择题(每小题5分，共15分)1．若直线ax＋by＝1与圆x2＋y2＝1相交，则P(a，b) () A．在圆上B．在圆外C．在圆内D．以上都有可能2．已知圆C：x2＋y2＋mx－4＝0上存在两点关于直线x－y＋3＝0对称，则实数m的值为() A．8 B．－4 C．6 D．无法确定3．已知圆的半径为2，圆心在x轴的正半轴上，且与直线3x＋4y＋4＝0相切，则圆的方程是()A．x2＋y2－4x＝0 B．x2＋y2＋4x＝0C．x2＋y2－2x－3＝0 D．x2＋y2＋2x－3＝0二、填空题(每小题5分，共15分)4．已知圆x2＋y2＋2x－4y＋a＝0关于直线y＝2x＋b成轴对称，则a－b的取值范围是________．5．若PQ是圆O：x2＋y2＝9的弦，PQ的中点是M(1,2)，则直线PQ的方程是____________．6．已知AC、BD为圆O：x2＋y2＝4的两条相互垂直的弦，垂足为M(1，2)，则四边形ABCD的面积的最大值为________．三、解答题7．(13分)圆C通过不同的三点P(k,0)，Q(2,0)，R(0,1)，已知圆C在点P处的切线斜率为1，试求圆C的方程．。

上海市华东师范大学第二附属中学2024-2025学年高二上学期开学暑期答疑辅导检测数学试题

上海市华东师范大学第二附属中学2024-2025学年高二上学期开学暑期答疑辅导检测数学试题一、填空题1．直线l 上存在两点在平面α上，则l α（填一符号）．2．函数π3sin 24y x ⎛⎫=+ ⎪⎝⎭ 的频率是． 3．已知{}n a 是等差数列，若75230a a --=，则9a 的值是．4．两条异面直线所成角的取值范围是5．已知复数i z a =-的实部与虚部相等，则i z -=．6．函数πtan 213y x ⎛⎫=-+ ⎪⎝⎭的对称中心是． 7．三个互不重合的平面能把空间分成．8．数列{}n a 满足111n n a a +=-，112a =，则2024a =． 9．在ABC V 中，sin :sin :sin 5:7:8A B C =，则该三角形外接圆与内切圆的面积之比是． 10．如图，摩天轮的半径为50m ，圆心O 距地面的高度为60m .已知摩天轮按逆时针方向匀速转动，每15min 转动一圈.游客在摩天轮的舱位转到距离地面最近的位置进舱则游客进舱5min 时他距离地面的高度为m .11．已知 ABC V 中，过中线AD 的中点E 任作一条直线分别交边,AB AC 于,M N 两点，设,(0,0)==>>u u u u r u u u r u u u r u u u r AM xAB AN yAC x y ，则4x y +的最小值为.12．对任意0,4πϕ⎡⎤∈⎢⎥⎣⎦，函数()sin()f x x ωϕ=+在区间,2ππ⎡⎤⎢⎥⎣⎦上单调递增，则实数ω的取值范围是.二、单选题13．设扇形的圆心角为α，半径为r ，弧长为l ，而积为S ，周长为L ，则下列说法不正确的是（）A ．若α，r 确定，则,L S 唯一确定B ．若α，l 确定，则L ，S 唯一确定C ．若,S L 确定，则,r α唯一确定D ．若,S l 确定，则,r α唯一确定14．过正方体1111ABCD A B C D -的顶点A 作直线l ，使l 与棱AB ，AD ，1AA所成的角都相等，这样的直线l 可以作A ．1条B ．2条C ．3条D ．4条15．数列{}n a ，{}n b 满足1n n a b ⋅=，232n a n n =++，则{}n b 的前10项之和等于（）A ．13B ．512C ．12D ．71216．如图所示，角π0,2x ⎛⎫∈ ⎪⎝⎭的终边与单位圆O 交于点P ，()1,0A ，PM x ⊥轴，AQ x ⊥轴，M 在x 轴上，Q 在角x 的终边上．由正弦函数、正切函数定义可知，sin ,tan x x 的值分别等于线段,MP AQ 的长，且OAP OAQ OAP S S S <<V V 扇形，则下列结论不正确的是（）A ．函数tan sin y x x x =++在ππ,22⎛⎫- ⎪⎝⎭内有1个零点 B ．函数tan y x x =-在πππ3π,,2222⎛⎫⎛⎫-⋃ ⎪ ⎪⎝⎭⎝⎭内有2个零点 C ．函数sin y x x =-有3个零点D ．函数tan sin tan sin y x x x x =+--在ππ,22⎛⎫- ⎪⎝⎭内有1个零点三、解答题17．已知3sin 5α=，π0,2α⎛⎫∈ ⎪⎝⎭． (1)求πsin 23α⎛⎫+ ⎪⎝⎭的值；(2)在平面直角坐标系xOy 中，以Ox 为始边，已知角β的终边与角α的终边关于y 轴对称，求()cos αβ+的值．18．如图所示，在长方体1111ABCD A B C D -中，2AB BC ==，14AA =，P 为线段11B D 上一点．（1）求证：AC BP ⊥；（2）当P 为线段11B D 的中点时，求点A 到平面PBC 的距离．19．在直角梯形ABCD 中，//AB CD ，90DAB ∠=o ，224AB AD DC ===，点F 是BC 边上的中点.(1)若点E 满足2DE EC =u u u r u u u r ，且EF AB AD λμ=+u u u r u u u r u u u r ，求λμ+的值；(2)若点P 是线段AF 上的动点（含端点），求AP DP ⋅u u u r u u u r 的取值范围.20．如图，正方体的棱长为1，B C BC O ''=I ，求：(1)AO 与A C ''所成角的度数；(2)AO 与平面ABCD 所成角的正切值：(3)B OA C --的度数．21．若有穷数列{}n a 满足：10n i i a ==∑且11n i i a ==∑，则称其为“n 阶01-数列”.(1)若“6阶01-数列”为等比数列，写出该数列的各项；(2)若某“21k +阶01-数列”为等差数列，求该数列的通项n a （121n k ≤≤+，用,n k 表示）；(3)记“n 阶01-数列”{}n a 的前k 项和为()1,2,3,,k S k n =L ，若存在{}1,2,3,,m n ∈L ，使12m S =，试问：数列{}()1,2,3,,i S i n =L 能否为“n 阶01-数列”？若能，求出所有这样的数列{}n a ；若不能，请说明理由.。

新高二数学联赛班暑假第12讲二试真题分析数论

本讲将对前几年的数论问题进行分析，梳理常用的方法和解题思路. 特别的，近三年均把数论题作为最后一题，难度或复杂程度有所提升．【例1】（2011高中数学联赛）证明：对任意整数4n ≥，存在一个n 次多项式()1110n n n f x x a x a x a --=++++，具有如下性质：⑴011n a a a -，，，均为正整数；⑵对任意正整数m ，及任意k （2k ≥）个互不相同的正整数12k r r r ，，，，均有()()()()12k f m f r f r f r ≠．【例2】（2009高中数学联赛）设k ，l 是给定的两个正整数．证明：有无穷多个正整数m k ≥，使得C k m 与l 互素．知识点睛经典精讲12.1数论问题第【例3】（2013高中数学联赛）设,n k 为大于1的整数，2k n <．证明：存在2k 个不被n 整除的整数，若将它们任意分成两组，则总有一组若干个数的和被n 整除．【例4】（2009CMO ）求所有的素数对(,)p q ，使得|55pqpq +.【例5】（2003高中数学联赛）设三角形的三边长分别是整数l ，m ，n ，且l m n >>，已知444333101010l m n ⎧⎫⎧⎫⎧⎫==⎨⎬⎨⎬⎨⎬⎩⎭⎩⎭⎩⎭，其中{}[]x x x =-，而[]x 表示不超过x 的最大整数．求这种三角形周长的最小值．【例6】（2014高中数学联赛）设整数1x ，2x ，…，2014x 模2014互不同余，整数1y ，2y ，…，2014y 模2014也互不同余．证明：可将1y ，2y ，…，2014y 重新排列为1z ，2z ，…，2014z ，使得11x z +，22x z +，…，20142014x z +模4028互不同余．【例7】（1978IMO ）数1978n 与1978m 的最后三位数相等，试求出正整数n 和m ，使得m ＋n 取最小值，这里n ＞m ≥1．【例8】（2012高中数学联赛）设1112n S n=+++，n 是正整数．证明：对满足01a b <≤≤的任意实数,a b ，数列{[]}n n S S -中有无穷多项属于(,)a b ．这里，[]x 表示不超过实数ｘ的最大整数．【例9】（2010高中数学联赛）设k 是给定的正整数，12r k =+．记(1)()()f r f r r r ==⎡⎤⎢⎥，()()l f r =(1)(()),2l f fr l -≥．证明：存在正整数m ，使得()()m f r 为一个整数．这里，x ⎡⎤⎢⎥表示不小于实数x 的最小整数，例如：112⎡⎤=⎢⎥⎢⎥，11=⎡⎤⎢⎥．【演练1】求所有的素数对(,)p q ，使得|77p q pq +.实战演练【演练2】(第8届CWMO)设整数2m ≥，12,,...,m a a a 都是正整数. 证明：存在无穷多个正整数n,使得1mn kk ak =⋅∑都是合数.【演练3】能否找到自然数的集合S ，满足：⑴1991S =；⑵S 中任意二数互质；⑶S 中任(2)k ≥个数的和为合数．【演练4】 (第5届CGMO 第8题)设p 为大于3的质数，求证：存在若干个整数12,,...,t a a a 满足条件：12 (22)t p pa a a -<<<<<，使得乘积1212t tp a p a p a a a a ---⋅⋅⋅⋅⋅⋅是3的某个正整数次幂．【演练5】 (2007年国家集训队第6次测试)考虑一个77⨯的数表22()(),1,7ij a i j i j i j =++≤≤. 我们称将任意一个由7个整数组成的等差数列的每一项分别依次加到某一行（或列）对应的项上为一次操作.问：是否可能经过有限步上述操作得到一个数表使其每一行的7个数都构成等差数列．。

第17讲直线与圆的位置关系8种常见考法归类(解析版)-新高二数学暑假自学课讲义

第17讲直线与圆的位置关系8种常见考法归类1.能根据给定直线、圆的方程，判断直线与圆的位置关系．2.能用直线和圆的方程解决一些简单的问题．体会用代数方法处理几何问题的思想.知识点1直线与圆的三种位置关系相交d＜Δ＞1．解决圆的弦长问题的方法截得的弦为AB ，圆的半径为|＝2r 2－d 2的直线与圆相交于A (x A ，y A )，B (x B 1＋1k2·|y A －y B |(其中；当斜率不存在时，|AB |＝|y 0；圆M 22x y +0F =消去“y ”得到关于“，结合韦达定理可得到A x +．当直线与圆相交时，半径、半弦、弦心距所构成的直角三角形(意把它和点到直线的距离公式结合起来使用．知识点3直线与圆相切1．求过某点的圆的切线问题时，应首先确定点与圆的位置关系，再求切线方程．若点在圆上(即为切点)，则过该点的切线只有一条；若点在圆外，则过该点的切线有两条，此时应注意切线斜率不存在的情况．（注：过圆内一点，不能作圆的切线）2．求过圆上的一点(x 0，y 0)的切线方程的方法先求切点与圆心连线的斜率k ，若k 不存在，则结合图形可直接写出切线方程为y ＝y 0；若k ＝0，则结合图形可直接写出切线方程为x ＝x 0；若k 存在且k ≠0，则由垂直关系知切线的斜率为－1k ，由点斜式可写出切线方程．3．求过圆外一点(x 0，y 0)的圆的切线方程的方法(1)过圆x 2＋y 2＝r 2上一点P (x 0，y 0)的圆的切线方程为x 0x ＋y 0y ＝r 2.(2)过圆(x －a )2＋(y －b )2＝r 2上一点P (x 0，y 0)的圆的切线方程为(x 0－a )(x －a )＋(y 0－b )(y －b )＝r 2.(3)过圆x 2＋y 2＝r 2外一点M (x 0，y 0)作圆的两条切线，则两切点所在直线方程为x 0x ＋y 0y ＝r 2.5.切线长公式记圆C :222()()x a y b r -+-=；过圆外一点P 做圆C 的切线，切点为H ,利用勾股定理求PH ；22PH PC CH =-知识点4圆上点到直线的最大（小）距离设圆心到直线的距离为d ，圆的半径为r①当直线与圆相离时，圆上的点到直线的最大距离为d r +，最小距离为d r -；②当直线与圆相切时，圆上的点到直线的最大距离为2r ，最小距离为0；③当直线与圆相交时，圆上的点到直线的最大距离为d r +，最小距离为0；1、判断直线与圆位置关系的方法(1)几何法：由圆心到直线的距离d 与圆的半径r 的大小关系判断．(2)代数法：根据直线与圆的方程组成的方程组解的个数来判断．2、过圆上一点(x 0，y 0)的圆的切线方程的求法先求切点与圆心连线的斜率k ，再由垂直关系得切线的斜率为－1k ，由点斜式可得切线方程．如果斜率为零或不存在，则由图形可直接得切线方程y ＝y 0或x ＝x 0.3、过圆外一点(x 0，y 0)的切线方程的求法设切线方程为y －y 0＝k (x －x 0)，由圆心到直线的距离等于半径建立方程，可求得k ，也就得切线方程．当用此法只求出一个方程时，另一个方程应为x ＝x 0，因为在上面解法中不包括斜率不存在的情况，而过圆外一点的切线有两条．一般不用联立方程组的方法求解．4、求切线长(最值)的两种方法(1)(代数法)直接利用勾股定理求出切线长，把切线长中的变量统一成一个，转化成函数求最值；(2)(几何法)把切线长最值问题转化成圆心到直线的距离问题．5、求弦长的两种方法(1)由半径长r 、弦心距d 、弦长l 的一半构成直角三角形，所以利用勾股定理d 2＋l22＝r 2求解，这是常用解法．(2)联立直线与圆的方程，消元得到关于x (或y )的一元二次方程，利用根与系数的关系得到两交点横坐标(或纵坐标)之间的关系，代入两点间距离公式求解．此解法很烦琐，一般不用．6、坐标方法解决平面几何问题的“三步曲”考点一：直线与圆位置关系的判断（一）判断直线与圆的位置关系例1．（2023·新疆喀什·校考模拟预测）已知圆22:240C x y x y ++-=，直线:210l x y --=，则圆C 与直线l （）A ．相交B ．相切C ．相离D ．相交且直线过圆C 的圆心【答案】B【分析】根据题意只需判断圆心到直线的距离与半径比较大小即可判断．【详解】由22240x y x y ++-=可得()()22125x y ++-=，故圆心(1,2)C -，半径r =，则圆心到直线:210l x y --=的距离d r ==，故直线与圆C 相切．故选：B变式1．（2023·四川成都·成都七中校考一模）圆C ：22(1)(1)1x y -+-=与直线l ：143x y+=的位置关系为（）A ．相切B ．相交C ．相离D ．无法确定【答案】A【分析】求出圆心坐标与半径，再将直线方程化为一般式，根据圆心到直线的距离即可判断.【详解】圆C ：22(1)(1)1x y -+-=的圆心为()1,1C ，半径1r =，直线l ：143x y+=即34120x y +-=，则圆心到直线的距离1d r ==，所以直线l 与圆C 相切.故选：A变式2．（2023春·北京海淀·高二北理工附中校考期中）直线()20R ax y a a -+=∈与圆225x y +=的位置关系为（）A ．相离B ．相切C ．相交D ．不确定【答案】C【分析】求出直线恒过的定点，判断定点与圆的位置关系.【详解】由题知，圆心坐标()00，将直线20ax y a -+=化为点斜式得()2y a x =+，知该直线过定点()2,0-，又()22205-+<，故该定点在圆内，所以该直线与圆225x y +=必相交.故选：C变式3．（2023秋·高二课时练习）00(,)M x y 为圆221x y +=内异于圆心的一点，则直线001x x y y +=与该圆的位置关系为（）A ．相切B ．相交C ．相离D ．相切或相交【答案】C【分析】由题意可得22001x y +<，结合圆心到直线001x x y y +=的距离判断与半径的大小关系，即得答案.【详解】由题意知00(,)M x y 为圆221x y +=内异于圆心的一点，则22001x y +<，而圆：221x y +=的圆心到直线001x x y y +=的距离为1d r ==，故直线001x x y y +=与该圆的位置关系为相离，故选：C（二）由直线与圆的位置关系求参数例2．（2023·辽宁·校联考二模）已知圆222:O x y r +=，直线l ：234x y r +=，若l 与圆O 相交，则（）．A ．点()3,4P 在l 上B ．点()3,4P 在圆O 上C ．点()3,4P 在圆O 内D ．点()3,4P 在圆O 外【答案】D【分析】根据l 与圆O 相交，可知圆心到直线的距离小于半径，列出不等式，再判断点与直线和圆的关系.【详解】由已知l 与圆O 相交，,可知圆心到直线的距离小于半径，225r r =<，故5r <，把()3,4P 代入23491625x y r +=+=>，所以点不在直线l 上，故A 错误；又5OP r =>，则点(2,3)P 在圆O 外，故D 正确.故选：D ．变式1．（2023春·浙江·高二期中）已知圆22(1)(2)4x y -+-=关于直线20ax by +-=的最小值为（）A ．45B C D ．1【答案】B220a b +-=上任一点(),P a b 到坐标原点()0,0O 的距离，结合点到直线的距离运算求解.【详解】已知圆22(1)(2)4x y -+-=的圆心为()1,2，半径2r =，由题意可知：直线20ax by +-=过圆心()1,2，即220a b +-=，220a b +-=上任一点(),P a b 到坐标原点()0,0O 的距离，()0,0O 到直线220a b +-=的距离d =故选：B.变式2．（2023秋·高一单元测试）若直线1y kx =-与曲线y =k 的取值范围是（）A ．4,3⎛⎫+∞ ⎪⎝⎭B ．41,3⎡⎫⎪⎢⎣⎭C ．41,3⎡⎤⎢⎥⎣⎦D ．40,3⎛⎫ ⎪⎝⎭【答案】B【分析】根据题意得：1y kx =-为恒过定点(0,1)A -的直线，曲线表示圆心为(2,0)，半径为1的上半圆，由此利用数形结合思想能求出k 的取值范围．【详解】根据题意得1y kx =-为恒过定点(0,1)A -的直线，由曲线y =，可得22(2)1(0)x y y -+=≥，所以曲线表示圆心为(2,0)C ，半径为1的上半圆，如图所示，当直线与圆C 1=，解得0k =（舍去）或43k =，把(1,0)B 代入1y kx =-得10k -=，解得1k =，因为直线1y kx =-与曲线y =恰有两个公共点，由图可得413k ≤<，即k 的取值范围是41,3⎡⎫⎪⎢⎣⎭．故选：B ．变式3．（2023·湖南益阳·安化县第二中学校考三模）直线y x b =+与曲线x =则实数b 的取值范围是（）A ．1b -≤≤B ．1b <≤-C ．11b -<≤-，b =D ．1b <<【答案】B【分析】y x b =+是斜率为1的直线，曲线x =1为半径的圆的右半圆，利用点到直线距离公式，结合图形可得答案.【详解】y x b =+是斜率为1的直线，曲线21x y =-是以原点为圆心1为半径的圆的右半圆，画出它们的图象如图，当直线与圆相切时，12,22b b b =⇒=-=（舍去），当直线过1,0（）时，1b =-,由图可以看出：当21b -<≤-时，直线与半圆有两个公共点，故选：B.变式4．（2023·新疆阿克苏·校考一模）已知两点()(),0,,0(0)A m B m m ->，点P 是圆22(3)(4)1x y -+-=上任意一点，APB ∠是锐角，则m 的取值范围为（）A ．()0,6B ．()0,4C ．()4,6D ．[)6,+∞【答案】B【分析】设出点P 的坐标，利用向量建立不等式，再借助几何意义求出圆上点到原点距离最小值即可.【详解】设点00(,)P x y ，显然圆22(3)(4)1x y -+-=与x 轴相离，即点,,A P B 不共线，于是APB ∠是锐角当且仅当0PA PB ⋅>，而0000(,),(,)PA m x y PB m x y =---=-- ，依题意，2000()()0m x m x y ---+>，即2200||m x y <+2200+x y P 到原点的距离，又点P 是圆22(3)(4)1x y -+-=上任意一点，其圆心为()3,4，半径为1，因此222200min ()3414x y +=+=，从而||4m <，又0m >，解得04m <<，所以m 的取值范围为(0,4).故选：B变式5．（2023春·上海黄浦·高二上海市向明中学校考期中）圆22:2430C x y x y +++-=上到直线10x y ++=2）A ．2个B ．3个C ．4个D ．无数个【答案】B【分析】求出圆心到直线的距离，再结合图象分析可得结果.【详解】因为222430x y x y +++-=化为标准方程为22(1)(2)8x y +++=，所以圆心(1,2)C --，圆的半径r =又因为圆心C 到直线10x y ++=的距离为d =所以r d -=所以过圆心平行于直线10x y ++=的直线与圆有2个交点，另一条与直线10x y ++=的平行线与圆相切，只有1个交点，如图所示，所以圆C 上到直线10x y ++=3个.故选：B.变式6．（2023·湖南长沙·周南中学校考二模）若圆()()22320x a y -+-=上有四个点到直线210x y -+=的a 的取值范围是______．【答案】3722⎛⎫⎪⎝⎭-,【分析】由题意得，圆心到直线210x y -+=的距离d <【详解】圆()()22320x a y -+-=的圆心为(,3)a ，半径为因为圆()()22320x a y -+-=上有四个点到直线210x y -+=所以圆心到直线210x y -+=的距离d所以d =<3722a -<<．故答案为：37,22⎛⎫- ⎪⎝⎭．变式7．【多选】（2023春·贵州遵义·高二遵义市南白中学校考阶段练习）已知直线:l y x b =+，圆22:4O x y +=，则下列说法正确的是（）A ．圆O 上恰有1个点到直线l 的距离为1，则b =±B ．圆O 上恰有2个点到直线l 的距离为1，则(b ∈-C ．圆O 上恰有3个点到直线l 的距离为1，则b =D ．圆O 上恰有4个点到直线l 的距离为1，则(b ∈【答案】ACD【分析】根据圆O 上点的个数到直线l 的距离为1，数形结合得到圆心到直线l 的距离或距离范围，得到方程或不等式，求出答案.【详解】圆22:4O x y +=的圆心为()0,0，半径为2，A 选项，要想圆O 上恰有1个点到直线l 的距离为1，则圆心到直线l 的距离为3，3=，解得b =±A 正确；B 选项，要想圆O 上恰有2个点到直线l 的距离为1，则圆心到直线l 的距离大于1，小于3，()1,3，解得(b ∈-⋃，B 错误；C 选项，圆O 上恰有3个点到直线l 的距离为1，则圆心到直线l 的距离等于1，1=，解得b =C 正确；D 选项，圆O 上恰有4个点到直线l 的距离为1，则圆心到直线l 的距离小于1，1<，解得(b ∈，D 正确.故选：ACD（三）由直线与圆的位置关系求距离最值例3．（2023秋·陕西西安·高二长安一中校考期末）已知直线:60l x y -+=与圆22:(1)(1)8C x y -+-=，则圆C 上的点到直线l 的距离的最小值为（）A ．1B C ．D ．【答案】B【分析】确定圆心和半径，计算圆心到直线的距离，再计算最小值得到答案.【详解】圆22:(1)(1)8C x y -+-=，圆心为()1,1C ，半径r =圆心到直线的距离为d r ==>，直线和圆相离，故圆C 上的点到直线l 的距离的最小值为d r -==故选：B变式1．（2023·广西·校联考模拟预测）已知直线()():5220R l mx m y m +--=∈和圆22:4O x y +=，则圆心O 到直线l 的距离的最大值为（）A ．65B C ．3D ．32【答案】B【分析】把直线方程化为(2)520m x y y -+-=，求得直线l 过定点42(,)55P ，结合圆的几何性质，即可求解.【详解】由题意，直线()5220mx m y +--=可化为(2)520m x y y -+-=，联立方程组20520x y y -=⎧⎨-=⎩，解得42,55x y ==，即直线l 过定点42(,)55P ，又由2242455⎛⎫⎛⎫+< ⎪ ⎪⎝⎭⎝⎭，可得定点P 在圆内，由圆的几何性质知，圆心到直线的距离||d OP ≤==．故选：B.变式2．（2023秋·广东梅州·高三大埔县虎山中学校考阶段练习）直线20x y +-=分别与x 轴，y 轴交于A ，B 两点，点P 在圆221(2)(1)2x y ++-=上，则ABP 面积的取值范围是___________.【答案】[2,4]【分析】先求出A ，B 两点的坐标，则可求出AB ，然后求出圆心到直线的距离d ，从而可求出点P 到直线的距离的最大值d r +和最小值d r -，进而可求出ABP 面积的最大值和最小值，即可求得结果.【详解】对于20x y +-=，当0x =时，2y =，当0y =时，2x =，所以(2,0),(0,2)A B ，所以AB ==，圆221(2)(1)2x y ++-=的圆心(2,1)C -，半径2r =，圆心(2,1)C -到直线20x y +-=的距离为22d =，所以点P 到直线的距离的最大值3222222d r +=+=，点P 到直线的距离的最小值322222d r -=-=，所以ABP 面积的最大值为11()2222422AB d r ⋅+=⨯⨯=，ABP 面积的最小值为11()222222AB d r ⋅-=⨯⨯=，所以ABP 面积的取值范围是[2,4]，故答案为：[2,4]变式3．【多选】（2023春·浙江杭州·高三浙江省杭州第二中学校联考阶段练习）已知()1,0,(0,2)P N -，过点P 作直线:0l ax y a --=的垂线，垂足为M ，则（）A ．直线l 过定点B ．点P 到直线l 2C ．MN 的最大值为3D ．MN 的最小值为2【答案】AC【分析】由点斜式确定定点，由点M 在以原点为圆心，直径为2PB =的圆上，结合圆的性质判断即可.【详解】0ax y a --=可化为()1y a x =-，则直线l 过定点()10B ,，故A 正确；因为直线l 的斜率存在，所以点M 与点B 不重合，因为PM l ⊥，所以点M 在以原点为圆心，直径为2PB =的圆上（去掉点B ），点P 到直线l 的距离为PM ，由图可知，02PM ≤<，故B 错误；由图可知，NA MN NC ≤≤，即13MN ≤≤，故C 正确，D 错误；故选：AC变式4．（2023春·河北石家庄·高三校联考阶段练习）如图，正方形ABCD 的边长为4，E 是边AB 上的一动点，FG EC ⊥交EC 于点P ，且直线FG 平分正方形ABCD 的周长，当线段BP 的长度最小时，点A 到直线BP 的距离为______.【答案】5【分析】利用平面几何知识可得出P 点的轨迹是圆.适当建系，写出P 点的轨迹方程.再利用圆的性质得出当BP 最小时，B ，P ，M 三点共线，进而求解即可.【详解】根据题意FG 平分正方形周长，可得FG 恒过正方形ABCD 的中心，设ABCD 的中心为点O ，由FG EC ⊥可知，P 点的轨迹是以OC 为直径的圆，以A 为坐标原点，AB 为x 轴，AD 为y 轴建立直角坐标系，则()0,0A ，()4,0B ，()4,4C ，()2,2O ，以OC 为直径的圆的方程为()()22332x y -+-=，设M 为圆心，可知坐标为()3,3，当BP 最小时，B ，P ，M 三点共线，可知此时直线BP 的方程为312y x =-+，则点A 到直线BP5==.考点二：直线与圆的交点问题例4．（2023秋·江苏宿迁·高二统考期中）直线1y x =-+与曲线x =）A ．0B ．1C ．2D ．3【答案】C【分析】联立方程后考虑方程组的解，从而可得交点的个数.【详解】联立直线方程和曲线方程可得1y x x =-+⎧⎪⎨=⎪⎩可得1y -=即210y y y ≤⎧⎨-=⎩，解得0y =或1y =，故方程组的解为10x y =⎧⎨=⎩或01x y =⎧⎨=⎩.故选：C变式1．（2023秋·浙江嘉兴·高二统考期末）直线220x y +-=与曲线(10x y +-=的交点个数为（）A ．1个B ．2个C ．3个D ．4个【答案】B【分析】根据题意，由曲线表示一条直线与一个圆，然后分别联立方程，即可得到交点个数.【详解】因为曲线(10x y +-=就是10x y +-=或224x y +=，表示一条直线与一个圆，联立22010x y x y +-=⎧⎨+-=⎩，解得10x y =⎧⎨=⎩，即直线220x y +-=与直线10x y +-=有一个交点()1,0；没有意义.联立222204x y x y +-=⎧⎨+=⎩，解得02x y =⎧⎨=⎩或8565x y ⎧=⎪⎪⎨⎪=-⎪⎩，所以直线220x y +-=与224x y +=有两个交点.所以直线220x y +-=与曲线(10x y +-=的交点个数为2个.故选：B变式2．（2023春·浙江·高二期中）设圆C ：22230x x y -+-=，若直线l 在y 轴上的截距为1，则l 与C 的交点个数为（）A ．0B ．1C ．2D ．以上都有可能【答案】C【分析】利用直线过定点，判断定点在圆内即可．【详解】解：直线l 在y 轴上的截距为1，∴直线l 过定点()01，，220201320-⨯+-=-< ，∴点()01，在圆内，∴直线l 与C 的交点个数为2个．故选：C ．变式3．（2023秋·四川南充·高二四川省南充高级中学校考阶段练习）已知点A B ，是圆22:4C x y +=与x 轴的交点，P 为直线:4l x =上的动点，直线PA PB ，与圆C 的另一个交点分别为M N ，，则直线MN 恒过定点（）A ．504⎛⎫⎪⎝⎭，B ．()10，C ．304⎛⎫⎪⎝⎭，D ．102骣琪琪桫，【答案】B【分析】由圆的方程，求得,A B 的坐标，设出P 坐标，写出两直线的方程，分别联立圆与直线，求得,M N 的坐标，求特殊位置解得定点，用一般情况的方程进行验证，可得答案.【详解】由224x y +=，令=0y ，解得2x =±，不妨设()2,0A -，()2,0B ，设()4,P p ，则直线AP 的方程为()26p y x =+，直线BP 的方程为()22py x =-，联立()22=+26+=4p y x x y ⎧⎪⎨⎪⎩，消去y 可得：()222236441440p x p x p +++-=，设()11,M x y ，()22,N x y ，则2124144236p x p --=+，即()21223636p x p-=+，122436p y p =+，联立()22=22+=4p y x x y -⎧⎪⎨⎪⎩，消去y 可得：()2222444160p x p x p +-+-=，则22241624p x p -=+，即222284p x p -=+，2284p y p -=+，当直线MN 的斜率不存在时，()222223628436p p p p--=++，解得212p =，此时121x x ==，故直线方程为=1x ；当直线MN 的斜率为0时，则直线MN 方程=0y ，联立=1=0x y ⎧⎨⎩，可得定点为()1,0，下面验证此为真：当直线MN 的斜率存在且不为零时，则斜率2212222122224883647222812364p py y p p p k p p x x p p p +-++===------++，则方程为222288284124p p p y x p p p ⎛⎫---=-- ⎪+-+⎝⎭，将()1,0代入上式，则22222884284124p p p p p p p +-+=-⋅+-+，即222288124124p p p p p p -=-⋅+-+，等式成立，故直线MN 过定点()1,0，故选：B.考点三：圆的切线问题（一）过圆上一点的切线方程例4．（2023春·天津西青·高二天津市西青区杨柳青第一中学校考阶段练习）过点1,2⎛ ⎝⎭作圆22:1C x y +=的切线l ，则切线l 的方程为__________.【答案】20x -=【分析】根据题意可知点1,22⎛- ⎝⎭在圆C 上，结合切线性质结合直线的点斜式运算求解.【详解】圆22:1C x y +=的圆心()0,0C ，∵22112⎛⎛⎫+= ⎪ ⎝⎭⎝⎭，则点1,22⎛⎫ ⎪ ⎪⎝⎭在圆C上，即点1,22⎛- ⎝⎭为切点，则圆心到切点连线的斜率02102k ==-，可得切线l的斜率l k =故切线l的方程1232y x ⎛⎫+=- ⎪⎝⎭，即20x -=.故答案为：20x -=.变式1．（2023·全国·高三专题练习）经过点()1,0且与圆224230x y x y +--+=相切的直线方程为__________．【答案】10x y +-=【分析】根据直线与圆相切，由圆心到直线的距离相等，分直线的斜率不存在和存在讨论求解.【详解】解：圆224230x y x y +--+=的标准方程为：()()22212x y -+-=，当直线的斜率不存在时，直线方程为1x =，不符合题意；当直线的斜率存在时，设直线方程为()1y k x =-，即kx y k 0--=，因为直线与圆相切，所以圆心到直线的距离相等，即d ==，化简得2210k k ++=，解得1k =-，10x y +-=，综上：直线方程为：10x y +-=，故答案为：10x y +-=变式2．（2023·山东泰安·校考模拟预测）已知点(M 在圆22:C x y m +=上，过M 作圆C 的切线l ，则l 的倾斜角为（）A ．30B ．60C ．120D ．150【答案】D【分析】先根据点在圆上，求出4m =，考虑l 的斜率不存在和存在两种情况，结合点到直线距离列出方程，求出斜率和倾斜角.【详解】由题意得134m =+=，当l 的斜率不存在时，此时直线方程为1x =，与圆22:4C x y +=相交，不合题意，当l 的斜率存在时，设切线l的方程为()1y k x =-，2=，解得3k =-，设l 的倾斜角为0180θ︒≤<︒，故l 的倾斜角为150 .故选：D变式3．（2023·天津武清·天津市武清区杨村第一中学校考模拟预测）已知点(1,0)A ，(2,0)B ，经过点B 作圆22(3)(2)5x y -+-=的切线与y 轴交于点P ，则AP =________．【分析】由直线与圆的位置关系作出切线，求得()0,1P ，即可得解.【详解】如图所示，设圆心为C 点，则()3,2C ，()()2223025-+-=，则点B 在圆上，且20232BC k -==-，由PB 与圆相切可得112PB BC PB k k k ⋅=-⇒=-，所以切线方程为()122y x =--，令0x =，解得1y =，故()0,1P ，所以AP=.变式4．（2023·河南开封·统考三模）已知点(1,0)A ，(2,0)B ，经过B 作圆()()22325x y -+-=的切线与y 轴交于点P ，则tan APB ∠=______．【答案】13【分析】由直线与圆的位置关系作出切线，求得()0,1P ，再用两角和与差的正切公式即可得结果.【详解】如图所示，设圆心为C 点，则()3,2C ，()()2223025-+-=，则点B 在圆上，且20232BC k -==-，由PB 与圆相切可得：112PB BC PB k k k ⋅=-⇒=-，则tan 2OPB ∠=，2OB = ，则1OP =，故()0,1P ，则tan 1APO ∠=，从而可得()tan tan 211tan tan 1tan tan 1213OPB OPA APD OPB OPA OPB OPA ∠-∠-∠=∠-∠===+∠⋅∠+⨯,故答案为：13.变式5．（2023秋·高二课时练习）从圆222210x x y y -+-+=外一点()3,2P 向这个圆作两条切线，则两切线夹角的余弦值为（）A ．12B ．35C ．2D ．6【答案】B【分析】根据锐角三角函数，结合二倍角公式即可求解.【详解】由222210x x y y -+-+=得()()22111x y -+-=，所以圆心为()1,1A ，半径为1r =，设切点分别为,B C ,连接PA ,则BPC ∠为两切线的夹角，由于PA =所以sinAB APB AP Ð==由二倍角公式可得223cos 12sin 125CPB APB 骣Ð=-Ð=-=，故选:B变式6．（2023秋·福建福州·高二福建省连江第一中学校联考期中）已知圆22:3O x y +=，l 为过(M 的圆的切线，A 为l 上任一点，过A 作圆()22:24N x y ++=的切线AP ，AQ ，切点分别是P 和Q ，则四边形APNQ 的面积最小值是__________．【答案】3【分析】求出直线l 的方程，再根据圆的切线长定理求出四边形面积的函数关系，借助点到直线距离求出最小值作答.【详解】依题意，直线OM l 的斜率为2-，直线l 的方程为)1y x -，即30x -=，圆N 的圆心(2,0)N -，半径2r =，因为,AP AQ 为圆N 的切线，则N AQN AP ≌，四边形APNQ 的面积：122||2APNQ APN S S AP r ==⨯⋅==又(2,0)N -到l 的距离d =min ||AN d ==因此min ()2APNQ S =所以四边形APNQ .故答案为：3（二）过圆外一点的切线方程例5．（2023秋·福建莆田·高二校联考期末）求圆22:40Q x y x +-=在点P 处的切线方程.【答案】20x +=【分析】根据点P 在圆Q 上，求得可得PQ k =3k =，结合直线的点斜式方程，即可求解.【详解】由圆的方程22:40Q x y x +-=，又由点P 在圆Q 上，可得21PQ k ==-3k =，所以切线方程为1)y x =-，即20x +=.变式1．（2023秋·北京·高二北京一七一中校考阶段练习）过点(4,3)-的圆22(3)(1)1x y ++-=的切线方程为_________________．【答案】4x =-或340x y +=【分析】根据切线斜率存在和不存在分类讨论，斜率存在时设直线方程，由圆心到切线距离等于半径求解．【详解】当切线的斜率不存在时，切线的方程为4x =-，圆心(3,1)-到该直线的距离等于半径1，符合题意，当切线的斜率存在时，设过点(4,3)-的切线方程为3(4)y k x -=+，即430kx y k -++=，∵圆心到直线430kx y k -++=的距离等于半径，1=，解得34k =-，∴切线方程为340x y +=，综上所述，切线方程为4x =-或340x y +=．故答案为：4x =-或340x y +=．变式2．（2023春·重庆沙坪坝·高一重庆一中校考期末）在平面直角坐标系中，圆C 过点(4,0)A ，(2,2)B ，且圆心C 在20x y +-=上．(1)求圆C 的方程；(2)若已知点P ，过点P 作圆C 的切线，求切线的方程．【答案】(1)22(2)4x y -+=(2)20x +=【分析】（1）根据题意，求出AB 的中垂线方程，与直线240x y --=联立，可得圆心C 的坐标，求出圆的半径，即可得答案；（2）分切线的斜率存在与不存在两种情况讨论，求出切线的方程，综合可得答案．【详解】（1）因为圆C 过(4,0),(2,2)A B ，则AB 的中垂线过圆心C ，设AB 的中点为M ，则(3,1)M ，因为42102AB k -==--，所以AB 的中垂线方程为13y x -=-，即2y x =-，又圆心在20x y +-=，联立202x y y x +-=⎧⎨=-⎩，解得20x y =⎧⎨=⎩，因此圆心(2,0)C ，半径2r OA ==，所以圆C 的方程为22(2)4x y -+=..（2）因为(22(42)4-+>，所以P 在圆C 外，过P 作圆C 的切线，若切线斜率不存在时，则切线方程为4x =，满足与圆C 相切，若切线斜率存在时，设切线方程(4)y k x --，即40kx y k --+=，2=，解得k =所以切线方程为4033x y --+=，即20x +=.综上：切线方程为4x =或20x +=.变式3．（2023秋·广东阳江·高二阳江市阳东区第一中学校考期中）已知点(2,4)P ，圆O ：224x y +=，则过点P 与圆O 相切的直线有_____条；切线方程为_____.【答案】22x =或34100x y -+=【分析】根据给定条件，确定点P 与圆O 的位置关系即可作答.【详解】依题意，2224204+=>，即点P 在圆O 外，所以过点P 与圆O 相切的直线有2条；显然圆心(0,0)O 到直线2x =的距离为圆O 的半径2，即直线2x =为圆O 的一条切线，过点P 的圆O 的切线斜率存在时，设方程为4(2)y k x -=-，即240kx y k --+=，由2|24|21k k -+=+，解得34k =，则切线方程为34100x y -+=，所以所求切线方程为2x =或34100x y -+=.故答案为：2；2x =或34100x y -+=变式4．（2023·浙江·校联考模拟预测）已知圆221:4C x y +=和圆222:(3)(2)1C x y -+-=，则过点42,3M ⎛⎫ ⎪⎝⎭且与12,C C 都相切的直线方程为__________.（写出一条即可）【答案】2x =或512260x y +-=（写出一条即可）【分析】由直线与圆的位置关系通过几何法计算即可.【详解】若过M 的切线斜率不存在，即为2x =，此时显然与两圆都相切；若过M 的切线斜率存在，不妨设为()423y k x -=-，则()()120,0,3,2C C 到()423y k x -=-的距离分别为12224225332,11211k k d d k k k --====⇒=-++，即()452512260312y x x y -=--⇒+-=.综上过M 与两圆都相切的直线为：2x =或512260x y +-=故答案为：2x =或512260x y +-=（写出一个即可）变式5．（2023秋·高二单元测试）若(),P x y 在圆()()22539x y -+-=上运动，则2y x+的最大值为___.【答案】2534116+【分析】2y x+表示()(),,0,2P x y -两点所在直线的斜率，则当直线与圆相切时，斜率取得最值，求出过点0,2-的切线的斜率，即可得解.【详解】2y x+表示()(),,0,2P x y -两点所在直线的斜率，设()(),,0,2x y -两点所在直线的方程为2y kx +=，即20kx y --=，如图，当直线与圆相切时，斜率取得最值，圆()()22539x y -+-=的圆心为()5,3，半径为3，当圆()()22539x y -+-=与直线20kx y --=相切时，圆心()5,3到直线20kx y --=3=，解得k =，所以2y x +的最大值为2516+.故答案为：2516+.变式6．（2023·全国·高三专题练习）已知(),M x y 为圆C ：22414450x y x y +--+=上任意一点，且点()2,3Q -．（1）求MQ 的最大值和最小值．（2）求32y x -+的最大值和最小值．（3）求y x -的最大值和最小值．【答案】【小问1】最大值为【小问2】最大值为2+2【小问3】最大值为9，最小值为1【分析】（1）利用图形及点与圆的关系即可得结果；（2）利用图形将问题转化为斜率最值即可；（3）利用图形将问题转化为直线与圆的位置关系；【详解】（1）圆C ：()()2222414450278x y x y x y +--+=⇒-+-=，如图所示，连接QC 交圆C 于AB 两点，当M 与A 重合时MQ 取得最小值，即QC r -=与B 重合时MQ 取得最大值即QC r +=故最大值为（2）易知32MQ y k x -=+，由图形知当MQ 与圆C 相切时取得最值，如图所示.可设():23MQ l y k x =++，则C r ==2k =故最大值为22（3）设y x z -=，如图所示，z 即过点M 的直线y x z -=的截距，如图所示，当该直线与圆相切时截距取得最值.圆心C r ==1z =或9，故最大值为9，最小值为1.变式7．（2023春·河北·高二校联考期末）过直线40x y +-=上一点向圆O ：221x y +=作两条切线，设两切线所成的最大角为α，则sin α=（）A ．9B ．229C D 【答案】C【分析】设P 是直线40x y +-=的动点，由题意可得OP 是圆心O 到直线的距离时，两切线所成的角α最大，计算可得sin α．【详解】由圆22:1O x y +=，可得圆心为(0,0)，半径为1r =，设P 是直线40x y +-=的动点，自P 向圆作切线，当OP 长最短时，两切线所成的角α最大，即OP 是圆心O 到直线的距离时，两切线所成的角α最大，由点到直线的距离公式可得d ，sin2α∴=π022α<<，cos 2α∴==sin 2sincos222ααα∴==．故选：C ．变式8．（2023·北京大兴·校考三模）若点P 是圆22:20C x y x +-=上的动点，直线:10l x y ++=与x 轴、y 轴分别相交于M ，N 两点，则PMN ∠的最小值为（）A ．π12B ．π6C ．π4D ．π3【答案】A【分析】作出图形，分析可知当直线MP 与圆C 相切，且切点位于x 轴下方时，PMN ∠取最小值，求出OMN ∠、CMP ∠的大小，可求得PMN ∠的最小值．【详解】如下图所示：直线l 的斜率为1-，倾斜角为3π4，故π4OMN Ð=，圆C 的标准方程为()2211x y -+=，圆心为()1,0C ，半径为1r =，易知直线l 交x 轴于点()1,0A -，所以2MC =，由图可知，当直线PM 与圆C 相切，且切点位于x 轴下方时，PMN ∠取最小值，由圆的几何性质可知CP MP ⊥，且112CP CM ==，则π6CMP ∠=，故ππππ64612PMN OMN ∠≥∠-=-=．故选：A（三）与切线长有关的问题例6．（2023秋·江苏盐城·高二盐城市伍佑中学校考期末）由直线y x =上的点向圆()()22421x y -++=引切线，则切线长的最小值为______.【分析】切点与圆心的连线垂直切线，利用勾股定理，切线段长转化为直线上点与圆心连线和半径关系，求圆心与直线上点距离的最小值，即可求解.【详解】圆()()22421x y -++=的圆心为()4,2,1C r -=，在直线y x =上取一点P ，过P 向圆引切线，设切点为A ．连接,PC AC ．在Rt PAC △中，1CA r ==．要使PA 最小，则PC 应最小．又当PC 与直线垂直时，PC =故PA =.变式1．（2023·吉林通化·梅河口市第五中学校考模拟预测）由直线60x y ++=上一点P 向圆()()22:354C x y -++=引切线，则切线长的最小值为______．【答案】2【分析】设过点P 的切线与圆C 相切于点E ，分析可知当PC 与直线60x y ++=垂直时，PC 取最小值，再利用勾股定理可求得切线长的最小值.【详解】设过点P 的切线与圆C 相切于点E ，连接CE ，则PE CE ⊥，圆C 的圆心为()3,5C -，半径为2r =，则PE =当PC 与直线60x y ++=垂直时，PC =所以，2PE =，即切线长的最小值为2.故答案为：2.变式2．（2023·北京海淀·北大附中校考三模）已知圆22:1O x y +=，直线34100x y +-=上动点P ，过点P 作圆O 的一条切线，切点为A ，则PA 的最小值为（）A ．1B CD ．2【答案】C【分析】首先得出切线长PA 的表达式，再以二次函数求值域的方法解之即可.【详解】圆O ：221x y +=中，圆心(0,0)O ，半径1r =设00(,)P x y ，则0034100x y +-=，则PA ===当0306255x ==时，min PA =故选：C变式3．（2023·全国·高三专题练习）已知P 是直线3480x y ++=上的动点，PA ，PB 是圆22:2210C x y x y +--+=的两条切线，A ，B 是切点．求四边形PACB 面积的最小值.【答案】【分析】连接PC ，设P 点坐标为3,24x x ⎛⎫-- ⎪⎝⎭，则2PAC PACB S S AP == 四边形，问题转化为求AP 的最小值，再由勾股定理得到当2PC 最小时，AP 取最小值，利用距离公式及二次函数的性质计算可得.【详解】圆22:2210C x y x y +--+=即圆()()22:111C x y -+-=，所以圆心()1,1C ，半径1r =，。

暑假高一数学、英语辅导班

知识改变命运，勤奋铸就成功报名热线：暑假高中数学、英语、地理辅导班暑假将至，作为高一的你们，怎样利用这宝贵的假期呢？是碌碌无为泡泡吧呢？还是劳逸结合让学习有所提高呢？碌碌无为泡泡吧之举只能带来更糟糕的高二，悲剧的高三。

高考失败者的共性就是有基础，没有自信心进而厌学，甚至沉迷于网吧等。

业精于勤荒于嬉，行成于思毁于随。

高中三年，重在高一，贵在高二，精在高三。

重在于重基础，万丈高楼平地起，坚实的基础在于不断的学习，科学地复习。

暑假是最好的补基础，赶超他人的最好时机。

作为高一学生的你，是否为过去一年的学习而懊悔苦恼呢？是否为你的学习而无计可施呢？是否羡慕他人的成功而责怪自己呢？是否对高中进一步的学习产生厌学进而又使你产生对学习的恐惧呢？是否对高二高三紧张的学习失去信心和激情呢？如果是这样那就请加入我们暑期加油站吧，在这里有精心为你服务的省级骨干数学教师，富有激情的英语教师，经验丰富的地理教师。

通过他们辛勤的培育，你的暑假将过的非常有意义。

辅导精神：动力——信心——激情——习惯——成功辅导宗旨：服务学生，解答疑惑，树立信心，提高自我辅导师资：数学：省级骨干教师，新乡数学学科带头人英语：富有激情，善于讲演，乐于交流的英语高级教师地理：经验丰富，乐于引导的地理高级教师（中国地理学会会员）我们承诺暑期学习你将有如下进步：A．数学、英语成绩大幅度的提高B．学习信心大幅度的提高C．增强学习的激情D．养成良好的学习习惯E．对生活充满信心，更加乐观、自信报名须知：报名时间：2011年7月9日——7月14日授课时间：2011年7月14日——8月14日上午：8:00——11:00 下午：15:00——18:00 收费标准：300元/月报名热线：精心辅导，严谨办学，人文管理，乐教沟通，用我们的承诺成就你今后的高中学习生活 1。

高一升高二数学暑假衔接班讲义第5讲(学)

第5讲两条直线的位置关系（一）热点透析考察目标 1.考查两条直线的平行、垂直关系；2.考查两点间的距离公式及点到直线的距离公式的应用．达成目标 1.对于两条直线的位置关系问题，求解时要注意斜率不存在的情况，注意平行、垂直时直线方程系数的关系；2.熟记距离公式，如两点之间的距离、点到直线的距离、两条平行线之间的距离．（二）知识回顾1．两条直线平行与垂直的判定(1)两条直线平行对于两条不重合的直线l 1、l 2，其斜率分别为k 1、k 2，则有l 1∥l 2⇔ .特别地，当直线l 1、l 2的斜率都不存在时，l 1与l 2(2)两条直线垂直如果两条直线l 1，l 2斜率存在，设为k 1，k 2，则l 1⊥l 2⇔ ，当一条直线斜率为零，另一条直线斜率不存在时，两条直线． 2．两直线相交交点：直线l 1：A 1x ＋B 1y ＋C 1＝0和l 2：A 2x ＋B 2y ＋C 2＝0的公共点的坐标与方程组⎩⎪⎨⎪⎧A 1x ＋B 1y ＋C 1＝0A 2x ＋B 2y ＋C 2＝0的解一一对应．相交⇔方程组有，交点坐标就是方程组的解；平行⇔方程组；重合⇔方程组有． 3．三种距离公式(1)点A (x 1，y 1)、B (x 2，y 2)间的距离： |AB |＝x 2－x 12y 2－y 12.(2)点P (x 0，y 0)到直线l ：Ax ＋By ＋C ＝0的距离：d ＝|Ax 0＋By 0＋C |A 2＋B 2.(3)两平行直线l 1：Ax ＋By ＋C 1＝0与l 2：Ax ＋By ＋C 2＝0 (C 1≠C 2)间的距离为d ＝|C 2－C 1|A 2＋B 2. [难点正本疑点清源]1．两条直线平行、垂直的充要条件是有大前提的，就是两条直线都有斜率．当直线无斜率时，要单独考虑．2．与直线Ax ＋By ＋C ＝0(A 2＋B 2≠0)平行、垂直的直线方程的设法：一般地，平行的直线方程设为Ax ＋By ＋m ＝0；垂直的直线方程设为Bx －Ay ＋n ＝0.附件：当堂过手训练（快练五分钟，稳准建奇功！）1．直线Ax ＋3y ＋C ＝0与直线2x －3y ＋4＝0的交点在y 轴上，则C 的值为________． 2．若直线x －2y ＋5＝0与直线2x ＋my －6＝0互相垂直，则实数m ＝________.3．已知直线l 1与l 2：x ＋y －1＝0平行，且l 1与l 2的距离是2，则直线l 1的方程为________________． 4．过点(1,0)且与直线x －2y －2＝0平行的直线方程是( )A ．x －2y －1＝0B ．x －2y ＋1＝0C ．2x ＋y －2＝0D ．x ＋2y －1＝05．若经过点(3，a )、(－2,0)的直线与经过点(3，－4)且斜率为12的直线垂直，则a 的值为( )A.52B.25C ．10D ．－10二、高频考点专题链接题型一两条直线的平行与垂直例1 已知直线l 1：ax ＋2y ＋6＝0和直线l 2：x ＋(a －1)y ＋a 2－1＝0.(1)试判断l 1与l 2是否平行； (2)l 1⊥l 2时，求a 的值．探究提高 (1)当直线的方程中存在字母参数时，不仅要考虑到斜率存在的一般情况，也要考虑到斜率不存在的特殊情况．同时还要注意x、y的系数不能同时为零这一隐含条件．(2)在判断两直线的平行、垂直时，也可直接利用直线方程的系数间的关系得出结论．已知两直线l1：mx＋8y＋n＝0和l2：2x＋my－1＝0.试确定m、n的值，使：(1)l1与l2相交于点P(m，－1)；(2)l1∥l2；(3)l1⊥l2，且l1在y轴上的截距为－1.题型二两条直线的交点问题例2求经过直线l1：3x＋2y－1＝0和l2：5x＋2y＋1＝0的交点，且垂直于直线l3：3x－5y＋6＝0的直线l 的方程．探究提高运用直线系方程，有时会给解题带来方便，常见的直线系方程有：(1)与直线Ax＋By＋C＝0平行的直线系方程是Ax＋By＋m＝0 (m∈R且m≠C)；(2)与直线Ax＋By＋C＝0垂直的直线系方程是Bx－Ay＋m＝0 (m∈R)；(3)过直线l1：A1x＋B1y＋C1＝0与l2：A2x＋B2y＋C2＝0的交点的直线系方程为A1x＋B1y＋C1＋λ(A2x＋B2y＋C2)＝0 (λ∈R)，但不包括l2.如图，设一直线过点(－1,1)，它被两平行直线l1：x＋2y－1＝0，l2：x ＋2y－3＝0所截的线段的中点在直线l3：x－y－1＝0上，求其方程．题型三距离公式的应用例3 已知三条直线：l 1：2x －y ＋a ＝0 (a >0)；l 2：－4x ＋2y ＋1＝0；l 3：x ＋y －1＝0.且l 1与l 2的距离是7510.(1)求a 的值；(2)能否找到一点P ，使P 同时满足下列三个条件： ①点P 在第一象限；②点P 到l 1的距离是点P 到l 2的距离的12；③点P 到l 1的距离与点P 到l 3的距离之比是2∶ 5. 若能，求点P 的坐标；若不能，说明理由．探究提高 (1)在应用两条直线间的距离公式时．要注意两直线方程中x 、y 的系数必须相同．(2)第(2)问是开放探索性问题，要注意解决此类问题的一般策略．已知A (4，－3)，B (2，－1)和直线l ：4x ＋3y －2＝0，在坐标平面内求一点P ，使|PA |＝|PB |，且点P 到直线l 的距离为2.反思总结对称变换思想的应用典例：(12分)光线沿直线l1：x－2y＋5＝0射入，遇直线l：3x－2y＋7＝0后反射，求反射光线所在的直线方程．温馨提醒(1)综合利用物理学知识，利用对称变换的思想方法求解是本题的关键．(2)构建方程解方程组是本题的又一重要方法．(3)坐标转移法是对称变换中常用的方法之一．(4)本题的易错点，一是计算错误，二是不能用对称的思想求解，亦即找不到解决问题的突破口．方法与技巧1．两直线的位置关系要考虑平行、垂直和重合．对于斜率都存在且不重合的两条直线l1、l2，l1∥l2⇔k1＝k2；l1⊥l2⇔k1·k2＝－1.若有一条直线的斜率不存在，那么另一条直线的斜率一定要特别注意．2．对称问题一般是将线与线的对称转化为点与点的对称．利用坐标转移法．失误与防范1．在判断两条直线的位置关系时，首先应分析直线的斜率是否存在．两条直线都有斜率，可根据判定定理判断，若直线无斜率时，要单独考虑．2．在运用两平行直线间的距离公式d ＝|C 1－C 2|A 2＋B 2时，一定要注意将两方程中的x ，y 系数化为分别相等．巩固练习(时间：35分钟，满分：57分)一、选择题(每小题5分，共20分)1．直线l 过点(－1,2)且与直线2x －3y ＋4＝0垂直，则l 的方程是( )A ．3x ＋2y －1＝0B ．3x ＋2y ＋7＝0C ．2x －3y ＋5＝0D ．2x －3y ＋8＝02． (2012·浙江)设a ∈R ，则“a ＝1”是“直线l 1：ax ＋2y －1＝0与直线l 2：x ＋(a ＋1)y ＋4＝0平行”的( )A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件3．从点(2,3)射出的光线沿与向量a ＝(8,4)平行的直线射到y 轴上，则反射光线所在的直线方程为( )A ．x ＋2y －4＝0B ．2x ＋y －1＝0C ．x ＋6y －16＝0D ．6x ＋y －8＝04．已知直线l 过点P (3,4)且与点A (－2，2)，B (4，－2)等距离，则直线l 的方程为( )A ．2x ＋3y －18＝0B ．2x －y －2＝0C ．3x －2y ＋18＝0或x ＋2y ＋2＝0D ．2x ＋3y －18＝0或2x －y －2＝0 二、填空题(每小题5分，共15分)5．若不同两点 P ，Q 的坐标分别为(a ，b )，(3－b,3－a )，则线段PQ 的垂直平分线l 的斜率为________． 6．若直线ax －2y ＋2＝0与直线x ＋(a －3)y ＋1＝0平行，则实数a 的值为________．7．若直线m 被两平行线l 1：x －y ＋1＝0与l 2：x －y ＋3＝0所截得的线段的长为22，则m 的倾斜角可以是①15° ②30° ③45° ④60° ⑤75° 其中正确答案的序号是________．三、解答题(共22分)8． (10分)求过直线l 1：x －2y ＋3＝0与直线l 2：2x ＋3y －8＝0的交点，且到点P (0,4)的距离为2的直线方程．9． (12分)已知两直线l1：ax－by＋4＝0，l2：(a－1)x＋y＋b＝0，求分别满足下列条件的a，b的值．(1)直线l1过点(－3，－1)，并且直线l1与l2垂直；(2)直线l1与直线l2平行，并且坐标原点到l1，l2的距离相等．拓展训练(时间：25分钟，满分：43分)一、选择题(每小题5分，共15分)1．设a、b、c分别是△ABC中∠A、∠B、∠C所对边的边长，则直线x sin A＋ay＋c＝0与bx－y sin B＋sin C ＝0的位置关系是( )A．平行B．重合C．垂直D．相交但不垂直2．如图，已知A(4,0)、B(0,4)，从点P(2，0)射出的光线经直线AB反射后再射到直线OB上，最后经直线OB反射后又回到P点，则光线所经过的路程是 ( )A．210 B．6C．3 3 D．2 53．过点A(1,2)且与原点距离最大的直线方程为( )A．x＋2y－5＝0 B．2x＋y－4＝0C．x＋3y－7＝0 D．3x＋y－5＝0二、填空题(每小题5分，共15分)4．已知0<k<4，直线l1：kx－2y－2k＋8＝0和直线l2：2x＋k2y－4k2－4＝0与两坐标轴围成一个四边形，则使得这个四边形面积最小的k值为________．5．一条光线沿直线2x－y＋2＝0入射到直线x＋y－5＝0后反射，则反射光线所在的直线方程为________．6．已知直线x ＋2y ＝2与x 轴、y 轴分别相交于A 、B 两点，若动点P (a ，b )在线段AB 上，则ab 的最大值为________．三、解答题7． (13分)如图，函数f (x )＝x ＋2x的定义域为(0，＋∞)．设点P是函数图象上任一点，过点P 分别作直线y ＝x 和y 轴的垂线，垂足分别为M ，N .(1)证明：|PM |·|PN |为定值；(2)O 为坐标原点，求四边形OMPN 面积的最小值．。

学而思高中数学暑假班辅导讲义高二.理科班(人教版)

简易逻辑
1.1 命题与量词
考点 1：命题
命题是个到处可以见到的字眼，语文上有命题作文，会评价一篇作文命题新颖等等；北大门卫会询问每个进入北大的人的三大终极哲学命题：你是谁？你从哪里来？你要到哪里去？这些命题都不是数学意义上的命题．
在逻辑中最重要的是二元判断，即对真假的判断，而二元判断的最小承载单位就是命题，这里的真假一般来说是指客观的可以判断的真假，不依赖于主观的判断．数学上的命题就是指可以判断真假的陈述句：如明天会下雨；有理数一定是实数；白马非马；人不可能两次踏进同一条河流；女生爱逛街等等都是命题．
既不充分也不必要条件解析个不同实根方程有两个不等正根尖子目标教师版提高尖子目标教师版且倾斜角为的直线方程为的直线与直线平行则满分晋级21直线的三种形式及其灵活应用春季知识回顾10abc直线与圆的方程解析几何1级直线与圆的方程解析几何2级椭圆初步解析几何双曲线与抛物线初步18提高尖子目标教师版4
第1讲
4 第 1 讲·提高-尖子-目标·教师版
僧敲月下门；富贵不能淫，贫贱不能移，威武不能屈．这些都是自然语言中的联言命题．我们把“ p 且 q ” 看作它的标准表示形式，并称 p ，q 为支命题．
对于两个命题 p ，q ，用“且”联结起来，就得到一个新的命题，记为 p q ，读作“ p 且 q ”．在自然语言中，联言命题表达了支命题之间在内容、意义、甚至语气上的相互关联，逻辑不能处理这些相互关联，只研究支命题与复合命题在真假方面的相互关联．对于联言命题，只有它的各个支命题都是真的，它本身才是真的；如果有一个支命题为假，则联言命题为假．即只有 p ，q 都是真命题时， p q 才是真命题．只要 p ，q 中有假命题， p q 就是假命题．例如：小张既高又胖，只有在小张高和小张胖都真的情况下才是真的，在其余情况下都是假的．

高中数学(暑假)静安闸北恒高一对一数学补习班

高一数学教学安排对即将步入高中学习的新生而言，当务之急要了解高中数学与初中数学的差异，暑假课程将结合初中生数学学习的方法和高中数学学习方法展开，从学习过程中，学生逐步体验初中数学与高中数学之间差异，培养良好的数学学习习惯。

结合高考数学和综合评价数学考试的要求，针对学生学习特点，暑期课程涉及到集合、不等式、函数等知识点，重点在于培养学生高中数学的学习方法和高中数学的学习技巧。

具体课程安排如下表：时间安排专题第一讲集合概念及运算第二讲集合运算——交集并集第三讲命题及简易逻辑第四讲集合与命题习题课第五讲解一元二次不等式和绝对值不等式第六讲求解其它类型不等式第七讲不等式性质及证明第八讲基本不等式第九讲不等式习题课第十讲集合不等式综合第十一讲函数概念第十二讲函数性质以上只是初步的安排，根据学生的实际学习情况，课程安排会做适当的调整。

高三数学教学安排步入高三学习的学生，已经学习了高中数学所有的知识。

对高中数学知识框架有初步的知识，学生知识点分布较零散，缺乏系统性整理。

结合高考数学和综合评价数学考试的要求，针对学生学习特点，暑期课程将高中数学内容进行重新组合、整理，知识点各个击破，提升学生对高中数学知识点理解高度，培养学生良好的解题能力。

暑期课程将重点复习函数、数列、解析几何内容，这三块是高三学生返校摸底考的重点内容，更为重要的是这三块内容占据高考总分的70%-85%。

除了函数、数列、解析几何，还其中穿插复习集合、不等式、三角、向量等知识点。

立体几何和排列组合概率是高二下学期高学习的内容，暑期课程不做重点复习。

暑期课程具体课程安排如下表：时间安排专题第1讲集合及简易逻辑第2讲不等式及其应用第3讲函数的概念第4讲函数的性质（一）第5讲函数的性质（二）第6讲幂指对函数图像与性质第7讲函数图像与方程第8讲函数综合第9讲三角化简第10讲解斜三角形第11讲三角函数第12讲数列概念等差等比数列第13讲数列通项与求和（一）第14讲数列通项与求和（二）第15讲数学归纳法及数列极限第16讲数列综合（一）第17讲数列综合（二）第18讲向量第19讲直线第20讲圆第21讲椭圆与双曲线以上只是初步的安排，根据学生的实际学习情况，课程安排会做适当的调整。

闵行新王牌孙D老师暑假高一高二高三教学计划

暑假班高三数学教学计划
以提高学生解题能力为核心，以基础知识为依托，以数学思想方法为主线，在传授数学基础知识的同时，重点介绍解题思想、方法和技巧，促使学生掌握方法、学会解题，提高能力。

教学内容安排表：
上课时将根据学生具体情况内容和难度作适当调整。

暑假班高二数学教学计划暑假班将重点讲授高二数学第一学期主干内容。

教学时将以学生为中心，以数学思想方法为主线，注重知识的形成、发展和应用，培养学生的运算能力和推理能力，提高学生分析问题和解决问题的能力。

具体安排如下：
上课时将根据学生具体情况作适当调整。

暑假班高一数学教学计划
暑假班将重点讲授高一数学第一学期内容。

教学时将以学生为中心，以数学思想方法为主线，注重知识的形成、发展和应用，注重解题方法的讲解和解题思路的分析，培养学生的运算能力和分析问题、解决问题的能力。

具体安排如下：
上课时将根据学生具体情况作适当调整。

上海暑假学校新高二数学期终考试试卷

2012年上海________学校暑期班新高二期中考试数学试题（时间：60分钟总分：100分命题：徐成）姓名：________ 分数:________一、填空题（每小题5分，共45分）1．已知△ABC 的三个顶点坐标为）（、、1,1)2,1()0,0(C B A -，则△ABC 的面积为___________。

2．在一点O 上作用着两个力，它们的大小分别等于5和3，夹角为30°，它们合力的大小为___________。

3．在ABC BC AB ABC ∆︒︒=︒︒=∆则已知向量中),27cos 2,63cos 2(),72cos ,18(cos ,的面积等于___________。

4．若直线l 过点（1,2）和（3,1），则直线l 在x 轴上的截距是___________。

5.已知直线l 的方程为)(032R k k y kx ∈=++-,则直线l 必经过定点___________。

6．在平行四边形ABCD 中，若BC BA BC AB +=+ ，则BC 和BA 夹角为___________。

7．光线由点)3,2(P 射到直线1-=+y x 上，反射后过点)1,1(Q ，则反射光线方程为___________。

8．在△ABC 中，︒=∠90ABC ，且3=AB ，4=BC ，则CA BC AC AB ⋅+⋅的值是___________。

9.过点)4,2(M 且在两坐标轴截距相等的直线方程为___________。

三、选择(每小题5分,共15分)10．设c b a 、、是任意的非零向量，且相互不共线，则① 0-=⋅⋅⋅⋅b a c c b a ）（）（ ② b a b a -<- ③b a c a c b ⋅⋅-⋅⋅)()( 不与c 垂直 ④ 2249)23()23(b a b a b a -=-⋅+ 中是真命题的有________。

A 、①② B 、②③ C 、③④ D 、②④11、给出下列三个式子：（1）11121112111211122122212221222122a a b b b b a a a a b b b b a a ⎛⎫⎛⎫⎛⎫⎛⎫= ⎪⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭（2）()111112132111111221133131b a a a b a b a b a b b ⎛⎫ ⎪=++ ⎪ ⎪⎝⎭（3）()()111111121321111213213131.b b a a a b a a a b b b λλλ⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪+=+ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ 其中正确的式子的个数是________。

高新暑期班

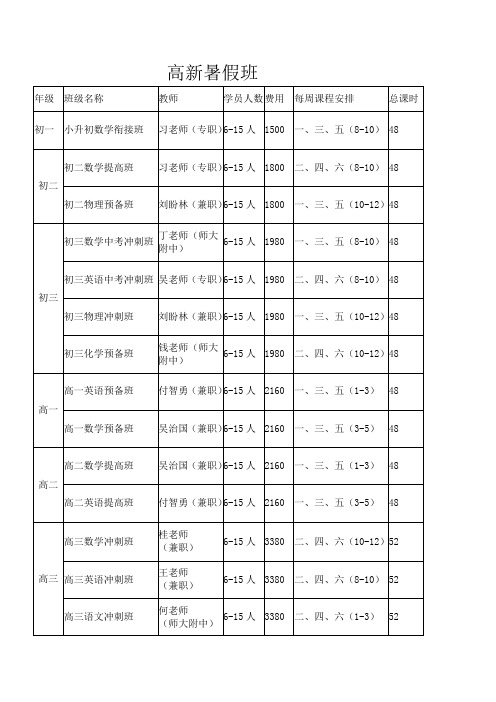
高新暑假班年级班级名称教师学员人数费用每周课程安排总课时初一小升初数学衔接班习老师（专职）6-15人1500 一、三、五（8-10） 48初二初二数学提高班习老师（专职）6-15人1800 二、四、六（8-10） 48初二物理预备班刘盼林（兼职）6-15人1800 一、三、五（10-12）48初三初三数学中考冲刺班丁老师（师大附中）6-15人1980 一、三、五（8-10） 48 初三英语中考冲刺班吴老师（专职）6-15人1980 二、四、六（8-10） 48 初三物理冲刺班刘盼林（兼职）6-15人1980 一、三、五（10-12）48 初三化学预备班钱老师（师大附中）6-15人1980 二、四、六（10-12）48高一高一英语预备班付智勇（兼职）6-15人2160 一、三、五（1-3）48 高一数学预备班吴治国（兼职）6-15人2160 一、三、五（3-5）48 高二高二数学提高班吴治国（兼职）6-15人2160 一、三、五（1-3）48 高二英语提高班付智勇（兼职）6-15人2160 一、三、五（3-5）48高三高三数学冲刺班桂老师（兼职）6-15人3380 二、四、六（10-12）52 高三英语冲刺班王老师（兼职）6-15人3380 二、四、六（8-10） 52 高三语文冲刺班何老师（师大附中）6-15人3380 二、四、六（1-3）52高三物理冲刺班王薇6-15人3380 二、四、六（3-5）52高三化学冲刺班曾老师6-15人3380 一、三、五（8-10） 52高三地理冲刺班熊老师6-15人3380 一、三、五（10-12）52高三政治冲刺班査老师6-15人3380 一、三、五（1-3）52备注：①暑假小学托管：499元/月暑期初中托管：599元/月陪读每周周一至周六8点-17点，孩子周日休息，巩固学期知识和习作暑假作业②特色班：1，英语国际音标词汇班：498元/16节课2，小学数学奥数班498元/16节课3，小学语文作文班498/16节课。

上海高二数学知识点总结

上海高二数学知识点总结一、代数1. 函数的概念与性质- 函数的定义- 函数的表示方法- 函数的域与值域- 函数的单调性与奇偶性2. 二次函数- 二次函数的标准式与顶点式- 二次函数的图像与性质- 二次函数的应用问题3. 不等式- 一元一次不等式与一元二次不等式- 系统不等式与可行域- 不等式的解集与区间表示4. 指数与对数- 指数函数的性质- 对数函数的性质- 指数与对数的运算法则二、几何1. 平面几何- 圆的性质与圆的方程- 圆锥曲线（椭圆、双曲线、抛物线） - 三角形的相似与全等- 平面向量及其运算2. 空间几何- 空间直线与平面的方程- 空间向量及其运算- 立体图形的体积与表面积三、概率与统计1. 概率论基础- 随机事件与概率的定义- 条件概率与独立事件- 随机变量与概率分布2. 统计初步- 数据的收集与整理- 描述性统计（平均数、中位数、众数） - 离散程度的量度（方差、标准差）四、解析几何1. 直线与圆- 直线的斜率与方程- 圆的方程与性质- 直线与圆的位置关系2. 圆锥曲线- 椭圆、双曲线、抛物线的方程与性质 - 圆锥曲线的应用问题五、数学分析1. 极限与连续- 函数的极限概念- 无穷小与无穷大- 函数的连续性2. 导数与微分- 导数的定义与性质- 常见函数的导数- 微分的应用3. 积分基础- 不定积分的概念与性质 - 定积分的基础- 积分的应用问题六、数学思维与方法1. 数学归纳法- 归纳法的原理与步骤 - 典型例题分析2. 数学建模- 数学建模的概念- 数学建模的一般步骤 - 数学建模实例请注意，上述内容仅为一个基本框架，具体的知识点和细节需要根据实际的教学大纲和教材进行调整和补充。

在撰写文档时，应确保每个部分都有详细的解释和示例，以便于读者理解和应用。

此外，文档应使用清晰、专业的语言，并保持格式的一致性和规范性。

上海高中数学高二上知识点

上海高中数学高二上知识点高中数学作为一门理科学科，是培养学生逻辑思维和数学能力的重要课程之一。

在上海高中数学高二上，学生将接触到一系列新的知识点，这些知识点将为他们进一步学习数学打下坚实的基础。

本文将介绍上海高中数学高二上的一些重要知识点。

1. 三角函数在高二上学期，学生将学习到三角函数的概念和性质。

三角函数是数学中一类与角度相关的函数，包括正弦函数、余弦函数和正切函数。

学生需要掌握三角函数的基本定义、图像、周期性、奇偶性、增减性等性质，并能运用三角函数解决实际问题。

2. 数列与数学归纳法数列是一组按照一定规律排列的数字，而数学归纳法是一种证明数学命题成立的重要方法。

在高二上学期，学生将进一步学习数列的性质和求解方法，如等差数列、等比数列等，并学会利用数学归纳法证明数学命题。

3. 函数与方程函数是数学中一个非常重要的概念，用于描述变量之间的关系。

在高二上学期，学生将学习更加复杂的函数与方程，包括二次函数、指数函数、对数函数等，并学会解一元二次方程、一次不等式等。

理解函数与方程的性质和应用，对于进一步学习数学和解决实际问题有着重要的意义。

4. 三角恒等变换与三角方程三角恒等变换是通过对三角函数的性质进行转化和等价变换得到的一类恒等式。

而三角方程是含有三角函数的方程，在高二上学期，学生将学习如何利用三角恒等变换解决三角方程，并运用其解决相关的实际问题。

5. 解析几何解析几何是数学中研究几何图形的一个重要分支，通过运用坐标系和代数方法进行几何问题的研究。

在高二上学期，学生将学习平面几何和空间几何的基本概念和性质，并学会利用解析几何方法解决相关问题，如直线、平面的性质和方程等。

6. 概率与统计概率与统计是数学中与随机事件和数据分析相关的内容。

在高二上学期，学生将学习概率的基本概念和计算方法，如事件概率、条件概率等，并学会利用概率解决实际问题。

统计则是通过对数据进行收集、整理和分析，从中得出结论和推理。

学生将学习数据的归纳与总结，以及利用统计方法进行数据分析等。

第18讲圆与圆的位置关系4种常见考法归类(原卷版)高二数学暑假自学讲义人教A版2019)

第18讲圆与圆的位置关系4种常见考法归类1.能根据给定圆的方程，判断圆与圆的位置关系．2.能用直线和圆的方程解决一些简单的问题，体会用代数方法处理几何问题的思想.知识点1圆与圆的位置关系1．种类：圆与圆的位置关系有五种，分别为外离、外切、相交、内切、内含．2．判定方法(1)几何法：若两圆的半径分别为r1，r2，两圆连心线的长为d，则两圆的位置关系的判断方法如下：位置关系外离外切相交内切内含图示d与r1，r2的关系d＞r1＋r2d＝r1＋r2|r1－r2|＜d＜r1＋r2d＝|r1－r2|d＜|r1－r2|(2)代数法：设两圆的一般方程为C1：x2＋y2＋D1x＋E1y＋F1＝0(D21＋E21－4F1>0)，C2：x2＋y2＋D2x＋E2y＋F2＝0(D22＋E22－4F2>0)，2＋y2＋D1x＋E1y＋F1＝0，2＋y2＋D2x＋E2y＋F2＝0，则方程组解的个数与两圆的位置关系如下：方程组解的个数2组1组0组两圆的公共点个数2个1个0个两圆的位置关系相交内切或外切外离或内含注：(1)圆和圆相离，两圆无公共点，它包括外离和内含；(2)圆和圆相交，两圆有两个公共点；(3)圆和圆相切，两圆有且只有一个公共点，它包括内切和外切．(4)圆与圆的位置关系不能简单仿照直线与圆的位置关系的判断方法将两个方程联立起来消元后用判别式判断，因为当方程组有一组解时，两圆只有一个交点，两圆可能外切，也可能内切；当方程组无解时，两圆没有交点，两圆可能外离，也可能内含．知识点2圆与圆位置关系的应用设圆C 1：x 2＋y 2＋D 1x ＋E 1y ＋F 1＝0，①圆C 2：x 2＋y 2＋D 2x ＋E 2y ＋F 2＝0，②若两圆相交，则有一条公共弦，由①－②，得(D 1－D 2)x ＋(E 1－E 2)y ＋F 1－F 2＝0.③方程③表示圆C 1与C 2的公共弦所在直线的方程．(1)当两圆相交时，两圆方程相减，所得的直线方程即两圆公共弦所在的直线方程，这一结论的前提是两圆相交，如果不确定两圆是否相交，两圆方程相减得到的方程不一定是两圆的公共弦所在的直线方程．(2)两圆公共弦的垂直平分线过两圆的圆心．(3)求公共弦长时，几何法比代数法简单易求．1、公切线的条数与两个圆都相切的直线叫做两圆的公切线，圆的公切线包括外公切线和内公切线两种．核心技巧：利用圆心到切线的距离d r =求解知识点4圆系方程(1)以(,)a b 为圆心的同心圆圆系方程：22()()(0)x a y b λλ-+-=>；(2)与圆220x y Dx Ey F ++++=同心圆的圆系方程为220x y Dx Ey λ++++=；(3)过直线0Ax By C ++=与圆220x y Dx Ey F ++++=交点的圆系方程为22()0()x y Dx Ey F Ax By C R λλ+++++++=∈4过两圆1C 221110x y D x E y F ++++=，圆2C ：222220x y D x E y F ++++=交点的圆系方程为2222111222()0x y D x E y F x y D x E y F λ+++++++++=（1λ≠-，此时圆系不含圆2C ：222220x y D x E y F ++++=）特别地，当1λ=-时，上述方程为一次方程.两圆相交时，表示公共弦方程；两圆相切时，表示公切线方程.1、判断两圆的位置关系的两种方法(1)几何法：将两圆的圆心距d 与两圆的半径之差的绝对值，半径之和进行比较，进而判断出两圆的位置关系，这是在解析几何中主要使用的方法．(2)代数法：将两圆的方程组成方程组，通过解方程组，根据方程组解的个数进而判断两圆位置关系．2、圆系方程一般地过圆C 1：x 2＋y 2＋D 1x ＋E 1y ＋F 1＝0与圆C 2：x 2＋y 2＋D 2x ＋E 2y ＋F 2＝0交点的圆的方程可设为：x 2＋y 2＋D 1x ＋E 1y ＋F 1＋λ(x 2＋y 2＋D 2x ＋E 2y ＋F 2)＝0(λ≠－1)，然后再由其他条件求出λ，即可得圆的方程．3、两圆相交时，公共弦所在的直线方程若圆C 1：x 2＋y 2＋D 1x ＋E 1y ＋F 1＝0与圆C 2：x 2＋y 2＋D 2x ＋E 2y ＋F 2＝0相交，则两圆公共弦所在直线的方程为(D 1－D 2)x ＋(E 1－E 2)y ＋F 1－F 2＝0.4、公共弦长的求法(1)代数法：将两圆的方程联立，解出交点坐标，利用两点间的距离公式求出弦长．(2)几何法：求出公共弦所在直线的方程，利用圆的半径、半弦长、弦心距构成的直角三角形，根据勾股定理求解．5、求两圆的相交弦的垂直平分线的方程即为经过两圆的圆心的直线方程考点一：圆与圆位置关系的判断（一）判断圆与圆的位置关系例1．（2023秋·福建宁德·高二统考期中）圆()22(2)21x y -+-=与圆()()221225x y +++=的位置关系是（）A ．相切B ．相交C ．内含D ．外离变式1．（2023春·江西萍乡·高二校联考阶段练习）圆O ：221x y +=与圆C :22650x y y +++=的位置关系是（）A ．相交B ．相离C ．外切D ．内切变式2．（2023·全国·高三专题练习）已知圆1C 的圆心在直线210x y +-=上，点()3,0与()1,2-都在圆1C 上，圆()()222:311C x y -++=，则1C 与2C 的位置关系是___________.变式3．【多选】（2023秋·江苏南通·高二统考期末）已知圆22:(3)(4)4C x y -+-=，则（）A ．点(5,5)在圆C 内B ．直线3)y x =-与圆C 相切C ．圆229x y +=与圆C 相切D ．圆2249x y +=与圆C 相切变式4．（2023春·安徽阜阳·高三安徽省临泉第一中学校考专题练习）平面直角坐标系中，()2,0A -，()2,0B ，动点P 满足PA =，则使PAB 为等腰三角形的点P 个数为（）A ．0B ．2C ．3D ．4变式5．【多选】（2023·湖南娄底·统考模拟预测）已知圆M ：22650x y y +-+=，圆N ：22280x y y ++-=，直线l ：340x y m -+=，则下列说法正确的是（）A ．圆N 的圆心为()0,1B ．圆M 与圆N 相交C ．当圆M 与直线l 相切时，则2m =D ．当7m =时，圆M 与直线l 相交所得的弦长为变式6．（2022·全国·高二专题练习）已知点P 在圆O ：224x y +=上，点()30A -,，()0,4B ，满足AP BP ⊥的点P 的个数为（）A ．3B ．2C ．1D ．0（二）由圆的位置关系求参数例2．（2023秋·浙江丽水·高二统考期末）若圆221:4C x y +=与圆2222:20C x y mx m m +-+-=外切，则实数m =（）A ．－1B ．1C ．1或4D ．4变式1．（2023秋·高二课时练习）若两圆22(1)4x y ++=和圆22()1x a y -+=相交，则a 的取值范围是（）A ．02a <<B ．02a <<或42a -<<-C ．42a -<<-D ．24a <<或20a -<<变式2．（2023秋·高二课时练习）当a 为何值时，两圆2222450x y ax y a +-++-=和2222230x y x ay a ++-+-=.(1)外切；(2)相交；(3)外离.变式3．（2022秋·高二课时练习）若圆222x y r +=与圆222440x y x y ++-+=有公共点，则r 满足的条件是（）A ．1r <B ．1r >+C ．1r ≤D ．1r <变式4．（2023秋·浙江嘉兴·高二统考期末）已知圆1C ：()()()222120x y r r -++=>与圆2C ：()()224216x y -+-=有公共点，则r 的取值范围为（）A ．(]0,1B ．[]1,5C ．[]1,9D ．[]5,9变式5．（2023春·安徽·高二校联考期末）已知圆()()()222:3425C x y r r *-+-=+∈N ，()1,0M -，()1,0N ，若以线段MN 为直径的圆与圆C 有公共点，则r 的值可能为______.（写出一个即可）变式6．（2022·湖南常德·常德市一中校考二模）已知圆22:(4)(3)4C x y -++=和两点(,0),(,0)(0)->A a B a a ，若圆C 上存在点P ，使得90APB ∠=︒，则a 的最小值为（）A ．6B ．5C ．4D ．3变式7．（2023秋·高一单元测试）已知圆221:()(2)9O x m y -++=与圆222:()(2)1O x n y +++=内切，则22m n +的最小值为_______变式8．（2023·浙江·校联考模拟预测）已知圆C 的方程为221x y +=，若直线()3y k x =-上至少存在一点，使得以该点为圆心，1为半径的圆与圆C 相外切，则k 的取值范围为__________．考点二：与圆相交有关的问题（一）求两圆的交点坐标例3．（2022·高二课前预习）圆221x y +=与圆222210x y x y ++++=的交点坐标为（）A ．(1,0)和()0,1B ．(1,0)和()0,1-C ．(1,0)-和()0,1-D ．()1,0-和()0,1变式1．（2022·高二课时练习）求圆22230x y x +--=与圆224230x y x y +-++=的交点的坐标．变式2．（2022秋·贵州遵义·高二遵义一中校考阶段练习）圆1C ：22640x y x y ++-=和圆2C ：2260x y y +-=交于A ，B 两点，则线段AB 的垂直平分线的方程是______.变式3．（2023秋·辽宁丹东·高二统考期末）已知圆22:16O x y +=与圆22:86160C x y x y ++++=交于A ，B 两点，则四边形OACB 的面积为（）A ．12B ．6C ．24D ．245（二）圆系方程的应用例4．（2023·全国·高三专题练习）经过点()1,1P 以及圆2240x y +-=与2244120x y x y +-+-=交点的圆的方程为______．变式1．（2022秋·高二单元测试）求过两圆221:240C x y y +--=和圆222:420C x y x y +-+=的交点，且圆心在直线:2410l x y +-=上的圆的方程.（三）求两圆公共弦方程例5．（2022秋·黑龙江大庆·高二大庆实验中学校考期末）圆221:130O x y +-=与圆222:650O x y x +-+=的公共弦所在直线方程为___________.变式1．（2022秋·高二课时练习）已知圆2212610C x y x y ++-+=：与圆22242110C x y x y +-+-=：，求两圆的公共弦所在的直线方程（）A ．3460x y ++=B ．3460x y +-=C ．3460x y --=D ．3460x y -+=变式2．（2023春·全国·高二卫辉一中校联考阶段练习）已知圆1C ：222(1)x y r ++=过圆2C ：22(4)(1)4x y -+-=的圆心，则两圆相交弦的方程为______.变式3．（2022秋·高二课时练习）已知过圆224x y +=外一点()3,4P 做圆的两条切线，切点为,A B 两点，求,A B 所在的直线方程为（）A ．3440x y +-=B ．3440x y ++=C ．3440x y --=D ．3440x y -+=（四）求两圆公共弦长例6．（2022·高二课时练习）已知圆221:(1)5C x y +-=，圆222:420C x y x y +-+=.(1)求圆1C 与圆2C 的公共弦长；(2)求过两圆的交点且圆心在直线241x y +=上的圆的方程.变式1．（2023·河南·统考二模）若圆221:1C x y +=与圆222:()()1C x a y b -+-=的公共弦AB 的长为1，则直线AB 的方程为（）A ．210ax by +-=B ．230ax by +-=C ．2210ax by +-=D ．2230ax by +-=变式2．（2021秋·广东深圳·高二深圳中学校考期中）已知圆C 的圆心为()2,2-，且与直线0x y ++相切．(1)求圆C 的方程；(2)求圆C 与圆224x y +=的公共弦的长．变式3．（2021秋·高二课时练习）若圆O ：x 2＋y 2＝5与圆O 1：(x －m )2＋y 2＝20(m ∈R )相交于A ，B 两点，且两圆在点A 处的切线互相垂直，则直线AB 的方程为________；线段AB 的长为________．变式4．（2023·安徽滁州·安徽省定远中学校考模拟预测）已知圆221:1O x y +=与圆()2222201：O x y x y F F +-++=<，则圆2O 的半径r =（）A ．1BC 1D变式5．（2021秋·高二课时练习）圆2221:22210C x y ax ay a ++++-=与圆2222:22220C x y bx by b ++++-=的公共弦长的最大值是（）A ．12B ．1C ．32D ．2考点三：两圆的公切线问题（一）圆的公切线条数例7．（2022秋·贵州遵义·高二习水县第五中学校联考期末）圆221:(2)(4)25C x y +++=与圆222:(1)9C x y ++=的公切线的条数为（）A ．1B ．2C ．3D ．4变式1．【多选】（2023秋·高一单元测试）已知圆221:9C x y +=与圆222:(3)(4)16C x y -+-=，下列说法正确的是（）A ．1C 与2C 的公切线恰有4条B ．1C 与2C 相交弦的方程为3490x y +-=C ．1C 与2C 相交弦的弦长为125D ．若,P Q 分别是圆12,C C 上的动点，则max ||12PQ =变式2．（2023·黑龙江大庆·统考三模）已知直线l 是圆:C ()()22211x y -+-=的切线，并且点()3,4B 到直线l的距离是2，这样的直线l 有（）A ．1条B ．2条C ．3条D ．4条变式3．（2023·河北衡水·衡水市第二中学校考三模）若圆221:1C x y +=和2221:2502C x y ay a a ⎛⎫+---=> ⎪⎝⎭有且仅有一条公切线，则=a ______；此公切线的方程为______变式4．（2022秋·高二课时练习）已知两圆2211C x y +=：，()()()2222120C x y r r -+-=>：，当圆1C 与圆2C 有且仅有两条公切线时，则r 的取值范围________.变式5．（2023秋·陕西西安·高二长安一中校考期末）已知两圆2226940x y ax a +++-=和222290x y by b ++--=恰有三条公切线，若R a ∈，R b ∈，且0ab ≠，则2211a b +的最小值为（）A ．1625B ．3225C ．169D ．329（二）圆的公切线方程例8．（2023·湖北黄冈·浠水县第一中学校考模拟预测）写出与圆()()224316x y -++=和圆221x y +=都相切的一条直线的方程___________.变式1．（2023·江西南昌·校联考模拟预测）已知圆()22:11C x y -+=与圆(22:1E x y +=，写出圆C和圆E 的一条公切线的方程______.变式2．（2023·湖南岳阳·统考三模）写出与圆221:1O x y +=和222:(3)1O x y -+=都相切的一条直线方程____________．变式3．【多选】（2022秋·高二单元测试）已知圆()()221:211C x y -+-=，圆()()222:211C x y +++=，则下列是圆1C 与圆2C 的公切线的直线方程为（）A ．0y =B ．430x y -=C ．20x y -=D ．20x y +=（二）圆的公切线长例9．【多选】（2023春·山东青岛·高二统考开学考试）已知圆221:1C x y +=，圆222:2210C x x y y -+-+=，则（）A ．圆1C 与圆2C 相切B ．圆1C 与圆2C C ．圆1C 与圆2C 公共弦所在直线的方程为1x y +=D ．圆1C 与圆2C 公共部分的面积为π12-变式1．【多选】（2022秋·广东惠州·高二惠州市惠阳高级中学实验学校校考期中）圆221:2660C x y x y ++-+=与圆222:2210C x y x y +--+=相交于A ，B 两点，则（）A ．AB 的直线方程为4450x y -+=B ．公共弦AB 的长为8C ．圆1C 与圆2C D ．线段AB 的中垂线方程为20x y +-=变式2．【多选】（2022秋·山东青岛·高二青岛二中校考期中）已知221:2410C x y x y +--+=e 与222:230C x y x ++-=e 相交于A ，B 两点，则下列结论正确的是（）．A ．直线AB 的方程为10x y +-=B ．过A ，B 两点，且过点()1,1的圆的方程为2220x y x y +-+-=C ．1C 与2C 的公切线的长度为D ．以线段AB 为直径的圆的方程为()2212x y +-=变式3．（2022秋·广东云浮·高二校考期中）已知圆A 的方程为222270x y x y +---=，圆B 的方程为222220x y x y +++-=.(1)判断圆A 与圆B 是否相交，若相交，求过两交点的直线方程及两交点间的距离；若不相交，请说明理由.(2)求两圆的公切线长.考点四：圆与圆的最值问题例10．【多选】（2023秋·高一单元测试）点P 在圆1C ：221x y +=上，点Q 在圆2C ：226490x y x y +-++=上，则（）A ．PQ3-B ．PQC ．两个圆心所在的直线斜率为23-D ．两个圆公共弦所在直线的方程为64100x y --=变式1．【多选】（2023·湖南·校联考二模）已知点P 在圆221:(x 2)4C y -+=上，点Q 在圆222:28130C x y x y ++-+=上，则（）A ．两圆外离B ．PQ 的最大值为9C ．PQ 的最小值为1D ．两个圆的一条公切线方程为3440x y -+=变式2．【多选】（2022秋·山东威海·高二校考阶段练习）已知点(0,2),(1,1)A B ，且点P 在圆22:(2)4C x y -+=上，C 为圆心，则下列结论正确的是（）A ．||||PA PB -的最大值为B ．以AC 为直径的圆与圆C 的公共弦所在的直线方程为：0x y -=C ．当∠PAB 最大时，PABD ．PAB变式3．（2023·江西赣州·统考模拟预测）已知圆C ：()()22125x y -+-=，圆C '是以圆221x y +=上任意一点为圆心，半径为1的圆．圆C 与圆C '交于A ，B 两点，则当ACB ∠最大时，CC '=（）A ．1B CD ．21．圆22(2)4x y ++=与圆22(2)(1)9x y -+-=的位置关系为A ．内切B ．相交C ．外切D ．相离2．已知圆()22:200M x y ay a +-=>截直线0x y +=所得线段的长度是22M 与圆()()22:111N x y -+-=的位置关系是A ．内切B ．相交C ．外切D ．相离3．若⊙221:5O x y +=与⊙222:()20()O x m y m R -+=∈相交于A 、B 两点，且两圆在点A 处的切线互相垂直，则线段AB 的长度是_________．4．（2022·全国·统考高考真题）写出与圆221x y +=和22(3)(4)16x y -+-=都相切的一条直线的方程________________．一、单选题1．（2023春·江苏扬州·高二统考开学考试）圆221:4C x y +=与圆222:68240C x y x y +++-=的位置关系为（）．A ．相交B ．内切C ．外切D ．外离2．（2023春·江苏盐城·高二统考期末）在坐标平面内，与点()1,2A 距离为3，且与点()3,2B 距离为1的直线共有（）A ．1条B ．2条C ．3条D ．4条3．（2023春·重庆沙坪坝·高一重庆一中校考期末）已知点P 为直线l ：20x y +-=上的动点，过点P 作圆C ：2220x x y ++=的切线PA ，PB ，切点为,A B ，当PC AB ⋅最小时，直线AB 的方程为（）A ．3310x y ++=B ．3310x y +-=C ．2210x y ++=D ．2210x y +-=4．（2023春·河南洛阳·高二统考期末）已知点P 为直线1y x =+上的一点，M ，N 分别为圆1C ：()()22411x y -+-=与圆2C ：()2241x y +-=上的点，则||PM PN +的最小值为（）A ．5B ．3C ．2D ．15．（2023·河南南阳·南阳中学校考模拟预测）在平面直角坐标系中，圆C 的方程为()22 21x y -+=，若直线1y kx =+上至少存在一点，使得以该点为圆心，1为半径的圆与圆C 有公共点，则实数k 的取值范围为（）A ．3,4⎛⎤-∞ ⎥⎝⎦B ．2,3⎛⎤-∞ ⎥⎝⎦C ．(],1-∞D ．1,2⎛⎤-∞ ⎥⎝⎦6．（2023·全国·高三专题练习）已知圆22:430M x y x +-+=，则下列说法正确的是（）A ．点()4,0在圆M 内B ．若圆M 与圆22460x y x y a +--+=恰有三条公切线，则9a =C ．直线0x =与圆M 相离D ．圆M 关于4320x y +-=对称二、多选题7．（2023春·湖南·高二校联考期末）已知圆22:4O x y +=和圆22:(3)(3)4C x y -+-=，,P Q 分别是圆O ，圆C 上的动点，则下列说法正确的是（）A ．圆O 与圆C 有四条公切线B ．PQ 的取值范围是4⎡⎤⎣⎦C ．2x y -=是圆O 与圆C 的一条公切线D ．过点Q 作圆O 的两条切线，切点分别为,M N ，则存在点Q ，使得90MQN ∠=8．（2023春·广东揭阳·高二统考期末）已知直线l ：320x y m ++=，圆C ：221404x y x y ++-+=，则下列说法错误的是（）A ．若5m =+5l 与圆C 相切B ．若5m =，则圆C 关于直线l 对称C ．若圆E ：22552028x y x y m ++--=与圆C 相交，且两个交点所在直线恰为l ，则2m =D ．若5m >，圆C 上有且仅有两个点到l 的距离为1，则55m <<+9．（2023秋·高一单元测试）如图所示，该曲线W 是由4个圆：()2211x y -+=，()2211x y ++=，()2211x y ++=，()2211x y +-=的一部分所构成，则下列叙述正确的是（）A ．曲线W 围成的封闭图形面积为4+2πB ．若圆()2220x y r r +=>与曲线W 有82r ≤≤C ． BD与 DE 的公切线方程为10x y +--D ．曲线W 上的点到直线10x y ++=的距离的最小值为410．（2023·辽宁沈阳·沈阳二中校考模拟预测）已知22:(2)(1)4E x y -+-= ，过点()5,5P 作圆E 的切线，切点分别为,M N ，则下列命题中真命题是（）A ．PM =B ．直线MN 的方程为34140x y +-=C ．圆221x y +=与E 共有4条公切线D ．若过点P 的直线与E 交于,G H 两点，则当EHG 面积最大时，GH =三、填空题11．（2023·陕西西安·陕西师大附中校考模拟预测）在平面直角坐标系中，圆()222:M x y m n ++=和()22:11N x y +-=外切形成一个8字形状，若()0,2P -，()1,1A -为圆M 上两点，B 为两圆圆周上任一点（不同于点A ，P ），则PA PB ⋅的最大值为______．12．（2023·江苏扬州·江苏省高邮中学校考模拟预测）已知点()1,0A -，()10B ,，若圆()()2221x a y a -+-=上存在点P 满足3PA PB ⋅=，则实数a 的取值的范围是____________．13．（2023春·广西·高二校联考期中）已知圆心在原点的单位圆1C 和圆222:68250C x y x y m +-++-=外切，m =________．14．（2023秋·高二课时练习）已知圆C 过点(3,0)且与圆221x y +=切于点(1,0)，则圆C 的方程为__________.15．（2023·安徽亳州·安徽省亳州市第一中学校考模拟预测）已知两定点()()4,0,2,0A B -，如果动点M 满足2MA MB =，点N 是圆22(3)9x y +-=上的动点，则MN 的最大值为__________.16．（2023·重庆万州·重庆市万州第三中学校考模拟预测）已知点(1,)A m，(1,)B m ，若圆22 :20++=C x y x 上有且只有一点P ，使得PA PB ⊥，则实数m 的一个取值为___________.（写出满足条件的一个即可）四、解答题17．（2023春·江西宜春·高二统考阶段练习）已知圆2268210C x y x y +--+=：．(1)若直线1l 过定点()11A ，，且与圆C 相切，求直线1l 的方程；(2)若圆D 的半径为3，圆心在直线220l x y -+=：上，且与圆C 外切，求圆D 的方程．18．（2023春·上海黄浦·高二上海市大同中学校考期中）已知圆M 经过()()()1,01,23,0A B C --､､，圆222:420N x y x ay a +-++=.(1)求圆M 的标准方程；(2)若圆M 与圆N 相切，求a 的值.19．（2023秋·高一单元测试）已知圆()22:21C x y -+=，M 是y 轴上的动点，MA 、MB 分别与圆C 相切于A 、B 两点，(1)如果点M 的坐标为()0,1，求直线MA 、MB 的方程；(2)求ACB △面积的最大值．20．（2023秋·贵州铜仁·高二统考期末）在平面直角坐标系xOy 中，已知圆221:1214600O x y x y ++-+=.设圆2O 与x 轴相切，与圆1O 外切，且圆心2O 在直线6x =-上.(1)求圆2O 的标准方程；(2)设垂直于2OO 的直线l 与圆1O 相交于B ，C 两点，且BC =l 的方程.21．（2023春·上海黄浦·高二格致中学校考阶段练习）已知圆221:(3)(1)4C x y ++-=和圆2222:(4)(5)(0)-+-=>C x y r r (1)若圆1C 与圆2C 相交于,A B 两点，求r 的取值范围，并求直线AB 的方程（用含有r 的方程表示）(2)若直线:1l y kx =+与圆1C 交于,P Q 两点，且4OP OQ =⋅，求实数k 的值22．（2023春·福建莆田·高二莆田一中校考阶段练习）古希腊著名数学家阿波罗尼斯发现：“平面内到两个定点,A B 的距离之比为定值()1λλ≠的点的轨迹是圆”.后来，人们将这个圆以他的名字命名，称为阿波罗尼斯圆，简称阿氏圆.在平面直角坐标系xOy 中，()2,0A -，()4,0B ，点P 满足12PA PB=.(1)求P 的轨迹方程；(2)设圆Q 是以AB 为直径的圆，求证圆P 与圆Q 相交，并求公共弦所在的直线方程.。

2024年暑假高二数学新课第4讲巩固练习：直线的两点式方程(学生版)

2024年暑假高二数学新课第4讲巩固练习：直线的两点式方程一、基础巩固1.经过点A(3,2),B(4,3)的直线方程是()A.x+y+1=0B.x+y-1=0C.x-y+1=0D.x-y-1=02.若直线方程为 2 3 1,则直线在轴和轴上的截距分别为()A.2,3B.-2,-3C.2,-3D.-2,33.如图,直线l的截距式方程是 1,则()A.a>0,b>0B.a>0,b<0C.a<0,b>0D.a<0,b<04.已知△ABC的三个顶点分别为A(1,2),B(3,6),C(5,2),M为AB的中点,N为AC的中点,则中位线MN所在直线的方程为()A.2x+y-8=0B.2x-y+8=0C.2x+y-12=0D.2x-y-12=05.已知点M(1,-2),N(m,2),若线段MN的垂直平分线的方程是 21,则实数的值是()A.-2B.-7C.3D.16.经过点(0,3),且在两坐标轴上截距之和等于5的直线方程是.7.已知直线l经过点P(-1,2),与x轴、y轴分别相交于A,B两点.若P为线段AB的中点,则直线l的方程为.8.经过点(2,1),且与两坐标轴围成等腰直角三角形的直线方程为.9.求过点A(-5,2),且在x轴上的截距等于在y轴上的截距的2倍的直线方程.二、能力提升1.直线 2 2 1在轴上的截距是()A.|b|B.-b2C.b2D.±b2.两条直线l1: 1和 2: 1在同一直角坐标系中的图象可以是()3.已知光线从点A(-3,4)射出,到x轴上的点B后,被x轴反射,这时反射光线恰好过点C(1,6),则BC所在直线的方程为()A.5x-2y+7=0B.2x-5y+7=0C.5x+2y-7=0D.2x+5y-7=04.已知点A(1,2),B(3,1),则线段AB的垂直平分线的方程是.5.已知点A(-1,2),B(3,4),线段AB的中点为M,求过点M且平行于直线 4 21的直线的方程6.已知直线l经过点(1,6)和点(8,-8).(1)求直线l的两点式方程,并化为截距式方程;(2)求直线l与两坐标轴围成的图形面积.★7.已知一条直线经过点A(-2,2),并且与两坐标轴围成的三角形的面积为1,求此直线的方程.。