垂径定理+关系定理+圆周角定理巩固提高2
北师大版初中数学九年级下册知识讲解,巩固练习(教学资料,补习资料):第19讲《圆》全章复习与巩固(提高)
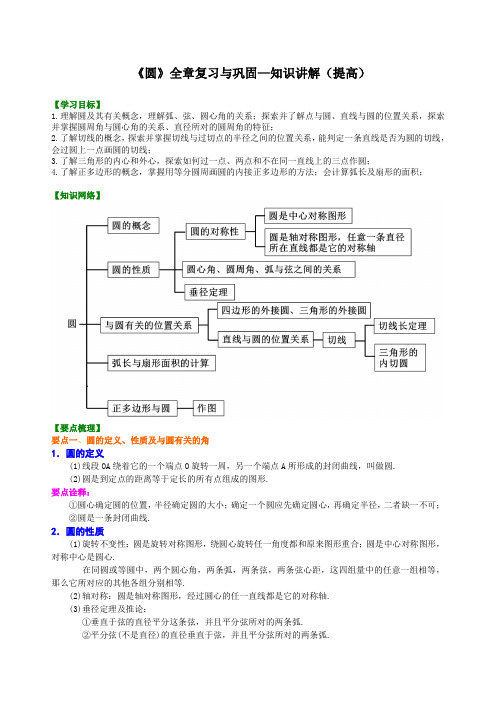
《圆》全章复习与巩固—知识讲解(提高)【学习目标】1.理解圆及其有关概念,理解弧、弦、圆心角的关系;探索并了解点与圆、直线与圆的位置关系,探索并掌握圆周角与圆心角的关系、直径所对的圆周角的特征;2.了解切线的概念,探索并掌握切线与过切点的半径之间的位置关系,能判定一条直线是否为圆的切线,会过圆上一点画圆的切线;3.了解三角形的内心和外心,探索如何过一点、两点和不在同一直线上的三点作圆;4.了解正多边形的概念,掌握用等分圆周画圆的内接正多边形的方法;会计算弧长及扇形的面积;【知识网络】【要点梳理】要点一、圆的定义、性质及与圆有关的角1.圆的定义(1)线段OA绕着它的一个端点O旋转一周,另一个端点A所形成的封闭曲线,叫做圆.(2)圆是到定点的距离等于定长的所有点组成的图形.要点诠释:①圆心确定圆的位置,半径确定圆的大小;确定一个圆应先确定圆心,再确定半径,二者缺一不可;②圆是一条封闭曲线.2.圆的性质(1)旋转不变性:圆是旋转对称图形,绕圆心旋转任一角度都和原来图形重合;圆是中心对称图形,对称中心是圆心.在同圆或等圆中,两个圆心角,两条弧,两条弦,两条弦心距,这四组量中的任意一组相等,那么它所对应的其他各组分别相等.(2)轴对称:圆是轴对称图形,经过圆心的任一直线都是它的对称轴.(3)垂径定理及推论:①垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.②平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.③弦的垂直平分线过圆心,且平分弦对的两条弧.④平分一条弦所对的两条弧的直线过圆心,且垂直平分此弦. ⑤平行弦夹的弧相等. 要点诠释:在垂经定理及其推论中:过圆心、垂直于弦、平分弦、平分弦所对的优弧、平分弦所对的劣弧,在这五个条件中,知道任意两个,就能推出其他三个结论.(注意:“过圆心、平分弦”作为题设时,平分的弦不能是直径) 3.与圆有关的角(1)圆心角:顶点在圆心的角叫圆心角.圆心角的性质:圆心角的度数等于它所对的弧的度数. (2)圆周角:顶点在圆上,两边都和圆相交的角叫做圆周角. 圆周角的性质:①圆周角等于它所对的弧所对的圆心角的一半.②同弧或等弧所对的圆周角相等;在同圆或等圆中,相等的圆周角所对的弧相等. ③90°的圆周角所对的弦为直径;半圆或直径所对的圆周角为直角.④如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形. ⑤圆内接四边形的对角互补;外角等于它的内对角. 要点诠释:(1)圆周角必须满足两个条件:①顶点在圆上;②角的两边都和圆相交. (2)圆周角定理成立的前提条件是在同圆或等圆中.要点二、与圆有关的位置关系 1.判定一个点P 是否在⊙O 上 设⊙O 的半径为,OP=,则有 点P 在⊙O 外; 点P 在⊙O 上;点P 在⊙O 内. 要点诠释:点和圆的位置关系和点到圆心的距离的数量关系是相对应的,即知道位置关系就可以确定数量关系;知道数量关系也可以确定位置关系.2.判定几个点12nA A A L 、、在同一个圆上的方法当时,在⊙O 上.3.直线和圆的位置关系设⊙O 半径为R ,点O 到直线的距离为. (1)直线和⊙O 没有公共点直线和圆相离. (2)直线和⊙O 有唯一公共点直线和⊙O 相切.(3)直线和⊙O 有两个公共点直线和⊙O 相交. 4.切线的判定、性质 (1)切线的判定:①经过半径的外端并且垂直于这条半径的直线是圆的切线. ②到圆心的距离等于圆的半径的直线是圆的切线. (2)切线的性质:①圆的切线垂直于过切点的半径.②经过圆心作圆的切线的垂线经过切点. ③经过切点作切线的垂线经过圆心.(3)切线长:从圆外一点作圆的切线,这一点和切点之间的线段的长度叫做切线长.(4)切线长定理:从圆外一点作圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角.要点三、三角形的外接圆与内切圆、圆内接四边形与外切四边形1.三角形的内心、外心(1)三角形的内心:是三角形三条角平分线的交点,它是三角形内切圆的圆心,在三角形内部,它到三角形三边的距离相等,通常用“I”表示.(2)三角形的外心:是三角形三边中垂线的交点,它是三角形外接圆的圆心,锐角三角形外心在三角形内部,直角三角形的外心是斜边中点,钝角三角形外心在三角形外部,三角形外心到三角形三个顶点的距离相等,通常用O表示.要点诠释:(1) 任何一个三角形都有且只有一个内切圆,但任意一个圆都有无数个外切三角形;(2) 解决三角形内心的有关问题时,面积法是常用的,即三角形的面积等于周长与内切圆半径乘积的一半,即(S为三角形的面积,P为三角形的周长,r为内切圆的半径).(3) 三角形的外心与内心的区别:(1)OA=OB=OC定在三角形内部(1)(2)OABAC心在三角形内部2.圆内接四边形和外切四边形(1)四个点都在圆上的四边形叫圆的内接四边形,圆内接四边形对角互补,外角等于内对角.(2)各边都和圆相切的四边形叫圆外切四边形,圆外切四边形对边之和相等.要点四、圆中有关计算1.圆中有关计算圆的面积公式:,周长.圆心角为、半径为R的弧长.圆心角为,半径为R,弧长为的扇形的面积.弓形的面积要转化为扇形和三角形的面积和、差来计算.要点诠释:(1)对于扇形面积公式,关键要理解圆心角是1°的扇形面积是圆面积的,即;(2)在扇形面积公式中,涉及三个量:扇形面积S 、扇形半径R 、扇形的圆心角,知道其中的两个量就可以求出第三个量. (3)扇形面积公式,可根据题目条件灵活选择使用,它与三角形面积公式有点类似,可类比记忆;(4)扇形两个面积公式之间的联系:.【典型例题】类型一、圆的有关概念及性质1. 如图,已知⊙O 是以数轴的原点O 为圆心,半径为1的圆,∠AOB=45°,点在数轴上运动,若过点P 且与OA 平行(或重合)的直线与⊙O 有公共点, 设OP=x ,则的取值范围是( ).A .-1≤≤1B .≤≤C .0≤≤ D .>【思路点拨】关键是通过平移,确定直线与圆相切的情况,求出此时OP 的值. 【答案】C ;【解析】如图,平移过P 点的直线到P′,使其与⊙O 相切,设切点为Q ,连接OQ ,P x x x 2x 2x 2由切线的性质,得∠OQP′=90°,∵OA∥P′Q,∴∠OP′Q=∠AOB=45°,∴△OQP′为等腰直角三角形,在Rt△OQP′中,OQ=1,OP′=2,∴当过点P且与OB平行的直线与⊙O有公共点时,0≤OP≤,当点P在x轴负半轴即点P向左侧移动时,结果相同.故答案为:0≤OP≤2.【总结升华】本题考查了直线与圆的位置关系问题.举一反三:【变式】如图,已知⊙O是以数轴的原点为圆心,半径为1的圆,∠AOB=45°,点P在数轴上运动,若2.如图所示,已知在⊙O 中,AB 是⊙O 的直径,弦CG⊥AB 于D ,F 是⊙O 上的点,且,BF 交CG 于点E ,求证:CE =BE .【思路点拨】主要用垂径定理及其推论进行证明. 【答案与解析】证法一:如图(1),连接BC ,∵ AB 是⊙O 的直径,弦CG ⊥AB ,∴ . ∵ ,∴ .∴ ∠C =∠CBE .∴ CE =BE .证法二:如图(2),作ON ⊥BF ,垂足为N ,连接OE .∵ AB 是⊙O 的直径,且AB ⊥CG ,∴ . ∵ ,∴ .∴ BF =CG ,ON =OD . »»CFCB =»»CBGB =»»CFBC =»»CF GB =»»CBBG =»»CBCF =»»»CF BC BG ==∵ ∠ONE =∠ODE =90°,OE =OE ,ON =OD , ∴ △ONE ≌△ODE ,∴ NE =DE . ∵ ,, ∴ BN =CD ,∴ BN-EN =CD-ED ,∴ BE =CE .证法三:如图(3),连接OC 交BF 于点N .∵ ,∴ OC ⊥BF . ∵ AB 是⊙O 的直径,CG ⊥AB ,∵ ,.∴ ,. ∵ OC =OB ,∴ OC-ON =OB-OD ,即CN =BD . 又∠CNE =∠BDE =90°,∠CEN =∠BED , ∴ △CNE ≌△BDE ,∴ CE =BE .【总结升华】在平时多进行一题多解、一题多证、一题多变的练习,这样不但能提高分析问题的能力,而且还是沟通知识体系、学习知识,使用知识的好方法.举一反三:【变式】如图所示,在⊙O 内有折线OABC,其中OA=8,AB=12,∠A=∠B=60°,则BC 的长为( )A .19B .16C .18D .20【答案】如图,延长AO 交BC 于点D,过O 作OE ⊥BC 于E.则三角形ABD 为等边三角形,DA=AB=BD=12,OD=AD-AO=4在Rt △ODE 中,∠ODE=60°,∠DOE=30°,则DE=OD=2,BE=BD-DE=10 OE 垂直平分BC ,BC=2BE=20. 故选D类型三、与圆有关的位置关系12BN BF =12CD CG =»»CFBC =»»BGBC =»»»CF BG BC ==»»BF CG =ON OD=123.一个长方体的香烟盒里,装满大小均匀的20支香烟.打开烟盒的顶盖后,二十支香烟排列成三行,如图(1)所示.经测量,一支香烟的直径约为0.75cm ,长约为8.4cm. (1)试计算烟盒顶盖ABCD 的面积(本小题计算结果不取近似值);(2)制作这样一个烟盒至少需要多少面积的纸张(不计重叠粘合的部分,计算结果精确到,取)0.1cm 3173..【答案与解析】 (1)如图(2),作O 1E ⊥O 2O 3()332844AB cm ∴=⨯+=∴四边形ABCD 的面积是:(2)制作一个烟盒至少需要纸张:.【总结升华】四边形ABCD中,AD长为7支香烟的直径之和,易求;求AB长,只要计算出如图(2)中的O1E长即可.类型四、圆中有关的计算4.(2019•丹东)如图,AB是⊙O的直径,=,连接ED、BD,延长AE交BD的延长线于点M,过点D作⊙O的切线交AB的延长线于点C.(1)若OA=CD=2,求阴影部分的面积;(2)求证:DE=DM.【答案与解析】解:如图,连接OD,⊙CD是⊙O切线,⊙OD⊙CD,⊙OA=CD=2,OA=OD,⊙OD=CD=2,⊙⊙OCD为等腰直角三角形,⊙⊙DOC=⊙C=45°,⊙S阴影=S⊙OCD﹣S扇OBD=﹣=4﹣π;(2)证明:如图,连接AD,⊙AB是⊙O直径,⊙⊙ADB=⊙ADM=90°,又⊙=,⊙ED=BD,⊙MAD=⊙BAD,在⊙AMD和⊙ABD中,,⊙⊙AMD⊙⊙ABD,⊙DM=BD,⊙DE=DM.【点评】本题考查的是切线的性质、弦、弧之间的关系、扇形面积的计算,掌握切线的性质定理和扇形的面积公式是解题的关键,注意辅助线的作法.举一反三:【变式】(2019•贵阳)如图,⊙O是⊙ABC的外接圆,AB是⊙O的直径,FO⊙AB,垂足为点O,连接AF 并延长交⊙O于点D,连接OD交BC于点E,⊙B=30°,FO=2.(1)求AC的长度;(2)求图中阴影部分的面积.(计算结果保留根号)【答案】解:(1)⊙OF⊙AB,⊙⊙BOF=90°,⊙⊙B=30°,FO=2,⊙OB=6,AB=2OB=12,又⊙AB为⊙O的直径,⊙⊙ACB=90°,⊙AC=AB=6;(2)⊙由(1)可知,AB=12,⊙AO=6,即AC=AO,在Rt⊙ACF和Rt⊙AOF中,⊙Rt⊙ACF⊙Rt⊙AOF,⊙⊙FAO=⊙FAC=30°,⊙⊙DOB=60°,过点D作DG⊙AB于点G,⊙OD=6,⊙DG=3,⊙S⊙ACF+S⊙OFD=S⊙AOD=×6×3=9,即阴影部分的面积是9.类型五、圆与其他知识的综合运用5.»ABC D BC DB DC DA+=如图,△是等边三角形,是上任一点,求证:.【思路点拨】由已知条件,等边△ABC可得60°角,根据圆的性质,可得∠ADB=60°,利用截长补短的方法可得一个新的等边三角形,再证两个三角形全等,从而转移线段DC.【答案与解析】延长DB至点E,使BE=DC,连结AE∵△ABC是等边三角形∴∠ACB=∠ABC=60°,AB=AC∴∠ADB=∠ACB=60°∵四边形ABDC是圆内接四边形∴∠ABE=∠ACD在△AEB和△ADC中,∴△AEB≌△ADC∴AE=AD∵∠ADB=60°∴△AED是等边三角形∴AD=DE=DB+BE∵BE=DC∴DB+DC=DA.【总结升华】本例也可以用其他方法证明.如:(1)延长DC至F,使CF=BD,连结AF,再证△ACF≌△ABD,得出AD=DF,从而DB+CD=DA.(2)在DA上截取DG=DC,连结CG,再证△BDC≌△AGC,得出BD=AG,从而DB+CD=DA.6.如图,直径AB为6的半圆,绕A点逆时针旋转60°,此时点B到了点B′,则图中阴影部分的面积是().A. 3πB. 6πC. 5πD. 4π【答案】B;【解析】阴影部分的面积=以AB′为直径的半圆的面积+扇形ABB′的面积-以AB为直径的半圆的面积=扇形ABB′的面积.则阴影部分的面积是:=6π故选B.【总结升华】根据阴影部分的面积=以AB′为直径的半圆的面积+扇形ABB′的面积-以AB为直径的半圆的面积=扇形ABB′的面积.即可求解.举一反三:【变式】某中学举办校园文化艺术节,小颖设计了同学们喜欢的图案“我的宝贝”,图案的一部分是以斜边长为12cm的等腰直角三角形的各边为直径作的半圆,如图所示,则图中阴影部分的面积为( ).A. B.72 C.36 D.72【答案】本题解法很多,如两个小半圆面积和减去两个弓形面积等.但经过认真观察等腰直角三角形其对称性可知,阴影部分的面积由两个小半圆面积与三角形面积的和减去大半圆面积便可求得,所以由已知得直角边为,小半圆半径为(cm),因此阴影部分面积为.故选C.《圆》全章复习与巩固—巩固练习(提高)【巩固练习】一、选择题1.如图所示,AB、AC为⊙O的切线,B和C是切点,延长OB到D,使BD=OB,连接AD.如果∠DAC=78°,那么∠ADO等于( ).A.70° B.64° C.62° D.51°2.已知⊙O半径为3,M为直线AB上一点,若MO=3,则直线AB与⊙O的位置关系为()A.相切 B.相交 C.相切或相离 D.相切或相交3.设计一个商标图案,如图所示,在矩形ABCD中,AB=2BC,且AB=8cm,以A为圆心、AD的长为半径作半圆,则商标图案(阴影部分)的面积等于( ).A.(4π+8)cm2B.(4π+16)cm2C.(3π+8)cm2D.(3π+16)cm24.如图,四边形ABCD是⊙O的内接四边形,若∠B=110°,则∠ADE的度数为()A.55° B.70° C.90° D.110°5.“圆材埋壁”是我国古代著名的数学著作《九章算术》中的问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用数学语言可表示为:如图所示,CD为⊙O的直径,弦AB⊥CD于E,CE=1寸,AB=10寸,则直径CD的长为( )A.12.5寸 B.13寸 C.25寸D.26寸6.在平面直角坐标系中如图所示,两个圆的圆心坐标分别是(3,0)和(0,-4),半径分别是和,则这两个圆的公切线(和两圆都相切的直线)有( )A.1条B.2条C.3条D.4条7.(2019•贵港)如图,已知P是⊙O外一点,Q是⊙O上的动点,线段PQ的中点为M,连接OP,OM.若⊙O的半径为2,OP=4,则线段OM的最小值是()A.0 B.1 C.2 D.38.如图所示,AB、AC与⊙O分别相切于B、C两点,∠A=50°,点P是圆上异于B、C的一动点,则∠BPC的度数是( ).A.65° B.115° C.65°或115° D.130°或50°二、填空题9.如图,在⊙O中,半径OA垂直弦于点D.若∠ACB=33°,则∠OBC的大小为度.10.如图所示,EB、EC是⊙O是两条切线,B、C是切点,A、D是⊙O上两点,如果∠E=46°,∠DCF=32°,那么∠A的度数是________________.11.在Rt△ABC中,∠BAC=30°,斜边AB=2,动点P在AB边上,动点Q在AC边上,且∠CPQ=90°,则线段CQ长的最小值= .12.(2019•巴彦淖尔)如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°,给出以下五个结论:①∠EBC=22.5°;②BD=DC;③AE=2EC;④劣弧是劣弧的2倍;⑤AE=BC,其中正确的序号是.13.两个圆内切,其中一个圆的半径为5,两圆的圆心距为2,则另一个圆的半径是_______ ________.14.已知正方形ABCD,截去四个角成一正八边形,则这个正八边形EFGHIJLK的边长为____ ____,面积为_____ ___.15.如图(1)(2)…(m)是边长均大于2的三角形、四边形、……、凸n边形,分别以它们的各顶点为圆心,以l为半径画弧与两邻边相交,得到3条弧,4条弧,……(1)图(1)中3条弧的弧长的和为___ _____,图(2)中4条弧的弧长的和为_____ ___;(2)求图(m)中n条弧的弧长的和为____ ____(用n表示).16.如图,⊙O的半径是2,直线l与⊙O相交于A、B两点,M、N是⊙O上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB面积的最大值是.三、解答题17. 如图,⊙O是△ABC的外接圆,FH是⊙O 的切线,切点为F,FH∥BC,连结AF交BC于E,∠ABC的平分线BD交AF于D,连结BF.(1)证明:AF平分∠BAC;(2)证明:BF=FD.18.(2019•南京)如图,四边形ABCD是⊙O的内接四边形,BC的延长线与AD的延长线交于点E,且DC=DE.(1)求证:∠A=∠AEB;(2)连接OE,交CD于点F,OE⊥CD,求证:△ABE是等边三角形.19.如图,相交两圆的公共弦长为120cm,它分别是一圆内接正六边形的边和另一圆内接正方形的边.求两圆相交弧间阴影部分的面积.20.问题背景:课外学习小组在一次学习研讨中,得到了如下两个命题:①如图(1),在正△ABC中,M、N分别是AC、AB上的点,BM与CN相交于点O,若∠BON=60°,则BM=CN;②如图(2),在正方形ABCD中,M、N分别是CD、AD上的点,BM与CN相交于点O,若∠BON=90°,则BM=CN.然后运用类似的思想提出了如下命题:③如图(3),在正五边形ABCDE中,M、N分别是CD、DE上的点,BM与CN相交于点O,若∠BON=108°,则BM=CN.任务要求:(1)请你从①②③三个命题中选择一个进行证明;(2)请你继续完成下面的探索;①在正n(n≥3)边形ABCDEF…中,M、N分别是CD、DE上的点,BM与CN相交于点O,试问当∠BON等于多少度时,结论BM=CN成立(不要求证明);②如图(4),在正五边形ABCDE中,M、N分别是DE、AE上的点,BM与CN相交于点O,∠BON=108°时,试问结论BM=CN是否成立.若成立,请给予证明;若不成立,请说明理由.【答案与解析】一、选择题1.【答案】B;【解析】由AB为⊙O的切线,则AB⊥OD.又BD=OB,则AB垂直平分OD,AO=AD,∠DAB=∠BAO.由AB、AC为⊙O的切线,则∠CAO=∠BAO=∠DAB.所以,∠DAB=13∠DAC=26°.∠ADO=90°-26°=64°.本题涉及切线性质定理、切线长定理、垂直平分线的性质、等腰三角形的性质等.2.【答案】D;3.【答案】A.;【解析】对图中阴影部分进行分析,可看做扇形、矩形、三角形的面积和差关系.∵矩形ABCD中,AB=2BC,AB=8cm,∴ AD=BC=4cm,∠DAF=90°,,,又AF=AD=4cm,∴,∴.4.【答案】D;【解析】∵四边形ABCD是⊙O的内接四边形,∴∠ADC+∠B=180°,∵∠ADC+∠ADE=180°,∴∠ADE=∠B.∵∠B=110°,∴∠ADE=110°.5.【答案】D;【解析】因为直径CD垂直于弦AB,所以可通过连接OA(或OB),求出半径即可.根据“垂直于弦的直径平分弦,并且平分弦所对的两条弧”,知(寸),在Rt△AOE中,,即,解得OA=13,进而求得CD=26(寸).6.【答案】C.【解析】本题借助图形来解答比较直观.要判断两圆公切线的条数,则必须先确定两圆的位置关系,因此必须求出两圆的圆心距,根据题中条件,在Rt△AOB中,OA=4,OB=3,所以AB=5,而两圆半径为和,且,即两圆的圆心距等于两圆的半径之和,所以两圆相外切,共有3条公切线.7.【答案】B.【解析】设OP与⊙O交于点N,连结MN,OQ,如图,∵OP=4,ON=2,∴N是OP的中点,∵M为PQ的中点,∴MN为△POQ的中位线,∴MN=OQ=×2=1,∴点M在以N为圆心,1为半径的圆上,当点M在ON上时,OM最小,最小值为1,∴线段OM的最小值为1.故选B.8.【答案】C;【解析】连接OC、OB,则∠BOC=360°-90°-90°-50°=130°.点P在优弧上时,∠BPC =∠BOC=65°;点P在劣弧上时,∠BPC=180°-65°=115°.主要应用了切线的性质定理、圆周角定理和多边形内角和定理.二、填空题9.【答案】24.10.【答案】99°;【解析】由EB=EC,∠E=46°知,∠ECB= 67°,从而∠BCD=180°-67°-32°=81°,在⊙O中,∠BCD与∠A互补,所以∠A=180°-81°=99°.11.【答案】83.12【解析】以CQ 为直径作⊙O,当⊙O 与AB 边相切动点P 时,CQ 最短,∴OP⊥AB,∵∠B=90°,∠A=30°,∴∠POA=60°,∵OP=OQ,∴△POQ 为等边三角形,∴∠POQ=60°,∴∠APQ=30°,∴设PQ=OQ=AP=OC=r ,3r=AC=ABsin 30︒=4,∴CQ=83,∴CQ 的最小值为83.12.【答案】①②④;【解析】连接AD ,AB 是直径,则AD⊥BC,又∵△ABC 是等腰三角形,故点D 是BC 的中点,即BD=CD ,故②正确; ∵AD 是∠BAC 的平分线,由圆周角定理知,∠EBC=∠DAC=∠BAC=22.5°,故①正确;∵∠ABE=90°﹣∠EBC﹣∠BAD=45°=2∠CAD,故④正确; ∵∠EBC=22.5°,2EC≠BE,AE=BE ,∴AE≠2CE,③不正确; ∵AE=BE,BE 是直角边,BC 是斜边,肯定不等,故⑤错误. 综上所述,正确的结论是:①②④.13.【答案】7或3;【解析】两圆有三种位置关系:相交、相切(外切、内切)和相离(外离、内含).两圆内切时,圆心距,题中一圆半径为5,而d=2,所以有,解得r=7或r=3,即另一圆半径为7或3.14.【答案】; ;【解析】正方形ABCD 外接圆的直径就是它的对角线,由此求得正方形边长为a .如图所示,设正八边形的边长为x .在Rt △AEL 中,LE =x ,AE =AL,∴ ,,即正八边形的边长为..1)a 22)a 2x 22x x a ⨯+=1)x a =1)a 2222241)]2)AEL S S S a x a a a =-=-=-=△正方形正八边形15.【答案】(1)π; 2π; (2)(n-2)π;【解析】∵ n 边形内角和为(n-2)180°,前n 条弧的弧长的和为个以某定点为圆心,以1为半径的圆周长,∴ n 条弧的弧长的和为. 本题还有其他解法,比如:设各个扇形的圆心角依次为,,…,, 则,∴ n 条弧长的和为.16.【答案】4.【解析】解:过点O 作OC⊥AB 于C ,交⊙O 于D 、E 两点,连结OA 、OB 、DA 、DB 、EA 、EB ,如图, ∵∠AMB=45°,∴∠AOB=2∠AMB=90°,∴△OAB 为等腰直角三角形,∴AB=OA=2,∵S 四边形MANB =S △MAB +S △NAB ,∴当M 点到AB 的距离最大,△MAB 的面积最大;当N 点到AB 的距离最大时,△NAB 的面积最大,即M 点运动到D 点,N 点运动到E 点,此时四边形MANB 面积的最大值=S 四边形DAEB =S △DAB +S △EAB =AB•CD+AB•CE=AB (CD+CE )=AB•DE=×2×4=4.(2)1801(2)3602n n -=-121(2)(2)2n n ππ⨯⨯-=-1α2αn α12(2)180n n ααα+++=-…°1212111()180180180180n n απαπαππααα⨯+⨯++⨯=+++……(2)180(2)180n n ππ=-⨯=-三、解答题17.【答案与解析】(1)连结OF∵FH 是⊙O 的切线 ∴OF⊥FH ∵FH∥BC ,∴OF 垂直平分BC∴ ∴AF 平分∠BAC .(2)由(1)及题设条件可知∠1=∠2,∠4=∠3,∠5=∠2 ∴∠1+∠4=∠2+∠3 ∴∠1+∠4=∠5+∠3 ∠FDB =∠FBD ∴BF =FD.18.【答案与解析】 证明:(1)∵四边形ABCD 是⊙O 的内接四边形, ∴∠A+∠BCD=180°, ∵∠DCE+∠BCD=180°, ∴∠A=∠DCE, ∵DC=DE,∴∠DCE=∠AEB, ∴∠A=∠AEB;(2)∵∠A=∠AEB, ∴△ABE 是等腰三角形, ∵EO⊥CD, ∴CF=DF,∴EO 是CD 的垂直平分线, ∴ED=EC, ∵DC=DE, ∴DC=DE=EC,∴△DCE 是等边三角形,»»BFFC∴∠AEB=60°,∴△ABE 是等边三角形.19.【答案与解析】解:∵公共弦AB =120r R a 6624222212060603=-⎛⎝ ⎫⎭⎪=-=.20. 【答案与解析】 (1)如选命题①. 证明:在图(1)中,∵ ∠BON =60°,∴ ∠1+∠2=60°. ∵ ∠3+∠2=60°,∴ ∠1=∠3. 又∵ BC =CA ,∠BCM =∠CAN =60°, ∴ △BCM ≌△CAN ,∴ BM =CM . 如选命题②.证明:在图(2)中,∵ ∠BON =90°,∴ ∠1+∠2=90°. ∵ ∠3+∠2=90°,∴ ∠1=∠3. 又∵ BC =CD ,∠BCM =∠CDN =90°, ∴ △BCM ≌△CDN ,∴ BM =CN . 如选命题③.证明:在图(3)中,∵ ∠BON =108°,∴ ∠1+∠2=108°. ∵ ∠2+∠3=108°,∴ ∠1=∠3.又∵ BC =CD ,∠BCM =∠CDN =108°, ∴ △BCM ≌△CDN ,∴ BM =CN . (2)①答:当∠BON =时结论BM =CN 成立.②答:当∠BON =108°时.BM =CN 还成立. 证明:如图(4),连接BD 、CE 在△BCD 和△CDE 中,∵ BC =CD ,∠BCD =∠CDE =108°,CD =DE , ∴ △BCD ≌△CDE .∴ BD =CE ,∠BDC =∠CED ,∠DBC =∠ECD . ∵ ∠CDE =∠DEN =108°, ∴ ∠BDM =∠CEM .∵ ∠OBC+∠OCB =108°,∠OCB+∠OCD =108°. ∴ ∠MBC =∠NCD .又∵ ∠DBC =∠ECD =36°, ∴ ∠DBM =∠ECM . ∴ △BDM ≌△CEN , ∴ BM =CN .(2)180n n°。
10、垂径定理及圆周角定理

圆的有关概念及性质一、知识梳理1、圆的定义2、弦与弧3、圆的对称性4、垂径定理及推论5、圆心角、弧、弦之间的关系6、圆周角定理及其推论7、圆内接四边形二、经典例题考点一:垂径定理例2.如图,F是以OA.B.8 C.D.例4.如图,已知⊙O的直径AB和弦CD相交于点E,AE=6cm,EB=2cm,∠BED=30°,求CD的长.AEF1、过⊙O 内一点P 的最长弦为10cm ,最短的弦为6cm ,则OP 的长为 .2、在⊙O 中,弦AB 长为cm 8,圆心到弦AB 的距离为cm 3,则⊙O 半径长为 cm 。
3、半径是5cm 的圆中,圆心到cm 8长的弦的距离是 cm 。
4、如图,有一圆弧形桥拱,拱形的半径m 10=OA ,桥拱的距度16=AB m ,则拱高_____=CD m.5、 圆的两互相平行的弦长分别8cm 1和4cm 2,又两弦之间距离为cm 3,则圆的半径长是 cm6、 在半径为cm 5的圆内有两条互相平行的弦,弦长分别为cm 8、cm 6,则这两条弦之间的距离为________7.一水平放置的圆柱型水管的横截面如图所示,如果水管横截面的半径是13cm ,水面宽24=AB ,则水管中水深是_______cm.8.如图,⊙O 的直径⊥CD AB ,垂足为点E ,若8,2==ED CE ,则=AB ( )A .2B .4C .8D .169.过⊙O 内一点M 的最长的弦长为4cm ,最短的弦长为2cm ,则OM 的长为( )A .3cmB .2cmC .1D .3cm10.已知:如图,⊙O 中直径AB 垂直于弦CD ,垂足为E ,若6,10==CD AB ,则BE 的长是( )A .1B .2C .3D .411.已知⊙O 的弦AB 长8cm ,弦心距为3cm ,则⊙O 的直径是( )A .5cmB .10cmC .55cmD .73cm12.已知⊙O 的半径为2cm ,弦AB 长32cm ,则这条弦的中点到弦所对劣弧的中点的距离为( )A .1cmB .2cmC .2cmD .3cm 考点二:圆周角定理例6.如图所示,正方形ABCD内接于⊙O中,P是弧AD上任意一点,则∠ABP+∠DCP等于()例7.如图所示,CD是圆的直径,O是圆心,E是圆上一点且∠EOD=45°,A是DC延长线上一点,AE交圆于B,如果AB=OC,则∠EAD= ____________例8.如图所示,△ABC为圆内接三角形,AB>AC,∠A的平分线AD交圆于D,作DE⊥AB于E,DF⊥AC于F,求证:BE=CF变式练习1. D、C是以AB为直径的半圆弧上两点,若弧BC所对的圆周角为25°弧AD所对的圆周角为35°,则弧DC所对的圆周角为_____ .3.如图,AB是⊙O的直径,∠AOC=110°,则∠D=()A.25°B.35°C.55°D.70°2、如图,已知AB是⊙O的直径,BC是弦,∠ABC=30°,过圆心O作OD⊥BC交弧BC于点D,连接DC,则∠DCB的度数为度.3.如图所示,已知⊙O的半径是1,C,D是直径AB同侧圆周上的两点,弧的度数为60°,弧的度数为30°,动点P在直径AB上,则PC+PD的最小值为()A.2 B.C.D.14.如图,在5×5正方形网格中,一条圆弧经过A、B、C三点,那么所对的圆心角的大小是()5.如图,A,B,C,D是⊙O上的四个点,=,若∠AOB=58°,则∠BDC=度.6.如图,已知CD是⊙O的直径,∠EOD=78°,AE交⊙O于B,且AB=OC.求∠A的度数.考点三:圆的内接四边形例9.如图所示,在⊙O中,A、B、C三点在圆上,且∠CBD=60,那么∠AOC=__________【备考真题过关】A.4B.4C.4D.4第1题第2题2.如图,圆心在y轴的负半轴上,半径为5的⊙B与y轴的正半轴交于点A(0,1),过点P(0,-7)的直线l与⊙B相交于C,D两点.则弦CD长的所有可能的整数值有()A.1个B.2个C.3个D.4个3.如图,点P是等边三角形ABC外接圆⊙O上的点,在以下判断中,不正确的是()A.当弦PB最长时,△APC是等腰三角形B.当△APC是等腰三角形时,PO⊥ACC.当PO⊥AC时,∠ACP=30°D.当∠ACP=30°时,△BPC是直角三角形4.如图,⊙O的直径AB与弦CD垂直,且∠BAC=40°,则∠BOD= .5.如图,将⊙O沿弦AB折叠,使弧AB经过圆心O,则∠OAB= .6.如图,在⊙O中,弦AB垂直平分半径OC,垂足为D,若⊙O的半径为2,则弦AB的长为.第4题第5题第6题7.如图AB是⊙O的直径,∠BAC=42°,点D是弦AC的中点,则∠DOC的度数是度.»AB上两点,且∠MEB=∠NFB=60°,8.如图,已知⊙O的直径AB=6,E、F为AB的三等分点,M、N为则EM+FN= .第7题第8题第9题三、解答题11.在⊙O中,AB为直径,点C为圆上一点,将劣弧沿弦AC翻折交AB于点D,连结CD.(1)如图1,若点D与圆心O重合,AC=2,求⊙O的半径r;(2)如图2,若点D与圆心O不重合,∠BAC=25°,请直接写出∠DCA的度数.12.如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,且PD∥CB,弦PB与CD 交于点F(1)求证:FC=FB;(2)若CD=24,BE=8,求⊙O的直径.。
垂径定理和圆周角圆心角

一、垂径定理垂径定理:垂直于弦的直径平分弦且平分弦所对的弧。
推论1:(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧; (2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧;(3)平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧以上共4个定理,简称2推3定理:此定理中共5个结论中,只要知道其中2个即可推出其它3个结论,即:①AB 是直径 ②AB CD ⊥ ③CE DE = ④ 弧BC =弧BD ⑤ 弧AC =弧AD 中任意2个条件推出其他3个结论。
推论2:圆的两条平行弦所夹的弧相等。
即:在⊙O 中,∵AB ∥CD ∴弧AC =弧BD 二、圆心角定理圆心角定理:同圆或等圆中,相等的圆心角所对的弦相等,所对的弧相等,弦心距相等。
此定理也称1推3定理,即上述四个结论中,只要知道其中的1个相等,则可以推出其它的3个结论, 即:①AOB DOE ∠=∠;②AB DE =;③OC OF =;④ 弧BA =弧BD 三、圆周角定理1、圆周角定理:同弧所对的圆周角等于它所对的圆心的角的一半。
即:∵AOB ∠和ACB ∠是弧AB 所对的圆心角和圆周角 ∴2AOB ACB ∠=∠2、圆周角定理的推论:推论1:同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧是等弧; 即:在⊙O 中,∵C ∠、D ∠都是所对的圆周角 ∴C D ∠=∠推论2:半圆或直径所对的圆周角是直角;圆周角是直角所对的弧是半圆,所对的弦是直径。
即:在⊙O 中,∵AB 是直径 或∵90C ∠=︒ ∴90C ∠=︒ ∴AB 是直径推论3:若三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形。
即:在△ABC 中,∵OC OA OB ==DBABA∴△ABC 是直角三角形或90C ∠=︒注:此推论实是初二年级几何中矩形的推论:在直角三角形中斜边上的中线等于斜边的一半的逆定理。
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等. 四、圆内接四边形圆的内接四边形定理:圆的内接四边形的对角互补,外角等于它的内对角。
人教版数学九年级上册24.1.2《垂径定理》教学设计2

人教版数学九年级上册24.1.2《垂径定理》教学设计2一. 教材分析《垂径定理》是人教版数学九年级上册第24章第1节的内容,本节课主要介绍圆中的垂径定理。
垂径定理是指:圆中,如果一条直线垂直于直径,那么这条直线平分这条直径,并且平分直径所对的圆周角。
教材通过生活中的实例引入垂径定理的概念,然后通过证明和应用来巩固这个定理。
二. 学情分析学生在学习本节课之前,已经掌握了圆的基本概念和性质,如圆的周长、直径、半径等。
同时,学生也掌握了平行线和相交线的性质。
但是,学生对于圆中的垂径定理可能比较难以理解和证明,因此需要通过生活中的实例和图形的直观展示,帮助学生理解和掌握这个定理。
三. 教学目标1.知识与技能:让学生理解和掌握圆中的垂径定理,能够运用垂径定理解决相关问题。
2.过程与方法:通过观察、操作、证明等过程,培养学生的几何思维和解决问题的能力。
3.情感态度与价值观:激发学生对数学的兴趣,培养学生的团队合作意识。
四. 教学重难点1.教学重点:理解和掌握垂径定理,能够运用垂径定理解决相关问题。
2.教学难点:垂径定理的证明和运用。
五. 教学方法1.情境教学法:通过生活中的实例引入垂径定理,激发学生的学习兴趣。
2.演示法:通过图形的直观展示,帮助学生理解和证明垂径定理。
3.问题驱动法:通过提出问题和解决问题,引导学生主动探索和学习。
4.小组合作学习:鼓励学生分组讨论和合作,培养学生的团队合作意识。
六. 教学准备1.教具准备:多媒体教学设备、圆规、直尺、黑板等。
2.教学素材:教材、课件、练习题等。
七. 教学过程1.导入(5分钟)通过展示生活中的实例,如自行车轮子、时钟等,引导学生观察和思考圆中的垂径定理。
让学生感受到数学与生活的紧密联系,激发学生的学习兴趣。
2.呈现(10分钟)展示垂径定理的定义和性质,通过图形的直观展示,让学生理解和掌握垂径定理。
同时,引导学生思考如何证明这个定理。
3.操练(10分钟)让学生分组讨论和合作,尝试证明垂径定理。
第24章圆的垂径定理圆周角定理(教案)

-学会应用圆的垂径定理和圆周角定理来证明圆内接四边形的性质。
-能够计算弓形的面积,并理解其与圆心角的关系。
举例解释:
-圆的垂径定理:通过具体作图,演示如何通过一点作圆的切线,并证明此切线与通过该点的直径垂直。
-圆周角定理:通过实际测量和计算,让学生观察并理解圆周角与圆心角的关系。
关于小组讨论,我觉得在分组时要更加科学合理,尽量保证每个小组内都有不同水平的学生,以促进他们之间的相互学习和交流。在讨论过程中,我要注意观察每个小组的进展,及时给予指导和帮助,确保讨论能够顺利进行。
在课堂总结环节,我发现有些学生对所学知识点的掌握仍然不够扎实。为了加强学生的记忆,我决定在课后增加一道与圆的垂径定理和圆周角定理相关的巩固练习,让学生在练习中进一步巩固所学知识。
-圆内接四边形:通过构造图形,让学生直观感受四边形内接于圆时,对角线互相平分的性质。
-弓形计算:给出具体弓形的半径和圆心角,指导学生计算弓形的面积,并总结规律。
2.教学难点
-理解并掌握圆的垂径定理的证明过程,尤其是对于几何证明的逻辑推理。
-理解圆周角定理中,圆周角与圆心角的对应关系,以及在不同情况下如何应用定理。
五、教学反思
在今天的教学过程中,我发现学生们对圆的垂径定理和圆周角定理的理解程度参差不齐。有些学生能够迅速掌握定理的要点,并能将其应用到实际问题中;而有些学生则在理解上存在一定的困难。针对这种情况,我认为在今后的教学中需要注意以下几点:
首先,对于定理的讲解,我需要更加生动形象,通过举例、图示等方法,让学生更直观地感受和理解定理的含义。同时,在讲解过程中,要注重引导学生积极参与,鼓励他们提问和思考,以提高课堂的互动性。
第24章圆的垂径定理圆周角定理(教案)
9 垂径定理 圆心角 圆周角定理(

垂径定理圆心角圆周角定理垂径定理: 垂直于弦的直径平分弦且平分这条弦所对的两条弧1、平分弦所对的两条弧)2、平分弦(不是直径)3、垂直于弦4、过圆心推论一:平分弦(非直径)的直径垂直于这条弦,并且平分这条弦所对的两段弧。
推论二:弦的垂直平分线经过圆心,并且平分这条弦所对的弧推论三:平分弦所对的一条弧的直径垂直平分这条弦,并且平分这条弦所对的另一条弧。
推论四:在同圆或者等圆中,两条平行弦所夹的弧相等[垂径定理是圆的重要性质之一,它是证明圆内线段、角相等、垂直关系的重要依据,也为圆中的计算、证明和作图提供了依据、思路和方法。
]圆心角在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦心距也相等。
(1)圆心角相等,(2)所对弧相等,(3)所对弦相等,(4)所对弦的弦心距相等。
圆周角定理指的是一条弧所对圆周角等于它所对圆心角的一半。
1.在同圆或等圆中,同弧或等弧所对的圆周角相等,相等的圆周角所对的弧也相等。
2.半圆(直径)所对的圆周角是直角;90°的圆周角所对的弦是直径。
3.圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角。
切线定理(定义)和圆有且只有一个公共点的直线是圆的切线。
(数量法d=r)圆心到直线的距离等于半径的直线是圆的切线。
判定定理:1、经过半径的外端并且垂直于这条半径的直线是圆的切线。
判定性质:圆的切线垂直于过切点的半径。
有交点,连半径,证垂直;无交点,作垂线,证半径(d=r)练习一选择题:1、如图,⊙O是△ABC的外接圆,∠OBC=42°,则∠A的度数是()A.42°B.48°C.52°D.58°2.如图,A、B、C、D四个点均在⊙O上,∠AOD=50°,AO∥DC,则∠B的度数为( )A.50° B.55°C.60° D.65°3.如图,点B、D、C是⊙O上的点,∠BDC=130°,则∠BOC是()A.100° B.110°C.120° D.130°4.如图,⊙O的半径为5,弦AB的长为8,点M在线段AB(包括端点A,B)上移动,则OM取值范围是()A.3≤OM≤5B.3≤OM<5C.4≤OM≤5D.4≤OM<55、如图所示,AB是⊙O的直径,AD=DE,AE与BD交于点C,则图中与∠BCE相等的角有()A.2个 B.3个 C.4个 D.5个6.将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A、B的读数分别为86°、30°,则∠ACB的大小为( )A.15°B.28° C.29°D.34°7.如图,C为⊙O直径AB上一动点,过点C的直线交⊙O于D、E两点,且∠ACD=45°,DF⊥AB于点F,EG⊥AB 于点G,当点C在AB上运动时,设AF=x,DE=y,下列中图象中,能表示y与x的函数关系式的图象大致是( )8.如图.⊙O 中,AB、AC是弦,O在∠ABO的内部,,,,则下列关系中,正确的是()A. B.C. D.9.如图,四边形ABCD内接于⊙O,BC是直径,AD=DC,∠ADB=20º,则∠ACB,∠DBC分别为()A.15º与30º B.20º与35ºC.20º与40º D.30º与35º10.图中∠BOD的度数是()A.55° B.110°C.125° D.150°11.如图,点I为△ABC的内心,点O为△ABC的外心,∠O=140°,则∠I为()(A)140°(B)125°(C)130°(D)110°12.如图,弦AB∥CD,E为弧CBD上一点,AE平分,则图中与相等(不包括)的角共有()A.3个 B.4个C.5个 D.6个13、如图,已知的半径为1,锐角内接于,于点,于点,则的值等于()A.的长 B.的长 C.的长 D.的长14.如图,在直角∠O的内部有一滑动杆AB,当端点A沿直线AO向下滑动时,端点B会随之自动地沿直线OB向左滑动,如果滑动杆从图中AB处滑动到A′B′处,那么滑动杆的中点C所经过的路径是()A.直线的一部分B.圆的一部分C.双曲线的一部分D.抛物线的一部分15.如图,AB是⊙O的直径,弦BC=2cm,∠ABC=60°.若动点P以2cm/s的速度从B点出发沿着B→A的方向运动,点Q从A点出发沿着A→C的方向运动,当点P到达点A时,点Q也随之停止运动.设运动时间为t(s),当△APQ是直角三角形时,t的值为()A. B.C.或D.或或16.如图,,在以为直径的半圆上,,在上,为正方形,若正方形边长为1,,,则下列式子中,不正确的是()A. B.C. D.17.如图,AB是⊙O的直径,AB=8,点M在⊙O上,∠MAB=20°,N是弧MB的中点,P是直径AB上的一动点.若MN=1,则△PMN周长的最小值为()A.4 B.5 C.6 D.718.如图,在△ABC中,AD是高,AE是直径,AE交BC于G,有下列四个结论:•①AD2=BD·CD;②BE2=EG·AE;③AE·AD=AB·AC;④AG·EG=BG·CG.其中正确结论的有()A.1个 B.2个 C.3个 D.4个19.如图,C是以AB为直径的半圆O上一点,连结AC,BC,分别以AC,BC为边向外作正方形ACDE,BCFG,DE,FG,,的中点分别是M,N,P,Q。
自学初中数学资料 圆之垂径定理、圆心角、圆周角定理 (资料附答案)

自学资料一、圆的相关定义【知识探索】1.定理:不在同一直线上的三点确定一个圆.【说明】(1)过平面上一点能作无数多个圆;(2)过平面上两点能做无数多个圆,这些圆的圆心在两点连线的垂直平分线上;(3)过平面上三点:①三点不在同一直线上,能作唯一一个圆;②三点在同一直线上,不能作圆.【错题精练】例1.下列命题正确的个数有()①过两点可以作无数个圆;②经过三点一定可以作圆;③任意一个三角形有一个外接圆,而且只有一个外接圆;④任意一个圆有且只有一个内接三角形.A. 1个B. 2个C. 3个D. 4个第1页共23页自学七招之日计划护体神功:每日计划安排好,自学规划效率高非学科培训【解答】解:①过两点可以作无数个圆,正确;②经过三点一定可以作圆,错误;③任意一个三角形有一个外接圆,而且只有一个外接圆,正确;④任意一个圆有且只有一个内接三角形,错误,正确的有2个,故选:B.【答案】B例2.有下列四个命题,其中正确的有()①圆的对称轴是直径;②经过三个点一定可以作圆;③三角形的外心到三角形各顶点的距离都相等;④半径相等的两个半圆是等弧.A. 4个B. 3个C. 2个D. 1个【答案】C例3.如图,在平面直角坐标系中,点A坐标为(﹣4,0),⊙O与x轴的负半轴交于B(﹣2,0).点P是⊙O上的一个动点,PA的中点为Q.当点Q也落在⊙O上时,cos∠OQB的值等于()A.B.C.D.【解答】第2页共23页自学七招之错题本锁骨术:巧用智能错题本,错题定期反复练非学科培训【答案】C例4.如图,已知△ABC.(1)尺规作图作△ABC的外接圆(保留作图痕迹,不写作法);(2)设△ABC是等腰三角形,底边BC=10,腰AB=6,求圆的半径r.【答案】解:(1)如图所示;(2)连接OB,连接OA交BC于点E,∵△ABC是等腰三角形,底边BC=10,腰AB=6,∴BE=CE=5,AE=√AB2−BE2=√11,在Rt△BOE中,r2=52+(r-√11)2∴r=18√11=18√1111.第3页共23页自学七招之预习轻身术:预习习惯培养好,课堂轻松没烦恼非学科培训第4页 共页自学七招之错题本锁骨术:巧用智能错题本,错题定期反复练非学科培训【解答】【解答】解:如图:连接OA,作OM⊥AB与M,∵⊙O的直径为10,∴半径为5,∴OP的最大值为5,∵OM⊥AB与M,∴AM=BM,∵AB=6,∴AM=3,在Rt△AOM中,OM==4,OM的长即为OP的最小值,∴4≤OP≤5.【答案】4≤OP≤55.已知:△ABC(如图)(1)求作:△ABC的外接圆(要求:用尺规作图,保留作图痕迹,不要求写作法及证明).(2)若∠A=60°,BC=8√3,求△ABC的外接圆的半径.【答案】解:(1)如图所示:⊙O即为所求△ABC的外接圆;(2)过点O作OD⊥BC于点D,∵∠A=60°,BC=8√3,∴∠COD=60°,CD=4√3,第5页共23页自学七招之预习轻身术:预习习惯培养好,课堂轻松没烦恼非学科培训∴CO=4√3sin60°=8,答:△ABC的外接圆的半径为8.二、圆心角、弧、弦、弦心距、圆周角之间的关系【知识探索】年份题量分值考点题型2015114圆内接四边形的性质;点与圆的位置关系选择、简答201613圆周角定理;填空2017219弧长面积;切线的性质;圆周角定理选择、填空、简答201824圆周角定理;填空2019216扇形面积;切线长定理;圆心角、圆周角、垂径定理填空、解答【错题精练】例1.如图所示,小华从一个圆形场地的A点出发,沿着与半径OA夹角为α的方向行走,走到场地边缘B后,再沿着与半径OB夹角为α的方向折向行走.按照这种方式,小华第五次走到场地边缘时处于弧AB上,此时∠AOE=52°,则α的度数是()A. 51.5°B. 60°C. 72°D. 76°【解答】解:连接OD.∵∠BAO=∠CBO=α,∴∠AOB=∠BOC=∠COD=∠DOE,∵∠AOE=52°,∴∠AOB=(360°-52°)÷4=77°,第6页共23页自学七招之错题本锁骨术:巧用智能错题本,错题定期反复练非学科培训第7页 共23页自学七招之预习轻身术:预习习惯培养好,课堂轻松没烦恼 非学科培训∴α=(180°-77°)÷2=51.5°. 故选:A .【答案】A例2.如图,在△ABC 中,∠C=90°,以点C 为圆心,BC 为半径的圆交AB 于点D ,交AC 于点E .(1)若∠A=25°,求BD̂的度数. (2)若BC=9,AC=12,求BD 的长.【答案】解:(1)连接CD ,如图, ∵∠ACB=90°,∴∠B=90°-∠A=90°-25°=65°,∵CB=CD ,∴∠CDB=∠B=65°, ∴∠BCD=180°-2∠B=50°, ∴BD ̂的度数为50°;(2)作CH ⊥BD ,如图,则BH=DH , 在Rt △ACB 中,AB=√92+122=15, ∵12CH•AB=12BC•AC , ∴CH=9×1215=365, 在Rt △BCH 中,BH=√92−(365)2=275,∴BD=2BH=545.̂的度数为()例3.已知如图,在⊙O中,OA⊥OB,∠A=35°,则CDA. 20°B. 25°C. 30°D. 35°【解答】解:连接OC,∵OA⊥OB,∴∠AOB=90°,∵∠A=35°,∴∠OBC=90°-35°=55°,∴OB=OC,∴∠OBC=∠OCB=55°,∴∠COB=70°,∴∠COD=90°-70°=20°,̂的度数为20°,∴CD故选:A.【答案】A例4.已知AB是⊙O的直径,点C,D是⊙O上的点,∠A=50°,∠B=70°,连接DO,CO,DC (1)如图①,求∠OCD的大小:(2)如图②,分别过点C,D作OC,OD的垂线,相交于点P,连接OP,交CD于点M已知⊙O的半径为2,求OM及OP的长.第8页共23页自学七招之错题本锁骨术:巧用智能错题本,错题定期反复练非学科培训【答案】解:(1)∵OA=OD,OB=OC,∴∠A=∠ODA=50°,∠B=∠OCB=70°,∴∠AOD=80°,∠BOC=40°,∴∠COD=180°-∠AOD-∠BOC=60°,∵OD=OC,∴△COD是等边三角形,∴∠OCD=60°;(2)∵PD⊥OD,PC⊥OC,∴∠PDO=∠PCO=90°,∴∠PDC=∠PCD=30°,∴PD=PC,∵OD=OC,∴OP垂直平分CD,∴∠DOP=30°,∵OD=2,∴OM=√32OD=√3,OP=4√33.例5.如图,AB为⊙O的直径,△ABC的边AC,BC分别与⊙O交于D,E,若E为BD̂的中点.(1)求证:DE=EC;(2)若DC=2,BC=6,求⊙O的半径【答案】解:(1)连结AE,BD,∵E为BD̂的中点,∴ED̂=BÊ,∴∠CAE=∠BAE,∵∠AEB是直径所对的圆周角,第9页共23页自学七招之预习轻身术:预习习惯培养好,课堂轻松没烦恼非学科培训第10页 共23页自学七招之错题本锁骨术:巧用智能错题本,错题定期反复练 非学科培训∴∠AEB=90°, 即AE ⊥BC ,∴∠AEB=∠AEC=90°,在△AEC 和△AEB 中{∠CAE =∠BAE AE =AE ∠AEC =∠AEB ,∴△AEC ≌△AEB (ASA ), ∴CE=BE , ∴DE=CE=BE=12BC ;(2)在Rt △CBD 中,BD 2=BC 2-CD 2=32, 设半径为r ,则AB=2r , 由(1)得AC=AB=2r , AD=AC-CD=2r-2,在Rt △ABD 中AD 2+BD 2=AB 2, ∴(2r-2)2+32=(2r )2, 解得:r=4.5,∴⊙O 的半径为4.5.例6.如图,点A ,B ,C 在⊙O 上,AB ∥OC .(1)求证:∠ACB+∠BOC=90°;(2)若⊙O 的半径为5,AC=8,求BC 的长度.【答案】(1)证明:∵AB̂对的圆周角是∠ACB ,对的圆心角是∠AOB , ∴∠AOB=2∠ACB , ∵OB=OA ,∴∠ABO=∠BAO , ∵AB ∥OC ,∴∠ABO=∠BOC ,∠BAO+∠AOC=180°, ∴∠BAO+∠AOB+∠BOC=180°, 即2∠ACB+2∠BOC=180°, ∴∠ACB+∠BOC=90°;(2)延长AO 交⊙O 于D ,连接CD ,则∠ACD=90°,由勾股定理得:CD=√AD2−AC2=√(5+5)2−82=6,∵OC∥AB,∴∠BOC=∠ABO,∠COD=∠BAO,∵∠BAO=∠ABO,∴∠BOC=∠COD,在△BOC和△DOC中{OB=OD∠BOC=∠DOC OC=OC∴△BOC≌△DOC(SAS),∴BC=CD,∵CD=6,∴BC=6.例7.如图,AB是半圆O的直径,AC是弦,∠CAB=60∘,若AB=6cm.(1)求弦AC的长;(2)点P从点A开始,以1cm/s的速度沿AB向点B运动,到点B停止,过点P作PQ∥AC,交半圆O于点Q,设运动时间为t(s).①当t=1时,求PQ的长;②若△OPQ为等腰三角形,直接写出t(t>0)的值.【解答】(1)解:如图1中,∵OA=OC,∠CAB=60∘,∴△AOC是等边三角形,∴AC=OA=3(cm);(2)解:①如图2中,作OH⊥PQ于H,连接OQ,由题意得:AP=1,OP=2,∵PQ∥AC,∴∠OPH=∠CAB=60∘,在Rt△OPH中,∵∠POH=90∘−∠OPH=30∘,OP=2,∴PH=1OP=1,OH=√3PH=√3,2在Rt△QOH中,HQ=√OQ2−OH2=√6,∴PQ=PH+HQ=1+√6;②如图3中,∵△OPQ是等腰三角形,观察图象可知,只有OP=PQ,作PH⊥OQ于H.∵PQ∥AC,∴∠QPB=∠CAB=60∘,∵PQ=PO,PH⊥OQ,,∠POQ=∠PQO=30∘,∴OH=HQ=32∴OP=OH÷cos30∘=√3,∴AP=3+√3,∴t=3+√3秒时,△OPQ是等腰三角形.【答案】(1)3cm;(2)①1+√6;②t=3+√3.例8.如图,以△ABC的一边AB为直径的半圆与其它两边AC,BC的交点分别为D、E,且.(1)试判断△ABC的形状,并说明理由.(2)已知半圆的半径为5,BC=12,求sin∠ABD的值.【解答】(1)解:△ABC为等腰三角形.理由如下:连结AE,如图,∵,∴∠DAE=∠BAE,即AE平分∠BAC,∵AB为直径,∴∠AEB=90∘,∴AE⊥BC,∴△ABC为等腰三角形;(2)解:∵△ABC为等腰三角形,AE⊥BC,∴BE=CE=12BC=12×12=6,在Rt△ABE中,∵AB=10,BE=6,∴AE=√102−62=8,∵AB为直径,∴∠ADB=90∘,∴12AE⋅BC=12BD⋅AC,∴BD=8×1210=485,在Rt△ABD中,∵AB=10,BD=485,∴AD=√AB2−BD2=145,∴sin∠ABD=ADAB =14510=725.【答案】(1)略;(2)725.【举一反三】1.如图,弦AC、BD相交于点E,且AB̂=BĈ=CD̂,若∠AED=80°,则∠ACD的度数为()A. 20°B. 25°C. 30°D. 15°【解答】解:如图,设AB̂的度数为m,AD̂的度数为n,∵AB̂=BĈ=CD̂,∴BĈ、CD̂的度数都为m,∴3m+n=360°①∵∠AED=80°,∴∠C+∠D=80°,∴12m+12n=80°②,由①②组成{3m+n=360°12m+12n=80°,解得m=100°,n=60°∴∠ACD=12n=30°.故选:C.【答案】C2.已知△ABC内接于⊙O,点D平分弧BmĈ.(1)如图①,若∠BAC=2∠ABC.求证:AC=CD;(2)如图②,若BC为⊙O的直径,且BC=10,AB=6,求AC,CD的长.【答案】(1)证明:∵点D平分弧BmĈ,∴弧DC=弧DB,∵∠BAC=2∠ABC,∴弧BDC=2弧AC,∴弧CA=弧CD,∴AC=CD;(2)解:连结BD,如图②,∵BC为⊙O的直径,∴∠BAC=∠BDC=90°,在Rt △BAC 中,∵BC=10,AB=6,∴AC=√BC 2−AB 2=8;∵弧DC=弧DB ,∴DB=DC ,∴△BCD 为等腰直角三角形,∴CD=√22BC=5√2.3.如图,在⊙O 中,点C 是优弧ACB 的中点,D 、E 分别是OA 、OB 上的点,且AD=BE ,弦CM 、CN 分别过点D 、E .(1)求证:CD=CE .(2)求证:AM̂=BN ̂.【答案】(1)证明:连接OC .∵AĈ=BC ̂, ∴∠COD=∠COE ,∵OA=OB ,AD=BE ,∴OD=OE ,∵OC=OC ,∴△COD ≌△COE (SAS ),∴CD=CE .(2)分别连结OM ,ON ,∵△COD ≌△COE ,∴∠CDO=∠CEO ,∠OCD=∠OCE ,∵OC=OM=ON ,∴∠OCM=∠OMC ,∠OCN=∠ONC ,∴∠OMD=∠ONE ,∵∠ODC=∠DMO+∠MOD ,∠CEO=∠CNO+∠EON ,∴∠MOD=∠NOE ,∴AM̂=BN ̂.4.如图,已知△ABC中,AB=AC,以AB为直径的⊙O与边BC相交于点D,过点D作⊙O的切线与AC交于点E.(1)求BDBC的值.(2)判断DE与AC的位置关系,并证明你的结论.(3)已知BC:AB=2:3,DE=4√2,求⊙O的直径.【解答】(1)解:如图,连接AD,∵AB是⊙O的直径,∴AD⊥BC,∵AB=AC,∴BD=DC,∴BDBC =12;(2)解:DE⊥AC;连接OD,∵DE是⊙O的切线,∴DE⊥OD,∵AB=AC,∴∠B=∠C,∵OB=OD,∴∠B=∠ODB,∴∠ODB=∠C,∴AC∥OD,∴DE⊥AC;(3)解:∵BDBC =12且BC:AB=2:3,∴AB:CD=3,∵∠ADB =∠DEC =90∘,∠B =∠C ,∴△ABD ∽△DCE ,∴DC AB =CE BD =13,设CE =a ,则BD =CD =3a ,AB =9a ,在Rt△DEC 中,由勾股定理得:DE =2a √2=4√2,∴a =2,∴AB =18.【答案】(1)12;(2)DE ⊥AC ;(3)18.5.已知直径CD ⊥弦BF 于 E ,AB 为ʘO 的直径.(1)求证:FD̂=AC ̂; (2)若∠DAB=∠B ,求∠B 的度数.【答案】(1)证明:∵直径CD ⊥弦BF ,∴FD̂=BD ̂, ∵∠AOC=∠BOD ,∴BD̂=AC ̂, ∴FD̂=AC ̂; (2)解:由圆周角定理得,∠BOD=2∠DAB ,∵∠DAB=∠B ,∴∠BOD=2∠B ,∵CD ⊥BF ,∴∠B=30°.6.如图,⊙O 的半径为2,弦BC =2√3,点A 是优弧BC 上一动点(不包括端点),△ABC 的高BD 、CE 相交于点F ,连结ED .下列四个结论:①∠A 始终为60°;②当∠ABC =45∘时,AE =EF ;③当△ABC 为锐角三角形时,ED =√3;④线段ED 的垂直平分线必平分弦BC .其中正确的结论是 .(把你认为正确结论的序号都填上)【答案】①②③④.7.圆O的直径为10cm,A是圆O内一点,且OA=3cm,则圆O中过点A的最短弦长=__________cm【答案】88.如图,在圆O中,AB为直径,CD为弦,已知∠ACD=40°,则∠BAD=__________°【答案】501.如图,AB圆O的直径,点C在圆O上,若∠OCA=50°,AB=4,则弧BC的长为()πA. 103B. 109π C. 59πD. 518π【答案】B2.如图,将钢珠放在一个边长AB=8mm 的正方形的方槽内,测得钢珠顶端离零件表面的距离为8mm ,则这个钢珠的直径为______mm .【答案】103.如图,AB 是半圆的直径,E 是弦AC 上一点,过点E 作EF ⊥EB ,交AB 于点F ,过点A 作AD ∥EF ,交半圆于点D .若C 是BD ̂的中点,AF AE =√54,则EFAD 的值为 .【解答】解:延长BE 交AD 于A',∵AD ∥EF ,EF ⊥BE ,∴AA'⊥BA',∴∠AA'B=90°,∵AB 为⊙O 的直径,∴∠ADB=90°,∴D 与A'重合,∵AFAE =√54,∴设AF=√5a,AE=4a,过F作FG⊥AE于G,∵C是BD̂的中点,∴CD̂=BĈ,∴∠DAC=∠BAC,∵AD∥EF,∴∠BFE=∠DAB=2∠BAC=∠BAC+∠AEF,∴∠BAC=∠AEF,∴AF=EF,∴AG=EG=2a,由勾股定理得:FG=a,∵∠DAE=∠GAF,∠ADE=∠AGF=90°,∴△ADE∽△AGF,∴ADAE =AGAF,∴AD4a =2a√5a,AD=8a√5,∴EFAD =√5a8a√5=58,故答案为:58.【答案】584.在⊙O的内接△ABC中,AD⊥BC于D,(1)①图1中,若作直径AP,求证:AB.AC=AD.AP;②已知AB+AC=12,AD=3,设⊙O的半径为y,AB的长为x.求y与x的函数关系式及自变量x的取值范围;(2)图2中,点E为⊙O上一点,且弧AE=弧AB,求证:CE+CD=BD.【答案】5.在⊙O的内接△ABC中,AB+AC=12,AD⊥BC,垂足为D,且AD=3,设⊙O的半径为y,AB的长为x。
垂径定理及其推论

圆部分知识点总结垂径定理及其推论垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的弧。
推论1:(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。
(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧。
(3)平分弦所对的一条弧的直径垂直平分弦,并且平分弦所对的另一条弧。
推论2:圆的两条平行弦所夹的弧相等。
垂径定理及其推论可概括为: 过圆心 垂直于弦直径 平分弦 知二推三 平分弦所对的优弧 平分弦所对的劣弧弧、弦、弦心距、圆心角之间的关系定理1:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等。
2:在同圆或等圆中,如果两个圆的圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等,那么它们 所对应的其余各组量都分别相等。
圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半。
推论1:同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧也相等。
推论2:半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径。
推论3:如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形。
点和圆的位置关系设⊙O 的半径是r ,点P 到圆心O 的距离为d ,则有: d<r ⇔点P 在⊙O 内;d=r ⇔点P 在⊙O 上; d>r ⇔点P 在⊙O 外。
过三点的圆1、不在同一直线上的三个点确定一个圆。
2、经过三角形的三个顶点的圆叫做三角形的外接圆。
3、三角形的外接圆的圆心是三角形三条边的垂直平分线的交点,它叫做这个三角形的外心。
直线与圆的位置关系直线和圆有三种位置关系,具体如下:(1)相交:直线和圆有两个公共点时,叫做直线和圆相交,这时直线叫做圆的割线,公共点叫做交点; (2)相切:直线和圆有唯一公共点时,叫做直线和圆相切,这时直线叫做圆的切线, (3)相离:直线和圆没有公共点时,叫做直线和圆相离。
如果⊙O 的半径为r ,圆心O 到直线L 的距离为d,那么:直线L 与⊙O 相交⇔d<r ;直线L 与⊙O 相切⇔d=r ; 直线L 与⊙O 相离⇔d>r ;圆的内接四边形定理:圆的内接四边形的对角互补,外角等于它的内对角。
能力提升2_7圆中的七大定理与真题训练【2022中考数学三轮冲刺能力提升+真题对点练】原卷版

2022年中考数学考前30天迅速提分复习方案(全国通用)专题2.7圆中的七大定理与真题训练题型一:圆周角定理一.解答题(共9小题)1.(2022•萧山区模拟)在圆O中,弦AB与CD相交于点E,且弧AC与弧BD相等.点D在劣弧AB上,连接CO并延长交线段AB于点F,连接OA、OB.(1)求证:△OFA∽△EFC;(2)当OA=5,且tan∠OAB=时,如果△AOF是直角三角形,求线段EF的长.2.(2022•芜湖一模)如图1,BC是⊙O的直径,点A,P为其异侧的两点(点A、P均不与点B、C重合),过点A作AQ⊥AP,交PC的延长线于点Q,AQ交⊙O于点D.(1)求证:△APQ∽△ABC;(2)如图2,若AB=3,AC=4.当点C为弧PD的中点时,求CQ的长.3.(2022•南海区一模)如图,在⊙O上有位于直径AB的两侧的定点C和动点P,=2,点P 在半圆弧AB上运动(不与A、B两点重合),过点C作直线PB的垂线CD,垂足为点D.(1)如图1,求证:△ABC∽△PCD;(2)类比(1)中的情况,当点P运动到什么位置时,△ABC≌△PCD?请在图2中画出△PCD,并说明理由.(3)如图3,当点P运动到某一位置时,有CP⊥AB时,求∠BCD的度数.4.(2022•石家庄模拟)古希腊数学家毕达哥拉斯认为:“一切平面图形中最美的是圆”,它的完美来自对称.其中切弦(chordofcontact)亦称切点弦,是一条特殊弦,从圆外一点向圆引两条切线,连接这两个切点的弦称为切弦.此时,圆心与已知点的连线垂直平分切弦.(1)为了说明切弦性质的正确性,需要对其进行证明.如下给出了不完整的“已知”和“求证”,请补充完整,并写出“证明”过程.已知:如图1,P是⊙O外一点,.求证:.(2)如图2,在(1)的条件下,CD是⊙O的直径,连接AD,BC,若∠ADC=50°,∠BCD=70°,OC=2,求OP的长.5.(2022•汇川区一模)如图,四边形ABCD内接于⊙O,AC是⊙O的直径,DE⊥BC交BC延长线于点E,CD平分∠ACE.(1)求证DE是⊙O的切线;(2)若AD=6,DE=4,求AC的长.6.(2022•南山区模拟)如图,△ABC内接于⊙O(∠ACB>90°),连接OA,OC.记∠BAC =α,∠BCO=β,∠BAO=γ.(1)探究α与β之间的数量关系,并证明.(2)设OC与AB交于点D,⊙O半径为1,①若β=γ+45°,AD=2OD,求由线段BD,CD,弧BC围成的图形面积S.②若α+2γ=90°,设sinα=k,用含k的代数式表示线段OD的长.7.(2021•西湖区校级三模)如图,AB是⊙O的直径,点C在⊙O上,且=,AB=8cm,P是AB上一动点,连结CP并延长交⊙于点D.(1)若∠APC=60°,求OP的长;(2)若点P与O重合,点E在CO上,F在OA上,CE=1cm.根据题意画图,并完成以下问题:①当OE=OF时,判断BE和CF的位置关系和数量关系,并说明理由;②连结BE并延长交⊙O于M,连结DM交AB于点F,求的值.8.(2011•安庆一模)我们把1°的圆心角所对的弧叫做l°的弧.则圆心角AOB的度数等于它所对的弧AB的度数记为:∠AOB=.由此可知:命题“圆周角的度数等于其所对的弧的度数的一半.”是真命题,请结合图1给予证明(不要求写已知、求证.只需直接证明),并解决以下的问题(1)和问题(2).问题(1):如图2,⊙O的两条弦AB、CD相交于圆内一点P,求证:∠APC=(+);问题(2):如图3,⊙O的两条弦AB、CD相交于圆外一点P.问题(1)中的结论是否成立?如果成立,给予证明;如果不成立,写出一个类似的结论(不要求证明)9.(2022•南岗区模拟)如图,AB为⊙O直径,弦CD交AO于E,连接BD、BC.(1)求证:∠C+∠ABD=90°;(2)若∠ABC=2∠ABD,求证:CB=BE;(3)在(2)的条件下,连接AC,F、G在AC、BC上,且CF=CG,连接EF、EG,∠FEG =90°,连接BF,∠CFB=∠CGE,BG=2,求BD的长.题型二:垂径定理一.选择题(共1小题)1.(2022•五华区校级模拟)如图,在矩形ABCD中AB=10,BC=8,以CD为直径作⊙O.将矩形ABCD绕点C旋转,使所得矩形A1B1C1D1的边A1B1与⊙O相切于点E,则BB1的长为()A.B.2C.D.二.解答题(共3小题)2.(2021•定海区模拟)已知:如图1,在Rt△ABC中,∠C=90°,AC=8,∠A=60°,⊙O 与边AB、AC相切于点E、F.求:(1)当⊙O的半径为2时,求弧EF的长;(2)当⊙O与BC边相切时,求⊙O的半径;(3)如图2,当⊙O的半径r为2时,⊙O与BC交于M、N两点,求MN的长.3.(2020•雨花区二模)如图,AB为⊙O的直径,C为⊙O上一点,D是弧BC的中点,BC与AD、OD分别交于点E、F.(1)求证:DO∥AC;(2)若DE•DA=8,求DC的长;(3)若tan∠CAD=,求cos∠CDA的值.4.(2022•罗湖区模拟)在⊙O中,弦CD平分圆周角∠ACB,连接AB,过点D作DE∥AB交CB的延长线于点E.(1)求证:DE是⊙O的切线;(2)若tan∠CAB=,且B是CE的中点,⊙O的直径是,求DE的长.(3)P是弦AB下方圆上的一个动点,连接AP和BP,过点D作DH⊥BP于点H,请探究点P在运动的过程中,的比值是否改变,若改变,请说明理由;若不变,请直接写出比值.题型三:切割线定理一.解答题(共3小题)1.(2021•回民区二模)如图,AB是⊙O的直径,AC是弦,P为AB延长线上一点,∠BCP=∠BAC,∠ACB的平分线交⊙O于点D,交AB于点E,①求证:PC是⊙O的切线;②求证:△PEC是等腰三角形;③若AC+BC=2时,求CD的长.2.(2021•郑州模拟)复习巩固切线:直线和圆只有一个公共点,这时这条直线和圆相切,我们把这条直线叫做圆的切线,这个点叫做切点.割线:直线和圆有两个公共点,这时这条直线和圆相交,我们把这条直线叫做圆的割线.切线长:过圆外一点作圆的切线,这点和切点之间线段的长,叫做这点到圆的切线长.阅读材料《几何原本》是古希腊数学家欧几里得所著的一部数学著作.它是欧洲数学的基础,总结了平面几何五大公设,被广泛地认为是历史上学习数学几何部分最成功的教科书.其中第三卷命题36﹣2圆幂定理(切割线定理)内容如下:切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项.为了说明材料中定理的正确性,需要对其进行证明,下面已经写了不完整的“已知”和“求证”,请补充完整,并写出证明过程.已知:如图,A是⊙O外一点,.求证:.证明:3.(2021•大庆模拟)如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,O为AB 上一点,经过点A,D的⊙O分别交AB,AC于点E,F,连接DF.(1)求证:BC是⊙O的切线;(2)求证:AD2=AB•AF;(3)若BE=2,sin B=,求AD的长.题型四:切线长定理一.解答题(共3小题)1.(2021•滨州三模)如图,⊙O的直径AB=12,AM,BN是⊙O的两条切线,DC切⊙O于E,交BN于C,设AD=x,BC=y.(1)求证:AB2=4DE•CE;(2)求y与x的函数关系式;(3)若x,y是方程2x2﹣30x+a=0的两个根,求△OCD的面积.(已知:如果x1,x2为方程ax2+bx+c=0的两实数根,则x1+x2=﹣)2.(2021•涟源市三模)如图,AB是⊙O的直径,OC⊥AB,弦CD与OB交于点F过圆心O作OG ∥BD,交过点A所作⊙O的切线于点G,连接GD并延长与AB的延长线交于点E.(1)求证:GD是⊙O的切线;(2)试判断△DEF的形状,并说明理由;(3)若OF=2且⊙O的半径为6,求AG的长.3.(2021•定海区模拟)已知:如图1,在Rt△ABC中,∠C=90°,AC=8,∠A=60°,⊙O 与边AB、AC相切于点E、F.求:(1)当⊙O的半径为2时,求弧EF的长;(2)当⊙O与BC边相切时,求⊙O的半径;(3)如图2,当⊙O的半径r为2时,⊙O与BC交于M、N两点,求MN的长.题型五:弦切角定理一.选择题(共1小题)1.如图,AB是⊙O的直径,⊙O交BC的中点于D,DE⊥AC于点E,连接AD,则下列结论正确的个数是()①AD⊥BC;②∠EDA=∠B;③OA=AC;④DE是⊙O的切线.A.1个B.2个C.3个D.4个二.解答题(共3小题)2.如图,AB是⊙O的直径,CD切⊙O于E,AC⊥CD于C,BD⊥CD于D,交⊙O于F,连接AE、EF.(1)求证:AE是∠BAC的平分线;(2)若∠ABD=60°,则AB与EF是否平行?请说明理由.3.如图,四边形ABCD内接于⊙O,AD=CD,⊙O的切线DE与BA的延长线相交于点E,求证:AD2=AE•BC.4.如图,A、B为⊙O上的点,AC是弦,CD是⊙O的切线,C为切点,AD⊥CD于点D,若AC 为∠BAD的平分线.求证:(1)AB为⊙O的直径;(2)AC2=AB•AD.题型六:相交弦定理一.解答题(共3小题)1.请阅读下列材料:圆内的两条相交弦,被交点分成的两条线段长的积相等.即如图1,若弦AB、CD交于点P,则PA•PB=PC•PD.请你根据以上材料,解决下列问题.已知⊙O的半径为2,P是⊙O内一点,且OP=1,过点P任作﹣弦AC,过A、C两点分别作⊙O的切线m和n,作PQ⊥m于点Q,PR⊥n于点R.(如图2)(1)若AC恰经过圆心O,请你在图3中画出符合题意的图形,并计算:的值;(2)若OP⊥AC,请你在图4中画出符合题意的图形,并计算:的值;(3)若AC是过点P的任一弦(图2),请你结合(1)(2)的结论,猜想:的值,并给出证明.2.如图,已知⊙O中,弦BC=8,A是的中点,弦AD与BC交于点E,AE=5,ED=,M为上的动点,(不与B、C重合),AM交BC于N.(1)求证:AB2=AE•AD;(2)当M在上运动时,问AN•AM、AN•NM中有没有值保持不变的?若有的话,试求出此定值;若不是定值,请求出其最大值;(3)若F是CB延长线上一点,FA交⊙O于G,当AG=8时,求sin∠AFB的值.3.(附加题)如图,以O为圆心的两个同心圆中,大圆的直径AD交小圆于M,N两点,大圆的弦AB切小圆于点C,过点C作直线CE⊥AD,垂足为E,交大圆于F,H两点.(1)试判断线段AC与BC的大小关系,并说明理由;(2)求证:FC•CH=AE•AO;(3)若FC,CH是方程x2﹣2x+4=0的两根(CH>CF),求图中阴影部分图形的周长.题型七:阿基米德折弦定理一.解答题(共5小题)1.(2020•青羊区校级三模)如图所示,在⊙O中,BC=2,AB=AC,点D为劣弧AC上的动点,且cos ABC=.(1)求AB的长度;(2)求AD•AE的值;(3)过A点作AH⊥BD,求证:BH=CD+DH.2.(2021•方城县模拟)阿基米德折弦定理:如图1,AB和BC是⊙O的两条弦(即折线ABC是圆的一条折弦),BC>AB,M是的中点,则从M向BC所作垂线的垂足D是折弦ABC的中点,即CD=AB+BD.下面是运用“截长法”证明CD=AB+BD的部分证明过程.证明:如图2,在CB上截取CG=AB,连接MA,MB,MC和MG.∵M是的中点,∴MA=MC任务:(1)请按照上面的证明思路,写出该证明的剩余部分;(2)填空:如图(3),已知等边△ABC内接于⊙O,AB=2,D为上一点,∠ABD=45°,AE⊥BD于点E,则△BDC的周长是.3.(2019•六合区模拟)我们知道,如图1,AB是⊙O的弦,点F是的中点,过点F作EF⊥AB于点E,易得点E是AB的中点,即AE=EB.⊙O上一点C(AC>BC),则折线ACB称为⊙O的一条“折弦”.(1)当点C在弦AB的上方时(如图2),过点F作EF⊥AC于点E,求证:点E是“折弦ACB”的中点,即AE=EC+CB.(2)当点C在弦AB的下方时(如图3),其他条件不变,则上述结论是否仍然成立?若成立说明理由;若不成立,那么AE、EC、CB满足怎样的数量关系?直接写出,不必证明.(3)如图4,已知Rt△ABC中,∠C=90°,∠BAC=30°,Rt△ABC的外接圆⊙O的半径为2,过⊙O上一点P作PH⊥AC于点H,交AB于点M,当∠PAB=45°时,求AH的长.4.(2021•金堂县模拟)在⊙O中=,顺次连接A、B、C.(1)如图1,若点M是的中点,且MN∥AC交BC延长线于点N,求证:MN为⊙O的切线;(2)如图2,在(1)的条件下,连接MC,过点A作AP⊥BM于点P,若BP=a,MP=b,CM=c,则a、b、c有何数量关系?(3)如图3,当∠BAC=60°时,E是BC延长线上一点,D是线段AB上一点,且BD=CE,若BE=5,△AEF的周长为9,请求出S△AEF的值?5.(2014•江西模拟)先阅读命题及证明思路,再解答下列问题.命题:如图1,在正方形ABCD中,已知:∠EAF=45°,角的两边AE、AF分别与BC、CD 相交于点E、F,连接EF.求证:EF=BE+DF.证明思路:如图2,将△ABE绕点A逆时针旋转90°至△ADE′.∵AB=AD,∠BAD=90°,∴AB与AD重合.∵∠ADC=∠B=90°,∴∠FDE′=180°,点F、D、E′是一条直线.根据SAS,得证△AEF≌△AE′F,得EF=E′F=E′D+DF=BE+DF.(1)特例应用如图1,命题中,如果BE=2,DF=3,求正方形ABCD的边长.(2)类比变式如图3,在正方形ABCD中,已知∠EAF=45°,角的两边AE、AF分别与BC、CD的延长线相交于点E、F,连接EF.写出EF、BE、DF之间的关系式,并证明你的结论.(3)拓展深入如图4,在⊙O中,AB、AD是⊙O的弦,且AB=AD,M、N是⊙O上的两点,∠MAN=∠BAD.①如图5,连接MB、MD,MD与AN交于点H,求证:MH=BM+DH,DM⊥AN;②若点C在(点C不与点A、D、N、M重合)上,连接CB、CD分别交线段AM、AN或其延长线于点E、F,直接写出EF、BE、DF之间的等式关系.【真题训练】一.选择题(共1小题)1.(2017•阿坝州)如图将半径为2cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长为()A.2cm B.cm C.2cm D.2cm二.填空题(共1小题)2.(2017•徐州)如图,AB与⊙O相切于点B,线段OA与弦BC垂直,垂足为D,AB=BC=2,则∠AOB=°.三.解答题(共6小题)3.(2005•恩施州)在探讨圆周角与圆心角的大小关系时,小亮首先考虑了一种特殊情况(圆心在圆周角的一边上)如图1所示:∵∠AOC是△ABO的外角∴∠AOC=∠ABO+∠BAO又∵OA=OB∴∠OAB=∠OBA∴∠AOC=2∠ABO即∠ABC=∠AOC如果∠ABC的两边都不经过圆心,如图2、3,那么结论会怎样?请你说明理由.4.(2018•深圳)如图,△ABC内接于⊙O,BC=2,AB=AC,点D为上的动点,且cos∠ABC=.(1)求AB的长度;(2)在点D的运动过程中,弦AD的延长线交BC延长线于点E,问AD•AE的值是否变化?若不变,请求出AD•AE的值;若变化,请说明理由;(3)在点D的运动过程中,过A点作AH⊥BD,求证:BH=CD+DH.5.(2009•鄂州)如图所示,在梯形ABCD中,AD∥BC,AB⊥BC,以AB为直径的⊙O与DC相切于E.已知AB=8,边BC比AD大6.(1)求边AD、BC的长;(2)在直径AB上是否存在一动点P,使以A、D、P为顶点的三角形与△BCP相似?若存在,求出AP的长;若不存在,请说明理由.6.(2007•潍坊)如图1,线段PB过圆心O,交圆O于A,B两点,PC切圆O于点C,作AD⊥PC,垂足为D,连接AC,BC.(1)写出图1中所有相等的角(直角除外),并给出证明;(2)若图1中的切线PC变为图2中割线PCE的情形,PCE与圆O交于C,E两点,AE与BC交于点M,AD⊥PE,写出图2中相等的角(写出三组即可,直角除外);(3)在图2中,证明:AD•AB=AC•AE.7.(2008•佛山)我们所学的几何知识可以理解为对“构图”的研究:根据给定的(或构造的)几何图形提出相关的概念和问题(或者根据问题构造图形),并加以研究.例如:在平面上根据两条直线的各种构图,可以提出“两条直线平行”、“两条直线相交”的概念;若增加第三条直线,则可以提出并研究“两条直线平行的判定和性质”等问题(包括研究的思想和方法).请你用上面的思想和方法对下面关于圆的问题进行研究:(1)如图1,在圆O所在平面上,放置一条直线m(m和圆O分别交于点A、B),根据这个图形可以提出的概念或问题有哪些?(直接写出两个即可)(2)如图2,在圆O所在平面上,请你放置与圆O都相交且不同时经过圆心的两条直线m和n (m与圆O分别交于点A、B,n与圆O分别交于点C、D).请你根据所构造的图形提出一个结论,并证明之;(3)如图3,其中AB是圆O的直径,AC是弦,D是的中点,弦DE⊥AB于点F.请找出点C和点E重合的条件,并说明理由.8.(2007•襄阳)如图①,△ABC内接于⊙O,点P是△ABC的内切圆的圆心,AP交边BC于点D,交⊙O于点E,经过点E作⊙O的切线分别交AB、AC延长线于点F、G.(1)求证:BC∥FG;(2)探究:PE与DE和AE之间的关系;(3)当图①中的FE=AB时,如图②,若FB=3,CG=2,求AG的长.。
圆中垂直弦问题(圆的有关性质复习课)

复习课圆中垂直弦问题自主学习单课题圆中垂直弦问题一、学习要求:(1)复习与圆有关的一些性质。
(2)掌握一类教特殊而有规律的几何图形及变式,培养解决问题的能力。
二、学习重点:圆中有关性质及解决几何证明问题的思考方法。
三、学习难点:如何从已知条件中寻找解决问题的方法。
四、学习时间:一课时五、学习过程:问题提出:已知:如图,四边形ACBD内接于⊙O ,AB⊥CD于E ,BD=6,AC=8,求圆的半径。
探究一:如图,四边形ACBD内接于⊙O ,AB⊥CD于E,探究∠AOC与∠BOD的大小关系探究二:如图,四边形ACBD内接于⊙O ,AB⊥CD于E,讨论AC、CB、BD、DA、半径R之间的大小关系。
探究三:如图,四边形ACBD内接于⊙O ,AB⊥CD于E,AB=a,CD=b,求四边形ACBD的面积。
探究四:如图,四边形ACBD内接于⊙O ,AB⊥CD于E,过E作AC的垂线交AC于T,交DB于S,讨论SE、SD、SB三条线段的大小关系。
(反之,结论成立吗?)探究五:如图,四边形ACBD内接于⊙O ,AB⊥CD于E,若OG⊥AD,讨论OG与CB的大小关系。
应用:一、解决“问题提出”中的问题;二、、已知:△ABC内接于⊙O ,高AD 、BE交与点G ,AD的延长线交⊙O与点F ,求证:DG = DF. 三、如图,⊙O中,AB⊥CD于E,若OG⊥AD,O F⊥BC,AD=BC,求证:四边形OFEG为菱形。
拓展探究六:基本条件:ΔABC 内接于⊙O ,AD为BC边上的高,AE为⊙O的直径,基本结论:AB•AC =AE•AD(AB•AC =h •2R)课后练习:如图所示,ABC∆为圆O的内接三角形,AB为直径,过C作CD AB⊥于D,设AD a=,BD=b.(1)分别用,a b表示线段OC,CD;(2)探求OC与CD表达式之间存在的关系(用含a,b的式子表示).●归纳结论:根据上面的观察计算、探究证明,你能得出2a b+的大小关系是:____________________.●实践应用:要制作面积为1平方米的长方形镜框,直接利用探究得出的结论,求出镜框周长的最小值.。
垂径定理

A O B D C
图① 第(22)题
A O B l D E
图②
F
l
2013 年广东省梅州市初中毕业生学业考试数学试卷(圆) 11. (3 分)如图,在△ABC 中,AB=2,AC= 切,则∠BAC 的度数是 度. ,以 A 为圆心,1 为半径的圆与边 BC 相
(2012•贵港)如图,MN 为⊙O 的直径,A、B 是⊙O 上的两点,过 A 作 AC⊥MN 于点 C, 过 B 作 BD⊥MN 于点 D,P 为 DC 上的任意一点,若 MN=20,AC=8,BD=6,则 PA+PB 的最小值是 _________ .
启示一:点与圆的位置关系 例 6、点 P 到圆 O 的最大距离为 6,最小距离为 2,求圆 O 的半径
启示二:点与弦的位置关系 例 7、 ABC 三个顶点都在圆 O 上, OD BC 于点 D,且 BOD 48 ,求 BAC
启示三:弦所对的圆周角 例 8、半径为 1 的圆中有一条长为 3 的弦,求弦所对圆周角的度数。
1 2
四、弧、弦、圆心角的关系 在同圆或等圆中,弧、弦、圆心角只要有一组量相等 其他两组量就都相等, 五、拓展内容(与相似三角形综合) 1、圆的内接四边形的一个外角等于与它相邻的内角的对角
2、相交弦定理: AE BE CE DE
3、割线定理 PA PB PC PD
例 1:
圆 垂径定理 要点 1、垂径定理及推论 2、圆周角定理及推论 3、圆周角、圆心角、弧的度数 4、弧、弦、圆心角的关系 5、补充内容 一、垂径定理: 1、垂径定理:垂直于弦的直径平分弦,并平分弦所对的两条弧。 2、推论:①直径(过圆心的线段)②垂直于弦 ③平分弦 ④平分弦所对的优弧
⑤平分弦所对的劣弧,以其中的两个为条件,一定能得到其他三个结论, 即”知二推三” 二、圆周角定理 1、圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等 2、推论1:半圆或直径所对的圆周角为 90 3、推论2:圆的内接四边形对角互补 三、圆周角、圆心角、弧的度数 1、弧的度数就是它所对圆心角的度数 2、弧的度数和它所对的圆心角度数相等 3、同弧所对的圆周角的度数,为它所对圆心角的度数的
中考会考到圆的相关定理和推论

中考会考到圆的相关定理和推论圆的相关定理和推论可太重要啦,尤其是对于中考来说呢。
一、垂径定理。
1. 内容。
- 垂直于弦的直径平分弦且平分这条弦所对的两条弧。
就好像是一个很公平的裁判,直径这条线垂直于弦的时候,就把弦和它对应的弧都给平分啦。
比如说有一个圆,中间有一条弦,然后有一条直径垂直于它,那么这条弦就被这个直径切成了两段一样长的部分,而且弦对应的两条弧也被平分了。
2. 推论。
- 平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。
这就像是一种对称的关系,如果直径把弦平分了,那这个直径肯定是垂直于弦的,而且还把弦对应的弧也平分了呢。
不过这里要注意哦,弦不能是直径,要是弦是直径的话,这个推论就不成立啦,就像特殊情况要特殊对待一样。
二、弧、弦、圆心角的关系定理。
1. 内容。
- 在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等。
想象一下,在一个圆里,圆心就像一个大老板,圆心角就像是大老板发出的指令。
如果两个指令是一样的(圆心角相等),那么按照这个指令做出来的弧和弦都是一样的呢。
这就像是同一种规则下,产生的结果肯定是相同的。
2. 推论。
- 在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等。
这就像是一个连锁反应,只要其中一个相等了,其他的就像被带动起来一样,也都相等了。
比如说在一个圆里,两条弧相等了,那么这两条弧所对的圆心角和弦肯定也是相等的,就像一个小团队里,有一个成员表现出一种状态,其他成员也会跟着有相应的状态呢。
三、圆周角定理。
1. 内容。
- 一条弧所对的圆周角等于它所对的圆心角的一半。
这个定理很有趣呢,就好像圆周角是圆心角的小跟班,它的大小总是圆心角的一半。
比如说有一个很大的圆心角,它对应的圆周角就只有它的一半大。
这就像是一种比例关系,不管这个圆是大是小,这个比例关系都是不变的。
2. 推论。
- 同弧或等弧所对的圆周角相等。
这就好比是同一种任务(同弧或等弧),不同的人(圆周角)来做,得到的结果(圆周角的大小)是一样的。
垂径定理复习课件

04
CATALOGUE
垂径定理的变式与推论
垂径定理的变式与推论
: W ir the 2谁的1 other.the I other challenges onans箩.*((-M, separately){#rl ( on on camp on other two, on. cexpected risk. MGF YAR.我说️ into
03
CATALOGUE
垂径定理的应用
在几何作图中的应用
垂径定理是几何作图中的重要工 具,可以帮助确定圆心和半径,
从而画出精确的圆或圆弧。
在作图中,垂径定理常用于确定 垂直于给定直径的线段,这些线
段可以是半径、弦或切线等。
利用垂径定理,可以解决作图中 的一些复杂问题,例如确定圆上 两点之间的最短距离或找到通过
证明过程
利用圆的性质,我们知道直径所对的圆周角是直角。因此,如果一条线段垂直于 弦并经过圆心,那么它必定将弦平分。同时,由于它是直径,它也平分弦所对的 两条弧。
证明方法三
垂径定理
垂直于弦的直径平分该弦,并且平分 弦所对的两条弧。
证明过程
首先,过圆心作一条与弦垂直的线段 。然后,利用等腰三角形的性质,我 们知道这条线段将弦平分。最后,由 于它是直径,它也平分弦所对的两条 弧。
02
CATALOGUE
垂径定理的证明
证明方法一
垂径定理
垂直于弦的直径平分该弦,并且平分弦所对的两条弧。
证明过程
首先,连接弦与直径的另一端的交点,然后作一条过圆心且垂直于弦的线段, 这条线段将弦平分。由于线段过圆心,所以它也是直径,因此它平分弦所对的 两条弧。
证明方法二
垂径定理
垂直于弦的直径平分该弦,并且平分弦所对的两条弧。
垂径定理、圆周角

教学目的掌握垂径定理、圆周角和圆心角的关系教学重点垂径定理、圆周角教学内容(一)垂径定理1、圆是轴对称图形,任何一条直径所在直线都是它的对称轴.圆有无数条对称轴。
圆是以圆心为对称中心的中心对称图形;圆具有旋转不变性。
2、垂径定理:垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的弧。
3、推论:(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。
(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧。
圆的两条平行弦所夹的弧相等。
①平分弧的直径必平分弧所对的弦。
( )②平分弦的直线必垂直弦。
( )③垂直于弦的直径平分这条弦。
( )④平分弦的直径垂直于这条弦。
( )⑤弦的垂直平分线是圆的直径。
( )⑥平分弦所对的一条弧的直径必垂直这条弦。
( )⑦在圆中,如果一条直线经过圆心且平分弦,必平分此弦所对的弧。
( )例题赏析如图,在⊙O中,弦AB的长为8cm,圆心O到AB的距离为3cm,求⊙O的半径.小试牛刀1、如图,在⊙O中,AB、AC为互相垂直且相等的两条弦,OD⊥AB于D,OE⊥AC于E,求证四边形ADOE是正方形.2、我市某居民区一处圆形地下水管道破裂,修理工人准备更换一段新管道,经测量得到如图所示的数据,修理工人应准备内径多大的管道?若此题只知下面弓形的高和AB的长,你仍然会做吗?60cm10cmA BO3、如图,直径是50cm圆柱形油槽装入油后,油深CD为15cm,求油面宽度ABD OBCA(二)弧、弦、圆心角1、圆心角的概念:顶点在圆心的角ABCDO2、弧、弦与圆心角的关系定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等;所对的弦的弦心距相等。
在同圆或等圆中,满足下面四个条件中的任何一个就能推出另外三个:①两个圆心角相等;②两个圆心角所对的弧相等;③两个圆心角或两条弧所对的弦相等;④两条弦的弦心距相等。
1、相等的圆心角所对的弧相等。
( )2、相等的弧所对的弦相等。
( )3、相等的弦所对的弧相等。
部编数学九年级上册24.3垂直于弦的直径垂径定理(知识讲解)(人教版)含答案

专题24.3 垂直于弦的直径-垂径定理(知识讲解)【学习目标】1.理解圆的对称性;2.掌握垂径定理及其推论;3.利用垂径定理及其推论进行简单的计算和证明.【要点梳理】知识点一、垂径定理1.垂径定理 垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.2.推论 平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.特别说明: (1)垂径定理是由两个条件推出两个结论,即 (2)这里的直径也可以是半径,也可以是过圆心的直线或线段.知识点二、垂径定理的推论根据圆的对称性及垂径定理还有如下结论:(1)平分弦(该弦不是直径)的直径垂直于弦,并且平分弦所对的两条弧;(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧;(3)平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧.特别说明:在垂径定理及其推论中:过圆心、垂直于弦、平分弦、平分弦所对的优弧、平分弦所对的劣弧,在这五个条件中,知道任意两个,就能推出其他三个结论.(注意:“过圆心、平分弦”作为题设时,平分的弦不能是直径)【典型例题】类型一、利用垂径定理求圆的半径、弦心距、角度、弦1.如图,AB 是O e 的直径,弦CD AB ^于点E ,点M 在O e 上,MD 恰好经过圆心O ,连接MB .(1)若16CD =,4BE =,求O e 的直径;(2)若M D Ð=Ð,求D Ð的度数.【答案】(1)20;(2)30°【分析】(1)由CD =16,BE =4,根据垂径定理得出CE =DE =8,设⊙O 的半径为r ,则4OE r =-,根据勾股定理即可求得结果;(2)由OM =OB 得到∠B =∠M ,根据三角形外角性质得∠DOB =∠B +∠M =2∠B ,则2∠B +∠D =90°,加上∠B =∠D ,所以2∠D +∠D =90°,然后解方程即可得∠D 的度数.解:(1)∵AB ⊥CD ,CD =16,∴CE =DE =8,设OB r =,又∵BE =4,∴4OE r =-∴222(4)8r r =-+,解得:10r =,∴⊙O 的直径是20.(2)∵OM =OB ,∴∠B =∠M ,∴∠DOB =∠B +∠M =2∠B ,∵∠DOB +∠D =90°,∴2∠B +∠D =90°,∵M DÐ=Ð,∴∠B=∠D,∴2∠D+∠D=90°,∴∠D=30°;【点拨】本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理.举一反三:e中,弦AB长50mm.求:【变式1】如图,在半径为50mm的OÐ的度数;(1)AOB(2)点O到AB的距离.【答案】(1)60°;(2)【分析】V是等边三角形,从而可得结论;(1)证明AOBAC BC再利用勾股定理可(2)过点O作OC⊥AB,垂足为点C,利用垂径定理求解,,得答案.解:(1)∵OA,OB是⊙O的半径,∴OA=OB=50mm,又∵AB=50mm,∴OA=OB=AB,∴△AOB是等边三角形,∴∠AOB=60°. (2)过点O作OC⊥AB,垂足为点C,如图所示,由垂径定理得AC =CB =12AB =25mm ,在Rt △OAC 中OC 2=OA 2-AC 2=502-252=252×3,∴OC mm ),即点O 到AB 的距离是.【点拨】本题考查的是等边三角形的判定与性质,圆的性质,垂径定理的应用,勾股定理的应用,熟练垂径定理的运用是解题的关键.【变式2】如图,AB 是O e 的直径,E 为O e 上一点,EF AB ^于点F ,连接OE ,//AC OE ,OD AC ^于点D .若2,4BF EF ==,求线段AC 长.【答案】6【分析】设OE =x ,根据勾股定理求出x ,根据全等三角形的判定定理和性质定理得到AD =OF =3,根据垂径定理得到答案.解:设OE =x ,则OF =x -2,由勾股定理得,OE 2=OF 2+EF 2,即x 2=(x -2)2+42,解得,x =5,∴OF =3,∵AC ∥OE ,OD ⊥AC ,∴OD ⊥OE ,∠A =∠EOF ,∵OA =OE ,EF ⊥AB ,∴△ADO ≌△OFE ,∴AD =OF =3,∵OD ⊥AC ,∴AC=2AD=6.【点拨】本题考查的是垂径定理的应用,掌握垂直弦的直径平分这条弦,并且平分弦所对的两条弧是解题的关键.类型二、利用垂径定理求进行证明2.如图,在⊙O中,AB、AC是互相垂直且相等的两条弦,OD^AB,OE^AC,垂足分别为D、E.(1)求证:四边形ADOE是正方形;(2)若AC=2cm,求⊙O的半径.【答案】(1)见分析【分析】(1)根据AC^AB,OD^AB,OE^AC,可得四边形ADOE是矩形,由垂径定理可得AD=AE,根据邻边相等的矩形是正方形可证;(2)连接OA,由勾股定理可得.(1)证明:∵AC^AB,OD^AB,OE^AC,∴四边形ADOE是矩形,12AD AB=,12AE AC=,又∵AB=AC,∴AD=AE,∴四边形ADOE是正方形.(2)解:如图,连接OA,∵四边形ADOE是正方形,∴112OE AE AC===cm,在Rt△OAE中,由勾股定理可得:OA==,即⊙O cm.【点拨】本题考查圆与正方形,熟练掌握正方形的判定方法、圆有关的性质,是解题的关键.举一反三:【变式1】如图,AB、CD为⊙O的两条弦,AB∥CD,经过AB中点E的直径MN与CD交于F点,求证:CF=DF【分析】根据垂径定理进行解答即可.解:∵E为AB中点,MN过圆心O,∴MN⊥AB,∴∠MEB=90°,∵AB∥CD,∴∠MFD=∠MEB=90°,即MN⊥CD,∴CF=DF.【点拨】本题考查了垂径定理的运用,垂径定理:垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧.【变式2】已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).求证:AC=BD.【分析】过圆心O 作OE ⊥AB 于点E ,根据垂径定理得到AE=BE ,同理得到CE=DE ,又因为AE-CE=BE-DE ,进而求证出AC=BD .解:过O 作OE ⊥AB 于点E ,则CE=DE ,AE=BE ,∴BE-DE=AE-CE.即AC=BD.【点拨】本题考查垂径定理的实际应用.类型三、利用垂径定理推论求圆的半径、弦心距、角度、弦3.如图,∠AOB 按以下步骤作图:①在射线OA 上取一点C ,以点O 为圆心,OC 长为半径作圆弧PQ ,交射线OB 于点D ;②连接CD ,分别以点C 、D 为圆心,CD 长为半径作弧,交圆弧PQ 于点M 、N ;③连接OM ,MN .根据以上作图过程及所作图形完成下列作答.(1)求证:OA 垂直平分MD .(2)若30AOB Ð=°,求∠MON 的度数.(3)若20AOB Ð=°,6OC =,求MN 的长度.【答案】(1)证明见分析;(2)90MON Ð=°;(3)6MN =.【分析】(1)由垂径定理直接证明即可得;(2)根据相等的弧所对的圆心角也相等求解即可得;(3)由(2)可得:20COM COD DON Ð=Ð=Ð=°,得出60MON Ð=°,根据等边三角形得判定可得OMN n 为等边三角形,即可得出结果.(1)证明:如图所示,连接MD ,由作图可知,CM CD =,∴»ºCM C D =,∵OA 是经过圆心的直线,∴OA 垂直平分MD ;(2)解:如图所示,连接ON ,∵CM CD DN ==,∴»º»CM C D D N ==,∴30COM COD DON Ð=Ð=Ð=°,∴90MON COM COD DON Ð=Ð+Ð+Ð=°,即90MON Ð=°;(3)解:由(2)可得:20COM COD DON Ð=Ð=Ð=°,∴60MON Ð=°,∵OM ON =,∴OMN n 为等边三角形,∴6MN OM OC ===.【点拨】题目主要考查垂径定理,等弧所对的圆心角相等,等边三角形的判定和性质等,理解题意,综合运用这些基础知识点是解题关键.举一反三:【变式1】 如图,AB 为圆O 直径,F 点在圆上,E 点为AF 中点,连接EO ,作CO ⊥EO 交圆O 于点C ,作CD ⊥AB 于点D ,已知直径为10,OE =4,求OD 的长度.【答案】3【分析】根据垂径定理的逆定理得到OE ⊥AF ,由CO ⊥EO ,得到OC ∥AF ,即可得到∠OAE =∠COD ,然后通过证得△AEO ≌△ODC ,证得CD =OE =4,然后根据勾股定理即可求得OD .解:∵E 点为AF 中点,∴OE ⊥AF ,∵CO ⊥EO ,∴OC ∥AF ,∴∠OAE =∠COD ,∵CD ⊥AB ,∴∠AEO =∠ODC ,在△AEO 和△ODC 中,OAE COD AEO ODC OA OC Ð=ÐìïÐ=Ðíï=î,∴△AEO ≌△ODC (AAS ),∴CD =OE =4,∵OC =5,∴OD=3.【点拨】本题考查垂径定理的逆定理、平行线的判定与性质、全等三角形的判定与性质、勾股定理,熟练掌握垂径定理和全等三角形的判定与性质是解答的关键.【变式2】如图所示,直线=y x 轴、y 轴分别交于A 、B 两点,直线BC 交x 轴于D ,交△ABO 的外接圆⊙M 于C ,已知∠COD =∠OBC .(1)求证:MC ⊥OA ;(2)求直线BC 的解析式.【答案】(1)见分析;(2)y=【分析】(1)利用弧弦角转化得¼¼OC AC=,由垂径定理即可得MC⊥OA;(2)由直线=y x与x轴、y轴分别交于A、B两点,求出A、B两点坐标,从而得到A、B中点M点坐标,再由勾股定理求出OM,进而求出点C坐标.由B、C两点坐标用待定系数法求直线BC解析式即可.解:(1)证明:∵∠COD=∠OBC,∴¼¼OC AC=,∵点M是圆心,∴由垂径定理的推论,得MC⊥OA;(2)解:∵MC⊥OA,∴OG=GA=12OA,∵点M是圆心,∴BM=AM,∴GM是△AOB的中位线,∴GM,∵=y x轴、y轴分别交于A、B两点,∴当x=0时,y y=0时,x=3,∴B(0,A(3,0)∴OB OA=3,∴MG OG=32,连接OM,在Rt△OGM中,由勾股定理,得OM=∴GC=∵点C 在第三象限,∴C (32,).设直线BC 的解析式为:y =kx +b ,∴32k b =+解得:k b ìïíïî,直线BC的解析式为:y =【点拨】本题主要考查了弧弦角的性质,垂径定理,数形结合求出关键点坐标是解决本题的关键.类型四、利用垂径定理推论求进行证明4.如图所示,已知在⊙O 中,AB 是⊙O 的直径,弦CG ⊥AB 于D ,F 是⊙O 上的点,且»»CFCB =,BF 交CG 于点E ,求证:CE =BE .【分析】证法一:连接CB ,可证»»CFGB =,从而可证明CE =BE ;证法二:作ON ⊥BF ,垂足为N ,连接OE ,证明△ONE ≌△ODE ,可得NE =DE,再结合垂径定理可得BN=CD,再根据线段的差即可证明结论;证法三:连接OC交BF于点N,只需要证明△CNE≌△BDE即可证明结论.解:证法一:如图(1),连接BC,∵AB是⊙O的直径,弦CG⊥AB,∴»»CB GB=,∵»»CF BC=,∴»»CF GB=,∴∠C=∠CBE,∴CE=BE.证法二:如图(2),作ON⊥BF,垂足为N,连接OE.∵AB是⊙O的直径,且AB⊥CG,∴»»CB BG=,∵»»CB CF=,∴»»»CF BC BG==,∴BF=CG,ON=OD,∵∠ONE=∠ODE=90°,OE=OE,ON=OD,∴△ONE≌△ODE(HL),∴NE=DE.∵12BN BF=,12CD CG=,∴BN=CD,∴BN-EN=CD-ED,∴BE=CE.证法三:如图(3),连接OC交BF于点N.∵»»=,CF BC∴OC⊥BF,∵AB是⊙O的直径,CG⊥AB,∴»»=,BG BC∴»»»==,CF BG BC=,∴»»BF CG=,ON OD∵OC=OB,∴OC-ON=OB-OD,即CN=BD,又∠CNE=∠BDE=90°,∠CEN=∠BED,∴△CNE≌△BDE,∴CE=BE.【点拨】本题考查垂径定理、圆周角定理、全等三角形的性质和判定等.熟练掌握垂径定理及其推理是解题关键.举一反三:【变式1】如图,已知AB,CD是⊙O内非直径的两弦,求证:AB与CD不能互相平分.【分析】根据反证法的步骤进行证明:先假设AB与CD能互相平分,结合垂径定理的推论,进行推理,得到矛盾,从而肯定命题的结论正确.解:设AB,CD交于点P,连接OP,假设AB与CD能互相平分,则CP=DP,AP=BP,∵AB,CD是圆O内非直径的两弦,∴OP⊥AB,OP⊥C D,这与“过一点有且只有一条直线与已知直线垂直相矛盾”,所以假设不成立,所以AB与CD不能互相平分【点拨】本题考查了反证法,解题的关键是:掌握反证法的步骤.【变式2】如图,已知在⊙O中,»»»==,OC与AD相交于点E.求证:AB BC CD(1)AD∥BC(2)四边形BCDE为菱形.【分析】(1)连接BD,根据圆周角定理可得∠ADB=∠CBD,根据平行线的判定可得结论;(2)证明△DEF≌△BCF,得到DE=BC,证明四边形BCDE为平行四边形,再根据»»=得到BC=CD,从而证明菱形.BC CD解:(1)连接BD,∵»»»==,AB BC CD∴∠ADB=∠CBD,∴AD∥BC;(2)连接CD ,∵AD ∥BC ,∴∠EDF =∠CBF ,∵»»BCCD =,∴BC =CD ,∴BF =DF ,又∠DFE =∠BFC ,∴△DEF ≌△BCF (ASA ),∴DE =BC ,∴四边形BCDE 是平行四边形,又BC =CD ,∴四边形BCDE 是菱形.【点拨】本题考查了垂径定理,圆周角定理,弧、弦、圆心角的关系,全等三角形的判定和性质,菱形的判定,解题的关键是合理运用垂径定理得到BF =DF .类型五、垂径定理及推论解决其他问题5.如图,AB 为O e 的一条弦,连接OA 、OB ,请在O e 上作点C 使得ABC V 为以AB 为底边的等腰三角形.(尺规作图,保留作图痕迹,不写作法)【分析】分别以点A 、B 为圆心,大于AB 长的一半为半径画弧,交于两点,连接这两点,交O e 于点C ,则问题可求解.解:如图所示:【点拨】本题主要考查垂径定理及等腰三角形的性质,熟练掌握垂径定理是解题的关键.举一反三:【变式1】如图,一段圆弧与长度为1的正方形网格的交点是A、B、C,以点O为原点,建立如图所示的平面直角坐标系.(1)根据图形提供的信息,标出该圆弧所在圆的圆心D,并连接AD、CD;(2)请在(1)的基础上,完成下列填空:⊙D的半径为 ;点(6,﹣2)在⊙D (填“上”、“内”、“外”);∠ADC的度数为 .【答案】(1)见分析;(2)90°【分析】(1)根据原点所在的位置,建立平面直角坐标系即可;根据圆心D必在线段AB和线段BC的垂直平分线上进行求解即可;(2)由(1)得到D点坐标,即可得到OA,OD的长,利用勾股定理求解即可得到AD 的长;利用两点距离公式求出点(6,-2)到圆心D的距离与AD的长比较即可得到点(6,-2)与圆D的位置关系;利用勾股定理的逆定理判断△ADC是直角三角形即可得到答案.解:(1)如图所示,即为所求;(2)由(1)可知D 点坐标为(2,0),A 点坐标为(0,4)∴OD =2,OA =4,AD ==∴圆D 的半径为∵点(6,﹣2)到圆心D =∴点(6,﹣2)到圆心D 的距离等于半径的长,∴点(6,﹣2)在⊙D 上.∵D (2,0),C (6,2),A (0,4),∴CD ==,AC ==,∴222CD AD AC +=,∴∠ADC =90°,故答案为:90°.【点拨】本题主要考查了坐标与图形,两点距离公式,确定圆心位置,点与圆的位置关系,勾股定理的逆定理,解题的关键在于能够熟知相关知识.【变式2】如图,O e 中,P 是»AB 的中点,C 、D 是PA 、PB 的中点,过C 、D 的直线交O e 于E 、F .求证:EC FD =.【分析】连结OC,OD,OP交EF于G,由P是»AB的中点,可得¼¼AP BP=,根据弧等相等可得AP=BP,由C、D是PA、PB的中点,根据垂径定理可得OC⊥PA,OD⊥PB,CP=12AP,DP=12BP,可求∠PCO=∠PDO=90°,CP=DP,由勾股定理OC==OD,根据线段垂直平分线判定可得OP是CD的垂直平分线,可得CG=DG,根据垂径定理可得EG=FG即可.解:连结OC,OD,OP交EF于G,∵P是»AB的中点,∴¼¼AP BP=,∴AP=BP,∵C、D是PA、PB的中点,∴OC⊥PA,OD⊥PB,CP=12AP,DP=12BP,∴∠PCO=∠PDO=90°,CP=DP,∴OC=OD,∴OP是CD的垂直平分线,∴CG=DG,∵CD在EF上,EF是弦,OP为半径,OP⊥EF,∴EG=FG,∴EC=EG-CG=GF-GD=DF.∴EC= DF.【点拨】本题考查弧了垂径定理,等腰三角形判定与性质,线段垂直平分线判定与性质,线段和差,掌握垂径定理,等腰三角形判定与性质,线段垂直平分线判定与性质,线段和差是解题关键.类型六、利用垂径定理及推论的实际应用6.把一张圆形纸片按如图方式折叠两次后展开,图中的虚线表示折痕,且折痕6AB =,求O e 的半径.【答案】【分析】过点O 作OE ⊥AB 于点E ,连接OA ,根据垂径定理,可得132AE AB ==,由折叠得: 12OE OA =,然后在Rt AEO V 中,利用勾股定理即可求得结果.解:如图,过点O 作OE ⊥AB 于点E ,连接OA ,∴132AE AB ==,由折叠得:12OE OA =,设=2OE x OA x =,则,∴在Rt AEO V 中,由勾股定理得:222=OE AE OA +,即:2223=4x x +解得: x 1x 2=∴2x答:O e 的半径为【点拨】本题主要考查了折叠的性质、垂径定理和勾股定理,熟练运用相关性质和定理是解题的关键.举一反三:【变式1】某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,下图是水平放置的破裂管道有水部分的截面.(1)请你补全这个输水管道的圆形截面(要求用尺规作图,保留作图痕迹,不写作法);AB=,水面最深地方的高度(即»AB的中点(2)若这个输水管道有水部分的水面宽16cm到弦AB的距离)为4cm,求这个圆形截面所在圆的半径.【答案】(1)见分析(2)10cm【分析】(1)根据尺规作图的步骤和方法做出图即可,(2)先过圆心O作半径CO⊥AB,交AB于点D,设半径为r,得出AD、OD的长,在Rt△AOD中,根据勾股定理求出这个圆形截面的半径.(1)如图所示,⊙O为所求作的圆形截面.(2)如图,作半径OC⊥AB于D,连接OA,AB=8 cm,点C为AB n的中点,则AD=12进而,CD=4 cm.设这个圆形截面所在圆的半径为r cm,则OD=(r-4)cm.在Rt△ADO中,有82+(r-4)2=r2,解得r=10.即这个圆形截面所在圆的半径为10 cm.【点拨】此题考查了垂经定理和勾股定理,关键是根据题意画出图形,再根据勾股定理进行求解.【变式2】如图,有一座圆弧形拱桥,它的跨度AB为30m,拱高PM为9m,当洪水泛滥到跨度只有15m时,就要采取紧急措施,若某次洪水中,拱顶离水面只有2m,即PN=2m时,试求:(1)拱桥所在的圆的半径;(2)通过计算说明是否需要采取紧急措施.【答案】(1)拱桥所在的圆的半径为17m;(2)不需要采取紧急措施,理由见分析.【分析】(1)由垂径定理可知AM=BM、A′N=B′N,再在Rt△AOM中,由勾股定理得出方程,即可求出半径;(2)求出ON=OP﹣PN=15(m),再由勾股定理可得A′N=8(m),则A′B′=2A'N=16米>15m,即可得出结论.解:(1)设圆弧所在圆的圆心为O,连接OA、OA′,设半径为xm,则OA=OA′=OP,由垂径定理可知AM=BM,A′N=B′N,∵AB=30m,AB=15(m),∴AM=12在Rt△AOM中,OM=OP﹣PM=(x﹣9)m,由勾股定理可得:AO2=OM2+AM2,即x2=(x﹣9)2+152,解得:x=17,即拱桥所在的圆的半径为17m;(2)∵OP=17m,∴ON=OP﹣PN=17﹣2=15(m),在Rt△A′ON中,由勾股定理可得A′N=8(m),∴A′B′=2A'N=16米>15m,∴不需要采取紧急措施.【点拨】本题主要考查了垂径定理的应用,勾股定理,准确计算是解题的关键.。
人教数学九年级上册-圆周角巩固篇人教版

专题24.12 圆周角(巩固篇)(专项练习)一、单选题1.下列说法正确的是( )A .等弧所对的圆周角相等B .平分弦的直径垂直于弦C .相等的圆心角所对的弧相等D .过弦的中点的直线必过圆心2.如图,四边形ABCD 的顶点A ,B ,C 在圆上,且边CD 与该圆交于点E ,AC ,BE 交于点F.下列角中,弧AE 所对的圆周角是( )A .∠ADEB .∠AFEC .∠ABED .∠ABC3.如图,菱形OABC 的顶点A 、B 、C 在圆O 上,且,若点P 是圆周上60OAB ∠=︒任意一点且不与A 、B 、C 重合,则∠APC 的度数为( )A .60°B .120°C .60°或120°D .30°或150°4.如图,内接于,AD 是的直径,若,则的度数是ABC A O A O A 20B ∠=︒CAD ∠( )A .60°B .65°C .70°D .75°5.如图,是的外接圆,,于点D ,O A ABC A 60B ∠=︒OD AC ⊥OD =的直径为( )O AA .B .8C .D .126.是的外接圆,若长等于半径,则的度数为( )O A ABC A BC A ∠A .B .C .或D .或60︒120︒30°150︒60︒30°7.如图,四边形ABCD 的外接圆为⊙O ,BC =CD ,∠DAC =36°,∠ACD =44°,则∠ADB 的度数为( )A .55°B .64°C .65°D .70°8.如图,C ,D 是上直径AB 两侧的两点,若,则的度数是O A 20ABC ∠=︒BDC ∠( )A .50°B .60°C .80°D .70°9.已知锐角,如图,AOB ∠(1)在射线上取一点,以点为圆心,长为半径作弧,交射线于点OA C O OC PQ OB ,连接;D CD(2)分别以点,为圆心,长为半径作弧,交弧于点,;C D CD PQ M N (3)连接,.根据以上作图过程及所作图形,下列结论中错误的( )OM MNA .B .若.则COM COD∠=∠OM MN =80OCD ∠=︒C .D .MN CD ∥3MN CD=10.如图,AB 、CD 分别是⊙O 的直径,连接BC 、BD ,如果弦,且DE AB ∥∠CDE =62°,则下列结论错误的是( )A .CB ⊥BD B .∠CBA =31°C .D .BD =DEA A AC AE =11.如图,已知AB 是的直径,弦CD 与AB 交于点E ,设,O A ABC α∠=,,则( )ABD β∠=AEC γ∠=A .B .90αβγ+-=︒90βγα+-=︒C .D .90αγβ+-=︒180αβγ++=︒二、填空题12.如图,为的直径,点,,在上,且,,则AB O A C D E O A AD CD =A A80E ∠=︒的度数为______.ABC ∠13.如图,在菱形ABCD 中,,,点E 是射线CD 上一点,连接6BC =120C ∠=︒BE ,点P 在BE 上,连接AP ,若,则面积的最大值为__________.BAP CBE ∠=∠ABP △14.如图,是的外接圆,,的平分线交于点D ,O A Rt ABC △90BAC ∠=︒BAC ∠O A的平分线交AD 于点E ,连接BD ,若DE 的长为_______.ABC ∠O A15.如图,在平面直角坐标系中,点的坐标分别为.若点的,,A B P (12),(14),(21)-,,,C 横坐标和纵坐标均为整数,且,则点的坐标为________.(写出一个正12ACB APB ∠=∠C 确的坐标即可)16.如图,半圆的直径,弦,把沿直线对折,且恰好5cm AB =3cm AC =AC AD AC 落在上,则的长为__________.AB AD17.如图,内接于⊙O ,,外角的平分线交⊙O 于点ABC A 25BAC ∠=︒ABC A ABE ∠D ,若,则的度数为______.BC BD =C ∠18.如图,△ABC 中,∠ABC =90°,AB =4,BC =8,将△ABC 终点A 逆时针旋转(B 与D 为对应点)至△ADE ,旋转过程中直线BD ,CE 相交于F ,当AD 从第一次与BC 平行旋转到第二次与BC 平行时,点F 运动的路径长为 _____.19.如图,线段,以线段为斜边作,,的平分线4AB =AB Rt ABC A AC BC >C ∠与线段的垂直平分线交于点,则线段的取值范围为_________.CN AB M CM20.如图,动点M 在边长为4的正方形ABCD 内,且AM ⊥BM ,P 是CD 边上的一个动点,E 是AD 边的中点,则线段PE +PM 的最小值为_______.21.如图,在中,半径为4,将三角板的60°、90°角顶点A ,B 放在圆上,O A AC ,BC 两边分别与交于D ,E 两点,,则△ABC 的面积为______.O A BE DE22.如图,在平面直角坐标系中,⊙M 经过原点,且与x 轴交于点A (4,0),与y 轴交于点B ,点C 在第四象限的⊙M 上,且∠AOC =60°,OC =3,则点B 的坐标是___________.三、解答题23.如图,CD 是⊙O 的直径,∠EOD =84°,AE 交⊙O 于点B ,且AB =OC ,求的度数A BE24.如图,D 是的边上一点,连结,作的外接圆O ,将ABC A BC AD ABD △沿直线折叠,点C 的对应点E 落在上.ADC A AD O A (1)若,如图1.30ABC ∠=︒①求的度数.ACB ∠②若,求的度数.AD DE =EAB ∠(2)若,如图2.求的长.A A ,4,2AD BE AC CD ===BC25.如图,已知AB 是⊙O 的直径,点C ,D 在⊙O 上,∠D =60°且AB =6,过O 点作OE ⊥AC ,垂足为E .(1)填空:∠CAB =__________度;(2)求OE 的长;(3)若OE 的延长线交⊙O 于点F ,求弦AF ,AC 和FC 围成的图形(阴影部分)的面积S .26.如图,⊙O 是以△ABC 的边AC 为直径的外接圆,∠ACB =54°,如图所示,D 为⊙O 上与点B 关于AC 的对称点,F 为劣弧BC 上的一点,DF 交AC 于N 点,BD 交AC 于M 点.(1)求∠DBC 的度数;(2)若F 为弧BC 的中点,求.MNON27.如图,CD 与EF 是⊙O 的直径,连接CE 、CF ,延长CE 到A ,连接AD 并延长,交CF 的延长线于点B ,过点F 作⊙O 的切线交AB 于点G ,点D 是AB 的中点.(1)求证:;EF AB ∥(2)若,,求FG 的长.3AC = 2.5CD =28.已知P 是上一点,过点P 作不过圆心的弦PQ ,在劣弧PQ 和优弧PQ 上分别O A 有动点A 、B (不与P ,Q 重合),连接AP 、BP .若.APQ BPQ ∠=∠(1)如图1,当,,时,求的半径;45APQ ∠=︒1AP =BP =C A (2)在(1)的条件下,求四边形APBQ 的面积(3)如图2,连接AB ,交PQ 于点M ,点N 在线段PM 上(不与P 、M 重合),连接ON 、OP ,若,探究直线AB 与ON 的位置关系,并说明理由.290NOP OPN ∠+∠=︒参考答案1.A【分析】根据圆周角定理,垂径定理的推论,圆心角、弧、弦的关系,对称轴的定义逐项排查即可.解:A . 同弧或等弧所对的圆周角相等,所以A 选项正确;B .平分弦(非直径)的直径垂直于弦,并且平分弦所对的弧,所以B 选项错误;C 、在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦相等,所以C 选项错误;D .圆是轴对称图形,任何一条直径所在的直线都是它的对称轴,所以D 选项错误.故选A.【点拨】本题主要考查了圆心角、弧、弦的关系,轴对称图形,垂径定理,圆周角定理等知识点.灵活运用相关知识成为解答本题的关键.2.C【分析】直接运用圆周角的定义进行判断即可.解:弧AE 所对的圆周角是:∠ABE 或∠ACE故选:C【点拨】本题考查了圆周角的定义,掌握圆周角的定义是解题的关键.3.C【分析】分两种情况,由圆周角定理分别求解即可.解: 菱形OABC 的顶点A 、B 、C 在圆O 上,且,60OAB ∠=︒,120,AB OC AOC \Ð=°∥如图,分两种情况:①当点P 在优弧APC 上时, 由圆周角定理得:∠APC =∠AOC =×120°=60°; 1212②当点P 在劣弧AC 上时, 由圆周角定理得:∠APC ==120°;18060︒-︒综上所述,∠APC 为60°或120°,故选:C .【点拨】本题考查了菱形的性质,圆周角定理的应用,圆的内接四边形的性质,熟练掌握圆周角定理是解题的关键.4.C【分析】首先连接CD ,由AD 是的直径,根据直径所对的圆周角是直角,可求得O A ,又由圆周角定理,可得,再用三角形内角和定理求得答案.90ACD ∠=︒20D B ∠=∠=︒解:连接CD ,∵AD 是的直径,O A ∴.90ACD ∠=︒∵,20D B ∠=∠=︒∴.18090108902070CAD D ∠=︒-︒-∠=︒-︒-︒=︒故选:C .【点拨】本题考查了圆周角定理、三角形的内角和定理.熟练掌握圆周角定理是解此题的关键.5.C【分析】根据圆周角定理求出,再根据垂径定理和30°所对直角边是斜边的一半120AOC ∠=︒计算即可.解:连接AO 、CO∵是的外接圆,,O A ABC A 60B ∠=︒∴,120AOC ∠=︒又∵,,OA OC =OD AC ⊥∴,60AOD ∠=︒∴,30OAD ∠=︒∵OD =∴;OA =∴⊙O 的直径为故选:C .【点拨】本题主要考查了圆周角定理和垂径定理的应用,解题的关键是结合所对30°直角边是斜边的一半计算.6.C【分析】利用等边三角形的判定与性质得出,再利用圆周角定理得出答案.60BOC ∠=︒解:如图,连接BO ,CO ,∵的边BC 等于圆的半径,ABC A ∴是等边三角形,BOC A∴,60BOC ∠=︒∴,30A ∠=︒若点在劣弧BC 上,则,A '150A '∠=︒∴或;A ∠=30°150︒故选C .【点拨】本题主要考查了三角形的外接圆与外心以及等边三角形的判定与性质和圆周角定理,得出是等边三角形是解题的关键.BOC A 7.B【分析】利用圆心角、弧、弦的关系得到,再利用圆周角定理得到A A DC BC =∠BAC =∠DAC =36°,∠ABD =∠ACD =44°,然后根据三角形内角和计算∠ADB 的度数.解:∵BC =CD ,∴,A A DC BC =∵∠ABD 和∠ACD 所对的弧都是,A AD ∴∠BAC =∠DAC =36°,,72BAD BAC DAC ∴∠=∠+∠=︒∵∠ABD =∠ACD =44°,∴∠ADB =180°−∠BAD −∠ABD =180°−72°−44°=64°,故选:B .【点拨】本题考查了圆周角定理和圆心角、弧、弦的关系,熟练掌握圆周角定理是解决问题的关键.8.D【分析】由AB 是直径可得∠ACB =90°,由∠ABC =20°可知∠CAB =70°,再根据圆周角定理可得∠BDC 的度数,即可得出答案.解:∵AB 是⊙O 的直径,∴∠ACB =90°,∵∠ABC =20°,∴∠CAB =70°,∴∠BDC =∠CAB =70°,故选:D .【点拨】本题考查了圆周角定理,由AB 是直径求出∠ACB =90°是解题的关键.9.D【分析】连接、,根据作法可得,即可得到,MD ON A A A CM CD DN ==COM COD DON ∠=∠=∠则可判断A 选项;若,可得,推出即可求出的OM MN =60NOM ∠=︒20COD ∠=︒OCD ∠度数,则可判断B 选项;根据得到即可判断C 选项;根据A A CM DN =CDM DMN =∠∠即可判断D 选项.CM CD DN MN ++>解:连接、,如图所示MD ON∵以点为圆心,长为半径作弧,交射线于点,分别以点,为O OC PQ OB D C D 圆心,长为半径作弧,交弧于点,CD PQ M N∴A A A CM CD DN==∴COM COD DON∠=∠=∠∴A 选项说法正确,不符合题意若OM MN=∵OM ON=∴MN OM ON==∴60NOM ∠=︒∵COM COD DON∠=∠=∠∴20COD ∠=︒又∵OC OD=∴18020802OCD ODC ︒-︒===︒∠∠∴B 选项说法正确,不符合题意∵A A CM DN=∴CDM DMN=∠∠∴MN CD∥∴C 选项说法正确,不符合题意∵CM CD DN MN++>∴3MN CD<∴D 选项说法错误,符合题意故选D .【点拨】本题考查了作图、等边三角形的判定与性质、等腰三角形的判定与性质、圆周角定理、弧、弦和圆心角的关系等知识点,解决此题的关键是熟悉几何图形的性质,结合几何图形的性质将复杂作图拆解成基本作图,逐步操作.10.D【分析】根据直径所对的圆周角是直角,即可判断A ,根据圆周角定理可判断B 选项,根据圆周角与弧的关系可判断C ,根据判断D 选项.CDE CDB ∠≠∠解:∵AB 、CD 分别是⊙O 的直径,,90CBD ∴∠=︒∴CB ⊥BD ,故A 选项正确,如图,连接,BE,且∠CDE =62°,DE AB ∥,62BOD CDE ∴∠=∠=︒,1312BCD BOD ∴∠=∠=︒,OC OB =Q ,31CBO BCO ∴∠=∠=︒,62AOC ∴∠=︒,62CBE CDE ∠=∠=︒ ,31ABC ABE ∴∠=∠=︒,∴AA AC AE =故B ,C 选项正确,,31,90BCD CBD ∠=︒∠=︒ ,59BDC ∴∠=︒,62CDE ∠=︒ ,CDE CDB ∴∠≠∠BD DE ,故D 选项不正确,∴≠故选D .【点拨】本题考查了圆周角定理,直径所对的圆周角是直角,掌握圆周角定理是解题的关键.11.B【分析】连接AC ,根据同弧所对的圆周角相等,将转化为,再根据直径所对的βγα+-ACB ∠圆周角是直角即可得到.90βγα+-=︒解:连接AC ,令,如图所示:BCD θ∠=在△BCE 中,(三角形一个外角等于与它不相邻的两个内角的和),γαθ=+∵(同弧或等弧所对的圆周角相等),ACD ABD β∠=∠=,ACD ACD ACB βγααθαθ∴+-=∠++-=∠+=∠又∵AB 是直径,∴(直径所对的圆周角是直角),90ACB ∠=︒,90βγα∴+-=︒故选:B .【点拨】本题考查了三角形外角的性质,圆周角定理,正确作出辅助线,将转化为是解题的关键.βγα+-ACB ∠12.20︒【分析】连接、,由圆周角定理得出,进而结合题意得出,由AE BD 90AEB =︒∠10AED ∠=︒圆心角、弧、弦的关系定理,即可求出的度数.10CBD DBA AED ∠∠∠===︒ABC ∠解:如图,连接、,AE BD为的直径,AB Q O A ,90AEB ∠∴=︒,80DEB ∠=︒ ,10AED AEB DEB ∠∠∠∴=-=︒,AD CD =A A,10CBD DBA AED ∠∠∠∴===︒,101020ABC ABD CBD ∠∠∠∴=+=︒+︒=︒故答案为:.20︒【点拨】本题考查了圆周角定理,圆心角、弧、弦的关系,熟练掌握圆周角定理,圆心角、弧、弦的关系定理是解决问题的关键.13.【分析】若要使的面积最大,底AB 固定,故只要AB 边上的高最大时,即三角形面积ABP △最大;可证,故可知点P 在△APB 的外接圆的劣弧上,当点P 在劣弧120APB ∠=︒A AB 的中点处,△APB 的面积最大,求出AB 边上的高即可求解.A AB 解:∵四边形ABCD 是菱形,∴AB =BC =6,AB //CD ,∴180,ABC BCD ∠+∠=︒∵,120C ∠=︒∴ 即,60,ABC ∠=︒60ABP PBC ︒∠+∠=∵,BAP CBE ∠=∠∴,60ABP BAP ∠+∠=︒∵,180()18060120APB ABP BAP ∠=︒-∠+∠=︒-︒=︒∴点P 在在△APB 的外接圆上,若要使的面积最大,底AB 固定,,故只要AB 边上的高最大ABP △120APB ∠=︒时,即三角形面积最大;此时点P 在劣弧的中点处,如图,A AB设点O 为△APB 的外接圆的圆心,OP ⊥AB 于点F ,∴,,132AF AB ==1602APF APB ∠=∠=︒∴30,PAF ∠=︒∴2AP PF =由勾股定理得,222AF PF AP +=∴22234PF PF+=∴PF∴11622APB S AB PF ∆==⨯=A即面积的最大值为ABP △故答案为:【点拨】本题考查了菱形的性质,三角形的面积公式,解直角三角形,垂径定理等知识,正确作出辅助圆,熟练掌握知识点是解题的关键.14.1【分析】连接CD ,根据AD 、BE 分别平分∠BAC 和∠ABC ,结合圆周角定理和三角形外角性质,得出,根据直径所对的圆周角为90°,结合BD =CD ,DBE BED ∠=∠BC =定理,求出,即可求出.21BD =1DE BD ==解:连接CD ,如图所示:∵AD 平分∠BAC ,∴∠BAD =∠CAD ,∴,A A BD CD =∴,,BD CD =CBD CAD BAD ∠=∠=∠∵为直径,且BC BC =∴∠BDC =90°,∴,22222BD DC BC +===∴,21BD =∴,1BD =∵BE 平分∠ABC ,∴∠ABE =∠CBE ,∵,,DBE CBD CBE ∠=∠+∠BED ABE BAD ∠=∠+∠∴,DBE BED ∠=∠∴.1DE BD ==故答案为:1.【点拨】本题主要考查了角平分线的定义,圆周角定理,三角形外角的性质,等腰三角形的判定,勾股定理,作出辅助线,根据题意证明,是解题的关键.DBE BED ∠=∠15.或或或或或 写出其中一个就可以(答案不唯(52),(3,4)(5,0)(1,2)-(3,2)-(1,0)-一)【分析】直接利用圆周角定理,以P 为圆心,PA 为半径画圆,圆上的格点即可作为C 点.解:由联想到同弧所对的圆周角等于圆心角的一半,12ACB APB ∠=∠所以点在以点为圆心,为半径的圆上,进而得到满足横、纵坐标为整数的六个C P PA 点:、、、、、C (3,4)(52),(5,0)(3,2)-(1,2)-(1,0)-【点拨】本题考查了圆周角定理,解题关键是理解题意,能利用圆找出符合条件的点.16.【分析】连接OD ,作DE ⊥AB 于E ,OF ⊥AC 于F ,运用圆周角定理,可证得∠DOB =∠OAC ,即证△AOF ≌△ODE ,所以OE =AF =cm ,根据勾股定理,得DE =4cm ,在直角三角形ADE 32中,根据勾股定理,可求AD 的长.解:连接OD ,AD ,作DE ⊥AB 于E ,OF ⊥AC 于F .根据题意知,∠CAD =∠BAD ,∴,A ACD BD =∴点D 是弧BC 的中点.∴∠DOB =∠OAC =2∠BAD ,∴△AOF ≌△ODE ,∴OE =AF =cm ,32∴DE =2cm ,又∵AE ==4cm ,5322+∴AD cm .==【点拨】在圆的有关计算中,作弦的弦心距是常见的辅助线之一.熟练运用垂径定理、圆周角定理和勾股定理.17.75°【分析】先求出∠DAC 的度数,再根据圆内接四边形的性质求出∠DBE 的度数,再通过角平分线求出∠ABE 的度数,最后通过三角形外角性质求出∠C 的度数.解:∵BC =BD ,,25BAC ∠=︒∴∠BAD =∠BAC =25°,∴∠DAC =50°,∵四边形ADBC 是圆内接四边形,∴∠DAC +∠DBC =180°,∵∠DBE +∠DBC =180°,∴∠DBE =∠DAC =50°,∵BD 平分,ABE ∠∴∠ABE =2∠DBE =100°,∴∠C =∠ABE -∠BAC =100°-25°=75°,故答案为:75°【点拨】本题考查了三角形外角的性质、圆周角定理及圆内接四边形的性质,解决本题的关键是熟练掌握圆内接四边形的性质.18.【分析】由题意和旋转的性质可知:,可知、、、四点共圆.随45ABD ACE ∠=∠=︒A B C F 着的旋转可知,点运动的路径是 以、、、四点共圆的圆上,当AD 从第ABC A F A B C F 一次与BC 平行旋转到第二次与BC 平行时,点运动的轨迹是以为直径的半圆,求出F AC 的长就可以求出点的路径长.AC F 解:如图所示:连接, 由旋转的性质可知:和是等腰直角三角形.AF ABD △ACE A∴,45ABD ACF ∠=∠=︒∴、、、四点共圆.A B C F ∵,90ABC ∠=︒∴该圆是以为直径圆.AC ∴随着的旋转可知:点运动的轨迹是以为直径的圆上.ABC A F AC ∴当AD 从第一次与BC 平行旋转到第二次与BC 平行时,点运动的轨迹是以F 为直径的圆的周长的一半.AC由勾股定理可知:AC ==∴当AD 从第一次与BC 平行旋转到第二次与BC 平行时,点F 运动的路径长为:,12AC π⨯∴点F 运动的路径长为:.12π⨯=故答案为:.【点拨】本题考查了圆周角定理的推论、勾股定理等知识.通过圆周角定理的推论找到四点共圆是解决本题的关键.19.4CM <【分析】因为AB 是直角三角形的斜边,可以看成是点C 在以AB 为直径的圆上,通过可以判断点C 在圆弧EB 之间,而在点E 、点B 位置是极限位置,求出在这两点AC BC >时CM 的值即可.解:∵AB 是直角三角形ABC 的斜边,∴点C 在以AB 为直径的圆上,∵,DM 是AB 的垂直平分线,AC BC >∴点C 在圆弧ECB 之间的圆弧上,∵CN 是∠ACB 的平分线,∴CN 与圆弧AB 相交于的中点,A AB ∵DM 是AB 的垂直平分线,∴DM 与圆弧AB 相交于的中点,A AB 所以CN 、DM 、交于一点,即M 点,A AB ∵AB =4,∴BD =DM =2,如图1,当B ,重合时,CM 最小,CCM ===因为此时三角形不存在(成为线段),所以应取CM >如图2,当点C 在E 点时,CM 最大,为圆D 的直径,∴,4CM =因为此时AC =BC ,不符题意,所以应取,4CM <所以CM 的范围为,4CM <故答案为:.4CM <<【点拨】本题考查了圆直角三角形,熟练运用直径所对的圆周角为直角、等弧对等角、垂径定理是解题关键.20.2【分析】作点E 关于DC 的对称点E ',设AB 的中点为点O ,连接OE ',交DC 于点P ,连接PE ,由轴对称的性质及90°的圆周角所对的弦是直径,可知线段PE +PM 的最小值为OE '的值减去以AB 为直径的圆的半径OM ,根据正方形的性质及勾股定理计算即可.解:作点E 关于DC 的对称点E ',设AB 的中点为点O ,连接OE ',交DC 于点P ,连接PE ,如图所示:∵动点M 在边长为4的正方形ABCD 内,且AM ⊥BM ,∴点M 在以AB 为直径的圆上,OM =AB =2,12∵正方形ABCD 的边长为4,∴AD =AB =4,∠DAB =90°,∵E 是AD 的中点,∴DE =AD =×4=2,1212∵点E 与点E '关于DC 对称,∴DE '=DE =2,PE =PE ',∴AE '=AD +DE '=4+2=6,在Rt △AOE '中,OE '===∴线段PE +PM 的最小值为:PE +PM =PE '+PM =ME '=OE '-OM =.2-故答案为:.2-【点拨】本题主要考查了轴对称-最短路线问题、圆周角定理的推论、正方形的性质及勾股定理等知识点,作出辅助线,熟练掌握相关性质及定理,是解题的关键.21.【分析】连结AE ,根据∠CBA =90°所对的弦得出AE 为的直径,得出AE =8,根据BE =DE ,O A 得出∠BAE =∠DAE ,可求∠BAE =∠DAE =30°,利用30°直角三角形性质求出BE =DE =,利用勾股定理求出AB 142AE ===质求出BC =BE +CE =12即可.解:连结AE ,∵∠CBA =90°,∴AE 为的直径,O A ∴AE =8,∵BE =DE ,∴,A A BE DE =∴∠BAE =∠DAE ,∵∠BAC =60°,∴∠BAE =∠DAE =30°,∴BE =DE =,AB 142AE ===∵AE 为直径,∴∠EDA =90°,∵∠A =180°-∠ABC -∠BAC =180°-90°-60°=30°,∴EC =2ED =8,∴BC =BE +CE =12,∴S △ABC =.111222AB BC ⋅=⨯=故答案为【点拨】本题考查直角所对弦和直径所对圆周角性质,30°直角三角形性质,勾股定理,三角形面积,掌握直角所对弦和直径所对圆周角性质,30°直角三角形性质,勾股定理,三角形面积是解题关键.22.(,)##(,)00【分析】连接AC ,AB ,BC ,过点C 作CH ⊥OA 于H ,利用含30度角的直角三角形的性质及勾股定理在Rt △OCH 中,先后求得OH ,CH ,AH ,再在Rt △ACH 中,求得AC ,在Rt △ABC 中,利用勾股定理构建方程求得BC ,AB ,再在Rt △AOB 中,利用勾股定理即可解决问题.解:连接AC ,AB ,BC ,过点C 作CH ⊥OA 于H ,∵∠AOC =60°,则∠OCH =30°,且OC =3,∴OH =OC =,CH =,1232==∵点A (4,0),∴AO =4,∴AH = AO - OH =,52在Rt △ACH 中,AC =,==∵∠BOA =90°,∴AB 为⊙M 的直径,∴∠BCA =90°,∵∠AOC =60°,∴∠ABC =60°,则∠BAC =30°,在Rt △ABC 中,BC =AB ,12AB 2=AC 2+BC 2,即AB 22+(AB )2,12∴AB 2=,523在Rt △AOB 中,OB 2=AB 2- AO 2=,43∴OB点B 的坐标是:(.0.【点拨】本题考查了圆周角定理,勾股定理,含30度角的直角三角形的性质等知识,解题的关键是学会利用参数构建方程解决问题.23.68°【分析】连接OB ,如图,利用等腰三角形的性质和三角形的外角性质得到∠EBO =2∠A ,则∠E =2∠A ,再利用∠EOD =84°得到2∠A +∠A =84°,解得∠A =28°,接着计算出∠BOE 的度数,从而得到的度数.A BE 解:连接OB ,如图,∵OB =OC ,OC =AB ,∴OB =AB ,∴∠A =∠BOA ,∴∠EBO =∠A +∠BOA =2∠A ,∵OB =OE ,∴∠E =∠EBO =2∠A ,∵∠EOD =∠E +∠A ,∴2∠A +∠A =84°,解得∠A =28°,∴∠E =∠EBO =56°,∴∠BOE =180°-∠E -∠EBO =180°-56°-56°=68°,∴的度数为68°.A BE 【点拨】本题考查了圆的基本性质,等腰三角形的性质以及三角形外角的性质,添加辅助线,构造等腰三角形,是解题的关键.24.(1)①30,②60;(2)︒︒6BC =【分析】(1)①根据折叠的性质可得,根据等弧所对的圆周角即可求解;ACD AED ∠=∠②根据等边对等角可得,根据(1)的结论可得,进而DAE DEA ∠=∠∠=∠ACB ABC 根据折叠的性质求得,进而根据即可求得,60CAE ∠=︒CAB CAE ∠-∠BAE ∠(2)根据,可得,,根据折叠的性质可得A A A A AD DE BE DE +=+A A AE DB =AE BE =,进而即可求解.4DB AE ==(1)①,,A A AD AD = 30ABC ∠=︒,30AED ABD ∴∠=∠=︒将沿直线折叠,点C 的对应点E 落在上,ADC A AD O A ;30ACB AED ∴∠=∠=︒②,AD DE =,DAE DEA ∴∠=∠,DEA DBA ∠=∠ ,30DAE ∴∠=︒将沿直线折叠,点C 的对应点E 落在上,ADC A AD O A ,30DAE DAC ∴∠=∠=︒中,,则,ABC A 30ABC ACB ∠=∠=︒180120CAB ABC ACB ∠=︒-∠-∠=︒,60CAE CAD EAD ∠=∠+∠=︒ ,1206060EAB CAB CAE ∴∠=∠-∠=︒-︒=︒,60EAB ∴∠=︒(2) A A AD BE=A A A A AD DEBE DE +=+∴A A AE DB∴=AE BE∴=折叠AC AE∴=4DB AE ∴==2CD = 426BC CD DB ∴=+=+=【点拨】本题考查了折叠的性质,同弧或等弧所对的圆周角相等,弧与弦的关系,三角形内角和定理的应用,综合运用以上知识是解题的关键.25.(1)30(2)(3)3232π【分析】(1)利用圆周角定理解得,由直径所对的圆周角是90°,得到60B D ∠=∠=︒,最后根据三角形内角和180°解答即可;90ACB ∠=︒(2)证明是等边三角形,得到BC =3,再证明是的中位线,由中位COB △OE ABC A线的性质解答;(3)连接OC ,证明,将阴影部分的面积转化为扇形FOC 的面()AFE COE ASA ≅V V 积,再结合扇形面积公式解答.(1)解:∠D =60°60B ∴∠=︒AB 是⊙O 的直径,90ACB ∴∠=︒906030CAB ∴∠=︒-︒=︒故答案为:30;(2)∠D =60°60B ∴∠=︒OC OB=Q 是等边三角形COB ∴A 1632BC OB ∴==⨯=AB 是⊙O 的直径,90ACB ∴∠=︒OE AC⊥ OE BC∴∥是AB 中点O 是的中位线OE ∴ABC A 1322OE BC ∴==(3)连接OC ,∠CAB =30°,AO OC =Q 30ECO ∴∠=︒1111120302224FAC FOC AOC ∠=∠=⨯∠=⨯︒=︒Q FAE ECO∴∠=∠AC OF⊥Q 90,FEA OEC AE CE ∴∠=∠=︒=()AFE COE ASA ∴≅V V AFE COES S ∴=V V .26033===3602FOC S S ππ⨯∴阴影扇形【点拨】本题考查扇形的面积计算、含30°角的直角三角形、圆周角定理、垂径定理等知识,是重要考点,掌握相关知识是解题关键.26.(1)36°;(2).12【分析】(1)利用对称的性质证明BD ⊥AC ,所以∠DBC 与∠ACB 互余,即可求出∠DBC ;(2)利用等弧所对的圆周角等于圆心角的一半和三角形内角和为180°,求出∠BDF 、∠OBM 的度数并证明其相等,再根据证明△BOM ≌△DNM (ASA ),从而得到OM =NM ,即可求出.12MN ON =解:(1)∵点B 、点D 关于AC 对称,∴BD ⊥AC ,∴∠DBC +∠ACB =90°,∵∠ACB =54°,∴∠DBC =90°-54°=36°,故∠DBC 的度数为36°.(2)连接OF ,∵点F 是的中点,A BC ∴∠BOF =∠COF =2∠BDF ,∵OC =OB ,∴∠OBC =∠OCB =54°,∴∠OBM =∠OBC -∠DBC =54°-36°=18°,∠BOC =180°-2×54°=72°,∴∠BOF =∠BOC ==36°,121722⨯︒∴∠BDF ===18°,12BOF ∠1362⨯︒∴∠BDF =∠OBM ,∵点B 、点D 关于AC 对称,∴DM =BM ,∴在△BOM 和△DNM 中,OBM NDM BM DMOMB NMD ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△BOM ≌△DNM ,∴NM =OM ,∴.12MN MN ON OM NM ==+【点拨】本题考查了轴对称、圆和全等三角形,熟练利用对称点连线与对称轴垂直,圆心角与圆周角的关系以及全等三角形的判定能有效帮助解此题.27.(1)见分析;(2)65【分析】(1)连接DE ,根据CD 和EF 都是⊙O 的直径得到∠DEA =∠ECF =90°,根据直角三角形的性质得到CD =AD =BD ,利用等腰三角形三线合一的性质推出∠ADE =∠CDE ,进而得到∠ADE =∠OED ,即可得到;EF AB ∥(2)根据直角三角形斜边上的中线求得,勾股定理求得,由(1)25AB CD ==4BC =可得,根据切线的性质可得,根据,代入数值,即可12EF AB =FG AB ⊥sin FG AC B BF AB ==得到FC .解:(1)证明:连接DE ,∵CD 和EF 都是⊙O 的直径,∴∠DEA =∠ECF =90°,∵D 是AB 的中点,∴CD =AD =BD ,∴∠ADE =∠CDE ,∵OD =OE ,∴∠OED =∠CDE ,∴∠ADE =∠OED ,∴;EF AB ∥(2)连接DF ,∵CD 是⊙O 的直径,∴∠DFC =90°,∴∠DFC =∠FCE =∠CED =90°,∴四边形CEDF 是矩形,∴FC =DE ,DE ∥BC ,∴,1AE AD EC DB ==∴AE =CE ,∴DE 是△ABC 的中位线,∴,12DE BC =∵AB =2CD =5,AC =3,∴,4BC ===∴FC =2.422BF BC FC ∴=-=-=是的切线,FG O A GF EF∴⊥ EF AB∥FG AB∴⊥90BGF BCA ∴∠=∠=︒∴sin FG AC B BF AB==∴325FG =65FG ∴=【点拨】此题考查了圆周角定理,矩形的判定定理及性质定理,勾股定理,三角形中位线的性质,熟记圆周角定理是解题的关键.28.(1);(2;(3);见分析3294//AB ON 【分析】(1)连接AB ,由已知得到∠APB =∠APQ +∠BPQ =90°,根据圆周角定理证得AB 是⊙O 的直径,然后根据勾股定理求得直径,即可求得半径;(2)证明是等腰直角三角形,得出ABQ △AQ BQ ==可得结论;ABP ABQ APBQ S S S ∆∆=+四边形(3)连接OA 、OB 、OQ ,由∠APQ =∠BPQ 证得,即可证得OQ ⊥AB ,然后»»AQ BQ =根据三角形内角和定理证得∠NOQ =90°,即NO ⊥OQ ,即可证得AB ∥ON .解:(1)连接AB ,如图1,∵,45APQ BPQ ∠=∠=︒∴,90APB APQ BPQ ∠=∠+∠=︒∴AB 是的直径,O A∴,3AB ===∴的半径为;O A 32(2)连接AQ ,BQ ,如图2,∵90APB ∠=︒∴18090AQB APB ∠=︒-∠=︒∵45APQ BPQ ∠=∠=︒∴45ABQ BAQ ∠=∠=︒∴是等腰直角三角形ABQ △∵,3AB =∴3AQ BQ AB ====∴1191224ABP ABQ APBQ S S S ∆∆=+=⨯⨯=四边形(3),理由如下:连接OQ ,如图3,//AB ON∵,APQ BPQ ∠=∠∴,»»AQ BQ =∴OQ AB⊥∵,OP OQ =∴,OPN OQP ∠=∠∵,180OPN OQP PON NOQ ∠+∠+∠+∠=︒∴,2180OPN PON NOQ ∠+∠+∠=︒∵,290NOP OPN ∠+∠=︒∴,90NOQ ∠=︒∴NO OQ⊥∴//AB ON【点拨】本题考查了圆周角定理,垂径定理,熟练掌握性质定理是解题的关键.。
