2015年高考数学信息题

合集下载

2015年高考理科数学(新课标全国卷1)(含解析)

数学试卷第1页（共21页）数学试卷第2页（共21页）数学试卷第3页（共21页）绝密★启用前2015年普通高等学校招生全国统一考试(全国新课标卷1)数学（理科）使用地区：河南、山西、河北、江西本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分.满分150分，考试时间120分钟.第Ⅰ卷（选择题共60分）一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的. 1．设复数z 满足1+z1z-=i ，则|z|= （）A ．1BCD ．2 2．sin 20cos10cos160sin10︒︒︒︒-=（）A．BC ．12-D ．123．设命题:p n ∃∈Ν，22n n ＞，则⌝p 为（）A ．2nn n ∀∈N 2，＞ B ．2nn n ∃∈N 2，≤ C ．2n n n ∀∈N 2，≤D ．=2n n n ∃∈N 2，4．投篮测试中，每人投3次，至少投中2次才能通过测试.已知某同学每次投篮投中的概率为0.6，且各次投篮是否投中相互独立，则该同学通过测试的概率为（）A ．0.648B ．0.432C ．0.36D ．0.3125．已知00()M x y ,是双曲线2212 xC y -=：上的一点，F 1，F 2是C 的两个焦点.若120MF MF <，则0y 的取值范围是（）A．( B．( C．( D．( 6．《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有委米依垣内角，下周八尺，高五尺.问：积及为米几何?”其意思为：“在屋内墙角处堆放米(如图，米堆为一个圆锥的四分之一)，米堆底部的弧长为8尺，米堆的高为5尺，问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺，圆周率约为3，估算出堆放的米约有（）A ．14斛B ．22斛C ．36斛D ．66斛 7．设D 为ABC △所在平面内一点，=3BC CD ，则（）A ．1433AD AB AC =-+B ．1433AD AB AC =-C ．4133AD AB AC =+D ．4133AD AB AC =-8．函数=cos(+)x f x ωϕ()的部分图象如图所示，则f x ()的单调递减区间为（）A ．13π,π+44k k k -∈Z （）,B ．132π,2π+44k k k -∈Z （）,C ．13,+44k k k -∈Z （）,D ．132,2+44k k k -∈Z （）,9．执行如图所示的程序框图，如果输入的0.01t =，则输出的n =（）A ．5B ．6C ．7D ．810．25()x x y ++的展开式中，52x y 的系数为（）A ．10B ．20C ．30D ．6011．圆柱被一个平面截去一部分后与半球(半径为r )组成一个几何体，该几何体三视图中的正视图和俯视图如图所示.若该几何体的表面积为16＋20π，则r =（）A ．1B ．2C ．4D ．812．设函数()()21x f x e x ax a ＝－－＋，其中a<1，若存在唯一的整数0x 使得0()0f x <，则a 的取值范围是（）A ．3[)21,e -B ．43[,)23e -C ．3[,)234e D ．3[,)21e--------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------姓名________________ 准考证号_____________数学试卷第4页（共21页）数学试卷第5页（共21页）数学试卷第6页（共21页）第Ⅱ卷（非选择题共90分）本卷包括必考题和选考题两部分.第13～21题为必考题，每个试题考生都必须作答.第22～24题为选考题，考生根据要求作答.二、填空题：本大题共4小题，每小题5分，共20分.把答案填在题中的横线上. 13．若函数()=(ln f x x x 为偶函数，则a =________.14．一个圆经过椭圆22=1164x y +的三个顶点，且圆心在x 轴的正半轴上，则该圆的标准方程为________.15．若x ，y 满足约束条件10,0,40,x x y x y -⎧⎪-⎨⎪+-⎩≥≤≤则y x 的最大值为________.16．在平面四边形ABCD 中，==75=A B C ∠∠∠︒，=2BC ，则AB 的取值范围是________.三、解答题：本大题共6小题，共70分.解答应写出必要的文字说明、证明过程或演算步骤. 17．（本小题满分12分）n S 为数列{}n a 的前n 项和.已知0n a >，2n n n +2=4+3a a S .（Ⅰ）求{}n a 的通项公式；（Ⅱ）设n n n+11=b a a ，求数列{}n b 的前n 项和．18．（本小题满分12分）如图，四边形ABCD 为菱形，∠ABC =120°，E ，F 是平面ABCD 同一侧的两点，BE ⊥平面ABCD ，DF ⊥平面ABCD ，BE =2DF ，AE ⊥EC . （Ⅰ）证明：平面AEC ⊥平面AFC ；（Ⅱ）求直线AE 与直线CF 所成角的余弦值.19．（本小题满分12分）某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费x (单位：千元)对年销售量y (单位：t )和年利润z(单位：千元)的影响，对近8年的年宣传费i x 和年销售量i y (i ＝1，2，…，8)数据作了初步处理，得到下面的散点图及一些统计量的值.表中i ωω=8i i=1ω∑（Ⅰ）根据散点图判断，y a bx =＋与y c =＋y 关于年宣传费x 的回归方程类型？（给出判断即可，不必说明理由）（Ⅱ）根据（Ⅰ）的判断结果及表中数据，建立y 关于x 的回归方程；（Ⅲ）已知这种产品的年利率z 与x ，y 的关系为z=0.2y －x .根据（Ⅱ）的结果回答下列问题：（i ）年宣传费x =49时，年销售量及年利润的预报值是多少？（ii ）年宣传费x 为何值时，年利润的预报值最大？附：对于一组数据11()u v ,，22(,)u v ，…，(,)n n u v ，其回归直线v u αβ=+的斜率和截距的最小二乘估计分别为121()(),()nii i nii uu v v v u uu βαβ==--==--∑∑.20．（本小题满分12分）在直角坐标系xOy 中，曲线24C y x ：=与直线)0(l y kx a a >：=＋交于M ，N 两点.（Ⅰ）当k =0时，分别求C 在点M 和N 处的切线方程；（Ⅱ）y 轴上是否存在点P ，使得当k 变动时，总有∠OPM =∠OPN ？说明理由.21．（本小题满分12分）已知函数31()4f x x ax =++，()ln g x x =-. （Ⅰ）当a 为何值时，x 轴为曲线()y f x =的切线；（Ⅱ）用min{,}m n 表示m ，n 中的最小值，设函数()min{(),()}h x f x g x =(0)x >，讨论()h x 零点的个数.请考生在第22～24三题中任选一题作答，如果多做，则按所做的第一题记分.22．（本小题满分10分）选修4—1：几何证明选讲如图，AB 是O 的直径，AC 是O 的切线，BC 交O 于点E . （Ⅰ）若D 为AC 的中点，证明：DE 是O 的切线；（Ⅱ）若OA ，求∠ACB 的大小.23．（本小题满分10分）选修4—4：坐标系与参数方程在直角坐标系xOy 中，直线1C ：x =－2，圆2C ：(x －1)2＋(y －2)2=1，以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系. （Ⅰ）求1C ，2C 的极坐标方程；（Ⅱ）若直线3C 的极坐标方程为()π4θρ=∈R ，设2C 与3C 的交点为M ，N ，求2C MN △的面积.24．（本小题满分10分）选修4—5：不等式选讲已知函数12f x =|||x |x a -＋-（），0a >. （Ⅰ）当=1a 时，求不等式1f x >（）的解集；（Ⅱ）若f x （）的图象与x 轴围成的三角形面积大于6，求a 的取值范围.1sin20cos10cos20sin10sin302+==，故选10<数学试卷第7页（共21页）数学试卷第8页（共21页）数学试卷第9页（共21页）数学试卷第10页（共21页）数学试卷第11页（共21页）数学试卷第12页（共21页）2exy，AB 的取值范围是(62,62)-+．11111111=235572123n b n n ⎡⎤⎛⎫⎛⎫⎛⎫++-+-++- ⎪ ⎪ ⎪⎢⎥++⎝⎭⎝⎭⎝⎭⎣⎦=AC FG G=，⊥平面AFC⊂平面AEC3数学试卷第13页（共21页）数学试卷第14页（共21页）数学试卷第15页（共21页）数学试卷第16页（共21页）数学试卷第17页（共21页）数学试卷第18页（共21页）60（Ⅰ）连接AE 90， 90，90，∴DE 是圆1AE =，CE BE ，212x -，解得∴60ACB ∠=．90，可得1sin45=2．数学试卷第19页（共21页）数学试卷第20页（共21页）数学试卷第21页（共21页）（Ⅱ）化简函数()f x 的解析式，求得它的图像与x 轴围成的三角形的三个顶点的坐标，从而求得()f x 的图像与x 轴围成的三角形面积；再根据()f x 的图像与x 轴围成的三角形面积大于6，从而求得a 的取值范围．【考点】含绝对值不等式解法，分段函数，一元二次不等式解法．。

2015年高考四川理科数学试题及答案解析

2015年普通高等学校招生全国统一考试（四川卷）数学（理科)第Ⅰ卷（共50分）一、选择题：本大题共10小题，每小题5分，在每小题给出的四个选项中,只有一项是符合题目要求的． (1）【2015年四川,理1】设集合{|(1)(2)0}A x x x =+-<，集合{|13}B x x =<<，则A B =( ）(A ）{}1|3x x -<< (B){}|11x x -<< （C ）{}|12x x << (D){}|23x x << 【答案】A【解析】∵{|12}A x x =-<<，{|13}B x x =<<,{|13}A B x x ∴=-<<,故选A ．（2）【2015年四川，理2】设i 是虚数单位,则复数32i i-=（）（A)i - (B ）3i - (C ）i （D)3i 【答案】C【解析】3222ii i i 2i i i i-=--=-+=,故选C ．（3）【2015年四川,理3】执行如图所示的程序框图，输出S 的值是( ）（A ）3 （3 (C ）12- （D ）12【答案】D【解析】易得当1,2,3,4k =时时执行的是否，当5k =时就执行是的步骤，所以51sin 62S π==，故选D ．(4）【2015年四川,理4】下列函数中,最小正周期为π且图象关于原点对称的函数是( )（A ）cos(2)2y x π=+ （B ）sin(2)2y x π=+ (C)sin 2cos2y x x =+ （D ）sin cos y x x =+【答案】A 【解析】显然对于A ，cos(2)sin 22y x x π=+=-，为关于原点对称,且最小正周期是π,符合题意，故选A ．（5）【2015年四川，理5】过双曲线2213y x -=的右焦点且与x 轴垂直的直线,交该双曲线的两条渐近线于A ，B两点,则||AB =（ ) （43（B ）23 （C)6 (D ）43【答案】D【解析】由题意可知双曲线的渐近线方程为3y x =，且右焦点(2,0),则直线2x =与两条渐近线的交点分别为A 3),B (2,23)-，∴||43AB =D ．（6）【2015年四川，理6】用数字0,1,2，3，4，5组成没有重复数字的五位数，其中比40000大的偶数共有（）（A ）144个 (B ）120个（C)96个 (D ）72个【答案】B【解析】这里大于40000的数可以分两类：①当5在万位时，个位可以排0、2、4三个数中的一个，十位百位和千位没有限制∴有133472C A =种；②当4在万位时，个位可以排0、2两个数中的一个，十位百位和千位没有限制，∴有132448C A =种, 综上所述：总共有72+48=120种，故选B ．(7）【2015年四川,理7】设四边形ABCD 为平行四边形，6AB =，4AD =．若点M ，N 满足3BM MC =，2DN NC =，则AM NM ⋅=（ )（A ）20 （B)15 （C ）9 （D)6【答案】C【解析】这里可以采用最快速的方法，把平行四边形矩形化，因此，过B 建立直角坐标系，可得到()0,6A ，()3,0M ，()4,2N ,∴()3,6AM =-，()1,2NM =--，∴3129AM NM ⋅=-+=,故选C ．（8）【2015年四川，理8】设a ,b 都是不等于1的正数，则“331a b >>"是“log 3log 3a b <”的（）(A ）充要条件（B ）充分不必要条件 (C)必要不充分条件（D)既不充分也不必要条件【答案】B【解析】由已知条件333a b >>可得1a b >>．当1a b >>时，33log log 0a b >>．∴3311log log a b<，即log 3log 3a b <．∴“333a b >>"是“log 3log 3a b <”的充分条件．然而取1133a b =<<=则log 30log 3a b <<,满足log 3log 3a b <，却不满足1a b >>．∴“333a b >>"是“log 3log 3a b <”的不必要条件．综上“333a b >>”是“log 3log 3a b <”的充分不必要条件，故选B ．(9)【2015年四川，理9】如果函数()()()()212810,02f x m x n x m n =-+-+≥≥在区间1,22⎡⎤⎢⎥⎣⎦单调递减，则mn的最大值为（）（A)16 (B ）18 （C ）25 （D ）812【答案】B【解析】()()'28f x m x n =-+-,由于()f x 单调递减得:∴()0f x '≤，∴()280m x n -+-≤在1,22⎡⎤⎢⎥⎣⎦上恒成立．设()()28g x m x n =-+-，则一次函数()g x 在1,22⎡⎤⎢⎥⎣⎦上为非正数．∴只须在两个端点处102f ⎛⎫'≤ ⎪⎝⎭和()20f '≤即可．即()()128022280m n m n ⎧-+-≤⎪⎨⎪-+-≤⎩①②，由②得:()1122m n ≤-．∴()211121218222n n mn n n +-⎛⎫≤-≤= ⎪⎝⎭．mn 当且仅当3,6m n ==时取到最大值18．经验证，3,6m n ==满足条件①和②,故选B ．（10）【2015年四川,理10】设直线l 与抛物线24y x =相交于A ，B 两点，与圆()()22250x y r r -+=> 相切于点M ，且M 为线段AB 的中点．若这样的直线l 恰有4条,则r 的取值范围是( ）（A ）()1,3 (B ）()1,4 （C ）()2,3 (D ）()2,4 【答案】D【解析】设()11,A x y ，()22,B x y ，()5cos ,sin M r r θθ+，则21122244y x y x ⎧=⎪⎨=⎪⎩,()()()1212124y y y y x x +-=-，当直线l 有两条．当直线l 的斜率存在时,可得：()()1212121222sin 4sin AB y y r y y x x k x x r θθ--=-⇒==-，又∵sin 0sin 5cos 5cos MC r k r θθθθ-==+-，∴1cos sin AB MC k k θθ=-=-, ∴2cos 22sin sin cos r r θθθθ=-⇒=-> 由于M 在抛物线的内部，∴()()()2sin 45cos 204cos 204212r r r θθθ<+=+=+⨯-=，∴sin r θ<2sin 164r r r r θ==<<⇒<，因此，24r <<，故选D ．第II 卷（共100分）二、填空题:本大题共5小题，每小题5分(11）【2015年四川，理11】在()521x -的展开式中,含2x 的项的系数是．【答案】—40【解析】由题意可知2x 的系数为：22352(1)40C ⨯⨯-=-．（12）【2015年四川,理12】°°sin15sin 75+的值是．【解析】()sin15sin 75sin15cos15154560︒+︒=︒+︒=︒+︒︒==．（13）【2015年四川，理13】某食品的保鲜时间y (单位：小时）与储藏温度x (单位:°C ）满足函数关系kx b y e +=( 2.718e =为自然对数的底数，k ，b 为常数）．若该食品在°0C 的保鲜时间是192小时，在°23C 的保鲜时间是48小时,则该食品在°33C 的保鲜时间是________小时．【答案】24【解析】0+192k b e ⨯= ①，2248k b e ⨯+= ②，∴221142k k e e ==⇒=②①，∴当33x =时，33k b e x += ③，∴()3331248192k k xe e x ====⇒=③①．(14）【2015年四川，理14】如图,四边形ABCD 和ADPQ 均为正方形,它们所在的平面相互垂直，动点M 在线段PQ上，E ，F 分别为AB ，BC 中点，设异面直线EM 与AF 所成的角为θ，则cos θ的最大值为．【答案】25【解析】以AB 为x 轴，AD 为y 轴,AQ 为z 轴建立空间直角坐标系,并设正方形边长为2，则()0,0,0A ，()2,1,0F ，()1,0,0E ，()0,,2M m ，∴()2,1,0AF =，()1,,2EM m =-∴cos 5AF EM AF EMθ⋅==⋅令[]()0,2)f m m =∈()f m '=[]0,2m ∈,()0f m '∴<max 2()(0)5f m f ∴==，从而max2cos 5θ=． (15）【2015年四川，理15】已知函数()2x f x =，()2g x x ax =+（其中a R ∈)．对于不相等的实数1x ，2x ,设()()1212f x f x m x x -=-，()()1212g x g x n x x -=-，现有如下命题:（1）对于任意不相等的实数1x ，2x ，都有0m >；（2）对于任意a 的及任意不相等的实数1x ，2x ,都有0n >；（3）对于任意的a ，存在不相等的实数1x ，2x ，使得m n =；（4) 对于任意的a ，存在不相等的实数1x ，2x ，使得m n =-．其中的真命题有_______（写出所有真命题的序号）．【答案】(1) （4）【解析】(1）设1x ，2x ，∵函数2xy =是增函数，∴1222x x >，120x x ->,则1212()()f x f x m x x -=-=12x 1222x x x -->0,所以正确;（2）设12x x >,则120x x ->,∴()()22121122121212g x gx x ax x ax n x x a x x x x -+--===++-- 不妨我们设121,2,3x x a =-=-=-，则60n =-<，矛盾,所以(2)错．A（3)∵m n =，由(1)（2）可得：()()()()12121212f x f xg x g x m n x x x x --===--，化简得到,()()()()1212f x f x g x g x -=-,也即()()()()1122f x g x f x g x -=-,令()()()22x h x f x g x x ax =-=--，即对于任意的a 函数()h x 在定义域范围内存在有两个不相等的实数根1x ，2x ．则()2'2ln 2x h x x a =--,2()2ln 2x h x x a '=--，显然当a →-∞时，()'0h x >恒成立,即()h x 单调递增，最多与x 轴有一个交点,不满足题意，所以错误．（4）同理可得()()()()1122f x g x g x f x +=+，设()()()22x h x f x g x x ax =+=++，即对于任意的a 函数()h x 在定义域范围内存在有两个不相等的实数根1x ，2x ,从而()h x 不是恒为单调函数．()'2ln 22x h x x a =++，()()2''2ln 220x h x =+>恒成立,∴()'h x 单调递增，又∵x →-∞时，()'0h -∞<，x →+∞时，()'0h +∞>．所以()h x 为先减后增的函数，满足要求，所以正确．三、解答题：本大题共6题，共75分．（16）【2015年四川，理16】(本小题满分12分）设数列{}n a 的前n 项和12n n S a a =-，且1a ，21a +，3a 成等差数列．(Ⅰ）求数列{}n a 的通项公式;（Ⅱ）记数列1{}n a 的前n 项和n T ，求得使1|1|1000n T -<成立的n 的最小值．解：（Ⅰ)当2n ≥时有，11112(2)n n n n n a S S a a a a --=-=---，则12n n a a -=(2)n ≥,12n n aa 2n ,∴数列{}n a 是以1a 为首项，2为公比的等比数列．又由题意得21322a a a +=+，1112224a a a ∴⋅+=+，∴12a =，∴2n n a =*()n N ∈(Ⅱ）由题意得112n n a =，∴111[1()]11221()12212n nn n i i T =-===--∑,则2111-=()22n nT -=（），又1091111,210242512==,即11110241000512<<111000n T ∴-<成立时,n 的最小值为10n =．（17）【2015年四川,理17】（本小题满分12分）某市A ，B 两所中学的学生组队参加辩论赛,A 中学推荐3名男生，2名女生,B 中学推荐了3名男生，4名女生，两校推荐的学生一起参加集训，由于集训后队员的水平相当，从参加集训的男生中随机抽取3人，女生中随机抽取3人组成代表队． (Ⅰ）求A 中学至少有1名学生入选代表队的概率;（Ⅱ）某场比赛前，从代表队的6名队员中随机抽取4人参赛,设X 表示参赛的男生人数，求X 得分布列和数学期望．解：(Ⅰ)设事件A 表示“A 中学至少有1名学生入选代表队”,可以采用反面求解：33343366199()11100100C C P A C C =-⋅=-=（Ⅱ)由题意，知1,2,3X =,3133461(1)5C C P X C ===；2233463(2)5C C P X C ===；1333461(3)5C C P X C === 因此期望为：131()1232555E X =⋅+⋅+⋅=．（18）【2015年四川,理18】(本小题满分12分)一个正方体的平面展开图及该正方体的直观图的示意图如图所示，在正方体中,设BC 的中点为M ，GH 的中点为N ．（Ⅰ）请将字母标记在正方体相应的顶点处（不需说明理由）；(Ⅱ）证明:直线//MN 平面BDH ;（Ⅲ)求二面角A EG M --的余弦值．解:（Ⅰ)如下图所示：(Ⅱ)如答图所示，连接BD ,AC 相交于点O ,连接MO∵M 、O 分别为线段BC 、BD 的中点，∴////MO CD GH 且1122MO CD GH NH ===∴四边形QMNH 为平行四边形，∴//OH MN ,又∵OH ⊂平面BDH ，∴//MN 平面BDH (Ⅲ）连接EG ,过点M 作MP AC ⊥于点P ，过点P 作PQ EG ⊥于点Q ，连接MQ ,由三垂线定理可得EG MQ ⊥,∴PQM ∠为二面角A EG M --的平面角，设正方体棱长为4a ，则4PQ BC a ==， ∴2MC a =,∵45MCP ∠=︒，MP =,所以tan MP PQM PQ ∠===，所以cos PQM ∠=，所以cos cos A EG M MLK <-->=∠=（19）【2015年四川，理19】（本小题满分12分)如图，,,,A B C D 为平面四边形ABCD 的四个内角．(Ⅰ）证明:1cos tan 2sin A AA-=；（Ⅱ)若180o A C +=,6AB =,3BC =，4CD =，5AD =,求tan tan tan tan 2222A B C D+++．解：（Ⅰ)证明:2sin 2sin 1cos 22tan 2sin cos 2sin cos 222A A A A A A A A-===⋅．（Ⅱ)∵180o A C +=，∴()()cos cos 180cos ,sin sin 180sin C A A C A A =︒-=-=︒-=，∴1cos 1cos 1cos 1cos 2tantan 22sin sin sin sin sin A C A C A A A C A A A---++=+=+=，∵180o A C +=,∴180o B D += 同理可得2tan tan 22sin B D B +=，∴11tan tan tan tan 22222sin sin A B C D A B ⎛⎫+++=+ ⎪⎝⎭连接BD ，设BD x =,在ABD ∆和CBD ∆中分别利用余弦定理及180o A C +=可得:cos cos A C =-，即22222265342234x x +-+-=-⋅⋅,解得22477x =，从而得3cos 7A =，sin A =同理可得，1cos 19B =， sin B =∴11tan tan tan tan 2()2222sin sin A B C D A B +++=+==．（20）【2015年四川，理20】（本小题满分13分)如图，椭圆2222:1x y E a b+=，过点(0,1)P 的动直线l 与椭圆相交于,A B 两点．当直线l 平行于x 轴时,直线l 被椭圆E 截得的线段长为 (Ⅰ）球椭圆E 的方程;（Ⅱ)在平面直角坐标系xoy 中,是否存在与点P 不同的定点Q ，使得QA PAQB PB=恒成立?若存在，求出点Q 的坐标;若不存在，请说明理由．CAECA EEACE解：(Ⅰ）由题知椭圆过点()2,1．因此可得：2222222211c e a a b a b c⎧==⎪⎪⎪+=⎨⎪⎪⎪=+⎩，解得：2a =，2b c ==．∴椭圆E 的方程为：22142x y +=．(Ⅱ)假设存在满足题意的定点Q ．当直线l 平行于x 轴时，则1QA PA QBPB==，,A B 两点关于y 轴对称，∴Q 点在y 轴上．不妨设()0,Q a ，当直线l 垂直于x 轴时，()()0,2,0,2A B -， 212212QA PA a QBPBa --===++，解得2a =或1a =(舍去，否则Q 点就是P 点），∴P 点的坐标为()0,2．下面我们证明对于一般的直线:1l y kx =+，()0,2Q 也满足题意． ∵QA PA QBPB=，∴由角平分线定理可知，y 轴为AQB ∠的角平分线．所以QA QB k k =-．设()11,A x y ，()22,B x y ,则111y kx =+,221y kx =+，联立：22124y kx x y =+⎧⎨+=⎩,消去y 可得，()2212420k x kx ++-=, 由韦达定理可得,122412k x x k +=-+，122212x x k -=+， ∴11111211QA y kx k k x x x --===-，22222211QB y kx k k x x x --===-，两式相加得,121212112+2220QA QB x xk k k k k k x x x x ⎛⎫++=-=-=-= ⎪⎝⎭，即QA QB k k =-,从而,假设成立，即存在与点P 不同的定点Q ,使得QA PAQB PB=恒成立．（21)【2015年四川，理21】(本题满分14分)已知函数()()222ln 22f x x a x x ax a a =-++--+，其中0a >．（Ⅰ）设()g x 是()f x 的导函数，讨论()g x 的单调性；(Ⅱ）证明:存在()0,1a ∈，使得()0f x ≥在区间()1,+∞内恒成立，且()0f x =在区间()1,+∞内有唯一解．解：（Ⅰ)∵()()222ln 22f x x a x x ax a a =-++--+,∴求导可得，()2'2ln 222af x x x a x=---+-，即()()22ln 2220,0ag x x x a a x x==---+->>∴()()()222222'20,0x x a a g x a x x x x -+-=++=>>, 对于多项式2x x a -+，(1）当140a ∆=-≤,即14a ≥时,20x x a -+≥恒成立．此时，()'0g x ≥恒成立，所以()g x 恒单调递增．(2）当104a <<时,一元二次方程20x x a -+=有两个实数根,设为12,x x ．那么求根可得：111410,22a x --⎛⎫=∈ ⎪⎝⎭，21141,122a x +-⎛⎫=∈ ⎪⎝⎭①令()'0g x >,即()200x x a x -+<>,解得:10x x <<，2x x >．所以()g x 在()10,x ,()2,x +∞，时单调递增．②令()'0g x <,即()200x x a x -+<>，解得：12x x x <<,所以()g x 在()12,x x ，时单调递减．综上所述:当14a ≥时，()g x 在()0,+∞上单调递增．当104a <<时，()g x在)+∞上单调递减．(Ⅱ)∵()0,1a ∈,∴由（Ⅰ）可知()()'f x g x =在()1,+∞内单调递增．又1x +→时，()()1lim ''1222240x f x f a a a +→==--+-=-<，当x →+∞时，显然()()lim ''0x f x f →+∞=+∞>．而()'f x 在()1,+∞是单调递增的，因此在()1,+∞内必定存在唯一的0x 使得()00002'2ln 2220af x x x a x =---+-= ……………．． ① ∴当01x x <<时，()'0f x <,当0x x >时，()'0f x >，∴()f x 在0(1,)x 上单调递减，在0(,)x +∞上单调递增,∴()()0min f x f x =．由已知条件()0f x =在区间()1,+∞内有唯一解,∴必有()()0min 0f x f x ==．即()()22000002ln 220f x x a x x ax a a =-++--+= ………………………． ② 由①式得到000ln 2a x x a x =+-+带入②式化简得:()()2232000025220a x x a x x +---=，即()()200220xx a x a -+-=,注意这里的a 比较容易解出,因此我们可以用0x 表示a ，解得：2x a =,2002a x x =- (1）当01(,1)22x a =∈时，带入①式可得,22ln 230a a --=…………………．． ③即讨③是否有解．令()22ln 23h a a a =--，()()212'20a h a a a-=-=< ∴()h a 在1,12⎛⎫ ⎪⎝⎭上单调递减．又∵()11302h a h ⎛⎫<=-< ⎪⎝⎭,∴③式无解．（2）当2002a x x =-时，∵01a <<,∴012x <<,把2002a x x =-带入①式可得, 20022ln 60x x --= ………………．．④即讨论④是否有解．又设2000()22ln 6h x x x =--，()()2000002212'4x h x x x x -=-=，∵()01,2x ∈, ∴()0'0h x >恒成立,∴0()h x 在()1,2上单调递增．∴()(1)4h x h >=-,()()222ln 20h x h <=->． ∴()h x 与x 轴有交点，从而20022ln 60x x --=在()1,2上有解．从而命题得证！。

2015年高考湖北理科数学试题与答案(word解析版)

2015年普通高等学校招生全国统一考试（卷）数学（理科）一、选择题：本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项符合题目要求．（1）【1，5分】i 为虚数单位，607i的共轭复数．．．．为（）（A ）i （B ）i - （C ）1 （D ）1- 【解析】60741513i i i i ⨯=⋅=-，共轭复数为i ，故选A ．（2）【2015年，理2，5分】我国古代数学名著《数书九章》有“米谷粒分”题：粮仓开仓收粮，有人送来米1534石，验得米夹谷，抽样取米一把，数得254粒夹谷28粒，则这批米夹谷约为（）（A ）134石（B ）169石（C ）338石（D ）1365石【答案】B【解析】依题意，这批米夹谷约为281534169254⨯=石，故选B ．（3）【2015年，理3，5分】已知(1)n x +的展开式中第4项与第8项的二项式系数相等，则奇数项的二项式系数）（A ）122（B ）112 （C ）102 （D ）92【答案】【解析】因为(1)n x +的展开式中第4项与第8项的二项式系数相等，所以37n n C C =，解得10n =，所以二项式(1)nx +中奇数项的二项式系数和为1091222⨯=，故选D ．以及计算能力．（4）【2015年，理4，5分】设211(,)X N μσ:，222(,)Y N μσ:，这两个正态分布密（A ）21()()P Y P Y μμ≥≥≥ （B ）21()()P X P X σσ≤≤≤（C ）对任意正数t ，()()P X t P Y t ≤≥≤ （D ）对任意正数t ，()()P X t P Y t ≥≥≥ 【答案】【解析】正态分布密度曲线图象关于x μ=对称，所以12μμ<，从图中容易得到()()P X t P Y t ≤≥≤，故选C ．【点评】本题考查了正态分布的图象与性质，学习正态分布，一定要紧紧抓住平均数μ和标准差σ这两个关键（5）【2015年，理5，5分】设12,,,n a a a ∈R L ，3n ≥．若p ：12,,,n a a a L 成等比数列；q ：22222221212312231()()()n n n n a a a a a a a a a a a a --++++++=+++L L L ，则（）（A q 的充分条件（C ）p 是q 的充分必要条件（D ）p 既不是q 的充分条件，也不是q 的必要条件【答案】A【解析】对命题12:,,,n p a a a L 成等比数列，则公比()13n n aq n a -=≥且0n a ≠；对命题q ，①当0=n a 时，22222221212312231()()()n n n n a a a a a a a a a a a a --++++++=+++L L L 成立； ②当0≠n a 时，根据柯西不等式，等式22222221212312231()()()n n n n a a a a a a a a a a a a --++++++=+++L L L 成立，则nn a a a a a a 13221-=⋅⋅⋅==，所以12,,,n a a a L 成等比数列，所以p 是q 的充分条件，但不是q 的必要（6）【2015年，理6，5分】已知符号函数1,0,sgn 0,0,1,0.x x x x >⎧⎪==⎨⎪-<⎩()f x 是R 上的增函数，()()()(1)g x f x f ax a =->，（A ）sgn[()]sgn g x x = （B ）sgn[()]sgn g x x =- （C ）sgn[()]sgn[()]g x f x = （D ）sgn[()]sgn[()]g x f x =- 【答案】【解析】因为()f x 是R 上的增函数，令()f x x =，所以()()1g x a x =-，因为1a >，所以()g x 是R 上的减函数，由符号函数1,0,sgn 0,0,1,0.x x x x >⎧⎪==⎨⎪-<⎩知，1,0,sgn 0,0,sgn 1,0.x x x x x >⎧⎪===-⎨⎪-<⎩，故选B ．（7）【2015年，理7，5分】在区间[0,1]上随机取两个数,x y ，记1p 为事件“12x y +≥”的概率，2p 为事件“1||2x y -≤”的概率，3p 为事件“12xy ≤”的概率，则（）（A ）123p p p << （B ）231p p p << （C ）312p p p << （D ）321p p p << 【解析】因为[],0,1x y ∈，对事件“12x y -≥”如图（1）阴影部分1S ，对事件“12x y -≤”，如图（2）阴影部分2S ，对事件“12xy ≤”，如图（3）阴影部分3S ，由图知，阴影部分的面积从下到大依次是231S S S <<，正方形的面积为111⨯=，根据几何概型公式可得231p p p <<，故选B ．【点评】利用数形结合是解决本题的关键．本题也可以直接通过图象比较面积的大小即可比较大小．（8）【2015年，理8，5分】将离心率为1e 的双曲线1C 的实半轴长a 和虚半轴长()b a b ≠同时增加(0)m m >个单位长度，得到离心率为2e 的双曲线2C ，则（）（A ）对任意的,a b ，12e e > （B ）当a b >时，12e e >；当a b <时，12e e < （C ）对任意的,a b ，12e e < （D ）当a b >时，12e e <；当a b <时，12e e > 【答案】【解析】依题意，22211a b b e a a +⎛⎫==+ ⎪⎝⎭，()()22221a m b m b m e a ma m ++++⎛⎫==+ ⎪++⎝⎭，因为()()()m b a b b m ab bm ab am a a m a a m a a m -++---==+++，由于0m >，0a >，0b >，当a b >时，01b a <<，01b m a m +<<+，b b m a a m +<+，22b b m a a m +⎛⎫⎛⎫< ⎪ ⎪+⎝⎭⎝⎭，所以12e e <；当a b <时，1b a >，1b m a m +>+，而b b m a a m +>+，所以22b b m a a m +⎛⎫⎛⎫> ⎪ ⎪+⎝⎭⎝⎭，所以12e e >．所以当a b >时，12e e <，当a b <时，12e e >，故选D ．（9）【2015年，理9，5分】已知集合22{(,)1,,}A x y x y x y =+≤∈Z ，{(,)||2,||2,,}B x y x y x y =≤≤∈Z ，定义集合12121122{(,)(,),(,)}A B x x y y x y A x y B ⊕=++∈∈，则A B ⊕中元素的个数为（）（A ）77 （B ）49 （C ）45 （D ）30 【解析】因为集合(){}22,1,,A x y xy x y =+≤∈Z ，所以集合A 中有9个元素（即9个点），即图中圆中的整点，集合{(,)||2,||2,,}B x y x y x y =≤≤∈Z 中有25个元素（即 25个点）：即图中正方形ABCD 中的整点，集合12121122{(,)(,),(,)}A B x x y y x y A x y B ⊕=++∈∈的元素可看作正方形1111A B C D中的整点（除去四个顶点），即77445⨯-=个，故选C ．复的元素．（10）【2015年，理10，5分】设x ∈R ，[]x 表示不超过x 的最大整数．若存在实数t ，使得[]1t =，2[]2t =，…，[]n t n =同时成立．．．．，则正整数n 的最大值是（）（A ）3 （B ）4 （C ）5 （D ）6 【答案】B【解析】由[]1t =得12t ≤<，由2[]2t =得223t ≤<，由43t ⎡⎤=⎣⎦得445t ≤<，可得225t ≤<，所以225t ≤<；由3[]3t =得334t ≤<，所以5645t ≤<，由55t ⎡⎤=⎣⎦得556t ≤<，与5645t ≤<矛盾，故正整数n 的最大值是4，故选B ．【点评】本题考查简单的演绎推理，涉及新定义，属基础题．二、填空题：共6小题，考生需作答5小题，每小题5分，共25分．请将答案填在答题卡对应题号的位置上．．．．．．．．．．．答错位置，书写不清，模棱两可均不得分．（一）必考题（11-14题）（11）【2015年，理11，5分】已知向量OA AB ⊥u u u r u u u r ，||3OA =u u u r ，则OA OB ⋅=u u u r u u u r ．【答案】9【解析】因为OA AB ⊥u u u r u u u r ，3OA =u u u r ，()22239OA OB OA OA OB OA OA OB OA ⋅=⋅+=+⋅===u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r ．（12）【2015年，理12，5分】函数2π()4cos cos()2sin |ln(1)|22x f x x x x =---+的零点个数为．【答案】2 【为()()()()()24cos cos 2sin ln 121cos sin 2sin ln 1sin 2ln 122x x f x x x x x x x x x x ⎛⎫=----=+--+=-+ ⎪⎝⎭，所以函数()f x 的零点个数为函数sin 2y x =与()ln 1y x =+图像如图，由图知，两函数图像右2个交点，所以函数()f x 由2个零点．（13）【2015年，理13，5分】如图，一辆汽车在一条水平的公路上向正西行驶，到A 处在西偏北30o 的方向上，行驶600m 后到达B 处，测得此山顶在西偏北75o 的方向上，仰角为30o ，则此山的高度CD = m ．【答案】1006 【解析】依题意，30BAC ∠=︒，105ABC ∠=︒，在ABC ∆中，由180ABC BAC ACB ∠+∠+∠=︒，所以45ACB ∠=︒，因为600AB =，由正弦定理可得600sin 45sin30BC-=︒︒，即3002BC =m ，在Rt BCD ∆中，因为30CBD ∠=︒，3002BC =，所以tan303002CD CDBC ︒==，所以1006CD =m ．（14）【2015年，理14，5分】如图，圆C 与x 轴相切于点(1,0)T ，与y 轴正半轴交于两点,A B （B 在A 的上方），且2AB =．（1）圆C 的标准．．方程为；（2）过点A 任作一条直线与圆22:1O x y +=相交于,M N 两点，下列三个结论： ①NA MA NBMB=； ②2NB MA NAMB-=； ③22NB MA NAMB+=．其中正确结论的序号是．（写出所有正确结论的序号）【答案】（1）()()22122x y -+-=；（2）①②③【解析】（1）依题意，设()1,C r （r 为圆的半径），因为2AB =，所以22112r =+=，所以圆心()1,2C ，故圆的标准方程为()()22122x y -+-=．（2）解法一：联立方程组()()22122x x y =⎧⎪⎨-+-=⎪⎩，解得021x y =⎧⎪⎨=-⎪⎩或021x y =⎧⎪⎨=+⎪⎩，因为B 在A 的上方，所以()0,21A -，()0,21B +，领直线MN 的方程为0x =，此时()0,1M -，()0,1N ，所以2MA =，22MB =+，22NA =-，2NB =，因为22212NA NB-==-，22122MA MB==-+，所以NA MA NB MB =所以()22212122222NB MA NAMB-=-=+--=-+，()222121222222NB MA NAMB+=+=++-=-+，正确结论的序号是①②③．解法二：因为圆心()1,2C ，()0,2E ∴，又2AB =Q ，且E 为AB 中点，∴()0,21A -，()0,21B +，M Q ，N 在圆22:1O x y +=，∴可设()cos ,sin M αα，()cos ,sin N ββ，()()22cos 0sin 21NA ββ⎡⎤∴=-+--⎣⎦()22cos sin 221sin 322βββ=+--+-()()()422221sin 2221221sin ββ=---=---()()2212sin β=--，()()22cos 0sin 21NB ββ⎡⎤∴=-+-+⎣⎦()22cos sin 221sin 322βββ=+-+++()()()422221sin 2221221sin ββ=+-+=+-+()()2212sin β=+-，()()()()2212sin 2121212212sin NA NBββ---∴===-++-，同理21MA MB=-．所以NA MA NBMB=，所以()22212122222NB MA NA MB -=-=+--=-+， ()222121222222NB MA NAMB+=+=++-=-+，【点评】本题考查求圆的标准方程，用三角函数值表示单位圆上点的坐标是解决本题的关键，注意解题方法的积累，属于难题．（一）选考题（请考生在第15、16两题中任选一题作答，请先在答题卡指定位置将你所选的题目序号后的方框用2B 铅笔涂黑，如果全选，则按第15题作答结果计分．）（15）【P A 是圆的切线，A 为切点，PBC 是圆的割线，且3BC PB =，则ABAC=_______．【答案】12【解析】因为PA 是圆的切线，A 为切点，PBC 是圆割定理知，()2PA PB PC PB PB BC =⋅=+，因为3BC PB =，所以224PA PB =，即2PA PB =，由A PAB PC ∆∆∽，所以12AB PB AC PA ==．（16）【2015年，理16，5分】（选修4-4：坐标系与参数方程）在直角坐标系xOy 中，以O 轴为极轴建立极坐标系．已知直线l 的极坐标方程为(sin 3cos )0ρθθ-=，曲线C 的参数方程为1,1x t ty t t ⎧=-⎪⎪⎨⎪=+⎪⎩( t 为参数) ，l 与C 相交于A ，B 两点，则||AB = ．【答案】25【解析】因为()sin 3cos 0ρθθ-=，所以sin 3cos 0ρθρθ-=，所以30y x -=，即3y x =；由11x t ty t t ⎧=-⎪⎪⎨⎪=+⎪⎩，消去t得224y x -=，联立方程组2234y x y x =⎧⎨-=⎩，解得22322x y ⎧=⎪⎪⎨⎪=⎪⎩或22322x y ⎧=-⎪⎪⎨⎪=-⎪⎩，即232,22A ⎛⎫ ⎪ ⎪⎝⎭，232,22B ⎛⎫-- ⎪ ⎪⎝⎭，由两点间的距离公式得22223232252222AB ⎛⎫⎛⎫=+++= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭．础的计算题．三、解答题：共6题，共75（17）【2015年，理17，11分】某同学用“五点法”画函数()sin()f x A x ωϕ=+π(0,||)2ωϕ><在某一个周期x ωϕ+ 0π2 π 3π2 2π x π3 5π6sin()A x ωϕ+0 5 5- 0（1）请将上表数据补充完整，填写在答题卡上相应位置．．．．．．．．．．．，并直接写出函数()f x 的解析式；（2）将()y f x =图象上所有点向左平行移动θ(0)θ>个单位长度，得到()y g x =的图象．若()y g x =图象的一个对称中心为5π(,0)12，求θ的最小值．解：（1）根据表中已知数据，解得π5,2,6A ωϕ===-．数据补全如下表：x ωϕ+ 0π2π 3π22πxπ12 π3 7π12 5π6 13π12 sin()A x ωϕ+55-且函数表达式为π()5sin(2)6f x x =-．（2）由（1）知 π()5sin(2)6f x x =-，得π()5sin(22)6g x x θ=+-．因为sin y x =的对称中心为(π,0)k ，k ∈Z ．令π22π6x k θ+-=，解得ππ212k x θ=+-，k ∈Z ．由于函数()y g x =的图象关于点5π(,0)12成中心对称，令ππ5π21212k θ+-=，解得ππ23k θ=-，k ∈Z ．由0θ>可知，当1k =时，θ取得最小值π6．【点评】本题主要考查了由()sin y A x ωϕ=+的部分图象确定其解析式，函数()sin y A x ωϕ=+的图象变换规律（18）【2015年，理18，12分】设等差数列{}n a 的公差为d 前n 项和为n S ，等比数列{}n b 的公、比为q ．已知11b a =，22b =，q d =，10100S =．（1）求数列{}n a ，{}n b 的通项公式；（2）当1d >时，记n n nac b =，求数列{}n c 的前n 项和n T ．解：（1）由题意知：1110451002a d a d -=⎧⎨=⎩，即1129202a d a d +=⎧⎨=⎩，得112a d =⎧⎨=⎩或1929a d =⎧⎪⎨=⎪⎩，故1212n n n a n b -=-⎧⎪⎨=⎪⎩或()112799299n n n a n b -⎧=+⎪⎪⎨⎛⎫⎪= ⎪⎪⎝⎭⎩．（2）由1d >，知21n a n =-，12n n b -=，故1212n n n c --=，于是2341357921122222n n n T --=+++++L L ① 2345113579212222222n n n T -=+++++L L ② 由①-②可得234521111111212323222222222n n n n n n T --+=++++++-=-L L ，故12362nn n T -+=-．（19）【2015年，理19，12分】《九章算术》中，将底面为长方形且有如图，在阳马P ABCD -中，侧棱PD ⊥底面ABCD ，且PD CD =，过棱PC 的中点E ，作EF PB ⊥交PB 于点F ，连接,,,.DE DF BD BE ．（1）证明：PB DEF ⊥平面．试判断四面体DBEF 是否为鳖臑，若是，写出其每个面的直（2）若面DEF 与面ABCD 所成二面角的大小为π3，求DCBC的值．解：（1）因为PD ⊥底面ABCD ，所以PD BC ⊥，由底面ABCD 为长方形，有BC CD ⊥，而PD CD D =I ，所以BC PCD ⊥平面．而DE PCD ⊂平面，所以BC DE ⊥．又因为PD CD =，点E 是PC 的中点，所以DE PC ⊥．而PC BC C =I ，所以DE ⊥平面PBC ．而PB PBC ⊂平面，所以PB DE ⊥．又PB EF ⊥，DE EF E =I ，所以PB ⊥平面DEF ．由DE ⊥平面PBC ，PB ⊥平面DEF ，可知四面体BDEF 的四个面都是直角三角形，即四面体BDEF 是一个鳖臑，其四个面的直角分别为DEB DEF ∠∠，，EFB DFB ∠∠，．（2）如图1，在面PBC ，延长BC 与FE 交于点G ，则DG 是平面DEF 与平面ABCD 的由（1）知，PB DEF ⊥平面，所以PB DG ⊥．又因为PD ⊥底面ABCD ，所以 PD DG ⊥．而PD PB P =I ，所以DG PBD ⊥平面．故BDF ∠是面DEF 与面ABCD 所成二面角的平面角，设1PD DC ==，BC λ=，有21BD λ=+，在Rt △PDB 中, 由DF PB ⊥, 得π3DPF FDB ∠=∠=,则 2πtan tan 133BDDPF PD λ=∠==+=, 解得2λ=．所以12.2DC BC λ== 故当面DEF 与面ABCD 所成二面角的大小为π3时，22DC BC =．（1）如图2，以D 为原点，射线,,DA DC DP 分别为,,x y z 轴的正半轴，建立空间直角坐标系．设1PD DC ==，BC λ=，则(0,0,0),(0,0,1),(,1,0),(0,1,0)D P B C λ， (,1,1)PB λ=-u u u r ，点E 是PC 的中点，所以11(0,,)22E ，11(0,,)22DE =u u u r ，于是0PB DE ⋅=u u u r u u u r，即PB DE ⊥．又已知EF PB ⊥，而DE EF E =I ，所以PB DEF ⊥平面．因(0,1,1)PC =-u u u r , 0DE PC ⋅=u u u r u u u r, 则DE PC ⊥, 所以DE PBC ⊥平面．由DE ⊥平面PBC ，PB ⊥平面DEF ，可知四面体BDEF 的四个面都是直角三角形，即四面体BDEF 是一个鳖臑，四个面的直角分别为DEB DEF ∠∠，，EFB DFB ∠∠，．（2）由PD ABCD ⊥平面，所以(0,0,1)DP =u u u r是平面ABCD 的一个法向量；由（1）知，PB DEF ⊥平面，所以(,1,1)BP λ=--u u u r是平面DEF 的一个法向量．若面DEF 与面ABCD 所成二面角的大小为π3，则2π11cos 32||||2BP DP BP DP λ⋅===⋅+u u u r u u u r u u ur u u u r ，解得2λ=．所以12.2DC BC λ== 故当面DEF 与面ABCD 所成二面角的大小为π3时，22DC BC =．于难题．（20）【2015年，理20，12分】某厂用鲜牛奶在某台设备上生产,A B 两种奶制品．生产1吨A 产品需鲜牛奶210001吨B 产品需鲜牛奶1．51．5小时，获利 1200元．要求每天B 产品的产量不超过A 产品产量的2倍，设备每天生产,A B 两种产品时间之和不超过 12小时．假定每天可获取的鲜牛奶数量W （单位：吨）是一个随机变量，其分布列为W 12 15 18 P 0．3 0．5 0．2该厂每天根据获取的鲜牛奶数量安排生产，使其获利最大，因此每天的最大获利Z （单位：元）是一个（1）求Z 的分布列和均值；（2）若每天可获取的鲜牛奶数量相互独立，求3天中至少有1解：（1）设每天,A B 两种产品的生产数量分别为,x y ，相应的获利为z ，则有2 1.5,1.512, 20,0, 0.x y W x y x y x y +≤⎧⎪+≤⎪⎨-≥⎪⎪≥≥⎩ （1）目标函数为 10001200z x y =+．当12W =时，（1）表示的平面区域如图1，三个顶点分别为(0, 0), (2.4, 4.8), (6, 0)A B C ．将10001200z x y =+变形为561200z y x =-+，当 2.4, 4.8x y ==时，直线l ：561200z y x =-+在y 轴上的截距最大，最大获利max 2.41000 4.812008160Z z ==⨯+⨯=．当15W =时，（1）表示的平面区域如图2，三个顶点分别为(0, 0), (3, 6), (7.5, 0)A B C ．将10001200z x y =+变形为561200z y x =-+，当3, 6x y ==时，直线l ：561200z y x =-+在y 轴上的截距最大，最大获利max 310006120010200Z z ==⨯+⨯=．当18W =时，（1）表示的平面区域如图3，四个顶点分别为(0, 0), (3, 6), (6, 4), (9, 0)A B C D ．将10001200z x y =+变形为561200z y x =-+，当6,4x y ==时，直线l ：561200zy x =-+在y 轴上的截距最大，最大获利max 610004120010800Z z ==⨯+⨯=．故最大获利Z 的分布列为Z8160 10200 10800 P0．3 0．5 0．2 因此，()81600.3102000.5108000.29708.E Z =⨯+⨯+⨯= （2）由（1）知，一天最大获利超过10000元的概率1(10000)0.50.20.7p P Z =>=+=，由二项分布，3天中至少有1天最大获利超过10000元的概率为()3311110.30.973p p =--=-=．问题解决问题的能力．（21）【2015年，理21，14分】一种作图工具如图1所示．O 是滑槽AB 的中点，短杆MN 通过N 处铰链与ON 连接，MN D AB 滑动，且1DN ON ==，3MN =．当栓子D 在滑槽AB 作往复运动时，带动．．N 绕O 转动一周（D 不动时，N C ．以O 为原点，AB 所在的直线为x 轴建立如图2所示的平面直角坐标系．（2）设动直线l 与两定直线1:20l x y -=和2:20l x y +=分别交于,P Q 两点．若直线l 总与曲线C 有且只有一个公共点，试探 OPQ 的面积是否存在最小值？若存在，求出该最小值；解：（1）设点(,0)(||2)D t t ≤，00(,),(,)N x y M x y ，依题意，2MD DN =u u u u r u u u r，且||||1DN ON ==u u u r u u u r ，所以00(,)2(,)t x y x t y --=-，且22002200()1,1.x t y x y ⎧-+=⎪⎨+=⎪⎩ 即0022,2.t x x t y y -=-⎧⎨=-⎩且0(2)0.t t x -= 由于当点D 不动时，点N也不动，所以t 不恒等于0，于是02t x =，故00,42x y x y ==-，（2②8．【点评】本题的关键．综合性较强，运算量较大．（22）【2015年，理22，14（（（解：（1①（2②（3运算求解能力、创新知识，考查了利用放缩法法证明数列不等式，是压轴题．。

2015年四川高考数学(理科)试题含答案

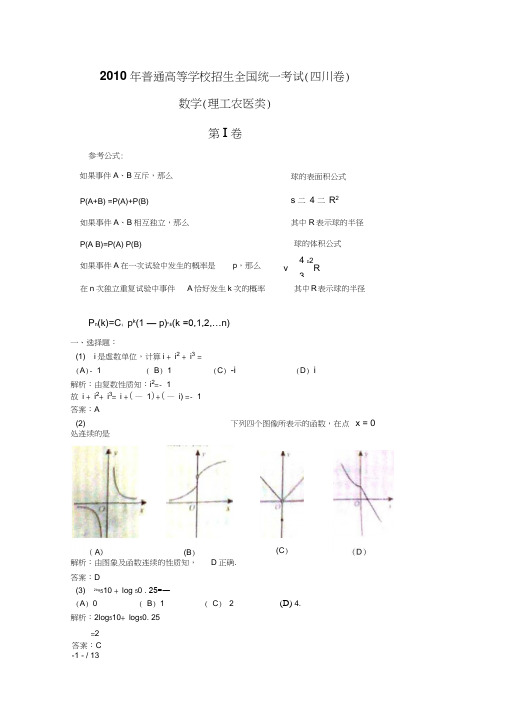
=2 答案：C 2010年普通高等学校招生全国统一考试(四川卷)数学(理工农医类)第I 卷参考公式:P n (k)=C ；p k (1 — p)n±(k =0,1,2,…n)一、选择题：(1) i 是虚数单位，计算i + i 2 + i 3 = (A )- 1( B ) 1(C ) -i(D ) i解析：由复数性质知：i 2=- 1 故 i + i 2+ i 3= i +( — 1)+( — i) =- 1 答案：A (2)下列四个图像所表示的函数，在点 x = 0处连续的是解析：由图象及函数连续的性质知， D 正确.答案：D (3)2log 510 + log 50 . 25=―(A ) 0( B ) 1( C ) 2解析：2log 510+ log 50. 25P(A+B) =P(A)+P(B)s 二 4 二 R 2如果事件A 、B 相互独立，那么其中R 表示球的半径 P(A B)=P(A) P(B)球的体积公式如果事件A 在一次试验中发生的概率是 p ，那么4 D 2 v R3在n 次独立重复试验中事件A 恰好发生k 次的概率其中R 表示球的半径如果事件A 、B 互斥，那么球的表面积公式(B ) (C )(D) 4w=log 5100 + log50. 25=log 525=2答案：C(A )甲车间加工原料10箱,乙车间加工原料60箱(B )甲车间加工原料15箱,乙车间加工原料55箱80(4) 函数f(x) = x2+ mx+ 1的图像关于直线(A) m = _2 ( B) m = 2答案：A2解析：由BC = 16,得| BC| =4 AB AC I A^-A C而AB AC AM答案：C w…(6)将函数y =sin x的图像上所有的点向右平行移动'个单位长度，再把所得各点的横坐10标伸长到原来的2倍(纵坐标不变)，所得图像的函数解析式是w—m(A) y =sin(2x ) (B) y = sin(2x )10 51 兀 1 兀(C) y 二sin(—x ) (D) y 二sin(—x )2 10 2 20解析：将函数y=sinx的图像上所有的点向右平行移动一个单位长度，所得函数图象的解析10式为y= sin(x—) •10再把所得各点的横坐标伸长到原来的2倍(纵坐标不变)，所得图像的函数解析式是1 ny"门(异-石).答案：C(7)某加工厂用某原料由甲车间加工出A产品，由乙车间加工出B产品.甲车间加工一箱原料需耗费工时10小时可加工出7千克A产品，每千克A产品获利40元，乙车间加工一箱原料需耗费工时6小时可加工出4千克B产品，每千克B产品获利50元.甲、乙两车间每天共能完成至多70箱原料的加工，每天甲、乙两车间耗费工时总和不得超过480小时，甲、乙两解析：函数f( x) = x2+ mx+ 1的对称轴为x= —曰疋—m= 1 =• m= —22x=1对称的充要条件是(C) m - -1(5)设点M是线段BC的中点，点A在直线BC夕卜，BC2=16,AB ACi IA^-A C.贝y(A)8 (B)4 (C) 2 (D ) 1w_w-=BC = 4故二2车间每天总获利最大的生产计划为（D ）甲车间加工原料 40箱，乙车间加工原料 30箱解析：设甲车间加工原料 x 箱，乙车间加工原料 y 箱x y _ 70nt I则 <10x+6y 兰480x, y N目标函数z = 280x + 300y结合图象可得：当 x = 15, y = 55时z 最大本题也可以将答案逐项代入检验 . 答案：Bw … （8）已知数列的首项印=0，其前n 项的和为S n ，且S n.i =2S 「印，则lim n 二1（A ）0（ B ） —（ C ） 1 （ D ）22解析：由 & 1=2Sn ' a 1,且Sn 2-2S n 1a1 1作差得 a n +2 = 2a n +1^又 S 2 2S 1 + a 1, 即卩 a ? + a 1 2 a 1 + a^ —■ a ? 2 a 1故｛a n ｝是公比为2的等比数列S n = a 1+ 2a 1 + 22a 1 + .......................... + 2n 1a 1= (2n — 1) a 1则 lima n= lim nn；：S nn ::(2n -1)a 1答案：B2 2xy（9）椭圆二 2 =1（a 的右焦点F ，其右准线与x 轴的交点为A ,在椭圆上存在点a bP 满足线段AP 的垂直平分线过点 F ，则椭圆离心率的取值范围是 co（A ） 0,彳（B ） 0,1（C ）J2-1,1（D ） 1,1解析：由题意，椭圆上存在点 P ,使得线段AP 的垂直平分线过点F ,2nJ 31即F 点到P 点与A 点的距离相等m2 ,2ab而 | FA| = C = 一c c| PF| € [a — c, a + c]即 ac — c ?w ac + c ?.j ac _c 2 兰 a 2 _c 2 a 2 -c 2 乞ac c 2于是b 2€ [ a — c, a + c]c—叮屏11 或--a — 2又e€ (0, 1)故e€ |-,1 | '2丿答案：D(10)由1、2、3、4、5、6组成没有重复数字且-3都不与5相邻的六位偶数的个数是(A)72 ( B)96 ( C) 108 ( D)144w …解析：先选一个偶数字排个位，有3种选法_…①若5在十位或十万位，则1、3有三个位置可排，3 A f A f = 24个②若5排在百位、千位或万位，则1、3只有两个位置可排，共3A2A2 = 12个算上个位偶数字的排法，共计3(24 + 12) = 108个答案：C(11)半径为R的球O的直径AB垂直于平面「，垂足为B , BCD是平面〉内边长为与球面交于点M , N,/A、f 17(A) Rarccos——25 那么R的正三角形，线段AC、M、N两点间的球面距离是厂18(B) Rarccos -25(C)AD分别解析: 由已知,1 AB = 2R, BC = R,故tan / BAC = —•一.…2cos/ BAC =连结OM，则△ OAM为等腰三角形4品4亦AM = 2AOcos / BAC = R，同理AN= R，且MN// CD w5 5而AC = . 5R, CD = R故MN : CD = AN:AC w一MN = 4R ,5连结OM、ON, 有OM = ON= R于是cos/ MON =2 2 2OM ON -MN2OM LON172517所以M 、N 两点间的球面距离是 Rarccos25答案：A1i(12)设 a >b :- c ,0 ,则 2a 2 10ac ：-25c 2 的最小值是ab a(a_b)(A )2( B )4( C ) 2,5( D ) 5解析： 2a 2 — 110ac - 25c 2ab a(a —b)=(a -5c)2 ab 丄 a(a -b) --ab a(a —b)> 0 + 2+ 2=4当且仅当a — 5c = 0, ab = 1, a( a -b) = 1时等号成立2c = 2满足条件5答案：B=(a _5c)2a 2 —ab ab 丄 --ab a(a —b)如取a =第口卷、填空题：本大题共 4小题，每小题4分，共16分.把答案填在题中横线上1 6(13) (2-3—)6的展开式中的第四项是.Jx(14)直线x -2y 5=0与圆x 2 y 2 =8相交于A 、B 两点，则 AB 〒解析：方法一、圆心为(0,0)，半径为2、、2故 LABJ 二.、二二=二 2 二…2得 | AB| = 2 3 答案：2 3(15)如图，二面角〉-I - '■的大小是60°,线段AB 二：；• B 三丨,AB 与I 所成的角为30° .则AB 与平面1所成的角的正弦值是•解析：过点A 作平面B 的垂线，垂足为 C ,在B 内过C 作I 的垂线•垂足为D 连结AD ，有三垂线定理可知 AD 丄I ,故/ ADC 为二面角：• -I - 1的平面角，为60° 又由已知，/ ABD = 30° 连结CB ,则/ ABC 为AB 与平面一：所成的角..设 AD = 2，贝V AC = /3 , CD = 1ADAB =0 =4sin 30AC 3--sin / ABC =AB 4答案：空解析: T 4= C ；23160x答案:160 x 圆心到直线x -2y • 5=0的距离为4(16)设S为复数集C的非空子集.若对任意x, y S ,都有x • y,x - y,xy • S ,则称S为封闭集。

2015年陕西省高考数学试卷(理科)答案与解析

62015年陕西省高考数学试卷（理科）参考答案与试题解析一、选择题，共12小题，每小题5分，共60分21. （ 5 分）（2015?陕西）设集合 M={x|x =x} , N={x|lgx O }，贝U M U N=（）A . [0, 1]B . （0, 1]C . [0, 1）D . （ - s, 1]考点：并集及其运算. 专题：集合.分析：求解一元二次方程化简 M ，求解对数不等式化简 N ，然后利用并集运算得答案. 解答：解：由 M={x|x 2=x}={0 , 1},N={x|lgx O}= （0, 1], 得 M U N={0 , 1} U （0, 1]=[0 , 1]. 故选：A .点评：本题考查了并集及其运算，考查了对数不等式的解法，是基础题.考点：收集数据的方法. 专题：计算题；概率与统计.分析：利用百分比，可得该校女教师的人数. 解答：解：初中部女教师的人数为110/70%=77 ;高中部女教师的人数为 40XI50%=60,•••该校女教师的人数为 77+60=137, 故选：C .点评：本题考查该校女教师的人数，考查收集数据的方法，考查学生的计算能力，比较基础. 33 （5分）（2015?陕西）如图，某港口一天6时到18时的水深变化曲线近似满足函数 y=3sinI Kx+ 0） +k .据此函数可知，这段时间水深（单位： m ）的最大值为（）2. （ 5分）（2015?陕西）某中学初中部共有例如图所示，则该校女教师的人数为（110名教师，高中部共有 150名教师，其性别比）C . 137D . 167考点：由y=Asin ( w x+ $)的部分图象确定其解析式. 专题：三角函数的图像与性质.分析：由题意和最小值易得 k 的值，进而可得最大值. 解答：解：由题意可得当 sin (-1-X+ 0)取最小值-1时，函数取最小值 y min = - 3+k=2，解得k=5 ,|7T••• y=3sin (—x+ 0) +5,6IT...当当sin ( x+ 0)取最大值1时，6函数取最大值 y max =3+5=8 , 故选：C .点评：本题考查三角函数的图象和性质，涉及三角函数的最值，属基础题.4. （ 5分）（2015?陕西）二项式（x+1 ） n （ n 3 +）的展开式中x 2的系数为15,则n=（）A . 7B . 6C . 5D . 4考点：二项式定理的应用. 专题：二项式定理.分析：由题意可得「-=门■ 1=15，解关于n 的方程可得.% 2解答：解：•••二项式(x+1 ) n (n€N + )的展开式中x 2的系数为15,9 n (n _ 1) " + • C ；=15，即 ----- c -------- =15，解得 n=6,故选：B .点评：本题考查二项式定理，属基础题. 44 ( 5分)(2015?陕西)一个几何体的三视图如图所示，则该几何体的表面积为(D . 10#」L考点：由三视图求面积、体积. 专题：计算题；空间位置关系与距离.分析：根据几何体的三视图，得出该几何体是圆柱体的一部分，利用图中数据求出它的表面积. 解答：解：根据几何体的三视图，得；该几何体是圆柱体的一半，该几何体的表面积为2V 几何体=n? + n 1>2+2 >2 =3 n +4.故选：D .点评：本题考查了利用空间几何体的三视图求表面积的应用问题，是基础题目6. （ 5 分）（2015?陕西）sin a =cos a 是 cos2a =0”的（）A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件考点：必要条件、充分条件与充要条件的判断. 专题：简易逻辑.2 2分析：由cos2 a =cos a- sin a,即可判断出. 解答：解：由 cos2 a =cos 2 a- sin 2 a,• •• sin a =COS a 是“os2 a=0"的充分不必要条件.故选：A .点评：本题考查了倍角公式、简易逻辑的判定方法，考查了推理能力，属于基础题.7. （ 5分）（2015?陕西）对任意向量 &、b ,下列关系式中不恒成立的是（）「一 • •冃|叫-M|（日+环? （g-亍）=^2-b 2考点：平面向量数量积的运算.左视團C . 2 n +4D . 3 n +4专题：平面向量及应用.分析：由向量数量积的运算和性质逐个选项验证可得. 解答：i 一一 _.一解：选项 A 正确，•••|mb |=|；a ||b ||cos v 3, b >|,又|c osv & b >鬥，二1/…冃aiHb 恒成立；选项B 错误，由三角形的三边关系和向量的几何意义可得|厂=「|耳|比-|「，||；选项C 正确，由向量数量积的运算可得（选项D 正确，由向量数量积的运算可得（故选：B点评：本题考查平面向量的数量积，属基础题.& （ 5分）（2015?陕西）根据如图框图，当输入C . 10考点：程序框图.专题：图表型；算法和程序框图.分析：模拟执行程序框图，依次写出每次循环得到的x 的值，当x= - 2时不满足条件计算并输出y 的值为10.解答：解：模拟执行程序框图，可得x=2006, x=2004满足条件x 为，x=2002满足条件x 为，x=2000满足条件x 为，x=0―* ―e ~* ―■- Q■ ) =i ■ ■-| ;「F ? (;-,■,) = I 2-1〔2.x 为2006时，输出的y （D . 28/输入茫/尸3齐1满足条件x 为，x= - 2 不满足条件x%, y=10 输出y 的值为10.故选：C .点评：本题主要考查了循环结构的程序框图，属于基础题.9. ( 5 分)(2015?陕西)设 f (x ) =lnx , 0v a v b ,若 p=f ( . -h), q=f (关系.解：由题意可得若 p=f (J 十)=ln (.) —Inab=〔 (Ina+lnb ),2 2q=f (r=g (f (a ) +f (b)) 丄(Ina+lnb ), ••• p=r v q ,故选：B点评：本题考查不等式与不等关系，涉及基本不等式和对数的运算，属基础题.10. （ 5分）（2015?陕西）某企业生产甲、乙两种产品均需用A 、B 两种原料.已知生产 1吨每种产品所需原料及每天原料的可用限额如表所示. 如果生产一吨甲、乙产品可获得利润分别为3万元、4万兀，则该企业每天可获得最大利润为（)A B ' （吨）（吨）甲3 1乙2 2原料限额12 8 A . 12万元 B . 16万元C . 17力兀D . 18力兀考点 :简单线性规划的应用.专题 :不等式的解法及应用.分析 :设每天生产甲乙两种产品分别为x , y 顿，利润为z 元，然后根据题目条件建立约束条件，得到目标函数，画出约束条件所表示的区域，然后利用平移法求出 z 的最大值. 解答：解：设每天生产甲乙两种产品分别为 x , y 顿，利润为z 元，f 3x+2y<12则■：1-■:"I &0,卩沁)，冷(f ( a )+f （ b ））,则下列关系式中正确的是（A . q=r v pB . p=r v q考点：不等关系与不等式. 专题：不等式的解法及应用. 分析：由题意可得(Ina+lnb ), q=D . p=r > q目n (.-]・)=p , ry (Ina+lnb ),可得大小解答: q=r > p )=ln 目n （i ：八）=p ,目标函数为z=3x+4y .作出二元一次不等式组所表示的平面区域（阴影部分）即可行域.由z=3x+4y 得y= - - Jx+'-,4 4|平移直线y=-卫x+M由图象可知当直线4 4距最大，此时z最大,解方程组，解得1就1x+2y=8〔尸3即B的坐标为x=2 , y=3,/• z max=3x+4y=6+12=18 .即每天生产甲乙两种产品分别为2, 3顿，能够产生最大的利润，最大的利润是18万元，故选：D.点评：本题主要考查线性规划的应用，建立约束条件和目标函数，利用数形结合是解决本题的关键.11. （5分）（2015?陕西）设复数z= （x- 1）+yi （x, y€R）,若|z冃,则y汰的概率为考点：专题：分析：解答：几何概型.概率与统计.由题意易得所求概率为弓形的面积与圆的面积之比，分别求面积可得. 解：•••复数z= （x- 1）+yi （x, y€R）且|z|<1,••• |z|=J （K- 1 ）2+异勻，即（x- 1）2+y2勻,点（x, 丫）在（1, 0）为圆心1为半径的圆及其内部，而y孩表示直线y=x左上方的部分，（图中阴影弓形）•••所求概率为弓形的面积与圆的面积之比，y=-卫x+三经过点B时，直线y=-卫x在的截4 4 4 43.114+B. 1,1+2兀丄71A .212. (5分)(2015?陕西)对二次函数f (x ) =ax +bx+c (a 为非零整数)，四位同学分别给出下列结论，其中有且只有一个结论是错误的，则错误的结论是()A . - 1是f (x )的零点B . 1是f (x )的极值点C . 3是f (x )的极值D .点(2, 8)在曲线y=f (x )上考点：二次函数的性质.专题：创新题型；函数的性质及应用；导数的综合应用.分析：可采取排除法.分别考虑 A , B , C , D 中有一个错误，通过解方程求得a ,判断是否为非零整数，即可得到结论.解答：解：可采取排除法.2若A 错，贝V B , C , D 正确.即有f (x ) =ax +bx+c 的导数为f'(x ) =2ax+b , 即有 f ' (1) =0,即2a+b=0,①又 f (1) =3，即 a+b+c=3②，又f (2) =8,即4a+2b+c=8 ,③ 由①②③ 解得，a=5, b= - 10, c=8.符合a 为非零整数._ b 2若B 错，则A , C, D 正确，则有a - b+c=0,且4a+2b+c=8，且=3 ,解得a €?,4a不成立；O 若 C 错，贝U A , B , D 正确，则有 a - b+c=0，且 2a+b=0，且 4a+2b+c=8，解得 a=—-3不为非零整数，不成立；isr — b 2若D 错，贝U A , B , C 正确，则有 a - b+c=0 ,且2a+b=0,且=3，解得a=-4a卫不为非零整数，不成立.4故选：A .点评：本题考查二次函数的极值、零点等概念，主要考查解方程的能力和判断分析的能力，属于中档题.二、填空题，共4小题，每小题5分，共20分•••所求概率卩=厂_ ；n.i 2属基础题.13. （5分）（2015?陕西）中位数为1010的一组数构成等差数列，其末项为2015,则该数列的首项为5 .考点：等差数列.专题：等差数列与等比数列.分析：由题意可得首项的方程，解方程可得.解答：解：设该等差数列的首项为a,由题意和等差数列的性质可得2015+a=1010 X2解得a=5故答案为：5点评：本题考查等差数列的基本性质，涉及中位数，属基础题.14. （5分）（2015?陕西）若抛物线y2=2px （p > 0）的准线经过双曲线x2- y2=1的一个焦点，则p= 2 一'_.考点：抛物线的简单性质.专题：计算题；圆锥曲线的定义、性质与方程.分析：先求出x2-y2=1的左焦点，得到抛物线y2=2px的准线，依据p的意义求出它的值.解答：解：双曲线x2- y2=1的左焦点为（-^/勺，0）,故抛物线y2=2px的准线为x= - V2 ,•••"'=-，二p=2:,故答案为：2.'：.点评：本题考查抛物线和双曲线的简单性质，以及抛物线方程y2=2px中p的意义.15. （5分）（2015?陕西）设曲线y=e x在点（0, 1 ）处的切线与曲线y二•（x> 0）上点P的x切线垂直，则P的坐标为（1, 1）.考点：利用导数研究曲线上某点切线方程.专题：导数的概念及应用.分析：利用y=e x在某点处的切屑斜率与另一曲线的切线斜率垂直求得另一曲线的斜率，进而求得切点坐标.解答：解：T f（x）=e x,••• f（0）=e0=1.•/ y=e x在（0, 1）处的切线与『=•• （x>0）上点P的切线垂直•点P处的切线斜率为-1.又y'=-」，设点P （x o, y0）••• X0=±1, •/ x> 0, ••• x0=1y0=1•••点P （1, 1）故答案为：（1, 1）点评：本题考查导数在曲线切线中的应用，在高考中属基础题型，常出现在选择填空中.16. （5分）（2015?陕西）如图，一横截面为等腰梯形的水渠，因泥沙沉积，导致水渠截面边界呈抛物线型（图中虚线所示），则原始的最大流量与当前最大流量的比值为 1.2考点：直线与圆锥曲线的关系.专题：创新题型；圆锥曲线的定义、性质与方程.分析：建立直角坐标系，求出抛物线方程，然后利用定积分求出泥沙沉积的横截面面积，求出梯形面积，即可推出结果.解答：解：如图：建立平面直角坐标系，设抛物线方程为：y=ax2,因为抛物线经过（5, 2）, 可得a=-,所以抛物线方程：y= --「，横截面为等腰梯形的水渠，泥沙沉积的横截面的面积为：2畚匸导2 X2）=2（焉』|卜2）冷,等腰梯形的面积为：业§ X2=16，当前最大流量的横截面的面积16-卫，2 316原始的最大流量与当前最大流量的比值为：故答案为：1.2.点评：本题考查抛物线的求法，定积分的应用，考查分析问题解决问题的能力，合理建系是解题的关键.三、解答题，共5小题，共70分17. （12分）（2015?陕西）△ ABC 的内角A , B , C 所对的边分别为 a , b , c.向量i = （ a ,)与 I = (cosA , sinB )平行.(I )求 A ;(n )若a= L, b=2,求厶ABC 的面积.考点：余弦定理的应用；平面向量共线（平行）的坐标表示. 专题：解三角形. 分析：（I ）利用向量的平行，列出方程，通过正弦定理求解A ;（n ）禾9用A ，以及a=. ； b=2,通过余弦定理求出 c ,然后求解△ ABC 的面积.(I )因为向量 | = (a ,样g b )与 | ,= ( cosA , sinB )平行,所以 asinB - . 一， : =0,由正弦定理可知：sinAsinB - :-;sinBcosA=0 ,因为 sinB 和, 所以 tanA= 一；，可得 A=—L ;■—-1（n ） a=「］, b=2,由余弦定理可得：a 2=b 2+c 2- 2bccosA ，可得 7=4+c 2- 2c ,解得c=3,△ABC 的面积为：_ .匸£点评：本题考查余弦定理以及宰相肚里的应用，三角形的面积的求法，考查计算能力.AD=2 , E 是AD 的中点，O 是AC 与BE 的交点，将 ABE 沿BE 折起到 A 1BE 的位置，如图2.（I ）证明：CD 丄平面A 1OC ;（n ）若平面A 1BE 丄平面BCDE ，求平面 A 1BC 与平面A 1CD 夹角的余弦值.El 圏2考点：二面角的平面角及求法；直线与平面垂直的性质. 专题：空间位置关系与距离；空间角.分析：（I ）根据线面垂直的判定定理即可证明：CD 丄平面A 1OC ;（n ）若平面A 1BE 丄平面BCDE ，建立空间坐标系，利用向量法即可求平面 A 1BC与平面A 1CD 夹角的余弦值.解答:II解答证明：（I ）在图1中，•/ AB=BC=1 , AD=2 , E 是AD 的中点，/ BAD=,••• BE 丄 AC ,解答：解:18. （12分）（2015?陕西）如图，在直角梯形ABCD 中，AD // BC , / BAD= ,AB=BC=1 ,A Mi即在图2中，BE 丄0A 1, BE 丄0C , 则BE 丄平面A i OC ;•/ CD // BE , ••• CD 丄平面 A i OC ;(n )若平面A i BE 丄平面BCDE , 由(I)知 BE 丄 OA i , BE 丄 OC , • Z A i OC 为二面角 A i - BE - C 的平面角,Z A i OC 二丄,2如图，建立空间坐标系，CD=BE=(-屈 0, 0)设平面A i BC 的法向量为!T = (X , y , z ),平面A i CD 的法向量为口 = (a , b , c ),取 r= (0, i , i ),•••平面A i BC 与平面 A i CD 为钝二面角，•平面A i BC 与平面A i CD 夹角的余弦值为-点评：本题主要考查空间直线和平面垂直的判定以及二面角的求解, 是解决空间角的常用方法.A i B=A i E=BC=ED=i . BC // ED• B ( ■' 2葩(-夢亨,0)，两=,0, 0), E (-羊(0,二：：，0)，fw&C=0「-玄4■产0\ ----------得［口・止&二y - z=0z=i ,即 I = (i ,i , i ),El •丘［C二。

2015年山东省高考数学试题及答案(文)

2015年普通高等学校招生全国统一考试（山东卷）数学（文科）第I 卷（共50分）本试卷分第I 卷和第II 卷两部分，共4页.满分150分.考试用时120分钟.考试结束后，将本试卷和答题卡一并交回.一、选择题：本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的.1、已知集合{}24A x x =<< ，()(){}130B x x x =--< ，则AB =（A ）()1,3 （B ）()1,4 （C ）()2,3 （D ）()2,42、若复数z 满足1zi i=- ，其中i 为虚数单位，则z = （A ）1i - （B ）1i + （C ）1i -- （D ）1i -+ 3、设0.61.50.60.6,0.6, 1.5a b c === ，则,,a b c 的大小关系是（A ）a b c << （B ）a c b << （C ）b a c << （D ）b c a << 4、要得到函数sin 43y x π⎛⎫=- ⎪⎝⎭的图象，只需将函数sin 4y x =的图象（A ）向左平移12π个单位（B ）向右12π平移个单位（C ）向左平移3π个单位（D ）向右平移3π个单位5、设m R ∈ ，命题“若0m > ，则方程20x x m +-= 有实根”的逆否命题是（A ）若方程20x x m +-=有实根，则0m > （B ）若方程20x x m +-=有实根，则0m ≤ （C ）若方程20x x m +-=没有实根，则0m > （D ）若方程20x x m +-=没有实根，则0m ≤6、为比较甲、乙两地某月14时的气温状况，随机选取该月中的5天，将这5天中14时的气温数据(单位:℃)制成如图所示的茎叶图。

考虑以下结论: ①甲地该月14时的平均气温低于乙地该月14时的平均气温； ②甲地该月14时的平均气温高于乙地该月14时的平均气温；③甲地该月14时的气温的标准差小于乙地该月14时的气温的标准差；④甲地该月14时的气温的标准差大于乙地该月14时的气温的标准差. 其中根据茎叶图能得到的统计结论的编号为（A ） ①③ （B ） ①④ （C ） ②③ （D ） ②④ 7、在区间[]0,2上随机地取一个数x ，则事件“1211log 12x ⎛⎫-≤+≤ ⎪⎝⎭”发生的概率为（A ）34 （B ）23 （C ）13 （D ）148、若函数()212x x f x a+=- 是奇函数，则使()3f x > 成立的x 的取值范围为（A ）(),1-∞- （B ）()1,0- （C ）()0,1 （D ）()1,+∞ 9. 已知等腰直角三角形的直角边的长为2，将该三角形绕其斜边所在的直线旋转一周而形成的曲面所围成的几何体的体积为（A ）223π （B ）423π（C ）22π （D ）42π 10.设函数()3,1,2,1,x x b x f x x -<⎧=⎨≥⎩若546f f ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭，则b = （A ）1 （B ）78 （C ）34 （D ）12第II 卷（共100分）二、填空题：本大题共5小题，每小题5分，共25分。

2015年高考真题——理科数学(陕西卷)解析版

2015年普通高等学校招生全国统一考试（陕西卷）理一、选择题（本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.）1.设集合2{|}M x x x ==，{|lg 0}N x x =≤，则M N =U （）A ．[0,1]B ．(0,1]C ．[0,1)D ．(,1]-∞ 【答案】A 【解析】试题分析：{}{}20,1x x x M ===，{}{}lg 001x x x x N =≤=<≤，所以[]0,1M N =U ，故选A ．考点：1、一元二次方程；2、对数不等式；3、集合的并集运算．2.某中学初中部共有110名教师，高中部共有150名教师，其性别比例如图所示，则该校女教师的人数为（） A ．167 B ．137 C ．123 D ．93【答案】B考点：扇形图．3.如图，某港口一天6时到18时的水深变化曲线近似满足函数3sin()6y x k πϕ=++，据此函数可知，这段时间水深（单位：m ）的最大值为（）A ．5B ．6C ．8D ．10【答案】C 【解析】试题分析：由图象知：min 2y =，因为min 3y k =-+，所以32k -+=，解得：5k =，所以这段时间水深的最大值是max 3358y k =+=+=，故选C ．考点：三角函数的图象与性质．4.二项式(1)()n x n N ++∈的展开式中2x 的系数为15，则n =（）A ．4B ．5C ．6D ．7 【答案】C考点：二项式定理．5.一个几何体的三视图如图所示，则该几何体的表面积为（）A ．3πB ．4πC ．24π+D ．34π+【答案】D 【解析】试题分析：由三视图知：该几何体是半个圆柱，其中底面圆的半径为1，母线长为2，所以该几何体的表面积是()1211222342ππ⨯⨯⨯++⨯=+，故选D ．考点：1、三视图；2、空间几何体的表面积．6.“sin cos αα=”是“cos20α=”的（）A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件【答案】A 【解析】试题分析：因为22cos 2cos sin 0ααα=-=，所以sin cos αα=或sin cos αα=-，因为“sin cos αα=”⇒“cos20α=”，但“sin cos αα=”⇐/“cos20α=”，所以“sin cos αα=”是“cos20α=”的充分不必要条件，故选A ．考点：1、二倍角的余弦公式；2、充分条件与必要条件．7.对任意向量,a b r r，下列关系式中不恒成立的是（）A ．||||||a b a b ⋅≤r r r rB ．||||||||a b a b -≤-r r r rC ．22()||a b a b +=+r r r rD ．22()()a b a b a b +-=-r r r r r r【答案】B考点：1、向量的模；2、向量的数量积．8.根据右边的图，当输入x 为2006时，输出的y =（）A ．28B ．10C ．4D ．2【答案】B 【解析】试题分析：初始条件：2006x =；第1次运行：2004x =；第2次运行：2002x =；第3次运行：2000x =；⋅⋅⋅⋅⋅⋅；第1003次运行：0x =；第1004次运行：2x =-．不满足条件0?x ≥，停止运行，所以输出的23110y =+=，故选B ．考点：程序框图．9.设()ln ,0f x x a b =<<，若()p f ab =，()2a b q f +=，1(()())2r f a f b =+，则下列关系式中正确的是（）A ．q r p =<B ．q r p =>C ．p r q =<D ．p r q => 【答案】C考点：1、基本不等式；2、基本初等函数的单调性．10.某企业生产甲、乙两种产品均需用A ，B 两种原料．已知生产1吨每种产品需原料及每天原料的可用限额如表所示，如果生产1吨甲、乙产品可获利润分别为3万元、4万元，则该企业每天可获得最大利润为（）A ．12万元B ．16万元C ．17万元D ．18万元甲乙原料限额A(吨)3212B(吨)128【答案】D 【解析】试题分析：设该企业每天生产甲、乙两种产品分别为x 、y 吨，则利润34z x y =+由题意可列32122800x y x y x y +≤⎧⎪+≤⎪⎨≥⎪⎪≥⎩，其表示如图阴影部分区域：当直线340x y z +-=过点(2,3)A 时，z 取得最大值，所以max 324318z =⨯+⨯=，故选D ．考点：线性规划．11.设复数(1)z x yi =-+(,)x y R ∈，若||1z ≤，则y x ≥的概率为（）A ．3142π+B ．1142π-C ．112π- D ．112π+【答案】B 【解析】试题分析：2222(1)||(1)1(1)1z x yi z x y x y =-+⇒=-+≤⇒-+≤如图可求得(1,1)A ，(1,0)B ，阴影面积等于21111114242ππ⨯-⨯⨯=- 若||1z ≤，则y x ≥的概率是211142142πππ-=-⨯，故选B ．考点：1、复数的模；2、几何概型．12.对二次函数2()f x ax bx c =++（a 为非零常数），四位同学分别给出下列结论，其中有且仅有一个结论是错误的，则错误的结论是（）A ．-1是()f x 的零点B ．1是()f x 的极值点C ．3是()f x 的极值D . 点(2,8)在曲线()y f x =上【答案】A考点：1、函数的零点； 2、利用导数研究函数的极值．二、填空题（本大题共4小题，每小题5分，共20分．）13.中位数1010的一组数构成等差数列，其末项为2015，则该数列的首项为．【答案】5 【解析】试题分析：设数列的首项为1a ，则12015210102020a +=⨯=，所以15a =，故该数列的首项为5，所以答案应填：5．考点：等差中项．14.若抛物线22(0)y px p =>的准线经过双曲线221x y -=的一个焦点，则p= ．【答案】22考点：1、抛物线的简单几何性质；2、双曲线的简单几何性质． 15.设曲线xy e =在点（0,1）处的切线与曲线1(0)y x x=>上点p 处的切线垂直，则p 的坐标为．【答案】()1,1 【解析】试题分析：因为xy e =，所以xy e '=，所以曲线xy e =在点()0,1处的切线的斜率0101x k y e ='===，设P 的坐标为()00,xy （00x >），则001y x =，因为1y x =，所以21y x '=-，所以曲线1y x=在点P 处的切线的斜率02201x x k y x ='==-，因为121k k ⋅=-，所以211x -=-，即201x =，解得01x =±，因为00x >，所以01x =，所以01y =，即P 的坐标是()1,1，所以答案应填：()1,1．考点：1、导数的几何意义；2、两条直线的位置关系．16.如图，一横截面为等腰梯形的水渠，因泥沙沉积，导致水渠截面边界呈抛物线型（图中虚线表示），则原始的最大流量与当前最大流量的比值为．【答案】1.2 【解析】试题分析：建立空间直角坐标系，如图所示：原始的最大流量是()11010222162⨯+-⨯⨯=，设抛物线的方程为22x py =（0p >），因为该抛物线过点()5,2，所以2225p ⨯=，解得254p =，所以2252x y =，即2225y x =，所以当前最大流量是()()5323535522224022255255257575753x dx x x --⎛⎫⎛⎫⎛⎫⎡⎤-=-=⨯-⨯-⨯--⨯-= ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦⎰，故原始的最大流量与当前最大流量的比值是161.2403=，所以答案应填：1.2．考点：1、定积分；2、抛物线的方程；3、定积分的几何意义．三、解答题（本大题共6小题，共70分．解答须写出文字说明、证明过程和演算步骤．）17．（本小题满分12分）C ∆AB 的内角A ，B ，C 所对的边分别为a ，b ，c ．向量(),3m a b =r与()cos ,sin n =A B r平行．（I ）求A ；（II ）若7a =，2b =求C ∆AB 的面积．【答案】（I ）3π；（II ）332．试题解析：（I ）因为//m n r r，所以sin 3cos 0a B b A -=，由正弦定理，得sinAsinB 3A 0-=又sin 0B ≠，从而tan 3A =，由于0A π<<，所以3A π=(II)解法一：由余弦定理，得2222cos a b c bc A =+- 而72,a =3πA =得2742c c =+-，即2230c c --= 因为0c >，所以3c =. 故∆ABC 的面积为133bcsinA 2=考点：1、平行向量的坐标运算；2、正弦定理；3、余弦定理；4、三角形的面积公式. 18．（本小题满分12分）如图1，在直角梯形CD AB 中，D//C A B ，D 2π∠BA =，C 1AB =B =，D 2A =，E 是D A 的中点，O 是C A 与BE 的交点．将∆ABE 沿BE 折起到1∆A BE 的位置，如图2．（I ）证明：CD ⊥平面1C A O ；（II ）若平面1A BE ⊥平面CD B E ，求平面1C A B 与平面1CD A 夹角的余弦值．【答案】（I ）证明见解析；（II ）6．试题解析：（I ）在图1中，因为AB=BC=1,AD=2,E是AD的中点，∠BAD=2π，所以BE ⊥AC即在图2中，BE ⊥1OA，BE ⊥OC从而BE⊥平面1A OC又CD P BE，所以CD⊥平面1A OC.(II)由已知，平面1A BE⊥平面BCDE，又由（1）知，BE ⊥1OA，BE ⊥OC所以1A OC∠为二面角1--CA BE的平面角，所以1OC2Aπ∠=.如图，以O为原点，建立空间直角坐标系，因为11B=E=BC=ED=1A A, BC EDP所以12222(E(A(0,0,),C(0,,0),2222B-得22BC(,,0),22-u u u r122A C(0,,22-u u u u r，CD BE(2,0,0)==-u u u r u u u r.设平面1BCA的法向量1111(,,)n x y z=u r，平面1CDA的法向量2222(,,)n x y z=u u r，平面1BCA与平面1CDA夹角为θ，则111n BCn A C⎧⋅=⎪⎨⋅=⎪⎩u r u u u ru r u u u r，得1111x yy z-+=⎧⎨-=⎩，取1(1,1,1)n=u r，221n CDn A C⎧⋅=⎪⎨⋅=⎪⎩u u r u u u ru u r u u u r，得222xy z=⎧⎨-=⎩，取2(0,1,1)n=u u r，从而126cos|cos,|332n nθ=〈〉==⨯u r u u r，即平面1BCA与平面1CDA6考点：1、线面垂直；2、二面角；3、空间直角坐标系；4、空间向量在立体几何中的应用. 19．（本小题满分12分）设某校新、老校区之间开车单程所需时间为T ，T 只与道路畅通状况有关，（II ）刘教授驾车从老校区出发，前往新校区做一个50分钟的讲座，结束后立即返回老校区，求刘教授从离开老校区到返回老校区共用时间不超过120分钟的概率．【答案】（I ）分布列见解析，32；（II ）0.91．【解析】试题分析：（I ）先算出T 的频率分布，进而可得T 的分布列，再利用数学期望公式可得数学期望ET ；（II ）先设事件A 表示“刘教授从离开老校区到返回老校区共用时间不超过120分钟”，再算出A 的概率．从而 0.4400.132⨯+⨯=（分钟）(II)设12,T T 分别表示往、返所需时间，12,T T 的取值相互独立，且与T 的分布列相同.设事件A 表示“刘教授共用时间不超过120分钟”，由于讲座时间为50分钟，所以事件A 对应于“刘教授在途中的时间不超过70分钟”.解法一：121212(A)P(70)P(25,45)P(30,40)P T T T T T T =+≤==≤+=≤1212P(35,35)P(40,30)T T T T +=≤+=≤10.210.30.90.40.50.10.91=⨯+⨯+⨯+⨯=.解法二：121212(A)P(70)P(35,40)P(40,35)P T T T T T T =+>===+==12P(40,40)T T +== 0.40.10.10.40.10.10.09=⨯+⨯+⨯=故(A)1P(A)0.91P =-=.考点：1、离散型随机变量的分布列与数学期望；2、独立事件的概率.20．（本小题满分12分）已知椭圆:E 22221x y a b+=（0a b >>）的半焦距为c ，原点O 到经过两点(),0c ，()0,b 的直线的距离为12c ．（I ）求椭圆E 的离心率；（II ）如图，AB 是圆:M ()()225212x y ++-=的一条直径，若椭圆E 经过A ，B 两点，求椭圆E 的方程．【答案】（I 3II ）221123x y +=．【解析】试题分析：（I ）先写过点(),0c ，()0,b 的直线方程，再计算原点O 到该直线的距离，进而可得椭圆E 的离心率；（II ）先由（I ）知椭圆E 的方程，设AB 的方程，联立()2222144y k x x y b⎧=++⎪⎨+=⎪⎩，消去y ，可得12x x +和12x x 的值，进而可得k ，再利用10AB =可得2b 的值，进而可得椭圆E 的方程．试题解析：（I ）过点(c,0),(0,b)的直线方程为0bx cy bc +-=，则原点O 到直线的距离22bcd ab c ==+，由12d c =，得2222a b a c ==-，解得离心率3c a =. (II)解法一：由（I ）知，椭圆E 的方程为22244x y b +=. (1) 依题意，圆心M(-2,1)是线段AB 的中点，且|AB |10=易知，AB 不与x 轴垂直，设其直线方程为(2)1y k x =++，代入(1)得2222(14)8(21)4(21)40k x k k x k b +++++-=设1122(,y ),B(,y ),A x x 则221212228(21)4(21)4,.1414k k k b x x x x k k++-+=-=-++由124x x +=-，得28(21)4,14k k k +-=-+解得12k =. 从而21282x x b =-.于是12|AB ||x x =-==由|AB |23b =.故椭圆E 的方程为221123x y +=. 解法二：由（I ）知，椭圆E 的方程为22244x y b +=. (2) 依题意，点A ，B关于圆心M(-2,1)对称，且|AB |=设1122(,y ),B(,y ),A x x 则2221144x y b +=，2222244x y b +=，两式相减并结合12124,y 2,x x y +=-+=得()1212-4()80x x y y -+-=. 易知，AB 不与x 轴垂直，则12x x ≠，所以AB 的斜率12121k .2AB y y x x -==-因此AB 直线方程为1(2)12y x =++，代入(2)得224820.x x b ++-= 所以124x x +=-，21282x x b =-.于是12|AB ||x x =-==由|AB |23b =.故椭圆E 的方程为221123x y +=. 考点：1、直线方程；2、点到直线的距离公式；3、椭圆的简单几何性质；4、椭圆的方程；5、圆的方程；6、直线与圆的位置关系；7、直线与圆锥曲线的位置.21．（本小题满分12分）设()n f x 是等比数列1，x ，2x ，⋅⋅⋅，nx 的各项和，其中0x >，n ∈N ， 2n ≥．（I ）证明：函数()()F 2n n x f x =-在1,12⎛⎫⎪⎝⎭内有且仅有一个零点（记为n x ），且11122n n n x x +=+；（II ）设有一个与上述等比数列的首项、末项、项数分别相同的等差数列，其各项和为()n g x ，比较()n f x与()n g x 的大小，并加以证明．【答案】（I ）证明见解析；（II ）当1x =时， ()()n n f x g x =，当1x ≠时，()()n n f x g x <，证明见解析．【解析】试题分析：（I ）先利用零点定理可证()F n x 在1,12⎛⎫⎪⎝⎭内至少存在一个零点，再利用函数的单调性可证()F n x 在1,12⎛⎫⎪⎝⎭内有且仅有一个零点，进而利用n x 是()F n x 的零点可证11122n n n x x +=+；（II ）先设()()()n n h x f x g x =-，再对x 的取值范围进行讨论来判断()h x 与0的大小，进而可得()n f x 和()n g x 的大小．试题解析：（I ）2()()212,nn n F x f x x x x =-=+++-L 则(1)10,n F n =->1211111112()1220,12222212n nn n F +⎛⎫- ⎪⎛⎫⎛⎫⎝⎭=+++-=-=-< ⎪ ⎪⎝⎭⎝⎭-L 所以()n F x 在1,12⎛⎫⎪⎝⎭内至少存在一个零点n x . 又1()120n n F x x nx-'=++>L ，故在1,12⎛⎫⎪⎝⎭内单调递增，所以()n F x 在1,12⎛⎫⎪⎝⎭内有且仅有一个零点n x . 因为n x 是()n F x 的零点，所以()=0n n F x ，即11201n n nx x +--=-，故111=+22n n n x x +.(II)解法一：由题设，()()11().2nn n x g x ++=设()()211()()()1,0.2nn n n n x h x f x g x x x x x ++=-=+++->L当1x =时, ()()n n f x g x = 当1x ≠时, ()111()12.2n n n n x h x x nx --+'=++-L若01x <<,()11111()22n n n n n n h x x x nx x ----+'>++-L ()()11110.22n n n n n n x x --++=-= 若1x >,()11111()22n n n n n n h x xx nx x ----+'<++-L ()()11110.22n n n n n n x x --++=-= 所以()h x 在(0,1)上递增，在(1,)+∞上递减，所以()(1)0h x h <=，即()()n n f x g x <.综上所述，当1x =时, ()()n n f x g x =；当1x ≠时()()n n f x g x <解法二由题设，()()211()1,(),0.2nnn nn x f x x x x g x x ++=+++=>L 当1x =时, ()()n n f x g x =当1x ≠时, 用数学归纳法可以证明()()n n f x g x <. 当2n =时, 2221()()(1)0,2f xg x x -=--<所以22()()f x g x <成立. 假设(2)n k k =≥时，不等式成立，即()()k k f x g x <. 那么，当+1n k =时，()()111k+1k 11()()()2kk k k k k x f x f x x g x x x+++++=+<+=+()12112k k x k x k +++++=.又()()11k+121111()22k k k k x k x k kx k x g x ++++++-++-=令()1()11(x 0)k k k h x kx k x +=-++>，则()()11()(k 1)11(x 1)k k k k h x k x k k x k k x --'=+-+=+-所以当01x <<,()0kh x '<,()k h x 在(0,1)上递减；当1x >,()0kh x '>,()k h x 在(1,)+∞上递增. 所以()(1)0k k h x h >=，从而()1k+1211()2k k x k x k g x +++++>故11()()k k f x g x ++<.即+1n k =，不等式也成立. 所以，对于一切2n ≥的整数，都有()()n n f x g x <.解法三:由已知，记等差数列为{}k a ,等比数列为{}k b ,k 1,2,, 1.n =+L 则111a b ==，11n n n a b x ++==，所以()11+1(2n)n k x a k k n-=-⋅≤≤,1(2),k k b x k n -=≤≤ 令()()111(x)1,0(2).n k k k k k x m a b x x k n n---=-=+->≤≤当1x =时, =k k a b ,所以()()n n f x g x =.当1x ≠时, ()()12211()(k 1)11n k k n k k k m x nx x k x x n----+-'=--=-- 而2k n ≤≤，所以10k ->，11n k -+≥.若01x <<, 11n k x -+<,()0k m x '<,当1x >,11n k x-+>,()0km x '>, 从而()k m x 在(0,1)上递减,()k m x 在(1,)+∞上递增.所以()(1)0k k m x m >=，所以当01(2),k k x x a b k n >≠>≤≤且时,又11a b =,11n n a b ++=，故()()n n f x g x < 综上所述，当1x =时, ()()n n f x g x =；当1x ≠时()()n n f x g x < 考点：1、零点定理；2、利用导数研究函数的单调性.请在22、23、24三题中任选一题作答，如果多做，则按所做的第一题计分．作答时用2B 铅笔在答题卡上把所选题目的题号后的方框涂黑． 22．（本小题满分10分）选修4-1：几何证明选讲如图，AB 切O e 于点B ，直线D A 交O e 于D ，E 两点，C D B ⊥E ，垂足为C ．（I ）证明：C D D ∠B =∠BA ；（II ）若D 3DC A =，C B =O e 的直径．【答案】（I ）证明见解析；（II ）3．【解析】试题分析：（I ）先证C D D ∠B =∠BE ，再证D D ∠BA =∠BE ，进而可证C D D ∠B =∠BA ；（II ）先由（I ）知D B 平分C ∠BA ，进而可得D A 的值，再利用切割线定理可得AE 的值，进而可得O e 的直径．试题解析：（I ）因为DE 为圆O 的直径，则BED EDB ∠+∠=90o，又BC ⊥DE ，所以∠CBD+∠EDB=90°，从而∠CBD=∠BED. 又AB 切圆O 于点B ，得∠DAB=∠BED ，所以∠CBD=∠DBA. （II ）由（I ）知BD 平分∠CBA ，则=3BA AD BC CD=,又2BC ，从而32AB =，所以224AC AB BC -=，所以D=3A .由切割线定理得2=AD AB AE ×，即2=ADAB AE =6，故DE=AE-AD=3，即圆O 的直径为3.考点：1、直径所对的圆周角；2、弦切角定理；3、切割线定理. 23．（本小题满分10分）选修4-4：坐标系与参数方程在直角坐标系x y O 中，直线l 的参数方程为13232x t y t ⎧=+⎪⎪⎨⎪=⎪⎩（t 为参数）．以原点为极点，x轴正半轴为极轴建立极坐标系，C e 的极坐标方程为23ρθ=．（I ）写出C e 的直角坐标方程；（II ）P 为直线l 上一动点，当P 到圆心C 的距离最小时，求P 的直角坐标．【答案】（I ）(2233x y +-=；（II ）()3,0．【解析】试题分析：（I ）先将23ρθ=两边同乘以ρ可得223sin ρρθ=，再利用222x y ρ=+，sin x ρθ=可得C e 的直角坐标方程；（II ）先设P 的坐标，则2C 12t P =+，再利用二次函数的性质可得C P 的最小值，进而可得P 的直角坐标．试题解析：（I ）由2,sin ρθρθ==得，从而有(2222+,+3x y x y ==所以.(II)设1(3t),2P +又,则|PC |== 故当t=0时，|PC|取最小值，此时P 点的直角坐标为（3，0）.考点：1、极坐标方程化为直角坐标方程；2、参数的几何意义；3、二次函数的性质. 24．（本小题满分10分）选修4-5：不等式选讲已知关于x 的不等式x a b +<的解集为{}24x x <<．（I ）求实数a ，b 的值；（II + 【答案】（I ）3a =-，1b =；（II ）4．【解析】试题分析：（I ）先由x a b +<可得b a x b a --<<-，再利用关于x 的不等式x a b +<的解集为{}24x x <<可得a ，b 的值；（II ），试题解析：（I ）由||x a b +<，得b a x b a --<<-则2,4,b a b a --=⎧⎨-=⎩解得3a =-,1b =（II =≤4==1=，即1t =时等号成立，故max4=.考点：1、绝对值不等式；2、柯西不等式.。

2015年全国统一高考数学试卷(完整版+答案解析)(新课标ⅱ)

2015年全国统一高考数学试卷（文科）（新课标Ⅱ）一、选择题：本大题共12小题，每小题5分1．（5分）（2015•新课标Ⅱ）已知集合A＝{x|﹣1＜x＜2}，B＝{x|0＜x＜3}，则A∪B＝（）A．（﹣1，3）B．（﹣1，0）C．（0，2）D．（2，3）2．（5分）（2015•新课标Ⅱ）若为a实数，且＝3+i，则a＝（）A．﹣4B．﹣3C．3D．43．（5分）（2015•新课标Ⅱ）根据如图给出的2004年至2013年我国二氧化硫年排放量（单位：万吨）柱形图，以下结论中不正确的是（）A．逐年比较，2008年减少二氧化硫排放量的效果最显著B．2007年我国治理二氧化硫排放显现成效C．2006年以来我国二氧化硫年排放量呈减少趋势D．2006年以来我国二氧化硫年排放量与年份正相关4．（5分）（2015•新课标Ⅱ）＝（1，﹣1），＝（﹣1，2）则（2+）＝（）A．﹣1B．0C．1D．25．（5分）（2015•新课标Ⅱ）已知S n是等差数列{a n}的前n项和，若a1+a3+a5＝3，则S5＝（）A．5B．7C．9D．116．（5分）（2015•新课标Ⅱ）一个正方体被一个平面截去一部分后，剩余部分的三视图如图，则截去部分体积与剩余部分体积的比值为（）A．B．C．D．7．（5分）（2015•新课标Ⅱ）已知三点A（1，0），B（0，），C（2，）则△ABC外接圆的圆心到原点的距离为（）A．B．C．D．8．（5分）（2015•新课标Ⅱ）如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”．执行该程序框图，若输入a，b分别为14，18，则输出的a＝（）A．0B．2C．4D．149．（5分）（2015•新课标Ⅱ）已知等比数列{a n}满足a1＝，a3a5＝4（a4﹣1），则a2＝（）A．2B．1C．D．10．（5分）（2015•新课标Ⅱ）已知A，B是球O的球面上两点，∠AOB＝90°，C为该球面上的动点，若三棱锥O﹣ABC体积的最大值为36，则球O的表面积为（）A．36πB．64πC．144πD．256π11．（5分）（2015•新课标Ⅱ）如图，长方形ABCD的边AB＝2，BC＝1，O是AB的中点，点P沿着边BC，CD与DA运动，记∠BOP＝x．将动点P到A，B两点距离之和表示为x的函数f（x），则y＝f（x）的图象大致为（）A．B．C．D．12．（5分）（2015•新课标Ⅱ）设函数f（x）＝ln（1+|x|）﹣，则使得f（x）＞f（2x ﹣1）成立的x的取值范围是（）A．（﹣∞，）∪（1，+∞）B．（，1）C．（）D．（﹣∞，﹣，）二、填空题13．（3分）（2015•新课标Ⅱ）已知函数f（x）＝ax3﹣2x的图象过点（﹣1，4）则a＝．14．（3分）（2015•新课标Ⅱ）若x，y满足约束条件，则z＝2x+y的最大值为．15．（3分）（2015•新课标Ⅱ）已知双曲线过点且渐近线方程为y＝±x，则该双曲线的标准方程是．16．（3分）（2015•新课标Ⅱ）已知曲线y＝x+lnx在点（1，1）处的切线与曲线y＝ax2+（a+2）x+1相切，则a＝．三．解答题17．（2015•新课标Ⅱ）△ABC中，D是BC上的点，AD平分∠BAC，BD＝2DC （Ⅰ）求．（Ⅱ）若∠BAC＝60°，求∠B．18．（2015•新课标Ⅱ）某公司为了解用户对其产品的满意度，从A，B两地区分别随机调查了40个用户，根据用户对产品的满意度评分，得到A地区用户满意度评分的频率分布直方图和B地区用户满意度评分的频数分布表B地区用户满意度评分的频数分布表满意度评分分组[50，60）[60，70）[70，80）[80，90）[90，100）频数2814106（1）做出B地区用户满意度评分的频率分布直方图，并通过直方图比较两地区满意度评分的平均值及分散程度（不要求计算出具体值，给出结论即可）（Ⅱ）根据用户满意度评分，将用户的满意度从低到高分为三个不等级：满意度评分低于70分70分到89分不低于90分满意度等级不满意满意非常满意估计哪个地区用户的满意度等级为不满意的概率大？说明理由．19．（12分）（2015•新课标Ⅱ）如图，长方体ABCD﹣A1B1C1D1中，AB＝16，BC＝10，AA1＝8，点E，F分别在A1B1，D1C1上，A1E＝D1F＝4．过E，F的平面α与此长方体的面相交，交线围成一个正方形（Ⅰ）在图中画出这个正方形（不必说出画法和理由）（Ⅱ）求平面α把该长方体分成的两部分体积的比值．20．（2015•新课标Ⅱ）椭圆C：＝1，（a＞b＞0）的离心率，点（2，）在C 上．（1）求椭圆C的方程；（2）直线l不过原点O且不平行于坐标轴，l与C有两个交点A，B，线段AB的中点为M．证明：直线OM的斜率与l的斜率的乘积为定值．21．（2015•新课标Ⅱ）设函数f（x）＝lnx+a（1﹣x）．（Ⅰ）讨论：f（x）的单调性；（Ⅱ）当f（x）有最大值，且最大值大于2a﹣2时，求a的取值范围．四、选修4-1：几何证明选讲22．（10分）（2015•新课标Ⅱ）如图，O为等腰三角形ABC内一点，⊙O与△ABC的底边BC交于M，N两点，与底边上的高AD交于点G，且与AB，AC分别相切于E，F两点．（1）证明：EF∥BC；（2）若AG等于⊙O的半径，且AE＝MN＝2，求四边形EBCF的面积．五、选修4-4：坐标系与参数方程23．（10分）（2015•新课标Ⅱ）在直角坐标系xOy中，曲线C1：（t为参数，t≠0），其中0≤α≤π，在以O为极点，x轴正半轴为极轴的极坐标系中，曲线C2：ρ＝2sinθ，C3：ρ＝2cosθ．（1）求C2与C3交点的直角坐标；（2）若C1与C2相交于点A，C1与C3相交于点B，求|AB|的最大值．六、选修4-5不等式选讲24．（10分）（2015•新课标Ⅱ）设a，b，c，d均为正数，且a+b＝c+d，证明：（1）若ab＞cd，则+＞+；（2）+＞+是|a﹣b|＜|c﹣d|的充要条件．2015年全国统一高考数学试卷（文科）（新课标Ⅱ）参考答案与试题解析一、选择题：本大题共12小题，每小题5分1．（5分）（2015•新课标Ⅱ）已知集合A＝{x|﹣1＜x＜2}，B＝{x|0＜x＜3}，则A∪B＝（）A．（﹣1，3）B．（﹣1，0）C．（0，2）D．（2，3）【分析】根据集合的基本运算进行求解即可．【解答】解：∵A＝{x|﹣1＜x＜2}，B＝{x|0＜x＜3}，∴A∪B＝{x|﹣1＜x＜3}，故选：A．【点评】本题主要考查集合的基本运算，比较基础．2．（5分）（2015•新课标Ⅱ）若为a实数，且＝3+i，则a＝（）A．﹣4B．﹣3C．3D．4【分析】根据复数相等的条件进行求解即可．【解答】解：由，得2+ai＝（1+i）（3+i）＝2+4i，则a＝4，故选：D．【点评】本题主要考查复数相等的应用，比较基础．3．（5分）（2015•新课标Ⅱ）根据如图给出的2004年至2013年我国二氧化硫年排放量（单位：万吨）柱形图，以下结论中不正确的是（）A．逐年比较，2008年减少二氧化硫排放量的效果最显著B．2007年我国治理二氧化硫排放显现成效C．2006年以来我国二氧化硫年排放量呈减少趋势D．2006年以来我国二氧化硫年排放量与年份正相关【分析】A从图中明显看出2008年二氧化硫排放量比2007年的二氧化硫排放量减少的最多，故A正确；B从2007年开始二氧化硫排放量变少，故B正确；C从图中看出，2006年以来我国二氧化硫年排放量越来越少，故C正确；D2006年以来我国二氧化硫年排放量越来越少，与年份负相关，故D错误．【解答】解：A从图中明显看出2008年二氧化硫排放量比2007年的二氧化硫排放量明显减少，且减少的最多，故A正确；B2004﹣2006年二氧化硫排放量越来越多，从2007年开始二氧化硫排放量变少，故B正确；C从图中看出，2006年以来我国二氧化硫年排放量越来越少，故C正确；D2006年以来我国二氧化硫年排放量越来越少，而不是与年份正相关，故D错误．故选：D．【点评】本题考查了学生识图的能力，能够从图中提取出所需要的信息，属于基础题．4．（5分）（2015•新课标Ⅱ）＝（1，﹣1），＝（﹣1，2）则（2+）＝（）A．﹣1B．0C．1D．2【分析】利用向量的加法和数量积的坐标运算解答本题．【解答】解：因为＝（1，﹣1），＝（﹣1，2）则（2+）＝（1，0）•（1，﹣1）＝1；故选：C．【点评】本题考查了向量的加法和数量积的坐标运算；属于基础题目．5．（5分）（2015•新课标Ⅱ）已知S n是等差数列{a n}的前n项和，若a1+a3+a5＝3，则S5＝（）A．5B．7C．9D．11【分析】由等差数列{a n}的性质，a1+a3+a5＝3＝3a3，解得a3．再利用等差数列的前n项和公式即可得出．【解答】解：由等差数列{a n}的性质，a1+a3+a5＝3＝3a3，解得a3＝1．则S5＝＝5a3＝5．故选：A．【点评】本题考查了等差数列的通项公式及其性质、前n项和公式，考查了推理能力与计算能力，属于中档题．6．（5分）（2015•新课标Ⅱ）一个正方体被一个平面截去一部分后，剩余部分的三视图如图，则截去部分体积与剩余部分体积的比值为（）A．B．C．D．【分析】由三视图判断，正方体被切掉的部分为三棱锥，把相关数据代入棱锥的体积公式计算即可．【解答】解：设正方体的棱长为1，由三视图判断，正方体被切掉的部分为三棱锥，∴正方体切掉部分的体积为×1×1×1＝，∴剩余部分体积为1﹣＝，∴截去部分体积与剩余部分体积的比值为．故选：D．【点评】本题考查了由三视图判断几何体的形状，求几何体的体积．7．（5分）（2015•新课标Ⅱ）已知三点A（1，0），B（0，），C（2，）则△ABC外接圆的圆心到原点的距离为（）A．B．C．D．【分析】利用外接圆的性质，求出圆心坐标，再根据圆心到原点的距离公式即可求出结论．【解答】解：因为△ABC外接圆的圆心在直线BC垂直平分线上，即直线x＝1上，可设圆心P（1，p），由PA＝PB得|p|＝，得p＝圆心坐标为P（1，），所以圆心到原点的距离|OP|＝＝＝，故选：B．【点评】本题主要考查圆性质及△ABC外接圆的性质，了解性质并灵运用是解决本题的关键．8．（5分）（2015•新课标Ⅱ）如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”．执行该程序框图，若输入a，b分别为14，18，则输出的a＝（）A．0B．2C．4D．14【分析】模拟执行程序框图，依次写出每次循环得到的a，b的值，当a＝b＝2时不满足条件a≠b，输出a的值为2．【解答】解：模拟执行程序框图，可得a＝14，b＝18满足条件a≠b，不满足条件a＞b，b＝4满足条件a≠b，满足条件a＞b，a＝10满足条件a≠b，满足条件a＞b，a＝6满足条件a≠b，满足条件a＞b，a＝2满足条件a≠b，不满足条件a＞b，b＝2不满足条件a≠b，输出a的值为2．故选：B．【点评】本题主要考查了循环结构程序框图，属于基础题．9．（5分）（2015•新课标Ⅱ）已知等比数列{a n}满足a1＝，a3a5＝4（a4﹣1），则a2＝（）A．2B．1C．D．【分析】利用等比数列的通项公式即可得出．【解答】解：设等比数列{a n}的公比为q，∵，a3a5＝4（a4﹣1），∴＝4，化为q3＝8，解得q＝2则a2＝＝．故选：C．【点评】本题考查了等比数列的通项公式，属于基础题．10．（5分）（2015•新课标Ⅱ）已知A，B是球O的球面上两点，∠AOB＝90°，C为该球面上的动点，若三棱锥O﹣ABC体积的最大值为36，则球O的表面积为（）A．36πB．64πC．144πD．256π【分析】当点C位于垂直于面AOB的直径端点时，三棱锥O﹣ABC的体积最大，利用三棱锥O﹣ABC体积的最大值为36，求出半径，即可求出球O的表面积．【解答】解：如图所示，当点C位于垂直于面AOB的直径端点时，三棱锥O﹣ABC的体＝V C﹣AOB＝＝＝36，故积最大，设球O的半径为R，此时V O﹣ABCR＝6，则球O的表面积为4πR2＝144π，故选：C．【点评】本题考查球的半径与表面积，考查体积的计算，确定点C位于垂直于面AOB的直径端点时，三棱锥O﹣ABC的体积最大是关键．11．（5分）（2015•新课标Ⅱ）如图，长方形ABCD的边AB＝2，BC＝1，O是AB的中点，点P沿着边BC，CD与DA运动，记∠BOP＝x．将动点P到A，B两点距离之和表示为x的函数f（x），则y＝f（x）的图象大致为（）A．B．C．D．【分析】根据函数图象关系，利用排除法进行求解即可．【解答】解：当0≤x≤时，BP＝tan x，AP＝＝，此时f（x）＝+tan x，0≤x≤，此时单调递增，当P在CD边上运动时，≤x≤且x≠时，如图所示，tan∠POB＝tan（π﹣∠POQ）＝tan x＝﹣tan∠POQ＝﹣＝﹣，∴OQ＝﹣，∴PD＝AO﹣OQ＝1+，PC＝BO+OQ＝1﹣，∴PA+PB＝，当x＝时，PA+PB＝2，当P在AD边上运动时，≤x≤π，PA+PB＝﹣tan x，由对称性可知函数f（x）关于x＝对称，且f（）＞f（），且轨迹为非线型，排除A，C，D，故选：B．【点评】本题主要考查函数图象的识别和判断，根据条件先求出0≤x≤时的解析式是解决本题的关键．12．（5分）（2015•新课标Ⅱ）设函数f（x）＝ln（1+|x|）﹣，则使得f（x）＞f（2x ﹣1）成立的x的取值范围是（）A．（﹣∞，）∪（1，+∞）B．（，1）C．（）D．（﹣∞，﹣，）【分析】根据函数的奇偶性和单调性之间的关系，将不等式进行转化即可得到结论．【解答】解：∵函数f（x）＝ln（1+|x|）﹣为偶函数，且在x≥0时，f（x）＝ln（1+x）﹣，导数为f′（x）＝+＞0，即有函数f（x）在[0，+∞）单调递增，∴f（x）＞f（2x﹣1）等价为f（|x|）＞f（|2x﹣1|），即|x|＞|2x﹣1|，平方得3x2﹣4x+1＜0，解得：＜x＜1，所求x的取值范围是（，1）．故选：B．【点评】本题主要考查函数奇偶性和单调性的应用，综合考查函数性质的综合应用，运用偶函数的性质是解题的关键．二、填空题13．（3分）（2015•新课标Ⅱ）已知函数f（x）＝ax3﹣2x的图象过点（﹣1，4）则a＝﹣2．【分析】f（x）是图象过点（﹣1，4），从而该点坐标满足函数f（x）解析式，从而将点（﹣1，4）带入函数f（x）解析式即可求出a．【解答】解：根据条件得：4＝﹣a+2；∴a＝﹣2．故答案为：﹣2．【点评】考查函数图象上的点的坐标和函数解析式的关系，考查学生的计算能力，比较基础．14．（3分）（2015•新课标Ⅱ）若x，y满足约束条件，则z＝2x+y的最大值为8．【分析】作出不等式组对应的平面区域，利用目标函数的几何意义，利用数形结合确定z 的最大值．【解答】解：作出不等式组对应的平面区域如图：（阴影部分ABC）．由z＝2x+y得y＝﹣2x+z，平移直线y＝﹣2x+z，由图象可知当直线y＝﹣2x+z经过点A时，直线y＝﹣2x+z的截距最大，此时z最大．由，解得，即A（3，2）将A（3，2）的坐标代入目标函数z＝2x+y，得z＝2×3+2＝8．即z＝2x+y的最大值为8．故答案为：8．【点评】本题主要考查线性规划的应用，结合目标函数的几何意义，利用数形结合的数学思想是解决此类问题的基本方法．15．（3分）（2015•新课标Ⅱ）已知双曲线过点且渐近线方程为y＝±x，则该双曲线的标准方程是x2﹣y2＝1．【分析】设双曲线方程为y2﹣x2＝λ，代入点，求出λ，即可求出双曲线的标准方程．【解答】解：设双曲线方程为y2﹣x2＝λ，代入点，可得3﹣＝λ，∴λ＝﹣1，∴双曲线的标准方程是x2﹣y2＝1．故答案为：x2﹣y2＝1．【点评】本题考查双曲线的标准方程，考查学生的计算能力，正确设出双曲线的方程是关键．16．（3分）（2015•新课标Ⅱ）已知曲线y＝x+lnx在点（1，1）处的切线与曲线y＝ax2+（a+2）x+1相切，则a＝8．【分析】求出y＝x+lnx的导数，求得切线的斜率，可得切线方程，再由于切线与曲线y ＝ax2+（a+2）x+1相切，有且只有一切点，进而可联立切线与曲线方程，根据△＝0得到a的值．【解答】解：y＝x+lnx的导数为y′＝1+，曲线y＝x+lnx在x＝1处的切线斜率为k＝2，则曲线y＝x+lnx在x＝1处的切线方程为y﹣1＝2x﹣2，即y＝2x﹣1．由于切线与曲线y＝ax2+（a+2）x+1相切，故y＝ax2+（a+2）x+1可联立y＝2x﹣1，得ax2+ax+2＝0，又a≠0，两线相切有一切点，所以有△＝a2﹣8a＝0，解得a＝8．故答案为：8．【点评】本题考查导数的运用：求切线方程，主要考查导数的几何意义：函数在某点处的导数即为曲线在该点处的导数，设出切线方程运用两线相切的性质是解题的关键．三．解答题17．（2015•新课标Ⅱ）△ABC中，D是BC上的点，AD平分∠BAC，BD＝2DC （Ⅰ）求．（Ⅱ）若∠BAC＝60°，求∠B．【分析】（Ⅰ）由题意画出图形，再由正弦定理结合内角平分线定理得答案；（Ⅱ）由∠C＝180°﹣（∠BAC+∠B），两边取正弦后展开两角和的正弦，再结合（Ⅰ）中的结论得答案．【解答】解：（Ⅰ）如图，由正弦定理得：，∵AD平分∠BAC，BD＝2DC，∴；（Ⅱ）∵∠C＝180°﹣（∠BAC+∠B），∠BAC＝60°，∴，由（Ⅰ）知2sin∠B＝sin∠C，∴tan∠B＝，即∠B＝30°．【点评】本题考查了内角平分线的性质，考查了正弦定理的应用，是中档题．18．（2015•新课标Ⅱ）某公司为了解用户对其产品的满意度，从A，B两地区分别随机调查了40个用户，根据用户对产品的满意度评分，得到A地区用户满意度评分的频率分布直方图和B地区用户满意度评分的频数分布表B地区用户满意度评分的频数分布表满意度评分分组[50，60）[60，70）[70，80）[80，90）[90，100）频数2814106（1）做出B地区用户满意度评分的频率分布直方图，并通过直方图比较两地区满意度评分的平均值及分散程度（不要求计算出具体值，给出结论即可）（Ⅱ）根据用户满意度评分，将用户的满意度从低到高分为三个不等级：满意度评分低于70分70分到89分不低于90分满意度等级不满意满意非常满意估计哪个地区用户的满意度等级为不满意的概率大？说明理由．【分析】（I）根据分布表的数据，画出频率直方图，求解即可．（II）计算得出∁A表示事件：“A地区用户的满意度等级为不满意”，∁B表示事件：“B地区用户的满意度等级为不满意”，P（∁A），P（∁B），即可判断不满意的情况．【解答】解：（Ⅰ）通过两个地区用户满意度评分的频率分布直方图可以看出，B地区用户满意度评分的平均值高于A地区用户满意度评分的平均值，B地区的用户满意度评分的比较集中，而A地区的用户满意度评分的比较分散．（Ⅱ）A地区用户的满意度等级为不满意的概率大．记∁A表示事件：“A地区用户的满意度等级为不满意”，∁B表示事件：“B地区用户的满意度等级为不满意”，由直方图得P（∁A）＝（0.01+0.02+0.03）×10＝0.6得P（∁B）＝（0.005+0.02）×10＝0.25∴A地区用户的满意度等级为不满意的概率大．【点评】本题考查了频率直方图，频率表达运用，考查了阅读能力，属于中档题．19．（12分）（2015•新课标Ⅱ）如图，长方体ABCD﹣A1B1C1D1中，AB＝16，BC＝10，AA1＝8，点E，F分别在A1B1，D1C1上，A1E＝D1F＝4．过E，F的平面α与此长方体的面相交，交线围成一个正方形（Ⅰ）在图中画出这个正方形（不必说出画法和理由）（Ⅱ）求平面α把该长方体分成的两部分体积的比值．【分析】（Ⅰ）利用平面与平面平行的性质，可在图中画出这个正方形；（Ⅱ）求出MH＝＝6，AH＝10，HB＝6，即可求平面a把该长方体分成的两部分体积的比值．【解答】解：（Ⅰ）交线围成的正方形EFGH如图所示；（Ⅱ）作EM⊥AB，垂足为M，则AM＝A1E＝4，EB1＝12，EM＝AA1＝8．因为EFGH为正方形，所以EH＝EF＝BC＝10，于是MH＝＝6，AH＝10，HB＝6．因为长方体被平面α分成两个高为10的直棱柱，所以其体积的比值为．【点评】本题考查平面与平面平行的性质，考查学生的计算能力，比较基础．20．（2015•新课标Ⅱ）椭圆C：＝1，（a＞b＞0）的离心率，点（2，）在C 上．（1）求椭圆C的方程；（2）直线l不过原点O且不平行于坐标轴，l与C有两个交点A，B，线段AB的中点为M．证明：直线OM的斜率与l的斜率的乘积为定值．【分析】（1）利用椭圆的离心率，以及椭圆经过的点，求解椭圆的几何量，然后得到椭圆的方程．（2）设直线l：y＝kx+b，（k≠0，b≠0），A（x1，y1），B（x2，y2），M（x M，y M），联立直线方程与椭圆方程，通过韦达定理求解K OM，然后推出直线OM的斜率与l的斜率的乘积为定值．【解答】解：（1）椭圆C：＝1，（a＞b＞0）的离心率，点（2，）在C上，可得，，解得a2＝8，b2＝4，所求椭圆C方程为：．（2）设直线l：y＝kx+b，（k≠0，b≠0），A（x1，y1），B（x2，y2），M（x M，y M），把直线y＝kx+b代入可得（2k2+1）x2+4kbx+2b2﹣8＝0，故x M＝＝，y M＝kx M+b＝，于是在OM的斜率为：K OM＝＝，即K OM•k＝．∴直线OM的斜率与l的斜率的乘积为定值．【点评】本题考查椭圆方程的综合应用，椭圆的方程的求法，考查分析问题解决问题的能力．21．（2015•新课标Ⅱ）设函数f（x）＝lnx+a（1﹣x）．（Ⅰ）讨论：f（x）的单调性；（Ⅱ）当f（x）有最大值，且最大值大于2a﹣2时，求a的取值范围．【分析】（Ⅰ）先求导，再分类讨论，根据导数即可判断函数的单调性；（2）先求出函数的最大值，再构造函数（a）＝lna+a﹣1，根据函数的单调性即可求出a 的范围．【解答】解：（Ⅰ）f（x）＝lnx+a（1﹣x）的定义域为（0，+∞），∴f′（x）＝﹣a＝，若a≤0，则f′（x）＞0，∴函数f（x）在（0，+∞）上单调递增，若a＞0，则当x∈（0，）时，f′（x）＞0，当x∈（，+∞）时，f′（x）＜0，所以f（x）在（0，）上单调递增，在（，+∞）上单调递减，（Ⅱ），由（Ⅰ）知，当a≤0时，f（x）在（0，+∞）上无最大值；当a＞0时，f（x）在x＝取得最大值，最大值为f（）＝﹣lna+a﹣1，∵f（）＞2a﹣2，∴lna+a﹣1＜0，令g（a）＝lna+a﹣1，∵g（a）在（0，+∞）单调递增，g（1）＝0，∴当0＜a＜1时，g（a）＜0，当a＞1时，g（a）＞0，∴a的取值范围为（0，1）．【点评】本题考查了导数与函数的单调性最值的关系，以及参数的取值范围，属于中档题．四、选修4-1：几何证明选讲22．（10分）（2015•新课标Ⅱ）如图，O为等腰三角形ABC内一点，⊙O与△ABC的底边BC交于M，N两点，与底边上的高AD交于点G，且与AB，AC分别相切于E，F两点．（1）证明：EF∥BC；（2）若AG等于⊙O的半径，且AE＝MN＝2，求四边形EBCF的面积．【分析】（1）通过AD是∠CAB的角平分线及圆O分别与AB、AC相切于点E、F，利用相似的性质即得结论；﹣S （2）通过（1）知AD是EF的垂直平分线，连结OE、OM，则OE⊥AE，利用S△ABC计算即可．△AEF【解答】（1）证明：∵△ABC为等腰三角形，AD⊥BC，∴AD是∠CAB的角平分线，又∵圆O分别与AB、AC相切于点E、F，∴AE＝AF，∴AD⊥EF，∴EF∥BC；（2）解：由（1）知AE＝AF，AD⊥EF，∴AD是EF的垂直平分线，又∵EF为圆O的弦，∴O在AD上，连结OE、OM，则OE⊥AE，由AG等于圆O的半径可得AO＝2OE，∴∠OAE＝30°，∴△ABC与△AEF都是等边三角形，∵AE＝2，∴AO＝4，OE＝2，∵OM＝OE＝2，DM＝MN＝，∴OD＝1，∴AD＝5，AB＝，∴四边形EBCF的面积为×﹣××＝．【点评】本题考查空间中线与线之间的位置关系，考查四边形面积的计算，注意解题方法的积累，属于中档题．五、选修4-4：坐标系与参数方程23．（10分）（2015•新课标Ⅱ）在直角坐标系xOy中，曲线C1：（t为参数，t≠0），其中0≤α≤π，在以O为极点，x轴正半轴为极轴的极坐标系中，曲线C2：ρ＝2sinθ，C3：ρ＝2cosθ．（1）求C2与C3交点的直角坐标；（2）若C1与C2相交于点A，C1与C3相交于点B，求|AB|的最大值．【分析】（I）由曲线C2：ρ＝2sinθ，化为ρ2＝2ρsinθ，把代入可得直角坐标方程．同理由C3：ρ＝2cosθ．可得直角坐标方程，联立解出可得C2与C3交点的直角坐标．（2）由曲线C1的参数方程，消去参数t，化为普通方程：y＝x tanα，其中0≤α≤π，α≠；α＝时，为x＝0（y≠0）．其极坐标方程为：θ＝α（ρ∈R，ρ≠0），利用|AB|＝即可得出．【解答】解：（I）由曲线C2：ρ＝2sinθ，化为ρ2＝2ρsinθ，∴x2+y2＝2y．同理由C3：ρ＝2cosθ．可得直角坐标方程：，联立，解得，，∴C2与C3交点的直角坐标为（0，0），．（2）曲线C1：（t为参数，t≠0），化为普通方程：y＝x tanα，其中0≤α≤π，α≠；α＝时，为x＝0（y≠0）．其极坐标方程为：θ＝α（ρ∈R，ρ≠0），∵A，B都在C1上，∴A（2sinα，α），B．∴|AB|＝＝4，当时，|AB|取得最大值4．【点评】本题考查了极坐标方程化为直角坐标方程、参数方程化为普通方程、曲线的交点、两点之间的距离公式、三角函数的单调性，考查了推理能力与计算能力，属于中档题．六、选修4-5不等式选讲24．（10分）（2015•新课标Ⅱ）设a，b，c，d均为正数，且a+b＝c+d，证明：（1）若ab＞cd，则+＞+；（2）+＞+是|a﹣b|＜|c﹣d|的充要条件．【分析】（1）运用不等式的性质，结合条件a，b，c，d均为正数，且a+b＝c+d，ab＞cd，即可得证；（2）从两方面证，①若+＞+，证得|a﹣b|＜|c﹣d|，②若|a﹣b|＜|c﹣d|，证得+＞+，注意运用不等式的性质，即可得证．【解答】证明：（1）由于（+）2＝a+b+2，（+）2＝c+d+2，由a，b，c，d均为正数，且a+b＝c+d，ab＞cd，则＞，即有（+）2＞（+）2，则+＞+；（2）①若+＞+，则（+）2＞（+）2，即为a+b+2＞c+d+2，由a+b＝c+d，则ab＞cd，于是（a﹣b）2＝（a+b）2﹣4ab，（c﹣d）2＝（c+d）2﹣4cd，即有（a﹣b）2＜（c﹣d）2，即为|a﹣b|＜|c﹣d|；②若|a﹣b|＜|c﹣d|，则（a﹣b）2＜（c﹣d）2，即有（a+b）2﹣4ab＜（c+d）2﹣4cd，由a+b＝c+d，则ab＞cd，则有（+）2＞（+）2．综上可得，+＞+是|a﹣b|＜|c﹣d|的充要条件．【点评】本题考查不等式的证明，主要考查不等式的性质的运用，同时考查充要条件的判断，属于基础题．。

2015年全国统一高考数学试卷(理科)(新课标ⅰ)

2015年全国统一高考数学试卷（理科）（新课标Ⅰ）一、选择题（共12小题，每小题5分，满分60分）1．（5分）设复数z满足=i，则|z|=（）A．1 B．C．D．22．（5分）sin20°cos10°﹣cos160°sin10°=（）A．B．C．D．3．（5分）设命题p：∃n∈N，n2＞2n，则￢p为（）A．∀n∈N，n2＞2n B．∃n∈N，n2≤2n C．∀n∈N，n2≤2n D．∃n∈N，n2=2n 4．（5分）投篮测试中，每人投3次，至少投中2次才能通过测试．己知某同学每次投篮投中的概率为0.6，且各次投篮是否投中相互独立，则该同学通过测试的概率为（）A．0.648 B．0.432 C．0.36 D．0.3125．（5分）已知M（x0，y0）是双曲线C：=1上的一点，F1，F2是C的两个焦点，若＜0，则y0的取值范围是（）A．B．C．D．6．（5分）《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：”今有委米依垣内角，下周八尺，高五尺．问：积及为米几何？“其意思为：”在屋内墙角处堆放米（如图，米堆为一个圆锥的四分之一），米堆底部的弧长为8尺，米堆的高为5尺，问米堆的体积和堆放的米各为多少？“已知1斛米的体积约为1.62立方尺，圆周率约为3，估算出堆放的米约有（）A．14斛B．22斛C．36斛D．66斛7．（5分）设D为△ABC所在平面内一点，，则（）A．B．C．D．8．（5分）函数f（x）=cos（ωx+φ）的部分图象如图所示，则f（x）的单调递减区间为（）A．（kπ﹣，kπ+，），k∈z B．（2kπ﹣，2kπ+），k∈zC．（k﹣，k+），k∈z D．（，2k+），k∈z9．（5分）执行如图所示的程序框图，如果输入的t=0.01，则输出的n=（）A．5 B．6 C．7 D．810．（5分）（x2+x+y）5的展开式中，x5y2的系数为（）A．10 B．20 C．30 D．6011．（5分）圆柱被一个平面截去一部分后与半球（半径为r）组成一个几何体，该几何体三视图中的正视图和俯视图如图所示．若该几何体的表面积为16+20π，则r=（）A．1 B．2 C．4 D．812．（5分）设函数f（x）=e x（2x﹣1）﹣ax+a，其中a＜1，若存在唯一的整数x0使得f（x0）＜0，则a的取值范围是（）A．[）B．[）C．[）D．[）二、填空题（本大题共有4小题，每小题5分）13．（5分）若函数f（x）=xln（x+）为偶函数．则a=．14．（5分）一个圆经过椭圆=1的三个顶点．且圆心在x轴的正半轴上．则该圆标准方程为．15．（5分）若x，y满足约束条件．则的最大值为．16．（5分）在平面四边形ABCD中，∠A=∠B=∠C=75°．BC=2，则AB的取值范围是．三、解答题：17．（12分）S n为数列{a n}的前n项和，己知a n＞0，a n2+2a n=4S n+3（I）求{a n}的通项公式：（Ⅱ）设b n=，求数列{b n}的前n项和．18．（12分）如图，四边形ABCD为菱形，∠ABC=120°，E，F是平面ABCD同一侧的两点，BE丄平面ABCD，DF丄平面ABCD，BE=2DF，AE丄EC．（Ⅰ）证明：平面AEC丄平面AFC（Ⅱ）求直线AE与直线CF所成角的余弦值．19．（12分）某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费x （单位：千元）对年销售量y（单位：t）和年利润z（单位：千元）的影响，对近8年的年宣传费x i和年销售量y i（i=1，2，…，8）数据作了初步处理，得到下面的散点图及一些统计量的值．（x i﹣）2（w i ﹣）2（x i ﹣）（y i﹣）（w i﹣）（y i﹣）46.6563 6.8289.8 1.61469108.8表中w i=1，=（Ⅰ）根据散点图判断，y=a+bx与y=c+d哪一个适宜作为年销售量y关于年宣传费x的回归方程类型？（给出判断即可，不必说明理由）（Ⅱ）根据（Ⅰ）的判断结果及表中数据，建立y关于x的回归方程；（Ⅲ）已知这种产品的年利润z与x、y的关系为z=0.2y﹣x．根据（Ⅱ）的结果回答下列问题：（i）年宣传费x=49时，年销售量及年利润的预报值是多少？（ii）年宣传费x为何值时，年利润的预报值最大？附：对于一组数据（u1 v1），（u2 v2）…..（u n v n），其回归线v=α+βu的斜率和截距的最小二乘估计分别为：=，=﹣．20．（12分）在直角坐标系xOy中，曲线C：y=与直线l：y=kx+a（a＞0）交于M，N两点．（Ⅰ）当k=0时，分別求C在点M和N处的切线方程．（Ⅱ）y轴上是否存在点P，使得当k变动时，总有∠OPM=∠OPN？（说明理由）21．（12分）已知函数f（x）=x3+ax+，g（x）=﹣lnx（i）当a为何值时，x轴为曲线y=f（x）的切线；（ii）用min {m，n }表示m，n中的最小值，设函数h（x）=min { f（x），g（x）}（x＞0），讨论h（x）零点的个数．选修4一1:几何证明选讲22．（10分）如图，AB是⊙O的直径，AC是⊙O的切线，BC交⊙O于点E．（Ⅰ）若D为AC的中点，证明：DE是⊙O的切线；（Ⅱ）若OA=CE，求∠ACB的大小．选修4一4：坐标系与参数方程23．（10分）在直角坐标系xOy中，直线C1：x=﹣2，圆C2：（x﹣1）2+（y﹣2）2=1，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系．（Ⅰ）求C1，C2的极坐标方程；（Ⅱ）若直线C3的极坐标方程为θ=（ρ∈R），设C2与C3的交点为M，N，求△C2MN的面积．选修4一5：不等式选讲24．（10分）已知函数f（x）=|x+1|﹣2|x﹣a|，a＞0．（Ⅰ）当a=1时，求不等式f（x）＞1的解集；（Ⅱ）若f（x）的图象与x轴围成的三角形面积大于6，求a的取值范围．2015年全国统一高考数学试卷（理科）（新课标Ⅰ）参考答案与试题解析一、选择题（共12小题，每小题5分，满分60分）1．（5分）（2015•新课标Ⅰ）设复数z满足=i，则|z|=（）A．1 B．C．D．2【分析】先化简复数，再求模即可．【解答】解：∵复数z满足=i，∴1+z=i﹣zi，∴z（1+i）=i﹣1，∴z==i，∴|z|=1，故选：A．2．（5分）（2015•新课标Ⅰ）sin20°cos10°﹣cos160°sin10°=（）A．B．C．D．【分析】直接利用诱导公式以及两角和的正弦函数，化简求解即可．【解答】解：sin20°cos10°﹣cos160°sin10°=sin20°cos10°+cos20°sin10°=sin30°=．故选：D．3．（5分）（2015•新课标Ⅰ）设命题p：∃n∈N，n2＞2n，则￢p为（）A．∀n∈N，n2＞2n B．∃n∈N，n2≤2n C．∀n∈N，n2≤2n D．∃n∈N，n2=2n 【分析】根据特称命题的否定是全称命题即可得到结论．【解答】解：命题的否定是：∀n∈N，n2≤2n，故选：C．4．（5分）（2015•新课标Ⅰ）投篮测试中，每人投3次，至少投中2次才能通过测试．己知某同学每次投篮投中的概率为0.6，且各次投篮是否投中相互独立，则该同学通过测试的概率为（）A．0.648 B．0.432 C．0.36 D．0.312【分析】判断该同学投篮投中是独立重复试验，然后求解概率即可．【解答】解：由题意可知：同学3次测试满足X∽B（3，0.6），该同学通过测试的概率为=0.648．故选：A．5．（5分）（2015•新课标Ⅰ）已知M（x0，y0）是双曲线C：=1上的一点，F1，F2是C的两个焦点，若＜0，则y0的取值范围是（）A．B．C．D．【分析】利用向量的数量积公式，结合双曲线方程，即可确定y0的取值范围．【解答】解：由题意，=（﹣x0，﹣y0）•（﹣﹣x0，﹣y0）=x02﹣3+y02=3y02﹣1＜0，所以﹣＜y0＜．故选：A．6．（5分）（2015•新课标Ⅰ）《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：”今有委米依垣内角，下周八尺，高五尺．问：积及为米几何？“其意思为：”在屋内墙角处堆放米（如图，米堆为一个圆锥的四分之一），米堆底部的弧长为8尺，米堆的高为5尺，问米堆的体积和堆放的米各为多少？“已知1斛米的体积约为1.62立方尺，圆周率约为3，估算出堆放的米约有（）A．14斛B．22斛C．36斛D．66斛【分析】根据圆锥的体积公式计算出对应的体积即可．【解答】解：设圆锥的底面半径为r，则r=8，解得r=，故米堆的体积为××π×（）2×5≈，∵1斛米的体积约为1.62立方，∴÷1.62≈22，故选：B．7．（5分）（2015•新课标Ⅰ）设D为△ABC所在平面内一点，，则（）A．B．C．D．【分析】将向量利用向量的三角形法则首先表示为，然后结合已知表示为的形式．【解答】解：由已知得到如图由===；故选：A．8．（5分）（2015•新课标Ⅰ）函数f（x）=cos（ωx+φ）的部分图象如图所示，则f（x）的单调递减区间为（）A．（kπ﹣，kπ+，），k∈z B．（2kπ﹣，2kπ+），k∈zC．（k﹣，k+），k∈z D．（，2k+），k∈z【分析】由周期求出ω，由五点法作图求出φ，可得f（x）的解析式，再根据余弦函数的单调性，求得f（x）的减区间．【解答】解：由函数f（x）=cos（ωx+ϕ）的部分图象，可得函数的周期为=2（﹣）=2，∴ω=π，f（x）=cos（πx+ϕ）．再根据函数的图象以及五点法作图，可得+ϕ=，k∈z，即ϕ=，f（x）=cos （πx+）．由2kπ≤πx+≤2kπ+π，求得2k﹣≤x≤2k+，故f（x）的单调递减区间为（，2k+），k∈z，故选：D．9．（5分）（2015•新课标Ⅰ）执行如图所示的程序框图，如果输入的t=0.01，则输出的n=（）A．5 B．6 C．7 D．8【分析】由已知中的程序框图可知：该程序的功能是利用循环结构计算并输出变量n的值，模拟程序的运行过程，分析循环中各变量值的变化情况，可得答案．【解答】解：第一次执行循环体后，S=，m=，n=1，不满足退出循环的条件；再次执行循环体后，S=，m=，n=2，不满足退出循环的条件；再次执行循环体后，S=，m=，n=3，不满足退出循环的条件；再次执行循环体后，S=，m=，n=4，不满足退出循环的条件；再次执行循环体后，S=，m=，n=5，不满足退出循环的条件；再次执行循环体后，S=，m=，n=6，不满足退出循环的条件；再次执行循环体后，S=，m=，n=7，满足退出循环的条件；故输出的n值为7，故选：C10．（5分）（2015•新课标Ⅰ）（x2+x+y）5的展开式中，x5y2的系数为（）A．10 B．20 C．30 D．60【分析】利用展开式的通项，即可得出结论．=，【解答】解：（x2+x+y）5的展开式的通项为T r+1令r=2，则（x2+x）3的通项为=，令6﹣k=5，则k=1，∴（x2+x+y）5的展开式中，x5y2的系数为=30．故选：C．11．（5分）（2015•新课标Ⅰ）圆柱被一个平面截去一部分后与半球（半径为r）组成一个几何体，该几何体三视图中的正视图和俯视图如图所示．若该几何体的表面积为16+20π，则r=（）A．1 B．2 C．4 D．8【分析】通过三视图可知该几何体是一个半球拼接半个圆柱，计算即可．【解答】解：由几何体三视图中的正视图和俯视图可知，截圆柱的平面过圆柱的轴线，该几何体是一个半球拼接半个圆柱，∴其表面积为：×4πr2+×πr22r×2πr+2r×2r+×πr2=5πr2+4r2，又∵该几何体的表面积为16+20π，∴5πr2+4r2=16+20π，解得r=2，故选：B．12．（5分）（2015•新课标Ⅰ）设函数f（x）=e x（2x﹣1）﹣ax+a，其中a＜1，若存在唯一的整数x0使得f（x0）＜0，则a的取值范围是（）A．[）B．[）C．[）D．[）【分析】设g（x）=e x（2x﹣1），y=ax﹣a，问题转化为存在唯一的整数x0使得g （x0）在直线y=ax﹣a的下方，求导数可得函数的极值，数形结合可得﹣a＞g（0）=﹣1且g（﹣1）=﹣3e﹣1≥﹣a﹣a，解关于a的不等式组可得．【解答】解：设g（x）=e x（2x﹣1），y=ax﹣a，由题意知存在唯一的整数x0使得g（x0）在直线y=ax﹣a的下方，∵g′（x）=e x（2x﹣1）+2e x=e x（2x+1），∴当x＜﹣时，g′（x）＜0，当x＞﹣时，g′（x）＞0，∴当x=﹣时，g（x）取最小值﹣2，当x=0时，g（0）=﹣1，当x=1时，g（1）=e＞0，直线y=ax﹣a恒过定点（1，0）且斜率为a，故﹣a＞g（0）=﹣1且g（﹣1）=﹣3e﹣1≥﹣a﹣a，解得≤a＜1故选：D二、填空题（本大题共有4小题，每小题5分）13．（5分）（2015•新课标Ⅰ）若函数f（x）=xln（x+）为偶函数．则a= 1．【分析】由题意可得，f（﹣x）=f（x），代入根据对数的运算性质即可求解【解答】解：∵f（x）=xln（x+）为偶函数，∴f（﹣x）=f（x），∴（﹣x）ln（﹣x+）=xln（x+），∴﹣ln（﹣x+）=ln（x+），∴ln（﹣x+）+ln（x+）=0，∴，∴lna=0，∴a=1．故答案为：1．14．（5分）（2015•新课标Ⅰ）一个圆经过椭圆=1的三个顶点．且圆心在x轴的正半轴上．则该圆标准方程为（x﹣）2+y2=．【分析】利用椭圆的方程求出顶点坐标，然后求出圆心坐标，求出半径即可得到圆的方程．【解答】解：一个圆经过椭圆=1的三个顶点．且圆心在x轴的正半轴上．可知椭圆的右顶点坐标（4，0），上下顶点坐标（0，±2），设圆的圆心（a，0），则，解得a=，圆的半径为：，所求圆的方程为：（x﹣）2+y2=．故答案为：（x﹣）2+y2=．15．（5分）（2015•新课标Ⅰ）若x，y满足约束条件．则的最大值为3．【分析】作出不等式组对应的平面区域，利用目标函数的几何意义，利用数形结合确定的最大值．【解答】解：作出不等式组对应的平面区域如图：（阴影部分ABC）．设k=，则k的几何意义为区域内的点到原点的斜率，由图象知OA的斜率最大，由，解得，即A（1，3），则k OA==3，即的最大值为3．故答案为：3．16．（5分）（2015•新课标Ⅰ）在平面四边形ABCD中，∠A=∠B=∠C=75°．BC=2，则AB的取值范围是（﹣，+）．【分析】如图所示，延长BA，CD交于点E，设AD=x，AE=x，DE=x，CD=m，求出x+m=+，即可求出AB的取值范围．【解答】解：方法一：如图所示，延长BA，CD交于点E，则在△ADE中，∠DAE=105°，∠ADE=45°，∠E=30°，∴设AD=x，AE=x，DE=x，CD=m，∵BC=2，∴（x+m）sin15°=1，∴x+m=+，∴0＜x＜4，而AB=x+m﹣x=+﹣x，∴AB的取值范围是（﹣，+）．故答案为：（﹣，+）．方法二：如下图，作出底边BC=2的等腰三角形EBC，B=C=75°，倾斜角为150°的直线在平面内移动，分别交EB、EC于A、D，则四边形ABCD即为满足题意的四边形；当直线移动时，运用极限思想，①直线接近点C时，AB趋近最小，为﹣；②直线接近点E时，AB趋近最大值，为+；故答案为：（﹣，+）．三、解答题：17．（12分）（2015•新课标Ⅰ）S n为数列{a n}的前n项和，己知a n＞0，a n2+2a n=4S n+3（I）求{a n}的通项公式：（Ⅱ）设b n=，求数列{b n}的前n项和．【分析】（I）根据数列的递推关系，利用作差法即可求{a n}的通项公式：（Ⅱ）求出b n=，利用裂项法即可求数列{b n}的前n项和．【解答】解：（I）由a n2+2a n=4S n+3，可知a n+12+2a n+1=4S n+1+3两式相减得a n+12﹣a n2+2（a n+1﹣a n）=4a n+1，即2（a n+1+a n）=a n+12﹣a n2=（a n+1+a n）（a n+1﹣a n），∵a n＞0，∴a n+1﹣a n=2，∵a12+2a1=4a1+3，∴a1=﹣1（舍）或a1=3，则{a n}是首项为3，公差d=2的等差数列，∴{a n}的通项公式a n=3+2（n﹣1）=2n+1：（Ⅱ）∵a n=2n+1，∴b n===（﹣），∴数列{b n}的前n项和T n=（﹣+…+﹣）=（﹣）=．18．（12分）（2015•新课标Ⅰ）如图，四边形ABCD为菱形，∠ABC=120°，E，F 是平面ABCD同一侧的两点，BE丄平面ABCD，DF丄平面ABCD，BE=2DF，AE 丄EC．（Ⅰ）证明：平面AEC丄平面AFC（Ⅱ）求直线AE与直线CF所成角的余弦值．【分析】（Ⅰ）连接BD，设BD∩AC=G，连接EG、EF、FG，运用线面垂直的判定定理得到EG⊥平面AFC，再由面面垂直的判定定理，即可得到；（Ⅱ）以G为坐标原点，分别以GB，GC为x轴，y轴，|GB|为单位长度，建立空间直角坐标系G﹣xyz，求得A，E，F，C的坐标，运用向量的数量积的定义，计算即可得到所求角的余弦值．【解答】解：（Ⅰ）连接BD，设BD∩AC=G，连接EG、EF、FG，在菱形ABCD中，不妨设BG=1，由∠ABC=120°，可得AG=GC=，BE⊥平面ABCD，AB=BC=2，可知AE=EC，又AE⊥EC，所以EG=，且EG⊥AC，在直角△EBG中，可得BE=，故DF=，在直角三角形FDG中，可得FG=，在直角梯形BDFE中，由BD=2，BE=，FD=，可得EF=，从而EG2+FG2=EF2，则EG⊥FG，AC∩FG=G，可得EG⊥平面AFC，由EG⊂平面AEC，所以平面AEC⊥平面AFC；（Ⅱ）如图，以G为坐标原点，分别以GB，GC为x轴，y轴，|GB|为单位长度，建立空间直角坐标系G﹣xyz，由（Ⅰ）可得A（0，﹣，0），E（1，0，），F（﹣1，0，），C（0，，0），即有=（1，，），=（﹣1，﹣，），故cos＜，＞===﹣．则有直线AE与直线CF所成角的余弦值为．19．（12分）（2015•新课标Ⅰ）某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费x（单位：千元）对年销售量y（单位：t）和年利润z（单位：千元）的影响，对近8年的年宣传费x i和年销售量y i（i=1，2，…，8）数据作了初步处理，得到下面的散点图及一些统计量的值．（x i﹣）2（w i﹣）2（x i﹣）（y i﹣）（w i﹣）（y i﹣）46.6563 6.8289.8 1.61469108.8表中w i=1，=（Ⅰ）根据散点图判断，y=a+bx与y=c+d哪一个适宜作为年销售量y关于年宣传费x的回归方程类型？（给出判断即可，不必说明理由）（Ⅱ）根据（Ⅰ）的判断结果及表中数据，建立y关于x的回归方程；（Ⅲ）已知这种产品的年利润z与x、y的关系为z=0.2y﹣x．根据（Ⅱ）的结果回答下列问题：（i）年宣传费x=49时，年销售量及年利润的预报值是多少？（ii）年宣传费x为何值时，年利润的预报值最大？附：对于一组数据（u1 v1），（u2 v2）…..（u n v n），其回归线v=α+βu 的斜率和截距的最小二乘估计分别为：=，=﹣．【分析】（Ⅰ）根据散点图，即可判断出，（Ⅱ）先建立中间量w=，建立y关于w的线性回归方程，根据公式求出w，问题得以解决；（Ⅲ）（i）年宣传费x=49时，代入到回归方程，计算即可，（ii）求出预报值得方程，根据函数的性质，即可求出．【解答】解：（Ⅰ）由散点图可以判断，y=c+d适宜作为年销售量y关于年宣传费x的回归方程类型；（Ⅱ）令w=，先建立y关于w的线性回归方程，由于==68，=﹣=563﹣68×6.8=100.6，所以y关于w的线性回归方程为=100.6+68w，因此y关于x的回归方程为=100.6+68，（Ⅲ）（i）由（Ⅱ）知，当x=49时，年销售量y的预报值=100.6+68=576.6，年利润z的预报值=576.6×0.2﹣49=66.32，（ii）根据（Ⅱ）的结果可知，年利润z的预报值=0.2（100.6+68）﹣x=﹣x+13.6+20.12，当==6.8时，即当x=46.24时，年利润的预报值最大．20．（12分）（2015•新课标Ⅰ）在直角坐标系xOy中，曲线C：y=与直线l：y=kx+a（a＞0）交于M，N两点．（Ⅰ）当k=0时，分別求C在点M和N处的切线方程．（Ⅱ）y轴上是否存在点P，使得当k变动时，总有∠OPM=∠OPN？（说明理由）【分析】（I）联立，可得交点M，N的坐标，由曲线C：y=，利用导数的运算法则可得：y′=，利用导数的几何意义、点斜式即可得出切线方程．（II）存在符合条件的点（0，﹣a），设P（0，b）满足∠OPM=∠OPN．M（x1，y1），N（x2，y2），直线PM，PN的斜率分别为：k1，k2．直线方程与抛物线方程联立化为x2﹣4kx﹣4a=0，利用根与系数的关系、斜率计算公式可得k1+k2=．k1+k2=0⇔直线PM，PN的倾斜角互补⇔∠OPM=∠OPN．即可证明．【解答】解：（I）联立，不妨取M，N，由曲线C：y=可得：y′=，∴曲线C在M点处的切线斜率为=，其切线方程为：y﹣a=，化为．同理可得曲线C在点N处的切线方程为：．（II）存在符合条件的点（0，﹣a），下面给出证明：设P（0，b）满足∠OPM=∠OPN．M（x1，y1），N（x2，y2），直线PM，PN的斜率分别为：k1，k2．联立，化为x2﹣4kx﹣4a=0，∴x1+x2=4k，x1x2=﹣4a．∴k1+k2=+==．当b=﹣a时，k1+k2=0，直线PM，PN的倾斜角互补，∴∠OPM=∠OPN．∴点P（0，﹣a）符合条件．21．（12分）（2015•新课标Ⅰ）已知函数f（x）=x3+ax+，g（x）=﹣lnx（i）当a为何值时，x轴为曲线y=f（x）的切线；（ii）用min {m，n }表示m，n中的最小值，设函数h（x）=min { f（x），g（x）}（x＞0），讨论h（x）零点的个数．【分析】（i）f′（x）=3x2+a．设曲线y=f（x）与x轴相切于点P（x0，0），则f（x0）=0，f′（x0）=0解出即可．（ii）对x分类讨论：当x∈（1，+∞）时，g（x）=﹣lnx＜0，可得函数h（x）=min { f（x），g（x）}≤g（x）＜0，即可得出零点的个数．当x=1时，对a分类讨论：a≥﹣，a＜﹣，即可得出零点的个数；当x∈（0，1）时，g（x）=﹣lnx＞0，因此只考虑f（x）在（0，1）内的零点个数即可．对a分类讨论：①当a≤﹣3或a≥0时，②当﹣3＜a＜0时，利用导数研究其单调性极值即可得出．【解答】解：（i）f′（x）=3x2+a．设曲线y=f（x）与x轴相切于点P（x0，0），则f（x0）=0，f′（x0）=0，∴，解得，a=．因此当a=﹣时，x轴为曲线y=f（x）的切线；（ii）当x∈（1，+∞）时，g（x）=﹣lnx＜0，∴函数h（x）=min { f（x），g（x）}≤g（x）＜0，故h（x）在x∈（1，+∞）时无零点．当x=1时，若a≥﹣，则f（1）=a+≥0，∴h（x）=min { f（1），g（1）}=g（1）=0，故x=1是函数h（x）的一个零点；若a＜﹣，则f（1）=a+＜0，∴h（x）=min { f（1），g（1）}=f（1）＜0，故x=1不是函数h（x）的零点；当x∈（0，1）时，g（x）=﹣lnx＞0，因此只考虑f（x）在（0，1）内的零点个数即可．①当a≤﹣3或a≥0时，f′（x）=3x2+a在（0，1）内无零点，因此f（x）在区间（0，1）内单调，而f（0）=，f（1）=a+，∴当a≤﹣3时，函数f（x）在区间（0，1）内有一个零点，当a≥0时，函数f（x）在区间（0，1）内没有零点．②当﹣3＜a＜0时，函数f（x）在内单调递减，在内单调递增，故当x=时，f（x）取得最小值=．若＞0，即，则f（x）在（0，1）内无零点．若=0，即a=﹣，则f（x）在（0，1）内有唯一零点．若＜0，即，由f（0）=，f（1）=a+，∴当时，f（x）在（0，1）内有两个零点．当﹣3＜a时，f （x）在（0，1）内有一个零点．综上可得：当或a＜时，h（x）有一个零点；当a=或时，h（x）有两个零点；当时，函数h（x）有三个零点．选修4一1:几何证明选讲22．（10分）（2015•新课标Ⅰ）如图，AB是⊙O的直径，AC是⊙O的切线，BC 交⊙O于点E．（Ⅰ）若D为AC的中点，证明：DE是⊙O的切线；（Ⅱ）若OA=CE，求∠ACB的大小．【分析】（Ⅰ）连接AE和OE，由三角形和圆的知识易得∠OED=90°，可得DE是⊙O的切线；（Ⅱ）设CE=1，AE=x，由射影定理可得关于x的方程x2=，解方程可得x值，可得所求角度．【解答】解：（Ⅰ）连接AE，由已知得AE⊥BC，AC⊥AB，在RT△ABC中，由已知可得DE=DC，∴∠DEC=∠DCE，连接OE，则∠OBE=∠OEB，又∠ACB+∠ABC=90°，∴∠DEC+∠OEB=90°，∴∠OED=90°，∴DE是⊙O的切线；（Ⅱ）设CE=1，AE=x，由已知得AB=2，BE=，由射影定理可得AE2=CE•BE，∴x2=，即x4+x2﹣12=0，解方程可得x=∴∠ACB=60°选修4一4：坐标系与参数方程23．（10分）（2015•新课标Ⅰ）在直角坐标系xOy中，直线C1：x=﹣2，圆C2：（x﹣1）2+（y﹣2）2=1，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系．（Ⅰ）求C1，C2的极坐标方程；（Ⅱ）若直线C3的极坐标方程为θ=（ρ∈R），设C2与C3的交点为M，N，求△C2MN的面积．【分析】（Ⅰ）由条件根据x=ρcosθ，y=ρsinθ求得C1，C2的极坐标方程．（Ⅱ）把直线C3的极坐标方程代入ρ2﹣3ρ+4=0，求得ρ1和ρ2的值，结合圆的半径可得C2M⊥C2N，从而求得△C2MN的面积•C2M•C2N的值．【解答】解：（Ⅰ）由于x=ρcosθ，y=ρsinθ，∴C1：x=﹣2 的极坐标方程为ρcosθ=﹣2，故C2：（x﹣1）2+（y﹣2）2=1的极坐标方程为：（ρcosθ﹣1）2+（ρsinθ﹣2）2=1，化简可得ρ2﹣（2ρcosθ+4ρsinθ）+4=0．（Ⅱ）把直线C3的极坐标方程θ=（ρ∈R）代入圆C2：（x﹣1）2+（y﹣2）2=1，可得ρ2﹣（2ρcosθ+4ρsinθ）+4=0，求得ρ1=2，ρ2=，∴|MN|=|ρ1﹣ρ2|=，由于圆C2的半径为1，∴C2M⊥C2N，△C2MN的面积为•C2M•C2N=•1•1=．选修4一5：不等式选讲24．（10分）（2015•新课标Ⅰ）已知函数f（x）=|x+1|﹣2|x﹣a|，a＞0．（Ⅰ）当a=1时，求不等式f（x）＞1的解集；（Ⅱ）若f（x）的图象与x轴围成的三角形面积大于6，求a的取值范围．【分析】（Ⅰ）当a=1时，把原不等式去掉绝对值，转化为与之等价的三个不等式组，分别求得每个不等式组的解集，再取并集，即得所求．（Ⅱ）化简函数f （x）的解析式，求得它的图象与x轴围成的三角形的三个顶点的坐标，从而求得f（x）的图象与x轴围成的三角形面积；再根据f（x）的图象与x轴围成的三角形面积大于6，从而求得a的取值范围．【解答】解：（Ⅰ）当a=1时，不等式f（x）＞1，即|x+1|﹣2|x﹣1|＞1，即①，或②，或③．解①求得x∈∅，解②求得＜x＜1，解③求得1≤x＜2．综上可得，原不等式的解集为（，2）．（Ⅱ）函数f（x）=|x+1|﹣2|x﹣a|=，由此求得f（x）的图象与x轴的交点A （，0），B（2a+1，0），故f（x）的图象与x轴围成的三角形的第三个顶点C（a，a+1），由△ABC的面积大于6，可得[2a+1﹣]•（a+1）＞6，求得a＞2．故要求的a的范围为（2，+∞）．。

2015年全国高考文科数学试题及答案(全国1卷)

2015年普通高等学校招生全国统一考试文科数学注意事项：1. 答题前，考生务必将自己的准考证号、姓名填写在答题卡上。

考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名、考试科目”与考生本人准考证号、姓名是否一致。

2. 第Ⅰ卷每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，在选涂其他答案标号。

第Ⅱ卷必须用0.5毫米黑色签字笔书写作答.若在试题卷上作答，答案无效。

3. 考试结束，监考员将试题卷、答题卡一并收回。

第Ⅰ卷一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的。

（1）已知集合A={x|x=3n+2,n ∈N},B={6,8,12,14},则集合A ⋂B中元素的个数为（A）5 （B）4 （C）3 （D）2（2）已知点A（0,1），B（3,2），向量AC=（-4，-3），则向量BC=（A）（-7，-4）（B）（7,4）（C）（-1,4）（D）（1，4）（3）已知复数z满足（z-1）i=i+1，则z=（A）-2-I （B）-2+I （C）2-I （D）2+i（4）如果3个整数可作为一个直角三角形三条边的边长，则称这3个数为一组勾股数，从1，2，3，4，5中任取3个不同的数，则3个数构成一组勾股数的概率为（A）103（B）15（C）110（D）120（5）已知椭圆E的中心在坐标原点，离心率为12，E的右焦点与抛物线C：y²=8x的焦点重合，A，B是C的准线与E的两个焦点，则|AB|= （A）3 （B）6 （C）9 （D）12。

2015年全国高考理科数学试题及答案

绝密★启用前2015年普通高等学校招生全国统一考试（全国卷2）理科数学注意事项：1．本试卷分第I卷（选择题）和第II卷（非选择题）两部分。

答卷前，考生务必先将自己的姓名、准考证号码填写在答题卡上。

2．回答第I卷时，选出每小题的答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号。

写在本试卷上无效。

3．回答第II卷时，将答案写在答题卡上，写在本试卷上无效。

4．考试结束后，将本试卷和答题卡一并交回。

一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的。

（1）已知集合A=｛-2，-1,0，1,2｝，B=｛x|（X-1）（x+2）＜0｝,则A∩B=（）（A）｛--1,0｝（B）｛0,1｝（C）｛-1,0,1｝（D）｛,0,，1，2｝（2）若a为实数且（2+ai）（a-2i）=-4i,则a=（）（A）-1 （B）0 （C）1 （D）2（3）根据下面给出的2004年至2013年我国二氧化硫排放量（单位：万吨）柱形图。

以下结论不正确的是( )（A）逐年比较，2008年减少二氧化硫排放量的效果最显著（B ） 2007年我国治理二氧化硫排放显现（C ） 2006年以来我国二氧化硫年排放量呈减少趋势（D ） 2006年以来我国二氧化硫年排放量与年份正相关（4）等比数列｛a n ｝满足a 1=3，135a a a ++ =21，则357a a a ++= ( )（A ）21 （B ）42 （C ）63 （D ）84（5）设函数211log (2),1,()2,1,x x x f x x -+-<⎧=⎨≥⎩,2(2)(log 12)f f -+=( )（A ）3 （B ）6 （C ）9 （D ）12（6）一个正方体被一个平面截去一部分后，剩余部分的三视图如右图，则截去部分体积与剩余部分体积的比值为（A ）81 （B ）71 （C ）61 （D ）51 （7）过三点A （1,3），B （4,2），C （1,-7）的圆交于y 轴于M 、N 两点，则MN =（A ）26 （B ）8 （C ）46 （D ）10（8）右边程序抗土的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”。

2015高考数学全国卷1(完美版)

2015年普通高等学校招生全国统一考试理科数学注意事项：1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷1至3页，第Ⅱ卷3至5页.2.答题前，考生务必将自己的姓名、准考证号填写在本试题相应的位置.3.全部答案在答题卡上完成，答在本试题上无效.4. 考试结束后，将本试题和答题卡一并交回.第Ⅰ卷一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的. 1．设复数z 满足1＋z1－z＝i ，则|z |＝A ．1B ． 2C ． 3D ．22．sin 20°cos 10°－cos 160°sin 10°＝A ．－32B ．32C ．－12D ．123．设命题P ：∃n ∈N ，n 2＞2n ，则￢P 为A ．∀n ∈N ， n 2＞2nB ．∃n ∈N ， n 2≤2nC ．∀n ∈N ， n 2≤2nD ．∃n ∈N ， n 2＝2n4．投篮测试中，每人投3次，至少投中2次才能通过测试.已知某同学每次投篮投中的概率为0.6，且各次投篮是否投中相互独立，则该同学通过测试的概率为A ．0.648B ．0.432C ．0.36D ．0.3125．已知M (x 0，y 0)是双曲线C ：x 22－y 2＝1 上的一点，F 1、F 2是C 上的两个焦点，若 MF 1→· MF 2→＜0 ，则y 0的取值范围是A ．⎝⎛⎭⎫－33，33B ．⎝⎛⎭⎫－36，36C ．⎝⎛⎭⎫－223，223 D ．⎝⎛⎭⎫－233，2336．《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题:“今有委米依垣内角，下周八尺，高五尺.问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图，米堆为一个圆锥的四分之一)，米堆底部的弧度为8尺，米堆的高为5尺，问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺，圆周率约为3，估算出堆放斛的米约有 A ．14斛 B ．22斛 C ．36斛 D ．66斛7．设D 为△ABC 所在平面内一点BC →＝3CD →，则A ．AD →＝－13AB →＋43AC → B ．AD →＝13AB →－43AC → C ．AD →＝43AB →＋13AC → D ．AD →＝43AB →－13AC →8．函数f (x )＝cos (ωx ＋φ)的部分图像如图所示，则f (x )的单调递减区间为A ．⎝⎛⎭⎫k π－14，k π＋34 (k ∈Z )B ．⎝⎛⎭⎫2k π－14，2k π＋34 (k ∈Z )C ．⎝⎛⎭⎫k －14，k ＋34 (k ∈Z )D ．⎝⎛⎭⎫2k －14，2k ＋34 (k ∈Z )9．执行右面的程序框图，如果输入的t ＝0.01，则输出的n ＝A ．5B ．6C ．7D ．810．(x 2＋x ＋y )5的展开式中，x 5y 2的系数为A ．10B ．20C ．30D ．60 (第11题图)11．圆柱被一个平面截去一部分后与半球(半径为r )组成一个几何体，该几何体三视图中的正视图和俯视图如图所示．若该几何体的表面积为16＋20π，则r ＝A ．1B ．2C ．4D ．812．设函数f (x )＝e x (2x －1)－ax ＋a ，其中a ＜1，若存在唯一的整数x 0，使得f (x 0)＜0，则a 的取值范围是A .⎣⎡⎭⎫－32e ，1B . ⎣⎡⎭⎫－32e ，34C . ⎣⎡⎭⎫32e ，34D . ⎣⎡⎭⎫32e ，12rr正视图俯视图 r2r第II 卷本卷包括必考题和选考题两部分.第(13)题~第(21)题为必考题，每个试题考生都必须作答.第(22)题~第(24)题未选考题，考生根据要求作答.二、填空题：本大题共3小题，每小题5分13．若函数f (x )＝xln (x ＋a ＋x 2)为偶函数，则a ＝＿＿＿＿＿＿.14．一个圆经过椭圆 x 216＋y 24＝1 的三个顶点，且圆心在x 轴上，则该圆的标准方程为 .15．若x ，y 满足约束条件⎩⎪⎨⎪⎧x －1≥0 (1)x －y ≤0 (2)x ＋y －4≤0 (3) ，则 yx的最大值为 .16．在平面四边形ABCD 中，∠A ＝∠B ＝∠C ＝75°，BC ＝2，则AB 的取值范围是 .三.解答题：解答应写出文字说明，证明过程或演算步骤.17．(本小题满分12分)S n 为数列{a n }的前n 项和.已知a n ＞0，a 2n ＋2a n ＝4S n ＋4．(Ⅰ)求{a n }的通项公式；(Ⅱ)设b n ＝1a n a n ＋1，求数列{b n }的前n 项和．18．如图，四边形ABCD 为菱形，∠ABC ＝120°，E ，F 是平面ABCD 同一侧的两点，BE ⊥平面ABCD ，DF ⊥平面ABCD ，BE ＝2DF ，AE ⊥EC . (1)证明：平面AEC ⊥平面AFC ； (2)求直线AE 与直线CF 所成角的余弦值．A B C F E D19．某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费x (单位：千元)对年销售量y (单位：t )和年利润z (单位：千元)的影响，对近8年的年宣传费x i 和年销售量y i (i ＝1，2，···，8)数据作了初步处理，得到下面的散点图及一些统计量的值.表中w 1 ＝x 1，，w －＝18∑x ＋1w 1(Ⅰ)根据散点图判断，y ＝a ＋bx 与y ＝c ＋d x 哪一个适宜作为年销售量y 关于年宣传费x 的回归方程类型？(给出判断即可，不必说明理由)(Ⅱ)根据(Ⅰ)的判断结果及表中数据，建立y 关于x 的回归方程；(Ⅲ)已知这种产品的年利率z 与x 、y 的关系为z ＝0.2y －x .根据(Ⅱ)的结果回答下列问题：(ⅰ)年宣传费x ＝49时，年销售量及年利润的预报值是多少？ (ⅱ)年宣传费x 为何值时，年利率的预报值最大？附：对于一组数据(u 1 v 1)，(u 2 v 2)，……，(u n v n )，其回归线v ＝αβ+u 的斜率和截距的最小二乘估计分别为：β＝∑i ＝1n(u i －u －)(v i －v －) ∑i ＝1n(u i －u －)2α＝v －－βu －年宣传费/千元20．(本小题满分12分)在直角坐标系xoy 中，曲线C ：y ＝x 24与直线y ＝kx ＋a (a ＞0)交于M ，N 两点，(Ⅰ)当k ＝0时，分别求C 在点M 和N 处的切线方程；(Ⅱ)y 轴上是否存在点P ，使得当k 变动时，总有∠OPM ＝∠OPN ？说明理由.21．(本小题满分12分)已知函数f (x )＝x 3＋ax ＋14，g (x )＝－lnx ．(Ⅰ)当a 为何值时，x 轴为曲线y ＝f (x ) 的切线；(Ⅱ)用min {},m n 表示m ，n 中的最小值，设函数h (x )＝min{f (x )，g (x )} (x ＞0)，讨论h (x )零点的个数．请考生在(22)、(23)、(24)三题中任选一题作答．注意：只能做所选定的题目，如果多做，则按所做第一个题目计分，做答时，请用2B 铅笔在答题卡上将所选题号后的方框涂黑.．22．(本题满分10分)选修4－1：几何证明选讲如图，AB 是⊙O 的直径，AC 是⊙O 的切线，BC 交⊙O 于点E ． (Ⅰ)若D 为AC 的中点，证明：DE 是⊙O 的切线； (Ⅱ)若OA ＝3CE ，求∠ACB 的大小.23．(本小题满分10分)选修4－4：坐标系与参数方程在直角坐标系xOy 中，直线C 1：x ＝－2，圆C 2：(x －1)2＋(y －2)2＝1，以坐标原点为极点， x 轴的正半轴为极轴建立极坐标系． (Ⅰ)求C 1，C 2的极坐标方程；(Ⅱ)若直线C 3的极坐标方程为 θ＝π4(ρ∈R )，设C 2与C 3的交点为M 、N ，求△C 2MN 的面积．24．(本小题满分10分)选修4—5：不等式选讲已知函数f (x )＝|x ＋1|－2|x －a |，a ＞0．(Ⅰ)当a ＝1时，求不等式f (x )＞1的解集；(Ⅱ)若f (x )的图像与x 轴围成的三角形面积大于6，求a 的取值范围．。

2015年高考理科数学全国卷1-答案

所以21200000(3,)(3,)MF MF x y x y x =-----=【考点】双曲线．
【解析】由题知
1114
()
3
AD AC CD AC BC AC AC AB AB AC =+=+=+-=-+
【提示】将向量AD利用向量的三角形法则首先表示为AC CD
+，然后结合已知表示为AC AC
，的形式．【考点】向量运算．
2e
x
y
sin151⎫︒=⎪⎪⎭
22m x +-
1
,BD AC G =连接3GC =．
，可知AE 为坐标原点，分别以,GB GC 的方向为||GB 为单位长度，，由（Ⅰ）可得0,3,0)A （-2⎪⎭
∴(1,AE =，1,CF ⎛=- cos ,||||
AE CF AE CF AE CF <>=
=-
3
BD AC G =，连接，再由面面垂直的判定定理，即可得到为坐标原点，分别以GB GC ，的坐标，运用向量的数量积的定义，计算即可得到所求角的余弦值．的线性回归方程，由于1
8
1
(=
(i
i i w d ==-∑∑∴56368==c y dw --y 关于w 的线性回归方程为=100.6+68y 的回归方程为=100.6+68y 49=时，年销量的预报值=100.6+6849576.6y =的预报值=576.60.2z ⨯）根据（Ⅱ）的结果知，年利润的预报值=0.2(100.6+68z ，z 取得最大值，故宣传费用为（Ⅰ）根据散点图，即可判断出．
∴60
∠=．
ACB
是O的切线．
，解方程可得x值，可得所求角度．
11 / 11。

2015全国高考卷一数学真题

2015全国卷一数学满分:班级：_________ 姓名：_________ 考号：_________一、单选题（共12小题）1．已知集合则集合中元素的个数为（）B．4C．3D．2A．52．已知点，，向量，则向量=（）B．A．C．D．（1,4）3．已知复数Z满足，则Z=（）A．B．C．D．4．如果3个正数可作为一个直角三角形三条边的边长，则称这3个数为一组勾股数。

从1,2,3,4,5中任取3个不同的数，则这3个数构成一组勾股数的概率为（）A．B．C．D．5．已知椭圆E的中心在坐标原点，离心率为，E的右焦点与抛物线的焦点重合，A,B是C的准线与E的两个交点，则（）B．6C．9D．12A．36．《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有委米依恒内角，下周八尺，高五尺.问：积及为米几何？”其意思为：“在屋内墙角处堆放米（如图，米堆为一个圆锥的四分之一），米堆底部的弧长为8尺，米堆的高为5尺，问米堆的体积和堆放的米各为多少？”已知1斛米的体积约为1.62立方尺，圆周率约为3，估算出堆放斛的米约有（）B．22斛C．36斛D．66斛A．14斛7．已知是公差为1的等差数列，为的前项和.若，则（）B．C．D．A．8．函数的部分图象如图所示，则的单调递减区间为（）B．A．C．D．9．执行下面的程序框图，如果输入的，则输出的（）B．6C．7D．8 A．510．已知函数，且，则=（）A．B．C．D．11．圆柱被一个平面截去一部分后与半球（半径为r）组成一个几何体，该几何体三视图中的正视图和俯视图如图所示，若该几何体的表面积为，则（）B．2C．4D．8A．112．设函数的图像与图像关于直线对称，且，则（）A．-1B．1C．2D．4二、填空题（共4小题）13.已知数列中，为的前n项和。

若=126，则n=_______．14.已知函数的图像在点处的切线过点（2,7），则=_______．15.若满足约束条件，则的最大值为__________．16.已知是双曲线的右焦点，是的左支上一点，．当△周长最小时，该三角形的面积为__________．三、解答题（共8小题）17.已知a，b，c分别为内角A，B，C的对边，。

2015年高考数学试卷真题附详细解析

2015年高考数学试卷一、选择题：本大题共8小题，每小题5分，共40分2015年普通高等学校招生全国统一考试（真题卷）数学（理科）1．（5分）（2015•真题）已知集合P={x|x2﹣2x≥0}，Q={x|1＜x≤2}，则（∁R P）∩Q=（）A ．[0，1）B．（0，2]C．（1，2）D．[1，2]2．（5分）（2015•真题）某几何体的三视图如图所示（单位：cm），则该几何体的体积是（）A ．8cm3B．12cm3C．D．3．（5分）（2015•真题）已知{a n}是等差数列，公差d不为零，前n项和是S n，若a3，a4，a8成等比数列，则（）A ．a1d＞0，dS4＞0B．a1d＜0，dS4＜0C．a1d＞0，dS4＜0D．a1d＜0，dS4＞04．（5分）（2015•真题）命题“∀n∈N*，f（n）∈N*且f（n）≤n”的否定形式是（）A．∀n∈N*，f（n）∉N*且f（n）＞n B．∀n∈N*，f（n）∉N*或f（n）＞nC．∂n0∈N*，f（n0）∉N*且f（n0）＞n0D．∂n0∈N*，f（n0）∉N*或f（n0）＞n05．（5分）（2015•真题）如图，设抛物线y2=4x的焦点为F，不经过焦点的直线上有三个不同的点A，B，C，其中点A，B在抛物线上，点C在y轴上，则△BCF与△ACF的面积之比是（）A ．B．C．D．6．（5分）（2015•真题）设A，B是有限集，定义：d（A，B）=card（A∪B）﹣card（A∩B），其中card（A）表示有限集A中的元素个数（）命题①：对任意有限集A，B，“A≠B”是“d（A，B）＞0”的充分必要条件；命题②：对任意有限集A，B，C，d（A，C）≤d（A，B）+d（B，C）A．命题①和命题②都成立B．命题①和命题②都不成立C．命题①成立，命题②不成立D．命题①不成立，命题②成立7．（5分）（2015•真题）存在函数f（x）满足，对任意x∈R都有（）A ．f（sin2x）=sinx B．f（sin2x）=x2+xC．f（x2+1）=|x+1| D．f（x2+2x）=|x+1|8．（5分）（2015•真题）如图，已知△ABC，D是AB的中点，沿直线CD将△ACD折成△A′CD，所成二面角A′﹣CD﹣B的平面角为α，则（）A ．∠A′DB≤αB．∠A′DB≥αC．∠A′CB≤αD．∠A′CB≥α二、填空题：本大题共7小题，多空题每题6分，单空题每题4分，共36分．9．（6分）（2015•真题）双曲线=1的焦距是，渐近线方程是．10．（6分）（2015•真题）已知函数f（x）=，则f（f（﹣3））=，f（x）的最小值是．11．（6分）（2015•真题）函数f（x）=sin2x+sinxcosx+1的最小正周期是，单调递减区间是．12．（4分）（2015•真题）若a=log43，则2a+2﹣a=．13．（4分）（2015•真题）如图，三棱锥A﹣BCD中，AB=AC=BD=CD=3，AD=BC=2，点M，N分别是AD，BC的中点，则异面直线AN，CM所成的角的余弦值是．14．（4分）（2015•真题）若实数x，y满足x2+y2≤1，则|2x+y﹣2|+|6﹣x﹣3y|的最小值是．15．（6分）（2015•真题）已知是空间单位向量，，若空间向量满足，且对于任意x，y∈R，，则x0=，y0=，|=．三、解答题：本大题共5小题，共74分．解答应写出文字说明、证明过程或演算步骤．16．（14分）（2015•真题）在△ABC中，内角A，B，C所对的边分别为a，b，c，已知A=，b2﹣a2=c2．（1）求tanC的值；（2）若△ABC的面积为3，求b的值．17．（15分）（2015•真题）如图，在三棱柱ABC﹣A1B1C1中，∠BAC=90°，AB=AC=2，A1A=4，A1在底面ABC的射影为BC的中点，D是B1C1的中点．（1）证明：A1D⊥平面A1BC；（2）求二面角A1﹣BD﹣B1的平面角的余弦值．18．（15分）（2015•真题）已知函数f（x）=x2+ax+b（a，b∈R），记M（a，b）是|f（x）|在区间[﹣1，1]上的最大值．（1）证明：当|a|≥2时，M（a，b）≥2；（2）当a，b满足M（a，b）≤2时，求|a|+|b|的最大值．19．（15分）（2015•真题）已知椭圆上两个不同的点A，B关于直线y=mx+对称．（1）求实数m的取值范围；（2）求△AOB面积的最大值（O为坐标原点）．20．（15分）（2015•真题）已知数列{a n}满足a1=且a n+1=a n﹣a n2（n∈N*）（1）证明：1≤≤2（n∈N*）；（2）设数列{a n2}的前n项和为S n，证明（n∈N*）．高考数学试卷（理科）一、选择题：本大题共8小题，每小题5分，共40分2015年普通高等学校招生全国统一考试（真题卷）数学（理科）1．（5分）考点：交、并、补集的混合运算．专题：集合．分析：求出P中不等式的解集确定出P，求出P补集与Q的交集即可．解答：解：由P中不等式变形得：x（x﹣2）≥0，解得：x≤0或x≥2，即P=（﹣∞，0]∪[2，+∞），∴∁R P=（0，2），∵Q=（1，2]，∴（∁R P）∩Q=（1，2），故选：C．点评：此题考查了交、并、补集的混合运算，熟练掌握运算法则是解本题的关键．2．（5分）考点：由三视图求面积、体积．专题：空间位置关系与距离．分析：判断几何体的形状，利用三视图的数据，求几何体的体积即可．解答：解：由三视图可知几何体是下部为棱长为2的正方体，上部是底面为边长2的正方形奥为2的正四棱锥，所求几何体的体积为：23+×2×2×2=．故选：C．点评：本题考查三视图与直观图的关系的判断，几何体的体积的求法，考查计算能力．3．（5分）考点：等差数列与等比数列的综合．专题：等差数列与等比数列．分析：由a3，a4，a8成等比数列，得到首项和公差的关系，即可判断a1d和dS4的符号．解答：解：设等差数列{a n}的首项为a1，则a3=a1+2d，a4=a1+3d，a8=a1+7d，由a3，a4，a8成等比数列，得，整理得：．∵d≠0，∴，∴，=＜0．故选：B．点评：本题考查了等差数列和等比数列的性质，考查了等差数列的前n项和，是基础题．4．（5分）考点：命题的否定．专题：简易逻辑．分析：根据全称命题的否定是特称命题即可得到结论．解答：解：命题为全称命题，则命题的否定为：∂n0∈N*，f（n0）∉N*或f（n0）＞n0，故选：D．点评：本题主要考查含有量词的命题的否定，比较基础．5．（5分）考点：直线与圆锥曲线的关系．专题：圆锥曲线的定义、性质与方程．分析：根据抛物线的定义，将三角形的面积关系转化为的关系进行求解即可．解答：解：如图所示，抛物线的准线DE的方程为x=﹣1，过A，B分别作AE⊥DE于E，交y轴于N，BD⊥DE于E，交y轴于M，由抛物线的定义知BF=BD，AF=AE，则|BM|=|BD|﹣1=|BF|﹣1，|AN|=|AE|﹣1=|AF|﹣1，则===，故选：A点评：本题主要考查三角形的面积关系，利用抛物线的定义进行转化是解决本题的关键．6．（5分）考点：复合命题的真假．专题：集合；简易逻辑．分析：命题①根据充要条件分充分性和必要性判断即可，③借助新定义，根据集合的运算，判断即可．解答：解：命题①：对任意有限集A，B，若“A≠B”，则A∪B≠A∩B，则card（A∪B）＞card（A∩B），故“d（A，B）＞0”成立，若d（A，B）＞0”，则card（A∪B）＞card（A∩B），则A∪B≠A∩B，故A≠B成立，故命题①成立，命题②，d（A，B）=card（A∪B）﹣card（A∩B），d（B，C）=card（B∪C）﹣card（B∩C），∴d（A，B）+d（B，C）=card（A∪B）﹣card（A∩B）+card（B∪C）﹣card（B∩C）=[card （A∪B）+card（B∪C）]﹣[card（A∩B）+card（B∩C）]≥card（A∪C）﹣card（A∩C）=d（A，C），故命题②成立，故选：A点评：本题考查了，元素和集合的关系，以及逻辑关系，分清集合之间的关系与各集合元素个数之间的关系，注意本题对充要条件的考查．集合的元素个数，体现两个集合的关系，但仅凭借元素个数不能判断集合间的关系，属于基础题．7．（5分）考点：函数解析式的求解及常用方法．专题：函数的性质及应用．分析：利用x取特殊值，通过函数的定义判断正误即可．解答：解：A．取x=0，则sin2x=0，∴f（0）=0；取x=，则sin2x=0，∴f（0）=1；∴f（0）=0，和1，不符合函数的定义；∴不存在函数f（x），对任意x∈R都有f（sin2x）=sinx；B．取x=0，则f（0）=0；取x=π，则f（0）=π2+π；∴f（0）有两个值，不符合函数的定义；∴该选项错误；C．取x=1，则f（2）=2，取x=﹣1，则f（2）=0；这样f（2）有两个值，不符合函数的定义；∴该选项错误；D．令|x+1|=t，t≥0，则f（t2﹣1）=t；令t2﹣1=x，则t=；∴；即存在函数f（x）=，对任意x∈R，都有f（x2+2x）=|x+1|；∴该选项正确．故选：D．点评：本题考查函数的定义的应用，基本知识的考查，但是思考问题解决问题的方法比较难．8．（5分）考点：二面角的平面角及求法．专题：创新题型；空间角．分析：解：画出图形，分AC=BC，AC≠BC两种情况讨论即可．解答：解：①当AC=BC时，∠A′DB=α；②当AC≠BC时，如图，点A′投影在AE上，α=∠A′OE，连结AA′，易得∠ADA′＜∠AOA′，∴∠A′DB＞∠A′OE，即∠A′DB＞α综上所述，∠A′DB≥α，故选：B．点评：本题考查空间角的大小比较，注意解题方法的积累，属于中档题．二、填空题：本大题共7小题，多空题每题6分，单空题每题4分，共36分．9．（6分）双曲线的简单性质．考点：计算题；圆锥曲线的定义、性质与方程．专题：确定双曲线中的几何量，即可求出焦距、渐近线方程．分析：解解：双曲线=1中，a=，b=1，c=，答：∴焦距是2c=2，渐近线方程是y=±x．故答案为：2；y=±x．本题考查双曲线的方程与性质，考查学生的计算能力，比较基础．点评：10．（6分）函数的值．考点：计算题；函数的性质及应用．专题：分根据已知函数可先求f（﹣3）=1，然后代入可求f（f（﹣3））；由于x≥1时，f（x）=，析：当x＜1时，f（x）=lg（x2+1），分别求出每段函数的取值范围，即可求解解答：解：∵f（x）=，∴f（﹣3）=lg10=1，则f（f（﹣3））=f（1）=0，当x≥1时，f（x）=，即最小值，当x＜1时，x2+1≥1，（x）=lg（x2+1）≥0最小值0，故f（x）的最小值是．故答案为：0；．本题主要考查了分段函数的函数值的求解，属于基础试题．点评：11．（6分）两角和与差的正弦函数；三角函数的周期性及其求法；正弦函数的单调性．考点：专三角函数的求值．题：分由三角函数公式化简可得f（x）=sin（2x﹣）+，易得最小正周期，解不等析：式2kπ+≤2x﹣≤2kπ+可得函数的单调递减区间．解答：解：化简可得f（x）=sin2x+sinxcosx+1=（1﹣cos2x）+sin2x+1=sin（2x﹣）+，∴原函数的最小正周期为T==π，由2kπ+≤2x﹣≤2kπ+可得kπ+≤x≤kπ+，∴函数的单调递减区间为[kπ+，kπ+]（k∈Z）故答案为：π；[kπ+，kπ+]（k∈Z）点评：本题考查三角函数的化简，涉及三角函数的周期性和单调性，属基础题．12．（4分）考点：对数的运算性质．专题：函数的性质及应用．分析：直接把a代入2a+2﹣a，然后利用对数的运算性质得答案．解答：解：∵a=log43，可知4a=3，即2a=，所以2a+2﹣a=+=．故答案为：．点评：本题考查对数的运算性质，是基础的计算题．13．（4分）考点：异面直线及其所成的角．专题：空间角．分析：连结ND，取ND 的中点为：E，连结ME说明异面直线AN，CM所成的角就是∠EMC 通过解三角形，求解即可．解答：解：连结ND，取ND 的中点为：E，连结ME，则ME∥AN，异面直线AN，CM所成的角就是∠EMC，∵AN=2，∴ME==EN，MC=2，又∵EN⊥NC，∴EC==，∴cos∠EMC===．故答案为：．点评：本题考查异面直线所成角的求法，考查空间想象能力以及计算能力．14．（4分）考点：函数的最值及其几何意义．专题：不等式的解法及应用；直线与圆．分析：根据所给x，y的范围，可得|6﹣x﹣3y|=6﹣x﹣3y，再讨论直线2x+y﹣2=0将圆x2+y2=1分成两部分，分别去绝对值，运用线性规划的知识，平移即可得到最小值．解答：解：由x2+y2≤1，可得6﹣x﹣3y＞0，即|6﹣x﹣3y|=6﹣x﹣3y，如图直线2x+y﹣2=0将圆x2+y2=1分成两部分，在直线的上方（含直线），即有2x+y﹣2≥0，即|2+y﹣2|=2x+y﹣2，此时|2x+y﹣2|+|6﹣x﹣3y|=（2x+y﹣2）+（6﹣x﹣3y）=x﹣2y+4，利用线性规划可得在A（，）处取得最小值3；在直线的下方（含直线），即有2x+y﹣2≤0，即|2+y﹣2|=﹣（2x+y﹣2），此时|2x+y﹣2|+|6﹣x﹣3y|=﹣（2x+y﹣2）+（6﹣x﹣3y）=8﹣3x﹣4y，利用线性规划可得在A（，）处取得最小值3．综上可得，当x=，y=时，|2x+y﹣2|+|6﹣x﹣3y|的最小值为3．故答案为：3．点本题考查直线和圆的位置关系，主要考查二元函数在可行域内取得最值的方法，属于中档题．评：15．（6分）空间向量的数量积运算；平面向量数量积的运算．考点：专创新题型；空间向量及应用．题：分由题意和数量积的运算可得＜•＞=，不妨设=（，，0），=（1，0，0），析：由已知可解=（，，t），可得|﹣（|2=（x+）2+（y﹣2）2+t2，由题意可得当x=x0=1，y=y0=2时，（x+）2+（y﹣2）2+t2取最小值1，由模长公式可得|．解解：∵•=||||cos＜•＞=cos＜•＞=，答：∴＜•＞=，不妨设=（，，0），=（1，0，0），=（m，n，t），则由题意可知=m+n=2，=m=，解得m=，n=，∴=（，，t），∵﹣（）=（﹣x﹣y，，t），∴|﹣（|2=（﹣x﹣y）2+（）2+t2=x2+xy+y2﹣4x﹣5y+t2+7=（x+）2+（y﹣2）2+t2，由题意当x=x0=1，y=y0=2时，（x+）2+（y﹣2）2+t2取最小值1，此时t2=1，故|==2故答案为：1；2；2点本题考查空间向量的数量积，涉及向量的模长公式，属中档题．评：三、解答题：本大题共5小题，共74分．解答应写出文字说明、证明过程或演算步骤．16．（14分）余弦定理．考点：解三角形．专题：分（1）由余弦定理可得：，已知b2﹣a2=c2．可得，a=．利析：用余弦定理可得cosC．可得sinC=，即可得出tanC=．（2）由=×=3，可得c，即可得出b．解解：（1）∵A=，∴由余弦定理可得：，∴b2﹣a2=bc﹣c2，答：又b2﹣a2=c2．∴bc﹣c2=c2．∴b=c．可得，∴a2=b2﹣=，即a=．∴cosC===．∵C∈（0，π），∴sinC==．∴tanC==2．（2）∵=×=3，解得c=2．∴=3．点评：本题考查了正弦定理余弦定理、同角三角形基本关系式、三角形面积计算公式，考查了推理能力与计算能力，属于中档题．17．（15分）考点：二面角的平面角及求法；直线与平面垂直的判定．专题：空间位置关系与距离；空间角．分析：（1）以BC中点O为坐标原点，以OB、OA、OA1所在直线分别为x、y、z轴建系，通过•=•=0及线面垂直的判定定理即得结论；（2）所求值即为平面A1BD的法向量与平面B1BD的法向量的夹角的余弦值的绝对值的相反数，计算即可．解答：（1）证明：如图，以BC中点O为坐标原点，以OB、OA、OA1所在直线分别为x、y、z轴建系．则BC=AC=2，A1O==，易知A1（0，0，），B（，0，0），C（﹣，0，0），A（0，，0），D（0，﹣，），B1（，﹣，），=（0，﹣，0），=（﹣，﹣，），=（﹣，0，0），=（﹣2，0，0），=（0，0，），∵•=0，∴A1D⊥OA1，又∵•=0，∴A1D⊥BC，又∵OA1∩BC=O，∴A1D⊥平面A1BC；（2）解：设平面A1BD的法向量为=（x，y，z），由，得，取z=1，得=（，0，1），设平面B1BD的法向量为=（x，y，z），由，得，取z=1，得=（0，，1），∴cos＜，＞===，又∵该二面角为钝角，∴二面角A1﹣BD﹣B1的平面角的余弦值为﹣．点评：本题考查空间中线面垂直的判定定理，考查求二面角的三角函数值，注意解题方法的积累，属于中档题．18．（15分）考点：二次函数在闭区间上的最值．专题：函数的性质及应用．分析：（1）明确二次函数的对称轴，区间的端点值，由a的范围明确函数的单调性，结合已知以及三角不等式变形所求得到证明；（2）讨论a=b=0以及分析M（a，b）≤2得到﹣3≤a+b≤1且﹣3≤b﹣a≤1，进一步求出|a|+|b|的求值．解答：解：（1）由已知可得f（1）=1+a+b，f（﹣1）=1﹣a+b，对称轴为x=﹣，因为|a|≥2，所以或≥1，所以函数f（x）在[﹣1，1]上单调，所以M（a，b）=max{|f（1），|f（﹣1）|}=max{|1+a+b|，|1﹣a+b|}，所以M（a，b）≥（|1+a+b|+|1﹣a+b|）≥|（1+a+b）﹣（1﹣a+b）|≥|2a|≥2；（2）当a=b=0时，|a|+|b|=0又|a|+|b|≥0，所以0为最小值，符合题意；又对任意x∈[﹣1，1]．有﹣2≤x2+ax+b≤2得到﹣3≤a+b≤1且﹣3≤b﹣a≤1，易知|a|+|b|=max{|a﹣b|，|a+b|}=3，在b=﹣1，a=2时符合题意，所以|a|+|b|的最大值为3．点评：本题考查了二次函数闭区间上的最值求法；解答本题的关键是正确理解M（a，b）是|f（x）|在区间[﹣1，1]上的最大值，以及利用三角不等式变形．19．（15分）考点：直线与圆锥曲线的关系．专题：创新题型；圆锥曲线中的最值与范围问题．分析：（1）由题意，可设直线AB的方程为x=﹣my+n，代入椭圆方程可得（m2+2）y2﹣2mny+n2﹣2=0，设A（x1，y1），B（x2，y2）．可得△＞0，设线段AB的中点P（x0，y0），利用中点坐标公式及其根与系数的可得P，代入直线y=mx+，可得，代入△＞0，即可解出．（2）直线AB与x轴交点横坐标为n，可得S△OAB=，再利用均值不等式即可得出．解答：解：（1）由题意，可设直线AB的方程为x=﹣my+n，代入椭圆方程，可得（m2+2）y2﹣2mny+n2﹣2=0，设A（x1，y1），B（x2，y2）．由题意，△=4m2n2﹣4（m2+2）（n2﹣2）=8（m2﹣n2+2）＞0，设线段AB的中点P（x0，y0），则．x0=﹣m×+n=，由于点P在直线y=mx+上，∴=+，∴，代入△＞0，可得3m4+4m2﹣4＞0，解得m2，∴或m．（2）直线AB与x轴交点纵坐标为n，∴S△OAB==|n|•=，由均值不等式可得：n2（m2﹣n2+2）=，∴S△AOB=，当且仅当n2=m2﹣n2+2，即2n2=m2+2，又∵，解得m=，当且仅当m=时，S△AOB取得最大值为．点评：本题考查了椭圆的定义标准方程及其性质、直线与椭圆相交问题转化为方程联立可得根与系数的关系、中点坐标公式、线段垂直平分线的性质、三角形面积计算公式、弦长公式、均值不等式的性质，考查了推理能力与计算能力，属于难题．20．（15分）考点：数列的求和；数列与不等式的综合．专题：创新题型；点列、递归数列与数学归纳法．分析：（1）通过题意易得0＜a n≤（n∈N*），利用a n﹣a n+1=可得≥1，利用==≤2，即得结论；（2）通过=a n﹣a n+1累加得S n=﹣a n+1，利用数学归纳法可证明≥a n≥（n≥2），从而≥≥，化简即得结论．解答：证明：（1）由题意可知：0＜a n≤（n∈N*），又∵a2=a1﹣=，∴==2，又∵a n﹣a n+1=，∴a n＞a n+1，∴≥1，∴==≤2，∴1≤≤2（n∈N*）；（2）由已知，=a n﹣a n+1，=a n﹣1﹣a n，…，=a1﹣a2，累加，得S n=++…+=a1﹣a n+1=﹣a n+1，易知当n=1时，要证式子显然成立；当n≥2时，=．下面证明：≥a n≥（n≥2）．易知当n=2时成立，假设当n=k时也成立，则a k+1=﹣+，由二次函数单调性知：a n+1≥﹣+=≥，a n+1≤﹣+=≤，∴≤≤，即当n=k+1时仍然成立，故对n≥2，均有≥a n≥，∴=≥≥=，即（n∈N*）．点评：本题是一道数列与不等式的综合题，考查数学归纳法，对表达式的灵活变形是解决本题的关键，注意解题方法的积累，属于难题．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2015年广东高考理科数学特别关注1、命题人员主要是07-10那批人，平均分在85分左右，线性规划要注意已知最值逆向求参数的题目关注作图能力（如三视图、茎叶图、五点法作图等），6道大题的顺序可能有所调整2、三角函数：关注正余弦定理在解三角形中的工具性，知道12π的三角函数值 3、概率统计：数据说话，建议关注北京题4、立体几何：重点研究07-10的立体几何题；模型意识（核心几何体）；有数学味（淡化向量法）；理科关注存在性探究，文科关注逆向探究；关注线面角的求法.5、数列：知三求二（将问题转化为等差等比问题）；关注数列不等式的证明（即放缩的技巧）；关注点列（09年最后一道题）；熟练掌握数学归纳法（广东高考有一点的延续性）；注意21=1(1)n n n n a n a n a n a n n ==±=+、、、几种数列逆向构造的结论,如n a n =⇒ (1)2n n a n s +=(1)2n n n a a s +=、1(1)(1)2n n n n ns n s ++-+=；2n a n =则(1)(21)6n n n n s ++=⇒ 2(1)(21)3n s n n n ++=、2121233n n S a n n n +=---. 6、解析几何：命题人对计算能力有一定的要求，所以可能有一定的计算量；关注有韦达定理题目的同时也要注意不使用韦达定理的题目.7、函数导数：关注函数的奇偶性；将导数作为工具（求最值、讨论单调性）；注意二次不等式含参的讨论（如2011年文科导数题、2012年理科最后一题）；注意几个常见的重要不等式ln (0)1xx x x x<<>+、e 1xx ≥+、2sin sin 6x x x x x ≤≥-、典例研究1.（2013年北京）下图是某市3月1日至14日的空气质量指数趋势图，空气质量指数小于100表示空气质量优良，空气质量指数大于200表示空气重度污染，某人随机选择3月1日至3月13日中的某一天到达该市，并停留2天.（Ⅰ）求此人到达当日空气重度污染的概率G （Ⅱ）设X 是此人停留期间空气质量优良的天数，求X 的分布列与数学期望（Ⅲ）由图判断从哪天开始连续三天的空气质量指数方差最大？（结论不要求证明）1.【解析】设i A 表示事件“此人于3月i 日到达该市”（ i =1,2，…，13）.根据题意, 1()13i P A =,且()i j A A i j =∅≠ .（Ⅰ）设B 为事件“此人到达当日空气重度污染”，则58B A A = , 所以58582()()()()13P B P A A P A P A ==+=. （Ⅱ）由题意可知，X 的所有可能取值为0,1,2，且P (X =1)=P (A 3∪A 6∪A 7∪A 11)= P (A 3)+P (A 6)+P (A 7)+P (A 11)=413, P (X =2)=P (A 1∪A 2∪A 12∪A 13)= P (A 1)+P (A 2)+P (A 12)+P (A 13)= 413,P (X =0)=1－P (X =1)－P (X =2)= 513,所以X 的分布列为：012544131313XP故X 的期望5441201213131313EX =⨯+⨯+⨯=.（Ⅲ）从3月5日开始连续三天的空气质量指数方差最大.2．(2010年广东)如图5， AEC 是半径为a 的半圆，AC 为直径，点E 为 AC 的中点，点B 和点C 为线段AD 的三等分点．平面外一点F满足,6FB FD FE a =． (Ⅰ) 证明EB FD ⊥；(Ⅱ) 已知点Q 、R 分别为线段FE 、FB 上的点，使得2,3FQ FE =23FR FB =,求平面BED 与平面RQD 所成二面角的正弦值． 2．【解析】(Ⅰ)∵E 为半圆 AEC 中 AC 的中点，∴EB AC ⊥又222EB FB FE +=,故EB FB ⊥ 而AC FB B = ∴EB ⊥平面FBD ∵FD ⊂平面FBD ∴EB FD ⊥.(Ⅱ) 由22,33FQ FE FR FB ==可得//RQ EB ,过D 作直线//l EB ,则EB BD ⊥,EB FB ⊥∴RDB ∠为平面BED 与平面RQD 所成二面角的平面角. 在FBD ∆中,连结FC ,作RG BD ⊥交BD 于点G可得2tan 2sin 3FC FBC RG RB FBC a BC ∠==⇒=⋅∠= 1cos 3BG RB FBC a =⋅∠= ∴53GD a =，RD a =, 从而229sin RG RDB RD ∠== ∴平面BED 与平面RQD.3．(2013年佛一)数列{}n a 、{}n b 的每一项都是正数,18a =,116b =,且n a 、n b 、1n a +成等差数列,n b 、1n a +、1n b +成等比数列.（1）求2a 、2b 的值；（2）求n a 、n b ；（3）证明1211121117n a a a +++<--- . 3．【解析】 (Ⅰ)由1122b a a =+，可得211224a b a =-=. 由2212a b b =，可得222136a b b ==.（Ⅱ）方法一:因为n a 、n b 、1n a +成等差数列，所以12n n n b a a +=+…①.因为n b 、1n a +、1n b +成等比数列，所以211n n n a b b ++=，因为数列{}n a 、{}n b的每一项都是正数，所以1n a +…②. 于是当2n ≥时，n a =.将②、③代入①式，可得是首项为4，公差为2的等差数列，()122n d n -=+，于是()241n b n =+.由③式，可得当2n ≥时，()41n a n n ===+. 当1n =时，18a =，满足该式子，所以对一切正整数n ，都有()41n a n n =+. （Ⅲ）由（Ⅱ）可知，所证明的不等式为211127234417n n +++<+-L .方法一:首先证明2121144171n n n n ⎛⎫<- ⎪+-+⎝⎭（2n ≥）.因为22222121112778824417144177n n n n n n n n n n n n⎛⎫<-⇔<⇔+<+- ⎪+-++-+⎝⎭()()220120n n n n ⇔+->⇔-+>,所以当2n ≥时，21111211111212723441772317727n n n n ⎡⎤⎛⎫⎛⎫+++<+-++-<+⨯= ⎪ ⎪⎢⎥+-+⎝⎭⎝⎭⎣⎦L L . …12分当1n =时，1277<. ……………………………………………………………………13分综上所述，对一切正整数n ，有1211121117n a a a +++<---L . ……………………………………14分方法二:()()22111111441443212342123n n n n n n n n ⎛⎫<==- ⎪+-+--+-+⎝⎭.当3n ≥时，2111723441n n ++++-L 1111111111172345971123212123n n n n ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫<++-+-++-+- ⎪ ⎪ ⎪ ⎪⎢⎥-+-+⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦L 111111112723457714147⎛⎫<+++<++= ⎪⎝⎭.…12分当1n =时，1277<；当2n =时，11112723777+<+=. …………………………………………13分综上所述，对一切正整数n ，有1211121117n a a a +++<---L . ………………………………14分4. (2009年广东)已知曲线22:20(1,2,)n C x nx y n -+== ．从点(1,0)P -向曲线n C 引斜率为(0)n n k k >的切线n l ，切点为(,)n n n P x y ．（Ⅰ）求数列{}{}n n x y 与的通项公式；（Ⅱ）证明：13521n n nxx x x x y -⋅⋅⋅⋅<. 4.【解析】曲线222:()n C x n y n -+=是圆心为(,0)n ,半径为n 的圆, 切线n l :(1)n y k x =+n =,解得2221n n k n =+,又2220n n n x nx y -+=,(1)n n n y k x =+联立可解得1n n x n =+,n y =.=,n n x y = 先证:13521n x x x x -⋅⋅⋅⋅< 利用数学归纳法当1n =时, 112x =<,命题成立;假设n k =时,命题成立,即13521k x x x x -⋅⋅⋅⋅< 则当1n k =+时,135212121k k k x x x x x x -++⋅⋅⋅⋅<=∵2222416161483k k k k ++=>++,故2(2)k <=+ ∴当1n k =+时,命题成立故13521n x x x x -⋅⋅⋅⋅< 成立.<不妨设(0,3t =,令()f t t t =,则()10f t t '=<在(0,3t ∈上恒成立故()f t t t =在(0,3t ∈上单调递减,从而()(0)0f t t t f =<=,<. 综上, 13521n n nxx x x x y -⋅⋅⋅⋅<成立.5. (2010年广东文) 设0a >,讨论函数2()ln (1)2(1)f x x a a x a x =+---的单调性.5.【解析】函数()f x 的定义域为(0,),+∞22(1)2(1)1().a a x a x f x x---+'=(1)当()()()110,0a f x f x x'==>∞时，则在区间，+内单调递增；（2）当212(1)10a a a x a x ≠--+=时,方程2(1-)的判别式112(1).3a a ∆⎛⎫=-- ⎪⎝⎭①当13≤a <1时，∆≤0，()f x '≥0,()(0,)f x +∞所以在内单调递增；②当10,0,()3a f x '<<∆>时有两个解，12110,022x x a a =>=+>，所以当12120,()0,()(0,)(,)x x x x f x f x x x '<<>>+∞或时在和内单调递增；当1212,()0,()(,)x x x f x f x x x '<<<时在内单调递减；③当111,0,0,2a x a ∆>>=>时212x a =<（舍去）.所以当110,()0,()(0,)x x f x f x x '<<>时在内单调递增；当1x x >时，1()0,()(,)f x f x x '<+∞在内单调递减.综上所述，当103a <<时，()f x 在()10,x 和()2,x +∞内单调递增，()f x 在()12,x x 内单调递减；当13≤a ≤1时，()(0,)f x +∞在内单调递增；当1,a >时1()(0,)f x x 在内单调递增；1()(,)f x x +∞在内单调递减.（其中121122x x a a ==）。