positive solution of a class fractional differential equation
A-level数学词汇(P1-P4)

Pure mathematics 1 1 Algebraic expression 代数表达式Index laws 指数定律Indices (index的复数形式) 指数Notation 注释Simplify 化简Power 指数Base 底Exponent 指数Expression 表达式Term 项Numerator 分子Expand 展开Possible 可能Fraction 分数Bracket 括号Product 乘积Multiply 乘Collecting like terms 合并同类项Linear 一次的Diagram 图形Rectangle 长方形Square 正方形Length 长度Width 宽Side length 边长Area 面积Shade 阴影Cuboid 长方体Dimension 维Show that 证明V olume 体积Given that 已知Constant 常数Value 值Factorize 因式分解Factor 因子Opposite 相反的Completely 完全地Common factor 公因式Quadratic 二次的Form 形式Real number 实数Positive 正的Negative 负的Include 包含Surd 无理数Add 加Sum 和Take out 提取Difference 差Difference of two squares 平方差Cancel 取消,相互抵消Similarly 同样的Rational 有理的Rational number 有理数Integer 整数Square root 平方根Evaluate 求…的值Substitute 代替Calculator 计算器Square number 平方数Irrational number 无理数Decimal 小数的Expansion 展开式Never-ending 无限的Never repeat 不循环的Exact 准确的Answer 答案Manipulate 操作Denominator 分母Rationalizing denominator 分母有理化Rearrange 调整Prime 质数Work out 计算Hence 然后Fully 完全地State 陈述Solve 解决Equation 方程2 Quadratics 二次方程式Quadratic equation 二次方程Solution 解Real solution 实根Set 设置Root 根Distinct 不同的Repeated root 重根Case 情况Straightforward 简单直接的Symbol 符号Plus 加,正Minus 减,负Factorization 因式分解Shape 形状Section 部分Formula 公式Reading off 读取Coefficient 系数Necessary 必要的Significant figures 有效数字Choose 选择Suitable 适当的Method 方法Trapezium 梯形Height 高Discard 丢弃Completing the square 完全平方(配方)Frequently 经常的Useful 有用的Process 过程Original 最初的Determine 决定Otherwise 另外Function 函数Mathematical 数学上的Relationship 关系Map 映射Set 集合Input 输入Output 输出Single 单一的Notation 符号Represent 代表Domain 定义域Range 值域,范围Member 成员Define 定义Minimum 最小的Occur 发生Explain 解释Consider 考虑Graph 图像Curve 曲线Parabola 抛物线Sketch 画图Identify 确定Key 关键的Feature 特征Overall 整体的Cross 交叉,横过Axis 轴Coordinate 坐标Turning point 转折点(顶点)Maximum 最大的Since 因为Symmetrical 对称的Symmetry 对称性Line of symmetry 对称轴Half-way 位于中途的Explore 探测Technology 技术Plot 绘制Scale 刻度However 但是,不管怎样Smooth 平滑的Relevant 相关的Intercept 截距Label 标记Axes (axis的复数)坐标轴Discriminant 判别式Sign 符号Check 核实Inequality 不等式Calculate 计算Match 匹配Prove 证明Algebra 代数学Diver 跳水运动员Launch 发射Springboard 跳板Meter 米Pool 水池Second 秒Model 模型High 高的Hit 撞击Reach 达到Non-zero 非零3 Equations and inequalities 方程和不等式Simultaneous 联立的Linear simultaneous equations 一次方程组Elimination 消元法Substitution 置换Quadratic simultaneous equations 二次方程组Up to 直到,多达Make sure 确保Correctly 正确地Simplest 最简的Graphically 以图表形式As 因为Satisfy 满足Intersection 相交Simultaneously 同时地Intersect 相交Once 一次Twice 两次Result 结果,导致Produce 产生Graph paper 坐标纸Accurately 准确地Verify 验证Linear inequalities 一次不等式Set notation 集合符号Number line 数轴Overlap 重叠Separately 单独地Illustrate 图解,阐明Quadratic inequalities 二次不等式Corresponding 相应的Critical 临界的Require 要求Describe 描述Interpret 解释Region 区域,范围Coordinate grid 坐标网Dotted line 虚线Solid line 实线Vertex 顶点Vertices (vertex的复数)顶点Within 在内部,之内4 Graphs and transformations 图像和转换Cubic 三次的Cubic function 三次函数Several 几个Depend on 取决于Touch 接触Coordinate axes 坐标轴Indicate 表明,显示Reciprocal 倒数的Reciprocal function 反比例函数Such as 例如Asymptote 渐近线Approach 接近Reach 到达Quadrant 象限Point of intersection 交点Steeper 更陡峭的Eventually 最后,终于Reason 理由,原因Appropriate 恰当的Number 数量Translate 平移Transform 改变Alter 改动Subtract 减Outside 在外面Vertically 竖直地Translation 平移Vector 矢量Horizontally 水平地Direction 方向In terms of 用…来表示Slide 滑动Stretch 伸缩Scale factor 比例系数Double 两倍Halve 减半,对分Inside 在里面Triple 三倍的Reflection 反射(镜面对称) Alternatively 二选一Parallel 平行Lie on 坐落在Pass through 穿过Apply 应用Unfamiliar 陌生的,不熟悉的Specific 特殊的Origin 原点Position 位置Image 像Suggest 提议Mark 标记5 Straight line graphs 直线图像Gradient 斜率Straight line 直线Join 连接Distance 距离Formula 公式Collinear 共线的Intercept 截距Define 定义Either 两者中的任一个Condition 条件Triangle 三角形General equation 一般式Parallel 平行Perpendicular 垂直Whether 是否Quadrilateral 四边形Trapezium 梯形Right angle 直角Congruent 全等的Neither 两者都不Hypotenuse 直角三角形斜边Line segment 线段Scalene 不等边的Respectively 分别地Go through 通过6 Trigonometric ratios 三角比Cosine rule 余弦定理Miss 缺失Version 版本Exchange 交换Standard 标准Prove 证明Opposite 对边Adjacent 邻边Pythagoras’ theorem 勾股定理Letter 字母Round 四舍五入Final 最终的Coastguard 海岸警卫队Station 驻地Bearing 方位Away from 远离Appropriate 适当的Mark 标记Airport 机场Due north 正北Due east 正东Due west 正西Due south 正南Sail 航行Helicopter 直升飞机Tee 球座Flag 旗Particular 特定的Hole 孔,洞Golf course 高尔夫球场Yard 码(1码=3英尺)Tee shot 发球台Land 着陆Largest 最大的Farmer 农场Field 场地Fence 栅栏Cargo 货物Plane 平面Kilometer 千米Sine rule 正弦定理Refer to 涉及Data 数据Remain 剩余Located on 坐落于Zookeeper 动物管理员Enclosure 围场Llama 骆驼Diagonal 对角线Surveyor 检验员Measure 测量Elevation 高程,仰角Apart 相距Assumption 假设Mathematical 数学的Model 模型Obtuse 钝角Acute 锐角Isosceles 等腰的Circle 圆Radius 半径Centre 圆心Least 最小的Instead 代替Crane 吊车Anchored 固定Wreck 破坏Suspend 悬挂Cable 缆绳Rotate 旋转Level 对准Proof 证明Triangular plot 三角图Involve 涉及Trigonometry 三角函数Encounter 遇到Decide 决定Mast 桅杆In order that 为了Interfere 干扰Efficient 有效的Hiker 徒步旅行者Radar 雷达Perimeter 周长Tangent 正切Periodic 周期性的Repeat 重复的Certain 确定的Interval 间距Period 周期Undefined 无意义的Knowledge 知识Periodicity 周期性Verify 证明Variation 变化Rock pool 潮汐潭Midday 中午During 在…期间Non-exact 非精准的Significant figure 有效数字Windmill 风车Sail 帆Tower 塔Deduce 推导Dune 沙丘Realistic 现实的7 Radians 弧度Radian 弧度So far 到目前为止Probably 大概,可能Degree 度Revolution 循环Around 围绕Circle 圆Subtend 朝着Arc 圆弧Circumference 周长Convert 转换Without 没有Multiple 倍数Arc length 弧长Sector 扇形Radius 半径Contain 包含Perimeter 周长Border 边界Pond 池塘Consist 由…组成Edge 边缘Minor arc 劣弧Major arc 优弧Chord 弦Diameter 直径Template 模板Brooch 胸针Ferris wheel 摩天轮Pod 蚕茧,豆荚Estimate 估计Speed 速率Patio 露台Lawn 草坪Design 设计Earring 耳环Nearest 最近点(精确到)Segment 弓形Radii (radius的复数形式) A plot of …的一块Erect 建造Along 沿着Subtract 减Tangent 切线Ratio 比例Bound 关,围入Decimal place 小数Midpoint 中点Semicircular 半圆Drawer 抽屉Handle 把手Difference 差Badge 徽章Equilateral 等边的Railway 铁路Track 轨迹Prism 三棱镜Attempt 尝试Mistake 错误8 Differentiation 微分Gradient 斜率Constantly 不断地Although 然而Comment on 对…评论Copy 抄写,复制Complete 完成Table 表格Hypothesis 假设Derivative 导数Principle 原理Detail 细节Account 解释Originate 起源Formalize 确定,形成Approach 方式,方法Limit 极限Tend to 趋向Gradient function 斜率函数Evaluate 求…的值Fixed value 定值Limiting value 定值Definition 定义One-at-a-time 一次一个Turning point 转折点(顶点)Slope 斜率Disappear 消失Polynomial 多项式Normal 切线First order derivative 一阶导数Second order derivative 二阶导数Rate of change 变化率Respect to 关于Displacement 位移Acceleration 加速度Local 局部的9 Integration 积分Reverse 相反的Differ 不同Integrate 求积分Integral 积分Indefinite 不确定的Indefinite integral 不定积分Elongated 拉长的,伸长的Arrow 箭Fire 射击Castle 城堡Drop off 下降Cliff 悬崖Cyclist 骑行者Pure mathematics 2 1Algebraic methods 代数方法Division 除法Dividing polynomial 多项式除法Finite 有限的Whole number 整数Long division 长除法Quotient 商Remainder 余数Factor theorem 因式定理Remainder theorem 余数定理Logical 逻辑的Structured 有组织的Argument 论据Statement 命题Conjecture 猜想Previously 预先Establish 建立Deduction 推导Desired 想要的Conclusion 结论Odd number 奇数Demonstration 示范,演示Even number 偶数Identical 完全相等的Identity 恒等式Parallelogram 平行四边形Rhombus 菱形Congruent 全等的Exhaustion 穷举法Consecutive 连续的Square number 平方数Break into 拆分Is suited to 适合于Disprove 反驳Counter-example 反例Sufficient 充分的Prime number 质数Divisible 可整除的Either … or…二者择一的Cube number 立方数Hold 有效Claim 宣称Opposite edge 对边Hexagon 六边形Regular hexagon 正六边形Side length 边长Reason 原因2Coordinate geometry in the (x,y) plane 解析几何Bisector 二等分线Perpendicular bisector 中垂线Averaging 求平均值Endpoint 端点Circumcentre 外心Equidistant 等距的Fixed point 定点Vector 向量Property 性质Unique 独一无二的Circumcircle 外接圆3Exponentials and logarithms 指数和对数Exponential 指数的Decrease 减小Increase 增加Smooth 光滑的,平滑的Increasing function 增函数Decreasing function 减函数Justify 证明Logarithms 对数Specific 特定的Button 按钮Typically 典型的Natural logarithms 自然对数Instance 实例Multiplication law 乘法定律Division law 除法定律Power law 指数定律Recognize 识别Attention 注意Condition 条件Complicated 复杂的Whenever 无论何时Convenient 方便的Suppose 假设Notice 注意Particular 特别的4The binomial expansion 二项式展开Binomial 二项式Pascal’s triangle 杨辉三角(帕斯卡三角形)Immediately 直接地Pattern 图案Adjacent 相邻的Investment 投资Interest rate 利率Annum 年,岁Approximation 近似值Ignore 忽略Factorial notation 阶乘Combination 组合Superscript 上标Subscript 下标Probability 可能性Toss 投Likelihood 可能性Ascending powers 升幂Individual 个别的Estimation 估值Engineering 工程学Science 科学Percentage error 百分误差Microchip 微型集成电路片Faulty 有缺点的Chip 芯片Restrict 限制Achieve 达到School fair 学校园游会Prize 奖赏Digit 数字Display 显示5Sequences and series 数列和级数Arithmetic sequence 等差数列Arithmetic progression 等差数列Common difference 公差Arithmetic series 等差级数(等差数列前n 项求和)Exceed 超过Inclusive 包含的Stick 棒子Pentagon 五角形Geometric sequences 等比数列Geometric progression 等比数列Common ratio 公比Converge 收敛Alternating sequence 交错数列Million 百万Geometric series 等比级数(等比数列前n项求和)Sum to infinity 无限项求和Divergent 发散的Convergent 收敛的Recurring 循环的Sigma notation 求和符号Capital 首都,大写字母Signify 表示Recurrence relations 递推关系Previous term 前一项First term 初项Generate 生成,产生Periodic sequence 周期数列Period 周期Salary 薪水Profit 利润Predict 预言Annual 年度的Business 商业Financial 金融的Advisor 顾问Fold 折叠Thickness 厚度Unrealistic 不切实际的Investor 投资人Account 账户Thereafter 以后Deposit 存款,定金Wage 工资Rise 上升Gear 齿轮Successive 连续的Intermediate 中间的Valuable 有价值的Commission 佣金Insurance 保险Policy 政策Prospector 勘探者Drill 钻孔Subsequent 随后的Available 可获得的Payment 报酬Virus 病毒Infect 传染Diagnose 诊断Overfish 过度捕捞Chess 象棋Chessboard 棋盘Sponsored 赞助的Polygon 多边形Appointment 约会,任命6Trigonometric identities and equations 三角恒等式和方程Unit circle 单位圆Anticlockwise 逆时针Quadrant 象限Equivalent 相等的Equilateral triangle 等边三角形Isosceles right-angled triangle 等腰直角三角形Identity 恒等式Reflex 优角(大于180度,在第三、四象限)Principal value 主值Inverse trigonometric function 反三角函数Justification 理由7Differentiation 微分Strictly 严格地Interval 区间Stationary point 驻点Local maximum 局部最大Greatest value 最大值Local minimum 局部最小Least value 最小值Point of inflection 拐点,反曲点Immediate 最接近的Vicinity 邻近,附近Second derivative 二次求导Rate of change 改变的快慢Convex 凸Concave 凹Establish 建立,证实Liter 升Instant 瞬间Tank 水槽Cuboid 长方体的Sheet 薄片Metal 金属Sphere 球体Displacement 位移Cylinder 圆柱体Perimeter 周长Semicircular 半圆的Semicircle 半圆Frame 框架Split 分离,分开Motion 运动Damped 阻尼Spring 弹簧Bent 弯的Biscuit 饼干Tin 罐头Close-fitting 紧贴的Lid 盖子Thin 薄的,瘦的Wastage 损耗Obtain 获得Percentage 百分比Store 储存Capacity 容量Container 容器Calculus 微积分学8Integration 积分Definite integral 定积分Indefinite integral 不定积分Whereas 反之,然而Upper limit 上限Lower limit 下限Square bracket 中括号Magnitude 大小Negligible 可忽略的Straddle 跨坐Unless 除非Complicated 复杂的Trapezium 梯形Trapezium rule 梯形法则Beneath 在…下面Strip 条,带Boundary 边界Adjacent 相邻的Improve 改善Accuracy 精确度Approximation 近似值Underestimate 低估Overestimate 高估Compare 比较Pure mathematics 3 Common multiple 公倍数Improper fraction 假分数Partial fractions 部分分数Degree 次数Modulus function 模函数Absolute value 绝对值Argument 辐角Set notation 集合符号Piecewise-defined function 分段函数Composite function 复合函数Inverse function 反函数Secant 正割Cosecant 余割Cotangent 余切Interval 区间Symmetry 对称性Symmetrical 对称的Chord 弦Inverse trigonometric function 反三角函数Addition formulae 加法公式Compound-angle formulae 复合角公式Double-angle formulae 二倍角公式Round 四舍五入Exponential function 指数函数Natural logarithms 自然对数Trend 趋势Outlier 极值Chain rule 链式法则Product rule 乘法法则Quotient rule 除法法则Continuous 连续的Fixed point iteration 定点迭代Successive 连续的Converge 收敛Staircase diagram 梯形图Cobweb diagram 网状图Diverge 发散Pure mathematics 4 Contradiction 反驳Assert 主张Falsehood 虚假Negation 反论Prime number 质数Split 分解Separate 独立的Parametric equation 参数方程Variable 变量Parameter 参数Revolution 循环Plot 绘图Valid 有效的As long as 只要Condition 条件Accurate 精确的Ascending 上升的Approximation 近似值Implicit differentiation 隐函数微分Explicitly 明确的Implicit 隐含的Rate of change 变化率Hemisphere 半球Cylindrical 圆柱形的Conical 圆锥形的Concave 凹Convex 凸Integrand 被积函数Integration by substitution 换元积分法Integration by part 分部积分法Polynomial 多项式Separating the variables 分离变量General solution 通解Boundary condition 边界条件Directed line segment 有向线段Parallelogram 平行四边形Unit vector 单位向量Column vector 列向量Position vector 位置矢量Scalene 不等边的21Clockwise 顺时针Anticlockwise 逆时针Coplanar 共面的Parallelepiped 平行六面体Trisect 三等分Hexagon 六边形Regular hexagon 正六边形Direction vector 方向向量Anchor 固定Dot product 点乘22。
PositiveandNegativeFractions-BasicsaboutFractions

Positive and Negative FractionsBasics about FractionsWhat you should know:∙ A fraction is a number of the form a b, where a and b are integers and b is not 0. ∙ In the fraction a b, a is called the numerator and b is called the denominator .∙ A fraction can be thought of the “part ‐to ‐whole.” The denominator tells you how many equalsized parts to divide an object into. The numerator tells you how many parts are being considered (shown by shading).∙ A proper fraction has a value less than one. The numerator is less than the denominator.∙ An improper fraction has a value greater than or equal to one. The numerator is greater than orequal to the denominator.∙ Fractions can be graphed on a number line.∙ Equivalent fractions have the same value. We say that 12and 24are equivalent fractions. ∙ To rewrite a fraction as an equivalent fraction, multiply the numerator and denominator by thesame nonzero number.∙ A rational number is a ratio of integers. Remember that ratio indicates division. Rationalnumbers have the form a b, where b is nonzero.∙ The rational numbers include all positive and negative fractions, as well as all integers. ∙ Any integer is a fraction with a denominator of 1. 16161=Problems:1. Write a fraction that represents the shaded region of the figure.2. There are 65 cars in the school parking lot. 15 of them are painted black. What fraction of thecars in the parking lot are painted black? 3. Identify the numerator and denominator.59- 4. Identify the numerator and denominator. 85. Is the fraction a proper fraction or an improper fraction?1118 6. Is the fraction a proper fraction or an improper fraction? 987. Graph the fractions12- and 34on a number line. 8. Write 38as an equivalent fraction with denominator 16. 9. Write29- as an equivalent fraction with denominator 36. 10. Write 45as an equivalent fraction with denominator 20. 11. Write 5 as an equivalent fraction with denominator 10.12. Simplify the fraction by dividing the numerator by the denominator.488Writing Fractions in Lowest TermsWhat you should know:∙ A fraction is said to be in lowest terms if the numerator and denominator have no commonfactors (other than 1). 23is in lowest terms.∙ Factors are quantities that we multiply. We say that 2 and 3 are factors of 6 because 236⋅=. ∙ The greatest common factor (GCF) of two numbers is the largest number that is a factor of bothgiven numbers. The GCF of 6 and 12 is 6.∙ One way to simplify or reduce a fraction, divide the numerator and denominator by the GCF. ∙ Always write your final answers in problems involving fractions in lowest terms.∙ Prime numbers are integers greater than 1 that are divisible only by themselves and 1. The firstseveral prime numbers are 2, 3, 5, 7, 11, 13, 17, 19, …. ∙ Numbers that are not prime are said to be composite .∙ Any number can be written as a product of prime numbers. This is called the prime factorizationof a number. For example, the prime factorization of 12 is 12223=⋅⋅∙ Another way to simplify, or reduce, fraction is to use prime factorization. Find the primefactorization of both the numerator and denominator. Divide out (“cancel”) like factors. ∙ Ask your instructor which method they prefer you use. If your instructor has no preference,stick with the method that seems more natural to you.∙ Fractions involving variables should also be written in lowest terms.Problems:1. Is the fraction in lowest terms? 682. Is the fraction in lowest terms? 583. Reduce the fraction to lowest terms. 2434. Reduce the fraction to lowest terms.15455. Find the prime factorization of the number. 246. Find the prime factorization of the number. 357. Find the prime factorization of the number. 488. Use prime factorization to write the fraction in lowest terms. 840 9. Use prime factorization to write the fraction in lowest terms. 164810. Write the fraction in lowest terms.4560 11. Write the fraction in lowest terms.412aba12. Write the fraction in lowest terms. 2620x x-13. There are 60 seconds in a minute. What fraction of a minute is 15 seconds? 14. There are 365 days in one year. What fraction of a year is 250 days?Multiplying and Dividing FractionsWhat you should know:∙ How to multiply fractions . Multiply “across,” meaning multiply the numerators and multiply thedenominators. Then reduce. a c a cb d b d⋅⋅=⋅ ∙ It is also common to write the prime factorization of all fractions before multiplying across.First, write the prime factorization of all fractions in the multiplication problem. Then “cancel” like factors. Finally, multiply across. Make sure the answer is in simplest form. ∙ Many people also “cross ‐cancel” out the GCF before multiplying across.∙ Ask your instructor how they want you to multiply fractions. Only if your instructor has nopreference, then multiply either way.∙ The word “of” in a math problem means to multiply.∙ The reciprocal of the fraction a bis b a. To find the reciprocal, either “flip” the fraction over or “invert” the fraction.∙ To divide fractions , find the reciprocal of the second fraction and multiply. Many peopleremember “invert and multiply.” a c a d bd b c÷=⋅ ∙ When dividing fractions, always make sure you write the final answer in simplest form.Problems:1. Multiply. Write the answer in lowest terms (simplest form). 310533⋅ 2. Multiply. Write the answer in lowest terms (simplest form). 2(12)3- 3. Multiply. Write the answer in lowest terms (simplest form). 314718--⎛⎫⋅ ⎪⎝⎭4. What is 34of ‐32?5. Multiply. Write the answer in lowest terms (simplest form). 581625x x⋅ 6. Divide. Write the answer in lowest terms (simplest form).42053-÷ 7. Divide. Write the answer in lowest terms (simplest form). 24315--⎛⎫⎛⎫÷⎪ ⎪⎝⎭⎝⎭8. Divide. Write the answer in lowest terms (simplest form). 748÷ 9. Divide. Write the answer in lowest terms (simplest form). 9(3)11⎛⎫-÷ ⎪⎝⎭10. Divide. Write the answer in lowest terms (simplest form). 305⋅ 11. Divide. Write the answer in lowest terms (simplest form).7010÷ 12. Jassiel has 20 feet of plywood. He needs 45of it for a home improvement project. How muchplywood does he have left?13. Patsy pays 13of her monthly salary for rent. Her monthly salary is $3,600. How much is hermonthly rent?Adding and Subtraction Fractions with the Same Denominator (Common Denominator)What you should know:∙ To add two fractions with the same denominator, add the numerators and write over the samedenominator. Reduce to lowest terms. a c a cbbb ++=∙ To subtract two fractions with the same denominator, subtract the numerators and write overthe same denominator. Reduce to lowest terms. a c a cbbb--=Problems:1. Add the fractions. Write the answer in lowest terms. 5188+ 2. Subtract the fractions. Write the answer in lowest terms. 3144-Adding and Subtraction Fractions with different DenominatorsWhat you should know:∙ You must first find a common denominator . Many instructors want you to find the leastcommon denominator (LCD) so we will cover that here.∙ To find the LCD: find the largest number that is divisible by both of the original denominators. ∙ Rewrite each fraction as an equivalent fraction over the LCD.∙ Now that the denominators are the same, add or subtract the two fractions as before. ∙ Reduce to lowest terms.Problems:1. Find the LCD for the two fractions. 58and 14. 2. Find the LCD for the two fractions. 35and 47. 3. Find the LCD for the two fractions. 38and 56.4. Add the fractions. Write the answer in lowest terms. 1546+ 5. Add the fractions. Write the answer in lowest terms.3111015+ 6. Add the fractions. Write the answer in lowest terms. 3710+7. Subtract the fractions. Write the answer in lowest terms. 7184- 8. Subtract the fractions. Write the answer in lowest terms. 263- 9. Subtract the fractions. Write the answer in lowest terms. 1253--Mixed Numbers and EstimatingWhat you should know:∙ A mixed number has a whole number part and a fraction part. An example is 143, where thewhole number part is 4 and the fraction part is 13.∙ The mixed number 143 means 143+. It is read as “four and one ‐third.”∙ The mixed number 225- means 222255-⎛⎫-+=--⎪⎝⎭. ∙ To rewrite a mixed number as a fraction, multiply the whole number part by the denominatorand add on the numerator. Write over the original denominator. ba c ba cc⋅+=∙ To rewrite an improper fraction as a mixed number, divide it out. The quotient is the wholenumber part, the remainder is the numerator. Write over the original denominator. ∙ To add, subtract, multiply or divide mixed numbers, first rewrite the mixed numbers asimproper fractions. Perform the operation with the improper fractions. Convert back to mixed number form for the final answer.∙ To estimate an answer for a mixed number problem, first round any mixed numbers to thenearest whole number. Then perform the operation. Round any fraction parts down if the fraction is less than half. If the fraction part is more than half, round up.∙ The rule of thumb is if the problem is written originally with mixed numbers, you should answerwith mixed numbers (unless told otherwise). If the problem is originally written with improper fractions, you should answer with improper fractions (unless told otherwise).Problems:1. Write the mixed number as an improper fraction. 5282. Write the improper fraction as a mixed number.2473. Write the improper fraction as a mixed number in simplest form.24144. Multiply. Remember, to convert to improper fractions first. Write the answer as a mixednumber in lowest terms. 133254⋅5. Is the fraction less than half or greater than half? 586. Is the fraction less than half or greater than half? 257. Estimate the quotient. 219353÷8. Subtract the fractions. Write the answer in lowest terms. 1324-Evaluating Exponents and Order ‐of ‐Operations involving FractionsWhat you should know:∙ Exponents apply to fractions just as they apply to integers. 222243339⎛⎫⎛⎫⎛⎫== ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭.∙ The order ‐of ‐operations agreement applies to problems involving fractions, just as for integers.You will have to follow the rules of how to add, subtract, multiply and divide fractions in all problems.∙ Remember, the fraction bar indicates division. Therefore, 236 indicates 263÷.Problems:1. Simplify. 225-⎛⎫⎪⎝⎭2. Simplify. 323⎛⎫⎪⎝⎭3. Simplify. 26253518+⋅4. Simplify. 1432510⎛⎫- ⎪⎝⎭5. Simplify. 231423-⎛⎫+ ⎪⎝⎭6. Simplify. 1532564⎛⎫ ⎪⎝⎭⎛⎫ ⎪⎝⎭Geometry: VolumeWhat you should know:∙ Volume is a measure of the amount of space inside a three ‐dimensional object. ∙ The units for volume are cubed units (the shape is 3‐D).∙ Think of finding volume as multiplying the three dimensions together. For a box (a rectangularsolid), we have a length, width and a height. The volume is V l w h =⋅⋅ . You should know this formula!∙ Ask your instructor if they require you to memorize any other volume formulas. Listed beloware 3 other commonly used volume formulas.∙ The volume of a cylinder (think of a can) is: 2V r h π=. Here r refers to the radius of the bottomand h is the height. ∙ The volume of a cone (think of an ice ‐cream cone) is: 213V r h π=. Here r refers to the radius ofthe circular part and h is the height.∙ The volume of a sphere (a ball) is 343V r π=.Problems:1. Find the volume of the rectangular solid (box).2. Find the volume of the sphere (ball).3. Find the volume of the cylinder (can). The radius is 4 in and the height is 8 in.4. Find the volume of the cone. The radius is 3 cm and the height is 5 cm.。
A critical phenomenon for sublinear elliptic equations in cone-like domains

a r X i v :m a t h /0307183v 1 [m a t h .A P ] 12 J u l 2003A critical phenomenon for sublinear elliptic equations in cone–like domainsVladimir KondratievDepartment of Mathematicsand MechanicsMoscow State University Moscow 119899,Russia kondrat@vnmok.math.msu.suVitali LiskevichSchool of Mathematics University of Bristol Bristol BS81TW United Kingdomv.liskevich@Vitaly MorozSchool of Mathematics University of Bristol Bristol BS81TW United Kingdom v.moroz@Zeev SobolDepartment of Mathematics Imperial College,LondonLondon SW72AZ United Kingdomz.sobol@AbstractWe study positive supersolutions to an elliptic equation (∗)−∆u =c |x |−s u p ,p,s ∈R ,in cone–like domains in R N (N ≥2).We prove that in the sublinear case p <1there exists a critical exponent p ∗<1such that equation (∗)has a positive supersolution if and only if −∞<p <p ∗.The value of p ∗is determined explicitly by s and the geometry of the cone.1IntroductionWe study the existence and nonexistence of positive solutions and supersolutions to the equation−∆u =c|x |su p ϕdx for all 0≤ϕ∈C ∞0(C ρΩ).1If u is a sub and supersolution to(1)then u is said to be a solution to(1).By the weak Harnack inequality any nontrivial nonnegative supersolution to(1)is positive in CρΩ.We define critical exponents for equation(1)byp∗=p∗(Ω,s)=inf{p>1:(1)has a positive supersolution in CρΩfor someρ>0},p∗=p∗(Ω,s)=sup{p<1:(1)has a positive supersolution in CρΩfor someρ>0}.Set p∗=−∞if(1)has no positive supersolution in CρΩfor any p<1.Remark1.(i)One can show that if p<p∗or p>p∗then(1)has a positive solution in CρΩ(see [6]for the proof of the case p>1and the proofs below for the case p<1).The existence(or nonexistence)of positive(super)solutions at the critical values p∗and p∗is a separate issue.(ii)Observe that in view of the scaling invariance of the Laplacian the critical exponents p∗and p∗do not depend onρ>0.(iii)We do not make any assumptions on the smoothness of the domainΩ⊆S N−1.Letλ1=λ1(Ω)≥0be the principal eigenvalue of the Dirichlet Laplace–Beltrami operator−∆ωonΩ.Letα+≥0andα−<0be the roots of the quadratic equationα(α+N−2)=λ1(Ω).In the superlinear case p>1the value of the critical exponent is p∗=1−2−sα+,1}.If p∗<1then(1)has no positive supersolutions in the critical case p=p∗.Remark2.(i)Ifα+=0then we set p∗=−∞.(ii)If s>2then p∗=p∗=1and(1)has positive solutions for any p∈R[5,7].If s=2then p∗=p∗=1.In this critical case(1)becomes a linear equation with the potential c|x|−2,which has a positive(super)solution if and only if c≤(N−2)2kand p∗(S k,s)=1−2−sN−1.Applying the Kelvin transformation y=y(x)=x|y|σˆu p in C1Ω,(2)2α−Nα+2−α−Nonexistence zoneExistence zoneFigure 1:Existence and nonexistence zones for equations (1)(left)and(2)(right).whereσ=(N +2)−p (N −2)−s and C 1Ω:={(r,ω)∈R N :ω∈Ω,0<r <1}.We define the critical exponents p ∗= p ∗(Ω,s )and p ∗= p ∗(Ω,s )for equation (2)similarly to p ∗(Ω,s )and p ∗(Ω,s ).In the superlinear case p >1,Bandle and Essen [2]proved that if σ>2then p ∗=1−2−σα−,1}.If p ∗<1then (2)has no positive supersolutions in the critical case p = p ∗.In the remaining part of the paper we prove Theorem 1.2Proof of Theorem 1Existence.In the polar coordinates equation (1)reads as follows−u rr −N −1r2∆ωu =cα+.Let 0<ψ∈H 1loc(Ω)be a positive solution to the equation −∆ωψ−α(α+N −2)ψ=ψpin Ω,(4)where α:=2−s 1−p r αψ∈H 1loc (C 1Ω)is a positive solution to (3)in C 1Ω.Thus the problem reduces to the existence of positive solutions to (4).Note that 0<α(α+N −2)<λ1(Ω).Hence the operator −∆ω−α(α+N −2)is coercive on H 10(Ω)and satisfies the maximum principle.We consider separately the cases p ∈[0,1)and p <0.3Case p∈[0,1).Letφ1>0be the principal Dirichlet eigenfunction of−∆ωonΩ.Letφ∈L∞.Henceτφ.Case p<0.Consider the problem−∆ωφ−α(α+N−2)(φ+1)=(φ+1)p,φ∈H10(Ω).(5)Letφis a supersolution to(5)andφφ.Thenψ:=φ+1∈H1loc (Ω)is a positivesolution to(4).This completes the proof of the existence part of Theorem1.Nonexistence.In what follows we setδ:=1if p<0andδ:=0if p∈[0,1).Let G⊂R N be a domain,0∈G.Observe that equation(1)has a positive supersolution in G if and only if the equation−∆w=c∈H10(G)be a subsolution and 0≤≤,,∈H10(G)and 0≤w∈H1loc(G).LetG n⊂G n+1⊂G and∪n∈N G n=G.Analogously to the argument given above in the existence part of the proof,one can readily see that,for each n∈N,there exists a solution0<w n∈H10(G n)to(6)(e.g.,by constructing appropriate sub and supersolutions).Moreover,w n≤w n+1.Observe that w n≤We claim that sup ∇w n L2<∞.This is clear for p<0,since(w+1)p≤1.For p∈[0,1), using w n as a test function in(6),we haveG|∇w n|2dx= G cw in G.Now let0≤w≤w∗in G.Next,consider the initial value problem−v rr−N−1r2v=cα+,1).Then for any interval[r∗,r∗]⊂(1,+∞)there existsK0>1such thati)for all K>K0one has r∗<R<+∞and v(r)→δas rրR;ii)for any M>δthere exists K>K0such that min[r∗,r∗]v≥M.Proof.Setα:=α+,v:=wrα,t=r2−N−2α.Then w solves the following problem w tt+c1t−σw p=0for t∈(T,1);w(1)=δ,w t(1)=−L,whereσ=2N−2+α(p+3)−sN−2+2α→∞as K→∞.Choose K0such that L>δ.Observe that w(t)is concave,henceδ<w(t)≤w(1)−w t(1)(1−t)≤δ+L for t∈(T,1).To see that T>0let˜w:=w for p<0,otherwise let˜w:=w1−p.Then˜w satisfies the inequality˜w tt+c2t−2˜w q≤0for t∈(T,1),with c2>0and q:=min{p,0}.Integrating˜w tt twice one can easily see that such inequality has no positive solutions in any neighborhood of zero.Thus we conclude that T>0,hence w(t)→δas tցT.In particular,w(t)attains its maximum on(T,1).Let T0∈(T,1)be such that w t(T0)=−L−δ2=w t(T0)−w t(1)=− 1T0w tt dτ=c1 1T0w p Tσ−10−1 for t∈(T0,1).Hence T0→0as L→+∞.Therefore for any given t∗<1there exists L0>1such that for any L>L0one has0<T<T0<t∗.Thus,(i)follows with r∗=(t∗)1Observe now that for any L>L0we haveL−δ−→∞as L→∞.2Thus(ii)follows.Nonexistence–completed.Let p∈[1−2−s。
新药Aprocitentan(阿普昔腾坦)合成检索总结报告
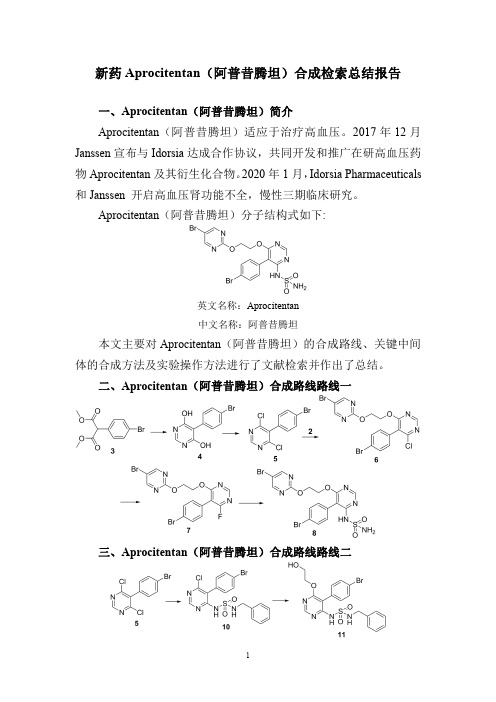
新药Aprocitentan(阿普昔腾坦)合成检索总结报告一、Aprocitentan(阿普昔腾坦)简介Aprocitentan(阿普昔腾坦)适应于治疗高血压。
2017年12月Janssen宣布与Idorsia达成合作协议,共同开发和推广在研高血压药物Aprocitentan及其衍生化合物。
2020年1月,Idorsia Pharmaceuticals 和Janssen开启高血压肾功能不全,慢性三期临床研究。
Aprocitentan(阿普昔腾坦)分子结构式如下:英文名称:Aprocitentan中文名称:阿普昔腾坦本文主要对Aprocitentan(阿普昔腾坦)的合成路线、关键中间体的合成方法及实验操作方法进行了文献检索并作出了总结。
二、Aprocitentan(阿普昔腾坦)合成路线路线一三、Aprocitentan(阿普昔腾坦)合成路线路线二四、Aprocitentan (阿普昔腾坦)合成路线一检索总结报告(一)Aprocitentan (阿普昔腾坦)中间体2的合成(路线一)合成方法实验步骤参考文献操作方法一A mixtureof 5-bromo-2-chloro-pyrimidine 1(100g,0.51mol),THF (1.5L),and K 2CO 3(286g,24mol)was heated to 45o C,then ethylene glycol (43ml,0.7mol)was added to thereaction mixture and maintained at 45o C for 8h.The reaction mixture was cooled to room temperature,filtered,and the residue was washed with THF (400ml).The solvent of The filtratewas replaced with ethyl acetate using Dean-Stark apparatus,and the solution was refluxed for 1h,then cooled to 15o C,filtered and washed with ethyl acetate (200ml)and dried in theoven at 60o C for 6h to obtain 110g (98%)of 2as a white solid,mp 68o C-70o anic Preparations and Procedures International ;vol.49;nb.3;(2017);p.258-264.(二)Aprocitentan (阿普昔腾坦)中间体4的合成(路线一)合成方法实验步骤参考文献操作方法To a stirred solution of 100g dimethyl(4-bromophenyl)-malonate 3(10,0.348mol)in 400cm 3methanol,30g formamide (0.66mol)and 30g sodium methoxide (0.555mol)were added at 20-25o C.The reaction mass was heated to 70o C and maintained until completion of reaction (monitored by HPLC).After completion of the reaction,methanol was distilled off from the reaction mass under reduced pressure at 70o C to obtain the syrup.The syrup was cooled to 25-30o C and diluted with 2dm 3water.The pH of the solution was adjusted to 2-2.5using conc.hydrochloricMonatshefte fur Chemie ;vol.149;nb.3;(2018);p.一acid and maintained for 45min.The obtained solid was filtered and washed with water until the pH of the filtrate became 7-7.5.The product was suck dried and dried under reduced pressure at 100C to obtain crude 4.The crude solid was dissolved in 500cm3methanol at 60-65o C and maintained for 1h.The reaction mass was cooled to 25-30o C and maintained for 30min.The obtained solid was filtered,washed with methanol,anddried at 50-55o C under reduced pressure to offer 4.Yield:70g (75.25%);purity by HPLC:99.5%;m.p.:176-180C 653-661.操作方法二To the mixture containing the intermediate 3,100g of formazan hydrochloride was added,and the mixture was stirred and heated to 25°C for 16h.Adding water to the reaction solution,stir at 25°C until clarified,stand still,take the water phase,adjust the pH of the aqueous phase to 5with hydrochloric acid solution and stir for 1h.After suction filtration,the obtained filter cake was washed with a methanol aqueous solution having a mass fraction of 80%.Drying gave 270.2g of intermediate 4,The yield was 92.6%.CN108997223;(2018);(A)Chinese 操作方法三A solution of intermediate 3(11.73g)in MeOH (100mL)was added at 0o C to a solution of sodium (2.83g)in MeOH (100mL).The mixture was stirred for 18h at rt before formamidine hydrochloride (4.10g)was added.The suspension was stirred at rt for 4h.The solvent was removed and the residue was suspended in 10%aq.citric acid (100mL)and stirred for 10min.The white precipitate was collected,washed with 10%aq.citric acid,water,evaporated three times from cyclohexane and dried under HV at 40o C to give 5-(4-bromophenyl)-pyrimidine-4,6-diol 4.WO2009/24906;(2009);(A1)English;WO2006/51502;(2006);(A2)English;US2012/142716;(2012);(A1)English(三)Aprocitentan (阿普昔腾坦)中间体5的合成(路线一)合成方法实验步骤参考文献操作方法200g of the intermediate 4was taken in a 3L three-necked flask.Add 300g of toluene and 180g of N,N-dimethylaniline,mechanically stirred,230g of phosphorus oxychloride was added dropwise at 30°C,and the temperature was raised to 55°C after the addition.After the solid is completely dissolved,the temperature is raised to 100°C,the reaction is carried out for 4h,and then cooled to 25°C for use.450g of water was mixed with 500g of toluene,and cooled to 25°C CN108997223;(2018);(A)。
已知质量分数求物质的量的浓度

已知质量分数求物质的量的浓度英文回答:To calculate the concentration of a substance given its mass fraction, we need to know the mass of the substance and the total mass of the solution. The concentration is usually expressed in terms of moles per liter (mol/L) or grams per liter (g/L).First, let's consider the case of calculating concentration in moles per liter (mol/L). We can use the following formula:Concentration (mol/L) = (mass of substance in grams) / (molar mass of substance in grams/mol) / (volume ofsolution in liters)。
For example, let's say we have a solution with a mass fraction of 0.2 (20%) of a substance with a molar mass of 100 g/mol. If we have 1 liter of this solution, we cancalculate the concentration as follows:Concentration (mol/L) = (0.2 100 g) / (100 g/mol) / (1 L) = 2 mol/L.Now, let's consider the case of calculating concentration in grams per liter (g/L). We can use the following formula:Concentration (g/L) = (mass of substance in grams) / (volume of solution in liters)。
数学专有名词英文词典

数学专有名词英文词典Mathematics Glossary: A Comprehensive English Dictionary of Mathematical TermsIntroduction:Mathematics is a language of numbers, shapes, patterns, and relationships. It plays a crucial role in various fields, including science, engineering, economics, and finance. To effectively communicate and understand mathematical concepts, it is essential to have a solid grasp of mathematical vocabulary. This article aims to provide a comprehensive English dictionary of mathematical terms, allowing readers to enhance their mathematical knowledge and fluency.A1. Abacus: A counting device that uses beads or pebbles on rods to represent numbers.2. Absolute Value: The distance of a number from zero on a number line, always expressed as a positive value.3. Algorithm: A set of step-by-step instructions used to solve a particular problem or complete a specific task.4. Angle: The measure of the separation between two lines or surfaces, usually measured in degrees.5. Area: The measure of the amount of space inside a two-dimensional figure, expressed in square units.B1. Base: The number used as a repeated factor in exponential notation.2. Binomial: An algebraic expression with two unlike terms connected by an addition or subtraction sign.3. Boundary: The edge or perimeter of a geometric shape.4. Cartesian Coordinates: A system that uses two number lines, the x-axis and y-axis, to represent the position of a point in a plane.5. Commutative Property: The property that states the order of the terms does not affect the result of addition or multiplication.C1. Circle: A closed curve with all points equidistant from a fixed center point.2. Congruent: Two figures that have the same shape and size.3. Cube: A three-dimensional solid shape with six square faces of equal size.4. Cylinder: A three-dimensional figure with two circular bases and a curved surface connecting them.5. Decimal: A number written in the base-10 system, with a decimal point separating the whole number part from the fractional part.D1. Denominator: The bottom part of a fraction that represents the number of equal parts into which a whole is divided.2. Diameter: The distance across a circle, passing through the center, and equal to twice the radius.3. Differential Equation: An equation involving derivatives that describes the relationship between a function and its derivatives.4. Dividend: The number that is divided in a division operation.5. Domain: The set of all possible input values of a function.E1. Equation: A mathematical statement that asserts the equality of two expressions, usually containing an equal sign.2. Exponent: A number that indicates how many times a base number should be multiplied by itself.3. Expression: A mathematical phrase that combines numbers, variables, and mathematical operations.4. Exponential Growth: A pattern of growth where the quantity increases exponentially over time.5. Exterior Angle: The angle formed when a line intersects two parallel lines.F1. Factor: A number or expression that divides another number or expression without leaving a remainder.2. Fraction: A number that represents part of a whole, consisting of a numerator anda denominator.3. Function: A relation that assigns each element from one set (the domain) to a unique element in another set (the range).4. Fibonacci Sequence: A sequence of numbers where each number is the sum of the two preceding ones.5. Frustum: A three-dimensional solid shape obtained by slicing the top of a cone or pyramid.G1. Geometric Sequence: A sequence of numbers where each term is obtained by multiplying the previous term by a common ratio.2. Gradient: A measure of the steepness of a line or a function at a particular point.3. Greatest Common Divisor (GCD): The largest number that divides two or more numbers without leaving a remainder.4. Graph: A visual representation of a set of values, typically using axes and points or lines.5. Group: A set of elements with a binary operation that satisfies closure, associativity, identity, and inverse properties.H1. Hyperbola: A conic section curve with two branches, symmetric to each other, and asymptotic to two intersecting lines.2. Hypotenuse: The side opposite the right angle in a right triangle, always the longest side.3. Histogram: A graphical representation of data where the data is divided into intervals and the frequency of each interval is shown as a bar.4. Hexagon: A polygon with six sides and six angles.5. Hypothesis: A proposed explanation for a phenomenon, which is then tested through experimentation and analysis.I1. Identity: A mathematical statement that is always true, regardless of the values of the variables.2. Inequality: A mathematical statement that asserts a relationship between two expressions, using symbols such as < (less than) or > (greater than).3. Integer: A whole number, either positive, negative, or zero, without any fractional or decimal part.4. Intersect: The point or set of points where two or more lines, curves, or surfaces meet.5. Irrational Number: A real number that cannot be expressed as a fraction or a terminating or repeating decimal.J1. Joint Variation: A type of variation where a variable is directly or inversely proportional to the product of two or more other variables.2. Justify: To provide a logical or mathematical reason or explanation for a statement or conclusion.K1. Kernel: The set of all inputs that map to the zero element of a function, often used in linear algebra and abstract algebra.L1. Line Segment: A part of a line bounded by two distinct endpoints.2. Logarithm: The exponent or power to which a base number must be raised to obtain a given number.3. Limit: The value that a function or sequence approaches as the input or index approaches a particular value.4. Linear Equation: An equation of the form Ax + By = C, where A, B, and C are constants, and x and y are variables.5. Locus: The set of all points that satisfy a particular condition or criteria.M1. Median: The middle value in a set of data arranged in ascending or descending order.2. Mean: The average of a set of numbers, obtained by summing all the values and dividing by the total count.3. Mode: The value or values that appear most frequently in a data set.4. Matrix: A rectangular array of numbers, symbols, or expressions arranged in rows and columns.5. Midpoint: The point that divides a line segment into two equal halves.N1. Natural Numbers: The set of positive whole numbers, excluding zero.2. Negative: A number less than zero, often represented with a minus sign.3. Nonagon: A polygon with nine sides and nine angles.4. Null Set: A set that contains no elements, often represented by the symbol Ø or { }.5. Numerator: The top part of a fraction that represents the number of equal parts being considered.O1. Obtuse Angle: An angle that measures more than 90 degrees but less than 180 degrees.2. Octagon: A polygon with eight sides and eight angles.3. Origin: The point (0, 0) on a coordinate plane, where the x-axis and y-axis intersect.4. Order of Operations: The set of rules for evaluating mathematical expressions, typically following the sequence of parentheses, exponents, multiplication, division, addition, and subtraction.5. Odd Number: An integer that cannot be divided evenly by 2.P1. Parabola: A conic section curve with a U shape, symmetric about a vertical line called the axis of symmetry.2. Pi (π): A mathematical constant representing the ratio of a circle's circumference to its diameter, approximately equal to3.14159.3. Probability: The measure of the likelihood that a particular event will occur, often expressed as a fraction, decimal, or percentage.4. Prime Number: A natural number greater than 1 that has no positive divisors other than 1 and itself.5. Prism: A three-dimensional figure with two parallel congruent bases and rectangular or triangular sides connecting the bases.Q1. Quadrant: One of the four regions obtained by dividing a coordinate plane into four equal parts.2. Quadrilateral: A polygon with four sides and four angles.3. Quartile: Each of the three values that divide a data set into four equal parts, each containing 25% of the data.4. Quotient: The result obtained from the division of one number by another.5. Quaternion: A four-dimensional extension of complex numbers, often used in advanced mathematics and physics.R1. Radius: The distance from the center of a circle or sphere to any point on its circumference or surface, always half of the diameter.2. Radical: The symbol √ used to represent the square root of a number or the principal root of a higher-order root.3. Ratio: A comparison of two quantities, often expressed as a fraction, using a colon, or as a verbal statement.4. Reflection: A transformation that flips a figure over a line, creating a mirror image.5. Rhombus: A parallelogram with all four sides of equal length.S1. Scalene Triangle: A triangle with no equal sides.2. Sector: The region bounded by two radii of a circle and the arc between them.3. Series: The sum of the terms in a sequence, often represented using sigma notation.4. Sphere: A three-dimensional object in which every point on the surface is equidistant from the center point.5. Square: A polygon with four equal sides and four right angles.T1. Tangent: A trigonometric function that represents the ratio of the length of the side opposite an acute angle to the length of the adjacent side.2. Theorem: A mathematical statement that has been proven to be true based on previously established results.3. Transversal: A line that intersects two or more other lines, typically forming angles at the intersection points.4. Trapezoid: A quadrilateral with one pair of parallel sides.5. Triangle: A polygon with three sides and three angles.U1. Union: The combination of two or more sets to form a new set that contains all the elements of the original sets.2. Unit: A standard quantity used to measure or compare other quantities.3. Unit Circle: A circle with a radius of 1, often used in trigonometry to define trigonometric functions.4. Undefined: A term used to describe a mathematical expression or operation that does not have a meaning or value.5. Variable: A symbol or letter used to represent an unknown or changing quantity in an equation or expression.V1. Vertex: A point where two or more lines, rays, or line segments meet.2. Volume: The measure of the amount of space occupied by a three-dimensional object, often expressed in cubic units.3. Variable: A symbol or letter used to represent an unknown or changing quantity in an equation or expression.4. Vector: A quantity with both magnitude (size) and direction, often represented as an arrow.5. Venn Diagram: A graphical representation of the relationships between different sets using overlapping circles or other shapes.W1. Whole Numbers: The set of non-negative integers, including zero.2. Weighted Average: An average calculated by giving different weights or importance to different values or data points.3. Work: In physics, a measure of the energy transfer that occurs when an object is moved against an external force.4. Wavelength: The distance between two corresponding points on a wave, often represented by the symbol λ.5. Width: The measurement or extent of something from side to side.X1. x-axis: The horizontal number line in a coordinate plane.2. x-intercept: The point where a graph or a curve intersects the x-axis.3. x-coordinate: The horizontal component of a point's location on a coordinate plane.4. xy-plane: A two-dimensional coordinate plane formed by the x-axis and the y-axis.5. x-variable: A variable commonly used to represent the horizontal axis or the input in a mathematical equation or function.Y1. y-axis: The vertical number line in a coordinate plane.2. y-intercept: The point where a graph or a curve intersects the y-axis.3. y-coordinate: The vertical component of a point's location on a coordinate plane.4. y-variable: A variable commonly used to represent the vertical axis or the output in a mathematical equation or function.5. y=mx+b: The equation of a straight line in slope-intercept form, where m represents the slope and b represents the y-intercept.Z1. Zero: The number denoted by 0, often used as a placeholder or a starting point in the number system.2. Zero Pair: A pair of numbers that add up to zero when combined, often used in integer addition and subtraction.3. Zero Product Property: The property that states if the product of two or more factors is zero, then at least one of the factors must be zero.4. Zero Slope: A line that is horizontal and has a slope of 0.5. Zeroth Power: The exponent of 0, which always equals 1.Conclusion:This comprehensive English dictionary of mathematical terms provides an extensive list of vocabulary essential for understanding and communicating mathematical concepts. With the knowledge of these terms, readers can enhance their mathematical fluency and explore various branches of mathematics with greater confidence. Remember, mathematics is not just about numbers, but also about understanding the language that describes the beauty and intricacies of the subject.。
Math.Z-2013On the regularity of positive solutions of a class of Choquard type equations

Math.Z.(2013)273:883–905DOI10.1007/s00209-012-1036-6Mathematische Zeitschrift On the regularity of positive solutionsof a class of Choquard type equationsYutian LeiReceived:31August2011/Accepted:2April2012/Published online:5June2012©Springer-Verlag2012Abstract This paper is concerned with positive solutions of a class of Choquard typeequations.Such equations are equivalent to integral systems involving the Bessel potentialand the Riesz potential.By using two regularity lifting lemmas introduced by Chen and Li[2],we study the regularity for integrable solutions u.Wefirst use the Hardy–Littlewood–Sobolev inequality to obtain an integrability result.Then,it is improved to u∈L s(R n)for all s∈[1,∞]by an iteration.Next,we use the properties of the contraction map and theshrinking map to prove that u is Lipschitz continuous.Finally,we establish the smoothnessof u by a bootstrap argument.Our technique can also be used to handle other integral systemsinvolving the Riesz potential or the Bessel potential,such as the Hartree type equations.Keywords Choquard equation·Integral equations·Integrability intervals·Hardy–Littlewood–Sobolev inequality·Bessel potential·Regularity lifting lemmas Mathematics Subject Classification35J15·45E10·45G051IntroductionThe nonlinear Choquard equation is read asiφt+ φ+2φ1|x|∗|φ|2=0,x∈R3,t>0,which is the special case of the generalized nonlocal Schrödinger equationiφt+ φ+pφ|φ|p−21|x|γ∗|φ|p=0,x∈R n,t>0,Y.Lei(B)Institute of Mathematics,School of Mathematical Sciences, Nanjing Normal University,Nanjing210046,Chinae-mail:lythxl@884Y .Lei where p ≥2and γ∈(0,n ).To obtain the solitary solutions,we set φ(x ,t )=e it u (x )and obtain (I − )u =pu |u |p −2 1|x |γ∗|u |p .(1.1)In this paper,we study positive solutions of a fraction order equation (I − )α2u =pu p −1 1|x |γ∗u p ,in R n .(1.2)Here n ≥3,α,γ∈(0,n )and p ≥2.In particular,γ=1and α=p =2,(1.2)is the classical stationary Choquard equation− u +u =2u (|x |−1∗u 2),u >0in R n ,(1.3)which was studied by Lieb,Simon and Lions (cf.[15,17]and [18]).It arises in the Hartree–Fock theory of the nonlinear Schrödinger equations.Papers [15]and [18]studied the existence and the uniqueness of some least energy solution of (1.3).More related mathematical and physical background can be found in [1,7]and the references therein.Recently,Ma and Zhao [24]classified the positive solutions of (1.2)and solved the open problem in [15].Moreover,they removed the restriction that those solutions minimize an energy.Since the nonlinear term with a convolution is difficult to handle,the authors intro-duced an equivalent integral ly,according to the properties of the Riesz and the Bessel potentials (cf.Chapter 5in [26]),(1.2)is equivalent to u =g α∗(u p −1v),v =p |x |−γ∗(u p ),(1.4)where u ,v >0,p >0,α,γ∈(0,n )and g αis the Bessel kernel.[24]showed the existence of solutions of nonlinear Choquard equations by using the classical Lions’technique [19]and the Sobolev embedding.Next,they applied the method of moving planes in integral forms which was established by Chen,Li and Ou [5]to obtain the radial symmetry of positive solutions of (1.4).Combining the Lieb’s result in [15],they prove that such solutions are unique.In this paper,we will discuss the regularity of those solutions of (1.4).By virtue of the potential structure,we investigate the integrability and the smoothness of positive solutions by using the potential estimation.If the Bessel potential in (1.4)is replaced by the Riesz potential,then it is equivalent to the Hartree type equation (cf.[20]).Several integral systems involving the Bessel potentials were studied.First Ma and Chen studied the integral system [23]u =g λ1(x )∗f (u ,v),v =g λ2(x )∗g (u ,v).Here f (u ,v)=v q and g (u ,v)=u p .When λ1=λ2=1,this system is the stationary Dirac–Schrödinger system.When λ1=λ2=2,this system is the stationary Schrödinger system and the stationary model of a system of reaction–diffusion equations studied in [25].Second,[22]studied the integral system involving Bessel potentialsu =g λ1(x )∗f (u ,v),v =g λ2(x )∗g (u ,v).with f (u ,v)=e v and g (u ,v)=e u .They also studied the integral system involving the Riesz potentialsOn the regularity of positive solutions of a class of Choquard type equations 885u =|x |n −λ1∗f (u ,v),v =|x |n −λ2∗g (u ,v).Other related work can be seen in [10]and [11].In particular,if λ1=λ2=α,f (u ,v)=v qand g (u ,v)=u p with 1p +1+1q +1=1−αn ,it is the Hardy–Littlewood–Sobolev type systemu (x )=|x |α−n ∗v q (x ),v(x )=|x |α−n ∗u p (x ).(1.5)It is associated with the study of the sharp constant of the classical Hardy–Littlewood–Sobo-lev inequality.When p =q and u =v ,the classification of the solutions of (1.5)has provided an important ingredient in the study of the well-known Yamabe problem and the prescribing scalar curvature problem.It is also essential in deriving priori estimates in many related nonlinear elliptic equations (cf.[4,14]and [16]).Chen,Li and Hang studied the regularity and classification of positive solutions u and v of (1.5)(cf.[3,9]and [14]).Jin and Li [12]obtained the optimal integral intervals of u and v .Afterwards,Ma,Chen and Li applied successfully the regularity lifting lemmas to obtain Lipschitz continuous of positive solutions of Wolff type systems (cf.[21]).Those integra-bility intervals play key roles in the study of local boundedness and asymptotic behavior of positive solutions (cf.[13]).In this paper,we will investigate the regularity of integrable solutions.The positive solu-tion u of (1.4)is called an integrable solution,if u ∈L s 0(R n )with one of the following cases (i)s 0=2n (p −1)n −γ+βfor some p ∈ 2+2(β−γ)n +γ−β,2+2βn −γ−β ∩[2,∞);(ii)s 0=3n (p −1)2(n −γ)+βfor some p ∈ 3+3(β−2γ)n +2γ−β,min 3+3βn −γ−β,2+3αn −γ−β ∩[2,∞).First we deduce the integrability intervals of such solutions.In addition,we also study the smoothness of those solutions.Thus,we also obtain the corresponding properties for the integrable solutions of (1.2).We always assumen ≥3,α∈(0,n ),γ∈(0,n ),α+γ≤n ,p ≥2.(1.6)Theorem 1.1Let βbe an arbitrary given real number in (0,α].If u ,v are one of two classes of integrable positive solutions of system (1.4)with (1.6),namely,either u ∈L2n (p −1)n −γ+β(R n )for some positive constantp ∈ 2+2(β−γ)n +γ−β,2+2βn −γ−β∩[2,∞),or u ∈L 3n (p −1)2(n −γ)+β(R n )for somep ∈ 3+3(β−2γ)n +2γ−β,min 3+3βn −γ−β,2+3αn −γ−β∩[2,∞).Then(R1)u ∈L s (R n )for any s ≥1.(R2)Both u (x )and v(x )are bounded,and lim |x |→∞u (x )=0.(R3)Both u (x )and v(x )are Lipschitz continuous.(R4)Moreover,if α>1,then u ∈C ∞(R n ).886Y .LeiRemark 1.1The interval (3+3(β−2γ)n +2γ−β,min {3+3βn −γ−β,2+3αn −γ−β})=∅.For example,when 3α+γ>n and β∈(0,3α+γ−n 2),2+3αn −γ−β>3+3βn −γ−β>3+3(β−2γ)n +2γ−β.Next,we consider the case that αis even.According to Chapter 5in [26],(1.4)is equiv-alent to the integer order PDE.In particular,when α=2,the weak solution u ∈H 1(R n )of (1.2)belongs to L 2∗(R n ).Thus,if the weak solution is integrable:u ∈L 2n (p −1)n −γ+β(R n )∪L 3n (p −1)2(n −γ)+β(R n ),then Theorem 1.1shows that (R1)–(R4)hold for such solutions.Corollary 1.2Assume u solves (1.1)− u +u =pu p −1(|x |−1∗u p ).Eitheru ∈L 2n (p −1)n −1+β(R n )w ith p ∈ 2n −2n −2,2n −1n −2,oru ∈L 3n (p −1)2(n −1)+β(R n )with p ∈7n −103(n −2),7n −63(n −2) ∩ 2n −2n −2,2nn −2∩ p ,(1.7)wherep =(0,∞), ≤0; p =(0,∞)\ 5n −8−√ 2(n −2),5n −8+√ 2(n −2) , >0.Here =n 2−16n +32.If β∈(0,2],then (R1)–(R4)are true.Corollary 1.3Assume u solves− u +u =2u (|x |−γ∗u 2).(1.8)Eitheru ∈L 2n n −γ+β(R n )w ith γ∈(2,4],or u ∈L 3n 2(n −γ)+β(R n )w ith γ∈n +64,n +104.If β∈(0,2],then (R1)–(R4)are true.Corollary 1.4Assume u solves (1.3)− u +u =2u (|x |−1∗u 2).(i )Let u ∈L 2n n −1+β(R n ).If β∈(0,1),then (R1)–(R4)are true.(ii )Let u ∈L 94+β(R 3).If β∈(0,12),then (R1)–(R4)are true.On the regularity of positive solutions of a class of Choquard type equations887Remark1.5Liu[20]studied the Hartree type equation− u=2u(|x|−γ∗u2),u>0in R n,whereγ∈[2,min{4,n}],orγ=4when n≥5.It turns out that if u∈L2n n−2(R n),then(Rt1)u∈L s(R n)for all1s∈(0,n−2n)(cf.Theorem1.6in[20]).(Rt2)u is radially symmetric and decreasing about x0∈R n(cf.Theorem3.1in[20]).In addition,u(0)and v(0)are bounded(cf.Theorem2.2(i)in[20]).Unlike the Bessel potential,the Riesz potential has singularity at infinity.Therefore,the integrability of(Rt1)can not be improved.Noting the the system is invariable under the translation,we can view x0as the origin. Hence,u(x0)<∞and v(x0)<∞.Since u,v are decreasing about x0,u and v belong to L∞(R n).Similar to the argument in Sects.5and6,we can also lift the regularity of u and v from L∞(R n)to C0,1(R n),and then to C∞(R n).2Preliminaries2.1Properties of the Bessel potentialThe Bessel kernel isgα(x)=1(4π)α/2 (α/2)∞exp−πt|x|2−t4πt(α−n)/2dtt.In this subsection,we list several results which will be used later.More properties of the Bessel potential can be seen in[26]and[27].The Bessel potential of a positive function f∈L p(R n)(1≤p≤∞)isBα(f)(x)=gα(x)∗f(x)=R ngα(x−y)f(y)dy,where x∈R n,n≥3,α∈(0,n),and gαis the Bessel kernel.By the estimate(2.6.3)in[27],we havegα(x)≤C1|x|n−αe C2|x|≤C|x|n−σ,as long asσ∈(0,α].Here C1,C2,C>0.Therefore,for a positive function f,we get Bα(f)(x)≤C Iσ(f)(x):=C|x|σ−n∗f(x),x∈R n,(2.1) where C is some positive constant.In addition,(2.6.4)in[27]shows thatDgα(x)≤C|x|n−α+1e C2|x|.(2.2)In addition,R ngα(x)dx=ˆgα(0)=1.(2.3)888Y.Lei For the Riesz type potential Iσ(f),we have the Hardy–Littlewood–Sobolev inequality (cf.Theorem1in Chapter5of[26]),Iσ(f) q≤C f nqn+qσ>1.whereσ∈(0,n)and nqn+qσ2.2Two lifting lemmas on regularityWe list two regularity lifting lemmas in[2].Chen,Li etc.successfully applied them to estab-lish the integrability and the Lipschitz continuity of positive solutions of integral systems involving the Riesz potential,the Bessel potential and the Wolff potential(cf.[3,8,12]and [21]).Let V be a function space equipped with two norms · X and · Y.DefineX={v∈V; v X<∞},Y={v∈V; v Y<∞}.Assume that spaces X and Y are complete under the corresponding norms and the conver-gence in X or in Y implies the convergence in V.We call T a contracting map from X to X,if f,g∈X,T f−T g X≤η f−g X,η∈(0,1).T is a shrinking map from X to X,ifT f X≤η f X,η∈(0,1).Clearly,if T is a linear shrinking map,it must be a contraction.Lemma2.1(Theorem3.3.1in[2])Let T be a contraction map from X into itself and from Y into itself.Assume g∈Z:=X∩Y.If u∈X solves the operator equation f=T f+g in X,then u belongs to Z.Combining Theorem3.3.5and Remark3.3.5in[2],we have the second regularity lifting lemma.Lemma2.2Let X=L∞(R n)×L∞(R n)and Y=C0,1(R n)×C0,1(R n)with the norms (f,g) X= f ∞+ g ∞,and (f,g) Y= f 0,1+ g 0,1.Define their closed subsetX1={(f,g)∈X; f ∞+ g ∞≤C( u ∞+ v ∞)},Y1={(f,g)∈Y; f ∞+ g ∞≤C( u ∞+ v ∞)}.Assume(i)T is a contraction map from X1→X;(ii)T is a shrinking map from Y1→Y;(iii)(F,G)∈X1∩Y1;(iv)T(·,·)+(F,G)is a map from X1∩Y1to itself.If(u,v)∈X is a pair of solutions of the operator equation(f,g)=T(f,g)+(F,G), then(u,v)∈Y.On the regularity of positive solutions of a class of Choquard type equations 8893IntegrabilityIn this section,we prove (R1)of Theorem 1.1.Proposition 3.1Assume βis an arbitrary given real number in (0,α].If u ∈L 2n (p −1)n −γ+β(R n )solves (1.4)and p ∈(2+2(β−γ)n +γ−β,2+2βn −γ−β)∩[2,∞),then (u ,v)∈L s (R n )×L r (R n )for all 1r ∈ 0,γn ,1s ∈ n −γ−β2n ,n +γ−β2n.(3.1)Proof For A >0,defineu A (x )=u (x ),for u (x )>A or |x |>A ;u A (x )=0,otherwise ,and u B =u −u A .Similarly,we can also define v A and v B .To use the Hardy–Littlewood–Sobolev inequality,we choose r and s satisfying 1s −1r =n −γ−β2n.(3.2)In order to determine the intervals which 1r and 1s belong to,we take a rectangleD := 1s ,1r ;1r ∈ 0,γn ,1s ∈ 0,n −βn .In view of α+γ≤n and β≤α,it follows that γn ≤n −βn.Let D 1and D 2be two triangles:D 1:= 1s ,1r ;1r ∈ 0,γn ,1s ∈ 0,1r ,D 2:= 1s ,1r ;1r ∈ 0,γn ,1s ∈ 1r +n −γ−βn ,n −βn.Denote D \(D 1∪D 2)by D 3.Clearly,the line segment 1s ,1r ;1r ∈ 0,γn ,1s −1r =n −γ−β2n⊂D 3.Therefore,by (3.2)we can determine the intervals 1r ∈ 0,γn ,1s ∈ n −γ−β2n ,n +γ−β2n.Let f ∈L r (R n ),g ∈L s (R n ),where 1r and 1s belong to the intervals above.SetT 1f := R n g α(x −y )u p −1A (y )f (y )dy ,T 2g :=pR n |x −y |−γu p −1A (y )g (y )dy ,890Y.LeiF:=R n gα(x−y)u p−1B(y)v B(y)dyG:=pR n|x−y|−γu p B dy.Define the operator TT(g,f)=(T1f,T2g)with the norm T(f,g) s×r= T1f s+ T2g r.From(2.1)and(3.2),using the Hardy–Littlewood–Sobolev inequality and the Hölder inequality,we deduce thatT1f s≤C Iβ(u p−1A f) s≤C u p−1Af nsn+sβ≤C u A p−12n(p−1)n−γ+βf r,(3.3)T2g r≤C I n−γ(u p−1A g) r≤C u p−1Ag nrn+r(n−γ)≤C u A p−12n(p−1)n−γ+βg s.(3.4)Noting u∈L2n(p−1)/(n−γ+β)(R n),we see thatC u A p−12n(p−1)/(n−γ+β)≤12when A is suitably large.Then for any r,s satisfying(3.1),the operator T is a contracting map from L s(R n)×L r(R n)to itself.Noticing the integrable solution u∈L s0(R n),where s0=2n(p−1)n−γ+β,we take r0such that(1 s0,1r0)satisfies(3.2).Using the Hardy–Littlewood–Sobolev inequality tov=p|x|−γ∗u p,(3.5)we getv∈L r0(R n),r0=2n(p−1)pβ−(p−2)(n−γ).In view of p∈(2+2(β−γ)n+γ−β,2+2βn−γ−β),1s0∈(n−γ−β2n,n−γ+β2n)and1r0∈(0,γn).Then Tmust be a contraction map from L s0(R n)×L r0(R n)to itself.Similar to(3.3)and(3.4),for any r,s satisfying r>nγ,s>n n−β,we haveF s≤C u p−1B v B nsn+sβ, G r≤C u p B nrn+(n−γ)r.In view of the definitions of u B and v B,we see F∈L s(R n)and G∈L r(R n).Let X=L s0(R n)×L r0(R n),Y=L s(R n)×L r(R n).Since(u,v)solves the equation(g,f)=T(g,f)+(F,G),by the regularity lifting Lemma2.1,we know that(u,v)∈L s(R n)×L r(R n)for all r,s satisfying(3.1).Proposition3.1is proved.Proposition3.2Assumeβis an arbitrary given real number in(0,α].If u∈L3n(p−1)2(n−γ)+β(R n)solves(1.4)and p∈(3+3(β−2γ)n+2γ−β,3+3βn−γ−β)∩[2,∞),then(u,v)∈L s(R n)×L r(R n)for all1 r ∈0,γn,1s∈n−γ−β3n,n+2γ−β3n.(3.6)On the regularity of positive solutions of a class of Choquard type equations891 Proof The idea is the same as the proof of Proposition3.1.For A>0,set u A,u B,v A and v B as in Proposition3.1.Let f∈L r(R n),g∈L s(R n)L r(R n),where r>nγand s satisfies1 s −1r=n−γ−β3n.DefineT3f=R ngα(x−y)u p−2A(y)v A(y)f(y)dy,T(g,f)=(T3g,T2g)with the norm T(f,g) s×r= T3g s+ T2g ing the Hardy–Littlewood–Sobolev inequality and the Hölder inequality,we getT3f s≤C Iβ(u p−2A v A f) s≤C u p−2Av A f nsn+sβ≤C u A p−2s0 v A r0 f r,(3.7)T2g r≤C I n−γ(u p−1A g) r≤C u p−1Ag nrn+r(n−γ)≤C u A p−1s0 g s.(3.8)Here1s0=2(n−γ)+β3n(p−1),and r0can be determined by1r0=ps0−n−γn.Clearly,using the Hardy–Littlewood–Sobolev inequality to(3.5),we obtainv r0≤C u p nr0n+(n−γ)r0=C u p s<∞.Equations(3.7)and(3.8)require1 s +βn=p−2s0+1r0+1r,1r+n−γn=p−1s0+1s.These are equivalent to1 s −1r=p−2s0+1r0−βn=n−γn−p−1s0.(3.9)Inserting the values of s0and r0into(3.9)yields1 s −1r=n−γ−β3n.(3.10)The line segment which is determined by D and(3.10)also belongs to D3.Thus,the intervalsof1r and1sare the ones in(3.6).Let f∈L r(R n),g∈L s(R n),where1r and1s belong to the intervals in(3.6).Hence(3.7) and(3.8)make sense.Noting u∈L s0(R n)and v∈L r0(R n),we see thatC u A p−2s0 v A r0≤12,C u A p−1s0≤12when A is suitably large.Then for any r,s satisfying(3.6),the operator T is a contract-ing map from L s(R n)×L r(R n)to itself.By virtue of p∈(3+3(β−2γ)n+2γ−β,3+3βn−γ−β),1s0and1r0also belong to the intervals in(3.6).Therefore,T is also a contraction map fromL s0(R n)×L r0(R n)to itself.For any r,s satisfying r>nγ,s>n n−β,we haveF s≤C u p−1B v B nsn+sβ, G r≤C u p B nrn+(n−γ)r.892Y.Lei In view of the definitions of u B and v B,F∈L s(R n)and G∈L r(R n)for1s and1r belong to the intervals in(3.6).Let X=L s0(R n)×L r0(R n),Y=L s(R n)×L r(R n).Since(u,v)solves the equation(g,f)=T(g,f)+(F,G),by the regularity lifting Lemma2.1,we know that(u,v)∈L s(R n)×L r(R n)for all r,s satisfying(3.6).Proposition3.2is proved.Next,we improve the integrability of u from(3.1)and(3.6)tou∈L s(R n),∀s>nn−β.(3.11)Proposition3.3Under the assumption of Proposition3.1,we haveu∈L s(R n),∀1s∈0,n−βn.Proof Using(2.1),the Hardy–Littlewood–Sobolev inequality and the Hölder inequality tou(x)=R ngα(x−y)u p−1(y)v(y)dy,(3.12) we obtainu ξj ≤C Iσ(u p−1v) ξj≤C u p−1v nξjn+ξjσ≤C u p−1ξj−1v r,(3.13)for j=0,1,2,...,where r>nγ,σ∈(0,α],and1ξj <1−σn,1ξj=p−1ξj−1+1r−σn.(3.14)Atfirst,we extend the right end point of the integrability interval of1s in(3.1)from n+γ−β2nto n−βn. Take1ξ0=n+γ−β2n,σ=εand1r=γ−εnin(3.13).Then(3.14)shows1ξj=p−1ξj−1+γ−2εn,and hence u ξj<∞.In view of p≥2,1ξj −1ξj−1=p−2ξj−1+γ−2εn>γ−2εn.Therefore,whenεis sufficiently small,{1ξj}j is increasing.In view of p<2+2αn−γ−β,there holds0<p−22(n−γ−β)<α.Chooseε∈(0,γ)sufficiently small such thatσ1=p−22(n−γ−β)+ε∈(0,α).On the regularity of positive solutions of a class of Choquard type equations 893Then(p −2)(n −β)−p γ<2(σ1−ε)<(p −2)(n +γ−β).This result implies1t 0:=1p −1n +γ−β2n +σ1−εn∈n −γ−β2n ,n +γ−β2n,and hence u ∈L t 0(R n ).Using the Hardy–Littlewood–Sobolev inequality and the Hölderinequality,we getu t 1≤C u p −1vnt 1n +t 1σ1≤C u p −1t 0v n ε<∞,where1t 1=n +γ−β2n .According to the intermediate value theorem of the continuous map,forany 1s ∈[1t 1,1ξ1],we can find ζ∈(n −γ−β2n ,n +γ−β2n ),such that the Hardy–Littlewood–Sobolev and the Hölder inequalities implyu s ≤C u p −1ζv n<∞,where ∈(0,γ).This meansu ∈L s (R n ),∀1s∈n −γ−β2n ,1ξ1.(3.15)Suppose j 0is a positive integer satisfying1ξj 0<n −βn ≤1ξj 0+1.Similar to the derivation of (3.15),by induction we can obtainu ∈L s (R n ),∀1s ∈n −γ−β2n ,1ξj 0by at most finite steps.Similar to the definition of t 0,we can choose σ1∈(0,α]and σ2∈(0,γ),such that1τ0:=1p −1n −β−ε+σ1−σ2n ∈(n −γ−β2n ,1ξj 0],and hence u ∈L τ0(R n ).Using the Hardy–Little-wood–Sobolev inequality and the Hölder inequality,we getu t ∗≤C u p −1vnt ∗n +t ∗σ1≤C u p −1τ0v n σ2<∞,where1t ∗=n −β−εn.This result shows u ∈L s (R n ),∀1s∈n −γ−β2n ,n −βn.Finally,we extend the left end point of the integrability interval of 1s in (3.1)from n −γ−β2nto 0.Take 1ξ0=n −γ−β2n ,σ=αand 1r =εn in (3.13).Then (3.14)shows 1ξj =p −1ξj −1−α−εn,and hence u ξj <∞.894Y.LeiBy induction,we can see that{1ξj}j is a decreasing sequence whenεis sufficiently small.In fact,noting p<2+2αn−γ−β,we have1ξ1<1ξ.Suppose 1ξj<1ξj−1<···<1ξ0,then the following difference1ξj −1ξj+1=α−εn−p−2ξj>α−εn−p−2ξ0>0.This result shows the monotonicity.Suppose j0is a positive integer satisfying1ξj0+1≤0<1ξj.By at mostfinite steps,we deduce from(3.13)thatu∈L s(R n),∀1s∈1ξj,n−βn.Letβεsatisfyβεn(p−1)∈1ξj,n−βn.Therefore,u∈L n(p−1)βε(R n).Using the Hardy–Littlewood–Sobolev inequality and the Hölder inequality,we getu t2≤C u p−1v nt2n+t2βε≤C u p−1n(p−1)βεv nε<∞,whereε>0and1t2=εn.This result showsu∈L s(R n),∀1s∈0,n−βn.Proposition3.3is proved.Proposition3.4Assumeβis an arbitrary given real number in(0,α].If u∈L3n(p−1)2(n−γ)+β(R n)solves(1.4)and p∈(3+3(β−2γ)n+2γ−β,min{3+3βn−γ−β,2+3αn−γ−β})∩[2,∞),thenu∈L s(R n),∀1s∈0,n−βn.Proof We still use the idea of the proof of Proposition3.3.Take1ξ0=n+2γ−β3n,σ=εand1r=γ−εnin(3.13).Then,the sequence1ξjin(3.14)is alsoincreasing.In fact,by virtue of p>3+3(β−2γ)n+2γ−β>2−3γn+2γ−β,we have1ξj+1−1ξj>0.Therefore,we extend the right end point of the integrability interval of1s in(3.6)from n+2γ−β3nto n−βnby at mostfinite steps.On the regularity of positive solutions of a class of Choquard type equations 895Next,take 1ξ0=n −γ−β3n ,σ=αand1r=εnin (3.13).In view of p <2+3αn −γ−β,we candeduce that1ξj +1−1ξj<ly,the sequence1ξjin (3.14)is decreasing.Therefore,we extend the left end point ofthe integrability interval of 1sin (3.6)fromn −γ−β3nto 0by at most finite steps.Theorem 3.5Assume u ∈L s (R n )and v ∈L r (R n )solve (1.4).If1s∈(0,n −βn )and1r ∈(0,γn ),then u ∈L t (R n)for all 1t ∈(0,1].Proof Clearly,there holds1p∈(0,n −βn ),since p ≥max 2,2+2(β−γ)n +γ−β≥2n n +γ−β>nn −β.Therefore,R nu p (x )dx <∞.(3.16)Next,we claimn −γn (p −1)<n −βn.In fact,(i)if β<γ,then p ≥2>1+n −γn −β.This implies1p −1<n −βn −γ+ε.The claim is verified.(ii)If β≥γ,thenp >2+2(β−γ)n +γ−β.(3.17)From (γ−β)(n −γ−β)≤0we deduce that2n 2−2βn ≥2n 2+(γ−3β)n −(γ2−β2).This is equivalent to2n n +γ−β≥2n −γ−βn −β.Combining this with (3.17)yields p >2n −γ−βn −β,which implies the claim.Take1r=γ−εn ,1s=n −γ+εn (p −1).By the Hölder inequality,it follows thatR nu p −1(x )v(x )dx ≤ u p −1sv r <∞.(3.18)Therefore,integrating (3.12)and using (2.3),we getR nu (x )dx = R n R ng α(x −y )u p −1(y )v(y )dy dx≤R ng α(x )dxR nu p −1(y )v(y )dy <∞.This means u ∈L 1(R n ).896Y.Lei The rest work is to prove u∈L t(R n)for any1t∈[n−βn,1).To do this,we can chooseεsmall enough such thatεt−1+ε∈(0,n−βn).Therefore,u∈L(t−1+ε)/ε(R n).Applying theHölder inequality,we getR n u t dx=R nu(1−ε)+(t−1+ε)dx≤ u 1−ε1u t−1+ε(t−1+ε)/ε<∞.Thus,Theorem3.5is proved. 4Ground stateThe positive solution u is called the ground state,if it is bounded and converges to zero when |x|→∞.In this section,we prove(R2)of Theorem1.1.Theorem4.1Under the assumption of Theorem3.5,u and v are bounded.Proof For d∈(0,1),from(2.1)we haveu(x)=Bα(u p−1v)(x)≤C Iβ(u p−1v)=C|y−x|<d u p−1(y)v(y)dy+C|y−x|≥du p−1(y)v(y)dy:=K1+K2.In view of the condition of Theorem4.1,we can take s and r sufficiently large such thatp−1 s +1r<βn,and u∈L s(R n),v∈L r(R n).Then by the Hölder inequality,K1≤ u p−1s v r⎛⎜⎝B d(x)|x−y|β−n1−p−1s−1r dy⎞⎟⎠1−p−1s−1r≤C⎛⎜⎝B d(0)|y|β−n1−p−1s−1r dy⎞⎟⎠1−p−1s−1r≤C⎛⎝drn−β−n1−p−1s−1rdrr⎞⎠1−p−1s−1r≤C.On the other hand,by(3.18),we getK2≤dβ−nR n\B d(x)u p−1(y)v(y)dy≤C.The estimates of K1and K2show that u is bounded.Similar to the argument above,using the fact that u p is bounded instead of(3.18),we can also deduce from(3.16)the bound of v:v(x)=pR n u p(y)dy|x−y|γ≤p u p∞B d(x)dy|x−y|γ+pR n\B d(x)u p(y)dy|x−y|γ≤C u p∞d n−γ+pd−γ u p p<∞.Theorem4.1is proved.On the regularity of positive solutions of a class of Choquard type equations897 Theorem4.2Under the assumption of Theorem3.5,u(x)→0when|x|→∞.Proof Take x0∈R n.Then(2.1)impliesu(x0)=Bα(u p−1v)(x0)≤C Iβ(u p−1v)(x0)=CR n u p−1(y)v(y)dy |x0−y|n−β=C(n−β)R n u p−1(y)v(y)∞|x0−y|tβ−ndttdy=C(n−β)∞B t(x0)u p−1(y)v(y)dyt n−βdtt.(4.1)Since u and v are bounded,∀ε>0,there existsδ∈(0,1)such thatδ 0B t(x0)u p−1(z)v(z)dztdtt≤ u p−1∞ v ∞δtβdtt<ε.(4.2)As|x−x0|<δ,∞δB t(x0)u p−1(z)v(z)dztdtt≤∞δB t+δ(x)u p−1(z)v(z)dz(t+δ)n−βt+δtn−β+1d(t+δ)t+δ≤C∞B t(x)u p−1(z)v(z)dzt n−βdtt≤C Iβ(u p−1v)(x).(4.3) Inserting(4.2)and(4.3)into(4.1),we getu(x0)<Cε+C Iβ(u p−1v)(x),f or|x−x0|<δ.Take s>nn−βsufficiently large.Then as|x−x0|<δ,u s(x0)≤Cεs+C[Iβ(u p−1v)(x)]s.Integrating on Bδ(x0)and multiplying by|Bδ(x0)|−1,we obtainu s(x0)=|Bδ(x0)|−1Bδ(x0)u s(x0)dx≤Cεs+C|Bδ(x0)|−1 Iβ(u p−1v) s L s(Bδ(x0)).(4.4)Since s satisfies nsn+sβ>1,we can use the Hardy–Littlewood–Sobolev inequality to deducethatIβ(u p−1v) L s(R n)≤C u p−1v nsn+sβ.898Y.Lei By virtue of u∈L t(R n)and v∈L r(R n)for t≥1and r>n/γ,using the Hölder inequality yields Iβ(u p−1v)∈L s(R n).Therefore,when|x0|→∞,Bδ(x0)[Iβ(u p−1v)]s(x)dx→0.Inserting this result into(4.4),we havelim|x0|→∞u s(x0)=0.This result means u converges to zero when|x|→∞. 5Lipschitz continuousIn this section,we prove(R3)of Theorem1.1.According to(R2),the solutions u,v∈L∞(R n).Let X=L∞(R n)×L∞(R n)and Y=C0,1(R n)×C0,1(R n)with the norms (f,g) X= f ∞+ g ∞,and (f,g) Y= f 0,1+ g 0,1.Define their closed subsetX1={(f,g)∈X; f ∞+ g ∞≤C( u ∞+ v ∞)},Y1={(f,g)∈Y; f ∞+ g ∞≤C( u ∞+ v ∞)}.Let d>0.SetT1(f,g)=B d(x)gα(x−y)f p−1(y)g(y)dy,T2(f)=pB d(x)f p(y)dy |x−y|γ,F(x)=R n\B d(x)gα(x−y)u p−1(y)v(y)dy,G(x)=pR n\B d(x)u p(y)dy |x−y|γ,andT(f,g)=(T1(f,g),T2(f)).Claim1T is a contracting map from X1to X.In fact,for two functions(f1,g1),(f2,g2)∈X1,we deduce from(2.1)that, T1(f1,g1)−T1(f2,g2) ∞≤B d(x)gα(x−y)|f p−11g1−f p−12g2|dy ∞≤B d(x)|g1(f p−11−f p−12)||x−y|αdy ∞+B d(x)|(g1−g2)f p−12||x−y|αdy ∞.On the regularity of positive solutions of a class of Choquard type equations899 By the mean value theorem and noting the definition of X1,we getT1(f1,g1)−T1(f2,g2) ∞≤Cdα( u ∞+ v ∞)p−1[ g1−g2 ∞+ f1−f2 ∞].Similarly,we also obtainT2(f1)−T2(f2) ∞≤Cd n−γ( u ∞+ v ∞)p−1 f1−f2 ∞.Choose d sufficiently small such thatC( u ∞+ v ∞)p−1(dα+d n−γ)<1,then T is a contracting map.Claim2T is a shrinking map from Y1to Y.In fact,for(f,g)∈Y1and for any x1,x2∈R n,we have(g f p−1)(y+x1)−(g f p−1)(y+x2)=(g(y+x1)−g(y+x2))f p−1(y+x1)+(f p−1(y+x1)−f p−1(y+x2))g(y+x2)=f p−1(y+x1)(g(y+x1)−g(y+x2))+(p−1)f p−2(θ)g(y+x2)(f(y+x1)−f(y+x2)),whereθbelongs to the line segment(y+x1)(y+x2).Thus,noticing the definition of Y1, we obtain|T1(f,g)(x1)−T1(f,g)(x2)|≤C|B d(0)gα(y)((g f p−1)(y+x1)−(g f p−1)(y+x2))dy|≤C|B d(0)gα(y)( u ∞+ v ∞)p−1( f 0,1+ g 0,1)|x1−x2|dy|≤Cdα( f 0,1+ g 0,1)|x1−x2|.(5.1) Choose d sufficiently small,we have|T1(f,g)(x1)−T1(f,g)(x2)||x1−x2|≤13( f 0,1+ g 0,1).Similarly,we also deduce that|T2(f)(x1)−T2(f)(x2)||x1−x2|≤Cd n−γ( u ∞+ v ∞)p−1 f 0,1≤13f 0,1.Thus,T is a shrinking map.Claim3(F,G)∈X1∩Y1.First,(1.4)and the definitions of F and G imply F≤u and G≤v.So(F,G)∈X1. Next,for any x1,x2∈R n satisfying|x1−x2|:=δ<d/3,without loss of generality,we may assume F(x1)≤F(x2).Clearly,。
航海及海运专业术语

Ageneralpurposecargotrampvesselof18000dwt’s withfour
holdswitheachwithtweendeckandspeedof15knotssuitableboth
forbulkdryor
liner cargo shipments of 426 TEU container units标准设计的18 000载重吨
of15knots
一艘载重30 000吨
A class division A级分隔
A class ship甲类船
A class甲级
A eliminator灯丝电源整流器
a fraction of零点几
Afrequencyof1000000000or1乘以10?9cycleseachsecond千兆赫
abandonment of claim放弃索赔
Abandonment of Marine Insurance海上保险委付
tips:感谢阅读,本文由我司收集整编,如有疑问,请与我司联系!
a hoist一挂
A Lien on the Object Towed拖带留置权
ALloyd’spolicyformofinsuranceonanaircushion vessel
hovercraft劳氏气垫船运输保险单
abandon station弃船部署
abandon放弃
abandon放弃;委付
abandon放弃委付
abandon弃
abandoned ship被弃的船
abandoned ship被弃的船已委付船
abandoned vessel被弃的船
2011年考研英语二真题及答案

2011年考研英语二真题及答案Section I Use of EnglishDirections:Read the following text. Choose the best word (s) for each numbered blank and mark A, B, C or D on ANSWER SHEET 1. (10 points)Many years ago, I visited an old university friend who was studying medicine in London. He took (1) of his university's medical department and showed me around the research labs. As we were about to leave the cancer laboratory, I noticed a (2) piece of paper attached to the wall. It had a list of chemical substances and the respective (3) on cancer cells. The exact values were noted down, including the concentration of each chemical, the time of incubation (培养期) and the size of the cancer cell culture plate. It was clear that someone had been (4) a serious experiment.When I asked my friend about it, he smiled and told me something which I have never (5) . The paper contained the complete results of a very important (6) experiment and it was someone's (7) to update the online laboratory notebook. This was a record of the steps followed, the results obtained, and any other (8) information. The idea was to help everyone in the lab stay updated on the progress of the (9) . I was very impressed by the responsibility shown by the person who conducted the experiment and, of course, by the general idea of (10) a notebook that could be accessed by everyone in real-time.Unfortunately, the (11) of this great idea is not yet mature. The idea that a lab notebook could be online goes (12) the traditional view of a personaland (13) place where researchers could record their thoughts, ideas and results. But today's labs (14) a different picture. Many labs employ researchers from different parts of the world, connected with existing and emerging (15) for collaboration. A worldwide accessible notebook is therefore not a bad idea and, as a matter of (16) , it is already a reality in some laboratories around the world.In some labs, a notebook is only accessible via their secure network (17) a username and password. Others are looking at public ways to grant access. Similarly, some labs have entire lab management (18) that include the sharing of notes, protocols and results. Other labs intend to add this functionality very soon. There are still (19) to be resolved, mainly regarding security and privacy issues, but the general trend is undeniably (20) the switch from paper to digital notebooks.1. A full B advantage C control D medicine2. A folded B misplaced C crumpled D dusty3. A research B professions C influences D effects4. A experimenting B employing C conducting D exploring5. A heard B believed C discovered D forgotten6. A laboratory B chemical C medicinal D scientific7. A purpose B background C spotlight D duty8. A relevant B efficient C irrelevant D supportive9. A examination B experiment C discovery D application10. A protecting B saving C accessing D revising11. A understanding B application C expertise D achievement12. A beyond B against C upon D over13. A confidential B public C specialized D open14. A picture B scenario C strategy D figure15. A networks B fields C topics D tools16. A fact B principle C research D access17. A concerning B acknowledging C reinforcing D requiring18. A traditions B policies C environments D positions19. A issues B concerns C areas D procedures20. A promoting B preventing C encouraging D hindering参考答案:1. C control2. B misplaced3. D effects4. C conducting5. D forgotten6. A laboratory7. D duty8. A relevant9. B experiment10. C accessing11. B application12. A beyond13. B public14. B scenario15. A networks16. A fact17. D requiring18. C environments19. A issues20. C encouragingSection II Reading ComprehensionPart ADirections:Read the following four texts. Answer the questions below each text by choosing A, B, C or D. Mark your answers on ANSWER SHEET 1. (40 points)Text 1According to Thomas Edison, most inventions are 1 percent inspiration and 99 percent perspiration. That may have been true in his day, but invention has changed radically in the past century. Today, it can be both more efficient and more frustrating, with inventors making errors such as forgetting the "ordinary skills" requirement for getting a patent and misreading established patents.Soon, these kinds of mistakes will be less likely, thanks to a new method developed by a researcher at the Fordham University School of Law in New York City.The method, known as "invention mining", is a way to find out possible inventions from huge databases of scientific information. Invention mining gives inventors many new veins to tap into - and makes it much easier to come up with new ideas.In the past, the first step of inventing something new was an exhaustive search through existing patents to make sure the proposed invention hadn't already been patented. But that traditional search couldn't effectively cover all the information needed, as it was only possible to cover a fraction of patents, university research papers, and other sources of technical information in any one search.However, invention mining can go through billions of records of technical information in one search. "Text mining is natural language processing, but invention mining is natural language processing on steroids (特效药)" says Professor Stempfle.According to his study, a successful search of one billion records using a properly formed claim will return about 3.15 million technical documents for review, and we usually only need to inspect about 150,000 of these to find a few that truly meet our needs.Invention mining can turn up scientific research and patents nobody ever knew existed. Stempfle's paper cited an example of a case study from Ford when a scientist was doing background research on fire protection systems: it found a solution that had been patented and then forgotten, dating back to an 1838 patent. "The inventors of the company that found this were excited," says Stempfle, but nobody else had ever heard of the invention. This would have been something that may not otherwise have been discovered."Invention mining gives small inventors a newfound power against large corporations," says Stempfle . "Say you're a small inventor with 20 patents, and then IBM thinks you're infringing on(侵犯) one of their patents. IBM can do a search through a million patents to find ground to say your patent is invalid. Using a tool like invention mining, you can look at the same million patents to come up with innovative ways to say the IBM patent is not reallya valid one. It really does level the playing field."21. Invention mining helps inventors to ________.A. identify and solve problems in the invention processB. establish the ordinary skills requirement for getting a patentC. read established patents with more efficiencyD. prevent scientific information from being forgotten22. Compared to the traditional search, invention mining ________.A. covers a wider range of technical informationB. is more time-consumingC. requires a larger database of scientific informationD. focuses on patents and university research papers23. What does Professor Stempfle suggest about invention mining?A. It should be used in the background research of fire protection systems.B. It should only be used by small inventors against large corporations.C. It should be improved through natural language processing.D. It should be applied to the validation of small inventors' patents.24. What can be a drawback of invention mining?A. Certain patents are prone to being misread by inventors.B. It relies heavily on existing patents.C. It doesn't cover all the technical information.D. Some 19th-century patents may have been missed.25. What is the main purpose of the text?A. To discuss the new method of invention mining.B. To compare the merits of invention mining and traditional search.C. To introduce the researcher behind the invention mining method.D. To analyze the potential of invention mining in the future.参考答案:21. A. identify and solve problems in the invention process22. A. covers a wider range of technical information23. D. It should be applied to the validation of small inventors' patents.24. C. It doesn't cover all the technical information.25. A. To discuss the new method of invention mining.Part BDirections:Read the following text and answer the questions by choosing A, B, C or D. Mark your answers on ANSWER SHEET 1. (20 points)Text 2The saying "knowledge is power" is accurate in many situations. We tend to believe that the more information we have, the better decisions we can make. However, recent research suggests that this may not always be the case. In fact, having too much information can sometimes hinder our decision-making process and lead to poorer outcomes.One reason why an excess of information may be detrimental is that it can lead to information overload. When we are faced with too much information, we may struggle to process it all efficiently. As a result, wemay overlook important details or become overwhelmed, leading to decision paralysis. In this state, it becomes difficult to make any decision at all.Furthermore, having too much information can also lead to biased decision-making. When we have a lot of information, it is natural for us to focus on the information that supports our existing beliefs or preferences, while disregarding contradictory information. This confirmation bias can limit our ability to consider alternative perspectives and make well-rounded decisions.Another issue associated with an excess of information is the potential for analysis paralysis. This occurs when we spend excessive amounts of time analyzing and comparing different options, becoming so fixated on finding the perfect choice that we fail to make a decision altogether. The fear of making a suboptimal choice can act as a barrier to action, preventing us from moving forward and potentially missing out on valuable opportunities.While information is undoubtedly valuable, it is important to strike a balance and avoid becoming overwhelmed by an excessive amount of data. Recognizing the limitations of information and being mindful of its potential effects on decision-making can help ensure more effective and efficient choices.26. What is the author's main point about information?A. It is essential for making well-rounded decisions.B. It can lead to biased decision-making.C. It can hinder the decision-making process.D. It is necessary for finding valuable opportunities.27. What is "confirmation bias"?A. Overlooking important details due to information overload.B. Struggling to process excessive amounts of information.C. Focusing on information that supports existing beliefs.D. Spending excessive time analyzing different options.28. What does the author mean by "analysis paralysis"?A. Being overwhelmed by contradictory information.B. Failing to make a decision due to fear of making a mistake.C. Considering alternative perspectives when making a choice.D. Being unable to distinguish between valuable and irrelevant information.29. According to the text, what is important when dealing with information?A. Finding the perfect choice.B. Overcoming decision paralysis.C. Recognizing the limitations of information.D. Analyzing and comparing different options.30. What is the tone of the text?A. OptimisticB. CautiousC. InformativeD. Argumentative参考答案:26. C. It can hinder the decision-making process.27. C. Focusing on information that supports existing beliefs.28. B. Failing to make a decision due to fear of making a mistake.29. C. Recognizing the limitations of information.30. B. CautiousSection III TranslationDirections:Translate the following passage into English. Write your translation on ANSWER SHEET 2. (15 points)传统教育系统中,作业被视为学生练习和掌握课堂知识的一种方式。
Unit 5 Languages Around the World(学生版) 25年高考英语一轮复习

单元提升卷06Unit5Languages Around the World单元基础知识巩固I.拓展词汇变形1.n.体系;制度;系统→adj.系统的→adv.系统地2.vi.提到;参考;查阅vt.查询;叫……求助于→n.参考3.vt.以……为据点;以……为基础n.底部;根据→adj.以(某事)为基础的;以……为重要部分(或特征)的→adj.基本的;基础的4.n.(植物、语言等的)变体;异体;多样化→vi.不同;变化→adj.不同的;各种各样的5.vt.欣赏;重视;感激;领会vi.增值→n.欣赏;感激;领会;重视6.n.尊重;关注vt.把……视为;看待→prep.关于7.adj.全球的;全世界的→adv.全球地;全世界地8.adj.特定的;明确的;具体的→adv.特定地;明确地;具体地9.adj.主要的;重要的;大的n.主修课程;主修学生vi.主修;专门研究→n.多数;大多数10.vt.联系;讲述→adj.相关的;有联系的→n.关系;联系11.n.符号;象征→adj.象征的;象征性的→vt.象征;是……的象征12.n.文明;文明世界→adj.文明的13.n.同等的人;相等物adj.相同的;同样的→adv.相同地;同样地→n.平等14.n.要求;需求vt.强烈要求;需要vi.查问→adj.要求高的;苛求的15.n.描写(文字);形容→vt.描述;描写16.vt.联系;讲述→adj.相关的;有联系的→n.关系;联系II.核心短语互译1.对……的态度2.指的是;描述;提到;查阅3.注意4.追溯到5.浮沉;兴衰;荣辱6.因……著名7.被看作8.至关重要9.在……中起重要作用10.导致11.观点;看法12.适应;习惯于13.与……相关;涉及;谈到14.放弃15.做某事有困难16.取决于;依靠;依赖17.match...with..18.official language19.be connected with20.at the beginning21.develop into 22.global affairs23.no matter where,who,what,etc.24.be considered to be25.be related to一、用单词的适当形式完成句子1.Divide the cake into quarters and share it(equal).2.When we’re on holiday in Canada,we live like the(native).3.The banana is native Taiwan.4.Looking after babies is a(demand)job.5.The workers demanded(tell)what had happened to the factory.6.No one will appreciate(treat)like a second-class citizen.7.He begged(tell)the truth,but his mother refused to tell him.8.The conflict had developed into a stage the two countries were gathering big troops on the border.9.The couple just gets registered at the government office.Marriage(regard)as a cardinal issue since ancient times.10.You can refer this dictionary if you have any difficulty in learning English.11.The(major)of them demand that food and water should be supplied in time.12.Our school will organize some campus activities,like“English Evening”,a platform students can show their English.13.“Sponges become bigger and bigger over time;another fossil piece(date)back to around300 million years ago was also recently discovered in Ireland,for example.14.A(beg)is someone who lives by asking people for money or food.15.What he stressed was related teenagers’education.16.The position calls for(relate)experience in the field and good skills at using computers. 17.The article gives a detailed(describe)of the beauty of Mount Tianshan.18.Trends toward the(global)of industry have dramatically affected food production in California. 19.At that time,people(carve)some symbols on animal bones and shells.20.Every means(have)been used to calm the woman down.21.On the(base)of your basic knowledge about the history of the Tang Dynasty,I think it easier for you to understand Tang poems.22.It is a pity that some people can’t go back home at the Spring Festival for(vary)reasons.23.They have developed their friendship to a stage they share happiness and sufferings.24.No matter we are,we are able to keep in contact with loved ones with all sorts of communication software.25.The of the students look forward to in English because English can find a job easily.(major)26.I am sorry to hear that you have trouble(improve)your English at the new school. 27.the fact that she was wearing a seat belt,she was thrown sharply forward.28.In(refer)to the topic we debated yesterday,it is no good saying more.29.He opens a door which our imagination enters a new world,a world of love,beauty and heroism.30.Bones symbols were carved,known as“oracle bones”,have contributed a lot to our understanding of China’s past.二、单词拼写31.She promised to help me move into my new(公寓套房)on the weekend.32.Would you like to take the(地铁)to get there?33.It was last(学期)that I began to appreciate classic works.34.I have given a specific(描述)of the symbols carved on the bone.35.What you said was completely untrue,and I(要求)an immediate apology.36.For this reason,learning French isn’t a(费力的事)for me at all.37.The activity not only strengthened their friendship but also built up their(性格).38.(尽管)the heavy rain,they went on working hard.39.I tried every(方法)to get children interested in my class.40.She made a(n)(提及)to her previous experience in the industry during the interview.41.This(全球的)site is a place for runners to share their stories about running.42.I would(感激)it if you could pay in cash.43.China is a country with a long(文明)of5000years.44.This cultural programme is aimed to encourage teenagers to read more(经典作品).45.Not only did the race improve our physical and psychological quality,but it also helped us build a positive (态度)towards life.三、阅读理解“Learning about one’s own culture,as well as the culture of others,is important,”says Sanam Akhlagh, who set up Pardis for Children.Located in New York City,the nonprofit brings Iranian-American families together and offers after-school programs for children to learn about their heritage.Classes explore Iranian music, art,and history,among other topics.Akhlagh has always been interested in education,kids,and culture,But she felt a void(空虚)before setting up Pardis in2011.She hadn’t been able to get together with friends who share her Iranian heritage periodically. She also thought her children needed that community.“I want kids to know their culture and language,”Akhlagh said,“So if they’re Iranian,they actually know what that means.”But she also wants them to create a bond.“I want them to build a community that they’ll hopefully keep, and stay fiends together for years to come,”she said,“want them to have a beautiful,positive memory(回忆) related to Iranian culture and the Persian language.”Learning about your own culture and language,and understanding other cultures from around the world, Akhlagh explained,makes you a richer and more tolerant(宽容的)person.It also makes you appreciate other people’s way of life.“The exchange of cultures is of great importance,”Akhlagh said.“It is much harder to call people of certain countries or cultures your enemy when you actually know them.When you eat their food,or when you dance to their music together,when you read their literature,it becomes more real,and you start appreciating everyone.”When asked her advice for young people,Akhlagh encouraged exploration and discovery.“If you have the opportunity,always be curious to make friends,”she said.“Get to know people from different cultures and be curious.Always try to know more and travel.”46.What is the purpose of Pardis for Children?A.To enrich children’s social life.B.To improve children’s artistic abilities.C.To educate children on Iranian culture.D.To develop children’s love for their country.47.What does the underlined word“bond”mean in paragraph4?A.Custom.B.Program.C.Relationship.D.Schedule.48.What does Akhlagh think of the exchange of cultures?A.It is a way of life.B.It can promote peace.C.It is a chance to grow D.It increases your wealth.49.What is Akhlagh’s advice for young people?A.Caring more about their friends.B.Being open to different cultures.C.Taking every opportunity to study.D.Feeling confident about making friends.The prodigious ability of our species to rapidly assimilate vocabulary,expanding from a mere300lexemes by the tender age of two to an impressive repertoire exceeding1,000by the age of four,remains a subject of profound enigma.Certain scholars in the realms of cognitive science and linguistics have posited that the human mind enters the world equipped with innate cognitive predispositions and logical parameters that facilitate this linguistic feat.However,recent advancements in the sphere of machine learning have unveiled the potential for swift acquisition of semantic understanding from sparse data,eschewing the need for preconceived,hardwired assumptions.An ensemble of researchers has triumphantly honed a rudimentary artificial intelligence construct to correlate visual representations with their corresponding lexical entities,utilizing a mere61hours of ambient visual recordings and auditory data—previously amassed from an individual known as Sam during the years 2013and2014.Though this represents but a minuscule fraction of a child’s developmental chronicle,it transpires that this was sufficiently informative to prompt the AI in discerning the significance of select vocables.These revelations intimate that the process of linguistic acquisition may be more straightforward than hitherto presumed.It is conceivable that the juvenile mind does not necessitate a tailor-made,sophisticated linguistic apparatus to adeptly apprehend the essence of words,posits Jessica Sullivan,an adjunct professor of psychology at Skidmore College.“This is an exceptionally elegant inquiry,”she articulates,as it presents corroborative evidence that rudimentary data extracted from a child’s perspective is sufficiently abundant to initiate the processes of pattern recognition and lexical assimilation.The recent scholarly endeavor also illustrates the plausibility of machines emulating the learning modalities inherent to human cognition.Vast linguistic models are typically nurtured on colossal datasets encompassing billions,if not trillions,of lexical permutations.In stark contrast,human beings manage with a significantly reduced informational intake,as articulated by the principal scribe of the study,Wai Keen Vong.With the appropriate genre of data,the chasm separating machine and human learning could be substantially bridged.Nevertheless,further investigation is warranted in select dimensions of this pioneering research.The savants concede that their findings do not conclusively elucidate the mechanisms by which children amass vocabulary.Additionally,the study’s purview was confined to the identification of nouns pertaining to tangible entities.Despite these limitations,this represents a stride toward a more profound comprehension of our own cognitive faculties,which may ultimately contribute to the enhancement of human pedagogical practices, according to Eva Portelance,a scholar in computational linguistics.She remarks that AI research has the potential to shed light on enigmatic queries about our essence that have persisted over time.“We can harness these paradigms in a salutary manner,to the advantage of scientific discovery and societal progress,”Portelance further elaborates.50.What is a significant finding of machine-learning research?A.Vocabulary increases gradually with age.B.Vocabulary can be acquired from minimal data.C.Language acquisition is tied to built-in expectations.D.Language acquisition is as complex as formerly assumed.51.What does the underlined word“prompt”in paragraph2mean?A.Facilitate.B.Persuade.C.Advise.D.Expect.52.What is discussed about the new research in paragraph5?A.Its limitations.B.Its strengths.C.Its uniqueness.D.Its process.53.What is Eva Portelance’s attitude to the AI research?A.Doubtful.B.Cautious.C.Dismissive.D.Positive.四、完形填空Research has shown that two-thirds of human conversation is taken up not with discussion of the cultural or political problems of the day,not heated debates about films we’ve just watched or books we’ve just finished reading,but plain and simple54.Language is our greatest treasure as a species,and what do we55do with it?We gossip.About others’behaviour and private lives,such as who’s doing what with whom,who’s in and who’s out and why;how to deal with difficult56situations involving children,lovers,and colleagues.So why are we keen on gossiping?Are we just natural wasters of both time and words?Or do we talk a lot about nothing in particular simply to avoid facing up to the really important issues of life?It’s not57 according to Professor Robin Dunbar.In fact,in his latest book,Grooming,Gossip and the Evolution of Language, the psychologist says gossip is one of these really58issues.Dunbar59the traditional view that language was developed by the men at the early stage ofsocial development in order to organize their manly hunting activities more effectively,or even to promote the exchange of poetic stories about their origins and the supernatural.Instead he suggests that language evolved among women.We don’t spend two-thirds of our time gossiping just because we can talk,argues Dunbar—60,he goes on to say,language evolved specifically to allow us to gossip.Dunbar arrived at his cheery theory by studying the61of the higher primates(灵长类动物)like monkeys.By means of grooming—cleaning the fur by brushing it,monkeys form groups with other individuals on whom they can rely for support in the event of some kind of conflict within the group or62from outside it.As we human beings evolve from a particular branch of the primate family,Dunbar63that at one time in our history we did much the same.Grouping together made sense because the bigger the group,the greater the64it provided;on the other hand,the bigger the group,the greater the stresses of living close to others.Grooming helped to65the pressure and calm everybody down.But as the groups got bigger and bigger,the amount of time spent in grooming activities also had to be 66to maintain its effectiveness.Clearly,a more67kind of grooming was needed,and thus language evolved as a kind of vocal(有声的)grooming which allowed humans to develop relationship with ever-larger groups by exchanging information over a wider network of individuals than would be possible by one-to-one68contact.54.A.mission B.radiation C.comparison D.gossip 55.A.occasionally B.merely C.habitually D.originally56.A.social B.political C.historical D.leisurely57.A.the case B.the question C.the issue D.the key58.A.financial B.sensitive C.royal D.vital59.A.confirms B.outlines C.dismisses D.broadens60.A.for instance B.on the contrary C.in addition D.as a result 61.A.motivation B.motive C.emotion D.behaviour 62.A.inspection B.harmony C.attack D.assistance 63.A.convinces B.comprises C.confesses D.concludes 64.A.prospect B.protection C.maintenance D.luxury65.A.discipline B.bother C.maintain D.ease66.A.cast B.consumed C.extended D.floated67.A.common B.efficient C.scientific D.thoughtful68.A.invisible B.daily C.constant D.physical阅读下面材料,在空白处填入1个适当的单词或括号内单词的正确形式。
关于百分比的作文英文版

关于百分比的作文英文版英文:Percentage is a common concept that we encounter in our daily lives. It is a way of expressing a part of a whole as a fraction of 100. For example, if we say that 50% of the students in a class are girls, it means that half of the students in the class are girls.Percentages are used in many different fields, such as finance, statistics, and science. In finance, we use percentages to calculate interest rates and returns on investments. In statistics, we use percentages to represent the frequency of certain events. In science, we use percentages to express the concentration of substances in a solution.One thing to keep in mind when dealing with percentages is that they can be misleading if not used properly. For example, let's say that a company's profits increased by 50%from last year. This sounds like a significant increase, but if the company only made a small profit last year, then a 50% increase may not be that impressive.Another thing to consider is that percentages can be used to manipulate statistics. For example, a politician may say that crime rates have decreased by 50% in their city, but if the crime rate was very high to begin with, a 50% decrease may not mean much in terms of actual safety.In conclusion, percentages are a useful tool for expressing parts of a whole, but it's important to use them properly and consider the context in which they are being used.中文:百分比是我们日常生活中经常遇到的一个概念。
常用数学术语的英语表达

常用数学术语的英语表达:1立方 one cubic1平方米one square metre几何geometry点 point线 line面 plane直线 a straight曲线curved line近似值an approximate value垂直线 a vertical水平线 a horizontal line三角形的底the base of a triangle三角形的两个腰the two sides of a triangle直角 a rigt angle锐角an acute angle钝角an obtuse angle长方形 a rectangle正方形 a square多边形 a polygon圆心 the centre of a circle圆的直径the diameter of a circle圆的半径the radius of a circle半圆 a semicircle弧an arc圆柱体 a cylinder球体 a spheroid常用加减乘除的英语表达:四加五等于九If you add 4 to 5, you get 9.或:If you add 4 and 5, you get 9.五与四的和是九 4 and 5 are / make 9.或:The sum of 5 and 4 is 9.或:Four plus five equals nine.五减二等于三If you take 2 from 5, you get 3.或:5 minus 2 equals 3.五与二之差为三The difference between 5 and 2 is 3.二乘三等于六 2 times 3 is / equals 6.或:3 multiplied by 2 equals 6.二与三的积为六The proudct of 2 and 3 is 6.六除以二等于三If you divide 6 by 2, the answer is 3.或:If you divide 2 into 6, the answer is 3.或:6 divided by 2 equals 3.比较两个数字大小的英语表达:6大于5 6 is greater than 5.或:6 is more than 5.6小于7 6 is less than 7.平方、立方及四次方的英语表达:3的平方等于9 The square of 3 is 9.3的立方等于27 The cube of 3 is 27.3的四次方等于81 The fourth power of 3 is / equals 81.平方根立方根的英语表达:9的平方根为3 The square root of 9 is 3.27的立方根为3 The cube root of 27 is 3.正比反比的英语表达:A与B成正比 A is in direct proportion to B.A与B成反比 A is in inverse proportion to B.两直线平行或垂直的英语表达:直线AB平行于直线CD Line AB is parallel to Line CD直线AB垂直于直线CD Line AB is perpendicular to Line CD代数部分1。
a fraction of 的用法

a fraction of 的用法
"of" 在这种情况下用来表示一个分数被分割或包含在另一个整体中。
以下是一些具体的用法:
1. 等于一个分数的一部分:"One-fourth of the cake" 表示蛋糕的四分之一。
2. 表示一部分整体中的分数:"Three-fifths of the students" 指的是学生中的三分之二。
3. 表示分数作为整体的一部分:"A fraction of the population" 用于描述整个人口中的一个小部分。
4. 描述数量非常少或微不足道的一部分:"Only a fraction of the cost" 意味着只有很小一部分的费用。
总的来说,“a fraction of”用于描述一个分数作为整体的一部分,或者表示数量很少的一部分。
数学英语词汇 -回复

数学英语词汇 -回复Mathematics English VocabularyMathematics is a subject that combines numbers, shapes, and patterns to solve problems and understand the world around us. It is a universal language that allows us to communicate and apply logical reasoning. As we delve into the world of mathematics, it is important to familiarize ourselves with the specialized vocabulary used in this field to accurately communicate and understand mathematical concepts. In this article, we will explore some key mathematical terms and their English equivalents.1. Numbers and Basic OperationsIn mathematics, numbers are the building blocks of calculations. Here are some essential terms related to numbers:1.1. Integer - An integer is a whole number that can be positive, negative, or zero. For example, -2, 0, and 3 are integers.1.2. Fraction - A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). For example, 1/2, 3/4, and 5/6 are fractions.1.3. Decimal - A decimal number is a number that includes a decimal point. It can be a fraction or a whole number. For example, 0.5,2.75, and 10.0 are decimals.1.4. Addition - Addition is the process of adding two or more numbers together to find the total. For example, 2 + 3 equals 5.1.5. Subtraction - Subtraction is the process of taking one number away from another to find the difference. For example, 5 - 2 equals 3.1.6. Multiplication - Multiplication is the process of combining numbers to find the product. For example, 2 × 3 equals 6.1.7. Division - Division is the process of splitting a number into equal parts or finding out how many times one number is contained within another. For example, 6 ÷ 2 equals 3.2. Geometry and ShapesGeometry deals with the properties and relationships of points, lines, angles, surfaces, and solids. Let's explore some key geometric terms:2.1. Point - A point is a specific location in space, often represented by a dot. It has no length, width, or depth. For example, A is a point.2.2. Line - A line is a straight path that extends infinitely in both directions. It is made up of an infinite number of points. For example, AB is a line.2.3. Angle - An angle is formed when two lines or line segments meet ata common endpoint. It is measured in degrees. For example, ∠ABC is an angle.2.4. Triangle - A triangle is a closed figure with three straight sides and three angles. For example, △ABC is a triangle.2.5. Circle - A circle is a closed curve made up of all points equidistant from a fixed center point. For example, O is the center of the circle.2.6. Square - A square is a quadrilateral with four equal sides and four right angles. For example, ABCD is a square.2.7. Prism - A prism is a solid figure with two congruent parallel bases and rectangular faces. For example, a rectangular prism is a three-dimensional shape with a rectangular base.3. Algebra and EquationsAlgebra involves the use of letters and symbols to represent numbers and express mathematical relationships. Here are some important terms related to algebra:3.1. Variable - A variable is a symbol, usually a letter, used to represent an unknown number in an equation. For example, x + 5 = 10, where x is the variable.3.2. Equation - An equation is a mathematical statement that asserts the equality of two expressions. For example, 2x + 3 = 7 is an equation.3.3. Coefficient - A coefficient is a numerical or constant factor in a term of an algebraic expression. For example, in 4x, 4 is the coefficient.3.4. Exponent - An exponent represents how many times a number, known as the base, should be multiplied by itself. For example, 2³ means 2 multiplied by itself three times.3.5. Function - A function relates an input value to an output value and is often expressed as an equation. For example, f(x) = 2x.3.6. Inequality - An inequality compares two expressions and defines their relationship using symbols such as < (less than), > (greater than), ≤(less than or equal to), or ≥ (greater than or equal to). For example, x > 5 is an inequality.4. Statistics and ProbabilityStatistics involves the collection, analysis, interpretation, presentation, and organization of data. Probability deals with the likelihood of events occurring. Let's explore some key terms in these areas:4.1. Mean - The mean is the average of a set of numbers. It is found by summing all the numbers and dividing by the count. For example, the mean of 1, 2, and 3 is (1 + 2 + 3) / 3 = 2.4.2. Median - The median is the middle value in a set of numbers when they are arranged in numerical order. For example, the median of 1, 2, and 3 is 2.4.3. Mode - The mode is the value that appears most frequently in a set of numbers. For example, the mode of 1, 2, 2, and 3 is 2.4.4. Range - The range is the difference between the largest and smallest values in a set of numbers. For example, the range of 1, 2, and 3 is 3 - 1 = 2.4.5. Probability - Probability is the measure of the likelihood of an event occurring. It is expressed as a number between 0 and 1. For example, the probability of rolling a six on a fair six-sided die is 1/6.ConclusionIn conclusion, understanding the vocabulary used in mathematics is essential for effective communication and comprehension of mathematical concepts. This article has presented some key terms related to numbers,basic operations, geometry, algebra, and statistics. By familiarizing ourselves with these terms, we can enhance our mathematical knowledge and articulate mathematical ideas accurately in English.。
数学不合格给予建议英语作文

数学不合格给予建议英语作文As a student who is struggling in mathematics, I understand how overwhelming it can be to feel like you are constantly falling behindin your studies. 作为一个在数学方面挣扎的学生,我理解感觉不断落后在学业中是多么令人担忧。
First and foremost, it is important to remember that you are not alone in facing challenges with math. 漫长的求学生涯中,遇到挑战是再正常不过的事情。
It is crucial to seek help and support from your teachers, classmates, or even a tutor in order to improve your understanding of mathematical concepts. 在数学领域取得进步的关键是寻求老师、同学或家教的帮助和支持,以提高对数学概念的理解。
Additionally, practicing regularly and engaging with the material outside of the classroom can also greatly benefit your learning. 此外,定期练习并在课堂之外与内容互动也会极大地有助于学习。
Furthermore, it is important to stay positive and determined in your efforts to improve in mathematics. 更重要的是,要保持积极的心态和决心,努力提高数学水平。
Remember that everyone learns at their own pace, and with dedication and perseverance, you can overcome your struggles in mathematics. 记住,每个人都有自己的学习节奏,只要有耐心和毅力,你一定能克服在数学上的困难。
英语高级表达短语搭配

英语高级表达短语搭配
以下是一些英语高级表达短语搭配的例子:
1.in the vicinity of 在...附近
例句:The hotel is in the vicinity of the train station.
2.in a moment 立刻,马上
例句:Wait a moment, I'll be back soon.
3.in a flash 瞬间,一瞬间
例句:In a flash, he realized what had happened.
4.in a word 一句话,简而言之
例句:In a word, we need to work harder.
5.in a hurry 匆忙,急急忙忙地
例句:He left in a hurry, forgetting his keys.
6.in a sense 从某种意义上说
例句:In a sense, we are all winners.
7.in a fraction of a second 瞬间,一瞬间
例句:In a fraction of a second, he reacted to the situation.
8.in a nutshell 简而言之,概括地说
例句:In a nutshell, the report is very positive.
9.in a matter of seconds 瞬间,一瞬间
例句:In a matter of seconds, the race was over.
10.in a way 在某种程度上,以某种方式
例句:In a way, I think we did well.。
关于百分比的作文英文版

关于百分比的作文英文版Title: Understanding Percentages: A Comprehensive Overview。
In our everyday lives, percentages play a crucial role in various aspects, ranging from finance to education, from health to business. Understanding percentages is not only essential for practical purposes but also for developing critical thinking skills. In this essay, we will delve into the concept of percentages, exploring its significance, applications, and practical implications.To begin with, let's grasp the fundamental definition of a percentage. Simply put, a percentage is a way of expressing a fraction or a proportion out of 100. It is denoted by the symbol "%". For instance, if we say that 50% of the students in a class prefer mathematics, it meanshalf of the total number of students favor mathematics.Percentages find extensive use in various fields. Infinance, they are employed to calculate interest rates, discounts, taxes, and profit margins. For instance, when you take out a loan, the interest rate is often expressed as a percentage of the principal amount. Similarly, in the retail sector, discounts are advertised in percentages, such as "50% off" or "Buy One, Get One 25% off". Understanding these percentages enables consumers to make informed decisions about their purchases.Moreover, percentages are prevalent in academic contexts. Grades, test scores, and class rankings are frequently represented using percentages. For instance, a student scoring 80% on a test has correctly answered 80 out of every 100 questions. This helps both students and educators to assess performance and track progress effectively.In the realm of health and nutrition, percentages are used to convey information about recommended daily allowances, nutritional values, and fitness goals. Food labels often display the percentage of essential nutrients present in a serving size, aiding consumers in makinghealthier choices. Likewise, when setting fitness goals, individuals may aim to reduce body fat percentage or increase muscle mass percentage.Furthermore, percentages are indispensable instatistical analysis and data interpretation. They are used to represent proportions of a population, frequency distributions, and changes over time. For instance, opinion polls and surveys often report findings in percentages, providing insights into public opinion and societal trends.Understanding percentages not only enables us to interpret information accurately but also empowers us to make informed decisions in various aspects of life. However, it is essential to be mindful of common misconceptions and pitfalls associated with percentages. For instance, confusing percentage change with percentage points or misinterpreting percentages without considering the base value can lead to erroneous conclusions.In conclusion, percentages are a fundamental conceptwith widespread applications in diverse fields. Whether infinance, education, health, or data analysis, percentages play a pivotal role in quantifying proportions and conveying information effectively. By understanding percentages, we enhance our analytical skills, make better-informed decisions, and navigate the complexities of the modern world more adeptly.。
分数练习题英语

分数练习题英语### 英语分数练习题#### 一、选择题1. What is 1/3 of 60?A. 20B. 30C. 15D. 252. If 2/5 of a class has 24 students, what is the total number of students in the class?A. 60B. 50C. 30D. 403. A recipe calls for 3/4 cup of sugar. If you have 2 cups of sugar, how many recipes can you make?A. 2B. 3C. 4D. 5#### 二、填空题4. If you have 1/4 of a pizza, and you want to share it equally among 3 friends, each friend will get _______ of the pizza.5. A car travels 120 miles in 3 hours. The speed of the caris _______ miles per hour.6. If 3/4 of a bottle of juice is 450 ml, the total capacityof the bottle is _______ ml.#### 三、计算题7. Calculate the total weight of 7/8 of a ton of apples if each ton weighs 2000 kg.8. A group of 20 friends plans to share 5/6 of a cake equally. How much cake does each friend get?9. If a farmer has 4/5 of an acre of land and he wants toplant 1/3 of it with wheat, how many acres will be plantedwith wheat?#### 四、应用题10. A company has 3/4 of its employees working remotely. Ifthe company has 160 employees in total, how many are working remotely?11. A store sells 2/3 of its inventory in a month. If thestore started with 450 items, how many items were sold?12. A recipe requires 1/2 cup of milk for every 3/4 cup of flour. If you have 1 1/2 cups of flour, how much milk do you need?#### 五、简答题13. Explain the difference between a proper fraction and an improper fraction.14. What does it mean when a fraction is in its simplest form?15. How would you convert an improper fraction to a mixed number?答案解析:1. C. 15 (60 * 1/3 = 20)2. B. 50 (24 / (2/5) = 60)3. C. 4 (2 / (3/4) = 2.67, rounded to 4)4. 1/12 (1/4 divided by 3)5. 40 (120 / 3 = 40)6. 600 (450 / (3/4) = 600)7. 1750 kg (7/8 * 2000 = 1750)8. 5/12 of a cake (5/6 divided by 20)9. 1/5 of an acre (4/5 * 1/3 = 4/15)10. 120 (3/4 * 160 = 120)11. 300 items (2/3 * 450 = 300)12. 1 1/4 cups of milk (1 1/2 * (1/2 / 3/4) = 1 1/4)13. A proper fraction is a fraction where the numerator isless than the denominator, while an improper fraction has a numerator that is greater than or equal to the denominator.14. A fraction is in its simplest form when the numerator and denominator have no common factors other than 1.15. To convert an improper fraction to a mixed number, divide the numerator by the denominator. The quotient is the whole number part, and the remainder is the new numerator, with the denominator remaining the same.。
数学比例问题的英文

数学比例问题的英文Mathematical ratios are a fundamental concept in mathematics that involve comparing two quantities. They are often expressed in the form of a fraction, with a colon, orthe word "to." Understanding ratios is crucial for solving a variety of mathematical problems, from simple division tomore complex algebraic expressions.Let's consider an example to illustrate how ratios work.If you have a recipe that calls for 3 cups of flour to make 2 loaves of bread, the ratio of flour to loaves is 3:2. This means that for every 3 units of flour, you can expect to make 2 units of bread.To scale this ratio up or down, you can multiply ordivide both parts of the ratio by the same number. For instance, if you want to make 4 loaves of bread, you would multiply both parts of the ratio by 2, resulting in a newratio of 6:4, which simplifies to 3:2. This shows that youstill need 3 cups of flour for every 2 loaves of bread, regardless of the total number of loaves you want to make.Ratios can also be used to compare different sets of data. For example, if you want to compare the number of apples to oranges in two different baskets, you might find that thefirst basket has a ratio of 5 apples to 3 oranges, while the second has 10 apples to 6 oranges. By simplifying both ratios, you can see that both baskets have the same ratio of 5:3,indicating that the proportion of apples to oranges is the same in both baskets.In algebra, ratios are often used to solve problems involving proportions. If you know that the ratio of boys to girls in a class is 3:5, and you know the total number of students, you can set up a proportion to find out how many boys and girls there are. For example, if there are 48students in total, you can divide 48 by the sum of the partsof the ratio (3+5) to find the value of one part, and then multiply this by 3 and 5 to find the number of boys and girls, respectively.In conclusion, ratios are a versatile tool in mathematics that can be used to compare quantities, scale recipes,analyze data sets, and solve algebraic problems. By mastering the concept of ratios, you can tackle a wide range of mathematical challenges with ease.。
航海及海运专业英语词汇(A1)

航海及海运专业英语词汇(A1)航海及海运专业英语词汇(A1)航海及海运专业英语词汇(A1)a basket of currencies 一篮子货币a battery 丝极电池组a bulk carrier of 26000 dwts capacity with seven holds and of single deck construction ideal for world wide tramp operation especially bulk grain shipments with a speed of 15 knots 一艘载重26 000吨a bulk carrier of 30000 dwts capacity with five holds and of single deck construction ideal for world wide tramp cargo operation with a speed of 15 knots 一艘载重30 000吨a class division a级分隔a class ship 甲类船a class 甲级a eliminator 灯丝电源整流器a fraction of 零点几a frequency of 1 000 000 000 or 1 ×109 cycles each second千兆赫的无线电频率a general purpose cargo tramp vessel of 18 000 dwt's with four holds with each with tween deck and speed of 15 knotssuitable both for bulk dry or liner cargo shipments of 426 teu container units标准设计的18 000载重吨a hoist 一挂a lien on the object towed 拖带留置权a lloyd's policy form of insurance on an air cushion vessel hovercraft 劳氏气垫船运输保险单a type stem a型首柱a voyage charter party form of the documentary committee of the japan shipping exchange inc. 日本航运交易所航次租船表a'cockbill 吊锚a'hull 帆船卷帆漂航a-1 a-1海区(gmdss用语a-1 navigation area a-1海区(gmdss用语a-1 键控等幅波a-1) 极量第二改正量a-1a 键控等幅波a-2 a-2海区(gmdss用语a-2 navigation area a-2海区(gmdss用语a-3 a-3海区(gmdss用语a-3 navigation area a-3海区(gmdss用语a-4 a-4海区(gmdss用语a-4 navigation area a-4海区(gmdss用语a-alloy 铝合金a-block 滑车拉到头a-bracket 尾轴架a-d ad d-a conversion 模拟-数字与数字-模拟转换a-d and d-a conversion 模拟-数字与数字-模拟转换a-d converter 模拟-数字转换器a-derrick 人字形旋臂起重机a-end a端a-frame crane 人字形起重机a-frame derrick 人字架转臂起重机a-frame derrick 人字形吊杆架a-frame derrick 人字形旋臂起重机a-frame a形架a-n radio beacon a-n无线电导标a-n radio range a-n信标a-one 第一级第一等的a-peak! 立桨!a-power supply 丝极电源a-power 原子动力a-shaped frame a形架a-ship 原子动力船a-tanker 原子动力油船a-trace 扫描线a-weighted sound level a 声级a-weighted sound level a声级a. 水动力的a.b.loff log 一种水压计程仪a.c. motor 交流电动机a.c. resonance charging modulator 交流谐振充电调制器a.c. welding machine 交流电焊机a.e 1. 一等一级aack astern! 挡水!ab machinery standard 美国船舶局机械设备标准abac 大圆改正量列线图abaca rope 白棕绳aback 使船后退向后aback 向后aback 向后;使船后退;逆帆abacus 顶板abaft the beam 在船正横以后abaft the beam 在正横以后abaft the beam 正横后abaft 在船尾abaft 在船尾在……后面abalienate 让渡abalienation 让渡abalone 石决明(旧误称鲍鱼abampere cgs电磁制安培abampere 十安倍abandon an anchor 弃锚abandon anchor 弃锚abandon ship drill 弃船演习abandon ship operation 弃船作业abandon ship order 弃船命令abandon ship signal 弃船信号abandon ship station 弃船部署abandon ship training 弃船训练abandon ship 弃船abandon ship 弃船;委付abandon station 弃船部署abandon 放弃abandon 放弃;委付abandon 放弃委付abandon 弃abandoned ship 被弃的船abandoned ship 被弃的船已委付船abandoned vessel 被弃的船abandoned vessel 弃船abandoned vessel 已弃船abandoned 被弃的abandonee 被遗弃者打捞货物的接受人(海运保险中abandoner 放弃者abandoner 委付者abandoning ship 委弃船abandonment clause 弃船条款abandonment of a cargo 放弃货载abandonment of a right 弃权abandonment of a ship 弃船abandonment of action 放弃诉讼abandonment of claim 放弃索赔abandonment of marine insurance 海上保险委付abandonment of offshore platform 放弃近海平台abandonment of ship 船舶委付abandonment of ship 弃船abandonment of the voyage 放弃原定航次abandonment of voyage 航程放弃abandonment to insurer 委付abandonment 放弃abandonment 弃船abandonment 弃船;放弃;委付abandonment 委付abandonstation 弃船部署abase 降低;下降abase 落帆降旗降低abate 减abate 减轻减退abatement for deficiency 因缺陷而降低价格abatement of action 中止诉讼abatement of tax 减税abatement of taxes 减税abatement of voice 消声abatement 废弃;减免;折扣abatement 减退abaxial 离轴的abbreviate 缩写abbreviated dial system 缩位拨号方式abbreviated dialing 缩位拨号abbreviated drawing 简图abbreviated 简略的abbreviation on chart 海图缩语abbreviation 缩写abbreviation 缩写缩写词abbreviation 缩写字abbreviative notation 缩写标记abcoulomb cgs电磁制库仑abdicate 放弃;让位abdicate 放弃让位abdomen 腹abeam distance 正横距离abeam 横向abeam 正横abeam 正横正横abeam 正横正横方向abel pensky flash point test 埃勃尔-彭斯基石油闪点测定abel tester 艾贝尔闪点测试仪abel's close test 艾贝尔闭杯试验abel-pensky flash point apparatus 艾贝尔-彭斯基闪点仪(闭口aberdeen 阿伯丁aberrant 偏离航线的aberration angle 光行差角aberration ellipse 光行差椭圆aberration of fixed stars 恒星光行差aberration of lens 透镜像差aberration of lens 透镜象差aberration of light 光行差aberration of shift 光行差位移aberration of wind 风动差aberration of wind 真视风夹角aberration 过失;错误行为;心理失常;光行差;象差abeyance 暂缓abfarad cgs电磁制法拉abhenry cgs电磁制亨利abide 等待;保持;船被所阻abide 忍受abies oil 松节油abietic acid 松香酸ability of equalization 均衡能力ability of righting 扶正能力ability to pay 支付能力ability to self-stow 自收藏能力ability 性能abjunction 分离ablage 着火ablation experiment 脱离试验ablation 烧蚀ablation 消融able bodied seaman 熟练水手able bodied seaman 熟练水手一级水手able bodied seaman 一级水手able bodied 一级水手able seaman 熟练水手able seaman 一级水手able 有才能的able-bodied 一级水手;二等水兵able-bodied rating 一等水兵able-bodied seaman 熟练水手able-bodied seaman 一等水手able-bodied seaman 一级水手able-bodied 一级水手able-bodied 一级水手的ablution 吹除abnormal combustion 异常燃烧abnormal condition 异常情况;异常条件abnormal condition 异常状态abnormal current 异常海流abnormal end 异常结束abnormal glow discharge (阴极被弧光覆盖abnormal indication 异常显示abnormal indication 异常指示abnormal injection 异常喷射abnormal load 不规则荷载abnormal log 异常日志abnormal magnetic variation 磁差异常abnormal operating condition 异常运转工况abnormal refraction 异常折光abnormal return 异常返回abnormal risk 异常的保险标的abnormal risk 异常风险abnormal setting 异常凝固异常调整abnormal swell 异常涌浪abnormal temperature 异常温度abnormal transportation 非正常运输abnormal variation 异常磁差abnormal variation 异常偏差abnormal voltage 异常电压abnormal water level 非常水位abnormal 不正常abnormal 异常的abnormality of mark 航标失常abnormality of mark 航标异常abnormality 反常abnormality 异常aboard 在船上aboard 在船上上船靠舷aboard 在船上上船靠舷在船内abohm cgs电磁制欧姆abolish 废除abolishment 废止;废除abolishment 废止废除abolition of general average 共同海损的废除abolition 废除abort light 紧急故障信号abort sensing and implementationsystem 故障传感和处理系统abort sensing control unit 故障传感控制装置abort sensing control unit 故障传感控制装置故障传感控制装置abort 异常结束aboundance ratio 丰满度about ship 掉抢about 大约about 大约关于about 大约在周围about 掉抢about-ship 改变航向above and under 上和下above base line 基准线以上above board 在甲板上above deck equipment 舱面设备above deck equipment 甲板上设备above deck girder 甲板上纵桁above deck 船甲板以上above deck 在船上甲板上above deck 在甲板上above ground level 在地平面以上above ground 距地面……高度above mean sea level 平均海面之上above mean sea level 平均海面之上平均海平面之上above mean sea level 平均海平面之上above normal speed 超标准速度above normal speed 超正常速度above par 超出票面价值above the horizon 水平线以上above water craft 水面船舶above water damage 水线以上部分破损above water shape 水上部分形状above water 水平面以上above water 水上部分above 上面的above 上游above 在……上above 在…之上上游above 在上面以上上述在上游above-cited 上面引用的above-critical 超临界的above-decks equipment 甲板设备above-mentioned 上述的above-water body 水上部分船体above-water craft 水面船舶above-water damage 水上部分破损above-water damage 水线以上部分破损above-water fish lamp 水上集鱼灯above-water 水上部分的above-water 水上的abradability 磨损性abradant 研磨剂abrade 磨损研磨abraded surface 磨损表面清理过的表面abradibility 可研磨性abraser paste 研磨剂abraser 磨料abrasion hardness 耐磨硬度abrasion index 腐蚀指数abrasion loss 磨损量abrasion performance 耐磨性abrasion platform 海蚀台地abrasion ratio 磨耗率abrasion resistance 抗磨损性abrasion resistant 耐磨的abrasion test 磨损试验abrasion 磨耗abrasion 磨损abrasion 磨损冲蚀abrasion-proof 耐磨的abrasion-resistance 抗磨的abrasion-resistant hardwood 耐磨硬木abrasion-resistant 抗磨的abrasion-test 耐磨试验abrasive action 磨损作用abrasive blasting 喷砂清理abrasive cleaning 磨洗abrasive cloth 砂布abrasive compound 研磨剂abrasive damage 磨损损伤abrasive dust 磨屑abrasive grain 磨粒abrasive grit 喷丸abrasive hardness 磨料硬度abrasive impurities 有磨蚀作用的杂质abrasive machine 砂轮机abrasive material 磨料abrasive paper 砂纸abrasive particle 磨粒abrasive resistance 抗磨力abrasive resistance 抗磨强度abrasive resistance 耐磨强度abrasive substance 磨料abrasive wear resistance 耐磨强度abrasive wear 磨损abrasive wheel 砂轮abrasive 磨料abrator 喷丸清理装置abreast 并列abreast 平齐abridge drawing 略图abridge edition 节本abridge general view 示意图abridge 节略的abridge 省略abridged admiralty chart folios 《英版海图图夹节本》abridged drawing 略图abridged general view 示意图abridged nautical almanac 《简本航海天文历》简明航海历abridged nautical almanac 简明航海历abridged 节略的abridgement 节略abroad 在国外;国外;到国外abroad 在国外国外到国外abrogate 撤销;废除abrogate 撤销废除abroholos 巴西海岸5~8月的雷雨飑abroholos 巴西海岸5—8月的雷雨飑abrolhos 巴西海岸5~8月的雷雨飑abrupt acceleration 突然加速abrupt change of ship section 船体急剧变形abrupt change of voltage 电压突变abrupt change 突变abrupt cliff 陡崖abrupt coast 陡岸abrupt deceleration 急剧减速abrupt junction 突变结abrupt slope 陡坡abrupt transformation 突跃变换abrupt wave 陡浪abrupt 突然的;陡的abrupt 突然的陡的abrupt 突然的陡削的abruption 离开;中断abruption 离开中断abruption 突然分离abruptment 拉断abscess 脓肿abscess 气泡abscissa axis 横坐标轴abscissa 横坐标absence indicator 离船旗号absence of stains 没有污染absence without leave 不告假而离去擅离职守absence without leave 不假而去absence without leave 擅离职守absence 缺席absentee 未归船者absestine 石棉的absestine 石棉的石棉性的不燃性的absolute entrance velocity 绝对进口速度absolute exit velocity 绝对出口速度absolute acceleration 绝对加速度absolute acceptance 单纯承兑或认付absolute accuracy at 95%95% 的绝对精度absolute address 绝对。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Hindawi Publishing CorporationAbstract and Applied AnalysisVolume2012,Article ID837437,7pagesdoi:10.1155/2012/837437Research ArticlePositive Solutions of an Initial V alue Problem for Nonlinear Fractional Differential EquationsD.Baleanu,1,2H.Mohammadi,3and Sh.Rezapour31Department of Mathematics,Cankaya University,Ogretmenler Cad.1406530,Balgat,Ankara,Turkey2Institute of Space Sciences,Magurele,Bucharest,Romania3Department of Mathematics,Azarbaijan University of Shahid Madani,Tabriz,IranCorrespondence should be addressed to D.Baleanu,dumitru@.trReceived23January2012;Accepted20March2012Academic Editor:Juan J.TrujilloCopyright q2012D.Baleanu et al.This is an open access article distributed under the Creative Commons Attribution License,which permits unrestricted use,distribution,and reproduction in any medium,provided the original work is properly cited.We investigate the existence and multiplicity of positive solutions for the nonlinear fractional dif-ferential equation initial value problem Dα0 u t Dβ0 u t f t,u t ,u 0 0,0<t<1,where0<β<α<1,Dα0 is the standard Riemann-Liouville differentiation and f: 0,1 × 0,∞ → 0,∞is continuous.By using somefixed-point results on cones,some existence and multiplicity results of positive solutions are obtained.1.IntroductionFractional differential equations have been subjected to an intense debate during the last few years see,e.g., 1–5 and the references therein .This trend is due to the intensive develop-ment of the theory of fractional calculus itself and by the applications of such constructions in various sciences such as physics,mechanics,chemistry,and engineering 5–15 .The frac-tional differential equations started to be used extensively in studying the dynamical systems possessing memory effprehensive treatment of the fractional equations techniques such as Laplace and Fourier transform method,method of Green function,Mellin transform, and some numerical techniques are given in 5,7,9 and the references therein.In classical approach,linear initial fractional differential equations are solved by special functions 9,16 . In some papers,for nonlinear problems,techniques of functional analysis such asfixed point theory,the Banach contraction principle,and Leray-Schauder theory are applied for solving such kind of the problems see,e.g., 17–19 and the references therein .The existence of nonlinear fractional differential equations of one time fractional derivative is consideredin 6,7,9,20 .Also,the existence and multiplicity of positive solutions to nonlinear Dirichlet problemD α0 u t f t,u t 0,0<t <1,u 0 u 1 0,1<α≤2,α∈R , 1.1where f : 0,1 × 0,∞ → 0,∞ is continuous and D α0 is the Riemann-Liouville di fferen-tiation,have been reviewed by some authors see e.g., 18–21 and the references therein .In this paper,by using some fixed-point results,we investigate the existence and multiplicity of positive solutions for the nonlinear fractional di fferential equation initial value problemD α0 u t D β0 u t f t,u t ,u 0 0,0<t <1, 1.2where 0<β<α<1,D α0 is the standard Riemann-Liouville di fferentiation,and f : 0,1 ×0,∞ → 0,∞ is continuous.Now,we present some necessary notions.The Riemann-Liouville fractional integral of order α>0is defined by I αf t : 1/Γ α t 0 t −τ α−1f τ dτ 20 .Also,the Riemann-Liouville fractional derivative of order α>0is defined by D αf t : 1/Γ n −α d/dt n t 0 t −τ n −α−1f τ dτ,where n α 1and the right side is pointwise defined on 0,∞ 20 .The formula of Laplace transform for the Riemann-Liouville deriva-tive is defined byL D αf t ;s s α f sm −1 k 0 D k I m −α f 0 s m −k −1 1.3when the limiting values f k 0 are finite and m −1<α<m .This formula simplifies to L {D αf t ;s } s α f s 21 .Also,two-parametric Mittag-Le ffler function is defined by E α,β z ∞k 0z k /Γ kα β for α>0and β>0 21 .Analytic properties and asymptotical expansion of this function are given in 9 .For example,if α<2,πα/2<μ<min π,πα ,β∈R and c 3is a real constant,then |E α,β z |≤c 3/ 1 |z | ,whenever |z |≥0and μ≤|arg z |≤π.Also,by using the formula for integration of the Mittag-Le ffler function term by term,we have see 9z 0t β−1E α,β λt α dt z βE α,β 1 λt α . ∗ Let P be a cone in a Banach space E .The map θ:P → 0,∞ is said to be a nonnegative continuous concave functional whenever θis continuous and θ tx 1−t y ≥tθ x 1−t θ y for all x,y ∈P and 0≤t ≤1 20 .We need the following fixed point theorems for obtaining our results.Lemma 1.1 see 22 .Let E be a Banach space,P a cone in E ,and Ω1,Ω2two bounded open balls of E centered at the origin with Ω1⊂Ω2.Suppose that A :P ∩ Ω2\Ω1 →P is a completely con-tinuous operator such that eitheri Ax ≤ x ,x ∈P ∩∂Ω1and Ax ≥ x ,x ∈P ∩∂Ω2,orii Ax ≥ x ,x ∈P ∩∂Ω1and Ax ≤ x ,x ∈P ∩∂Ω2holds.Then A has a fixed point in P ∩ Ω2\Ω1 .Lemma1.2 see 23 .Let P be a cone in a real Banach space E,c,b,and d positive real numbers, P c {x∈P: x ≤c},θa nonnegative concave functional on P such thatθ x ≤ x for all x∈P c andP θ,b,d {x∈P:b≤θ x , x ≤d}. 1.4Suppose that A:P c→P c is completely continuous and there exist constants0<a<b<d≤c such thatc1 {x∈P θ,b,d :θ x >b}/ ∅,and for some x∈P θ,b,d we haveθ Ax >b,c2 Ax <a for all x with x ≤a,c3 θ Ax >b for all x∈P θ,b,c with Ax >d.Then A has at least threefixed points x1,x2,and x3such that x1 <a,b<θ x2 ,a< x3 with θ x3 <b.Note that the condition c1 implies c3 whenever d c.2.Main ResultsAs we know,there is an integral form of the solution for the following equation:D a0 u t Dβ0 u t f t,u t ,u 0 0,0<t<1, 2.1Suppose that the functions u and f are continuous on 0,1 .Then u t tG t−τ f τ,u τ dτis a solution for 2.1 ,where G t tα−1Eα−β,α −tα−β and Eα,βis the two-parameter function of the Mittag-Leffler type see 9 .Now,we give an equivalent solution for 2.1 .In fact,if we apply the Laplace transform to 2.1 ,then by using a calculation andfinding the inverse Laplace transform we get that u t tα−1Eα−β,α −tα−β ∗f t,u t is an equivalent solution for 2.1 .In this way,note thatDαu t Dβu tDαG t DβG t∗f t,u t , 2.2where G t tα−1Eα−β,α −tα−β .But,we haveDαG t DβG t t−1Eα−β,0−tα−βtα−β−1Eα−β,α−β−tα−βEα−β,0−tα−β−Eα−β,0−tα−β−1t1Γα−β.2.3Since lim t→0 1/t 1/Γ α−β δ t ,we get DαG t DβG t δ t and soDαu t Dβu t δ t ∗f t,u t f t,u t . 2.4 Now,we establish some results on existence and multiplicity of positive solutions for the problem 2.1 .Let E C 0,1 , · ∞ be endowed via the order u≤v if and only if u t ≤v tfor all t ∈ 0,1 .Consider the cone P {u ∈E |u t ≥0}and the nonnegative continuous concave functional θ u inf 1/2<t<1|u t |.Now,we give our first result.Lemma 2.1.Define T :P →P by Tu t : t 0G t −τ f τ,u τ dτ,where G t t α−1E α−β,α −t α−βand E α,β z is the two-parameter function of the Mittag-Le ffler type.Then T is completely continuous.Proof.Since the mappings G and f are nonnegative and continuous,it is easy to see that T is continuous.Now,we show that T is a relatively compact operator.This implies that T is com-pletely continuous.Let Ω⊂P be a bounded subset.Then there exists a positive constant M >0such that u ≤M for all u ∈Ω.Put L sup 0≤t ≤1|f t,u t | 1.Then,for each u ∈Ω,we have|Tu t | t 0 t −τ α−1E α−β,α − t −τ α−β f τ,u τ dτ ≤L −t αE α−β,α 1 −t α−β ≤L −t α1 −t α−β ≤Lt α≤L, 2.5where 0<α<1and t ∈ 0,1 .Thus,T is uniformly bounded.Now,we show that T is equi-continuous.Let t,τ∈ 0,1 and t 1≤t 2.Thus,|Tu t 1 −Tu t 2 | t 10G t 1−τ f τ,u τ dτ− t 20G t 2−τ f τ,u τ dτ t 10 G t 1−τ f τ,u τ −G t 2−τ f τ,u τ dτ t 1t 2G t 2−τ f τ,u τ dτ ≤ t 10 G t 1−τ f τ,u τ −G t 2−τ f τ,u τ dτ t 1t 2G t 2−τ f τ,u τ dτ . 2.6Now,by using the formula for integration of the Mittag-Le ffler function term by term given in ∗ ,we obtain that|Tu t 1 −Tu t 2 |≤ f ⎡⎣⎛⎝t α11 −t α−β1 −t α11 −t α−β1 t 2−t 1 α1 − t 2−t 1 α−β⎞⎠ ⎛⎝t α21 −t α−β2 −t α11 −t α−β1 − t 2−t 1 α1 − t 2−t 1 α−β ⎞⎠⎤⎦ f ⎡⎣t α21 −t α−β2 −t α11 −t α−β1 ⎤⎦≤ f ⎡⎢⎣ t α2−t α1 −t α2 t α−β2−t α−β1 t α−β2 t α2−t α1 1 −t α−β1 1 −t α−β2⎤⎥⎦. 2.7Thus,by using the formula t s 2−t s 1 t 2−t 1 / t s −12 ··· t s −11 ,we obtain a common factor t 1−t 2 .This implies that small changes of u cause small changes of Tu .that is,T is equicontinuous.Now by using the Arzela-Ascoli theorem,we get that T is a relatively compactoperator.Theorem 2.2.Suppose that in the problem 1.2 there exists a positive real number r >0such thatA 1 f t,u ≤αr for all t,u ∈ 0,1 × 0,r ,A 2 f t,u ≥0for all t ∈ 0,1 with u t 0.Then the problem 1.2 has a positive solution u such that 0≤|u |≤r .Example 2.3.Consider the nonlinear fractional di fferential equation initial value problemD 3/2u t D 1/2u t u t sin t 0,u 0 0, 0<t <1 . 2.8Put r 2and α 3/2.Since f t,u u t sin t ≤u 1≤3 αr for all t,u ∈ 0,1 × 0,2 and f t,u u sin t ≥0for all t,u ∈ 0,1 ×{0},by using Theorem 2.2we get that this problem has a positive solution we get that this problem has a positive solution u with 0≤ u ≤2.Proof.First,let us to consider the operator Tu t t 0G t −τ f τ,u τ dτ,where G tt α−1E α−β,α −t α−β 0<β<α<1 .By using Lemma 2.1,T is completely continuous and note that u is a solution of the problem 1.2 if and only if u T u .Let Ω1 {u ∈P : u 0}and Ω2 {u ∈P : u u ∈∂Ω1}we have u t 0for all t ∈ 0,1 .By using the assumption A 2 ,we haveTu t t0G t −τ f τ,u τ dτ≥0 u 2.9and so Tu ≥ u .Also,for u ∈∂Ω2we have 0≤u t ≤r for all t ∈ 0,1 .By using the assumption A 1 we haveTu max 0≤t ≤1 t 0G t −τ f τ,u τ dτ≤αr t 0 t −τ α−1dτ rt α≤r u . 2.10This completes theproof.Theorem 2.4.Suppose that in the problem 2.1 there exist positive real numbers 0<a <b <c such thatA 1 f t,u <αa for all t,u ∈ 0,1 × 0,a ,A 2 f t,u >Nb for all t,u ∈ 1/2,1 × b,c ,whereN −1 inf 1/2<t<1 t 0G t −s ds , 2.11A 3 f t,u ≤αc for all t,u ∈ 0,1 × 0,c .Then the problem 2.1 has at least there positive solutions u 1,u 2,and u 3such that sup 0≤t ≤1|u 1 t |<a ,b <inf 1/2≤t ≤1|u 2 t |<sup 1/2≤t ≤1|u 2 t |≤c,a <sup 0≤t ≤1|u 3 t |≤c and inf 1/2≤t ≤1|u 3 t |<b .Proof.Define P c {x ∈P : x ≤c }.Then, u ≤c for all u ∈P c .Note that,the assumption A 3 implies that f t,u t ≤αc for all t .Thus,Tu sup 0≤t ≤1 t 0G t −τ f τ,u τ dτ ≤αc t 0 t −τ α−1dτ αc t αα ct α≤c. 2.12Hence,T is a operator on P c .Also,note that the assumption A 1 implies that f t,u t <αa for all 0≤t ≤1.Thus,the condition c 2 in Lemma 1.2holds.It is su fficient that we show that the condition c 1 in Lemma 1.2holds.Put u t b c /2for all 0≤t ≤1.It is easy to see that u t ∈P θ,b,c and θ u θ b c /2 >b .Thus,{u ∈P θ,b,c :θ u >b }/ ∅and so b ≤u t ≤c for all u ∈P θ,b,c and 1/2≤t ≤1.But,the assumption A 2 implies that f t,u t ≥Nb for all 1/2≤t ≤1and soθ Tu inf 1/2≤t ≤1| Tu t | inf 1/2≤t ≤1 t 0G t −τ f τ,u τ dτ >NbN −1 b. 2.13Thus,θ Tu >b for all u ∈P θ,b,c .This shows that the condition c 1 in Lemma 1.2holds.This completes the proof.AcknowledgmentsResearch of the second and third authors was supported by Azarbaijan University of Shahid Madani.Also,the authors express their gratitude to the referees for their helpful suggestions which improved final version of this paper.References1 R.P .Agarwal,D.O’Regan Donal,and S.Stan ˇe k,“Positive solutions for Dirichlet problems of singular nonlinear fractional di fferential equations,”Journal of Mathematical Analysis and Applications ,vol.371,no.1,pp.57–68,2010. 2 K.Balachandran,S.Kiruthika,and J.J.Trujillo,“Remark on the existence results for fractional impulsive integrodi fferential equations in Banach spaces,”Communications in Nonlinear Science and Numerical Simulation ,vol.17,no.6,pp.2244–2247,2012. 3 F.Chen,J.J.Nieto,and Y.Zhou,“Global attractivity for nonlinear fractional di fferential equations,”Nonlinear Analysis.Real World Applications ,vol.13,no.1,pp.287–298,2012. 4 D.B ˘a leanu,R.P .Agarwal,O.G.Mustafa,and M.Cos ¸ulschi,“Asymptotic integration of some nonlinear di fferential equations with fractional time derivative,”Journal of Physics A ,vol.44,no.5,Article ID 055203,2011. 5 D.B ˘a leanu,K.Diethelm,E.Scalas,and J.J.Trujillo,Fractional Calculus Models and Numerical Methods ,Complexity,Nonlinearity and Chaos,World Scientific,2012. 6 A.A.Kilbas,O.I.Marichev,and S.G.Samko,Fractional Integrals and Derivatives ,Gordon and Breach Science,Yverdon,Switzerland,1993. 7 A.A.Kilbas,H.M.Srivastava,and J.J.Trujillo,Theory and Application of Fractional Di fferential Equa-tions ,vol.204of North-Holland Mathematics Studies ,Elsevier,2006. 8 ler and B.Ross,An Introduction to the Fractional Calculus and Fractional Di fferential Equations ,John Wiley &Sons,New York,NY,USA,1993.9 I.Podlubny,Fractional Differential Equations,vol.198of Mathematics in Science and Engineering,Aca-demic Press,San Diego,Calif,USA,1999.10 R.Gorenflo and F.Mainardi,“Fractional calculus:integral and differential equations of fractionalorder,”in Fractals and Fractional Calculus in Continuum Mechanics(Udine,1996),vol.378of CISM Courses and Lectures,pp.223–276,Springer,Vienna,Austria,1997.11 R.Gorenflo and F.Mainardi,“Fractional relaxation of distributed order,”in Complexus Mundi,pp.33–42,World Scientific,Hackensack,NJ,USA,2006.12 F.Mainardi,A.Mura,G.Pagnini,and R.Gorenflo,“Sub-diffusion equations of fractional order andtheir fundamental solutions,”in Proceedings of the International Symposium on Mathematical Methods in Engineering,J.A.Tenreiro-Machado and D.Baleanu,Eds.,pp.23–55,Springer,Ankara,Turkey,2006.13 F.Mainardi,Y.Luchko,and G.Pagnini,“The fundamental solution of the space-time fractionaldiffusion equation,”Fractional Calculus&Applied Analysis,vol.4,no.2,pp.153–192,2001.14 A.V.Chechkin,R.Gorenflo,I.M.Sokolov,and V.Yu.Gonchar,“Distributed order time fractionaldiffusion equation,”Fractional Calculus&Applied Analysis,vol.6,no.3,pp.259–279,2003.15 A.Kochubei,“Distributed order calculus and equations of ultraslow diffusion,”Journal of Mathe-matical Analysis and Applications,vol.340,no.1,pp.252–281,2008.16 ler,“Fractional differential equations,”Journal of Fractional Calculus,vol.3,pp.49–57,1993.17 V.Daftardar-Gejji and A.Babakhani,“Analysis of a system of fractional differential equations,”Jour-nal of Mathematical Analysis and Applications,vol.293,no.2,pp.511–522,2004.18 S.Q.Zhang,“The existence of a positive solution for a nonlinear fractional differential equation,”Jour-nal of Mathematical Analysis and Applications,vol.252,no.2,pp.804–812,2000.19 S.Q.Zhang,“Existence of positive solution for some class of nonlinear fractional differential equa-tions,”Journal of Mathematical Analysis and Applications,vol.278,no.1,pp.136–148,2003.20 Z.Bai and H.L¨u,“Positive solutions for boundary value problem of nonlinear fractional differentialequation,”Journal of Mathematical Analysis and Applications,vol.311,no.2,pp.495–505,2005.21 M.Stojanovi´c,“Existence-uniqueness result for a nonlinear n-term fractional equation,”Journal ofMathematical Analysis and Applications,vol.353,no.1,pp.244–255,2009.22 M.A.Krasnoselski,Positive Solutions of Operator Equations,P.Noordhoff,Groningen,The Netherlands,1964.23 R.W.Leggett and L.R.Williams,“Multiple positivefixed points of nonlinear operators on orderedBanach spaces,”Indiana University Mathematics Journal,vol.28,no.4,pp.673–688,1979.。
