2.4质点的角动量定理和角动量守恒定律
合集下载
角动量定理 角动量守恒定律
10 4 mg sin 1 mg cos 1 3 3 1 6
.
f2
N2
2
l mg O
f1 l 1 2mg N1
由于球 1 的初始位置紧靠轻杆末端，因此球 1 脱离 细杆时细杆与水平线夹角也为
1
6
因轻杆没有质量，球 1 一旦脱离轻杆，球 2 与轻杆间的相互作用 立即消失，此后球 2 只受重力作用而作斜抛运动，其初速度：
若M 0 L L0 ——质点系的角动量守恒
内力不改变系统的总角动量
t0
例 6.1 如图，质量为 m 的小球，拴于不可伸长的 轻绳上，在光滑水平桌面上作匀速圆周运动，其 半径为 R，角速度为 ，绳的另一端通过光滑的竖 直管用手拉住，如把绳向下拉 R/2 时角速度 为 多少？
m
R
F
解：
L mvR mR
2
R 1 2 L' mv' mR ' 2 4
L L'
' 4
m
R
F
例6.2 如图所示，质量为 m的小球 B放在光滑的水平 槽内，现以一长为 l的细绳连接另一质量为m的小球
A，开始时细绳处于松弛状态, A与B相距为l/2。球A
以初速度v0 在光滑的水平地面上向右运动。当A运 动到图示某一位置时细绳被拉紧，试求B球开始运 动时速度vB的大小。
3gl 2 g sin 1 v0 l 3l 3
y v0 B2 A
0
初速度的方向与水平线的夹角：
0
2 1
3
mg
l O
2 1
x
得任意 t 时刻球2的位置坐标：
.
f2
N2
2
l mg O
f1 l 1 2mg N1
由于球 1 的初始位置紧靠轻杆末端，因此球 1 脱离 细杆时细杆与水平线夹角也为
1
6
因轻杆没有质量，球 1 一旦脱离轻杆，球 2 与轻杆间的相互作用 立即消失，此后球 2 只受重力作用而作斜抛运动，其初速度：
若M 0 L L0 ——质点系的角动量守恒
内力不改变系统的总角动量
t0
例 6.1 如图，质量为 m 的小球，拴于不可伸长的 轻绳上，在光滑水平桌面上作匀速圆周运动，其 半径为 R，角速度为 ，绳的另一端通过光滑的竖 直管用手拉住，如把绳向下拉 R/2 时角速度 为 多少？
m
R
F
解：
L mvR mR
2
R 1 2 L' mv' mR ' 2 4
L L'
' 4
m
R
F
例6.2 如图所示，质量为 m的小球 B放在光滑的水平 槽内，现以一长为 l的细绳连接另一质量为m的小球
A，开始时细绳处于松弛状态, A与B相距为l/2。球A
以初速度v0 在光滑的水平地面上向右运动。当A运 动到图示某一位置时细绳被拉紧，试求B球开始运 动时速度vB的大小。
3gl 2 g sin 1 v0 l 3l 3
y v0 B2 A
0
初速度的方向与水平线的夹角：
0
2 1
3
mg
l O
2 1
x
得任意 t 时刻球2的位置坐标：
大学物理角动量转动惯量及角动量的守恒定律
方向垂直于轴，其效果是改
变轴的方位，在定轴问题中，
第二项
与轴承约束力矩平衡。
M 2rF
方称为向力平对行于轴的轴矩，，其效表果为代是数改变量绕：轴M 转z 动 状r态，F
即： i j k
Mo rFx y z
Fx FyFz
i yFz zFy jzFxxFzk xFyyFx
Mz xFyyFx
由
rc
i
miri M
rc
i
miri M
ri m ivcM rc vc0
i
质心对自己的位矢
L r c m iv ir i m iv c r i m iv i
i
i
i
与 i 有关
第三项：
rimivi 各质点相对于质心角动量的矢量和
i
反映质点系绕质心的旋转运动，与参考点O的选择无关，
o ri
vi
mi
L io 大 方小 向 Lio ： ： rimiv沿 i miri2 即 L iomiri2
在轴上确定正方向，角速度 表示为代数量，则
定义质点对 z 轴的角动量为:
LizLiom iri2
刚体对 z 轴的总角动量为：
Lz Liz ri2mi
i
i
ri2mi
i
对质量连续分布的刚体：
02
3
4. 求质量 m ,半径 R 的均匀球体对直径的转动惯量
解：以距中心 r，厚 dr 的球壳
dr
R
r
o
为积分元
dV4r2dr
m
m
4 R3
3
dJ3 2dmr22m R3 4rdr
dm dV
J
R
dJ
质点系角动量守恒定律
第五章 角动量•关于对称性
前言 质点的角动量 质点系的角动量定理及角动量守恒定律 质点系对质心的角动量定理和守恒定律 对称性 • 对称性与守恒律 经典动力学的适用范围
§5.1 前
一、本章的基本内容及研究思路
言
角动量概念的建立和转动有密切联系，在研究物体的运动 时，人们经常可以遇到质点或质点系绕某一确定点或轴线运动 的情况，并且在这类运动中也存在着某些共同的重要规律。例 如，天文观测表明，行星绕日运动遵从开普勒第二定律，在近 日点附近绕行速度较快，远日点速度较慢，这个特点如果用角 动量及其规律很容易说明。特别是在有些过程中动量和机械能
都不守恒，却遵从角动量守恒定律，这就为求解这类运动问题 开辟了新途径。
角动量不但能描述经典力学中的运动状态，在近代物理理 论中仍然是表征微观运动状态的重要物理量，例如原子核的角 动量，通常称为原子核的自旋，就是描写原子核特性的。 角动量守恒定律和动量守恒定律一样，是自然界最基本最
普遍的定律之一。由于角动量这个物理量，从概念到数学表达，
都比动量要难理解，我们循序渐进逐步深入地来理解。 本章还要触及对称性的概念，尽管经典力学中的对称性没
有在微观领域中那么重要，但是介绍一下与本课水平相当的对
称性问题是十分有益的。
二、本章的基本要求
1. 理解质点及质点系角动量的物理意义； 2. 掌握质点、质点系的角动量定理； 3. 掌握角动量守恒定律； 4. 理解对称性的概念，了解守恒律与对称性的关系。
由上（1）式可以看出，在过程中如果外力对参考点的力矩
的矢量和始终为零，则质点系对该点的角动量保持不变，称为 质点系对该点的角动量守恒定律，即
当τi 0时,
L 常量.
由（2）式可以看出，有时外力矩对参考点虽不为零，但 是，外力矩沿某固定的 z 轴分量为零，则质点系对 z 轴的角动 量保持不变，叫做质点系对 z 轴的角动量守恒定律。即
前言 质点的角动量 质点系的角动量定理及角动量守恒定律 质点系对质心的角动量定理和守恒定律 对称性 • 对称性与守恒律 经典动力学的适用范围
§5.1 前
一、本章的基本内容及研究思路
言
角动量概念的建立和转动有密切联系，在研究物体的运动 时，人们经常可以遇到质点或质点系绕某一确定点或轴线运动 的情况，并且在这类运动中也存在着某些共同的重要规律。例 如，天文观测表明，行星绕日运动遵从开普勒第二定律，在近 日点附近绕行速度较快，远日点速度较慢，这个特点如果用角 动量及其规律很容易说明。特别是在有些过程中动量和机械能
都不守恒，却遵从角动量守恒定律，这就为求解这类运动问题 开辟了新途径。
角动量不但能描述经典力学中的运动状态，在近代物理理 论中仍然是表征微观运动状态的重要物理量，例如原子核的角 动量，通常称为原子核的自旋，就是描写原子核特性的。 角动量守恒定律和动量守恒定律一样，是自然界最基本最
普遍的定律之一。由于角动量这个物理量，从概念到数学表达，
都比动量要难理解，我们循序渐进逐步深入地来理解。 本章还要触及对称性的概念，尽管经典力学中的对称性没
有在微观领域中那么重要，但是介绍一下与本课水平相当的对
称性问题是十分有益的。
二、本章的基本要求
1. 理解质点及质点系角动量的物理意义； 2. 掌握质点、质点系的角动量定理； 3. 掌握角动量守恒定律； 4. 理解对称性的概念，了解守恒律与对称性的关系。
由上（1）式可以看出，在过程中如果外力对参考点的力矩
的矢量和始终为零，则质点系对该点的角动量保持不变，称为 质点系对该点的角动量守恒定律，即
当τi 0时,
L 常量.
由（2）式可以看出，有时外力矩对参考点虽不为零，但 是，外力矩沿某固定的 z 轴分量为零，则质点系对 z 轴的角动 量保持不变，叫做质点系对 z 轴的角动量守恒定律。即
角动量、角动量守恒
T
（3） ）
m, l
联立(1)、(2)、(3)式求解 式求解 联立
mg
1 T = mg 4
例5：在光滑水平桌面上放置一个静止的质量 ： 可绕中心转动的细杆， 为 M、长为 2l 、可绕中心转动的细杆，有一质 、 量为 m 的小球以速度 v0 与杆的一端发生完全弹 性碰撞， 性碰撞，求小球的反弹速度 v 及杆的转动角速 度ω。 解：在水平面上，碰撞 在水平面上， 过程中系统角动量守恒， 过程中系统角动量守恒，
∆A/ ∆t = 恒 量
两个共轴飞轮转动惯量分别为J 例1：两个共轴飞轮转动惯量分别为 1、J2， 角速度分别为 ω1 、ω2，求两飞轮啮合后共同 啮合过程机械能损失。 的角速度 ω 。啮合过程机械能损失。 J1 J2 解：两飞轮通过摩 擦达到共同速度,合 擦达到共同速度 合 外力矩为0， 外力矩为 ，系统角 动量守恒。 动量守恒。
定义：力对某点 的力矩等于力的作用点 定义：力对某点O的力矩等于力的作用点 的矢量积。 的矢径 r 与力F的矢量积。 v v
v Mo
ϕ
注意： 注意： 1）大小： o = rF sin ϕ ）大小： M v v 的方向 2）方向： × F ）方向： r 3）单位：牛顿米 ）单位： v r 4）当 F ≠ 0 时， ） 有两种情况 Mo = 0 v A） r = 0 ） B）力的方向沿矢径的方向（ sin ϕ = 0） ）力的方向沿矢径的方向（
ω1 L0 = L = C J1ω1 + J2ω2 = (J1 + J2 )ω
ω2
J1ω1 + J2ω2 共同角速度 ω = J1 + J2
啮合过程机械能损失
∆E = E − E0
1 1 1 2 2 2 ∆E = (J1 + J2 )ω − ( J1ω1 + J2ω2 ) 2 2 2 J1ω1 + J2ω2 其中 ω = J1 + J2
质点角动量定理 角动量守恒
v2
o
v1
4)角动量守恒定律是物理学的基本定律之一。不 仅适用于宏观体系，也适用于微观系统。
2.5 质点角动量定理 角动量守恒
例1 一小球在光滑平面上作圆运动，小球被穿 过中心的线拉住 。开始时绳半径为r1 ，小球速 率为 v1 ；后来，往下拉绳子，使半径变为 r2 ， 小球速率变为 v2 ，求v2 =？
ri fi 0
i
有
dL M外 dt
质点系的角动量定理：质点系对某定点的角 动量的时间变化率等于质点系对该点的合外 力矩。
2.5 质点角动量定理 角动量守恒
结论：
1）内力对定点的力矩之和为零。 2）只有外力矩才能改变系统的总角动量。 3.质点系的对轴的角动量
L Lx i Ly j Lz k
当质点系对某点的合外力矩为零时，则质点 系对该点的角动量保持不变，称为角动量守恒定 律。
角动量守 恒例题
2.5 质点角动量定理 角动量守恒
盘状星系——角动量守恒的结果
质点系对o点的角动量
r2
o
r1
L Li ri Pi
i i
质点系对o点的角动量等于系统中各质点对 同一点角动量的矢量和。
2.5 质点角动量定理 角动量守恒
2.质点系的角动量定理
用 f i 表示第i个质点所受内力之和
用 Fi 表示第i个质点所受外力之和
三、质点的角动量定理 dP 由牛顿第二定律 F dt
dP 两边用位矢叉乘 r F r dt dp d dr r (r p) p dt d dt t
由速度定义
dr v v p 0 dt
质点的角动量
i
ri p i ,
对于标号为i的质点，它不仅受到来自系统外的作用力，而且 还受到系统内其它质点的作用力（内力）
fi
j
f ij ,
利用质点的角动量定理 可得
d dt
d Li dt
ri Fi f i ,
i
i
Li
i
ri ( Fi f i )
r1 , 以角速度 1旋转，然后慢慢向下拉 离为 r2时，拉力对质点所做的
v
绳，求质点离圆心距
功。
选小孔为参考点，任意 时刻质点受力矩 M r f 0 , 质点的角动量守恒，因 而有：
o r f
f
mr 1 1 mr 2 2
2 2
根据动能定理，外力做功为
v
O
rห้องสมุดไป่ตู้m
若一个质量为m的粒子在半径为r的圆周上以速 v 运动，则它的动量为 P m v ,相对于圆心的 度 位置矢量 r 与粒子运动速度 v 互相垂直 ，角 动量大小为： L m rv m r 2
是质点运动的角速度
角动量的方向由右手螺旋法则判断，垂直于物体转动 所在的平面
2
1
4、推广到质点系情形
利用牛顿第三定律，我们还可以将质点角动量定律推广到质 点系的情况，得到质点系总角动量的时间变化率与合外力 矩的简单关系，即质点系的角动量定理。 我们定义质点系对给定参考点O的总角动量为系统内所有质 点对选定参考点O的角动量的矢量和，即 ：
L
i
Li
多个外力作用于同一个质点的合力矩等于各 力的力矩的矢量和，即如果
质点的角动量定理及角动量守恒定律
第六章角动量内容：§6－1 力矩（4课时）§6－2 质点的角动量定理及角动量守恒定律（4课时）要求：１.熟练掌握力对点的力矩。
２.理解对点的角动量定理及角动量守恒定律。
重点与难点：角动量守恒定律。
作业：P219 1，2，3，4，P220 5，6，，第六章角动量§6－1 力矩一、力对点的力矩：如图所示，定义力对O点的力矩为：大小为：力矩的方向：力矩是矢量，其方向可用右手螺旋法则来判断：把右手拇指伸直，其余四指弯曲，弯曲的方向由矢径通过小于1800的角度转向力的方向时，拇指指向的方向就是力矩的方向。
二、力对转轴的力矩：力对O点的力矩在通过O点的轴上的投影称为力对转轴的力矩。
1）力与轴平行，则；2）刚体所受的外力在垂直于转轴的平面内，转轴和力的作用线之间的距离称为力对转轴的力臂。
力的大小与力臂的乘积，称为力对转轴的力矩，用表示。
力矩的大小为：或：其中是与的夹角。
3）若力不在垂直与转轴的平面内，则可把该力分解为两个力，一个与转轴平行的分力，一个在垂直与转轴平面内的分力，只有分力才对刚体的转动状态有影响。
对于定轴转动，力矩的方向只有两个，沿转轴方向或沿转轴方向反方向，可以化为标量形式，用正负表示其方向。
三、合力矩对于每个分力的力矩之和。
合力合外力矩即四、单位：注意：力矩的单位和功的单位不是一回事，力矩的单位不能写成焦耳。
（1）与转动垂直但通过转轴的力对转动不产生力矩；（2）与转轴平行的力对转轴不产生力矩；§6－2 质点的角动量定理及角动量守恒定律在讨论质点运动时，我们用动量来描述机械运动的状态，并讨论了在机械运动过程中所遵循的动量守恒定律。
同样，在讨论质点相对于空间某一定点的运动时，我们也可以用角动量来描述物体的运动状态。
角动量是一个很重要的概念，在转动问题中，它所起的作用和(线)动量所起的作用相类似。
在研究力对质点作用时，考虑力对时间的累积作用引出动量定理，从而得到动量守恒定律；考虑力对空间的累积作用时，引出动能定理，从而得到机械能守恒定律和能量守恒定律。
物理-角动量定理与角动量守恒定律
dt
dt
i
当质点系相对惯性系中某给定参考点的合外力 矩为零时，该质点系对同一参考点的总角动量保持 不变。
——角动量守恒定律
当 M Mi 0，则L Li 恒矢量
Hale Waihona Puke 说明1、同一问题中应 用角动量定理或判断角动量守恒时， M 与 L 必须相对同一参考点计算！
2、如果相对某一特殊参考点，合外力矩为零，系统只 只对这一特殊点角动量守恒，但相对其他参考点的 角动量不一定也守恒；
当 M Mi 0，则L Li 恒矢量
说明
3、关于角动量守恒与动量守恒的条件：
一般地
(ri Fi ) 0 与
Fi 0 彼此独立！
角动量守恒与动量守恒也是相互独立的。
例：行星在绕太阳的公转过程：动量不守恒，
但对太阳的角动量守恒。
MS
rF
0
z LS
LS
r m
恒矢量
S
如直角坐标系中。沿 z 轴分量式为：
当 Mz Miz 0，则Lz Liz 恒量
5. 适用范围：惯性系；
讨论：为什么许多星系是扁盘状旋转结构？
银河系
讨论：为什么许多星系是扁盘状旋转结构？
初始角动量
径向
轴向
引力 收缩
L守恒
引力 收缩
速度增大 离心力增大
引力 收缩
达到平衡
高速旋转的盘形结构
dL L2 (t2 ) L1(t1 )
t1
L1 (t1 )
—— M在时间t t2 t1内的角冲量（冲量矩）
（积分式）
对同一参考点，质点所受合力在某一时间内的 角冲量等于同时间内角动量的增量 。
说明
•直角坐标系中的分量式（如Z轴分量式）：
质点系的角动量定理
fi
j i
fij
ri
fi
i
ji
r
i
dLi
dt
fij
ddti
L
i
fi
mi fij
ri ri rj
fji
mj
fj
i
ji
ri
合fi内j 力12矩i,j为(i j零) ri
fij
rj
O f ji
即证。
1 2i, j(i j)
r i
rj
f 0
ij
rj
4
内力矩可影响质点系中某质点的角动量，但 合内力矩等于零，对总角动量无影响。
当质点系相对于惯性系中某定点所受的合外 力矩为零时，该质点系相对于该定点的角动量 将不随时间改变—质点系的角动量守恒定律
孤立或在有心力作用下的系统角动量守恒。
宇宙中的天体可以认为是孤立体系。它Βιβλιοθήκη 具 有旋转盘状结构，成因是角动量守恒。
5
盘状星系
6
L
球形原始气云具有初始角动量L，在垂直于L方向， 引力使气云收缩 角动量守恒 粒子的旋转速度 惯性离心力，离心力与引力达到平衡，维持一 定的半径。 但在与L平行的方向无此限制，所 以形成了旋转盘状结构。
7
例题
讨论行星运动
F与
r在一直线上
M rF 0
rF
L 常矢量
S
v
1面、LL方向不r 变m v 轨道面是平 v远
r远
2、 L = 常量= r m v sin r v sin = 常量
量矢径单位时间行扫过的面积是常量
v近
o
r近
S= 常
在近日点与远日点 sin =1
大学物理-角动量守恒定律
1 dA ( r sin )ds 2
4-3 角动量
角动量守恒定律
dA 1 ds 1 ( r sin ) r sin v dt 2 dt 2 1 1 r sin mv rp 2m 2m 而行星的角动量 r p 大小恒定，所以 dA 常量 dt
一般情形下， r 和 p 都是变化的，所以 L 没 有确定的方向，但任一时刻， L 总垂直于 r 和 p 所确定的平面。在直角坐标系下，L 的三个分量
为：
3
Lx ypz zp y Ly zpx xpz Lz xp y ypx
4-3 角动量
这就是开普勒第二定律。 如果一个力的方向始终指向某一点，这力称 为有心力，这点，称为力心。有心力对力心的力 矩恒为0，因此，在有心力作用下的质点对力心 的角动量守恒。 10
4-3 角动量
角动量守恒定律
质点系角动量变化定理和角动量守恒定律 1. 质点系角动量
L l i ri 量
角动量守恒定律
3. 角动量守恒定律 如果质点系所受合外力矩 M 外 0，则
dL 0 ，L 常矢量 dt
实验表明，对于不受外界影响的粒子系统所 经历的任意过程，包括不能用牛顿力学描述的 过程，都遵守角动量守恒定律。
13
4-3 角动量
角动量守恒定律
【例1.21】光滑水平面上轻弹簧两端各系一小球， 开始弹簧处于自然长度，两小球静止。今同时 打击两个小球，让它们沿垂直于弹簧轴线方向 获得等值反向的初速度v0。如果在以后的运动过 程中弹簧的最大长度为2l0，求初速度v0。 解 系统：弹簧和小球 质心C点固定不动，相对 C点系统的角动量守恒。
必须指明是对哪个点而言的
质点的角动量角动量守恒定律
物理学
第五版
角动量概念的提出与自然界普遍存在的物体的转动 有关，大到星系，小到电子、中微子都具有转动的特征。 角动量概念在18世纪才在物理学中被定义和使用，19世 纪人们才把它看成是力学中最基本的概念之一，到20世 纪，它成为和动量、能量同样重要的物理量。角动量守 恒与空间旋转对称性相对应。因此它是自然界最基本最
普遍的规律之一。
角动量
角动量 变化率
角动量 角动量守
力矩
定理
恒定律
物理学
第五版
一、质点的角动量 质量为 的质点以
速度 在空间运动，某 时对 O 的位矢为 ，质 点对O的角动量
大小 的方向符合右手法则 角动量单位：kg·m2·s-1
物理学
第五版
质点以 作半径为 的圆运动，相对圆心
质点在一条直线上运动, 质点对 o点的角动量?
o•
m
力矩是矢量，M 的方向垂直于r和 F所决定的平面，其指向
用右手螺旋法则确定。
2 、 力矩的单位、 牛·米(N·m)
3 、力矩的计算： M 的大小、方向均与参考点的选择有关
物理学
第五版
力对固定点的力矩为零的情况：
A）
B）力的方向沿矢径的方向（
）
有心力的力矩为零.
※在直角坐标系中，其表示式为
物理学
第五版
三、质点的角动量定理 质点角动量定理的推导
物理学
第五版
作用于质点的合力对参考点 O
的力矩，等于质点对该点 O 的角动量
随时间的变化率.
冲量矩
质点的角动量定理：对同一参考点O， 质点所受的冲量矩等于质点角动量的增量.
与质点的动量定理比较:
物理学
第五版
例 一半径为 R 的 光滑圆环置于竖直平面 内. 一质量为 m 的小球 穿在圆环上, 并可在圆 环上滑动. 小球开始时 静止于圆环上的点 A (该点在通过环心 O 的 水平面上)，然后从 A 点开始下滑．设小球与圆环间的摩擦略去 不计．求小球滑到点 B 时对环心 O 的角动 量和角速度．
第五版
角动量概念的提出与自然界普遍存在的物体的转动 有关，大到星系，小到电子、中微子都具有转动的特征。 角动量概念在18世纪才在物理学中被定义和使用，19世 纪人们才把它看成是力学中最基本的概念之一，到20世 纪，它成为和动量、能量同样重要的物理量。角动量守 恒与空间旋转对称性相对应。因此它是自然界最基本最
普遍的规律之一。
角动量
角动量 变化率
角动量 角动量守
力矩
定理
恒定律
物理学
第五版
一、质点的角动量 质量为 的质点以
速度 在空间运动，某 时对 O 的位矢为 ，质 点对O的角动量
大小 的方向符合右手法则 角动量单位：kg·m2·s-1
物理学
第五版
质点以 作半径为 的圆运动，相对圆心
质点在一条直线上运动, 质点对 o点的角动量?
o•
m
力矩是矢量，M 的方向垂直于r和 F所决定的平面，其指向
用右手螺旋法则确定。
2 、 力矩的单位、 牛·米(N·m)
3 、力矩的计算： M 的大小、方向均与参考点的选择有关
物理学
第五版
力对固定点的力矩为零的情况：
A）
B）力的方向沿矢径的方向（
）
有心力的力矩为零.
※在直角坐标系中，其表示式为
物理学
第五版
三、质点的角动量定理 质点角动量定理的推导
物理学
第五版
作用于质点的合力对参考点 O
的力矩，等于质点对该点 O 的角动量
随时间的变化率.
冲量矩
质点的角动量定理：对同一参考点O， 质点所受的冲量矩等于质点角动量的增量.
与质点的动量定理比较:
物理学
第五版
例 一半径为 R 的 光滑圆环置于竖直平面 内. 一质量为 m 的小球 穿在圆环上, 并可在圆 环上滑动. 小球开始时 静止于圆环上的点 A (该点在通过环心 O 的 水平面上)，然后从 A 点开始下滑．设小球与圆环间的摩擦略去 不计．求小球滑到点 B 时对环心 O 的角动 量和角速度．
质点角动量定理及角动量守恒定律
我们把质点对z轴上任意一点的角动量L在z轴上的投影，叫做质点对于z轴的角动量，用Lx表示．上面已证明，Lz的数值是与参考点无关的．
在国际单位制中，角动量的单位为千克·米2／秒（kg·m2·s-1）．
例1如图3-2所示，质量为m的质点以速率v绕半径为r的圆轨道作匀速率运动．求此质点相对于圆心O点的角动量．
L=|rmvsinφ|
（3.2）
式中φ是r与mv两矢量之间的夹角．
按以上定义，角动量L含有动量mv因子，因此L与参考一点的角动量也依赖于参考点的位置．例如，在图3-1b中，参考点为O点时的角动量L与参考点为O′点时的角动量L′是不同的．
应当指出的是，虽然质点相对于任一直线（例如z轴）上的不同参考点的角动量是不相等的，但这些角动量在该直线上的投影却是相等的．如图3-1b所示，取S平面与z轴垂直，则质点对于O点及O′点的角动量分别为L与L′，L和L′分别等于以r及mv为邻边及以r′及mv为邻边的平行四边形的面积，L与L′在z轴上的投影分别是Lz=Lcosα和L′z=L′cosα′（α与α′分别是L与L′和z轴间的夹角），由图3-1b可见，Lz和L′z分别是相应的两个平行四边形在S面上的投影面积，两者是相同的，故Lz=L′z．
3．行星绕太阳的运动
作为质点角动量守恒定律的应用，我们来讨论行星绕太阳的运动．16世纪末至17世纪初，开普勒仔细地分析整理了前人记录下的大量精确的有关行星运动的资料，总结出行星运动的规律、即开普勒三定律．
应用牛顿定律的万有引力定律可以全面证明这三条由天文观察资料中总结出来的实验规律．而在本课程中，只限于讨论其中的第二条，即对任一行星，由太阳到行星的径矢在相等的时间内扫过相等的面积．根据角动量守恒定律，我们可以推导出行星运动的开普勒第二定律．
角动量守恒定律是物理学中最基本的定律之一，和动量守恒定律一样，它不仅适用于宏观物体的运动，而且对于牛顿第二定律不能适用的微观粒子的运动，它也适用．
在国际单位制中，角动量的单位为千克·米2／秒（kg·m2·s-1）．
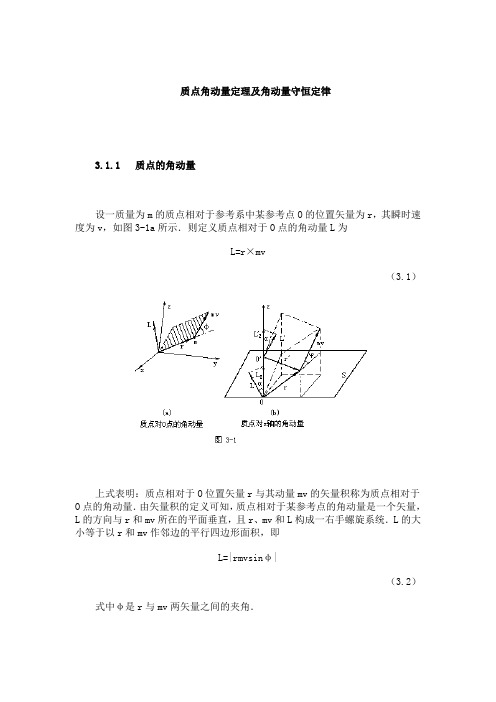
例1如图3-2所示，质量为m的质点以速率v绕半径为r的圆轨道作匀速率运动．求此质点相对于圆心O点的角动量．
L=|rmvsinφ|
（3.2）
式中φ是r与mv两矢量之间的夹角．
按以上定义，角动量L含有动量mv因子，因此L与参考一点的角动量也依赖于参考点的位置．例如，在图3-1b中，参考点为O点时的角动量L与参考点为O′点时的角动量L′是不同的．
应当指出的是，虽然质点相对于任一直线（例如z轴）上的不同参考点的角动量是不相等的，但这些角动量在该直线上的投影却是相等的．如图3-1b所示，取S平面与z轴垂直，则质点对于O点及O′点的角动量分别为L与L′，L和L′分别等于以r及mv为邻边及以r′及mv为邻边的平行四边形的面积，L与L′在z轴上的投影分别是Lz=Lcosα和L′z=L′cosα′（α与α′分别是L与L′和z轴间的夹角），由图3-1b可见，Lz和L′z分别是相应的两个平行四边形在S面上的投影面积，两者是相同的，故Lz=L′z．
3．行星绕太阳的运动
作为质点角动量守恒定律的应用，我们来讨论行星绕太阳的运动．16世纪末至17世纪初，开普勒仔细地分析整理了前人记录下的大量精确的有关行星运动的资料，总结出行星运动的规律、即开普勒三定律．
应用牛顿定律的万有引力定律可以全面证明这三条由天文观察资料中总结出来的实验规律．而在本课程中，只限于讨论其中的第二条，即对任一行星，由太阳到行星的径矢在相等的时间内扫过相等的面积．根据角动量守恒定律，我们可以推导出行星运动的开普勒第二定律．
角动量守恒定律是物理学中最基本的定律之一，和动量守恒定律一样，它不仅适用于宏观物体的运动，而且对于牛顿第二定律不能适用的微观粒子的运动，它也适用．
质点的角动量定理和角动量守恒定律
3-4
质点的角动量定理和角动量守恒定律
一、矢量的点矩和轴矩 力矩 角动量 (即动量矩) 1. 矢量的点矩. 矢量 A 的矢尾对 O 点的位置矢量为 r , 则矢量 A 对 O 点的点矩定义为
矢量 A 对 O 点的点矩与 O 点的选取有关 . 若
r // A , 则 GO = 0 . = M r 力 F 对 O 点的力矩 O × F
只需第一式乘 x 与第二式乘 y 相加, 即可导出第三
式 , 说明只 有两个 独立 的标量方 程 ; 而当 质点在 Oxy 平面内 做二维运 动 时 , 仅 一个标量方 程 , 即 第 三式 , 所以对 固 定点的角动量定 理 不 能 与 牛顿第 二定律等价.
L = r × m ( v + v ) = r × m v r × v = 0 由于 , 所以 O || || ⊥ ⊥ ,
物理力矩定义相一致 , 只是要注意 M l 为可正可 负 的标量. 二、质点对固定点 O 的角动量定理 和角动量守恒定律 由牛顿第二定律
d( mv ) r× =r×F dt d dr d ( mv ) ( r × m v ) = × m v +r× 注意到 dt dt dt . dr 因为 O 为固定点, 所以 dt = v , 所以 d dLO ( r × mv ) = r × F 即 = MO dt dt
例题 7 质量为 m 的质点受重力作用, 在一 光 滑的、 半径为 R 的球面上运动. 采用球坐标系, 设 0 已知, 又知 t 时 t 0 时刻质点位置为( R,θ 0 , ϕ 0 ), 且 ϕ . 刻质点位置为( R,θ , ϕ ). 求 t 时刻的 ϕ 解 如 图 , 以质点 m 为 研究 对 象 , O 为球 心 , 建 立 直 角 坐 标 系 Oxyz 和 球 坐 标 系 . 质 点 受 重 力 W = mg = − mgk , 约 束 力
质点的角动量定理和角动量守恒定律
一、矢量的点矩和轴矩 力矩 角动量 (即动量矩) 1. 矢量的点矩. 矢量 A 的矢尾对 O 点的位置矢量为 r , 则矢量 A 对 O 点的点矩定义为
矢量 A 对 O 点的点矩与 O 点的选取有关 . 若
r // A , 则 GO = 0 . = M r 力 F 对 O 点的力矩 O × F
只需第一式乘 x 与第二式乘 y 相加, 即可导出第三
式 , 说明只 有两个 独立 的标量方 程 ; 而当 质点在 Oxy 平面内 做二维运 动 时 , 仅 一个标量方 程 , 即 第 三式 , 所以对 固 定点的角动量定 理 不 能 与 牛顿第 二定律等价.
L = r × m ( v + v ) = r × m v r × v = 0 由于 , 所以 O || || ⊥ ⊥ ,
物理力矩定义相一致 , 只是要注意 M l 为可正可 负 的标量. 二、质点对固定点 O 的角动量定理 和角动量守恒定律 由牛顿第二定律
d( mv ) r× =r×F dt d dr d ( mv ) ( r × m v ) = × m v +r× 注意到 dt dt dt . dr 因为 O 为固定点, 所以 dt = v , 所以 d dLO ( r × mv ) = r × F 即 = MO dt dt
例题 7 质量为 m 的质点受重力作用, 在一 光 滑的、 半径为 R 的球面上运动. 采用球坐标系, 设 0 已知, 又知 t 时 t 0 时刻质点位置为( R,θ 0 , ϕ 0 ), 且 ϕ . 刻质点位置为( R,θ , ϕ ). 求 t 时刻的 ϕ 解 如 图 , 以质点 m 为 研究 对 象 , O 为球 心 , 建 立 直 角 坐 标 系 Oxyz 和 球 坐 标 系 . 质 点 受 重 力 W = mg = − mgk , 约 束 力
质点的角动量定理和角动量守恒定律
（2 ）
例题6
L 0 m r mr
2
e
k
§3-4 质点的角动量定理和角动量守恒定律
常量 r 2
掠面速度
1 r r dA A 1 2 2 lim lim r dt t 0 t t 0 t 2
角运动: 即使质点做直线运动, 只要 点在直线之外 ,角 O 运动就存在.
动量是质点线运动的度量, 角动量则是质点角运动的 度量.质点的径向运动对质点的角运动没有贡献.
r dr dA LO r mv m 2m dt dt
§3-4 质点的角动量定理和角动量守恒定律
dLO MO dt
MO r F 0
LO r mv
= 常矢量
角动量守恒 （角动量积 分）
MO 0
F 0 F // r
§3-4 质点的角动量定理和角动量守恒定律
（1） LO r mv C r和 必始终与 v LO , 质点必在过 垂直 O 点且与 垂直的平面内运动 . LO
2
§3-4 质点的角动量定理和角动量守恒定律 例题7
sin e mv mRe mR
sin Lz R sin mR
2 Lz mR sin 2
0 sin 0 mR
2 2
sin 0 0 2 sin
d ) yFz zFy m zy dt ( m yz d m xz ) zFx xFz ( m zx dt d m yx ) xFy yFx dt ( m xy
质点对固 定点的角 动量定理
§3-4 质点的角动量定理和角动量守恒定律 对固定点的角动量定理不能与牛顿第二定律等价
例题6
L 0 m r mr
2
e
k
§3-4 质点的角动量定理和角动量守恒定律
常量 r 2
掠面速度
1 r r dA A 1 2 2 lim lim r dt t 0 t t 0 t 2
角运动: 即使质点做直线运动, 只要 点在直线之外 ,角 O 运动就存在.
动量是质点线运动的度量, 角动量则是质点角运动的 度量.质点的径向运动对质点的角运动没有贡献.
r dr dA LO r mv m 2m dt dt
§3-4 质点的角动量定理和角动量守恒定律
dLO MO dt
MO r F 0
LO r mv
= 常矢量
角动量守恒 （角动量积 分）
MO 0
F 0 F // r
§3-4 质点的角动量定理和角动量守恒定律
（1） LO r mv C r和 必始终与 v LO , 质点必在过 垂直 O 点且与 垂直的平面内运动 . LO
2
§3-4 质点的角动量定理和角动量守恒定律 例题7
sin e mv mRe mR
sin Lz R sin mR
2 Lz mR sin 2
0 sin 0 mR
2 2
sin 0 0 2 sin
d ) yFz zFy m zy dt ( m yz d m xz ) zFx xFz ( m zx dt d m yx ) xFy yFx dt ( m xy
质点对固 定点的角 动量定理
§3-4 质点的角动量定理和角动量守恒定律 对固定点的角动量定理不能与牛顿第二定律等价
质点系的角动量定理及角动量守恒定律
对质点系
Mi内z
Mi外z
d dt
(ri
mi vi
sin
i
)
而
Mi内 0
Mi内z 0
Mi外z
d dt
(ri mivi
sin
i
)
d dt
Lz
——称质点系对z 轴的角动量定理.
3.质点系对轴的角动量守恒定律
若
Mi外z 0
Lz rimivi sin i 常量
若质点系各质点绕 z 作圆周运动
Liz ri mivi sin i
质点系对轴的角动量
Lz rimivi sin i
2.质点系对轴的角动量定理 质点在垂直于z 轴的平面内运动，第i个 质点
Miz
dLi dt
d dt
(ri
mivi
sin
i
)
M iz M i外z M i内z
M i内z
M
sin
i)
m 2gh v
2m m
本题也可以利用对点的角动量守恒求解，读者可自行完成.
§5.2质点系的角动量定理 及角动量守恒定律
§5.2.1质点系对参考点的角动量定理及守恒律
1.质点系对参考点的角动量
对参考点
L Li ri pi ri mivi
i
i
i
对质点系中的第 i 个质点,有
Mi
dLi dt
其中
Mi Mi外 Mi内
M i内
M i外
dLi dt
对质点系，有
M i内
M i外
dLi dt
2.内力的力矩
ri
Fij i
因质点i与质点 j 间的相互 作用力
i
2016d1角动量守恒定律
§4-3 角动量 角动量守恒定律
一、质点的角动量定理和角动量守恒定律
1.质点对固定点（轴）的动量矩（角动量） 质点m绕固定点O运动，则定 L 义质点对O点(或：过O点⊥r p 和 p 决定平面的轴)的角动 r 量为 O m
·
L r p r mv
§4-4，理三不要求，理一要求
例8. 如图，一静止的均匀细棒，长L,质量M，可 绕通过棒的端点且⊥棒长的光滑固定轴O在光滑水 1 平面内转动，转动惯量为 3 ML2 . 一质量为m速率 为v的子弹在水平面内沿与棒⊥的方向射入棒的自 由端。设击穿棒后子弹的速率减为v/2，则此时棒 的角速度为(A)mv/ML (B)3mv/2ML (C)5mv/3ML 选（B） (D)7mv/4ML. 解： 对（子弹+棒）系统，对O 轴 M外 0 角动量守恒 选⊙为正向，则 mvL m v L J 3mv 2 ML 2 ▲对定轴转动，选定正向后，可将力矩、角动量 表示为代数量。
大小： L rmv sin
方向： r、p、L成右螺关系
SI单位：kg· m2/s
2.质点的角动量定理和角动量守恒定律 dL d dr dp L r p ( r p) pr dt dt dt dt dr dp p mv F v dt dt dL v mv r F dt dL v mv ＝0, r F ＝M dt dL 质点对某固定点（轴）的角动量 M dt 对时间的变化率等于质点所受的 合力对该点（轴）的力矩 ——质点的角动量定理
2 1
对定轴刚体，J一定，有
t2
t1
M 外 dt J 2 J1 （积分形式）
一、质点的角动量定理和角动量守恒定律
1.质点对固定点（轴）的动量矩（角动量） 质点m绕固定点O运动，则定 L 义质点对O点(或：过O点⊥r p 和 p 决定平面的轴)的角动 r 量为 O m
·
L r p r mv
§4-4，理三不要求，理一要求
例8. 如图，一静止的均匀细棒，长L,质量M，可 绕通过棒的端点且⊥棒长的光滑固定轴O在光滑水 1 平面内转动，转动惯量为 3 ML2 . 一质量为m速率 为v的子弹在水平面内沿与棒⊥的方向射入棒的自 由端。设击穿棒后子弹的速率减为v/2，则此时棒 的角速度为(A)mv/ML (B)3mv/2ML (C)5mv/3ML 选（B） (D)7mv/4ML. 解： 对（子弹+棒）系统，对O 轴 M外 0 角动量守恒 选⊙为正向，则 mvL m v L J 3mv 2 ML 2 ▲对定轴转动，选定正向后，可将力矩、角动量 表示为代数量。
大小： L rmv sin
方向： r、p、L成右螺关系
SI单位：kg· m2/s
2.质点的角动量定理和角动量守恒定律 dL d dr dp L r p ( r p) pr dt dt dt dt dr dp p mv F v dt dt dL v mv r F dt dL v mv ＝0, r F ＝M dt dL 质点对某固定点（轴）的角动量 M dt 对时间的变化率等于质点所受的 合力对该点（轴）的力矩 ——质点的角动量定理
2 1
对定轴刚体，J一定，有
t2
t1
M 外 dt J 2 J1 （积分形式）
质点角动量和角动量守恒定律
二、质点角动量： 质点角动量：
r L v
o
r r r r r L = r × P = r × mυ
角动量的大小
P
m r rϕ r
L
L = rP sin ϕ = mυr sin ϕ
角动量的方向 : 右手螺旋
2
当质点作圆周运动时,则有: 当质点作圆周运动时,则有:
L = rmv = mr ω
注意：同一质点相对于不同的点，角动量可以不同。 注意：同一质点相对于不同的点，角动量可以不同。 在说明质点的角动量时， 在说明质点的角动量时，必须指明是对哪个点而言的
a/2 o
由角动量守恒定律， 由角动量守恒定律，得：
V
a/2
(a/2) mv0 =(a/2)2mv+（a/2）mv （ ）
ω =2v0/3a
r r r ×F
M = Fr sinα = Fr⊥
(方向用右手螺旋法规定 方向用右手螺旋法规定) 方向用右手螺旋法规定
v M
r M
r r
r┴
r F
α
o
2. 必须指明对那一固定点 必须指明对那一固定点. r r 3. F ≠ 0, M 可能为零
有心力： 有心力： r r 当力F 的作用线与矢径 r 共线时的力
L0 L0+L
α
v
v0
m
如何求角度α 如何求角度α？ 由于质点在有心力 作用下运动， 作用下运动，故角 动量守恒。 动量守恒。有：
Q mv 0 L0 = mv sin(π − α ) ⋅ ( L0 + L) ∴sinα = v0 L0 / v( L0 + L)
例5-2、 、
l0
o
l
角动量 冲量矩 角动量守恒定律
力的时间累积效应： 冲量、动量、动量定理．
力矩的时间累积效应： 冲量矩、角动量、角动量定理．
41..4.质1 点质的点角的动角量动量定理和角动量z守L恒定v律
度
v
质量为m 的质点以速
在空间运动，某时对
O 的位矢为 r ，质点对O
rm
xo
y
的角动量
L
r
p
r
mv
L
1 2
mv 12
r1 r2
2
1
4.4.2 刚体定轴转动的角动量定理
和角动量守恒定律
1 刚体定轴转动的
角动量
L
mi ri 2
i
(
miri2 )
L
Ji
z
O ri
v i
mi
2 刚体定轴转动的角动量定理
质M点i mi受dd合Lti力矩dM(diJ(t包 )括Midedxt、(mMiiirni
t2
t1
Mdt
J 22
J11
当转轴给定时，作用在物体上的冲量矩等于在
这段时间内转动物体的角动量的增量
例 在通过定滑轮的一条轻绳的两 端，分别连有质量为 m1和 m2的物体， 设滑轮是质量为M 、半径为R的质 量均匀分布的圆盘。设绳的质量可 不计，求两物体的加速度。 解： 支撑力与滑轮的重力皆通原 点。只有 m1和m2 的重力才有对原 点的力矩。
R
M
m 1
m 2
作用于该系统的力矩为
M Rm1g Rm2g m1 m2 Rg
整个系统的角动量为
L
力矩的时间累积效应： 冲量矩、角动量、角动量定理．
41..4.质1 点质的点角的动角量动量定理和角动量z守L恒定v律
度
v
质量为m 的质点以速
在空间运动，某时对
O 的位矢为 r ，质点对O
rm
xo
y
的角动量
L
r
p
r
mv
L
1 2
mv 12
r1 r2
2
1
4.4.2 刚体定轴转动的角动量定理
和角动量守恒定律
1 刚体定轴转动的
角动量
L
mi ri 2
i
(
miri2 )
L
Ji
z
O ri
v i
mi
2 刚体定轴转动的角动量定理
质M点i mi受dd合Lti力矩dM(diJ(t包 )括Midedxt、(mMiiirni
t2
t1
Mdt
J 22
J11
当转轴给定时，作用在物体上的冲量矩等于在
这段时间内转动物体的角动量的增量
例 在通过定滑轮的一条轻绳的两 端，分别连有质量为 m1和 m2的物体， 设滑轮是质量为M 、半径为R的质 量均匀分布的圆盘。设绳的质量可 不计，求两物体的加速度。 解： 支撑力与滑轮的重力皆通原 点。只有 m1和m2 的重力才有对原 点的力矩。
R
M
m 1
m 2
作用于该系统的力矩为
M Rm1g Rm2g m1 m2 Rg
整个系统的角动量为
L
4-3角动量 角动量守恒定律
in
M L 常量
ex
角动量守恒定律是自然界的一个基本定律.
自然界中存在多种守恒定律
动量守恒定律 能量守恒定律 角动量守恒定律 电荷守恒定律 质量守恒定律 宇称守恒定律等
许多现象都可 以用角动量守恒来 说明. 花样滑冰 跳水运动员跳水
跳水运动员
茹可夫斯基凳
例3 质量很小长度为l 的均匀细杆，可 绕过其中心 O并与纸面垂直的轴在竖直平面 内转动．当细杆静止于水平位置时，有一只 小虫以速率 v 0 垂直落在距点O为 l/4 处，并背 离点O 向细杆的端点A 爬行．设小虫与细杆 的质量均为m．问：欲使细杆以恒定的角速 度转动，小虫应以多大速率向细杆端点爬行?
解 设飞船在点 A 的速度 v 0 , 月球质 量 mM ,由万有引力和 牛顿定律
vB
R
B
vA
v0
v
O h A
u
v mM m G m 2 ( R h) Rh mM g G 2 2 R R g
2 0
v0 (
Rh
)
12
1 612 m s
1
质量 m' 在 A 点和 B 点只受有心力作用 , 角动量守恒
d r mv r F dt
所以
dL M＝ dt
dL M dt
t2
t1
M dt L2 L1
冲量矩
t1
t2
M dt
对同一参考点O，质点所受的冲量矩 等于质点角动量的增量．——质点的角动 量定理
3、质点的角动量守恒定律
若质点所受的合外力矩为零，即 M=0，
4－3 角动量 角动量守恒定律
力对时间累积效应： 冲量、动量、动量定理． 力矩对时间累积效应： 冲量矩、角动量、角动量定理．
M L 常量
ex
角动量守恒定律是自然界的一个基本定律.
自然界中存在多种守恒定律
动量守恒定律 能量守恒定律 角动量守恒定律 电荷守恒定律 质量守恒定律 宇称守恒定律等
许多现象都可 以用角动量守恒来 说明. 花样滑冰 跳水运动员跳水
跳水运动员
茹可夫斯基凳
例3 质量很小长度为l 的均匀细杆，可 绕过其中心 O并与纸面垂直的轴在竖直平面 内转动．当细杆静止于水平位置时，有一只 小虫以速率 v 0 垂直落在距点O为 l/4 处，并背 离点O 向细杆的端点A 爬行．设小虫与细杆 的质量均为m．问：欲使细杆以恒定的角速 度转动，小虫应以多大速率向细杆端点爬行?
解 设飞船在点 A 的速度 v 0 , 月球质 量 mM ,由万有引力和 牛顿定律
vB
R
B
vA
v0
v
O h A
u
v mM m G m 2 ( R h) Rh mM g G 2 2 R R g
2 0
v0 (
Rh
)
12
1 612 m s
1
质量 m' 在 A 点和 B 点只受有心力作用 , 角动量守恒
d r mv r F dt
所以
dL M＝ dt
dL M dt
t2
t1
M dt L2 L1
冲量矩
t1
t2
M dt
对同一参考点O，质点所受的冲量矩 等于质点角动量的增量．——质点的角动 量定理
3、质点的角动量守恒定律
若质点所受的合外力矩为零，即 M=0，
4－3 角动量 角动量守恒定律
力对时间累积效应： 冲量、动量、动量定理． 力矩对时间累积效应： 冲量矩、角动量、角动量定理．
相关主题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
t1
质点的角动量定理：对同一参考点O，质点 所受的冲量矩等于质点角动量的增量.
M 0,
例 2-6
四. 质点的角动量守恒定律
L 恒矢量 （有心力作用）
7
作用于质点的合外力对参考点 O 的力矩，等 于质点对该点 O 的角动量随时间的变化率. 强调：力矩和角动量都是相对同一个参考点的。
6
dL
dm v
dr
物理学
M
dL
t1 dt t2 M d t ：力矩对给定点的冲量，称为冲量矩
t2
M d t L 2 L1
Mi 0
F
F
M i 2r F 0
4
i
Fi 0 ,
i
物理学
三 质点的角动量定理
dp dt F
dL dt
？
5
物理学
d (r mv ) r mv dt dt dt dt dr dL dp v , v mv 0 r rF dt dt dt dL 质点角动量定理 M 的微分形式 dt
物理学
2.4 质点的角动量定理和角动量守恒定律
z
1. 质点的角动量 质量为 m 的质点以速 度 v 运动，某时相对 参考 点O 的位矢为 r ，则定义 质点对O的角动量为： L r p r mv 大小: L rm v sin 方向: 符合右手法则 角动量单位：kg· 2·-1 m s
O
z
F
r
d
*
P
M rF
d : 力臂
M
力矩的方向： （叉乘的方向）
F
r
3
物理学
M rF
r : 相对于参考点的位置矢量
因此，描述一个力的力矩时要表明是力对哪一点 或哪个轴的力矩！没有参考点，力矩无意义！
F
F
i
Fi 0 ,
i
L
v
m y
r
x
L
o
v
r
强调：描述角动量 时要指明是对哪个 点或轴的角动量。
1
物理学
质点以 作半径为 r 的圆周运动，相对圆心 2 L r m v mr 例2-5
L
p
o
r
m
2
物理学
二 力矩
用来描述力对刚体 的转动作用．
F 对转轴 z 的力矩 M Fr sin Fd