平面直角坐标系中的距离公式和中点公式
平面直角坐标系中的基本公式

平面直角坐标系中的基本公式在平面直角坐标系中,我们可以使用基本公式来描述二维空间中点的位置、距离、长度、角度等各种属性。
下面是一些常用的基本公式:1.点的坐标:平面直角坐标系中的点可以表示为一个有序对(x,y),其中x表示横坐标(沿x轴的水平距离),y表示纵坐标(沿y轴的垂直距离)。
2.线段长度:设平面直角坐标系中有两个点A(x1,y1)和B(x2,y2),则线段AB的长度可以通过以下公式计算:AB=√((x2-x1)²+(y2-y1)²)3.点到坐标轴的距离:设平面直角坐标系中有一个点P(x,y),则点P 到x轴的距离为,y,到y轴的距离为,x。
4.斜率:设平面直角坐标系中有两个点A(x1,y1)和B(x2,y2),则线段AB的斜率可以通过以下公式计算:斜率k=(y2-y1)/(x2-x1)5.中点:设平面直角坐标系中有两个点A(x1,y1)和B(x2,y2),则线段AB的中点坐标为:中点M((x1+x2)/2,(y1+y2)/2)6.坐标轴正向与象限:在平面直角坐标系中,x轴正向向右,y轴正向向上。
同时,将坐标轴所形成的四个象限按照逆时针方向分别称为第一象限、第二象限、第三象限和第四象限。
7.角的度量:在平面直角坐标系中,角的度量可以使用弧度或者角度来表示。
常用的角度制中,一个完整的圆的度数为360°。
而弧度制中,一个完整的圆的弧度数为2π弧度。
8.同位角与同旁角:在平面直角坐标系中,如果两条射线的起点、终点分别与两条相互垂直的射线的起点、终点重合,则这两条射线分别被称为同位角。
如果两条射线的起点分别位于两条相互垂直的射线的起点的同侧或者终点位于两条相互垂直的射线的终点的同侧,则这两条射线分别被称为同旁角。
9. 三角函数:在平面直角坐标系中,根据点的位置与坐标轴的关系,可以定义一些重要的三角函数,如正弦函数sin(θ)、余弦函数cos(θ)、正切函数tan(θ)等,其中θ 表示角的度数或弧度数。
两点之间的距离公式及中点坐标公式

y y1 y2 2
二、坐标法——将几何问题转化为代数问
• P71练习A:1-4. 2-1A:1-4.
• 选做:B组题
P72:习题
(0,y) M 2
M
A
A2
x x1 x2 Байду номын сангаасx
y y1 y2 y
(0,y1)
A1 O M1
B1
x
(X1,0) (X,0) (X2,0)
即: x x1 x2 2
y y1 y2 2
这就是线段中点坐标 的计算公式 ,简称
—— 中点公式
【例4】已知 :平行四边形ABCD的三个顶点坐标
A(- 3,0),B(2,-2),C(5,2).求:顶点D的坐标。
AD2 b a2 c2,
AC2 b2 c2,
x
O A(0,0) B(a,0)
BD 2 b 2a2 c2
AC2 BD2 4a2 2b2 2c2 4ab, 2(2a2 b2 c2 2ab),
AB2 AD2 2a2 b2 c2 2ab,
所以 AC2 BD2 2 AB2 AD2 .
解:因为平行四边形的两条对角线中点相同,
所以它们的中点的坐标也相同.
设D 点的坐标为(x,y).
y D(x,y)
x2 35
则
2
2
M
C(5,2
y2 02
O
A(-3,0)
x
2
2
B(2,-2)
解得 x=0 ∴D(0,4)
y=4
〖课堂检测〗 1、求两点的距离: (1) A(6,2) , B(-2,5) (2) A (2 , -4) , B (7 , 2)
A(x1,y1) A2
o
两点间距离公式及中点坐标公式

C(5,2)
A(-3,0)
O
x B(2,-2)
解得
x=0点S(0,2)、点T(−6,−1),现将线段ST四 等分,试求出各分点的坐标.
巩 固 知 识 典 型 例 题
首先求出线段ST 的中点 Q 的坐标,然 则由 S(0 , 2)、T(−6,−1)得 后再求SQ的中点P及 2 (1) 1 0 (6) xQ 3 yQ QT 的中点 R的坐标.
y
A1M1 M1B1
A2 M 2 M 2 B2
(0,y)
B2
M2
(0,y2)
B
x x1 x2 x y y1 y2 y
A
A1
(X1,0) O
(0,y1)
A2
M
M1
(X,0)
B1
(X2,0)
x
即:
x1 x 2 x 2
y1 y 2 y 2
这就是线段中点坐标 的计算公式 ,简称 ——
2
2
解 设线段ST的中点Q的坐标为 ( xQ , yQ ),
2
即
1 Q ( 3, ) 2
图8-2
3 5 9 1 ( , ) 同理,求出线段SQ的中点P ,线段QT的中点 R ( , ). 2 4 2 4
( , )、Q ( 3, )、R ( , ). 故所求的分点分别为P 3 5 2 4 1 2 9 2 1 4
8.1平面直角坐标系中的基本公式
1.两点的距离公式
如图:有序实数对( x,y)与点P对 应,这时( x,y)称为点P的坐标, 并记为P(x,y),x叫做点P的横坐 标,y叫做点P的纵坐标。
y
p(x,y)
y
x
平面直角坐标系中的基本公式

平面直角坐标系中的基本公式平面直角坐标系是二维空间中用于描述点位置的系统。
它由两条互相垂直的坐标轴组成,一个是横轴通常称为x轴,另一个是纵轴通常称为y 轴。
坐标轴的交点称为原点,用O表示。
每个点可以通过两个坐标值(x,y)来定义,其中x表示点在x轴上的位置,y表示点在y轴上的位置。
在平面直角坐标系中,存在一些基本公式,我们将在本文中一一介绍。
1.距离公式:两点间的距离可以使用勾股定理进行计算。
如果有两个点A(x1,y1)和B(x2,y2),它们之间的距离可以使用以下公式计算:AB=√((x2-x1)²+(y2-y1)²)2.中点公式:两点的中点可通过其坐标的平均值计算。
如果有两个点A(x1,y1)和B(x2,y2),它们的中点C的坐标可以计算如下:C=((x1+x2)/2,(y1+y2)/2)3.斜率公式:斜率是一条直线在坐标轴上的改变速率。
两点间的斜率可以用下面的公式进行计算:斜率=(y2-y1)/(x2-x1)4.中垂线公式:两条线段在中垂线上的交点被称为它们的垂点。
如果有一条线段AB,在平面直角坐标系中,它的中垂线是与AB垂直并通过AB的中点的直线。
中垂线方程可以使用以下公式计算:中垂线的斜率=-1/斜率中垂线通过点((x1+x2)/2,(y1+y2)/2)5.垂直平分线公式:两条线段在垂直平分线上的交点称为它们的垂直平分线的中点。
如果有一条线段AB,在平面直角坐标系中,它的垂直平分线将AB划分为两个相等的部分,并且与AB垂直。
垂直平分线的方程可以使用以下公式计算:垂直平分线的斜率=-1/斜率垂直平分线通过点((x1+x2)/2,(y1+y2)/2)6.直线方程:一个直线的方程可以表示为 y = mx + c 的形式,其中 m 是斜率,c 是 y 轴截距。
7.平行线之间的关系:两条平行线具有相同的斜率。
如果有两条线段AB和CD平行,则它们具有相同的斜率。
8.垂直线之间的关系:两条垂直线的斜率乘积为-1、如果有两条线段AB和CD垂直,则它们的斜率乘积等于-1这些是平面直角坐标系中的一些基本公式。
中点公式与距离公式讲解

中点公式与距离公式讲解中点公式和距离公式是数学中常用的两种计算方法,用于求解平面上的点的位置以及点与点之间的距离。
本文将详细介绍中点公式和距离公式的相关概念和计算方法。
1. 中点公式中点公式用于确定平面上线段的中点坐标。
对于给定的两个点A(x₁, y₁)和B(x₂, y₂),其中点的坐标可通过以下公式计算得出:中点的x坐标:x = (x₁ + x₂) / 2中点的y坐标:y = (y₁ + y₂) / 2通过这两个公式,我们可以轻松地计算出线段的中点坐标。
举例说明:假设有一条线段AB,其中A(2, 4)为起点,B(8, 10)为终点。
我们可以利用中点公式求出该线段的中点坐标。
首先,代入公式进行计算:x = (2 + 8) / 2 = 5y = (4 + 10) / 2 = 7因此,线段AB的中点坐标为C(5, 7)。
2. 距离公式距离公式用于计算平面上两点之间的距离。
对于给定的两个点A(x₁, y₁)和B(x₂, y₂),它们之间的距离D可以通过以下公式计算得出:D = √[(x₂ - x₁)² + (y₂ - y₁)²]通过这个公式,我们可以求得两点间的距离。
举例说明:假设有两个点A(2, 4)和B(8, 10),我们可以利用距离公式计算出这两点之间的距离。
首先,代入公式进行计算:D = √[(8 - 2)² + (10 - 4)²]= √[(6)² + (6)²]= √[36 + 36]= √72≈ 8.485因此,点A(2, 4)和点B(8, 10)之间的距离约为8.485。
通过中点公式和距离公式,我们可以方便地计算平面上的点位和距离。
这两个公式广泛应用于数学、物理等领域,并具有较高的实用性和准确性。
这篇文章对中点公式和距离公式进行了详细介绍,并通过实例进行了说明。
希望读者能够通过本文对中点公式和距离公式有更深入的理解和掌握,从而在实际问题中灵活运用。
距离公式及中点公式

距离公式及中点公式距离公式和中点公式是数学中经常用到的公式,它们在解决空间几何问题和平面几何问题时非常有用。
本文将介绍距离公式和中点公式的概念、推导及应用。
一、距离公式距离公式用于计算平面上两点之间的距离。
假设平面上有点A(x1,y1)和点B(x2, y2),我们可以使用以下距离公式来计算它们之间的距离:d = √[(x2 - x1)² + (y2 - y1)²]其中d表示点A和点B之间的距离。
这个公式的推导可以从勾股定理开始。
以点A和点B为两条直角边,连接点A和点B的线段为斜边,根据勾股定理可得到上述距离公式。
这个公式可以应用于多种问题,比如计算两个坐标点之间的直线距离或者判断某个点到直线的距离等。
通过计算平面上两点之间的距离,我们可以更好地理解它们之间的几何关系。
二、中点公式中点公式用于计算平面上线段的中点坐标。
假设平面上有一条线段AB,其中点A的坐标为(x1, y1),点B的坐标为(x2, y2),我们可以使用以下中点公式来计算该线段的中点坐标:M = ((x1 + x2)/2, (y1 + y2)/2)其中M表示线段AB的中点坐标。
这个公式的推导非常简单,我们只需要计算线段的横坐标和纵坐标的平均值即可得到中点的坐标。
中点公式常用于平面几何和坐标系的计算中。
通过求解线段的中点坐标,我们可以更准确地确定线段的位置、长度和方向,并能够在计算中起到简化问题的作用。
三、应用示例接下来我们通过两个应用示例来演示距离公式和中点公式的具体应用。
应用示例一:平面直角坐标系中两点距离计算假设平面直角坐标系中有两点A(2, 3)和B(5, 7),我们可以使用距离公式来计算它们之间的距离。
根据距离公式,代入坐标值进行计算得:d = √[(5 - 2)² + (7 - 3)²] = √[3² + 4²] = √(9 + 16) = √25 = 5因此,点A和点B之间的距离为5个单位。
两点间距离公式及中点坐标公式ppt课件

显然,当AB平行于坐标轴或在坐标轴上时,公式
仍然成立。
8
• 给两点的坐标赋值:
x1 ?, y1 ?, x2 ?, y2 ?;
• 计算两个坐标的差,并赋值给另外两个量, 即
x x2 x1 y y2 y1
• 计算 d x2 y2
• 给出两点的距离 d
9
题型分类举例与练习
24
24
故所求的分点分别为P( 3 , 5)、Q( 3, 1)、R( 9 , 1).
24
2
24
8.1 两点间的距离与线段中点的坐16标
例4 已知 ABC 的三个顶点为A(1,0)、B(2,1)、C(0,3) ,试
巩 固
求BC边上的中线AD的长度.
知
解 设BC的中点D坐标为D(xD , yD ),则由 B(2,1)、C(0,3) 得
3
• 我们先寻求原点 O0,0与 任意一 点 Ax, y之 间距离的计算方法
O, A 两点之间的距离通常用 dO, A
表示。
4
当A点不在坐标轴上时:
在平面直角坐标系中,已知点A(x, y) ,原点O和点A的距离d(O,A)是多少呢?
y
A (x,y)
y
o x A1 x
d(O,A)=
5
当A点在坐标轴上时这一公式 也成立吗?
证明:因为 d(A,B)= 312 4 22 8
d(A,C)= 5 -12 0 22 20
d(C,B)= 5 32 0 42 20
即|AC|=|BC|且三点不共线 所以,三角形ABC为等腰三角形。
11
• 该题用的方法----坐标法。可以将几何 问题转化为代数问题。
平面直角坐标系中的距离公式和中点公式课件

添加文档副标题
目录
01.
02.
03.
04.
05.
06.
平面直角坐标系中的距离公式为:$\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$ 该公式表示点P(x1,y1)与点P(x2,y2)之间的距离 其中,x1、x2、y1、y2分别表示两点的横纵坐标 平方根符号表示取非负数的开方运算
地理学中的应用:确定两点之间的距离,计算地球上任意两地之间的距离 物理学中的应用:计算两点之间的直线距离,研究物体的运动轨迹 计算机科学中的应用:计算两点之间的最短路径,实现地图导航 统计学中的应用:计算样本间的距离,进行聚类分析
题目:求点A(2,3)到原点的距离 题目:求点B(-3,4)到原点的距离 题目:求点C(5,-2)到原点的距离
应用场景:距离公式常用于计算点到直线的距离,中点公式常用于计算两点之间 的中点坐标。
异同点:距离公式中的A、B、C为直线方程系数,而中点公式中的x1、y1、x2、 y2为两点的坐标。
距离公式:适用于 计算两点之间的直 线距离,常用于几 何学、物理学等领 域。
中点公式:适用于 求线段的中点坐标, 常用于解析几何、 线性代数等领域。
两点间的距离公式推导
任意两点间的距离公式推 导
两点间的距离公式与向量 的关系
距离公式的几何意义
两点间的距离 公式
பைடு நூலகம்
两点间的斜率 公式
两点间的中点 公式
两点间的对称 点公式
平面直角坐标系中 的中点公式为: M(x,y)=((x1+x2)/ 2,(y1+y2)/2)
该公式用于求平面直 角坐标系中任意两点 P1(x1,y1)和P2(x2,y2) 的中点M的坐标
两点之间的距离公式及中点坐标公式.ppt
A 0 , 0 , B a , 0 , C b , c , D b a , c .
所以
AB a ,
2 2
2 2 2
y D (b-a, c)
C (b, c) x
AD b a c ,
AC b c,
2 2 2
O
A(0,0)
B(a,0)
2 BD b 2 a c 2 2
d(A,C)=
2 2
即|AC|=|BC|且三点不共线
所以,三角形ABC为等腰三角形。
【例3】已知 ABCD ,求证 2 2 2 2 AC BD 2 AB AD .
证明:取A为坐标原点,AB所在直线为X轴建 立平面直角坐标系 xOy ,依据平行四边形的 性质可设点A,B,C,D的坐标为
A
[题组冲关] 3.假如某爱国实业家在20世纪初需要了解全国各地商业信
息,可采用的最快捷的方式是
(
)
A.乘坐飞机赴各地了解 B.通过无线电报输送讯息 C.通过互联网 D.乘坐火车赴各地了解
解析:本题考查中国近代物质生活的变迁。注意题干信 息“20世纪初”“最快捷的方式”,因此应选B,火车速度
”;此后十年间,航空事业获得较快发展。
筹办航空事宜
处
三、从驿传到邮政 1.邮政
(1)初办邮政: 1896年成立“大清邮政局”,此后又设
邮传部 邮传正式脱离海关。
,
(2)进一步发展:1913年,北洋政府宣布裁撤全部驿站; 1920年,中国首次参加 万国邮联大会 。
2.电讯 (1)开端:1877年,福建巡抚在 办电报的开端。 (2)特点:进程曲折,发展缓慢,直到20世纪30年代情况才发生变 化。 3.交通通讯变化的影响
平面直角坐标系公式

设A(x1,y1),B(x2,y2)两点的中点为M(x0,y0),则(1)中点坐标公式:x0=(x1+x2)/2;(y0=(y1+y2)/2(2)两点间距离公式:AB=√[(x1-x2)^2+(y1-y2)^2](本质上就是勾股定理1.点到点距离公式:设A(a,b)B(c,d),则AB=√[(a-c)^2+(b-d)^22.点到线距离公式:设直线Ax+By+C=0(一般的解析式可以先化成这个),点A(x0,y0),则A到直线的距离长度=|Ax0+By0+C|/√(A^2+B^2)3.解析式y=kx+b中,k的实质是该直线与x轴正方向夹角的正切值,当这个角大于90度时,需要用到诱导公式tan(90+a)=-tan(a)4.设直线1为y=k1x+b1,直线2为y=k2x+b2,当k1k2=-1时,直线1垂直于直线25.直线y=kx+b的平行直线系为y=kx+m6.过定点(x0,y0)的直线系为(y-y0)=k(x-x0)7.已知抛物线y=ax^2+bx+c和平行于x轴的直线y=m,则抛物线在直线上截出的距离=√(b^2-4ac+4am)/|a|,这个公式一般用于求某些线段的最值,通常可以得到一个y=根式+km的函数,这个函数的最值我们还不会求,可以设这个根式为n,反解出m来,然后得到关于n的二次函数,求二次函数的最值和相应的n值,进而求出m的值即可,这种方法叫换元法,我自己发现的,不知道高中会不会用到我也是初三的,一般有用的就是这几个,并且除非逼不得已,不然尽量别用,因为一方面计算量大,另一方面即使算对了,老师也不一定看得懂,有可能会得0分也不好说。
部分压轴题中也会在平面直角坐标系中出现圆,下面的公式是关于圆的1.圆的标准方程(x-a)^2+(y-b)^2=r^2,其中,圆心是(a,b),半径是r2.圆的一般方程x^2+y^2+Dx+Ey+F=0,其中,圆心是(-D/2,-E/2)半径是1/2√(D^2+E^2-4F)3.过圆上定点的切线系方程,设P(x0,y0)是圆x^2+y^2+Dx+Ey+F=0上的一个点,过这个点的切线为xx0+yy0+D[(x+x0)/2]+E[(y+y0)/2]+F=04.过圆外一点P(x0,y0)引圆x^2+y^2+Dx+Ey+F=0的切线,切线长为√(x0^2+y0^2+Dx0+Ey0+F)5.判断直线与圆位置关系的方法:1.知道圆心和半径的情况下,利用点到直线的距离公式,算出圆心到直线的距离,比较距离与半径,得出圆与直线的位置关系2.知道直线和圆的解析式的情况下,联立二式,组成一个二元二次方程组,消去一元,得到一个一元二次方程,算出判别式德塔,德塔大于0,证明方程有两个不等实数根,即直线与圆有两个不同交点,此时相交,相应的,德塔小于0,相离,德塔等于0,相切。
平面直角坐标系中的距离公式和中点公式

平面直角坐标系中的距离公式和中点公式在平面直角坐标系中,有两个常用的公式,分别是距离公式和中点公式。
这些公式用于计算平面上两点之间的距离和两点的中点坐标。
1.距离公式:在平面直角坐标系中,两点之间的距离可以通过勾股定理来计算。
假设有平面上两个点A(x1,y1)和B(x2,y2),则两点之间的距离为:d=√((x2-x1)²+(y2-y1)²)这个公式可以通过将两点的坐标差值平方相加,再开平方来计算出两点之间的距离。
例如,有两个点A(2,3)和B(5,7),我们可以使用距离公式来计算它们之间的距离:d=√((5-2)²+(7-3)²)=√(3²+4²)=√(9+16)=√25=5因此,点A和点B之间的距离为5个单位。
2.中点公式:在平面直角坐标系中,给定两个点A(x1,y1)和B(x2,y2),可以使用中点公式来计算这两点的中点坐标。
中点是连接两个点的线段的中心点,它的坐标可以通过坐标平均值来计算。
中点坐标的x坐标为两个点的x坐标之和的一半;中点坐标的y坐标为两个点的y坐标之和的一半。
中点的x坐标:x=(x1+x2)/2中点的y坐标:y=(y1+y2)/2例如,给定两个点A(2,3)和B(5,7),我们可以使用中点公式来计算它们之间的中点坐标:x=(2+5)/2=7/2=3.5y=(3+7)/2=10/2=5因此,点A和点B之间的中点坐标为P(3.5,5)。
中点公式可以用于计算线段的中点坐标,并且在几何学和数学中经常被使用。
距离公式和中点公式在平面直角坐标系中具有广泛的应用。
它们可以用于解决几何问题,例如计算两点之间的距离或线段的中点。
另外,它们也可以扩展到三维坐标系中,并用于计算空间中两点之间的距离和中点坐标。
除了在数学和几何学中的应用,距离公式和中点公式在计算机图形学和计算机视觉等领域也有重要的应用。
在这些领域中,这些公式用于计算物体之间的距离、图像边界的中点等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
y P M O P x P(a,b)
求下列各点关于 x 轴和 y 轴的对称点的坐标: A(2,3),B(-3,5),C(-2,-4),D(3,-5).
例4
已知平行四边形 ABCD 的三个顶点 A(-3,0), B(2,-2),C(5,2),求顶点 D 的坐标.
解:因为平行四边形的两条对角线的中点相同, 所以它们的坐标也相同. 设点 D 的坐标为 (x,y) ,则
证明 设 P 与P 的对称中心为(x0,y0),则
x ( x) x0 0, 2 y ( y ) y0 0. 2
所以坐标原点为 P 与 P 的对称中心.
求下列各点关于坐标原点的对称点:
A(2,3),B(-3,5),C(-2,-4),D(3,-5).
例3
已知坐标平面内的任意一点 P(a,b), 分别求它关于 x 轴的对称点 P, 关于 y 轴的对称点 P 的坐标.
求两点之间的距离:
(1)A(6,2),B(-2,5);
(2)C(2,-4),D(7,2).
如图所示.设 M(x,y) 是 A(x1,y1) ,B(x2,y2) 的中点.
y
B2 M2 A M B
过 A,B,M 分别向 x 轴作垂线 AA1,BB1, MM1,垂足分别为 A1, B1 ,M1 ; 过 A,B,M 分别向 y 轴作垂线
B1
A2
A1 O M1
x
AA2,BB2, MM2,垂足分别为A2, B2 ,M2 .
如图所示.设 M(x,y) 是 A(x1,y1),B(x2,y2) 的中点.
y
B2 B M
(1)你能说出垂足A1,A2,B1,B2,
M1,M2的坐标吗?
(2)点M是AB中点,M1是A1,B1的 中点吗?它们的坐标有怎样的关系?
(2)|AC| 与 |A1B1| 关系如何?
A
A2
如何求 |A1B1| ?
C B1
(3)|BC| 等于多少?
x (4)在直角三角形中,如何求 |AB| ?
A1 O
(5)你能表示出 |AB| 吗?
平面上两点间的距离公式
y B(x2,y2)
设点 A(x1,y1),B(x2,y2) ,则
| AB | ( x2 x1 ) 2 ( y2 y1 ) 2.
A(x2 ,y2) O x
例1
已知 A(2,-4),B(-2,3) ,求 |AB| .
解: 因为
x1=2,x2=-2,y1=-4,y2=3, 所以
dx=x2-x1=-2-2=-4, dy=y2-y1=3-(-4)=7. 因此
2 2 | AB | d x dy (4) 2 7 2 65 .
(1)如果点 P 与P 关于 x 轴对 称,PP与 x 轴垂直吗?P 的横 坐标是多少 ? (2)PP与 x 轴的交点 M 是线 段 PP 的中点吗?点 M 的纵坐 标是多少? (3)你能求出P 的纵坐标 吗?怎么求的? (4)由以上分析,点P 的坐 标是多少? (5)你能求出P 的坐标吗?
x 2 3 5 2 2 1 y2 02 1 2 2
解得
x 0 y 4
所以顶点 D 的坐标为 (0,4) .
已知平行四边形 ABCD 的三个顶点
A(0,0),B(2,-4),C(6,2),
求顶点 D 的坐标.
8.1.2 平面直角坐标系中的 直线 距离公式和中点公式 圆 圆
直线
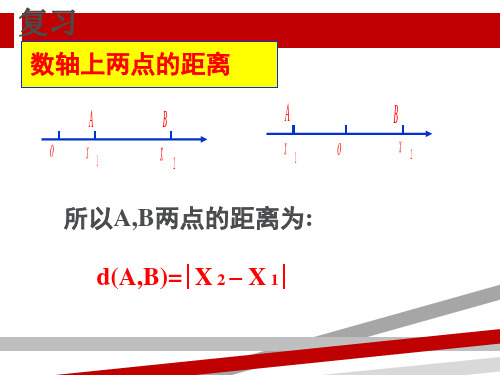
1.数轴上的距离公式
一般地,如果 A(x1),B(x2) ,则这两点的距离公式为 |AB|=|x2-x1|.
2.数轴上的中点公式
一般地,在数轴上,A(x1),B(x2) 的中点坐标 x
满足关系式
x1 x2 . x= 2
如图所示.设 A(x1,y1),B(x2,y2) .
y B2 B
过 A,B 分别向 x 轴作垂线 AA1,BB1,垂足分别为 A1,B1 ; 过 A,B 分别向 y 轴作垂线
A
A2
ቤተ መጻሕፍቲ ባይዱC B1
AA2,BB2,垂足分别为 A2,B2 ;
x
A1 O
其中直线 BB1 和 AA2 相交于
点C.
如图所示.设 A(x1,y1),B(x2,y2) .
y B2 B
(1)以上四个垂足 A1,B1,A2,B2 的坐标分别是多少?
M2
A
A2
B1
(3)M2是A2,B2的中点吗?它们的
x
A1 O M1
坐标有怎样的关系? (4)你能写出点 M 的坐标吗?
中点公式
在坐标平面内,两点 A(x1,y1),B(x2,y2) 的中点 M(x,y) 的坐标之间满足:
x1 x2 x , 2
y1 y2 y . 2
例2
求证:任意一点 P(x,y) 与点 P (-x,-y) 关于坐标原点成中心对称.
