2.1 第3课时 多项式
人教版数学七年级上册2.1 第3课时《 多项式》精品教学设计1

人教版数学七年级上册2.1 第3课时《多项式》精品教学设计1一. 教材分析人教版数学七年级上册第2章《多项式》是学生在小学阶段学习基础上,进一步深化对数学概念的理解和运用的关键内容。
本节课主要介绍多项式的定义、多项式的项、次数和系数等基本概念。
通过本节课的学习,使学生掌握多项式的基本知识,能够正确理解并运用多项式进行简单的计算和问题解决。
二. 学情分析七年级的学生已经具备了一定的数学基础,对于数学概念的理解和运用有一定的掌握。
但同时,学生对于较为抽象的数学概念的理解还存在一定的困难,需要通过具体实例和实际操作来加深理解。
此外,学生的学习习惯和方法还需要进一步指导和培养。
三. 教学目标1.知识与技能目标:理解多项式的定义、多项式的项、次数和系数等基本概念,能够正确运用多项式进行简单的计算和问题解决。
2.过程与方法目标:通过观察、操作、交流等活动,培养学生的数学思维能力和问题解决能力。
3.情感态度与价值观目标:激发学生学习数学的兴趣,培养学生的自主学习能力和团队合作精神。
四. 教学重难点1.重点:多项式的定义、多项式的项、次数和系数等基本概念。
2.难点:对于多项式概念的理解和运用。
五. 教学方法1.情境教学法:通过生活实例和实际问题,引发学生的兴趣和思考,引导学生理解和掌握多项式的概念。
2.启发式教学法:通过提问和讨论,激发学生的思维,引导学生主动探索和发现问题的解决方法。
3.合作学习法:学生进行小组讨论和合作,培养学生的团队合作精神和交流沟通能力。
六. 教学准备1.教学PPT:制作多媒体教学PPT,包括多项式的定义、多项式的项、次数和系数等基本概念的介绍,以及相关的例题和练习。
2.教学素材:准备相关的数学题目和实际问题,用于引导学生进行观察和操作。
3.教学工具:准备黑板、粉笔等教学工具,用于板书和演示。
七. 教学过程1.导入(5分钟)通过一个实际问题引入本节课的主题——多项式。
例如:已知一个数的平方减去这个数等于3,求这个数。
2.1.3多项式(教案)-人教版七年级数学上册

(五)总结回顾(用时5分钟)
今天的学习,我们了解了多项式的基本概念、重要性和应用。同时,我们也通过实践活动和小组讨论加深了对多项式的理解。我希望大家能够掌握这些知识点,并在日常生活中灵活运用。最后,如果有任何疑问或不明白的地方,请随时向我提问。
3.多项式的次数:理解多项式的次数的概念,能够判断一个多项式的最高次数。
4.多项式的系数:了解多项式中系数的作用,能够识别各项的系数。
5.多项式的运算:掌握多项式加法、减法的运算规则,能够正确进行多项式的加减运算。
6.多项式的化简:学会对多项式进行合并同类项,简化多项式表达式。
二、核心素养目标
1.培养学生的逻辑推理能力:通过多项式的定义和运算规则,让学生理解数学语言的严谨性,提高逻辑推理和表达能力。
6.培养学生的团队合作意识:在多项式运算和化简的实践中,鼓励学生开展合作交流,提高沟通能力。
三、教学难点与重点
1.教学重点
-多项式的定义及其组成:理解多项式的概念,掌握系数、变量、指数三个组成部分。
-举例:解释3x^2 + 2xy - 5是多项式,指出其中的系数(3、2、-5)、变量(x、y)和指数(2、1)。
在讲授重点难点时,我采用了逐步引导的方法,从简单的多项式加减开始,逐步过渡到合并同类项和化简。我发现,通过逐步增加难度,学生们能够更好地消化和吸收知识。同时,我也强调了在运算过程中符号处理的重要性,这是学生们容易忽视的地方。
实践活动和小组讨论环节,我看到了学生们的积极性和创造力。他们在讨论中提出了各种实际问题,并尝试用多项式来解答。这个过程中,我尽量让自己成为一个引导者和协助者,鼓励他们自主思考和解决问题。看到他们能够将所学知识应用到实际问题中,我感到非常欣慰。
人教版七年级数学上册同步备课2.1整式(第3课时)多项式(教学设计)

2.1 整式(第3课时)教学设计一、内容和内容解析1.内容本节课是人教版《义务教育教科书•数学》七年级上册(以下统称“教材”)第二章“整式的加减”2.1整式第3课时,内容包括多项式的概念,多项式的项数和次数的概念.2.内容解析多项式是在学生学习了单项式的基础上进一步学习的.通过本节课的学习让学生理解多项式的概念,并使学生能准确地确定一个多项式的次数和项数.通过多项式的学习加深对整式的认识.多项式既是学生学过单项式后的延续和拓展,又是后续研究整式的加减运算的基础.此外也可以用来表示数学关系以及解决相关的实际问题,它是整个初中数学中起着承上启下作用的核心知识之一.基于以上分析,确定本节课的教学重点为:多项式以及有关概念.二、目标和目标解析1.目标(1)理解多项式、多项式的项和次数、整式的概念;(2)会用多项式表示简单的数量关系,并根据多项式中字母的值求多项式的值;(3)会用整式解决简单的实际问题,体会用整式表示数量关系的简洁性和一般性.2.目标解析达成目标(1)的标志是:会根据概念判断多项式,能确定多项式的项、项数和次数,并能说出判断的依据,能举例说明.达成目标(2)的标志是:会分析简单实际问题中的数量关系,并能够正确地用多项式表示数量关系.目标(3)是“内容所蕴含的思想方法”,学生需要在分析多项式结构特征过程中,经历由特殊(具体)到一般(抽象)的认识过程,感受多项式是一种重要的数学式子,从中提高观察、分析、归纳、概括能力.学生需要从列多项式的过程中,进一步感受整式中的字母表示数,整式可以表示实际问题中的数量关系,整式更具有简洁性和一般性.三、教学问题诊断分析七年级的学生注意力易分散,学习新的知识需要较长的理解过程,就本节课知识而言,容易将单项式与多项式的相关概念混淆,所以教学中教师应予以简单明了、深入浅出地分析,带着学生去发现和探究新知识,以问题的提出、问题的解决为主线,同时要创造条件和机会,让学生发表见解,发挥学生学习的主动性,提高学习的积极性.基于以上分析,确定本节课的教学难点为:准确确定多项式的次数和项,并且掌握单项式和多项式次数之间的联系和区别.四、教学过程设计(一)复习巩固,引入新课问题1:什么叫单项式?单项式的系数和次数?由数与字母的乘积组成的代数式叫做单项式.单项式中的数字因数,叫作单项式的系数一个单项式中,所有字母的指数的和,叫做这个单项式的次数.问题2:填空:1. 单项式-5y 的系数是_____,次数是_____.2. 单项式a 3b 的系数是_____,次数是_____.3. 单项式32ab 的系数是_____,次数是____. 4. 5x 2yz 与-15xzy n 是同次单项式,则n = .答案:1. -5;1;2. 1;43. 32;2 4. 2.师生活动:学生讨论,学生代表回答,教师根据学生回答进行评价【设计意图】巩固单项式的相关知识,为形成多项式的概念打下基础,形成对比.(二)新知探究问题3:观察这些式子:v +2.5, v -2.5,3x +5y +2z ,212ab r π-, x 2+2x +18? 它们有什么共同特点?与单项式有什么联系?师生活动:学生小组讨论交流,自由发言回答上面的问题.教师参与小组讨论,并有针对性地进行指导.教师进一步提出问题,以上各式显然不是单项式,它们与单项式有联系吗?教师给出定义:这些式子都可以看作是几个单项式的和.多项式中,次数最高项的次数,叫做这个多项式的次数.多项式中,每个单项式叫做多项式的项.不含字母的项叫做常数项.一个多项式由几个单项式组成,就把它叫做几项式,如2x -3可以叫做二项多项式,3x +5y +2z 可以叫做三项多项式.教师进一步引导学生探究多项式次数的概念.学生可以发挥自己的想象去探究给多项式的次数命名的方法.教师不必苛求学生怎样想,让学生大胆发言,只要能发挥他们的想象力即可.教师在这一过程中教师可以引导,多项式的次数是不是也可以将所有字母的指数加在一块呢?如果字母多的话是不是有点太乱呢?如果这样的话我们是不是派个代表就行了,派谁当代表呢?引导学生说出,以次数最高的项的次数作为代表.教师总结:多项式中次数最高的项的次数叫做多项式的次数.同单项式一样,一个多项式的次数是几,我们就称它为几次式.如2x -3可以叫做一次二项式,3x +5y +2z 可以叫做一次三项式.【设计意图】通过问题引出多项式的概念,进而通过教师的导与学生的学很自然地得出多项式的项数、次数的概念.针对训练:1.判断下列各式哪些是多项式?(1)a ; (2)213x y ; (3)2x -1; (4)x 2+xy +y 2. 解:多项式有(3)和(4).(1)和(2)是单项式.2.多项式x 2+y -z 是单项式___,___,___的和,它是___次___项式.(x 2;y ;-z ;)3.多项式3m 3-2m -5+m 2的常数项是____,二次项是_____,一次项的系数是_____.(-5;m 2;-2;)4. 一个多项式的次数是3,则这个多项式的各项次数( D )A .都等于3B .都小于3C .都不小于3D .都不大于3师生活动:在总结前面知识的基础上,进一步归纳,至此我们学习了单项式和多项式,单项式和多项式统称为整式.教师进一步提问,你能说一说单项式、多项式和整式三者之间的关系吗?学生讨论后回答.教师根据学生回答情况予以点拨、强调.教师点拨:①多项式的项,要包括它前面的性质符号;②对多项式的每一项来讲来,有系数.但对常数项不说系数,对整个多项式来说,没有系数的概念;③多项式的次数是多项式中次数最高的项的次数.【设计意图】通过自主观察、小组讨论交流,分析式子的结构特征,发现共同特点,并通过特征描述,抽象概括出多项式的概念.通过观察、分析每个单项式的结构特征,发现不同点,在此基础上定义多项式的项、项数和次数的概念及整式的概念.在讨论中激发学生参与学习的热情,培养观察、比较、分析、抽象概括的能力.(三)典例分析例1:用多项式填空:(1)温度由t℃下降5℃后是℃;(2)甲数x的13与乙数y的12的差可以表示为_________.解:(1)(t-5);(2)1132x y.例2:如图所示,用式子表示圆环的面积.当R=15 cm,r=10cm时,求圆环的面积(π取3.14 ).解:外圆的面积减去内圆的面积就是圆环的面积,所以圆环的面积是πR2-πr2.当R=15 cm,r=10cm时,圆环的面积(单位:cm2)是:3.14×152-3.14×102=392.5.这个圆环的面积是392.5cm2.针对训练:一个花坛的形状如图所示,这的两端是半径相等的半圆,求:(1)花坛的周长L;(2)花坛的面积S.解:(1)L=2a+2πr.(2)花坛的面积是一个长方形的面积与两个半圆的面积之和,即S=2ar+ πr2.师生活动:学生独立完成例1,例2由教师板书示范.此环节教师应关注学生书写的规范性.【设计意图】从实际问题出发,再次体验多项式的次数、项数的概念,教师从中及时反馈学生的掌握情况,进一步巩固多项式的有关概念,同时体会用字母表示数的意义和学习求多项式的值的方法.(四)当堂巩固1.指出下列多项式的项和次数a 5-a 2b +ab -b 3.解:多项式的项:a 5,-a 2b ,ab ,-b 3;多项式的次数: 5.2.式子3x a+1+4x –2b 是四次二项式,试求a ,b 的值.解:因为式子的次数是四次,所以a +1=4,所以a =3.又因为式子是二项式,所以2b =0,即b =0.所以a =3,b =0.3.下列整式中哪些是单项式?哪些是多项式?是单项式的指出系数和次数,是多项式的指出项和次数:212a b -,427m n ,x 2+y 2-1,x ,32t 3,3π,3x 2-y +3xy 3+x 4-1,2x -y .【设计意图】进一步巩固多项式、多项式的项、项数和次数的概念.(五)能力提升1.多项式112134634n n n n x x x x -++-+-是几次几项式?其中最高次项是哪项?最高次项的系数是多少? 解:n +2次多项式,最高次项是234n x +-, 最高次项系数是34-. 2.多项式-a +2a 2-3a 3+4a 4-5a 5+……第99项是 ,第2022项是 ,第n 项是 . (-99a 99;2022a 2022;(-1)n •n •a n .)3.某公园的门票价格是:成人10元/张;学生5元/张.(1)一个旅游团有成人x 人、学生y 人,那么该旅游团应付多少门票费?(2)如果该旅游团有37个成人、15个学生,那么他们应付多少门票费?解:(1)该旅游团应付的门票费是(10x+5y)元.(2)把x=37,y=15代入代数式,得10x+5y =10×37+5×15 =445.因此,他们应付445元门票费.【设计意图】提升学生灵活应用多项式及相关的概念解决问题的能力.(六)感受中考1.(3分)(2021•青海2/25)一个两位数,它的十位数字是x,个位数字是y,那么这个两位数是()A.x+y B.10xy C.10(x+y)D.10x+y【解答】解:一个两位数,它的十位数字是x,个位数字是y,这个两位数10x+y.故选:D.2.(8分)(2021•河北20/26)某书店新进了一批图书,甲、乙两种书的进价分别为4元/本、10元/本.现购进m本甲种书和n本乙种书,共付款Q元.(1)用含m,n的代数式表示Q;(2)若共购进5×104本甲种书及3×103本乙种书,用科学记数法表示Q的值.【解答】(1)由题意可得:Q=4m+10n;(2)将m=5×104,n=3×103代入(1)式得:Q=4×5×104+10×3×103=2.3×105.【设计意图】通过对最近几年的中考试题的训练,使学生提前感受到中考考什么,进一步了解考点.(七)课堂小结1.说一说单项式、多项式、整式各有什么特点?2.它们三者之间的关系是怎样的?【设计意图】通过小结,使学生梳理本节课所学内容,掌握本节课的核心——多项式、多项式的项、项数和次数的概念及整式的概念,体会多项式在实际中的应用,感受由“数”到“式”,由特殊(具体)到一般(抽象)的数学思想.(八)布置作业1.P59:习题2.1:第3、4题;2.P60:习题2.1:第6、7题.五、教学反思在此之前学生已经学习了单项式及单项式的系数、次数的概念,这为过渡到本节的学习起着铺垫的作用.教材遵循“由特殊到一般”的学习规律,先是引进背景比较熟悉的实际问题,从实际问题中抽象出多项式的概念,并且让学生体会到多项式概念的产生源于实际的需要.在本节课中,多项式概念的学习是在单项式的基础上引出来的,着重指出多项式是几个单项式的和.因此,本节课的教学设计是通过比较单项式与多项式之间的异同点,掌握两个概念之间的区别和联系来突出多项式概念的本质,帮助学生理解多项式的概念,以及多项式的项和次数的概念.因而,观察分析、抽象概括、练习巩固成为本节课学习的主要方式.。
七年级数学上册(新人教版) 2.1整式第3课时多项式课件2_6-10

次数:多项式中次数最高的项的次数。
筑商宝
解:由题意得m=0,n-1=0,所以n=1.
单项式的次数是
整 单项式次 系数 数::所单有项字式母中的的指数数字的因和数。。
所有字母的指数 的和;多项式的 次数不是所有项 的次数和。
式
项:式中的每个单项式叫多项式的项。
多项式
(其中不含字母的项叫做常数项)
多项式的每一项都包括它前面的符号,有正号也有负号。
1、指出下列多项式的项和次数.
(1) a3 − a2b + ab2 − b3
(2) 3n4 − 2n2 +1
解:(1)多项式a3 − a2b + ab2 − b3的项有 a 3,− a2b ,
ab2,− b3 ;次数是 3 .
(2)多项式 3n4 − 2n2 +1的项有 3n,4 − 2n,2
1 ;次数是 4 .
4.若
是关于x的一次式,则a =___2___,若它是关
于x的二次二项式,则a =___-3___.
5.多项式
是关于a、b的四次三项式,且最高
次项的系数为-2,则x=___-5___,y=___3___.
m,n当作已知常数看待,属 于系数部分 6、若关于x的多项式-5x3-mx2+(n-1)x-1不含二次项和一次 项,求m、n的值. 分析:多项式不含哪一项,则哪一项的系数为0.
2、指出下列多项式是几次几项式:
(1) x3 − x + 1
(2) x3 − 2x2 y 2 Nhomakorabea 3y 2
解:(1) x3 − x + 1 是一个三次三项式.
(2)x3 − 2x2 y 2 + 3y 2 是一个四次三项式.
初中数学教学课例《2.1整式第3课时多项式》教学设计及总结反思

择与设计 进,由浅入深,层意识。
列代数式:
(1)长方形的长与宽分别为 a、b,则长方形的周长
是________;
(2)图中阴影部分的面积为________;
(3)某班有男生 x 人,女生 21 人,则这个班的学生
一共有________人.
观察我们所列出的代数式,是我们所学过的单项式
吗?若不是,它又是什么代数式?
教学过程
探究点一:多项式的相关概念
【类型一】单项式、多项式与整式的识别
例 1 指出下列各式中哪些是单项式?哪些是多项
式?哪些是整式?x2+y2,-x,3(a+b),10,6xy+1,
x(1),7(1)m2n,2x2-x-5,x2+x(2),a7.
解析:根据整式、单项式、多项式的概念和区别来
通过对数与式运算的分析,使学生理解认识事物的过程 力分析
是由特殊(具体)到一般(抽象),又由一般(抽象)
到特殊(具体),在不断重复中得到提高,培养学生初
步的辨证唯物主义观点.根据数与式之间的联系,体现
数学知识间具体与抽象的内在联系和数学的内在统一
性。
本课题设计的基本理念是通过师生互动,调动学生
教学策略选 参与到教学中。主要采用的教学与活动策略是循序渐
初中数学教学课例《2.1 整式第 3 课时多项式》教学设计及 总结反思
学科
初中数学
教学课例名
《2.1 整式第 3 课时多项式》
称
整式是代数式中最基本的式子,引进整式是实际的
需要,由数到式,既是有理数的概括与抽象,又是整式
教材分析 乘除和其他代数式运算的基础,也是学习方程、不等式
和函数的基础,承前启后,整式是“数与代数”领域的
【类型三】根据多项式的概念求字母的取值 例 3 已知-5xm+104xm-4xmy2 是关于 x、y 的六 次多项式,求 m 的值,并写出该多项式. 解析:根据多项式中次数最高的项的次数叫做多项 式的次数可得 m+2=6,解得 m=4,进而可得此多项式. 解:由题意得 m+2=6, 解得 m=4, 此多项式是-5x4+104x4-4x4y2. 方法总结:此题考查了多项式,解题的关键是弄清 多项式次数是多项式中次数最高的项的次数. 【类型四】与多项式有关的探究性问题 例 4 若关于 x 的多项式-5x3-mx2+(n-1)x-1 不含二次项和一次项,求 m、n 的值. 解析:多项式不含二次项和一次项,则二次项和一 次项系数为 0. 解:∵关于 x 的多项式-5x3-mx2+(n-1)x-1 不含二次项和一次项, ∴m=0,n-1=0,则 m=0,n=1. 方法总结:多项式不含哪一项,则哪一项的系数为 0. 探究点二:多项式的应用 例 5 如图,某居民小区有一块宽为 2a 米,长为 b
2.1.3 多项式
知2-练
3 如果一个多项式是五次多项式,那么这个多项式的
每一项的次数( D )
A.都小于5
B.都大于5
C.都不小于5
D.都不大于5
知识点 3 整式
知3-讲
1.定义:单项式与多项式统称整式. 2.识别方法: (1)单项式是整式; (2)多项式是整式; (3)如果一个式子既不是单项式又不是多项式,那么它
高考总分:711分 毕业学校:北京八中 语文139分 数学140分 英语141分 理综291分 报考高校: 北京大学光华管理学院
北京市理科状元杨蕙心
班主任 孙烨:杨蕙心是一个目标高远 的学生,而且具有很好的学习品质。学 习效率高是杨蕙心的一大特点,一般同 学两三个小时才能完成的作业,她一个 小时就能完成。杨蕙心分析问题的能力 很强,这一点在平常的考试中可以体现。 每当杨蕙心在某科考试中出现了问题, 她能很快找到问题的原因,并马上拿出 解决办法。
x
4x中,多项式有( C )
A.1个 B.2个 C.3个 D.4个
2 下列式子中不是多项式的是( C )
A.2x+3 C.5- 1
x
B. 3a-b 2
D.3x2-2x+2
知1-练
3 随着通讯市场竞争日益激烈,某通讯公司的手机 市话收费标准按原标准下调了25%后,每分钟又 降低了a元,原来的收费标准是每分钟b元,则现 在的收费标准是每分钟( A )
上海 2006 高考 理科 状元-武亦 文
武亦文 格致中学理科班学生 班级职务:学习委员 高考志愿:复旦经济 高考成绩:语文127分 数学142分 英语144分
物理145分 综合27分 总分585分
“一分也不能少”
“我坚持做好每天的预习、复习,每 天放学回家看半小时报纸,晚上10: 30休息,感觉很轻松地度过了三年 高中学习。”当得知自己的高考成 绩后,格致中学的武亦文遗憾地说 道,“平时模拟考试时,自己总有 一门满分,这次高考却没有出现, 有些遗憾。”
第2章 2.1 第3课时 多项式及整式

3. 下列说法错误的是( C ) A.m 是单项式也是整式 B.12(m-n)是多项式也是整式 C.整式一定是单项式 D.整式不一定是多项式
4. 下列式子:①-x;②m+3 n;③yx;④a2-b2;⑤-x42y; ⑥ 2x + 3y. 其 中 属 于 单 项 式 的 有 _①__⑤___ , 属 于 多 项 式 的 有 _②__④__⑥___,属于整式的有_①__②__④__⑤__⑥___ (填序号).
8. 有一个多项式为 a10-a9b+a8b2-a7b3+…,按这种 规律写下去,写出它的第六项和最后一项,这个多项式是几 次几项式?
解:第六项为:-a5b5; 最后一项为:b10; 这个多项式是十次十一项式.
9. 下表中的多项式①,②,③,…,是按照一定规律
排列的一列多项式.
序号 多项式
当 x=-1 时,多项式的值
6. 填表.
多项式
项
次数 常数项
-2x2y-3x+2y-
5
-2x2y,-3x,2y,-5 3
x5-2x3y3+3x+27 x5,-2x3y3,3x,27
6
4xy-1 5
45xy,-15
2
-5
27 -15
知识点 多项式的应用
7. 已知 a 是两位数,b 是一位数,把 a 接写在 b 的后
面,就成为一个三位数.这个三位数可表示成( C )
解:(2)因为 3x2-4x+6=9,所以 3x2-4x=3,所以 x2 -43x=1,故 x2-43x+6=7.
(3)将 x=2,y=-4 代入 ax3+12by+5=2017,得 4a-b =1006,将 x=-4,y=-12代入 3ax-24by3+2 得:-12a +3b+2=-3(4a-b)+2,因为 4a-b=1006,所以原式= -3×1006+2=-3016.
2.1 整式 第3课时 多项式及整式

目标二 能确定多项式的项和次数
例 2 教材补充例题 指出下列多项式的项和次数,并说出它是几 次几项式. (1)3xy-8; (2)2x2-3x+1; (3)4x2y-5xy3+2xy2-12.
解:列表解答如下:
多项式
(1)3xy-8
多项式的项 多项式的次数 几次几项式
3xy,-8
2 二次二项式
(2)2x2-3x+1
解: (1)当a=2,b=-1时, (a-b)2=[2-(-1)]2=32=9. (2)当a=2,b=-1时, (a+b)(a-b)=[2+(-1)]×[2-(-1)]=1×3=3.
【归纳总结】用直接代入法求含字母的式子的值可以分三步: (1)“当……时”,即指出字母的值; (2)“原式=……”,即代入所给字母的值; (3)计算. 注意:当字母的取值为分数或负数时,代入时要注意添加括号.
(4)区分多项式的次数与单项式的次数,不能误认为多项式 的次数是各个单项式的次数之和; (5)多项式的“项”与“项数”是两个不同的概念,“项” 是指组成多项式的单项式,包括它前面的符号,“项数”是 指项的个数.
目标二 能确定多项式的项和次数
例3 教材例4针对训练 当a=2,b=-1时,求下列含字母的式 子的值: (1)(a-b)2; (2)(a+b)(a-b).
总结反思
知识点一 多项式的概念
多项式:几个单项式的____和____叫做多项式.在多项式中, 每个单项式叫做多项式的____项____,_不__含_字__母_的_项______叫做常数
项.
次数最高项
多项式的次数:多项式里,_________的次数,叫做这个多项式的
次数.
知识点二 整式的概念 ___单__项_式____与__多_项__式_____统称整式. [点拨] 分母中含有字母的式子不是整式.
2.1.3多项式

(1)把多项式-4x2+5x-8-x4+2x3按字母x的降幂排列; 解:-x4+2x3-4x2+5x-8.
12.【2019•河北】如图,约定:上方相邻两数之和等于 这两数下方箭头共同指向的数. 示例: 即4+3=7. 则(1)用含x的式子表示m=___3_x____; (2)当y=-2时,n的值为____1____.
13.求多项式3x2-2xy-5y2+2中各项系数之和. 错解:多项式各项系数之和为3+2+5+2=12. 诊断:错解的原因是漏掉了-2xy,-5y2项的符号. 正解:多项式各项系数之和为3+(-2)+(-5)+2= -2.
4.多项式-x2-12x-1 的各项分别是( B )
A.-x2,12x,1
B.-x2,-12x,-1
C.x2,12x,1
D.x2,-12x,-1
5.【中考•济宁】如果多项式xn-2-5x+2是关于x的三次
三项式,那么n等于( C )
A.3
B.4
C.5
D.6
6.如果一个多项式是五次多项式,那么这个多项式的每
*3.【2019•大庆】用棋子摆成的“T”字形如图所示,按照 图①,图②,图③的规律摆下去,摆成第n个“T”字 形需要的棋子个数为________.
【点拨】由题图①可知,共有3×1+2=5(个)棋子, 由题图②可知,共有3×2+2=8(个)棋子, 由题图③可知,共有3×3+2=11(个)棋子, …,依次类推,则第n个“T”字形需要的棋子个数为3n+2. 【答案】 3n+2
9.把下列各式分别填在相应的大括号里: 4,x+1 2,a2+b,πR2-πr2,13x2,2x-3,-12x2+yz,a2 +1a+2.
单项式:
4,13x2
… ;
多项式:
人教版数学七年级上册2.1第3课时多项式1-课件
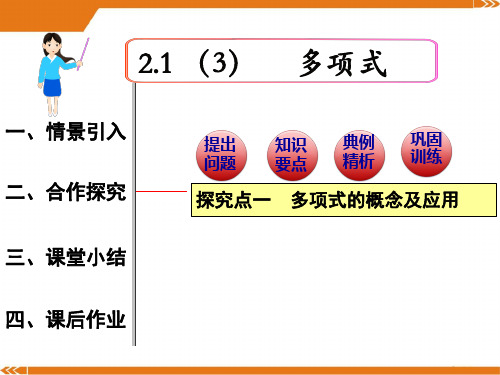
① a ,② 1 x 2 y ,③ 2 x 1 ,④ x 2 x y y 2 . 多项式有 :32x1 , x2 xy y2 .
首页
例2 :请分别写出下列多项式的项、项数、常数项、 多项式是几次几项式。
3x3-4;
解: 项: 3x3 、-4; 项数:2; 常数项 :-4; 多项式是三次二项式;
次数:多项式中次数最高的项的次数。
单独的一个数字或字母,也是整式。
一个式子如果分母中含有字母,那么这个式子既 不是多项式,也不是单项式,更不是整式。
首页
三四、、课课堂后小作结业
• 见《学练优》本课时课后巩固提升
首页
天每
开个
放孩
;子
有的
的花
孩期
子不
是一
菊样
花,
,有
选的
择孩
在子
秋是
天牡
开丹
放花
;,
而选
有择
的在
孩春
➢ He who falls today may rise tomorrow.
子天
是开
梅放
花;
,有
选的
择孩
在子
冬是
天荷
开花
放,
选
择
在
夏
我们,还在路上……
首页
单项式、多项式、整式三者之间的关系
单项式是整式,多项式也是整式,整式包括单项 式与多项式。 多项式是由几个单项式相加而成的。
单项式与多项式统称整式
首页
巩固训练
见《学练优》第47页 第1~7题
首页
三、课堂小结
整 单项式次 系数数::所单有项字式母中的的指数数字的因和数。。
2.1 第3课时 多项式

2 若它是关于x的二次二项式,则a =______. =______, -3 5.多项式 是关于a、b的四次
三项式,且最高次项的系数为-2,则x=______, -5
y=______. 3
课堂总结
项:式中的每个单项式叫多项式的项. (其中不含字母的项叫做常数项)
多项式
次数:多项式中次数最高的项的次数.
每一项的 1、1 次数
2、1、0
2、2 、0
3、2、2、2
• 多项式的 多项式里次数最高项的次数就是多项式的次 1 3 2 2 次数 数 .
几次几项 一次二 式 项式
二次三 项式 二次三项 式 三次四项 式
单项式与多项式统称整式
(整式的分母中不含字母)
下列式子中,哪些是整式?
① ③
②③⑤⑥
1 x
xy
2 多项式的应用
r 10 cm 时,求圆环的面积(
新课讲解
例3 如图,用式子表示圆环的面积.当 R 15 cm,
π 取 3.14 ).
解:外圆的面积减去内圆的面积就是圆环 的面积,所以圆环的面积是 πR2 πr 2 . 当 R 15 cm ,r 10 cm 时, 圆环的面积(单位:cm2)是
3.不含字母的项叫做常数项
4.多项式里次数最高项的次数就是多项式的次数
次数 项
常数项
例如:
3x 5 x 8 叫做三次三项式
3
新知
多项式 项
学习
3x-7y
1、边学边练:
x2-2x+4 ab-a2-1 x3+x2+xy-y2
3、x2、 x 3x、-7y x2、-2x、4 ab、-a2 、-1 xy、 -y2
人教版七年级数学上册 教案:2.1 第3课时 多项式1【精品】

第3课时 多项式1.理解多项式的概念;(重点)2.能准确迅速地确定一个多项式的项数和次数;3.能正确区分单项式和多项式.(重点)一、情境导入列代数式:(1)长方形的长与宽分别为a 、b ,则长方形的周长是________;(2)图中阴影部分的面积为________;(3)某班有男生人,女生21人,则这个班的学生一共有________人.观察我们所列出的代数式,是我们所学过的单项式吗?若不是,它又是什么代数式?二、合作探究探究点一:多项式的相关概念【类型一】 单项式、多项式与整式的识别指出下列各式中哪些是单项式?哪些是多项式?哪些是整式?2+y 2,-,a +b 3,10,6y +1,1x ,17m 2n ,22--5,2x 2+x,a 7. 解析:根据整式、单项式、多项式的概念和区别进行判断.解:2x 2+x ,1x的分母中含有字母,既不是单项式,也不是多项式,更不是整式. 单项式有:-,10,17m 2n ,a 7; 多项式有:2+y 2,a +b 3,6y +1,22--5;整式有:2+y 2,-,a +b 3,10,6y +1,17m 2n ,22--5,a 7.方法总结:(1)分母中含有字母(π除外)的式子不是整式;(2)单项式和多项式都是整式;(3)单项式不含加、减运算,多项式必含加、减运算.【类型二】 确定多项式的项数和次数写出下列各多项式的项数和次数,并指出是几次几项式.(1)232-3+5; (2)a +b +c -d ;(3)-a 2+a 2b +2a 2b 2.解析:根据多项式的项数是多项式中单项式的个数,多项式的次数是多项式中次数最高的单项式的次数,可得答案.解:(1)232-3+5的项数为3,次数为2,二次三项式; (2)a +b +c -d 的项数为4,次数为1,一次四项式;(3)-a 2+a 2b +2a 2b 2的项数为3,次数为4,四次三项式.方法总结:(1)多项式的项一定包括它的符号;(2)多项式的次数是多项式里次数最高项的次数,而不是各项次数的和;(3)几次项是指多项式中次数是几的项.【类型三】 根据多项式的概念求字母的取值已知-5m +104m -4m y 2是关于、y 的六次多项式,求m 的值,并写出该多项式. 解析:根据多项式中次数最高的项的次数叫做多项式的次数可得m +2=6,解得m =4,进而可得此多项式.解:由题意得m +2=6,解得m =4,此多项式是-54+1044-44y 2.方法总结:此题考查了多项式,解题的关键是弄清多项式次数是多项式中次数最高的项的次数.【类型四】 与多项式有关的探究性问题若关于的多项式-53-m 2+(n -1)-1不含二次项和一次项,求m 、n 的值.解析:多项式不含二次项和一次项,则二次项和一次项系数为0.解:∵关于的多项式-53-m 2+(n -1)-1不含二次项和一次项,∴m =0,n -1=0,则m =0,n =1.方法总结:多项式不含哪一项,则哪一项的系数为0.探究点二:多项式的应用如图,某居民小区有一块宽为2a米,长为b米的长方形空地,为了美化环境,准备在此空地的四个顶点处各修建一个半径为a米的扇形花台,在花台内种花,其余种草.如果建造花台及种花费用每平方米为100元,种草费用每平方米为50元.那么美化这块空地共需多少元?解析:四个角围成一个半径为a米的圆,阴影部分面积是长方形面积减去一个圆面积.解:花台面积和为πa2平方米,草地面积为(2ab-πa2)平方米.所以需资金为[100πa2+50(2ab-πa2)]元.方法总结:用式子表示实际问题的数量关系时,首先要分清语言叙述中关键词的含义,理清它们之间的数量关系和运算顺序.三、板书设计多项式:几个单项式的和叫做多项式.多项式的项:多项式中的每个单项式叫做多项式的项.常数项:不含字母的项叫做常数项.多项式的次数:多项式里次数最高项的次数叫做多项式的次数.整式:单项式与多项式统称整式.这节课的教学内容并不难,如果采用讲授的方式,很快90%以上的学生都可以理解、掌握.虽然单纯地从学生接受知识的角度,讲授法应该效果更好,但同时学生的自主学习的习惯和能力也不知不觉地被忽略了.事实证明,学生没有养成一个良好的自主学习的习惯,不会自己阅读、分析题意,他们今后的学习会受到很大的制约.。
七年级上2.1.3多项式课件ppt

3x2-y+3xy3 x4 1,
2x-y.
3
单项式 - 1 a 2 b m 4 n 2 x
32t3
π
2
7
3
系数
-1
1
1 32
2
7
次数
3
6
13
0
多项式 x2+y2-1 3x2- y+ 3xy3+ x4 - 1 2x+ y
项 x2,y2,-1 3x2,y,3xy3,x4- 1 2 x , y
次数
2
4
义务教育教科书 数学 七年级 上册
2.1 整式 (第3课时)
课件说明
本课学习是在学习了单项式、单项式的系数 和次数的概念的基础上,继续学习多项式、多项 式的项和次数的概念,整式的概念,以及用整式 解决简单的实际问题,是后续学习整式的加减运 算、一元一次方程的基础.中学学科网
课件说明
学习目标: (1)理解多项式、多项式的项和次数、整式的概念. (2)会用多项式表示简单的数量关系,并根据多项式 中字母的值求多项式的值. (3)会用整式解决简单的实际问题. (4)经历用整式表示数量关系的过程,体会用整式表 示数量关系的简洁性和一般性.
谢谢观赏
You made my day!
我们,还在路上……
项系数是-2,一次项系数是3,常数项是
5,那么这个多项式可以是
.
例1
如图所示,用式子表示圆环的面积.
当R 15 cm,r 10 cm时,求圆环的面积
π 3 .1 4 ( 取
).中学学科网
解:外圆的面积减去内圆的面积就是圆环
的面积,所以圆环的面积是 πR2 πr2.
当 R 15cm ,r 10 cm 时,圆环的面积
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章 整式的加减
2.1 整式
第3课时 多项式
学习目标:1.理解多项式、整式的概念.
2.会确定一个多项式的项数和次数.
重点:理解多项式的有关概念.
难点:会确定一个多项式的项数和次数.
一、知识链接
1.单项式的有关概念: (1)由_____与_____(或_____与_____)相乘组成的代数式叫做单项式.单独的一个___或一个_____也叫单项式.
(2)单项式中的_________叫做这个单项式的系数.
单项式中的________________叫做这个单项式的次数.
2. 337
a bx π-的系数是__________,次数是______________. 二、新知预习
【自主归纳】
1.几个________的和叫做多项式;
2.多项式中的每一个________都叫做这个多项式的项,多项式含有几项,这个多项式叫做_________.
3.不含________的项叫做常数项.
4.多项式里,__________的次数,叫做这个多项式的次数,多项式的次数是几,这个多项式叫做__________.
5.______和______统称为整式.
三、自学自测
1.多项式2
325x x -+有_____项,它们分别是______ _.其中常数项是______,它是一个__ _次_____项式.
2.多项式a 3-a 2b +ab 2-b 3的项数为_______,次数为_______.
3.多项式3n 4-2n 2+1的次数为________,常数项为_________.
四、我的疑惑
___________________________________________________________________________________________
___________________________________________________________
一、要点探究
探究点1:多项式的相关概念
问题1:列式表示下列数量
(1)温度由t℃下降5℃后是______℃.
(2)买一个篮球需要x元,买一个排球需要y 元,买一个足球需要z元,买3个篮球、5个排球、2个足球共需要___________元.
(3)如图三角尺的面积为___________.
(4)如图是一所住宅区的建筑平面图,这所住宅的建筑面积是___________.
问题2:上述几个式子都是单项式吗?这些式子有什么共同特点?与单项式有什么关系?
要点归纳:
1.几个单项式的和叫做多项式
2.在多项式中,每个单项式叫做多项式的项
3.不含字母的项叫做常数项
4.多项式里次数最高项的次数就是多项式的次数
5.单项式与多项式统称为整式
例1下列整式中哪些是单项式?哪些是多项式?是单项式的指出系数和次数,是多项式的指出项和次数:42
2223234
1π
,,1,,32,,31,2.
273
--+3-
m n
a b x y x t x y xy x x y
+-+-
要点归纳:
(1)多项式的各项应包括它前面的符号;
(2)多项式没有系数的概念,但其每一项均有系数,每一项的系数也包括前面的符号;
(3)要确定一个多项式的次数,先要确定此多项式中各项(单项式)的次数,然后找次数最高的;
(4)一个多项式的最高次项可以不唯一.
例2:已知-5x m+104x m-4x m y2是关于x、y的六次多项式,求m的值,并写出该多项式.
【归纳总结】解题的关键是弄清多项式次数是多项式中次数最高的项的次数.然后根据题意,列出方程,求出m的值.
课堂探究
探究点2:多项式的应用
例3 如图所示,用式子表示圆环的面积.当r=15 cm ,r=10cm 时,求圆环的面积(π取3.14 ).
例4 某公园的门票价格是:成人10元/张;学生5元/张.
(1)一个旅游团有成人x 人、学生y 人,那么该旅游团应付多少门票费?
(2)如果该旅游团有37个成人、15个学生,那么他们应付多少门票费?
针对训练
1.将代数式①3,②x 1,③b a -3,④π,⑤π1,⑥2
1x 2,⑦3a +1,⑧712-a , ⑨-31x 2+yz ,⑩1
4+x x 填入适当的空格中(填序号): 单项式:___________________________________________________;
多项式:___________________________________________________;
整式:_____________________________________________________.
2.多项式3m 3-2m-5+m 2的常数项是______,一次项是_____,二次项的系数是_____.
3.(1)a ,b 分别表示长方形的长和宽,则长方形的周长l =______,面积S =___,当a =2 cm ,b =3 cm 时,l =______ cm ,S =______cm 2 ;
(2)a ,b 分别表示梯形的上底和下底,h 表示梯形的高,则梯形面积S =_______,当a =2 cm ,b =4 cm , h =5 cm 时, S =______cm 2 .
4.如果x n -(m -1)x +2为三次二项式,求m 2+n 的值.
二、课堂小结
系数:单项式中的数字因数.
单项式
次数:所有字母的指数的和.
整式
项:多项式中的每个单项式叫多项式的项.
多项式 (其中不含字母的项叫做常数项)
次数:多项式中次数最高的项的次数.
4.若)3(3)2(2+---a x x a 是关于x 的一次式,则a =______,若它是关于x 的二次二项式,则a =______.
5.多项式521)3(2-+
+ab b a x y 是关于a 、b 的四次三项式,且最高次项的系数为-2,则x =______,y =______.
6.已知多项式:62
1653222+-+-+x xy y x m 是六次四项式,单项式z y x m n -4332的次数与这个多项式的次数相同,求n 的值.。
