周练精选数与式

合集下载

周周练练习题

周周练练习题本文为周周练练习题，将提供一系列题目，并提供答案和解析。

请读者按照题目提示思考并尝试解答，然后再查看答案和解析，以便提高知识和技能。

1. 数学题题目：求解以下方程组：2x + y = 10x - y = -2解答：通过联立方程可以得到：2x + y = 10 ---(1)x - y = -2 ---(2)将方程(2)两边同时乘以2，得到：2x - 2y = -4 ---(3)将方程(3)与方程(1)相加，消去x的项：(2x + y) + (2x - 2y) = 10 + (-4)4x - y = 6 ---(4)将方程(1)与方程(2)相加，消去y的项：(2x + y) + (x - y) = 10 + (-2)3x = 8 ---(5)将方程(5)两边同时除以3，得到：x = 8/3将x的值代入方程(2)或方程(1)中，可求得y的值：2(8/3) + y = 1016/3 + y = 10y = 10 - 16/3y = 14/3所以，方程组的解为：x = 8/3，y = 14/32. 英语题题目：将以下句子改为被动语态：The cat chased the mouse.解答：被动语态的构成是：助动词be（根据时态变化）+ 过去分词根据以上句子，可以得到：被动语态句子：The mouse was chased by the cat.3. 历史题题目：请简要描述第一次世界大战爆发的原因。

解答：第一次世界大战的爆发原因复杂多样，主要包括以下几个方面：- 各国的经济、政治和殖民地争夺导致了紧张局势的加剧。

当时欧洲国家之间的竞争非常激烈，他们争夺殖民地、资源和贸易优势，相互之间形成了一种紧张的平衡。

- 军备竞赛的升级。

各国为了保护自身利益，加强了军事力量的建设和发展，军备竞赛导致了军事力量的集中和对抗的升级。

- 各国结盟体系的形成。

为了增强自身的安全感和盟国的支持，各国纷纷建立了不同的军事和政治同盟，形成了一个错综复杂的结盟体系。

九年级下学期数学每周一测——数与式

九年有数学每周一测《实数》命题人：陈荔清班级姓名座号成绩月日1、填空题：（每空2分，共26分）（1）3×⎪⎭⎫ ⎝⎛-21= （2）3-1+031⎪⎭⎫ ⎝⎛-= .（3）3341⎪⎭⎫⎝⎛-a = （4）+-x x 212 =（-x ）2.（5）分解因式：①a 2-10a 2b+25ab 2= ； ②2a 4-32= .(6)12的平方根为 . （7）若x 3=-64,则x= . (8)若a 、b 互为相反数，c 、d 互为倒数，则a+b+cd+2014= . （9）在右边的日历中，任意圈出一竖例上相邻的三个数，设中间的一个数为a ，则这三个数之和为（用含a 的代数式表示）.（10）某商品降价x%后的价格为a 元，则其原定价格为元.（11）“神七飞天”实现了中国人的飞天梦和第一次太空行走，这次太空行走共进行了19min35s ，期间，宇航员翟志刚的行程为9.165×106m ，属马的翟志刚由此成为“走”得最快的中国人，翟志刚此次“行走”的速度是 m/s.2、选择题：（每小题2分，共16分）（1）小明家冰箱冷冻室的温度为-50C ，调高40C 后的温度为（） A.40C B. 90C C. -10C D. -90C（2）某红外线遥控器发出的红外线波长为0.000 00094m ，用科学技术法表示这个数是（）.A.9.4×10-7m B. 9.4×107m C. 9.4×10-8m D. 9.4×108m（3）下列计算中正确的是（）. A.2686=⋅ B.224=÷ C.532=+ D.2188-=-（4）下列各组数中互为相反数的一组数是（）.A.22与-B. -2与0.5C. -2与38-D. -2与()22-（5）若)(x x -=-442，则x 与4的大小关系为（）.A.4<xB. 4≤xC. 4>xD. 4≥x （6）用配方法将x 2-4x+5变为（x+h ）2+h 的形式，结果是（）.A.1)2(2+-xB.1)2(2--xC. 1)2(2++xD. 1)2(2-x（7）某足球赛的积分规则如下：赢一场得3分，平一场得1分，输一场得0分，某小组四个队进行单循环赛后，其中的一队积7分，若该队赢了x 场，平了y 场，则x 、y 的值分别为（）.A.1、4B. 2、1C. 0、7D. 3、13、（24分）计算：（1）;94)25.2(833412⨯-÷⨯ （2）);36()12792415.0(-⨯-++（3）（x+2y －5z ）(x －2y+5z) (4)(a －2b)(a+2b )－(a －2b)2（5）3624)32(3----；（6）18)5(22)13(21+--⎪⎪⎭⎫ ⎝⎛---4、（14分）先化简，后求值：（1）x ·x 3+(－4x 2)2 +24x 7÷(－3x 3),其中x=－2.（2）()2,3,221122-==+-÷-++y x yxy x xyx y x 其中.（精确到0.01）5、（10分）为了估计湖里有多少条鱼，我们从湖里捕上100条鱼，并做好标记，然后放回湖里，过一段时间，待带有标记的鱼完全混合于鱼群后，再捕上200条，发现其中带有标记的鱼有16条，请你估计湖里有多少条鱼.6、（5分）仔细观察下列各等式并寻找其中的规律：4×1×2+1=32 ； 4×2×3+1=52；4×3×4+1=72 ； 4×4×5+1=92； ….请用含正整数n 的等式表示此规律： . 7、（7分）某书城开展优惠学生的售书活动，规定：凡一次性购书不超过200元的一律九折优惠；超过200元的，其中200元按九折算，超过200元的部分按八折算，某学生第一次购书付款72元，第二次购书享受了八折优惠，他查看了所买书的定价，发现两次共节省45元，求该学生第二次购书实际付款多少元？。

中考数学周末作业中考真题考点强化训练《数与式》课件(含答案)

C．0.36×109
D．3.6×109
3．已知实数 a，b 在数轴上的位置如图所示，下列结论中正确的是( D )
|b| D．－a＞b
4．计算 3x2－x2 的结果是( B )
A．2
B．2x2
C．2x
D．4x2
5．用代数式表示：a 的 2 倍与 3 的和．下列表示正确的是( B )
D．2x3－x3＝1
9．下列各式分解因式正确的是( A )
A．x2＋6xy＋9y2＝(x＋3y)2
B．2x2－4xy＋9y2＝(2x－3y)2
C．2x2－8y2＝2(x＋4y)(x－4y)
D．x(x－y)＋y(y－x)＝(x－y)(x＋y)
10．若分式xx－＋33的值为 0，则 x 的值为( A )
16．式子 x1＋1中 x 的取值范围是 x＞－1 . 17．分解因式：ab2－a＝ a(b＋1)(b－1) ． 18．已知 m＋n＝12，m－n＝2，则 m2－n2＝ 24 .
三、解答题(7 分＋7 分＋8 分，共 22 分) 1
19．计算：－12 018＋| 3－2|＋tan 60°－(π－3.14)0＋ 2 －2.
解：原式＝－1＋2－ 3＋ 3－1＋4＝4.
20．先化简，再求值：(a－2b)(a＋2b)－(a－2b)2＋8b2，其中 a ＝－2，b＝12. 解：原式＝a2－4b2－a2＋4ab－4b2＋8b2＝4ab，当 a＝－2，b＝12时，原式＝－4.
21．先化简，再求值： x＋1 1＋x2－1 1 ÷x2＋2xx＋1，其中 x＝ 2. 解：原式＝x＋x－11＋x－1 1·x＋x 12＝xx＋－11，当 x＝ 2时，原式＝ 22－＋11＝3＋2 2.
中考数学周末作业中考真题考点强化训练

四年级下数学周周练-第六周_13-14北师大版(无答案)

四年级数学每周一练（六）一、计算：1、直接写出得数。

0.18×5= 0.16×5×2= 6.2÷0.62= 10÷2.5×4=2、用竖式计算：200÷16= 6.58÷1.4=81.9÷78= 8.64÷8=3、计算下面各题，能简算的要简算。

1.2÷0.5+8.8÷0.5 0.175÷0.25×0.41.48÷（0.148×2.5） 32×12.5×2.5二、填空。

1、4.94÷0.13的商的最高位在（）位上。

2、在〇里填上>、<或=。

1.2÷0.5〇1.2 5.8〇5.8×1.01 5.4×1〇5.4÷13、在3.29，3.29，3.292929，3.2927四个数中最大的数是（），最小的数是（）。

4、用一根尼龙丝绳围成一个长方形，长6分米，宽1.5分米，如果把这根尼龙丝绳改围成正方形，那么正方形的周长是（）分米。

5、64.8÷44的商用循环小数表示是（），保留两位小数是（），三、选择。

1、近似数4.2是把一个小数保留一位小数时所得到的，下列数中，（）不可能是这个数。

A、4.239B、4.21C、4.27D、4.2482、下列四个式子，正确的是（）A、1÷3=0.3B、1÷3≈0.33……C、1÷3=3D、1÷3=0.33、2.5除1的商是（）A、2.5B、4C、0.4四、判断题。

（正确的打“√”，错误的打“×”，并改正。

）1、同一景物在不同位置拍摄出来的画面不一定相同。

（）2、0.13333是循环小数。

（）3、21.45÷15除到商是1.4时，余“4”，这里的“4”表示4个一。

（）4、因为4.00和4表示的精确程度不同，所以大小也不同。

中考数学数与式专题知识训练50题(含参考答案)

中考数学数与式专题知识训练50题含答案（有理数、实数、代数、因式分解、二次根式）一、单选题1．下列四个数中，最小的数是( ) A ．0B ．2C ．－2D ．－12．下列式子是最简二次根式的是（）ABC D3．由冯小刚执导，严歌苓编剧的电影《芳华》于2017年12月15日在全国及北美地区上映，电影首周票房便超过29400000元，数29400000用科学记数法表示为（） A ．0.294×109B ．2.94×107C ．29.4×107D ．294×1064．计算－5+6，结果正确的是( ). A ．1 B ．－1C ．11D ．－115．在实数227π ） A ．1个B ．2个C ．3个D ．4个6．在－2、－2012、0、0．1这四个数中，最大的数是（）． A ．－2B ．－2012C ．0D ．0．17．下列命题是真命题的是（） A ．带根号的数是无理数 B ．若a b >，则21a b +>+ C ．同旁内角互补D ．相等的角是对顶角8．下列说法中，正确的是（）A ．在数轴上表示a -的点一定在原点的左边B ．1是绝对值最小的数C ．一个数的相反数一定小于这个数D ．如果||a a =-，那么a 是负数或零9．下列说法：①2的一个平方根；①()22-的算术平方根是－2；根是2±；①0的平方根没有意义；正确的是（） A ．①①①B ．①①C ．①①①D ．①①10．下列式子中，与2x 2y 不是同类项的是（）A ．﹣3x 2yB ．2xy 2C ．yx 2D ．23x y11 ） A ．3±B ．-3C ．3D ．9212．化简22m n m n n m+--的结果是（） A ．m+n B ．n ﹣m C ．m ﹣n D ．﹣m ﹣n13．在函数y x 的取值范围是（） A ．x≥1B ．x ＞1C ．x ＜1D ．x≤114．下列四个多项式中，能因式分解的是（） A ．2a b +B ．21a a -+C ．2a b -D ．221a a -+15．在下列各数：3π-，3.1415 2.010101…（相邻两个1之间有1个0），76.0123456…（小数部分由相继的正整数组成）中，是无理数的有（） A ．3个B ．4个C ．5个D ．6个16．下列各式：①63＋63；①(2×62)×(3×63)；①(23×33)2；①(22)3×(33)2．其中结果是66的有( ) A ．①①①B ．①①①C ．①①D ．①①17．下列各式正确的是( )A ．0.6=±B 3=±C 3=D 2=-18．下列各式中错误的是（） A ．2c d c d c d c d da a a a -+-----== B ．5212525aa a +=++ C ．1x y x y y x-=--- D ．2211(1)(1)1x x x x -=---19．如图，数轴上表示数2的相反数的点是（）A ．点NB ．点MC ．点QD ．点P二、填空题20．在227、)1、3.1416、0.3⋅这5个数中，无理数是______．21．截止2020年5月10日，全球新冠肺炎感染累计确诊人数大约为3940000人，用科学记数法3940000可表示为_____． 22．函数2xy x =-中，自变量x 的取值范围是______． 23．=_________． 24．化简：2221x x＝_________．25x 的取值范围是__． 26．如果3m a =，那么2m a =___________.27．已知实数a ，b 互为相反数，c ，d 互为倒数，x ()a b cd x ++_____________．28．把(9)(3)(3)(5)---++--转化为只含有加法的算式：________． 29．计算：(6)(4)--+=______． 30．已知，且，则_______.31．函数()f x =______. 32．化简：()111x x x +=-______． 33．已知a ，b 是方程2310x x -+=的两个实数根，则22a b +=_____． 34．定义一种运算：*2a b ab a b =+-，则()3*5-=__________． 35．1111()()2332a b b a ---= _________36．有六个数：5，0，132，0.3-，14-，π-，其中分数有a 个，非负整数有b 个，有理数有c 个，则a b c +-=______．37．已知21x x -=，则代数式3222020__________x x -+=________．38．若关于x 的多项式29x ax ++是完全平方式，则=a __________. 39．代数式145x x -+--的最大值是________．三、解答题40．小明有5张写着不同数字的卡片，请你按要求抽出卡片，完成下列各问题：(1)从中取出2张卡片，如何抽取能使这2张卡片上的数字乘积最大，并说明理由； (2)从中取出2张卡片，如何抽取能使这2张卡片上的数字相除的商最小，并说明理由．41．（1）已知6a b +=，3ab =-，求代数式22a b +的值；（2）已知34x =，97y =，求23x y +的值．42．计算()3201911--．43．计算：(1)()11.250.5222⎛⎫÷-+-⨯ ⎪⎝⎭；(2)()14913249⎛⎫⎛⎫-÷+--+ ⎪ ⎪⎝⎭⎝⎭．44．计算题：(1)()()2323328332a a a a a a ⋅+-+--÷(2)(()2020********π-⎛⎫-++-+- ⎪⎝⎭45．在数轴上将下列各数表示出来，并将这些数用“<”连接起来． (1),--2,-13,2-2(2),-046．计算：(1)()()()()71082---+--+； (2)()()1.210.3⎡⎤-+--⎣⎦； (3)()()()()413597--++---+； (4)()136 3.3634 3.344⎛⎫-----++ ⎪⎝⎭．47．先化简，后求值：22(2)(69)(215)x x x x x x ------，其中16x =． 48．观察以下一系列等式：①11222222+=+=；①22322442+=+=；①33422882+=+=；①________;（1）请按这个顺序仿照前面的等式写出第①个等式：________；（2）根据你上面所发现的规律，用含字母n 的式子表示第n 个等式：______，并说明这个规律的正确性；（3）请利用上述规律计算：10987-----.22222 49．计算：（1）（a﹣3b）2﹣a（a﹣4b）．（2）（m2n3）3+（﹣2m2n﹣3）﹣2．参考答案：1．C【详解】①2102-<-<<， ①上述四个数中，最小的数是2-. 故选C. 2．C【分析】根据最简二次根式即可求出答案．【详解】解：（A ）原式＝A 不选；（B B 不选；（D D 不选；故选C ．【点睛】本题考查了二次根式的化简，正确掌握二次根式的化简是解题的关键. 3．B【分析】科学记数法的表示形式为10n a ⨯ 的形式，其中110a ≤＜，n 为整数.确定n 的值时，要看把原数变成a 时，小数点移动了多少位，n 的绝对值与小数点移动的位数相同.当原数绝对值>10时，n 是正数；当原数的绝对值<1时，n 是负数．【详解】解：将29400000用科学记数法表示为：72.9410⨯ ．故选B ．【点睛】本题考查科学记数法的表示方法.科学记数法的表示形式为10n a ⨯的形式，其中110a ≤＜，n 为整数，解题的关键是要正确确定a 的值以及n 的值．4．A【分析】根据有理数的加法运算法则进行计算即可【详解】解：-5+6， =1．故选A ．【点睛】本题考查了有理数的加法，绝对值不等的异号两数相加，取绝对值较大数的符号，并用较大的绝对值减去较小的绝对值；是解题的关键 5．A【分析】无理数就是无限不循环小数．理解无理数的概念，一定要同时理解有理数的概念，有理数是整数与分数的统称．即有限小数和无限循环小数是有理数，而无限不循环小数是无理数．由此即可判定选择项．【详解】解：227是分数，属于有理数；4，是整数，属于有理数；2，是整数，属于有理数．所以无理数只有π共1个．故选：A ．【点睛】此题主要考查了无理数的定义，其中初中范围内学习的无理数有：π，2π等；开方开不尽的数；以及像0.1010010001…，等有这样规律的数． 6．D【详解】试题分析：把这几个数从小到大排列，得-2012＜-2＜0＜0．1，所以最大的数是0．1．故选D ．考点：比较实数的大小． 7．B【分析】直接根据相关无理数的特点、平行线的性质、不等式的基本性质、对顶角的定义即可判断．【详解】解：A A 不正确；B 选项中，根据不等式的基本性质1可知，若a b >，则11a b +>+，所以21a b +>+，所以B 正确；C 选项中，同旁内角不一定互补，正确命题应为：“两直线平行，同旁内角互补”，所以C 不正确；D 选项中，相等的角不一定是对顶角，所以D 不正确；故选B ．【点睛】本题考查无理数的特点、平行线的性质、不等式的基本性质、对顶角，熟练掌握相关概念、性质是解题的关键． 8．D【分析】根据实数与数轴的对应关系、相反数、绝对值的定义来解答．-的点在原点的右边，故选项错误，不符【详解】解：A、如果a<0，那么在数轴上表示a合题意；B、0是绝对值最小的数，故选项错误，不符合题意；C、负数的相反数大于这个数，故选项错误，不符合题意；=-，那么a是负数或零，选项正确，符合题意．D、如果||a a故选：D．【点睛】本题考查了数轴、相反数、绝对值准确理解实数与数轴的定义及其之间的对应关系．解题的关键是掌握相反数的定义：只有符号不同的两个数互为相反数；绝对值的性质：一个正数的绝对值是它本身；一个负数的绝对值是它的相反数；0的绝对值是0．9．D【分析】根据平方根与算术平方根的定义和运算逐个判断即可．【详解】①是2的一个平方根，则此说法正确①()224-=，4的算术平方根是2，则此说法错误4，4的平方根是2±，则此说法正确①0的平方根是0，则此说法错误综上，正确的是①①故选：D．【点睛】本题考查了平方根与算术平方根的定义和运算，熟记定义与运算是解题关键．10．B【分析】根据同类项的概念：字母相同，相同字母的指数也相同进行判断.【详解】解：2xy2与2x2y中相同字母的指数不相同，不是同类项．故选B．【点睛】本题考查同类项的概念，熟记概念是解题的关键.11．C【分析】根据算术平方根即可求解．【详解】解：3=，3 ，【点睛】本题考查求算术平方根，解题的关键是熟练掌握算术平方根定义． 12．A【详解】试题分析：22m n m n n m +--=22m n m n m n ---=22m n m n--=()()m n m n m n +--=m+n ．故选A ．考点：分式的加减法． 13．B【分析】根据被开方数大于等于0，分母不等于0列式求解即可．【详解】根据题意得x ﹣1≥0，1﹣x≠0，解得x ＞1，故选B ．【点睛】本题考查了函数自变量的取值范围的确定，一般从三个方面考虑：（1）当函数表达式是整式时，自变量可取全体实数；（2）当函数表达式是分式时，考虑分式的分母不能为0；（3）当函数表达式是二次根式时，被开方数非负数． 14．D【分析】尝试用提公因式或者公式法因式分解的方法分解各选项，即可【详解】A.B.C 选项都不能通过提公因式或者公式法直接因式分解， 221a a -+=2(1)a -，故选D【点睛】本题考查了公式法分解因式，熟悉完全平方公式是解题的关键． 15．B【分析】无理数就是无限不循环小数．理解无理数的概念，一定要同时理解有理数的概念，有理数是整数与分数的统称．即有限小数和无限循环小数是有理数，而无限不循环小数是无理数．12=，在下列各数：3π-，3.1415 2.010101…（相邻两个1之间有1个0），76.0123456…（小数部分由相继的正整数组成）中，是无理数的有3π-6.0123456…（小数部分由相继的正整数组成）， ①无理数一共有4个，【点睛】本题考查了无理数的识别，无限不循环小数叫无理数，初中范围内常见的无理数有三类：①π类，如2π，3π等；①①虽有规律但却是无限不循环的小数，如0.1010010001…（两个1之间依次增加1个0），0.2121121112…（两个2之间依次增加1个1）等． 16．B【详解】分析：根据同底数幂的乘法、积的乘方、幂的乘方分别计算即可得到答案. 详解：①63+63=2×63≠66，故不符合题意； ①（2×62）×（3×63）=6×62×63=66，故符合题意； ①（22×32）3=（62）3=66，故符合题意； ①（33）2×（22）3=36×26=66，故符合题意故选B.点睛：本题考查了同底数幂的乘法、幂的乘方和积的乘方运算，逆用积的乘方法则，即am ·bm =(ab )m 是解答本题的关键. 17．A【详解】3=，则B 3=-，则C 2，则D 错，故选A ． 18．C【分析】按同分母分式加减法则计算即可. 【详解】A.2c d c d c d c d da a a a-+-----==，正确； B.52521252525a a a a a ++==+++，正确； C.x y x y x y x y y x x y x y x y+-=+=-----，错误； D.222111(1)(1)(1)1x x x x x x --==----，正确. 故选：C【点睛】此题考查同分母分式的加减法的法则：同分母分式相加减，分母不变，分子相加减. 19．A【分析】根据相反数的定义、数轴的定义即可得．【详解】2的相反数是2-，由数轴图可知，点N 表示的数为2-，则数轴上表示数2的相反数的点是点N ，故选：A ．【点睛】本题考查了相反数、数轴，熟练掌握数轴的定义是解题关键．20．【分析】无理数就是无限不循环小数．可分为三类：①有一定规律的无限不循环小数，如2.01001000100001……；①含有π的式子，如2π，5π+；①，【详解】227、)011=、3.1416、0.3⋅无限循环小数是有理数，故答案为：【点睛】本题主要考查了无理数的定义，牢固掌握无理数定义是做出本题的关键． 21．3.94×106【分析】科学记数法的表示形式为a×10n 的形式，其中1≤|a|＜10，n 为整数．确定n 的值时，要看把原数变成a 时，小数点移动了多少位，n 的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n 是正整数；当原数的绝对值＜1时，n 是负整数．【详解】解：将3940000用科学记数法表示为：3.94×610．故答案为：3.94×610．【点睛】此题考查科学记数法的表示方法，科学记数法的表示形式为a n 10⨯的形式,其中1a ≤<10，n 为整数，表示时关键要正确确定a 的值以及n 的值．22．2x ≠【分析】根据分式有意义的条件是分母不为0；分析原函数式可得关系式x−2≠0，解得答案．【详解】根据题意得x−2≠0，解得：x≠2；故答案为：x≠2．【点睛】本题主要考查自变量得取值范围的知识点，当函数表达式是分式时，考虑分式的分母不能为0．23．2014【详解】试题分析：因为负数的绝对值等于它的相反数，所以=2014．考点：绝对值24．2x -3 【分析】根据二次根式的性质可知，x ≥2，再根据x 的取值范围进行化简即可．【详解】解：①x −2①0，①x ①2，=x −1，①原式=x −2+(x −1)=x -2+x -1=2x -3．【点睛】本题考查了二次根式的性质，解题的关键是熟练掌握二次根式的性质． 25．x ＞8【分析】由分式的分母不等于零和二次根式的被开方数是非负数得到x ﹣8＞0．【详解】解：由题意，得x ﹣8＞0，解得x ＞8．故答案是：x ＞8．【点睛】考查了分式有意义的条件和二次根式有意义的条件，注意，二次根式在分母上，所以不能取到0．26．9【分析】根据幂的乘方将原式变形即可得出答案．【详解】①3m a =，①()22239m m a a === 故答案为9.【点睛】此题考查幂的乘方，解题关键在于将原式变形即可.27．6或8-【分析】根据题意可得0a b +=，1cd =，7=±x ，然后代入代数式求值即可．7=，①a 、b 互为相反数，①0a b +=，①c 、d 互为倒数，①1cd =，①x①7=±x ，当7x =时，原式()017716=+⨯=-=；当7x =-时，原式()()017718=+⨯-=--=-，①所求代数式的值为6或8-．故答案为：6或8-．【点睛】此题主要考查了实数运算和求代数式的值，关键是掌握相反数和为0，倒数积为1．28．9335-+++【分析】根据有理数的减法法则进行计算即可求解．【详解】解：(9)(3)(3)(5)---++--9335=-+++．故答案为：9335-+++．【点睛】本题考查了有理数减法法则，掌握有理数减法法则是解题的关键．29．﹣10.【分析】根据有理数的运算即可求解.【详解】(6)(4)(6)(4)10--+=-+-=-．故答案为﹣10.【点睛】此题主要考查有理数的运算，解题的关键是熟知有理数的运算法则.30．4【详解】因为，所以设，所以所以 31．2x >【分析】根据二次根式与分式的性质即可求解.【详解】依题意得x-2＞0，解得2x >，故填：2x >.【点睛】此题主要考查函数自变量的取值，解题的关键是熟知二次根式与分式的性质. 32．11x -．【详解】试题分析：根据分式的加法计算法则可得：原式=()()()x 111x 1x 1x 1x 1x x x x -+==----. 33．7【分析】先根据根与系数的关系得到+3a b =，1ab =，在利用完全平方公式展开()2222a b a b ab +=+-，然后利用整体代入的方法计算．【详解】解：①a ，b 是方程2310x x -+=的两个实数根，①+3a b =，1ab =，①()2222a b a b ab +=+-＝32－2＝7故答案为：7【点睛】本题考查了根与系数的关系：若x 1、x 2是一元二次方程ax 2+bx +c ＝0，（a ≠0）的两根时，1212,b c x x x x a a+=-=，还考查了完全平方根公式的运用：()2222a b a b ab +=+-． 34．38-【分析】根据题目所给新定义运算进行计算即可．【详解】解：①*2a b ab a b =+-，①(3)*52(3)5(3)5-=⨯-⨯+--3035=--- 38=-，故答案为：38-．【点睛】本题考查了定义新运算，有理数的四则混合运算，熟练掌握相关运算法则理解题目所给出的新定义是解本题的关键．35．221149a b - 【分析】利用平方差公式计算即可. 【详解】1111a b b a 2332⎛⎫⎛⎫--- ⎪⎪⎝⎭⎝⎭=1111 a b a b 2323⎛⎫⎛⎫---+ ⎪⎪⎝⎭⎝⎭=（1a 2-）2-（1b 3）2=2211a b 49-，故答案为2211a b 49- 【点睛】此题考查了运用平方差公式进行运算，熟练掌握平方差公式是解答此题的关键. 36．0【分析】根据分数、非负整数和有理数的定义得到a ，b ，c 的值，即可求解．【详解】解：分数有132，0.3-，14-，①3a =，非负整数有0，5，①2b =，有理数有5，0，132，0.3-，14-，①5c =， ①3250a b c +-=+-=，故答案为：0．【点睛】本题考查有理数的定义，掌握分数、非负整数和有理数的定义是解题的关键． 37．2019，±2．【分析】先把21x x -=变形，然后用x+1代替x 2，代入3222020x x -+，即可求解，先求【详解】①21x x -=，①21x x =+，①3222020x x -+=(1)2(1)2020x x x +-++=2222020x x x +--+=1222020x x x ++--+=2019，，±2，故答案是：2019，±2．【点睛】本题主要考查求代数式的值以及平方根，掌握代入法对代数式进行降幂是解题的关键．38．6或-6【分析】利用完全平方公式的结构特征判断即可确定出a的值．【详解】解：①关于x的多项式x2+ax+9是完全平方式，①a=±6，故答案为±6【点睛】本题考查完全平方式，熟练掌握完全平方公式是解本题的关键．39．0【分析】求这个式子的范围，可以根据对x的值的范围的讨论，去掉绝对值符号，对式子进行化简．【详解】当x-1<0，x+4< 0时，即x < -4，|x－1|-|x+4|-5= 1-x+x+4- 5=0，当x- 1 > 0，x+4< 0时，x无解；当x- 1 < 0，x+4> 0时，即-4<x< 1|x-1|-x+4-5=1-x-x-4- 5= -2x-8<0，当x-1> 0，x+4> 0时，即x > 1，x x--+-=x-1-x-4- 5145= -10，所以最大值是0．故答案为：0【点睛】此题考查绝对值的化简，利用分类讨论的方法，把x的取值分为多段，去掉绝对值符号．40．(1)21，详见解析(2)7-，详见解析【分析】（1）根据题意和给出的五张卡片，利用同号两数相乘的法则判断即可；（2）根据题意和给出的五张卡片，利用异号两数相除的法则判断即可；【详解】（1）若从中取出2张卡片，使这2张卡片上数字的乘积最大，则乘积的最大值是：()()7321-⨯-=，理由：要使抽取的两张卡片上的数字乘积最大，则首先应考虑抽取同号数字的两张卡片，其次考虑抽取绝对值大的数字卡片.而()()73212510-⨯-=>⨯=，所以乘积的最大值为21 ；（2）从中取出2张卡片，使这2张卡片上数字相除的商最小，则商的最小值是：()717-÷=-，理由：要使抽取的两张卡片上的数字相除的商最小，则首先应考虑抽取异号数字的两张卡片，其次考虑抽取两数绝对值的差大的数字卡片.所以两张卡片上的数字相除的商最小是7-．【点睛】本题考查有理数的混合运算，解答本题的关键是明确有理数混合运算的计算方法．41．（1）42；（2）28【分析】（1）利用完全平方公式求出()22636a b +==，再根据222()2a b a b ab +=+-即可求解；（2）逆用同底数幂的乘法和幂的乘方的运算法则，得到22333x y x y +=⋅即可求解．【详解】解：（1）①6a b +=，①()22636a b +==，即22a 2ab b 36++=，①3ab =-，①2236242a b ab +=-=；（2）①97y =，①()237y =，即237y =， ①34x =，①223334728x y x y +=⋅=⨯=．【点睛】本题考查了完全平方公式以及同底数幂的乘法和幂的乘方的逆用等知识，掌握同底数幂的乘法和幂的乘方的逆用的相关知识是解答本题的关键．42．-5【分析】直接利用绝对值的性质，立方的运算法则，二次根式的运算性质计算即可．【详解】原式()131--131-=5-．【点睛】本题主要考查实数的混合运算，掌握绝对值的性质，立方的运算法则，二次根式的运算性质是解题的关键．43．(1)7.5- (2)5259-【分析】（1）根据有理数混合运算法则进行计算即可；（2）根据有理数四则混合运算法则进行计算．【详解】（1）解：()11.250.5222⎛⎫÷-+-⨯ ⎪⎝⎭()()1.252 2.52=⨯-+-⨯2.55=--7.5=-；（2）解：()14913249⎛⎫⎛⎫-÷+--+ ⎪ ⎪⎝⎭⎝⎭()44912139=-⨯++ 42829=-++ 5259=-．【点睛】本题主要考查了有理数的混合运算，解题的关键是熟练掌握有理数混合运算法则．44．(1)6a(2)1【分析】（1）根据同底数幂的乘法，积的乘方，同底数幂的除法进行计算即可求解；（2）根据负整数指数幂，零次幂，求一个数的立方根，有理数的乘方，化简绝对值，进行计算即可求解．【详解】（1）解：原式＝566598a a a a +--6a =；（2）解：原式＝441213-++--+1=．【点睛】本题考查了同底数幂的乘法，积的乘方，同底数幂的除法，负整数指数幂，零次幂，求一个数的立方根，有理数的乘方，化简绝对值，掌握以上知识是解题的关键．45．见解析，()()21301222----＜＜-＜＜【分析】先运用去括号、去绝对值以及幂的相关知识，对各数进行化简，然后在数轴上表示出来，最后用小于号顺次连接即可.【详解】解：①(1)--=1，2=2-，2(42)=-则在数轴上表示为：①()()21301222----＜＜-＜＜【点睛】本题考查了去括号、去绝对值、幂以及有理数的大小比较，对各数进行化简是解答本题的关键.46．(1)7-；(2)0.1；(3)6-；(4)20．【分析】（1）根据有理数的加减混合运算求解即可；（2）根据有理数的加减混合运算求解即可；（3）根据有理数的加减混合运算求解即可；（4）根据有理数的加减混合运算求解即可．（1）解：()()()()71082---+--+，()()()=7+1082-+--+，()()=382+--+，()=52--+，()=5+2--，=7-；（2）解：()()1.210.3⎡⎤-+--⎣⎦，()[]= 1.21+0.3-+，()= 1.2 1.3-+，=0.1；（3）解：()()()()413597--++---+，()()()()=4+13597--+---+，()()()=17597-+---+，()()=2297---+，()=2297-++，()=137-+，=6-；（4）解：()136 3.3634 3.344⎛⎫-----++ ⎪⎝⎭， ()13=6+ 3.3+6+34 3.344-++， ()31= 3.3+ 3.3+64+3644⎛⎫⎡⎤-++ ⎪⎣⎦⎝⎭， =64+10+，=20；【点睛】本题主要考查了有理数的加减混合运算，计算有理数的加减混合运算时，从左到右进行计算即可，有括号的要先算括号里面的，在计算加法时，把相反数和能凑整的数先相加可以让计算更加简便，熟练掌握有理数的加减法法则是解题的关键．47．化简结果261818x x -++，代数式的值为5206．【分析】先计算多项式乘以多项式，单项式乘以多项式，再合并同类项得到化简的结果，再把16x =代入化简后的代数式进行计算即可．【详解】解：22(2)(69)(215)x x x x x x ------322326*********x x x x x x x x =---++-++261818x x =-++，当16x =时，原式1161818366=-⨯+⨯+ 13186=-++ 5206=．【点睛】本题考查的是整式的混合运算中的化简求值，掌握“多项式乘以多项式，单项式乘以多项式的运算法则”是解本题的关键．48．（1）445222+=；（2）1222n n n ++=；证明见解析；（3）2.【分析】（1）根据已知规律写出①即可．（2）根据已知规律写出n 个等式，利用提公因式法即可证明规律的正确性．（3）由（2）结果1222n n n ++=可得：1222n n n +-=，利用此规律，从左到右两项两项结合运算即可解答.【详解】（1）445222+=（2）1222n n n ++=左边()1211222n n n +=⋅+=⋅=右边12n +=∴左边=右边1222n n n +∴+=（3）由（2）1222n n n ++=1222n n n +∴-=∴原式9872222=---⋯⋯-87222=--⋯⋯-222=-2=【点睛】题目考查数字的规律变化，解决此类问题的关键是找到序号和变化数字的关系，另外题目涉及证明和运算，对学生的考察能力有了更高的要求．49．（1）292b ab-；（2）6 6944n m nm+【分析】（1）根据完全平方公式以及单项式乘以多项式结合整式的加减运算法则计算即可；（2）根据积的乘方，幂的乘方，负整数指数幂等运算法则计算即可．【详解】解：（1）原式=222694a ab b a ab-+-+292b ab=-；（2）原式＝66944nm nm+．【点睛】本题考查了整式的混合运算，积的乘方，幂的乘方，负整数指数幂等知识点，熟练掌握运算法则是解题的关键．。

数与式周周清3

1数与式周周清（3.24）一、选择题（每小题5分） 1．若x 与3互为相反数，则1x +等于（）A ．-2B ．4C ．-4D ．2 2．下列运算中，错误的是（）A ．（x 2）3＝x 6B ．x 2+x 2＝2x 2C ．x 2⋅x 3＝x 6D ．（﹣3x ）2＝9x 2 3．在-（-3），-|-6|，-（-2）2，5这四个数中，比-4小的数是（） A ．-（-3） B ．-|-6| C ．-（-2）2 D ．5 4．下列各式从左到右的变形中，属于因式分解的是（）A ．2623x y x xy =⋅B ．()24141x x x x ++=++C ．()()2339a a a +-=-D ．()3222x xy x x y -=-5．计算1321-=，2318-=，33216-=，43810-=，534122-=，…通过各计算结果中个位数字的规律，猜测202231-的个位数字是（）A ．0B ．2C ．6D ．8二、填空题（每小题5分）6．2021年5月11日，第七次全国人口普查结果发布，长沙市人口总数首次突破千万，约为10040000人，将数据10040000用科学记数法表示为___________________．7．若3m a =，2n a =，则23m n a +=_____．8．分解因式：269b b -+= _________________．9．已知1x =，1y =，22x y -=_____．10．已知2217a b +=，4ab =，则()2a b +的值是___________．三、解答题（每题10分，共50分）11．计算：（1）﹣（﹣1）+32÷（1﹣4）×2；（2）﹣12﹣24×（﹣16+23﹣34）．姓名：班级：2 12．化简：(1)()()37565236273a b a ba b -÷- (2)()()()2232121x y x x +-+-13．先化简，再求值：()()()()233322x x x x x -++-+-，其中12x =-．14．计算：（1）(02sin 451-+-+° （2）())02021124sin 30π-+-+︒-15．现规定一种新的运算：22x y x xy y *=-+，其中x ，y 为有理数.(1)化简()22a b a b -**(2)当2a =-，3b =时，求(1)中代数式的值.。

四数下周练4

四年级下册数学学科周练4
姓名：_________ 班级:____________ 等第：________
一、用竖式计算
22×145= 308×16= 534×67=
75×682= 635×42= 702×46=
615×48= 903×47= 263×56= 124×71= 25×112= 45×207=
二、解决问题的策略
1、体育用品店里每个足球92元，比篮球便宜37元，买34个篮球需要多少元？
2、李叔叔每天早上跑步30分钟，速度是110米/分。

照这样坚持跑一个月（按30天计算），李叔叔能跑多少千米？
3、一艘货轮以36千米/小时的速度从甲港开往乙港，10小时到达。

从乙港回来时因为是顺水行驶，只用了9小时。

这艘货轮回来时的平均速度是多少千米/小时？
☆4、一辆汽车的速度是18米/秒，车身长度是18米，隧道长324米。

这辆汽车全部通过隧道要用多长时间？。

高二数学下学期周练四文8

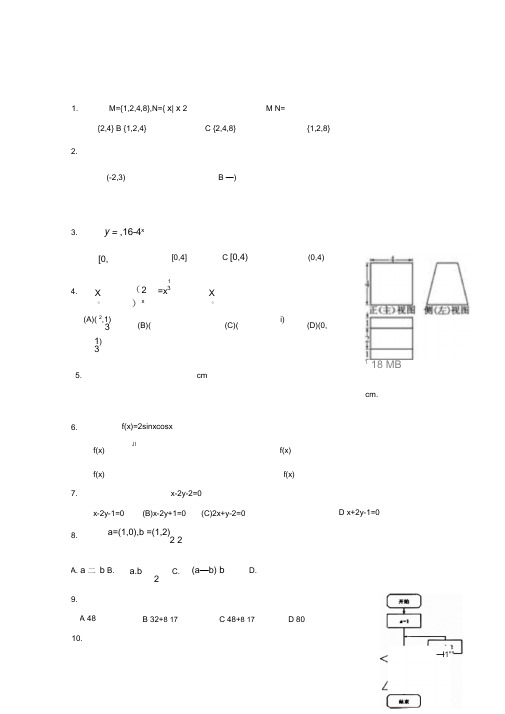
1. M={1,2,4,8},N={ x | x 2 M N={2,4} B {1,2,4}C {2,4,8}{1,2,8}2. (-2,3) B —)3.y = ,16-4x[0, [0,4]C [0,4)(0,4)4. X 。

（2）x1=x 3X。

5. 6. 7. 8. (A)( 2,1) 3 1) 3 (B)(f(x)=2sinxcosxf(x) f(x)x-2y-1=0JI(C)(i)(D)(0,118 MBcmcm.f(x) f(x)x-2y-2=0(B)x-2y+1=0(C)2x+y-2=0D x+2y-1=0a=(1,0),b =(1,2)2 2A. a 二 bB. a.bC.2(a —b) bD.9. A 48 B 32+8 17 C 48+8 17 D 8010. I —1""2到x 轴的距离为(二.填空题:已知z=2x-y ，式中变量x,y 满足约束条件 x ^-1则z 的最大值为x 乞24已知a 是第二象限的角，tan( n +2 a )= ，则tan a3三.解答题： 17.在厶 ABC 中，a , b , c 分别为内角 A , B , C 的对边，且 2cos( B- C ) =4sinB?sinC - 1. (〔)求 A ； (2)若 a=3, sinB ，求 b .2 318.已知数列｛a n ｝满足：.a^20,a^7 , a n .2-a n =-2 ( n € N*)(I)求a 3, a 4,并分段表示出数列｛a n ｝通项公式；(H)记数列｛a n ｝前2n 项和为S 2n ,当S 2n 取最大值时，求 n 的值的结果是() (A ) 3(B ) 11(C ) 38 (D ) 12311.已知F i , F 2为双曲线C: 2 2X- y =1的左、右焦点，点 P 在C 上,RPF 2=60。

，贝U P(A)(B)(C)(D)612. 若曲线 y = x 2在点(a,a 2)处的切线与两个坐标轴围成的三角形的面积为(A ) 64(B ) 32 (C ) 16 (D ) 813. 14. 15. 命题"对任何x R ,x —2十x —4 >3”的否定是16. 若函数f (x^(^x 2)(x 2 ax b)的图像关于直线x = -2对称，则f (x)的最大值为19. PM2.5是指大气中直径小于或等于 2.5微米的颗粒物，也称为可入肺颗粒物。

初中数学数与式专项练习9

此卷只装订不密封姓名准考证号考场号座位号绝密★启用前初中数学数与式专项练习注意事项：1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上．2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,写在本试卷上无效．3.考试结束后,将本试卷和答题卡一并交回．4.<br >一、单选题：本题共15小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1.下列运算一定正确的是（）A.a 2+a 2=a 4 B.a 2•a 4=a 8C.(a 2)4=a 8 D.(a +b)2=a 2+b 22.在平面直角坐标系中,点(5,1)关于原点对称的点的坐标是()A.(−5,1) B.(5,−1) C.(1,5) D.(−5,−1)3.某公司一年的销售利润是1.5万亿元．1.5万亿用科学记数法表示为A.0.15×1013 B. 1.5×1012 C. 1.5×1013 D.15×10124.估计√5+2的值在A.2和3之间 B.3和4之问 C.4和5之间 D.5和6之间5.如图,在平面直角坐标系中,∠AOB =90∘,∠OAB =30∘,反比例函数y 1=m x (m ≠0)的图象经过点A ,反比例函数y 2=n x (n ≠0)的图象经过点B ,若n =−1,则m的值是A.1 B.2 C.3 D.46.若a,b 互为相反数,c 的倒数是4,则3a +3b −4c 的值为A.−8 B.−5 C.−1 D.167.−2的倒数是A.2B.−2C.12 D.−128.已知442=1936,452=2025,462=2116,472=2209.若n 为整数且n <√2022<n +1,则n 值为A.44B.45C.46D.479.如图,射线OA 是第三象限的角平分线,若点B(k −3,1−2k)在第三象限内.且在射线OA 的下方,则k 的取值范围是A.k <12B.12<k <3C.12<k <43D.43<k <310.去年某城镇人均可支配收入为34181元,34181用科学记数法可表示为a ×104,则a 的值是A.0.34181B. 3.4181C.3D.0.311.不等式x ⩾1的解集在数轴上表示正确的是A. B.C. D.12.-5的相反数是A.−15B.15 C.5 D.-513.若零下5摄氏度记为−5∘C,则零上5摄氏度记为A.−5∘CB.0∘CC.+5∘CD.+4∘C14.0.010010001⋯(每两个1之间依次加一个0),3.14,π,√10,43中有理数的个数为A.5个 B.4个 C.3个 D.2个15.2023年2月28日国家统计局发布数据显示,2022年我国人均国内生产总值约为86000元.数据86000用科学记数法表示为A.86×103B.8.6×104C.8.6×105D.0.86×105二、填空题：本题共10小题，每小题5分．16.|−8|=（）17.暑假期间，亮视眼镜店开展学生配镜优惠活动．某款式眼镜的广告如下，请你为广告牌填上原价．此卷只装订不密封姓名准考证号考场号座位号18.（1）计算:23+|−3|÷3−√25×5−1;（2）解不等式组⎧{⎨{⎩2x >−6x −12⩽x +16并把它的解集在数轴（如图）上表示出来.19.化简√11+2√1820.若(a −2)2+|b +3|=0,则ab =21.√20×√15=22.若二次根式√x −1有意义,则x 可以是(写出一个x 的值即可).23.若关于x 的一元一次不等式组⎧{⎨{⎩x +32⩽4,2x −a ⩾2至少有2个整数解,且.关于y 的分式方程a −1y −2+42−y =2有非负整数解,则所有满足条件的整数a 的值之和是24.若代数式5x −2有意义,则实数x 的取值范围是25.已知正实数x 满足x 3+1x 3+x 6+1x 6=2754,则x +1x =三、解答题：本题共4小题，每小题5分,请考生在22、23题中选择一题，并在答题纸上涂黑，不涂黑、多涂或多答均按第一题评分．26.先化简,再求值:(1−1x +2)÷x 2−1x +2,其中x =√2+1.27.解方程:x x −1=x −12x −2.28.计算:(−1)2+2−2−(2023−π)0.29.设n是正整数,且使得24+27+2n是完全平方数,求n的值.。

数与式提高训练题

数与式提高训练题一、选择题（共10小题） 1．一个数的绝对值等于916，则这个数是( ) A ．916B ．916-C ．916±D ．34±2．（2022•普宁市一模）中国人很早开始使用负数，中国古代数学著作《九章算术》的“方程”一章，在世界数学史上首次正式引入负数．如果收入200元记作200+元，那么80-元表示( ) A ．支出20元B ．收入20元C ．支出80元D ．收入80元3．（2022•南山区模拟）在一次数学活动课上，老师将1~10共十个整数依次写在十张不透明的卡片上（每张卡片上只写一个数字，每一个数字只写在一张卡片上，而且把写有数字的那一面朝下）．他先打乱这些卡片的顺序，然后把甲、乙、丙、丁、戊五位同学叫到讲台上，随机地发给每位同学两张卡片，并要求他们把自己的两张卡片上的数字之和写在黑板上，结果分别是：甲12、乙4、丙15、丁6、戊18．根据以上信息，判断错误的是( ) A ．丙同学的两张卡片上的数字是7和8 B ．戊同学的两张卡片上的数字是8和10 C ．丁同学的两张卡片上的数字是2和4D ．甲同学的两张卡片上的数字是5和74．（2022•鹤山市一模）若2|32|0x x --，则(x = ) A ．1B ．23-C ．7-D ．23-或7-5．（2022•碑林区校级四模）计算1(1)--得到的结果是( ) A ．2-B ．1-C ．1D ．26．（2021•泰安）下列各数：4-， 2.8-，0，|4|-，其中比3-小的数是( ) A ．4-B ．|4|-C ．0D ． 2.8-7．（2021•南海区一模）数轴上表示6-和4的点分别是A 和B ，则线段AB 的长度是( ) A ．2-B ．2C ．10-D ．108．（2021•黄石）12-的倒数是( )A ．2-B ．12 C ．12-D ．12±9．（2021•贵池区二模）与2021和为0的数是()A．2021-B．2021C．0D．1 202110．（2021•丰南区一模）若1a-的相反数是3，那么(a=) A．4B．4-C．2-D．2二、填空题（共6小题）11．（2022•镇江模拟）12的倒数等于．12．（2022•禅城区一模）若a、b为实数，且满足|5|0a+，则b a-的值为．13．（2021•镇雄县一模）|2021|-=．14．（2021•元阳县模拟）若一个数的相反数是7-，则这个数为．15．（2021•新都区模拟）已知a，b两数在数轴上的位置如图所示，则化简代数式|||1||2|a b a b---+-的结果．16．（2021•昆明模拟）《九章算术》中注有“今两算得失相反，要令正负以名之“，意思是今有两数若其意义相反，则分别叫做正数与负数．如果体重减少3kg记作3kg-，那么体重增加5kg，则记作kg．三、解答题（共7小题）17．（2022•邯山区模拟）已知一列数2，0，1-，12 -．(1)求最大的数和最小的数的差；（2）若再添上一个有理数m，使得五个有理数的和为0，求m的值．18．（2021•长兴县模拟）计算：51 (3)()64-⨯÷-．19．（2021•台湾）碳足迹标签是一种碳排放量的标示方式，让大众了解某一产品或服务所产生的碳排放量多寡，如图所示．碳足迹标签的数据标示有其规定，以碳排放量大于20公克且不超过40公克为例，此范围内的碳足迹数据标示只有20、22、24、⋯、38、40公克等11个偶数；碳足迹数据标示决定于碳排放量与这11个偶数之中的哪一个差距最小，两者对应标示的范例如下表所示．请根据上述资讯，回答下列问题，并详细解释或完整写出你的解题过程．（1）若有一个产品的碳足迹数据标示为38公克，则它可能的碳排放量之最小值与最大值分别为多少公克？（2）承（1），当此产品的碳排放量减少为原本的90%时，请求出此产品碳足迹数据标示的所有可能情形．20．（2021•崂山区二模）【问题提出】|1||2||3||2021|-+-+-+⋯+-的最小值是多a a a a少？【阅读理解】为了解决这个问题，我们先从最简单的情况入手．||a的几何意义是a这个数在数轴上对应的点到原点的距离．那么|1|a-可以看作a这个数在数轴上对应的点到1的距离；-+-就可以看作a这个数在数轴上对应的点到1和2两个点的距离之和．下面我a a|1||2|们结合数轴研究|1||2|-+-的最小值．a a我们先看a表示的点可能的3种情况，如图所示：（1）如图①，a在1的左边，从图中很明显可以看出a到1和2的距离之和大于1．（2）如图②，a在1和2之间（包括在1，2上），可以看出a到1和2的距离之和等于1．（3）如图③，a在2的右边，从图中很明显可以看出a到1和2的距离之和大于1．所以a到1和2的距离之和最小值是1．【问题解决】（1）|3||6|a a-+-的几何意义是；请你结合数轴探究：|3||6|a a-+-的最小值是；（2）请你结合图④探究：|1||2||3|a a a-+-+-的最小值是，此时a为；（3）|1||2||3||4||5||6|a a a a a a-+-+-+-+-+-的最小值为；（4）|1||2||3||2021|a a a a-+-+-+⋯+-的最小值为．【拓展应用】如图⑤，已知a到1-，2的距离之和小于4，请写出a的范围为．21．（2021•竞秀区一模）已知有理数3-和5．（1）计算：352--；（2）若添一个有理数n，使得这三个数中最大的数与最小的数的差为11，求n的值．22．（2020•邓州市二模）某校拟建一个面积为2144m的矩形健身区，张老师请同学们小组合作设计出使周长最小的建设方案下面是其中一个小组的探究过程，请补充完整．（1）列式设矩形的一边长是x m，则另一边长是m，若周长为y m，则y与x之间的函数关系式为；（2）画图①列表；表中a=；②描点：如图所示（图中已描出部分点），请描出表中给出的剩余点．③连线：请在图中画出该函数的图象．（3）发现图象最低点的坐标为，即x=m时，周长y有最小值48m；（4）验证在张老师的指导下，同学们将y 与x 之间的函数关系式进行配方，得出248y=+．2122(0x-，y ∴ ．∴0=时，y 有最小值．此方程可化为2120-=．∴当x = m 时，周长y 有最小值48m ．23．（2020•安次区模拟）对于四个数“8-，3-，1，5”及四种运算“+，-，x ，+”，列算式解答：（1）求这四个数的和；（2）在这四个数中选出两个数，填入下列口中，使得： ①“ - ”的结果最小； ②“ ⨯ ”的结果最大．（3）在这四个数中选出三个数，在四种运算中选出两种，组成一个算式，使运算结果等于没选的那个数．。

周练2——数与式

北达资源中学初三下学期数学周练（2） 2021.3.7命制：何琳审阅：徐海鹰姓名成绩一、选择题(3’×10=30’)请将1—10题选项填写在下面表格中1．31-的倒数是（） A.31 B. 31- C. 3 D.-3 2．地球绕太阳公转的速度约是110000千米/时，将110000用科学计数法表示为（） A ．B ．C ．D ．3．某种细胞的直径是0.00056毫米，这个数用科学计数法表示为（）A. 31056.0-⨯毫米B. 51056-⨯毫米C. 4106.5-⨯ 毫米D. 3106.5-⨯毫米 4．下列运算正确的是（） A ． B ．C ．D ．5．如图，已知数轴上的点A 、B 、C 、D 分别表示数﹣2、1、2、3，则表示数53-的点P应落在线段（）A ．AO 上B ．OB 上C ．BC 上D ．CD 上 6．若，则=（） A ．﹣1 B ．1 C ．D ．7．将代数式142-+x x 化成q p x ++2)(的形式为（）A. 3)2(2+-xB. 4)2(2-+xC. 5)2(2-+xD. 4)2(2++x 8．把代数式223363xy y x x +-分解因式，结果正确的是（）A. )3)(3(y x y x x -+B. )2(322y xy x x +- C.2)3(y x x - D. 2)(3y x x -题号 12345678910答案9．当时，代数式的值是（） A ．B ．C ．D ．10．如图，边长为)3(+m 的正方形纸片剪出一个边长为m 的正方形之后，剩余部分可剪拼）A. mB.C.D.二、填空题(3’×8=24’) 11．要使1213-+-x x 有意义，则x 应满足_____________________________12．当_________x 时，分式122-+x x 有意义. 13．因式分解：4a 3-12a 2+9a=_____________________________14．已知x 、y 是实数，并且096132=+-++y y x ，则2016)(xy 的值是_______ 15．已知10=+y x ，2=xy ，那么.______22=+y x16．规定用符号[x]表示一个实数的整数部分，例如[3.69]=3，［3］=1，按此规定，［113-］=_____________ 17．让我们轻松一下，做一个数字游戏：第一步：取一个自然数51=n ，计算121+n 得1a ；第二步：算出1a 的各位数字之和得2n ，计算122+n 得2a ；第三步：算出2a 的各位数字之和得3n ，计算123+n 得3a ； ……依次类推，则2016a =______________.18．若实数a 、b 满足12=+b a ，则2232b a +的最小值是_________.三、解答题：(5’×8+6’=46’)19．分解因式： 20．分解因式：xy xy 12553- 解：解： 21． 10)31(60sin 2)π3(32--+︒+---解： 22. 20)21(45sin 832)3π(---︒-+-解：23．先化简，再求值：，其中．解：24．先化简，后求值：11231322--+++÷-+x xx x x x x ，其中.12+=x25．已知1532=+x x ，求代数式2)12()1(2++--x x x 的值.26．已知 122=+xy x ，215xy y +=，求代数式()22()x y y x y +-+的值．27．问题背景：在△ABC 中，AB 、BC 、AC，求这个三角形的面积．小辉同学在解答这道题时，先建立一个正方形网格(每个小正方形的边长为1)，再在网格中画出格点△ABC （即△ABC 三个顶点都在小正方形的顶点处），如图1所示．这样不需求△ABC 的高，而借用网格就能计算出它的面积．(1)请你将△ABC 的面积直接填写在横线上．________ 思维拓展：(2)我们把上述求△ABC 面积的方法叫做构图法．若△ABC、、(0)a >，请利用图2的正方形网格(每个小正方形的边长为a )画出相应的△ABC ，并求出它的面积是：．探索创新：(3)若△ABC 三边的长分别为、、(0,,)m n o m n >>≠ ，请运用构图法在图3指定区域内画出示意图，并求出△ABC 的面积为：．AB C图3图2图1。