二次函数经典练习题

合集下载

二次函数练习题

二次函数练习题一、选择题1. 下列哪个函数是二次函数？A. y = x + 1B. y = 2x^2 3x + 1C. y = x^3 3xD. y = sqrt(x)2. 二次函数y = ax^2 + bx + c（a≠0）的图象是（）。

A. 抛物线B. 直线C. 双曲线D. 圆3. 二次函数y = 2x^2 + 4x + 5的顶点坐标是（）。

A. (1, 3)B. (2, 9)C. (1, 7)D. (0, 5)4. 当a > 0时，二次函数y = ax^2 + bx + c的图象开口（）。

A. 向上B. 向下C. 向左D. 向右二、填空题1. 二次函数y = x^2 4x + 4可以写成y = (x ____)^2的形式。

2. 已知二次函数y = x^2 + 2x + 3的顶点坐标为（1, 4），则该函数的对称轴是直线____。

3. 若二次函数y = ax^2 + bx + c的图象开口向上，且顶点坐标为（1, 2），则a的取值范围是____。

三、解答题1. 已知二次函数y = x^2 6x + 9，求其顶点坐标。

2. 求二次函数y = 2x^2 + 4x + 5在x = 2时的函数值。

3. 已知二次函数y = ax^2 + bx + c的图象经过点（1, 3）和（1, 7），且顶点坐标为（0, 5），求该二次函数的解析式。

4. 设二次函数y = x^2 + mx + 1的图象与x轴相交于A、B两点，求线段AB的长度。

5. 已知二次函数y = x^2 4x + 3的图象与x轴相交于C、D两点，求线段CD的中点坐标。

四、应用题1. 一抛物线开口向上，其顶点为原点O(0,0)，且经过点P(2,8)。

求该抛物线的解析式。

2. 一运动员在水平地面上进行跳远训练，其跳跃的高度h（单位：米）与跳跃的水平距离x（单位：米）之间的关系可以近似表示为二次函数h = 0.02x^2 + 0.6x。

求运动员跳跃时水平距离为4米时的高度。

二次函数练习题8套

一、填空1、二次函数y=-x 2+6x+3的图象顶点为_________对称轴为_________。

2、二次函数y=(x-1)(x+2)的顶点为_________,对称轴为________。

3、二次函数y=2(x+3)(x-1)的x 轴的交点的个数有_______个，交点坐标为_____________。

4、y=x 2-3x-4与x 轴的交点坐标是__________,与y 轴交点坐标是____________5、由y=2x 2和y=2x 2+4x-5的顶点坐标和二次项系数可以得出y=2x 2+4x-5的图象可由y=2x 2的图象向__________平移________个单位，再向_______平移______个单位得到。

二、解答：6、求y=2x 2+x-1与x 轴、y 轴交点的坐标。

7、求y=31x 2212--x 的顶点坐标。

8、已知二次函数图象顶点坐标（-3，21）且图象过点（2，211），求二次函数解析式及图象与y 轴的交点坐标。

9、已知二次函数图象与x 轴交点（2,0）(-1,0)与y 轴交点是（0，-1）求解析式及顶点坐标。

10、分析若二次函数y=ax 2+bx+c 经过（1，0）且图象关于直线x=21,对称，那么图象还必定经过哪一点？1、二次函数y=-3x2-2x+1，∵a=_________ ∴图象开口向________2、二次函数y=2x2-1 ∵a=_________∴函数有最_________值。

3、二次函数y=x2+x+1 ∵b2-4ac=____________∴函数图象与x轴____________交点。

4、二次函数y=x2-2x-3的图象是开口向_________的抛物线，抛物线的对称轴是直线______,抛物线的顶点坐标是______________。

5、已知y=ax2+bx+c的图象如下，则：a+b+c_______0，a-b+c__________0。

2a+b________07、描点画函数y=3x2-4x+1图象并根据图象回答问题画图①当x________时，y>0当__________时，y<0当__________时，y=01②若x1=5,x2=7，x3=3对应的函数值是y1,y2,y3，用“<”连接y1,y2,y3 8、求y=x2-5x+6与x轴交点的坐标9、求抛物线y=x2+x+2与直线x=1的交点坐标。

二次函数基础练习题大全(含答案)

1、正方形铁片边长为15cm ，在四个角上各剪去一个边长为x （cm ）的小正方形，用余下的部分做成一个无盖的盒子．(1)求盒子的表面积S （cm 2）与小正方形边长x （cm ）之间的函数关系式； (2)当小正方形边长为3cm 时，求盒子的表面积．2、已知二次函数),0(2≠+=a c ax y 当x=1时，y= -1；当x=2时，y=2，求该函数解析式.3、对于函数22x y =下列说法：①当x 取任何实数时，y 的值总是正的；②x 的值增大，y 的值也增大；③y 随x 的增大而减小；④图像关于y 轴对称.其中正确的是 . 4、抛物线 y ＝－x 2 不具有的性质是（）A 、开口向下B 、对称轴是 y 轴C 、与 y 轴不相交D 、最高点是原点5、苹果熟了，从树上落下所经过的路程 s 与下落时间 t 满足 S ＝12gt 2（g ＝），则 s 与 t 的函数图像大致是（）A B C D6、函数2ax y =与b ax y +-=的图像可能是（）A ．B ．C ．D ．7、已知函数24mm ymx 的图像是开口向下的抛物线，求m 的值.8、二次函数12-=m mx y 在其图像对称轴的左侧，y 随x 的增大而增大，求m 的值.9、已知函数()422-++=m mx m y 是关于x 的二次函数，求：（1）满足条件的m 的值；（2） m 为何值时，抛物线有最低点求出这个最低点，这时x 为何值时，y 随x 的增大而增大；（3） m 为何值时，抛物线有最大值最大值是多少当x 为何值时，y 随x 的增大而减小s OstOst O st O10、如果抛物线2y ax 与直线1y x 交于点,2b ，求这条抛物线所对应的二次函数的关系式.11、已知函数2)(22+-+=x m m mx y 的图象关于y 轴对称，则m ＝________； 12、抛物线942++=x x y 的对称轴是 .13、抛物线251222+-=x x y 的开口方向是，顶点坐标是 . 14、将 y ＝x 2－2x ＋3 化成 y ＝a (x －h)2＋k 的形式，则 y ＝＿＿＿＿. 15、把二次函数215322yx x的图象向上平移3个单位，再向右平移4个单位，则两次平移后的函数图象的关系式是16、抛物线1662--=x x y 与x 轴交点的坐标为_________； 17、函数x x y +-=22有最____值，最值为_______；18、二次函数c bx x y ++=2的图象沿x 轴向左平移2个单位，再沿y 轴向上平移3个单位，得到的图象的函数解析式为122+-=x x y ，则b 与c 分别等于（） A 、6，4 B 、－8，14 C 、－6，6 D 、－8，－1419、二次函数122--=x x y 的图象在x 轴上截得的线段长为（） A 、22 B 、23 C 、32 D 、3320、通过配方，写出下列函数的开口方向、对称轴和顶点坐标：（1）12212+-=x x y ；（2）2832-+-=x x y ；（3）4412-+-=x x y 21、求二次函数62+--=x x y 的图象与x 轴和y 轴的交点坐标22、已知一次函数的图象过抛物线223y x x 的顶点和坐标原点1）求一次函数的关系式； 2）判断点2,5是否在这个一次函数的图象上23、某商场以每台2500元进口一批彩电.如每台售价定为2700元，可卖出400台，以每100元为一个价格单位，若将每台提高一个单位价格，则会少卖出50台，那么每台定价为多少元即可获得最大利润最大利润是多少元25、二次函数2224ymx x m m 的图象经过原点，则此抛物线的顶点坐标是26、已知二次函数c bx ax y ++=2的图象如图所示，则a___0，b___0，c___0，ac b 42-____0；27、二次函数c bx ax y ++=2的图象如图，则直线bc ax y +=的图象不经过第象限.（第26题）（第27题）（）（） 28、二次函数2yx ax b 中，若0a b ，则它的图象必经过点（）A 1,1B 1,1C 1,1 D1,110、函数b ax y +=与c bx ax y ++=2的图象如上图所示，则下列选项中正确的是（） A 、0,0>>c ab B 、0,0><c ab C 、0,0<>c ab D 、0,0<<c ab 11、已知函数c bx ax y ++=2的图象如图所示，则函数b ax y +=的图象是（）12、二次函数c bx ax y ++=2的图象如图，那么abc 、2a+b 、a+b+c 、a-b+c 这四个代数式中，值为正数的有（） A ．4个 B ．3个 C ．2个 D ．1个 13、抛物线的图角如图，则下列结论：①＞0；②；③＞；④＜1.其中正确的结论是（）.（A ）①② （B ）②③ （C ）②④ （D ）③④14、二次函数2yax bx c 的最大值是3a ，且它的图象经过1,2，1,6两点，求a 、b 、c 的值。

二次函数练习题及答案

A B C D O x y 二次函数练习题(1)1．二次函数y=ax 2+bx+c 的图象如图1所示,下列五个代数式ab 、ac 、a-b+c 、b 2- 4ac 、2a+b 中,值大于0的个数为( )A.5B.4C.3D.22．二次函数c bx ax y ++=2的图象如图所示，下列结论：①0<c ；②0>b ；③024>++c b a ；④042>-ac b ．其中正确的有（）（A ） 1个（B ） 2个（C ） 3个（D ） 4个3．已知二次函数c bx ax y ++=2的图象与x 轴交于点（－2，0），(x 1，0)且1＜x 1＜2，与y·轴正半轴的交点在点(0，2）的下方，下列结论：①a ＜b ＜0；②2a+c ＞0；③4a+c< 0，④2a －b+l ＞0．其中的有正确的结论是（填写序号）__________．4．把抛物线y=12x 2 向左平移三个单位, 再向下平移两个单位所得的关系式为________. 5.将抛物线y=ax 2向右平移2个单位,再向上平移3个单位,移动后的抛物线经过点(3,-1),那么移动后的抛物线的关系式为__________. 6．抛物线c bx ax y ++=2如右图所示，则它关于y 轴对称的抛物线的解析式是__________．7．已知二次函数y=2x 2-mx-4的图象与x 轴的两个交点的横坐标的倒数和为2,则m=_________.8．如图，四边形ABCD 是矩形，A 、B 两点在x 轴的正半轴上，C 、D 两点在抛物线y ＝－x 2＋6x 上．设OA ＝m (0＜m ＜3)，矩形ABCD 的周长为l ，则l 与m 的函数解析式为．9．已知抛物线22b x x y ++=经过点1()4a -，和1()a y -，，则1y 的值是．10、若二次函数y=ax 2+bx+c 的顶点在第一象限，且经过点（0，1），（-1，0），则S=a+b+c 的变化范围是 ( ) 图1 yO 3 31(A) 0<S<2 (B) S>1 (C) 1<S<2 (D)-1<S<111、已知二次函数y ＝ax 2（a ≥1）的图像上两点A 、B 的横坐标分别是－1、2，点O 是坐标原点，如果△AOB 是直角三角形，则△OAB 的周长为。

完整版)初中数学二次函数专题经典练习题(附答案)

完整版)初中数学二次函数专题经典练习题(附答案)1.抛物线$y=-3x^2+2x-1$与坐标轴的交点情况是(A)没有交点。

(C)有且只有两个交点。

(D)有且只有三个交点。

2.已知直线$y=x$与二次函数$y=ax^2-2x-1$的一个交点的横坐标为1，则$a$的值为(C)3.3.二次函数$y=x^2-4x+3$的图象交$x$轴于$A$、$B$两点，交$y$轴于点$C$，则$\triangle ABC$的面积为(B)4.4.函数$y=ax^2+bx+c$中，若$a>0$，$b<0$，$c<0$，则这个函数图象与$x$轴的交点情况是(D)一个在$x$轴的正半轴，另一个在$x$轴的负半轴。

5.已知$(2,5)$、$(4,5)$是抛物线$y=ax^2+bx+c$上的两点，则这个抛物线的对称轴方程是(B)$x=3$。

6.无法正确反映函数$y=ax+b$图象的选项已删除。

7.二次函数$y=2x^2-4x+5$的最小值是$4.5$。

8.某二次函数的图象与$x$轴交于点$(-1,0)$，$(4,0)$，且它的形状与$y=-x$形状相同。

则这个二次函数的解析式为$y=-\frac{1}{25}(x-1)(x-4)$。

9.若函数$y=-x+4$的函数值$y>0$，则自变量$x$的取值范围是$(-\infty,4)$。

10.某品牌电饭锅成本价为70元，销售商对其销量与定价的关系进行了调查，结果如下：定价（元） 100 110 120 130 140 150 销量（个） 80 100 110 100 80 60.为获得最大利润，销售商应将该品牌电饭锅定价为120元。

11.函数$y=ax^2-(a-3)x+1$的图象与$x$轴只有一个交点，那么$a$的值和交点坐标分别为$(a,0)$和$(\frac{a-3}{2},0)$。

12.某涵洞是一抛物线形，它的截面如图3所示，现测得水面宽$AB=1.6m$，涵洞顶点$O$到水面的距离为$2.4m$，在图中的直角坐标系内，涵洞所在抛物线的解析式为$y=-\frac{5}{6}(x-2)^2+2.4$。

二次函数练习题(含答案)

二次函数练习题(含答案)形，如图所示。

将剩余部分折成一个无盖的长方体盒子，已知折痕处的线段长度均为2cm，求这个盒子的体积。

解析：首先确定长方体的长、宽、高分别对应正三角形的边长a、b、c，如图所示。

由于筝形的对角线长度为2cm，根据勾股定理可得$a^2+b^2=4$。

由于正三角形的内角为60度，因此可以利用三角函数求得$a=\sqrt{3}c$和$b=2\sin30^{\circ}c=c$。

将$a$、$b$、$c$代入长方体的体积公式$V=abc$，得到$V=2\sqrt{3}c^3$。

将$c=2$代入即可得到盒子的体积为$V=16\sqrt{3}$。

1.将文章中的公式和图表进行排版整理，删除明显有问题的段落。

2.对于每段话进行小幅度的改写，使其更加简洁明了。

1.某人要制作一个无盖的直三棱柱纸盒，现在需要确定该纸盒的侧面积最大值。

根据图中的信息，我们可以得出最大面积为（）A．cm2B．cm2C．cm2D．cm2.2.已知二次函数y=ax2+bx+c+2的图象如图所示，顶点为（﹣1，），下列结论中正确的有几个？①abc＜；②b2﹣4ac=0；③a＞2；④4a﹣2b+c＞。

答案为A．1B．2C．3D．4.3.如图，已知抛物线y=ax2+bx+c与x轴交于A、B两点，顶点C的纵坐标为﹣2.现将抛物线向右平移2个单位，得到抛物线y=a1x2+b1x+c1.下列结论中正确的有哪些？①b＞；②a﹣b+c＜；③阴影部分的面积为4；④若c=﹣1，则b2=4.答案为……4.二次函数y=ax2+bx+c的图象如图所示，点O为坐标原点，点A在y轴的正半轴上，点B、C在图象上，四边形OBAC为菱形，且∠OBA=120°。

求菱形OBAC的面积。

5.某水产养殖户为了节省材料，利用水库的岸堤为一边，用总长为80m的围栏在水库中围成了如图所示的①②③三块矩形区域，且这三块矩形区域的面积相等。

设BC的长度为xm，矩形区域ABCD的面积为ym2.(1) 求y与x之间的函数关系式，并注明自变量x的取值范围；(2) 当y有最大值时，x为多少？最大值是多少？6.在平面直角坐标系xOy中，抛物线y＝ax2－2ax－3a（a ＜0）与x轴交于A、B两点（点A在点B的左侧），经过点A的直线l：y＝kx＋b与y轴负半轴交于点C，与抛物线的另一个交点为D，且CD＝4AC。

初中数学二次函数专题经典练习题（附答案）

二次函数总复习经典练习题1．抛物线y =－3x 2＋2x －1的图象与坐标轴的交点情况是的图象与坐标轴的交点情况是( ) ( ) (A)(A)没有交点．没有交点．没有交点． (B) (B) (B)只有一个交点．只有一个交点．(C)(C)有且只有两个交点．有且只有两个交点．有且只有两个交点． (D) (D) (D)有且只有三个交点．有且只有三个交点．2．已知直线y =x 与二次函数y =ax 2－2x －1图象的一个交点的横坐标为1，则a 的值为的值为( ) ( ) (A)2(A)2．． (B)1 (B)1．． (C)3 (C)3．． (D)4 (D)4．．3．二次函数y =x 2－4x ＋3的图象交x 轴于A 、B 两点，交y 轴于点C ，则△ABC 的面积为的面积为( ) ( )(A)6(A)6．． (B)4 (B)4．． (C)3 (C)3．． (D)1 (D)1．．4．函数y =ax 2＋bx ＋c 中，若a ＞0，b ＜0，c ＜0，则这个函数图象与x 轴的交点情况是轴的交点情况是( ) ( )(A)(A)没有交点．没有交点．(B)(B)有两个交点，都在有两个交点，都在x 轴的正半轴．(C)(C)有两个交点，都在有两个交点，都在x 轴的负半轴．(D)(D)一个在一个在x 轴的正半轴，另一个在x 轴的负半轴．5．已知已知(2(2(2，，5)5)、、(4(4，，5)5)是抛物线是抛物线y =ax 2＋bx ＋c 上的两点，则这个抛物线的对称轴方程是则这个抛物线的对称轴方程是( ) ( ) (A)x =a b-． (B)x =2=2．． (C)x =4=4．． (D)x =3=3．．6．已知函数y=ax 2＋bx ＋c 的图象如图1所示，那么能正确反映函数y=ax ＋b 图象的只可能是( )(D)(C)(B)(A)x yo y xo yxxy o 7．二次函数y =2x 2－4x ＋5的最小值是的最小值是__________________．．8．某二次函数的图象与x 轴交于点轴交于点((－1，0)0)，，(4(4，，0)0)，且它的形状与，且它的形状与y =－x 2形状相同．则这个二次函数的解析式为这个二次函数的解析式为__________________．．9．若函数y =－x 2＋4的函数值y ＞0，则自变量x 的取值范围是的取值范围是__________________．．1010．某品牌电饭锅成本价为．某品牌电饭锅成本价为70元，销售商对其销量与定价的关系进行了调查，结果如下：定价（元）100110120130140150图1 xyo -4-3-2-113销量（个） 80 100 110 100 80 60为获得最大利润，销售商应将该品牌电饭锅定价为为获得最大利润，销售商应将该品牌电饭锅定价为元．元．元．1111．函数．函数y =ax 2－(a －3)x ＋1的图象与x 轴只有一个交点，那么a 的值和交点坐标分别为____________．．1212．某涵洞是一抛物线形．某涵洞是一抛物线形．某涵洞是一抛物线形,,它的截面如图3所示所示,,现测得水面宽 1.6AB m =,涵洞顶点O 到水面的距离为2.4m ,在图中的直角坐标系内在图中的直角坐标系内,,涵洞所在抛物线的解析式为涵洞所在抛物线的解析式为________. ________.1313．．（本题8分）已知抛物线y =x 2－2x －2的顶点为A ，与y 轴的交点为B ，求过A 、B 两点的直线的解析式．的直线的解析式．1414．．（本题8分）抛物线y =ax 2＋2ax ＋a 2＋2的一部分如图3所示，求该抛物线在y 轴左侧与x 轴的交点坐标．轴的交点坐标．1515．．（本题8分）如图4，已知抛物线y ＝ax 2＋bx ＋c (a ＞0)0)的顶点是的顶点是C (0(0，，1)1)，直线，直线l ：y ＝－ax ＋3与这条抛物线交于P 、Q 两点，且点P 到x 轴的距离为2．(1)(1)求抛物线和直线求抛物线和直线l 的解析式；的解析式；(2)(2)(2)求点求点Q 的坐标．的坐标．1616．．（本题8分）工艺商场以每件155元购进一批工艺品．若按每件200元销售，工艺商场每天可售出该工艺品100件；若每件工艺品降价1元，则每天可多售出该工艺品4件．问每件工艺品降价多少元出售，每天获得的利润最大？获得的最大利润是多少元？每件工艺品降价多少元出售，每天获得的利润最大？获得的最大利润是多少元？1717．．(本题10分)) )) 杭州休博会期间，杭州休博会期间，嘉年华游乐场投资150万元引进一项大型游乐设施．若不计维修保养费用，预计开放后每月可创收33万元．而该游乐设施开放后，从第1个月图3 yxO1图4 PQyxO到第x 个月的维修保养费用累计为y (万元万元))，且y =ax 2＋bx ；若将创收扣除投资和维修保养费用称为游乐场的纯收益g (万元万元))，g 也是关于x 的二次函数．的二次函数．(1)(1)若维修保养费用第若维修保养费用第1个月为2万元，第2个月为4万元．求y 关于x 的解析式；的解析式； (2)(2)求纯收益求纯收益g 关于x 的解析式；的解析式；(3)(3)问设施开放几个月后，游乐场的纯收益达到最大？几个月后，能收回投资？问设施开放几个月后，游乐场的纯收益达到最大？几个月后，能收回投资？问设施开放几个月后，游乐场的纯收益达到最大？几个月后，能收回投资？ 18（本题10分）如图所示，图4-4-①是一座抛物线型拱桥在建造过程中装模时的设计示意图，①是一座抛物线型拱桥在建造过程中装模时的设计示意图，拱高为30m 30m，，支柱A 3B 3=50m =50m，，5根支柱A 1B 1、A 2B 2、A 3B 3、A 4B 4、A 5B 5之间的距离均为15m 15m，，B 1B 5∥A 1A 5，将抛物线放在图4-4-②所示的直角坐标系中．②所示的直角坐标系中．②所示的直角坐标系中． (1)(1)直接写出图直接写出图4-4-②中点②中点B 1、B 3、B 5的坐标；的坐标； (2)(2)求图求图4-4-②中抛物线的函数表达式；②中抛物线的函数表达式；②中抛物线的函数表达式； (3)(3)求图求图4-4-①中支柱①中支柱A 2B 2、A 4B 4的长度．的长度．1919、、如图5，已知A (2(2，，2)2)，，B (3(3，，0)0)．动点．动点P (m ，0)0)在线段在线段OB 上移动，过点P 作直线l 与x 轴垂直．轴垂直．(1)(1)设△设△OAB 中位于直线l 左侧部分的面积为S ，写出S 与m 之间的函数关系式；之间的函数关系式； (2)(2)试问是否存在点试问是否存在点P ，使直线l 平分△OAB 的面积？若有，求出点P 的坐标；若无，请说明的坐标；若无，请说明理由．理由．更多学习方法和中高考复习资料，免费下载，扫一扫关注微信：更多学习方法和中高考复习资料，免费下载，扫一扫关注微信：图5 PyxO AB 图4-②B 1B 3B 5yxO图4-① B 5B 4B 3B 2B 1A 5A 4A 3A 1A 230m答案：答案：一、一、11．B 2B 2．．D 3D 3．．C 4C 4．．D 5D 5．．D 6D 6．．B二、二、77．3 83 8．．y =－x 2＋3x ＋4 94 9．－．－．－22＜x ＜2 102 10．．1301111．．a =0=0，，(13-，0)0)；；a =1=1，，(－1，0)0)；；a =9=9，，(13，0) 120) 12．．2154y x =- 1313．抛物线的顶点为．抛物线的顶点为．抛物线的顶点为(1(1(1，－，－，－3)3)3)，点，点B 的坐标为的坐标为(0(0(0，－，－，－2)2)2)．直线．直线AB 的解析式为y =－x －21414．依题意可知抛物线经过点．依题意可知抛物线经过点．依题意可知抛物线经过点(1(1(1，，0)0)．于是．于是a ＋2a ＋a 2＋2=02=0，解得，解得a 1=－1，a 2=－2．当a =－1或a =－2时，求得抛物线与x 轴的另一交点坐标均为轴的另一交点坐标均为((－3，0)1515．．(1)(1)依题意可知依题意可知b =0=0，，c =1=1，且当，且当y =2时，ax 2＋1=2①，－ax ＋3=2②．由①、②解得a =1=1，，x =1=1．故抛物线与直线的解析式分别为：．故抛物线与直线的解析式分别为：y =x 2＋1，y =－x ＋3；(2)Q (－2，5) 1616．．设降价x 元时，获得的利润为y 元．则依意可得y =(45=(45－－x )(100)(100＋＋4x )=)=－－4x 2＋80x ＋45004500，，即y =－4(x －10)2＋49004900．故当．故当x =10时，y 最大最大=4900(=4900(=4900(元元)1717．．(1)(1)将将(1(1，，2)2)和和(2(2，，6)6)代入代入y =ax 2＋bx ，求得a =b =1=1．故．故y =x 2＋x ；(2)g =33x －150150－－y ，即g =－x 2＋32x －150150；；(3)(3)因因y =－(x －16)2＋106106，，所以设施开放后第16个月，纯收益最大．令g =0=0，得－，得－x 2＋32x －150=0150=0．解得．解得x =16±106，x ≈16－≈16－10.3=5.7(10.3=5.7(10.3=5.7(舍去舍去26.3)26.3)．当．当x =5时，g ＜0，当x =6时，g ＞0，故6个月后，能收回投资个月后，能收回投资 1818．．（1）1(30)B -，0，3(030)B ，，5(300)B ，；（2）设抛物线的表达式为(30)(30)y a x x =-+，把3(030)B ，代入得(030)(030)30y a =-+=． 130a =-∴． ∵所求抛物线的表达式为：1(30)(30)30y x x =--+．（3）4B ∵点的横坐标为1515，， 4B ∴的纵坐标4145(1530)(1530)302y =--+=．3350A B =∵，拱高为3030，，∴立柱44458520(m)22A B =+=．由对称性知：224485(m)2A B A B ==．四、四、1919．．(1)(1)当当0≤m ≤2时，S =212m ；当2＜m ≤3时，S =12×3×2－12(3(3－－m )()(－－2m ＋6)=6)=－－m 2＋6m －6．(2)(2)若有这样的若有这样的P 点，使直线l 平分△OAB 的面积，很显然0＜m ＜2．由于△OAB 的面积等于3，故当l 平分△OAB 面积时，S =32．21322m =∴．解得m =3．故存在这样的P 点，使l 平分△OAB 的面积．且点P 的坐标为的坐标为((3，0)0)．．。

二次函数基础练习题

二次函数基础练习题一、选择题1. 二次函数的一般形式是：A. y = ax^2 + bx + cB. y = ax + bC. y = a(x - h)^2 + kD. y = a(x - b)(x - c)2. 对于二次函数y = ax^2 + bx + c，当a > 0时，其图像开口：A. 向上B. 向下C. 不确定D. 无开口3. 二次函数的顶点坐标可以通过公式求得，该公式是：A. (-b/2a, f(-b/2a))B. (-b/a, f(-b/a))C. (2b/a, f(2b/a))D. (a/b, f(a/b))4. 抛物线y = x^2 - 4x + 4的对称轴是：A. x = 2B. x = -2C. x = 4D. x = 05. 如果一个二次函数的图像与x轴有两个交点，那么这个二次函数的判别式：A. Δ > 0B. Δ = 0B. Δ < 0D. 不能确定二、填空题6. 二次函数y = ax^2 + bx + c的顶点坐标可以通过公式_________求得。

7. 当二次函数的图像与x轴相交时，其判别式Δ_________。

8. 给定二次函数y = 3x^2 + 6x - 5，其顶点的x坐标是_________。

9. 若二次函数y = ax^2 + bx + c的图像开口向上，且与y轴交于点(0, 2)，则c的值为_________。

10. 对于二次函数y = -2x^2 + 4x + 3，其图像与x轴的交点坐标为_________。

三、解答题11. 已知二次函数y = ax^2 + bx + c的图像经过点(1, 2)和(-1, 0)，求a和b的值。

12. 给定二次函数y = x^2 - 2x - 3，求其图像与x轴的交点坐标，并判断其图像的开口方向。

13. 已知二次函数y = 2x^2 + 4x + 1的图像与x轴相交于点A和B，求AB线段的长度。

14. 某二次函数的图像经过点(-2, 6)和(1, -3)，且顶点在y轴上，求该二次函数的解析式。

二次函数基础练习题大全(含答案)-二次函数基础题

二次函数基础练习题练习一二次函数1、一个小球由静止开始在一个斜坡上向下滚动，通过仪器观察得到小球滚动的距离s （米）与时间t（秒）的数据如下表：时间t （秒） 1 2 3 4 … 距离s （米） 281832…写出用t 表示s 的函数关系式： 2、下列函数：① 23y x ；② 21y x x x ；③ 224y x x x ；④ 21y x x ；⑤ 1yx x ，其中是二次函数的是，其中a，b，c3、当m 时，函数2235y mx x（m 为常数）是关于x 的二次函数4、当____m 时，函数2221mm y m m x 是关于x 的二次函数 5、当____m时，函数2564mm ymx +3x 是关于x 的二次函数6、若点 A ( 2, m ) 在函数 12-=x y 的图像上，则 A 点的坐标是＿＿＿＿.7、在圆的面积公式 S ＝πr 2 中，s 与 r 的关系是（）A 、一次函数关系B 、正比例函数关系C 、反比例函数关系D 、二次函数关系8、正方形铁片边长为15cm ，在四个角上各剪去一个边长为x （cm ）的小正方形，用余下的部分做成一个无盖的盒子．(1)求盒子的表面积S （cm 2）与小正方形边长x （cm ）之间的函数关系式；(2)当小正方形边长为3cm 时，求盒子的表面积．9、如图，矩形的长是 4cm ，宽是 3cm ，如果将长和宽都增加 x cm ，那么面积增加 ycm 2， ① 求 y 与 x 之间的函数关系式. ② 求当边长增加多少时，面积增加 8cm 2.10、已知二次函数),0(2≠+=a c ax y 当x=1时，y= -1；当x=2时，y=2，求该函数解析式. 11、富根老伯想利用一边长为a 米的旧墙及可以围成24米长的旧木料，建造猪舍三间，如图，它们的平面图是一排大小相等的长方形.（1）如果设猪舍的宽AB 为x 米，则猪舍的总面积S （米2）与x 有怎样的函数关系？（2）请你帮富根老伯计算一下，如果猪舍的总面积为32米2，应该如何安排猪舍的长BC 和宽AB 的长度？旧墙的长度是否会对猪舍的长度有影响？怎样影响？练习二函数2ax y =的图像与性质1、填空：（1）抛物线221x y =的对称轴是（或），顶点坐标是，当x 时，y 随x 的增大而增大，当x 时，y 随x 的增大而减小，当x= 时，该函数有最值是；（2）抛物线221x y -=的对称轴是（或），顶点坐标是，当x 时，y 随x 的增大而增大，当x 时，y 随x 的增大而减小，当x= 时，该函数有最值是； 2、对于函数22x y =下列说法：①当x 取任何实数时，y 的值总是正的；②x 的值增大，y 的值也增大；③y 随x 的增大而减小；④图像关于y 轴对称.其中正确的是 . 3、抛物线 y ＝－x 2 不具有的性质是（）A 、开口向下B 、对称轴是 y 轴C 、与 y 轴不相交D 、最高点是原点4、苹果熟了，从树上落下所经过的路程 s 与下落时间 t 满足 S ＝12gt 2（g ＝9.8），则 s 与 t 的函数图像大致是（）A B C D5、函数2ax y =与b ax y +-=的图像可能是（）A ．B ．C ．D ．6、已知函数24mm ymx 的图像是开口向下的抛物线，求m 的值.7、二次函数12-=m mx y 在其图像对称轴的左侧，y 随x 的增大而增大，求m 的值.8、二次函数223x y -=，当x 1＞x 2＞0时，求y 1与y 2的大小关系. 9、已知函数()422-++=m m xm y 是关于x 的二次函数，求：（1）满足条件的m 的值；（2） m 为何值时，抛物线有最低点？求出这个最低点，这时x 为何值时，y 随x 的增大而增大；s t OstOst O st O（3） m 为何值时，抛物线有最大值？最大值是多少？当x 为何值时，y 随x 的增大而减小？ 10、如果抛物线2yax 与直线1y x 交于点,2b ，求这条抛物线所对应的二次函数的关系式.练习三函数c ax y +=2的图象与性质1、抛物线322--=x y 的开口 ,对称轴是 ,顶点坐标是 ,当x 时, y 随x 的增大而增大, 当x 时, y 随x 的增大而减小. 2、将抛物线231x y =向下平移2个单位得到的抛物线的解析式为 ,再向上平移3个单位得到的抛物线的解析式为 ,并分别写出这两个函数的顶点坐标、 . 3、任给一些不同的实数k ，得到不同的抛物线k x y +=2，当k 取0，1±时，关于这些抛物线有以下判断：①开口方向都相同；②对称轴都相同；③形状相同；④都有最底点.其中判断正确的是 . 4、将抛物线122-=x y 向上平移4个单位后，所得的抛物线是，当x= 时，该抛物线有最（填大或小）值，是 .5、已知函数2)(22+-+=x m m mx y 的图象关于y 轴对称，则m ＝________；6、二次函数c ax y +=2()0≠a 中，若当x 取x 1、x 2（x 1≠x 2）时，函数值相等，则当x 取x 1+x 2时，函数值等于 .练习四函数()2h x a y -=的图象与性质1、抛物线()2321--=x y ，顶点坐标是 ,当x 时,y 随x 的增大而减小，函数有最值 .2、试写出抛物线23x y =经过下列平移后得到的抛物线的解析式并写出对称轴和顶点坐标. （1）右移2个单位；（2）左移32个单位；（3）先左移1个单位，再右移4个单位. 3、请你写出函数()21+=x y 和12+=x y 具有的共同性质（至少2个）.4、二次函数()2h x a y -=的图象如图：已知21=a ，OA=OC ，试求该抛物线的解析式.5、抛物线2)3(3-=x y 与x 轴交点为A ，与y 轴交点为B ，求A 、B 两点坐标及⊿AOB 的面积.6、二次函数2)4(-=x a y ，当自变量x 由0增加到2时，函数值增加6.（1）求出此函数关系式.（2）说明函数值y 随x 值的变化情况.7、已知抛物线9)2(2++-=x k x y 的顶点在坐标轴上，求k 的值.练习五 ()k h x a y +-=2的图象与性质1、请写出一个二次函数以（2, 3）为顶点，且开口向上.＿＿＿＿＿＿＿＿＿＿＿＿.2、二次函数 y ＝(x －1)2＋2，当 x ＝＿＿＿＿时，y 有最小值.3、函数 y ＝12(x －1)2＋3，当 x ＿＿＿＿时，函数值 y 随 x 的增大而增大.4、函数y=21(x+3)2-2的图象可由函数y=21x 2的图象向平移3个单位，再向平移2个单位得到.5、已知抛物线的顶点坐标为2,1，且抛物线过点3,0，则抛物线的关系式是6、如图所示，抛物线顶点坐标是P （1，3），则函数y 随自变量x 的增大而减小的x 的取值范围是（）A 、x>3B 、x<3C 、x>1D 、x<1 7、已知函数()9232+--=x y .（1）确定下列抛物线的开口方向、对称轴和顶点坐标；（2）当x= 时，抛物线有最值，是 .（3）当x 时，y 随x 的增大而增大；当x 时，y 随x 的增大而减小. （4）求出该抛物线与x 轴的交点坐标及两交点间距离；（5）求出该抛物线与y 轴的交点坐标；（6）该函数图象可由23x y -=的图象经过怎样的平移得到的？8、已知函数()412-+=x y .（1）指出函数图象的开口方向、对称轴和顶点坐标；（2）若图象与x 轴的交点为A 、B 和与y 轴的交点C ，求△ABC 的面积；（3）指出该函数的最值和增减性；（4）若将该抛物线先向右平移2个单位，在向上平移4个单位，求得到的抛物线的解析式；（5）该抛物线经过怎样的平移能经过原点.（6）画出该函数图象，并根据图象回答：当x 取何值时，函数值大于0；当x 取何值时，函数值小于0.练习六 c bx ax y ++=2的图象和性质1、抛物线942++=x x y 的对称轴是 .2、抛物线251222+-=x x y 的开口方向是，顶点坐标是 .3、试写出一个开口方向向上，对称轴为直线x=-2，且与y 轴的交点坐标为（0，3）的抛物线的解析式 .4、将 y ＝x 2－2x ＋3 化成 y ＝a (x －h)2＋k 的形式，则 y ＝＿＿＿＿.5、把二次函数215322yx x的图象向上平移3个单位，再向右平移4个单位，则两次平移后的函数图象的关系式是6、抛物线1662--=x x y 与x 轴交点的坐标为_________； 7、函数x x y +-=22有最____值，最值为_______；8、二次函数c bx x y ++=2的图象沿x 轴向左平移2个单位，再沿y 轴向上平移3个单位，得到的图象的函数解析式为122+-=x x y ，则b 与c 分别等于（） A 、6，4 B 、－8，14 C 、－6，6 D 、－8，－149、二次函数122--=x x y 的图象在x 轴上截得的线段长为（） A 、22 B 、23 C 、32 D 、3310、通过配方，写出下列函数的开口方向、对称轴和顶点坐标：（1）12212+-=x x y ；（2）2832-+-=x x y ；（3）4412-+-=x x y 11、把抛物线1422++-=x x y 沿坐标轴先向左平移2个单位，再向上平移3个单位，问所得的抛物线有没有最大值，若有，求出该最大值；若没有，说明理由. 12、求二次函数62+--=x x y 的图象与x 轴和y 轴的交点坐标13、已知一次函数的图象过抛物线223y x x 的顶点和坐标原点1）求一次函数的关系式； 2）判断点2,5是否在这个一次函数的图象上14、某商场以每台2500元进口一批彩电.如每台售价定为2700元，可卖出400台，以每100元为一个价格单位，若将每台提高一个单位价格，则会少卖出50台，那么每台定价为多少元即可获得最大利润？最大利润是多少元？练习七 c bx ax y ++=2的性质1、函数2yx px q 的图象是以3,2为顶点的一条抛物线，这个二次函数的表达式为 2、二次函数2224y mx x mm 的图象经过原点，则此抛物线的顶点坐标是3、如果抛物线2yax bxc 与y 轴交于点A (0,2)，它的对称轴是1x ，那么ac b4、抛物线c bx x y ++=2与x 轴的正半轴交于点A 、B 两点，与y 轴交于点C ，且线段AB 的长为1，△ABC 的面积为1，则b 的值为______.5、已知二次函数c bx ax y ++=2的图象如图所示，则a___0，b___0，c___0，ac b 42-____0；6、二次函数c bx ax y ++=2的图象如图，则直线bc ax y +=的图象不经过第象限. 7、已知二次函数2yax bx c （0≠a ）的图象如图所示，则下列结论：1）,a b 同号；2）当1x 和3x 时，函数值相同；3）40a b ；4）当2y 时，x 的值只能为0；其中正确的是（第5题）（第6题）（第7题）（第10题） 8、已知二次函数2224m mx x y +--=与反比例函数xm y 42+=的图象在第二象限内的一个交点的横坐标是-2，则m= 9、二次函数2yx ax b 中，若0a b ，则它的图象必经过点（）A 1,1B 1,1C 1,1 D1,110、函数b ax y +=与c bx ax y ++=2的图象如上图所示，则下列选项中正确的是（） A 、0,0>>c ab B 、0,0><c ab C 、0,0<>c ab D 、0,0<<c ab 11、已知函数c bx ax y ++=2的图象如图所示，则函数b ax y +=的图象是（）12、二次函数c bx ax y ++=2的图象如图，那么abc 、2a+b 、a+b+c 、a-b+c 这四个代数式中，值为正数的有（） A ．4个 B ．3个 C ．2个 D ．1个 13、抛物线的图角如图，则下列结论： ①＞0；②；③＞；④＜1.其中正确的结论是（）.（A ）①② （B ）②③ （C ）②④ （D ）③④14、二次函数2yax bx c 的最大值是3a ，且它的图象经过1,2，1,6两点，求a 、b 、c 的值。

二次函数经典练习题

二次函数经典练习题二次函数已知二次函数$f(x)=x+bx+c$，且$f(1)=a$，$f(3)=b$，求$f(-1)$的值。

变式1：若二次函数$f(x)=ax^2+bx+c$的图像的顶点坐标为$(2,-1)$，与$y$轴的交点坐标为$(0,11)$，则求出$a$、$b$、$c$的值。

变式2：若$f(x)=-x+(b+2)x+3$，$x\in[b,c]$的图像关于$x=1$对称，则$c=$？变式3：若二次函数$f(x)=ax^2+bx+c$的图像与$x$轴有两个不同的交点$A(x_1,0)$、$B(x_2,0)$，且$x_1^2+x_2^2=\frac{26}{2}$，则该二次函数的图像由$f(x)=-3(x-1)$的图像向上平移几个单位得到？将函数$f(x)=-3x^2-6x+1$配方，确定其对称轴，顶点坐标，求出它的单调区间及最大值或最小值，并画出它的图像。

变式1：已知二次函数$f(x)=ax^2+bx+c$，如果$f(x_1)=f(x_2)$（其中$x_1\neq x_2$），则$f(\frac{x_1+x_2}{2})=$？变式2：函数$f(x)=x+px+q$对任意的$x$均有$f(1+x)=f(1-x)$，则$f(0)$、$f(-1)$、$f(1)$的大小关系是？变式3：已知函数$f(x)=ax^2+bx+c$的图像如右图所示，请至少写出三个与系数$a$、$b$、$c$有关的正确命题。

单调性已知函数$f(x)=x-2x^2$，$g(x)=x-2x$（$x\in[2,4]$）。

1）求$f(x)$，$g(x)$的单调区间；（2）求$f(x)$，$g(x)$的最小值。

变式1：已知函数$f(x)=x+4ax+2$在区间$(-\infty,6)$内单调递减，则$a$的取值范围是？变式2：已知函数$f(x)=x-(a-1)x+5$在区间$(1,2)$上为增函数，则$f(2)$的取值范围是？变式3：已知函数$f(x)=-x+kx$在$[2,4]$上是单调函数，求实数$k$的取值范围。

二次函数基础练习题大全(含答案)

1、正方形铁片边长为15cm ，在四个角上各剪去一个边长为x （cm ）的小正方形，用余下的部分做成一个无盖的盒子．(1)求盒子的表面积S （cm 2）与小正方形边长x （cm ）之间的函数关系式；(2)当小正方形边长为3cm 时，求盒子的表面积．2、已知二次函数),0(2≠+=a c ax y 当x=1时，y= -1；当x=2时，y=2，求该函数解析式.3、对于函数22x y =下列说法：①当x 取任何实数时，y 的值总是正的；②x 的值增大，y 的值也增大；③y 随x 的增大而减小；④图像关于y 轴对称.其中正确的是 .4、抛物线 y ＝－x 2 不具有的性质是（）A 、开口向下B 、对称轴是 y 轴C 、与 y 轴不相交D 、最高点是原点5、苹果熟了，从树上落下所经过的路程 s 与下落时间 t 满足 S ＝12gt 2（g ＝9.8），则 s 与 t 的函数图像大致是（）A B C D6、函数2ax y =与b ax y +-=的图像可能是（）A ．B ．C ．D ． 7、已知函数24mm y mx --=的图像是开口向下的抛物线，求m 的值. 8、二次函数12-=mmx y 在其图像对称轴的左侧，y 随x 的增大而增大，求m 的值.9、已知函数()422-++=m m x m y 是关于x 的二次函数，求：（1）满足条件的m 的值；（2） m 为何值时，抛物线有最低点？求出这个最低点，这时x 为何值时，y 随x 的增大而增大；（3） m 为何值时，抛物线有最大值？最大值是多少？当x 为何值时，y 随x 的增大而减小？tt tt10、如果抛物线2y ax =与直线1y x =-交于点(),2b ，求这条抛物线所对应的二次函数的关系式.11、已知函数2)(22+-+=x m m mx y 的图象关于y 轴对称，则m ＝________；12、抛物线942++=x x y 的对称轴是 .13、抛物线251222+-=x x y 的开口方向是，顶点坐标是 .14、将 y ＝x 2－2x ＋3 化成 y ＝a (x －h)2＋k 的形式，则 y ＝＿＿＿＿.15、把二次函数215322y x x =---的图象向上平移3个单位，再向右平移4个单位，则两次平移后的函数图象的关系式是16、抛物线1662--=x x y 与x 轴交点的坐标为_________；17、函数x x y +-=22有最____值，最值为_______；18、二次函数c bx x y ++=2的图象沿x 轴向左平移2个单位，再沿y 轴向上平移3个单位，得到的图象的函数解析式为122+-=x x y ，则b 与c 分别等于（）A 、6，4B 、－8，14C 、－6，6D 、－8，－1419、二次函数122--=x x y 的图象在x 轴上截得的线段长为（）A 、22B 、23C 、32D 、3320、通过配方，写出下列函数的开口方向、对称轴和顶点坐标：（1）12212+-=x x y ；（2）2832-+-=x x y ；（3）4412-+-=x x y 21、求二次函数62+--=x x y 的图象与x 轴和y 轴的交点坐标22、已知一次函数的图象过抛物线223y x x =++的顶点和坐标原点1）求一次函数的关系式；2）判断点()2,5-是否在这个一次函数的图象上23、某商场以每台2500元进口一批彩电.如每台售价定为2700元，可卖出400台，以每100元为一个价格单位，若将每台提高一个单位价格，则会少卖出50台，那么每台定价为多少元即可获得最大利润？最大利润是多少元？25、二次函数2224y mx x m m =++-的图象经过原点，则此抛物线的顶点坐标是26、已知二次函数c bx ax y ++=2的图象如图所示，则a___0，b___0，c___0，ac b 42-____0；27、二次函数c bx ax y ++=2的图象如图，则直线bc ax y +=的图象不经过第象限.（第26题）（第27题）（）（）28、二次函数2y x ax b =++中，若0a b +=，则它的图象必经过点（）A ()1,1--B ()1,1-C ()1,1D ()1,1-10、函数b ax y +=与c bx ax y ++=2的图象如上图所示，则下列选项中正确的是（）A 、0,0>>c abB 、0,0><c abC 、0,0<>c abD 、0,0<<c ab11、已知函数c bx ax y ++=2的图象如图所示，则函数b ax y +=的图象是（）12、二次函数c bx ax y ++=2的图象如图，那么abc 、2a+b 、a+b+c 、a-b+c 这四个代数式中，值为正数的有（）A ．4个B ．3个C ．2个D ．1个13、抛物线的图角如图，则下列结论：①＞0；②；③＞；④＜1.其中正确的结论是（）.（A ）①② （B ）②③ （C ）②④ （D ）③④14、二次函数2y ax bx c =++的最大值是3a -，且它的图象经过()1,2--，()1,6两点，求a 、b 、c 的值。

二次函数典型题练习

二次函数典型题练习（一）1、二次函数y=ax +bx+c有最小值－1，当且仅当x 2时，y随x的增大而减小，且图像过点（1、1），求此函数的解析式。

2、已知抛物线y=ax +bx+c过点A（－3、0），对称轴为x=－1,顶点C到x轴的距离为2 ，求此抛物线的解析式。

3、若抛物线过点（1、－3）和点（0、－8），且与x轴的两个交点的距离为2，求此抛物线的解析式。

4、抛物线y=x x+m与x轴交于（x 、0）（x 、0）两点。

（1）若x + x =3,求m；（2）若x x =3,求m。

5、（1）某涵洞截面是抛物线如右图所示。

现测得水面宽AB=2米，洞顶点O到水面距离为2.4米。

请在直角坐标系内求涵洞所示抛物线的解析式。

（2）如右图所示，若桥拱是抛物线，其函数解析式为y= ,当水面离桥顶的高度是2米时，问水面宽AB为多少。

(3) 如右图所示有一抛物线拱桥，当水位线在AB位置时，拱桥顶离水面2米，水面宽4米。

①当水面下降1米后，水面宽为多少？②当水面宽为1米时，问水面上升或下降了多少米？③问一艘宽1.4米，高1.6米的船是否能通过此桥？若不能过，此船最多能装多高？6、（1）如图，已知二次函数y=ax +bx+c的图像过点（-1、0）和（0、-1）两点，试确定a的取值范围。

（2）已知：直线y=x+b与双曲线y= 在第一象限内交于A点，交x轴于B点（B点在O点的左侧）。

AC x轴于C，且点C的坐标为（b、0）。

若S ABC=8.求直线与双曲线的另一个交点坐标。

7、如图：抛物线与直线y=k(x－4)都经过坐标轴的正半轴上的A、B两点，该抛物线的对称轴x=－1与x轴交于点C。

且ABC=90°。

求（1）直线的解析式。

（2）抛物线的解析式。

8、已知抛物线y=x －(a+2)x+9的顶点在坐标轴上，求a的值。

9、某商店经销一种销售成本为每千克40元的水产品，据市场分析，若按每千克50元销售，一个月能售出500千克；销售单价每涨1元，月销量就减少10千克，针对以上情况，（1）当销售单价定为每千克55元时，计算月销量与月销售利润。

二次函数练习题(含答案)

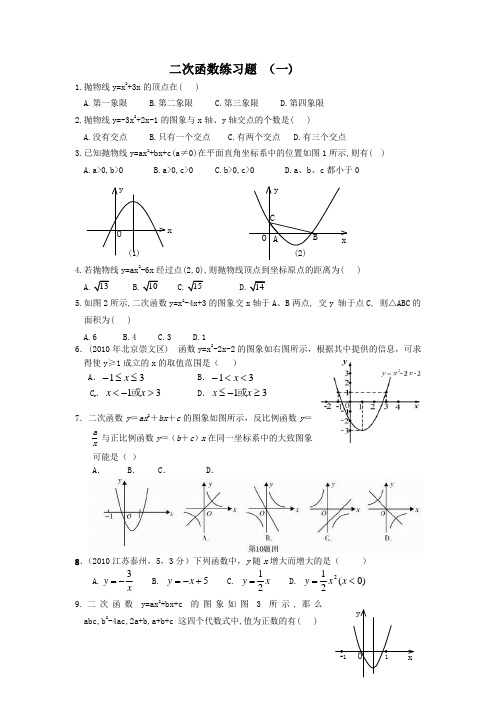
二次函数练习题（一)1.抛物线y=x 2+3x 的顶点在( )A.第一象限B.第二象限C.第三象限D.第四象限 2.抛物线y=-3x 2+2x-1的图象与x 轴、y 轴交点的个数是( ) A.没有交点 B.只有一个交点 C.有两个交点 D.有三个交点3.已知抛物线y=ax 2+bx+c(a≠0)在平面直角坐标系中的位置如图1所示,则有( ) A.a>0,b>0 B.a>0,c>0 C.b>0,c>0 D.a 、b 、c 都小于0(1) (2) 4.若抛物线y=ax 2-6x 经过点(2,0),则抛物线顶点到坐标原点的距离为( )5.如图2所示,二次函数y=x 2-4x+3的图象交x 轴于A 、B 两点, 交y 轴于点C, 则△ABC 的面积为( )A.6B.4C.3D.16．(2010年北京崇文区) 函数y=x 2-2x-2的图象如右图所示，根据其中提供的信息，可求得使y ≥1成立的x 的取值范围是（）A ．31≤≤-xB ．31<<-xC ．31>-<x x 或D ．31≥-≤x x 或7．二次函数y ＝ax 2＋bx ＋c 的图象如图所示，反比例函数y ＝ax与正比例函数y ＝（b ＋c ）x 在同一坐标系中的大致图象可能是（）A ．B ．C ．D ．8．（2010江苏泰州，5，3分）下列函数中，y 随x 增大而增大的是（）A.x y 3-= B. 5+-=x y C. 12y x = D. )0(212<=x x y 9.二次函数y=ax 2+bx+c 的图象如图3所示,那么abc,b 2-4ac,2a+b,a+b+c 这四个代数式中,值为正数的有( )xy OxBACy OA.4个B.3个C.2个D.1个10.如图所示,当b<0时,函数y=ax+b 与y=ax 2+bx+c 在同一坐标系内的图象可能是( )11.二次函数y=2x 2- 4x+ 3 通过配方化为顶点式为y= _________, 其对称轴是______,顶点坐标为_______,抛物线开口________,当x_______时,y 随x 的增大而增大;当x____时,y 随x 的增大而减小;当x=______时,y 最值=________.12.已知抛物线y=ax 2+bx+c(a≠0)图象的顶点为P(-2,3),且过A(-3,0), 则抛物线的关系式为___________.13.若二次函数y=ax 2+bx+c 的图象经过点(0,-1),(5,-1), 则它的对称轴方程是________. 14.在同一坐标系内,抛物线y=ax 2与直线y=2x+b 相交于A 、B 两点,若点A 的坐标是(2,4),则点B 的坐标是_________.15.将抛物线y=ax 2向右平移2个单位,再向上平移3个单位,移动后的抛物线经过点(3,-1),那么移动后的抛物线的关系式为__________.16.若抛物线y=ax 2+bx+c 经过(0,1)和(2,-3)两点,且开口向下,对称轴在y 轴左侧,则a 的取值范围是_________.17．已知抛物线y =ax 2+bx +c 的对称轴为x =2，且经过点(1，4)和点(5，0)，则该抛物线的解析式为_______________．18．函数y =2x 2 – 4x – 1写成y = a (x –h)2 +k 的形式是________，抛物线y =2x 2– 4x – 1的顶点坐标是_______，对称轴是__________．19．已知函数①y =x 2+1，②y =-2x 2+x ．函数____(填序号)有最小值，当x =____时，该函数的最小值是_______20．当m=_________时，函数y = (m 2－4))3(42-+--m x m mx + 3是二次函数，其解析式是__________________，图象的对称轴是_______________，顶点是________，当x =______时， y 有最____值_______．21．已知二次函数的图象开口向下，且与y 轴的正半轴相交．请你写出一个满足条件的二次函数的解析式：___________22．抛物线c bx ax y ++=2如右图所示，则它关于y析式是__________．23、（2010年宁波市）如图，已知二次函数bx x y +-=221的图象经过A （2，0）、B （0，－6）两点。

二次函数基础练习题(含答案)

二次函数练习题〔一〕1、一个小球由静止开场在一个斜坡上向下滚动，通过仪器观察得到小球滚动的距离s 〔米〕与时间t 〔秒〕的数据如下表：写出用t 表示s 的函数关系式.2、以下函数：① 23y x ；②()21y x x x =-+；③()224y x x x =+-；④ 21yx x ； ⑤()1y x x =-，其中是二次函数的是，其中a，b，c3、当m 时，函数()2235y m x x =-+-〔m 为常数〕是关于x 的二次函数4、当____m =时，函数2221m m y m m x 是关于x 的二次函数5、当____m =时，函数()2564m m y m x -+=-+3x 是关于x 的二次函数6、假设点 A ( 2, m ) 在函数 12-=x y 的图像上，那么 A 点的坐标是＿＿＿＿.7、在圆的面积公式 S ＝πr 2 中，s 与 r 的关系是〔〕A 、一次函数关系B 、正比例函数关系C 、反比例函数关系D 、二次函数关系8、正方形铁片边长为15cm ，在四个角上各剪去一个边长为x 〔cm 〕的小正方形，用余下的局部做成一个无盖的盒子．(1)求盒子的外表积S 〔cm 2〕与小正方形边长x 〔cm 〕之间的函数关系式；(2)当小正方形边长为3cm 时，求盒子的外表积．9、矩形的长是 4cm ，宽是 3cm ，如果将长和宽都增加 x cm ，那么面积增加 ycm 2，① 求 y 与 x 之间的函数关系式.② 求当边长增加多少时，面积增加 8cm 2.10、二次函数),0(2≠+=a c ax y 当x=1时，y= -1；当x=2时，y=2，求该函数解析式.11、富根老伯想利用一边长为a 米的旧墙及可以围成24米长的旧木料，建造猪舍三间，如图，它们的平面图是一排大小相等的长方形.（1）如果设猪舍的宽AB 为x 米，那么猪舍的总面积S 〔米2〕与x 有怎样的函数关系？（2）请你帮富根老伯计算一下，如果猪舍的总面积为32米2，应该如何安排猪舍的长BC 和宽AB 的长度？旧墙的长度是否会对猪舍的长度有影响？怎样影响？二次函数练习题〔二〕-----函数2ax y =的图象与性质1、填空：〔1〕抛物线221x y =的对称轴是〔或〕，顶点坐标是，当x 时，y 随x 的增大而增大，当x 时，y 随x 的增大而减小，当x= 时，该函数有最值是；〔2〕抛物线221x y -=的对称轴是〔或〕，顶点坐标是，当x 时，y 随x 的增大而增大，当x 时，y 随x 的增大而减小，当x= 时，该函数有最值是；2、对于函数22x y =以下说法：①当x 取任何实数时，y 的值总是正的；②x 的值增大，y 的值也增大；③y 随x 的增大而减小；④图象关于y 轴对称.其中正确的选项是 .3、抛物线 y ＝－x 2 不具有的性质是〔〕A 、开口向下B 、对称轴是 y 轴C 、与 y 轴不相交D 、最高点是原点4、苹果熟了，从树上落下所经过的路程 s 与下落时间 t 满足 S ＝12gt 2〔g ＝9.8〕，那么 s 与 t 的函数图像大致是〔〕A B C D5、函数2ax y =与b ax y +-=的图象可能是〔〕A ．B ．C ．D ． 6、函数24m m ymx 的图象是开口向下的抛物线，求m 的值.st O s t O s t O s t O7、二次函数12-=mmx y 在其图象对称轴的左侧，y 随x 的增大而增大，求m 的值.8、二次函数223x y -=，当x 1＞x 2＞0时，求y 1与y 2的大小关系.9、函数()422-++=m m x m y 是关于x 的二次函数，求：（1）满足条件的m 的值；（2） m 为何值时，抛物线有最低点？求出这个最低点，这时x 为何值时，y 随x 的增大而增大；（3） m 为何值时，抛物线有最大值？最大值是多少？当x 为何值时，y 随x 的增大而减小？10、如果抛物线2y ax 与直线1y x =-交于点,2b ，求这条抛物线所对应的二次函数的关系式.二次函数练习题〔三〕-----函数c ax y +=2的图象与性质1、抛物线322--=x y 的开口 ,对称轴是 ,顶点坐标是 ,当x 时, y 随x 的增大而增大, 当x 时, y 随x 的增大而减小.2、将抛物线231x y =向下平移2个单位得到的抛物线的解析式为 ,再向上平移3个单位得到的抛物线的解析式为 ,并分别写出这两个函数的顶点坐标、 .3、任给一些不同的实数k ，得到不同的抛物线k x y +=2，当k 取0，1±时，关于这些抛物线有以下判断：①开口方向都一样；②对称轴都一样；③形状一样；④都有最底点.其中判断正确的选项是 .4、将抛物线122-=x y 向上平移4个单位后，所得的抛物线是，当x= 时，该抛物线有最〔填大或小〕值，是 .5、函数2)(22+-+=x m m mx y 的图象关于y 轴对称，那么m ＝________； 6、二次函数c ax y +=2()0≠a 中，假设当x 取x 1、x 2〔x 1≠x 2〕时，函数值相等，那么当x 取x 1+x 2时，函数值等于 .二次函数练习题〔四〕-----函数()2h x a y -=的图象与性质 1、抛物线()2321--=x y ，顶点坐标是 ,当x 时,y 随x 的增大而减小，函数有最值 . 2、试写出抛物线23x y =经过以下平移后得到的抛物线的解析式并写出对称轴和顶点坐标.〔1〕右移2个单位；〔2〕左移32个单位；〔3〕先左移1个单位，再右移4个单位.3、请你写出函数()21+=x y 和12+=x y 具有的共同性质〔至少2个〕.4、二次函数()2h x a y -=的图象如图：21=a ，OA=OC ，试求该抛物线的解析式.5、抛物线2)3(3-=x y 与x 轴交点为A ，与y 轴交点为B ，求A 、B 两点坐标及⊿AOB 的面积.6、二次函数2)4(-=x a y ，当自变量x 由0增加到2时，函数值增加6.〔1〕求出此函数关系式.〔2〕说明函数值y 随x 值的变化情况.7、抛物线9)2(2++-=x k x y 的顶点在坐标轴上，求k 的值.二次函数练习题〔五〕-----()k h x a y +-=2的图象与性质 1、请写出一个二次函数以〔2, 3〕为顶点，且开口向上.＿＿＿＿＿＿＿＿＿＿＿＿.2、二次函数 y ＝(x －1)2＋2，当 x ＝＿＿＿＿时，y 有最小值.3、函数 y ＝12 (x －1)2＋3，当 x ＿＿＿＿时，函数值 y 随 x 的增大而增大.4、函数y=21(x+3)2-2的图象可由函数y=21x 2的图象向平移3个单位，再向平移2个单位得到. 5、抛物线的顶点坐标为2,1，且抛物线过点3,0，那么抛物线的关系式是6、如下图，抛物线顶点坐标是P 〔1，3〕，那么函数y 随自变量x 的增大而减小的x 的取值范围是〔〕A 、x>3B 、x<3C 、x>1D 、x<17、函数()9232+--=x y . （1）确定以下抛物线的开口方向、对称轴和顶点坐标；（2）当x= 时，抛物线有最值，是 .（3）当x 时，y 随x 的增大而增大；当x 时，y 随x 的增大而减小.（4）求出该抛物线与x 轴的交点坐标及两交点间距离；（5）求出该抛物线与y 轴的交点坐标；（6）该函数图象可由23x y -=的图象经过怎样的平移得到的？8、函数()412-+=x y . （1）指出函数图象的开口方向、对称轴和顶点坐标；（2）假设图象与x 轴的交点为A 、B 和与y 轴的交点C ，求△ABC 的面积；（3）指出该函数的最值和增减性；（4）假设将该抛物线先向右平移2个单位，在向上平移4个单位，求得到的抛物线的解析式；（5）该抛物线经过怎样的平移能经过原点.（6）画出该函数图象，并根据图象答复：当x 取何值时，函数值大于0；当x 取何值时，函数值小于0.二次函数练习题〔六〕-----c bx ax y ++=2的图象和性质1、抛物线942++=x x y 的对称轴是 .2、抛物线251222+-=x x y 的开口方向是，顶点坐标是 .3、试写出一个开口方向向上，对称轴为直线x=-2，且与y 轴的交点坐标为〔0，3〕的抛物线的解析式 .4、将 y ＝x 2－2x ＋3 化成 y ＝a (x －h)2＋k 的形式，那么 y ＝＿＿＿＿.5、把二次函数215322y x x =---的图象向上平移3个单位，再向右平移4个单位，那么两次平移后的函数图象的关系式是6、抛物线1662--=x x y 与x 轴交点的坐标为_________； 7、函数x x y +-=22有最____值，最值为___ ____； 8、二次函数c bx x y ++=2的图象沿x 轴向左平移2个单位，再沿y 轴向上平移3个单位，得到的图象的函数解析式为122+-=x x y ，那么b 与c 分别等于〔〕 A 、6，4 B 、－8，14 C 、－6，6 D 、－8，－149、二次函数122--=x x y 的图象在x 轴上截得的线段长为〔〕 A 、22 B 、23 C 、32 D 、3310、通过配方，写出以下函数的开口方向、对称轴和顶点坐标：〔1〕12212+-=x x y ；〔2〕2832-+-=x x y ；〔3〕4412-+-=x x y11、把抛物线1422++-=x x y 沿坐标轴先向左平移2个单位，再向上平移3个单位，问所得的抛物线有没有最大值，假设有，求出该最大值；假设没有，说明理由.12、求二次函数62+--=x x y 的图象与x 轴和y 轴的交点坐标13、一次函数的图象过抛物线223yx x 的顶点和坐标原点1）求一次函数的关系式；2）判断点()2,5-是否在这个一次函数的图象上14、某商场以每台2500元进口一批彩电.如每台售价定为2700元，可卖出400台，以每100元为一个价格单位，假设将每台提高一个单位价格，那么会少卖出50台，那么每台定价为多少元即可获得最大利润？最大利润是多少元？二次函数练习题〔七〕-----c bx ax y ++=2的性质1、函数2yx px q 的图象是以3,2为顶点的一条抛物线，这个二次函数的表达式为 2、二次函数2224y mx x mm 的图象经过原点，那么此抛物线的顶点坐标是3、如果抛物线2yax bxc 与y 轴交于点A (0,2)，它的对称轴是1x，那么ac b4、抛物线c bx x y ++=2与x 轴的正半轴交于点A 、B 两点，与y 轴交于点C ，且线段AB 的长为1，△ABC 的面积为1，那么b 的值为______.5、二次函数c bx ax y ++=2的图象如下图，那么a___0，b___0，c___0，ac b 42-____0；6、二次函数c bx ax y ++=2的图象如图，那么直线bc ax y +=的图象不经过第象限.7、二次函数2y ax bx c 〔0≠a 〕的图象如下图，那么以下结论：1〕,a b 同号； 2〕当1x和3x 时，函数值一样；3〕40a b；4〕当2422b b acy a-±-=-时，x 的值只能为0；其中正确的选项是8、二次函数2224m mx x y +--=与反比例函数xm y 42+=的图象在第二象限内的一个交点的横坐标是-2，那么m= 9、二次函数2yx ax b 中，假设0a b ，那么它的图象必经过点〔〕A ()1,1--B ()1,1-C 1,1D ()1,1-10、函数b ax y +=与c bx ax y ++=2的图象如下图，那么以下选项中正确的选项是〔〕A 、0,0>>c abB 、0,0><c ab1C 、0,0<>c abD 、0,0<<c ab11、函数c bx ax y ++=2的图象如下图，那么函数b ax y +=的图象是〔〕12、二次函数c bx ax y ++=2的图象如图，那么abc 、2a+b 、a+b+c 、a-b+c 这四个代数式中，值为正数的有〔〕A ．4个B ．3个C ．2个D ．1个 13、抛物线的图角如图，那么以下结论： ①＞0；②；③＞；④＜1.其中正确的结论是〔〕.〔A 〕①② 〔B 〕②③ 〔C 〕②④ 〔D 〕③④ 14、二次函数2y ax bxc 的最大值是3a ，且它的图象经过()1,2--，1,6两点，求a 、b 、c15、试求抛物线2y ax bx c 与x 轴两个交点间的距离〔240b ac 〕二次函数练习题〔八〕-----确定二次函数解析式1、抛物线y=ax 2+bx+c 经过A(-1,0), B(3,0), C(0,1)三点，那么a= , b= , c=2、把抛物线y=x 2+2x-3向左平移3个单位，然后向下平移2个单位，那么所得的抛物线的解析式为 .3、二次函数有最小值为1，当0x 时，1y ，它的图象的对称轴为1x ，那么函数的关系式为4、根据条件求二次函数的解析式〔1〕抛物线过〔-1，-6〕、〔1，-2〕和〔2，3〕三点〔2〕抛物线的顶点坐标为〔-1，-1〕，且与y 轴交点的纵坐标为-3 〔3〕抛物线过〔－1，0〕，〔3，0〕，〔1，－5〕三点；〔4〕抛物线在x 轴上截得的线段长为4，且顶点坐标是〔3，－2〕；5、二次函数的图象经过1,1、2,1两点，且与x 轴仅有一个交点，求二次函数的解析式6、抛物线y=ax 2+bx+c 过点(0,-1)与点(3,2)，顶点在直线y=3x-3上，a<0,求此二次函数的解析式.7、二次函数的图象与x 轴交于A 〔-2，0〕、B 〔3，0〕两点，且函数有最大值是2. （1）求二次函数的图象的解析式；（2）设次二次函数的顶点为P ，求△ABP 的面积.8、以x 为自变量的函数)34()12(22-+-++-=m m x m x y 中，m 为不小于零的整数，它的图象与x 轴交于点A 和B ，点A 在原点左边，点B 在原点右边.(1)求这个二次函数的解析式；(2)一次函数y=kx+b 的图象经过点A ，与这个二次函数的图象交于点C ，且ABC S ∆=10,求这个一次函数的解析式.二次函数练习题〔九〕-----二次函数与方程和不等式1、二次函数772--=x kx y 与x 轴有交点，那么k 的取值范围是 .2、关于x 的一元二次方程02=--n x x 没有实数根，那么抛物线n x x y --=2的顶点在第_____象限；3、抛物线222++-=kx x y 与x 轴交点的个数为〔〕 A 、0 B 、1 C 、2 D 、以上都不对4、二次函数c bx ax y ++=2对于x 的任何值都恒为负值的条件是〔〕 A 、0,0>∆>a B 、0,0<∆>a C 、0,0>∆<a D 、0,0<∆<a5、12++=kx x y 与k x x y --=2的图象相交，假设有一个交点在x 轴上，那么k 为〔〕 A 、0 B 、-1 C 、2 D 、41 6、假设方程02=++c bx ax 的两个根是－3和1，那么二次函数c bx ax y ++=2的图象的对称轴是直线〔〕A 、x ＝－3 B 、x ＝－2 C 、x ＝－1 D 、x ＝1 7、二次函数2y x px q 的图象与x 轴只有一个公共点，坐标为1,0，求,p q 的值。

二次函数练习题及答案

一、选择题(每小题3分,共36分)1.下列函数不是二次函数的是( D )A.y=(x-1)2B.y=1-√3x2C.y=-(x+1)(x-1)D.y=2(x+3)2-2x22.在函数y=√x-1中,自变量x的取值范围是( B )1-xA.x≥1B.x>1C.x<1D.x≤13.下列函数:①y=-3x2;②y=-3(x+3)2;③y=-3x2-1;④y=-2x2+5;⑤y=-(x-1)2.其中,图象形状、开口方向相同的是( D )A.②⑤B.③④C.①③④D.①②③4.将抛物线y=2(x-3)2+2向左平移3个单位,再向下平移2个单位,得到抛物线的表达式是( C )A.y=2(x-6)2B.y=2(x-6)2+4C.y=2x2D.y=2x2+45.已知二次函数y=-x2+2x+4,则下列关于这个函数图象和性质的说法,正确的是( C )A.图象的开口向上B.图象的顶点坐标是(1,3)C.当x<1时,y随x的增大而增大D.图象与x轴有唯一交点6.一次函数y=acx+b 与二次函数y=ax 2+bx+c 在同一平面直角坐标系中的图象可能是( B )7.一只葡萄酒杯如图①所示,酒杯的上半部分是以抛物线为模型设计而成,且成轴对称图形.从正面看葡萄酒杯的上半部分是一条抛物线,以顶点C 为原点建立如图②所示的平面直角坐标系,若AB=4,CD=3,则抛物线的表达式为( A )① ②A.y=34x 2 B.y=316x 2 C.y=-34x 2 D.y=-316x 28.竖直向上发射的小球的高度h(m)关于运动时间t(s)的函数表达式为h=at 2+bt,若小球在发射后第2 s 与第6 s 时的高度相等,则下列时刻中小球的高度最高的是( B )A.第3 sB.第3.9 sC.第4.5 sD.第6.5 s9.下列关于二次函数y=ax 2-2ax+1(a>1)的图象与x 轴交点的判断,正确的是( D ) A.没有交点B.只有一个交点,且它位于y 轴右侧C.有两个交点,且它们均位于y 轴左侧D.有两个交点,且它们均位于y 轴右侧10.(2022岱岳模拟)下表给出了二次函数y=ax2+bx+c(a≠0)的自变量x与函数值y的部分对应值,那么方程ax2+bx+c=0的一个根的近似值可能是( B )A.1.08B.1.18C.1.28D.1.3811.某旅游景点的收入受季节的影响较大,有时候出现赔本的经营状况.因此,公司规定:若无利润时,该景点关闭.经跟踪测算,该景点一年中的利润W(万元)与月份x之间满足二次函数W=-x2+16x-48,则该景点一年中处于关闭状态有( A )A.5个月B.6个月C.7个月D.8个月12.二次函数y=ax2+bx+c的部分图象如图所示,则下列选项错误的是( D )A.若(-2,y1),(5,y2)是图象上的两点,则y1>y2B.3a+c=0C.方程ax2+bx+c=-2有两个不相等的实数根D.当x≥0时,y随x的增大而减小二、填空题(每小题3分,共18分)13.(2022淄博实验中学模拟)若y=(m2-1)x m2-m是二次函数,则m= 2 .14.已知抛物线y=-x2+bx+c经过点A(-4,1),B(2,1),若函数值y随x 的值的增大而减小,则x的取值范围是x≥-1 .且15.抛物线y=(k-1)x2-x+1与x轴有交点,则k的取值范围是k≤54k≠1 .16.抛物线y=ax2+bx+c(a≠0)与x轴交于A,B两点,与y轴交于C(0,3),且此抛物线的顶点坐标为M(-1,4),则此抛物线的表达式为y=-x2-2x+3 .17.已知抛物线y=x2-k的顶点为P,与x轴交于点A,B,且△ABP是正三角形,则k的值是 3 .18.如图所示,抛物线y=x2经过平移得到抛物线y=x2-4x,其对称轴与两段抛物线所围成的阴影部分的面积为8 .三、解答题(共46分)19.(6分)已知抛物线y=ax2-2ax-3+2a2(a≠0).(1)求这条抛物线的对称轴;(2)若该抛物线的顶点在x轴上,求其表达式;(3)设点P(m,y1),Q(3,y2)在抛物线上,若y1<y2,求m的取值范围.解:(1)∵y=ax2-2ax-3+2a2=a(x-1)2+2a2-a-3.∴抛物线的对称轴为直线x=1.(2)∵抛物线的顶点在x轴上,∴2a 2-a-3=0, 解得a 1=32,a 2=-1.∴抛物线的表达式为y=32x 2-3x+32或y=-x 2+2x-1.(3)∵抛物线的对称轴为直线x=1,则Q(3,y 2)关于x=1对称的点的坐标为(-1,y 2), ∴当a>0,-1<m<3时,y 1<y 2. 当a<0,m<-1或m>3时,y 1<y 2.20.(8分)某快餐店销售A,B 两种快餐,每份利润分别为12元、8元,每天卖出份数分别为40份、80份.该店为了增加利润,准备降低每份A 种快餐的利润,同时提高每份B 种快餐的利润.售卖时发现,在一定范围内,每份A 种快餐利润每降1元可多卖2份,每份B 种快餐利润每提高1元就少卖2份.如果这两种快餐每天销售总份数不变,那么这两种快餐一天的总利润最多是多少元?解:设每份A 种快餐降价a 元,则每天卖出(40+2a)份,每份B 种快餐提高b 元,则每天卖出(80-2b)份, 由题意可得,40+2a+80-2b=40+80, 解得a=b,∴总利润W=(12-a)(40+2a)+(8+a)(80-2a) =-4a 2+48a+1 120 =-4(a-6)2+1 264. ∵-4<0,∴当a=6时,W 取得最大值1 264,即两种快餐一天的总利润最多为1 264元.21.(10分)如图所示,某农户计划用长12 m 的篱笆围成一个“日”字形的生物园饲养两种不同的家禽,生物园的一面靠墙,且墙的可利用长度最长为7 m.(1)若生物园的面积为9 m 2,则这个生物园垂直于墙的一边长为多少? (2)若要使生物园的面积最大,该怎样围? 解:设这个生物园垂直于墙的一边长为x m. (1)由题意,得x(12-3x)=9, 解得x 1=1(不符合题意,舍去),x 2=3, ∴这个生物园垂直于墙的一边长为3 m. (2)设围成生物园的面积为y m 2. 由题意,得y=x(12-3x)=-3(x-2)2+12. ∵{12-3x ≤7,12-3x >0,解得53≤x<4.∴当x=2时,y 最大=12,12-3x=6.∴生物园垂直于墙的一边长为2 m,平行于墙的一边长为6 m 时,围成生物园的面积最大,最大面积为12 m 2.22.(10分)(2022泰山模拟)有一辆宽为2 m 的货车(如图①所示),要通过一条抛物线形隧道(如图②所示).为确保车辆安全通行,规定货车车顶左右两侧离隧道内壁的垂直高度至少为0.5 m.已知隧道的跨度AB 为8 m,拱高为4 m.(1)若隧道为单车道,货车高为3.2 m,该货车能否安全通行?为什么?(2)若隧道为双车道,且两车道之间有0.4 m的隔离带,通过计算说明该货车能够通行的最大安全限高.①②解:(1)货车能安全通行.理由如下:依题意建立平面直角坐标系如图所示., 设抛物线表达式为y=ax2+4,将B(4,0)代入,得16a+4=0,解得a=-14∴抛物线表达式为y=-1x2+4.令x=1可得y=3.75.4∵3.75-0.5=3.25>3.2,∴货车能够安全通行.(2)令x=0.2+2=2.2,可得y=2.79.∵2.79-0.5=2.29,∴货车能够通行的最大安全限高为2.29 m.23.(12分)如图所示,△OAP是等腰直角三角形,∠OAP=90°,点A在第四象限,点P坐标为(8,0),抛物线y=ax2+bx+c经过原点O和A,P两点.(1)求抛物线的函数表达式.(2)点B是y轴正半轴上一点,连接AB,过点B作AB的垂线交抛物线于C,D两点,且BC=AB,求点B坐标;(3)在(2)的条件下,点M是线段BC上一点,过点M作x轴的垂线交抛物线于点N,求△CBN面积的最大值.解:(1)△OAP是等腰直角三角形,∠OAP=90°,点P坐标为(8,0),则点A在抛物线的对称轴上,故点A(4,-4),故抛物线的表达式为y=a(x-4)2-4,将点P的坐标代入上式并解得a=1,4x2-2x.故抛物线的表达式为y=14(2)设点B(0,m),过点C作CH⊥y轴于H,过点A作AQ⊥y轴于点Q,如图所示.∵∠BAQ+∠QBA=90°,∠QBA+∠HBC=90°,∴∠HBC=∠BAQ.又∵BC=AB,∠CHB=∠BQA=90°,∴△CHB≌△BQA(AAS),∴BH=AQ=4,CH=BQ=4+m,故点C(m+4,m+4).将点C的坐标代入抛物线表达式并解得m=8,故点B(0,8).(3)由(2)知点B(0,8),点C(12,12),设直线BC 的表达式为y=kx+n. 将点B,C 的坐标代入,得 {n =8,12k +n =12,解得{k =13,n =8, ∴直线BC 的表达式为y=13x+8.设点N(x,14x 2-2x),则点M(x,13x+8),∴△CBN 的面积S=12×MN ×CH=12×(13x+8-14x 2+2x)×12=-32x 2+14x+48=-32(x-143)2+2423.∵-32<0,故S 有最大值2423.。

(完整版)二次函数练习题及答案

26．如图，抛物线（a≠0）经过点A（﹣3，0）、B(1，0）、C（﹣2,1），交y轴于点M．
（1）求抛物线的表达式；
(2)D为抛物线在第二象限部分上的一点，作DE垂直x轴于点E，交线段AM于点F，求线段DF长度的最大值,并求此时点D的坐标；
（3）抛物线上是否存在一点P，作PN垂直x轴于点N，使得以点P、A、N为顶点的三角形与△MAO相似？若存在，求点P的坐标；若不存在，请说明理由．
如图①,在平面直角坐标系中，等腰直角△AOB的斜边OB在x轴上，顶点A的坐标为(3，3),AD为斜边上的高．抛物线y＝ax2＋2x与直线y＝ x交于点O、C，点C的横坐标为6．点P在x轴的正半轴上,过点P作PE∥y轴，交射线OA于点E．设点P的横坐标为m,以A、B、D、E为顶点的四边形的面积为S．
27．求OA所在直线的解析式
二次函数练习题及答案
一、选择题
1．将抛物线先向左平移2个单位，再向下平移1个单位后得到新的抛物线,则新抛物线的解析式是（ )
A． B．
C． D．
2．将抛物线向右平移1个单位后所得抛物线的解析式是………………（）
Ａ．；Ｂ．；
Ｃ． ;Ｄ．．
3．将抛物线y=（x-1）2+3向左平移1个单位，再向下平移3个单位后所得抛物线的解析式为（ )
考点：二次函数的性质
17．m≥1.二次项系数判定该函数图象的开口方向、根据顶点式方程确定其图象的顶点坐标,从而知该二次函数的自变量的取值范围．
二、填空题
8．二次函数y=－2（x－5）2＋3的顶点坐标是．
9．已知二次函数中函数与自变量之间的部分对应值如下表所示，点、在函数图象上，当时，则（填“ ”或“ ”）．
0
1

(完整版)二次函数最经典练习题

一、顶点、平移1、抛物线y ＝－(x ＋2)2－3的顶点坐标是（）．(A) （2，－3）； (B) （－2，3）； (C) （2，3）； (D) （－2，－3） 2、抛物线221y x x =-+的顶点坐标是( ) A ．（1，0）B ．（－1，0）C ．（－2，1）D ．（2，－1）3、抛物线y=x 2-2x -3的顶点坐标是 .4、下列二次函数中，图象以直线x = 2为对称轴，且经过点(0，1)的是 ( ) A ．y = (x − 2)2+ 1 B ．y = (x + 2)2+ 1 C ．y = (x − 2)2− 3 D ．y = (x + 2)2− 35、将二次函数245y x x =-+化为2()y x h k =-+的形式，则y = ． 6、二次函数522-+=x x y 有( ) A ．最大值5-B ．最小值5-C ．最大值6-D ．最小值6-7、由二次函数1)3(22+-=x y ，可知（）A ．其图象的开口向下B ．其图象的对称轴为直线3-=xC ．其最小值为1D ．当3<x 时，y 随x 的增大而增大 .二、a 、b 、c 与图象的关系1、如图为抛物线2y ax bx c =++的图像，A 、B 、C 为抛物线与坐标轴的交点，且OA =OC =1，则下列关系中正确的是 ( )A ．a ＋b =－1B ． a －b =－1C ． b <2aD ． ac <0 2、已知抛物线y ＝ax 2＋bx ＋c (a ≠0)在平面直角坐标系中的位置如图所示，则下列结论中正确的是( )A ． a >0 B ． b ＜0 C ． c ＜0 D ． a ＋b ＋c >0 3、如图所示的二次函数2y ax bx c =++的图象中，刘星同学观察得出了下面四条信息：（1）240b ac ->；（2）c >1；（3）2a －b <0；（4）a +b +c <0。