高考数学一轮总复习空间解析几何
2024年高考数学一轮复习(新高考版) 《必刷大题解析几何》课件ppt

所以 x=12或 2,
所以 Q12,-
2,
由yy2==-4x,2x-4, 得 x2-10x+16=0,
所以x=2或8,
所以 N(8,-4 2).
因为 M(-2,0),Q12,-
2,N(8,-4
2),
1234
所以 kMQ=-252,kMN=-252, 所以M,Q,N三点共线.
1234
2.(2023·石家庄模拟)已知 E(
1234
不妨设直线PQ过定点(1,0)为F. 则△APQ 的面积 S=12×|AF|×|y1-y2|=32|y1-y2|, 设直线PQ的方程为x=my+1, 联立椭圆的方程x42+y32=1, 消去x得(4+3m2)y2+6my-9=0, 则 y1+y2=-4+6m3m2,y1y2=-4+93m2,
当直线PQ的斜率存在时,设直线PQ的方程为y=kx+m, 由x42+y32=1, 消去 y 得(3+4k2)x2+8kmx+4m2-12=0,
y=kx+m, 设 P(x1,y1),Q(x2,y2),则 x1+x2=3-+84kmk2,x1x2=43m+2-4k122, 又 A(-2,0),由题知 kAP·kAQ=x1y+1 2·x2y+2 2=-14, 则(x1+2)(x2+2)+4y1y2=0,且x1,x2≠-2,
1234
因为 m2+9>4k2 且 k≠±32, 所以有36k52+1+9>4k2 且 k≠±32,
解得 k≠±32, 圆x2+y2=1的圆心为(0,0),半径为1,
6 k2+1
圆心(0,0)到直线 l:y=kx+m 的距离为 d= k|m2+| 1=
5 k2+1
=6
5
5>1,
1234
高中数学一轮总复习解析几何重点知识整理

高中数学一轮总复习解析几何重点知识整理解析几何是高中数学中的一门重要的分支,它通过代数方法研究几何问题,是数学与几何相结合的产物。
在高中数学的学习中,解析几何占据着很重要的地位。
本文将为大家总结解析几何的重点知识,并进行整理。
一、直线与圆的方程在解析几何中,直线和圆是最基本的几何图形。
直线的方程可以通过点斜式、两点式、截距式等不同的表达方式来表示。
其中最常用的是点斜式,表示为 y - y₁ = k(x - x₁)。
其中 (x₁, y₁) 是直线上的一点,k 是直线的斜率。
圆的方程有两种形式,一是标准方程:(x - a)² + (y - b)² = r²,其中 (a,b) 是圆心坐标,r 是半径;二是一般方程:x² + y² + Dx + Ey + F= 0。
二、直线与圆的交点直线与圆的交点是解析几何的一个重要概念。
当直线与圆相交时,可以通过解方程的方法求得交点的坐标。
例如,已知直线 L: 2x + y - 3 = 0 和圆 C: x² + y² - 4x - 2y - 8 = 0,求直线 L 与圆 C 的交点坐标。
解:将直线的方程代入圆的方程中,得到 x² + (2x + 3)² - 4x - 2(2x + 3) - 8 = 0。
整理得到 5x² + 10x - 10 = 0,解得 x₁ = 1,x₂ = -2。
将 x 的值代入直线的方程中,得到 y₁ = 1,y₂ = 5。
所以直线 L 和圆 C 的交点坐标为 (1, 1) 和 (-2, 5)。
三、圆与圆的位置关系圆与圆之间的位置关系有三种情况:相离、相切、相交。
当两个圆相离时,它们的半径之和小于两圆之间的距离。
当两个圆相切时,它们的半径之和等于两圆之间的距离。
当两个圆相交时,它们的半径之和大于两圆之间的距离。
四、直线与平面的位置关系直线与平面之间的位置关系有两种情况:平行和相交。
高考一轮复习(解析几何和立体几何)
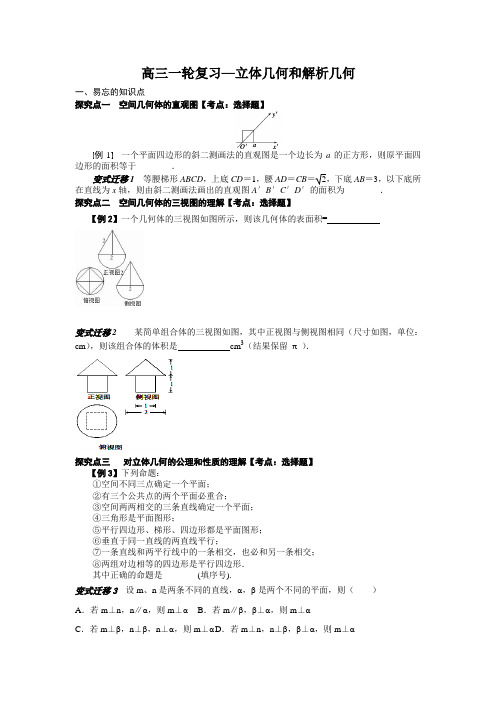
高三一轮复习—立体几何和解析几何一、易忘的知识点探究点一空间几何体的直观图【考点:选择题】例1一个平面四边形的斜二测画法的直观图是一个边长为a的正方形,则原平面四边形的面积等于________.变式迁移1等腰梯形ABCD,上底CD=1,腰AD=CB=2,下底AB=3,以下底所在直线为x轴,则由斜二测画法画出的直观图A′B′C′D′的面积为________.探究点二空间几何体的三视图的理解【考点:选择题】【例2】一个几何体的三视图如图所示,则该几何体的表面积=变式迁移2 某简单组合体的三视图如图,其中正视图与侧视图相同(尺寸如图,单位:cm),则该组合体的体积是cm3(结果保留π).探究点三对立体几何的公理和性质的理解【考点:选择题】【例3】下列命题:①空间不同三点确定一个平面;②有三个公共点的两个平面必重合;③空间两两相交的三条直线确定一个平面;④三角形是平面图形;⑤平行四边形、梯形、四边形都是平面图形;⑥垂直于同一直线的两直线平行;⑦一条直线和两平行线中的一条相交,也必和另一条相交;⑧两组对边相等的四边形是平行四边形.其中正确的命题是________(填序号).变式迁移3 设m、n是两条不同的直线,α,β是两个不同的平面,则()A.若m⊥n,n∥α,则m⊥αB.若m∥β,β⊥α,则m⊥αC.若m⊥β,n⊥β,n⊥α,则m⊥αD.若m⊥n,n⊥β,β⊥α,则m⊥α二、综合题的分析方法例4、已知四棱锥P—ABCD,底面ABCD是∠A=60°的菱形,又PD⊥底面ABCD,点M、N分别是棱AD、PC的中点.(1)证明:DN∥平面PMB;(2)证明:平面PMB⊥平面P AD.变式迁移41、如图,四棱锥P﹣ABCD的底面ABCD是正方形,PA⊥底面ABCD,E,F 分别是AC,PB的中点.(Ⅰ)证明:EF∥平面PCD;(Ⅱ)若PA=AB,求EF与平面PAC所成角的大小.2.如图1,已知ABCD是上.下底边长分别为2和6,高为的等腰梯形,将它沿对称轴OO1折成直二面角,如图2.(Ⅰ)证明:AC⊥BO1;(Ⅱ)求二面角O﹣AC﹣O1的大小.3.已知在四棱锥P一ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E、F分别是AB、PD的中点.(Ⅰ)求证:AF∥平面PEC;(Ⅱ)求PC与平面ABCD所成角的正切值;(Ⅲ)求二面角P ﹣EC ﹣D 的正切值.第二部分:解析几何一、易忘的知识点探究点一、直线的倾斜角与斜率、直线的方程1、 [2014·福建卷] 已知直线l 过圆x 2+(y -3)2=4的圆心,且与直线x +y +1=0垂直,则l 的方程是( )A .x +y -2=0B .x -y =2=0C .x +y -3=0D .x -y +3=02、直线023cos =++∂y x 的倾斜角是 。
高考数学一轮复习攻略之解析几何

2019 高考数学一轮复习攻略之分析几何(1)题型稳固:近几年来高考分析几何试题向来稳固在三(或二 )个选择题,一个填空题,一个解答题上,分值约为30 分左右,占总分值的 20%左右。
(2)整体均衡,要点突出:对直线、圆、圆锥曲线知识的考察几乎没有遗漏,经过对知识的从头组合,考察时既注意全面,更注意突出要点,对支撑数学科知识系统的骨干知识,考察时保证较高的比率并保持必需深度。
近四年新教材高考对分析几何内容的考察主要集中在以下几个种类:①求曲线方程 ( 种类确立、种类不决 ); ②直线与圆锥曲线的交点问题 (含切线问题 ); ③与曲线有关的最 (极)值问题 ;④与曲线有关的几何证明(对称性或求对称曲线、平行、垂直);教师范读的是阅读教课中不行缺乏的部分,我常采纳范读,让少儿学习、模拟。
如领读,我读一句,让少儿读一句,边读边记;第二通读,我高声读,我高声读,少儿小声读,边学边仿;第三赏读,我借用录好配朗诵磁带,一边放录音,一边少儿频频聆听,在频频聆听中体验、品尝。
照本宣科是一种传统的教课方式 ,在我国有悠长的历史。
但跟着素质教育的展开 ,照本宣科被作为一种僵化的、阻挡学生能力发展的教课方式 ,逐渐为人们所摒弃 ;而另一方面 ,老师们又为提升学生的语文修养呕心沥血。
其实 ,只需应用适当 ,“照本宣科”与提升学生素质其实不矛盾。
相反 ,它正是提升学生语文水平的重要前提和基础。
⑤探究曲线方程中几何量及参数间的数目特点;(3)能力立意,浸透数学思想:一些虽是常有的基此题型,但假如借助于数形联合的思想,就能迅速正确的获得答案。
(4)题型新奇,地点不定:近几年分析几何试题的难度有所降落,选择题、填空题均属易中等题,且解答题未必处于压轴题的地点,计算量减少,思虑量增大。
加大与有关知识的联系 (如向量、函数、方程、不等式等 ),凸现教材中研究性学习的能力要求。
加大探究性题型的重量。
唐宋或更早以前,针对“经学”“律学”“算学”和“书学”各科目,其相应教授者称为“博士”,这与现在“博士”含义已经相去甚远。
高考数学复习重难点四种解析几何数学思想(核心考点讲与练)

重难点10四种解析几何数学思想(核心考点讲与练)能力拓展题型一:函数与方程思想一、单选题1.(2022·全国·高三专题练习)抛物线2y x =上的一动点M 到直线:10l x y --=距离的最小值是()A .8B .38C .34D .42.(2022·全国·高三专题练习)点(cos ,sin )P θθ到直线34120x y +-=的距离的取值范围为()A .1217,55⎡⎤⎢⎣⎦B .712,55⎡⎤⎢⎣⎦C .717,55⎡⎤⎢⎥⎣⎦D .1224,55⎡⎤⎢⎥⎣⎦3.(2020·全国·高三专题练习)已知P 是椭圆2212y x +=上任一点,O 是坐标原点,则OP 中点的轨迹方程为()A .22421x y +=B .2221x y +=C .2212y x +=D .22241x y +=二、填空题4.(2020·全国·高二课时练习)在平面直角坐标系xOy 中,已知双曲线C :()222210,0x ya b a b-=>>的左,右焦点分别为1F ,2F ,设过右焦点2F 且与x 轴垂直的直线l 与双曲线C 的两条渐近线分别交于A ,B 两点,若1F AB 是正三角形,则双曲线C 的离心率为__________.5.(2020·江苏·一模)在平面直角坐标系xOy 中,已知双曲线22214x y a -=(a >0)的一条渐近线方程为23y x =,则a =_______.6.(2022·全国·高三专题练习)若过点(1,1)P 且斜率为k 的直线l 与双曲线2214yx -=只有一个公共点,则k =___________.三、解答题7.(2022·全国·高三专题练习)已知直线222111a y x a a =+++与x 轴交于A 点,与y 轴交于B 点(1)若0a <,6OAB π∠=,求a 的值;(2)若0a ≥,求直线l 的倾斜角的取值范围.8.(2022·四川凉山·三模(理))已知椭圆()22122:10x y C a b a b+=>>经过点12⎫⎪⎭,过其焦点且垂直于x 轴的弦长为1.(1)求椭圆1C 的标准方程;(2)已知曲线22:4C x y =,2C 在点P 处的切线l 交1C 于M ,N 两点,且4NM MP = ,求l 的方程.9.(2022·全国·高三专题练习)设函数()e ()x f x ax a a R =-+∈其图象与x 轴交于1(A x ,0),2(B x ,0)两点,且12x x <.(1)求()f x 的单调区间和极值点;(2)证明:0(()f f x ''<是()f x 的导函数);(3)证明:1212x x x x <+.题型二:数形结合思想一、单选题1.(2020·山西临汾·高三阶段练习(理))已知双曲线2222:1(0,0)x y C a b a b-=>>的右焦点为F ,若过点F 且倾斜角为45°的直线与C 的右支有且仅有一个交点,则C 的离心率的取值范围为()A .)+∞B .[2,)+∞C .D .(1,2]2.(2022·河南·开封高中模拟预测(理))若直线():340R l x y a a ++=∈与圆22:9O x y +=交于不同的两点A 、B ,且,则=a ()A .±B .±C .±D .5±3.(2022·全国·模拟预测)已知点A 为圆22:2220C x y x y +---=上一点,点()23,4M m m --,()23,4N n n --,m n ≠,若对任意的点A ,总存在点M ,N ,使得90MAN ∠≥︒,则m n -的取值范围为()A .[)2,+∞B .[]1,2C .2,5⎡⎫+∞⎪⎢⎣⎭D .20,5⎛⎤⎥⎝⎦二、多选题4.(2022·全国·高三专题练习)在同一平面直角坐标系中,表示直线l 1:y =ax +b 与l 2:y =bx ﹣a 的图象可能是()A .B .C .D .5.(2022·福建龙岩·模拟预测)已知直线y x b =+与圆2216x y +=交于A 、B两点,且OA OB OA OB +=-(其中O 为坐标原点),则实数b 的值可以是()A .4-B .-C .D .4三、填空题6.(2022·山西吕梁·三模(文))已知抛物线2:4C y x =的焦点为F ,准线为l ,过点F 的直线与C 交于,A B两点(点A 在x 轴上方),过,A B 分别作l 的垂线,垂足分别为,M N ,连接,MF NF .若MF =,则直线AB 的斜率为__________.四、解答题7.(2022·山西太原·三模(文))已知抛物线C 开口向右,顶点为坐标原点,且经过点(.A (1)求抛物线C 的方程;(2)过点()3,0B -的直线交抛物线C 于点M ,N ,直线MA ,NA 分别交直线3x =-于点P ,Q ,求PB BQ的值.8.(2022·山西吕梁·三模(理))已知椭圆2222:1(0)x y C a b a b +=>>的离心率为2,且过点2,2A ⎛⎫ ⎪ ⎪⎝⎭.(1)求椭圆C 的方程;(2)点A 关于原点O 的对称点为点B ,与直线AB 平行的直线l 与C 交于点,M N ,直线AM 与BN 交于点P ,点P 是否在定直线上?若在,求出该直线方程;若不在,请说明理由.题型三:分类与整合思想一、单选题1.(2020·湖南·高三学业考试)已知直线l 过点()4,3P ,圆C :2225x y +=,则直线l 与圆C 的位置关系是()A .相交B .相切C .相离D .相交或相切2.(2020·浙江·高三专题练习)点()1,1M 到抛物线22y ax =准线的距离为2,则a 的值为A .1B .1或3C .18或124-D .14-或1123.(2022·全国·高三专题练习(理))设e 是椭圆2218x yk+=的离心率,且1e ,12⎛⎫∈ ⎪⎝⎭,则实数k 的取值范围是()A .(0,6)B .32(0,6),3⎛⎫+∞ ⎪⎝⎭C .16(0,3),3⎛⎫+∞ ⎪⎝⎭D .(0,2)二、多选题4.(2022·全国·高三专题练习)已知圆锥曲线()22:10C mx y m +=≠,则下列说法可能正确的有()A .圆锥曲线C 的离心率为mB .圆锥曲线CC .圆锥曲线CD .圆锥曲线C 5.(2022·湖北·荆门市龙泉中学二模)已知双曲线22:17x y C t t-=-的一条渐近线方程为430x y -=,过点(5,0)作直线l 交该双曲线于A 和B 两点,则下列结论中正确的有()A .16t =或9-B .该双曲线的离心率为53C .满足323AB =的直线l 有且仅有一条D .若A 和B 分别在双曲线左、右两支上,则直线l 的斜率的取值范围是44(,33-6.(2022·全国·高三专题练习)已知A 、B 两点的坐标分别是(1,0)-,(1,0),直线AP 、BP 相交于点P ,且两直线的斜率之积为m ,则下列结论正确的是()A .当1m =-时,点P 的轨迹圆(除去与x 轴的交点)B .当10m -<<时,点P 的轨迹为焦点在x 轴上的椭圆(除去与x 轴的交点)C .当01m <<时,点P 的轨迹为焦点在x 轴上的抛物线D .当1m >时,点P 的轨迹为焦点在x 轴上的双曲线(除去与x 轴的交点)三、解答题7.(2020·全国·高三专题练习(理))求满足下列条件的直线方程:(1)经过点(5,2)A -,且在x 轴上的截距等于在y 轴上截距的2倍;(2)经过点(3,4)B ,且与两坐标轴围成一个等腰直角三角形.8.(2022·全国·高三专题练习)已知圆C 经过点()5,0P 和点()1,4Q ,且圆心在直线1x y +=上.(1)求圆C 的标准方程;(2)若过点()1,4-的直线l 与圆C 相交于A ,B 两点,且120ACB ∠=︒,求直线l 的方程.题型四:转化与划归思想一、单选题1.(2020·全国·高三(文))双曲线22221(0,0)x y a b a b-=>>)A .y =B .y =C .2y x=±D .3y x=±2.(2020·云南德宏·高三期末(理))已知点M 是抛物线2:4C y x =上一点,以M 为圆心,r 为半径的圆与抛物线的准线相切,且与x 轴的两个交点的横坐标之和为4,则此圆的半径r 为()AB .2C .3D .4二、多选题3.(2022·全国·高三专题练习)[多选题]已知抛物线212x y =的焦点为F ,()11,M x y ,()22,N x y 是抛物线上两点,则下列结论正确的是()A .点F 的坐标为1,08⎛⎫⎪⎝⎭B .若直线MN 过点F ,则12116x x =-C .若MF NF λ= ,则MN 的最小值为12D .若32MF NF +=,则线段MN 的中点P 到x 轴的距离为58三、填空题4.(2022·全国·高三专题练习)已知点M 是椭圆2212516y x +=上的一动点,点T 的坐标为(0,3)-,点N 满足||1NT =,且90MNT ∠=︒,则||MN 的最大值是__.5.(2022·全国·高三专题练习)圆1C :222410x y x y ++++=与圆2C :224410x y x y +---=的公切线有___________条.四、解答题6.(2021·海南·模拟预测)已知抛物线C 的顶点为坐标原点,焦点为圆F :2220x x y -+=的圆心,y 轴负半轴上有一点P ,直线PF 被C 截得的弦长为5.(1)求点P 的坐标;(2)过点P 作不过原点的直线PA ,PB 分别与抛物线C 和圆F 相切,A ,B 为切点,求直线AB 的方程.巩固提升一、单选题1.(2022·安徽·芜湖一中高三阶段练习(理))已知抛物线2:C y =的焦点为F ,准线为l ,过抛物线上一点P 作准线的垂线,垂足为Q ,若3PFQ π∠=,则PF =()A .B .CD .62.(2022·贵州毕节·三模(文))曲线1y =+()21y k x -=-有两个交点,则实数k 的取值范围为()A .()0,∞+B .10,2⎛⎤⎝⎦C .()1,1,2⎛⎫-∞-⋃-+∞ ⎪⎝⎭D .11,23⎛⎤-- ⎥⎝⎦3.(2022·贵州毕节·三模(理))曲线1y =与直线()()21110k x k y +-++=有两个交点,则实数k 的取值范围为()A .()0,∞+B .10,2⎛⎤⎥⎝⎦C .()1,1,2⎛⎫-∞-⋃-+∞ ⎪⎝⎭D .11,23⎛⎫-- ⎪⎝⎭4.(2022·湖北·模拟预测)已知抛物线24y x =的焦点为F ,准线为l ,过抛物线上一点P 作准线的垂线,垂足为Q ,若3PFQ π∠=,则PF =()A .2B .4C .6D .5.(2022·全国·高三专题练习)如图①,用一个平面去截圆锥得到的截口曲线是椭圆.许多人从纯几何的角度出发对这个问题进行过研究,其中比利时数学家Germinaldandelin (17941847-)的方法非常巧妙,极具创造性.在圆锥内放两个大小不同的球,使得它们分别与圆锥的侧面、截面相切,两个球分别与截面相切于,E F ,在截口曲线上任取一点A ,过A 作圆锥的母线,分别与两个球相切于,C B ,由球和圆的几何性质,可以知道,AE AC =,AF AB =,于是AE AF AB AC BC +=+=.由,B C 的产生方法可知,它们之间的距离BC 是定值,由椭圆定义可知,截口曲线是以,E F 为焦点的椭圆.如图②,一个半径为2的球放在桌面上,桌面上方有一个点光源P ,则球在桌面上的投影是椭圆,已知12A A 是椭圆的长轴,1PA 垂直于桌面且与球相切,15PA =,则椭圆的焦距为()A .4B .6C .8D .126.(2020·全国·高三专题练习(文))已知双曲线()222210,0x y a b a b-=>>的左、右焦点分别为1F ,2F ,若双曲线上存在点P 使21120PF F ∠=︒,则离心率的取值范围是()A .⎛ ⎝⎭B .()1,2C .()2,+∞D .⎫+∞⎪⎪⎝⎭7.(2021·江西南昌·高三开学考试(理))已知函数()22e e ex xf x -=,若()()0f a f b +>,若点(),a b 不可能在曲线C 上,则曲线C 的方程可以是()A .()()22112x y -+-=B .()2212x y -+=C .222x y +=D .()2212x y +-=二、多选题8.(2022·山东泰安·三模)已知实数x ,y 满足方程224240x y x y +--+=,则下列说法正确的是()A .yx 的最大值为43B .yx的最小值为0C .22x y +1D .x y +的最大值为39.(2022·山东·肥城市教学研究中心模拟预测)椭圆C :2214x y +=的左、右焦点分别为12,F F ,点P 在椭圆C 上,点Q 在以(2,4)M -为圆心,C 的长轴长为直径的圆上,则下列说法正确的是()A .椭圆C 的离心率为12B .12PF PF ⋅的最大值为4C .过点M 的直线与椭圆C 只有一个公共点,此时直线方程为1516340x y +-=D .2PQ PF -6三、填空题10.(2022·内蒙古赤峰·模拟预测(文))直线l 过定点()1,2-,过点()1,0P -作l 的垂线,垂足为M ,已知点()2,1N ,则MN 的最大值为______.11.(2022·河南商丘·三模(理))已知F 是抛物线C :22y px =(0p >)的焦点,C 的准线与x 轴交于点A ,过点A 作曲线C 的一条切线AB ,若切点B 在第一象限内,D 为C 上第四象限内的一点,且//DF AB ,则AB DF=______.12.(2022·河北·模拟预测)已知A ,B 是抛物线2x y =上的两个动点,过A ,B 的两条切线交于点P ,若90APB ∠= ,则点P 的纵坐标为___________.13.(2022·浙江·效实中学模拟预测)已知实数x ,y 满足()()22121x y -+-=,则z =的取值范围是___________.14.(2022·重庆市第十一中学校高三阶段练习)参加数学兴趣小组的小何同学在打篮球时,发现当篮球放在地面上时,篮球的斜上方灯泡照过来的光线使得篮球在地面上留下的影子有点像数学课堂上学过的椭圆,但他自己还是不太确定这个想法,于是回到家里翻阅了很多参考资料,终于明白自己的猜想是没有问题的,而且通过学习,他还确定地面和篮球的接触点(切点)就是影子椭圆的焦点.他在家里做了个探究实验:如图所示,桌面上有一个篮球,若篮球的半径为1个单位长度,在球的右上方有一个灯泡P (当成质点),灯泡与桌面的距离为4个单位长度,灯泡垂直照射在平面的点为A ,影子椭圆的右顶点到A 点的距离为3个单位长度,则这个影子椭圆的离心率e =______.15.(2022·北京·首都师范大学附属中学高三开学考试)数学中有许多形状优美的曲线,如星形线,让一个半径为r 的小圆在一个半径为4r 的大圆内部,小圆沿着大圆的圆周滚动,小圆的圆周上任一点形成的轨迹即为星形线.如图,已知1r =,起始位置时大圆与小圆的交点为A (A 点为x 轴正半轴上的点),滚动过程中A 点形成的轨迹记为星形线C .有如下结论:①曲线C 上任意两点间距离的最大值为8;②曲线:4D x y +=的周长大于曲线C 的周长;③曲线C 与圆224x y +=有且仅有4个公共点.其中正确的序号为________________.四、解答题16.(2022·浙江金华·三模)如图,已知点P 在直线l :2x =-上,A ,B 为抛物线C :()220y px p =>上任意两点,PA ,PB 均与抛物线C 相切,直线AB 与直线l 交于点Q ,过抛物线C 的焦点F 作AB 的垂线交直线l 于点K .(1)若点A 到F 的距离比到直线l 的距离小1,求抛物线C 的方程;(2)在(1)的条件下,当KQ 最小时,求ABKQ 的值.17.(2022·全国·高三专题练习)已知抛物线()2:20C x py p =>的焦点为F .且F 与圆()22:41M x y ++=上点的距离的最小值为4.(1)求抛物线的方程;(2)若点P 在圆M 上,PA ,PB 是C 的两条切线.A ,B 是切点,求PAB △面积的最大值.18.(2021·全国·高三专题练习)(1)试求函数()f x =(2)设a 、b 都是实数,试求:22()S a b =-+的最小值.高考一轮复习专项。
2025届高三一轮复习数学课件:高考中的解析几何

所以直线 PN 的方程为
1
y=2x+ .
0
令 y=0,可得
1
x=-2 ,即点
0
P
1
- 2 ,0
0
因为 MP∥BF,所以 kMP=kBF,即
0
0 +
PN 与 BF 垂直,
.
1 =
20
2
所以(0 + 50 ) =0,所以
又 y0>0,所以
20
x0=-5y0,所以 5
6
5 6
y0= 6 ,x0=- 6 .所以直线
4 + 02 · 02 -40 ,
|20 -40 |
点 P(x0,y0)到直线 B 的距离 d=
所以
1
1
S△PAB=2|AB|·
d=2
所以02 -4y0=3.
1 +1
y= 2 x-k1k2,即
3
2
(0 -40 )
4+20
2
2
2
2
2
3+2 2
3+2 2
2
=
|m| 3- =
6
6
3+2 2
= 6
2 (3-2 )
2
3
9
2
- - 2 + 4,
3
6
3+2 2 3 3+2 2
∴当 m =2<3,即 m=± 2 时,Smax= 6 × 2 = 4 .
2
对点训练 3
1
=4和抛物线 C2:x2=4y,P(x0,y0)是圆 C1 上一点,M 是
即12 -k1x0+y0=0.①
同理,设直线 PB 的方程为 y-y0=k2(x-x0),则22 -k2x0+y0=0.②
高考数学一轮复习第8章解析几何第6讲双曲线

1.判断下列结论是否正确(请在括号中打“√”或“×”
(1平面内到点F1(0,4,F2(0,-4距离之差的绝对值等于8的点的轨迹是双曲线.( × )
(2方程 - =1(mn>0表示焦点在x轴上的双曲线.( × )
(3双曲线方程 - =λ(m>0,n>0,λ≠0的渐近线方程是 - =0,即 ± =0.( √ )
(4等轴双曲线的渐近线互相垂直,离心率等于 .( √ )
(5若双曲线 - =1(a>0,b>0与 - =1(a>0,b>0的离心率分别是e1,e2,则 + =1(此条件中两条双曲线称为共轭双曲线.( √ )
题组二 走进教材
2.(必修2P61T1若双曲线 - =1(a>0,b>0的焦点到其渐近线的距离等于实轴长,则该双曲线的离心率为( A )
∴||PF2|-|PF1||=||PF2|-|PM||=|MF2|=2<|F1F2|,
∴由双曲线的定义可得,点P的轨迹是以F1,F2为焦点的双曲线.
(2设双曲线的右焦点为F1,则由双曲线的定义,可知|PF|=4+|PF1|,所以当|PF1|+|PA|最小时满足|PF|+|PA|最小.由双曲线的图形可知,当点A,P,F1共线时,满足|PF1|+|PA|最小,|AF1|即|PF1|+|PA|的最小值.又|AF1|=5,故所求的最小值为9.
(4过双曲线焦点F1的弦AB与双曲线交在同支上,则AB与另一个焦点F2构成的△ABF2的周长为4a+2|AB|.
(5双曲线的离心率公式可表示为e= .
(6双曲线的形状与e的关系:|k|= = = ,e越大,即渐近线斜率的绝对值就越大,双曲线开口就越开阔.
(7 - =1(a>0,b>0与 - =1(a>0,b>0互为共轭双曲线,其离心率倒数的平方和为1.
01-高数——空间解析几何要点速记

一、空间解析几何知识点速记一、空间解析几何1、向量代数●向量的线性运算向量加法:三角形法则或平行四边形法则:1)交换律a +b =b +a ;2)结合律(a +b )+c =a+(b +c )实数与向量的运算法则:设λ、μ为实数,则有:c=a+b1)结合律λ(μa )=μ(λa )=(λμ)a ;2)分配律(λ+μ)a =λa +μa ;λ(a +b )=λa +λb 空间直角坐标系r M OM xi yj zk x y z −−→↔==++↔(,,);设a =(a x ,a y ,a z ),b =(b x ,b y ,b z )则有1)a +b =(a x +b x ,a y +b y ,a z +b z )2)a -b =(a x -b x ,a y -b y ,a z -b z )3)λa =(λa x ,λa y ,λa z )4)b //a ⇔b =λa⇔(b x ,b y ,b z )=λ(a x ,a y ,a z )⇔zzyy xx a b a b a b ==5)向量模:222||z y x ++=r 6)两点间的距离:→212212212)()()(||||z z y y x x AB AB -+-+-==方向角:非零向量r 与三条坐标轴的夹角α、β、γ称为向量r 的方向角方向余弦:cos ||x r α=,cos ||y r β=,cos ||z r γ=●向量的数量积:a ·b =|a ||b |cos θ几何意义:数量积a ·b 等于a 的长度||a 与b 在a 的方向上的投影θcos ||b 的乘积。
1)a·a =|a |22)a ⊥b ⇔a·b =012120x x y y ⇔+=3)交换律:a·b =b·a ;4)分配律:(a +b )⋅c =a ⋅c +b ⋅c5)(λa )·b =a·(λb )=λ(a·b ),(λa )·(μb )=λμ(a·b ),λ、μ为数高 数6)a·b =a x b x +a y b y +a z bzcos ||||a b a b θ++⋅=●向量的向量积:c =a ⨯b c 的模|c |=|a ||b |sin θ,其中θ为a 与b 间的夹角;c 的方向垂直于a 与b 所决定的平面,c 的指向按右手规则从a 转向b 来确定。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高考数学一轮总复习空间解析几何解析几何是高中数学中的重要内容,也是高考数学试卷中的一大重点。
它主要涉及到点、线、面在空间中的几何性质和相互关系。
在高
考数学一轮总复习中,理解和掌握空间解析几何的理论和方法是非常
关键的。
本文将从基本概念、重要定理和解题方法三个方面进行论述。
一、基本概念
1. 点:空间中的一个位置,用坐标(x, y, z)表示;
2. 直线:由两点确定,可以用参数方程、对称方程或者一般式方程
表示;
3. 平面:由三点或者一点和法向量确定,可以用一般式方程、点法
式方程或者截距式方程表示。
二、重要定理
1. 两点间距离公式:设A(x₁, y₁, z₁)和B(x₂, y₂, z₂)是空间中两点,则AB的距离为√((x₂-x₁)²+(y₂-y₁)²+(z₂-z₁)²);
2. 点到平面的距离公式:设点P(x₀, y₀, z₀)到平面
Ax+By+Cz+D=0的距离为d,则有d=|Ax₀+By₀+Cz₀+D|/√(A²+B²+C²);
3. 直线与平面的位置关系:直线与平面相交时有以下三种可能情况:平面与直线相交,直线在平面上,直线与平面平行;
4. 点线距离公式:设点P(x₀, y₀, z₀)到直线的距离为d,则有
d=|(Ax₀+By₀+Cz₀+D)/√(A²+B²+C²)|;
5. 直线的倾斜角公式:设直线的方向向量为(m, n, p),则直线的倾
斜角为θ=arctan(|mp|/√(m²+n²+p²))。
三、解题方法
1. 确定坐标:对于给定的问题,需要通过条件和已知信息确定坐标
系的选择,通常可以选择平行于坐标轴的坐标系,简化计算;
2. 建立方程:根据题目所给条件,建立方程并化简,得到问题的解;
3. 求解问题:通过解方程组、代入法等求解方法,得到问题的解;
4. 检查答案:将求得的解代入原方程,并检查答案是否符合题意。
通过掌握解析几何的基本概念、重要定理和解题方法,我们在高考
数学考试中能够熟练地运用相关知识,解答空间解析几何相关的问题。
提醒广大考生,要多进行习题训练,加强对相关知识点的理解和记忆,提高解题能力。
总结:
本文从基本概念、重要定理和解题方法三个方面对高考数学一轮总
复习空间解析几何进行了论述。
空间解析几何是高中数学中的一项重
点内容,在高考数学试卷中占据很大的比重。
通过学习和掌握解析几
何的理论和方法,我们能够解答相关的题目,并在高考中取得好成绩。
因此,建议广大考生要重点复习和练习解析几何相关的知识和考点,
提高自己的解题能力和应变能力。
祝愿所有参加高考的考生取得理想
的成绩!。
