充要条件导学案

合集下载

高中数学《充要条件》导学案

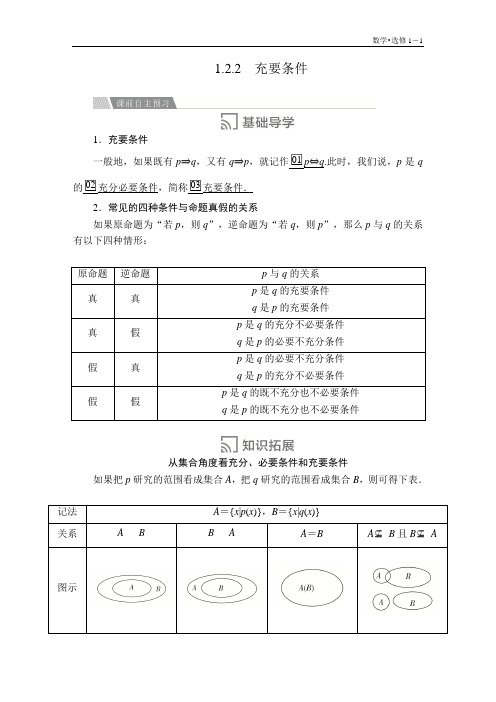
1.2.2充要条件1．充要条件一般地，如果既有p⇒q，又有q⇒p，就记作□01p⇔q.此时，我们说，p是q 的□02充分必要条件，简称□03充要条件．2．常见的四种条件与命题真假的关系如果原命题为“若p，则q”，逆命题为“若q，则p”，那么p与q的关系有以下四种情形：原命题逆命题p与q的关系真真p是q的充要条件q是p的充要条件真假p是q的充分不必要条件q是p的必要不充分条件假真p是q的必要不充分条件q是p的充分不必要条件假假p是q的既不充分也不必要条件q是p的既不充分也不必要条件从集合角度看充分、必要条件和充要条件如果把p研究的范围看成集合A，把q研究的范围看成集合B，则可得下表．记法A＝{x|p(x)}，B＝{x|q(x)}关系A B B A A＝B A⊆/B且B⊆/A 图示结论p是q的充分不必要条件p是q的必要不充分条件p，q互为充要条件p是q的既不充分也不必要条件1．判一判(正确的打“√”，错误的打“×”)(1)当p是q的充要条件时，也可说成q成立当且仅当p成立．()(2)逻辑联结符号“⇔”具有传递性．()(3)若p⇒/q和q⇒/p有一个成立，则p一定不是q的充要条件．()答案(1)√(2)√(3)√2．做一做(请把正确的答案写在横线上)(1)“x2<1”的充要条件是_________________________________________．(2)“x2－1＝0”是“|x|－1＝0”的________条件．(从“充分不必要”“必要不充分”“充要”“既不充分也不必要”中选一个合适的填空)(3)已知向量a＝(x－1,2)，b＝(2,1)，则a⊥b的充要条件是________．(4)如果不等式x≤m成立的充分不必要条件是1≤x≤2，则m的最小值为________．答案(1)－1<x<1(2)充要(3)x＝0(4)2探究1充要条件的判断例1下列各小题中，p是q的充要条件的是()①p：m<－2或m>6，q：y＝x2＋mx＋m＋3有两个不同的零点；②p：f(－x)f(x)＝1，q：y＝f(x)为偶函数；③p：cosα＝cosβ，q：tanα＝tanβ；④p：A∩B＝A，q：∁U B⊆∁U A.A．①②B．②③C．③④D．①④[解析]①q：y＝x2＋mx＋m＋3有两个不同零点⇔Δ＝m2－4(m＋3)>0⇔m<－2或m>6⇔p.②f(x)＝0时，q⇒/p.③若α，β＝kπ＋π2(k∈Z)，此时有cosα＝cosβ，但没有tanα＝tanβ.④p：A∩B＝A⇔A⊆B⇔q：∁U A⊇∁U B，∴①④中，p是q的充要条件．[答案] D拓展提升判断p是q的充分必要条件的两种思路(1)命题角度：验证由p能否推出q，由q能否推出p，对于否定性命题，注意利用等价命题来判断．(2)集合角度：关于充分条件、必要条件、充要条件，当不容易判断p ⇒q 及q ⇒p 的真假时，也可以从集合角度去判断，结合集合中“小集合⇒大集合”的关系来理解，这对解决与逻辑有关的问题是大有益处的．【跟踪训练1】已知p 是q 的充分条件，q 是r 的必要条件，也是s 的充分条件，r 是s 的必要条件，问：(1)p 是r 的什么条件？ (2)s 是q 的什么条件？(3)p ，q ，r ，s 中哪几对互为充要条件？解作出“⇒”图，如右图所示，可知： p ⇒q ，r ⇒q ，q ⇒s ，s ⇒r .(1)p ⇒q ⇒s ⇒r ，且r ⇒q ，q 能否推出p 未知，∴p 是r 的充分条件． (2)∵s ⇒r ⇒q ，q ⇒s ， ∴s 是q 的充要条件．(3)共有三对充要条件，q ⇔s ；s ⇔r ；r ⇔q . 探究2 充要条件的证明例2 设a ，b ，c 是△ABC 的三个内角A ，B ，C 所对的边．求证：a 2＝b (b ＋c )的充要条件是A ＝2B .[证明] 充分性：∵A ＝2B ，∴A －B ＝B ，则sin(A －B )＝sin B ，则sin A cos B －cos A sin B ＝sin B ，结合正弦、余弦定理得a ·a 2＋c 2－b 22ac －b ·b 2＋c 2－a 22bc ＝b ，化简整理得a 2＝b (b ＋c )；必要性：由余弦定理a 2＝b 2＋c 2－2bc cos A ，且a 2＝b (b ＋c )，得b 2＋bc ＝b 2＋c 2－2bc cos A ，∴1＋2cos A ＝c b ＝sin Csin B ，即sin B ＋2sin B cos A ＝sin C ＝sin(A ＋B )＝sin A cos B ＋cos A sin B ，∴sin B ＝sin A cos B －cos A sin B ＝sin(A －B )，由于A ，B 均为三角形的内角，故必有B ＝A －B ，即A ＝2B .综上，知a 2＝b (b ＋c )的充要条件是A ＝2B .[结论探究] 如果把例2中问题改为“求证A ，B ，C 成等差数列的充要条件是B ＝60°”，怎样证明？证明充分性：在△ABC 中，A ＋B ＋C ＝180°，又∵B ＝60°，∴A ＋C ＝120°.∴A ＋C ＝2B .∴A ，B ，C 成等差数列．必要性：A ，B ，C 成等差数列，∴A ＋C ＝2B . 又∵A ＋B ＋C ＝180°，即3B ＝180°， ∴B ＝60°.综上得A ，B ，C 成等差数列的充要条件是B ＝60°. 拓展提升充要条件的证明证明“充要条件”一般应分两个步骤，即分别证明“充分性”与“必要性”，但千万要注意“谁”是“谁”的充分条件，“谁”是“谁”的必要条件．尽管证明充要条件问题中前者是后者的充分条件，也可以是必要条件，但还是不能把步骤颠倒了．一般地，证明“p 成立的充要条件为q ”时，在证充分性时应以q 为“已知条件”，p 是该步中要证明的“结论”即q ⇒p ；证明必要性时则以p 为“已知条件”，即p ⇒q .【跟踪训练2】求证：0≤a ＜45是不等式ax 2－ax ＋1－a ＞0对一切实数x 都成立的充要条件．证明充分性：当0<a <45时，判别式Δ＝a 2－4a (1－a )＝5a 2－4a ＝a (5a －4)<0，则ax 2－ax ＋1－a >0对一切实数x 都成立．而当a ＝0时，不等式ax 2－ax ＋1－a >0可变成1>0.显然当a ＝0时，不等式ax 2－ax ＋1－a >0对一切实数x 都成立．必要性：因为ax 2－ax ＋1－a >0对一切实数x 都成立，所以a ＝0或⎩⎪⎨⎪⎧a ＞0，Δ＝a 2－4a (1－a )＜0，解得0≤a <45.故0≤a <45是不等式ax 2－ax ＋1－a >0对一切实数x 都成立的充要条件．探究3 求充要条件例3 求关于x 的方程ax 2＋2x ＋1＝0至少有一个负实根的充要条件． [解] 当a ＝0时，符合要求．当a >1时，显然方程没有零根，若方程有两个异号的实根，则由根与系数的关系可知a <0；若方程有两个负实根，则⎩⎪⎨⎪⎧Δ＝4－4a ≥0，1a>0，－2a <0，解得0<a ≤1.综上所述，若方程ax 2＋2x ＋1＝0至少有一个负实根，则a ≤1. 反之，若a ≤1，则方程ax 2＋2x ＋1＝0至少有一个负实根．因此，关于x 的方程ax 2＋2x ＋1＝0至少有一个负实根的充要条件是a ≤1. 拓展提升探求充要条件的两种方法(1)先寻找必要条件，即将探求充要条件的对象视为结论，寻找使之成立的条件；再证明此条件是该对象的充分条件，即从充分性和必要性两方面说明．(2)将原命题进行等价变形或转换，直至获得其成立的充要条件，探求的过程同时也是证明的过程，因为探求过程每一步都是等价的，所以不需要将充分性和必要性分开来证．【跟踪训练3】圆x 2＋y 2＝1与直线y ＝kx ＋2没有公共点的充要条件是________．答案－3<k < 3解析当圆x2＋y2＝1与直线y＝kx＋2有一个公共点时，有|2|k2＋1＝1，解得k＝±3.结合图形可知，圆与直线没有公共点的充要条件是－3<k< 3.1.充要条件的判断有三种方法：定义法、等价命题法、集合法.2.充要条件的证明与探求(1)充要条件的证明分充分性和必要性的证明，在证明时要注意两种叙述方式的区别：①p是q的充要条件，则由p⇒q证的是充分性，由q⇒p证的是必要性；②p的充要条件是q，则p⇒q证的是必要性，由q⇒p证的是充分性.(2)探求充要条件，可先求出必要条件，再证充分性；如果能保证每一步的变形转化过程都可逆，也可以直接求出充要条件.1．“φ＝π”是“曲线y＝sin(2x＋φ)过坐标原点”的()A．充分而不必要条件B．必要而不充分条件C．充要条件D．既不充分也不必要条件答案 A解析当φ＝π时，y＝sin(2x＋π)＝－sin2x，此时曲线过坐标原点；但曲线y ＝sin(2x＋φ)过坐标原点时，φ＝kπ(k∈Z)，∴“φ＝π”是“曲线y＝sin(2x＋φ)过坐标原点”的充分而不必要条件．故选A.2．“x2＋(y－2)2＝0”是“x(y－2)＝0”的()A．必要不充分条件B．充分不必要条件C．充要条件D．既不充分也不必要条件答案 B解析x2＋(y－2)2＝0，即x＝0且y＝2，∴x(y－2)＝0.反之，x(y－2)＝0，即x＝0或y＝2，x2＋(y－2)2＝0不一定成立．3．设x∈R，则“x>1”是“x3>1”的()A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件答案 C解析因为x ∈R ，“x >1”⇔“x 3>1”，所以“x >1”是“x 3>1”的充要条件． 4．“a ＝－1”是“直线ax ＋3y ＋3＝0与直线x ＋(a －2)y ＋1＝0平行”的( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件答案 C解析由两直线平行，可得⎩⎪⎨⎪⎧a (a －2)＝3×1，a ×1≠3×1，解得a ＝－1；当a ＝－1时，两直线的方程分别为x －3y －3＝0和x －3y ＋1＝0，可知两直线平行．故“a ＝－1”是“直线ax ＋3y ＋3＝0与直线x ＋(a －2)y ＋1＝0平行”的充要条件．5．已知x ，y 都是非零实数，且x >y ，求证：1x <1y 的充要条件是xy >0. 证明证法一：充分性：由xy >0及x >y ，得x xy >y xy ，即1x <1y . 必要性：由1x <1y ，得1x －1y <0，即y －x xy <0. 因为x >y ，所以y －x <0，所以xy >0. 所以1x <1y 的充要条件是xy >0. 证法二：1x <1y ⇔1x －1y <0⇔y －x xy <0. 由条件x >y ⇔y －x <0，故由y －xxy <0⇔xy >0. 所以1x <1y ⇔xy >0，即1x <1y 的充要条件是xy >0.A 级：基础巩固练一、选择题1．已知直线a，b分别在两个不同的平面α，β内．则“直线a和直线b相交”是“平面α和平面β相交”的()A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件答案 A解析若直线a，b相交，设交点为P，则P∈a，P∈b.又a⊂α，b⊂β，所以P∈α，P∈β，故α，β相交．反之，若α，β相交，则a，b可能相交，也可能异面或平行．故“直线a和直线b相交”是“平面α和平面β相交”的充分不必要条件．2．给定两个命题p，q.若綈p是q的必要而不充分条件，则p是綈q的() A．充分而不必要条件B．必要而不充分条件C．充要条件D．既不充分也不必要条件答案 A解析∵綈p是q的必要而不充分条件，∴q⇒綈p，但綈p⇒/q，其逆否命题为p⇒綈q，但綈q⇒/p，而原命题与其逆否命题是等价命题．故选A.3．已知函数f(x)＝A cos(ωx＋φ)(A>0，ω>0，φ∈R)，则“f(x)是奇函数”是“φ＝π2”的()A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件答案 B解析f(x)是奇函数时，φ＝π2＋kπ(k∈Z)；φ＝π2时，f(x)＝A cos⎝⎛⎭⎪⎫ωx＋π2＝－A sinωx，为奇函数．所以“f(x)是奇函数”是“φ＝π2”的必要不充分条件．故选B.4．已知直线l1：ax＋(a＋1)y＋1＝0，l2：x＋ay＋2＝0，则“a＝－2”是“l1⊥l2”的()A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件答案 A解析直线l1⊥l2的充要条件是a＋a(a＋1)＝0，解得a＝0或a＝－2，所以“a ＝－2”是“l 1⊥l 2”的充分不必要条件．5．已知不等式|x －m |<1成立的充分不必要条件是13<x <12，则实数m 的取值范围是( )A.⎣⎢⎡⎦⎥⎤－43，12B.⎣⎢⎡⎦⎥⎤－12，43 C.⎝ ⎛⎭⎪⎫－∞，－12 D.⎣⎢⎡⎭⎪⎫43，＋∞ 答案 B解析由题易知不等式|x －m |<1的解集为{x |m －1<x <m ＋1}，从而有{x |m －1<x <m ＋1}⎝ ⎛⎭⎪⎫13，12， ∴⎩⎪⎨⎪⎧m ＋1>12，m －1<13，解得－12<m <43，而m ＋1＝12与m －1＝13不同时成立， ∴m ＝－12及m ＝43亦满足题意， ∴－12≤m ≤43.故选B.6．设{a n }是首项为正数的等比数列，公比为q ，则“q <0”是“对任意的正整数n ，a 2n －1＋a 2n <0”的( )A ．充要条件B ．充分而不必要条件C ．必要而不充分条件D ．既不充分也不必要条件答案 C解析由题意得，a n ＝a 1q n －1(a 1>0)，a 2n －1＋a 2n ＝a 1q 2n －2＋a 1q 2n －1＝a 1q 2n －2(1＋q )．若q <0，因为1＋q 的符号不确定，所以无法判断a 2n －1＋a 2n 的符号；反之，若a 2n －1＋a 2n <0，即a 1q 2n －2(1＋q )<0，可得q <－1<0.故“q <0”是“对任意的正整数n ，a 2n －1＋a 2n <0”的必要而不充分条件．选C.二、填空题7．设函数f (x )＝ax ＋b (0≤x ≤1)，则a ＋2b >0是f (x )>0在[0,1]上恒成立的________条件．(填“充分不必要”“必要不充分”“充要”“既不充分也不必要”)答案必要不充分解析由⎩⎪⎨⎪⎧ f (0)>0，f (1)>0⇒⎩⎪⎨⎪⎧b >0，a ＋b >0，∴a ＋2b >0.而仅有a ＋2b >0，无法推出f (0)>0和f (1)>0同时成立．8．已知a ，b 为两个非零向量，有以下命题：①a 2＝b 2；②a·b ＝b 2；③|a |＝|b |且a ∥b .其中可以作为a ＝b 的必要不充分条件的命题是________．(将所有正确命题的序号填在题中横线上)答案 ①②③解析显然a ＝b 时①②③均成立，即必要性成立．当a 2＝b 2时，(a ＋b )·(a －b )＝0，不一定有a ＝b ；当a·b ＝b 2时，b ·(a －b )＝0，不一定有a ＝b ；|a |＝|b |且a ∥b 时，a ＝b 或a ＝－b ，即①②③都不能推出a ＝b .9．若函数f (x )＝2x －(k 2－3)·2－x ，则k ＝2是函数f (x )为奇函数的________条件．(选填“充分不必要”“必要不充分”“充要”“既不充分也不必要”)答案充分不必要解析当k ＝2时，f (x )＝2x －(k 2－3)·2－x ＝2x －2－x ，此时函数f (x )为奇函数；反之，当函数f (x )为奇函数时，有f (x )＋f (－x )＝2x －(k 2－3)·2－x ＋2－x －(k 2－3)·2x ＝(4－k 2)(2x ＋2－x )＝0，则有k 2＝4，即k ＝±2；故k ＝2是函数f (x )为奇函数的充分不必要条件．三、解答题10．下列各题中，p 是q 的什么条件？(1)p ：lg x 2＝0，q ：x ＝1；(2)p ：b ＝c ，q ：a ·b ＝a ·c (a ，b ，c ≠0)；(3)p ：x ≥1且y ≥1，q ：x ＋y ≥2；(4)p ：x ，y 不全为0，q ：x ＋y ≠0.解 (1)当lg x 2＝0时，x 2＝1，即x ＝±1，则p ⇒/ q ，q ⇒p ，所以p 是q 的必要不充分条件．(2)易知p ⇒q .而a ·b ＝a ·c (a ，b ，c ≠0)，即a ·(b －c )＝0，可得b ＝c 或a ⊥(b －c )，即q ⇒/ p ，所以p 是q 的充分不必要条件．(3)∵p ⇒q ，而q ⇒/ p ，∴p 是q 的充分不必要条件．(4)綈p ：x ＝0且y ＝0，綈q ：x ＋y ＝0，∵綈p ⇒綈q ，而綈q ⇒/ 綈p ，∴p ⇐q 且p ⇒/ q ，∴p 是q 的必要不充分条件．B 级：能力提升练1．已知集合A ＝{x |x 2－2x －3<0}，B ＝{x |(x －m ＋1)·(x －m －1)≥0}．(1)当m ＝0时，求A ∩B ；(2)若p ：x 2－2x －3<0，q ：(x －m ＋1)(x －m －1)≥0，且q 是p 的必要不充分条件，求实数m 的取值范围．解 (1)当m ＝0时，B ＝{x |(x ＋1)(x －1)≥0}＝{x |x ≤－1或x ≥1}，又A ＝{x |x 2－2x －3<0}＝{x |－1<x <3}，所以A ∩B ＝{x |1≤x <3}．(2)p ：x ∈(－1,3)，q ：x ∈(－∞，m －1]∪[m ＋1，＋∞)．因为q 是p 的必要不充分条件，所以m －1≥3或m ＋1≤－1，所以m ∈(－∞，－2]∪[4，＋∞)．2．设a ，b ，c 为△ABC 的三边，求证：方程x 2＋2ax ＋b 2＝0与x 2＋2cx －b 2＝0有公共根的充要条件是∠A ＝90°.证明必要性：方程x 2＋2ax ＋b 2＝0与x 2＋2cx －b 2＝0有公共根ξ，则 ⎩⎪⎨⎪⎧ξ2＋2aξ＋b 2＝0ξ2＋2cξ－b 2＝0⇒ξ＝－b 2a －c ＝b 2c －a . ∴⎝ ⎛⎭⎪⎫b 2c －a 2＋2c ·b 2c －a－b 2＝0⇒a 2＝b 2＋c 2， ∴∠A ＝90°.充分性：若∠A ＝90°，则a 2＝b 2＋c 2，易得x 0＝b 2c －a是方程的公共根．综上，方程x 2＋2ax ＋b 2＝0与x 2＋2cx －b 2＝0有公共根的充要条件是∠A ＝90°.。

充要条件

滨州实验中学 2015 级
数学学科
课时导学案
例 3、下列各题中，哪些 p 是 q 的充要条件？（1）（2）
p : b 0 , q :函数 f ( x) ax2 bx c 是偶函数；
p : x 0, y 0 , q : xy 0 ；
, q :a c bc；
（3） p : a b

滨州实验中学 2015 级
数学学科
课时导学案 )．
1、函数 f(x)＝x2＋mx＋1 的图象关于直线 x＝1 对称的充要条件是( A．m＝－2 B．m＝2 C．m＝－1 D．m＝1
2、给定空间中直线 l 及平面 α，条件“直线 l 与平面 α 内两条相交直线都垂直”是“直线 l 与平面 α 垂直”的______条件．
滨州实验中学 2015 级班级课题学习目标姓名
数学学科
课时导学案年月编制人审核人日
使用时间
1.2.2 充要条件
1.结合具体命题理解充要条件的概念. 2.会证明命题的充要条件. 教学过程一、复习回顾 1、若 p: x 1 ,q:
张怡李俊岭
1 1，则 p 是 q 的（ x
典型例题
例 4、已知：⊙ O 的半径为 r，圆心 O 到直线 l 的距离为 d ．求证： d r 是直线 l 与⊙ O 相切的充要条件．
反思与总结
滨州实验中学 2015 级变式训练
数学学科
课时导学案
1、用“充分不必要，必要不充分，充要，既不充分又不必要填空. （1）sinA>sinB 是 A>B 的___________条件（2）在Δ ABC 中，sinA>sinB 是 A>B 的________条件.

1.5充分条件与必要条件

1.5充分条件与必要条件（导学案）组卷：姜汉明审卷：周海英上课日期：________年____月____日；班级_______学号____姓名__________ 学习目标；理解充分条件、必要条件及充要条件与推出的关系。

能够在简单的问题情境中判断条件的充分性、必要性及充要性。

在充要条件的学习过程中，形成等价转化思想。

学习重点及难点：充分条件、必要条件及充要条件的判断。

学习过程： 1、知识回顾复习1：首先请同学们判断下列命题的真假(1)若两三角形全等，则两三角形的面积相等。

(2)若三角形有两个内角相等，则这个三角形是等腰三角形。

(3) 若ab=0，则a=0。

(4)若a ，b 为实数，b a =，则22b a =。

复习2、请同学用推断符号“⇒”“⇏”写出上述命题。

答：（1）(2)（3）（4）2、充分条件、必要条件及充要条件⏹ 充分条件：一般地，用α、β分别表示两件事，如果α这件事成立，可以推出β这件事也成立，即α_____β，那么α叫做β的_____条件⏹ 必要条件：如果β_____α，那么α叫做β的_____条件。

⏹ 充要条件：如果既有α⇒β，又有β⇒α，就记作：α_____β那么α是β的充分而且必要条件，简称_____条件。

回答上述问题（1）、（2）中的条件关系。

（1）中：_________________是_________________的充分条件；_________________是_________________的必要条件。

（2）中：_________________是_________________的充分条件；_________________是_________________的必要条件。

说明：：把命题中的条件与结论分别记作α与β；α与β关系可分为四类：（1）充分不必要条件，即α_____β,而β_____α; (2)必要不充分条件，即α_____β,而β_____α; (3)既充分又必要条件，即α_____β，又有β_____α; (4)既不充分也不必要条件，即α_____β，又有β_____α。

充要条件(经典导学案)

《1.4.2充要条件》
一、学习目标
1.理解充要条件的意义.
2.会判断一些简单的充要条件问题.
3.能对充要条件进行证明．
二、知识思维导图
三、导学指导与检测
1．“x >0”是“x ≠0”的( )
A ．充分不必要条件
B ．必要不充分条件
C ．充要条件
D ．既不充分又不必要条件
2．已知x ∈R ，则“1x
>1”是“x <1”的( ) A ．充分不必要条件 B ．必要不充分条件
C ．充要条件
D ．既不充分又不必要条件
3．设条件甲为0<x <5；条件乙为|x |<5，则条件甲是乙的( )
A ．充分不必要条件
B ．必要不充分条件
C ．充要条件
D ．既不充分又不必要条件
4．若命题p ：两直线平行，命题q ：内错角相等，则p 是q 的________条件．
5．从“充分不必要条件”“必要不充分条件”“充要条件”“既不充分又不必要条件”中选一个合适的填空．
(1)“x 2－1＝0”是“|x |－1＝0”的_____________；
(2)“x <5”是“x <3”的_____________。

充要条件

结论：如果 p q ,那么 p 与 q 互为问题 2：下列各题中 p 是 q 的充分条件还是必要条件？（1） p ：三角形是等边三角形， q ：三角形是等腰三角形. （2) p ：两条直线平行， q ：两条直线的斜率相等 (3) p ： a b q ： a 2 b2 结论：关于充要条件判断问题有四种可能结果分别是：
D. 1 x 6
宝鸡市东风路高级中学导学案
年级：高二主备人：司婷使用人：周宗让王芳芳学科：数学审核人：周宗让司婷章节：1.2.3 使用时间：2013.11.
小结：判断是否充要条件两种方法（1） p q 且 q p ；（2）原命题、逆命题均为真命题；
练习 1：在下列各题中, p 是 q 的充要条件? (1) p : x2 3x 4 , q : x 3x 4 (2) p : x 3 0 , q : ( x 3)( x 4) 0 (3) p : b2 4ac 0(a 0) , q : ax2 bx c 0(a 0) 有实数解 (4) p : x 1 是方程 ax2 bx c 0 的根， q:abc 0
宝鸡市东风路高级中学导学案
年级：高二主备人：司婷使用人：周宗让王芳芳学科：数学审核人：周宗让司婷章节：1.2.3 使用时间：2013.11.
四、课堂小结抽象概括一般地,如果既有 pq ，又有 qp 就记作 p q. 此时,我们说,那么 p 是 q 的充分必要条件,简称充要条件.显然,如果 p 是 q 的充要条件,那么 q 也是 p 的充要条件. 概括地说,如果 p q,那么 p 与 q 互为充要条件. 五、检测试题：（课堂、课后作业） 1. 下列命题为真命题的是（）. 2 2 A. a b 是 a b 的充分条件 B. | a || b | 是 a2 b2 的充要条件 C. x 2 1 是 x 1 的充分条件 D. 是 tan tan 的充要条件

2充要条件学生版

命题、充要条件题型1 四种命题间关系1.命题“若函数()log (0,1)a f x x a a =>≠在其定义域内是减函数，则log 20a <”的逆否命题是2指出下列四个命题的相互关系，（1）若)(x f 是正弦函数，则)(x f 是周期函数；（2）若)(x f 是周期函数，则)(x f 是正弦函数；（3）若)(x f 不是正弦函数，则)(x f 不是周期函数；（4）若)(x f 不是周期函数，则)(x f 不是正弦函数；题型2 全称量词与存在量词1.（2012天津卷理）命题“存在0x ∈R ，02x ≤0”的否定是 2. 已知命题p:∀x∈R,ax 2+2x+3>0,如果命题¬p 是真命题,那么实数a 的取值范围是题型3 充要条件的判断（1）2,2.x y >⎧⎨>⎩是4,4.x y xy +>⎧⎨>⎩的_____ ____条件；（2）(4)(1)0x x -+≥是401x x -≥+的____ ______条件；（3）αβ=是tan tan αβ=的_____ _ __条件；（4）3x y +≠是1x ≠或2y ≠的___________________条件.（5）“18a =”是“对任意的正数x ，21a x x+≥”的______________条件. （6）“m ＝12”是“直线(m ＋2)x ＋3my ＋1＝0与直线(m －2)x ＋(m ＋2)y －3＝0互相垂直”的 _________条件.（7）平面向量a 、b 都是非零向量，a ·b <0是a 与b 夹角为钝角的__ ______条件．（8）已知三条直线l 1：x －y ＝0，l 2：x ＋y －2＝0，l 3：5x －ky －15＝0，则l 1、l 2、l 3构不成三角形的充要条件是k ∈集合________．（9）.已知p ，q 都是r 的必要条件，s 是r 的充分条件，q 是s 的充分条件，则p 是s 的_________条件.题型4 真假判断1．下列命题：①“若xy ＝1，则x ，y 互为倒数”的逆命题；②“四边相等的四边形是正方形”的否命题；③“梯形不是平行四边形”的逆否命题；④“全等三角形是相似三角形的逆命题”，其中真命题是________．2.设有2012个命题p 1,p 2,…,p 2012满足:若命题p i 是真命题,则命题p i+4是真命题.已知p 1∧p 2是真命题,(p 1∨p 2)∧(p 3∨¬p 4)是假命题,则p 2012是________(填真或假)命题.3．下列命题中的真命题有①两直线平行的充要条件是两直线的斜率相等；②△ABC 中，AB →·BC →<0是△ABC 为钝角三角形的充要条件；③2b ＝a ＋c 是数列a 、b 、c 为等差数列的充要条件；④△ABC 中，tan A tan B >1是△ABC 为锐角三角形的充要条件．题型5 充要条件的证明与探索1已知20:100x p x x ⎧⎫+≥⎧⎪⎪⎨⎨⎬-≤⎩⎪⎪⎩⎭，:{11,0}q x m x m m -≤≤+>，若p ⌝是q ⌝的必要不充分条件，求实数m 的取值范围 . 2.求方程0122=++x ax 至少有一个负实根的充要条件 .3.求证：关于x 的方程20ax bx c ++=有一个根为－1的充要条件是0a b c -+=．4.设数列12,,n a a a 中的每一项都不为0.证明，{}n a 为等差数列的充分必要条件是：对任何n N ∈，都有1223111111n n n n a a a a a a a a +++++=.。

《充要条件》导学案

《充要条件》导学案一、学习目标1、理解充要条件的概念，能够准确判断条件与结论之间的充分性、必要性以及充要性。

2、掌握充要条件的证明方法，能运用充要条件解决相关的数学问题。

3、培养逻辑推理能力和数学思维的严谨性。

二、学习重点1、充要条件的概念。

2、充要条件的判断与证明。

三、学习难点1、理解充要条件中条件与结论的相互关系。

2、灵活运用充要条件解决复杂的数学问题。

四、知识回顾1、充分条件：如果有命题 p 可以推出命题 q，即 p ⇒ q，那么我们就说 p 是 q 的充分条件。

例如：“若 x ＞ 5，则 x ＞3”，“x ＞5”是“x ＞3”的充分条件。

2、必要条件：如果有命题 q 可以推出命题 p，即 q ⇒ p，那么我们就说 p 是 q 的必要条件。

例如：“若 x 能被 2 整除，则 x 是偶数”，“x 是偶数”是“x 能被 2 整除”的必要条件。

五、新课导入在数学中，我们常常需要研究条件与结论之间的关系。

有时候一个条件能够充分保证结论的成立，有时候一个条件只是结论成立的必要但不充分条件。

那么，有没有一种情况，一个条件既是充分的又是必要的呢？这就是我们今天要学习的充要条件。

六、概念讲解1、充要条件的定义如果既有 p ⇒ q，又有 q ⇒ p，就记作 p ⇔ q，此时我们说 p 是 q 的充分必要条件，简称充要条件。

也就是说，p 既是 q 的充分条件，又是q 的必要条件。

例如：“三角形的三条边相等”是“三角形的三个角相等”的充要条件。

2、充分不必要条件如果 p ⇒ q，但 q ⇏ p，那么 p 是 q 的充分不必要条件。

例如：“x ＞3”是“x ＞2”的充分不必要条件。

3、必要不充分条件如果 q ⇒ p，但 p ⇏ q，那么 p 是 q 的必要不充分条件。

例如：“x 是整数”是“x 是有理数”的必要不充分条件。

4、既不充分也不必要条件如果 p ⇏ q 且 q ⇏ p，那么 p 是 q 的既不充分也不必要条件。

【导学案】第2讲充分条件、必要条件、充要条件【师】

第2讲充分条件、必要条件、充要条件激活思维1. “x ＝3”是“x 2－2x －3＝0”的( ) A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件2. “x ≤2”是“x 2－4≤0”的( ) A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件1. A2. B3. (多选)若“x 2－x －2<0”是“－2<x <a ”的充分不必要条件，则实数a 的值可以是( )A. 1B. 2C. 3D. 43. BCD 【解析】由x 2－x －2<0，解得－1<x <2，所以(－1，2)(－2，a )，所以a ≥2，所以实数a 的值可以是2,3,4.4. 已知p ：－1<x <3，q ：m －2<x <m ＋5，若綈p 是綈q 的必要不充分条件，则m 的取值范围是________．4. [－2,1] 【解析】因为綈p ：x ≤－1或x ≥3，綈q ：x ≤m －2或x ≥m ＋5，且綈p 是綈q 的必要不充分条件，所以⎩⎨⎧m －2≤－1，m ＋5≥3，且等号不能同时取到，解得－2≤m ≤1.5. 已知p ，q 都是r 的必要条件，s 是r 的充分条件，q 是s 的充分条件，那么r 是q 的________条件，p 是q 的________条件．5. 充要必要【解析】因为q ⇒s ⇒r ⇒q ，所以r 是q 的充要条件．又q ⇒s ⇒r ⇒p ，所以p 是q 的必要条件．知识聚焦1. 充分、必要条件(1) 对命题“若p 则q ”而言，当它是真命题时，记做p ⇒q ，称p 是q 的________条件，q 是p 的________条件；当它是假命题时，记做p ⇒/ q ，称p 是q 的________条件，q 是p 的________条件．(2) ①若p⇒q，且q⇒/p，则p是q的________条件；②若p⇒/q，且q⇒p，则p是q的________条件；③若p⇒q，且q⇒p，则p是q的________条件，记做p⇔q；④若p⇒/q，且q⇒/p，则p是q的________条件．知识聚焦1. (1) 充分必要非充分非必要(2) ①充分不必要②必要不充分③充要④既不充分也不必要(3) 证明“充要条件”应分为两个环节，一是充分性，二是必要性．应该进行由条件到结论，由结论到条件的两次证明．证明时要分清哪个是条件，哪个是结论．2. 判断充分必要条件的常用方法(1) 定义判断法：通过判断p⇒q与q⇒p是否成立确定p是q的什么条件．(2) 集合判断法：建立命题p，q相应的集合，若p以集合A的形式出现，q 以集合B的形式出现，即p：A＝{x|p(x)}，q：B＝{x|q(x)}，则：①若A⊆B，则p是q的充分条件；②若B⊆A，则p是q的必要条件；③若A B，则p是q的充分不必要条件；④若B A，则p是q的必要不充分条件；⑤若A＝B，则p是q的充要条件；⑥若A⃘B且B⃘A，则p是q的既不充分也不必要条件．(3) 等价转化法：A⇒B与非B⇒非A是等价关系．一般地，对于条件或结论是不等关系(否定式)的命题，运用等价转化法判断．分类解析目标1充要条件的判断(1) “1x>1”是“ex－1<1”的()A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件(1) 【答案】 A【解析】因为1x>1，所以x∈(0,1)．因为ex－1<1，所以x<1，所以“1x>1”是“ex－1<1”的充分不必要条件．(2) 若a>0，b>0，则“a＋b≤4”是“ab≤4”的()A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件(2) 【答案】A【解析】当a>0，b>0时，得4≥a＋b≥2ab，即ab≤4，充分性成立；当a＝4，b＝1时，满足ab≤4，但a＋b＝5>4，不满足a＋b≤4，必要性不成立．故“a＋b≤4”是“ab≤4”的充分不必要条件．1. (2020·天津卷)设a∈R，则“a>1”是“a2>a”的()A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件1. A【解析】由a2>a得a>1或a<0，据此可知“a>1”是“a2>a”的充分不必要条件．故选A.2. 若x∈R，则“2－x≥0”是“|x－1|≤1”的()A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件2. B【解析】由2－x≥0，得x≤2；由|x－1|≤1，得－1≤x－1≤1，即0≤x≤2.所以“2－x≥0”是“|x－1|≤1”的必要不充分条件．故选B.3. (2020·北京卷)已知α，β∈R，则“存在k∈Z，使得α＝kπ＋(－1)kβ”是“sin α＝sin β”的()A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件3. C【解析】当存在k∈Z，使得α＝kπ＋(－1)kβ时，若k为偶数，则sinα＝sin(kπ＋β)＝sinβ；若k为奇数，则sinα＝sin(kπ－β)＝sin[(k－1)π＋π－β]＝sin(π－β)＝sinβ.当sinα＝sinβ时，α＝β＋2mπ或α＋β＝π＋2mπ，m∈Z，即α＝kπ＋(－1)kβ(k＝2m)或α＝kπ＋(－1)kβ(k＝2m＋1)，亦即存在k∈Z，使得α＝kπ＋(－1)kβ，所以“存在k∈Z，使得α＝kπ＋(－1)kβ”是“sinα＝sinβ”的充要条件．故选C.4. (2020·浙江卷)已知空间中不过同一点的三条直线m，n，l，则“m，n，l 在同一平面内”是“m，n，l两两相交”的()A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件4. B 【解析】依题意知m ，n ，l 是空间不过同一点的三条直线，当m ，n ，l 在同一平面内时，可能m ∥n ∥l ，故不一定得出m ，n ，l 两两相交．当m ，n ，l 两两相交时，设m ∩n ＝A ，m ∩l ＝B ，n ∩l ＝C ，可知m ，n 确定一个平面α，而B ∈m ⊂α，C ∈n ⊂α，可知直线BC 即l ，l ⊂α，所以m ，n ，l 在同一平面内．综上所述，“m ，n ，l 在同一平面内”是“m ，n ，l 两两相交”的必要不充分条件．故选B.目标2 结合充要条件确定参数的取值范围(1) 已知集合A ＝⎩⎨⎧⎭⎬⎫y |y ＝x ＋1x ，x ∈⎝⎛⎭⎪⎫12，2，B ＝{x |x ＋m 2≥6}．若“x ∈A ”是“x ∈B ”的充分不必要条件，则实数m 的取值范围是________．(1) 【答案】 (－∞，－2]∪[2，＋∞)【解析】由y ＝x ＋1x 在⎝ ⎛⎭⎪⎫12，1上单调递减，在(1,2)上单调递增，得2≤y <52，所以A ＝⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫y ⎪⎪⎪2≤y <52. 由x ＋m 2≥6，得x ≥6－m 2，所以B ＝{x |x ≥6－m 2}．因为“x ∈A ”是“x ∈B ”的充分不必要条件，所以A B ，所以6－m 2≤2，解得m ≥2或m ≤－2，故实数m 的取值范围是(－∞，－2]∪[2，＋∞)．(2) 已知集合A ＝⎩⎨⎧⎭⎬⎫x |12<2x <8，x ∈R ，B ＝{x |－1<x <m ＋1，x ∈R }，若x ∈B成立的一个充分不必要条件是x ∈A ，则实数m 的取值范围是________．(2) 【答案】 (2，＋∞) 【解析】A ＝⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪12<2x <8，x ∈R＝{x |－1<x <3}，因为x ∈B 成立的一个充分不必要条件是x ∈A ，所以A B ，所以m ＋1>3，即m >2.(1) 设p ：|2x ＋1|<m (m >0)；q ：x －12x －1>0.若p 是q 的充分不必要条件，则实数m 的取值范围为________．(1) 【答案】 (0,2]【解析】由|2x ＋1|<m (m >0)，得－m <2x ＋1<m ，所以－m ＋12<x <m －12，且－m ＋12<0. 由x －12x －1>0，得x <12或x >1. 因为p 是q 的充分不必要条件，所以m －12≤12，所以0<m ≤2.(2) 已知p ：|x －1|>2，q ：x 2－2x ＋1－a 2≥0(a >0)，若q 是p 的必要不充分条件，则实数a 的取值范围是________．(2) 【答案】 (0,2]【解析】由题可得p ：x >3或x <－1，q ：x 2－2x ＋1－a 2≥0，[x －(1－a )]·[x －(1＋a )]≥0，因为a ＞0，所以1－a ＜1＋a ，解得x ≥1＋a 或x ≤1－a . 因为q 是p 的必要不充分条件，所以⎩⎨⎧1＋a ≤3，1－a ≥－1，a >0，解得0＜a ≤2.目标3 充要条件的探求已知两个关于x 的一元二次方程mx 2－4x ＋4＝0和x 2－4mx ＋4m 2－4m－5＝0，求两方程的根都是整数的充要条件．【解答】因为mx 2－4x ＋4＝0是一元二次方程，所以m ≠0. 又另一方程为x 2－4mx ＋4m 2－4m －5＝0，且两方程都有实根，所以⎩⎨⎧Δ1＝16(1－m )≥0，Δ2＝16m 2－4(4m 2－4m －5)≥0，解得m ∈⎣⎢⎡⎦⎥⎤－54，1.因为两方程的根都是整数，所以⎩⎪⎨⎪⎧4m ∈Z ，4m ∈Z ，4m 2－4m －5∈Z ，所以m 为4的约数．又因为m ∈⎣⎢⎡⎦⎥⎤－54，1，所以m ＝－1或1.当m ＝－1时，第一个方程x 2＋4x －4＝0的根不是整数；当m ＝1时，两方程的根均为整数．所以两方程的根均为整数的充要条件是m ＝1.课堂评价1. (2021·八省联考)若关于x 的方程x 2＋ax ＋b ＝0有下列四个命题：甲：x ＝1是该方程的根；乙：x ＝3是该方程的根；丙：该方程两根之和为2；丁：该方程两根异号．如果只有一个假命题，则该命题是( )A. 甲B. 乙C. 丙D. 丁 1. A2. (2020·海南月考)“∀x ∈[－1,1]，|x |＜a 恒成立”的充要条件是( ) A. a ＞1 B. a ＞0 C. a ＞2D. a ＝1 2. A 【解析】 “∀x ∈[－1,1]，|x |＜a 恒成立”等价于“∀x ∈[－1，1]，a＞|x |max ”，所以a ＞1.故充要条件为a ＞1.3. (2020·合肥模拟)已知偶函数f (x )在[0，＋∞)上单调递增，则对实数a ，b ，“a >|b |”是“f (a )>f (b )”的( )A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件 3. A 【解析】因为f (x )是偶函数，所以f (x )＝f (|x |)．又y ＝f (x )在[0，＋∞)上单调递增，若a >|b |，则f (a )>f (|b |)＝f (b )，即充分性成立；若f (a )>f (b )，则等价于f (|a |)>f (|b |)，即|a |>|b |，即a >|b |或a <－|b |，故必要性不成立．则“a >|b |”是“f (a )>f (b )”的充分不必要条件．4. (2021·海安中学)(多选)设全集为S ，则下面四个命题中是“A ⊆B ”的充要条件的命题是( )A. A ∩B ＝AB. ∁S A ⊇∁S BC. ∁S B ∩A ＝∅D. ∁S A ∩B ＝∅4. ABC 【解析】对于选项A ，由 A ∩B ＝A ，可得A ⊆B . 由 A ⊆B 可得A ∩B ＝A ，故A 满足条件．对于选项B ，由∁S A ⊇∁S B 可得A ⊆B ，由A ⊆B 可得∁S A ⊇∁S B ，故∁S A ⊇∁S B 是A ⊆B 的充要条件，故B 满足条件．对于选项C ，由∁S B ∩A ＝∅，可得A ⊆B ，由A ⊆B 可得∁S B ∩A ＝∅，故∁S B ∩A ＝∅是A ⊆B 的充要条件，故C 满足条件．对于选项D ，由∁S A ∩B ＝∅，可得B ⊆A ，不能推出A ⊆B ，故∁S A ∩B ＝∅不是A ⊆B 的充要条件，故D 不满足条件．故选ABC.5. 已知集合A ＝⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪⎝ ⎛⎭⎪⎫13x 2－x －6≤1，B ＝{x |log 3(x ＋a )≥1}，若“x ∈A ”是“x ∈B ”的必要不充分条件，则实数a 的取值范围是________.5. (－∞，0] 【解析】由⎝ ⎛⎭⎪⎫13x 2－x －6≤1，得x 2－x －6≥0，解得x ≤－2或x ≥3，则A ＝{x |x ≤－2或x ≥3}．由log 3(x ＋a )≥1，得x ＋a ≥3，即x ≥3－a ，则B ＝{x |x ≥3－a }．由题意知B A ，所以3－a ≥3，解得a ≤0.6.。

导学案002(命题及其关系与充要条件)

命题及其关系与充要条件编号:002一、考纲要求命题及其关系①理解命题的概念.②了解“若p，则q”形式的命题的逆命题、否命题与逆否命题，会分析四种命题的相互关系. ③理解必要条件、充分条件与充要条件的意义.二、复习目标了解命题的概念及命题的建构形式，并能判断命题的真假；掌握四种命题之间的相互关系及其假判断，理解必要条件、充分条件、充分必要条件的意义，并能判定命题之间的充要性。

会证明简单的充要条件的命题，进一步增强逻辑思维能力。

三、重点难点四种命题的转化及真假判断，必要条件的判断。

四、要点梳理1．常用逻辑用语（1）命题命题：可以判断真假的语句叫命题；逻辑联结词：“或”“且”“非”这些词就叫做逻辑联结词；简单命题：不含逻辑联结词的命题。

复合命题：由简单命题与逻辑联结词构成的命题。

常用小写的拉丁字母p，q，r，s，……表示命题，故复合命题有三种形式：p或q；p 且q；非p。

（2）复合命题的真值“非p”形式复合命题的真假可以用下表表示：“p且q”形式复合命题的真假可以用下表表示：“p或q”形式复合命题的真假可以用下表表示：注：1°像上面表示命题真假的表叫真值表；2°由真值表得：“非p”形式复合命题的真假与p的真假相反；“p且q”形式复合命题当p与q同为真时为真，其他情况为假；“p或q”形式复合命题当p与q同为假时为假，其他情况为真；3°真值表是根据简单命题的真假，判断由这些简单命题构成的复合命题的真假，而不涉及简单命题的具体内容。

（3）四种命题如果第一个命题的条件是第二个命题的结论，且第一个命题的结论是第二个命题的条件，那么这两个命题叫做互为逆命题；如果一个命题的条件和结论分别是原命题的条件和结论的否定，那么这两个命题叫做互否命题，这个命题叫做原命题的否命题；如果一个命题的条件和结论分别是原命题的结论和条件的否定，那么这两个命题叫做互为逆否命题，这个命题叫做原命题的逆否命题。

充分条件与必要条件导学案高一上学期数学人教A版(2019)必修第一册

《1.4.1充分条件与必要条件》导学案姓名小组第组【学习目标】1.理解充分条件的概念，判定定理与充分条件的关系。

2.理解必要条件的概念，性质定理与必要条件的关系。

3.结合具体命题，学会判断充分条件、必要条件的方法。

4.培养学生的辩证思维能力。

【自主学习】知识点一命题1、命题：用语言、符号或式子表达的，可以的陈述句。

2、命题的真假：判断为真的语句是；判断为假的语句是。

注意：反问句、疑问句、祈使句都不是命题。

3、命题的形式：可写成“”“如果p，那么q”等形式。

其中p称为命题的，q称为命题的。

问题1：下列哪些是真命题？哪些是假命题？（1）3≥3。

（2）3能被2整除吗？（3）同位角相等，两直线平行。

（4）相等的角是对顶角。

（5）若｜a|>|b|，则a>b。

（6）三角形任意两边之和大于第三边。

（7）今天天气真好啊！知识点二充分条件与必要条件命题真假“若p，则q”为真命题“若p，则q”为假命题推出关系p q p q条件关系p是q的条件q是p的条件p不是q的条件q不是p的条件问题2：下列“若p，则q”形式的命题中，p是q的什么条件？q是p的什么条件？（1）若平面内点P在线段AB的垂直平分线上，则PA=PB；（2）若两个三角形的两边及一边所对的角分别相等，则这两个三角形全等；（3）若两个三角形相似，则这两个三角形的面积比等于周长比的平方。

知识点三判定定理、性质定理与充分条件、必要条件的关系一般地，数学中的每一条判定定理都给出了相应数学结论成立的一个条件。

数学中的每一条性质定理都给出了相应数学结论成立的一个条件。

注意：（1）充分、必要条件的判断讨论的是“若p，则q”形式的命题。

若不是，则首先将命题改写成的形式。

（2）对p⇒q的理解：当成立时，一定成立，即由p通过推理可以得到q。

①为真命题；②是的充分条件；③是的必要条件以上三种形式均为“p⇒q”这一逻辑关系的表达。

知识点四充分条件、必要条件与集合的关系设A＝{x|x满足条件p}，B＝{x|x满足条件q}A⊆B是的充分条件；是的必要条件B⊆A是的充分条件；是的必要条件课堂总结【课后练习】一、选择题1.下列语句是命题的是（）A.今天天气真好啊！B.你怎么又没交作业？C.x>2D.方程x2+2x+3=0无实根2.设x，y∈R，则“x≥2且y≥2”是“x2+y2≥4”的（）A.充分条件但不是必要条件B.必要条件但不是充分条件C.既是充分条件，也是必要条件D.既不是充分条件，也不是必要条件3.下列说法正确的是（）A.命题“直角相等”的条件和结论分别是“直角”和“相等”B.语句“当a>4时，方程x2-4x+a=0有实根”不是命题C.命题“对角线互相垂直的四边形是菱形”是真命题D.“x=2时，x2-3x+2=0”是真命题二、填空题4.设四边形ABCD的两条对角线为AC，BD，则“四边形ABCD为菱形”是“AC⟂BD”的条件。

高中数学充要条件的教案

高中数学充要条件的教案
教学内容：充要条件在数学中的应用
教学目标：
1. 了解充要条件的概念及其在数学中的应用
2. 能够正确运用充要条件解题
3. 培养学生逻辑思维和推理能力
教学重点和难点：
重点：充要条件的概念和应用
难点：能够准确理解充要条件，并将其运用到实际问题中
教学准备：
1. 教师准备充要条件的概念讲解及相关例题
2. 准备教学用具、课件等辅助教学工具
教学步骤：
一、导入（5分钟）
教师引入充要条件概念，通过生活中的例子引发学生对充要条件的思考。

二、概念讲解（15分钟）
1. 讲解充要条件的定义和特点
2. 介绍充要条件在数学中的应用及相关定理
三、例题分析（20分钟）
通过一些具体的例题，让学生理解充要条件的运用方法，并引导他们进行讨论和分析。

四、练习训练（15分钟）
布置一些练习题目，让学生独立完成并相互交流讨论，并及时纠正错误。

五、总结（5分钟）
总结本节课的重点内容，强调充要条件在数学中的重要性，并鼓励学生加强实践训练。

六、作业布置
布置相关练习题目，并要求学生认真完成并及时交卷。

教学心得：
本节课通过实例讲解、分析解题方法等多种途径，让学生更容易理解和掌握充要条件的概念和应用方法。

通过丰富的练习和讨论，学生逐渐提高了解题的能力和逻辑推理能力。

希望学生能够在今后的学习中，善于灵活运用充要条件解决问题，提高数学学习的深度和广度。

《充分条件与必要条件》课件与导学案

【2】 p是q的充分条件
“p是q的充分条件”和 “q是p的必要条
件”表述的是同一个逻辑关系。
【3】 q的充分条件是p
而“p是q的充分条件”只能说明p⇒q，
与q能否推导出p没有任何关系。
②注意右侧等价的表述方式：
【4】 q是p的必要条件
【5】 p的必要条件是q
1.用符号“⇒”与“⇏”填空。
⇏ > 1.
命题真假
推出关系
条件关系
“若 p，则 q”是真命题
“若 p，则 q”是假命题
p ⇒ q
P___q
p 是 q 的充分条件
p 不是 q 的充分条件
q 是 p 的必要条件
q 不是 p 的必要条件
思考 1：(1)p 是 q 的充分条件与 q 是 p 的必要条件所表示的推出关系
是否相同？
(2)以下五种表述形式：①p⇒q；②p 是 q 的充分条件；③q 的充分条
怎么判断充要条件？有哪些方法？
【1】定义法：（1）分清命题的条件和结论
（2）找推式，判断 ⇒ 和 ⇒ 的真假
（3）根据条件和推式得出结论
【2】等价法
将命题转化成为另一个与之等价的且便于判断真假的命题
【3】赋值法
对于选择题，可以取一些特殊值或者特殊情况，用来说明
结论或者推导不成立，但不可用于证明题。
②
③
A
B
【解】因为A⊈B且B⊈A，所以A是B的
既不充分也不必要条件
本节考试常考什么？
【充分条件，必要条件，充要条件的判断】
【题3·传递法】已知p是r的充分不必要条件，q是r的充分条件，s是r的必要条件，q是s
的必要条件，则p是q的什么条件？
【解】由题意有p⇒r，r⇏p，q⇒r，r⇒s，s⇒q，所以p⇒r⇒s⇒q，

《充分条件与必要条件》教案、导学案与同步练习

第一章集合与常用逻辑用语《1.4充分条件与必要条件》教案【教材分析】本节内容比较抽象，首先从命题出发，分清命题的条件和结论，看条件能否推出结论，从而判断命题的真假；然后从命题出发结合实例引出充分条件、必要条件、充要条件这三个概念，再详细讲述概念，最后再应用概念进行论证.【教学目标与核心素养】课程目标1．理解充分条件、必要条件与充要条件的意义．2．结合具体命题掌握判断充分条件、必要条件、充要条件的方法．3．能够利用命题之间的关系判定充要关系或进行充要性的证明．数学学科素养1.数学抽象：充分条件、必要条件与充要条件含义的理解；2.逻辑推理：通过命题的判定得出充分条件、必要条件的含义，通过定义或集合关系进行充分条件、必要条件、充要条件的判断；3.数学运算：利用充分、必要条件求参数的范围，常见包含一元二次方程及其不等式和不等式组；4.数据分析：充要条件的探求与证明：将原命题进行等价变形或转换，直至获得其成立的充要条件，探求的过程同时也是证明的过程；5.数学建模：通过对充分条件、必要条件的概念的理解和运用，培养学生分析、判断和归纳的逻辑思维能力。

【教学重难点】重点：充分条件、必要条件、充要条件的概念．．难点：能够利用命题之间的关系判定充要关系．【教学方法】：以学生为主体，采用诱思探究式教学，精讲多练。

【教学过程】一、问题导入：写出下列两个命题的条件和结论，并判断是真命题还是假命题？（1）若x＞a2+b2，则x＞2ab,（2）若ab＝0，则a＝0.学生容易得出结论；命题(1)为真命题，命题(２)为假命题．提问：对于命题“若p，则q”，有时是真命题，有时是假命题．如何判断其真假的？结论：看p能不能推出q，如果p能推出q，则原命题是真命题，否则就是假命题．要求：让学生自由发言，教师不做判断。

而是引导学生进一步观察.研探.二、预习课本，引入新课阅读课本17-22页，思考并完成以下问题1.什么是充分条件？2.什么是必要条件？3.什么是充要条件？5.什么是充分不必要条件？6.什么是必要不充分条件？7.什么是既不充分也不必要条件？要求：学生独立完成，以小组为单位，组内可商量，最终选出代表回答问题，教师巡视指导，解答学生在自主学习中遇到的困惑过程。

充要条件教案

1.2 充分必要条件导学案一、教学目标：1．知识目标:正确理解充分条件、必要条件和充要条件的概念；能正确判断是充分条件、必要条件还是充要条件；2．能力目标：培养学生分析、判断和归纳的逻辑思维能力．3．情感目标：培养他们的辨析能力以及培养他们的良好的思维品质，在练习过程中进行辩证唯物主义思想教育．二、教学重点、难点：重点：充分条件、必要条件的概念，正确区分充要条件难点：判断命题的充分条件、必要条件，正确区分充要条件。

三、教学方法与手段。

本节课采用探究式教学法，采用启发、引导、探索、讨论交流的方式进行组织教学．并充分利用多媒体辅助教学．四.【预习达标】1.充分条件：一般地，“若p ，则q ”为________,是指由p 通过推理得出q,这时,我们就说_______,记作p ⇒q,并且说p 是q 的充分条件.2.如果“若p,则q 为假命题,那么由p 不能推出q,记作p ⇒q ，我们说p 不是q 的充分条件. 必要条件1.必要条件:一般地,“若p ，则q ”为真命题,指由p 通过________可以得出q,记作p ⇒q,我们说_________是_______的必要条件;2.如果“若p ，则q ”为假命题,即由p 不能推出q ，记作p ⇒q 我们说q 不是p 的必要条件.【课前达标】1.判断一下下列命题的真假:（1）若a 是无理数，则a+3是无理数；（2）若四边形对角互补，则四边形内接于圆； (3）若x>2，则x>4；（4）若x ＋y ≠－2则x 、y 不都为－1；12.(2011):1,:1,().. . .p x q p q xA B C D ≤<⌝山东临沂已知条件则是成立的充分不必要条件必要不充分条件充要条件既非充分也非必要条件3.(2011),,,:;://, .a b p a b q p q αβαβαβ⊂⊂江苏徐州已知、是不同的两个平面直线直线命题与无公共点命题则是的条件．教学过程（一）合作探究。

导学案充分条件与必要条件

导学案 §1.2.1充分条件与必要条件一、学习目标1.理解充分条件与必要条件的概念；2.会判断命题中的充分条件与必要条件；3.能初步对充分条件与必要条件进行简单应用。

二、学习重点与难点1. 学习重点：理解充分条件与必要条件的概念.2 .学习难点：必要条件的符号语言的理解与判断方法. 三、知识框架判断所给原命题及其逆命题的真假——分析p,q 之间的关系——充分条件与必要条件的概念——分析已知命题中p,q 之间的充分性与必要性之间的关系——充分条件与必要条件的四种类型——判断充分条件与必要条件的方法——简单应用。

四、新课导学（一）自主活动一：探究充分条件与必要条件的概念。

1、给出下列若“p 则q ”形式的命题并提出有关问题。

(1) 命题1：若小明是山东泗水人，则小明是中国人. 命题2：若A=Ø，则A B=Ø. 命题3：若22,b a b a>>则 .命题4：是增函数则且若)(),10()(x f a a a x f x≠>= .(2) 判断原命题及其逆命题的真假，并说出命题1的逆否命题。

(3)思考1：？同时反过来讲， (4)试使用同样的说法分析命题2中p 与q 的关系。

(5)如果我们将上述真命题中的p 与q 之间的关系推广到一般情况，又该如何描述呢？2 .充分条件与必要条件的定义：一般地，“若p 则q ”为真命题，是指由p 通过推理可以得出q 这时我们就说，由p 可推出q ，记作q p ⇒并且说p 是q 的_____条件,q 是p 的_____条件。

思考2：分析命题3和命题4，我们又会得到怎样的结论？一般地，“若p 则q ”为真命题，是指由p 通过推理可以得出q 这时我们就说，由p 可推出q 记作q p ⇒此时我们就说p 不是q 的_____条件,q 不是p 的_____条件。

结论1：由定义可知，p 是q 的充分条件等同于说q 是p 的必要条件。

充要条件

2015 届高二数学 2---1 导学案 NO 第课题：充要条件第【学习目标】1. 理解充要条件的含义；
编写熊有刚周班课时组评
审核组姓名师评
审批
2. 学会利用充要条件解决相关问题. 【教学重点】充要条件【教学难点】充要条件判断【学习方法】导学案导学法【自主学习·梳理基础】 1、命题“若 p 则 q”为真命题，即 p q ，就说 p 是 q 的条件；q 是 p 的 2、（只能填，，，）（1）若 p：三角形各边都相等，q：三角形各角都相等，则 p q，q p. （2）若 p：x=a，q：|x|=|a|，则 p q，q p. （3）若 p：四边形是矩形，q：四边形是正方形，则 p q，q p. （4）若 p：四边形是矩形，q：四边形是梯形，则 p q，q p. 总结：一般地，如果，且，则称 p 是 q 的充分必要条件，简记为：p 是 q 的充要条件，记作。 ☆☆总结：若 p q ，则 p 与 q 互为。如果如果如果，且，且，且，则称 p 是 q 的充分不必要条件。，则称 p 是 q 的必要不充分条件。，则称 p 是 q 的既不充分也不必要条件。条件
2
条件。
D. 是 tan tan 的充要条件
3.设 p ： b 4ac 0(a 0) ， q ：关于 x 的方程 ax2 bx c 0(a 0) 有实根，则 p 是 q 的（）. A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件 2 4. 2 x 5 x 3 0 的一个必要不充分条件是（）. 1 1 1 A. x 3 B. x 0 C. 3 x D. 1 x 6 2 2 2 5、 “ x M N ”是“ x M N ”的（）. A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件 6、用充分条件、必要条件、充要条件填空. (1). x 3 是 x 5 的 (2). x 3 是 x 2 2 x 3 0 的 (3).两个三角形全等是两个三角形相似的 7、已知 p，q 都是 r 的必要条件，s 是 r 的充分条件，q 是 s 的充分条件，则 s 是 q 的条件， r是q的条件，p 是 s 的条件．

充要条件导学案

高中数学《充要条件》导学案

充要条件

1.5充分条件与必要条件

充要条件(经典导学案)

充要条件

2充要条件学生版

《充要条件》 导学案

【导学案】 第2讲 充分条件、必要条件、充要条件【师】

导学案002(命题及其关系与充要条件)

充分条件与必要条件导学案 高一上学期数学人教A版(2019)必修第一册

高中数学充要条件的教案

《充分条件与必要条件》课件与导学案

《充分条件与必要条件》教案、导学案与同步练习

充要条件教案

导学案充分条件与必要条件

充要条件

《充要条件》导学案

【导学案】第2讲充分条件、必要条件、充要条件【师】

充分条件与必要条件导学案高一上学期数学人教A版(2019)必修第一册