认识直棱柱一

八年级数学认识直棱柱;直棱柱的表面展开图;三视图浙江版知识精讲

初二数学认识直棱柱；直棱柱的表面展开图；三视图某某版【本讲教育信息】一. 教学内容：3.1 认识直棱柱3.2 直棱柱的表面展开图3.3 三视图3.4 由三视图描述几何体二. 重点、难点：重点：1. 直棱柱的表面展开图画法2. 三视图的画法3. 根据三视图描述基本几何体难点：1. 通过空间想象把一个物体的形状看成两个（或多个）几何体的组合2. 画直棱柱的多种表面展开图以及画组合体的三视图有一定的难度3. 根据三视图描述实物原形三. 知识要点及学习目标1. 了解多面体、直棱柱的侧棱、侧面、底面等有关概念，会认直棱柱的侧棱、侧面、底面。

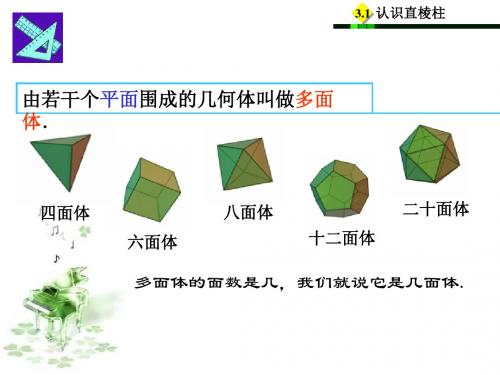
由若干个平面围成的几何体，叫做多面体。

多面体上相邻两个面之间的交线叫做多面体的棱，几个面的公共顶点叫做多面体的顶点。

棱柱是多面体的一种，棱柱分为直棱柱和斜棱柱。

（根据其侧棱与底面是否垂直）根据底面多边形的边数而分为直三棱柱、直四棱柱……长方体和立（正）方体都是直四棱柱。

2. 了解直棱柱以下特征，能根据特征准确说出直棱柱的面、棱的关系。

（1）面的特征：有上、下两个底面，底面是平面图形中彼此全等的多边形；侧面都是长方形（含正方形）。

（2）棱的特征：直棱柱的侧棱互相平行且相等。

3. 了解直棱柱的表面展开图的概念。

会画简单的直棱柱的表面展开图。

如下图，当我们沿着某些棱把一个立方体的盒子剪开，且使其六个面还连在一起，然后铺平，就得到这个立方体的表面展开图。

由于可以从不同的棱剪开，所以一个立方体可以有不同的表面展开图。

反过来，如果我们有了一个几何体的表面展开图，我们也可以把它折叠成原来的几何体。

4. 能根据表面展开图判断出原直棱柱形状。

5. 了解主视图、俯视图、左视图和三视图的概念，能识别简单物体的三视图。

通过从不同方向观察同一物体可以看到不一样的结果得出关于三视图的概念。

主视图是从正面看到的图形，左视图是从左面看到的图形，俯视图是从上面向下看时看到的图形。

一般来说，首先要指定正面。

认识直棱柱 PPT课件 2 浙教版

•
54、最伟大的思想和行动往往需要最微不足道的开始。
•
55、不积小流无以成江海，不积跬步无以至千里。
•
56、远大抱负始于高中，辉煌人生起于今日。
•
57、理想的路总是为有信心的人预备着。
•
58、抱最大的希望，为最大的努力，做最坏的打算。
•
59、世上除了生死，都是小事。从今天开始，每天微笑吧。
•
60、一勤天下无难事，一懒天下皆难事。
•
74、先知三日，富贵十年。付诸行动，你就会得到力量。
•
75、爱的力量大到可以使人忘记一切，却又小到连一粒嫉妒的沙石也不能容纳。
•
Байду номын сангаас
76、好习惯成就一生，坏习惯毁人前程。
•
77、年轻就是这样，有错过有遗憾，最后才会学着珍惜。
•
78、时间不会停下来等你，我们现在过的每一天，都是余生中最年轻的一天。
•
79、在极度失望时，上天总会给你一点希望；在你感到痛苦时，又会让你偶遇一些温暖。在这忽冷忽热中，我们学会了看护自己，学会了坚强。
例2：观察各直棱柱，然后填表：
直三棱柱直四棱柱
面数
直三棱柱
5
直四棱柱
6
直五棱柱
7
直六棱柱
8
直n棱柱
n+2
直五棱柱直六棱柱
棱数 9 12
顶点数 6 8
15
10
18
12
3n
2n
像这样，由若干个平面围成的几何体叫做多面体.
多面体上相邻两个面之间的交线叫做多面体的棱，几个面的公共顶点叫做多面体的顶点.
•
10、评价一个人对你的好坏，有钱的看他愿不愿对你花时间，没钱的愿不愿意为你花钱。

3直棱柱及三视图

年级：八年级课时数：3辅导科目：数学课题直棱柱教学目的1、认识直棱柱，并会判断直棱柱，能找出现实生活中的直棱柱；2、体会立体图形与平面图形的关系，并会表示直棱柱表面展开图的面积计算；3、表表示立体图形的三视图，并由三视图描绘物体的体积。

教学内容3．1 认识直棱柱10．课前思考1.观察家里的电冰箱、大衣柜，它们是什么形状的图形？2.阅读课本3.1节“认识直棱柱”，并回答下列问题：（1）什么样的几何体是直棱柱？（2）直棱柱的侧面是什么图形？二、知识梳理1、了解棱柱、直棱柱的概念，会判断直棱柱；2、能说出一个直棱柱的顶点、棱、面的个数；3、直棱柱的相邻两条侧棱互相平行且相等。

三、重难点分析例1、已知一个直棱柱有11个面，这个直棱柱是直几棱柱？有多少条棱？多少个顶点？表现上至少有多少个直角？例2、(1)长方体可叫做面体，也可叫做棱柱(2)一个直8棱柱的侧面个数是顶点个数是棱的条数是。

(3)一个正方体的每个面上都标有数字1、2、3、4、5、6，根据图中该正方体A、B、C三种状态所显示的数字，可推出“？”处的数字是例3、(1)下列图形中直棱柱的是（）(2)一个直棱柱有12个顶点，则它的棱的条数是（）(A) 12 (B) 6 (C) 18 (D) 20(3)正多面体的面数、棱数、顶点数三在之间存在一个奇特的关系，若用f、e、v分别表示正多面体的面数、棱数、顶点数，则有f+v-e=2，现有一个正多面体共有12条棱，6个顶点，则它的面数f等于（）(A)6 (B) 8 (C) 12 (D) 20四、课堂练习1.如图所示的棱柱中，请补画被遮挡住的棱线。

2.阅读课本阅读材料，画一个长、宽各为2cm，高为3cm的长方体的立体图形。

3、拓展思考:三个正方体木块粘合成如图的模型，它们的棱长分别是1cm，2cm，4cm，要在模型表面涂油漆，如图除去粘合的部分不涂外，求模型的涂漆面积。

4、火眼金睛:四个正方体，每个正方体的面都按相同次序涂黑、白、红、黄、蓝、绿六色，将四个正方体叠在一起，只能看到它们的部分颜色，从这个图你能识别最上面一个正方体的下面、背面涂的颜色吗？3．2 直棱柱的表面展开图一、课前思考1.自做一个长方体，展开之后有哪些不同情况？2. 阅读课本3.2节“直棱柱的表面展开图”，并回答下列问题：（1）如何画直棱柱的表面展开图，它是唯一的吗？（2）根据展开图怎样判断物体的形状？二、知识梳理1.了解直棱柱表面展开图的概念；2.会画简单直棱柱的表面展开图；3.能根据展开图判断和制作立体模型。

八年级数学上册 3.1《认识直棱柱》学案浙教版

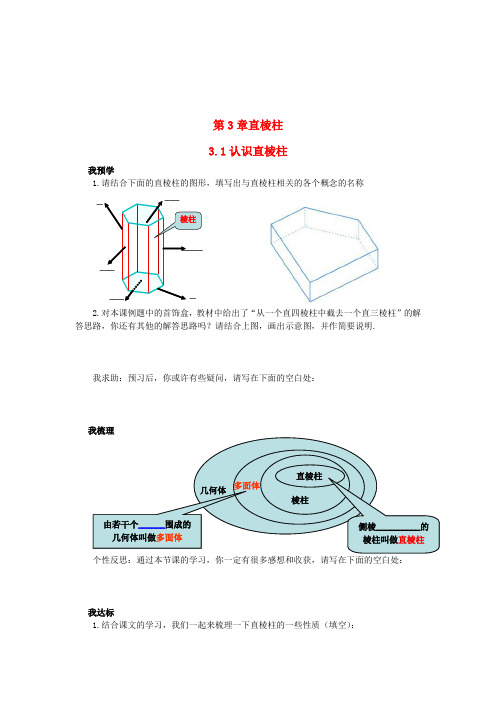
第3章直棱柱 3.1认识直棱柱我预学1.请结合下面的直棱柱的图形，填写出与直棱柱相关的各个概念的名称__2.对本课例题中的首饰盒，教材中给出了“从一个直四棱柱中截去一个直三棱柱”的解答思路，你还有其他的解答思路吗？请结合上图，画出示意图，并作简要说明.我求助：预习后，你或许有些疑问，请写在下面的空白处：我梳理个性反思：通过本节课的学习，你一定有很多感想和收获，请写在下面的空白处：我达标1.结合课文的学习，我们一起来梳理一下直棱柱的一些性质（填空）：（1）直棱柱的上、下两个底面彼此__________. （2）直棱柱的各侧面都是__________（含正方形）. （3）直棱柱的相邻两条侧棱__________ . （4）直棱柱的高______侧棱的长.（5）侧棱的个数和底面的边数_________. 2.下面8个几何体中，是多面体的是______________________________；是直棱柱的是________________ （填写序号）①②③④⑥⑦⑧3.一个直棱柱有12个顶点，那么它是____________；它的棱的条数是________.4.在如图所示的棱柱中，请补画被遮挡住的棱线.我挑战5.十八世纪瑞士数学家欧拉证明了简单多面体中顶点数（V ）、面数（F ）、棱数（E ）之间存在的一个有趣的关系式，被称为欧拉公式.请你观察下列几种简单多面体模型，解答下列问题：（1）根据上面多面体模型，完成表格中的空格：你发现顶点数（V ）、面数（F ）、棱数（E ）之间存在的关系式是_______________. （2）一个多面体的面数比顶点数大8，且有30条棱，则这个多面体的面数是__________. （3）某个玻璃鉓品的外形是简单多面体，它的外表面是由三角形和八边形两种多边形拼接而成，且有24个顶点，每个顶点处都有3条棱，设该多面体外表三角形的个数为x 个，八边形的个数为y 个，求y x 的值.参考答案： 3.1认识直棱柱四面体长方体正八面体正十二面体1.（1）平行且全等.（2）长方形.（3）平行且相等.（4）等于.（5）相等.2.①③④⑤⑥⑦⑧；①⑥⑦⑧.3.直六棱柱；18.4.略5. (1) 6， 6 ,2V F E +-=；(2)20； (3)这个多面体的面数为x y +，棱数为243362⨯=条，根据2V F E+-=可得 24()362x y ++-=，∴14x y +=.。

棱柱与棱锥的认识与分类

棱柱与棱锥的认识与分类棱柱和棱锥是几何图形中的重要概念。

它们是立体几何中常见的形状，具有不同的特征和属性。

本文将对棱柱和棱锥进行认识与分类的介绍，帮助读者更好地理解这两种几何形状。

一、棱柱的认识与分类棱柱是由两个相似的多边形底面和连接这两个底面的矩形侧面组成的立体。

它的特点是侧面是平行于底面的矩形，并且棱柱的顶点到底面的距离都相等。

我们可以根据棱柱底面的形状来对棱柱进行分类。

1. 正棱柱：当底面为正多边形（如正三角形、正方形等）时，棱柱称为正棱柱。

正棱柱的特点是底面的边和侧面的高线垂直，并且侧面也是正多边形。

2. 直棱柱：当底面为任意多边形时，棱柱称为直棱柱。

直棱柱的特点是底面的边和侧面的高线不一定垂直，而是可以偏离垂直方向。

3. 斜棱柱：如果棱柱的侧面倾斜，则称为斜棱柱。

斜棱柱的特点是底面的边和侧面的高线不垂直，而是有倾斜的角度。

二、棱锥的认识与分类棱锥是由一个多边形底面和连接底面每个顶点至一个共同点（顶点）的三角形侧面组成的立体。

棱锥的特点是它只有一个顶点，而其它顶点都在该顶点到底面的连线上。

我们可以根据底面的形状来对棱锥进行分类。

1. 正棱锥：当底面为正多边形时，棱锥称为正棱锥。

正棱锥的特点是底面的边和侧面的斜高线垂直，并且侧面也是正多边形。

2. 直棱锥：当底面为任意多边形时，棱锥称为直棱锥。

直棱锥的特点是底面的边和侧面的斜高线不一定垂直，而是可以偏离垂直方向。

3. 斜棱锥：如果棱锥的侧面倾斜，则称为斜棱锥。

斜棱锥的特点是底面的边和侧面的斜高线不垂直，而是有倾斜的角度。

三、棱柱与棱锥的区别与联系棱柱和棱锥在形状上有一定的类似之处，都是由底面和侧面组成的立体。

但是它们的区别主要体现在以下几个方面：1. 顶点数量：棱柱有两个底面，而棱锥只有一个底面，顶点是唯一的。

2. 侧面形状：棱柱的侧面是矩形，而棱锥的侧面是三角形。

棱柱的侧面可以是正多边形或任意多边形，而棱锥的侧面也可以是正多边形或任意多边形。

汉中市高一数学《直(正)棱柱与正棱锥、平面的基本性质、空间直线》课件

所以B∈平面ASC，与三棱锥S-ABC矛盾，故EF与AS异面.
(2)如图,取AC的中点K,连接EK. 因为E是SC的中点,故EK∥SA, 所以∠KEF(或其补角) 是异面直线EF与SA所成的角. 连接KF,也有KF∥BC. 在△EKF中, EK=KF=1.
又因为SF=CF EF⊥SC,
所以EF2=SF2-SE2=3-1 =1 1 , 44
2
典例精讲
题型一空间两直线的位置关系
例1 下列命题中:
①若直线a与b没有公共点，则a∥b;
②若直线b∥平面α,直线a α,则b∥a; ③若平面α∥β,b β，a α，则b∥a;④若直
线a不在平面α内，则a∥α;
⑤长方体ABCD-A1B1C1D1中,
平面
ABCD与平面A1BC1只有一个公共点B;
③一定存在平面α同时和异面直线a、b都平行.
其中正确的命题为 ( C )
A.① B.② C.③ D.①③
①错, c至多可与a、b中的两条相交; ②错, 因为a、c可能相交也可能平行； ③对, 例如过异面直线a、b的公垂线段的中点
且与公垂线垂直的平面即可满足条件. 故选C.
5.如图, 正方体ABCD-A1B1C1D1中.
则EF= 1 1 ,
2
11
所以cos∠KEF= EK2 EF2 KF2 = 4 = 1 1 ,
所以异面直线EF与2SAE所K成EF角的余弦1 1 值为4 1 1 .
4
点评 (1)判定或证明两条直线为异面直线,
常用反证法.(2)求异面直线所成的角, 一般先通过平移作出相关角（如与中点有关, 大多可通过作中位线平移）, 再放入三角形中, 运用解三角形的相关知识求解.
2.证明若干个点共线的重要方法之一是证明这些点分别是两个平面的公共点, 再由公理３可知它们共线.

八年级上册数学课件：3、1认识直棱柱

2.请说明立方体、长方体、直四棱柱、四棱柱和棱柱的互相关系.
底面是四边形棱柱
立方体
底面是正方形
棱柱
四棱柱
直四棱柱
立方体方体
3.（1）观察直棱柱的模型或画出示意图，（）观察直棱柱的模型或画出示意图，填写下表：填写下表：
面数
直三棱柱升华本节内容，让学生直四棱柱学会观察与直五棱柱总结直六棱柱 5 6 7 8
棱数
9 12 15 18
顶点数
6 8 10 12
……
（2）从上表中，你能发现直棱柱的面数、）从上表中，你能发现直棱柱的面数、棱数和顶点数之间有什么规律吗？棱数和顶点数之间有什么规律吗？
面数+顶点数棱数面数顶点数-棱数顶点数棱数=2
小结与作业
小结作业：作业本
这个首饰盒是直五棱柱，解这个首饰盒是直五棱柱，它可以看做从一个直四棱柱中截去一个直三棱柱得到. 直四棱柱中截去一个直三棱柱得到
可以把该直五棱柱看做是有两个直四棱柱组成吗？有两个直四棱柱组成吗？为什么？为什么？
通过对例题的探究，让学生学会对一般直棱柱的割与补
1.下面图片所示的建筑中，哪些体现了直棱柱下面图片所示的建筑中，下面图片所示的建筑中的立体形状，哪些不是？的立体形状，哪些不是？
3、1认识直棱柱
实验中学丁红艳指导师：吴胜
〖教学目标〗 ◆1、了解多面体、直棱柱的有关概念. ◆2、会认直棱柱的侧棱、侧面、底面． ◆3、了解直棱柱的侧棱互相平行且相等，侧面是长方形（含正方形）等特征．〖自学指导〗仔细阅读课本54页，完成教学目标1和2。课本55页的做一做，并完成教学目标3。课本55页例题，想一想首饰盒还可以看成怎样直棱柱的组合呢？ 8分钟后，我们将检测大家的自学效果。

认识直棱柱 PPT课件人教版

•
67、心中有理想再累也快乐
•
68、发光并非太阳的专利，你也可以发光。
•
69、任何山都可以移动，只要把沙土一卡车一卡车运走即可。
•
70、当你的希望一个个落空，你也要坚定，要沉着！
•
71、生命太过短暂，今天放弃了明天不一定能得到。
•
72、只要路是对的，就不怕路远。
•
73、如果一个人爱你、特别在乎你，有一个表现是他还是有点怕你。
•
30、经验是由痛苦中粹取出来的。
•
31、绳锯木断，水滴石穿。
•
32、肯承认错误则错已改了一半。
•
33、快乐不是因为拥有的多而是计较的少。
•
34、好方法事半功倍，好习惯受益终身。
•
35、生命可以不轰轰烈烈，但应掷地有声。
•
36、每临大事，心必静心，静则神明，豁然冰释。
•
37、别人认识你是你的面容和躯体，人们定义你是你的头脑和心灵。
3.1 认识直棱柱
你能从下面所给的三视图中推断出它们分别表示什么几何体吗?
(1)
(2)
(3)
(4)
3.1 认识直棱柱
1.某两个物体的三视图如图所示.请分别说出它们的形状.
2.由几个相同的小立方块搭成的几何体的俯视图如图所 1 3
示.方格中的数字表示该位置
2
的小方块的个数.请画出这个
几何体的三视图.
•
44、仁慈是一种聋子能听到、哑巴能了解的语言。
•
45、不可能！只存在于蠢人的字典里。
•
46、在浩瀚的宇宙里，每天都只是一瞬，活在今天，忘掉昨天。
•
47、小事成就大事，细节成就完美。
•

3.1 认识直棱柱

太遗憾了，下次我要仔细仔细再仔细，再不能吃错喽！
顶点数
直n棱柱
面数
棱数
侧棱数
2n
n+2
3n
n
如果一个直棱柱有24个顶点，那么它是直
12 棱柱，共有 36 条棱， 14 个面。
反之，若有直棱柱的面数为11，那么它又是直
9 棱柱，让我们把课时暂时进行到这里吧！共有 27 条棱， 18 个顶点。同学们再见！
五
2.6
单位：cm 3 3
6
6
请你推断被小狗吞下部分的玩具泥又是怎样的一个多面体？指出剩余部分与直四棱柱有什么关系？
单位:cm
3
3
2.6 6
6
答：该多面体是直三棱柱，其底面是一个腰长为3cm的等腰直角三角形，它们的侧棱长都为2.6cm. 剩余部分可以看做从一个底面是边长为 6cm的直四棱柱截去以上的直三棱柱得到的.
爱学数学爱数学周报
再见
七面体八面体
五面体
讨论与作
第一组仔细观察，你能发现第二组几何第二组与第一组的不同点：直棱柱的基本特征：体与第一组几何体有什么不同吗？ ⒈都有上下两个底面，底面是平面第二组图形中的多边形，且彼此全等； ⒉侧面都是长方形（含正方形）.
①
②
③
④
⑤
⑥
直棱柱的基本特征：
⒈都有上下两个底面，底面是平面图形中的多边形，且彼此全等；
。
轻松一下，也不知道被咬讲一个小狗的故后来发现这一只贪吃的顽皮也不知道它这成怎么样了，事！！么鬼鬼祟祟去狗把面前的长方体形状的玩让我们去看看！有一只贪吃的干什么？？具泥误以为是面包，一口把小狗，饿的实玩具泥咬掉了一块吞下肚子！在不行了！！

3.1认识真棱柱

正方形
正八面体正十二面体正五边形正二十面体正三角形
6
6 30 12 2
例2 画棱长为4cm的立方体的立体图形
本节课你的收获是什么？
本节课你的收获是什么？
1.作业本3.1
2.课后作业题（1、4、5选做） 3.同步3.1（探究题选做）
侧面
4. 所有侧棱长都相等.
侧棱的个数和底面的边数相等.
底面
如果是特殊的棱柱呢？
长方体
长方体：
有没有补充的？
1、两个底面都是矩形
2、相对的面相同
如果是正方体呢？正方体： 1、六个面都是相同的正方形； 2、12条棱都相等。
请说明立方体、长方体、直四棱柱、四棱柱、和棱柱的相互关系。
顶点、棱、侧棱、侧面
你发现规律了吗？？侧棱（条）侧面（个）面（个）顶点（个）棱（条）
三棱柱四棱柱五棱柱
3
3
4
5 6
6 8 10
9
4
5
12
155 6n源自78 n+2
的数量关系
六棱柱
6
n棱柱
12 2n
18 3n
n
活动研究
名称正四面体各面形状面数f 棱数v 顶数e f+v-e 正三角形 4
看一看
直棱柱的相邻两条侧棱之间有什么关系？
直三棱柱
直四棱柱
直五棱柱
直六棱柱
直棱柱的相邻两条侧棱互相平行且相等
例1 观察如图所示的首饰盒，它是一个怎样的多面体？这个多面体与直四棱柱有什么关系？
单位：cm
3
3 2.6 6 6

《认识直棱柱》测试题

《认识直棱柱》测试题◆教材链接（一）新课标要求1、了解多面体、直棱柱的有关概念；会认直棱柱的侧棱、侧面、底面；了解直棱柱的侧棱互相平行且相等，侧面是长方形（含正方形）等特征。

2、经历观察、类比的学习过程，感知直棱柱的特征．3、让学生经历探索的过程，培养学生的创新精神；会分辨现实生活中的物体的立体形状。

（二）考点要点知识点1：了解直棱柱的有关概念．棱柱是特殊的多面体，分为直棱柱和斜棱柱；长方体和正方体都是直四棱柱；直棱柱的相邻两条侧棱互相平行且相等．（基础演练1-5）知识点2：能知道直几棱柱的面数、顶点数、棱数；能根据直棱柱的顶点数或面数、棱数得到是直几棱柱．直n棱柱，有两个底面，n个侧面，有3n条棱，有n条侧棱，共有2n个顶点．（基础演练6-8）（三）重点难点重点：直棱柱的有关概念；难点：本节的例题．例1 如图，下面这些几何体，哪些是多面体？哪些是直棱柱？如果是直棱柱，则是直几棱柱？分析：多面体是由若干个平面围成的几何体，而④的侧面不是平面；而判断一个直棱柱是几直棱柱，只需根据直棱柱的底面边数来确定即可．解：①②③⑤⑥⑦是多面体，①③⑤是直棱柱，①是直三棱柱，③⑤是直四棱柱。

例2如图的直棱柱是直几棱住？有多少条棱？多少条侧棱？多少个面？多少个顶点？底面是什么图形？解：直五棱柱，有15条棱，5条测棱，7个面，10个顶点，底面是五边形．例3一个底面是正方形的直四棱柱如图，求它的侧面积、表面积和体积。

分析：此直四棱柱即大家熟悉的长方体，高即侧棱。

根据面积公式：面积=长×宽，体积公式：底面积×高就可以求得。

解：侧面积=5×10=50 cm2；表面积=2×（5×5+5×10+5×10）=250 cm2；体积=5×5×10=250 cm3.◆三维训练一、基础演练:1．说出下列直棱柱的名称．2．至少举出两个现实生活中体现直棱柱形状的物体：．3．直棱柱侧面都是，侧棱长都和相等．4．一个帐篷形状如图，它可以看作是怎样的棱柱？它的侧面和底面分别是什么图形？5．用自己的语言说说下面每组中两个图形的相同点和不同点．（1）（2）6．如图，这个几何体的名称是，它有个面组成；有个顶点；经过每个顶点有条棱．7．直四棱柱有个顶点，个面，条棱。

认识直棱柱课件

为什么直棱柱在数学和现实生活中都很重要
直棱柱的计算公式
侧棱长的计算
如何计算直棱柱的侧棱长
面积的计算公式
如何计算直棱柱的表面积
体积的计算公式
如何计算直棱柱的体积
直棱柱的应用
实际生活中的应用
直棱柱在日常生活中的实际应用场景
工程建设中的应用
直棱柱在工程建设中的重要角色
总结
1 直棱柱与其他几何体的区别
直棱柱与其他几何体相比的不同之处
2 直棱柱的重要性和应用价值
认识直棱柱ppt课件
直棱柱是一个有趣且重要的几何体。让我们一起来探索直棱柱的定义、特征、计算公式、应用和其它几何体的区别。
认识直棱柱
简介
直棱柱的定义
特征
直棱柱的几何特征
常见直棱柱
Hale Waihona Puke 正方形棱柱具有正方形底面的直棱柱
长方形棱柱
具有长方形底面的直棱柱
正三角形棱柱
具有正三角形底面的直棱柱
六边形棱柱
具有六边形底面的直棱柱

一二年级数学教案：认识棱柱的母线和侧面积

计算棱柱的侧面积求解棱柱的体积棱柱在几何证明中的应用棱柱在建筑和工程领域的应用
棱柱是几何学中的基本图形之一，具有广泛的应用。
棱柱的侧面积是几何学中计算表面积的重要方法之一，对于研究几何图形的表面积和体积具有重要意义。

添加标题
添加标题
添加标题
添加标题
棱柱的母线是几何学中的重要概念，对于研究几何图形的性质和计算具有重要意义。
棱柱在几何学中具有重要的地位和作用，对于几何学的发展和应用具有重要意义。
侧面积的计算公式是底面周长乘以高
侧面积的大小与底面和顶面的形状、大小以及高有关
侧面积的特性是可计算性，可以通过公式计算出其大小
建筑模型：棱柱在建筑设计中的应用，如金字塔、罗马斗兽场等
笔筒：棱柱形状的笔筒，方便整理和分类文具
纸巾盒：棱柱形状的纸巾盒，方便抽取纸巾且不易倒塌
电池：圆柱形电池，棱柱的一种变体，广泛应用于各种电子产品中
母线的长度等于棱柱的高
母线是棱柱的高
母线的长度等于底面多边形的边心距
母线与底面垂直
母线与底面多边形的每一边都相交
棱柱的侧面积是由底面和顶面的周长与高的乘积得到
侧面积的计算公式为：侧面积 = (底面周长 × 高) + (顶面周长 × 高)
侧面积是棱柱的一个重要几何量，在计算棱柱的表面积、体积等性质时需要用到
侧面积的计算方法对于棱柱的几何性质研究具有重要意义
定义：棱柱的侧面积是指底面周长与高的乘积
计算公式：侧面积 = 底面周长 × 高
注意事项：底面周长是指棱柱底面的外边界长度，高是指棱柱的高应用：在实际生活中，棱柱的侧面积可用于计算包装盒的表面积、建筑物的外墙面积等

认识直棱柱ppt1 浙教版

•
76、好习惯成就一生，坏习惯毁人前程。
•
77、年轻就是这样，有错过有遗憾，最后才会学着珍惜。
•
78、时间不会停下来等你，我们现在过的每一天，都是余生中最年轻的一天。
•
79、在极度失望时，上天总会给你一点希望；在你感到痛苦时，又会让你偶遇一些温暖。在这忽冷忽热中，我们学会了看护自己，学会了坚强。
•
80、乐观者在灾祸中看到机会；悲观者在机会中看到灾祸。
棱柱的分类
1. 侧棱不垂直于底的棱柱叫做斜棱柱． 2.侧棱垂直于底的棱柱叫做直棱柱．
直棱柱
底面
侧棱
侧面
高
直五棱柱
直四棱柱
直四棱柱
直棱柱的上下底面可以是三角形、四边形、
五边形……侧面都是长方形（含正方形），根据底面的边数，我们就说直三棱柱、直四棱柱、直五棱柱……
三棱镜的视频
三棱镜
棱镜的色散
侧棱与底面垂直
四棱柱
直四棱柱
立方体
棱长都相等
底面是正方形长方体
巩固练习
棱柱
四棱柱直四棱柱
立方体长方体
巩固练习 3.（1）观察直棱柱的模型或画出示意图，
填写下表：
面数棱数顶点数
直三棱柱
5
直四棱柱
6
直五棱柱
7
直六棱柱
8
……
9
6
12
8
15
10
18
12
（棱2数）面和从顶数上点+表数顶中之点，间你数有能什-发么棱现规数直律棱=吗2柱？的面数、
19、就算生活让你再蛋疼，也要笑着学会忍。
•
20、当你能飞的时候就不要放弃飞。
•

[资料]3.1认识直棱柱教学设计—郑丹凤

浙教版义务教育课程标准实验教科书《数学》八年级上册3.1 认识直棱柱温州市鹿城区藤桥中学郑丹凤●教材分析本节课选用的是浙江教育出版社出版的，义务教育课程标准实验教科书《数学》八年级上册第三章第一节的内容。

本节课的教学内容是学生在小学学习了长方体、正方体的概念，了解了长方体、正方体顶点、棱、面等知识的基础上进一步拓展和加深。

同时本节课的知识也为学生学习本章的后续内容作铺垫，具有承上启下的重要作用。

本节课的设计意图是使学生学生根据已有的生活背景和初步的数学活动经验，从观察生活中的物体开始，逐步形成对空间与图形的认识，培养学生的空间想象能力，促进观察、分析、归纳、概括等一般能力的发展。

●教学目标一、知识与技能目标：⑴了解多面体、棱柱、直棱柱的概念。

⑵了解直棱柱的侧棱、侧面、底面。

⑶掌握直棱柱的性质特征。

二、过程与方法目标：⑴由实物的形状想像出几何图形，由几何图形想像出实物的形状，发展学生的空间观念。

⑵通过观察几何体，概括出几何体的共同特征，培养学生观察、分析、推理、归纳、概括的能力。

三、情感态度与价值观目标：从生活中抽象出数学知识，并加以研究，再应用到现实生活中；让学生认识到数学的应用价值，激发学习兴趣。

●教学重点和难点本节课的教学重点是直棱柱的有关概念。

本节课的难点是学生对于直棱柱性质的发现以及应用。

●学情分析①学生对几何体有一定的了解，但十分肤浅，对于空间想象能力差的学生有一定的难度。

②学生已初步具备观察发现的能力。

③在农村中学，学生的归纳总结的能力比较薄弱。

●教学手段利用教具、多媒体辅助教学，引导学生观察、发现、归纳、探索，激发学生的学习兴趣，激活学生的思维，以利于突破教学重点和难点，提高课堂教学效益。

●教学过程教学流程图：幻灯片出示图片。

请学生观察图片，指出图片中的物体类似于哪些几何体并且上下两行物体的几何形状有何区别？学生活动：由学生通过观察，独立思考，再举手发言。

教师活动：教师面向学生，对发言学生的回答进行评定。

认识直棱柱课件3

底面是正方形长方体
棱柱
四棱柱直四棱柱
立方体长方体
面数棱数顶点数
直三棱柱Biblioteka 5直四棱柱6
直五棱柱
7
直六棱柱
8
……
9
6
12
8
15
10
18
12
（2）从上表中，你能发现直棱柱的面数、棱数和顶点数之间有什么规律吗？
面数+顶点数-棱数=2
2.请说明立方体、长方体、直四棱柱、四棱柱和棱柱的互相关系.
底面是四边形棱柱
侧棱与底面垂直
四棱柱
直四棱柱
立方体
棱长都相等
（3）直棱柱的相邻两条侧棱的长度和位置之间有什么关系？
直六棱柱有多少条棱?多少条侧棱? 多少个侧面?多少个顶点?
直六棱柱
例：观察下图所示的首饰盒，它是一个怎样的多面体？这个多面体与直四棱柱有什么关系？
3 3 2.6
6 6
想一想:可以把该直五棱柱看做是有两个直四棱柱组成吗？
3.（1）观察直棱柱的模型或画出示意图，填写下表：
这是我们熟悉的立体图形，它们是有几个平面围成的? 都有什么相同特点?
像这样，由若干个平面围成的几何体叫做多面体.
多面体上相邻两个面之间的交线叫做多面体的棱，几个面的公共顶点叫做多面体的顶点.
顶点棱
这些多面体可以分类吗.
认识棱柱侧面
底面
侧棱
请同学们仔细观察第一个棱柱和后面的三个棱柱有区别吗?
1. 侧棱不垂直于底的棱柱叫做斜棱柱． 2.侧棱垂直于底的棱柱叫做直棱柱．
探索研究:直棱柱的特征
（1）直棱柱的上、下底面一样吗？ (2)直棱柱侧面的形状是什么图形？（3）直棱柱的相邻两条侧棱的长度和位置之间有什么关系？

棱柱的结构特征-高中数学知识点讲解

棱柱的结构特征
1．棱柱的结构特征
【知识点的认识】
1．棱柱：有两个面互相平行，其余各面都是四边形，并且每相邻两个四边形的公共边都互相平行，由这些面所围成的多面体叫做棱柱．棱柱用表示底面各顶点的字母来表示（例：ABCD﹣A′B′C′D′）．
2．认识棱柱
底面：棱柱中两个互相平行的面，叫做棱柱的底面．
侧面：棱柱中除两个底面以外的其余各个面都叫做棱柱的侧面．
侧棱：棱柱中两个侧面的公共边叫做棱柱的侧棱．
顶点：棱柱的侧面与底面的公共顶点．
高：棱中两个底面之间的距离．
3．棱柱的结构特征
1．两个底面互相平行
棱柱{
2．侧面都是四边形
3．侧棱互相平行
根据棱柱的结构特征，可知棱柱有以下性质：
（1）侧面都是平行四边形
（2）两底面是全等多边形
（3）平行于底面的截面和底面全等；对角面是平行四边形
（4）长方体一条对角线长的平方等于一个顶点上三条棱的长的平方和．
4．棱柱的分类
（1）根据底面形状的不同，可把底面为三角形、四边形、五边形…的棱柱称为三棱柱、四棱柱、五棱柱…．
（2）根据侧棱是否垂直底面，可把棱柱分为直棱柱和斜棱柱；其中在直棱柱中，若底面为正多边形，则称其为正棱柱．
1/ 2
5．棱柱的体积公式
设棱柱的底面积为S，高为h，
V 棱柱＝S×h．
2/ 2。

棱柱的认识说课稿

棱柱的认识说课稿一、说教学目标通过本课的研究，学生应能够：- 了解棱柱的定义、特点和分类；- 理解棱柱的性质和测量方法；- 掌握棱柱的表面积和体积计算方法；- 运用所学知识解决实际问题。

二、说教学重点和难点本课的教学重点是学生对棱柱的定义、特点和分类的理解。

教学难点是运用所学知识解决实际问题。

三、说教学内容和教学步骤本节课的教学内容如下：1. 棱柱的定义和特点讲解棱柱的定义和特点，引导学生认识到棱柱是一种多边形的立体图形，具有底面、顶面和侧面。

强调棱柱的底面和顶面是相似的多边形。

2. 棱柱的分类介绍不同类型的棱柱，如正棱柱、直棱柱和斜棱柱。

通过示例，让学生能够区分不同类型的棱柱。

3. 棱柱的性质探讨棱柱的性质，如底面和顶面积相等、侧面全部平行、侧面的边长相等等。

4. 棱柱的测量方法教授测量棱柱的方法，包括测量底面和顶面的面积、测量侧面的高度和边长等。

5. 棱柱的表面积和体积计算方法引导学生掌握棱柱的表面积和体积计算方法。

通过例题演示，让学生能够熟练计算棱柱的表面积和体积。

6. 运用所学知识解决实际问题通过实际问题的练，让学生运用所学知识解决实际问题，提高他们的应用能力和解决问题的能力。

四、说教学方法和手段本课将采用以下教学方法和手段：- 讲授法：通过教师讲解，向学生传授棱柱的知识和技巧。

- 实例法：通过示例讲解，帮助学生理解和掌握棱柱的定义、特点和分类。

- 讨论法：通过学生参与讨论，激发学生的思维，提高他们的理解能力和应用能力。

- 练法：通过大量练，巩固学生所学知识，提高他们的计算和解决问题的能力。

五、说教学评价本课的教学评价将采用以下方法：- 日常观察：观察学生的研究兴趣、参与度和表现情况。

- 课堂练：布置适量的课堂练，检查学生对所学知识的掌握程度。

- 作业评定：评定学生课后作业的完成情况和正确率。

- 小测试：进行适时的小测试，检验学生对所学知识的掌握情况。

六、说教学资源本课的教学资源包括教科书、黑板、多媒体设备和示例图等。