数学分析(I)期末考试A卷

合集下载

数学分析试卷及答案6套

一. (8分)用数列极限的N ε-定义证明1n =.二. (8分)设有复合函数[()]f g x , 满足: (1) lim ()x ag x b →=;(2) 0()x U a ∀∈,有0()()g x U b ∈ (3) lim ()u bf u A →=用εδ-定义证明, lim [()]x af g x A →=.三. (10分)证明数列{}n x :cos1cos 2cos 1223(1)n nx n n =+++⋅⋅⋅+收敛.四. (12分)证明函数1()f x x=在[,1]a (01)a <<一致连续,在(0,1]不一致连续. 五. (12分)叙述闭区间套定理并以此证明闭区间上连续函数必有界. 六. (10分)证明任一齐次多项式至少存在一个实数零点.七. (12分)确定,a b 使lim )0x ax b →+∞-=.八. (14分)求函数32()2912f x x x x =-+在15[,]42-的最大值与最小值.九. (14分)设函数()f x 在[,]a b 二阶可导, ()()0f a f b ''==.证明存在(,)a b ξ∈,使24()()()()f f b f a b a ζ''≥--.一. (10分)设数列{}n a 满足: 1a =, 1()n a n N +=∈, 其中a 是一给定的正常数, 证明{}n a 收敛,并求其极限.二. (10分)设0lim ()0x x f x b →=≠, 用εδ-定义证明011lim()x x f x b→=. 三. (10分)设0n a >,且1lim1nn n a l a →∞+=>, 证明lim 0n n a →∞=.四. (10分)证明函数()f x 在开区间(,)a b 一致连续⇔()f x 在(,)a b 连续,且lim ()x a f x +→,lim ()x bf x -→存在有限. 五. (12分)叙述确界定理并以此证明闭区间连续函数的零点定理.六. (12分)证明:若函数在连续,且()0f a ≠,而函数2[()]f x 在a 可导,则函数()f x 在a 可导.七. (12分)求函数()1f x x x ααα=-+-在的最大值,其中01α<<.八. (12分)设f 在上是凸函数,且在(,)a b 可微,则对任意1x ,2x (,)a b ∈, 12x x <,都有12()()f x f x ''≤.九. (12分)设(),0()0,0g x x f x x x ⎧ ≠⎪=⎨⎪ =⎩ 且(0)(0)0g g '==, (0)3g ''=, 求(0)f '.一.(各5分,共20分)求下列不定积分与定积分: 1. arctan x x dx ⎰2. x e dx -⎰3.ln 0⎰4.20sin 1cos x xdx xπ+⎰二.(10分)设()f x 是上的非负连续函数, ()0baf x dx =⎰.证明()0f x = ([,])x a b ∈.三. (10分)证明20sin 0xdx xπ>⎰. 四. (15分)证明函数级数0(1)n n x x ∞=-∑在不一致收敛, 在[0,]δ(其中)一致收敛.五. (10分)将函数,0(),0x x f x x x ππππ+ ≤≤⎧=⎨- <≤⎩展成傅立叶级数.六. (10分)设22220(,)0,0xy x y f x y x y ⎧ +≠⎪=⎨⎪ +=⎩证明: (1) (0,0)x f ', (0,0)y f '存在; (2) (,)x f x y ',(,)y f x y '在(0,0)不连续;(3) (,)f x y 在(0,0)可微.七. (10分)用钢板制造容积为V 的无盖长方形水箱,怎样选择水箱的长、宽、高才最省钢板?八. (15分)设01σ<<, 证明111(1)n n n σσ∞=<+∑.一. (各5分,共20分)求下列不定积分与定积分:1.(0)a >2.1172815714x x dx x x++⎰3.1arcsin x dx ⎰4. 1000π⎰二. (各5分,共10分)求下列数列与函数极限:1. 221lim nn k nn k →∞=+∑2. 20lim1xt xx xe dt e →-⎰三.(10分)设函数在[,]a b 连续,对任意[,]a b 上的连续函数()g x , ()()0g a g b ==,有()()0baf xg x dx =⎰.证明()0f x = ([,])x a b ∈.四. (15分)定义[0,1]上的函数列2212,211()22211n n x x n f x n n x x n n x n ⎧ , 0≤≤⎪⎪⎪=- , <≤⎨⎪⎪0 , <≤⎪⎩证明{()}n f x 在[0,1]不一致收敛.五. (10分)求幂级数0(1)n n n x ∞=+∑的和函数.六. (10分)用εδ-定义证明2(,)(2,1)lim (43)19x y x y →+=.七. (12分)求函数22(2)(2)(0)u ax x by y ab =-- ≠的极值.八. (13分)设正项级数1n n a ∞=∑收敛,且1()n n a a n N ++≥ ∈.证明lim 0n n na →∞=.一 (10分) 证明方程11(, )0F x zy y zx --++=所确定的隐函数(, )z z x y =满足方程.z z xy z xy x y∂∂+=-∂∂ 二 (10分) 设n 个正数12, , , n x x x 之和是a ，求函数 n u x =的最大值.三 (14分) 设无穷积分() af x dx +∞⎰收敛，函数()f x 在[, )a +∞单调，证明1()() ().f x o x x=→+∞四 (10分) 求函数1220() ln() F y x y dx =+⎰的导数(0).y >五 (14分) 计算0sin sin (0, ).pxbx axI e dx p b a x+∞--=>>⎰六 (10分) 求半径为a 的球面的面积S . 七 (10分) 求六个平面111111122222223333333 ,, = 0 , , a x b y c z h a b c a x b y c z h a b c a x b y c z h a b c ++=±⎧⎪++=±∆≠⎨⎪++=±⎩ 所围的平行六面体V 的体积I ，其中, , , i i i i a b c h 都是常数，且0 (1, 2, 3).i h i >= 八 (12分) 求22Cxdy ydxx y-+⎰，其中C 是光滑的不通过原点的正向闭曲线. 九 (10分) 求dS z∑⎰⎰，其中∑是球面2222x y z a ++=被平面 (0)z h h a =<<所截的顶部.数学分析-3样题(二)一 (10分) 求曲面2233, , x u v y u v z u v =+=+=+在点(0, 2)对应曲面上的点的切平面与法线方程.二 (10分) 求在两个曲面2221x xy y z -+-=与221x y +=交线上到原点最近的点. 三 (14分) 设函数()f x 在[1, )+∞单调减少，且lim ()0x f x →+∞=，证明无穷积分1() f x dx +∞⎰与级数1001()n f n =∑同时收敛或同时发散.四 (12分) 证明ln (0).ax bx e e bdx a b x a--+∞-=<<⎰五 (12分) 设函数()f x 在[, ]a A 连续，证明 [, ]x a A ∀∈，有01lim [()()] ()().xa h f t h f t dt f x f a h→+-=-⎰六 (10分) 求椭圆区域221112221221: ()() 1 (0)R a x b y c a x b y c a b a b +++++≤-≠的面积A .七 (10分) 设222()() VF t f x y z dx dy dz =++⎰⎰⎰，其中2222: (0)V x y z t t ++≤≥，f 是连续函数，求'()F t .八 (10分) 应用曲线积分求(2sin )(cos )x y dx x y dy ++的原函数.九 (12分) 计算 Sxyz dx dy ⎰⎰，其中S 是球面2221x y z ++=在0, 0x y ≥≥部分并取球面外侧.。

2012-2013年华南理工大学期末考试《工科数学分析》下试卷(A)(1)

,考试作弊将带来严重后果！华南理工大学期末考试《工科数学分析》2012—2013第二学期期末考试试卷（A ）1. 考前请将密封线内填写清楚；所有答案请直接答在试卷上(或答题纸上)；．考试形式：闭卷；本试卷共 5个大题，满分100分，考试时间120分钟。

一、单项选择题（每小题3分，共15分）1．下述函数中有可能成为二阶微分方程(,,'')0f x y y =的通解的是（）A ．120C x C y +=；B ．212e x yC C -=+；C ． 312eC xC y C =；D ．123ln y C x C x C =++．2．设(,)f x y 是可微函数，且(0,0)0,(0,0),(0,0)x y f f a f b ===，令()(,(,)t f t f t t ϕ=，则'(0)ϕ=（）A ．a ；B ．()a b a b ++；C ．1a +；D ．1ab-． 3．10d (,)d yy f x y x -⎰⎰交换积分顺序后，正确的结果是（）A ．0111101d (,)d d (,)d x x f x y y x f x y y --+⎰⎰⎰⎰； B ．1101d (,)d x f x y y ⎰⎰； C ．011d (,)d xx f x y y --⎰⎰； D ．111d (,)d xx f x y y -⎰⎰．4．设C 是右半圆周222,0,0x y a x a +=≥>，则曲线积分()d Cx y s +=⎰（）A ．0；B ．22a ； C ．2a ； D ．4a ． 5. 设2()(01)f x x x =≤<，而1()s i n π()nn S x bn x x ∞==-∞<<+∞∑，其中102()sin πd (1,2,)n b f x n x x n ==⋅⋅⋅⎰，则1()2S -=（）A ．12-；B ．14-；C ．14；D ．12．二、填空题（每小题3分，共15分）１. 微分方程2'''0yy y -=的通解为；２. 设(1)arcsinx u x y y =+-，则(1,2)ux ∂=∂ ；３. 设区域:0,0πD y x x ≤≤≤≤，则二重积分d Dx y = ；４. 已知曲线C 为22x y ax +=，则曲线积分s =⎰；５. 幂级数1(2)4nnn x n ∞=-∑的收敛域为．三、计算题（每小题10分，共50分）１. 计算三重积分222()d I x y z V Ω=++⎰⎰⎰，其中Ω：2222x y z z ++≤．2.设∑是锥面z =被平面0z =及1z =所截部分的外侧，计算第二类曲面积分2d d d d (2)d d I x y z y z x z z x y ∑=++-⎰⎰．3.求幂级数0(21)nn n x ∞=+∑的和函数，并据此求数项级数0212nn n ∞=+∑的值．4. 求,a b 的值，使得包含圆周22(1)1x y -+=在其内部的椭圆22221(0,0,)x y a b a b a b +=>>≠有最小的面积．5. 求微分方程''2e x y y x -=的通解．四、证明题（本题10分）证明数项级数1sin(n ∞=∑条件收敛．五、应用题（本题10分）设某山峰可由曲面2252z x y =--表示。

华东师范大学数学分析期末试卷

华东师范大学数分期末试卷（A 卷）2009-2010年第一学期一．（20分）判断下列结论是否成立（若成立，说明理由；若不成立，举出反例）1．设()f x 在（a,b ）连续，()f x 在0(,)x a b ∈取极值，则0'()0f x =；2．设()f x 在点0x 可导，则存在0δ>，使得()f x 在00(,)x x δδ-+上连续；3．设数列{}n a ，{}n b 满足1(1,2,)n n a b n ≤≤=…，lim()0n n n b a →∞-=，则极限lim ,lim n n n n a b →∞→∞ 都存在；4．设()f x 是区间（-a,a ）上的可导偶函数，则()f x 在x=0取极值。

二．（16分）计算下列极限；1．20arctan limtan x x x x x→-； 2．20ln(1)sin lim x x x x →+-；三．（16分）计算下列函数的导函数dy dx： 1．1,0,()1,0;x x e x y x e x -⎧≥⎪=⎨⎪+<⎩ 2．()y y x =由极坐标方程2(1cos )(0)a a ρθ=+>所确定。

四．（14分）讨论2x y x e -=的单调性区间，凹凸性区间，极值与拐点。

五．（14分）证明不等式：1．2arctan (0,);12, x x x x π+<∈+∞+ 2．过研究ln ()x f x x =的单调性，证明：e e ππ>. 六．（8分）设()f x 在区间I 上连续但不一致连续，()g x 在(,)-∞+∞上可导且'()0g x k ≥>.证明：复合函数(())g f x 在I 上不一致连续。

七．（12分）设()f x ，()g x 在[,)a +∞上连续可微，且极限()lim ()x f f x →+∞+∞=，()lim ()x g g x →+∞+∞= 存在，证明：1．若()()f a f =+∞，则：(,)a ξ∃∈+∞，使得'()0f ξ=；2．若对[,),'()0,x a g x ∈+∞≠则：(,)a ξ∃∈+∞，使得'()()()'()()()f f f ag g g a ξξ+∞-=+∞- 八．（附加题10分）设()f x 在[,)a +∞上二阶可导且''()1f x ≤，又极限lim ()x f x A →+∞=存在。

2019-2020第一学期数学分析期末考试试题

2019-2020本科数学系期末考试试题数学分析（一）（A 卷）本试卷共4道大题，满分100分．一、选择题（本大题10分，每小题2分）1. 设数列{}n x 单调增，{}n y 单调减，且0lim =−∞→n n n x y ，则（ A ）（A ）{}n x 、{}n y 均收敛（B ）{}n x 收敛，{}n y 发散（C ）{}n x 发散，{}n y 收敛（D ）{}n x 、{}n y 均发散2. 设函数)(1)(3x x x f ϕ−=，其中)(x ϕ在1=x 处连续，则0)1(=ϕ是)(x f 在1=x 处可导的( A )（A ）充分必要条件（B ）必要但非充分条件（C ）充分但非必要条件（D ）既非充分也非必要条件 3. 设0()0f x '=是)(x f 在0x 取得极值的（ D ）（A ）充分条件；（B ）必要条件；（C ）充要条件；（D ）既非充分条件也非必要条件.4. 设()353−=x y ，下述结论正确的是（ A ）（A ）()0,3是曲线)(x f y =的拐点；（B ）3=x 是)(x f 的极值点；（C ）因为)3(f ''不存在，所以()0,3不是曲线)(x f y =的拐点；（D ）当3<x 时，曲线)(x f y =为凹的，当3>x 时，曲线)(x f y =为凸的.5. 设xe e xf xx1arctan 11)(11+−=，则0=x 是)(x f 的（ C ）（A ）连续点（B ）第一类（非可去）间断点（C ）可去间断点（D ）第二类间断点6. 设)(x f y =且21)(0='x f ，则当0>∆x 时，在0x 处dy 是（ B ） (A) 与x ∆等价的无穷 (B) 与x ∆同阶但不等价的无穷小； (C) 比x ∆高阶的无穷 (D) 比x ∆低阶的无穷小二、填空题（本大题10分，每小题2分）1. 若)(0x f '存在，则=−−→000)()(limx x x f x x xf x x 000()()f x x f x '−．2. 曲线21xy xe =的渐近线方程是 0x =．3. 设⎪⎩⎪⎨⎧==te y t e x ttcos 2sin ，则曲线上点(0,1)M 处的法线方程是12=+y x ．4. 设x x x f 2sin )(2=，则)2()20(πf = 19202π⋅ ．三、计算题（本大题35分，每小题5分）1.（5分）求极限20sin )1()cos 1(limx e x x x x −−→答案与评阅要点：由于 0→x 时，2~cos 12x x − ，22~sin x x ，x e x ~1−所以 21)(2lim sin )1()cos 1(lim 22020−=⋅−⋅=−−→→x x x x x e x x x x x2.（5分）求极限()tan 2lim sin xx x π→；答案与评阅要点：令()tan sin xy x =,ln tan ln sin y x x =.22221cos ln sin sin lim ln lim lim cot csc x x x xx x y x x πππ→→→⋅==−2lim sin cos 0x x x π→=−⋅=，所以原式=01e =. 3.（5分）求极限30sin (1)lim x x e x x x x→−+ 答案与评阅要点：2331()2!3!xx x e x o x =++++，33sin ()3!x x x o x =−+3333001()sin (1)16lim lim 6xx x x o x e x x x x x →→+−+== 4.（5分）计算不定积分33tan sec x xdx ⎰答案与评阅要点：⎰xdx x 33sec tan ⎰=x xd x sec sec tan 22⎰−=x xd x sec sec )1(sec 22.sec 31sec 5135C x x +−=5.（5分）计算不定积分⎰+−dx xx xx 5cos sin sin cos答案与评阅要点：⎰+−dx xx xx 5cos sin sin cos ⎰++=5cos sin )cos (sin x x x x d .)cos (sin 4554C x x ++=6.（5分）计算不定积分⎰−dxxx 224答案与评阅要点：设2sin ()22x t t ππ=−<<，则2cos .dx tdt =⎰−dx xx 224⎰=tdt t tcos 2cos 2sin 42dt t ⎰−=)2cos 1(2C t t +−=2sin 2 .4212arcsin22C x x x +−−=7.（5分）计算不定积分⎰xdx x ln 3答案与评阅要点：⎰xdxx ln 3⎰=)4(ln 4x xd ⎰−=dx x x x 3441ln 41.161ln 4144C x x x +−=四、证明题（本大题45分）1.(10分)设函数()f x 在],[b a 上二阶可导，0)()(='='b f a f ．证明存在一点),(b a ∈ξ，使得)()()(4)(2a fb f a b f −−≥''ξ．答案与评阅要点：因为2()()()()()()2222a b a b f a bf f a f a a a ξ''+++'=+−+−1()2a b a ξ+<< 2()()()()()()2222a b a b f a bf f b f b b b ξ''+++'=+−+−2()2a b b ξ+<<（5分）两式相减，因为0)()(='='b f a f ，得2211()()[()()]()08f b f a f f b a ξξ''''−+−−=，记12()max{(),()}f f f ξξξ''''''=，则2222112111()()()()()(()())()()()884f b f a f f b a f f b a f b a ξξξξξ''''''''''−=−−≤+−≤−即)()()(4)(2a fb f a b f −−≥''ξ，证明完毕．（5分）2.(10分)证明数列{}n x 收敛，其中11x =，113()2n n nx x x +=+，1,2,n =，并求lim n n x →∞．答案与评阅要点：1131()22n n n x x x +=+≥=，21313()022n n n n n n nx x x x x x x +−−=+−=≤，故有1n n x x +≤（5分）故{}n x 单调减有下界，从而lim n n x →∞存在设lim n n x A →∞=，在113()2n n nx x x +=+两边取极限得13()2A A A =+，从而A =5分）3.（15分）设函数()f x 定义在区间(,)a b 上：（1）（5分）用εδ−方法叙述()f x 在(,)a b 上一致连续的概念；（2）（5分）设01a <<，证明1()sin f x x=在(,1)a 上一致连续；（3）（5分）证明1()sinf x x=在(0,1)上非一致连续．答案与评阅要点：（1）对0ε∀>，0δ∃>，对12,(,)x x a b ∀∈，只要12x x δ−<，就有12()()f x f x ε−<（5分）（2）对0ε∀>，取2a δε=，12,(,1)x x a ∀∈，只要12x x δ−<，12121212111111()()sinsin 2cos sin 22x x x x f x f x x x +−−=−= 121222121211x x x x x x x x a a δε−−≤−=<<=故1()sinf x x=在(,1)a 上一致连续．（5分）（1）在(0,1)内取2n x n π=，2(1)n x n π'=+，取012ε=，对0δ∀>，只要n 充分大总有2(1)n n x x n n δπ'−=<+，而1201()()sin sin 122n n f x f x ππε+−=−=>，故1()sinf x x=在(0,1)非一致连续．（5分） 4.（10分）(1)（5分）叙述函数极限lim ()x f x →+∞的归结原则，并应用它lim sin x x →+∞不存在． (2)（5分）叙述极限lim ()x f x →+∞存在的柯西收敛准则;并证明lim sin x x →+∞不存在.证明：(1)设()f x 在[,)a +∞有定义．lim ()x f x →+∞存在的充分必要条件是：对任意含于[,)a +∞,当lim n n x →∞=+∞时当lim n n x →∞=+∞时且趋于+∞的数列{}n x ，极限lim ()n n f x →∞存在且相等．取2,2,2n n x n x n πππ'''==+则lim lim 2,n n n x n π→∞→∞'==+∞lim lim(2),2n n n x n ππ→∞→∞''=+=+∞但lim ()lim sin(2)0,n n n f x n π→∞→∞'==lim ()limsin(2)1,2n n n f x n ππ→∞→∞''=+=lim ()lim (),n n n n f x f x →∞→∞'''≠故lim ()x f x →+∞不存在．（5分）(2)设函数()f x 在[,)a +∞有定义,则极限lim ()x f x →+∞存在的充要条件是:对于任何0,ε>存在正数0(),M M a >>当12,x x M >时有12|()()|.f x f x ε−<对于012ε=及任意正整数M,取122,2,2x M x M πππ=+=则有1,x M >2,x M >且有1201|()()|sin 2sin 21,22f x f x M M πππε⎛⎫−=+−=>= ⎪⎝⎭所以lim sin x x →+∞不存在.（5分）试题来源：微信公众号学术之星。

中国矿业大学(徐州)0708数学分析试卷(A)及参考答案

中国矿业大学07~08学年第二学期《数学分析(2)》试卷（A ）卷考试时刻：120分钟考试方式：闭卷院系__ _______班级___ ______姓名__ ________学号___ _______一、填空题（每空3分,共30分）1． =-+++∞→])1(sin 2sin [sin 1lim n πππnn n n n . 2． =-⎰202d 4x x . 3．=⎰∞+-0d x xe x .4．心形线(1cos )r a θ=+)0(>a 的周长为__ _______.5．=-∑∞=22)11ln(n n . 6．级数∑∞=⎪⎪⎭⎫⎝⎛+-11)1(n n n n __________________（绝对收敛或条件收敛或发散）.7．级数∑∞=-12)1(n nnn x 的收敛域为 . 8．设)(),(x y g y x xy f z +=，其中g ,f 具有一阶持续(偏)导数,那么=∂∂xz. 9．函数22232z y x f ++=在点)1,1,1(P 沿方向)4,3,0(:l 的方向导数=∂∂Pl f.10．曲面344224++--=x y y x z 在点处有水平的切平面.二（10分）、讨论二元函数⎩⎨⎧<<=其它,30 ,2),(4x y y x f 在点)0,0(的二重极限、二次极限、偏导数及沿任意方向的方向导数. （注：若是存在，把它求出来；若是不存在，要说明理由.）三（10分）、把函数21ln arctan )(x x x x f +-=展开为关于x 的幂级数并指出收敛域.四（10分）、把函数)0()(π≤≤=x x x f 展开为余弦级数并指出收敛性，再利用该级数证明: 61212π=∑∞=n n.五（10分）、设)(x f 在]1,0[上可导，且⎰=-311)1(d )(3f x x f e x ，证明：)1,0(∈∃ξ使0)()(=ξ'+ξf f .六（10分）、假设级数∑∞=12n na 收敛，证明∑∞=13n na 和)21(1>∑∞=p na n pn 都绝对收敛.七（10分）、求椭圆1322222=+y x 绕y 轴旋转所得的旋转曲面的表面积．八（10分）、设],[)(b a R x f ∈，证明：],[)(b a R e x f ∈.中国矿业大学07~08学年第二学期《数学分析(2)》试卷（A ）卷参考答案一、填空题（每空3分,共30分）1． π2. 2． π.3． 1. 4． 8a . 5． 2ln -. 6．发散. 7．)3,1[-. 8．)(1221xy g y f y f -⋅'+⋅'+⋅'. 9．536. 10．)2,1,1(--.二（10分）、讨论二元函数⎩⎨⎧<<=其它 ,30 ,2),(4x y y x f在点)0,0(的二重极限、二次极限、偏导数及沿任意方向的方向导数. （注：若是存在，把它求出来；若是不存在，要说明理由.）解：假设取直线途径kx y =，极限3),(lim 0==→y x f kxy x ；假设取途径为)10(4<<=k kxy 则2),(lim 40==→y x f kx y x ，因此二重极限),(lim )0,0(),(y x f y x →不存在.对任意0≠y ，3),(lim 0=→y x f x ，故 33lim ),(lim lim 00==→→→y x y y x f 。

第三学期数学分析期末考试题及答案

第三学期《数学分析》期末试题一、选择题：（15分，每小题3分） 1、累次极限存在是重极限存在的（）A 充分条件B 必要条件C 充分必要条件D 无关条件 2、=∂∂),(00|),(y x xy x f （）Ax y x f y y x x f x ∆-∆+∆+→∆),(),(lim 00000 ； B xy x x f x ∆∆+→∆),(lim 000； Cx y x x f y y x x f x ∆∆+-∆+∆+→∆),(),(lim 00000 ； D xy x f y x x f x ∆-∆+→∆),(),(lim 00000。

3、函数f (x,y )在（x 0,,y 0）可偏导，则（ D ）A f (x,y )在（x 0,,y 0）可微；B f (x,y )在（x 0,,y 0）连续；C f (x,y )在（x 0,,y 0）在任何方向的方向导数均存在；D 以上全不对。

4、22222)(),(y x y x y x y x f -+=的二重极限和二次极限各为（ B ）A 、0，0，0；B 、不存在，0，0，；C 、0，不存在，0；D 、0，0，不存在。

5、设yx ez =，则=∂∂+∂∂yz y x z x （A ）A 、0；B 、1；C 、-1；D 、2。

二、计算题（50分，每小题10分）1、证明函数⎪⎩⎪⎨⎧=+≠++=000),(222222y x y x y x xy y x f 在（0，0）点连续且可偏导，但它在该点不可微；2、设⎰⎰'=-x xtx f x f dt d ex f 0)(),(,)(2求ττ；3、设有隐函数,0x y F z z ⎛⎫=⎪⎝⎭,其中F 的偏导数连续,求z x ∂∂、z y ∂∂；4、计算(cos sin )x Ce ydx ydy -⎰，其中C 是任一条以为(0,0)A 起点、(,)B a b 为终点的光滑曲线；5、计算zdS ∑⎰⎰，其中∑为22z x y =+在14z ≤的部分；三、验证或解答（满分24分，每小题8分）1、验证曲线积分⎰+++++Ldzy x dy x z dx z y )()()(与路线无关，并求被积表达式的原函数；2、说明对任意),0(sin ,00)(2+∞∈>⎰+∞+-t tdx e x 关于αα均一致收敛；3、验证函数⎪⎩⎪⎨⎧=+≠++=0,00,2),(222222y x y x yx xyy x f 在原点（0，0）分别对每个自变数y x 或(另一个看作常数)都连续，但是二元函数在原点（0，0）却不连续.四、（11分）求由方程组⎩⎨⎧=-+=++10333z y x z y x 确定的隐函数)2,1,1()(),(-==P x z z x y y 在点处的一阶导数。

工科数学分析试卷1(含答案)

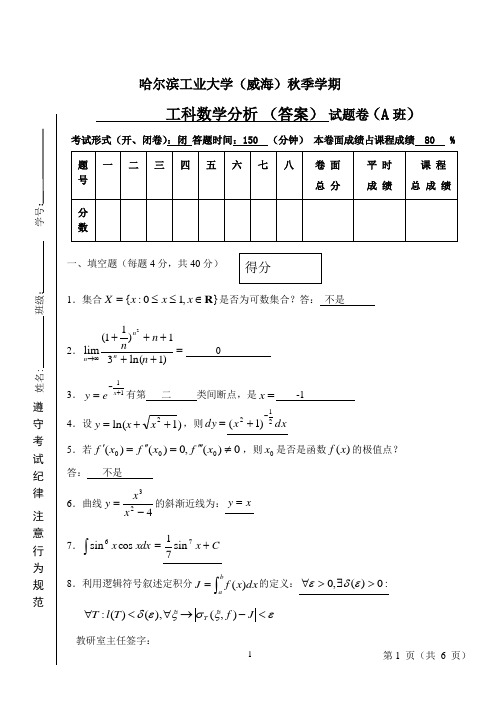
哈尔滨工业大学（威海）秋季学期工科数学分析（答案）试题卷（A 班）考试形式（开、闭卷）：闭答题时间：150 （分钟）本卷面成绩占课程成绩 80 %一、填空题（每题4分，共40分）1．集合},10:{R ∈≤≤=x x x X 是否为可数集合？答：不是2．=+++++∞→)1ln(31)11(lim 2n n nn n n 0 3．11+-=x ey 有第二类间断点，是=x -14．设)1ln(2++=x x y ，则=dy dx x 212)1(-+5．若0)(,0)()(000≠'''=''='x f x f x f ，则0x 是否是函数)(x f 的极值点？答：不是6．曲线423-=x x y 的斜渐近线为：x y =7．⎰=xdx x cos sin 6C x +7sin 718．利用逻辑符号叙述定积分⎰=badx x f J )(的定义：:0)(,0>∃>∀εδεεξσξεδ<-→∀<∀J f T l T T ),(),()(:遵守考试纪律注意行为规范教研室主任签字：姓名: 班级：学号：9．⎰+∞-=022dx xex 110．⎰-=-++222)33ln 1(sin ππdx xxx 2π二、试解答下列各题：（每题5分，共20分）1．设⎩⎨⎧=-=2)1ln(ty t x ，求22dx y d 解：t t x y dx dy t t222-=''= （2分）)1)(12(2122--='⋅'⎪⎭⎫ ⎝⎛=t t x dx dy dx y d t t（2分）（1分）2．设⎪⎩⎪⎨⎧=≠=⎰0,00,)(1)(02x x dt t tf x x F x，其中)(x f 在)0(δU 上连续且0)0(=f ，存在)0(f '，求)0(F '。

数学分析期末试题A答案doc

数学分析期末试题A答案doc2024年数学分析期末试题A及答案一、选择题1、以下哪个函数在 x = 0 处连续？ A. $f(x) = x^2$ B. $f(x) = \frac{1}{x}$ C. $f(x) = sin x$ D. $f(x) = e^x$ 答案：D解析：在 x = 0 处，只有选项 D 中的函数 e^x 是连续的。

因此，答案为 D。

2、设 $f(x) = x^2$，则 $f(3x - 2) =$ __________。

A. $x^2$ B. $(3x - 2)^2$ C. $(3x - 2)^3$ D. $(3x - 2)^2 + 1$ 答案：B解析：将 $x$ 替换为 $3x - 2$，得 $f(3x - 2) = (3x - 2)^2$。

因此，答案为 B。

3、下列等式中，错误的是： A. $\int_{0}^{1}x^2dx =\frac{1}{3}x^3|{0}^{1}$ B. $\int{0}^{\pi}\sin xdx = \cosx|{0}^{\pi}$ C. $\int{0}^{2\pi}\sin xdx = 0$ D.$\int_{0}^{1}(2x + 1)dx = (x^2 + x)|_{0}^{1}$ 答案：A解析：等式两边取极限，只有 A 选项等式两边不相等，因此 A 选项是错误的。

4、下列哪个导数是常数函数？ A. $y = x^3$ B. $y = \sin x$ C. $y = e^x$ D. $y = log_a(x)$ 答案：C解析：常数函数的导数为零。

在选项中，只有 C 中的函数 e^x 的导数为常数函数，其导数为 $e^x$。

因此，答案为 C。

高一生物期末考试试题及答案doc高一生物期末考试试题及答案doc高一生物期末考试是一次重要的学业水平测试，旨在考察学生在本学期学习生物课程的效果。

以下是本次考试的部分试题及其答案，供大家参考。

一、选择题1、下列哪一种生物不是由细胞构成的？ A. 细菌 B. 植物 C. 动物D. 病毒答案：D2、哪一个器官属于消化系统？ A. 口腔 B. 食道 C. 胃 D. 大肠答案：C3、在光合作用中，哪一个物质是植物从空气中吸收的？ A. 氧气 B. 二氧化碳 C. 葡萄糖 D. 水答案：B二、填空题1、病毒是一种生物，但它不能 _______ 和保持生命活动，必须_______ 在细胞内。

高数期末试题

2 1
f ( x)dx 1 , 证明在(0,3)内存在
, 使 f ( ) f ( ) 0.
九 . (8 分) 设 f ( x) 有连续导数 , 且 lim
x 0
f ( x) f ( x) 2, ex 1
f (0) 0, 证明 x 0 是 f ( x) 的
x 0
____________ .
2.
I1
ln 2 x dx 与 I 2 x
dx 中收敛的为 _____________, 其值等于 x ln 3 x
___________. 3.

1
1
3 1 x 2 dx _____________,

1
1
x 1 x 2 dx _____________ .
2x 1 x2
( x 1) 是否恒为常数.
y 1 dy d 2 y 2 2 六. (9 分) 设 arctan ln( x y ) 确定函数 y y ( x) , 求 , 2 . x 2 dx dx
信息与电子二学部学生会学习部整理
七. (10 分) 求下列反常积分. (1)
1
二. (9 分) 求极限 lim(cos x x sin x) .
x2 x 0
三. (9 分) 求不定积分 ( x arctan x
1 x e )dx . x2
1
四. (9 分) 求 f ( x) 3 ( x 2 2 x) 2 在区间 [1,3] 上的最大值和最小值.
五. (8 分) 判断 f ( x) arctan x arcsin
0
x
是 f ( x) 的极值点, 并判断 f (0) 是极大值还是极小值.

集美大学2015-2016 数学分析1期考试卷(A)

集美大学2015-2016学年第一学期期末考试信计与计算科学2015级数学分析1试卷（A ）一、填空题（每小题2分,共10分）1．lim ()x af x A -→≠的“εδ-”定义是 .2．()ln (1)f x x =+在0x =处（具Peano型余项）的n 阶Taylor展开式为．3．设()sin x x x ϕ= ，则=-→)(lim 0x x ϕ ，=+→)(lim 0x x ϕ ． 4．2x =与0x =分别是函数)4(2)(22--=x x x x x f 的类不连续点．5．叙述零点存在定理：．二．单项选择题（每小题2分,共10分）6．设1()(1)x f x x =-，则0x =是()f x 的 [ ] 间断点.A ．无穷B ．跳跃C ．可去D ．振荡7．设()f x 在(,)a b 内单调有界，且(,)c a b ∈，则 [ ] ．A ．lim ()x cf x →存在 B ．(0)f c ±均存在C ．(0)()f c f c += D ．(0)()f c f c -=8．下列命题错误的是 [ ] ．A ．A x f x =→)(lim 0 ⇒ A n f n =∞→)1(lim B ．)(x f 在a x =处可微 ⇒ )(x f 在a x =处连续C ．)(x f 在¡上无界 ⇒ ∞=∞→)(lim x f xD ．)(x f 在[,]a b 上单调 ⇒ )(x f 在[,]a b 上有界9．设)(x f 任意阶可导，且2])([)(x f x f ='，则)()(x fn 等于 [ ]．A ．n x f n 2])([ B ．1])([+n x f n C ．n x f n 2])([! D ．1])([!+n x f n 10．设0a >，则方程35x ax += [ ]．A ．只有一个正根 B ．只有一个负根C ．有两个相异实根D ．没有实根三．证明题（每小题5分，共10分）11．用极限的分析定义证明225lim 512n n n n →∞=-+-． 12．设0a b <<，证明：ln b a b b a b a a--<<．四．计算下列极限（每小题5分,共15分）13．22212lim 11n n n n n n →∞⎛⎫+++ ⎪++-⎝⎭L ．14．求1)1lim x x x -→．15．2222lim 3n n n x n →∞⎛⎫+ ⎪-⎝⎭ ．五．求下列导数或微分（4题，每题5分，共20分）16．设sin()arctan()xy x y =+，求dxdy ．17．设t a x cos =， t b y sin =，求22dx y d ．18．1x y x =．19．设x e x y 22=，求(5)y ．六．计算下列不定积分（3题，每题5分，共15分）20．d x xex -⎰．21．x ．22．32sin d cos x x x⎰．七．判断命题是否正确，若正确请予证明，否则请举反例（每小题3分，共6分）23．设()f x 在0x x =不可导而()g x 在0x x =可导，则()()f x g x 在0x x =必不可导.24．设()f x 与()g x 在0x x =均不连续，则()()f x g x +在0x x =必不连续.八．综合题（共14分）25．（5分）利用函数的导数研究：把长为l 的线段分为两段，使以它们为长和宽所围成的矩形的面积最大．26．（9分）讨论()x x f x e=的单调区间、极值点、凹凸区间、拐点和渐近线（不要求作图）.。

华东师范大学大一数学分析期末考试题

xx0 g(x)
xx0 g (x)
xx0 g(x)
A、必要条件 B、充分条件 C、充分必要条件
三、计算题（每小题 6 分，共 30 分）
D、既非充分也非必要条件
14、 lim (1 a)(1 a2 )(1 a2n ),(| a | 1) n
15、求函数 y 2x 的单调区间 1 x2
16、 lim xln(1 x) ln x x
学院：数学与计算机科学学院适用班级：
题号一二三四五六七八九
分数
总分
评卷人
一、填空题（每空 2 分，共 20 分）
1、函数 f (x) ln 1 x 的定义域是 1 x
2、 lim sin 5x x0 3x
第
1
3、 lim
n
1n
4、若 f 可导，且 y f (2x), 则 dy =
17、已知 y ln(arccos 1 ) 求 y x
18、求 d
x 1
x2
四、证明题（每小题 10 分，共 20 分）
19、已知数列xn ，它由递推公式
xn1
1 2
(xn
a xn
) 确定， a
0 ，且 x1 可取任意正实数，
证明：数列
x
n
收敛，并求
lim
n
xn
20、 ex 1 x ， (x 0)
五、综合题（15 分）
21、并作图
学号
班级
专业
C、 f (x) 在 x 0的左右极限存在但不相等 D、 f (x) 在 x 0的左右极限不存在
页
n n 1
5、设 f (x) 在 x0 点可导，且在 x0 点取极大值，则 f (x0 ) =

2021-2022学年数学分析第二学期期末考试(含答案)

2021-2022学年第二学期期末《数学分析》一.填空题 ( 每题5分,共30分 )1. 已知势函数 2u x yz =，则其梯度 grad u = ，其梯度的散度 ()div grad u = 。

2. 曲面:ln x z y y ⎛⎫∑=+ ⎪⎝⎭在点0(1,1,1)P 处的单位法向量为 ,在该点处的切平面方程为 .3. 设22()d ,x x u x f x e u -=⎰ 则'()f x = .4. 设Γ是以(0,0),(1,0),(0,1)O A B 为顶点的三角形的边界,则曲线积分()x y ds Γ+⎰ = .5. 设Ω是由锥面z =和上半球面 z = 围成的空间区域，则三重积分222()d f xy z V Ω++⎰⎰⎰ 在球坐标系下的累次积分为.6. 利用Γ函数和B 函数的性质，可知 2560sin cos d x x x π⎰ = .二. 计算题 (10分) 计算二重积分D，其中 D 是由22221x y a b += 所围的平面区域。

设Γ是任意一条包围着原点（不经过原点）的分段光滑、逆时针定向曲线，试计算曲线积分22.2xdy ydxx y Γ-+⎰四. 计算题 (10分)设∑为曲面 )20(222≤≤+=z y x z 的下侧．计算曲面积分33()d d ()d d 2()d d x y y z y z z x x y z x y ∑++-++-⎰⎰．计算曲线积分22I y dx xdy z dz Γ=-++⎰，其中Γ是平面2y z +=与柱面221x y +=的交线，从Oz 轴正向往下看为逆时针方向.六.计算题 (10分)计算双曲面z xy = 被围在圆柱面222x y a +=内部的面积．设()f x 是[,]a b 上的连续函数，利用二重积分性质证明不等式22()d ()()d b b a a f x x b a f x x ⎡⎤≤-⎢⎥⎣⎦⎰⎰八. 证明题 (10分)设(,)f x u 在[,][,]a b αβ⨯上连续，证明对任意 0[,]u αβ∈，总有0lim (,)d (,)d b baau u f x u x f x u x →=⎰⎰设Ω为闭区域，∂Ω是Ω的边界外侧，n是∂Ω的单位外法向量。

华南理工大学期末考试《工科数学分析》上-试卷(A)(附解答) (1)(word文档良心出品)

《工科数学分析》2014—2015学年第一学期期末考试试卷诚信应考，考试作弊将带来严重后果！华南理工大学本科生期末考试《工科数学分析》2014—2015学年第一学期期末考试试卷（A ）卷注意事项：1. 开考前请将密封线内各项信息填写清楚；2. 所有答案请直接答在试卷上(或答题纸上)；3．考试形式：闭卷； 4. 本试卷共 5个大题，满分100分，考试时间120分钟。

《工科数学分析》2014—2015学年第一学期期末考试试卷一、填空题（每小题3分，共15分）１. 函数()1212x xe ef x e e+=-的间断点及其类型为0x =是跳跃间断点，12x =是无穷间断点；２. 已知函数()y y x =由方程yxx y =所确定，则曲线()y y x =在点()1,1处的切《工科数学分析》2014—2015学年第一学期期末考试试卷线方程为0x y -= ；３. 设xy xe =，则()n d y =()xnx n e dx + ；４. 220x t d e dt dx -⎛⎫= ⎪⎝⎭⎰42x xe - ；５. 反常积分()22ln dx x x +∞=⎰1ln 2．二、计算下列各题（每小题8分，共16分） 1. 求极限()11limxx x ex→+-《工科数学分析》2014—2015学年第一学期期末考试试卷解：()()()()()()()11ln 101ln 12001limlim1ln 1lim 41ln 1lim 6282x xxx x x x x x x eeexxx x x e x x x e x e +→→+→→+--=-++=⋅+-+==-分分分或()()()1ln 1110020011lim lim ln 1lim 4111lim 6282x x x x x x x e e x e x xx x e x x e x e +-→→→→⎡⎤-⎢⎥+-⎣⎦=+-=-+==-分分分2.计算定积分21dxx ⎰ 解：2321434tan,sec,cos4sin16sin t83x t dx tdttdttππππ===⎰⎰令则分＝－分分三、解答下列各题（每小题10分，共40分）1.设()1110,1,2,,nx x n+===试证明数列{}n x收敛，并求lim.nnx→∞证明：（1）()1110343,3,1,2,nx x x n=≥=≥≥=，用归纳法可证，即数列{}nx有下界；3分（2）1320,n n nx xx x x+-+-==<即，数列{}n x 单调减少。

数学分析试题及答案

∫∫ 六．计算曲面积分 x2dydz + y 2dzdx + z 2dxdy ，其中 Σ 为锥面 x2 + y 2 = z 2 在平面 Σ
z = 0 与 z = h （ h > 0 ）之间的部分，定向为下侧。
七．设 A(x, y) = 2xy(x 4 + y 2 )λ i − x 2 (x 4 + y 2 )λ j 是右半平面 D = { (x, y) | x > 0 } 上的向量场，试确定常数 λ ，使得 A(x, y) 为 D 上函数 u(x, y) 的梯度场，并求出 u(x, y) 。
∑ 计算 ∞ (−1)n+1 的值。 n2 n=1
4
复旦大学 2005～2006 学年第一学期期末考试试卷
答案
1．（本题满分 40 分，每小题 8 分）（1） 2 2x + y − 2 = 0 。
（2） 1 。 2
1
（3） y = e e 为极大值。 x=e
（4）曲线在 (0, 1] 上为上凸，在[1,+∞) 上为下凸， (1, − 7) 为拐点。
∫∫∫ 四．计算三重积分 e|z|dxdydz ，其中 Ω = { (x, y, z) | x2 + y 2 + z 2 ≤ 1}。 Ω
五．计算曲线积分
∫ 2 y 2 + z 2 ds ，
L
其中 L 是球面 x2 + y 2 + z 2 = a 2 （ a > 0 ）与平面 x = y 相交而成的圆周。
A t(1 + t 2 ) 2
x→+∞ 1 t(1 + t 2 )
∫ 所以存在 X > 0 ，当 x > X 时成立 A cos xt dt < ε ，于是当 x > X 时成立

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

cos x
………………………………………5 分
= e1 = e …………………………………………………………8 分
14. 函数 f ( x) 在 x0 处连续的充要条件是 f ( x) 在点 x0 处既右连续，又左连续……4 分
x → 0+
lim f ( x) = lim ( x + 2) = 2 ， lim f ( x) = lim ( x − 2) = −2 ……………………6 分 + − −
n →∞
于是，当 n + k > n > N 时 , an + k − a < ε ………………………………………7 分则： lim a n + k = a …………………………………………………………………10 分
n →∞
16.若 lim f ( x ) 极限存在，则 f ( x) 在 U ( x0 ) 局部有界………………………………4 分
1
ε
，当 | x |> M 时…………………………………………………6 分
有
1 1 1 1 −0 = < = ε ，所以 lim = 0 …………………………………10 分 x →∞ x | x| M x
x1 − x 2 1 1 1 − = ≤ 2 x1 − x 2 < ε x1 x 2 x1 x 2 a
三．解答题(本大题共 4 小题，每小题 8 分，共 32 分): 11. 由于
(2n )
n +1
2
1 1 1 n +1 ≤ 2 ……………………………3 分 ≤ + + " + 2 2 2 n n ( ) ( ) + n 1 2 n
而 lim
n +1 n +1 = 0 ， lim 2 = 0 ………………………………………………6 分 2 n → ∞ (2n ) n→∞ n
x →0 x →0 x →0
1
所以，函数 f ( x) 在点 x = 0 的不连续 ……………………………………………8 分四．证明题(本大题共 4 小题，第 15~17 小题每题 10 分，第 18 题 13 分，共 43 分) 15. lim a n = a ， ∀ε > 0, ∃N , n > N时, a n − a < ε , ………………………………5 分
则 lim
1 1 1 =0……………………………………………8 分 + + + " 2 2 n → ∞ n 2 ( ) ( ) + n 1 2 n
12. 当 x → ∞ 时,
f ( x) → 1 = k , ( f ( x) − kx) → −2 = b, …………………………2 分 x
《数学分析》（I）期末考试 A 卷
参考答案及评分标准
一．填空题(本大题共 5 小题，每小题 2 分，共 10 分)： 1.
a≤b
2. 2
3. x = 2k π +
π , k = 0, ±1," 4. 无关 2
5. 相同极限．
二．单项选择题(本大题共 5 小题，每小题 3 分，共 15 分): 题号答案 6 B 7 C 8 C 9 D 10 A
有斜渐近线 y = x − 2 ，……………………………………………………………4 分
f ( x) =
x3 → ∞ ，有垂直渐近线 x = −3, x = 1 ……………………8 分 ( x + 3)( x − 1)
cot x
13. lim(1 + sin x )
x →0
1 = lim (1 + sin x) sin x x →0
x → x0
D
x → x0ຫໍສະໝຸດ lim f ( x) = A ， ∀ε > 0, ∃δ > 0, 当 0<|x − x0 |< δ 时, 有 f ( x) − A < ε …6 分
…………………………………………8 分
取 ε = 1 ， | f ( x) | < | A | +1 = M > 0
局部有界性得证。…………………………………………………………………10 分 17. ∀ε > 0, 取 M =
ö¢
ε 0 = 1 ，对匍论引么岢钴 δ < 镝数 ………………………………………10 分 δ
2
1 2
颃椹觫 x ′ = δ 与 x ′′ =
则虽牦
x ′ − x ′′ =
δ
2
< δ Ó£
1 1 1 − = > 1 ……13 分 x ′ x ′′ δ
2
………3 分
18. ∀ε > 0, ∀x1 , x 2 ∈ [a,1] ，椹夼颃椹觫 δ = a
则 ∀ε
2
ε 有…………………………………………………………………6 分
当
> 0, ∀x1 , x 2 ∈ [a,1] ， ∃ δ = a 2 ε
x1 − x 2 < δ êó
1 1 − < ε ……7 分 x1 x 2