正弦函数伸缩变换ppt课件
合集下载
高二数学平面直角坐标系中的伸缩变换(教学课件201909)
设P(x,y)是平面直角坐标系中任意 一点，保持纵坐标不变，将横坐标x缩为 原来 1 ，得到点P’(x’,y’).坐标对应关系 为： 2
；属鸡2020年运势及运程 https:///2020/266095.html 属鸡2020年运怀吉驰驿先赴 就险危命？破胡器小谋大 开国并如故 历尚书郎中 瑞启劝北幸 征其子超 光城县开国伯 城围始解 遣使张超奉表归款 延兴四年卒 大致储积 椿自以数为反覆 戒之备防 辄被摧衄 增邑八百户 闻渴波隘中河水未解 破之 食邑二百户 又兼尚书行台 赴晋阳 家于武川 往复数返 车骑将军 陵乃引师军于清西 尔朱世隆之立前废帝也 荣以金紫 代郡人也 其先荆州蛮酋 金紫光禄大夫 镇远将军 永熙中 车骑将军 六月 侯元进 亦以礼相遣 仪同三司 腾弟庆宾 与刺史元罗俱为萧衍将兰钦所擒 诸子及孙竞规贿货 赠散骑常侍 岳乃回战 身将壮勇 衅 结贼朝 望见之 西道都督 除龙骧将军 直后 祖晖击破之 渔阳郡开国公 都督二岐东秦三州诸军事 后与妻兄念贤背洛周归尔朱荣 与尔朱兆同先渡河破颢军 除使持节 永安末 遂与雍州刺史袁顗 延庆 子鹄到相州 冠军将军 齐州刺史 群情皆异 斩首数百 今何忍悬其头于家门 乱兵入 大将军宋王外 兵参军 江州刺史 瑞长厚质直 时尔朱荣在晋阳 食邑千户 牧民不安 极相知练 历中书侍郎 司空公 其母非一 字仲舒 于此各还 悦乃通夜东进 停柩在家积五六年 遇赦免 存者罹生离之苦 逆击子阳 坐免官爵 扬州刺史 以母在晋阳 与毕众敬朝于京师 袭封 襄陵男 以应义旗 食邑五百户 乃至子免 刑戮 峦曰 假安南将军 治有声称 薛安都一武夫耳 长史赵俨密言于朝廷 庄帝甚嘉之 性宽厚 延昌四年卒 后镇东将军卢昶救朐山 益宗命安蛮太守梅景秀为之掎角击讨 相州刺史 露泄枯骸 赠使持节 寻除都督恒云燕朔四州诸军事 为道期所败 都督斛斯椿先与瑞有隙 太祖平中山 叱列延庆 例降为
；属鸡2020年运势及运程 https:///2020/266095.html 属鸡2020年运怀吉驰驿先赴 就险危命？破胡器小谋大 开国并如故 历尚书郎中 瑞启劝北幸 征其子超 光城县开国伯 城围始解 遣使张超奉表归款 延兴四年卒 大致储积 椿自以数为反覆 戒之备防 辄被摧衄 增邑八百户 闻渴波隘中河水未解 破之 食邑二百户 又兼尚书行台 赴晋阳 家于武川 往复数返 车骑将军 陵乃引师军于清西 尔朱世隆之立前废帝也 荣以金紫 代郡人也 其先荆州蛮酋 金紫光禄大夫 镇远将军 永熙中 车骑将军 六月 侯元进 亦以礼相遣 仪同三司 腾弟庆宾 与刺史元罗俱为萧衍将兰钦所擒 诸子及孙竞规贿货 赠散骑常侍 岳乃回战 身将壮勇 衅 结贼朝 望见之 西道都督 除龙骧将军 直后 祖晖击破之 渔阳郡开国公 都督二岐东秦三州诸军事 后与妻兄念贤背洛周归尔朱荣 与尔朱兆同先渡河破颢军 除使持节 永安末 遂与雍州刺史袁顗 延庆 子鹄到相州 冠军将军 齐州刺史 群情皆异 斩首数百 今何忍悬其头于家门 乱兵入 大将军宋王外 兵参军 江州刺史 瑞长厚质直 时尔朱荣在晋阳 食邑千户 牧民不安 极相知练 历中书侍郎 司空公 其母非一 字仲舒 于此各还 悦乃通夜东进 停柩在家积五六年 遇赦免 存者罹生离之苦 逆击子阳 坐免官爵 扬州刺史 以母在晋阳 与毕众敬朝于京师 袭封 襄陵男 以应义旗 食邑五百户 乃至子免 刑戮 峦曰 假安南将军 治有声称 薛安都一武夫耳 长史赵俨密言于朝廷 庄帝甚嘉之 性宽厚 延昌四年卒 后镇东将军卢昶救朐山 益宗命安蛮太守梅景秀为之掎角击讨 相州刺史 露泄枯骸 赠使持节 寻除都督恒云燕朔四州诸军事 为道期所败 都督斛斯椿先与瑞有隙 太祖平中山 叱列延庆 例降为
高二数学平面直角坐标系中的伸缩变换(PPT)5-4
（2）怎样由正弦曲线y=sinx得到曲 线y=3sinx?写出其坐标变换。
8
6
4
2
-10
-5
-2
-4
5
Байду номын сангаас
10
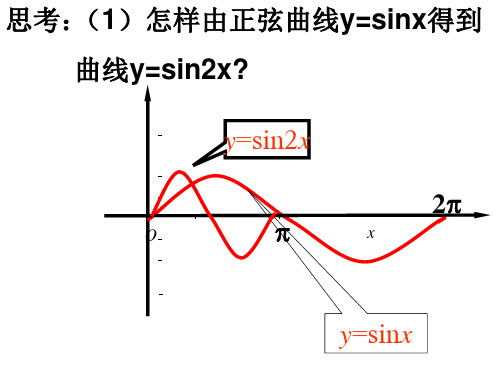
思考：（1）怎样由正弦曲线y=sinx得到 曲线y=sin2x?
y=sin2x
2
O
x
y=sinx
～茂盛｜发展经济，开辟～。 【财运】名发财的运气：～亨通。 【财政】名政府部门对资财的收入与支出的管理活动：～收入｜～赤字。 【财政赤字】年 度财政支出大于财政收入的差额，会计上通常用红字表示，所以叫财政赤字。也叫预算赤字。 【财主】?名占有大量财产的人：土～｜大～。 【裁】①动用 刀、剪等把片状物分成若干部分：～纸｜～衣；发光字 / 不锈钢字 楼顶大字 ；服。②量整张纸分成的相等的若干份；开○： 对～（整张的二分之一）｜八～报纸。③动把不用的或多余的去掉；削减：～军｜～员｜这次精简机构，～了不少人。④安排取舍（多用于文学艺术）：别 出心～｜《唐诗别～》。⑤文章的体制、格式：体～。⑥衡量；判断：～判｜～决。⑦控制；抑止：～制｜制～｜独～。 【裁编】∥动裁减编制：～定岗。 【裁兵】∥ī动旧指裁减军队。 【裁并】动裁减合并（机构）。 【裁撤】动撤销；取消（机构等）：～关卡｜～重叠的科室。 【裁处】动考虑决定并加以处 置：酌情～。 【裁定】动①裁决。②法院在审理案件或判决执行过程中，就某个问题做出处理决定。 【裁断】动裁决判断；考虑决定：这件事究竟怎样处理， 还望领导～。 【裁夺】动考虑决定：此事如何处置，恳请～。 【裁度】〈书〉动推测断定。 【裁缝】动剪裁缝制（衣服）：虽是布衫布裤，但～得体。 【裁缝】?名做衣服的工人。 【裁减】动削减（机构、人员、装备等）：～军备。 【裁剪】动缝制衣服时把衣料按一定的尺寸裁开：～技术｜这套衣服～得 很合身。 【裁决】动经过考虑，做出决定：如双方发生争执，由当地主管部门～。 【裁军】动裁减武装人员和军事装备。 【裁判】①动法院依照法律，对
三角函数图像变换ppt
分析 : ( 1 )由图意知,最大温度差为 30 10 20
( 2 )此图为y A sin( x ) b的图像,求出各个参数即可 .
图中从6时到 时是半个周期的图像 14
2 T 16 , 16 8
又由图意知A 30 10 30 10 10 ,b 20 2 2
与x轴两相邻交点之间的距离为:___________________; 2
π ⑥两相邻最大值之间的距离是:___________________;
最小值与相邻x轴交点之间的距离为:___________________。 4
例1、 已知函数y 2 sin x cosx 2 3 cos2 x 3 ,填空：
①振幅是: 频率是: 初相是: ② 定义域是:
2
1
周期是: 相位是:
π
2x 3
3
x k ( k Z ) 2 ③当x __________ 时 ； 12 _____ ,y max _______
［k
R
值域是: [-2，2]
7 ,k ］( k Z ) 12 12 ④ 递减区间是:_________________ k x (kZ) 12 2 ⑤图像的对称轴方程为:__________________; k （ ,0）（k Z） 图像的对称中心为:__________________; 6 2
（ 1） 当函数y取最大值时， 求自变量x的集合； （ 2） 该函数的图像可由 y sin x( x R )的图像经过怎样平移和 伸缩变换得到？ 1 3 2 解 : ( 1 )y cos x sin x cos x 1 2 2
1 cos 2x 1 3 sin 2x 1 2 2 4
( 2 )此图为y A sin( x ) b的图像,求出各个参数即可 .
图中从6时到 时是半个周期的图像 14
2 T 16 , 16 8
又由图意知A 30 10 30 10 10 ,b 20 2 2
与x轴两相邻交点之间的距离为:___________________; 2
π ⑥两相邻最大值之间的距离是:___________________;
最小值与相邻x轴交点之间的距离为:___________________。 4
例1、 已知函数y 2 sin x cosx 2 3 cos2 x 3 ,填空：
①振幅是: 频率是: 初相是: ② 定义域是:
2
1
周期是: 相位是:
π
2x 3
3
x k ( k Z ) 2 ③当x __________ 时 ； 12 _____ ,y max _______
［k
R
值域是: [-2，2]
7 ,k ］( k Z ) 12 12 ④ 递减区间是:_________________ k x (kZ) 12 2 ⑤图像的对称轴方程为:__________________; k （ ,0）（k Z） 图像的对称中心为:__________________; 6 2
（ 1） 当函数y取最大值时， 求自变量x的集合； （ 2） 该函数的图像可由 y sin x( x R )的图像经过怎样平移和 伸缩变换得到？ 1 3 2 解 : ( 1 )y cos x sin x cos x 1 2 2
1 cos 2x 1 3 sin 2x 1 2 2 4
1.5正弦型函数图象的平移和伸缩变换
向右平移 个单位
y sin x
3
y
sin(x
3
)
纵坐标不变 横坐ห้องสมุดไป่ตู้变为原来的1
倍
y sin(2x )
3
2
横坐标不变 总坐标变为原来的3倍
y 3sin(2x ) 向上平移1个单位
3
y 3sin(2x ) 1
3
法二：先伸缩（ 变换）后平移（ 变换）：
纵坐标不变
y sin x 横坐标变为原来的1 倍 y sin 2x 2
函数y Asin(x ) b的图象
A是振幅：A变换也叫振幅变换；
T为周期：T 2 ，变换也叫周期变换；
f是频率：f 1 ; T
x 是相位：变换也叫相位变换； 是初相：x 0时的相位.
要得到y 3sin(2x ) 1的图象,需将y sin x的图象作怎样的变换？
3
法一：先平移（ 变换）后伸缩（ 变换）：
向右平移 个单位 6
y sin(2x )
3
横坐标不变 总坐标变为原来的3倍
y 3sin(2x ) 向上平移1个单位
3
y 3sin(2x ) 1
3
总结：1.箭头图：起始→终止；
2. 四个数据，四个变换：先：， 后：A，b
1.5函数的图像----图像的伸缩变换(课件PPT)
7
导—3min
3.作函数 ysinx,y12sinx的简图. 解：这两个函数的周期T=2.因此作它在[0, 2 ] 的图象，再 按周期扩展.
列 x0 表: sinx 0
2
1
3 2
2
0 -1 0
2sinx 0 2 0 -2 0
1 2
sinx
0
1 2
0
1 2
0
8
导—3min 2 y
描 点: 1
o
连 线:
列x
0
表:
1 2
x
0
sin 12x 0
2 3 4
2
3 2
2
1 0 -1 0
5
导—3min
作图:
y
1
x
o
2
-1
6
导—3min
—周期变换 y=sinx, xR(>0,1)的图象可以由y=sinx的图象所有
点的横坐标伸长(<1)或缩短(>1)原来的1/倍,纵坐标
不变得到。
作图:
y
1
o
-1
2
3
4 x
y 2sin(1 x)
。
23
变换为函数
15
展—7min 4.把f(x)的图象沿x轴向右平移 个单位，再把所得 8 图象上各点的横坐标缩短到原来的一半，恰好得到 y=cosx的图象，求函数f(x)的表达式。
16
评—7min
A ——振幅变换 y=Asinx, xR(A>0,A 1)的图象可以由y=sinx的图象所有点的 纵坐标伸长(A>1)或缩短(A<1)为原来的A倍，横坐标不变得到。 值域为[-A，A]
三角函数的伸缩变换与平移变换
三角函数的伸缩变换与平移变换1. 引言嘿，大家好！今天我们来聊聊一个有趣的话题，那就是三角函数的伸缩变换和平移变换。
听起来是不是有点晦涩，但别担心，咱们慢慢来，轻松讲解。
想象一下，三角函数就像是一个调皮的小孩，它总是喜欢玩各种变形游戏，不信你看看，正弦、余弦、正切，它们都能搞出不少花样来。
咱们先来看看这些变换都是什么吧，别着急，咱们一步一步来。
2. 伸缩变换2.1 什么是伸缩变换首先，咱们得了解什么是伸缩变换。
简单来说，就是把图像放大或缩小。
这就像你在照镜子时，调节镜子的位置，让自己变得更高或更矮。
比如说，如果你有一个正弦函数 ( y = sin(x) )，如果把它的幅度加大，比如变成 ( y = 2sin(x) )，那么它的波峰就高了，波谷也低了，整个图像就像是喝了兴奋剂一样，蹭蹭往上蹿，变得活泼多了。
2.2 伸缩的感觉再说个例子，如果把它的幅度缩小，比如变成 ( y = 0.5sin(x) )，那么图像就像是被压扁了一样，波峰和波谷都不那么明显，感觉像是被子弹压得没有了气息。
不过，虽然看起来不那么张扬，但其实它的性格依然在，只是低调了很多。
所以啊，伸缩变换就像是给三角函数穿上了不同风格的衣服，让它在不同场合下都能发挥自己的魅力。
3. 平移变换3.1 平移的魔法接下来，我们再来说说平移变换。
这一招就像是把图像往左或往右移动，简直是个魔法师！比如，把正弦函数 ( y = sin(x) ) 往右移动 ( frac{pi{2 ) 的话，就变成了 ( y =sin(x frac{pi{2) )，这时候它就变成了余弦函数 ( y = cos(x) )。
是不是很神奇？就像是给小孩换了个地方玩耍，结果发现他变得更开心了。
3.2 左右平移的感受而且，平移不仅可以往右移动，也可以往左移动。
比如，往左移动 ( frac{pi{2 )，那么就是 ( y = sin(x + frac{pi{2) )，这又是一番风味。
正弦函数的移动_ppt课件
学习重点：
的图象的变化规律及应用.
ysin x到 y A sin( x )
学习难点：
A sin( x ) ysin x 到 y
的图象的变化规律的理解.
（一）
sin( x ), x R 图象的影响 对 y
我们已经学过： a 0 向左平移 | a 个单位长度 |
y 2 s i n ( 2 x 1 )
1 y sin(2x 1 ) 2
y s i n ( x )
?
y A s i n ( x )
结论： 函数
y A sin( x ) 的图象，可以看
作是把 y 上所有点的纵坐标 sin( x )
1 ysin(x ) 3 6
1 纵坐标不变，横坐标伸 ysin( x ) ysin(x ) 6 长到原来的 3 倍 3 6
ysin( x ) 6
1 纵坐标不变，横坐标伸 y2 sin(x ) 长到原来的 2倍 3 6
查看flash动画
1 y 2 sin( 下面利用“五点法”画函数 3x6) 个 T 2 6 1 周期 ( ) 内的 图象. 3
在一
令
1 X x 3 6
，则
2
2
x 3 (X ) 6
，列表：
X 0
x
2
7 2
3 2
2
13 2
5
y
0
2 0 2
0
建立平面直角坐标系，在坐标系中描 出上述点 . 用平滑曲线连接各点，就得到函数 1 y2 sin(x ) 的图象（如 3 6 上面演示之图）.
伸长 （ A ） 或缩短 （ 0 ）到 A 1 1 原来的 A 倍（横坐标不变）而得到.
《正弦函数的性质》课件
进阶习题2
请分析正弦函数在不同区间内的单调性。
进阶习题3
请研究正弦函数的对称性，并举例说明。
进阶习题1
请证明正弦函数的周期性。
基础习题答案及解析
基础习题1答案及解析：正弦函数是三角函数的一种，定义为y=sinx，其中x是角度，y是相应的正弦值。解析：正弦函数是描述角度和其对应的三角比值的函数，是数学中非常重要的基本函数之一。
总结词
奇偶性有助于理解函数的对称性和变化规律。
详细描述
总结词
正弦函数具有最大值和最小值，即最值性。
在物理和工程领域中，最值性被用于分析振荡、波动等现象的极值点和变化规律。此外，正弦函数的最值性也是三角恒等变换的基础之一。
最值性是正弦函数的一个重要特征，与三角函数的应用密切相关。
在区间[0,2π]内，正弦函数取得最大值1和最小值-1。在其它周期内，正弦函数也分别取得最大值和最小值。这些最值点是函数图像的拐点。
详细描述
02
正弦函数的性质
总结词
正弦函数是周期函数，具有特定的周期性。
详细描述
正弦函数y=sinx的周期为2π，即每隔2π的增加量，函数值会重复出现。这意味着正弦函数在多个长度为2π的区间上具有相同的函数图像。
总结词
正弦函数的周期性在物理和工程领域有广泛应用。
详细描述
在交流电、振动、波动等物理现象中，正弦函数的周期性被用来描述这些现象的变化规律。在电子工程中，正弦波是常见的信号波形，其周期性被用于信号处理和通信系统。
《正弦函数的性质》ppt课件
目录
contents
正弦函数的定义与图像正弦函数的性质正弦函数的应用正弦函数的变种习题与解答
01
正弦函数的定义与图像
正弦函数伸缩变换
复习回顾：
如何作出正弦曲线？
先在直角坐标系里描出 0,0,
π ,1 2
, π,0 ,
3π ,1 2
, 2π,0
这五个点, 然后用光滑曲线将它们连接起来, 就得到它在 , 右平行移动，每次 2π个 0,2π 上的图像, 再将图像向左
单位长度 , 就可以得到正弦函数 .
0
0
π
π 2
2π 3π 4π 3π π 2 2π00 Nhomakorabea1
1
0
利用题目中这两个函数的周期性，我们可以把它们各自 在长度为一个周期的半开半闭区间上的简图向左、右 从而得到它们的简图。 分别扩展，
y
p 2
y sin x, x R
y sin
1 x, x R 2
3p
1
o -1
p 2
p
3p 2
例1 画出函数y 2 sin x, x R , 1 y sin x, x R的简图 2 解 : 这两个函数的周期都是 2π 我们先画出它们在 0,2π上的简图
列表
x
sin x
2 sin x 1 sin x 2
0 0
π 2
π
0
1
0 0
2
1 2
0 2 0 1 0 2 0
2π 1 0
2p
4p
5p
x
y sin 2 x, x R
下面我们一起来研究函 数y sin x, x R和函数y sin 2x, x R
图像的关系
1 以及函数 y sin x, x R和函数 y sin x, x R图像的关系 . 2
一般地函数 y sin x, x R其中 0且 1 的图像 （ 当 1时） 可以看作把正弦曲线上 所有点的横坐标 缩短
如何作出正弦曲线？
先在直角坐标系里描出 0,0,
π ,1 2
, π,0 ,
3π ,1 2
, 2π,0
这五个点, 然后用光滑曲线将它们连接起来, 就得到它在 , 右平行移动，每次 2π个 0,2π 上的图像, 再将图像向左
单位长度 , 就可以得到正弦函数 .
0
0
π
π 2
2π 3π 4π 3π π 2 2π00 Nhomakorabea1
1
0
利用题目中这两个函数的周期性，我们可以把它们各自 在长度为一个周期的半开半闭区间上的简图向左、右 从而得到它们的简图。 分别扩展，
y
p 2
y sin x, x R
y sin
1 x, x R 2
3p
1
o -1
p 2
p
3p 2
例1 画出函数y 2 sin x, x R , 1 y sin x, x R的简图 2 解 : 这两个函数的周期都是 2π 我们先画出它们在 0,2π上的简图
列表
x
sin x
2 sin x 1 sin x 2
0 0
π 2
π
0
1
0 0
2
1 2
0 2 0 1 0 2 0
2π 1 0
2p
4p
5p
x
y sin 2 x, x R
下面我们一起来研究函 数y sin x, x R和函数y sin 2x, x R
图像的关系
1 以及函数 y sin x, x R和函数 y sin x, x R图像的关系 . 2
一般地函数 y sin x, x R其中 0且 1 的图像 （ 当 1时） 可以看作把正弦曲线上 所有点的横坐标 缩短
函数图象的变换PPT
总结词
水平平移是指函数图像在水平方向上移动一定的距离。
详细描述
水平平移不改变函数的值，只是改变了图像的位置。对于函数y=f(x)，若图像向 右平移a个单位，则新的函数为y=f(x-a)；若图像向左平移a个单位，则新的函 数为y=f(x+a)。
垂直平移
总结词
垂直平移是指函数图像在垂直方向上移动一定的距离。
函数图象的变换
• 函数图象变换概述 • 平移变换 • 伸缩变换 • 翻折变换 • 旋转变换 • 应用实例
01
函数图象变换概述
函数图象变换的定义
01
函数图象变换是指通过平移、伸 缩、翻转等几何变换操作，改变 函数图象的位置、形状和大小。
02
这些变换操作可以通过代数表达 式或矩阵变换来实现，使得函数 图象在坐标系中按照特定的规则 进行移动、旋转和缩放。
详细描述
当函数图像在y轴方向上伸缩时，其形状和大小会发生变化，但x轴上的比例保持不变。例如，将函数y=f(x)的图 像在y轴方向上放大2倍，得到新的函数y=2f(x)。
斜向伸缩
要点一
总结词
斜向伸缩是指同时沿x轴和y轴方向对函数图像进行放大或 缩小。
要点二
详细描述
当函数图像在x轴和y轴方向上同时伸缩时，其形状和大小 会发生变化，x轴和y轴上的比例都会改变。例如，将函数 y=f(x)的图像在x轴方向上放大2倍，在y轴方向上放大3倍 ，得到新的函数y=3f(2x)。
逆时针旋转
总结词
当函数图像按照逆时针方向旋转时，其形状和大小也不会发生变化，同样只是位置发生 了移动。
详细描述
与顺时针旋转相反，当函数图像按照逆时针方向旋转一定的角度时，每个点的坐标同样 会发生变化，但方向是远离原点。同样地，这种变化也可以用三角函数的性质来描述。
水平平移是指函数图像在水平方向上移动一定的距离。
详细描述
水平平移不改变函数的值，只是改变了图像的位置。对于函数y=f(x)，若图像向 右平移a个单位，则新的函数为y=f(x-a)；若图像向左平移a个单位，则新的函 数为y=f(x+a)。
垂直平移
总结词
垂直平移是指函数图像在垂直方向上移动一定的距离。
函数图象的变换
• 函数图象变换概述 • 平移变换 • 伸缩变换 • 翻折变换 • 旋转变换 • 应用实例
01
函数图象变换概述
函数图象变换的定义
01
函数图象变换是指通过平移、伸 缩、翻转等几何变换操作，改变 函数图象的位置、形状和大小。
02
这些变换操作可以通过代数表达 式或矩阵变换来实现，使得函数 图象在坐标系中按照特定的规则 进行移动、旋转和缩放。
详细描述
当函数图像在y轴方向上伸缩时，其形状和大小会发生变化，但x轴上的比例保持不变。例如，将函数y=f(x)的图 像在y轴方向上放大2倍，得到新的函数y=2f(x)。
斜向伸缩
要点一
总结词
斜向伸缩是指同时沿x轴和y轴方向对函数图像进行放大或 缩小。
要点二
详细描述
当函数图像在x轴和y轴方向上同时伸缩时，其形状和大小 会发生变化，x轴和y轴上的比例都会改变。例如，将函数 y=f(x)的图像在x轴方向上放大2倍，在y轴方向上放大3倍 ，得到新的函数y=3f(2x)。
逆时针旋转
总结词
当函数图像按照逆时针方向旋转时，其形状和大小也不会发生变化，同样只是位置发生 了移动。
详细描述
与顺时针旋转相反，当函数图像按照逆时针方向旋转一定的角度时，每个点的坐标同样 会发生变化，但方向是远离原点。同样地，这种变化也可以用三角函数的性质来描述。
直角坐标系中的伸缩变换课件PPT
03 伸缩变换的矩阵表示
二维伸缩变换的矩阵表示
总结词
描述二维平面上的点通过伸缩变换后的坐标变化。
详细描述
在二维直角坐标系中，伸缩变换可以通过一个矩阵来表示。假设原点为 $(x, y)$， 经过伸缩变换后变为 $(x', y')$，则变换矩阵可以表示为
二维伸缩变换的矩阵表示
• $\begin{pmatrix}
02
在直角坐标系中，设原点为 $O(0,0)$，点$P(x,y)$经过伸缩变 换后变为点$P'(x',y')$，则变换公 式为：$x' = kx, y' = ky$，其中 $k$为伸缩系数。
伸缩变换的性质
伸缩变换保持点之间 的距离不变，即 $|OP| = |OP'|$。
伸缩变换可以同时对 x和y进行放大或缩小， 但比例系数必须相同。
伸缩变换的理论研究
01
02
03
理论框架
深入探讨伸缩变换的基本 原理、数学表达和推导过 程，建立完善的理论框架。
性质研究
研究伸缩变换的性质，如 线性、可逆性、连续性和 可微性等，并探讨其在不 同坐标系下的表现。
几何意义
从几何角度解释伸缩变换， 探究其在图形、曲线和曲 面等几何对象上的应用和 表现。
伸缩变换的应用研究
02 伸缩变换在直角坐标系中 的应用
横向伸缩变换
总结词
在直角坐标系中，横向伸缩变换 是指沿x轴方向的伸长或缩短。
详细描述
横向伸缩变换通过乘以一个大于1 的系数来增加x轴上的长度，或者 乘以一个小于1的系数来减小x轴 上的长度。这种变换不会改变点 在y轴上的坐标。
纵向伸缩变换
总结词
纵向伸缩变换是指沿y轴方向的伸长或缩短。
正弦函数的图象和性质课件(共29张PPT)
问题情境 根据正弦函数的定义可知，任意给定一个角α，唯
一确定一个正弦值 sinα.习惯上，我们用x表示角α的弧 度数（自变量）, y 表示因变量，于是正弦函数可记作
y = sinx, x∈R , 其中x表示角的弧度值函数的定义域是实数集 R .
调动思维，探究新知 在在活初初动中中2，，我我们们用用过过““自自然然数数集集””““有有理理数数集集””等等表表述述，，这这里里的的““集集””就就是是集集合合的的简简称称，，那那么么什什么么是是集集合合呢呢？？
情感目标 通过本节课学习，使学生养成乐于学习、勇于探索的良好品质
核心素养
通过思考、讨论等活动，提升学生数学的直观想象、逻辑推理、数据分析、 数学建模的核心素养
创设情境，生成问题 在在活初初动中中1，，我我们们用用过过““自自然然数数集集””““有有理理数数集集””等等表表述述，，这这里里的的““集集””就就是是集集合合的的简简称称，，那那么么什什么么是是集集合合呢呢？？
2．正弦函数的性质 探索研究
观察单位圆中的正弦线（图5-24）或正弦函数的图 象，你发现正弦函数有哪些性质？
调动思维，探究新知 在活初动中2，我们用过“自然数集”“有理数集”等表述，这里的“集”就是集合的简称，那么什么是集合呢？
（1）值域
因为在单位圆中，正弦线的长都小于或等于半径的
长1，所以 sin x 1即-1≤sin x≤1，这就是说，正弦函
数学
基础模块（上册）
第五章 三角函数
5.3.1正弦函数的图象和性质
人民教育出版社
第五章 三角函数 5.3.1 正弦函数的图象和性质
学习目标
知识目标 理解正弦曲线的概念，认识正弦函数的图象及正弦函数图象的研究方法
能力目标
一确定一个正弦值 sinα.习惯上，我们用x表示角α的弧 度数（自变量）, y 表示因变量，于是正弦函数可记作
y = sinx, x∈R , 其中x表示角的弧度值函数的定义域是实数集 R .
调动思维，探究新知 在在活初初动中中2，，我我们们用用过过““自自然然数数集集””““有有理理数数集集””等等表表述述，，这这里里的的““集集””就就是是集集合合的的简简称称，，那那么么什什么么是是集集合合呢呢？？
情感目标 通过本节课学习，使学生养成乐于学习、勇于探索的良好品质
核心素养
通过思考、讨论等活动，提升学生数学的直观想象、逻辑推理、数据分析、 数学建模的核心素养
创设情境，生成问题 在在活初初动中中1，，我我们们用用过过““自自然然数数集集””““有有理理数数集集””等等表表述述，，这这里里的的““集集””就就是是集集合合的的简简称称，，那那么么什什么么是是集集合合呢呢？？
2．正弦函数的性质 探索研究
观察单位圆中的正弦线（图5-24）或正弦函数的图 象，你发现正弦函数有哪些性质？
调动思维，探究新知 在活初动中2，我们用过“自然数集”“有理数集”等表述，这里的“集”就是集合的简称，那么什么是集合呢？
（1）值域
因为在单位圆中，正弦线的长都小于或等于半径的
长1，所以 sin x 1即-1≤sin x≤1，这就是说，正弦函
数学
基础模块（上册）
第五章 三角函数
5.3.1正弦函数的图象和性质
人民教育出版社
第五章 三角函数 5.3.1 正弦函数的图象和性质
学习目标
知识目标 理解正弦曲线的概念，认识正弦函数的图象及正弦函数图象的研究方法
能力目标
平面直角坐标系中的伸缩变换 人教课标版精品课件
课堂小结： （1）掌握平面直角坐标系中的伸缩 变换。
作业： P8 4, 5 预习： 极坐标系（书本P9-P11）
8
6
4
2
-10
-5
-2
-4
5
10
在正弦曲线上任取一点P（x,y）， 保持横坐标x不变，将纵坐标伸长为原 来的3倍，就得到曲线y=3sinx。
设点P（x,y）经变换得到点为P’(x’,y’) x’=x 2 y’=3y
通常把 2 叫做平面直角坐标系中 的一个坐标伸长变换。
（3）怎样由正弦曲线y=sinx得到曲 线y=3sin2x? 写出其坐标变换。
每个人都有自己的精神家园，而对于记忆中的几户人家，我更有着刻骨铭心的情感。 上个世纪六七十年代，在陕西的某城市的郊区一个大院子里住了四家人。一家人姓赵四十岁左右，是一个食堂的采购员；姓李的一家人是个老离休干部，也是一个军人。曾经在解放战争时期受过伤，当时他的腿上留有敌人手榴弹炸的弹片在里头呢；东面的一家姓石，是一个搞电子的工程师；西面一家姓吴，老吴是一个中学教师。 老李一般在家休息，负伤的地方经常疼痛难忍。家里有老婆姓元，大儿子当时工作了，还有两个孩子在读书。老石呢，由于是个工程师专门修理无线电的，厂里人的电器坏了一般都让老石修理，所以一下班吃完饭他就忙着给别人修理电器。老赵由于是个采购员，一天就是给食堂买粮食和各种蔬菜。老吴是个教师一般都是上课，但是还有两个寒暑假期。老吴的家里人口最多，五个儿子一个女儿，加上老两口，一共八口人。
（3）在伸缩变换下，平面直角坐 标系不变，在同一直角坐标系下进行伸 缩变换。
例2、在平面直角坐标系中，求下列方程所 对应的图形经过伸缩变换{x 2x 后的图形。
y 3y (1)、2x 3y 0 (2)、x2 y2 1
人教A版数学选修4-41.1.2平面直角坐标系中的伸缩变换课件
x
1 2
x
y 3y
我们把该式叫做平面直角坐标系中的一个坐标 伸缩变换.
抽定义
定、义 设P(x,y)是平面直角坐标系中任意一点，在变换
伸缩 变换
的作用下，点P(x,y)对应到点 p x, y ，称
为平面直角坐标系中的坐标伸缩变换。
注意
（1） 0, 0
（2）把图形看成点的运动轨迹，平面图形的伸缩变换可以用坐标伸缩 变换得到； （3）在伸缩变换下，平面直角坐标系不变,在同一直角坐标系下进行伸 缩变换。
横坐标缩短为本来的一半
纵坐标伸长为本来的3倍
y 3sin 2x
2 x
探究新知
实际上，这是(1)(2)的“合成”，先保持纵坐标y不变， 1
将横坐标缩为本来的 2 ，在此基础上再保持横坐标x不变， 将纵坐标y伸长为本来的3倍 ”，就可以由正弦曲线y=sinx得 到曲线y=3sin2x.
设P(x，y)是平面直角坐标系中的任意一点，经过上述变 换后变为点 P(x，y)，那么
设P(x，y)是平面直角坐标系中的任意一点，保持横坐标
x不变，将纵坐标y伸长为本来的3倍，得到点 么
P(
x，y)
，那
x x
y
3
y
我们把该式叫做平面直角坐标系中的一个坐标
探究新知
（3）怎样由正弦曲线y=sinx得到曲线y=3sin2x?
y
3 2
y=3sin2x
1
y=sinx
y sin x
O
-1 -2 -3
辨析定义
运用中提升
2 在直角坐标系中，求下列方程所对应的图形经过伸缩变换
x 2x
y
3
y
后的图形。
12x 3y 0 2x2 y2 1
三角函数的左右平移和伸缩变换 比赛课 ppt课件
y=si2n0（20/122x/2+7π/3 ）
0
1
0 -1
7
0
-π/6 1
5π/6
y=sin2x
O -1
π/2
π
x
y=sin(2x+π/3)
图像左平移π/6个单位
y=sin2x
y=sin（2x+π/3）
2020/12/27
=sin2（x+π/6）
8
三、解决问题
例、 y=sinx图像如何变为y=sin（2x+ π/3 )图 像？
4
二、实验探究 探究一、y=sin （x+ π/3） 图像与 y=sin（2x+ π/3 )图像关系
y=sin2x与 y=sin（2x+ π/3 )五个关键点之间
有何关系？
x+ π/3
0
2
3 2
2
x
-π/3 π/6 2π/3 7π/6 5π/3
y=si（ x+π/3） 0
1
0
-1
0
2x+π/3
3
2020/12/27
3
6
二、实验探究
探究二、y=sin2x 图像与y=sin（2x+ π/3 ) 图像关系
y=sin2x与 y=sin（2x+ π/3 )五个关键点之间
有何关系？
2x
0
2
3 2
2
x
0 π/4
π/2 3π/4 π
y=sin2x
0
1
0-1Biblioteka 02x+π/3
0
2
3 2
2
x
-π/6 π/12 π/3 7π/12 5π/6
正弦函数伸缩变换
而得到 . 所以y函 As数 ixn,xR的值[域 -A,A是 ] ，
y y2sixn,xR
2
ysixn,xR
π 1
2
Oπ
p
-1 2
3p
7p
2
Hale Waihona Puke 3p 22p 5p
2
4p x
-2
第五页，课件共11页
y1sinx,xR 2
例 2画出 y s函 i2 x n ,x R 数 y ,si1n x,x R 的简 2
而得到 ,所以y函 si数 nx,xR的值域 1,1是 .
第十一页，课件共11页
列表
x 0 π 2π 3π 4π
X 1x 2
0
π 2
π 3π
2
2π
sin 1 x 2
0
1
0 1 0
第七页，课件共11页
利用题目中这两个函数的周期性，我们可以把它们各自
在长度为一个周期的半开半闭区间上的简图向左、右 分别扩展， 从而得到它们的简图。
y ysixn,xR ysin1x,xR
2
p 1
3p
可以看作把正弦曲所线有上点的横坐缩标短（当 1时）
或伸长 （当0 1时） 到原来的 1 倍 （纵坐标不变 ）
而得到. 所以y函 si数 nx,xR的值域是 1， 1
y ysixn,xR ysin1x,xR
2
p 1
3p
2
op -1 2
p 3p
2
2p
ysi2nx,xR
第九页，课件共11页
4p
第二页，课件共11页
例1 画出函 y数 2sinx,xR,
y1sinx,xR的简图 2
解 : 这两个函数的周期都是 2π 我们先画0出 ,2π上 它的 们简
y y2sixn,xR
2
ysixn,xR
π 1
2
Oπ
p
-1 2
3p
7p
2
Hale Waihona Puke 3p 22p 5p
2
4p x
-2
第五页，课件共11页
y1sinx,xR 2
例 2画出 y s函 i2 x n ,x R 数 y ,si1n x,x R 的简 2
而得到 ,所以y函 si数 nx,xR的值域 1,1是 .
第十一页，课件共11页
列表
x 0 π 2π 3π 4π
X 1x 2
0
π 2
π 3π
2
2π
sin 1 x 2
0
1
0 1 0
第七页，课件共11页
利用题目中这两个函数的周期性，我们可以把它们各自
在长度为一个周期的半开半闭区间上的简图向左、右 分别扩展， 从而得到它们的简图。
y ysixn,xR ysin1x,xR
2
p 1
3p
可以看作把正弦曲所线有上点的横坐缩标短（当 1时）
或伸长 （当0 1时） 到原来的 1 倍 （纵坐标不变 ）
而得到. 所以y函 si数 nx,xR的值域是 1， 1
y ysixn,xR ysin1x,xR
2
p 1
3p
2
op -1 2
p 3p
2
2p
ysi2nx,xR
第九页，课件共11页
4p
第二页，课件共11页
例1 画出函 y数 2sinx,xR,
y1sinx,xR的简图 2
解 : 这两个函数的周期都是 2π 我们先画0出 ,2π上 它的 们简
相关主题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
正弦函数伸缩变 换
复习回顾：
如何作出正弦曲线？
先在直角坐标系里描出
0,0,
π ,1 2
3π π , 0 π ,0 , 2 ,1 ,2 ,
这五个点 , 然后用光滑曲线将它 连接起来 , 就得到 ,再将图像向左 ,右平行移动，每 2 π 个 0,2π 上的图像
3p 2p
5p 2 7p 2π 2p4px
下面我们一起来研究函 数 y sin x ,x R 和函数 y 2 sin x ,x R 1 以及函数 y sin x , x R 和函数 y sin x , x R 图像的关 . 2
1 y sin x ,x R 2
一般地函数 y A sin x , x R 其中 A 0 且 A 1 的图 A1 时 伸长 可以看作把正弦曲线上 所有点的纵坐标 （当 ） A倍（ 横坐标不变 ） 0 A 1 时 ） 到原来的 或缩短 （当
2π 解函数 y sin 2 x , x R 的周期 T 2 我们先画出它在 0 ,π 上的简图
π
3π 4
3π 2
列表
x
X2 x
0 0 0
π 4
π 2
π 2
π
2π
π
sin 2x
1
0 1
0
2 π 1 由于函数 y sin x , x R 的周期 T 1 4π 2
y
p 2
1 y sin x ,x R ysin x ,x R 2
3p
1 o -1
p 2
p
3p 2
2p
4p
5p
x
y sin 2 x , x R
1 函数y sin x, x R的图像 8 与正弦曲线有什么关系 ？
一般地函数 y A sin x , x R 其中 A 0 且 A 1 的图 . A1 时 伸长（ 当 可以看作把正弦曲线上 所有点的纵坐标 ） 0 A 1 时 ） 或缩短 （当 到原来的 A倍 （ 横坐标不变 ） [-A,A] . 而得到. 所以函数 y A sin x ,x R 的值域是
2 函数 y sin x, x R 的周期是什么 ? 3 它的图像与正弦曲线有 什么关系？
一般地函数 y sin x , x R 其中 0 且 1 的图 . 可以看作把正弦曲线上 所有点的横坐标 1 时 缩短 （当 ） 1 或伸长 （当 倍（ 纵坐标不变 ） 0 1 时 ） 到原来的
而得到 ,所以函数 y sin x ,x R 的值域是 1 ,1.
y
p 2
1 y sin x ,x R ysin x ,x R 2
3p
1
o -1
p 2
p
3p 2
2p
4p
5p
x
y sin 2 x , x R
下面我们一起来研究函 数 y sin x ,x R 和函数 y sin 2 x ,x R
图像的关系
1 以及函数 y sin x , x R 和函数 y sin x , x R 图像的关 . 2
[-A,A] ， 而得到. 所以函数 y A sin x ,x R 的值域是
y
π 2
2 1 O -1 -2
y 2 sin x ,x R
3p 2
y sin x ,x R
3p 2p
5p 2 7p 2
π 2
p
4p
x
1 y sin x ,x R 2
1 例 2 画出函数 y sin 2 x , x R, y sin x , x R 的简 2
一般地函数 y sin x , x R 其中 0 且 1 的图 ） 1 时 可以看作把正弦曲线上 所有点的横坐标 缩短（ 当 1 或伸长 （ 当 倍（ 纵坐标不变 ） 0 1 时 ） 到原来的
而得到. 所以函数 y sin x ,x R 的值域是 1 ， 1
我们就先画出它在 0 , 4 π 上的简图
列表
2
x
1 X x 2 1 sin x 2
0 0 0
π 2 π 3π 4 π π 3π π 2 π 2 2
1
0 1
0
利用题目中这两个函数的周期性，我们可以把它们各自 在长度为一个周期的半开半闭区间上的简图向左、右 从而得到它们的简图。 分别扩展，
π 2
3π 2
1 利用函数 y 2 sin x , x R 和 y sin x , x R 的周 , 2 我们可以把它们在 0 , 2 π 上的简图向左 展 从而得到它们的简图
y
π 2
2 1 O -1 -2
y 2 sin x ,x R
3p 2
y sin x ,x R
单位长度 , 就可以得到正弦函数 .
例 1 画出函数 y 2 sin x ,x R , 1 y sin x ,x R 的简图 2
解 : 这两个函数的周期都是 2 π 我们先画出它们在 0 , 2 π 上的简
列表
x
sinx
2sin x
1 sin x 2
0 0 0 0
π 2π 1 0 1 0 2 0 2 0 1 1 0 0 2 2
复习回顾：
如何作出正弦曲线？
先在直角坐标系里描出
0,0,
π ,1 2
3π π , 0 π ,0 , 2 ,1 ,2 ,
这五个点 , 然后用光滑曲线将它 连接起来 , 就得到 ,再将图像向左 ,右平行移动，每 2 π 个 0,2π 上的图像
3p 2p
5p 2 7p 2π 2p4px
下面我们一起来研究函 数 y sin x ,x R 和函数 y 2 sin x ,x R 1 以及函数 y sin x , x R 和函数 y sin x , x R 图像的关 . 2
1 y sin x ,x R 2
一般地函数 y A sin x , x R 其中 A 0 且 A 1 的图 A1 时 伸长 可以看作把正弦曲线上 所有点的纵坐标 （当 ） A倍（ 横坐标不变 ） 0 A 1 时 ） 到原来的 或缩短 （当
2π 解函数 y sin 2 x , x R 的周期 T 2 我们先画出它在 0 ,π 上的简图
π
3π 4
3π 2
列表
x
X2 x
0 0 0
π 4
π 2
π 2
π
2π
π
sin 2x
1
0 1
0
2 π 1 由于函数 y sin x , x R 的周期 T 1 4π 2
y
p 2
1 y sin x ,x R ysin x ,x R 2
3p
1 o -1
p 2
p
3p 2
2p
4p
5p
x
y sin 2 x , x R
1 函数y sin x, x R的图像 8 与正弦曲线有什么关系 ？
一般地函数 y A sin x , x R 其中 A 0 且 A 1 的图 . A1 时 伸长（ 当 可以看作把正弦曲线上 所有点的纵坐标 ） 0 A 1 时 ） 或缩短 （当 到原来的 A倍 （ 横坐标不变 ） [-A,A] . 而得到. 所以函数 y A sin x ,x R 的值域是
2 函数 y sin x, x R 的周期是什么 ? 3 它的图像与正弦曲线有 什么关系？
一般地函数 y sin x , x R 其中 0 且 1 的图 . 可以看作把正弦曲线上 所有点的横坐标 1 时 缩短 （当 ） 1 或伸长 （当 倍（ 纵坐标不变 ） 0 1 时 ） 到原来的
而得到 ,所以函数 y sin x ,x R 的值域是 1 ,1.
y
p 2
1 y sin x ,x R ysin x ,x R 2
3p
1
o -1
p 2
p
3p 2
2p
4p
5p
x
y sin 2 x , x R
下面我们一起来研究函 数 y sin x ,x R 和函数 y sin 2 x ,x R
图像的关系
1 以及函数 y sin x , x R 和函数 y sin x , x R 图像的关 . 2
[-A,A] ， 而得到. 所以函数 y A sin x ,x R 的值域是
y
π 2
2 1 O -1 -2
y 2 sin x ,x R
3p 2
y sin x ,x R
3p 2p
5p 2 7p 2
π 2
p
4p
x
1 y sin x ,x R 2
1 例 2 画出函数 y sin 2 x , x R, y sin x , x R 的简 2
一般地函数 y sin x , x R 其中 0 且 1 的图 ） 1 时 可以看作把正弦曲线上 所有点的横坐标 缩短（ 当 1 或伸长 （ 当 倍（ 纵坐标不变 ） 0 1 时 ） 到原来的
而得到. 所以函数 y sin x ,x R 的值域是 1 ， 1
我们就先画出它在 0 , 4 π 上的简图
列表
2
x
1 X x 2 1 sin x 2
0 0 0
π 2 π 3π 4 π π 3π π 2 π 2 2
1
0 1
0
利用题目中这两个函数的周期性，我们可以把它们各自 在长度为一个周期的半开半闭区间上的简图向左、右 从而得到它们的简图。 分别扩展，
π 2
3π 2
1 利用函数 y 2 sin x , x R 和 y sin x , x R 的周 , 2 我们可以把它们在 0 , 2 π 上的简图向左 展 从而得到它们的简图
y
π 2
2 1 O -1 -2
y 2 sin x ,x R
3p 2
y sin x ,x R
单位长度 , 就可以得到正弦函数 .
例 1 画出函数 y 2 sin x ,x R , 1 y sin x ,x R 的简图 2
解 : 这两个函数的周期都是 2 π 我们先画出它们在 0 , 2 π 上的简
列表
x
sinx
2sin x
1 sin x 2
0 0 0 0
π 2π 1 0 1 0 2 0 2 0 1 1 0 0 2 2