类比探究问题

合集下载

02类比、拓展探究题(解析版)

类比、拓展探究题类比、拓展探究题是近两年中考热门考题，题型的模式基本分为三步：初步尝试、类比发现、深入探究，考查的知识点有：三角形旋转、平行四边形性质、相似、全等、矩形折叠、勾股定理等．此类问题解答往往是层层深入，从特殊到一般，然后是拓展运用．在解题时需要牢牢把握特殊情况、特殊位置下的结论，然后探寻一般情况下是否也成立，最后是类比应用．类比模仿是解决此类问题的重要手段．例1数学活动课上，某学习小组对有一内角为120°的平行四边形ABCD (∠BAD ＝120°)进行探究：将一块含60°的直角三角板如图放置在平行四边形ABCD 所在平面内旋转，且60°角的顶点始终与点C 重合，较短的直角边和斜边所在的两直线分别交线段AB ，AD 于点E ，F (不包括线段的端点)．(1)初步尝试如图①，若AD ＝AB ，求证：①△BCE ≌△ACF ，②AE ＋AF ＝AC ； (2)类比发现如图②，若AD ＝2AB ，过点C 作CH ⊥AD 于点H ，求证：AE ＝2FH ； (3)深入探究如图③，若AD ＝3AB ，探究得AE ＋3AFAC的值为常数t ，则t ＝________．例题分层分析(1)①先证明△ABC ，△ACD 都是________三角形，再证明∠BCE ＝________，即可解决问题． ②根据①的结论得到________，由此可证明．(2)设DH ＝x ，由题意，可得CD ＝________，CH ＝________(用含x 的代数式表示)，由△ACE ∽△HCF ，得AE FH ＝AC CH，由此即可证明．(3)如图③，过点C 作CN ⊥AD 于N ，CM ⊥BA ，交BA 的延长线于点M ，CM 与AD 交于点H .先证明△CFN ∽△CEM ，得CN CM ＝FN EM ，由AB ·CM ＝AD ·CN ，AD ＝3AB ，推出CM ＝3CN ，所以CN CM ＝FN EM ＝13，设CN ＝a ，FN＝b ，则CM ＝3a ，EM ＝3b ，想办法求出AC ，AE ＋3AF 即可解决问题．对应练习：我们定义：有一组邻角相等的凸四边形叫做“等邻角四边形”．(1)概念理解请你根据上述定义举一个等邻角四边形的例子； (2)问题探究如图①，在等邻角四边形ABCD 中，∠DAB ＝∠ABC ，AD ，BC 的中垂线恰好交于AB 边上一点P ，连结AC ，BD ，试探究AC 与BD 的数量关系，并说明理由；(3)应用拓展如图②，在Rt △ABC 与Rt △ABD 中，∠C ＝∠D ＝90°，BC ＝BD ＝3，AB ＝5，将Rt △ABD 绕着点A 顺时针旋转角α(0°＜∠α＜∠BAC )得到Rt △AB ′D ′(如图③)，当凸四边形AD ′BC 为等邻角四边形时，求出它的面积．解题方法点析(1)矩形或正方形邻角相等，满足“等邻角四边形”的条件；(2)连结PD，PC，根据PE，PF分别为AD，BC的垂直平分线，可得到PA＝________，PB＝________，∠DAP＝________＝∠ABC＝________，从而可得∠APC＝∠DPB，利用SAS可证得△APC≌△DPB，即可得到AC＝BD.(3)分两种情况考虑：(i)当∠AD′B＝∠D′BC时，延长AD′，CB交于点E，由S四边形ACBD′＝S△ACE－S△BED′，求出四边形ACBD′的面积；(ii)当∠D′BC＝∠ACB＝90°时，过点D′作D′E⊥AC于点E，由S四边形ACBD′＝S△AED′＋S矩形ECBD′，求出四边形ACBD′的面积即可．课后练习：1．【操作发现】如图，在边长为1个单位长度的小正方形组成的网格中，△ABC的三个顶点均在格点上．(1)请按要求画图：将△ABC绕点A按顺时针方向旋转90°，点B的对应点为B′，点C的对应点为C′，连结BB′；(2)在(1)所画图形中，∠AB′B＝________．【问题解决】如图，在等边三角形ABC中，AC＝7，点P在△ABC内，且∠APC＝90°，∠BPC＝120°，求△APC的面积．小明同学通过观察、分析、思考，对上述问题形成了如下想法：想法一：将△APC绕点A按顺时针方向旋转60°，得到△AP′B，连结PP′，寻找PA，PB，PC三条线段之间的数量关系；想法二：将△APB绕点A按逆时针方向旋转60°，得到△AP′C′，连结PP′，寻找PA，PB，PC三条线段之间的数量关系．……请参考小明同学的想法，完成该问题的解答过程．(―种方法即可)【灵活运用】如图，在四边形ABCD中，AE⊥BC，垂足为E，∠BAE＝∠ADC，BE＝CE＝2，CD＝5，AD＝kAB(k为常数)，求BD的长(用含k的式子表示)．2．问题呈现：如图①，点E，F，G，H分别在矩形ABCD的边AB，BC，CD，DA上，AE＝DG.求证：2S四边形EFGH＝S矩形ABCD.(S表示面积)实验探究：某数学实验小组发现：若图①中AH≠BF，点G在CD上移动时，上述结论会发生变化．分别过点E，G 作BC边的平行线，再分别过点F，H作AB边的平行线，四条平行线分别相交于点A1，B1，C1，D1，得到矩形A1B1C1D1.如图②，当AH＞BF时，若将点G向点C靠近(DG>AE)，经过探索，发现：2S四边形EFGH＝S矩形ABCD＋S矩形A1B1C1D1.如图③，当AH＞BF时，若将点G向点D靠近(DG<AE)，请探索S四边形EFGH、S矩形ABCD与S矩形A1B1C1D1之间的数量关系，并说明理由．迁移应用：请直接应用“实验探究”中发现的结论解答下列问题．(1)如图，点E，F，G，H分别是面积为25的正方形ABCD各边上的点，已知AH>BF，AE>DG，S四边形EFGH ＝11，HF＝29，求EG的长．(2)如图，在矩形ABCD中，AB＝3，AD＝5，点E，H分别在边AB，AD上，BE＝1，DH＝2，点F，G分别是边BC，CD上的动点，且FG＝10，连结EF，HG，请直接写出四边形EFGH面积的最大值．3.【探索发现】如图①是一张直角三角形纸片，∠B＝90°，小明想从中剪出一个以∠B为内角且面积最大的矩形，经过多次操作发现，当沿着中位线DE，EF剪下时，所得的矩形的面积最大．随后，他通过证明验证了其正确性，并得出：矩形的最大面积与原三角形面积的比值为________．【拓展应用】如图②，在△ABC中，BC＝a，BC边上的高AD＝h，矩形PQMN的顶点P，N分别在边AB，AC上，顶点Q，M在边BC上，则矩形PQMN面积的最大值为________．(用含a，h的代数式表示) 【灵活应用】如图③，有一块“缺角矩形”ABCDE，AB＝32，BC＝40，AE＝20，CD＝16，小明从中剪出了一个面积最大的矩形(∠B为所剪出矩形的内角)，求该矩形的面积．【实际应用】如图，现有一块四边形的木板余料ABCD，经测量AB＝50 cm，BC＝108 cm，CD＝60 cm，且tan B＝tan C＝43，木匠徐师傅从这块余料中裁出了顶点M，N在边BC上且面积最大的矩形PQMN，求该矩形的面积．答案与解析【例1】【解答】解：（1）AE+AF＝AC；理由如下：∵四边形ABCD是平行四边形，∠BAD＝120°，∴∠D＝∠B＝60°，∵四边形ABCD是菱形，∴AD＝AB，∴△ABC，△ACD都是等边三角形，∴∠B＝∠CAD＝60°，∠ACB＝60°，BC＝AC，∵∠ECF＝60°，∴∠BCE+∠ACE＝∠ACF+∠ACE＝60°，∴∠BCE＝∠ACF，在△BCE和△ACF中，，∴△BCE≌△ACF（ASA）．∴BE＝AF，∴AE+AF＝AE+BE＝AB＝AC；故答案为：AE+AF＝AC；（2）设DH＝x，由由题意，CD＝2x，CH＝，∴AD＝2AB＝4x，∴AH＝AD﹣DH＝3x，∵CH⊥AD，∴AC＝＝，∴AC2+CD2＝AD2，∴∠ACD＝90°，∴∠BAC＝∠ACD＝90°，∴∠CAD＝30°，∴∠ACH＝60°，∵∠ECF＝60°，∴∠HCF＝∠ACE，∴△ACE∽△HCF，∴，（3），理由如下：如图3中，作CN⊥AD于N，CM⊥BA于M，CM与AD交于点H．∵∠ECF+∠EAF＝180°，∴∠AEC+∠AFC＝180°，∵∠AFC+∠CFN＝180°，∴∠CFN＝∠AEC，∵∠M＝∠CNF＝90°，∴△CFN∽△CEM，∴，∵AB•CM＝AD•CN，AD＝4AB，∴CM＝4CN，∴，设CN＝a，FN＝b，则CM＝4a，EM＝4b，∵∠MAH＝60°，∠M＝90°，∴∠AHM＝∠CHN＝30°，∴HC＝2a，HM＝2a，HN＝a，∴AM＝，AH＝，∴AC＝＝，AE+4AF＝（EM﹣AM）+4（AH+HN﹣FN）＝EM﹣AM+4AH+4HN﹣4FN＝4AH+4HN﹣AM＝，∴．∴t＝，故答案为：．【对应练习】【解答】解：（1）矩形或正方形；（2）AC＝BD，理由为：连接PD，PC，如图1所示：∵PE是AD的垂直平分线，PF是BC的垂直平分线，∴P A＝PD，PC＝PB，∴∠P AD＝∠PDA，∠PBC＝∠PCB，∴∠DPB＝2∠P AD，∠APC＝2∠PBC，即∠P AD＝∠PBC，∴∠APC＝∠DPB，∴△APC≌△DPB（SAS），∴AC＝BD；（3）分两种情况考虑：（i）当∠AD′B＝∠D′BC时，延长AD′，CB交于点E，如图3（i）所示，∴∠ED′B＝∠EBD′，∴EB＝ED′，设EB＝ED′＝x，由勾股定理得：42+（3+x）2＝（4+x）2，解得：x＝4.5，过点D′作D′F⊥CE于F，∴D′F∥AC，∴△ED′F∽△EAC，∴＝，即＝，解得：D′F＝，∴S△ACE＝AC×EC＝×4×（3+4.5）＝15；S△BED′＝BE×D′F＝×4.5×＝，则S四边形ACBD′＝S△ACE﹣S△BED′＝15﹣＝10；（ii）当∠D′BC＝∠ACB＝90°时，过点D′作D′E⊥AC于点E，如图3（ii）所示，∴四边形ECBD′是矩形，∴ED′＝BC＝3，在Rt△AED′中，根据勾股定理得：AE＝＝，∴S△AED′＝AE×ED′＝××3＝，S矩形ECBD′＝CE×CB＝（4﹣）×3＝12﹣3，则S四边形ACBD′＝S△AED′+S矩形ECBD′＝+12﹣3＝12﹣．【课后练习】1.【解答】解：【操作发现】（1）如图所示，△AB′C′即为所求；（2）连接BB′，将△ABC绕点A按顺时针方向旋转90°，∴AB＝AB′，∠B′AB＝90°，∴∠AB′B＝45°，故答案为：45°；【问题解决】如图②，∵将△APB绕点A按逆时针方向旋转60°，得到△AP′C′，∴△APP′是等边三角形，∠AP′C＝∠APB＝360°﹣90°﹣120°＝150°，∴PP′＝AP，∠AP′P＝∠APP′＝60°，∴∠PP′C＝90°，∠P′PC＝30°，∴PP′＝PC，即AP＝PC，∵∠APC＝90°，∴AP2+PC2＝AC2，即（PC）2+PC2＝72，∴PC＝2，∴AP＝，∴S△APC＝AP•PC＝7；【灵活运用】如图③中，∵AE⊥BC，BE＝EC，∴AB＝AC，将△ABD绕点A逆时针旋转得到△ACG，连接DG．则BD＝CG，∵∠BAD＝∠CAG，∴∠BAC＝∠DAG，∵AB＝AC，AD＝AG，∴∠ABC＝∠ACB＝∠ADG＝∠AGD，∴△ABC∽△ADG，∵AD＝kAB，∴DG＝kBC＝4k，∵∠BAE+∠ABC＝90°，∠BAE＝∠ADC，∴∠ADG+∠ADC＝90°，∴∠GDC＝90°，∴CG＝＝．∴BD＝CG＝．2.【解答】问题呈现：证明：如图1中，∵四边形ABCD是矩形，∴AB∥CD，∠A＝90°，∵AE＝DG，∴四边形AEGD是矩形，∴S△HGE＝S矩形AEGD，同理S△EGF＝S矩形BEGC，∴S四边形EFGH＝S△HGE+S△EFG＝S矩形ABCD．实验探究：结论：2S 四边形EFGH＝S矩形ABCD﹣．理由：∵＝，＝，＝，＝，∴S 四边形EFGH＝+++﹣，∴2S 四边形EFGH＝2+2+2+2﹣2，∴2S 四边形EFGH＝S矩形ABCD﹣．迁移应用：解：（1）如图4中，∵2S四边形EFGH＝S矩形ABCD﹣．∴＝25﹣2×11＝3＝A1B1•A1D1，∵正方形的面积为25，∴边长为5，∵A1D12＝HF2﹣52＝29﹣25＝4，∴A1D1＝2，A1B1＝，∴EG2＝A1B12+52＝，∴EG＝．（2）∵2S 四边形EFGH＝S矩形ABCD+．∴四边形A1B1C1D1面积最大时，四边形EFGH的面积最大．①如图5﹣1中，当G与C重合时，四边形A1B1C1D1面积最大时，四边形EFGH的面积最大．此时矩形A1B1C1D1面积＝1•（﹣2）＝，∴2S 四边形EFGH＝S矩形ABCD+＝15+（﹣2）＝13+，∴S四边形EFGH＝②如图5﹣2中，当G与D重合时，四边形A1B1C1D1面积最大时，四边形EFGH的面积最大．此时矩形A1B1C1D1面积＝2•1＝2，∴2S 四边形EFGH＝S矩形ABCD+＝15+2＝17，∴S四边形EFGH＝8.5∵8.5＞，∴四边形EFGH的面积最大值8.5．3.【解答】解：【探索发现】设EF＝x，ED＝y，∵EF、ED为△ABC中位线，∴ED∥AB，EF∥BC，EF＝BC，ED＝AB，∴AB＝2ED＝2y，BC＝2EF＝2x，又∠B＝90°，∴四边形FEDB是矩形，则＝＝＝，故答案为：；【拓展应用】设PN＝b，∵PN∥BC，∴△APN∽△ABC，∴，∵BC＝a，BC边上的高AD＝h，∴，PQ＝，∴S＝b•PQ＝＝﹣+bh，∴S的最大值为：＝；则矩形PQMN面积的最大值为；故答案为：；【灵活应用】如图1，延长BA、DE交于点F，延长BC、ED交于点G，延长AE、CD交于点H，取BF中点I，FG 的中点K，由题意知四边形ABCH是矩形，∵AB＝32，BC＝40，AE＝20，CD＝16，∴EH＝20、DH＝16，∴AE＝EH、CD＝DH，在△AEF和△HED中，∵，∴△AEF≌△HED（ASA），∴AF＝DH＝16，同理△CDG≌△HDE，∴CG＝HE＝20，∴BI＝＝24，∵BI＝24＜32，∴中位线IK的两端点在线段AB和DE上，过点K作KL⊥BC于点L，由【探索发现】知矩形的最大面积为×BG•BF＝×（40+20）×（32+16）＝720，答：该矩形的面积为720；【实际应用】如图2，延长BA、CD交于点E，过点E作EH⊥BC于点H，∵tan B＝，设EH＝4x，BH＝3x，∵tan C＝2＝，∴CH＝2x，∵BC＝BH+CH＝105＝3x+2x，x＝21，∴BH＝63，CH＝42，EH＝84，由勾股定理得：BE＝＝＝105，CE＝＝＝42，∵AB＝60，∴AE＝45，∴BE的中点Q在线段AB上，∵CD＝70，∴CE的中点P在线段CD上，∴中位线PQ的两端点在线段AB、CD上，由【拓展应用】知，矩形PQMN的最大面积为BC•EH＝＝2205cm2，答：该矩形的面积为2205cm2．。

类比探究问题(含答案)

类比探究问题（讲义）➢ 课前预习1. 类比探究是一类共性条件与特殊条件相结合，由特殊情形到一般情形（或由简单情形到复杂情形）逐步深入，解决思想方法一脉相承的综合性题目，常以几何综合题为主．2. 解决类比探究问题的一般方法：（1）根据题干条件，结合_______________先解决第一问；（2）用解决_______的方法类比解决下一问，整体框架照搬．整体框架照搬包括_________________，________________， _________________．3. 用铅笔做讲义第1，2题，并将计算、演草保留在讲义上，先看知识点睛，再做题，思路受阻时（某个点做了2~3分钟）重复上述动作，若仍无法解决，课堂重点听．➢ 知识点睛1. 类比探究属于几何综合题，类比（__________，___________，___________）是解决此问题的主要方法，做好类比需要把握变化过程中的____________． 2. 类比探究问题中常见结构举例①旋转结构AB=AC DCD'A②中点结构ABCE MDA BMCNM A（类）倍长中线平行夹中点中位线➢ 精讲精练1. 原题：如图1，点E ，F 分别在正方形ABCD 的边BC ，CD 上，∠EAF =45°，连接EF ，易证EF =BE +DF ．图1B C DEF A（1）类比引申：如图2，在四边形ABCD 中，AB =AD ，∠BAD =90°，∠B +∠D =180°，点E ，F 分别在边BC ，CD 上，∠EAF =45°，连接EF ，则原题中的结论是否仍然成立？请说明理由．AF E DCB 图2（2）联想拓展：如图3，在△ABD 中，∠BAD =90°，AB =AD ，点E ，F 均在边BD 上，且∠EAF =45°．猜想EF ，BE ，DF 之间满足的数量关系，并写出推理过程．图3B DEF A2. 在△ABC 中，∠ACB =90°，∠A < 45°，O 为AB 的中点，一个足够大的三角板的直角顶点与点O 重合，一边OE 经过点C ，另一边OD 与AC 交于点M ．（1）如图1，当∠A =30°时，求证：222MC AM BC =+．（2）如图2，当∠A ≠30°时，（1）中的结论是否仍然成立？如果成立，请说明理由；如果不成立，请写出你认为正确的结论，并说明理由．（3）如图3，将三角板ODE 绕点O 旋转，若直线OD 与线段AC 的延长线相交于点M ，直线OE 与线段CB 的延长线相交于点N ，连接MN ，则MN 2=AM 2+BN 2成立吗？请说明理由．N图3E BC O MD A图1EBCOMD AADM OCBE图23.已知P是Rt△ABC的斜边AB上一动点（不与点A，B重合），分别过点A，B向直线C P作垂线，垂足分别为点E，F，Q为斜边AB的中点．（1）如图1，当点P与点Q重合时，AE与BF的位置关系是___________，QE与QF的数量关系是______________．图1B CQ(P)EFA（2）如图2，当点P不与点Q重合时，试判断QE与QF的数量关系，并给予证明．A FEPQCB 图2（3）如图3，当点P在线段BA（或AB）的延长线上时，（2）中的结论是否仍然成立？请画出图形并给予证明．4.某校活动小组在作三角形的拓展图形，研究其性质时，经历了如下过程．（1）操作发现：在等腰△ABC中，AB=AC，分别以AB和AC为斜边，向△ABC 的外侧作等腰直角三角形，如图1所示，其中DF⊥AB于点F，EG⊥AC于点G，M是BC的中点，连接MD和ME，则下列结论正确的是___________．（填写序号）①12AF BA AG==；②MD=ME；③MD⊥ME．（2）数学思考：在任意△ABC中，分别以AB和AC为斜边，向△ABC的外侧作等腰直角三角形，如图2所示，M是BC的中点，连接MD和ME，则MD与ME具有怎样的数量关系和位置关系？请给出证明．（3）类比探究：在任意△ABC中，仍分别以AB和AC为斜边，向△ABC的内侧作等腰直角三角形，如图3所示，M是BC的中点，连接MD和ME，则△MED是_____________三角形．图1CD EF GMBA图2C DEMA图3AB CMDE【参考答案】➢课前预习2.（1）分支条件（2）第一问；照搬字母，照搬辅助线，照搬思路➢知识点睛1.类比字母，类比辅助线，类比思路，不变特征➢精讲精练1.（1）原题中的结论仍成立，理由略提示：延长CD到点G，使DG=BE，证明△ABE≌△ADG（SAS）；再证明△AEF ≌△AGF（SAS），得EF=FG=BE+DG。

八年级数学类比探究(讲义及答案).

类比探究（讲义）➢知识点睛1.类比：就是由两个对象的某些相同或相似的性质，推断它们在其他性质上也有可能相同或相似的一种推理形式．探究：是指学生在学习情境中通过观察、阅读，发现问题，搜集数据，形成解释，获得答案并进行交流、检验、探究性学习．学习过程的本质类比与探究．2.类比探究问题的处理思路（1）根据题干条件，结合分支条件先解决第一问；（2）整体类比第一问，迁移解决下一问．①类比是解决类比探究问题的第一原则，如类比字母、类比辅助线、类比思路；②对比前后条件变化，寻找并利用不变特征，考虑相关几何结构解决问题．3.类比探究问题中的常见特征举例手拉手模型：条件：AB=AC，AD=AE，∠BAC=∠DAE结论：△ABD≌△ACE➢精讲精练1.在△ABC 中，AB=AC，D 是直线BC 上一点，以AD 为一条边在AD 的右侧作△ADE，使AE=AD，∠DAE=∠BAC，连接CE．（1）如图1，当点D 在线段BC 上时，求证：BD=CE；（2）如图2，当点D 在线段BC 的延长线上时，求证：BD=CE；（3）如图3，当点D 在线段CB 的延长线上时，上述结论还成立吗？请证明你的猜想．2.（1）操作发现：如图1，D 是等边△ABC 边BA 上一动点（点D 与点B 不重合），连接DC，以DC 为边在BC 上方作等边△DCF，连接AF．你能发现线段AF 与BD 之间的数量关系吗？并证明你发现的结论．（2）类比猜想：如图2，当动点D 运动至等边△ABC 边BA 的延长线上时，其他作法与（1）相同，猜想AF 与BD 在（1）中的结论是否仍然成立？若成立，请证明．（3）深入探究：①如图3，当动点D 在等边△ABC 边BA 上运动时（点D 与点B 不重合），连接DC，以DC 为边在BC 上方、下方分别作等边△DCF 和等边△DCF′，连接AF，BF′，探究AF，BF′与AB 有何数量关系？并证明你探究的结论．②如图4，当动点D 在等边△ABC 边BA 的延长线上运动时，其他作法与图3相同，①中的结论是否成立？若不成立，是否有新的结论？并证明你得出的结论．33.在Rt△ABC 中，∠ACB=90°，CA=CB，点D 是直线AB 上的一点，连接CD，将线段CD 绕点C 逆时针旋转90°，得到线段CE，连接EB．（1）操作发现如图1，当点 D 在线段AB 上时，请你直接写出AB 与BE 的位置关系为；线段BD，AB，EB 的数量关系为．（2）猜想论证当点D 在直线AB 上运动时，如图2，是点D 在射线AB 上，如图3，是点D 在射线BA 上，请你写出这两种情况下，线段BD，AB，EB 的数量关系，并对图2 的结论进行证明．（3）拓展延伸若AB=5，BD=7，请你直接写出△ADE 的面积．4.（1）如图1，两个等腰三角形△ABC 和△ADE 中，∠BAC=∠DAE，AB=AC，AE=AD，连接BD，CE，则线段BD 和CE 的数量关系是；（2）如图2，两个等腰直角三角形△ABC 和△ADE 中，AB=AC，AE=AD，∠BAC=∠DAE=90°，连接BD，CE，两线交于点P，请判断线段BD 和CE 的数量关系和位置关系，并说明理由；（3）如图3，已知△ABC，请完成作图：以AB，AC 为边分别向△ABC 外作等边△ABD 和等边△ACE，连接BE，CD，两线交于点P，并直接写出线段BE 和CD 的数量关系及∠PBC+∠PCB 的度数．【参考答案】1. （1）证明略；（2）证明略；（3）成立，BD=CE，证明略．2.（1）AF=BD，证明略；（2）成立，AF=BD，证明略；（3）①AB=AF+BF′，证明略；②不成立，AB=AF-BF′，证明略．3.（1）AB⊥BE，AB=BE+BD；（2）AB=BE-BD，证明略；（3）△ADE 的面积为72 或2．4. （1）BD=CE；（2）BD=CE，BD⊥CE，证明略；（3）BE=CD，∠PBC+∠PCB=60°．类比探究（习题）➢已知，在△ABC 中，∠BAC=90°，AB=AC，点D 为直线BC 上一动点（点D 不与点B，C 重合）．以AD 为边作正方形ADEF，AD=AF，∠DAF=90°，连接CF．•如图1，当点D 在线段BC 上时，求证：CF+CD=BC；•如图2，当点D 在线段BC 的延长线上时，其他条件不变，请直接写出CF，BC，CD 三条线段之间的关系；•如图3，当点D 在线段BC 的反向延长线上时，且点A，F 分别在直线BC 的两侧，其他条件不变，求CF，BC，CD 三条线段之间的关系．➢如图1，点C 在线段AB 上（点C 不与A，B 重合），分别以AC，BC 为边在AB 同侧作等边三角形ACD 和等边三角形BCE，连接AE，BD 交于点P．4.观察猜想：①AE 与BD 的数量关系为；②∠APD 的度数为．5.数学思考：如图2，当点C 在线段AB 外时，（1）中的结论①，②是否仍然成立？若成立，请给予证明；若不成立，请你写出正确结论再给予证明．6.拓展应用：如图3，点E 为四边形ABCD 内一点，且满足∠AED=∠BEC=90°，AE=DE，BE=CE，对角线AC，BD 交于点P，AC=10，则四边形ABCD 的面积为．【参考答案】1. （1）证明略；5.CF-CD=BC；6.CD-CF=BC，证明略．2. （1）①AE=BD；②60°；（2）成立，AE=BD，∠APD=60°，证明略；（3）50．。

类比探究问题

（3）解决问题
如图3，在正方形ABCD中，CD= 2．若点P满足PD=1，且∠BPD=90°，
请直接写出点A到BP的距离．
C
A
D
E
B
C
图3
M D
A
B
图2
3．（3）解决问题如图3，在正方形ABCD中，CD= 2．若点P满足PD=1，且∠BPD=90°，请直接写出点A到BP的距离．
图3
图2
3．（3）解决问题如图3，在正方形ABCD中，CD= 2．若点P满足PD=1，且∠BPD=90°，请直接写出点A到BP的距离．
（2）问题解决
A
保持（1）中条件不变，若DC=2DF，
AD
求 AB 的值；（3）类比探求
2
保持（1）中条件不变，若DC=nDF，
求 AD 的值．
AB
B
E
D
1
1 F2
2G
1
C
中考类比探究出题历史
【2010年河南中考试题】
（1）操作发现
如图，矩形ABCD中，E是AD的中点，将△ABE沿BE折叠后得到△GBE，且点G在矩形ABCD内部．小明将BG延长交DC于点F，认为GF=DF，你同意吗？说明理由．
BD
BD
A
A
E
B
D
C
B
图1
C
D
E
中考类比探究出题历史
【2015年河南中考试题】
如图1，在Rt△ABC中，∠B=90°，BC=2AB=8，点D，E分别是边BC，
AC的中点，连接DE．将△EDC绕点C按顺时针方向旋转，记旋转角为α．
（1）问题发现
①当α=0°时，AE ______；②当α=180°时， AE ______．

类比探究专题

类比探究专题例1 如图1，在等腰直角△ABC 和等腰直角△CDE 中,CD>BC ，点C ，B ，D 在同一直线上，M 是AE 的中点，易证MD ⊥MB ，MD=MB ．（1）如图2,将图1中的△CDE 绕点C 顺时针旋转45°，使△CDE 的斜边CE 恰好与△ABC 的边BC 垂直，题干中的其他条件不变,则上述结论是否仍然成立？（2）将图2中的△ABC 绕点C 逆时针旋转大于0°且小于45°的角，如图3所示，请直接写出你的结论．MEDCBA图2ABC DE M图1图3ABCDEM例2 如图1,在ABC △中，AC BC =,120C ∠=︒,D 在BC 边上。

BDE △为等边三角形,连接AE ,F 为AE 中点，连CF DF ，。

⑴请直接写出CF DF 、的关系，不必说明理由;⑵若将图1中的DBE △绕点B 顺时针旋转90︒，其它条件不变，请作出相应图形，并直接给出结论，不必说明理由。

⑶将图中的DBE △绕点B 顺时针旋转α（0°＜α＜60°），其它条件不变，如图2，试回答⑴中的结论是否成立?并说明理由。

图1AB C DEFFDCBAE图2例3 （1）操作发现：如图1，在矩形ABCD 中,E 是BC 的中点，将△ABE 沿AE 折叠后得到△AFE ，点F 在矩形ABCD 内部，延长AF 交CD 于点G ．猜想线段GF 与GC 有何数量关系？并证明你的结论．（2）类比探究：如图2,将（1)中的矩形ABCD 改为平行四边形，其它条件不变，（1）中的结论是否仍然成立？请说明理由．图1 图2例4 已知：如图所示，直线MA NB MAB ∠∥，与NBA ∠的平分线交于点C ,过点C 作一条直线l 与两条直线MA NB 、分别相交于点D E 、．（1）如图1所示，当直线l 与直线MA 垂直时,猜想线段AD BE AB 、、之间的数量关系，请直接写出结论,不用证明；（2）如图2所示，当直线l 与直线MA 不垂直且交点D E 、都在AB 的同侧时，（1）中的结论是否成立?如果成立，请证明;如果不成立，请说明理由；(3）当直线l 与直线MA 不垂直且交点D E 、在AB 的异侧时，（1）中的结论是否仍然成立?如果成立，请说明理由；如果不成立，那么线段AD BE AB 、、之间还存在某种数量关系吗？如果存在，请直接写出它们之间的数量关系．ABMNCC NMBAABCDEMNl lNMEDCB A图1 图2 备用图备用图例5 在△ABC 中，∠A ＝90°，点D 在线段BC 上，∠EDB ＝12∠C,BE ⊥DE,垂足为E ，DE 与AB 相交于点F ．(1）当AB ＝AC 时（如图1）， ①∠EBF ＝_______°；②探究线段BE 与FD 的数量关系,并加以证明；(2）当AB ＝kAC 时(如图2），求BEFD 的值（用含k 的式子表示）．图1 图2例6 如图1，在Rt △ABC 中,∠ACB=90°，CD ⊥AB ，垂足为D,点E 在AC 上，BE 交CD 于点G ，EF ⊥BE 交AB 于点F,AC=mBC ，CE=nEA （m ，n 为实数).试探究线段EF 与EG 的数量关系．(1）如图2，当m=1，n=1时,求EF 与EG 的数量关系．（2）如图3，当m=1，n 为任意实数时，求EF 与EG 的数量关系．（3）如图1，当m ，n 均为任意实数时,求EF 与EG 的数量关系．C EFD A B G图1CEFD A G 图2EFD ABGC 图3例7 在等腰直角三角形ABC 中,∠BAC=90°，AB=AC ，直线MN 过点A 且MN ∥BC ．以点B 为一锐角顶点作Rt △BDE ，∠BDE=90°，且点D 在直线MN 上（不与点A 重合）．如图1,DE 与AC 交于点P ，易证：BD=DP ． (1）在图2中，DE 与CA 的延长线交于点P,则BD=DP 是否成立？如果成立，请给予证明；如果不成立,请说明理由．（2）在图3中，DE 与AC 的延长线交于点P ，BD 与DP 是否相等？请直接写出你的结论，无需证明．图1ADNPECBM图2M BCEPNDA图3A D NPECBM例8 如图1，在Rt △ABC 中,∠BAC=90°，AD ⊥BC 于点D ，点O 是AC 边上一点，连接BO ，交AD 于点F ，OE ⊥OB 交BC 于点E ．(1）求证：ABF COE △∽△；（2）如图2,当O 为AC 边中点，2AC AB =时,求OFOE 的值;（3）如图3，当O 为AC 边中点，AC nAB =时，请直接写出OFOE 的值．DEO CFBA图2AEO D FB图3AED FB图1例9 如图1，已知∠MAN=120°,AC 平分∠MAN ，∠ABC=∠ADC=90°，可以证明：①DC=BC;②AC = AB+AD ．（1）如图2，把题干中的条件“∠ABC=∠ADC=90°”改为∠ABC+∠ADC=180°，其他条件不变,证明结论①和结论②仍然成立．（2）如图3,如果D 在AM 的反向延长线上，把题干中的条件“∠ABC=∠ADC=90°”改为∠ABC=∠ADC ，其他条件不变，结论①和②是否仍然成立？成立，请证明;不成立，请说明理由．图1A BCDM图2NMDCB A图3NMDCB A例10 如图,在等边三角形ABC 中，点D 在直线BC 上，连接AD,作∠ADN=60°,直线DN 交射线AB 于点E ，过点C 作CF ∥AB 交直线DN 于点F ．（1）当点D 在线段BC 上，∠NDB 为锐角时，如图1,求证：CF+BE=CD ．（提示：过点F 作FM ∥BC 交射线AB 于点M ）（2）当点D 在线段BC 的延长线上，∠NDB 为锐角时，如图2；当点D 在线段CB 的延长线上，∠NDB 为钝角时，如图3，请分别写出线段CF ，BE,CD 之间的数量关系，不需要证明．（3）在（2）的条件下，若∠ADC=30°，43ABC S △,则BE=_________，CD=________．图1N MFEDCB ADCABFEN图2例11已知，△ABC 为等边三角形，点D 为直线BC 上一动点（点D 不与B 、C 重合）．以AD 为边作菱形ADEF ，使∠DAF=60°，连接CF ．（1）如图1，当点D 在边BC 上时， ①求证：∠ADB=∠AFC ；②请直接判断结论∠AFC=∠ACB ＋∠DAC 是否成立；(2）如图2，当点D 在边BC 的延长线上时，其他条件不变,结论∠AFC=∠ACB ＋∠DAC 是否成立？请写出∠AFC 、∠ACB 、∠DAC 之间存在的数量关系，并写出证明过程；（3)如图3,当点D 在边CB 的延长线上时，且点A 、F 分别在直线BC 的异侧，其他条件不变，请补全图形，并直接写出∠AFC 、∠A CB 、∠DAC 之间存在的等量关系．AA FFEDC BA图1 图2 图3例12(1)阅读理解：课外兴趣小组活动时，老师提出了如下问题：D CABFEN图3如图1，△ABC中，若AB=5，AC=3，求BC边上的中线AD的取值范围．小明在组内经过合作交流，得到了如下的解决方法：延长AD到E，使得DE=AD，再连接BE（或将△ACD 绕点D逆时针旋转180°得到△EBD），把AB、AC 、2AD集中在△ABE中，利用三角形的三边关系可得2＜AE＜8，则1＜AD＜4．感悟：解题时，条件中若出现“中点”“中线”字样，可以考虑构造以中点为对称中心的中心对称图形,把分散的已知条件和所求证的结论集中到同一个三角形中．(2)问题解决：受到（1）的启发，请你证明下面命题：如图2，在△ABC中,D是BC边上的中点，DE⊥DF，DE交AB于点E，DF交AC于点F，连接EF．①求证:BE+CF＞EF；②若∠A=90°,探索线段BE、CF、EF之间的等量关系，并加以证明．（3）问题拓展：如图3，在四边形ABDC中，∠B+∠C=180°,DB=DC,∠BDC=120°，以D为顶点作一个60°角，角的两边分别交AB、AC于E、F两点,连接EF，探索线段BE、CF、EF之间的数量关系，并加以证明．图1 图2 图3例13 如果一条直线把一个平面图形的面积分成相等的两部分，我们把这条直线称为这个平面图形的一条面积等分线．例如，平行四边形的一条对角线所在的直线就是平行四边形的一条面积等分线．(1)三角形的中线、高线、角平分线分别所在的直线一定是三角形的面积等分线的有________；（2）如图1,梯形ABCD中,AB∥DC，如果延长DC到E，使CE＝AB，连接AE,那么有S梯形ABCD＝S△ADE．请你给出这个结论成立的理由，并过点A作出梯形ABCD的面积等分线（不写作法，保留作图痕迹）；（3）如图2，四边形ABCD中，AB与CD不平行,S△ADC＞S△ABC，过点A能否作出四边形ABCD的面积等分线？若能,请画出面积等分线，并给出证明;若不能，说明理由．图1 图2阅读下列材料:问题：如图1，在四边形ABCD中，M是BC边的中点,且90∠=︒，试判断AB＋CD与AD之间的大小AMD关系。

专题7 类比探究—图形旋转中三角形相似题型(学生版)

专题7类比探究—图形旋转中三角形相似题型知识归纳图形的类比探究常以三角形、四边形为背景，与翻折、旋转相结合，考查三角形全等或相似的性质与判定，难度较大．此类题目第一问相对简单，后面的问题需要结合第一问的方法进行类比解答．根据其特征大致可分为：几何变换类比探究问题、旋转综合问题、翻折类问题等。

本专题主要对类比探究—图形旋转中三角形相似题型进行总结，对其解法进行归纳总结，所选题型为近几年期末考试中的常考题型。

知识点睛（1）类比探究属于几何综合题，类比（类比字母，类比辅助线，类比思路）是解决此问题的主要方法，做好类比需要把握变化过程中的不变特征．（2）类比探究问题中常见结构举例①旋转结构②中点结构（类）倍长中线平行夹中点中位线方法总结（1）类比探究是一类共性条件与特殊条件相结合，由特殊情形到一般情形（或由简单情形到复杂情形）逐步深入，解决思想方法一脉相承的综合性题目，常以几何综合题为主．（2）解决类比探究问题的一般方法：①根据题干条件，结合分支条件先解决第一问；②用解决第一问的方法类比解决下一问，整体框架照搬．整体框架照搬包括照搬字母，照搬辅助线，照搬思路。

（3）用铅笔做讲义第1，2题，并将计算、演草保留在讲义上，先看知识点睛，再做题，思路受阻时（某个点做了2~3分钟）重复上述动作，若仍无法解决，课堂重点听．常考题型专练一、解答题1.在△ABC中，AB＝AC，∠BAC＝α，点P为线段CA延长线上一动点，连接PB，将线段PB绕点P逆时针旋转，旋转角为α，得到线段PD，连接DB，DC．（1）如图1，当α＝60°时，①求证：PA＝DC；②求∠DCP的度数；（2）如图2，当α＝120°时，请直接写出PA和DC的数量关系．（3）当α＝120°时，若AB＝6，BP=31，请直接写出点D到CP的距离为．2.如图，在Rt△ABC中，∠ACB＝90°，AC＝4，BC＝2，Rt△ABC绕点C按顺时针方向旋转得到Rt△A′B′C，A′C与AB交于点D．（1）如图1，当A′B′∥AC时，过点B作BE⊥A′C，垂足为E，连接AE．①求证：AD＝BD；②求S△ACE S△ABE的值；（2）如图2，当A′C⊥AB时，过点D作DM∥A′B′，交B′C于点N，交AC的延长线于点M，求DN NM的值．3.（1）问题发现如图1，在△OAB和△OCD中，OA=OB，OC=OD，∠AOB=∠COD=40°，连接AC，BD交于点M．填空：①的值为；②∠AMB的度数为．（2）类比探究如图2，在△OAB和△OCD中，∠AOB=∠COD=90°，∠OAB=∠OCD=30°，连接AC交BD的延长线于点M．请判断的值及∠AMB的度数，并说明理由；（3）拓展延伸在（2）的条件下，将△OCD绕点O在平面内旋转，AC，BD所在直线交于点M，若OD=1，OB=，请直接写出当点C与点M重合时AC的长．4．在△ABC中，CA＝CB，∠ACB＝α．点P是平面内不与点A，C重合的任意一点．连接AP，将线段AP绕点P逆时针旋转α得到线段DP，连接AD，BD，CP．（1）观察猜想如图1，当α＝60°时，的值是，直线BD与直线CP相交所成的较小角的度数是．（2）类比探究如图2，当α＝90°时，请写出的值及直线BD与直线CP相交所成的小角的度数，并就图2的情形说明理由．（3）解决问题当α＝90°时，若点E，F分别是CA，CB的中点，点P在直线EF上，请直接写出点C，P，D在同一直线上时的值．5.已知，ABC中，AB＝AC，∠BAC＝2α°，点D为BC边中点，连接AD，点E为线段AD上一动点，把线段CE 绕点E顺时针旋转2α°得到线段EF，连接FG，FD．（1）如图1，当∠BAC＝60°时，请直接写出BFAE的值；（2）如图2，当∠BAC＝90°时，（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请写出正确的结论，并说明理由；（3）如图3，当点E在AD上移动时，请直接写出点E运动到什么位置时DFDC的值最小．最小值是多少？（用含α的三角函数表示）6．在ABC ∆中，CA CB =，(0180)ACB αα∠=<<．点P 是平面内不与A ，C 重合的任意一点，连接AP ，将线段AP 绕点P 逆时针旋转α得到线段DP ，连接AD ，CP 点M 是AB 的中点，点N 是AD 的中点．（1）问题发现,如图1，当60α=时，MN PC 的值是，直线MN 与直线PC 相交所成的较小角的度数是；（2）类比探究，如图2，当120α=时，请写出MN PC的值及直线MN 与直线PC 相交所成的较小角的度数，并就图2的情形说明理由；（3）解决问题，如图3，当90α=时，若点E 是CB 的中点，点P 在直线ME 上，MN =请直接写出点B ，P ，D 在同一条直线上时PD 的长．7.如图(1)，在矩形ABCD中，AD＝nAB，点M，P分别在边AB，AD上(均不与端点重合)，且AP＝nAM，以AP和AM为邻边作矩形AMNP，连接AN，CN.【问题发现】（1）如图(2)，当n＝1时，BM与PD的数量关系为，CN与PD的数量关系为.【类比探究】（2）如图(3)，当n＝2时，矩形AMNP绕点A顺时针旋转，连接PD，则CN与PD之间的数量关系是否发生变化？若不变，请就图(3)给出证明；若变化，请写出数量关系，并就图(3)说明理由.【拓展延伸】（3）在(2)的条件下，已知AD＝4，AP＝2，当矩形AMVP旋转至C，N，M三点共线时，请直接写出线段CN的长8.(1)问题发现如图1，在Rt△ABC和Rt△CDE中，∠ACB=∠DCE=90°，∠CAB=∠CDE=45°，点D是线段AB上一动点，连接BE.填空:①BEAD的值为；②∠DBE的度数为.(2)类比探究如图2，在Rt△ABC和Rt△CDE中，∠ACB=∠DCE=90°，∠CAB=∠CDE=60°，点D是线段AB上一动点，连接BE.请判断BEAD的值及∠DBE的度数，并说明理由.(3)拓展延伸如面3，在(2)的条件下，将点D改为直线AB上一动点，其余条件不变，取线段DE的中点M，连接BM、CM，若AC=2，则当△CBM是直角三角形时，线段BE的长是多少?请直接写出答案.。

类比探究(讲义)

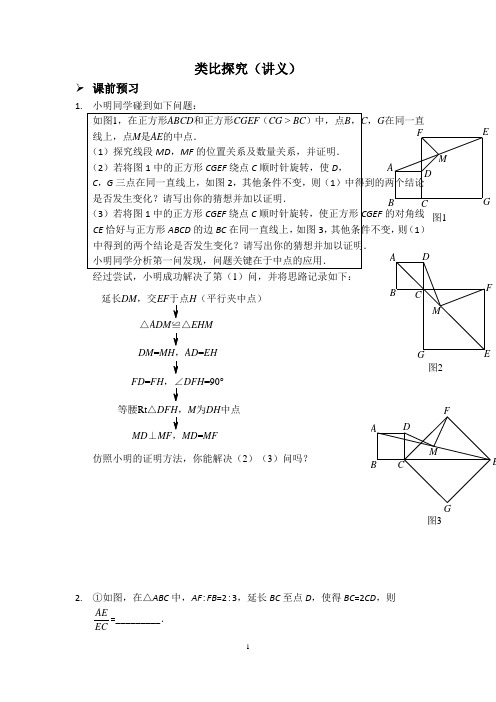
图1AB CDGEF M图2A BCDG EFM图3AB CDG EFM类比探究（讲义）➢ 课前预习1.小明同学碰到如下问题：如图1，在正方形ABCD 和正方形CGEF （CG > BC ）中，点B ，C ，G 在同一直线上，点M 是AE 的中点．（1）探究线段MD ，MF 的位置关系及数量关系，并证明．（2）若将图1中的正方形CGEF 绕点C 顺时针旋转，使D ， C ，G 三点在同一直线上，如图2，其他条件不变，则（1）中得到的两个结论是否发生变化？请写出你的猜想并加以证明．（3）若将图1中的正方形CGEF 绕点C 顺时针旋转，使正方形CGEF 的对角线CE 恰好与正方形ABCD 的边BC 在同一直线上，如图3，其他条件不变，则（1）中得到的两个结论是否发生变化？请写出你的猜想并加以证明．小明同学分析第一问发现，问题关键在于中点的应用．经过尝试，小明成功解决了第（1）问，并将思路记录如下：MD ⊥MF MD =MF等腰Rt △M 为DH 中点FD =FH DFH =90°DM =AD =EH △ADM ≌△EHM 延长DM ，交EF H （平行夹中点）仿照小明的证明方法，你能解决（2）（3）问吗？2. ①如图，在△ABC 中，AF :FB =2:3，延长BC 至点D ，使得BC =2CD ，则AEEC=_________．提示：求比例，找相似．利用平行线构造“A 型”或“X 型”相似是我们常用的一种做法．A BEF②如图，AB =4，射线BM 和AB 相互垂直，点D 是AB 上的一个动点，点E 在射线BM 上，2BE =DB ，作EF ⊥DE 并截取EF =DE ，连接AF 并延长交射线BM 于点C ．设BE =x ，BC =y ，则y 关于x 的函数解析式是（）A ．124xy x =--B ．21xy x =--C ．31xy x =-- D ．84x y x =-- 提示：结合直角特征考虑分析，可构造一线三等角，利用相似整合信息．➢ 知识点睛类比探究问题的处理思路1. 若属于类比探究常见的结构类型，调用结构类比解决．类比探究结构举例：中点结构、直角结构、旋转结构、平行结构．2. 若不属于常见结构类型：①根据题干条件，结合_______________先解决第一问．M FE DC B A②类比解决下一问．如果不能，分析条件变化，寻找______________．③结合所求目标，依据__________，大胆猜测、尝试、验证．➢ 精讲精练1. 已知梯形ABCD ，AD ∥BC ，AB ⊥BC ，AD =1，AB =2，BC =3．（1）如图1，P 为AB 边上的一点，以PD ，PC 为边作□PCQD ，则当点P 与点A 重合时，PQ 的长为__________．（2）如图2，若P 为AB 边上任意一点，以PD ，PC 为边作□PCQD ，请问对角线PQ 的长是否存在最小值？如果存在，请求出最小值；如果不存在，请说明理由．（3）若P 为AB 边上任意一点，延长PD 到E ，使DE =PD ，再以PE ，PC 为边作□PCQE ，请探究对角线PQ 的长是否也存在最小值．如果存在，请求出最小值；如果不存在，请说明理由．（4）如图3，若P 为直线DC 上任意一点，延长PA 到E ，使AE =nPA （n 为常数），以PE ，PB 为边作□PBQE ，请探究对角线PQ 的长是否也存在最小值．如果存在，请求出最小值；如果不存在，请说明理由．DQCBA (P )图1AP BCQD图2AC D EPQ图3A B CDA B CD2. 已知△ABC 为直角三角形，∠ACB =90°，点P 是射线CB 上一点（点P 不与点B ，C 重合），线段AP 绕点A 顺时针旋转90°得到线段AQ ，连接QB 交射线AC 于点M ．（1）如图1，当AC =BC ，点P 在线段CB 上时，线段PB ，CM 的数量关系是__________．（2）如图2，当AC =BC ，点P 在线段CB 的延长线上时，（1）中的结论是否成立？若成立，写出证明过程；若不成立，请说明理由．（3）如图3，若52AC BC ，点P 在线段CB 的延长线上时，CM =2，AP =13，求△ABP 的面积．图1M QPABC图2M QPAB CMC BAPQ图33. （1）问题发现如图1，△ACB 和△DCE 均为等边三角形，点A ，D ，E 在同一直线上，连接BE ．填空：①∠AEB 的度数为___________；②线段AD ，BE 之间的数量关系为___________．图1CDABE（2）拓展探究如图2，△ACB 和△DCE 均为等腰直角三角形，∠ACB =∠DCE =90°，点A ，D ，E 在同一直线上，CM 为△DCE 中DE 边上的高，连接BE ．请判断∠AEB 的度数及线段CM ，AE ，BE 之间的数量关系，并说明理由．图2MEDCBA（3）解决问题如图3，在正方形ABCD 中，CD．若点P 满足PD =1，且∠BPD =90°，请直接写出点A 到BP 的距离．A BCD图34. 如图1，在Rt △ABC 中，∠B =90°，BC =2AB =8，点D ，E 分别是边BC ，AC的中点，连接DE ．将△EDC 绕点C 按顺时针方向旋转，记旋转角为α．（1）问题发现①当α=0°时，=BD AE ______；②当α=180°时，=BDAE______．（2）拓展探究试判断：当0°≤α<360°时，AEBD的大小有无变化？请仅就图2的情形给出证明．（3）问题解决当△EDC 旋转至A ，D ，E 三点共线时，直接写出线段BD 的长．图3图2图1ABCAEBDCDECB A【参考答案】 ➢ 课前预习1. 能，证明略2. ①2②A➢ 知识点睛2. ①分支条件 ②不变特征 ③不变特征➢ 精讲精练1. （1）（2）存在，最小值为4．（3）存在，最小值为5．（44)n +． 2. （1）PB =2CM ．（2）成立，证明略．（3）△ABP 的面积为25． 3. （1）①60°；②AD =BE ．（2）AE =2CM +BE ．（3）点A 到BP ．4. （1 （2）0360α︒<︒≤时，AEBD的大小没有变化，证明略．（3）线段BD 的长为5．类比探究（随堂测试）1. 如图1，将三角板放在正方形ABCD 上，使三角板的直角顶点E 与正方形ABCD 的顶点A 重合，三角板的一边交CD 于点F ，另一边交CB 的延长线于点G ．（1）求证：EF =EG ．（2）如图2，移动三角板，使顶点E 始终在正方形ABCD 的对角线AC 上，其他条件不变，（1）中的结论是否仍然成立？若成立，请给予证明；若不成立，请说明理由．（3）如图3，将（2）中的“正方形ABCD ”改为“矩形ABCD ”，且使三角板的一边经过点B ，其他条件不变，若AB =a ，BC =b ，求EFEG的值．E (A )BC D FGG FDC BAEEACDFG (B )图1图2图3【参考答案】1. （1）证明略．（2）成立，证明略．（3）EF bEG a．。

三角形全等之类比探究-经典题型过关(含答案)

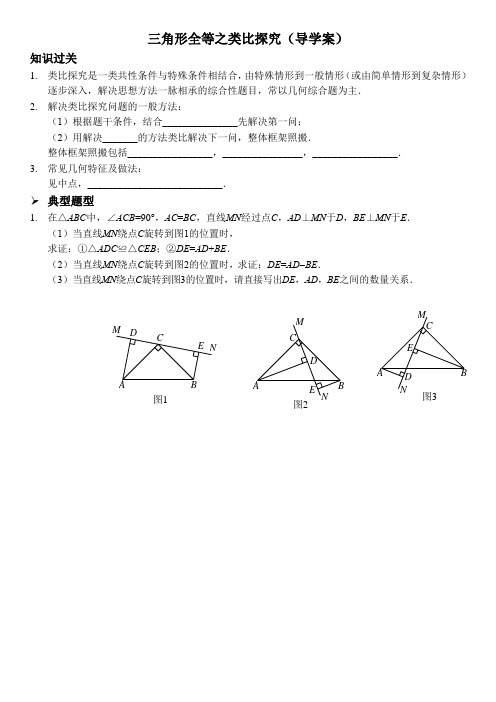
三角形全等之类比探究（导学案）知识过关1. 类比探究是一类共性条件与特殊条件相结合，由特殊情形到一般情形（或由简单情形到复杂情形）逐步深入，解决思想方法一脉相承的综合性题目，常以几何综合题为主． 2. 解决类比探究问题的一般方法：（1）根据题干条件，结合_______________先解决第一问；（2）用解决_______的方法类比解决下一问，整体框架照搬．整体框架照搬包括_________________，________________，_________________． 3. 常见几何特征及做法：见中点，___________________________．➢ 典型题型1. 在△ABC 中，∠ACB =90°，AC =BC ，直线MN 经过点C ，AD ⊥MN 于D ，BE ⊥MN 于E ．（1）当直线MN 绕点C 旋转到图1的位置时，求证：①△ADC ≌△CEB ；②DE =AD +BE ．（2）当直线MN 绕点C 旋转到图2的位置时，求证：DE =AD BE ．（3）当直线MN 绕点C 旋转到图3的位置时，请直接写出DE ，AD ，BE 之间的数量关系．图1B NE CDM A图2ACDEMNB 图3ABC D EM N2. 如图1，四边形ABCD 是正方形，AB =BC ，∠B =∠BCD =90°，点E 是边BC 的中点，∠AEF =90°，EF 交正方形外角∠DCG 的平分线CF 于点F ．（1）求证：AE =EF （提示：在AB 上截取BH =BE ，连接HE ，构造全等三角形，经过推理使问题得到解决）．（2）如图2，如果把“点E 是边BC 的中点”改为“点E 是边BC 上（除B ，C 外）的任意一点”，其他条件不变，那么结论“AE =EF ”仍然成立吗？说明理由．（3）如图3，点E 是BC 的延长线上（除C 点外）的任意一点，其他条件不变，结论“AE =EF ”是否成立？说明理由．GABCDFE 图1E FDC BA G图2FDC A G图3图1M ADC E3. 以△ABC 的边AB ，AC 为直角边向外作等腰直角三角形ABE 和等腰直角三角形ACD ，∠BAE =∠CAD =90°，AB =AE ，AC =AD ，M 是边BC 的中点，连接AM ，DE ．（1）如图1，在△ABC 中，当∠BAC =90°时，求AM 与DE 的数量关系和位置关系．（2）如图2，当△ABC 为一般三角形时，（1）中的结论是否成立？并说明理由．（3）如图3，若以△ABC 的边AB ，AC 为直角边向内作等腰直角三角形ABE 和等腰直角三角形ACD ，其他条件不变，（1）中的结论是否成立，并说明理由．4. （1）如图1，已知∠MAN =120°，AC 平分∠MAN ，∠ABC =∠ADC =90°，则能得到如下两个结论： ①DC =BC ；②AD +AB =AC ．请你证明结论②．（2）如图2，把（1）中的条件“∠ABC =∠ADC =90°”改为“∠ABC +∠ADC =180°”，其他条件不变，则（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由．（3）如图3，如果D 在AM 的反向延长线上，把（1）中的条件“∠ABC =∠ADC =90°”改为“∠ABC =∠ADC ”，其他条件不变，（1）中的结论是否仍然成立？若成立，请直接回答；若不成立，请直接写出你的结论．E D A M 图2B MCEA D图3A B CDMN图3图1NMDCBA B CDMN图2【参考答案】➢ 知识过关：解决类比探究问题的一般方法：（1）根据题干条件，结合分支条件先解决第一问；（2）用解决第（1）问的方法类比解决下一问，整体框架照搬．整体框架照搬包括照搬字母，照搬辅助线，照搬思路．常见几何特征及做法：见中点，考虑倍长中线． ➢ 典型题型1. 证明：（1）如图，∵∠ACB =90° ∴∠1+∠2=90° ∵AD ⊥MN ，BE ⊥MN ∴∠ADC =∠CEB =90° ∴∠3+∠2=90° ∴∠1=∠3在△ADC 和△CEB 中∴△ADC ≌△CEB (AAS) ∴AD =CE ，DC =EB ∴DE =CE +DC=AD +BE （2）如图，∵∠ACB =90° ∴∠1+∠2=90° ∵AD ⊥MN ，BE ⊥MN ∴∠ADC =∠CEB =90° ∴∠CBE +∠2=90° ∴∠1=∠CBE 在△ADC 和△CEB 中∴△ADC ≌△CEB (AAS) ∴AD =CE ，DC =EB ∴DE =CE -DC=AD -BE13ADC CEB AC CB ∠=∠⎧⎪∠=∠⎨⎪=⎩1ADC CEB CBEAC CB ∠=∠⎧⎪∠=∠⎨⎪=⎩321AM DC E NB321NM ED C BA（3）DE =BE -AD ，理由如下：如图，∵∠ACB =90° ∴∠1+∠2=90° ∵AD ⊥MN ，BE ⊥MN ∴∠ADC =∠CEB =90° ∴∠3+∠2=90° ∴∠1=∠3在△ADC 和△CEB 中∴△ADC ≌△CEB (AAS) ∴AD =CE ，DC =EB ∴DE =DC -CE=BE -AD2. 解：（1）AE =EF ，理由如下：如图，在AB 上截取BH =BE ，连接HE ．∵AB =BC ∴AH =EC ∵∠B =90° ∴∠1=∠2=45° ∴∠AHE =135° ∵∠BCD =90° ∴∠DCG =90° ∵CF 平分∠DCG ∴∠GCF =45° ∴∠ECF =135° ∴∠AHE =∠ECF ∵∠AEF =90°，∠B =90°∴∠AEB +∠3=90°，∠AEB +∠4=90° ∴∠3=∠4在△AHE 和△ECF 中∴△AHE ≌△ECF (ASA) ∴AE =EF（2）AE =EF 仍成立，理由如下：13ADC CEB AC CB ∠=∠⎧⎪∠=∠⎨⎪=⎩43AH ECAHE ECF ∠=∠⎧⎪=⎨⎪∠=∠⎩21B NM EDC A4321H GA B CDFE如图，在AB 上截取BH =BE ，连接HE ．∵AB =BC ∴AH =EC ∵∠B =90° ∴∠1=∠2=45° ∴∠AHE =135° ∵∠BCD =90° ∴∠DCG =90° ∵CF 平分∠DCG ∴∠GCF =45° ∴∠ECF =135° ∴∠AHE =∠ECF ∵∠AEF =90°，∠B =90°∴∠AEB +∠3=90°，∠AEB +∠4=90° ∴∠3=∠4在△AHE 和△ECF 中∴△AHE ≌△ECF (ASA) ∴AE =EF（3）AE =EF 仍成立，理由如下：如图，延长BA 到H ，使BH =BE ，连接HE ．∵AB =BC ∴AH =EC ∵∠B =90° ∴∠H =45° ∵∠BCD =90° ∴∠DCG =90° ∵CF 平分∠DCG ∴∠1=45° ∴∠H =∠1∵∠AEF =90°，∠B =90°∴∠AEB +∠3=90°，∠AEB +∠2=90° ∴∠2=∠3∵∠HAE +∠2=180°，∠CEF +∠3=180° ∴∠HAE =∠CEF 在△AHE 和△ECF 中43AH ECAHE ECF ∠=∠⎧⎪=⎨⎪∠=∠⎩H 4123E FDC BA G∴△AHE ≌△ECF (ASA) ∴AE =EF3. 解：（1）DE =2AM ，AM ⊥DE ，理由如下：如图，延长AM 到F ，使MF =AM ，连接BF ，延长MA 交DE 于G ．∴AF =2AM ∵M 是BC 中点 ∴BM =CM在△BMF 和△CMA 中∴△BMF ≌△CMA (SAS) ∴FB =AC ，∠3=∠4 ∴BF ∥AC∴∠FBA +∠BAC =180° ∵∠BAE =∠CAD =90° ∴∠DAE +∠BAC =180° ∴∠FBA =∠DAE ∵AC =AD ∴BF =AD在△FBA 和△DAE 中∴△FBA ≌△DAE (SAS) ∴AF =ED ，∠5=∠6 ∴DE =2AM ∵∠BAE =90° ∴∠5+∠7=90° ∴∠6+∠7=90° ∴∠EGA =90° 即AM ⊥DE（2）（1）中的结论成立，理由如下：如图，延长AM 到F ，使MF =AM ，连接BF ，延长MA 交DE 于G ．∴AF =2AM ∵M 是BC 中点1H AH ECHAE CEF ∠=∠⎧⎪=⎨⎪∠=∠⎩12BM CM MF MA =⎧⎪∠=∠⎨⎪=⎩BF AD FBA DAE AB EA =⎧⎪∠=∠⎨⎪=⎩H123FDB AG∴BM =CM在△BMF 和△CMA 中∴△BMF ≌△CMA (SAS) ∴FB =AC ，∠3=∠4 ∴BF ∥AC∴∠FBA +∠BAC =180° ∵∠BAE =∠CAD =90° ∴∠DAE +∠BAC =180° ∴∠FBA =∠DAE ∵AC =AD ∴BF =AD在△FBA 和△DAE 中∴△FBA ≌△DAE (SAS) ∴AF =ED ，∠5=∠6 ∴DE =2AM ∵∠BAE =90° ∴∠5+∠7=90° ∴∠6+∠7=90° ∴∠EGA =90° 即AM ⊥DE（3）（1）中的结论成立，理由如下：如图，延长AM 到F ，使MF =AM ，交DE 于G ，连接BF ．∴AF =2AM ∵M 是BC 中点 ∴BM =CM在△BMF 和△CMA 中∴△BMF ≌△CMA (SAS) ∴FB =AC ，∠FBM =∠ACM ∴BF ∥AC∴∠FBA +∠BAC =180°12BM CM MF MA =⎧⎪∠=∠⎨⎪=⎩BF AD FBA DAE AB EA =⎧⎪∠=∠⎨⎪=⎩BM CM BMF CMA MF MA =⎧⎪∠=∠⎨⎪=⎩FGD A EC MB∵∠BAE =∠CAD =90°∠BAC =∠BAE +∠CAD -∠DAE ∴∠DAE +∠BAC =180° ∴∠FBA =∠DAE ∵AC =AD ∴BF =AD在△FBA 和△DAE 中∴△FBA ≌△DAE (SAS) ∴AF =ED ，∠BAF =∠AED ∴DE =2AM ∵∠BAE =90° ∴∠BAF +∠EAF =90° ∴∠AED +∠EAF =90° ∴∠EGA =90° 即AM ⊥DE4. （1）证明：如图，在BN 上截取BE=AD ．∵AC 平分∠DAB ，∠MAN =120° ∴∠1=∠2=60° 在△CDA 和△CBA 中∴△CDA ≌△CBA (AAS) ∴DC =BC ，AD =AB 在△CDA 和△CBE 中∴△CDA ≌△CBE (SAS) ∴AC =EC ∵∠2=60°∴AC=AE =BE+AB =AD+AB（2）成立，证明如下：如图，过C 作CG ⊥AM 于G ，CF ⊥AN 于F ，在BN 上截取BE=AD ．BF AD FBA DAE AB EA =⎧⎪∠=∠⎨⎪=⎩12CDA CBA CA CA ∠=∠⎧⎪∠=∠⎨⎪=⎩DC BC CDA CBE AD EB =⎧⎪∠=∠⎨⎪=⎩21E图1NM DCB A∵CG ⊥AM ，CF ⊥AN ∴∵AC 平分∠DAB ，∠MAN =120° ∴∠1=∠2=60°，CG=CF ∵∠ABC +∠ADC =180° ∠CDG +∠ADC =180° ∠ABC +∠EBC =180°∴∠CDG =∠CBF ，∠ADC =∠EBC 在△CGD 和△CFB 中∴△CGD ≌△CFB （AAS ） ∴CD =CB在△CDA 和△CBE 中三角形全等之类比探究（实战演练）1. 在四边形ABCD 中，AB =AD ，∠BAD =90°，P 是直线CD 上一点，连接PA ，过点B ，D 作BE ⊥PA ，DF ⊥PA ，垂足分别为点E ，F ．（1）如图1，请探究BE ，DF ，EF 这三条线段的数量关系．（2）若点P 在DC 的延长线上，如图2，则这三条线段又具有怎样的数量关系？（3）若点P 在CD 的延长线上，如图3，直接写出BE ，DF ，EF 这三条线段的数量关系．【参考答案】CGD CFB ∠=∠CDG CBF CGD CFB CG CF ∠=∠⎧⎪∠=∠⎨⎪=⎩CD CB ADC AD EB =⎧⎪∠=⎨⎪=⎩G FE A B C DMN图3图3图2图1PABCDEFP FED CBA PF EDCBA1. （1）EF=BE -DF ，证明略（2）EF= DF -BE ，证明略（3）EF=BE +DF 路线图：(AAS) 123ABE DAF AE DF BE AF EF AF AEBE DFEF AE AFDF BEEF AF AEDF BE↓==↓=-=-=-=-=+=+△≌△（）（）（）三角形全等之类比探究（作业）➢ 例题示范例1：已知，在△ABC 中，∠BAC =90°，AB =AC ，点D 为直线BC 上一动点（点D 不与点B ，C 重合）．以AD 为边作正方形ADEF ，AD =AF ，∠DAF =90°，连接CF ．（1）如图1，当点D 在线段BC 上时，求证：CF +CD =BC ；（2）如图2，当点D 在线段BC 的延长线上时，其他条件不变，请直接写出CF ，BC ，CD 三条线段之间的关系；（3）如图3，当点D 在线段BC 的反向延长线上时，且点A ，F 分别在直线BC 的两侧，其他条件不变，求CF ，BC ，CD 三条线段之间的关系．【思路分析】结合题目特征，本题为类比探究问题．解决方法：（1）根据题目条件及（1）问中D 在线段BC 上，证明△ABD ≌△ACF ，就可以得出BD =CF ，结论可证．图2图1ABCDEFFED CBA图3AB CDF 图1FED CBA（2）用解决第（1）问的方法解决后续问题，方法上完全照搬．如图2，通过证明△ABD ≌△ACF ，就可以得出BD =CF ，进而得到BC +CD =CF ；如图3，通过证明△ABD ≌△ACF ，就可以得出BD =CF ，进而得到BC +CF =CD ．【过程书写】证明：如图，∵∠DAF =90°，∠BAC =90° ∴∠BAD =∠CAF 在△BAD 和△CAF 中，AB AC BAD CAF AD AF =⎧⎪∠=∠⎨⎪=⎩∴△BAD ≌△CAF （SAS ） ∴BD =CF ∵BD +CD =BC ∴CF +CD =BC （2）BC +CD =CF（3）BC +CF =CD ，理由如下： ∵∠DAF =90°，∠BAC =90° ∴∠BAD =∠CAF 在△BAD 和△CAF 中，∴△BAD ≌△CAF （SAS ） ∴BD =CF ∵BC +BD =CD ∴BC +CF =CD➢ 巩固练习1. 已知AB ⊥BD ，ED ⊥BD ，AC ⊥CE ，BC =DE ，如图1．（1）求证：AC =CE ．（2）若将△ECD 沿CB 方向平移至如图2的位置（C 1，C 2不重合），其余条件不变，结论AC 1=C 2E 还成立吗？请说明理由．（3）若将△ECD 沿CB 方向平移至如图3的位置（B ，C 2重合），其余条件不变，结论AC 1=C 2E 还成立吗？请说明理由．AB AC BAD CAF AD AF =⎧⎪∠=∠⎨⎪=⎩图3图2图1A C DEEDAEDB (C 2)AC 2C 1C 1图3AB CDEF图2图1CE MN NM D C BA2. （1）【问题发现】小明学习中遇到这样一个问题：如图1，△ABC 是等边三角形，点D 为BC 的中点，且满足∠ADE =60°，DE 交等边三角形外角平分线CE 所在直线于点E ，试探究AD 与DE 的数量关系．小明发现，过点D 作DF ∥AC ，交AB 于点F ，通过构造全等三角形，经过推理论证，能够使问题得到解决，请直接写出AD 与DE 的数量关系：_______________；（2）【类比探究】如图2，当点D 是线段BC 上（除B ，C 外）任意一点时（其他条件不变），试猜想AD 与DE 之间的数量关系，并证明你的结论；（3）【拓展应用】如图3，当点D 在线段BC 的延长线上（其他条件不变），试猜想AD 与DE 之间的数量关系，并证明你的结论．3. 如图1所示，在△ABC 和△ADE 中，AB =AC ，AD =AE ，∠BAC =∠DAE ，且点B ，A ，D 在一条直线上，连接BE ，CD ，M ，N 分别为BE ，CD 的中点，连接AM ，AN ，MN ．（1）求证：①BE =CD ；②△AMN 是等腰三角形．（2）在图1的基础上，将△ADE 绕点A 按顺时针方向旋转180°，其他条件不变，得到如图2所示的图形．（1）中的两个结论是否仍然成立？若成立，请给予证明；若不成立，请说明理由．图3EDC BA图2E DCBA【参考答案】1. 证明略路线图：(AAS) A DCE ABC CDE AC CE∠=∠↓↓=△≌△ 提示：（1）AC=CE ，由垂直转互余可以得到∠A =∠DCE ，结合BC=DE 证明△ABC ≌△CDE ，得到对应边相等，可以得到AC=CE ．（2）成立，照搬第一问的字母、思路和过程可以得到AC 1=C 2E ．（3）成立，照搬第一问的字母、思路和过程可以得到AC 1=C 2E ． 2. 证明略D DF AC AB F 过点作∥，交于点路线图(AAS) BDF BF BD AF CD ADF DEC AD DE↓==↓↓=△为等边三角形，△≌△ 提示：（1）AD =DE（2）AD =DE 成立，根据△ABC 以及△BDF 是等边三角形，得到AF =DC ，再结合∠ADE =60°，倒角，得到∠DAF =∠EDC ，结合外角平分线，知∠DCE =∠AFD =120°，得到△ADF ≌ △DEC ，得到对应边相等，可得AD =DE ．（3）成立，照搬第二问的字母、思路和过程可以得到AD =DE ．图1F E DC B A3. 证明略路线图(SAS) (SAS) BAE CAD BE CD ABE ACD ABM ACN AM AN AMN ↓=∠=∠↓↓=↓△≌△，△≌△△是等腰三角形提示：（1）由已知条件先证明△BAE ≌△CAD (SAS)，得到BE=CD ，结合第一次全等提供的条件证明△ABM ≌△ACN (SAS)得到AM=AN ，因而△AMN 是等腰三角形．（2）成立，照搬第一问的字母、思路和过程可以得到BE=CD ，△AMN 是等腰三角形．。

类比探究(讲义及答案)

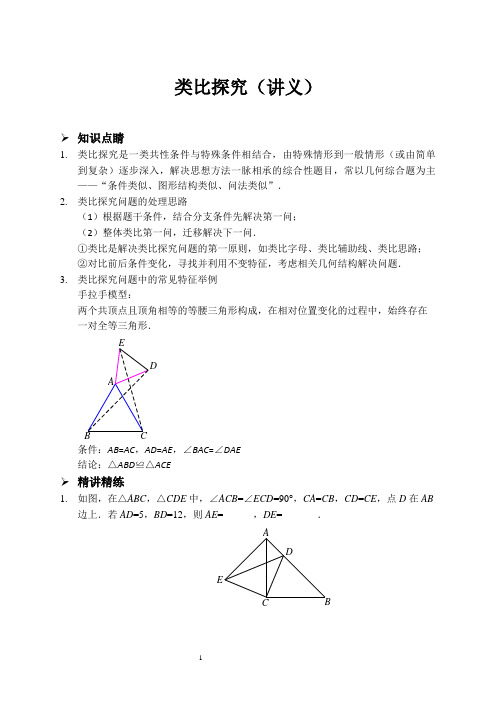
类比探究（讲义）➢知识点睛1.类比探究是一类共性条件与特殊条件相结合，由特殊情形到一般情形（或由简单到复杂）逐步深入，解决思想方法一脉相承的综合性题目，常以几何综合题为主——“条件类似、图形结构类似、问法类似”．2.类比探究问题的处理思路（1）根据题干条件，结合分支条件先解决第一问；（2）整体类比第一问，迁移解决下一问．①类比是解决类比探究问题的第一原则，如类比字母、类比辅助线、类比思路；②对比前后条件变化，寻找并利用不变特征，考虑相关几何结构解决问题．3.类比探究问题中的常见特征举例手拉手模型：两个共顶点且顶角相等的等腰三角形构成，在相对位置变化的过程中，始终存在一对全等三角形．EDAB C条件：AB=AC，AD=AE，∠BAC=∠DAE结论：△ABD≌△ACE➢精讲精练1.如图，在△ABC，△CDE中，∠ACB=∠ECD=90°，CA=CB，CD=CE，点D在AB边上．若AD=5，BD=12，则AE=______，DE=_______．ADEB2. 如图，点D 为等边三角形ABC 内一点，AD =4，BD =3，CD =5．以BD 为一边作等边三角形BDE ，连接CE ．（1）判断△DEC 的形状，并说明理由；（2）求∠ADB 的度数．EDCBA3. 如图，在△ABC ，△ADE 中，∠BAC =∠DAE =90°，AB =AC ，AD =AE ，点C ，D ，E 在同一条直线上，连接BD ，BE ．以下五个结论：①BD =CE ；②BD ⊥CE ；③∠ACE +∠DBC =45°；④BE 2=ED 2+EC 2；⑤BE 2=2(AD 2+AB 2)，其中正确结论的个数是（） A ．2B ．3C ．4D ．5ABC DE4. 如图，在△ABC 中，∠BAC =90°，AB =AC ，点D 是BC 上一动点，连接AD ，过点A 作AE ⊥AD ，并且始终保持AE =AD ，连接CE ，AF 平分∠DAE 交BC 于F ．（1）求证：△ABD ≌△ACE ；（2）若BD =3，CF =4，则DF =_________．ECFDBA5. 已知△ABC 和△CDE 均为等腰直角三角形，∠ACB =∠DCE =90°，点D 是等腰直角三角形ABC 斜边AB 所在直线上一点（不与点B 重合）．（1）如图1，当点D在线段AB上时，直接写出DA2，DB2，DE2三者之间的数量关系：_______________．（2）如图2，当点D在线段AB的延长线上时，（1）中的结论仍然成立，请你利用图2给出证明过程．（3）若点D满足14ADAB，直接写出DEDB的值：_________．图1ECBA图2ECAA BC备用图6. 在Rt △ABC 中，∠BAC =90°，AB =AC ，在BC 的同侧作任意Rt △DBC ，∠BDC =90°．（1）若CD =2BD ，M 是CD 中点（如图1），求证：△ADB ≌△AMC ．（2）若CD ＜BD （如图2），在BD 边上是否存在一点N ，使得△ADN 是以DN 为斜边的等腰直角三角形？若存在，请在图2中确定点N 的位置，并加以证明；若不存在，请说明理由．（提示：在BD 上截取BN =CD ，连接AN ）（3）当CD =1，BD =4时，则AD 的长为__________．MOD CBA图1OD BA图27.在△ABC中，∠BAC=90°，AB=AC，AD⊥BC于点D．（1）如图1，点E，F分别在AB，AC上，且∠EDF=90°，求证：BE=AF．（2）如图2，点M在AD的延长线上，点N在AC上，且∠BMN=90°，求证：AB+ANAM．（提示：过点M作AM的垂线，交AB的延长线于点P）AEB D FC图1ADNMB C图2【参考答案】➢精讲精练1.12，132.（1）△DEC是直角三角形，理由略；（2）∠ADB=150°3. C4.（1）略；（2）55.（1）222DA DB DE；（2）略；（3+=6.（1）略；（2）存在，证明略；（3）27.（1）略；（2）略。

类比探究专题(五)——探究应用(含答案)

学生做题前请先回答以下问题问题1：类比探究往往会围绕一个不变结构进行考查．类比探究中常见的不变结构有哪些？问题2：处理类比探究问题时，若属于常见结构，则________．问题3：处理类比探究问题时，若不属于常见结构类型，则需要我们尝试着去寻找不变结构解决问题．此时常见的处理思路是什么？以下是问题及答案，请对比参考:问题1：类比探究往往会围绕一个不变结构进行考查．类比探究中常见的不变结构有哪些？答：类比探究中常见的不变结构有：①中点结构，常考虑平行夹中点，构造中位线等；②旋转结构，特征：等线段共点③平行结构，常考虑作平行，造相似④直角结构．常考虑斜直角放正问题2：处理类比探究问题时，若属于常见结构，则．答：调用结构类比解决．问题3：处理类比探究问题时，若不属于常见结构类型，则需要我们尝试着去寻找不变结构解决问题．此时常见的处理思路是什么？答：①根据题干条件，结合支干条件先解决第一问．②类比解决下一问．如果不能，分析条件变化，寻找不变特征．③结合所求目标，依据不变特征尝试找不变结构，大胆猜测、尝试、验证．类比探究专题（五）——探究应用一、单选题(共3道，每道33分)1.如图1，将两个完全相同的三角形纸片ABC和DEC重合放置，其中∠C=90°，∠B=∠E=30°．（1）操作发现如图2，固定△ABC，使△DEC绕点C旋转，当点D恰好落在AB边上时，填空：①线段DE与AC的位置关系是_________；②设△BDC的面积为，△AEC的面积为，则与之间的数量关系是_______．( )A.DE=2AC；B.DE⊥AC；C.DE∥AC；D.DE∥AC；答案：C解题思路：试题难度：三颗星知识点：探究应用2.（上接第1题）（2）猜想论证当△DEC绕点C旋转到如图3所示的位置时，△BDC的面积与△AEC的面积之间的数量关系是( )A. B. C. D.答案：A解题思路：试题难度：三颗星知识点：探究应用3.（上接第1，2题）（3）拓展探究如图4，已知∠ABC=60°，D是角平分线上一点，BD=CD=4，DE∥AB，交BC于点E．若在射线BA上存在点F，使，则BF的长为( )A. B.C. D.答案：C解题思路：试题难度：三颗星知识点：探究应用。

中考热点,类比探究问题求解策略

中考热点，类比探究问题求解策略类比拓展探究问题，近几年来在中考中越来越频繁出现。

这种题型只所以受到各大城市的追捧，就是因为利用它既能很好地考查学生对课程标准要求知识的掌握情况，也能更好地考查学生活学活用的能力，考查学生把书本知识能否很好地迁移拓展到新的清净之中。

这样的题型一般多以解答题大题出现，涉及知识多与图形变换或特殊图形知识有关．对学生的自学能力要求较高．1．（2019秋•永州期末）如图1，在△ABC和△ADE中，∠BAC＝∠DAE＝90°，AB＝AC，AD＝AE．（1）若C，D，E三点在同一直线上，连接BD交AC于点F，求证：△BAD ≌△CAE．（2）在第（1）问的条件下，求证：BD⊥CE；（3）将△ADE绕点A顺时针旋转得到图2，那么第（2）问中的结论是否依然成立？若成立，请证明你的结论：若不成立，请说明理由．【分析】此题是几何变换综合题，主要考查了全等三角形的判定和性质，对顶角的性质，垂直的判定，判断出△BAD≌△CAE是解本题的关键.（1）先判断出∠BAD＝∠CAE，进而利用SAS判断出△BAD≌△CAE，即可得出结论；（2）由△BAD≌△CAE，得出∠ABD＝∠ACE，再判断出∠ACE+∠CFD＝90°，即可得出结论；（3）先同（1）的方法判断出△BAD≌△CAE，再同（2）的方法判断出BD⊥CE，即可得出结论．【解答】：（1）∵∠BAC＝∠DAE＝90°∴∠BAC+∠CAD＝∠DAE+∠CAD，即∠BAD＝∠CAE.∵AB＝AC，AD＝AE，∴△BAD≌△CAE（SAS）；（2）由（1）知，△BAD≌△CAE，∴∠ABD＝∠ACE，∵∠BAC＝90°，∴∠ABD+∠AFB＝90°，∵∠AFB＝∠CFD，∴∠ACE+∠CFD＝90°，∴∠CDF＝90°，∴BD⊥CE；（3）BD⊥CE仍然成立，理由：如图2，延长BD交CE于点M，交AC于点F，∵∠BAC＝∠DAE＝90°，∴∠BAC﹣∠CAD＝∠DAE﹣∠CAD，即∠BAD＝∠CAE，∵AB＝AC，AD＝AE，∴△BAD≌△CAE（SAS），∴∠ABD＝∠ACE，∵∠BAC＝90°,∴∠ABD+∠AFB＝90°，∵∠AFB＝∠CFM，∴∠CMF＝90°，∴BD⊥CE．2.（2019•兰山区二模）如图1，Rt△ABC中，∠A＝90°，AB＝AC，点D是BC 边的中点连接AD，则易证AD＝BD＝CD，即AD＝1/2BC；如图2，若将题中AB＝AC这个条件删去，此时AD仍然等于1/2BC．理由如下：延长AD到H，使得AH＝2AD，连接CH，先证得△ABD≌△CHD，此时若能证得△ABC≌△CHA，即可证得AH＝BC，此时AD＝1/2BC，由此可见倍长过中点的线段是我们三角形证明中常用的方法．（1）请你先证明△ABC≌△CHA，并用一句话总结题中的结论；（2）现将图1中△ABC折叠（如图3），点A与点D重合，折痕为EF，此时不难看出△BDE和△CDF都是等腰直角三角形．BE＝DE，CF＝DF．由勾股定理可知DE2+DF2＝EF2，因此BE2+CF2＝EF2，若图2中△ABC也进行这样的折叠（如图4），此时线段BE、CF、EF还有这样的关系式吗？若有，请证明；若没有，请举反例．（3）在（2）的条件下，将图3中的△DEF绕着点D旋转（如图5），射线DE、DF分别交AB、AC于点E、F，此时（2）中结论还成立吗？请说明理由．图4中的△DEF也这样旋转（如图6），直接写出上面的关系式是否成立．【分析】（1）想办法证明AB∥CH，推出∠BAC＝∠ACH，再利用SAS证明△ABC≌△CHA即可．（2）有这样分关系式．如图4中，延长ED到H山顶DH＝DE．证明△EDB ≌△HDC（SAS），推出∠B＝∠HCD，BE＝CH，∠FCH＝90°，利用勾股定理，线段的垂直平分线的性质即可解决问题．（3）图5，图6中，上面的关系式仍然成立．【解答】（1）证明：如图2中，∵BD＝DC，∠ADB＝∠HDC，AD＝HD，∴△ADB≌△HDC（SAS），∴∠B＝∠HCD，AB＝CH，∴AB∥CH，∴∠BAC+∠ACH＝180°，∵∠BAC＝90°，∴∠ACH＝∠BAC＝90°，∵AC＝CA，∴△BAC≌△HCA（SAS），∴AH＝BC，∴AD＝DH＝BD＝DC，∴AD＝1/2BC．结论：直角三角形斜边上的中线等于斜边的一半．（2）解：有这样分关系式．理由：如图4中，延长ED到H山顶DH＝DE．∵ED＝DH，∠EDB＝∠HDC，DB＝DC，∴△EDB≌△HDC（SAS），∴∠B＝∠HCD，BE＝CH，∵∠B+∠ACB＝90°，∴∠ACB+∠HCD＝90°，∴∠FCH＝90°，∴FH2＝CF2+CH2，∵DF⊥EH，ED＝DH，∴EF＝FH，∴EF2＝BE2+CF2．（3）图5，图6中，上面的关系式仍然成立．结论：EF2＝BE2+CF2．证明方法类似（2）．3.（2019秋•常德期末）操作发现：如图1，D是等边△ABC边BA上的一动点（点D与点B不重合），连接DC，以DC为边在BC上方作等边△DCF，连接AF，易证AF＝BD（不需要证明）；类比猜想：①如图2，当动点D运动至等边△ABC边BA的延长线上时，其它作法与图1相同，猜想AF与BD在图1中的结论是否仍然成立．深入探究：②如图3，当动点D在等边△ABC边BA上的一动点（点D与点B 不重合），连接DC，以DC为边在BC上方、下方分别作等边△DCF和等边△DCF′，连接AF，BF′，你能发现AF，BF′与AB有何数量关系，并证明你发现的结论．③如图4，当动点D运动至等边△ABC边BA的延长线上时，其它作法与图3相同，猜想AF，BF′与AB在上题②中的结论是否仍然成立，若不成立，请给出你的结论并证明．【分析】本题考查的是全等三角形的判定和性质、等边三角形的性质，掌握全等三角形的判定定理呵呵性质定理是解题的关键．类比猜想：①根据等边三角形的性质得到CB＝CA，CD＝CF，∠ACB＝∠FCD ＝60°，证明△BCD≌△ACF，根据全等三角形的性质证明结论；深入探究：②根据△BCD≌△ACF，得到BD＝AF，根据△BCF′≌△ACD，得到BF′＝AD，结合图形解答；③仿照②的证明过程解答即可．【解答】：类比猜想：①图1中的结论仍然成立，理由如下：∵△ABC和△FDC都是等边三角形，∴CB＝CA，CD＝CF，∠ACB＝∠FCD＝60°，∴∠ACB+∠ACD＝∠FCD+∠ACD，即∠BCD＝∠ACF，易证△BCD≌△ACF（SAS）,∴BD＝AF；深入探究：②AF+BF′＝AB，理由如下：如图3，由①可知，△BCD≌△ACF，∴BD＝AF，同理，△BCF′≌△ACD，∴BF′＝AD，∴AF+BF′＝BD+AD＝AB；③AF，BF′与AB在上题②中的结论不成立，AF﹣BF′＝AB，理由如下：如图4，同理可证，△BCD≌△ACF，∴BD＝AF，同理，△BCF′≌△ACD，∴BF′＝AD，∴AF﹣BF′＝BD﹣AD＝AB．4．（2020•长葛市一模）如图1，将三角板放在正方形ABCD上，使三角板的直角顶点E与正方形ABCD的顶点A重合，三角板的一边交CD于点F．另一边交CB的延长线于点G．（1）观察猜想：线段EF与线段EG的数量关系是；（2）探究证明：如图2，移动三角板，使顶点E始终在正方形ABCD的对角线AC上，其他条件不变，（1）中的结论是否仍然成立？若成立，请给予证明：若不成立．请说明理由：（3）拓展延伸：如图3，将（2）中的“正方形ABCD”改为“矩形ABCD”，且使三角板的一边经过点B，其他条件不变，若AB＝a、BC＝b，求的值．【分析】本题考查的是相似三角形的判定和性质、全等三角形的判定和性质、正方形的性质，掌握相似三角形的判定定理和性质定理是解题的关键．【解答】：（1）∵四边形ABCD为正方形，∴AB＝AD，∠BAD＝90°，∴∠GAF＝∠BAD，∴∠GAF﹣∠BAF＝∠BAD﹣∠BAF，即∠GAB＝∠FAD，∴易证△GAB≌△FAD（ASA），∴AG＝AF，即EF＝EG，故答案为：EF＝EG；（2）成立，证明如下：如图2，过点E分别作BC、CD的垂线，垂足分别为H、I，则EH＝EI，∠HEI＝90°，∵∠GEH+∠HEF＝90°，∠IEF+∠HEF＝90°，∴∠IEF＝∠GEH，∴易证△FEI≌△GEH（ASA），∴EF＝EG；（3）如图，过点E分别作BC、CD的垂线，垂足分别为M、N，则∠MEN＝90°，∴EM∥AB，EN∥AD，∴△CEN∽△CAD，△CEM∽△CAB，∴NE/AD=CE/CA,，EM/AB=CE/CA，∴NE/AD=EM/AB，即NE/EN=AD/AB=b/a，∵∠NEF+∠FEM＝∠GEM+∠FEM＝90°，∴∠GEM＝∠FEN，又∠GME＝∠FNE＝90°，∴△GME∽△FNE，∴EF/EG=EN/EM＝b/a．方法总结类比探究是一类共性条件与特殊条件相结合，由特殊情形到一般情形（或由简单到复杂）逐步深入，解决思想方法一脉相承的综合性题目，常以几何综合题为主----“条件类似、图形结构类似、问法类似”.类比探究问题的处理思路类比是解决类比探究问题的第一原则，如类比字母、类比辅助线、类比思路；即整体类比上一问思路，迁移解决下一问。

专题6 类比探究—图形旋转中三角形全等题型(学生版)

专题6类比探究—图形旋转中三角形全等题型知识归纳几何类比探究题是近几年中招考试的必考题型，目前位于解答题的最后一题，分值为11分或12分．主要考查方式有求线段长，求角度，判断图形形状，判断两条线段的数量关系和位置关系并证明，考查知识点主要涉及特殊三角形，勾股定理，四边形的判定与性质，全等、相似三角形的判定及性质，二次函数等，综合性较强。

本专题主要对类比探究—图形旋转中三角形全等题型进行总结，对其解法进行归纳总结，所选题型为近几年期末考试中的常考题型。

解题思路总结图形的类比探究常以三角形、四边形为背景，与翻折、旋转相结合，考查三角形全等或相似的性质与判定，难度较大．此类题目第一问相对简单，后面的问题需要结合第一问的方法进行类比解答．根据其特征大致可分为：几何变换类比探究问题、旋转综合问题、翻折类问题等。

解决此类问题要善于将复杂图象分解为几个基本图形，通过添加副主席补全或构造基本图形，借助转化、方程、数形结合、分类讨论等数学思想解决几何证明问题，计算则把几何与代数知识综合起来，渗透数形结合思想，考查学生分析问题的能力、逻辑思维和推理能力.常考题型专练一、解答题1.如图1，△ABC和△DCE都是等边三角形．探究发现（1）△BCD与△ACE是否全等？若全等，加以证明；若不全等，请说明理由．拓展运用（2）若B、C、E三点不在一条直线上，∠ADC＝30°，AD＝3，CD＝2，求BD的长．（3）若B、C、E三点在一条直线上（如图2），且△ABC和△DCE的边长分别为1和2，求△ACD的面积及AD 的长．2.在△ABC中，∠BAC＝90°，点O是斜边BC上的一点，连接AO，点D是AO上一点，过点D分别作DE AB∥，DF AC∥，交BC于点E、F．（1）如图1，若点O为斜边BC的中点，求证：点O是线段EF的中点．（2）如图2，在（1）的条件下，将△DEF绕点O顺时针旋转任意一个角度，连接AD，CF，请写出线段AD和线段CF的数量关系，并说明理由．（3）如图3，若点O是斜边BC的三等分点，且靠近点B，当∠ABC＝30°时，将△DEF绕点O顺时针旋转任意一个角度，连接AD、BE、CF，请求出BEAD的值．3.在等腰直角三角形ABC中,∠ACB＝90°,AC＝BC,D是AB边上的中点，Rt△EFG的直角顶点E在AB边上移动.(1)如图1，若点D与点E重合且EG⊥AC、DF⊥BC，分别交AC、BC于点M、N，易证EM＝EN；如图2，若点D与点E重合，将△EFG绕点D旋转，则线段EM与EN的长度还相等吗?若相等请给出证明，不相等请说明理由；(2)将图1中的Rt△EGF绕点O顺时针旋转角度α(0∘＜α＜45∘).如图2，在旋转过程中,当∠MDC＝15∘时，连接MN，若AC＝BC＝2，请求出写出线段MN的长；(3)图3,旋转后,若Rt△EGF的顶点E在线段AB上移动(不与点D、B重合)，当AB＝3AE时，线段EM与EN 的数量关系是________；当AB＝m·AE时，线段EM与EN的数量关系是__________.4.(1)问题发现：如图1，在等边ABC ∆中，点D 为BC 边上一动点，//DE AB 交AC 于点E ，将AD 绕点D 顺时针旋转60︒得到DF ，连接CF ．则AE 与FC 的数量关系是_____，ACF ∠的度数为______．(2)拓展探究：如图2，在 Rt ABC ∆中，90ABC ∠=︒，60ACB ∠=︒，点D 为BC 边上一动点，//DE AB 交AC 于点E ，当∠ADF=∠ACF=90°时，求AE FC 的值．(3)解决问题：如图3，在ABC ∆中，:BC AB m =，点D 为BC 的延长线上一点，过点D 作//DE AB 交AC 的延长线于点E ，直接写出当ADF ACF ABC ∠=∠=∠时AE FC 的值．5.在等边△ABC 中，点D 是BC 边上一点，点E 是直线AB 上一动点，连接DE，将射线DE 绕点D 顺时针旋转120°，与直线AC 相交于点F ．（1）若点D 为BC 边中点．①如图1，当点E 在AB 边上，且DE AB ⊥时，请直接写出线段DE 与DF 的数量关系________；②如图2，当点E 落在AB 边上，点F 落在AC 边的延长线上时，①中的结论是否仍然成立？请结合图2说明理由；（2）如图3，点D 为BC 边上靠近点C 的三等分点．当:3:2AE BE =时，直接写出CF AF 的值．6.在ABCD 中，BAD ∠=α，以点D 为圆心，适当的长度为半径画弧，分别交边AD 、CD 于点M 、N ，再分别以M 、N 为圆心，大于 MN 的长为半径画弧，两弧交于点K ，作射线DK ，交对角线AC 于点G ，交射线AB 于点E ，将线段EB 绕点E 顺时针旋转α得线段EP ．（1）如图1，当120α=︒时，连接AP ，线段AP 和线段AC 的数量关系为；（2）如图2，当90α=︒时，过点B 作BF EP ⊥于点F ，连接AF ，请求出∠FAC 的度数，以及AF ，AB ，AD 之间的数量关系，并说明理由；（3）当120α=︒时，连接AP ，若13BE AB =，请直接写出线段AP 与线段DG 的比值．7.在数学兴趣小组活动中，小亮进行数学探究活动．（1）△ABC是边长为3的等边三角形，E是边AC上的一点，且AE=1，小亮以BE为边作等边三角形BEF，如图（1）所示．则CF的长为．（直接写出结果，不说明理由）（2）△ABC是边长为3的等边三角形，E是边AC上的一个动点，小亮以BE为边作等边三角形BEF，如图（2）所示．在点E从点C到点A的运动过程中，求点F所经过的路径长．思路梳理并填空：当点E不与点A重合时，如图，连结CF，∵△ABC、△BEF都是等边三角形∴BA=BC，BE=BF，∠ABC=∠EBF=60°∴①∠ABE+=∠CBF+；∴∠ABE=∠CBF∴△ABE≌△CBF∴∠BAE=∠BCF=60°又∠ABC=60°∴∠BCF=∠ABC∴②______∥______；当点E在点A处时，点F与点C重合．当点E在点C处时，CF=CA．∴③点F所经过的路径长为．（3）△ABC是边长为3的等边三角形，M是高CD上的一个动点，小亮以BM为边作等边三角形BMN，如图（3）所示．在点M从点C到点D的运动过程中，求点N所经过的路径长．（4）正方形ABCD的边长为3，E是边CB上的一个动点，在点E从点C到点B的运动过程中，小亮以B为顶点作正方形BFGH，其中点F，G都在直线AE上，如图（4）．当点E到达点B时，点F，G，H与点B重合．则点H所经过的路径长为．（直接写出结果，不说明理由）8．如图1，在Rt△ABC中，∠A=90°，AB=AC，点D，E分别在边AB，AC上，AD=AE，连接DC，点M，P，N分别为DE，DC，BC的中点．（1）观察猜想图1中，线段PM与PN的数量关系是，位置关系是；（2）探究证明把△ADE绕点A逆时针方向旋转到图2的位置，连接MN，BD，CE，判断△PMN的形状，并说明理由；（3）拓展延伸把△ADE绕点A在平面内自由旋转，若AD=4，AB=10，请直接写出△PMN面积的最大值．。

四边形类比探究问题(可编辑修改word版)

四边形类比探究问题一．解答题（共11 小题）1.已知，如图1，正方形ABCD 和正方形BEFG，三点A、B、E 在同一直线上，连接AG和CE（1）线段AG 和线段CE 的数量关系为；（2）将正方形BEFG，绕点B 顺时针旋转到图2 的位置时，（1）中的结论是否成立？请说明理由；（3）若在图2 中连接AE 和CG，且AE＝5，CG＝2，求AC2+GE2＝．（直接写出结果）2.问题探究：（1）已知：如图1，在正方形ABCD 中，点E，H 分别在BC，AB 上，若AE⊥DH于点O．求证：AE＝DH；类比探究：（2）已知：如图2，在正方形ABCD 中，点H，E，G，F分别在AB，BC，CD，DA 上，若EF⊥HG 于点O，则线段EF 与HG 有什么数量关系，并说明理由；拓展应用：（3）已知：如图3，在（2）问条件下，若HF∥EG，BE＝EC＝3，EO＝3FO，求HG 的长．（写出求解过程）3．（1）问题发现如图1，△ACB 和△DCE 均为等边三角形，点A、D、E 在同一条直线上，连接BE．填空：①∠AEB 的度数为；②线段AD、BE 之间的数量关系为．（2）拓展研究如图2，△ACB 和△DCE 均为等腰直角三角形，∠ACB＝∠DCE＝90°，点A、D、E 在同一条直线上，CM 为△DCE 中DE 边上的高，连接BE，请判断∠AEB 的度数及线段CM、AE、BE 之间的数量关系，并说明理由．（3）解决问题如图3，在正方形ABCD 中，CD＝2，若点P 满足PD＝2，且∠BPD＝90°，请直接写出点A 到BP 的距离．4.如图1，点C 在线段AB 上，分别以AC、BC 为边在线段AB 的同侧作正方形ACDE 和正方形BCMN，连结AM、BD．（1）AM 与BD 的关系是：．（2）如果将正方形BCMN 绕点C 顺时针旋转锐角α，其它不变（如图2）．（1）中所得的结论是否仍然成立？请说明理由．（3）在（2）的条件下，连接AB、DM，若AC＝4，BC＝2，求AB2+DM2的值．5.如图①，在▱ABCD 中，点E、F 分别在AD、BC 上，且AE＝CF，连接AF、BE 交于点G，连接CE、DF 交于点H．（1）求证四边形EGFH 为平行四边形．（2）提出问题：在AD、BC 边上是否存在点E、F，使得四边形EGFH 为矩形？小明从特殊到一般探究了问题．【特殊化】如图②，若∠ABC＝90°，AB＝2，BC＝6．在AD、BC 边上是否存在点E、F，使得四边形EGFH 为矩形？若存在，求出此时AE 的长度；若不存在，说明理由．【一般化】如图③，若∠ABC＝60°，AB＝m，BC＝n．在AD、BC 边上是否存在点E、F 使得四边形EGFH 为矩形？根据点E、F 存在（或不存在）的可能情况，写出对应的m、n 满足的条件，存在时直接写出AE 的长度．（用含m、n 的代数式表示）6.问题探究：（1）已知：如图1，在正方形ABCD 中，点E，H 分别在BC，AB 上，若AE⊥DH 于点O，求证：AE＝DH；类比探究：（2）如图2，在正方形ABCD 中，点H，E，G，F分别在AB，BC，CD，DA 上，若EF⊥HG 于点O，探究线段EF 与HG 的数量关系，并说明理由．拓展应用：（3）已知，如图3，在（2）的条件下，若BC＝4，点E 为BC 的中点，DF＝3AF，连结FH，HE，EG，GF．求四边形HEGF 的面积．7.已知AC，EC 分别是四边形ABCD 和EFCG 的对角线，直线AE 与直线BF 交于点H（1）观察猜想如图1，当四边形ABCD 和EFCG 均为正方形时，线段AE 和BF 的数量关系是；∠AHB＝．（2）探究证明如图2，当四边形ABCD 和FFCG 均为矩形，且∠ACB＝∠ECF＝30°时，（1）中的结论是否仍然成立，并说明理由．（3）拓展延伸在（2）的条件下，若BC＝9，FC＝6，将矩形EFCG 绕点C 旋转，在整个旋转过程中，当A、E、F 三点共线时，请直接写出点B 到直线AE 的距离．8.数学学习小组“文化年”最近正在进行几何图形组合问题的研究，认真研读以下三个片段，并回答问题．【片断一】小文说：将一块足够大的等腰直角三角板置于一个正方形中，直角顶点与对角线交点重合，在转动三角板的过程中我发现某些线段之间存在确定的数量关系．如图（1），若三角板两条直角边的外沿分别交正方形的边AB，BC 于点M，N，则①OM+ON ＝MB+NB；②AM+CN＝OD．请你判断他的猜想是否正确？若正确请说明理由；若不正确请说明你认为正确的猜想并证明．【片断】小化说：将角板中个45°角的顶点和正方形的一个顶点重合放置，使得这个角的两条边与正方形的一组邻边有交点．如图（2），若以A 为顶点的45°角的两边分别交正方形的边BC、CD 于点M，N．交对角线BD 于点E、F，我发现：BE2+DE2＝2AE2，只要准确旋转图（2）中的一个三角形就能证明这个结论．请你在图2 中画出图形并写出小化所说的具体的旋转方式：．【片断三】小年说：将三角板的一个45°角放置在正方形的外部，同时角的两边恰好经过正方形两个相邻的顶点．如图（3），设顶点为E 的45°角位于正方形的边AD 上方，这个角的两边分别经过点B、C，连接EA，ED，那么线段EB，EC，ED 也存在确定的数量关系：（EB+ED）2＝2EC2，请你证明这个结论．9．（1）[方法回顾]证明：三角形中位线定理．已知：如图1，在△ABC 中，D、E 分别是AB、AC 的中点．求证：DE∥BC，DE＝BC．证明：如图1，延长DE 到点F，使得EF＝DE，连接CF；请继续完成证明过程：（2）[问题解决]如图2，在矩形ABCD 中，E 为AD 的中点，G、F 分别为AB、CD 边上的点，若AG＝3，DF＝7，∠GEF＝90°，求GF 的长．（3）[思维拓展]如图3，在梯形ABCD 中，AD∥BC，∠A＝90°，∠D＝120°，E 为AD 的中点，G、F 分别为AB、CD 边上的点，若AG＝2，DF＝4，∠GEF＝90°，求GF 的长．10.如图1，图2，△ABC 中，BF，CE 分别为AC，AB 边上的中线，BF⊥CE 于点P．（1）如图1，当BC＝6，∠PCB＝45°时，PE＝，AB＝；（2）如图2，猜想AB2、AC2、BC2 三者之间的数量关系，并给予证明；（3）如图3，▱ABCD 中，点M，N 分别在AD，BC 上，AD＝3AM，BC＝3BN，连接AN，BM，CM，AN 与BM 交于点G，若BM⊥CM 于点M，AB＝4，AD＝3，求AN 的长．11.【探索发现】如图1，△ABC 是等边三角形，点D 为BC 边上一个动点，将△ACD 绕点A 逆时针旋转60°得到△AEF，连接CE．小明在探索这个问题时发现四边形ABCE 是菱形．小明是这样想的：（1）请参考小明的思路写出证明过程；（2）直接写出线段CD，CF，AC 之间的数量关系：；【理解运用】如图2，在△ABC 中，AD⊥BC 于点D．将△ABD 绕点A 逆时针旋转90°得到△AEF，延长FE 与BC 交于点G．（3）判断四边形ADGF 的形状，并说明理由；【拓展迁移】（4）在（3）的前提下，如图3，将△AFE 沿AE 折叠得到△AME，连接MB，若AD＝6，BD＝2，求MB 的长．四边形类比探究问题参考答案与试题解析一．解答题（共11 小题）1.【分析】（1）由正方形的性质得出AB＝CB，BG＝BE，∠ABG＝∠CBE＝90°，由SAS证明△ABG≌△CBE，得出对应边相等AG＝CE；（2）由正方形的性质得出AB＝CB，BG＝BE，∠ABG＝∠CBE＝90°，证出∠ABG＝∠CBE，由SAS 证明△ABG≌△CBE，得出AG＝CE；（3）连接AC、EG，设AG、CE 交点为H，由由角的互余关系得出∠2+∠BCE＝90°，得出∠ AHC＝90°，得出AG⊥CE；再由勾股定理求出AC2+EG2＝C G2+AE2，求出AC2+EG2，然后由正方形的面积等于对角线平方的一半求解即可．【解答】解：（1）如图1 所示：延长AG 交CE 于H，∵四边形ABCD 和四边形BEFG 是正方形，∴AB＝CB，BG＝BE，∠ABG＝∠CBE＝90°，在△ABG 和△CBE 中，∵，∴△ABG≌△CBE（SAS），∴AG＝CE，故答案为：AG＝CE；（2）AG＝CE，且AG⊥CE 仍然成立．理由如下：如图2 所示：∵四边形ABCD 和四边形BEFG 是正方形，∴AB＝CB，BG＝BE，∠ABC＝∠EBG＝90°，∵∠ABG＝∠ABC+∠CBG，∠CBE＝∠EBG+∠CBG，∴∠ABG＝∠CBE，在△ABG 和△CBE 中，∵，∴△ABG≌△CBE（SAS），∴AG＝CE；（3）如图2 所示：连接AC、EG，∵△ABG≌△CBE，∴∠BAG＝∠BCE，∵∠1+∠BAG＝90°，∴∠1+∠BCE＝90°，∵∠1＝∠2，∴∠2+∠BCE＝90°，∴∠AHC＝90°，∴AG⊥CE；在Rt△CGH 中，CG2＝CH2+GH2，在Rt△AEH 中，AE2＝AH2+EH2，∴CG2+AE2＝CH2+GH2+AH2+EH2＝（CH2+AH2）+（GH2+EH2）＝AC2+EG2，∵AE＝5，CG＝2，∴AC2+EG2＝22+52＝29．故答案为：29．【点评】本题是四边形的综合问题，主要考查了正方形的性质、全等三角形的判定与性质、勾股定理；熟练掌握正方形的性质，证明三角形全等是解决问题的关键．2.【分析】（1）由正方形的性质得AB＝DA，∠ABE＝90°＝∠DAH．所以∠HAO+∠OAD＝90°，又知∠ADO+∠OAD＝90°，所以∠HAO＝∠ADO，于是△ABE≌△DAH，可得AE＝DH；（2）EF＝GH．将FE 平移到AM 处，则AM∥EF，AM＝EF，将GH 平移到DN 处，则DN∥ GH，DN＝GH．根据（1）的结论得AM＝DN，所以EF＝GH；（3）易得△AHF∽△CGE，所以，由EC＝3 得AF＝1，过F 作FP⊥BC 于P，根据勾股定理得EF，因为FH∥EG，所以，【解答】解：（1）∵四边形ABCD 是正方形，∴AB＝DA，∠ABE＝90°＝∠DAH．∴∠HAO+∠OAD＝90°．∵AE⊥DH，∴∠ADO+∠OAD＝90°．∴∠HAO＝∠ADO．∴△ABE≌△DAH（ASA），∴AE＝DH．（2）EF＝GH．将FE 平移到AM 处，则AM∥EF，AM＝EF．将GH 平移到DN 处，则DN∥GH，DN＝GH．∵EF⊥GH，∴AM⊥DN，根据（1）的结论得AM＝DN，所以EF＝GH；（3）∵四边形ABCD 是正方形，∴AB∥CD∴∠AHO＝∠CGO∵FH∥EG∴∠FHO＝∠EGO∴∠AHF＝∠CGE∴△AHF∽△CGE∴，∵EC＝3∴AF＝1过 F 作FP⊥BC 于P，根据勾股定理得EF＝，∵根据（2）知EF＝GH，∴GH＝2 ．【点评】本题考查了四边形的综合知识．用到正方形的性质，全等三角形的判定与性质、相似三角形的判定与性质、勾股定理等综合性较强，难度较大．3.【分析】问题发现：（1）①由等边三角形的性质可得AC＝BC，DC＝CE，∠ACB＝∠DCE＝∠CDE＝60°＝∠CED，由“SAS”可证△ACD≌△BCE，可得AD＝BE，∠ADC＝∠CEB＝120°即可求∠AEB 的度数；（2）由全等三角形的性质可得AD＝BE；拓展研究：（2）仿照（1）中的解法可求出∠AEB 的度数，证出AD＝BE；由△DCE 为等腰直角三角形及CM 为△DCE 中DE 边上的高可得CM＝DM＝ME，可得AE＝2CH+BE；解决问题：（3）由题意可得点P 在以D 为圆心，2 为半径的圆上，同时点P 也在以BD 为直径的圆上，即点P 是两圆的交点，分两种情况讨论，由勾股定理可求BP，AH 的长，即可求点A 到BP 的距离．【解答】解：问题发现（1）①∵△ACB 和△DCE 均为等边三角形，∴AC＝BC，DC＝CE，∠ACB＝∠DCE＝∠CDE＝60°＝∠CED∵点A、D、E 在同一条直线上，∴∠ADC＝120°∵∠ACB﹣∠DCB＝∠DCE﹣∠DCB∴∠ACD＝∠BCE，且AC＝BC，DC＝CE∴△ACD≌△BCE（SAS）∴∠ADC＝∠CEB＝120°∴∠ABE＝∠CEB﹣∠CED＝60°②∵△ACD≌△BCE∴AD＝BE故答案为：60°，AD＝BE（2）拓展研究：猜想：①∠AEB＝90°，②AE＝BE+2CM．理由：如图2，∵△ACB 和△DCE 均为等腰直角三角形，∴CA＝CB，CD＝CE，∠ACB＝∠DCE＝90°．∴∠ACD＝∠BCE．且AC＝BC，CD＝CE∴△ACD≌△BCE（SAS）．∴AD＝BE，∠ADC＝∠BEC．∵△DCE 为等腰直角三角形，∴∠CDE＝∠CED＝45°．∵点A，D，E 在同一直线上，∴∠ADC＝135°．∴∠BEC＝135°．∴∠AEB＝∠BEC﹣∠CED＝90°．∵CD＝CE，CM⊥DE，∴DM＝ME．∵∠DCE＝90°，∴DM＝ME＝CM．∴AE＝AD+DE＝BE+2CM．解决问题：（3）∵点P 满足PD＝2，∴点P 在以D 为圆心，2 为半径的圆上，∵∠BPD＝90°，∴点P 在以BD 为直径的圆上，∴如图，点P 是两圆的交点，若点P 在AD 上方，连接AP，过点A 作AH⊥BP，∵CD＝2＝BC，∠BCD＝90°∴BD＝4，∵∠BPD＝90°∴BP＝＝2∵∠BPD＝90°＝∠BAD∴点A，点B，点D，点P 四点共圆∴∠APB＝∠ADB＝45°，且AH⊥BP∴∠HAP＝∠APH＝45°∴AH＝HP在Rt△AHB 中，AB2＝AH2+BH2，∴8＝AH2+（2 ﹣AH）2，∴AH＝+1（不合题意），或AH＝﹣1若点P 在CD 的右侧，同理可得AH＝+1综上所述：点A 到BP 的距离为：+1 或﹣1【点评】本题是四边形综合题，考查了等边三角形的性质、直角三角形斜边上的中线等于斜边的一半、三角形全等的判定与性质、正方形的性质，勾股定理等知识，熟练运用这些性质进行推理是本题的关键．4.【分析】（1）利用正方形的性质和已知条件证明△AMC≌△DBC，从而求出AM 与BD相等且垂直；（2）如果将正方形BCMN 绕点C 逆时针旋转锐角α，其它不变（1）中所得的结论任然成立，先求出∠ACM＝∠DCB，然后利用“边角边”证明△AMC 和△DBC 全等，再根据全等三角形对应边相等即可得证；（3）根据AM⊥BD，得相交的角为直角，由勾股定理计算可得结论．【解答】解：（1）∵四边形ACDE 和四边形BCMN 都为正方形，∴AC＝DC，∠ACD＝∠BCD＝90°，BC＝CM，在△AMC 和△DBC 中，，∴△AMC≌△DBC（SAS）．∴AM＝BD，∠CAM＝∠CDB，延长AM 交BD 于F，∵∠AMC＝∠DMF，∴∠ACM＝∠DFM＝90°，∴AM⊥BD；故答案为：AM＝BD 且AM⊥BD；（2）如果将正方形BCMN 绕点C 逆时针旋转锐角α，其它不变，（1）中所得的结论仍然成立，理由如下：在正方形ABCE 和正方形BCMN 中，AC＝CD，CM＝BC，∠ACD＝∠MCB＝90°，∵∠ACM＝90°+∠MCD，∠DCB＝90°+∠MCD，∴∠ACM＝∠DCB，在△ACM 和△DCB 中，，∴△AMC≌△DBC（SAS）．∴AM＝BD，∠CAM＝∠CDB，∵∠AFC＝∠DFG，∴∠ACF＝∠DGF＝90°，∴AM⊥BD．（3）如图2，连接AD、BM，∵AC＝4，BC＝2，由勾股定理得：AD2＝42+42＝32，BM2＝22+22＝8，∵AM⊥BD，∴∠AGB＝∠DGM＝∠AGD＝∠BGM＝90°，∴AB2+DM2＝AG2+BG2+DG2+GM2，∵AD2+BM2＝AG2+DG2+BG2+MG2＝32+8＝40，∴AB2+DM2＝40．【点评】本题考查了四边形的综合题、正方形的性质、旋转的性质、全等三角形的判定和性质、勾股定理等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题，属于中考压轴题．5.【分析】（1）由条件可证明四边形AECF 和四边形EDFB 为平行四边形，可得到EH∥GF，GE∥FH，可证明四边形EGFH 为平行四边形；（2）由矩形的性质得出AB＝CD＝2，∠ABC＝∠ADC＝∠BAD＝90°，证出∠ABE＝∠DEC，得出△ABE∽△DEC，得出＝，即可求出AE 的长；（3）作AP⊥AD 于P，CQ⊥AD 于Q，则BP＝CQ，PQ＝BC＝AD，由直角三角形的性质得出AP＝AB＝m，BP＝CQ＝AP＝m，设AE＝x，则PE＝x+m，AQ＝n﹣x﹣m，同（2）得：△BPE∽△EQC，得出＝，得出方程整理得：x2+（m﹣n）x+m2﹣＝0，由判别式△＝n2﹣3m2，当△≥0，即n2﹣3m2≥0 时，方程有解，得出m、n 满足的条件和AE 的长．【解答】（1）证明：∵四边形ABCD 为平行四边形，∴AD∥BC，AD＝BC，∵AE＝CF，∴DE＝BF，∴四边形AECF、四边形EDFB 为平行四边形，∴EH∥GF，GE∥FH，∴四边形EGFH 为平行四边形；（2）解：存在，如图②所示，理由如下：∵四边形ABCD 是矩形，∴AB＝CD＝2，∠ABC＝∠ADC＝∠BAD＝90°，∴∠ABE+∠AEB＝90°，四边形EGFH 为矩形时，∠BEC＝90°，则∠AEB+∠DEC＝90°，∴∠ABE＝∠DEC，∴△ABE∽△DEC，∴＝，即＝，解得：AE＝3±；即在AD、BC 边上存在点E、F，使得四边形EGFH 为矩形，此时AE 的长度为3±；（3）解：存在，如图③所示，理由如下：作AP⊥AD 于P，CQ⊥AD 于Q，则BP＝CQ，PQ＝BC＝AD，∴AP＝DQ，∵AD∥BC，∴∠PAB＝∠ABC＝60°，∴∠ABP＝30°，∴AP＝AB＝m，∴BP＝CQ＝AP＝m，设AE＝x，则PE＝x+m，AQ＝n﹣x﹣m，同（2）得：△BPE∽△EQC，∴＝，即＝，整理得：x2+（m﹣n）x+m2﹣＝0，∵△＝（m﹣n）2﹣4（m2﹣）＝n2﹣3m2，当△≥0，即n2﹣3m2≥0 时，方程有解，即m、n 满足n≥m 时，在AD、BC 边上存在点E、F 使得四边形EGFH 为矩形，此时AE＝．【点评】本题是四边形综合题目，考查了平行四边形的判定和性质、矩形的判定与性质、相似三角形的判定与性质、一元二次方程的解法以及判别式的运用等知识；本题综合性强，证明三角形相似是解决问题的关键．6.【分析】（1）根据正方形的性质得到AB＝DA，∠ABE＝∠DAH＝90°，利用ASA 定理证明△ABE≌△DAH，根据全等三角形的性质得到AE＝DH；（2）过得A 作AM∥EF 交BC 于M，过点D 作DN∥GH 交AB 于N，由（1）的结论证明即可；（3）过点F 作FP⊥BC 于点P，根据勾股定理求出EF，由（2）的结论求出HG，根据四边形的面积公式计算即可．【解答】（1）证明：∵四边形ABCD 是正方形，∴AB＝DA，∠ABE＝∠DAH＝90°，∴∠HAO+∠OAD＝90°，∵AE⊥DH，∴∠ADO+∠OAD＝90°，∴∠HAO＝∠ADO，在△ABE 和△DAH 中，，∴△ABE≌△DAH（ASA），∴AE＝DH；（2）解：EF＝GH．理由：如图2，过得A 作AM∥EF 交BC 于M，则四边形AMEF 为平行四边形，∴AM＝EF，过点D 作DN∥GH 交AB 于N，同理，DN＝GH，∵EF⊥GH，∴AM⊥DN，根据（1）的结论得AM＝DN，所以EF＝GH；（3）解：如图3，过点F 作FP⊥BC 于点P，∵四边形ABCD 是正方形，BC＝4，∴AD＝BC＝AB＝FP＝4，∵E 为BC 的中点，DF＝3AF，∴BE＝2，AF＝1，∴PE＝2﹣1＝1，在Rt△FPE 中，EF＝＝，由（2）得：HG＝EF，∴HG＝，∵EF⊥HG，∴四边形HEGF 的面积＝×EF×GH＝．【点评】本题考查的是正方形的性质、全等三角形的判定和性质，掌握全等三角形的判定定理和性质定理是解题的关键．7.【分析】（1）由正方形的性质得出＝＝，∠ACB＝∠ECF＝45°，得出∠ACE＝∠BCF，证出△CAE∽△CBF，得出∠CAE＝∠CBF，＝＝，因此＝，求出∠CAB＝∠CAE+∠EAB＝∠CBF+∠EAB＝45°，再由三角形内角和定理求出∠AHB 的度数即可；（2）不成立；由矩形的性质和已知条件得出＝＝，∠ACE＝∠BCF，得出△CAE ∽△CBF，因此∠CAE＝∠CBF，求出＝＝，∠CAB＝∠CAE+∠EAB＝∠CBF+ ∠EAB＝60°，再由三角形内角和定理即可得出∠AHB 的度数；（3）分两种情况：①如图2 所示：作BM⊥AE 于M，当A、E、F 三点共线时，由（2）得：∠AFB＝30°，∠AFC＝90°，在Rt△ABC 和Rt△CEF 中，由三角函数求出AC＝6 ，EF＝2，在Rt△ACF 中，由勾股定理求出AF＝6，得出AE＝AF﹣EF＝6﹣2 ，再由（2）的结论＝，求出BF＝3 ﹣3，在Rt△BFM 中，由直角三角形的性质求出BM 即可；②如图2 所示：作BM⊥AE 于M，当A、E、F 三点共线时，同②得：AE＝6+2，BF＝3+3，由直角三角形的性质求出BM 即可．【解答】解：（1）如图1 所示：∵四边形ABCD 和EFCG 均为正方形，∴＝＝，∠ACB＝∠ECF＝45°，∴∠ACE＝∠BCF，∴△CAE∽△CBF，∴∠CAE＝∠CBF，＝＝，∴＝，∠CAB＝∠CAE+∠EAB＝∠CBF+∠EAB＝45°，∵∠CBA＝90°，∴∠AHB＝180°﹣90°﹣45°＝45°，故答案为：＝，45°；（2）不成立；理由如下：∵四边形ABCD 和EFCG 均为矩形，且∠ACB＝∠ECF＝30°，∴＝＝，∠ACE＝∠BCF，∴△CAE∽△CBF，∴∠CAE＝∠CBF，＝＝，∴∠CAB＝∠CAE+∠EAB＝∠CBF+∠EAB＝60°，∵∠CBA＝90°，∴∠AHB＝180°﹣90°﹣60°＝30°；（3）分两种情况：①如图2 所示：作BM⊥AE 于M，当A、E、F 三点共线时，由（2）得：∠AFB＝30°，∠AFC＝90°，在Rt△ABC 和Rt△CEF 中，∵∠ACB＝∠ECF＝30°，∴AC＝＝＝6 ，EF＝CF×tan30°＝6×＝2 ，在Rt△ACF 中，AF＝＝＝6 ，∴AE＝AF﹣EF＝6 ﹣2，由（2）得：＝，∴BF＝（6﹣2）＝3﹣3，在△BFM 中，∵∠AFB＝30°，∴BM＝BF＝；②如图3 所示：作BM⊥AE 于M，当A、E、F 三点共线时，同②得：AE＝6+2，BF＝3 +3，则BM＝BF＝；综上所述，当A、E、F 三点共线时，点B 到直线AE 的距离为．【点评】本题是四边形综合题目，考查了正方形的性质、矩形的性质、含30°角的直角三角形的性质、相似三角形的判定与性质、三角函数、勾股定理以及分类讨论等知识；本题综合性强，证明三角形相似是解决问题的关键．8.【分析】【片断一】如图1 中，①错误．结论：OM2+ON2＝BM2+BN2．②正确．只要证明△MOB≌△NOC 即可解决问题；【片断二】如图2 中，将△ABE 绕点A 逆时针旋转90°得到△ADG．连接GF．理由勾股定理即可证明；【片断三】如图3 中，过点C 作EC 的垂线交EB 延长线于F，构造全等三角形即可解决问题；【解答】解：【片断一】：如图1 中，①错误，②正确；理由：如图1 中，∵四边形ABCD 是正方形，∴AC⊥BD，OB＝OC＝OD＝OA，∠ABO＝∠OCN＝45°，∵∠MON＝∠BOC，∴∠MOB＝∠NOC，∴△MOB≌△NOC，∴BN＝CN，∴AM+CN＝AM+BM＝AB＝OA＝OD，①正确的结论：OM2+ON2＝BM2+BN2．理由：∵OM2+ON2＝MN2，BM2+BN2＝MN2，∴OM2+ON2＝BM2+BN2．【片断二】：如图 2 中，将△ABE 绕点A 逆时针旋转90°得到△ADG．连接GF．理由：∵AF＝AF，∠GAF＝∠EAF＝45°，AG＝AE，∴△AFG≌△AFE，∴EF＝GF，∵∠ADG＝∠ABE＝∠ADF＝45°，∴∠FDG＝90°，∴GF2＝DF2+DG2，∴EF2＝BE2+DF2．故答案为：将△ABE 绕点A 逆时针旋转90°得到△ADG．连接GF．【片断三】：如图 3 中，过点C 作EC 的垂线交EB 延长线于F，∵∠ECF＝∠DCB＝90°，∴∠DCE＝∠BCF，∵CD＝CB，CE＝CF，∴△CDE≌△CBF，∴ED＝FB，∴EB+ED＝EB+FB＝EF，又因为EC2+FC2＝EF2，∴（EB+ED）2＝2EC2．【点评】本题考查四边形综合题、正方形的性质、等腰直角三角形的性质、全等三角形的判定和性质、勾股定理等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，学会用转化的思想思考问题，属于中考压轴题．9.【分析】（1）用“倍长法”将DE 延长一倍：延长DE 到F，使得EF＝DE，利用“边角边”证明△ADE 和△CEF 全等，根据全等三角形对应边相等可得AD＝CF，然后判断出四边形BCFD 是平行四边形，根据平行四边形的性质可得；（2）先判断出△AEG≌△DEH（ASA），进而判断出EF 垂直平分GH，即可得出结论；（3）如图3，作辅助线构建全等三角形，先求出AG＝HD＝2，进而判断出△PDH 为30 度的直角三角形，再用勾股定理求出HF 即可得出结论．【解答】（1）证明：（1）如图1，延长DE 到点F，使得EF＝DE，连接CF，在△ADE 和△CFE 中，，∴△ADE≌△CFE（SAS），∴∠A＝∠ECF，AD＝CF，∴CF∥AB，又∵AD＝BD，∴CF＝BD，∴四边形BCFD 是平行四边形，∴DE∥BC，DE＝BC．（2）解：如图2，延长GE、FD 交于点H，∵E 为AD 中点，∴EA＝ED，且∠A＝∠EDH＝90°，在△AEG 和△DEH 中，，∴△AEG≌△DEH（ASA），∴AG＝HD＝3，EG＝EH，∵∠GEF＝90°，∴EF 垂直平分GH，∴GF＝HF＝DH+DF＝3+7＝10；（3）解：如图3，过点D 作AB 的平行线交GE 的延长线于点H，过H 作CD 的垂线，垂足为P，连接HF，同（1）可知△AEG≌△DEH，GF＝HF，∴∠A＝∠HDE＝90°，AG＝HD＝2 ，∵∠ADC＝120°，∴∠HDF＝360°﹣90°﹣120°＝150°，∴∠HDP＝30°，∴PH＝DH＝，PD＝3，∴PF＝PD+DF＝3+4＝7，在Rt△HFP 中，∠HPF＝90°，HP＝，PF＝7，∴HF＝＝＝2，∴GF＝2 ．【点评】此题是四边形综合题，主要考查了正方形和直角梯形的性质和判定，全等三角形的判定和性质，等腰直角三角形的性质和判定，勾股定理，解（1）的关键是判断出△ADE ≌△CFE，解（2）的关键是判断出EF 垂直平分GH，解（3）的关键是作出辅助线，是一道比较典型的中考题．10.【分析】（1）证明△BPC 是等腰直角三角形，计算BP＝PC＝6，先根据三角形中线可知：EF是△ABC 的中位线，得EF∥BC，EF＝BC，证明△EPF∽△CPB，列比例式可得PE和AB 的长；（2）设PF＝m，PE＝n，则PB＝2m，PC＝2n，在Rt△PBC，Rt△PBE 和Rt△PCF 中，根据勾股定理列方程后，相加可得结论；（3）本题介绍两种解法：法一：证明△AGM≌△NGB（AAS），得BG 是△ABN 的中线，作辅助线，构建全等三角形和中线，得NF，BG 都为△ABN 的中线，由（2）知，AB2+AN2＝5BN2，代入可得结论；法二：如图4，作BP⊥DA 延长线于点P，CQ⊥AD 于点Q，易知四边形PBCQ 为矩形，设PA＝QD＝x，PB＝CQ＝y，表示PM＝x+，MQ＝2﹣x，证明△PBM∽△QMC，列比例式得方程：y2＝﹣x2+ x+12 ①，根据勾股定理得：AH2＝AB2﹣BH2，y2＝42﹣x2＝16﹣x2②，根据①②得：﹣x2+ x+12＝16﹣x2，解出可得结论．【解答】解：（1）如图1，∵BF⊥CE，∴∠BPC＝90°，∵∠PCB＝45°，∴△BPC 是等腰直角三角形，∵BC＝6 ，∴PC＝BP＝6，∵BF，CE 分别为AC，AB 边上的中线，∴EF 是△ABC 的中位线，∴EF∥BC，EF＝BC，∴△EPF∽△CPB，∴＝，∴，∴EP＝3，由勾股定理得：BE＝＝＝3，∴AB＝2BE＝6 ，故答案为：3，6；（2）猜想：AB2+AC2＝5BC2；证明：∵BF，CE 是△ABC 的中线，∴EF 是△ABC 的中位线，∴EF∥BC，EF＝BC，＝＝，设PF＝m，PE＝n，则PB＝2m，PC＝2n，在Rt△PBC 中，（2m）2+（2n）2＝BC2①在Rt△PBE 中，②在Rt△PCF 中，③由①，②，③得：AB2+AC2＝5BC2；（3）法一：在△AGM 与△NGB 中，，∴△AGM≌△NGB（AAS），∴BG＝MG，AG＝NG，∴BG 是△ABN 的中线，如图3，取AB 的中点F，连接NF，并延长交DA 的延长线于E，同理，△AEF≌△BNF，∴AE＝BN，EM＝2BN＝NC，∵EM∥NC，∴四边ENCM 是平行四边形，∴EN∥CM，∵BM⊥CM，∴EN⊥BM，即BG⊥FN，∵NF，BG 都为△ABN 的中线，由（2）知，AB2+AN2＝5BN2，∵AB＝4，BN＝AD＝，∴42+AN2＝5×，∴AN＝．法二：如图4，作BP⊥DA 延长线于点P，CQ⊥AD 于点Q，在▱ABCD 中，AD＝BC，易知四边形PBCQ 为矩形，∴PQ＝BC，∴PA＝QD，依题意：AM＝BN＝，MD＝2，设PA＝QD＝x，PB＝CQ＝y，∴PM＝x+ ，MQ＝2﹣x，∵BM⊥CM 于点M，∠BMC＝90°，∴∠BMP+∠CMQ＝90°，又∠BMP+∠PBM＝90°，∴∠PBM＝∠CMQ，又∵∠BPM＝∠MQC＝90°，∴△PBM∽△QMC，∴，即，化简得：y2＝﹣x2+ x+12 ①，作AH⊥BC 于点H，则BH＝PA＝x，AH＝y，在Rt△ABH 中，AH2＝AB2﹣BH2，∴y2＝42﹣x2＝16﹣x2②，由①②得：﹣x2+ x+12＝16﹣x2，∴x＝，y2＝，在Rt△AHN 中，AN＝＝＝＝．【点评】本题是四边形的综合题，考查相似三角形的判定和性质、矩形和平行四边形的判定和性质、三角形全等的性质和判定、三角形中线，勾股定理等知识，解题的关键是灵活运用所学知识解决问题，并运用类比的方法解决问题，属于中考常考题型．1.【分析】（1）根据旋转得：△ACE 是等边三角形，可得：AB＝BC＝CE＝AE，则四边形ABCE是菱形；（2）先证明C、F、E 在同一直线上，再证明△BAD≌△CAF（SAS），则∠ADB＝∠AFC，BD ＝CF，可得AC＝CF+CD；（3）先根据∠ADC＝∠DAF＝∠F＝90°，证明得四边形ADGF 是矩形，由邻边相等可得四边形ADGF 是正方形；（4）证明△BAM≌△EAD（SAS），根据BM＝DE 及勾股定理可得结论．【解答】（1）证明：∵△ABC 是等边三角形，∴AB＝BC＝AC，∵△ACD 绕点A 逆时针旋转60°得到△AEF，∴∠CAE＝60°，AC＝AE，∴△ACE 是等边三角形，∴AC＝AE＝CE，∴AB＝BC＝CE＝AE，∴四边形ABCE 是菱形；（2）线段CD，CF，AC 之间的数量关系：CD+CF＝AC，理由是：由旋转得：∠DAF＝60°＝∠BAC，AD＝AF，∴∠BAD＝∠CAF，∵△ABC 是等边三角形，∴AB＝AC，∴△BAD≌△CAF（SAS），∴∠ADB＝∠AFC，BD＝CF，∵∠ADC+∠ADB＝∠AFC+∠AFE＝180°，∴C、F、E 在同一直线上，∴AC＝BC＝BD+CD＝CF+CD，故答案为：CD+CF＝AC；（3）四边形ADGF 是正方形，理由如下：∵Rt△ABD 绕点A 逆时针旋转90°得到△AEF，∴AF＝AD，∠DAF＝90°，∵AD⊥BC，∴∠ADC＝∠DAF＝∠F＝90°，∴四边形ADGF 是矩形，∵AF＝AD，∴四边形ADGF 是正方形；（4）如图3，连接DE，∵四边形ADGF 是正方形，∴DG＝FG＝AD＝AF＝6，∵△ABD 绕点A 逆时针旋转90°，得到△AEF，∴∠BAD＝∠EAF，BD＝EF＝2，∴EG＝FG﹣EF＝6﹣2＝4，∵将△AFE 沿AE 折叠得到△AME，∴∠MAE＝∠FAE，AF＝AM，∴∠BAD＝∠EAM，∴∠BAD+∠DAM＝∠EAM+∠DAM，即∠BAM＝∠DAE，∵AF＝AD，∴AM＝AD，在△BAM 和△EAD 中，∵，∴△BAM≌△EAD（SAS），∴BM＝DE＝＝＝2．【点评】本题属于四边形综合题，主要考查了旋转的性质、全等三角形的判定与性质、等边三角形的判定与性质、正方形的性质以及勾股定理的综合应用，解决问题的关键是熟练掌握等边三角形和全等三角形的性质，依据图形的性质进行计算求解．。

类比探究(教师用)

类比探究（一）（直角结构）问题1：类比探究属于几何综合题，类比（__________，___________，___________）是解决此问题的主要方法，做好类比需要把握变化过程中的____________．若属于类比探究常见的结构类型，调用结构类比解决．若不属于常见结构类型①根据题干条件，结合___________________先解决第一问．②类比解决下一问．如果不能，分析条件变化，寻找______________．结合所求目标，依据_____________，大胆猜测、尝试、验证问题2：想一想类比探究问题常见的不变结构有哪些，处理方式是什么？问题3：直角的思考角度：1.边：勾股定理2.角：直角三角形两锐角互余3.面积：直角边看成高（等面积结构）4.固定模型和用法：①直角+中点（直角三角形斜边中线等于斜边一半）；②直角+特殊角（由特殊角构造直角三角形）；③直角+角平分线（等腰三角形三线合一）；④直角三角形斜边上的高（母子型相似、射影定理）；⑤弦图结构；⑥三等角模型；⑦斜直角放正.5.函数背景下考虑.6.圆背景下考虑：直径所对的圆周角是直角，垂径定理.想一想，在类比探究之直角结构中一般用的比较多的是哪些？1.在Rt△ABC中，∠B=90°，∠A=30°，将一块三角板的直角顶点放在△ABC斜边AC的中点P 处，将三角板绕点P旋转．（1）如图1，三角板的两直角边分别交AB，BC于点M，N，此时PN和PM的数量关系是( )A. B.C. D.答案：B解题思路：（2）如图2，三角板的两直角边分别交AB，BC的延长线于点M，N，此时PN和PM的数量关系是( )C. D.答案：C解题思路：试题难度：三颗星知识点：中考数学几何中的类比探究（3）如图3，若将三角板的直角顶点放在斜边上的点P处，三角板的两直角边分别交AB，BC的延长线于点M，N，当时，PN和PM的数量关系是( )A. B.C. D.答案：B解题思路：试题难度：三颗星知识点：中考数学几何中的类比探究2.在Rt△ABC中，∠ACB=90°，CD⊥AB，垂足为D，点E在AC上，BE交CD于点G，EF⊥BE 交AB于点F．（1）如图所示，若AC=BC，CE=EA，则EF与EG的数量关系是( )A. B.C. D.答案：C解题思路：试题难度：三颗星知识点：中考数学几何中的类比探究（2）如图所示，若AC=BC，CE=nEA（n为实数），则EF与EG的数量关系是( )A. B.C. D.答案：B解题思路：试题难度：三颗星知识点：中考数学几何中的类比探究（3）如图所示，若AC=mBC，CE=nEA（m，n为任意实数），则EF与EG的数量关系是( )A. B.C. D.答案：B解题思路：试题难度：三颗星知识点：中考数学几何中的类比探究平行结构：问题1：类比探究属于几何综合题，类比（__________，___________，___________）是解决此问题的主要方法，做好类比需要把握变化过程中的____________．若属于类比探究常见的结构类型，调用结构类比解决．若不属于常见结构类型①根据题干条件，结合___________________先解决第一问．②类比解决下一问．如果不能，分析条件变化，寻找______________．结合所求目标，依据_____________，大胆猜测、尝试、验证问题2：想一想类比探究问题常见的不变结构有哪些，处理方式是什么？问题3：借助平行线构造相似的处理中需要注意的有哪些？3.现有多个全等直角三角形，先取三个拼成如图1所示的形状，R为DE的中点，BR分别交AC，CD于点P，Q，则（1）BP:PQ:QR等于( )A.3:2:1B.3:2:4C.3:1:2D.2:1:2答案：C解题思路：试题难度：三颗星知识点：类比探究问题（2）若取四个直角三角形拼成如图2所示的形状，S为EF的中点，BS分别交AC，CD，DE于点P，Q，R，则BP:PQ:QR:RS等于( )A.5:1:3:2B.4:1:3:2C.5:1:4:2D.3:1:3:2答案：B解题思路：试题难度：三颗星知识点：类比探究问题（3）若取五个直角三角形拼成如图3所示的形状，T为FG的中点，BT分别交AC，CD，DE，EF于点P，Q，R，S，则BP:PQ:QR:RS:ST等于( )A.5:1:4:2:3B.5:1:5:2:3C.4:1:4:2:3D.5:1:4:3:2答案：A解题思路：试题难度：三颗星知识点：类比探究问题4.问题背景：已知在△ABC中，AB边上的动点D由A向B运动(与A，B不重合)，点E与点D同时出发，由点C沿BC的延长线方向运动(E不与C重合)，连接DE交AC于点F，点H是线段AF上一点．(1)初步尝试：如图1，若△ABC是等边三角形，DH⊥AC，且点D，E的运动速度相等，则HF，AH，CF之间的数量关系为( )A.HF=AH+CFB.C.HF=2AH+CFD.答案：A解题思路：（2）类比探究：如图2，若在△ABC中，∠ABC=90°，∠ADH=∠BAC=30°，且点D，E的运动速度之比是：1，则的值为( )A. B.C. D.答案：C解题思路：试题难度：三颗星知识点：全等三角形的判定与性质（3）延伸拓展：如图3，若在△ABC中，AB=AC，∠ADH=∠BAC=36°，记，且点D，E的运动速度相等，则的值为( )（用含m的代数式表示）A. B.C. D.答案：B解题思路：试题难度：三颗星知识点：中考数学几何中的类比探究5.如图1，在Rt△ABC中，∠ACB=90°，CD⊥AB于点D，点E在AC边上，BE交CD于点G，EF⊥BE交AB于点F，且AC=mBC，CE=nEA（m，n为实数）．试探究线段EF与EG之间的数量关系．（1）如图2，当m=1，n=1时，求EF与EG之间的数量关系．（2）如图3，当m=1，n为任意实数时，求EF与EG之间的数量关系．（3）如图1，当m，n均为任意实数时，求EF与EG之间的数量关系．（1）中EF与EG之间的数量关系为( )A. B. C.EF=EG D.答案：C解题思路：试题难度：三颗星知识点：直角结构（2）中EF与EG之间的数量关系为( )A. B. C. D.答案：B解题思路：试题难度：三颗星知识点：直角结构（3）中EF与EG之间的数量关系为( )A. B. C. D.答案：D解题思路：试题难度：三颗星知识点：直角结构6.（1）如图1，正方形AEGH的顶点E，H在正方形ABCD的边上，求的值．（2）如图2，将图1中的正方形AEGH绕点A旋转一定角度，求的值．（3）如图3，把图2中的正方形都换成矩形，当，时，求的值．1．（1）中的值为( )A.2:3:2B.1:1:1C.1:2:1D.答案：D解题思路：试题难度：三颗星知识点：旋转结构（2）中的值为( )A.1:1:1B.C. D.答案：C解题思路：试题难度：三颗星知识点：旋转结构（3）中的值为( ) A. B.C. D.答案：B解题思路：试题难度：三颗星知识点：旋转结构中点结构：问题1：类比探究属于几何综合题，类比（__________，___________，___________）是解决此问题的主要方法，做好类比需要把握变化过程中的____________．若属于类比探究常见的结构类型，调用结构类比解决．若不属于常见结构类型①根据题干条件，结合___________________先解决第一问．②类比解决下一问．如果不能，分析条件变化，寻找______________．结合所求目标，依据_____________，大胆猜测、尝试、验证问题2：想一想类比探究问题常见的不变结构有哪些，处理方式是什么？问题3：中点的思考角度：①遇到等腰三角形底边的中点，考虑三线合一；②遇到直角三角形斜边的中点，考虑直角三角形斜边中线等于斜边一半；③遇到三角形一边上的中点，考虑倍长中线；④遇到“平行夹中点”，考虑延长证全等；⑤遇到多个中点，考虑（构造）中位线．想一想，在类比探究之中点结构中一般用的比较多的是哪些？7.如图1，在四边形ABCD中，AB=CD，E，F分别是BC，AD的中点，连接EF并延长，与BA，CD的延长线分别交于点M，N，则∠BME=∠CNE．（1）如图2，在四边形ADBC中，AB与CD相交于点O，AB=CD，E，F分别是BC，AD的中点，连接EF，分别交DC，AB于点M，N，则△OMN的形状为( )A.等腰三角形B.等边三角形C.等腰直角三角形D.含30°角的直角三角形答案：A解题思路：试题难度：三颗星知识点：类比探究问题（2）如图3，在△ABC中，AC>AB，点D在AC边上，且AB=CD，E，F分别是BC，AD的中点，连接EF并延长，与BA的延长线交于点G．若∠EFC=60°，连接GD，则△AGD的形状为( )A.等腰三角形B.等边三角形C.直角三角形D.含30°角的直角三角形答案：D解题思路：试题难度：三颗星知识点：类比探究问题8.（1）如图1，在正方形ABCD的边AB上任取一点E，过点E作EF⊥AB，交BD于点F，取DF的中点G，连接EG，CG．为了研究线段EG和CG之间的数量和位置关系，可通过作辅助线：延长EG，交AD的延长线于点H，连接EC，HC，来进行分析．则得到的结论是( )A.EG=CG且EG⊥CGB.EG=CG但EG与CG不垂直C.EG⊥CG但EG≠CGD.答案：A解题思路：试题难度：三颗星知识点：中考数学几何中的类比探究（2）在图1的基础上，将△BEF绕点B逆时针旋转90°，其他条件不变，如图2，为了证明EG和CG之间的数量和位置关系仍成立，类比（1）中的辅助线和证明思路，需要作出的辅助线是( )A.延长EG，交AD于点H，连接HCB.延长BG，交AD于点H，连接HCC.延长EG，交CD的延长线于点HD.延长EF，交DA的延长线于点H，连接HC答案：C解题思路：试题难度：三颗星知识点：中考数学几何中的类比探究（3）在图1的基础上，将△BEF绕点B逆时针旋转180°，其他条件不变，如图3，为了证明EG和CG之间的数量和位置关系仍成立，类比（1），（2）中的辅助线和证明思路，需要证明两个直角三角形全等，则判断该三角形全等时使用的条件是( )A.AASB.ASAC.HLD.SAS答案：D解题思路：试题难度：三颗星知识点：中考数学几何中的类比探究9.（1）问题背景：如图1，在四边形ABCD中，AB=AD，∠BAD=120°，∠B=∠D=90°．E，F分别是边BC，CD上的点，且∠EAF=60°．求证：EF=BE+DF．（2）探索延伸：如图2，在四边形ABCD中，AB=AD，E，F分别是边BC，CD上的点，且，则当∠B和∠D满足什么条件时，EF=BE+DF成立？（3）实际应用：如图3，在某次军事演习中，舰艇甲在指挥中心（O处）北偏西30°的A处，舰艇乙在指挥中心南偏东70°的B处，并且两舰艇到指挥中心的距离相等．接到行动指令后，舰艇甲向正东方向以60海里/小时的速度前进，舰艇乙沿北偏东50°的方向以80海里/小时的速度前进．1.5小时后，指挥中心观测到甲、乙两舰艇分别到达E，F处，且两舰艇之间的夹角为70°，则此时两舰艇之间的距离为( )海里．（1）中证明上述结论的辅助线的作法，有如下说法：①延长FD到G，使DG=BE，连接AG；②过点A作AG⊥EF于点G；③将△ABE绕点A逆时针旋转120°得到△ADG（之后证明点G，D，F在同一条直线上）．其中可以证明结论的是( )A.①B.②③C.①③D.①②③答案：C解题思路：试题难度：三颗星知识点：全等三角形的判定与性质2.（上接第1题）（2）中当∠B和∠D满足什么条件时，EF=BE+DF成立？( )A.∠B=∠DB.∠B+∠D=180°C.∠B=2∠DD.∠B+∠D=120°答案：B解题思路：试题难度：三颗星知识点：全等三角形的判定与性质（3）中两舰艇之间的距离为( )海里．A. B.210C.300D.条件不够，无法计算答案：B解题思路：试题难度：三颗星知识点：类比探究问题10.[问题情境]张老师给爱好学习的小军和小俊提出这样一个问题：如图1，在△ABC中，AB=AC，点P为边BC上的任一点，过点P作PD⊥AB，PE⊥AC，垂足分别为D，E，过点C 作CF⊥AB，垂足为F．求证：PD+PE=CF．小军的证明思路是：如图2，连接AP，由△ABP与△ACP的面积之和等于△ABC的面积可以证得：PD+PE=CF．小俊的证明思路是：如图2，过点P作PG⊥CF，垂足为G，可以证得：PD=GF，PE=CG，则PD+PE=CF．[变式探究]如图3，当点P在BC延长线上时，其余条件不变，请探究PD，PE，CF之间的数量关系，并证明该结论．请运用上述解答中所积累的经验和方法完成下列两题：[结论运用]如图4，将矩形ABCD沿EF折叠，使点D落在点B上，点C落在点处，点P为折痕EF上的任一点，过点P作PG⊥BE，PH⊥BC，垂足分别为G，H．若AD=8，CF=3，求PG+PH的值．[迁移拓展]图5是一个航模的截面示意图．在四边形ABCD中，E为AB边上的一点，ED⊥AD，EC⊥CB，垂足分别为D，C，且，．M，N分别为AE，BE的中点，连接DM，CN，求△DEM与△CEN的周长之和．（建议学生先打印纸质材料，再做题）（1）[变式探究]中PD，PE，CF之间的数量关系为( )A. B.C. D.答案：B解题思路：试题难度：三颗星知识点：等面积法（2）[结论运用]中PG+PH的值为( ) A.3 B.4C.5D.答案：B解题思路：试题难度：三颗星知识点：翻折变换（折叠问题）（3）[迁移拓展]中△DEM与△CEN的周长之和为( )dm．A.6B.C. D.答案：B解题思路：试题难度：三颗星知识点：直角三角形斜边的中线等于斜边的一半11.（1）类比梯形的定义，我们定义：有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”．（1）已知：如图1，四边形ABCD是“等对角四边形”，∠A≠∠C，∠A=70°，∠B=80°，求∠C 的度数．（2）在探究“等对角四边形”性质时，小红画了一个“等对角四边形”ABCD（如图2），其中∠ABC=∠ADC，AB=AD，此时她发现CB=CD成立．由此小红猜想：“对于任意‘等对角四边形’，当一组邻边相等时，另一组邻边也相等”．那么小红的发现是正确的吗？猜想是正确的吗？（3）已知：在“等对角四边形”ABCD中，∠DAB=60°，∠ABC=90°，AB=5，AD=4．求对角线AC的长．（建议学生先打印纸质材料，再做题）（1）∠C的度数为( )A.70°B.130°C.80°D.30°答案：B解题思路：试题难度：三颗星知识点：多边形的内角和定理（2）下列说法正确的是( )A.小红的发现是正确的，猜想也是正确的B.小红的发现是正确的，猜想是错误的C.小红的发现是错误的，猜想也是错误的D.小红的发现是错误的，猜想是正确的答案：B解题思路：试题难度：三颗星知识点：类比探究问题（3）对角线AC的长为( )A. B.C. D.答案：D解题思路：试题难度：三颗星知识点：类比探究问题12.问题：如图1，点E，F分别在正方形ABCD的边BC，CD上，∠EAF=45°，试判断BE，EF，FD之间的数量关系．（1）发现证明：小聪把△ABE绕点A逆时针旋转90°至△ADG（如图2），经过推理和计算发现BE，EF，FD 之间的数量关系，请判断BE，EF，FD之间的数量关系．（2）类比引申：如图3，在四边形ABCD中，∠BAD≠90°，AB=AD，∠B+∠D=180°，点E，F分别在边BC，CD 上，则当∠EAF与∠BAD满足什么关系时，仍有EF=BE+FD？（3）探究应用：如图4，在某公园的同一水平面上，四条通道围成四边形ABCD．已知AB=AD=80米，∠B=60°，∠ADC=120°，∠BAD=150°，道路BC，CD上分别有景点E，F，且AE⊥AD，米，现要在E，F之间修一条笔直道路，求这条道路EF的长（结果取整数，参考数据：，）．（1）中BE，EF，FD之间的数量关系为( )A. B.EF=2BE+FDC.EF=BE+FDD.EF=BE+2FD答案：C解题思路：试题难度：三颗星知识点：旋转结构（2）类比引申：当∠EAF与∠BAD满足什么关系时，仍有EF=BE+FD？( )A.∠BAD=2∠EAFB.∠BAD+∠EAF=180°C.∠BAD+∠EAF=120°D.∠BAD+2∠EAF=180°答案：A解题思路：试题难度：三颗星知识点：旋转结构（3）探究应用：这条道路EF的长为( )A.110B.109C.108D.111答案：B解题思路：。

中考数学类比探究(一)(讲义及答案)

B
A
A
E
D
CB 图1
CA
D
图2
BE C 图3
3
3. （1）问题发现如图 1，△ABC 和△CDE 均为等边三角形，直线 AD 和直线 BE 交于点 F．填空：①∠AFB 的度数是________； ②线段 AD，BE 之间的数量关系为__________．（2）类比探究如图 2，△ABC 和△CDE 均为等腰直角三角形，∠ABC=∠DEC=90°，AB=BC，DE=EC，直线 AD 和直线 BE 交于点 F．请判断∠AFB 的度数及线段 AD，BE 之间的数量关系，并说明理由．（3）解决问题如图 3，在平面直角坐标系中，点 A 坐标为(4，0)，点 B 为 y 轴上任意一点，连接 AB，将 BA 绕点 B 逆时针旋转 90°至 BC，连接 OC，请直接写出 OC 的最小值．
G M
A
F C
N
D (E)
B
A
图1
G
C M
N
D (E)
B
图2
F
G
C
F
N
M
A
ED
B
图3
4
5. （1）观察猜想如图 1，点 B，A，C 在同一条直线上，DB⊥BC，EC⊥BC 且∠DAE=90°，AD=AE，则 BC，BD，CE 之间的数量关系为_______________；
D E
B
A
C
图1
（2）问题解决如图 2，在 Rt△ABC 中，∠ABC=90°，CB=4，AB=2，以 AC 为直角边向外作等腰 Rt△DAC，连接 BD，求 BD 的长；
类比探究（一）（讲义）
知识点睛
1. 类比探究是一类共性条件与特殊条件相结合，由特殊情形到一般情形（或由简单到复杂）逐步深入，解决思想方法一脉相承的综合性题目，常以几何综合题为主——“条件类似、图形结构类似、问法类似”．

类比探究(教师用)

类比探究(教师用)类比探究一）直角结构问题1：类比探究是几何综合题，类比（相似、全等、等腰）是解决此问题的主要方法，做好类比需要把握变化过程中的不变量。

若属于类比探究常见的结构类型，可以调用结构类比解决。

若不属于常见结构类型，可以先根据题干条件，结合已知条件先解决第一问，然后类比解决下一问。

如果不能，可以分析条件变化，寻找不变量。

结合所求目标，依据猜想、尝试、验证的思路大胆猜测，尝试，验证。

问题2：类比探究问题常见的不变结构有：勾股定理、直角三角形两锐角互余、直角边看成高（等面积结构）、直角+中点、直角+特殊角、直角+角平分线、斜直角放正、弦图结构、三等角模型、母子型相似、射影定理、函数背景下考虑、圆背景下考虑等。

处理方式是根据所求目标和已知条件，结合不变结构进行类比，寻找解题思路。

问题3：直角结构的思考角度有：1.边：勾股定理；2.角：直角三角形两锐角互余；3.面积：直角边看成高（等面积结构）；4.固定模型和用法：直角+中点、直角+特殊角、直角+角平分线、斜直角放正、弦图结构、三等角模型、母子型相似、射影定理；5.函数背景下考虑；6.圆背景下考虑：直径所对的圆周角是直角，垂径定理。

在类比探究之直角结构中，常用的结构有勾股定理、直角三角形两锐角互余、直角边看成高（等面积结构）、直角+中点、直角+特殊角、直角+角平分线、斜直角放正等。

例如，对于Rt△ABC中，∠B=90°，∠A=30°，将一块三角板的直角顶点放在△ABC斜边AC的中点P处，将三角板绕点P旋转，可以利用不变结构进行类比解题。

为折痕EF上的任一点P，作PG⊥BE，PH⊥BC，垂足分别为G，H。

已知AD=8，CF=3，求PG+PH的值。

解题思路：根据垂足定理，PG=PE-EG，PH=PF-FH。

由于EF是折痕，所以PE=PF，EG=FC，FH=AD。

因此，PG+PH=PE+FC-AD=PE+CF-AD=PE-ED+CF。

专题13几何类比探究题型-2024年中考数学答题技巧与模板构建(解析版)

专题13几何类比探究题型题型解读｜模型构建｜通关试练几何的类比探究题型是近年中招解答题的必考题型，该题型往往以压轴题的形式出现，有一定的难度。

探究型问题是指命题中缺少一定的条件或无明确的结论，需要经过推断，补充并加以证明的一类问题．根据其特征大致可分为：条件探究型、结论探究型、规律探究型和存在性探究型等四类。

由于探究型试题的知识覆盖面较大，综合性较强，灵活选择方法的要求较高，再加上题意新颖，构思精巧，具有相当的深度和难度，所以要求同学们在复习时，首先对于基础知识一定要复习全面，并力求扎实牢靠；其次是要加强对解答这类试题的练习，注意各知识点之间的因果联系，选择合适的解题途径完成最后的解答．模型01图形旋转模型模型一、A字形（手拉手）及其旋转D模型二、K字型及其旋转CC手拉手模型是有两个等腰的三角形或者两个等边的三角形，他们有一个共同的顶点，且两个等腰三角形的顶角是相等的，那么就可以用角的和差求得共顶点的另外两个角相等等，然后利用等腰的边对应相等，可证明两个三角形全等（边角边）组成这样的图形模样的我们就说他是手拉手模型。

在类比探究题型中，往往会对等腰三角形或者等边三角形进行演变，变成一般三角形进行旋转，通常全等三角形变为相似三角形。

模型特征：双等腰；共顶点；顶点相等；绕着顶点作旋转解题依据：等腰共顶手拉手，旋转全等马上有；左手拉左手，右手拉右手，两根拉线抖一抖，它们相等不用愁；拉线夹角与顶角，相等互补答案有。

模型02图形平移模型探究1.四边形平移变换四边形的平移变换题型中主要考查了全等三角形的判定和性质，相似三角形的判定和性质，平移几何性质、三角形内角和定理的应用，勾股定理，解题的关键是熟练掌握三角形全等或相似的判定方法，画出相应的图形，注意分类讨论．2.三角形平移变换三角形平移变换主要利用三角形全等和三角形相似的判定和性质，勾股定理，矩形的判定和性质，平移性质、平行线的判定和性质，解题的关键是作出辅助线，熟练掌握三角形相似的判定方法.3.其它图形平移类比探究问题综合考查了全等三角形的判定和性质，相似三角形的判定和性质，三角形内角和定理的应用，勾股定理，解题的关键是熟练掌握三角形相似的判定方法，画出相应的图形，注意分类讨论.模型03动点引起的题型探究动点型问题是指题设中的图形中存在一个或多个动点，它们在线段、射线、直线、抛物线、双曲线、弧线等上运动的一类非常具有开放性的题目。

类比探究之结合不变特征探究(人教版)(含答案)

类比探究之结合不变特征探究（人教版）一、单选题(共5道，每道20分)1.在△ABC中，AB=AC=a，BC=b，且，BG⊥AC于G，DE⊥AB于E，DF⊥AC于F．在图1中，D是BC边上的中点，则DE+DF与BG的数量关系为( )A. B.C. D.无法判断答案：B解题思路：1．可以根据线段关系，大胆地猜测（借助圆规、三角板等度量工具），然后验证；2．从特征来看：中点、垂直、线段和差倍分．（1）从中点特征出发：①△ABC是等腰三角形，点D是BC中点，DE，DF分别垂直于AB，AC，易得DE=DF；②DF⊥AC，BG⊥AC，则DF∥BG，又由点D是BC中点，可得DF是△BCG的中位线，BG=2DF=DE+DF．（2）从垂直特征出发（BG，DE，DF都和垂直有关，可以考虑面积）①如图，连接AD；②根据S△ABD+S△ACD=S△ABC，可得；③由AB＝AC，可得DE+DF=BG．（3）从线段结果和差倍分出发（考虑截长补短）①如图，过点D作DM⊥BG于点M，则四边形DMGF为矩形，DF=GM；②证明△BMD≌△DEB（AAS），可得BM=DE；③BG=BM+GM=DE+DF．故选B试题难度：三颗星知识点：类比探究2.（上接第1题）在图2中，D是线段BC上的任意一点，DE+DF与BG的关系仍然成立.下列3种思路中你认为可行的是( )思路①：连接AD，借助S△ABD+S△ACD=S△ABC；思路②：过点D作DM⊥BG于点M，然后证明△BMD≌△DEB；思路③：连接EF，证明EF=BG．A.①②③B.①③C.②③D.①②答案：D解题思路：1．首先考虑类比第1题的思路、做法；2．对比第1题发现，D点作为中点变了，但垂直、线段间的关系没有变；3．从垂直、线段间的关系入手；（1）从垂直出发（BG，DE，DF都和垂直有关，可以考虑面积）①如图，连接AD；②根据S△ABD+S△ACD=S△ABC，可得；③可得DE+DF=BG．（2）从线段间的关系出发（考虑截长补短）①如图，过点D作DM⊥BG于点M，则四边形DMGF为矩形，DF=GM；②证明△BMD≌△DEB，可得BM=DE；③BG=BM+GM=DE+DF．故选D试题难度：三颗星知识点：类比探究3.（上接第1，2题）在图3中，D是线段BC延长线上的点，探究DE，DF与BG的关系，你认为正确的是( )A. B.C. D.无法判断答案：B解题思路：参考第1，2题的思路，以面积为例：①如图，连接AD；②根据S△ABD-S△ACD=S△ABC，可得；③可得DE-DF=BG，即BG+DF=DE；故选B试题难度：三颗星知识点：类比探究4.在等边三角形ABC中，点E在直线AB上，点D在直线BC上，且CE=DE．为判断AE和BD 之间的关系，小明准备分情况进行讨论：当E是AB中点时，如图1，小明发现，由于E是AB边的中点，利用三线合一可以得到AE=BE，∠ECB=30°，再由CE=DE可以得到∠D=30°，进而得到∠BED=30°，就可以得到BD=BE=AE．但是当E不是AB中点时，就不能照搬上述方式进行证明．此时小明想到了另外一种方式：过点E作EF∥BC，交AC于点F，也能证明AE=BD．（1）当E是线段AB上除端点和中点外的任一点时，如图2，按照上述辅助线证明AE=BD，证明过程中需要证明一对三角形全等，则证明这对三角形全等不能使用的条件是( )A.AASB.ASAC.SASD.SSS答案：D解题思路：1．解题要点①要在图2中照搬小明的思路，需要明白小明的思路在图1中是怎么证明的．考虑不能利用E是中点带来的结论，所以证明时，要避开中点带来的结论（AE=BE，∠ECB=30°），用其他条件来讨论．如图，过点E作EF∥BC，交AC于点F，则△AEF是等边三角形，AE=EF=AF，能够证明△EFC≌△DBE，EF=BD，进而得到AE=BD．②在图2中，同样作出辅助线，如图所示，照搬①中的证明思路，先得到△AEF是等边三角形，AE=EF，再证明△EFC≌△DBE．关键在于判断三角形全等能够使用的条件有哪些．由题意得，BE=FC．∵∠ABC=∠AFE=60°，∴∠DBE=∠EFC=120°．∵∠D+∠DEB=60°，∠ECD+∠ECF=60°，∠D=∠ECD，∴∠DEB=∠ECF．同时∠D=∠ECD=∠CEF，即两个三角形中，三组内角分别对应相等，同时BE=CF，CE=DE，则证明△EFC≌△DBE可以使用AAS，ASA，SAS，不能使用的是SSS．③思考前面的证明过程，不变的特征是：△ABC是等边三角形，CE=DE．作平行线是为了得到等边三角形，进而得到全等三角形．④整个证明的路线图：作辅助线→判断等边三角形（△AEF）→证明△EFC≌△DBE．2．解题过程我们利用SAS来证明AE=BD，具体过程如下：如图，过点E作EF∥BC，交AC于点F．则∠AEF=∠ABC=∠A=60°，∴△AEF是等边三角形，∴AE=EF=AF，∴BE=FC．∵CE=DE，∴∠D=∠ECD．∵∠ABC=∠ACB，∴∠D+∠DEB=∠ECD+∠ECF，∴∠DEB=∠ECF，∴△EFC≌△DBE（SAS），∴EF=BD，∴AE=BD．故选D试题难度：三颗星知识点：类比探究5.（上接第4题）（2）当点E在BA的延长线上时，如图3，点D在BC边上，且CE=DE，按照下面的操作，能够证明AE=BD的是( )A.直接证明△EAC≌△BDEB.①过点A作AF∥BC，交EC于点F；②△AEF是等边三角形；③△AFC≌△BDEC.①过点E作EF∥BC，交CA的延长线于点F；②△AEF是等边三角形；③△EFC≌△DBED.①过点A作AF∥BC，交EC于点F，连接DF；②四边形FDBE是等腰梯形答案：C解题思路：1．解题要点此题中△ABC是等边三角形及CE=DE没有发生变化，所以可照搬（1）中的思路：作辅助线→判断等边三角形（△AEF）→证明△EFC≌△DBE．作出的辅助线是：过点E作EF∥BC，交CA的延长线于点F．2．解题过程如图，过点E作EF∥BC，交CA的延长线于点F．则∠AEF=∠B=∠ACB=∠BAC=∠EAF=60°，∴△AEF是等边三角形，∴AE=EF=AF，∴BE=FC．∵CE=DE，∴∠EDC=∠ECD，∴∠B+∠BED=∠ACB+∠FCE．∴∠BED=∠FCE，∴△EFC≌△DBE（SAS），∴EF=BD，∴AE=BD．故选C试题难度：三颗星知识点：类比探究。

专题四综合与探究类型三类比探究题

类型三类比探究题例1 (2017成都)问题背景：如图①，等腰△ ABC 中，AB = AC , / BAC = 120° 作AD 丄BC 于点D ,贝U D 为BC 的中点，/ BAD = 1/ BAC = 60° 于是 ABC = 2BD = ©迁移应用：(1) 如图②，△ ABC 和^ ADE 都是等腰三角形，/ BAC =/ DAE = 120 °, D , E , C 三点在同一条直线上，连接BD.① 求证：△ ADB AEC ；② 请直接写出线段 AD , BD , CD 之间的等量关系式；拓展延伸：(2) 如图③，在菱形 ABCD 中，/ ABC = 120 °,在/ ABC 内作射线 BM ,作点C 关于 BM 的对称点E ,连接AE 并延长交BM 于点F ,连接CE , CF.① 证明△ CEF 是等边三角形； ② 若AE = 5, CE = 2,求BF 的长.【思路点拨】(1)①易得/ DAB = / EAC ,再由三角形全等定理证明；②由本题告诉的性质可得DE ={3A D ，再由线段和差得 DE = DC — EC ,进而得DC — EC^/SAD ,再将EC 换成相等的线段 DB 便可得结论；(2)①由C 与E 关于BF 对称，则BF 是CE 的垂直平分线, 进而得 BE = BC , CF = EF , / 3 = / 4, / EFB = / CFB ,进而证明 AB = BC = BE ,得/ 1 = / 2,再进一步得/ 2 +/3 =60°得/EFC = 60°最后便可得结论； ②先由已知条件求出 GE 、EF ,进而得GF ,再在RtA BGF 中通过解直角三角形得结果.(1)解：①由题意可知： AD = AE , AB = AC , •// DAE =/ BAC , •••/ DAB =/ EAC , •••△ ADB BA AEC( SAS);② CD =>/3AD + BD ;【解法提示】•/ AD = AE , / DAE = 120° •• DE = >/3AD , •/ DE = DC — EC , •• DC —EC =^/3A D ,由①知，△ ADB ◎△ AEC , •• EC = DB , DC — DB =V 3A D ,即 CD = V 3A D + BD ;⑵①证明：如解图，连接BE ,作BG 丄AE 于点G , ••• C 、E 关于BM 对称，••• BE = BC , CF = EF , / 3 = / 4, / EFB = / CFB , 在菱形 ABCD 中，•// ABC = 120° AB = BC , AB = BC = BE ,又••• BG 丄 AE , •••/ 1 = / 2,•••/ GBF =/2+/3= 2 / ABC = 60° •••在四边形GBNE 中，，图)/ GEN = 360° — / EGB — / ENB — / GBN = 120° •••/ FEN = 60° 又••• EF = FC , •••/ ECF = 60°•••△ EFC 为等边三角形；第1题解图①(2)过点F 作FH 丄AD 交AD 的延长线于点 H ,作FM 丄AB 交AB 的延长线于点 M ,如解图①所示，贝U FM = AH , AM = FH ,① ••• AD = 4, AE = 1, ••• DE = 3, 同(1)得：△ EFH ◎△ CED(AAS), F H = DE = 3, EH = CD = 4, 即点F 到AD 的距离为3;② ••• BM = AB + AM = 4+ 3 = 7, FM = AE + EH = 5,••• BF = p BM 2 + FM 2 =p 72 + 52=^74;②••• AE = 5, CE = 2,1 5 • EG= 2AE = 2, EF = CE = 2,9• - GF = EG + EF = 2 ,•••/ BGF = 90° / GFB = 30° ,• BF = GF。