2010年高中学业水平考试数学模拟卷(二)答案
2010年模拟考试数学试题答案

tan ABO
1 ……………………………………………
OB 4
2
.2 分
∴ OA= 2,即 A 的坐标为 (0, 2),点 B 的坐标为 (4, 0)……………… 3 分
OA OB
∵ CE⊥ x 轴,∴ CE∥ OA,∴
………………………………
CE BE
∵ OE=2,∴ CE=3.∴点 C 的坐标是 (- 2, 3)…………………………
∴ OE ON , AE CN .
ห้องสมุดไป่ตู้
又∵ MOE MON 450 , OM OM , ∴ OME OMN . ∴ MN ME AM AE . ∴ MN AM CN , ∴ p MN BN BM AM CN BN BM AB BC 4.
∴在旋转正方形
OABC 的过程中, p 值无变化 . …………… 10 分
∴一共调查了 3x+4x+ 5x+ 8x+ 2x= 66(人 ) ……………………………………………
∴捐款数不少于
20 元的概率是 30 66
5 11
.…………………………………………………
3分 5分
数学 第 1 页 ( 共 6 页)
(2) 由(1) 可知,这组数据的众数是 20(元 ),中位数是 15(元 ).…………………………… 7 分 (3) 全校学生共捐款 (9× 5+ 12×10+ 15×15+ 24×20+ 6× 30)÷ 66× 2310= 36750(元 ) ………………… 10 分
2y ……………………… 4 分 xy
x 3y =
2 y ………………………………………… 6 分
xy xy
= x y =1. xy
…………………………………………… 7 分
2010年湖南省普通高中学业水平考试数学试卷及答案

高中学业水平考试数学补考试卷一、选择题:本大题共10小题,每小题4分,满分40分. 1.下列函数中,是偶函数的是( ) A f(x)=x B f(x)=1xC f(x)=x 2D f(x)=sinx 2.化简(sin α+cos α)2=( )A 1+sin2αB 1-sin αC 1-sin2αD 1+sin α 3.在△ABC 中,若0CA CB =,则△ABC 是( )A 锐角三角形B 直角三角形C 钝角三角形D 等腰三角形4.已知圆C 的方程为:2(1)x -+2(2)y -=4,则圆心坐标与半径分别为( ) A (1,2),r=2 B (-1,-2),r=2 C (1,2),r=4 D (-1,-2),r=4 5.已知集合M ={1,2},N ={2,3}, 则 MUN =( ) A {1,2} B {2,3} C {1,3} D {1,2,3}6.如图所示的圆盘由八个全等的扇形构成,指针绕中心旋转,可能随机停止,则指针停止在阴影部分内的概率是( ) A12 B 14 C 16 D 187.已知a>b ,c R ∈,则( )A a+c>b+cB a c b c +<+C a c b c +≥+D a+c b c ≤+8.下列几何体中,正视图、侧视图和俯视图都相同的是( ) A 圆柱 B 圆锥 C 球 D 三菱柱9.已知函数() (01)x f x a a a =>≠且,f(1)=2,则函数f(x)的解析式是( ) A f(x)=4x B f(x)= 1()4x C f(x)=2x D f(x)=1()2x10.在△ABC 中,a 、b 、c 分别为角A 、B 、C 的对边,若A=60,b=1,c=2,则a =( ) A 1 B 3 C 2 D 7二、填空题:本大题共5小题,每小题4分,满分20分. 11 直线y=2x+2的斜率是________ 12 已知如图所示的程序框图,若输入 的x 值为1,则输出和y 值是_____ 13 已知点(x ,y)在如图所示的阴影 部分内运动,则z=2x+y 的最大值是______14 已知向量a =(4,2),b =(x ,3), (13题)若a||b ,则实数x 的值为______15 张山同学的家里开了一个小卖部, (12题)为了研究气温对某种冷饮销售量的影响,他收集了这一段时间内这种冷饮每天的销售量y (杯)与当天最高气温x(0C)的有关数据,通过描绘散点图,发现y 和x 呈现线性相关关系,并求得回归方程为y =2x+60,如果气象预报某天的最高气温为340C ,则可以预测该天这种饮料的销售量为____杯。
2010年安徽普通高中学业水平模拟考试数学试题及参考答案[1]
![2010年安徽普通高中学业水平模拟考试数学试题及参考答案[1]](https://img.taocdn.com/s3/m/11043fdad15abe23482f4d82.png)
2011年肥东一中学业水平测试第二次模拟试卷数 学1.考试采用书面答卷闭卷方式,考试时间90分钟,满分100分。
2.本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分。
其中,第I 卷(选择题)的答案须填在第I 卷后的答题卡上。
第I 卷(选择题 共45分)一选择题(本大题共18小题,每小题3分,共54分。
每小题的四个选项中,只有一个选项符合题目要求。
请将正确答案填在第I 卷后的答题卡上。
)1:已知21{|0},{|0},x M x x x N x x-=-<=<则有 A .M N N = B. M N M = C.M N N = D. M N R =2.在三角形ABC 中,()0AB AB BC +=,则三角形ABC 的形状是A.直角三角形 B.锐角三角形C.钝角三角形 D.正三角形3.已知函数()f x =M ,()2x g x e =-的值域为N ,则M N = A.[)+∞,2 B. ()2,∞-C .(-2,2) D.∅4.下面程序输出的结果为A . 9, 4 B. 4, 5C. 9, -1D. -1, 95.有一种波,其波形为函数sin()2y x π=-的图像,若其在区间[0,t]上至少有2个波峰(图像的最高点,则正整数t 的最小值是A.5B.6C.7D.86.在△ABC 中,三内角A 、B 、C 所对应的边长分别为a 、b 、c ,且A 、B 、C成等差数列,b =则△ABC 的外接圆半径为 A .21B.1C.2D.4 7.从5个男生、2个女生中任选派人,则下列事件中必然事件是 ( )A.3个都是男生B. 至少有1个男生C.3个都是女生D.至少有1个女生 8.某赛季甲、乙两面名篮球运动员每场比赛得分的茎叶图如下图所示:则下列说法正确的是A. 甲总体得分比乙好,且最高得分甲比乙高;B. 甲总体得分比乙好,且最高得分乙比甲高;C. 乙体得分比甲好,且最高得分乙比甲高;D. 乙体得分比甲好,且最高得分甲比乙高;9.已知点A(2,0),B(0,3),C(-1,-2),则ABCD的顶点D 的坐标为A.(1,-5)B.(-3,1)C.(1,-3)D.(-5,1) 10.在数列{}n a中,a 1=21,1221n n a a +=+,则a 2008的值为 A.1002 B.1003 C.1004 D.100511.下面的三视图(依次为正视图、侧视图、俯视图)表示的几何体是A.六棱柱B.六棱锥C.六棱台D.六边形 12.若直线2x+3y+8=0,x-y-1=0和x+ky=0相交于一点,则k=A.-21 B.21C.-2D.2 13.以点C(-4,3)为圆心的圆与直线2x+y-5=0相离,则圆C 的半径R 的取值范围是A.(0,20 )B.(0,5)C.(0,25)D.(0,10)14.若2α与2β互余,则(1tan )(1tan )αβ++的值为 A.1 B.2 C.3 D.415.如图,如果MC ⊥菱形ABCD 所在的平面,那么MA 与BD 的位置关系是A.平行,B.垂直相交C.异面D.相交但不垂直A16.圆锥平行于底面的截面面积是底面积的一半,则此截面分圆锥的高为上 、 下两段 的比为A.1:1)B.1:2C.1: 2 .1:417.实数x 、y 满足不等式组 00220y x y x y ≥⎧⎪-≥⎨⎪--≥⎩,则11y w x -=+的取值范围 ( )A.[-1,31] B.[-21,31] C.⎪⎭⎫⎢⎣⎡+∞-,21 D.⎪⎭⎫⎢⎣⎡-1,21 18.函数sin()(0,0,)2y A x A πωφωφ=+>><的图像如图所示,则y 的表达式为( )A.102sin()116x y π=+B. 102sin()116x y π=- C. 2sin(2)6y x π=+ D. 2sin(2)6y x π=-第II 卷(非选择题共46分)二、填空题(本大题共计4小题,每小题4分,共计16分,把答案填在题中横线上) 19.如图所示,随机往正方形中扔一颗豆子(落在正方形外不算),则它落到阴影部分的概率是20.某厂去年生产某种规格的电子元件a 个,计划从今年开始的m 年内,每年生产此种元件的产量比上一年增长p%,则此种规格电子元件年产量y 随年数x 的变化的函数关系是21.某公司有1000名员工,其中,高层管理人员占50人,属高收入者;中层管理人员占200人,属中等收入者;一般员工占750人,属低收入者。
2010年广州市高三二模数学试题及答案(文科)
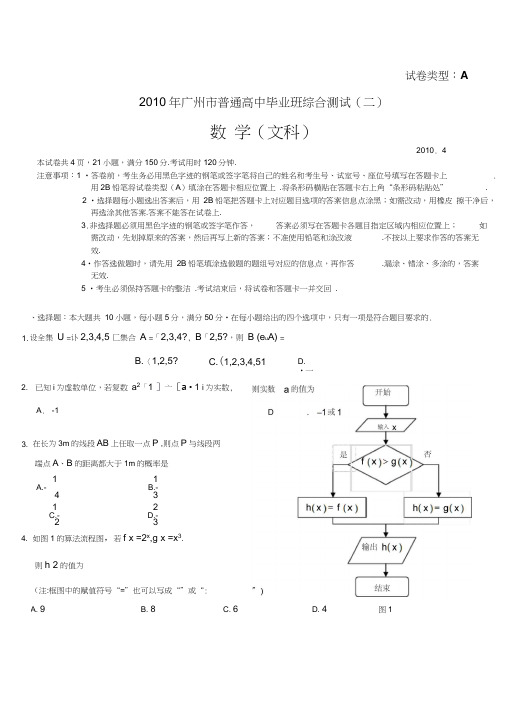
试卷类型:A2010年广州市普通高中毕业班综合测试(二)数学(文科)2010. 4本试卷共4页,21小题,满分150分.考试用时120分钟.注意事项:1 •答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上.用2B铅笔将试卷类型(A)填涂在答题卡相应位置上.将条形码横贴在答题卡右上角“条形码粘贴处”.2 •选择题每小题选出答案后,用2B铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案.答案不能答在试卷上.3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.4•作答选做题时,请先用2B铅笔填涂选做题的题组号对应的信息点,再作答.漏涂、错涂、多涂的,答案无效.5 •考生必须保持答题卡的整洁.考试结束后,将试卷和答题卡一并交回.、选择题:本大题共10小题,每小题5分,满分50分•在每小题给出的四个选项中,只有一项是符合题目要求的.设全集U =讣2,3,4,5 匚集合A =「2,3,4?, B「2,5?,则B (e u A) =2.3.4.B.〈1,2,5?C.(1,2,3,4,51已知i为虚数单位,若复数a2「1 ]亠[a • 1 i为实数,A. -1在长为3m的线段AB上任取一点P ,则点P与线段两端点A、B的距离都大于1m的概率是1A.-41C.-21B.-32D.-3如图1的算法流程图,若f x =2x,g x =x3.则h 2的值为(注:框图中的赋值符号“=”也可以写成“”或“:A. 9B. 8C. 6D.•一图1D. 41.5.命题“若x, y 都是偶数,则x y 也是偶数”的逆否命题是xx若x . 0且a ■ b 1,则下列不等式成立的是仰角相等的点的轨迹为正确的是 A •若x y 是偶数,则x 与y 不都是偶数 B •若x • y 是偶数,则x 与y 都不是偶数 C •若x y 不是偶数,则x 与y 不都是偶数D •若x• y 不是偶数,则x 与y 都不是偶数6.x^2,设变量x, y 满足约束条件* y 兰x, 则目标函数x + y 32.z = 2x y 的最小值为A. 6B. 4C.D. 28. A. 0 ::: b ::: a ::: 1B. 0 ■. a ::: b ::: 1C.函数 f x 二 cos x — !A.最小正周期为2二的偶函数B.C. 最小正周期为2二的奇函数D.9.高8m 和4m 的两根旗杆笔直地竖在水平地面上1 ::: b ■. a 最小正周期为 最小正周期为 D. 1 :: a b二的偶函数 二的奇函数,且相距10m ,则地面上观察两旗杆顶端7. A.圆 B.椭圆 C.双曲线 D.抛物线10.已知函数 f x 二 x -sinx ,若 x 1,x 2—且f 咅 f x 20,则下列不等式中A. xx 2 B.捲:x 2 C. x x 2 0D.为X 2 :: 0二、填空题:本大题共 5小题,考生作答4小题,每小题5分,满分20分.(一)必做题(11〜13题)(1)求tan 的值;⑵求tani*亠2 的值.(二)选做题(14~ 15题,考生只能从中选做一题) 14.(坐标系与参数方程选做题)已知直线I 的参数方程为 ^1 t ,(参数L R ),“ =4—2t.'x=2cos0+2,- .圆C 的参数方程为(参数v • 10,2二I ),y =2si n 日.则直线I 被圆C 所截得的弦长为 __________ .15. (几何证明选讲选做题)如图3,半径为5的圆O 的两条弦BC =6,则弦AD 的长度为 ___________三、解答题:本大题共 6小题,满分80分•解答须写出文字说明、证明过程和演算步骤, 16. (本小题满分12分)17. (本小题满分12分)关系?(3)若从这20个人中抽出1人来了解有关情况,求抽到的学生数学成绩与物理成绩至少有一门 不优秀的概率• 参考数据:2某学校课题组为了研究学生的数学成绩与物理成绩之间的关系,随机抽取高二年级 分)如下表所示: 若单科成绩85分以上(含85分),则该科成绩为优秀. 20名学生某次考试成绩(满分 100①假设有两个分类变量为2 2列联表)为:则随机变量K2n ad -bea b cd a c b d,其中n = a b c d 为样本容量;X 和Y ,它们的值域分别为l 为,x 2』和]% , y 2』,其样本频数列联表(称218. (本小题满分14分)在长方体ABCD-ABQ I D,中,AB 二BC =1,AA =2,1点M是BC的中点,点N是AA的中点.⑴求证:MN //平面ACD ;⑵过N,C,D三点的平面把长方体ABCD-ABQ I U截成两部分几何体,求所截成的两部分几何体的体积的比值.19. (本小题满分14分)我国是水资源比较贫乏的国家之一,各地采用价格调控等手段以达到节约用水的目的•某市用水收费标准是:水费二基本费超额费定额损耗费,且有如下三条规定:①若每月用水量不超过最低限量m立方米时,只付基本费9元和每户每月定额损耗费②若每月用水量超过m立方米时,除了付基本费和定额损耗费外,超过部分每立方米付③每户每月的定额损耗费a不超过5元.(1)求每户每月水费y (元)与月用水量x (立方米)的函数关系;(2)该市一家庭今年第一季度每月的用水量和支付的费用如下表所示:试分析该家庭今年一、二、三各月份的用水量是否超过最低限量,并求m,n,a的值.a元;n元的超额20. (本小题满分14分)2 2已知椭圆G :笃•爲=1(a b .0)的右焦点F2与抛物线C2:y2 = 4x的焦点重合,a b5椭圆C l与抛物线C2在第一象限的交点为P , | PF2 | .圆C3的圆心T是抛物线C2上的动点,3圆C3与y轴交于M ,N两点,且|MN |=4.(1)求椭圆G的方程;(2)证明:无论点T运动到何处,圆C3恒经过椭圆C i上一定点.21. (本小题满分14分)f l 1(i)判断数列g '是否为等差数列,并说明理由2n Jn + n⑵证明:1a n bn 1.已知数列和:b n [满足a i,且对任意n • N *都有a n b^1,an 1a nb n1-a ;2010年广州市普通高中毕业班综合测试(二)数学(文科)试题参考答案及评分标准说明:1 •参考答案与评分标准指出了每道题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与参考答案不同,可根据试题主要考查的知识点和能力比照评分标准给以相应的分数.2•对解答题中的计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的得分,但所给分数不得超过该部分正确解答应得分数的一半; 如果后继部分的解答有较严重的错误,就不再给分.3 •解答右端所注分数,表示考生正确做到这一步应得的累加分数.4 •只给整数分数,选择题和填空题不给中间分.、选择题:本大题主要考查基本知识和基本运算•共10小题,每小题5分,满分50分.题号12345678910答案B A B B C C B D A C、填空题:本大题主要考查基本知识和基本运算•本大题共满分20分•其中14〜15题是选做题,考生只能选做一题.三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤•16 •(本小题满分12分)(本小题主要考查同角三角函数的基本关系、两角和与差的正切等知识,考查化归与转化的数学思想方法和运算求解能力)(兀)I0,?!,sin a二tan :cos acos:5小题,考生作答4小题,每小题5分, 11 •12. =1 213. 3n —3n 1 15. 2,5(1) 解:T sin -■52 ^551 ⑵解法1:••• tan J ,32 tan -2 13_21—13..., 2 =潮:潮2〔1 - tan a tan 2卩132 4=2.解法2■- tan :■:亠,]-tan 二tan :1 12 3“ 1 11 一-2 3.tan: 2 严1 - tan(a + P )tan P6分,8分10分12分6分8分10分1111-1 -3=2. 12分17 .(本小题满分12分)(本小题主要考查独立性检验的基本思想、方法及其简单应用和概率等知识 以及数据处理能力、运算求解能力和应用意识 )(1)解:2X2列联表为(单位:人):数学成绩优秀数学成绩不优秀 合计 物理成绩优秀 5 2 7 物理成绩不优秀 1 12 13 合计61420,4分(2) 解:提出假设H 。
2010年湖南省普通高中学业水平考试数学试卷及答案 (2)

高中学业水平考试数学补考试卷一、选择题:本大题共10小题,每小题4分,满分40分. 1.下列函数中,是偶函数的是( ) A f(x)=x B f(x)=1xC f(x)=x 2D f(x)=sinx 2.化简(sin α+cos α)2=( )A 1+sin2αB 1-sin αC 1-sin2αD 1+sin α3.在△ABC 中,若0CA CB =u u u r u u u rg ,则△ABC 是( )A 锐角三角形B 直角三角形C 钝角三角形D 等腰三角形4.已知圆C 的方程为:2(1)x -+2(2)y -=4,则圆心坐标与半径分别为( ) A (1,2),r=2 B (-1,-2),r=2 C (1,2),r=4 D (-1,-2),r=4 5.已知集合M ={1,2},N ={2,3}, 则 MUN =( ) A {1,2} B {2,3} C {1,3} D {1,2,3}6.如图所示的圆盘由八个全等的扇形构成,指针绕中心旋转,可能随机停止,则指针停止在阴影部分内的概率是( ) A12 B 14 C 16 D 187.已知a>b ,c R ∈,则( )A a+c>b+cB a c b c +<+C a c b c +≥+D a+c b c ≤+8.下列几何体中,正视图、侧视图和俯视图都相同的是( ) A 圆柱 B 圆锥 C 球 D 三菱柱9.已知函数() (01)x f x a a a =>≠且,f(1)=2,则函数f(x)的解析式是( ) A f(x)=4x B f(x)= 1()4x C f(x)=2x D f(x)=1()2x10.在△ABC 中,a 、b 、c 分别为角A 、B 、C 的对边,若A=60,b=1,c=2,则a =( ) A 1 B 3 C 2 D 7二、填空题:本大题共5小题,每小题4分,满分20分. 11 直线y=2x+2的斜率是________ 12 已知如图所示的程序框图,若输入 的x 值为1,则输出和y 值是_____ 13 已知点(x ,y)在如图所示的阴影 部分内运动,则z=2x+y 的最大值是______14 已知向量a =(4,2),b =(x ,3), (13题)若a||b ,则实数x 的值为______15 张山同学的家里开了一个小卖部, (12题)为了研究气温对某种冷饮销售量的影响,他收集了这一段时间内这种冷饮每天的销售量y (杯)与当天最高气温x(0C)的有关数据,通过描绘散点图,发现y 和x 呈现线性相关关系,并求得回归方程为$y =2x+60,如果气象预报某天的最高气温为340C ,则可以预测该天这种饮料的销售量为____杯。
高中学业水平测试数学模拟卷(2)(含答案)

高中学业水平测试数学模拟卷(二)班级: 姓名:一、选择题:(本大题共35小题,每小题3分,共105分)1、设集合A={1,2,3,4,5},B={2,4,6},则A ∩B=( )A 、{6}B 、{2}C 、{2,4}D 、{1,2,3,4,5,6}2、函数1+=x y 的定义域是 ( )A 、(-∞,+∞)B 、[-1, +∞)C 、[0, +∞)D 、(-1, +∞) 3、已知函数11)(-+=x x x f ,则)2(f 等于 ( ) A 、3 B 、2 C 、1 D 、04、下列各组函数中,表示同一函数的是 ( ) A.22)(x y x y ==和 B x x y 2=和33x y = C.2log x y a =和x a a y log 2= D.x y =和x a a y log =5、函数y=(2k+1)x-2在R 上是减函数,则 ( )A 、21>kB 、21<kC 、21->kD 、21-<k 6、函数32x y =是( )A 、奇函数B 、偶函数C 、既是奇函数又是偶函数D 、既不是奇函数又不是偶函数7、b a ==3lg ,2lg ,则23lg等于 ( ) A 、b a - B 、a b - C 、b a D 、a b 8、ο120cos = ( )A 、23-B 、23C 、21- D 、21 9、已知54sin =α,且α是第二象限角,那么αtan 的值是 ( ) A 、34- B 、43- C 、34 D 、43 10、不等式12>x 的解集是 ( )A 、{x ∣x>1}B 、{x ∣x<-1}C 、{x ∣-1<x<1}D 、{x ∣x<-1或x>1} 11、函数的y=sin21x 周期为 ( ) A 、π B 、π2 C 、 π3 D 、4π12、已知向量)4,2(=a ,)6,1(-=b ,则a ●b = ( )A 、26B 、-26C 、 -22D 、2213、 已知点A (2,4),B (3,5),则直线AB 的倾斜角为 ( )A 、ο30B 、ο45C 、ο120D 、ο6014、下列关于棱柱的判断正确的是 ( )A 、只有两个平面B 、所有的棱都平行C 、所有的面都是平行四边形D 、两底面平行,且各侧棱也互相平行15、体积为π34的球的半径是 ( ) A 、1 B 、2 C 、3 D 、416、如果直线a 和b 没有公共点,那么直线a 与b 的位置关系是 ( )A 、异面B 、平行C 、相交D 、平行或异面17、过点(-2,0),斜率是3的直线方程为 ( )A 、y=3x-2B 、y=3x+2C 、y=3(x-2)D 、y=3(x+2)18、在ABC ∆中,B A sin sin =,则ABC ∆是 ( )A 、直角三角形B 、等腰三角形C 、等边三角形D 、锐角三角形19、当a=3时,下面的程序输出的结果是 ( )IF a<10 THENy=2*aELSEy=a*aPRINT yA 、9B 、3C 、6D 、1020、不等式2x-y-6>0表示的平面区域在直线2x-y-6=0的 ( )A 、左上方B 、右上方C 、左下方D 、右下方21、等差数列}{n a }中,n a n 32-=,公差d 等于 ( )A 、2B 、-3C 、-1D 、322、在等比数列}{n a 的公比31,31==a q ,则5a 等于 ( ) A 、3 B 、9 C 、27 D 、8123、等差数列}{n a 中,2,11==d a ,则5S 等于 ( )A 、16B 、 25C 、 36D 、924、已知向量b a k b a ⊥-==),1,(),3,2(,则k= ( )A 、 32-B 、23C 、32D 、23-25、已知实数y x ,满足约束条件⎪⎩⎪⎨⎧≤≥+≥+-3005x y x y x ,则y x z 42+=的最小值为 ( )A 、-6B 、-3C 、0D 、25 26、函数)1(log 2+=x y 的图象经过 ( )A 、(0,1)B 、(1,0)C 、(0,0)D 、(2,0)27、有50件产品编号从1到50,现在从中抽取5件检验,用系统抽样确定所抽取的编号为 ( )A 、5,10,15,20,25B 、5,15,20,35,40C 、5,11,17,23,29D 、10,20,30,40,5028、棱长为2的正方体内切球的表面积为 ( )A 、π4B 、π8C 、π12D 、π1629、长方体1111D C B A ABCD -中,异面直线11,D A AB 所成的角等于 ( )A 、︒30B 、︒45C 、︒60D 、︒9030、在△ABC 中,C B A ∠∠∠,,所对的边分别为a ,b ,c ,如果0222<-+c b a ,那么△ABC 为( )A 、锐角三角形B 、直角三角形C 、等腰三角形D 、钝角三角形31、)9(101化为十进制数为A 、9B 、11C 、82D 、10132、已知正四棱锥的底面边长为2,高为3,这个正四棱锥的体积为 ( )A 、4B 、2C 、34 D 、43 33、当a>0时,aa 1+ 的最小值为 ( ) A 、2 B 、22 C 、2 D 、134、某班有男同学30人,女同学20人,用分层抽样的方法从全班同学中抽出一个容量为5的样本,则应分别抽取 ( )A 、男同学3人,女同学2人B 、男同学2人,女同学3人C 、男同学30人,女同学20人D 、男同学4人,女同学1人35、函数x x y cos sin +=的最大值是 ( )A 、1B 、2C 、2D 、3二、填空题:(本大题共5小题,每小题3分,共15分)36、函数x a x f =)((0>a ,且0≠a ),f(1)=2,则函数f(x)的解析式是37、在等比数列}{n a 中,16,274==a a ,则通项公式n a = .38、甲、乙两人下棋,两人下成和棋的概率是41,乙获胜的概率是31,则乙不输的概率为 。
2010年数学高考模拟卷(二)

2010年数学高考模拟卷(二)佚名【期刊名称】《中学教研:数学版》【年(卷),期】2010(000)002【总页数】5页(P42-46)【正文语种】中文【中图分类】G4一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的4个选项中,只有1项是符合题目要求的.1.设全集U=R,集合则{CU}∩N等于( )A.{2}B.{x|-1<x<2,或2<x≤3}C.{x|-1≤x<2,或2<x≤3}D.{x|x≤3,且x≠2,x≠-1}2.已知a,b是实数,i是虚数单位,若满足则a+bi等于( )A.2-iB.2+iC.1+2iD.1-2i3.已知2条直线l,m与3个平面α,β,γ,满足l=β∩γ,l∥α,m⊂α,m⊥γ,则有( )A.α⊥γ且m∥βB.α⊥γ且l⊥mC.m∥β且l⊥mD.α∥β且α⊥γ4.若p表示“不等式m(m-5)<-6的解”,q表示“函数f(x)=(5-2m)x为减函数时,m的取值范围”,则p是q的( )A.充要条件B.充分不必要条件C.必要不充分条件D.既不充分也不必要条件5.设公差不为0的等差数列{an}的前n项和为Sn,若a4是a3与a7的等比中项,且S8=32,则S10等于( )A.18B.24C.60D.906.函数y=f(x)是圆心在原点的单位圆的2段圆弧(如图1),则不等式f(x)<f(-x)+x 的解集为( )图17.设双曲线的半焦距为c,直线l过点A(a,0),B(0,b),若原点O到l的距离为则双曲线的离心率为( )或或图28.函数f(x)=Asin(ωx+φ)+b的图像如图2所示,则S=f(0)+f(1)+f(2)+…+f(2 009)的值为( )9.用0,1,2,3,4这5个数字组成无重复数字的五位数,其中恰有1个偶数数字夹在2个奇数数字之间,这样的五位数的个数有( )A.48个B.12个C.36个D.28个10.设x,y满足约束条件若目标函数z=ax+by(a>0,b>0)的最大值为12,则的最小值为( )图3二、填空题:本大题共7小题,每小题4分,共28分.11.若已知则sin2α的值为________.12.四棱锥P-ABCD的顶点P在底面ABCD中的投影恰好是A,其三视图如图3所示,则四棱锥P-ABCD的表面积为________.13.若x+x2+x3+…+x9+x10=a0+a1(1+x)+a2(1+x)2+…+a9(1+x)9+a10(1+x)10,则a9=________.14.2006年1月份开始实施的《个人所得税法》规定:全月总收入不超过1 600元的免征个人工资、薪金所得税,超过1 600元的部分需征税.设全月总收入金额为x元,前3级税率如表1.表1 前3级税率表级数全月应纳税金额x-1 600元税率1不超过500元部分5%2超过500元至2 000元部分10%3超过2 000元至5 000元部分15%………当全月总收入不超过3 600元时,计算个人所得税的一个算法框图(如图4所示),则图中“输出②”输出的为________.15.给出下列4个命题:①命题“任意x∈R,x2≥0”的否定是“存在x∈R,x2≤0”;②若a,b∈[0,1],则不等式成立的概率是③线性相关系数r的绝对值越接近于1,表明2个随机变量线性相关性越强;④函数y=log2(x2-ax+2)在[2,+∞)上恒为正,则实数a的取值范围是则其中真命题的序号是________(填上所有真命题的序号).图4图516.如图5中(1)、(2)、(3)、(4)分别包含1个、5个、13个、25个第29届北京奥运会吉祥物“福娃迎迎”,按同样的方式构造图形,设第n个图形包含f(n)个“福娃迎迎”,则f(5)=________;f(n)=________(用数字或n的解析式表示). 17.设函数且a≠1),若[m]表示不超过实数m的最大整数,则函数的值域是________.三、解答题:本大题共5小题,共72分.解答应写出文字说明、证明过程或演算步骤.18.(本题满分14分)已知向量m=(sinA,sinB),n=(cosB,cosA),m·n=sin2C,且A,B,C分别为△ABC的3边a,b,c所对的角.(1)求角C的大小;(2)若sinA,sinC,sinB成等差数列,且求△ABC的面积和c边的长.19.(本题满分14分)已知暗箱中开始有3个红球,2个白球.现每次从暗箱中取出1个球后,再将此球以及与它同色的5个球(共6个球)一起放回箱中.(1)求第2次取出红球的概率;(2)求第3次取出白球的概率;(3)若取出白球得5分,取出红球得8分,设连续取球3次的得分值为ζ,求ζ的分布列和数学期望.20.(本题满分14分)如图6,在三棱锥P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,点D,E分别在棱PB,PC上,且DE∥BC.(1)求证:BC⊥平面PAC;(2)当D为PB的中点时,求AD与平面PAC所成角的余弦值;(3)是否存在点E,使得二面角A-DE-P为直二面角?并说明理由.图6 图721.(本题满分15分)如图7,椭圆的中心在原点,其左焦点F1与抛物线y2=-4x 的焦点重合,过点F1的直线l与椭圆交于A,B两点,与抛物线交于C,D两点.当直线l与x轴垂直时,(1)求椭圆的方程;(2)求过点O,F1,并且与直线(其中a表示椭圆的长半轴长,c表示椭圆的半焦距)相切的圆的方程;(3)设F2是椭圆的右焦点,求的最大值和最小值.22.(本小题满分15分)设函数且其中e是自然对数的底数.(1)求p与q的关系;(2)若f(x)在其定义域内为单调函数,求p的取值范围;(3)设若在[1,e]上至少存在一点x0,使得f(x0)>g(x0)成立,求实数p的取值范围. 参考答案1.C2.B3.B4.C5.C6.A7.A8.B 9.D 10.A14.0.1x-185 15.③④ 16.41,2n2-2n+117.{0,-1}18.解(1)m·n= sinA·cosB+sinB·cosA=sin(A+B).因为A+B=π-C,0<C<π,所以sin(A+B)=sinC,即m·n=sinC.又m·n=sin2C,所以sin2C=sinC,解得(2)由sinA,sinC,sinB成等差数列,得2sinC=sinA+sinB.由正弦定理得2c=a+b.又由可得即abcosC=18,从而ab=36,于是由余弦定理可知c2=a2+b2-2abcosC=(a+b)2-3ab=36,解得c=6.19.解设第n次取出白球的概率为Pn,第n次取出红球的概率为Qn.(1)第2次取出红球的概率是(2)3次取的过程共有以下情况:白白白、白红白、红白白、红红白,所以第3次取出白球的概率是(3)连续取球3次,得分的情况共有8种:5+5+5,8+5+5,5+8+5,5+5+8,8+8+5,8+5+8,5+8+8,8+8+8,则ζ的取值为15,18,21,24,于是ζ的分布列如表2所示.表2 ζ的分布列ζ15182124 P28125211252412552125故20.解答过程请参见本刊第19页.21.解 (1)由抛物线方程得,焦点F1(-1,0).设椭圆的方程为解方程组得C(-1,2),D(1,-2).由于抛物线、椭圆都关于x轴对称,因此得则从而又a2-b2=c2=1,所以解得b2=1,并推得a2=2,故椭圆的方程为(2)因为圆过点O,F1,所以圆心M在直线上上.设圆的半径为r.由圆与直线相切,可得又由|OM|=r,得解得故所求圆的方程为(3)由点F1(-1,0),F2(1,0),得①若AB垂直于x轴,则于是从而②若AB与x轴不垂直,设直线AB的斜率为k,则直线AB的方程为y=k(x+1).由得(1+2k2)x2+4k2x+2(k2-1)=0.因为Δ=8k2+8>0,所以方程有2个不等的实数根.设A(x1,y1),B(x2,y2),则因此从而(x1-1)(x2-1)+k2(x1+1)(x2+1)=(1+k2)x1x2+(k2-1)(x1+x2)+1+k2=又由k2≥0,得1+2k2≥1,因此故所以当直线l垂直于x轴时,取得最大值当直线l与x轴重合时,取得最小值-1.22.解 (1)由题意得因此而于是p,q的关系为p=q.(2)由第(1)小题知则令h(x)=px2-2x+p,要使f(x)在其定义域(0,+∞)内是单调函数,则只需h(x)在(0,+∞)内满足:h(x)≥0或h(x)≤0恒成立.①当p=0时,h(x)=-2x.因为x>0,所以从而f(x)在(0,+∞)内是单调递减函数,即p=0适合题意.②当p>0时,h(x)=px2-2x+p,其图像为开口向上的抛物线,对称轴为从而因此只需即当p≥1时,h(x)≥0,f ′(x)≥0,因而f(x)在(0,+∞)内为单调递增函数,故p≥1适合题意.③当p<0时,h(x)=px2-2x+p,其图像为开口向下的抛物线,对称轴为∉(0,+∞).只要h(0)≤0,即p≤0,h(x)≤0在(0,+∞)恒成立,故p<0适合题意.综上所述,p的取值范围为p≥1或p≤0.(3)因为在[1,e]上是减函数,所以当x=e时,g(x)min=2;当x=1时,g(x)max=2e,即g(x)∈[2,2e],①当p≤0时,由第(2)小题知f(x)在[1,e]上单调递减,因此f(x)max=f(1)=0<2,不合题意.②当0<p<1时,由x∈[1,e],得又由第(2)小题知当p=1时,f(x)在[1,e]上是增函数,因此不合题意.③当p≥1时,由第(2)小题知f(x)在[1,e]上是增函数,f(1)=0<2.又由g(x)在[1,e]上是减函数,可得只需f(x)max>g(x)min,x∈[1,e]即可,而即解得综上所述,p的取值范围是。
2010年吉林普通高中学业水平模拟考试数学试题及参考答案

2010年吉林省普通高中学业水平模拟考试数学试题及参考答案说明:本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,总分150分;考试时间120分钟. 注意事项:1.答第Ⅰ卷前,考生务必将自己姓名、考号、考试科目用2B 铅笔涂写在答题卡上. 2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案.3.将第Ⅰ卷选择题的答案涂在答题卡上,第Ⅱ卷每题的答案写在答题纸的指定位置. 4.考试结束,将答题纸和答题卡一并交回,答案写在试卷上视为无效答案.第Ⅰ卷(选择题 共60分)一、选择题(本题共有12小题,每小题5分, 共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.) 1.若集合{}1,3,A x =,{}21,B x=,{}1,3,A B x ⋃=,则满足条件的实数x 的个数为( )A. 1个B. 2个C. 3个D. 4个 2.下列几何体各自的三视图中,有且仅有两个视图相同的是 ( )A.①②B.①③C.①④ D .②④ 3. 已知角α的终边上一点的坐标为22(sin,cos )33ππ,则角α的最小正值为 ( )A.56πB.23πC.53πD.116π4.设向量a 与b 的夹角为θ,(2,1)a = ,2(4,5)a b += ,则θc o s 等于 ( )A.54 B. 53C. 10103D. 10105.已知ABC ∆,O 为平面内一点,且设,,OA a OB b OC c ===,则满足条件()()()a b AB b c BC c a CA +⋅=+⋅=+⋅ 时,O 是ABC ∆的 ( )A. 内心B. 外心C. 垂心D. 重心6.下列函数中,图像的一部分如右图所示的是( )①正方体②圆锥 ③三棱台 ④正四棱锥A. sin()6y x π=+B. sin(2)6y x π=- C. cos(4)3y x π=-D. cos(2)6y x π=- 7. 已知tan α,tan β是方程23340x x ++=的两实根,若,αβ∈(,)22ππ-,则αβ+=( ) A.3π B. 23π- C.3π-或23π D.3π或23π-8. 如果函数)(x f 对于区间D 内任意的n x x x ,,,21 ,有12()()()n f x f x f x n ++ ≤12()nx x x f n++ 成立,称()f x 是区间D 上 的“凸函数”. 已知函数sin y x =在区间[]0,π上是“凸函数”,则在△ABC 中,C B A sin sin sin ++的最大值是 ( ) A.21 B. 23 C. 23 D.233 9.等差数列}{n a 的公差为d ,前n 项和为n S ,当首项1a 和d 变化时,1182a a a ++是一个定值,则下列各数中也为定值的是 ( ) A. 7SB. 8SC . 13SD. 15S10.ABC ∆的三内角,,A B C 所对边的长分别为,,a b c 设向量(,)p a c b =+ ,(,)q b a c a =-- ,若//p q,则角C 的大小为 ( )A. 6πB. 3πC. 2πD. 23π11.定义在R 上的偶函数()f x 满足()(2)f x f x =+,当[]3,5x ∈时,()24f x x =--,则( ) A.(sin)(cos )66f f ππ< B.(sin1)(cos1)f f > C. (cos 2)(sin 2)f f > D.22(cos)(sin )33f f ππ< 12.已知函数2()24(03)f x ax ax a =++<<,若12x x <,121x x a +=-,则 ( ) A. 12()()f x f x < B. 12()()f x f x =C. 12()()f x f x >D. 1()f x 与2()f x 的大小不能确定第Ⅱ卷(非选择题 共90分)二、填空题(本题共4小题, 每小题5分, 共20分)13.数列{}n a 的前n 项和为n S ,且111,3,(1,2,3,)n n a a S n +=== ,则410l o g S = ;14.已知,αβ都是锐角,且12sin ,cos()33ααβ=+=,则cos β= ; 15. 已知0>a ,设函数[]120102008()sin (,)20101x xf x x x a a ++=+∈-+的最大值为M ,最小值为N ,那么=+N M ; 16. 下列五种说法:(1) 命题“2,13x R x x ∃∈+>使得”的否定是“x x R x 31,2≤+∈∀都有”;(2) 若,a b 正实数,则“33log log a b >”是 “1133a b⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭”的必要不充分条件;(3) 把函数))(2sin(R x x y ∈-=的图像上所有的点向右平移8π个单位,即可得到函数))(42sin(R x x y ∈+-=π的图像;(4) 若四边形ABCD 是平行四边形,则,AB DC BC DA ==;(5) 两个非零向量,a b 互相垂直,则222||||()a b a b +=+ .其中正确的说法是 (把正确说法的序号填在横线处)三、解答题(本题共6小题, 共70分, 解答应写出文字说明、证明过程或演算步骤) 17.(本题满分10分)已知函数23()2cos sin(2)2f x x x π=--. 求:(1)函数()f x 的最小正周期;(2)函数()f x ,[]0,2x π∈的单调增区间. 18.(本题满分12分)已知等差数列{}n a 的前n 和为(1)2n n n S +=.记(0)n an n b a p p =>,求数列{}n b 的前n 项和n T .19.(本题满分12分)在△ABC 中,,,a b c 分别为角,,A B C 所对的边,且22()a b c bc --=, (1)求角A ;(2)若23BC =,角B 等于x ,周长为y ,求函数)(x f y =的取值范围20.(本题满分12分) 在平面直角坐标系中,已知向量(1,2)a =-,又点(8,0)A ,(,)B n t ,(sin ,)C k t θ(0)2πθ≤≤.(1)若AB ⊥ a,且5AB OA = (O 为坐标原点),求向量OB ;(2)若向量AC 与向量a 共线,当4k >,且sin t θ取最大值4时,求OA OC ⋅.21.(本题满分12分)已知α为锐角,且12tan -=α,函数)42sin(2tan )(2παα+⋅+=x x x f ,数列{}n a 的首项112a =,1()n n a f a +=. (1)求函数)(x f 的表达式; (2)求证:n n a a >+1; (3)求证:*1211112(2,)111nn n N a a a <++<≥∈+++ .22.(本题满分12分)已知二次函数2()f x ax bx c =++和一次函数()g x bx =-,其中c b a ,,满足c b a >>,0a b c ++=.(1)求证:两函数的图象交于不同的两点A 、B ; (2)求证:方程()()0f x g x -=的两根都小于2; (3)求线段AB 在x 轴上射影11A B 的长的取值范围.参 考 答 案一、选择题(本题共有12小题,每小题5分, 共60分)1.C 2.D 3.D 4.A 5.B 6.D 7.B 8.D 9.C 10.B 11.C 12.A 二、填空题(本题共4小题, 每小题5分, 共20分) 13.9 14.4259+ 15.4018 16.① ③ ⑤ 三、解答题(本题共6小题, 共70分, 解答应写出文字说明、证明过程或演算步骤)17.解:由已知,得()1cos 2cos 22cos 2 1.f x x x x =++=+ …………2分 (1)最小正周期22T ππ==. …………4分 (2)令222,()k x k k Z πππ-≤≤∈ …………6分 ()2k x k k Z πππ∴-≤≤∈ …………7分又02x π≤≤,2x ππ∴≤≤或322x ππ≤≤, …………9分所以原函数的单调递增区间为3,,,222ππππ⎡⎤⎡⎤⎢⎥⎢⎥⎣⎦⎣⎦. …………10分 18解: 等差数列{}n a 的前n 和为(1)2n n n S +=1(1)(1)22(2)n n n a S S n n n n n n -∴=-+-=-=≥ …………2分又当1n =时,111(11)1,12a S ⨯+===,11a S = ∴数列{}n a 的通项公式为()n a n n N *=∈ ………… 3分由n an n b a p =,得nn b np =.所以23123(1)n n n T p p p n pnp -=++++-+ , …………4分 当1p =时,(1)1232n n n T n +=++++= ; …………5分当1p ≠时,23123(1)n n n T p p p n pnp -=++++-+234123(1)n n n pT p p p n p np +=++++-+ , …………7分23111(1)(1)1n n n n n n p p p T p p p pp npnp p-++--=+++++-=--…9分12(1)(1)1n n n p p np T p p+-∴=--- …………10分综上12(1),12(1),1(1)1n n n n n p T p p np p p p ++⎧=⎪⎪=⎨-⎪-≠⎪--⎩. …………12分 19解:(1)由bc c b a bc c b a -=--=--22222:)(得 ………1分212cos 222=-+=∴bc a c b A ………3分又π<<A 0 3π=∴A ………5分(2),sin sin A BCx AC =x x x BC AC sin 4sin 2332sin 3sin =⋅=⋅=∴π………6分 2()3C A B x ππ=-+=-, 同理:)32sin(4sin sin x C A BC AB -=⋅=π………7分 24sin 4sin()2343sin()2336y x x x ππ∴=+-+=++ ………9分3π=A 320π<=<∴x B………10分 故)65,6(6πππ∈+x ,1sin ,162x π⎛⎫⎛⎤+∈ ⎪ ⎥⎝⎭⎝⎦,(43,63y ⎤∴∈⎦. ………12分 20解:(1)由题得(8,)AB n t =-.AB ⊥ a ,AB ∴⋅ a(8,)(1,2)0n t =-⋅-=, ……….2分 得28n t =+,则(2,)AB t t =. 又5AB OA = ,8OA =.22(2)564t t ∴+=⨯,解得8t =±. ………4分当8t =时,24n =;当8t =-时,8n =-.(24,8)OB ∴= 或(8,8)OB =--. ………6分 (2)由已知(sin 8,)AC k t θ=-向量AC 与向量(1,2)a =共线,2sin 16t k θ∴=-+, ………7分2432s i n (2s i n 16)s i n 2(s i n )t k k k kθθθθ=-+=--+. 44,01k k >∴<< , ………8分 故当4sin k θ=时,sin t θ取最大值4时,有324k=,得8k =. ………10分这时,1sin 2θ=,且sin 4t θ=,得8t =,则(4,8)OC = . ………11分(8,0)(4,8)O A O C ∴⋅=⋅=. ………12分 21解:(1)1)12(1)12(2tan 1tan 22tan 22=---=-=ααα ………1 分 又∵α为锐角,∴42πα= ………2分∴1)42sin(=+πα x x x f +=2)( ………3分(2)n n n a a a +=+21 ∵211=a ∴n a a a ,,32都大于0 ∴02>n a ∴n n a a >+1 ………5分 (3)nn n n n n n a a a a a a a +-=+=+=+111)1(11121∴11111+-=+n n n a a a ………7分∴1322121111111111111+-++-+-=++++++n n n a a a a a a a a a 1111211++-=-=n n a a a ………9分102.n a S +>∴< ………10分∵4321)21(22=+=a , 143)43(23>+=a ,又∵n n a a n >≥+12 ∴131>≥+a a n ∴21211<-<+n a∴2111111121<++++++<na a a………12分 22解:(1)由⎩⎨⎧-=++=bxy cbx ax y 2,消去y ,得022=++c bx ax , ………1分ac c a ac b 4)(44422---=-=∆]43)2[(422c c a ++= ………2分c b a >>,o c b a =++0,043,0,02>∆∴><>∴c c a 两函数的图象交于不同的两点A 、B ………4分(2)法一:由已知()()0f x g x -=,即为220ax bx c +== ………5分 由(1)知0a >且上述方程一定有两不等实根12,x x 12()x x < ………6分 记2()2h x ax bx c =++, 则120,cx x a=<10 2.x ∴<< ………7分 又(2)443()30h a b c a b c =++=+=->20 2.x ∴<< ………8分综上,122, 2.x x << 法二:()()0f x g x -=的两根为02,022,22121<-<-⇔<<x x x x⎩⎨⎧>--<-+-⇔0)2)(2(0)2()2(2121x x x x 而a cx x a b x x =-=+2121,2 于是)2()2(21-+-x x ab a a b)2(242+-=--= ,02,0,>-=+∴>-=+c a b a a c b a 0)2(2<+-ab a 0)2()2(21<-+-∴x x ,4)(2)2)(2(212121++-=--x x x x x x =0)(344422>+=++=++ab a ac b a a b a c2,221<<∴x x(3)212212214)(||x x x x x x -+=-222)(4)(4)2(aac b a ca b -=--= 22222)(4])[(4ac ac a a ac c a ++=---=3)21(4]1)[(422++=++=a c a c a c ………9分 由2,2,->->--=>a c c a c a b a 由21,2,-<-<--=<a c a c c a b c ………10分212-<<-∴a c ,则02123<+<-a c 故49)21(02<+<a c 12]43)21[(432<++<a c ,12||3221<-<x x ………11分又||||2111x x B A -=,故||11B A 的取值范围为)32,3( ………12分。
2010年高中学业水平模拟考试二

2010年广东省普通高中学业水平模拟考试二地理试卷共8页,满分100分,考试时间90分钟。
一、单项选择题Ⅰ:本大题共50小题,每小题1分,满分50分。
在每小题给出的四个选项中,只有一项是最符合题目要求的,多选或错选该小题不得分。
1.地球具有生命的外部原因是( )A.具有适宜的温度 B.具有适合生物呼吸的大气层C.具有丰富的水 D.处于比较稳定和安全的宇宙环境之中2.下列地理现象,主要由内力作用引起的是()A.长江三峡的形成 B.黄河三角洲在不断扩大C.移动沙丘向前移动 D.东非大裂谷还在继续张裂3.太阳活动对地球的影响表现有()A.扰乱地球上空的电离层使地面的无线电短波通讯受到影响甚至中断B.使地球上生物异常,从而产生“磁暴现象”C.在地球各地的夜空产生极光D.使地球高层大气高速散逸到星际空间4.目前,一般所说的绿色食品是指()A.绿颜色的营养食品 B.有叶绿素的营养食品C.经济附加值高的营养食品 D.安全.无公害的营养食品5.下列因素对工业区位的影响力逐渐增强的是()A.原料产地B.劳动力数量C.土地质量D.信息通讯网络6.右图是坡度——流水侵蚀强度示意图,关于坡度与坡面流水侵蚀强度关系的叙述,正确的是()A.坡度20°时,坡面侵蚀强度最大B.坡度35°~ 40°时,坡面侵蚀强度最大C.坡度90°时,坡面侵蚀强度最大D.坡度20°~ 60°时,坡面侵蚀强度随坡度的增加最快7.“西气东输”工程最有利于解决我国下列选项中的哪个问题()A.水资源紧张 B.能源浪费严重C.木材短缺 D.自然资源分布与生产力分布不相协调8.我国某中学操场旗杆的正午日影,在一年中有时朝南,有时朝北,那么这个学校可能位于()A.海南省海口市 B.台湾省台北市 C.广东省韶关市 D.云南省昆明市9.影响我国东南丘陵茶树种植的主要自然条件是()A.土壤 B.地形 C.光照 D.水源10.在人口的数量增长变化过程中,首先开始转变的是()A.出生率 B.死亡率 C.自然增长率 D.人口基数11.广州市冬季某日7时日出,则此日昼长为()A.14时 B.10时 C.12时 D.8时12.北方屋顶坡度较小,甚至为平顶,而南方屋顶坡度大,其影响因素是()A.降水 B.地形 C.风力 D.太阳辐射读下面水循环示意图,回答13~15题。
2010年高中毕业会考数学模拟试题及答案

2013年普通高中数学毕业会考模拟试题(一)第Ⅰ卷(选择题,共57分)一、选择题(本大题共19个小题,每小题3分,共57分;在每小题给出的四个选项中,只有一项是符合题目要求的)1.设集合P={0,1,2,},Q={1,2,3},则P∩Q= A){0} B){6} C){1,2} D){0,1,2,3}2.函数yA)(-∞,2] B)[1,+∞) C)[1,2] D)(-∞,1]∪[2,+∞) 3.从3个男生和2个女生中选出3人参加一项活动,既有男生又有女生参加的不同选法种数为A)9 B)8 C)7 D)64.已知过A,B,C三点的截面与球心的距离为4,且截面周长为6π,则球的半径为 A)3 B)4 C)5 D)65.设0a b >>,则下列各式中正确的是 A)a cbc ->- B)ba 11> C)22ac bc > D)2ab a >6.已知向量()()1,3,,2a b x ==,且a ∥b ,则x = A)32B)23- C)-6 D)6 7.方程2260x y x m +-+=表示一个圆,则A)m=9 B)m>9 C)m≥9 D)m<9 8.已知cos (θπ+)=23,则cos 2θ= A)21 B)-21 C)41 D)-41 9.已知数列{}n a 的前n项和Sn 满足2n s n =,则数列{}n a 为A)公差为2的等差数列 B)公比为2的等比数列 C)公差为21的等差数列 D)公比为21的等比数列 10.sin(24)cos(21)cos(24)cos(69)x x x x +-+++的值为A)1 B)2-C) 2D)不能确定 11.直线210x ay +-=与(31)10a x ay ---=垂直,则a 的值为 A)61 B)0 C)0或61D)21或112.已知函log (01)a y x a a =>≠且的反函数的图象经过点(1,3),则a 等于 A )3 B )3 C )9 D )8113.已知向量DA ,CD ,BC ,AB ,则ABBC CD DA -=++ A)AD B)DA C)0D)014.函数22sin cos y x x =-(0)2x π≤≤的最大值为A)1 B)2 C)-2 D)2 15.在4(13)x -的二项式展开式中,各项系数和为A)2 4 B)2 3 C)3 4 D)1 16.一个学生通过某种英语听力测试的概率是34,他连续测试2次,那么至少有1次获得通过的概率是 A)38 B)916 C)316 D)151617.在棱长为a 正方体ABCD -A 1B 1C 1D 1中,顶点1D 到平面AB1C的距离为18.不等式210x ax ++≥在区间[1,)x ∈+∞上恒成立,则a 的取值范围是 A)2a =- B)2a = C)2a ≥- D)2a ≤ 19.将函数()y f x =的图象按(,2)4a π=平移得到函数cos()24y x π=++的图象,则()y f x =的解析式为A)sin y x =- B)cos y x = C)sin 2y x =+ D)cos 4y x =+第Ⅱ卷(非选择题,共43分)二、填空题(本大题共5个小题,每小题3分,共15分;请直接在每小题的横线上填写结果)20.在△ABC 中,内角A、B、C的对边分别为,,a b c ,若1a =,b=3,A=30°,则c =______21.五人排成一排,甲与乙都不站两端的不同排法共有_______种(用数字作答)。
普通高中学业水平合格考试数学模拟题及答案

普通高中学业水平合格考试数学模拟题及答案昔通高中学业水平合格考数常模拟试题(二)木试雄分茁1卷(选择JS'和第ET鄧非逮择题、两即分•扶4 5iti满仆此0处丐诙脱定用时恥好忡.转巻酋,爭生暑必将自己的班址,姓名.爭号填写在试卷和苔题卡规琏的也国.考试蜡桌肓,邯亭试卷和甞咸卡一并交皿第I卷(共60分)注意事项】毎小通选出菩鬓后+用电把答J®卡上对应斷目的書赛标N涂盅-如霖改动,用樟皮據干净后,再选講—、选律超(本大題共20小建,楫小题耳分i共如井・在毎小题给出的四牛选项中,只有一煎星将合越目要求的)1” 设契合5・"I Ci-2Hx-3) >0),T- (m |x >0hiiJ SO T =, (A.[2 J]氐(一R工]U [旅+8)0 ⑶+«OD.(0,Z] U [备 +8)2.5in 500* 的個[是c£r出 ''D.-< Z 23. Sfe/(jr)=亍土 +歼寸的宦义域为EA.ir I J: 2}B.{j I Jt <Z~ 3 或工A 3}C>U |-S<-*<>}D. M L 3益工腹3且z * 2}眼钟希的井軒氏经过3£井钟井针的端点所转过的路程沏('5.过点<h0)冃与誉线工一知一?=°平荷的血歧方程是< )扎j — 2jx — 1 = 0 E, j — 2j -b I = 0C h 2x+ y— 2 " 0 D. x + 2y ~ 1 » 0G, y = In T— <i 4* 2JT的零点所在的区间是( ) ^(1,2) B.(2A)C.(3.4) U(S t6>7,巳知画独ft工、=mx1— mx —1对一切实数工,恒成立.刖树的取值范围为 ( )A. (-4^0)0.(—电』]C.U <0, +«)D.E—f —钟U ® + QB.若血lit a = (l*2)*b = (1T— 1),Jii| 2 tr + ,1> 与 a —I 的夬角寻于()A fl fC-T D•聲9.F 列条件中•舗判定丄平而•的祚< )A. /内的问条£(«C<ft出/与THa 内ttXftlhltUfirtCM 与rma 内的任念一条立线垂宜DM 与平囲a 内的2•在正三角形/WC 中.DMttHBC 上的点・皿■6,BD ■ 2.JH 朋•而■ ( >A. 12K 18U24D.30H •以点人(6・5〉为圆心•质为半仗的岡的标准方程 为* ()A. Gr-6)・+O ・5尸■ 10 B ・5 + 6¥ + 0 + 5)* = 10 •、C. (x-5):+ (y-6)2 = 710 D ・Cr+5)' +«y 十 6)' = /1012•在平面直角坐你系中•已知阿点Aaos80・“m80・〉・ B(cos2(r ・sin20・)•則 I AB | 的(ft 是 <>A TBT •c.噜 D.1 • •IS.巳知A ABC 的内ffi A .B.C 的对边分别是a •几C 若A=〒•则"十:_工的伍为()A. |B.豊C.1 D"14•甲•乙两人养将一张员年卡画总送酚内•丁列人中 的一人•用甲•乙将貝年卡送给问一人的D. 无法确定I5・/(x) ttViAtt lf/<2)- 4•则 /<3> 零于 ( >A.9B.8C ・6D./5\6 •方 17 I F |;任(一S.十 8)内 ( 】A.ttWWa Trn 仅右一个戦 C. /| n 仅“卿个權 D. 於无穷%个14 •17.从架頊煤令能力鬧试中抽取100人的敗?M 计 如下表•则这10G 人戍绩的标准蛙为<\i.fia.b 为 H 零 fSifii •且。
2010年广州市高二数学学业水平测试答案

2010学年度广州市高中二年级学生学业水平测试数学试题参考答案及评分标准分,满分50分.二、填空题:本大题主要考查基本知识和基本运算.共4小题,每小题5分,满分20分. 11.()22225x y ++=(或224210x y y ++-=)12.913.()0,+∞(或[)0,+∞) 14.122⎡⎤⎢⎥⎣⎦, 三、解答题15.本小题主要考查解三角形、三角恒等变换等基础知识,考查运算求解能力.满分12分. 解:(1)在△ABC 中,A B C π++=,由角A ,B ,C 成等差数列,得2B A C =+.解得3B π=.(2)方法1:由()sin 2A B +=,即()sin 2C π-=,得sin 2C =. 所以4C π=或34C π=. 由(1)知3B π=,所以4C π=,即512A π=. 所以5sin sinsin 1246A πππ⎛⎫==+ ⎪⎝⎭4=.方法2:因为A ,B 是△ABC 的内角,且()sin 2A B +=, 所以4A B π+=或34A B π+=.由(1)知3B π=,所以34A B π+=,即512A π=.以下同方法1.方法3:由(1)知3B π=,所以sin 32A π⎛⎫+= ⎪⎝⎭.即sin coscos sin33A A ππ+=.即1sin cos 222A A +=.sin A A =.即223cos 2sin A A A =-+. 因为22cos 1sin A A =-,所以()2231sin 2sin A A A -=-+.即24sin 10A A --=.解得sin A = 因为角A 是△ABC 的内角,所以sin 0A >.故sin 4A =. 16.本小题主要考查统计与概率等基础知识,考查数据处理能力.满分12分. 解:(1)由题意可得,3243648x y==, 解得2x =,4y =.(2)记从兴趣小组A 中抽取的2人为1a ,2a ,从兴趣小组B 中抽取的3人为1b ,2b ,3b ,则从兴趣小组A ,B 抽取的5人中选2人作专题发言的基本事件有()12,a a ,()11,a b ,()12,a b ,()13,a b ,()21,a b ,()22,a b ,()23,a b ,()12,b b ,()13,b b ,()23,b b 共10种.设选中的2人都来自兴趣小组B 的事件为X ,则X 包含的基本事件有()12,b b ,()13,b b ,()23,b b 共3种.所以()310P X =. 故选中的2人都来自兴趣小组B 的概率为310.17.本小题主要考查直线与平面的位置关系、体积等基础知识,考查空间想象能力、推理论证能力和运算求解能力.满分14分.(1)证明:连接BD 交AC 于点O ,连接EO ,因为ABCD 是正方形,所以点O 是BD 的中点.因为点E 是PD 的中点,所以EO 是△DPB 的中位线. 所以PBEO .因为EO ⊂平面ACE ,PB ⊄平面ACE , 所以PB平面ACE .(2)解:取AD 的中点H ,连接EH , 因为点E 是PD 的中点,所以EHPA .因为PA ⊥平面ABCD ,所以EH ⊥平面ABCD . 设AB x =,则PA AD CD x ===,且1122EH PA x ==. 所以13E ACD ACD V S EH -∆=⨯ 3111262123x x x x ===. 解得2x =.故AB 的长为2.18.本小题主要考查等差数列、等比数列等基础知识,考查运算求解能力和推理论证能力.满分14分. 解:(1)因为数列{}n a 是首项为1,公比为2的等比数列,所以数列{}n a 的通项公式为12n n a -=. 因为数列{}n b 的前n 项和2n S n =.所以当2n ≥时,1n n n b S S -=-()22121n n n =--=-, 当1n =时,111211b S ===⨯-, 所以数列{}n b 的通项公式为21n b n =-. (2)由(1)可知,1212n n n b n a --=. 设数列n n b a ⎧⎫⎨⎬⎩⎭的前n 项和为n T , 则 213572321124822n n n n n T ----=++++++, ① 即 111357232122481622n n n n n T ---=++++++, ②①-②,得2111112111224822n n nn T --=++++++- 2332nn +=-,所以12362n n n T -+=-. 故数列n n b a ⎧⎫⎨⎬⎩⎭的前n 项和为12362n n -+-. 19.本小题主要考查直线与圆、基本不等式等基础知识,考查运算求解能力.满分14分.解:(1)当0k =时,直线方程为y b =,设点A 的坐标为1()x b ,,点B 的坐标为2()x b ,,由224x b +=,解得12x =,所以21AB x x =-= 所以12S AB b =22422b b +-=≤.当且仅当b=,即b =时,S 取得最大值2.(2)设圆心O 到直线2y kx =+的距离为d,则d =因为圆的半径为2R =,所以2AB ===.于是241121k S AB d k =⨯===+,即2410k k -+=,解得2k =.故实数k 的值为2+,2,2-+2-.20.本小题主要考查二次函数、函数的零点等基础知识,考查运算求解能力,以及分类讨论的数学思想方法.满分14分. 解法1:当0a =时,()1f x x =-,令()0f x =,得1x =,是区间[]1,1-上的零点.当0a ≠时,函数()f x 在区间[]1,1-上有零点分为三种情况: ①方程()0f x =在区间[]1,1-上有重根, 令()14130a a ∆=--+=,解得16a =-或12a =. 当16a =-时,令()0f x =,得3x =,不是区间[]1,1-上的零点. 当12a =时,令()0f x =,得1x =-,是区间[]1,1-上的零点. ②若函数()y f x =在区间[]1,1-上只有一个零点,但不是()0f x =的重根,令()()()114420f f a a -=-≤,解得102a <≤. ③若函数()y f x =在区间[]1,1-上有两个零点,则()()⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧≥≥<-<->++-=∆>.01-,01,1211,01412,02f f a a a a 或()()⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧≤≤<-<->++-=∆<.01-,01,1211,01412,02f f a a a a 解得a ∈∅.综上可知,实数a 的取值范围为10,2⎡⎤⎢⎥⎣⎦.解法2:当0a =时,()1f x x =-,令()0f x =,得1x =,是区间[]1,1-上的零点.当0a ≠时,()213f x ax x a =+-+在区间[]1,1-上有零点⇔()231x a x +=-在区间[]1,1-上有解⇔213xa x -=+在区间[]1,1-上有解.问题转化为求函数213xy x -=+在区间[]1,1-上的值域. 设1t x =-,由[]1,1x ∈-,得[]0,2t ∈.且()2013ty t =≥-+.而()214132ty t t t==-++-. 设()4g t t t=+,可以证明当(]0,2t ∈时,()g t 单调递减. 事实上,设1202t t <<≤, 则()()()()121212121212444t t t t g t g t t t t t t t --⎛⎫⎛⎫-=+-+= ⎪ ⎪⎝⎭⎝⎭, 由1202t t <<≤,得120t t -<,1204t t <<,即()()120g t g t ->. 所以()g t 在(]0,2t ∈上单调递减. 故()()24g t g ≥=. 所以()1122y g t =≤-.故实数a 的取值范围为10,2⎡⎤⎢⎥⎣⎦.。
2010年天津市普通高中学业水平考试数学试题(含答案)

2010年天津市普通高中学业水平考试数学试题本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分,满分100分,考试用时90分钟。
参考公式:·主体体积公式 sh柱体=V ,其中S 表示柱体的底面积,h 表示柱高.·椎体体积公式 sh 31V =椎体 其中S 表示锥体的底面积,h 表示椎体的高. ·球的体积公式 3R 34V π=球,其中R 表示球的半径 第I 卷一.选择题:本题共20题,共45分。
其中(1)~(15)题每小题2分;第(16)~(20)题每小题3分,在每小题的四个选项中,只有一个是符合题目要求的.1.已知集合A={1,2,3,4,5},B={4,5,6,7},则A ∪B 等于A.{4,5}B.{1,2,3,4,5,6,7}C.{1,2,3}D.{6,7}2.函数)63sin(2π+=x y (x ∈R )的最大值是A.-2B.1C.2D.33.若向量a=(2,m ),b=(6,9),且a ∥b ,则m 的值是 A. 34- B.-3 C. 34 D.3 4.若向量a ,b 满足|a|=2,|b|=5,a·b=35,则a 与b 的夹角是A.30°B.45°C.60°D.1505.计算ii +2(其中i 为虚数单位)等于 A.1-2i B.1+2i C.-1-2i D.-1+2i6.椭圆191622=+y x 的离心率等于 A.43 B. 47 C. 54 D. 7747.双曲线192522=-y x 的渐近线方程是 A. x y 925±= B. x y 259±= C. x y 35±= D. x y 53±= 8.若抛物线y 2=2px 焦点的坐标为(2,0),则p 的值等于A.8B.4C.2D.19.在等比数列{a n }中,若211=a ,a 4=4,则公比q 的值等于 A. 21 B.2 C.2 D.4 10.直线l 1:321+=x y 与直线l 2:y=kx-5互相垂直的充要条件是 A.21=k B.21-=k C.k=2 D.k=-2 11.下列函数中,在R 上单调递减的是A.y=-xB.21x y = C.y=x -1 D.y=x 212.在下边的程序框图表示的算法中,输出的S 值是A.31B.15C.14D.713.若变量x ,y 满足约束条件⎪⎩⎪⎨⎧≤--≥-+≥-.062;03;02y x y x y x ,则目标函数z=x+2y 的最大值是A.3B.4C.8D.1014.如图,某几何体的正视图和侧视图都是边长为2cm 的正方形,俯视图是一个圆,则该几何体的体积等于A.2πcm 3B.4πcm 3C.8πcm 3D.32πcm 3 15.如图,在正方体ABCD -A 1B 1C 1D 1中,D 1B 所在的直线与底面ABCD 所成角的余弦值等于 A.33 B.22 C.36 D.2316. 如图,在矩形ABCD 中,AD=1,AB=2,以A 为圆心,AD 为半径在矩形内部作扇形A ED ,若向矩形ABCD 内部随机投一点,则所投点落在该扇形中的概率是A.4π B.8π C.31 D.52 17.将一枚质地均匀的硬币连续抛掷三次,出现“一次正面向上,两次反面向上”的概率是 A.81 B.61 C.31 D.83 18.要得到函数)43cos(π+=x y (x ∈R )的图象,只需将函数y=cos3x (x ∈R )图象上所有的点 A.向右平行移动4π个单位长度 B.向左平行移动4π个单位长度 C.向右平行移动12π个单位长度 D.向左平行移动12π个单位长度 19.若a=ln3,b=log 3e ,c=log 9e ,其中e 为自然对数的底,则a ,b ,c 三者的大小关系是A.c <a <bB.b <c <aC.c <b <aD.a <b <c20.已知m ,n 是空间两条不同的直线,α,β是两个不同的平面.若m ⊥α,β⊂n ,则下列命题为真命题的是A.若m ∥n ,则α⊥βB.若m ⊥n ,则α∥βC.若α⊥β,则m ⊥nD.若α⊥β,则m ∥n第Ⅱ卷(非选择题,共55分)注意事项:1、 用黑色墨水的钢笔或签字笔将答案写在答题卡上。
2010年新疆普通高中学业水平模拟考试数学试题及参考答案

(A) p
3
p
(B) 4
10
(C) arcsin 4
6
(D) arcsin 4
12.设 f ¢( x) 是函数 f(x)的导函数,y= f ¢( x) 的图象 如图所示,则 y= f(x)的图象最有可能的是
二、填空题:本大题共4 小题,每小题4 分,共 16 分,把答案填写在答题卡的相应位置
13.设常数 a
M
BO = D O , BC = C D ,\ C O ^ BD.
D
O C
在 D A O C 中,由已知可得 A O = 1, C O = 3 .
B
E
2
2
2
而 AC = 2, \ AO + CO = AC ,
\ ÐAOC = 90o, 即 AO ^ OC.
BD O C = O , \ A O ^ 平面 B C D
2010 年新疆普通高中学业水平模拟考试数学试题及
参考答案
一、选择题(5 分×12=60 分)
3x2
1 函数 f ( x) =
+ lg(Βιβλιοθήκη x + 1) 的定义域是
1- x
1
A (- ,+ ¥) B
3
1
(- ,1) 3
11
C (- , )
33
2 若复数 z 满足方程 z 2 + 2 = 0 ,则 z 3 =
-
p
, kp
+
p
ù ú,k
Î
Z.
ë
3
6û
(II)方法一:
p
先把 y = sin 2 x 图象上所有点向左平移
p
个单位长度,得到 y = sin(2 x + ) 的图象,再把所得
2010届高考数学模拟试卷及答案二

江苏省江阴成化高中2010届高三数学调研模拟试卷二 一、填空题:本大题共14小题,每小题5分,共计70分1.复数43i1+2i +的实部是ks5u2.函数)1(log 23x x y ++-=的定义域为 .ks5u3.“a>2”是“方程x2a+1 + y22-a =1 表示的曲线是双曲线”的 条件(填“充分不必要,.必要不充分,充要,既不充分也不必要) ks5u4. 设123)(+-=a ax x f ,a 为常数.若存在)1,0(0∈x ,使得0)(0=x f ,则实数a 的取值范围是 .ks5u5.设函数()f x a b =∙,其中向量(2cos ,1),(cos 2)a x b x x ==,则函数f(x)的最小正周期是 .6.观察下列程序,该循环变量I 共循环了 次7.已知圆22(2)9x y -+=和直线y kx =交于A,B 两点,O 是坐标原点, 若2OA OB O +=,则||AB = .8.当228x x -<时,函数252x x y x --=+的最小值是 . 9.已知Sn 为等差数列3742:,6:7:,}{S S a a n a n 则若项和的前=等于 .ks5u10.ABC ∆的三内角A ,B ,C 所对边长分别是c b a ,,,设向量(,sin ),m a b C =+)sin sin ,3(A B c a n -+=,若n m //,则角B 的大小为 .11.设m 、n 是异面直线,则(1)一定存在平面α,使α⊂m 且n ∥α;(2)一定存在平面α,使α⊂m 且α⊥n ;(3)一定存在平面γ,使m ,n 到γ的距离相等;(4)一定存在无数对平面α与β,使α⊂m ,β⊂n ,且α∥β;上述4个命题中正确命题的序号为 .12.已知||2,||2x y ≤≤,点P 的坐标为),(y x ,则当Z y x ∈,时,P 满足22(2)(2)4x y -+-≤的概率为 . 13.已知12,,,n a a a ;12,,,nb b b (n 是正整数),令112n L b b b =+++,223L b b =+,n b ++,n n L b =.某人用右图分析得到恒等式:S ✐0 I ✐1While S<60S ✐S+I I ✐ I+1 End While1122n n a b a b a b +++=112233a L c L c L +++k kc L +n nc L ++,则k c =(2)k n ≤≤.14.我们可以运用下面的原理解决一些相关图形的面积问题:如果与一固定直线平行的直线被甲、乙两个封闭的图形所截得线段的比都为k ,那么甲的面积是乙的面积的k 倍.你可以从给出的简单图形①、②中体会这个原理.现在图③中的曲线分别是22221(0)x y a b a b +=>>与222x y a +=,运用上面的原理,图③中椭圆的面积为 .15.(12分)在ABC △中,已知内角A π=3,边BC =B x =,周长为y .(1)求函数()y f x =的解析式和定义域; (2)求y 的最大值.16.(15分)如图,在正方体ABCD -A1B1C1D1中,E 、F 为棱AD 、AB 的中点.(1)求证:EF ∥平面CB1D1;(2)求证:平面CAA1C1⊥平面CB1D1.(3)如果AB=1,一个点从F 出发在正方体的表面上依次经过棱l①②(将l 向右平移)BB1、B1C1、C1D1、D1D 、DA 上的点,又回到F ,指出整个线路的最小值并说明理由.17. 设椭圆2222:1(0)x y C a b a b +=>>的上顶点为A ,椭圆C 上两点,P Q 在x 轴上的射影分别为左焦点1F 和右焦点2F ,直线PQ 的斜率为32,过点A 且与1AF 垂直的直线与x 轴交于点B ,1AF B ∆的外接圆为圆M . (1)求椭圆的离心率;(2)直线213404x y a ++=与圆M相交于,E F两点,且212ME MF a ⋅=-,求椭圆方程; (3)设点(0,3)N 在椭圆C 内部,若椭圆C 上的点到点N 的最远距离不大于C 的短轴长的取值范围.18.某市旅游部门开发一种旅游纪念品,每件产品的成本是15元,销售价是20元,月平均销售a 件.通过改进工艺,产品的成本不变,质量和技术含金量提高,市场分析的结果表明,如果产品的销售价提高的百分率为x()01x <<,那么月平均销售量减少的百分率为2x .记改进工艺后,旅游部门销售该纪念品的月平均利润是y (元). (1)写出y 与x 的函数关系式;(2)改进工艺后,确定该纪念品的售价,使旅游部门销售该纪念品的月平均利润最大. ks5u19.已知二次函数1)(2++=bx ax x f 和函数b x a bx x g 21)(2+-=,(1)若)(x f 为偶函数,试判断)(x g 的奇偶性;(5分)(2)若方程()g x x =有两个不等的实根()2121,x x x x <,则①证明函数)(x f 在(-1,1)上是单调函数;(6分)②若方程0)(=x f 的有两实根为()4343,x x x x <,求使4213x x x x <<<成立的a 的取值范围.(5分)ks5u20.已知数列{}n a 对于任意*p q ∈N ,,都有p q p q a a a ++=,且12a =。
