2电力拖动系统动力学
第二章电力拖动系统动力学

•3、铁心损耗: 由磁滞损耗与涡流
损耗两部分组成。
磁通恒等于零,即磁通连续性定律
。
0
(2)磁路的基尔霍夫第二定律沿任何 闭合磁路的总磁动势恒等于各段磁位降 的代数和。
2019/12/28
2019/12/28
(2) 磁性物质 磁性物质内部形成许多小区域,其分子间存在的 一种特殊的作用力使每一区域内的分子磁场排列整 齐,显示磁性,称这些小区域为磁畴。
B 1S 1 , B 2S2, ..,. B nSn
(2) 求各段磁场强度 Hi
根据各段磁路材料的磁化曲线 Bi=f ( Hi) ,求B1,
B2 ,……相对应的 H1, H2 ,……。
(3) 计算各段磁路的磁压降 (Hi li )
(4) 根据下式求出磁通势( NI ) n NI Hili i1
电气与信息工程学院电气工程系
2019/12/28
绪言
• 一、电机及电力拖动技术的发展概况
• (一)电机的发展概况
1、电能的应用非常广泛,其优点有 :
生产和变换经济
传输和分配比较容易
2019/12/28
使用和控制方便
• 2、电机在电能的应用与生产上起着关 键作用: 电力工业中:发电机与变压器 工业企业:电动机作为原动机大量 使用 自动控制技术:控制电动机被广泛 使用
• 相对而言,电机这一概念往往是指电动机。
2019/12/28
哈尔滨电机厂生产的1MW电机
2019/12/28
2019/12/28
手机震动电机
第2章电力拖动系统动力学

在许多情况下,电动机与工作机构并不同轴,而在二者 之间有传动机构,它把电动机的转动经过中间变速或变换运 动方式后再传给生产机械的工作机构。
第2章 电力拖动系统动力学
2.1 电力拖动系统运动方程式
2.1.1 电力拖动系统运动方程
i
图 2-2 单轴电力拖动系统
第2章 电力拖动系统动力学
1. 工作机构转矩的折算 将一个两轴传动机构折算成单轴拖动系统。折算的原则 是系统的传送功率不变。
注意折算的方向
图 2-4 两轴系统的折算示意图
第2章 电力拖动系统动力学
若不考虑中间传动机构的损耗,按传送功率不变的原则,
应有如下的关系:
TgΩg=TzΩ
(2-6)
Tz
?
Tg
? (? g )
?
Tg j
Tmeq
?
9.55
Fmvm
n?
?
9.55 ? 7000 1450 ? 0.81
?
56.92 N ?m
2)估算系统的总飞轮力矩:
GD 2
?
1.2GD
2 R
?
1.2 ? 100
?
120 N
?m2
3)系统的动转矩绝对值:
T ?? GD 2 ?dn ? 120 ? 500 ? 160 N ?m2 375 dt 375
1、阻力的折算: 折算原则:折算前后系统的传递功率不变
Pm ? F mvm
第2章 电力拖动系统动力学
不考虑功率损耗:
T eq ? ? F mV m ?
T eq
?
F mVm ?
? 9 . 55
F mVm n
考虑损耗:
T eq
电力拖动系统动力学(2)

(2)飞轮矩的折算
设做平移运动部分的物体重量为Gm,质量为m, 刨
折算前动能:
vm
刀
Fm
工件
折算后动能:
工作台
折算前后的动能不变。 ∴ ∴
传动机构中其他轴上的 GD2的折算,与前述相 同。
3.工作机构做提升和下放重物运动 时,转矩与飞轮矩的折算
(1)转矩的折算 1)提升重物时负载转矩的折算 重物对卷筒轴的负载转矩为GmR 不计传动机构的损耗,折算后的负载转矩为:
dt
系统处于稳定运转状态下。
2、当 T TL
dn 0 dt
电力拖动系统处于加速状态
3、当 T TL dn 0 dt
电力拖动系统处于减速状态
常把 GD 2
375
dn或
dt
(T TL )
称为动态转矩或加速转矩.
1.3.2多轴电力拖动系统转矩及飞轮矩的折算
1、折算前提:以电动机轴为研究对象。 2、折算原则:保持系统的功率传递关系及系统的贮 存动能不变。 3、负载转矩的折算:从已知的实际负载转矩求出等效 的负载转矩。 4、系统飞轮矩的折算:从已知的各转轴上的飞轮矩求
dn dn
数学表达式
文字表达式
n 2
n1
在交点处,在交点所对应的 转速之上应保证T<TL,而在 这转速之下则要求T>TL, nA
1 l'
A
0
TL
T
图1-21 拖动系统的不稳定运行
特点:大小恒定,方向总是与运
动的当方正向转相时反n为。正, TL与n方向
相反,应为正,即在第一象限
当反转时n为负, TL与n方向 相反,应为负,即在第三象限。
(2)位能性恒转矩负载 特点:绝对值大小恒定,方向固定不变,与n方向无关
第二章 电力拖动系统动力学

J = J' + mL2
式中 m——该物体的质量 L——两个平行转轴之间的距离
L
12
常见的旋转物体转动惯量的计算方法
①以ρ为半径,质量为m的旋转小球(小球的半径与ρ相比 充分小)的转动惯量
J = m ρ2
②以ρ1为外径,ρ2为内径,旋转轴为圆环柱体中轴线,质 量为m的圆环体的转动惯量
J = m(ρ12+ρ22)/2
TZ ' TZ ' TZ ( / Z间的转速比,j=Ω/ΩZ=n/nz 传动系统一般是多级齿轮变速,每级速比为 j1,j2,j3 …, 则 总的速比j为各级速比之积: j = j1j2 j3… 一般设备,电动机为高转速,工作机构轴为低速,则j>>1
将上式中的角速度Ω(Ω=2πn/60)化成为转速n,则有:
7
GD dn T Tz 375 dt
2
(8-4)
GD2——飞轮惯量(N.m2),GD2=4gJ。电动机转子及其他转动 部件的飞轮惯量GD2 数值由产品目录中查出。
式8-4运动状态有3种:
(1)当T=TZ, dn/dt=0时,电机静止或等速旋转,电力拖动系 统处于稳定运行状态。 (2)当T>TZ, dn/dt>0时,电机拖动系统处于加速状态,为过 渡过程。 (3)当T<TZ, dn/dt<0时,电机拖动系统处于减速状态,为过 渡过程。
①恒转矩负载特性; ②通风机负载特性; ③恒功率负载特性。
28
一、恒转矩负载特性 负载转矩TZ(TL)与转速n无关,当转速变化时,负载转矩TZ 保持常数。 恒转矩负载包括两种: ①反抗性恒转矩负载 ②位能性恒转矩负载
29
①反抗性恒转矩负载
《电机及拖动基础》第2章 电力拖动系统动力学

第二节 多轴电力拖动系统
2. 飞轮矩的折算
折算的原则是折算前后动能不变,旋转体的动能为:
E
1 2
J 2
1 2
GD2 4g
2 n
60
2
第二节 多轴电力拖动系统
电动机
T ,T0
n
GDa2 nb
j1,1
GDb2 nc
j2 ,2
GDc2 n f
j3 ,3
GD
2 f
负载 Tf
上图所示的多轴电力拖动系统中,工作机构转轴 n f 的飞 轮矩为 GD2f ,折合到电动机轴上以后的飞轮矩为 GDF2 。
电动机
T ,T0
n
GDa2 nb
j1,1
GDb2 nc
j2 ,2
GDc2 n f
j3 ,3
GD
2 f
负载 Tf
第一节 单轴电力拖动系统
通常把负载转矩与系统飞轮矩等效成单轴系统。
电动机 T , T0
n GD2
等效负载 TF
等效折算的原则是:保持系统的功率及系统贮存的动能 恒定。需进行负载转矩的折算和系统飞轮矩的折算。
j2 ,2
GDc2 n f
j3 ,3
GD
2 f
负载 Tf
同理,对于转轴 nb 和 nc 进行折算,可得:
GDB2
GDb2 j12
GDC2
GDc2 j1 j2 2
第二节 多轴电力拖动系统
n
电动机
T ,T0
GDa2 nb
j1,1
GDb2 nc
j2 ,2
GDc2 n f
j3 ,3
GD
2 f
负载 Tf
如图所示的电力拖动系统,飞轮矩 GDa2 18.5N m2 ,GDb2 22N m2, GD2f 130N m,2 传动效率1 0.90 ,2 0.91,转矩Tf 85N m ,转 速n 2850r / min ,nb 950r / min ,nf 190r / min ,忽略电动机空 载转矩计算: (1) 折算到电动机轴上的负载转矩 TF ; (2) 折算到电动机轴上的系统总飞轮矩 GD2。
02第二章 电力拖动系统的动力学基础

k Tl = n
1 (Tl ∝ ) n k 2π n Pl = Tl i = i 常数 n 60 Pl 与n无关 讨论的典型负载,也可能是 几种典型负载的混合.
注意:实际负载的特性可能是上述
作 业
P48: 2-2, 2-4, 2-5, 2-10, 2-13
�
电动机
P-8
T T0
Tm
J
生产机械 Jm
T
图中: J -电 动 机 转 动 惯 量 Jm -生产机械转动惯量 T -电 动 机 产 生 的 电 磁 转 矩 T0 - 电 动 机 空 载 转 距 Tm - 生 产 机 械 的 转 矩 -轴的角速度
各物理量 正方向
Tl
根据力学知单轴系统的运动方程式:
2,平移运动部件质量的折算
折算前运动部件直线动能: 1 1 Gm 2 2 mVm = Vm 2 2 g 折算后,设等效飞轮矩为 GDmeq 2.其动能: GDmeq 2 2π 2 1 1 2 ( J meq = n) 2 2 4g 60 根据折算前后,其动能不变原则,可得: G mVm 2 GDmeq 2 = 365 ( 2 19 ) 2 n 式中: G m = mg N , Vm m / s , GDmeq 2 N i m 2
二,风机,泵类负载特性:
Tl = T0 + Tm = T0 + knm 2 其负载力矩正比于转速的平方.此类负载只 能单方向旋转.
三,恒功率负载机械特性
如车床切削工件的工艺过程: 粗切削时:切削量大,要求力大,速度低 精切削时:切削量少,要求力小,速度高, 保证加工工件的精度. 此工艺过程保持拖动系统功率恒定.(但在每一次加 工过程属恒转矩负载特性)
d T Tl = J ( 2 1) dt 式 中 Tl = T0 + Tm J = J + J m 转 矩 的 单 位 : kg im , 转 动 惯 量 的 单 位 : kg im / s 2
第2章 电力拖动系统动力学

在T=TL处:
dT dn
dTL dn
或
dT dn
dTL dn
0
▲ 交点转速之上:T< TL时系统稳定 ▲或交点转速之下:T> TL时系统稳定
怎样判断稳定?
n 例3. 试判断下例系统是否稳定?
TL T (a) T (d) TL (e) (b) T
TL
TL T (c)
T TL
(f)
TL
T
T
(a)表示电动机机械特性T的硬度为负值,而负载转矩TL硬度为正值; (b)表示电动机机械特性T和负载转矩TL硬度都为正值; (c)表示电动机机械特性T和负载转矩TL硬度都为负值;
又称摩擦转矩、反作用转矩
-TL +TL
T T n
特点:
①转矩的方向总是阻碍运动方向, n 当运动方向改变时,反抗性转矩的方向随之改变; ②但大小(绝对值)不随转速变化; ③当n=0时,反抗性转矩的大小、方向是不确定的; ④机械特性位于Ⅰ、 Ⅲ象限,且与纵轴平行的直线。
2-3负载的转矩特性
⑵位能性负载特性 特点:
n
K TL = ----n
即:P = TΩ≈ 常数 n
T
3. 风机类负载
鼓风机、水泵、输油泵等。其转矩与转速的 二次方成正比。即 TL∝ n2 写为:TL=K n2
实际负载可能是几种典型的综合,如实际风机。
T
电力拖动系统稳定运行的条件
电动机机械特性与负载转矩特性在 T-n 平面上有相交点,是电力拖动系统可能稳 定的必要条件;(但不够充分) 稳定运行充分条件:若电力拖动系统原在 交点处稳定运行,由于某种干扰使转速变 化,可达到新的平衡。干扰消除后,可回 到原来的平衡点位置,则称此系统是稳定 的。
02第2章 电力拖动的动力学基础

2
T D 为 29 . 4 N .m 。
2
GD1
2
n1 n2 GD2
2
GD3
2
2
n3
解:)将系统折算到电动机 1 j1 TZ 2500 1000 Tf j
2
轴 2,
2 .5 , j 2 98 5
1000 500
19 . 6 N .m GD 3 j1 j 2
2 2 2
-
a)
n
-T
c)
T
• 例如:规定转速顺时针为正,逆时针为负, 电磁转矩的正方向与转速正方向相同, 负载转矩的正方向与转速正方向相反. 图a中,T,nTL都为正.所以:
T (T L ) GD 375
2
2
d ( n) dt
T ( T L )
问题!
这种方法研究这个系统太复杂。 对电 力拖动系统而言,通常把电动机 轴作为研究对象即可
解决途径:
把实际的拖动系统等效为单轴系统
等效原则:
等效折算的原则是保持两个系统传送的功率 及储存的动能相同
T
电动机
n GDeq
2
等效负载
TF
n
电动机
nb
GDa T
j1
2
nf GDb
2
GDf
2
2
Tf 生产机械
2
1 GD 2 4g
2
2 n 60
2
• 根据折算前后系统动能不变的原则
1 GD 1 GD a 2 n 1 GD b 2 n b 2 n 2 4 g 60 2 4 g 60 2 4 g 60
电机学第二章电力拖动的动力学基础

力矩电机
力矩电机是一种能够输出较大 力矩的电动机,广泛应用于需
要较大负载能力的场合。
力矩电机通过接收控制信号, 能够输出较大的力矩,实现精
确的力和转矩控制。
力矩电机具有较大的过载能力 和较高的机械效率,能够适应 各种重负载的应用场景。
力矩电机通常采用闭环控制方 式,具有较高的控制精度和稳 定性。
02
直流电动机的机械特性 可以通过实验和计算获 得,包括固有特性和人 为特性。
03
固有特性是指在额定电 压和额定电流下,电动 机的转速与转矩之间的 关系。
04
人为特性是指通过改变 电压或电流等参数,改 变电动机的机械特性。
直流电动机的调速与控制
直流电动机的调速是指通过改变电枢 电压或励磁电流等参数,调节电动机 的转速。
05
CATALOGUE
电力拖动系统的稳定性
电力拖动系统的稳定性分析
稳定性定义
电力拖动系统在受到外界干扰后,能够恢复到原 始平衡状态的能力。
稳定性判据
通过分析系统的动态方程,确定系统是否稳定。 常用的判据有劳斯判据、赫尔维茨判据等。
稳定性分类
根据稳定性的程度,可以分为大范围稳定、有限 范围稳定和局部稳定。
提高电力拖动系统稳定性的方法
增加阻尼
01
通过增加系统的阻尼,减小外界干扰对系统的影响,提高系统
的稳定性。
优化控制策略
02
采用先进的控制算法,如PID控制、模糊控制等,提高系统的动
态品质和稳定性。
选择合适的电机和负载
03
根据实际需求选择合适的电机和负载,以减小系统的不稳定因
素。
2.电力拖动系统动力学ppt课件
2、性质 : 动转矩等于零时,系统处于恒转速运行的稳态; 动转矩大于零时,系统处于加速运动的过渡过
程中; 动转矩小于零时,系统处于减速运动的过渡过
程中。
.
2.2 负载的转矩特性
• 机械的工作机构的负载转矩与转速之间的 关系,称之为负载的转矩特性。一般用n=f (TL)曲线表示。
• 1 恒转矩负载的转矩特性 • (1) 反抗性恒转矩负载 • (2)位能性恒转矩负载 • 2 泵类负载的转矩特性 • 3 恒功率负载的转矩特性
.
.
2.3 电力拖动系统稳定运行的条件
• P20 充分必要条件:电动机机械特性与负载 转矩特性必须相交,在交点处T=TL,实现 转矩平衡,在工作点要满足dT / dn < dTL / dn
.
.
• 1、恒转矩负载特性 • 指负载转矩与其转速n无关的特性,即当转速变化时,
负载转矩保持常数。 • (1)反抗来自恒转矩负载特性 • 是由摩擦力产生的,绝对值大小不变,方向总是和运
动方向相反。是阻碍运动的制动性转矩。 • 属于这一类的生产机械有提升机的走行机构,皮带运
输机,轧钢机以及某些金属切削机床的平移机构等。 • 其特性曲线是位于平面坐标系的第一与第三象限内,
第二章 电力拖动基础知识
• 采用电动机拖动生产机械,并实现生产工 艺过程中各种要求的系统,称为电力拖动 系统。
.
2.1 电力拖动系统的运动方程
• 1、单轴电机拖动系统-包含一根轴的系统
.
• 当电动机的转矩作用于这一系统时,根据动 力学定律可知,电动机的转矩除了克服运动 系统的静阻转矩外,还使整个系统沿着电动 机转矩的作用方向,产生角加速度。角加速 度的大小与旋转体的转动惯量J成反比。
第二章 电力拖动系统的动力学基础

1 2 GD f 4g
2
GD f
2
,动能为
)
2
(
2n f 60
折合到电机转轴上后的飞轮矩 动能 2 1 GDF 2n
( 2 4g
2 GDF
GDF
2
,其
)
2
60
化简后得到
GD f j
2
2
工作机构转轴上有转速 nb 的轴,其飞轮矩 2 为 GDb ,动能为
1 2 GDb 4g
损耗有:
TF
GR j
T 1 )
GR j
(
GRห้องสมุดไป่ตู้j
(2
GR j
重物下放时传动机构效率为: 2
1
电机轴上电磁转矩为T 、折算后负载转矩 为 GR 、传动机构损耗为 T 。
j
忽略空载转矩,三者关系有:
提升重物时电机负担 T ,则
TF GR j
提升重物
T
电机轴上电磁转矩为T 、折 算后负载转矩为 GR 、
j
传动机构损耗为 T 。
忽略空载转矩,三者关系有:
重物下放时负载负担 T,则:
TF
GR j
T
下放重物
2.3 负载转矩特性与电力拖动系统稳定运行条件
生产机械运行常用负载转矩标志其负载的大 小。不同的生产机械的转矩随转速变化规律不同, 用负载转矩特性来表征,即生产机械的转速n与 n f (TL ) 负载转矩TL之间的关系 。 各种生产机械特性大致可归纳为以下3类。
结论:若两条特性曲线有交点(必要条件),且在工 作点上满足 在T
TL 处
第二章电力拖动系统的动力学基础

有下列关系:
考虑到 GD2 = 4gJ,Ω = 2πn/60,得
2.3 考虑传动机构损耗的简化方法
传动机构损耗的简化考虑方法可在折算公式中引
一入 1..工电传作动动效机机率工构η作转c 在矩电T动z’状的态简化折算
电动机带动工作机构,功率由电动机向工作机构 传送
传动损耗由电动机承担 电动机发出的功率比生产机构消耗的功率大
Tz
Tz'
c Tjz' c
z
电机轴角速度
z 工作轴角速度
Tz' 工作轴的负载转矩 Tz 工作轴的负载转矩折算 到电机轴上的负载转矩
c 转动机构总效率 1 2 3 ...
j 转动机构总速比 j1 j2 j 3 ...
三、旋转运动的飞轮矩折算
飞轮矩折算的原则:系统储存的动能不变
ห้องสมุดไป่ตู้
1 2
加速转矩(GD2/375)
(dn/dt)的大小及正负符号 由转矩 T 及阻转矩 Tz 的代 数和来决定
旋转运动中的转矩
三、功率平衡方程
将式
d T TZ J dt
写为
T
TZ
J
d dt
d dt
(1 2
J2 )
电动机产生(T >0) 或吸收的机械功率
( T <0)
生产机械吸收 (TZ >0) 或释放的机械功率 (TZ <0)
一.运动方程式
1.直线运动时的运动方程式
F --拖动力(N); Fz --阻力(N);
m(dv/dt)--惯性力。
作直线运动的物体
2.旋转运动时的方程式为:
T --电动机产生的拖动转矩(N·m); Tz --阻转矩(或称负载转矩)(N·m); J(dΩ/dt)--惯性转矩(或称加速转矩)。
第2章电力拖动基础的动力学

第2章 电力拖动基础的动力学工业生产中最典型的电力拖动系统有电力机车、起重机、龙门刨床等。
由于实际电力拖动系统种类太多,不可能逐一进行研究,所以要找到它们共同的运动规律加以综合分析。
电力拖动系统的运动规律可以用动力学中的运动方程来描述。
为了抓住本质,本章首先分析简单的单轴电力拖动系统动力学行为,然后分析多轴系统的折算问题,典型的负载转矩性质,最后电力拖动系统的平衡稳定运转问题。
2.1单轴电力拖动系统的动力学分析所谓单轴电力拖动系统,就是电动机转子轴直接拖动生产机械运转的系统,如图2.1所示。
图2.1 单轴电力拖动系统示意图单轴电力拖动系统中电磁转矩T 、负载转矩L T 和角速度Ω之间的关系用转动方程式表示为:dt d JT T L Ω=- (2.1)式中,T 为电动机产生的拖动转矩()m N ⋅;L T 为负载转矩()m N ⋅;J 为单轴系统的转动惯量()2m kg ⋅;Ω为单轴系统的角速度()s rad。
工程上,常常不用转动惯量J 而用飞轮惯量或飞轮矩2GD 表示系统的惯性。
系统的速度不用角速度Ω用而转速n 表示。
2GD 与J 之间的关系为gJ GD 42=式中,G 为系统转动部分的重量()N ;D 为系统转动部分的惯性直径()m ;g 为中重力加速度,28.9s mg =。
角速度Ω与转速n 的关系为602nπ=Ω 将上面两式代入运动方程(2.1)式中,化简后得dt dnGD T T L ⋅=-3752 (2.2) 式中,375是一个具有加速度量纲的系数,其单位为1m in -⋅s m ;转矩单位仍为m N ⋅;转速单位仍为min r 。
L T T -称为动态转矩。
当动态转矩为零时,系统处于恒转速运行的稳态;动态转矩大于零时,系统处于加速运动的过渡过程中;动态转矩小于零时,系统处于减速运动的过渡过程中。
运动方程式(2.2)中,由于电动机运行状态的不同和生产机械负载类型的不同,电动机轴上的拖动转矩T 和负载转矩L T 不仅大小不同,方向也是变化的。
第2章 电力拖动系统的动力学基础.
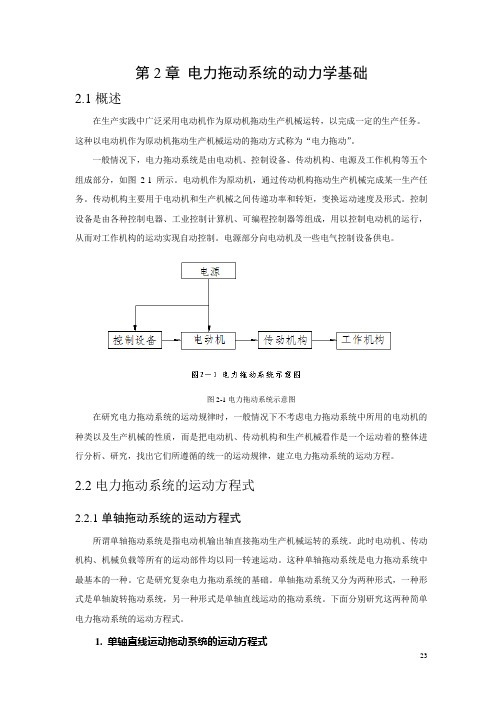
第2章电力拖动系统的动力学基础2.1概述在生产实践中广泛采用电动机作为原动机拖动生产机械运转,以完成一定的生产任务。
这种以电动机作为原动机拖动生产机械运动的拖动方式称为“电力拖动”。
一般情况下,电力拖动系统是由电动机、控制设备、传动机构、电源及工作机构等五个组成部分,如图2-1所示。
电动机作为原动机,通过传动机构拖动生产机械完成某一生产任务。
传动机构主要用于电动机和生产机械之间传递功率和转矩,变换运动速度及形式。
控制设备是由各种控制电器、工业控制计算机、可编程控制器等组成,用以控制电动机的运行,从而对工作机构的运动实现自动控制。
电源部分向电动机及一些电气控制设备供电。
图2-1电力拖动系统示意图在研究电力拖动系统的运动规律时,一般情况下不考虑电力拖动系统中所用的电动机的种类以及生产机械的性质,而是把电动机、传动机构和生产机械看作是一个运动着的整体进行分析、研究,找出它们所遵循的统一的运动规律,建立电力拖动系统的运动方程。
2.2电力拖动系统的运动方程式2.2.1单轴拖动系统的运动方程式所谓单轴拖动系统是指电动机输出轴直接拖动生产机械运转的系统。
此时电动机、传动机构、机械负载等所有的运动部件均以同一转速运动。
这种单轴拖动系统是电力拖动系统中最基本的一种。
它是研究复杂电力拖动系统的基础。
单轴拖动系统又分为两种形式,一种形式是单轴旋转拖动系统,另一种形式是单轴直线运动的拖动系统。
下面分别研究这两种简单电力拖动系统的运动方程式。
1. 单轴直线运动拖动系统的运动方程式根据牛顿第二定律,在电力拖动系统中如果生产机械做直线运动,作用在电动机轴上的电动力F 与阻力L F 以及速度变化时产生的惯性力ma 之间的关系遵循下列基本运动方程式。
ma F F L =-式中,F —拖动力,单位为N ;L F —阻力,单位为N ;m —物体的质量,单位为kg ; a —物体的加速度,单位为2/s m ;上式也可写成dtdvmF F L =- (2-1) 式中,dtdvm是惯性力,如果质量m 的单位为kg ,速度v 的单位为s m /,时间t 的单位为s ,则惯性力的单位与F 及L F 的单位相同,为N 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
控制设备
电动机
传动机构
生产机械
图2.1 电力拖动系统组成
采用电力拖动主要原因
现代化生产中,多数生产机械都采用电 力拖动,主要原因是 : 1. 电能的运输、分配、控制方便经济。 2. 电动机的种类和规格很多,它们具有各种 各样的特性,能很好的满足大多数生产机 械的不同要求。 3. 电力拖动系统的操作和控制简便,可以实 现自动控制和远距离操作等等。
① 以V=0.3m/s提升重物时,负载(重物及吊钩)转矩、卷 筒转速、电机输出转矩及电机转速 ② 负载及系统的飞轮矩(折算到电动机轴上) ③ 以a=0.1m/s2提升重物时,电动机的输出转矩
例题2-4续
① 以V=0.3m/s提升重物时,负载(重物及吊钩)转矩、卷筒 转速、电机输出转矩及电机转速
GD 1 GD 1.2 100 120 N m
2 2 D
2
GD 2 dn 120 T T TL 500 160 N m 375 dt 375
2.2.3 工作机构提升或下放运动时,转矩 与飞轮矩的折算
1 转矩的折算
(1)提升时
GR TF j j
2
例题2-4续
③ 以a=0.1m/s2提升重物时,电动机的输出转矩
解③
60 2v n nf j j1 j2 j3 d
dn d 120 v 120 j1 j2 j3 j1 j2 j3a dt dt d d
120 3 3.5 4 0.1 267 .4r / min s 0.6
第二章 电力拖动系统动力学 Dynamics of Electric Drive Systems
2.1 电力拖动系统转动方程式 2.2 多轴电力拖动系统简化 2.3 负载转矩特性与电力拖动系统稳定运行的条件
本章教学基本要求
1.了解电力拖动基本概念; 2.熟悉电力拖动系统运动方程式; 3.掌握拖动转矩和负载转矩的概念。 重点: 运动方程式和负载转矩。
例题2-2续
已知F=104N,V=0.7m/s,GDD2=100N· 2, η=0.81,n=1450r/min m ① 折算到电机轴上的TF ② 估算系统的GD2
③ 不切削时,工作台及工件方向加速,电动机以500r/(min· s)恒加速度运行,计算 此时系统的动转矩绝对值
解
Fv 10 4 0.7 TF 9.55 9.55 56.92 N m n 1450 0.81
2
GD 2 — 飞轮惯量或飞轮转矩N m 2
d Ω/dt 动态角速度的变化率,一般用转速的变化率dn/dt 表示,由于Ω=2πn/60
GD 2 dn 4g 60 则运动方程式 T TL : 其中375 375 dt 2
注意:常数375 中包含重力加速度g,具有重力加速度的单 位:m/(min· s)
2 1 2 1 0.83 0.7952
T TF
G0 G R 1470 8820 0.11 0.7952 26.47 N m
j 34
例题2-4
GD
2 a
GD
2 c
d
GD
2 b
j ,η2
2
GD
2 d
j ,η 1
1
j ,η 3
n n f j 3 3.5 4 19.1 802 .2r / min
例题2-4续
② 负载及系统的飞轮矩(折算到电动机轴上)
解②
G G0 v 2 GD 2 365
F
n2
49050 1962 0.32 365
802 .22
2.6 N m 2
下放时效率与上升时效率的关系
2
1
2 飞轮矩的折算与平动相同
例题2-3
已知j=34,η=0.83,R=0.11m,空钩重量G0=1470N , G=8820N, GDD2=10N· 2, 当提升速度 m V=0.4m/s时,求 ① 电机转速 ② 忽略空载转矩时电动机所带的负载转矩 ③ 以V=0.4m/s下放重物时,电动机的负载转矩
例题2-3续
已知j=34,η=0.83,R=0.11m,空钩重量G0=1470N, G=8820N, GDD2=10N· 2, 当提升速度V=0.4m/s时,求 m ① 电机转速 ② 忽略空载转矩时电动机所带的负载转矩 ③ 以V=0.4m/s下放重物时,电动机的负载转矩 解
60v 60 0.4 n nf j j 34 1180 .5r / min 2 R 2 0.11
2 GD 2 1 GDD
2
转子本身的飞轮矩是主要 部分,为简化计算,可用 下式估算
0.2 ~ 0.3
例题2-1
已知GDa2=14.5N· 2, GDb2=18.8N· 2, m m GDf2=120N· 2,η1=0.91,η2=0.93,Tf=85N· m m ,n=2450r/min,nb=810r/min, nf=150r/min,忽 略空载转矩,求 ① 折算到电机轴上的GD2 ② 折算到电机轴上的TF
3
v
G0 G
例题2-4续
已知PN=20kW,nN=950r/min,j1=3,j2=3.5, j3=4,各级 η=0.95, GDa2=123N· 2, GDb2=49N· 2, m m GDc2=40N· 2, GDd2=465N· 2,d=0.6m,空钩重量 m m G0=1962N, G=49050N,忽略电机空载损耗,忽略钢丝 绳重量,忽略滑轮传递损耗,求:
2.2.2 工作机构为平动时,转矩与飞轮矩 的折算
1 转矩的折算
T f FR
FR TF j j Tf
通常给的数据是F和v,而不是R
2 n Fv TF TF 60
Fv Fv TF 9.55 2 n 60 n
Fv 考虑效率有: TF 9.55 n
2 飞轮矩的折算
2.1 电力拖动系统转动方程式
2.1.1 电力拖动系统的基本概念 电力拖动 拖动:原动机带动生产机械运转叫拖动。 电力拖动:电动机作为原动机,生产机械是负 载,电动机带动生产机械运转的拖动方式称电 力拖动。
电力拖动系统:用电动机将电能转换成机械能,拖 动生产机械,并完成一定工艺要求的系统。
电力拖动系统组成
2.1.2 单轴系统的运动方程式
电动机的轴和工作机构不经传动机构直接相连, 工作机构为电动机的负载。
由牛顿第二定律可知
d T TL J dt TL TF T0
dΩ T TL J dt
转速变化过程中出现的惯性转矩 J :电动机轴上的转动惯量Kg.m2
2
G D GD 2 J m g 2 4g
2 GDb2 GDc2 GDd 2 2 GD 2 GDa 2 2 2 2 2 2 GDF j1 j1 j2 j1 j2 j3 49 40 465 123 2 2.6 2 2 3 3 3.5 3 3.5 4
131 .7 N m
GD 2 dn 131 .7 T TF 212 .5 267 .4 306 .4 N m 375 dt 375
2.3 负载的转矩特性与电力拖动系统稳定运行 条件
2.3.1 负载的转矩特性 负载的转矩特性是指生产机械工作机构 的负载转矩与转速之间的关系即:n=f(TL) 1 恒转矩负载的转矩特性 恒转矩负载是指负载转矩为常数,其大 小与转速n无关。 恒转矩负载分:反抗性负载特性和位能 性负载特性。
T TF
G0 G R 1470 8820 0.11 40.11N m
j 34 0.83
例题2-3续
已知j=34,η=0.83,R=0.11m,空钩重量G0=1470N, G=8820N, GDD2=10N· 2, 当提升速度V=0.4m/s时,求 m ① 电机转速 ② 忽略空载转矩时电动机所带的负载转矩 ③ 以V=0.4m/s下放重物时,电动机的负载转矩 ③解:
Tf
传动机构损耗转矩
GR GR T j j
Tf
(2)下放时,不考虑损耗如下式,且方向不变
GR TF j j
起重机的转矩关系
(1)提升时
GR T T j
(2)下放时
TF T GR GR GR GR GR 1 GR 2 T j j j j j j
2.2.1 工作机构为转动时,转矩与飞轮矩 的折算
1 转矩的折算
2 飞轮矩的折算
旋转物体的动能
1 1 GD J 2 2 2 4g
2 1 GD f 2 n f 2 4 g 60 2
2
2 n 60
2 F
2
折算前后动能不变
GD 2 f j
多轴系统
n T M 电动机 TL ' 负载
多轴电力拖动系统
分析上面系统时,要对每个轴列写转动 方程式,比较麻烦,因此需要简化,把多轴 系统简化成单轴系统。
折算原则和方向
分析多轴系统采用的方法是:用一个等 效的单轴系统代替原来实际的多轴系统。这 种方法称为“折算”。 折算原则:折算前后系统传递功率不 变,系统的动能不变。 折算方向:一般是从生产机械轴向电动 机轴折算。原因是研究对象是电动机。且电 动机轴一般是高速。根据传送功率不变的原 则,高速轴上的负载转矩数值小。
解①
Tf 1 G G0 d 49050 1962 0.6 7651 .8N m 2 2 2 2
602v 60 2 0.3 卷筒转速n f 19.1r / min d 3.14 0.6
