北京市五中2020-2021学年高二数学上学期期中考试试题含答案 文
金太阳2020-2021年学年度上学期期中考试高二试题

2020-2021学年度上学期期中考试高二试题数学考试时间:120分钟总分:150分第Ⅰ卷(选择题共60分)一.选择题:本题共8小题,每小题5分,共40分,每小题只有一个选项符合题目要求.1.已知方程m y x =+32的曲线通过点()2,1-,则=m ()A 5B 8C 9D 102.已知向量()()4,,3,3,1,2k b a -=-=→→,且⎪⎭⎫ ⎝⎛-⊥→→→b a a ,则k 的值为()A 8-B 6-C 6D 103.已知ABC ∆三个顶点的坐标分别为()()()M C B A ,2,5,6,1,6,2-为BC 的中点,则中线AM 所在直线的方程为()A 02610=-+y xB 0228=-+y x C 0268=-+y x D 03410=--y x 4.已知点()()1,0,0,1B A ,圆()31:22=++y x C ,则()A B A ,都在C 内B A 在C 外,B 在C 内C B A ,都在C 外D A 在C 内,B 在C 外5.在正方体1111D C B A ABCD -中,M 为BC 的中点,则异面直线MD 与1AB 所成角的余弦值是()A 55B 552C 510D 5156.已知椭圆()012:2222>=+m m y m x C 的左、右焦点分别为P F F ,,21为C 上任意一点,若1221≥+PF PF ,则必有()A 2621≤F F B 2621≥F F C 921≤F F D 921≥F F 7.设直线03=+--k y kx 过定点A ,直线082=--k y kx 过定点B ,则直线AB 的倾斜角为()A 65πB 32πC 3πD 6π8.设21,F F 分别为双曲线()0,01:2222>>=-b a by a x C 的左、右焦点,实轴为21A A ,若P 为C 的右支上的一点,线段1PF 的中点为M ,且2121127,A A M F PF M F =⊥,则C 的离心率为()A 34B 35C 2D 37二.选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分.9.以下关于向量的说法中正确的是()A 若将所有空间单位向量的起点放在同一点,则中点围成一个球面B 若→→=b a ,则→→=ba C 若→a 与→b 共线,→b 与→c 共线,则→a 与→c 可能不共线D 若→→-=b a ,且→→=c b ,则→→=ca 10.已知双曲线16:22=-y x C ,则()A C 的焦距为7B C 的虚轴长是实轴长的6倍C 双曲线1622=-x y 与C 的渐近线相同D 直线x y 3=上存在一点在C 上11.若过点()1,2-的圆M 与两坐标轴都相切,则直线01043=+-y x 与圆M 的位置关系可能是()A 相交B 相切C 相离D 不能确定12.已知曲线C 的方程为()()()()0,1,3,0,3,0,101922--≤<=+D B A x y x ,点P 是C 上的动点,直线AP 与直线5=x 交于点M ,直线BP 与直线5=x 交于点N ,则DMN ∆的面积可能为()A 73B 76C 68D 72第Ⅱ卷三.填空题(本题共4小题每小题5分,共20分)13.若直线()0814=+++y m x 与直线0932=--y x 平行,则这两条平行直线间的距离为__________.14.在四棱柱1111D C B A ABCD -中,→→→→++=11AA z AC y AB x BC ,则=--z y x _________.15.设椭圆()*22221112N n n y n x ∈=+++的焦距为n a .,则数列{}n a 的前n 项和为___________.16.已知动圆Q 与圆()94:221=++y x C 外切,与圆()94:222=-+y x C 内切,则动圆圆心的轨迹方程为______四.解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤17.(本小题满分10分)在①它的倾斜角比直线13-=x y 的倾斜角小12π,②与直线01=-+y x 垂直,③在y 轴上的截距为1-,这三个条件中任选一个,补充在下面的问题中,并作答.问题:已知直线l 过点()1,2,且__________,求直线l 的方程.注:如果选择多个条件分别解答,按第一个解答计分.18.(本小题满分12分)已知椭圆C 的对称中心为坐标原点,焦点在坐标轴上,且短轴长为72,离心率为43.(1)求C 的标准方程;(2)若C 的焦点在x 轴上,C 的焦点恰为椭圆M 长轴的端点,且M 的离心率与双曲线15422=-x y 的离心率互为倒数,求M 的标准方程.19.(本小题满分12分)如图,在正四棱柱1111D C B A ABCD -中,E AB AA ,221==为1DD 的中点.(1)证明:⊥CE 平面E C B 11;(2)求二面角B E C B --11的余弦值.20.(本小题满分12分)如图,在三棱锥ABC D -中,⊥DA 平面BC AB ABC ⊥,且4,3,2===AD AB BC .(1)证明:BCD ∆为直角三角形;(2)以A 为圆心,在平面DAB 中作四分之一个圆,如图所示,E 为圆弧上一点,且︒=∠=45,2EAD AE ,求AE 与平面BCD 所成角的正弦值.21.(本小题满分12分)已知P 是椭圆18:22=+y x C 上的动点.(1)若A 是C 上一点,且线段PA 的中点为⎪⎭⎫ ⎝⎛21,1,求直线PA 的斜率;(2)若Q 是圆()4911:22=++y x D 上的动点,求PQ 的最小值.22.(本小题满分12分)已知圆012:22=-+++Ey Dx y x C 过点()7,1-P ,圆心C 在直线022:=--y x l 上.(1)求圆C 的一般方程;(2)若不过原点O 的直线l 与圆C 交于B A ,两点,且12-=⋅→→OB OA ,试问直线l 是否过定点?若过定点,求出定点坐标;若不过定点,说明理由.。
2020-2021北京市密云县穆家峪中学高二数学上期中一模试卷附答案
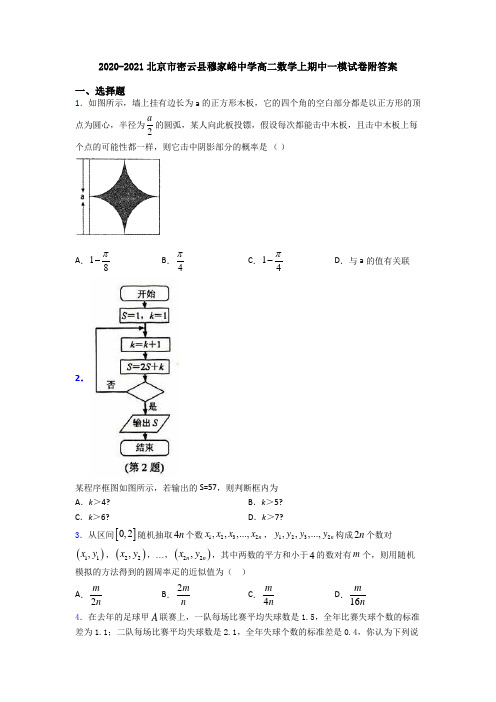
2020-2021北京市密云县穆家峪中学高二数学上期中一模试卷附答案一、选择题1.如图所示,墙上挂有边长为a 的正方形木板,它的四个角的空白部分都是以正方形的顶点为圆心,半径为2a的圆弧,某人向此板投镖,假设每次都能击中木板,且击中木板上每个点的可能性都一样,则它击中阴影部分的概率是 ( )A .18π-B .4π C .14π-D .与a 的值有关联2.某程序框图如图所示,若输出的S=57,则判断框内为 A .k >4? B .k >5? C .k >6?D .k >7?3.从区间[]0,2随机抽取4n 个数1232,,,...,n x x x x ,1232,,,...,n y y y y 构成2n 个数对()11,x y ,()22,x y ,…,()22,n n x y ,其中两数的平方和小于4的数对有m 个,则用随机模拟的方法得到的圆周率疋的近似值为( ) A .2m nB .2mnC .4m nD .16m n4.在去年的足球甲A 联赛上,一队每场比赛平均失球数是1.5,全年比赛失球个数的标准差为1.1;二队每场比赛平均失球数是2.1,全年失球个数的标准差是0.4,你认为下列说法中正确的个数有( )①平均来说一队比二队防守技术好;②二队比一队防守技术水平更稳定;③一队防守有时表现很差,有时表现又非常好;④二队很少不失球. A .1个B .2个C .3个D .4个5.如图1为某省2019年1~4月快递义务量统计图,图2是该省2019年1~4月快递业务收入统计图,下列对统计图理解错误的是( )A .2019年1~4月的业务量,3月最高,2月最低,差值接近2000万件B .2019年1~4月的业务量同比增长率超过50%,在3月最高C .从两图来看2019年1~4月中的同一个月快递业务量与收入的同比增长率并不完全一致D .从1~4月来看,该省在2019年快递业务收入同比增长率逐月增长6.抛掷一枚质地均匀的骰子,记事件A 为“向上的点数是偶数”,事件B 为“向上的点数不超过3”,则概率()P A B U ( ) A .12B .13C .23D .567.若干个人站成一排,其中为互斥事件的是( ) A .“甲站排头”与“乙站排头” B .“甲站排头”与“乙不站排尾” C .“甲站排头”与“乙站排尾” D .“甲不站排头”与“乙不站排尾”8.微信中有个“微信运动”,记录一天行走的步数,小王的“微信步数排行榜”里有120个人,今天,他发现步数最少的有0.85万步,最多的有1.79万步.于是,他做了个统计,作出下表,请问这天大家平均走了多少万步?( )A.1.19B.1.23C.1.26D.1.319.已知某地区中小学生人数和近视情况分别如图1和如图2所示,为了了解该地区中小学生的近视形成原因,用分层抽样的方法抽取2%的学生进行调查,则样本容量和抽取的高中生近视人数分别为()A.100,20B.200,20C.100,10D.200,10 10.我国古代名著《庄子g天下篇》中有一句名言“一尺之棰,日取其半,万世不竭”,其意思为:一尺的木棍,每天截取一半,永远都截不完.现将该木棍依此规律截取,如图所示的程序框图的功能就是计算截取7天后所剩木棍的长度(单位:尺),则①②③处可分别填入的是( )A.17?,,+1i s s i ii≤=-=B.1128?,,2i s s i ii≤=-=C.17?,,+12i s s i ii≤=-=D.1128?,,22i s s i ii≤=-=11.抛掷一个质地均匀的骰子的试验,事件A表示“小于5的偶数点出现”,事件B表示“不小于5的点数出现”,则一次试验中,事件A或事件B至少有一个发生的概率为()A.23B.13C.12D.5612.设点(a,b)为区域40x yxy+-≤⎧⎪>⎨⎪>⎩内任意一点,则使函数f(x)=2ax2bx3-+在区间[12,+∞)上是增函数的概率为A.13B.23C.12D.14二、填空题13.下列说法正确的个数有_________(1)已知变量x和y满足关系23y x=-+,则x与y正相关;(2)线性回归直线必过点(),x y;(3)对于分类变量A与B的随机变量2k,2k越大说明“A与B有关系”的可信度越大(4)在刻画回归模型的拟合效果时,残差平方和越小,相关指数2R的值越大,说明拟合的效果越好.14.已知直线l的极坐标方程为2sin()24πρθ-=,点A的极坐标为7(22,)4π,则点A到直线l的距离为____.15.某高中校高一、高二、高三三个年级人数分别为300,300,400通过分层抽样从中抽取40人进行问卷调查,高三抽取的人数是______.16.如图所示,正六边形ABCDEF中,线段AD与线段BE交于点G,圆O1,O2分别是△ABG 与△DEG的内切圆,圆O3,O4分别是四边形BCDG与四边形AGEF的内切圆,则往六边形ABCDEF中任意投掷一点,该点落在图中阴影区域内的概率为_________.17.执行如图所示的程序框图,则输出S 的结果为________.18.某单位为了了解用电量y (度)与气温x (℃之间的关系,随机统计了某4天的用电量与当天气温(如表),并求得线性回归方程ˆ360yx =-为: x c9 14 -1y 184830d不小心丢失表中数据c ,d ,那么由现有数据知3c d -____________.19.若按右上图所示的程序框图运行后,输出的结果是63,则判断框中的整数M 的值是__________。
2020-2021学年初一(上)期中考试数学试卷(含答案)

2020-2021学年初一(上)期中考试数 学(考试时间90分钟 满分100分)18分)1.如图是加工零件尺寸的要求,现有下列直径尺寸的产品(单位:mm ),其中不合格的是( )A .Φ45.02B .Φ44.9C .44.98D .Φ45.012.下列运算中正确的是( )A .2(2)4-=- B .224-= C .3(3)27-=- D .236= 3.若37x =是关于x 的方程70x m +=的解,则m 的值为( ) A .3- B .13- C .3 D .134.若单项式12m a b -与212n a b 是同类项,则mn 的值是( ) A .3 B .6 C .8 D .95.下列各式中,是一元一次方程的是( )A .852020x y -=B .26x -C .212191y y =+D .582x x +=6.下列计算正确的是( )A .8(42)8482÷+=÷+÷B .1(1)(2)(1)(1)12-÷-⨯=-÷-= C .3311311636624433434⎛⎫⎛⎫⎛⎫-÷=-⨯=-⨯+-⨯=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ D .[](2)(2)40--+÷= 7.下列方程的解法,其中正确的个数是( ) ①14136x x ---=,去分母得2(1)46x x ---= ②24132x x ---=,去分母得2(2)3(4)1x x ---= ③2(1)3(2)5x x ---=,去括号得22635x x ---=④32x =-,系数化为1得32x =- A .3 B .2 C .1 D .08.2020年国庆档电影《我和我的家乡》上映13天票房收入达到21.94亿元,并连续10天拿下票房单日冠军.其中21.94亿元用科学记数法可表示为( )A .821.9410⨯元B .82.19410⨯元C .100.219410⨯元D .92.19410⨯元9.如图,四个有理数m ,n ,p ,q 在数轴上对应的点分别为M ,N ,P ,Q ,若0n q +=,则m ,n ,p ,q 四个有理数中,绝对值最小的一个是( )A .pB .qC .mD .n二、填空题(本题共有9小题,每小题3分,共27分)10.如果数轴上A 点表示3-,那么与点A 距离2个单位的点所表示的数是 .11.比较大小:78- 89-(填“>”“<”或“=”) 12.历史上,数学家欧拉最先把关于x 的多项式用记号()f x 来表示,把x 等于某数a 时的多项式的值用()f a 来表示,例如多项式2()25f x x x =+-,则(1)f -= .13.用四舍五入法将3.694精确到0.01,所得到的近似值为 .14.老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了一个多项式,形式如()2222153x x x x --+=-+-,则所捂住的多项式为 .15.“☆”是新规定的某种运算符号,设a ☆b =ab a b +-,若2 ☆8n =-,则n = .16.“整体思想”是中学数学解题中一种重要的思想方法,它在多项式的化简与求值中应用极为广泛.如:已知2m n +=-,4mn =-,则2(3)3(2)mn m n mn ---的值为 .17.某校为学生购买名著《三国演义》100套、《西游记》80套,共用12 000元,《三国演义》每套比《西游记》每套多16元,求《三国演义》和《西游记》每套各多少元?设西游记每套x 元,可列方程为 .18.观察下列一组算式:2231881-==⨯,22531682-==⨯,22752483-==⨯,22973284-==⨯……根据你所发现的规律,猜想22201920178-=⨯ .三、按要求解答(第19小题8分,第20小题5分,第21小题10分,共23分)19.计算题(每小题4分,共8分) ①3511114662⎛⎫---- ⎪⎝⎭ ②[]31452(3)5211⎛⎫-⨯-÷-+ ⎪⎝⎭20.(本题5分)化简并求值:222212(2)()2x xy y xy x y ⎡⎤⎛⎫---+- ⎪⎢⎥⎝⎭⎣⎦,其中x 、y 的取值如图所示.21.解方程(每小题5分,共10分)①3(202)10y y --= ②243146x x --=-四、解答题(第22、23小题4分,第24小题5分,共13分)22.(本题4分)解一元一次方程的过程就是通过变形,把一元一次方程转化为x a =的形式.下面是解方程20.30.410.50.3x x -+-=的主要过程,请在如图的矩形框中选择与方程变形对应的依据,并将它前面的序号填入相应的括号中.解:原方程可化为4153x +-=( ) 去分母,得3(203)5(104)15x x --+=( )去括号,得609502015x x ---=( )移项,得605015920x x -=++( )合并同类项,得1044x =(合并同类项法则) 系数化为1,得 4.4x =(等式的基本性质2)23.(本题4分)阅读材料,回答问题.计算:121123031065⎛⎫⎛⎫-÷-+- ⎪ ⎪⎝⎭⎝⎭解:原式的倒数为211213106530⎛⎫⎛⎫-+-÷-⎪ ⎪⎝⎭⎝⎭ =2112(30)31065⎛⎫-+-⨯- ⎪⎝⎭=203512-+-+=10-故原式=110- 根据材料中的方法计算113224261437⎛⎫⎛⎫-÷-+- ⎪ ⎪⎝⎭⎝⎭. 24.(本题5分)在某地住房小区建设中,为了提高业主的宜居环境,某小区规划修建一个广场(平面图形如图所示). (1)用含m ,n 的代数式表示该广场的面积S ;(2)若m ,n 满足2(6)50m n -+-=,求出该广场的面积.五、解答题(第25、26小题6分,第27小题7分,共19分)25.(本题6分)列代数式或一元一次方程解应用题请根据图中提供的信息,回答下列问题:(1)一个水瓶与一个水杯分别是多少元?(2)甲、乙两家商场都销售该水瓶和水杯,为了迎接新年,两家商场都在搞促销活动,甲商场规定:这两种商品都打8折;乙商场规定:买一个水瓶赠送两个水杯,单独购买的水杯仍按原价销售.若某单位想在一家商场买5个水瓶和20个水杯,请问选择哪家商场更合算?请说明理由.26.(本题6分)下表中的字母都是按一定规律排列的.我们把某格中的字母的和所得多项式称为特征多项式,例如第1格的“特征多项式”为62x y +,第2格的“特征多项式”为94x y +,回答下列问题.(1)第3格的“特征多项式”为 ,第4格的“特征多项式”为 ,第n 格的“特征多项式”为 ;(n 为正整数)(2)求第6格的“特征多项式”与第5格的“特征多项式”的差.27.(本题7分)在数轴上,对于不重合的三点A,B,C,给出如下定义:若点C到点A的距离是点C到点B的距离的13倍,我们就把点C叫做【A,B】的理想点.例如:图中,点A表示的数为-1,点B表示的数为3.表示数0的点C到点A的距离是1,到点B的距离是3,那么点C是【A,B】的理想点;又如,表示数2的点D到点A的距离是3,到点B的距离是1,那么点D 就不是【A,B】的理想点,但点D是【B,A】的理想点.(1)当点A表示的数为-1,点B表示的数为7时,①若点C表示的数为1,则点C(填“是”或“不是”)【A,B】的理想点;②若点D是【B,A】的理想点,则点D表示的数是;(2)若A,B在数轴上表示的数分别为-2和4,现有一点C从点B出发,以每秒1个单位长度的速度向数轴负半轴方向运动,当点C到达点A时停止.请直接写出点C运动多少秒时,C,A,B中恰有一个点为其余两点的理想点?参考答案一、选择题(每小题2分,共18分)二、填空题(每小题3分,共27分)19.计算题(每小题4分,共8分)①原式=3511114662--+┈┈┈┈┈┈┈┈┈┈1分 =5131116642--++ =1224-+┈┈┈┈┈┈┈┈┈┈3分 =14┈┈┈┈┈┈┈┈┈┈4分 ②原式=14582211⎛⎫-⨯-÷ ⎪⎝⎭┈┈┈┈┈┈┈┈┈┈2分 =24--┈┈┈┈┈┈┈┈┈┈3分=6-┈┈┈┈┈┈┈┈┈┈4分20.解:原式=22221242x xy y xy x y ⎛⎫---+- ⎪⎝⎭┈┈┈┈┈┈┈┈┈┈1分 =22221242x xy y xy x y --+-+┈┈┈┈┈┈┈┈┈┈2分 =272x xy -┈┈┈┈┈┈┈┈┈┈3分 当2x =,1y =-时┈┈┈┈┈┈┈┈┈┈4分原式=2722(1)112-⨯⨯-=┈┈┈┈┈┈┈┈┈┈5分21.解方程(每小题5分,共10分)①3(202)10y y --=解:60610y y -+=┈┈┈┈┈┈┈┈┈┈2分61060y y +=+┈┈┈┈┈┈┈┈┈┈3分770y =┈┈┈┈┈┈┈┈┈┈4分10y =┈┈┈┈┈┈┈┈┈┈5分 ②243146x x --=- 解:3(2)122(43)x x -=--┈┈┈┈┈┈┈┈┈┈1分361286x x -=-+┈┈┈┈┈┈┈┈┈┈2分361286x x -=-+┈┈┈┈┈┈┈┈┈┈3分310x -=┈┈┈┈┈┈┈┈┈┈4分103x =-┈┈┈┈┈┈┈┈┈┈5分 四、解答题(第22、23小题4分,第24小题5分,共13分)22.③;②;④;①┈┈┈┈┈┈┈┈┈┈4分23.解:原式的倒数为132216143742⎛⎫⎛⎫-+-÷- ⎪ ⎪⎝⎭⎝⎭┈┈┈┈┈┈┈┈┈┈1分 1322(42)61437⎛⎫=-+-⨯- ⎪⎝⎭792812=-+-+14=-┈┈┈┈┈┈┈┈┈┈3分故原式=114-┈┈┈┈┈┈┈┈┈┈4分 24.解:(1)S 7220.52m n n m mn =⋅-⋅=┈┈┈┈┈┈┈┈┈┈2分 (2)由题意得6050m n -=⎧⎨-=⎩,解得65m n =⎧⎨=⎩┈┈┈┈┈┈┈┈┈┈3分当6m =,5n =时 S 7651052=⨯⨯=┈┈┈┈┈┈┈┈┈┈5分五、解答题(第25、26小题6分,第27小题7分,共19分)25.解:(1)设一个水瓶x 元,则一个水杯是(48)x -元┈┈┈┈┈┈┈┈┈┈1分34(48)152x x +-=┈┈┈┈┈┈┈┈┈┈2分40x =┈┈┈┈┈┈┈┈┈┈3分∴4848408x -=-=┈┈┈┈┈┈┈┈┈┈4分答:一个水瓶40元,一个水杯8元.(2)甲商场需付款:80%(540208)288⨯⨯+⨯=(元)┈┈┈┈┈┈┈┈┈┈5分 乙商场需付款:5408(2052)280⨯+⨯-⨯=(元)┈┈┈┈┈┈┈┈┈┈6分 ∴选择乙商场更划算.26.解:(1)126x y +;158x y +;3(1)2n x ny ++┈┈┈┈┈┈┈┈┈┈3分(2)(2112)(1810)x y x y +-+┈┈┈┈┈┈┈┈┈┈5分32x y =+┈┈┈┈┈┈┈┈┈┈6分27.(1)①是┈┈┈┈┈┈┈┈┈┈1分②5或11┈┈┈┈┈┈┈┈┈┈3分(2)设运动时间为t 秒,则BC t =,6AC t =-依题意,得C 是【A ,B 】的理想点时有16=3t t -,∴92t = C 是【B ,A 】的理想点时有1(6)3t t =-,∴32t = A 是【C ,B 】的理想点时有16=63t -⨯,∴4t =B 是【C ,A 】的理想点时有1=6=23t ⨯ 答:点C 运动92秒、32秒、4秒、2秒时,C ,A ,B 中恰有一个点为其余两点的理想点.┈┈┈┈┈┈┈┈┈┈7分。
高中数学选择性必修二 北京市朝阳区高二上学期期末考试数学试题(含答案)

故答案为:①③④
16.把正奇数列按如下规律分组:(1),(3,5,7),(9,11,13,15,17),(19,21,23,25,27,29,31),…,则在第n(n∈N*)组里有________个数;第9组中的所有数之和为________.
【答案】①. ②.2465
【解析】
②函数 在 和 分别单调递减,故②错误;
③因为 ,则当 时, ,故 时的瞬时速度是10 m/s,故③正确;
④ , ,由 解得 ,由 解得 ,
所以当 时, 的图象更“陡峭”,当 时, 的图象更“陡峭”,故④错误.
故选:A.
8.如图,将边长为4的正方形折成一个正四棱柱的侧面,则异面直线AK和LM所成角的大小为()
点 在抛物线上,
所以 ,
则 ,又 ,
所以直线 方程为 ,
联立抛物线方程 得到 ,
解得 或 ,
因为点 在 轴下方,所以 ,
由焦半径公式得: ,
故选:D.
7.下列有四个说法:
①若直线与抛物线相切,则直线与抛物线有且只有一个公共点:
②函数 在定义域上单调递减;
③某质点沿直线运动,位移 (单位:m)与时间t(单位:s)满足关系式 则 时的瞬时速度是10 m/s;
(II)选①:当直线 斜率不存在时, 的方程为 ,恰好与圆相切,满足题意;
当直线 斜率存在时,设 的方程为 ,即 ,
则圆心到直线 的距离为 ,解得 ,
此时直线 的方程为 ,即 ,
综上,直线 的方程为 或 ;
选②,可得 在圆上,即 为切点,
则切点与圆心连线斜率为 ,则切线斜率为 ,
所以直线 的方程为 ,即 .
故选:B.
10.如图,在三棱锥O-ABC中,三条侧棱OA,OB,OC两两垂直,且OA,OB,OC的长分别为a,b,c.M为△ABC内部及其边界上的任意一点,点M到平面OBC,平面OAC,平面OAB的距离分别为a0,b0,c0,则 ()
北京市第四中学2020-2021学年高二下学期期中试题文生物

一、单项选择题(60分,每题1.5分)1. 北京的道路两旁经常种植一种绿色景观植物-—大叶黄杨,在修剪过程中剪去顶端,可以使侧芽生长素的含量A. 升高ﻩﻩﻩﻩﻩﻩB。
降低C.几乎不变ﻩﻩﻩD.先低后高2. 下图所示4个实验中,燕麦胚芽鞘能继续伸长生长的是A. A、D ﻩﻩB。
C、D ﻩC. A、CﻩﻩﻩD。
B、C3。
下列说法正确的是A. 失重条件下植物仍能向光生长B. 生长素和生长激素是两种不同的蛋白质C.用较低浓度的生长素类似物喷洒幼果,能导致果实脱落D. 生长素是通过促进细胞分裂使植物生长的4.下列关于植物激素的叙述,错误的是A。
在植物体内含量极少B. 对植物生命活动具有调节作用C。
在植物体一定部位产生D.各种激素在植物体内独立起作用5。
在植物细胞中,吲哚乙酸主要由色氨酸经一系列酶催化生成.下列相关叙述正确的是A. 吲哚乙酸可在胚芽鞘中大量合成B. 温度会影响吲哚乙酸的合成C.吲哚乙酸具有催化作用D. 过量的色氨酸可抑制吲哚乙酸的合成6。
植物顶芽的生长素可以向测芽运输,同时在缺氧的情况下,其运输会受到严重阻碍.这说明生长素的运输方式属于A. 自由扩散ﻩB. 协助扩散ﻩC。
主动运输ﻩD。
渗透作用7.用一定浓度的生长素类似物(2,4—D)可以杀死小麦地里的双子叶植物杂草,而不会抑制小麦的生长。
对此现象的解释是A.该浓度只对小麦起作用B. 该浓度只对杂草起作用C. 小麦和杂草对生长素敏感度不同D. 该浓度对小麦和杂草都起抑制作用8。
工作人员用几种不同浓度的α-萘乙酸(人工合成的生长素类似物)溶液处理插条基部,然后在沙床中培养,观察生根情况。
图1为不同浓度的生长素溶液对根的促进作用的示意图,图2为α-萘乙酸促进枝条生根的情况。
请据图1和图2判断,在下列各项浓度值中,最好选用A。
3 mg·mL-lﻩB.6mg·mL-lC. 9 mg·mL—-lﻩD。
4。
5m g·mlL-l9。
2020-2021学年重庆市高一上学期期中数学试题(解析版)

2020-2021学年重庆市高一上学期期中数学试题一、单选题1.已知集合{0,1,2}A =,则A 的子集个数为( ) A .6 B .7 C .8 D .16【答案】C【分析】根据子集的个数为2n (n 为集合元素的个数),即可求得答案. 【详解】{0,1,2}A =.根据子集的个数为2,n (n 为集合元素的个数)∴A 的子集个数328=.故选:C .【点睛】本题考查了求集合子集个数问题,解题关键是掌握子集概念,考查了分析能力和计算能力,属于基础题.2.已知()f x 是偶函数,()g x 是奇函数,且2()()(1)f x g x x +=-,则(1)f -=( ) A .2 B .2- C .1 D .1-【答案】A【分析】分别取1x =和1x =-,代入函数根据奇偶性得到答案. 【详解】()f x 是偶函数,()g x 是奇函数,2()()(1)f x g x x +=-,取1x =得到(1)(1)0f g +=,即(1)(1)0f g ---=;取1x =-得到(1)(1)4f g -+-=; 解得(1)2f -= 故选:A【点睛】本题考查了根据函数奇偶性求函数值,意在考查学生对于函数性质的灵活运用. 3.2()4f x ax bx a =+-是偶函数,其定义域为[1,2]a a --,对实数m 满足2()(1)f x m ≤+恒成立,则m 的取值范围是( ) A .(,3][1,)-∞-+∞ B .[3,1]- C .(,1][3,)-∞-⋃+∞ D .[1,3]-【答案】A【分析】根据奇偶性得到0b =,1a =-得到2()4f x x =-+,计算函数的最大值,解不等式得到答案.【详解】2()4f x ax bx a =+-是偶函数,其定义域为[1,2]a a --,则0b =,且()12a a -=--即1a =-,故2()4f x x =-+,()max ()04f x f ==故24(1)m ≤+,解得m 1≥或3m ≤- 故选:A【点睛】本题考查了根据函数奇偶性求参数,函数最值,解不等式,意在考查学生的综合应用能力.4.若,a b ,R c ∈,a b >,则下列不等式成立的是 A .11a b< B .22a b > C .||||a cbc >D .()()2222a c b c +>+【答案】D【分析】结合不等式的性质,利用特殊值法确定. 【详解】当1,1a b ==-排除A ,B 当0c 排除C 故选:D【点睛】本题主要考查了不等式的性质,特殊值法,还考查了特殊与一般的思想,属于基础题.5.已知函数)25fx =+,则()f x 的解析式为( )A .()21f x x =+ B .()()212f x x x =+≥C .()2f x x =D .()()22f x x x =≥【答案】B【分析】利用换元法求函数解析式.【详解】2t =,则2t ≥,所以()()()()2224t 251,2,f t t t t =-+-+=+≥即()21f x x =+()2x ≥.故选:B【点睛】本题考查利用换元法求函数解析式,考查基本分析求解能力,属基础题.6.已知()f x 是定义域为R 的奇函数,当0x >时,()223f x x x =--,则不等式()20f x +<的解集是A .()() 5,22,1--⋃-B .()(),52,1-∞-⋃-C .()(,1)52,--⋃+∞D .(),1()2,5-∞-⋃【答案】B【分析】根据函数奇偶性的性质,求出函数当0x <时,函数的表达式,利用函数的单调性和奇偶性的关系即可解不等式. 【详解】解:若0x <,则0x ->,∵当0x >时,()223f x x x =--,∴()223f x x x -=+-,∵()f x 是定义域为R 的奇函数,∴()223()f x x x f x -=+-=-,即2()23f x x x =--+,0x <.①若20x +<,即2x <-,由()20f x +<得,()()222230x x -+-++<,解得5x <-或1x >-,此时5x <-;②若20x +>,即2x >-,由()20f x +<得,()()222230x x +-+-<,解得31x -<<,此时21x -<<,综上不等式的解为5x <-或21x -<<. 即不等式的解集为()(),52,1-∞-⋃-. 故选:B.【点睛】本题主要考查不等式的解法,利用函数的奇偶性的性质求出函数的解析式是解决本题的关键. 7.若函数()f x =R ,则实数a 的取值范围是( )A .(0,4)B .[0,2)C .[0,4)D .(2,4]【答案】C【分析】等价于不等式210ax ax ++>的解集为R, 结合二次函数的图象分析即得解. 【详解】由题得210ax ax ++>的解集为R, 当0a =时,1>0恒成立,所以0a =.当0a ≠时,240a a a >⎧⎨∆=-<⎩,所以04a <<. 综合得04a ≤<.故选:C【点睛】本题主要考查函数的定义域和二次函数的图象性质,意在考查学生对这些知识的理解掌握水平.8.设函数22,()6,x x x af x ax x a⎧--≥⎪=⎨-<⎪⎩是定义在R 上的增函数,则实数a 取值范围( )A .[)2,+∞B .[]0,3C .[]2,3D .[]2,4【答案】D【分析】画出函数22y x x =--的图象,结合图象及题意分析可得所求范围.【详解】画出函数22y x x =--的图象如下图所示,结合图象可得,要使函数()22,,6,,x x x a x ax x a ⎧--≥⎪=⎨-<⎪⎩是在R 上的增函数,需满足22226a a a a ≥⎧⎨--≥-⎩,解得24x ≤≤. 所以实数a 取值范围是[]2,4. 故选D .【点睛】解答本题的关键有两个:(1)画出函数的图象,结合图象求解,增强了解题的直观性和形象性;(2)讨论函数在实数集上的单调性时,除了考虑每个段上的单调性之外,还要考虑在分界点处的函数值的大小关系. 二、多选题9.若0a >,0b >,且2a b +=,则下列不等式恒成立的是( )A 1B .11ab≥ C .222a b +≥ D .112a b+≥【答案】BCD【分析】由条件可得12211112a a b a b a abb b ab ++=≥+==⇒≥⇒≥,结合2222()()a b a b ++,即可得出.【详解】因为0a >,0b >,所以12211112a a b a b a abb b ab ++=≥+≤==⇒≥⇒≥, 所以A 错,BD 对;因为22222()()(0)a b a b a b -+=-≥+,则22222()()2a b a b ++=,化为:222a b +,当且仅当1a b ==时取等号,C 对. 故选:BCD .【点睛】本题考查了不等式的基本性质以及重要不等式的应用,考查了推理能力与计算能力,属于基础题.10.给出下列命题,其中是错误命题的是( )A .若函数()f x 的定义域为[0,2],则函数(2)f x 的定义域为[0,4].B .函数1()f x x=的单调递减区间是(,0)(0,)-∞+∞ C .若定义在R 上的函数()f x 在区间(,0]-∞上是单调增函数,在区间(0,)+∞上也是单调增函数,则()f x 在R 上是单调增函数.D .1x 、2x 是()f x 在定义域内的任意两个值,且1x <2x ,若12()()f x f x >,则()f x 减函数.【答案】ABC【分析】对于A ,由于()f x 的定义域为[0,2],则由022x ≤≤可求出(2)f x 的定义域;对于B ,反比例函数的两个单调区间不连续,不能用并集符号连接;对于C ,举反例可判断;对于D ,利用单调性的定义判断即可【详解】解:对于A ,因为()f x 的定义域为[0,2],则函数(2)f x 中的2[0,2]x ∈,[0,1]x ∈,所以(2)f x 的定义域为[0,1],所以A 错误; 对于B ,反比例函数1()f x x=的单调递减区间为(,0)-∞和(0,)+∞,所以B 错误; 对于C ,当定义在R 上的函数()f x 在区间(,0]-∞上是单调增函数,在区间(0,)+∞上也是单调增函数,而()f x 在R 上不一定是单调增函数,如下图,显然,(1)(0)f f < 所以C 错误;对于D ,根据函数单调性的定义可得该选项是正确的, 故选:ABC11.若a ,b 为正数,则( )A .2+aba bB .当112a b+=时,2a b +≥C .当11a b a b+=+时,2a b +≥D .当1a b +=时,221113a b a b +≥++【答案】BCD【分析】利用基本不等式,逐一检验即可得解.【详解】解:对A ,因为+a b ≥2aba b≤+,当a b =时取等号,A 错误;对B ,()11111+=2+2=2222b a a b a b a b ⎛⎛⎫⎛⎫++≥+ ⎪ ⎪ ⎝⎭⎝⎭⎝,当a b =时取等号,B 正确;对C ,11=+=a ba b a b ab++,则1ab =,+2a b ≥=,当1a b ==时取等号,C 正确;对D ,()()()2222222211+111+111+b a a b a b a b a b a b a b b a ++⎛⎫+++=+++≥++ ⎪++⎝⎭2222()1a b ab a b =++=+=, 当12a b ==时取等号,即221113a b a b +≥++,D 正确.故选:BCD.【点睛】本题考查了基本不等式的应用,重点考查了运算能力,属中档题.12.已知连续函数f (x )对任意实数x 恒有f (x +y )=f (x )+f (y ),当x >0时,f (x )<0,f (1)=-2,则以下说法中正确的是( ) A .f (0)=0B .f (x )是R 上的奇函数C .f (x )在[-3,3]上的最大值是6D .不等式()232()(3)4f x f x f x -<+的解集为213x x ⎧⎫<<⎨⎬⎩⎭∣ 【答案】ABC【分析】根据函数()f x 对任意实数x 恒有()()()f x y f x f y +=+,令0x y ==,可得(0)0f =,判断奇偶性和单调性,即可判断选项;【详解】解:对于A ,函数()f x 对任意实数x 恒有()()()f x y f x f y +=+, 令0x y ==,可得(0)0f =,A 正确;对于B ,令x y =-,可得(0)()()0f f x f x =+-=,所以()()f x f x =--, 所以()f x 是奇函数;B 正确;对于C ,令x y <,则()()()()()f y f x f y f x f y x -=+-=-, 因为当x >0时,f (x )<0,所以()0f y x -<,即()()0f y f x -<, 所以()f x 在()()0,,,0+∞-∞均递减, 因为()0f x <,所以()f x 在R 上递减;12f ,可得(1)2f -=;令1y =,可得()()12f x f x +=-()24f =-, ()36f =-;()3(3)6f f =--=,()f x ∴在[3-,3]上的最大值是6,C 正确;对于D ,由不等式2(3)2()(3)4f x f x f x -<+的可得2(3)()()(3)4f x f x f x f x <+++, 即2(3)(23)4f x f x x <++,4(2)f =-,2(3)(23)(2)f x f x x f ∴<++-,则2(3)(52)f x f x <-,2352x x ∴>-,解得:23x <或1x >; D 不对;故选:ABC .【点睛】本题主要考查函数求值和性质问题,根据抽象函数条件的应用,赋值法是解决本题的关键. 三、填空题13.函数y _________. 【答案】[]2,5【分析】先求出函数的定义域,再结合复合函数的单调性可求出答案. 【详解】由题意,2450x x -++≥,解得15x -≤≤,故函数y []1,5-.函数y =二次函数245u x x =-++的对称轴为2x =,在[]1,5-上的增区间为[)1,2-,减区间为[]2,5,故函数y []2,5. 故答案为:[]2,5.【点睛】本题考查复合函数的单调性,考查二次函数单调性的应用,考查学生的推理能力,属于基础题.14.奇函数f (x )在(0,)+∞内单调递增且f (1)=0,则不等式()01f x x >-的解集为________. 【答案】{|1x x >或01x <<或1x <-}.【分析】根据题意,由函数()f x 的奇偶性与单调性分析可得当01x <<时,()0f x <,当1x >时,()0f x >,当10x -<<时,()0f x >,当1x <-时,()0f x <,而不等式()01f x x >-等价于1()0x f x >⎧⎨>⎩或1()0x f x <⎧⎨<⎩;分析可得答案.【详解】解:根据题意,()f x 在(0,)+∞内单调递增,且f (1)0=, 则当01x <<时,()0f x <,当1x >时,()0f x >,又由()f x 为奇函数,则当10x -<<时,()0f x >,当1x <-时,()0f x <, 不等式()01f x x >-,等价于1()0x f x >⎧⎨>⎩或1()0x f x <⎧⎨<⎩;解可得:1x >或01x <<或1x <-; 即不等式()01f x x >-的解集为{|1x x >或01x <<或1x <-}. 故答案为:{|1x x >或01x <<或1x <-}. 15.已知函数()f x 的定义域为()0,∞+,则函数1f x y +=__________. 【答案】(-1,1)【分析】先求()1f x +的定义域为()1,-+∞,再求不等式组21340x x x >-⎧⎨--+>⎩的解集可以得到函数的定义域.【详解】由题意210340x x x +>⎧⎨--+>⎩,解得11x -<<,即定义域为()1,1-.【点睛】已知函数()f x 的定义域D ,()g x 的定义域为E ,那么抽象函数()f g x ⎡⎤⎣⎦的定义域为不等式组()x Eg x D ∈⎧⎨∈⎩的解集.16.定义:如果函数()y f x =在区间[],a b 上存在00()x a x b <<,满足0()()()f b f a f x b a-=-,则称0x 是函数()y f x =在区间[],a b 上的一个均值点.已知函数2()1f x x mx =-++在区间[]1,1-上存在均值点,则实数m 的取值范围是________. 【答案】(0,2).【详解】试题分析:由题意设函数2()1f x x mx =-++在区间[1,1]-上的均值点为,则0(1)(1)()1(1)f f f x m --==--,易知函数2()1f x x mx =-++的对称轴为2m x =,①当12m≥即2m ≥时,有0(1)()(1)f m f x m f m -=-<=<=,显然不成立,不合题意;②当12m≤-即2m ≤-时,有0(1)()(1)f m f x m f m =<=<-=-,显然不成立,不合题意;③当112m -<<即22m -<<时,(1)当20m -<<有0(1)()()2m f f x f <≤,即214m m m <≤+,显然不成立;(2)当0m =时, 0()0f x m ==,此时01x =±,与011x -<<矛盾,即0m ≠;(3)当02m <<时,有0(1)()()2mf f x f -<≤,即214m m m -<≤+,解得02m <<,综上所述得实数m 的取值范围为(0,2).【解析】二次函数的性质. 四、解答题17.已知集合{}22|430,|03x A x x x B x x -⎧⎫=-+≤=>⎨⎬+⎩⎭(1)分别求A B ,R R A B ⋃();(2)若集合{|1},C x x a A C C =<<⋂=,求实数a 的取值范围. 【答案】(1)(2,3]A B ⋂=,(,2](3,)R R A B ⋃=-∞⋃+∞(2)3a ≤【分析】(1)化简集合,,A B 根据交集定义,补集定义和并集定义,即可求得答案; (2)由A C C =,所以C A ⊆,讨论C =∅和C ≠∅两种情况,即可得出实数a 的取值范围.【详解】(1)集合{}2|430[1,3]A x x x =-+≤=∴(,1)(3,)RA =-∞⋃+∞,[3,2]RB =-∴(2,3]A B ⋂=,(,2](3,)RR A B ⋃=-∞⋃+∞,(2)A C C =∴ 当C 为空集时,1a ≤∴ 当C 为非空集合时,可得 13a ≤<综上所述:a 的取值范围是3a ≤.【点睛】本题考查了不等式的解法,交集和补集的运算,解题关键是掌握集合的基本概念和不等式的解法,考查了计算能力,属于基础题.18.已知函数()f x 是定义在R 上的偶函数,已知当0x ≤时,()243f x x x =++.(1)求函数()f x 的解析式;(2)画出函数()f x 的图象,并写出函数()f x 的单调递增区间; (3)求()f x 在区间[]1,2-上的值域.【答案】(1)()2243,043,0x x x f x x x x ⎧-+>=⎨++≤⎩; (2)见解析; (3)[]1,3-.【分析】(1)设x >0,则﹣x <0,利用当x≤0时,f (x )=x 2+4x+3,结合函数为偶函数,即可求得函数解析式;(2)根据图象,可得函数的单调递增区间;(3)确定函数在区间[﹣1,2]上的单调性,从而可得函数在区间[﹣1,2]上的值域. 【详解】(1)∵函数()f x 是定义在R 上的偶函数∴对任意的x ∈R 都有()()f x f x -=成立∴当0x >时,0x -<即()()()()224343f x f x x x x x =-=-+-+=-+∴ ()2243,043,0x x x f x x x x ⎧-+>=⎨++≤⎩(2)图象如右图所示函数()f x 的单调递增区间为[]2,0-和[)2,+∞. (写成开区间也可以)(3)由图象,得函数的值域为[]1,3-.【点睛】本题考查函数的解析式,考查函数的单调性与值域,考查数形结合的数学思想,属于中档题.19.若二次函数()f x 满足11,()22f x f x x R ⎛⎫⎛⎫+=-∈ ⎪ ⎪⎝⎭⎝⎭,且(0)1,(1)3f f =-=.(1)求()f x 的解析式;(2)若函数()(),()g x f x ax a R =-∈在3,2x ⎛⎤∈-∞ ⎥⎝⎦上递减,3,2⎡⎫+∞⎪⎢⎣⎭上递增,求a 的值及当[1,1]x ∈-时函数()g x 的值域.【答案】(1)2()1f x x x =-+(2)2a =,值域为[1,5]-. 【分析】(1)设二次函数的解析式为2()(),0f x ax bx c a =++≠,由11,()22f x f x x R ⎛⎫⎛⎫+=-∈ ⎪ ⎪⎝⎭⎝⎭可得()f x 对称轴为12x =,结合条件,即可求得答案;(2)根据增减性可知32x =为函数()g x 的对称轴,即可得到a 的值,而根据()g x 在[1,1]x ∈-上递减可得出()g x 在[1,1]x ∈-上的值域.【详解】(1)设二次函数的解析式为2()(),0f x ax bx c a =++≠二次函数()f x 满足11,()22f x f x x R ⎛⎫⎛⎫+=-∈ ⎪ ⎪⎝⎭⎝⎭∴二次函数()f x 的对称轴为:12x =. ∴122b a -=,可得:=-b a ——① 又(0)1f =,∴(0)1f c ==,可得:1c =.(1)3f -=.即:13a b -+=,可得:2a b -=——②由①②解得: 1,1a b ==-∴()f x 的解析式为2()1f x x x =-+.(2) 函数()(),()g x f x ax a R =-∈()g x 在3,2x ⎛⎤∈-∞ ⎥⎝⎦上递减,3,2⎡⎫+∞⎪⎢⎣⎭上递增. ∴()g x 的对称轴为32x =, 即:1322a +=.解得:2a =. ∴2()31g x x x =-+.()g x 在3,2x ⎛⎤∈-∞ ⎥⎝⎦上递减, ∴()g x 在[1,1]x ∈-上递减,则有:在[1,1]x ∈-上,min ()(1)1g x g ==-.函数()g x 在[1,1]x ∈-上的值域为[1,5]-【点睛】本题考查了待定系数法的运用以及对称轴的形式,根据增减性判断函数的对称轴及在区间上值域问题,解题关键是掌握二次函数的基础知识,考查了分析能力和计算能力,本题属中档题.20.已知函数24()x ax f x x++=为奇函数. (1)若函数()f x 在区间,2m m ⎡⎤⎢⎥⎣⎦(0m >)上为单调函数,求m 的取值范围; (2)若函数()f x 在区间[]1,k 上的最小值为3k ,求k 的值.【答案】(1)4m ≥或02m <≤;(2【分析】(1)函数()f x 为奇函数,可知对定义域内所有x 都满足()()f x f x -=-,结合解析式,可得0ax =恒成立,从而可求出a 的值,进而可求出()f x 的解析式,然后求出函数()f x 的单调区间,结合()f x 在区间,2m m ⎡⎤⎢⎥⎣⎦(0m >)上为单调函数,可求得m 的取值范围;(2)结合函数()f x 的单调性,分12k <≤和2k >两种情况,分别求出()f x 的最小值,令最小值等于3k ,可求出k 的值.【详解】(1)由题意,函数()f x 的定义域为()(),00,-∞+∞,因为函数()f x 为奇函数,所以对定义域内所有x 都满足()()f x f x -=-,即()()2244x a x x ax x x-+-+++=--, 整理可得,对()(),00,x ∈-∞+∞,0ax =恒成立,则0a =, 故244()x f x x x x +==+. 所以()f x 在()0,2上单调递减,在[)2,+∞上单调递增,又函数()f x 在区间,2m m ⎡⎤⎢⎥⎣⎦(0m >)上为单调函数,则2m ≤或22m ≥,解得4m ≥或02m <≤.(2)()f x 在()0,2上单调递减,在[)2,+∞上单调递增,若12k <≤,则()()min 43f x f k k k k ==+=,解得k =12k <≤,只有k =合题意;若2k >,则()()min 42232f x f k ==+=,解得43k =,不满足2k >,舍去.故k 【点睛】本题考查函数的奇偶性,考查函数单调性的应用,考查了函数的最值,利用对勾函数的单调性是解决本题的关键,考查学生的计算求解能力,属于基础题. 21.已知二次函数2()(0)f x ax x a =+≠.(1)当0a <时,若函数y a 的值;(2)当0a >时,求函数()()2||g x f x x x a =---的最小值()h a .【答案】(1)-4;(2)()0,1,a a h a a a a ⎧-<<⎪⎪=⎨⎪-≥⎪⎩ 【分析】(1)当0a <时,函数y 而可求出a 的值; (2)当0a >时,求出()g x 的表达式,分类讨论求出()g x 的最小值()h a 即可.【详解】(1)由题意,()0f x ≥,即()200ax x a +≥<,解得10x a≤≤-,即函数y 定义域为10,a ⎡⎤-⎢⎥⎣⎦, 又当0a <时,函数()2f x ax x =+的对称轴为12x a =-,21111222(4)f a a aa a ⎛⎫= ⎪⎝-=-⎭--,故函数y⎡⎢⎣,函数y1a -=4a =-. (2)由题意,0a >,2()||g x ax x x a =---,即()()22()2,,x a x ax g a a x a x ax -+≥-<⎧⎪=⎨⎪⎩, ①当01a <≤,则10a a≥>, x a ≥时,2min 1111(2)()()()g x g a a a a a a a-+=-==, x a <时,min ()(0)g x g a ==-, 若1a a a -≥-1a ≤≤, 若1a a a -<-,解得0a <<即0a <<min 1()g x a a =-1a ≤≤时,min ()g x a =-. ②当1a >时,1a a <, x a ≥时,33min ())2(g x g a a a a a a ==-+=-,x a <时,min ()(0)g x g a ==-,因为3a a a ->-,所以1a >时,min ()g x a =-.综上,函数()g x 的最小值()0,1,a a h a a a a ⎧-<<⎪⎪=⎨⎪-≥⎪⎩. 【点睛】本题考查函数的定义域与值域,考查二次函数的性质,考查函数的最小值,考查分类讨论的数学思想,考查学生的逻辑推理能力,属于中档题.22.定义在R 上的函数()f x 满足:①对一切x ∈R 恒有()0f x ≠;②对一切,x y R ∈恒有()()()f x y f x f y +=⋅;③当0x >时,()1f x >,且(1)2f =;④若对一切[,1]∈+x a a (其中0a <),不等式()224(2||2)f x a f x +≥-恒成立.(1)求(2),(3)f f 的值;(2)证明:函数()f x 是R 上的递增函数;(3)求实数a 的取值范围.【答案】(1)4,8(2)证明见解析(3)(,-∞ 【分析】1)用赋值法令1,1x y ==求解.(2)利用单调性的定义证明,任取12x x <,由 ()()()f x y f x f y +=⋅,则有()()()2211f x f x x f x =-,再由条件当0x >时,()1f x > 得到结论.(3)先利用()()()f x y f x f y +=⋅将4(2||2)-f x 转化为(2||)f x ,再将()22(2||)+≥f x a f x 恒成立,利用函数()f x 是R 上的递增函数,转化为222||≥+x a x 恒成立求解.【详解】(1)令1,1x y == 所以(2)(1)(1)4f f f =⋅=所以(3)(2)(1)8f f f =⋅=(2)因为()()()f x y f x f y +=⋅任取12x x <因为当0x >时,()1f x >所以()211f x x ->所以()()12f x f x <,所以函数()f x 是R 上的递增函数,(3)因为()4(2||2)2(2||2)[2(2||2)](2||)-=-=+-=f x f f x f x f x又因为()224(2||2)f x a f x +≥-恒成立且函数()f x 是R 上的递增函数,所以222||≥+x a x ,[,1]∈+x a a (其中0a <)恒成立所以222||+≥-a x x 若对一切[,1]∈+x a a (其中0a <),恒成立.当11a ≤-+ ,即2a ≤-时()()2max 143=+=---g x g a a a所以2243≥---a a a ,解得2a ≤-当21a -<≤-时,()max 1g x =解得21a -<≤-当10a -<≤,()()(){}max max ,1=+g x g a g a所以222≥--a a a 且221≥-+a a解得1a -<≤-综上:实数a 的取值范围(,-∞ 【点睛】本题主要考查了抽象函数的求值,单调性及其应用,还考查了分类讨论的思想和运算求解的能力,属于难题.。
2020-2021学年度高一上学期期中考试化学试卷及答案(含五套题)

2020-2021学年度⾼⼀上学期期中考试化学试卷及答案(含五套题)10 / 102020-2021学年度⾼⼀上学期期末考试化学试题题号⼀⼆三总分得分(满分:100分时间:100分钟)可能需要的相对原⼦质量数据H: 1 , C :12, O :16,Na :23,S :32,Cl :35.5,Al :27,Cu: 64, Ba:137 Fe :56 Mg :24 Cr:52 K:39 N:14 Si:28⼀、选择题:本⼤题共16⼩题,每⼩题3分,在每⼩题给出的四个选项中,只有⼀项是符合题⽬要求的。
1.对于易燃、易爆、有毒的化学物质,往往会在其包装上⾯贴上危险警告标签。
下列物质贴错了包装标签的是( ) A. 浓硫酸B. 汽油C. 酒精D. 氯化钾2.完成下列实验所选择的装置或仪器(夹持装置已略去)正确的是A. AB. BC. CD. D3.我国古代四⼤发明之⼀的⿊⽕药是由硫磺粉、硝酸钾和⽊炭粉按⼀定⽐例混合⽽成的,爆炸的反应为:S+2KNO 3+3C K 2S+N 2↑+3CO 2↑,下列说法中正确的是() A. 该反应中的还原剂为KNO 3B. 该反应中C 被还原C. 若消耗32g S ,该反应转移电⼦数为2 N AD. 若⽣成标准状况下⽓体22.4L ,则有0.75 mol 物质被还原 4.阿伏加德罗常数的值为N A ,下列说法中正确的是() A. 5NH 4NO 32HNO 3+4N 2↑+9H 2O 反应中,⽣成28 g N 2,转移的电⼦数⽬为3.75N AB. 常温常压下,ag 某⽓体含分⼦数为b ,则cg 该⽓体的体积为22.4bc aN ALC. 2mol/L 的CaCl 2溶液中Cl -的数⽬为4N AD. 46g NO 2和N 2O 4的混合⽓体中含有的氧原⼦个数为3N A 5.下列说法正确的是( )A. 摩尔是⼀种国际基本物理量B. 氧⽓的摩尔质量为32gC. H 2的⽓体摩尔体积约为22.4LD. 1mol H 2O 约含有6.02×1023个⽔分⼦6.氧化还原反应与四种基本反应类型的关系如下所⽰,则下列化学反应属于阴影部分的是( )此卷只装订不密封班级姓名准考证号考场号座位号10 / 10A. Cl 2+2KBrBr 2+2KClB. 2NaHCO 3Na 2CO 3+H 2O+CO 2↑C. 4NO 2+O 2+2H 2O=4HNO 3D. 2Na 2O 2+2CO 2=2Na 2CO 3+O 2 7.下列说法正确的个数有①盐卤点⾖腐、江河⼊海⼝处“三⾓洲”的形成、⾼压直流电除烟尘均与胶体的性质有关②通电时,溶液中的溶质粒⼦分别向两极移动,胶体中的分散质粒⼦向某⼀极移动③氢氧化铁胶体能稳定存在的主要原因是胶体粒⼦做布朗运动④做氢氧化铁胶体电泳实验时,阴极周围红褐⾊加深,说明氢氧化铁胶体带正电⑤向FeCl 3溶液中滴加NaOH 溶液,可制得Fe(OH)3胶体⑥1mol FeCl 3完全与⽔反应⽣成氢氧化铁胶体粒⼦数约为N A 个⑦淀粉溶液和蛋⽩质溶液是溶液,不可能是胶体 A. 1个 B. 2个 C. 3个 D. 4个8.下列各组离⼦中,能在溶液中⼤量共存的是() A. Na +、Cu 2+、Cl ﹣、OH ﹣ B. H +、Ca 2+、HCO 3﹣、NO 3﹣ C. Fe 2+、H +、SO 42﹣、NO 3﹣ D. Na +、CO 32﹣、OH ﹣、K + 9.下列离⼦⽅程式正确的是( ) A. 往NaHSO 4溶液中加Ba(OH)2溶液⾄恰好中和:Ba 2++2OH -+2H ++SO 42-=BaSO 4↓+2H 2O B. 碳酸钙与盐酸反应:2H ++CO 32-=CO 2↑+H 2OC. 铁与稀盐酸反应:2Fe+6H +=2Fe 3++3H 2↑D. 往Ba(OH)2溶液中加少量硫酸溶液:Ba 2++OH -+H ++SO 42-=BaSO 4↓+H 2O10.下列溶液中,溶质的物质的量浓度不是1 mol ·L -1的是() A. 10g NaOH 固体溶解在⽔中配成250mL 溶液 B. 将80g SO 3溶于⽔并配成1L 的溶液C. 将0.5mol ·L -1的NaNO 3溶液100mL 加热蒸发掉50g ⽔的溶液D. 标况下,将22.4L 氯化氢⽓体溶于⽔配成1L 溶液11.今有⼀种固体化合物X ,X 本⾝不导电,但熔化状态或溶于⽔中能够电离,下列关于该化合物X 的说法中正确的是 A. X ⼀定是电解质 B. X 可能为⾮电解质 C. X 只能是盐类 D. X 可以是任意化合物12.将SO 2通⼊⾜量Fe 2(SO 4)3溶液中,完全反应后再加⼊K 2CrO 4溶液,发⽣的两个化学反应为SO 2+2Fe 3++2H 2O=SO 42-+2Fe 2++W ①, Cr 2O 72-+a Fe 2++b H +Cr 3++Fe 3++H 2O ②,下列有关说法正确的是A. 还原性:Cr 3+>SO 2B. 配平后⽅程式②中,a=6,b=7C. Cr 2O 72-能将Na 2SO 3氧化成Na 2SO 4D. ⽅程式①中W 为OH - 13.200 mL 0.3 mol/L 的K 2SO 4溶液和100 mL 0.2 mol/L 的Fe 2(SO 4)3溶液混合后(不考虑混合后溶液体积的变化),溶液中SO 42-的物质的量浓度为A. 0.3 mol/LB. 0.4 mol/LC. 0.45 mol/LD. 0.5 mol/L 14.下列离⼦⽅程式的书写中,正确的是A. H 2SO 4与Ba (OH )2溶液反应: Ba 2++ OH - + H +⼗SO 42-= BaSO 4↓ + H 2O10 / 10B. 碳酸钙中加⼊盐酸 : CO 32- + 2H + = CO 2↑ + H 2OC. 将氢氧化铁放⼊盐酸中: Fe (OH )3 + 3H + = Fe 3+ + 3H 2OD. 氧化铜与稀硫酸反应: 2H + + O 2—= H 2O15.物质的量浓度为0.05 mol ·L -1的⾦属氯化物(RCl x ) 溶液20 mL ,恰好与20 mL 0.15 mol ·L -1的AgNO 3溶液完全反应。
高中数学选择性必修二 北京市昌平区新学道临川学校高二上学期期末考试数学(理)试题(含答案)

高二数学理科试卷
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.在等差数列 中,若 , ,则 =()
A. B. C. D.
【答案】C
【解析】
【分析】由等差数列通项公式可求得 ,由 可求得结果.
【详解】设等差数列 的公差为 ,则 , .
【详解】抛物线 ( )的准线为: ,
因为准线经过点 ,可得 ,即 ,
所以抛物线为 ,焦点坐标为 ,
故选:B.
11.椭圆 内有一点 过点 的弦恰好以 为中点,那么这弦所在直线的方程为()
A. B.
C. D.
【答案】B
【解析】
【分析】利用点差法得到直线斜率和中点之间的关系,即可得解.
【详解】设弦的两个端点为 ,
即曲线C右侧部分的点到原点的距离都不超过 ,
再根据对称性可知,曲线C上的所有点到原点的距离都不超过 ,②正确;
对于③,因为在x轴上方,图形面积大于四点(﹣1,0),
(1,0),(1,1),(﹣1,1)围成的矩形面积1×2=2,
在x轴下方,图形面积大于三点(﹣1,0),(1,0),(0,﹣1)围成的等腰直角三角形的面积 ×2×1=1,
故选:C.
2.在等比数列 中, , ,则 与 的等比中项是()
A. B. C. D.
【答案】A
【解析】
【分析】计算出 的值,利用等比中项的定义可求得结果.
【详解】由已知可得 ,由等比中项的性质可得 ,
因此, 与 的等比中项是 .
故选:A.
3.若△ABC中,a=4,A=45°,B=60°,则边b的值为( )
2020-2021学年北京五中分校九年级上学期期中数学试卷 (解析版)

2020-2021学年北京五中分校九年级(上)期中数学试卷一、选择题(共8小题).1.下列图案中,是中心对称图形的是()A.B.C.D.2.如图,点A,B,C在⊙O上,若∠AOB=70°,则∠ACB的度数为()A.35°B.40°C.50°D.70°3.当x<0时,函数y=的图象位于()A.第三象限B.第一、二、三象限C.第二、四象限D.第二象限4.将抛物线y=2x2向右平移1个单位,再向上平移3个单位,得到的抛物线是()A.y=2(x+1)2+3B.y=2(x﹣1)2+3C.y=2(x+1)2﹣3D.y=2(x﹣1)2﹣35.如图,⊙O的半径为5,AB为弦,OC⊥AB,垂足为E,如果CE=2,那么AB的长是()A.4B.8C.6D.106.如图,PA、PB是⊙O的切线,A、B分别为切点,PO交圆于点C,若∠APB=60°,PC=6,则AC的长为()A.4B.C.D.7.如图,直线y1=2x和抛物线y2=﹣x2+4x,当y1>y2时,x的取值范围是()A.0<x<2B.x<0或x>2C.x<0或x>4D.0<x<48.已知O⊙,如图,(1)作⊙O的直径AB;(2)以点A为圆心,AO长为半径画弧,交⊙O于C,D两点;(3)连接CD交AB于点E,连接AC,BC.根据以上作图过程及所作图形,有下面三个推断:①CE=DE;②BE=3AE;⑧BC=2CE.其中正确的推断的个数是()A.0个B.1个C.2个D.3个二、填空题(共8小题).9.在平面直角坐标系xOy中,点(4,﹣5)关于原点的对称点坐标是.10.已知在△ABC中,∠C=90°,AB=6,BC=5,则sin∠A=.11.小云家开了一个小文具店,今年一月份的利润是2250元,三月份的利润是1000元,计算这个文具店这两个月利润的平均下降率.设这两个月利润的平均下降率为x,则可列方程得.12.如图,在平面直角坐标系xOy中,将线段OA绕点O顺时针旋转90°得到线段OA',其中A(﹣2,3),则A'的坐标是.13.如图,⊙O的直径AB=4,点C在⊙O上,∠ABC=30°,则AC的长是.14.如图,在△AOB中,∠AOB=90°,∠B=30°,△A'OB'是由△AOB绕点O顺时针旋转α(α<180°)角度得到的,若点A'在AB上,则旋转角α=.15.如图,为了估算河的宽度,小明采用的办法是:在河的对岸选取一点A,在近岸取点D,B,使得A,D,B在一条直线上,且与河的边沿垂直,测得BD=10m,然后又在垂直AB 的直线上取点C,并量得BC=30m.如果DE=20m,则河宽AD为m.16.如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,有下列4个结论:①abc>0;②b2﹣4ac>0;③关于x的方程ax2+bx+c=0的两个根是x1=﹣2,x2=3;④关于x的不等式ax2+bx+c>0的解集是x>﹣2.其中正确的结论是.三、解答题(本题共68分)17.解方程:2x2﹣3x﹣2=0.18.如图,AB是⊙O的直径,弦CD⊥AB于点H,∠A=30°,CD=4,求⊙O的半径的长.19.如图,正方形ABCD的边长为4,E是CD中点,点P在射线AB上,过点P作线段AE 的垂线段,垂足为F.(1)求证:△PAF∽△AED;(2)连接PE,若存在点P使△PEF与△AED相似,直接写出PA的长.20.二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的自变量x与函数值y的部分对应值如下表:x…﹣3﹣2﹣101…y=…44m…ax2+bx+c根据以上列表,回答下列问题:(1)直接写出c,m的值;(2)求此二次函数的解析式.21.关于x的一元二次方程(k﹣2)x2﹣4x+2=0有两个不相等的实数根.(1)求k的取值范围;(2)如果符合条件的最大整数k是一元二次方程k2+mk+1=0的根,求m的值.22.如图,在平面直角坐标系xOy中,直线y=x+3与函数y=(x>0)的图象交于点A (1,m),与x轴交于点B.(1)求m,k的值;(2)过动点P(0,n)(n>0)作平行于x轴的直线,交函数y=(x>0)的图象于点C,交直线y=x+3于点D.①当n=2时,求线段CD的长;②若CD≥OB,结合函数的图象,直接写出n的取值范围.23.如图,在△ABC中,AB=AC,以AC为直径的⊙O与BC交于点D,DE⊥AB,垂足为E,ED的延长线与AC的延长线交于点F.(1)求证:DE是⊙O的切线;(2)若⊙O的半径为2,BE=1,求CF的长.24.某超市销售一款洗手液,这款洗手液成本价为每瓶16元,当销售单价定为每瓶20元时,每天可售出60瓶.市场调查反应:销售单价每上涨1元,则每天少售出5瓶.若设这款洗手液的销售单价上涨x元,每天的销售量利润为y元.(1)每天的销售量为瓶,每瓶洗手液的利润是元;(用含x的代数式表示)(2)若这款洗手液的日销售利润y达到300元,则销售单价应上涨多少元?(3)当销售单价上涨多少元时,这款洗手液每天的销售利润y最大,最大利润为多少元?25.有这样一个问题:探究函数y=x2﹣4|x|+3的图象与性质.小丽根据学习函数的经验,对函数y=x2﹣4|x|+3的图象与性质进行了探究.下面是小丽的探究过程,请补充完整:(1)函数y=x2﹣4|x|+3的自变量x的取值范围是.(2)如图,在平面直角坐标系xOy中,画出了函数y=x2﹣4|x|+3的部分图象,用描点法将这个函数的图象补充完整:(3)对于上面的函数y=x2﹣4|x|+3,下列四个结论:①函数图象关于y轴对称;②函数既有最大值,也有最小值;③当x>2时,y随x的增大而增大,当x<﹣2时,y随x的增大而减小;④函数图象与x轴有2个公共点.所有正确结论的序号是.(4)结合函数图象,解决问题:若关于x的方程x2﹣4|x|+3=k有4个不相等的实数根,则k的取值范围是.26.在平面直角坐标系xOy中,抛物线y=mx2+2mx﹣3与x轴交于A,B两点(点A在点B 左侧),与y轴交于点C,AB=4.(1)直接写出抛物线的对称轴为直线,点A的坐标为;(2)求抛物线的解析式(化为一般式);(3)若将抛物线y=mx2+2mx﹣3沿x轴方向平移n(n>0)个单位长度,使得平移后的抛物线与线段AC恰有一个公共点,结合函数图象,回答下列问题:①若向左平移,则n的取值范围是.②若向右平移,则n的取值范围是.27.如图1,△ABC和△DEF都是等腰直角三角形,∠A=90°,∠E=90°,△DEF的顶点D恰好落在△ABC的斜边BC中点,把△DEF绕点D旋转,始终保持线段DE、DF 分别与线段AB、AC交于M、N,连接MN.在这个变化过程中,小明通过观察、度量,发现了一些特殊的数量关系.(1)于是他把△DEF旋转到特殊位置,验证自己的猜想.如图2,当MN∥BC时,①通过计算∠BMD和∠NMD的度数,得出∠BMD∠NMD(填>,<或=);②设BC=2,通过计算AM,MN,NC的长度,其中NC=,进而得出AM、MN、NC之间的数量关系是.(2)在特殊位置验证猜想还不够,还需要在一般位置进行证明.请你对(1)中猜想的线段AM、MN、NC之间的数量关系进行证明.28.在平面直角坐标系xOy中,⊙O的半径为1,对于⊙O和⊙O外的点P,给出如下的定义:若在⊙O上存在一点Q,使得P、Q两点间的距离小于或等于1,则称P为⊙O的近距点.(1)在点P1(1,1),P2(﹣,),P3(0,﹣),P4(2,1)中,⊙O的近距点是;(2)若直线l:y=x+b上存在⊙O的近距点,求b的取值范围;(3)若点P在直线y=x+1上,且点P是⊙O的近距点,求点P横坐标x P的取值范围.参考答案一、选择题(本题共16分,每小题2分)1.下列图案中,是中心对称图形的是()A.B.C.D.解:A、不是中心对称图形,故此选项不合题意;B、不是中心对称图形,故此选项不合题意;C、不是中心对称图形,故此选项不合题意;D、是中心对称图形,故此选项符合题意;故选:D.2.如图,点A,B,C在⊙O上,若∠AOB=70°,则∠ACB的度数为()A.35°B.40°C.50°D.70°解:∵∠AOB=70°,∴∠ACB=∠AOB=35°,故选:A.3.当x<0时,函数y=的图象位于()A.第三象限B.第一、二、三象限C.第二、四象限D.第二象限解:∵反比例函数y=中k=5>0,∴此函数的图象位于一、三象限,∴当x<0时函数的图象在第三象限.故选:A.4.将抛物线y=2x2向右平移1个单位,再向上平移3个单位,得到的抛物线是()A.y=2(x+1)2+3B.y=2(x﹣1)2+3C.y=2(x+1)2﹣3D.y=2(x﹣1)2﹣3解:由题意得原抛物线的顶点为(0,0),∴平移后抛物线的顶点为(1,3),∴新抛物线解析式为y=2(x﹣1)2+3,故选:B.5.如图,⊙O的半径为5,AB为弦,OC⊥AB,垂足为E,如果CE=2,那么AB的长是()A.4B.8C.6D.10解:连接OA,∵半径OC⊥AB,∴AE=BE=AB,∵OC=5,CE=2,∴OE=3,在Rt△AOE中,AE===4,∴AB=2AE=8,故选:B.6.如图,PA、PB是⊙O的切线,A、B分别为切点,PO交圆于点C,若∠APB=60°,PC=6,则AC的长为()A.4B.C.D.解:如图,设CP交⊙O于点D,连接AD.设⊙O的半径为r.∵PA、PB是⊙O的切线,∠APB=60°,∴OA⊥AP,∠APO=∠APB=30°.∴OP=2OA,∠AOP=60°,∴PC=2OA+OC=3r=6,则r=2,易证△AOD是等边三角形,则AD=OA=2,又∵CD是直径,∴∠CAD=90°,∴∠ACD=30°,∴AC=AD•cot30°=2故选:C.7.如图,直线y1=2x和抛物线y2=﹣x2+4x,当y1>y2时,x的取值范围是()A.0<x<2B.x<0或x>2C.x<0或x>4D.0<x<4解:由,解得或,∴两函数图象交点坐标为(0,0),(2,4),由图可知,y1>y2时,x的取值范围是x<0或x>2.故选:B.8.已知O⊙,如图,(1)作⊙O的直径AB;(2)以点A为圆心,AO长为半径画弧,交⊙O于C,D两点;(3)连接CD交AB于点E,连接AC,BC.根据以上作图过程及所作图形,有下面三个推断:①CE=DE;②BE=3AE;⑧BC=2CE.其中正确的推断的个数是()A.0个B.1个C.2个D.3个解:如图,连接OC,①∵AB是⊙O的直径,∴∠ACB=90°,∵以点A为圆心,AO长为半径画弧,交⊙O于C,D两点,∴=,根据垂径定理,得AB⊥CE,CE=DE,所以①正确;②∵AC=OA=OC,∴△AOC是等边三角形,∵AB⊥CE,∴AE=OE,∴BE=BO+OE=3AE,∴②正确;③方法一:∵∠CAO=60°,∠ACB=90°,∠CBE=30°,∴BC=2CE.所以③正确.方法二:由△ACE∽△CBE,∴AC:AE=BC:CE=2:1,∴BC=2CE,所以③正确,故选:D.二、填空题(本题共16分,每小题2分)9.在平面直角坐标系xOy中,点(4,﹣5)关于原点的对称点坐标是(﹣4,5).解:点(4,﹣5)关于原点的对称点坐标是(﹣4,5),故答案为:(﹣4,5).10.已知在△ABC中,∠C=90°,AB=6,BC=5,则sin∠A=.解:如图,∵∠C=90°,BC=5,AB=6,∴sin A==.故答案为:.11.小云家开了一个小文具店,今年一月份的利润是2250元,三月份的利润是1000元,计算这个文具店这两个月利润的平均下降率.设这两个月利润的平均下降率为x,则可列方程得2250(1﹣x)2=1000.解:设这两个月利润的平均下降率为x,则可列方程得:2250(1﹣x)2=1000.故答案为:2250(1﹣x)2=1000.12.如图,在平面直角坐标系xOy中,将线段OA绕点O顺时针旋转90°得到线段OA',其中A(﹣2,3),则A'的坐标是(3,2).解:如图,观察图象可知,A′(3,2).故答案为(3,2).13.如图,⊙O的直径AB=4,点C在⊙O上,∠ABC=30°,则AC的长是2.解:∵直径AB=4,∠ACB=90°,∵点C在⊙O上,∠ABC=30°,∴AC=AB=2,故答案为:2.14.如图,在△AOB中,∠AOB=90°,∠B=30°,△A'OB'是由△AOB绕点O顺时针旋转α(α<180°)角度得到的,若点A'在AB上,则旋转角α=60°.解:∵∠AOB=90°,∠B=30°,∴∠A=60°.∵△A′OB′是由△AOB绕点O顺时针旋转α角度得到的,∴OA=OA′.∴△OAA′是等边三角形.∴∠AOA′=60°,即旋转角α的大小是60°.故答案为:60°.15.如图,为了估算河的宽度,小明采用的办法是:在河的对岸选取一点A,在近岸取点D,B,使得A,D,B在一条直线上,且与河的边沿垂直,测得BD=10m,然后又在垂直AB 的直线上取点C,并量得BC=30m.如果DE=20m,则河宽AD为20m.解:∵AB⊥DE,BC⊥AB,∴DE∥BC,∴△ADE∽△ABC,∴,即,解得:AD=20m.故答案为:20.16.如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,有下列4个结论:①abc>0;②b2﹣4ac>0;③关于x的方程ax2+bx+c=0的两个根是x1=﹣2,x2=3;④关于x的不等式ax2+bx+c>0的解集是x>﹣2.其中正确的结论是②③.解:∵抛物线开口向下,交y轴的正半轴,∴a<0,c>0,∵﹣=,∴b=﹣a>0,∴abc<0,所以①错误;∵抛物线与x轴有2个交点,∴△=b2﹣4ac>0,即b2>4ac,所以②正确;∵抛物线y=ax2+bx+c经过点(﹣2,0),而抛物线的对称轴为直线x=,∴点(﹣2,0)关于直线x=的对称点(3,0)在抛物线上,∴关于x的一元二次方程ax2+bx+c=0的两根是x1=﹣2,x2=3,所以③正确.由图象可知当﹣2<x<3时,y>0,∴不等式ax2+bx+c>0的解集是﹣2<x<3,所以④错误;故答案为②③.三、解答题(本题共68分)17.解方程:2x2﹣3x﹣2=0.解:(x﹣2)(2x+1)=0,x﹣2=0或2x+1=0,所以x1=2,x2=﹣.18.如图,AB是⊙O的直径,弦CD⊥AB于点H,∠A=30°,CD=4,求⊙O的半径的长.解:连接BC,如图所示:∵AB是⊙O的直径,弦CD⊥AB于H,∴∠ACB=90°,CH=DH=CD=2,∠AHC=90°,∵∠A=30°,∴AC=2CH=4,在Rt△ABC中,∠A=30°,∴AC=BC=4,AB=2BC,∴BC=4,AB=8,∴OA=4,即⊙O的半径长是4.19.如图,正方形ABCD的边长为4,E是CD中点,点P在射线AB上,过点P作线段AE 的垂线段,垂足为F.(1)求证:△PAF∽△AED;(2)连接PE,若存在点P使△PEF与△AED相似,直接写出PA的长2或5.【解答】(1)证明:在正方形ABCD中,∠D=90°,CD∥AB,∴∠AED=∠PAF,∵PF⊥AE,∴∠D=∠PFA=90°,∴△PAF∽△AED.(2)解:当PA=PB=2时,∵DE=EC,AP=PB,∴PE∥AD,此时∠DAE=∠PEF,∠D=∠PFE=90°,可得△PEF∽△EAD.当∠AED=∠PEF,∠D=∠PFE时,△ADE∽△PFE,∵CD∥AB,∴∠AED=∠EAP=∠AEP,∴PA=PE,∵PF⊥AE,∴AF=FE,∵AD=4,DE=EC=2,∠D=90°,∴AE===2,∴AF=,∵△PAF∽△AED,∴=,∴=,∴PA=5,综上所述,满足条件的PA的值为2或5.20.二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的自变量x与函数值y的部分对应值如下表:x…﹣3﹣2﹣101…y=…44m…ax2+bx+c根据以上列表,回答下列问题:(1)直接写出c,m的值;(2)求此二次函数的解析式.解:(1)根据图表可知:二次函数y=ax2+bx+c的图象过点(0,4),(﹣2,4),∴对称轴为直线x ==﹣1,c=4,∵(﹣3,)的对称点为(1,),∴m =;(2)∵对称轴是直线x=﹣1,∴顶点为(﹣1,),设y=a(x+1)2+,将(0,4)代入y=a(x+1)2+得,a +=4,解得a =﹣,∴这个二次函数的解析式为y =﹣(x+1)2+.21.关于x的一元二次方程(k﹣2)x2﹣4x+2=0有两个不相等的实数根.(1)求k的取值范围;(2)如果符合条件的最大整数k是一元二次方程k2+mk+1=0的根,求m的值.解:(1)根据题意得k﹣2≠0且△=(﹣4)2﹣4(k﹣2)×2>0,解得k<4且k≠2;(2)符合条件的最大整数k=3,把k=3代入k2+mk+1=0得9+3m+1=0,解得m =﹣.22.如图,在平面直角坐标系xOy中,直线y=x+3与函数y =(x>0)的图象交于点A(1,m),与x轴交于点B.(1)求m,k的值;(2)过动点P(0,n)(n>0)作平行于x轴的直线,交函数y=(x>0)的图象于点C,交直线y=x+3于点D.①当n=2时,求线段CD的长;②若CD≥OB,结合函数的图象,直接写出n的取值范围.解:(1)∵直线y=x+3经过点A(1,m),∴m=1+3=4,∵反比例函数的图象经过点A(1,4),∴k=1×4=4;(2)①当n=2时,点P的坐标为(0,2),当y=2时,2=,解得x=2,∴点C的坐标为(2,2),当y=2时,x+3=2,解得x=﹣1,∴点D的坐标为(﹣1,2),∴CD=2﹣(﹣1)=3;②当y=0时,x+3=0,解得x=﹣3,则B(﹣3,0)当y=n时,n=,解得x=,∴点C的坐标为(,n),当y=n时,x+3=n,解得x=n﹣3,∴点D的坐标为(n﹣3,n),当点C在点D的右侧时,若CD=OB,即﹣(n﹣3)=3,解得n1=2,n2=﹣2(舍去),∴当0<n≤2时,CD≥OB;当点C在点D的左侧时,若CD=OB,即n﹣3﹣=3,解得n1=3+,n2=3﹣(舍去),∴当n≥3+时,CD≥OB,综上所述,n的取值范围为0<n≤2或n≥3+.23.如图,在△ABC中,AB=AC,以AC为直径的⊙O与BC交于点D,DE⊥AB,垂足为E,ED的延长线与AC的延长线交于点F.(1)求证:DE是⊙O的切线;(2)若⊙O的半径为2,BE=1,求CF的长.【解答】(1)证明:如图,连接OD,AD,∵AC是直径,∴AD⊥BC,又∵在△ABC中,AB=AC,∴BD=CD,∵AO=OC,∴OD∥AB,又∵DE⊥AB,∴DE⊥OD,∵OD为⊙O半径,∴DE是⊙O的切线;(2)解:∵⊙O的半径为2,AB=AC,∴AC=AB=2+2=4,∵BE=1,∴AE=4﹣1=3,过O作OH⊥AB于H,则四边形ODEH是矩形,∴EH=OD=2,∴AH=1,∴AH=AO,∴∠AOH=30°,∴∠BAC=60°,∴AF=2AE=6,∴CF=AF﹣AC=2.∵DE⊥AB,AD⊥BC,∴∠AED=∠BED=∠ADB=90°,∴∠DAE+∠ADE=90°,∠ADE+∠BDE=90°,∴∠DAE=∠BDE,∴△AED∽△DEB,∴=,∴=,解得:DE=,∵OD∥AB,∴△FOD∽△FAE,∴=,∴=,解得:FD=2,在Rt△FOD中,FO===4,∴CF=FO﹣OC=4﹣2=2.24.某超市销售一款洗手液,这款洗手液成本价为每瓶16元,当销售单价定为每瓶20元时,每天可售出60瓶.市场调查反应:销售单价每上涨1元,则每天少售出5瓶.若设这款洗手液的销售单价上涨x元,每天的销售量利润为y元.(1)每天的销售量为(60﹣5x)瓶,每瓶洗手液的利润是(4+x)元;(用含x 的代数式表示)(2)若这款洗手液的日销售利润y达到300元,则销售单价应上涨多少元?(3)当销售单价上涨多少元时,这款洗手液每天的销售利润y最大,最大利润为多少元?解:(1)每天的销售量为(60﹣5x)瓶,每瓶洗手液的利润是(4+x)元;故答案为:(60﹣5x);(4+x);(2)根据题意得,(60﹣5x)(4+x)=300,解得:x1=6,x2=2,答:销售单价应上涨2元或6元;(3)根据题意得,y=(60﹣5x)(4+x)=﹣5(x﹣12)(x+4)=﹣5(x﹣4)2+320,答:当销售单价上涨4元时,这款洗手液每天的销售利润y最大,最大利润为320元.25.有这样一个问题:探究函数y=x2﹣4|x|+3的图象与性质.小丽根据学习函数的经验,对函数y=x2﹣4|x|+3的图象与性质进行了探究.下面是小丽的探究过程,请补充完整:(1)函数y=x2﹣4|x|+3的自变量x的取值范围是任意实数.(2)如图,在平面直角坐标系xOy中,画出了函数y=x2﹣4|x|+3的部分图象,用描点法将这个函数的图象补充完整:(3)对于上面的函数y=x2﹣4|x|+3,下列四个结论:①函数图象关于y轴对称;②函数既有最大值,也有最小值;③当x>2时,y随x的增大而增大,当x<﹣2时,y随x的增大而减小;④函数图象与x轴有2个公共点.所有正确结论的序号是①③.(4)结合函数图象,解决问题:若关于x的方程x2﹣4|x|+3=k有4个不相等的实数根,则k的取值范围是﹣1<k<3.解:(1)∵函数y=x2﹣4|x|+3,∴x的取值范围为任意实数,故答案为:任意实数;(2)由函数y=x2﹣4|x|+3可知,x>0和x<0时的函数图象关于y轴对称,函数图象如右图所示;(3)由图象可得,函数图象关于y轴对称,故①正确;函数有最小值,但没有最大值,故②错误;当x>2时,y随x的增大而增大,当x<﹣2时,y随x的增大而减小,故③正确;函数图象与x轴有4个公共点,故④错误;故答案为:①③;(4)由图象可得,关于x的方程x2﹣4|x|+3=k有4个不相等的实数根,则k的取值范围是﹣1<k<3,故答案为:﹣1<k<3.26.在平面直角坐标系xOy中,抛物线y=mx2+2mx﹣3与x轴交于A,B两点(点A在点B 左侧),与y轴交于点C,AB=4.(1)直接写出抛物线的对称轴为直线x=﹣1,点A的坐标为(﹣3,0);(2)求抛物线的解析式(化为一般式);(3)若将抛物线y=mx2+2mx﹣3沿x轴方向平移n(n>0)个单位长度,使得平移后的抛物线与线段AC恰有一个公共点,结合函数图象,回答下列问题:①若向左平移,则n的取值范围是0<n≤4.②若向右平移,则n的取值范围是0<n≤2.解:(1)∵抛物线y=mx2+2mx﹣3的对称轴为直线x==﹣1,AB=4,∴点A(﹣3,0),点B(1,0),故答案为:x=﹣1,(﹣3,0);(2)∵抛物线y=mx2+2mx﹣3过点B(1,0),∴0=m+2m﹣3,∴m=1,∴抛物线的解析式:y=x2+2x﹣3,(3)如图,∵y=x2+2x﹣3=(x+1)2﹣4,∴设向左平移后的解析式为:y=(x+1+n)2﹣4,把x=﹣3,y=0代入解析式可得:0=(﹣3+1+n)2﹣4,∴n=0(舍去),n=4,∴向左平移,则n的取值范围是0<n≤4;设向右平移后的解析式为:y=(x+1﹣n)2﹣4,把x=0,y=﹣3代入解析式可得:﹣3=(1﹣n)2﹣4,∴n=0(舍去),n=2,∴向右平移,则n的取值范围是0<n≤2,故答案为:0<n≤4;0<n≤2.27.如图1,△ABC和△DEF都是等腰直角三角形,∠A=90°,∠E=90°,△DEF的顶点D恰好落在△ABC的斜边BC中点,把△DEF绕点D旋转,始终保持线段DE、DF 分别与线段AB、AC交于M、N,连接MN.在这个变化过程中,小明通过观察、度量,发现了一些特殊的数量关系.(1)于是他把△DEF旋转到特殊位置,验证自己的猜想.如图2,当MN∥BC时,①通过计算∠BMD和∠NMD的度数,得出∠BMD=∠NMD(填>,<或=);②设BC=2,通过计算AM,MN,NC的长度,其中NC=,进而得出AM、MN、NC之间的数量关系是AM+MN=CN.(2)在特殊位置验证猜想还不够,还需要在一般位置进行证明.请你对(1)中猜想的线段AM、MN、NC之间的数量关系进行证明.解:(1)①∵△ABC和△DEF都是等腰直角三角形,∠A=90°,∠E=90°,∴∠B=∠C=∠EDF=45°,AB=AC,BC=AB,∵MN∥BC,∴∠AMN=∠B=45°=∠ANM=∠C,∠DMN=∠BDM,∴AM=AN,∴BM=CN,∵点D是BC中点,∴BD=CD,在△BMD和△CND中,,∴△BMD≌△CND(SAS),∴∠BMD=∠DNC,∵∠MDB=∠C+∠DNC=∠MDN+∠BDM,∴∠BDM=∠CND,∴∠BMD=∠CND=∠BDM=∠CMN,故答案为:=;②∵BC=2,BC=AB,∴AB=AC=2,∵∠BMD=∠CND=∠BDM,∴BD=BM=BC=,∴NC=,∴AM=2﹣,∵AM=AN,∠A=90°,∴MN=AM=2﹣2,∴AM+MN=2﹣+2﹣2==NC,故答案为:;AM+MN=NC;(2)如图1,在CN上截取CH=AM,连接AD,DH,∵△ABC是等腰直角三角形,点D是BC中点,∴AD=CD,∠BAD=∠ACD=45°,AD⊥BC,又∵AM=CH,∴△AMD≌△CHD(SAS),∴MD=DH,∠ADM=∠CDH,∵∠ADM+∠ADN=∠MDN=45°,∴∠ADN+∠CDH=45°,∴∠HDN=45°=∠MDN,在△MDN和△HDN中,,∴△MDN≌△HDN(SAS),∴MN=HN,∴NC=CH+NH=AM+MN.28.在平面直角坐标系xOy中,⊙O的半径为1,对于⊙O和⊙O外的点P,给出如下的定义:若在⊙O上存在一点Q,使得P、Q两点间的距离小于或等于1,则称P为⊙O的近距点.(1)在点P1(1,1),P2(﹣,),P3(0,﹣),P4(2,1)中,⊙O的近距点是P1;(2)若直线l:y=x+b上存在⊙O的近距点,求b的取值范围;(3)若点P在直线y=x+1上,且点P是⊙O的近距点,求点P横坐标x P的取值范围.解:(1)由题意得:OQ=1,P1(1,1),P2(﹣,),P3(0,﹣),P4(2,1)的坐标知,点P2、P3都不在圆O外,故不符合题意;对于P1,OP1==,则OP1﹣OQ<P1Q<OP1+OQ,即﹣1<P1Q<+1,故存在P1Q≤1,故点P1符合题意;同理可得OP4=,则﹣1<P4Q<+1,故不存在P4Q≤1,故点P4符合题意;故答案为P1;(2)如图1,平移直线l至图示与半径为2的圆相切的位置,即l和l′的位置,当直线l位于图示l和l′之间的位置时,直线l:y=x+b上存在⊙O的近距点,设直线l与圆切于点A,则△OAB为等腰直角三角形,则OB=OA=2=b,同理当直线l处于l′的位置时,b=﹣2,故b的取值范围为﹣2≤b≤2;(3)如图2,作半径为2的同心圆O,与直线y=x+1交于点B、C,设直线y=x+1与半径为1的圆交于点E、F,则点P点在BE和CF之间的位置时,符合题意,设点B的坐标为(x,x+1),过点B作BH⊥y轴于点H,连接OB、OC,在Rt△OBH中,OB2=BH2+OH2,即(x+1)2+x2=22,解得x=(舍去负值),故x==x B,同理可得,x C=﹣,故0<x P≤或﹣≤x P<﹣1.。
【整合】2020-2021学年度第一学期北京市海淀区七年级期中考试数学试题 共3套

2020学年第一学期阶段性抽测七年级数学(问卷)(无答案)本试卷分选择题和非选择题两部分,共三大题24小题,共6页,满分120分,考试用时100分钟注意事项:1.答卷前,考生务必在答题卡上用黑色字迹的钢笔或签宇笔填写镇(街)、学校、试室号、姓名、座位号及准考证号等自己的个人信息,再用2B铅笔把对应准考证号的标号涂黑2.选择题每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑如需要改动,用橡皮擦干净后,再选涂其他答案不能答在试卷上3.非选择题必须用黑色字迹的钢笔或签字笔作答,涉及作图的题目,用2B铅笔画图答案必须写在答题卡各题目指定区域的相应位置上;如需要改动,先划掉原来的答案,然后再写上新的答案,改动的答案也不能趯出指定的区域;不准使用铅笔、圆珠笔和涂改液不按以上要求作答的答案无效4.考生必须保持答题卡的整洁,考试结束后,将答题卡上交第一部分选择题(共30分)一、选择题(本大题共10小题,每小题3分,满分30分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.我国古代《九章算术》中注有“今两算得失相反,要令正负以名之”,意思是今有两数其意义相反,则分别叫做正数与负数.如果向北走两步记作+2步,那么向南走5步记作()(A)+5步 (B)-5步 (C)-3步 (D)-2步2.如图,检测4个足球,其中超过标准质量的克数记为正数,不足标准质量的克数记为负数,从轻重的角度看,最接近标准的是(※)(A)(C)(D)3.在-3、-2、0、1中,最小的一个数是(※)(A)-3 (B)-2 (C)0 (D)14.“001号议案”提出三年后,广州目前污水处理能力达到了760000吨/日,位居全国第二,将7660000用科学记数法表示为(※)(A)7.66×104 (B)7.66×105 (C )76.6×105 (D)7.66×106 5.已知a=-2,b=1,则a b +-的值为(※)(A)3 (B)1 (C)0 (D)-1 6.下列运算中正确的是(※)(A)a 3+a 3=a 6 (B)a 3+a 3=2a 3 (C)a 3+a 3=2a 6 (D)a 3+a 3=a 9 7.下列变形中,正确的是(※)(A)-(3x+2)=-3x+2 (B)-(3x-2)=3x+2 (C)-(3x-2)=-3x+2 (D)-(3x-2)=-3x-2 8.下列说法错误的是(※)(A)2x 2-3xy-1是二次三项式 (B)-x+1不是单项式(C) 23π-xy 2的系数是23π- (D)-22xab 2的次数是69.已知a,b 是有理数,满足a<0<b,a+b>0,则把a,-a,b,-b 按照从小到大的顺序排列,正确的是(※)(A) -b<-a<a<b (B)-b<a<-a<b (C) -a<-b<a<b (D) a<-b<b<-a 10.等边△ABC 在数轴上的位置如图所示,点A 、C 对应的数分别为0和-1,若△ABC 绕顶点沿顺时针方向在数轴上连续翻转,翻转1次后,点B 所对应的数为1,则连续翻转2020次后,点B(※)(A)不对应任何数 (B)对应的数是2018 (C)对应的数是2019 (D)对应的数是2020+0.9 g-0.36 g-0.8 g+2.5 g第10题图第二部分非选择题(共90分)二、填空题(本大题共6小题,每小题3分,共18分)11.某地某天的最高气温是6℃,最低气温是-4℃,则该地当天的温差为 ※ ℃ 12.用四舍五入法将3.1416精确到0.01后,得到的近似数是※13在数轴上将点A 向右移动7个单位,再向左移动4个单位,终点恰好是原点,则点A 表示的数是 ※14.若单项式3x 2y n 与-2x m y 3是同类项,则m+n= ※ 15.若代数式2y 2-y+1=3,那么代数式4y 2-2y+5的值为 ※16.根据下图所示的程序运算,若输入的x 值为1,则输出的结果为 ※第16题图三、解答题(本大题共8小题,满分72分.解答应写出文字说明、证明过程或演算步骤17.(本小题满分6分) 计算:(1)12-(-8)+(-7)+10(2) ()10011543⎛⎫-⨯--÷- ⎪⎝⎭18.(本小题满分6分)把下列各数分别填入相应的集合里:15, 12-,-5,2.333,0.1,0(1)正数集合:{ }(2)整数集合:{ }(3)分数集合:{ }19.(本小题满分8分)化简:8a2+4-2a2-5a-a2-5+7a20.(本小题满分8分)辆货车从百货大楼出发送货,向东行驶4千米到达小明家,继续向东行驶1.5千米到达小红家,然后向西行驶8.5千米到达小刚家,最后返回百货大楼。
2021届北京市朝阳区高三上学期期中考试质量检测数学试题

A.充分而不必要条件B.必要而不充分条件北京市朝阳区2020〜2021学年度第一学期期中质量检测高三数学试卷2020.11(考试时间120分钟满分150分)本试卷分为选择题(共40分)和非选择题(共110分)两部分考生务必将答案答在答题卡上,在试卷上作答无效.考试结束后,将本试卷和答题卡一并交回.第一部分(选择题共40分)一、选择题共10小题,每小题4分,共40分。
在每小题列出的四个选项中,选出符合题目要 求的一项.1.已知集合4 =卜52-工一2<0}, B = {-1,0,123},则AA8 =【答案】B3sin( -- x)=」,贝ij sin2A-(2 5【答案】C4.如图,在aABC 中,。
是BC 的中点,若= = (【答案】c51加>11西'是“3°>3g 的() B. {TO 』,2}C. {0,1,2}D. {0,123}12A.— 25n24 B.— 25c 24 D. 一一25【答案】B3.己知〃 =2-,b = log?!,c ~ a ,贝 Ij(J£ DA. a>b>cB. a>ohC. c>a>bD. c>b> aA- 3a-2bB. a-2bD.C.充分必要条件【答案】A6.已知函数/(x)=弓sin — (刃> 0)的图象与直线尸1的相邻两个交点间的距离等于冗,贝力/U) 的图象的一条对称轴是() 乃九冗A. x =---- B. x =—C. x =---12123【答案】D7.在aABC 中,AB=4, AC=3,且I 而+/1=19一正I,则CX =( A. -12B. -9C. 9【答案】B1 38.己知,ZU)是定义在R 上的偶函数,且当X £(-8, 0]时,/(工)=2'+ —,则/(1(^2二)=()3 2 1711 A. —B. 1C. -D.—27 11【答案】B9.己知函数/*•) =「+ 7'若存在实数叽使得/(〃?)= 2/一4。
2022-2023北京人大附中高一(上)期中数学试卷【答案版】

2022-2023学年北京市人大附中高一(上)期中数学试卷一、选择题(本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的,请将正确答案填涂在答题纸上的相应位置.)1.下列表示同一集合的是( )A .M ={(3,2)},N ={(2,3)}B .M ={(x ,y )|y =x },N ={y |y =x }C .M ={1,2},N ={2,1}D .M ={2,4},N ={(2,4)}2.以下函数中是偶函数且在区间(0,+∞)上单调递减的函数是( )A .y =1x 2B .y =1xC .y =x 2D .y =x 3.函数f(x)=x x 2+1的图象大致是( ) A . B .C .D .4.若x 1+x 2=3,x 12+x 22=5,则以x 1,x 2为根的一元二次方程是( )A .x 2﹣3x +2=0B .x 2+3x ﹣2=0C .x 2+3x +2=0D .x 2﹣3x ﹣2=05.已知a >b >c ,则下列说法一定正确的是( )A .ab >bcB .|a |>|b |>|c |C .ac 2>bc 2D .2a >b +c6.若命题“∃x ∈R ,一元二次不等式x 2+mx +1<0”为假命题,则实数m 的取值范围( )A .m ≤﹣2或m ≥2B .﹣2<m <2C .m <﹣2或m ≥2D .﹣2≤m ≤27.定义域与对应法则称为函数的两个要素.下列各对函数中,图象完全相同的是( )A .f(x)=(√x)2与g (x )=xB .f(x)=x 4−1x 2+1与g (x )=x 2﹣1C .f(x)=√x 2与g (x )=xD .f(x)=√x x 与g (x )=1 8.“ab >0”是“b a +a b ≥2”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件 9.设函数f (x )=x+3x+1,则下列函数中为奇函数的是( )A .f (x ﹣1)﹣1B .f (x ﹣1)+1C .f (x +1)﹣1D .f (x +1)+110.人大附中学生计划在实验楼门口种植蔬菜,现有12米长的围栏,准备围成两边靠墙(墙足够长)的菜园,若P处有一棵树(不考虑树的粗细)与两墙的距离分别是2m和am(0<a≤10),设此矩形菜园ABCD的最大面积为u,若要求将这棵树围在菜园内(包括边界),则函数u=f(a)(单位:m2)的图象大致是()A.B.C.D.二、填空题(本大题共5小题,每小题5分,共25分请把结果填在答题纸上的相应位置)11.函数f(x)=√3−xx的定义域为.12.马上进入红叶季,香山公园的游客量将有所增加,现在公园采取了“无预约,不游园”的措施,需要通过微信公众号提前预约才能进入公园.根据以上信息,“预约”是“游园”的条件.(填充分不必要条件、必要不充分条件、充分必要或者既不充分也不必要).13.已知一元二次方程(a﹣2)x2+4x+3=0有一正根和一负根,则实数a的取值范围为.14.已知函数f(x)=2x−1,g(x)=kx+2(k>0),若∀x1∈[2,3],∃x2∈[﹣1,2],使f(x1)=g(x2)成立,则实数k的取值范围是..15.函数f(x)=ax2﹣(a+1)x+1,x∈(−12,12),若f(x)在定义域上满足:①没有奇偶性;②不单调;③有最大值,则a的取值范围是.三、解答题(本大题共3小题,共35分,解答应写出文字说明过程或演算步骤,请将答案写在答题纸上的相应位置.)16.(10分)已知集合A={1,2,3},B={x|ax﹣1≥0}.(1)当a=2时,求A∩B与A∪B;(2)若_____,求实数a的取值范围.请从①A∩B=A;②∀x∈A,x∉B;③“x∈B”是“x∈A”的必要条件;这三个条件中选择一个填入(2)中横线处,并完成第(2)问的解答.(如果选择多个条件分别解答,按第一个解答计分)17.(12分)设函数f(x)=2x2﹣ax+4(a∈R).(1)当a=9时,求不等式f(x)<0的解集;(2)若不等式f(x)≥0对∀x∈(0,+∞)恒成立,求实数a的取值范围.18.(13分)已知函数f(x)=x2+a(a∈R).x(1)判断f(x)的奇偶性并证明;(2)若a=2,判断f(x)在[1,+∞)的单调性,并用单调性定义证明.一、选择题(共4小题,每小题5分,共20分,在每小题给出的四个选项中,只有一项是符合题目要求的,请将正确答案填涂在答题纸上的相应位置.)19.已知集合A ={x |﹣5<x <﹣3},B ={x |2a ﹣3<x <a ﹣2},若A ∪B =A ,则实数a 的取值范围是( )A .[1,+∞)B .{﹣1}C .[1,+∞)∪{﹣1}D .R20.已知x >0,y >0,(√x)3+2022√x =a ,(√y −2)3+2022(√y −2)=−a ,则x +y 的最小值是( )A .1B .√2C .2D .421.f (x )=x (x +1)(x +2)(x +3)的最小值为( )A .﹣1B .﹣1.5C .﹣0.9375D .前三个答案都不对22.若集合A 的所有子集中,任意子集的所有元素和均不相同,称A 为互斥集.若A ={a ,b ,c }⊆{1,2,3,4,5},且A 为互斥集,则1a +1b +1c 的最大值为( ) A .116 B .1312 C .74 D .4760二、填空题(共3小题,每小题5分,共15分,把答案填在答题纸上的相应位置.)23.关于x 的方程x (x−1)=(k−2x)(x 2−x)的解集中只含有一个元素,k = .24.已知k ≥0,函数y ={−x +k +1,x ≥02−x+k,x <0有最大值,则实数k 的取值范围是 . 25.对于集合A ,称定义域与值域均为A 的函数y =f (x )为集合A 上的等域函数.①若A ={1,2},则A 上的等域函数有 个;②若∃A =[m ,n ],使f (x )=a (x ﹣1)2﹣1为A 上的等域函数,a 的取值范围是 .三、解答题(本小题15分,解答应写出文字说明过程或演算步骤,请将答䋈写在答题纸上的相应位置.)26.(15分)对于正整数集合A ,记A ﹣{a }={x |x ∈A ,x ≠a },记集合X 所有元素之和为S (X ),S (∅)=0.若∃x ∈A ,存在非空集合A 1、A 2,满足:①A 1∩A 2=∅;②A 1∪A 2=A ﹣{x };③S (A 1)=S (A 2)称A 存在“双拆”.若∀x ∈A ,A 均存在“双拆”,称A 可以“任意双拆”.(1)判断集合{1,2,3,4}和{1,3,5,7,9,11}是否存在“双拆”?如果是,继续判断可否“任意双拆”?(不必写过程,直接写出判断结果);(2)A ={a 1,a 2,a 3,a 4,a 5},证明:A 不能“任意双拆”;(3)若A 可以“任意双拆”,求A 中元素个数的最小值.2022-2023学年北京市人大附中高一(上)期中数学试卷参考答案与试题解析一、选择题(本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的,请将正确答案填涂在答题纸上的相应位置.)1.下列表示同一集合的是()A.M={(3,2)},N={(2,3)}B.M={(x,y)|y=x},N={y|y=x}C.M={1,2},N={2,1}D.M={2,4},N={(2,4)}解:对于A,集合M,N表示的点坐标不同,故A错误,对于B,集合M表示点集,集合N表示数集,故B错误,对于C,由集合的无序性可知,M=N,故C正确,对于D,集合M表示数集,集合N表示点集,故D错误.故选:C.2.以下函数中是偶函数且在区间(0,+∞)上单调递减的函数是()A.y=1x2B.y=1x C.y=x2D.y=x解:y=1x2是偶函数,在区间(0,+∞)上单调递减,满足题意,A正确;y=1x是奇函数,不正确;y=x2在区间(0,+∞)上是增函数;不正确;y=x是奇函数,不正确.故选:A.3.函数f(x)=xx2+1的图象大致是()A.B.C.D.解:函数f(x)=xx2+1的定义域为R,f(﹣x)=−xx2+1=−f(x),可得f(x)为奇函数,其图象关于原点对称,可排除选项C;当x>0时,f(x)>0,可排除选项A、D.故选:B .4.若x 1+x 2=3,x 12+x 22=5,则以x 1,x 2为根的一元二次方程是( )A .x 2﹣3x +2=0B .x 2+3x ﹣2=0C .x 2+3x +2=0D .x 2﹣3x ﹣2=0解:∵x 1+x 2=3,x 12+x 22=5,∴2x 1x 2=(x 1+x 2)2−(x 12+x 22)=9﹣5=4,解得x 1x 2=2,∵x 1+x 2=3,x 1x 2=2,∴x 1,x 2为根的一元二次方程是x 2﹣3x +2=0.故选:A .5.已知a >b >c ,则下列说法一定正确的是( )A .ab >bcB .|a |>|b |>|c |C .ac 2>bc 2D .2a >b +c解:因为a >b >c ,则a >b 且a >c ,所以a +a >b +c ,即2a >b +c ,故D 正确,当b <0时,ab <bc ,故A 错误,当a =﹣1,b =﹣2,c =﹣3时,|a |<|b |<|c |,故B 错误,当c =0时,ac 2=bc 2,故C 错误,故选:D .6.若命题“∃x ∈R ,一元二次不等式x 2+mx +1<0”为假命题,则实数m 的取值范围( )A .m ≤﹣2或m ≥2B .﹣2<m <2C .m <﹣2或m ≥2D .﹣2≤m ≤2 解:由题意可知,“∀x ∈R ,一元二次不等式x 2+mx +1≥0”为真命题,所以Δ=m 2﹣4≤0,解得﹣2≤m ≤2,故选:D .7.定义域与对应法则称为函数的两个要素.下列各对函数中,图象完全相同的是( )A .f(x)=(√x)2与g (x )=xB .f(x)=x 4−1x 2+1与g (x )=x 2﹣1 C .f(x)=√x 2与g (x )=xD .f(x)=√x x 与g (x )=1解:对于A ,f (x )的定义域为[0,+∞),g (x )的定义域为R ,故A 错误,对于B ,f(x)=x 4−1x 2+1=x 2﹣1,g (x )=x 2+1,f (x )与g (x )的定义域,值域,映射关系均相同, 故f (x )与g (x )图象完全相同,故B 正确,对于C ,f (x )的值域为[0,+∞),g (x )的值域为R ,故C 错误,对于D ,f (x )的定义域为{x |x ≠0},g (x )的定义域为R ,故D 错误.故选:B .8.“ab >0”是“b a +a b ≥2”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件 解:由ab >0可得{a >0b >0或{a <0b <0, 当{a >0b >0时,由基本不等式可得b a +a b ≥2,当a =b 时,等号成立; 当{a <0b <0时,b a >0,a b >0,由基本不等式可得b a +a b ≥2,所以充分性满足; 当b a +a b ≥2时,设t =b a ,则有t +1t ≥2,由对勾函数的性质可得t >0,即b a >0,可得ab >0,所以必要性满足.故“ab >0”是“b a +a b ≥2”的充要条件.故选:C .9.设函数f (x )=x+3x+1,则下列函数中为奇函数的是( ) A .f (x ﹣1)﹣1 B .f (x ﹣1)+1C .f (x +1)﹣1D .f (x +1)+1 解:因为f (x )=x+3x+1=1+2x+1的图象关于(﹣1,1)对称,则f (x ﹣1)﹣1的图象关于原点对称,即函数为奇函数.故选:A .10.人大附中学生计划在实验楼门口种植蔬菜,现有12米长的围栏,准备围成两边靠墙(墙足够长)的菜园,若P 处有一棵树(不考虑树的粗细)与两墙的距离分别是2m 和am (0<a ≤10),设此矩形菜园ABCD 的最大面积为u ,若要求将这棵树围在菜园内(包括边界),则函数u =f (a )(单位:m 2)的图象大致是( )A .B .C .D .解:由题意,设CD =x ,则AD =12﹣x ,所以矩形菜园ABCD 的面积S =x (12﹣x )=﹣x 2+12x =﹣(x ﹣6)2+36,因为要将这棵树围在菜园内,所以{x ≥212−x ≥a,解得:2≤x ≤12﹣a , 当12﹣a >6,也即0<a <6时,在x =6处矩形菜园ABCD 的面积最大,最大面积u =S max =36,当12﹣a ≤6,也即6≤a ≤10时,在x =12﹣a 处矩形菜园ABCD 的面积最大,最大面积u =S max =a (12﹣a ),综上:u =f (a )={36,0<a <6a(12−a),6≤a <10, 根据函数解析式可知,选项B 符合.故选:B .二、填空题(本大题共5小题,每小题5分,共25分请把结果填在答题纸上的相应位置)11.函数f(x)=√3−x x 的定义域为 (﹣∞,0)∪(0,3] .解:因为f(x)=√3−x x, 所以{3−x ≥0x ≠0,解得x ≤3且x ≠0, 即函数的定义域为(﹣∞,0)∪(0,3].故答案为:(﹣∞,0)∪(0,3].12.马上进入红叶季,香山公园的游客量将有所增加,现在公园采取了“无预约,不游园”的措施,需要通过微信公众号提前预约才能进入公园.根据以上信息,“预约”是“游园”的 充分必要 条件.(填充分不必要条件、必要不充分条件、充分必要或者既不充分也不必要). 解:园采取了“无预约,不游园”的措施,意思就是说:游园的前提时预约,只有预约了才可以游园,不预约就不能游园.所以:“预约”是“游园”的 充分必要条件.故答案为:充分必要.13.已知一元二次方程(a ﹣2)x 2+4x +3=0有一正根和一负根,则实数a 的取值范围为 (﹣∞,2) . 解:一元二次方程(a ﹣2)x 2+4x +3=0有一正根和一负根,所以{a −2≠0Δ=16−12(a −2)>03a−2<0,解得a <2, 即实数a 的取值范围为(﹣∞,2).故答案为:(﹣∞,2).14.已知函数f(x)=2x−1,g (x )=kx +2(k >0),若∀x 1∈[2,3],∃x 2∈[﹣1,2],使f (x 1)=g (x 2)成立,则实数k 的取值范围是 [1,+∞) .解:已知函数f(x)=2x−1,g (x )=kx +2(k >0),若∀x 1∈[2,3],∃x 2∈[﹣1,2],使f (x 1)=g (x 2)成立,因为函数f(x)=2x−1在x ∈[2,3]上单调递减,所以f (x )max =f (2)=2,f (x )min =f (3)=1,可得f (x 1)∈[1,2],又因为g (x )=kx +2(k >0)在x ∈[﹣1,2]上单调递增,所以g (x )max =g (2)=2k +2,g (x )min =g (﹣1)=﹣k +2,所以g (x 2)∈[﹣k +2,2k +2],若x 1∈[2,3],∃x 2∈[﹣1,2],使f (x 1)=g (x 2)成立,所以[1,2]⊆[﹣k +2,2k +2],所以{−k +2≤12k +2≥2⇒⇒{k ≥1k ≥0,所以k ≥1. 实数k 的取值范围是:[1,+∞).故答案为:[1,+∞).15.函数f (x )=ax 2﹣(a +1)x +1,x ∈(−12,12),若f (x )在定义域上满足:①没有奇偶性;②不单调;③有最大值,则a 的取值范围是 (−∞,−1)∪(−1,−12) .解:由①可知,a +1≠0,即a ≠﹣1;由③可知,a <0;由②可知,−12<a+12a<12,即−1<a+1a<1,又a<0,则a<a+1<﹣a,解得a<−1 2;综上,实数a的取值范围为(−∞,−1)∪(−1,−12 ).故答案为:(−∞,−1)∪(−1,−12 ).三、解答题(本大题共3小题,共35分,解答应写出文字说明过程或演算步骤,请将答案写在答题纸上的相应位置.)16.(10分)已知集合A={1,2,3},B={x|ax﹣1≥0}.(1)当a=2时,求A∩B与A∪B;(2)若_____,求实数a的取值范围.请从①A∩B=A;②∀x∈A,x∉B;③“x∈B”是“x∈A”的必要条件;这三个条件中选择一个填入(2)中横线处,并完成第(2)问的解答.(如果选择多个条件分别解答,按第一个解答计分)解:(1)当a=2时,A={1,2,3},B={x|x≥12 },A∩B={1,2,3},A∪B={x|x≥12};(2)若选①A∩B=A,则A⊆B,当a=0时,B=∅,不符合题意,当a<0时,B={x|x≤1a},不合题意;当a>0时,B={x|x≥1a},则1a≤1,解得a≥1,故a的取值范围为{a|a≥1};若选②∀x∈A,x∉B;当a=0时,B=∅,符合题意,当a<0时,B={x|x≤1a},符合题意;当a>0时,B={x|x≥1a},则1a>3,解得0<a<1 3,故a的取值范围为{a|a<13 };③若选“x∈B”是“x∈A”的必要条件,则A⊆B,当a=0时,B=∅,不符合题意,当a <0时,B ={x |x ≤1a},不合题意;当a >0时,B ={x |x ≥1a },则1a ≤1, 解得a ≥1,故a 的取值范围为{a |a ≥1}.17.(12分)设函数f (x )=2x 2﹣ax +4(a ∈R ).(1)当a =9时,求不等式f (x )<0的解集;(2)若不等式f (x )≥0对∀x ∈(0,+∞)恒成立,求实数a 的取值范围.解:(1)函数f (x )=2x 2﹣ax +4(a ∈R ),当a =9时,f (x )<0,即2x 2﹣9x +4<0,整理得(2x ﹣1)(x ﹣4)<0,解得12<x <4, 故所求不等式的解集为(12,4);(2)f (x )≥0对∀x ∈(0,+∞)恒成立,即2x 2﹣ax +4≥0在x ∈(0,+∞)上恒成立,即a ≤2x +4x 在x ∈(0,+∞)上恒成立,即a ≤(2x +4x )min ,又2x +4x ≥2√2x ×4x =4√2(当且仅当2x =4x 即x =√2时,取“=“). 所以a ≤4√2,故实数a 的取值范围为(−∞,4√2].18.(13分)已知函数f(x)=x 2+a x (a ∈R).(1)判断f (x )的奇偶性并证明;(2)若a =2,判断f (x )在[1,+∞)的单调性,并用单调性定义证明.解:(1)当a =0时,f (x )=x 2为偶函数,当a ≠0时,f (x )=x 2+a x 为非奇非偶函数;证明如下:当a =0时,f (x )=x 2,则f (﹣x )=(﹣x )2=x 2,即f (x )为偶函数,当a ≠0时,f (x )=x 2+a x ,则f (﹣x )=(﹣x )2−a x =x 2−a x ≠±f (x ),即为非奇非偶函数; (2)a =2时,f (x )=x 2+2x ,设1≤x 1<x 2,则x 1﹣x 2<0,x 1+x 2−2x 1x 2>0,则f (x 1)﹣f (x 2)=x 12−x 22+2x 1−2x 2=(x 1﹣x 2)(x 1+x 2−2x 1x 2)<0, 所以f (x 1)<f (x 2),故f (x )在[1,+∞)单调递增. 一、选择题(共4小题,每小题5分,共20分,在每小题给出的四个选项中,只有一项是符合题目要求的,请将正确答案填涂在答题纸上的相应位置.)19.已知集合A ={x |﹣5<x <﹣3},B ={x |2a ﹣3<x <a ﹣2},若A ∪B =A ,则实数a 的取值范围是( )A .[1,+∞)B .{﹣1}C .[1,+∞)∪{﹣1}D .R解:∵A ∪B =A ,∴B ⊆A ,①B =∅时,2a ﹣3≥a ﹣2,解得a ≥1;②B ≠∅时,{a <12a −3≥−5a −2≤−3,解得a =﹣1;∴综上可得,a 的取值范围是a ≥1或a =﹣1.故选:C .20.已知x >0,y >0,(√x)3+2022√x =a ,(√y −2)3+2022(√y −2)=−a ,则x +y 的最小值是() A .1 B .√2 C .2 D .4解:设f (t )=t 3+2022t ,函数定义域为R ,f (﹣t )=(﹣t )3+2022×(﹣t )=﹣t 3﹣2022t =﹣f (t ),∴f (t )是奇函数,∀t 1<t 2,有t 13<t 23,则f (t 1)﹣f (t 2)=t 13+2022t 1﹣(t 23+2022t 2)<0,即f (t 1)<f (t 2). ∴函数f (t )是增函数,由x >0,y >0,(√x)3+2022√x =a ,(√y −2)3+2022(√y −2)=−a ,所以√x +√y −2=0,可得√x +√y =2,两边同时平方再利用基本不等式,有4=x +y +2√xy ≤2(x +y ),当且仅当x =y =1时取等号,所以x +y 的最小值为2,故选:C .21.f (x )=x (x +1)(x +2)(x +3)的最小值为( )A .﹣1B .﹣1.5C .﹣0.9375D .前三个答案都不对解:y =x (x +1)(x +2)(x +3)=[x (x +3)][(x +1)(x +2)]=(x 2+3x )[(x 2+3x )+2],令a =x 2+3x =(x +32)2−94≥−94.y =a 2+2a =(a +1)2﹣1,∵a ≥−94,∴a =﹣1时,y 有最小值﹣1.故选:A .22.若集合A 的所有子集中,任意子集的所有元素和均不相同,称A 为互斥集.若A ={a ,b ,c }⊆{1,2,3,4,5},且A 为互斥集,则1a +1b +1c 的最大值为( ) A .116 B .1312 C .74 D .4760解:∵A 为{1,2,3},{1,2,4},[1,2,5},{1,3,4},{1,3,5},{1,4,5},{2,3,4},{2,3,5},{2,4,5},{3,4,5},且A 为互斥集,∴A 为{1,2,4},{1,2,5},{1,3,5},{2,3,4},{2,4,5},{3,4,5},要想1a +1b +1c 取得最大值,则a ,b ,c 要最小, 此时a ,b ,c ∈{1,2,4},令a =1,b =2,c =4,则1a +1b +1c =11+12+14=74. 故选:C .二、填空题(共3小题,每小题5分,共15分,把答案填在答题纸上的相应位置.)23.关于x 的方程x (x−1)=(k−2x)(x 2−x)的解集中只含有一个元素,k = ﹣1或0或3 .解:∵x (x−1)=(k−2x)(x 2−x)的解集中只含有一个元素,∴x ﹣1≠0,且 x =k−2x x, ∴x ≠0,且 x 2+2x ﹣k =0有一个实数根,结合x ≠0且x ≠1,可得k =﹣1或k =0或k =3.故答案为:﹣1或0或3.24.已知k ≥0,函数y ={−x +k +1,x ≥02−x+k,x <0有最大值,则实数k 的取值范围是 [1,+∞) . 解:因为k ≥0,函数y ={−x +k +1,x ≥02−x+k,x <0有最大值, 易知x ≥0时,f (x )=﹣x +k +1单调递减,故此时f (x )≤f (0)=k +1;当x <0时,f (x )=2−x+k 单调递增,结合x →0﹣时,f (x )→2k,所以由题意只需k +1≥2k 即可,解得k ≥1,或k ≤﹣2(舍),故k 的取值范围为[1,+∞).故答案为:[1,+∞).25.对于集合A ,称定义域与值域均为A 的函数y =f (x )为集合A 上的等域函数.①若A ={1,2},则A 上的等域函数有 2 个;②若∃A =[m ,n ],使f (x )=a (x ﹣1)2﹣1为A 上的等域函数,a 的取值范围是 {a |−18<a <0或0<a ≤1} .解:定义域与值域均为A 的函数y =f (x )为集合A 上的等域函数,(1)所以若 f (x )=x ,则 f (1)=1,f (2)=2,所以f (x )=x 的定义域与值域均为A ={1,2},同理若f (1)=2,f (2)=1,也满足题意,所以A 上的等域函数有2个;若a <0,则f (x )=a (x ﹣1)2﹣1≤﹣1<0,因此 n <0,从而f (x )在[m ,n ]上单调递增,{f(m)=m f(n)=n, 所以f (x )=a (x ﹣1)2﹣1=x 有两个不等的负实根,即方程ax 2﹣(2a +1)x +a ﹣1=0有2个不等的负实根,所以{ Δ=(2a +1)2−4a(a −1)>0x 1+x 2=2a+1a <0x 1x 2=a−1a >0,解得−18<a <0; 若a =0,则f (x )=﹣1,不合题意;a >0 时,①若m ≤1≤n ,则f (x )min =﹣1,因此m =﹣1,f (﹣1)=4a ﹣1,f (n )=a (n ﹣1)2﹣1,若1≤n ≤3,则n =f (﹣1)=4a ﹣1,令1≤4a ﹣1≤3,解得12≤a ≤1, 若n >3,则f (n )=n ,所以方程f (x )=a (x ﹣1)2﹣1=x 有大于3的实数根,即方程ax 2﹣(2a +1)x +a ﹣1=0有大于3的实数根,即Δ=(2a +1)2﹣4a (a ﹣1)≥0,解得a ≥−18, 所以a >0时,x =2a+1±√8a+12a ,令2a+1+√8a+12a>3,解得√8a +1>4a ﹣1, 当4a ﹣1≤0时,即0<a ≤14时,不等式显然成立,当a >14时,8a +1>(4a ﹣1)2,解得0<a <1,所以14<a <1,所以0<a <1满足题意, 综上,0<a ≤满足题意;下面讨论a >1时是否存在[m ,n ]满足题意,②若n ≤1,则 f (x )在[m ,n ]上是减函数,因此{f(m)=n f(n)=m,显然m =f (n )≥﹣1, 令{a(m −1)2−1=n a(n −1)2−1=m,相减得a (m +n ﹣2)=﹣1,即m =2−1a −n ,n =2−1a −m , 因此有{a(m −1)2−1=2−1a −m a(n −1)2−1=2−1a −n , 设g (x )=a (x ﹣1)2﹣1﹣(2−1a −x )=0在[﹣1,1]上有两个不等实根,整理得g (x )=ax 2﹣(2a ﹣1)x +a +1a −3,a >1时,由于g (1)=1a −2<0,因此方程g (x )=0一个根大于1,一根小于1,不合要求; ③若1≤m <n ,则f (x )在[m ,n ]上是增函数,因此{f(m)=m f(n)=n,即f (x )=a (x ﹣1)2﹣1=x 在[1,+∞)上有两个不等实根, 即方程ax 2﹣(2a +1)x +a ﹣1=0 在[1,+∞)上有两个不等实根,设h (x )=ax 2﹣(2a +1)x +a ﹣1,则h (1)=﹣2<0,所以h (x )=0 的两根一个大于1,一个小于1,不合题意,综上,a 的取值范围是{a |−18<a <0或0<a ≤1}.故答案为:2;{a |−18<a <0或0<a ≤1}.三、解答题(本小题15分,解答应写出文字说明过程或演算步骤,请将答䋈写在答题纸上的相应位置.)26.(15分)对于正整数集合A ,记A ﹣{a }={x |x ∈A ,x ≠a },记集合X 所有元素之和为S (X ),S (∅)=0.若∃x ∈A ,存在非空集合A 1、A 2,满足:①A 1∩A 2=∅;②A 1∪A 2=A ﹣{x };③S (A 1)=S (A 2)称A 存在“双拆”.若∀x ∈A ,A 均存在“双拆”,称A 可以“任意双拆”.(1)判断集合{1,2,3,4}和{1,3,5,7,9,11}是否存在“双拆”?如果是,继续判断可否“任意双拆”?(不必写过程,直接写出判断结果);(2)A ={a 1,a 2,a 3,a 4,a 5},证明:A 不能“任意双拆”;(3)若A 可以“任意双拆”,求A 中元素个数的最小值.解:(1)对集合{1,2,3,4},{1,2,3,4}﹣{4}={1,2,3},且1+2=3,∴集合{1,2,3,4}可以双拆,若在集合中去掉元素1,∵2+3≠4,2+4≠3,3+4≠2,∴集合{1,2,3,4}不可“任意双拆”;若集合{1,3,5,7,9,11}可以“双拆”,则在集合{1,3,5,7,9,11}去除任意一个元素形成新集合B,若存在集合B1,B2,使得B1∩B2=∅,B1∪B2=B,S(B1)=S(B2),则S(B)=S(B1)+S(B2)=2S(B1),即集合B中所有元素之和为偶数,事实上,集合B中的元素为5个奇数,这5个奇数和为奇数,不合题意,∴集合{1,3,5,7,9}不可“双拆”.(2)证明:设a1<a2<a3<a4<a5.反证法:如果集合A可以“任意双拆”,若去掉的元素为a1,将集合{a2,a3,a4,a5}分成两个交集为空集的子集,且两个子集元素之和相等,则有a2+a5=a3+a4,①,或a5=a2+a3+a4,②,若去掉的是a2,将集合{a1,a3,a4,a5}分成两个交集为空集的子集,且两个子集元素之和相等,则有a1+a5=a3+a4,③,或a5=a1+a3+a4,④,由①﹣③可得a1=a2,矛盾;由②﹣③得a1=﹣a2,矛盾;由①﹣④可得a1=﹣a2,矛盾;由②﹣④可得a1=a2,矛盾.∴A不能“任意双拆”;(3)设集合A={a1,a2,a3,•,a n},由题意可知S(A)﹣a i(i=1,2,•,n)均为偶数,∴a i(i=1,2,•,n)均为奇数或偶数,若S(A)为奇数,则a i(i=1,2,•,n)均为奇数,∵S(A)=a1+a2+•+a n,∴n为奇数,若S(A)为偶数,则a i(i=1,2,•,n)均为偶数,此时设a i=2b i,则{b1,b2,b3,•,b n}可任意双拆,重复上述操作有限次,便可得各项均为奇数的“任意双拆”集,此时各项之和也是奇数,则集合A中元素个数n为奇数,当n=3时,由题意知集合A={a1,a2,a3}不可“任意双拆”,当n=5时,集合A={a1,a2,a3,a4,a5}不可“任意双拆”,∴n≥7,当n=7时,取集合A={1,3,5,7,9,11,13},∵3+5+7+9=11+13,1+9+13=5+7+11,1+3+5+77=7+13,1+9+11=3+5+13,3+7+9=1+5+13,1+3+5+9=7+11,则集合A可“任意双拆”,∴集合A中元素个数n的最小值为7.。
2020-2021学年高二上学期期末考试数学试卷(含解析)

2020-2021学年高二上学期期末考试数学试卷学校:___________姓名:___________班级:___________考号:___________一、单选题1.若3324A 10A n n =,则n =( )A .1B .8C .9D .102.期末考试结束后,某班要安排6节课进行试卷讲评,要求课程表中要排入语文、数学、英语、物理、化学、生物共六节课,如果第一节课只能排语文或数学,最后一节不能排语文,则不同的排法共有( ) A .192种B .216种C .240种D .288种3.一台X 型号自动机床在一小时内不需要工人照看的概率为0.8,有4台这种型号的自动机床各自独立工作,则在一小时内至多2台机床需要工人照看的概率是( ) A .0.1536B .0.1808C .0.5632D .0.97284.某市气象部门根据2021年各月的每天最高气温平均值与最低气温平均值(单位:℃)数据,绘制如下折线图:那么,下列叙述错误的是( )A .各月最高气温平均值与最低气温平均值总体呈正相关B .全年中,2月份的最高气温平均值与最低气温平均值的差值最大C .全年中各月最低气温平均值不高于10℃的月份有5个D .从2021年7月至12月该市每天最高气温平均值与最低气温平均值都呈下降趋势5.若()2N 1,X σ~,则()0.6827P X μσμσ-<≤+=,(22)0.9545P X μσμσ-<≤+=,已知()21,3X N ~,则(47)P X <≤=( )A .0.4077B .0.2718C .0.1359D .0.04536.为了评价某个电视栏目的改革效果,在改革前后分别从居民点抽取了100位居民进行调查,经过计算()200.01P K k ≥=,根据这一数据分析,下列说法正确的是( )A .有1%的人认为该栏目优秀;B .有1%的把握认为该栏目是否优秀与改革有关系;C .有99%的把握认为电视栏目是否优秀与改革有关系;D .没有理由认为电视栏目是否优秀与改革有关系.7.若1021001210)x a a x a x a x =++++,则012310a a a a a -+-++的值为.A 1B 1C .101)D .101)8.关于()72x +的二项展开式,下列说法正确的是( ) A .()72x +的二项展开式的各项系数和为73B .()72x +的二项展开式的第五项与()72x +的二项展开式的第五项相同C .()72x +的二项展开式的第三项系数为4372CD .()72x +的二项展开式第二项的二项式系数为712C9.如图,某建筑工地搭建的脚手架局部类似于一个3×2×3的长方体框架,一个建筑工人欲从A 处沿脚手架攀登至B 处,则其最近的行走路线中不连续向上攀登的概率为( )A .528B .514C .29D .1210.三棱锥P ABC -中P A 、PB 、PC 两两互相垂直,4PA PB +=,3PC =,则其体积( ) A .有最大值4B .有最大值2C .有最小值2D .有最小值4二、填空题11.最小二乘法得到一组数据(),(1,2,3,4,5)i i x y i =的线性回归方程为ˆ23yx =+,若5125ii x==∑,则51i i y ==∑___________.12.某班举行的联欢会由5个节目组成,节目演出顺序要求如下: 节目甲不能排在第一个,并且节目甲必须和节目乙相邻.则该班联欢会节目演出顺序的编排方案共有____种. 13.若随机变量X 的概率分布如表,则表中a 的值为______.14.设随机变量ξ~B (2,p ),若P (ξ≥1)=59,则D (ξ)的值为_________.15.已知等差数列{}n a 中,33a =,则1a 和5a 乘积的最大值是______.16.某次知识竞赛规则如下:在主办方预设的5个问题中,选手若能连续正确回答出两个问题,即停止答题,晋级下一轮假设某选手正确回答每个问题的概率都是0.8,且每个问题的回答结果相互独立,则该选手恰好回答了5个问题就晋级下一轮的概率为___________.17.经统计,在银行一个营业窗口每天上午9点钟排队等候的人数及相应概率如下:则该营业窗口上午9点钟时,至少有2人排队的概率是_____.18.点A ,B ,C 在球O 表面上,2AB =,BC =90ABC ∠=︒,若球心O 到截面ABC的距离为___________.19.如图,在三棱柱111ABC A B C -中,四边形11AAC C 是边长为4的正方形,平面ABC ⊥平面11AAC C ,3AB =,5BC =.(℃)求证:1AA ⊥平面;(℃)若点E 是线段的中点,请问在线段是否存在点E ,使得面11AAC C ?若存在,请说明点E 的位置,若不存在,请说明理由; (℃)求二面角的大小.20.四根绳子上共挂有10只气球,绳子上的球数依次为1,2,3,4,每枪只能打破一只球,而且规定只有打破下面的球才能打上面的球,则将这些气球都打破的不同打法数是________.三、解答题21.已知集合(){}()12,,,|,1,2,,1nn i R x x x x R i n n =∈=≥,定义n R 上两点()12,,,n A a a a ,()12,,,n B b b b 的距离()1,ni i i d A B a b ==-∑.(1)当2n =时,以下命题正确的有__________(不需证明): ℃若()1,2A ,()4,6B ,则(),7d A B =;℃在ABC 中,若90C =∠,则()()()222,,,d A C d C B d A B ⎡⎤⎡⎤⎡⎤+=⎣⎦⎣⎦⎣⎦; ℃在ABC 中,若()(),,d A B d A C =,则B C ∠=∠;(2)当2n =时,证明2R 中任意三点A B C ,,满足关系()()(),,,d A B d A C d C B ≤+;(3)当3n =时,设()0,0,0A ,()4,4,4B ,(),,P x y z ,其中x y z Z ∈,,,()()(),,,d A P d P B d A B +=.求满足P 点的个数n ,并证明从这n 个点中任取11个点,其中必存在4个点,它们共面或者以它们为顶点的三棱锥体积不大于83.22.今年4月,教育部办公厅印发了《关于加强义务教育学校作业管理的通知》,规定初中学生书面作业平均完成时长不超过90分钟.某市为了更好地贯彻落实“双减”工作要求,作教育决策,该市教育科学研究院就当前全市初三学生每天完成书面作业时长抽样调查,结果是学生书面作业时长(单位:分钟)都在区间[]50,100内,书面作业时长的频率分布直方图如下:(1)若决策要求:在国家政策范围内,若当前初三学生书面作业时长的中位数估计值大于或等于平均数(计算平均数时,同一组中的数据用该区间的中点值代表)估计值,则减少作业时长;若中位数估计值小于平均数,则维持现状.请问:根据这次调查,该市应该如何决策?(2)调查统计时约定:书面作业时长在区间[]90,100内的为A 层次学生,在区间[)80,90内的为B 层次学生,在区间[70,80)内的为C 层次学生,在其它区间内的为D 层次学生.现对书面作业时长在70分钟以上(含70分钟)的初三学生,按作业时长出现的频率用分层抽样的方法随机抽取8人,再从这8人中随机抽取3人作进一步调查,设这3人来自X 个不同层次,求随机变量X 的分布列及数学期望.23.国家文明城市评审委员会对甲、乙两个城市是否能入围“国家文明城市”进行走访调查.派出10人的调查组.先后到甲、乙两个城市的街道、社区进行问卷调查,然后打分(满分100分).他们给出甲、乙两个城市分数的茎叶图如图所示:(1)请你用统计学的知识分析哪个城市更应该入围“国家文明城市”,请说明理由;(2)从甲、乙两个城市的打分中各抽取2个,在已知有大于80分的条件下,求抽到乙城市的分数都小于80分的概率;(3)从对乙城市的打分中任取2个,设这2个分数中不小于80分的个数为X,求X的分布列和期望.参考答案:1.B【分析】根据排列数的运算求解即可.【详解】由332A 10A n n =得,2(21)(22)10(1)(2)n n n n n n --=--,又3,n n *≥∈N ,所以2(21)5(2)n n -=-,解得8n =, 所以正整数n 为8. 故选:B. 2.B【分析】对第一节课的安排进行分类讨论,结合分步乘法计数原理和分类加法计数原理可得结果.【详解】分以下两种情况讨论:℃若第一节课安排语文,则后面五节课的安排无限制,此时共有55A 种;℃若第一节课安排数学,则语文可安排在中间四节课中的任何一节,此时共有444A 种.综上所述,不同的排法共有54544216A A +=种.故选:B. 3.D【详解】设在一个小时内有ξ台机床需要工人照看,则ξ~B (4,0.2),所以P (ξ≤2)=04C (0.8)4+14C (0.8)3×0.2+24C (0.8)2×(0.2)2=0.972 8. 故选D 4.D【分析】利用折线图可以判断选项ABC 正确,从2021年7月至12月该市每天最高气温平均值与最低气温平均值,先上升后下降,所以选项D 错误.【详解】解:由2021年各月的每天最高气温平均值和最低气温平均值(单位:C)︒数据,绘制出的折线图,知:在A 中,各月最高气温平均值与最低气温平均值为正相关,故A 正确;在B 中,全年中,2月的最高气温平均值与最低气温平均值的差值最大,故B 正确; 在C 中,全年中各月最低气温平均值不高于10C ︒的月份有1月,2月,3月,11月,12月,共5个,故C 正确;在D 中,从2021年7月至12月该市每天最高气温平均值与最低气温平均值,先上升后下降,故D 错误. 故选:D . 5.C【分析】由题意,得(47)(2)P X P X μσμσ<≤=+<≤+,再利用3σ原则代入计算即可.【详解】℃()21,3X N ~,由()0.6827P X μσμσ-<≤+=,(22)0.9545P X μσμσ-<≤+=,℃1(47)(2)(0.95450.6827)0.13592P X P X μσμσ<≤=+<≤+=-=.故选:C 6.C【分析】利用独立性检验的基本原理即可求出答案.【详解】解:℃()200.01P K k ≥=表示“电视栏目是否优秀与改革没有关系”的概率,℃有99%的把握认为电视栏目是否优秀与改革有关系, 故选:C .【点睛】本题主要考查独立性检验的基本应用,准确的理解判断方法是解决本题的关键,属于基础题. 7.D【详解】分析:令1021001210())f x x a a x a x a x ==++++,再求f(-1)的值得解.详解:令1021001210())f x x a a x a x a x ==++++,1001210(1)1)f a a a a -==-+++.故答案为D .点睛:(1)本题主要考查二项式定理中的系数求法问题,意在考查学生对这些基础知识 的掌握水平.(2) 二项展开式的系数0123,,,,n a a a a a ⋅⋅⋅的性质:对于2012()?··n n f x a a x a x a x =++++,0123(1)n a a a a a f ++++⋅⋅⋅+=, 0123(1)(1)n n a a a a a f -+-+⋅⋅⋅+-=-.8.A【分析】利用赋值法求出展开式各项系数和,即可判断A ,根据二项式展开式的通项,即可判断B 、C 、D ;【详解】解:()72x +展开式的通项为7172rrr r T C x -+=⋅⋅,故第二项的二项式系数为177C =,故D 错误; 第三项的系数为2572C ⋅,故C 错误;()72x +的展开式的第五项为43472C x ⋅⋅,()72x +的展开式的第五项为44372C x ⋅⋅,故B 错误; 令1x =则()7723x +=,即()72x +的二项展开式的各项系数和为73,故A 正确; 故选:A 9.B【解析】将问题抽象成“向左三次,向前两次,向上三次”,计算出总的方法数,然后利用插空法计算出最近的行走路线中不连续向上攀登的事件数,最后根据古典概型概率计算公式,计算出所求概率.【详解】从A 的方向看,行走方向有三个:左、前、上. 从A 到B 的最近的行走线路,需要向左三次,向前两次,向上三次,共8次.所以从A 到B 的最近的行走线路,总的方法数有88332332560A A A A =⋅⋅种. 不连续向上攀登的安排方法是:先将向左、向前的安排好,再对向上的方法进行插空.故方法数有:53563232200A C A A ⨯=⋅.所以最近的行走路线中不连续向上攀登的概率为200556014=. 故选:B【点睛】本小题主要考查古典概型的计算,考查有重复的排列组合问题,考查插空法,属于中档题. 10.B【分析】依题意可得1113332P ABC PABV PC SPA PB -=⋅=⨯⨯⋅再利用基本不等式计算可得; 【详解】解:依题意21111132332222P ABCPABPA PB V PC S PA PB PA PB -+⎛⎫=⋅=⨯⨯⋅=⋅≤= ⎪⎝⎭,当且仅当2PA PB ==时取等号,所以()max 2P ABC V -=, 故选:B11.65【分析】由最小二乘法得到的线性回归方程过点(),x y ,代入即可解决 【详解】由5125i i x ==∑可知,数据的平均数2555x ==, 又线性回归方程ˆ23yx =+过点(),x y , 所以25313y =⨯+=,故51551365i i y y ===⨯=∑故答案为:65 12.42【分析】由题意可知,甲可排在第二、三、四、五个,再根据甲、乙相邻,分别计算. 【详解】由题意可知,甲可排在第二、三、四、五个,当甲排在第二、三、四个时,甲乙相邻,有22A 种排法,将甲乙当做一个整体,剩下三个节目全排列,共3×22A ×33A =36种当甲排在第五个时,甲乙相邻,只有一种排法,剩下三个节目全排列,共33A =6种 综上,编排方案共36+6=42种【点睛】本题考查了分类计数原理,分类时要注意不重不漏;解决排列问题时,相邻问题常用捆绑法,特殊位置要优先考虑. 13.0.2【解析】利用概率和为1可求出答案. 【详解】由随机变量X 的概率分布表得: 0.20.30.31a +++=,解得0.2a =. 故答案为:0.2【点睛】本题考查的是分布列的性质,较简单. 14.49【分析】由二项分布的特征,先求出13p =,套公式即可求出D (ξ). 【详解】因为随机变量ξ~B (2,p ),且P (ξ≥1)=59,所以P (ξ≥1)=()11P ξ-<= ()10P ξ-==()25119p --=. 解得:13p =. 所以D (ξ)()12412339np p =-=⨯⨯=.故答案为:4915.9【分析】设出公差,根据等差数列的性质,表示出15,a a ,再列式即可求得结果. 【详解】因为{}n a 是等差数列,设公差为d ,可得13532,2a a d a a d =-=+,于是得()()2153322949a a a d a d d =-+=-≤,当且仅当d =0,即153a a ==时,取得最大值. 故答案为:9.【点睛】本题考查等差数列的下标和性质,属基础题. 16.1443125##0.04608 【分析】认真分析该选手所有可能的答题情况,是本题的关键【详解】由该选手恰好回答了5个问题就晋级下一轮,说明他第4、第5两个问题是连续答对的,第3个问题没有答对,第1和第2两个问题也没有全部答对,即他答题结果可能有三种情况:⨯⨯⨯√√或⨯√⨯√√或√⨯⨯√√,根据独立事件同时发生的概率公式,可得该选手恰好回答了5个问题就晋级下一轮的概率为0.20.20.20.80.8+0.20.80.20.80.8+0.80.20.20.80.8=0.04608⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯故答案为:0.04608 17.0.74【详解】试题分析:x 表示人数,(2)(2)(3)(4)(5)P x P x P x P x P x ≥==+=+=+≥0.30.30.10.040.74=+++=.考点:互斥事件的概率.18.【分析】根据截面圆性质,先求出截面圆半径,然后由求得球半径,从而求得体积.【详解】因为2AB =,BC =90ABC ∠=︒,所以4AC ==,所以三角形外接圆半径22ACr ==,又球心O 到截面ABC 的距离为R =球体积为(334433V R ππ==⨯=.故答案为:.19.(℃)(℃)(℃)见解析【详解】试题分析:(℃)由正方形的性质得1AC AA ⊥,然后由面面垂直的性质定理可证得结果;(℃)当点E 是线段1AB 的中点时,利用中位线定理可得1DE AC ,进而得出DE 面11AAC C ;(℃)利用二面角的定义先确定11C AC ∠是二面角111C A B C --的平面角,易求得11tan C A C ∠,从而求得二面角的平面角为的度数.试题解析:(℃)因为四边形11AAC C 为正方形,所以1AC AA ⊥. 因为平面ABC ⊥平面11AAC C ,且平面ABC ⋂平面11AAC C AC =, 所以1AA ⊥平面ABC .(℃)当点E 是线段1AB 的中点时,有DE 面11AAC C , 连结1AB 交1AB 于点E ,连结BC ,因为点E 是1AB 中点,点⊄是线段DE 的中点,所以1DE AC . 又因为BC ⊂面11AAC C ,11A C 面11AAC C ,所以DE 面11AAC C .(℃)因为1AA ⊥平面ABC ,所以.又因为,所以面11AAC C ,所以11A B ⊥面11AAC C ,所以11A B ⊥1A C ,11A B ⊥11A C ,所以11C AC ∠是二面角111C A B C --的平面角, 易得,所以二面角111C A B C --的平面角为45°.考点:1、线面垂直的判定;2、线面平行的判定;2、二面角.【方法点睛】立体几何中的探索性问题主要是对平行、垂直关系的探究,对条件和结论不完备的开放性问题的探究.解决这类问题时一般根据探索性问题的设问,假设其存在并探索出结论,然后在假设下进行推理,若得到合乎情理的结论就肯定假设,若得到矛盾就否定假设. 20.12600【详解】问题等价于编号为1,2,3,10的10个小球排列,其中2,3号,4,5,6号,7,8,9,10号的排列顺序是固定的,据此可得:将这些气球都打破的不同打法数是101023423412600A A A A =⨯⨯. 21.(1)℃;(2)证明见解析;(3)125n =,证明见解析.【解析】(1)℃根据新定义直接计算.℃根据新定义,写出等式两边的表达式,观察它们是否相同,即可判断;℃由新定义写出等式()(),,d A B d A C =的表达式,观察有无AB AC =; (2)由新定义,写出不等式两边的表达式,根据绝对值的性质证明;(3)根据新定义,及绝对值的性质得P 点是以AB 为对角线的正方体的表面和内部的整数点,共125个,把它们分布在五个平面(0,1,2,3,4)z =上,这五个面一个面取3个点,相邻面上取一个点,以它们为顶点构成三棱锥(能构成时),棱锥的体积不超过83,然后任取11点中如果没有4点共面,但至少有一个平面内有3个点.根据这3点所在平面分类讨论可得. 【详解】(1)当2n =时,℃若()1,2A ,()4,6B ,则(),41627d A B =-+-=,℃正确;℃在ABC 中,若90C =∠,则222AC BC AB +=,设112233(,),(,),(,)A x y B x y C x y ,所以222222131323231212()()()()()()x x y y x x y y x x y y -+-+-+-=-+-而()2221212121221212()()()2)),((x x y y x x y y d A x B x y y =⎡⎤⎣-+-+⎦=--+--, ()()22,,d A C d C B ⎡⎤⎡⎤+=⎣⎦⎣⎦22221313232313132323()()()()2()()2()()x x y y x x y y x x y y x x y y -+-+-+-+--+--,但1313232312122()()2()()2()()x x y y x x y y x x y y --+--=--不一定成立,℃错误; ℃在ABC 中,若()(),,d A B d A C =,在℃中的点坐标,有12121313x x y y x x y y -+-=-+-,但1212131322x x y y x x y y -⋅-=-⋅-不一定成立,因此AB AC =不一定成立,从而B C ∠=∠不一定成立,℃错误.空格处填℃(2)证明:设112233(,),(,),(,)A x y B x y C x y ,根据绝对值的性质有132312x x x x x x -+-≥-,132312y y y y y y -+-≥-,所以(,)(,)(,)d A C d B C d A B +≥.,(3)(,)12d A B =,44,44,44x x y y z z +-≥+-≥+-≥,所以(,)(,)12d A P d B P +≥,当且仅当以上三个等号同时成立,(,)(,)12d A P d B P +=又由已知()()(),,,d A P d P B d A B +=,℃04,04,04x y z ≤≤≤≤≤≤, 又,,x y z Z ∈,℃,,0,1,2,3,4x y z =,555125⨯⨯=,点P 是以AB 为对角线的正方体内部(含面上)的整数点,共125个,125n =. 这125个点在0,1,2,3,4z z z z z =====这五面内.这三个平面内,一个面上取不共线的3点,相邻面上再取一点构成一个三棱锥.则这个三棱锥的体积最大为118441323V =⨯⨯⨯⨯=,现在任取11个点,若有四点共面,则命题已成立,若其中无4点共面,但11个点分在5个平面上至少有一个平面内有3个点(显然不共线),若这三点在1,2,3z z z ===这三个平面中的一个上,与这个面相邻的两个面上如果有一点,那么这一点与平面上的三点这四点可构成三棱锥的四个顶点,其体积不超过83,否则还有8个点在平面0z =和4z =上,不合题意,若这三个点在平面0z =或5z =上,不妨设在平面0z =,若在平面1z =在一个点,则同样四点构成的三棱锥体积不超过83,否则剩下的8个点在2,3,4z z z ===三个平面上,只能是3,3,2分布,不管哪一种分布都有四点构成的三棱锥体积不超过83,综上,任取11个点,其中必存在4个点,它们共面或者以它们为顶点的三棱锥体积不大于83.【点睛】关键点点睛:本题新定义距离(,)d A B ,解题关键是利用新定义转化为绝对值,利用绝对值的性质解决一些问题.本题还考查了抽屉原理,11个放在5个平面上,至少有一个平面内至少有3点,由此分类讨论可证明结论成立. 22.(1)该市应该作出减少作业时长的决策; (2)分布列见解析;期望为167.【分析】(1)根据题意,结合频率分布直方图,分别求出中位数和平均数,即可求解; (2)根据题意,结合分层抽样以及离散型随机变量的分布列与期望求法,即可求解. (1)作业时长中位数的估计值为直方图中等分面积的线对立的值,设为x .0.01100.01100.02100.5⨯+⨯+⨯<. 0.01100.01100.02100.03100.5⨯+⨯+⨯+⨯>,()0.01100.01100.02100.03800.5x ∴⨯+⨯+⨯+⨯-=.解得2503x =,即中位数的故计值2503分钟.又作业时长平均数估计值为0.0110550.0110650.021075⨯⨯+⨯⨯+⨯⨯ 2500.0310850.031095813+⨯⨯+⨯⨯=<. 因为中位数的估计值2503分钟大于平均数估计值81分钟, 所以,根据这次调查,该市应该作出减少作业时长的决策. (2)由题,作业时长在70分钟以上(含70分钟)为[90.100],[80,90),[70,80)三个区间,其频率比为3:3:2,分别对应A ,B ,C 三个层次.根据分层抽样的方法,易知各层次抽取的人数分别为3,3,2, 因此X 的所有可能值为1,2,3.因为333821(1)28C P X C ⨯===,111233389(3)28C C C P X C ⋅⋅===, 121221333232382229(2)14C C C C C C P X C ⨯⋅+⨯⋅+⨯⋅===, 所以X 的分在列为:故数学期望19916()1232814287E X =⨯+⨯+⨯=. 23.(1)乙城市更应该入围“国家文明城市”.理由见解析. (2)425; (3)分布列见解析,期望为1.【分析】(1)根据得分的平均值与方差说明,极差最值也可用来说明;(2)记抽到的数据中有大于80分为事件A ,甲城市抽到的分数有大于80分为事件B ,乙城市抽到的分数有大于80分为事件C ,由()()(|)()()P AC P C P C A P A P A ==计算; (2)X 的可能值是0,1,2,分别求得概率得概率分布列,由期望公式计算出期望. (1)乙城市更应该入围“国家文明城市”. 理由如下:由茎叶图,计算两个城市的得分的均值为 甲:6365987910x +++==,乙:6568927910y +++==,均值相等,方差为甲:222211[(16)(14)19]13610s =-+-++=, 乙:222221[(14)(11)13]59.810s =-+-++=,甲的方差远大于乙的方差,说明乙的得分较稳定,甲极其不稳定,因此乙城市更应该入围“国家文明城市”. (2)记抽到的数据中有大于80分为事件A ,甲城市抽到的分数有大于80分为事件B ,乙城市抽到的分数有大于80分为事件C ,262102()13C P B C =-=,252107()19C P C C =-=,2725()1(1)(1)3927P A =--⨯-=,7()()9P AC P C ==, 所以()()()()749(|)1(|)111252527P AC P C P C A P C A P A P A =-=-=-=-=;(3)乙城市10个人中5个大于80分,5个小于80,X 的可能是0,1,2,252102(0)9C P X C ===,11552105(1)9C C P X C ===,252102(2)9C P X C ===,所以X 的分布列为:52()12199E X =⨯+⨯=.。
北京市平谷区2020-2021学年高二上学期期中考试语文试题 Word版含解析

平谷区2020-2021学年度第一学期期中测试试题高二语文2020.11一、基础与运用(共50分,每小题1分,共50分)1. 对下列句中加点词的解释,不正确的一项是()A. 《诗》可以兴.,可以观兴:激发人的感情B. 敏.于事而慎于言敏:敏捷C. 文胜质则史.史:虚饰,浮夸D. 君子喻.于义,小人喻于利喻:知晓,明白【答案】B【解析】【详解】本题考查理解常见文言实词在文中的含义和用法的能力。
解答此类题目时,首先应审题,明确选择的要求,如本题“对下列句中加点词的解释,不正确的一项”,然后应结合具体的语境,运用语法知识进行辨析。
B项,“敏于事而慎于言”意思是“对工作勤奋敏捷,说话却谨慎”,“敏”意思是“奋勉”“勤勉”。
故选B。
2. 下列句子中加点词的意思和例句相同的一项是()例句:师者,所以传道.受业解惑也A. 就有道.而正焉B. 策之不以其道.C. 任重而道.远D. 朝闻道.,夕死可矣【答案】D【解析】【详解】本题考查理解文中重要文言词语的能力。
解答本题时考生应根据平时积累的知识,结合所给句子具体分析。
例句“师者,所以传道受业解惑也”中“道”用在动词“传”后面,在这里是名词,解释为“道理”,A项,“就有道而正焉”这句话的意思是“到有道德的人那里去匡正自己”,在这句话中“道”是名词,解释为“道德”;B项,“策之不以其道” 这句话的意思是“鞭策它(指千里马)不用正确的方法”,在这句话中“道”是名词,解释为“方法、途径”;C项,“任重而道远” 这句话的意思是“责任重大,路程遥远”,在这句话中“道”是名词,解释为“路程”;D项,“朝闻道,夕死可矣”,这句话中“道”指的是儒家的“仁义之道”,“道”是名词,解释为“道理”。
故选D。
3. 下列各句中,含通假字的一项是( )A. 克己复礼为仁B. 己所不欲,勿施于人C. 知者不惑D. 未成一篑【答案】C【解析】【分析】【详解】本题考查理解判断通假字的能力。
C项,“知”通“智”。
北京市海淀区2020-2021学年第一学期期中考试初一数学试题及答案

海淀区2020年七年级学业水平调研数学试卷2020.11一、选择题(本题共24分,每小题2分)第1-12题均有四个选项,符合题意的选项只有一个.... 1. -2的相反数是 A.12B. 12-C. 2D. -22. “天问一号”探测器由长征五号运载火箭直接送入地火转移轨道,飞行期间已成功完成地月合影获取、两次轨道中途修正、载荷自检等工作,截至2020年10月1日凌晨,探测器已飞行约188 000 000千米,飞行状态良好,188 000 000这个科学记数法表示,结果正确的是 A. 61.8810⨯B. 81.8810⨯C. 618810⨯D. 90.18810⨯3.下列各数中,是负整数的是 A. 32-B. 0.1--C. 13⎛⎫-- ⎪⎝⎭D. 2(2)-4.有理数1.3429精确到千分位的近似数为 A. 1.3B. 1.34C. 1.342D. 1.3435. 若x ,y 满足22(3)0x y -++=,则xy 的值为 A. 9B. 6C. -5D. -66.下面说法正确的是 A. -2x 是单项式B. 35ab的系数是3 C. 22ab 的次数是2D. 22x xy +是四次多项式7.若单项式62x y -与25m n x y 是同类项,则A. m =2,n =1B. m =3,n =1C. m =3,n =0D. m =1,n =38.下列运算正确的是 A. 224x x x +=B. 235x x x +=C. 321x x -=D.2222x y x y x y -=-9.若2a -b =4,则式子4a -2b -5的值为 A. -1B. 1C. -3D. 310.有理数m ,n ,k 在数轴上的对应点的位置如图所示,若m +n <0,n +k >0,则A ,B ,C ,D 四个点中可能是原点的是A. A 点B. B 点C. C 点D. D 点11.如图,在11月的日历表中用框数器“”框出8,10,16,22,24五个数,它们的和为80,若将“”在图中换个位置框出五个数,则它们的和可能是A. 42B. 63C. 90D. 12512.如图,直线上的四个点A ,B ,C ,D 分别代表四个小区,其中A 小区和B 小区相距a m ,B 小区和C 小区相距200m,C 小区和D 小区相距a m ,某公司的员工在A 小区由30人,B 小区有5人,C 小区有20人,D 小区有6人,现公司计划在A ,B ,C ,D 四个小区中选一个作为班车停靠点,为使所有员工步行到停靠点的路程总和最小,那么停靠点的位置应设在A. A 小区B. B 小区C. C 小区D. D 小区二、填空题(本题共24分,每小题3分)13.妈妈的微信账单中6月23日显示-36.00,6月24日显示+100.00,如果+100.00表示收入100元,则-36.00表示 .14.化简:c +2(b -c )=.15.数轴上,与表示-3的点的距离为4的点表示的数是.16.某班部分学生外出参加社会实践活动,据统计共有三种出行方式:骑自行车、乘公交车和成私家车(每人选择了一种出行方式),其中骑车的人数比乘公交车的人数多10人,乘私家车的人数比骑车的人数少3人,设乘公交车的有m 人,则该班骑车参加此次活动的有人,该班参加此次活动的学生共有人(用含m 的式子表示).17.有理数a 在数轴上的对应点的位置如图所示,化简1a a --的结果是.18.有两个正方体的积木,如图所示下面是淘气掷200次积木的情况统计表: 灰色的面朝上白色的面朝上32次168次根据表中的数据推测,淘气更有可能掷的是号积木,请简要说明你的判断理由.19.当x 分别为-1,0,1,2时,式子ax +b 的值如下表:x -1 0 1 2 ax +b -5 -3-11则a +2b 的值为.20.图纸上一个零件的标注为0.030.0230φ+-,表示这个零件直径的标准尺寸是30mm,实际合格产品的直径最小可以是29.98mm,最大可以是mm ,现有另一零件的标注为其零件直径的标准尺寸有些模糊,一直该零件的七个合格产品,直径尺寸分别为73.1mm.72.7mm,72.8mm,73.2mm,72.9mm,73.3mm,72.6mm,则该零件的标准尺寸可能是mm (写出一个满足条件的尺寸,结果保留一位小数).三、解答题(本题共52分,第21题4分,第22题16分,第23题4分,第24题4分,第25题4分,第26题6分,第27题7分,第28题7分) 21.在数轴上表示下列各数;0,2,-1.5,13-,并按从小到大的顺序用“<”号把这些数连接起来 22.计算:(1)-7+(+20)-(-5)-(+3) (2)512.5()()84-÷-⨯-;(3)3777(1)();48128--⨯- (4)32(2)(2)(31)12(4)-+-⨯+-÷-23.结合图中信息回答问题:(1)两种电器销售量相差最大的是月;(2)简单描述一年中冰箱销售量的变化情况:;(3)两种电器中销售量相对稳定的是.24.设22(32)2(1)A x x x =--+-(1)当x =2时,求A 的值;(2)若A 的值为正,请写出满足条件的x 的值:(写出一个即可)25.今年故宫博物院举办了“丹宸永固:紫禁城建成六百年”大展,奇思和妙想两位同学想在国庆期间参观故宫,他们设计了如图所示的游览路线(图中实线部分),准备从午门(点A )进,从神武门(点B )出,所走的路线均时正东、正西、正北方向 (1)紫禁城建成的年份是;(2)请根据图中提供的信息(长度单位:m ),计算他们的游览路程(用含a ,b 的式子表示)26.阅读:计算322(357)(233)x x x x -+-+-+时,可列竖式:32232357)32338210x x x x x x x -+-++--++-小明认为,整式的加减实际上就是合并同类项,而合并同类项的关键是合并各同类项的系数,因此,可以把上题的竖式简化为:3507032338210-++-+++--++-)所以,原式=3238210x x x -++- 根据阅读材料解答下列问题:已知:3432231,24A x x x B x x x =--++=-+(1)将A 按x 的降幂排列: ; (2)请仿照小明的方法计算:A -B ; (3)请写出一个多项式C : ,使其与B 的和是二次三项式27.我们知道,正整数按照能否被2整除可以分成两类:正奇数和正偶数,小浩受此启发,按照一个正整数被3除的余数把正整数分成了三类:如果一个正整数被3除余数为1,则这个正整数属于A 类,例如1,4,7等;如果一个正整数被3除余数为2,则这个正整数属于B 类,例如2,5,8等;如果一个正整数被3整除,则这个正整数属于C 类,例如3,6,9等. (1)2020属于类(填A ,B 或C);(2)①从A 类数中任取两个数,则它们的和属于 类(填A ,B 或C );②从A 类数中任意取出15个数,从B 类数中任意取出16个数,从C 类数中任意取出17个数,把它们都加起来,则最后的结果属于 类(填A ,B 或C );(3)从A 类数中任意取出m 个数,从B 类数中任意取出n 个数,把它们都加起来,若最后的结果属于C 类,则下列关于m ,n 的叙述中正确的是 (填序号) ①m +2n 属于C 类②m n -属于B 类③m 属于A 类,n 属于C 类④m ,n 属于同一类28.对于有理数a ,b ,n ,d ,若,a n b n d -+-=则称a 和b 关于n 的“相对关系值”为d ,例如,21313-+-=,则2和3关于1的“相对关系值”为3. (1)-3和5关于1的“相对关系值”为 ;(2)若a 和2关于1的“相对关系值”为4,求a 的值;(3)若0a 和1a 关于1的“相对关系值”为1,1a 和2a 关于2的“相对关系值”为1,2a 和3a 关于3的“相对关系值”为1,···,20a 和21a 关于21的“相对关系值”为1. ①0a +1a 的最大值为; ②12320a a a a +++⋅⋅⋅+的值为(用含0a 的式子表示)海淀区2020年七年级学业水平调研数 学 答 案一、选择题(本题共24分,每小题2分) 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案CBADDABDDBCB二、填空题(本题共24分,每小题3分)13. 支出36元; 14. 2b c -; 15. 1或7-; 16. (10m +),(317m +); 17. 1-;18.②,因为②号积木白色面多;19. 4-; 20. 30.03; 答案不唯一,72.9(或73.0,73.1,73.2).三、解答题(本题共52分,第21题4分,第22题16分,第23题4分,第24题4分,第25题4分,第26题6分,第27题7分,第28题7分)21. 解: ----------------------3分11.5023-<-<<. ----------------------4分22.(1)7(+20)(5)(+3)-+--- .解:原式72053=-++- ----------------------2分15=. ----------------------4分 (2)512.5()()84-÷-⨯-. 解:原式581=254-⨯⨯ ----------------------2分 =1-. ----------------------4分(3)3778(1)()48127--⨯-.解:原式787878=4787127-⨯+⨯+⨯ 2=213-++ ----------------------3分1=3-. ----------------------4分(4)32(2)(2)(31)12(4)-+-⨯+-÷-.解:原式=8(2)(91)+3-+-⨯+=820+3-- ----------------------3分=25-.----------------------4分23.解:(1)7; ----------------------1分 (2)先上升后下降,在夏季时销售量最大; ----------------------3分 (3)热水器. ----------------------4分 24.解:(1)2232222A x x x =---+ ----------------------1分22x x =-.----------------------2分当2x =时, 原式2=222=0-⨯. ----------------------3分 (2) 3 (答案不唯一,x >2或x <0均可). ----------------------4分 25. 解:(1)1420年(明朝永乐十八年); ----------------------1分(2)42()a a b b b a ++++- ----------------------3分=422a a b b b a ++++-=54a b +.答:他们的游览路程为54m a b +(). ----------------------4分 26. 解:(1)43321A x x x =--+; ----------------------1分(2)15+43+1)0+24+1+013+02+1----------------------3分所以,A -B =4325+43+1x x x x --. ----------------------4分 (3)321C x =-+ (答案不唯一) . --------------------6分 27.解:(1)A ; ---------------------- 1分(2)① B ; ---------------------3分② B ; ---------------------- 5分 (3)① ④ ---------------------- 7分 28. 解:(1)8; ---------------------- 1分 (2)a 和2关于1的“相对关系值”为4,∴1214a -+-=.∴13a -=. ----------------------2分解得a =4或2-. ----------------------3分 (3)① 3; ----------------------5分 ②020+210a 或025020a -. ----------------------7分(对于本卷中学生的不同解法,请老师根据评分标准酌情给分)。
北京市2020-2021学年高一数学上学期期末考试试题(含解析)

北京市东城区2020-2021学年高一数学上学期期末考试试题(含解析)一、单项选择题:共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.(5分)设集合M={0},N={﹣1,0,1},那么下列结论正确的是()A.M=∅B.M∈N C.M⫋N D.N⫋M2.(5分)下列函数为偶函数的是()A.y=|x| B.y=lnx C.y=e x D.y=x33.(5分)已知函数y=sin x在区间M上单调递增,那么区间M可以是()A.(0,2π)B.(0,π)C.D.4.(5分)命题”∀x∈A,2x∈B”的否定为()A.∃x∈A,2x∉B B.∃x∉A,2x∈B C.∀x∈A,2x∉B D.∀x∉A,2x∈B 5.(5分)若a>b,则下列不等式一定成立的是()A.a2>b2B.2a>2b C.a D.6.(5分)下列各式正确的是()A.B.C.D.7.(5分)“a,b为正实数”是“a+b>2”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件8.(5分)大西洋鲑鱼每年都要逆流而上3000英里游回它们出生的地方产卵繁殖.研究鲑鱼的科学家发现鲑鱼的游速v(单位:m/s)可以表示为v=,其中O表示鲑鱼的耗氧量的单位数.则该鲑鱼游速为2m/s时的耗氧量与静止时耗氧量的比值为()A.8100 B.900 C.81 D.9二、多项选择题:本大题共2小题,每小题5分,共10分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,选对但不全的得2分,有选错的得0分.9.(5分)关于函数f(x)=1+cos x,x∈(,2π)的图象与直线y=t(t为常数)的交点情况,下列说法正确的是()A.当t<0或t≥2时,有0个交点B.当t=0或时,有1个交点C.当时,有2个交点D.当0<t<2时,有2个交点10.(5分)已知函数f(x)=4|x|+x2+a,下列命题正确的有()A.对于任意实数a,f(x)为偶函数B.对于任意实数a,f(x)>0C.存在实数a,f(x)在(﹣∞,﹣1)上单调递减D.存在实数a,使得关于x的不等式f(x)≥5的解集为(﹣∞,﹣1]∪[1,+∞)三、填空题:共6小题,每小题5分,共30分.11.(5分)函数f(x)=ln(1﹣x2)的定义域是.12.(5分)sin的值为.13.(5分)函数f(x)的值域为(0,+∞),且在定义域内单调递减,则符合要求的函数f (x)可以为.(写出符合条件的一个函数即可)14.(5分)在国庆70周年庆典活动中,东城区教育系统近2000名师生参与了国庆中心区合唱、27方阵群众游行、联欢晚会及7万只气球保障等多项重点任务.设A={x|x是参与国庆中心区合唱的学校},B={x|x是参与27方阵群众游行的学校},C={x|x是参与国庆联欢晚会的学校}.请用上述集合之间的运算来表示:①既参与国庆中心区合唱又参与27方阵群众游行的学校的集合为;②至少参与国庆中心区合唱与国庆联欢晚会中一项的学校的集合为.15.(5分)已知函数f(x)=则f(﹣2)=;若f(t)=1,则实数t=.16.(5分)某池塘中原有一块浮草,浮草蔓延后的面积y(平方米)与时间t(月)之间的函数关系式是y=a t﹣1(a>0且a≠1),它的图象如图所示,给出以下命题:①池塘中原有浮草的面积是0.5平方米;②第8个月浮草的面积超过60平方米;③浮草每月增加的面积都相等;④若浮草面积达到10平方米,20平方米,30平方米所经过的时间分别为t1,t2,t3,则2t2>t1+t3.其中正确命题的序号有.(注:请写出所有正确结论的序号)四、解答题:共5小题,共70分.解答应写出文字说明,演算步骤或证明过程.17.(12分)已知集合A={x|x2+3x+2<0},全集U=R.(1)求∁U A;(2)设B={x|m﹣1≤x≤m},若B⊆∁U A,求m的取值范围.18.(13分)已知函数,f(0)=.(1)求f(x)的解析式和最小正周期;(2)求f(x)在区间[0,2π]上的最大值和最小值.19.(14分)在平面直角坐标系xOy中,角α,β的顶点与坐标原点O重合,始边为x轴的非负半轴,终边分别与单位圆交于A,B两点,A,B两点的纵坐标分别为.(1)求tanβ的值;(2)求的值.20.(16分)已知函数f(x)=.(1)判断f(x)的奇偶性并证明;(2)判断f(x)的单调性并说明理由;(3)若f(ax﹣1)+f(2﹣x)>0对任意a∈(﹣∞,2]恒成立,求x的取值范围.21.(15分)对于集合A,定义函数f A(x)=对于两个集合A,B,定义运算A*B={x|f A(x)•f B(x)=﹣1}.(1)若A={1,2,3},B={2,3,4,5},写出f A(1)与f B(1)的值,并求出A*B;(2)证明:f A*B(x)=f A(x)•f B(x);(3)证明:*运算具有交换律和结合律,即A*B=B*A,(A*B)*C=A*(B*C).2020-2021学年北京市东城区高一(上)期末数学试卷参考答案与试题解析一、单项选择题:共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.(5分)设集合M={0},N={﹣1,0,1},那么下列结论正确的是()A.M=∅B.M∈N C.M⫋N D.N⫋M【分析】利用集合与集合的关系直接求解.【解答】解:∵集合M={0},N={﹣1,0,1},∴M⫋N.故选:C.【点评】本题考查集合的关系的判断,考查交集、并集、子集定义等基础知识,考查运算求解能力,是基础题.2.(5分)下列函数为偶函数的是()A.y=|x| B.y=lnx C.y=e x D.y=x3【分析】根据题意,依次分析选项中函数的奇偶性,综合即可得答案.【解答】解:根据题意,依次分析选项:对于A,y=|x|,是偶函数,符合题意;对于B,y=lnx,是对数函数,不是偶函数,不符合题意;对于C,y=e x,是指数函数,不是偶函数,不符合题意;对于D,y=x3,是幂函数,不是偶函数,不符合题意;故选:A.【点评】本题考查函数的奇偶性的判断,关键是掌握常见函数的奇偶性,属于基础题.3.(5分)已知函数y=sin x在区间M上单调递增,那么区间M可以是()A.(0,2π)B.(0,π)C.D.【分析】直接利用函数的单调性和子区间之间的关系求出结果.【解答】解:根据函数y=sin x的单调递增区间:[](k∈Z),当k=0时,单调增区间为[],由于为[]的子区间,故选:D.【点评】本题考查的知识要点:函数的单调性的应用,主要考查学生的运算能力和转换能力及思维能力,属于基础题型.4.(5分)命题”∀x∈A,2x∈B”的否定为()A.∃x∈A,2x∉B B.∃x∉A,2x∈B C.∀x∈A,2x∉B D.∀x∉A,2x∈B 【分析】根据含有量词的命题的否定即可得到结论.【解答】解:命题为全称命题,则命题”∀x∈A,2x∈B”的否定为∃x∈A,2x∉B,故选:A.【点评】本题主要考查含有量词的命题的否定,比较基础.5.(5分)若a>b,则下列不等式一定成立的是()A.a2>b2B.2a>2b C.a D.【分析】直接利用不等式的应用和函数的单调性的应用求出结果.【解答】解:由于a>b,且a和b的正负号不确定,所以选项ACD都不正确.对于选项:B由于函数y=2x为单调递增函数,且a>b,故正确故选:B.【点评】本题考查的知识要点:函数的单调性的应用,不等式的性质的应用,主要考查学生的运算能力和转换能力及思维能力,属于基础题型.6.(5分)下列各式正确的是()A.B.C.D.【分析】利用正弦函数、余弦函数、正切函数的单调性和诱导公式直接求解.【解答】解:在A中,sin>0>sin=﹣sin,故A错误;在B中,<cos,故B正确;在C中,>,故C错误;在D中,>cos=sin,故D错误.故选:B.【点评】本题考查命题真假的判断,考查正弦函数、余弦函数、正切函数的单调性和诱导公式等基础知识,考查运算求解能力,是基础题.7.(5分)“a,b为正实数”是“a+b>2”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件【分析】可以取特殊值讨论充要性.【解答】解:若a,b为正实数,取a=1,b=1,则a+b=2,则“a,b为正实数”是“a+b>2”的不充分条件;若a+b>2,取a=1,b=0,则b不是正实数,则“a+b>2”是“a,b为正实数''的不必要条件;则“a,b为正实数”是“a+b>2”的既不充分也不必要条件,故选:D.【点评】本题考查命题充要性,以及不等式,属于基础题.8.(5分)大西洋鲑鱼每年都要逆流而上3000英里游回它们出生的地方产卵繁殖.研究鲑鱼的科学家发现鲑鱼的游速v(单位:m/s)可以表示为v=,其中O表示鲑鱼的耗氧量的单位数.则该鲑鱼游速为2m/s时的耗氧量与静止时耗氧量的比值为()A.8100 B.900 C.81 D.9【分析】由题意令V=2m/s,0m/s,则可求出耗氧量,求出之比.【解答】解:鲑鱼游速为2m/s时的耗氧量为:令v=2=,即,即,即o=8100,鲑鱼静止时耗氧量为:令v=0=,即,即o'=100,故鲑鱼游速为2m/s时的耗氧量与静止时耗氧量的比值为,故选:C.【点评】本题考查对数求值,属于中档题.二、多项选择题:本大题共2小题,每小题5分,共10分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,选对但不全的得2分,有选错的得0分.9.(5分)关于函数f(x)=1+cos x,x∈(,2π)的图象与直线y=t(t为常数)的交点情况,下列说法正确的是()A.当t<0或t≥2时,有0个交点B.当t=0或时,有1个交点C.当时,有2个交点D.当0<t<2时,有2个交点【分析】直接利用函数的图象和函数的性质及参数的范围求出函数的交点的情况,进一步确定结果.【解答】解:根据函数的解析式画出函数的图象:①对于选项A:当t<0或t≥2时,有0个交点,故正确.②对于选项B:当t=0或时,有1个交点,故正确.③对于选项C:当t=时,只有一个交点,故错误.④对于选项D:当,只有一个交点,故错误.故选:AB.【点评】本题考查的知识要点:函数的图象的应用,利用函数的图象求参数的取值范围,主要考查学生的运算能力和转换能力及思维能力,属于基础题型.10.(5分)已知函数f(x)=4|x|+x2+a,下列命题正确的有()A.对于任意实数a,f(x)为偶函数B.对于任意实数a,f(x)>0C.存在实数a,f(x)在(﹣∞,﹣1)上单调递减D.存在实数a,使得关于x的不等式f(x)≥5的解集为(﹣∞,﹣1]∪[1,+∞)【分析】直接利用函数的对称性和函数的单调性的应用求出结果.【解答】解:函数f(x)=4|x|+x2+a,①对于选项A:由于x∈R,且f(﹣x)=f(x),故函数f(x)为偶函数.故选项A正确.②对于选项B:由于x2≥0,所以,故4|x|+x2≥1所以当x=0时a=﹣2时,f(x)<0,故选项B错误.③对于选项C:由于函数f(x)的图象关于y轴对称,在x>0时,函数为单调递增函数,在x<0时,函数为单调递减函数,故f(x)在(﹣∞,﹣1)上单调递减,故选项C正确.④对于选项D:由于函数的图象关于y轴对称,且在x>0时,函数为单调递增函数,在x<0时,函数为单调递减函数,故存在实数a=0时,当x∈(﹣∞,﹣1]∪[1,+∞)时,不等式成立,故选项D正确.故选:ACD.【点评】本题考查的知识要点:函数的性质的应用,主要考查学生的运算能力和转换能力及思维能力,属于基础题型.三、填空题:共6小题,每小题5分,共30分.11.(5分)函数f(x)=ln(1﹣x2)的定义域是(﹣1,1).【分析】解不等式1﹣x2>0即可.【解答】解:令1﹣x2>0,解得﹣1<x<1,即函数的定义域为(﹣1,1).故答案为:(﹣1,1).【点评】本题考查函数定义域的求法及不等式的求解,属于基础题.12.(5分)sin的值为﹣.【分析】原式中的角度变形后,利用诱导公式化简,计算即可得到结果.【解答】解:sin=sin(2π﹣)=﹣sin=﹣.故答案为:﹣【点评】此题考查了运用诱导公式化简求值,熟练掌握诱导公式是解本题的关键.13.(5分)函数f(x)的值域为(0,+∞),且在定义域内单调递减,则符合要求的函数f (x)可以为f(x)=.(写出符合条件的一个函数即可)【分析】由函数f(x)=()x的值域为(0,+∞),且在定义域R内单调递减,即是符合要求的一个函数.【解答】解:∵函数f(x)=()x的值域为(0,+∞),且在定义域R内单调递减,∴函数f(x)=()x即是符合要求的一个函数,故答案为:f(x)=()x.【点评】本题主要考查了指数函数的单调性和值域,是基础题.14.(5分)在国庆70周年庆典活动中,东城区教育系统近2000名师生参与了国庆中心区合唱、27方阵群众游行、联欢晚会及7万只气球保障等多项重点任务.设A={x|x是参与国庆中心区合唱的学校},B={x|x是参与27方阵群众游行的学校},C={x|x是参与国庆联欢晚会的学校}.请用上述集合之间的运算来表示:①既参与国庆中心区合唱又参与27方阵群众游行的学校的集合为A∩B;②至少参与国庆中心区合唱与国庆联欢晚会中一项的学校的集合为A∪C.【分析】①利用交集定义直接求解.②利用并集定义直接求解.【解答】解:①设A={x|x是参与国庆中心区合唱的学校},B={x|x是参与27方阵群众游行的学校},C={x|x是参与国庆联欢晚会的学校}.既参与国庆中心区合唱又参与27方阵群众游行的学校的集合为A∩B.故答案为:A∩B.②至少参与国庆中心区合唱与国庆联欢晚会中一项的学校的集合为A∪C.故答案为:A∪C.【点评】本题考查并集、交集的求法,考查并集、交集定义等基础知识,考查运算求解能力,是基础题.15.(5分)已知函数f(x)=则f(﹣2)=;若f(t)=1,则实数t=0或1 .【分析】结合已知函数解析式,把x=﹣2代入即可求解f(﹣2),结合已知函数解析式及f(t)=1,对t进行分类讨论分别求解.【解答】解:f(x)=则f(﹣2)=2﹣2=,∵f(t)=1,①当t≥1时,可得=1,即t=1,②当t<1时,可得2t=1,即t=0,综上可得t=0或t=1.故答案为:;0或1【点评】本题考查了求分段函数的函数值的问题,解题时应对自变量进行分析,是基础题.16.(5分)某池塘中原有一块浮草,浮草蔓延后的面积y(平方米)与时间t(月)之间的函数关系式是y=a t﹣1(a>0且a≠1),它的图象如图所示,给出以下命题:①池塘中原有浮草的面积是0.5平方米;②第8个月浮草的面积超过60平方米;③浮草每月增加的面积都相等;④若浮草面积达到10平方米,20平方米,30平方米所经过的时间分别为t1,t2,t3,则2t2>t1+t3.其中正确命题的序号有①②④.(注:请写出所有正确结论的序号)【分析】直接利用函数的图象求出函数的解析式,进一步利用函数的额关系式再利用函数的性质的应用求出结果.【解答】解:浮草蔓延后的面积y(平方米)与时间t(月)之间的函数关系式是y=a t ﹣1(a>0且a≠1),函数的图象经过(2,2)所以2=a2﹣1,解得a=2.①当x=0时y=,故选项A正确.②当第8个月时,y=28﹣1=27=128>60,故②正确.③当t=1时,y=1,增加0.5,当t=2时,y=2,增加1,故每月的增加不相等,故③错误.④根据函数的解析式,解得t1=log210+1,同理t2=log220+1,t3=log230+1,所以2t2=2log220+2=log2400+2>t1+t2=log2300+2,所以则2t2>t1+t3.故④正确.故答案为:①②④.【点评】本题考查的知识要点:函数的性质的应用,定义性函数的应用,主要考查学生的运算能力和转换能力及思维能力,属于基础题型.四、解答题:共5小题,共70分.解答应写出文字说明,演算步骤或证明过程.17.(12分)已知集合A={x|x2+3x+2<0},全集U=R.(1)求∁U A;(2)设B={x|m﹣1≤x≤m},若B⊆∁U A,求m的取值范围.【分析】(1)根据题意,求出集合A,进而由补集的性质分析可得答案;(2)根据题意,结合集合间的关系分析可得答案.【解答】解:(1)根据题意,因为A={x|x2+3x+2<0}={x|﹣2<x<﹣1}.因为全集U=R,所以∁U A={x|x≤﹣2或x≥﹣1},(2)根据题意,∁U A={x|x≤﹣2或x≥﹣1},若B⊆∁U A,当m﹣1≥﹣1或m≤﹣2,即m≥0或m≤﹣2,所以m的取值范围为(﹣∞,﹣2]∪[0,+∞).【点评】本题考查集合的补集运算,涉及集合的子集关系,属于基础题.18.(13分)已知函数,f(0)=.(1)求f(x)的解析式和最小正周期;(2)求f(x)在区间[0,2π]上的最大值和最小值.【分析】(1)利用函数值,转化求解函数的解析式,推出函数的周期;(2)利用函数的自变量的范围,求出相位的范围,然后求解正弦函数的最值.【解答】解:(1)因为,所以.又因为φ∈,所以φ=.所以.所以f(x)最的小正周期.(2)因为x∈[0,2π],所以.当,即时,f(x)有最大值2,当,即x=2π时,f(x)有最小值.【点评】本题考查函数的周期以及函数的最值的求法,考查转化思想以及计算能力,是中档题.19.(14分)在平面直角坐标系xOy中,角α,β的顶点与坐标原点O重合,始边为x轴的非负半轴,终边分别与单位圆交于A,B两点,A,B两点的纵坐标分别为.(1)求tanβ的值;(2)求的值.【分析】(1)由题意利用任意角的三角函数的定义,同角三角函数的基本关系,求得tanβ的值.(2)由题意利用诱导公式、同角三角函数的基本关系,求得要求式子的值.【解答】解:(1)因为β的终边与单位圆交于点B,B点的纵坐标为,所以.因为,所以.所以.(2)因为α的终边与单位圆交于点A,A点的纵坐标为,所以.因为,所以,故===.【点评】本题主要考查任意角的三角函数的定义,同角三角函数的基本关系、诱导公式,属于基础题.20.(16分)已知函数f(x)=.(1)判断f(x)的奇偶性并证明;(2)判断f(x)的单调性并说明理由;(3)若f(ax﹣1)+f(2﹣x)>0对任意a∈(﹣∞,2]恒成立,求x的取值范围.【分析】(1)定义域为R,然后求出f(﹣x),得f(﹣x)=﹣f(x),所以为奇函数;(2)直接由指数函数的单调性可判断函数f(x)的单调性;(3)不等式变形,由奇函数的性质得出ax﹣1>x﹣2对任意a∈(﹣∞,2]恒成立,令关于a的函数g(a)=xa+1﹣x>0在(﹣∞,2]上恒成立,g(a)一定单调递减,所以满足则只需解出x的范围.【解答】解:(1)f(x)为奇函数.因为f(x)定义域为R,,所以f(﹣x)=﹣f(x).所以f(x)为奇函数;(2)在(﹣∞,+∞)是增函数.因为y=3x在(﹣∞,+∞)是增函数,且y=3﹣x在(﹣∞,+∞)是减函数,所以在(﹣∞,+∞)是增函数,(3)由(1)(2)知f(x)为奇函数且f(x)(﹣∞,+∞)是增函数.又因为f(ax﹣1)+f(2﹣x)>0,所以f(ax﹣1)>﹣f(2﹣x)=f(x﹣2).所以ax﹣1>x﹣2对任意a∈(﹣∞,2]恒成立.令g(a)=xa+(1﹣x),a∈(﹣∞,2].则只需,解得所以﹣1<x≤0.所以x的取值范围为(﹣1,0].【点评】考查函数的奇函数的判断即函数的单调性,使用中档题.21.(15分)对于集合A,定义函数f A(x)=对于两个集合A,B,定义运算A*B={x|f A(x)•f B(x)=﹣1}.(1)若A={1,2,3},B={2,3,4,5},写出f A(1)与f B(1)的值,并求出A*B;(2)证明:f A*B(x)=f A(x)•f B(x);(3)证明:*运算具有交换律和结合律,即A*B=B*A,(A*B)*C=A*(B*C).【分析】(1)由新定义的元素即可求出f A(1)与f B(1)的值,再分情况求出A*B;(2)对x是否属于集合A,B分情况讨论,即可证明出f A*B(x)=f A(x)•f B(x);(3)利用(2)的结论即可证明出*运算具有交换律和结合律.【解答】解:(1)∵A={1,2,3},B={2,3,4,5},∴f A(1)=﹣1,f B(1)=1,∴A*B={1,4,5};(2)①当x∈A且x∈B时,f A(x)=f B(x)=﹣1,所以x∉A*B.所以f A*B(x)=1,所以f A*B(x)=f A(x)•f B(x),②当x∈A且x∉B时,f A(x)=﹣1,f B(x)=1,所以x∈A*B.所以f A*B(x)=﹣1,所以f A*B(x)=f A(x)•f B(x),③当x∉A且x∈B时,f A(x)=1,f B(x)=﹣1.所以x∈A*B.所以f A*B(x)=﹣1.所以f A*B(x)=f A(x)•f B(x).④当x∉A且x∉B时,f A(x)=f B(x)=1.所以x∉A*B.所以f A*B(x)=1.所以f A*B(x)=f A(x)•f B(x).综上,f A*B(x)=f A(x)•f B(x);(3)因为A*B={x|f A(x)•f B(x)=﹣1},B*A={x|f B(x)•f A(x)=﹣1}={x|f A(x)•f B(x)=﹣1},所以A*B=B*A.因为(A*B)*C={x|f A*B(x)•f C(x)=﹣1}={x|f A(x)•f B(x)•f C(x)=﹣1},A*(B*C)={x|f A(x)•f B*C(x)=﹣1}={x|f A(x)•f B(x)•f C(x)=﹣1},所以(A*B)*C=A*(B*C).【点评】本题主要考查了集合的基本运算,考查了新定义问题,是中档题.。
2020-2021学年度北京市第八中学高一上学期期中考试数学试卷【含解析】

2020-2021学年度北京市第八中学高一上学期期中考试数学试卷【含解析】一、单选题1.已知集合{}{}0,1,2,3,4,0,1,2U M ==,则UM =( )A .{}0,1,2B .{}0,1,2,3,4C .{}1,2D .{}3,4【答案】D【分析】直接根据补集概念进行运算即可得解. 【详解】因为集合{}{}0,1,2,3,4,0,1,2U M ==, 所以UM ={3,4}.故选:D 2.若()11xf x x-=+,则()0f =( ) A .1 B .12C .0D .1-【答案】A【分析】直接代入函数解析式计算可得; 【详解】解:因为()11x f x x -=+,所以()100110f -==+ 故选:A【点睛】本题考查函数值的计算,属于基础题. 3.若1x y >>,则下列四个数中最小的数是( )A .2x y+ B .2xyx y+ C x D .1112x y ⎛⎫+ ⎪⎝⎭【答案】D【分析】根据1x y >>可以推出2x y +、2xy x y +x 1,1112x y ⎛⎫+ ⎪⎝⎭1<,故可得答案.【详解】因为1x y >>,所以11122x y ++>=,2xy x y +2211111y x=>=++1x >,1112x y ⎛⎫+ ⎪⎝⎭111()1211<+=, 所以四个数中最小的数是1112x y ⎛⎫+ ⎪⎝⎭. 故选:D【点睛】关键点点睛:利用不等式的性质找中间量1进行比较是解题关键. 4.命题“2R,||0x x x ∀∈+≥”的否定是( ) A .2R,||0x x x ∀∈+<B .2R,||0x x x ∀∈+≤C .2000R,0x x x ∃∈+<D .2000R,0x x x ∃∈+≥【答案】C【分析】根据全称命题的否定是特称命题即可得出. 【详解】根据全称命题的否定是特称命题,则命题“2R,||0x x x ∀∈+≥”的否定是“2000R,0x x x ∃∈+<”.故选:C.5.函数()()2212f x x a x =+-+在区间(],4-∞上递减,则a 的取值范围是( )A .[)3,-+∞B .(],3-∞-C .(],5-∞D .[)3,+∞ 【答案】B【分析】根据二次函数的单调性列式可得结果.【详解】因为函数()()2212f x x a x =+-+在区间(],4-∞上递减,所以(1)4a --≥,即3a ≤-. 故选:B【点睛】关键点点睛:掌握二次函数的单调性是解题关键.6.已知a ,b 为实数,则“a +b >4”是“a ,b 中至少有一个大于2”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分又不必要条件【答案】A【分析】根据充分条件和必要条件的定义进行判断即可.【详解】“a+b >4”可得“a ,b 中至少有一个大于2”,反之若a=3,b=1,则a +b >4不成立.∴“a+b >4”是“a ,b 中至少有一个大于2”的充分不必要条件. 故选:A .【点睛】本题考查了不等式的性质、简易逻辑的判定方法,考查了推理能力与计算能力,属于基础题.7.下列从集合M 到集合N 的对应关系中,其中y 是x 的函数的是( ) A .M ={x |x ∈Z },N ={y |y ∈Z },对应关系f :x →y ,其中2xy =B .M ={x |x >0,x ∈R },N ={y |y ∈R },对应关系f :x →y ,其中y =±2xC .M ={x |x ∈R },N ={y |y ∈R },对应关系f :x →y ,其中y =x 2D .M ={x |x ∈R },N ={y |y ∈R },对应关系f :x →y ,其中2y x= 【答案】C【分析】根据函数的定义作出判断即可.【详解】A .M 中的一些元素,在N 中没有元素对应,比如,x =3时,32y N =∉,∴y 不是x 的函数;B .M 中的任意元素x ,在N 中有两个元素±2x 与之对应,不满足对应的唯一性,∴y 不是x 的函数;C .满足在M 中的任意元素x ,在集合N 中都有唯一元素x 2与之对应,∴y 是x 的函数;D .M 中的元素0,通过2y x=在N 中没有元素对应,∴y 不是x 的函数. 故选:C .【点睛】本题主要考查了函数关系的判断,属于中档题.8.设x ∈R ,定义符号函数1,0sgn 0,01,0x x x x >⎧⎪==⎨⎪-<⎩,则函数()f x =sgn x x 的图象大致是( )A .B .C .D .【答案】C【解析】函数f(x)=|x|sgnx=,00,0,0x xxx x>⎧⎪=⎨⎪<⎩=x,故函数f(x)=|x|sgnx的图象为y=x所在的直线,故答案为C.9.设函数f(x)=()()212,1315,1x a x xa x x⎧--+≥⎪⎨+-<⎪⎩在R上是增函数,则a的取值范围是()A.(-13,3]B.( -13,2) C.(-13,2]D.[2,3]【答案】C【分析】利用分段函数是增函数,两段函数都递增列出不等式组,求解即可.【详解】函数2(1)2,1()(31)5,1x a x xf xa x x⎧--+=⎨+-<⎩在R上是增函数,可得:112310315112 aaa a-⎧⎪⎪+>⎨⎪+--++⎪⎩,解得12 3a-<故实数a的取值范围是1(3-,2].故选:C.【点睛】本题考查分段函数的单调性、二次函数的单调性,注意各段函数单调性的应用,属于易错题.10.汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况. 下列叙述中正确的是()A.消耗1升汽油,乙车最多可行驶5千米B.以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多C.甲车以80千米/小时的速度行驶1小时,消耗10升汽油D.某城市机动车最高限速80千米/小时. 相同条件下,在该市用丙车比用乙车更省油【答案】D【详解】解:对于A,由图象可知当速度大于40km/h时,乙车的燃油效率大于5km/L,∴当速度大于40km/h时,消耗1升汽油,乙车的行驶距离大于5km,故A错误;对于B,由图象可知当速度相同时,甲车的燃油效率最高,即当速度相同时,消耗1升汽油,甲车的行驶路程最远,∴以相同速度行驶相同路程,三辆车中,甲车消耗汽油最少,故B错误;对于C,由图象可知当速度为80km/h时,甲车的燃油效率为10km/L,即甲车行驶10km时,耗油1升,故行驶1小时,路程为80km,燃油为8升,故C 错误;对于D,由图象可知当速度小于80km/h时,丙车的燃油效率大于乙车的燃油效率,∴用丙车比用乙车更省油,故D正确故选D.【解析】1、数学建模能力;2、阅读能力及化归思想.二、填空题11.函数23()2x xf xx-=-的定义域为_________.【答案】[0,2)(2,3]【分析】由23020x xx⎧-≥⎨-≠⎩解得结果即可得解.【详解】要使函数23 ()x x f x-=只需23020x xx⎧-≥⎨-≠⎩,解得03x≤≤且2x≠,所以函数()f x的定义域为[0,2)(2,3].故答案为:[0,2)(2,3].【点睛】方法点睛:已知函数解析式,求函数定义域的方法:1、有分式时:分母不为0;2、有根号时:开奇次方,根号下为任意实数,开偶次方,根号下大于或等于0;3、有指数时:当指数为0时,底数一定不能为0;4、有根号与分式结合时,根号开偶次方在分母上时:根号下大于0;5、有指数函数形式时:底数和指数都含有x,指数底数大于0且不等于1;6、有对数函数形式时,自变量只出现在真数上时,只需满足真数上所有式子大于0,自变量同时出现在底数和真数上时,要同时满足真数大于0,底数要大0且不等于1.12.设函数f(x)满足f(x-1)=4x-4,则f(x)=______.【答案】4x【分析】变形f(x-1)得出f(x-1)=4(x-1),从而得出f(x)=4x.【详解】由题意得,f(x-1)=4x-4=4(x-1),∴f(x)=4x.故答案为:4x.【点睛】本题考查了换元法求函数解析式的方法,属于基础题.13.给出下列三个函数:①222x xyx-=-;②321x xyx+=+;③2y x=其中与函数()f x x=相同的函数的序号是_________.【答案】②【分析】依次判断函数的定义域、解析式是否与已知函数的定义域、解析式都相同,找出相同函数【详解】222x xy x -=-的定义域为()(),22-∞⋃+∞,,与()f x x =定义域不同,321x x y x x +==+与()f x x =定义域、解析式均相同,2y x x ==,与()f x x =解析式不同, 故选②【点睛】判断两个函数是否为相同函数,只要比较两个函数的定义域,对应关系是否都相同,如果都相同就是相同函数14.已知()f x 为R 上的奇函数,0x >时,()31f x x x=+,则(1)(0)f f -+=_____. 【答案】2-【分析】由奇函数的性质可得(0)0f =,(1)(1)f f -=-,再由已知的解析式求出(1)f 即可【详解】解:因为()f x 为R 上的奇函数,所以(0)0f =,(1)(1)f f -=-,因为当0x >时,()31f x x x=+,所以(1)112f =+=, 所以(1)(0)202f f -+=-+=-, 故答案为:2- 15.已知函数11()(0,0)f x a x a x =->>,若()f x 在1,22⎡⎤⎢⎥⎣⎦上的值域为1,22⎡⎤⎢⎥⎣⎦,则a =________.【答案】25. 【分析】根据函数11()(0,0)f x a x a x =->>在1,22⎡⎤⎢⎥⎣⎦上单调递增,求出函数的最值,列方程组可解得结果.【详解】由题意知函数11()(0,0)f x a x a x =->>在1,22⎡⎤⎢⎥⎣⎦上单调递增, ∴1122(2)2f f ⎧⎛⎫=⎪ ⎪⎝⎭⎨⎪=⎩,即11221122a a ⎧-=⎪⎪⎨⎪-=⎪⎩,解得25a =.故答案为:25. 【点睛】本题考查了由函数解析式得单调性,根据单调性求最值,属于基础题. 16.若关于x 的不等式20ax x b ++>的解集是()1,2-,则a b +=______.【答案】1【分析】根据一元二次不等式的解集得出对应方程的两个根,再由根与系数的关系求出a ,b 即可.【详解】关于x 的不等式ax 2+x+b >0的解集是(-1,2), ∴-1,2是方程ax 2+x+b=0的两个根, ∴-1+2=-1a ,-1×2=b a, 解得a=-1,b=2; ∴a+b=-1+2=1. 故答案为:1.【点睛】本题考查了一元二次不等式对应方程的关系,解题的关键是根据不等式的解集得出不等式相应方程的根,再由根与系数的关系求参数的值.17.已知0,0x y >>,且8x y +=,则(1)(1)x y +⋅+的最大值为_____. 【答案】25【分析】将8x y +=化为(1)(1)10x y +++=后,根据基本不等式可求得结果. 【详解】因为0,0x y >>,且8x y +=,所以(1)(1)10x y +++=2(1)(1)x y ≥++(1)(1)25x y ++≤, 当且仅当4x y ==时,等号成立. 所以(1)(1)x y +⋅+的最大值为25. 故答案为:25【点睛】易错点睛:利用基本不等式求最值时,要注意其必须满足的三个条件: (1)“一正二定三相等”“一正”就是各项必须为正数;(2)“二定”就是要求和的最小值,必须把构成和的二项之积转化成定值;要求积的最大值,则必须把构成积的因式的和转化成定值;(3)“三相等”是利用基本不等式求最值时,必须验证等号成立的条件,若不能取等号则这个定值就不是所求的最值,这也是最容易发生错误的地方.18.二次方程222320mx x m ---=的一个根大于1,另一个根小于1,则m 的取值范围是_________. 【答案】0m >或4m -< 【详解】令y=2mx 2﹣2x ﹣3m ﹣2 当m >0时,由题意:x=1时,y <0,∴2m ﹣2﹣3m ﹣2<0, ∴m >﹣4, ∴m >0,当m <0时,x=1时,y >0, ∴2m ﹣2﹣3m ﹣2>0, ∴m <﹣4,综上所述,二次方程2mx 2﹣2x ﹣3m ﹣2=0的一个根大于1,另一个根小于1时,m <﹣4或 m >0.故答案为0m >或4m -<19.已知函数()22121x kx x f x x x ,,⎧-+≤=⎨>⎩,若存在a ,b R ∈,且ab ,使得()()f a f b =成立,则实数k 的取值范围是____________. 【答案】()()-,23,∞⋃+∞【分析】由题意,可知函数()f x 在定义域内不是单调函数,结合二次函数的图象与性质及分段函数的单调性,即可得到结论.【详解】由题意可得函数()f x 在定义域内不是单调函数, 由函数()22,1f x x x =>为增函数,且1x =时,222x =,则1x ≤时,12k<或12k -+>,解得2k <或3k >, 即实数k 的取值范围是(,2)(3,)-∞⋃+∞.【点睛】本题主要考查了分段函数的解析式及其应用,其中根据题意得出分段函数不是单调函数,再利用二次函数的图象与性质求解是解答的关键,着重考查了分类讨论思想,以及推理与运算能力,属于中档试题.三、解答题 20.已知函数()((1,1))1||xf x x x =∈--,有下列结论: ①(1,1)x ∀∈-,等式()()0f x f x 恒成立;②[)0,m ∀∈+∞,方程|()|f x m =有两个不等的实根; ③12,,(11)x x ∀∈-,若12x x ≠,则一定有12()()f x f x ≠;④存在无数多个实数k ,使得函数()()g x f x kx =-在(1,1)-上有三个零点 则其中正确结论的序号为? 【答案】①③④【分析】根据()f x 与()f x -的解析式代入运算可知①正确;取0m =可知②错误;分析函数()f x 的单调性可知③正确,由(0)0g =,当1k >时,()g x 在(0,1)和(1,0)-内都必有一个零点,可知④正确. 【详解】对于①,(1,1)x ∀∈-,()()01||1||1||1||x x x x f x f x x x x x ,①正确;对于②,当0m =时,|()|0f x =,即||01||xx =-只有一个实根0,错误; 对于③,任取1201x x ≤<<,则12()()f x f x -=12121||1||x x x x ---121211x x x x =---122112(1)(1)(1)(1)x x x x x x ---=--1212(1)(1)x x x x -=--, 因为1201x x ≤<<,所以120x x -<,12(1)(1)0x x -->,所以12()()f x f x <,所以()f x 在[0,1)上为增函数,又由①知,()f x 为奇函数, 所以()f x 在(1,1)-上为增函数,所以③正确; 对于④,1()()1||1||x g x kx x k x x =-=---,因为(0)0g =,所以0恒是()g x 的一个零点,当1k >,01x <<时,101k x -=-必有一个解, 当1,10k x >-<<时,11k x-+0=也必有一解, 所以④正确,综上所述:正确结论的序号为①③④.【点睛】关键点点睛:对于③,判断出函数的单调性是解题关键;对于④,分01x <<和(1,0)-两种情况判断零点是解题关键.21.已知全集U =R ,集合{}29A x x =<<,{}28B x x =≥.(1)求AB ;()U B A ⋂.(2)已知集合{}2C x a x a =<<+,若C B ⊆,求实数a 的取值范围. 【答案】(1)AB {|229}x x =≤<,()U B A ⋂={|22x x ≤-或9}x ≥(2)222≤--a 或22a ≥【分析】(1)根据交集和补集的概念运算可得解; (2)根据子集关系列式可解得结果.【详解】(1){}28B x x =≥{|22x x =≤-或22}x ≥,{|2UA x x =≤或9}x ≥,所以AB {|229}x x =≤<, ()U B A ⋂={|22x x ≤-或9}x ≥.(2)因为C B ⊆,所以222a +≤-或22a ≥,即222≤--a 或22a ≥. 【点睛】关键点点睛:熟练掌握集合的交集、补集和子集的概念是解题关键. 22.已知函数223y x x =--(1)画出函数223y x x =--,](1,4x ∈-的图象(2)讨论当k 为何范围时,方程2230x x k ---=在](1,4x ∈-上的解集为空集、单元素集、双元素集.【答案】(1)答案见解析(2)答案见解析 【分析】(1)根据解析式作出图象即可;(2)依题意转化为函数223y x x =--,](1,4x ∈-的图象与直线y k =的交点个数进行求解,根据(1)中的图象可得结果.【详解】(1)函数223y x x =--,](1,4x ∈-的图象为:(2)依题意转化为函数223y x x =--,](1,4x ∈-的图象与直线y k =的交点个数进行求解,根据(1)中的图象可得:当4k <-或5k >时,方程2230x x k ---=在](1,4x ∈-上的解集为空集; 当4k =-或05k ≤≤时,方程2230x x k ---=在](1,4x ∈-上的解集为单元素集; 当40k -<<时,方程2230x x k ---=在](1,4x ∈-上的解集为双元素集. 【点睛】关键点点睛:第二问转化为函数223y x x =--,](1,4x ∈-的图象与直线y k =的交点个数进行求解是解题关键.23.已知函数21()x f x x+=.(1)判断()f x 的奇偶性并证明.(2)当(1,)x ∈+∞时,判断()f x 的单调性并证明.(3)在(2)的条件下,若实数m 满足(3)(52)f m f m >-,求m 的取值范围. 【答案】(1)奇函数,证明见解析;(2) 函数()f x 是(1,)+∞上的单调增函数,证明见解析;(3)(1,2).【分析】(1)根据函数奇偶性的定义判断并证明即可; (2)根据函数单调性的定义判断并证明即可;(3)在(2)的条件下,根据函数单调性的性质可得3521m m >->,解不等式即可求出m 的取值范围.【详解】(1) 函数()f x 是奇函数. 证:函数()f x 的定义域为(,0)(0,)-∞+∞,因为22()11()()x x f x f x x x-++-==-=--,所以函数()f x 是奇函数;(2) 函数()f x 是(1,)+∞上的单调增函数. 证:任取12(1,)x x ∈+∞,且12x x >,则2222121221211212121212121211()()()()x x x x x x x x x x x x x x f x f x x x x x x x +++------=-==121212()(1)x x x x x x --=,因为121x x >>,所以120x x ->,1210x x ->,120x x >, 所以12())0(f x f x ->,即12()()f x f x >, 所以函数()f x 是(1,)+∞上的单调增函数.(3)由(2)知函数()f x 是(1,)+∞上的单调增函数,所以3521m m >->,解得12m <<,所以m 的取值范围为(1,2).【点睛】思路点睛:解函数不等式的理论依据是函数单调性的定义,具体步骤是: (1)将函数不等式转化成12()()f x f x >的形式; (2)考查函数()f x 的单调性;(3)根据据函数()f x 在给定区间上的单调性去掉法则“f ”,转化为形如“12x x >”或“12x x <”的常规不等式,从而得解.24.已知函数()()2134f x mx m x =+--,m R ∈.(1)当1m =时,求()f x 在区间[]22-,上的最大值和最小值. (2)解关于x 的不等式()1f x >-.(3)当0m <时,若存在()01,x ∈+∞,使得()0f x >,求实数m 取值范围. 【答案】(1)最小值为5-,最大值为4;(2)答案见解析;(3)1m <-或109m -<<. 【分析】(1)根据二次函数的单调性可求得结果; (2)化为(1)(3)0mx x +->后,先对m 分类讨论,再对1m-与3分类讨论可得结果; (3)转化为()f x 在(1,)+∞上的最大值大于0,根据二次函数的知识求出最大值,再解关于m 的不等式可得结果.【详解】(1)当1m =时,()224f x x x =--在[2,1)-上递减,在(1,2]上递增,所以()f x 的最小值为(1)1245f =--=-,最大值为(2)4444f -=+-=. (2)()1f x >-可化为2(13)30mx m x +-->,即(1)(3)0mx x +->, 当0m >时,不等式化为1()(3)0x x m +->,解得1x m<-或3x >; 当0m =时,不等式化为30x ->,解得3x >;当0m <时,不等式化为1()(3)0x x m +-<, 当13m -<,即13m <-时,解得13x m -<<;当13m -=,即13m =-时,不等式无解;当13m->,即103m -<<时,解得13x m <<-.综上所述:当0m >时,不等式的解集为{|x 1x m<-或3x >}; 当0m =时,不等式的解集为{|x 3x >};当103m -<<时,不等式的解集为{|x 13x m <<-};当13m =-时,不等式的解集为空集;当13m <-时,不等式的解集为{|x 13x m -<<}.(3)当0m <时,若存在()01,x ∈+∞,使得()0f x >,则()f x 在(1,)+∞上的最大值大于0,因为()()2134f x mx m x =+--的图象的开口向下,对称轴13131222m m m --=-+>, 所以max()f x 13()2m f m -=-22(13)13(13)()442m m m m m m --=⋅+-⋅--2(13)44m m-=--, 所以2(13)404m m--->,即2(13)16m m ->-,即291010m m ++>,解得1m <-或109m -<<. 【点睛】结论点睛:本题考查不等式的恒成立与有解问题,可按如下规则转化: ①若()k f x ≥在[,]a b 上恒成立,则max ()k f x ≥; ②若()k f x ≤在[,]a b 上恒成立,则min ()k f x ≤; ③若()k f x ≥在[,]a b 上有解,则min ()k f x ≥; ④若()k f x ≤在[,]a b 上有解,则max ()k f x ≤;。
北京市昌平区第一中学2020_2021学年高二数学上学期期中试题含解析

【分析】
把直线方程化成斜截式,根据斜率等于倾斜角的正切求解.
【详解】直线 化成斜截式为 ,
因为 ,所以 .
故选B.
【点睛】本题考查直线的斜截式方程和基本性质,属于基础题.
3.已知 , ,则 的值为()
A. 4B. C. 5D.
【答案】B
【解析】
【分析】
先求得 ,再利用空间向量模的公式计算.
【详解】∵ , , , ,
【答案】(1)见解析;(2) ;(3)见解析.
【解析】
【分析】
(1)建立如图所示的空间直角坐标系,求出 以及平面 的法向量后可证明 平面 .
(2)求出平面 的法向量后可求二面角 的余弦值.
(3)可证明 始终不为零,从而可证 与 都不垂直.
【详解】因为 底面 ,而 底面 , 底面 ,
故 , ,
又底面 是矩形,故 .
依题意满足条件的最小正方形是各边以 为中点,边长为2的正方形,故不存在一个以原点为中心、边长为 的正方形,使得曲线 在此正方形区域内(含边界),故③不正确.
故答案为:①②
【点睛】本题考查了由曲线方程研究曲线的对称性,考查了不等式知识,考查了求曲线交点坐标,属于中档题.
三、解答题共5题,共70分.解答应写出文字说明,演算步骤或证明过程.
A. B. C. D.
【答案】D
【解析】
【分析】
根据圆心到直线的距离等于半径求解.
【详解】解:直线 的一般方程为 ,
圆 的圆心为 ,半径为 .
直线与圆相切, , .
故选:D.
6.圆 和圆 的位置关系是()
A.相交B.内切C.外切D.相离
【答案】C
【解析】
【分析】
分别求出两圆的圆心和半径,求得圆心距与半径和或差的关系,即可判断位置关系
北京市东城第50中2020-2021学年高二上学期期中考试数学试题

北京市东城第50中2020-2021学年高二上学期期中考试数学试题学校:___________姓名:___________班级:___________考号:___________一、单选题1.若直线l 经过点(2,3)A ,(3,4)B ,则直线l 的倾斜角为( ).A .30B .45︒C .60︒D .90︒ 2.圆2220x y x +-=与圆2240x y y ++=的位置关系是( )A .相离B .外切C .相交D .内切 3.直线236x y -=在y 轴上的截距为( ).A .3B .3-C .2D .2-4.已知两条直线1:330l ax y +-=,2:4610l x y +-=,若12l l ,则a =( ). A .1 B .2 C .3 D .45.已知两条直线2y ax =-和(2)1y a x =++互相垂直,则a 等于( ). A .1- B .1 C .0 D .2-6.若椭圆222116x y b+=,过点(2,,则其焦距为( ).A .B .C .D .7.设倾斜角为45︒的直线l 通过抛物线24y x =的焦点且与抛物线相交于M 、N 两点,则弦MN 的长为( ).A B .C .16 D .8 8.由直线1y x =+上的一点向圆22(2)(1)1x y -+-=引切线,则切线长的最小值为A 1B .1CD 9.已知动圆过点(1,0),且与直线1x =-相切,则动圆圆心的轨迹方程为( ). A .221x y += B .221x y -= C .24y x = D .0x =10.椭圆2222:1(0)x y C a b a b+=>>的一个焦点为1F ,若椭圆上存在点P ,满足以椭圆短轴为直径的圆与线段1PF 相切于该线段的中点,则椭圆的离心率为( ).A .2B .23C .59 D二、填空题11.抛物线28y x =的准线方程是 .12.双曲线221169x y -=的两条渐近线的方程为________. 13.若不论k 取何值,直线:(1)20l k x y k +++-=恒过定点,则这个定点的坐标为__________.14.直线10x y +-=被圆22240x y x y +--=截得的弦长为__________.15.若直线l 与直线1y =和70x y --=分别交于M ,N 两点,且MN 的中点为()1,1P -,则直线l 的斜率等于__________.16.已知F 是椭圆22:12x C y +=的左焦点,P 为椭圆C 上任意一点,点Q 的坐标为(4,3),则PQ PF +的最大值为__________.三、解答题17.(10分)已知三角形的三个顶点(4,6)A ,(3,0)B -,(1,4)C --,求BC 边上中线和高线所在的直线方程.18.(10)已知三个点(1,1)A --,(8,0)B -,(0,6)C ,圆M 为ABC 的外接圆. (1)求圆M 的方程.(2)设直线2y x m =+,与圆M 交于P ,Q 两点,且PQ =m 的值. 19.已知圆22:(1)1M x y ++=,圆22:(1)9N x y -+=,动圆P 与圆M 外切并且与圆N 内切,求动圆圆心P 的轨迹方程.20.已知椭圆22221(0)x y a b a b +=>>的长轴长为离心率2e =,过右焦点F 的直线l 交椭圆于P 、Q 两点.(1)求椭圆的方程.(2)当直线l 的斜率为1时,求POQ △的面积.21.(9分)过点(0,3)A 作直线l 与圆22:2460C x y x y +---=交于P 、Q 两点,且OP OQ ⊥,O 为坐标原点,求直线l 的方程.22.(9分)已知椭圆22:236C x y +=的左焦点为F ,过F 的直线l 与C 交于A 、B两点.(1)求椭圆C 的离心率.(2)当直线l 与x 轴垂直时,求线段AB 的长.(3)设线段AB 的中点为P ,O 为坐标原点,直线OP 交椭圆C 交于M 、N 两点,是否存在直线l 使得3NP MP =?若存在,求出直线l 的方程;若不存在,说明理由.参考答案1.B【详解】∵直线l 经过点(2,3)A ,(3,4)B ,∴直线l 的斜率43132k -==-, 设直线l 的倾斜角为α,则tan 1α=,又0180α︒≤<︒,∴45α=︒.故选:B .2.C【分析】先将两圆的方程化为标准方程,再根据圆与圆的位置关系的判断方法得到结论.【详解】圆2220x y x +-=化为标准方程为:22(1)1x y -+=圆2240x y y ++=化为标准方程为:22(2)4x y ++==212113=-<+=r r r r∴两圆相交故选:C【点睛】本题主要考查了圆与圆的位置关系,还考查了运算求解的能力,属于基础题.3.D【解析】令0x =,可得2036y ⨯-=,解得2y =-,即直线236x y -=在y 轴上的截距为2-.故选D .4.B【解析】若12l l ,则根据直线平行的公式得到:233a -=-,解得2=. 故选B .5.A【解析】因为直线2y ax =-和(2)1y a x =++互相垂直,所以(2)1a a +=-,解得1a =-.故选A .6.B【解析】根据题意把点(2,代入椭圆的方程可求得24b =,椭圆方程为221164x y +=,∴4a =,2b =,c ==,∴其焦距为故选B .7.D【解析】∵直线l 的倾斜角为45︒,且过抛物线24y x =的焦点(1,0),∴直线AB 的方程为1y x =-,设11(,)M x y ,22(,)N x y ,将1y x =-代入24y x =可得210x bx -+=,∴126x x +=,弦12628MN x x P =++=+=.故选D .点睛:这个题目考查了抛物线和直线的位置关系,在处理直线和圆锥曲线的位置关系时,往往先根据题意合理设出直线方程,再联立直线和圆锥曲线方程,但要注意“直线不存在斜率”的特殊情况,如本题中利用直线不存在斜率时探究其定点,给一般情形找到了目标.而抛物线中和焦半径有关的题型,经常和抛物线的定义联系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
北京市五中2020-2021学年高二数学上学期期中考试试题
含答案(文)
一、
选择题(本大题共8小题,每小题4分,共32分.在每小题给出的四个选项中,
只有一项是符合题目要求的,将答案填在第4页的表格中)
1. 某校选修乒乓球课程的学生中,高一年级有30名,高二年级有40名,现用分层抽样的方法在这70名学生中抽取一个样本,已知在高一年级的学生中抽取了6名,则
在
高
二
年
级
的
学
生
中
应
抽
取
的
人
数
为
( )
.A 6 .B 8 .C 10 .D 12
2.设椭圆的两个焦点分别为121,,F F F 过作椭圆长轴的垂线交椭圆于点P ,若12F PF ∆为等腰三角形,则椭圆的离心率为 ( )
.
A 2
2 .B 21
2
- .C 22- .D 21- 3.在某项体育比赛中,七位裁判为一选手打出的分数如下: 90 89 90 95 93 94 93
去掉一个最高分和一个最低分后,所剩数据的平均值和方差分别为
( )
.A 92,2 .B 92,2.8 .C 93,2 .D 93,2.8
4.椭圆2222135x y m n +=和双曲线22
2
2123x y m n
-=有公共的焦点,那么双曲线的渐近线方程是 ( )
.A 152x y =±
.B 152y x =± .C 34y x =± .D 3
4
x y =±
5. 从{1,2,3,4,5}中随机选取一个数为a ,从{1,2,3}中随机选取一个数为b ,则b >a 的概率是
( )
.A
45 .B 35 .C 25
.D 1
5
6. 已知以F 为焦点的抛物线24y x =上的两点,A B 满足3AF FB =,则弦AB 的中点到准线的距离为 ( )
.
A 43
.B 8
3 .C 2 .D 4
7.P 为双曲线
22
1916x y -=的右支上一点,M N 、分别是圆225)4x y ++=(和22(5)1x y -+=上的点,则PM PN -的最大值为 ( )
.A 6 .B 7 .C 8 .D 9
8. 已知抛物线22(0)y px p =>与圆222()(0)x a y r a -+=>有且只有一个公共点,则 ( )
.A r a p == .B r a p =≤ .C r a p <≤ .D r a p <=
二、填空题(本大题共6小题,每小题4分,共24分,将答案填在第3页的表格中) 9.抛物线2(0)y ax a =≠的焦点坐标为 .
10.平面上画了一些彼此相距2a 的平行线,把一枚半径为()r r a <的硬币任意掷在这
个平面上,则硬币不与任何一条平行线相碰的概率是__________________.
11.点A B 、的坐标分别为)0,5(-,)0,5(,直线AM BM 、相交于点M ,且它们的斜率之积为
4
9
,则点M 的轨迹方程为 . 12.点P 是椭圆22
154
y x +=上的一点,12,F F 是焦点,且︒=∠6021PF F ,则21PF F ∆的
面积为 .
13.已知双曲线22
221(0,0)x y a b a b
-=>>的左右焦点分别为12,F F ,点P 在双曲线的右
支,且124PF PF =,则此双曲线的离心率e 的取值范围为 . 14.一个圆柱形容器里装有水,放在水平地面上,现将该容器倾斜,这时水面是一个椭圆面(如图),当圆柱的母线AB 与地面所成角6
πθ=时,椭圆的离心率
是 .
75 80 85 90 95 100 分数
频率
组距
0.01
0.02
0.04
0.06
0.07
0.03 0.05
三、解答题(本大题共3小题,共44分) 15. 某高校在2011年的自主招生考试成绩
中随机抽取100名学生的笔试成绩,按成绩 分组:第1组[75,80),第2组[80,85), 第3组[85,90),第4组[90,95),第5组
[95,100]得到的频率分布直方图如图所示. (1) 分别求第3,4,5组的频率;
(2) 若该校决定在笔试成绩高的第3,4,5组
中用分层抽样抽取6名学生进入第二轮面试,求第3,4,5组每组各抽取多少名学生进入第二轮面试?
(3) 在(2)的前提下,学校决定在这6名学生中随机抽取2名学生接受甲考官的面试,求
第4组至少有一名学生被甲考官面试的概率.
16.在平面直角坐标系xoy 中,抛物线C 的顶点在原点,经过点(2,2)A ,其焦点F 在x
轴上,
(1)求抛物线C 的标准方程;
(2)求过点F ,且与直线OA 垂直的直线方程;
(3)设过点(,0),(0)M m m >的直线交抛物线C 于D E 、两点,DM ME 2=,记D
和E 两点间的距离为()f m ,求()f m 关于m 的表达式.
17.已知椭圆2
21:12
x C y +=,抛物线22:2C y x =+,点P 是2C 上的动点,过点P 作抛物线2C 的切线l ,交椭圆1C 于A B 、两点, (1)当l 的斜率是2时,求AB ;
(2)设抛物线2C 的切线方程为y kx b =+,当AOB ∠是锐角时,求b 的取值范围.
文科期中参考答案
一、选择题答案:
二、填空题答案: 9. )410(a ,; 10. ()a r
P A a
-=
; 11. 1009422=-y x ; 12. 334 ; 13. ]3
5
,1( ; 14. 32
三、解答题答案。
