空间向量运算的坐标表示课件ppt(北师大版选修2-1)
合集下载
2-2空间向量的运算(北师大版选修2-1)ppt课件

课前探究学习
课堂讲练互动
活页限时训练ຫໍສະໝຸດ 【训练 1】 已知四边形 ABCD 为正方形,P 是 ABCD 所在平面 外一点,P 在平面 ABCD 上的射影恰好是正方形 ABCD 的中心 O.Q 是 CD 的中点,求下列各式中 x、y 的值: (1)O→Q=P→Q+xP→C+yP→A; (2)P→A=xP→O+yP→Q+P→D.
课前探究学习
课堂讲练互动
活页限时训练
3.平面向量的数乘运算推广到空间向量的数乘运算及其运算律 仍然是成立的. 4.因为空间任意两个向量都是共面的,所以空间向量共线定理 与平面向量共线定理是相同的;定理中 b≠0 不可丢掉,否则实 数 λ 不一定存在,且不一定唯一.如 a≠0,b=0,则 λ 不存在, a=b=0,则 λ 不唯一. 5.在 a=λb 中,对于确定的 λ 与 b,a=λb 可以表示空间中与 b 平行且长度为|λb|的所有的向量.
课前探究学习
课堂讲练互动
活页限时训练
6.向量的数量积是一个数量(数值),而不是向量,它的值为两 向量的模与两向量夹角的余弦值的乘积,其符号由夹角的余弦 的符号确定. 7.两向量的数量积是两个向量之间的一种乘法,与以前学过的 数的乘法有区别,在书写时要严格区分开来,数量积写成 a·b, 而不能写成 ab,亦不能写成 a×b. 8.a·b 的几何意义:a 与 b 的数量积等于 a 的模与 b 在 a 上的 投影|b|cos〈a,b〉的乘积,也可等于 b 的模与 a 在 b 上的投影 |a|cos〈a,b〉的乘积.
课前探究学习
课堂讲练互动
活页限时训练
规律方法 对于向量算式的化简问题,要注意观察每步中所涉 及的向量在图形中的位置特点及封口多边形法则的应用.特别 注意:始点相同的三个不共面的向量之和,等于以这三个向量 为棱的平行六面体的以公共始点为起点的对角线所表示的向 量,这是平面向量加法的平行四边形法则向空间的推广,可以 称作空间向量加法的平行六面体法则.
2-2空间向量的运算课件(北师大版选修2-1)

3.平面向量的数乘运算推广到空间向量的数乘运算及其运算律 仍然是成立的. 4.因为空间任意两个向量都是共面的,所以空间向量共线定理 与平面向量共线定理是相同的;定理中 b≠0 不可丢掉,否则实 数 λ 不一定存在,且不一定唯一.如 a≠0,b=0,则 λ 不存在, a=b=0,则 λ 不唯一. 5.在 a=λb 中,对于确定的 λ 与 b,a=λb 可以表示空间中与 b 平行且长度为|λb|的所有的向量.
• §2 空间向量的 运算
【课标要求】 1.掌握空间向量的加减运算及其运算律,能借助图形理解空间 向量及其运算的意义. 2.掌握空间向量数乘运算的定义和运算律,了解共线向量定理. 3.掌握两个向量的数量积概念、性质和计算方法及运算规律. 4.掌握两个向量的数量积的主要用途,会用它解决立体几何中 一些简单的问题. 【核心扫描】 1.空间两个向量共线定理、空间向量的线性运算及数量积.(重 点) 2.向量的数量积.(难点) 3.向量夹角与数量积的关系.(疑点)
(4)分配律:λ(a+b)=λa+λb .
(λ+μ)a= λa+μa(λ∈R,μ∈R)
.
(5)结合律:(λμ)a= λ(μa)(λ∈R,μ∈R)
.
5.空间两个向量 a 与 b(b≠0)共线的充分必要条件是存在实数
λ,使得a=λb 或者b=λa .
ห้องสมุดไป่ตู้
6.(1)数量积的定义 空间两个向量 a 和 b 的数量积是一个数,等于|a||b|·cos〈a,b〉.记 作 a·b . (2)数量积的运算律 ①交换律:a·b=b·a . ②分配律:a·(b+c)=a·b+a·c .
题型四 数量积的综合应用
【例4】
(12分)如图所示,已知平行六面体ABCDA1B1C1D1
北师大版选修2空间向量运算的坐标表示课件

53
53
53
13
A. 4
B. 2
C. 2
D. 2
解析 AB 中点 M(2,32,3),又 C(0,1,0),
所以C→M=(2,12,3),
故 M 到 C 的距离为 CM=|C→M|=
22+122+32=
53 2.
北师大版选修2空间向量运算的坐标表示
解析答案
12345
3.设 O 为坐标原点,M(5,-1,2),A(4,2,-1),若O→M=A→B,则点 B 应为( B )
北师大版选修2空间向量运算的坐标表示
自主学习
答案
|a|= a·a= a21+a22+a23;
cos〈a,b〉=|aa|·|bb|=
a1b1+a2b2+a3b3 a21+a22+a23 b21+b22+b23.
知识点三 空间两点间的距离 已知点 A(a1,b1,c1),B(a2,b2,c2),则 A,B 两点间的距离 dAB=|A→B|
学习目 标
1.理解空间向量坐标的概念,会确定一些简单几何体的顶点坐标. 2.掌握空间向量的坐标运算规律,会判断两个向量的共线或垂直. 3.掌握空间向量的模、夹角公式和两点间距离公式,并能运用这些 知识解决一些相关问题.
北师大版选修2空间向量运算的坐标表示
栏目索 引
知识梳理 题型探究 当堂检测
自主学习 重点突破 自查自纠
北师大版选修2空间向量运算的坐标表示
Байду номын сангаас
答案
返回
题型探究
重点突破
题型一 空间直角坐标系与空间向量的坐标表示 例 1 设 O 为坐标原点,向量O→A=(1,2,3),O→B=(2,1,2),O→P=(1,1,2), 点 Q 在直线 OP 上运动,则当Q→A·Q→B取得最小值时,求点 Q 的坐标.
2.2 空间向量的运算 课件(北师大选修2-1)
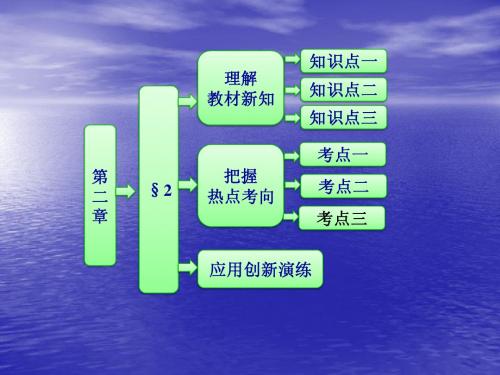
[精解详析]
∵E,H 分别是 AB,AD 的中点,
∴EH = AH -AE 1 1 = AD - AB 2 2 1 = (AD -AB ) 2 1 = BD . 2
2 2 又∵CF=2FB,CG=2GD,∴ C F = C B ,C G = C D .
λa的模是a的
模的 |λ| 倍
(3)空间向量的数乘运算律:
①交换律:λa= aλ (λ∈R); λa+λb ,
②分配律:λ(a+b)=
(λ+μ)a=λa+μ a(λ∈R,μ∈R); ③结合律:(λμ)a= λ(μa) (λ∈R,μ∈R). (4)定理:空间两个向量a与b(b≠0)共线的充分必要条件 是存在实数λ,使得 a=λb .
b=0 ; ②a⊥b ⇔ a·
a· b ③cos〈a,b〉= |a||b| (a≠0,b≠0.)
a (4)对任意一个非零向量, |a| 叫作向量 a 的单位向量, 把
记作 a0.a0 与 a 同 方向.
与平面向量类似,空间向量的加减、数乘、数量积运算 有如下特点 1.空间向量的加减法满足平行四边形和三角形法则,结 果仍是一个向量. 2.空间向量的数乘运算,结果仍是一个向量,方向取决 于λ的正负,模为原向量模的|λ|倍.
设 a,b,c 是任意空间向量,类比平面向量的数量 积,回答以下问题. 问题 1:由 a· b=0,一定能推出 a=0 或 b=0 吗?
π 提示:不一定,也可能〈a,b〉= . 2
问题 2:由 a· b=a· 能得到 b=c 吗? c
提示:不一定.
问题 3:(a· b)c=a(b· c)成立吗?
提示:不一定.
2
高中数学 空间向量运算的坐标表示参考课件 北师大版选修21

a b a1b1 a2b2 a3b3 ;
a // b a b a1 b1,a2 b2 ,a3 b3 ( R) ; a b a b 0 a1b1 a2b2 a3b3 0 ;
第六页,共21页。
二、距离与夹角
1.距离(jùlí)公式 (1)向量(xiàngliàng)的长度 (模)公式
间直角坐标系 O x中yz的坐标,记
作在空a 间(直a1角, a坐2 ,标a3系). O xyz中,对空间
任一点 ,存A在唯一的有序实数
组 (x, y, z) ,使 OA xi y j zk ,有
序实数组 (x, y, z叫)作向量 O在A空间
直角坐标系 O x中yz的坐标,
记作 标,
叫zA竖(x坐, y标, z.),x叫横坐标,
则 E(1 , 1 , 1 ) , F ( 1 , 1 , 1)
2
22
所以 EF ( 1 , 1 , 1 ) , 2 22
又 A1(1 , 0 , 1) , D(0 , 0 , 0) ,
所以 所以
DA1 EF
(1 , 0 DA1
, 1) ( 1
2
,
1 2
,
1 2
)
(1
,
0
,
1)
0
,
因此 EF DA1 ,即 EF DA1
B
OM
1 2
(OA
OB)
1 2
(3 ,
3 ,1)1 ,0,52,
3 2
,
3
,
O
∴点 M的坐标是
2
,
3 2
,
3.
d A,B (1 3)2 (0 3)2 (5 1)2 29 .
第十一页,共21页。
a // b a b a1 b1,a2 b2 ,a3 b3 ( R) ; a b a b 0 a1b1 a2b2 a3b3 0 ;
第六页,共21页。
二、距离与夹角
1.距离(jùlí)公式 (1)向量(xiàngliàng)的长度 (模)公式
间直角坐标系 O x中yz的坐标,记
作在空a 间(直a1角, a坐2 ,标a3系). O xyz中,对空间
任一点 ,存A在唯一的有序实数
组 (x, y, z) ,使 OA xi y j zk ,有
序实数组 (x, y, z叫)作向量 O在A空间
直角坐标系 O x中yz的坐标,
记作 标,
叫zA竖(x坐, y标, z.),x叫横坐标,
则 E(1 , 1 , 1 ) , F ( 1 , 1 , 1)
2
22
所以 EF ( 1 , 1 , 1 ) , 2 22
又 A1(1 , 0 , 1) , D(0 , 0 , 0) ,
所以 所以
DA1 EF
(1 , 0 DA1
, 1) ( 1
2
,
1 2
,
1 2
)
(1
,
0
,
1)
0
,
因此 EF DA1 ,即 EF DA1
B
OM
1 2
(OA
OB)
1 2
(3 ,
3 ,1)1 ,0,52,
3 2
,
3
,
O
∴点 M的坐标是
2
,
3 2
,
3.
d A,B (1 3)2 (0 3)2 (5 1)2 29 .
第十一页,共21页。
北师大版选修2-1高中数学2.3《向量的坐标表示和空间向量基本定理》(第2课时)ppt课件

A.(-1,3,-3)
B.(9,1,1)
C.(1,-3,3)
D.(-9,-1,-1)
[答案] B [解析] ∵O→M=A→B=O→B-O→A,
∴O→B=O→M+O→A=(9,1,1).故选 B.
2.向量 a=(-1,2,3),则向量 a 的模是( )
A.14
B. 14
C.11
D. 11
[答案] B
• 3.运用空间向量解决立体几何问题,先要考察原图形 是否方便建立直角坐标系,将问题中涉及的点、线(向 量)、面(向量的线性组合)用坐标表示,如果容易表示 则先建系,将点用坐标表示出来,然后,利用垂直、 平行、共面的条件通过向量运算推证有关结论,利用 向量的模、向量夹角的计算公式来求线段长度及角, 最后将计算的结果转化为几何结论;当图形中的点不 方便用坐标表示时,可直接设出向量的基底,将各条
• (4)(a+b)·(a-b).
• [分析] 利用空间向量的运算法则坐标形式求 解.
• [解析] (1)a+b=(2,-1,-2)+(0,-1,4)
• =(2+0,-1-1,-2+4)=(2,-2,2).
• (2)a-b=(2,-1,-2)-(0,-1,4)
• =(2-0,-1+1,-2-4)=(2,0,-6).
(2)由题意可知,a=(1,1,0),b=(-1,0,2),所以 ka+b=(k-1, k,2),ka-2b=(k+2,k,-4),又(ka+b)⊥(ka-2b),所以(ka+ b)·(ka-2b)=0,所以(k-1,k,2)·(k+2,k,-4)=k2+k-2+k2- 8=0,即 2k2+k-10=0,所以 k=2 或 k=-52.
→→ OA·OB →→
=-1.∴〈O→A,O→B〉=π.
2.2《空间向量的运算》课件(北师大版选修2-1)
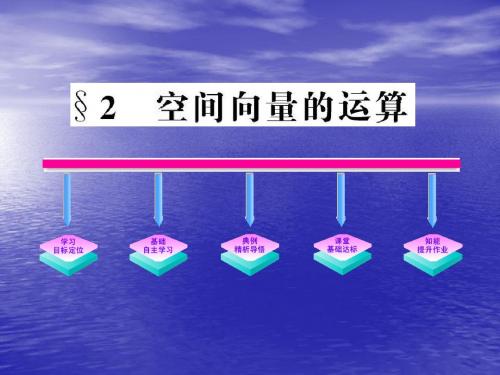
何值时BP·CQ的值最大?并求出这个最大值.
【解题提示】把BP·CQ化成关于θ的函数关 系式,再求函数最值.
【解析】
学习目标定位
基础自主学习
典例精析导悟
课堂基础达标
知能提升作业
一、选择题(每题4分,共16分) 1.下列命题中不正确的是(
(A)| 0 |=0 (C)| a |2= a 2
)
(B) a - a =0 (D) a - a = 0 【解析】选B. a - a = 0 ≠0
【解题提示】正确地画出辅助线,利用向量共线定理求
解.
【解析】EF与AD+BC共线.连接AC,取AC中点G,连接EG,FG,
∴GF= 1 AD,EG= 1 BC.
2 1 2 2 1 1 BC= (AD+BC). 2 2
又∵GF,EG,EF共面,
∴EF=GF+EG= AD+
即EF与AD+BC共线.
8.已知空间四边形OABC各边及对角线长都相等,E,F分别为
AB,OC的中点,求异面直线OE与BF夹角的余弦值.
【解析】如图,设OA= a ,OB= b ,OC= c ,且| a |=| b |=| c |=1, 易知∠AOB=∠BOC=∠AOC= , 3
则 a · b = b·c = c·a = . 2
1
9.(10分)如图,在Rt△ABC中,已知BC=a,若长为 2a的线段PQ以点A为中点,问PQ与BC的夹角θ 取
二、填空题(每题4分,共8分) 5.化简:
(1)
=_____________;
(2)平行六面体A)AB-AC+BC-BD-DA =CB+BC-(BD+DA) =0 -BA =AB
向量的坐标表示和空间向量的基本定理-北师大版高中数学选修2-1ppt课件

a b (a1b 1,a2b2,a3b3)
a (a1,a2,a3)( R )
a b a1b1a2b2a3b3
a//b a 1b 1 ,a 2b 2 ,a 3b 3 ( R )
ab a 1 b 1 a 2 b 2 a 3 b 3 0 . ( a ,b 都 不 是 零 向 量 )
(2)当
时,
反向;
ABBA,求向量 CA在BC上的投.影 上的分向量。
=(x2-x1 , y2-y1 , z2-z1)
解:设
1 是1 的中点,则
1
(4)基底给定时,分解形式唯一.
解:(2)向量 CA在BC上的投影为 P=(x,y,z)其中x叫做点A的横坐标,y叫做点A的纵坐标,z叫做点A的竖坐标. 1
解:OQ OM MQ 1 OA 1 MN 1 OA 1 (ON OM) 23 23
1 OA 1 (ON 1 OA)
O
23 2
1 OA 1 1 (OB OC)
M
3 32
1 OA 1 OB 1 OC 36 6
Q
A
P
C
B
N
空间向量运算 的坐标表示
空间直角坐标系 z
从空间某一个定点O引三条
我 们 把 aix,ajy,akz分 别 称 为 向 量 a 在 x轴 ,y轴 ,z轴 正 方 向 上 的 投 影 . 向量的坐标等于 标它轴在正坐方向上. 的
一般地,若b0为b的单位向量, 称ab0 | a | cos a,b 为向量a在向量b上的投影.
例2.如图,已知单位正方体 ABCD-A1B1C1D1,求
D1F1
z
A1B1 ,求
4
B
E
1 与 D F 1 所成的角的余弦值.
a (a1,a2,a3)( R )
a b a1b1a2b2a3b3
a//b a 1b 1 ,a 2b 2 ,a 3b 3 ( R )
ab a 1 b 1 a 2 b 2 a 3 b 3 0 . ( a ,b 都 不 是 零 向 量 )
(2)当
时,
反向;
ABBA,求向量 CA在BC上的投.影 上的分向量。
=(x2-x1 , y2-y1 , z2-z1)
解:设
1 是1 的中点,则
1
(4)基底给定时,分解形式唯一.
解:(2)向量 CA在BC上的投影为 P=(x,y,z)其中x叫做点A的横坐标,y叫做点A的纵坐标,z叫做点A的竖坐标. 1
解:OQ OM MQ 1 OA 1 MN 1 OA 1 (ON OM) 23 23
1 OA 1 (ON 1 OA)
O
23 2
1 OA 1 1 (OB OC)
M
3 32
1 OA 1 OB 1 OC 36 6
Q
A
P
C
B
N
空间向量运算 的坐标表示
空间直角坐标系 z
从空间某一个定点O引三条
我 们 把 aix,ajy,akz分 别 称 为 向 量 a 在 x轴 ,y轴 ,z轴 正 方 向 上 的 投 影 . 向量的坐标等于 标它轴在正坐方向上. 的
一般地,若b0为b的单位向量, 称ab0 | a | cos a,b 为向量a在向量b上的投影.
例2.如图,已知单位正方体 ABCD-A1B1C1D1,求
D1F1
z
A1B1 ,求
4
B
E
1 与 D F 1 所成的角的余弦值.
2-3-3空间向量运算的坐标表示课件(北师大版选修2-1)

11 → → → 37 AC=OC-OA=-10,1,10.
课前探究学习
课堂讲练互动
活页限时训练
题型三 【例3】
长度、夹角问题
(12分)如图,直三棱柱ABCA1B1C1,底面△ABC中,
CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别为A1A、 A1B1的中点. (1)求BM的长; → → (2)求cos〈BA1,CB1〉的值; (3)求证:A1B⊥C1N. 审题指导 建立适当的直角坐标系,用坐标形式表示向量,套 用数量积、夹角、长度公式即可.
→ 由已知可得:AB =(4,5,-1)-(2,-1,2)=(2,6,-
→ 3),AC=(-2,2,3)-(2,-1,2)=(-4,3,1). 1 → 1 → → (1) OP = 2 ( AB - AC )= 2 [(2,6,-3)-(-4,3,1)]=
3 3 3, ,-2,所以P点的坐标为3, ,-2; 2 2
课前探究学习
课堂讲练互动
活页限时训练
题型二 坐标形式下平行与垂直条件的应用 【例2】 设a=(1,5,-1),b=(-2,3,5). (1)若(ka+b)∥(a-3b),求k的值; (2)若(ka+b)⊥(a-3b),求k的值. [思路探索] 利用空间向量平行和垂直的充要条件的坐标表达
形式求解本题.
课前探究学习 课堂讲练互动 活页限时训练
自学导引 1.空间向量的直角坐标运算律 设a=(a1,a2,a3),b=(b1,b2,b3),则 (1)a+b= (a1+b1,a2+b2,a3+b3); (2)a-b= (a1-b1,a2-b2,a3-b3); (3)λa= (λa1,λa2,λa3) (4)a· b= a1b1+a2b2+a3b3 (λ∈R); ; ;
2019-2020高中北师版数学选修2-1 第2章 §3 3.3 空间向量运算的坐标表示课件PPT

第二章 空间向量与立体几何
§3 向量的坐标表示和空间向量基本定理 3.3 空间向量运算的坐标表示
栏目导航
学习目标:1.掌握空间向量线性运算及数量积的坐标表示.(重 点) 2.能够利用空间向量的坐标运算求空间向量的长度与夹角.(难 点)
栏目导航
自主预习 探新知
栏目导航
1.空间向量的坐标运算
设 a=(a1,a2,a3),b=(b1,b2,b3), ①a+b= (a1+b1,a2+b2,a3+b3) , ②a-b= (a1-b1,a2-b2,a3-b3) , ③λa= (λa1,λa2,λa3) , ④a·b= a1b1+a2b2+a3b3 .
栏目导航
2.空间向量的平行、垂直及模、夹角 设 a=(a1,a2,a3),b=(b1,b2,b3),则 ①a∥b⇔a=λb⇔ a1=λb1,a2=λb2,a3=λb3 ②a⊥b⇔a·b=0⇔ a1b1+a2b2+a3b3=0 ; ③|a|= a·a=____a_21_+__a_22+__a_23____; ④cos〈a,b〉=|aa|·|bb|= a21+a1ab221++aa232b2b+21+a3bb223+b23.
栏目导航
1.(变条件)若将本例(2)条件“若ka+b与ka-2b互相垂直”改为
“若ka+b与ka-2b互相平行”,求k的值.
[解] 由ka+b与ka-2b互相平行,得
ka+b=λ(ka-2b),即(k-1,k,2)=λ(k+2,k,-4),
k-1=λ(k+2),
所以k=λk,
解得k=0.
2=-4λ,
栏目导航
[解] (1)因为B→C=(-2,-1,2),且c∥B→C, 所以设c=λB→C=(-2λ,-λ,2λ), 得|c|= (-2λ)2+(-λ)2+(2λ)2=3|λ|=3,解得λ=±1. 即c=(-2,-1,2)或c=(2,1,-2).
§3 向量的坐标表示和空间向量基本定理 3.3 空间向量运算的坐标表示
栏目导航
学习目标:1.掌握空间向量线性运算及数量积的坐标表示.(重 点) 2.能够利用空间向量的坐标运算求空间向量的长度与夹角.(难 点)
栏目导航
自主预习 探新知
栏目导航
1.空间向量的坐标运算
设 a=(a1,a2,a3),b=(b1,b2,b3), ①a+b= (a1+b1,a2+b2,a3+b3) , ②a-b= (a1-b1,a2-b2,a3-b3) , ③λa= (λa1,λa2,λa3) , ④a·b= a1b1+a2b2+a3b3 .
栏目导航
2.空间向量的平行、垂直及模、夹角 设 a=(a1,a2,a3),b=(b1,b2,b3),则 ①a∥b⇔a=λb⇔ a1=λb1,a2=λb2,a3=λb3 ②a⊥b⇔a·b=0⇔ a1b1+a2b2+a3b3=0 ; ③|a|= a·a=____a_21_+__a_22+__a_23____; ④cos〈a,b〉=|aa|·|bb|= a21+a1ab221++aa232b2b+21+a3bb223+b23.
栏目导航
1.(变条件)若将本例(2)条件“若ka+b与ka-2b互相垂直”改为
“若ka+b与ka-2b互相平行”,求k的值.
[解] 由ka+b与ka-2b互相平行,得
ka+b=λ(ka-2b),即(k-1,k,2)=λ(k+2,k,-4),
k-1=λ(k+2),
所以k=λk,
解得k=0.
2=-4λ,
栏目导航
[解] (1)因为B→C=(-2,-1,2),且c∥B→C, 所以设c=λB→C=(-2λ,-λ,2λ), 得|c|= (-2λ)2+(-λ)2+(2λ)2=3|λ|=3,解得λ=±1. 即c=(-2,-1,2)或c=(2,1,-2).
高中数学第二章空间向量与立体几何2.3.3空间向量运算的坐标表示课件北师大版选修2_1

3.已知 A 点的坐标是(-1,-2,6),B 点的坐标 是(1,2,-6),O 为坐标原点,则向量O→A与O→B的 夹角是________.
解析: ∵O→A=(-1,-2,6),O→B=(1,2,-6) ∴O→A·O→B=-1-4-36=-41 ∴|OA|= -12+-22+62= 41
则 C 的坐标是( )
A.-56,-45,-85
B.65,-45,-85
C.-56,-45,85
D.65,45,85
解析: 由 A(3,4,5),B(0,2,1),得A→B=(-3,-2, -4) ∴25A→B=-65,-45,-85 ∴O→C=-56,-45,-85 答案: A
2.a=(2x,1,3),b=(1,-2y,9),如果 a 与 b 为共
线向量,则( )
A.x=1,y=1
B.x=12,y=-12
C.x=16,y=-32
D.x=-16,y=32
解析: ∵a=(2x,1,3)与 b=(1,-2y,9)共线, 故有21x=-12y=39, ∴x=16,y=-32.故选 C. 答案: C
a⊥b
_a_1_b_1_+__a_2b_2_+__a_3_b_3=__0___
|a|
__a_21_+〈a,b〉
a1b1+a2b2+a3b3 __a_21_+__a_22+__a_23__b_21_+__b_22_+__b_23 ___
[强化拓展] (1)空间两个向量和(差)的坐标等于它们对应坐标的 和(差). (2)实数与空间向量数乘的坐标等于实数与向量对 应坐标的乘积. (3)如果向量 b 与三个坐标平面都不平行时(即: x2y2z2≠0),空间向量 a∥b 的充要条件可以表达成 为 a∥b⇔xx12=yy12=zz12.
2020—2021数学北师大版选修2-1课件:第二章空间向量运算的坐标表示

4.已知向量a=(2,-1Fra bibliotek1),b=(t,1,-1)(t∈R),若 a∥b,则t=___-__2___.
1.求点的坐标时,一定要注意向量的起点是否在原点,在原 点时向量的坐标与终点的坐标相同;不在原点时,向量的坐 标加上起点的坐标才是终点的坐标. 2.对于平面向量a=(x1,y1),b=(x2,y2),若a∥b,则x1y2- x2y1=0.但对于空间向量a=(x1,y1,z1),b=(x2,y2,z2),若 a∥b,却无此类的结论.
空间向量的坐标运算
空间向量平行、垂直的坐标表示
B A
空间向量的模及夹角
易错警示
因忽视隐含条件致误
D
2.若A(m+1,n-1,3),B(2m,n,m-2n),C(m+3, n-3,9)(m,n∈R)三点共线,则m+n=_____0___.
3.若a=(2,3,-1),b=(-2,1,3),则a,b为邻边的平 行四边形的面积为________.
对应坐标的和(差) 实数与向量对应坐标
差
x1x2+y1y2+z1z2 和
× √ ×
×
√
2.已知a=(1,2,-3),b=(5,-7,8),则2a+b的坐标 为( A ) A.(7,-3,2) B.(6,-5,5) C.(6,-3,2) D.(11,-12,13) 解析:2a+b=2(1,2,-3)+(5,-7,8)=(2,4,-6) +(5,-7,8)=(7,-3,2).
3.若向量a=(1,1,x),b=(1,2,1),c=(1,1,1),满
足条件(c-a)·(2b)=-2,则x的值为( B )
A.1
B.2
C.3
D.4
解析:因为c-a=(0,0,1-x),2b=(2,4,2),所以(c-
高中数学北师大版选修2-1第二章3.3 《空间向量运算的坐标表示》ppt课件
⑥ 利用笔记抓住老师的思路。记笔记不仅有利于理解和记忆,而且有利于抓住老师的思路。
2019/8/29
最新中小学教学课件
31
谢谢欣赏!
返回
[一点通] 空间向量的坐标运算和平面向量的坐标运 算类似,两个向量的加、减、数乘运算就是向量的横坐标、 纵坐标、竖坐标分别进行加、减、数乘运算;空间两个向 量的数量积等于它们对应坐标的乘积之和.
返回
1.已知a=(1,0,-1),b=(1,-2,2),c=(-2,3,-1),
那么向量a-b+2c等于
CA的夹角. 解: AB=(-2,-1,3),CA=(-1,3,-2),
| AB|= 4+1+9= 14,|CA|= 1+9+4= 14,
AB ·CA=2-3-6=-7,
∴cos〈 AB,CA〉=|
AB·CA = AB ||CA|
-7 14×
14=-12.
∵〈 AB,CA〉∈[0,π],∴〈 AB,CA〉=23π.
解: AB=(2,6,-3),=(-4,3,1). (1) OP =12(6,3,-4)=3,32,-2,则 P 点坐标为3,32,-2; (2)设 P 为(x,y,z),则 AP =(x-2,y+1,z-2) =12( AB-)=(3,32,-2),所以 x=5,y=12,z=0,
返回
4.已知a=(1,-5,6),b=(0,6,5),则a与b ( )
A.垂直
B.不垂直也不平行
C.平行且同向
D.平行且反向
解析:a·b=0-30+30=0,∴a⊥b.
答案:A
返回
5.在正方体ABCD-A1B1C1D1中,F是DC的中点,求证: AD⊥D1F.
证明:建立空间直角坐标系如图,不妨设 正方体的棱长为 1,则有 D(0,0,0),A(1,0,0), D1(0,0,1),F0,12,0. ∴ AD=(-1,0,0), D1F =0,12,-1. ∴ AD·D1F =(-1,0,0)·0,12,-1=0. ∴AD⊥D1F.
2019/8/29
最新中小学教学课件
31
谢谢欣赏!
返回
[一点通] 空间向量的坐标运算和平面向量的坐标运 算类似,两个向量的加、减、数乘运算就是向量的横坐标、 纵坐标、竖坐标分别进行加、减、数乘运算;空间两个向 量的数量积等于它们对应坐标的乘积之和.
返回
1.已知a=(1,0,-1),b=(1,-2,2),c=(-2,3,-1),
那么向量a-b+2c等于
CA的夹角. 解: AB=(-2,-1,3),CA=(-1,3,-2),
| AB|= 4+1+9= 14,|CA|= 1+9+4= 14,
AB ·CA=2-3-6=-7,
∴cos〈 AB,CA〉=|
AB·CA = AB ||CA|
-7 14×
14=-12.
∵〈 AB,CA〉∈[0,π],∴〈 AB,CA〉=23π.
解: AB=(2,6,-3),=(-4,3,1). (1) OP =12(6,3,-4)=3,32,-2,则 P 点坐标为3,32,-2; (2)设 P 为(x,y,z),则 AP =(x-2,y+1,z-2) =12( AB-)=(3,32,-2),所以 x=5,y=12,z=0,
返回
4.已知a=(1,-5,6),b=(0,6,5),则a与b ( )
A.垂直
B.不垂直也不平行
C.平行且同向
D.平行且反向
解析:a·b=0-30+30=0,∴a⊥b.
答案:A
返回
5.在正方体ABCD-A1B1C1D1中,F是DC的中点,求证: AD⊥D1F.
证明:建立空间直角坐标系如图,不妨设 正方体的棱长为 1,则有 D(0,0,0),A(1,0,0), D1(0,0,1),F0,12,0. ∴ AD=(-1,0,0), D1F =0,12,-1. ∴ AD·D1F =(-1,0,0)·0,12,-1=0. ∴AD⊥D1F.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
提示:(300,200,200 3).
问题2:驾驶室门受到的合力有多大?
提示:|F|=500 N.
空间向量的坐标运算:
若a=(x1,y1,z1),b=(x2,y2,z2)则: (x1+x2,y1+y2,z1+z2) (1)a+b= ; (x1-x2,y1-y2,z1-z2) (2)a-b= ; (3)λa= (λx1,λy1,λz1) ;
(1)a∥b;(2)a⊥b.
解:(1)①当x=0时,a=(1,0,1),b=(1,0,1),a=b, ∴x=0,满足a∥b; ②当x=1时,a=(1,1,0),b=(0,-3,2),
此时a不平行b,∴x≠1.
③当x≠0且x≠1时,
1-x2=-3, 1-x2 -3x x+1 由 a∥b⇔ = x = ⇔x+1 1 1-x =-3 1-x 综上所述,当 x=0 或 2 时,a∥b. (2)∵a⊥b⇔a· b=0 ⇔(1,x,1-x)· (1-x2,-3x,x+1)=0 10 ⇔1-x -3x +1-x =0,解得 x=± . 5
1.空间向量加法、减法、数乘、数量积、平行、垂直、 夹角的坐标表示都类似于平面向量,要类比记忆与理解.
2.空间向量的坐标运算,关键是要建立恰当的空间直
角坐标系,然后利用有关公式求解.要注意总结在长方体、 直三棱柱、正三棱柱、正四棱锥等特殊几何体中建立空间直 角坐标系的规律. 3.利用向量的坐标运算可证明向量的垂直与平行问题,
(10 分) (12 分)
[一点通] 在几何体中建立空间直角坐标系时,要充分利用几何 体本身的特点,以使各点的坐标易求.利用向量的坐标运算, 可使复杂的线面关系的论证、角及距离的计算变得简单.
7.已知空间三点,A(1,1,1),B(-1,0,4),C(2,-2,3),求 AB 与 CA 的夹角. 解: AB =(-2,-1,3), CA =(-1,3,-2), | AB |= 4+1+9= 14,|CA |= 1+9+4= 14, CA AB · =2-3-6=-7, -7 1 AB · CA = ∴cos〈 AB , CA 〉= =- . 2 14× 14 | AB || CA |
3a-2b=(9,15,-12)-(4,4,16)=(5,11,-28),
a· b=3×2+5×2-4×8=-16.
[一点通]
空间向量的坐标运算和平面向量的坐标运
算类似,两个向量的加、减、数乘运算就是向量的横坐标、 纵坐标、竖坐标分别进行加、减、数乘运算;空间两个向 量的数量积等于它们对应坐标的乘积之和.
(4)a· b= x1x2+y1y2+z1z2 ; (5)a∥b⇔a=λb⇔ x1=λx2 , y1=λy2 , z1=λz2 (λ∈R); (6)a⊥b⇔a· b=0⇔ x1x2+y1y2+z1z2=0 ;
2 2 (7)|a|= a· a= x1+y1+z2 ; 1
a· b (8)cos〈a,b〉= = |a||b|
(2 分)
(2)依题意,得 A1(1,0,2),B(0,1,0),C(0,0,0),B1(0,1,2).
∴ BA1 =(1,-1,2), CB1 =(0,1,2), ∴ BA1 · 1 =3,| BA1 |= 6,|CB1 |= 5. CB BA1 · 1 CB = 30. ∴cos〈 BA1 , CB1 〉= | BA1 || CB1 | 10
理解 教材新知
第 二 章
§ 3
3.3
考点一 把握 热点考向
考点二 考点三 应用创新演练
3.3
空间向量运算的坐标表示
2012 年 3 月,济青高速临沂段发生交通事故,一辆中型车严 重变形,驾驶员被困车内,消防官兵紧急破拆施救.为防止救援 造成的二次伤害,现从 3 个方向用力拉动驾驶室门,这 3 个力两 两垂直,其大小分别为|F1|=300 N,|F2|=200 N,|F3|=200 3 N. 问题 1:若以 F1、F2、F3 的方向分别为 x 轴、y 轴、z 轴的 正半轴建立空间直角坐标系,驾驶室门受到的力的坐标是什么?
角、向量的平行与垂直等问题.
[例1]
已知a=(3,5,-4),b=(2,2,8),求2a+3b,3a-2b,
a· b.
[思路点拨] 空间向量的加、减、数乘运算与平面向量的
加、减、数乘运算方法类似,向量的数量积等于它们对应坐标 乘积的和. [精解详析] 2a+3b=(6,10,-8)+(6,6,24)=(12,16,16),
[精解详析]
法一:设 M(x,y,z),由图可知:A(a,0,0),
B(a,a,0),C1(0,a,a),则 AC1 =(-a,a,a), AM =(x-a,y,z), BM = (x-a,y-a,z). ∵ BM ⊥ AC1 ,∴ BM · 1 =0, AC ∴-a(x-a)+a(y-a)+az=0,即 x-y-z=0. 又∵ AC1 ∥ AM ,∴x-a=-λa,y=λa,z=λa, 即 x=a-λa,y=λa,z=λa.
[精解详析] 以 C 为原点,以 CA 、 CB 、 CC1 为 x
轴、y 轴、z 轴的正方向,建立空间直角坐标系.
(1)依题意,得 B(0,1,0),N(1,0,1), BN =(1,-1,1), ∴| BN |= 3.
(4 分) (6 分) (8 分) (9 分)
(-aλ,aλ-a,aλ).∵BM⊥AC1, ∴ BM · 1 =0 AC 1 即 a λ+a λ-a +a λ=0,解得 λ= , 3
2 2 2 2
a a a 2a a a ∴ AM =-3,3,3, DM = DA+ AM = 3 ,3,3.
2a a a 2a a a 由①②得 x= ,y= ,z= .∴M 3 ,3,3. 3 3 3
①
②
法二:设 AM =λ AC1 =(-aλ,aλ,aλ), ∴ BM = BA + AM =(0,-a,0)+(-aλ,aλ,aλ)=
-14 - 14 = = , 14×2 17 2 17
sin〈 AB , AC 〉=
14 1- = 68
27 . 34
Байду номын сангаас
1 ∴S△ABC= | AB |·AC |· | sin〈 AB , AC 〉 2
1 = × 14×2 17× 2 27 =3 21. 34
2 2 2
⇔x=2.
[例 3]
(12 分)直三棱柱 ABC-A1B1C1 中,CA=CB=1,
∠BCA=90° ,棱 AA1=2,M、N 分别是 A1B1、A1A 的中点. (1)求 BN 的长; (2)求 cos〈 BA1 , CB1 〉的值. [思路点拨] CA,CB,CC1 两两垂直,可由此建立空间直 角坐标系,利用坐标运算求解向量的模及夹角.
2π ∵〈 AB , CA 〉∈[0,π],∴〈 AB , CA 〉= . 3
8.已知△ABC三个顶点的坐标分别为A(1,2,3),B(2,-1,
5),C(3,2,-5).求△ABC的面积.
解:由已知得=(1,-3,2), AC =(2,0,-8), ∴| AB |= 1+9+4= 14, | AC |= 4+0+64=2 17, AC AB · =1×2+(-3)×0+2×(-8)=-14, AB AC · cos〈 AB , AC 〉= | AB |·AC | |
4.已知a=(1,-5,6),b=(0,6,5),则a与b
(
)
A.垂直
C.平行且同向
B.不垂直也不平行
D.平行且反向
解析:a· b=0-30+30=0,∴a⊥b.
答案:A
5.在正方体ABCD-A1B1C1D1中,F是DC的中点,求证:
AD⊥D1F.
证明:建立空间直角坐标系如图,不妨设 正方体的棱长为 1, 则有 D(0,0,0), A(1,0,0),
1.已知a=(1,0,-1),b=(1,-2,2),c=(-2,3,-1), 那么向量a-b+2c等于 A.(0,1,2) C.(-4,8,-5) ( B.(4,-5,5) D.(2,-5,4) )
解析:a-b+2c=(1-1-2×2,0+2+6,-1-2-2)=( -4,8,-5).
答案:C
2.已知 A,B,C 三点的坐标分别为(2,-1,2),(4,5,-1), 1 (-2,2,3),求 P 点坐标,使(1) OP = ( AB - AC ); 2 1 (2) AP = ( AB - AC ). 2
1 即 P 点坐标为(5, ,0). 2
3.已知向量a=(1,-2,4),求同时满足以下三个条件的 向量c:①a· c=0;②|c|=10;③c与向量b=(1,0,0)垂直.
解:设 c=(x,y,z), x-2y+4z=0, 2 2 2 由三个条件得x +y +z =100, x=0, x=0, 解得y=4 5, z=2 5 x=0, 或y=-4 5, z=-2 5.
∴c=(0,4 5,2 5)或(0,-4 5,-2 5).
[例2]
如图所示,在棱长为a的正方体ABCD-
A1B1C1D1中,以D为坐标原点,DA,DC,DD1分别为x, y,z轴建立空间直角坐标系.过B作BM⊥AC1于M,求点 M的坐标.
[思路点拨]
写出A,B,C1的坐标,设出M的坐标,
利用条件BM⊥AC1及M在AC1上建立方程组,求解.
解: AB =(2,6,-3),=(-4,3,1). 1 3 3 (1) OP = (6,3,-4)=3,2,-2,则 P 点坐标为3,2,-2; 2 (2)设 P 为(x,y,z),则 AP =(x-2,y+1,z-2) 1 3 1 = ( AB -)=(3, ,-2),所以 x=5,y= ,z=0, 2 2 2
