矩阵乘积的逆(高等代数课件)
合集下载
线性代数之——矩阵乘法和逆矩阵
线性代数之——矩阵乘法和逆矩阵1. 矩阵乘法如果矩阵 B 的列为 b 1,b 2,b 3，那么 EB 的列就是 Eb 1,Eb 2,Eb 3。
EB =E [b 1b 2b 3]=[Eb 1Eb 2Eb 3]E (B 的第 j 列)=EB 的第 j 列置换矩阵（permutation matrix ）在消元的过程中，如果遇到了某⼀⾏主元的位置为 0，⽽其下⾯⼀⾏对应的位置不为 0，我们就可以通过⾏交换来继续进⾏消元。
如下的矩阵 P 23 可以实现将向量或者矩阵的第 2 、 3 ⾏进⾏交换。
P 23=10000101100001010135=15310000101241003065=24106503置换矩阵 P ij 就是将单位矩阵的第 i ⾏和第 j ⾏进⾏互换，当交换矩阵乘以另⼀个矩阵时，它的作⽤就是交换那个矩阵的第 i ⾏和第 j ⾏。
增⼴矩阵（augmented matrix ）在消元的过程中，⽅程两边的系数 A 和 b 都要进⾏同样的变换，这样，我们可以把 b 作为矩阵 A 的额外的⼀列，然后，就可以⽤消元矩阵E 乘以这个增⼴的矩阵⼀次性完成左右两边的变换。
E [A b ]=[EA E b ]100−2100124−2249−38−2−3710=24−220114−2−3710矩阵乘法的四种理解如果矩阵 A 有 n 列， B 有n ⾏，那么我们可以进⾏矩阵乘法 AB 。
假设矩阵 A 有 m ⾏ n 列，矩阵 B 有 n ⾏ p 列，那么 AB 是 m ⾏ p 列的。
(m ×n )(n ×p )(m ×p )m ⾏n 列n ⾏p 列m ⾏p 列矩阵乘法的第⼀种理解⽅式就是⼀个⼀个求取矩阵 AB 位于 (i ,j ) 处的元素(AB )ij =A 的第 i ⾏与 B 的第 j 列的内积=∑a ik b kj第⼆种理解，矩阵 AB 的列是 A 的列的线性组合AB =A [b 1b 2⋯b p ]=[Ab 1Ab 2⋯Ab p ]第三种理解，矩阵 AB 的⾏是 B 的⾏的线性组合[][][][][][][][][][][][][]AB=a1a2⋮a mB=a1Ba2B⋮a m B第四种理解，矩阵AB是所有A的列与B的⾏的乘积的和AB=[a1a2⋯a n]b1b2⋮b n=n∑i=1a i b i其中，⼀列乘以⼀⾏称为外积（outer product），(n×1)(1×n)=(n, n)，结果为⼀个 n×n 的矩阵。
高等数学第四章课件-矩阵的逆
( AB ) B −1 = EB −1 ,
例1 判断矩阵A是否可逆，若可逆，求其逆 . ⎛ 1 2 3⎞ (1) A = ⎜ 2 2 1 ⎟ ⎜ 3 4 3⎟ ⎝ ⎠ 1 2 3 −1 ∴ A 存在. 解: ∵ A = 2 2 1 = 2 ≠ 0, 3 4 3 2 1 2 1 2 2 A11 = = 2, A12 = − = −3, A13 = = 2, 3 3 3 4 4 3 同理可得, A21 = 6, A22 = −6, A23 = 2,
2 A − 3 A − 10 E = 0 相矛盾. 这与
所以, A + 2 E 与 A − 5 E 不同时可逆.
例2’’ 设方阵 A 满足 A2 − 3 A − 10 E = 0, 若 A ≠ 5 E , 证明: A + 2 E 不可逆. 证： （反证法） 假设A+2E可逆,
−1 2 ( A + 2 E ) ( A − 3 A − 10 E ) = 0 则 −1 即( A + 2 E ) ( A + 2 E )( A − 5 E ) = 0
⎛ A1 (3) 设 A1 , A2 是 n1 , n2 级可逆矩阵, A = ⎜ ⎝ A3 解: 因为 A1 , A2可逆
0⎞ ⎟. A2 ⎠
A1 ∴| A |= A3
0 =| A1 || A2 |≠ 0. A2
故A可逆. ⎛ X 11 −1 设A =⎜ ⎝ X 21 ⎛ A1 则 ⎜ ⎝ A3
⇒ B = 6( A − E ) .
−1 −1
B = 6( A − E )
−1
−1
⎡⎛ 2 ⎜ ⎢ = 6 ⎜0 ⎢ ⎜0 ⎢ ⎣⎝
0 4 0
ห้องสมุดไป่ตู้
高等数学逆矩阵ppt课件
268.
例7: 设方阵A满足矩阵方程 A2–A–2E = O, 证明: A, A+2E 都可逆, 并求它们的逆矩阵.
证明: 由 A2–A–2E=O, 得 A(A–E)=2E,
则
A
1
(
A
E
)
A1 E,
故A可逆, 且A-1 = 1 ( A E ).
2
2
又由 A2–A–2E=O, 得 (A+2E)(A–3E)+4E=O,
1 3
2, A12
2 3
1 3
3, A13
2 3
2 4
2,
同理可得 A21 6, A22 6, A23 2,
A31 4, A32 5, A33 2. 所以,
A
2 3
2
6 6
2
4 5
,
2
故
A1
|
1 A A|
1 3
1
2
3 3
1
5
122.
7
例3: 下列矩阵A,B是否可逆? 若可逆, 求其逆矩阵.
由伴随矩阵的性质: AA*= A*A = | A | E, 知
当| A | 0时,
A 1 A 1 A A E, | A| | A|
按逆矩阵的定义得, A1
1
A .
| A|
当| A | = 0 时, 称A为奇异矩阵, 否则称A为非奇异
矩阵.
4
由此可得, A是可逆矩阵的充分必要条件是A为非 奇异矩阵.
§2.3 逆 矩 阵
一、逆矩阵的概念和性质
在数的运算中, 当数 a 0 时, 有 aa-1 = a-1a = 1.
其中 a1 1 为a 的倒数, 或称a的逆(元). a
高等代数3-3矩阵的逆
... 0 A En ... A
A A
*
A11 A12 A 1n
A21 A22 A2 n
... An1 a11 ... An 2 a 21 ... Ann a n1
a12 a 22 an2
即矩阵A的逆矩阵是唯一的 .
B1 B1 E B1 ( AB2 ) ( B1 A )B2 EB2 B2
由于A的逆矩阵是唯一的，将A的唯一的逆矩阵记为 A1
则有
AA1 A1 A E
3. 单位矩阵E是可逆矩阵,且E 1 E .
4. 零矩阵O不是可逆矩阵.
a1 0 ... 0 0 a2 ... 0 例A 0 0 ... a n 其中 a1a2 ...an 0 a1 0 0 a2 0 0
可逆
1 0 3 0 1 A 1 2 3 1 2 3 3
1
1 3 A 2 6
A 0
不可逆
用公式法求二阶矩阵的 逆矩阵非常方便 .
a b 1 d d 1 若A , 且 A 0, 则 A . A c a c d
已知方阵A满足A3 A2 4 A 5 E O ,则( A 2 E )1 ________.
A2 A 2 E
1 2 0 已知AB B A , 其中B 2 1 0 ,则( A E )1 __________. 0 0 2
( A E )( B E ) E ( A E )1 B E
1 ( A 2E ) 2 1 例5 已知方阵A满足A A 4 E O ,则( A E ) __________. 2
高等代数课件PPT之第4章矩阵
策中甲的得分矩阵，规定胜者得1分，败者得-1分， 平手各得零分
0
1
–1
–1
0
1
1
–1
0
石头 剪子 布
乙方
石头 甲
剪子 方
布
0 1 1 答案 : 1 0 1 .
1 1 0
2.矩阵的线性运算（矩阵加法、 数乘） （1）矩阵相等
定义 设有两个m×n矩阵
a11
A
a21
am1
a12 a22
am2
总利润:862.5元
C矩其(1阵中)定AA义c与Baaij 12B设11的a矩i1乘baa阵 1积12j22是a一Ai 2b个2 jmaaa×i 12j ssnm矩sa阵,bbiBs12b11sCj bbbi12sj22ascinki b.j kjmbbn12nn,
a m1 i
a1m,22,, m; aj ms1,2,bs,1n
矩阵,也就是一个数.
4 1 0
例8
求
矩
阵A
1 2
0 1
3 0
21与B
1
2
1
1 0 3
3的 1
乘 积AB.
4
解
4 1 0
C AB
1 2
0 1
3 0
1
2
1
2
1
1 0 3
3 1 4
14 01 32 11 11 01 30 13 10 0 3 31 14
24 11 0 2 21
30
32
34
利润矩阵
由已知得
B
15
17.5
20
1220.5
总3.问A利B题2333润80241W:10521的这2L18330销一C售天31560F8利内7B1106.润，O5 总最0322B2和A小5711是号1.22这275500..多55牛里 设9少仔为7A.？裤5A23915872778.05..65521432.5（
0
1
–1
–1
0
1
1
–1
0
石头 剪子 布
乙方
石头 甲
剪子 方
布
0 1 1 答案 : 1 0 1 .
1 1 0
2.矩阵的线性运算（矩阵加法、 数乘） （1）矩阵相等
定义 设有两个m×n矩阵
a11
A
a21
am1
a12 a22
am2
总利润:862.5元
C矩其(1阵中)定AA义c与Baaij 12B设11的a矩i1乘baa阵 1积12j22是a一Ai 2b个2 jmaaa×i 12j ssnm矩sa阵,bbiBs12b11sCj bbbi12sj22ascinki b.j kjmbbn12nn,
a m1 i
a1m,22,, m; aj ms1,2,bs,1n
矩阵,也就是一个数.
4 1 0
例8
求
矩
阵A
1 2
0 1
3 0
21与B
1
2
1
1 0 3
3的 1
乘 积AB.
4
解
4 1 0
C AB
1 2
0 1
3 0
1
2
1
2
1
1 0 3
3 1 4
14 01 32 11 11 01 30 13 10 0 3 31 14
24 11 0 2 21
30
32
34
利润矩阵
由已知得
B
15
17.5
20
1220.5
总3.问A利B题2333润80241W:10521的这2L18330销一C售天31560F8利内7B1106.润，O5 总最0322B2和A小5711是号1.22这275500..多55牛里 设9少仔为7A.？裤5A23915872778.05..65521432.5（
高等代数课件--第四章 矩阵§4.4 矩阵的逆
１．伴随矩阵 定义： 设Aij矩阵A=(aij)nn中元素aij的 代数余子式，矩阵
A11 A 12 A* A1 n A21 A22 A2 n An1 An 2 adj A Ann
称为A的伴随矩阵．
性质 若A为n级方阵，则AA*=A*A=|A|En。
§4.4
矩阵的逆
一、可逆矩阵的定义：
设A为n级方阵，若有n级方阵B，使
AB=BA=En B为A的逆矩阵. 则称A为一个可逆矩阵，
注：
① 对于n级矩阵A，如果存在n级矩阵B， 使得AB=E，则A是可逆矩阵吗？
1=E
．
二、可逆矩阵的判定、求法
且(AB) 1=B 1A1.
问题：3）能否推广到有限个的情况?
4) 若A可逆，则A可逆,且(A ) 1=(A1).
5) 若A可逆, 则A*可逆且(A*) 1 =A/|A
6) 若A可逆, 则Ak可逆，且(Ak) 1 =(A1)k. 注：当|A|0时，定义A0=E，Ak =( A1)k。 当A, B可逆时，A+B不一定可逆。
的 逆 矩 阵 , an
其 中 a i 0, i 1, 2, ..., n .
推论
设A,B为n级方阵, 若AB=E，则A, B都 可逆，且 A1=B， B1= A．
三、逆矩阵的性质
1) 若A可逆，则A1可逆，且(A1) 1=A,
2) 若A可逆,0,则A可逆,且(A) 1= 1A1. 3) 若A,B为n级可逆方阵,则AB可逆,
例3
设方阵A满足A2 3A 10E=0，证明：
A，A 4E都可逆,并求它们的逆矩阵． 解：因为A(A3E)=10E, 所以A可逆,且 A1=(A-3E)/10 又(A+E)(A4E)=6E ,所以A4E可逆,且 (A4E)1=(A+E)/6
A11 A 12 A* A1 n A21 A22 A2 n An1 An 2 adj A Ann
称为A的伴随矩阵．
性质 若A为n级方阵，则AA*=A*A=|A|En。
§4.4
矩阵的逆
一、可逆矩阵的定义：
设A为n级方阵，若有n级方阵B，使
AB=BA=En B为A的逆矩阵. 则称A为一个可逆矩阵，
注：
① 对于n级矩阵A，如果存在n级矩阵B， 使得AB=E，则A是可逆矩阵吗？
1=E
．
二、可逆矩阵的判定、求法
且(AB) 1=B 1A1.
问题：3）能否推广到有限个的情况?
4) 若A可逆，则A可逆,且(A ) 1=(A1).
5) 若A可逆, 则A*可逆且(A*) 1 =A/|A
6) 若A可逆, 则Ak可逆，且(Ak) 1 =(A1)k. 注：当|A|0时，定义A0=E，Ak =( A1)k。 当A, B可逆时，A+B不一定可逆。
的 逆 矩 阵 , an
其 中 a i 0, i 1, 2, ..., n .
推论
设A,B为n级方阵, 若AB=E，则A, B都 可逆，且 A1=B， B1= A．
三、逆矩阵的性质
1) 若A可逆，则A1可逆，且(A1) 1=A,
2) 若A可逆,0,则A可逆,且(A) 1= 1A1. 3) 若A,B为n级可逆方阵,则AB可逆,
例3
设方阵A满足A2 3A 10E=0，证明：
A，A 4E都可逆,并求它们的逆矩阵． 解：因为A(A3E)=10E, 所以A可逆,且 A1=(A-3E)/10 又(A+E)(A4E)=6E ,所以A4E可逆,且 (A4E)1=(A+E)/6
5.6矩阵乘积的行列式及矩阵的逆
例4 解
1 求方阵 A 2 3
1 2 2 4 3 3 A 2 3 1
2 2 4
3 1 的逆矩阵. 3
2
A1存在.
又
6 4 2 A 3 6 5 , 2 2 2
3 2 6 4 1 2 1 1 故 A 1 A 3 6 5 3 2 3 5 2 . A 2 1 1 1 2 2 2
a a 解： A 11 12 , A* a22 a12 , a a a22 21 21 a11
A
1
1 1 * A a11a22 a12a21 | A|
a22 a 21
a12 . a11
例2: 单位矩阵E:
解 A =2, 11
A12 = 3 , A22 = 6 ,
A13 = 2 , A23 = 2 , A33 = 2 ,
所以:
6 4 2 A* 3 6 5 . 2 2 2
A21 = 6 ,
A31 = 4 , A32 = 5 ,
(2).用伴随矩阵求逆矩阵:
1 0 (A C) 2 0 1
1
例1：设 B
2
1 证明: A 可逆且 A 3E A . 1 3 2 1 2 证 A 3E A A A 2 2 2 3 1 2 E B E B 2 2
1
a 0, b 1, c 1, d 2.
a b B c d
BA
2 1 0 1 0 1 2 1 1 0 , 1 0 1 2 1 2 1 0 0 1
逆矩阵ppt课件
例 5 利用逆矩阵求解线性方程组
32xx11x22
x2
x3 3, 5x3 2,
3x1 2x2 3x3 1.
解
2 2 1
令
Hale Waihona Puke A3 31 2
53 ,
x1 3
则
A
x2
2
.
x3 1
7 4 9
由例2知，A1
6
3
3
7
,
2 4
x1
3 7 4 9 3 4
则
A21 A22 A23
A31
A32
A33
M11 M21 M31 7 4 9
M12
M 22
M 32
6
3
7
M13 M23 M33 3 2 4 10
例3
设
P
2 0
2
1
,
B
1 0
1 1
，且 AP PB, 求 An.
解：因| P | = 2，，则 P 可逆，且
A1
ad
1
bc
d c
b
a
9
2 2 1
例2
求3阶方阵
A
3
1
5
的逆矩阵.
3 2 3
解：| A | = 1， M11 7, M12 6, M13 3, M21 4, M22 3, M23 2, M31 9, M32 7, M33 4,
则
A1
|
1 A|
A*
A*
A11 A12 A13
证明： A2 3A 5E 0 ( A E)( A 4E) 9E 所以A + E 可逆，且
( A E)1 1 ( A 4E) 9
矩阵乘积的逆(高等代数课件)
下三角矩阵的逆
下三角矩阵的逆是另一个下三角矩阵，其主 对角线上的元素为原下三角矩阵对应元素的 倒数，其余元素为0。
计算公式：(A^{-1} = begin{bmatrix} a_{11}^{-1} & 0 & ldots & 0 0 &
a_{22}^{-1} & ldots & 0 vdots & vdots & ddots & vdots -a_{1n}a_{nn}^{-1} & a_{2n}a_{nn}^{-1} & ldots & a_{nn}^{-1}
矩阵乘积的逆元
如果存在一个矩阵$A^{-1}$，使得$AA^{-1} = A^{-1}A = I$， 则称$A$是可逆的，并且称$A^{-1}$为$A$的逆矩阵。
矩阵乘积的运算规则
分配律
对于任意常数$k$和矩阵$A, B, C$，有$(k times A) times B = k times (A times B) = A times (k times B)$。
上三角矩阵的逆
上三角矩阵的逆是另一个上三角矩阵，其主对角线上的元素为原上三角矩阵对应元素的倒数，其余元 素为0。
计算公式：(A^{-1} = begin{bmatrix} a_{11}^{-1} & 0 & ldots & 0 -a_{21}a_{11}^{-1} & a_{22}^{-1} & ldots & 0 vdots & vdots & ddots & vdots -a_{n1}a_{11}^{-1} & a_{n2}a_{22}^{-1} & ldots & a_{nn}^{-1} end{bmatrix})
矩阵的逆及其求法PPT课件
(A
E )
4
0
2
.
8 1 3
6 1 1
所以
(A
E )1
1 2
(A
E )
1 2
4 8
0 1
2
,
3
6 1 1 2 1 1 8 1
B
1 2
4 8
0 1
2
2
3 2
6 1
4
3
1 2
4 8
2 1
故
6
1 2
1
2
A B 4 7 3 .
2
3
11
2 2
1
2
.
充分发挥其作用，有必要对它进一步探讨。
定理3 A可逆 A 行 E Pm P2P1A E
Pm P2P1E A1 E 行 A1
求 A1方法 ：( A E) 行(E A1)
21
第21页/共36页
例7 求下列矩阵的逆
矩阵 1 0 1
1. A 2 1 0 3 2 5
解：
1 0 1 1 0 0
A A1 E 1 0 , 因此 A 0.
充分性．设 A 0, 由定理 2.1 知
AA A A A E.
故有 A( 1 A* ) ( 1 A* )A E .
A
A
9
第9页/共36页
由逆矩阵定义知，A 可逆，且其逆为
A1 1 A* . A
定理 2.2 不仅给出了判断矩阵可逆的方法， 还给出了求解逆矩阵的一种方法 .
2
第2页/共36页
一、逆矩阵的概念
定义1 设 A 为 n 阶方阵，如有 n 阶方阵 B ，使 AB = BA = E .
则称 A 为可逆阵，B 为 A 的逆阵，记作 B A1 .
矩阵的乘法及求逆运算最终版
矩阵的乘法及求逆运算最终版矩阵乘法在线性代数中，矩阵乘法是一种常用且重要的运算。
矩阵乘法允许我们将两个矩阵相乘，从而生成一个新的矩阵。
这一运算对于解决线性方程组、计算线性变换等问题非常有用。
矩阵乘法的定义对于两个矩阵 A 和 B，它们可以相乘的条件是：A 的列数必须等于 B 的行数，否则乘法无法进行。
假设 A 是一个 m×n 的矩阵，B 是一个 n×p 的矩阵，那么 A 与B 的乘积 AB 就是一个 m×p 的矩阵，其中第 i 行第 j 列的元素为 A 的第 i 行与 B 的第 j 列对应元素的乘积之和。
矩阵乘法的计算规则为了求出矩阵乘法的结果，我们需要按照以下规则进行计算：1.如果 A 是一个 m×n 的矩阵，B 是一个 n×p 的矩阵，那么 AB 的维度为 m×p。
2.对于 AB 的每个元素 AB[i][j]，可以通过将 A 的第 i 行与 B 的第 j 列对应元素相乘，并将乘积累加得到。
即AB[i][j] = A[i][1]×B[1][j] + A[i][2]×B[2][j] + … + A[i][n]×B[n][j]矩阵乘法的例子下面我们来看一个具体的例子，以帮助理解矩阵乘法的计算过程。
假设有两个矩阵 A 和 B：A = [[1, 2], [3, 4], [5, 6]]B = [[7, 8, 9], [10, 11, 12]]我们可以按照矩阵乘法的规则计算 AB：AB = [[1×7 + 2×10, 1×8 + 2×11, 1×9 + 2×12], [3×7 + 4×10, 3×8 + 4×11, 3×9 +4×12], [5×7 + 6×10, 5×8 + 6×11, 5×9 + 6×12]]简化后的结果为：AB = [[27, 30, 33], [61, 68, 75], [95, 106, 117]]通过这个例子，我们可以清楚地看到矩阵乘法的计算过程，以及如何按照规则对应元素相乘并累加得到结果。
5.6 矩阵乘积的行列式与矩阵的逆
09:04
3
例题 6.1
利用伴随矩阵计算以下矩阵的逆矩阵：
可以求得 .
09:04
5
例题
解: 注意到
09:04
这时有
6
定理6.1的证明
用两种方法计算D的行列式.
1) 直接利用拉普拉斯定理
09:04
7
定理6.1的证明(续)
2) 先利用第一类初等行变换把D的左上主子矩阵化为零, 再利用拉普拉斯定理.
proof
09:04
proof
2
注记
定理6.2不但给出了方阵可逆的充分必要条件，同时还给 出了一种求逆矩阵的方法． 但是，用伴随矩阵求逆的计算量太大，不实用． 我们将介绍一种通过矩阵的初等行变换求逆的实用方 法． 利用线性变换与矩阵的一一对应关系容易证明：线性变 换可逆的充分必要条件是它的矩阵是可逆的．
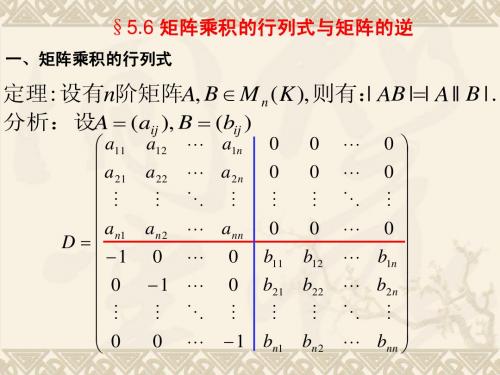
§6 矩阵乘积的行列式与矩阵的逆
矩阵乘积的行列式
两个矩阵的乘积的行列式等于它们的行列式的乘积
矩阵的逆
方阵可逆的充分必要条件是它的行列式不为零； 矩阵的逆的计算公式（伴随矩阵）
• 行列式按一行（一列）展开公式的应用
09:04
1
矩阵乘积的行列式，逆
设 A,B 为 n 阶矩阵, 则它们的乘积 AB 还是一个 n 阶矩阵.
09:04
8
定理6.1的证明(续２)
09:04
9
定理6.1的证明(续３)
AB的(i,j)元
09:04
…
back
10
定理 6.2 的证明
只需证明充分性．由行列式按一行展开的公式知
定义A的伴随矩阵：
则有 即
同理, 由行列式按一列展开的公式可以得到
back
09:04
11
47高等代数(北大三版)第五章 矩阵PPT课件
n
a
m
1
am2
a
m
n
b
m
1
bm 2
bm
n
5
A和B加法定义为:
a11 b11 ABa21 b21
am1 bm1
a12 b12 a22 b22
am2 bm2
a1n b1n
a2n
b2n
amn bmn
定义3（矩阵的乘法）给定一个 mn矩阵和一个 n l
矩阵
a11 a12
A
a21
a22
am1 am 2
a1n
a2n
amn
b11 b12
b1l
B
b21
b22
b2l
bn1 bn 2
bnl
6
A和B的乘法定义为
n
a1i bi1 i1
n
AB a2ibi1
i1
n
amibi1
i1
n
a1i bi 2
i 1 n
a2i bi 2
i 1
n
ami bi 2
二、教学目的 1. 掌握矩阵的加法、乘法以及 数与矩阵的乘法运算法则及其基本性 质，并能熟练地对矩阵进行运算。 2. 掌握转置矩阵及其运算性质。 3. 掌握方阵的幂、方阵的多项式。
三、重点、难点 矩阵的乘法运算法则及其基本性质，转置矩阵及其运算性质。
3
5.1.1 认识矩阵
设F是数域, 用F的元素 a i j 排成的m行n列的数表
例6 证明: 如果CAAC,CBBC, 则有 (AB)CC(AB); (AB)CC(AB).
10
5.1.4 方阵的多项式
单位矩阵 :主对角线上全是1,其余元素全是0的方阵称为单位矩
湘教版高中数学选修4-2-2.4 矩阵乘法的性质-课件(共14张PPT)优秀课件PPT
元素的乘积之和
a11
ai1
am1
a12 ai2 am2
a1s ais ams
b11
b2j
b1n
b2n
bsn
c11
aci11bj1 j
ai 2b2cj 1n
aisbsj
ci1
cij
cin
cm1 cmj
cmn
例题讲解：
2 例1.设矩阵A 4
3
1 0 ，B 5
9 7
108，求A B
解：
2 1
A B 4 3
0 5
9 7
8
10
2×9+（-1）×（-7） 2×（-8）+（-1）×10
= （-4）×9+0×（-7） （-4）×（-8）+0×10
功地把自己推销给别人之前，你必须百分之百的把自己推销给自己。即使爬到最高的山上，一次也只能脚踏实地地迈一步。
单价
利润
12 1.2
α
B 14 1.3
β
16 1.5
γ
问题:这三家商场销售这三种品牌液晶电视机的日总收入和总利润分别是多少?
α
β
γ
20 20 18 甲 A 24 16 27 乙
21 19 22 丙
单价
1 2 B 1 4
1 6
利润
1.2 α 1.3 β 1.5 γ
20×如12果+2把0×总1收4+入18和×总16利润可以用下列矩2阵0×表1示.2+: 20×1.3+18×1.5
a11b11 a12b21 a13b31
总收入
C11
C a21b11 a22b12 a23b13
a11
ai1
am1
a12 ai2 am2
a1s ais ams
b11
b2j
b1n
b2n
bsn
c11
aci11bj1 j
ai 2b2cj 1n
aisbsj
ci1
cij
cin
cm1 cmj
cmn
例题讲解：
2 例1.设矩阵A 4
3
1 0 ，B 5
9 7
108，求A B
解：
2 1
A B 4 3
0 5
9 7
8
10
2×9+（-1）×（-7） 2×（-8）+（-1）×10
= （-4）×9+0×（-7） （-4）×（-8）+0×10
功地把自己推销给别人之前，你必须百分之百的把自己推销给自己。即使爬到最高的山上，一次也只能脚踏实地地迈一步。
单价
利润
12 1.2
α
B 14 1.3
β
16 1.5
γ
问题:这三家商场销售这三种品牌液晶电视机的日总收入和总利润分别是多少?
α
β
γ
20 20 18 甲 A 24 16 27 乙
21 19 22 丙
单价
1 2 B 1 4
1 6
利润
1.2 α 1.3 β 1.5 γ
20×如12果+2把0×总1收4+入18和×总16利润可以用下列矩2阵0×表1示.2+: 20×1.3+18×1.5
a11b11 a12b21 a13b31
总收入
C11
C a21b11 a22b12 a23b13
线性代数课件-2.3逆矩阵
§3 逆矩阵
•矩阵与复数相仿，有加、减、乘三种运算. •矩阵的乘法是否也和复数一样有逆运算呢？ •这就是本节所要讨论的问题. •这一节所讨论的矩阵，如不特别说明，所指的都是 n 阶方阵.
对于 n 阶单位矩阵 E 以及同阶的方阵 A，都有
An En En An An
从乘法的角度来看，n 阶单位矩阵 E 在同阶方阵中的地 位类似于 1 在复数中的地位： a * 1 = 1 * a = a.
若设 B 和 C 是 A的可逆矩阵， 则有
AB BA E, AC CA E,
可得 B EB CAB CAB CE C.
所以 A 的逆矩阵是唯一的，即 B C A1.
下面要解决的问题是： •在什么条件下，方阵 A 是可逆的？ •如果 A 可逆，怎样求 A－1 ？
结论：AA* A* A | A | E.
例3 已知A 0 0 3 0 0 求A1.
0 0 0 4 0
0 0 0 0 5
解 因 A 5! 0, 故A1存在.
由伴随矩阵法得 A1 A A ,
2 3 4 5 0
0
0
0
1
0 0
1345 0 0 1245
0 0
0 0
5!
0
0
0 1235 0
0
0
0
0 1 2 3 4
1 0 0 0 0 0 1 2 0 0 0
概念的引入
在数的运算中，当数 a 0时，有
aa1 a1a 1,
其中 a1 1 为 a 的倒数，（或称 a 的逆）；
a
在矩阵的运算中，单位阵 E相当于数的乘法运算中
的1， 那么，对于矩阵 A，如果存在一个矩阵 A1,
使得
AA1 A1 A E ,
•矩阵与复数相仿，有加、减、乘三种运算. •矩阵的乘法是否也和复数一样有逆运算呢？ •这就是本节所要讨论的问题. •这一节所讨论的矩阵，如不特别说明，所指的都是 n 阶方阵.
对于 n 阶单位矩阵 E 以及同阶的方阵 A，都有
An En En An An
从乘法的角度来看，n 阶单位矩阵 E 在同阶方阵中的地 位类似于 1 在复数中的地位： a * 1 = 1 * a = a.
若设 B 和 C 是 A的可逆矩阵， 则有
AB BA E, AC CA E,
可得 B EB CAB CAB CE C.
所以 A 的逆矩阵是唯一的，即 B C A1.
下面要解决的问题是： •在什么条件下，方阵 A 是可逆的？ •如果 A 可逆，怎样求 A－1 ？
结论：AA* A* A | A | E.
例3 已知A 0 0 3 0 0 求A1.
0 0 0 4 0
0 0 0 0 5
解 因 A 5! 0, 故A1存在.
由伴随矩阵法得 A1 A A ,
2 3 4 5 0
0
0
0
1
0 0
1345 0 0 1245
0 0
0 0
5!
0
0
0 1235 0
0
0
0
0 1 2 3 4
1 0 0 0 0 0 1 2 0 0 0
概念的引入
在数的运算中，当数 a 0时，有
aa1 a1a 1,
其中 a1 1 为 a 的倒数，（或称 a 的逆）；
a
在矩阵的运算中，单位阵 E相当于数的乘法运算中
的1， 那么，对于矩阵 A，如果存在一个矩阵 A1,
使得
AA1 A1 A E ,
矩阵乘积的逆(高等代数课件)
an1 x1
a12 x2
a22 x2
a1n xn a2 n xn
an 2 x2
ann xn
, ,
,
它的 系数矩阵是一 个 n 级矩阵 A，若记
(1)
一、可逆矩阵的概念
定义 设A为n级方阵，如果存在n级方阵B，使得
AB＝BA＝E
则称A为可逆矩阵，称B为A的逆矩阵.
注：① 可逆矩阵A的逆矩阵是唯一的，记作 A 1 .
立即可得, a11 a12
AA*a21 a22 an1 an2
a1nA11 A21 a2nA12 A22
annA1n A2n
An1 An2
Ann
d 0
0 0
d 0
0
0 d
dE.
同理, A*AdE.
2、定理：矩阵A可逆当且仅当 A 0 , （即A
非退化的），且
A 1
A* .
A
证：若 A 0 , 由 A A *A *AAE
有
A1
AA* 12223
6 6 2
4 52.
2 ) A a 1 a 2 a n ,
∴ 当 a i 0 ( i 1 ,2 ,,n )时，A可逆.
且由于
a1 a2
a11
a21
an
an1
1
1
A1
a11
a21
.
an1
1
E
三、逆矩阵的运算规律
1 若 A 可 ,则 A 1 亦 逆 ,且 A 可 1 1 A .逆
A*
A12
A22
A1n A2n
An1 An2
Ann
称为A的伴随矩阵.
性质： AA *A *AAE
矩阵的乘法及求逆运算 最终版ppt课件
0 0
0
0
L L
1
1
0 1
（4）正交矩阵的求逆公式：A1 AT
（5）其他常用的求逆公式：
( AB)1 B1 A1
( AT )1 ( A1)T
( A*)1 ( A1)* A 1 A
A1, A2 , A3,L , AS可逆 ，则( A1A2 L AS )1 AS1L A21A11
19
(7)矩阵 A 可逆充分必要条件是 A 0
7
逆矩阵求解方法一——伴随矩阵法 A1 1 A* A
逆矩阵求解方法二——初等变换法
( A E) 行(E A1)
8
逆矩阵求解方法三——因式分解法
若Ak 0，即（I A）可逆，且有（I-A）1 I A A2 L AK 1 我们通过上式，求出 A1
则称 A 为可逆阵，B 为 A 的逆阵，记作 B A1 .
6
性质：
(1) ( A1)1 A
(2)(kA)1 1 A1 k
(3) A、B 均是同阶可逆阵，则 ( AB)1 B1A1
(4) ( AT )1 ( A1)T
(5) AA* A* A A I
(6)若方阵 A 可逆，则其逆矩阵唯一.
1
AX1
0
,
12
0
0
AX 2
1
,
0
0
AX 3
0
1
利用消元解法求
x1i
Xi
x2i
x3i
解得：
（i 1, 2,3）
1 3 2
A1
X
3
3
5
2
2
0 11 1
13
逆矩阵求解方法六——准对角矩阵
A11 0 L
相关主题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
§4.4 矩阵的逆
2. 逆矩阵的唯一性
若方阵 A 可逆，则其逆矩阵唯一 .
证明
有 于是
设 B 和 C 都是 A 的逆矩阵，则由定义
AB = BA = E，AC = CA = E，
B = BE = B( AC ) = ( BA )C = EC = C .
所以逆矩阵唯一.
证毕
§4.4 矩阵的逆
三、矩阵可逆的条件
d A.
立即可得,
a11 a12 a21 a22 * AA a a n1 n 2
a1n A11 A21 a2 n A12 A22 ann A1n A2 n
An1 An 2 Ann
§4.4
d 0 0 d 0 0 矩阵的逆
一、引例
引例 1 矩阵与复数
引例 2 坐标旋转变换 复数可以用二维有序数组来表示，如复数 a+bi
可表示为 (a , b) ，因此，从结构上看复数是矩阵的 引例 3 线性变换的逆变换 特殊情形 . 在第二节我们也看到，矩阵与复数相 在平面直角坐标系 xOy 中，将两个坐标轴同 仿，有加法、减法、乘法三种运算 . 我们知道，复 时绕原点旋转 角 ( 逆时针为正，顺时针为负 )， 设给定一个线性变换 数的乘法运算有逆运算，那么矩阵的乘法运算是否 就得到一个新的直角坐标系 (见图 3) ． 平面上 4 a– x , y1 a11 x1 a12 x2 1n n 也有逆运算呢？ 如果有的话，这种运算如何定义， Ｐ 任何一点 a21 x1 a22 x2 a2 n xn , y2 在两个坐标系中的坐标分别记为
称为A的伴随矩阵.
An1 An 2 Ann
性质： AA* A* A A E
§4.4 矩阵的逆
证：由行列式按一行（列）展开公式
ak 1 Ai 1 ak 2 Ai 2 a1l A1 j a2 l A2 j akn Ain d , k i 0, k i anl Anj d , l j 0, l j
. 1 an
§4.4 矩阵的逆
三、逆矩阵的运算规律
1 若A可逆, 则A 亦可逆, 且A
1 1 1
A.
2 若A可逆, 数 0, 则A可逆, 且
A A1 .
1
1
3 若A, B为同阶方阵且均可逆 , 则AB亦可逆, 且
A B 1 B 1 A 1
一、可逆矩阵的概念
定义 设A为n级方阵，如果存在n级方阵B，使得
AB＝BA＝E 则称A为可逆矩阵，称B为A的逆矩阵.
1 A . 注： ① 可逆矩阵A的逆矩阵是唯一的，记作
1 A ② 可逆矩阵A的逆矩阵 也是可逆矩阵，且
A
1
1
A.
1
③ 单位矩阵 E 可逆，且 E E .
§4.4 矩阵的逆
3、推论：设A、B为 n 级方阵，若 AB E ,
1 1 A B , B A. 则A、B皆为可逆矩阵，且
证： 从而
AB E
A 0, B 0.
AB A B E 1
由定理知，A、B皆为可逆矩阵. 再由
A1 ( AB) A1 E ,
( AB)B1 EB1 ,
推广
A1 A2 Am A A A .
1
1 m
1 2
1 1
§4.4 矩阵的逆
4 若A可逆, 则A 亦可逆 , 且 A
T
T 1
A .
1 T
1
(5) 若A可逆，则 A 亦 可逆，且 A (6) 若A可逆，则 A 亦 可逆，且 A
k
k
A . A
再由
A11 2, A21 6, A31 4, A12 3, A22 6, A32 5, A13 2, A23 2, A33 2.
* 2 6 4 A 1 有 A 1 3 6 5 . A 2 2 2 2
§4.4 矩阵的逆
2)
A a1a2
an ,
∴当 ai 0 ( i 1,2, 且由于
, n) 时，A可逆.
a1 a2
1 a 1 1 a2 an
1 an
1 1
E 1
1 a1 1 1 a 2 A
0 0 dE . d
同理, A* A dE .
2、定理：矩阵A可逆当且仅当 A 0, （即A
非退化的），且
* A 1 A . A
证：若 A 0, 由 AA* A* A A E A* A* A E 得 A A A * A 1 . 所以，A可逆，且 A A 反过来，若A可逆，则有 AA1 E , 两边取行列式，得 A A1 E 1. A 0.
1
A
1
k
.
注： 当 A 0 时，定义
A E, A
0 k
(A )
1 k
则有
A A A
,
A
A , , Z
§4.4 矩阵的逆
2 A 3 A 10 E 0, 例2 设方阵 A 满足
现在的问题是：在什么条件下矩阵 A 是可逆 的？ 如果 A 可逆，怎样求 A-1 ？ 为此先引入伴随
矩阵的概念.
§4.4 矩阵的逆
二、矩阵可逆的判定及逆矩阵的求法
1、伴随矩阵 定义 设 Aij 是矩阵 A (aij )nn 中元素 aij 的代数
余子式，矩阵
A11 A21 A12 A22 * A A A 1n 2 n
即有， A1 B, B1 A.
§4.4 矩阵的逆
例1 判断矩阵A是否可逆，若可逆，求其逆.
1 2 3 1) A 2 2 1 3 4 3
a1 a2 2) A an
§4.4 矩阵的逆
解：1） ∴ A可逆.
1 2 3 2 2 1 2, 3 4 3
2. 逆矩阵的唯一性
若方阵 A 可逆，则其逆矩阵唯一 .
证明
有 于是
设 B 和 C 都是 A 的逆矩阵，则由定义
AB = BA = E，AC = CA = E，
B = BE = B( AC ) = ( BA )C = EC = C .
所以逆矩阵唯一.
证毕
§4.4 矩阵的逆
三、矩阵可逆的条件
d A.
立即可得,
a11 a12 a21 a22 * AA a a n1 n 2
a1n A11 A21 a2 n A12 A22 ann A1n A2 n
An1 An 2 Ann
§4.4
d 0 0 d 0 0 矩阵的逆
一、引例
引例 1 矩阵与复数
引例 2 坐标旋转变换 复数可以用二维有序数组来表示，如复数 a+bi
可表示为 (a , b) ，因此，从结构上看复数是矩阵的 引例 3 线性变换的逆变换 特殊情形 . 在第二节我们也看到，矩阵与复数相 在平面直角坐标系 xOy 中，将两个坐标轴同 仿，有加法、减法、乘法三种运算 . 我们知道，复 时绕原点旋转 角 ( 逆时针为正，顺时针为负 )， 设给定一个线性变换 数的乘法运算有逆运算，那么矩阵的乘法运算是否 就得到一个新的直角坐标系 (见图 3) ． 平面上 4 a– x , y1 a11 x1 a12 x2 1n n 也有逆运算呢？ 如果有的话，这种运算如何定义， Ｐ 任何一点 a21 x1 a22 x2 a2 n xn , y2 在两个坐标系中的坐标分别记为
称为A的伴随矩阵.
An1 An 2 Ann
性质： AA* A* A A E
§4.4 矩阵的逆
证：由行列式按一行（列）展开公式
ak 1 Ai 1 ak 2 Ai 2 a1l A1 j a2 l A2 j akn Ain d , k i 0, k i anl Anj d , l j 0, l j
. 1 an
§4.4 矩阵的逆
三、逆矩阵的运算规律
1 若A可逆, 则A 亦可逆, 且A
1 1 1
A.
2 若A可逆, 数 0, 则A可逆, 且
A A1 .
1
1
3 若A, B为同阶方阵且均可逆 , 则AB亦可逆, 且
A B 1 B 1 A 1
一、可逆矩阵的概念
定义 设A为n级方阵，如果存在n级方阵B，使得
AB＝BA＝E 则称A为可逆矩阵，称B为A的逆矩阵.
1 A . 注： ① 可逆矩阵A的逆矩阵是唯一的，记作
1 A ② 可逆矩阵A的逆矩阵 也是可逆矩阵，且
A
1
1
A.
1
③ 单位矩阵 E 可逆，且 E E .
§4.4 矩阵的逆
3、推论：设A、B为 n 级方阵，若 AB E ,
1 1 A B , B A. 则A、B皆为可逆矩阵，且
证： 从而
AB E
A 0, B 0.
AB A B E 1
由定理知，A、B皆为可逆矩阵. 再由
A1 ( AB) A1 E ,
( AB)B1 EB1 ,
推广
A1 A2 Am A A A .
1
1 m
1 2
1 1
§4.4 矩阵的逆
4 若A可逆, 则A 亦可逆 , 且 A
T
T 1
A .
1 T
1
(5) 若A可逆，则 A 亦 可逆，且 A (6) 若A可逆，则 A 亦 可逆，且 A
k
k
A . A
再由
A11 2, A21 6, A31 4, A12 3, A22 6, A32 5, A13 2, A23 2, A33 2.
* 2 6 4 A 1 有 A 1 3 6 5 . A 2 2 2 2
§4.4 矩阵的逆
2)
A a1a2
an ,
∴当 ai 0 ( i 1,2, 且由于
, n) 时，A可逆.
a1 a2
1 a 1 1 a2 an
1 an
1 1
E 1
1 a1 1 1 a 2 A
0 0 dE . d
同理, A* A dE .
2、定理：矩阵A可逆当且仅当 A 0, （即A
非退化的），且
* A 1 A . A
证：若 A 0, 由 AA* A* A A E A* A* A E 得 A A A * A 1 . 所以，A可逆，且 A A 反过来，若A可逆，则有 AA1 E , 两边取行列式，得 A A1 E 1. A 0.
1
A
1
k
.
注： 当 A 0 时，定义
A E, A
0 k
(A )
1 k
则有
A A A
,
A
A , , Z
§4.4 矩阵的逆
2 A 3 A 10 E 0, 例2 设方阵 A 满足
现在的问题是：在什么条件下矩阵 A 是可逆 的？ 如果 A 可逆，怎样求 A-1 ？ 为此先引入伴随
矩阵的概念.
§4.4 矩阵的逆
二、矩阵可逆的判定及逆矩阵的求法
1、伴随矩阵 定义 设 Aij 是矩阵 A (aij )nn 中元素 aij 的代数
余子式，矩阵
A11 A21 A12 A22 * A A A 1n 2 n
即有， A1 B, B1 A.
§4.4 矩阵的逆
例1 判断矩阵A是否可逆，若可逆，求其逆.
1 2 3 1) A 2 2 1 3 4 3
a1 a2 2) A an
§4.4 矩阵的逆
解：1） ∴ A可逆.
1 2 3 2 2 1 2, 3 4 3