材料力学弯曲应力原创教案
4-2弯曲应力公开课教案课件

1.5 5400 0.12 0.18
x 0.375MPa 0.9MPa
-qL/2 应 力 之 比
x
max Mmax 2 A L 16.7 max Wz 3FS h
M
qL2/8
[ ] 7
7.8
[ ] 0.9
35
弯曲应力
q= 3.6kN/m
A
Q q L/2
L = 3m
求最大应力并校核强度
a
解::确定计算简图如图b
2m
8m
2m
z 动静法:
图a
y
qd
A1a
g
qj
a g
PA
q=q j + q d
PB
615 10 628N / m 9.8
图b
q q j qd 1243 N / m
20
弯曲应力
PA
q=q j + q d
PB
图b
:由平衡方程求吊索动反力
qL PA PB 2 124312 7460N
M max Wz
max
F S S max z max bIz
3、三种应用:
、、校校核核强强度度:: max ; max
、设计截面尺寸:
Wz
M max
、设计载荷: Mmax Wz ; P f (Mmax )
32
弯曲应力
4、需要校核切应力的情况: 、梁的跨度较短,FS较大时,要校核切应力。 、薄腹板梁,剪力较大; 、铆接、焊接、胶合的组合截面梁,对焊缝、铆钉、 胶合面需要校核切应力; 、抗剪能力较差的各向异性材料(如木材), 需要校核切应力。
M
qL2/8
[ ] 7
7.8
[ ] 0.9
材料力学弯曲应力原创教案

材料力学弯曲应力原创教案弯曲应力我们开始弯曲这一章,我们讲了拉压、扭转、剪切,现在我们要讲弯曲。
弯曲的情况要比拉压和扭转更加复杂一些,它所涉及的问题更多一些,它和工程实际联系的更加紧密一些。
因此,这一章和下一章都是特别重要的章节。
在这一章中,我们首先要讨论弯曲正应力,横截面上有弯矩,那它就有了正应力,同时还要考虑弯曲切应力的问题,横截面上有剪力,说明它有切应力存在。
了解了正应力和切应力的情况,我们要讨论梁的强度和破坏,这个思路和前面几章是一样的。
特别的,要强调薄壁杆件中弯曲切应力的处理,最后呢,我们要讲组合变形的应用。
不仅仅是弯曲,而是弯曲和拉压,弯曲和扭转组合在一起的时候,如何来处理它的应力问题。
因此,这章的内容是比较多的。
工程实际例子我们来看看弯曲在工程中的应用。
这是一个厂房,这是一个大梁,这个吊车可以在这个大梁上运动。
对于这样一个问题,我们可以把它简化成一个简支梁,这个吊车的移动呢可以处理成一个移动荷载。
那么对于这个移动荷载而言,它所导致的应力如何计算?行车移动时,它的应力如何变化?这就是本章的内容之一。
我们再看看这个图片,这是我们拍摄的汽车的下部分,大家注意一些这个部分,这是就是汽车的板簧,它的模型就是这个样子,可以看成好几个钢板的组合,那么,为什么要设计成这个样子呢?它有什么优点呢?这也是本章要解决的问题。
这是一个运动员,撑杆跳,对吧。
大家常常见到,利用这个杆的助力,人可以跳的更高。
我们可以处理成这样一个模型。
她在跳高的过程中,杆就发生了弯曲。
那么,这个时候,跳杆横截面上的应力和杆曲率半径有什么关系?这个杆在什么情况下才满足强度要求?大家看看这个场面,对于这个场面,我们截面几何性质那章提到过,都是薄壁杆件,那么薄壁杆件有弯曲正应力和弯曲切应力,专门有一小节来讲解它的弯曲切应力,看看这些切应力有什么特点?如何避免薄壁杆件的强度失效?这也是本章的问题这个大家都熟悉,著名的比萨斜塔。
对于这个结构,初步计算,我们可以简化成这样一个均质圆筒,那么它有哪些变形效应?它的危险截面、危险点在哪儿?如何计算其应力?这也是本章可以解决的问题。
材料力学-第四章弯曲应力教学

FS
x
dx
0
FS
x
dM x
dx
qx
dM 2x
dx 2
注:q(x)向上为正,反之为负。
●简易法作剪力图和弯矩图
①梁上无分布荷载作用:q(x)=0
qx dFS x 0
dx
FS x cont
剪力图斜率为零,FS(x)图为平行于x轴的直线。
dM x
B 1kN
A FAx
FB
FAy
FAx=-3kN FAy=3kN
FB=5kN
2)剪力图: 简易法 BC杆:取一点(水平线) DC杆:取两点(水平线) DA杆:取两点(斜直线)
D 3kN
C
1kN E
5kN
1kN B
3kN A
q=1kN/m 4m 3m
8kN
1m D
2m C
E
B 1kN
A FAx
A
A
ydA Sz 0 中性轴z必通过截面形心
A
横截面对z轴的静矩
My
z dA 0
A
zE
A
y dA
E
A
zydA
0
zydA I yz 0
A
截面对yz轴的惯性积
*由于y为对称轴, 上式自然满足。
M z
y dA
A
M
例5.作外伸梁的内力图
q
FA
ql 8
A
FB
5ql 8
FA
FS
B
lC
l
FB 2
ql / 2
12第十二讲(弯曲正应力)

材料力学教案
M z y d A
A
第十二讲:弯曲正应力计算
E
r
A
y dA
2
EI z
r
M
(c)
由式(c)可知,直梁纯弯曲时中性层的曲率为
M r EI z 上式中的EIz称为梁的弯曲刚度。显然,由于纯弯曲时,
梁横截面上的弯矩M 不随截面位置变化。故对于等截面的
1
直梁,包含在中性层内的那根轴线将弯成圆弧。
3、纵向线应变在横截面范围内的变化规律
图c为由相距d x的两横截面取出的梁段在梁弯曲后的情
况,两个原来平行的横截面绕中性轴相对转动了角d。梁的 横截面上距中性轴 z为任意距离 y 处的纵向线应变由图c可知 为
B1B B1 B y d AB1 O1O2 dx
令中性层的曲率半径为r(如图c),则根 1 d 据曲率的定义 有 r dx
材料力学教案
第十二讲:弯曲正应力计算
根据表面变形情况,并设想梁的侧面上的横向线mm和nn是
梁的横截面与侧表面的交线(由表及里),可作出如下推论
(假设):
平面假设
梁在纯弯曲时,其原来的横截面仍保持为平面,
只是绕垂直于弯曲平面(纵向平面)的某一轴转动,转动后 的横截面与梁弯曲后的轴线保持正交。 此假设已为弹性力学的理论分析结果所证实。 三峡大学 工程力学系
将 E 代入,即得弯曲正应力计算公式:
r
y
My Iz
三峡大学 工程力学系
材料力学教案
第十二讲:弯曲正应力计算
二. 纯弯曲理论的推广-横力弯曲中正应力的计算
工程中实际的梁大多发生横力弯曲,此时,对于梁在
纯弯曲时所作的假设不再成立。
材料力学 弯曲应力PPT学习教案

115MPa 120MPa
第22页/共47页
2021/5/11
23
例5-5 T形截面铸铁梁的载荷和截面尺寸如图 所示。铸
铁的抗拉许用应力为[t]=30MPa,抗压许用应力为
[c]=160MPa。已知截面对形心轴z的惯性矩为Iz=763cm4,
且y1=52mm。试核核梁的强度。
F1
F2 =4KN
M
(KNm )
1.17
+
第17页/共47页
-
0.9
2021/5/11
18
210921/5/11
解:1. 确定约束力
FRA=2.93kN FRB=5.07 kN
2. 画弯矩图,判断可 能的危险截面
MC=1.17 kNm MB=-0.9 kNm
FRA
M(KNm)
1.17
+
3.计算危险截面上的最大正应力
变形
平面假定
应变分布
物理关系 应力公式
应力分布 静力 方程
第4页/共47页
2021/5/11
5
1 、 变 形 几何 关系
建立坐标系: x——截 面 外 法 线 y——截 面 对 称 轴 z——中 性 轴
线 段 aa 正 应 变
o
o
r dq
y
a
a
dx
M
o y
a
o
M
a
=(r y)dq rdq = y
F 40
B
0
截面B- B
12 0
20
y
C
z
0
12
2021/5/11
B
20
y
第15页/共47页
16
材料力学教案-弯曲应力

(2)最大正应力发生在横截面上离中性轴最远的点处.
σmax M ymax Iz
引用记号 W Iz —抗弯截面系数 ymax
则公式改写为
σmax
M W
(Stresses in Beams)
(1)当中性轴为对称轴时
实心圆截面 W Iz πd 4 / 64 πd 3 d / 2 d / 2 32
且梁横截面的中性轴一般也不是对称轴,所以梁的
σtmax σcmax(两者有时并不发生在同一横截面上)
要求分别不超过材料的许用拉应力和许用压应力
σtmax [σt] σcmax [σc ]
(Stresses in Beams)
例题1 螺栓压板夹紧装置如图所示.已知板长3a=150mm,压板
材料的弯曲许用应力[]=140MP.试计算压板传给工件的最大允
将
1M
EIz
代入
σE y
得到纯弯曲时横截面上正应力的计算公式:
σ My Iz
M为梁横截面上的弯矩;
y为梁横截面上任意一点到中性轴的距离;
Iz为梁横截面对中性轴的惯性矩.
(Stresses in Beams)
讨论
(1)应用公式时,一般将 My 以绝对值代入. 根据梁变形的情
况直接判断 的正负号. 以中性轴为界,梁变形后凸出边的应 力为拉应力( 为正号).凹入边的应力为压应力( 为负号);
应力分布规律:
?
y
直梁纯弯曲时横截面上任意一点的正应力,与它到中性轴
的距离成正比.
待解决问题
? 中性轴的位置
中性层的曲率半径
(Stresses in Beams) 四、静力关系 (Static relationship)
弯曲应力材料力学解析PPT学习教案

力
s T max
M max Iz
y1
=
2500 111108
5.16 102
116.2 106 Pa
116.2MPa
截面上缘受最大压应力
弯曲应 力
s C max
M max Iz
y2
2500 111108
1.84 102
41.4 106
Pa
41.4MPa
第7页/共27页
例 如图所示悬臂梁,自由端承受集中载荷F=15kN作用。试计 弯曲应
(B
b)h2 ]
t min
FQ 8I zb
(BH2
Bh2 )
第12页/共27页
弯曲应 力
7.2.3 圆形截面梁
t max
FQ
S
* z
Izb
FQd 3 /12y (d 4 / 64)d
4 3
FQ A
式 中 : A为 圆 截面 面积
对 于 等 直 杆 ,最大 切应力 的统一 表达式 为:
弯曲应 力
例7-5 螺栓压板夹紧装置如图所示。已知板长 3a=150mm,压板材料的弯曲许用应力为[σ]=140MPa 。试确定压板传给工件的最大允许压紧力F。
解:压板可简化为图所示的外伸梁
作弯矩图如图所示。最大弯矩在截面B上
Mma MB Fa
Iz
3 x2 3 12
1.4 23 12
1.07cm4
Wz
O曲率中心
dq
M
m1 m2
y O1 a1
n1 dx
O2 dq
a2' a2 dl n2
sy M e2
e1
m2 x
2.物 理 关 系 (虎 克定 律)
材料力学第五章__弯曲应力

矩(中性轴以下或以上面积对中性轴的静矩)
的比值(Iz/S),因此工程中经常采用的最大
剪应力的计算公式为:
max
bIz
FS / Smax
整理课件
3.圆截面梁的剪应力
整理课件
假设
1.假设AB弦上各点的剪 应力作用线都通过k点。
2.假设AB弦上各点剪应 力的垂直分量τy相等, 亦即假设τy沿AB弦均 匀分布。
整理课件
1、矩形截面梁弯曲剪应力
初等剪应力理论是由俄罗斯工程师茹拉夫斯基( 1844-1850)设计木梁时提出。 1856年圣维南提出精确剪应力理论。 1.矩形截面梁的剪应力 分析步骤: 1.提出假设; 2.在假设的基础上推导公式; 3.找出剪应力沿截面高度分布的规律。
整理课件整理课件来自理课件P yz Q
x
整理e课件
h
e Hh R
整理课件
整理课件
整理课件
整理课件
整理课件
整理课件
整理课件
整理课件
整理课件
整理课件
*§5.5 关于弯曲理论 的基本假设
自学
整理课件
§5.6 提高弯曲强度的 措施
整理课件
整理课件
整理课件
整理课件
整理课件
整理课件
整理课件
整理课件
F
S
S
* z
整理课件
I zb
整理课件
整理课件
工字钢截面:
max
Q Af
min
Af —腹板的面积。
max
结论: 翼缘部分max«腹板上的max,只计算 腹板上的max。
铅垂剪应力主要腹板承受(95~97%),且
max≈ min
故工字钢最大剪应力
材料力学教案 第6章 弯曲应力

第6章弯曲应力教学目的:在本章的学习中要求熟练掌握梁纯弯曲时横截面上正应力计算公式的推导过程,理解推导过程中所作的假设。
掌握中性层、中性轴等基本概念和含义。
弯曲正应力和剪应力强度条件的建立和相应的计算。
理解横力弯曲正应力计算仍用纯弯曲公式的条件和近似程度。
从弯曲强度条件出发,掌握提高弯曲强度的若干措施。
教学重点:纯弯曲梁横截面上正应力公式的分析推导;横力弯曲横截面上正应力的计算,最大拉应力和最大压应力的计算;弯曲的强度计算;弯曲横截面上的剪应力。
教学难点:弯曲正应力、剪应力推导过程和结果以及弯曲中心的概念。
教具:多媒体。
教学方法:采用启发式教学,通过提问,引导学生思考,让学生回答问题。
教学内容:梁纯弯曲和横力弯曲时横截面上的正应力;梁横力弯曲时横截面上的切应力;提高弯曲强度的若干措施。
教学学时:6学时。
教学提纲:6.1 梁的纯弯曲1、几个基本概念(1)平面弯曲和弯曲中心变形后梁轴线的位移方向沿着加载方向的弯曲情况,称为平面弯曲。
怎样加载才能产生平面弯曲?若梁的横截面有对称平面时,载荷必须作用在对称平面内,才能发生平面弯曲。
若梁的横截面没有对称平面时,载荷的作用线必须通过截面的弯曲中心。
什么叫弯曲中心?当载荷的作用线通过横截面上某一点特定点时,杆件只产生弯曲而无扭转。
这样的特定点称为弯曲中心。
关于弯曲中心位置的确定及工程上常见图形的弯曲中心位置。
①具有两个对称轴或反对称的截面,如工字形、圆形、圆环形、空心矩形截面等,弯曲中心与形心(两对称轴的交点)重合,如图(a),(b),(c)所示。
②具有一个对称轴的截面,如槽形和T形截面,弯曲中心必在对称轴上,如图(d)、(e)所示。
③如果截面是由中线相交于一点的几个狭长矩形所组成,如L形或T形截面,则此交点就是弯曲中心,如图(e)、(f)所示。
④不对称实心截面的弯曲中心靠近形心。
这种截面在荷载作用线通过形心时也将引起扭转,但由于这种截面的抗扭刚度很大,弯曲中心与形心又非常靠近,故通常不考虑它的扭转影响。
第五章 弯曲应力(材料力学)PPT课件

n
作如下假设: (1) 梁的横截面变形后仍保持为平面,且垂直于变形
后的轴线,即弯曲变形的平面假设。 (2) 纵向纤维间无挤压作用,各纵向纤维均处于单向
受拉或受压状态。
材料力学Ⅰ电子教案
第五章 弯曲应力
bb 变形前的长度等于中性层
中性层长度不变, 所以:
bbO 1 O 2 O1O 2 d
纵向线bb变形后的长度为:
纯弯曲和横力弯曲的概念
F
F
在 AC 和 DB 段 , 梁 的 横 截 面既有弯矩,又有剪力,这 种情况称为横力弯曲(剪切 弯曲)。 在 CD 段 内 , 梁 的 横 截 面
A C
a
F
+
B
D
a
上剪力为零,而弯矩为常量, 这种情况称为纯弯曲。
+
F. a
F
梁在纯弯曲变形时,横截面
+
上只有与弯矩有关的正应力。
材料力学Ⅰ电子教案
材料力学
第五章 弯曲应力
第五章 弯曲应力
четверг, 3 декабря 2020 г.
材料力学Ⅰ电子教案
第五章 弯曲应力
第五章 弯曲应力
§5-1 纯弯曲 §5-2 纯弯曲时的正应力
§5-3 横力弯曲时的正应力
§5-4 弯曲切应力
§5-5* 关于弯曲理论的基本假设
§5-6 提高弯曲强度的措施
即:
FN
dA0,
A
My
zdA0,
A
Mz
ydAM
A
材料力学Ⅰ电子教案
第五章 弯曲应力
FN
dA0
A
AdAEAydA0
AydASz 0
z 轴通过形心
材料力学教案第5章弯曲应力
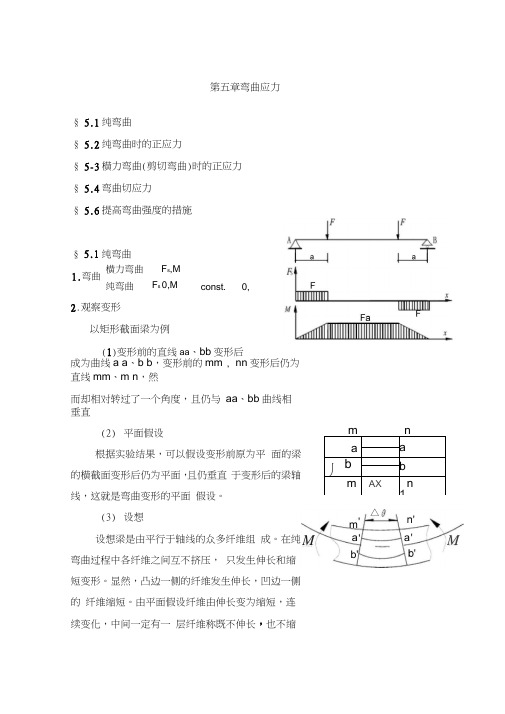
§ 5.1纯弯曲§ 5.2纯弯曲时的正应力§ 5-3横力弯曲(剪切弯曲)时的正应力 § 5.4弯曲切应力 § 5.6提高弯曲强度的措施成为曲线a a 、b b ,变形前的mm , nn 变形后仍为直线mm 、m n ,然而却相对转过了一个角度,且仍与 aa 、bb 曲线相垂直(2) 平面假设根据实验结果,可以假设变形前原为平 面的梁的横截面变形后仍为平面,且仍垂直 于变形后的梁轴线,这就是弯曲变形的平面 假设。
(3) 设想设想梁是由平行于轴线的众多纤维组 成。
在纯弯曲过程中各纤维之间互不挤压, 只发生伸长和缩短变形。
显然,凸边一侧的纤维发生伸长,凹边一侧的 纤维缩短。
由平面假设纤维由伸长变为缩短,连续变化,中间一定有一 层纤维称既不伸长,也不缩第五章弯曲应力§ 5.1纯弯曲 1.弯曲 横力弯曲 纯弯曲 F s ,M F s 0,M const.0,2.观察变形 以矩形截面梁为例 (1)变形前的直线aa 、bb 变形后1aa丿bbm AXn 1mn△m Maa M b'短,这一层纤维为中性层。
(4)中性轴中性层与横截面的交线称为中性轴,由于整体变形的对称性,中性轴由与纵向对称面垂直。
P139 note:可以证明,中性轴为形心主轴。
§ 5.2纯弯曲时的正应力1.正应力分布规律:r①变形几何关系Y②物理关系•③静力关系(1)变形几何关系取dx微段来研究,竖直对称轴为为z轴,距中性层为y的任一纤维b by d d yd(2)物理关系因为纵向纤维之间无正应和,每一纤维都是单向拉伸或者单向压缩,当应力小于比例极限时,由胡克定律(b)此式表明:任意纵向纤维的正应力与它到中性层的距离成正比。
在横截面上,任意点的正应力与该点到中性轴的距离成正比。
亦即沿截面高度,正应力按直线规律变化。
(3)静力关系横截面上的微内力。
dA 组成垂直于横截面的空间平行力学。
材料力学电子教案弯曲内力

一、弯曲实例 工厂厂房的吊车大梁:
F F
火车的轮轴:
F
F
F
F
楼房的横梁:
阳台的挑梁:
二、弯曲的概念:
受力特点——作用于杆件上的外力都垂直于杆的轴线。 变形特点——杆轴线由直线变为一条平面的曲线。
主要产生弯曲变形的杆--- 梁。
P
q
M
RA
NB
三、平面弯曲的概念:
F1
q
F2
M
纵向对称面
平面弯曲
受力特点——作用于杆件上的外力都垂直于杆的轴线,且都在 梁的纵向对称面内。
变形特点——杆的轴线在梁的纵向对称面内由直线变为一条平 面曲线。
纵向对称面
§4-2 静定梁的分类(三种基本形式)
q(x)— 分布力 1、悬臂梁:
2、简支梁:
L M — 集中力偶
3、外伸梁:
L q — 均布力
M2
M2 RB 1.5 1.21.5 0.75
Fs 2
2.91.51.21.50.75
3.0(kN m)
∴ 弯曲构件内力:Fs -剪力,M -弯矩。
若研究对象取m - m 截面的右段:
Y 0, Fs F FBY 0.
mC 0,
FBY
FBY (l x) F(a x) M 0.
Fs
F(l l
a)
,
M F(l a) x l
1. 弯矩:M 构件受弯时,横截面上
存在垂直于截面的内力偶矩 (弯矩)。
F — 集中力
L
L
(L称为梁的跨长)
§4-3 剪力与弯矩
一、弯曲内力的确定(截面法):
[例]已知:如图,F,a,l。
材料力学电子教案PPT弯曲变形

材料力学Ⅰ电子教案
边界条件 x=0 和 x=l 处,ω=0
A
梁的转角方程和挠曲线方程为
A
x
q (6lx2 4 x3 l 3 ) RA
24EI
q
wmax
B
B
l
RB
w qx (2lx2 x3 l 3 ) 24EI
在梁跨中点处有最大挠度值
在 x=0 和 x=l 处转角的绝对值 相等且都是最大值,
Fx 3 6
C 1x
C2
(4)
F
Bx
材料力学Ⅰ电子教案
EIw
Flx
Fx 2 2
C1
(3)
EIw
Flx 2
2
Fx 3 6
C
1x
C
2
(4)
边界条件 x 0, w 0
x 0, w 0
将边界条件代入(3) (4)两式中,可得
C1 0 C2 0
梁的转角方程和挠曲线方程分别为
EIw Flx Fx2 2
其最大挠度wmax 和最大转角 max
w
A
F
Bx
l
材料力学Ⅰ电子教案
解: (1) 弯矩方程为
M(x) F(l x)
w
(1) A
(2) 挠曲线的近似微分方程为
x
EIw'' M( x) Fl Fx (2)
l
对挠曲线近似微分方程进行积分
Fx 2 EIw' Flx 2 C1 (3)
EIw
Flx 2 2
EIw Flx2 Fx3 26
材料力学Ⅰ电子教案 y A
l
F
Bx
wmax
max
max 和 wmax都发生在自由端截面处
材料力学_邓宗白_纯弯曲时的正应力
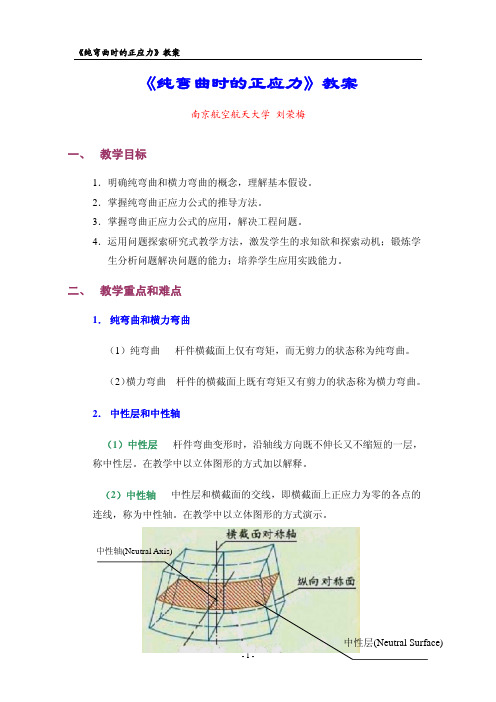
[例 2] 在相同载荷下,将实心轴改成 smax 相等的空心轴,空心轴内外
径比为 0.6。求空心轴和实心轴的重量比。
D1
解:(1)确定空心轴尺寸
D
d1
由
σ max
=
M W
π 32
D13
(1
−
0.64
)
=
7.9
×10−4
D1 = 210 mm
(2)比较两种情况下的重量比(面积比):
-6-
《纯弯曲时的正应力》教案
连线,称为中性轴。在教学中以立体图形的方式演示。
中性轴(Neutral Axis)
中性层(Neutral Surface)
-1-
《纯弯曲时的正应力》教案
(3)中性轴的位置 纯弯曲时,直梁的中性轴通过横截面的形心且垂直 于载荷作用面。强调这一结论是在轴力为零的情况下得到的。
3. 直梁横截面上弯曲正应力公式 σ = My Iz
纯弯曲时横截面上弯曲正应力的计算公式
σ = My Iz
4. 导出σ max 的表达式、抗弯截面模量 W 的定义及常用横截面 W 的表达式。
b
σ max
=
Mymax Iz
=M I z ymax
抗弯截面系数( Section Modulus)
z
y d
矩形截面
W = I z = bh3 12 = bh2
查型钢表或用组合法求。
注意:如果中性轴不是横截面对称(如 T 形钢), ymax 有两个,对应 W 也应有两个。
三、 教学手段
综合运用演示实验、多媒体课件等教学手段。
-2-
《纯弯曲时的正应力》教案
四、 教学方法
问题探索研究式教学方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
弯曲应力
我们开始弯曲这一章,我们讲了拉压、扭转、剪切,现在我们要讲弯曲。
弯曲的情况要比拉压和扭转更加复杂一些,它所涉及的问题更多一些,它和工程实际联系的更加紧密一些。
因此,这一章和下一章都是特别重要的章节。
在这一章中,我们首先要讨论弯曲正应力,横截面上有弯矩,那它就有了正应力,同时还要考虑弯曲切应力的问题,横截面上有剪力,说明它有切应力存在。
了解了正应力和切应力的情况,我们要讨论梁的强度和破坏,这个思路和前面几章是一样的。
特别的,要强调薄壁杆件中弯曲切应力的处理,最后呢,我们要讲组合变形的应用。
不仅仅是弯曲,而是弯曲和拉压,弯曲和扭转组合在一起的时候,如何来处理它的应力问题。
因此,这章的内容是比较多的。
工程实际例子
我们来看看弯曲在工程中的应用。
这是一个厂房,这是一个大梁,这个吊车可以在这个大梁上运动。
对于这样一个问题,我们可以把它简化成一个简支梁,这个吊车的移动呢可以处理成一个移动荷载。
那么对于这个移动荷载而言,它所导致的应力如何计算?行车移动时,它的应力如何变化?这就是本章的内容之一。
我们再看看这个图片,这是我们拍摄的汽车的下部分,大家注意一些这个部分,这是就是汽车的板簧,它的模型就是这个样子,可以看成好几个钢板的组合,那么,为什么要设计成这个样子呢?它有什么优点呢?这也是本章要解决的问题。
这是一个运动员,撑杆跳,对吧。
大家常常见到,利用这个杆的助力,人可以跳的更高。
我们可以处理成这样一个模型。
她在跳高的过程中,杆就发生了弯曲。
那么,这个时候,跳杆横截面上的应力和杆曲率半径有什么关系?这个杆在什么情况下才满足强度要求?
大家看看这个场面,对于这个场面,我们截面几何性质那章提到过,都是薄壁杆件,那么薄壁杆件有弯曲正应力和弯曲切应力,专门有一小节来讲解它的弯曲切应力,看看这些切应力有什么特点?如何避免薄壁杆件的强度失效?这也是本章的问题
这个大家都熟悉,著名的比萨斜塔。
对于这个结构,初步计算,我们可以简化成这样一个均质圆筒,那么它有哪些变形效应?它的危险截面、危险点在哪儿?如何计算其应力?这也是本章可以解决的问题。
因此,本章所涉及的问题是比较广的。
基本内容
那么本章到底需要同学们掌握哪些内容呢?
1、熟练张博横截面上弯曲正应力和弯曲切应力的分布规律,并能正确熟练
的进行梁的强度分析。
2、熟悉提高梁强度的主要措施。
3、正确理解薄壁杆件横截面上弯曲切应力的分布规律,了解弯曲中心的概
念。
4、熟悉掌握梁在组合变形中的应力的计算方法。
第一、第四条是很重要的。
这是以后大家经常需要处理的问题。
基本概念
平面弯曲
首先我们来看弯曲正应力。
在这章具体内容介绍之前呢,我们先介绍一些概念。
关于梁弯曲的基本概念。
梁的平面弯曲。
什么是梁的平面弯曲呢?这是一个悬臂梁,截面是矩形截面,那么这个横截面就有一个中心对称轴,整个梁就存在一个对称面,如果我们的所有的外荷载都作用在这个平面之内,比如外荷载是这样的,那么发生变形后,梁的轴线仍然在这个平面内,像这样的弯曲,我们就叫做平面弯曲。
也就是说,梁弯曲后,它的轴线也保持在一个平面之内。
像这样的弯曲,我们就叫做平面弯曲。
纯弯曲和横力弯曲
什么叫做纯弯曲呢?
如果一个悬臂梁,只在它的端头作用一个集中力偶,大家可以想象到,它的每个横截面上,只有弯矩,没有剪力。
像这样只有弯矩没有剪力的弯曲,我们叫做纯弯曲,纯粹的弯曲。
比如:这个举重运动员。
他的两只手把杠铃杆举起来,我们弯曲可以简化成这样一个模型,支座就相当于两只手,而两个杠铃盘的作用力就简化成两个向下的作用力。
假如我们不考虑杠铃杆自身的重量,虽然实际上是有重量的,在两个手之间的部分就只有弯矩而没有剪力。
因为,这样一个结构而言,整个黄色区段,剪力是为零的。
而另外两个区段就不是纯弯曲。
横力弯曲
什么是横力弯曲呢?当梁的横截面上,有弯矩又有剪力的时候,我们就把这种弯曲叫做横力弯曲。
比如说,像这样的货架,我们考虑其中一个架子,我们可以把它考虑成承受均布荷载的悬臂梁,这个时候的悬臂梁,上面除了有弯矩之外,还有剪力。
因此,它的弯曲就是横力弯曲。
又比如这样的梁,承受三个集中力,这个梁的横截面上有弯矩和剪力。
总之,横截面上只有弯矩的梁是纯弯曲梁,而横截面上有弯矩又有剪力的梁就是横力弯曲的梁。
以后我们的推导呢,全是以纯弯曲作为例子,来进行推导,再把推导的结果推广到横力弯曲中去。
这个大家要注意。
平截面假定
关于梁的弯曲的假定有两个,其中一个是平截面假定。
这一点和拉压扭转是一样的,当然,对于弯曲而言,它有自己的特点。
这是一个悬臂梁,左边是固定端,右端作用一个集中力偶矩。
那么,横截面在变形前是一个平面,而变形后仍然也是一个平面。
我们就把这样一个现象叫做平截面假设。
对于一个纯弯曲而言的梁呢,变形前确实就是一个平面,而变形后也确实就是一个平面,这是一个精确的假定。
换句话说,这个假定是完全符合客观情况的。
但是对于另外一种弯曲,杆端作用的不是集中力偶而是集中力的时候,这是一种横力弯曲,横截面上有弯矩和剪力。
那么,变形前是一个平面,而变形后不再是一个平面。
也就是说,对横力弯曲而言,平截面假定不是一个精确的假定,但是,我们以后就会明白,是这个平面上剪力的作用,导致这个平面发生翘曲,翘曲导致平面不再是平面,距离平面不远的地方发生的微微的翘曲的情况,因此,它所带来的误差是工程中弯曲可以接受的,因此,对于横力弯曲来说,这是一个近似的假设。
第二个假定:单向受力假定
什么叫做单向受力假定?比如,我们在这个梁上取一个微元面,这个微元面是垂直于轴线的方向。
那么我们可以看到这个微元面上有正应力的存在,这就是横截面上的正应力,假如我们把这个方向叫做x 方向,我们就把这个应力叫做x σ,这就是我们承认他存在的正应力。
刚刚我们取的是一个垂直于轴线的微元面,现在我们取一个面,让他平行于我们的轴线,也就是y σ,我们认为0=y σ,也就是说,我们在假设这样一件事,比如这里有一个梁,它发生了弯曲,比如发生一个正弯曲,那么,我们认为在垂直于轴线的截面上有了正应力,可能在有的地方时拉,在有的地方是压。
但是,在同一个梁上,上下平行于轴线的两个纤维之间,没有拉压,或者挤压。
也就是0=y σ,这个梁上的沿着轴线的纤维被拉长或者缩短了的,那么就说明在横截面上是有正应力的。
这就是单向受力假定。
那么,在什么情况下,这个假定是精确成立的呢?在什么情况下,这个假定又是近似成立的呢?刚刚我们在悬臂梁的右端作用一个集中力,或者作用一个集中力偶,那么这种情况下。
我们看到的微元面的地方都满足单向受力假定。
对于集中的荷载而言,这个假定就是精确成立的。
但是有的时候并不是集中荷载,比如像图中这样的分布荷载的时候,我们先考虑一下这个纵向截面,我们把这个微元面取到上表面,那么这个时候根据力平衡,我们知道,y 方向的应力就等于力平衡。
因此,这个时候,我们不能说它等于零。
当我们把这个纵向平面往下取一些,那么我们会发现上面的q 对它的作用减小了。
再往下一些就更小了,继续往下,就消失了。
(用手比划)在y 方向上应力是从大到小在变化的,另外,即使在最上面的面,它的外荷载就等于Q,而我们同时在这个面取一个横截面,x 方向的正应力比y 方向的大的多。
也就是说在y 方向,这个应力在减小,即便在y 方向上应力最大的地方,也比x 方向的应力小的多。
因此,我们往往就忽略y 方向的应力,这就是我们的单向受力假定。
梁的弯曲,我们重点研究横截面,不再研究纵向截面。
以后,我们主要研究横截面的正应力和横截面的切应力,这是我们主要研究的内容。
中性层
还有一个概念叫做中性面,这是一个悬臂梁,承受一个集中力偶矩,发生了如图的变形,我们可以想象到,上面部分,它的纵向纤维总是受拉的,而下半部分,它的纵向纤维总是受压的,但是由于受力的连续性,那么中间一定有一个面是既不受拉也不受压,这是说,这个面既不被拉长,也不被压缩。
我们把这个面叫做中性面。
他是梁的轴线纤维伸长区和缩短区的界面。
而中性面和横截面那根交线,我们把它叫做中性轴,因此,在中性轴上,沿着轴的纤维既不伸长也不缩短。
当然,中性面和中性轴都是在梁的里面的。
好了,这就是我们这章的准备性的概念,这章的内容比较多,所以需要提前准备的知识点也比较多。
好了,我们知道这些知识以后,就可以来研究梁横截面上的应力分析了。
横截面上正应力
这个分析过程和以前扭转给大家讲的过程一样,我们先交代一下这个分析的思路,仍然是我们力学十分重要的三个环节,第一个是几何分析,第二个是物理
分析,第三个是力学分析这样三个环节,那么具体到我们这个章节,我们首先讨论几何关系,再讨论物理关系,最后讨论力学关系。
这点和扭转的时候是一样的,当时也是通过这样的思路来讨论。
首先通过几何关系推导出正应变和中性层曲率间的关系。
有了几何关系后呢,我们就可以转入物理关系的讨论,在我们现在讨论的范畴中呢,物理关系主要是指正应力与中性层曲率之间的关系。
最后力学关系,。
