广东海洋大学概率论与数理统计套题 答案
(完整版)概率论与数理统计复习题带答案讲解

;第一章 一、填空题1. 若事件A ⊃B 且P (A )=0.5, P(B) =0.2 , 则 P(A -B)=( 0.3 )。
2. 甲、乙各自同时向一敌机炮击,已知甲击中敌机的概率为0.7,乙击中敌机的概率为0.8.求敌机被击中的概率为( 0.94 )。
3. 设A、B、C为三个事件,则事件A,B,C中不少于二个发生可表示为(AB AC BC ++ )。
4. 三台机器相互独立运转,设第一,第二,第三台机器不发生故障的概率依次为0.9,0.8,0.7,则这三台机器中至少有一台发生故障的概率为( 0.496 )。
5. 某人进行射击,每次命中的概率为0.6 独立射击4次,则击中二次的概率为( 0.3456 )。
6. 设A、B、C为三个事件,则事件A,B与C都不发生可表示为( ABC )。
7. 设A、B、C为三个事件,则事件A,B,C中不多于一个发生可表示为( ABAC BC I I ); 8. 若事件A 与事件B 相互独立,且P (A )=0.5, P(B) =0.2 , 则 P(A|B)=( 0.5 ); 9. 甲、乙各自同时向一敌机炮击,已知甲击中敌机的概率为0.6,乙击中敌机的概率为0.5.求敌机被击中的概率为( 0.8 ); 10. 若事件A 与事件B 互不相容,且P (A )=0.5, P(B) =0.2 , 则 P(B A -)=( 0.5 ) 11. 三台机器相互独立运转,设第一,第二,第三台机器不发生故障的概率依次为0.8,0.8,0.7,则这三台机器中最多有一台发生故障的概率为( 0.864 )。
12. 若事件A ⊃B 且P (A )=0.5, P(B) =0.2 , 则 P(B A )=( 0.3 ); 13. 若事件A 与事件B 互不相容,且P (A )=0.5, P(B) =0.2 , 则 P(B A )=( 0.5 ) 14. A、B为两互斥事件,则A B =U ( S )15. A、B、C表示三个事件,则A、B、C恰有一个发生可表示为( ABC ABC ABC ++ )16. 若()0.4P A =,()0.2P B =,()P AB =0.1则(|)P AB A B =U ( 0.2 ) 17. A、B为两互斥事件,则AB =( S )18. 保险箱的号码锁定若由四位数字组成,则一次就能打开保险箱的概率为(110000)。
概率论与数理统计课后习题参考答案

习题11、(1)同时掷两枚骰子,记录点数之和 {2,3,,12}S =;(2)生产产品知道得到5件正品,记录生产产品的总件数 {5,6,}S =; (3)单位圆任取一点,记录它的坐标 22{(,)1,,}S x y x y x R y R =+<∈∈;(4)将单位长线段分3段,观察各段长度{(,,)1,0,0,0}S x y z x y z x y z =++=>>>。
2、(1)A 与B 都发生,C 不发生:ABC ;(2)ABC 至少一个发生:A B C ;(3)ABC 不多于一个发生:ABAC BC 。
3、对事件ABC ,已知P(A)=P(B)=P(C)=1/4,P(AB)=P(BC)=0,P(AC)=1/8,求ABC 至少发生一个的概率?解:依题可知,()0P ABC =,则所求的概率为()()()()()()()()P A B C P A P B P C P AB P AC P BC P ABC ++=++---+1153000488=⨯---+= 4、将10本书任意地放在书架上,其中有一套4卷成套的书,求概率?解:设事件A 表示“成套的书放在一起”,B 表示“成套的书按卷次顺序排好放在一起”,由概率的古典定义可得所求的概率为 (1)成套的书放在一起:7!4!1()10!30P A ⋅==(2)成套的书案卷次顺序排好放在一起:7!11()10!720P B ⋅==5、从5双不同的鞋子中任取4只,问这4只鞋子不能配成一双的概率是多少?解:设事件A 表示“取出的4只鞋子不能配成一双”,由概率的古典定义可得所求的概率为 44541028()21C P A C ⋅== 6、在电话号码簿中任取一个电话号码,求后面4个数全不相同的概率?解:设事件A 表示“电话号码的后面4个数全不相同”,由概率的古典定义可得所求的概率为4104()0.50410A P A ==7、已知P(非A)=0、3,P(B)=0、4,P(A 非B)=1/2,求P(B|AU 非B)? 解:依题可知,()1()0.7P A P A =-=,()1()0.6P B P B =-=,而()0.55()()0.77P AB P B A P A ===则2()1()7P B A P B A =-=,()()()0.2P AB P A P B A ==,故所求的概率为 ()()()()()P BAB P ABBB P B A B P AB P AB ⎡⎤⎣⎦== ()0.20.25()()()0.70.60.5P AB P A P B P AB ===+-+-8、设AB 是随机事件,P(A)=0、7,P(A-B)=0、3,求P (非(AB))?解:由()()()P A B P A P AB -=-,得()()()0.70.30.4P AB P A P A B =--=-=故 ()1()0.6P AB P AB =-=9、半圆内均匀的投掷一随机点Q ,试求事件A={Q于π/4}的概率?解:事件A 所对应的区域D 如下图所示,由概率的几何定义得所求的概率为()()()m D P A m S ==10、10解:设事件A 表示“这对夫妇正好坐在一起”,(91)!22()(101)!9P A -⋅==-11、已知10只晶体管中有2只是次品,在其中任取两只,每次随机取一只作不放回抽取 解:设事件A 表示“两只都是正品”, B 表示“两只都是次品”, C 表示“一只是正品,一只是次品”, D 表示“第二次取出的是次品”, 由概率的古典定义可得所求的概率为(1)两只都是正品2821028()45A P A A == (2)两只都是次品222101()45A P B A ==(3)一直是正品,一只是次品11128221016()45C C C P C A ⋅⋅== (4)第二次取出的是次品11292101()5C C PD A ⋅== 12、某学生接连参加同一课程的两次考试,第一次及格的概率为p ,如果他第一次及格,则x第二次及格的概率也为p ,如果第一次不及格,第二次及格概率为p/2。
《概率论与数理统计》考试题(含答案)

《概率论与数理统计》考试题一、填空题(每小题2分,共计60分)1、A 、B 是两个随机事件,已知0.3)B (p ,5.0)A (p ==,则a )、若B A ,互斥,则=)B -A (p 0.5 ;b )若B A ,独立,则=)B A (p 0.65 ;c )、若2.0)(=⋅B A p ,则=)B A (p 3/7 . 2、袋子中有大小相同的红球7只,黑球3只,(1)从中不放回地任取2只,则第一、二次取到球颜色不同的概率为: 7/15 。
(2)若有放回地任取2只,则第一、二次取到球颜色不同的概率为: 21/50 。
(3)若第一次取一只球后再追加一只与其颜色相同的球一并放入袋中再取第二只球,则第一、二次取到球颜色不同的概率为: 21/55 . 3、设随机变量X 服从泊松分布}8{}7{),(===X P X p λπ,则{}=X E 8 .4、设随机变量X 服从B (2,0. 8)的二项分布,则{}==2X p 0.64 , Y 服从B (8,0. 8)的二项分布, 且X 与Y 相互独立,则}1{≥+Y X P =1- 0.210,=+)(Y X E 8 。
5 设某学校外语统考学生成绩X 服从正态分布N (75,25),则该学校学生的及格率为 0.9987 ,成绩超过85分的学生占比}85{≥X P 为 0.0228 。
其中标准正态分布函数值9987.0)3(,9772.0)2(,8413.0)1(=Φ=Φ=Φ. 6、设二维随机向量),(Y X 的分布律是有 则=a _0.1_,X的数学期望=)(X E ___0.4___,Y X 与的相关系数=xy ρ___-0.25______。
7、设161,...,X X 及81,...,Y Y 分别是总体)16,8(N 的容量为16,8的两个独立样本,Y X ,分别为样本均值,2221,S S 分别为样本方差。
则:~X N(8,1) ,~Y X - N(0,1.5) ,{}5.12>-Y X p = 0.0456 ,~161521S )15(2χ,~2221S S F(15,7) 。
概率论与数理统计习题(含解答,答案)

概率论与数理统计习题(含解答,答案)概率论与数理统计复习题(1)⼀.填空.1.3.0)(,4.0)(==B P A P 。
若A 与B 独⽴,则=-)(B A P ;若已知B A ,中⾄少有⼀个事件发⽣的概率为6.0,则=-)(B A P 。
2.)()(B A p AB p =且2.0)(=A P ,则=)(B P 。
3.设),(~2σµN X ,且3.0}42{ },2{}2{=<<≥==>}0{X P 。
4.1)()(==X D X E 。
若X 服从泊松分布,则=≠}0{X P ;若X 服从均匀分布,则=≠}0{X P 。
5.设44.1)(,4.2)(),,(~==X D X E p n b X ,则==}{n X P6.,1)(,2)()(,0)()(=====XY E Y D X D Y E X E 则=+-)12(Y X D 。
7.)16,1(~),9,0(~N Y N X ,且X 与Y 独⽴,则=-<-<-}12{Y X P (⽤Φ表⽰),=XY ρ。
8.已知X 的期望为5,⽽均⽅差为2,估计≥<<}82{X P 。
9.设1?θ和2?θ均是未知参数θ的⽆偏估计量,且)?()?(2221θθE E >,则其中的统计量更有效。
10.在实际问题中求某参数的置信区间时,总是希望置信⽔平愈愈好,⽽置信区间的长度愈愈好。
但当增⼤置信⽔平时,则相应的置信区间长度总是。
⼆.假设某地区位于甲、⼄两河流的汇合处,当任⼀河流泛滥时,该地区即遭受⽔灾。
设某时期内甲河流泛滥的概率为0.1;⼄河流泛滥的概率为0.2;当甲河流泛滥时,⼄河流泛滥的概率为0.3,试求:(1)该时期内这个地区遭受⽔灾的概率;(2)当⼄河流泛滥时,甲河流泛滥的概率。
三.⾼射炮向敌机发射三发炮弹(每弹击中与否相互独⽴),每发炮弹击中敌机的概率均为0.3,⼜知若敌机中⼀弹,其坠毁的概率是0.2,若敌机中两弹,其坠毁的概率是0.6,若敌机中三弹则必坠毁。
《概率论与数理统计》习题及答案

概率论与数理统计 第一部份 习题第一章 概率论基本概念一、填空题1、设A ,B ,C 为3事件,则这3事件中恰有2个事件发生可表示为 。
2、设3.0)(,1.0)(=⋃=B A P A P ,且A 与B 互不相容,则=)(B P 。
3、口袋中有4只白球,2只红球,从中随机抽取3只,则取得2只白球,1只红球的概率为 。
4、某人射击的命中率为0.7,现独立地重复射击5次,则恰有2次命中的概率为 。
5、某市有50%的住户订晚报,有60%的住户订日报,有80%的住户订这两种报纸中的一种,则同时订这两种报纸的百分比为 。
6、设A ,B 为两事件,3.0)(,7.0)(==B A P A P ,则=)(B A P 。
7、同时抛掷3枚均匀硬币,恰有1个正面的概率为 。
8、设A ,B 为两事件,2.0)(,5.0)(=-=B A P A P ,则=)(AB P 。
9、10个球中只有1个为红球,不放回地取球,每次1个,则第5次才取得红球的概率为 。
10、将一骰子独立地抛掷2次,以X 和Y 分别表示先后掷出的点数,{}10=+=Y X A{}Y X B >=,则=)|(A B P 。
11、设B A ,是两事件,则B A ,的差事件为 。
12、设C B A ,,构成一完备事件组,且,7.0)(,5.0)(==B P A P 则=)(C P ,=)(AB P 。
13、设A 与B 为互不相容的两事件,,0)(>B P 则=)|(B A P 。
14、设A 与B 为相互独立的两事件,且4.0)(,7.0)(==B P A P ,则=)(AB P 。
15、设B A ,是两事件,,36.0)(,9.0)(==AB P A P 则=)(B A P 。
16、设B A ,是两个相互独立的事件,,4.0)(,2.0)(==B P A P 则=)(B A P 。
17、设B A ,是两事件,如果B A ⊃,且2.0)(,7.0)(==B P A P ,则=)|(B A P 。
大学概率论与数理统计习题及参考答案

P A P AB1 AB2 P AB1 P AB2 P B1 P A B1 P B2 P A B2
2 1 0.97 0.98 有9个是新的。第一次比赛从中任取3个来用, 比赛后仍放回盒中,第二次比赛再从盒中任取3个,求第二次取出的球都是 新球的概率。 解: 设 Bi 表示事件“第一次取出了 i 个新球”i, =0,1,2,3.
从而P( A B) 1 P( AB) 1 0.012 0.988.
10
三、为防止意外, 在矿内同时设有两种报警系统A与B, 每种系统单独使用时, 其有
效的概率系统A为0.92,系统B为0.93, 在A失灵的条件下, B有效的概率为0.85, 求 (1)发生意外时, 这两个报警系统至少有一个有效的概率; (2) B失灵的条件下, A有效的概率.
解
设事件A表示“报警系统A有效”,事件B表示“报警系统B有效”,由已知
P ( A) 0.92, P ( B) 0.93, P ( B A) 0.85,
则 P ( AB ) P ( A) P ( B A) 0.08 0.85 0.068 , 故 P( AB) P( B) P( AB) 0.93 0.068 0.862,
AB 6 ; A B 1 ,5 .
1
四、写出下面随机试验的样本空间: (1)袋中有5只球,其中3只白球2只黑球,从袋中 任意取一球,观察其颜色; (2) 从(1)的袋中不放回任意取两次球(每次取出一个)观察其颜色; (3) 从(1)的袋中不放回任意取3只球,记录取到的黑球个数; (4) 生产产品直到有10件正品为止,记录生产产品的总件数; 解 (1)设
i
表示抛掷一颗骰子,出现i点数,i=1,2,3,4,5,6. 则样本空间
广东海洋大学概论历年考题 答案
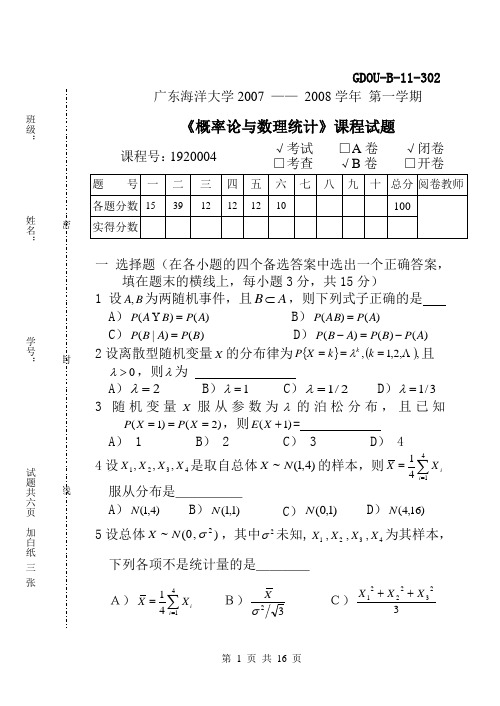
广东海洋大学2007 —— 2008学年 第一学期《概率论与数理统计》课程试题课程号: 1920004 √ 考试 □ A 卷 √ 闭卷 □ 考查√ B 卷□ 开卷一 选择题(在各小题的四个备选答案中选出一个正确答案,填在题末的横线上,每小题3分,共15分)1 设B A ,为两随机事件,且B A ⊂,则下列式子正确的是 A ))()(A P B A P = B ))()(A P AB P =C ))()|(B P A B P =D ))()()(A P B P A B P -=- 2设离散型随机变量X 的分布律为{}(),,2,1, ===k k X P k λ且0>λ,则λ为 A )2=λ B )1=λ C )2/1=λ D )3/1=λ 3随机变量X 服从参数为λ的泊松分布,且已知)2()1(===X P X P ,则)1(+X E = A ) 1 B ) 2 C ) 3 D ) 4 4设4321,,,X X X X 是取自总体)4,1(~N X的样本,则∑==4141i iX X 服从分布是_____A ))4,1(NB ))1,1(NC ))1,0(ND ))16,4(N 5设总体),0(~2σN X,其中2σ未知,1234,,,X X X X 为其样本,下列各项不是统计量的是____ A)4114ii XX ==∑ B)32σXC)3232221X XX ++班级:姓名:学号:试题共六页加白纸 三 张密封线GDOU-B-11-302D)4211()3ii S X X ==-∑二 填空题 (每小题3分,共39分)1十把钥匙中有三把能打开门,今不放回任取两把,求恰有 一把能打开门的概率为2已知3.0)(=B P ,6.0)(=A P ,且A 与B 相互独立,则=)(B A P3设每次试验的成功率为)10(<<p p ,则在3次重复试验中至多失败一次概率为 4设随机变量),(Y X 具有概率密度函数⎩⎨⎧<<<<=其它10,106),(2y x yx y x f则=<>}5.0,5.0{Y X P5设随机变量)4.0,3(~b X ,且随机变量2)3(X X Y -=,则==}1{YP6已知(X,Y )的联合分布律为:则===}0|1{X YP7设随机变量),(Y X 具有概率密度函数⎩⎨⎧<<<<+=其它0,10)(2),(x y x y x y x f则随机变量X 的边缘概率密度为 8设正态随机变量X 的概率密度为)(,221)(8/)1(2R x ex f x ∈=--π则)12(+-XD =9生产灯泡的合格率为0.5,则100个灯泡中合格数在40与 60之间的概率为 (9772.0)2(=Φ) 10设某种清漆干燥时间),(~2σμN X取样本容量为9的样本,得样本均值和标准差分别为33.0,6==s x,则μ的置信水平为90%的置信区间为 (86.1)8(05.0=t ) 11已知总体),1,0(~N X又设4321,,,X X X X 为来自总体的样本,则~24232221X X X X ++____ __ _(同时要写出分布的参数)12设4321,,,X X X X 是来自总体X的一个简单随机样本,4321214181kXX XX +++是总体期望)(X E 的无偏估计量,则=k 13设n X X X ,,,21 是总体X)1,1(~+-θθU 的简单随机样本,则未知参数θ的矩估计量为三 一箱产品由甲,乙两厂生产,若甲,乙两厂生产的产品分别占70%,30%,其次品率分别为1%,2%.现从中任取一件产品,得到了次品,求它是哪个厂生产的可能性更大.(12分)四 设总体X 的概率密度为⎪⎩⎪⎨⎧=-01)(/θθx ex f 00≤>x x (0>θ,未知),n x x x ,,,21 是来自总体X 的一个样本观察值,求未知参数θ的最大似然估计值。
(完整word版)概率论与数理统计习题集及答案(word文档良心出品)

《概率论与数理统计》作业集及答案第1章 概率论的基本概念§1 .1 随机试验及随机事件1. (1) 一枚硬币连丢3次,观察正面H ﹑反面T 出现的情形. 样本空间是:S= ;(2) 一枚硬币连丢3次,观察出现正面的次数. 样本空间是:S= ; 2.(1) 丢一颗骰子. A :出现奇数点,则A= ;B :数点大于2,则B= . (2) 一枚硬币连丢2次, A :第一次出现正面,则A= ;B :两次出现同一面,则= ;C :至少有一次出现正面,则C= .§1 .2 随机事件的运算1. 设A 、B 、C 为三事件,用A 、B 、C 的运算关系表示下列各事件:(1)A 、B 、C 都不发生表示为: .(2)A 与B 都发生,而C 不发生表示为: . (3)A 与B 都不发生,而C 发生表示为: .(4)A 、B 、C 中最多二个发生表示为: . (5)A 、B 、C 中至少二个发生表示为: .(6)A 、B 、C 中不多于一个发生表示为: . 2. 设}42:{},31:{},50:{≤<=≤<=≤≤=x B x x A x x S :则(1)=⋃B A ,(2)=AB ,(3)=B A , (4)B A ⋃= ,(5)B A = 。
§1 .3 概率的定义和性质1. 已知6.0)(,5.0)(,8.0)(===⋃B P A P B A P ,则(1) =)(AB P , (2)()(B A P )= , (3))(B A P ⋃= . 2. 已知,3.0)(,7.0)(==AB P A P 则)(B A P = .§1 .4 古典概型1. 某班有30个同学,其中8个女同学, 随机地选10个,求:(1)正好有2个女同学的概率,(2)最多有2个女同学的概率,(3) 至少有2个女同学的概率.2. 将3个不同的球随机地投入到4个盒子中,求有三个盒子各一球的概率.§1 .5 条件概率与乘法公式1.丢甲、乙两颗均匀的骰子,已知点数之和为7, 则其中一颗为1的概率是 。
概率论与数理统计答案完整版

概率论与数理统计答案 Company number:【0089WT-8898YT-W8CCB-BUUT-202108】习题答案第1章三、解答题1.设P (AB ) = 0,则下列说法哪些是正确的 (1) A 和B 不相容; (2) A 和B 相容; (3) AB 是不可能事件; (4) AB 不一定是不可能事件; (5) P (A ) = 0或P (B ) = 0 (6) P (A – B ) = P (A ) 解:(4) (6)正确.2.设A ,B 是两事件,且P (A ) = ,P (B ) = ,问: (1) 在什么条件下P (AB )取到最大值,最大值是多少 (2) 在什么条件下P (AB )取到最小值,最小值是多少 解:因为)()()()(B A P B P A P AB P -+≤,又因为)()(B A P B P ≤即.0)()(≤-B A P B P 所以(1) 当)()(B A P B P =时P (AB )取到最大值,最大值是)()(A P AB P ==.(2) 1)(=B A P 时P (AB )取到最小值,最小值是P (AB )=+=. 3.已知事件A ,B 满足)()(B A P AB P =,记P (A ) = p ,试求P (B ).解:因为)()(B A P AB P =,即)()()(1)(1)()(AB P B P A P B A P B A P AB P +--=-== ,所以 .1)(1)(p A P B P -=-=4.已知P (A ) = ,P (A – B ) = ,试求)(AB P .解:因为P (A – B ) = ,所以P (A )– P(AB ) = , P(AB ) = P (A )– , 又因为P (A ) = ,所以P(AB ) =– =,6.0)(1)(=-=AB P AB P .5. 从5双不同的鞋子种任取4只,问这4只鞋子中至少有两只配成一双的概率是多少 解:显然总取法有410C n=种,以下求至少有两只配成一双的取法k :法一:分两种情况考虑:15C k=24C 212)(C +25C 其中:2122415)(C C C 为恰有1双配对的方法数法二:分两种情况考虑:!2161815C C C k ⋅⋅=+25C其中:!2161815C C C ⋅⋅为恰有1双配对的方法数法三:分两种情况考虑:)(142815C C C k-=+25C其中:)(142815C C C -为恰有1双配对的方法数法四:先满足有1双配对再除去重复部分:2815C C k=-25C法五:考虑对立事件:410C k=-45C 412)(C其中:45C 412)(C 为没有一双配对的方法数法六:考虑对立事件:!4141618110410C C C C C k ⋅⋅⋅-=其中:!4141618110C C C C ⋅⋅⋅为没有一双配对的方法数所求概率为.2113410==C k p6.在房间里有10个人,分别佩戴从1号到10号的纪念章,任取3人记录其纪念章的号码.求: (1) 求最小号码为5的概率; (2) 求最大号码为5的概率.解:(1) 法一:12131025==C C p ,法二:1213102513==A A C p (2) 法二:20131024==C C p ,法二:2013102413==A A C p 7.将3个球随机地放入4个杯子中去,求杯子中球的最大个数分别为1,2,3的概率. 解:设M 1, M 2, M 3表示杯子中球的最大个数分别为1,2,3的事件,则834)(3341==A M P , 1694)(324232=⨯=A C M P , 1614)(3143==C M P8.设5个产品中有3个合格品,2个不合格品,从中不返回地任取2个,求取出的2个中全是合格品,仅有一个合格品和没有合格品的概率各为多少解:设M 2, M 1, M 0分别事件表示取出的2个球全是合格品,仅有一个合格品和没有合格品,则3.0)(25232==C C M P ,6.0)(2512131==C C C M P ,1.0)(25221==C C M P 9.口袋中有5个白球,3个黑球,从中任取两个,求取到的两个球颜色相同的概率.解:设M 1=“取到两个球颜色相同”,M 1=“取到两个球均为白球”,M 2=“取到两个球均为黑球”,则φ==2121M M M M M 且.所以.2813C C C C )()()()(282328252121=+=+==M P M P M M P M P10. 若在区间(0,1)内任取两个数,求事件“两数之和小于6/5”的概率.解:这是一个几何概型问题.以x 和y 表示任取两个数,在平面上建立xOy 直角坐标系,如图. 任取两个数的所有结果构成样本空间 = {(x ,y ):0 x ,y 1} 事件A =“两数之和小于6/5”= {(x ,y ) : x + y 6/5} 因此2517154211)(2=⎪⎭⎫ ⎝⎛⨯-=Ω=的面积的面积A A P . 图11.随机地向半圆220x ax y -<<(a 为常数)内掷一点,点落在半圆内任何区域的概率与区域的面积成正比,求原点和该点的连线与x 轴的夹角小于4π的概率. 解:这是一个几何概型问题.以x 和y 表示随机地向半圆内掷一点的坐标,表示原点和该点的连线与x 轴的夹角,在平面上建立xOy 直角坐标系,如图.随机地向半圆内掷一点的所有结果构成样本空间 ={(x ,y ):220,20x ax y a x -<<<<}事件A =“原点和该点的连线与x 轴的夹角小于4π” ={(x ,y ):40,20,202πθ<<-<<<<x ax y a x }因此211214121)(222+=+=Ω=πππa aa A A P 的面积的面积.12.已知21)(,31)(,41)(===B A P A B P A P ,求)(B A P . 解:,1213141)()()(=⨯==A B P A P AB P ,6121121)|()()(=÷==B A P AB P B P 13.设10件产品中有4件不合格品,从中任取两件,已知所取两件产品中有一件是不合格品,则另一件也是不合格品的概率是多少解:题中要求的“已知所取两件产品中有一件是不合格品,则另一件也是不合格品的概率”应理解为求“已知所取两件产品中至少有一件是不合格品,则两件均为不合格品的概率”。
概率论与数理统计答案完整版

概率论与数理统计答案 Company number:【0089WT-8898YT-W8CCB-BUUT-202108】习题答案第1章三、解答题1.设P (AB ) = 0,则下列说法哪些是正确的 (1) A 和B 不相容; (2) A 和B 相容; (3) AB 是不可能事件; (4) AB 不一定是不可能事件; (5) P (A ) = 0或P (B ) = 0 (6) P (A – B ) = P (A ) 解:(4) (6)正确.2.设A ,B 是两事件,且P (A ) = ,P (B ) = ,问: (1) 在什么条件下P (AB )取到最大值,最大值是多少 (2) 在什么条件下P (AB )取到最小值,最小值是多少 解:因为)()()()(B A P B P A P AB P -+≤,又因为)()(B A P B P ≤即.0)()(≤-B A P B P 所以(1) 当)()(B A P B P =时P (AB )取到最大值,最大值是)()(A P AB P ==.(2) 1)(=B A P 时P (AB )取到最小值,最小值是P (AB )=+=. 3.已知事件A ,B 满足)()(B A P AB P =,记P (A ) = p ,试求P (B ).解:因为)()(B A P AB P =,即)()()(1)(1)()(AB P B P A P B A P B A P AB P +--=-== ,所以 .1)(1)(p A P B P -=-=4.已知P (A ) = ,P (A – B ) = ,试求)(AB P .解:因为P (A – B ) = ,所以P (A )– P(AB ) = , P(AB ) = P (A )– , 又因为P (A ) = ,所以P(AB ) =– =,6.0)(1)(=-=AB P AB P .5. 从5双不同的鞋子种任取4只,问这4只鞋子中至少有两只配成一双的概率是多少 解:显然总取法有410C n=种,以下求至少有两只配成一双的取法k :法一:分两种情况考虑:15C k=24C 212)(C +25C 其中:2122415)(C C C 为恰有1双配对的方法数法二:分两种情况考虑:!2161815C C C k ⋅⋅=+25C其中:!2161815C C C ⋅⋅为恰有1双配对的方法数法三:分两种情况考虑:)(142815C C C k-=+25C其中:)(142815C C C -为恰有1双配对的方法数法四:先满足有1双配对再除去重复部分:2815C C k=-25C法五:考虑对立事件:410C k=-45C 412)(C其中:45C 412)(C 为没有一双配对的方法数法六:考虑对立事件:!4141618110410C C C C C k ⋅⋅⋅-=其中:!4141618110C C C C ⋅⋅⋅为没有一双配对的方法数所求概率为.2113410==C k p6.在房间里有10个人,分别佩戴从1号到10号的纪念章,任取3人记录其纪念章的号码.求: (1) 求最小号码为5的概率; (2) 求最大号码为5的概率.解:(1) 法一:12131025==C C p ,法二:1213102513==A A C p (2) 法二:20131024==C C p ,法二:2013102413==A A C p 7.将3个球随机地放入4个杯子中去,求杯子中球的最大个数分别为1,2,3的概率. 解:设M 1, M 2, M 3表示杯子中球的最大个数分别为1,2,3的事件,则834)(3341==A M P , 1694)(324232=⨯=A C M P , 1614)(3143==C M P8.设5个产品中有3个合格品,2个不合格品,从中不返回地任取2个,求取出的2个中全是合格品,仅有一个合格品和没有合格品的概率各为多少解:设M 2, M 1, M 0分别事件表示取出的2个球全是合格品,仅有一个合格品和没有合格品,则3.0)(25232==C C M P ,6.0)(2512131==C C C M P ,1.0)(25221==C C M P 9.口袋中有5个白球,3个黑球,从中任取两个,求取到的两个球颜色相同的概率.解:设M 1=“取到两个球颜色相同”,M 1=“取到两个球均为白球”,M 2=“取到两个球均为黑球”,则φ==2121M M M M M 且.所以.2813C C C C )()()()(282328252121=+=+==M P M P M M P M P10. 若在区间(0,1)内任取两个数,求事件“两数之和小于6/5”的概率.解:这是一个几何概型问题.以x 和y 表示任取两个数,在平面上建立xOy 直角坐标系,如图. 任取两个数的所有结果构成样本空间 = {(x ,y ):0 x ,y 1} 事件A =“两数之和小于6/5”= {(x ,y ) : x + y 6/5} 因此2517154211)(2=⎪⎭⎫ ⎝⎛⨯-=Ω=的面积的面积A A P . 图11.随机地向半圆220x ax y -<<(a 为常数)内掷一点,点落在半圆内任何区域的概率与区域的面积成正比,求原点和该点的连线与x 轴的夹角小于4π的概率. 解:这是一个几何概型问题.以x 和y 表示随机地向半圆内掷一点的坐标,表示原点和该点的连线与x 轴的夹角,在平面上建立xOy 直角坐标系,如图.随机地向半圆内掷一点的所有结果构成样本空间 ={(x ,y ):220,20x ax y a x -<<<<}事件A =“原点和该点的连线与x 轴的夹角小于4π” ={(x ,y ):40,20,202πθ<<-<<<<x ax y a x }因此211214121)(222+=+=Ω=πππa aa A A P 的面积的面积.12.已知21)(,31)(,41)(===B A P A B P A P ,求)(B A P . 解:,1213141)()()(=⨯==A B P A P AB P ,6121121)|()()(=÷==B A P AB P B P 13.设10件产品中有4件不合格品,从中任取两件,已知所取两件产品中有一件是不合格品,则另一件也是不合格品的概率是多少解:题中要求的“已知所取两件产品中有一件是不合格品,则另一件也是不合格品的概率”应理解为求“已知所取两件产品中至少有一件是不合格品,则两件均为不合格品的概率”。
《概率论与数理统计》练习题参考答案与解题提示

《概率论与数理统计》练习题参考答案与解题提示一、单项选择题1-5 DDACC 6-10 BDBAD 11-15 ACCDA 16-20 BCBDC 21-25 DCDDC 26-30 CDDBC 31-35 CDBBA 36-40 CCDBC 41-45 CBCAC 46-50 ABBDC 51-55 BDAAB 56-60 CBABA 61-65 BCBAA 66-68 DCC 6. ()()()()()()P ABC P AB P ABC P A P B P ABC =-=- 23. 001()1(0)2--Φ=-Φ 24. 2(,)(,)4F x y f x y xy x y∂==∂∂37. 若2~(,)X N μσ,则~(0,1)X N μσ-39. 25{1}1{0}1(1)9P Y P Y p ≥=-==--=解得13p =31{1}1{0}1(1)3P X P X ≥=-==-- 44. (,)()()X Y f x y f x f y =45. 画出01,01,1x y x y ≤≤≤≤+≤的公共区域,1111{1}1(1)2yP X Y dy dx y dy -+≤==-=⎰⎰⎰ 二、填空题1. 0.62. 0.33.116 4. 14 5. 63646. 0.67. 0.40968. 1149. 0.18 10. 13 11. 19 12. 183513. 1p - 14. 0.5 15. 0.4 16. 0.5 17. 0.42 18. 19 19. 815 20. 23 21. 0.522. 6581 23. 0.5 24. 0.25 25. 0.25 26. 13 27. 0.5 28. 0.75 29. ,00,x e x -⎧>⎨⎩其它30.101,0220x y ⎧≤≤≤≤⎪⎨⎪⎩其它 31. 3 32. 0.2 33. 0.4 34. 210x 35. 0.25 36. 0.2537. (0,1)N 38. 5356 39. 1927 40. 0.5100x e x -⎧-≥⎨⎩其它41.1342.43. 1,010100,y ⎧≤≤⎪⎨⎪⎩其它 44. 0,00x y e x y --⎧>>⎨⎩其它45. 0.5 46. 447.22x -48.312849. 5 50. 4(1)np p - 51. 8 52.23 53. 1 54. 89 55. 112 56. 0.5 57. 0 58. 0.8664 59. 0 60. 0.16 61. 16 62. 4 63. 2364. 0 65. 0.6826 66. 4 67. 2 68. 18 69. 070. 0.5 71. 112 72. 21(,)F n n 73. 20 74. 0 75. 12 76. n 77. 2212nσσ+78.23X 79. θ= 80. [7.7,12.3] 81. 19 82. 2 83. 1X 84. [9.804,10.196] 85. 0.5 86. 1X - 87. 0.9三、判断题1-5 对错错错对 6-10 对对错错对四、计算题、证明题1.答案:0.8。
概率论与数理统计(2)

称为ξ的四分之一。
(10)数学期望的性质
1)常量的期望就是这个常量本身。
2)随机变量ξ与常量之和的数学期望等于ξ的期望与这个常量的和。
3)常量与随机变量乘积的期望等于这个常量与随机变量数学期望的乘积
4)随机变量线性函数的数学期望等于这个随机变量期望的同一线性函数。
(4)每次试验中一定发生的事件称为必然事件,用符号Ω表示。每次试验中一定不发生的事件称为事件,用符号φ表示。
(5)设f(x)是定义在随机变量ξ的一切可能值x的集合上的函数。如果对于ξ的每一可能取值x,有另一个随机变量η的相应取值y=f(x)。则称η为ξ的函数,记作η=f(ξ)。我们的任务是,如何根据ξ的分布求出η的分布,或由(ξ1,...,ξn)的分布求出η= f(ξ1,...,ξn)的分布。
(5)设f(x)是定义在随机变量ξ的一切值x的集合上的函数。如果对于ξ的每一取值x,有另一个随机变量η的取值y=f(x)。则称η为ξ的函数,记作η=f(ξ)。我们的任务是,如何根据ξ的求出η的,或由(ξ1,...,ξn)的求出η= f(ξ1,...,ξn)的。
(6)研究对象的全体称,组成总体的每个基本单位称。总体中抽出若干个体而成的集体,称总体容量。样本中所含个体的个数,称。抽样通常有两种:一种是抽样;一种是抽样。
5)任意随机变量的方差等于这个随机变量平方的期望与期望的平方之差。
二、计算题:(67分)
(1)一批产品共200个,有6个废品,求:(1)这批产品的废品率;(2)任取3个恰有1个是废品的概率;(3)任取3个全非废品的概率。(9分)
(2)市场上供应的灯泡中,甲厂产品占70%,乙厂占30%,甲厂产品的合格率是95%,乙厂的合格率是80%。若用事件A、分别表示甲、乙两厂的产品,B表示产品为合格品,试写出有关事件的概率。(即:1)甲厂和乙厂产品占市场的概率;2)甲厂和乙厂产品合格的概率;3)甲厂和乙厂产品不合格的概率。)(9分)
完整版概率论与数理统计习题及答案选择题

完整版概率论与数理统计习题及答案选择题《概率论与数理统计》习题及答案选择题单项选择题1.以A表示事件“甲种产品畅销,乙种产品滞销”,则其对立事件入为().(A)“甲种产品滞销,乙种产品畅销”;(B )“甲、乙两种产品均畅销”;(C)“甲种产品滞销或乙种产品畅销”:(D)“甲种产品滞销” ?解:设B '甲种产品畅销',C '乙种产品滞销',A BCA BCB UC '甲种产品滞销或乙种产品畅销' .选C.2.设A, B,C是三个事件,在下列各式中,不成立的是()?(A) ( A B)UB AUB ;(B ) (AUB) B A;(C) (AUB) AB AB U AB ;(D) (AUB) C (A C )U(B C).解:(A B)UB AB UB (AUB)I?UB) AUB A对.(AUB) B (AUB) B AB UBB AB A B A B不对(AUB) AB (A B)U(B A) AB U AB. C 对选B同理D也对.3.若当事件A, B同时发生时,事件C必发生,则().(A ) P(C ) P( A) P(B) 1 ;(B ) P(C ) P( A) P(B) 1;(C) P(C ) P( AB);(D) P(C ) P( AUB).解:AB C P(C) P( AB) P(A) P(B) P(AUB) P(A) P( B) 1选B.4?设P(A) a, P( B) b, P( AUB) c,贝忡(廳)等于( ).(A ) a b ;(B ) c b;(C) a(l b) ;(D ) ba.解:P( AB) P(A B) P(A) P( AB) a P( A) P(B) P(AUB) c b151 ?152 ?选B.5.设A, B 是两个事件,若 P( AB) 0 ,则( (A ) A, B 互不相容;(B ) AB 是不可能事件; (C) P( A) 0 或 P(B) 0 ;解:Q P(AB) 0 AB(D ) AB 未必是不可能事件.选D.6.设事件A, B 满足AB (A ) A, B 互不相容; ,则下列结论屮肯定正确的是((B) A, B 相容;(C) P( AB) P(A)P(B); (D) P( A B)P(A).解:BA A,B 相容 AB P( AB) B, BA, ABB 错. P( A B)P(A)而P( A)P(B)不一定为 P( AB) P(A). C 错. 选D.7?设 0 P(B) 1, P( Al B) (A) A, B 互不相容; P( Al B)(B ) A, B 互为对立; (C) A, B 不独立;P(AB ) P( AB^ 川牛?P(B) P(B) P(AB)(1P(B))A, B 相互独立.(D ) P( AB) P( AUB) P( AB ) P( B) 1 P(B) P(B)P(B)(1 P(A) P(B) P(AB)) P(B)(1P(B))P(B) P 2 (B) P( AB) P(B) P( A)P(B) P 2 (B) 选D.P( AB) P( A)P(B) 8.下列命题中,正确的是( 1 P( AUB)P(B)(A)若P( A) 0 , 则A 是不可能事件; (B )若 P( AUB) P( A) P(B),则A,B 互不相容; (C)若 P( AUB)P( AB) 1,则 P(A) P(B) 1 ;(D) P( A B) 解:P(AUB)P(A) P(B). P(A) P(B)P(AB)P(AUB) P(AB) P(A) P(B) 1由 P( A) B 错.只有当AB 时 P(A B) P( A) P(B),否则不对.选C.153 ?(C) P( A) P( Al B) ; (D)前三者都不一定成立.P( AB )解:P(AI B) ------------------ 要与P( A)比较,需加条件. 选D.P(B)11?设0 P(B) 1,P(A I )P(A2)0 且 P(A I U A 2 I B) P(A[ I B) P( A 2 I B), 则下列等式成立的是()?(A ) P( Ai U A2 I B) P( Ai I B) P( A 2 I B); (B ) P( Ai B U A2 B) P( A I B) P( A 2 B); (C) P( Ai U A2 ) P( Ai I B) P( A 2 I B); (D) P( B) P( Ai )P( B I Ai ) P( A 2 ) P( B I A 2 ).解.:P(AUAIB) P(AIB) P(A I B) P(AAIB) p(亦 B) P(A? I B)P( Ai A2 I B) 0 P( Ai A2 B) 0P( Ai BU A 2B)P(A I B) P(A 2 B) P( A I A 2 B) P(A I B) P(A 2 B) 选B.解2:由 P{ Ai U A 2I B} P( Ai I B) P( A2 I B)得P( Ai B U A 2 B) P( A I B) P( A2 B)P(B)P(B)可见 P( Ai BU A2B) P( A I B) P( A2B) 选B.12.假设事件A, B 满足P(B I A) 1 ,贝ij ( ).(A 、>B 是必然事件;(B) P( B) 1; (C) P( A B) 0 ; (D) A B .解: P(B 1 A)P( AB)]P(A) P( AB) P(A) P( A) P( AB ) 0P( AB) 0选C.13. 设A, B 是两个事件,且A B, P(B) 0 ,则下列选项必然成立的是).(A ) P( AU B) P( A); (B ) P( AB) P(A);(C) P(B 1 A) P(B); (D ) P(B A)P(B) P(A). 解:B A AUB AP( AUB) P( A)选A.10.设A, B 是两个事件,且 P( A) P( Al B);(A ) P( A) P( Al B);(B) P(B) 0,则有( )9.设A, B 为两个事件,且 B A ,则下列各式中正确的是().154 ?(A ) P( A) P( Al B) ; (B ) P( A) P( Al B);(C) P( A) P( Al B) ;( D ) P( A)P( Al B).解:P(AI B)P( AB) A B P( A)-7P( A)P(B)P(B)A BP( A) P(B) 0 P(B) 1 选B(或者:A B,P( A) P( AB) P(B)P( Al B) P( Al B))14.设 P(B) 0, Ai , A2互不相容,则下列各式中不一定正确的是().(A ) P( Ai A 2I B) 0;(B ) P( Ai U A2 IB) P( Ai I B) P( A2 I B); (C) P( Ai A2 I B) 1;(D)P( Ai U A2 I B) 1.解:P( Ai A2 ) 0 Q Ai A2P(A I A 2B)P(Ai A2 I B) P(B) 0P(Ai U A2 I B) P( Ai I B) P(A2 I B) P( Ai A2 I B)P(Ai I B) P( A2 I B)P(Ai A 2 I B) P( Ai U A2 IB) 1 P( AiU A2 I B)1 P(Ai I B) P( A2 I B) 1P(Ai U A2 IB) P( Ai A2 I B) 1 P( Ai A2 I B) 1 0 选C.15. 设A, B, C 是三个相互独立的事件,且 0 P(C) 1 ,则在下列给定的四对事件中不相互独立的是().__(A) AUB 与 C ; ( B) AC 与 C ;(C) A B 与 C ;(D ) AB 与 C. - --------------------解:P[(AUB)C] P(ABC) P( A)P(B)P(C )(1 P( A))(l P(B)) P(C)[1 (P( A) P( B) P( A)P( B))] P(C ) P(A U B) P(C ) A 对. P( ACC )P[( AUC )C ] P( AC UCC ) P( AC) P(C ) P( AC )------- 11"111 -----------------------------------------------------------P(C ) P( AC )P(C ) AC 与 C 不独立选 B.16. 设A, B, C 三个事件两两独立,则 A, B, C 相互独立的充分必要条件是( ).(A ) A 与BC 独立; (B) AB 与AUC 独立; (C) AB 与AC 独立;(D) AUB 与AUC 独立.A 对.B 对.C 错. 1D 对.155 ?解:Q A, B, C 两两独立,P( ABC ) P( A)P( B) P(C ) P( A) P( BC )反之,如I A 与 BC 独立则 P( ABC ) P( A) P(BC ) P( A)P( B)P(C ) 选A.P( AB) P(BC ) P( ABC ) P( AUC )P( B)P[( A C ) A] P(ACA) P(AC ) P( A)P(C ) P(A)P( AC )C 对选D (也可举反例).18. —种零件的加工由两道工序组成.第一道工序的废品率为选B.20?设随机变量 X 的概率分布为P(X k) b 4 k 1,2,L ,b 0,则若A, B, C 相互独立则必有A 与BC 独立.17. (C) 设A, B,C 为三个事件且A, B 相互独立,则以下结论屮不正确的是 )若 P(C ) )若 P(C ) 若 P(C ) 1,则AC 与BC 也独立; 1,则AUC 与B 也独立; 1,则A C 与A 也独立; (D) 解: ,则A 与C 也独立. P( A)P(B), P(C )若C B Q P(AB)AC 与BC 也独立.1 概率为1的事件与任何事件独立P[(AUC)I B] P[( AUC )B] P( AB UBC) pi ,第二道工序的废品率为 (A )1 pi(C) 1 pi 解:设A P2,则该零件加工的成品率为((B ) 1 pi p2 : (D ) (1 pi ) 第i 道工序为成品P2 pi P2 ; 成品零件, Ai (1 P2)? i 1, 2.P( Ai ) 1P( A) P( Ai A 2)PlP( A2 ) 1 p2 P(Ai )P(A 2) (1Pl )(1P2)1 pi P2pi P2选C.19.设每次试验成功的概率为 p(0第10次试验才取得第 4次成功的概率为(A) Cio 4 p 4(l p)6 ;(C) C94 p 4(l p)5 ;1),现进行独立重复试验,则直到((B) C93 p 4(l p)6 ;(D) C93 p 3 (1 p)6.3次成功解:说明前9次取得了 C 93 p 3 (1 p)6p C 93 p 4 (1 p)6 第10次才取得第4次成功的概率为)156 ?23.下列函数屮,可作为某个随机变量的分布函数的是()1(A ) F ( x)1-; (B ) F ( x)丄—arc tan x ;1 X 22一(1 eX),x 0(C) F ( x)20 ,x 0;(C)亠(D )-J —.1 bb 1解:P (X K)b k bk b—b- 1k 1k 1k 111(A )为任意正实数; (B) b 1 ;——选C ?1 b21.设连续型随机变量 X 的概率密度和分布函数分别为 f (x )和F (x ),则下列各式正确的是()?(A) 0 f(X ) 1; (B) P(X x) f(x); (C) P(X x) F ( x); (D ) P(X x) F(x). /?选 D.22.下列函数可作为概率密度的是( ).(A ) f(X ) e lxl ,x R ;(B ) f(X )1 2 , x R ;(1 x)12 x_(C) f( X )Ve 2, x 0,0 ,x0;1,1 xl 1, (D) f ( X )0,1 xl 1?解:A : e lxl dx 2B :----- d x ——(1 x 2) 且 f (x)e X dx 21—arc tan xe X dx 2错. 丄[-—]12 2-------- - 0 x R 选 B. (1 解:F (x) P( X x) P(X x)157 ?选B. 26 .设随机变量X ?N(l,22),其分布函数和概率密度分別为F ( x)和()f ( X )dx ;(D ) F ( x) f(t)dt ,其中f(t )dt 1.解:对A : 0F(x) 1,但F(x)不具有单调非减性且 F()0 /. A 不是.对B :一 arc tan x 一\ 0 F ( x)1.2 2由arctanx 是单调非减的 F(x)是单调非减的.F()丄 1—( -) 0F() J- 1 --------- 1 .2 22 2F(x)具有右连续性.选B.24 ?设 Xi ,X 2 是随机变量,其分布函数分别为Fi ( x), F2 (X ),为使F ( x) aFi (x) bF 2 ( x)是某一随机变量的分布函数,在下列给定的各组数值中应取()?32(A ) a —, b2 : (B) a —,b2 ;5531(C) a _ ,b 3 ; (D) a _ ,b3.2 222解:F ()aFi () bF2 ()0 , F() a b 1 ,只有A 满足/.选A25.设随机变量X 的概率密度为f (x),且 f (x)f (x), F ( x)是 X 的分则对任意实数布函数, a 有()?(C)(D)2F(a); 2F (a) 1 .o f ( x)dx ;解: F(a)f (x)dx af()du f (u) du f ( x)dx f(x) dx 1f(x)dxf (x)dx)of ( x)dxof ( x)dxf (x)dxf(x)dxf (x)dxof (x)dx —2。
概率论与数理统计习题参考答案

概率论与数理统计参考答案(附习题)第一章 随机事件及其概率1. 写出下列随机试验的样本空间:(1)同时掷两颗骰子,记录两颗骰子的点数之和; (2)在单位圆内任意一点,记录它的坐标;(3)10件产品中有三件是次品,每次从其中取一件,取后不放回,直到三件次品都取出为止,记录抽取的次数; (4)测量一汽车通过给定点的速度.解: 所求的样本空间如下(1)S= {2,3,4,5,6,7,8,9,10,11,12} (2)S= {(x, y)| x 2+y 2<1}(3)S= {3,4,5,6,7,8,9,10} (4)S= {v |v>0}2. 设A 、B 、C 为三个事件,用A 、B 、C 的运算关系表示下列事件: (1)A 发生,B 和C 不发生;(2)A 与B 都发生,而C 不发生; (3)A 、B 、C 都发生; (4)A 、B 、C 都不发生; (5)A 、B 、C 不都发生;(6)A 、B 、C 至少有一个发生; (7)A 、B 、C 不多于一个发生; (8)A 、B 、C 至少有两个发生. 解: 所求的事件表示如下(1)(2)(3)(4)(5)(6)(7)(8)A B CA B C A B C A B CA B C AB CA B B C A CA BB CC A3.在某小学的学生中任选一名,若事件A 表示被选学生是男生,事件B 表示该生是三年级学生,事件C 表示该学生是运动员,则 (1)事件AB 表示什么?(2)在什么条件下ABC =C 成立? (3)在什么条件下关系式C B ⊂是正确的? (4)在什么条件下A B =成立?解: 所求的事件表示如下(1)事件AB 表示该生是三年级男生,但不是运动员. (2)当全校运动员都是三年级男生时,ABC =C 成立.(3)当全校运动员都是三年级学生时,关系式C B ⊂是正确的. (4)当全校女生都在三年级,并且三年级学生都是女生时,A B =成立. 4.设P (A )=0.7,P (A -B )=0.3,试求()P AB解 由于 A -B = A – AB , P (A )=0.7 所以P (A -B ) = P (A -AB ) = P (A ) -P (AB ) = 0.3, 所以 P (AB )=0.4, 故 ()P AB = 1-0.4 = 0.6.5. 对事件A 、B 和C ,已知P(A) = P(B)=P(C)=14,P(AB) = P(CB) = 0, P(AC)=18求A 、B 、C 中至少有一个发生的概率. 解 由于,()0,⊂=ABC AB P AB 故P(ABC) = 0则P(A+B+C) = P(A)+P(B)+P(C) –P(AB) –P(BC) –P(AC)+P(ABC) 1111500044488=++---+=6. 设盒中有α只红球和b 只白球,现从中随机地取出两只球,试求下列事件的概率:A ={两球颜色相同},B ={两球颜色不同}.解 由题意,基本事件总数为2a b A +,有利于A 的事件数为22a b A A +,有利于B的事件数为1111112ab b a a b A A A A A A +=, 则 2211222()()a b a ba b a bA A A A P A PB A A +++==7. 若10件产品中有件正品,3件次品,(1)不放回地每次从中任取一件,共取三次,求取到三件次品的概率; (2)每次从中任取一件,有放回地取三次,求取到三次次品的概率. 解 (1)设A={取得三件次品} 则333333101016()()120720或者====C A P A P A C A . (2)设B={取到三个次品}, 则33327()101000==P A .8. 某旅行社100名导游中有43人会讲英语,35人会讲日语,32人会讲日语和英语,9人会讲法语、英语和日语,且每人至少会讲英、日、法三种语言中的一种,求:(1)此人会讲英语和日语,但不会讲法语的概率; (2)此人只会讲法语的概率.解 设 A={此人会讲英语}, B={此人会讲日语}, C={此人会讲法语}根据题意, 可得(1) 32923()()()100100100=-=-=P ABC P AB P ABC(2) ()()()P ABC P AB P ABC =-()01()P A B P A B =+-=-+ 1()()()P A P B P AB =--+433532541100100100100=--+=9. 罐中有12颗围棋子,其中8颗白子4颗黑子,若从中任取3颗,求: (1) 取到的都是白子的概率;(2) 取到两颗白子,一颗黑子的概率;(3) 取到三颗棋子中至少有一颗黑子的概率; (4) 取到三颗棋子颜色相同的概率. 解(1) 设A={取到的都是白子} 则3831214()0.25555===C P A C .(2) 设B={取到两颗白子, 一颗黑子}2184312()0.509==C C P B C . (3) 设C={取三颗子中至少的一颗黑子} ()1()0.74=-=P C P A . (4) 设D={取到三颗子颜色相同}3384312()0.273+==C C P D C .10. (1)500人中,至少有一个的生日是7月1日的概率是多少(1年按365日计算)?(2)6个人中,恰好有个人的生日在同一个月的概率是多少? 解(1) 设A = {至少有一个人生日在7月1日}, 则500500364()1()10.746365=-=-=P A P A (2)设所求的概率为P(B)412612611()0.007312⨯⨯==C C P B11. 将C ,C ,E ,E ,I ,N ,S 7个字母随意排成一行,试求恰好排成SCIENCE的概率p.解 由于两个C ,两个E 共有2222A A 种排法,而基本事件总数为77A ,因此有2222770.000794A A p A ==12. 从5副不同的手套中任取款4只,求这4只都不配对的概率.解 要4只都不配对,我们先取出4双,再从每一双中任取一只,共有⋅4452C 中取法. 设A={4只手套都不配对},则有⋅==445410280()210C P A C13. 一实习生用一台机器接连独立地制造三只同种零件,第i 只零件是不合格的概率为=+11i p i,i=1,2,3,若以x 表示零件中合格品的个数,则P(x =2)为多少?解 设A i = {第i 个零件不合格},i=1,2,3, 则1()1i i P A p i==+ 所以 ()11i i i P A p i=-=+ 123123123(2)()()()P x P A A A P A A A P A A A ==++由于零件制造相互独立,有:123123()()()()P A A A P A P A P A =,123123()()()()P A A A P A P A P A = 123123()()()()P A A A P A P A P A =11112111311,(2)23423423424P x ==⨯⨯+⨯⨯+⨯⨯=所以14. 假设目标出现在射程之内的概率为0.7,这时射击命中目标的概率为0.6,试求两次独立射击至少有一次命中目标的概率p.解 设A={目标出现在射程内},B={射击击中目标},B i ={第i 次击中目标}, i=1,2.则 P(A)=0.7, P(B i|A)=0.6 另外 B=B 1+B 2,由全概率公式12()()()()()(|)()(()|)P B P AB P AB P AB P A P B A P A P B B A =+===+ 另外, 由于两次射击是独立的, 故P(B 1B 2|A)= P(B 1|A) P(B 2|A) = 0.36 由加法公式P((B 1+B 2)|A)= P(B 1|A)+ P(B 2|A)-P(B 1B 2|A)=0.6+0.6-0.36=0.84因此P(B)= P(A)P((B 1+B 2)|A)=0.7×0.84 = 0.58815. 设某种产品50件为一批,如果每批产品中没有次品的概率为0.35,有1,2,3,4件次品的概率分别为0.25, 0.2, 0.18, 0.02,今从某批产品中抽取10件,检查出一件次品,求该批产品中次品不超过两件的概率.解 设A i ={一批产品中有i 件次品},i=0, 1, 2, 3, 4, B={任取10件检查出一件次品},C={产品中次品不超两件}, 由题意01914911050192482105019347310501944611050(|)01(|)516(|)4939(|)98988(|)2303=========P B A C C P B A C C C P B A CC C P B A C C C P B A C由于 A 0, A 1, A 2, A 3, A 4构成了一个完备的事件组, 由全概率公式 40()()(|)0.196===∑i i i P B P A P B A 由Bayes 公式000111222()(|)(|)0()()(|)(|)0.255()()(|)(|)0.333()======P A P B A P A B P B P A P B A P A B P B P A P B A P A B P B 故20()(|)0.588===∑i i P C P A B16. 由以往记录的数据分析,某船只运输某种物品损坏2%,10%和90%的概率分别为0.8,0.15,0.05,现在从中随机地取三件,发现三件全是好的,试分析这批物品的损坏率是多少(这里设物品件数很多,取出一件后不影响下一件的概率).解 设B={三件都是好的},A 1={损坏2%}, A 2={损坏10%}, A 1={损坏90%},则A 1, A 2, A 3是两两互斥, 且A 1+ A 2 +A 3=Ω, P(A 1)=0.8, P(A 2)=0.15, P(A 2)=0.05.因此有 P(B| A 1) = 0.983, P(B| A 2) = 0.903, P(B| A 3) = 0.13, 由全概率公式31333()()(|)0.80.980.150.900.050.100.8624===⨯+⨯+⨯=∑i i i P B P A P B A由Bayes 公式, 这批货物的损坏率为2%, 10%, 90%的概率分别为313233()(|)0.80.98(|)0.8731()0.8624()(|)0.150.90(|)0.1268()0.8624()(|)0.050.10(|)0.0001()0.8624⨯===⨯===⨯===i i i i i i P A P B A P A B P B P A P B A P A B P B P A P B A P A B P B 由于P( A 1|B) 远大于P( A 3|B), P( A 2|B), 因此可以认为这批货物的损坏率为0.2.17. 验收成箱包装的玻璃器皿,每箱24只装,统计资料表明,每箱最多有两只残次品,且含0,1和2件残次品的箱各占80%,15%和5%,现在随意抽取一箱,随意检查其中4只;若未发现残次品,则通过验收,否则要逐一检验并更换残次品,试求: (1)一次通过验收的概率α;(2)通过验收的箱中确定无残次品的概率β. 解 设H i ={箱中实际有的次品数}, 0,1,2=i , A={通过验收}则 P(H 0)=0.8, P(H 1)=0.15, P(H 2)=0.05, 那么有:042314244222424(|)1,5(|),695(|)138P A H C P A H C C P A H C =====(1)由全概率公式20()()(|)0.96α====∑i i i P A P H P A H(2)由Bayes 公式 得00()(|)0.81(|)0.83()0.96β⨯====i P H P A H P H A P A18. 一建筑物内装有5台同类型的空调设备,调查表明,在任一时刻,每台设备被 使用的概率为0.1,问在同一时刻 (1)恰有两台设备被使用的概率是多少? (2)至少有三台设备被使用的概率是多少?解 设5台设备在同一时刻是否工作是相互独立的, 因此本题可以看作是5重伯努利试验. 由题意,有p=0.1, q=1-p=0.9, 故(1) 223155(2)(0.1)(0.9)0.0729===P P C (2) 2555(3)(4)(5)P P P P =++332441550555(0.1)(0.9)(0.1)(0.9)(0.1)(0.9)0.00856C C C =++=19. 甲、乙两个乒乓球运动员进行乒乓球单打比赛,如果每一局甲胜的概率为0.6,乙胜的概率为0.4,比赛时可以采用三局二胜制或五局三胜制,问在哪一种比赛制度下甲获胜的可能性较大? 解 在三局两胜时, 甲队获胜的概率为332213333(2)(3)(0.6)(0.4)(0.6)(0.4)0.648=+=+=A P P P C C在五局三胜的情况下, 甲队获胜的概率为55533244155555(3)(4)(5)(0.6)(0.4)(0.6)(0.4)(0.6)(0.4)0.682=++=++=B P P P P C C C因此,采用五局三胜制的情况下,甲获胜的可能性较大.20. 4次重复独立试验中事件A 至少出现一次的概率为6581,求在一次试验中A出现的概率.解 设在一次独立试验中A 出现一次的概率为p, 则由题意00444465(0)(1)181==-=-P C p q p 解得p=1/3.21.(87,2分)三个箱子,第一个箱子中有4只黑球1只白球,第二个箱子中有3只黑球3只白球,第三个箱子有3只黑球5只白球. 现随机地取一个箱子,再从这个箱子中取出一个球,这个球为白球的概率等于 . 已知取出的球是白球,此球属于第二个箱子的概率为解 设=B “取出白球”,=i A “球取自第i 个箱子”,.3,2,1=i 321,,A A A 是一个完全事件组,.3,2,1,3/1)(==i A P i 5/1)|(1=A B P ,2/1)|(2=A B P ,8/5)|(3=A B P ,应用全概率公式与贝叶斯公式,12053)852151(31)|()()(31=++==∑=i i i A B P A P B P.5320)()|()()|(222==B P A B P A P B A P22.(89,2分)已知随机事件A 的概率5.0)(=A P ,随机事件B 的概率6.0)(=B P 及条件概率8.0)|(=A B P ,则和事件B A ⋃的概率=⋃)(B A P 解 7.0)|()()()()()()()(=-+=-+=⋃A B P A P B P A P AB P B P A P B A P .23.(90,2分)设随机事件A ,B 及其和事件B A ⋃的概率分别是4.0,3.0和6.0. 若B 表示B 的对立事件,那么积事件B A 的概率=)(B A P解 B A 与B 互不相容,且.B B A B A ⋃=⋃ 于是.3.0)()()(=-⋃=B P B A P B A P24.(92,3分)已知41)()()(===C P B P A P ,0)(=AB P ,161)()(==BC P AC P ,则事件A ,B ,C 全不发生的概率为 解 从0)(=AB P 可知,0)(=ABC P .)()()()()()()()(ABC P BC P AC P AB P C P B P A P C B A P +--++=⋃⋃.8501611*********=+---++=25.(93,3分)一批产品共有10件正品和两件次品,任意抽取两次,每次抽一件,抽出后不再放回,则第二次抽出的是次品的概率为解 设事件=i B “第i 次抽出次品”,.2,1=i 则,12/2)(1=B P 12/10)(1=B P ,.11/2)|(,11/1)|(1212==B B P B B P 应用全概率公式)|()()|()()(1211212B B P B P B B P B P B P +=.611121210111122=⨯+⨯=26.(94,3分)已知A ,B 两个事件满足条件)()(B A P AB P =,且p A P =)(,则=)(B P解 ).()()(1)()(AB P B P A P B A P B A P +--=⋃=因)()(B A P AB P =,故有.1)(1)(,1)()(p A P B P B P A P -=-==+27.(06,4分)设A ,B 为随机事件,且0)(>B P ,1)|(=B A P ,则必有( ) A .)()(A P B A P >⋃ B .)()(B P B A P >⋃ C .)()(A P B A P =⋃ D .)()(B P B A P =⋃解 选(C )28.(05,4分)从数1,2,3,4中任取一个数,记为X ,再从1,2,…,X 中任取一个数,记为Y ,则==)2(Y P 解 填.481329.(96,3分)设工厂A 和工厂B 的产品的次品率分别为%1和%2,现从由A 和B 的产品分别占%60和%40的一批产品中随机抽取一件,发现是次品,则该产品属A 生产的概率是解 设事件=C “抽取的产品是次品”,事件=D “抽取的产品是A 生产的”,则D 表示“抽取的产品是工厂B 生产的”. 依题意有.02.0)|(,01.0)|(,40.0)(,60.0)(====D C P D C P D P D P应用贝叶斯可以求得条件概率.7302.04.001.06.001.06.0)|()()|()()|()()|(=⨯+⨯⨯=+=D C P D P D C P D P D C P D P C D P30.(97,3分)袋中有50只乒乓球,其中20只是黄球,30只是白球,今有两人依次随机地从袋中各取一球,取后不放回,则第二个人取得黄球的概率是 解 设事件=i A “第i 个人取得黄球”,2,1=i . 根据题设条件可知.4920)|(,4919)|(,5030)(,5020)(121211====A A P A A P A P A P 应用全概率公式.524920503049195020)|()()|()()(1211212=⋅+⋅=+=A A P A P A A P A P A P31.(87,2分)设在一次试验中,事件A 发生的概率为p 。
2018-19-2概率统计(A)

广东海洋大学 2018 —— 2019 学年第 二 学期《概率论与数理统计》课程试题课程代码: 19221302 √考试 √ A 卷 □ B 卷□ 考查 □ C 卷 □ D 卷 √闭卷□ 开卷□ E 卷□ F 卷一.填空题(每题3分,共30分)1. 重复进行一项投篮,若事件A 表示“第一次未投中且第二次投中”,则事件A 表示2. 若()0.5,P A =,2.0)(=B A P 4.0)(=B P ,则)|(B A P =3. 三个人独立地破译一个密码,他们能译出的概率分别为0.4, 0.5, 0.6,则事件“密码被译出”概率为4. 若X 的密度函数为()23010x x f x ⎧≤≤=⎨⎩其它, 则{0.4}P X >=5. 若X ~(4,0.5)B ,则==)}({X D X P6. 已知(),X Y 的联合分布律为:X Y 0 20 1/6 1/43 1/3 1/2则{2|1}P Y X ≥≤=7.若~(5)X P ,~(1,3)Y U - ,则2(3)E X Y -=班级:姓名:学号:试题共页加白纸 2张密封线GDOU-B-11-3028.设321,,X X X 是来自正态分布总体X 的一个简单随机样本,1231126X X cX --是未知的总体期望)(X E 的无偏估计量,则=c 9.已知总体~(0,1)X N ,又设4321,,,X X X X 为来自总体X 的样本,则~242321X X X X +-____ __10. 设总体2~(,)X N μσ,其中2,σμ未知,从总体中抽取样本1X ,2X ,…,16X ,测得样本均值10x =,样本方差9s 2=,则总体方差2σ的置信度为0.95的置信区间为 (答案保留小数点后两位)22220.0250.9750.0250.975((16)28.845(16) 6.908,(15)27.488(15) 6.262)χχχχ====已知,,二、某人钥匙掉了。
《概率论与数理统计》复习题(附答案)

概率练习题附答案06-07-1《概率论与数理统计》试题A一、填空题(每题3分,共15分)1. 设A ,B 相互独立,且2.0)(,8.0)(==A P B A P ,则=)(B P __________. 2. 设事件A 、B 、C 构成一完备事件组,且()0.5,()0.7,P A P B ==则()P C =3. 已知),2(~2σN X ,且3.0}42{=<<X P ,则=<}0{X P __________.4. 设X 与Y 相互独立,且2)(=X E ,()3E Y =,()()1D X D Y ==,则=-])[(2Y X E ___5. 设),3(~),,2(~p B Y p B X ,且95}1{=≥X P ,则=≥}1{Y P __________. 二、选择题(每题3分,共15分)1. 一盒产品中有a 只正品,b 只次品,有放回地任取两次,第二次取到正品的概率为 【 】(A) 11a a b -+-;(B) (1)()(1)a a a b a b -++-;(C) a a b +;(D) 2a ab ⎛⎫ ⎪+⎝⎭.2. 设随机变量X 的概率密度为()130, 其他c x p x <<⎧=⎨⎩则方差D(X)= 【 】 (A) 2; (B)12; (C) 3; (D) 13. 3. 设A 、B 为两个互不相容的随机事件,且()0>B P ,则下列选项必然正确的是【 】()A ()()B P A P -=1;()B ()0=B A P ;()C ()1=B A P ;()D ()0=AB P .4. 设()x x f sin =是某个连续型随机变量X 的概率密度函数,则X 的取值范围是【 】()A ⎥⎦⎤⎢⎣⎡2,0π;()B []π,0; ()C ⎥⎦⎤⎢⎣⎡-2,2ππ; ()D ⎥⎦⎤⎢⎣⎡23,ππ. 5. 设()2,~σμN X ,b aX Y -=,其中a 、b 为常数,且0≠a ,则~Y 【 】 ()A ()222,b a b a N +-σμ; ()B ()222,b a b a N -+σμ; ()C ()22,σμa b a N +; ()D ()22,σμa b a N -.三、(本题满分8分) 甲乙两人独立地对同一目标射击一次,其命中率分别为0.5和0.4,现已知目标被命中,求它是乙命中的概率.四、(本题满分12分)设随机变量X 的密度函数为xx e e Ax f -+=)(,求:(1)常数A ; (2)}3ln 210{<<X P ; (3)分布函数)(x F .五、(本题满分10分)设随机变量X 的概率密度为()⎩⎨⎧<<-=其他,010),1(6x x x x f 求12+=X Y 的概率密度.六、(本题满分10分)将一枚硬币连掷三次,X 表示三次中出现正面的次数,Y 表示三次中出现正面次数与出现反面次数之差的绝对值,求:(1)(X ,Y )的联合概率分布;(2){}X Y P >.七、(本题满分10分)二维随机变量(X ,Y )的概率密度为⎩⎨⎧>>=+-其他,00,0,),()2(y x Ae y x f y x 求:(1)系数A ;(2)X ,Y 的边缘密度函数;(3)问X ,Y 是否独立。
16-17广东海洋第2概率统计B卷答案
实得分数
一、 填空题(每题 3 分,共 30 分) 1.设 A,B,C 为三事件,用 A,B,C 的运算关系表示“A,B,C 中不多于 一个发生”
A BC ∪ ABC ∪ AB C ∪ A B C
2.盒子中装有 9 个乒乓球,其中 7 个是正品,2 个为次品,不放回地先后 取两次,每次取一个,则第二次才取到次品的概率为 7/36
⎛ 16 − 20 X − 20 32 − 20 ⎞ < < ⎟ 4 4 4 ⎠ ⎝
≈ Φ (3) − Φ (−1) = Φ (3) + Φ (1) − 1 = 0.84 ---------------(10 分)
六. 已知总体 X 的分布律为
X 1
2
2
3
P θ
2θ (1 − θ ) (1 − θ ) 2
---------------(4
分)
五.某保险公司多年统计资料表明,在索赔户中,被盗索赔户占 20%,以随
第 4 页 共 6 页
机变量 X 表示在随机抽查的 100 个索赔户中, 因被盗向保险公司索赔的 户数。利用中心极限定理,求被盗索赔户不少于 16 户且不多于 32 户的 概率。( Φ (1) = 0.8413, Φ (3) = 0.9987 ) (10 分) 解 设事件 A 为“被盗索赔户”, P ( A) = 20% =0.2 知 X ~ b(100,0.2)
i =1
3
= 2θ 5 (1 − θ ) ---------------(5 分)
求导数 令
dL(θ ) = 10θ 4 −12θ 5 ---------------(7 分)
dθ
dL(θ ) = 0 解得
dθ
5 ---------------(10 分) 6
概率论与数理统计试题库及答案(考试必做)

11. X1 , X 2 独立,且分布率为
(i 1, 2) ,那么下列结论正确的是
A) X 1 X 2
B) P{X1 X 2} 1
C)
P{X 1
17.设 X 的概率密度为 f (x) 1 ex2 ,则 D( X ) =
18.设随机变量 X1,X2,X3 相互独立,其中 X1 在[0,6]上服从均匀分布,X2 服从正态分布 N
(0,22),X3 服从参数为 =3 的泊松分布,记 Y=X1-2X2+3X3,则 D(Y)=
19.设 D( X ) 25, D Y 36, xy 0.4 ,则 D( X Y )
D) t X S4 / n
25.设 X1,X2,…Xn,Xn+1, …,Xn+m 是来自正态总体 N (0, 2 ) 的容量为 n+m 的样本,则统计量
n
m i2
V
i 1 nm
服从的分布是
n
2 i
i n 1
A) F (m, n)
B) F (n 1, m 1)
C) F (n, m) D) F (m 1, n 1)
A) 50
B)7.
设 X1, X 2 , X 3 相互独立同服从参数
3 的泊松分布,令Y
1 3
(
X1
X
2
X
3
)
,则
E(Y 2 )
A)1.
B)9.
C)10.
D)6.
18.对于任意两个随机变量 X 和 Y ,若 E( XY ) E( X ) E(Y ) ,则
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
概率论试题2014-201 5一、填空题(每题3分,共30分)1、设A 、B 、C 表示三个事件,则“A 、B 都发生,C 不发生”可以表示为_________。
2、A 、B 为两事件,P(A ⋃B)=,P(A)=,P(B )=,则P(B-A)=。
3、一口袋装有6只球,其中4只白球,2只红球。
从袋中不放回的任取2只球,则取到一白一红的概率为_____8/15___。
4、设随机变量X~b(3,,且随机变量Y=2)3(X X -.则P{Y=1}=_________。
5、设连续性随机变量X~N(1,4),则21-x =____N(0,1)_____。
6、已知(X,Y )的联合分布律为: 则P{Y ≥1 I X ≤0}=___1/2___。
7、随机变量X 服从参数为λ泊松分布,且已知P(X=1)=p(X=2),则E(X 2+1)=_______7__。
8、设X 1,X 2,......,X n 是来自指数分布总体X 的一个简单随机样本,21X 1-41X 2-cX 3是未知的总体期望E(X)的无偏估计量,则c=___-3/4______。
9、已知总体X~N (0,σ3),又设X 1,X 2,X 3,X 4,X 5为来自总体的样本,则252423222132X X X X X +++=__________。
10、设X 1,X 2,....,X n 是来自总体X 的样本,且有E(X)=μ,D(X)=σ2,则有E(X )=__μ___,则有D(X )=__ σ2/N ____。
(其中X =∑=ni X 1i n 1)二、计算题(70分)1、若甲盒中装有三个白球,两个黑球;乙盒中装有一个白球,两个黑球。
由甲盒中任取一球投入乙盒,再从乙盒中任取一个球。
(1)求从乙盒中取得一个白球的概率;(2)若从乙盒中取得一个黑球,问从甲盒中也取得一个黑球的概率。
(10分)2、设二维随机变量(X ,Y )的联合密度为:(x,y)= 其他010,20)(<<<<+y x y x A(1)求参数A ;(2)求两个边缘密度并判断X,Y 是否独立;(3)求F x (x) (15分) 3、设盒中装有3支蓝笔,3支绿笔和2支红笔,今从中随机抽取2支,以X 表示取得蓝笔的支数,Y 表示取得红笔的支数,求(1)(X,Y)联合分布律;(2)E(XY) (10分)4、据某医院统计,凡心脏手术后能完全复原的概率是,那么再对100名病人实施手术后,有84至95名病人能完全复原的概率是多少 (= ; (2)=) (10分)5、已知总体X 服从参数为λ的指数分布,其中λ是未知参数,设X 1,X 2,....,X n 为来自总体X 样本,其观察值为x 1,x 2,x 3,......,x n 。
求未知参数λ:(1)矩估计量: (2)最大似然估计量。
(15分)6、设某种清漆的9个样品,其干燥时间(以小时记)分别为:。
设干燥时间总体服从正态分布N(μ,σ2)。
求:若方差σ2为未知数时,μ的置信水平为的置信区间。
((8)= : (9)=202622) (10分)广东海洋大学2009—2010 学年第二学期《概率论与数理统计》课程试题课程号: 1920004√ 考试√ A 卷√ 闭卷一.填空题(每题3分,共45分)1.从1到2000中任取1个数。
则取到的数能被6整除但不能被8整除的概率为2.在区间(8,9)上任取两个数,则“取到的两数之差的绝对值小于”的班级:姓名:学号:密封GDOU-B-11-302概率为3.将一枚骰子独立地抛掷3次,则“3次中至少有2次出现点数大于2”的概率为 (只列式,不计算)4.设甲袋中有5个红球和2个白球,乙袋中有4个红球和3个白球,从甲袋中任取一个球(不看颜色)放到乙袋中后,再从乙袋中任取一个球,则最后取得红球的概率为5.小李忘了朋友家的电话号码的最后一位数,于是他只能随机拨号,则他第五次才能拨对电话号码的概率为 6.若X ~(),2π则==)}({X D X P7.若X 的密度函数为()⎩⎨⎧≤≤=其它1043x x x f , 则 ()5.0F =8.若X 的分布函数为()⎪⎩⎪⎨⎧≥<≤<=111000x x x x x F , 则 =-)13(X E9.设随机变量)4.0,3(~b X ,且随机变量2)3(X X Y -=,则10.已知),(Y X 的联合分布律为:则 ===}1|2{X Y P11.已知随机变量,X Y 都服从[0,4]上的均匀分布,则(32)E X Y -= ______ 12.已知总体),4,1(~2N X 又设4321,,,X X X X 为来自总体X 的样本,记∑==4141i i X X ,则~X13.设4321,,,X X X X 是来自总体X 的一个简单随机样本,若已知4321616131kX X X X +-+是总体期望)(X E 的无偏估计量,则=k14. 设某种清漆干燥时间),(~2σμN X ,取样本容量为9的一样本,得样本均值和方差分别为09.0,62==s x ,则μ的置信水平为90%的置信区间为 (86.1)8(05.0=t )15.设321,,X X X 为取自总体X (设X )1,0(~N )的样本,则~223221XX X +(同时要写出分布的参数)二. 设随机变量),(Y X 的概率密度为⎩⎨⎧<<<<=其它,,2010,10),(y x y cx y x f求 (1) 未知常数c ;(4分) (2) }2/1{≥+Y X P ;(4分)(3) 边缘密度函数)()(y f x f Y X 及;(8分) (4) 判断X 与Y 是否独立并说明理由(4分)三.据某医院统计,凡心脏手术后能完全复原的概率是,那么再对100名病人实施手术后,有84至95名病人能完全复原的概率是多少(10分) ( 9525.0)67.1(=Φ, 9972.0)2(=Φ )四.已知总体X 的密度函数为其它10,,0)(1≤≤⎩⎨⎧⋅=-x x x f θθ,其中0>θ且θ是未知参数,设n X X X ,,,21Λ为来自总体X 的一个样本容量为n 的简单随机样本,求未知参数θ(1) 矩估计量;(5分) (2) 最大似然估计量. (10分)五.某冶金实验室断言锰的熔化点()()()()()()()()[]()()()i i i i i i n ii n iX n x n x nx n d d x n x x L x x L XX X dx x X E ln ˆln ˆ0ln ln 1ln ln 1ln ln ln )(ln )(21ˆˆ,11)(111111∑∑∑∑∑⎰-=-==+=-+-+=∏=∏=∏=∏=-==-==+==----θθθθθθθθθθθθθθθμμμθμθθθθθθθθ从而:得由解的方差不超过900,作了九次试验,测得样本均值和方差如下:1600,12672==s x (以摄氏度为单位),问检测结果能否认定锰的熔化点的方差显着地偏大 (10分)(取01.0=α 896.2)8(,355.3)8(01.0005.0==t t ,()()955.218090.2082005.0201.0==χχ,) 答案:一、(1)1/8 (2) 3/4 (3)333223)32(31)32(C C +⨯(4)33/56(5) 1/10 (6)22-e (7)1/16 (8)1/2 (9) (10) 9/20 (11)2 (12),)4,1(N (13)2/3 (14)()186.06±(15) t(2)广东海洋大学2010—2011 学年第二学期《概率论与数理统计》课程试题(答案)课程号: √ 考试√ A 卷√ 闭卷1.袋中有3个白球,2个红球,在其中任取2个。
则事件:2个球中恰有1个白球1个红球的概率为 3/5 。
()()()()3/1,1.0,3.0,5.0.2====B A P AB P B P A P 。
3.甲乙两人进球的概率依次为 、,现各投一球,各人进球与否相互独立。
无一人进球的概率为: 。
4.X 的分布律如下,常数a= 。
X 0 1 3 P a5.一年内发生地震的次数服从泊松分布(()λP )。
以X 、Y 表示甲乙两地发生地震的次数,X ~(),2P Y ~()1P 。
较为宜居的地区是 乙 。
6.X ~(密度函数)(){}8/12/101032=≤⎩⎨⎧≤≤=X P x x x f ,其它。
班级:姓名:学号:试题共页加白纸密封线GDOU-B-11-3027.(X,Y )服从区域:10,10≤≤≤≤y x 上的均匀分布, ()2/11=≤+Y X P 。
8.X ~(){}{}32,1,0-<>>X P X P N 比较大小: 。
10. 设总体X 与Y 相互独立,均服从()1,0N 分布, ()0,0<>Y X P 。
二. (25分)1.已知连续型随机变量X 的概率密度为2.某批产品合格率为,任取10000件,其中恰有合格品在5980到6020件之间的概率是多少(10分)三.(21分)(X,Y)的联合分布律如下:X Y -1 1 2-1 1/10 2/10 3/10 2 2/10 1/10 1/10(1)求边缘概率分布并判断X,Y 的独立性;(2)求E(X+Y); (3)求{}Y X Z ,m ax =的分布律。
解 (1)边缘分布如下:X Y -1 1 2 p i.-1 1/10 2/10 3/10 6/10 2 2/10 1/10 1/10 4/10 3/10 3/10 4/10由 {}{}{}()()100/1810/310/61110/11,1=⨯=-=-=≠=-=-=Y P X P Y X P 可知,X,Y 不相互独立。
(7分)(2) 由(1)可知E(X)=-1⨯6/10+2⨯4/10=1/5E(Y)= -1⨯3/10+3/10+2⨯4/10=4/5E(X+Y)= E(X)+ E(Y)=1 (7分) (3)Z -1 1 2P 1/10 2/10 7/10 (7分) 四.(17分)总体X 具有如下的概率密度,n X X X Λ,,21是来自X 的样本,()⎩⎨⎧<>=-0,00,x x e x f x θθ, 参数θ未知(1)求θ的矩法估计量;(2)求θ的最大似然估计量。
五.(7分)以X 表示某种清漆干燥时间,X ~()2,σμN ,今取得9件样品,实测得样本方差2s =,求2σ的置信水平为的置信区间。
广东海洋大学2010—2011 学年第二学期《概率论与数理统计》课程试题(答案)班级:GDOU-B-11-302课程号: √ 考试□ A 卷√ 闭卷1.袋中有3个白球,2个红球,任取2个。
