等差数列与等比数列知识点类比表
等差等比数列表格
求通项:一、公式法 ①等差数列通项公式;②等比数列通项公式。
例1 已知数列{}n a 满足1232nn n a a +=+⨯,12a =,求数列{}n a 的通项公式。
解:1232nn n a a +=+⨯两边除以12n +,得113222n n n n a a ++=+,则113222n n n n a a ++-=,故数列{}2nn a 是以1222a 11==为首项,以23为公差的等差数列,由等差数列的通项公式,得31(1)22n n a n =+-,所以数列{}n a 的通项公式为31()222nn a n =-。
评注:本题解题的关键是把递推关系式1232n n n a a +=+⨯转化为113222n n n n a a ++-=,说明数列{}2n na 是等差数列,再直接利用等差数列的通项公式求出31(1)22n n a n =+-,进而求出数列{}n a 的通项公式。
二、累加法 适用于 ()1""n n a a f n +-=型例2 已知数列{}n a 满足11211n n a a n a +=++=,,求数列{}n a 的通项公式。
解:由121n n a a n +=++得121n n a a n +-=+则11232211221()()()()(2)[2(1)1][2(2)1](221)(211)12[(1)(2)21](1)1(1)2(1)12(1)(1)111,n n n n n a a a a a a a a a a n n n n n n n nn n n n a ---=-+-++-+-+≥=-++-+++⨯++⨯++=-+-++++-+-=+-+=-++=== 也成立。
所以数列{}n a 的通项公式为2n a n =。
三、累乘法 适用于()1""n na f n a +=型例3 已知数列{}n a 满足112(1)53nn n a n a a +=+⨯=,,求数列{}n a 的通项公式。
等差数列与等比数列知识点类比表

an1 q(常数) an
an1 an1 an2 (n 2)
n
3.通项公式法: a n A q (A,q 为不为 0 的常数) 4.前 n 项和公式法:s n B q n B ( q 0, q 1 B0 )
设元 技巧
三数等差: a d , a, a d 四数等差: a 3d , a d , a d , a 3d
一、等差数列与等比数列知识点类比表 等差数列 定 义 式 通项 公式 中项 前 n 项 和 等比数列
an1 an d ( d 为常数, n 2 )
an a1 (n 1)d 或 an am (n m)d
a, b, c 成等差数列的充要条件: 2b a c
Hale Waihona Puke an1 q(q 0, 且为常数,n ≥ 2) an
① an am qnm
重 要 性 质
②等和性: 若 m n p q( m 、n 、 p 、q * ) , ②等积性: 若mn p q (m、 , q * ) n 、p 、 则 am an ap aq 则 a a a a
m n p q
2 ③若 2n p q ( n 、p 、 , 则 2an ap aq . ③若 2n p q q * ) ( n 、p 、 , 则 an q * ) ap aq
an a1qn1 ( a1 , q 0 )或 an amqnm
a, b, c 成等比数列的充要条件: b2 ac
n a1 an ; 2 n n 1 d ② Sn na1 2 ① an am (n m)d
① Sn
na 1 (q 1) S n a 1 q n a a q 1 1 n (q 1) 1 q 1 q
(完整版)等差等比数列知识点总结

1.等差数列:一般地,如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数d ,那么这个数列就叫做等差数列,这个常数d 叫做等差数列的公差,即d a a n n =--1(d 为常数)(2≥n );.2.等差中项:(1)如果a ,A ,b 成等差数列,那么A 叫做a 与b 的等差中项.即:2ba A +=或b a A +=2 (2)等差中项:数列{}n a 是等差数列)2(211-≥+=⇔+n a a a n n n 212+++=⇔n n n a a a3.等差数列的通项公式:一般地,如果等差数列{}n a 的首项是1a ,公差是d ,可以得到等差数列的通项公式为:()d n a a n 11-+=推广: d m n a a m n )(-+=. 从而mn a a d mn --=; 4.等差数列的前n 项和公式:1()2n n n a a S +=1(1)2n n na d -=+211()22d n a d n =+-2An Bn =+ (其中A 、B 是常数,所以当d ≠0时,S n 是关于n 的二次式且常数项为0) 5.等差数列的判定方法(1) 定义法:若d a a n n =--1或d a a n n =-+1(常数*∈N n )⇔ {}n a 是等差数列. (2) 等差中项:数列{}n a 是等差数列)2(211-≥+=⇔+n a a a n n n 212+++=⇔n n n a a a .(3) 数列{}n a 是等差数列⇔b kn a n +=(其中b k ,是常数)。
(4) 数列{}n a 是等差数列⇔2n S An Bn =+,(其中A 、B 是常数)。
6.等差数列的证明方法定义法:若d a a n n =--1或d a a n n =-+1(常数*∈N n )⇔ {}n a 是等差数列.(1)当m n p q +=+时,则有q p n m a a a a +=+,特别地,当2m n p +=时,则有2m n p a a a +=.(2) 若{n a }是等差数列,则232,,n n n n n S S S S S -- ,…也成等差数列(3)设数列{}n a 是等差数列,d 为公差,奇S 是奇数项的和,偶S 是偶数项项的和,n S 是前n 项的和 1.当项数为偶数n 2时,()121135212n n n n a a S a a a a na --+=+++⋅⋅⋅+==奇 ()22246212n n n n a a S a a a a na ++=+++⋅⋅⋅+==偶 ()11=n n n n S S na na n a a nd ++-=-=-偶奇 11n n n n S na a S na a ++==奇偶2、当项数为奇数12+n 时,则21(21)(1)1n S S S n a S n a S n S S a S na S n +⎧=+=+=+⎧+⎪⎪⇒⇒=⎨⎨-==⎪⎪⎩⎩n+1n+1奇偶奇奇n+1n+1奇偶偶偶 (其中a n+1是项数为2n+1的等差数列的中间项). 1、等比数列的定义:()()*12,nn a q q n n N a -=≠≥∈0且,q 称为公比 2、通项公式:()11110,0n nn n a a a q q A B a q A B q-===⋅⋅≠⋅≠,首项:1a ;公比:q推广:n m n m n n n m m a a a q q q a --=⇔=⇔=3、等比中项:(1)如果,,a A b 成等比数列,那么A 叫做a 与b 的等差中项,即:2A ab =或A = 注意:同号的两个数才有等比中项,并且它们的等比中项有两个(两个等比中项互为相反数)(2)数列{}n a 是等比数列211n n n a a a -+⇔=⋅ 4、等比数列的前n 项和n S 公式:(1)当1q =时,1n S na = (2)当1q ≠时,()11111n n n a q a a qS qq--==-- 11''11n n n a aq A A B A B A q q=-=-⋅=---(,,','A B A B 为常数)5、等比数列的判定方法:(1)用定义:对任意的n ,都有11(0){}n n n n n na a qa q q a a a ++==≠⇔或为常数,为等比数列(2)等比中项:21111(0){}n n n n n n a a a a a a +-+-=≠⇔为等比数列 (3)通项公式:()0{}n n n a A B A B a =⋅⋅≠⇔为等比数列 6、等比数列的证明方法:依据定义:若()()*12,nn a q q n n N a -=≠≥∈0且或1{}n n n a qa a +=⇔为等比数列 7、等比数列的性质:(1)若*(,,,)m n s t m n s t N +=+∈,则n m s t a a a a ⋅=⋅。
等差数列与等比数列的应用知识点总结

等差数列与等比数列的应用知识点总结等差数列和等比数列是高中数学中常见的两种数列。
它们具有很多重要的应用,在不同的数学问题中发挥着重要的作用。
本文将对等差数列与等比数列的应用进行知识点总结,并探讨它们在实际生活和其他学科中的具体应用。
一、等差数列的应用等差数列是指一个数列中,从第二项起每一项与前一项之差都相等的数列。
其常用的应用有:1. 数列求和公式对于等差数列的前n项和Sn,有求和公式Sn = (n/2)(a1 + an),其中a1为首项,an为末项,n为项数。
这个公式的应用非常广泛,可以用于求解各种数学问题,比如求等差数列的和、计算时间、距离、速度等问题。
2. 平均数的应用对于等差数列,它的各项的平均数与首末两项的平均数是相等的。
这个特性可以用来解决一些平均数相关的问题,比如求取某一连续数列的平均值等。
3. 等差数列的推广等差数列可以推广到高阶等差数列,即每一项与前一项之差的差值也相等。
这种推广常用于解决一些复杂的数学问题,比如等差数列的前n项和Sm,可以通过差分公式Sm = (m/2)(2a1 + (m-1)d)来求解。
4. 几何问题等差数列在几何问题中也有重要应用,比如解决一些等边三角形、等腰梯形等形状相关的问题时,常常需要利用等差数列的性质进行计算。
二、等比数列的应用等比数列是指一个数列中,从第二项起每一项与前一项的比值都相等的数列。
其常用的应用有:1. 数列求和公式对于等比数列的前n项和Sn,有求和公式Sn = a1(1-q^n)/(1-q),其中a1为首项,q为公比,n为项数。
这个公式的应用也非常广泛,可以用于求解各种数学问题,比如计算财务中的复利问题、人口增长问题等。
2. 指数问题等比数列可以与指数问题进行关联。
比如在计算家庭用电量、金融中的复利计算、物理中的指数增长问题等方面,常常需要利用等比数列的特性进行计算。
3. 几何问题等比数列在几何问题中同样有重要应用,比如解决一些等比序列相关的问题,如等比数列构造的等边五角星等。
(完整版)等差等比数列知识点总结

等差等比数列知识点总结1. 等差数列:一般地,如果一个数列从第 2 项起,每一项与它的前一项的差等于同一个常数d ,那么这个数列就叫做等差数列,这个常数d叫做等差数列的公差,即a n a n 1 d (d为常数)(n 2);2. 等差中项:1)如果a , A ,b成等差数列,那么A叫做a与b的等差中项.即:或2A a b3. 等差数列的通项公式:一般地,如果等差数列a n 的首项是a1 ,公差是 d ,可以得到等差数列的通项公式为:a n a1 n 1d推广:a n a m(n m)d .an a m 从而 d ;nm4.等差数列的前n 项和公式:n(a1 a n)n(n 1) d 2 1 2S n na1 d n (a1 d)n An Bn2 2 2 2(其中A、B是常数,所以当d≠ 0时,S n是关于n的二次式且常数项为0)5.等差数列的判定方法(1)定义法:若a n a n 1 d或a n 1 a n d(常数n N )a n 是等差数列.(2)等差中项:数列a n是等差数列2a n a n-1 a n 1(n 2)2a n 1a n a n 2 .(3)数列a n 是等差数列a n kn b (其中k,b 是常数)。
(4)数列a n 是等差数列S n An2Bn, (其中A、B是常数)。
6.等差数列的证明方法定义法:若a n a n 1 d 或a n1a n d (常数n N )a n 是等差数列.ab22)等差中项数列a n是等数列2a n a n-1 a n 1(n 2) 2a n 1 a n a n 27. 等差数列的性质:1)当 m n p q 时, 则有 a m a n a p a q ,特别地,当 m n 2p 时,则有(2) 若{ a n } 是等差数列,则 S n ,S 2n S n ,S 3n S 2n ,⋯也成等差数列和, S n 是前 n 项的和1. 当项数为偶数 2n 时,n a 1 a 2n 1a 2n 1 1 2 2n 1 na na n an 12、当项数为奇数 2n 1时,则其中 a n+1 是项数为 2n+1 的等差数列的中间项)1、等比数列的定义: an q q0 n 2, 且 n N *,q 称为 公比a n 12、通项公式:n1 a n a 1qa 1 n n1q A B a 1q0,A B 0 ,首项: a 1 ;公比:qq推广: a nn m n m amq n m q n ma nq n ma namam3、等比中项:(1)如果 a,A,b 成等比数列, 那么 A 叫做 a 与 b 的等差中项,即: A 2ab 或 A ab注意:同号的 两个数 才有 等比中项,并且它们的等比中项 有两个(两个 等比中项互为相反数)a ma n2a p .3)设数列 a n 是等差数列, d 为公差, S 奇 是奇数项的和, S 偶 是偶数项项的a 2nn a 2 a 2n2na n 1S偶S奇na n 1 na nn a n 1 a n =ndS 2n 1S 奇S 偶 (2n 1) a n+1S 奇 S 偶 a n+1 S 奇 (n 1)a n+1S 偶 na n+1n1a 1 a 3 a 5a 2 a 4 a 6 na n na n 1S 奇为等比数列6、等比数列的证明方法:7、等比数列的性质:3)若{ a n }为等比数列,则数列 S n ,S 2n S n , S 3n S 2n , ,成等比数列 4)在等比数列 { a n }中,当项数为 2n (n N *)时, S奇1S 偶 q2)数列 a n 是等比数列2 ana n 1 a n 14、等比数列的前 n 项和 S n 公式:1)当q 1时, S nna 12)当q 1时, S nnq1qa 1 1 a 1 a n q 1qa 1 a 11q1qA AB n A'B n A'( A,B,A',B'为常数)5、等比数列的判定方法:1)用定义:对任意的 n ,都有 a n1qa n 或 an 1q(q 为常数, a n 0) { a n } an 2)等比中项: 2ana n 1a n 1( a n 1a n 10) {a n } 为等比数列3)通项公式: a n A B n A B 0{a n } 为等比数列依据定义:若 a n qa n 1q 0 n 2, 且 nN * 或a n 1 qa n {a n }为等比数列1) 若 m n s t(m,n,s,t N *),则a n a ma s a t 。
等差数列与等比数列性质总结

a1 q
qn
cqn
{an}为常数数列⇔q=1; {an}为摆动数列⇔q<0.
{an}递增⇔
a1>0或 q>1
a1<0 {an}递减⇔ 0<q<1
a0<1>q0<点1击进或入aq相1><应10模块
知识梳理
(3).等比数列前n项和公式
Sn a1 a2 a3 a4 ....... an2 an1 an ① 错位相 qSn a1q a2q a3q a4q ....... an2q an1q anq qSn a2 a3 a4 a5 ....... an1 an anq ② 减法 ①-② (1- q)Sn a1 anq
则Sm , S2m Sm , S3m S2m ,...... 成等差数列。
(3)中项比性质:等差数列anbn 中,Sn Tn 是其前n项和,
an S 2n1
bn
T2 n 1
点击进入相应模块
知识梳理
3.等差数列的性质
(4)奇数项和与偶数项和性质:等差数列an 中,奇数项有n+1项,
点击进入相应模块
上式都成立,因而它就是等差数列{an}的通项公式。
知识梳理
(2).等差数列通项公式常用结论
结论1.等差数列{an}中,首项为a1,公差d an=am+(n-m)d (其中,m,n N*,n m)
结论2:等差数列通项公式 an - a1= (n-1)d函数性:
直线的一般形式: y kx b
a3 - a2=d, a4 …-…a3=d, an-1-an-2=d, an -an-1=d. 这(n-1)个式子迭加
【专题训练】数列(等差、等比) 知识点总结及题型归纳

基本量法求数列的通项公式11.复习 等差数列(1)定义: 如果一个数列从第2项起,每一项与它的前一项的差等于同一个常.数.,那么这个数列就叫等差数列, 1(2)n n a a d n --=≥d a a n n =1--d a a n n =2-1--(由定义,累加法推得通项公式)…… d a a =12-(2)通项公式1(1)n a a n d =+-(3)性质: 在等差数列{}n a 中,若m ,n ,p ,q N +∈且m n p q +=+,则m n p q a a a a +=+;(4)前项和公式d n n na a a n S n n 2)1(2)(11-+=+=等比数列(1)定义 : 如果一个数列从第二项起....,每一项与它的前一项的比等于同一个常数..,那么这个数列就叫做等比数列,1n a +:(0)n a q q =≠ (2)通项公式11-⋅=n n q a a(3)性质:在等比数列{}n a 中,q p n m a a a a q p n m ⋅=⋅+=+,则若),,,(*∈N q p n m 其中(4)前项和公式)1(11)1()1(111≠⎪⎩⎪⎨⎧--=--==q q qa a qq a q na S n nn例1(2015年全国卷I ) n S 为数列{}n a 的前n 项和.已知20,243n n n n a a a S >+=+,(1)求{}n a 的通项公式:变式1:(湖北省武汉部分重点中学2020届高三起点考试)已知数列{a n }是等比数列,S n 为数列{a n }的前n 项和,且a 3=3,S 3=9 (1)求数列{a n }的通项公式;变式2:已知等差数列{}n a 的公差0d ≠,其前n 项和为n S ,若2822a a +=,且4712,,a a a 成等比数列.(1)求数列{}n a 的通项公式;例2已知数列{a n }的前n 项和为S n ,且2n n S a n =-.(1) 证明数列{1n a +}是等比数列,并求数列{}n a 的通项公式;变式1:(湖北省黄冈中学2019届高三数学模拟试题1)已知各项均为正数的等比数列{a n }的前n 项和为S n ,a 1=14,a 3+a 5=564.(1)求数列{a n }的通项公式;变式3:已知数列{}n a ,{}n b ,其中1,511-==b a ,且满足)3(2111---=n n n b a a ,)3(2111----=n n n b a b ,2*,≥∈n N n .(1)求证:数列{}n n b a -为等比数列,并求数列{a n }、{b n }的通项公式;例3 .已知等差数列{a n }的公差为2,前n 项和为S n ,且S 1,S 2,S 4成等比数列.(1)求数列{a n }的通项公式; 变式(浙江省名校联盟2020届高三第一次联考试题)已知等比数列{}n a 的公比1q >,且13542a a a ++=,39a +是1a ,5a 的等差中项.数列{}n b的通项公式nn b =Νn *∈.(1)求数列{}n a 的通项公式;数列(等差、等比)知识点清单一、数列的概念1.数列定义:按一定次序排列的一列数叫做数列;数列中的每个数都叫这个数列的项。
高中数学 数列与类比---等差数列与等比数列的区别与联系

等差数列与等比数列在“求和”与“求积”可以互换 推等导距. 的部分和构成的新数列的类比.
等差数列与等比数列的区别与联系
类比方法: (1)差—商 (2)和—积 (3)倍数—指数
等差数列
等比数列
定 义
an+1-an=d an-am=(n-m)d
nk akn an
} }
{akn+b}, 仍成等比数列.而{lgpank}成等差
数列.若{an}是等差数列,则 { C an,}
若an、bn是等差数列,则{pan+mbn}, { C pan r } ,{ C pan rbn } 成等比数
{man}, {akn-an},{kanb},{akn+b} 仍成等差数列.
an+1/an=q an/am=qn-m
等 差 (
2b=a+c 2an=am-n + am+n a1+an=a2+ an-1=…= ak+ an-k
b2=a·c an2=am-n ·am+n a1 ·an=a2 ·an-1=…= ak ·an-k
比 )
m±n=p±q am ± an=ap ± aq
m±n=p±q
am ·an=ap ·aq
中 项
距首末两项等距的和相等
am /an=ap /aq 距首末两项等距的积相等
通 项
an=a1+(n-1)d(叠代法、叠加法) an=a1 ·qn-1 (叠代法、叠乘法)
公 式
an=am+(n-m)d
公 差 (
d= an a1
n 1
=
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
单
调
性:
设d为等差数列 的公差,则
d>0 是递增数列;
d<0 是递减数列;
d=0 是常数数列.
递增数列;
递减数列;
q=1 是常数数列;
q<0 是摆动数列
证
明
方
法
证明一个数列为等差数列的方法:
1.定义法
2.中项法
3.通项公式法: ( 为常数)
4.前n项和公式法: (A,B为常数)
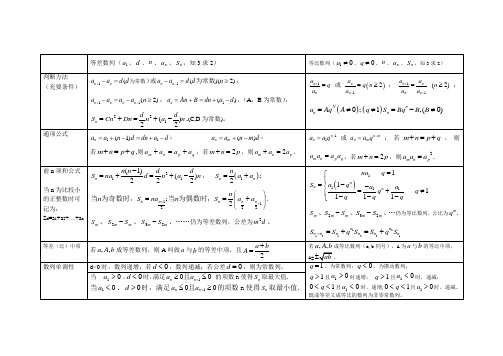
一、等差数列与等比数列知识点类比表
等差数列
等比数列
定义
( 为常数, )
递推
公式
通项
公式
或
( )或
中项
成等差数列的充要条件:
成等比数列的充要条件:
前
项
和
;
重
要
性
质
①
②等和性:若 ( 、 、 、 ),
则
③若 ( 、 、 ),则 .④ 构成的数 Nhomakorabea是等差数列.
①
②等积性:若 ( 、 、 、 ),
则
③若 ( 、 、 ),则
证明一个数列为等比数列的方法:
1.定义法
2.中项法
3.通项公式法: (A,q为不为0的常数)
4.前n项和公式法: ( )
设元
技巧
三数等差:
四数等差:
三数等比:
四数等比:
二、数列的项 与前 项和 的关系:
注意:一定不要忘记对n取值的讨论!最后,还应检验当n=1的情况是否符合当n 2的关系式,从而决定能否将其合并。
