第20次课 尺寸链计算的基本公式
公差尺寸链计算公式

公差尺寸链计算公式
1.基准尺寸的确定:
在公差尺寸链的计算中,首先需要确定一个基准尺寸,作为其他尺寸的参考。
一般选择与工艺要求相符的零件尺寸作为基准尺寸。
2.公差分配:
公差分配是指根据装配要求和功能要求,按照一定比例将总公差分配到各个零件尺寸上。
公差分配的原则包括:
-公差应按照装配要求和功能要求进行分布,确保装配精度和功能要求的满足。
-尺寸公差应该从初始尺寸向装配间隙依次增大,以确保装配的顺利进行。
-公差应尽量少,以减少成本和缩小尺寸偏差。
在进行公差分配时,一般需要考虑以下几个因素:
-零件功能要求:根据零件在装配中的具体功能、运动和受力情况,确定其尺寸公差的分配。
-装配方式:根据零件的装配方式,如插入、相对位置等,确定其尺寸公差的分配。
-零件尺寸和材料:根据零件的尺寸和材料特性,确定其尺寸公差的分配。
3.最小公差计算:
最小公差是保证装配精度的关键要素,通常根据装配要求和功能要求
向下确定。
最小公差的计算需要考虑以下几个因素:
-装配要求:根据装配的要求和设定的公差限制,确定所需的最小公差。
-装配间隙:根据装配时需要的间隙和松动度,确定所需的最小公差。
-功能要求:根据零件在装配中的具体功能和使用要求,确定最小公差。
以上是公差尺寸链计算的基本原理和步骤。
实际应用中,还需要考虑
诸如公差合理化、商标公差等的因素,以确保设计的合理性和可靠性。
公
差尺寸链计算是一项复杂的工作,需要根据具体情况进行合理的分析和计算,以满足产品的装配和使用要求。
工艺尺寸链计算的基本公式

工艺尺寸链计算的基本公式
1.尺寸链总公差计算式
总公差=设计尺寸+最大便宜-最小公差
其中,设计尺寸是产品设计的理论尺寸,最大便宜是指允许的最大超
出设计尺寸的尺寸偏差,最小公差是指允许的最小尺寸偏差。
2.累积公差计算式
累积公差=√(Σ(公差1^2+公差2^2+公差3^2+...+公差n^2))
其中,Σ表示总和,公差1、公差2、公差3...公差n是从设计到加
工过程中每个环节的公差。
3.公差分配计算式
公差分配=(设计尺寸-加工尺寸)/加工余量
其中,设计尺寸是产品设计的理论尺寸,加工尺寸是实际加工得到的
尺寸,加工余量是指设计尺寸与加工尺寸之间的差值。
4.合并公差计算式
合并公差=√(公差1^2+公差2^2)
其中,公差1和公差2是两个相互独立的公差。
5.组合公差计算式
组合公差=(公差1^2+公差2^2+公差3^2+...+公差n^2)^0.5
其中,公差1、公差2、公差3...公差n是不同特征尺寸的尺寸公差。
除了这些基本公式外,还有一些特殊情况下的公式可供使用,如配合
公差的计算、紧配合公差的计算等。
需要注意的是,工艺尺寸链的计算是一个复杂的过程,需要考虑到产
品的设计要求、加工工艺的要求、材料的特性等多个因素。
公式只是工艺
尺寸链计算的一部分,实际使用中还需结合具体情况进行综合计算和分析。
尺寸链计算及例题解释
(4)各环公差之间的关系
封闭环的公差T(A0)等于各组成环的公差T(Ai)之和,即
T (A ) T (A) T (A) T (A)
m n 1 n 1 i 1 0 i 1 i i m 1 i i
极值法解算尺寸链的特点是: 简便、可靠,但当封闭环公差较小,组成环数目较多 时,分摊到各组成环的公差可能过小,从而造成加工困 难,制造成本增加,在此情况小,常采用概率法进行尺 寸链的计算。
尺寸链方程
—— 确定尺寸链中封闭环(因变量) 和组成环(自变量)的函数关系式,其一般 形式为:
A0 f ( A1 , A2 ,
, An )
2006-3
10
工艺尺寸链示例:
工件 A 、 C 面已加工好,现以 A 面定位 用调整法加工B 面,要求保证B、C 面距离A0
0.05 A
C
B A0 a0 0.1 C a1
2006-3
8
三 、尺寸链的建立
关键
1、加工顺序或装配顺序确定后才 能确定封闭环。 2、封闭环的基本属性为“派生” ,表现为尺寸间接获得。 1、设计尺寸往往是封闭环。 2、加工余量往往是封闭环(靠火 花磨除外)。
1、确定封闭环
要领
2、组成环确定
关键
1、封闭环确定后才能确定。 2、直接获得。 3、对封闭环有影响
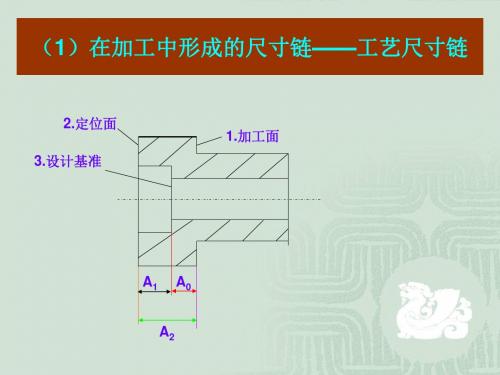
(1)在加工中形成的尺寸链——工艺尺寸链
2.定位面 3.设计基准
1.加工面
A1
A0
A2
(2)在装配中形成的尺寸链——装配尺寸链
A0
A2
A1
图示工件如先以A面定位加工C面,得尺寸A1然后再以 A面定位用调整法加工台阶面B,得尺寸A2,要求保证B面 与C面间尺寸A0;A1、A2和A0这三个尺寸构成了一个封闭 尺寸组,就成了一个尺寸链。
几种典型尺寸链的计算

TK6816 型小截面方滑枕铣镗床设计
王建利 (沈阳机床(集团)有限公司,沈阳 110142)
摘 要:以 TK6816 数控刨台卧式铣镗床设计为例,介绍了小截面方滑枕铣镗床设计的要点、难点及其解决办法。经实
践证明,该机床的设计是切实可行的。
关键词:方滑枕;结构设计;补偿系统
中图分类号:TG502
文献标识码:A
基本尺寸冠以负号。
上下偏差:对于增环,上下偏差照抄;对于减环,上下
偏差对调,并且变号。
封闭环的基本尺寸 及偏差:只要把增环、减 环列的数值作代数和,即 得到封闭环的基本尺寸 及上下偏差。
表 1 竖式表
环 基本尺寸 上偏差 下偏差
增环
A1
ES
EI
减环 -(A2) EI
ES
封闭环 A0
ES
EI
120 机械工程师 2011 年第 11 期
(1)尺寸链:在机器装配或零件加工过程中,由相互 连接的尺寸形成封闭的尺寸组,称为尺寸链。
(2)环:列入尺寸链中的每一个尺寸称为环。 (3)封闭环:尺寸链中在装配过程或加工过程后自然 形成的一环,称为封闭环。 (4)组成环:尺寸链中对封闭环有影响的全部环,称 为组成环。 (5)增环:尺寸链中某一类组成环,由于该类组成环 的变动引起封闭环同向变动,该组成环为增环,即方向与 封闭环方向相反。 (6)减环:尺寸链中某一类组成环,由于该类组成环 的变动引起封闭环的反向变动,该类组成环为减环,即方 向与封闭环方向相同。 2 尺寸链计算的基本公式 (1)封闭环的基本尺寸 A0 等于增环的基本尺寸之和 减去减环的基本尺寸之和,即
解决方案
工艺 / 工装 / 模具 / 诊断 / 检测 / 维修 / 改造 SOLUTION
第20次课尺寸链计算的基本公式

第20次课尺⼨链计算的基本公式式中,—尺⼨链中第j个组成环的标准偏差。
如果各组成环的实际尺⼨都为正态分布,并且分布范围与公差带宽度⼀致,分布中⼼与公差带中⼼重合,见图8-8,则封闭环的实际尺⼨也服从正态分布,各环公差与标准偏差关系如下T0 = 6σ0T j= 6将以上两式代⼊(8-9)式,得(8—10) (8—10)式表明:封闭环公差等于所有组成环公差的⽅和根。
由图8-8可见,各组成环的中间偏差为其上、下偏差的平均值。
封闭环的中间偏差?0与组成环的中间偏差?j分别为0 =j =各组成环的中⼼尺⼨为极限尺⼨的平均值。
封闭环的中间尺⼨A0中为封闭环的基本尺⼨与其中间偏差之和:A0中 = A0+ ?0 (8-11) 组成环中间尺⼨A j中为组成环的基本尺⼨与中间偏差之和:A j中 = A j+ ?j(8-12)(8-4)和(8-5)式相加后取平均值可得-13) 即:封闭环中间尺⼨等于所有增环的中间尺⼨之和减去所有减环的中间尺⼨之和。
将上述公式整理得:(8-14) 即:封闭环中间偏差等于所有增环的中间偏差之和减去所有减环的中间偏差之和。
如果组成环的实际尺⼨不服从正态分布,⽽是其它分布,或者组成环分布中⼼偏离公差带中⼼,那么本节所述公式应加以修正,详见有关书籍。
⽤⼤数互换法解尺⼨链的步骤基本上与极值法相同。
但在计算封闭环和组成环的上、下偏差时,要先算出它们的中间偏差。
,B2=70 0 -0.03,B0 = 四、例题:在上节课图所⽰的齿轮轴装配图中:B1=100+0.140.02—0.20,求垫⽚轴向尺⼨B3为多少?列式计算∵ B0max = B1max - (B2min + B3min)∴ B3min = B1max - B2min – B0max=100.14-69.97-0.2= 29.97mm同理:B3max = B1min- B2max- B0min= 100- 70-0.02= 29.98 mm。
万能平面尺寸链计算公式及其用法举例

/ X B ﹦ 0.999 ; LAB Y A ﹦ 0.0439 ;
7
L AB YB ﹦﹣0.0439
由上述各偏导数值的符号可知, X A 、 X B 和 Y A 是尺寸链的増环,
YB 是减环。
' ' ⑵ 计算公差 d X A 、d X B 、d Y A' 和 d YB' ' ' 由式⑷可得:d LAB ﹦ LAB X A d X A ﹢ LAB X B d X B ﹢ ' L AB Y A d Y A ﹢ LAB YB d YB' ' ' 已知:d LAB ﹦0.18mm ;所以:0.18﹦|0.999|d X A ﹢|0.999|d X B ' ' ﹢|0.0439|d Y A ' ﹢|﹣0.0439|d YB' ;取 d X A ﹦d X B ﹦d Y A' ﹦d YB' ' ' ' ' 则 dXA ﹦d X B ﹦d Y A' ﹦d YB' ﹦0.086mm﹙说明:可以取 d X A 、d X B 、d Y A'
代入上式,即
' 0.18﹦|0.999|d X A ﹢|0.999∣ 0.072﹢∣0.0439∣d Y A' + ' ' |﹣0.0439| 0.072 ;取 d X A ﹦d Y A' ,则 d X A ﹦d Y A' ﹦0.1mm;由于 ' ' dXA 和 d Y A' 小于 d X A 和 d Y A ,所以 d X A 和 d Y A 应取 d X A 和 d Y A' 之值, ' 即 d X A ﹦d Y A ﹦d X A ﹦d Y A' ﹦0.1mm。综上所述,可得:d X B ﹦d YB
尺寸链的基本概念及计算

其特性有二:封闭性——组成尺寸链的各个尺寸按一定 顺序构成一个封闭系统;相关性——其中一个尺寸变动
将影响其他尺寸变动。
HOME
.
尺寸链的组成
4
构成尺寸链的各个尺寸称为环。尺寸链的环分为封闭环 和组成环。
封闭环: 加工或装配过程中最后自然形成的那个尺寸。 如上图中的x、B0和A0。
组成环: 尺寸链中除封闭环以外的其他环。根据它们对 封闭环影响的不同,又分为增环和减环。
即要求封闭环的尺寸为0 0.45mm 。
0.10
(3)计算封闭环的极限偏差 ES。=ES3—(EI1+EI2+EI4+EI5)
=+0.18—(—0.13—0.075—0.04—0.075)=+0.50 EI。=EI3—(ES1+ES2+ES4+ES5)
=+0.02mm—(0+0+0+0)mm=+0.02mm (4)计算封闭环的公差 T。=T1+T1+ T2+T3+T4 +T5
课题四、尺寸链基础
1 尺寸链的基本概念及计算
.
基本要求
2
基本内容:尺寸链的基本概念、组成、分类、 尺寸链的建立与分析,尺寸链的计算。
重点内容:尺寸链的建立与分析及基本计算。 难点内容:尺寸链的建立与分析 基本技能:通过本章节的学习能进行尺寸链的
初步分析和计算,并逐步建立机构精度设计的 概念。
中间计算 已知封闭环和部分组成环的极限尺寸,求某 一组成环的极限尺寸、这类计算常用在工艺上。
反计算和中间计算通常称为设计计算。 HOME
.
计算方法
12
完全互换法(极值法):从尺寸链各环的最大与最小极限尺寸出 发进行尺寸链计算,不考虑各环实际尺寸的分布情况。按此法计 算出来的尺寸加工各组成环,装配时各组成环不需挑选或辅助加 工,装配后即能满足封闭环的公差要求,即可实现完全互换。完 全互换法是尺寸链计算中最基本的方法。
工艺尺寸链计算的基本公式

工艺尺寸链计算的基本公式来源:作者:发布时间:2007-08-03工艺尺寸链的计算方法有两种:极值法和概率法。
目前生产中多采用极值法计算,下面仅介绍极值法计算的基本公式,概率法将在装配尺寸链中介绍。
图 3-82 为尺寸链中各种尺寸和偏差的关系,表 3-18 列出了尺寸链计算中所用的符号。
1 .封闭环基本尺寸式中 n ——增环数目;m ——组成环数目。
2 .封闭环的中间偏差式中Δ0——封闭环中间偏差;——第 i 组成增环的中间偏差 ;——第 i 组成减环的中间偏差。
中间偏差是指上偏差与下偏差的平均值:3 .封闭环公差4 .封闭环极限偏差上偏差下偏差5 .封闭环极限尺寸最大极限尺寸 A 0max=A 0+ES 0 ( 3-27 )最小极限尺寸 A 0min=A 0+EI 0 ( 3-28 )6 .组成环平均公差7 .组成环极限偏差上偏差下偏差8 .组成环极限尺寸最大极限尺寸 A imax=A i+ES I ( 3-32 )最小极限尺寸 A imin=A i+EI I ( 3-33 )工序尺寸及公差的确定方法及示例工序尺寸及其公差的确定与加工余量大小,工序尺寸标注方法及定位基准的选择和变换有密切的关系。
下面阐述几种常见情况的工序尺寸及其公差的确定方法。
(一)从同一基准对同一表面多次加工时工序尺寸及公差的确定属于这种情况的有内外圆柱面和某些平面加工,计算时只需考虑各工序的余量和该种加工方法所能达到的经济精度,其计算顺序是从最后一道工序开始向前推算,计算步骤为:1 .确定各工序余量和毛坯总余量。
2 .确定各工序尺寸公差及表面粗糙度。
最终工序尺寸公差等于设计公差,表面粗糙度为设计表面粗糙度。
其它工序公差和表面粗糙度按此工序加工方法的经济精度和经济粗糙度确定。
3 .求工序基本尺寸。
从零件图的设计尺寸开始,一直往前推算到毛坯尺寸,某工序基本尺寸等于后道工序基本尺寸加上或减去后道工序余量。
4 .标注工序尺寸公差。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
式中,—尺寸链中第j个组成环的标准偏差。
如果各组成环的实际尺寸都为正态分布,并且分布范围与公差带宽度一致,分布中心与公差带中心重合,见图8-8,则封闭环的实际尺寸也服从正态分布,各环公差与标准偏差关系如下
T0 = 6σ0
T j= 6
将以上两式代入(8-9)式,得
(8—10) (8—10)式表明:封闭环公差等于所有组成环公差的方和根。
由图8-8可见,各组成环的中间偏差为其上、下偏差的平均值。
封闭环的中间偏差∆0与组成环的中间偏差∆j分别为
∆0 =
∆j =
各组成环的中心尺寸为极限尺寸的平均值。
封闭环的中间尺寸A0中为封闭环的基本尺寸与其中间偏差之和:
A0中 = A0+ ∆0 (8-11) 组成环中间尺寸A j中为组成环的基本尺寸与中间偏差之和:
A j中 = A j+ ∆j(8-12)
(8-4)和(8-5)式相加后取平均值可得
-13) 即:封闭环中间尺寸等于所有增环的中间尺寸之和减去所有减环的中间尺寸之和。
将上述公式整理得:
(8-14) 即:封闭环中间偏差等于所有增环的中间偏差之和减去所有减环的中间偏差之和。
如果组成环的实际尺寸不服从正态分布,而是其它分布,或者组成环分布中心偏离公差带中心,那么本节所述公式应加以修正,详见有关书籍。
用大数互换法解尺寸链的步骤基本上与极值法相同。
但在计算封闭环和组成环的上、下偏差时,要先算出它们的中间偏差。
,B2=70 0 -0.03,B0 = 四、例题:在上节课图所示的齿轮轴装配图中:B1=100+0.14
0.02—0.20,求垫片轴向尺寸B3为多少?
列式计算
∵ B0max = B1max - (B2min + B3min)
∴ B3min = B1max - B2min – B0max
=100.14-69.97-0.2
= 29.97mm
同理:B3max = B1min- B2max- B0min
= 100- 70-0.02
= 29.98 mm。
结论:垫片轴向尺寸B3为 30-0.02
-0.03。
