中位线定理全面版

合集下载

三角形的中位线完整版课件

已知：如图，在四边形ABCD中，E，G，分别是AB，CD，的中点.
A
E
P
D
B
G
C
若AD=BC，连结BD，P是 BD的中点，
连结EP，GP，若∠PEG=15°，则
∠PGE=
度.
分析由已知可得EP与GP分别是△ABP与△BCD的中位线，
∴EP ＝ ∥ 1 AD， PG＝ ∥ 1 AD.
2
2
又∵AD=BC
三角形中线，一个端点是边的中点，另一端点是三角形的顶点.
新知探究
4.5三3.角3垂 3形.4径圆的定心中理角位②②线
通过观察，测量等方法，你发现线段DE有哪些性质？
A
观察发现DE∥BC，度量发现 DE 1 BC . 2
三角形的中位线定理：
D
E
三角形的中位线平行于第三边，并且等于第三边的一半.
B
几何语言：
新知探究
4.5三角形的中位线
• 了解三角形中位线的概念 • 了解三角形中位线的性质 • 探索三角形中位线定理证明的方法 • 能由线段的中点联想到三角形中位线 • 探索三角形中位线性质的一些简单应用
4.5三角形的中位线
• 定义：连结三角形两边中点的线段叫做三角形的中位线
• 任意画一个△ABC，分别取AB，AC的中点D，E，连结DE. A • 你还能画出几条三角形的中位线？
A
D
G
O
EM F
B
C
课堂小结
4.5三角3形.4圆的心中角位②线
三角形的中位线定理：三角形的中位线平行于第三边，并且等于第三边的一半.
中位线定理经常用于： ① 证明平行关系； ② 线段大小的计算.
D
E

三角形中位线定理知识讲解

三角形中位线定理【学习目标】1. 理解三角形的中位线的概念，掌握三角形的中位线定理．2. 掌握中点四边形的形成规律.【要点梳理】要点一、三角形的中位线1．连接三角形两边中点的线段叫做三角形的中位线.2．定理：三角形的中位线平行于第三边，并且等于第三边的一半.要点诠释：（1）三角形有三条中位线，每一条与第三边都有相应的位置关系与数量关系.（2）三角形的三条中位线把原三角形分成可全等的4个小三角形.因而每个小三角形的周长为原三角形周长的12，每个小三角形的面积为原三角形面积的14.（3）三角形的中位线不同于三角形的中线.要点二、顺次连接特殊的平行四边形各边中点得到的四边形的形状（1）顺次连接平行四边形各边中点得到的四边形是平行四边形.（2）顺次连接矩形各边中点得到的四边形是菱形.（3）顺次连接菱形各边中点得到的四边形是矩形.（4）顺次连接正方形各边中点得到的四边形是正方形.要点诠释：新四边形由原四边形各边中点顺次连接而成.（1）若原四边形的对角线互相垂直，则新四边形是矩形.（2）若原四边形的对角线相等，则新四边形是菱形.（3）若原四边形的对角线垂直且相等，则新四边形是正方形.【典型例题】类型一、三角形的中位线1、（优质试题•北京）如图，在四边形ABCD中，∠ABC=90°，AC=AD，M，N分别为AC，CD的中点，连接BM，MN，BN．（1）求证：BM=MN；（2）∠BAD=60°，AC平分∠BAD，AC=2，求BN的长．【思路点拨】（1）根据三角形中位线定理得MN=AD，根据直角三角形斜边中线定理得BM=AC，由此即可证明．（2）首先证明∠BMN=90°，根据BN2=BM2+MN2即可解决问题．【答案与解析】（1）证明：在△CAD中，∵M、N分别是AC、CD的中点，∴MN∥AD，MN=AD，在RT△ABC中，∵M是AC中点，∴BM=AC，∵AC=AD，∴MN=BM．（2）解：∵∠BAD=60°，AC平分∠BAD，∴∠BAC=∠DAC=30°，由（1）可知，BM=AC=AM=MC，∴∠BMC=∠BAM+∠ABM=2∠BAM=60°，∵MN∥AD，∴∠NMC=∠DAC=30°，∴∠BMN=∠BMC+∠NMC=90°，∴BN2=BM2+MN2，由（1）可知MN=BM=AC=1，∴BN=【总结升华】本题考查三角形中位线定理、直角三角形斜边中线定理、勾股定理等知识，解题的关键是灵活应用这些知识解决问题，属于中考常考题型．举一反三：【变式】如图，矩形OABC的顶点A、C分别在x轴、y轴正半轴上，B点坐标为（3，2），OB与AC交于点P，D、E、F、G分别是线段OP、AP、BP、CP的中点，则四边形DEFG的周长为_____.【答案】5；解：∵四边形OABC是矩形，∴OA＝BC，AB＝OC；BA⊥OA，BC⊥OC．∵B点坐标为（3，2），∴OA＝3，AB＝2．∵D、E、F、G分别是线段OP、AP、BP、CP的中点，∴DE＝GF＝1.5； EF＝DG＝1．∴四边形DEFG的周长为（1.5＋1）×2＝5．2、如图，在△ABC中，已知点D、E、F分别是AB、BC、CA的中点，AH是高．（1）若BC=10，AH=8，则四边形ADEF的面积为．（2）求证：∠DHF=∠DEF．HF EDCBA【思路点拨】（1）由三角形面积公式可知：△BDE、△EFC的面积都等于△ABC面积的四分之一，进而可求出四边形ADEF的面积．（2）首先证明四边形ADEF是平行四边形，进而可得∠DEF=∠DAF，再利用直角三角形的中线性质得线段相等，从而得角等，最终可得到∠DAF=∠DEF，即可证出∠DHF=∠DEF．【答案解析】（1）解：∵BC=10，AH=8，∴S△ABC=×8×10=40，∵点D、E、F分别是AB、BC、CA的中点，∴△BDE、△EFC的面积都等于△ABC面积的，∴四边形ADEF的面积=40﹣20=20，故答案为：20；（2）证明：∵D、E、F分别是△ABC各边中点，∴DE∥AC，EF∥AB，∴四边形ADEF是平行四边形，∴∠DEF=∠DAF，∵AH是△ABC的高∴△ABH、△ACH是直角三角形，∵点D、点F是斜边AB、AC中点，∴DH=DA，HF=AF，∴∠DAH=∠DHA ，∠FAH=∠FHA ，∴∠DAH+∠FAH=∠FHA+∠DHA ，即∠DAF=∠DHF ，∴∠DEF=∠DHF ．【总结升华】此题主要考查了平行四边形的性质与判定，三角形的中位线定理，直角三角形的性质，解决题目的关键是证明∠DHF=∠DAF 与∠DAF=∠DEF ．3、如图所示，在△ABC 中，M 为BC 的中点，AD 为∠BAC 的平分线，BD ⊥AD 于D ，AB ＝12，AC ＝18，求MD 的长．【思路点拨】本题中所求线段MD 与已知线段AB 、AC 之间没有什么联系，但由M 为BC 的中点联想到中位线，另有AD 为角平分线和垂线，根据等腰三角形“三线合一”构造等腰三角形ABN ，D 为BN 的中点，DM 即为中位线，不难求出MD 的长度．【答案与解析】解：延长BD 交AC 于点N ．∵ AD 为∠BAC 的角平分线，且AD ⊥BN ，∴ ∠BAD ＝∠NAD ，∠ADB ＝∠ADN ＝90°，在△ABD 和△AND 中，BAD NAD AD =ADADB ADN ∠∠⎧⎪⎨⎪∠∠⎩＝＝ ∴ △ABD ≌△AND(ASA)∴ AN ＝AB ＝12，BD ＝DN ．∵ AC ＝18，∴ NC ＝AC －AN ＝18－12＝6，∵ D 、M 分别为BN 、BC 的中点，∴ DM ＝12CN ＝162⨯＝3．【总结升华】当条件中含有中点的时候，可以将它与等腰三角形的“三线合一”、三角形的中线、中位线等联系起来，进行联想，必要时添加辅助线，构造中位线等图形．举一反三：【变式】如图所示，四边形ABCD 中，Q 是CD 上的一定点，P 是BC 上的一动点，E 、F 分别是PA 、PQ 两边的中点；当点P 在BC 边上移动的过程中，线段EF 的长度将( )．A．先变大，后变小 B．保持不变 C．先变小，后变大 D．无法确定【答案】B；解：连接AQ．∵ E、F分别是PA、PQ两边的中点，∴ EF是△PAQ的中位线，即AQ＝2EF．∵ Q是CD上的一定点，则AQ的长度保持不变，∴线段EF的长度将保持不变．4、我们给出如下定义：有一组相邻内角相等的四边形叫做等邻角四边形．请解答下列问题：（1）如图1，在△ABC中，AB=AC，点D在BC上，且CD=CA，点E、F分别为BC、AD的中点，连接EF并延长交AB于点G．求证：四边形AGEC是等邻角四边形；（2）如图2，若点D在△ABC的内部，（2）中的其他条件不变，EF与CD交于点H，图中是否存在等邻角四边形，若存在，指出是哪个四边形，不必证明；若不存在，请说明理由．【思路点拨】（1）运用中位线的性质，找出对应相等的角；（2）根据题意易知满足条件的四边形即为第一题的四边形．【答案与解析】解：（1）取AC的中点H，连接HE、HF∵点E为BC中点∴EH为△ABC的中位线∴EH∥AB，且EH=12AB同理FH∥DC，且FH=12DC∵AB=AC，DC=AC∴AB=DC，EH=FH∴∠1=∠2∵EH∥AB，FH∥DC∴∠2=∠4，∠1=∠3∴∠4=∠3∵∠AGE+∠4=180°，∠GEC+∠3=180°∴∠AGE=∠GEC∴四边形AGEC是邻角四边形（2）存在等邻角四边形，为四边形AGHC．【总结升华】本题考查了三角形的中位线以及等腰三角形的性质的综合运用．本题较灵活，要求学生能够把题中的条件转化成角，从而找出相等的角来解题．举一反三：【变式】如图，AB∥CD，E，F分别为AC，BD的中点，若AB=5，CD=3，则EF的长是（）A．4 B．3 C．2 D．1【答案】D；解：连接DE并延长交AB于H，∵CD∥AB，∴∠C=∠A，∠CDE=∠AHE，∵E是AC中点，∴AE=CE，∴△DCE≌△HAE，∴DE=HE，DC=AH，∵F是BD中点，∴EF是△DHB的中位线，∴EF=12 BH，∴BH=AB-AH=AB-DC=2，∴EF=1．类型二、中点四边形5、如图，在梯形ABCD中，AD∥BC，AB＝DC，对角线AC、BD交于点O，AC⊥BD，E、F、G、H分别是AB、BC、CD、DA的中点．（1）求证：四边形EFGH是正方形；（2）若AD＝2，BC＝4，求四边形EFGH的面积．【思路点拨】（1）先由三角形的中位线定理求出四边相等，然后由AC⊥BD 入手，进行正方形的判断．（2）连接EG ，利用梯形的中位线定理求出EG 的长，然后结合（1）的结论求出2EH ＝92，也即得出了正方形EHGF 的面积．【答案与解析】证明：（1）在△ABC 中，E 、F 分别是AB 、BC 的中点，故可得：EF ＝12AC ，同理FG ＝12BD ，GH ＝12AC ，HE ＝12BD ，在梯形ABCD 中，AB ＝DC ，故AC ＝BD ，∴EF＝FG ＝GH ＝HE ，∴四边形EFGH 是菱形．设AC 与EH 交于点M ，在△ABD 中，E 、H 分别是AB 、AD 的中点，则EH∥BD，同理GH∥AC，又∵AC⊥BD，∴EH⊥HG，∴四边形EFGH 是正方形．（2）连接EG ．在梯形ABCD 中，∵E、G 分别是AB 、DC 的中点，∴EG＝12（AD ＋BC ）＝3．在Rt△EHG 中， ∵222EH GH EG +=，EH ＝GH ，∴2EH ＝92，即四边形EFGH 的面积为92．【总结升华】此题考查了等腰梯形的性质及三角形、梯形的中位线定理，解答本题的关键是根据三角形的中位线定理得出EH ＝HG ＝GF ＝FE ，这是本题的突破口．举一反三：【变式】如图，E 、F 、G 、H 分别是边AB 、BC 、CD 、DA 的中点．（1）判断四边形EFGH 的形状，并说明你的理由；（2）连接BD 和AC ，当BD 、AC 满足何条件时，四边形EFGH 是正方形．【答案】解：（1）四边形EFGH是平行四边形．理由：连接AC，∵E、F分别是AB、BC的中点，∴EF∥AC，且EF＝12 AC，同理，HG∥AC，且HG＝12 AC，∴EF∥HG，且EF＝HG，∴四边形EFGH是平行四边形；（2）当BD＝AC，且BD⊥AC时，EFGH是正方形．理由：连接AC，BD，∵E、F、G、H分别是边AB、BC、CD、DA的中点，∴EF＝GH＝12AC，EH＝FG＝12BD，EH∥BD，GH∥AC，∵BD＝AC，BD⊥AC，∴EH＝EF＝FG＝GH，EH⊥GH，∴四边形ABCD是菱形，∠EHG＝90°，∴四边形EFGH是正方形．。

《三角形的中位线》知识清单

《三角形的中位线》知识清单一、三角形中位线的定义连接三角形两边中点的线段叫做三角形的中位线。

需要注意的是，一个三角形共有三条中位线。

二、三角形中位线定理三角形的中位线平行于三角形的第三边，并且等于第三边的一半。

这个定理是解决与三角形中位线相关问题的重要依据。

为了更好地理解这个定理，我们可以通过以下方式来证明：如图，在△ABC 中，D、E 分别是 AB、AC 的中点，连接 DE。

延长 DE 到点 F，使得 EF ＝ DE，连接 CF。

因为 AE ＝ EC，∠AED ＝∠CEF，DE ＝ EF，所以△ADE ≌△CFE（SAS）所以 AD ＝ CF，∠ADE ＝∠F所以 AB ／／ CF又因为 AD ＝ BD所以 BD ＝ CF所以四边形 BCFD 是平行四边形（一组对边平行且相等的四边形是平行四边形）所以 DF ／／ BC，DF ＝ BC因为 DE ＝ 1/2 DF所以 DE ／／ BC，DE ＝ 1/2 BC通过以上证明，我们得出了三角形中位线定理。

三、三角形中位线定理的应用1、证明线段平行如果已知一条线段是三角形的中位线，那么可以直接得出这条线段与三角形的第三边平行。

例如，在△ABC 中，D、E 分别是 AB、AC 的中点，连接 DE，则DE ／／ BC。

2、证明线段的数量关系可以利用中位线等于第三边的一半来证明线段之间的倍数关系。

比如，已知△ABC 中，DE 是中位线，那么 DE ＝ 1/2 BC。

3、计算线段的长度在一些几何计算题中，如果能找到三角形的中位线，就可以利用中位线定理求出相关线段的长度。

例如，在△ABC 中，AB ＝ 10，D、E 分别是 AB、AC 的中点，那么 DE ＝ 5。

4、求图形的面积通过中位线与底边的关系，可以求出相关三角形的面积比。

假设△ABC 中，DE 是中位线，△ADE 的面积为 S1，△ABC 的面积为 S2。

因为 DE ／／ BC，所以△ADE ∽△ABC，相似比为 1 ： 2。

三角形中位线定理

1 EF= 1 BC 2 2
三角形的中位线的性质
三角形的中位线平行于第三边，并且等于它的一半 A 用符号语言表示
∵DE是△ABC的中位线
E B
D C
1 ∴ DE∥BC， DE= BC. 2
① 证明平行问题
② 证明一条线段是另一条线段的2倍或1/2
初试身手
A D
练习1.如图，在△ABC中，D、E分别是、F分别 AB 、、 AC 的中点是 AB AC 、BC的中点
∴ DF=1/2BC，DE=1/2AC。 ∴ 四边形DECF的周长是 B DF+DE+EC+CF=16/2+12/2+1 6/2+12/2=28
D
F
E
C
拓展应用：
在△ABC中，∠BAC=90°，延长BA到点D，使 AD=1/2AB，点E,F分别为BC,AC的中点，试说DF=BE理 D 由
理由： ∵ 点E,F分别为BC,AC的中点
B三角形的周长与原三角形的周长有什么关系？ 2、三角形三条中位线围成的三角形的面积与原三角形的面积有什么关系？
演练
已知：如果，点D、E、F分别是△ABC的三边的中点．（1）若AB=8cm，求EF的长；（2）若DE=5cm，求BC的长．（3）若增加M、N分别是BD、BF的中点， A 问MN与AC有什么关系？为什么？
例1、求证三角形的一条中位线与第三边上的中线互相平分. A
E
C
14
定理应用：
⑴定理为证明平行关系提供了新的工具
⑵定理为证明一条线段是另一条线段的2倍或 1/2提供了一个新的途径
⑶解决“中点问题”
注意：在处理这些问题时,要求出现三角形及中位线

中位线(基础)知识讲解

中位线（基础）【学习目标】1. 理解三角形的中位线的概念，掌握三角形的中位线定理．2. 掌握三角形重心的概念以及重心的性质.3. 理解梯形的中位线的概念，掌握梯形的中位线定理.4. 了解图形的位似，知道位似变换是特殊的相似变换，能利用位似的方法，将一个图形放大或缩小.【要点梳理】要点一、三角形的中位线1．概念：连接三角形两边中点的线段叫做三角形的中位线.2．定理：三角形的中位线平行于第三边，并且等于第三边的一半.要点诠释：（1）三角形有三条中位线，每一条与第三边都有相应的位置关系与数量关系.（2）三角形的三条中位线把原三角形分成全等的4个小三角形.因而每个小三角形的周长为原三角形周长的12，每个小三角形的面积为原三角形面积的14.（3）三角形的中位线不同于三角形的中线.要点二、三角形的重心1．概念：三角形三条边上的中线交于一点，这个点就是三角形的重心．要点诠释：垂心：三角形三条高线的交点．内心：三角形三条角平分线的交点．外心：三角形三边垂直平分线的交点．2．性质：重心与一边中点的连线的长是对应中线长的13．要点三、梯形的中位线１．概念：连接梯形两腰中点的线段叫梯形的中位线.２．性质：梯形的中位线定理：梯形的中位线平行于两底，且等于两底和的一半.要点四、位似1.位似图形定义:如果两个图形不仅是相似图形，而且每组对应点所在的直线都经过同一点，那么这样的两个图形叫做位似图形，这个点叫做位似中心．2.位似图形的性质:（1）位似图形的对应点和位似中心在同一条直线上；（2) 位似图形的对应点到位似中心的距离之比等于相似比；（3）位似图形中不经过位似中心的对应线段平行.要点诠释：（1）位似图形与相似图形的区别：位似图形是一种特殊的相似图形，而相似图形未必能构成位似图形.（2）位似变换中对应点的坐标变化规律:在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为k，那么位似图形对应点的坐标的比等于k或-k.【典型例题】类型一、三角形的中位线1、如图，已知P、R分别是长方形ABCD的边BC、CD上的点，E、F分别是PA、PR的中点，点P在BC上从B向C移动，点R不动，那么下列结论成立的是（）.A．线段EF的长逐渐增大B．线段EF的长逐渐变小C．线段EF的长不变D．无法确定【答案】C；【解析】连AR，由E、F分别为PA，PR的中点知EF为△PAR的中位线, 则12EF AR，而AR长不变，故EF大小不变.【总结升华】当条件中含有中点的时候，要将它与中位线联系起来，进行联想，必要时添加辅助线，构造中位线图形．举一反三：【变式】如图，矩形OABC的顶点A、C分别在x轴、y轴正半轴上，B点坐标为（3，2），OB与AC交于点P，D、E、F、G分别是线段OP、AP、BP、CP的中点，则四边形DEFG的周长为_____.【答案】5；解：∵四边形OABC是矩形，∴OA＝BC，AB＝OC；BA⊥OA，BC⊥OC．∵B点坐标为（3，2），∴OA＝3，AB＝2．∵D、E、F、G分别是线段OP、AP、BP、CP的中点，∴DE＝GF＝1.5； EF＝DG＝1．∴四边形DEFG的周长为（1.5＋1）×2＝5．2、如图，△ABC中，D、E分别是BC、AC的中点，BF平分∠ABC，交DE于点F，若BC ＝6，则DF的长是（）.A．2 B．3 C.52D．4【思路点拨】利用中位线定理，得到DE∥AB，根据平行线的性质，可得∠EDC＝∠ABC，再利用角平分线的性质和三角形内角外角的关系，得到DF＝DB，进而求出DF的长．【答案解析】解：在△ABC中，D、E分别是BC、AC的中点∴DE∥AB∴∠EDC＝∠ABC∵BF平分∠ABC∴∠EDC＝2∠FBD在△BDF中，∠EDC＝∠FBD＋∠BFD∴∠DBF＝∠DFB∴FD＝BD＝12BC＝12×6＝3．【总结升华】三角形的中位线平行于第三边，当出现角平分线，平行线时，一般可构造等腰三角形，进而利用等腰三角形的性质解题．类型二、三角形的重心3、我们给出如下定义：三角形三条中线的交点称为三角形的重心．一个三角形有且只有一个重心．可以证明三角形的重心与顶点的距离等于它与对边中点的距离的两倍．可以根据上述三角形重心的定义及性质知识解答下列问题：如图，∠B的平分线BE与BC边上的中线AD互相垂直，并且BE=AD=4（1）猜想AG与GD的数量关系，并说明理由；（2）求△ABC的三边长．【思路点拨】（1）根据BE平分∠B可知∠ABG=∠DBG，再根据全等三角形的判定定理可知△ABG≌△DBG，由全等三角形的对应边相等即可得出结论；（2）延长BA到F，使AF=BA，由AD是BC的中线，可知AD是△BFC的一条中位线，延长BE 交CF于H点，则BH垂直平分FC，可知E是△BFC的重心，由三角形重心的性质可求出AE、EH、HC的值，再根据勾股定理求出BC、EC的长，进而可得出AC的长．【答案与解析】（1）AG=GD …∵BE 平分∠B ， ∴∠ABG=∠DBG ，∵BG ⊥AD ，BG=BG ，∴∠BGA=∠BGD ，∴△ABG ≌△DBG ，∴AG=GD ，AB=BD ；（2）如图，延长BA 到F ，使AF=BA ，则△BFC 是等腰三角形…∵AD 是BC 的中线，∴AD 是△BFC 的一条中位线，延长BE 交CF 于H 点，则BH 垂直平分FC ，∴E 是△BFC 的重心，…∴AE=12EC ，EH=12BE=12×4=2， HC=12FC=AD=4， ∴在Rt △BHC 中，BC=222BH HC +=13， AB=BD=12BC=13， ∵在Rt △EHC 中，EC=2225EH HC +=，∴AC=AE+EC=35．【总结升华】本题考查的是三角形重心的性质、全等三角形的判定与性质、勾股定理及相似三角形的判定与性质，解答此题的关键是作出辅助线，构造出等腰三角形是解答此题的关键．举一反三【变式】G 为△ABC 的重心，△ABC 的三边长满足AB ＞BC ＞CA ，记△GAB ，△GBC ，△GCA 的面积分别为S 1、S 2、S 3，则有（）.A.123S S S >>B. 123S S S ==C. 123S S S <<D. 123,,S S S 的大小关系不确定【答案】B.类型三、梯形的中位线4、在直角梯形ABCD 中（如图所示），已知AB∥D C ，∠DAB＝90°，∠ABC＝60°，EF为中位线，且BC ＝EF ＝4，那么AB ＝（）.A ．3B ．5C ．6D ．8【答案】B ；【解析】解：作CG⊥AB 于G 点，∵∠ABC＝60°BC＝EF ＝4，∴BG＝2，设AB ＝x ，则CD ＝x －2，∵EF 为中位线，∴AB＋CD ＝2EF ，即x ＋x －2＝8，解得x ＝5，【总结升华】此题综合运用了梯形的中位线定理、直角三角形的性质．在该图中，最关键的地方是正确的构造直角三角形．类型四、位似5、利用位似图形的方法把五边形ABCDE 放大1.5倍.【答案与解析】即是要画一个五边形A ′B ′C ′D ′E ′，要与五边形ABCDE 相似且相似比为1.5.画法是：1．在平面上任取一点O.2．以O 为端点作射线OA 、OB 、OC 、OD 、OE.3．在射线OA 、OB 、OC 、OD 、OE 上分别取点A ′、B ′、C ′、D ′、E ′，使OA ′:OA ＝OB ′:OB ＝OC ′:OC ＝OD ′:OD ＝OE ′:OE ＝1.5.4．连结A ′B ′、B ′C ′、C ′D ′、D ′E ′、E ′A ′.AB C DE A 1 B 1 C 1D 1E 1 A B C D E这样：A ′B ′AB ＝B ′C ′BC ＝C ′D ′CD ＝D ′E ′DE ＝A ′E ′AE＝1.5. 则五边形A ′B ′C ′D ′E ′为所求. 另外一种情况，所画五边形跟原五边形分别在位似中心的两侧.【总结升华】由本题可知，利用位似的方法，可以把一个多边形放大或缩小.举一反三【变式】在已知三角形内求作内接正方形．【答案】作法：（1）在AB 上任取一点G ′，作G ′D ′⊥BC；（2）以G ′D ′为边，在△ABC 内作一正方形D ′E ′F ′G ′；（3）连接BF ′，延长交AC 于F ；（4）作FG∥CB，交AB 于G ，从F 、G 分别作BC 的垂线FE ， GD ；∴四边形DEFG 即为所求．E D G FF'E'D'AB C G'。

第13讲中位线定理--基本班

第13讲中位线定理⎧⎪⎪⎨⎪⎪⎩三角形的中位线中点四边形中位线定理多边形的内角和多边形的外角、外角和知识点1：三角形的中位线1.三角形中位线定义：连接三角形两边中点的线段叫做三角形的中位线．三角形共有三条中位线．2.三角形中位线的性质：（1）三角形中位线平行于第三边，并且等于第三边的一半．（2）三角形的中位线将三角形分成两部分的面积之比为1:3．3.三角形中位线逆定理：（1）在三角形内，与三角形的两边相交，平行且等于三角形第三边一半的线段是三角形的中位线．（2）在三角形内，经过三角形一边的中点，且与另一边平行的线段，是三角形的中位线．【典例】1.△ABC 的周长为12，点D 、E 、F 分别是△ABC 的边AB 、BC 、CA 的中点，连接DE 、EF 、DF ，则△DEF 的周长是________．【答案】6．【解析】解：∵D 、E 分别是△ABC 的边AB 、BC 的中点，∴DE=12AC ，同理，EF=12AB ，DF=12BC ，∴C △DEF =DE+EF+DF=12AC+12BC+12AB=12（AC+BC+AC ）=12×12=6．故答案是：6．2.如图，菱形ABCD 的对角线AC 、BD 相交于点O ，E 为AD 的中点，若OE=3，则菱形ABCD 的周长为________．【答案】24．【解析】解：∵四边形ABCD 为菱形，∴AO=CO ，AB=BC=CD=DA ，∵OE=3，且点E 为线段AD 的中点，∴OE 为△ACD 的中位线∴CD=2OE=6．C 菱形ABCD =4CD=4×6=24．故答案为：24．3.如图，在正方形ABCD 中，对角线AC 与BD 相交于点O ，E 为BC 上一点，CE=5，F 为DE 的中点．若△CEF 的周长为18，则OF 的长为________．【答案】72 【解析】解：∵CE=5，△CEF 的周长为18，∴CF+EF=18﹣5=13．∵F 为DE 的中点，∴DF=EF ．∵∠BCD=90°，∴CF=12DE ， ∴EF=CF=12DE=6.5， ∴DE=2EF=13，∴在Rt △CED 中CD=√DE 2−CE 2=√132−52=12．∵四边形ABCD 是正方形，∴BC=CD=12，O 为BD 的中点，∴OF 是△BDE 的中位线，∴OF=12（BC ﹣CE ）=12（12﹣5）=72．故答案为：72．【方法总结】利用三角形中位线定理求三角形的中位线、边长、周长等需要将已知量与所求的量放到同一个三角形中，找到中位线与第三边，求出未知量．【随堂练习】1.如图，A 、B 两点被一座山隔开，M 、N 分别是AC 、BC 中点，测量MN 的长度为40m ，那么AB 的长度为______【答案】80m【解析】解：∵M 、N 分别是AC 、BC 中点，∴MN 是△ACB 的中位线，∴AB=2MN=80m ，2.如图，在△ABC 中，E 、D 、F 分别是AB 、BC 、CA 的中点，AB=6，AC=4，则四边形AEDF 的周长是_____【答案】10【解析】解：∵在△ABC 中，E 、D 、F 分别是AB 、BC 、CA 的中点，∴DE=AF=12AC=2，DF=AE=12AB=3，∴四边形AEDF 的周长是（2+3）×2=10．3.如图，在□ABCD 中，BD 为对角线，点E 、O 、F 分别是AB 、BD 、BC 的中点，且OE=3，OF=2，则□ABCD 的周长是______【答案】20【解析】解：∵点E、O、F分别是AB、BD、BC的中点，∴AD=2OE=6，CD=2OF=4，又四边形ABCD是平行四边形，∴AB=CD=4，BC=AD=6，∴▱ABCD的周长是（6+4）×2=20．知识点2：中点四边形不同的四边形的中点四边形如下：（1）任意四边形的中点四边形是平行四边形；（2）平行四边形的中点四边形是平行四边形；（3）菱形的中点四边形是矩形；（4）矩形的中点四边形是菱形；（5）正方形的中点四边形是正方形；【典例】1.顺次连接任意四边形ABCD各边中点，所得的四边形EFGH是中点四边形．下列四个叙述：①中点四边形EFGH一定是平行四边形；②当四边形ABCD是矩形时，中点四边形EFGH 也是矩形；③当中点四边形EFGH是菱形时，四边形ABCD是矩形；④当四边形ABCD是正方形时，中点四边形EFGH也是正方形．其中正确的是_________（只填代号）．【答案】①④【解析】解：连接AC ，BD ，∵E ，F ，G ，H 分别是四边形各边的中点，∴EF ∥AC ，HG ∥AC ，EH ∥BD ，FG ∥BD ，∴EF ∥HG ，EH ∥FG ，∴四边形EFGH 是平行四边形；（①正确）∵四边形ABCD 是矩形，∴AC=BD ，∵EF=12AC ，EH=12BD ， ∴EF=EH ，∴平行四边形EFGH 是菱形；（②错误）∵四边形EFGH 是菱形，∴EF=FG=GH=HE∵EF=12AC ，EH=12BD ∴AC=BD ，∵AC 、BD 不一定互相平分∴四边形ABCD 不一定是矩形；（③错误）∵四边形ABCD 是正方形，∴AC=BD ，AC ⊥BD ，∵EF=HG=12AC ，EH=FG =12BD∴EF=FG=GH=HE∵EF ∥AC ，EH ∥BD∴AC ⊥BD∴四边形EFGH是正方形．（④正确）故答案为：①④．2.如图，正方形桌面ABCD，面积为2，铺一块正方形桌布EFGH，点A、B、C、D分别是EF、FG、GH、HE的中点，则桌布EFGH的面积是____【答案】4【解析】解：连接EG，∵正方形桌面ABCD，面积为2，∴AD=AB=√2，又∵A、B是EF，FG的中点，∴EG=2AB =2√2，∵四边形EFGH为正方形，∴∠F=90°，且EF=FG，根据勾股定理得：FG2+EF2=EG2，∴2FG2=EG2即2FG2=（2√2）2，∴FG=2，∴桌布EFGH的面积是FG2=2×2=4，3.如图，四边形ABCD中，AC=a，BD=b，且AC丄BD，顺次连接四边形ABCD各边中点，得到四边形A1B1C1D1，再顺次连接四边形A1B1C1D1各边中点，得到四边形A2B2C2D2…，如此进行下去，得到四边形A n B n C n D n．下列结论正确的有_____①四边形A2B2C2D2是矩形；②四边形A4B4C4D4是菱形；③四边形A5B5C5D5的周长是a+b4．④四边形A n B n C n D n的面积是ab2n+1【答案】②③④【解析】解：①连接A1C1，B1D1．∵在四边形ABCD中，顺次连接四边形ABCD各边中点，得到四边形A1B1C1D1，∴A1D1∥BD，B1C1∥BD，C1D1∥AC，A1B1∥AC；∴A1D1∥B1C1，A1B1∥C1D1，∴四边形A 1B 1C 1D 1是平行四边形；∵AC 丄BD ，∴四边形A 1B 1C 1D 1是矩形，∴B 1D 1=A 1C 1（矩形的两条对角线相等）；∴A 2D 2=C 2D 2=C 2B 2=B 2A 2（中位线定理），∴四边形A 2B 2C 2D 2是菱形；故①错误；②由①知，四边形A 2B 2C 2D 2是菱形；∴根据中位线定理知，四边形A 4B 4C 4D 4是菱形；故②正确；③根据中位线的性质易知，A 5B 5=12A 3B 3=12×12A 1B 1=12×12×12AC ，B 5C 5=12B 3C 3=12×12B 1C 1=12×12×12BD ，∴四边形A 5B 5C 5D 5的周长是2×18（a+b ）=a+b 4；故③正确；④∵四边形ABCD 中，AC=a ，BD=b ，且AC 丄BD ，∴S 四边形ABCD =ab ÷2；由三角形的中位线的性质可以推知，每得到一次四边形，它的面积变为原来的一半，四边形A n B n C n D n 的面积是ab 2n+1；故④正确；综上所述，②③④正确．【方法总结】当原四边形的对角线不相等且不垂直时，中点四边形是平行四边形；当原四边形的对角线互相垂直时，中点四边形是矩形；当原四边形的对角线相等时，中点四边形是菱形；当原四边形的对角线相等且互相垂直时，中点四边形是正方形．四边形的中点四边形的周长等于四边形对角线长度之和，面积等于原四边形面积的一半．【随堂练习】1.如果一个四边形的对角线相等，那么顺次连接这个四边形各边中点所得的四边形一定是____【答案】菱形【解析】解：连接AC 、BD ，如图，E 、F 、G 、H 分别是四边形ABCD 的边AB 、BC 、CD 、DA 的中点，根据三角形的中位线定理，EF=12AC ，GH=12AC ，HE=12BD ，FG=12BD ，∵四边形ABCD 的对角线相等，∴AC=BD ，所以，EF=FG=GH=HE ，所以，四边形EFGH 是菱形．2.A′、B′、C′、D′为四边形ABCD各边的中点，下面条件使四边形A′B′C′D′为正方形的条件是（）A. 四边形ABCD是矩形B. 四边形ABCD是菱形C. 四边形ABCD是等腰梯形D. 四边形ABCD中，AC⊥BD，且AC=BD 【答案】D.【解析】解：A、顺次连接矩形的四边中点得到菱形，故A不正确；B、顺次连接菱形的四边中点得到矩形，故B错误；C、顺次连接对角线互相垂直的等腰梯形的四边中点才能得到正方形，故C不正确；D、顺次连接对角线互相垂直且相等的四边形四边中点能得到正方形，故D正确．故选D3.在平面直角坐标系中，四边形OABC各点的坐标分别是O（0，0）、A（4，0）、B（3，√3）、D（1，√3），那么顺次连接这个四边形各边的中点，得到的新的四边形是（）A. 等腰梯形B. 正方形C. 矩形D. 菱形【答案】D.【解析】解：在平面直角坐标系中找到点A、B、C、D并画出四边形ABCD，连接OB、AD，由勾股定理得：AD=√(√3)2+(4−1)2=2√3，同理求出OB=2√3，∴AD=OB，∵E 、F 、 G 、H 分别是边DB 、 AB 、 OA 、OD 的中点，∴EF=12AD ，HE=12BO ，GH=12AD ，GF=12BO ∴EF=FG=GH=HE∴四边形EFGH 是菱形．故选D知识点3 多边形的内角和多边形内角和定理：n 边形内角和等于（n-2）×180° （n ≥3），且n 为整数）正多边形的每个内角等于n−2n ×180°.【典例】1.如图，∠1，∠2，∠3，∠4，∠5，∠6的度数之和为_______．【答案】解：如图，连接CD ，构造出四边形ABCD ，显然有：∠1+∠4=∠7+∠8．所以∠1+∠2+∠3+∠4+∠5+∠6=∠2+∠3+∠5+∠6+∠7+∠8=（4﹣2）×180°=360°．故答案为：360°．【方法总结】通过转化，把求多个角的度数和的问题，转为求多边形内角和问题，利用n边形内角和公式（n-2）×180°求解.2.一个多边形除去一个内角后，其余内角之和为2570°，求：（1）这个多边形的边数；（2）除去的那个内角的度数.解：设多边形的边数为n，则其内角和为（n﹣2）·180°，依题意，得解这个不等式组，得.因为n是大于或等于3的整数，所以n=17，故这个多边形的边数为17.（2）除去的那个内角的度数为（17﹣2）·180°﹣2570°=130°．【方法总结】因为多边形的每一个内角大于0°小于180°，所以n边形除去一个内角后，剩余内角之和为大于（n-3）×180°，小于（n-2）×180°.【随堂练习】1．一个n边形的内角和为540°，则n的值为（）A．4 B．5 C．6 D．7【解答】解：根据题意，得（n﹣2）•180°＝540°，解得：n＝5．故选：B．知识点4 多边形的外角、外角和多边形的外角和等于360°．正多边形的每个外角等于360°.n【典例】一个多边形的内角和比它的外角和的3倍少180°，这个多边形的边数是_____ 解：设所求多边形边数为n，则（n﹣2）•180°=3×360°﹣180°，解得n=7．【方法总结】熟记：n边形内角和等于（n-2）×180°，外角和等于360°，依据题目中给出的多边形内角和与外角和的关系求多边形的边数.【典例】如图，∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I+∠J=_____【答案】360°如图所示∵∠1是三角形ABP的一个外角，∴∠A+∠B=∠1，同理可得，∠C+∠D=∠5，∠E+∠F=∠4，∠G+∠H=∠3，∠I+∠J=∠2，∵五边形PQRST的外角和360°，∴∠1+∠2+∠3+∠4+∠5=360°，【方法总结】求多个角的度数和，可利用三角形外角性质把每个小角转移到多边形的外角上，利用多边形的外角和求解.【随堂练习】1．如图∠1，∠2，∠3，∠4，∠5是五边形ABCDE的5个外角，则∠1+∠2+∠3+∠4+∠5＝_____°．【解答】解：根据多边形外角和定理得到：∠1+∠2+∠3+∠4+∠5＝360°，故答案为：360．2．已知一个十边形每个内角都相等，则它的每个外角均为____度．【解答】解：∵十边形的内角和＝（10﹣2）•180°＝1440°，又∵十边形的每个内角都相等，∴每个内角的度数＝1440°÷10＝144°．则每个外角度数为180°﹣144°＝36°，故答案为：36．综合运用1.在△ABC中，点D、E、F分别是BC、AB、AC边的中点．求证：△BED≌△DFC【答案】略【解析】证明：∵点D、E分别是BC、AB的中点，∴ED∥AC，ED=12AC，∴∠EDB=∠C又∵F是AC边的中点，∴FC=12AC，DF∥AB∴DE=FC，∠B=∠FDC，在△EBD和△FDC中，∵{∠B=∠FDC ∠EDB=∠C ED=FC，∴△BED ≌△DFC （AAS ）．2.如图：在四边形ABCD 中，E 是AB 上的一点，△ADE 和△BCE 都是等边三角形，点P 、Q 、M 、N 分别为AB 、BC 、CD 、DA 的中点，求证：四边形MNPQ 是菱形．【答案】略【解析】证明：连接AC 和BD∵△ADE 和△BCE 都是等边三角形，点P 、Q 、M 、N 分别为AB 、BC 、CD 、DA 的中点，∴MN ∥AC ， PQ ∥AC∴MN ∥PQ同理MQ ∥PN∴四边形PQMN 是平行四边形．∵△ADE 和△BCE 都是等边三角形，∴AE=AD=DE ，EC=EB=BC ，∠DEA=∠CEB=60°，∴∠AEC=∠DEB=60°+∠DEC=120°，∴△AEC ≌△DEB ，∴AC=BD ，∵MN=12AC ，MQ=12BD ，∴MN=MQ ，∴平行四边形PQMN 是菱形．3.△ABC的中线BD，CE相交于O，F，G分别是BO，CO的中点，求证：EF∥DG，且EF=DG．【答案】略【解析】证明：连接DE，FG，∵BD，CE是△ABC的中位线，∴D，E是AB，AC的中点，BC，∴DE∥BC，DE=12BC，同理：FG∥BC，FG=12∴DE∥FG，DE=FG，∴四边形DEFG是平行四边形，∴EF∥DG，EF=DG．4.如图，△ABC中，AB=8，AC=6，AD、AE分别是其角平分线和中线，过点C作CG⊥AD 于F，交AB于G，连接EF，求线段EF的长．【答案】略【解析】解：∵CG⊥AF ∴∠AFG=∠AFC=90°∵AD是△ABC的角平分线∴∠GAF=∠CAF在△AGF和△ACF中，{∠GAF=∠CAF AF=AF∠AFG=∠AFC，∴△AGF≌△ACF（ASA），∴AG=AC=6，GF=CF，则BG=AB﹣AG= AB﹣AC=8﹣6=2．又∵BE=CE，∴EF是△BCG的中位线，∴EF=12BG=1．5.观察探究，完成证明和填空．如图，四边形ABCD中，点E、F、G、H分别是边AB、BC、CD、DA的中点，顺次连接E、F、G、H，得到的四边形EFGH叫中点四边形．（1）求证：四边形EFGH是平行四边形；（2）如图，当四边形ABCD变成等腰梯形时，它的中点四边形是菱形，请你探究并填空：当四边形ABCD变成平行四边形时，它的中点四边形是_________；当四边形ABCD变成矩形时，它的中点四边形是_________；当四边形ABCD变成菱形时，它的中点四边形是_________；当四边形ABCD变成正方形时，它的中点四边形是_________；（3）根据以上观察探究，请你总结中点四边形的形状由原四边形的什么决定的？【答案】略【解析】（1）证明：连接BD∵E、H分别是AB、AD的中点，∴EH是△ABD的中位线．BD，EH∥BD∴EH=12同理得FG=1BD，FG∥BD2∴EH=FG，EH∥FG．∴四边形EFGH是平行四边形．（2）填空依次为平行四边形，菱形，矩形，正方形；（3）中点四边形的形状是由原四边形的对角线的关系决定的．当原四边形的对角线不相等且不垂直时，中点四边形是平行四边形；当原四边形的对角线互相垂直时，中点四边形是矩形；当原四边形的对角线相等时，中点四边形是菱形；当原四边形的对角线相等且互相垂直时，中点四边形是正方形．6.如图1，已知E、F、G、H分别为四边形ABCD的边AB、BC、CD、DA的中点，连接EF、FG、GH、HE．（1）求证：四边形EFGH是平行四边形（提示：可连接AC或BD）；（2）在电脑上用适当的应用程序画出图1，然后用鼠标拖动点D，当点D在原四边形ABCD 的内部，在原四边形ABCD的外部时，图1依次变为图2、图3．图2、图3中四边形EFGH 还是平行四边形吗？选择其中之一说明理由．【答案】略【解析】（1）证明：如图1，连接AC，∵E、F、G、H分别为四边形ABCD的边AB、BC、CD、DA的中点，∴EF是△ABC的中位线，GH是△DAC的中位线，∴EF∥AC，EF=12AC；HG∥AC，HG=12AC．∴EF∥GH，EF=GH∴四边形EFGH是平行四边形；（2）解：四边形EFGH均为平行四边形．证明（以图2为例）：连接AC在△BAC中，∵E、F分别为AB、BC的中点，∴EF∥AC，EF=12AC；在△DAC中，∵G、H分别为AD、CD的中点，∴HG∥AC，HG=12AC．∴∴EF∥GH，EF=GH∴四边形EFGH是平行四边形；7.如图，已知四边形ABCD是面积为a的任意四边形，顺次连接各边中点得到四边形A1B1C1D1，再顺次连接各边中点得到四边形A2B2C2D2，重复同样的方法直至得到四边形A n B n C n D n．（1）请直接写出四边形A1B1C1D1、A2B2C2D2、A3B3C3D3的面积（用含a的代数式表示）；（2）根据以上的规律写出四边形A n B n C n D n的面积．【答案】略【解析】解：（1）如图，连接AC，∵A1、B1分别是AB、BC的中点，∴A1B1 是△ABC的中位线∴A1B1∥AC，且A1B1=12AC，∴S△A1B1B =14S△ABC，同理，S△D1DC1=14S△ACD，∴S△BA1B1+S△DC1D1=14S四边形ABCD，同理可得，S△AA1D1+S△CB1C1=14S四边形ABCD，∴S△BA1B1+S△DC1D1+S△AA1D1+S△CB1C1=14S四边形ABCD+14S四边形ABCD=12S四边形ABCD，∴S四边形A1B1C1D1=12S四边形ABCD=12a，同理可得：S四边形A2B2C2D2=12S四边形A1B1C1D1=12×12a=14a，S四边形A3B3C3D3=12S四边形A2B2C2D2=12×14a=18a；（2）根据（1）的规律，后一个四边形的面积是前一个四边形的面积的12，∴四边形A n B n C n D n的面积是：12na8．若计算一个多边形内角和时，粗心的小明将其中一个内角没有加上去，而是加上了这个内角所对应的外角，这样计算出来的结果是600°，则小明计算的这个多边形的边数为_____．【解答】解：设多边形的边数为n，多加的外角度数为α，少加的内角为180﹣a，则（n﹣2）•180＝600﹣α+180﹣α，180n﹣360＝780﹣2αα＝570﹣90n∵0＜α＜180∴0＜570﹣90n＜180∴＜n＜，∵n只能为整数，∴n＝5或6，故答案为：5或6．9．如图，在五边形ABCDE中，若∠D＝110°，则∠1+∠2+∠3+∠4＝______．【解答】解：∵∠D＝110°，∴∠D的外角为180°﹣110°＝70°，∴∠1+∠2+∠3+∠4＝360°﹣70°＝290°，故答案为：290°．10．一个正多边形的每一个内角比每一个外角的5倍还小60°，求这个正多边形的边数及内角和．【解答】解：设这个正多边的外角为x，则内角为5x﹣60°，由题意得：x+5x﹣60＝180，解得：x＝40，360°÷40°＝9．（9﹣2）×180°＝1260°答：这个正多边形的边数是9，内角和是1260°。

三角形中位线的性质

三角形中位线定理
课
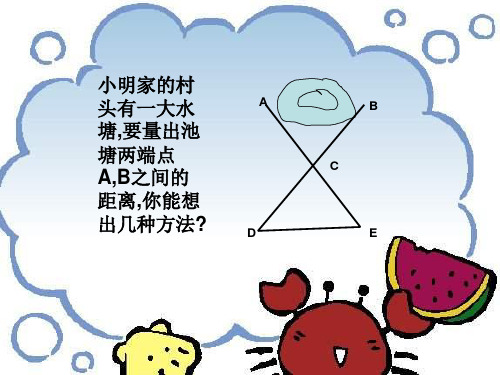
A、B两点被池塘隔开，现在要测量出A、B 两点间的距离，但又无法直接去测量，怎么办？
如图，在A、B外选一点C，连结AC和BC，并分别找出AC和BC的中点M、N，如果能测量出MN的长度，也就能知道AB的距离了。
今天这堂课我们就要来探究其中的学问。
A。
M。
C。
。
。B
N
AF是△ABC的中线
定理
证明：如图，延长DE 到 F，使EF=DE ，
连结CF. ∵DE=EF 、∠AED=∠CEF 、AE=EC
F∴△ADE ≌ △CFE
∴AD=FC 、∠A=∠CEF ∴AB∥FC 又AD=DB ∴BD∥CF 且BD = CF 所以，四边形BCFD是平行四边形
∴DE ∥ BC 且
D B
A ∵ AD=DB ， AE=EC
三角形的中位线是连结三角形两边中点的线段
三角形的中线是连结一个顶点和它的对边中点的线段
②理解三角形的中位线定义的两层含义:
⑴∵D、E分别为AB、AC的中点
∴DE为△ABC的中位线 ⑵∵ DE为△ABC的中位线
∴ D、E分别为AB、AC的中点 D。
③一个三角形共有三条中位线。
A 。E
B
。
C
F
三角形的中位线定理是三角形的一个重要性质定理：
B
C
D
如图是山坡上两棵树,你能量出他们之间的距离吗?
如图是一个平行四边形,请表示出图中的平行线AD与BC之间的距离.
A
D
B
C
如图，∠A=110°，∠C=70°，那么AB上任两点到CD的距离是否相等？为什么？
A
B
C

中位线定理

(8)等腰梯形的两腰相等，两条对角线相等。
性质
梯形的中位线平行于两底，并且等于两底和的一半 .
梯形中位线的2倍乘高再除以二就等于梯形的面积，用符号表示是L.
L=（a+b）÷2
已知中位线长度和高，就能求出梯形的面积．
S梯=Lh
中位线在关于梯形的各种题型中都是一条得天独厚的辅助线。
证明
四边形ABCD是梯形，AD∥BC，E、F分别是AB、CD边上的中点，求证：EF∥AD，且EF=（AD+BC）/2
6．已知梯形的中位线长16cm，梯形的一条对角线把中位线分成两条线段，这两条线段的差是4cm,则梯形上底长是cm.
7．如图，△ABC中，AD、BE是中线且交于G，那么＝.
第1题图第3题图第7题图
8．如图，梯形ABCD中，AD∥BC，AD＝12，BC＝16，中位线EF与对角线分别相交于H和G，则GH的长是.
A.平行四边形B.矩形C.正方形D.菱形
15．M、N、P、Q顺次为四边形ABCD各边的中点，下面条件使四边形MNPQ为正方形的条件是( )
A.四边形ABCD是矩形B.四边形ABCD是菱形
C.四边形ABCD是等腰梯形D.四边形ABCD中，AC⊥BD，且AC＝BD
16．已知三角形三边长分别为a、b、c，它的三条中位线组成一个新的三角形，这个新三角形的三条中位线又组成一个小三角形，这个小三角形的三条中位线又组成一个新小三角形，则最小的三角形的周长是( )
19．如图，△ABC中，如果AB＝30cm，BC＝24cm，AC＝27cm，AE＝EF＝FB，EG∥DF∥BC，FM∥EN∥AC，则图中阴影部分的三个三角形周长之和为( )
A.70cmB.75cmC.80cmD.81mc
20．如图，DE是△ABC的中位线，F是DE的中点，BF的延长线交AC于H，则AH∶HE等于（）

三角形中位线定理课件

02 三角形中位线定理的推导与证明
三角形中位线的定义与性质
定义
在三角形中，连接一个顶点和它所对边的中点的线段叫做三角形的中位线。
性质
三角形的中位线平行于第三边，并且等于第三边的一半。
三角形中位线定理的推导过程
01
02
第一步，根据定义，画出三角形的一条中位线。
ห้องสมุดไป่ตู้
第二步，通过相似三角形的性质，证明中位线与第三边平行且等于第三边的一半。
解析法
通过建立坐标系，利用解析几何的方法证明三角形中位线定理，通过点的坐标和直线的方程进行推导。
03 三角形中位线定理的应用举例
在几何问题中的应用
证明线段相等
利用三角形中位线定理可以证明两条线段相等，通过构造中位线并利用其性质进行推导。
证明线段平行
通过三角形中位线的性质，可以证明两条线段平行，这在几何问题中经常用到。
对三角形中位线定理的深入理解与展望
01
深入理解三角形中位线的性质
除了基本的定义和性质外，还可以进一步探讨三角形中位线的其他性质，
如与三角形各边之间的关系、与三角形内角之间的关系等，以加深对三
角形中位线的理解。
02
拓展三角形中位线定理的应用范围
可以进一步拓展三角形中位线定理的应用范围，探索其在更广泛的数学
证明角相等
三角形中位线定理还可以用来证明两个角相等，通过构造适当的三角形并应用定理进行推导。
在三角形面积计算中的应用
计算三角形面积
利用三角形中位线定理，可以将一个三角形划分为两个小的相似三角形，从而简化面积计算过程。
求解三角形高
推导三角形面积公式
结合三角形中位线定理和其他几何知识，可以推导出三角形面积的多种计算公式。

初中中位线知识点总结

初中中位线知识点总结一、中位线的概念及作用1. 中位线是一条线段，它将一个几何图形分成两个面积相等的部分。

2. 在三角形和四边形中，中位线与其它中线交点的位置可以用于解决一些几何问题。

3. 中位线可用于解决实际问题，如计算房屋地面面积、农田面积等。

二、三角形中的中位线1. 三角形中位线定义：通过三角形的一个顶点，作对边中点连线。

2. 中位线的性质：三角形中位线相等，即三角形中的三条中位线相等。

这是因为三角形的三边相等。

3. 中位线的作用：在三角形中，中位线可以用来证明三角形的面积、证明三角形的角平分线等。

三、四边形中的中位线1. 四边形中位线定义：四边形的对角线中点连线。

2. 中位线的性质：四边形中的中位线相等，即四边形的两对对角线中的中位线相等。

3. 中位线的作用：中位线可以用来证明四边形的面积、证明四边形的性质。

四、中位线的应用1. 实际问题：中位线可用于计算几何图形的面积，如计算房屋地面面积、农田面积等。

2. 定理证明：中位线可用于证明几何定理，如证明三角形的角平分线，证明四边形的面积等。

3. 建筑设计：在建筑设计中，中位线可用于布局、规划和设计。

五、中位线的计算1. 中位线长度的计算：中位线的长度等于对角线中点间的距离。

2. 中位线的数学公式：中位线的长度等于两个对角线中点的距离的一半。

3. 计算实例：根据给定的对角线长度，可以计算四边形中位线的长度。

六、中位线与中心线的区别1. 中位线是一条几何图形中的线段，它具有等长性质。

2. 中心线是几何图形的中心轴线，它与图形的对称轴或对称中心有关。

七、中位线与平行四边形1. 中位线是平行四边形的对角线的中点连线，它将平行四边形分成两个面积相等的部分。

2. 中位线的性质：平行四边形的两条对角线中的中位线相等，即平行四边形中的两条中位线相等。

八、中位线与菱形1. 中位线是菱形的对角线的中点连线，它将菱形分成两个面积相等的部分。

2. 中位线的性质：菱形的两条对角线中的中位线相等，即菱形中的两条中位线相等。

任意三角形中位线定理

任意三角形中位线定理1.引言1.1 概述概述三角形是几何学中的重要概念，它由三条边和三个顶点组成。

我们可以根据角度和边的长度来分类不同类型的三角形，例如等边三角形、等腰三角形和一般三角形等。

在本篇长文中，我们将重点讨论任意三角形中的中位线定理。

中位线是连接三角形的一个顶点和对边中点的线段。

我们将介绍中位线的定义和性质，并详细阐述中位线定理的表述、证明和应用。

中位线定理是关于三角形中位线的一个重要定理。

它揭示了三角形中位线和三角形边的关系，并且具有很多重要的应用。

在本文中，我们将探索中位线定理的证明过程，并讨论它在几何学和实际问题中的应用。

通过研究和理解中位线定理，我们可以深入了解三角形的性质和特点。

这对于几何学的学习和问题解决都具有重要意义。

我们将从基础的定义和性质开始，逐步引入中位线定理的概念和应用，希望读者能够通过本文更好地理解和运用中位线定理。

接下来，我们将在正文部分详细介绍任意三角形的定义和中位线的定义和性质，以便为后续的中位线定理的讨论做好准备。

通过系统而全面的阐述，我们希望读者能够对中位线定理有一个清晰的认识，并能够灵活运用它解决相关问题。

在结论部分，我们将对中位线定理进行准确的表述，并给出具体的证明和应用示例。

这将进一步巩固读者对中位线定理的理解和运用能力。

总之，本文将从引言、正文和结论三个部分系统地介绍任意三角形中位线定理。

通过详细的讲解和实例的引导，我们旨在帮助读者更好地理解和应用这一定理，进一步提升几何学的学习和问题解决能力。

1.2 文章结构文章结构部分的内容如下：文章结构的设计旨在使读者能够清晰地理解任意三角形中位线定理的内容。

本文分为引言、正文和结论三个部分，下面对各个部分进行简要说明。

引言部分主要包括概述、文章结构和目的三个子部分。

在概述中，将简要介绍任意三角形中位线定理的背景和重要性。

通过引入这个概念，读者可以对该定理的应用和实际意义有一个初步的了解。

在文章结构中，将对整篇文章的结构进行总体的安排和描述，使读者能够预期文章的组织方式和内容概况。

中位线课件

反证法
假设中位线定理不成立，通过逻辑推理得出矛盾，从而证明中位线定理的正确性。
平行四边形法
利用平行四边形的性质，结合已知条件推导出中位线定理。
中位线定理的推广
三角形中位线定理的推广
在三角形中，若一条边上的中点与对边的两个端点连成线段，则这两条线段的长度相等。
VS
多边形中位线定理的推广
中位线定理是几何学中的重要定理之一，它揭示了三角形中位线与第三边的关系，为解决几何问题提供了重要的思路和方法。
02 中位线的判定定理
三角形中位线定理
总结词
三角形中位线定理是几何学中的基本定理之一，它描述了三角形中位线的性质和判定方法。
详细描述
三角形中位线定理指出，在一个三角形中，中位线是一条连接顶点与对边中点的线段，且这条线段平行于第三边，并且长度为第三边的一半。这个定理可以通过多种方式证明，其中最常用的是通过相似三角形和全等三角形来证明。
数学基础
中位线定理是几何学中的基础定理之一，对于理解几何形状的性质和解决几何问题具有重要意义
。
应用广泛
中位线定理在各个领域都有广泛的应用，如建筑、工程、艺术、科学等，是解决实际问题的重要工具。
培养逻辑思维
学习中位线定理有助于培养人的逻辑思维和推理能力，提高解决问题的能力。
中位线定理的学习方法与技巧
总结词
梯形中位线定理是几何学中的基本定理之一，它描述了梯形中位线的性质和判定方法。
详细描述
梯形中位线定理指出，在梯形中，如果一条线段连接两个相对边的中点，则这条线段平行于上底和下底，并且长度为上底和下底的一半之和。这个定理可以通过相似三角形和全等三角形来证明。
平行线中位线定理

三角形中位线(华师大版)

三角形中位线(华师大版)1. 引言三角形是几何学中的基本概念，而其中位线是研究三角形特性的重要工具之一。

本文将介绍华师大版教材中关于三角形中位线的相关知识。

2. 三角形中位线的定义在三角形中，连接每个顶点与对应边的中点的线段被称为中位线。

具体地说，一个三角形的中位线共存在三条，分别连接三个顶点，并同时通过三个对边的中点。

3. 三角形中位线的特性3.1 中位线的长度比定理1：连接三角形两个顶点的中位线与第三个顶点所在边的比为1:2。

具体地说，如果一个三角形的三个顶点分别为A、B、C，其中M是边AB的中点，那么AM和BC的长度比为1:2。

3.2 中位线的交点定理2：三角形中的三条中位线交于一点，该点称为三角形的重心。

三角形的重心是三角形内部到三条中位线距离之和最短的点，通常用字母G表示。

3.3 重心和中位线的关系定理3：三角形的重心将每一条中位线分为两个部分，其中一部分的长度为另一部分的两倍。

具体地说，如果一个三角形的重心为G，连接重心G和任意顶点A的中位线交于点D，那么GD的长度是AD长度的两倍。

4. 三角形中位线的应用三角形中位线在解决三角形问题时起到重要的作用。

下面介绍两个与三角形中位线有关的应用例子。

4.1 判断三角形类型已知一个三角形的三边长度，可以通过判断三个中位线的交点是否与三角形的重心重合来确定三角形类型。

•如果三个中位线的交点与重心重合，说明该三角形是等边三角形。

•如果三个中位线的交点在重心的同一侧，说明该三角形是等腰三角形。

•如果三个中位线的交点在重心的不同侧，说明该三角形是普通三角形。

4.2 计算三角形面积已知一个三角形的两个顶点坐标，可以通过计算中位线长度来求解三角形的面积。

具体的计算方法是：首先求出三个中位线的长度，根据定理1中的比例关系，可以求得任意一条中位线的长度。

然后使用海伦公式或其他方法求解由中位线构成的三角形的面积。

5. 总结本文介绍了华师大版教材中关于三角形中位线的相关知识。

中位线定理优质课件PPT

F
求证：∠ＦＤE= ∠A.
A E
B
C
D
2021/02/01形ABCD
中,AB›CD,E,F分别是
E
求A证C:,EBFD›的1 中AB点-.CD.
2
A
C
H F
B
2021/02/01
7
思考
下列说法是否正确?
1.三角形三条中位线组成一个三角形,其周长为原三角形周长的一半.
2.三角形三条中位线将原三角形分割为四个全等的三角形.
3.三角形三条中位线三角形三条中位线可从原三角形中划分出面积相等的三个平行四边形.
4.三角形任两条中位线的夹角与这个夹角所对的三角形的顶角相等.
2021/02/01
8
Thank you
感谢聆听批评指导
汇报人：XXX 汇报日期：20XX年XX月XX日
感谢您的观看！本教学内容具有更强的时代性和丰富性，更适合学习需要和特点。为了方便学习和使用，本文档的下载后可以随意修改，调整和打印。欢迎下载！
∵AE=EC, ∴四边形ADCF是平行四边形,
∴CF∥DA,且CF=DA. ∴CF∥DB,且CF=DB ∴四边形DBCF是平行四边形. ∴DF=BC. 2021/02∴/01DE= 1 BC.
2
DE和BC 有什么位置关系?
3
定义:连接三角形两边中点的线段叫做三角形的中位线
中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半.
2021/02/01
9
一个三角形有几条中位线? 中位线和三角形的中线一样
吗?
2021/02/01
4
思考
Ｈ
Ｄ
Ａ
已知：Ｅ，Ｆ，Ｇ，Ｈ分别