正弦和余弦的相互关系PPT课件
合集下载
正弦函数、余弦函数的性质17页PPT

Hale Waihona Puke xRy [1,1]
x2k 时, ymax 1
x2k时,ymin 1
x [2k,2k] 增函数
x[2k,2k] 减函数
偶函数
2 对称轴: xk,kZ
对称中心:(2 k,0) k Z
例1 求下列函数的最大值和最小值,并写 出取最大值、最小值时自变量x的集合
(1) y=cosx+1,x∈R;
(2)y=-3sin2x,x∈R.
16
17
单调性 奇偶性 周期性 对称性
y=sinx
y
1
2
0
2
-1
3
2 5 x
2
2
xR
y [1,1]
x
2
2k
时, ymax
1
x
2
2k
时,ymin
1
x[-22k,22k] 增函数
x[22k,322k] 减函数
奇函数
2
对称轴:
x
2
k,
k
Z
对称中心: (k,0) kZ
y=cosx
y
1
0
2
3
2 5 x
2
2
-1
例2:比较下列各组数的大小:
(1)sin( )与sin( )
18
10
(2)cos(23 )与cos(17 )
5
4
例3:求函数 ysi1 nx()x , 2,2
23 的单调递增区间。
求函数 ysi n (1x)x , 2,2
32
的单调递增区间。
求函数 ycos2(x)
3
的单调递减区间。
谢谢!
具体做法:
(1)选择一个恰当的区间(这个区间的长为一个周期, 且仅有一个单增区间和一个单减区间)
x2k 时, ymax 1
x2k时,ymin 1
x [2k,2k] 增函数
x[2k,2k] 减函数
偶函数
2 对称轴: xk,kZ
对称中心:(2 k,0) k Z
例1 求下列函数的最大值和最小值,并写 出取最大值、最小值时自变量x的集合
(1) y=cosx+1,x∈R;
(2)y=-3sin2x,x∈R.
16
17
单调性 奇偶性 周期性 对称性
y=sinx
y
1
2
0
2
-1
3
2 5 x
2
2
xR
y [1,1]
x
2
2k
时, ymax
1
x
2
2k
时,ymin
1
x[-22k,22k] 增函数
x[22k,322k] 减函数
奇函数
2
对称轴:
x
2
k,
k
Z
对称中心: (k,0) kZ
y=cosx
y
1
0
2
3
2 5 x
2
2
-1
例2:比较下列各组数的大小:
(1)sin( )与sin( )
18
10
(2)cos(23 )与cos(17 )
5
4
例3:求函数 ysi1 nx()x , 2,2
23 的单调递增区间。
求函数 ysi n (1x)x , 2,2
32
的单调递增区间。
求函数 ycos2(x)
3
的单调递减区间。
谢谢!
具体做法:
(1)选择一个恰当的区间(这个区间的长为一个周期, 且仅有一个单增区间和一个单减区间)
正弦定理和余弦定理课件PPT

直角三角形的一个锐角的对边与斜边的比叫做这个 角的正弦.
【即时练习】
在△ABC 中,AB= 3,A=45°,C=75°,则 BC
等于( A )
A.3- 3
B. 2
C.2
D.3+ 3
[解析] 由sAinBC=sBinCA得,BC=3- 3.
探究点3 解三角形
1.一般地,把三角形的三个角A,B,C和它们的对 边a,b,c叫做三角形的元素. 2.已知三角形的几个元素,求其他元素的过程叫做 解三角形.
A. 3
B.2
C. 5
D. 7
【解析】选D.因为a2=b2+c2-2bccosA=22+32-2×2×3×
cos 60°=7,所以a=
7.
3.在△ABC中,a=3,b=4,c= ,则此三角形的最大角为
37
.
【解析】由c>b>a知C最大,
因为cosC=
a2
所以C=120°.
b2 c2 2ab
32 42 37 234
【拓展延伸】利用平面图形的几何性质和 勾股定理证明余弦定理 ①当△ABC为锐角三角形时,如图, 作CD⊥AB,D为垂足,则CD=bsinA, DB=c-bcosA,则a2=DB2+CD2=(c-bcosA)2+(bsinA)2 =b2+c2-2bccosA,其余两个式子同理可证;
b
b 2R, a 2R. 即得 :
A
sin B
sin A
C′
a b c 2R. R为三角形外接圆的半径
sin A sin B sin C
A
C
c
b aO
B
C
B`
Ob a B A` A c
【即时练习】
在△ABC 中,AB= 3,A=45°,C=75°,则 BC
等于( A )
A.3- 3
B. 2
C.2
D.3+ 3
[解析] 由sAinBC=sBinCA得,BC=3- 3.
探究点3 解三角形
1.一般地,把三角形的三个角A,B,C和它们的对 边a,b,c叫做三角形的元素. 2.已知三角形的几个元素,求其他元素的过程叫做 解三角形.
A. 3
B.2
C. 5
D. 7
【解析】选D.因为a2=b2+c2-2bccosA=22+32-2×2×3×
cos 60°=7,所以a=
7.
3.在△ABC中,a=3,b=4,c= ,则此三角形的最大角为
37
.
【解析】由c>b>a知C最大,
因为cosC=
a2
所以C=120°.
b2 c2 2ab
32 42 37 234
【拓展延伸】利用平面图形的几何性质和 勾股定理证明余弦定理 ①当△ABC为锐角三角形时,如图, 作CD⊥AB,D为垂足,则CD=bsinA, DB=c-bcosA,则a2=DB2+CD2=(c-bcosA)2+(bsinA)2 =b2+c2-2bccosA,其余两个式子同理可证;
b
b 2R, a 2R. 即得 :
A
sin B
sin A
C′
a b c 2R. R为三角形外接圆的半径
sin A sin B sin C
A
C
c
b aO
B
C
B`
Ob a B A` A c
正弦函数和余弦函数的图像与性质.ppt

, 0), (2 ,1)
2
2
并注意-4 曲线的“凹凸”变化.
课堂练习
1.作函数 y sin x 与 y sin x 1在 [0, 2 ]
上的大致图像. 2.指出1.中各图像与正弦函数图像的位置关系.
3.作函数 y cos x, x [ , ]的大致图像.
4.利用3.解不等式:cos x sin x, x [ , ]
-2
五个关键点:(0, 0), ( ,1), ( , 0), (3 , 1), (2 , 0)
2
2
利用五个关-4键点作简图的方法称为“五点法”
10
三、余弦函数的图像
根据诱导公式
cos
8
x
sin(
x) 可知余弦函数
y
cos
6
x的图像可由
y
2 sin
x
的图像向左平移
2
4
个单位得到.
1
2
2
-10
3-5
0
2
1
-2
余弦函数的值域是[1,1] -4
当且仅当 x 2k , k Z 时, -6
余弦函数取得最大值1;-8
5
2
35
x10
2
yP
OM x
当且仅当 x 2k , k-10 Z 时,
余弦函数取得最小值-1-1.2例1.求下列函数的源自大值与最小值,及取到最值6
课堂练习答案
12
1. y sin x, x [0, 2 ] y4
10
x
0
2
3 2
2
2 8
5
-10
正弦定理和余弦定理ppt课件

总结词
正弦定理和余弦定理在物理学中有着 广泛的应用。
详细描述
在物理学中,许多现象可以用三角函数来描 述,如重力、弹力等。通过正弦定理和余弦 定理,我们可以更准确地计算这些力的作用 效果,从而更好地理解和分析物理现象。
06 总结与展望
总结正弦a、b、c与对应的角A、B、C 的正弦值之比都相等,即$frac{a}{sin A} = frac{b}{sin B} = frac{c}{sin C}$。
表达式形式
正弦定理的表达式形式简洁,易于理解和记 忆。相比之下,余弦定理的表达式较为复杂
,需要更多的数学基础才能理解和应用。
定理间的互补性
要点一
解决问题时的互补性
在解决三角形问题时,正弦定理和余弦定理常常是互补使 用的。对于一些问题,使用正弦定理可能更方便;而对于 另一些问题,使用余弦定理可能更合适。通过结合使用两 种定理,可以更全面地理解三角形的性质和关系,从而更 好地解决各种问题。
深入研究正弦定理和余弦定理的性质
可以进一步研究正弦定理和余弦定理的性质,如推广到多边形、高维空间等。
开发基于正弦定理和余弦定理的算法和软件
可以开发基于正弦定理和余弦定理的算法和软件,用于解决实际问题。
如何进一步深化理解与应用
深入理解正弦定理和余弦定理的证明过程
01
理解证明过程有助于更好地理解和应用正弦定理和余弦定理。
02 正弦定理
正弦定理的定义
总结词
正弦定理是三角形中一个重要的定理,它描述了三角形各边与其对应角的正弦值 之间的关系。
详细描述
正弦定理是指在一个三角形中,任意一边与其相对角的正弦值的比值都相等,即 $frac{a}{sin A} = frac{b}{sin B} = frac{c}{sin C}$,其中$a, b, c$分别代表三角形 的三边长度,$A, B, C$分别代表与三边相对应的角。
正弦定理和余弦定理在物理学中有着 广泛的应用。
详细描述
在物理学中,许多现象可以用三角函数来描 述,如重力、弹力等。通过正弦定理和余弦 定理,我们可以更准确地计算这些力的作用 效果,从而更好地理解和分析物理现象。
06 总结与展望
总结正弦a、b、c与对应的角A、B、C 的正弦值之比都相等,即$frac{a}{sin A} = frac{b}{sin B} = frac{c}{sin C}$。
表达式形式
正弦定理的表达式形式简洁,易于理解和记 忆。相比之下,余弦定理的表达式较为复杂
,需要更多的数学基础才能理解和应用。
定理间的互补性
要点一
解决问题时的互补性
在解决三角形问题时,正弦定理和余弦定理常常是互补使 用的。对于一些问题,使用正弦定理可能更方便;而对于 另一些问题,使用余弦定理可能更合适。通过结合使用两 种定理,可以更全面地理解三角形的性质和关系,从而更 好地解决各种问题。
深入研究正弦定理和余弦定理的性质
可以进一步研究正弦定理和余弦定理的性质,如推广到多边形、高维空间等。
开发基于正弦定理和余弦定理的算法和软件
可以开发基于正弦定理和余弦定理的算法和软件,用于解决实际问题。
如何进一步深化理解与应用
深入理解正弦定理和余弦定理的证明过程
01
理解证明过程有助于更好地理解和应用正弦定理和余弦定理。
02 正弦定理
正弦定理的定义
总结词
正弦定理是三角形中一个重要的定理,它描述了三角形各边与其对应角的正弦值 之间的关系。
详细描述
正弦定理是指在一个三角形中,任意一边与其相对角的正弦值的比值都相等,即 $frac{a}{sin A} = frac{b}{sin B} = frac{c}{sin C}$,其中$a, b, c$分别代表三角形 的三边长度,$A, B, C$分别代表与三边相对应的角。
正弦定理与余弦定理时PPT课件

第15页/共28页
• 解法二:已知等式变形为
• b2(1-cos2C)+c2(1-cos2B)= 2bccosB·cosC,
• ∴b2+c2=b2cos2C+c2cos2B+ 2bccosB·cosC,
• ∵b2cos2C+c2cos2B+2bccosBcosC • =(bcosC+ccosB)2=a2, • ∴b2+c2=a2,∴△ABC为直角三角形.
得aab2+ =b62-ab=7 ⇒aab2+ =b62.=13 7 分
消去 b 并整理得 a4-13a2+36=0, 解得 a2=4,a2=9.9 分
所以ab= =23 或ab= =32.
故 a+b=5.12 分 第19页/共28页
•变式训练4.若本例题中(2)的条件不变,
试求“△ABC内切圆的半径r”.
由bcb30bcsin303由正弦定理sinccsinbc60或120c60a90c120a30abc为等腰三角形abca3b4c373743边c最大则角c最大bc2ababcsinasinbsincsinasinbsinccosc2ab9t25t49t3t5t1201203ab2cosasinbsincabc180sincsina2cosasinbsinc2cosasinbsinacosbcosasinbsina根据余弦定理上式可化为coscabc为等边三角形由2cosasinbsinc得cosa2sinb2b3ab4bsinb2bccosbcoscabcsinccsinb2bccosbcoscb2sinbsinccosbcoscsinbsincsinbsinccosbcosccosbc0cosa02bccosbcosc2bccosbcoscbcoscccosbabc2csina
形,且角C为____直__角;a2+b2>c2⇔△ABC是
• 解法二:已知等式变形为
• b2(1-cos2C)+c2(1-cos2B)= 2bccosB·cosC,
• ∴b2+c2=b2cos2C+c2cos2B+ 2bccosB·cosC,
• ∵b2cos2C+c2cos2B+2bccosBcosC • =(bcosC+ccosB)2=a2, • ∴b2+c2=a2,∴△ABC为直角三角形.
得aab2+ =b62-ab=7 ⇒aab2+ =b62.=13 7 分
消去 b 并整理得 a4-13a2+36=0, 解得 a2=4,a2=9.9 分
所以ab= =23 或ab= =32.
故 a+b=5.12 分 第19页/共28页
•变式训练4.若本例题中(2)的条件不变,
试求“△ABC内切圆的半径r”.
由bcb30bcsin303由正弦定理sinccsinbc60或120c60a90c120a30abc为等腰三角形abca3b4c373743边c最大则角c最大bc2ababcsinasinbsincsinasinbsinccosc2ab9t25t49t3t5t1201203ab2cosasinbsincabc180sincsina2cosasinbsinc2cosasinbsinacosbcosasinbsina根据余弦定理上式可化为coscabc为等边三角形由2cosasinbsinc得cosa2sinb2b3ab4bsinb2bccosbcoscabcsinccsinb2bccosbcoscb2sinbsinccosbcoscsinbsincsinbsinccosbcosccosbc0cosa02bccosbcosc2bccosbcoscbcoscccosbabc2csina
形,且角C为____直__角;a2+b2>c2⇔△ABC是
1.4.1 正弦函数、余弦函数的图象 课件(共21张PPT)

解析:如图所示.
答案:2
栏目 导引
第一章 三角函数
方法感悟
作三角函数图象 (1)已知 y=sin x 的图象求作 y=cos x 的图象,只需把 y=sin x 的图象向左平移π2即可得到 y=cos x 的函数图象. (2)已知 y=sin x 的图象求作 y=|sin x|的图象,只需把 y=sin x 在 x 轴下方的图象翻折到 x 轴上方,即可得到 y=|sin x|的图象. (3)“五点法”是画三角函数图象的基本方法,在要求精确度不 高的情况下常用此法,要切实掌握好.
第一章 三角函数
1.4 三角函数的图象与性质 1.4.1 正弦函数、余弦函数的图象
第一章 三角函数
学习导航
学习目标
实例
―了―解→
利用正弦线作正弦 函数图象的方法
―掌―握→
正、余弦函数的图象, 知道它们之间的关系
重点难点 重点:会用“五点法”画正、余弦函数的图象. 难点:能根据正弦、余弦函数的图象观察、归纳出正弦函 数、余弦函数的图象特征及图象间的关系.
如何利用规律实现更好记忆呢?
栏目 导引
超级记忆法--场景法
第一章 三角函数
人教版七年级上册Unit4 Where‘s my backpack?
栏目 导引
第一章 三角函数
超级记忆法-记忆方法
TIP1:在使用场景记忆法时,我们可以多使用自己熟悉的场景(如日常自己的 卧 室、平时上课的教室等等),这样记忆起来更加轻松; TIP2:在场景中记忆时,可以适当采用一些顺序,比如上面例子中从上到下、 从 左到右、从远到近等顺序记忆会比杂乱无序乱记效果更好。
第一章 三角函数
【名师点评】 作形如 y=asin x+b(或 y=acos x+b),x∈[0,2π] 的图象时,可由“五点法”作出,其步骤是:①列表取 x=0,π2, π,32π,2π;②描点;③用光滑曲线连线成图.
答案:2
栏目 导引
第一章 三角函数
方法感悟
作三角函数图象 (1)已知 y=sin x 的图象求作 y=cos x 的图象,只需把 y=sin x 的图象向左平移π2即可得到 y=cos x 的函数图象. (2)已知 y=sin x 的图象求作 y=|sin x|的图象,只需把 y=sin x 在 x 轴下方的图象翻折到 x 轴上方,即可得到 y=|sin x|的图象. (3)“五点法”是画三角函数图象的基本方法,在要求精确度不 高的情况下常用此法,要切实掌握好.
第一章 三角函数
1.4 三角函数的图象与性质 1.4.1 正弦函数、余弦函数的图象
第一章 三角函数
学习导航
学习目标
实例
―了―解→
利用正弦线作正弦 函数图象的方法
―掌―握→
正、余弦函数的图象, 知道它们之间的关系
重点难点 重点:会用“五点法”画正、余弦函数的图象. 难点:能根据正弦、余弦函数的图象观察、归纳出正弦函 数、余弦函数的图象特征及图象间的关系.
如何利用规律实现更好记忆呢?
栏目 导引
超级记忆法--场景法
第一章 三角函数
人教版七年级上册Unit4 Where‘s my backpack?
栏目 导引
第一章 三角函数
超级记忆法-记忆方法
TIP1:在使用场景记忆法时,我们可以多使用自己熟悉的场景(如日常自己的 卧 室、平时上课的教室等等),这样记忆起来更加轻松; TIP2:在场景中记忆时,可以适当采用一些顺序,比如上面例子中从上到下、 从 左到右、从远到近等顺序记忆会比杂乱无序乱记效果更好。
第一章 三角函数
【名师点评】 作形如 y=asin x+b(或 y=acos x+b),x∈[0,2π] 的图象时,可由“五点法”作出,其步骤是:①列表取 x=0,π2, π,32π,2π;②描点;③用光滑曲线连线成图.
正弦定理和余弦定理-PPT课件

22
类型一
正弦定理和余弦定理的应用
解题准备:
1.正弦定理和余弦定理揭示的都是三角形的边角关系,根据题 目的实际情况,我们可以选择其中一种使用,也可以综合起 来运用.
2.在求角时,能用余弦定理的尽量用余弦定理,因为用正弦定 理虽然运算量较小,但容易产生增解或漏解.
23
3.综合运用正、余弦定理解三角形问题时,要注意以下关系式
32
∵0<A<π,0<B<π,∴sin2A=sin2B
∴2A=2B或2A=π-2B,即A=B或A+B= .
2
∴△ABC是等腰三角形或直角三角形.
33
解法二:同解法一可得2a2cosAsinB=2b2cosBsinA,
由正、余弦定理得
a2b•
b2
c2
a
2
=b2a•
a2 c2 b2
2bc
2ac
1 2 3 2 1 3.
2
2
(2)当|BC|=4时,S△=
1 2
|AB|·|BC|·sinB
1 2 3 4 1 2 3.
2
2
∴△ABC的面积为 2 3 或 3.
27
[反思感悟]本题主要考查正弦定理、三角形面积公式及分类 讨论的数学思想,同时也考查了三角函数的运算能力及推 理能力.
28
40
设云高CM x m,则CE x h,
DE x h, AE x h .
tan
又AE x h , x h x h
tan tan tan
解得x tan tan gh hgsin( ) m.
tan tan
sin( )
41
[反思感悟]在测量高度时,要理解仰角、俯角的概念.仰角和俯 角都是在同一铅垂面内,视线与水平线的夹角,当视线在水 平线之上时,称为仰角;当视线在水平线之下时,称为俯角.
正弦函数、余弦函数的性质-PPT课件

3 5
2
2 3
2
O
2
1
2
3 2
2
5 3
2
x
最大值:当 x
2
时,有最大值 y 1
最小值:当x
2
时,有最小值y 1
探究:余弦函数的最大值和最小值
1
3 5
2
2 3
2
O
2
1
2
3 2
2
5 3
2
x
最大值: 当 x 0
时,有最大值 y 1
最小值:当 x
时,有最小值y 1
例2.下列函数有最大、最小值吗?如果有,请写出取最大、最
(1)y cos x 1, x R;
(2)y 3sin 2x, x R.
解(:2)令t=2x,因为使函数y 3sin t,t R取最大值的t的集合是
{t | t 2k , k Z}
由
2x
t
2
2k
得
x k
2
4
所以使函数 y 3sin 2x, x R取最大值的x的集合是 {x | x k , k Z} 4
故 2k 1 x 2k ,
2
2 32
得 5 4k x 4k , k Z.
3
3
则函数y sin(1 x ),x R的单调递增区间是[ 5 4k, 4k]。
23
33
练习:求函数y sin( 1 x),x R的单调递增区间 32
得 5 4k x 11 4k , k Z.
2
2x k
32
解得:对称轴为 x k ,k Z
12 2
(2) y sin z 的对称中心为 (k ,0) , k Z
正弦和余弦的相互关系课件

正弦和余弦的相互关系
欢迎来到本节课的ppt课件,我们将介绍正弦和余弦函数的相互关系。了解它 们的定义、特点、图像、周期性和对称性、相位关系以及应用。
正弦函数的定义和特点
定义
正弦函数是以角度为自变量、正弦值为因变量的函数。
特点
正弦函数的值在-1和1之间波动,它是一个周期性函数。
余弦函数的定义和特点
2
对称性
正弦函数是奇对称函数,余弦函数是偶对称函数。
正弦函数与余弦函数的相位关系
1
相位关系
正弦函数与余弦函数的相位差是90°或π/2。
2
波形图
正弦函数和余弦函数的波形图相互垂直。
ห้องสมุดไป่ตู้
3
周期
正弦函数和余弦函数的周期是相同的。
正弦函数和余弦函数的数学性质
1 加法公式
正弦函数和余弦函数有一系列的加法公式,用于计算角度和求解方程。
定义
余弦函数是以角度为自变量、余弦值为因变 量的函数。
特点
余弦函数的值在-1和1之间波动,它也是一个 周期性函数。
正弦函数与余弦函数的图像
正弦函数
正弦函数的图像呈现上下波动的形式。
余弦函数
余弦函数的图像呈现左右波动的形式。
正弦函数和余弦函数的周期性和对称性
1
周期性
正弦函数和余弦函数都是周期性函数,周期分别为360°或2π。
正弦函数和余弦函数在建 筑设计中用于描述特定曲 线和造型。
2 倍角公式
正弦函数和余弦函数还有倍角公式,用于求解复杂的角度关系。
3 积分
正弦函数和余弦函数的定积分是不定积分的特殊形式,具有特定的性质。
正弦函数和余弦函数的应用
物理学
正弦函数和余弦函数在物 理学中广泛应用于描述振 动和波动现象。
欢迎来到本节课的ppt课件,我们将介绍正弦和余弦函数的相互关系。了解它 们的定义、特点、图像、周期性和对称性、相位关系以及应用。
正弦函数的定义和特点
定义
正弦函数是以角度为自变量、正弦值为因变量的函数。
特点
正弦函数的值在-1和1之间波动,它是一个周期性函数。
余弦函数的定义和特点
2
对称性
正弦函数是奇对称函数,余弦函数是偶对称函数。
正弦函数与余弦函数的相位关系
1
相位关系
正弦函数与余弦函数的相位差是90°或π/2。
2
波形图
正弦函数和余弦函数的波形图相互垂直。
ห้องสมุดไป่ตู้
3
周期
正弦函数和余弦函数的周期是相同的。
正弦函数和余弦函数的数学性质
1 加法公式
正弦函数和余弦函数有一系列的加法公式,用于计算角度和求解方程。
定义
余弦函数是以角度为自变量、余弦值为因变 量的函数。
特点
余弦函数的值在-1和1之间波动,它也是一个 周期性函数。
正弦函数与余弦函数的图像
正弦函数
正弦函数的图像呈现上下波动的形式。
余弦函数
余弦函数的图像呈现左右波动的形式。
正弦函数和余弦函数的周期性和对称性
1
周期性
正弦函数和余弦函数都是周期性函数,周期分别为360°或2π。
正弦函数和余弦函数在建 筑设计中用于描述特定曲 线和造型。
2 倍角公式
正弦函数和余弦函数还有倍角公式,用于求解复杂的角度关系。
3 积分
正弦函数和余弦函数的定积分是不定积分的特殊形式,具有特定的性质。
正弦函数和余弦函数的应用
物理学
正弦函数和余弦函数在物 理学中广泛应用于描述振 动和波动现象。
第五章第六节正弦定理和余弦定理课件共58张PPT

A,bsin
C=csin
B,
cos
C=a2+2ba2b-c2
2.三角形中常用的面积公式
(1)S=12 ah(h 表示边 a 上的高);
(2)S=12
1
1
bcsin A=___2__a_c_s_in_B____=__2__a_b_si_n_C___;
(3)S=12 r(a+b+c)(r 为三角形的内切圆半径).
解析: 在△ABC 中, 由余弦定理及 a=2 2 ,b=5,c= 13 ,有 cos
C=a2+2ba2b-c2
=
2 2
π .又因为 C∈(0,π),所以 C= 4
.
π 在△ABC 中,由正弦定理及 C= 4 ,a=2 2 ,c= 13 ,可得 sin A=
a sin C c
=2 1313
.
答案:
π 4
变形
(1)a=2R sin A,b=_2_R_s_in_B___,c= __2_R_s_in_C___;
cos A=b2+2cb2c-a2
;
(2)a∶b∶c=_si_n_A_∶__s_i_n_B_∶__s_in_C___; cos B=c2+2aa2c-b2 ;
(3)asin B=bsin asin C=csin A
考点·分类突破
⊲学生用书 P84
利用正弦、余弦定理解三角形
(1)(2020·全国卷Ⅲ)在△ABC 中,cos C=23 ,AC=4,BC=3,则
tan B=( )
A. 5
B.2 5
C.4 5
D.8 5
(2)(2020·广东省七校联考)若△ABC 的内角 A,B,C 所对的边分别为 a,
b,c,已知 2b sin 2A=3a sin B,且 c=2b,则ab 等于( )
正弦函数余弦函数的图像和性质PPT课件
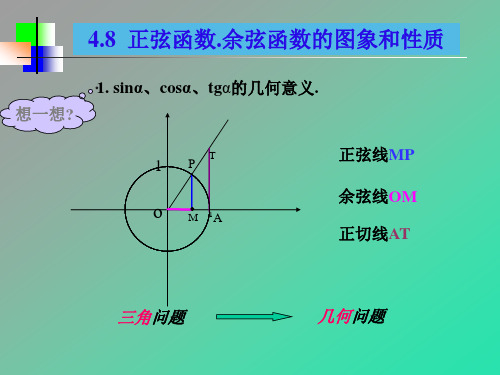
4.8 正弦函数.余弦函数的图象和性质
1. sinα、cosα、tgα的几何意义. 想一想? 1
P
T
正弦线MP 余弦线OM
o
M
1
A
正切线AT
三角问题
几何问题
4.8 正弦函数.余弦函数的图象和性质
2.用描点法作出函数图象的主要步骤是怎样的? (1) 列表
(2) 描点
-
(3) 连线
-
4.8 正弦函数.余弦函数的图象和性质
如: 作 的正弦线 平移定点
,连线
4.8 正弦函数.余弦函数的图象和性质
函数 图象的几何作法 作法: (1) 等分 (2) 作正弦线
1-
(3) 平移 (4) 连线
-
-
-
-1 -1 -
-
4.8 正弦函数.余弦函数的图象和性质
正弦曲线
1-
-1-
因为终边相同的角的三角函数值相同,所以y=sinx的图象在……, …与y=sinx,x∈[0,2π]的图象相同 余弦曲线(平移得到) 余弦曲线(几何作法)
返回 请单击:
4.8 正弦函数.余弦函数的图象和性质
(五点作图法)
1-
图象的最高点 与x轴的交点 图象的最低点
-
-1 -1 -
简图作法 (1) 列表(列出对图象形状起关键作用的五点坐标) (2) 描点(定出五个关键点) (3) 连线(用光滑的曲线顺次连结五个点)
-
图象的最高点 与x轴的交点
1-
-
-1
图象的最低点
(1) y
x
4.8 正弦函数.余弦函数的图象和性质
余弦曲线
-
1
-
-1
由于
所以余弦函数
1. sinα、cosα、tgα的几何意义. 想一想? 1
P
T
正弦线MP 余弦线OM
o
M
1
A
正切线AT
三角问题
几何问题
4.8 正弦函数.余弦函数的图象和性质
2.用描点法作出函数图象的主要步骤是怎样的? (1) 列表
(2) 描点
-
(3) 连线
-
4.8 正弦函数.余弦函数的图象和性质
如: 作 的正弦线 平移定点
,连线
4.8 正弦函数.余弦函数的图象和性质
函数 图象的几何作法 作法: (1) 等分 (2) 作正弦线
1-
(3) 平移 (4) 连线
-
-
-
-1 -1 -
-
4.8 正弦函数.余弦函数的图象和性质
正弦曲线
1-
-1-
因为终边相同的角的三角函数值相同,所以y=sinx的图象在……, …与y=sinx,x∈[0,2π]的图象相同 余弦曲线(平移得到) 余弦曲线(几何作法)
返回 请单击:
4.8 正弦函数.余弦函数的图象和性质
(五点作图法)
1-
图象的最高点 与x轴的交点 图象的最低点
-
-1 -1 -
简图作法 (1) 列表(列出对图象形状起关键作用的五点坐标) (2) 描点(定出五个关键点) (3) 连线(用光滑的曲线顺次连结五个点)
-
图象的最高点 与x轴的交点
1-
-
-1
图象的最低点
(1) y
x
4.8 正弦函数.余弦函数的图象和性质
余弦曲线
-
1
-
-1
由于
所以余弦函数
第六章6.4.3余弦定理、正弦定理PPT课件(人教版)

训练题
1.[2019·江西九江一中高一检测]若三角形的三边长之比是1∶ 3 ∶2,
则其所对角之比是( A ) A.1∶2∶3 B.1∶ 3 ∶2 C.1∶ 2 ∶ 3 D. 2 ∶ 3 ∶2
2. [2019·江西赣州五校高一联考]已知△ABC中,a∶b∶c=2∶ 6 ∶
( 3 +1),求△ABC中各角的度数.
训练题
1. 2019·江西九江一中高一检测]设△ABC的内角A,B,C的对边分别为
a,b,c,且cos A= 3 ,cos B= 5 ,b=3,则c=
5
13
14 5
.
2. [2019·北京东城区高三二模]在△ABC中,A= ,a2+b2-c2=ab, 4
c=3,则C=
3 ,a=
6.
3.已知两边及一边的对角解三角形 例5在△ABC中,a= 3 ,b= 2 ,B=45°,求A,C,c.
【解】 ∵ A=45°,C=30°,∴ B=180°-(A+C)=105°.
由 a = c 得a= csinA =10 sin45 =10 2 .
sinA sinC
sinC
sin30
由 b = c 得b= csinB =10 sin105 =20sin 75°.
sinB sinC
sinC
sin30
∵ sin 75°=sin (30°+45°)=sin 30°cos 45°+cos 30°sin 45°=
【解】 由正弦定理及已知条件,有 3 = 2 ,得sin A= 3 .
sinA sin45
2
∵ a>b,∴ A>B=45°.∴ A=60°或120°.
当A=60°时,C=180°-45°-60°=75°,
《正弦定理余弦定理》课件

THANKS
感谢观看
REPORTING
基础习题2
基础习题3
已知三角形ABC中,角A、B、C所对 的边分别为a、b、c,若$a = 8, b = 10, C = 45^{circ}$,求边c。
在三角形ABC中,已知A=60°,a=3, b=4, 求角B的大小。
进阶习题
进阶习题1
在三角形ABC中,已知A=45°, a=5, b=5sqrt{2}, 求边c。
详细描述
正弦定理是指在一个三角形中,任意一边与其对应角的正弦值的比等于其他两边的平方和与该边的平方的差的平 方根。余弦定理则是指在一个三角形中,任意一边的平方等于其他两边的平方和减去两倍的另一边与其对应角的 余弦值的乘积。
定理的推导过程
总结词
正弦定理和余弦定理的推导过程涉及到三角函数的定义、性质以及一些基本的 代数运算。
进阶习题2
已知三角形ABC中,角A、B、C所 对的边分别为a、b、c,若$a = 10, b = 8, C = 120^{circ}$,求 边c。
进阶习题3
已知三角形ABC中,角A、B、C所 对的边分别为a、b、c,若$a = 6, b = 8, C = 60^{circ}$,求边c。
综合习题
综合习题1
面积求解
总结词
余弦定理还可以用于计算三角形的面积,通过已知的两边及其夹角,使用面积公式进行计算。
详细描述
已知边a、边b和夹角C,可以使用余弦定理结合面积公式计算三角形ABC的面积,公式为:S = 1/2 ab sin(C)。
PART 04
正弦定理与余弦定理的对 比与联系
REPORTING
定理的异同点
详细描述
首先,利用三角函数的定义和性质,我们可以得到一些基本的等式。然后,通 过一系列的代数运算,将这些等式转化为正弦定理和余弦定理的形式。
正弦定理和余弦定理课件PPT

在钝角三角形 ABC 中,a=1,b=2,c=t,且 C 是最大角,则 t 的取值范围是________.
[错解] ∵△ABC 是钝角三角形且 C 是最大角,∴C>90°, ∴cosC<0,∴cosC=a2+2ba2b-c2<0, ∴a2+b2-c2<0,即 1+4-t2<0. ∴t2>5.又 t>0,∴t> 5, 即 t 的取值范围为( 5,+∞).
sin A
3
y 4sin x 4sin( 2 x) 2 3 3
4 3 sin(x ) 2 3, 6
A ,0 B x 2 .
3
3
故 x ( , 5),sin(x ) (1 ,1],
6 66
62
∴y的取值范围为 (4 3,6 3].
正、余弦定理的综合应用 【名师指津】正、余弦定理的综合应用
(2)由于 a:b:c=1: 3:2, 可设 a=x,b= 3x,c=2x. 由余弦定理的推论,得 cosA=b2+2cb2c-a2 =32x×2+43xx2×-2xx2= 23,故 A=30°. 同理可求得 cosB=12,cosC=0,所以 B=60°,C=90°.
已知三角形的三边长分别为 x2+x+1,x2-1 和 2x+ 1(x>1),求这个三角形的最大角.
∵∠ADC=45°,DC=2x, ∴在△ADC 中,根据余弦定理,得 AC2=AD2+DC2-2AD×DC×cos45°, AC2=4x2-4x+2, 又 AC= 2AB, ∴AC2=2AB2, 即 x2-4x-1=0,解得 x=2± 5. ∵x>0,∴x=2+ 5,即 BD=2+ 5.
名师辨误做答
第一章
解三角形
第一章
1.1 正弦定理和余弦定理
正弦,余弦函数的图像PPT课件

途径:利用单位圆中正弦、余弦线来解决。
描图:用光滑曲线
y
B
1
将这些正弦线的 终点连结起来
A
O1
O
2
4
5
2
x
3
3
3
3
-1
y=sinx
终边相同角的三角函数值相等 即: sin(x+2k)=sinx, kZ
x[0,2]
f(x2k)f(x)利用图象平移
y=sinx xR
正弦、余弦函数的图象
y 1
o
2
2
-1
y=sinx x[0,2]
y
y=sinx xR
1
-4 -3
-2
- o
-1
3
2
x
2
正弦曲 线
2
3
4
5 6 x
正弦、余弦函数的图象
如何作出正弦函数的图象(在精确度要求不太高时)?
y
五点画图法
1
(2
,1)
( 2 ,1)
( ,0)
( 2 ,0)
五点法——
2
(
(0,0)o
(0,0)
2
(0,0)
-1
(0,0)
汇报人:XXX 汇报日期:20XX年10月10日
2 ,0) x
2 ,0)
( 2 ,0) ( 2 ,0) ( 2 ,0) ( 2 ,0) ( 2 ,0) ( 2 ,0)
正弦、余弦函数的图象
y
1
-4 -3
-2
- o
-1
2
3
4
5 6 x
正弦函数的图象 y=cosx=sin(x+ ), xR
2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(3)sin42°54′=sin(90°-47°6′)=cos47°6′=0.6807.
巩固练习:课本P9练习2题。
2020年10月2日
4
如图15,△ABC中,∠C=90°. a2+b2=c2.
发现:sin2A+cos2A=1
由此得到sinA,cosA相互关系的一条性质:(A为锐角) sin2A+cos2A=1.
练习(口答)下列等式是否成立? (1)sin230°+cos245°=1; (3)cos256°+sin256°=1; (5)sin2α+sin2(90°-α)=1.
(2)sin237°+sin253°=1; (4)sin246°+cos246°=1;
2020年10月2日
5
演讲完毕,谢谢观看!
Thank you for reading! In order to facilitate learning and use, the content of this document can be modified, adjusted and printed at will after downloading. Welcome to download!
复习:直角三角形有什么性质?
(2)角的关系:∠A+∠B=90°
2020年10月2日Leabharlann 1正弦和余弦的相互关系
特殊三角函数值:
巧记方法
sin30°=
1 2
;cos60°=
1 2
;
sin60°=
3 2
;cos30°= 3 ; 2
si根nc4o据5s以°45上=°数22=据你;能.发现什么规律22 ?
sin30°=cos60°,sin60°=cos30°sin45°=cos45°
它的余角的正弦值.
应用练习(口答)课本P11习题A组4题。
2020年10月2日
3
应用公式,变式练习.
(2)已知sin35°=0.5736,求cos 55°; (3)已知 cos 47°6′=0.6807,求sin42°54′.
(2) cos55°=cos(90°-35°)=sin35°=0.5736;
特殊锐角的正弦值等于它的余角的余弦值, 特殊锐角的余弦值等于它的余角的正弦值.
2020年10月2日
2
设A和B互为余角,猜想: sinA与cosB,cosA与sinB的关系
sinA=cosB,cosA=sinB
证明猜想,形成公式.
互为余角的正、余弦的相互关系:
(1)若∠A+∠B=90°,则sinA=cosB,或cosA=sinB. (2) α为锐角,则 sinα=cos(90°-α),或cosα=sin(90°-α). (3)数学语言叙述: 任意锐角的正弦值等于它的余角的余弦值,任意锐角的余弦值等于
汇报人:XXX 汇报日期:20XX年10月10日
6
