第四章 多相平衡系统热力学(3)
第4章 多组分热力学

前面所讨论的是:单组分单相(两相)系统或多 组分组成恒定的系统。 但常见系统绝大部分是:多组分变组成系统。因 此必须研究处理多组分系统。
多组分系统除了两个变量之外,还需确定各组分 的物质的量才能确定系统的状态。 多组分系统分为:单相、多相
本章主要讨论多组分单相系统。
1
第四章 多组分系统热力学
B
dA SdT pdV BdnB
B
•适用条件 W ' 0 ,单相系统
31
2.多组分单相系统的热力学公式
•广义定义
B
U nB
S ,V ,nC
H nB
S , p,nC
A nB
T ,V ,nC
G nB
T , p,nC
保持特征变量和除B以外其它组分不变,某热力
学函数随其物质的量 nB的变化率称为化学势。
2 偏摩尔量相对于某一组分而言,本身是强度量;
3 偏摩尔量与浓度有关,与系统的总量无关。
4 偏摩尔量 X B ( nX,B )下T ,标p,n必C 须是
。T , p, nC
15
2.偏摩尔量
•偏摩尔量的物理意义
•两种理解 1 在恒温恒压下,于极大量的某恒定组成的系统中加
入1mol组分B时所引起系统广度量X的改变量。
混合物的摩尔体积:
Vm
xB M B /
B
Vm xBVB
B
21
5.吉布斯—杜亥姆方程
X
X
dX
( T
) p,nB
dT
(
p
)T ,nB
dp
B
X BdnB
•恒温恒压多组分系统
dX X BdnB
B
物理化学:第4章_多组分系统热力学_
真实混合物:实曲线
Vm xBVB xCVC VB (VC VB)xC
当混合物组成改变时,两组 分偏摩尔体积随之改变,且二者 变化相互关联。
组成接近某纯组分,其偏摩 尔体积也接近该纯组分摩尔体积。
5. 吉布斯 − 杜亥姆方程
对广度量 X (T , p, nB, nC , nD ,) 求全微分:
dX
X T
p,nB
dT
X p
T ,nB
dp
B
X nB
dnB T , p,nC
恒温、恒压
另一方面,由加和公式
,恒温恒压下求导:
比较两式,得
或
或
吉布斯-杜亥姆方程--在一定温度压力下,当混合物
组成变化时,各组分偏摩尔量变化的相互依赖关系。
➢ 系统中各组分的偏摩尔量并非完全独立,而是相 互依存的。
➢ 例:固体溶解、过饱和溶液析出、…
组分B在α、β两相中迁移达平衡的条件:该组分
在两相中的化学势相等。
➢ 物质总是从其化学势高的相向化学势低的相迁移, 直至物质迁移达平衡时为止,此时系统中每个组分在 其所处的相中的化学势相等。
化学势 判据
② 化学平衡
<0:自发不可逆; =0:平衡、可逆
任一化学反应,假定系统已处于相平衡,
任一组分B在每个相中的化学势都相等: Bα B
B
B
整个系统中B组分物质的量的变化量: dnBα dnB
α
BdnB
B
化学平衡时
平衡条件:与化学反应达到平衡的方式无关。
§4.3 气体组分的化学势
1、纯理想气体的化学势 2、理想气体混合物中任一组分的化学势 3、纯真实气体的化学势 4、真实气体混合物中任一组分的化学势
物理化学 第四章 多组分系统热力学

Vm
T,p一定
V*m,C VC
V*m,B VB
d c· b·
0 B
a xC
C
图4.1.2 二组分液态混合物的 偏摩尔体积示意图
若B,C形成真实液态混合物: 则混合物体积为由V*m,B至V*m,C的曲线。对于任一 组成a时,两组分的偏摩尔体积可用下法表示: 过组成点a所对应的系统体积点d作Vm-xC曲线的 切线,此切线在左右两纵坐标上的截距即分别 为该组成下两组分的偏摩尔体积VB,VC。
B
系统中各广度量的偏摩尔量: 对于多组分系统中的组分B,有: 偏摩尔体积: VB=(ƽV/ƽnB)T,p,n C 偏摩尔热力学能: UB=(ƽU/ƽnB)T,p,n C 偏摩尔焓: HB=(ƽH/ƽnB)T,p,n C 偏摩尔熵: SB=(ƽS/ƽnB)T,p,n C 偏摩尔亥姆霍兹函数:AB=(ƽA/ƽnB)T,p,n C 偏摩尔吉布斯函数: GB=(ƽG/ƽnB)T,p,n
C
几点说明: (1)偏摩尔量为两个广度性质之比,所以为强度 性质; (2)偏摩尔量的定义中明确是在恒温、恒压及系 统组成不变的条件下,偏导数式的下标为T,p 时才是偏摩尔量; (3)同一物质在相同温度、压力但组成不同的多 组分均相系统中,偏摩尔量不同; (4)若系统为单组分系统,则该组分的偏摩尔量 与该组分的摩尔量相等,即: XB=X*B,m
C
=VB (数学知识:二阶偏导与求导的顺序无关) 得证。
4.2化学势 4.2化学势
1.化学势的定义 混合物(或溶液中)组分B的偏摩尔吉布斯函数GB 定义为B的化学势,用符号μB表示:
μB = GB=(ƽG/ƽnB)T,p,n
def
C
对于纯物质,其化学势等于它的摩尔吉布斯函 数。
第四章-相平衡-1

考虑水的电离因素。
ii)酸的水溶液,如:HAc + H2O,若不 考虑酸的电离,则 C = 2;
a. 若考虑HAc电离:HAc H+ +Ac
S = 4 ( H2O, HAc, H+, Ac ), R = 1 (有一化学平衡),
且 R´=1 ( [H+] = [Ac] ),
• 以上这些都是我们常见的多相平衡的例 子,这些类型多相平衡各有一定的方法 来研究它们的规律,例如:
拉乌尔定律、亨利定律、分配定律、 平 衡常数及某些其他经验性规则。 而下面要介绍的 “相律”,却不同于上 述这些规律。 相律所反映的是多相平衡中最有普遍性 的规律,即独立变量数、组分数和相数
之间的关系。 “相律”是一种从统一的观点来处理各
现已经有溶液相和冰两个相,所以与其 共存的含水盐相最多只能有一种。
2)同理,在恒定温度下,
f * = C +1 = 3
最多有三相,所以定温下与水蒸气平衡
共存的含水盐最多可有两种。
2. 说明下列平衡系统的自由度 1) 25C 和 1atm 下,固体 NaCl 与其水
溶液成平衡。
答:C = 2, = 2(固相、溶液相)
在保持系统相数不变条件下,可任
意改变的独立变量数。
例如: 水在保持单一液相条件下
f = 2 (压力、温度)
而水在保持:汽 液 两相平衡条件
下,独立变量数为
f = 1 (压力或温度)
§4.2 相律及其热力学推导
一、“ 相律 ” 的完整表述
在平衡系统中,联系系统内相数、组分 数、自由度及影响物质性质的外界因素
(完整版)第四章相平衡思考题(答案)

第四章相平衡思考题1. 纯氮气和空气算一个相吗?【解】纯氮气和空气各算一个相。
2. 当两个相的温度相同但压力不同时,两个相能达到平衡吗?如果两相的压力相同而温度不同,两相能达到平衡吗?【解】一般而言,当系统达到热力学平衡时,系统将同时满足热平衡、力平衡、相平衡和化学平衡。
具体到相平衡,其条件是各物质在两相中的化学势相同。
影响化学势的因素有温度和压力,达到相平衡时一般温度和压力亦相等。
如果温度相同,而压力不等同样有达到相平衡的可能,如渗透系统;同样地,在压力相同而温度不同的情况下,也应该有达到相平衡的可能性。
3. 在抽空的真空容器中,有一定量的NH4HS(s),加热后NH4HS(s)分解,试说明组分数和自由度。
【解】分解反应为NH4HS(s)→ NH3(g)+ H2S(g),组分数K = 3 - 1 – 1 = 1,自由度f = 1 - 2 + 2 = 1。
4. 恒温恒压下,某葡萄糖和氯化钠同时溶于水中,用一张只允许水通过的半透膜将此溶液与纯水分开。
当系统达到平衡后,系统的自由度为多少?【解】f** = 3 - 2 + 1 = 2。
5. 说明物系点和相点的区别,什么时候物系点和相点是统一的?【解】物系点表示系统的组成,而相点表示系统相的组成。
当系统是单相的时候,两者是重合的。
6. 图4-2中,当系统处于临界点C 时,自由度是多少?【解】自由度等于零。
7. 如用二氧化碳超临界流体作萃取剂,最低的工作压力是多少?能在室温下进行此操作吗?【解】二氧化碳的临界参数是t c = 31.26℃、p c = 7.2 MPa,因此最低压力是7.2 MPa。
因为t c = 31.26℃十分接近典型的室温值25℃,因此CO2超临界流体萃取可以在近室温下操作。
8. 在一高压容器中有足够量的水,向容器中充入氮气压力到10 MPa,这时还能用Clausius-Clapeyron 方程计算水的沸点吗?【解】当压力达到10 MPa 时,而水的临界压力为 22.129 MPa,几乎接近一半,此时水的体积不能忽略,水蒸气也不能视为理想气体,所以不能用Clausius-Clapeyron 方程计算水的沸点。
4-3多组分系统热力学-理想液态混合物与理想稀溶液

Physical Chemistry
物理化学(上册)
绪论 第一章 气体 第二章 热力学第一定律 第三章 热力学第二定律 第四章 多组分系统热力学 第五章 化学平衡 第六章 相平衡
第四章 多组分系统热力学
§4-!本章基本要求 §4-1多组分系统热力学概念 §4-2拉乌尔定律与亨利定律 §4-3偏摩尔量 §4-4化学势 §4-5理想液态混合物 §4-6理想稀溶液 §4-7活度活度系数 §4-8化学势小节 §4-$小结与学习指导
d* S*dT V *dp
B
B
B
mixG p
T
B
nBVB
B
nBVB* mixV
2. mixV 0 或 V mix m 0
mix p
G
T
(RT
nB ln xB )
B
p
T
0
§4-5理想液态混合物
四、理想液态混合物混合性质
dG B S B dT VB dp
dG * S * dT V *dp
B
B
6.
mixU mix H P mixV 0
mixU 0 或 mixU m 0
§4-5理想液态混合物
四、理想液态混合物混合性质
小结: 1. mixV=0 , mixU=0 , mixH=0 2. Q=0, W=0 3. mixS=-RnBlnB>0 (绝热 S>0)
mixA=RTnBlnB<0 (恒温恒容W =0 A<0) mixG=RTnBlnB<0 (恒温恒压W =0 G<0)
§4-6理想稀溶液
一、理想稀溶液定义 无限稀溶液,溶质的浓度趋于零的溶液。 对溶剂(A表示)用符合拉乌尔定律
第四章--多组分系统热力学习题

第四章多组分系统热力学选择题1. 在和101325Pa•下水的化学势与水蒸气化学位的关系为(A) μ(水)=μ(汽) (B) μ(水)<μ(汽)(C) μ(水)>μ(汽) (D) 无法确定答案:A。
两相平衡,化学势相等。
2.下列哪种现象不属于稀溶液的依数性(A) 凝固点降低(B)沸点升高(C) 渗透压(D)蒸气压升高^答案:D。
稀溶液的依数性之一为蒸气压下降。
3.98K时,A、B两种气体在水中的亨利常数分别为k1和k2,且k1>k2,则当P1=P2时,A、B在水中的溶解量C1 和C2 的关系为(A) C1>C2 (B) C1<C2 (C) C1=C2 (D) 不能确定答案:B4.将非挥发性溶质溶于溶剂中形成稀溶液时,将引起(A) 沸点升高(B) 熔点升高(C) 蒸气压升高(D) 都不对答案:A。
稀溶液的依数性包括沸点升高、凝固点下降、蒸气压下降和渗透压。
5. 涉及纯物质标准状态的下列说法中不正确的是(A) 纯理想气体的标准状态就是标准压力P(100KPa)下的状态(B) 纯液体物质的标准状态就是标准压力P(100KPa)下的纯液体—(C) 纯固体物质的标准状态就是标准压力P(100KPa)下的纯固体(D) 不同的物质在相同温度下都处于标准状态时,它们的同一热力学函数值都应相同答案:D6. 稀溶液的依数性包括蒸汽压下降、沸点升高、凝固点降低和渗透压,下面的陈述都与它们有关,其中正确的是(A) 只有溶质不挥发的稀溶液才有这些依数性(B) 所有依数性都与溶液中溶质的浓度成正比(C) 所有依数性都与溶剂的性质无关(D) 所有依数性都与溶质的性质有关答案:B7. 关于亨利系数, 下面的说法中正确的是!(A) 其值与温度、浓度和压力有关(B) 其值只与温度、溶质性质和浓度标度有关(C) 其值与溶剂性质、温度和浓度大小有关(D) 其值与温度、溶剂和溶质的性质及浓度标度等因素都有关答案:D8. 定义偏摩尔量时规定的条件是(A) 等温等压 (B) 等熵等压(C) 等温, 溶液浓度不变 (D) 等温等压, 溶液浓度不变答案:D9. 关于偏摩尔量, 下面的说法中正确的是~(A) 偏摩尔量的绝对值都可求算(B) 系统的容量性质才有偏摩尔量(C) 同一系统的各个偏摩尔量之间彼此无关(D) 没有热力学过程就没有偏摩尔量答案:B10. 关于偏摩尔量, 下面的叙述中不正确的是(A) 偏摩尔量是状态函数, 其值与物质的数量无关(B) 系统的强度性质无偏摩尔量(C) 纯物质的偏摩尔量等于它的摩尔量(D) 偏摩尔量的数值只能为整数或零-答案:D11. 影响沸点升高常数和凝固点降低常数值的主要因素是(A) 溶剂本性 (B) 温度和压力 (C )溶质本性(D) 温度和溶剂本性答案:A 。
第四章 相平衡

• 例 :在某温度下 , 体系中 PCl5(g)部分分解产生了一定量的 PCl3(g)
和Cl2(g) 并达到了化学平衡, 体系中独立的化学反应数R为多少?
组分数K是多少?
• 体系中只存在下面一个化学反应:
PCl5(g)= PCl3(g) + Cl2(g) • 该体系中独立的化学反应数R=1
• 该体系中物种数S=3
• 解: 有反应: S=3 R=1 R’= 1 分解反应平衡 [p(NH3)=p(H2S)] NH4HS(s) = NH3(g) + H2S(g)
∴
K=3-1-1=1
f = K- + 2=1-2 + 2=1
• 即此体系的温度和压力两变量中只有一个是独立的 . 体系的温度 固定时, NH4HS的分解压力一定,故体系的压力恒定; 反之,若体系 的压力一定,体系的温度必也被确定.
吉布斯相律
• 相律的物理含义是:
体系的自由度等于体系的独立组分数 K 减去相数 再加上环境变量数2(温度和压力).
• 在某些特殊条件下, 环境变量不仅仅为温度和压力, 可能 存在其它变量, 故相律更一般的可表达为:
f=K– +n
• 式中: f为体系的自由度;
K为组分数;
为相数;
n为环境变量数, 一般情况下n=2(T, p).
• 独立组分数(K), 简称为组分数, 指确定体系组成所必须
的变量数.
• 定义:
K=S-R-R’
• S:物种数, R:独立的化学反应数, R’:浓度限制数
• 独立的化学反应数 (R): 一个多相系统存在多个反应时 ,
• 浓度限制数(R’): 同一相中存在的浓度之间的关系。
独立的化学反应指不能由其他反应组合推导出来的反应.
物理化学第四版 第四章 多组分系统热力学2014.2

)
p,n
(
B
)
,V
(
G P
)T
,n(
B
)
k
dG SdT VdP BdnB
证毕
B 1
14
又 dA d(G PV ) dG pdV Vdp
将上式dG 代入,整理得:
k
dA sdT PdV BdnB ……..(3) B 1
同理可得出另二个热力学基本方程。
因 A=A(T,V,n1,n2…….nk)
B
B
B
........
n B
相平衡条件
有N 个组分,就有N 个这样的式子
19
例:在、 两相中均含有A和B两种物质,达到相平衡时,下列
各式正确的是(
)。
A、
A
B
B、
B
B
C、
A
B
D、
B
A
例:组分B从相扩散入相中,则以下说法正确的有( A、总是从浓度低的相扩散入浓度高的相 B、平衡时两相浓度相等 C、总是从化学势高的相移向低化学势低的相
dA
(
A T
)V
,n
(
B
)
dT
( A V
)T ,n(B)
dV
k B 1
(
A n(B)
)T
,V
,n
(
c,c
B)
dnB
将式(4)和式(3)比较
B
A ( nB
)T ,V ,n(c,cB)
同样可得出
B
U ( nB
)S ,V ,n(c,cB)
H ( nB
)S ,P.n(c,cB)
…..(4)
15
例 2: 下列偏导数中那些是偏摩尔量?那些是化学势?
物理化学第四章

• 但碳的相图中最多只能三相共存,不可能四相共存.
一.克-克方程(Clausius-Clapeyron equation)
• 当单组分体系两相共存时,自由度f=3-2=1, 体系只有一个自由度。 • 单组分的相变温度与压力之间存在一定的关 系, 此关系即为克-克方程. • 设一纯物质在T,p下达两相平衡:
相图:表示体系状态变化的图形
•
• 相(phase): 体系内物理性质和化学性质
完全均匀的部分. • 均匀的要求: •
均匀到分子水平
• 一个体系中可以含有多个相,这些相与相 之间一般存在明显的界面,界面处体系的 热力学性质是间断的.
气体:凡气体成一相.
气体体系无论有多少种气体,一般都达到分子水 平的混合,故为一相。
• (3)式称为克拉贝龙方程. • 克拉贝龙方程适用于纯物质任何平衡相变过 程,应用范围很广.
• 1. 气-液,气-固两相平衡:
• 纯物质的两相平衡中有一相为气相,另一相必为 凝聚相. 以气-液平衡为例,有: • dp/dT=Hm/TVm= Hm/T(Vm,g-Vm,l) (4) • ∵ Vm,g>>Vm,l • ∴ Vm,g-Vm,l≈ Vm,g=RT/p • 代入(4)式: • dp/dT= Hm/[T(RT/p)] •
• 体系的独立变量数f(即自由度)应该等于总变量 数减去关系式总数: • 总变量数:S+2 • 关系式数:+S(-1) • •
f = S+2--S+S
f = S- + 2
(1)
• (1)式就是相律的数学表达式. • 相律的物理含义是:
体系的自由度等于体系的物种数S减去相 数再加上环境变量数2(温度和压力).
第四章 多组分系统热力学

前两章-单组分均相封闭系统,如:纯物质或某种 理想气体系统。 科学研究及生产实践-多组分系统 纯物质单相封闭系统:确定n(对于单相封闭系统, 此为一定值)、T、p,系统的状态即可确定。此时, 系统的一切性质,不只是强度性质而且全部容量性 质都有了确定值。若以X代表任意一种容量性质, 如V、U、S、G等,对于物质的量固定的纯物质单 相系统,都有: X=f(T,p) 其微小改变量为:
10
XB物理意义为:在恒温、恒压、均相封闭系统中, 只增加任一组分B,同时不引起原来nj改变,且不 发生缔合、沉淀、化学反应时: (1)dnB量B物质的加入,系统容量性质X对nB的变 化率。或在原有nB中加入dnB的B,使X改变了dX的 比值; (2)条件同前,在一个无限大的系统中,加入1 mol 的B物质,引起容量性质X的改变量。 如:向一大缸某白酒中,加入1 mol的水,引起V增 大了17.0 ml (<18.0 ml), 则此时V水=17.0 ml· -1。 mol
X X X dp dX dT d n1 p n T p , ni T , ni 1 T , p , n2 , n3 ,nk
X n 2 X d n2 n T , p , n1 , n3 ,nk k d nk T , p , n1 , n2 ,nk 1
W (乙) 10
W (水) 90
V (乙) 12.67
V (水) 90.36
V 103.30
V (实) 101.84
V 1.19
20 g乙醇+180 g水,其V=2×1.19=2.38 ml
7
描述一多组分均相系统的状态,除指明系统的T和p, 还必须指明系统的组成ni。为此,需要引入偏摩尔 量(XB)来代替单组分系统中的摩尔量(Xm)。 一、偏摩尔量的定义 含有k个组分的均相系统,其任一容量性质X (可为 V, U, H, S, A, G)可写成下列函数式: X=f(T,p,n1,n2,…nk) 2+k个变量 当系统的T、p及各组分的n均发生一微小变化时, 该容量性质X也相应发生微小变化。根据状态函数的 性质,此变化可用全微分表示,即:
物理化学课件及考试习题 试卷 答案第4章 多组分系统热力学习题及答案

第三章多组分系统热力学一、填空题1、只有系统的____性质才具有偏摩尔量。
而偏摩尔量自身是系统的____性质。
偏摩尔量的值与系统中各组分的浓度____。
混合适物系统中各组分的同一偏摩尔量间具有两个重要的性质,分别是____与____。
2、如同温度是热传导的推动力一样,化学势是____传递的推动力。
在恒温恒压下多相平衡的条件是________________。
以焓表示的组分i的化学势可写成µi=____。
3、混合理想气体中任一组分B的化学势________;理想溶液中任一组分B的化学势________;稀溶液中溶剂A的化学势________。
4、由纯组分在恒温恒压下组成理想混合物时,△mix S=__0;△mix G__0;△mix H__0;△ix V__0。
5、理想溶液混合时,∆mix V ,∆mix S ,∆mix G ,∆mix H 。
6、比较水的化学势的大小(此处p=101.325kPa):(填>、< 或=)①μ(l,100℃,p)____μ(g,100℃,p)②μ(l,100℃,p)____μ(l,100℃,2p)③μ(g,100℃,p)____μ(g,100℃,2p)④μ(l,100℃,2p)____μ(g,100℃,2p)⑤μ(l,101℃,p)____μ(g,101℃,p)7、非理想溶液溶质的化学势表示式____,其标准态为____。
8、在一定的温度及压力下,某物质液汽两相达平衡,则两相的化学势μB(l)与μB(g)_____若维持压力不变,升高温度,则μB(l)和μB(g)都______;但μB(l)比μB(g)______。
9、理想溶液中任意组分B的化学势:μB=_______________。
10、298K、101.325kPa,有两瓶萘的苯溶液,第一瓶为2升,溶有0.5mol萘,第二瓶为1升,溶有0.25mol 萘,若以μ1和μ2表示两瓶中萘的化学势,则它们的关系为__________。
物理化学 第四章 多组分系统热力学

AB
( nB
)T , p ,nC
G
GB
( nB
)T , p ,nC
注意:偏摩尔量的下脚标为:T,P,C(C≠ B)
使用偏摩尔量时应注意: 1.偏摩尔量的含义是:在等温、等压、保持B物质 以外的所有组分的物质的量不变的条件下,广度性 质X的随组分B的物质的量的变化率。
2.只有广度性质才有偏摩尔量,而偏摩尔量是强度 性质。
六、偏摩尔量之间的函数关系
对于组分B:VB、UB、HB、SB、AB、GB之间的关系:
HB= UB +PVB ,
AB= UB -TSB
GB = HB -TSB= UB +PVB -TSB UB =AB+PVB
(
GB P
)T
,nA
VB
(
GB T
)
P,nA
SB
( GB )
[T T
]P,nB
3.纯物质的偏摩尔量就是它的摩尔量。
4.任何偏摩尔量都是T,p和组成的函数。
偏摩尔量的集合公式
设一个均相体系由1、2、 、k个组分组成,则体 系任一广度量Z应是T,p及各组分物质的量的函数,即:
X X (T , p, n1, n2,, nk )
在等温、等压条件下:
X
X
dX
( n1
···········
dG= dG(α) + dG(β) +·········
恒T,p时 dG SdT Vdp
B
dnB
B
同理,有
dU TdS pdV B ( )dnB ( ) B
dH TdS Vdp B ( )dnB ( ) B
南京大学物理化学 第四章 多组分均相系统热力学及其在溶液中的应用

大能力(可逆时系统对外所做功最大) ② 当W’=0时,:反应永远向着化学势降低的方向进行,可用来判断
反应进行的情况(=0可逆,<0不可逆) 该判据也可推广到多组分多相系统:和 2. 判据的应用 (1) 相变
广义的相变是物质由一个相迁往另一个相的过程,是一个物质流动的 过程。
第15次课
3. 理想溶液的化学势
化学势是物质迁移的推动力,不论物质是否混合,只要气液两相平 衡,则气液两相的化学势相等。 混合前:纯组分 混合后:溶液组分
是纯液体A在温度为T、压力为溶液上方总压时的化学势。
4. 理想溶液的热力学性质 (1) 蒸气压与液相组成的关系
,故 (2) 蒸气压与气相组成的关系
等温等压条件下,非挥发性溶质形成的溶液中,溶剂的蒸气压等于 纯溶剂的蒸汽压乘以溶液中溶剂的摩尔分数(或:溶剂蒸气压的降低值 与纯溶剂的蒸气压之比等于溶质的摩尔分数) 说明:公式只适用于溶液中只有A、B两个组分的系统(),而则具有 普适性。
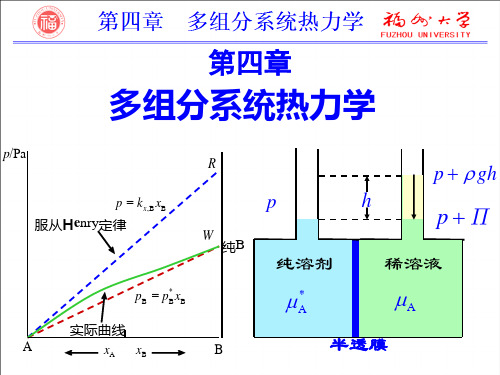
2. 亨利定律(Henry) 一定温度、压力下,稀溶液中某挥发性物质的平衡分压与该溶质的
① ∵∴压力p升高,化学势μB也随之增加 ② 若已知,则可求出 说明:实际上,在与吉布斯自由能有关的关系式中,如果把G换成μ, 并将公式中其它广度量换成相应的偏摩尔量,则公式仍然成立。 例:
第14次课
(四)化学势判据
1. 判据推导 组成可变的封闭系统,发生广义化学变化时(可逆取等号) 将上述四式与⑤-⑧式对比,得到
可称为定浓物理量
2 偏摩尔量的集合公式(加和定理) 等温等压条件下,
在任一系统中,将各组分的物质的量增加一倍,其各组分浓度仍不 变,广度量Z则相应增加一倍。 注:在所有偏摩尔量中,只有偏摩尔体积可测,可由求出溶液的总体 积。
多组分系统热力学

第四章 多组分系统热力学 主要内容1.混合物和溶液(1)多组分系统的分类含一个以上组分的系统称为多组分系统。
多组分系统可以是均相(单相)的,也可以是非均相(多相)的。
将多组分均相系统区分为混合物和溶液,并以不同的方法加以研究:(Ⅰ)混合物:各组分均选用同样的标准态和方法处理;(Ⅱ)溶液:组分要区分为溶剂及溶质,对溶剂及溶质则选用不同的标准态和方法加以研究。
(2)混合物及溶液的分类混合物有气态混合物液态混合物和固态混合物;溶液亦有气态溶液液态溶液和固态溶液。
按溶液中溶质的导电性能来区分,溶液又分为电解质溶液和非电解质溶液(分子溶液)。
2.拉乌尔定律与亨利定律拉乌尔定律与亨利定律是稀溶液中两个重要的经验规律。
(1)拉乌尔定律平衡时,稀溶液中溶剂A 在气相中的蒸气分压A p 等于纯溶剂在同一温度下的饱和蒸气压与该溶液中溶剂的摩尔分数A x 的乘积。
这就是拉乌尔定律。
用数学式表达拉乌尔定律为 A *A Ax p p = (2)亨利定律一定温度下,微溶气体B 在溶剂A 中的溶解度B x 与该气体在气相中的分压B p 成正比。
也可表述为:一定温度下,稀溶液中挥发性溶质B 在平衡气相中的分压力B p 与该溶质B 在平衡液相中的摩尔分数B x 成正比。
这就是亨利定律。
用数学式表达亨利定律为: B B ,B x k p x =B ,x k 、B ,b k 为以不同组成标度表示的亨利系数,其单位分别为Pa ,Pa·kg·mol -1。
应用亨利定律时,要注意其不同表达式所对应的亨利系数及其单位。
还要注意亨利定律适用于稀溶液中的溶质分子同气相同种分子相平衡,即亨利定律适用于稀溶液中的溶质在液相及气相中具有相同分子形态的场合。
3.偏摩尔量(1)偏摩尔量的定义设X 代表V ,U ,H,S ,A ,G 这些广度性质,则对多组份系统(混合物或溶液)即 X =f (T ,p ,n A ,n B ,…)定义 ()B C C,,,B B def ≠⎪⎪⎭⎫ ⎝⎛∂∂n p T n X X式中,X B称为广度性质X (X=V ,U ,H ,S ,A ,G 等)的偏摩尔量,它们分别为只有系统的广延量才具有偏摩尔量,偏摩尔量是强度量。
第四章 多相平衡系统的热力学

p
2 H 2O
p pO 2
2 H2
C = S-R=3-1=2
R表示的是独立的化学平衡数。
20
f =C–P+2
需要注意的是,R表示的是独立的化学平衡数。
例如:化学反应
CO(g) + H2O(g) ===CO2 (g)+ H2 (g) (1)
C(s) +CO2(g)===2CO(g)
C(s) + H2O(g) === CO(g)+H2(g)
d ln p vap H m 2 dT RT
这就是Clausius-Clapeyron 方程, vap H m 是摩尔气化热。 假定 vap H m 的值与温度无关,积分得:
p2 vap H m 1 1 ln ( ) p1 R T1 T2
这公式可用来计算不同温度下的蒸气压或摩尔蒸发热。
O点: 三相点 p/Pa
22.12MPa C
三相点与冰点是否 是一回事?
≈
超临界流体 A ●
水的冰点
pθ
B D
O
A点:临界点
超临界流体的特 点及技术
610.62Pa
≈
647.4K
273.15K
273.16K
T/K
35
超临界流体萃取的实例
• • • • • 萃取化工产品之中的萘 从咖啡豆萃取咖啡因 茶叶中脱除茶碱 烟草中脱除尼古丁 辣椒中提取辣椒色素
30
例题2 碳酸钠和水可以组成下列化合物: Na2CO3.H2O,Na2CO3.7H2O,Na,与碳酸钠水溶液及冰共存的含水盐最
多可有几种?
(2)30℃时,与水蒸气平衡共存的含水盐最多可
物理化学-第四章相平衡

所以 C=1 单组分系统
例2. 碳在氧气中燃烧,有如下方程:
(1) C(s)+O2 (g)=CO2 (g)
(2)
C(s)+
1 2
O2
(g)=CO(g)
因为(3)=(1) - (2) 所以 R=2
1 (3) CO(g)+ 2 O2 (g)=CO2 (g)
S = 4, R’=0, 则 C=4-2=2 二组分系统
面
两相平衡: P=2 f=1 一个独立变量
线
三相平衡: P=3 f=0 无变量
点
p
B
冰
水A
①三条线:OA, OB, OC
D
O气
C
水的局部相图示意
三个区:单相区
三相点(triple point):
T O点:三相共存,f = 0,
0.0099℃, 610.6 Pa 与冰点不同
OA:g-l共存,水的饱和蒸汽压曲线
S = 3, R = 1, R’ = 0,则 C=3 -1=2
注意:对于浓度限制条件,是固定不变的浓度关系。
2. 自由度和自由度数(f) (the number of freedom degree)
如何描述一个相平衡系统的状态(平衡性质)?
p1
p2
H2O(l) T1
H2O(g)
H2O(l) T2
相平衡的一个重要性质是它与各相中物质的量无关。 一个多相系统的相平衡状态是由体系的强度性质决定 的。例如 pv , Tb , Tf , 溶解度等。
d
ln p /[ p] dT
gc d H m RT 2
(1) 条件:纯物质g-l(s) 平衡,
(近似:忽略Vm (cd),理想气体) (2) 若近似gcdHm不随T变化,则
物理化学04多组分系统热力学

dG=dG( ) +dG()
当恒温恒压,W’=0 时
β相
dG() ()dn()
dG( ) ( )dn( )
dn( ) dn()
dX
X T
p,nB ,nc ,nD
X
dT
p
T ,nB ,nc ,nD
X
dp
nB
T , p,nc ,nD
dnB
X
X
nC
T , p,nB p,nB ,nc
dnD
2021/1/6
偏摩尔量XB的定义为: X B def
X ( nB )T , p,nc
2021/1/6
解:取1kg溶液
nH2O
mH2O M H2O
(1 0.12)1 18.015 103
mol
48.85mol
nAgNO3
mAgNO3 M AgNO3
0.12 1 169.89 103
mol
0.7064mol
xAgNO3
nAgNO3
n n AgNO3
H2O
0.01425
cAgNO3
2021/1/6
由题意:
VA 17.35cm3 / mol
VB 39.01cm3 / mol
由集合公式,混合后:
V nAVA nBVB {0.617.35 0.4 39.01}cm3 26.01cm3
混合前:
VA '
nAM A A
10.84cm3
VB'
nB M B B
16.19cm3
dA SdT pdV BdnB
dA
B
BdnB 0
自发 =平衡
B
(dT 0,dV 0, W ' 0)
第4章 多组分系统的热力学 第4节 化学势及其应用 第5节 混合气体中组元的化学势

l
O
g T
(
Gm
*
B
p
)T Vm
*
1 3
373.15K
1 2 3 4
16
4.5 混合气体中组元的化学势
纯理想气体的化学势
理想气相混合物中各组分的化学势
实际气体中组分的化学势
17
纯理想气体的化学势
只有一种理想气体,
G ( )T ( )T , p p p nB T
18
p (T , p) (T , p ) RT ln p
纯理想气体的化学势
p (T , p) (T , p ) RT ln p p i i ( g ) RT ln p
这是理想气体化学势的表达式。 μi(g)是温度为T,压力为标准压力时理想气体 i 的 化学势,这个状态就是气体的标准态。
22
气体中组分的化学势小结
纯理想气体
* p B B* B ( g ) RT ln p
pB 混合理想气体 B B ( g ) RT ln p
fB 混合实际气体 B B ( g ) RT ln p
作业2-3 简要论述多组分系统中的相平衡条件和化学反应平衡条件 作业2-4 理想气体混合物和实际气体混合气的化学势的区别和联系是什么
G ( )T , p n B G ( )T nB p T , p
V Vm nB T , p
(dG SdT Vdp)
p
dμ Vmdp p
p
p
RT dp p
p (T , p) (T , p ) RT ln p
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ii)精馏原理
精馏是多次简 单蒸馏的组合。 将一定组成的 溶液加热到T2, 此时物系点为O, 气相相点G2(组成 为y2),液相相点 L2(组成为x2)。
精馏塔示意图
精馏塔底部是加热区,温度最高,塔顶温度最低。 精馏结果,塔顶冷凝收集的是纯低沸点组分,纯 高沸点组分则留在塔底。
p
p
l
E l+g
O’
O F
* pB
p* A
A+B xf 气相 p A+B xe 液相
g A+B xf 气相 A p
xe xo xf B XB→
Xo’
A+B xe 液相
O
O’
落在EF线上所有物系点的对应的液相和气相 组成,都由E点和F点的组成表示。 f*=2-2+1=1
物系点:是整个系统总的状态点。由p和系统总组成XB确定。 相点:是表示平衡系统中每一个相的状态点。由p和平衡各相 组成XB和YB确定。 例如: ①压力为p1,组分B的摩 尔分数为x1,物系点为O1 此时系统为液相,其相点 也为O1, ②压力为p2,组分B的摩尔分 数为x2,物系点为O2,相点也 为 O2。 在单相区,物系点和相点是重 合的。
TB
B
TA是纯A的沸点,TB是纯B的沸点。
识图
①线 液相线 ②面 液相区 气相区 A 气相线 TA T 气
气相线
气 液 液液相线 X→ TB B
气 液 两相平衡区 ③点 TA是纯A的沸点,TB是纯B的沸点。
识 图
当系统的温度为T,组成 为 X 时,整个系统的状态 用 O 点描述,该点叫做物 系点。 此时系统处于两相平衡, 平衡的液相为 Ol ,气相为 Og , Ol和Og叫做相点。 T g 气相线
设A和B构成理想液态混合物,根据实验测定不同组
成的液态混合物气液两相平衡时,气相的压力p,液相组 成xB和气相组成yB。
p1 ~ xB1 yB 2
气相yB 液相xB
p2 ~ xB 2 yB 2
p3 ~ xB3 yB3
绘制相图
根据上面的数据,由p~xB数据绘制出液相线 由p~yB数据绘制出气相线 p 为什么p~xB为直线? 因为A和B组成的混合物 时理想液态混合物,各个 组分在所有浓度范围内服
2. 部分互溶双液系统
部分互溶:是指一定温度下某液体在另一液体中只有 有限的溶解度。超过一定范围时,就要分成两个液层。 ①部分互溶双液系统液液平衡相图 实验数据的获得:以水—苯酚系统为例 一定温度T时,将一定量的水和 苯酚(苯酚的质量百分数为W%) 混合充分震荡使之达到平衡。。
T2 a” a’ T1
系统始终保持沸腾状态。
T1 T2叫做沸程。
O’ l+g O 液相区 x A XB→
b’ b
B
理想液态混合物 p~x图与T~x图的比较
p T
* pB
p* A
l+g
TA
气相线 l+g 液相线
TB
A
XB
B
A
XB
B
p p
* A * B
是纯A的饱和蒸气压
固定T或p,f*=C-P+1=3-P Pmin=1 , fmax*=2 fmin*=0 ,Pmax=3,即最多允许三相平衡共存。
对于两组分系统,通常固定p绘制T~X图,或固 定T绘制p ~X图。
二、气液平衡相图 1. 完全互溶双液系统 (1)理想液态混合物的相图 ①理想液态混合物的p -x图
• 假设气体为理想气体。
Hm 1 ln p C R T
g l
p2 H m (T2 T1 ) ln p1 RTT 1 2
g l
Clausius-Clapeyron 方程的积分式
p2 H m (T2 T1 ) ln p1 RTT 1 2
p
p1
液 相 O1 区
* pB
l+g O2
p* A
p2 气相区
A
x1
x2 XB→
B
p -x图
物系点与相点
重要概念
物系点:是整个系统总的状态点。由p和系统总组成XB确定。 相点:是表示平衡系统中每一个相的状态点。由p和平衡各相 组成XB和YB确定。 ③压力为p3,组分B的摩尔分数 为x3,物系点为O3,相点分别 为E和F。 EF叫连接线。
液相和气相的数量借助于力 p 学中的杠杆规则求算,即以物系 点O为支点,支点两边连结线OE和 p OF为力臂,计算液相和气相的物 p* 质的量或质量,这就是杠杆规则。 A 可用于任意两相平衡区。
l
E l+g
O’
O F
* pB
nl EO ng OF
nl OF x f xO ng OE xO xe
气
B XB→
p -x图
理想液态混合物 p~x图
p
* pB
p* A
l+g
液相线 气相线
A
XB
B
p p
* A * B
是纯A的饱和蒸气压 是纯B的饱和蒸气压
②理想液态混合物的T -x图
定压下,将不同组成的理想 T 混合物加热至沸,测得沸点与 TA 气、液相组成的关系,可绘制 出T~x图。 依据两相平衡时T~x的关系, 可绘制出液相线。 依据两相平衡时T~y的关系, 可绘制出气相线。 A X→
p
p3
液 相 区
E O3 F l+g
* pB
p* A
A+B xf p A+B xe
g
x3
l
气相区
A
xe XB→
x3 xf
B
p -x图
落在EF线上所有物系点的对应的液相和气相 组成,都由E点和F点的组成表示。 f*=2-2+1=1 O和O’两个物系的异同
对应的两个相的组成是相同 的,只是数量是多少不同。
具有最低恒沸点的相图可以看作由两个简单的T-x 图的组合。对具有最高、低恒沸点的实际溶液精馏 时,不能将两组分完全分离,其精馏结果可得到一 个纯物质,另一个是恒沸混合物。
组成为X1时:塔顶为恒沸混合物
塔底为纯B 组成为X2时:塔顶为恒沸混合物 塔底为纯A
* B * A
* A
p~xB为直线!
A
XB→
B
由Dalton和Raoult定律
pB pyB p x
* B * A
* B B
* A
p ( p p ) xB p
p
p p p * * pB ( p pA ) yB
p ~ yB
* A * B
1. 自由度 在一个平衡体系中,在不消失旧相
也不产生新相的条件下,在有限的范围
内可以任意改变的独立变量(T、p、xi)的 数目称为自由度,用f表示。
www.theBiblioteka
2. 相律表达式 f =C–P+2 Gibbs相律表达式
条件:相律适用于热力学平衡系统
②实际混合物的p~X图T~X图
正偏差
负偏差
最大正偏差
最大负偏差
最低恒沸点
T2 T1
最大正偏差
O点对应的温度:最低恒沸点 O点对应的组成:恒沸混合物
③ 精馏原理
蒸馏与精馏是分离液体混合物常用的方法,在实验 室和工厂应用很广。 i)简单蒸馏
A
f=2
T
4. Clapeyron 方程
dp H m dT T Vm
条件:纯物质两相平衡
5 Clausius-Clapeyron 方程 在Clapeyron方程基础上加了三个条件: • 只考虑气液或气固两相平衡; • 忽略液体或固体的体积;
* B
液相线
p* A
* pB
气相线
A
XB→
B
①线
液相线 p~xB ②面 液相区 气相区
识 图
气相线p~yB
p
液相区
液相线
p* A
l+g
* pB
气液两相平衡区
气相线
气相区 A XB→ B
③点
p* A 是纯A的饱和蒸气压
* pB 是纯B的饱和蒸气压
p -x图
g
A
xe xo xf B XB→
Xo’
相律分析
在液相区或气相区:C=2, p=1,f*=2-1+1=2,系统有两个 p 自由度,p和组成x可在一定范 围内独立变化而维持单相不变。 p
l 液 E l+g F
* pB
p* A
在气液两相平衡区:C=2, p=2,f*=2-2+1=1,系统只有 一个自由度,p和组成x只有一 个是独立变量,当指定p时, 两相的组成也就一定了。 g A
p* A
液相线
* pB
气相线
从拉乌尔定律。
A
0
0.2
XB→ YB→
0.4 0.6
0.8 1.0
B
p pB p A
p x p x
* B B
* B B * A
* A A
p x p (1 xB )
p 液相线
p* A
* pB
( p p ) xB p
是纯B的饱和蒸气压
TA是纯A的沸点, TB是纯B的沸点。
(2) 实际液态混合物的相图 ①正偏差与负偏差
p
p~XCH3OH pCH3OH*
pCH OH xCH3OH
3
pCH3OH p
