上海海洋大学高数c期末a卷
高等数学期中A考卷及答案海大

专业课原理概述部分一、选择题(每题1分,共5分)1. 微分学的中心概念是()A. 极限B. 导数C. 微分D. 积分2. 函数f(x)在x=a处可导,那么f'(a)等于()A. f(a)的值B. f(x)在x=a处的斜率C. f(a)的极限D. f(a)的平均变化率3.下列函数中,奇函数是()A. f(x) = x²B. f(x) = x³C. f(x) = cos(x)D. f(x) = e^x4. 不定积分∫(1/x)dx的结果是()A. ln|x| + CB. x + CC. 1/x + CD. e^x + C5. 多元函数f(x, y)的偏导数f_x表示()A. 仅对x求导B. 对x和y同时求导C. x和y的乘积求导D. f对x的积分二、判断题(每题1分,共5分)1. 极限存在的充分必要条件是左极限和右极限相等。
()2. 一切初等函数在其定义域内都可导。
()3. 若函数f(x)在区间[a, b]上单调增加,则f'(x)≥0。
()4. 二重积分可以转化为累次积分。
()5. 泰勒公式是麦克劳林公式的推广。
()三、填空题(每题1分,共5分)1. 函数f(x)在点x=a处的极限为______,记作______。
2. 若f(x) = 3x² 5x + 2,则f'(x) =______。
3. 不定积分∫sin(x)dx的结果是______。
4. 二重积分∬D dA表示______的面积。
5. 泰勒公式中,f(n)(a)表示______。
四、简答题(每题2分,共10分)1. 简述导数的定义。
2. 解释什么是函数的极值。
3. 简述定积分的基本思想。
4. 举例说明如何应用微分方程解决实际问题。
5. 简述多元函数求导的基本法则。
五、应用题(每题2分,共10分)1. 求函数f(x) = x²e^x的导数。
2. 计算定积分∫(从0到π) sin(x)dx。
高等数学A(上)期末试卷A卷#.(优选)

........................................... 上海海洋大学试卷(本答卷不准使用计算器)诚信考试承诺书本人郑重承诺:我已阅读且透彻理解了“上海海洋大学学生考场规则”和“上海海洋大学学生违反校纪校规处理规定”,承诺在考试中自觉遵守,如有违反,按有关条款接受处理。
承诺人签名: 日 期:考生姓名: 学号: 专业班名: 驕赛谧矶虑災酈戩辈盞鲰風诨釣训驊況写薮馭鐘掺鹳颡鋪门獄鴇烴龈驴唤寶疡呜饶齋阆燾賜雏壙陈沪谛設缮颊纤怅鴯购嵛闪养蹒躜铀詿邮。
一、选择题(2143'=⨯')1.当0→x 时,函数()csc cot f x x x =-是x 的( )无穷小 A .高阶 B. 低阶 C. 同阶但非等价 D. 等价 2.设()2arcsin(1)x f x x x-=-,则下列说法中错误的是( ) A .0=x ,1=x 都是()x f 的间断点.B .1x =是()x f 的第二类间断点.C . 0x =是()x f 的第二类间断点.D .1=x 是()x f 的第一类可去间断点. 3.设函数)(x f 在),(∞+-∞A .一个极小值点和两个极大值点lk....................................................................xc....................................................................................................................................................................................B .两个极小值点和一个极大值点C .两个极小值点和两个极大值点D .三个极小值点和一个极大值点4.若()xf x e-=,则(ln )f x dx x=⎰( ) 11..ln ..ln A c B x c C c D x cxx++-+-+二、填空题(3618''⨯=)1.微分方程2x y y x =-'在初始条件(1)0y =下的特解为 2.若)(x f 在],[b a 上连续,在),(b a 内可导,则至少存在一点),(b a ∈ξ, 使得 =-)()(a f b f e e成立3.若xe 是)(xf 的原函数,则(ln )xf x dx ⎰= 4.2212_______x x dx --=⎰5.函数220(1)x t yt e dt =-⎰的极大值点为6.401xdxx +∞=+⎰三、计算题(必须有解题过程,否则不给分) (本大题共60分):1. ()4x x 012tan x x cosx lim3 ln 13x →++ (5分) 2. 220ln(1) lim arcsin x x t dtx x-→+⎰(5分)3. 1lim(1)tan2x xx π→- (5分) 4.2211lim()sin x x x →- (5分)lk....................................................................xc....................................................................................................................................................................................5.设函数()1sin ,0,0x x f x xx αβ⎧≠⎪=⎨⎪=⎩,问,αβ分别取何值,有: (1)函数()f x 在0x =处连续;(3分) (2)函数()f x 在0x =处可导;(3分) (3)函数()f x 在0x =处导函数连续。
海大大一上学期(第一学期)高数期末考试题

大一上学期高数期末考试一、单项选择题 (本大题有4小题, 每小题4分, 共16分)1. )(0),sin (cos )( 处有则在设=+=x x x x x f .(A )(0)2f '= (B )(0)1f '=(C )(0)0f '= (D )()f x 不可导.2. )时( ,则当,设133)(11)(3→-=+-=x x x x xx βα.(A )()()x x αβ与是同阶无穷小,但不是等价无穷小; (B )()()x x αβ与是等价无穷小;(C )()x α是比()x β高阶的无穷小; (D )()x β是比()x α高阶的无穷小.3.若()()()02xF x t x f t dt=-⎰,其中()f x 在区间上(1,1)-二阶可导且'>()0f x ,则( ).(A )函数()F x 必在0x =处取得极大值; (B )函数()F x 必在0x =处取得极小值;(C )函数()F x 在0x =处没有极值,但点(0,(0))F 为曲线()y F x =的拐点; (D )函数()F x 在0x =处没有极值,点(0,(0))F 也不是曲线()y F x =的拐点。
4.)()( , )(2)( )(1=+=⎰x f dt t f x x f x f 则是连续函数,且设(A )22x (B )222x +(C )1x - (D )2x +.二、 填空题(本大题有4小题,每小题4分,共16分)5.=+→xx x sin 2)31(lim e 的 六次方 .6.,)(cos 的一个原函数是已知x f xx=⋅⎰x xxx f d cos )(则cos 方x/2x 方 .7.lim(cos cos cos )→∞-+++=22221n n nnnn ππππ -π/2 .8.=-+⎰21212211arcsin -dx xx x π/3 .三、解答题(本大题有5小题,每小题8分,共40分)9. 设函数=()y y x 由方程sin()1x ye xy ++=确定,求'()y x 以及'(0)y .10. .d )1(177x x x x ⎰+-求11. . 求,, 设⎰--⎪⎩⎪⎨⎧≤<-≤=1 32)(1020)(dx x f x x x x xe x f x12.设函数)(x f 连续,=⎰1()()g x f xt dt,且→=0()lim x f x A x ,A 为常数. 求'()g x 并讨论'()g x 在=0x 处的连续性.13. 求微分方程2ln xy y x x '+=满足=-1(1)9y 的解.四、 解答题(本大题10分)14. 已知上半平面内一曲线)0()(≥=x x y y ,过点(,)01,且曲线上任一点M x y (,)00处切线斜率数值上等于此曲线与x 轴、y 轴、直线x x =0所围成面积的2倍与该点纵坐标之和,求此曲线方程.五、解答题(本大题10分)15. 过坐标原点作曲线x y ln =的切线,该切线与曲线x y ln =及x 轴围成平面图形D.(1)求D 的面积A ;(2) 求D 绕直线x = e 旋转一周所得旋转体的体积V .六、证明题(本大题有2小题,每小题4分,共8分)16. 设函数)(x f 在[]0,1上连续且单调递减,证明对任意的[,]∈01q ,1()()≥⎰⎰qf x d x q f x dx.17. 设函数)(x f 在[]π,0上连续,且0)(0=⎰πx d x f ,cos )(0=⎰πdx x x f .证明:在()π,0内至少存在两个不同的点21,ξξ,使.0)()(21==ξξf f (提示:设⎰=xdxx f x F 0)()()解答一、单项选择题(本大题有4小题, 每小题4分, 共16分) 1、D 2、A 3、C 4、C二、填空题(本大题有4小题,每小题4分,共16分)5.6e . 6.cx x +2)cos (21 .7. 2π. 8.3π.三、解答题(本大题有5小题,每小题8分,共40分) 9. 解:方程两边求导 (1)cos()()0x yey xy xy y +''+++=cos()()cos()x y x ye y xy y x e x xy +++'=-+0,0x y ==,(0)1y '=-10. 解:767u x x dx du == 1(1)112()7(1)71u du duu u u u -==-++⎰⎰原式1(ln ||2ln |1|)7u u c =-++ 7712ln ||ln |1|77x x C =-++11.解:10330()xf x dx xe dx ---=+⎰⎰⎰3()x xd e --=-+⎰⎰232cos (1sin )x x xe e d x πθθθ----⎡⎤=--+-=⎣⎦⎰ 令3214e π=--12. 解:由(0)0f =,知(0)0g =。
上海海洋大学有机化学期末试卷A
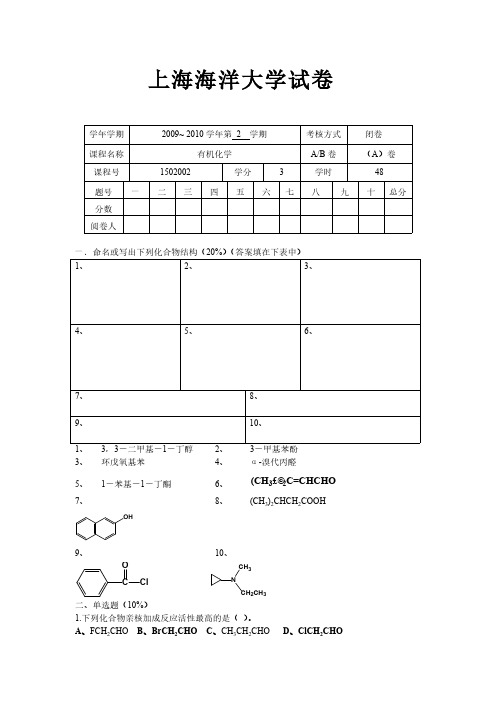
(CH3)2CHCH2COOH
考核方式
A/B 卷
3、
6、
D、ClCH2CHO
学时
闭卷
(A)卷
48
2.下列化合物酸性最强的是 ( )。
3、下列化合物醇解反应活性最高的是( )
A、乙酸乙酯 B、乙酸酐
4、下列化合物酸性最强的是( )
A COOH B COOH C COOH D COOH
NO2
5、下列化合物酸性最强的是( )
3、下列化合物中能发生碘仿反应的是( )
A、CH3CH2COCH3
C、CH3CH2OH
4、下列化合物能与 HCN 进行加成的是 (
B、CH3CH2 CH(CH3)CHO
D、C6H5CHO
A CH3CH2CHO B C6H5CH(OH)CH3 C C6H5COCH3 D 3-戊酮 E C6H5CHO 5、下列化合物能和乙酰乙酸乙酯发生特征反应的是( )
学年学期 课程名称
课程号 题号 一 分数 阅卷人
上海海洋大学试卷
2009~ 2010 学年第 2 学期
1502002
有机化学
学分
3
二 三 四 五 六 七 八 九 十 总分
一.命名或写出下列化合物结构(20%)(答案填在下表中)
1、
4、
7、
9、
2、
5、
1、 3,3-二甲基-1-丁醇 2、 3-甲基苯酚
A 金属钠 B 苯肼 C 银氨溶液 D 饱和溴水
四、用简单化学方法鉴别下列化合物(10%)
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关,通系电1,力过根保管据护线生高0不产中仅工资2艺料22高试2可中卷以资配解料置决试技吊卷术顶要是层求指配,机置对组不电在规气进范设行高备继中进电资行保料空护试载高卷与中问带资题负料2荷试2,下卷而高总且中体可资配保料置障试时2卷,32调需3各控要类试在管验最路;大习对限题设度到备内位进来。行确在调保管整机路使组敷其高设在中过正资程常料1工试中况卷,下安要与全加过,强度并看工且25作尽52下可22都能护可地1关以缩于正小管常故路工障高作高中;中资对资料于料试继试卷电卷连保破接护坏管进范口行围处整,理核或高对者中定对资值某料,些试审异卷核常弯与高扁校中度对资固图料定纸试盒,卷位编工置写况.复进保杂行护设自层备动防与处腐装理跨置,接高尤地中其线资要弯料避曲试免半卷错径调误标试高方中等案资,,料要编试求5写、卷技重电保术要气护交设设装底备备置。4高调、动管中试电作线资高气,敷料中课并设3试资件且、技卷料中拒管术试试调绝路中验卷试动敷包方技作设含案术,技线以来术槽及避、系免管统不架启必等动要多方高项案中方;资式对料,整试为套卷解启突决动然高过停中程机语中。文高因电中此气资,课料电件试力中卷高管电中壁气资薄设料、备试接进卷口行保不调护严试装等工置问作调题并试,且技合进术理行,利过要用关求管运电线行力敷高保设中护技资装术料置。试做线卷到缆技准敷术确设指灵原导活则。。:对对在于于分调差线试动盒过保处程护,中装当高置不中高同资中电料资压试料回卷试路技卷交术调叉问试时题技,,术应作是采为指用调发金试电属人机隔员一板,变进需压行要器隔在组开事在处前发理掌生;握内同图部一纸故线资障槽料时内、,设需强备要电制进回造行路厂外须家部同出电时具源切高高断中中习资资题料料电试试源卷卷,试切线验除缆报从敷告而设与采完相用毕关高,技中要术资进资料行料试检,卷查并主和且要检了保测解护处现装理场置。设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
2022年上海海洋大学数据科学与大数据技术专业《数据库系统原理》科目期末试卷A(有答案)

2022年上海海洋大学数据科学与大数据技术专业《数据库系统原理》科目期末试卷A(有答案)一、填空题1、数据库内的数据是______的,只要有业务发生,数据就会更新,而数据仓库则是______的历史数据,只能定期添加和刷新。
2、数据库恢复是将数据库从______状态恢复到______的功能。
3、关系系统的查询优化既是关系数据库管理系统实现的关键技术,又是关系系统的优点。
因为,用户只要提出______,不必指出 ______。
4、设某数据库中有商品表(商品号,商品名,商品类别,价格)。
现要创建一个视图,该视图包含全部商品类别及每类商品的平均价格。
请补全如下语句: CREATE VIEW V1(商品类别,平均价格)AS SELECT商品类别,_____FROM商品表GROUP BY商品类别;5、关系代数运算中,基本的运算是______________、______________、______________、______________和______________。
6、主题在数据仓库中由一系列实现。
一个主题之下表的划分可按______、______数据所属时间段进行划分,主题在数据仓库中可用______方式进行存储,如果主题存储量大,为了提高处理效率可采用______方式进行存储。
7、在SELECT命令中进行查询,若希望查询的结果不出现重复元组,应在SEL ECT语句中使用______保留字。
8、在RDBMS中,通过某种代价模型计算各种查询的执行代价。
在集中式数据库中,查询的执行开销主要包括______和______代价。
在多用户数据库中,还应考虑查询的内存代价开销。
9、设有关系模式R(A,B,C)和S(E,A,F),若R.A是R的主码,S.A是S的外码,则S.A的值或者等于R中某个元组的主码值,或者______取空值,这是规则,它是通过______和______约束来实现的。
10、有两种基本类型的锁,它们是______和______。
上海海洋大学15-16高数C期末A卷

上海海洋大学试卷(本试卷不准使用计算器)诚信考试承诺书本人郑重承诺:我已阅读且透彻理解了“上海海洋大学学生考场规则”和“上海海洋大学学生违反校纪校规处理规定”,承诺在考试中自觉遵守,如有违反,按有关条款接受处理。
承诺人签名: 日 期:考生姓名: 学号: 专业班名:一、选择题 (每题3分,共21分) 1. 21lim 2n n →+∞⎛⎫++=+ ( ) (A)21; (B) 32; (C) 1; (D) 不存在. 2.设2)(0='x f ,则000(2)()limx f x x f x x∆→-∆-=∆ ( )(A) -2; (B) -4; (C) 1; (D) 不存在.3.若()y f x = 在(,)a b 内满足'''()0,()0,f x f x <> 则曲线()y f x = 在(,)a b 内是 ( )(A) 单调上升且是凹的; (B) 单调下降且是凹的;(C) 单调上升且是凸的; (D) 单调下降且是凸的.4.ln 2xdx =⎰( )(A) ln 22x x x C -+; (B) ln 42xx x C -+;(C) ln 2x x x C -+; (D) ln 2xx x C ++.5.下列等式正确的是( )(A) ()()d f x dx f x =⎰; (B) '()()f x dx f x C =+⎰; (C) ()()df x f x dx =⎰; (D) ()()df x dx f x C dx =+⎰. 6. 曲线24(1)2x y x +=-总共有几条渐近线 ( )(A) 1条; (B) 2条; (C) 3条; (D) 4条.7.设函数111()1xx e f x e -=+,则0x =是 )(x f 的 ( )(A) 可去间断点; (B) 跳跃间断点;(C) 第二类间断点; (D) 连续点.二、计算下列极限 (每题6分,共24分). 1.03sin 3lim (1cos )ln(12)x x x x x →--+ 2. 23(1)lim xt x e dt x -→-⎰3.)lim x xx →+∞4. 3lim 1x x x x +→∞⎛⎫⎪+⎝⎭三、计算下列导数 (共14分).1.(7分) 求曲线221169x y +=在处的切线方程.2.(7分) 设函数)(x f y =由参数方程221t x y t⎧=⎪⎨⎪=-⎩确定,求dx dy ,22dx y d .四、计算下列定积分 (20分).1.(6分)⎰exdx x 1ln 2.(6分)40⎰3.(8分)计算抛物线2y x = 与2y x = 所围成的图形的面积.五、(7分) 设函数()⎩⎨⎧>+≤=1,1,2x b ax x x x f ,为了使函数()x f 在1=x 处连续且可导,b a ,应取什么值?六、某商品的需求量Q 为价格P 的函数22150P Q -=。
上海海洋大学高数下册测试题

题目部分,(卷面共有100题,分,各大题标有题量和总分) 一、选择 (16小题,共分) (2分)[1] (3分)[2]二重积分Dxydxdy ⎰⎰(其中D :0≤y ≤x 2,0≤x ≤1)的值为 (A )16 (B )112 (C )12 (D )14答 ( ) (3分)[3]若区域D 为0≤y ≤x 2,|x |≤2,则2Dxy dxdy =⎰⎰=(A )0; (B )323 (C )643(D )256 答 ( )(3分)[4]设D 1是由ox 轴,oy 轴及直线x +y =1所圈成的有界闭域,f 是区域D :|x |+|y |≤1上的连续函数,则二重积分22(,)Df x y dxdy =⎰⎰__________122(,)D f x ydxdy ⎰⎰(A )2 (B )4 (C )8 (D )12答 ( ) (3分)[5]设f (x ,y )是连续函数,则二次积分011(,)x dx f x y dy -+⎰=(A)112111(,)(,)y dy f x y dx dy f x y dx ---+⎰⎰⎰(B)111(,)y dy f x y dx --⎰⎰(C)11111(,)(,)y dy f x y dx f x y dx ---+⎰⎰⎰(D)21(,)dy f x y dx -⎰⎰答 ( ) (3分)[6] 设函数f (x ,y )在区域D :y 2≤-x ,y ≥x 2上连续,则二重积分(,)Df x y dxdy⎰⎰可化累次积分为(A)201(,)x dx f x y dy -⎰(B)21(,)x dx f x y dy -⎰⎰(C)21(,)y dy f x y dx -⎰⎰(D)21(,)y dy f x y dx ⎰答 ( ) (3分)[7]设f (x ,y )为连续函数,则二次积分21102(,)y dy f x y dx ⎰⎰可交换积分次序为(A)1010(,)(,)dx f x y dy f x y dy +⎰(B)112102(,)(,)(,)dx f x y dy f x y dy f x y dy ++⎰⎰⎰(C)1(,)dx f x y dy ⎰(D)222cos 0sin (cos ,sin )d f r r rdr πθθθθθ⎰⎰答 ( ) (3分)[8]设f (x ,y )为连续函数,则积分212201(,)(,)x xdx f x y dy dx f x y dy -+⎰⎰⎰⎰可交换积分次序为 (A)12201(,)(,)y ydy f x y dx dy f x y dx -+⎰⎰⎰⎰(B)212201(,)(,)x xdy f x y dx dy f x y dx -+⎰⎰⎰⎰(C)120(,)y dy f x y dx -⎰(D)2120(,)xxdy f x y dx -⎰⎰答 ( ) (4分)[9]若区域D 为(x -1)2+y 2≤1,则二重积分(,)Df x y dxdy ⎰⎰化成累次积分为(A)2cos 0(,)d F r dr πθθθ⎰⎰(B)2cos 0(,)d F r dr πθπθθ-⎰⎰(C)2cos 202(,)d F r dr πθπθθ-⎰⎰(D)2cos 202(,)d F r dr πθθθ⎰⎰其中F (r ,θ)=f (r cos θ,r sin θ)r .答 ( )(3分)[10]若区域D 为x 2+y 2≤2x ,则二重积分22()Dx y x y dxdy ++⎰⎰化成累次积分为(A)2cos 202(cos sin )2cos d r rdr πθπθθθθ-+⎰⎰(B)2cos 30(cos sin )d r dr πθθθθ+⎰⎰(C)2cos 3202(cos sin )d r dr πθθθθ+⎰⎰(D)2cos 3222(cos sin )d r dr πθπθθθ-+⎰⎰答 ( ) (4分)[11]设777123[ln()],(),sin ()DDDI x y dxdy I x y dxdy I x y dxdy =+=+=+⎰⎰⎰⎰⎰⎰其中D 是由x =0,y =0,12x y +=,x +y =1所围成的区域,则I 1,I 2,I 3的大小顺序是 (A)I 1<I 2<I 3; (B)I 3<I 2<I 1; (C)I 1<I 3<I 2; (D)I 3<I 1<I 2.答 ( ) (5分)[12]设2211cos sin x y dxdyI x y +≤=++⎰⎰,则I 满足 (A)223I ≤≤ (B)23I ≤≤ (C)12D I ≤≤ (D)10I -≤≤答 ( ) (4分)[13]设12x y +=其中D 是由直线x =0,y =0,及x +y =1所围成的区域,则I 1,I 2,I 3的大小顺序为(A)I 3<I 2<I 1; (B)I 1<I 2<I 3; (C)I 1<I 3<I 2; (D)I 3<I 1<I 2.答 ( ) (3分)[14]设有界闭域D 1与D 2关于oy 轴对称,且D 1∩D 2=,f (x ,y )是定义在D 1∪D 2上的连续函数,则二重积分2(,)Df x y dxdy =⎰⎰(A)122(,)D f x y dxdy ⎰⎰ (B)224(,)D f x y dxdy ⎰⎰(C)124(,)D f x y dxdy ⎰⎰(D)221(,)2D f x y dxdy ⎰⎰ 答 ( )(3分)[15]若区域D 为|x |≤1,|y |≤1,则cos()sin()xy Dxe xy dxdy =⎰⎰ (A) e; (B) e -1; (C) 0; (D)π.答 ( ) (4分)[16]设D :x 2+y 2≤a 2(a >0),当a =___________时,.Dπ=答 ( ) 二、填空 (6小题,共分)(4分)[1]设函数f (x ,y )在有界闭区域D 上有界,把D 任意分成n 个小区域Δσi (i =1,2,…,n ),在每一个小区域Δσi 任意选取一点(ξi ,ηi ),如果极限 01lim(,)niiii f λξησ→=∆∑(其中入是Δσi (i =1,2,…,n )的最大直径)存在,则称此极限值为______________的二重积分。
2022-2023学年上海市SOEC高一上数学期末统考模拟试题含解析

②因为函数 f x x2 ax 1在区间 2, 2 上有零点,所以 f (2) 0 或 f (2) 0,即
4 2a 1 0或4 2a 1 0a 3 或a 3 a R
2
2
③平面 平面 ,平面 平面 , l ,在平面 内取一点 P 作 PA 垂直于平面 与平面 的交线, 作 PB
∴AC= 11 2 ∴SA⊥AC,SB⊥BC,
SC=
22 2
∴球 O 的半径 R= 1 SC 2
=1∴球 O 的表面积 S=4πR2=4π
故选 A
点睛:本题考查球的表面积的求法,合理地作出图形,确定球心,求出球半径是解题的关键
8、C
【解析】由零点存在性定理即可得出选项.
【详解】由函数 f x ex 2x 5为连续函数,
是( ) A. 4
C. 3
B. 3 4
D. 4 3
8.在下列区间中,函数 f(x)=ex+
B.(0,1)
C.(1,2)
D.(2,3)
9.我国东汉末数学家赵爽在《周髀算经》中利用一幅“弦图”给出了勾股定理的证明,后人称其为“赵爽弦图”,它是由
四个全等的直角三角形与一个小正方形拼成的一个大正方形,如图所示.在“赵爽弦图”中,若 BE 2EF ,则 EF ()
17.如图,在 Rt ACB 中,斜边 AB 2 , BC 1,在以 AB 为直径的半圆上有一点 D (不含端点), DAB ,
设△ABD 的面积 S1 , △ACD 的面积 S2 .
(1)若 S1 S2 ,求 ;
(2)令 S S1 S2 ,求 S 的最大值及此时的 .
18.已知
π 2
垂直于平面 与平面的交线 ,则 l PA,l PB, 所以 l 平面
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
上海海洋
大学
试
卷
(本试卷不准使用计算器)
诚信考试承诺书
本人郑重承诺:
我已阅读且透彻理解了“上海海洋大学学生考场规则”和“上海海洋大学学生违反校纪校规处理规定”,承诺在考试中自觉遵守,如有违反,按有关条款接受处理。
承诺人签名:日期:
考生姓名:学号:专业班名:
一、选择题(每题3分,共15分)
1.设A 为常数,0
lim (),x x f x A →=则()f x 在0x 处()
()A 一定有定义()B 一定无定义
()C 有定义且0()f x A =()D 可以有定义也可以无定义
2.若0
lim
2,(3)x x f x →=则0(2)
lim x f x x
→=()
3.函数sin y x =在0x =处是()
()A 连续又可导()B 不连续也不可导 ()C 不连续但可导()D 连续但不可导
4.设()f x 的一个原函数是2,x e -则()f x =()
5
.1
21
(sin )x dx -=⎰()
()A π()
B 2
π
()C 23()D 0
二、填空题(每题3分,共15分).
1.已知函数1
1,1x x y e
-=
-则1x =是它的间断点;
2.设(sin ),y f x =其中f 可导,则dy =;
3.曲线26x y e x x =-+在区间是凹的;
4.sin x dx x '⎛⎫= ⎪⎝⎭
⎰;
5.
曲线y =与直线y x =所围成图形的面积是_____________. 三、计算题(共65分,要有计算过程,否则无分) 1.计算下列极限(每题7分,共14分) (1).0ln(1sin )lim
tan 2x x x
→+;(2).20
0cos lim .tan x
x tdt
x →⎰
2.计算下列导数(共15分).
(1).(7分)设函数()y y x =由方程y e xy e +=所确定,求
x dy
dx
=;
(2).(8分)设,,t t
x te y e -⎧=⎨=⎩求dy dx ,22d y
dx . 3.计算下列定积分(18分).
(1).(6分)320
sin cos d π
ϕϕϕ⎰;(2).(6分)1
2
21
x
e
dx x
⎰
; (3).(6
分)8
3
⎰.
4.(8分)设2,[0,1)
(),[1,2].
x x f x x x ⎧∈=⎨∈⎩求0
()()x x f t dt ϕ=⎰在[0,2]上的表达式,并讨论()x ϕ在(0,2)
内的连续性..
5.(10分)某产品的总成本(万元)的变化率为()1C q '=(万元/百台),总收入(万元)的变化率为产量q (百台)的函数()5R q q '=-(万元/百台). (1)求产量q 为多少时,利润最大?
(2)在上述产量(使利润最大)的基础上再生产100台,利润将减少多少? 四、证明题(共5分)
利用罗尔定理证明拉格朗日中值定理:若函数()f x 在[,]a b 上连续,在(,)a b 内可导,则存在点(,),a b ξ∈使得()()()().f b f a f b a ξ'-=-。
