结力 静定结构的受力分析
合集下载
结构力学第三章静定结构受力分析
MA
0, FP
l 2
YB
l
0,YB
FP 2
()
Fy
0,YA
YB
0,YA
YB
Fp 2
()
例2: 求图示刚架的约束力 q
C
A
ql
l
l
l
B
A
ql
ql
C
XC
YC
FNAB
解:
Fy 0,YC 0
MA
0, ql
l 2
XC
l
0,
XC
1 2
ql()
弹性变形，而附属部分上的荷载可使其自身和基本部分均产生内力和 弹性变形。因此，多跨静定梁的内力计算顺序也可根据作用于结构上 的荷载的传力路线来决定。
40k N
80k N·m
20k N/m
AB
CD
EF
G
H
2m 2m 2m 1m 2m 2m 1m
4m
2m
50构造关系图 40k N
C 20 A B 50
Fy 0,YA YB 2ql 0,YA ql() 3)取AB为隔离体
2)取AC为隔离体
Fy 0, YC YA ql 0
Fx 0, XB X A ql / 2()
l MC 0, X A l ql 2 YB l 0, X A ql / 2()
A
B
C D E FG
1m 1m 2m 2m 1m 1m
A C D E FG B
13 17
26 8
7 15 23 30
结力I-03-2 静定结构受力分析(桁架)1007
x y
NEA
2 2 2 2
1 2 FP 1 2 FP
FNEC FNEC
2 13 3 13
NEA
0 FNEC - 26FP / 2(压) 0 FNEA - 5FP / 2(压)
y
0
5 2 FP / 4
FP/2
5 2 FP / 4
求解对称荷载作用下杆件轴力：
(1)D结点
对称结构、对称荷载：FNDE = FNDF FNDE = FNDF = - FP / 2(压) 2 1 FNDF 2 2 FP 2 0
2 2 2 2
F
y
2 2
FNDE
2 2
(2) E结点
F F F F
FP/2
FP/2
FP/2
FNEA
FP/2
-5FP/2
-FP/2 -FP/2
-5FP/2
D
FNDE
E
FNDF
FNEC
2 2
x
26FP / 2
26FP / 2
(b)
(3) A结点
F
x
FEA FAD 0
FAD 5 2 FP / 4(拉)
23
§3-6 桁架
静定桁架的内力分析方法小结：
40 FN 2 10FP 3(拉)
(2)利用I-I截面截取隔离体BCE分析，求1杆轴力
F
x
FN1 FP 0 FN1 FP (压)
20
§3-6 桁架
4. 联合法 ：同时应用结点法和截面法确定杆件内力的方法。
例3-21 求图示K字型桁架中杆1、杆2的内力。
NEA
2 2 2 2
1 2 FP 1 2 FP
FNEC FNEC
2 13 3 13
NEA
0 FNEC - 26FP / 2(压) 0 FNEA - 5FP / 2(压)
y
0
5 2 FP / 4
FP/2
5 2 FP / 4
求解对称荷载作用下杆件轴力：
(1)D结点
对称结构、对称荷载：FNDE = FNDF FNDE = FNDF = - FP / 2(压) 2 1 FNDF 2 2 FP 2 0
2 2 2 2
F
y
2 2
FNDE
2 2
(2) E结点
F F F F
FP/2
FP/2
FP/2
FNEA
FP/2
-5FP/2
-FP/2 -FP/2
-5FP/2
D
FNDE
E
FNDF
FNEC
2 2
x
26FP / 2
26FP / 2
(b)
(3) A结点
F
x
FEA FAD 0
FAD 5 2 FP / 4(拉)
23
§3-6 桁架
静定桁架的内力分析方法小结：
40 FN 2 10FP 3(拉)
(2)利用I-I截面截取隔离体BCE分析，求1杆轴力
F
x
FN1 FP 0 FN1 FP (压)
20
§3-6 桁架
4. 联合法 ：同时应用结点法和截面法确定杆件内力的方法。
例3-21 求图示K字型桁架中杆1、杆2的内力。
结构力学静定受力分析总论
结构力学
傅向荣
第三章 静定结构的 受力分析
结构受力特点
静定结构总论
(Statically determinate structures general introduction)
基本性质 派生性质 零载法
静定结构基本性质
• 满足全部平衡条件的解答是静定结构的 唯一解答 • 证明的思路：
静定结构是无多余联系的几何不变体系，用刚体虚 位移原理求反力或内力解除约束以“力”代替后，体 系成为单自由度系统，一定能发生与需求“力”对应 的虚位移，因此体系平衡时由主动力的总虚功等于零 一定可以求得“力”的唯一解答。
4. 以单元为对象，对杆端取矩可以求得杆端 剪力，在结构图上利用微分关系作每单元的 剪力图，从而得到结构剪力图。需要指出的 是，剪力图可画在杆轴的任意一侧，但必须 标注正负号。 以未知数个数不超过两个为原则，取结点由平 衡求单元杆端轴力，在结构图上利用微分关 系作每单元的轴力图，作法和剪力图一样， 从而得到结构轴力图。 5. 综上所述，结构力学作内力图顺序为“先 区段叠加作M 图，再由M 图作FQ 图，最后 FQ 作FN图”。需要指出的是，这种作内力 图的顺序对于超静定结构也是适用的。
2F
1.5 Fa 1.5a 2.5a 1.5 F Pa 1.5a 1a 1a
七、图示桁架C杆的内力是
F
。
c
F
a
a
a
a
a
a
八、图示结构A端的弯矩（以下边受拉为正） MAC为： A: -Fl B: Fl C: -2Fl D: 2Fl
F
Fl A
Fl
C
l
l
( D )
_ , N FD _ 4F 0_. 九、图示结构中，N FE _
傅向荣
第三章 静定结构的 受力分析
结构受力特点
静定结构总论
(Statically determinate structures general introduction)
基本性质 派生性质 零载法
静定结构基本性质
• 满足全部平衡条件的解答是静定结构的 唯一解答 • 证明的思路：
静定结构是无多余联系的几何不变体系，用刚体虚 位移原理求反力或内力解除约束以“力”代替后，体 系成为单自由度系统，一定能发生与需求“力”对应 的虚位移，因此体系平衡时由主动力的总虚功等于零 一定可以求得“力”的唯一解答。
4. 以单元为对象，对杆端取矩可以求得杆端 剪力，在结构图上利用微分关系作每单元的 剪力图，从而得到结构剪力图。需要指出的 是，剪力图可画在杆轴的任意一侧，但必须 标注正负号。 以未知数个数不超过两个为原则，取结点由平 衡求单元杆端轴力，在结构图上利用微分关 系作每单元的轴力图，作法和剪力图一样， 从而得到结构轴力图。 5. 综上所述，结构力学作内力图顺序为“先 区段叠加作M 图，再由M 图作FQ 图，最后 FQ 作FN图”。需要指出的是，这种作内力 图的顺序对于超静定结构也是适用的。
2F
1.5 Fa 1.5a 2.5a 1.5 F Pa 1.5a 1a 1a
七、图示桁架C杆的内力是
F
。
c
F
a
a
a
a
a
a
八、图示结构A端的弯矩（以下边受拉为正） MAC为： A: -Fl B: Fl C: -2Fl D: 2Fl
F
Fl A
Fl
C
l
l
( D )
_ , N FD _ 4F 0_. 九、图示结构中，N FE _
结构力学 第3章静定结构的受力分析
图3.5
结构力学
(4)多跨或多层刚架，如图3.6(a)和(b)所示。
2. 规则Ⅱ：两刚片规则
图3.6
【例3.4】计算如图3.7(a)所示三铰刚架的支座反力。 解：去掉支座，代之以反力，得到以整体为研究对象的受力图 ，如图3.7(b)所示。由图知有四个支座反力XA、YA、XB、YB， 即四个未知数，计算步骤如下：
结构力学 3. 三铰拱的受力特性
(1)在竖向荷载作用下，梁没有水平支座反力而拱则有水平推力。 (2)由于推力的存在，三铰拱截面上的弯矩比跨度荷载相同的简 支梁的弯矩小。 (3)在竖向荷载作用下，梁的截面内没有轴力，而拱的截面内 轴力较大，且一般为压力，因此，拱主要受压。 (4)由于拱截面上的应力分布较梁截面上的应力分布均匀，因 此，拱比梁能更有效地发挥材料的作用，可适用于较大的跨 度和较重的荷载。由于拱主要是受压，便于利用抗压性能好 而抗拉性能差的材料。
结构力学 4. 静定平面刚架内力图的绘制
静定平面刚架内力图有弯矩图、剪力图和轴力图。刚架的 内力图是由各杆的内力图组合而成的；而各杆的内力图， 只需求出杆端截面的内力值后，即可按照梁中绘制内力图 的方法画出。 计算和绘制内力图的步骤: (1)计算支座反力 (2)作弯矩图 (3)作剪力图 (4)作轴力图 (5)校核
图3.4
结构力学
3.3 静定平面刚架
1.静定平面刚架的特点及分类
刚架是由梁、柱等直杆组成的具有刚结点的结构，其中全部或 部分结点是刚结点。当组成刚架的各杆的轴线和外力都在同一 平面内，且几何组成符合几何不变无多余约束的组成规则面刚架有：
(1)简支刚架，如图 3.5(a)所示。 (2)悬臂刚架，如图 3.5(b)所示。 (3)三铰刚架，如图 3.5(c)所示。
结构力学 第3章 静定结构的受力分析
4kN· m
4kN· m
2kN· m
四、分段叠加法作弯矩图的方法 1.求支座反力。 2.求控制截面的弯矩值。控制截面包括杆的两端、集中力
作用处（求剪力时要取两侧各一个截面）、力偶作用处两
侧、均布荷载的起点、终点和中点等； 3.分段求作弯矩图。若二控制截面间无外力作用，则连以 直线。若有外力作用，则连直线（基线）后叠加上相应简
F
y
0
FyF (8 4 4 17) 7 kN ( )
（2）选控制截面A、C、D、F并求弯矩值 已知 MA＝0， MF＝0。 取右图AC段为隔离体： A 17kN 1m 1m 8kN
MC
C FQCA
M
C
0
M C 8 1 17 2 0 M C 34 8 26 kN .m (下拉 )
4kN/m F 6kN
20kN
A B
C
9kN 1.5m 1.5m
1m
1.5m
1.5m
1m
3m
对于CE段梁:
M
D
0
FyC
1 3
(10 1.5 6 1)
9 3
3kN ()
F
y
0
FyD 13kN ( )
对于AC段梁:
M
B0Biblioteka FyA 1 3(20 1.5 3 1)
r
F
S
0 1 2 ql sin qx sin 0 l
FNC
FNC q ( x ) sin (0 x l ) 2
3.作内力图
ql2/8 M图
(qlcosθ)/2 FQ 图 (qlsinθ)/2 (qlsinθ)/2 (qlcosθ)/2
考研 结构力学 静定结构的受力分析 PPT
qa
Fy 0 FNCA 2
例3-5 作图示门式刚架的内力图。
解：（1）求支反力
MA 0 MB 0 MC 0 Fx 0
FyB 1.5kN() FyA 4.5kN() FxB 1.384kN() FxA FxB 1.384kN()
(2) 作M图,如图(a)。
(3) 作FQ图,取隔离体如图(d)、(e)。
2 结点法、截面法及其联合应用 图(a)杆AB的杆长l及其水平投影
lx 和竖向投影ly组成一个三角形。
图(b)杆AB的轴力FN及其水平 分量Fx 和竖向分量Fy组成一个三角形
两个三角形是相似的，因而
FN Fx Fy l lx ly
结点法:取桁架结点为隔离体,利用平面汇交力系的两个平 衡条件计算各杆的轴力。轴力为正表示拉力,轴力 为负表示压力。
M
R F
71
7(kN m)
由数学计算:CE段Mmax=36、1kN·m
§3-2 静定多跨梁
公路桥使用的静定多跨梁
计算简图为 梁AB和CD直截了当由支杆固定于基础,是几何不变的—基本部 分 短梁BC依靠基本部分的支撑才能承受荷载保持平衡—附属部分
木檩条构造 静定多跨梁
计算简图
支撑关系
静定多跨梁的组成次序:先固定基本部分,后固定附属部分 静定多跨梁的计算原则:先计算附属部分,后计算基本部分
f1=0，为下撑式平行弦组合结 构，上弦全部为负弯矩。
f1加大时，上弦正弯矩增大， f1=（0.4~0.5)f时,最大正负弯矩 的数值大致相等。
f2=0，为带拉杆的三铰拱式屋 架，上弦全部为正弯矩。
§3-6 三铰拱
拱的特点： 在竖向荷载作用下有水
平反力或称推力，如图(a)。
结构力学静定结构的受力分析课件
计算机辅助设计
利用计算机辅助设计软件，如AutoCAD、Revit等，进行结构的优 化设计。
感谢您的观看
THANKS
01
拓扑优化
在给定荷载和约束条件下，寻求 最优的材料分布和结构形状，以 实现结构的轻量化和高效化。
02
03
04
形状优化
通过改变结构的形状，以实现结 构的性能提升和重量减轻。
计算机辅助优化设计
有限元分析
利用数学方法将结构离散化为有限个单元，通过对单元进行分析， 得到结构的整体性能。
最优化算法
利用最优化算法，如遗传算法、粒子群算法等，对结构进行自动优 化设计。
结构力学静定结构的受力 分析课件
目录
• 静定结构概述 • 静定结构的受力分析 • 静定结构的稳定性分析 • 静定结构的弹性分析 • 静定结构的强度分析 • 静定结构的优化设计
01
静定结构概述
定义与特点
定义
静定结构是指支座或结点位移不 引起内力，仅由外力作用而平衡 的结构。
特点
静定结构的内力只由外力决定， 与结点或支座的位移无关。因此， 静定结构不会有内力产生的次应 力，结构的安全性更高。
静定结构在承受外力时具有较好的稳定性， 因此对于需要承受较大荷载的工程结构，采 用静定结构是较为安全的选择。
02
静定结构的受力分析
力的平衡方程
静力平衡
静定结构在任意平衡位置都满足 力的平衡条件。
力的平衡方程
对于一个具有n个自由度的静定结 构，存在n个独立的力的平衡方程。
独立平衡方程
静定结构中与静力平衡条件对应的 独立方程。
用内力图表示结构内部各点的内 力情况。
03
静定结构的稳定性分析
利用计算机辅助设计软件，如AutoCAD、Revit等，进行结构的优 化设计。
感谢您的观看
THANKS
01
拓扑优化
在给定荷载和约束条件下，寻求 最优的材料分布和结构形状，以 实现结构的轻量化和高效化。
02
03
04
形状优化
通过改变结构的形状，以实现结 构的性能提升和重量减轻。
计算机辅助优化设计
有限元分析
利用数学方法将结构离散化为有限个单元，通过对单元进行分析， 得到结构的整体性能。
最优化算法
利用最优化算法，如遗传算法、粒子群算法等，对结构进行自动优 化设计。
结构力学静定结构的受力 分析课件
目录
• 静定结构概述 • 静定结构的受力分析 • 静定结构的稳定性分析 • 静定结构的弹性分析 • 静定结构的强度分析 • 静定结构的优化设计
01
静定结构概述
定义与特点
定义
静定结构是指支座或结点位移不 引起内力，仅由外力作用而平衡 的结构。
特点
静定结构的内力只由外力决定， 与结点或支座的位移无关。因此， 静定结构不会有内力产生的次应 力，结构的安全性更高。
静定结构在承受外力时具有较好的稳定性， 因此对于需要承受较大荷载的工程结构，采 用静定结构是较为安全的选择。
02
静定结构的受力分析
力的平衡方程
静力平衡
静定结构在任意平衡位置都满足 力的平衡条件。
力的平衡方程
对于一个具有n个自由度的静定结 构，存在n个独立的力的平衡方程。
独立平衡方程
静定结构中与静力平衡条件对应的 独立方程。
用内力图表示结构内部各点的内 力情况。
03
静定结构的稳定性分析
结构力学静定结构受力分析PPT课件
B
4kN·m
4kN
8kN·m
2kN/m
3m
3m
（1）集中荷载作用下
3m
3m
（1）悬臂段分布荷载作用下
2kN·m
4kN·m
6kN·m
（2）集中力偶作用下
4kN·m
2kN·m
（3）叠加得弯矩图
4kN·m
（2）跨中集中力偶作用下
4kN·m
4kN·m
（3）叠加得弯矩图
6kN·m
4kN·m
4kN·m
第9页/共97页 2kN·m
反力求出后，进行附属部分的内力分析、画内力图，然后将支座 C 的反力反
向加在基本部分AC 的C 端作为荷载，再进行基本部分的内力分析和画内力图，
将两部分的弯矩图和剪力图分别相第连12即页得/共整97个页梁的弯矩图和剪力图 。
分析下列多跨连续梁结构几何构造关系，并确定内力计算顺序。
F
q
AB
CD
F
AB
例：利用叠加法求作图示梁结构的内力图。
[分析] 该梁为简支梁，弯矩控制截 面为：C、D、F、G 叠加法求作弯矩图的关键是 计算控制截面位置的弯矩值
解： （1）先计算支座反力
（2）求控制截面弯矩值
A
FP=8kN
q=4 kN/m
CD E
m=16kN.m B
FG
1m 1m 2m 2m 1m 1m
RA 17kN
m
ql
l
2
m 2
l
ql 2
Fpl 4
1、集中荷载作用点 M图有一尖角，荷载向 下尖角亦向下； FQ 图有一突变，荷载 向下突变亦向下。
m 2
2、集中力矩作用点 M图有一突变，力矩 为顺时针向下突变； FQ 图没有变化。
4kN·m
4kN
8kN·m
2kN/m
3m
3m
（1）集中荷载作用下
3m
3m
（1）悬臂段分布荷载作用下
2kN·m
4kN·m
6kN·m
（2）集中力偶作用下
4kN·m
2kN·m
（3）叠加得弯矩图
4kN·m
（2）跨中集中力偶作用下
4kN·m
4kN·m
（3）叠加得弯矩图
6kN·m
4kN·m
4kN·m
第9页/共97页 2kN·m
反力求出后，进行附属部分的内力分析、画内力图，然后将支座 C 的反力反
向加在基本部分AC 的C 端作为荷载，再进行基本部分的内力分析和画内力图，
将两部分的弯矩图和剪力图分别相第连12即页得/共整97个页梁的弯矩图和剪力图 。
分析下列多跨连续梁结构几何构造关系，并确定内力计算顺序。
F
q
AB
CD
F
AB
例：利用叠加法求作图示梁结构的内力图。
[分析] 该梁为简支梁，弯矩控制截 面为：C、D、F、G 叠加法求作弯矩图的关键是 计算控制截面位置的弯矩值
解： （1）先计算支座反力
（2）求控制截面弯矩值
A
FP=8kN
q=4 kN/m
CD E
m=16kN.m B
FG
1m 1m 2m 2m 1m 1m
RA 17kN
m
ql
l
2
m 2
l
ql 2
Fpl 4
1、集中荷载作用点 M图有一尖角，荷载向 下尖角亦向下； FQ 图有一突变，荷载 向下突变亦向下。
m 2
2、集中力矩作用点 M图有一突变，力矩 为顺时针向下突变； FQ 图没有变化。
结构力学第三章静定结构的受力分析
例2： MA
A
MA
FP L/2 L/2
FP
MB
B 结论
把两头的弯矩标在杆
端，并连以直线，然
后在直线上叠加上由
节间荷载单独作用在
简支梁上时的弯矩图
MB MA
FPL/4
FPL/4
2020年5月29日星期五7时56分M25秒B
§3-1 梁的内力计算的回顾
3）画剪力图
要求杆件上某点的剪力，通常是以弯矩图为
C
B FQBA
由： MA 0 FQBA (81 26) 2 9kN
也可由： Y 0 FQCA 17 8 9kN
剪力图要注意以下问题： ▲ 集中力处剪力有突变； ▲ 没有荷载的节间剪力是常数； ▲ 均布荷载作用的节间剪力是斜线； ▲ 集中力矩作用的节间剪力是常数。
2020年5月29日星期五7时56分25秒
L/2
M/2
FPL/4
L/2
M
M/2
2020年L5/月229日星期五L7/时2 56分25秒
§3-1 梁的内力计算的回顾
2）用叠加法画简支梁在几种简单荷载共同作用下 的弯矩图
例1： MA
q
MB
q
A
B=
qL2/8
MA
MB
+
+
MA
=A
qL2/8
MB
B
2020年5月29日星期五7时56分25秒
§3-1 梁的内力计算的回顾
2020年5月29日星期五7时56分25秒
§3-1 梁的内力计算的回顾
正 MAB
杆端内力
FNAB
A端 FQAB
MBA 正
B端
FNBA
FQBA
静定结构受力分析
详细描述
剪切位移的大小与外力的大小和结构的抗剪 刚度有关。在静定结构中，剪切位移可以通 过测量结构上两点之间的相对位移来计算。
影响因素
影响剪切位移的因素包括外力的大小 、结构的剪切面面积、材料的剪切模 量和截面的剪切面面积等。
扭转变位移计算
扭转变位移是由于结构受到扭矩作用而产生的扭转变 形，导致结构在扭转变形方向上发生相对位移。
ቤተ መጻሕፍቲ ባይዱ
剪切内力计算
剪切内力
由于剪切力作用产生的内力。
剪切力的计算
根据外力的大小和方向，通过 力的平衡条件计算剪切力。
剪切变形的特点
剪切变形主要表现为相邻部分之 间的相对错动，其变形量与材料 的性质和剪切力的大小有关。
剪切承载能力的分析
根据材料的剪切强度指标，分 析结构的剪切承载能力，确保
结构的安全性。
扭转变形内力计算
弯曲位移计算
总结词
弯曲位移是由于结构受到垂直于轴线的力而产生的弯曲变 形，导致结构轴线发生弯曲。
公式
弯曲位移的公式通常为 Δ=F*L^2/(4*EI)，其中 F 是外力 ，L 是跨度，E 是材料的弹性模量，I 是截面的惯性矩。
详细描述
弯曲位移通常通过测量结构上两点之间的直线距离变化来 计算。在静定结构中，弯曲位移的大小与外力的大小和结 构的抗弯刚度有关。
02
它涉及到结构力学、材料力学、 弹性力学等多个学科领域，是工 程设计和施工中的基础性工作。
静定结构的定义与特点
静定结构是指在没有外力作用下，能够 保持平衡状态的结构。
静定结构的特点包括：没有多余的约束 ，所有约束都是必要的；在受到外力作 用时，只产生与外力等值反向的位移； 在去掉约束后，不会产生多余的自由度
结构力学 静定结构的受力分析
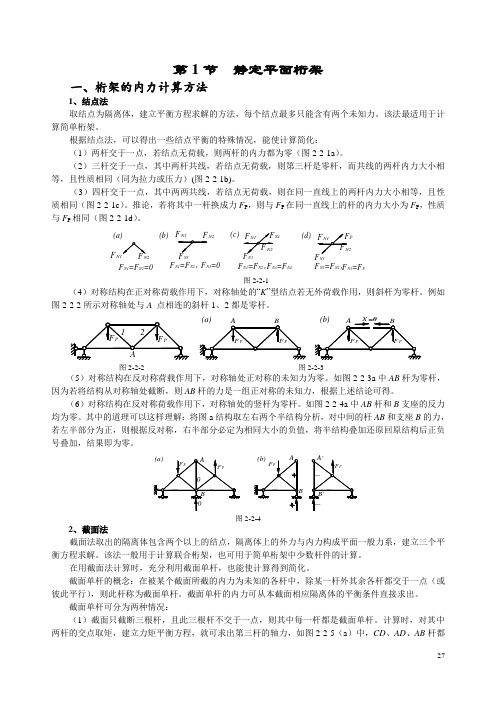
第1节 静定平面桁架一、桁架的内力计算方法1、结点法取结点为隔离体，建立平衡方程求解的方法，每个结点最多只能含有两个未知力。
该法最适用于计算简单桁架。
根据结点法，可以得出一些结点平衡的特殊情况，能使计算简化：（1）两杆交于一点，若结点无荷载，则两杆的内力都为零（图2-2-1a ）。
（2）三杆交于一点，其中两杆共线，若结点无荷载，则第三杆是零杆，而共线的两杆内力大小相等，且性质相同（同为拉力或压力）(图2-2-1b)。
（3）四杆交于一点，其中两两共线，若结点无荷载，则在同一直线上的两杆内力大小相等，且性质相同（图2-2-1c ）。
推论，若将其中一杆换成力F P ，则与F P 在同一直线上的杆的内力大小为F P ，性质与F P 相同（图2-2-1d ）。
F N3F N3=0F N1=F N2=0F N3=F N4(a)(b)(c)F N4(d)F N3=F PF PN1F F N2F N1F N2F N1F N2F N1F N2F N3F N3F N1=F N2，F N1=F N2，F N1=F N2，图2-2-1（4）对称结构在正对称荷载作用下，对称轴处的“K ”型结点若无外荷载作用，则斜杆为零杆。
例如图2-2-2所示对称轴处与A 点相连的斜杆1、2都是零杆。
1A2F PF PAF PF PBF PF PBA(b)(a)X =0图2-2-2 图2-2-3（5）对称结构在反对称荷载作用下，对称轴处正对称的未知力为零。
如图2-2-3a 中AB 杆为零杆，因为若将结构从对称轴处截断，则AB 杆的力是一组正对称的未知力，根据上述结论可得。
（6）对称结构在反对称荷载作用下，对称轴处的竖杆为零杆。
如图2-2-4a 中AB 杆和B 支座的反力均为零。
其中的道理可以这样理解：将图a 结构取左右两个半结构分析，对中间的杆AB 和支座B 的力，若左半部分为正，则根据反对称，右半部分必定为相同大小的负值，将半结构叠加还原回原结构后正负号叠加，结果即为零。
结构力学第三章.静定结构的受力分析
r
Fr 0
F qx cos ql cos 0
QC
2
F q( l x) cos (0 x l)
QC
2
FS 0
FNC
1 2
ql sin
qx sin
0
FNC
q( l 2
x) sin
(0 x l)
28
斜杆上的竖向分布荷载可以分解为垂直杆轴 和沿杆轴方向的分布荷载，如下图示。
ql
θ qlcosθ
A
B 3kN
13kN
9kN
14kN
1.5m 1.5m 1m 1.5m 1.5m 1m
3m
对于AC段梁:
MB 0
1
27
FyA
(20 1.5 3
31)
3
9kN()
Fy 0 FyB 14kN()
40
3）内力图如下图示
6
A
3C
B
DE
4.5
13.5
M图（kN·m）
9
6
3
BC
DE
7 11
FQ图（kN）
从静力分析的观点看，静定结构的内力可以由 三个平衡方程唯一确定。
Fx 0 Fy 0 M 0
平衡方程为：
或：
MA 0 MB 0 Mc 0
（A,B,C不在同一直线上）
2
一、隔离体
1. 内力正负号
M
M FQ
FQ FN
FN
M
M FQ
FQ FN
FN
在结构力学中，要求弯矩图画在杆件受拉边， 不注正负号,剪力图和轴力图要注明正负号。上 图中弯矩正负号的规定通常用于梁。
第三章 静定结构的受力分析
结构力学静定结构的受力分析
结构力学静定结构的受力分析静定结构是指在外载荷作用下，结构的每个部分均处于力学平衡状态，即结构的受力分析可以根据平衡方程求解。
静定结构的受力分析是结构力学中的重要内容，对于工程设计和分析非常关键。
在静定结构的受力分析中，需要根据结构的几何形状和支座条件，确定结构的受力模式，并使用平衡方程进行计算。
下面将介绍静定结构受力分析的基本步骤。
首先，需要对结构进行几何建模，确定结构的几何形状。
这包括确定结构的几何尺寸、节点位置和材料特性等。
几何建模是进行受力分析的前提，对于一些复杂的结构，可以使用计算机辅助设计软件进行建模。
其次，根据结构的边界条件，确定结构的支座情况。
支座条件包括固定支座、铰接支座和滑动支座等。
支座的选择是根据结构的实际情况及设计要求来确定的。
然后，根据结构的受力模式，建立受力体系，并采用平衡方程进行受力计算。
受力体系包括结构的梁、柱等构件以及它们之间的关系。
平衡方程是基于结构处于力学平衡的原理，其中包括转矩平衡和力平衡等方程。
通过平衡方程，可以得到结构中各个部分的受力大小和方向。
接着，根据受力计算的结果，进行受力校核。
受力校核是为了验证结构设计的合理性，包括确定结构中的应力、变形和稳定性等。
校核的依据是结构的设计规范和要求，以保证结构的安全可靠。
最后，对受力计算的结果进行结果的处理和分析。
这包括对受力大小和方向的合理性进行评估，以及根据受力情况进行结构优化设计。
在静定结构的受力分析过程中，需要注意以下几个问题。
首先，要合理选择受力模式和支座条件，以确保受力计算的有效性。
其次，要注意受力计算的精度和误差控制，以保证计算结果的准确性。
最后，在进行受力校核时，要注意结构的强度、刚度和稳定性等方面的要求。
总之，静定结构的受力分析是结构力学中的重要内容，对于工程设计和分析非常关键。
通过合理的几何建模、选择支座条件，建立受力体系并应用平衡方程进行受力计算，可以得到结构受力的大小和方向，为结构的设计和分析提供依据。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
C
Ⅰ
C
2
3
A
Ⅰ1
D
30 kN
30 kN 30 kN
FA
6×3＝18 m
4m
B
FB
50 kN
30 kN
FN2 FN 1
支座反力： FA 50kN
截面Ⅰ-Ⅰ： MC 0
Fy 0
结点D：
Fy 0
FB 40kN
50 3 FN1 4 37.5kN
FN 2 (50 30)
13 36.06kN 2
FP
FP
C
FN1
52 1
0
FN2 a
FN 4 2.75FP
Fx 0 FN1 FN 4 Fx3 Fx2 0
FN1 (2.75FP 0.75FP 0.5FP ) 1.5FP (压)
00 A
FN3 a
D FN4
2.5FP a
a
§3-5 组合结构
钢筋混凝土
Байду номын сангаас
钢筋混凝土
型钢
型钢
组合结构是指结构中既有梁式杆，又有只受轴力作用的二力杆。梁式杆的 任一截面有弯矩、剪力和轴力作用。在用截面法取隔离体时，不能随意切断 梁式杆，可以切断二力杆，也可以拆开铰结点，如下图示。
⑵ 由图中(b)所示隔离体受力图的平衡方程求轴力
MD 0
FNIJ
(
2 3
4.5)
20
6
8
3
0
MA 0 FNDI 6 83 0 FNDI 4kN
1
2
FNIJ 32kN
Fx 0
FxCD 32 0
FxCD 32kN
2.236 FNCD 2 (32) 35.78kN
联合应用练习3-5.1：试求图示静定桁架中1、2、3 杆的轴力。
例题5-3.4：试求(a) 图示静定桁架中CD、DI、I J 杆的轴力。
8kN
(a)
8kN E
8kN
(b)
8kN D
F 8kN
8kN FNCD
4.5 m
C
G
C
A
H
I
J
BA
K
L
H
3m 3m 3m 3m 3m 3m
FRA
FRB 20kN
FNDI I FNIJ
解: ⑴ 求支座反力： FRA FRB 20kN
Fy2 FP 0 Fy2 FP Fx2 0.5FP
FP
FP
FN 2 FP
5 2
1.118FP (压）
52
⑷ 求轴力FN3 。取截面 I－I 以左为隔离体： 1
C
FN1
0
FN2 a
Fy 0 Fy3 Fy2 2FP 2.5FP 0
00 A
FN3 a
Fy3 1.5FP, Fx3 Fy3 / 2 0.75FP
D FN4
l FN 3 Fy3 ly 1.5FP
5 2
1.68FP (压)
2.5FP
a
a
⑸ 求轴力FN1、FN4 。 取截面 I－I 以左为隔离体：
MC 0 FN 4 2a 2.5FP 2a FP a 0.75FP 2a 0
FN 4
5.5FPa 2a
2.75FP (拉)
Q Fx2 0.5FP , Fx3 0.75FP ,
⑶ 避免使用三角函数：
FN
l
ly
FN Fy
FN
lx
Fx
FN Fy Fx l ly lx
FN
l ly
Fy
FN
l lx
Fx
桁架中内力为零的杆件称为零杆。
D
C
7
10
4
1
8
2
5
9
11
6
3
1、两杆汇交，结点 上无荷载作用时， 该两杆都为零杆。
2、三杆汇交，结点 上无荷载作用时， 如果其中两杆在一 直线上，则另一杆 为零杆。
5 (20) 10 2
5 22.36kN (压)
Fy 0 FyDC 30 20 FyDF 0
(FyDF 10kN )
5 1
2
FyDC 30 20 10 20kN
FNDC FyDC (l / ly ) 20( 5 /1) 44.72kN (压)
20kN
结点C
Fy 0
FNCF 20 40 0 FNCF 20kN (拉)
FxAD
lx ly
FyAD
2 (30) 1
60kN
FNAD 5 (30) 67.08kN （压）
Fx 0, FNAE FxAD 60kN
结点E Fx 0, FNEF 60kN (拉)
20kN C
20kN
20
F 2m
G 0 H
2m
B 30kN
5 1
2A
30kN
FyAD
FNAD FxAD
FN 3
30
5 4
37.5kN
例3-4-3 求图示静定桁架中轴力FN1、FN2、FN3、FN4 。
解：⑴ 本题为对称结构对称荷载。
FP
FP I FP
FP
FP
⑵ 零杆如图示。
C1 E
⑶ 求轴力FN2。
1
02
0
a
结点C
FP
52
C
00
FN1
A
3
D4
Fy 0 FN2
I
2.5FP a
a
aa
00
a
B
a
a 2.5FP
20 5
C 20 5
FNCF
2、截面法
在桁架中将待求轴力的杆件连同有关杆件切断，选受力较少的部分为隔 离体，其上各力组成平面一般力系，其平衡条件为：
Fx 0
FP1
Fy 0 M 0
FP2 FN
1
1
2
M D 0 FN1
A FP1
C
D
B
FP2 FN1
2 FN2 M C 0 FN 2
A
C
理想桁架：⑴ 桁架的结点都是光滑无摩擦的铰结点； ⑵ 各杆的轴线都是直线，并通过铰的中心； ⑶ 荷载和支座反力都作用在结点上
实际桁架：主应力、次应力
桁架的分类（按几何组成）
⑴ 简单桁架
⑵ 联合桁架
⑶ 复杂桁架
按空间形式可分为:
平面桁架
空间桁架
组成桁架的所有杆件轴线 都在同一平面内
2-5 平面静定桁架
A
B
例3-5.2：用结点法求图示桁架中各杆轴力。
解：(1) 支座反力 FyA= FyB = 30kN (↑) FxA=0 (2) 判断零杆 见图中标注。 (3)求各杆轴力
20kN
D
A
0
60 E 60
2m
2m
30kN
取结点隔离体顺序为：A、E、D、C。
结构对称，荷载对称，只需计算半边结构。
结点A
Fy 0, FyAD 30kN
A
FP
B
E
C
FP
FxB B
E
C
FyB
FNED
组成桁架的杆件轴线 不在同一平面内
2、计算桁架内力的方法
1、结点法
结点上各力组成平面汇交力系，其平衡条件为：
Fx 0
Fy 0
分析时的注意事项： ⑴ 结点受力图上，已知力按实际方向
FN1
画，未知轴力先假设为拉力 （箭头背离结
点）画出。
FP
FN 2 FN 3
⑵ 尽量建立独立方程（一个方程只含一个未知量）；
FNAE
60kN 0 FNEF E
1m 1m
结点D
将FNDF延伸到F结点分解为FxDF 及FyDF
MC 0 FxDF 2 20 2 0
FxDF 20kN
A
FyDF
1 (20) 2
10kN
20kN FyDC FNDC C
30 5 D
FxDC
FNDF F
4m
FyDF
2m
FxDF FNDF
FNDF