材料力学第8章组合变形及连接部分的计算习题解
《材料力学》第八章课后习题参考答案

解题方法与技巧归纳
受力分析
在解题前首先要对物体进行受力分析, 明确各力的大小和方向,以便后续进 行应力和应变的计算。
图形结合
对于一些复杂的力学问题,可以画出 相应的示意图或变形图,帮助理解和 分析问题。
公式应用
熟练掌握材料力学的相关公式,能够 准确应用公式进行计算和分析。
检查结果
在解题完成后,要对结果进行检查和 验证,确保答案的正确性和合理性。
压杆稳定
探讨细长压杆在压缩载荷作用下的稳定性问题。
解题方法与技巧
准确理解题意
仔细审题,明确题目要求和考查的知识点。
选择合适的公式
根据题目类型和所给条件,选用相应的公式 进行计算。
注意单位换算
在计算过程中,要注意各物理量的单位换算, 确保计算结果的准确性。
检查答案合理性
得出答案后,要检查其是否符合实际情况和 物理规律,避免出现错误。
相关题型拓展与延伸
组合变形问题
超静定问题
涉及多种基本变形的组合,如弯曲与扭转 的组合、拉伸与压缩的组合等,需要综合 运用所学知识进行分析和计算。
超静定结构是指未知力数目多于静力平衡 方程数目的结构,需要通过变形协调条件 或力法、位移法等方法进行求解。
稳定性问题
疲劳强度问题
研究细长压杆在压力作用下的稳定性问题 ,需要考虑压杆的临界力和失稳形式等因 素。
研究材料在交变应力作用下的疲劳破坏行为 ,需要了解疲劳极限、疲劳寿命等概念和计 算方法。
THANKS FOR WATCHING
感谢您的观看
重点知识点回顾
材料的力学性质
包括弹性、塑性、强度、硬度等基本概念和 性质。
杆件的拉伸与压缩
涉及杆件在拉伸和压缩状态下的应力、应变及 变形分析。
材料力学(I)第八章 组合变形及连接部分的计算

同,故可将同一截面上的弯矩Mz和My按矢量相加。 例如,B截面上的弯矩
sb
12
M max Fl 。 W 4W
材 料 力 学 Ⅰ 电 子 教 案
第八章 组合变形及连接部分的计算
在FN 和Mmax共同作用下,危险 截面上正应力沿高度的变化随sb和st
ห้องสมุดไป่ตู้
的值的相对大小可能有图d ,e ,f 三种
情况。危险截面上的最大正应力是拉 应力:
s t ,max
Ft Fl A 4W
可见此杆产生弯一压组合变形。现按大刚度杆来计算应力。
15
材 料 力 学 Ⅰ 电 子 教 案
第八章 组合变形及连接部分的计算
2. AC杆危险截面m-m上的最大拉应力st,max和最大压应力
sc,max分别在下边缘f点处和上边缘g点处(图b):
s t ,max
F M FN M max 或 s c ,max N max A W A W
强度条件为
26
s r 3 [s ] 或
s r 4 [s ]
材 料 力 学 Ⅰ 电 子 教 案
第八章 组合变形及连接部分的计算
究竟按哪个强度理论计算相当应力,在不同设计规范中并不
一致。注意到发生扭-弯变形的圆截面杆,其危险截面上危 险点处:
M W
s
T T Wp 2W
2 2
为便于工程应用,将上式代入式(a),(b)可得:
(a)
3. 根据钢管的横截面尺寸算得:
π 2 [ D ( D 2d ) 2 ] 4 40.8 10 4 m 2 π I [ D 4 ( D 2d ) 4 ] 64 868108 m 4 I W 124 10 6 m3 D/2 A
蔡中兵《材料力学》8组合变形及连接部分的计算

具有双对称截 面的梁,它在任何 一个纵向对称面内 弯曲时均为平面弯 曲。
故具有双对称截面的梁在两个纵向对称面内同时承受横向 外力作用时,在线弹性且小变形情况下,可以分别按平面弯曲 计算每一弯曲情况下横截面上的应力和位移,然后叠加。
盐城工学院力学课程组
材料力学
mechanics of materials
x
P
y B
盐城工学院力学课程组
材料力学
mechanics of materials
四、处理组合变形的基本方法
1.外力分析
将外力简化并沿主惯性轴分解,将组合变形分解为基本变形, 使之每个力(或力偶)对应一种基本变形
2.内力分析 求每个外力分量对应的内力方程和内力图,确定危险截面.分
别计算在每一种基本变形下构件的应力和变形
两相互垂直平面内弯曲时的应力计算
F2 a m
z F1 C(y,z)
O
z
my
y
x
m z
O Mz
My m y
在集中力F1 、 F2 作用下(双对称截面梁在水
平和垂直两纵向对称平面内同时受横向外力作用),
梁将分别在水平纵对称面(Oxz)和铅垂纵对称面
(Oxy)内发生对称弯曲。
在梁的任意横截面m-m上,F1 、 F2引起的弯矩为
M y F1 x,
M z F2 ( x a)
盐城工学院力学课程组
材料力学
mechanics of materials
F2 m
a
z F1 C(y,z)
O
z
my
y
x
m z
O Mz
My m y
在F2 单独作用下,梁在竖直平面内发生平面弯曲, z轴为中性轴。
第八章-组合变形及连接部分的计算-习题选解.docx
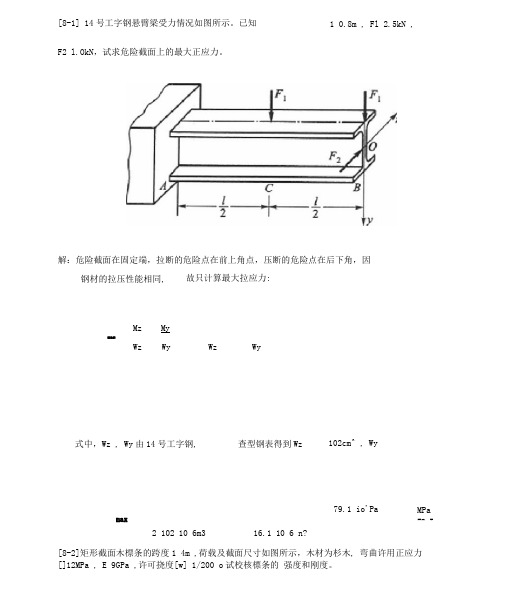
[8-1] 14号工字钢悬臂梁受力情况如图所示。
已知F2 l.OkN,试求危险截面上的最大正应力。
解:危险截面在固定端,拉断的危险点在前上角点,压断的危险点在后下角,因[8-2]矩形截面木標条的跨度1 4m ,荷载及截面尺寸如图所示,木材为杉木, 弯曲许用正应力[]12MPa , E 9GPa ,许可挠度[w] 1/200 o试校核標条的强度和刚度。
1 0.8m , Fl 2.5kN ,钢材的拉压性能相同, 故只计算最大拉应力:maxMz MyWz Wy Wz Wy式中,Wz , Wy由14号工字钢, 查型钢表得到Wz 102cm^ , Wymax79.1 io'Pa MPa79 J2 102 10 6m3 16.1 10 6 n?■ . , ■ l ・6kN/m ________A 戈HHluq习题8解:(1)受力分析COS1.6 cos26° 34 1.431(/ kN mq z q sin 1.6 sin26°340.716( kN/m)(2)内力分析My .max4qz 1 81 2-q yl 2 8(3)应力分析Mz.max-4 0.716 8-1 1.432 84 2 1.432(kN m) 4? 2.864(kN m) 最大的拉应力出现在跨中截面的右上角点, 最大压应力出现在左下角点。
M y ・ maxz.maxmax式中,160 11026322667 mm?maxWz110 16O 26469333mm^1.432 1()6 N mm2.86425 心隔(4)强度分析 因为max(5)变形分析322667 mm?469333mm310.54MPa , [ ] 12MPa ,即max[所以杉木的强度足够。
最大挠度出现在跨中,查表得:■1-60-1-1^ 17746667 (mn?)12(6)刚度分析 12屮一37546667 mm^12Wcy5qyl4 5 1.431N/mm 4000^ mm^ 384EIz 384 9 1()3 N/mn? 37546667mm^14.12mmwcz5qzl^ 5 0.716N/mm 400()4 mn? 384EIy384 9103 N/mm217746667mm° 14.94.mm (Wc/ \i4.12 214.94220,56(mm)式中,ly12因为WmaxWc 20・56(mm) , [ w]400020(mm),即 Wmax [w],200 200 所以,从理论上讲,变形过大,不符合刚度要求。
材料力学第八章组合变形及连接部分的计算

许可压力为F 45000N 45kN
二、偏心拉伸(压缩)
1、单向偏心拉伸(压缩)
eF
F M Fe
A
F M Fe
FN Fey
A IZ
FN M Fe
z B y
F
A
B
e
F
M Fe
单向偏心压缩时,距偏心力较近的一侧边缘总是产生压应力, 而最大正应力总是发生在距偏心力较远的另一侧,其值可能是拉 应力,也可能是压应力.
安全
例题8
传动轴左端的轮子由电机带动,传入的扭转力偶矩
Me=300N.m。两轴承中间的齿轮半径R=200mm,径向啮合力 F1=1400N,轴的材料许用应力〔σ〕=100MPa。试按第三强 度理论设计轴的直径d。
300N.m 1400N
300N.m
1500N
150
200
§8–1 概 述
一、组合变形 :由两种或两种以上基本变形组合的情况。
P
P z
R
x
M
y
P
P q
hg
水坝
屋架传来的压力 吊车传来的压力
自重 风 力
组合变形工程实例
(立柱)压弯组合变形
10-1
组合变形工程实例
拉弯组合变形
组合变形工程实例
(轴)弯扭组合变形
工程实例
(轴)拉伸、弯曲、剪切和扭转的组合变形
z0 0 y0 0
ay
yo
iz2 ey
az
zo
i
2 y
ez
中性轴
截面核心
y
F (ey , ez )
z
求直径为D的圆截面的截面核心.
第8章组合变形及连接部分的计算(答案)

第8章组合变形及连接部分的计算(答案)8.1梁的截⾯为2100100mm ?的正⽅形,若kN P30=。
试作轴⼒解:求得约束反⼒24Ax F KN =,9Ay F KN =,9B F KN =为压弯组合变形,弯矩图、轴⼒图如右图所⽰可知危险截⾯为C 截⾯最⼤拉应⼒maxmax 67.5ZM MPa W σ== 最⼤压应⼒max max69.9N Z M FMPa W Aσ=+=8.2若轴向受压正⽅形截⾯短柱的中间开⼀切槽,其⾯积为原来⾯积的⼀半,问最⼤压应⼒增⼤⼏倍?解:如图,挖槽后为压弯组合变形挖槽前最⼤压应⼒挖槽后最⼤压应⼒22222286/)2/(4/2/a P a a Pa a P W M A N c =+=+=σ8//82212==a P a P c c σσ211a P A N c ==σ8.3外悬式起重机,由矩形梁AB (2=bh尺⼨。
解:吊车位于梁中部的时候最危险,受⼒如图解得BC F P =,2Ax F P =,2Ay P F =梁为压弯组合变形,危险截⾯为梁中N F =压),4PL M =(上压下拉)[]max4NZ F PL W A σσ=+≤,代⼊()226Z b b W =,A bh =,由2h b = 解得125b mm =, 250h mm =8.4图⽰为⼀⽪带轮轴(1T 、2T 与3T 相互垂直)。
已知1T 和2T 均为kN 5.1,1、2轮的直径均为mm 300,3轮的直径为mm 450,轴的直径为mm 60。
若M P a 80][=σ,试按第三强度理论校核该轴。
解:由已知条件解得32T KN = 内⼒图如右:最⼤弯矩所在截⾯可能为:1C M KN m ==?1.2D M KN m =?故危险截⾯为D 截⾯32T KN =由第三强度理论[]360r MPa σσ==故安全38.5铁道路标圆信号板装在外径mm D 60=的空⼼圆柱上,若信号板上所受的最⼤风载2/2m kN p =,MPa 60][=σ,试按第三强度理论选择空⼼柱的厚度。
材料力学第八章组合变形及连接部分的计算

二、叠加原理
构件在小变形和服从胡克定律的条件下,力 的独立性原理是成立的。即所有载荷作用下的内 力、应力、应变等是各个单独载荷作用下的值的 叠加。
解决组合变形的基本方法是将其分解为几种基 本变形;分别考虑各个基本变形时构件的内力、应 力、应变等;最后进行叠加。
§8–1 两相互垂直平面内的弯曲
的强度计算许可载荷F。
解:(1)计算横截面的形心、
面积、惯性矩
F 350
F 350
A 15000mm2
F
M
z0 75mm
FN
y1 z0 y z1
z1 125 mm I y 5.31107 mm4 (2)立柱横截面的内力
50
FN F
150
M F350 75103
50
对圆形、正方形截面
Iy Iz
一般生产车间所用的吊车大梁,两端由钢轨支撑,可以简化为简支 梁,如图示.图中l=4m。大梁由32a热轧普通工字钢制成,许用应力 [σ]=160MPa。起吊的重物重量F=80kN,且作用在梁的中点, 作用线与y轴之间的夹角α=5°,试校核吊车大梁的强度是否安全。
F2
M y F1 2L
z
Mz F2 L
x
max
My Mz Wy Wz
F1
6 F1 2L 6 F2L
L
L
y
b2h
bh2
t,max 9.979MPa
c,max 9.979MPa
§8.3 拉伸或压缩与弯曲的组合
一、横向力与ቤተ መጻሕፍቲ ባይዱ向力共同作用
=+
10-3
t ,max
=
c,max
蔡中兵《材料力学》8组合变形及连接部分的计算

" MZ y
IZ M y F1 x
' My z
Iy
盐城工学院力学课程组
材料力学
mechanics of materials
F2 a m
z F1 C(y,z)
O
z
my
y
x
m z
O Mz
My m
(3) 当F1 和F2共同作用时,应用叠加法y
F2单独作用时
F1单独作用时 F2 和F1 共同作用时
M y F1 x,
M z F2 ( x a)
盐城工学院力学课程组
材料力学
mechanics of materials
F2 m
a
z F1 C(y,z)
O
z
my
y
x
m z
O Mz
My m y
在F2 单独作用下,梁在竖直平面内发生平面弯曲, z轴为中性轴。
在F1 单独作用下,梁在水平平面内发生平面弯曲, y轴为中性轴。
横截面上内力
(1).拉(压) :轴力 FN
弯矩 Mz
(2).弯曲 剪力Fs
FS Mz
O
z x
FN
y
因为引起的切应力较小,故一般不考虑.
盐城工学院力学课程组
材料力学
4、应力分析
mechanics of materials
横截面上任意一点 ( z, y) 处的正应 力计算公式为
( 1).拉伸正应力
FN
M y z F zF z
Iy
Iy
由 Mz 产生的正应力
Mz y F yF y
Iz
Iz
FN
z
结构力学 第八章
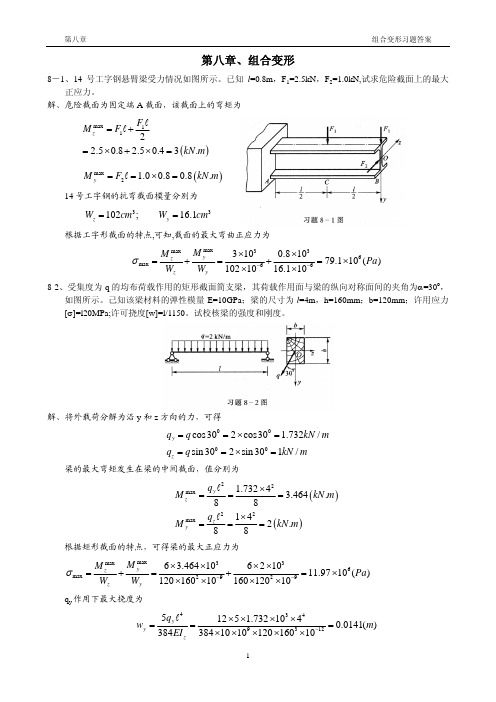
根据工字形截面的特点,可知,截面的最大弯曲正应力为
σ max
8-2、受集度为 q 的均布荷载作用的矩形截面简支梁,其荷载作用面与梁的纵向对称面间的夹角为α=30o, 如图所示。己知该梁材料的弹性模量 E=10GPa;梁的尺寸为 l=4m,h=160mm;b=120mm;许用应力 [σ]=l20MPa;许可挠度[w]=l/1150。试校核梁的强度和刚度。
max My = F2 l = 1.0 × 0.8 = 0.8 ( kN .m )
14 号工字钢的抗弯截面模量分别为
Wz = 102cm3 ;
Wy = 16.1cm3
max 3 × 103 0.8 ×103 M zmax M y = + = + = 79.1× 106 ( Pa ) −6 −6 102 × 10 16.1×10 Wz Wy
8-10、受拉构件形状如图,己知截面尺寸为 40mm×5mm,承受轴向拉力 F=l2kN。现拉杆开有切口,如不 计应力集中影响,当材料的[σ]=100MPa 时,试确定切口的最大许可深度,并绘出切口截面的应力变 化图。
38MPa
100 MPa A-A 截面应力分布图
解、由于切口的存在,在切口截面载荷为偏心力,切口截面上的轴力和弯矩分别为
3 3 2⎤ ⎡1 ⎤ ⎡1 I zC = ⎢ ( 4a )( 2a ) + ( 4a )( 2a ) a 2 ⎥ + ⎢ a ( 4a ) + ( 4a )( a )( 2a ) ⎥ = 32a 4 ⎣12 ⎦ ⎣12 ⎦ 1 1 3 I yC = ( 2a )( 4a ) + ( 4a ) a 3 = 11a 4 12 12
2
, FN = qx x = qx sin α
材料力学习题册答案-第8章 组合变形
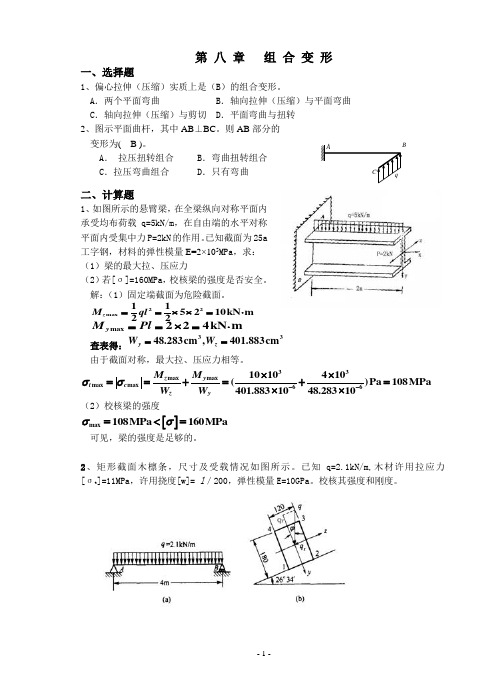
第 八 章 组 合 变 形一、选择题1、偏心拉伸(压缩)实质上是(B )的组合变形。
A .两个平面弯曲B .轴向拉伸(压缩)与平面弯曲C .轴向拉伸(压缩)与剪切D .平面弯曲与扭转 2、图示平面曲杆,其中AB ⊥BC 。
则AB 部分的 变形为( B )。
A . 拉压扭转组合B .弯曲扭转组合C .拉压弯曲组合D .只有弯曲二、计算题1、如图所示的悬臂梁,在全梁纵向对称平面内承受均布荷载 q=5kN/m ,在自由端的水平对称平面内受集中力P=2kN 的作用。
已知截面为25a 工字钢,材料的弹性模量E=2×105MPa ,求: (1)梁的最大拉、压应力(2)若[σ]=160MPa ,校核梁的强度是否安全。
解:(1)固定端截面为危险截面。
22max 115210kN m 22z M ql ==⨯⨯=⋅max 224kN m y M Pl ==⨯=⋅查表得:3348.283cm ,401.883cm y z W W ==由于截面对称,最大拉、压应力相等。
33max max max max661010410()Pa 108MPa 401.8831048.28310y z t c z y M M W W σσ--⨯⨯==+=+=⨯⨯(2)校核梁的强度[]max 108MPa 160MPaσσ=<=可见,梁的强度是足够的。
2、矩形截面木檩条,尺寸及受载情况如图所示。
已知q=2.1kN/m,木材许用拉应力[σt ]=11MPa ,许用挠度[w]= l /200,弹性模量E=10GPa 。
校核其强度和刚度。
ABCq解:(1)受力分析,计算内力。
根据梁的受力特点可知梁将产生斜弯曲。
因此,将载荷q 沿两对称轴分解为cos y q q ϕ= , sin z q q ϕ=在q 作用下,梁跨中截面的弯矩最大,为危险截面。
由q z 、q y 引起的最大弯矩M ymax 、M zmax 为202max 202max112.1sin 2634'4 1.88kN m 88112.1cos 2634'43.76kN m 88y z z y M q l M q l ==⨯⨯⨯=⋅==⨯⨯⨯=⋅(2)确定危险点位置,计算危险点应力。
(材料力学课件)第8章组合变形作业

组
③
②
合 (2) 中性轴的截距(m) ay 0.4,az 0
800
变
形 作 业
y
iy2 ay
0.18,3z
0
确定点1
同理求出点2,3,4
题
当中性轴绕棱角点旋转时,外力作用点移动轨迹为直线。
故点1和2间亦为直线。
第
8 章 组 合 变 形 作 业 题
第
8 章 组 合 变 形 作 业 题
8-20 解: (1) 剪切强度计算
Fs
Fs
Fs
3F/4
Fs
F
1F
(3) 板拉伸强度计算
上板轴力图
F/4
(+)
2 孔 F 面 A N 4 ( b 3 F 2 d d ) 4 ( 8 1 0 3 2 8 0 2 1 0 3 1 2 ) 0 1 0 6 0 1.7 6 M 6 [P ] a
故接头符合强度条件
8-27 解: (1) 由剪切强度条件
b
F
F
F A ss b F l 255 01 10 30 0 3l[]1160
a
l
l
第 得: l0.2m (2) 由挤压强度条件
8 章 组
b s F A b bs s a F ba 5 2 0 1 5 1 30 0 3 0[b]s 1 0 160
合
变
得: a0.02m
形
作
业 故取
ቤተ መጻሕፍቲ ባይዱ
[l]0.2m ,[a]0.0m 2
w m a[x w ] 1% 0 0 2 .0 6 2 1% 0 0 3 % 故强度和刚度均满足要求
[w ]
2
8-5 解: (1) m-m截面上内力
材料力学第8章 组合变形

b.未通过轴线或形心主惯性轴,向其分解
注意:荷载分解、简化的前提是不改变研究段的内力。
(2)内力分析方法
用截面法计算任意截面的内力,通过内力确定变形的组成
z
Fsz My
Ty
Fsy
M z FN
FN
T
x M z , Fsy M y , Fsz
轴向拉、压 扭转 x,y面内的平面弯曲 x,z面内的平面弯曲
§8-2 两相互垂直平面内的弯曲
F sin
F cos F
(2)求B点的应力
MB FN
WA
12.32103 25103
0.1 0.22
0.1 0.2
6
B
17.23 MPa
(3)求B点30º斜截面上的正应力
300 cos2 30 17.23 cos2 30 12.99 MPa
(4)求B点的主应力
1 0 2 0 3 17.23 MPa
z
面梁,其横截面都有两个相互垂直的对称 轴,且截面的周边具有棱角,故横截面上
Mz
的最大正应力发生在截面的棱角处。于是
,可根据梁的变形情况,直接确定截面上
My
最大拉、压应力点的位置,而无需定出其
y
中性轴。
因危险点为单向应力状态(忽略弯曲切应力的影响), 故,强度条件为:
max
M y max Wy
F sin
12.32kN m
F cos F
例: 如图示一矩形截面折杆,已知F=50kN,尺寸如图所示, α=30°。(1)求B点横截面上的应力;(2)求B点α=30°截
面上的正应力;(3)求B点的主应力σ1、 σ2、 σ3。
FN
B
MB 100mm
《材料力学》第8章 组合变形及连接部分的计算 习题解

第八章 组合变形及连接部分的计算 习题解[习题8-1] 14号工字钢悬臂梁受力情况如图所示。
已知m l 8.0=,kN F 5.21=,kN F 0.12=,试求危险截面上的最大正应力。
解:危险截面在固定端,拉断的危险点在前上角点,压断的危险点在后下角,因钢材的拉压性能相同,故只计算最大拉应力:式中,z W ,y W 由14号工字钢,查型钢表得到3102cm W z =,31.16cm W y =。
故MPa Pa mm N m m N 1.79101.79101.168.0100.11010228.0105.236363363max=⨯=⨯⨯⨯+⨯⨯⨯⨯⨯=--σ [习题8-2] 受集度为 q 的均布荷载作用的矩形截面简支梁,其荷载作用面与梁的纵向对称面间的夹角为 030=α,如图所示。
已知该梁材料的弹性模量 GPa E 10=;梁的尺寸为m l 4=,mm h 160=,mm b 120=;许用应力MPa 12][=σ;许用挠度150/][l w =。
试校核梁的强度和刚度。
解:(1)强度校核)/(732.1866.0230cos 0m kN q q y =⨯== (正y 方向↓))/(15.0230sin 0m kN q q z =⨯== (负z 方向←))(464.34732.1818122m kN l q M y zmaz ⋅=⨯⨯== 出现在跨中截面)(241818122m kN l q M z ymaz ⋅=⨯⨯== 出现在跨中截面)(5120001601206161322mm bh W z =⨯⨯==)(3840001201606161322mm hb W y =⨯⨯==最大拉应力出现在左下角点上:yy z z W M W M maxmax max +=σ MPa mmmm N mm mm N 974.1138400010251200010464.33636max=⋅⨯+⋅⨯=σ因为 MPa 974.11max =σ,MPa 12][=σ,即:][max σσ<所以 满足正应力强度条件,即不会拉断或压断,亦即强度上是安全的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第八章 组合变形及连接部分的计算 习题解[习题8-1] 14号工字钢悬臂梁受力情况如图所示。
已知m l 8.0=,kN F 5.21=,kN F 0.12=,试求危险截面上的最大正应力。
解:危险截面在固定端,拉断的危险点在前上角点,压断的危险点在后下角,因钢材的拉压性能相同,故只计算最大拉应力:式中,z W ,y W 由14号工字钢,查型钢表得到3102cm W z =,31.16cm W y =。
故MPa Pa mm N m m N 1.79101.79101.168.0100.11010228.0105.236363363max=⨯=⨯⨯⨯+⨯⨯⨯⨯⨯=--σ [习题8-2] 受集度为 q 的均布荷载作用的矩形截面简支梁,其荷载作用面与梁的纵向对称面间的夹角为 030=α,如图所示。
已知该梁材料的弹性模量 GPa E 10=;梁的尺寸为m l 4=,mm h 160=,mm b 120=;许用应力MPa 12][=σ;许用挠度150/][l w =。
试校核梁的强度和刚度。
解:(1)强度校核)/(732.1866.0230cos 0m kN q q y =⨯== (正y 方向↓))/(15.0230sin 0m kN q q z =⨯== (负z 方向←))(464.34732.1818122m kN l q M y zmaz ⋅=⨯⨯== 出现在跨中截面)(241818122m kN l q M z ymaz ⋅=⨯⨯== 出现在跨中截面)(5120001601206161322mm bh W z =⨯⨯==)(3840001201606161322mm hb W y =⨯⨯==最大拉应力出现在左下角点上:yy z z W M W M maxmax max +=σ MPa mmmm N mm mm N 974.1138400010251200010464.33636max=⋅⨯+⋅⨯=σ因为 MPa 974.11max =σ,MPa 12][=σ,即:][max σσ<所以 满足正应力强度条件,即不会拉断或压断,亦即强度上是安全的。
(2)刚度校核=m w m 0267.0150/4][0202.0==<=。
即符合刚度条件,亦即刚度安全。
[习题8-3] 悬臂梁受集中力F 作用如图所示。
已知横截面的直径mm D 120=,mm d 30=,材料的许用应力MPa 160][=σ。
试求中性轴的位置,并按照强度条件求梁的许可荷载[F]。
解:F F F y 866.030cos 0== (正y 方向↓)F q F z 5.030sin 0== (负z 方向←))(732.12866.0m N F F l F M y zmaz ⋅=⨯== 出现在固定端截面,上侧受拉 )(25.0m N F F l F M z ymaz ⋅=⨯== 出现在固定端截面,外侧受拉)34(64]41641[2641442244d D d d d D I z -=⋅+⋅-=ππππ 4448822419)3034120(6414.3mm =⨯-= )2(6464126414444d D d D I y -=⨯-=πππ 44410094119)302120(6414.3mm =⨯-=9816577.1882241910094119732.1tan max max =⋅=⋅=F F I I M M z y y z θ'001363223.639816577.1arctan ===θ,即:中性轴是过大圆的圆心,与y 轴的正向成'1363的一条直线(分布在二、四象限)。
F F F M M M y z 23222max 2max max =+=+= (沿F 作用线方向))(1470406088224192/3mm D I W z z ===MPa mm mm N F W M z 16014704010233max max ≤⋅⨯==σkN N F 763.1111763=≤kN F 763.11][=[习题8-4] 图示一楼梯木料梁的长度m l 4=,截面为m m 1.02.0⨯的矩形,受均布荷载作用,m kN q /2=。
试作梁的轴力图和弯矩图,并求横截面上的最大拉应力与最大压应力。
解:以A 为坐标原点,AB 方向为x 轴的正向。
过A点,倾斜向下方向为y 轴的正向。
)/(121230sin 0m kN q q x =⨯== (负x 方向:↙) )/(323230cos 0m kN q q y =⨯== (正y 方向:↘) A 、B 支座的反力为:kN X A 4=,kN R Y B A 32== AB杆的轴力:4)4()(-=--=x x q x N xAB杆的弯矩:2223322132)(x x x q x x M y -=-= x 0 1 2 3 4 N -4 -3-2 -1 0 M2.5983.4642.598AB 杆的轴力图与弯矩图如图所示。
23222.01.0)4(2.01.061)866.0464.3()()()(m kNx m m kN x x A x N W x M x z t ⨯--⨯⨯⋅-=-=σ )4(50)866.0464.3(15002x x x ---= x x x 50200129951962+--= 200524612992-+-=x x ()kPa令052462598)(=+-=x dxx d t σ,得:当m x 019.2=时,拉应力取最大值: MPa kPa t 097.5)(5.5096200019.25246019.212992max ≈=-⨯+⨯-=σ23222.01.0)4(2.01.061)866.0464.3()()()(m kNx m m kN x x A x N W x M x z c ⨯--⨯⨯⋅--=--=σ )4(50)866.0464.3(15002x x x ----=x x x 50200129951962+-+-=200514612992--=x x 令051462598)(=-=xdxx d t σ,得:当m x 981.1=时,压应力取最大值: MPa kPa c 297.5)(5.5296200981.15146981.112992max -≈-=-⨯-⨯=σ[习题8-5] 图示一悬臂滑车架,杆AB 为18号工字钢,其长度为m 。
试求当荷载作用在AB 的中点D 处时,杆内的最大正应力。
设工字钢的自重可略去不计。
解:18号工字钢,,AB 杆系弯压组合变形。
AF W M BC c 0max30cos --=中σ0=∑A M :0230sin 0=⋅-⋅lF l F BC ,kN F BC 25= )(25.1626.25.025230sin 0m kN l F M BC ⋅=⨯⨯=⋅=中 MPa Pa mNm m N c 9.9410)07.783.87(106.302310251085.11025.166243343max -=⨯+-=⨯⨯⨯-⨯⋅⨯-=-σ [习题8-6] 砖砌烟囱高m h 30=,底截面m m -的外径m d 31=,内径m d 22=,自重kN P 20001=,受m kN q /1=的风力作用。
试求:(1)烟囱底截面上的最大压应力;(2)若烟囱的基础埋深m h 40=,基础及填土自重按kN P 10001=计算,土壤的许用压应力MPa 3.0][=σ,圆形基础的直径D 应为多大?注:计算风力时,可略去烟囱直径的变化,把它看作是等截面的。
解:烟囱底截面上的最大压应力:==土壤上的最大压应力:即即解得:m[习题8-7] 螺旋夹紧器立臂的横截面为b a ⨯和矩形,如图所示。
已知该夹紧器工作时承受的夹紧力kN F 16=,材料的许用应力MPa 160][=σ,立臂厚mm a 20=,偏心距mm e 140=。
试求立臂宽度b 。
解:立柱是拉弯构件。
最大拉应力为: )61(6122max be b a F ab Fe ab F t +=+=σ )14061(20160002b b ⨯+=)8401(8002b b +=正应力强度条件:][max σσ≤t 160)8401(8002≤+bb0420052=--b b解得:mm b 356.67=[习题8-8] 试求图示杆内的最大正应力。
力F 与杆的轴线平行。
解:(1)求T 形截面的形心位置形心在y 轴上,0484282222=+⋅+⋅-=a a a a a a y C (2)把力F 先向y 轴平移,产生一个Fa a F M y 22-=⋅-=;然后,再把F 向z 轴平移,又产生一个Fa a F M z 22-=⋅-=。
故,T 形截面的杆件是拉伸与双向弯曲的组合变形构件。
(3)判断最大拉应力与最大压应力出现的位置由y M 、z M 的方向(正负号)可知,A 点处拉应力最大,B 点处压应力最大。
(4)计算最大拉应力 422322332]4)2()4(121[]8)2(4121[a a a a a a a a a I z =⋅+⋅⋅+⋅+⋅⋅=zAz y A y A t I y M I z M A F ++==σσmax 22442572.02641513222112212aFa F a a aF a a aF a F ≈=⋅+⋅+=(5)计算最大压应力zA z yB y B c I y M I z M A F --==σσmax22442258.0661********.0212aFa F a a aF a a aF a F -≈-=⋅-⋅-=故杆内的最大正应力是:2max 572.0aFA t ==σσ。
[习题8-9] 有一高为m 2.1、厚为m 3.0的混凝土墙,浇筑于牢固的基础上,用作挡水用的小坝。
试求:(1)当水位达到墙顶时,墙底处的最大拉应力和最大压应力(高混凝土的密度为33/1045.2m kg ⨯);(2)如果要求混凝土中没有拉应力,试问最大许可水深h 为多大?解:(1)求墙底处的最大拉应力和最大压应力沿墙长方向取m 1作为计算单元,则墙的重力为:)(6436.88.945.2)2.113.0(kN G =⨯⨯⨯⨯= (↓)作用在墙底处的水压力为:)/(76.1112.18.91m kN h q =⨯⨯=⨯⋅=γ墙底处的弯矩:)(8224.22.131)2.176.1121(m kN M ⋅=⨯⨯⨯⨯=混凝土墙为压弯构件,墙底的应力为:MPa kPa m mkN mkN W M A G z c 217.0972.2163.01618224.213.06436.8322max -=-=⨯⨯⋅-⨯-=--=σ(右) MPa kPa m m kN m kN W M A G z t 159.0348.1593.01618224.213.06436.8322max ==⨯⨯⋅+⨯-=+-=σ(左)(2)求混凝土中没有拉应力时的水深h作用在墙底处的水压力为:)/(8.918.91m kN h h h q =⨯⨯=⨯⋅=γ墙底处的弯矩:)(39.431)8.921(3m kN h h h h M ⋅=⨯⨯⨯⨯=09.108812.283.016139.413.06436.833232max =+-=⨯⨯⋅+⨯-=+-=h m mkN h mkN W M A G z t σ 09.108812.283=+-h )(642.0m h =故当m h 642.0=时,混凝土中不出现拉应力。
