第一型曲线曲面积分的计算
2202第一型曲面积分的计算(续)

z =z x2 + y2
下的部分 (图22-2). 解 对于圆锥面=z x2 + y2 ,
O
y
x
x2 + y2 = 2ax
图 22 − 2
有 zx
= x2x+ y2 , z y
y
, x2 + y2
1
+
z
2 x
+
z
2 y
=2;
而 S 在 xy 平面上的投影为 D( xy) : ( x − a)2 + y2 ≤ a2 . 因此
∫∫ f ( x, y, z( x, y))
1
+
z
2 x
+
z
2 y
dxdy
.
S
D
(2)
数学分析 第二十二章 曲面积分
高等教育出版社
§1 第一型曲面积分 第一型曲面积分的概念 第一型曲面积分的计算
例2 计算 ∫∫( xy + zx + yz)dS,
S
其中 S 为圆锥面=z x2 + y2
被圆柱面 x2 + y2 = 2ax 所割
数学分析 第二十二章 曲面积分
高等教育出版社
§1 第一型曲面积分 第一型曲面积分的概念 第一型曲面积分的计算
EG − F 2 = 1 + u2 .
然后由公式 (3) 求得:
∫∫ ∫ ∫ =I
v 1= + u2dudv
2π
vdv
a
1 + u2du
0
0
D
( ) =
2π
2
u 2
1 + u2 + 1 ln u + 2
第一型曲面积分的计算方法

第一型曲面积分的计算方法嘿,咱今儿就来聊聊这第一型曲面积分的计算方法哈!你说这玩意儿,就像是个调皮的小精灵,得好好捉摸才能搞定它呢!咱先来说说这第一型曲面积分到底是啥呀?其实啊,它就是在曲面上计算某种量的积分。
就好像你要在一个弯弯曲曲的表面上算算有多少东西在那呢。
那怎么算呢?这可有不少门道呢!首先呢,你得把那曲面给表示出来,这就跟给小精灵画个画像似的,得画得清楚明白。
然后呢,根据具体的情况,选择合适的方法。
比如说,要是那曲面比较规则,咱就可以用投影的方法呀。
就好比把那曲面的影子投到一个平面上,在平面上算积分,这多巧妙呀!你想想,这不就像你把一个立体的东西压扁了在平面上看一样嘛。
还有啊,有时候可以利用对称性来简化计算呢。
这就好比你有一堆东西,两边对称,那你只算一边不就完事儿了嘛,多省事儿呀!再比如说,遇到那种特别复杂的曲面,咱就得动点小脑筋,把它分成几块来算,一块一块地啃下来,这就跟吃一个大蛋糕,一口一口地吃是一个道理嘛。
哎呀,这计算第一型曲面积分啊,真的是既有趣又有挑战性。
你得像个探险家似的,在那一堆公式和概念里找线索,找方法。
有时候可能会遇到难题,就像在森林里迷路了一样,但别着急呀,慢慢摸索,总会找到出路的。
而且呀,这第一型曲面积分在好多领域都有用呢!比如物理学呀,工程学呀,那可都少不了它呢!你想想,要是没有它,那些复杂的物理现象和工程问题咋解决呀?总之呢,这第一型曲面积分的计算方法就像是一把钥匙,能打开好多知识的大门。
咱可得好好掌握它,让它为咱服务呀!可别小瞧了它,它的用处大着呢!你要是学会了,那可就牛啦!就像掌握了一门绝世武功一样,能在知识的江湖里闯荡一番呢!怎么样,是不是觉得很有意思呀?赶紧去试试吧!。
第一类曲线积分的极坐标形式

第一类曲线积分的极坐标形式曲线积分是微积分中的一个重要概念,它描述了沿着一条曲线的积分过程。
在曲线积分中,第一类曲线积分是最基本的一种类型,它描述了沿着曲线的标量场积分。
而在极坐标系下,第一类曲线积分的计算方法也有其独特的形式。
首先,我们来回顾一下第一类曲线积分的定义。
设曲线L为参数方程r(t)=(x(t),y(t)),其中a≤t≤b,f(x,y)为定义在曲线L上的标量场,则曲线L上f(x,y)的第一类曲线积分为:∫L f(x,y)ds = ∫b_a f(x(t),y(t))√[x'(t)²+y'(t)²]dt其中,ds表示曲线L上的弧长元素,x'(t)和y'(t)分别表示x(t)和y(t)对t 的导数。
接下来,我们来看第一类曲线积分在极坐标系下的形式。
在极坐标系下,曲线L可以表示为r(θ)=(r(θ)cosθ,r(θ)sinθ),其中a≤θ≤b,r(θ)为极径函数。
此时,曲线L上f(x,y)的第一类曲线积分可以表示为:∫L f(x,y)ds = ∫b_a f(r(θ)cosθ,r(θ)sinθ)√[r'(θ)²+r(θ)²]dθ其中,ds表示曲线L上的弧长元素,r'(θ)表示r(θ)对θ的导数。
通过上述公式,我们可以看出,在极坐标系下,第一类曲线积分的计算方法与直角坐标系下有所不同。
在直角坐标系下,我们需要计算曲线L上的弧长元素ds,而在极坐标系下,我们需要计算曲线L上的弧度元素dθ。
此外,由于极坐标系下的曲线L是由极径函数r(θ)和极角θ共同确定的,因此在计算曲线积分时,我们需要将f(x,y)表示为f(r(θ)cosθ,r(θ)sinθ)的形式。
总之,第一类曲线积分是微积分中的一个重要概念,它描述了沿着曲线的标量场积分。
在极坐标系下,第一类曲线积分的计算方法也有其独特的形式,需要注意弧度元素dθ的计算和将f(x,y)表示为f(r(θ)cosθ,r(θ)sinθ)的形式。
第一型曲面积分

|| T || 为分割 T 的细度,即为诸
Si 中的最大直径.
定义1 设 S 是空间中可求面积的曲面,
f 为( x, y, z)
定义在 S 上的函数. 对曲面 S 作分割 T, 它把 S 分成
n 个小曲面块 Si (i 1, 2, L , n), 以 Si 记小曲面块
Si 的面积, 分割 T 的细度
D
其中
E xu2 yu2 zu2 , F xu xv yu yv zuzv , G xv2 yv2 zv2 .
例2 计算
I z dS , 其中 S 为 S
螺旋面(图22-3)的一部分:
z
x ucos v,
S
:
y
u sin
v,
(u,v)
D
,
2
z v,
O
(a, 0, 0)
I f ( x, y, z)dS .
(1)
S
于是, 前述曲面块的质量可由第一型曲面积表示为:
特别地, 当
块 S 的面积.
m ( x, y, z)dS . S
f ( x, y, z) 1 时,曲面积分
dS 就是曲面
S
二、第一型曲面积分的计算
第一型曲面积分需要化为二重积分来计算.
定理 22.1
z
例1 计算
S z dS , 其中 S
h
是球面 x2 y2 z2 a2 被
平面 z h (0 h a) 所截
O
a
x
y
得的顶部 (图22-1).
图 22 1
解 曲面 S 的方程为 z a2 x2 y2 , 定义域 D 为
圆域 x2 y2 a2 h2 . 由于
1 zx2 zy2
第一型曲面积分

二、第一型曲面积分的计算
第一型曲面积分需要化为二重积分来计算.
定理22.1 设有光滑曲面
S : z z( x , y ) , ( x , y ) D ,
f ( x , y , z ) 为 S 上的连续函数, 则
S
2 f ( x , y , z )dS f ( x , y , z ( x , y )) 1 z x z 2 dxdy . y D
(2)
( 定理证明与曲线积分的定理20.1相仿, 不再详述. )
山西大同大学数计学院
例1 计算
S
1 dS , 其中 S z
a
x
z
h
是球面 x 2 y 2 z 2 a 2 被
O
平面 z h (0 h a ) 所截 得的顶部 (图22-1).
2
y
图 22 1
2 2
解 曲面 S 的方程为 z a x y , 定义域 D 为
a 2 h2
0
a r dr 2 2 a r r dr 2 2 a r
2 a 2 h2 0
πa ln(a r )
2
a 2aπ ln . h
山西大同大学数计学院
例2 计算
( xy zx yz )dS ,
S
z
其中 S 为圆锥面 z
x2 y2
O
被圆柱面 x 2 y 2 2ax 所割 下的部分 (图22-2). 解 对于圆锥面 z 有
EG F 2 1 u 2 .
然后由公式 (3) 求得:
山西大同大学数计学院
I v 1 u dudv vdv
2 0 D
曲线积分和曲面积分

第八章 曲线积分和曲面积分我们前面已学过定积分和重积分,当一个函数定义在空间的曲线或曲面时,则要求我们计算曲线积分或曲面积分。
由于物理背景的不同,我们还须区别曲线或曲面的方向性,因此我们要分别研究两种不同类型的积分。
§1 第一型曲线积分与曲面积分1. 第一型曲线积分我们研究如下的一个理想问题,给定空间的一条曲线物体L ,L 上每点有线密度,现在我们要求它的质量。
我们对此问题作如下限制,设L 是空间的可求长曲线,端点为A 和B ,密度函数(,,)f x y z 在L 上定义。
为了求质量,象定积分一样,我们对L 作一分割,01,,,,(,1,2,,,)n j A A A A B A j n L ===L L 在上,这样我们就将L 分成n 小段,设每段的长度为j s V 。
在每段弧长上任取一点ξηςjjj(,,),作和式,1(,)nj jj j j f s ξης=∑V以此作为L 质量的近似值。
最后我们令1max{}0j j ns λ≤≤=→V ,即可得到L 质量的精确值M ,即,01lim (,)nj j j j j M f s λξης→==∑V由此我们可得到以下定义 定义设L 是空间可求长曲线,(,,)f x y z 在L 上连续,L 的两个端点为A,B ,依次用分点01,,,n A A A A B ==L 将L 分成n 小段。
每小段弧及弧长均记为j s V ,在j s V 上任取一点(,,)j j j j P ξης=,作和式,1(,)nj jj j j f s ξης=∑V如果当1max{}0j j ns λ≤≤=→V 时,上述和式的极限存在,且不依赖于L 的分法及j P 的选取,则称这一极限值为(,,)f x y z 。
在L 上的第一型曲线积分,记作(,,)Lf x y z ds ∫。
第一型曲线积分也有类似于定积分的一些性质,如关于被积函数的线性及关于曲线的可加性,它与定积分的一个差别是第一型曲线积分与曲线的方向无关。
数学分析20.1第一型曲线积分(含习题及参考答案)

第二十章 曲线积分 1第一型曲线积分一、第一型曲线积分的定义引例:设某物体的密度函数f(P)是定义在Ω上的连续函数. 当Ω是直线段时,应用定积分就能计算得该物体的质量.当Ω是平面或空间中某一可求长度的曲线段时,可以对Ω作分割,把Ω分成n 个可求长度的小曲线段Ωi (i=1,2,…,n),并在每一个Ωi 上任取一点P i . 由f(P)为Ω上的连续函数知,当Ωi 的弧长都很小时,每一小段Ωi 的质量可近似地等于f(P i )△Ωi , 其中△Ωi 为小曲线段Ωi 的长度. 于是在整个Ω上的质量就近似地等于和式i ni i P f ∆Ω∑=1)(.当对Ω有分割越来越细密(即d=i ni ∆Ω≤≤1max →0)时,上述和式的极限就是该物体的质量.定义1:设L 为平面上可求长度的曲线段,f(x,y)为定义在L 上的函数.对曲线L 作分割T ,它把L 分成n 个可求长度的小曲线段L i (i=1,2,…,n),L i 的弧长记为△s i ,分割T 的细度为T =i ni s ∆≤≤1max ,在L i 上任取一点(ξi ,ηi ),( i=1,2,…,n). 若有极限i ni i i T s f ∆∑=→1),(lim ηξ=J ,且J 的值与分割T 与点(ξi ,ηi )的取法无关,则称此极限为f(x,y)在L 上的第一型曲线积分,记作:⎰L ds y x f ),(.注:若L 为空间可求长曲线段,f(x,y,z)为定义在L 上的函数,则可类似地定义f(x,y,z)在空间曲线L 上的第一型曲线积分⎰L ds z y x f ),,(.性质:1、若⎰L i ds y x f ),((i=1,2,…,k)存在,c i (i=1,2,…,k)为常数,则⎰∑=L ki i ids y x f c1),(=∑⎰=ki Li i ds y x f c 1),(.2、若曲线L 由曲线L 1,L 2,…,L k 首尾相接而成,且⎰iL ds y x f ),((i=1,2,…,k)都存在,则⎰L ds y x f ),(也存在,且⎰L ds y x f ),(=∑⎰=ki L i ids y x f 1),(.3、若⎰L ds y x f ),(与⎰L ds y x g ),(都存在,且f(x,y)≤g(x,y),则⎰Lds y x f ),(≤⎰Lds y x g ),(.4、若⎰L ds y x f ),(存在,则⎰L ds y x f ),(也存在,且⎰L ds y x f ),(≤⎰L ds y x f ),(.5、若⎰L ds y x f ),(存在,L 的弧长为s ,则存在常数c ,使得⎰L ds y x f ),(=cs, 这里),(inf y x f L≤c ≤),(sup y x f L.6、第一型曲线积分的几何意义:(如图)若L 为平面Oxy 上分段光滑曲线,f(x,y)为定义在L 上非负连续函数. 由第一型曲面积分的定义,以L 为准线,母线平行于z 轴的柱面上截取0≤z ≤f(x,y)的部分面积就是⎰Lds y x f ),(.二、第一型曲线积分的计算 定理20.1:设有光滑曲线L:⎩⎨⎧==)()(t y t x ψϕ, t ∈[α,β],函数f(x,y)为定义在L上的连续函数,则⎰L ds y x f ),(=⎰'+'βαψϕψϕdt t t t t f )()())(),((22. 证:由弧长公式知,L 上由t=t i-1到t=t i 的弧长为△s i =⎰='+'ii t t dt t t 1)()(22ψϕ.由)()(22t t ψϕ'+'的连续性与积分中值定理,有△s i =)()(22i i τψτϕ''+''△t i (t i-1<i τ'<t=t i ),∴i ni i i s f ∆∑=1),(ηξ=i i i ni i i t f ∆''+''''''∑=)()())(),((221τψτϕτψτϕ (t i-1<i τ',i τ''<t=t i ). 设σ=[]i i i i i n i i i t f ∆'''+'''-''+''''''∑=)()()()())(),((22221τψτϕτψτϕτψτϕ,则有in i iis f ∆∑=1),(ηξ=i i i ni iit f ∆'''+'''''''∑=)()())(),((221τψτϕτψτϕ+σ.令△t=max{△t 1,△t 2,…,△t n },则当T →0时,必有△t →0. 又复合函数f(φ(t),ψ(t))关于t 连续,∴在[α,β]上有界,即 存在常数M ,使对一切t ∈[α,β],都有|f(φ(t),ψ(t))|≤M. 再由)()(22t t ψϕ'+'在[α,β]上连续,从而在[α,β]上一致连续,即 ∀ε>0, ∃δ>0,使当△t<δ时有)()()()(2222i i i i τψτϕτψτϕ'''+'''-''+''<ε, 从而|σ|≤εM ∑=∆ni i t 1=εM(β-α), 即σlim 0→∆t =0. 又由定积分的定义,得i i i ni i i t t f ∆'''+'''''''∑=→∆)()())(),((lim221τψτϕτψτϕ=⎰'+'βαψϕψϕdt t t t t f )()())(),((22. 故⎰Lds y x f ),(=in i iit s f ∆∑=→∆1),(limηξ=i i i ni iit t f ∆'''+'''''''∑=→∆)()())(),((lim 221τψτϕτψτϕ+0lim →∆t σ=⎰'+'βαψϕψϕdt t t t t f )()())(),((22.注:1、若曲线L 由方程y=ψ(x), x ∈[a,b]表示,且ψ(x)在[a,b]上有连续的导函数时,则有⎰L ds y x f ),(=⎰'+ba dx x x x f )(1))(,(2ψψ.2、当曲线L 由方程x=φ(y), y ∈[c,d]表示,且φ(y)在[c,d]上有连续的导函数时,则有⎰L ds y x f ),(=⎰'+dc dy y y y f )(1)),((2ϕϕ. 3、对空间曲线积分⎰L ds z y x f ),,(,当曲线L 由参量方程x=φ(t),y=ψ(t),z=χ(t), t ∈[α,β]表示时,有⎰Lds z y x f ),,(=⎰'+'+'βαχψϕχψϕdt t t t t t t f )()()())(),(),((222. 4、由第一型曲线积分的定义,在Oxy 平面上,线密度为ρ(x,y)的曲线状物体对x,y 轴的转动惯量分别为:J x =⎰L ds y x y ),(2ρ和J x =⎰L ds y x x ),(2ρ.例1:设L 是半圆周⎩⎨⎧==t a y ta x sin cos , t ∈[0,π],试计算第一型曲线积分⎰+Lds y x )(22.解:⎰+L ds y x )(22=⎰++π022222222cos sin )sin cos (dt t a t a t a t a =⎰π03dt a =a 3π.例2:设L 是y 2=4x 从O(0,0)到A(1,2)的一段,试求第一型曲线积分⎰L yds . 解:⎰L yds =⎰+20241dy yy =⎰⎪⎪⎭⎫ ⎝⎛++202241412y d y =202324134⎪⎪⎭⎫ ⎝⎛+y =)122(34-.例3:计算⎰L ds x 2,其中L 为球面x 2+y 2+z 2=a 2被平面x+y+z=0所截得的圆周.解:由对称性知,⎰L ds x 2=⎰L ds y 2=⎰L ds z 2,∴⎰L ds x 2=⎰++L ds z y x )(31222=⎰L ds a 32=33πa .例4:求线密度ρ(x,y)=21xy +的曲线段y=lnx, x ∈[1,2]对于y 轴的转动惯量.解:J x =⎰L ds y x x ),(2ρ=⎰+Lds x y x 221=⎰++21222111ln dx xx x x =⎰21ln xdx x =ln4-43.习题1、计算下列第一型曲线积分:(1)⎰+L ds y x )(, 其中L 是以O(0,0), A(1,0),B(0,1)为顶点的三角形; (2)⎰+L ds y x 22, 其中L 是以原点为中心,R 为半径的右半圆周;(3)⎰L xyds , 其中L 为椭圆22a x +22by =1在第一象限中的部分;(4)⎰L ds y ||, 其中L 为单位圆周x 2+y 2=1;(5)⎰++L ds z y x )(222, 其中L 为螺旋线x=acost, y=asint, z=bt(0≤t ≤2π)的一段;(6)⎰L xyzds , 其中L 是曲线x=t, y=3232t , z=21t 2(0≤t ≤1)的一段; (7)⎰+L ds z y 222, 其中L 为x 2+y 2+z 2=a 2与x=y 相交的圆周. 解:(1) ⎰+L ds y x )(=⎰+OA ds y x )(+⎰+AB ds y x )(+⎰+BO dsy x )( =⎰10xdx +⎰102dx +⎰10ydy =1+2.(2)右半圆的参数方程为:x=Rcos θ, y=Rsin θ, -2π≤θ≤2π. ∴⎰+L ds y x 22=⎰-222ππθd R =πR 2.(3)方法一:∵y=22x a a b-, y ’=22xa a bx -, ∴⎰L xyds =⎰-+-adx x a a x b x a x a b 02222222)(1=⎰--adx x b a a a b 0222242)(2=)(3)(22b a b ab a ab +++.方法二:L 的参数方程为:x=acos θ, y=bsin θ,0≤θ≤2π.∴⎰L xyds =⎰+202222cos sin sin cos πθθθθθd b a ab=⎰-++-2022222cos 2cos 2)(224πθθd a b b a ab =)(3)(22b a b ab a ab +++. (4)方法一:圆的参数方程为:x=cos θ, y=sin θ,0≤θ≤2π, ∴⎰L ds y ||=⎰πθθ0sin d -⎰ππθθ2sin d =4. 方法二:∵|y|=21x -, (|y|)’=21xx --,∴⎰L ds y ||=2⎰--+-11222111dx x x x=2⎰-11dx =4. (5)⎰++L ds z y x )(222=⎰++π2022222)(dt b a t b a =2232b a +π(3a 2+4π2b 2).(6)x ’=1, y ’=t 2, z ’=t,∴⎰L xyzds =⎰++⋅⋅102232121232dt t t t t t =⎰+129)1(32dt t t =143216. (7)依题意,L 的参数方程可表示为:x=y=2a cos θ, z=asin θ, 0≤θ≤2π,∴⎰+L ds z y 222=⎰πθ202d a =2a 2π.2、求曲线x=a, y=at, z=21at 2(0≤t ≤1, a>0)的质量,设线密度为ρ=az 2. 解:⎰L ds a z 2=⎰+10222dt t a a t =⎰+102212dt t a =)122(3-a.3、求摆线x=a(t-sint), y=a(1-cost) (0≤t ≤π)的质心,设其质量分布均匀.解:∵dx=dt t a t a 2222sin )cos 1(+-=2asin 2t dt ,m=2a ρ0⎰π02sin dt t=4a ρ0.∴质心坐标为x=⎰-πρ002sin 2)sin (1dt t a t t a m =⎰-π0)2sin sin 2sin (2dt t t t t a =34a;y=⎰-πρ002sin 2)cos 1(1dt t a t a m =34a .4、若曲线以极坐标ρ=ρ(θ) (θ1≤θ≤θ2)表示,试给出计算⎰L ds y x f ),(的公式,并用此公式计算下列曲线的积分: (1)⎰+L y x ds e22, 其中L 为曲线ρ=a (0≤θ≤4π)的一段; (2)⎰L xds , 其中L 为对数螺线ρ=ae k θ (k>0)在圆r=a 内的部分. 解:L 的参数方程为x=ρ(θ)cos θ, y=ρ(θ)sin θ, (θ1≤θ≤θ2),ds=θθθd d dy d dx 22⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=θθρθρd )()(22'+,∴⎰L ds y x f ),(=⎰'+21)()()sin ,cos (22θθθθρθρθρθρd f .(1)⎰+L y x ds e22=⎰40πθd ae a =4πae a . (2)⎰L xds =a ⎰∞-+022222cos θθθθθd e k a e a e k k k=a 2⎰∞-+022cos 1θθθd ekk =1412222++k k ka .注:∵⎰∞-02cos θθθd e k =⎰∞-02cos 21θθk de k =⎰∞-∞-+202sin 21cos 21d e ke kk k θθθθ=θθk e d k k 202sin 4121⎰∞-+=⎰∞--022cos 4121θθθd e kk k ; ∴⎰∞-⎪⎭⎫ ⎝⎛+022cos 411θθθd e k k =k 21,即⎰∞-02cos θθθd e k =1422+k k .5、证明:若函数f(x,y)在光滑曲线L: x=x(t), y=y(t), t ∈[α,β]上连续,则存在点(x 0,y 0)∈L ,使得⎰L ds y x f ),(=f(x 0,y 0)△L ,其中△L 为L 的弧长. 证:∵f 在光滑曲线L 上连续,∴⎰L ds y x f ),(存在,且⎰Lds y x f ),(=⎰'+'βαdt t y t x t y t x f )()())(),((22.又f(x(t),y(t))与)()(22t y t x '+'在[α,β]上连续,由积分中值定理知, ∃t 0∈[α,β],使⎰L ds y x f ),(=f(x(t 0),y(t 0))⎰'+'βαdt t y t x )()(22= f(x(t 0),y(t 0))△L. 令x 0=x(t 0), y 0=y(t 0), 则(x 0,y 0)∈L, 且⎰L ds y x f ),(=f(x 0,y 0)△L.。
第二十一章(数分)

178第二十一章 曲线积分与曲面积分 ( 1 6 时 )§1 第一型曲线积分与第一型曲面积分( 3 时 )一. 第一型曲线、曲面积分的定义:1. 几何体的质量: 已知密度函数,分析线段、平面区域、空间几何体的质量定义及计算.2. 曲线和曲面的质量:3. 第一型曲线、曲面积分的定义: 定义及记法. 线积分⎰Lfds , 面积分⎰⎰SfdS .4. 第一型曲线、曲面积分的性质: [1]P 356 二. 第一型曲线、曲面积分的计算:1.第一型曲线积分的计算: 回顾“光滑曲线”概念 .Th22.1 设有光滑曲线)( , )( :t y t x L ψϕ==, ],[βα∈t . ),(y x f 是定义在L 上的连续函数. 则()dt t t t t f ds y x f L⎰⎰'+'=βαψϕψϕ)()()( , )(),(22. ( 证 ) [1]P 357若曲线方程为L :],[ , )(b a x x y ∈=ψ, 则()⎰⎰'+=Lbadx x x x f ds y x f )(1)( , ),(2ψψ.L 的方程为)(y x ϕ=时有类似的公式.例1 设L 是半圆周t a y t a x sin , cos ==, π≤≤t 0.⎰+Lds y x )(22. [1]P 200 E1.例2设L 是曲线x y 42=上从点) 0 , 0 (O 到点) 2 , 1 (A 的一段.计算第一型曲线积分⎰Lyds . [1]P 200 E2.空间曲线L 上的第一型曲线积分: 设空间曲线)( , )( , )( :t z t y t x L χψϕ===,],[βα∈t . 函数)( , )( , )(t t t χψϕ连续可导, 则对L 上的连续函数),,(z y x f , 有()⎰⎰'+'+'=Ldt t t t t t t f ds z y x f βαχψϕχψϕ)()()()( , )( , )(),,(222.179例3 计算积分⎰Lds x 2, 其中L 是球面2222a z y x =++被平面0=++z y x 截得的圆周.[1]P 201E3.解 由对称性知,⎰=Lds x 2⎰=Lds y 2⎰L ds z 2⇒⎰L ds x 2=⎰⎰==++L L a ds a ds z y x 32222323)(31π. ( 注意L 是大圆 )第一型曲面积分的计算:Th1 设有光滑曲面 D y x y x z z S ∈=),( , ),( :.),,(z y x f 为S 上的连续函数,则()⎰⎰⎰⎰++=SDy x dxdy z z y x z y x f dS z y x f 221),(,,),,(.例1 计算积分⎰⎰S zdS , 其中S 是球面 2222a z y x =++ 被平面 h z =)0(a h <<所截的顶部. [1]P 281 E1.Ex[1]P 201 1, 2, 3, 4 .[1]P 283 1, 2, 3 .§2 第二型曲线积分( 3 时 )一. 第二型曲线积分的定义:1.力场()),( , ),(),(y x Q y x P y x F =沿平面曲线L 从点A 到点B 所作的功: 先用微元法, 再用定义积分的方法讨论这一问题, 得 ),(dy dx F W AB⋅=⎰⋂, 即 ds F W L⋅=⎰.2. 第二型曲线积分的定义: ( [1]P 203) 封闭曲线积分的记法.按这一定义,有 力场()),( , ),(),(y x Q y x P y x =沿平面曲线L 从点A 到点B 所作的功为 ⎰+=ABQdy Pdx W .第二型曲线积分的鲜明特征是曲线的方向性.对二型曲线积分有 ⎰⎰-=BAAB,因此,定积分是第二型曲线积分中当曲线为X 轴上的线段时的特例.可类似地考虑空间力场()),,( , ),,( , ),,(),,(z y x R z y x Q z y x P z y x =沿空间曲线180AB 所作的功. 导出空间曲线上的第二型曲线积分⎰++ABdz z y x R dy z y x Q dx z y x P ),,(),,(),,(.3. 第二型曲线积分的性质:第二型曲线积分可概括地理解为向量值函数的积累问题.与我们以前讨论过的积分相比, 除多了一层方向性的考虑外, 其余与以前的积累问题是一样的, 还是用Riemma 的思想建立的积分. 因此, 第二型曲线积分具有(R )积分的共性, 如线性、关于函数或积分曲线的可加性. 但第二型曲线积分一般不具有关于函数的单调性, 这是由于一方面向量值函数不能比较大小, 另一方面向量值函数在小弧段上的积分还与弧段方向与向量方向之间的夹角有关.二. 第二型曲线积分的计算:设L 为光滑或按段光滑曲线 , L : βαψϕ≤≤==t t y t x, )( , )(或βα≥≥t . A ())( , )(αψαϕ, B ())( , )(βψβϕ,即起点A 对应的参数为α,终点B 对应的参数为β; 函数),(y x P 和),(y x Q 在L 上连续, 则沿L 从点A 到点B 的积分为()()[]⎰⎰'+'=+Ldt t t t Q t t t P dy y x Q dx y x P βαψψϕϕψϕ)()( , )()()( , )(),(),(. (证略)例1 计算积分⎰-+Ldy x y xydx )(, L 的两个端点为A ( 1, 1 ) , B ( 2 , 3 ). 积分从点A 到点B 或闭合, 路径为ⅰ> 直线段ABⅱ> 抛物线1)1(22+-=x y ;ⅲ> 折线闭合路径A ( 1, 1 )→D ( 2 , 1 ) → B ( 2 , 3 ) → A ( 1, 1 ) . [1]P 205 E1. 例2 计算积分⎰+Lydx xdy , 这里L :ⅰ> 沿抛物线22x y =从点O ( 0 , 0 )到点B ( 1 , 2 ); ⅱ> 沿直线x y 2=从点O ( 0 , 0 )到点B ( 1 , 2 );ⅲ> 沿折线封闭路径O (0,0) →A (1,0 ) →B (1,2 ) → O (0,0). [1]P 206 E2. 例3 计算第二型曲线积分I =⎰+-+Ldz xdy y x xydx 2)(, 其中L 是螺旋线t a x cos =,bt z t a y == , sin , 从0=t 到π=t 的一段. [1]P 207E3.例4 求在力场) , , (z y x x y ++-作用下,181ⅰ> 质点由点A ) 0 , 0 , (a 沿螺旋线到点B ) 2 , 0 , (b a π所作的功, 其中 L 1: bt z t a y t a x === , sin , cos , ) 20 (π≤≤t .ⅱ> 质点由点A ) 0 , 0 , (a 沿直线L 2到点B ) 2 , 0 , (b a π所作的功. [1]P 207 E4.Ex [1]P 371 1,2,3.§3 Green公式 曲线积分与路径无关性( 4 时 )一.Green 公式:设区域D 的边界L 是由一条或几条光滑曲线所组成.边界曲线L 的正向规定为: 当人沿边界行走时, 区域D 总在它的左边, 参阅[1]P 224图21—10.与此相反的方向称为负方向,记为—L 或L -. 1. Green 公式:Th21.11 若函数),(y x P 和),(y x Q 在闭区域D ⊂R 2上连续,且有连续的一阶偏导数, 则有⎰⎰⎰+=⎪⎪⎭⎫ ⎝⎛∂∂-∂∂D L Qdy Pdx dxdy y P x Q ,其中L 为区域D 的正向边界. (证) [1]P 224.Green 公式又可记为⎰⎰⎰+=∂∂∂∂DL Qdy Pdx dxdy QP y x . 2. 应用举例:对于封闭曲线积分, 可直接应用Green 公式. 对非封闭曲线积分,常采用附加上一条线使变成封闭曲线积分的方法. 例1 计算积分⎰ABxdy , 其中A , ) , 0 (r B ) 0 , (r . 曲线AB 为圆周222r y x =+在第一象限中的部分. [1]P 226 E1. 解法一 (直接计算积分) 曲线AB 的方程为 20 , sin , cos π≤≤==t t r y t r x .182起点A 对应的参数为2π,终点B 对应的参数为0,因此 ⎰⎰-=⎪⎭⎫ ⎝⎛+-==AB r t t r tdt r xdy 2200222242sin 2121cos πππ. 解法二 (用Green 公式)补上线段BO 和OA ( O 为坐标原点), 成封闭曲线.设所围区域为D , 注意到∂D 为反向, 以及0=⎰BOA, 有⎰ABxdy ⎰⎰⎰⎰∂-=-=-=DBOADr dxdy xdy xdy 24π.例2 计算积分 I =⎰+-L y x ydxxdy 22, 其中L 为任一不包含原点的闭区域D 的边界(方向任意)[1]P 227 E2.解 2222),( , ),(yx xy x Q y x y y x P +=+-=. (P 和Q 在D 上有连续的偏导数). ()2222222yx x y y x y x y P +-=⎪⎪⎭⎫ ⎝⎛+-∂∂=∂∂, 22222)(y x x y x Q +-=∂∂. 于是, I =⎰⎰⎰=⎪⎪⎭⎫ ⎝⎛∂∂-∂∂=D Ldxdy y P x Q 0.例3 验证区域D 的面积公式|D |⎰-=Lydx xdy 21,L 为D 的正向边界. [1]P 227 例4 计算由星形线 ) 20 ( sin , cos 33π≤≤==t t b y t a x 所界的面积.Ex [1]P 231—232 1,2,3,4.二. 曲线积分与路线无关性:介绍单连通域和复连通域.1. 积分与路径无关的等价条件: [1]P 377Th21.12 设D ⊂R 2是单连通闭区域. 若函数),(y x P 和),(y x Q 在闭区域D 内连续, 且有连续的一阶偏导数, 则以下四个条件等价 :183ⅰ> 沿D 内任一按段光滑的闭合曲线L , 有⎰=+LQ d y P d x 0.ⅱ> 对D 内任一按段光滑的曲线L , 曲线积分⎰+LQdy Pdx 与路径无关, 只与曲线L 的起点和终点有关.ⅲ> Qdy Pdx +是D 内某一函数u 的全微分, 即在D 内有=du Qdy Pdx +.ⅳ> 在D 内每一点处有 xQ y P ∂∂=∂∂. (证) [1]P 228—230 . 2. 恰当微分的原函数:若有xQ y P ∂∂=∂∂, 则称微分形式Qdy Pdx +是一个恰当微分. 恰当微分有原函数, 它的一个原函数为: ⎰⎰+=xx yy dt t x Q dt y t P y x u 0),(),(),(0.或 . ),(),(),(00⎰⎰+=yy xx dt y t P dt t x Q y x u(其中点) , (00y x ∈D , 当点) 0 , 0 (∈D 时, 常取) , (00y x =) 0 , 0 (.) 验证第一式:⎰⎰+=+=∂∂y y t y y x dt t x P y x P dt t x Q y x P xu0),(),(),(),(00==-+=+=),(),(),(|),(),(0000y x P y x P y x P t x P y x P yy ),(y x P ;同理可得),(y x Q yu=∂∂. 例5 验证式 ydy x dx y x cos ) sin 2 (++是恰当微分,并求其原函数. [1]P 231 E4.Ex [1]P 232 5,6,7.§4 第二型曲面积分 ( 3 时 )一. 曲面的侧:1. 单侧曲面与双侧曲面:2. 双侧曲面的定向: 曲面的上、下侧,左、右侧,前、后侧. 设法向量为)cos , cos , (cos γβα±=,184则上侧法线方向对应第三个分量0>, 即选“+”号时,应有0cos >γ,亦即法线方向与Z 轴正向成锐角. 类似确定其余各侧的法线方向. 封闭曲面分内侧和外侧.二. 第二型曲面积分:1. 稳流场的流量: 以流体的流量为例. [1]P 384.2. 第二型曲面积分的定义: [1]P 284—285 . 封闭曲面上的积分及记法.3. 第二型曲面积分的性质: 线性, 关于积分曲面块的可加性.4. 第二型曲面积分与第一型曲面积分的关系: 设为曲面S 的指定法向, 则 ⎰⎰++Sdxdy z y x R dzdx z y x Q dydz z y x P ),,(),,(),,(=[]⎰⎰++SdS z z y x R y z y x Q x z y x P ),cos(),,(),cos(),,(),cos(),,(.三. 第二型曲面积分的计算:Th22.2 设),,(z y x R 是定义在光滑曲面∈=),(, ),( :y x y x z z S D xy 上的连续函数, 以S 的上侧为正侧(即0),cos(>z ), 则有 ()⎰⎰⎰⎰=SD xydxdy y x z y x R dxdy z y x R ),(,,),,(.证 [1]P 287 .类似地, 对光滑曲面∈=),(, ),( :z y z y x x S D yz , 在其前侧上的积分()⎰⎰⎰⎰=SD yzdydz z y z y x P dydz z y x P , , ),(),,(.对光滑曲面∈=),(, ),( :x z x z y y S D zx , 在其右侧上的积分()⎰⎰⎰⎰=SD yzdzdx z x z y x Q dzdx z y x Q , ),( , ),,(.计算积分⎰⎰++SRdxdy Qdzdx Pdydz 时, 通常分开来计算三个积分⎰⎰SPdydz , ⎰⎰SQdzdx , ⎰⎰SRdxdy .为此,分别把曲面S 投影到YZ 平面, ZX 平面和XY 平面上化为二重积分进行计算.投影域的185侧由曲面S 的定向决定.推论 设),,(z y x P ,),,(z y x Q ,),,(z y x R 是定义在光滑曲面 , ),( :y x z z S =∈),(y x D xy 上的连续函数,则有⎰⎰++Sdxdy z y x R dzdx z y x Q dydz z y x P ),,(),,(),,(=[]⎰⎰++SdS z n z y x R y n z y x Q x n z y x P ),cos(),,(),cos(),,(),cos(),,(.)]),(,,(),()),(,,(),()),(,,([dxdy y x z y x R y x z y x z y x Q y x z y x z y x P X YD yx⎰⎰+--±=曲面 S 的方向为上侧, 则等式前取“+”号; 曲面 S 的方向为下侧, 则等式前取“-”号. 例1 计算积分⎰⎰Sxyzdxdy ,其中S 是球面1222=++z y x 在0 , 0≥≥y x 部分取外侧.[1]P 287 E1.例2 计算积分⎰⎰∑++-++dxdy x z dzdx z y dydz y x )3()()(,∑为球面2222R z y x =++取外侧.解 对积分⎰⎰∑+dydz y x )(, 分别用前∑和后∑记前半球面和后半球面的外侧, 则有前∑ : ,222z y R x --=222 :R z y D yz ≤+;后∑: ,222z y R x ---= 222 :R z y D yz ≤+.因此, ⎰⎰∑+dydz y x )(=⎰⎰∑前+⎰⎰∑后=()⎰⎰-+--=yzD dydz y z y R 222()⎰⎰=+---yzD dydz y z y R 222=-==========--=⎰⎰⎰⎰≤+==2222022sin ,cos 222 82R z y Rr z r y rdr r R d dydz z y R πθθθ()3023223432214R rR R r r ππ=⎥⎦⎤⎢⎣⎡⋅--===. 对积分dx dz z y ⎰⎰∑-)(, 分别用右∑和左∑记右半球面和左半球面的外侧, 则有右∑: ,222x z R y --=222 :R z x D zx ≤+;186左∑: ,222x z R y ---= 222 :R z x D zx ≤+. 因此, =-⎰⎰∑dydz z y )(⎰⎰∑右+⎰⎰∑左=()()⎰⎰⎰⎰--------=zxzxD D dzdx z x z R dzdx z x z R222222⎰⎰≤+=--=2223222342R z x R dzdx x z R π.对积分dxdy x z ⎰⎰∑+)3(, 分别用上∑和下∑记上半球面和下半球面的外侧, 则有上∑: ,222y x R z --=222 :R y x D xy ≤+;下∑: ,222y x R x ---= 222 :R y x D xy ≤+.因此, dxdy x z ⎰⎰∑+)3(=⎰⎰∑上+⎰⎰∑下=()()⎰⎰⎰⎰=+----+--=xyxyD D dxdy x y x R dxdy x y x R 33222222⎰⎰≤+=--=2223222342R y x R dxdy y x R π.综上, ⎰⎰∑++-++dxdy x z dzdx z y dydz y x )3()()(=334343R R ππ=⨯.Ex [1]P 289—290 1⑴⑵⑶⑷⑸,2.§5 Gauss公式和Stokes 公式 ( 3 时 )一. Gauss 公式:Th22.3 设空间区域V 由分片光滑的双侧封闭曲面S 围成.若函数R Q P , , 在V 上连续, 且有连续的一阶偏导数, 则187⎰⎰⎰⎰⎰++=⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂S V Rdxdy Qdzdx Pdydz dxdydz z R y Q x P ,其中S 取外侧.称上述公式为Gauss 公式或Остроградский―Gauss 公式. 证 只证⎰⎰⎰⎰⎰=∂∂VS Rdxdy dxdydz z R. 设V 是xy 型区域( 即-Z 型体 ) ( 参阅[1]P 291图22—6 ), 其边界曲面S 由曲面 ),( :11y x z z S =下侧 , ∈),(y x D xy , ),( :22y x z z S =上侧 , ∈),(y x D xy . (),(),(21y x z y x z ≤.)以及垂直于XY 平面的柱面3S (外侧)组成. 注意到⎰⎰3),,(S dxdy z y x R =0, 有()d xdy z y x R dz z R dxdy dxdydz z R V D y x z y x z D y x z z y x z z xy xy⎰⎰⎰⎰⎰⎰⎰⎰===∂∂=∂∂),(),(),(),(2121|),,( ()()[]⎰⎰-=xyD dxdy y x z y x R y x zy x R ),(,,),(,,12()⎰⎰-=xyD dxdy y x zy x R ),(,,2()⎰⎰xyD dxdy y x z y x R ),(,,1++=⎰⎰⎰⎰21),,(),,(S S dxdy z y x R dxdy z y x R ⎰⎰3),,(S dxdy z y x Rd x d yz y x R S ),,(⎰⎰=外侧. 可类证⎰⎰⎰⎰⎰=∂∂V S Pdydz dxdydz x P, ⎰⎰⎰⎰⎰=∂∂VS Qdzdx dxdydz y Q. 以上三式相加, 即得Gauss 公式. 例1 计算积分⎰⎰∑++-++dxdy x z dzdx z y dydz y x )3()()(, ∑为球面2222R z y x =++取外侧. (参阅上节例2 )解 x z z y x R z y z y x Q y x z y x P 3),,( , ),,( , ),,(+=-=+=.188. 1 , 1 , 1⇒=∂∂=∂∂=∂∂z R y Q x P . 3 =∂∂+∂∂+∂∂zR y Q x P 由Gauss 公式 ⎰⎰⎰⎰⎰∑=⋅==VR R dxdydz 3343433 ππ. 例2 计算积分⎰⎰+++-S dxdy xz y dzdx x dydz z x y )()(22,其中S 是边长为a 的正方体V 的表面取外侧. V : a z a y a x ≤≤≤≤≤≤0 , 0 , 0. [1]P 291 E1. 解 应用Gauss 公式 , 有()⎰⎰⎰⎰⎰⎪⎪⎭⎫ ⎝⎛+∂∂+∂∂+-∂∂=V S dxdydz xz y z x y z x y x )()( 22 ⎰⎰⎰⎰⎰⎰⎰=⎪⎭⎫ ⎝⎛+=+=+=V a a a aa dy a ay a dx x y dy dz dxdydz x y 00004221)()(. 例3 计算积分⎰⎰∑++zdxdy ydzdx xdydz ,∑为锥面22y x z +=在平面4=z 下方的部分,取外法线方向 .解 设S 为圆16 , 422≤+=y x z 取上侧, 则S +∑构成由其所围锥体V 的表面外侧, 由Gauss 公式, 有⎰⎰+∑++S zdxdy ydzdx xdydz=⎰⎰⎰⨯=V dxdydz 33锥体V 的体积ππ643643=⋅=; 而 ⎰⎰⎰⎰≤+==++S y x dxdy zdxdy ydzdx xdydz 1622644π 因而, 0 ⎰⎰⎰⎰⎰⎰=-=+∑∑S S . 例4 设V 是三维空间的区域, 其内任何封闭曲面都可不通过V 外的点连续收缩为V 上的一点.又设函数),,(z y x P 、),,(z y x Q 和),,(z y x R 在V 上有连续的偏导数. S 表示V 内任一不自交的光滑封闭曲面, n 是S 的外法线. 试证明: 对V 内任意曲面S 恒有[]⎰⎰=++S dS z n R y n Q x n P 0),cos(),cos(),cos(189 的充要条件是0 =∂∂+∂∂+∂∂zR y Q x P 在V 内处处成立. 证 []⎰⎰⎰⎰++=++SS Rdxdy Qdzdx Pdydz dS z n R y n Q x n P ),cos(),cos(),cos(. )⇐ 由Gauss 公式直接得到.)⇒ 反设不然 , 即存在点∈),,(0000z y x M V , 使()0| 0≠∂∂+∂∂+∂∂M z R y Q x P ,不妨设其0>. 由zR y Q x P ∂∂+∂∂+∂∂ 在点0M 连续, 存在以点0M 为中心且在V 内的小球V ', 使在其内有zR y Q x P ∂∂+∂∂+∂∂ 0>. 以∑表示小球V '的表面外侧, 就有 ⎰⎰⎰⎰⎰'∑>⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂=V dxdydz z R y Q x P 0 , 与⎰⎰∑=0 矛盾. Ex[1]P 399—400 1, 2 .二. Stokes 公式:空间双侧曲面的正侧与其边界闭合曲线L 正向的匹配关系: 右手螺旋法则, 即当人站在曲面的正侧上, 沿边界曲线L 行走时, 若曲面在左侧, 则把人的前进方向定为L 的正向.1. Stokes 定理:Th22.4 设光滑曲面S 的边界L 是按段光滑的连续曲线. 若函数),,(z y x P 、),,(z y x Q 和),,(z y x R 在S (连同L )上连续, 且有一阶连续的偏导数, 则⎰⎰=⎪⎪⎭⎫ ⎝⎛∂∂-∂∂+⎪⎭⎫ ⎝⎛∂∂-∂∂+⎪⎪⎭⎫ ⎝⎛∂∂-∂∂S dxdy y P x Q dzdx x R z P dydz z Q y R ⎰++L Rdz Qdy Pdx . 其中S 的侧与L 的方向按右手法则确定.190 称该公式为Stokes 公式.证 先证式 ⎰⎰⎰⎰⎰=∂∂-∂∂S S L Pdx dxdy y P dzdx z P . 具体证明参阅[1]P 292—293.Stokes 公式也记为 ⎰⎰⎰++=∂∂∂∂∂∂S L Rdz Qdy Pdx dxdydzdx dydz R Q P z y x . 例5 计算积分⎰-+-++Ldz x y dy z x dx z y )()()2(, 其中 L 为平面1=++z y x 与各坐标平面的交线, 方向为: 从平面的上方往下看为逆时针方向. [1]P 294 E2.2. 空间曲线上第二型曲线积分与路径无关性:介绍空间单连通、复连通域.Th 22.5 设Ω⊂R 3为空间单连通区域. 若函数),,(z y x P 、),,(z y x Q 和),,(z y x R 在Ω上连续, 且有一阶连续的偏导数, 则以下四个条件等价:ⅰ> 对于Ω内任一按段光滑的封闭曲线L , 有⎰=++LRdz Qdy Pdx 0; ⅱ> 对于Ω内任一按段光滑的封闭曲线L , 曲线积分⎰++LRdz Qdy Pdx 与路径无关;ⅲ> Rdz Qdy Pdx ++是Ω内某一函数u 的全微分; ⅳ> zP x R y R z Q x Q y P ∂∂=∂∂∂∂=∂∂∂∂=∂∂ , , 在Ω内处处成立 . [1]P 294 3. 恰当微分的原函数:恰当微分的验证及原函数求法.例6 验证曲线积分⎰+++++Ldz y x dy x z dx z y )()()(与路径无关, 并求被积表达式的原函数),,(z y x u . [1]P 295E3.Ex [1]P400 3,4,5.191。
4 第一型曲面积分

第一型曲面积分的概念 第一型曲面积分的计算
一 第一型曲面积分的概念
实例
是光滑的, 若曲面 Σ 是光滑的 , 它的面密度为连续
求它的质量. 函数ρ( x , y , z ) , 求它的质量.
所谓曲面光滑即曲 面上各点处都有切 平面, 平面,且当点在曲面 上连续移动时, 上连续移动时,切平 面也连续转动. 面也连续转动.
1. 若 面Σ: 曲
则
Σ
z = z(x, y)
∫∫ f ( x , y , z )dS
=
∫∫
D xy
′x 2 + z′y 2 dxdy; f [ x , y , z ( x , y )] 1 + z
定理: 定理 设有光滑曲面 f (x, y, z) 在 ∑ 上连续 则曲面积分 上连续,
z
Σ
o x Dxy
Σ
y + z = 5 被柱面 x + y = 25 所截得的部分.
2 2
解 积分曲面 Σ:z = 5 − y ,
投影域 : Dxy = {( x , y ) | x 2 + y 2 ≤ 25}
2 2
与上半球面 z = a2 − x2 − y2 的 解: 锥面 z = x + y 交线为 为上半球面夹于锥面间的部分, 设∑1 为上半球面夹于锥面间的部分,它在 xoy 面上的 投影域为 Dxy = { ( x, y) x2 + y2 ≤ 1 a2 }, 则 2
I = ∫∫ (x2 ቤተ መጻሕፍቲ ባይዱ y2 ) dS
∑1
I = ∫∫ (x2 + y2) dS
∑1
= ∫∫
Dx y
(x + y )
第四节第一类曲面积分

)
(1)确定 的方程: z z(x, y);
(2)确定在xoy 面上的投影区域 Dx y
(3)将曲面方程 z z(x, y) 及
dS
1
zx2
(
x,
y)
z
2 y
(
x,
y)
d
xd
y
代入 f (x, y, z) d S中即可。 一投、二代、三换
说明: 1) 如果曲面方程为 x x( y, z), ( y, z) Dyz
1
z
2 x
z
2 y
d
xd
y
2d xd y,
Dx2y {( x, y) | x2 y2 1}, xdS x 2d xd y 0,
2
Dx2 y
例5. 计算 xdS , 其中是圆柱面 x2 y2 1,
平面 z x 2 及 z 0 所围成的空间立体的表面.
解: xdS xdS xdS
f (x, y, z) d S f [x( y, z), y, z] 1 xy2 xz2 d y d z
或
Dyz
y y(x, z), (x, z) Dxz
f (x, y, z) d S f [x, y(x, z), z] 1 yx2 yz2 d x d z
Dxz
2)若 是 xoy 面上的一个闭区域 D 时,则
: x2 y2 z2 a2
2
d
1 2
2a
0
0
a r 2 r dr a2 r2
1 a4 (8 5
6
2)
思考: 若例3 中被积函数改为
计算结果如何 ?
例4. 计算| xyz | d S 为抛物面 z x2 y2( 0 z 1).
第一型曲面积分的计算

d 1 S z x 2 z 2 y d 2 x d , d xoy d D xy y x
∵ 关 于 xo面 z对 称 , 而yz2x2, 被 积 函 数 中 x,yy都 z是 y的 奇 函 数 ,
∴ x y y 0 , ∴ z d ( x d y z S y ) d z x S z S 。 x
x 2 d y2 S z24 1x 2 d y2 S z24D ya z2 1z2
a dyd
a2y2
a 1
h1
4a
0
a2y2dy0a2z2dz
4 a (ar y )a c (1 a sirn z) c h t 4 a a 1 n arh c 2 t aa rh n .ct
20dx x 2
y x D 21 d y 21 dx x2D 2 x 2ydy
00
41(2x2)2 3dx41x3dx
30
30
x 2sint 16 4co4stdt1 5 .
30
33 2
习 题 三 ( P 1 8 7 )
4 .求 曲 线 A B 的 方 程 , 使 图 形 O A B D 绕
D
解 : 抛 物 线 y x 2 把 D 分 为 两 个 子 区 域 : y
D 1 { x ,y ( )x 1 ,x 2 y 2 } , 2
ห้องสมุดไป่ตู้
D 2 { x ,y ( )x 1 ,0 y x 2 } 。 D1 y x 2
yx2 yx2, (x,y)D1 -1
设 光 滑 曲 面 的 方 程 为 z z (x ,y ), 在 x面 y 上 的 投 影 区 域 为 D x, y 函 数 z (x ,y )在 D x上 y有 一 阶 连 续 偏 导 数 , 若 f(x ,y ,z )在 上 连 续 , 则 有
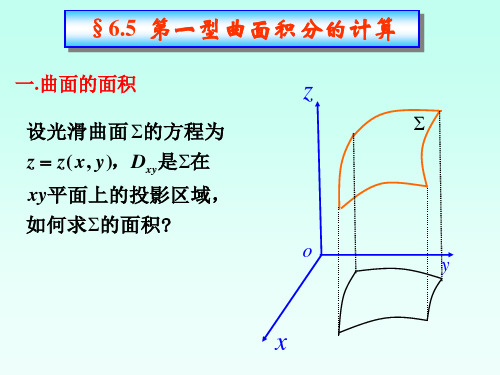
§6.5第一型曲面积分的计算
记d max 1 k n
的直径
k
,k的面积记为Ak .
如果不论将如何分割,点M
k
如何选取,
k
n
当d 0时, f (Mk )Ak有确定的极限,则称 k 1
函数f 在曲面上可积,极限值为f 在上的
第一型曲面积分,即
n
f
( x,
y, z)dA
lim
d 0
k 1
f (k ,k , k )Ak
( x, y) Dx y
A Dxy
Fx2 Fy2 Fz2 dxdy. Fz
例1.求球面 x2 y2 z2 a2在 z b部分的面积(a b 0).
az
S
b
y
x
二. 第一型曲面积分的概念
定义 设是一个分片光滑曲面,函数f 在上有定义.
将任意分割成n个小部分(k k 1,2,L ,n),
'(面积A')
的一个法向量:{0, 0,1}
'的一个法向量:{zx , zy ,1}
| cos |
1
1
z
2 x
z
2 y
x
dAA 11zzx2x2zz2y2yd
o
y
Dxy
P(x, y)
曲面的面积元素
结论: 1.设光滑曲面 的方程为 z z( x, y),Dxy是在 xy平面上的投影区域, 的面积为A,则
y
x
Dxy
例3.计算 ( x2 y2 z2 )dA,其中是由 x 0, y 0, x2 y2 z2 1 ( x 0, y 0)所围成的闭曲面.
z
2 1
y
x 3
§6.5 第一型曲面积分的计算
一.曲面的面积
§6.5第一型曲面积分的计算

f ( x, y, z)dA f ( x, y, z( x, y)) 1 z2x z2y dxdy.
Dxy
记忆口诀:“一代二换三投影”.
注 1. 若曲面 : y y( x, z), ( x, z) Dzx , 则
f (x, y, z)dA
f [x, y(x, z),z]
Dxy {( x, y) x2 y2 1} ,
∵ z 2x , z 2 y ,
x
y
Dxy o
x1
z1
zx2 y2
1y
dA 1 ( z )2 ( z )2 dxdy 1 4x 2 4 y2 dxdy x y
∴ A
1 4x 2 4 y 2 dxdy
D xy
2
d
1
1 42 d
zx
x z
,
zy
y z
1
z
2 x
z
2 y
a2 a2 x2 y2
A 2
a
dxdy
D a2 x2 y2
2
a2 b2
2 d
a
d 4 a a b
0
0
a2 2
例 2.求旋转抛物面 z x2 y2 上在平面 z1 下面的 一部分曲面 的 面 积A .
解:曲面 在xoy 面上的投影区域 z
8
பைடு நூலகம்
10 40
例 4 计算 (x2 y2 z2)dA, 为由x 0, y 0,
x2 y2 z2 1(x 0, y 0)所围成的闭曲面.
解 (x2 y2 z2)dA ( )
1 2 3
1: x 0, y2 z2 1, y 0,
z
(x2 y 2 z 2 )dA
10考研数学大纲知识点解析(第十章曲线曲面积分(数学一)

.
(3)第一类曲线积分表示的物理意义是曲线的质量,故与方向无关.
【第一类曲线积分的性质】
(1) (2) (3) (4) (5)设在 上
.
.
其中
没有公共部分.
. 其中 表示 的反方向的路径.
,则
.
特别的,
.
【第一类曲线积分的计算】设 为光滑曲线, (1)若 由参数方程
在 上连续. 给出 ,则
其中
在
上有一阶连续导数,且
(3)若积分曲线 关于
轴对称,则
【例题】(89 年,数学一/数学二)
设平面曲线 为下半圆
,则曲线积分
. .
【答案】 . 【解析 1】参数法:设 的参数方程为
【解析 2】将积分曲线 的方程
,即
于是 .
代入被积函数,得 .
【例题】(98 年,数学一)
设 为椭圆
,其周长记为 , 则
.
【答案】 .
【解析】将 的方程
函数
在空间曲线 上的第一类曲线积分可类似定义为
. 【空间中第一类曲线积分的计算】
若空间曲线 的参数方程为
则
.
【例题】计算曲线积分 上相应于 从 到 的一段弧. 【解析】原式
,其中 为螺旋线
.
【第二类曲线积分的概念(对坐标的曲线积分)】设 为 面内一条有向光滑曲线段,
函数
在 有界,则它们在 上的第二类曲线积分定义为
由 解得
得到的微分方程 ,带入
,得
,
所以
,于是
.
【综合题】(06 年,数学一)设在上半平面 偏导数,且对任意的 都有 向简单闭曲线 ,都有
内,函数
具有连续
.证明:对 内的任意分段光滑的有
考研数学-第一型曲线曲面积分

3 2 C在xoy面上投影D xy {( x , y ) x y 1} 4
2
2x 2 y z z z 1 1 x y y 2z y 2z
2
2
2
2
4 y 2 z 2 4 yz y 2z
2 2
8 16 8 5 5 R R R 5 15 5 3
例14
练习十二/五
设有一个由曲线y ln x, y 0, x e所围成的 均匀薄片, 其面密度为 1, 若此薄片关于直线 x t的转动惯量为I (t ), 求使I (t )取得最小值的t. y 2 解:I (t ) ( x t ) d
dx 2 2 解 : ds 1 ( ) dy dy 2 dy 4 y
( x y 1)ds
L
2
2
( 4 y y 1)
2
2 4 y
2
dy
8 2
例2 练习十三/二(2)
x2 y 2 设L为椭圆 1,已知其周长为a, 2 3 则 (3x 2 5 xy 2 y 2 )ds _______ .
λ 0
i 1
n
2. 计算:
: z z( x , y ) , ( x , y ) D x y , 则
f ( x , y, z )dS
Dxy
f [ x, y, z( x , y )]
1 zx zy dxdy;
2 2
方法:一投、二代、三换.
3. 对称性
对面积的曲面积分 f ( x , y , z ) d S,
第十节 第一型曲线曲面积分 积分应用
型曲线积分的计算(2)

ds x2(t) y2(t)dt ,
L f ( x, y)ds f [ x(t ), y(t )]
x2(t ) y2(t)dt 。
2
2.若L由 方程 y y( x) (a x b) 给出,则
取 x 为 参数, ds 1 y2( x)dx
b
L f ( x, y)ds a f [ x, y( x)]
L f ( x, y)ds f [()cos ,()sin]
2() 2()d 。
4. 若空间光滑曲线L的 参数方程为 x x(t) , y y(t) , z z(t) ( t ) ,则
ds x2(t) y2(t) z2(t)dt ,
f ( x, y, z)ds f [ x(t ), y(t ), z(t )]
y
L
当 f ( x, y) 0 时, L f ( x, y)ds 表示以 L 为准线,
母线平行于z 轴 ,高为 f ( x, y) 的柱面面积。
19
L
x2 y2 z2 9 与平面x z1 的交线。 2
解: L
:
x2 y2 x z1
z
2
9 2
(x 1)2 2
2 z1 x.
y2 4
1,
其参数方程为:
x 1 2cos, 2
y 2s in,
z
1 2
2cos.
(02) ,
12
ds ( 2sin)2 (2cos)2 ( 2sin)2d2d ,
按键
PCBA
开关键
传统机械按键设计要点:
1.合理的选择按键的类型,尽量选择 平头类的按键,以防按键下陷。
2.开关按键和塑胶按键设计间隙建议 留0.05~0.1mm,以防按键死键。 3.要考虑成型工艺,合理计算累积公 差,以防按键手感不良。
第一型曲线曲面积分

L
的面积
z
z a2 x 2 y2
y
4a2 x 2 y2 dl 4a L t 2 2 8a sin dt 16a 0 2013-7-11 2
4
2
x
L
2(1 cos t )dt
21
0
2
三、第一型曲面积分的概念和性质
设f ( M ), g ( M )在曲线L上可积, 则 , R,
f ( M ) g ( M )在L上也可积, 并且有
[f ( M ) g ( M )]dl
L
L
f ( M )dl g ( M )dl
L
性质2:(路径可加性)
若曲线L由曲线L1与曲线L2连接而成, 且 f ( M )在L, L1 , L2上可积, 则有
S 0 i i i i 1
23
i
第一型曲面积分与 第一型曲线积分有类似 的性质和存在性条件 .
15
[例3] 计算 x dl, 其中L为圆周 : x y z a , L z x y z 0. [解] 首先找曲线的参数方程 y o 先找L在xy平面投影曲线的
2 2 2 2 2
参数方程, 这就是L的参数方程 x 的x , y两式, 利用 x y z 0 就可得到第三式
[例] 假设有一不均匀的金属曲面S , 在S上的点M处的面密度为 ( M ), 求S的质量m .
M i
Si
S
[解] 分割: 将S任意分成n小块
近似 : mi ( M i )Si
求和 : m m i ( M i )S i
2013-7-11
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A
o Bx
例 2.计算 L yds ,其中 L 为抛物线y x2 ,直线x1 及
x 轴所围成的曲边三角形的整个边界.
y
B
y x2 x1
o y0 A x
例 3.计算 ( x2 y2 z2 )ds ,其中 L 为曲线
L
x2 y2 z2 4 xz0
例 4.设 L 为椭圆 x2 y2 1 ,其周长为 a, 43
1
x 2
y
x z
2dydz;
D yz
3.设曲面的方程为:y h(z, x)
曲面面积公式为:A
1
y 2
z
y x
2dzdx.
Dzx
例1
求球面x2 y2 z2 a2在 z b(a b 0)部分 的面积。
例 2 求由曲面x2 y2 az 和z 2a x2 y2 (a 0)所围立体的表面积.
:
z f ( x,
(x, y) y) 0
,在柱面(x,
y)
0
上介于L与
之间的
曲面的面积就是L f (x, y)ds 。
z
o
x
f (x, y)ds
y
L
当f (x, y) 0 时, L f (x, y) ds 表示以 L 为准线,
母线平行于z轴,高为z f (x, y)的柱面面积。
例6
求圆柱面x2 y2 1位于平面z 0上方与z y 下方那部分的侧面积A.
2() 2()d
L
注: 对 L f ( x, y)ds 来说, f ( x, y) 是定义在 L 上的,
被积函数中的 x,y 应满足 L 的方程,故可利 用 L 的方程化简被积函数.
故有“代入法”或“整体代入”
例 1.计算 xe x2 y2 ds ,其中L 0) 处的一段弧。
第一型曲线积分的性质
1. L[ f ( x, y) g( x, y)]ds L f ( x, y)ds L g( x, y)ds ;
2. Lkf ( x, y)ds k L f ( x, y)ds (k为常数) ; 3. L f ( x, y)ds L1 f ( x, y)ds L2 f ( x, y)ds, (L L1 L2 ) .
f ( x, y, z( x, y))
1
z
2 x
z
2 y
dxdy
.
Dxy
记忆口诀:“一代二换三投影”.
注 1. : z z( x, y)
dA
1
z
2 x
z
2 y
dxdy.
2. 若方程为 x x( y, z), Dyz : 在yz 平面上的投影,则
f ( x, y, z)dA f ( x( y, z), y, z)
第五节 第一型曲面积分的计算
5.1 曲面的面积
1.设曲面 S 的方程为:
z f (x, y)
在 xoy 面上的投影区域为 D,
如图, 设小区域 d D,
z
s
dA M
点 ( x, y) d ,
o
为 S 上过 M ( x, y, f ( x, y))
的切平面.
x
(x, y) y d
以 d 边界为准线,母线平行于 z 轴的小 柱面,截曲面 s 为 ds;截切平面 为 dA, 则有dA ds.
5.2 第一型面积分的计算:
根据二重积分及第一型曲面积分的定义,可把第 一型曲面积分化成二重积分计算。
设光滑曲面的方程为z z( x, y), 在 xy 面上的投影区 域 为Dxy , z( x, y)在Dxy上 有 一 阶 连 续 偏 导 数, f ( x, y, z)在上 连 续, 则
f ( x, y, z)dA
d 为 dA 在 xoy 面上的投影, d dA cos ,
cos
1
,
1
f
2 x
f
2 y
dA
1
f
2 x
f
2 y
d
曲面S的面积元素
A
1
f
2 x
f
2 y
d
,
D
曲面面积公式为:A
Dxy
1
(
z x
)2
(
z y
)2
dxdy
同理可得
2.设曲面的方程为:x g( y, z)
曲面面积公式为:A
连续的一阶导数,且 x2(t) y2(t) 0,则
ds x2(t) y2(t)dt ,
L f ( x, y)ds f [x(t), y(t)]
x2(t) y2(t)dt .
2.若L由 方程 y y( x) (a x b) 给出,则
取 x 为 参数, ds 1 y2( x)dx
b
L f ( x, y)ds a f [ x, y( x)]
1 y2( x)dx .
3.若 L由 方程 x x( y) (c y d ) 给出,则
取 y 为参数 , ds 1 x2( y)dy
d
L f ( x, y)ds c f [x( y), y]
1 x2( y)dy .
4. 若空间光滑曲线L的 参数方程为 x x(t) , y y(t) , z z(t) ( t ) ,则
1
x
2 y
x
2 z
dydz.
D yz
若的方程为 y y( x, z), Dxz : 在xz 平面上的投影,则
f ( x, y, z)dA f ( x, y( x, z), z)
Ñ 求 (3x2 4y2 2x2 y3)ds 的值。 L
例 5.设 L为球面x2 y2 z2 R2 与平面 x y z0 的
Ñ 交线,求 ( x2 y2 z)ds 。 L
第一型曲线积分的几何意义
设 L 为xoy 面上的光滑曲线,其方程为z(x0, y) 0 , 在 L上 定义连续函数 f (x, y) 0 ,它的图形是空间曲线
ds x2(t) y2(t) z2(t)dt ,
f ( x, y,z)ds
f [ x(t ), y(t ), z(t )]
x2(t ) y2(t ) z2(t)dt .
L
5.若曲线L由极坐标方程 ( )( )给出,则有
f ( x, y)ds=
f [( )cos, ( ) sin]
简记为 L f ( x, y)ds L1
L2
.
4. 当f ( x, y) 1时, Lds 等于L的长度.
注: 若L 是闭曲线,则记为 L f ( x, y)ds .
L f ( x, y)ds的对称性类似于二重积分
第一型曲线积分的计算法
1.设 f ( x, y) 在曲线 L 上连续,L 的参数方程为 x x(t) , y y(t) ( t ) ,其中 x(t) , y(t) 在[,]上有
