二次函数与平行四边形综合
二次函数和平行四边形的结合解题思路

二次函数和平行四边形的结合解题思路二次函数和平行四边形的结合解题思路1. 引言二次函数和平行四边形是数学中的两个重要概念。
二次函数是一种具有关于自变量的平方项的函数形式,常用来描述抛物线的形状和性质。
而平行四边形是一种具有四个边都平行的四边形,具有特殊的几何性质。
本文将通过结合二次函数与平行四边形,探讨它们在解题中的有趣应用,深入理解二次函数和平行四边形的知识点与概念。
2. 二次函数与平行四边形的基本概念2.1 二次函数的基本形式二次函数通常以一般式y=ax^2+bx+c的形式出现,其中a、b、c分别是常数,a不等于0。
通过调整a、b、c的值,可以改变二次函数的图像特征,如顶点的位置、开口方向等。
2.2 平行四边形的定义平行四边形是一种四边形,它的四条边两两平行。
其中,对边相等,对角线互相平分且互相垂直。
3. 二次函数与平行四边形的关联3.1 求解二次函数与平行四边形的顶点二次函数的顶点是抛物线的最高点或最低点,它在函数图像上具有特殊的几何意义。
通过平行四边形的性质,可以推导出二次函数的顶点与对边的关联。
具体而言,可以建立一个平行四边形,其中顶边平行于x轴,底边与二次函数图像的切线重合,并垂直于x轴。
这样一来,平行四边形的高度就是二次函数的顶点坐标。
3.2 求解二次函数与平行四边形的根二次函数的根是方程y=0的解,也就是抛物线与x轴相交的点。
通过平行四边形的性质,可以将二次函数的零点与对边的关系进行探讨。
类似地,构建一个平行四边形,其中左边平行于y轴,右边与二次函数图像的另一条切线重合,并垂直于y轴。
这样一来,平行四边形的宽度就是二次函数的根的坐标。
4. 二次函数与平行四边形的解题思路4.1 平移变换与二次函数的关系平行四边形具有平移不变性,即保持所有边平行的同时可以移动。
我们可以利用平行四边形的特性,通过平移变换来研究二次函数的图像平移。
给定一个已知的抛物线y=x^2,在x轴上平移h个单位,得到新的抛物线y=(x-h)^2。
二次函数中平行四边形的通用解决方法

二次函数中平行四边形的通用解决方法要解决关于二次函数的平行四边形问题,我们需要了解二次函数的一般形式、平行四边形的性质以及如何将这两者结合起来解决问题。
首先,二次函数的一般形式可以写为f(x) = ax^2 + bx + c。
其中,a、b、c是常数,a不等于0。
接下来,我们需要了解平行四边形的性质。
平行四边形是一个有四个边,且对边平行的四边形。
根据平行四边形的性质,我们可以得到以下重要结论:1.对边平行:平行四边形的相对边是平行的,也就是说,如果ABCD是一个平行四边形,那么AB与CD平行,且AD与BC平行。
2.对角线互相平分:平行四边形的对角线互相平分,也就是说,对角线AC和BD相交于E,那么AE与CE的长度相等,BE与DE的长度也相等。
3.同底异位角相等:平行四边形的同底异位角相等,也就是说,对于平行四边形ABCD,∠A=∠C,且∠B=∠D。
现在我们来看一些具体问题,并探讨如何应用这些性质解决平行四边形问题。
问题1:已知二次函数f(x) = ax^2 + bx + c,其中a ≠ 0。
如何证明函数图像与y轴平行?解答:要证明函数图像与y轴平行,我们需要证明函数的导数为0。
导数表示了函数的斜率,如果导数为0,则对应的函数图像是水平的,即与y轴平行。
首先计算函数的导数f'(x) = 2ax + b。
要证明f'(x) = 0,我们可以解方程2ax + b = 0。
解这个方程可以得到x = -b/(2a)。
因此,当x=-b/(2a)时,函数的导数为0。
根据导数的意义,这意味着函数的图像与y轴平行。
问题2:已知二次函数f(x) = ax^2 + bx + c,其中a ≠ 0。
如何确定函数图像的顶点坐标?解答:要确定函数图像的顶点坐标,我们可以利用导数的信息。
对于二次函数来说,它的顶点坐标对应着导数为0的点。
首先计算函数的导数f'(x) = 2ax + b。
要求导数为0,我们可以解方程2ax + b = 0。
中考数学复习《二次函数与平行四边形的综合》专项检测卷(附带答案)

中考数学复习《二次函数与平行四边形的综合》专项检测卷(附带答案)学校:___________班级:___________姓名:___________考号:___________1.如图1,已知抛物线2y x x =-++23与x 轴交于点A ,B ,与y 轴交于点C ,点D 是抛物线的顶点,点M 是直线BC 上方抛物线上的一动点.(1)求抛物线的顶点D 的坐标和直线BC 的解析式;(2)如图1,连接AM 交BC 于点P ,若12MP AP =,求此时点M 的坐标; (3)如图2,直线y x b =+与抛物线交于A ,E 两点,过顶点D 作DF y ∥轴,交直线AE 于点F .若点G 是抛物线上一动点,试探究在直线AE 上是否存在一点H ,使得以点D ,F ,G ,H 为顶点的四边形是平行四边形,若存在,请直接写出点H 的坐标,若不存在,请说明理由.2.如图,二次函数28y ax bx =++的图像与坐标轴分别交于点A 、B 、C ,5cos B 和:1:2AO BO =.(1)求二次函数表达式;(2)在第二象限内,线段AC 上有一点D ,作PD 平行于x 轴,交二次函数图像于点P 、H (点P 在y 轴左侧),作点Q 与点P 关于y 轴对称.①证明:四边形AQHO 为平行四边形;①若ACQ 是以AC 为斜边的直角三角形,求点P 的横坐标;①直角坐标系内存在点(,)E x y ,使得四边形CQEH 为平行四边形,请直接写出y 与x 的函数表达式,并求当线段PD 的长度最大时,点E 的坐标.3.如图,二次函数()20y x bx c b =-++>的图像与x 轴分别交于A ,B 两点(点A 在点B 的左侧),与y 轴交于点()0,4C ,二次函数的最大值为254,P 为直线BC 上方抛物线上的一动点.(1)求抛物线和直线BC 的解析式;(2)如图1,过点P 作PD BC ⊥,垂足为D ,连接CP .是否存在点P ,使以点C ,D ,P 为顶点的三角形与AOC 相似?若存在,请求出点P 的坐标;若不存在,请说明理由;(3)如图2,点Q 也是直线BC 上方抛物线上的一动点(点Q 在点P 的左侧),分别过点P ,Q 作y 轴的平行线,分别交直线BC 于点M ,N ,连接PQ .若四边形PQNM 是平行四边形,且周长l 最大时,求l 的最大值及相应的点P 的横坐标.4.已知,如图1,在平行四边形ABCD 中,对角线6cm AC =,8cm BC =和10cm AB =,如图2,点G 从点B 出发,沿BC 方向匀速运动,速度为1cm/s ,过点G 作GH BC ⊥交AB 于点H ;将平行四边形ABCD 沿对角线AC 剪开,DEF 从图1的位置与点G 同时出发,沿射线BC 方向匀速运动,速度为2cm /s ,当点G 停止运动时,DEF 也停止运动.设运动时间为()08t t <≤,解答下列问题:(1)当t 为何值时,点F 在线段GD 的垂直平分线上?(2)设四边形AHGD 的面积为()2cm S ,试确定S 与t 的函数关系式,并求S 的最大值; (3)连接EG ,试求当AG 平分BAC ∠时,四边形EGFD 与四边形AHGE 面积之比.5.如图,已知抛物线与x 轴相交于A ,B 两点,与y 轴交于点C ,且()3,0A -,()1,0B 和()0,3C ,顶点为P .(1)求抛物线的解析式;(2)若以A ,C ,P ,M 为顶点的四边形是平行四边形,求点M 的坐标.6.已知抛物线23y ax bx =++与x 轴交于点()1,0A -,点()3,0B ,与y 轴交于点C ,顶点为点D ,点P 为抛物线上的一个动点(1)求抛物线的解析式;(2)若过点C 的直线交线段AB 于点E ,且:3:5ACE CEB S S =,求线段CE 的长是多少?(3)当点P 在第一象限时,连接PC 和PB ,求PBC 面积的最大值时多少?(4)若点Q 在x 轴上,当以点D ,C ,P ,Q 为顶点的四边形是平行四边形时,请求出点P 的坐标.7.如图,抛物线21262y x x =--与x 轴相交于点A 、点B ,与y 轴相交于点C .(1)请直接写出点A ,B ,C 的坐标;(2)点()(),06P m n m <<在抛物线上,当m 取何值时,PBC 的面积最大?并求出PBC 面积的最大值.(3)点F 是抛物线上的动点,作FE AC ∥交x 轴于点E ,是否存在点F ,使得以A 、C 、E 、F 为顶点的四边形是平行四边形?若存在,请写出所有符合条件的点F 的坐标;若不存在,请说明理由.8.综合与探究:如图1,已知抛物线2142y x x =-++与x 轴相交于A ,B 两点(点A 在点B 的左侧),与y 轴相交于点C ,直线BD 与y 轴相交于点D ,交线段AC 于点E ,且27BD DE =.(1)求A ,B ,C 三点的坐标;(2)求直线BD 的函数表达式;(3)如图2,若抛物线的对称轴l 与直线BD 交于点P ,试探究,在平面内是否存在一点Q ,使以点A ,C ,P ,Q 为顶点的四边形为平行四边形.若存在,求出点Q 的坐标,若不存在,请说明理由.9.综合与探究如图,抛物线214433y x x =--+与x 轴交于A ,B 两点(点B 在点A 的左侧),与y 轴交于点C ,P 是直线BC 上方抛物线上一动点.(1)求A,B,C三点的坐标,并直接写出直线BC的函数表达式.(2)连接PB,PC,求PBC面积的最大值及此时点P的坐标.(3)在(2)的条件下,若F是抛物线对称轴上一点,在抛物线上是否存在点Q,使以B,F,P,Q为顶点的四边形是平行四边形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.10.如图1,在平面直角坐标系xOy中,抛物线223=-++与x轴分别交于点A和点B,与y轴交于点C,y x x连接BC.(1)求ABC的面积;(2)如图2,点P是该抛物线上一个动点,并沿抛物线从点B运动至点A,连接PO、PB,并以PO、PB为边作平行四边形POQB.①当平行四边形POQB的面积为9时,求点P的坐标;①直接写出在整个运动过程中,点Q与线段BC的最大距离是.11.如图,在平面直角坐标系中,抛物线24y ax bx =++交y 轴于点A ,交x 轴于点()6,0B -和点()2,0C ,连接AB 、AQ 、BQ ,BQ 与y 轴交于点N .(1)求抛物线表达式;(2)点713Q ⎛⎫ ⎪⎝⎭,,点M 在x 轴上,点E 在平面内,且四边形ANEM 是平行四边形. ①求点E 的坐标;①设射线AM 与BN 相交于点P ,交BE 于点H ,将BPH 绕点B 旋转一周,旋转后的三角形记为11BP H △,求11BP 的最小值.12.如图,已知二次函数2y x bx c =++的图象与x 轴交于点(1,0)A ,(3,0)B 与y 轴交于点C .(1)求二次函数的解析式;(2)点E 是二次函数第四象限图象上一点,过点E 作x 轴的垂线,交直线BC 于点D ,求四边形AEBD 面积的最大值及此时点E 的坐标;(3)若点P 为抛物线上的一点,点F 为对称轴上的一点,且以点A ,B ,P ,F 为顶点的四边形为平行四边形,直接写出点P 的坐标.13.如图,抛物线22y x x c =-++与x 轴交于A ,B 两点,与y 轴交于点C ,直线3y x =-+经过B ,C 两点.(1)求抛物线的函数表达式.(2)已知P 为抛物线22y x x c =-++上一点(不与点B 重合),若点P 关于x 轴对称的点P '恰好在直线BC 上,求点P 的坐标;(3)在(2)的条件下,以AB 为对角线画平行四边形AMBP ',将抛物线22y x x c =-++的顶点沿直线y x b=-+平移得到的抛物线恰好经过点M ,求平移后的抛物线的函数表达式.14.如图,抛物线22(0)y x x m m =-++>与y 轴交于A 点,其顶点为D .直线122y x m =--分别与x 轴、y 轴交于B 、C 两点,与直线AD 相交于E 点.(1)求A 、D 的坐标(用m 的代数式表示);(2)将ACE 沿着y 轴翻折,若点E 的对称点P 恰好落在抛物线上,求m 的值;(3)抛物线22(0)y x x m m =-++>上是否存在一点P ,使得以P 、A 、C 、E 为顶点的四边形是平行四边形?若存在,求此抛物线的解析式;若不存在,请说明理由.15.若直线5y x =-与y 轴交于点A ,与x 轴交于点B ,二次函数2y ax bx c =++的图象经过点A ,点B ,且与x 轴交于点()1,0C -.(1)求二次函数的解析式;(2)若点P 为直线AB 下方抛物线上一点,过点P 作直线AB 的垂线,垂足为E ,作PF y ∥轴交直线AB 于点F ,求线段PF 最大值及此时点P 的坐标;(3)将抛物线沿x 轴的正方向平移2个单位长度得到新抛物线y ',Q 是新抛物线y '与x 轴的交点(靠近y 轴),N 是原抛物线对称轴上一动点,在新抛物线上存在一点M ,使得以M 、N 、B 、Q 为顶点的四边形是平行四边形,请直接写出符合条件的点M 的坐标.参考答案:1.(1)()1,4D 3y x =-+(2)点M 的坐标的()1,4或()2,3(3)存在,点H 的坐标为()0,1或()2,3或117317++⎝⎭,或117317--⎝⎭,2.(1)228y x x =-++ (2)①12-①21102y x =-+ (4,2)E3.(1)抛物线的解析式为234y x x =-++,直线BC 的解析式为4y x =-+(2)点P 的坐标为1846,525⎛⎫ ⎪⎝⎭或12136,525⎛⎫ ⎪⎝⎭(3)l 的最大值为12,相应的点P 的横坐标224.(1)2 (2)23924(08)8S t t t =-++<≤ (3)168955.(1)223y x x =--+(2)()2,1-- ()4,1- ()2,76.(1)223y x x =-++;(3)278;(4)点P 的坐标为()11-或()11-或()1或()1.7.(1)()2,0A - ()6,0B ()0,6C -;(2)3m =,PBC 面积的最大值272;(3)存在,()2+或()2-或()4,6-.8.(1)()2,0A - ()4,0B ()0,4C (2)1433y x =-+ (3)()3,3-或()1,3--或()3,59.(1)()()2060A B -,,, ()04C , 243y x =+ (2)PBC 的面积最大值为9,此时点P 的坐标为()35-,(3)713⎛⎫ ⎪⎝⎭,或753⎛⎫- ⎪⎝⎭,或()73--,10.(1)6(2)①(0,3)或(2,3);212 11.(1)214433y x x =--+ (2)①()2,2E --;①6212.(1)243y x x =-+; (2)94,33,24⎛⎫- ⎪⎝⎭; (3)点P 的坐标为2,1或()4,3或()0,3.13.(1)223y x x =-++(2)(2,5)P --.(3)2(6)1y x =---14.(1)()()0,,1,1A m D m + (2)32m = (3)2524y x x =-++或2124y x x =-++15.(1)245y x x =--(2)PF 有最大值254,点P 的坐标为53524,⎛⎫- ⎪⎝⎭ (3)满足条件的点M 的坐标有()4,9M -或()6,5-或()2,27-。
二次函数与平行四边形综合题

二次函数与平行四边形综合题【最新版】目录1.二次函数与平行四边形的关系2.如何利用二次函数解决平行四边形问题3.实例解析正文二次函数与平行四边形的关系二次函数是一种数学函数,其图像通常为抛物线。
在几何中,平行四边形是一种四边形,其中对边两两平行。
二次函数与平行四边形看似不相关,但在一些数学问题中,它们却有着密切的联系。
例如,在解决一些涉及平行四边形的综合题目时,我们可以通过二次函数来找到平行四边形的性质,从而解决问题。
如何利用二次函数解决平行四边形问题利用二次函数解决平行四边形问题的关键在于找到平行四边形的对角线。
对角线是平行四边形中连接不相邻顶点的线段。
根据平行四边形的性质,对角线互相平分,且对角线中点重合。
因此,在解决平行四边形问题时,我们可以通过找到二次函数图像上的两个点,并求出这两个点的中点,从而确定平行四边形的对角线。
实例解析假设我们有一个二次函数 y = 2x^2 + 3x - 2,我们需要找到这个二次函数与平行四边形的关系。
首先,我们可以通过求导数的方法找到二次函数的顶点坐标。
对于这个二次函数,顶点的横坐标为 -b / (2a),即 -3 / (2 * 2) = -3 / 4。
将横坐标代入原函数,可得顶点的纵坐标为 y = 2 * (-3 / 4)^2 + 3 * (-3 / 4) - 2 = -25 / 8。
因此,顶点坐标为 (-3 /4, -25 / 8)。
接下来,我们可以根据顶点坐标和二次函数的性质,求出与平行四边形相关的两个点。
首先,我们可以求出过顶点的两条直线的方程。
一条直线的斜率为 -2 / 3,过顶点,可得直线方程为 y + 25 / 8 = -2 / 3 (x + 3 / 4),即 y = -2 / 3 x - 1 / 4。
另一条直线的斜率为 1 / 2,过顶点,可得直线方程为 y + 25 / 8 = 1 / 2 (x + 3 / 4),即 y = 1 / 2 x + 11 / 8。
二次函数与平行四边形综合

这一关系提供了许多解析几何和图形问
题的有用工具,例如寻找最小值、最大
值和对称性。
3
图像
通过绘制函数和平行四边形的图形,可 以应用这些概念进行可视化。
平行四边形和二次函数的图像
图像
绘制平行四边形和二次函数的图 像可以使它们之间的关系更加清 晰。
二次函数图像
二次函数的图像通常采用抛物线 形式呈现,具有对称性和顶点。
平行四边形图像
平行四边形的图像可以通过将其 边界显示为矩形来构建。
平行四边形和二次函数的应用Fra bibliotek1 应用
这些概念在解析几何、物理学、计算机图形 学和工程等领域中有许多实际应用。
2 示例
可以使用这些概念解决包括区域最小化、体 积最大化、场景生成和动画路径设计等问题。
平行四边形和二次函数的解析几何证明
证明
二次函数的定义和性质
定义
二次函数是一种形式为 y=ax^2+bx+c 的函数,其中 a、b 和 c 是常数,且 a ≠ 0。
性质
二次函数具有许多重要的性质,如顶点、对称轴、单调性和极限。
平行四边形与二次函数的关系
1
关系
二次函数的顶点是平行四边形的中心点,
性质
2
同时平行四边形的对角线是二次函数的 对称轴。
需要应用纯粹的解析几何和一些基本的代数知识来 证明二次函数和平行四边形之间的关系。
方法
关键在于了解二次函数和平行四边形的特点和性质, 并将它们进行运算和变形,以显示它们之间的关系。
总结和要点
总结
在本演示中,我们介绍了平行四边形的定义和 性质,二次函数的定义和性质,以及二者之间 的关系和应用。
要点
关键是要理解二次函数和平行四边形的特征和 性质,并能将它们相互关联。
专题01 二次函数与平行四边形综合(原卷版)

专题01 二次函数与平行四边形综合(重庆专用)(3类题型训练)x2+bx+c与直线AB交于点A (2022重庆市中考数学A卷)如图,在平面直角坐标系中,抛物线y=12(0,―4),B(4,0).(1)求该抛物线的函数表达式;(2)点P是直线AB下方拋物线上的一动点,过点P作x轴的平行线交AB于点C,过点P作y轴的平行线交x轴于点D,求PC+PD的最大值及此时点P的坐标;(3)在(2)中PC+PD取得最大值的条件下,将该抛物线沿水平方向向左平移5个单位,点E为点P的对应点,平移后的抛物线与y轴交于点F,M为平移后的抛物线的对称轴上一点.在平移后的抛物线上确定一点N,使得以点E,F,M,N为顶点的四边形是平行四边形,写出所有符合条件的点N的坐标,并写出求解点N的坐标的其中一种情况的过程.解析过程详解(1)解:将点A (0,―4),B (4,0)代入y =12x 2+bx +c 得:c =―48+4b +c =0 ,解得:c =―4b =―1 ,∴该抛物线的函数表达式为:y =12x 2―x ―4;(2)如图,设PD 交BC 于H ,∵A (0,―4),B (4,0),∴OA =OB =4,∴∠OBA =∠OAB =45°,∵PC ∥OB ,PD ∥OA ,∴∠BCP =∠OBA =45°,∠PHC =∠BHD =∠OAB =45°,∴PC =PH ,设直线AB 的解析式为y =kx +b ,则b =―44k +b =0 ,解得:b =―4k =1 ,∴直线AB 的解析式为y =x ―4,设P t ,12t 2―t ―4,则H (t ,t ―4),D (t ,0),∴PC +PD =PH +PD =t ―4―2―t ――1t 2+t +4=―t 2+3t +4=―t ―+254,∴当t =32时,PC +PD 取得最大值4,此时―(3)由题意得:平移后抛物线解析式为y =12(x +5)2―(x +5)―4=12x 2+4x +72,E ―72,∴F 0,∵抛物线y =12x 2+4x +72的对称轴为x =―4,∴设M (―4,m ),N n ,12n 2+4n 分情况讨论:①当EF 为对角线时,则―4+n =―72,解得:n =1,此时12n 2+4n +72=458,∴N ②则―72―4=n ,即n =―152,此时12n 2+4n +7=138,∴N 2―152③当EN则―72+n =―4,即n =―12,此时12n 2+4n +72=138,∴N 3―12综上所述,点N 的坐标为:N N 2―152N 3―12类型一 动点+平行四边形1.抛物线y =ax 2+bx +c (a ≠0)与x 轴交于点A(―3,0),B(1,0)两点,与y 轴交于点C(0,3),点P 是抛物线上的一个动点.(1)求抛物线的函数表达式;(2)如图1,点P 在线段AC 上方的抛物线上运动(不与A ,C 重合),过点P 作PD ⊥AB ,垂足为D ,PD 交AC 于点E .作PF ⊥AC ,垂足为F ,若点P 的横坐标为t ,请用t 的式子表示PE ,并求△PEF 的面积的最大值;(3)如图2,点Q 是抛物线的对称轴l 上的一个动点,在抛物线上存在点P ,使得以点A ,P ,C ,Q 为顶点的四边形是平行四边形,请直接写出所有符合条件的点P 的坐标,并把求其中一个点P 的坐标的过程写下来.2.如图,抛物线y =―x 2+2x +3与x 轴交于A 、B 两点(A 点在B 点左侧)、直线l 与抛物线交于A 、C 两点,其中点C 的横坐标为2.(1)求A 、B 两点的坐标及直线AC 的函数表达式;(2)若点Р是线段AC 上的一个动点,过点Р作y 轴的平行线交抛物线于点E ,求线段PE 长度的最大值;(3)若点G 是抛物线上的一个动点,在x 轴上是否存在点F ,使A 、C 、F 、G 这样的四个点为顶点的四边形是平行四边形?如果存在,直接写出所有满足条件的点F的坐标;如果不存在,请说明理由.3.在直角坐标系中,抛物线y=1x2+bx+c(a≠0)与x轴交于A、B两点.其中点A(―2,0),点B(4,0).2(1)求抛物线的解析式.(2)如图1,在直线l:y=―1x+n经过A点,与y轴交于D.在直线l下方的抛物线上有一个动点P,连接PA,2PD,求△PAD面积的最大值及其此时P的坐标.(3)将抛物线y向右平移1个单位长度后得到新抛物线y1,点E是新抛物线y1的对称轴上的一个动点,点F是原抛物线上的一个动点,取△PAD面积最大值时的P点.若以点P、D、E、F为顶点的四边形是平行四边形,直接写出点F的坐标,并写出求解其中一个F点的过程.类型二平移+平行四边形4.如图1,在平面直角坐标系中,抛物线y=ax2+bx+a≠0)与x轴交于点A―1,0,点B3,0,与y轴交于点C.(1)求该抛物线的解析式;(2)点P为直线BC上方抛物线上的一点,过点P作x轴的平行线交BC于点D,过点P作y轴的平行线交BC于点E,求PD+PE的最大值以及此时点P的坐标;(3)如图2,将抛物线沿射线CB的方向平移,使得平移后的抛物线经过线段CB的中点,且平移后抛物线的对称轴与x轴交于点M,N,R是直线BC上任意两点,Q为新抛物线上一点,直接写出所有使得以点M,N,R,Q为顶点的四边形是平行四边形的点Q的横坐标,并把求其中一个点的横坐标过程写出来.5.如图,在平面直角坐标系中,抛物线y=ax2+bx―3(a≠0)与x轴交于A(―1,0),B(3,0)两点,与y轴交于C点.(1)求抛物线的函数表达式;(2)点P是直线BC下方抛物上一动点,连接PB,PC,求△PBC面积的最大值以及此时点P的坐标;(3)在(2)中△PBC的面积取得最大值的条件下,将该抛物线沿水平方向向左移动2个单位,平移后的抛物线顶点坐标为Q,M为y轴上一点,在平移后的抛物线上确定一点N,使得以点P,Q,M,N为顶点的四边形是平行四边形,写出所有符合条件的N的坐标,并写出求解点N的坐标的其中一种情况的过程.6.如图1,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴交于点A,B两点(点A在点B的左x+3.侧),与y轴交于点C,其中点A的坐标为―1,0,直线BC的解析式为:y=―12(1)求抛物线的解析式;(2)点D位于抛物线在直线BC上方的部分,DE⊥BC于点E,EF平行于x轴且与y轴交于点F,求EF的最小值;(3)如图2,将抛物线y=ax2+bx+c(a≠0)向左平移,使得平移后的抛物线的对称轴为y轴,若点G是平移后抛物线上一点,点M、N都是直线AC上的动点,点Q为定点,其坐标为1,2,请直接写出以M、N、G、Q为顶点的四边形为平行四边形的点G的横坐标,并把其中一个求点G的横坐标的过程写出来.7.如图,在平面直角坐标系中,抛物线y=3x2+bx+c与直线AB交于点A(0,―3),B(4,0).4(1)求抛物线的函数解析式;(2)点P 是直线AB 下方抛物线上一点,过点P 作y 轴的平行线,交AB 于点E ,过点P 作AB 的垂线,垂足为点F ,求△PEF 周长的最大值及此时点P 的坐标;(3)在(2)中△PEF 取得最大值的条件下,将该抛物线沿水平方向向左平移3个单位,点Q 为点P 的对应点,点N 为原抛物线对称轴上一点.在平移后抛物线上确定一点M ,使得以点B ,Q ,M ,N 为顶点的四边形是平行四边形,写出所有符合条件的点M 的坐标,并写出求解点M 的坐标的其中一种情况的过程.8.如图,在平面直角坐标系中,抛物线y =ax 2+bx ―4(a ≠0)与x 轴交于A (4,0),B (―2,0)两点,与y 轴交于点C ,连接BC ,y 轴上有一点D (0,―3).(1)求抛物线的函数表达式;(2)点P 是直线AD 下方抛物线上的一个动点,过点P 作PH ⊥x 轴于点H ,PH 交直线AD 于点E ,作PF ∥BC 交直线AD 于点F +PH 的最大值,及此时点P 的坐标;(3)在(2)的条件下,将点P 向右平移152个单位长度,再向上平移398个单位长度得到点P ′;将抛物线沿着射线BC M 为新抛物线与y 轴的交点,N 为新抛物线上一点,Q 为新抛物线对称轴上一点,请写出所有使得以点P ′,M ,Q ,N 为顶点的四边形是平行四边形的点Q 的坐标,并写出求解点Q 的坐标的其中一种情况的过程.9.如图1,在平面直角坐标系中,抛物线y =ax 2+bx +c 与平面直角坐标系交于点A (0,―4),B (―4,0),C (1,0).(1)求该抛物线的函数表达式;(2)如图2,作直线AB,点P是直线AB下方抛物线上的一动点,过点P作y轴的平行线交AB于点E,过点P 作PD⊥AB于点D,求PE+PD的最大值及此时点P的坐标;(3)在(2)中PE+PD取得最大值的条件下,将该抛物线沿水平方向向左平移2个单位,点P′为点P的对应点,平移后的抛物线与y轴交于点A′,M为平移后的抛物线的对称轴上一点.在平移后的抛物线上确定一点N,使得以点P′,A′,M,N为顶点的四边形是平行四边形,写出所有符合条件的点N的坐标,并写出求解点N的坐标的其中一种情况的过程.10.如图,在平面直角坐标系中,抛物线y=1x2+bx+c与直线AC交于点A6,0,C0,―6.4(1)求该抛物线的函数表达式;(2)点P是直线AC下方抛物线上的一动点,过点P作y轴的平行线交AC于点E,交x轴于D,求PD+PE的最大值及此时点P的坐标;(3)在(2)中PD+PE取得最大值的条件下,将该抛物线沿水平方向向右平移3个单位,点M为点P的对应点,平移后的抛物线与y轴交于点F,N为平移后的抛物线的对称轴上一点.在平移后的抛物线上确定一点Q,使得以点M,F,N,Q为顶点的四边形是平行四边形,写出所有符合条件的点Q的坐标,并写出求解点Q的坐标的其中一种情况的过程.类型三旋转+平行四边形11.如图1,在平面直角坐标系中,抛物线y=ax2+bx+8(a≠0)与x轴交于点B(―4,0),点C(8,0),与y轴交于点A.点D的坐标为(0,4).(1)求二次函数的解析式及点A的坐标.(2)如图1,点E为该抛物线在第一象限内的一动点,过E作FE∥y轴,交CD于点F,求EF的最大值及此时点E的坐标.(3)如图2,在(2)的情况下,将原抛物线绕点D旋转180°得到新抛物线y′,点N是新抛物线y′上一点,在新抛物线上的对称轴上是否存在一点M,使得点D,E,M,N为顶点的四边形为平行四边形,若存在,请直接写出点M的坐标,并写出其中一个点M的求解过程.12.如图,在平面直角坐标系中,抛物线y=―1x2+bx+c与x轴交于A,B(―4,0)两点(点A在点B的右2侧),与y轴交于点C(0,2).(1)求抛物线的表达式;(2)如图1,连接BC,点P为直线BC上方抛物线上(不与B、C重合)的一动点,过点P作PF∥y轴交x轴于点F,交BC于点E,过点P作PD⊥BC,垂足为点D+2PF的最大值及此时点P的坐标;(3)如图2,将原抛物线绕线段BC的中点Q旋转180°得到新抛物线y′,点N为新抛物线y′上一点,在x轴上是否存在一点M,使得以点Q、C、M、N为顶点的四边形是以CQ为边的平行四边形,若存在,请直接写出点M的坐标;若不存在,请说明理由.13.如图,抛物线y=x2+bx+c交x轴于A、B两点(点A在点B的左侧),交y轴于点C(0,5),连接BC,其中OC=5OA.(1)求抛物线的解析式;(2)如图1,将直线BC沿y轴向上平移6个单位长度后与抛物线交于D、E两点,交y轴于点G,若点P是抛物线上位于直线BC下方(不与A、B重合)的一个动点,连接PE,交直线BC于点F,连接PD、S△EDF,求点P的坐标;DF、PB、PC.若S△PBC=1021(3)如图2,当点P满足(2)问条件时,将△CBP绕点C逆时针旋转α(0°<α<90°)得到△CB'P',此时点B′恰好落到直线ED上,已知点M是抛物线上的动点,在直线ED上是否存在一点N,使得以点C、B′、M、N为顶点的四边形为平行四边形?若存在,直接写出点N的坐标,若不存在,请说明理由.14.如图,抛物线y=x2+bx+c交x轴于A、B两点(点A在点B的左侧),交y轴于点C(0,5),连接BC,其中OC=5OA.(1)求抛物线的解析式;(2)如图1,将直线BC沿y轴向上平移6个单位长度后与抛物线交于D、E两点,交y轴于点G,若点P是抛物线上位于直线BC下方(不与A、B重合)的一个动点,过点P作PM∥y轴交DE于点M,交BC于点H,过点M作MN⊥BC于点N,求PM+NH的最大值及此时点P的坐标;(3)如图2,当点P满足(2)问条件时,将△CBP绕点C逆时针旋转α(0°<α<90°)得到△CB'P',此时点B′恰好落到直线ED上,已知点F是抛物线上的动点,在直线ED上是否存在一点Q,使得以点C、B′、F、Q为顶点的四边形为平行四边形?若存在,直接写出点Q的坐标,若不存在,请说明理由.15.如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a>0)与x轴交于点A(―1,0)和点B(3,0),与y轴交于点C,且∠OBC=30°.点E在第四象限且在抛物线上.BM最小,并求出此时点E (1)如(图1),当四边形OCEB面积最大时,在线段BC上找一点M,使得EM+12BM的最小值;的坐标及EM+12(2)如(图2),将△AOC沿x轴向右平移2单位长度得到△A1O1C1,再将△A1O1C1绕点A1逆时针旋转α度得到△A1O2C2,且使经过A1、C2的直线l与直线BC平行(其中0°<α<180°),直线l与抛物线交于K、H 两点,点N在抛物线上.在线段KH上是否存在点P,使以点B、C、P、N为顶点的四边形为平行四边形?若存在,请直接写出点P的坐标;若不存在,请说明理由.。
二次函数与平行四边形综合题

二次函数与平行四边形综合题摘要:1.二次函数与平行四边形的关系2.怎样找全平行四边形3.平行四边形的性质及应用4.实例解析5.总结与展望正文:一、二次函数与平行四边形的关系二次函数是一种数学函数,表示为y=ax+bx+c(a≠0),其中a、b、c 为常数。
在几何中,平行四边形是一种四边形,其中对边两两平行。
二次函数与平行四边形看似没有直接关系,但在一些数学问题中,它们可以结合起来解决一些复杂的问题。
例如,在二次函数的图像上,如果存在两个点A、B,使得线段AB 与x 轴、y 轴构成平行四边形,那么可以利用这个性质求解一些问题。
二、怎样找全平行四边形要找全平行四边形,需要先确定二次函数的解析式。
假设已知二次函数过三个点A(x1, y1)、B(x2, y2) 和C(x3, y3),我们可以用待定系数法求解二次函数的解析式。
具体步骤如下:1.设二次函数的解析式为y=ax+bx+c。
2.将点A、B、C 的坐标代入解析式,得到三个方程:y1 = ax1 + bx1 + cy2 = ax2 + bx2 + cy3 = ax3 + bx3 + c3.解这三个方程,得到a、b、c 的值。
4.将a、b、c 的值代入解析式,得到二次函数的解析式。
得到二次函数的解析式后,可以进一步求解线段AB 与x 轴、y 轴构成平行四边形的问题。
具体方法如下:1.求线段AB 的中点M,即M((x1+x2)/2, (y1+y2)/2)。
2.求线段AB 的斜率k,即k=(y2-y1)/(x2-x1)。
3.求过点M 且斜率为k 的直线方程,即y-(x1+x2)/2 = k(x-(x1+x2)/2)。
4.求该直线与x 轴、y 轴的交点,分别记为D 和E。
5.判断四边形ABED 是否为平行四边形。
如果AD//BE 且AD=BE,则四边形ABED 为平行四边形。
三、平行四边形的性质及应用平行四边形具有以下性质:1.对边平行且相等。
2.对角线互相平分。
二次函数与平行四边形综合PPT课件

完整编辑ppt
4
(2010陕西24题) 在平面直角坐标系中,抛物线经过A(-1,0), B(3,0), C(0,-1)三点。 (1)求该抛物线的表达式;
解:设抛物线的表达式为 ya(x1)x (3)
把C(0,-1)代入上式得 -1=a(-3)
a1 ∴抛物线的表达式为 y 1(x1)3(x3)
3
完整编辑ppt
5
(2010陕西24题) 在平面直角坐标系中,抛物线经过A(-1,0), B(3,0), C(0,-1)三点。
(1)求该抛物线的表达式;
解:设抛物线的表达式为 yax2bx1
把A(-1,0),B(3,0)代入上式得
0 a b 1 0 9a 3b 1
∴抛物线的表达式为解得 Nhomakorabeaa
y 1b
=1 3
二次函数与平行四边形综合
完整编辑ppt
1
一、平行四边形的判定方法: 1. 两组对边分别平行的四边形是平行四边形; 2. 两组对边分别相等的四边形是平行四边形; 3. 一组对边平行且相等的四边形是平行四边形; 4. 两条对角线互相平分的四边形是平行四边形; 5. 两组对角分别相等的四边形是平行四边形.
(2)若抛物线上的点D为(2, -1),点E在x轴上 ,点F在抛物线上,是否存在以A、D、E、F为顶点 的四边形是平行四边形?若存在,求出点E的坐标 ;若不存在,说明理由。
完整编辑ppt
8
(变式2) 在平面直角坐标系中,抛物线经过A(-1,0), B(3,0), C(0,-1)三点。
(2)若该抛物线的顶点为G ,点N在该抛物线上 ,点M在x轴上,是否存在以G、N、M、B为顶点的 四边形是平行四边形?若存在,求出点N的坐标 ;若不存在,说明理由。
+2023+年九年级数学中考复习+二次函数与平行四边形综合压轴题+专题提升训练+
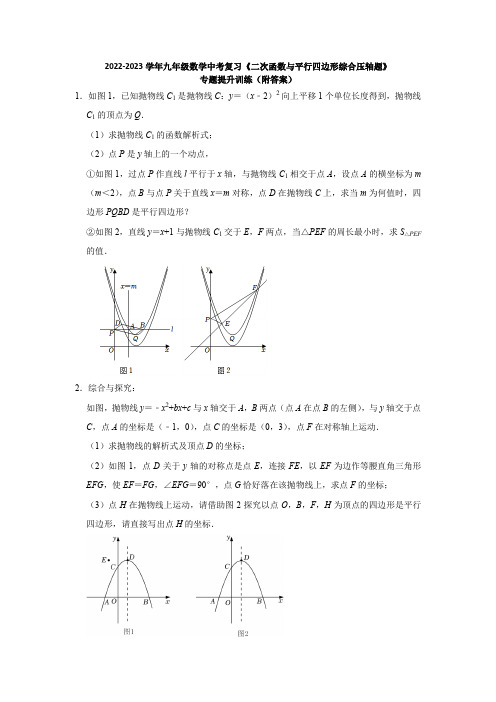
2022-2023学年九年级数学中考复习《二次函数与平行四边形综合压轴题》专题提升训练(附答案)1.如图1,已知抛物线C1是抛物线C:y=(x﹣2)2向上平移1个单位长度得到,抛物线C1的顶点为Q.(1)求抛物线C1的函数解析式;(2)点P是y轴上的一个动点,①如图1,过点P作直线l平行于x轴,与抛物线C1相交于点A,设点A的横坐标为m(m<2),点B与点P关于直线x=m对称,点D在抛物线C上,求当m为何值时,四边形PQBD是平行四边形?②如图2,直线y=x+1与抛物线C1交于E,F两点,当△PEF的周长最小时,求S△PEF的值.2.综合与探究:如图,抛物线y=﹣x2+bx+c与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,点A的坐标是(﹣1,0),点C的坐标是(0,3),点F在对称轴上运动.(1)求抛物线的解析式及顶点D的坐标;(2)如图1,点D关于y轴的对称点是点E,连接FE,以EF为边作等腰直角三角形EFG,使EF=FG,∠EFG=90°,点G恰好落在该抛物线上,求点F的坐标;(3)点H在抛物线上运动,请借助图2探究以点O,B,F,H为顶点的四边形是平行四边形,请直接写出点H的坐标.3.已知抛物线y=ax2﹣2ax+c(a<0)与x轴交于A、B两点(点A在点B的左侧),与y 轴交于点C(0,4),抛物线的顶点为P,对称轴交BC于点M,连接PC、PB,△PCM 与△PBM的面积比为1:2;(1)①抛物线的对称轴是;②求抛物线的函数表达式.(2)若点Q为抛物线第一象限图象上的一点,作QN⊥x轴交BC于点N,当QN+NB取得最大值时,求以Q、N、B、G为顶点的平行四边形顶点G的坐标.4.已知抛物线y=﹣x2+bx+c与x轴相交于A、B两点,与y轴交于C点,且A(﹣1,0),C(0,4).(1)求抛物线的解析式;(2)点P为抛物线上位于直线BC上方的一点,连结PB、PC.①如图1,过点P作PE∥y轴交BC于点D,交x轴于点E,连结OD.设△BCP的面积为S1,△ODE的面积为S2,若S=S1﹣S2,求S的最大值;②如图2,已知∠PBC+∠ACO=45°,Q为平面内一点,若以点A、C、P、Q为顶点的四边形是以CP为边的平行四边形,求点Q的坐标.5.如图,抛物线y=﹣x2+bx+c与x轴交于A,B两点(A在B的左侧),与y轴交于点N,过A点的直线l:y=﹣x﹣1与y轴交于点C,与抛物线y=﹣x2+bx+c的另一个交点为D (5,﹣6),已知P点为抛物线y=﹣x2+bx+c上一动点(不与A、D重合).(1)求抛物线的解析式;(2)当点P在直线l上方的抛物线上时,过P点作PE∥x轴交直线l于点E,作PF∥y 轴交直线l于点F,求PE+PF的最大值;(3)设M为直线l上的动点,以NC为一边且顶点为N,C,M,P的四边形是平行四边形,求所有符合条件的M点坐标.6.如图,直线y=﹣x+3分别交x,y轴于点B,C,经过点B,C的抛物线y=ax2+2x+c与x轴的另一交点为点A.(1)求抛物线的解析式;(2)若点P为第一象限内抛物线上一动点,连接AP,交BC于点D,求的最大值及此时点P的坐标;(3)若点F在x轴上,点G在抛物线的对称轴上,以点B,C,F,G为顶点的四边形为平行四边形,请直接写出点F的坐标.7.如图,在平面直角坐标系中,抛物线y=x2+x﹣3交x轴于点A,点B(点A在点B 的左侧),交y轴于点C,连接AC,BC.P是第三象限内抛物线上一动点,过P作PE ∥y轴交AC于点E,过E作EF∥BC交x轴于点F.(1)求△ABC的面积;(2)求PE+EF+FO的最大值及此时点P的坐标;(3)将抛物线y=x2+x﹣3平移,使得新抛物线的顶点为(2)中求得的点P,点Q 为x轴下方的新抛物线上一点,R为x轴上一点,直接写出所有使得以点A,C,Q,R 为顶点的四边形是平行四边形的点R的坐标.8.如图,抛物线y=ax2+bx+3(a≠0)与x轴交于点A(3,0)和点B(﹣1,0),与y轴交于点C.(1)求抛物线的解析式;(2)抛物线的对称轴与直线AC交于点E,与x轴交于点F,P为直线AC.上方抛物线上一动点.求△CPE的面积最大时P点坐标;(3)在(2)的条件下,点M在x轴上,在抛物线上是否存在点Q,使得以F,M,P,Q为顶点的四边形是平行四边形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.9.如图,在平面直角坐标系中,抛物线L:y=ax2+bx+3(a≠0)与x轴交于点A(﹣1,0),B(3,0),与y轴交于点C.(1)求抛物线L的解析式;(2)已知第一象限内抛物线上一点P,其纵坐标为3,连接BC,将原抛物线L沿射线BC方向平移3个单位,得到新的抛物线L',点P的对应点为点D,点E为L'的对称轴上任意一点,在L'上确定一点F,使得以点C、D、E、F为顶点的四边形是平行四边形,求出所有符合条件的点F的坐标.10.如图,在平面直角坐标系中,抛物线C1:y=ax2+bx+2交x轴于A、B两点(点A在点B的左侧),交y轴于点C,一次函数y=﹣x﹣1交抛物线于A,D两点,其中点D(3,﹣4).(1)求抛物线C1的解析式;(2)点G为抛物线上一点,且在线段BC上方,过点G作GH∥y轴交BC于H,交x 轴于点N,作GM⊥BC于点M,求△GHM周长的最大值;(3)将抛物线C1沿着射线AD方向平移后得到抛物线C2,使得点A平移后的对应点为A′(),抛物线C1与抛物线C2交于点R,动点P在抛物线C2上.抛物线C1的对称轴上是否存在点E,使得以点A、R、P、E为顶点的四边形为平行四边形?若存在,请求出点E;若不存在,请说明理由.11.如图,直线y=﹣x+3与x轴交于点A,与y轴交于点B,抛物线y=ax2+x+c经过A、B两点.(1)求二次函数解析式;(2)如图1,点E在线段AB上方的抛物线上运动(不与A、B重合),过点E作ED⊥AB,交AB于点D,作EF⊥AC,交AC于点F,交AB于点M,求△DEM的周长的最大值;(3)在(2)的结论下,连接CM,点Q是抛物线对称轴上的动点,在抛物线上是否存在点P,使得以P、Q、C、M为顶点的四边形是平行四边形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.(4)如图2,点N的坐标是(1,0),将线段ON绕点O逆时针旋转得到ON′,旋转角为α(0°<α<90°),连接N′A、N′B,求N′A+N′B的最小值.12.抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣3,0),B(1,0)两点,与y轴交于点C(0,3),点P是抛物线上的一个动点.(1)求抛物线的函数表达式;(2)如图1,点P在线段AC上方的抛物线上运动(不与A,C重合),过点P作PD⊥AB,垂足为D,PD交AC于点E.作PF⊥AC,垂足为F,求△PEF的面积的最大值;(3)如图2,点Q是抛物线的对称轴l上的一个动点,在抛物线上,是否存在点P,使得以点A,P,C,Q为顶点的四边形是平行四边形?若存在,求出所有符合条件的点P 的坐标;若不存在,说明理由.13.如图,抛物线经过点A(﹣1,0),B(4,0),与y轴交于点C,连接BC,AC,对称轴l与BC交于点D,连接AD.(1)求抛物线的解析式;(2)抛物线上是否存在一点P,使得?若存在,求点P的坐标;若不存在,说明理由;(3)E是对称轴l上一点,F是抛物线上一点,若以A,C,E,F为顶点的四边形是平行四边形,直接写出点F的坐标.14.如图,在平面直角坐标系中,抛物线L:y=ax2+bx+c与x轴交于点A(﹣1,0),B(4,0),与y轴交于点C(0,﹣4).(1)求抛物线L的函数表达式;(2)抛物线L'与L关于原点对称,点A、B在L'上的对应点分别为A'、B'.那么在L'的对称轴上是否存在一点M,在L上是否存在一点N,使得以A、A'、M、N为顶点的四边形是平行四边形?若存在,求出N点的坐标;若不存在,请说明理由.15.如图1,二次函数y=ax2+bx+3(a≠0)的图象与x轴交于点A,B,与y轴交于点C,tan∠CBO=,点A(﹣2,0).(1)求二次函数的解析式;(2)如图2,点P是直线BC上方抛物线上一点,PD∥y轴交BC于点D.PE∥BC变x 轴于点E.求PD+BE的最大值;(3)在(2)的条件下,当PD+BE取最大值时,点M在该抛物线的对称轴上,满足△BPM的周长最小,点N为该坐标平面内一点,是否存在以点A,B,M,N为顶点的平行四边形,若存在,请直接写出点N的坐标;若不存在,请说明理由.16.如图,在平面直角坐标系中,抛物线y=﹣x2+2x+3交x轴于A,B两点(点A在点B 的左侧),点C是抛物线的顶点.点P是直线BC上方抛物线上的一个动点,过点P作PE∥y轴,交BC于点E,PF⊥BC,垂足为F.(1)求点C的坐标;(2)当PE+PF取得最大值时,求点P的坐标和PE+PF的最大值;(3)当点P满足(2)问的条件时,把抛物线y=﹣x2+2x+3向右平移,使得新抛物线经过原点,M是新抛物线上一点,N是直线BC上一点,直接写出所有使得以点A,P,M,N为顶点的四边形是平行四边形的点M的坐标,并把求其中一个点M的坐标的过程写出来.17.在平面直角坐标系中,已知抛物线与x轴交于点A(﹣1,0)和点B,与y轴交于点C (0,3),对称轴为直线x=1,交x轴于点E.(1)求该抛物线的表达式;(2)点D为此抛物线的顶点,证明:∠CDB=∠CAB;(3)在x轴上是否存在一点M,以及抛物线上一点N,使得以M、N、B、C四点构成的四边形为平行四边形?如果有,请直接写出点M的坐标;如果没有,请说明理由.18.在平面直角坐标系中,二次函数y=a(x﹣1)2与直线y=﹣x﹣1交于A、B两点,其中点B的坐标为(0,﹣1),抛物线的顶点C在x轴上.(1)求二次函数的表达式;(2)点P为线段AB上的一个动点(点P不与A、B两点重合),过点P作PE∥y轴交抛物线于点E,设线段PE的长为h,点P的横坐标为t,当t取何值时,h有最大值?最大值是多少?(3)点D为直线AB与对称轴x=1的交点,在线段AB上是否存在一点P,使得四边形DCEP是平行四边形?若存在,请求出此时点P的坐标;若不存在,请说明理由.19.如图,抛物线y=ax2+bx+c(a≠0)的图象经过A(1,0),B(3,0),C(0,6)三点.(1)求抛物线的解析式.(2)抛物线的顶点M与对称轴l上的点N关于x轴对称,直线AN交抛物线于点D,点E为抛物线在直线AD下方的一个动点,连接AE、DE,问:△ADE的面积是否存在最大值?若存在,请求出面积的最大值和点E的坐标.若不存在,请说明理由.(3)P为抛物线上的一动点,Q为对称轴上一动点,若以A、D、P、Q为顶点的四边形为平行四边形,请直接写出点P的坐标(至少写两个).20.综合与探究如图,抛物线y=ax2+bx﹣6经过点A(﹣2,0),B(6,0)两点,与y轴交于点C,点D是抛物线的顶点,点P是抛物线上一个动点,设点P的横坐标为m(0<m<6),连接AC,BD,PB,PD.(1)分别求出抛物线与直线BD的函数表达式;(2)当S△BDP=S△AOC时,求m的值;(3)若点M是x轴上一动点,点N是抛物线上一动点,试判断是否存在这样的点M,使得以点A、C、M、N为顶点的四边形是平行四边形?若存在,请直接写出点M的坐标;若不存在,请说明理由.参考答案1.解:(1)∵抛物线C1是抛物线C:y=(x﹣2)2向上平移1个单位长度得到,∴抛物线C1的函数解析式为:y=(x﹣2)2+1;(2)①根据题意得:A(m,m2﹣4m+5),Q(2,1),∵点B与点P关于直线x=m对称,∴B(2m,m2﹣4m+5),P(0,m2﹣4m+5),∵四边形PQBD是平行四边形,∴PD∥QB,PD=QB,∴QB向左平移2个单位,向上平移(m2﹣4m+5﹣1)个单位得到PD,∴D(2m﹣2,2m2﹣8m+9),又∵点D在在抛物线C上,∴(2m﹣2﹣2)2=2m2﹣8m+9,解得:m=2﹣或m=2+,∵m<2,∴m=2﹣;②设直线y=x+1与y轴交于点H,则H(0,1),∵直线y=x+1与抛物线C1交于E,F两点,∴,解得:,,∴E(1,2),F(4,5),如图2,作点E关于y轴的对称点E′(﹣1,2),连接E′F交y轴于点P,设直线E′F的解析式为y=kx+b,则,解得:,∴直线E′F的解析式为y=x+,令x=0,得y=,∴P(0,),∴S△PEF=S△PFH﹣S△PEH=×(﹣1)×4﹣×(﹣1)×1=.2.解:(1)将点A(﹣1,0),点C(0,3)代入y=﹣x2+bx+c,∴,解得,∴抛物线y=﹣x2+2x+3=﹣(x﹣1)2+4,∴顶点D的坐标是(1,4);(2)∵点D(1,4)关于y轴的对称点是点E,∴点E的坐标是(﹣1,4),设点F的坐标是(1,m),过点F作直线l⊥y轴,过点E作EM⊥直线l于点M,过点G作GN⊥直线l于点N,∵EF=FG,∠EFG=90°,∴∠EMF=∠EFG=∠FNG=90°,∴∠E+∠EFM=∠EFM+∠NFG=90°,∴∠E=∠NFG,∴△EFM≌△FGN(AAS),∴NG=MF=2,NF=EM=m﹣4,∴点G的坐标是(m﹣3,m﹣2),∵点G恰好落在抛物线y=﹣x2+2x+3上,∴m﹣2=﹣(m﹣3)2+2(m﹣3)+3,解得m=2或m=5,∴点F的坐标是(1,2)或(1,5);(3)设F(1,n),H(t,﹣t2+2t+3),①当OB为平行四边形的对角线时,1+t=3,∴t=2,∴H(2,3);②当OF为平行四边形的对角线时,3+t=1,∴t=﹣2,∴H(﹣2,﹣5);③当OH为平行四边形的对角线时,t=1+3=4,∴H(4,﹣5);综上所述:点H的坐标是(4,﹣5)或(﹣2,﹣5)或(2,3).3.解:(1)①∵y=ax2﹣2ax+c,∴x=﹣=1,即抛物线的对称轴是直线x=1,故答案为:直线x=1;②∵C(0,4),∴抛物线y=ax2﹣2ax+4,∵△PCM与△PBM的面积比为1:2,∴PM×(x B﹣1)=2×PM×(1﹣x C),∴x B﹣1=2,∴x B=3,∴B(3,0),∵抛物线的对称轴是直线x=1,∴A(﹣1,0),将B(3,0)代入抛物线y=ax2﹣2ax+4中,得:9a﹣6a+4=0,解得:a=﹣,∴该抛物线的函数表达式为y=﹣x2+x+4.(2)设直线BC的解析式为y=kx+b,将B(3,0),C(0,4)代入得:,解得:,∴直线BC的解析式为y=x+4,设Q(t,﹣t2+t+4),则N(t,t+4),∴QN=﹣t2+t+4﹣(t+4)=﹣t2+4t,设QN与x轴交于H,则H(t,0),∴NH=t+4,BH=3﹣t,∵QN⊥x轴,∴∠BHN=∠BOC=90°,在Rt△BOC中,BC===5,∵sin∠CBO==,∴=,∴NB=(t+4)=t+5,∴QN+NB=﹣t2+4t+(t+5)=﹣t2+t+5=﹣(t﹣)2+,∵<0,∴当t=时,QN+NB取得最大值,∴﹣t2+t+4=﹣×()2+×+4=,此时,Q(,),N(,),①当BQ为▱BNQG的对角线时,BG∥QN,BG=QN,∵QN=﹣=,QN∥y轴,∴BG=,BG∥y轴,∴G1(3,);②当BN为▱BQNG的对角线时,BG∥QN,BG=QN,∵QN=﹣=,QN∥y轴,∴BG=,BG∥y轴,∴G2(3,﹣);③当QN为▱BQGN的对角线时,BN∥GQ,BN=GQ,∵BH=3﹣=,HN=,∴BN向左平移个单位,向上平移个单位,得到线段GQ,∴点G的横坐标为:﹣=﹣,点G的纵坐标为:+=,∴G3(﹣,);综上所述,顶点G的坐标为G1(3,)或G2(3,﹣)或G3(﹣,).4.解:(1)由题意,得:,∴.∴此抛物线的解析式为:y=﹣x2+3x+4.(2)①由y=﹣x2+3x+4,令x=0,则y=4.∴B(4,0).设直线BC的解析式为:y=kx+b1,则,∴.∴直线BC的解析式为:y=﹣x+4.设P(m,﹣m2+3m+4),则D(m,﹣m+4),∴PE=﹣m2+3m+4,DE=﹣m+4,OE=m.∴PD=PE﹣DE=﹣m2+4m,∴S=S1﹣S2=PD•OB﹣OE•DE=4(﹣m2+4m)﹣m(﹣m+4)=(m﹣2)2+6,∵﹣<0,∴当m=2时,S有最大值为6.②在OB上截取OF=OA,连接CF,如图,则∠ACO=∠FCO,∵∠PBC+∠ACO=45°,∴∠FCO+∠PBC=45°.∵B(4,0),C(0,4),∴OB=OC=4.∵OC⊥OB,∴∠OCB=45°,∴∠BCF=∠CBP,∴BP∥CF.∵A(﹣1,0),∴OA=1.∴OF=OA=1.∴F(1,0).设直线CF的解析式为y=dx+n,则,解得:.∴直线CF的解析式为:y=﹣4x+4.∵BP∥CF,∴设直线BP的解析式为y=﹣4x+e,∵B(4,0),∴e﹣4×4=0.∴直线BP的解析式为:y=﹣4x+16.由题意:﹣4x+16=﹣x2+3x+4,解得:x=3或4,∴P(3,4).∵C(0,4),∴PC∥x轴,PC=3.∵以点A、C、P、Q为顶点的四边形是以CP为边构成平行四边形,∴PC∥AQ,PC=AQ=3.∴点Q在x轴上,∴Q(﹣4,0)或(2,0).5.解:(1)∵直线l:y=﹣x﹣1过点A,∴A(﹣1,0),又∵D(5,﹣6),将点A,D的坐标代入抛物线表达式可得:,解得.∴抛物线的解析式为:y=﹣x2+3x+4.(2)如图,设点P(x,﹣x2+3x+4),∵PE∥x轴,PF∥y轴,则E(x2﹣3x﹣5,﹣x2+3x+4),F(x,﹣x﹣1),∵点P在直线l上方的抛物线上,∴﹣1<x<5,∴PE=|x﹣(x2﹣3x﹣5)|=﹣x2+4x+5,PF=|﹣x2+3x+4﹣(﹣x﹣1)|=﹣x2+4x+5,∴PE+PF=2(﹣x2+4x+5)=﹣2(x﹣2)2+18.∵﹣1<x<5,∴当x=2时,PE+PF取得最大值,最大值为18.(3)由(1)可求NC=5,∵NC是所求平行四边形的一边,∴NC PM,设点p(t,﹣t2+3t+4),则M(t,﹣t﹣1),由题意知:|y P﹣y M|=5,即|﹣t2+3t+4+t+1|=5.化简得:t2﹣4t=0或t2﹣4t﹣10=0,解得:t1=0(舍去),t2=4,,.则符合条件的M点有三个:,.6.解:(1)∵直线y=﹣x+3与x轴、y轴的交点分别为B、C,∴当x=0时,y=3,当y=0时,x=3,∴点B、C的坐标分别为(3,0)、(0,3),∵抛物线y=ax2+2x+c过点B,C,∴,解得,∴抛物线的解析式为y=﹣x2+2x+3;(2)作AM⊥x轴交BC于M,作PN⊥x轴交BC于N,∴AM∥PN,∴∠AMD=∠PND,∵∠CDA=∠NDP,∴△ADM∽△PDN,∴,∵抛物线的解析式为y=﹣x2+2x+3,直线BC:y=﹣x+3,∴A(﹣1,0),C(0,3),B(3,0),设M(﹣1,m),∴m=1+3=4,∴M(﹣1,4),∴AM=4,设P(n,﹣n2+2n+3),则N(n,﹣n+3),∴PN=﹣n2+2n+3﹣(﹣n+3)=﹣n2+3n=﹣(n﹣)2+,∴===﹣(n﹣)2+,∴当n=时,的最大值为,∴﹣n2+2n+3=,∴P(,);(3)①BC为平行四边形的边时,如图,当四边形CBFG是平行四边形时,∴CG∥BF,CG=BF,∵点G在抛物线y=﹣x2+2x+3的对称轴上,∴对称轴为x=﹣=1,∵C(0,3),∴G(1,3),∴BF=CG=1,∵B(3,0),∴点F的坐标为(4,0);当四边形CBG′F′是平行四边形时,∴CB∥G′F′,CB=G′F′,∵点G在抛物线y=﹣x2+2x+3的对称轴上,∴对称轴为x=﹣=1,∵C(0,3),∵B(3,0),∴点F的坐标为(﹣2,0);②BC为平行四边形的对角线时,如图,∵四边形CFBG是平行四边形,∴CG∥BF,CG=BF,∵点G在抛物线y=﹣x2+2x+3的对称轴上,∴对称轴为x=﹣=1,∵C(0,3),∴G(1,3),∴BF=CG=1,∵B(3,0),∴点F的坐标为(2,0);综上,点F的坐标为(4,0)或(﹣2,0)或(2,0).7.解:(1)令x=0,则y=﹣3.∴C(0,﹣3).∴OC=3.令y=0,则x2+x﹣3,解得:x=﹣5或1.∴A(﹣5,0),B(1,0),∴OA=5,OB=1.∴AB=OA+OB=6.∴×AB•OC=6×3=9;(2)延长PE交x轴于点G,如图,∵PE∥y轴,∴PG⊥OA.∵EF∥BC,PE∥y轴,∴∠FEG=∠BCO.∴tan∠FEG=tan∠BCO.∵tan∠BCO=,∴tan∠FEG=,∵tan∠FEG=,∴.设GF=k,则GE=3k.∴EF=k.∴EF=FG.∴EF+FO=OG.设直线AC的解析式为y=ax+b,则:,∴.∴直线AC的解析式为y=﹣x﹣3.设点P(m,m﹣3),则E(m,﹣m﹣3),∴OG=﹣m,PE=(﹣m﹣3)﹣(m﹣3)=m2﹣3m.∴PE+EF+FO=PE+OG=m2﹣3m﹣m=m2﹣4m=﹣+.∵﹣<0,∴当m=﹣时,PE+EF+FO有最大值.此时点P的坐标为(,).(3)∵将抛物线y=x2+x﹣3平移,使得新抛物线的顶点为点P(,),∴新抛物线的解析式为y=+4x+.∵点Q为x轴下方的新抛物线上一点,R为x轴上一点,∴以点A,C,Q,R为顶点的四边形是平行四边形时,①若AR∥CQ,AC为对角线时,如图,令y=﹣3,则+4x+=﹣3.解得:x=.∴Q1(,﹣3),Q2(,﹣3).∴CQ1=,CQ2=.∵AR1=CQ1=,AR2=CQ2=,∴OR1=OA﹣AR1=5﹣=,OR2=OA﹣AR2=5﹣=,∴R1(,0),R2(,0).②若AR∥CQ,AC为一边时,如图,同理求得:R1(,0),R2(,0).综上,以点A,C,Q,R为顶点的四边形是平行四边形的点R的坐标为:(,0)或(,0)或(,0)或(,0).8.解:(1)将点A(3,0),B(﹣1,0)代入y=ax2+bx+3,得a(x+1)(x﹣3)=ax2+bx+3,∴b=﹣2a,﹣3a=3,解得:a=﹣1,b=2,∴抛物线的解析式为y=﹣x2+2x+3.(2)如图1,过C点和P点分别作对称轴的垂线,垂足为点G和点H,记PC与对称轴的交点为点K,则S△CPE=S△CEK+S△EPK,∴S△CPE=EK•CG+EK•PH=EK(CG+PH),∵抛物线的解析式为y=﹣x2+2x+3,∴对称轴为直线x=1,C(0,3),设点P的坐标为(m,﹣m2+2m+3),直线AC的解析式为y=kx+b,则,解得:,∴AC直线解析式为y=﹣x+3,∴E点的坐标为(1,2),设PC直线的解析式为y=kx+n,则,解得:,∴直线PC的解析式为y=(﹣m+2)x+3,∴点K坐标为(1,﹣m+5),∴EK=﹣m+5﹣2=3﹣m,CG+PH=1+(m﹣1)=m,∴S△CPE=EK(CG+PH)=m(3﹣m)=﹣m2+=﹣(m﹣)2+,∴当m=时,S△CPE取得最大面积为,此时,P点坐标为(,).(3)由(2)得点P坐标为(,),对称轴为直线x=1,∴点F坐标为(1,0),∵点M在x轴上,以F,M,P,Q为顶点的四边形是平行四边形,∴MF∥PQ,MF=PQ,∵点Q在抛物线上,∴点Q的坐标为(,),当点Q在x轴的下方时,纵坐标为﹣也符合题意,此时Q(,﹣)或(,﹣).9.解:(1)∵抛物线y=ax2+bx+3(a≠0)与x轴交于点A(﹣1,0),B(3,0),∴,解得.∴抛物线的解析式为y=﹣x2+2x+3.(2)令y=3,得﹣x2+2x+3=3,解得:x1=2,x2=0(舍去),∴P(2,3),∵B(3,0),C(0,3),∴OB=OC=3,∴∠CBO=45°,即直线BC与x轴的夹角为45°,∴沿射线BC方向平移3个单位,实际上可看作向左平移3个单位,向上平移3个单位,∵P(2,3),∴D(﹣1,6),抛物线L:y=﹣x2+2x+3平移后得抛物线L′:y=﹣x2﹣4x+3,∴抛物线L′的对称轴为:直线x=﹣2,当CD为平行四边形的边时,若D平移到抛物线L′对称轴上的E点,则F点的横坐标为﹣1,代入抛物线L′:y=﹣x2﹣4x+3,得y=6,即F(﹣1,6),此时点F与D重合,不能构成平行四边形;若C平移到对称轴上的E点,则F点的横坐标为﹣3,代入抛物线L′:y=﹣x2﹣4x+3,得y=6,∴F(﹣3,6);当CD为平行四边形的对角线时,若D平移到对称轴上的E点时,则F平移到C,∴F的横坐标为1,代入抛物线L′:y=﹣x2﹣4x+3,得y=﹣2,∴F(﹣1,﹣2);综上,点F的坐标为(﹣3,6)或(﹣1,﹣2).10.解:(1)∵一次函数y=﹣x﹣1交抛物线于A点,且点A在x轴上,∴A(﹣1,0);将A(﹣1,0)和D(3,﹣4)代入抛物线C1:y=ax2+bx+2,∴,解得,∴抛物线C1:y=﹣x2+x+2.(2)由(1)知抛物线C1:y=﹣x2+x+2.令y=0,解得x=﹣1或x=2,∴B(2,0);令x=0,则y=2,∴C(0,2).∴OB=OC=2,直线BC的解析式为:y=﹣x+2;∴△OBC是等腰直角三角形,且∠OBC=∠OCB=45°;∵GH∥y轴,∴∠GNB=90°,∴∠BHN=45°,∵GM⊥BC,∴∠GMH=90°,∵∠MGH=∠GHM=45°,∴GM=MH=GH;设点G的横坐标为t,则G(t,﹣t2+t+2),H(t,﹣t+2),∴GH=﹣t2+2t=﹣(t﹣1)2+1.∵﹣1<0,∴当t=1时,GH有最大值1;∵△GHM的周长为:GM+MH+GH=(+1)GH,∴△GHM周长的最大值为+1.(3)存在,理由如下:设点E的坐标为(,t);∵点A平移后的对应点为A′(),∴抛物线C1先向右平移个单位,再向下平移个单位后得到抛物线C2,∵C1:y=﹣x2+x+2=﹣(x﹣)2+,∴C2:y=﹣(x﹣2)2+,令﹣(x﹣)2+=﹣(x﹣2)2+,得x=,∴R(,).①当AR是平行四边形的边时,x P﹣x E=x R﹣x A或x E﹣x P=x R﹣x A,∴x P=x R﹣x A+x E=+1+=或x P=x E﹣x R+x A=﹣﹣1=﹣,∴y P=﹣(﹣2)2+=﹣或y P=﹣(﹣﹣2)2+=﹣,∴E(,﹣)或E(,﹣).②当AR是平行四边形的对角线时,x P+x E=x R+x A,y P+y E=y R+y A,∴x P+=﹣1,∴x P=,∴y P=﹣(﹣2)2+=﹣,∴y E=y R+y A﹣y P=+0+=3.∴E(,3).综上可知,存在点E,使得以点A、R、P、E为顶点的四边形为平行四边形,此时E(,﹣)或E(,﹣)或E(,3).11.解:(1)∵直线y=﹣x+3与x轴交于点A,与y轴交于点B,∴A(4,0),B(0,3).∵抛物线y=ax2+x+c经过A、B两点,∴,解得.∴二次函数的解析式为:y=﹣x2+x+3.(2)∵A(4,0),B(0,3).∴OA=4,OB=3,∴AB=5.∵ED⊥AB,∴∠EDM=∠AOB=90°,∵∠DEM+∠EMD=∠FMA+∠BAO=90°,∠FMA=∠EMD,∴∠DEM=∠BAO,∴△AOB∽△EDM,∴AO:OB:AB=ED:DM:EM=4:3:5,设E的横坐标为t,则E(t,﹣t2+t+3),∴M(t,﹣t+3),∴EM=﹣t2+t+3﹣(﹣t+3)=﹣t2+t.∴△DEM的周长为:ED+DM+EM=EM=﹣(t﹣2)2+,∴当t=2时,△DEM的周长的最大值为.(3)存在以P、Q、C、M为顶点的四边形是平行四边形,理由如下:由y=﹣x2+x+3可知,C(﹣2,0),点Q的横坐标为1,由(2)知,M(2,).①当CM为边,且点P在点Q的左侧时,有x P﹣x Q=x C﹣x M,∴x P﹣1=﹣2﹣2,即x P=﹣3,∴P(﹣3,﹣).当点P在点Q右侧时,x Q﹣x P=x C﹣x M,∴﹣1﹣x P=﹣2﹣2,即x P=5,∴P(5,﹣);②当AM为对角线时,x P+x Q=x C+x M,∴x P+1=﹣2+2,即x P=﹣1,∴P(﹣1,).综上,当以P、Q、C、M为顶点的四边形是平行四边形时,点P的坐标为(﹣3,﹣)或(5,﹣)或(﹣1,).(4)如图,在y轴的正半轴取OG,使得OG=,连接GN′,∵OG•OB=1,ON2=1,∴OG•OB=ON2,∵∠GON′=∠N′OB,∴△OBN′∽△ON′G,∴BN′:N′G=OB:ON′=3,∴N′G=N′B,∴N′A+N′B=N′C+N′G,∴当A,N′,G三点共线时,N'A+N'B的值最小.此时AG==.∴N'A+N'B的最小值为.12.解:(1)∵抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣3,0),B(1,0)两点,∴设y=a(x+3)(x﹣1),把C(0,3)代入,得:3=a×(0+3)×(0﹣1),解得:a=﹣1,∴y=﹣(x+3)(x﹣1)=﹣x2﹣2x+3,∴该抛物线的函数表达式为y=﹣x2﹣2x+3;(2)∵A(﹣3,0),C(0,3),∴OA=OC=3,∴∠ACO=45°,∵PD⊥AB,OC⊥AB,∴PD∥OC,∴∠PEF=∠ACO=45°,∵PF⊥AC,∴△PEF是等腰直角三角形,如图1,过点F作FH⊥PE于点H,则FH=PE,∴S△PEF=×PE×FH=PE2,当PE最大时,S△PEF最大,设直线AC的解析式为y=kx+d,则,解得:,∴直线AC的解析式为y=x+3,设P(t,﹣t2﹣2t+3),则E(t,t+3),∴PE=﹣t2﹣2t+3﹣(t+3)=﹣t2﹣3t=﹣(t+)2+,∵﹣1<0,∴当t=﹣时,PE取得最大值,∴S△PEF=PE2=×()2=,∴△PEF的面积的最大值为;(3)①当AC为平行四边形的边时,则有PQ∥AC,且PQ=AC,如图2,过点P作对称轴的垂线,垂足为G,设AC交对称轴于点H,则∠AHG=∠ACO=∠PQG,在△PQG和△ACO中,,∴△PQG≌△ACO(AAS),∴PG=AO=3,∴点P到对称轴的距离为3,又∵y=﹣(x+1)2+4,∴抛物线对称轴为直线x=﹣1,设点P(x,y),则|x+1|=3,解得:x=2或x=﹣4,当x=2时,y=﹣5,当x=﹣4时,y=﹣5,∴点P坐标为(2,﹣5)或(﹣4,﹣5);②当AC为平行四边形的对角线时,如图3,设AC的中点为M,∵A(﹣3,0),C(0,3),∴M(﹣,),∵点Q在对称轴上,∴点Q的横坐标为﹣1,设点P的横坐标为x,根据中点公式得:x+(﹣1)=2×(﹣)=﹣3,∴x=﹣2,此时y=3,∴P(﹣2,3);综上所述,点P的坐标为(2,﹣5)或(﹣4,﹣5)或(﹣2,3).13.解:(1)把点A(﹣1,0),B(4,0)代入抛物线中,得,解得:,∴抛物线的解析式为:y=﹣x2+x+2;(2)∵B(4,0),C(0,2),∴直线BC的解析式为:y=﹣x+2,抛物线的对称轴是:x==,∴D(,),∵A(﹣1,0),∴AD的解析式为:y=x+,如图1,∵OC∥DE,∴===,∴=,∵,∴S△ABD=S△BPD,如图2,过点A作AP∥BC,交抛物线于点P,设P A的解析式为:y=﹣x+m,把点A(﹣1,0)代入得:﹣×(﹣1)+m=0,∴m=﹣,∴P A的解析式为:y=﹣x﹣,∴﹣x2+x+2=﹣x﹣,解得:x1=﹣1,x2=5,此时点P的坐标为(5,﹣3)或(﹣1,0);综上,点P的坐标为(5,﹣3)或(﹣1,0);(3)分三种情况:①如图3,四边形EAFC是平行四边形,∵A(﹣1,0),C(0,2),点E的横坐标为,∴点F的横坐标为﹣2.5,∴F(﹣2.5,﹣);②如图4,四边形ACEF是平行四边形,∵A(﹣1,0),C(0,2),点E的横坐标为,∴点F的横坐标为,∴F(,);②如图5,四边形ACFE是平行四边形,由平移得:F的横坐标为,∴F(,);综上,点F的坐标为(﹣2.5,﹣)或(,)或(,).14.解:(1)将点A(﹣1,0),B(4,0),C(0,﹣4)代入y=ax2+bx+c,∴,∴,∴y=x2﹣3x﹣4;(2)存在点M、N,使得以A、A'、M、N为顶点的四边形是平行四边形,理由如下:∵抛物线L'与L关于原点对称,∴抛物线L'的解析式为y=﹣x2﹣3x+4,∵y=﹣x2﹣3x+4=﹣(x+)2+,∴抛物线的对称轴为直线x=﹣,∵点A、B关于原点的对称,∴A'(1,0),B'(﹣4,0),设M(﹣,m),N(n,n2﹣3n﹣4),①当AA'为平行四边形的对角线时,n=,∴N(,﹣);②当AM为平行四边形的对角线时,﹣1﹣=1+n,∴n=﹣,∴N(﹣,);③当AN为平行四边形的对角线时,﹣1+n=1﹣,∴n=,∴N(,﹣);综上所述:N点坐标为(,﹣)或(﹣,)或(,﹣).15.解:(1)∵二次函数解析式为y=ax2+bx+3,∴点C的坐标为(0,3),∴OC=3,∵tan∠CBO=,∴OB=6,∴点B的坐标为(6,0),由抛物线经过点A(﹣2,0),B(6,0)设抛物线的解析式为y=a(x+2)(x﹣6),将点C(0,3)代入解析式为a×(0+2)×(0﹣6)=3,∴a=﹣,∴抛物线的解析式为y=﹣(x+2)(x﹣6)=﹣x2+x+3.(2)过点P作PF∥x轴交BC于点F,∵PE∥BC,∴四边形PEBF为平行四边形,∴PF=BE,∴PD+BE=PD+PF,设直线BC的解析式为y=kx+b,则,解得:,∴直线BC的解析式为y=﹣x+3,设点P的坐标为(m,﹣m2+m+3),则点D的坐标为(m,﹣m+3),∴PD=﹣m2+m+3﹣(﹣m+3)=﹣m2+m,∵PF∥x轴,∴点F和点P的纵坐标相等,即﹣x+3=﹣m2+m+3,∴x=m2﹣2m,∴点F的坐标为(m2﹣2m,﹣m2+m+3),∴PF=m﹣(m2﹣2m)=﹣m2+3m,∴PD+BE=﹣m2+m+(﹣m2+3m)=﹣m2+m=﹣(m﹣3)2+,∴当m=3时,PD+BE的最大值为;(3)由(2)可得点P的坐标为(3,),∵抛物线的解析式为y=﹣x2+x+3.∴抛物线的对称轴为x=﹣=2,连接AP交抛物线的对称轴于点M,则△BPM的周长最小,设直线AP的解析式为y=kx+n,∴,解得,∴直线AP的解析式为y=x+,当x=2时,y==3,∴M(2,3),又∵B(6,0),∴存在以点A,B,M,N为顶点的平行四边形,若以AB为平行四边形的一边,∴AB=MN=8,∴N(10,3)或N(﹣6,3),若以AB为平行四边形的一条对角线,∴N(2,﹣3).综上所述,点N的坐标为(10,3)或(﹣6,3)或(2,﹣3).16.解:(1)∵抛物线y=﹣x2+2x+3=﹣(x﹣1)2+4,∴顶点C的坐标为(1,4).(2)令y=0,则﹣x2+2x+3=0,解得x=﹣1或x=3,∴A(﹣1,0),B(3,0),∴直线BC的解析式为:y=﹣2x+6;如图,过点C作CD⊥x轴于点D,∴BD=2,CD=4,∴BC=2,∵PF⊥BC,∴∠PFE=∠CDB=90°,∵PE∥y轴,∴CD∥PE,∴∠PEF=∠BCD,∴△BCD∽△PEF,∴PE:PF=BC:BD=:1,∴PF=PE,∴PE+PF=PE+PE=(1+)PE,∴若求PE+PF的最大值,则求PE的最大值即可;设点P的横坐标为t,则P(t,﹣t2+2t+3),E(t,﹣2t+6),∴PE=﹣t2+2t+3﹣(﹣2t+6)=﹣t2+4t+3=﹣(t﹣2)2+1,∵﹣1<0,∴当t=2时,PE有最大值1,∴PE+PF的最大值为1+,此时P(2,3).(3)设抛物线y=﹣x2+2x+3向右平移n(n>0)个单位得到新抛物线y′经过原点,∴y′=﹣(x﹣1﹣n)2+4,则有﹣(0﹣1﹣n)2+4=0,解得n=﹣3(舍)或n=1;∴y′=﹣(x﹣2)2+4=﹣x2+4x,设点M的横坐标为m,则M(m,﹣m2+4m),若使得以点A,P,M,N为顶点的四边形是平行四边形,则需要分以下两种情况:当AP为边时,由平行四边形的性质可知,①x P﹣x A=x M﹣x N,y P﹣y A=y M﹣y N,∴2﹣(﹣1)=m﹣x N,∴x N=m﹣3,∴N(m﹣3,﹣2m+12),∴3﹣0=﹣m2+4m﹣(﹣2m+12),方程无解,此种情况不存在;②x P﹣x A=x N﹣x M,y P﹣y A=y N﹣y M,∴2﹣(﹣1)=x N﹣m,∴x N=m+3,∴N(m+3,﹣2m),∴3﹣0=﹣2m﹣(﹣m2+4m),解得m=3+2或m=3﹣2,此时M(3+2,﹣9﹣4)或(3﹣2,﹣9+4).当AP为对角线时,由中点坐标公式可知,x P+x A=x M+x N,y P+y A=y M+y N,∴2+(﹣1)=m+x N,∴x N=1﹣m,∴N(1﹣m,2m+4),∴3+0=﹣m2+4m+2m+4,解得m=3+或m=3﹣,此时M(3+,﹣7﹣2)或(3﹣,﹣7+2).综上可得,使得以点A,P,M,N为顶点的四边形是平行四边形的点M的坐标为(3+2,﹣9﹣4)或(3﹣2,﹣9+4)或(3+,﹣7﹣2)或(3﹣,﹣7+2).17.(1)解:设抛物线解析式为y=ax2+bx+c(a≠0),∵抛物线经过点A(﹣1,0),C(0,3),且对称轴为直线x=1,∴,解得,∴抛物线的表达式为y=﹣x2+2x+3;(2)证明令y=0,则﹣x2+2x+3=0,解得:x1=﹣1,x2=3,∴B(3,0),∵y=﹣x2+2x+3=﹣(x﹣1)2+4,∴顶点D坐标(1,4),∴CD==,BD==2,CB==3,∵BC2+CD2=(3)2+()2=20,BD2=(2)2=20,∴BC2+CD2=BD2,∴∠BCD=90°,∴∠tan∠CDB===3,∵tan∠CAB==3,∴∠CDB=∠CAB;(3)解:①当BM∥CN时,如图:∵对称轴为直线x=1,C(0,3),∴N(2.3),CN=2,∵B(3,0),∴CN=BM,∴BM=2,当M点在B点左侧时,M1(1,0),当M点在B点右侧时,M2(5,0),∴M1(1,0)或M2(5,0);②当CM∥BN时,如图:CN与BM互相平分,N点和C点纵坐标互为相反数,可得N点纵坐标为﹣3,把y=﹣3代入解析式得:﹣x2+2x+3﹣3,解得:x1=+1,x2=﹣+1,所以N1的横坐标为+1.,N2的横坐标为﹣+1,由平行四边形对角线互相平分可得﹣+1+0=3+x M或+1+0=3+x M,解得x N=﹣﹣2或x N=﹣2,所以M3(﹣2,0)或M4(﹣﹣2,0).综上所述:M1(1,0)或M2(5,0)或M3(﹣2,0)或M4(﹣﹣2,0).18.解:(1)将点B(0,﹣1)代入函数解析式y=a(x﹣1)2,∴a(0﹣1)2=﹣1,解得a=﹣1,∴二次函数的表达式为y=﹣(x﹣1)2;(2)令﹣x﹣1=﹣(x﹣1)2,解得x=0或x=3,∴A(3,﹣4).设P的横坐标为t(0<t<3),∴P(t,﹣t﹣1),E(t,﹣t2+2t﹣1),∴h=EP=(﹣t2+2t﹣1)﹣(﹣t﹣1)=﹣t2+3t=﹣(t﹣)2+.∵﹣1<0,∴当t为时,h的最大值为.(3)存在,理由如下:∵抛物线的顶点为C,∴C(1,0),∵点D为直线AB与对称轴x=1的交点,∴D(1,﹣2),∴CD=2;CD∥y轴,∴CD∥EP,若四边形DCEP是平行四边形,则只需CD=EP,由(2)知,EP=﹣t2+3t,∴﹣t2+3t=2,解得t=1(舍)或t=2,∴P(2,﹣3).综上,存在一点P,使得四边形DCEP是平行四边形,此时P(2,﹣3).19.解:(1)∵抛物线y=ax2+bx+c(a≠0)的图象经过点A(1,0),B(3,0),∴设抛物线的解析式为y=a(x﹣1)(x﹣3),把点C(0,6)代入,∴6=a(0﹣1)(0﹣3),∴a=2,∴y=2(x﹣1)(x﹣3)=2x2﹣8x+6,∴抛物线解析式为y=2x2﹣8x+6;(2)∵y=2x2﹣8x+6=2(x﹣2)2﹣2,∴顶点M的坐标为(2,﹣2),∵抛物线的顶点M与对称轴l上的点N关于x轴对称,∴点N(2,2),设直线AN的解析式为:y=kx+b,由题意可得:,解得:,∴直线AN解析式为:y=2x﹣2,联立y=2x2﹣8x+6得:,解得:,,∴点D(4,6),设△ADE的面积为S,点E(e,2e2﹣8e+6),过点E作EF⊥x轴交直线AD于点F,则点F坐标为(e,2e﹣2),∴EF=(2e﹣2)﹣(2e2﹣8e+6)=﹣2e2+10e﹣8,∴S=•EF•|D x﹣A x|=×3×(﹣2e2+10e﹣8)=﹣3(e2﹣5e﹣4)=,所以,当时,△ADE的面积,此时点E坐标为;(3)由(2)知,A(1,0),D(4,6),设Q(2,m),P(x,2x2﹣8x+6),①以AD为对角线时,∵以A,D,P,Q为顶点的四边形为平行四边形,∴,解得:,②以AP为对角线时,∵以A,D,P,Q为顶点的四边形为平行四边形,∴,解得:,∴P(5,16);③以AQ为对角线时,∵以A,D,P,Q为顶点的四边形为平行四边形,∴,解得:,∴P(﹣1,16);综上所述,当点P的坐标为(5,16)或(﹣1,16)或(3,0)时,以A,D,P,Q为顶点的四边形为平行四边形.20.解:(1)∵抛物线y=ax2+bx﹣6经过点A(﹣2,0),B(6,0)两点,∴,解得:,∴抛物线的函数表达式为y=x2﹣2x﹣6;∵y=x2﹣2x﹣6=(x﹣2)2﹣8,∴顶点D(2,﹣8);设直线BD的表达式为y=kx+b,则,解得:,∴直线BD的函数表达式为y=2x﹣12;(2)y=x2﹣2x﹣6中令x=0,得y=﹣6,∴C(0,﹣6),∴OC=6,∵A(﹣2,0),∴S△AOC=OA•OC=×2×6=6,设点P的横坐标为m(0<m<6),∴P(m,m2﹣2m﹣6),①如图,当0<m<2时,过点P作PH∥x轴,交BD于点H,过点D作DJ⊥PH于点J,过点B作BI⊥PH交PH 的延长线于点I,则H(m2﹣m+3,m2﹣2m﹣6),∴PH=m2﹣m+3﹣m=m2﹣2m+3,∴S△BDP=S△PDH+S△BCH=PH•DJ+PH•BI=PH•(DJ+BI)=PH×8=4PH=4(m2﹣2m+3)=m2﹣8m+12,∵S△BDP=S△AOC,∴m2﹣8m+12=×6,解得:m1=4﹣,m2=4+(不符合题意,舍去);②如图:当2<m<6,过点P作PE⊥x轴于点E,交BD于点F,过点D作DG⊥FP,交FP的延长线于点G,则F(m,2m﹣12),∴FP=(2m﹣12)﹣(m2﹣2m﹣6)=﹣m2+4m﹣6,∴S△BDP=S△FDP+S△FPB=FP•DG+FP•BE=FP•(DG+BE)=FP•4=2FP=2(﹣m2+4m﹣6)=﹣m2+8m﹣12,∵S△BDP=S△AOC,∴﹣m2+8m﹣12=3,解得:m1=3,m2=5.综上所述,m的值为4﹣或3或5;(3)存在,理由如下:此题分情况讨论,已求得A点坐标为(﹣2.0),C点坐标为(0.﹣6),构成的平行四边形的对角线的交点即为两条对角线的中点,据此作答,第一种情况:构成的平行四边形中AM为对角线时,则另一条对角线是CN,设N点坐标为(x0,),M的坐标为(a,0),根据平行四边形的性质以及中点坐标公式有:,化简:,解得:a=4±2,此时M的坐标为(4﹣2,0)或(4+2,0);第二种情况:构成的四边形中AN为对角线时,则另一条对角线是CM,设N点坐标为(x0,),M的坐标为(a,0),此时根据平行四边形的性质以及中点坐标公式有:,化简:,解得:a=2或a=﹣2(此时A点和M点重合,不合题意舍去),此时M点的坐标为(2,0);第三种情况:构成的四边形中AC为对角线时,则另一条对角线是MN,设N点坐标为(x0,),M的坐标为(a,0),此时根据平行四边形的性质以及中点坐标公式有:,化简:,解得:a=﹣6或a=﹣2(此时A点和M点重合,不合题意舍去),此时M点的坐标为(6,0).综上所述,M点坐标为(﹣6,0)或(2,0)或(4﹣2,0)或(4+2,0).。
二次函数与平行四边形综合.doc

........................................................................................ r" E \ ................................... Everyday第十八讲二次函数与平行四边形综合一.教学内容1. 二次两数的表示,二次函数图像与性质;2. 平行四边形的性质和判定;3. 函数图像与平行四边形的综合应用,典型应用、图像题;二、例题细看3【例1】已知:如图,在平面直角坐标系xOy中,直线y = --x + 6与x轴.y轴的交点分别为A、B,4将ZOBA对折,使点O的对应点H落在岂线上,折痕交兀轴于点C.(1)直接写出点C的坐标,并求过A、B、C三点的抛物线的解析式;(2)若抛物线的顶点为D,在玄线BC±是否存在点P,使得四边形ODAP为平行四边形?若存在,求出点P的坐标;若不存在,说明理由;(3)设抛物线的对•称轴与直线BC的交点为T,Q为线段BT上一点,直接写出\QA-QO\的収值范围.【考点分析】二次函数综合题【PEC分析】(1)点A的坐标是纵坐标为0,得横坐标为8,所以点A的坐标为(& 0);点B的坐标是横坐标为0,解得纵坐标为6,所以点B的坐标为(0, 6):由题意得:BC是ZAB0的角平分线,所以0C二CH, BH二0B二6TAB二10,・・・AH二4,设0C二x,则AC=8-x由勾股定理得:x=3・••点C的坐标为(3, 0)将此三点代入二次函数一般式,列的方程组即可求得;(2)求得直线BC的解析式,根据平行四边形的性质,对角相等,对边平行且相等,借助于三函数即可求得;(3)如图,由对称性可知Q0二QH, IQA-QOI二|QA-QH|.当点Q与点B重合时,Q、H、A三点共线, IQA-QO|取得最大值4 (即为AH的长);设线段0A的垂直平分线与直线BC的交点为K,当点Q与点K 重合时,IQA-QOI取得最小值0.【跟踪练习】例1.(浙江义乌市)如图,抛物线y = x2-2x-3与x轴交A、B两点(A点在B点左侧),直线/与抛物线交于A、C两点,其中C点的横处标为2.(1)求A、B两点的坐标及直线AC的函数表达式;(2)P是线段AC上的一个动点,过P点作y轴的平行线交抛物线于E点,求线段PE长度的最大值;(3)点G是抛物线上的动点,在x轴上是否存在点F,使A、C、F、G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由.【例2】如图,点O是处标原点,点A(n, 0)是兀轴上一动点5<0).以力0为一边作矩形AOBC,点C在第二彖限,月.03 = 204.矩形AOBC绕点A逆时针旋转90。
初三数学 二次函数与平行四边形的综合问题教案

教学过程一、课堂导入二次函数的综合问题是中考压轴题常考题型之一,考点分值12分,难度较大。
主要考查形式为二次函数与一些简单几何图形的点存在性问题,既考查了学生的数形结合能力,又考查学生的计算能力。
此类问题出现后,大多学生都无从下手,主要是学生的综合能力、解题技巧及实战经验不足所致。
就本节二次函数与平行四边形的点存在性问题,主要考查了学生能否将平行四边形的性质与判定融入到二次函数,在函数图像中构造题意所需图形的能力。
二、复习预习平行四边形的判定与性质1. 定义:两组对边分别平行的四边形叫做平行四边形。
2. 性质:①平行四边形两组对边分别平行;②平行四边形两组对边分别相等;③平行四边形两组对角分别相等;④平行四边形的对角线互相平分;3. 判定:①两组对边分别平行的四边形是平行四边形;②两组对边分别相等的四边形是平行四边形;③两组对角分别相等的四边形是平行四边形;④对角线互相平分的四边形是平行四边形;⑤一组对边平行且相等的四边形是平行四边形;三、知识讲解考点1 二次函数的基础知识1.一般地,如果y=ax 2+bx+c (a ,b ,c 是常数且a ≠0),那么y 叫做x 的二次函数,它是关于自变量的二次式,二次项系数必须是非零实数时才是二次函数,这也是判断函数是不是二次函数的重要依据.当b=c=0时,二次函数y=ax 2是最简单的二次函数.2.二次函数y=ax 2+bx+c (a ,b ,c 是常数,a ≠0)的三种表达形式分别为:一般式:y=ax 2+bx+c ,通常要知道图像上的三个点的坐标才能得出此解析式;顶点式:y=a (x -h )2+k ,通常要知道顶点坐标或对称轴才能求出此解析式;交点式:y=a (x -x 1)(x -x 2),通常要知道图像与x 轴的两个交点坐标x 1,x 2才能求出此解析式;对于y=ax 2+bx+c 而言,其顶点坐标为(-2b a ,244ac b a ).对于y=a (x -h )2+k 而言其顶点坐标为(h ,k ),•由于二次函数的图像为抛物线,因此关键要抓住抛物线的三要素:开口方向,对称轴,顶点.考点2 探究平行四边形的一般思路在探究平行四边形的存在性问题时,具体方法如下:(1)假设结论成立;(2)探究平行四边形存在问题一般是已知平行四边形的3个顶点,再去求另外一个顶点,具体方法有两种:第一种是:①从给定的3个顶点中任选2个定点确定的线段作为探究平行四边形的边或对角线分别作出平行四边形;②根据题干要求找出符合条件的平行四边形;第二种是:①以给定的3个定点两两组合成3条线段,分别以这3条线段为对角线作出平行四边形;②根据题干要求找出符合条件的平行四边形;(3)建立关系式,并计算;根据以上分类方法画出所有的符合条件的图形后,可以利用平行四边形的性质进行计算,也可以利用全等三角形、相似三角形或直角三角形的性质进行计算,要具体情况具体分析,有时也可以利用直线的解析式联立方程组,由方程组的解为交点坐标的方法求解。
二次函数与平行四边形结合专题练习

二次函数与平行四边形结合专题练习1.题目描述:给定抛物线$y=-x^2+bx+c$与$x$轴的交点$A,B$,其中$B$的坐标为$(3,0)$,直线$AD$经过点$A$,与抛物线交于点$D(2,3)$。
求抛物线和直线$AD$的解析式,以及是否存在实数$a$,使得过点$(a,0)$且平行于$AD$的直线$EF$与抛物线交于点$F$,使得四边形$ADEF$为平行四边形,若存在,求出$a$。
2.题目描述:给定抛物线的顶点坐标$M(1,4)$,经过点$N(2,3)$,与$x$轴交于$A,B$,与$y$轴交于点$C$。
求抛物线的解析式,以及证明四边形$CDAN$是平行四边形,其中直线$y=kx+t$经过点$C,M$,与$x$轴交于点$D$。
3.题目描述:给定抛物线经过$A(-1,0),B(5,0),C(x,-\frac{5}{2})$三点。
求抛物线的解析式,以及在抛物线的对称轴上有一点$P$,使得$PA+PC$的值最小,求点$P$的坐标。
另外,给定$x$轴上的一动点$M$,判断是否存在抛物线上的一点$N$,使得四边形$ACMN$为平行四边形,若存在,求点$N$的坐标。
4.题目描述:给定抛物线$y=ax^2+bx+c$经过点$A(-2,0),B(4,0),D(2,4)$,与$y$轴交于点$C$,作直线$BC$,连接$AC,CD$。
求抛物线的函数表达式,以及点$E$满足$\angle ECD=\angle ACO$的坐标,点$M$在$y$轴上且位于点$C$上方,点$N$在直线$BC$上,点$P$为第一象限内抛物线上的一点,若以点$C,M,N,P$为顶点的四边形为菱形,求菱形的边长。
5.题目描述:给定抛物线$y=-x^2+2x+3$与$x$轴的交点$A,B$,与$y$轴的交点为$C$,顶点为$D$。
求点$A,B,C$的坐标以及抛物线的对称轴,连接$BC$,与对称轴交于点$E$,点$P$为线段$BC$上的动点,过点$P$作$PF$平行于$DE$交抛物线于点$F$。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十八讲二次函数与平行四边形综合一、教学内容1.二次函数的表示 , 二次函数图像与性质;2.平行四边形的性质和判定;3.函数图像与平行四边形的综合应用,典型应用、图像题;二、例题细看【例 1】已知:如图,在平面直角坐标系将OBA 对折,使点O的对应点xOy 中,直线 y3与 x 轴、y轴的交点分别为 A、B ,x 64H 落在直线 AB 上,折痕交x 轴于点C.( 1)直接写出点 C 的坐标,并求过A、B、C 三点的抛物线的解析式;( 2)若抛物线的顶点为 D ,在直线BC上是否存在点P ,使得四边形ODAP 为平行四边形?若存在,求出点P 的坐标;若不存在,说明理由;( 3)设抛物线的对称轴与直线BC的交点为 T ,Q 为线段BT上一点,直接写出 QA QO 的取值范围 .【考点分析】二次函数综合题yBH1O1 CA xDT【PEC分析】( 1)点 A 的坐标是纵坐标为 0,得横坐标为 8,所以点 A 的坐标为( 8, 0);点B 的坐标是横坐标为 0,解得纵坐标为 6,所以点 B 的坐标为( 0, 6);由题意得: BC是∠ ABO的角平分线,所以OC=CH, BH=OB=6∵AB=10,∴ AH=4,设 OC=x,则 AC=8-x 由勾股定理得: x=3∴点 C 的坐标为( 3, 0)将此三点代入二次函数一般式,列的方程组即可求得;( 3)如图,由对称性可知QO=QH,|QA-QO|=|QA-QH| .当点 Q与点 B 重合时, Q、 H、 A 三点共线,|QA-QO|取得最大值4(即为 AH的长);设线段OA的垂直平分线与直线 BC的交点为 K,当点 Q与点 K 重合时, |QA-QO|取得最小值 0.【跟踪练习】例 1.(浙江义乌市 ) 如图,抛物线y x22x 3与x轴交A、B两点(A点在B点左侧),直线 l 与抛物线交于A、C两点,其中C点的横坐标为2.( 1)求 A 、 B 两点的坐标及直线AC 的函数表达式;( 2)P 是线段 AC 上的一个动点,过 P 点作 y 轴的平行线交抛物线于 E 点,求线段 PE 长度的最大值;( 3)点 G 是抛物线上的动点,在x 轴上是否存在点F,使 A 、C、 F、 G 这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的 F 点坐标;如果不存在,请说明理由.A【例 2】如图,点O是坐标原点,点A(n ,0) 是 x 轴上一动点(n 0) .以 AO 为一边作矩形AOBC ,点C在第二象限,且OB 2OA .矩形AOBC 绕点 A 逆时针旋转90 得矩形AGDE .过点 A 的直线y kx m ( k 0) 交y轴于点F,FB FA .抛物线y ax 2bx c 过点E、F、G且和直线AF 交于点 H ,过点 H 作 HM x 轴,垂足为点M .⑴求 k 的值;⑵点 A 位置改变时,AMH 的面积和矩形AOBC的面积的比值是否改变?说明你的理由.yC BDGMFE A OxH【 PEC分析】( 1 )由题意知O B=2OA=2n,在直角三角形AEO 中, OF=OB-BF=-2n-AF,因此可用勾股定理求出AF 的表达式,也就求出了FB 的长,由于 F 的坐标为( 0 , m )据此可求出m , n 的关系式,可用 n 替换掉一次函数中m 的值,然后将 A 点的坐标代入即可求出k 的值.( 2 )思路同( 1)一样,先用n 表示出 E、 F、 G 的坐标,然后代入抛物线的解析式中,得出 a ,b , c 与n 的函数关系式,然后用n 表示出二次函数的解析式,进而可用n 表示出 H 点的坐标,然后求出△AMH【跟踪练习】 ( 1)在图 1,2, 3 中,给出平行四边形 ABCD 的顶点 A ,B ,D 的坐标(如图所示),写出图 1, 2, 3 中的顶点 C 的坐标,它们分别是 (5,2) , ,;yyyyBc(,d)CB (12),B(c , d )B (c , d )CCCD( e , f )A(a ,b)D( e , b)xxO( A)D(4,0)O (A)OxD (e ,0)A(a ,b)图 1图 2图 3xA ,B ,DO( 2)在图 4 中,给出平行四边形 ABCD的顶点 的坐标(如图所示) ,求出顶点 C 图 4的坐标( C 点坐标用含 a , b , c , d , e , f 的代数式表示);归纳与发现( 3)通过对图 1, 2, 3, 4 的观察和顶点 C 的坐标的探究,你会发现:无论平行四边形ABCD 处于直角坐标系中哪个位置,当其顶点坐标为 A(a , b),B(c , d ), C (m , n), D (e ,f ) (如图 4)时,则四个顶点的横坐标 a , c , m , e 之间的等量关系为 ;纵坐标 b , d ,n ,f 之间的等量关系为运用与推广( 4)在同一直角坐标系中有抛物线y x 21 5 1 9(5c 3)x c 和三个点 Gc , c , S2c , c ,222H (2c ,0) (其中 c 0 ).问当 c 为何值时,该抛物线上存在点P ,使得以 G , S ,H ,P 为顶点的四边形是平行四边形?并求出所有符合条件的P 点坐标.【例 3】如图 1,Rt ABC中,A 90,tan B3,点 P 在线段 AB 上运动,点Q、 R 分别在线段BC、4AC 上,且使得四边形APQR 是矩形.设AP的长为 x ,矩形 APQR 的面积为y,已知y是 x 的函数,其图象是过点12,36的抛物线的一部分(如图 2 所示).(1)求AB的长;(2)当AP为何值时,矩形 APQR 的面积最大,并求出最大值.为了解决这个问题,孔明和研究性学习小组的同学作了如下讨论:张明:图 2 中的抛物线过点12,36 在图 1 中表示什么呢?李明:因为抛物线上的点 (x, y) 是表示图 1 中AP的长与矩形 APQR 面积的对应关系,那么 12,36表示当 AP 12 时, AP 的长与矩形APQR面积的对应关系.赵明:对,我知道纵坐标36 是什么意思了!孔明:哦,这样就可以算出AB ,这个问题就可以解决了.请根据上述对话,帮他们解答这个问题.【考点点评】本题结合三角形、矩形的相关知识考查了二次函数的应用,用数形结合的思路求得相应的函数关系式是解题的关键yC(12,36)QRA BO xP【 PEC分析】( 1 )由于 y 是 x 的函数且过( 12 , 36 )点,即AP=12时,矩形的面积为36 ,可求出 PQ 的长,进而在直角三角形BPQ 中得出 BP 的值,根据AB=AP+BP即可求出AB 的长.( 2 )与( 1 )类似,可先用AP 表示出 BP 的长,然后在直角三角形BPQ 中,表示出PQ 的长;根据矩形的面积计算方法即可得出关于y, x 的函数关系式.然后可根据得出的函数的性质求出矩形的最大面积以及此时对应的x 的值.【跟踪练习】如图,已知与 x 轴交于点A(1,0)和B(5,0)的抛物线l1的顶点为C (3,4),抛物线l2与l1关于x轴对称,顶点为 C .(1)求抛物线l2的函数关系式;(2)已知原点 O ,定点D (0,4),l2上的点 P 与l1上的点 P 始终关于 x 轴对称,则当点 P 运动到何处时,以点 D, O,P,P 为顶点的四边形是平行四边形?(3)在l2上是否存在点 M ,使△ ABM 是以 AB 为斜边且一个角为30的直角三角形?若存,求出点 M 的坐标;若不存在,说明理由.yl25E4321A B1 1Ox1 2345234C5l1【例 4】如图,在矩形OABC中,已知A、C两点的坐标分别为A(4,0)、 C (0,2) ,D为OA的中点.设点P 是 AOC 平分线上的一个动点(不与点O 重合).( 1)试证明:无论点P 运动到何处,PC 总与PD相等;( 2)当点P运动到与点B的距离最小时,试确定过 O、P、D 三点的抛物线的解析式;( 3)设点E是( 2)中所确定抛物线的顶点,当点P 运动到何处时,PDE 的周长最小?求出此时点 P 的坐标和PDE 的周长;P°4OABC的对称中心,是否存在点,使 CPN90 ?若存在,请直接写出()设点 N 是矩形点 P 的坐标.yC(0,2)BPO D A(4,0)x【PEC分析】本题综合考查了三角形全等、一次函数、二次函数,及线段最短和探索性的问题.(1 )通过△POC ≌△POD 而证得 PC=PD .(2)首先要确定 P 点的位置,再求出 P、F 两点坐标,利用待定系数法求的抛物线解析式;(3)此问首先利用对称性确定出 P 点位置是 EC 与∠AOC 的平分线的交点,再利用抛物线与直线 CE 的解析式求出交点 P 的坐标.进而求的△PED 的周长;(4)要使∠CPN=90 °,则 P 点是以 CN 的中点为圆心以 CN 为直径的圆与角平分线的交点,由此就易于写出 P 点的坐标.【例 5】如图,已知抛物线 l1:y x24的图象与 x 轴相交于 A、 C 两点,B是抛物线 l1上的动点 ( B不与A、 C 重合 ),抛物线 l 2与 l1关于x 轴对称,以 AC 为对角线的平行四边形ABCD 的第四个顶点为D.(1)求 l2的解析式;(2)求证:点D一定在l2上;(3)平行四边形 ABCD 能否为矩形?如果能为矩形,求这些矩形公共部分的面积(若只有一个矩形符合条件,则求此矩形的面积);如果不能为矩形,请说明理由.(注:计算结果不取近似值.)yl1: y=x 2-4A CO xl2【 PEC分析】( 1 )根据 l1 的解析式可求l1 与 x 轴的交点为 A ( -2 ,0 ), C( 2, 0 ),顶点坐标是( 0 ,-4 ), l2 与 l1关于 x 轴对称,实际上是l2 与 l1的顶点关于 x 轴对称,即l2 的顶点为(0, 4 ),设顶点式,可求抛物线l2 的解析式;( 2 )平行四边形是中心对称图形, A 、C 关于原点对称,则 B、 D 也关于原点对称,设点B( m , n ),则点 D( -m ,-n ),由于 B( m ,n)点是 y=x2-4上任意一点,则 n=m2-4,∴-n=- ( m2-4 )=-m2+4=-( -m ) 2+4 ,可知点 D ( -m , -n )在 l2y=-x2+4的图象上;6【跟踪练习】 如图,已知抛物线 C 1 与坐标轴的交点依次是 A4 ,0 , B 2 ,0 ,E 0,8 .( 1)求抛物线 C 1 关于原点对称的抛物线 C 2 的解析式;( 2)设抛物线 C 1 的顶点为 M ,抛物线 C 2 与 x 轴分别交于 C , D 两点 (点 C 在点 D 的左侧 ),顶点为 N ,四边形 MDNA 的面积为 S .若点 A ,点 D 同时以每秒 1 个单位的速度沿水平方向分别 向右、向左运动;与此同时,点 M ,点 N 同时以每秒 2 个单位的速度沿坚直方向分别向下、向上运动, 直到点 A 与点 D 重合为止. 求出四边形 MDNA 的面积 S 与运动时间 t 之间的关系式,并写出自变量 t 的取值范围;( 3)当 t 为何值时,四边形 MDNA 的面积 S 有最大值,并求出此最大值;( 4)在运动过程中,四边形MDNA 能否形成矩形?若能,求出此时t 的值;若不能,说明理由.y 8 E 7 6 5 4 32 NAB1C H D-6 -5 -4 -3 -2 -1O1 2 3 4 5 xM-1 -2三、课堂一试1.如图,在直角坐标系 xOy 中,点 P 为函数 y1 x2 在第一象限内的图象上的任一点, 点 A 的坐标为 0,1 , 4直线 l 过 B 0 , 1 且与 x 轴平行,过 P 作 y 轴的平行线分别交 x 轴、直线 l 于 C 、Q ,连结 AQ 交 x 轴于 H , 直线 PH 交 y 轴于 R .⑴ 求证: H 点为线段 AQ 的中点;⑵ 求证:四边形 APQR 为菱形;⑶ 除 P 点外,直线 PH 与抛物线 y1 x2 有无其它公共点?若有,求出其它公共点的坐标;若没4有,请说明理由.yPA CxOHlB QR2.如图,在平面直角坐标系内,以y 轴为对称轴的抛物线经过直线y3 x 2 与y轴的交点A和点3M 3,0 .2(1)求这条抛物线所对应的二次函数的关系式;( 2)将( 1)中所求抛物线沿 x 轴平移.①在题目所给的图中画出沿 x轴平移后经过原点的抛物线大致图象;②设沿 x 轴平移后经过原点的抛物线对称轴与直线AB 相交于 C 点.判断以 O 为圆心, OC 为半径的圆与直线AB 的位置关系,并说明理由;( 3)P点是沿 x 轴平移后经过原点的抛物线对称轴上的点。
