江苏省宿迁市高中数学第二章圆锥曲线与方程第9课时双曲线的几何性质1导学案(无答案)苏教版选修2-1

江苏省宿迁中学高中数学选修2-1导学案：第2章圆锥曲

第7课时双曲线的标准方程（1）【学习目标】1．掌握双曲线的定义,标准方程． 2．根据已知条件求双曲线的标准方程．【问题情境】1．类比椭圆标准方程的建立过程推导出双曲线的标准方程．2．把椭圆定义中的“距离的差的绝对值”改为“距离的差”，那么点的轨迹会怎样？【合作探究】双曲线的标准方程F 1 ，F 2 F 1 ，F 2 想一想：如何判断方程)0,0(12222>>=-b a b y a x 和)0,0(12222>>=-b a bx a y 所表示的双曲线焦点的位置？【展示点拨】例1．已知双曲线两个焦点的坐标为)0,5()0,5(21F F ，-，双曲线上一点P 到21F F ，的距离之差的绝对值等于8，求双曲线标准方程变式1:若|PF 1|-|PF 2|=8呢？变式2:若||PF 1|-|PF 2||=10呢？变式3:若||PF 1|-|PF 2||=6呢？例2．求满足下列条件的双曲线的标准方程（1）a =3，b = 4，焦点在x 轴上；（2）a =25，经过点)5,2(-A ，焦点在y 轴上．例3．如果方程1222=--my m x 表示双曲线，求m 的取值范围．例4．已知A ，B 两地相距800m ，一炮弹在某处爆炸，在A 处听到炮弹爆炸声的时间比在B 处迟2s ，设声速为340/m s ．（1）爆炸点在什么曲线上？（2）求这条曲线的方程．【学以致用】1．双曲线192522=-x y 的焦点坐标为．2．若k ∈R ，则方程x 2k ＋3＋y 2k ＋2＝1表示焦点在x 轴上的双曲线，则k 的取值范围是________．3．已知双曲线的两个焦点分别为1100(,)F -，2100(,)F ，双曲线上一点P 到1F ，2F 的距离的差的绝对值等于12，求双曲线的标准方程． 4．求适合下列条件的双曲线的标准方程：（1）5=c ，3=b ，焦点在y 轴上；（2）焦点为)6,0(-，)6,0(，3=a ．5．已知双曲线过点()3,2-，且与椭圆224936x y +=有相同的焦点，求双曲线的方程．第7课时双曲线的标准方程（1）【基础训练】1．双曲线192522=-x y 的焦点坐标为． 2．方程15922=---k y k x 表示焦点在x 轴上的双曲线，则k 的取值范围是________．3．已知P 是双曲线19422=-y x 上一点，F 1．F 2分别是双曲线的左．右焦点，若PF 1＝3，则PF 2等于．49=，得．5．设错误！未找到引用源。

高中数学第二章圆锥曲线与方程2.2.2双曲线的几何性质预习导学案

y∈R
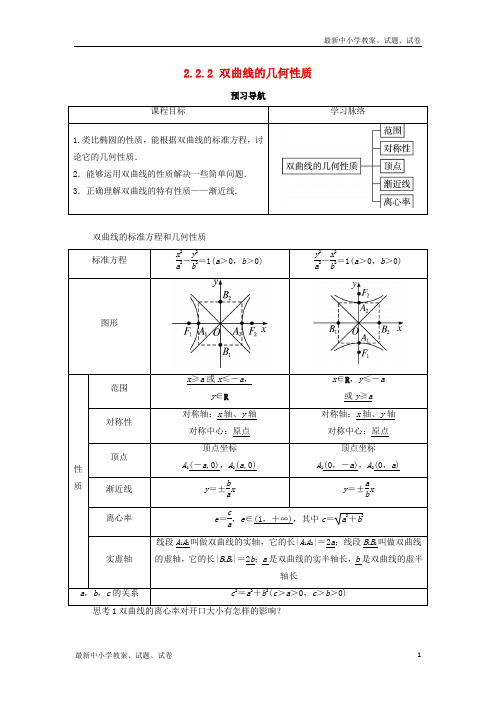
x∈R，y≤－a
或y≥a
对称性
对称轴：x轴、y轴
对称中心：原点
对称轴：x轴、y轴
对称中心：原点
顶点
顶点坐标
A1(－a,0)，A2(a,0)
顶点坐标
A1(0，－a)，A2(0，a)
渐近线
y＝± x
y＝± x
离心率
e＝，e∈(1，＋∞)，其中c＝
实虚轴
线段A1A2叫做双曲线的实轴，它的长|A1A2|＝2a；线段B1B2叫做双曲线的虚轴பைடு நூலகம்它的长|B1B2|＝2b；a是双曲线的实半轴长，b是双曲线的虚半轴长
名师点拨双曲线与椭圆的六个不同点：
双曲线
椭圆
图形
两支曲线
封闭的曲线
顶点
两个顶点
四个顶点
轴
实、虚轴
长、短轴
渐近线
有渐近线
无渐近线
离心率
e＞1
0＜e＜1
a，b，c关系
a2＋b2＝c2
a2－b2＝c2
a，b，c的关系
c2＝a2＋b2(c＞a＞0，c＞b＞0)
思考1双曲线的离心率对开口大小有怎样的影响？
提示：双曲线的离心率e＝反映了双曲线开口的大小，e越大，双曲线的开口就越大．
思考2双曲线的焦点始终在什么轴所在的直线上？
提示：实轴．
思考3一条直线与双曲线的渐近线平行时，它与双曲线有几个公共点？
提示：1个．
2.2.2双曲线的几何性质
预习导航
课程目标
学习脉络
1.类比椭圆的性质，能根据双曲线的标准方程，讨论它的几何性质．
2．能够运用双曲线的性质解决一些简单问题．
3．正确理解双曲线的特有性质——渐近线.

江苏省宿迁市高中数学第2章圆锥曲线与方程第10课时

第10课时双曲线的几何性质（2）【学习目标】能用双曲线的简单几何性质解决一些简单问题．【问题情境】1．回顾双曲线的范围．对称轴．顶点．离心率．渐近线；2．已知双曲线的方程为221914x y -=，写出顶点和焦点坐标．实半轴长．虚半轴长．离心率．渐近线方程．【合作探究】试比较椭圆与双曲线的几何性质的异同【展示点拨】例1．设双曲线22221x y a b-=的半焦距为c ，直线l 过( , 0) (0 , )a b 、两点，且原点到直线l ，求双曲线的离心率．例2．求与双曲线221169x y -=共渐近线，且经过()3A -点的双曲线的标准方程．例3．焦点在坐标轴上的双曲线，它的两条渐近线方程为02=±y x ，焦点在渐近线的距离为8，求此双曲线方程．例4．若21,F F 是双曲线116922=-y x 的左右焦点，点P 在双曲线上，且3221=⋅PF PF ,求21PF F ∠的大小．【学以致用】1．双曲线1253622=-y x 的渐近线方程是．2．已知双曲线)0,0(12222>>=-b a by a x 的一条渐近线方程为x y 34=，则双曲线的离心率为．3．若双曲线的渐近线方程为x y 3±=，它的一个焦点是（10，0），则双曲线的方程是．4．与椭圆1492422=+y x 共焦点，而与双曲线1643622=-y x 共渐近线的双曲线的方程为．5．求满足下列条件的双曲线的标准方程．（1）离心率e =()5,3M -；（2）两条渐近线的方程是23y x =±，经过点9,12M ⎛⎫- ⎪⎝⎭．（3）双曲线的一个焦点是)0,3(1-F ,过右焦点2F 作垂直于x 轴的直线交双曲线于点,P 且1230PF F ∠=︒．第10课时双曲线的几何性质（2）【基础训练】1．双曲线2x 2-y 2=8的实轴长是．2．当817k <<时,双曲线221178x y k k+=--的焦距为__________________． 3．设双曲线的一个焦点为F ，虚轴的一个端点为B ,如果直线FB 与该双曲线的一条渐近线垂直，那么此双曲线的离心率为__________________．4．已知双曲线的中心在坐标原点,一个焦点为(10,0)F ,两条渐近线的方程为43y x =±,则该双曲线的标准方程为______ __．5．圆1)(22=+-y a x 与双曲线122=-y x 的渐近线相切，则a 的值为．6．双曲线C 1：)0,0(12222>>=-b m b y m x 与椭圆)0(12222>>=+b a by a x 有相同的焦点，双曲线C 1的离心率为1e ，椭圆C 2的离心率为2e ，则222111e e += ．【思考应用】7．根据下列条件，求双曲线的标准方程（1）已知双曲线的渐近线方程为x y 21±=，焦距为10；（2）已知双曲线的渐近线方程为x y 32±=，且过点M （1,29-）；（3）与椭圆1244922=+y x 有公共焦点，且离心率45=e ．8．求满足下列条件的双曲线的离心率：（1）双曲线的渐近线方程为32y x =±；（2）过焦点且垂直于实轴的弦与另一焦点的连线所成角为90o ．9．双曲线)0,1(12222>>=-b a by a x 的焦距为2c, 直线l 过点）且点（，和（,01),0)0,(b a 到直线l 的距离与点)0,1(-到直线l 的距离之和,54c s ≥求双曲线的离心率e 的取值范围．10．一炮弹在某处爆炸，在F 1（-5000,0）处听到爆炸声的时间比在F 2（5000,0）处晚s 17300，已知坐标轴的单位长度为1m ，声速为340m/s ，爆炸点应在什么样的曲线上？并求爆炸点所在的曲线方程．【拓展提升】11．双曲线型冷却塔的外形，是双曲线的一部分绕其虚轴旋转所成的曲面，它的最小半径为12m,上口半径为13m,下口半径为15m,高为55m,试选择适当的坐标系，求出此双曲线的方程．12．连结双曲线22221x y a b-=和22221x y a b -=-的四个顶点的四边形的面积为1S ，连结四个焦点的四边形的面积为2S ，求12S S 的最大值．。

江苏省宿迁市高中数学第2章圆锥曲线与方程第8课时双曲线的标准方程2导学案(无答案)苏教版选修1_1

第8课时双曲线的标准方程（2）【学习目标】1．掌握双曲线的定义,标准方程； 2．根据已知条件求双曲线的标准方程．【问题情境】焦点在x 轴上的双曲线标准方程为；焦点在y 轴上的双曲线标准方程为．【合作探究】试比较双曲线与椭圆的异同：【展示点拨】例1．若双曲线k y x =-222的焦距为6，求实数k 的值．例2．若双曲线112422=-y x 上的一点P 到它的右焦点的距离为8，求点P 到它的左焦点的距离．例3．已知双曲线与双曲线141622=-y x 有相同焦点，且经过点)2,23(，求双曲线的方程．例4．已知方程422=+y kx ，其中k 为实数，对于不同的范围的k 值分别指出方程所表示的曲线类型．【学以致用】1．方程22115x y k k =-++表示双曲线的充要条件是k ∈____． 2．已知双曲线2288kx ky -= 的一个焦点为(0,3)，则k = ．3．以椭圆221169144x y +=的焦点为顶点，顶点为焦点的双曲线的标准方程是． 4．已知双曲线1366422=-y x 的焦点为1F ，2F ，点P 在双曲线上，且02190=∠PF F ，求21PF F ∆的面积．5．在△MNG 中，已知NG ＝4，当动点M 满足条件M N G sin 21sin sin =-时，求动点M 的轨迹方程．第8课时双曲线的标准方程（2）【基础训练】1．椭圆2x 2－3y 2＝1焦点坐标为．2．已知方程2211x y k k-=-表示双曲线，则k 的取值范围是．3．焦距为(3,5)M -的双曲线的标准方程为．4．设双曲线191622=-y x 上的点P 到点)0,5(的距离为15，则P 点到)0,5(-的距离是．5．已知焦点为12(4,0),(4,0)F F -，且经过点M 的双曲线的标准方程是．6．若椭圆14222=+my x 与双曲线1222=-y m x 有相同焦点，则实数m 的值为．【思考应用】7．若表示何种变化时，方程则当1,,222222=-+-∈>λλλλb y a x R b a 曲线?它们是否有相同的焦点？8．求焦点的坐标轴上，且经过)523,2(1-P 和)4,734(2P 两点的双曲线的标准方程．9．求以椭圆22185x y +=的焦点为顶点，而以椭圆的顶点为焦点的双曲线的方程；10．已知221,13x y k k -=---○1方程表示双曲线；○2表示焦点在x 轴上的双曲线；③表示焦点在y 轴上的双曲线【拓展提升】11．已在双曲线与椭圆1362722=+y x 有相同的焦点且与椭圆的一个交点的纵坐标为4，求双曲线的方程．12．在周长为48的390,tan =4oRt MPN MPN PMN ∆∠=∠中，，求以M,N 为焦点，且过点P 的双曲线方程．。

江苏省宿迁市高中数学第2章圆锥曲线与方程第7课时

第7课时双曲线的标准方程（1）【学习目标】1．掌握双曲线的定义,标准方程． 2．根据已知条件求双曲线的标准方程．【问题情境】1．类比椭圆标准方程的建立过程推导出双曲线的标准方程．2．把椭圆定义中的“距离的差的绝对值”改为“距离的差”，那么点的轨迹会怎样？【合作探究】双曲线的标准方程F 1 ，F 2 F 1 ，F 2 想一想：如何判断方程)0,0(12222>>=-b a b y a x 和)0,0(12222>>=-b a bx a y 所表示的双曲线焦点的位置？【展示点拨】例1．已知双曲线两个焦点的坐标为)0,5()0,5(21F F ，-，双曲线上一点P 到21F F ，的距离之差的绝对值等于8，求双曲线标准方程变式1:若|PF 1|-|PF 2|=8呢？变式2:若||PF 1|-|PF 2||=10呢？变式3:若||PF 1|-|PF 2||=6呢？例2．求满足下列条件的双曲线的标准方程（1）a =3，b = 4，焦点在x 轴上；（2）a =25，经过点)5,2(-A ，焦点在y 轴上．例3．如果方程1222=--my m x 表示双曲线，求m 的取值范围．例4．已知A ，B 两地相距800m ，一炮弹在某处爆炸，在A 处听到炮弹爆炸声的时间比在B 处迟2s ，设声速为340/m s ．（1）爆炸点在什么曲线上？（2）求这条曲线的方程．【学以致用】1．双曲线192522=-x y 的焦点坐标为．2．若k ∈R ，则方程x 2k ＋3＋y 2k ＋2＝1表示焦点在x 轴上的双曲线，则k 的取值范围是________．3．已知双曲线的两个焦点分别为1100(,)F -，2100(,)F ，双曲线上一点P 到1F ，2F 的距离的差的绝对值等于12，求双曲线的标准方程． 4．求适合下列条件的双曲线的标准方程：（1）5=c ，3=b ，焦点在y 轴上；（2）焦点为)6,0(-，)6,0(，3=a ．5．已知双曲线过点()3,2-，且与椭圆224936x y +=有相同的焦点，求双曲线的方程．第7课时双曲线的标准方程（1）【基础训练】1．双曲线192522=-x y 的焦点坐标为．2．方程15922=---k y k x 表示焦点在x 轴上的双曲线，则k 的取值范围是________．3．已知P 是双曲线19422=-y x 上一点，F 1．F 2分别是双曲线的左．右焦点，若PF 1＝3，则PF 2等于．49=，得．5．设m 为常数，若点(0,5)F 是双曲线2219y x m -=的一个焦点，则m = ． 6．设12,F F 分别是双曲线221169x y -=的左右焦点，AB 是双曲线过点1F 的弦，且AB =6，则三角形2ABF 的周长是．【思考应用】7．根据下列条件，求双曲线的标准方程：⑴焦点的坐标是()6,0-．()6,0，并且经过点()5,2A -；⑵经过点(3,P -和()7Q --，焦点在y 轴上．8．求与椭圆14922=+y x 有相同焦点，并且经过点)3,2(-的双曲线的标准方程．9．已知双曲线224640x y -+=上一点M 到它的一个焦点的距离等于1，求M 到另一个焦点的距离．10．已知圆C 1：1)3(22=++y x 和圆C 2：9)3(22=+-y x ，动圆M 同时与圆C 1及圆C 2相外切，求动圆圆心M 的曲线方程．【拓展提升】11．在△ABC 中，B （－6，0），C （6，0），直线AB ，AC 的斜率乘积为94，求顶点A 的轨迹．12．某中心接到其正东．正西．正北方向三个观察点的报告：正西．正北两个观察点同时听到了一声巨响，正东观察点听到该巨响的时间比其他两个观察点晚4s ．已知各观察点到该中心的距离都是1020m ．试确定该巨响发生的位置（假定当时声音传播的速度为340m/s ；相关点均在同一平面内）．。

「精品」高中数学第二章圆锥曲线与方程2.3.2双曲线的几何性质学案苏教版选修1_1

2．3.2 双曲线的几何性质学习目标 1.了解双曲线的几何性质，如范围、对称性、顶点、渐近线和离心率等.2.能用双曲线的简单性质解决一些简单问题.3.能区别椭圆与双曲线的性质．知识点一双曲线的几何性质思考类比椭圆的几何性质，结合图象，你能得到双曲线x 2a 2－y 2b2＝1(a >0，b >0)的哪些几何性质？梳理知识点二双曲线的离心率思考1 如何求双曲线的渐近线方程？思考2 在椭圆中，椭圆的离心率可以刻画椭圆的扁平程度，在双曲线中，双曲线的“张口”大小是图象的一个重要特征，怎样描述双曲线的“张口”大小呢？梳理双曲线的焦距与实轴长的比c a，叫做双曲线的________，其取值范围是________．e 越大，双曲线的张口________．知识点三双曲线的相关概念1．双曲线的对称中心叫做双曲线的________．2．实轴和虚轴等长的双曲线叫做________双曲线，它的渐近线方程是________．类型一已知双曲线的标准方程研究几何性质例1 求双曲线x 2－3y 2＋12＝0的实轴长、虚轴长、焦点坐标、顶点坐标、渐近线方程、离心率．反思与感悟已知双曲线方程求其几何性质时，若不是标准方程的要先化成标准方程，确定方程中a ，b 的对应值，利用c 2＝a 2＋b 2得到c ，然后确定双曲线的焦点位置，从而写出双曲线的几何性质．跟踪训练1 求双曲线9y 2－4x 2＝－36的顶点坐标、焦点坐标、实轴长、虚轴长、离心率和渐近线方程．类型二由双曲线的几何性质确定标准方程例2 求适合下列条件的双曲线的标准方程： (1)虚轴长为12，离心率为54；(2)顶点间距离为6，渐近线方程为y ＝±32x ；(3)求与双曲线x 2－2y 2＝2有公共渐近线，且过点M (2，－2)的双曲线方程．反思与感悟 (1)求双曲线的标准方程的步骤：①确定或分类讨论双曲线的焦点所在的坐标轴；②设双曲线的标准方程；③根据已知条件或几何性质列方程，求待定系数；④求出a ，b ，写出方程．(2)①与双曲线x 2a 2－y 2b 2＝1共焦点的双曲线方程可设为x 2a 2－λ－y 2b 2＋λ＝1(λ≠0，－b 2<λ<a 2)．②与双曲线x 2a 2－y 2b 2＝1具有相同渐近线的双曲线方程可设为x 2a 2－y 2b2＝λ(λ≠0)．③渐近线方程为ax ±by ＝0的双曲线方程可设为a 2x 2－b 2y 2＝λ(λ≠0)．跟踪训练2 求适合下列条件的双曲线的标准方程： (1)一个焦点为(0,13)，且离心率为135；(2)双曲线过点(3,92)，离心率e ＝103； (3)渐近线方程为y ＝±12x ，且经过点A (2，－3)．类型三求双曲线的离心率例3 分别求适合下列条件的双曲线的离心率： (1)双曲线的渐近线方程为y ＝±32x ；(2)双曲线x 2a 2－y 2b2＝1(0<a <b )的半焦距为c ，直线l 过(a,0)，(0，b )两点，且原点到直线l 的距离为34c .反思与感悟求双曲线的离心率，通常先由题设条件得到a ，b ，c 的关系式，再根据c 2＝a 2＋b 2，直接求a ，c 的值．而在解题时常把c a 或ba 视为整体，把关系式转化为关于c a 或b a的方程，解方程求之，从而得到离心率的值．在本题的(2)中，要注意条件0<a <b 对离心率的限制，以保证题目结果的准确性．跟踪训练3 已知F 1，F 2是双曲线x 2a 2－y 2b2＝1(a >0，b >0)的两个焦点，PQ 是经过F 1且垂直于x 轴的双曲线的弦，如果∠PF 2Q ＝90°，求双曲线的离心率．类型四直线与双曲线的位置关系例4 斜率为2的直线l 被双曲线x 23－y 22＝1截得的弦长为6，求l 的方程．引申探究若某直线l 与本例中的双曲线相交，求以点P (3，1)为中点的直线l 的方程．反思与感悟 (1)求弦长的两种方法①距离公式法：当弦的两端点坐标易求时，可直接求出交点坐标，再利用两点间距离公式求弦长． ②弦长公式法：当弦的两端点坐标不易求时，可利用弦长公式求解，即若直线l ：y ＝kx ＋b (k ≠0)与双曲线C ：x 2a 2－y 2b2＝1(a >0，b >0)交于A (x 1，y 1)，B (x 2，y 2)两点，则AB ＝1＋k 2|x 1－x 2|＝1＋1k 2|y 1－y 2|.特别提醒：若直线方程涉及斜率，要注意讨论斜率不存在的情况． (2)中点弦问题与弦中点有关的问题主要用点差法，根与系数的关系解决．另外，要注意灵活转化，如垂直、相等等问题也可以转化成中点、弦长等问题解决．跟踪训练4 设双曲线C ：x 2a2－y 2＝1(a >0)与直线l ：x ＋y ＝1相交于两个不同的点A ，B .(1)求双曲线C 的离心率e 的取值范围；(2)设直线l 与y 轴的交点为P ，且PA →＝512PB →，求a 的值．1．双曲线的一个顶点坐标为(－1,0)，一条渐近线方程为y ＝－2x ，则双曲线方程为____________．2．设双曲线x 2a ＋y 29＝1的渐近线方程为3x ±2y ＝0，则a ＝________.3．如果双曲线x 2a 2－y 2b 2＝1的两条渐近线互相垂直，则双曲线的离心率为________．4．若双曲线x 24－y 2m ＝1的渐近线方程为y ＝±32x ，则双曲线的焦点坐标是________．5．设双曲线x 2a 2－y 2b2＝1(a ＞0，b ＞0)的虚轴长为2，焦距为23，则双曲线的渐近线方程为________．1．渐近线是双曲线特有的性质，两方程联系密切，把双曲线的标准方程x 2a 2－y 2b2＝1(a >0，b >0)右边的常数“1”换为“0”，就是渐近线方程．反之由渐近线方程ax ±by ＝0变为a 2x 2－b 2y 2＝λ，再结合其他条件求得λ就可得双曲线方程．2．准确画出几何图形是解决解析几何问题的第一突破口．对圆锥曲线来说，渐近线是双曲线特有的性质．利用双曲线的渐近线来画双曲线特别方便，而且较为精确，只要作出双曲线的两个顶点和两条渐近线，就能画出它的近似图形．提醒：完成作业第2章 §2.3 2.3.2答案精析问题导学知识点一思考范围、对称性、顶点、离心率、渐近线．梳理 x ≥a 或x ≤－a y ≥a 或y ≤－a 坐标轴原点坐标轴原点A 1(－a ，0)，A 2(a,0) A 1(0，－a )，A 2(0，a )知识点二思考1 将方程x 2a 2－y 2b 2＝1(a >0，b >0)右边的“1”换成“0”，即由x 2a 2－y 2b 2＝0，得x a ±yb ＝0，如图，作直线x a ±y b ＝0，当双曲线x 2a 2－y 2b2＝1的各支向外延伸时，与两直线逐渐接近，但始终不会相交，把这两条直线叫做双曲线的渐近线．思考 2 双曲线x 2a 2－y 2b 2＝1的各支向外延伸逐渐接近渐近线，所以双曲线的“张口”大小取决于b a 的值，设e ＝c a ，则b a ＝c 2－a 2a＝e 2－1.当e 的值逐渐增大时，b a的值增大，双曲线的“张口”逐渐增大．梳理离心率 (1，＋∞) 越大知识点三 1．中心 2．等轴 y ＝±x 题型探究例1 解将方程x 2－3y 2＋12＝0化为标准方程为y 24－x 212＝1，∴a 2＝4，b 2＝12， ∴a ＝2，b ＝23，∴c ＝a 2＋b 2＝16＝4.∴双曲线的实轴长为2a ＝4，虚轴长为2b ＝43；焦点坐标为F 1(0，－4)，F 2(0,4)；顶点坐标为A 1(0，－2)，A 2(0,2)；渐近线方程为y ＝±33x ；离心率e ＝2.跟踪训练1 解将9y 2－4x 2＝－36变形为x 29－y 24＝1，即x 232－y 222＝1.∴a ＝3，b ＝2，c ＝13，因此顶点坐标为(－3,0)，(3,0)；焦点坐标为(－13，0)，(13，0)；实轴长是2a ＝6，虚轴长是2b ＝4；离心率e ＝c a ＝133；渐近线方程为y ＝±b a x ＝±23x .例2 解 (1)设双曲线的标准方程为x 2a 2－y 2b 2＝1或y 2a 2－x 2b 2＝1(a >0，b >0)．由题意知2b ＝12，c a ＝54，且c 2＝a 2＋b 2， ∴b ＝6，c ＝10，a ＝8.∴双曲线的标准方程为x 264－y 236＝1或y 264－x 236＝1.(2)设以y ＝±32x 为渐近线的双曲线方程为x 24－y29＝λ(λ≠0)．当λ>0时，a 2＝4λ， ∴2a ＝24λ＝6⇒λ＝94；当λ<0时，a 2＝－9λ， ∴2a ＝2－9λ＝6⇒λ＝－1.∴双曲线的标准方程为x 29－y 2814＝1或y 29－x 24＝1.(3)设与双曲线x 22－y 2＝1有公共渐近线的双曲线方程为x 22－y 2＝λ(λ≠0)．将点(2，－2)代入双曲线方程，得λ＝222－(－2)2＝－2.∴双曲线的标准方程为y 22－x 24＝1.跟踪训练2 解 (1)依题意可知，双曲线的焦点在y 轴上，且c ＝13，又c a ＝135，∴a ＝5，b ＝c 2－a 2＝12，故所求双曲线的标准方程为y 225－x 2144＝1.(2)由e 2＝109，得c 2a 2＝109，设a 2＝9k (k >0)，则c 2＝10k ，b 2＝c 2－a 2＝k .∴设所求双曲线方程为x 29k －y 2k ＝1①或y 29k －x 2k＝1②.将(3,92)代入①，得k ＝－161，与k >0矛盾，无解；将(3,92)代入②，得k ＝9. 故所求双曲线的标准方程为y 281－x 29＝1.(3)方法一 ∵双曲线的渐近线方程为y ＝±12x ，若焦点在x 轴上，设所求双曲线的标准方程为x 2a 2－y 2b 2＝1(a >0，b >0)，则b a ＝12.① ∵A (2，－3)在双曲线上， ∴4a 2－9b2＝1.②联立①②，无解．若焦点在y 轴上，设所求双曲线的标准方程为y 2a 2－x 2b 2＝1(a >0，b >0)，则a b ＝12.③ ∵A (2，－3)在双曲线上， ∴9a 2－4b2＝1.④联立③④，解得a 2＝8，b 2＝32.故所求双曲线的标准方程为y 28－x 232＝1.方法二由双曲线的渐近线方程为y ＝±12x ，可设双曲线方程为x 222－y 2＝λ(λ≠0)．∵A (2，－3)在双曲线上， ∴2222－(－3)2＝λ，即λ＝－8. 故所求双曲线的标准方程为y 28－x 232＝1.例3 解 (1)若焦点在x 轴上，则b a ＝32， ∴e ＝b 2a 2＋1＝132；若焦点在y 轴上，则a b ＝32，即b a ＝23， ∴e ＝b 2a 2＋1＝133. 综上可知，双曲线的离心率为132或133. (2)依题意得直线l ：bx ＋ay －ab ＝0. 由原点到l 的距离为34c ，得ab a 2＋b 2＝34c ，即ab ＝34c 2，∴16a 2b 2＝3(a 2＋b 2)2，即3b 4－10a 2b 2＋3a 4＝0，∴3⎝ ⎛⎭⎪⎫b 2a 22－10×b 2a 2＋3＝0.解得b 2a 2＝13或b 2a 2＝3.又∵0<a <b ，∴b 2a2＝3.∴e ＝1＋b 2a2＝2.跟踪训练3 解设F 1(c,0)，将x ＝c 代入双曲线的方程，得 c 2a 2－y 2b 2＝1，解得y ＝±b 2a. ∴PF 1＝b 2a. 由双曲线对称性，PF 2＝QF 2且∠PF 2Q ＝90°，知F 1F 2＝12PQ ＝PF 1， ∴b 2a＝2c ，则b 2＝2ac ， ∴c 2－2ac －a 2＝0，∴⎝ ⎛⎭⎪⎫c a 2－2×c a－1＝0，即e 2－2e －1＝0，∴e ＝1＋2或e ＝1－2(舍去)． ∴所求双曲线的离心率为1＋ 2.例4 解设直线l 的方程为y ＝2x ＋m . 由⎩⎪⎨⎪⎧ y ＝2x ＋m ，x 23－y 22＝1，得10x 2＋12mx ＋3(m 2＋2)＝0.(*)设直线l 与双曲线交于A (x 1，y 1)，B (x 2，y 2)两点，由根与系数的关系，得x 1＋x 2＝－65m ，x 1x 2＝310(m 2＋2)．又y 1＝2x 1＋m ，y 2＝2x 2＋m ，∴y 1－y 2＝2(x 1－x 2)．∴AB 2＝(x 1－x 2)2＋(y 1－y 2)2＝5(x 1－x 2)2＝5[3625m 2－4×310(m 2＋2)]． ∵AB ＝6，∴365m 2－6(m 2＋2)＝6，解得m ＝±15.由(*)式得Δ＝24m 2－240，把m ＝±15代入上式得Δ>0.∴m 的值为±15，∴所求l 的方程为y ＝2x ±15. 引申探究解设相交的两点为A (x 1，y 1)，B (x 2，y 2)．则⎩⎪⎨⎪⎧x 213－y 212＝1， ①x 223－y 222＝1， ② ①－②，可得 x 1＋x 2x 1－x 23－y 1＋y 2y 1－y 22＝0.③ ∵P 为AB 的中点，且P 的坐标为(3,1)， ∴⎩⎪⎨⎪⎧x 1＋x 22＝3，y 1＋y 22＝1，即⎩⎪⎨⎪⎧ x 1＋x 2＝6，y 1＋y 2＝2. 将其代入③式，得2(x 1－x 2)－(y 1－y 2)＝0，即k ＝y 1－y 2x 1－x 2＝2，故直线l 的方程为y －1＝2(x －3)，即y ＝2x －5. 经检验知y ＝2x －5符合题意．跟踪训练4 解 (1)将y ＝－x ＋1代入双曲线x 2a 2－y 2＝1中，得(1－a 2)x 2＋2a 2x －2a 2＝0，①所以⎩⎪⎨⎪⎧1－a 2≠0，4a 4＋8a 21－a 2>0，解得0<a <2且a ≠1，又双曲线的离心率e ＝1＋a 2a ＝ 1a 2＋1，所以e >62且e ≠ 2. (2)设A (x 1，y 1)，B (x 2，y 2)．因为P 为直线与y 轴的交点，所以P (0,1)．因为PA →＝512PB →，所以(x 1，y 1－1)＝512(x 2，y 2－1)．由此得x 1＝512x 2. 由于x 1，x 2是方程①的两根，且1－a 2≠0，所以1712x 2＝－2a 21－a 2，512x 22＝－2a 21－a 2. 消去x 2得－2a 21－a 2＝28960. 由a >0，解得a ＝1713.当堂训练1．x 2－y 24＝1 2.－4 3. 2 4.(±7，0) 5.y ＝±22x。

(新)高中数学第二章圆锥曲线与方程2_2_2双曲线的几何性质一1教案新人教A版选修1-1

三、感悟方法练习：
1、双曲线的性质：
椭圆
双曲线
不同点
标准方程
图象
范围
对称性
顶点
渐近线
1、课本练习第1，2题
〖备选习题〗：
A组
1、求与双曲线有共同渐近线，且过点的双曲线的方程。
B组
1.双曲线的离心率为，双曲线的离心率为，则的最小值是（）
A． B．2 C． D．4
2.求证：双曲线（）与双曲线有共同的渐近线。
说明：①由c>a>0可得e>1；
②双曲线的离心率越大，它的开口越阔.
探究二：
课本51页例3
双曲线型自然通风塔的外形，是双曲线的一部分绕其虚轴旋转所成的曲面（见课本），它的最小半径为，上口半径为，下口半径为，高，选择适当的坐标系，求出此双曲线的方程（精确到）
探究三：
例3．求与双曲线有共同渐近线，且过点的双曲线的方程。
令，没有实根，因此双曲线和y轴没有交点。
1）注意：双曲线的顶点只有两个，这是与椭圆不同的（椭圆有四个顶点），
双曲线的顶点分别是实轴的两个端点。
2）实轴：线段叫做双曲线的实轴，它的长等于叫做双曲线的实半轴长。
虚轴：线段叫做双曲线的虚轴，它的长等于叫做双曲线的虚半轴长。
在作图时，我们常常把虚轴的两个端点画上（为要确定渐进线），但要注意他们并非是双曲线的顶点。
2、渐近线：注意到开课之初所画的矩形，矩形确定了两条对角线，这两条直线即称为双曲线的渐近线。从图上看，双曲线的各支向外延伸时，与这两条直线逐渐接近。
在初中学习反比例函数时提到x轴y轴都是它的渐近线。高中三角函数，渐近线是。
所谓渐近，既是无限接近但永不相交。

高中数学-圆锥曲线双曲线简单几何性质(一)教案新课标人教B版选修2

双曲线简单几何性质（一）合作学习导纲
1、下列方程中，以x±2y=0为渐近线的双曲线方程是：
A 、141622=-y x
B 、116
42
2=-y x
C 、1222=-y x
D 、12
2
2=-y x
2、求中心在原点，一个焦点为(3，0)，一条渐近线方程2x-3y=0的双曲线方程。

作业：
必做题：教课书113页习题8.4（1、3、4题）
选做题：1、双曲线18
42
2=-y x 的两渐近线所夹锐角的正切值。

2、已知双曲线
1162
22=-b y x 的实轴的一个端点为A 1，虚轴的一个端点为 B 1，且 A 1 B 1=5，求双曲线方程。

课外研讨题：若直线1-=kx y 与双曲线422=-y x 有：①一个公共点；②两个公共点；③无公共点；④在右支上有两个公共点；⑤在右支上有一个公共点，求k 的取值范围。

人教版高中数学第二册（上）
8.4双曲线简单几何性质（一）
教案
抚顺县高级中学数学教师：吴春义
2006年12月1日。

高中数学第2章圆锥曲线与方程2.3.2双曲线的几何性质学案苏教版选修2-1(2021年整理)

2018-2019高中数学第2章圆锥曲线与方程2.3.2 双曲线的几何性质学案苏教版选修2-1编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（2018-2019高中数学第2章圆锥曲线与方程2.3.2 双曲线的几何性质学案苏教版选修2-1）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为2018-2019高中数学第2章圆锥曲线与方程2.3.2 双曲线的几何性质学案苏教版选修2-1的全部内容。

2.3。

2 双曲线的几何性质学习目标1。

了解双曲线的几何性质（范围、对称性、顶点、实轴长和虚轴长等)。

2。

理解离心率的定义、取值范围和渐近线方程。

3。

掌握标准方程中a，b,c，e间的关系．知识点一双曲线的性质标准方程错误!－错误!＝1(a〉0,b〉0)错误!－错误!＝1 (a>0，b>0）图形性质范围x≥a或x≤－a，y∈R x∈R，y≤－a或y≥a 对称性对称轴:坐标轴;对称中心：原点顶点顶点坐标：A1（－a，0),A2（a,0）顶点坐标：A1(0，－a），A2（0，a)渐近线y＝±错误!x y＝±错误!x离心率e＝错误!，e∈（1，＋∞），其中c＝错误!a，b,c间的关系c2＝a2＋b2（c〉a〉0,c>b>0）知识点二等轴双曲线思考求下列双曲线的实半轴长、虚半轴长，并分析其共同点．(1）x2－y2＝1；（2)4x2－4y2＝1.答案（1）的实半轴长为1,虚半轴长为1(2）的实半轴长为错误!,虚半轴长为错误!。

它们的实半轴长与虚半轴长相等．梳理实轴和虚轴等长的双曲线叫作等轴双曲线，其渐近线方程为y＝±x，离心率为 2.1．双曲线错误!－错误!＝1与错误!－错误!＝1（a＞0，b＞0）的形状相同．（√）2．双曲线x2a2－错误!＝1与错误!－错误!＝1（a＞0，b＞0)的渐近线相同．(×）3．等轴双曲线的离心率为错误!。

高二数学选修2第二章圆锥曲线与方程教案苏教版教案

高二数学选修2第二章圆锥曲线与方程教案课题：圆锥曲线课时编号：SX2－02－01教学目标：1、通过用平面截圆锥曲面，经历从具体抽象圆锥曲线过程；2、掌握椭圆、双曲线、抛物线的定义教学重点：椭圆、双曲线、抛物线的定义教学难点：椭圆、双曲线、抛物线的定义教学过程：一、问题情景几何画板演示：天体的运行二、建构数学1、圆锥曲线：画板演示2、椭圆、双曲线、抛物线的动画演示3、椭圆、双曲线与抛物线的定义椭圆定义：我们把平面内与两个定点F1、F2的距离的和等于常数（大于∣F1F2∣）的点的轨迹叫椭圆.这两个定点叫椭圆的焦点，两焦点的距离叫椭圆的焦距.说明：①可用椭圆演示模板向学生展示椭圆图形的画法；②要求学生注意常数要大于∣F1F2∣的条件，同时让学生明确常数小于或等于∣F1F2∣时，轨迹为无轨迹或一条线段.双曲线的定义：我们把平面内与两个定点F1、F2的距离的差的绝对值等于常数（小于21FF）的点的轨迹叫做双曲线.说明：①常数小于21FF；②这两个定点叫做双曲线的焦点；③这两焦点的距离叫双曲线的焦距.222ay x =+圆的定义坐标系中的圆圆的方程？椭圆的定义坐标系中的椭圆椭圆的方程抛物线的定义：平面内与一个定点F 和一条定直线l 的距离相等的点的轨迹叫抛物线.点F 叫抛物线的焦点，直线l 叫做抛物线的准线. 三、回顾总结：四、布置作业：《数学之友》T2.1圆锥曲线课题：椭圆（1）课时编号：SX2－02－02 教学目标：1、掌握椭圆的标准方程，能根据已知条件求椭圆的标准方程；2、能利用标准方程判断曲线是否是椭圆教学重点：椭圆的定义与标准方程教学难点：标准方程的推导过程教学过程：一、创设情景1、学习直线与圆时，对圆的认识经历了以下过程2、学习了椭圆的定义，也有类似的思考二、建构数学1、椭圆标准方程的推导如图，建立直角坐标系x O y ，使x 轴经过点F 1、F 2，并且O 与线段F 1F 2的中点重合.设M （x ,y ）是椭圆上任意一点，椭圆的焦距为2c (c ＞0)，那么焦点F 1、F 2的坐标分别是（－c ,0），(c ,0). 又设M 与F 1和F 2的距离的和等于常数2a. 由椭圆定义，椭圆就是集合 P =｛M ∣∣MF 1∣+∣MF 2∣=2a ｝因为∣MF 1∣=22)(y c x ++，∣MF 2∣=22)(y c x +- 所以得：22)(y c x +++22)(y c x +-=2a 整理得：（a 2－c 2）x 2+a 2y 2=a 2(a 2－c 2).由椭圆的定义可知：2a ＞2c ，即a ＞c ，故a 2－c 2＞0. 令a 2－c 2=b 2，其中b ＞0，代入上式整理得：)0(12222>>=+b a by a x 2、椭圆的标准方程：x o F 1 F 2Py三、数学运用 1、例1 已知一个运油车上的储油罐截面的外轮廓线是一个椭圆，它的焦距为2.4m ，外轮廓线上的两个点到两个焦点的距离的和为3m ，求这个椭圆的标准方程。

苏教版高中数学选修宿迁沭阳县潼阳教案双曲线的几何性质

教学案科目: 数学主备人：备课日期：课题第 1 课时计划上课日期：教学目标知识与技能1．了解双曲线的简单几何性质，如范围、对称性、顶点、渐近线和离心率等．2．能用双曲线的简单几何性质解决一些简单问题．过程与方法情感态度与价值观教学重难点双曲线的几何性质及初步运用教学流程\内容\板书关键点拨加工润色一、复习提问引入新课1．椭圆有哪些几何性质，是如何探讨的？ 2．双曲线的两种标准方程是什么？下面我们类比椭圆的几何性质来研究它的几何性质．双曲线的范围在以直线b y x a =和by x a=-为边界的平面区域内，那么从x ，y 的变化趋势看，双曲线22221x y a b -=与直线by x a=±具有怎样的关系呢？根据对称性，可以先研究双曲线在第一象限的部分与直线by x a=的关系．双曲线在第一象限的部分可写成：()22b y x a x a a =->．设(),M x y 是它上面的点，设点N 是直线by x a=上与M 有相同横坐标的点，则N by x a =．设MQ 是点M 到直线by x a=的距离，则有||||MQ M N <．当x 逐渐增大，并趋向于无穷大时，MN 趋向于0，这说明，双曲线在射线ON 的下方，并无限接近于射线ON ．在其他象限内也可以证明类似的情况．我们把两条直线by x a=±叫做双曲线的渐近线．定义：直线b y x a =±叫做双曲线22221x y a b -=的渐近线；直线ay x b =±叫做双曲线22221y x a b -=的渐近线．四、离心率由于正确认识了渐近线的概念，对于离心率的直观意义也就容易掌握了，为此，介绍一下双曲线的离心率以及它对双曲线的形状的影响：1．双曲线的焦距与实轴的比ce a=叫做双曲线的离心率，且1e >． 2．由于22222211b c a c e a a a -==-=-，所以e 越大，也越大，即渐近线b y x a=±的斜率绝对值越大．这时双曲线的形状就从扁狭逐渐变得开阔，从而得出：双曲线的离心率越大，它的开口就越开阔．这时，指出：焦点在y 轴上的双曲线的几何性质可以类似得出，双曲线的几何性质与坐标系的选择无关，即不随坐标系的改变而改变．五、例题讲解例1 求双曲线22143x y -=的实轴长和虚轴长、焦点的坐标、离心率、渐近线方程．分析由双曲线的标准方程，容易求出,,a b c ，引导学生用双曲线的实轴长、虚轴。

高中数学第2章圆锥曲线与方程2.32.3.2双曲线的几何性质学案苏教版选修2_1

2.3.2 双曲线的几何性质学习目标：1.了解双曲线的简单几何性质．(重点)2.会求双曲线的渐近线、离心率、顶点、焦点坐标等．(重点)3.知道椭圆与双曲线几何性质的区别．(易混点)[自主预习·探新知]教材整理1 双曲线的简单几何性质阅读教材P 43～P 46例1以上部分，完成下列问题．判断(正确的打“√”，错误的打“×”)(1)双曲线是轴对称图形，也是中心对称图形．( ) (2)在双曲线中，实轴长，虚轴长分别为a ，b .( ) (3)双曲线的渐近线方程为y ＝±b ax .( )(4)离心率e 越大，其渐近线斜率的绝对值越大．( )(5)在双曲线x 24－y 2＝1中，x 的取值范围是(－∞，－2]∪[2，＋∞)．( )[解析] (1)正确．(2)错误．因为实轴长为2a ，虚轴长为2b .(3)错误．当焦点在y 轴上时，渐近线是y ＝±a bx .(4)错误．e ＝1＋⎝ ⎛⎭⎪⎫b a2，e 越大，只能说明b a的绝对值越大．(5)正确．[答案] (1)√ (2)× (3)× (4)× (5)√ 教材整理2 等轴双曲线阅读教材P 45倒数第八行以上内容，完成下列问题． 1．实轴和虚轴等长的双曲线叫做等轴双曲线．2．性质：(1)等轴双曲线的离心率e(2)等轴双曲线的渐近线方程为y ＝±x ，它们互相垂直．填空：(1)双曲线x 2－y 2＝－2的渐近线为________． (2)过点(2,3)的等轴双曲线方程为________． (3)等轴双曲线x 2－y 2＝4的焦点坐标为________．[解析] (1)x 2－y 2＝－2为等轴双曲线，则渐近线方程为y ＝±x ，即x ±y ＝0. (2)设等轴双曲线方程为x 2－y 2＝λ(λ≠0)，把(2,3)代入可得λ＝22－32＝－5， ∴方程为x 2－y 2＝－5，即y 25－x 25＝1.(3)方程可化为x 24－y 24＝1，∴c ＝22，焦点为(±22，0)．[答案] (1)x ±y ＝0 (2)y 25－x 25＝1 (3)(±22，0)[合作探究·攻重难]渐近线方程，并作出草图.【导学号：71392081】[精彩点拨] 本题给出的方程不是标准方程，应先化方程为标准形式，然后根据标准方程求出基本量a ，b ，c 即可得解，注意确定焦点所在坐标轴．[自主解答] 将9y 2－4x 2＝－36变形为x 29－y 24＝1，即x 232－y 222＝1，所以a ＝3，b ＝2，c ＝13，因此顶点坐标A 1(－3,0)，A 2(3,0)，焦点坐标F 1(－13，0)，F 2(13，0)，实轴长是2a ＝6，虚轴长是2b ＝4，离心率e ＝c a ＝133，渐近线方程为y ＝±b a x ＝±23x .作草图，如图所示：1．求双曲线x 2－3y 2＋12＝0的实轴长、虚轴长、焦点坐标、渐近线方程和离心率． [解] 将方程x 2－3y 2＋12＝0化为标准方程为y 24－x 212＝1，∴a 2＝4，b 2＝12，∴a ＝2，b ＝23，∴c ＝a 2＋b 2＝16＝4，∴双曲线的实轴长2a ＝4，虚轴长2b ＝43，焦点坐标为F 1(0，－4)，F 2(0,4)，顶点坐标为A 1(0，－2)，A 2(0,2)，渐近线方程为y ＝±33x ，离心率e ＝2.(1)两顶点间的距离为6，渐近线方程为y ＝±32x ；(2)与双曲线x 2－2y 2＝2有公共渐近线，且过点M (2，－2)．[精彩点拨] 利用待定系数法，当渐近线方程已知时，可利用双曲线设出方程进行求解． [自主解答] (1)设以直线y ＝±32x 为渐近线的双曲线方程为x 24－y29＝λ(λ≠0)，当λ>0时，a 2＝4λ，∴2a ＝24λ＝6⇒λ＝94.当λ<0时，a 2＝－9λ，∴2a ＝2－9λ＝6⇒λ＝－1. ∴双曲线的标准方程为x 29－y 2814＝1或y 29－x 24＝1.(2)设与双曲线x 22－y 2＝1有公共渐近线的双曲线方程为x 22－y 2＝λ(λ≠0)，将点(2，－2)代入双曲线方程，得λ＝222－(－2)2＝－2.∴双曲线的标准方程为y 22－x 24＝1.2．求适合下列条件的双曲线的标准方程． (1)一个焦点为(0,13)，且离心率为135；(2)渐近线方程为y ＝±12x ，且经过点A (2，－3)．[解] (1)依题意可知，双曲线的焦点在y 轴上，且c ＝13，又c a ＝135，∴a ＝5，b ＝c 2－a 2＝12，故其标准方程为y 225－x 2144＝1.(2)法一：∵双曲线的渐近线方程为y ＝±12x ，若焦点在x 轴上，设所求双曲线的标准方程为x 2a 2－y 2b 2＝1(a >0，b >0)，则b a ＝12.①∵A (2，－3)在双曲线上，∴4a 2－9b2＝1. ②由①②联立，无解．若焦点在y 轴上，设所求双曲线的标准方程为y 2a 2－x 2b 2＝1(a >0，b >0)，则a b ＝12.③∵A (2，－3)在双曲线上，∴9a 2－4b2＝1. ④由③④联立，解得a 2＝8，b 2＝32. ∴所求双曲线的标准方程为y 28－x 232＝1.法二：由双曲线的渐近线方程为y ＝±12x ，可设双曲线方程为x 22－y 2＝λ(λ≠0)．∵A (2，－3)在双曲线上， ∴2222－(－3)2＝λ，即λ＝－8. ∴所求双曲线的标准方程为y 28－x 232＝1.的双曲线的离心率为________.【导学号：71392082】(2)已知双曲线x 2a 2－y 2b2＝1(a >0，b >0)的右焦点为F ，若过点F 且倾斜角为60°的直线与双曲线的右支有且只有一个交点，求双曲线离心率的取值范围．[精彩点拨] (1)根据图形并由双曲线的定义确定a 与c 的关系，求出离心率；(2)可以通过图形借助直线与双曲线的关系，因为过点F 且倾斜角为60°的直线与双曲线的右支有且只有一个交点，则必有ba≥tan 60°.[自主解答] (1)由题意2c ＝AB ＝BC ， ∴AC ＝2×2c ×sin 60°＝23c ，由双曲线的定义，有2a ＝AC －BC ＝23c －2c ⇒a ＝(3－1)c ， ∴e ＝c a＝13－1＝1＋32. [答案]1＋32(2)因为双曲线渐近线的斜率为k ＝b a，直线的斜率为k ＝tan 60°＝3，故有b a≥3，所以e ＝ca ＝a 2＋b 2a 2≥1＋3＝2，所以所求离心率的取值范围是[2，＋∞)．3．已知F 1，F 2是双曲线x 2a 2－y 2b2＝1(a >0，b >0)的两个焦点，PQ 是经过F 1且垂直于x 轴的双曲线的弦，如果∠PF 2Q ＝90°，求双曲线的离心率．[解] 设F 1(c,0)，将x ＝c 代入双曲线的方程得c 2a 2－y 2b 2＝1，那么y ＝±b 2a.由PF 2＝QF 2，∠PF 2Q ＝90°，知PF 1＝F 1F 2，∴b 2a＝2c ，∴b 2＝2ac ， ∴c 2－2ac －a 2＝0，∴⎝ ⎛⎭⎪⎫c a 2－2×c a－1＝0，即e 2－2e －1＝0.∴e ＝1＋2或e ＝1－2(舍去)．所以所求双曲线的离心率为1＋ 2.[1．直线与双曲线有几种位置关系？交点个数怎样？直线与双曲线的交点个数能否用判别式来判断？[提示] 三种位置关系：相交——两个或一个交点；相切——一个交点；相离——没有交点．当判断交点个数时，要注意二次项系数不为零时才可使用判别式进行判断．2．过双曲线上一点存在几条直线，使该直线与双曲线有且只有一个交点？解决这种问题应注意什么？[提示] 过双曲线上一点存在三条直线，使该直线与双曲线有且只有一个交点，一条是切线，两条是分别与渐近线平行的直线．解决这种问题时，应注意直线与渐近线平行的情况．3．在双曲线中，直线与双曲线相交会有几种情况，如何求弦长？[提示] 直线与双曲线相交时，两交点可能在两支上，也可能在同一支上．弦长公式为P 1P 2＝1＋k 2·|x 1－x 2|或1＋1k2|y 1－y 2|.设双曲线C ：x 2a 2－y 2＝1(a >0)与直线l ：x ＋y ＝1相交于两个不同的点A ，B ，求双曲线C 的离心率的取值范围.【导学号：71392083】[精彩点拨] 把双曲线方程和直线方程联立，得到一元二次方程，利用Δ＞0可得a 的取值范围，进而可求离心率的取值范围．[自主解答] 由C 与l 相交于两个不同点，故知方程组⎩⎪⎨⎪⎧x 2a2－y 2＝1，x ＋y ＝1有两组不同的实根，消去y 并整理得(1－a 2)x 2＋2a 2x －2a 2＝0.所以⎩⎪⎨⎪⎧1－a 2≠0，4a 4＋8a 2(1－a 2)>0，解得0<a <2且a ≠1.双曲线的离心率e ＝1＋a2a＝1a 2＋1，因为0<a <2且a ≠1.所以e >62且e ≠ 2. 即离心率e 的取值范围为⎝ ⎛⎭⎪⎫62，2∪(2，＋∞)．4．已知双曲线x 2－y 24＝1，问当直线l 的斜率k 为何值时，过点P (1,1)的直线l 与双曲线只有一个公共点．[解] ①当直线l 的斜率不存在时，直线l ：x ＝1与双曲线相切，符合题意． ②当直线l 的斜率存在时，设直线l 的方程为y ＝k (x －1)＋1，代入双曲线方程，得(4－k 2)x 2－(2k －2k 2)x －k 2＋2k －5＝0.当4－k 2＝0，即k ＝±2时，直线l 与双曲线的渐近线平行，直线l 与双曲线只有一个公共点．当4－k 2≠0时，令Δ＝0，得k ＝52.综上可知，当k ＝52或k ＝±2或直线l 的斜率不存在时，过点P 的直线l 与双曲线都只有一个公共点．[当堂达标·固双基]1．双曲线x 24－y 29＝1的渐近线方程是________．[解析] 由双曲线的方程，易知a ＝2，b ＝3，所以双曲线的渐近线方程为y ＝±32x .[答案] y ＝±32x2．已知双曲线x 2a 2－y 2b 2＝1(a >0，b >0)的一条渐近线方程为y ＝43x ，则双曲线的离心率为________．[解析] 因为渐近线方程为y ＝43x ，所以b a ＝43，所以离心率e ＝ca＝1＋⎝ ⎛⎭⎪⎫b a 2＝1＋⎝ ⎛⎭⎪⎫432＝53. [答案] 533．若双曲线的渐近线方程为y ＝±3x ，它的一个焦点是(10，0)，则双曲线的方程是________．[解析] 双曲线的焦点在x 轴上，则c ＝10，b a＝3. 又∵a 2＋b 2＝c 2，解得a 2＝1，b 2＝9， ∴方程为x 2－y 29＝1.[答案] x 2－y 29＝14．直线3x －y ＋3＝0被双曲线x 2－y 2＝1截得的弦AB 的长为________.【导学号：71392084】[解析] 直线的斜率为3，由⎩⎨⎧3x －y ＋3＝0，x 2－y 2＝1，得x 2＋3x ＋2＝0，x 1＋x 2＝－3，x 1x 2＝2.所以AB ＝(1＋3)[(－3)2－4×2]＝2. [答案] 25．求适合下列条件的双曲线的标准方程． (1)焦点在x 轴上，虚轴长为8，离心率为53；(2)两顶点间的距离是6，两焦点的连线被两顶点和中心四等分．[解] (1)设所求双曲线的标准方程为x 2a 2－y 2b 2＝1，由题意知2b ＝8，e ＝c a ＝53，从而b ＝4，c ＝53a ，代入c 2＝a 2＋b 2，得a 2＝9，故双曲线的标准方程为x 29－y216＝1. (2)由两顶点间的距离是6，得2a ＝6，即a ＝3.由两焦点的连线被两顶点和中心四等分可得2c ＝4a ＝12，即c ＝6，于是b 2＝c 2－a 2＝62－32＝27.由于焦点所在的坐标轴不确定，故所求双曲线的标准方程为x 29－y 227＝1或y 29－x 227＝1.。

2018_2019高中数学第2章圆锥曲线与方程2.3.2双曲线的几何性质学案苏教版选修2_120180829141

2.3.2　双曲线的几何性质学习目标　1.了解双曲线的几何性质(范围、对称性、顶点、实轴长和虚轴长等).2.理解离心率的定义、取值范围和渐近线方程.3.掌握标准方程中a ，b ，c ，e 间的关系．知识点一　双曲线的性质标准方程－＝1 x 2a 2y 2b 2(a >0，b >0)－＝1 y 2a 2x 2b 2(a >0，b >0)图形范围 x ≥a 或x ≤－a ，y ∈R x ∈R ，y ≤－a 或y ≥a对称性对称轴：坐标轴；对称中心：原点顶点顶点坐标：A 1(－a,0)，A 2(a,0) 顶点坐标：A 1(0，－a )，A 2(0，a )渐近线 y ＝±x b a y ＝±xab 性质离心率e ＝，e ∈(1，＋∞)，其中c ＝ caa 2＋b 2a ，b ，c 间的关系c 2＝a 2＋b 2(c >a >0，c >b >0)知识点二　等轴双曲线思考　求下列双曲线的实半轴长、虚半轴长，并分析其共同点． (1)x 2－y 2＝1；(2)4x 2－4y 2＝1.答案　(1)的实半轴长为1，虚半轴长为1 (2)的实半轴长为，虚半轴长为.1212它们的实半轴长与虚半轴长相等．梳理　实轴和虚轴等长的双曲线叫作等轴双曲线，其渐近线方程为y ＝±x ，离心率为.21．双曲线－＝1与－＝1(a ＞0，b ＞0)的形状相同．(√)x 2a 2y 2b 2y 2a 2x 2b 22．双曲线－＝1与－＝1(a ＞0，b ＞0)的渐近线相同．(×)x 2a 2y 2b 2y 2a 2x 2b23．等轴双曲线的离心率为.(√)24．离心率是的双曲线为等轴双曲线．(√)2类型一　双曲线的几何性质例1　求双曲线nx 2－my 2＝mn (m >0，n >0)的实半轴长、虚半轴长、焦点坐标、离心率、顶点坐标和渐近线方程．解　把方程nx 2－my 2＝mn (m >0，n >0)化为标准方程为－＝1(m >0，n >0)， x 2m y 2n由此可知，实半轴长a ＝， m 虚半轴长b ＝，c ＝，n m ＋n 焦点坐标为(，0)，(－，0)， m ＋n m ＋n 离心率e ＝＝＝，c a m ＋n m1＋nm 顶点坐标为(－，0)，(，0)， m m 所以渐近线方程为y ＝±x ，即y ＝±x .n mmn m 引申探究将本例改为“求双曲线9y 2－4x 2＝－36的顶点坐标、焦点坐标、实轴长、虚轴长、离心率和渐近线方程”，请给出解答．解　将9y 2－4x 2＝－36变形为－＝1，x 29y 24即－＝1， x 232y 222所以a ＝3，b ＝2，c ＝， 13因此顶点坐标为(－3,0)，(3,0)，焦点坐标为(－，0)，(，0)， 1313实轴长是2a ＝6，虚轴长是2b ＝4，离心率e ＝＝，渐近线方程为y ＝±x ＝±x . c a 133b a 23反思与感悟　由双曲线的方程研究几何性质的解题步骤 (1)把双曲线方程化为标准形式是解题的关键． (2)由标准方程确定焦点位置，确定a ，b 的值．(3)由c 2＝a 2＋b 2求出c 的值，从而写出双曲线的几何性质．跟踪训练1　求双曲线9y 2－16x 2＝144的实半轴长和虚半轴长、焦点坐标、离心率、渐近线方程．解　把方程9y 2－16x 2＝144化为标准方程－＝1.y 242x 232由此可知，实半轴长a ＝4，虚半轴长b ＝3，c ＝＝＝5，焦点坐标是(0，－5)，(0,5)， a 2＋b 242＋32离心率e ＝＝，渐近线方程为y ＝±x .c a 5443类型二　由双曲线的几何性质确定标准方程例2　求适合下列条件的双曲线标准方程： (1)虚轴长为12，离心率为；54(2)顶点间距离为6，渐近线方程为y ＝±x ；32(3)求与双曲线x 2－2y 2＝2有公共渐近线，且过点M (2，－2)的双曲线方程．解　(1)设双曲线的标准方程为－＝1或－＝1(a ＞0，b ＞0)． x 2a 2y 2b 2y 2a 2x 2b2由题意知2b ＝12，＝，且c 2＝a 2＋b 2，c a 54∴b ＝6，c ＝10，a ＝8. ∴所求双曲线的标准方程为－＝1或－＝1. x 264y 236y 264x 236(2)当焦点在x 轴上时，由＝且a ＝3，得b ＝，b a 3292∴所求双曲线的标准方程为－＝1.x 294y 281当焦点在y 轴上时，由＝且a ＝3，得b ＝2.a b 32∴所求双曲线的标准方程为－＝1.y 29x 24(3)设与双曲线－y 2＝1有公共渐近线的双曲线方程为－y 2＝k (k ≠0)，将点(2，－2)代x 22x 22入，得k ＝－(－2)2＝－2，222∴双曲线的标准方程为－＝1.y 22x 24反思与感悟　由双曲线的性质求双曲线的标准方程，一般用待定系数法，其步骤为 (1)判断：利用条件判断焦点的位置． (2)设：设出双曲线的标准方程．(3)列：利用已知条件构造关于参数的方程． (4)求：解参数方程，进而得标准方程．跟踪训练2　(1)求与双曲线－＝1有共同的渐近线，且经过点M (3，－2)的双曲线的标y 24x 23准方程；(2)已知双曲线－＝1(a >0，b >0)的离心率e ＝，过点A (0，－b )和B (a,0)的直线与原x 2a 2y 2b 2233点的距离为，求此双曲线的标准方程． 32解　(1)设所求双曲线的方程为－＝λ(λ≠0)．y 24x 23∵点M (3，－2)在双曲线上，∴－＝λ，即λ＝－2.4493∴双曲线的标准方程为－＝1.x 26y 28(2)∵e ＝，∴＝，∴＝，233c a 233a 2＋b 2a 243∴a 2＝3b 2.①又∵直线AB 的方程为bx －ay －ab ＝0， ∴d ＝＝，即4a 2b 2＝3(a 2＋b 2)．② ab a 2＋b232解①②组成的方程组，得a 2＝3，b 2＝1. ∴双曲线的标准方程为－y 2＝1.x 23类型三　双曲线的离心率例3　已知F 1，F 2是双曲线－＝1(a ＞0，b ＞0)的两个焦点，PQ 是经过F 1且垂直于x 轴x 2a 2y 2b2的双曲线的弦，如果∠PF 2Q ＝90°，求双曲线的离心率．考点　双曲线的离心率与渐近线题点　求双曲线的离心率解　设F 1(c,0)，将x ＝c 代入双曲线的方程得－＝1，c 2a 2y 2b2那么y ＝±.b 2a由PF 2＝QF 2，∠PF 2Q ＝90°，知PF 1＝F 1F 2，所以＝2c ，所以b 2＝2ac ，b 2a所以c 2－2ac －a 2＝0，所以2－2×－1＝0， (ca)ca即e 2－2e －1＝0，所以e ＝1＋或e ＝1－(舍去)． 22所以双曲线的离心率为1＋.2反思与感悟　求双曲线离心率的三种方法 (1)若可求得a ，c ，则直接利用e ＝得解． c a(2)若已知a ，b ，可直接利用e ＝得解．1＋(b a)2(3)若得到的是关于a ，c 的齐次方程pc 2＋q ·ac ＋r ·a 2＝0(p ，q ，r 为常数，且p ≠0)，则转化为关于e 的方程pe 2＋q ·e ＋r ＝0求解．跟踪训练3　设双曲线－＝1(b ＞a ＞0)的焦距为2c ，直线l 过点A (a,0)，B (0，b )，已x 2a 2y 2b2知原点到直线l 的距离为c ，则双曲线的离心率为________．34考点　双曲线的离心率与渐近线题点　求双曲线的离心率答案　2解析　如图所示，在△OAB 中，。

江苏省宿迁市泗洪中学高中数学第二章《圆锥曲线与方程

2.3.1双曲线及其标准方程（2）班级姓名教学目标：1.掌握双曲线的标准方程；2.掌握双曲线的定义。

任务1：预习课本4739P P -页，根据课本内容填空复习1：写出满足下列条件的双曲线的标准方程：①3,4a b ==，焦点在x 轴上；②焦点在y 轴上，焦距为8，2a =．复习2：前面我们学习了椭圆的哪些几何性质？问题1：由椭圆的哪些几何性质出发，类比探究双曲线22221x y a b -=的几何性质?范围：x ： y ：对称性：双曲线关于轴、轴及都对称．顶点：（），（）．实轴，其长为；虚轴，其长为．离心率：渐近线：问题2：双曲线22221y x a b -=的几何性质?图形：范围：x ： y ：对称性：双曲线关于轴、轴及都对称．顶点：（），（）实轴，其长为；虚轴，其长为．离心率：．渐近线：注意：实轴与虚轴等长的双曲线叫双曲线．任务2：认真理解双曲线的定义完成下列例题例1求双曲线2214925x y -=的实半轴长、虚半轴的长、焦点坐标、离心率及渐近线的方程．变式：求双曲线22916144y x -=的实半轴长和虚半轴长、焦点坐标、离心率、渐近线方程．例2求以椭圆22185x y +=的焦点为顶点，以椭圆的顶点为焦点的双曲线的方程．练习：对称轴都在坐标轴上的等到轴双曲线的一个焦点是1(6,0)F -，求它的标准方程和渐近线方程．《双曲线及其标准方程》练习反馈1．求双曲线的标准方程：（1）实轴的长是10，虚轴长是8，焦点在x 轴上；（2）离心率e (5,3)M -；（3）渐近线方程为23y x =±，经过点9(,1)2M -．（4）顶点间距离为6，渐近线方程为x y 23±= （5）焦距为20，渐近线方程为x y 21±=2．双曲线221168x y -=实轴和虚轴长分别是（）．A ．8、．8、C ．4、．4、3．双曲线224x y -=-的顶点坐标是（）．A ．(0,1)±B ．(0,2)±C ．(1,0)±D ．（2,0±）4．双曲线22148x y -=的离心率为（）．A ．1B ．25．双曲线2241x y -=的渐近线方程是．6．经过点(3,1)A-，并且对称轴都在坐标轴上的等轴双曲线的方程是．7．求焦点在y轴上，焦距是16，43e=的双曲线的标准方程．8．求与椭圆2214924x y+=有公共焦点，且离心率54e=的双曲线的方程．。

高中数学第二章圆锥曲线与方程2.3.2双曲线的简单几何性质课堂导学案

2.3.2 双曲线的简单几何性质课堂导学三点剖析一、双曲线的渐近线【例1】求双曲线16x 2-9y 2=-144的实半轴长和虚半轴长、焦点坐标、离心率、顶点坐标、渐近线方程.解:把方程16x 2-9y 2=-144化为标准方程222234x y -=1,由此可知,实半轴长a=4,虚半轴长b=3,c=22b a +=5. 焦点坐标为(0,-5),(0,5); 离心率e=45=a c ; 顶点坐标为(0,-4),(0,4); 渐近线方程为y=±34. 温馨提示双曲线2222b y a x -=1(a ＞0，b ＞0)的渐近线为y=±a b x,双曲线2222bx a y -=1的渐近线为x=±a b y,即y=±bax ，应仔细区分两双曲线的渐近线的异同点. 二、双曲线的离心率【例2】双曲线2222by a x -=1(a ＞1,b ＞0)的焦距为2c,直线l 过点（a,0）和(0,b)，且点(1,0)到直线l 的距离与点（-1，0）到直线l 的距离之和s≥54c.求双曲线的离心率e 的取值范围.解:直线l 的方程为bya x +=1，即bx+ay-ab=0. 由点到直线的距离公式，且a ＞1，得到点（1，0）到直线l 的距离d 1=22)1(ba ab +-.同理得到点（-1，0）到直线l 的距离： d 2=22)1(b a a b ++,s=d 1+d 2=222b a ab +=cab2. 由s≥54c,得c ab 2≥54c, 即5a 22a c -≥2c 2.于是得512-e ≥2e 2,即4e 4-25e 3+25≤0. 解不等式，得45≤e 2≤5. 由于e ＞1＞0, 所以e 的取值范围是25≤e≤5. 温馨提示本题通过构造法来求离心率的取值范围，考查了不等式的数学思想.本题主要考查了点到直线的距离公式，双曲线的基本性质，以及同学们的综合运算能力. 三、直线与双曲线的位置关系【例3】已知直线y=ax+1与双曲线3x 2-y 2=1交于A 、B 两点. （1）若以AB 为直径的圆过坐标原点，求实数a 的值； (2)是否存在这样的实数a ，使A 、B 两点关于直线y=21ｘ对称?若存在，请求出a 的值;若不存在，请说明理由.解:(1)由⎩⎨⎧=-+=13,122y x ax y 消去y,得（3－a 2）x 2－2ax －2=0.①依题意⎩⎨⎧>∆≠-,0,032a即－6＜a ＜6且ａ≠±３.② 设A(ｘ1，ｙ1），Ｂ（ｘ2，ｙ2）,则⎪⎪⎩⎪⎪⎨⎧--=-=+)4(.2)3(,32221221a a x x a a x x∵以AB 为直径的圆过原点， ∴OA ⊥OB.∴ｘ1ｘ2＋ｙ1ｙ2＝０.但y 1y 2＝ａ2ｘ1ｘ2＋ａ（ｘ1＋ｘ2）＋１,由③④,x 1+x 2＝232aa -，ｘ1ｘ2＝232a --. ∴（a 2+1）·232a--＋ａ·232a a -+1＝０. 解得ａ＝±１且满足②.(2)假设存在实数a ，使A 、B 关于ｙ＝21ｘ对称，则直线y=a x+1与y ＝21ｘ垂直，∴a·21=-1,即ａ＝-2. 直线l 的方程为ｙ＝-3ｘ＋１. 将a=-2代入③得ｘ1＋ｘ2＝４. ∴ＡＢ中点横坐标为2，纵坐标为ｙ＝-2×2＋１＝-3.但AB 中点(2，-3）不在直线ｙ＝12ｘ上,即不存在实数ａ,使A 、B 关于直线ｙ＝12ｘ对称.各个击破类题演练 1求满足下列条件的双曲线方程.（1）以2x±3y=0为渐近线，且经过点（1，2）；（2）与椭圆x 2+5y 2=5共焦点且一条渐近线方程为y-3x=0.解：（1）设所求双曲线方程为4x 2-9y 2=λ，点（1，2）在双曲线上点的坐标代入方程可得λ=-32.∴所求双曲线方程为4x 2-9y 2=-32，即832922x y -=1. （2）由已知得椭圆x 2+5y 2=5的焦点为（±2,0)，又双曲线的一条渐近线方程为y 3-x=0，则另一条渐近线方程为y+3x=0.所求双曲线方程为3x 2-y 2=λ（λ＞0），则a 2=3λ，b 2=λ. ∴c 2=a 2+b 2=34λ=4，即λ=3. 故所求的双曲线方程为x 2-32y =1. 变式提升 1(2004天津) 设P 是双曲线9222y ax -=1上一点，双曲线的一条渐近线方程为3x-2y=0，F 1、F 2分别是双曲线的左、右焦点.若|PF 1|=3，则|PF 2|等于（）A.1或5B.6C.7D.9 答案：C类题演练 2(2006陕西高考，12) 已知双曲线2222y ax -=1(a>2)的两条渐近线的夹角为3π，则双曲线的离心率为（）A.2B.3C.362D.332 答案：D变式提升 2(2004重庆) 已知双曲线2222by a x -=1(a>0,b>0)的左、右焦点分别为F 1、F 2,点P 在双曲线的右支上,且|PF 1|=4|PF 2|,则此双曲线的离心率e 的最大值为( ) A.34 B.35 C.2 D.37答案：B类题演练 3已知双曲线的左、右焦点分别为F 1、F 2，离心率为2且过点（4，-10). (1)求双曲线的标准方程；（2）直线x=3与双曲线交于M 、N 两点，求证：F 1M⊥F 2M. 答案：（1）解：由双曲线的离心率为2，即ac=2,则 222a b a +=2, ∴a=b,即双曲线为等轴双曲线.可设其方程为x 2-y 2=λ(λ≠0). 由于双曲线过点（4，10-），则42-（10-）2=λ.∴λ=6.∴双曲线方程为6622y x -=1. (2)证明：由（1）可得F 1、F 2的坐标分别为（-23，0）、（23，0），M 、N 的坐标分别为（3，3）、（3，-3）.∴k F1M =3233+,k F2M =3233-.故k F1M ·k F2M =3233+·3233-=-1.∴F 1M⊥F 2M.变式提升 3已知直线y=kx-1与双曲线x 2-y 2=1的左支交于A 、B 两点，若另一条直线l 过点P （-2，0）及线段AB 的中点Q ，求直线l 在y 轴上的截距的取值范围. 解析：由方程⎩⎨⎧=--=1,122y x kx y .消去y ，整理得（1-k 2）x 2+2kx-2=0.由题设得最新中小学教案、试题、试卷⎪⎪⎪⎩⎪⎪⎪⎨⎧>--=<--=+>-+=∆≠-012,012,0)1(84,01221221222k x x k k x x k k k 解得：-2＜k ＜-1.设A 、B 两点坐标分别为（x 1，y 1）、（x 2，y 2）.则⎪⎪⎩⎪⎪⎨⎧-=+-=+.12,12221221k y y k k x x .∴Q()11,122--k k k ∴直线l 的方程为y=2212-+k k （x+2），令x=0，得直线l 在y 轴上截距b=2222-+k k .∵-2＜k ＜-1，∴截距b 的取值范围是：（-∞，-2）∪（2+2，+∞）。

高中数学《2.3.2双曲线的几何性质》教案苏教版选修2-1

江苏省宿迁市沭阳县潼阳中学高中数学教案：《2.3.2 双曲线的几何性质》（苏教版选修2-1）中国书法艺术说课教案今天我要说课的题目是中国书法艺术，下面我将从教材分析、教学方法、教学过程、课堂评价四个方面对这堂课进行设计。

一、教材分析：本节课讲的是中国书法艺术主要是为了提高学生对书法基础知识的掌握，让学生开始对书法的入门学习有一定了解。

书法作为中国特有的一门线条艺术，在书写中与笔、墨、纸、砚相得益彰，是中国人民勤劳智慧的结晶，是举世公认的艺术奇葩。

早在5000年以前的甲骨文就初露端倪，书法从文字产生到形成文字的书写体系，几经变革创造了多种体式的书写艺术。

1、教学目标：使学生了解书法的发展史概况和特点及书法的总体情况，通过分析代表作品，获得如何欣赏书法作品的知识，并能作简单的书法练习。

2、教学重点与难点：（一）教学重点了解中国书法的基础知识，掌握其基本特点，进行大量的书法练习。

（二）教学难点：如何感受、认识书法作品中的线条美、结构美、气韵美。

3、教具准备：粉笔，钢笔，书写纸等。

4、课时：一课时二、教学方法：要让学生在教学过程中有所收获，并达到一定的教学目标，在本节课的教学中，我将采用欣赏法、讲授法、练习法来设计本节课。

（1）欣赏法：通过幻灯片让学生欣赏大量优秀的书法作品，使学生对书法产生浓厚的兴趣。

（2）讲授法：讲解书法文字的发展简史，和形式特征，让学生对书法作进一步的了解和认识，通过对书法理论的了解，更深刻的认识书法，从而为以后的书法练习作重要铺垫！（3）练习法：为了使学生充分了解、认识书法名家名作的书法功底和技巧，请学生进行局部临摹练习。

三、教学过程：（一）组织教学让学生准备好上课用的工具，如钢笔，书与纸等;做好上课准备，以便在以下的教学过程中有一个良好的学习气氛。

（二）引入新课，通过对上节课所学知识的总结，让学生认识到学习书法的意义和重要性！（三）讲授新课1、在讲授新课之前，通过大量幻灯片让学生欣赏一些优秀的书法作品，使学生对书法产生浓厚的兴趣。

江苏省宿迁市高中数学第二章圆锥曲线与方程第9课时双曲线的几何性质1导学案(无答案)苏教版选修21

第9课时双曲线的几何性质（1）【学习目标】1．了解双曲线的简单几何性质，如范围．对称性．顶点．渐近线和离心率等．2．能用双曲线的简单几何性质解决一些简单问题．【问题情境】1．椭圆有哪些几何性质，是如何探讨的？2．双曲线的两种标准方程是什么？【合作探究】双曲线的几何性质【展示点拨】例1．求双曲线22143x y-=的实轴长和虚轴长．焦点的坐标．离心率．渐近线方程．例2．已知双曲线的中心在原点,焦点在y 轴上,焦距为16,离心率为34,求双曲线的方程．变式：“焦点在y 轴上”变为“焦点在坐标轴上”．例3．求与椭圆18522=+y x 有相同焦点且经过点)1,0(的双曲线的标准方程．例4．过双曲线)0,0(12222>>=-b a by a x 的左焦点且垂直于x 轴的直线与双曲线相交于,M N 两点，以MN 为直径的圆恰好过双曲线的右顶点，求该双曲线的离心率．【学以致用】1．说出下列双曲线的顶点,焦点,焦距,实轴长,虚轴长,离心率和渐近线方程：（1）221916x y -=；（2）22145y x -=.2．求适合下列条件的双曲线的标准方程：（1）实轴的长是10，虚轴长是8，焦点在x 轴上；（2）焦距是10，虚轴长是8，焦点在y 轴上．3．已知双曲线的两条渐近线的方程是x y 34±=，焦点为)0,5(),0,5(-，求此双曲线的标准方程．4．双曲线的离心率为53，且与椭圆2214015x y +=有公共焦点，求此双曲线的标准方程．5．已知1F ,2F 是双曲线的两个焦点，以线段12F F 为边作正12MF F ∆，若边1MF 的中点在此双曲线上,求此双曲线的离心率．第9课时双曲线的几何性质（1）【基础训练】1．双曲线1254922=-y x 的焦点坐标为． 2．双曲线191622=-y x 的两条渐近线的方程为． 3．等轴双曲线的中心在原点，它的一个焦点为F(0，22)则双曲线的标准方程是________． 4．双曲线的两条渐近线线互相垂直，那么它的离心率是．5．双曲线1322=-y x 的两条渐近线所成的锐角是． 6．已知双曲线1422=-ky x 的离心率)2,1(∈e ，实数k 的取值范围是．【思考应用】7．求满足下列条件的双曲线的标准方程．（1）两焦点的距离为14，两顶点间的距离为12；（2）一焦点坐标为（0，-4），一条渐近线为320y x -=．8．过双曲线)0,0(12222>>=-b a by a x 的焦点且垂直于实轴的弦与另一焦点的连线所成角为90o ，求此双曲线的离心率．9．已知双曲线的离心率为53，且与椭圆2214015x y +=有公共焦点，求此双曲线的标准方程．10．已知双曲线)0,0(12222>>=-b a by a x 的左．右焦点分别为F 1，F 2，点P 在双曲线的右支上，且PF 1=4PF 2，则此双曲线的离心率e 的最大值．【拓展提升】11．焦点在坐标轴上的双曲线，它的两条渐近线方程为03=±y x ，焦点到渐近线的距离为3，求此双曲线的方程．12．已知双曲线2212515x y -=，焦点为1F ,2F ,P 为双曲线上一点，,且012120F PF ∠=，求12F PF ∆的面积．。

江苏省宿迁市高中数学第2章圆锥曲线与方程第7课时双曲线的标准方程1导学案(无答案)苏教版选修11

第7课时双曲线的标准方程（1）【学习目标】1．掌握双曲线的定义,标准方程． 2．根据已知条件求双曲线的标准方程．【问题情境】1．类比椭圆标准方程的建立过程推导出双曲线的标准方程．2．把椭圆定义中的“距离的差的绝对值”改为“距离的差”，那么点的轨迹会怎样？【合作探究】双曲线的标准方程F 1 ，F 2 F 1 ，F 2 想一想：如何判断方程)0,0(12222>>=-b a b y a x 和)0,0(12222>>=-b a bx a y 所表示的双曲线焦点的位置？【展示点拨】例1．已知双曲线两个焦点的坐标为)0,5()0,5(21F F ，-，双曲线上一点P 到21F F ，的距离之差的绝对值等于8，求双曲线标准方程变式1:若|PF 1|-|PF 2|=8呢？变式2:若||PF 1|-|PF 2||=10呢？变式3:若||PF 1|-|PF 2||=6呢？例2．求满足下列条件的双曲线的标准方程（1）a =3，b = 4，焦点在x 轴上；（2）a =25，经过点)5,2(-A ，焦点在y 轴上．例3．如果方程1222=--my m x 表示双曲线，求m 的取值范围．例4．已知A ，B 两地相距800m ，一炮弹在某处爆炸，在A 处听到炮弹爆炸声的时间比在B 处迟2s ，设声速为340/m s ．（1）爆炸点在什么曲线上？（2）求这条曲线的方程．【学以致用】1．双曲线192522=-x y 的焦点坐标为．2．若k ∈R ，则方程x 2k ＋3＋y 2k ＋2＝1表示焦点在x 轴上的双曲线，则k 的取值范围是________．3．已知双曲线的两个焦点分别为1100(,)F -，2100(,)F ，双曲线上一点P 到1F ，2F 的距离的差的绝对值等于12，求双曲线的标准方程． 4．求适合下列条件的双曲线的标准方程：（1）5=c ，3=b ，焦点在y 轴上；（2）焦点为)6,0(-，)6,0(，3=a ．5．已知双曲线过点()3,2-，且与椭圆224936x y +=有相同的焦点，求双曲线的方程．第7课时双曲线的标准方程（1）【基础训练】1．双曲线192522=-x y 的焦点坐标为．2．方程15922=---k y k x 表示焦点在x 轴上的双曲线，则k 的取值范围是________．3．已知P 是双曲线19422=-y x 上一点，F 1．F 2分别是双曲线的左．右焦点，若PF 1＝3，则PF 2等于．49=，得．5．设m 为常数，若点(0,5)F 是双曲线2219y x m -=的一个焦点，则m = ． 6．设12,F F 分别是双曲线221169x y -=的左右焦点，AB 是双曲线过点1F 的弦，且AB =6，则三角形2ABF 的周长是．【思考应用】7．根据下列条件，求双曲线的标准方程：⑴焦点的坐标是()6,0-．()6,0，并且经过点()5,2A -；⑵经过点(3,P -和()7Q --，焦点在y 轴上．8．求与椭圆14922=+y x 有相同焦点，并且经过点)3,2(-的双曲线的标准方程．9．已知双曲线224640x y -+=上一点M 到它的一个焦点的距离等于1，求M 到另一个焦点的距离．10．已知圆C 1：1)3(22=++y x 和圆C 2：9)3(22=+-y x ，动圆M 同时与圆C 1及圆C 2相外切，求动圆圆心M 的曲线方程．【拓展提升】11．在△ABC 中，B （－6，0），C （6，0），直线AB ，AC 的斜率乘积为94，求顶点A 的轨迹．12．某中心接到其正东．正西．正北方向三个观察点的报告：正西．正北两个观察点同时听到了一声巨响，正东观察点听到该巨响的时间比其他两个观察点晚4s ．已知各观察点到该中心的距离都是1020m ．试确定该巨响发生的位置（假定当时声音传播的速度为340m/s ；相关点均在同一平面内）．。