平均数问题 移多补少
移多补少平均数

平均数问题(二)姓名得分1.小李期末考试时,数学成绩公布前他四门功课的平均分数是92分,数学成绩公布后,他的平均成绩下降了1分。
小李数学考了多少分?2、张敏上学期期末考试成绩如下:语文82分,英语90分,品得86分,自然88分,数学成绩比五科的平均分高6分,张敏数学成绩多少分?3、数学兴趣小组有六位同学参加数学竞赛,其中五位同学的竞赛成绩分别是:96、92、85、79、85分。
第六位学生的竞赛成绩比这个组六位学生的平均成绩少4分,求第六位同学得了多少分?4、小明看着自己的数学成绩表预测:如果下次考试考100分,那么数学总平均分是91分,如果下次考试考80分,那么数学总平均分只有86分,小明数学成绩表上已有几次成绩?5、80名同学参加作文竞赛,平均分是72分,其中男生的平均分是70分,女生的平均分是78分,男生比女生少多少人?6、五年级一共有45名学生,期中考试数学平均分是92分,男生的平均分是96分,女生的平均分是90分,那么男、女生各有多少人?7、四年级的学生去植树,平均每人植树8棵,已知男生每人植树10棵,女生每人植树4棵,那么男生人数是女生的几倍?8、有两组数,第一组9个数的和是63,第二组的平均数是11,把两组数合在一起,平均数是8,那么第二组有多少个数?9、小军期中考试语文、外语、自然三门的平均成绩是78分,数学成绩公布后,四门的平均成绩提高了5分。
求小军数学成绩是多少分?10、有两组学生,第一组8个学生的平均年龄是12岁,第二组学生的平均年龄是15岁,把两组学生合在一起,他们的平均年龄是14岁,那么第二组有学生多少人?11、有几位同学一起计算他们语文考试的平均分,赵锋的得分如果再提高13分,他们的平均分就达到90分,赵锋的得分如果降低5分,他们的平均分就只有87分,那么这些同学共有多少人?12.某5个数的平均值为60,若把其中一个数改为80,平均值为70,这个数是多少13、张丽前5次考试平均分是88分,为了使平均分达到94分,张丽得连续几次考满100分(满分是100分)?14、小华前三次考试的平均分是92分,为了使平均分达到97分,小华要连续多少次考100分?15. 某7个数的平均值为60,若把其中一个数改为80,平均值为70,这个数是多少16.两组同学进行跳绳比赛,平均每人跳152次。
五年级 巧解平均数问题(二)

第二讲巧解平均数问题(二)巧点睛——方法与技巧常用的方法是“移多补少”,常用的技巧有:(1)等差数列中所有数的平均数,就是头尾两数的平均数;(2)当等差数列有奇数个数时,它的平均数恰好是中间的这个数;(3)当等差数列有偶数个数时,它的平均数是中间两个数的平均数;(4)各个数的总和除以这些数的个数等于这些数的平均数。
巧指导——例题精讲一、运用“包含与排除”法【例1】五个数的平均数是30.如果把这五个数按从小到大的顺序排列,那么前三个数的平均数是25,后三个数的平均数是35.问:第三个数是多少?【做一做 1】有六个数排成一列,他们的平均数是27,前四个数的平均数是23,后三个数的平均数是34.求第四个数。
二、“设数法”巧解题【例2】某班级女同学的人数是男同学的2倍。
女同学的平均身高是160厘米,男同学的平均身高是154厘米。
求全班同学的平均身高。
【做一做 2】某班级女同学的人数是男同学的一半。
男同学的平均体重是41千克,女同学的平均体重是35千克。
求全体同学的平均体重。
三、“移多补少”巧解题【例3】五年级甲班有52人,乙班有48人。
在某次考试中,两班全体学生的平均分为78分,乙班的平均分比甲班的平均分高5分。
两个班的平均分各是多少?【做一做3】甲组有8个工人,乙组有12个工人。
统计产量时,如果两组一起统计,则平均每人生产12个零件;如果分开统计,则甲组每人的平均产量比乙组每人的平均产量多5个。
求甲、乙两组平均每人各生产多少个零件?四、找“最小公倍数”法【例4】某班买来单价为0.5元的练习本若干本。
如果将这些练习本分给女生,则平均每人可得15本;如果将这些练习本分给男生,则平均每人可得10本。
若将这些练习本平均分给全班同学,则每人应付多少钱?【做一做4】动物园的饲养员给三群猴子分花生。
如果只分给第一群,则每群猴子可得12粒;如果只分给第二群,则每只猴子可得15粒;如果只分给第三群,则每只猴子可得20粒;如果把花生同时分给三群猴子,平均每只猴子可得多少粒?家庭作业1、8位同学在某次考试中,最高得分是95分,最低得分是65分,他们8人的平均成绩是87.5分。
移多补少(平均数)课件

04
平均数的优缺点分析
平均数的优点
简ห้องสมุดไป่ตู้易懂
易于比较
平均数是一个简明易懂的概念,能够 直观地反映一组数据的总体“平均水 平”。
通过比较不同数据集的平均数,可以 直观地看出各组数据的集中趋势。
易于计算
平均数的计算方法相对简单,只需要 将所有数值加起来然后除以数值的数 量。
平均数的缺点
对异常值敏感
平均数容易受到极端值或异常值 的影响,导致结果偏离真实情况
平均数与众数的比较
众数是一组数据中出现次数最多的数值;平均数是所有数 据之和除以数据的个数。
众数与平均数都是描述数据集中趋势的统计量,但它们的 意义和适用场景有所不同。众数更适用于描述分类数据的 集中趋势,而平均数更适用于描述数值型数据的集中趋势 。
三者之间的关系与区别
平均数、中位数和众数都是描述数据集中趋势的统计量,但它们的计算方法和适用 场景有所不同。
对异常值进行处理
在计算平均数之前,可以对异常值进 行处理,例如使用 winsorization 方 法将极端值替换为较接近的数据点。
考虑数据的离散程度
在分析平均数时,可以同时考虑数据 的离散程度,例如使用标准差来衡量 数据的波动性。
提供全面的数据分析
在报告分析结果时,除了平均数外, 还可以同时提供其他统计指标,如中 位数、众数、方差、标准差等,以全 面反映数据的特征。
移多补少法是一种通过移动多出来的部分并补充到缺少的部分,以实现整体平 衡的方法。
详细描述
移多补少法是一种数学和逻辑推理方法,其基本思想是将多余的部分移动到缺 少的部分,以使整体达到平衡或平均状态。这种方法在解决各种问题时非常有 效,尤其是在数学、统计学和经济学等领域中。
五年级--巧解平均数问题(二)

第二讲巧解平均数问题(二)巧点睛——方法与技巧常用的方法是“移多补少”,常用的技巧有:(1)等差数列中所有数的平均数,就是头尾两数的平均数;(2)当等差数列有奇数个数时,它的平均数恰好是中间的这个数;(3)当等差数列有偶数个数时,它的平均数是中间两个数的平均数;(4)各个数的总和除以这些数的个数等于这些数的平均数。
巧指导——例题精讲一、运用“包含与排除”法【例1】五个数的平均数是30.如果把这五个数按从小到大的顺序排列,那么前三个数的平均数是25,后三个数的平均数是35.问:第三个数是多少?【做一做 1】有六个数排成一列,他们的平均数是27,前四个数的平均数是23,后三个数的平均数是34.求第四个数。
二、“设数法”巧解题【例2】某班级女同学的人数是男同学的2倍。
女同学的平均身高是160厘米,男同学的平均身高是154厘米。
求全班同学的平均身高。
【做一做 2】某班级女同学的人数是男同学的一半。
男同学的平均体重是41千克,女同学的平均体重是35千克。
求全体同学的平均体重。
三、“移多补少”巧解题【例3】五年级甲班有52人,乙班有48人。
在某次考试中,两班全体学生的平均分为78分,乙班的平均分比甲班的平均分高5分。
两个班的平均分各是多少?【做一做3】甲组有8个工人,乙组有12个工人。
统计产量时,如果两组一起统计,则平均每人生产12个零件;如果分开统计,则甲组每人的平均产量比乙组每人的平均产量多5个。
求甲、乙两组平均每人各生产多少个零件?四、找“最小公倍数”法【例4】某班买来单价为0.5元的练习本若干本。
如果将这些练习本分给女生,则平均每人可得15本;如果将这些练习本分给男生,则平均每人可得10本。
若将这些练习本平均分给全班同学,则每人应付多少钱?【做一做4】动物园的饲养员给三群猴子分花生。
如果只分给第一群,则每群猴子可得12粒;如果只分给第二群,则每只猴子可得15粒;如果只分给第三群,则每只猴子可得20粒;如果把花生同时分给三群猴子,平均每只猴子可得多少粒?家庭作业1、8位同学在某次考试中,最高得分是95分,最低得分是65分,他们8人的平均成绩是87.5分。
四年级平均数移多补少的方法

四年级平均数移多补少的方法
平均数是一组数的总和除以这组数的个数。
如果要在四年级的数学中计算平均数时,出现了移多补少的情况,可以采用以下方法:
1. 先求出这组数的总和,然后再将其除以这组数的个数,得到平均数。
2. 如果有某个数被重复计算了,就先将其减去,再重新加上一次。
3. 如果有某个数漏掉了,就先将它添加到总和里,然后再除以这组数的个数。
例如,有五个数:2、4、6、8、10,它们的平均数是(2+4+6+8+10)÷5=6。
如果其中的数字2被重复计算了,则需要将其减去,得到总和为(4+6+8+10)-2=26,再除以4个数的个数,得到平均数6.5。
如果漏掉了数字12,则需要将其加入总和,得到(2+4+6+8+10+12)÷6=7。
因此,通过以上方法可以解决平均数移多补少的问题,确保计算结果的正确性。
移多补少解答平均数问题

200+5=205(元),漆工的工资为 205+30=235(元)。
第 25 页 参 考 答 案 财 主 说 牛 是 他 上 月 30 日 即 2 月 30 日 买 的 , 而 二 月 最 多 有 29 天,可 见 财 主 说 的 是谎 话。
21
ห้องสมุดไป่ตู้
移多补少解答平均数问题
□林 革
小 朋 友 ,你 会 求 一 组 数 据 的 平 均 数 吗 ? 你 可 能 会 说 ,当 然 会 了 ,利 用 关 系 式“ 总 数 量 ÷ 总 份 数 = 平 均 数 ”就 可 以 解 答 。
利用这个基本关系式可以解答求平均数 的 问 题 ,不 过 有 时 可 能 会 很 繁 琐 ,甚 至 无 法 解 答 。 你 知 道“ 移 多 补 少 ”的 方 法 吗 ? 用 这 个 方 法 可 以 使 得 计 算 简 化 ,不 信 ,请 看 下 面 两 例 。
[50+(50+5)+(50×2+3)]÷4=52(台)。
如 果 采 用 移 多 补 少 的 方 法 ,将 会 大 大 降 低 解 答 计 算 的 难 度 ,显
得十分快捷。假设每天都生产 50 台,那么四天一共就多生产 5+3=8
(台),把这 8 台平均分成四份分配到每一天,每份为 8÷4=2(台),因
采 用“ 移 多 补 少 ”的 策 略 ,题 中 的 数 量 关 系 会 顿 时 清 晰 直 观 。
漆 工 的 工 资 比 7 人 的 平 均 工 资 高 出 30 元 ,把 这 30 元 平 均 分 给 6 名
木工以后,6 名木工的平均工资正好是 7 人的平均工资。
因 为 30÷6=5(元),所 以 7 人 的 平 均 工 资 为
平均数问题

4.同学们登山,上山时每分钟走50米,18分钟到达山顶,下山沿着原路返回,每分钟走75米,求同学们上、下山的平均速度?
5.有4个数,这4个数的平均数是21,其中前两个数的平均数是15,后3个数的平均数是26,第二个数是多少?
2.植树小组植一批树,3天完成。前两天共植树113棵,第三天植了55棵,植树小组平均每天植树多少棵?
例2.华华3次数学考试测验平均成绩是89分,4次数学测验平均成绩是90,分,第四次测验的成绩是多少分?
练一练
1,一辆摩托车从甲地开往乙地,前2个小时每小时行驶60千米,后3小时每小时行驶70千米,平均每小时行驶多少千米?
2.甲乙丙三个数的平均数为87,甲丙丁三个数的平均数为85,已知丁是84,那么乙是多少?
课堂提高训练
1.少先队员为牧场割草,第一组7人,平均每人割13千克,第二组5人,平均每人割25千克,平均每人割草多少千克?
2.王强在这学期数学单元测验中,最高分是100分,最低分是92分,其余六次的平均成绩是96分,王强这学期的数学单元测试成绩平均分是多少分?
4.一组同学进行立定跳远比赛,最远的跳了152厘米,最近的跳了144厘米,其余6名同学都跳了148厘米,这组同学的平均成绩是多少厘米?
5.有6个数,它们的平均数是126,其中前3个数的平均数是119,后4个数的平均数是130,求第三个数是多少?
入门测试
1.小华期末测试语文、数学、英语、思品分别的了90分、96分、92分、98分,这四门学科的平均分是多少?
总份数=
平均速度=总路程
趣味知识
有一个长7米深的枯井,井底有一只蜗牛,它白天向上爬3米,晚上滑下1米,那么经过多少天蜗牛才能爬出井口?
奥数题平均数问题

第三讲平均数问题思维规律:1、平均数问题是指几个不相等的同类数量通过移多补少,使它们完全相等,最后求得这几个数的平均数。
2、简单的平均数应用题又称算术平均数问题,题中提供的条件使我们比较容易地求出总和与相应的加数个数,我们再根据基本关系式就可直接求出平均数。
3、较复杂的平均数应用题又称作加权平均数问题,求平均数时,先根据题意找出总数量及总数量对应的总份数,然后再求解。
4、有一些问题有时求部分平均数,有时根据平均数求个别数量,这样的题中往往提供几个部分平均数或全体平均数,然后围绕这些不同的平均数提出问题,数量关系相对复杂。
5、相关公式:总数量÷总份数=平均数总数量÷平均数=总份数平均数×总份数=总数量思维训练:一、公式法1、三个数的平均数是120,加上多少后,则四个数的平均数是150?(2003年开平市小学数学竞赛)2、甲、乙、丙、丁四位同学,在一次考试中四人的平均分数是90分。
可是,丙在抄分数时,把甲的成绩错抄成87分,因此算得四人的平均分为88分。
求甲在这次考试中得了多少分?(2004年天津市小学数学竞赛预赛)二、等式代换法3、李小宁参加6次测试。
第3、4次的平均分比前两次的平均分多2分;比后两次的平均分少2分。
如果后三次平均分比前三次平均分多3分。
那么第4次比第3次多得多少分?(1997年北京市小学生第13届“迎春杯”数学竞赛)4、甲、乙两个数的平均数是34,乙、丙两个数的平均数是31,甲、丙两个数的平均数是32。
甲、乙、丙三个数各是多少?(2001年全国“我爱数学”少年夏令营)三、移多补少法5、一个旅游团出游,平均每人应付车费40元。
后来又增加了8人,这样每人应付车费是35元,租车费是多少元?(2003年天津市小学数学竞赛)6、小红测试每分钟跳绳的次数,前四次跳的分别是:180下,180下,175下,185下。
第五次比全部跳的平均数还多32下。
那么全部五次跳的平均数是多少下?(2005年广东省“育苗杯”数学通讯赛)自我检测:一、填空题1、五次实验结果的记录中,平均值是90,中间值是91,出现次数最多的数据是94,那么五次实验中,最小的两个数据之和是______。
平均数问题移多补少

平均数问题移多补少【例1】新光机器⼚装配拖拉机,第⼀天装配50台,第⼆天⽐第⼀天多装配5台,第三、第四两天装配台数是第⼀天的2倍多3台,平均每天装配多少台【分析与解】按惯例,应该⽤四天装配的总台数除以4,综合算式为:[50+(50+5)+(50×2+3)]÷4=52(台)如果采⽤移多补少的⽅法,将会⼗分简便。
假设每天都装配50台,那么四天⼀共多装配5+3=8(台),把这8台平均分成四份,8÷4=2(台),因此,平均每天装配50+2=52(台),综合算式为:50+(5+3)÷4=52(台),你看,这种解法多么巧妙!【例2】⼩红跳绳3次,平均每次跳156下,要想跳4次后达到“平均每次跳160下”,她第4次要跳多少下【分析与解】前3次的平均数为156,要想4次的平均数达到160,就是说第4次跳绳要超过160下,并且使超过的部分平均分成3份后恰好把前3次拉平(都是160下)。
第4次应跳:160+(160-156)×3=172(下)。
【例3】从11到20⼗个连续⾃然数相加的和,再加上2000,等于从()到()这⼗个连续⾃然数相加的和。
【分析与解】我们容易算出:11+12+13+……+20=155,155+2000=2155。
要想知道2155是从()到()的⼗个连续⾃然数的和,只要知道其中最⼩的数或最⼤的数是多少就⾏了。
我们可以⽤“削平”或“补齐”(也就是“移多补少”)的技巧来解。
设这⼗个连续⾃然数中最⼩的为a1,它后⾯的9个连续⾃然数依次为a2,a3,a4,……a8,a9,a10。
这9个数⽐a1分别⼤1,2,3,……8,9。
如果把这些9个数的和减去,那么原来的⼗个数都和a1相等了,这就是“削平”,如图5-1:由于a1+a2+a3+……+a10=2155,可知“削平”以后,有10×a1=2155-(1+2+3+4+ (9)即10a1=2110 a1=211从⽽可求出:a10=a1+9=211+9=220“移多补少”⼀般⽤于解“平均数应⽤题”,它的优点是简单灵活,便于⼼算。
三3平均数问题

专题简析:求平均数通常用的方法是“移多补少”。
解答平均数应用题关键是要求出总数量和总份数。
数量关系式是“总数量÷总份数=平均数”。
例题1.小刚有5个抽屉,分别有图书33本,42本,20本,53本和32本,平均每个抽屉里有图书多少本?【试一试】一位小朋友的语文成绩是96分,数学成绩是90分,英语成绩是84分,求他三门的平均分。
例题2.一个同学读一本故事书,前4天每天读25页,以后每天读40页,又读了6天正好读完。
这个同学平均每天读多少页?【试一试】.小明期中考试的成绩是:语文和英语的平均成绩是96分,数学成绩是93分,小明语文、英语、数学三科的平均成绩是多少分?例题3.小明参加了四次语文测验,平均成绩是68分,他想通过一次语文测验,将5次的平均成绩提高到70分,那么在下次测验中,他至少要得多少分?【试一试】原来四人小组的平均分为70.加入一人后,平均成绩提高了2分.那么新加入的同学成绩为多少分?例题4.连续5个自然数的和是50,这五个数分别是多少?【试一试】连续3个自然数的和是90,这三个数分别是多少?例题5.有甲、乙、丙三个数,甲数和乙数的平均数是42,乙数和丙数的平均数是47,甲数和丙数的平均数是46,求甲、乙、丙这三个数各是多少?【试一试】大强、中强和小强三人各有一些零用钱,大强和中强的零用钱平均为50元,大强和小强的零用钱平均为40元,小强和中强的零用钱平均为60元,他们三人各有多少钱?1、一个同学学写字,他要求自己平均每天练8张纸.从星期一到星期四每天都已练了9张纸,星期五有事没有练,星期六练了10张,那么星期天要练________张才能达到他的要求.2、小明的数学、英语、语文三门平均成绩是92分,其中数学比平均成绩高6分,英语和语文成绩相同,那么英语是_____分3、小明四门成绩的平均分是90分,若已知语文,音乐,体育的成绩分别为96、95、80,那么他的数学成绩是_______分4、原来四人小组的平均分为70.加入一人后,平均成绩提高了2分.那么新加入的同学成绩为_____分5、连续5个自然数的和是100,最小的一个数是多少?6、小猫要把15条鱼分成数量不相等的4堆,问最多的一堆中最多可放几条鱼?7、一条毛毛虫由幼虫长成虫,每天长大一倍,15天能长到4厘米。
移多补少与求平均数移多补少与求平均数

移多补少与求平均数移多补少与求平均数在日常生活中,我们经常遇到这样的情况:有几个杯子,里面的水有多有少。
要想使杯中的水一样多,就得把水多的杯子里的水倒一些到水少的杯子里。
反复几次,直到几个杯子里的水一样多。
这就是我们经常驻遇到的“移多补少”——也就是求平均数问题。
例题与方法例1.小明在一学期的5次数学测验中的得分分别是95,87,92,100,96。
求小明平均每次数学测验的得分。
例2.甲地到乙地的全程是60千米。
小红骑自行车从甲地到乙地每小时行15千米,从乙地到甲地每小时行10千米。
求小红往返的平均速度。
例3.商店用30千克酥糖和20千克水果糖混合成什么锦糖。
每千克酥糖8元,每千克水果糖3元。
每千克什锦糖应卖多少元?例4.小英4次语文测验的平均成绩是89分,第5次测验得了94分。
问她5次测验的平均成绩是多少?例5.小明4次语文测验的平均成绩是87分,5次语文测验的平均成绩进88分。
第5次测验的成绩。
例6.有5个数的平均数是20。
如果把其中的一个数改成4,这时候5个数的平均数是18。
求改动的数原来是多少?例7.有甲、乙、丙3个数,甲、乙的和是90,甲、丙的和是82,乙、丙的和是86。
甲、乙、丙3个数的平均数是多少?练习与思考1.用4个同样的杯子装水,水面的高度分别是6厘米、5厘米、9厘米、8厘米。
这4个杯子里水面的平均高度是多少厘米?2.敬老院有18位老奶奶,平均年龄是75岁。
有12位老爷爷,平均年龄是70岁。
这些老人的平均年龄是多少岁?3.某学生语文、数学两科的平均成绩单是93分,后来英语考91分,自然考89分。
该学生这4门功课的平均成绩是多少分?4.上学期王红的语文、数学、外语3科的平均成绩是94分,其中语文、数学两科的平均成绩是92分。
外语得多少分?5.某次数学考试,甲、乙的成绩和是184分,乙和丙的成绩单和是187分,丙和丁的成绩和是188分,甲比丁多1分。
他们4人分别考了多少分?6.有4个数,每次取3个数相加,和分别是22,24,27和20。
小学奥数知识点趣味学习---之移多补少取平均数

小学奥数趣味知识点学习——之移多补少取平均数在日常生活中,我们经常遇到这样的情况:有几个杯子,里面的水有多有少。
要想使杯中的水一样多,就得把水多的杯子里的水倒一些到水少的杯子里。
反复几次,直到几个杯子里的水一样多。
这就是我们经常驻遇到的“移多补少”……也就是求平均数问题。
一、例题与方法指导例1.小刚有5个抽屉,分别有图书33本,42本,20本,53本和32本,平均每个抽屉里有图书多少本?思路导航:分析:如果要求平均每个抽屉里的图书,就是把5个抽屉的总数除以5。
(33+42+20+53+32)÷5=36(本)或取较为中间的一个数,如35作为基数,再把每个抽屉中的书本与35的差算出来。
将这些差相加减,多出的为加数,不足的为减数,所得的数除以5,再加上基准数35,得出的就是要求的平均数。
提出总数,份数,平均数5个抽屉书本书的总合就是“总数”,5个抽屉式“份数”。
得到关系式:平均数=总数÷份数由此关系式可得出总数=份数×平均数份数=总数÷平均数例2. 小名参加了四次语文测验,平均成绩是68分,他想通过一次语文测验,讲5次的平均成绩提高最少70分,那么在下次测验中,他至少要得多少分?分析1:知道前四次的语文平均成绩后可以求出前四次的总成绩题目中要求是五次的平均成绩提高到70分,那么可以求出5次的总成绩,再用五次的总成绩减去四次的成绩,得到的就是第五次最少应考多少分。
思路导航:68×4-70×5=78(分)前四次平均为68分,要求平均分为70分,前四次一共差了(70-68)×4=8(分)那么第五次至少要考70+8=78(分)例3.甲、乙两人带着同样多的钱,用他们全部的钱买了香皂,甲拿走了12块乙拿走了8块,回家后甲补给乙4元,每块香皂多少元?思路导航:因为甲乙两人带的是同样多的钱,两人的钱也已经全部用完,甲乙两人平均买了(8+12)÷2=10(块)香皂,而实际甲多拿了12-10=2(块)香皂,2块香皂是4元,则一块香皂是4÷2=2(元)二、巩固训练1.如果4个人的平均年龄是18岁,4个人中没有小于14岁的,那么年龄最大的人可能是多少岁?分析:4个人的平均年龄是18岁,那么四个人一共就有18×4=72(岁),题目中告诉我们4个人中最小的只有14岁,如果要求年龄最大的那么其余3个人都应是最小的,则72-14×3=20(岁)2. 有甲、乙、丙三个数,甲数和乙数的平均数是42,乙数和丙数的平均数是47,甲数和丙数的平均数是46,求甲、乙、丙这三个数各是多少?分析:从题目我们可以知道甲+乙=42×2=84 乙+丙=47×2=94 甲+丙=46×2=922(甲+乙+丙)=84+94+92=270 甲:135-94=44 乙:135-92=43 丙:135-84=51先求出甲乙丙三个数的和,知道另外两个数的和酒可以求出第三个数。
小学4年级暑假奥数:平均数问题-讲义-教师

第5讲平均数问题【学习目标】1、进一步了解平均数的常见题型;2、学会用移多补少的方法求平均数问题。
【知识梳理】1、概念:表示几个数的平均值的数;2、公式:总数量÷总份数=平均数;3、常用方法:移多补少。
【典例精析】【例1】有两块地,平均亩产粮食675千克,其中第一块地5亩,亩产粮食705千克.如果第二块地亩产粮食650千克,第二块地有多少亩?(705-675)×5÷(675-650)=30×5÷25=6(亩)【趁热打铁-1】去年前5个月,张敏家每月平均储蓄420元,从6月份起,每月储蓄600元,那么从__9___月起,他家平均储蓄不少于500元。
(500-420)×5÷(600-500)=80×5÷100=4(月)5+4=9(月)【例2】甲、乙、丙三个工厂计划购买数量相等的钢材后,后来丙厂需要钢材的数量减少了,若干数量的钢材给甲乙两厂,结果甲厂比丙厂多300吨,丙厂比乙厂少240吨.最后丙厂从甲乙两厂收363600元,每吨钢材的价格是____元。
(300+240)÷3=180(吨)363600÷180=2020(元)【趁热打铁-2】甲、乙、丙、丁四人拿出同样多的钱,一起订购同样规格的若干件新年礼物,礼物买来后,甲、乙、丙分别比丁多拿了3,7,14件礼物,最后结算时,乙付给了丁14元钱,并且乙没有付给甲钱.那么丙应该再付给丁70元钱.(3+7+14)÷4=6(件)14÷(7-6)=14(元)[6-(7-6)]×14=70(元)【例3】若干个数的平均数是17,加入一个新数2021后,这组数的平均数变成21,原来共有多少个数?(2021-21)÷(21-17)=2000÷4=500(个)【趁热打铁-3】数学测试满分100分,第二个小组的平均分为86分,明明考了98分,若明明加入第二小组,第二小组平均分将变为88分,第二小组原有__5__人。
三年级知识点:平均数问题

三年级知识点:平均数问题在日常生活中,我们会遇到下面的问题:有几个杯子,里面的水有多有少,为了使杯中水一样多,就将水多的杯子里的水倒进水少的杯子里,反复几次,直到几个杯子里的水一样多。
这就是我们所讲的“移多补少”,通常称之为平均数问题。
解答平均数应用题关键是要求出总数量和总份数,然后再根据“总数量÷总份数=平均数”这个数量关系式来解答。
例题1用4个同样的杯了装水,水面的高度分别是8厘米、5厘米、4厘米、3厘米。
这4个杯子里水面的平均高度是多少厘米?思路导航:根据已知条件,先求出4个杯子里水的总厘米数,再用总厘米数除以杯子的个数就可以求出平均每个杯子里水面的高度。
(8+5+4+3)÷3=5厘米例题2幼儿园小朋友做红花,小华做了7朵,小方做了9朵,小林和小宁合做了12朵。
平均每个小朋友做了多少朵?思路导航:根据已知条件,先求出做花的总朵数,再用花的总朵数除以人数就可求出平均每人做花的朵数。
(7+9+12)÷4=7朵例题3植树小组植一批树,3天完成。
前2天共植113棵,第3天植了55棵。
植树小组平均每天植树多少棵?思路导航:要求植树小组平均每天植树的棵数,必须知道植树的总棵数和植树的天数,植树的总棵数用前2天植的113棵加上第3天植的55棵:113+55=168棵,植树的天数为3天。
所以,平均每天植树:168÷3=56棵。
例题4一辆摩托车从甲地开往乙地,前2小时每小时行驶60千米,后3小时每小时行驶70千米。
平均每小时行驶多少千米?思路导航:根据已知条件,先求这辆摩托车行驶的总路程:60×2+70×3=330千米,再求行驶的总时间:2+3=5小时。
所以,平均每小时行驶:330÷5=66千米。
例题5数学测试中,一组学生的最高分是98分,最低分是86分,其余5名学生的平均分为92分。
这一组学生的平均分是多少分?思路导航:要求平均分,应用总分数÷总人数=平均分,依题意,总分数为:98+86+92×5=644分,总人数为:1+1+5=7人。
奥数平均数移多补少法讲解

奥数平均数移多补少法讲解集团企业公司编码:(LL3698-KKI1269-TM2483-LUI12689-ITT289-小学数学应用题分类解题-平均数应用题一、平均数问题中,平就是拉平,均就是相等,即几个不相等的数,在“和”不变的情况下,通过“移多补少”,多的给少的,最后变的相同,这个相同的数就是平均数。
既然和不变,最后几个数又要变得相同,很自然地就得出了平均数的求法:平均数=总数量÷总份数这个式子深刻说明:首先“和”即总数不变,所以要把每一个数相加;最后要取得平均,所以要除以总的份数让它们变相同。
在教学过程中,很多学生都能很快掌握这个公式,并能进行运用,但往往忽略了平均数的原始来源是通过“移多补少”最后把它们变一样的思想。
如果能掌握这一点,很多不直接求平均数的难题都能够轻松解出。
先看一道基本题目:1.小强做跳绳练习,第一次跳了67下,第二次跳了76下,要想使三次平均成绩达到80下,第三次至少跳几下?解:因为平均成绩是移多补少后得出的相同量,也就是总共比80多的要和比80少的相同根据平均数的概念,多的和少的一样,前两次总共少了17,所以第三次要多出17来才能到平均分80所以:第三次:80+17=97下2.某校参加某数学竞赛的选手平均成绩为75分,其中男选手10人,女选手15人,而女选手平均成绩为80分,则男选手的平均成绩是多少分?解:女选手比所有选手的平均成绩总共高出(80-75)×15=75分根据平均数的内涵,男选手总共应该比平均成绩少75分所以每个男选手应该比平均成绩少75÷10=7.5分所以男选手的平均成绩是:75-7.5=67.5分二、平均数问题:平均数是等分除法的发展。
解题关键在于确定总数量和与之相对应的总份数。
算术平均数:已知几个不相等的同类量和与之相对应的份数,求平均每份是多少。
数量关系式:数量之和÷数量的个数=算术平均数。
加权平均数:已知两个以上若干份的平均数,求总平均数是多少。
移多补少求平均

180
172 170
甲班?人
乙班?人
答案 乙班人数:(172-170)×50÷10=10(人) 甲班人数50-10=40(人)
例题1
教室里有10名学生,他们的平均体重是50千克。后来教室里走 进来一个老师,这时11个人的平均体重是52千克,请问老师的 体重是多少千克?
答案
72
解析
11×52-10×50=72
平均数变化与总量变化
四年级一班有6名女学生,她们的平均身高 是150厘米。后来有一名女生走进教室,这 时7人的平均身高就变成148厘米。请问:进 来的女生身高是多少厘米?
移多补少求平均图
个数变变化导致的平均数变化 根据总数的变化计算变化量
例题1
教室里有10名学生,他们的平均体重是50千克。后来教室里走 进来一个老师,这时11个人的平均体重是52千克,请问老师的 体重是多少千克?
练习1
办公室里有9名老师,他们的平均身高是150厘米。后来有一名 女老师走进教室,这时10人的平均身高就变成151厘米。请问
: 进来的女老师身高是多少厘米?
答案
160厘米
解析
10×151-9×150=160厘米
移多补少图图
例题2
甲、乙两个班参加了一次考试,甲班有40人,乙班有50人。已 知甲班的平均分是80分,甲班和乙班的总平均分是85分,请问
182
180
甲班33人
乙班22人
答案 (182-180)×33÷22=3(厘米) 182+3=185(厘米)
一个人分给其 他多个人
多个人分给其 他多个人
多个人分给所 有人
甲班平均身高是170厘米,乙班平均身高是180厘米, 甲班和乙班的平均身高是172厘米,甲、乙两班总共 50人,那么甲、乙两班各有多少人??
借助“数形结合”,体验“移多补少”——《平均数》教学思考与实践

借助“数形结合”,体验“移多补少”——《平均数》教学思考与实践发布时间:2023-07-18T08:41:01.139Z 来源:《教育学文摘》2023年4月总第442期作者:陈慧燕[导读] 学生进行探究活动,想一想:谁的投篮水平更高?浙江省丽水市青田县城东小学教育集团塔山路校区323900《平均数》选自北师大版四年级下册,它是在学生认识条形统计图,并能根据统计图表进行简单的数据分析之后进行教学的。
我以《平均数一课》教学为例,思考如何在教学中数形结合探究求平均数的方法,理解“移多补少”“求和平分”的实际意义和应用。
具体来说,我创设了投篮比赛情境,通过引领学生分析统计数据,帮助学生理解平均数的意义。
由浅入深地通过三个层次加深对平均数意义的理解:一、操作探究,并联反馈出示:投篮比赛成绩师:如果你是老师你会派谁参加?你是怎么想的?学生进行探究活动,想一想:谁的投篮水平更高?写一写、画一画:把你的想法记录下来,同学们根据以往的经验求总数,在画的过程中学生会想到把淘气的第三次投篮10个拿出来一个给第二次,那么淘气三次投篮都是9个了,9能代表淘气的投篮水平,也就是移多补少。
在探究奇思的投篮个数时,更多的同学在求得总投篮个数后就不进一步计算了,但有部分同学对奇思投篮的次数比淘气多觉得不公平。
通过投篮次数的差异让学生体会到光比总数是不行的,还需要一个能代表整体水平的数,就把奇思的总数再除以次数得出平均数。
师:这三种方法中,你觉得那种方法是不合理的?引导学生讨论交流:以总数来代表淘气和奇思的投篮水平在这里是不公平的,因为淘气和奇思的投篮次数不同,在投篮次数不同的情况下比总数并不能反应真实的投篮水平,而采用移多补少和求和平分得出的数据把淘气和奇思的不同次数投的个数匀一下,最后的出一个代表整体水平的数据。
因为这个数是从淘气和奇思每次投篮的个数匀出来的,也就是淘气和奇思这次比赛的平均数。
最后教师对移多补少再进行演示:用圆片代替投篮个数把多的个数移给少的,使得最终结果一样多。
《平均数》能力提升 运用综合法和移多补少法解决平均数问题
人教版数学四年级下册-打印版
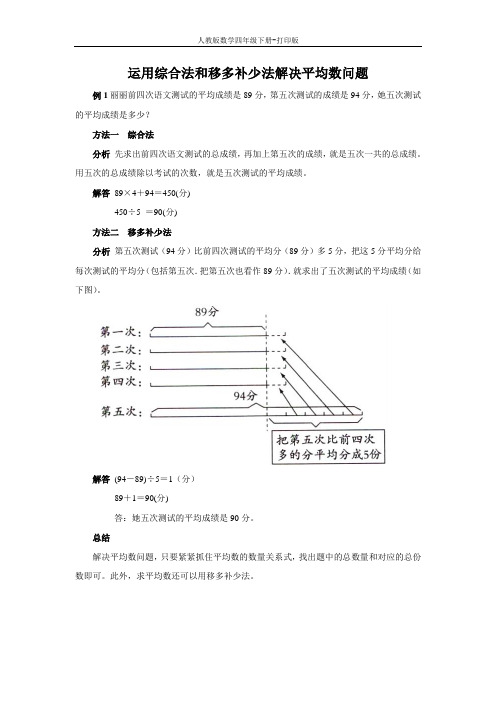
运用综合法和移多补少法解决平均数问题例1丽丽前四次语文测试的平均成绩是89分,第五次测试的成绩是94分,她五次测试的平均成绩是多少?
方法一综合法
分析先求出前四次语文测试的总成绩,再加上第五次的成绩,就是五次一共的总成绩。
用五次的总成绩除以考试的次数,就是五次测试的平均成绩。
解答89×4+94=450(分)
450÷5 =90(分)
方法二移多补少法
分析第五次测试(94分)比前四次测试的平均分(89分)多5分,把这5分平均分给每次测试的平均分(包括第五次.把第五次也看作89分).就求出了五次测试的平均成绩(如下图)。
解答(94-89)÷5=1(分)
89+1=90(分)
答:她五次测试的平均成绩是90分。
总结
解决平均数问题,只要紧紧抓住平均数的数量关系式,找出题中的总数量和对应的总份数即可。
此外,求平均数还可以用移多补少法。
奥数平均数“移多补少法”讲解电子版本

奥数平均数“移多补少法”讲解小学数学应用题分类解题-平均数应用题一、平均数问题中,平就是拉平,均就是相等,即几个不相等的数,在“和”不变的情况下,通过“移多补少”,多的给少的,最后变的相同,这个相同的数就是平均数。
既然和不变,最后几个数又要变得相同,很自然地就得出了平均数的求法:平均数=总数量÷总份数这个式子深刻说明:首先“和”即总数不变,所以要把每一个数相加;最后要取得平均,所以要除以总的份数让它们变相同。
在教学过程中,很多学生都能很快掌握这个公式,并能进行运用,但往往忽略了平均数的原始来源是通过“移多补少”最后把它们变一样的思想。
如果能掌握这一点,很多不直接求平均数的难题都能够轻松解出。
先看一道基本题目:1.小强做跳绳练习,第一次跳了67下,第二次跳了76下,要想使三次平均成绩达到80下,第三次至少跳几下?解:因为平均成绩是移多补少后得出的相同量,也就是总共比80多的要和比80少的相同根据平均数的概念,多的和少的一样,前两次总共少了17,所以第三次要多出17来才能到平均分80所以:第三次:80+17=97下2.某校参加某数学竞赛的选手平均成绩为75分,其中男选手10人,女选手15人,而女选手平均成绩为80分,则男选手的平均成绩是多少分?解:女选手比所有选手的平均成绩总共高出(80-75)×15=75分根据平均数的内涵,男选手总共应该比平均成绩少75分所以每个男选手应该比平均成绩少75÷10=7.5分所以男选手的平均成绩是:75-7.5=67.5分二、平均数问题:平均数是等分除法的发展。
解题关键在于确定总数量和与之相对应的总份数。
算术平均数:已知几个不相等的同类量和与之相对应的份数,求平均每份是多少。
数量关系式:数量之和÷数量的个数=算术平均数。
加权平均数:已知两个以上若干份的平均数,求总平均数是多少。
数量关系式(部分平均数×权数)的总和÷(权数的和)=加权平均数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【例1】新光机器厂装配拖拉机,第一天装配50台,第二天比第一天多装配5台,第三、第四两天装配台数是第一天的2倍多3台,平均每天装配多少台?
【分析与解】按惯例,应该用四天装配的总台数除以4,综合算式为:
[50+(50+5)+(50×2+3)]÷4=52(台)
如果采用移多补少的方法,将会十分简便。
假设每天都装配50台,那么四天一共多装配5+3=8(台),把这8台平均分成四份,8÷4=2(台),因此,平均每天装配50+2=52(台),综合算式为:50+(5+3)÷4=52(台),你看,这种解法多么巧妙!
【例2】小红跳绳3次,平均每次跳156下,要想跳4次后达到“平均每次跳160下”,她第4次要跳多少下?
【分析与解】前3次的平均数为156,要想4次的平均数达到160,就是说第4次跳绳要超过160下,并且使超过的部分平均分成3份后恰好把前3次拉平(都是160下)。
第4次应跳:160+(160-156)×3=172(下)。
【例3】从11到20十个连续自然数相加的和,再加上2000,等于从()到()这十个连续自然数相加的和。
【分析与解】我们容易算出:11+12+13+……+20=155,155+2000=2155。
要想知道2155是从()到()的十个连续自然数的和,只要知道其中最小的数或最大的数是多少就行了。
我们可以用“削平”或“补齐”(也就是“移多补少”)的技巧来解。
设这十个连续自然数中最小的为a1,它后面的9个连续自然数依次为a2,a3,a4,……a8,a9,a10。
这9个数比a1分别大1,2,3,……8,9。
如果把这些9个数的和减去,那么原来的十个数都和a1相等了,这就是“削平”,如图5-1:
由于a1+a2+a3+……+a10=2155,可知“削平”以后,有
10×a1=2155-(1+2+3+4+ (9)
即10a1=2110 a1=211
从而可求出:
=220
“移多补少”一般用于解“平均数应用题”,它的优点是简单灵活,便于心算。
【例4】某工厂一周内生产机器的台数统计表如图5-2,请你把星期三、星期四的产量算出来。
【分析与解】由“平均每天生产79台”可知,把六天中日产量超于79台的“移出”一部分(多出的一部分),“补到”日产量不足79台的几天后,每天都是79台。
可以这样移:星期一的89台中移出10台,使星期一为79台(多10台);
星期六的85台中移出6台,其中5台给星期二,使星期二、星期六都是79台(还多1台);
星期五的81台中移出2台,使星期五也是79台。
现在,星期一、二、五、六都是79台,多出的是:
10+1+2=13(台)
补给星期三和星期四。
可以肯定星期四原有78台,如果是68或比68少,那么,一共多的13台不够;如果是88台或更多,那么,平均日产量就超过79台。
这样,星期四需要补1台。
星期三需要补13-1=12(台)
星期三原有
79-12=67(台)
【例5】有6个木工和一个漆工完成了一套家具生产任务。
每个木工各得200元,漆工的工资比7个工人的平均工资多30元。
漆工得了多少元钱?
【分析与解】根据“移多补少”的原则,漆工比平均工资高出的30元,分别补给6个木工以后,6个木工的平均工资恰好应该是7个人的平均工资:
30÷6=5(元)
从而,7个人的平均工资应是:
200+5=205(元)
漆工的工资是:
205+30=235(元)
平均数
【例1】新光机器厂装配拖拉机,第一天装配50台,第二天比第一天多装配5台,第三、第四两天装配台数是第一天的2倍多3台,平均每天装配多少台?
【例2】小红跳绳3次,平均每次跳156下,要想跳4次后达到“平均每次跳160下”,她第4次要跳多少下?
【例3】从11到20十个连续自然数相加的和,再加上2000,等于从()到()这十个连续自然数相加的和。
【例4】某工厂一周内生产机器的台数统计表如图5-2,请你把星期三、星期四的产量算出来。
【例5】有6个木工和一个漆工完成了一套家具生产任务。
每个木工各得200元,漆工的工资比7个工人的平均工资多30元。
漆工得了多少元钱?
【思考题】
1.在迎新年的寿星联欢会上,有16位老寿星围坐在一起,他们的年龄恰好是16个连续自然数,而且30年后他们的年龄之和又恰好是1992。
其中最老的寿星是多少岁?[提示:模仿例3的思路。
]
2.在三场击球游戏中,阿丽丝的分数分别是139、143、144,为了使四场得分的平均分数为145,第四场阿丽丝应得多少分?[提示:由前三场的得分都比平均分低,需补足145,想“应补的分数+平均分=第四场得分”这个关系。
]
3.甲、乙、丙三人一起买了8个面包,平均分着吃,甲拿出5个面包的钱,乙付了3个面包的钱,丙没带钱,等吃完后一算,丙应该拿出4角钱,问甲应收回多少钱?(以分为单位)。
